FOCUS FEATURE: - Ricerca sull'intelligenza artificiale specializzata al MIT

FOCUS FEATURE:
Network Communication in the Brain

Path-dependent connectivity, not modularity,
consistently predicts controllability of structural
brain networks

Shubhankar P. Patankar1, Jason Z. Kim1, Fabio Pasqualetti2, and Danielle S. Bassett

1,3,4,5,6,7,8

1Department of Bioengineering, University of Pennsylvania, Philadelphia, PA USA
2Department of Mechanical Engineering, University of California, Riverside, CA USA
3Department of Neuroscience, University of Pennsylvania, Philadelphia, PA USA
4Department of Electrical and Systems Engineering, University of Pennsylvania, Philadelphia, PA USA
5Department of Neurology, University of Pennsylvania, Philadelphia, PA USA
6Department of Physics and Astronomy, University of Pennsylvania, Philadelphia, PA USA
7Department of Psychiatry, University of Pennsylvania, Philadelphia, PA USA
8Santa Fe Institute, Santa Fe, NM USA

Keywords: Community structure, Network dynamics, Linear systems, Network control, Block
modeling, Communication

ABSTRACT

The human brain displays rich communication dynamics that are thought to be particularly
well-reﬂected in its marked community structure. Yet, the precise relationship between
community structure in structural brain networks and the communication dynamics that
can emerge therefrom is not well understood. In addition to offering insight into the
structure-function relationship of networked systems, such an understanding is a critical
step toward the ability to manipulate the brain’s large-scale dynamical activity in a targeted
maniera. We investigate the role of community structure in the controllability of structural
brain networks. At the region level, we ﬁnd that certain network measures of community
structure are sometimes statistically correlated with measures of linear controllability.
Tuttavia, we then demonstrate that this relationship depends on the distribution of network
edge weights. We highlight the complexity of the relationship between community structure
and controllability by performing numerical simulations using canonical graph models with
varying mesoscale architectures and edge weight distributions. Finalmente, we demonstrate that
weighted subgraph centrality, a measure rooted in the graph spectrum, and which captures
higher order graph architecture, is a stronger and more consistent predictor of controllability.
Our study contributes to an understanding of how the brain’s diverse mesoscale structure
supports transient communication dynamics.

AUTHOR SUMMARY

A central question in network neuroscience is how the structure of the brain constrains the
patterns of communication dynamics that underlie function. At the mesoscale of network
organization, this question has been examined through the lens of modularity. Recent work
has demonstrated a diversity in the mesoscale architecture of the human connectome.
Further diversity in the characterization of structural brain networks is introduced by the fact
that the distribution of edge weights in a network depends on the precise empirical
measurement whose value is assigned to an edge. This paper explores network controllability
in light of the variety of community interaction motifs and edge weight distributions that may
be used to characterize structural brain networks.

a n o p e n a c c e s s

j o u r n a l

Citation: Patankar, S. P., Kim, J. Z.,
Pasqualetti, F., & Bassett, D. S. (2020).
Path-dependent connectivity, non
modularity, consistently predicts
controllability of structural brain
networks. Network Neuroscience, 4(4),
1091–1121. https://doi.org/10.1162
/netn_a_00157

DOI:
https://doi.org/10.1162/netn_a_00157

Supporting Information:
https://doi.org/10.1162/netn_a_00157

Received: 15 Febbraio 2020
Accepted: 15 Luglio 2020

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Danielle S. Bassett
dsb@seas.upenn.edu

Handling Editor:
Daniel Graham

Copyright: © 2020
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza

The MIT Press

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

Complex System:
A collection of interconnected
components that interact in
non-trivial ways.

Modularity:
The property of nodes in networks to
be separated into groups based on
shared connections.

Community Structure:
The segregation of network nodes
into groups, that are referred to as
communities or modules.

The brain is a complex system of interconnected components that can be studied at a va-
riety of spatial and temporal scales (Betzel & Bassett, 2017). Signals between communicating
neuronal populations propagate along the white-matter structure of the brain and give rise to
the complex repertoire of functional dynamics that underlie cognition (Bassett & Gazzaniga,
2011; Chialvo, 2010; Fries, 2015; Tononi, Boly, Massimini, & Koch, 2016). A key goal of
network neuroscience is to elucidate the relationship between brain network structure and
function (Bansal, Medaglia, Bassett, Vettel, & Muldoon, 2018; Honey, Kötter, Breakspear, &
Sporns, 2007; Honey et al., 2009; Sporns, Tononi, & Edelman, 2000). At any scale of inter-
est, the patterns of interconnectivity between components constrain the functional dynamics
that may evolve on the underlying network topology (Wang & Kennedy, 2016), and thus the
patterns of communication between neural units. Infatti, structural brain networks display
striking features such as small-worldness (Bassett & Bullmore, 2017), hierarchical organization
(Meunier, Lambiotte, & Bullmore, 2010), spatial and topological scaling relationships (Bassett
et al., 2010), and modularity (Sporns & Betzel, 2016). Modularity, in particular, is a commonly
studied feature of interest at the mesoscale of brain network organization that impacts potential
patterns of communication.

The term “mesoscale” refers to the topological level higher than that of a single node, Ma
lower than that of the entire network. Community detection techniques have been applied
extensively to both structural and functional brain networks in order to group together nodes
that share common features; each group is commonly referred to as a community or module.
The predominant view is that the brain is composed of assortative modules, in which nodes
connect densely to other nodes within their own community and sparsely to nodes outside
of their community. Assortative modules are observed across species ranging from humans
(Sporns, 2013; van den Heuvel & Sporns, 2011) and nonhuman primates such as macaques
(Harriger, van den Heuvel, & Sporns, 2012), to the nematode C. elegans (Towlson, Vértes,
Ahnert, Schafer, & Bullmore, 2013), and are thought to enable information integration and
segregation in support of ﬂexible cognition and behavior (Park & Friston, 2013). Tuttavia,
the ﬁeld’s focus on assortative modules could in part be an artifact of our methodologies;
popular community detection algorithms expressly seek internally dense and externally sparse
subnetworks and are agnostic to other forms of mesoscale structure (Newman, 2006; Newman
& Girvan, 2004; Rosvall & Bergstrom, 2008). Recent work has suggested that while most brain
communities are indeed assortative, others form disassortative and core-periphery structures
(Betzel, Medaglia, & Bassett, 2018; Faskowitz & Sporns, 2019; Faskowitz, Yan, Zuo, & Sporns,
2018; Pavlovic, Vértes, Bullmore, Schafer, & Nichols, 2014) (Figura 1). The existence of such a
diverse mesoscale architecture could explain the diversity of the brain’s functional repertoire
(Betzel et al., 2018; Deco, Tononi, Boly, & Kringelbach, 2015).

Yet, precisely how the community structure of brain networks constrains, supports, and ex-
plicates the communication dynamics that we observe in empirical measurements is not well
understood. Whole-brain models of neural dynamics provide an avenue to bridge this knowl-
edge gap by stipulating how neural activity propagates along the underlying structural network
(Andrea, Misic, & Sporns, 2018; C. W. Lynn & Bassett, 2019). Further insight into how transient
dynamics evolve on networks can be obtained by perturbing the dynamical model with exoge-
nous inputs. Linear systems theory and its associated network control framework can be used
to probe the relationship between the structure of networks and the transient dynamics that
they support (Kailath, 1980; Liu, Slotine, & Barabási, 2011) (Figure 2B). The approach requires
that the brain be represented as a network of regions connected by edges, which are commonly
derived from empirical estimates reﬂecting the strength, volume, or integrity of white matter
tracts (Bassett & Sporns, 2017; Bassett, Zurn, & Gold, 2018) (Figure 2A). Control inputs, Quale

Network Neuroscience

1092

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

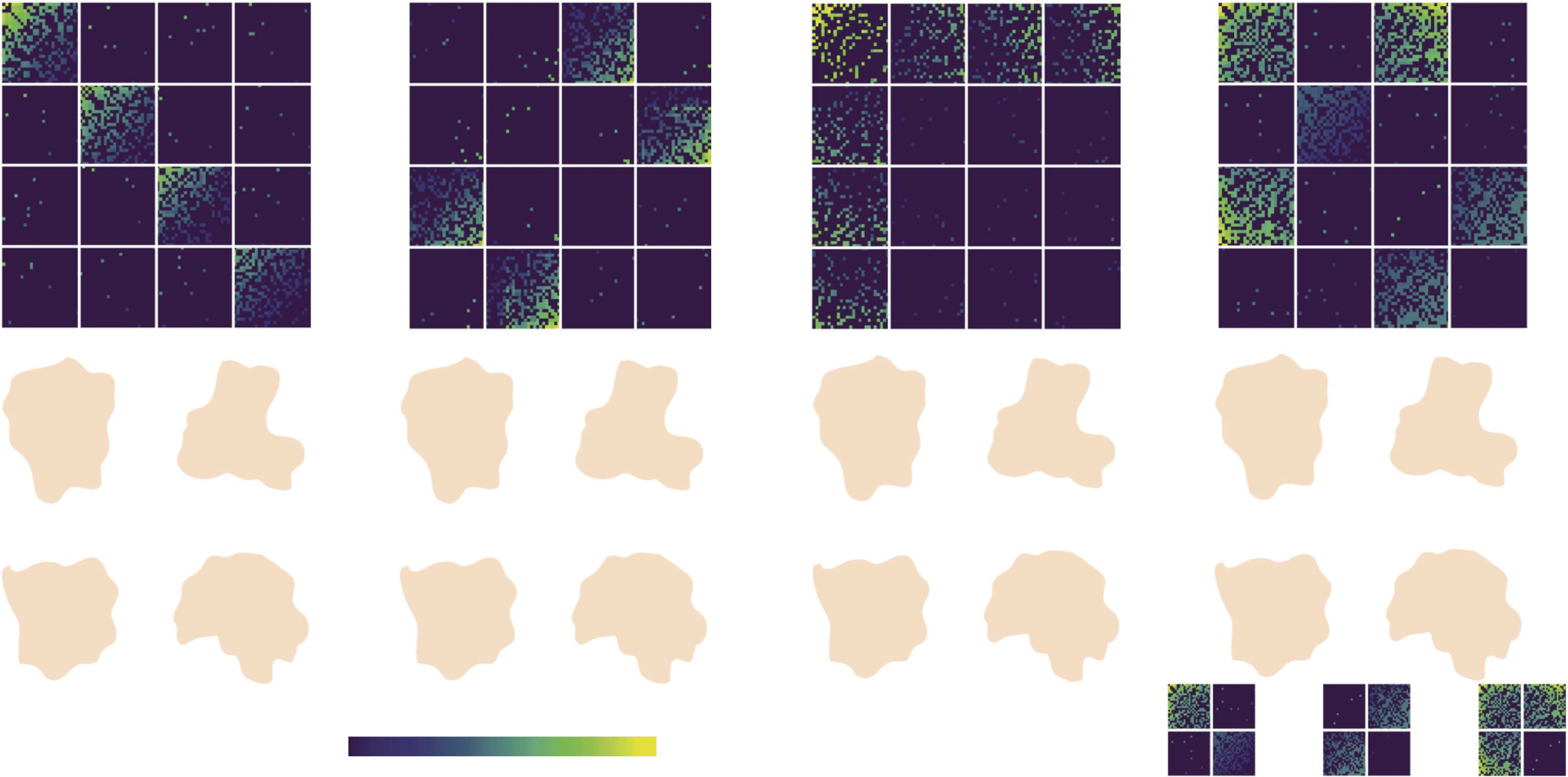
Figura 1. Structural brain networks exhibit a diversity of mesoscale architectures. (UN) Assortative communities are internally densely and
externally sparsely connected, whereas (B) disassortative communities are internally sparsely but externally densely connected. (C) Core-
periphery organization is characterized by a dense core of well-connected nodes, and a periphery of sparsely connected nodes. (D) Structural
brain networks have been observed to possess a mixed mesoscale architecture that combines assortative, disassortative, and core-periphery
organization [Figure reproduced with permission from Betzel et al. (2018)].

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

are representative of changing levels of activity, can then be added to network nodes to study
the evolution of activity dynamics (Gu et al., 2015; Tang & Bassett, 2018) (Figure 2C). From
a biophysical perspective, these inputs may represent an endogenous shift in neural activity
from one cognitive state to another (Cornblath et al., 2019; Gu et al., 2015), or even direct
exogenous inputs such as during electrical stimulation (Khambhati et al., 2019; Stiso et al.,
2019).

We hypothesize that brain regions have different controllability statistics depending on the
extent to which they participate in interactions with nodes from other communities. We reason
that a diversity in connections ought to lead to greater ability for a node to control the rest of the
rete. To test this hypothesis, we partition brain regions into communities by applying the
weighted stochastic block model (WSBM) to structural connectivity matrices extracted from
noninvasive magnetic resonance imaging (MRI) measurements in humans. Block modeling is
a ﬂexible community detection technique that is able to uncover diverse mesoscale motifs be-
yond the commonly studied assortative type (Aicher, Jacobs, & Clauset, 2014; Hastings, 2006).
The connectivity matrices we study encode networks whose nodes represent brain regions.
Edges can represent diverse estimates of internode connections, such as white matter stream-
line counts between regions, mean quantitative anisotropy (QA) values along the streamlines,
and generalized fractional anisotropy values (GFA) (Hagmann et al., 2007; Smith, Tournier,
Calamante, & Connelly, 2012; Tuch, 2004; Yeh, Verstynen, Wang, Fernández-Miranda, &

Network Neuroscience

1093

Community structure does not explain network controllability

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

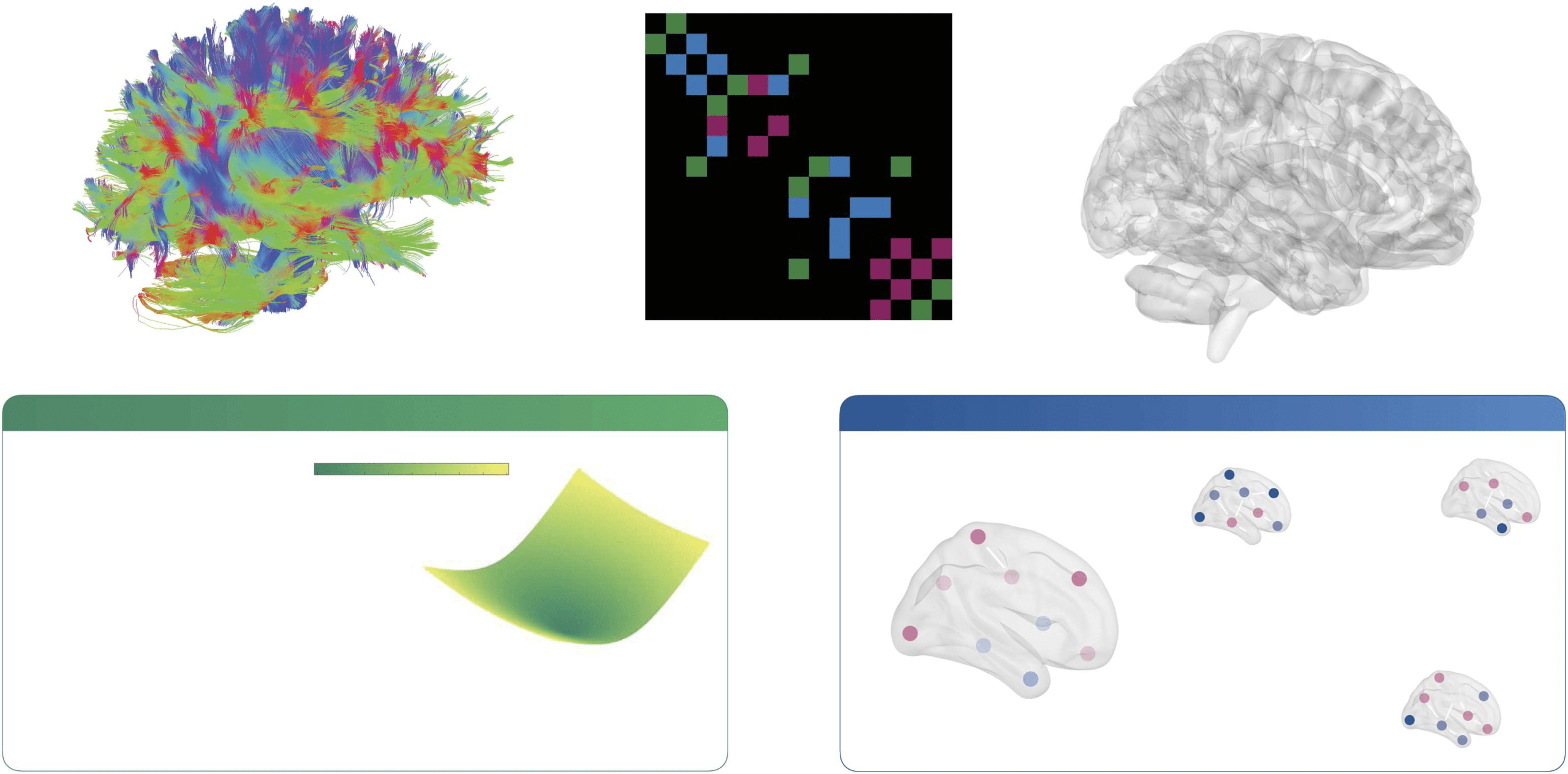
Figura 2. Schematic of methods and approach. (UN) A variety of empirical measurements are used to estimate and study brain network
structure. This data is then compiled into a weighted network adjacency matrix A whose entries Aij describe the connection strength of
region i and region j, thus characterizing the brain’s structural network. (B) While brain dynamics are nonlinear, linearization is a convenient
modeling approach that has been demonstrated to yield biologically meaningful insights, and one that allows us to systematically investigate
relationships between model parameters and model behavior. Linear systems theory provides a natural language in which to characterize state
transitions in the brain. (C) The level of activity in each brain region is combined into a state vector x and modeled using a linear dynamical
system. Linear control theory can be used to assess the effect of exogenous inputs on the brain’s functional dynamics. Controllability may
be quantiﬁed using metrics such as average and modal controllability, and the minimum energy required to effect a state transition [Figura
reproduced with permission from C. W. Lynn & Bassett (2019)].

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Tseng, 2013). Unfortunately, there is no consensus in the ﬁeld yet regarding whether one type
of edge weight has more utility than another type of edge weight, and therefore the literature
contains studies that use a variety. The distribution of edge weights in the network depends
on the precise quantity that the edge represents, and this fact hampers formal comparison of
results across studies. Per esempio, structural brain networks with QA values (Kim et al., 2018;
Stiso et al., 2019) and those with streamline counts have differing edge weight distributions.
Both have been previously used for network control-theoretic studies (Cornblath et al., 2019;
Gu et al., 2015; Jeganathan et al., 2018; Karrer et al., 2020; Kim et al., 2018; W. H. Lee,
Rodrigue, Glahn, Bassett, & Frangou, 2019; Shine et al., 2019; Stiso et al., 2019), but di-
rect comparisons between the two have not been performed. Here we seek to obtain a more
comprehensive understanding of the relations between community structure and controllabil-
ity that is independent of the choice of edge weight, and the associated differences in edge
weight distribution. Così, we use multiple data sets containing networks with distinct edge
deﬁnitions.

We further hypothesize that disrupting the amount of a particular mesoscale motif such
as assortativity, disassortativity, or core-peripheriness in a network ought to result in a motif-
speciﬁc controllability proﬁle. We perform numerical simulations to gradually alter the

Network Neuroscience

1094

Community structure does not explain network controllability

mesoscale structure of networks along speciﬁc continuums of interest while preserving their
binary density and the distribution from which network edge weights are drawn. At each stage,
we examine their controllability. In one set of simulations we alter the binary topology on an
axis ranging from disassortative to assortative. In another set of simulations, network topol-
ogy ranges from disassortative to core-periphery. We perform both sets of simulations on net-
works where edge weights are drawn from the normal distribution as well as the geometric
distribution. The latter distribution is an example of a fat-tailed distribution, which resembles
the weighted degree distributions of many biologically observed networks (Broido & Clauset,
2019). If binary topology of networks is the key driver of controllability, we expect to observe
that regardless of the choice of distribution used to assign edge weights, similar alterations to
network topology along a structural continuum ought to similarly affect patterns of network
controllability.

MATHEMATICAL FRAMEWORK

While brain network dynamics are known to be nonlinear (Figure 2B) (Rabinovich, Varona,
Selverston, & Abarbanel, 2006), the simpliﬁcation to a linearized network model is often a
useful approximation (Abdelnour, Voss, & Raj, 2014; Galán, 2008). We offer a discussion
of the utility of the linear framework in the Discussion section; for a more comprehensive
discussion we point the reader to the Supporting Information.

A linear model may be created by linearizing the nonlinear system of interest about a ﬁxed
point. System dynamics are then characterized in terms of deviations about this ﬁxed point.
Linear modeling provides a tractable simpliﬁcation for the analysis of nonlinear dynamical
systems, allowing the use of well-developed theoretical tools from linear systems and con-
trol theory to investigate network dynamics in response to exogenous control inputs (Kailath,
1980). In the context of brain networks, the linear model allows one to study how signals can
propagate along structural links connecting brain regions.

Suppose we have a node set V = {1, · · · , N} with undirected weighted edges E ⊆ V × V,
compiled in a graph G = (V, E ) and represented by a symmetric weighted adjacency matrix
A ∈ Rn×n. Elements of V denote brain regions and elements of E represent the strengths of the
connections between them. The dynamics of a discrete-time linear time-invariant (LTI) system
are written as

X(T + 1) = Ax(T) + Bu(T),

(1)

where A is the n × n symmetric and weighted network adjacency matrix, which acts as the
system matrix in the LTI framework, and B is an n × k matrix, where k is the number of inde-
pendent control inputs. A full control set implies that all n network nodes receive input, for
instance, in the case when B = In, the identity matrix of dimension n. The terms x(T) and u(T)
represent the state of the system and the exogenous input at time t, rispettivamente (see Discussion
section for biophysical interpretations of x(T) and u(T)).

A particularly useful element of the linear control framework is the matrix deﬁned as,

WC(T) =

T−1
∑
t=0

AtBB⊤(A⊤)T

(2)

called the ﬁnite time controllability Gramian, where T refers to the time horizon of control
(Kailath, 1980). The Gramian plays a vital role in determining the unique control input of

Graph:
A mathematical description of a
rete, where elements are
represented as nodes, E
interactions between elements
are represented as edges.

Network Neuroscience

1095

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

minimum energy that transitions the network state from some initial state x0 at t = 0 to a ﬁnal
state x f at a later time t = T (Karrer et al., 2020; Stiso et al., 2019). We create target state
vectors by placing a 1 in x f corresponding to the location of each brain region i in turn, and 0s
elsewhere. These one-hot vectors may be thought to represent the activation of a single brain
region with a full control set. With x0 = 0, the minimum energy of the input required to attain
a state x f at time T is written as

Ei = x f

⊤WC

−1(T)x f .

(3)

We demonstrate in the Supporting Information that the energies thus computed, by perform-
ing N state transitions to N one-hot vectors, form an upper bound on the energy required to
perform arbitrary non-negative state transitions.

In addition to the useful energy-related interpretation, other controllability metrics are of-
ten deﬁned using the Gramian (Pasqualetti, Zampieri, & Bullo, 2014). Average controllability,
which is the average energy input over all possible target states (Marx, Koenig, & Georges,
2004; Shaker & Tahavori, 2012), is one such metric. It has been used in previous studies
examining the controllability of structural brain networks (Bernhardt et al., 2019; Jeganathan
et al., 2018; B. Lee, Kang, Chang, & Cho, 2019; W. H. Lee et al., 2019; Shine et al., 2019). Av-
erage controllability is proportional to the trace of the inverse of the controllability Gramian,
Tr(W−1
C ). In practice, Tuttavia, this quantity is replaced by the trace of the controllability
Gramian, Tr(WC), since computing the inverse of WC is typically ill conditioned, and the
two quantities satisfy a bounded relation of inverse proportionality (Pasqualetti et al., 2014;
Summers & Lygeros, 2014). We compute average controllability for an individual node by set-
ting B = bi, where bi is a one-hot vector with a 1 in the location corresponding to the node.
Smaller values of average controllability for a node may be thought of as implying that the
network is less controllable on average from that node.

Another controllability measure that is often used in the context of structural brain networks
is modal controllability (Gu et al., 2015; Karrer et al., 2020; Khambhati et al., 2019; Pasqualetti
et al., 2014; Shine et al., 2019; Stiso et al., 2019). Modal controllability quantiﬁes the extent
to which a network’s eigenmodes, weighted by the rate of their decay, are inﬂuenced by input
v2
into a brain region. For a node i, modal controllability is deﬁned as: φi = ∑N
j=1
ij
(Karrer et al., 2020). We note that this functional form of modal controllability is deﬁned specif-
ically for symmetric matrices. Here, λj represents an eigenvalue of the weighted adjacency
matrix and vij represents the i-th component of the j-th eigenvector of A. Since the weighted
adjacency matrix is symmetric, all of its eigenvalues are real. The eigenvectors of A represent
independent directions in the state-space along which system dynamics evolve according to
the rate speciﬁed by the corresponding eigenvalues. A quickly decaying mode is harder to
control since, intuitively, it requires more input energy to sustain its activity. Di conseguenza, Questo
metric has been previously described as a measure of the controllability to the “hard-to-reach”
states of a system (Cornblath et al., 2019; Gu et al., 2015; Tang et al., 2017).

1 − λ2

j (UN)

(cid:17)

(cid:16)

In order to ensure comparability of time scales across networks, we scale the network adja-
cency matrices by their largest eigenvalues. In this study we set T = 4 for average controllability
and minimum energy computations. Tuttavia, we demonstrate that our results remain robust
to a broad range of choices of T in the Supporting Information. We also note that whereas
average/modal controllability consider control from a single node, minimum control energy
considers controllability from a larger node set. All minimum control energy results presented
in this paper are computed using a full control set, B = In.

Network Neuroscience

1096

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

RESULTS

Relationship between Network Controllability and Community Structure for Edge Weights Drawn from
a Normal Distribution

Results presented in this section are obtained from analyses performed on Data Set 1 (Vedere
subsection Data in the Methods for details), which is comprised of structural brain networks
where edges represent estimates of mean quantitative anisotropy (QA) values. An element
[Aij] of the weighted adjacency matrix for these networks represents the mean QA weighting
across streamlines connecting two regions i and j. Note that edge weights with QA values
approximate a normal distribution.

Measures of Controllability are not Consistently Correlated with Measures of Modularity for Structural
Prior work has reported a statistical
Brain Networks with Normally Distributed Edge Weights
correlation between some controllability metrics and modularity, a summary measure of as-
sortative community structure (Tang et al., 2017); yet, importantly in that study results held
even after regressing out the effects of modularity. Here we began our investigation by assess-
ing whether controllability of structural brain networks is statistically related to community
structure in a different data set than the one used by Tang et al., and when using a larger set
of measures of a network’s community structure. Speciﬁcally, we compute three metrics of
network control for each brain region: minimum control energy to activate the region, average
controllability, and modal controllability. We then study the relationships between these mea-
sures, and the weighted variant of the participation coefﬁcient and the intramodule strength
Z-score. Participation coefﬁcient measures the diversity of the distribution of a node’s strength
among network modules. A value of 0 for a node implies that all its connection strength is
associated with other nodes in its own module, whereas a value of 1 implies that connec-
tion strength is distributed uniformly among all modules. Intramodule strength Z-score mea-
sures the connectivity strength of a node to other nodes in its own module (Guimerà & Nunes
Amaral, 2005; Rubinov & Sporns, 2011). We compute participation coefﬁcient for brain re-
gions and the intramodule strength Z-score after partitioning the networks into communities
by using the weighted stochastic block model (WSBM). We use the normal distribution as the
choice of prior for the edge weight distribution when applying the WSBM, since edge weights
in QA-weighted networks are approximately normally distributed.

We begin by testing the relationships between participation coefﬁcient and the intramodule
strength Z-score, and the three measures of network controllability. We observe that participa-
tion coefﬁcient relates negatively with minimum control energy (ρ = −0.807, p ≈ 0) and with
modal controllability (ρ = −0.810, p ≈ 0), whereas it relates positively with average control-
lability (ρ = 0.815, p ≈ 0). Allo stesso modo, intramodule strength Z-score relates negatively with both
minimum control energy (ρ = −0.338, p ≈ 0) and modal controllability (ρ = −0.323, p ≈ 0),
and relates positively with average controllability (ρ = 0.244, p ≈ 0). These observations sug-
gest the presence of a statistical relationship between community structure and controllability.

Tuttavia, it is possible for community structure and controllability to be related due the
inﬂuence of a third variable. We hypothesize that node strength could be such a shared driver
since prior work has reported a correlation between network controllability and node strength
(Gu et al., 2015; Jeganathan et al., 2018; W. H. Lee et al., 2019; Muldoon et al., 2016). In this
dataset, node strength relates negatively with minimum control energy (ρ = −0.998, p ≈ 0)
and with modal controllability (ρ = −0.998, p ≈ 0), whereas it relates positively with average
controllability (ρ = 0.986, p ≈ 0). Inoltre, we ﬁnd that node strength is also positively

Network Neuroscience

1097

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 3. Relationships between metrics of regional controllability and metrics of community structure for edge weights approximating
a normal distribution. (UN, B, C) Participation coefﬁcient does not relate in a statistically signiﬁcant manner with minimum control energy
(ρ = −0.052, p = 0.426) when accounting for node strength. D'altra parte, correlations between participation coefﬁcient with average
(ρ = 0.192, p = 0.003) and modal controllability (ρ = −0.132, p = 0.044) survive corrections for node strength. (D, E, F) Intramodule strength
Z-score follows a similar pattern; it does not relate with minimum control energy (ρ = −0.089, p = 0.174), but relates signiﬁcantly with
average (ρ = −0.530, p ≈ 0) and modal controllability (ρ = 0.165, p = 0.011). Each dot in the scatter plots represents the mean value of a
controllability and modularity measure across 24 (8 subjects in triplicate) network instantiations for a single brain region resulting in 234 dati
points.

related to both participation coefﬁcient (ρ = 0.807, p ≈ 0) and intramodule strength Z-score
(ρ = 0.333, p ≈ 0). Di conseguenza, node strength may be the potential driver of any relationship
between community structure and controllability.

Therefore, we run partial Spearman correlations between metrics of community structure
and controllability, correcting for node strength (Figura 3). We ﬁnd that when node strength

Network Neuroscience

1098

Community structure does not explain network controllability

is accounted for, participation coefﬁcient no longer relates to minimum control energy (ρ =
−0.052, p = 0.426) (Figure 3A). It continues to relate signiﬁcantly with average controllability
(ρ = 0.192, p = 0.003) and modal controllability (ρ = −0.132, p = 0.044) (Figure 3B, C).
Intramodule strength Z-score follows a similar trend; it does not relate signiﬁcantly with min-
imum control energy (ρ = −0.089, p = 0.174), but continues to relate with average control-
lability (ρ = −0.530, p ≈ 0) and modal controllability (ρ = 0.165, p = 0.011) even when
controlling for node strength (Figure 3D, E, and F).

From the ﬁndings in this section, we conclude that for the examined structural brain net-
works where edge weights are approximately normally distributed, region-level measures of
modularity such as participation coefﬁcient and intramodule strength Z-score correlate in a
statistically signiﬁcant manner with average and modal controllability, but not with minimum
control energy.

Numerical Simulations Using Edges Drawn from a Normal Distribution Next, we seek to better
understand the relationship between controllability and community structure by parsing com-
munity structure into distinct motifs, such as assortativity, or core-peripheriness. We generate
synthetic networks with a speciﬁcally determined community structure and examine their con-
trollability. In silico experiments where network topologies are precisely enforced and edge
weights are drawn from distributions with precisely known parameters are useful benchmarks
in understanding the relationship between mesoscale organization and controllability. We be-
gin by generating networks with a 2 × 2 block structure in their adjacency matrices, and with
normally distributed edge weights (see subsection Numerical Simulations in the Methods for
details).

Recall that when the diagonal blocks of a network are denser relative to the off-diagonal
blocks, networks possess an assortative block structure (Figure 1A). By contrast, when the off-
diagonal blocks are denser relative to the diagonal blocks, network communities interact dis-
assortatively (Figure 1B). Another form of mesoscale topology is the core-periphery structure
(Figure 1C). Nodes in the core are connected more densely to each other than they are to the
rest of the network. Nodes in the periphery predominantly connect with nodes in the core
but not with each other. We quantify the notion of modularity in the form of the modularity
quality index (Q), which is a network-level measure of how well a given community partition
segregates nodes into modules. It quantiﬁes the extent of modularity by relating the observed
strength of within-module connections in a network to the strength of within-module connec-
tions expected under a null model (Newman & Girvan, 2004). The quantity Q can be positive
or negative, with positive values implying the presence of an assortative community structure
(Newman, 2006). We characterize the relationship between Q and the fraction of network
edges inside of modules (or the core) in the Supporting Information.

In the ﬁrst set of simulations, we generate networks on a range from disassortative to assor-
tative (see subsection Numerical Simulations in the Methods for details). At each point along
the structural continuum, we generate an ensemble of 100 different sparse weighted networks
with a known value of the modularity quality index Q. Primo, for each network in the ensemble
we compute the mean of the 234 obtained values of minimum control energy, average control-
lability, and modal controllability. Minimum control energy and average controllability values
are computed using T = 4 as the choice of time horizon for consistency. We then compute
the mean for each of the three network-level controllability metrics across the 100 network in-
stantiations in the ensemble. We observe that as network topology becomes more assortative
from disassortative, minimum control energy and average controllability ﬁrst decrease, E

Network Neuroscience

1099

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

then increase with a minimum value at Q ≈ 0 (Figure 4A, and B). The trough corresponds to
Q ≈ 0 where the network topology is random. Modal controllability has no discernible trend
with changing network topology along the disassortative-assortative continuum (Figure 4C).

In the second set of simulations, we generate networks on a range from disassortative to
core (see subsection Numerical Simulations in the Methods for details). Along this structural
continuum, when the fraction of edges in the core ([1, 1]-block) is closer to 0, a network is
disassortative, whereas when the fraction is closer to 1, it has a dense core reminiscent of a
core-periphery network. Networks are nearly random when the fraction is 1/3 for the 2 × 2
block adjacency matrix with a single on-diagonal block ([2, 2]-block) having zero density. In
terms of the modularity quality index Q, the extremes correspond to values of −0.5 (disas-
sortative) E 0 (core), rispettivamente. The extent of disassortativity and coreness is in balance
when Q ≈ −0.28. Similar to the ﬁrst set of simulations, we generate 100 network instantia-
tions as the topology gradually changes from disassortative to more core-like. Lo osserviamo
as networks become more core-like, mean minimum control energy increases (Figure 4D).
There is little change in the mean control energy value in the disassortative regime; how-
ever, this is followed by a sharp rise past Q ≈ −0.20. Average controllability, in contrast, ﬁrst
decreases gradually to Q ≈ −0.28, followed by a sharp increase (Figure 4E). Similar to the
disassortative-assortative structural continuum, modal controllability does not exhibit a signif-
icant trend along the disassortative-core continuum (Figure 4F).

In summary, disruptions to particular mesoscale motifs in networks where edges are drawn

from a normal distribution result in motif-speciﬁc proﬁles of network controllability.

Relationship Between Network Controllability and Community Structure for Edge Weights Drawn from
a Fat-Tailed Distribution

In the context of structural brain networks, multiple empirical estimates may be used to quan-
tify the strength of connections between two regions, such as white-matter streamline counts
between regions, mean quantitative anisotropy (QA) values along the streamlines, and gen-
eralized fractional anisotropy (GFA) values. These measures reﬂect the strength, volume, O
integrity of white-matter tracts connecting one region of the brain to another. This diversity in
the characterization of structural networks introduces further complexity in the modeling of
large-scale communication dynamics in the brain. The distribution of edge weights in a struc-
tural brain network is contingent on the choice of edge deﬁnition, which has the potential to
cause conﬂict in results that relate network topology to controllability.

In order to examine the relationship between the edge weight distribution that underlies a
mesoscale topology and network controllability, we next turn to brain networks with an edge
weight distribution distinct from the already examined normal distribution from Data Set 1.
Results presented in this section are obtained from analyses performed on Data Set 2 (Vedere
subsection Data in the Methods for details), which is comprised of structural brain networks
where edges represent estimates of streamline counts between regions. An element [Aij] Di
an adjacency matrix for these networks represents the number of streamlines connecting two
brain regions i and j. Edge weights with streamline counts approximate a fat-tailed distribu-
zione. Recent work has indicated that real-world networks with fat-tailed distributions can often
be approximated using the log-normal distribution (Broido & Clauset, 2019). Di conseguenza, we
use the log-normal distribution as the choice of edge weight distribution prior when infer-
ring communities using the weighted stochastic block model (WSBM). We demonstrate the

Network Neuroscience

1100

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 4. Controllability for normally weighted networks as a function of changing mesoscale topology. (UN, B) As network topology changes
from disassortative to assortative, mean network control energy and average controllability ﬁrst decrease, and then increase tracing out
U-shaped curves. Their values are the lowest when Q ≈ 0, which corresponds to the point of randomness. Networks with a balance be-
tween disassortativity and coreness occur when Q ≈ −0.28. (D) Minimum control energy increases as networks become less disassortative
and more core-like. (E) Average controllability ﬁrst decreases and then rapidly increases past Q ≈ −0.28. (C, F) Modal controllability, on the
other hand, exhibits no discernible trends with changing network topology. Each point in the scatter plots represents a Z-scored mean network
controllability value computed across 100 network instantiations at each Q-value. Error bars correspond to the standard deviation of the mean
controllability value for networks in a given ensemble.

Network Neuroscience

1101

Community structure does not explain network controllability

robustness of our results to the choice of the edge weight distribution prior in the Supporting
Information.

Measures of Controllability are not Consistently Correlated with Measures of Modularity for Structural
Similar to our observations in struc-
Brain Networks with a Fat-Tailed Distribution of Edge Weights
tural brain networks with normally distributed edge weights (Data Set 1), here we ﬁnd that the
participation coefﬁcient relates negatively with minimum control energy (ρ = −0.433, p ≈ 0)
and with modal controllability (ρ = −0.435, p ≈ 0), and positively with average controllability
(ρ = 0.450, p ≈ 0) for networks with a fat-tailed edge weight distribution (Data Set 2). Intramod-
ule strength Z-score relates negatively with both minimum control energy (ρ = −0.638, p ≈ 0)
and modal controllability (ρ = −0.630, p ≈ 0), and relates positively with average controlla-
bility (ρ = 0.565, p ≈ 0). These observations, yet again, suggest the presence of a statistical
relationship between community structure and controllability.

Similar to Data Set 1, Tuttavia, it is possible for these statistical relations between control-
lability and community structure to be driven by a third variable such as node strength. Infatti
in Data Set 2, we also observe that node strength is related to measures of network control-
lability. Node strength relates negatively with minimum control energy (ρ = −0.993, p ≈ 0)
and modal controllability (ρ = −0.993, p ≈ 0), and relates positively with average control-
lability (ρ = 0.984, p ≈ 0). Node strength is also a predictor of the participation coefﬁcient
(ρ = 0.440, p ≈ 0) and the intramodule strength Z-score (ρ = 0.625, p ≈ 0). Similar to ear-
lier analyses, we run partial Spearman correlations in order to account for the effects of node
strength when characterizing the relationship between measures of controllability and those
of community structure. We ﬁnd that participation coefﬁcient no longer signiﬁcantly relates to
minimum control energy (ρ = 0.038, p = 0.563) (Figure 5A), average controllability (ρ = 0.103,
p = 0.117) (Figure 5B), or modal controllability (ρ = 0.023, p = 0.728) (Figure 5C). Intramod-
ule strength Z-score continues to relate in a statistically signiﬁcant manner with minimum
control energy (ρ = −0.190, p = 0.004) (Figure 5D) and average controllability (ρ = −0.366,
p ≈ 0) (Figure 5E), but not with modal controllability (ρ = −0.110, p = 0.095) (Figure 5F)
when accounting for the effect of node strength.

From the ﬁndings in this section, we conclude that for structural brain networks with a
fat-tailed edge weight distribution, region-level minimum control energy and average con-
trollability are related in a statistically signiﬁcant manner with intramodule strength Z-score.
Tuttavia, unlike Data Set 1 no measure of controllability relates with participation coefﬁcient
in a statistically signiﬁcant manner. Therefore, the hypothesized relationship between a node’s
participation in the community structure, and its associated controllability metrics, is not gen-
eral and is also strongly contingent on the distribution from which network edges are drawn.

In parallel to the previ-
Numerical Simulations Using Edges Drawn from a Geometric Distribution
ous set of numerical simulations on networks with normally distributed edge weights, we next
sought to describe the relationship between mesoscale architecture and network controllabil-
ity for networks with a fat-tailed edge weight distribution. We use the geometric distribution
as a representative fat-tailed distribution when drawing network edge weights.

In the ﬁrst set of simulations, we generate networks on a range from disassortative to as-
sortative. At each value of the modularity quality index Q, we generate an ensemble of 100
sparse weighted networks with edge weights drawn from the geometric distribution (see sub-
section Numerical Simulations in the Methods for details). We begin by computing the mean

Network Neuroscience

1102

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 5. Relationships between metrics of regional controllability and metrics of community structure for edge weights approximating
a fat-tailed distribution. (UN, B, C) Participation coefﬁcient does not relate in a statistically signiﬁcant manner with minimum control energy
(ρ = 0.038, p = 0.563), average controllability (ρ = 0.103, p = 0.117), or modal controllability (ρ = 0.023, p = 0.728). (D, E) Intramodule
strength Z-score relates signiﬁcantly with minimum control energy (ρ = −0.190, p = 0.004) and average controllability (ρ = −0.366, p ≈ 0).
(F) It does not relate with modal controllability (ρ = −0.110, p = 0.095). Each point in the scatter plots represents the mean value of a
controllability and modularity measure across 24 (8 subjects in triplicate) network instantiations for a single brain region resulting in 234 dati
points.

of the nodal values of minimum control energy, average controllability, and modal controlla-
bility. We then compute the mean for each of the three controllability measures across the 100
instantiations in an ensemble, and repeat this process at every Q value.

We observe that as the network topology becomes more assortative from disassortative,
minimum control energy and modal controllability ﬁrst increase, and then decrease with a

Network Neuroscience

1103

Community structure does not explain network controllability

peak at Q ≈ 0, which corresponds to the point of randomness (Figure 6A, and C). Average
controllability, on the other hand, follows the opposite trend, and is the highest at points of
greatest disassortativity and assortativity, with a low at Q ≈ 0 (Figure 6B). Importantly, IL
trends in network controllability observed for networks with a fat-tailed distribution (Figura 6)
of edge weights are not similar to those observed for networks with a normal distribution of
edge weights (Figura 4).

In the second set of simulations, we generate networks on a range from disassortative
to core-like (see subsection Numerical Simulations in the Methods for details). Along this
structural continuum, when the modularity quality Q index is closer to −0.5, a network is
disassortative, whereas when the index is closer to 0, it has a dense core reminiscent of a
core-periphery network. Networks are nearly random when the index is −0.28. We ﬁnd that
networks with increasingly dense cores have lower mean minimum control energy and mean
modal controllability (Figure 6D, and F). Average controllability, in contrast, increases with an
increasingly dense core (Figure 6E). Trends in the mean network controllability values along
the disassortative-core continuum appear to form traces of U-shaped curves.

For networks where edge weights are drawn from the geometric distribution, disruptions to
particular mesoscale motifs results in motif-speciﬁc proﬁles of network controllability. How-
ever, these proﬁles are distinct from those observed for networks with normally distributed
edge weights. Had binary topology been a unique predictor of network controllability, IL
trends in the curves in Figures 4 E 6 would have been similar for similarly altered networks
along the continuums.

Weighted Subgraph Centrality as a Predictor of Network Controllability

Based on the results thus far, and contrary to the initial hypothesis, the extent of a node’s
participation in the network’s community structure is not a consistent predictor of its metrics
of controllability. Inoltre, at the network level, binary topology does not uniquely de-
termine controllability. It is apparent that the distribution of edge weights is as important to
network controllability as the binary distribution of edges themselves. Since modularity and
controllability do not uniquely explain one another, perhaps a different but complementary
feature of network organization relates the two. Since eigenvalues and eigenvectors fully and
uniquely describe a matrix, the spectrum of the weighted network adjacency matrix, Quale
acts as the system matrix A for our discrete-time LTI system, encodes all features of the net-
work including those that consistently predict controllability. Therefore, we hypothesize that a
node-level metric that is rooted in the graph spectrum ought to relate to controllability statistics
regardless of the distribution of edge weights, or the binary distribution of edges.

With a full control set B = In, the controllability Gramian can be written as,

WC(T) =

T−1
∑
t=0

At BB⊤(A⊤)t =

T−1
∑
t=0

A2t = I + A2 + A4 + · · · .

(4)

Inoltre, in a weighted adjacency matrix A, the entry in the i-th row and j-th column of An
represents the strength of closed walks from node j to node i along paths of length n. Subgraph
centrality (SC) is a measure of centrality deﬁned for unweighted networks that incorporates
higher order path lengths through a factorial discounted sum of the powers of the adjacency

Network Neuroscience

1104

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 6. Controllability for weighted networks with a geometric distribution of edge weights as a function of changing mesoscale topol-
ogy. (UN, C) As network topology changes from disassortative to assortative, the mean network control energy and modal controllability ﬁrst
increase and then decrease on either side of Q ≈ 0, which marks the point of randomness. (B) By contrast, average controllability exhibits
the opposite trend; ﬁrst decreasing and then increasing as networks become more assortative from disassortative. (D, F) Along the continuum
from disassortativity to coreness, minimum control energy and modal controllability decrease, whereas (E) average controllability increases.
Each point in the scatter plots represents a Z-scored mean network controllability value computed across 100 network instantiations. Error
bars correspond to the standard deviation of the mean controllability value for networks in a given ensemble.

Network Neuroscience

1105

Community structure does not explain network controllability

matrix (Estrada & Rodríguez-Velázquez, 2005). We extend the deﬁnition of subgraph centrality
to a weighted adjacency matrix A in order to compute weighted subgraph centrality as follows:

WSC(io) =

∞
∑
k=0

(Ak)ii
k!

= 1 + (UN)ii +

(A2)ii
2!

(A3)ii
3!

(A4)ii
4!

+ · · · .

(5)

We note that Equation 5 can also be written in terms of the eigenvalues and eigenvectors of A
(Estrada & Rodríguez-Velázquez, 2005).

WSC(io) =

∞
∑
k=0

(Ak)ii
k!

∞
∑
k=0

λk
j

vi
j

(cid:16)
k!

N
∑
j=1






(cid:17)






(6)

where N is the number of network nodes, and λj and vj are an eigenvalue and associated
eigenvector, rispettivamente. Practically, we compute weighted subgraph centrality by noting that
the above deﬁnition is equivalent to selecting the diagonal entries of the matrix exponential
of A, WSC(io) = [expm (UN)]ii. Since minimum control energy and average controllability
are explicitly deﬁned in terms of the controllability Gramian, and since modal controllabil-
ity is deﬁned explicitly in terms of the network spectrum, Equations 4, 5, E 6 suggest that
the weighted variant of subgraph centrality is a promising node-level predictor of measures
of network controllability. Hence, in the results that follow, we compute weighted subgraph
centrality on the weighted adjacency matrix A.

We test weighted subgraph centrality to examine whether it is an accurate predictor of con-
trollability that generalizes across structural brain network datasets with distinct edge weight
distributions. Initially we note that weighted subgraph centrality is related negatively with min-
imum control energy (ρ = −0.998, p ≈ 0) and modal controllability (ρ = −0.999, p ≈ 0), E
positively with average controllability (ρ = 0.992, p ≈ 0) for Data Set 1, in which the edge
weight distribution approximates a normal distribution. Tuttavia, it is also related to node
strength (ρ = 0.998, p ≈ 0). In order to account for the effects of node strength, we perform
partial Spearman rank correlations, and ﬁnd that weighted subgraph centrality continues to
relate negatively with minimum control energy (ρ = −0.461, p ≈ 0) (Figure 7A) and modal
controllability (ρ = −0.795, p ≈ 0) (Figure 7C), and positively with average controllability
(ρ = 0.707, p ≈ 0) (Figure 7B).

We then repeat the analyses performed above on Data Set 2, where the distribution of edge
weights approximates a fat-tailed distribution. We ﬁnd that weighted subgraph centrality re-
lates negatively with minimum control energy (ρ = −0.999, p ≈ 0) and modal controllability
(ρ = −0.999, p ≈ 0), and positively with average controllability (ρ = 0.994, p ≈ 0). Since
it also relates to node strength (ρ = 0.993, p ≈ 0), we examine partial Spearman correla-
tions between weighted subgraph centrality and measures of network controllability. Similar
to results with Data Set 1, we ﬁnd that weighted subgraph centrality continues to predict mea-
sures of network controllability in a statistically signiﬁcant manner for Data Set 2. It relates
negatively with minimum control energy (ρ = −0.898, p ≈ 0) (Figure 7D) and modal control-
lability (ρ = −0.954, p ≈ 0) (Figure 7F), and positively with average controllability (ρ = 0.806,
p ≈ 0) (Figure 7E). Additionally, we examine the robustness of weighted subgraph centrality
in predicting controllability of potentially directed structural brain networks in the Supporting
Information. We also examine performance in an independent high resolution data set (Data
Set 3) to verify generalizability of the weighted subgraph centrality–controllability relationship.

Network Neuroscience

1106

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 7. Relationships between metrics of regional controllability and weighted subgraph centrality for networks approximating normal and
fat-tailed distributions of edge weights. (UN, B, C) Weighted subgraph centrality is related in a statistically signiﬁcant manner to controllability
when controlling for node strength in networks with normally distributed edge weights. (UN, C) It relates negatively with minimum control
energy (ρ = −0.461, p ≈ 0) and modal controllability (ρ = −0.795, p ≈ 0), E (B) positively with average controllability (ρ = 0.707, p ≈ 0).
(D, E, F) Weighted subgraph centrality is also related in a statistically signiﬁcant manner to controllability when controlling for node strength
in networks with a fat-tailed distribution of edge weights. The relationships follow similar trends as networks with normally distributed edge
pesi; (D) negative with minimum control energy (ρ = −0.898, p ≈ 0) E (F) modal controllability (ρ = −0.954, p ≈ 0), and positive
con (F) average controllability (ρ = 0.806, p ≈ 0). Each point in the scatter plots represents the mean value of a controllability measure and
weighted subgraph centrality across 24 (8 subjects in triplicate) network instantiations for a single brain region resulting in 234 data points.

In summary, unlike participation coefﬁcient and intramodule strength Z-score, weighted
subgraph centrality reliably and signiﬁcantly explains measures of network controllability re-
gardless of the distribution of network edge weights.

Network Neuroscience

1107

Community structure does not explain network controllability

DISCUSSION

The topology of structural brain networks shapes and constrains the patterns of signaling
between distant neuronal populations (Ritter, Schirner, McIntosh, & Jirsa, 2013; Schirner,
McIntosh, Jirsa, Deco, & Ritter, 2018). These patterns, in turn, give rise to the diverse and
complex large-scale functional dynamics of the brain that underlie cognition (Bansal, Nakuci,
& Muldoon, 2018; Griffa & Van den Heuvel, 2018). In this study, we sought to probe the rela-
tionship between brain network structure and the transient communication dynamics that the
topology can support at the mesoscale of network organization.

While the structure-function relationship for brain networks is of interest at all scales of
network organization, recent advances in community detection techniques have made the
mesoscale particularly relevant (Betzel et al., 2018; Faskowitz et al., 2018). Distinct motifs of
mesoscale structure serve different roles in the context of communication dynamics; assortative
(or modular) interactions allow for information integration and segregation (Goñi et al., 2013;
Park & Friston, 2013), core-periphery motifs with rich-club hubs (Colizza, Flammini, Serrano, &
Vespignani, 2006) allow for information broadcast and receipt (van den Heuvel, Kahn, Goñi, &
Sporns, 2012; van den Heuvel & Sporns, 2013), while disassortative motifs support information
transmission. Controllability, by contrast, inﬂuences state transitions (Towlson et al., 2018), E
has been related to the notion of cognitive control, where the brain shifts from one cognitive
state to another (Cornblath et al., 2019). Through our numerical simulations, we demonstrate
that distinct features of community structure are likely to be implicated in distinct aspects of
neural computation.

A mesoscale feature is any topological feature that cannot be explained by the local neigh-
borhood of a node, and is better explained by larger neighborhoods around the node than it
is by the total global architecture (Lohse, Bassett, Lim, & Carlson, 2014; Schlesinger, Turner,
Grafton, Mugnaio, & Carlson, 2017). Much of the literature has focused on modularity and core-
periphery structure as the canonical forms of mesoscale structure (Girvan & Newman, 2002;
Newman & Girvan, 2004). But our results suggest that another distinct form of mesoscale
structure must be considered, and that is the feature that drives controllability statistics (Kim
et al., 2018). Here we demonstrate that weighted subgraph centrality can potentially assess
this distinct dimension of mesoscale architecture in future studies.

Recent work has sought to deﬁne measures of network topology, such as disassortativity
and core-peripheriness, both at the scale of nodes and at the scale of communities (Foster,
Foster, Grassberger, & Paczuski, 2010; C. Sarkar & Jalan, 2018; S. Sarkar, Henderson, &
Robinson,2013; Zhang, Guo, & Yi, 2015). A natural direction to extend this work is to exam-
ine the distribution of eigenvalues as the network topology gradually alters to become more
assortative or core-periphery from disassortative. Moments of the eigenvalue distribution such
as the mean, variance, skewness, and kurtosis may hold valuable insights into the behavior of
network control metrics as functions of mesoscale architecture and edge weight distribution.
More theoretical work is needed in order to relate the spectra of weighted graphs to properties
of network controllability. Recent work has attempted to create closed-form characterizations
of spectral properties for both assortative (Van Mieghem, Wang, Ge, Tang, & Kuipers, 2010)
and core-periphery networks. Inoltre, since structural brain networks simultaneously pos-
sess a variety of community interaction motifs (Betzel et al., 2018), future work might involve
characterizing the effects of mixed interactions in numerical simulations similar to those per-
formed in this work.

Controllability statistics cannot be explained simply by node strength, nor can they be ex-
plained by mesoscale structure. Through our results, we verify that node strength is a signiﬁcant

Network Neuroscience

1108

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

predictor of network controllability in the classes of graphs we study. Tuttavia, it does not
uniquely explain controllability. In all our analyses, after verifying the dependence of con-
trollability on node strength, we proceed to regress out its effects when examining any de-
pendence on other metrics of interest. We demonstrate in the Supporting Information that
weighted subgraph centrality correlates more strongly, as well as linearly, with measures of
network controllability than node strength does across a range of values of the time horizon
of control. Additionally, whereas weighted subgraph centrality survives corrections for node
strength, and continues to signiﬁcantly predict controllability, modularity often does not. Questo
distinction indicates that weighted subgraph centrality explains parts of network controllability
that neither node strength nor any modularity metric we evaluated are able to.

Our results indicate that higher order path-dependent network structure, as captured by
weighted subgraph centrality, is strongly related to transient communication dynamics. In-
deed, it explains controllability better than descriptive statistics such as node strength and
measures of modularity. At the network-level, communicability is able to separate patients of
stroke from healthy controls (Crofts et al., 2011). Communicability metrics have been shown
to be sensitive indicators of lesions in patients with relapsing-remitting multiple sclerosis (Y. Li
et al., 2013). It has also been shown that communicability is disrupted in patients of Alzheimer’s
disease (Lella et al., 2018). Weighted subgraph centrality is the weighted extension of the no-
tion of self-communicability. The consistently strong relationship between weighted subgraph
centrality and measures of network controllability suggests that statistics derived from linear
control theory (such as average and modal controllability, and minimum energy) are also likely
useful tools in investigating the disruptions to brain network dynamics in disease.

The distinction between modularity and controllability impacts our interpretation of previ-
ous reports that provide evidence that these two features change appreciably over normative
neurodevelopment. A naive hypothesis could be that the change in modularity drives a change
in controllability, or vice versa. Tuttavia, Tang et al. show that their network controllability
results hold after regressing out modularity (Tang et al., 2017). Inoltre, we ﬁnd more gen-
erally using multiple data sets and systematic variation of network modularity in simulations,
that the two variables cannot be explained by one another. In the context of development, our
results suggest that the process of brain development may reﬂect a more complex optimiza-
tion function that coordinates a change in modularity alongside a change in controllability.
What that function is, and what the mechanism of coordination is, remains to be clearly spec-
iﬁed, but would be an important area for future work. The distinction between modularity and
controllability also calls for care when interpreting reports of either of these features changing
as a function of aging (Baum et al., 2017), training (Arnemann et al., 2015), treatment (Baliki,
Babbitt, & Cherney, 2018; Tao & Rapp, 2019), injury (Gratton, Nomura, Pérez, & D’Esposito,
2012), or disease (Vértes et al., 2012).

Biophysical Interpretation of Model Parameters

In the discrete-time LTI framework, the variable x(T) is a real N-dimensional vector, whose
i-th element corresponds to the level of activity of brain region i. The level of activity of
each brain region can be deﬁned in multiple ways, such as the average blood oxygen level-
dependent (BOLD) signal from functional magnetic resonance imaging (fMRI) (Braun et al.,
2019; Cui et al., 2020), or the average electrical activity from electrophysiological recordings
(Khambhati et al., 2019; Stiso et al., 2019). As for the inputs, the variable u(T) represents
independent control inputs whose inﬂuence can be linearly separated from the activity along
white-matter tracts. For instance, these inﬂuences may be endogenous neurotransmitter activity

Network Neuroscience

1109

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

(Braun et al., 2019), task-based internal modulation of the brain state (Cornblath et al., 2020;
Cui et al., 2020), or exogenous inputs such as pharmacological agents (Braun et al., 2019), di-
rect electrical stimulation, or transcranial magnetic stimulation (Khambhati et al., 2019; Stiso
et al., 2019).

Hence, while the most immediate and straightforward interpretation of u(T) is as an ex-
ternal electrical or pharmacological perturbation, we do not discount the possibility of other
internal neural mechanisms (per esempio., local dynamics of gray-matter neurons) that are independent
of and take advantage of these white-matter tracts to inﬂuence global dynamics. Keeping both
possibilities in mind, we refer to u(T) as the “exogenous input” for conceptual tractability. In
aggiunta, if it is easier for an exogenous input to globally inﬂuence the system by changing
the activity of a node (less energetic cost, more spread of activity), then it is similarly easier
for the endogenous activity of that node to globally inﬂuence the system. If the endogenous
nodal activity is generated by a process that is independent of the white-matter tracts, it can
be modeled as a separate input u(T) to the linear dynamical system without making additional
assumptions beyond an interpretation of exogenous inputs.

In the context of structural brain networks and computations of control energy for state tran-
sitions, more work is needed to neurobiologically motivate the choices for initial and target
stati. Prior work has made imaging-based choices for states to model cognitive states of the
brain, such as band-limited power (Stiso et al., 2019) or beta weights from a general linear
model of BOLD activation from fMRI (Braun et al., 2019). Alternatively, binary activation of
regions corresponding to functional modules has also been examined (Betzel, Gu, Medaglia,
Pasqualetti, & Bassett, 2016). Tuttavia, since the focus of this paper is to examine network
controllability from the perspective of network community structure, a thorough investigation
of state-pair choices is beyond the current scope. Our speciﬁc choice here is motivated by prior
work probing the generic control properties of a system by formulating an inﬂuence maximiza-
tion problem (C. Lynn & Lee, 2016). We compute minimum control energies by performing n
state transitions to n one-hot vectors for each brain region i, such that the energies Ei form an
upper bound on the energy required to perform arbitrary non-negative state transitions x∗ (Vedere
Supporting Information for more discussion).

Methodological Considerations

The choice of the weighted stochastic block model (WSBM) to uncover network communi-
ties is motivated by the desire to uncover community interaction motifs extending beyond the
traditionally examined assortative type. We hypothesized that disruptions to speciﬁc motifs
ought to result in motif-speciﬁc proﬁles of network controllability. In the context of empiri-
cal brain data, the WSBM uncovers a diverse community structure reﬂecting the diversity of
the functional dynamics supported. The WSBM is an incredibly ﬂexible community detection
technique. Tuttavia, this ﬂexibility comes at the price of having to choose a number of param-
eters a priori, including the number of communities that are anticipated to exist in the network,
and a prior regarding the nature of the edge weight distribution. We ﬁx the number of com-
munities by sweeping over a range of values and choosing the value that maximizes the likeli-
hood of observing the given network data. Additionally, we verify salient analyses performed
in the paper in the Supporting Information with a different choice of edge weight distribution
prior.

In our network-level numerical simulations, we adopt the geometric distribution as a rep-
resentative fat-tailed distribution from which to draw edge weights. The geometric distribution

Prior:
The probability distribution or
density on the causes of data that
encode beliefs about those causes
prior to observing the data.

Network Neuroscience

1110

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

is the discrete counterpart to the exponential distribution. Another fat-tailed distribution that
is commonly explored in network neuroscience is the scale-free distribution characterized by
a power-law (Sizemore, Giusti, & Bassett, 2016; Wu-Yan et al., 2018). Tuttavia, recent work
has demonstrated that scale-free networks are not as ubiquitous as previously thought, and that
the exponential distribution is often a suitable alternative (Broido & Clauset, 2019). Our mo-
tivation in considering the normal and geometric distributions was to examine controllability
of networks with two different edge weight distributions. Future work could characterize con-
trollability performance explicitly for networks with a scale-free distribution of edge weights,
instead of relying on a stand-in fat-tailed distribution (Wu-Yan et al., 2018).

While a linear model of network dynamics lends itself well to control-theoretic studies
of communication dynamics, empirical results have shown that brain activity is nonlinear
(Rabinovich et al., 2006). Tuttavia, recent work has demonstrated that a linear approxima-
tion is often useful (Galán, 2008; Honey et al., 2009; Muldoon et al., 2016). Inoltre, IL
linear framework can be adapted to incorporate more complex features of neural dynamics
(UN. Li, Cornelius, Liu, Wang, & Barabási, 2017; Yang et al., 2019; Zañudo, Yang, & Albert,
2017). Similar to the WSBM, applying linear network control theory to empirical data involves
setting a variety of hyperparameters, such as the time horizon over which control is exerted, IL
target state vector in computations of minimum control energy, or the normalization scheme
employed. Our hyperparameter choices are motivated by the desire to investigate and compare
network topology across datasets with very distinct edge weight distributions. Di conseguenza, we
choose a nonzero short time horizon after scaling down the network adjacency matrices by
their largest eigenvalues. This step ensures that the fastest evolving modes across systems stay
consistent. Tuttavia, we note the need for further work to motivate parameter choices from a
neurophysiological perspective.

Our results demonstrate that the choice of empirical measurement that is used to charac-
terize structural edges in brain networks is crucial to investigations of network control. For
instance, whereas results derived from quantitative anisotropy (QA) weighted networks may
lead us to conclude that modularity as measured by the participation coefﬁcient and average
controllability are related (Figura 3), streamline count weighted networks present contrary re-
sults (Figura 5). It is unclear if one type of empirical estimate for network edges in structural
brain networks is better than another. It is possible that some measures better assess signal
speed, others better assess bundle volume, and yet others better assess microstructure integrity
(Johansen-Berg, 2010). Perhaps the choice of edge weight deﬁnition also has implications for
community detection. For instance, are network partitions likely to be different depending on
the distribution of edge weights? More work is needed to contextualize the impact of edge
weights on our interpretations of modularity, core-periphery structure, and network control-
lability, and their relationships to communication, computation, and dynamics. The WSBM
continues to remain a promising tool in this endeavor since it is comprised of a generative
model with a prior over the edge weight distribution built into its framework.

CONCLUSION

We began with the hypothesis that the extent of a node’s participation in the network com-
munity structure ought to be related to its controllability. We ﬁnd that modularity as measured
by the participation coefﬁcient and intra-module strength Z-score is a signiﬁcant predictor of
average and modal controllability for structural brain networks where the distribution of edge
weights approximates a normal distribution. For these networks, neither participation coefﬁ-
cient nor intra-module strength Z-score are related with minimum control energy. For networks

Network Neuroscience

1111

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

where edge weights approximate a fat-tailed distribution, we ﬁnd that participation coefﬁcient
is not related in a statistically signiﬁcant manner with any measure of network controllability.
Intra-module strength Z-score is related with minimum control energy and average controlla-
bility, but not with modal controllability.

By contrast, weighted subgraph centrality is a statistically robust predictor of network con-
trollability, regardless of the distribution of network edge weights. The relationships between
weighted subgraph centrality and measures of network controllability, indicate that higher or-
der path-dependent network structure predicts transient communication dynamics. At the net-
work level, through numerical simulations, we demonstrate that binary topology alone is not
a predictor of mean network controllability. Along a structural continuum from disassortative
to assortative, or from disassortative to core, mean controllability proﬁles are heavily depen-
dent on the distribution of network edge weights. Our study contributes to an understanding
of how the diverse mesoscale structural architecture of the brain, characterized by a variety
of community interaction motifs and edge weight distributions, supports transient dynamics in
the brain.

METHODS

Data

Structural brain networks used in the analyses are constructed from diffusion spectrum imaging
(DSI) data acquired in triplicate from eight subjects (mean age 27 ± 5 years, two female, two
left handed) along with T1-weighted anatomical scans at each scanning session. DSI scans
sampled 257 directions using a Q5 half-shell acquisition scheme with a maximum b-value
S
mm2 and an isotropic voxel size of 2.4 mm. Axial acquisition with the following
Di 5,000
parameters was employed: repetition time (TR) = 11.4 S, echo time (TE) = 138 ms, 51 slices,
ﬁeld of view (FoV) (231, 231, 123 mm). All participants volunteered with informed consent
in accordance with the Institutional Review Board/Human Subjects Committee, University of
California, Santa Barbara. Data acquisition and network construction methods are described
elsewhere in further detail (Gu et al., 2015).

The data contain brain networks where edges represent diverse estimates of inter-node
connections, including white-matter streamline counts between regions, mean quantitative
anistropy (QA) values along the streamlines, and generalized fractional anisotropy (GFA) val-
ues. The choice of edge deﬁnition has implications for the distribution of edge weights in the
networks. Streamline counts have a fat-tailed edge weight distribution, whereas QA values are
normally distributed. In the present study, we investigate the implications of edge weight dis-
tribution on network controllability by using networks with QA values as well as streamline
conta. We refer to networks with QA values as Data Set 1, and to networks with streamline
counts as Data Set 2.

Additionally, we repeat salient analyses in the Supporting Information on a higher resolution
dataset, henceforth termed Data Set 3. This dataset is acquired from 10 healthy human subjects
as part of an ongoing data collection effort at the University of Pennsylvania; the subjects
provided informed consent in writing, in accordance with the Institutional Review Board of
the University of Pennsylvania. Similar to Data Set 2, Data Set 3 is comprised of structural brain
networks where edges reﬂect streamlines counts between regions.

For Data Set 3, all scans are acquired on a Siemens Magnetom Prisma 3 Tesla scanner with
a 64-channel head/neck array at the University of Pennsylvania. All participants volunteered
with informed consent in accordance with the Institutional Review Board/Human Subjects

Network Neuroscience

1112

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

Committee, University of Pennsylvania. Each data acquisition session includes both a diffusion
spectrum imaging (DSI) scan as well as a high-resolution T1-weighted anatomical scan. IL
diffusion scan is 730-directional with a maximum b-value of 5,010 S
mm2 and TE/TR = 102/4,300
ms, which includes 21 b = 0 images. Matrix size is 144 × 144 with a slice number of 87. Field
of view is 260 × 260 mm2 and slice thickness is 1.80 mm. Acquisition time per DTI scan
È 53 : 24 min, using a multiband acceleration factor of 3. The anatomical scan is a high-
resolution three-dimensional T1-weighted sagittal whole-brain image using a magnetization
prepared rapid acquisition gradient-echo (MPRAGE) sequence. It is acquired with TR = 2,500
ms; TE = 2.18 ms; ﬂip angle = 7 degrees; 208 slices; 0.9 mm thickness. More detail on data
acquisition and processing is available elsewhere (Kim et al., 2018).

Weighted Stochastic Block Model

In our effort to probe the relationship between network controllability and the mesoscale archi-
tecture of structural brain networks, the ﬁrst step is to partition the networks into communities.
We apply block modeling to infer network partitions from data. Block models uncover diverse
mesoscale architectures (Aicher et al., 2014; Hastings, 2006), which may have implications
for network controllability. The model assumes that connections between nodes are made
independently of one another, and that the probability of a connection between two nodes
depends only on the communities to which the nodes are assigned. Fitting the model involves
estimating the parameters that maximize the likelihood of observing a given network.

The stochastic block model (SBM) seeks to partition the nodes of a network into K commu-
nities. Let zi ∈ {1, · · · , K} indicate the community label of node i. Under the block model,
the probability Pij = θzi,zj that any two nodes i and j are connected depends only on their
community labels, zi and zj, where zi, zj ∈ {1, · · · , K}. To ﬁt the block model to the observed
data in A, we estimate θrs for all pairs of communities {R, S} ∈ {1, · · · , K} and the community
labels zi. Assuming that the placement of edges is independent of one another, the likelihood
of the SBM having generated a network is

P(UN | {zi}, {θrs}) = ∏
io,j

(θzizj )Aij(1 − θzizj)1−Aij.

(7)

Fitting the SBM involves determining the parameters {zi} E {θrs}. Tuttavia, the SBM is
limited to binary networks. By contrast, the weighted stochastic block model (WBSM) (Aicher,
Jacobs, & Clauset, 2013; Aicher et al., 2014; Hastings, 2006) incorporates edge weights into
its framework, making weighted graphs such as brain networks accessible to block models for
community detection (Betzel et al., 2018; Faskowitz & Sporns, 2019; Faskowitz et al., 2018;
Pavlovic et al., 2014).

In the weighted variant (WSBM) of the block model, the likelihood function in Equation 7

is modiﬁed to

P(UN | {zi}, {θrs}) ∝ exp

∑
io,j

(cid:18)

T(Aij) . η(θzizj )

(cid:19)

(8)

In the binary case (SBM), T and η correspond to the vector-valued function of sufﬁcient
statistics and the vector-valued function of natural parameters for the Bernoulli distribution,
rispettivamente. Different choices of T and η can allow for the edge weights to be drawn from
different distributions of the exponential family. The WSBM, just like its classical variant, È
parameterized by the set of community assignments, {zi}, and the parameters {θrs}. The dif-
ference is that each θzizj now speciﬁes the parameters governing the weight distribution of the

Network Neuroscience

1113

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

edge zizj, and not the probability of edge existence. For the normal distribution, the vector-
valued function of sufﬁcient statistics is T = [X, x2, 1], while the vector-valued function of
natural parameters is η = [µ/σ2, −1/2σ2, µ2/(2P)2]. Edges are now parameterized by a mean
zizj). Di conseguenza, the likelihood function in Equation 7 can be
and variance, θzizj = (µzizj
modiﬁed to read

, σ2

UN | {zi}, {µrs}, {σ2

rs}

(cid:0)

= ∏
io,j

(cid:1)

esp

(cid:18)

Aij ·

µzi,zj
σ2
zizj

− A2
ij ·

1
2σ2

zizj

− 1 ·

µ2
zi,zj
σ2
zizj

(cid:19)

(9)

for edge weights drawn from the normal distribution.

An additional challenge in ﬁtting block models to data is the handling of sparse networks
(Aicher et al., 2014). This is particularly important for brain networks since the neural connec-
tome is sparse and most entries in the adjacency matrix A are zero. This sparsity is handled
by modeling edge weights as described above, and separately modeling edge presence with
a Bernoulli distribution. If Te and ηe represent the edge existence distribution, and Tw and ηw
the edge weight distribution, the likelihood function for A, can be written as:

logP(UN | {zi}, {θrs}) = α ∑
io,j∈E

Te(Aij) . ηe(θzizj) + (1 − α) ∑
io,j∈W

Tw(Aij) . ηw(θzizj).

(10)

In Equation 10, E is the set of all edges and W is a subset of E representing the weighted
edges. A variational Bayes algorithm is then used to estimate the model parameters from data,
as outlined in Aicher et al. (2013) and Aicher et al. (2014).

Tuttavia, this pipeline is still incomplete as ﬁtting the WSBM to a network requires that the
number of blocks K in the community structure be chosen a priori. A data-driven approach can
help determine the suitable number of blocks present. Since the WSBM is a generative model,
we can estimate the likelihood of observing a connectivity matrix A for different values of K.
The K that maximizes the likelihood of observing the data is chosen as the parameter value
when inferring network partitions downstream. For Data Set 1 and Data Set 2, we run the
WSBM on all structural connectivity matrices derived from the eight subjects (8 subjects ×
3 = 24 matrices) while sweeping over a range of K values from K = 6 to K = 15. Since the
WSBM is not deterministic, we run 10 iterations for each subject for each trial at each choice
of K. We ﬁnd that data likelihood is maximized when K = 12 for networks with normally
distributed edge weights (Data Set 1) with a Gaussian edge weight prior, and when K = 14
for networks with a fat-tailed edge weight distribution (Data Set 2) with a log-normal edge
weight prior. A by-product of the process of selecting K is the partitions of the networks into
communities that we seek. At the K that maximizes data likelihood, each network already has
10 instantiations of partitions. The network partition chosen for the analyses is the one that
is the most central out of all, as deﬁned by variation of information (Faskowitz et al., 2018).
For Data Set 3, we run 25 iterations of the WSBM for each K and ﬁnd that the likelihood is
maximized when K = 10 with a log-normal edge weight distribution prior.

Code to infer community structure from networks using the WSBM is freely available at

http://tuvalu.santafe.edu/~aaronc/wsbm/ (Aicher et al., 2013, 2014).

Network Neuroscience

1114

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

Network Statistics

Recall that our hypotheses depend on the quantiﬁcation of the extent to which nodes par-
ticipate in interactions with nodes from other communities. We compute the participation
coefﬁcient (Guimerà & Nunes Amaral, 2005), and intramodule strength Z-score (Guimerà &
Nunes Amaral, 2005) to quantify this extent based on the WSBM-generated partitions of brain
networks.

The participation coefﬁcient for a node i is deﬁned as

PCi = 1 −

K
∑
z=1 (cid:0)

κiz
κi (cid:1)

(11)

where κiz is the strength of connection of node i to nodes in community z, and κi is the total
strength of node i. The term K is the number of communities in the partition. Intramodule
strength Z-score (Z) for node i is deﬁned as

Zi =

κizi − ¯κzi
σκzi

(12)

¯κzi
where κizi is the strength of connection of node i to other nodes in its own community zi,
È
is the average strength of connection of all nodes in module zi to other nodes in zi, and σκzi
the standard deviation of κizi. We compute these metrics using freely available code from the
Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/) (Rubinov & Sporns,
2010).

At the network level, the modularity quality index Q measures how well a given partition
of a network compartmentalizes its nodes into modules (Newman, 2006; Newman & Girvan,
2004). We use this measure in conjunction with numerical simulations to quantify the extent
of modularity at the network level. Q is deﬁned as:

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Q = ∑
ij (cid:2)

Aij − Nij

zi, zj

(cid:3)

(cid:0)

(cid:1)

(13)

where Nij is the expected strength of connections between nodes i and j under the Newman–
Girvan null model, which is designed to quantify assortativity (Newman, 2006). The Kronecker
delta function equals 1 when the two nodes belong to the same community, and equals zero
otherwise.

Numerical Simulations

In order to generate networks with speciﬁc edge weight distributions and binary topologies,
we make use of a 2 × 2 block structure, and specify the binary density of each block separately.
When the fraction of total edges inside of the on-diagonal blocks exceeds the fraction in the
off-diagonal blocks, the network has an assortative community structure. By contrast, Quando
the fraction of total edges in the off-diagonal blocks exceeds the fraction inside of the diagonal
blocks, the network has a disassortative community structure. If the fraction of edges inside
of the block in the [1, 1] position is higher than the fractions for the three remaining blocks,
the network has a core-periphery architecture. Upon ﬁxing the value of the fraction of total
edges inside of a block of interest, the remaining edges are distributed across the network such
that the network’s binary density remains 0.1485, which is the mean density of structural brain
networks from Data Set 1.

Network Neuroscience

1115

Community structure does not explain network controllability

For each edge, a corresponding weight value is drawn from a prespeciﬁed distribution,
either a normal distribution or a family of geometric distributions (see below). Edges drawn
from the normal distribution are parameterized by µ = 0.5 and σ = 0.12 (Wu-Yan et al.,
2018). The geometric distribution was chosen as a representative of the family of fat-tailed dis-
tributions that are ubiquitous in biological systems (Broido & Clauset, 2019; Sizemore et al.,
2016; Wu-Yan et al., 2018). Geometric distributions are parameterized by a single number p,
which represents the probability of success of a Bernoulli trial. Weights are then assigned to
edges by incrementing the value of an edge until the ﬁrst failure of a Bernoulli trial. Therefore,
when p is closer to 0 edge weights tend to remain small, and when p is closer to 1 edge weights
tend to take on large values.

During the course of numerical simulations along a structural continuum from disassortative
to assortative, or from disassortative to core-periphery, new networks are created at each stage
with new binary densities for the four blocks. In the case of the continuum from disassortative
to assortative networks, the fraction of total edges in the on-diagonal blocks is gradually altered.
When this fraction is 0, all network edges lie in the off-diagonal blocks giving the network a
disassortative architecture. By contrast, when the fraction is 1 and all edges lie inside of the
on-diagonal blocks, the network is perfectly modular and possesses an assortative mesoscale
structure. In the case of the continuum from disassortative to core-periphery networks, the frac-
tion inside of the [1, 1]-block is gradually altered, and the [2, 2]-block is left empty. When the
fraction of total edges inside of the [1, 1]-block is 0, the network is disassortative, whereas when
the fraction is 1, the network only has a single densely connected core. Alternatively, this pro-
cess may be thought of as moving edges from the off-diagonal blocks to either the on-diagonal
blocks, or the [1, 1]-block, depending on the structural continuum under consideration.

At each stage along the continuum, 100 networks are created using the set of parameters that
deﬁne the network topology of the ensemble. The process of creating ensembles is intended to
ensure roughly similar degree distributions for networks across a structural continuum. In case
of simulations for networks with geometrically distributed edge weights, a further constraint
is enforced. In order to align network topology to the network geometry, when drawing edge
weights for the numerical simulations, we use multiple geometric distributions. For each block
in the 2 × 2 block adjacency matrix, p is chosen to be the desired binary density (fraction
of total edges) corresponding to the block (Wu-Yan et al., 2018). We summarize the extent
of modularity in each network in an ensemble along the continuum by using the modularity
quality index Q. Since networks are generated with partitions that are known a priori, we do
not perform a repartitioning of the networks in order to determine Q. We characterize the
relationship between Q, and the fraction of edges inside of modules (as well as inside the
core) in the Supporting Information.

CITATION DIVERSITY STATEMENT

Recent work in neuroscience and other ﬁelds has identiﬁed a bias in citation practices such
that papers from women and other minorities are under-cited relative to the number of such
papers in the ﬁeld (Caplar, Tacchella, & Birrer, 2017; Chakravartty, Kuo, Grubbs, & McIlwain,
2018; Dworkin et al., 2020; Maliniak, Powers, & Walter, 2013; Thiem, Sealey, Ferrer, Trott, &
Kennison, 2018). Here we sought to proactively consider choosing references that reﬂect the
diversity of the ﬁeld in thought, form of contribution, genere, race, geography, and other factors.
We used automatic classiﬁcation of gender based on the ﬁrst names of the ﬁrst and last authors
(Dworkin et al., 2020), with code freely available at https://github.com/dalejn/cleanBib. Pos-
sible combinations for the ﬁrst and senior authors include male/male, male/female, female/

Network Neuroscience

1116

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

male, and female/female. After excluding self-citations to the ﬁrst and senior authors of our
current paper, the references in this work contain 58.6% male/male, 8% male/female, 18.4%
female/male, 3.4% female/female, E 11.5% unknown citation categorizations. We look for-
ward to future work that could help us better understand how to support equitable practices
in science.

ACKNOWLEDGMENTS

The authors gratefully acknowledge helpful discussions with Jennifer Stiso, Dr. Eli J. Cornblath,
Dr. Xiasong He, and Dr. Ann Sizemore-Blevins.

SUPPORTING INFORMATION

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00157.

AUTHOR CONTRIBUTIONS

S.P.P. performed the simulations, analyzed the data, made the ﬁgures, and wrote the paper.
J.Z.K. contributed analytical solutions. J.Z.K., F.P., and D.S.B. participated in discussions and
edited the paper.

FUNDING INFORMATION

Danielle S. Bassett would like to acknowledge support from the John D. and Catherine T.
MacArthur Foundation, the Alfred P. Sloan Foundation, the ISI Foundation, the Paul Allen
Foundation, the Army Research Laboratory (W911NF-10-2-0022), the Army Research Ofﬁce
(Bassett-W911NF-14-1-0679, Grafton-W911NF-16-1-0474, DCIST- W911NF-17-2-0181), IL
Ofﬁce of Naval Research, the National Institute of Mental Health (2-R01-DC-009209-11, R01
MH112847, R01-MH107235, R21-M MH-106799), the National Institute of Child Health and
Human Development (1R01HD086888-01), National Institute of Neurological Disorders and
Stroke (R01 NS099348), and the National Science Foundation (BCS-1441502, BCS-1430087,
NSF PHY-1554488 and BCS-1631550).

REFERENCES

Abdelnour, F., Voss, H. U., & Raj, UN. (2014). Network diffusion ac-
curately models the relationship between structural and func-
tional brain connectivity networks. NeuroImage, 90, 335–347.
https://doi.org/10.1016/j.neuroimage.2013.12.039

Aicher, C., Jacobs, UN. Z., & Clauset, UN. (2013). Adapting the stochas-
tic block model to edge-weighted networks. arXiv:1305.5782
Aicher, C., Jacobs, UN. Z., & Clauset, UN. (2014). Learning latent block
structure in weighted networks. Journal of Complex Networks
(2015), 3(2), 221–248. https://doi.org/10.1093/comnet/cnu026
Andrea, A., Misic, B., & Sporns, O. (2018). Communication dynam-
ics in complex brain networks. Nature Reviews Neuroscience, 19.
Arnemann, K. L., Chen, UN. J., Novakovic-Agopian, T., Gratton, C.,
Nomura, E. M., & D’Esposito, M. (2015). Functional brain net-
work modularity predicts response to cognitive training after
brain injury. Neurology, 84(15), 1568–1574.
Baliki, M. N., Babbitt, E. M., & Cherney, l. R.

(2018). Brain net-
work topology inﬂuences response to intensive comprehensive
aphasia treatment. NeuroRehabilitation, 43(1), 63–76.

Bansal, K., Medaglia, J. D., Bassett, D. S., Vettel, J. M., & Muldoon,
S. F.
(2018). Data-driven brain network models differentiate
variability across language tasks. PLoS Computational Biology,
14(10), e1006487–e1006487. https://doi.org/10.1371/journal
.pcbi.1006487

Bansal, K., Nakuci, J., & Muldoon, S. F. (2018). Personalized brain
network models for assessing structure-function relationships.
Current Opinion in Nuerobiology, 52, 42–47.

Bassett, D. S., & Bullmore, E. T. (2017). Small-world brain networks
revisited. The Neuroscientist, 23(5), 499–516. https://doi.org
/10.1177/1073858416667720
Bassett, D. S., & Gazzaniga, M. S.

(2011). Understanding com-
plexity in the human brain. Trends in Cognitive Sciences, 15(5),
200–209. https://doi.org/0.1016/j.tics.2011.03.006

Bassett, D. S., Greenﬁeld, D. L., Meyer-Lindenberg, A., Weinberger,
D. R., Moore, S. W., & Bullmore, E. T. (2010). Efﬁcient physical
embedding of topologically complex information processing net-
works in brains and computer circuits. PLoS Computational Biol-
ogy, 6(4), 1–14. https://doi.org/10.1371/journal.pcbi.1000748

Network Neuroscience

1117

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353–364. https://doi.org/10.1038/nn.4502
Bassett, D. S., Zurn, P., & Gold, J. IO. (2018). On the nature and use of
models in network neuroscience. Nature Reviews Neuroscience,
19(9), 566–578.

Baum, G. L., Ciric, R., Roalf, D. R., Betzel, R. F., Moore, T. M.,
Shinohara, R. T., . . . Satterthwaite, T. D.
(2017). Modular seg-
regation of structural brain networks supports the development
of executive function in youth. Current Biology, 27(11), 1561–
1572.e8. https://doi.org/10.1016/j.cub.2017.04.051

Bernhardt, B. C., Fadaie, F., Liu, M., Caldairou, B., Gu, S.,
Jefferies, E., . . . Bernasconi, N. (2019). Temporal lobe epilepsy.
Neurology, 92(19), e2209–e2220. https://doi.org/10.1212/WNL
.0000000000007447

Betzel, R. F., & Bassett, D. S.

(2017). Multi-scale brain networks.
NeuroImage, 160, 73–83. https://doi.org/10.1016/j.neuroimage
.2016.11.006

Betzel, R. F., Gu, S., Medaglia, J. D., Pasqualetti, F., & Bassett, D. S.
(2016). Optimally controlling the human connectome: The role
of network topology. Scientiﬁc Reports, 6(1), 30770. https://doi
.org/10.1038/srep30770

Betzel, R. F., Medaglia, J. D., & Bassett, D. S.

(2018). Diversity
of meso-scale architecture in human and non-human connec-
tomes. Nature Communications, 9(1), 346. https://doi.org/10
.1038/s41467-017-02681-z

Braun, U., Harneit, A., Pergola, G., Menara, T., Schaefer, A., Betzel,
R. F., . . . Tost, H.
(2019). Brain state stability during work-
ing memory is explained by network control theory, modu-
lated by dopamine D1/D2 receptor function, and diminished in
schizophrenia. arXiv, 1906, 09290.

Broido, UN. D., & Clauset, UN. (2019). Scale-free networks are rare.
Nature Communications, 10(1), 1017–1017. https://doi.org/10
.1038/s41467-019-08746-5

Caplar, N., Tacchella, S., & Birrer, S.

(2017). Quantitative evalu-
ation of gender bias in astronomical publications from citation
conta. Nature Astronomy, 1(6), 0141.

Chakravartty, P., Kuo, R., Grubbs, V., & McIlwain, C. (2018). #Commu-
nicationSoWhite. Journal of Communication, 68(2), 254–266.
Chialvo, D. R. (2010). Emergent complex neural dynamics. Nature
Physics, 6(10), 744–750. https://doi.org/10.1038/nphys1803
Colizza, V., Flammini, A., Serrano, M. A., & Vespignani, UN. (2006).
Detecting rich-club ordering in complex networks. Nature
Physics, 2, 110–115.

Cornblath, E. J., Ashourvan, A., Kim, J. Z., Betzel, R. F., Ciric, R.,
Adebimpe, A., . . . Bassett, D. S. (2020). Temporal sequences of
brain activity at rest are constrained by white matter structure and
modulated by cognitive demands (Vol. Epub Ahead of Print).
Cornblath, E. J., Tang, E., Baum, G. L., Moore, T. M., Adebimpe,
(2019). Sex differences
A., Roalf, D. R., . . . Bassett, D. S.
in network controllability as a predictor of executive function
in youth. NeuroImage, 188, 122–134. https://doi.org/10.1016/j
.neuroimage.2018.11.048

Crofts, J., Higham, D., Bosnell, R., Jbabdi, S., Matthews, P., Behrens,
T., & Johansen-Berg, H. (2011). Network analysis detects changes
in the contralesional hemisphere following stroke. NeuroIm-
age, 54(1), 161–169. https://doi.org/10.1016/j.neuroimage.2010
.08.032

Cui, Z., Stiso, J., Baum, G. L., Kim, J. Z., Roalf, D. R., Betzel, R. F., . . .
Sauerthwaite, T. D.
(2020). Optimization of energy state tran-
sition trajectory supports the development of executive func-
tion during youth. eLife, 9, e53060. https://doi.org/10.7554/eLife
.53060

Deco, G., Tononi, G., Boly, M., & Kringelbach, M. l. (2015). Re-
thinking segregation and integration: contributions of whole-
brain modelling. Nature Reviews Neuroscience, 16(7), 430–439.
https://doi.org/10.1038/nrn3963

Dworkin, J. D., Linn, K. A., Teich, E. G., Zurn, P., Shinohara, R. T., &
Bassett, D. S. (2020). The extent and drivers of gender imbalance
in neuroscience reference lists. bioRxiv. https://doi.org/10.1101
/10.1101/2020.01.03.894378

Estrada, E., & Rodríguez-Velázquez, J. UN. (2005). Subgraph central-
ity in complex networks. Physical Review E, 71, 056103. https://
doi.org/10.1103/PhysRevE.71.056103

Faskowitz, J., & Sporns, O. (2019). Mapping the community struc-
ture of the rat cerebral cortex with weighted stochastic block
modeling. Brain Structure and Function. https://doi.org/10.1007
/s00429-019-01984-9

Faskowitz, J., Yan, X., Zuo, X.-N., & Sporns, O. (2018). Weighted
stochastic block models of the human connectome across the
life span. Scientiﬁc Reports, 8(1), 12997. https://doi.org/10.1038
/s41598-018-31202-1

Foster, J. G., Foster, D. V., Grassberger, P., & Paczuski, M.

(2010).
Edge direction and the structure of networks. Atti del
National Academy of Sciences of the United States of America,
107(24), 10815–10820.

Fries, P.

(2015). Rhythms for cognition: Communication through
coherence. Neuron, 88(1), 220–235. https://doi.org/10.1016/j
.neuron.2015.09.034

Galán, R. F. (2008). On how network architecture determines the
dominant patterns of spontaneous neural activity. PLoS ONE,
3(5), 1–10. https://doi.org/10.1371/journal.pone.0002148

Girvan, M., & Newman, M. E.

(2002). Community structure in
social and biological networks. Proceedings of the National
Academy of Sciences of the United State of the America, 99(12),
7821–7826.

Goñi,

J., Avena-Koenigsberger, A., Velez de Mendizabal, N.,
(2013). Ex-
van den Heuvel, M. P., Betzel, R. F., & Sporns, O.
ploring the morphospace of communication efﬁciency in com-
plex networks. PLoS ONE, 8(3), 1–10. https://doi.org/10.1371
/journal.pone.0058070

Gratton, C., Nomura, E. M., Pérez, F., & D’Esposito, M. (2012). Fo-
cal brain lesions to critical locations cause widespread disruption
Journal of Cognitave
of the modular organization of the brain.
Nueroscience Neurosci, 24(6), 1275–1285.

Griffa, A., & Van den Heuvel, M. P.

(2018). Rich-club neurocir-
cuitry: Function, evolution, and vulnerability. Dialogues Clinical
Neuroscience, 2, 121–132.

Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Yu, UN. B., Kahn,
UN. E., . . . Bassett, D. S. (2015). Controllability of structural brain
networks. Nature Communications, 6(1), 8414. https://doi.org
/10.1038/ncomms9414

Guimerà, R., & Nunes Amaral, l. UN. (2005). Functional cartography
of complex metabolic networks. Nature, 433(7028), 895–900.
https://doi.org/10.1038/nature03288

Network Neuroscience

1118

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

Hagmann, P., Kurant, M., Gigandet, X., Thiran, P., Wedeen, V. J.,
Meuli, R., & Thiran, J.-P. (2007). Mapping human whole-brain
structural networks with diffusion MRI. PLoS One, 2(7), 1–9.
https://doi.org/10.1371/journal.pone.0000597

Harriger, L., van den Heuvel, M. P., & Sporns, O. (2012). Rich club
organization of macaque cerebral cortex and its role in network
communication. PLoS One, 7(9), 1–13. https://doi.org/10.1371
/journal.pone.0046497

Hastings, M. B. (2006). Community detection as an inference prob-
lem. Physical Reviews E, 74, 035102. https://doi.org/10.1103
/PhysRevE.74.035102

Honey, C. J., Kötter, R., Breakspear, M., & Sporns, O. (2007). Net-
work structure of cerebral cortex shapes functional connectivity
on multiple time scales. Proceedings of the National Academy of
Scienze, 104(24), 10240–10245. https://doi.org/10.1073/pnas
.0701519104

Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J. P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Proceedings
of the National Academy of Sciences, 106(6), 2035–2040. https://
doi.org/10.1073/pnas.0811168106

Jeganathan, J., Perry, A., Bassett, D. S., Roberts, G., Mitchell, P. B.,
& Breakspear, M.
(2018). Fronto-limbic dysconnectivity leads
to impaired brain network controllability in young people with
bipolar disorder and those at high genetic risk. NeuroImage:
Clinical, 19, 71–81. https://doi.org/10.1016/j.nicl.2018.03.032
(2010). Behavioural relevance of variation in
white matter microstructure. Current Opinion in Neurology,
23(4), 351–358.

Johansen-Berg, H.

Kailath, T. (1980). Linear Systems. Prentice Hall.
Karrer, T. M., Kim, J. Z., Stiso, J., Kahn, UN. E., Pasqualetti, F., Habel,
U., & Bassett, D.
(2020). A practical guide to methodological
considerations in the controllability of structural brain networks.
Journal of Neural Engineering. http://iopscience.iop.org/10.1088
/1741-2552/ab6e8b

Khambhati, UN. N., Kahn, UN. E., Costantini, J., Ezzyat, Y., Solomon,
E. A., Gross, R. E., . . . Bassett, D. S. (2019). Functional control
of electrophysiological network architecture using direct neuro-
stimulation in humans. Network Neuroscience, 3(3), 848–877.
Kim, J. Z., Soffer, J. M., Kahn, UN. E., Vettel, J. M., Pasqualetti, F., &
Bassett, D. S.
(2018). Role of graph architecture in controlling
dynamical networks with applications to neural systems. Nature
Physics, 14(1), 91–98. https://doi.org/10.1038/nphys4268

Lee, B., Kang, U., Chang, H., & Cho, K.-H.

control architecture of complex brain networks.
154–162. https://doi.org/10.1016/j.isci.2019.02.017

(2019). The hidden
iScience, 13,

Li, Y., Jewells, V., Kim, M., Chen, Y., Moon, A., Armao, D., . . .
Shen, D. (2013). Diffusion tensor imaging based network analysis
detects alterations of neuroconnectivity in patients with clinically
early relapsing-remitting multiple sclerosis. Human Brain Map-
ping, 34(12), 3376–3391. https://doi.org/10.1002/hbm.22158
Liu, Y.-Y., Slotine, J.-J., & Barabási, A.-L. (2011). Controllability of
complex networks. Nature, 473(7346), 167–173. https://doi.org
/10.1038/nature10011

Lohse, C., Bassett, D. S., Lim, K. O., & Carlson, J. M. (2014). Resolv-
ing anatomical and functional structure in human brain organi-
zation: Identifying mesoscale organization in weighted network
representations. PLoS Computational Biology, 10(10), e1003712.
Lynn, C., & Lee, D. D. (2016). Maximizing inﬂuence in an ising net-
lavoro: A mean-ﬁeld optimal solution. In D. D. Lee, M. Sugiyama,
U. V. Luxburg, IO. Guyon, & R. Garnett (Eds.), Advances in neu-
ral information processing systems 29 (pag. 2495–2503). Curran
Associates, Inc.

Lynn, C. W., & Bassett, D. S. (2019). The physics of brain network
structure, function and control. Nature Reviews Physics, 1(5),
318–332. https://doi.org/10.1038/s42254-019-0040-8

Maliniak, D., Powers, R., & Walter, B. F. (2013). The gender citation
gap in international relations. International Organization, 67(4),
889–922.

Marx, B., Koenig, D., & Georges, D. (2004). Optimal sensor and ac-
tuator location for descriptor systems using generalized gramians
and balanced realizations. Negli Atti del 2004 American
Control Conference (Vol. 3, P. 2729–2734). https://doi.org/10
.23919/ACC.2004.1383878

Meunier, D., Lambiotte, R., & Bullmore, E.

(2010). Modular and
hierarchically modular organization of brain networks. Fron-
tiers in Neuroscience, 4, 200. https://doi.org/10.3389/fnins.2010
.00200

Muldoon, S. F., Pasqualetti, F., Gu, S., Cieslak, M., Grafton, S. T.,
Vettel, J. M., . . . Bassett, D. S. (2016). Stimulation-based control
of dynamic brain networks. PLoS Computational Biology, 12(9),
1–23. https://doi.org/10.1371/journal.pcbi.1005076

Newman, M. E. J.

(2006). Modularity and community structure
in networks. Proceedings of the National Academy of Sciences,
103(23), 8577–8582. https://doi.org/10.1073/pnas.0601602103
(2004). Finding and evaluating
Physical Reviews E, 69,

community structure in networks.
026113. https://doi.org/10.1103/PhysRevE.69.026113

Newman, M. E. J., & Girvan, M.

Park, H.-J., & Friston, K.

(2013). Structural and functional brain
networks: From connections to cognition. Scienza, 342(6158).
https://doi.org/10.1126/science.1238411

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Lee, W. H., Rodrigue, A., Glahn, D. C., Bassett, D. S., & Frangou,
S. (2019). Heritability and cognitive relevance of structural brain
controllability. Cerebral Cortex, bhz293.

Pasqualetti, F., Zampieri, S., & Bullo, F. (2014). Controllability met-
rics, limitations and algorithms for complex networks. IEEE Trans-
actions on Control of Network Systems, 1(1), 40–52.

Lella, E., Amoroso, N., Lombardi, A., Maggipinto, T., Tangaro, S.,
Bellotti, R., & Initiative, UN. D. N. (2018). Communicability dis-
ruption in AlzheimerâŁ™s disease connectivity networks. Jour-
nal of Complex Networks, 7(1), 83–100. https://doi.org/10.1093
/comnet/cny009

Li, A., Cornelius, S. P., Liu, Y.-Y., Wang, L., & Barabási, A.-L. (2017).
The fundamental advantages of temporal networks. Scienza,
358(6366), 1042–1046. https://doi.org/10.1126/science.aai7488

Pavlovic, D. M., Vértes, P. E., Bullmore, E. T., Schafer, W. R., &
Nichols, T. E. (2014). Stochastic blockmodeling of the modules
and core of the caenorhabditis elegans connectome. PLoS One,
9(7), 1–16. https://doi.org/10.1371/journal.pone.0097584
I., Varona, P., Selverston, UN.

I., & Abarbanel,
H. D. IO. (2006). Dynamical principles in neuroscience. Reviews
of Modern Physics, 78, 1213–1265. https://doi.org/10.1103
/RevModPhys.78.1213

Rabinovich, M.

Network Neuroscience

1119

Community structure does not explain network controllability

Ritter, P., Schirner, M., McIntosh, UN. R., & Jirsa, V. K. (2013). IL
virtual brain integrates computational modeling and multimodal
neuroimaging. Brain Connectivity, 3(2), 121–145.

Rosvall, M., & Bergstrom, C. T. (2008). Maps of random walks on
complex networks reveal community structure. Atti del
National Academy of Sciences, 105(4), 1118–1123. https://doi
.org/10.1073/pnas.0706851105

Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003
Rubinov, M., & Sporns, O. (2011). Weight-conserving characteriza-
tion of complex functional brain networks. NeuroImage, 56(4),
2068–2079. https://doi.org/10.1016/j.neuroimage.2011.03.069
Sarkar, C., & Jalan, S. (2018). Spectral properties of complex net-
works. Chaos: An Interdisciplinary Journal of Nonlinear Science,
28(10), 102101. https://doi.org/10.1063/1.5040897

Sarkar, S., Henderson, J. A., & Robinson, P. UN.

(2013). Spectral
characterization of hierarchical network modularity and limits of
modularity detection. PLoS One, 8(1), 1–11. https://doi.org/10
.1371/journal.pone.0054383

Schirner, M., McIntosh, UN. R., Jirsa, V., Deco, G., & Ritter, P. (2018).
Inferring multi-scale neural mechanisms with brain network
modelling. Elife, 7.

Schlesinger, K. J., Turner, B. O., Grafton, S. T., Mugnaio, M. B., &
Carlson, J. M. (2017). Improving resolution of dynamic commu-
nities in human brain networks through targeted node removal.
PLoS One, 12(12), e0187715.

Shaker, H. R., & Tahavori, M. (2012). Optimal sensor and actuator
location for unstable systems. Journal of Vibration and Control.
Shine, J. M., Breakspear, M., Campana, P. T., Ehgoetz Martens, K. A.,
Shine, R., Koyejo, O., . . . Poldrack. R. UN. (2019). Human cogni-
tion involves the dynamic integration of neural activity and neu-
romodulatory systems. Nature Neuroscience, 22(2), 289–296.
https://doi.org/10.1038/s41593-018-0312-0

Sizemore, A., Giusti, C., & Bassett, D. S.

(2016). Classiﬁcation
of weighted networks through mesoscale homological features.
Journal of Complex Networks, 5(2), 245–273. https://doi.org/10
.1093/comnet/cnw013

Smith, R. E., Tournier, J.-D., Calamante, F., & Connelly, UN. (2012).
Anatomically-constrained tractography: Improved diffusion mri
streamlines tractography through effective use of anatomical in-
formation. NeuroImage, 62(3), 1924–1938. https://doi.org/10
.1016/j.neuroimage.2012.06.005

Sporns, O. (2013). Network attributes for segregation and integra-
tion in the human brain. Current Opinion in Neurobiology, 23(2),
162–171. https://doi.org/10.1016/j.conb.2012.11.015

Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual
Review of Psychology, 67(1), 613–640. https://doi.org/10.1146
/annurev-psych-122414-033634
Sporns, O., Tononi, G., & Edelman, G.

(2000). Theoretical Neu-
roanatomy: Relating Anatomical and Functional Connectivity
in Graphs and Cortical Connection Matrices. Cerebral Cortex,
10(2), 127–141. https://doi.org/10.1093/cercor/10.2.127

Stiso, J., Khambhati, UN. N., Menara, T., Kahn, UN. E., Stein, J. M.,
Das, S. R., . . . Bassett, D. S. (2019). White matter network archi-
tecture guides direct electrical stimulation through optimal state
transitions. Cell Reports, 28(10), 2554–2566.e7. https://doi.org
/10.1016/j.celrep.2019.08.008

Summers, T. H., & Lygeros, J. (2014). Optimal sensor and actuator
IFAC Proceedings
placement in complex dynamical networks.
Volumes, 47(3), 3784–3789. https://doi.org/10.3182/20140824
-6-ZA-1003.00226

Tang, E., & Bassett, D. S. (2018). Colloquium: Control of dynam-
ics in brain networks. Reviews of Modern Physics, 90, 031003.
https://doi.org/10.1103/RevModPhys.90.031003

Tang, E., Giusti, C., Baum, G. L., Gu, S., Pollock, E., Kahn, UN. E., . . .
Bassett, D. S. (2017). Developmental increases in white matter
network controllability support a growing diversity of brain dy-
namics. Nature Communications, 8(1), 1252. https://doi.org/10
.1038/s41467-017-01254-4

Tao, Y., & Rapp, B.

(2019). The effects of lesion and treatment-
related recovery on functional network modularity in post-stroke
dysgraphia. Neuroimage Clinical, 23, 101865.

Thiem, Y., Sealey, K. F., Ferrer, UN. E., Trott, UN. M., & Kennison, R.
(2018). Just Ideas? The Status and Future of Publication Ethics in
Philosophy: A White Paper (Tech. Rep.).

Tononi, G., Boly, M., Massimini, M., & Koch, C. (2016). Integrated
information theory: From consciousness to its physical substrate.
Nature Reviews Neuroscience, 17(7), 450–461. https://doi.org
/10.1038/nrn.2016.44

Towlson, E. K., Vértes, P. E., Ahnert, S. E., Schafer, W. R., &
Bullmore, E. T.
(2013). The rich club of the C. elegans neu-
ronal connectome. Journal of Neuroscience, 33(15), 6380–6387.
https://doi.org/10.1523/JNEUROSCI.3784-12.2013

Towlson, E. K., VÃ©rtes, P. E., Yan, G., Chew, l. Y., Walker, D. S.,
Schafer, W. R., et al.
(2018). Caenorhabditis elegans and the
network control framework—FAQs. Philosophical Transactions
of the Royal Society of London B Biol Sci, 373(1758), 20170372.
Tuch, D. S. (2004). Q-ball imaging. Magnetic Resonance in Medi-
cine, 52(6), 1358–1372. https://doi.org/10.1002/mrm.20279
van den Heuvel, M. P., Kahn, R. S., Goñi, J., & Sporns, O. (2012).
High-cost, high-capacity backbone for global brain communica-
zione. Proceedings of the National Academy of Sciences, 109(28),
11372–11377. https://doi.org/10.1073/pnas.1203593109

van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organization
of the human connectome. Journal of Neuroscience, 31(44),
15775–15786. https://doi.org/10.1523/JNEUROSCI.3539-11.2011
van den Heuvel, M. P., & Sporns, O. (2013). Network hubs in the
human brain. Trends in Cognitive Sciences, 17(12), 683–696.
https://doi.org/10.1016/j.tics.2013.09.012

Van Mieghem, P., Wang, H., Ge, X., Tang, S., & Kuipers, F. UN.
(2010). Inﬂuence of assortativity and degree-preserving rewiring
on the spectra of networks. The European Physical Journal B,
76(4), 643–652. https://doi.org/10.1140/epjb/e2010-00219-x

Vértes, P. E., Alexander-Bloch, UN. F., Gogtay, N., Giedd, J. N.,
Rapoport, J. L., & Bullmore, E. T. (2012). Simple models of human
brain functional networks. Proceedings of the National Academy
of Science of the United States of America, 109(15), 5868–5873.
Wang, X.-J., & Kennedy, H. (2016). Brain structure and dynamics
across scales: In search of rules. Current Opinion in Neurobiol-
ogy, 37, 92–98. https://doi.org/10.1016/j.conb.2015.12.010

Wu-Yan, E., Betzel, R. F., Tang, E., Gu, S., Pasqualetti, F., & Bassett,
D. S. (2018). Benchmarking Measures of Network Controllability

Network Neuroscience

1120

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Community structure does not explain network controllability

on Canonical Graph Models. Journal of Nonlinear Science. https://
doi.org/10.1007/s00332-018-9448-z

Yang, Y., Lee, J. T., Guidera, J. A., Vlasov, K. Y., Pei, J., Brown, E. N.,
. . . Shanechi, M. M. (2019). Developing a personalized closed-
loop controller of medically-induced coma in a rodent model.
Journal of Neural Engineering, 16(3), 036022. https://doi.org/10
.1088/1741-2552/ab0ea4

Yeh, F.-C., Verstynen, T. D., Wang, Y., Fernández-Miranda, J. C., &
Tseng, W.-Y. IO. (2013). Deterministic diffusion ﬁber tracking im-

proved by quantitative anisotropy. PLoS One, 8(11). https://doi
.org/10.1371/journal.pone.0080713
Zañudo, J. G. T., Yang, G., & Albert, R.

(2017). Structure-based
control of complex networks with nonlinear dynamics. Proceed-
ings of the National Academy of Sciences, 114(28), 7234–7239.
https://doi.org/10.1073/pnas.1617387114

Zhang, Z., Guo, X., & Yi, Y.

(2015). Spectra of weighted scale-
free networks. Scientiﬁc Reports, 5(1), 17469. https://doi.org/10
.1038/srep17469

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
4
1
0
9
1
1
8
6
6
9
8
6
N
e
N
_
UN
_
0
0
1
5
7
P
D