Feedforward Chemical Neural
Network: An In Silico Chemical
System That Learns XOR
Astratto
Inspired by natural biochemicals that perform complex
information processing within living cells, we design and simulate a
chemically implemented feedforward neural network, which learns
by a novel chemical-reaction-based analogue of backpropagation. Nostro
network is implemented in a simulated chemical system, Dove
individual neurons are separated from each other by semipermeable
cell-like membranes. Our compartmentalized, modular design allows
a variety of network topologies to be constructed from the same
building blocks. This brings us towards general-purpose, adaptive
learning in chemico: wet machine learning in an embodied dynamical
system.
Drew Blount*,**
Wild Me
†
Peter Banda
University of Luxembourg
Christof Teuscher
Portland State University
‡
Darko Stefanovic§
University of New Mexico
Keywords
Chemical reaction network, cellular
compartment learning, feedforward, error
backpropagation, linearly inseparable
function
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
UN
R
T
l
/
_
UN
_
0
0
2
3
3
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1 introduzione
Just as neural networks were inspired by models of the brain and a desire to emulate and understand
its computational power, chemical computation looks to the cell and other biological systems, hop-
ing to comprehend and harness the information-processing dynamics that drive life [13, 15, 31]. In
this view, each living cell is a powerful chemical computer, capable of dynamic resource allocation,
repair, reproduction, and sometimes even motility. We wish to understand chemical computation,
with the ultimate goal of building synthetic chemical networks capable of adaptation and learning.
Inoltre, a programmable wet computer could have myriad medical applications, particularly
in smart drug delivery [17, 37, 59]: We imagine a tiny chemical computer injected into a patient,
perhaps in its own cellular membrane, that dynamically reasons about the chemical composition
of the patientʼs blood and releases drugs as appropriate. This is a particularly potent option, con-
sidering that such chemical computers would likely be implemented using biocompatible synthetic
DNA strands [55].
There have been many projects on developing chemical computers in simulated environments over
the past two decades [9, 15, 16, 29, 58]. Several models of chemical neural networks have been explored
[11, 24, 25, 32], but so far these networks have been static in their behavior, incapable of learning.
* Contact author.
** Wild Me, 1726 North Terry Street, Portland, OR 97217. E-mail: me@drew.computer
† Luxembourg Centre for Systems Biomedicine, University of Luxembourg, Luxembourg. E-mail: peter.banda@uni.lu
‡ Department of Electrical and Computer Engineering, Portland State University, Portland, OR 97201. E-mail: teuscher@pdx.edu
§ Department of Computer Science and Center for Biomedical Engineering, University of New Mexico, Albuquerque, NM 87131.
© 2017 Massachusetts Institute of Technology Artificial Life 23: 295–317 (2017) doi:10.1162/ARTL_a_00233
D. Blount et al.
Feedforward Chemical Neural Network
In our previous work we proposed several binary and analogue chemical perceptrons [4, 6, 7].
These were the first simulated chemical systems capable of fully autonomous learning. We used
chemical reaction networks (CRNs), which are unstructured macroscopic chemistries, where interactions
between symbolic species follow realistic reaction-kinetic laws. In these CRNs, single perceptrons
were able to learn two-input linearly separable functions, and we also tackled time series learning and
prediction by introducing chemical delay lines, which store the past inputs (concentrations) and feed
them to underlying perceptrons [3, 46].
Having developed a family of individual chemical perceptrons, we wish to design a method for
connecting these in a more computationally powerful network. The network should be modular,
such that networks with different topologies are constructed from different combinations of the
same parts. As neural networks have been shown to be powerful machine learners, we hope that
a network of single chemical perceptrons could be a step towards the first general-use reprogram-
mable chemical computer.
We achieve this goal with the feedforward chemical neural network (FCNN), a network of cell-like
compartments, each containing a chemical neuron as a module. Communication between nodes
in the network is achieved by permeation through the walls of these compartments, facilitating
the networkʼs feedforward and backpropagation mechanisms.
Like standard single-layer perceptrons, each of our individual chemical perceptrons can learn the
linearly separable binary two-input logic functions, such as AND and OR, but they are incapable of
learning the linearly inseparable functions XOR and XNOR [45]. Here, we demonstrate that the FCNN
learns each of these functions. To our knowledge, it is the first chemical system able to learn a
linearly inseparable function.
The FCNN has the simplest feedforward neural network topology: one hidden layer with two
hidden neurons, the same as the first classical neural network to learn XOR via backpropagation [53].
For more complex learning problems, we show how the FCNNʼs modular design can be applied to
topologies with more, or larger, hidden layers. Using an FCNN is as simple as injecting a few species
into its outermost chemical container and measuring the concentration of an output species. By
modulating the concentrations of injected species, different inputs can be provided, the network
can be trained to new tasks, and its learning rate can be annealed.
Built on a realistic model of chemical dynamics, the FCNN is a step towards reusable, reprogram-
mable chemical computers and a possible union of biochemistry and computer science. The project
is also driven by a desire to better understand, through emulation and analogy, the information
processing that occurs naturally in living systems. In this sense, the FCNN is an exploration of
how relatively simple chemical reaction networks can embody computation, self-modification, E
apprendimento.
1.1 Related Work
Several projects have already implemented static, non-adapting neural networks in simulated chem-
ical systems, especially using DNA-based models [10, 11, 25, 26, 32, 44, 51]. Hjelmfelt et al. [26] E
Otakamo et al. [47], Per esempio, both use schemes where connection weights are encoded in the
concentrations of catalysts, which in turn speed up or slow down the relative consumption of the
input chemical in parallel reactions. Most previous work encodes binary values by considering
whether chemicals are present in the system above a certain threshold. We have taken the same
approach here.
While Hjelmfelt et al. [26] and others have made important progress in implementing various
components of the familiar feedforward neural network, such as a chemical activation function with
sigmoidal properties, all of the above-mentioned projects focus only on the forward propagation of
informazione, and not the backward propagation of the error. In each case, learning either is not
considered, or is performed by an external, non-chemical system that computes the weights for a
formal neural network before converting them to molecular concentrations to serve as parameters
for the chemical implementation [32, 51]. For a system to be truly useful, the real challenge is to
296
Artificial Life Volume 23, Numero 3
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
UN
R
T
l
/
_
UN
_
0
0
2
3
3
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
implement chemical adaptation, where a reinforcement signal triggers reactions that then modify the
systemʼs own behavior.
Several groups have designed chemical systems based on learning models other than neural net-
works, such as decision trees [48] and least-squares regression (LSR) [34]. McGregor et al. [42] dem-
onstrated how in silico evolution can be used used to develop artificial chemistries capable of
learning some particular fixed function. Lakin et al.ʼs scheme for rudimentary learning in an enzy-
matic chemistry [34] is equivalent to non-negative least-squares regression and achieves learning
within a chemical system (and similarly for our more recent learning scheme based on buffered
DNA strand displacement chemistry [35, 36]). Our FCNN differs from these architectures in
two important ways. Primo, it enjoys the conceptual advantages of the neural network model itself,
which is perhaps the most widely used and well-researched machine learning paradigm, and there-
fore represents a good model to use as the backbone of a general-purpose adaptable computer.
Secondo, the FCNN is built from modular and composable components, so that it or something
similar could be the scalable basis of future networks that are much larger and capable of more
complex computation, whereas previous chemical computers have generally been limited-purpose
and not scalable.
Chiang et al. [12] proposed a construction method for chemical reaction networks to represent
reconfigurable logic functions. As opposed to our work, the reconfiguration is performed manually
by changing the concentrations of certain control species. Wu et al. [60] surveyed a wide range of
DNA-based logic gates and their applications in biotechnology and biomedicine. Fernando et al. [21]
proposed a system based on gene regulatory networks embedded in Escherichia coli and demonstrated
that even single-celled organisms could carry out associative learning.
2 Chemical Formalism
2.1 The Chemical Reaction Network
Our simulated chemical system consists of chemical species and reactions between them, along with
rate coefficients governing the speed of those reactions. In this model, also known as a chemical
reaction network (CRN) [18, 26], there is no notion of space, as each species is considered only in
terms of its concentration in a uniformly mixed chemical bath where pressure, volume, and temper-
ature are constant. The chemical species are completely abstract, without any defined molecular
structure or atomic components. Their behavior is fully described by the reaction network, whose
dynamics are deterministic, given the speciesʼ concentrations and the reaction coefficients.
Our CRN uses both catalytic and non-catalytic reactions, and has no notion of reaction revers-
ibility, questo è, reactions go one way. Non-catalytic reactions follow the mass action law, which states
that the rate of a chemical reaction is the product of the concentrations of the reactants and a pos-
→ P, where substrates S1 and S2 combine
itive reaction rate k. For the elementary reaction S1 + S2
to form product P without any intermediate reactions, the reaction rate d[P]/dt is
(cid:2)
d P½
dt
(cid:2)
¼ − d S1½
dt
(cid:2)
¼ − d S2½
dt
¼ k S1½
(cid:2) S2½
(cid:2):
(1)
Square brackets around a species symbol denote the concentration of that species in the system.
In catalytic reactions, the catalyst, a chemical species, drives the reaction without being consumed
by it. If substrate S turns into product P in the presence of catalyst E, denoted S →E P, then so-called
Michaelis-Menten kinetics [14, 43] approximates the reaction rate,
(cid:2)
d P½
dt
¼ kcat E½
(cid:2) S½ (cid:2)
Km þ S½ (cid:2)
;
where kcat, Km 2 ℝ+ are rate constants.
Artificial Life Volume 23, Numero 3
(2)
297
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
UN
R
T
l
/
_
UN
_
0
0
2
3
3
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
We allow annihilation reactions, which remove chemicals from the system. These reactions work
like any other, but produce the null product E, which does not signify disappearance of matter, Ma
simply an inert species that does not further interact with other species in the system.
These different types of chemical reactions then give rise to a system of ordinary differential
equations (ODEs) over the concentrations of species within our system. This system of ODEs
mathematically defines our chemical reaction network.
2.2 Cell-like Compartments
Since Aristotle, Pasteur, and more recently Maturana and Varela [41], cellular compartmentali-
zation has been considered a central characteristic of living systems; this is a major motivation
behind the modern study of “protocells” [52]. The analogy of the cell as a self-contained, self-
sustaining regulatory machine is a familiar one, and the most basic requirement for such a machine
is compartmentalization—separation from the outside world. Hence, much effort has gone into
determining the salient characteristics of a cell and simulating cells in the field of artificial life
[20, 28, 54, 56]. For these reasons, cells have been a common component of several significant
accomplishments in chemical computing [8, 15, 57].
In our artificial chemistry, we introduce cell-like compartments, used as containers for each of the
individual chemical neurons composing the FCNN. Interaction between neurons is facilitated by
permeation across the walls of these compartments. We defined the permeation dynamics of these
compartment walls with reactionlike rules that we call channels.
Channels can be either reactive or inert. In the first case, a species is allowed to enter the com-
partment wall, but a different species emerges on the other side. Chemically, we imagine a molecule
that reacts with a cell wall as it passes through it. In the other case, a species passing through an
inert channel is not changed; it simply travels from one side of the membrane to the other. A given
compartment wall can have any number of channels of either type.
In modeling membrane permeation, it is common to consider the pressure inside the cell, O, in un
similar vein, the numbers of particular molecules within it [30, 54]. In the latter case, a chemical
species S permeates into a cell more slowly if there is already a high concentration of S in the cell.
Inoltre, if a cellʼs total volume is constrained, species can permeate into it only up to a certain
point, when the cell becomes “full.” More detailed models also consider solute permeability, vis-
cosity, hydraulic conductivity [33], pH, and temperature.
We make several simplifying assumptions regarding the dynamics of our cell-like compartments.
Primo, each compartmentʼs internal pressure is assumed constant, meaning that the total volume of
species entering or exiting through permeation is much smaller than the total volume of the con-
tainer; in other words, there is a large amount of some inert solvent inside each compartment.
Secondo, we assume that permeation rules are inherently one-way; if a species passes from side A
of a container wall to side B, it does so aware only of the state on side A. This means that perme-
ation is not osmotic, or equilibrium-seeking, but conceptually more akin to so-called active transport
across cell walls. Third, since we consider chemical species only in terms of their concentrations,
other physical parameters such as temperature and viscosity are beyond the scope of our model.
Having thus simplified the chemical picture, channel permeation rates follow mass-action kinetics:
The rate of permeation is exactly proportional to the concentration of the source species in the
source container and a permeability constant k.
We introduce a notation for channels. Consider two example channels through the wall of
container C,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
UN
R
T
l
/
_
UN
_
0
0
2
3
3
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
ð
C : S2←S1
(cid:1)
0
0
→S
C : S
2
1
Þ;
(cid:3)
:
(3)
In the parentheses, the first species is always inside C, and the second outside. The arrow denotes
← S1) is a reactive channel in which S1 passes into C,
the direction of permeation. Here C : (S2
298
Artificial Life Volume 23, Numero 3
D. Blount et al.
Feedforward Chemical Neural Network
turning into S2 in the process, while C : (S1
0 .
turning into S2
0 → S2
0) is a reactive channel in which S1
0 passes out of C,
It should be noted that the computational use of cells and their membranes is the central object
of study in the field of P systems, or membrane systems, which are abstracted chemical systems where
different reactions occur in different cells, with communication between cells via membrane perme-
ation [49, 50]. The work presented here is somewhat similar to P systems, so it is important to
understand key differences between the two models. Our approach to chemistry is less abstracted
than that taken in P systems: The chemical objects of P systems are strings that “react” through
rewriting rules akin to Chomskyʼs context-free grammars [49]. P systems successfully demonstrated
the theoretical computational power of chemically inspired systems of a certain type, but omissions
such as reaction-kinetic models generally make P systems unwieldy for the design of viable chemical
computers.
Our goal is to use the systems of ODEs that describe our CRNs to construct autonomously
learning neural networks. Each phase of the operation of a multilayered perceptron, such as “cal-
culate linear sum,” and “update weights,” is only qualitatively emulated by our ODEs—we do not
aim to reproduce the mathematics of neural networks in a one-to-one fashion in chemistry. Così,
our chemical perceptrons are mathematically distinct from perceptrons [22]. Inoltre, chemical
reactions representing each operation run continuously and in parallel, rather than discretely and in
sequence. Because our network is a large, nonlinear system of ODEs, there are generally no analytic
solutions for, Dire, what concentration of Y will be present in our system a set time after it is started
with given initial conditions. We therefore use numerical ODE solvers as the backbone of our analysis
(see Section 6).
Previous results on the theoretical power of perceptrons and neural networks (per esempio., Hornikʼs
proof that feedforward perceptrons are universal approximators [27]) start with the mathematical
definitions of the models, and thus rely upon assumptions (as basic as y = (cid:2)wi xi) that are not valid
in our chemical perceptrons. Inoltre, our scalable network construction is restricted to treelike
topologies, a restriction that is generally not made in the study of classical perceptrons. Così, Questo
work demonstrates the robustness of the general conceptual framework behind neural networks,
and that the mathematical particulars of a neural networkʼs implementation are perhaps less impor-
tant than the general, functional relationships between its parts.
In the spirit that drove the early history of neural networks, we consider in this article the same
problem that is the focus of Rumelhartʼs classic exposition of backpropagation [53]: solving XOR
with a one-hidden-layer, two-hidden-unit feedforward perceptron. In Section 6 we will use this
early result from classical multilayer perceptrons as a benchmark against our FCNN.
3 Chemical Neurons
The chemical neuron we chose as the building block for FCNNs is the analogue asymmetric signal
perceptron (AASP) [4]. Two new variants of the AASP are used, one for hidden neurons and one for
the output neuron. As a reference throughout this section and the rest of the article, Tavolo 1 lists all
chemical species in the FCNN. Tables listing all reactions, reaction rate constants, and permeation
channels are provided in the Online Supplementary Material (http://www.mitpressjournals.org/
doi/suppl/10.1162/ARTL_a_00233).
3.1 Our Chemical Neuron: The AASP
Our previous work [4] introduced the AASP and described its mechanism and motivation in depth.
Because both our hidden and output neurons (described in Sections 3.2.1 E 3.2.2) are modified
versions of the AASP, here we describe those features of the AASP that are relevant to the FCNN.
We present the two-input AASP, but the model can be easily extended by treating additional inputs
analogously to the first two.
Artificial Life Volume 23, Numero 3
299
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
UN
R
T
l
/
_
UN
_
0
0
2
3
3
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
Tavolo 1. Chemical Species in the FCNN.
Function
Inputs
Output
Weights
Input (clock) signal
Learning signal
Production records
Weight adjusters
Indiv. weight decreasers
Inert input transmit*
Binary threshold*
Penalty*
Error signal*
Backprop. signals*
Feedforward signal#
Feedforward output#
Species
X1, X2
Y
W0, W1, W2
Sin
SL
X1Y, X2Y, SinY
W ⊕
, W ⊖
⊖
⊖
, W1
W0
⊖
, W2
0
0
, X2
X1
0
, Sin
T
P
E⊕
, E ⊖
⊖
⊕
, P1
P1
⊕
, P2
⊖
, P2
SF
F
Notes. *: Output neuron only; #: hidden neuron only.
3.1.1 Input
Each component of the input vector is represented by a species Xi . Although the AASP accepts
continuous input values, it also operates very well as a binary-input perceptron. In questo caso, we inject
only those Xi whose value is 1, at a preset input concentration, and do not inject the Xi whose value
È 0.
Under this input encoding, the zero input (Xi = 0 for all i ) corresponds to no chemical injection,
which poses problems for a system that should react to such an input because the zero input is
indistinguishable from no input at all. We therefore include a special clock signal Sin with every input,
alerting the perceptron to the input event. Though Sin is necessary only to recognize the zero input,
it is included with all inputs for the sake of consistency. We will see later that Sin is also useful in the
weight integration.
3.1.2 Input-Weight Integration
Here we encounter a common problem in mapping mathematical structures to chemical systems,
the representation of negative numbers. As chemical species cannot exist in negative concentrations,
an arbitrary real number, such as a perceptronʼs input weight, cannot be represented by a straight-
forward mapping to a concentration of a single species.
300
Artificial Life Volume 23, Numero 3
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
UN
R
T
l
/
_
UN
_
0
0
2
3
3
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
In our earliest models of chemical perceptrons, we solved this problem by associating each
weight with two species, one to encode positive weight values and one for negative [6]. To reduce
the size and complexity of the chemical system, we have since used a scheme that requires only one
species per weight. For this we must sacrifice the straightforward linear relationship between the
weight of a formal perceptron and concentrations of weight species in a chemical system—hence
the name asymmetric signal perceptron. Our ASP is not only simpler than its predecessors, but also
learns more accurately [7].
Like a formal perceptronʼs weights, our chemical perceptronsʼ weights determine the persistent
state of the system and, when adjusted, modulate the mapping from input to output. With reactions
between the weight species Wi , input species Xi , and output species Y, we wish to qualitatively
reproduce the simple linear sum
y ¼ w0 þ w1x1 þ w2x2
(4)
in such a way that it reproduces the functionality of negative weights.
What we require of each Wi is simply that, in the presence of Xi, the output Y be either increased
or decreased depending on the concentration of Wi. This is achieved by a race between two
ʼs transformation into Y. In the second,
reactions that consume Xi. In the first, Wi catalyzes Xi
Xi and Y annihilate:
Xi →Wi Y þ Xi Y ;
Xi þ Y →E:
(5)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
UN
R
T
l
/
_
UN
_
0
0
2
3
3
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The first reaction, which produces Y as a function of Xi and Wi , also produces a record-keeping
species XiY. This species is later used in the weight-update stage of learning, as will be described in
Sezione 3.1.3. XiY is merely another abstract species in our artificial chemistry, and should not be
interpreted as a molecular complex containing both Xi and Y. The clock species Sin is already pres-
ent in every injection, so it is used as the constant multiplicative coefficient of the bias W0. In terms
of Equation 5, Sin
Based on the reaction rate laws as described by Equations 1 E 2, we see that [Y ]ʼs rate of
= X0.
change d [Y ]/dt during the input-weight integration is the sum of two terms for each input:
(cid:2)
d Y½
dt
¼
(cid:4)
X
io
(cid:2) Wi
½
½
kc;i Xi
½
Km;i þ Xi
(cid:2)
(cid:2)
(cid:5)
;
− ka;i Xi
½
(cid:2) Y½
(cid:2)
(6)
where each k is a reaction rate constant. The terms inside the sum are the rates of the reactions in
Equazione 5; their signs are opposite because one reaction produces Y and the other consumes it.
Because the first reactionʼs rate is proportional to [Wi], a large [Wi] will result in the first reaction
producing Y faster than the second reaction consumes it. In questo caso, the net effect of the two
reactions is to increase [Y ]. When [Wi] is small, the second reaction dominates and [Y ] decreases.
Così, the concentration of the weight species Wi determines if the presence of Xi serves to increase
or decrease the final output.
Note that upon input injection, each (Wi , Xi) pair is simultaneously producing and annihilating
the same Y. A consequence of this is another difference between chemical and formal percep-
trons: Weight strengths are relative, as each copy of the second reaction above will proceed at a
rate proportional to [Y ], which is constantly changing in a manner dependent on every input
weight. This sharing of Y by the various inputs, as well as the two reactions above, is diagrammed
in Figure 1.
Although we cannot determine the nonlinear dynamics of [Y ] without running an ODE solver,
the nature of the chemical reaction network enforces a lower bound of zero and an upper bound
Artificial Life Volume 23, Numero 3
301
D. Blount et al.
Feedforward Chemical Neural Network
Figura 1. Reactions in the input-weight integration of a two-input AASP. Dotted arrows denote a catalyst, Per esempio,
signifying Xi →Wi Y þ XiY. Each weight catalyzes a reaction turning its associated input into Y, while that input and Y simul-
taneously annihilate each other at a different rate. Reproduced from our article on the AASP [4].
equal to the sum of the input concentrations, (cid:2)
as weights go to infinity.
io [Xi]. The upper bound is asymptotically reached
3.1.3 Apprendimento
Chemical implementations of the input-weight integration are not new [25, 32], but our previous work
was the first to implement autonomous learning [6]. In an AASP, learning starts with the injection of a
desired output species ^Y, and ultimately updates each weight in the appropriate direction by a magnitude
relative to that input dimensionʼs influence on the most recent output Y combined with an analogue
of an error. This scheme is described below, and illustrated in its entirety in Figure 2.
The first step of the learning process is reading the output of the AASP. After input injection, IL
integration reactions are allowed to run for a preset period of time, chosen so that the injected input
species are fully consumed. In our simulations, this lasted 50 time steps. At the end of this period,
the concentration of Y in the AASP is read as its output. The next step in the AASPʼs learning
process is determining the correctness of this output. This is accomplished by injecting the desired
output species ^Y at the desired Y concentration. Upon this injection, Y and ^Y quickly annihilate
each other in equal proportions via the reaction
Y þ ^Y → E:
(7)
This reaction consumes all of whichever species has the lower initial concentration, and the remaining
speciesʼ concentration will be equal to the difference in initial concentrations, questo è, it will be an
analogue of the error. We then use whichever species remains to create weight-changing species with
the appropriate sign, in a slower reaction than the above, to ensure something akin to execution order:
⊕;
^Y → W
Y →SL W ⊖;
(8)
where the learning-signal species SL, also injected with ^Y, ensures that Y is transformed into W
only
after ^Y ʼs injection. This process, by which the output is compared with the desired output to produce
weight-adjustment species, is illustrated in Figure 2a. Similar processes are used to calculate error and
weight-adjustment signals in both the hidden and output neurons in the FCNN.
⊖
Once weight-adjustment signals are produced, all neuron types behave identically, adjusting their
ith weight in proportion to both the adjustment signal and the ith input dimensionʼs influence on
302
Artificial Life Volume 23, Numero 3
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
UN
R
T
l
/
_
UN
_
0
0
2
3
3
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
Figura 2. The three components of the weight-update mechanism of an AASP. (UN ) Y is compared with Ŷ, and the
appropriately signed error species is produced. (B) The positive error species (the result of [Y ] < [Ŷ]) is transformed
directly into each weight species. (c) The negative error species is transformed into annihilator species, which decrease
each weight. In both (b) and (c), the record-keeping species XiY catalyze the reactions, ensuring that the ith weight
is adjusted somewhat proportionally to the impact that the ith input had on Y. Nodes represent species, solid lines
are reactions, dashed lines are catalysts, and E stands for no or inert species.
the most recent production of Y. This qualitatively reproduces the so-called delta rule of classic per-
ceptron learning [22].
In Section 3.1.2, we introduced the species XiY, which is produced as a record of the influence of
Xi and Wi on the production of Y. Via catalysis, we use this species to emulate the delta rule: The
adjust the concentration of weight Wi through productive
weight-adjustment species W
and annihilatory reactions, respectively, each catalyzed by XiY. Thus, weight adjustment is achieved
by the reactions
and W
⊖
⊕
W ⊕ →Xi Y Wi ;
W ⊖ →Xi Y W ⊖
W ⊖
i
i
þ Wi → E:
;
(9)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The main difference between this method and the classical delta rule is that, because XiY ʼs produc-
tion is influenced positively by Wi, and XiY also catalyzes Wiʼs adjustment, larger Wi will be adjusted
relatively more than smaller ones. Thus, larger weights are adjusted more than smaller ones. We
reproduce the effect that the i th weight is adjusted proportionally to both the difference between
desired and actual output, and the most recent ith input signal.
Note that it takes an intermediate species and two reactions for W
to annihilate Wi. This is
simply because the hypothetical reaction W ⊖ þ Wi →Xi Y E , with two reactants and a catalyst, would
require the collision of three molecules in the same instant. As such three-molecule interactions are
unlikely, we do not use them in our designs.
⊖
Artificial Life Volume 23, Number 3
303
D. Blount et al.
Feedforward Chemical Neural Network
3.2 Two Breeds of AASP
To accommodate communication between neurons in FCNNs, we had to modify the original AASP
design. This resulted in two related breeds: one for hidden neurons, which has a modulated output
schedule and accepts backpropagated error signals; and another for the output neuron, modified to
initialize the cascading backpropagation reactions. We discuss the means by which these neurons are
connected to each other to achieve feeding forward and backpropagation in Sections 4.2 and 4.3, but
here we first discuss the details that distinguish our output and hidden neurons from each other
and the AASP.
3.2.1 The Hidden Chemical Neuron
The hidden chemical neuron (HCN) is the modular component from which FCNNs of various topol-
ogies are constructed. It has two differences from the AASP as presented in Section 3.1, one each to
facilitate feeding forward and backpropagation.
The AASP produces output Y constantly, as the input dimensions are gradually integrated
through the series of reactions in Section 3.1.2. It is designed to receive input signals instantaneously,
however, so in a network context we cannot simply feed forward a hidden neuronʼs output as it is
produced. In practice, we have found that AASPs perform poorly with their input injected gradually
over time.
Thus, we introduce a feedforward species SF, which arrives in an HCNʼs chemical system when its
output Y is meant to feed forward. The details of this will be discussed along with the rest of the
network in Section 4.2, but for now it is enough to know that the following reaction occurs in each
HCN:
Y →SF F;
(10)
where F is the species that is later fed forward. Thus, the next neuron receives an input signal that is
more sudden than the relatively gradual output of the HCN, and this action is induced by SF.
In learning, an HCN has less work to do than an AASP. An AASP reasons about its output and a
, but hidden neurons receive error
⊕
-
desired output to produce the weight-update species W
signals through backpropagation, not through a direct comparison of the outputs. Thus, the W
and W
-producing reactions of an AASP, illustrated in Figure 2a, are omitted from the HCN.
and W
⊖
⊕
⊖
3.2.2 The Output Chemical Neuron
The output chemical neuron (OCN) has a different learning mechanism from the AASP. As the current
FCNN is designed to learn binary functions, such as XOR, inserting a desired-output species to in-
stigate learning, as Figure 2a shows, is somewhat ineffective. For example, if the binary threshold is
0.5, the error will be minuscule if the actual output is, say, 0.499. This was not a serious problem in
the single AASP, but the OCNʼs error signal must not only update its own weights, but propagate
backwards as well. The reactions involving backpropagation will be discussed in Section 4.3; here,
we explain the method by which weight-changing signals are produced within the OCN.
The OCNʼs learning phase begins with the external evaluation of its output. A penalty species P
is injected only if the OCNʼs output is incorrect, that is, on the wrong side of the binary threshold
that is used to interpret chemical concentrations as binary values. Along with P, the AASPʼs learning
signal SL is injected. Further, a threshold species T is injected in concentration equivalent to the
binary threshold. T communicates the binary threshold to the OCN, and behaves somewhat anal-
ogously to the desired-output species ^Y in the AASP (Section 3.1.3).
The goal of the OCNʼs error-evaluating reactions, diagrammed in Figure 3, is to amplify small
continuous-valued errors to emulate distinct binary-valued errors. This is done in two stages. First,
Y and T annihilate in a fast reaction. Whichever is left over encodes whether Y was above or below
the threshold, and whether the weights should be increased or decreased. Thus, SL catalyzes rela-
tively slow reactions from Y and T to signed error species E
, respectively.
and E
⊖
⊕
304
Artificial Life Volume 23, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
Figure 3. The weight-update mechanism for a two-input AASP. The process is started by the injection of the penalty
signal P. The annihilatory comparison of the output Y and the threshold T determines whether the weights will be
increased or decreased. Nodes represent species, solid lines are reactions, dashed lines are catalysts, and E stands
for no or inert species.
Whichever E species is more prevalent tells whether the weights should be increased or decreased,
but their absolute magnitudes might be very small. We then amplify these signals autocatalytically
while consuming the penalty species P:
P →E⊕
P →E⊖
E⊕ þ W ⊕;
E⊖ þ W ⊖:
⊕
⊖
Note that E
tions are illustrated in the bottom half of Figure 3.
) is both catalyst and product, and W
(E
(11)
⊕
⊖
(W
) is also produced. The above equa-
The autocatalytic reactions ensure that the total amount of weight change is not limited by the
initial difference between [Y ] and [T ], which is encoded in the [E]s. The total amount of weight
change is bounded, however, by the injected concentration of P, as it is the only reactant creating
W
. Thus, we can achieve annealing by decreasing the concentration of successive injec-
tions of P. To summarize the error-evaluating reactions: The initial difference between [Y ] and [T ]
determines the sign of the weight adjustment, and [P ] determines the magnitude.
or W
⊕
⊖
4 Networking
This section discusses the methods by which AASPs are connected to make a FCNN. We first
describe the networkʼs topology, both as a neural network and as a series of chemical containers;
and then its mechanisms of feeding forward signals and error backpropagation.
4.1 Constructing the Network Topology
With neurons in nested compartments and links across compartment walls, our networks are topo-
logically trees, each wall being a branch and the outermost compartment being the root (Figure 4).
Figure 4. FCNNs have treelike topologies.
Artificial Life Volume 23, Number 3
305
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
Figure 5. An alternative scheme places all hidden neurons as sibling subcompartments of the output neuron, illustrated
for an all-to-all network topology.
The outermost compartment (1 in the figure) corresponds to the output layer in a feedforward multi-
layer perceptron, and for a given set of nested compartments, the deepest compartments (4–7 in
the figure) correspond to the input layer. We cannot construct arbitrary feedforward networks,
because in our treelike networks each node can feed forward to only one node in the next layer.
This nested architecture enables the FCNNʼs modularity. Each neuron is guaranteed to share a
permeable wall with any neuron to which it is connected in the network, so messages that must pass
from one neuron to another do not need to be “addressed”—they passively permeate from parent
to child or vice versa. This makes the architecture scalable. The signal species between different pairs
of neurons can be chemically identical because the signaling occurs in distinct compartments.
For this reason, the number of species in the FCNN is sublinear in the size of the network.
If we wished to make arbitrary feedforward topologies, that would be possible provided we
included distinct signal species for every linkage in the neural network. This could be achieved
by placing all hidden neurons, regardless of their level in the network, as sibling subcompartments
within the larger output neuron (Figure 5). Feedforward and backpropagation signals would travel
between hidden neurons via this shared compartment. As long as there are unique signal species for
each link in the network, this design allows arbitrary feedforward network topologies.
0
Figure 6. A simplified diagram of the feedforward action of a two-input, one-hidden-layer, two-hidden-neuron FCNN.
species are injected into the outer layer and permeate into the input layer, turning into the reactive Xi input
The inert Xi
species in the process. Each inner compartment produces Y, which then permeates into the outer compartment
as it is transformed into the appropriate Xi. This feedforward process is modulated by unshown species SF and F;
see Section 3.2.1.
306
Artificial Life Volume 23, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
In the simulation results presented in this article, we used a simple two-hidden-neuron, one-
hidden-layer topology to solve XOR (Figure 6). This topology is consistent with either of the above
paradigms. As we are more interested in the modularity afforded by a treelike topology, we
implement backpropagation and feeding forward in ways generalizable to treelike designs.
4.2 The Forward Pass
4.2.1 Injection
Each of an FCNNʼs input neurons is contained in a subcompartment of the output neuron. In the
interest of keeping the systemʼs input-output protocol as straightforward as possible, all injections
are made directly into the outermost compartment, rather than precisely into any of its subcompart-
ments. Yet the input species must be consumed only by reactions in the input-layer nodes, and
because the output compartment contains an AASP, any input species Xi are automatically con-
0 is injected instead that
sumed whenever they are present within it. Therefore, an inert species Xi
permeates into the input compartments. These compartments have channels that convert each inert
to the reactive input species Xi, which are then immediately treated by the hidden neurons as
Xi
input (Figure 6):
0
(cid:1)
0
C : Xi ←X
i
(cid:3)
for C an input compartment:
(12)
Similarly, each hidden neuron needs to receive a feedforward species SF (described in Section 3.2.1),
which must be injected from outside the system so that every neuron in a given layer receives this
1 ,
signal simultaneously. In an FCNN with n hidden layers, we require a set of feedforward species SF
2 , …, SF
n , which transform into the basic signal species SF when permeating into compartments
SF
of the appropriate layer:
C : SF ←Si
F
; C in the ith hidden layer:
(13)
Once SF permeates into a given hidden neuron, that neuronʼs output Y is transformed into the
j C.
feedforward species F. If this HCN is the i th neuron in the jth hidden layer, say it is in container i
Then F permeates outward into C, turning into the corresponding input species Xi in the process:
Y →SF F
ð
i C : F→Xi
Þ;
i C is the ith subcompartment of C:
Simultaneously, the OCN receives its signal species Sin by recycling the HCNʼs SF:
iC : SF →Sin
ð
Þ;
iC is the ith subcompartment of C:
(14)
(15)
Thus, SF plays two roles: It alerts the hidden neurons to feed forward their output, and then by
the above permeation alerts the neurons in the next layer to begin processing input. With these
reactions, the output Y of each hidden chemical neuron feeds forward. This process is illustrated
in Figure 7, which shows (in silico) experimental concentration-versus-time data for the species in
the feedforward process, in each neuron in a simple one-hidden-layer FCNN.
4.3 Backpropagation
Backpropagation is the algorithm that first learned XOR and popularized the modern feedforward
neural network [53]. Again, our chemical system does not exactly reproduce the classic formulae
Artificial Life Volume 23, Number 3
307
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Concentration-versus-time plot in the example FCNN with two HCNs (a, b) and one OCN (c), illustrating the
0
0
, X2
HCNsʼ outputs feeding forward and becoming the OCNʼs input. At time zero the inputs X1
are injected
to the OCN (not shown in (c)). They then permeate into each HCN, transforming into the input species. Note the
initial spikes in concentrations of X1, X2, and Sin in (a) and (b). After the injection of an SF signal at time 40, each HCNʼs
output permeates out to the OCN, transforming into the appropriate input species and Sin. Axis units are arbitrary.
0
, and Sin
308
Artificial Life Volume 23, Number 3
D. Blount et al.
Feedforward Chemical Neural Network
defining this process, and we focus instead on chemically reproducing the important conceptual
relationships between parts.
To review, classical backpropagation proceeds in three steps:
1. The output perceptronʼs error e = ^y − y is calculated, where ^y and y are the desired and
actual outputs.
2. Moving backwards, each perceptronʼs error is calculated as the sum of the errors that it
has affected, weighted by the connecting weights. In our topologically restricted multilayer
= ejwji , where
perceptrons, each node only feeds forward to one other, so this reduces to ei
wji is the weight from perceptron i to j, and ej is already known.
3. Each weight is updated proportionally to this error, the weightʼs own magnitude, and the
most recent output of the source perceptron: Dwji ∝ eiwji yi, where yi is the last output of
perceptron i.
The first step above is emulated by the OCNʼs internal reactions, described in Section 3.2.2.
These reactions produce weight-update species that encode the sign and magnitude of the networkʼs
overall error.
The OCN generates input-specific error signals to be backpropagated to the previous layer in the
network. These reactions are also implemented in any HCN with deeper layers of HCNs inside it,
that is, all neurons where a signal should be backpropagated. In such neurons, the weight-adjustment
species W
, in addition to changing weights, produce input-specific backpropagation
signals. This production is catalyzed by the weight species Wi ,
and W
⊖
⊕
W ⊕ →Wi P⊕
i
W ⊖ →Wi P⊖
i
;
;
(16)
⊕
so the ith backpropagation signal P i
ith weight and the overall adjustment species W
⊖
or P i
⊕
and W
⊖
.
is produced in an amount positively correlated with the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. A diagram of the backpropagation action of a one-hidden-layer, two-hidden-neuron FCNN. The weight-
adjusting species in the outer OCN (right of figure) produce signed, input-specific penalty species Pi. The penalty
species then permeate into the hidden neuronsʼ compartments, becoming those neuronsʼ weight-changing species
in the process.
Artificial Life Volume 23, Number 3
309
D. Blount et al.
Feedforward Chemical Neural Network
⊕
The signed, dimension-specific penalty species P i
then propagates backwards through
the network via permeation channels. Since the purpose of these signals is to adjust weights,
⊕
they are simply transformed to the species W
as they permeate into the appropriate
subcontainers:
⊖
or P i
and W
⊖
(cid:1)
iC : W ⊕←P⊕
i
iC : W ⊖←P⊖
i
(cid:1)
(cid:3)
(cid:3)
;
;
iC is the ith subcompartment of C:
(17)
Thus, in the one-hidden-layer case, the concentration of the weight-changing species W
⊖
and
W
in the outer compartment, and
(b) the weight Wi connecting the two compartments. This relationship is diagrammed in Figure 8.
in the ith inner compartment is related to (a) W
and W
⊖
⊕
⊕
5 Methodology
5.1 Rate and Permeation Constants
We have so far specified the reactants, products, and catalysts in each reaction, but every reaction
also has at least one dimensionless rate coefficient, which describes its speed (k in Equations 1 and 2).
Here we discuss how those rate coefficients have been set in our simulations. Tables listing all
reaction rates can be found in the Online Supplementary Material.
As each AASP (Section 3.1) contains around twenty distinct rate constants, the rate parameter
space is prohibitively large and complex to explore via exhaustive search. In our previous work [4]
we searched for these constants with a standard genetic algorithm. As both the hidden and output
chemical neurons share most of their reactions with the AASP, those reactions are set to the rates
found by the method described in [4].
Unlike with the AASP, we found success in setting the rate constants introduced in this article by
hand. Our intuition in doing so was based on the intended function of each reaction, and which
reactions should occur faster or slower than others. To illustrate the intuitive setting, consider the
case when two species annihilate in order to determine which had the larger initial concentration, and
then the remaining species is transformed into another to perform a task dependent on the initial
comparison. This is the case when Y and T are compared in the OCNʼs error-calculating mechanism
(Figure 3): Whichever species remains after annihilation is meant to turn into an appropriately signed
error species. In such cases, the comparison reaction should be faster than the follow-up reactions,
dependent on that comparison. Otherwise, the second reaction would execute before the compar-
ison had been meaningfully made. These manually set rate constants, as well as those set by the
genetic algorithm, are listed in the Online Supplementary Material.
5.2 Simulation Details
The FCNN is a large system of ODEs. As such systems are generally unsolvable analytically, we use
numerical Runge-Kutta-type ODE solvers to observe the FCNNʼs behavior. We used a fixed-time-
step solver with a step size of 0.1, chosen for speed as well as stability. All simulations were run on
the COEL web-based chemical modeling and simulation framework [2, 5].
In the interest of modularity and flexibility, COELʼs ODE solvers do not consider the FCNN as
a whole. Rather, the contents of each compartment are simulated semi-independently, each by a
separate ODE solver. Several solvers then communicate with each other as needed. This allows
us to use different solvers for different compartments, or even to have compartments solved by
entirely different types of simulations. When using adaptive time-step-size ODE solvers, the com-
partments are synchronized by imposing the slowest compartmentʼs time-step size on the other
compartments, and so all of the chemical concentrations in the FCNN are updated in unison.
310
Artificial Life Volume 23, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. Blount et al.
6 Results
Feedforward Chemical Neural Network
As our goal is to learn linearly inseparable functions in a chemical neural network, we built the first
FCNN in the classic one-hidden-layer, two-hidden-neuron network topology first shown to learn
XOR [53]. We will refer to this topology, with rate constants set as described in Section 5.1, simply as
the FCNN in this section.
The FCNN successfully learns each of the 16 binary two-input logic functions. In a single
learning run, it was trained to a given logic function with 2,000 random inputs and corresponding
penalty injections (described in Section 4). We generated inputs randomly from {0, 1}2 and later
injected a threshold species T with concentration 0.6 and a penalty P as appropriate, 2,000 times
consecutively. The concentration of the penalty species, which is analogous to a learning rate,
was annealed by a factor of 0.0008 at each injection (see the Online Supplementary Material
for further details).
The FCNNʼs accuracy at each of the 2,000 consecutive iterations was averaged over 10,000 train-
ing runs to produce accuracy-versus-time data for each logic function shown in Figure 9. Figure 10
shows an example of the FCNN converging to a solution of XOR.
The most important results are the FCNNʼs performance on XOR and XNOR, which, because of
their linear inseparability, cannot be learned by a single perceptron [45]. On the 2,000th iteration,
the FCNNʼs accuracy on XOR and XNOR is 100.00% and 98.05%, respectively. Averaged over all
16 functions, the FCNN is 99.88% accurate by the 2,000th learning iteration.
As can be seen in Figure 10, the FCNN converges to learn inseparable functions in a relatively
short period of time. The 14 separable functions are almost perfectly learned by the 600th learning
iteration, but it takes until around iteration 1,200 to learn XOR. XNOR is not perfectly learned even by
iteration 2,000. We see this as confirmation that linear inseparability is a challenging feature to learn.
Nonetheless, the FCNN learns about as quickly as the original multilayer perceptrons that solved
XOR: Rumelhartʼs classic multilayer perceptron took roughly 1,000 learning iterations [53].
The difference in performance between XOR and XNOR can be explained by the FCNNʼs asym-
metric treatment of the input values 0 and 1. As can be seen in Figure 10, the functions !X1 and !X2
Figure 9. Average accuracy of the FCNN on each of the 16 binary two-input logic functions. An FCNN with one hidden layer
and two hidden neurons was run 10,000 times on each of the 16 functions. Each run started with random initial weights
and was trained for 2,000 learning iterations. The data points represent the proportion of correct answers the system
produced on a given learning iteration. Six of the functions are labeled; the remaining ten overlap in the top left of the graph.
Note that the FCNN learns equally well any two functions that are quivalent after switching the names of X1 and X2.
Artificial Life Volume 23, Number 3
311
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 10. An example of weights and output concentration converging in the OCN as an FCNN learns XOR over 300
learning iterations. Note that when the weights reach a fixed point around the 250th iteration, the output [Y ] oscillates
around 0.6, which in this case is the binary threshold. In this simulation, inputs were cycled in the fixed order ((0, 0),
(1, 0), (0, 1), (1, 1)) for the purpose of illustration—once the function is learned, [Y] oscillates as the system produces
the correct (thresholded) output stream 0, 1, 1, 0 (zoomed in the smaller plot).
are learned almost identically well by the FCNN. This is because the FCNN architecture is symmetric
on input; each input dimension behaves according to the same logic. Its architecture is not symmetric
on negation, however, because 1 and 0 values are treated fundamentally differently. Consider the fact
that the output species Y is ultimately produced by the two input species X1 and X2, as well as the
signal species Sin (Sections 3.1.1 and 4.2). For this reason, it is easier for the FCNN to learn to output
0 when it is given the input (0, 0) (i.e., when only Sin is present at injection) than to learn to output 1.
Unlike its building block, the AASP (Section 3.1), the FCNN in this context behaves as a binary
perceptron. Thus, we compare its performance on the binary logic functions not with the AASP, but
with our previous binary single chemical perceptrons: the SASP (standard ASP), an automatically
thresholded version, the TASP (thresholded ASP) [7], the WLP, and the WRP [6]. The two more
recent models, the SASP and the TASP, represent the state of the art in binary chemical perceptrons;
although the TASP is more accurate, the SASP is more similar to the FCNN because of its lack of
automatic output thresholding. As shown in Table 2, the FCNN is significantly more capable than
any of them.
Thus, the FCNN is the first simulated chemical system to autonomously learn linearly inseparable
functions. As shown by Minsky and Papert [45], single perceptrons cannot learn such functions,
because, as binary classifiers, they can only divide the input space along a hyperplane. In common
312
Artificial Life Volume 23, Number 3
D. Blount et al.
Feedforward Chemical Neural Network
Table 2. Accuracy of FCNN versus single chemical perceptrons.
XOR
XNOR
16-function average
FCNN
100.00
98.05
99.88
WLP
57.61
57.79
94.71
WRP
61.88
61.12
95.18
SASP
50.53
51.02
93.40
TASP
59.00
57.86
94.80
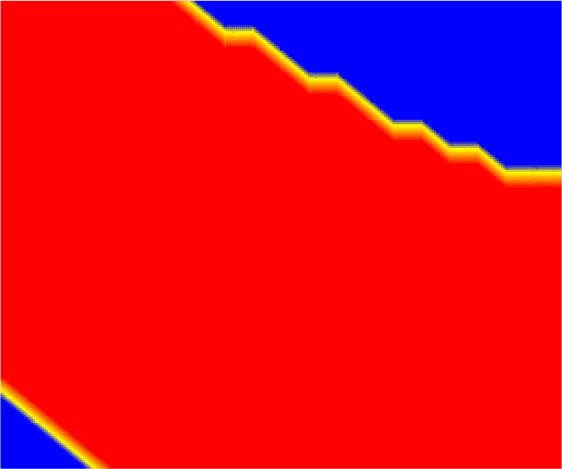
Figure 11. Response surface of an FCNN that learned XOR. Input [X] values of 1.0 correspond to TRUE, and 0.0 to FALSE, so
the accuracy of the FCNN is defined only by its response at the corners of the plots. The plot on the left shows the
FCNNʼs output value at each ([X1], [X2]), while the plot on the right shows the same data thresholded by 0.6—the
output values above the threshold correspond to TRUE (red region), and those below indicate FALSE (blue regions).
Jagged lines in the right figure are an artefact of our sampling technique.
with a multilayer perceptron, the FCNN does not have this constraint. To illustrate this, we mapped
the response surface of an FCNN after it had successfully learned to compute XOR, as shown in
Figure 11.
7 Conclusion
We have presented a hierarchical, compartmentalized artificial chemical system that is capable of
autonomous learning. The feedforward chemical neural network (FCNN) is, to our knowledge, the first
simulated chemical system to learn a linearly inseparable function. It does so by a chemical analogue
of backpropagation. This is demonstrated in the classic example of the XOR binary function, which
the FCNN learns perfectly in under 1,500 learning iterations, 100% of the time.
Each chemical neuron in the FCNN is a modified version of the AASP from our previous
work. Neurons are distinguished from each other by their compartmentalization in nested cell-like
containers. This nesting constrains FCNNs to treelike topologies, but allows modular design. Inter-
neuron communication, facilitating feeding forward and backpropagation, is mediated by selective
permeation of signal species through the compartment walls.
Each hidden neuron is chemically identical in the species and reactions that occur within them.
Thus, the FCNN brings us closer to a world where we might build a whole class of general-purpose
chemical computers from the same scalable, composable components.
Artificial Life Volume 23, Number 3
313
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
Because they follow textbook reaction rate laws, the chemical reaction networks we have de-
signed (i.e., each individual chemical neuron) are directly translatable to wet chemistries thanks to
advances in DNA strand-displacement circuits [55]. Translating our cell-like containers, along with
their reactive channels, into a wet implementation would be more challenging, as the problem of
constructing chemical membranes has no straightforward solution. We are hopeful that current work
in synthesizing bilayer lipid membranes will develop such a solution.
One technical complication in the FCNN design worth addressing is the manual injection of the
feedforward signal species SF. Ideally, a chemical neural network could operate completely indepen-
dently once receiving input and a desired output signal. We are hopeful of developing mechanisms
by which SF could be generated periodically within the FCNN, perhaps using chemical oscillators
such as the Lotka-Volterra predator-prey system [38, 39].
Another direction for further research is optimizing the modules of the FCNN. In our previous
work, we have developed a small family of single chemical perceptrons—we have already mentioned
the (standard) asymmetric signal perceptron [7], the thresholded asymmetric signal perceptron [7],
and the analogue ASP [3]. We have explored network architectures with many of these as building
blocks, shown in our Online Supplementary Materials. Though we have presented the best-
performing architecture we have tested, it is possible that there are yet better components for
the FCNN than our current hidden and output neurons.
In our previous work we have developed chemical perceptrons that incorporate delay lines to
learn patterns in time series [3, 46]. Integrating these into an FCNN would add a temporal dimen-
sion to the networkʼs pattern-recognition capabilities, which would enable us to tackle standard neu-
ral network and reservoir computing benchmark time series such as NARMA [1], Mackey-Glass
[19, 40], and the Hénon map [23].
Another logical extension of this work is to explore the FCNN model on larger networks, with
either more hidden layers, more neurons per layer, or both. Larger FCNNs are expected to tackle
more complex problems, and it is an open question how many layers and neurons per layer are
necessary for the FCNN to solve certain tasks, as its behavior and performance will likely differ
somewhat from classically implemented neural networks.
It bears repeating that the FCNN is not a chemical transcription of a neural network, but an anal-
ogy. As discussed with our results in Section 6, the FCNN we used here to solve XOR converged about
as quickly as Rumelhart, Hinton, and Williamsʼs first XOR-solving network [53]. It would be interesting
to explore if the FCNN generally converges faster or slower than classical neural nets. Our analogue
of input-weight integration, mathematically written in the language of ODEs, is highly nonlinear.
The importance of this research is the hope of a reprogrammable chemical computer. Like the
formal multilayered perceptron, the FCNN has two modes: simply processing output when given an
input, and learning via backpropagation of errors. A wet implementation of the FCNN, once trained
to learn a task, could perform that task reliably as long as desired. The chemical computer could
then, at any time, be retrained to perform any other task of which it is capable.
As parallelization becomes ever more prominent in computing, it is difficult not to be tempted by
the possibility of molecule-scale chemical computers. Such tiny machines could conceivably be com-
bined in molar amounts—on the scale of 1023—to perform naturally distributed, parallel computing.
Furthermore, the liquid nature of chemical computers and the possibility of constructing them
from bio-compatible DNA strands [55] open profound possibilities for patient-embedded bio-
chemical computers. A fleet of cell-size machines could monitor chemical concentrations in the
bloodstream, modulating the release of some drug accordingly. With time-series integration, bio-
chemical computers could keep a record of changes in a biological system and act as diagnostic aids
and tools in preventative medicine.
There has already been significant research into medical uses of computational chemical net-
works. One recent result [61] presented a chemical logic circuit that tests for the presence of par-
ticular microRNA molecules and the absence of others, effectively identifying a HeLa cancer cell.
The authors designed a bespoke chemical logic circuit for this purpose, but this is exactly the type
of computation an FCNN excels at learning. A standardized model of a programmable chemical
314
Artificial Life Volume 23, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
computer would trivialize the design of such medical machines, whose potential has only begun to
be explored.
Acknowledgments
This material is based upon work supported by the National Science Foundation under grants
1318833, 1518833, and 1518861.
References
1. Atiya, A. F., & Parlos, A. G. (2000). New results on recurrent network training: Unifying the algorithms
and accelerating convergence. IEEE Transactions on Neural Networks, 11(3), 697–709.
2. Banda, P., Blount, D., & Teuscher, C. (2014). COEL: A web-based chemistry simulation framework. In
S. Stepney & P. Andrews (Eds.), CoSMoS 2014: Proceedings of the 7th Workshop on Complex Systems Modelling
and Simulation (pp. 35–60). Frome, UK: Luniver Press.
3. Banda, P., & Teuscher, C. (2014). An analog chemical circuit with parallel-accessible delay line for learning
temporal tasks. In H. Sayama, J. Rieffel, S. Risi, R. Doursat, & H. Lipson (Eds.), ALIFE 14: The Fourteenth
Conference on the Synthesis and Simulation of Living Systems (pp. 482–489). Cambridge, MA: MIT Press.
4. Banda, P., & Teuscher, C. (2014). Learning two-input linear and nonlinear analog functions with a simple
chemical system. In O. H. Ibarra, L. Kari, & S. Kopecki (Eds.), Unconventional Computing and Natural
Computing Conference (pp. 14–26). Basel, Switzerland: Springer International Publishing.
5. Banda, P., & Teuscher, C. (2016). COEL: A cloud-based reaction network simulator. Frontiers in Robotics and
AI, 3(13), 13.
6. Banda, P., Teuscher, C., & Lakin, M. R. (2013). Online learning in a chemical perceptron. Artificial Life,
19(2), 195–219.
7. Banda, P., Teuscher, C., & Stefanovic, D. (2014). Training an asymmetric signal perceptron through
reinforcement in an artificial chemistry. Journal of The Royal Society Interface, 11(93), 20131100.
8. Basu, S., Gerchman, Y., Collins, C. H., Arnold, F. H., & Weiss, R. (2005). A synthetic multicellular system
for programmed pattern formation. Nature, 434(7037), 1130–1134.
9. Berry, G., & Boudol, G. (1992). The chemical abstract machine. Theoretical Computer Science, 96(1), 217–248.
10. Bray, D. (1995). Protein molecules as computational elements in living cells. Nature, 376(6538), 307–312.
11. Buchler, N. E., Gerland, U., & Hwa, T. (2003). On schemes of combinatorial transcription logic. Proceedings
of the National Academy of Sciences of the United States of America, 100(9), 5136–5141.
12. Chiang, H.-J. K., Jiang, J.-H. R., & Fagesy, F. (2014). Building reconfigurable circuitry in a biochemical
world. In Biomedical Circuits and Systems Conference (BioCAS) (pp. 560–563). New York: IEEE.
13. Condon, A., Harel, D., Kok, J. N., Salomaa, A., & Winfree, E. (Eds.) (2009). Algorithmic Bioprocesses. Berlin,
Heidelberg: Springer.
14. Copeland, R. A. (2002). Enzymes: A practical introduction to structure, mechanism, and data analysis (2nd ed.).
New York: Wiley.
15. Dittrich, P. (2005). Chemical computing. In J.-P. Banatre, P. Fradet, J.-L. Giavitto, & O. Michel (Eds.),
Unconventional programming paradigms (pp. 19–32). Berlin, Heidelberg: Springer.
16. Dittrich, P., Ziegler, J., & Banzhaf, W. (2001). Artificial chemistries: A review. Artificial Life, 7(3), 225–275.
17. Douglas, S. M., Bachelet, I., & Church, G. M. (2012). A logic-gated nanorobot for targeted transport of
molecular payloads. Science, 335(6070), 831–834.
18. Érdi, P., & Tóth, J. (1989). Mathematical models of chemical reactions: Theory and applications of deterministic and
stochastic models. Manchester, UK: Manchester University Press.
19. Farmer, J. D., & Sidorowich, J. J. (1987). Predicting chaotic time series. Physical Review Letters, 59,
845–848.
20. Fellermann, H., Rasmussen, S., Ziock, H.-J., & Solé, R. V. (2007). Life cycle of a minimal protocell—a
dissipative particle dynamics study. Artificial Life, 13(4), 319–345.
Artificial Life Volume 23, Number 3
315
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
21. Fernando, C. T., Liekens, A. M. L., Bingle, L. E. H., Beck, C., Lenser, T., Stekel, D. J., & Rowe, J. E.
(2009). Molecular circuits for associative learning in single-celled organisms. Journal of the Royal Society,
Interface / the Royal Society, 6(34), 463–469.
22. Haykin, S. (2009). Neural networks and learning machines (3rd ed.). New York: Prentice Hall.
23. Hénon, M. (1976). A two-dimensional mapping with a strange attractor. Communications in Mathematical
Physics, 50(1), 69–77.
24. Hjelmfelt, A., & Ross, J. (1992). Chemical implementation and thermodynamics of collective neural
networks. Proceedings of the National Academy of Sciences of the United States of America, 89(1), 388–391.
25. Hjelmfelt, A., Weinberger, E. D., & Ross, J. (1991). Chemical implementation of neural networks and
Turing machines. Proceedings of the National Academy of Sciences of the United States of America, 88(24),
10983–10987.
26. Horn, F., & Jackson, R. (1972). General mass action kinetics. Archive for Rational Mechanics and Analysis,
47(2), 81–116.
27. Hornik, K., Stinchcombe, M., & White, H. (1989). Multilayer feedforward networks are universal
approximators. Neural Networks, 2(5), 359–366.
28. Hutton, T. J. (2007). Evolvable self-reproducing cells in a two-dimensional artificial chemistry. Artificial Life,
13(1), 11–30.
29. Jiang, H., Riedel, M. D., & Parhi, K. K. (2012). Digital signal processing with molecular reactions. IEEE
Design & Test of Computers, 29(3), 21–31.
30. Kargol, M., & Kargol, A. (2003). Mechanistic formalism for membrane transport generated by osmotic
and mechanical pressure. General Physiology and Biophysics, 22(1), 5168.
31. Katz, E. (Ed.) (2012). Biomolecular information processing: From logic systems to smart sensors and actuators.
Weinheim, Germany: Wiley-VCH.
32. Kim, J., Hopfield, J. J., & Winfree, E. (2004). Neural network computation by in vitro transcriptional
circuits. In L. K. Saul, Y. Weiss, & L. Bottou (Eds.), Advances in neural information processing systems, vol. 17
(pp. 681–688). Cambridge, MA: MIT Press.
33. Kleinhans, F. (1998). Membrane permeability modeling: Kedem-Katchalsky vs a two-parameter formalism.
Cryobiology, 37(4), 271–289.
34. Lakin, M. R., Minnich, A., Lane, T., & Stefanovic, D. (2014). Design of a biochemical circuit motif for
learning linear functions. Journal of the Royal Society Interface, 11(101), 20140902.
35. Lakin, M. R., & Stefanovic, D. (2015). Supervised learning in an adaptive DNA strand displacement circuit.
In A. Phillips & P. Yin (Eds.), DNA computing and molecular programming (pp. 154–167). Berlin, Heidelberg:
Springer International Publishing.
36. Lakin, M. R., & Stefanovic, D. (2016). Supervised learning in adaptive DNA strand displacement networks.
ACS Synthetic Biology, 5(8), 885–897.
37. LaVan, D. A., McGuire, T., & Langer, R. (2003). Small-scale systems for in vivo drug delivery. Nature
Biotechnology, 21(10), 1184–1191.
38. Lotka, A. (1920). Undamped oscillations derived from the law of mass action. Journal of the American
Chemical Society, 42(8), 1595–1599.
39. Lotka, A. J. (1956). Elements of mathematical biology: Formerly published under the title “Elements of physical biology”
(1924). New York: Dover.
40. Mackey, M. C., & Glass, L. (1977). Oscillation and chaos in physiological control systems. Science,
197(4300), 287–289.
41. Maturana, H., & Varela, F. (1980). Autopoiesis and cognition: The realization of the living. Dordrecht, Holland: D. Reidel.
42. McGregor, S., Vasas, V., Husbands, P., & Fernando, C. (2012). Evolution of associative learning in
chemical networks. PLoS Computational Biology, 8(11), 1–19.
43. Michaelis, L., & Menten, M. L. (1913). Die Kinetik der Invertinwirkung. Biochemische Zeitschrift, 49, 333–369.
44. Mills, A. P., Yurke, B., & Platzman, P. M. (1999). Article for analog vector algebra computation. Biosystems,
52(1–3), 175–180.
316
Artificial Life Volume 23, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. Blount et al.
Feedforward Chemical Neural Network
45. Minsky, M., & Papert, S. (1972). Perceptrons: An introduction to computational geometry. Cambridge, MA: MIT
Press.
46. Moles, J., Banda, P., & Teuscher, C. (2015). Delay line as a chemical reaction network. Parallel Processing
Letters, 25(1), 1540002.
47. Okamoto, M., Sakai, T., & Hayashi, K. (1987). Switching mechanism of a cyclic enzyme system: Role as
a chemical diode. Biosystems, 21(1), 1–11.
48. Pei, R., Matamoros, E., Liu, M., Stefanovic, D., & Stojanovic, M. N. (2010). Training a molecular
automaton to play a game. Nature Nanotechnology, 5(11), 773–777.
49. Păun, G. (2000). Computing with membranes. Journal of Computer and System Sciences, 61(1), 108–143.
50. Păun, G., & Rozenberg, G. (2002). A guide to membrane computing. Theoretical Computer Science, 287(1),
73–100.
51. Qian, L., Winfree, E., & Bruck, J. (2011). Neural network computation with DNA strand displacement
cascades. Nature, 475(7356), 368–372.
52. Rasmussen, S. (2009). Protocells: Bridging nonliving and living matter. Cambridge, MA: MIT Press.
53. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by backpropagating
errors. Nature, 323(6088), 533–536.
54. Shirt-Ediss, B. (2011). Dynamical systems analysis of a protocell lipid compartment. In G. Kampis,
I. Karsai, & E. Szathmáry (Eds.), Advances in artificial life. Darwin meets von Neumann, 10th European Conference on
Artificial Life ECAL 2009, Part I (pp. 230–239). Heidelberg: Springer.
55. Soloveichik, D., Seelig, G., & Winfree, E. (2010). DNA as a universal substrate for chemical kinetics.
Proceedings of the National Academy of Sciences of the United States of America, 107(12), 5393–5398.
56. Suzuki, K., & Ikegami, T. (2009). Shapes and self-movement in protocell systems. Artificial Life, 15(1),
59–70.
57. Tamsir, A., Tabor, J. J., & Voigt, C. A. (2010). Robust multicellular computing using genetically encoded
NOR gates and chemical ‘wires’. Nature, 469(7329), 212–215.
58. Tominaga, K., Watanabe, T., Kobayashi, K., Nakamura, M., Kishi, K., & Kazuno, M. (2007). Modeling
molecular computing systems by an artificial chemistry—its expressive power and application. Artificial Life,
13(3), 223–247.
59. Win, M. N., & Smolke, C. D. (2008). Higher-order cellular information processing with synthetic RNA
devices. Science, 322(5900), 456–460.
60. Wu, C., Wan, S., Hou, W., Zhang, L., Xu, J., Cui, C., Wang, Y., Hu, J., & Tan, W. (2015). A survey of
advancements in nucleic acid-based logic gates and computing for applications in biotechnology and
biomedicine. Chemical Communications, 51, 3723–3734.
61. Xie, Z., Wroblewska, L., Prochazka, L., Weiss, R., & Benenson, Y. (2011). Multi-input RNAi-based logic
circuit for identification of specific cancer cells. Science, 333(6047), 1307–1311.
Artificial Life Volume 23, Number 3
317
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
3
3
2
9
5
1
6
6
6
6
5
9
a
r
t
l
/
_
a
_
0
0
2
3
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3