Evolutionary and Estimation of Distribution
Algorithms for Unconstrained, Constrained,
and Multiobjective Noisy Combinatorial
Optimisation Problems
Aishwaryaprajna
School of Computer Science, University of Birmingham, Birmingham,
United Kingdom
aishwaryaprajna@gmail.com
Jonathan E. Rowe
School of Computer Science, University of Birmingham, Birmingham,
United Kingdom and The Alan Turing Institute, London, United Kingdom
J.E.Rowe@cs.bham.ac.uk
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
e
D
tu
e
v
C
o
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
C
o
_
UN
_
0
0
3
2
0
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
https://doi.org/10.1162/evco_a_00320
Astratto
We present an empirical study of a range of evolutionary algorithms applied to var-
ious noisy combinatorial optimisation problems. There are three sets of experiments.
The first looks at several toy problems, such as OneMax and other linear problems.
We find that UMDA and the Paired-Crossover Evolutionary Algorithm (PCEA) are the
only ones able to cope robustly with noise, within a reasonable fixed time budget. In
the second stage, UMDA and PCEA are then tested on more complex noisy problems:
SubsetSum, Knapsack, and SetCover. Both perform well under increasing levels of
noise, with UMDA being the better of the two. In the third stage, we consider two
noisy multiobjective problems (CountingOnesCountingZeros and a multiobjective
formulation of SetCover). We compare several adaptations of UMDA for multiob-
jective problems with the Simple Evolutionary Multiobjective Optimiser (SEMO) E
NSGA-II. We conclude that UMDA, and its variants, can be highly effective on a va-
riety of noisy combinatorial optimisation, outperforming many other evolutionary
algorithms.
Keywords
Noisy combinatorial optimisation, noisy multiobjective optimisation, expected run-
time, crossover, estimation of distribution algorithms, NSGA-II.
1
introduzione
Realistic optimisation problems are often affected with noisy fitness measurements. IL
recent theoretical analyses of evolutionary algorithms (EAs) on noisy problems defined
in discrete spaces are mostly focused on simple and classical benchmark problems, come
as OneMax. Harder and more realistic combinatorial problems such as Knapsack or
SetCover, in presence of noisy fitness evaluations, are not easily amenable to theoreti-
cal analysis. This article discusses a thorough empirical analysis of an array of EAs on
several simple and harder noisy combinatorial problems. This study attempts to iden-
tify which EAs to choose when solving realistic noisy combinatorial problems.
Noise may affect fitness evaluation in a number of ways. It may be considered as
prior, in which the search point is randomly tampered with, and fitness evaluation is
Manuscript received: 4 agosto 2021; revised: 5 Luglio 2022 E 2 Febbraio 2023; accepted: 19 Febbraio 2023.
© 2023 Istituto di Tecnologia del Massachussetts
Evolutionary Computation 31(3): 259–285
Aishwaryaprajna and J.E. Rowe
performed on the noisy search point. Alternatively, posterior noise (which will be the
focus of our study) is where a random value gets added to the fitness of a search point
during the optimisation process. The same search string would have a different fitness
value each time it is being evaluated. With more complex combinatorial problems (per esempio.,
ones with constraints) the noise may enter in different ways (per esempio., in the evaluation of
those constraints).
An early theoretical result by Droste (2004) examined the performance of the hill-
climber (1 + 1)-EA on OneMax with prior noise. This was generalised to the (μ + λ)-EA
by Gießen and Kötzing (2016), showing that populations can help in both prior and pos-
terior noise. They show the (1 + 1)-EA, Tuttavia, can tolerate posterior Gaussian noise
only when the variance is very small (less than 1/(4 log n)). It has been recognised for a
long time that the population size can affect the ability of an EA to handle noise (Gold-
berg et al., 1991; Rattray and Shapiro, 1997). A more recent theoretical study by Dang and
Lehre (2015) shows that a low mutation rate enables a particular mutation-population
algorithm to handle arbitrary posterior noise for the OneMax problem in polynomial
time, although the bounds given are large. Allo stesso modo, the compact genetic algorithm
(cGA) is shown to handle noise with (large) polynomial runtime (Friedrich et al., 2015).
A better asymptotic runtime for OneMax with posterior Gaussian noise is proved for
the Paired-Crossover Evolutionary Algorithm (PCEA) which just uses crossover, E
no mutation (Prügel-Bennett et al., 2015).
Ovviamente, it is possible to handle noise simply by resampling the fitness of a poten-
tial solution many times, and taking the average as an estimate of the true fitness. Sup-
pose the noisy problem is defined by taking a deterministic fitness function and adding
Gaussian noise with mean 0 and variance σ 2. There is a general result (Akimoto et al.,
2015) that states if the runtime of a black-box algorithm on a problem with no noise is T ,
then σ 2 log T samples are required at each step leading to a runtime of σ 2T log T . Nel
case of OneMax, the most efficient algorithm (Anil and Wiegand, 2009) has a runtime of
(cid:2)(n/ log n). Using this algorithm with resampling, gives a runtime for noisy OneMax
Di (cid:2)(σ 2n). By contrast, the PCEA algorithm (Prügel-Bennett et al., 2015), when σ 2 = n,
has a runtime of O(N(log n)2) which is already faster than the resampling algorithm.
It has been suggested by Doerr and Sutton (2019) that using the median rather than
mean provides a better estimate when resampling, but this is significant only when the
variance is small (less than a constant).
A recent study by Rowe and Aishwaryaprajna (2019) of a new voting algorithm on
OneMax shows a runtime of O(n log n), when the variance of the noise distribution is
P 2 = O(N) and in O(P 2 log n) when the noise variance is greater than this. This upper
bound is the best proven runtime that we are aware of to date. Some empirical results
show that the use of voting in population-based algorithms (UMDA, PCEA, and cGA)
are effective for large population sizes. The voting algorithm is shown to solve the Jump
function, which has a fitness gap next to the global optimum, in O(n log n) fitness eval-
uations with high probability any gap size m < (1 − α)n where, the constant α ∈ [ 1
2 , 1].
The performance of voting algorithm and the cGA are also analysed for other variants
of the Jump function in the recent paper by Witt (2021). However, in our work, problems
with fitness gaps have not been considered.
In this article, we are interested in whether any of the algorithms with polyno-
mial theoretical runtimes for noisy OneMax would be capable of solving combinatorial
problems with added noise in practice, when given a reasonable but fixed time budget.1
1This article is an extended version of Aishwaryaprajna and Rowe (2019).
260
Evolutionary Computation Volume 31, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
EAs and EDAs for Solving Noisy Combinatorial Problems
We proceed in three stages. First, we will experimentally compare a collection of algo-
rithms on noisy OneMax and noisy Linear problems, to see which can find solutions
within a reasonable amount of time (to be defined below), bearing in mind that the
asymptotic bounds for some of these algorithms, while polynomial, are actually very
large. Second, we will take those algorithms which pass this first test, and see how
well they handle noise in three combinatorial problems: SubsetSum, Knapsack, and
SetCover. We choose these, as they have a “packing” structure which might make them
amenable to algorithms which can solve noisy OneMax efficiently. We generate random
problem instances within the “easy” regime (so that the algorithms can be expected to
solve them when there is no noise) and then empirically study how they degrade with
added Gaussian noise.
There has been considerable research in the last decades on stochastic combinato-
rial optimisation problems, like the stochastic knapsack problem (refer to Steinberg and
Parks, 1979; Sniedovich, 1980; Ross and Tsang, 1989; Henig, 1990; Carraway et al., 1993;
Fortz et al., 2013; and Bianchi et al., 2009 for a survey). In stochastic knapsack formula-
tions, in some instances the profits are considered as random variables (Steinberg and
Parks, 1979; Sniedovich, 1980; Carraway et al., 1993; Henig, 1990), as well as, the distri-
bution of weights are known in some formulations (Fortz et al., 2013). This means, that
the approaches in handling stochastic problems involve having access to more details
of the problem, for example, the distribution of the decision variables is known. How-
ever, in this article, we assume that the noise contribution to the fitness value is part of
the black-box, and so we do not have access to details such as the noise distribution, or
the exact distribution of the decision variables.
In the last stage of our analysis, we look at noisy multiobjective problems. Initially,
we analyse the performance of a collection of multiobjective algorithms on a toy mul-
tiobjective problem COCZ without and with high levels of noise and we attempted to
identify which algorithms perform better. We study the simple hill-climber algorithm
SEMO, the popular NSGA-II, and some other algorithms designed on the basis of our
previous experimental results. We compare our algorithms on the basis of the perfor-
mance indicator, hypervolume, which provides an analysis of the spread of the non-
dominated solutions found, in a reasonable time budget. We then formulate the noisy
constrained SetCover problem as a multiobjective problem and we empirically analyse
the performance of the better algorithms on this.
It should be noted that in our empirical results, while error bars are not always
shown, the Mann–Whitney test was used on all relevant comparisons, and results are
significant at the 95% level unless explicitly indicated.
Notation: We use the convention that [expr] equals 1 if expr is true, and 0 otherwise.
2
Problem Definitions—Noisy Single Objective Problems
The problems studied in this article are defined on a Boolean search space of bit strings
of length n. Let N (0, σ ) denote a random number drawn from a normal distribution with
mean zero, and standard deviation σ , which will be freshly generated at each fitness
function evaluation.
2.1 Unconstrained Single-Objective Noisy Problems
The first problem is OneMax, whose fitness function is defined as,
OneMax(x) =
n(cid:2)
i=1
xi.
Evolutionary Computation Volume 31, Number 3
261
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Aishwaryaprajna and J.E. Rowe
The fitness function is to be maximised, so the optimum would be the all-ones string,
1n.
When the fitness evaluation is tampered with random noise, the fitness function
becomes as follows,
NoisyOneMax(x) =
n(cid:2)
i=1
xi + N (0, σ ).
The WeightedLinear problem is defined with reference to n positive weights
w1, . . . , wn as follows, where the fitness is to maximised,
WeightedLinear(x) =
n(cid:2)
i=1
xiwi,
with corresponding noisy variant,
NoisyWeightedLinear(x) =
n(cid:2)
i=1
xiwi + N (0, σ ).
In generating random problem instances, we draw the weights uniformly at ran-
dom from the range 1, . . . , 100. Thus we avoid more extreme instances such as BinVal
(in which wi = 2i−1 for each i = 1, . . . , n). The reason for this is that when the distribu-
tion of weights is highly skewed, the addition of noise is irrelevant for those bits with
very high weights, yet completely overwhelms bits with weights lower than the typi-
cal noise level. Thus most algorithms will find the more significant bits, and fail on the
remainder.
With reference to n positive weights w1, . . . , wn and a target θ , the SubsetSum prob-
lem is defined as,
SubsetSum(x) = |θ −
n(cid:2)
i=1
xiwi|.
In presence of noisy fitness evaluations, the fitness function can be written as follows,
NoisySubsetSum(x) = |θ −
n(cid:2)
i=1
xiwi| + N (0, σ ).
SubsetSum can be seen as a generalisation of the WeightedLinear problem (in
which the target is θ = 0). In our experiments, we generate instances by choosing
weights uniformly at random from 1, . . . , 100. We take the target to be two-thirds of
the sum of the weights (we have run experiments for other choices of θ and found that
they do not significantly affect the empirical observations).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2.2 Constrained Single-Objective Noisy Problems
The Knapsack problem is defined with respect to a set of positive weights w1, . . . , wn,
a capacity C and positive profits p1, . . . , pn as follows,
Knapsack(x) =
(cid:3) (cid:4)
n
i=1 xipi
(cid:4)
(cid:4)
if
n
i=1 xiwi ≤ C
C −
n
i=1 xiwi otherwise.
Random instances choose weights and profits uniformly from 1, . . . , 100, and the ca-
pacity is two-thirds of the sum of the weights. We consider two noisy variants of
262
Evolutionary Computation Volume 31, Number 3
EAs and EDAs for Solving Noisy Combinatorial Problems
the Knapsack problem. The first version simply considers posterior additive noise as
before:
NoisyKnapsackV1(x) = Knapsack(x) + N (0, σ ).
In the second version, the presence of noise in the judgement with respect to the
weights is considered,
Wσ (x) =
n(cid:2)
i=1
xiwi + N (0, σ ).
If this (noisy) weight does not exceed the capacity, we then evaluate (noisily), the profit.
Otherwise we return the excess weight:
NoisyKnapsackV2(x) =
(cid:3) (cid:4)
n
i=1 xipi + N (0, σ )
if Wσ (x) ≤ C
C − Wσ (x)
otherwise.
Note that noise is added to the weight just once, when the constraint is checked, and
the same value used to report the fitness value, in the case the constraint is violated.
The SetCover problem finds a minimal covering of m elements with a collection
of sets from n predefined subsets. A Boolean matrix aij with n-rows and m-columns is
used to define the n subsets c1, . . . , cn:
ai,j = [i ∈ cj ].
The optimal collection of the sets would have the least number of the sets needed to
cover all the m elements. The SetCover problem has several real-world applications
such as the airline crew scheduling problem.
The problem can be defined as a constrained single-objective one, as well as a single-
objective problem with a penalty term. The problem can also be defined as a multiob-
jective problem (discussed later).
The ConstrainedSetCover problem has a constraint that checks if the solution
covers each of the m elements. The optimal solution would have the least number of
sets needed to cover all the m elements. It is defined as follows,
ConstrainedSetCover(x) =
n(cid:2)
j =1
xj
subject to
n(cid:2)
j =1
xj aij ≥ 1, i ∈ 1, . . . , m.
For comparison-based algorithms, we always prefer feasible solutions instead of in-
feasible solutions. Two feasible solutions are compared by their fitness values, whereas
two infeasible solutions by their constraint violations. The noisy version of the problem
arises if the judgements regarding the number of elements uncovered and the number
of the subsets required is noisy.
NoisyConstrainedSetCover(x) =
n(cid:2)
j =1
xj + N (0, σ )
subject to
n(cid:2)
j =1
xj aij + N (0, σ ) ≥ 1, i ∈ 1, . . . , m.
Evolutionary Computation Volume 31, Number 3
263
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Aishwaryaprajna and J.E. Rowe
The fitness function of SetCover problem can also be defined by including a penalty
term such that, if elements are under-covered by the considered collection of sets, a huge
penalty μ is incurred.
PenaltySetCover(x) =
n(cid:2)
j =1
xj + μ
(cid:2)
i
(cid:5)
(cid:6)
max
0,
1 −
(cid:7)(cid:8)
aij xj
.
n(cid:2)
j =1
This gives rise to a corresponding noisy variant:
NoisyPenaltySetCover(x) =
n(cid:2)
j =1
xj + μ
(cid:2)
i
(cid:5)
(cid:6)
max
0,
1 −
n(cid:2)
j =1
(cid:7)(cid:8)
aij xj
+ N (0, σ ).
3 Algorithms Chosen for Noisy Single-Objective Optimisation
The (1 + 1)-EA
3.1
The (1 + 1)-EA uses a bitwise mutation operator that produces an offspring by flipping
each bit of the parent string independently with probability 1/n. This can be considered
as a randomised or stochastic hill-climber which considers only one point in the search
space at a time and proceeds by trying to find a point which has a superior function
value. In each iteration, only one function evaluation takes place. The expected runtime
of the (1 + 1)-EA solving the non-noisy OneMax is O(n log n). The runtime remains
polynomial in the posterior Gaussian noise case for σ 2 < 1/(4 log n), so we do not expect
this algorithm to cope with anything but the smallest noise levels (Gießen and Kötzing,
2016).
3.2 Mutation-Population Algorithm
It has long been recognised that populations can help an EA handle noise. The paper
by Goldberg et al. (1991) developed a population sizing equation and instigated the
adoption of variance-based population sizing. Rattray and Shapiro (1997) showed that
in weak selection limit, effects of Gaussian noise could be overcome by an appropriate
increase of the population size. More recently, a population-based, non-elitist EA was
analysed by Dang and Lehre to study how it optimises the noisy OneMax problem with
uniform, Gaussian and exponential posterior noise distributions (Dang and Lehre, 2015,
2016). They considered a recently developed fitness-level theorem for non-elitist pop-
ulations to estimate the expected running time for the said problems in noisy environ-
ment. In the case of additive Gaussian noise N (0, σ 2) with mutation rate χ
3σ n and
n
population size λ = bσ 2 ln n (where a and b are constants), the considered algorithm
optimises the OneMax problem in expected time O(σ 7n ln(n) ln(ln (n))). Similar results
were shown for uniform and exponential noise distributions. Note that this is poten-
tially very large, when the noise is large—in excess of n4.5 when σ =
n, although of
course this is an upper bound, and we do not know the constants.
= a
√
3.3 Compact Genetic Algorithm (cGA)
The compact GA (cGA) is an EDA, introduced by Harik et al. (1999). cGA is able to av-
erage out the noise and optimise the noisy OneMax problem in expected polynomial
time, when the noise variance σ 2 is bounded by some polynomial in n, as suggested in
Friedrich et al. (2015). The paper introduced the concept of graceful scaling in which
264
Evolutionary Computation Volume 31, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
EAs and EDAs for Solving Noisy Combinatorial Problems
the runtime of an algorithm scales polynomially with noise intensity, and suggested
that cGA is capable of achieving this. It is also suggested that there is no threshold
point in noise intensity at which the cGA algorithm begins to perform poorly (by which
they mean having super-polynomial runtime). They proved that cGA is able to find
the optimum of the noisy OneMax problem with Gaussian noise of variance σ 2 after
n log n), with probability 1 − o(1). Note that
O(Kσ 2
this upper bound is in excess of n3 when σ =
n log Kn) steps when K = ω(σ 2
n.
√
√
√
3.4
Population-Based Incremental Learning (PBIL)
The algorithm PBIL, proposed by Baluja (1994), combines genetic algorithms and com-
petitive learning for optimising a function. We have included this algorithm as it is in
some ways similar to the cGA, so we might expect it to have similar performance. We
are not aware of any theoretical analysis of this algorithm on noisy problems. The run-
time of PBIL on OneMax is known to be O(n3/2 log n), for suitable choice of λ (Wu et al.,
2017).
3.5 Univariate Marginal Distribution Algorithm (UMDA)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Univariate Marginal Distribution Algorithm (UMDA) proposed by Mühlenbein
(1997) belongs to the EDA schema. In some ways, it is therefore similar to cGA and PBIL.
However, it can also be viewed as generalising the genepool crossover scheme, in which
bits are shuffled across the whole population (within their respective string positions).
We have included UMDA then, to see if its behaviour is more like cGA and PBIL on the
one hand (which emphasise an evolving distribution over bit values), or like PCEA on
the other (which emphasises crossover). The UMDA algorithm initialises a population
of λ solutions, and sorts the population according to the fitness evaluation of each candi-
date solution. The best μ members of the population are selected to calculate the sample
distribution of bit values in each position. The next population is generated from this
distribution. There are two variants of UMDA, depending on whether the probabilities
are constrained to stay away from the extreme values of 0 and 1, or not. It is known
that if the population size is large enough (that is, (cid:3)(
n log n)), then this handling of
probabilities at the margins is not required (Witt, 2017). Since we will work with a large
population (to match the PCEA algorithm described below), we will not employ margin
handling, unless otherwise stated. In our experiments we will take μ = λ/2. We are not
aware of any theoretical results concerning UMDA on problems with posterior noise,
but the runtime on OneMax is known to be O(n log n) for μ = (cid:2)(
n log n)—see Witt
(2017).
√
√
3.6
Paired-Crossover EA (PCEA)
Recently, the recombination operator has been suggested to be considerably beneficial
in noisy evolutionary search. Prügel-Bennett et al. (2015) considered the problem of
√
solving OneMax with noise of order σ =
n and analysed the runtime of an evolution-
ary algorithm consisting only of selection and uniform crossover, the paired-crossover
n log n then the required num-
EA (PCEA). They show that if the population size is c
ber of generations is O
), with the proba-
bility of failure at O(1/nc ). The proof in that paper can be generalised to the case of
σ ≥
n, to give a runtime of O(σ 2 log n). It is not known what happens for lower lev-
els of noise, though it is shown that in the absence of noise, PCEA solves OneMax in
O(n(log n)2).
, giving a runtime of O(cn
(cid:10)
n log n
(cid:10)
2
log n
(cid:9)√
√
√
(cid:9)
Evolutionary Computation Volume 31, Number 3
265
Aishwaryaprajna and J.E. Rowe
Table 1: Function evaluation budgets allowed for noisy OneMax experiments with dif-
ferent noise levels.
σ
budget
σ
budget
1
38392
6
64079
2
41066
7
70736
3
44477
8
79034
4
50728
9
86078
5
56851
10
93638
4
Experiments—Simple Noisy Problems
4.1 Noisy ONEMAX
We investigate the performance of the algorithms described above, in solving the noisy
OneMax problem. In the literature, some theoretical proofs exist for the expected run-
time of specific algorithms on solving the noisy OneMax problem with additive poste-
rior Gaussian noise (Prügel-Bennett et al., 2015; Dang and Lehre, 2015; Akimoto et al.,
2015; Friedrich et al., 2017; Lucas et al., 2017; Qian et al., 2018; Dang-Nhu et al., 2018;
Doerr and Sutton, 2019; Doerr, 2020). We are interested in the algorithms’ performances
given a reasonable but fixed runtime budget across a wide range of noise levels, from
σ = 0 up to σ =
n.
√
To address the question of what constitutes a reasonable budget, we compared the
known theoretical results of our algorithms on noisy OneMax. PCEA has the lowest
proven upper bound on its runtime, compared with the other algorithms for which re-
sults exist. We therefore allowed each algorithm to have twice the number of fitness
evaluations that PCEA requires (on average) to find the optimum, as a reasonable bud-
get. The function evaluation budgets calculated in this way are given in Table 1.
√
The population size for the PCEA is taken to be 10
n log n according to the theoret-
ical proofs and empirical study by Prügel-Bennett et al. (2015). According to the proofs
by Dang and Lehre (2015), the population size λ = σ 2 log n is chosen for the mutation-
population algorithm. According to the paper by Friedrich et al. (2015), the parameter
K = 7σ 2
n log n is considered for cGA. In presence of additive posterior noise, PBIL
and UMDA have not yet been studied much. For PBIL, the population size is taken as
λ = 10n (following the theoretical requirement of Wu et al., 2017). From these, we select
the best μ = λ/2 individuals. In case of UMDA, the total number of generated candi-
n log n, so that the effective population
dates in a particular generation is chosen as 20
size is the same as for PCEA. All these parameter settings are retained for all of our
experiments in simple and constrained noisy combinatorial optimisation problems.
√
√
Figure 1 illustrates a comparison of all of the considered algorithms while solv-
ing the noisy OneMax problem for problem size n = 100. Different levels of Gaussian
additive noise with mean 0 and standard deviation σ = 1 to 10 are considered in this ex-
periment. It can be seen that PCEA and UMDA are resistant to these noise levels as they
are capable of finding the global optimum within the given budget. The runtimes for
these two algorithms are shown in Figure 2. However, (1 + 1)-EA, mutation-population
algorithm, PBIL, and cGA are not able to cope with even these small levels of noise
within the given fixed budget of function evaluations. For these experiments, we run
the algorithms until the population converges (which they will, since we do not handle
probability margins). The Mann–Whitney U-test is performed on the samples of best
results achieved and the runtimes of the algorithms, with the null hypothesis that they
are from distributions with equal medians. For each data point, the null hypothesis is
rejected at a 5% significance level.
266
Evolutionary Computation Volume 31, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
EAs and EDAs for Solving Noisy Combinatorial Problems
Figure 1: Comparison of the algorithms while solving the noisy OneMax for different
noise levels.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2: Runtime comparison of UMDA and PCEA for noisy OneMax.
4.2 Noisy WEIGHTEDLINEAR Problem
Maximising the WeightedLinear problem, as defined in Section 2, has only one global
optimum, the sum of all the weights. The OneMax problem is a special case of the
WeightedLinear problem when all the weights are units. However, optimising the
WeightedLinear problem is difficult as the bits with heavier weights get optimised
with a higher preference than the bits with lower weights.
The plot in Figure 3 illustrates the performance comparison of all of the consid-
ered algorithms while solving the noisy WeightedLinear problem for the problem size
n = 100. Random problem instances were studied with 100 randomly chosen weights
between 1 and 100. The results for a typical problem are shown in Figure 3 with aver-
ages over 100 runs. The standard deviation of the Gaussian noise is shown as multiples
of the square root of the sum of the weights. The function evaluation budget allowed
Evolutionary Computation Volume 31, Number 3
267
Aishwaryaprajna and J.E. Rowe
Figure 3: Comparison of algorithms while solving noisy WeightedLinear.
Table 2: Function evaluation budgets allowed for noisy WeightedLinear experiments.
σ
budget
σ
budget
1
47096
6
49954
2
46801
7
50876
3
47704
8
51429
4
48350
9
52794
5
48682
10
53310
to each of the algorithms are fixed at twice the average runtime of PCEA at each noise
level (see Table 2).
As evident from Figure 3, the curves of PCEA and UMDA are coincident, showing
that they can cope with the noise well and are resistant up to these levels of noise. The
runtime of UMDA and PCEA are plotted in Figure 4. However, the performance of
the (1 + 1)-EA and mutation-population algorithm worsen with increasing noise. Even
with relatively small noise levels, the cGA and PBIL are not able to solve the problem
within twice the runtime of PCEA.
It is evident from the empirical results of these simple noisy problems that uniform
crossover-based PCEA and UMDA can cope with noise significantly better than the
other algorithms. At this point, it is interesting to note that, UMDA employs a mecha-
nism similar to genepool crossover, where at each bit position, the offspring bit is obtained
by recombination of that bit across the whole parent population. It is hypothesised that
these two algorithms are therefore highly similar in operation.
5
Experiments—Noisy Combinatorial Problems
5.1 Noisy SUBSETSUM
Given the success of UMDA and PCEA on the noisy toy problems, and the failure of the
others to cope with even modest levels of noise, we now move to the second stage of
the study considering only UMDA and PCEA.
268
Evolutionary Computation Volume 31, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
EAs and EDAs for Solving Noisy Combinatorial Problems
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4: Runtime comparison of UMDA and PCEA for noisy WeightedLinear.
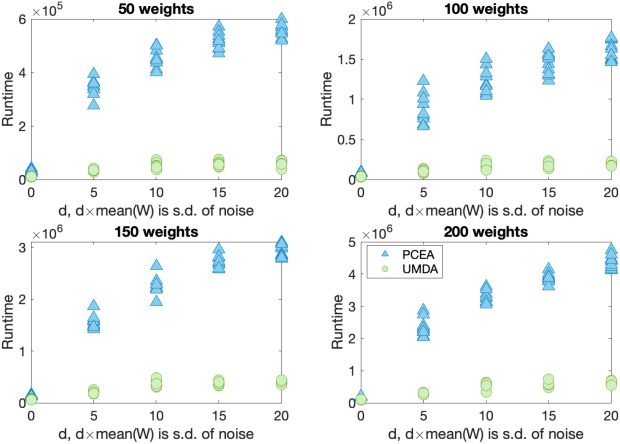
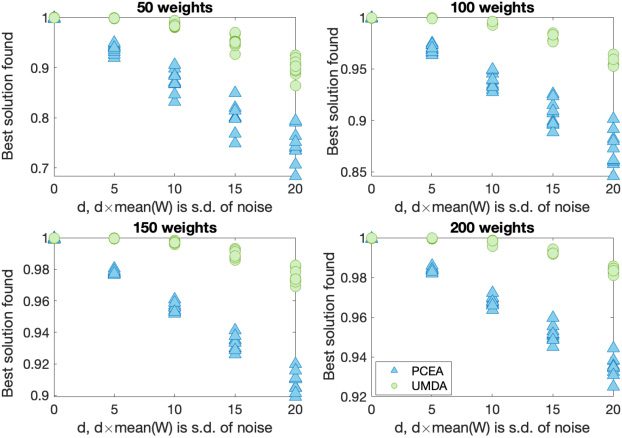
For the noisy SubsetSum problem, a range of problem sizes is considered with 50,
100, 150, and 200 weights, each lying between 1 and 100, and chosen uniformly at ran-
dom. Corresponding to each problem size, 10 different problems are considered. The
target θ is considered to be two-thirds of the sum of all the weights in the set. The ad-
ditive Gaussian noise considered in the SubsetSum problem is centered at zero and is
considered to have standard deviation of integral multiples of the mean of the weights,
viz., 5 × mean(W ), 10 × mean(W ), 15 × mean(W ), and 20 × mean(W ).
The NoisySubsetSum problem being a minimisation problem, if we obtain the (non-
noisy) fitness value of zero, we obtain the global optimum. Both the algorithms are able
to find the global optimum for these problems and their corresponding noise levels.
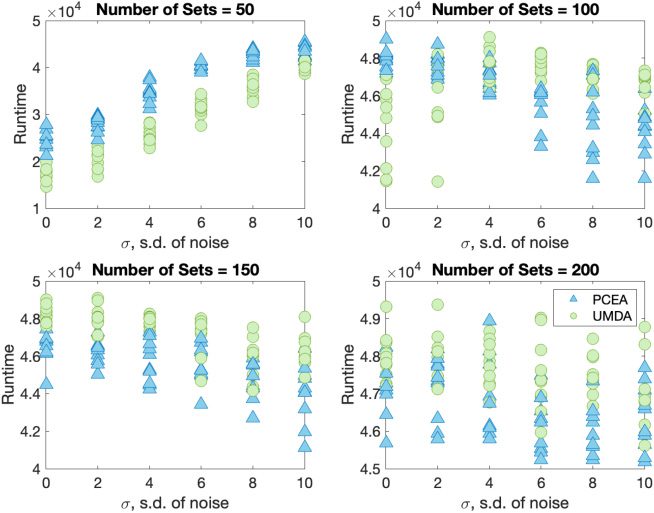
We therefore plot the runtime (averaged over 100 runs) to find the optimum against
the standard deviation of the noise (see Figure 5). Using the Mann–Whitney U-test, it is
observed that UMDA has the better runtime.
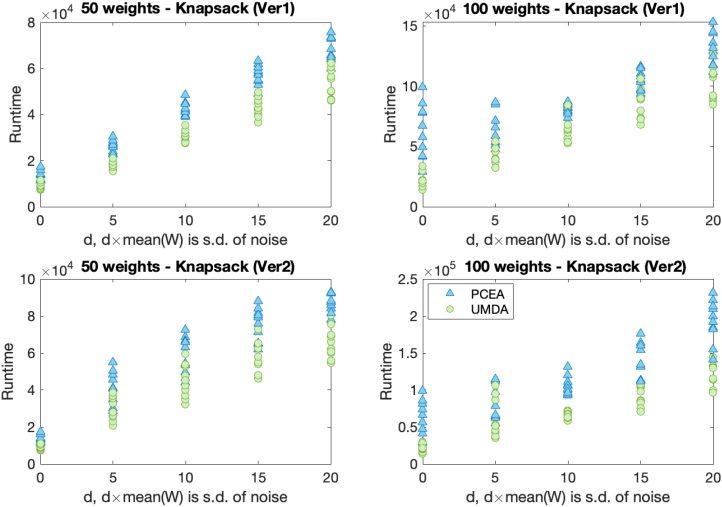
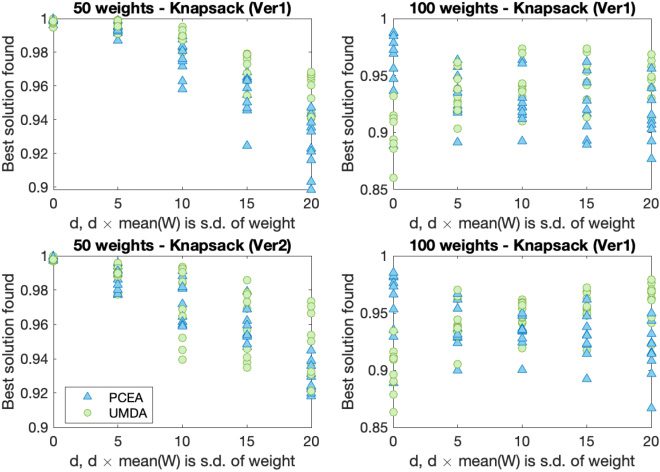
5.2 Noisy KNAPSACK (Version 1)
For the first version of the noisy Knapsack problem, uncorrelated (see Figures 6 and 7)
and strongly correlated (see Figures 10 and 11) problem instances have been studied.
For the uncorrelated instances, 50, 100, 150, and 200 weights (randomly chosen between
1 and 100) with associated profits (in the same range) are considered. For each problem
size, 10 different problems are considered. The maximum capacity of the knapsack is
taken to be two-thirds of the sum of all the weights considered. For the strongly corre-
lated instances, 10 problems each of sizes 50 and 100, described in Pisinger (2005), are
considered.
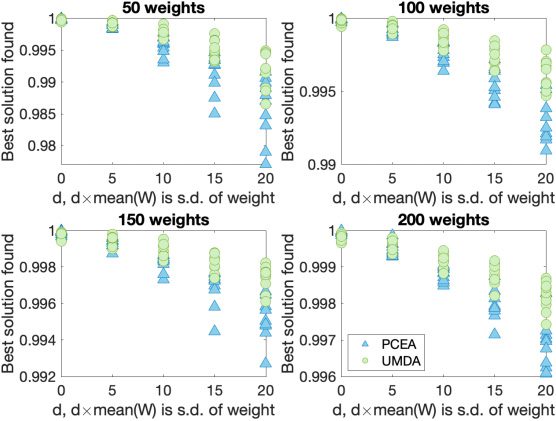
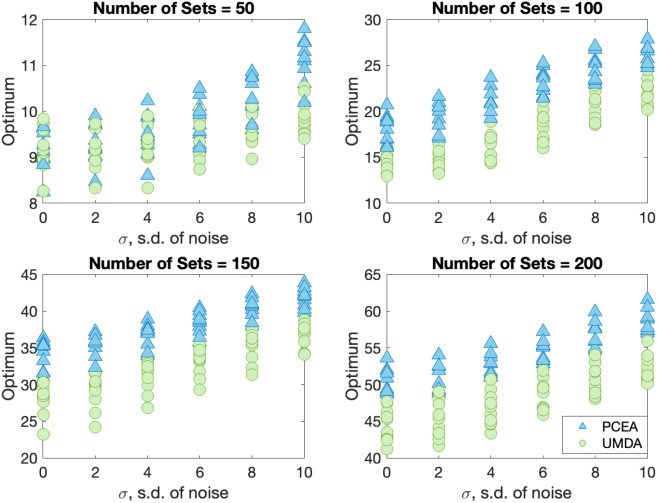
When noise is added, neither algorithm finds the optimal solution, so we record
the best solution found (as assessed by non-noisy fitness function). For each problem
instance, we plot (in Figures 6 and 10) the best solution found (averaged over 100 runs)
as a fraction of the best solution ever encountered for that problem instance. This en-
ables us to make meaningful comparisons between problem instances. The best known
Evolutionary Computation Volume 31, Number 3
269
Aishwaryaprajna and J.E. Rowe
Figure 5: Runtime comparison of UMDA (circles) and PCEA (triangles) while solving
instances of the noisy SubsetSum problem.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6: Solution quality of UMDA (circles) and PCEA (triangles) while solving in-
stances of NoisyKnapsackV1.
solution for each problem instance has a scaled fitness value of 1. Figures 7 and 11 show
the time taken (on average) to locate the best found solution in each case. We can ob-
serve in Figures 6 and 7, that both the algorithms can find good, though not optimal
solutions, for NoisyKnapsackV1 with significant levels of noise.
Observations from the Mann–Whitney U-test show that UMDA is slightly better
than PCEA with these parameter settings for larger noise levels.
270
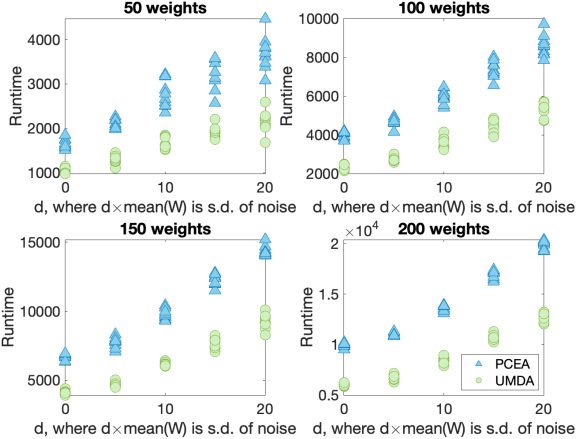
Evolutionary Computation Volume 31, Number 3
EAs and EDAs for Solving Noisy Combinatorial Problems
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7: Comparison of runtime of UMDA (circles) and PCEA (triangles) while solving
the NoisyKnapsackV1.
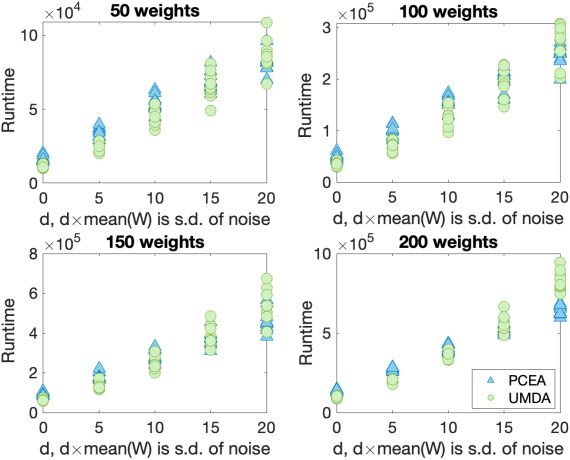
5.3 Noisy KNAPSACK (Version 2)
When the measurements of the weights is uncertain, as well as the profits, this creates a
more complex noise model for the Knapsack problem. In the first stage, the total weight
of the proposed solution is compared against the capacity, and this is done with added
noise. Hence it may be thought that the proposed solution is feasible when in fact it is
not. If it is considered feasible, then the benefit (total profit) is calculated, again with
added noise.The same problem instances are considered as in the previous version of
the Knapsack problem.
Figures 8 and 10 depict how the best (non-noisy) solution varies for different prob-
lem sizes. This value is scaled with respect to the best value found when there is no
noise. The Mann–Whitney U-test shows that the best solution achieved and correspond-
ing runtime of UMDA is better than PCEA in these particular parameter settings. The
runtime required to find these values is shown in Figures 9 and 11, and we see that
UMDA finds its best solution considerably faster than PCEA.
5.4 Noisy CONSTRAINEDSETCOVER and PENALTYSETCOVER
The ConstrainedSetCover problem is solved by initially finding the feasible solutions
and then minimising the number of the selected sets. This lexicographic ordering is
achieved in the selection mechanism of the considered algorithms.
In PCEA, the child with least uncovered elements is selected. When both of the
children have the same number of uncovered elements, the child with the minimum
number of sets goes to the next population. In UMDA, the sorting of the population is
based on the above mentioned lexicographic ordering. We consider margin handling in
UMDA for all the following experiments in single objective-optimisation.
The alternative PenaltySetCover problem handles the constraint within the
penalty function, hence creating a single objective. For both versions of the noisy
Evolutionary Computation Volume 31, Number 3
271
Aishwaryaprajna and J.E. Rowe
Figure 8: Solution quality of UMDA (circles) and PCEA (triangles) while solving the
NoisyKnapsackV2.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9: Comparison of runtime of UMDA (circles) and PCEA (triangles) while solving
the NoisyKnapsackV2.
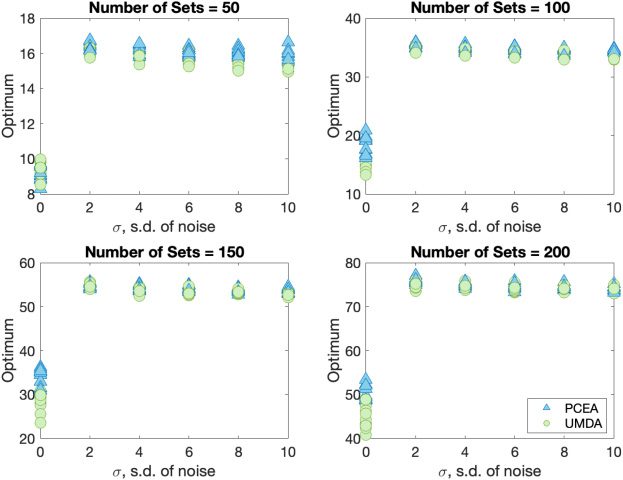
SetCover problem, a range of 40 problem instances (10 for each problem size) are run
with 100 elements and 50, 100, 150, and 200 subsets are available to cover those elements.
The problems are created by randomly generating subsets, where the probability of
272
Evolutionary Computation Volume 31, Number 3
EAs and EDAs for Solving Noisy Combinatorial Problems
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Figure 10: Solution quality of UMDA (circles) and PCEA (triangles) while solving the
NoisyKnapsack for strongly correlated problem instances.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 11: Comparison of runtime of UMDA (circles) and PCEA (triangles) while solving
the NoisyKnapsack for strongly correlated problem instances.
Evolutionary Computation Volume 31, Number 3
273
Aishwaryaprajna and J.E. Rowe
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 12: Solution quality of UMDA (circles) and PCEA (triangles) while solving the
ConstrainedSetCover.
including any element in any subset is p. This is set so that the probability of there
being cover is large:
Therefore, we take:
(1 − (1 − p)n)m = 1 − δ.
p = 1 − (1 − (1 − δ)1/m)1/n.
We have chosen δ = 0.001. All the algorithms are run until 50,000 function evaluations
are reached. An average of 30 runs are reported. Figure 12 reports the best feasible so-
lution found in the fixed budget of function evaluations. As evident from the figure,
neither of the algorithms can handle noise well. The noisy feasibility check significantly
worsens the optimum found even for small standard deviations of noise.
The parameters considered for solving the PenaltySetCover are chosen the same
as the ConstrainedSetCover. For each problem, we plot the best feasible solution
found so far in the given function evaluation budget and the runtime in Figures 13 and
14. It is interesting that both the algorithms can solve the noisy instances in a scalable
manner, with UMDA typically producing better quality solutions.
6 Noisy Combinatorial Multiobjective Problems
In this section, we empirically examine the performances of several evolutionary algo-
rithms on noisy combinatorial multiobjective problems. Much of the previous work on
multiobjective optimisation (especially in the context of noise) has concerned continu-
ous problems (Goh et al., 2010; Shim et al., 2013; Fieldsend and Everson, 2015; Falcón-
Cardona and Coello, 2020). In this article, we focus on discrete problems, but with
additive (posterior) Gaussian noise.
274
Evolutionary Computation Volume 31, Number 3
EAs and EDAs for Solving Noisy Combinatorial Problems
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Figure 13: Best solution found in stipulated budget of function evaluations by UMDA
(circles) and PCEA (triangles) for NoisyPenaltySetCover.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 14: Runtime of UMDA (circles) and PCEA (triangles) for best solution found
while solving NoisyPenaltySetCover.
Evolutionary Computation Volume 31, Number 3
275
Aishwaryaprajna and J.E. Rowe
A noisy multiobjective combinatorial problem in the search space of binary strings
may be defined as follows,
f (x) = (f1(x) + N (0, σ ), f2(x) + N (0, σ ), . . . , fk (x) + N (0, σ )),
where, x ∈ {0, 1}n is a candidate solution. The objectives f1(x), f2(x), . . . , fk (x) are con-
flicting in nature, so there does not necessarily exist an optimal solution that will
minimise all the objectives simultaneously. Instead, there exists a set of nondominat-
ing solutions known as the Pareto optimal solution set where none of the objectives may
be improved without worsening at least one of the other objectives. In the context of
noisy multiobjective optimisation, the goal is to find the set of Pareto optimal solutions,
as defined in the absence of noise; however, the challenge is that each time a compari-
son is made, noise is applied. This is particularly problematic for algorithms that make
use of an archive of nondominated solutions, as it is easy for a solution to be incorrectly
placed in the archive due to the noise.
In order to assess how successfully we have approximated the true Pareto optimal
set, we measure the spread of a set of nondominated solutions on the basis of the fre-
quently used hypervolume performance indicator (Zitzler and Thiele, 1998). Where we
seek to minimise each objective, this is a measure of the area (or volume) of the region
bounded below by a set of candidate solutions simultaneously and bounded above by
a reference point r in the objective space. The reference point r is chosen to be the max-
imum value each objective function can attain in each corresponding dimension of the
objective space; that is, r = (max f1, max f2, . . . , max fk ). Conversely, for maximisation
problems, we take the volume between the candidate set and a lower bounding refer-
ence point (in the case of non-negative objectives, it is common to take the origin as the
reference point). We use hypervolume of the population as an indicator of the spread
of the nondominated solutions in each generation of the considered algorithms.
In this article, we have studied two noisy multiobjective problems. The first is based
on the toy benchmark problem Counting Ones Counting Zeroes (COCZ), in which the
first objective function counts the number of ones in a string, and the second objective
function counts the number of ones in the first m bits and the number of zeroes in the
remainder. We seek to maximise both objectives.
NoisyCOCZ(x) =
(cid:11)
n(cid:2)
i=1
xi + N (0, σ ),
m(cid:2)
xi +
n(cid:2)
i=1
i=m+1
(cid:12)
(1 − xi ) + N (0, σ )
.
The Pareto optimal front consists of strings of the form 1m∗(n−m).
The second problem is a multiobjective version of SetCover problem, with the ob-
jective function and the constraint as defined in ConstrainedSetCover as the two ob-
jective functions. These objectives are conflicting in nature. The first objective minimises
the number of sets required to cover all the m elements of the target set, and the second
objective minimises the number of uncovered elements. The noisy version of the mul-
tiobjective SetCover problem is defined as follows,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
NoisyMultiobjectiveSetCover(x) =
(cid:11)
n(cid:2)
j =1
xj + N (0, σ ),
(cid:2)
⎡
⎣
n(cid:2)
i
j =1
Recall that [expr] equals 1 when expr is true and 0 otherwise.
⎤
(cid:12)
⎦+ N (0, σ )
.
aij xj = 0
276
Evolutionary Computation Volume 31, Number 3
EAs and EDAs for Solving Noisy Combinatorial Problems
7 Algorithms Chosen for Noisy Multiobjective Combinatorial
Problems
7.1
Simple Evolutionary Multiobjective Optimiser (SEMO)
SEMO (Laumanns et al., 2004) is one of the simplest evolutionary algorithms designed
for multiobjective optimisation in discrete search space. To the best of our knowledge,
it has not previously been used to solve noisy problems. SEMO is a simple population-
based algorithm using one-bit mutation, and a variable population size (representing
the current nondominated solutions found). The algorithm starts with adding an initial
solution x ∈ {0, 1}n chosen uniformly at random to the population P . Then a solution y is
chosen randomly from P and mutated with a one-bit flip to obtain y(cid:7)
is dominated
by anything in P it is discarded. Otherwise it is added to P and all the solutions that
y(cid:7)
dominates in P are discarded. Then a new y is chosen from P and the process is
repeated. One of the great challenges SEMO will face due to noisy dominance relations
is that, often good solutions will be discarded and bad solutions will be retained in P .
. If y(cid:7)
7.2 Nondominated Sorting Genetic Algorithm—II (NSGA-II)
NSGA-II, by Deb et al. (2002), sorts the population into nondominated fronts in each
generation. Based on nondominated sorting and using a crowding heuristic to break
ties, the best half of individuals become the parent population of the next generation.
In case of noisy function evaluations, nondominated sorting will be affected and worse
solutions will appear in better nondominated fronts. We use the same algorithm struc-
ture as defined in Deb et al. (2002) except considering noisy function evaluations during
the selection process.
7.3 Variants of Multiobjective Univariate Marginal Distribution Algorithm
(moUMDA)
From our experiments in noisy single-objective combinatorial problems, UMDA and
PCEA show significantly better performance in handling noise compared with the
other algorithms we tried, with UMDA generally producing better quality solutions.
From these results, we hypothesise that a multiobjective version of UMDA (denoted
moUMDA) may be able to handle large levels of noise in noisy combinatorial multi-
objective problems if proper diversification mechanisms are employed. In order to in-
vestigate this, we have considered several versions of moUMDA in our analysis with
different diversification techniques.
Pelikan et al. (2005) introduced a version of UMDA to address multiobjective
problems which used nondominated sorting in the selection mechanism. They also
Evolutionary Computation Volume 31, Number 3
277
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Aishwaryaprajna and J.E. Rowe
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
experimented with clustering methods, to help the algorithm generate solutions across
the Pareto front. We have followed this idea, and studied several versions of UMDA
adapted for multiobjective problems. Where nondominated sorting and crowding are
used for selection, these are implemented identically to NSGA-II. We also consider mak-
ing use of an archive, and in using hypervolume as a criterion in selection:
moUMDA without duplicates: Uses nondominated sorting (with crowding to break
ties) for selection. Maintains diversity by disallowing duplicates when generating
the population. See Algorithm 2.
moUMDA with clustering: Uses nondominated sorting (with crowding to break
ties) for selection. Clusters the selected population members (using either K-
means or Hierarchical Agglomeration), and produces a frequency vector for each
cluster. Generates next population from these, in proportion to the number of
items within each cluster. See Algorithm 3.
278
Evolutionary Computation Volume 31, Number 3
EAs and EDAs for Solving Noisy Combinatorial Problems
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
moUMDA with Pareto archive: Maintains an archive of nondominated solutions
and uses this to generate the frequency vector for the next population. Uses
nondominated sorting (with crowding to break ties) for selection, and updates
the archive with the selected items. See Algorithm 4.
moUMDA with hypervolume comparison operator: Uses binary tournament se-
lection, comparing solutions initially by Pareto dominance. If neither dominates
the other, then select the one with the better hypervolume indicator value. See
Algorithm 5.
8
Experiments—Noisy Multiobjective Problems
Following the same strategy as for single objective problems, we initially choose a wide
range of evolutionary multiobjective algorithms to compare their performances on a toy
problem: noisy CountingOnesCountingZeroes (COCZ). The algorithms considered
for solving COCZ consists of SEMO, NSGA-II and several versions of multiobjective
UMDA (moUMDA) as described above. Depending on their performances on this prob-
lem, we selected a smaller set of the better performing algorithms for the multiobjective
noisy SetCover problem.
Evolutionary Computation Volume 31, Number 3
279
Aishwaryaprajna and J.E. Rowe
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 15: Comparison of the hypervolume of population while solving the noisy COCZ
with n = 30, m = 15.
Some recent studies claim that multiobjective evolutionary approaches are useful
in solving single objective optimisation problems (Segura et al., 2016). For example,
the multiobjective version of SetCover could enable us to find good solutions to the
original single-objective version (by looking at solutions generated which do not violate
the constraints). Here, we consider whether this approach is also helpful in the context
of noise.
√
8.1 Noisy COUNTINGONESCOUNTINGZEROES (COCZ)
In this subsection, we solve a toy multiobjective problem, the noisy COCZ with n =
30, m = 15 and with additive Gaussian noise centered at zero and having standard
deviations σ = 0, 1, 3, 5, 7, 9, 11, 13, and 15. We set the parameter μ = λ/2, where
λ = 20
n log n for all the versions of moUMDA. For NSGAII, the parent population
n log n. All the algorithms are run for 50,000 function evaluations and
size is set as 10
the mean of 30 runs are reported. The best hypervolume of the population found so far
in the fixed budget of function evaluations are reported in Figure 15. The Pareto op-
timal front would contain 215 elements and the best possible hypervolume is 780. We
have used the dimension-sweep algorithm and the source code by Fonseca et al. (2006)
for hypervolume calculation in the experiments.
√
The results shown in Figure 15 show that SEMO is the worst performing algorithm,
even when there is no noise, and the performance degrades slightly as noise is increased.
The Pareto Archive algorithm (PAmoUMDA) is the next worst. Although it does not
degrade too much with added noise, it is still clearly worse than the other algorithms.
280
Evolutionary Computation Volume 31, Number 3
EAs and EDAs for Solving Noisy Combinatorial Problems
The remaining algorithms have rather similar performance, but we can still dis-
tinguish different behaviours by looking at the zoomed in section of the plot in Fig-
ure 15. The version of moUMDA that uses the hypervolume comparison operator
(moUMDAHCO) performs very well when there is little or no noise. However, its per-
formance degrades considerably as the level of noise increases. The same is true for
NSGAII. When the noise reaches a standard deviation of σ = 15, these two algorithms
are the worst of the remaining ones.
The plain moUMDA and the version forbidding duplicates in the population both
have the curious property that their performance improves with the presence of low
levels of noise, and then degrades at higher levels of noise. We speculate that low levels
of noise allow for much more diversity in the populations. At high levels of noise (σ =
15) they are the best performing algorithms, along with the two versions of moUMDA
that use clustering (moUMDA-Kmeans and moUMDA-HAC). The moUMDA with no
duplicates is marginally the best overall at this level of noise.
8.2 Noisy Multiobjective SETCOVER
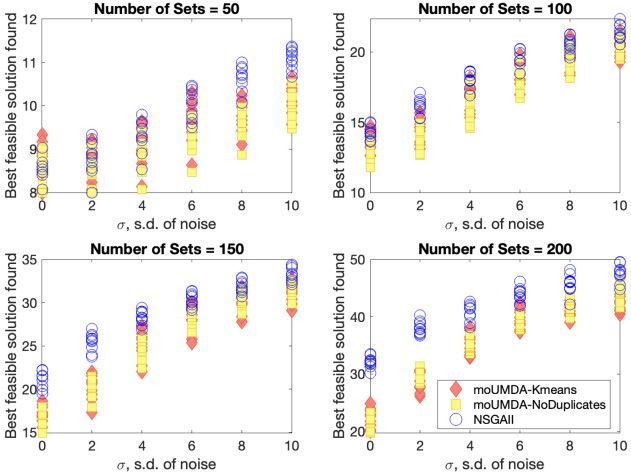
In this section, we compare the performance of three of our multiobjective algorithms,
viz., NSGA-II, moUMDA with no duplicates allowed, and moUMDA employing K-
means clustering, on the noisy multiobjective SetCover problem. We have chosen these
algorithms based on their behaviours on the COCZ. These were amongst the best al-
gorithms we tried on that problem. There being little to distinguish the two different
clustering methods, we have chosen to test just one of these (K-means clustering). We
have selected the “no duplicates” version of moUMDA, as this gave a small advantage
over the plain moUMDA. And we have kept NSGAII as this is a standard algorithm for
any multiobjective problem.
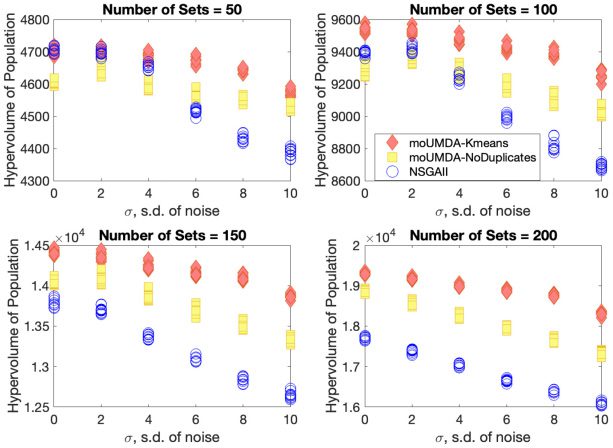
All the algorithms are run for 50,000 function evaluations. The best hypervolume
of the population obtained in the fixed function evaluation budget for each of 30 runs
is shown in Figure 16. We observe that the clustering algorithm, moUMDA-Kmeans,
handles high levels of noise significantly better than other algorithms. It is evident that
the performance of NSGA-II becomes worse as the standard deviation of noise increases
and the problem size increases and indeed is the worst of the three algorithms on this
problem.
We also consider the multiobjective formulation of noisy SetCover as a means to
solve the standard single objective problem. To this end, we consider the quality of the
best feasible solutions found by each algorithm, averaged over the 30 runs. The results
are plotted in Figure 17. Again, the two versions of moUMDA perform better than NS-
GAII. A comparison with Figure 13 shows that this approach can indeed produce better
quality results than the single objective formulation.
9 Conclusion
We have empirically studied a range of evolutionary algorithms on a set of noisy prob-
lems. The (1 + 1)-EA, as expected, fails to cope with any degree of posterior noise.
Interestingly, some algorithms (the mutation-population algorithm and cGA), where
there is a theoretical polynomial runtime for noisy OneMax, fail to be useful in practice
compared with some other algorithms. PBIL performs somewhat similar to cGA. The
Paired-Crossover Evolutionary algorithm handles noise well on both the simple test
problems, and on the noisy combinatorial problems we have tried. Interestingly, UMDA
also handles these cases well, with even a slightly better performance than PCEA. This
may be due to the fact that UMDA has a strong selection method (truncation selection)
Evolutionary Computation Volume 31, Number 3
281
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Aishwaryaprajna and J.E. Rowe
Figure 16: Best hypervolume of population obtained for MultiobjectiveSetCover.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 17: Best feasible solution found while solving the noisy MultiobjectiveSet-
Cover.
than PCEA (which uses a tournament on pairs of offspring). Of course, parameter val-
ues on each could be tweaked to produce slightly different results; our key finding is
that these are the only algorithms we have tried that seem remotely practical for such
problems. It seems likely that UMDA’s performance is more due to its relationship with
282
Evolutionary Computation Volume 31, Number 3
EAs and EDAs for Solving Noisy Combinatorial Problems
crossover algorithms (such as the genepool crossover), rather than considered as an
EDA (such as PBIL).
We are not aware of any previously published results on noisy combinatorial mul-
tiobjective problems. We carefully selected a set of multiobjective algorithms on the ba-
sis of the performance on noisy COCZ and tested them on the noisy multiobjective
SetCover. We observe that multiobjective UMDA with a simple diversity mechanism
that allows no duplicate solutions in the population is effective at solving the noisy Set-
Cover problem in both constrained and multiobjective forms. UMDA can also benefit
from using a clustering approach when dealing with noisy multiobjective problems.
References
Aishwaryaprajna, and Rowe, J. E. (2019). Noisy combinatorial optimisation by evolutionary al-
gorithms. In Proceedings of the Genetic and Evolutionary Computation Conference Companion
(GECCO), pp. 139–140.
Akimoto, Y., Astete-Morales, S., and Teytaud, O. (2015). Analysis of runtime of optimization algo-
rithms for noisy functions over discrete codomains. Theoretical Computer Science, 605:42–50.
10.1016/j.tcs.2015.04.008
Anil, G., and Wiegand, R. P. (2009). Black-box search by elimination of fitness functions. In Pro-
ceedings of the Tenth ACM SIGEVO Workshop on Foundations of Genetic Algorithms, pp. 67–78.
Baluja, S. (1994). Population-based incremental learning: A method for integrating genetic search based
function optimization and competitive learning. Technical Report. Department of Computer Sci-
ence, Carnegie-Mellon University, Pittsburgh, Pennsylvania.
Bianchi, L., Dorigo, M., Gambardella, L. M., and Gutjahr, W. J. (2009). A survey on metaheuris-
tics for stochastic combinatorial optimization. Natural Computing, 8(2):239–287. 10.1007/
s11047-008-9098-4
Carraway, R. L., Schmidt, R. L., and Weatherford, L. R. (1993). An algorithm for maximizing
target achievement in the stochastic knapsack problem with normal returns. Naval Research
Logistics, 40(2):161–173. 10.1002/nav.3220400203
Dang, D., and Lehre, P. K. (2016). Runtime analysis of non-elitist populations: From classical op-
timisation to partial information. Algorithmica, 75(3):428–461. 10.1007/s00453-015-0103-x
Dang, D.-C., and Lehre, P. K. (2015). Efficient optimisation of noisy fitness functions with
population-based evolutionary algorithms. In Proceedings of the 2015 ACM Conference on
Foundations of Genetic Algorithms XIII, pp. 62–68.
Dang-Nhu, R., Dardinier, T., Doerr, B., Izacard, G., and Nogneng, D. (2018). A new analysis
method for evolutionary optimization of dynamic and noisy objective functions. In Proceed-
ings of the Genetic and Evolutionary Computation Conference, pp. 1467–1474.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A fast and elitist multiobjective genetic
algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2):182–197. 10.1109/
4235.996017
Doerr, B. (2020). Exponential upper bounds for the runtime of randomized search heuristics.
In International Conference on Parallel Problem Solving from Nature, pp. 619–633. Vol. 12270.
10.1007/978-3-030-58115-2_43
Doerr, B., and Sutton, A. M. (2019). When resampling to cope with noise, use median, not mean.
In Proceedings of the Genetic and Evolutionary Computation Conference, pp. 242–248.
Droste, S. (2004). Analysis of the (1 + 1) ea for a noisy onemax. In Genetic and Evolutionary Com-
putation Conference, pp. 1088–1099.
Evolutionary Computation Volume 31, Number 3
283
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Aishwaryaprajna and J.E. Rowe
Falcón-Cardona, J. G., and Coello, C. A. C. (2020). Indicator-based multi-objective evolutionary
algorithms: A comprehensive survey. ACM Computing Surveys, 53(2):1–35.
Fieldsend, J. E., and Everson, R. M. (2015). The rolling tide evolutionary algorithm: A multiobjec-
tive optimizer for noisy optimization problems. IEEE Transactions on Evolutionary Computa-
tion, 19(1):103–117. 10.1109/TEVC.2014.2304415
Fonseca, C. M., Paquete, L., and López-Ibánez, M. (2006). An improved dimension-sweep algo-
rithm for the hypervolume indicator. In IEEE International Conference on Evolutionary Compu-
tation, pp. 1157–1163.
Fortz, B., Labbé, M., Louveaux, F., and Poss, M. (2013). Stochastic binary problems with sim-
ple penalties for capacity constraints violations. Mathematical Programming, 138(1):199–221.
10.1007/s10107-012-0520-4
Friedrich, T., Kötzing, T., Krejca, M. S., and Sutton, A. M. (2015). The benefit of recombination in
noisy evolutionary search. In K. Elbassioni and K. Makino (Eds.), Algorithms and computation,
pp. 140–150. Springer Berlin Heidelberg.
Friedrich, T., Kötzing, T., Krejca, M. S., and Sutton, A. M. (2017). The compact genetic algorithm
is efficient under extreme Gaussian noise. IEEE Transactions on Evolutionary Computation,
21(3):477–490.
Gießen, C., and Kötzing, T. (2016). Robustness of populations in stochastic environments. Algo-
rithmica, 75(3):462–489.
Goh, C. K., Tan, K. C., Cheong, C. Y., and Ong, Y.-S. (2010). An investigation on noise-induced fea-
tures in robust evolutionary multi-objective optimization. Expert Systems with Applications,
37(8):5960–5980. 10.1016/j.eswa.2010.02.008
Goldberg, D. E., Deb, K., and Clark, J. H. (1991). Genetic algorithms, noise, and the sizing of
populations. Urbana, 51:61801.
Harik, G. R., Lobo, F. G., and Goldberg, D. E. (1999). The compact genetic algorithm. IEEE Trans-
actions on Evolutionary Computation, 3(4):287–297. 10.1109/4235.797971
Henig, M. I. (1990). Risk criteria in a stochastic knapsack problem. Operations Research, 38(5):820–
825. 10.1287/opre.38.5.820
Laumanns, M., Thiele, L., and Zitzler, E. (2004). Running time analysis of multiobjective evolu-
tionary algorithms on pseudo-Boolean functions. IEEE Transactions on Evolutionary Compu-
tation, 8(2):170–182. 10.1109/TEVC.2004.823470
Lucas, S. M., Liu, J., and Pérez-Liébana, D. (2017). Efficient noisy optimisation with the multi-
sample and sliding window compact genetic algorithms. In IEEE Symposium Series on Com-
putational Intelligence, pp. 1–8.
Mühlenbein, H. (1997). The equation for response to selection and its use for prediction. Evolu-
tionary Computation, 5(3):303–346.
Pelikan, M., Sastry, K., and Goldberg, D. E. (2005). Multiobjective hboa, clustering, and scalability.
In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation, pp. 663–
670.
Pisinger, D. (2005). Where are the hard knapsack problems? Computers & Operations Research,
32(9):2271–2284.
Prügel-Bennett, A., Rowe, J., and Shapiro, J. (2015). Run-time analysis of population-based evolu-
tionary algorithm in noisy environments. In Proceedings of the 2015 ACM Conference on Foun-
dations of Genetic Algorithms XIII, pp. 69–75.
284
Evolutionary Computation Volume 31, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
EAs and EDAs for Solving Noisy Combinatorial Problems
Qian, C., Yu, Y., Tang, K., Jin, Y., Yao, X., and Zhou, Z.-H. (2018). On the effectiveness of sampling
for evolutionary optimization in noisy environments. Evolutionary Computation, 26(2):237–
267. 10.1162/evco_a_00201
Rattray, M., and Shapiro, J. (1997). Noisy fitness evaluation in genetic algorithms and the dy-
namics of learning. In R. K. Belew and M. D. Vose (Eds.), Foundations of Genetic Algorithms,
pp. 117–139. Morgan Kaufmann.
Ross, K. W., and Tsang, D. H. (1989). The stochastic knapsack problem. IEEE Transactions on Com-
munications, 37(7):740–747. 10.1109/26.31166
Rowe, J. E., and Aishwaryaprajna (2019). The benefits and limitations of voting mechanisms in
evolutionary optimisation. In Proceedings of the 15th ACM/SIGEVO Conference on Foundations
of Genetic Algorithms, pp. 34–42.
Segura, C., Coello, C. A. C., Miranda, G., and León, C. (2016). Using multi-objective evolution-
ary algorithms for single-objective constrained and unconstrained optimization. Annals of
Operations Research, 240(1):217–250. 10.1007/s10479-015-2017-z
Shim, V. A., Tan, K. C., Chia, J. Y., and Mamun, A. A. (2013). Multiobjective optimization with
estimation of distribution algorithm in a noisy environment. Evolutionary Computation,
21(1):149–177. 10.1162/EVCO_a_00066
Sniedovich, M. (1980). Preference order stochastic knapsack problems: Methodological issues.
Journal of the Operational Research Society, 31(11):1025–1032. 10.1057/jors.1980.189
Steinberg, E., and Parks, M. (1979). A preference order dynamic program for a knapsack problem
with stochastic rewards. Journal of the Operational Research Society, 30(2):141–147. 10.1057/
jors.1979.27
Witt, C. (2017). Upper bounds on the runtime of the univariate marginal distribution algorithm
on onemax. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO),
pp. 1415–1422.
Witt, C. (2021). On crossing fitness valleys with majority-vote crossover and estimation-of-
distribution algorithms. In Proceedings of the 16th ACM/SIGEVO Conference on Foundations
of Genetic Algorithms, pp. 1–15.
Wu, Z., Kolonko, M., and Möhring, R. H. (2017). Stochastic runtime analysis of the cross-
entropy algorithm. IEEE Transactions on Evolutionary Computation, 21(4):616–628. 10.1109/
TEVC.2017.2667713
Zitzler, E., and Thiele, L. (1998). Multiobjective optimization using evolutionary algorithms—A
comparative case study. In International Conference on Parallel Problem Solving from Nature,
pp. 292–301. Vol. 1498.
Evolutionary Computation Volume 31, Number 3
285
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
1
3
2
5
9
2
1
5
5
6
3
9
e
v
c
o
_
a
_
0
0
3
2
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3