Evaluating Explanations: How Much Do Explanations
from the Teacher Aid Students?
Danish Pruthi1∗ Rachit Bansal2 Bhuwan Dhingra3
Livio Baldini Soares3 Michael Collins3 Zachary C. Lipton1
Graham Neubig1 William W. Cohen3
1 Carnegie Mellon University, USA 2 Delhi Technological University, India
3 Google Research, USA
{ddanish, zlipton, gneubig}@cs.cmu.edu, racbansa@gmail.com
{bdhingra, liviobs, mjcollins, wcohen}@google.com
Astratto
While many methods purport to explain pre-
dictions by highlighting salient features, what
aims these explanations serve and how they
ought to be evaluated often go unstated. In
this work, we introduce a framework to quan-
tify the value of explanations via the accuracy
gains that they confer on a student model
trained to simulate a teacher model. Cru-
cially, the explanations are available to the
student during training, but are not available
at test time. Compared with prior proposals,
our approach is less easily gamed, enabling
principled, automatic, model-agnostic evalu-
ation of attributions. Using our framework,
we compare numerous attribution methods
for text classification and question answer-
ing, and observe quantitative differences that
are consistent (to a moderate to high degree)
across different student model architectures
and learning strategies.1
1
introduzione
The success of deep learning models, together with
the difficulty of understanding how they work,
has inspired a subfield of research on explaining
predictions, often by highlighting specific input
features deemed somehow important to a pre-
diction (Ribeiro et al., 2016; Sundararajan et al.,
2017; Shrikumar et al., 2017). For instance, we
might expect such a method to highlight spans like
‘‘poorly acted’’ and ‘‘slow-moving’’ to explain a
prediction of negative sentiment for a given movie
revisione. Tuttavia, there is little agreement in the
literature as to what constitutes a good explana-
∗Part of this work was done at Google.
1Code for the evaluation protocol: https://github
zione (Lipton, 2016; Jacovi and Goldberg, 2021).
Inoltre, various popular methods for generat-
ing such attributions disagree considerably over
which tokens to highlight (Tavolo 1). With so many
methods claimed to confer the same property while
disagreeing so markedly, one path forward is to
develop clear quantitative criteria for evaluating
purported explanations at scale.
The status quo for evaluating so-called expla-
nations skews qualitative—many proposed tech-
niques are evaluated only via visual inspection
of a few examples (Simonyan et al., 2014;
Sundararajan et al., 2017; Shrikumar et al.,
2017). While several quantitative evaluation tech-
niques have recently been proposed, many of
these are easily gamed (Treviso and Martins,
2020; Hase et al., 2020).2 Some depend upon the
model outputs corresponding to deformed exam-
ples that lie outside the support of the training
distribution (DeYoung et al., 2020), and a few
validate explanations on specifically crafted tasks
(Poerner et al., 2018).
In this work, we propose a new framework,
where explanations are quantified by the degree
to which they help a student model in learn-
ing to simulate the teacher on future examples
(Figura 1). Our framework addresses a coherent
goal, is model-agnostic and broadly applicable
across tasks, E (when instantiated with models
as students) can easily be automated and scaled.
Our method is inspired by argumentative mod-
els for justifying human reasoning, which posit
that the role of explanations is to communicate
information about how decisions are made, E
thus to enable a recipient to anticipate future
2See §7 for a comprehensive discussion on existing
.com/danishpruthi/evaluating-explanations.
metrics, and how they can be gamed by trivial strategies.
359
Operazioni dell'Associazione per la Linguistica Computazionale, vol. 10, pag. 359–375, 2022. https://doi.org/10.1162/tacl a 00465
Redattore di azioni: Trevor Cohn. Lotto di invio: 6/2021; Lotto di revisione: 11/2021; Pubblicato 4/2022.
C(cid:3) 2022 Associazione per la Linguistica Computazionale. Distribuito sotto CC-BY 4.0 licenza.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
T
l
UN
C
_
UN
_
0
0
4
6
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Tavolo 1: Overlap among the top-10% tokens selected by different explanation techniques for sentiment
analysis. In each row, for a given technique, we tabulate the fraction of explanatory tokens that overlap
with other explanations. Value of
implies perfect overlap and 0.0 denotes no overlap.
find attention-based explanations and integrated
gradients (Sundararajan et al., 2017) to be the
most effective, and vanilla gradient-based saliency
maps and LIME to be the least effective. Further,
we observe moderate to high agreement among
rankings obtained by varying student architec-
tures and learning strategies in our framework.
For question answering, we validate the effective-
ness of student learners on both human-produced
explanations collected by Lamm et al. (2021),
and automatically generated explanations from a
SpanBERT model (Joshi et al., 2020).
2 Explanation as Communication
2.1 An Illustrative Example
In our framework, we view explanations as a com-
munication channel between a teacher T and a stu-
dent S, whose purpose is to help S to predict T ’s
outputs on a given input. As an example, con-
sider the case of graduate admissions: An aspirant
submits their application x and subsequently the
admission committee T decides whether the can-
didate is to be accepted or not. The acceptance
criterion, fT (X), represents a typical black box
function—one that is of great interest to future
aspirants.3 To simulate the admission criterion, UN
student S might study profiles of several appli-
cants from previous iterations, x1, . . . , xn, E
their admission outcomes fT (x1), . . . , fT (xn).
Let A(fS, fT ) be the simulation accuracy, questo è,
the accuracy with which the student predicts the
3Our illustrative example assumes that the admission
decision depends solely upon the student application, E
ignores how other competing applicants might affect the
outcome.
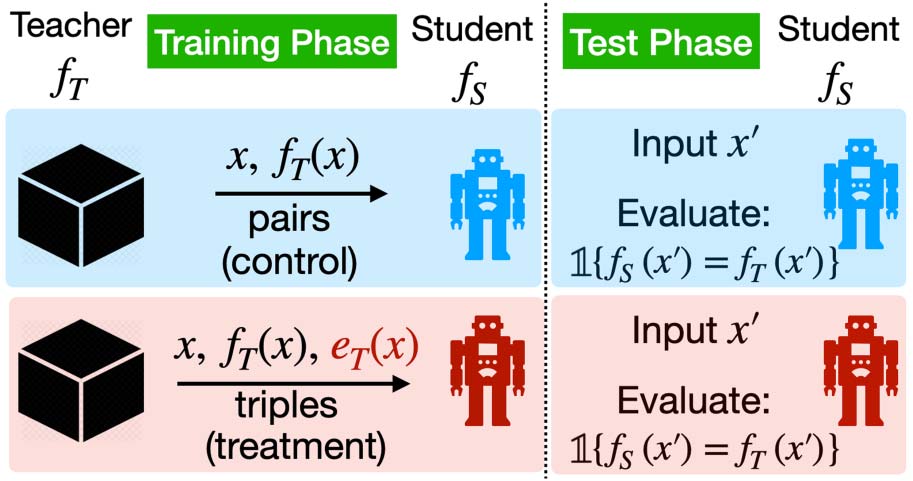
Figura 1: The proposed framework for quantifying
explanation quality. Student models learn to mimic the
teacher, with and without explanations (provided as
‘‘side information’’ with each example). Explanations
are effective if they help students to better approximate
the teacher on unseen examples for which explanations
are not available. Students and teachers could be either
models or people.
decisions (Mercier and Sperber, 2017). Our frame-
work is similar to human studies conducted by
Hase and Bansal (2020), who evaluate if expla-
nations help predict model behavior. Tuttavia,
here we focus on protocols that do not rely on
human-subject experiments.
Using our framework, we conduct extensive
experiments on two broad categories of NLP
text classification and question answer-
compiti:
ing. For classification tasks, we compare seven
widely used input attribution techniques, covering
gradient-based methods (Simonyan et al., 2014;
Sundararajan et al., 2017), perturbation-based
techniques (Ribeiro et al., 2016), attention-based
explanations (Bahdanau et al., 2015), and other
popular attributions (Shrikumar et al., 2017;
Dhamdhere et al., 2019). These comparisons
lead to observable quantitative differences—we
360
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
T
l
UN
C
_
UN
_
0
0
4
6
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
teacher’s decisions on unseen future applications
(defined formally below in §2.2).
using the explanations, questo è, explanations are
only available during training, not at test time.
Now suppose each previous admission outcome
was supplemented with an additional explanation
eT (X) from the admission committee, intended to
help S understand the decisions made by T . Ide-
alleato, these explanations would enhance students’
understanding about the admission process, E
would help students simulate the admission de-
cisions better, leading to a higher accuracy. Noi
argue that the degree of improvement in sim-
ulation accuracy is a quantitative indicator of
the utility of the explanations. Note that generic
explanations or explanations that simply encode
the final decision (per esempio., ‘‘We received far too
many applications …’’) are unlikely to help stu-
dents simulate fT (X), as they provide no addi-
tional information.
2.2 Quantifying Explanations
For concreteness, we assume a classification task,
and for a teacher T , we let fT denote a model
that computes the teacher’s predictions. Let S
be a student (either human or a machine), Poi
T could teach S to simulate fT by sampling
n examples, x1, . . . , xn, and sharing with S a
dataset ˆD containing its associated predictions
{(x1, ˆy1), . . . , (xn, ˆyn)}, where ˆyi = fT (xi), E
S could then learn some approximation of fT
from this data:
fS, ˆD = learn(S, ˆD).
Additionally, we assume that for a given teacher
T , an explanation generation method can generate
an explanation eT (X) for any example x which is
some side information that potentially helps S in
predicting fT (X). We use ˆE to denote a dataset of
explanation-augmented examples, questo è,
ˆE = {(x1, eT (x1), ˆy1), . . . , (xn, eT (xn), ˆyn)},
and the student learner can make use of this side
information during training, to learn a classifier
fS, ˆE = learn(S, ˆE).
Note that none of the learning tasks discussed
above involve the ‘‘gold’’ label y for any instance
X, only the prediction ˆy for x, produced by the
teacher. While the student S can use the explana-
tions for learning, all the classifiers fT , fS, ˆD, E
fS, ˆE predict labels given only the input x, without
In our framework the benefit of explanations is
measured by how much they help the student to
simulate the teacher. In particular, we quantify the
ability of a student fS to simulate a teacher using
the simulation accuracy:
UN(fS, fT ) = Ex [ 1{fS(X) = fT (X)} ] ,
(1)
where the expected agreement between student
and teacher is computed over test examples.
Better explanations will lead to higher values
of A(fS, ˆE, fT ) than the accuracy associated
with learning to simulate the teacher without
explanations, namely, UN(fS, ˆD, fT ).
So far, for a given teacher model, our criteria
for explanation quality depends upon the choice
of the student model (S), its learning procedure,
and the number of examples used to train it (N).
To reduce the reliance on a given student, we
could assume that the student S is drawn from
a distribution of students Pr(S), and extend our
framework by considering the expected benefit for
a random student averaged over various values of
N. In practice, we experiment with a small set of
diverse students (per esempio., models with different sizes,
architectures, learning procedures) and consider
different values of n.
2.3 Automated Teachers and Students
In principle, T and S could be either people or
algorithms. Tuttavia, quantitative measurements
are easier to conduct when T and (particolarmente)
S are algorithms. In particular, imagine that T
(which for example could be a BERT-based clas-
sifier) identifies an explanation eT (X) that is some
subset of tokens in a document x that are rele-
vant to the prediction (acquired by, Per esempio,
any of the explanation methods mentioned in
the introduction) and S is some machine learner
that makes use of the explanation. The value of
teacher-explanations for S can then be assessed
via standard evaluation of explanation-aware stu-
dent learners, using predicted labels instead of
gold labels. This value can then be compared to
other schemes for producing explanations (per esempio., In-
tegrated gradients). Albeit, an important concern
in automated evaluation is that, by design, IL
obtained results are contingent on the student
modello(S) and how explanations are incorporated
by the student model(S).
361
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
T
l
UN
C
_
UN
_
0
0
4
6
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Tavolo 2: Example of annotated rationales in sentiment analysis and referential equalities in QA.
Another apparent ‘‘bug’’ in this framework is
that in the automated case, one could obtain a
perfect simulation accuracy with an explanation
that communicates all the weights of the teacher
classifier fT to the student.4 We propose two
approaches to address this problem. Primo, we
simply limit explanations to be of a form that
people can comprehend—for example, spans in a
document x. Questo è, we consider only popular
formats of explanations that are considered to
be human understandable (see §3 for details and
Tavolo 2 for examples). Secondly, we experiment
with a diverse set of student models (per esempio., networks
with architectures different from the original
teacher model), which precludes trivial weight-
copying solutions.
2.4 Discussion
In our framework, two design choices are crucial:
(io) students do not have access to explanations
at test time; E (ii) we use a machine learning
model as a substitute for student learner. These
two design choices differentiate our framework
from similar communication games proposed by
Treviso and Martins (2020) and Hase and Bansal
(2020). When explanations are available at test
time, they can leak the teacher output directly
or indirectly, thus corrupting the simulation task.
Both genuine and trivial explanations can encode
the teacher output, making it difficult to discern
the quality of explanations.5 The framework of
Treviso and Martins (2020) is affected by this
4All the weights of the model can be thought of as a
complete explanation, and is a reasonable choice for simpler
models, per esempio., a linear-model with a few parameters.
5A trivial explanation may highlight the first input token
if the teacher output is 0, and the second token if the output
È 1. Such explanations, termed as ‘‘Trojan explanations’’,
are a problematic manifestation of several approaches, COME
issue, which is probably only partially addressed
by enforcing constraints on the student. Prevent-
ing access to explanations while testing solves
this problem and offers flexibility in choosing
student models.
Substituting machine learners for people al-
lows us to train student models on thousands of
examples, in contrast to the study by Hase and
Bansal (2020), Dove (human) students were
trained on only 16 O 32 examples. As a con-
sequence, the observed differences among many
explanation techniques were statistically insignif-
icant in their studies. While human subject ex-
periments are a valuable complement to scalable
automatic evaluations, it is expensive to conduct
sufficiently large-scale studies; people’s precon-
ceived notions might impair their ability to sim-
ulate the models accurately;6 and lastly these
preconceived notions might bias performance for
different people differently.
3 Learning with Explanations
Our student-teacher framework does not specify
how to use explanations while training the student
modello. Below, we examine two broad approaches
to incorporate explanations: attention regulariza-
tion and multitask learning. Our first approach
regularizes attention values of the student model
to align with the information communicated in
explanations. In the second method, we pose the
learning task for the student as a joint task of
prediction and explanation generation, expecting
discussed in Chang et al. (2020) and Jacovi and Goldberg
(2021).
6We speculate this effect to be pronounced when the
models’ outputs and the true labels differ only over a few
samples.
362
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
T
l
UN
C
_
UN
_
0
0
4
6
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
to improve prediction due to the benefits of multi-
task learning. We show that both of these methods
indeed improve student performance when using
human-provided explanations (and gold labels) for
classification tasks. We explore variants of these
two approaches for question answering tasks.
Quello
Classification Tasks The training data for
the student model consists of n documents
x1, . . . , xn, and the output
to be learned,
y1, . . . , yn, comes from the teacher,
È,
yi = fT (xi), along with teacher-explanations
eT (x1), . . . , eT (xn). In this work, we consider
teacher explanations in the form of a binary vector
eT (xi), such that eT (xi)j = 1 if the jth token in
document xi is a part of the teacher-explanation,
E 0 otherwise (Vedi la tabella 2 for an example).7
To incorporate explanations during training, we
suggest two different approaches. Primo, noi usiamo
attention regularization, where we add a reg-
ularization term to our loss to reduce the KL
divergence between the attention distribution of
the student model (αstudent) and the distribution of
the teacher-explanation (αexp):
(2)
R(cid:4) = −λ KL(αexp (cid:5) αstudent),
where the explanation distribution (αexp) is uni-
form over all the tokens in the explanation and
(cid:3) elsewhere (Dove (cid:3) is a very small constant).
When dealing with student models that employ
multi-headed attention, which use multiple differ-
ent attention vectors at each layer of the model
(Vaswani et al., 2017), we take αstudent to be the
attention from the [CLS] token to other tokens in
the last layer, averaged across all attention heads.
Several past approaches have used attention reg-
ularization to incorporate human rationales, con
an aim to improve the overall performance of
the system for classification tasks (Bao et al.,
2018; Zhong et al., 2019) and machine translation
(Yin et al., 2021).
Secondo, we use explanations via multitask
apprendimento, where the two tasks are prediction
and explanation generation (a sequence labeling
problem). Formalmente,
loss can be
written as:
the overall
⎡
⎤
L = −
N(cid:2)
i=1
⎢
⎣log p(yi|xi; θ)
(cid:9)
(cid:6)
(cid:7)(cid:8)
classify
+ log p(NO|xi; φ, θ)
(cid:9)
(cid:6)
(cid:7)(cid:8)
explain
⎥
⎦
.
7Explanations that generate a continuous ‘‘importance’’
score for each token can also be used as per this definition,
per esempio., by selecting the top-k% tokens from those scores.
363
As in multitask learning, if the task of prediction
and explanation generation are complementary,
then the two tasks would benefit from each other.
As a corollary, if the teacher-explanations offer no
additional information about the prediction, Poi
we would see no benefit from multitask learning
(appropriately so). For most of our classification
esperimenti, we use BERT (Devlin et al., 2019)
with a linear classifier on top of the [CLS] vector
to model p(sì|X; θ). To model p(e|X; φ θ) noi usiamo
a linear-chain CRF (Lafferty et al., 2001) on top
of the sequence vectors from BERT. Note that we
share the BERT parameters θ between classifica-
tion and explanation tasks. In prior work, similar
multitask formulations have been demonstrated to
effectively incorporate rationales to improve clas-
sification performance (Zaidan and Eisner, 2008)
and evidence extraction (Pruthi et al., 2020).
Question Answering Let the question q consist
of m tokens q1 . . . qm, along with passage x that
provides the answer to the question, consisting
of n tokens x1, . . . , xn. Let us define a set of
question phrases Q and passage phrases P to be
Q = {(io, j) : 1 ≤ i ≤ j ≤ m}
P = {(io, j) : 1 ≤ i ≤ j ≤ n}.
We consider a subset of QED explanations (Lamm
et al., 2021), which consist of a sequence of
one or more ‘‘referential equality annotations’’
e1 . . . e|e|. Formalmente, each referential equality an-
notation ek for k = 1 . . . |e| is a pair (φk, πk) ∈
Q × P, specifying that phrase φk in the ques-
tion refers to the same thing in the world as
the phrase πk in the passage (Vedi la tabella 2 for
an example).
To incorporate explanations for question answer-
ing tasks, we use the two approaches discussed
for text classification tasks, namely, attention reg-
ularization and multitask learning. Since the expla-
nation format for question answering is different
from the explanations in text classification, we
use a lossy transformation, where we construct a
binary explanation vector, Dove 1 corresponds to
tokens that appear in one or more referential equal-
ities and 0 otherwise. Given the transformation,
both these approaches do not use the alignment
information present in the referential equalities.
To exploit the alignment information provided
by referential equalities, we introduce and append
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
T
l
UN
C
_
UN
_
0
0
4
6
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Student Model
BERT-base
600
75.5
900
79.0
1200
81.1
w/ explanations used via
multitask learning
attention regularization
75.2
81.5
80.0
83.1
82.5
84.0
Tavolo 3: Simulation accuracy of a student model
when trained with and without explanations
from human experts for sentiment analysis. Noi
note that both the proposed methods to learn
with explanation improve performance: Attention
regularization leads to large gains, whereas mul-
titask learning requires more examples to yield
improvements.
the standard loss with attention alignment loss:
R(cid:4)
= −λ log
⎛
⎝ 1
|e|
|e|(cid:2)
k=1
αstudent[φk → πk]
⎞
⎠ ,
where ek = (φk, πk) is the kth referential equality,
and αstudent[φk → πk]) is the last layer average
attention originating from tokens in φk to tokens in
πk. The average is computed across all the tokens
in φk and across all attention heads. The underly-
ing idea is to increase attention values correspond-
ing to the alignments provided in explanations.
4 Human Experts as Teachers
Below, we discuss the results upon applying
our framework to explanations and output from
human teachers to confirm if expert explanations
improve the student models’ performance.
Setup There exist a few tasks where researchers
have collected explanations from experts besides
the output label. For the task of sentiment analysis
on movie reviews, Zaidan et al. (2007) collected
‘‘rationales’’ where people highlighted portions
of the movie reviews that would encourage (O
discourage) readers to watch (or avoid) the movie.
In another recent effort, Lamm et al. (2021) col-
lected ‘‘QED annotations’’ over questions and
the passages from the Natural Questions (NQ)
dataset (Kwiatkowski et al., 2019). These anno-
tations contain the salient entity in the question
and their referential mentions in the passage that
need to be resolved to answer the question. For
both these tasks, our student-learners are pre-
trained BERT-base models, which are further
Student Model
500
1500
2500
BERT-base
w/ explanations used via
multitask learning
attention regularization
attention alignment loss
28.9
43.7
49.0
29.7
31.2
37.3
42.7
47.2
49.6
49.2
52.6
54.0
Tavolo 4: Simulation performance (F1 score) Di
a student model when trained with and without
explanations from human experts for question
answering. We find that attention regulariza-
tion and attention alignment loss result in large
improvements upon incorporating explanations.
fine-tuned with outputs and explanations from
human experts.
Results Our suggested methods to learn from
explanations indeed benefit from human explana-
zioni. For the sentiment analysis task, Attenzione
regularization boosts performance, as depicted
in Table 3. For instance, attention regulariza-
tion improves the accuracy by an absolute 6
points, for 600 examples. The performance ben-
efits, unsurprisingly, diminish with increasing
training examples—for 1200 examples, the atten-
tion regularization improves performance by 2.9
points. While attention regularization is imme-
diately effective, the multitask learning requires
more examples to learn the sequence labeling task.
We do not see any improvement using multitask
learning for 600 examples, but for 900 E 1200
training examples, we see absolute improvements
Di 1 E 1.4 points, rispettivamente.
We follow up our findings to validate if the
simulation performance of the student model is
correlated with explanation quality. To do so, we
corrupt human explanations by unselecting the
marked tokens with varying noising probabilities
(ranging from 0 A 1, in steps of 0.1). We train stu-
dent models on corrupted explanations using at-
tention regularization and find their performance
to be highly negatively correlated with the amount
of noise (Pearson correlation ρ = −0.72). Questo
study verifies that our metric is correlated with (an
admittedly simple notion of) explanation quality.
For the question-answering task, we measure
the F1 score of the student model on the test set
carved from the QED dataset. As one can observe
from Table 4, both attention regularization and at-
tention alignment loss improve the performance,
364
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
T
l
UN
C
_
UN
_
0
0
4
6
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
T
l
UN
C
_
UN
_
0
0
4
6
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Tavolo 5: We evaluate the effectiveness of attribution methods for sentiment analysis using simulation
accuracy of student models trained with these explanations on varying amounts of data (§5.2). Each
method selects top-10% ‘‘important’’ tokens for each example. We find attention-based explanations to
be most effective, followed by integrated gradients. We also tabulate the average rank as per our metric.
Statistically significant differences (p-value < 0.05) from the no-explanation control are underlined.
whereas multitask learning is not effective.8 At-
tention regularization and attention alignment loss
improve F1 score by 2.3 and 8.4 points for 500
examples, respectively. The gains decrease with
increasing examples (e.g., the improvement due to
attention alignment loss is 5 points on 2500 exam-
ples, compared to 8.4 points with 500 examples).
The key takeaway from these experiments (with
explanations and outputs from human experts) is
that we observe benefits with the learning proce-
dures discussed in previous section. This provides
support to our proposal to use these methods for
evaluating various explanation techniques.
5 Automated Evaluation of Attributions
Here, we use a machine learning model as our
choice for the teacher, and subsequently train
student models using the output and explanations
produced by the teacher model. Such a setup
allows us to compare attributions produced by
different techniques for a given teacher model.
5.1 Setup
For
sentiment analysis, we use BERT-base
(Devlin et al., 2019) as our teacher model and train
it on the IMDb dataset (Maas et al., 2011).
The accuracy of the teacher model is 93.5%.
8We speculate that multitask learning might require more
than 2500 examples to yield benefits. Unfortunately, for the
QED dataset, we only have 2500 training examples.
We compare seven commonly used methods for
producing explanations. These techniques in-
clude LIME (Ribeiro et al., 2016), gradient-based
saliency methods, that is, gradient norm and gra-
dient × input (Simonyan et al., 2014), DeepLIFT
(Shrikumar et al., 2017),
layer conductance
(Dhamdhere et al., 2019), integrated gradients
(I.G.) (Sundararajan et al., 2017), and attention-
based explanations (Bahdanau et al., 2015). More
details about
these explanation techniques are
provided in the Appendix.
For each explanation technique to be compa-
rable to others, we sort the tokens as per scores
assigned by a given explanation technique, and
use only the top-k% tokens. This also ensures
that across different explanations, the quantity
of information from the teacher to the student
per example is constant. Additionally, we evaluate
no-explanation, random-explanation, and trivial-
explanation baselines. For random explanations,
we randomly choose k% tokens, and for triv-
ial explanations, we use the first k% tokens for
the positive class, and the next k% tokens for
the negative class. Such trivial explanations en-
code the label and can achieve perfect scores for
many evaluation protocols that use explanations at
test time.
Corresponding to each explanation type, we
train 4 different student models—comprising
BERT and BiLSTM based models—using out-
puts and explanations from the teacher. The test
365
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
t
l
a
c
_
a
_
0
0
4
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Table 6: Evaluatin different attribution methods for sentiment analysis using the simulation accuracy of
BiLSTM-based student models trained with these explanations on varying amounts of data (§5.2). We
find attention-based explanations, integrated gradients, and layer conductance to be effective techniques.
The rankings are largely consistent with those attained using transformer-based student models (Table 5).
Statistically significant differences (p-value < 0.05) from the no-explanation control are underlined.
set of the teacher model is divided to construct
train, development, and test splits for the student
model. We train student models with explanations
by using attention regularization and multitask
learning. We vary the amount of training data
available and note the simulation performance of
student models.
For the question answering task, we use the
Natural Questions dataset (Kwiatkowski et al.,
2019). The teacher model is a SpanBERT-based
model that is trained jointly to answer the question
and produce explanations (Lamm et al., 2021).
We use the model made available by the authors.
The test set of Natural Questions is split to form
the training, development, and test set for the
student model. We use a BERT-base QA model
as our student model to evaluate the value of
teacher explanations.
5.2 Main Results
We evaluate different explanation generation
methods based upon the simulation accuracy of
various student models for two NLP tasks: text
classification and question answering.
For the sentiment analysis task, we present
the simulation performance of BERT-base and
BERT-large student models in Table 5, and BiL-
STM and BiLSTM+Attention student models in
Student Model
BERT
w/ explanations used via
250
1K 4K 16K
25.0 37.7 52.6 61.6
27.6 42.8 54.4 62.3
attention regularization
attention alignment loss 32.9 46.9 55.5 62.2
Table 7: Simulation performance (F1 score) of
a student model when trained with and with-
out explanations from the SpanBERT QA model
(the teacher model in this case). We find these
explanations to be effective across both the learn-
ing strategies.
Table 6. From these two tables, we first note that
attention-based explanations are effective, result-
ing in large and statistically significant improve-
ments over the no-explanation control. We see an
improvement of 1.4 to 2.6 points for transformer-
based student models (Table 5), and up to 7 points
for the Bi-LSTM student model (Table 6).
While it may seem that attention is effective
because it aligns most directly with attention regu-
larization learning strategy, we note that the trends
from multitask learning corroborate the same con-
clusion for different student models—especially
the Bi-LSTM student model, which does not even
use the attention mechanism, and therefore cannot
366
Bi-LSTM w/ Attention Student Models
BS, ED, HS
LR
16, 128, 256,
2.5 × 10−3
16, 64, 256,
0.5 × 10−2
64, 256, 256,
0.5 × 10−2
32, 128, 768,
2.5 × 10−3
None
LIME
Grad Norm
Grad×Inp.
DeepLIFT
Layer Cond.
I.G.
Attention
MTL AR Rank MTL AR Rank MTL AR Rank MTL AR Rank
8.0
83.9
5.5
84.3
3.0
84.1
6.5
84.0
5.5
84.0
3.5
84.7
1.5
84.8
2.0
84.7
79.9
80.8
81.2
80.6
81.7
83.8
83.6
81.8
80.0
81.0
81.5
81.3
82.1
82.3
82.4
82.1
82.3
83.4
83.9
83.4
83.5
83.7
84.1
83.7
77.4
79.4
79.4
79.0
79.0
80.2
80.3
80.6
79.7
80.3
80.5
80.0
81.2
82.0
82.3
82.6
84.1
84.9
85.0
83.9
84.6
85.1
84.9
85.5
84.6
85.0
84.7
84.8
84.9
84.7
84.8
85.3
7.5
5.0
4.0
7.5
5.0
1.5
3.5
2.0
8.0
5.0
5.0
6.5
5.5
3.0
1.5
1.5
8.0
4.5
5.5
5.0
3.5
4.5
3.0
2.5
Table 8: Gauging the sensitivity of our framework to different hyperparameter values of student
models. We note the simulation accuracies of 4 BiLSTM with attention student models with varying
batch size (BS), learning rate (LR), embedding dimension (ED), and hidden size (HS). We incorporate
explanations via multi-task learning (MTL) over 4K examples and attention regularisation (AR) on 2K
examples. The average rank correlation coefficient τ between all five configurations (including one
from Table 6) is 0.95. Statistically significant differences (p-value < 0.05) from the no-explanation
control are underlined.
incorporate explanations using attention regular-
ization. Besides attention explanations, we also
find integrated gradients and layer conductance
to be effective techniques. Qualitatively inspect-
ing a few examples, we notice that attention and
integrated gradients indeed highlight spans that
convey the sentiment of the review.
Lastly, we see that trivial explanations do not
outperform the control experiment, confirming
that our framework is robust to such gamifica-
tion attempts. These explanations would result
in a perfect score for the protocol discussed in
Treviso and Martins (2020). The metric by
Hase et al. (2020) would be undefined in the
case when 100% of the explanations trivially leak
the label—in the limiting case (when all but one
explanation leak the label trivially), the metric
would result in a high score, which is unintended.
For the question answering task, we observe
from Table 7 that explanations from SpanBERT
QA model are effective, as indicated by both
the approaches to learn from explanations. The
performance benefit of using attention alignment
loss with 250 examples is 7.9 absolute points, and
these gains decrease (unsurprisingly) with increas-
ing number of training examples. For instance, the
gain is only 2.9 points for 4000 examples and the
benefits vanish with 16000 training examples.
5.3 Analysis
Here, we analyze the the effect of different instan-
tiations of our framework—namely, sensitivity to
the choice of student architectures, their hyper-
parameters, learning strategies, and so forth. Ad-
ditionally, we examine the effect of varying the
percentage of explanatory tokens (k in top-k to-
kens) on the results obtained from our framework.
Varying Student Models
and Learning
Strategies We evaluate the agreement among
attribution rankings obtained using (i) different
learning strategies; and (ii) different student
models. We compute the Kendall rank corre-
lation coefficient τ to measure the agreement
among different attribution rankings.9 We report
different τ values for varying combinations of
student models and learning strategies in the
Appendix (Table 10). The key takeaways from
this investigation are twofold: first the rank cor-
relation between rankings produced using the two
learning strategies—attention regularization (AR)
and multi-task learning (MTL)—for the same
student model is 0.64, which is considered a high
agreement. This value is obtained by averaging
τ values from 3 different student models that
9Note that τ lies in [−1, 1] with 1 signifying perfect
agreement and −1 perfect disagreement.
367
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
t
l
a
c
_
a
_
0
0
4
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
can use both these learning strategies. Second,
the rank correlation among rankings produced
using different student models (given the the
same learning strategy) is also high—we report
average values of 0.65 and 0.47 when we use
AR and MTL learning strategies, respectively.
For completion, we also compute τ for all
distinct combinations across student models and
learning strategies (21 combinations in total) and
obtain an average value of 0.52. Overall, we
observe high agreement among different rankings
attained through different instantiations of our
student-teacher framework.
Sensitivity to Hyperparameters We examine
the sensitivity of our framework to different hy-
perparameter values of the student models. For
BiLSTM-based student models, we perform a
random search over different values of four
hyperparameters, that is, number of embedding
dimensions (ED ∈ {64, 128, 256, 512}), num-
ber of hidden size (HS ∈ {256, 512, 768, 1024}),
batch size (BS ∈ {8, 16, 32, 64}) and learning rate
(LR ∈ {0.5 × 10−3, 1 × 10−3, 2.5 × 10−3, 0.5 ×
10−2}). From all possible configurations above,
we randomly sample 4 configurations and train
a BiLSTM with attention student model corre-
sponding to each configuration. The simulation
accuracy of student models with different choices
of hyperparameters are presented in Table 8. For a
given hyperparameter configuration, we average
the ranks across the two learning strategies. We
compute the Kendall rank correlation coefficient
τ among rankings obtained using different hyper-
parameter configurations (including the default
(cid:18)
5
configuration from Table 6, thus resulting in
2
comparisons). We obtain a high average correla-
tion of 0.95, suggesting that our framework yields
largely consistent ranking of attributions across
varying hyperparameters.
(cid:17)
Varying the Percentage of Explanatory Tokens
To examine the effect of k in selecting top-k%
tokens, we evaluate the simulation performance
of BERT-base students trained with varying val-
ues of k ∈ {5, 10, 20, 40} on 2000 examples.10
For these values of k, we corroborate the same
trend, that is, attention-based explanations are the
most effective, followed by integrated gradients
10Note that k is not a parameter of our framework,
but controls the number of explanatory tokens for each
attribution.
Sufficiency ↓
Explanations Value Rank
Comprehensive. ↑
Rank
Value
Random
Trivial
LIME
Grad Norm
Grad×Inp.
DeepLIFT
Layer Cond.
I.G.
Attention
0.29
0.29
0.06
0.25
0.33
0.39
0.11
0.13
0.11
6
7
1
5
8
9
2
4
3
0.04
0.04
0.32
0.11
0.06
0.06
0.24
0.17
0.28
9
8
1
5
7
6
3
4
2
Table 9: Comparing attribution methods as per the
sufficiency (lower the better) and comprehensive-
ness metrics proposed in (DeYoung et al., 2020).
(see Table 11 in the Appendix). We also perform
an experiment where we consider the entire at-
tention vector to be an explanation, as it does
not lose any information due to thresholding. For
500 examples, we see a statistically significant
improvement of 0.9 over the top-10% attention
variant (p-value = 0.03), the difference shrinks
with increasing numbers of training examples
(0.1 for 2000 examples).
5.4 Comparison With Other Benchmarks
For completeness, we compare the ranking of
explanations obtained through our metrics with
existing metrics of sufficiency and comprehen-
siveness introduced in (DeYoung et al., 2020).
The sufficiency metric computes the average
difference in the model output upon using the
input example versus using the explanation alone
(fT (x) − fT (e)), while the comprehensiveness
metric is the average of fT (x) − fT (x\e) over
the examples. Note that using these metrics is not
ideal as they rely upon the model output on de-
formed input instances that lie outside the support
of the training distribution.
We present
these metrics for different ex-
planations in Table 9. We observe that LIME
outperforms other explanations on both the suf-
ficiency and comprehensiveness metrics. We
attribute this to the fact that LIME explanations
rely on attributions from a surrogate linear model
trained on perturbed sentences, akin to the inputs
used to compute these metrics. The average rank
correlation of rankings obtained by our metrics
(across all students and tasks) with the rankings
from these two metrics is moderate (τ = 0.39),
368
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
t
l
a
c
_
a
_
0
0
4
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
which indicates that the two proposals produce
slightly different orderings. This is unsurprising
as our protocol, in principle, is different from the
compared metrics.
Ideally, we would like to link this comparison
with some notion of user preference. This aspira-
tion to evaluate inferred associations with users is
similar to that of evaluating latent topics for topic
models (Chang et al., 2009). However, directly
asking users for their preference (for one expla-
nation versus the other) would be inadequate, as
users would not be able to comment upon the
faithfulness of the explanation to the computation
that resulted in the prediction. Instead, we con-
duct a study inspired from our protocol, that is,
where users simulate the model with and with-
out explanations.
5.5 Human Students
As discussed in §2.4, it is difficult to ‘‘train’’ peo-
ple using a small number of input, output, expla-
nation triples to understand the model sufficiently
to simulate the model (on unseen examples) better
than the control baseline. A recent study trained
students with 16 or 32 examples, and tested if
students could simulate the model better using
different explanations, however the observed dif-
ferences among techniques were not statistically
significant (Hase and Bansal, 2020). Here, we at-
tempt a similar human study, where we present
each crowdworker 60 movie reviews, and for 40
(out of 60) reviews we supplement explanations
of the model predictions. The goal for the work-
ers is to understand the teacher model and guess
the output of the model on the 20 unseen movie
reviews for which explanations are unavailable.
In our case, the teacher model accurately pre-
dicts 93.5% of the test examples, therefore to avoid
crowdworkers conflating the task of simulation
with that of sentiment prediction, we over-sample
the error cases such that our final setup comprises
50% correctly classified and 50% incorrectly clas-
sified reviews. We experiment with 3 different
attribution techniques: attention (as it is one of
the best performing explanation technique as per
our protocol), LIME (as it is not very effective
according to our metrics, but nonetheless is a
popular technique), and random (for control). We
divide a total of 30 crowdworkers in three cohorts
corresponding to each explanation type. The av-
erage simulation accuracy of workers is 68.0%,
69.0%, and 75.0% using LIME, attention, and ran-
dom explanations, respectively. However, given
the large variance in the performance of workers
in each cohort, the differences between any pair of
these explanations is not statistically significant.
The p-value for random vs LIME, random vs at-
tention and LIME vs attention is 0.35, 0.14, and
0.87 respectively.
This study, similar to past human-subject ex-
periments on model simulatability, concludes that
explanations do not definitively help crowdwork-
ers to simulate text classification models. We
speculate that it is difficult for people to simu-
late models, especially when they see a few fixed
examples. A promising direction for future work
could be to explore interactive studies, where peo-
ple could query the model on inputs of their choice
to evaluate any hypotheses they might conjecture.
6 Limitations and Future Directions
There are a few important limitations of our work
that could motivate future work in this space.
First, our current experiments only compare ex-
planations that are of the same format. More work
is required to compare explanations of different
formats, for example, comparing natural language
explanations to the top-k% highlighted tokens, or
even comparing two methods to produce natural
language explanations. To make such compar-
isons, one would have to ensure that different
explanations (potentially with different formats)
communicate comparable bits of information, and
subsequently develop learning strategies to train
student models.
Second, validating the results of any automated
evaluation with human judgement of explana-
tion quality remains inherently difficult. When
people evaluate input attributions (or any form
of explanations) qualitatively,
they can deter-
mine whether the attributions match their intu-
ition about what portions of the input should be
important to solve the task (i.e., plausibility of
explanations), but it is not easy to evaluate if
the highlighted portions are responsible for the
model’s prediction. Going forward, we think that
more granular notions of simulatability, coupled
with counterfactual access to models (where peo-
ple can query the model), might help people bet-
ter assess the role of explanations.
Third, while we observe moderate to high agree-
ment among attribution rankings across different
369
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
t
l
a
c
_
a
_
0
0
4
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
student architectures and learning schemes, it is
conceivable that different explanations are favored
based on the choice of student model. This is a
natural drawback of using a learning model for
evaluation as the measurement could be sensitive
to its design. Therefore, we recommend users to
average simulation results over a diverse set of stu-
dent architectures, training examples, and learn-
ing strategies; and, wherever possible, validate
explanation quality with its intended users.
Lastly, an interesting future direction is to
train explanation modules to generate explana-
tions that optimize our metric, that is, learning
to produce explanations based on the feedback
from the students. To start with, an explanation
generation module could be a simple transfor-
mation over the attention heads of the teacher
model (as attention-based explanations are effec-
tive explanations as per our framework). Learning
explanations can be modeled as a meta-learning
problem, where the meta-objective is the few-shot
test performance of the student trained with in-
termediate explanations, and this performance
could serve as a signal to update the explana-
tion generation module using implicit gradients as
in (Rajeswaran et al., 2019).
7 Related Work
Several papers have suggested simulatability as
an approach to measure interpretability (Lipton,
2016; Doshi-Velez and Kim, 2017). In a survey
on interpretability, Doshi-Velez and Kim (2017)
propose the task of forward simulation: Given
an input and an explanation, people must predict
what a model would output for that instance.
Chandrasekaran et al. (2018) conduct human-
studies to evaluate if explanations from Visual
Question Answering (VQA) models help users
predict the output. Recently, Hase and Bansal
(2020) perform a similar human-study across text
and tabular classification tasks. Due to the na-
ture of these two studies, the observed differences
with and without explanation, and among different
explanation types, were not significant. Con-
ducting large-scale human studies poses several
challenges, including the considerable financial
expense and the logistical challenge of recruit-
ing and retaining participants for unusually long
tasks (Chandrasekaran et al., 2018). By automat-
ing students in our framework, we mitigate such
challenges, and observe quantitative differences
among methods in our comparisons.
Closest
in spirit
to our work, Treviso and
Martins (2020) propose a new framework to assess
explanatory power as the communication success
rate between an explainer and a layperson (which
can be people or machines). However, as a part of
their communication, they pass on explanations
during test time, which could easily leak the label,
and the models trained to play this communication
game can learn trivial protocols (e.g., explainer
generating a period for positive examples and a
comma for negative examples). This is probably
only partially addressed by enforcing constraints
on the explainer and the explainee. Our setup does
not face this issue as explanations are not available
at test time.
To counter
the effects of
leakage due to
explanations, Hase et al.
(2020) present a
Leakage-Adjusted Simulatability (LAS) metric.
Their metric quantifies the difference in perfor-
mance of the simulation models (analogous to
our student models) with and without explana-
tions at test time. To adjust for this leakage, they
average their simulation results across two dif-
ferent sets of examples, ones that leak the label,
and others that do not. Leakage is modeled as a
binary variable, which is estimated by whether
a discriminator can predict the answer using the
explanation alone. It is unclear how the average
of simulation results solves the problem, espe-
cially when trivial explanations leak the label.
Interpretability Benchmarks DeYoung et al.
(2020) introduce the ERASER benchmark to as-
sess how well the rationales provided by models
align with human rationales, and also how faith-
ful
these rationales are to model predictions.
To measure faithfulness, they propose two met-
rics: comprehensiveness and sufficiency. They
compute sufficiency by calculating the model
performance using only the rationales, and com-
prehensiveness by measuring the performance
without the rationales. This approach violates the
i.i.d assumption, as the training and evaluation
data do not come from the same distribution. It
is possible that the differences in model perfor-
mance are due to distribution shift rather than the
features that were removed. This concern is also
highlighted by Hooker et al. (2019), who instead
evaluate interpretability methods via their Re-
mOve And Retrain (ROAR) benchmark. Because
370
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
t
l
a
c
_
a
_
0
0
4
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
the ROAR approach uses explanations at test time,
it could be gamed: Depending upon the predic-
tion, an adversarial teacher could use a different
pre-specified ordering of important pixels as an
explanation. Lastly, Poerner et al. (2018) present
a hybrid document classification task, where the
sentences are sampled from different documents
with different class labels. The evaluation metric
validates if the important tokens (as per a given in-
terpretation technique) point to the tokens from the
‘‘right’’ document, that is, one with the same label
as the predicted class. This protocol, too, relies on
model output for out-of-distribution samples (i.e.,
hybrid documents), and is very task-specific.
8 Conclusion
We have formalized the value of explanations
as their utility in a student-teacher framework,
measured by how much they improve the stu-
dent’s ability to simulate the teacher. In our
setup, explanations are provided by the teacher
as additional side information during training,
but are not available at test time, thus prevent-
ing ‘‘leakage’’ between explanations and output
labels. Our proposed evaluation confirms the
value of human-provided explanations, and cor-
relates with a (simplistic) notion of explanation
quality. Additionally, we conduct extensive ex-
periments that measure the value of numerous
previously-proposed schemes for producing ex-
planations. Our experiments result in clear quan-
titative differences between different explanation
methods, which are consistent, to a moderate to
high degree, across different choices. Among ex-
planation methods, we find attention to be the most
effective. For student models, we find that both
multitask and attention-regularized student learn-
ers are effective, but attention-based learners are
more effective, especially in low-resource settings.
Acknowledgments
We are grateful
to Jasmijn Bastings, Katja
Filippova, Matthew Lamm, Mansi Gupta, Patrick
Verga, Slav Petrov, and Paridhi Asija for insight-
ful discussions that shaped this work. We also
thank the TACL reviewers and action editor for
providing high-quality feedback that improved
our work considerably. Lastly, we acknowledge
Chris Alberti for sharing explanations from the
SpanBERT model.
References
Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua
Bengio. 2015. Neural machine translation
by jointly learning to align and translate.
3rd International Conference on Learning
Representations, ICLR.
Yujia Bao, Shiyu Chang, Mo Yu, and Regina
atten-
Barzilay. 2018. Deriving machine
In Proceed-
tion from human rationales.
ings of
the 2018 Conference on Empirical
Methods in Natural Language Processing,
pages 1903–1913. https://doi.org/10
.18653/v1/D18-1216
Arjun Chandrasekaran, Viraj Prabhu, Deshraj
Yadav, Prithvijit Chattopadhyay, and Devi
Parikh. 2018. Do explanations make VQA
models more predictable to a human? In
Proceedings of the 2018 Conference on Empir-
ical Methods in Natural Language Processing,
pages 1036–1042. https://doi.org/10
.18653/v1/D18-1128
Jonathan Chang, Sean Gerrish, Chong Wang,
Jordan Boyd-graber, and David Blei. 2009.
Reading tea leaves: How humans interpret topic
models. In Advances in Neural Information
Processing Systems, volume 22.
Shiyu Chang, Yang Zhang, Mo Yu, and Tommi
S. Jaakkola. 2020. Invariant rationalization. In
the 37th International Con-
Proceedings of
ference on Machine Learning, ICML 2020,
13-18 July 2020, Virtual Event, volume 119
of Proceedings of Machine Learning Research,
pages 1448–1458.
Jacob Devlin, Ming-Wei Chang, Kenton Lee, and
Kristina Toutanova. 2019. BERT: Pre-training
of deep bidirectional transformers for language
understanding. In Proceedings of the 2019 Con-
ference of the North American Chapter of the
Association for Computational Linguistics: Hu-
man Language Technologies, Volume 1 (Long
and Short Papers), pages 4171–4186.
Jay DeYoung, Sarthak Jain, Nazneen Fatema
Rajani, Eric Lehman, Caiming Xiong, Richard
Socher, and ByronC.Wallace. 2020. ERASER: A
benchmark to evaluate rationalized NLP mod-
els. In Proceedings of the 58th Annual Meeting
of the Association for Computational Linguis-
tics, pages 4443–4458. https://doi.org
/10.18653/v1/2020.acl-main.408
371
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
t
l
a
c
_
a
_
0
0
4
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Kedar Dhamdhere, Mukund Sundararajan, and
Qiqi Yan. 2019. How important is a neuron.
In 7th International Conference on Learning
Representations, ICLR.
Finale Doshi-Velez and Been Kim. 2017. Towards
a rigorous science of interpretable machine
learning. arXiv preprint arXiv:1702.08608.
Peter Hase and Mohit Bansal. 2020. Evaluating
explainable AI: Which algorithmic explana-
tions help users predict model behavior? In
Proceedings of the 58th Annual Meeting of
the Association for Computational Linguistics,
pages 5540–5552. https://doi.org/10
.18653/v1/2020.acl-main.491
Peter Hase, Shiyue Zhang, Harry Xie, and Mohit
Bansal. 2020. Leakage-adjusted simulatability:
Can models generate non-trivial explanations
of their behavior in natural language? In Find-
the Association for Computational
ings of
Linguistics: EMNLP 2020, pages 4351–4367.
Sara Hooker, Dumitru Erhan, Pieter-Jan Kindermans,
and Been Kim. 2019. A benchmark for inter-
pretability methods in deep neural networks.
In Advances in Neural Information Process-
ing Systems, pages 9737–9748. https://
doi.org/10.18653/v1/2020.findings
-emnlp.390
Alon Jacovi and Yoav Goldberg. 2021. Aligning
Interpretations with their Social
Faithful
Attribution. Transactions of
the Association
for Computational Linguistics, 9:294–310.
https://doi.org/10.1162/tacl a 00367
Mandar Joshi, Danqi Chen, Yinhan Liu, Daniel
S. Weld, Luke Zettlemoyer, and Omer Levy.
2020. SpanBERT: Improving pre-training by
representing and predicting spans. Transactions
of
the Association for Computational Lin-
guistics, 8:64–77. https://doi.org/10
.1162/tacl_a_00300
Tom Kwiatkowski, Jennimaria Palomaki, Olivia
Redfield, Michael Collins, Ankur Parikh, Chris
Illia Polosukhin,
Alberti, Danielle Epstein,
Jacob Devlin, Kenton Lee, Kristina Toutanova,
Llion Jones, Matthew Kelcey, Ming-Wei
Chang, Andrew Dai, Jakob Uszkoreit, Quoc
Le, and Slav Petrov. 2019. Natural questions:
a benchmark for question answering research.
Transactions of the Association for Computa-
tional Linguistics, 7:453–466. https://doi
.org/10.1162/tacl_a_00276
John Lafferty, Andrew McCallum, and Fernando
C. N. Pereira. 2001. Conditional random fields:
Probabilistic models for segmenting and label-
ing sequence data. 18th International Confer-
ence on Machine Learning 2001 (ICML 2001),
pages 282–289.
Matthew Lamm, Jennimaria Palomaki, Chris
Alberti, Daniel Andor, Eunsol Choi, Livio
Baldini Soares, and Michael Collins. 2021.
QED: A framework and dataset for explana-
tions in question answering. Transactions of
the Association for Computational Linguistics,
9:790–806. https://doi.org/10.1162
/tacl_a_00398
Zachary C. Lipton. 2016. The mythos of model
interpretability. ACM Queue, 16(3):31–57.
https://doi.org/10.1145/3236386
.3241340
Andrew L. Maas, Raymond E. Daly, Peter
T. Pham, Dan Huang, Andrew Y. Ng, and
Christopher Potts. 2011. Learning word vec-
tors for sentiment analysis. In Proceedings of
the 49th Annual Meeting of the Association for
Computational Linguistics: Human Language
Technologies, pages 142–150.
Hugo Mercier and Dan Sperber. 2017. The Enigma
of Reason, Harvard University Press.
Nina Poerner, Hinrich Sch¨utze, and Benjamin
Roth. 2018. Evaluating neural network expla-
nation methods using hybrid documents and
morphosyntactic agreement. In Proceedings
of the 56th Annual Meeting of the Associa-
tion for Computational Linguistics (Volume 1:
Long Papers), pages 340–350. https://doi
.org/10.18653/v1/P18-1032
Danish Pruthi, Bhuwan Dhingra, Graham Neubig,
and Zachary C. Lipton. 2020. Weakly-and
semi-supervised evidence extraction. Findings
of
the Association for Computational Lin-
guistics: EMNLP 2020, pages 3965–3970.
https://doi.org/10.18653/v1/2020
.findings-emnlp.353
Aravind Rajeswaran, Chelsea Finn, Sham
and Sergey Levine. 2019.
M. Kakade,
Meta-learning with implicit gradients. In Ad-
Information Processing
vances
in Neural
372
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
t
l
a
c
_
a
_
0
0
4
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Systems 32: Annual Conference on Neural In-
formation Processing Systems, pages 113–124.
https://doi.org/10.18653/v1/2020
.blackboxnlp-1.10
Marco Tulio Ribeiro, Sameer Singh, and Carlos
Guestrin. 2016. ‘‘why should I trust you?’’:
Explaining the predictions of any classifier. In
Proceedings of the 22nd ACM SIGKDD Inter-
national Conference on Knowledge Discovery
and Data Mining, pages 1135–1144.
Avanti Shrikumar, Peyton Greenside, and Anshul
Kundaje. 2017. Learning important features
through propagating activation differences. In
the 34th International Con-
Proceedings of
ference on Machine Learning, ICML 2017,
Sydney, NSW, Australia, 6–11 August 2017,
volume 70 of Proceedings of Machine Learn-
ing Research, pages 3145–3153.
Karen Simonyan, Andrea Vedaldi, and Andrew
Zisserman. 2014. Deep inside convolutional
networks: Visualising image classification mod-
els and saliency maps. In 2nd International Con-
ference on Learning Representations, ICLR.
Mukund Sundararajan, Ankur Taly, and Qiqi
Yan. 2017. Axiomatic attribution for deep net-
works. In Proceedings of the 34th Interna-
tional Conference on Machine Learning, ICML,
volume 70 of Proceedings of Machine Learn-
ing Research, pages 3319–3328.
Marcos V. Treviso and Andr´e F. T. Martins. 2020.
The explanation game: Towards prediction
explainability through sparse communication.
the Third BlackboxNLP
In Proceedings of
Workshop on Analyzing and Interpreting Neu-
ral Networks for NLP, BlackboxNLP@EMNLP
2020, Online, November 2020, pages 107–118.
Ashish Vaswani, Noam Shazeer, Niki Parmar,
Jakob Uszkoreit, Llion Jones, Aidan N. Gomez,
Łukasz Kaiser, and Illia Polosukhin. 2017. Atten-
tion is all you need. In Advances in neural infor-
mation processing systems, pages 5998–6008.
Kayo Yin, Patrick Fernandes, Danish Pruthi,
Aditi Chaudhary, Andr´e F. T. Martins, and
Graham Neubig. 2021. Do context-aware trans-
lation models pay the right attention? In
Joint Conference of the 59th Annual Meet-
ing of
the Association for Computational
Linguistics and the 11th International Joint
Conference on Natural Language Processing
(ACL-IJCNLP). Virtual. https://doi.org
/10.18653/v1/2021.acl-long.65
Omar Zaidan and Jason Eisner. 2008. Modeling
annotators: A generative approach to learning
from annotator rationales. In Proceedings of
the 2008 Conference on Empirical Methods in
Natural Language Processing, pages 31–40.
https://doi.org/10.3115/1613715
.1613721
Omar Zaidan, Jason Eisner, and Christine Piatko.
2007. Using ‘‘annotator rationales’’ to im-
prove machine learning for text categorization.
In Human Language Technologies 2007: The
Conference of the North American Chapter
of the Association for Computational Linguis-
tics; Proceedings of
the Main Conference,
pages 260–267.
Ruiqi Zhong, Steven Shao,
and Kathleen
McKeown. 2019. Fine-grained sentiment anal-
ysis with faithful attention. arXiv preprint
arXiv:1908.06870.
373
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
t
l
a
c
_
a
_
0
0
4
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplementary Material
9 Explanation Types
We examine the following attribution methods:
LIME Locally Interpretable Model-agnostic
Explanations (Ribeiro et al., 2016), or LIME, are
explanations produced by a linear interpretable
model that is trained to approximate the original
black box model in the local neighborhood of
the input example. For a given example, several
samples are constructed by perturbing the input
string, and these samples are used to train the lin-
ear model. We draw twice as many samples as the
number of tokens in the example, and select the top
words that explain the predicted class. We set the
number of features for the linear classifier to be
2k, where k is the number of tokens to be selected.
Gradient-based Saliency Methods Several pa-
pers, both in NLP and computer vision, use
gradients of the log-likelihood of the predicted
label to understand the effect of infinitesimally
small perturbations in the input. While no pertur-
bation of an input string is infinitesimally small,
nonetheless, researchers have continued to use this
metric. It is most commonly used in two forms:
grad norm, i.e., the (cid:9)2 norm of the gradient w.r.t.
the token representation, and grad × input (also
called grad dot), i.e., the dot product of the gra-
dient w.r.t the token representation and the token
representation.
Integrated Gradients Gradients capture only
the effect of perturbations in an infinitesi-
mally small neighborhood, integrated gradients
(Sundararajan et al., 2017), instead compute and
integrate gradients along the line joining a starting
reference point and the given input example. For
each example, we integrate the gradients over 50
points on the line.
Layer Conductance Dhamdhere et al. (2019)
introduce and extend the notion of conductance
to compute neuron-level importance scores. We
apply layer conductance on the first encoder layer
of our teacher model and aggregate the scores to
define the attributions over the input tokens.
DeepLIFT DeepLIFT uses a reference for the
model input and target, and measures the con-
tribution of each input feature in the pair-wise
difference from this reference (Shrikumar et al.,
2017). It addresses the limitations of gradient-
based attribution methods, for regimes with zero
and discontinuous gradients. It backpropagates
the contributions of neurons using multipliers as
in partial derivatives. We use a reference input
(embeddings) of all zeros for our experiments.
Attention-based Explanations Attention mech-
anisms were originally introduced by Bahdanau
et al. (2015) to align source and target tokens
in neural machine translation. Because attention
mechanisms allocate weight among the encoded
tokens, these coefficients are sometimes thought
of intuitively as indicating which tokens the model
focuses on when making a prediction.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
t
l
a
c
_
a
_
0
0
4
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
374
Table 10: The Kendall rank correlation coefficient, τ , comparing rankings obtained through different
settings of our metric. We also compute correlations with the sufficiency and comprehensiveness metrics
from the ERASER benchmark (DeYoung et al., 2020). MTL and AR denote Multitask Learning and
Attention Regularization. Values can range from −1.0 (perfect disagreement) to
(perfect agreement).
Across different students and different learning strategies, the rankings obtained are highly correlated.
Value of k
LIME
Gradient Norm
Gradient × Input
Layer Conductance
Integrated Gradients
Attention
Attention Regularization
5%
93.0
92.8
92.5
93.6
94.1
94.7
10%
20%
40%
92.6
92.4
92.2
93.5
93.6
95.2
92.5
90.6
92.6
93.4
93.6
95.3
92.0
90.6
92.8
92.9
93.1
94.6
Multitask Learning
10%
20%
40%
92.6
93.1
92.7
92.9
93.3
94.4
92.5
92.9
92.5
92.5
93.1
94.7
91.8
93.0
91.3
92.3
92.1
94.9
5%
92.8
93.1
92.4
92.2
93.4
94.0
Table 11: Simulation accuracy of a BERT-base student model, examining the effect of k in selecting
top-k% explanatory tokens. Student model without explanations obtains a simulation accuracy of 92.6.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
6
5
2
0
0
6
9
7
1
/
/
t
l
a
c
_
a
_
0
0
4
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
375