Deciphering Undersegmented Ancient Scripts Using Phonetic Prior
Jiaming Luo
CSAIL, MIT
j luo@csail.mit.edu
Frederik Hartmann
University of Konstanz
frederik.hartmann
@uni-konstanz.de
Enrico Santus
Bayer
enrico.santus@bayer.com
Regina Barzilay
CSAIL, MIT
regina@csail.mit.edu
Yuan Cao
Google Brain
yuancao@google.com
Astratto
Most undeciphered lost languages exhibit two
characteristics that pose significant decipher-
ment challenges: (1) the scripts are not fully
segmented into words; (2) the closest known
language is not determined. We propose a
that handles both of
decipherment model
these challenges by building on rich linguis-
tic constraints reflecting consistent patterns in
historical sound change. We capture the natural
phonological geometry by learning character
embeddings based on the International Pho-
netic Alphabet (IPA). The resulting generative
framework jointly models word segmentation
and cognate alignment, informed by phono-
logical constraints. We evaluate the model on
both deciphered languages (Gothic, Ugaritic)
and an undeciphered one (Iberian). The ex-
periments show that incorporating phonetic
geometry leads to clear and consistent gains.
Additionally, we propose a measure for lan-
guage closeness which correctly identifies
related languages for Gothic and Ugaritic. For
Iberian, the method does not show strong evi-
dence supporting Basque as a related language,
concurring with the favored position by the
current scholarship.1
1
introduzione
All the known cases of lost language decipherment
have been accomplished by human experts,
oftentimes over decades of painstaking efforts.
At least a dozen languages are still undeciphered
today. For some of those languages, even the most
fundamental questions pertaining to their origins
1Code and data available at https://github.com
/j-luo93/DecipherUnsegmented/.
69
and connections to known languages are shrouded
in mystery, igniting fierce scientific debate among
humanities scholars. Can NLP methods be helpful
in bringing some clarity to these questions? Recente
work has already demonstrated that algorithms can
successfully decipher lost languages like Ugaritic
and Linear B (Luo et al., 2019), relying only on
non-parallel data in known languages—Hebrew
and Ancient Greek, rispettivamente. Tuttavia, these
methods are based on assumptions that are not
applicable to many undeciphered scripts.
The first assumption relates to the knowledge
of language family of the lost language. Questo
information enables us to identify the closest
living language, which anchors the decipherment
processi. Inoltre, the models assume significant
proximity between the two languages so that a
significant portion of their vocabulary is matched.
The second assumption presumes that word
boundaries are provided that uniquely define the
vocabulary of the lost language.
One of the famous counterexamples to both of
these assumptions is Iberian. The Iberian scripts
are undersegmented with inconsistent use of word
dividers. Allo stesso tempo, there is no definitive
consensus on its close known language—over
the years, Greek, Latin, and Basque were all
considered as possibilities.
in questo documento, we introduce a decipherment
approach that relaxes the above assumptions. IL
model is provided with undersegmented inscrip-
tions in the lost language and the vocabulary in a
known language. No assumptions are made about
the proximity between the lost and the known
languages and the goal is to match spans in the
lost texts with known tokens. As a byproduct
of this model, we propose a measure of language
closeness that drives the selection of the best target
language from the wealth of world languages.
Operazioni dell'Associazione per la Linguistica Computazionale, vol. 9, pag. 69–81, 2021. https://doi.org/10.1162/tacl a 00354
Redattore di azioni: Hinrich Sch¨utze. Lotto di invio: 7/2020; Lotto di revisione: 8/2020; Pubblicato 02/2021.
C(cid:2) 2021 Associazione per la Linguistica Computazionale. Distribuito sotto CC-BY 4.0 licenza.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Given the vast space of possible mappings
and the scarcity of guiding signal in the input
dati, decipherment algorithms are commonly
informed by linguistic constraints. These cons-
traints reflect consistent patterns in language
change and linguistic borrowings. Examples of
previously utilized constraints include skewness
of vocabulary mapping, and monotonicity of
character-level alignment within cognates. Noi
further expand the linguistic foundations of
decipherment models, and incorporate phonologi-
cal regularities of sound change into the matching
procedure. For instance, a velar consonant [k]
is unlikely to change into a labial [M]. Another
important constraint in this class pertains to sound
preservation,
the size of phonological
inventories is largely preserved during language
evolution.
Quello
È,
Our approach is designed to encapsulate these
constraints while addressing the segmentation
issue. We devise a generative framework that
jointly models word segmentation and cognate
alignment. To capture the natural phonological
geometry, we incorporate phonological features
into character representations using the Inter-
national Phonetic Alphabet (IPA). We introduce
a regularization term to explicitly discourage
the reduction of the phonological system and
employ an edit distance-based formulation to
model the monotonic alignment between cognates.
The model is trained in an end-to-end fashion to
optimize both the quality and the coverage of the
matched tokens in the lost texts.
The ultimate goal of this work is to evaluate the
model on an undeciphered language, specifically
Iberian. Given how little is known about
IL
lingua, it is impossible to directly assess pre-
diction accuracy. Therefore, we adopt two com-
plementary evaluation strategies to analyze model
performance. Primo, we apply the model to deci-
phered ancient languages, Ugaritic and Gothic,
which share some common challenges with
Iberian. Secondo, we consider evaluation scenarios
that capitalize on a few known facts about Iberian,
such as personal names, and report the model’s
accuracy against these ground truths.
The results demonstrate that our model can
robustly handle unsegmented or undersegmented
scripts. In the Iberian personal name experiment,
our model achieves a top 10 accuracy score
Di 75.0%. Across all the evaluation scenarios,
incorporating phonological geometry leads to
70
clear and consistent gains. For instance, the model
informed by IPA obtains 12.8% increase in
Gothic-Old Norse experiments. We also demon-
strate that the proposed unsupervised measure of
language closeness is consistent with historical
linguistics findings on known languages.
2 Related Work
Non-parallel Machine Translation At a high
level, our work falls into research on non-parallel
machine translation. One of the important recent
advancements in that area is the ability to induce
accurate crosslingual lexical representations with-
out access to parallel data (Lample et al., 2018B,UN;
Conneau and Lample, 2019). This is achieved by
aligning embedding spaces constructed from large
amounts of monolingual data. The size of data for
both languages is key: High-quality monolingual
embeddings are required for successful matching.
This assumption, Tuttavia, does not hold for
ancient languages, where we can typically access
a few thousands of words at most.
Decoding Cipher Texts Man-made ciphers
have been the focal point for most of the early work
on decipherment. They usually use EM algo-
rithms, which are tailored towards these specific
types of ciphers, most prominently substitution
ciphers (Knight and Yamada, 1999; Knight et al.,
2006). Later work by Nuhn et al. (2013), Hauer
et al. (2014), and Kambhatla et al. (2018) addresses
the problem using a heuristic search procedure,
guided by a pretrained language model. To the
best of our knowledge, these methods developed
for tackling man-made ciphers have so far not
been successfully applied to archaeological data.
One contributing factor could be the inherent
complexity in the evolution of natural languages.
Deciphering Ancient Scripts Our research is
most closely aligned with computational decipher-
ment of ancient scripts. Prior work has already
featured several successful instances of ancient
language decipherment previously done by human
experts (Snyder et al., 2010; Berg-Kirkpatrick
and Klein, 2013; Luo et al., 2019). Our work
incorporates many linguistic insights about the
structure of valid alignments introduced in prior
lavoro, such as monotonicity. We further expand the
linguistic foundation by incorporating phonetic
regularities that have been beneficial in early,
pre-neural decipherment work (Knight et al.,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2006). Tuttavia, our model is designed to handle
challenging cases not addressed by prior work,
where segmentation of the ancient scripts is
unknown. Inoltre, we are interested in dead
languages without a known relative and introduce
an unsupervised measure of language closeness
that enables us to select an informative known
language for decipherment.
3 Model
We design a model for the automatic extraction
of cognates2 directly from unsegmented or under-
segmented texts (detailed setting in Section 3.1).
In order to properly handle the uncertainties
caused by the issue of segmentation, we devise a
generative framework that composes the lost texts
using smaller units—from characters to tokens,
and from tokens to inscriptions. The model is
trained in an end-to-end fashion to optimize both
the quality and the coverage of the matched tokens.
To help the model navigate the complex
search space, we consider the following linguistic
properties of sound change, including phonology
and phonetics in our model design:
• Plausibility of
sound change: Similar
sounds rarely change into drastically different
sounds. This pattern is captured by the
natural phonological geometry in human
speech sounds and we incorporate relevant
phonological features into the representation
of characters.
• Preservation of
sounds: The size of
phonological inventories tends to be largely
preserved over time. This implies that total
disappearance of any sound is uncommon. In
light of this, we use a regularization term to
discourage any sound loss in the phonological
system of the lost language.
• Monotonicity of alignment: The alignment
between any matched pair is predominantly
monotonic, which means that character-level
alignments do not cross each other. Questo
property inspires our edit distance-based
formulation at the token level.
2Throughout this paper, the term cognate is liberally used
to also include loanwords, as the sound correspondences in
cognates and loanwords are both regular, although usually
different.
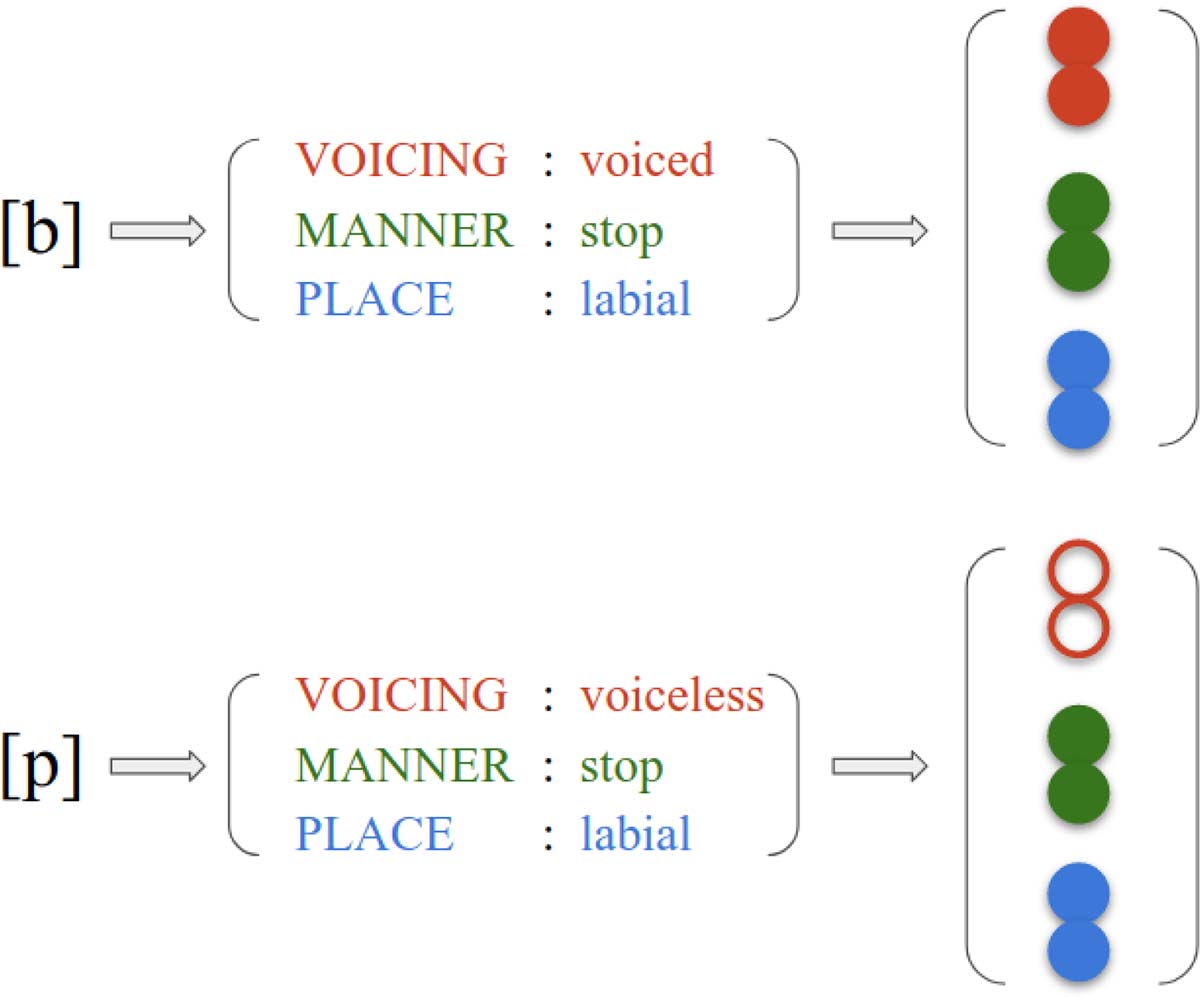
To reason about phonetic proximity, we need
to find character representation that explicitly
reflects its phonetic properties. One such repre-
sentation is provided by the IPA, where each
character is represented by a vector of pho-
nological features. As an example, consider IPA
representation for two phonetically close charac-
ters [B] E [P] (See Figure 3), which share
two identical coordinates. To further refine this
representation, the model learns to embed these
features into a new space, optimized for the
decipherment task.
3.1 Problem Setting
are given a
list of unsegmented or
Noi
undersegmented inscriptions X = {X} in the lost
lingua, and a vocabulary, questo è, a list of tokens
Y = {sì} in the known language. For each lost text
X, the goal is to identify a list of non-overlapping
spans {X} that correspond to cognates in Y. Noi
refer to these spans as matched spans and any
remaining character as unmatched spans.
We denote the character sets of the lost and the
known languages by C L = {cL} and C K = {cK},
rispettivamente. To exploit the phonetic prior, IPA
transcriptions are used for C K, while ortho-
graphic characters are used for C L. For this paper,
we only consider alphabetical scripts for the lost
language.3
3.2 Generative Framework
We design the following generative framework
to handle the issue of segmentation. It jointly
models segmentation and cognate alignment,
which requires different treatments for matched
spans and unmatched spans. An overview of the
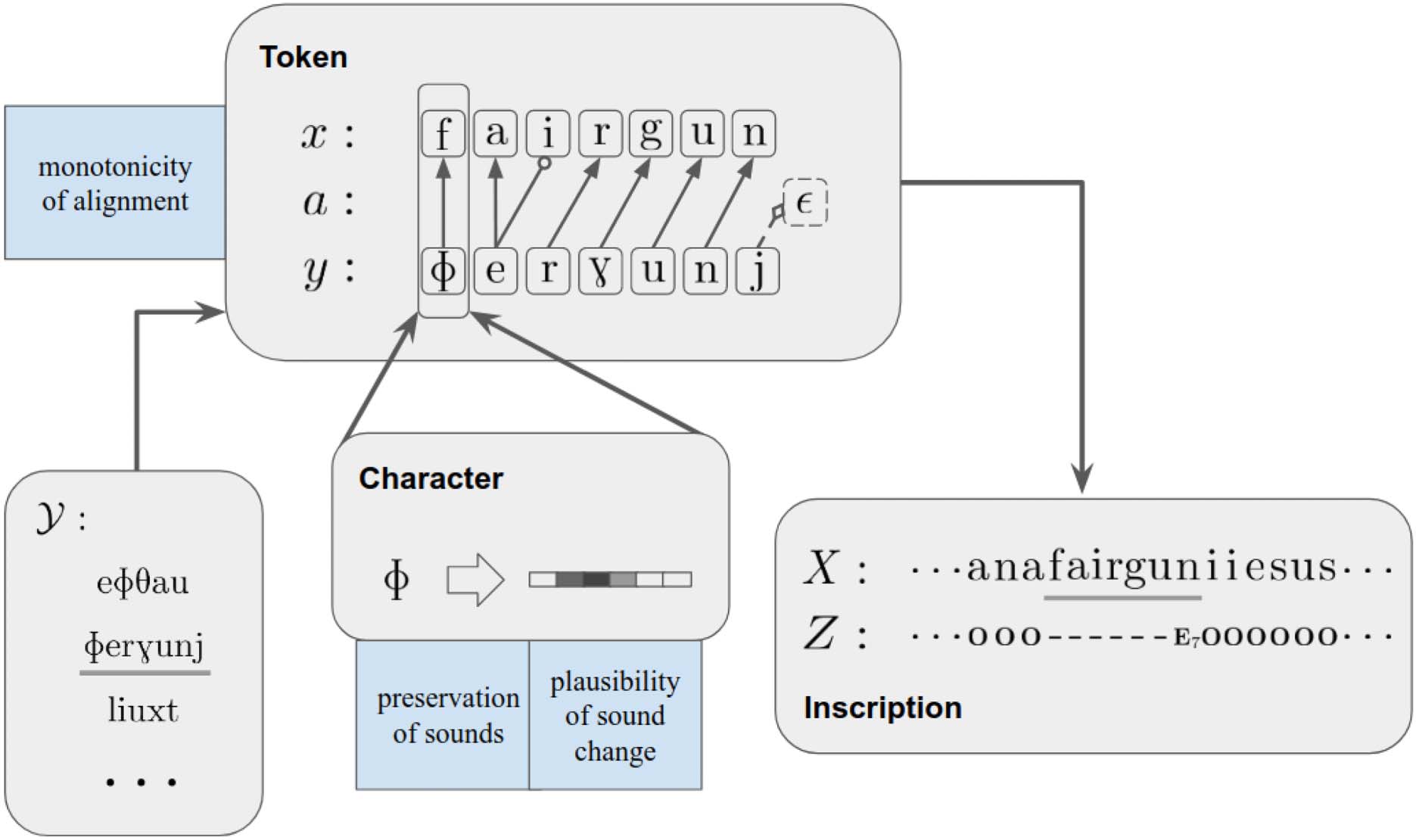
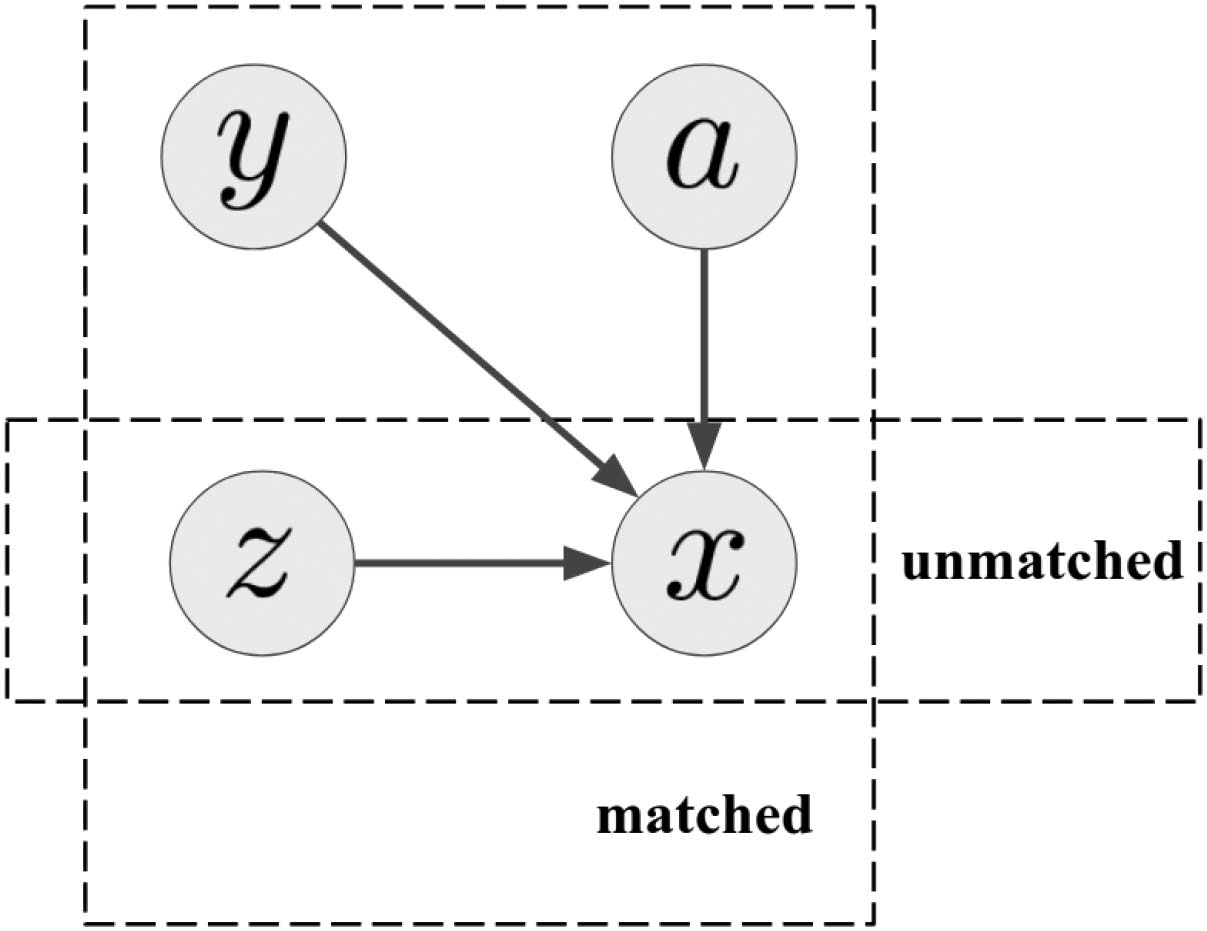
framework is provided in Figure 1 and a graphical
model representation in Figure 2.
For matched spans, we introduce two latent
variables: y representing the corresponding
cognate in the known language and a indicating
the character alignment between x and y (Vedere
the Token box in Figure 1). More concretely,
a = {aτ } is a sequence of indices, with aτ
representing the aligned position for yτ in x. IL
lost token is generated by applying a character-
level mapping to y according to the alignment
3Given that the known side uses IPA, an alphabetical
system, having an alphabetical system on the lost side makes
it much easier to enforce the linguistic constraints in this
paper. For other types of scripts, it requires more thorough
investigation, which is beyond the scope of this work.
71
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 1: An overview of our framework, which generates the lost texts from smaller units—from
characters to tokens and from tokens to inscriptions. Character mappings are first performed on the
phonetic alphabet of the known language. Based on these mappings, a token y in the known vocabulary
Y is converted into a token x in the lost language according to the latent alignment variable a. Lastly,
all generated tokens, together with characters in unmatched spans, are concatenated to form a lost
inscription. Blue boxes display the corresponding linguistic properties associated with each level of
modeling.
provided by a. For unmatched spans, we assume
each character is generated in an independent
and identically distributed fashion under a uniform
distribution p0 = 1
|C L| .
Whether a span is matched or not is indicated by
another latent variable z, and the corresponding
span is denoted by xz. More specifically, each
character in an unmatched span is tagged by
z = O, whereas the entirety of a matched span of
length l is marked by z = El at the end of the span
(see the Inscription box in Figure 1). All spans are
then concatenated to form the inscription, con un
corresponding (sparse) tag sequence Z = {z}.
Under this framework, we arrive at the follow-
ing derivation for the marginal distribution for
each lost inscription X:
(cid:2)
(cid:5)(cid:3) (cid:4)
(cid:5)(cid:3) (cid:4)
(cid:3) (cid:4)
(cid:5)
Pr(X) =
Pr(z)
p0
Z
z∈Z
z∈Z
z=O
z∈Z
z(cid:4)=O
72
Pr(xz|z)
,
(1)
Figura 2: A graphical model representation for
our framework to generate a span x. Charac-
ters in unmatched spans are generated in an
independent and identically distributed fashion
whereas matched spans are additionally condi-
tioned on two latent variables: y representing a
known cognate and a the character-level align-
ment between x and y.
where Pr(xz|z (cid:4)= O) is further broken down into
individual character mappings:
Pr(xz|z (cid:4)= O) =
∝
≈
=
(cid:2)
(cid:2)
y∈Y
(cid:2)
a∈A
(cid:2)
Pr(sì)Pr(UN) · Pr(xz|sì, z, UN)
Pr(xz|sì, z, UN)
a∈A
y∈Y
(cid:2)
max
UN
max
UN
y∈Y
(cid:2)
y∈Y
Pr(xz|sì, z, UN)
(cid:4)
Pr(xaτ
τ
|yτ ),
(2)
Note that we assume a uniform prior for both y
and a, and use the maximum to approximate the
sum of Pr(xz|sì, z, UN) over the latent variable a. UN
is the set of valid alignment values to be detailed
in § 3.2.2.
3.2.1 Phonetics-aware Parameterization
The character mapping distributions are specified
come segue:
|yτ = cK
Prθ(xaτ = cL
io )
j
j ) · EK(cK
EL(cL
io )
(cid:6)
∝exp
T
(cid:7)
,
(3)
where T is a temperature hyperparameter, EL(·)
and EK(·) are the embedding functions for the lost
characters and the known characters, rispettivamente,
and θ is the collection of all trainable parameters
(cioè., the embeddings).
In order to capture the similarity within cer-
tain sound classes, we use IPA embeddings to
represent each IPA character in the known lan-
guage. More specifically, each IPA character is re-
presented by a vector of phonological features.
The model learns to embed these features into a
new space and the full IPA embedding for cK
is composed by concatenating all of its rele-
vant feature embeddings. For the example in
Figura 3, the phone [B] can be represented as
the concatenation of the voiced embedding, IL
stop embedding, and the labial embedding.
This compositional structure encodes the na-
tural geometry existent in sound classes (Stevens,
2000) and biases the model towards utilizing such
a structure. By design, the representations for [B]
E [P] are close as they share the same values
for two out of three feature groups. This structural
bias is crucial for realistic character mappings.
For
character cL
the lost
lingua, we represent each
j as a weighted sum of IPA embeddings
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 3: An illustration of IPA embeddings.
Each phone is first represented by a vector of
phonological features. The model first embeds
each feature and then IPA embedding is ob-
tained by concatenating all its relevant feature
embeddings. For instance, the phone [B] can be
represented as the concatenation of the voiced,
stop, and the labial embeddings.
on the known side. Specifically,
EL(cL
j ) =
(cid:2)
io
wi,j · EK(cK
io ),
(4)
Dove {wi,j} are learnable parameters.
3.2.2 Monotonic Alignment and Edit Distance
Individual characters in the known token y are
token x according to the
mapped to a lost
alignment variable a. The monotonic nature of
character alignment between cognate pairings
motivates our design of an edit distance-based
formulation to capture the dominant mechanisms
involved in cognate pairings:
substitutions,
deletions, and insertions (Campbell, 2013). In
addition to aτ taking the value of an integer
signifying the substituted position, aτ can be
(cid:3), which indicates that yτ is deleted. To model
insertions, aτ = (aτ,1, aτ,2) can be two4 adjacent
indices in x.
This formulation inherently defines a set A of
valid values for the alignment. Firstly, they are
monotonically increasing with respect to τ , con
the exception of (cid:3). Secondly, they cover every
index of x, which means every character in x is
accounted for by some character in y. The Token
box in Figure 1 showcases such an example with
4Insertions of even longer character sequences are rare.
73
all three types of edit operations. More concretely,
we have the following alignment model:
Pr(xaτ
|yτ ) =
⎧
⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎩
|yτ )
ccPrθ(xaτ
Prθ((cid:3)|yτ )
Prθ(xaτ,1
·αPrθ(xaτ,2
|yτ )
(substitution)
(deletion)
|yτ )
(insertion)
where α ∈ [0, 1] is a hyperparameter to control
the use of insertions.
3.3 Objective
Given the generative framework, our training
objective is designed to optimize the quality of the
extracted cognates, while matching a reasonable
proportion of the text.
Quality We aim to optimize the quality of
matched spans under the posterior distribution
Pr(Z|X), measured by a
scoring function
Φ(X, Z). Φ(X, Z) is computed by aggregating
the likelihoods of these matched spans normalized
by length. The objective is defined as follows:
Q(X) = EZ∼Pr(Z|X)Φ(X, Z),
(cid:2)
Φ(X, Z) =
φ(xz, z),
z∈Z
z(cid:4)=O
φ(xz, z) = Pr(xz|z)
1
|xz | .
(5)
(6)
(7)
This term encourages the model to explicitly focus
on improving the probability of generating the
matched spans.
Regularity and Coverage The regularity of
sound change, as stated by the Neogrammarian
hypothesis (Campbell, 2013), implies that we need
to find a reasonable number of matched spans. A
achieve this goal, we incur a penalty if the expected
coverage ratio of the matched characters under the
posterior distribution falls below a given threshold
rcov:
(cid:13)
(cid:12)
cov(X)
(cid:14)
X∈X
rcov −
Ωcov(X ) = max
|X |
cov(X) = EZ∼Pr(Z|X)Ψ(X, Z),
(cid:2)
(cid:2)
Ψ(X, Z) =
ψ(xz, z) =
|xz|.
, 0.0
(8)
(9)
z∈Z
z(cid:4)=O
z∈Z
z(cid:4)=O
Note that the ratio is computed on the entire
corpus X instead of individual texts X because
the coverage ratio can vary greatly for different
74
individual texts. The hyperparameter rcov controls
the expected overlap between two languages,
which enables us to apply the method even
when languages share some loanwords but are
not closely related.
Preservation of Sounds The size of phono-
logical inventories tends to be largely preserved
over time. This implies that total disappearance
of any sound is uncommon. To reflect this ten-
dency, we introduce an additional regularization
term to discourage any sound loss. The intuition
is to encourage any lost character to be mapped
to exactly one5 known IPA symbol. Formalmente, we
have the following term
(cid:2)
(cid:15) (cid:2)
(cid:16)
Pr(cL|cK) − 1.0
2.
Ωloss(C L, C K) =
cL
cK
Final Objective Putting the terms together, we
have the following final objective:
S(X ; C L, C K) =
(cid:13)
Q(X) + λcovΩcov(X )
X∈X
+λlossΩloss(C L, C K),
(10)
where λcov and λloss are both hyperparameters.
3.4 Training
Training with the final objective involves either
finding the best latent variable, as in Equation (2),
or computing the expectation under a distribution
that involves one latent variable, as in Equation (5)
and Equation (8). In entrambi i casi, we resort to dy-
namic programming to facilitate efficient compu-
tation and end-to-end training. We refer interested
readers to Appendix A.1 for more detailed
derivations. We illustrate one training step in
Algorithm 1.
4 Experimental Setup
Our ultimate goal is to evaluate the decipherment
capacity for unsegmented lost languages, without
information about a known counterpart. Iberian
fits both of these criteria. Tuttavia, our ability
to evaluate decipherment of Iberian is limited
because a full ground truth is not known. There-
fore, we supplement our evaluation on Iberian with
more complete evaluation on lost languages with
known translation, such as Gothic and Ugaritic.
5We experimented with looser constraints (per esempio., with at
least instead of exactly one correspondence), but obtained
worse results.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Algorithm 1: One training step for our decipherment model
Input: One batch of lost inscriptions ˜X , entire known vocabulary Y = {sì}
Parameters: Feature embeddings θ
io ) ← ComputeCharDistr(θ)
1: Pr(cL
j
|cK
2: Pr(X|sì) ← EditDistDP
X, sì, Pr(cL
io )
(cid:15)
j
3: S( ˜X ; C L, C K) ← WordBoundaryDP
Pr(X|sì)
4: θ ← SGD(S)
|cK
(cid:15)
(cid:16)
(cid:16)
(cid:9) Compute character mapping distributions (Sezione 3.2.1)
(cid:9) Compute token alignment probability (Sezione 3.2.2)
(cid:9) Compute final objective (Sezione 3.3)
(cid:9) Backprop and update parameters
Language
Family
Gothic
Ugaritic
Iberian
Germanic
Semitic
unclassified
Fonte
Wulfila†
Snyder et al. (2010)
Hesperia‡
#Tokens Segmentation Situation Century
40,518
7,353††
3,466‡‡
unsegmented
segmented
undersegmented
3–10 AD
14–12 BC
6–1 BC
† http://www.wulfila.be/gothic/download/.
†† http://hesperia.ucm.es/. Iberian language is semi-syllabic, but this database has already
transliterated the inscriptions into Latin scripts.
‡ This dataset directly provides the Ugaritic vocabulary, cioè., each word occurs exactly once.
‡‡ Since the texts are undersegmented and we do not know the ground truth segmentations, Questo
represents the number of unsegmented chunks, each of which might contain multiple tokens.
Tavolo 1: Basic information about the lost languages.
4.1 Languages
We focus our description on the Gothic and
Iberian corpora that we compiled for this paper.
Ugaritic data was reused from the prior work
on decipherment (Snyder et al., 2010). Tavolo 1
provides statistics about
these languages. A
evaluate the validity for our proposed language
proximity measure, we additionally include six
known languages: Spanish (Romance), Arabic
(Semitic), Hungarian (Uralic), Turkish (Turkic),
classical Latin (Latino-Faliscan), and Basque
(isolate).
Gothic Several
features of Gothic make it
an ideal candidate for studying decipherment
models. Because Gothic is fully deciphered,
we can compare our predictions against ground
truth. Like Iberian, Gothic is unsegmented. Its
alphabet was adapted from a diverse set of
languages: Greek, Latin, and Runic, but some
characters are of unknown origin. The latter were
in the center of decipherment efforts on Gothic
(Zacher, 1855; Wagner, 2006). Another appealing
feature of Gothic is its relatedness to several
known Germanic languages that exhibit various
degree of proximity to Gothic. The closest is
its reconstructed ancestor Proto-Germanic, con
Old Norse and Old English being more distantly
related to Gothic. This variation in linguistic
proximity enables us to study the robustness of
decipherment methods to the historical change in
the source and the target.
Iberian Iberian serves as a real test scenario
for automatic methods—it is still undeciphered,
withstanding multiple attempts over at
least
two centuries. Iberian scripts present two issues
facing many undeciphered languages
today:
undersegmentation and lack of a well-researched
relative. Many theories of origin have been
proposed in the past, most notably linking Iberian
to Basque, another non-Indo-European language
on the Iberian peninsula. Tuttavia, due to a lack
of conclusive evidence, the current scholarship
favors the position that Iberian is not genetically
related to any living language. Our knowledge of
Iberian owes much to the phonological system
proposed by Manuel G´omez Moreno in the mid
20th century, based on fragmentary evidences
such as bilingual coin legends (Sinner and Velaza,
2019). Another area with a broad consensus relates
to Iberian personal names, thanks to a key Latin
epigraph, Ascoli Bronze, which recorded the grant
of Roman citizenship to Iberian soldiers who had
fought for Rome (Mart´ı et al., 2017). We use these
personal names recorded in Latin as the known
vocabulary.
75
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
WR†
Proto-Germanic (PG)
Old Norse (ON)
Old English (OE)
Known language
0.213 / 0.397 / 0.597
0.312 / 0.478 / 0.610
0.391 / 0.508 / 0.643
0.435 / 0.544 / 0.682
0.046 / 0.204 / 0.497
0.128 / 0.328 / 0.474
0.169 / 0.404 / 0.495
0.250 / 0.447 / 0.533
avg††
0.360 / 0.450 / 0.652
0.398 / 0.513 / 0.637
0.438 / 0.549 / 0.662
0.482 / 0.574 / 0.693
0.338 / 0.482 / 0.633
0.148 / 0.346 / 0.500
0.419 / 0.522 / 0.661
0%
0.820 / 0.749 / 0.863
25% 0.752 / 0.734 / 0.826
50% 0.752 / 0.736 / 0.848
75% 0.761 / 0.732 / 0.866
avg‡
0.771 / 0.737 / 0.851
† Short for whitespace ratio.
‡ Averaged over all whitespace ratio values.
†† Averaged over all known languages.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Tavolo 2: Main results on Gothic in a variety of settings using A@10 scores. All scores are reported in the
format of triplets, corresponding to base / partial / full models. Generalmente, more phonological
knowledge about the lost language, more segmentations improve the model performance. The choice of
the known language also plays a significant role as Proto-Germanic has a noticeably higher score than
the other two choices.
4.2 Evaluation
Stemming and Segmentation Our matching
process operates at the stem level for the known
lingua, instead of full words. Stems are more
consistently preserved during language change or
linguistic borrowings. While we always assume
that gold stems are provided for the known
lingua, we estimate them for the lost language.
The original Gothic texts are only segmented
into sentences. To study the effect of having
varying degrees of prior knowledge about the
word segmentations, we create separate datasets
by randomly inserting ground truth segmentations
(cioè., whitespaces) with a preset probability to
simulate undersegmentation scenarios.
Model Variants
In multiple decipherment
scenarios, partial
information about phonetic
assignments is available. This is the case with
both Iberian and Gothic. Therefore, we evaluate
performance of our model with respect to available
phonological knowledge for the lost language.
The base model assumes no knowledge while
the full model has full knowledge of the
phonological system and therefore the character
mappings. For
experiment, we
the Gothic
additionally experiment with a partial model
that assumes that we know the phonetic values
for the characters k, l, M, N, P, S, and t. IL
sound values of these characters can be used as
prior knowledge as they closely resemble their
original counterparts in Latin or Greek alphabets.
These known mappings are incorporated through
an additional term which encourages the model to
match its predicted distributions with the ground
truths.
In scenarios with full segmentations where it is
possible to compare with previous work, we report
the results for the Bayesian model proposed by
Snyder et al. (2010) and NeuroCipher by Luo
et al. (2019).
Metric We evaluate the model performance
using top K accuracy (A@K) scores. The pre-
diction (cioè., the stem-span pair) is considered
correct if and only if the stem is correct and the the
span is the prefix of the ground truth. For instance,
the ground truth for the Gothic word garda has the
stem gard spanning the first four letters, matching
the Old Norse stem garð. We only consider the
prediction as correct if it correctly matches garð
and the predicted span starts with the first letter.
5 Results
Decipherment of Undersegmentated Texts
Our main results on Gothic in Table 2 demon-
strate that our model can effectively extract
cognates in a variety of settings. Averaged over
all choices of whitespace ratios and known
languages (bottom right), our base/partial/
full models achieve A@10 scores of 0.419/
0.522/0.661, rispettivamente. Not surprisingly, access
to additional knowledge either about phonological
mappings and/or segmentation lead to improved
performance. See Table 5 for an example of model
predictions.
76
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
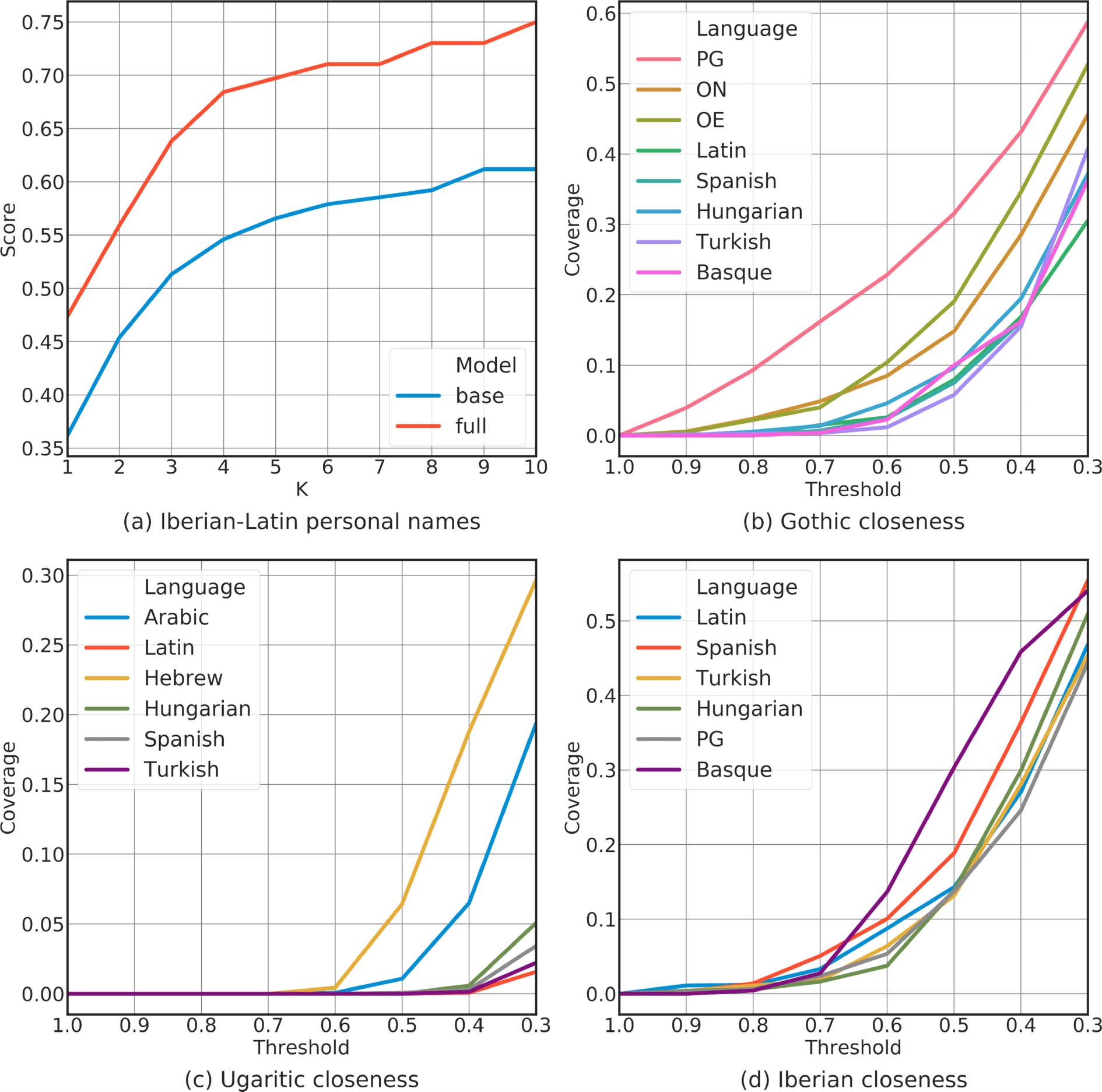
Figura 4: (UN) A@K scores on Iberian using personal name recorded in Latin; (B), (C), E (D): Closeness
plots for Gothic, Ugaritic and Iberian, rispettivamente.
The choice of the known language also plays
a significant role. On the closest language pair
Gothic-PG, A@10 reaches 75% even without
assuming any phonological knowledge about the
lost language. As expected, language proximity
directly impacts the complexity of the decipher-
ment tasks which in turn translates into lower
model performance on Old English and Old Norse.
These results reaffirm that choosing a close known
language is vital for decipherment.
IL
results on Iberian shows
that our
model performs well on a real undeciphered
language with undersegmented texts. As shown in
Figure 4a, base model reaches 60% in P@10
while full model reaches 75%. Note that Iberian
is non-Indo-European with no genetic relationship
with Latin, but our model can still discover regular
correspondences for this particular set of personal
names.
Ablation Study To investigate the contribution
of phonetic and phonological knowledge, we
conduct an ablation study using Gothic/Old Norse
(Tavolo 4). The IPA embeddings consistently
improve all the model variants. As expected, IL
gains are most noticeable (+12.8%) for the hardest
matching scenario where no prior information is
available (base model). As expected, Ωloss is vital
77
Lost
Known
Ugaritic†
Hebrew
Gothic
ON
PG
OE
–
–
0.604
0.659
0.778
Bayesian
NeuroCipher
base
–
0.753 0.543 0.313
0.865 0.558 0.472
† A@1 is reported for Ugaritic to make direct
comparison with previous work. A@10 is still
used for Gothic experiments.
Tavolo 3: Results for comparing base model with
previous work. Bayesian and NeuroCipher
are the models proposed by Snyder et al. (2010)
and Luo et al. (2019), rispettivamente. Ugaritic results
for previous work are taken from their papers.
For NeuroCipher, we run the authors’ public
implementation to obtain the results for Gothic.
IPA
Ωloss
base
partial
full
+
−
+
+
+
−
0.435
0.307
0.000
0.544
0.490
0.493
0.682
0.599
0.695
Tavolo 4: Ablation study on the pair Gothic-ON.
Both IPA embeddings and the regularization on
sound loss are beneficial, especially when we do
not assume much phonological knowledge about
the lost language.
Inscription
ammuhsaminhaidau
ammuhsaminhaidau
ammuhsaminhaidau
ammuhsaminhaidau
Matched stem
xaið
xaið
raið
braið
Tavolo 5: One example of top 3 model predictions
for base on Gothic-PG in WR 0% setting.
Spans are highlighted in the inscriptions. IL
first row presents the ground truth and the others
are the model predictions. Green color is used
for correct predictions and red for incorrect
ones.
for base but unnecessary for full which has
readily available character mapping.
Comparison with Previous Work To compare
with the state-of-the-art decipherment models
(Snyder et al., 2010; Luo et al., 2019), we
consider the version of our model that operates
con 100% whitespace ratio for the lost language.
Tavolo 3 demonstrates that our model consistently
78
outperforms the baselines for both Ugaritic and
Gothic. For instance, it reaches over 11% gain
for Hebrew/Ugaritic pair and over 15% for
Gotchic/Old English.
Identifying Close Known Languages Next we
evaluate model’s ability to identify a close known
language to anchor the decipherment process.
We expect that for a closer language pair, IL
predictions of the model will be more confident
while matching more characters. We illustrate this
idea with a plot that charts character coverage
(cioè., what percentage of the lost texts are matched
regardless of its correctness) as a function of
prediction confidence value (cioè., probability of
generating this span normalized by its length).
As Figure 4b and Figure 4c illustrate, the model
accurately predicts the closest languages for both
Ugaritic and Gothic. Inoltre, languages within
the same family as the lost language stand out
from the rest.
The picture is quite different for Iberian (Vedere
Figure 4d). No language seems to have a pro-
nounced advantage over others. This seems to
accord with the current scholarly understanding
that Iberian is a language isolate, with no estab-
lished kinship with others. Basque somewhat
stands out from the rest, which might be attributed
to its similar phonological system with Iberian
(Sinner and Velaza, 2019) and very limited
vocabulary overlap (numeral names)
(Aznar,
2005) which doesn’t carry over to the lexical
system.6
6 Conclusions
We propose a decipherment model
to extract
cognates from undersegmented texts, without
assuming proximity between lost and known lan-
guages. Linguistics properties are incorporated
into the model design, such as phonetic plausibil-
ity of sound change and preservation of sounds.
Our results on Gothic, Ugaritic, and Iberian
shows that our model can effectively handle
undersegmented texts even when source and
target languages are not related. Additionally, we
introduce a method for identifying close languages
that correctly finds related languages for Gothic
and Ugaritic. For Iberian, the method does not
show strong evidence supporting Basque as a
6For true isolates, whether the predicted segmentations
are reliable despite the lack of cognates is beyond our current
scope of investigation.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
related language, concurring with the favored
position by current scholarship.
Potential applications of our method are not
limited to decipherment. The phonetic values of
lost characters can be inferred by mapping them
to the known cognates. These values can serve as
the starting point for lost sound reconstruction
and more investigation is needed to establish
the effectiveness of
their efficacy. Inoltre,
incorporating phonological feature embeddings
provides a path for future improvement for cog-
nate detection in computational historical
lin-
guistics (Rama and List, 2019). Currently our
method operates on a pair of languages. A
simultaneously process multiple languages as it
is common in the cognate detection task, more
work is needed to modify our current model and
its inference procedure.
Ringraziamenti
We sincerely thank Noem´ı Moncunill Mart´ı for
her invaluable guidance on Iberian onomastics,
and Eduardo Ordu˜n Aznar for his tremendous
help on the Hesperia database and the Vasco-
Iberian theories. Special thanks also go to Ignacio
Fuentes and Carme Huertas for the insightful
discussions. This research is based upon work
supported in part by the Office of the Director
of National
Intelligenza
Intelligenza (ODNI),
Advanced Research Projects Activity (IARPA),
via contract # FA8650-17-C-9116. The views
and conclusions contained herein are those of
the authors and should not be interpreted as
necessarily representing the official policies,
either expressed or implied, of ODNI, IARPA,
or the U.S. Government. The U.S. Government
is authorized to reproduce and distribute reprints
for governmental purposes notwithstanding any
copyright annotation therein.
Riferimenti
Eduardo Ordu˜na Aznar. 2005. Sobre algunos
ib´ericos.
numerales
textos
posibles
Palaeohispanica, 5:491–506.
en
Taylor Berg-Kirkpatrick and Dan Klein. 2013.
Decipherment with a million random restarts.
IL 2013 Conference on
Negli Atti di
in Natural Language
Empirical Methods
in lavorazione, pages 874–878. Associazione per
Linguistica computazionale.
79
toolkit.
Negli Atti di
2006. NLTK: IL
natural
Steven Bird.
IL
lingua
COLING/ACL 2006 Interactive Presentation
Sessions, pages 69–72. Association for Compu-
linguistica nazionale. DOI: https://doi
.org/10.3115/1225403.1225421
Lyle Campbell. 2013. Historical Linguistics.
Edinburgh University Press.
Christos Christodouloupoulos and Mark Steedman.
2015. A massively parallel corpus: The bible in
100 languages. Language Resources and Eval-
uazione, 49(2):375–395. DOI: https://doi
.org/10.1007/s10579-014-9287-y,
PMID: 26321896, PMCID: PMC4551210
Alexis Conneau and Guillaume Lample. 2019.
Cross-lingual language model pretraining. In
Advances in Neural Information Processing
Sistemi, pages 7059–7069.
Bradley Hauer, Ryan Hayward, and Grzegorz
Kondrak. 2014. Solving substitution ciphers
with combined language models. In Procedi-
ings of COLING 2014, the 25th International
Conference on Computational Linguistics:
Documenti tecnici, pages 2314–2325, Dublin,
Ireland. Dublin City University and Association
for Computational Linguistics.
Nishant Kambhatla, Anahita Mansouri Bigvand,
and Anoop Sarkar. 2018. Decipherment of
substitution ciphers with neural
lingua
models. Negli Atti del 2018 Confe-
rence on Empirical Methods in Natural Lan-
guage Processing, pages 869–874, Brussels,
Belgium. Association for Computational Lin-
https://doi.org/10
guistics. DOI:
.18653/v1/D18-1102
Kevin Knight, Anish Nair, Nishit Rathod, E
Kenji Yamada. 2006. Unsupervised analysis
for decipherment problems. Negli Atti
of the COLING/ACL 2006 Main Conference
Poster Sessions, pages 499–506, Sydney,
Australia. Association
for Computational
Linguistica. DOI: https://doi.org/10
.3115/1273073.1273138
Kevin Knight and Kenji Yamada. 1999. UN
deciphering
approach
computational
unknown scripts. Unsupervised Learning in
Elaborazione del linguaggio naturale.
A
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Guillaume Lample, Alexis Conneau, Ludovic
Denoyer, and Marc’Aurelio Ranzato. 2018UN.
Unsupervised machine
using
monolingual corpora only.
translation
Guillaume Lample, Alexis Conneau, Marc’Aurelio
Ranzato, Ludovic Denoyer, and Herv´e J´egou.
2018B. Word translation without parallel data.
In International Conference on Learning
Representations.
Jiaming Luo, Yuan Cao, and Regina Barzilay.
2019. Neural decipherment via minimum-
In
flow: From ugaritic to linear b.
cost
Proceedings of the 57th Annual Meeting of
the Association for Computational Linguistics,
pages 3146–3155, Florence, Italy. Association
for Computational Linguistics.
Noem´ı Moncunill Mart´ı and others. 2017.
Indigenous naming practices in the western
Mediterranean: The case of Iberian. Studia
Antiqua et Archaeologica, 23(1):7–20.
David R. Mortensen, Siddharth Dalmia, E
Patrick Littell. 2018. Epitran: Precision G2P
for many languages. Negli Atti di
IL
Eleventh International Conference on Lan-
guage Resources and Evaluation (LREC 2018),
Paris, France. European Language Resources
Association (ELRA).
Malte Nuhn, Julian Schamper, and Hermann
Ney. 2013. Beam search for solving substi-
tution ciphers. Negli Atti di
the 51st
Annual Meeting of the Association for Compu-
linguistica nazionale (Volume 1: Documenti lunghi),
pages 1568–1576, Sofia, Bulgaria. Association
for Computational Linguistics.
Taraka Rama and Johann-Mattis List. 2019.
fast cognate
An automated framework for
detection and bayesian phylogenetic inference
in computational historical
In
Proceedings of the 57th Annual Meeting of
the Association for Computational Linguistics,
pages 6225–6235, Florence,
Italy. Associ-
ation for Computational Linguistics. DOI:
https://doi.org/10.18653/v1/P19
-1627
linguistics.
Jes´us Rodr´ıguez Ramos. 2014. Nuevo ´ındice
cr´ıtico de formantes de compuestos de tipo
onom´astico ´ıberos. Arqueoweb: Revista sobre
Arqueolog´ıa en Internet, 15(1):7–158.
Donald A. Ringe. 2017. From Proto-Indo-
European to Proto-Germanic. Oxford.
Alejandro Garcia Sinner and Javier Velaza. 2019.
Palaeohispanic Languages and Epigraphies.
Oxford University Press.
Benjamin Snyder, Regina Barzilay, and Kevin
Knight. 2010. A statistical model for lost
language decipherment. Negli Atti del
48esima Assemblea Annuale dell'Associazione per
Linguistica computazionale, pages 1048–1057,
Uppsala, Sweden. Associazione per il calcolo-
linguistica nazionale. DOI: https://doi.org
/10.1093/oso/9780198792581.001.0001
Kenneth N. Stevens. 2000. Acoustic phonetics,
volume 30. CON Premere.
Larry Trask. 2008. Etymological Dictionary of
Basque. http://www.bulgari-istoria
-2010.com/Rechnici/baski-rechnik
.pdf.
Norbert Wagner. 2006. Zu got. hv, q und ai, au.
Historische Sprachforschung/Historical Lin-
guistics, pages 286–291.
Julius Zacher. 1855. Das Gothische Alphabet
Vulfilas und das Runen Alphabet:
eine
Sprachwissenschaftliche Untersuchung, FA
Brockhaus.
A Appendices
A.1 Derivations for Dynamic Programming
We show the derivation for Pr(X) here—other
quantities can be derived in a similar fashion.
Given any X with length n, let pi(X) be the
probability of generating the prefix subsequence
X:io, and pi,z(X) be the probability of generating
X:i using z as the last
latent variable. By
definition, we have
Pr(X) = pn(X).
(cid:2)
pi(X) =
pi,z(X).
z
(11)
(12)
pi,z can be recursively computed using the
following equations:
pi,O = Pr(O) · p0 · pi−1.
pi,El = Pr(El) · Pr(xi−l+1:l|El) · pi−l.
(13)
(14)
80
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A.2 Data Preparation
Stemming Gothic stemmers are developed
based on the documentations of Gomorphv2.7
Stemmers for Proto-Germanic, Old Norse and
Old English are derived from relevant Wikipedia
entries on their grammar and phonology. For all
other languages, we use the Snowball stemmer
from NLTK (Bird, 2006)
IPA Transcription We use the CLTK library8
for Old Norse and Old English, and a rule-based
converter for Proto-Germanic based on (Ringe,
2017, pag. 242–260). Basque transcriber is based
on its Wikipedia guide for transcription, and all
other languages are transcribed using Epitran
(Mortensen et al., 2018). The ipapy library9
is used to obtain their phonetic features. There are
7 feature groups in total.
Known vocabulary For Proto-Germanic, Old
Norse, and Old English, we extract the information
from the descendant trees in Wiktionary.10 All
matched stems with at least four characters form
the known vocabulary. It resulted in 7883, 10,754
E 11,067 matches with Gothic inscriptions, E
613, 529, 627 unique words in the vocabularies
for Proto-Germanic, Old Norse, and Old English,
rispettivamente. For Ugaritic-Hebrew, we retain
stems with at least three characters due to its
shorter average stem length. For the Iberian-
Latin personal name experiments, we take the list
provided by Ramos (2014) and select the elements
that have both Latin and Iberian correspondences.
We obtain 64 unique Latin stems in total. For
Basque, we use a Basque etymological dictionary
(Trask, 2008), and extract Basque words of
unknown origins to have a better chance to match
Iberian tokens.
For all other known languages used for
the closeness experiments, we use the Book
of Genesis in these languages compiled by
Christodouloupoulos and Steedman (2015) E
take the most frequent stems. The number of
stems is chosen to be roughly the same as
the actual close relative,
in order to remove
any potential impact due to different vocabulary
sizes. For instance, for the Gothic experiments in
Figure 4b, this number is set to be 600 since the
PG vocabulary has 613 parole.
A.3 Training Details
Architecture For the majority of our exper-
iments, we use a dimensionality of 100 for each
feature embedding, making the character embed-
ding of size 700 (there are 7 feature groups). For
ablation study without IPA embeddings, each
character is directly represented by a vector of
size 700 instead. To compare with previous work,
we use the default setting from Neurocipher
which has a hidden size of 250, and therefore for
our model we use a feature embedding size of 35,
making it 245 for each character.
Hyperparameters We use SGD with a learning
rate of 0.2 for all experiments. Dropout with
a rate of 0.5 is applied after the embedding
layer. The length for matched spans l in the
range [4, 10] for most experiments and [3, 10] for
Ugaritic. Other settings include T = 0.2, λcov =
10.0, λcov = 100.0. We experimented with two
annealing schedules for the insertion penalty
α: ln α is annealed from 10.0 A 3.5 or from
0.0 A 3.5. These values are chosen based on
our preliminary results, representing an extreme
(10.0), a moderate (3.5), or a non-existent (0.0)
penalty. Annealing last for 2000 steps, and the
modello
is trained for an additional 1000 step
afterwards. Five random runs are conducted for
each setting and annealing schedule, and the best
result is reported.
7http://www.wulfila.be/gomorph/gothic
/html/.
8http://cltk.org/.
9https://github.com/pettarin/ipapy.
10https://www.wiktionary.org/.
81
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
5
4
1
9
2
4
2
4
1
/
/
T
l
UN
C
_
UN
_
0
0
3
5
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3