David Temperley - Ricerca sull'intelligenza artificiale specializzata al MIT

David Temperley
Eastman School of Music
26 Gibbs St.
Rochester, NY 14604 USA
dtemperley@esm.rochester.edu

An Evaluation System
for Metrical Models

In the young and rapidly expanding ﬁeld of music
artiﬁcial intelligence, one particularly active area of
research has been metrical analysis (also known as
meter-ﬁnding, beat tracking, beat induction,
rhythm parsing, and rhythm transcription)—the
problem of extracting metrical information from
music. Infatti, it would probably be fair to say that
no problem in the ﬁeld has attracted as much at-
tention and energy as this one. Tavolo 1 shows a list
Di 25 studies that present computational models of
metrical analysis. (The table includes all published
studies—not master’s and Ph.D. theses—that I have
been able to identify and obtain. It includes only
models that have been implemented or at least
completely speciﬁed; well-known models in music
theory such as Lerdahl and Jackendoff’s (1983) are
excluded for this reason. Also excluded are models
that identify tempo only without identifying actual
beat locations, such as Brown 1993. In cases where
several studies present close variants of a single
modello, only one study is listed.)

The models in Table 1 reﬂect a variety of per-
spectives on the metrical analysis problem. They
might be categorized along several different lines.
One fundamental distinction concerns the nature
of the input; until recently, almost all systems
worked from symbolic (‘‘note’’) input of some kind,
but in the last few years several models have been
proposed which operate directly from audio data.
Some models assume a quantized input (for exam-
ple, with durations represented by small integer
values), whereas some allow the ﬂuctuations in
timing characteristic of human performance; some
models generate just a single level of beats,
whereas others generate several. Ovviamente, IL
models might also be categorized in terms of their
approach (rule-based, connectionist, oscillator-
based, probabilistic, eccetera.), but this is a more com-
plex matter, so I do not consider it in Table 1.

Perhaps the most basic question to address about
a model—though it is not always addressed—is its

Computer Music Journal, 28:3, pag. 28–44, Autunno 2004
(cid:1) 2004 Istituto di Tecnologia del Massachussetts.

goal. Some metrical analysis systems are clearly in-
tended to model human cognition; others are sim-
ply designed to solve the practical problem of
meter-ﬁnding in whatever way seems most effec-
tive. The importance of meter-ﬁnding as a cogni-
tive process seems self-evident; meter is a basic
part of musical experience and has been shown to
inﬂuence other aspects of music cognition as well,
such as melodic similarity (Gabrielsson 1973), ex-
pectation (Jones et al. 2002), harmony perception
(Temperley 2001), performance expression (Sloboda
1983; Palmer 1997), and performance errors (Palmer
and Pfordresher 2003). Tuttavia, the practical prob-
lem is important as well. In particular, generating
music notation for a piece requires identiﬁcation of
its meter. As argued in Temperley (2001), if we
conceive of a metrical structure as a multi-leveled
framework of beats (whole-note beats, half-note
beats, and so on, down to the smallest rhythmic
level in the piece), the metrical structure of a piece
essentially provides the information required to
rhythmically notate it. E, precisely because of
the central role of metrical structure in music cog-
nition (as argued above), it will inevitably come
into play in other problems of musical engineering.
Per esempio, tasks such as matching queries to a
musical database, categorizing pieces by style or
mood, or generating an accompaniment for a mel-
ody will surely require the consideration of metri-
cal information.

Whatever the goals and assumptions of a metri-

cal model, an important and obvious question to
ask is, ‘‘How good is it?’’ That is, what percentage
of the time does it actually produce the correct re-
sult? (The ‘‘correct result’’ can be deﬁned as the
metrical structure inferred by competent listeners.
There might, Ovviamente, be some subjective differ-
ences among listeners; one might also take the mu-
sic notation for the piece to represent its meter. Ma
in most cases, I would argue, there will be agree-
ment among these sources.) If a model is intended
as a practical tool for meter-ﬁnding, the importance
of this question hardly needs defending. If the
model is intended as a hypothesis about cognition,

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Tavolo 1. Models of Metrical Analysis

Reference

Longuet-Higgins and Steedman (1971)
Longuet-Higgins (1976)
Steedman (1977)
Chafe et al. (1982)
Longuet-Higgins and Lee (1982)
Povel and Essens (1985)
Desain and Honing (1989)
Allen and Dannenberg (1990)
Lee (1991)
Miller et al. (1992)
Rosenthal (1992)
Rowe (1993)
Large and Kolen (1994)
McAuley (1994)
Parncutt (1994)
Scheirer (1998)
Temperley and Sleator (1999)
Cemgil et al. (2000UN, 2000B)
Dixon (2001UN)
Eck (2001)
Goto (2001)
Raphael (2001)
Sethares and Staley (2001)
Spiro (2002)
van Zaanen et al. (2003)

Input: Audio
or Symbolic?

symbolic
symbolic
symbolic
symbolic
symbolic
symbolic
symbolic
symbolic
symbolic
symbolic
symbolic
symbolic
symbolic
symbolic
symbolic
audio
symbolic
symbolic
symbolic or audio
symbolic
audio
symbolic
audio
symbolic
symbolic

Input: Quantized
or Performed?

Output:
Multiple Levels?

quantized
performed
quantized
performed
quantized
quantized
performed
performed
quantized
quantized
performed
performed
performed
performed
quantized
performed
performed
performed
performed
quantized
performed
performed
performed
quantized
quantized

yes
yes
yes
yes
yes
NO
yes
NO
yes
yes
yes
yes
yes
NO
NO
NO
yes
yes
NO
NO
yes
yes
yes
yes
yes

the relevance of its level of performance is less
clear. A model could perform perfectly, producing
exactly the correct structure (cioè., the one inferred
by most listeners) In 100 percent of cases, and yet
bear no resemblance whatsoever to the cognitive
process of meter-ﬁnding; a model that was only
correct 20 percent of the time might still turn out
to capture important aspects of the cognitive pro-
cess. Yet it seems to be generally accepted in cogni-
tive science that the level of performance of a
cognitive model is at least one valid criterion to
consider in evaluating it, though there are certainly
others. (One might consider, Per esempio, how well
the model accords with other experimental evi-
dence about the cognitive process, whether the
model’s architecture and computational demands
are psychologically plausible, and so on.) Given
two cognitive models A and B, otherwise equal in

cognitive plausibility, if model A’s output is much
better (closer to that of humans) than model B’s,
this surely gives model A greater credibility as a
hypothesis about cognition.

In short, the level of performance of a metrical
model is of central importance to the practical goal
and of at least some importance to the cognitive
goal. Given the large number of metrical models
that have been proposed, Poi, it seems worthwhile
to examine the quality of their performance. IL
aim of the current article is actually not to answer
this issue directly, but rather to address a prelimi-
nary question: ‘‘How can we decide how good a
metrical model is?’’ In what follows, I propose a
system for evaluating metrical models with the
goal of measuring their performance and comparing
their strengths and weaknesses in this regard.

Temperley

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Four Requirements for an Evaluation System

The problem at hand exempliﬁes a commonly oc-
curring situation in artiﬁcial intelligence and other
ﬁelds. The ultimate goal is to develop systems that
can retrieve some kind of information from data;
many models are available for the task, and we
wish to be able to evaluate their success. For such
an evaluation system, I submit that four things are
necessario: an agreed-upon way of representing the
kind of information to be retrieved; a suitably large
and representative corpus of data; correct analyses
of the corpus (representing the information to be
retrieved); and an agreed-upon way of comparing a
model’s analyses of the corpus to the correct analy-
ses and scoring the model on its success at match-
ing the correct analyses.

It is useful to consider a successful solution to
the evaluation problem in another domain—com-
putational linguistics. Since the birth of the ﬁeld, UN
central project in computational linguistics has
been the development of systems for natural-
language parsing—recovering syntactic information
from written or spoken text. Until recently, pro-
gress in this area was hindered by the difﬁculty of
evaluating models and comparing one model to an-
other. In the early 1990s, this problem was largely
solved by the development of the Penn Treebank
(Marcus et al. 1993). The Penn Treebank is a cor-
pus of several million words of naturally occurring
text gathered from both written and spoken
fonti. The treebank is accompanied by syntactic
analyses done by experts—a ‘‘constituent struc-
ture’’ for each sentence showing noun phrases, verb
frasi, clauses, eccetera. Metrics have been proposed
for comparing ‘‘treebank-style’’ analyses (Black et
al. 1991), and programs are available that take two
analyses of a set of sentences—the correct analysis
set (known as a ‘‘goldﬁle’’) and one produced by a
model to be evaluated (a ‘‘testﬁle’’)—and evaluate
how well the testﬁle analyses match those of the
goldﬁle.

For the problem of natural-language parsing, Poi,
it can be seen that all four of the requirements listed
above have been met. This achievement has led to a
surge of progress in natural-language parsing. (For
discussion, see Manning and Schu¨ tze 2000.) In

what follows, I consider possible solutions to these
four requirements for the metrical-model evalua-
tion problem.

Previous Work on the Evaluation
of Metrical Models

For the most part, issues of evaluation have re-
ceived little attention in the literature on metrical
analysis. Many studies present no quantitative per-
formance measures for the models presented. Nel
last few years, Tuttavia, some important proposals
have been offered in this area.

The appropriate way of evaluating a metrical
model depends on the nature of the model. Noi
might distinguish ﬁrst between models accepting
only quantized input and those accepting per-
formed input. In quantized-input models, time-
points are generally represented as multiples of a
short rhythmic value or ‘‘base unit,’’ such as a
sixteenth-note. Such models generally assume that
the metrical structure is perfectly regular through-
fuori. In such a case, each level of the metrical struc-
ture can be characterized by two numbers: one
indicating its period (in base units), or the distance
between beats; the other indicating the phase
(again in base units)—how long after the beginning
of the piece the ﬁrst beat occurs. A level generated
by the model could be said to be correct if its pe-
riod and phase exactly match one of the levels in
the correct metrical structure. This is essentially
the approach used by Desain and Honing (1999).
Desain and Honing evaluate three metrical models
(the model of Longuet-Higgins and Lee 1982 E
two later variants of it) using three test corpora: UN
set of randomly generated rhythms, a set of ‘‘metri-
cal’’ rhythms (in which each note is exactly one
beat long at some metrical level), and a corpus of
national anthem melodies. Each of the three mod-
els tested generates only a single beat level. For
each model, the authors present data regarding the
proportion of input cases for which the model’s
beat matches the main beat level in the correct
structure (in both period and phase); they also pres-
ent data comparing the model’s beat to other beat
levels in the correct structure. (Van Zaanen et al.

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2003 use the same anthem corpus and a similar
testing strategy.) Desain and Honing’s approach
seems very sensible for evaluating quantized-input
models. In what follows, we focus mainly on
performed-input models; as can be seen from Table
1, most models in recent years have addressed per-
formed input.

An approach to evaluating performed-input met-
rical models is presented by Cemgil et al. (2000B).
This requires data in which the locations of beats
are explicitly indicated. (Just one level of beats is
assumed.) Assume that the correct beat level for a
piece is S (cid:2) s1, s2, . . ., sI (where each sn is the time
point of a beat), and the model’s output beat level
is T (cid:2) t1, t2, . . ., tJ. The score W for the closeness of
any two beats si and tj is expressed using a Gaus-
sian window function (so that two exactly simulta-
neous beats receive a score of 1). The similarity
function between S and T is then

R max W (S , T )
j
(IO (cid:3) J) / 2

• 100

This formula takes each correct beat, pairs it with
the closest beat to it in the model’s output, E
adds together the W scores for these beat pairs.
This is then divided by the average of I and J
(which means that the model’s output will be pe-
nalized if it has many more beats than the correct
structure) and multiplied by 100. The result is a
single number that roughly indicates the percent-
age of correct beats that were matched by the
model’s beats. Using this evaluation technique,
Cemgil et al. (2000B) tested their own model on
keyboard performances of the Beatles song ‘‘Yester-
day,’’ played multiple times by different performers
and under different tempo instructions (fast, nor-
mal, or slow). (The model was essentially given the
correct initial tempo and phase.) Dixon (2001B)
later tested his model against that of Cemgil et al.
using a similar evaluation method and the same
insieme di dati, and he reported overall scores of 94 (cid:4) 9
for his model versus 91 (cid:4) 7 for the model of Cem-
gil et al.

A somewhat similar approach is proposed by

Goto and Muraoka (1997) for testing an audio-input
metrical model. The system requires that the audio
input be supplemented with markers, added by

hand, indicating the correct beat locations. Goto
and Muraoka present an audio-input model that
outputs multiple levels of beats; the model is eval-
uated in the following way. For each correct beat
Cn, the closest beat Bm in the model’s output is
found, and an error is calculated, which is the time
difference between Cn and Bm as a proportion of the
interval between correct beats. The longest cor-
rectly tracked portion of the piece is found (cioè., IL
longest span in which the error is less than a cer-
tain value). The test set consisted of 40 songs (from
popular music recordings without drums), each at
least 1 min long, by a variety of artists. The au-
thors deﬁne a correct analysis as one in which
(1) the longest correctly tracked portion begins no
later than 45 sec after the beginning of the piece
and extends to the end, E (2) the mean, variance,
and maximum of the error are within certain val-
ues. (Per esempio, the mean error must be less than
0.2.) By this criterion, the model analyzed 87.5 per-
cent of the input songs correctly at the quarter-note
level.

The approaches of Cemgil et al. and Goto and
Muraoka offer valuable contributions toward the
evaluation of performed-input metrical models.
Tuttavia, they also encounter certain difﬁculties.
In particular, they require the location of every beat
to be exactly speciﬁed, when in fact the exact loca-
tion of beats is often somewhat indeterminate.
Consider a MIDI ﬁle of a classical piece generated
from a piano performance (or an audio ﬁle, for that
matter). There will likely be many chords in which
several notes are understood as simultaneous and
coinciding with a certain beat. But most likely they
will not be played exactly simultaneously; so where
exactly is the beat? There may also be beats with
no coinciding note, so again the exact location of
the beat is uncertain. This problem can be solved
by having human annotators provide the beat infor-
mation according to their intuition. But this solu-
tion is far from ideal; such hand-annotation is
time-consuming and also somewhat subjective. It
seems that, in evaluating a metrical analysis, we
should focus on the aspects of the metrical struc-
ture that are clear and uncontroversial. Certain
beats correspond with certain notes, and other
beats may be in between but not necessarily at

Temperley

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

determinate locations. (Concrete examples of this
will be given later.)

One method that addresses this problem is what

could be called the ‘‘score-time’’ system. In this
system, the correct metrical structure for a piece is
used to generate a quantized rhythmic representa-
tion such that each event has a correct location or
‘‘score-time’’ in the piece. Per esempio, if quarter-
note beats are deﬁned as integers, a note on the
ﬁrst quarter-note beat is at score-time 0.0, a note
on the next beat is at 1.0, and a note one eighth-
note later is at 1.5. Such a system for rhythmic rep-
resentation has been used for various purposes—for
esempio, in score-performance matching (Heijink
et al. 2000). A metrical model could then operate
by assigning a score time to each note; the model
could be evaluated according to (Per esempio) IL
proportion of notes that were assigned the correct
score-time. Notice that such a model need not de-
cide the exact location of indeterminate beats that
contain no notes. Tuttavia, this system in effect
only represents one level of meter: generally the
main beat level or ‘‘tactus.’’ Score-times do not in-
dicate higher metrical levels, per esempio., whether tactus
beats are grouped in duples or triples (though such
information could be indicated in other ways; Vedere
for example Cemgil et al. 2000UN). This measure is
also rather inﬂexible. If a model inserted one extra
beat near the beginning of the piece, then all of the
score-times for subsequent events would be judged
as incorrect, which seems unduly harsh.

In what follows, I propose an alternative ap-
proach to metrical evaluation. This builds on the
‘‘score-time’’ idea, but allows multiple metrical
levels and also permits a more ﬂexible comparison
of metrical analyses. It should be stated at the out-
set that the system is intended primarily for
symbolic-input models. Whether it will also be
useful for audio-input models is an open question; IO
return to this at the end of the article.

A Representation System

We must ﬁrst consider how to represent the input
data—the data to be analyzed. Following many
other models, I will assume a representation con-

sisting of a list of notes encoded with ‘‘ontime’’ and
‘‘offtime’’ (both in msec) and pitch (in integer nota-
zione, with middle C (cid:2) 60). Such a representation,
similar to a MIDI ﬁle, is sometimes known as a
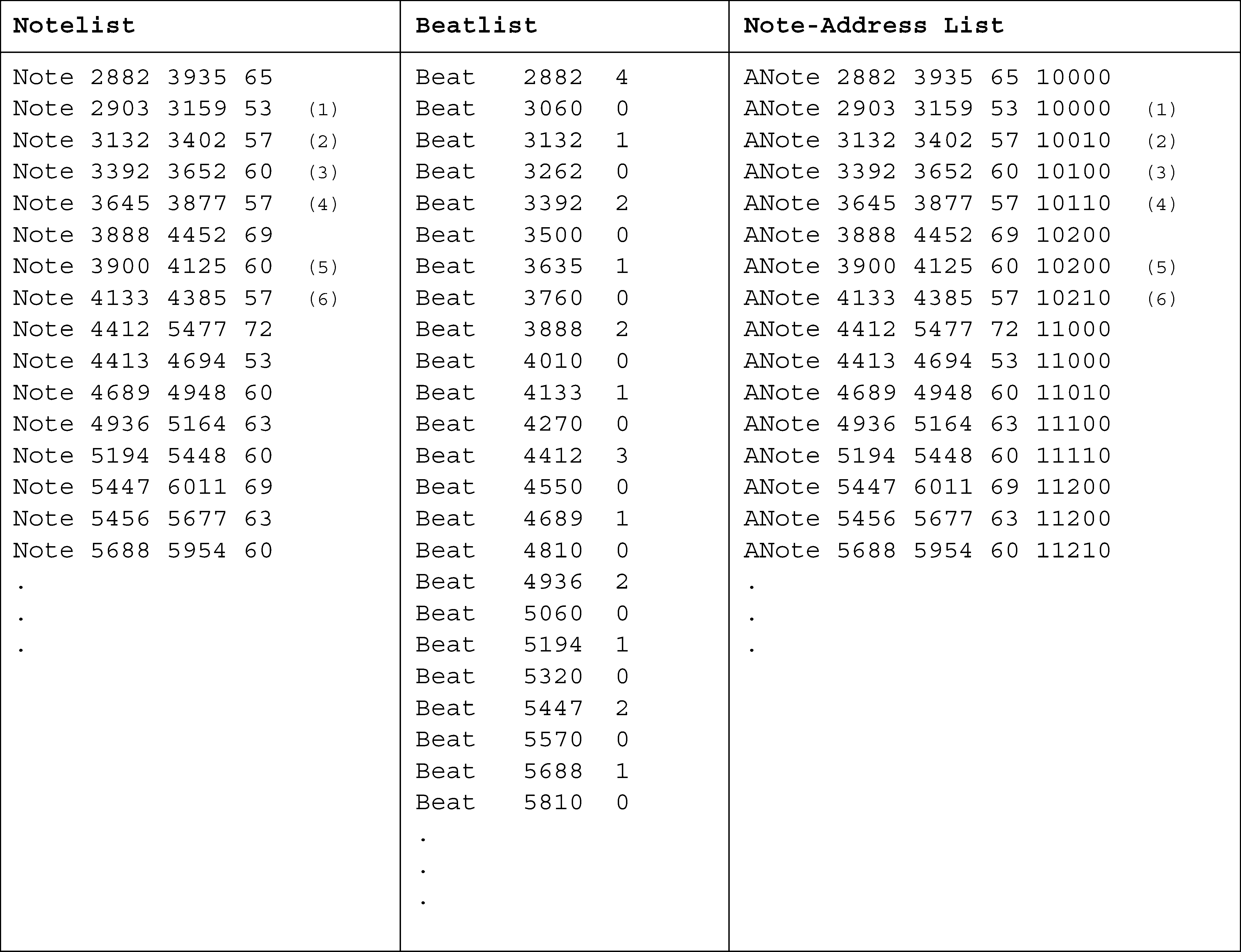
‘‘notelist.’’ Figure 1 shows the opening of a Mozart
piano sonata; the leftmost column below the score
shows the notelist for the ﬁrst two measures. (IL
numbers in parentheses have been added for refer-
ence in the following discussion.) Notice that this
system does not assume that the events are quan-
tized (except at the very low level of msec); the no-
telist in Figure 1 was generated from a performance
on a MIDI keyboard, and it can be seen that the
timing is somewhat irregular.

We now turn to the representation of the metri-
cal structure itself. Most metrical models produce
some kind of representation of beats aligned with
the music that was given as input. Beats are simply
points in time, subjectively understood as accented,
though not necessarily coinciding with any event.
Some systems (as discussed above) generate several
levels of beats, or—to put it another way—beats of
varying strength, where ‘‘strong’’ beats are present
at higher levels and ‘‘weak’’ beats only at lower
levels. A metrical structure can be represented
graphically as a framework of dots (Lerdahl and
Jackendoff 1983), as shown in Figure 1 above the
staff. In Temperley and Sleator (1999), we proposed
encoding such a structure as a list of beat state-
menti, each one with a timepoint and a level num-
ber representing the highest level at which that
beat is present; the ‘‘beatlist’’ for the ﬁrst two mea-
sures of the metrical grid in Figure 1 is shown in
the middle column below the score. We assume a
structure of ﬁve metrical levels, numbered 0–4,
with higher numbers representing higher levels;
level 2 is the ‘‘tactus’’ or main beat, the quarter-
note level in this case. (The assumption of ﬁve lev-
els seems optimal for common-practice music in
general, though some pieces may call for more or
fewer levels; see Lerdahl and Jackendoff 1983 E
Temperley 2001 for discussion.)

Given this representation scheme, one possible
idea for an evaluation system is as follows. Let us
assume a corpus of pieces or excerpts encoded in
notelist format. Each excerpt could be annotated

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figura 1. Mozart, Sonata
KV 332, IO, mm. 1–5, show-
ing metrical grid (above
the staff), notelist, beatlist,
and note-address list.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

with the correct beatlist; this could then be com-
pared with a beatlist generated by the model being
tested (similar to the approaches of Goto and Mu-
raoka 1997 and Cemgil et al. 2000B). A problem
arises here, as has already been mentioned: the lo-
cation of beats is often indeterminate. In Figure 1,
the ﬁrst notes in the right hand and the left hand
are understood as coinciding with the ﬁrst beat, Ma
they are not exactly simultaneous. Is the beat lo-
cated at 2882, 2903, or somewhere in between?

(The beatlist in Figure 1 arbitrarily aligns the beat
with the ﬁrst of these two onsets.) Inoltre,
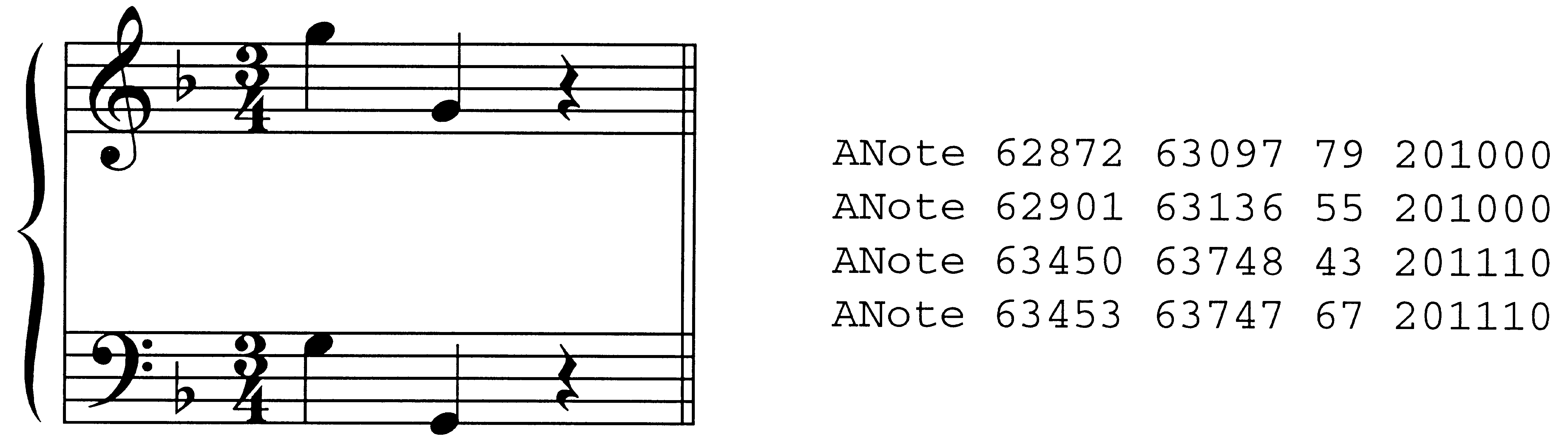
many beats have no coinciding note. In Figures 2a
and 2b (excerpts from later in the same piece),
where exactly is the second quarter-note beat of
M. 12, or the third quarter-note beat in m. 40? IL
same could be said of all the level-0 beats in Figure
1, none of which coincide with notes. Infatti, one
might question whether level-0 beats are even pres-
ent in this passage. The location of these indeter-

Temperley

Figura 2. Three excerpts
from Mozart, Sonata KV
332, IO, showing note-
address lists at right.

(Figures 2a and 2b show
ﬁve-value note-addresses;
Figure 2c shows six-value
note addresses.)

(UN) M. 12

(B) M. 40

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

minate beats could perhaps be determined in
perceptual terms—we do have some intuitions
about where the second beat of m. 12 occurs (prob-
ably roughly halfway between the ﬁrst and third
quarter-note beats)—but for a human annotator to
produce the correct answer would be quite difﬁ-
cult.

As suggested earlier, for the purposes of metrical

evaluation, we should focus on what is uncontro-
versial. And some things do seem uncontroversial:
in Figure 2a, the notes of the ﬁrst chord fall on the
beat, even though they may not be exactly simulta-
neous. This is followed by an empty beat (Anche se
its exact timepoint is indeterminate), followed by
another chord on the third beat of the measure.
(Notice also that the exact location of beat 2 of m.
12 is not needed for the purpose of converting the
beatlist into notation. As long as it is known that
the ﬁrst chord coincides with the ﬁrst level-2 beat
of the measure, and the second chord with the
third level-2 beat, with one other level-2 beat
somewhere in between, this is all that is required.)
One representation system that meets this re-
quirement is what I will call the ‘‘note-address’’
system—shown in the right-hand column of Figure
1 for the opening of the Mozart sonata excerpt. It
can be seen that the list of events here includes all
the information of the original notelist, ma il
Note statements have become ANote statements,
consisting of an ontime, offtime, pitch, and ‘‘note
address’’—a number representing the note’s posi-
tion in the metrical grid. This number should re-
ally be thought of as a ﬁve-valued vector, but it can
be represented as a single integer, as none of the
values ever exceed 9 except for the leftmost one.
(We assume ﬁve levels for now, though in principle
more or fewer could be used.) Each value in the
vector corresponds to a level of the metrical grid
(the rightmost value corresponds to level 0). IL
value represents the number of beats at that level
that have elapsed at that point in the piece since
the previous beat at the next level up.

As an example, consider the ﬁrst six eighth notes
of the left hand, indicated by the numbers in paren-
theses. For the quarter-note level (corresponding to
the third digit from the right in the note addresses),
the ﬁrst and second of these notes have the value 0

(no quarter-note beats have occurred since the last
dotted-half-note beat), the third and fourth have
value 1 (one beat has occurred), and the ﬁfth and
sixth have value 2 (two beats have occurred). IL
highest-level (leftmost) value of the address, Quale
is always set to 1 at the start of the piece, repre-
sents the number of highest-level beats that have
elapsed in the piece as a whole (since there is no
higher level from which to count). Eventually this
could become a 2- or 3-digit number, producing ad-
dresses like 20-1-0-0-0 (as in Figure 2b). One could
actually assign addresses to the beats themselves;
in a perfectly regular duple grid, this would be
equivalent to counting binary numbers (10000,
10001, 10010, 10011, 10100, . . .), with the excep-
tion that the leftmost digit is not binary. Tuttavia,
if we assign addresses only to notes, we avoid the
earlier-discussed problem of having to decide on
the location of indeterminate beats.

The note-address system also solves the problem

created by nominally simultaneous notes. As ob-
served earlier, the notes of a chord are generally un-
derstood as occurring on the same beat (and would
be represented that way in notation), yet they are
rarely performed exactly simultaneously. Thus as-
signing the ‘‘beat’’ to a single timepoint is difﬁ-
cult—indeed impossible, if we want all the notes of
the chord to be represented as coinciding with the
beat. The solution provided by the note-address
system can be seen in Figure 1. In m. 1, the ﬁrst
right-hand and ﬁrst left-hand notes can be given
the same address, even though they do not exactly
coincide, representing that they are understood as
being simultaneous in metrical terms and should
be notated that way.

One further reﬁnement of the note-address sys-
tem is needed. It is generally accepted in metrical
theory that not all notes necessarily coincide with
beats; some, like trills, turns, and grace notes, are
‘‘extrametrical’’ (Temperley 2001). Figure 2c shows
an example from m. 8 of the Mozart excerpt. Two
notes in the right-hand (notated in small note-
heads, as is customary) do not really occur on any
beat. To accommodate extrametrical notes, we in-
troduce one further (rightmost) digit of the note-
address. This digit is 0 for any note that coincides
with a beat; for a note that is between two beats,

Temperley

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

the address of the note is the address of the previ-
ous beat, except with 1 as the ﬁnal digit. If there
are multiple, non-coinciding notes between the two
beats, the ﬁnal digit of their addresses reﬂects their
ordering in time: the ﬁrst extrametrical note in Fig-
ure 2c is labeled 410111, the second 410112. (Prob-
lems would arise if there were more than nine
non-coinciding notes between two beats, but this
seems unlikely to occur.) A note address therefore
has six values, which we will refer to as levels 4, 3,
2, 1, 0 (for the ﬁve metrical levels), and –1 (the ex-
trametrical level).

The note-address system is not perfect. For one
thing, not only does it fail to represent the location
of beats with no coinciding note, it sometimes
even fails to represent their existence. In Figure 2a,
Per esempio, there is no explicit indication of the
second beat of the measure (which would be at ad-
dress 61100). In questo caso, the existence of the miss-
ing beat is implicit in the fact that the following
note has the address 61200; this implies that there
must have been a 61100 anche. A more worrisome
case is shown in Figure 2b. Here, the third beat of
M. 40 is not represented even implicitly. If we just
looked at the note addresses for the passage (even
including the address of the following downbeat,
210000), we could not even be certain that m. 40
were a triple-meter measure. We should bear in
mente, Poi, that certain errors metrical models
might make would not be recognized under the
note-address system: Per esempio, if a metrical
model omitted the third beat in m. 40, or added a
fourth beat (or an extra ten beats) at the end of the
measure. The seriousness of this problem is un-
clear; it depends on how often metrical models ac-
tually make these kinds of errors. (The problem
could be addressed in various ways, Per esempio, by
supplementing each highest-level beat with infor-
mation about the duple or triple divisions of the
grid at each level.) Some other limitations of the
note-address system will be discussed in later sec-
zioni.

The Corpus

In selecting a corpus for testing, two considerations
are important. Primo, the criteria used in assembling

the corpus should be as systematic as possible.
Rather than selecting 20 pieces that one knows and
happens to have handy, one should, if possible, Di-
vise objective criteria for inclusion in the corpus.
(The danger is, Ovviamente, that those pieces we
know and have handy are likely to be the ones we
used, or at least thought about, in developing our
model.)

Another requirement is that the corpus should be

a representative sample of the larger corpus that
the models to be tested were designed to analyze.
This is problematic in the current case. Many mod-
els have speciﬁcally addressed themselves to
‘‘common-practice’’ music (roughly speaking,
Western art music from 1700 A 1900). (Even here,
there may not be total agreement on what
common-practice music includes.) Other models
have sought to accommodate other kinds of music,
such as jazz, rock, and non-Western music
(Scheirer 1998; Cemgil et al. 2000B; Goto 2001; Se-
thares and Staley 2001). Così, I certainly do not
claim that the corpus proposed below would be a
suitable or fair one for all of the models listed in
Tavolo 1.

In Temperley (2001), I presented the ‘‘Kostka-
Payne Corpus’’ (hereafter the KP Corpus)—a set of
46 excerpts from the common-practice repertoire
taken from the workbook accompanying Stefan
Kostka’s and Dorothy Payne’s textbook Tonal Har-
mony (1995). The corpus includes all excerpts from
the workbook of at least eight measures in length;
it contains a total of 541 notated measures and
9,057 notes. Although the corpus is not especially
big (a larger one would certainly be desirable), Esso
has two important advantages: the excerpts were
selected by an objective criterion; and they span a
range of periods, genres, and composers within the
common-practice idiom, so that the corpus can be
considered a reasonably good sample of common-
practice music. Noteﬁles were generated for all the
excerpts in the corpus; these noteﬁles are quan-
tized (cioè., generated from notation) and thus have
perfectly regular timing (using tempi that seemed
reasonable to me). Tuttavia, for the 19 excerpts
from the corpus for solo piano, I had a skilled
(doctoral-level) pianist perform the excerpts and
generated noteﬁles from those as well. (We will call

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

this the KP Performed Corpus.) In the quantized
noteﬁles, no extrametrical notes were included; In
the performed noteﬁles, the performer was allowed
to include whatever extrametrical notes were de-
sired. The performances contained a few extrane-
ous notes (performance errors) that were
subsequently deleted from the performed ﬁles (ow-
ing to the difﬁculty of deciding on the ‘‘correct’’
metrical location of these); notes erroneously omit-
ted from the performed ﬁles were not restored.

Note-address ﬁles were generated for all excerpts
in the corpus (both the quantized ﬁles and the per-
formed ones) using the format shown in earlier ex-
amples (speciﬁcally, the six-value address format
shown in Figure 2c). This was done by running the
input ﬁles through the Melisma meter-ﬁnding pro-
gram (discussed later), sometimes adjusting the pa-
rameters in ad hoc ways to get the output as close
to correct as possible and then hand-correcting any
remaining errors. With very few exceptions, Questo
was unproblematic: it was clear, both for the quan-
tized ﬁles and the performed ﬁles, what the correct
address of each note should be. It was sometimes
not obvious which metrical level should be deﬁned
as the tactus (level 2); I used my own musical judg-
ment for these decisions. (In some slow move-
menti, Per esempio, the length of the tactus beats if
the notation were taken literally—e.g., quarter-note
beats in a 2/4 meter—would be over two seconds,
beyond most estimates for the upper range of the
perceived tactus.) Note-addresses were encoded
only up to the notated measure indicated in the
score; ‘‘hypermetrical’’ levels (above the measure)
were not included owing to their subjective nature.

Comparing Goldﬁles and Testﬁles

We now have a way of representing metrical struc-
tures (the note-address system), a corpus of data,
and correct analyses of the data in the required for-
mat. The ﬁnal requirement is a way of comparing a
note-address ﬁle produced by a metrical model (UN
‘‘testﬁle’’) with the correct analysis (the ‘‘goldﬁle’’).
We assume for now that the goldﬁle and testﬁle
contain exactly the same events (identiﬁed by their

pitches and timepoints), though we will modify
this assumption slightly below. Therefore, there
should be no difﬁculty in matching events in the
goldﬁle with their corresponding events in the test-
ﬁle. The problem is to compare the note addresses
for corresponding events between the two ﬁles.

One very simple approach would be to use ‘‘ex-
act matching,’’ that is, to score the testﬁle on the
proportion of its events that are assigned exactly
the same address in the goldﬁle. This would be a
fairly harsh and unforgiving metric. Per esempio,
suppose a model erroneously inserted an extra mea-
sure at the beginning of the piece but otherwise an-
alyzed the piece exactly correctly. The leftmost
value of each note address after the inserted mea-
sure would be incorrect (one greater in the testﬁle
than in the goldﬁle), so almost every note address
in the piece would be incorrect—though the
model’s analysis was in fact almost completely cor-
rect. (A similar problem arises with the ‘‘score-
time’’ method of meter representation, as discussed
earlier.)

A fairer approach would be to assign the testﬁle a

score for every level, indicating the proportion of
events that were correctly labeled at that level.
This is the approach taken here, implemented in a
program called compare-na. This program takes as
input two note-address ﬁles, a goldﬁle and a test-
ﬁle. For every level L that is present in the note-
addresses in the goldﬁle (except for the top level—
this is explained later), a score is assigned that
indicates the proportion of events whose note-
address value at level L is the same in the testﬁle
as in the goldﬁle. The program also produces an
overall score, which is simply the average of the in-
dividual level scores. (It is not clear how meaning-
ful this is. One could also consider a weighted
score, with some levels—e.g., the tactus level—
weighted more than others. Alternatively, as I
prefer, one could simply take the level scores indi-
vidually as indicators of the model’s success at the
tactus level, higher levels, and lower levels.)

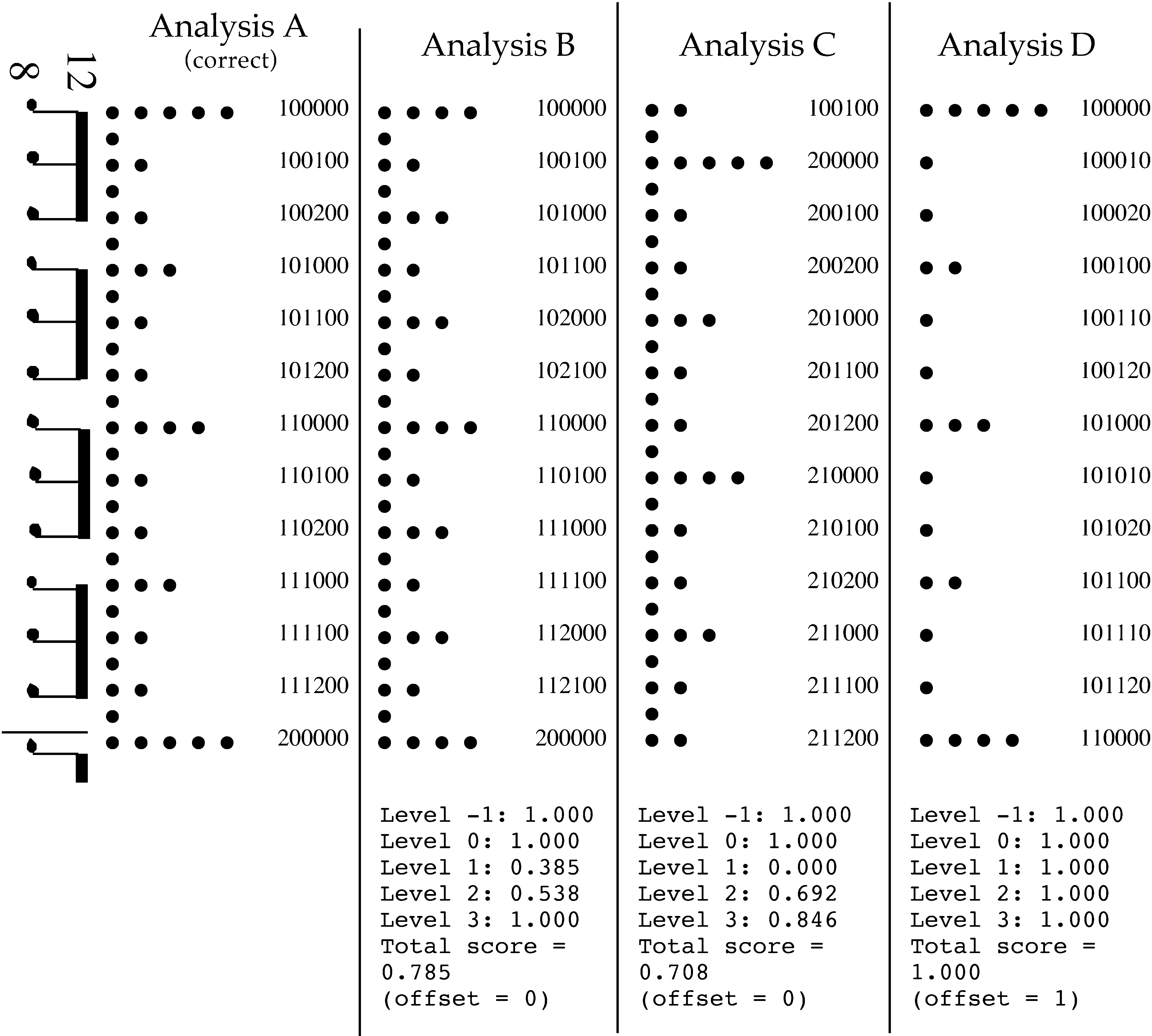
An example is shown in Figure 3 to give a ﬂavor

of this scoring system. A rhythmic pattern is
shown at left—a simple eighth-note pattern in a
12/8 meter. Four analyses are shown in the form of

Temperley

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figura 3. A rhythmic pat-
tern showing four analyses
as metrical grids and note-
address lists. Analysis A is

the correct analysis. For
analyses B, C, and D, IL
scores for each analysis
compared to analysis A,

according to the note-
address evaluation system,
are shown below.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

metrical grids, the correct one (analysis A) E
three incorrect ones; the note-address list implied
by each grid (for each note of the pattern) is shown
at the right. The scores yielded by compare-na for
analyses B, C, and D, when compared with analysis
UN, are shown below each analysis. In all four analy-
ses, no notes are analyzed as extrametrical, così
the rightmost digit is 0 for all notes. Because all
analyses agree totally with analysis A for level –1,
they all receive a score of 1.000 at this level. In
analyses B and C, as in analysis A, every note is an-
alyzed as coinciding with a level 1 beat, so the
second-from-the-right digit is 0 for all notes as
BENE. (We will discuss analysis D in a moment.)

In analysis B, only level 2 of the metrical grid is
incorrect: in essence, the passage is analyzed as 6/4
instead of 12/8. In questo caso, the level-2 values of
the addresses are mostly incorrect, as are the level-

1 values, leading to low scores for level 2 (0.538)
and level 1 (0.385). In analysis C, levels 2, 3, E 4
are all ‘‘out-of-phase’’ by one eighth-note beat (as if
the piece was notated in 12/8 with the barlines one
note too late). Many of the address values at levels
2 E 3 are now incorrect, as are all of the level 1
values. Values for levels 0 and –1, Tuttavia, are un-
affected.

These examples point out an important, E
rather counterintuitive, aspect of the note-address
system. What would normally be thought of as an
error at a particular metrical level will generally af-
fect not only the address values at that level, Ma
the values at the next lower level as well. For this
reason, also, it seems superﬂuous to compare the
highest metrical levels of the addresses, because
any difference in this level will cause differences at
the next level down. Thus the evaluation system

Computer Music Journal

compares note-addresses only up to and including
the second-highest level present in the goldﬁle.
(Notice the address assigned to the upbeat in

analysis C. For the ﬁrst beat in the piece, we assign
a value of 1 to the highest level present in the
beatlist; all other values are set to 0 except for the
highest level at which that beat is present—level 1
in this case—which is set to 1.)

Important questions arise here regarding how the
similarity between two metrical structures should
be judged. By one criterion, analyses A and C in
Figura 3 are very similar: both reﬂect a 12/8 metri-
cal structure, and the structures are also the same
in terms of the periods (intervals between beats) at
each level. Yet the metrical strength of each event
is incorrect; Infatti, from this point of view, analy-
sis C is maximally incorrect. In analysis B, IL
‘‘time signature’’ (the duple/triple relationships
among levels) is incorrect, but at least some of the
events have the correct metrical strength. Which of
these two analyses is more similar to analysis A?
The note-address system, along with the compari-
son method proposed here, seems to give fairly in-
tuitive results regarding the similarity between
structures. Per esempio, analysis B scores higher
overall than analysis C here (0.785 versus 0.708), COME
I think it should. Tuttavia, there may be no single
correct answer in this regard; it may depend on the
speciﬁc goals for which the model is intended.

Suppose, for the rhythmic pattern shown in Fig-
ure 3, a model produced the output shown in anal-
ysis D. This analysis essentially matches analysis
UN, except that the levels of the two analyses are
not aligned: the tactus (dotted quarter note) is level
2 in the goldﬁle but level 1 in the testﬁle. It is un-
clear how this situation should be handled. If the
two address lists were compared exactly as they
are, the testﬁle would receive the very low overall
score of 0.462. This solution is surely too harsh;
analysis D is not as incorrect as a score of 0.462
would suggest.

Another approach would be to compare each
level in the testﬁle with whichever level in the
goldﬁle addresses it matches most closely. This is
the approach taken by compare-na: different ‘‘off-
sets’’ of the testﬁle relative to the goldﬁle are tried,
and the one is chosen that yields the best match.

The program also outputs the offset value that was
chosen; an offset of 1 means that level L in the
goldﬁle was matched to level L–1 in the testﬁle. A
an offset of 1, analysis D yields a perfect overall
score of 1.000. (Level –1 in the goldﬁle has no cor-
responding level in the testﬁle; all address values
not explicitly indicated in the testﬁle are assumed
to be 0.) Some might consider this approach too
forgiving. Generally, the perception of a certain
beat level as the tactus or main beat is assumed to
be an important aspect of metrical cognition; IL
correct identiﬁcation of this level might well be re-
garded as part of the meter-ﬁnding problem. (One
solution would be to consider different alignments
of the goldﬁle and testﬁle addresses, but factoring
in a penalty for level misalignment.)

The compare-na program also contains a toler-
ance parameter for timing. Some models, ad esempio
the model of Temperley and Sleator (1999), slightly
alter the timepoints of events. One reason for this
is that it allows the notes of a chord—rarely played
exactly simultaneously—to be made simultaneous
and thus aligned with the same beat. Once the time-
points of an event are altered in the testﬁle, Questo
could cause problems for the matching of events
between the testﬁle and the goldﬁle. The tolerance
parameter addresses this problem; if the tolerance
È 50 msec, a goldﬁle event with an onset time of
T can be matched to any testﬁle event of the same
pitch with an onset time of T (cid:4) 50 msec. (If for
some reason no matching testﬁle event within the
speciﬁed tolerance is found for a goldﬁle event,
that goldﬁle is judged as unmatched at all levels.)

Given a series of outputs (from different pieces or
excerpts) from compare-na, the program tally-na av-
erages the ﬁgures for each level over the entire cor-
pus (weighting each excerpt in the corpus equally).
A sample output of tally-na is shown below:

level–1: average proportion correct (cid:2) 0.998 (46)
level 0: average proportion correct (cid:2) 0.966 (46)
level 1: average proportion correct (cid:2) 0.928 (46)
level 2: average proportion correct (cid:2) 0.899 (44)
level 3: average proportion correct (cid:2) 0.814 (29)
Overall corpus score (cid:2) 0.931; number with zero
offset (cid:2) 36 out of 46

The numbers in parentheses indicate the number
of excerpts for which that level was eligible for

Temperley

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

evaluation in the goldﬁle data. (Bear in mind that
the goldﬁle addresses only reﬂect levels that are ex-
plicitly indicated in the notation, and also that the
highest level of the addresses is never evaluated.
This means that, Per esempio, level 3 is only eligi-
ble for evaluation if level 4 is present in the goldﬁle
addresses.) An overall corpus score is also given,
which simply averages all the overall scores for
each excerpt. The program also gives information
about how many testﬁle analyses reﬂected the cor-
rect (‘‘zero’’) level offset.

Experiments with Melisma

As an illustration of the evaluation system pro-
posed above, I present an evaluation of the meter-
ﬁnding program proposed by Temperley and Sleator
(1999), part of the Melisma system for music analy-
sis (Temperley 2001). A brief description is needed
of the Melisma metrical model. The model is a
preference rule system that considers a large num-
ber of possible analyses and chooses the one that is
optimal on balance with regard to several criteria.
The main criteria are as follows: (1) prefer for beats
at each level to be aligned with event-onsets, IL
more onsets the better; (2) prefer for beats to be
aligned with longer events; (3) prefer for beats to be
regularly spaced at each level. (At the tactus level,
‘‘regularity’’ simply implies that each beat inter-
val—between two adjacent beats—should be close
in length to the previous beat interval; at higher
and lower levels, regularity refers to the relation-
ship between levels, cioè., a consistently duple or tri-
ple relationship between levels is preferred.) IL
model contains about a dozen user-settable param-
eters (regarding the relative weight of the prefer-
ence rules and other things); these were set on a
trial-and-error basis, before any testing was done
using the KP Corpus.

Tavolo 2 shows results of some tests performed on
both the KP Corpus and the KP Performed Corpus.
For each corpus, the ﬁrst row shows, for each level,
the number of excerpts for which that level was el-
igible for consideration. Next is shown the perfor-
mance statistics for the Melisma model using the

default parameters of the model (as deﬁned in the
most recently released 2001 version of the system).
Recall that the score for each level indicates a sim-
ple average of the scores for that level over all the
excerpts. Not surprisingly, the overall performance
on the KP ﬁles (0.931) was somewhat higher than
on the KP-performed ﬁles (0.908)—recall that the
former is generated from notation, the latter from
MIDI keyboard performances—though the differ-
ence is not very large. Regarding the values for dif-
ferent levels, it should be remembered that errors
at one level are mainly reﬂected in the scores for
the next level down, so the relatively low scores for
levels 2 E 3 in the KP Corpus mainly indicate er-
rors at levels 3 E 4. (The high score for level 3 SU
the KP Performed Corpus is surprising, but only
nine of the performed excerpts contained eligible
data for level 3, so the sample was fairly small.)

As a further test, the Melisma program was run
on piano renditions of the Beatles songs ‘‘Michelle’’
and ‘‘Yesterday’’ using the performances used for
testing by Cemgil et al. (2000B) and Dixon (2001B).
(MIDI ﬁles of these are publicly available online at
www.nici.kun.nl/mmm/archives.) Cemgil et al.
and Dixon used many performances of the same
two songs; the current test just used one perfor-
mance of each song (the ﬁrst performance by the
ﬁrst subject in the ‘‘classical’’ category, played at a
‘‘normal’’ tempo). Correct note-address ﬁles were
generated, and these were compared with the out-
put of the Melisma program. The results are shown
in Table 3. On ‘‘Yesterday,’’ the tactus level was
largely correct (as indicated by the high values for
level 1), as were lower levels; level 3 was not as
good, as it switched from duple meter to triple me-
ter for one section of the piece. On ‘‘Michelle,’’ the
program’s analysis was almost completely correct;
the only errors were due to a few triplet-quarter
notes, and a few ‘‘smudged’’ chords (in which notes
intended as simultaneous were not interpreted as
such by the program).

As well as allowing comparison between models,
the evaluation system proposed here might greatly
facilitate the development and improvement of
models. It is now very easy, Per esempio, to make a
change in the Melisma meter system, run the sys-
tem on the KP Corpus, generate note-address ﬁles

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Tavolo 2. Tests of the Melisma Meter Model on the Kostka-Payne Corpus Using the Note-Address
Evaluation System

Corpus and Model Used

Level 3

Level 2

Level 1

Level 0

Level –1

Correct
Offset

Overall
Score

KP Corpus (46 excerpts)

# of excerpts with data

Melisma score

With default parameters
Without length factor
With harmonic factor

0.814
0.664
0.707

0.899
0.774
0.926

0.928
0.895
0.921

0.966
0.955
0.965

0.998
0.997
0.997

KP Performed Corpus (19 excerpts)

# of excerpts with data

Melisma score

With default parameters
Without length factor
With harmonic factor

0.984
0.620
0.892

0.778
0.524
0.855

0.922
0.740
0.880

0.945
0.850
0.947

0.960
0.937
0.963

—

36
36
37

—

15
13
15

—

0.931
0.877
0.923

—

0.908
0.743
0.909

Tavolo 3. Tests of the Melisma Model on Beatles Songs

Input piece

Level 3

Level 2

Level 1

Level 0

Level –1

‘‘Yesterday’’
‘‘Michelle’’

0.836
1.000

0.755
0.971

0.958
0.971

0.986
0.980

1.000
1.000

Correct
Offset?

Yes
Yes

Overall
Score

0.907
0.984

automatically from the resulting beatlists, E
compare these to the correct note-address ﬁles to
see if the change resulted in better, worse, or un-
changed performance.

As an example, one might wonder how crucial

the consideration of length (the preference for
aligning beats with longer notes) is for the meter-
ﬁnding process. This was examined by altering a
parameter of the Melisma system so that all notes
are assumed to be just 0.1 sec in length (shorter
than the vast majority of actual notes)—thus, in ef-
fect, removing length distinctions between notes.
The results are shown in Table 2. For the KP Cor-
pus, ignoring note-length distinctions results in a
fairly modest decrease in performance from 0.931
A 0.877; for the KP Performed Corpus, the loss of
length information had a greater effect, riducendo
performance from 0.908 A 0.743.

Efforts are also underway to improve the Me-
lisma model through the incorporation of other fac-
tori. One obvious factor to include is harmony. È

generally agreed that harmonic structure can
greatly inﬂuence metrical structure (particularly at
higher metrical levels), in that strong beats tend to
be perceived at points of harmonic change (Lerdahl
and Jackendoff 1983; Temperley 2001). To incorpo-
rate the inﬂuence of harmony, the KP Corpus was
run through the Melisma harmony program, creat-
ing a harmonic analysis of segments labeled with
roots; the notelists plus harmonic information were
then ‘‘piped’’ back into the meter program, modi-
ﬁed to include a preference for strong beats on
changes of harmony. After some parameter tweak-
ing, the best performance that could be obtained is
shown in Table 2 for both the KP Corpus and the
KP Performed Corpus. For both corpora, it can be
seen that the score for level 2 is indeed somewhat
improved, but scores for levels 3 E 1 are wors-
ened; overall, the ‘‘harmonic-factor’’ model and the
default model are roughly equal in performance
(the difference between their overall scores is less
di 1 percent for both the quantized and per-

Temperley

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

formed corpora). In situations such as this, a larger
corpus would be desirable; differences in perfor-
mance of 1 percent are probably not signiﬁcant on
the KP Corpus. (It would also be desirable to have
one large portion of the corpus for model develop-
ment and parameter-tuning, and another ‘‘held-
out’’ portion for testing.)

Conclusions

It is hoped that the system presented here will fa-
cilitate the testing and comparison of metrical
models. Although the system does have certain
limitations, as discussed above, it offers a rational
way of comparing metrical structures whose results
accord reasonably well with intuition. The KP Cor-
pus presented here also has limitations, particolarmente
the fact that it represents only common-practice
music, which may not be fair to the aims of some
metrical models. Ovviamente, the note-address sys-
tem could also be used with a different corpus (COME
illustrated by the tests on Beatles songs presented
above), providing that the corpus is annotated with
note-address information. Notice that the system
does not in any way require note addresses with
ﬁve levels; it could function perfectly well with,
Dire, three levels.

Perhaps the greatest limitation of the note-

address system is that it is limited to symbolic in-
put. This is unfortunate, given the considerable
number of models proposed in recent years that
take audio data as input. The note-address system
could, in principle, be used with audio models. IL
problem is that the indeterminacy of beat locations
encountered with symbolic input is vastly greater
with audio input. Even with a single note, under-
stood as coinciding with a beat, it is often unclear
where exactly the note begins (and thus where the
beat is located). To solve this problem, the input
ﬁles would have to be annotated with markers in-
dicating the beat positions; at this point the ap-
proach becomes very similar to that of Goto and
Muraoka (1997). Tuttavia, the idea of note ad-
dresses might still be useful; even with audio in-
put, one might argue that some beat locations are
more certain than others (per esempio., the location of a beat

that coincides with a note is more certain than a
beat that does not), and a metrical model should
perhaps only be evaluated on its identiﬁcation of
the more certain ones. Another problem is that, In
the symbolic-input case, the model is given the ad-
dress locations—i.e., the note onsets—whereas in
the audio-input case, it is part of the model’s task
to ﬁnd these locations. (In the audio situation, UN
model might assert an address where there was not
one or fail to assert one where there was one.)
Così, the usefulness of the note-address system for
audio-input metrical models remains to be seen.

Ringraziamenti

Thanks are due to Henkjan Honing for valuable

feedback on an earlier version of this article.

Riferimenti

Allen, P., and R. Dannenberg. 1990. ‘‘Tracking Musical

Beats in Time.’’ Proceedings of the 1990 Internazionale
Computer Music Conference. San Francisco: Interna-
tional Computer Music Association, pag. 140–143.
Black, E., et al. 1991. ‘‘A Procedure for Quantitatively

Comparing the Syntactic Coverage of English Gram-
mars.’’ Proceedings of the Fourth DARPA Speech and
Natural Language Workshop. San Francisco: Morgan
Kauffman, pag. 306–311.

Brown, J. C. 1993. ‘‘Determination of the Meter of Musi-
cal Scores by Autocorrelation.’’ Journal of the Acousti-
cal Society of America 94:1953–1957.

Cemgil, UN. T., P. Desain, and B. Kappen. 2000UN. ‘‘Rhythm

Quantization for Transcription.’’ Computer Music
Journal 24(2):60–76.

Cemgil, UN. T., et al. 2000B. ‘‘On Tempo Tracking: Tem-

pogram Representation and Kalman Filtering.’’ Journal
of New Music Research 29:259–273.

Chafe, C., B. Mont-Reynaud, and L. Rush. 1982. ‘‘Toward
an Intelligent Editor of Digital Audio: Recognition of
Musical Constructs.’’ Computer Music Journal
6(1):30–41.

Desain, P., and H. Honing. 1989. ‘‘The Quantization of

Musical Time: A Connectionist Approach.’’ Computer
Music Journal 13(3):56–66.

Desain, P., and H. Honing. 1999. ‘‘Computational Models

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

of Beat Induction: The Rule-Based Approach.’’ Journal
of New Music Research 28:29–42.

Dixon, S. 2001UN. ‘‘Automatic Extraction of Tempo and
Beat from Expressive Performances.’’ Journal of New
Music Research 30:39–58.

Dixon, S. 2001B. ‘‘An Empirical Comparison of Tempo

Trackers.’’ Eighth Brazilian Symposium on Computer
Music, n.p., 832–840.

Eck, D. 2001. ‘‘A Positive-Evidence Model for Rhythmi-
cal Beat Induction.’’ Journal of New Music Research
30:187–200.

McAuley, J. 1994. ‘‘Time as Phase: A Dynamic Model of
Time Perception.’’ Proceedings of the Sixteenth An-
nual Meeting of the Cognitive Science Society. Hills-
dale, NJ: Erlbaum, pag. 607–612.

Mugnaio, B. O., D. l. Scarborough, and J. UN. Jones. 1992.

‘‘On the Perception of Meter.’’ In M. Balaban,
K. Ebcioglu, and O. Laske, eds. Understanding Music
with AI: Perspectives on Music Cognition. Cambridge,
Massachussetts: AAAI Press, pag. 428–447.

Palmer, C. 1997. ‘‘Music Performance.’’ Annual Review

of Psychology 48:115–138.

Gabrielsson, UN. 1973. ‘‘Studies in Rhythm.’’ Acta Univ-

Palmer, C., and P. Q. Pfordresher. 2003. ‘‘Incremental

ersitatis Upsaliensis 7:3–19.

Goto, M. 2001. ‘‘An Audio-Based Real-Time Beat Track-
ing System for Music with or without Drum-Sounds.’’
Journal of New Music Research 30:159–171.

Goto, M., and Y. Muraoka. 1997. ‘‘Issues in Evaluating

Beat Tracking Systems.’’ IJCAI-97 Workshop in Issues
in AI and Music—Evaluation and Assessment, n.p.,
9–16.

Heijink, H., et al. 2000. ‘‘Make Me a Match: An Evalua-
tion of Different Approaches to Score-Performance
Matching.’’ Computer Music Journal 24(1):43–56.

Jones, M. R., et al. 2002. ‘‘Temporal Aspects of Stimulus-
Driven Attending in Dynamic Arrays.’’ Psychological
Scienza 13:313–319.

Planning in Sequence Production.’’ Psychological Re-
view 110:683–712.

Parncutt, R. 1994. ‘‘A Perceptual Model of Pulse Salience
and Metrical Accent in Musical Rhythms.’’ Music Per-
ception 11:409–464.

Povel, D.-J., and P. Essens. 1985. ‘‘Perception of Tempo-

ral Patterns.’’ Music Perception 2:411–440.

Raphael, C. 2001. ‘‘Automated Rhythm Transcription.’’
Proceedings of the 2nd Annual International Sympo-
sium on Music Information Retrieval. Bloomington,
Indiana: Indiana University, pag. 99–107.

Rosenthal, D. 1992. ‘‘Emulation of Human Rhythm Per-

ception.’’ Computer Music Journal 16(1):64–76.

Rowe, R. 1993. Interactive Music Systems. Cambridge,

Kostka, S., and D. Payne. 1995. Workbook for Tonal Har-

Massachusetts: CON Premere.

mony. New York: McGraw–Hill.

Large, E. W., and J. F. Kolen. 1994. ‘‘Resonance and the
Perception of Musical Meter.’’ Connection Science
6:177–208.

Lee, C. 1991. ‘‘The Perception of Metrical Structure:

Experimental Evidence and a Model.’’ In P. Howell,
R. West, and I. Cross, eds. Representing Musical Struc-
ture. London: Academic Press, pag. 59–127.

Lerdahl, F., and R. Jackendoff. 1983. A Generative The-
ory of Tonal Music. Cambridge, Massachusetts: MIT
Press.

Longuet-Higgins, H. C. 1976. ‘‘Perception of Melodies.’’

Nature 263:646–653.

Longuet-Higgins, H. C., and C. S. Lee. 1982. ‘‘The Per-

ception of Musical Rhythms.’’ Perception 11:115–128.
Longuet–Higgins, H. C., and M. J. Steedman. 1971. ‘‘On
Interpreting Bach.’’ Machine Intelligence 6:221–41.
Equipaggio, C. D., and H. Schu¨ tze. 2000. Foundations of
Statistical Natural Language Processing. Cambridge,
Massachusetts: CON Premere.

Marcus, M. P., B. Santorini, and M. UN. Marcinkiewicz.

1993. ‘‘Building a Large Annotated Corpus of English:
The Penn Treebank.’’ Computational Linguistics
19:313–330.

Scheirer, E. D. 1998. ‘‘Tempo and Beat Analysis of

Acoustic Musical Signals.’’ Journal of the Acoustical
Society of America 103:588–601.

Sethares, W. A., and T. W. Staley. 2001. ‘‘Meter and Peri-
odicity in Musical Performance.’’ Journal of New Mu-
sic Research 30:149–158.

Sloboda, J. UN. 1983. ‘‘The Communication of Musical
Metre in Piano Performance.’’ Quarterly Journal of
Experimental Psychology 35:377–396.

Spiro, N. 2002. ‘‘Combining Grammar-Based and

Memory-Based Models of Perception of Time Signa-
ture and Phase.’’ In C. Anagnostopoulou, M. Ferrand,
e A. Smaill, eds. Music and Artiﬁcial Intelligence.
Berlin: Springer, pag. 183–194.

Steedman, M. 1977. ‘‘The Perception of Musical Rhythm

and Metre.’’ Perception 6:555–569.

Temperley, D. 2001. The Cognition of Basic Musical
Structures. Cambridge, Massachusetts: CON Premere.
Temperley, D., and D. Sleator. 1999. ‘‘Modeling Meter
and Harmony: A Preference-Rule Approach.’’ Com-
puter Music Journal 23(1):10–27.

van Zaanen, M., R. Bod, and H. Honing. 2003. ‘‘A

Memory-Based Approach to Meter Induction.’’ Pro-
ceedings of ESCOM 2003, n.p., pag. 250–253.

Temperley

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
8
3
2
8
1
8
5
4
1
3
7
0
1
4
8
9
2
6
0
4
1
7
9
0
6
2
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Appendix A

All of the materials (data ﬁles and programs) Di-
scribed here are available at the Melisma Web site,
www.link.cs.cmu.edu/melisma. (Programs are writ-
ten in C and are available in source form.) These
include the following:

1. Noteﬁles for the complete KP Corpus

(noteﬁles/kp) and KP Performed Corpus
(noteﬁles/kp-perf). (These ﬁles are also
available as MIDI ﬁles: midiﬁles/kp,
midiﬁles/kp-perf.)

2. The correct note-address ﬁles for the KP

Corpus and KP Performed Corpus (naﬁles/
kp-correct, naﬁles/kp-perf-correct).

3. compare-na: a program that compares two
note-address ﬁles and evaluates their simi-
larity.

4. tally-na: a program that takes a series of

outputs of compare-na and averages them.

5. The source code for the Melisma meter-

ﬁnding program.

6. gen-add: a program for generating note-

address ﬁles from the ‘‘note-beat ﬁles’’ (note-
list plus beatlist) produced by the Melisma
meter program. (This could be useful for
those who wish to experiment with modiﬁ-
cations of the Melisma program. It may also
be useful, perhaps with some alterations, A
those whose models already produce a note-
beat ﬁle or something similar to it and who
wish to convert this to note-address format.)