Communicated by Richard Andersen
Computing Optical Flow in the Primate Visual
System
H. Taichi Wang
Bimal Mathur
Science Center, Rockwell International, Thousand Oaks, CA 91360, USA
Christof Koch
Computation and Neural Systems Program,
Divisions of Biology and Engineering and Applied Sciences, 21 6-76,
California Institute of Technology, Pasadena, CA 91 125, USA
Computing motion on the basis of the time-varying image intensity is
a difficult problem for both artificial and biological vision systems. Noi
show how gradient models, a well known class of motion algorithms,
can be implemented within the magnocellular pathway of the primate’s
visual system. Our cooperative algorithm computes optical flow in
two steps. In the first stage, assumed to be located in primary visual
cortex, local motion is measured while spatial integration occurs in
the second stage, assumed to be located in the middle temporal area
(MT). The final optical flow is extracted in this second stage using
population coding, such that the velocity is represented by the vector
sum of neurons coding for motion in different directions. Our theory,
relating the single-cell to the perceptual level, accounts for a number of
psychophysical and electrophysiological observations and illusions.
1 introduzione
In recent years, a number of theories have been advanced at both the
computational and the psychophysical level, explaining aspects of bi-
ological motion perception (for a review see Ullman 1981; Nakayama
1985; Hildreth and Koch 1987). One class of motion algorithms exploit
the relation between the spatial and the temporal intensity change at
a particular point (Fenneman and Thompson 1979; Horn and Schunck
1981; Marr and Ullman 1981; Hildreth 1984). In this article we address
in detail how these algorithms can be mapped onto neurons in striate
and extrastriate primate cortex (Ballard et al. 1983).
Our neuronal implementation is derived from the most common ver-
sion of the gradient algorithm, proposed within the framework of ma-
chine vision (Horn and Schunck 1981). Due to the ”aperture” prob-
lem inherent in their definition of optical flow, only the component of
Neural Cornputation 1, 92-103 (1989) @ 1989 Massachusetts Institute of Technology
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
N
e
C
o
1
9
8
9
1
1
9
2
P
D
.
.
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Computing Optical Flow in the Primate Visual System
93
motion along the local spatial brightness gradient can be recovered. In
their formulation, optical flow is then computed by minimizing a two-
part quadratic variational functional. The first term forces the final op-
tical flow to be compatible with the locally measured motion compo-
nent (“constraint line term”), while the second term imposes the con-
straint that the final flow field should be as smooth as possible. Such as
“smoothness” O “continuity” constraint is common to most early vision
algorithms.
2 A Neural Network Implementation
Commensurate with this method, and in agreement with psychophys-
ical results (e.g. Welch 19891, our network extracts the optical flow in
two stages (Fig. 1). In a preliminary stage, the time-varying image
Z ( io , j ) is projected onto the retina and relayed to cortex via two neu-
ronal pathways providing information as to the spatial location of image
caratteristiche ( S neurons) and temporal changes in these features (T neurons):
S ( io , j ) = V 2 G * IO ( io , j ) and T ( io , j ) = a(V*G*I(io, j) )/ & , Dove * is the convo-
lution operator and G the 2-D Gaussian filter (Enroth-Cugell and Robson
1966; Marr and Hildreth 1980; Marr and Ullman 1981). In the first pro-
cessing stage, the local motion information is represented using a set of n
ON-OFF orientation- and direction-selective cells U , each with preferred
direction indicated by the unit vector o k :
where t is a constant and Vk is the spatial derivative along the direction
Ok. This derivative is approximated by projecting the convolved image
S ( io , j ) onto a “simple” type receptive field, consisting of a 1 by 7 pixel
positive (ON) subfield adjacent to a 1 by 7 pixel negative (OFF) subfield.
The cell U responds optimally if a bar or grating oriented at right angles
to Ok moves in direction Ok. Note that U is proportional to the product of
a transient cell ( T ) with a sustained simple cell with an odd-symmetric
receptive field, with an output proportional to the magnitude of local
component velocity (as long as \V&'(z,j)l > t). At each location i , j , N
such neurons code for motion in n directions. Equazione (2.1) differs from
the standard gradient model in which U = – T / V k S , by including a gain
control term, T, such that U does not diverge if the stimulus contrast de-
creases to zero. t is set to a fixed fraction of the square of the maximal
magnitude of the gradient V S for all values of z,j. Our gradient-like
scheme can be approximated for small enough values of the local con-
trast (i.e. if lVS(io,j)12 < e), by -T(z,j)VkS(z,j). Under this condition, our
model can be considered a second-order model, similar to the correlation
or spatio-temporal energy models (Hassenstein and Reichardt 1956; Pog-
gio and Reichardt 1973; Adelson and Bergen 1985; Watson and Ahumada
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
n
e
c
o
1
9
8
9
1
1
9
2
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
94
H. Taichi Wang, Bimal Mathur, Christof Koch
1985). We also require a set of n ON-OFF orientation- but not direction-
selective neurons E , with E ( i , j , k ) = IVkS(i, j ) ] , where the absolute value
ensures that these neurons only respond to the magnitude of the spatial
gradient, but not to its sign.
We assume that the final optical flow field is computed in a second
stage, using a population coding scheme such that the velocity is repre-
sented within a set of n‘ neurons V at location i , j , each with preferred
direction Ok with V(i, j) = ETLl V ( i , j , k)@k. Note that the response of any
individual cell V ( i , j , k ) is not the projection of the velocity field V(i, j)
onto Ok. For any given visual stimulus, the state of the V neurons is de-
termined by minimizing the neuronal equivalent of the above mentioned
variational functional. The first term, enforcing the constraint that the fi-
nal optical flow should be compatible with the measured data, has the
form:
k ) -
(2.2)
where cos(k’ - k ) is a shorthand for the cos of the angle between @k’ and
@k. The term E2(i, j , k ) ensures that the local motion components U ( i , j , k )
only have an influence when there is an appropriate oriented local pat-
tern; thus E2 prevents velocity terms incompatible with the measured
data from contributing significantly to Lo. In order to sharpen the ori-
entation tuning of E , we square the output of E (the orientation tuning
curve of E has a half-width of about 60”).
The smoothness term, minimizing the square of the first derivative of
the optical flow (Horn and Schunck 1981) takes the following form:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
n
e
c
o
1
9
8
9
1
1
9
2
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Our algorithm computes the state of the V neurons that minimizes Lo +
XLI (A is a free parameter, usually set at 10). We can always find
this state by evolving V ( i , j , k ) on the basis of the steepest descent rule:
dV/at = -a(& + XLI)/dV. Since the variational functional is quadratic
in V, the right hand side in the above differential equation is linear in
V. Conceptually, we can think of the coefficients of this linear equation
as synaptic weights, while the left hand side can be interpreted as a ca-
pacitive term, determining the dynamics of our model neurons. In other
words, the state of the V neurons evolve by summating the synaptic con-
tribution from E , U and neighboring V neurons and updating its state
accordingly. Thus, the system ”relaxes” into its final and unique state.
To mimic neuronal responses more accurately, the output of our model
neurons S, T , E , U , and V is set to zero if the net input is negative.
Computing Optical Flow in the Primate Visual System
95
K i l K K - 1
. . . 1i.j) lir . . .
. . . . . . . . . . . . . . . .
u. E
90"
I
i
b
V
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
n
e
c
o
1
9
8
9
1
1
9
2
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
270"
MT NEURON
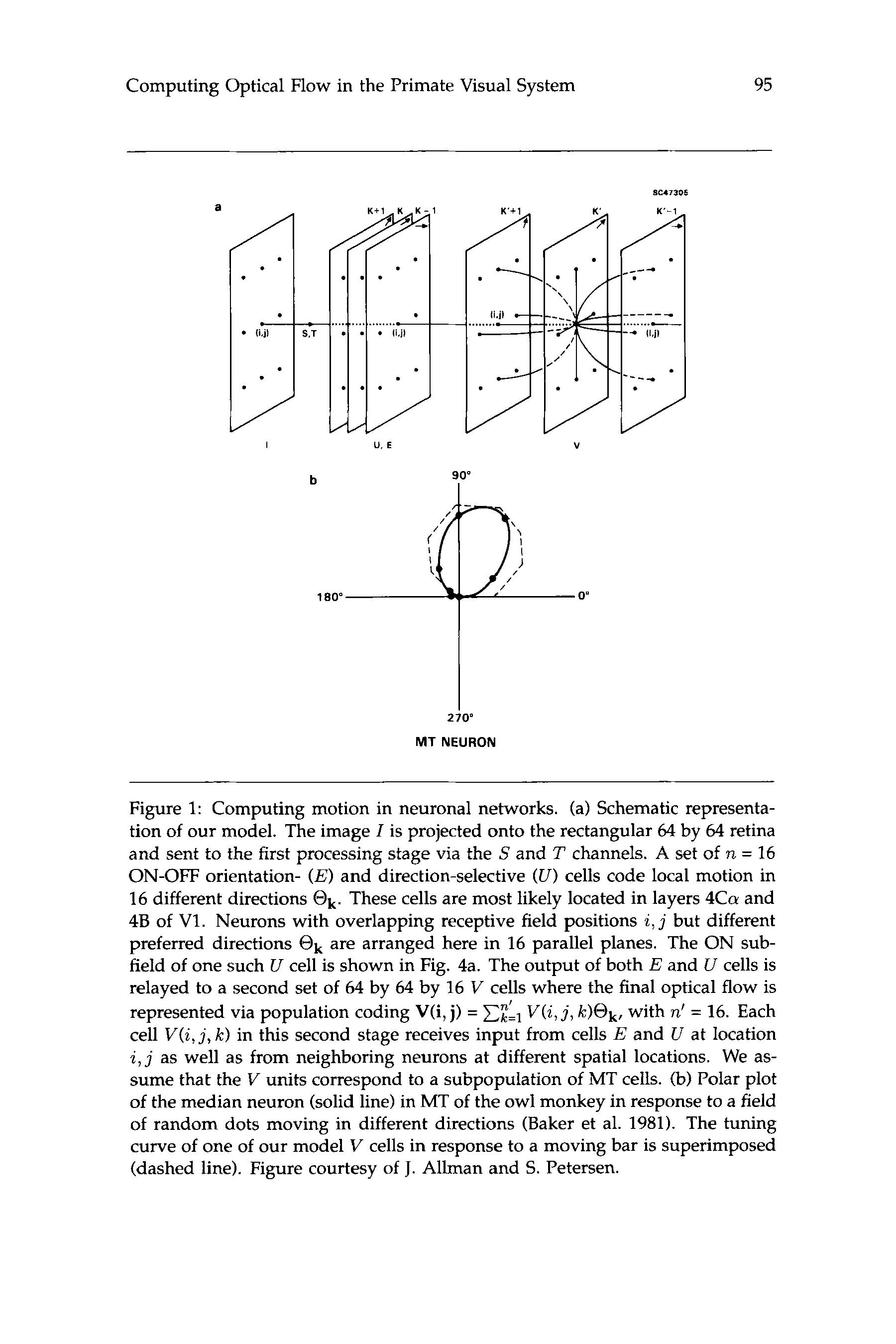
Figure 1: Computing motion in neuronal networks. (a) Schematic representa-
tion of our model. The image Z is projected onto the rectangular 64 by 64 retina
and sent to the first processing stage via the S and T channels. A set of n = 16
ON-OFF orientation- ( E ) and direction-selective (U) cells code local motion in
16 different directions @k. These cells are most likely located in layers 4Ca and
48 of V1. Neurons with overlapping receptive field positions i, j but different
preferred directions @k are arranged here in 16 parallel planes. The ON sub-
field of one such U cell is shown in Fig. 4a. The output of both E and U cells is
relayed to a second set of 64 by 64 by 16 V cells where the final optical flow is
V ( i , j , k ) @ k , with n' = 16. Each
represented via population coding V(i, j) = J&
cell V ( i , j , k ) in this second stage receives input from cells E and U at location
i , j as well as from neighboring neurons at different spatial locations. We as-
sume that the V units correspond to a subpopulation of MT cells. (b) Polar plot
of the median neuron (solid line) in MT of the owl monkey in response to a field
of random dots moving in different directions (Baker et al. 1981). The tuning
curve of one of our model V cells in response to a moving bar is superimposed
(dashed line). Figure courtesy of J. Allman and S. Petersen.
96
H. Taichi Wang, Bimal Mathur, Christof Koch
3 Physiology and Psychophysics
Since the magnocellular pathway in primates is the one processing mo-
tion information (Livingstone and Hubel 1988; DeYoe and Van Essen
1988) we assume that the U and E neurons would be located in layers
4Ca and 4B of V1 (see also Hawken et al. 1988) and the V neurons in area
MT, which contains a very high fraction of direction- and speed-tuned
neurons (Allman and Kass 1971; Maunsell and Van Essen 1983). All 2n
neurons U and E with receptive field centers at location i, j then project
to the n’ MT cells V in an excitatory or inhibitory (via interneurons) man-
ner, depending on whether the angle between the preferred direction of
motion of the pre- and post-synaptic neuron is smaller or larger than
190”1.’ Anatomically, we then predict that each MT cell receives input
from V1 (or V2) cells located in all different orientation-columns. The
smoothness constraint of equation (3) results in massive interconnections
among neighboring V cells (Fig. la).
Our model can explain a number of perceptual phenomena. When
two identical square gratings, oriented at a fixed angle to each other, are
moved perpendicular to their orientation (Fig. 2a), human observers see
the resulting plaid pattern move coherently in the direction given by the
intersection of their local constraint lines (“velocity constraint combina-
tion rule”; in the case of two gratings moving at right angle at the same
velocity, the resultant is the diagonal; Adelson and Movshon 1982). The
response of our network to such an experiment is illustrated in figure 2:
the U cells only respond to the local component of motion (component se-
lectivity; Fig. 2b), while the V cells respond to the global motion (Fig. 2c),
as can be seen by computing the vector sum over all V cells at every lo-
cation (pattern selectivity; Fig. 2d). About 30% of all MT cells do respond
in this manner, signaling the motion of the coherently moving plaid pat-
tern (Movshon et al. 1985). In fact, under the conditions of rigid motion
in the plane observed in Adelson and Movshon’s experiments, both their
“velocity space combination rule” and the “smoothness” constraint con-
verge to the solution perceived by human observers (for more results see
Wang et al. 1989). Given the way the response of the U neurons vary with
visual contrast (equation 2.1), our model predicts that if the two gratings
making up the plaid pattern differ in contrast, the final pattern velocity
will be biased in the direction of the component velocity of the grating
with the larger contrast. Recent psychophysical experiments support this
conjecture (Stone et al. 1988). It should be noted that the optical flow field
is not represented explicitly within neurons in the second stage, but only
implicitly, via vector addition.
Our algorithm reproduces both “motion capture” (Ramachandran and
‘The app;opriate weight of the synaptic connection between U and V is codk -
k’)U(k’)E ( k ). Various biophysical mechanisms can implement the required multi-
plicative interaction as well as the synaptic power law (Koch and Poggio 1987).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
n
e
c
o
1
9
8
9
1
1
9
2
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computing Optical Flow in the Primate Visual System
97
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
n
e
c
o
1
9
8
9
1
1
9
2
p
d
.
.
.
.
.
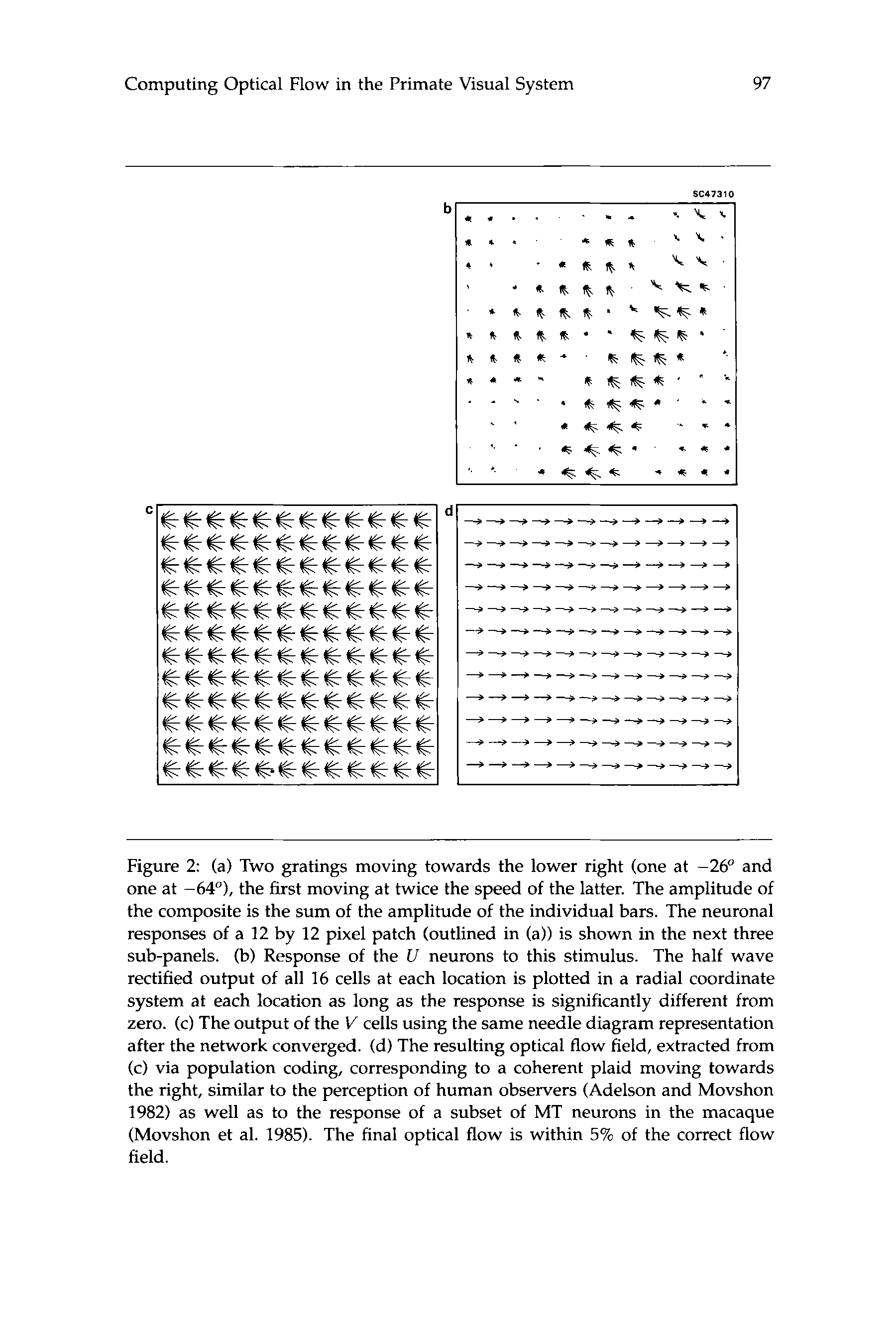
Figure 2: (a) Two gratings moving towards the lower right (one at -26" and
one at -64"), the first moving at twice the speed of the latter. The amplitude of
the composite is the sum of the amplitude of the individual bars. The neuronal
responses of a 12 by 12 pixel patch (outlined in (a)) is shown in the next three
sub-panels. (b) Response of the U neurons to this stimulus. The half wave
rectified output of all 16 cells at each location is plotted in a radial coordinate
system at each location as long as the response is significantly different from
zero. (c) The output of the V cells using the same needle diagram representation
after the network converged. (d) The resulting optical flow field, extracted from
(c) via population coding, corresponding to a coherent plaid moving towards
the right, similar to the perception of human observers (Adelson and Movshon
1982) as well as to the response of a subset of MT neurons in the macaque
(Movshon et al. 1985). The final optical flow is within 5% of the correct flow
field.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
98
H. Taichi Wang, Bimal Mathur, Christof Koch
Anstis 1983; see Wang et al. 1989) and “motion coherence” (Williams and
Sekuler 19841, as illustrated in figure 3. As demonstrated previously,
these phenomena can be explained, at least qualitatively, by a smoothness
or local rigidity constraint (Yuille and Grzywacz 1988; Biilthoff et al.
1989). Finally, y motion, a visual illusion first reported by the Gestalt
psychologists (Lindemann 1922; Kofka 1931; for a related illusion in man
and fly see Bulthoff and Gotz 1979), is also mimicked by our algorithm.
This illusion arises from the initial velocity measurement stage and does
not rely on the smoothness constraint.
Cells in area MT respond well not only to motion of a bar or grating
but also to a moving random dot pattern (Albright 1984; Allman et al.
1985). Similarly, our algorithm detects a random-dot figure moving over
a stationary random-dot background, as long as the spatial displacement
between two consecutive frames is not too large (Fig. 4). An interesting
distinction arises between direction-selective cells in V1 and MT. While
the optimal orientation in V1 cells is always perpendicular to their op-
timal direction, this is only true for about 60% of MT cells (type I cells;
Albright 1984; Rodman and Albright 1988). 30% of MT cells respond
strongly to flashed bars oriented parallel to the cells’ preferred direction
of motion (type I1 cells). If we identify our V cells with this MT subpop-
ulation, we predict that type I1 cells should respond to an extended bar
(or grating) moving parallel to its edge (Fig. 4).
4 Discontinuities in the Optical Flow
The major drawback of all motion algorithms is the degree of smooth-
ness required, smearing out any discontinuities in the optical flow field,
such as those arising along occluding objects or along a figure-ground
boundary. It has been shown previously how this can be dealt with by
introducing the concept of line processes which explicitly code for the
presence of discontinuities in the motion field (Hutchinson et al. 1988;
see also Poggio et al. 1988). If the spatial gradient of the optical flow
between two neighboring points is larger than some threshold, the flow
field “is broken”; that is the process or ”neuron” coding for a motion
discontinuity at that location is switched on and no smoothing occurs. If
little spatial variation exists, the discontinuity remains off. The perfor-
mance of the original version of the Horn and Schunck version is greatly
improved using this idea (Hutchinson et al. 1988). Perceptually, it is
known that the visual system uses motion to segment different parts of
visual scenes (Baker and Braddick 1982; van Doorn and Koenderink 1983;
Hildreth 1984). But what about the possible cellular correlate of line pro-
cesses? Allman and colleagues (Allman et al. 1985) first described cells in
area MT in the owl monkey whose “true” receptive field extended well
beyond the classical receptive field as mapped with bar or spot stim-
uli. About half of all MT cells have an antagonistic direction-selective
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
n
e
c
o
1
9
8
9
1
1
9
2
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computing Optical Flow in the Primate Visual System
99
I
SC47304
I
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .
...................
.. I C C C e . . r r . * c C I . . .
* t e < e % G F
C f
F e q C e
-
eF-€ c c c c c F F-
. * ' C C C C .
.. ' F C C E ,
...... C I
...................
. . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . .
. * r . * .
.
.
.
.
.
.
.
.
I
I
I
1
Figure 3: (a) In "motion coherence," a cloud of dots is perceived to move in the
direction of their common motion component. In this sequence, all dots have
an upward velocity component, while their horizontal velocity component is
random. (b) The final velocity field only shows the motion component common
to all dots. Humans observe the same phenomena (Williams and Sekuler 1984).
(c) In 7-motion, a dark stimulus flashed onto a homogenously lit background
appears to expand (Lindemann 1922; Kofka, 1931). It will disappear with a
motion of contraction. (d) Our algorithm perceives a similar expansion when
a disk appears. The contour of the stimulus is projected onto the final optical
flow.
surround, such that the response of the cell to motion of a random dot
display or an edge within the center of the receptive field can be modi-
fied by moving a stimulus within a very large surrounding region. The
response depends on the difference in speed and direction of motion
between the center and the surround, and is maximal if the surround
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
n
e
c
o
1
9
8
9
1
1
9
2
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
100
H. Taichi Wang, Bimal Mathur, Christof Koch
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
.
,
.
.
.
.
.
.
.
. . . .
. . . . .
. . . .
. . . . . . . . , t
. . . .
. . . . .
. . . . .
. .
. . . . .
. . . .
. . . . .
' 6 , * & . . . . . . .
. . . .
. . . . . . . . . . . . . . . . . . .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
'
I
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
n
e
c
o
1
9
8
9
1
1
9
2
p
d
.
.
.
.
.
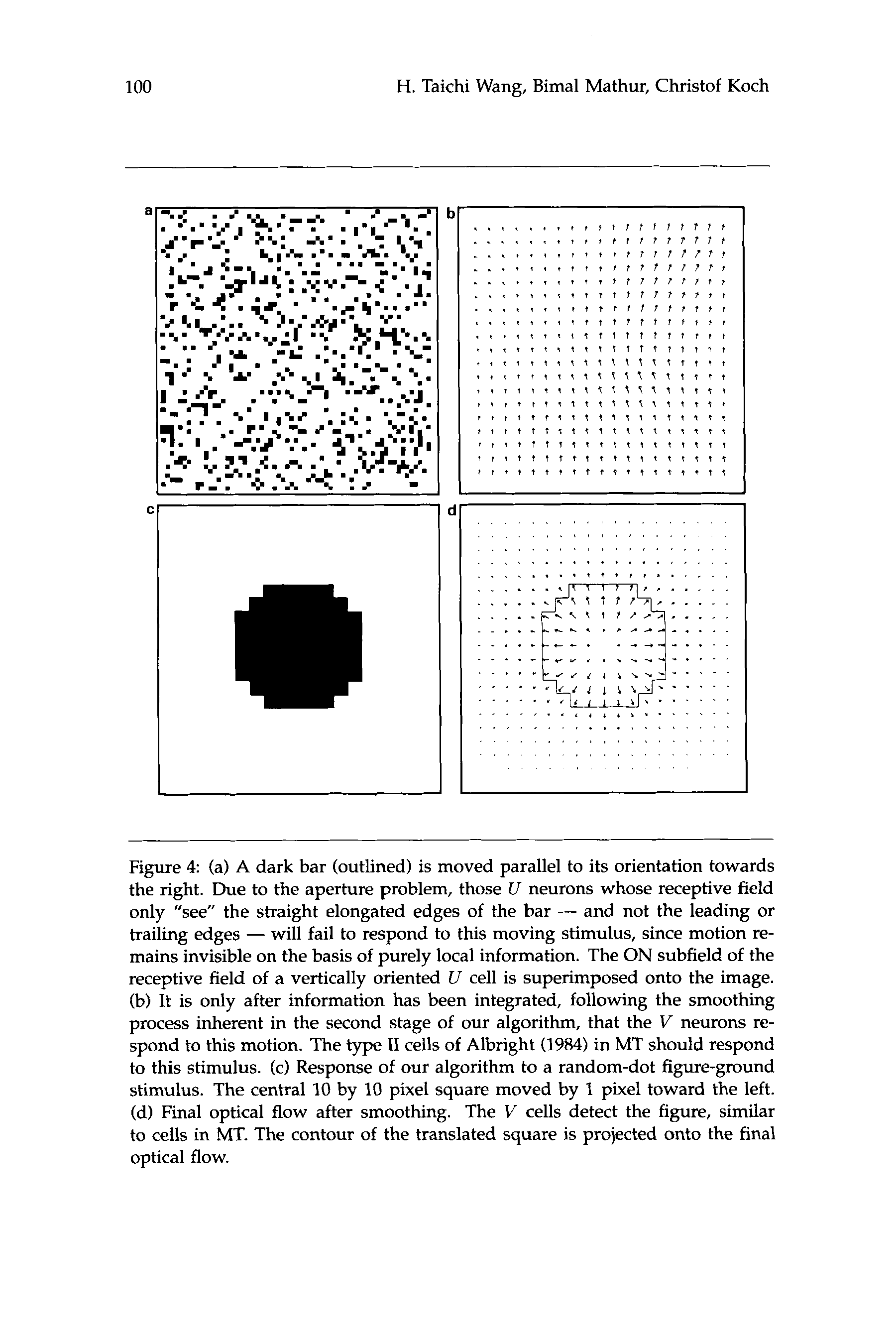
Figure 4 (a) A dark bar (outlined) is moved parallel to its orientation towards
the right. Due to the aperture problem, those U neurons whose receptive field
only "see" the straight elongated edges of the bar - and not the leading or
trailing edges - will fail to respond to this moving stimulus, since motion re-
mains invisible on the basis of purely local information. The ON subfield of the
receptive field of a vertically oriented U cell is superimposed onto the image.
(b) It is only after information has been integrated, following the smoothing
process inherent in the second stage of our algorithm, that the V neurons re-
spond to this motion. The type I1 cells of Albright (1984) in MT should respond
to this stimulus. (c) Response of our algorithm to a random-dot figure-ground
stimulus. The central 10 by 10 pixel square moved by 1 pixel toward the left.
(d) Final optical flow after smoothing. The V cells detect the figure, similar
to cells in MT. The contour of the translated square is projected onto the final
optical flow.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computing Optical Flow in the Primate Visual System
101
moves at the same speed as the stimulus in the center but in the oppo-
site direction. Thus, tantalizing hints exist as to the possible neuronal
basis of motion discontinuities.
Recently, two variations of Horn and Schuncks (1981) original algo-
rithm have been proposed, based on computational considerations (Uras
et al. 1988; Yuille and Grzywacz 1988). Both algorithms can be mapped
onto the neuronal network we have proposed, with minimal changes ei-
ther in the U stage (Uras et al. 1988) or by increasing the connectivity
among more distant V cells (Yuille and Grzywacz 1988). It remains an
open challenge to provide both psychophysical and electrophysiologi-
cal evidence to evaluate the validity of these and similar schemes (e.g.
Nakayama and Silverman 1988). We are currently trying to extend our
model to account for the intriguing phenomena of ”motion transparency,”
such as when two fields of random dots moving in opposite directions
are perceived to form the 3-D motion field associated with a transparent
and rotating cylinder (Siege1 and Andersen 1988).
Acknowledgments
We thank John Allman, David Van Essen, and Alan Yuille for many
fruitful discussions and Andrew Hsu for computing the figure-ground
response. Support for this research came from NSF grant EET-8700064,
ONR Young Investigator Award and NSF Presidential Young Investigator
Award to C.K.
References
Adelson, E.H. and J.R. Bergen. 1985. Spatio-temporal Energy Models for the
Perception of Motion. J. Opt. SOC. Am. A 2, 284299.
Adelson, E.H. and J.A. Movshon. 1982. Phenomenal Coherence of Moving
Visual Patterns. Nature 200, 523-525.
Albright, T.L. 1984. Direction and Orientation Selectivity of Neurons in Visual
Area MT of the Macaque. 1. Neurophysiol. 52, 1106-1130.
Allman, J.M. and J.H. Kass. 1971. Representation of the Visual Field in the
Caudal Third of the Middle Temporal Gyms of the Owl Monkey (Aotus
trivirgatus). Bruin Res. 31, 85-105.
Allman, J., F. Miezin, and E. McGuinness. 1985. Direction- and Velocity-specific
Responses from Beyond the Classical Receptive Field in the Middle Tempo-
ral Area (MT). Perception 14, 105-126.
Ballard, D.H., G.E. Hinton, and T.J. Sejnowski. 1983. Parallel Visual Computa-
tion. Nature 306, 21-26.
Baker, C.L. and O.J. Braddick. 1982. Does Segregation of Differently Moving
Areas Depend on Relative or Absolute Displacement. Vision Res. 7,851-856.
Baker, J.F., S.E. Petersen, W.T. Newsome, and J.M. Allman. 1981. Visual Re-
sponse Properties of Neurons in Four Extrastriate Visual Areas of the Owl
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
n
e
c
o
1
9
8
9
1
1
9
2
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
102
H. Taichi Wang, Bimal Mathur, Christof Koch
Monkey (Aotus trivirgatus): A Quantitative Comparison of Medial, Dor-
somedial, Dorsolateral, and Middle Temporal Areas. J. Neurophysiol. 45,
397416.
Bulthoff, H.H., J.J. Little, and T. Poggio. 1989. Parallel Computation of Motion:
Computation, Psychophysics and Physiology. Nature, in press.
Bulthoff, H.H. and K.G. Gotz. 1979. Analogous Motion Illusion in Man and
Fly. Nature 278, 636-638.
DeYoe, E.A. and D.C. Van Essen. 1988. Concurrent Processing Streams in
Monkey Visual Cortex. Trends Neurosci. 11, 219-226.
Enroth-Cugell, C. and J.G. Robson. 1966. The Contrast Sensitivity of Retinal
Ganglion Cells of the Cat. 1. Physiol. (Lond.) 187, 517-552.
Fennema, C.L. and W.B. Thompson. 1979. Velocity Determination in Scenes
Containing Several Moving Objects. Comput. Graph. Image Proc. 9,301-315.
Hassenstein, B. and W. Reichardt. 1956. Systemtheoretische Analyse der Zeit-,
Reihenfolgen- und Vorzeichenauswertung bei der Bewegungsperzeption des
Russelkafers Chlorophanus. Z. Naturforschung l l b , 513-524.
Hildreth, E.C. 1984. The Measurement of Visual Motion. Cambridge, MA: MIT
Press.
Hildreth, E.C. and C. Koch. 1987. The Analysis of Visual Motion. Ann. Rev.
Neurosci. 10, 4777.53
Horn, B.K.P. and B.G. Schunck. 1981. Determining Optical Flow. Artif. Intell.
17, 185-20
Hutchinson, J., C. Koch, J. Luo, and C. Mead. 1988. Computing Motion using
Analog and Binary Resistive Networks. I E E E Computer 21, 52-61.
Koch, C. and T. Poggio. 1987. Biophysics of Computation. In: Synaptic Func-
tion, eds. G.M. Edelman, W.E. Gall, and W.M. Cowan, 637-698. New York
John Wiley.
Kofka, K. 1931. In: Handbuch der normalen und pathologischen Physiologie
12, eds. A. Bethe et al. Berlin: Springer.
Lindemann, E. 1922. Experimentelle Untersuchungen uber das Enstehen und
Vergehen von Gestalten. Psych. Forsch. 2, 5-60.
Livingstone, M. and D. Hubel. 1988. Segregation of Form, Color, Movement,
and Depth: Anatomy, Physiology and Perception. Science 240, 740-749.
Marr, D. and E.C. Hildreth. 1980. Theory of Edge Detection. Proc. R. SOC. Lond.
B 297, 181-217.
Marr, D. and S. Ullman. 1981. Directional Selectivity and its Use in Early Visual
Processing. Proc. R. SOC. Lond. B 211, 151-180.
Maunsell, J.H.R. and D. Van Essen. 1983b. Functional Properties of Neurons
in Middle Temporal Visual Area of the Macaque Monkey. 11. Binocular
Interactions and Sensitivity to Binocular Disparity. J. Neurophysiol. 49,1148-
1167.
Movshon, J.A., E.H. Adelson, M.S. Gizzi, and W.T. Newsome. 1985. The Anal-
ysis of Moving Visual Patterns. In: Exp. Brain Res. Suppl. 11: Pattern Recog-
nition Mechanisms, eds. C. Chagas, R. Gattass, and C. Gross, 117-151. Hei-
delberg: Springer.
Nakayama, K. 1985. Biological Motion Processing: A Review. Vision Res. 25,
625-660.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
n
e
c
o
1
9
8
9
1
1
9
2
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computing Optical Flow in the Primate Visual System
103
Nakayama, K. and G.H. Silverman. 1988. The Aperture Problem-11.
Spatial
Integration of Velocity Information along Contours. Vision Res. 28, 747-75
Poggio, T., E.B. Gamble, and J.J. Little. 1988. Parallel Integration of Visual
Modules. Science 242 337-340.
Poggio, T. and W. Reichardt. 1973. Considerations on Models of Movement
Detection. Kybernetik 13, 223-227.
Ramachandran, V.S. and S.M. Anstis. 1983. Displacement Threshold for Co-
herent Apparent Motion Motion in Random-dot Patterns. Vision Res. 12,
1719-1724.
Rodman, H. and T. Albright. 1989. Single-unit Analysis of Pattern-motion
Selective Properties in the Middle Temporal Area (MT). Exp. Brain Res., in
press.
Siegel, R.M. and R.A. Andersen. 1988. Perception of Three Dimensional Struc-
ture from Motion in Monkey and Man. Nature 331, 259-261.
Stone, L.S., J.B. Mulligan, and A.B. Watson. 1988. Neural Determination of the
Direction of Motion: Contrast Affects the Perceived Direction of Motion.
Neurosci. Abstr. 14, 502.5.
Ullman, S. 1981. Analysis of Visual Motion by Biological and Computer Sys-
tems. I E E E Computer 14, 57-69.
Uras, S., F. Girosi, A. Verri, and V. Torre. 1988. A Computational Approach to
Motion Perception. Btol. Cybern. 60, 79-87.
van Doorn, A.J. and J.J. Koenderink. 1983. Detectability of Velocity Gradients
in Moving Random-dot Patterns. Vision Res. 23, 799-804.
Wang, H.T., B. Mathur, A. Hsu, and C. Koch. 1989. Computing Optical Flow in
the Primate Visual System: Linking Computational Theory with Perception
and Physiology. In: The Computing Neurone, eds. R. Durbin, C. Miall, and
G. Mitchinson. Reading: Addison-Wesley. In press.
Watson, A.B. and A.J. Ahumada. 1985. Model of Human Visual-motion Sensing.
J. Opt. SOC. Am. A 2, 322-341.
Welch, L. 1989. The Perception of Moving Plaids Reveals Two Motion Process-
ing Stages. Nature, in press.
Williams, D. and R. Sekuler. 1984. Coherent Global Motion Percepts from
Stochastic Local Motions. Vision Res. 24, 55-62.
Yuille, A.L. and N.M. Grzywacz. 1988. A Computational Theory for the Per-
ception of Coherent Visual Motion. Nature 333, 71-73.
Received 28 October; accepted 6 December 1988.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
9
2
8
1
1
8
3
5
n
e
c
o
1
9
8
9
1
1
9
2
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3