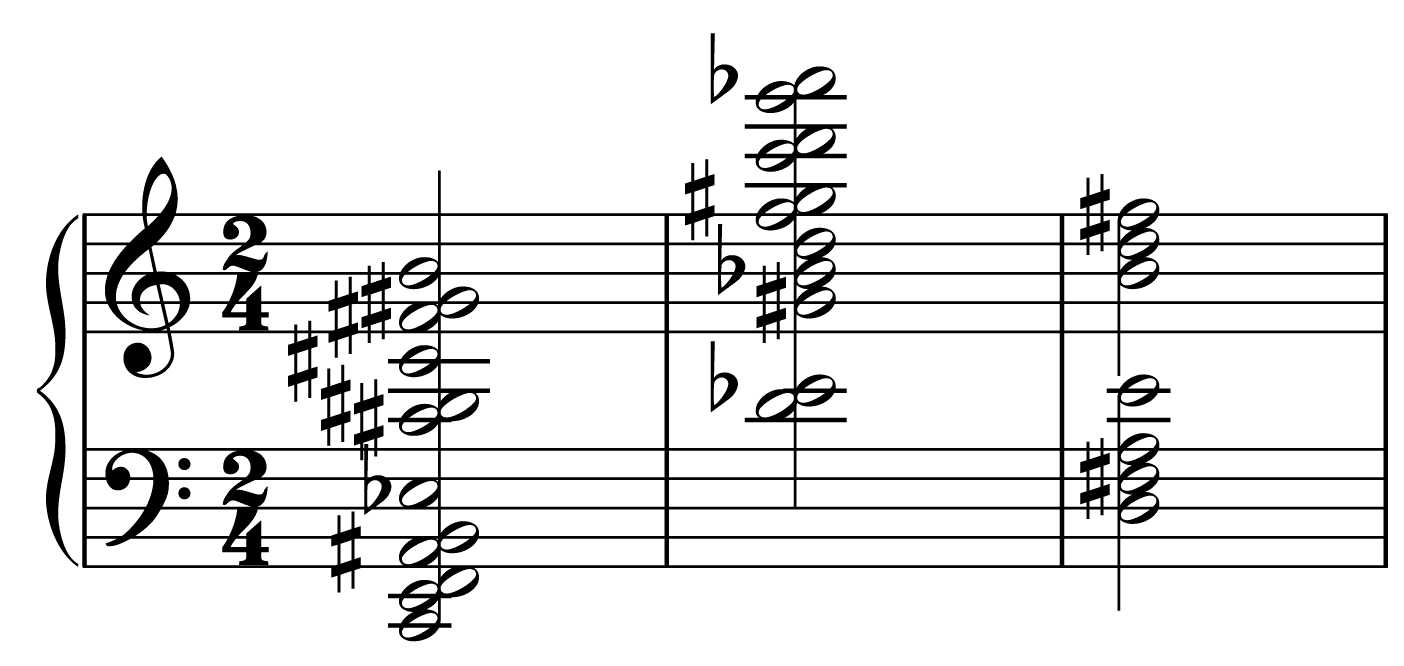Christopher Ariza - Ricerca sull'intelligenza artificiale specializzata al MIT

Christopher Ariza
New York University
Graduate School of Arts and Science,
Music Department
24 Waverly Place, Room 268
New York, New York 10003 USA
ariza@ﬂexatone.net

The Xenakis Sieve as
Object: A New Model and a
Complete Implementation

In numerous publications from 1965 A 1992, com-
poser, architect, and theorist Iannis Xenakis (1922–
2001) developed an elegant and powerful system for
creating integer-sequence generators called sieves.
Xenakis used sieves (cribles) for the generation of
pitch scales and rhythm sequences in many compo-
sitions, and he suggested their application to a vari-
ety of additional musical parameters. Though sieves
are best calculated with the aid of a computer, NO
complete implementation has been widely distrib-
uted. Xenakis’s published code is incomplete and
insufﬁcient for broad use.

This article demonstrates a new object-oriented
model and Python implementation of the Xenakis
sieve. This model introduces a bi-faceted represen-
tation of the sieve, expands Xenakis’s use of logic
operators, employs a practical notation, produces
sieve segments and transpositions, and easily inte-
grates within higher-level systems. This modular
implementation is deployed within athenaCL, UN
cross-platform, open-source, interactive command-
line environment for algorithmic composition using
Csound and MIDI. High-level, practical interfaces
have been developed to provide athenaCL users with
sieve-based tools for the algorithmic generation of
pitches, rhythms, and general parameter values.

Definition of the Sieve

Xenakis’s theory changed over the course of his
many writings on the sieve. Procedures, notation,
and nomenclature varied as the theory developed,
yet often with inconsistent and unexplained usage.
To avoid the complexity of Xenakis’s presentation,
a sieve will be deﬁned with a new model and nota-
zione. New terms and concepts are introduced to re-
place Xenakis’s sometimes-inconsistent usage.
Alternative theoretical treatments of the sieve have
been proposed by others (Riotte 1979; Squibbs 1996;

Computer Music Journal, 29:2, pag. 40–60, Estate 2005
© 2005 Istituto di Tecnologia del Massachussetts.

Gibson 2001; Jones 2001; Andreatta 2003), Anche se
none have integrated a complete software model.
A sieve is a formula consisting of one or more
residual classes combined by logic operators. UN
residual class consists of two integer values, a mod-
ulus (M) and a shift (IO). The modulus can be any pos-
itive integer greater than or equal to 0; the shift, for
a modulus M greater than 0, can be any integer from
0 to M–1. A modulus and shift will be notated M@I,
read “modulus M at shift I.” A shift I greater than or
equal to M is replaced by the common residue, or I
% M. (All computational examples in this article
are given in the Python programming language,
where the “%” is the modulus operator. For ex-
ample: 13 % 12 == 1.)

The residual class deﬁnes an inﬁnite number se-
quence. Given a sequence generated by M@I, each
value in the sequence modulus M is equal to I. For
esempio, the residual class 3@0 deﬁnes an inﬁnite
sequence consisting of all integers x where x % 3 ==
0. The resulting sieve sequence is [ . . . , –6, –3, 0, 3,
6, . . . ]. A residual class with the same modulus and
a shift of 1, notated 3@1, produces a sequence
Dove, for each value x, X % 3 == 1, O [ . . . , –5, –2, 1,
4, 7, . . . ]. For any modulus M, there exist M unique
shifts (the values 0 to M–1). For each shift of M, UN
sequence of equally spaced integers is produced,
where the difference between any adjacent integers
is always M. A residual class produces a periodic se-
quence with a period equal to M.

Although modulus by zero, and thus zero-division,
is typically undeﬁned for real numbers (and an error
for computers), the residual class 0@0 is permitted,
deﬁning the empty sieve sequence: []. The residual
class 1@0, the complement of 0@0, deﬁnes the inﬁ-
nite integer sequence (cid:1).

Logic operators are used to combine residual
classes. Four operators are permitted: union (“or”),
intersection (“and”), symmetric difference (“xor”),
and complementation (“not”). Union, intersection,
and symmetric difference are binary operators;
complementation is a unary operator. The logic op-
erators will be notated “|” for union, “&” for inter-

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

section, “^” for symmetric difference, and “-” for
complementation.

Per esempio, the sieve 3@0 | 4@0 produces the
union of two residual classes, or the sieve sequence
[ . . . , 0, 3, 4, 6, 8, 9, 12, . . . ]. The intersection of the
same residual classes, notated 3@0 & 4@0, produces
the sieve sequence [ . . . , 0, 12, 24, . . . ]. The sym-
metric difference, or the values in each residual
class and not in both residual classes, notated 3@0 ^
4@0, produces the sieve sequence [ . . . , –3, 3, 4, 6, 8,
9, 15, . . . ].

Unlike union, intersection, and symmetric differ-

ence, unary complementation operates on a single
residual class or a group of residual classes. Binary
complementation is not permitted. The sieve se-
quence of a complemented residual class, –M@I, È
the sequence of all integers not in M@I. A residual
class under complementation, –M@I, is equivalent
to the union of all residual classes of the modulus (IO
from 0 to M–1) excluding the complemented resid-
ual class. Per esempio, –3@0 is equal to the sieve
3@1 | 3@2, or the sieve sequence [ . . . , –7, –5, –4, –2,
–1, 1, 2, 4, 5, 7, . . . ]. Likewise, –5@2 is equivalent to
the sieve 5@0 | 5@1 | 5@3 | 5@4.

Operator precedence, from most- to least-binding,

is in the following order: unary complementation,
intersection, symmetric difference, union. By using
braces (“{“ and “}") as delimiters, a sieve can employ
unlimited nesting. A delimited collection of resid-
ual classes is always evaluated before residual classes
on the same hierarchical level. Per esempio: 7@1 |
3@2 & 4@3 & –9@1 is evaluated 7@1 | {3@2 & 4@3 &
{–9@1}}. A delimited group can be complemented.

There exist two types of sieves: simple and com-

plex. A simple sieve uses at most a two-level, O-
dered grouping of residual classes, in which the
inner level uses intersection, the outer level uses
union, and complemented residual classes are never
intersected. A maximally simple sieve is made of
any number of single residual classes combined
only by union. A complex sieve uses residual
classes with any combination of logic operators at
any hierarchical level, with hierarchical levels of
unlimited depth.

A sieve ﬁlters the set of all integers to produce
an inﬁnite sieve sequence. As all residual classes
are periodic, all sieves are periodic. The period of a

sieve is equal to the lowest common multiple
(LCM) of all residual class moduli. In caso di
some sieves, the period is easily apparent. The sieve
3@2 | 4@1, Per esempio, has a period of 12. Nel
case of other sieves, Tuttavia, the period can be so
large as to be practically unrecognizable.

A sieve segment, or a ﬁnite contiguous section of a
sieve sequence, can be extracted for practical deploy-
ment. Rather than ﬁltering the all-integer set, a sieve
segment ﬁlters a ﬁnite range of integers. The set of
integers ﬁltered will be called z and is speciﬁed z =
[UN, . . . , B], where a is the minimum, and b is the
maximum. The sieve 3@2 | 4@1 with z = [–37, . . . ,
–25], produces the sieve segment [–37, –35, –34, –31,
–28, –27, –25].

The integers of a sieve segment can be thought of
as points; the remaining integers found in z but not
in the sieve segment can be thought of as slots. An
integer representation of a sieve segment provides
only the points, ignoring the slots. The internal slots
between integers can be deduced; external slots be-
yond the minimum and maximum of the sieve seg-
ment, Tuttavia, cannot be determined without
knowledge of z. If external slots are not represented,
Per esempio, the segment may appear symmetrical
Quando, in terms of its z-relative position, it is not.
There are four practical representations, or for-
mats, of a sieve segment. Three are slot-discarding:
integer, width, and unit segments; one is slot-
retaining: binary segments. Integer segments dis-
card external slots and may distort z-relative position.
Width segments measure the distance from one
point to the next, counting the point itself and the
intervening slots. Width segments, like integer seg-
menti, discard external slots and may distort z-
relative position. Unit segments map z to the unit
interval and translate segment points into real num-
bers between 0 E 1. Because unit segments do not
treat points as integers, both internal and external
slots are discarded, and z, normally discrete, becomes
a continuous range. A unit segment contains no in-
formation on the number of slots between points, yet
accurate proportional spacing, including z-relative
position, is retained. Binary segments retain all
slots, both internal and external, and thus provide
the must complete representation. Figura 1 summa-
rizes the features of sieve segment representations.

Ariza

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 1. Sieve segment for-
mats for sieve 3@2 | 4@1,
where z = [7, . . . , 16].

Format

Sieve segment

[8, 9, 11, 13, 14]

[1, 2, 2, 1]

integer

width

unit

binary

[0.11, 0.22, 0.44, 0.66, 0.77]

continuous

[0, 1, 1, 0, 1, 0, 1, 1, 0, 0]

discrete

Internal

External

slots

retain

discard

retain

slots

discard

retain

z-relative

position

discard

retain

A sieve can be transposed by any integer. A sieve
transposition is created by adding the transposition
value to the shift of each residual class in the sieve.
Per esempio, the sieve 5@2 & 2@0 produces the
sieve sequence [ . . . , 2, 12, 22, 32, 42, 52, . . . ]. If
this sieve is transposed by a value of 4, the sieve
5@1 & 2@0 results (modulus reduction of 5@6 &
2@4), producing the sieve sequence [ . . . , 6, 16, 26,
36, 46, 56, . . . ]. A transposition value will be
called n.

When z is discrete (integer, width, and binary seg-
menti), the integer step can be mapped to any value.
The integer step will be called the elementary dis-
placement, or ELD. When z is continuous (unit seg-
menti), points can function as ﬂoating-point scalars
of any value. Così, what a sieve creates is a sequence
of points on a line, a sequence of proportions between
these points, or a distribution of points within a
range. This sequence can be treated as an ordered or
unordered collection.

Simple and complex sieves can undergo compres-
sion. There are two forms of compression: by inter-
section and by segment. Compression always
results in the production of a maximally simple
sieve. A maximally simple sieve cannot be further
compressed. A sieve that has not been compressed
is an expanded sieve.

A simple sieve can be compressed by intersection.
Compression by intersection is a process of combin-
ing all residual classes within inner intersection
groups into a single residual class. A maximally
simple sieve, a collection of single residual classes
combined by union, risultati. Compression by inter-
section is non-lossy: sieve segments produced with
any z will be identical for both compressed and ex-
panded sieves.

A complex sieve can be compressed only by seg-

ment. Compression by segment requires generating
a sieve segment from a complex sieve, then re-
sampling the values within this set to produce a
maximally simple sieve. Compression by segment
can be lossy. The compressed and expanded sieves
will generate identical sieve segments only for the z
provided during compression. Segments generated
with the compressed sieve beyond this z may devi-
ate from segments generated with the expanded
sieve. Increasing the size of z, and thus the size of
the segment sampled, improves the quality of com-
pression. Compression by segment with a z-length
equal to the sieve period, or even multiple periods,
may not result in a compressed sieve that, Quando
compared to the expanded sieve, produces identical
segments for all z.

Sieve compression is deﬁned by two theorems pro-
vided by Xenakis. Primo, any two non-complemented
residual classes under intersection can be reduced
to a single residual class. It follows that any number
of residual classes, if intersected, can be reduced to
a single residual class. This is compression by inter-
section. Secondo, any ﬁnite integer set can be ex-
pressed as a maximally simple sieve. This is
compression by segment.

The Xenakis sieve is a set theory of inﬁnite peri-

odicities. This sieve is a unique structure. Cer-
tainly, the concept of selecting a collection of
numbers by removing elements from a set is com-
mon in mathematics (Hawkins 1958). Few mathe-
matical sieves, Tuttavia, have the sole goal of
creating geometrically and aesthetically pleasing
structures for sonic deployment. As Xenakis states,
“the image of a line with points on it, which is close
to the musician and to the tradition of music, È
very useful” (Xenakis 1996, P. 147). Such an image
is provided by the sieve.

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

History and Foundations of the Sieve

In 1963, Aaron Copland invited Xenakis to teach at
the Berkshire Music Center at Tanglewood. Xenakis’s
notes and sketches from that summer contain his
ﬁrst experiments with sieves (Barthel-Calvet 2001).
As a result of a Ford Foundation grant, Xenakis
lived in Berlin from the fall of 1963 to the spring of
1964. During this time, he developed sieve theory
ulteriore (Barthel-Calvet 2001). Xenakis’s theory of
sieves can be seen in the context of his interest in
number sequences, his use of logic operators with
screens and groups, and his desire to develop
“outside-time” musical structures.

The sieve produces numerical sequences. Xenakis’s

interest in the musical deployment of numerical
sequences has been frequently demonstrated. An
example can be seen in his prominent use of the Fi-
bonacci series in his early compositions Zyia (1952)
and Sacriﬁc (1953; see Solomos 2002, pag. 26–29).
Xenakis may have had a similar interest in the se-
ries of prime numbers. The sieve of Eratosthenes of
Cyrene (C. 276–c. 194 BCE), a well-known method
of generating prime numbers (Horsely 1772), may
have inspired Xenakis’s sieve (Flint 1989).

The sieve of Eratosthenes can be explained through

the following steps: (1) list a range of ordered inte-
gers starting from 1; (2) let M be 2; (3) then select M:
this value is prime; (4) eliminate all values that are
multiples of M (cioè., M × 2, M × 3, M × 4, . . . ); (5) set
M to the next available (cioè., not eliminated) value;
(6) if integers remain, return to step 3. After M ex-
hausts all available values, only primes will remain.
This process has features in common with the Xe-

nakis sieve. The collected multiples of M are simi-
lar to the periodic integers deﬁned by a residual
class; combining these prime-number multiples is
similar to the union of multiple residual classes.
Multiples are used here, Tuttavia, to generate slots,
not points, and they exclude their ﬁrst multiple (IL
prime).

The sieve combines structures with logic opera-
tori. Xenakis’s writings collected in the 1963 edi-
tion of Musiques Formelles demonstrate similar
combinations with different materials. Chapter 2,
“Markovian Stochastic Music,” introduces the con-
cept of screens (1963; 1990, P. 51). A screen repre-

sents a moment in time with a two-dimensional
plane of frequency and intensity; this plane can be
populated with events, or what Xenakis calls grains.
Xenakis employs the logic operators union, inter-
section, and complementation to “envisage in all its
generality the manner of combining and juxtaposing
screens” (1963; 1992, P. 57). Analogique A (1958)
and Analogique B (1959) are offered by Xenakis as
demonstrations of this technique (1963; 1992,
pag. 98–108). The sieve might be seen as a one-
dimensional screen. In chapter 3, “Symbolic Mu-
sic,” logic operators are further used by Xenakis to
combine groups of musical materials. The pitch
groups of Herma (1960–1961), for solo piano, are of-
fered by Xenakis as a demonstration of this tech-
nique (Xenakis 1963; 1992, P. 175).

The sieve is a generator of outside-time struc-
tures. To Xenakis, a structure that is outside-time is
unique regardless of order or temporal deployment.
This contrasts with an “in-time” structure, Quale
only retains identity in an ordered or temporal de-
ployment (1992, P. 207). Using the standard trans-
formations of a twelve-tone row as an example, UN
retrograde transformation is an “in-time” operation,
whereas inversion, in producing new intervals, is an
“outside-time” operation: “of the four forms of the
series, only the inversion of the intervals is related
to an outside-time structure” (Xenakis 1992, P. 193).
Xenakis, taking an historic view, often lamented
the decline of outside-time structures to in-time
structures in Western music. He offered the sieve as
an antidote.

Xenakis wrote frequently about sieves. There are
at least ﬁve unique discussions of the sieve; each is
found in multiple translations and editions. (Through-
out this article, each discussion will be referenced
by the date of the earliest document, followed,
when necessary, by the date of the actual citation.)
Sieves were ﬁrst introduced in “La voie de la
recherche et de la question” (Xenakis 1965), pub-
lished in Preuve and later reprinted in Kéleütha
(1994). Xenakis further demonstrated the sieve in
“Vers une philosophie de la Musique,” published
in French in Gravesaner Blätter (1966), Revue
d’Esthétique (1968), and as chapter 6 in Musique
Architecture (Xenakis 1976). This text, detailing the
application of sieves in Nomos Alpha (1965–1966),

Ariza

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

was later translated to English by John and Amber
Challifour and included in the 1971 edition of For-
malized Music as chapter VIII. A detailed presenta-
tion of sieves occurs in the 1967 article “Vers une
métamusique,” published ﬁrst in La Nef, and sub-
sequently republished as chapter ﬁve of Musique
Architecture (Xenakis 1976). The ﬁrst English trans-
lation by G. W. Hopkins was published in Tempo in
1970 and was included in the 1971 English edition of
Formalized Music as chapter VII, “Towards a Meta-
music.” Sieves are also discussed in “Redécouvrir le
Temps” (Xenakis 1988). In 1989, excerpts from this
article, translated into English by Roberta Brown,
appeared in Perspectives of New Music as “Con-
cerning Time.” The complete text, titled “Concern-
ing Time, Space and Music,” was included as
chapter X in the 1992 edition of Formalized Music.
The article “Sieves” (Xenakis 1990), translated
into English by John Rahn, was ﬁrst published in
Perspectives of New Music. Nearly the same article
is included as chapter XI in the 1992 edition of For-
malized Music. “Sieves” (Xenakis 1990) includes
the only published software implementation of the
sieve, written in the C language. Chapter XI of For-
malized Music, titled “Sieves: A User’s Guide,” in-
cludes nearly the same software implementation.
Xenakis frequently mentioned composing with

sieve structures. Xenakis describes sieve-based
pitch structures in Akrata (1964–1965; Xenakis
1966), Nomos Alpha (1965–1966; Xenakis 1966),
Jonchaies (1977; Varga 1996, P. 164), Pléïades (1978;
Varga 1996, P. 180), and Aïs (1979; Varga 1996,
P. 165). Xenakis describes sieve-based time struc-
tures in Psappha (1975; Emmerson 1976, P. 24) E
Komboï (1981; Varga 1996, P. 71). In addition to Xe-
nakis’s explicit statements, analysts have found
sieve structures in numerous compositions includ-
ing Eonta (1963; Barthel-Calvet 2000), Anaktoria
(1969; Solomos 1996 P. 93), Persephassa (1969;
Harley 2004, P. 64), Pléïdes (1978; Harley 2004,
P. 121) Pour la Paix (1981; Solomos 1996, P. 93),
Embelllie (1981; Solomos 1996, P. 93), Mists (1981;
Squibbs 1996, 2002), Neküia (1981; Gibson 2001),
Serment-Orkos (1981; Solomos 1996, P. 93), À R.
(Hommage à Maurice Ravel) (1987; Squibbs 1996,
P. 61), Tetora (1990; Jones 2001), and Paille in the
Wind (1992; Solomos 1996, P. 93).

Two Models of the Sieve

Xenakis offers two sieve models. The ﬁrst model,
the complex sieve, is described in his earliest writ-
ing (Xenakis 1965, 1966, 1967, 1988). The second
modello, the simple sieve, is found only in his last
treatment of the topic and its accompanying soft-
ware implementation (Xenakis 1990). È interessante notare,
this second model fails to incorporate aspects of the
original, and Xenakis provides no explanation for
this difference. The models differ in their allowed
logic operators and their levels of residual class
nesting.

Xenakis’s ﬁrst model was based on the manual
calculation of sieves. Xenakis (1966; 1992, P. 234)
provides an image of a hand-written diagram on
graph paper labeled “Nomos alpha Sieves.” Each
column of the graph is treated as an integer unit and
is clearly labeled “ELD = 1/4 tone.” Numerous par-
allel, horizontal lines are used to calculate the sieve.
Each line illustrates a residual class segment (con
points marked as vertical tick-marks) and is labeled
with a logic operation such as “∩ (5,2).” By applying
the logic operator of each line to the previous line,
the ﬁnal sieve segment is realized. Xenakis men-
tions this technique elsewhere: when introducing
the sieve in a later document, he describes setting
the ELD to both a “semitone or a millimeter,” and
notating a sieve on graph paper (Xenakis 1990; 1992,
P. 269). This tedious process has been duplicated by
analysts of Xenakis’s music (Vriend 1981, pag. 55–57;
Harley 2004, P. 43).

Intersection, union, and unary complementa-
tion operators are employed in the ﬁrst model (Xe-
nakis 1965, 1966, 1967, 1988). In the second
modello (Xenakis 1990), Tuttavia, both in prose and
in code, there is no mention or example of com-
plementation. Xenakis says nothing about this
omission.

In the ﬁrst model, logic operators are permitted in
any combination, within any hierarchical level. IL
following complex sieve is an example:

{–M@I & M@I & {–M@I | M@I}} | M@I & M@I

The second model exclusively uses two-level or-
dered groups. The inner level consists only of inter-
sections, the outer level consists only of unions, E

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

complementation is not used. The following simple
sieve is an example:

M@I & M@I & M@I | M@I | M@I & M@I

It can be suggested that Xenakis ordered group-
ings and reduced the use of logic operators because
it became apparent that these features were not for-
mally necessary to produce all segments. Further,
software implementation may have encouraged the
deﬁnition of a simpler, easily computable model.
Two proofs, introduced with the second model (Xe-
nakis 1990), support this claim.

all common logic operators, including symmetric
difference (after Amiot et al. 1986), are permitted.
This model reformulates Xenakis’s reduction algo-
rithms into the concept of compression, a method
of moving from a complex to a maximally simple
sieve. Though these features are not formally neces-
sary to produce all sets, the expressive power of the
sieve formula is expanded by their use. This nota-
tional convenience is, Infatti, an essential feature of
the model.

Xenakis (1990; 1992, P. 275) provides an algo-

The Notation of the Sieve

rithm for sieve compression by segment: the deriva-
tion of a sieve from an arbitrary integer set. As
mentioned earlier, this proof demonstrates that any
ﬁnite set of integers can be generated by a maxi-
mally simple sieve: a sieve created exclusively from
the union of residual classes. Così, intersection,
complementation, and multiple levels of nesting are
not required to construct a sieve of any complexity
and may be deemed superﬂuous. Union is the only
necessary logic operator.

In Xenakis’s second model, complementation is re-
moved, yet intersection is retained. This peculiarity
is explained by Xenakis’s algorithm for compression
by intersection. This proof demonstrates that any
number of residual classes, upon intersection, can be
reduced to a single residual class (1990; 1992, P. 271).
Intersection, in the second model, is used not out

of necessity, but as a notational convenience. For
esempio, the following simple sieve (Xenakis 1992,
P. 274) contains four groups of intersections joined
by union:

3@2 & 4@7 & 6@11 & 8@7 | 6@9 & 15@18 | 13@5 &

8@6 & 4@2 | 6@9 & 15@19

Applying compression by intersection, this sieve

is reduced to a maximally simple sieve. The last
pair of residual classes, having no points in com-
mon, reduces to the null residual class 0@0:

24@23 | 30@3 | 104@70 | 0@0

The new model presented here combines both
Xenakis’s ﬁrst and second models. Complex and
simple sieves are incorporated into a single, bi-
faceted object. All forms of hierarchical nesting and

The notation of a sieve is important. To a user, IL
logic formula is the primary interface, and its nota-
tion directly affects the utility of the model. A sieve
notation must include a means of specifying a resid-
ual class as a modulus and a shift, symbols for the
logic operators, and symbols to delimit residual
class groups.

Xenakis uses one notation, with slight variation,
for complex sieves (1965, 1966, 1967, 1988). Shifts
are represented as subscripts of the modulus. (In
some instances, this notation is reversed, with the
modulus represented as a subscript of the shift; Vedere
Xenakis 1965.) Traditional logic symbols are used:
∪ for union, ∩ for intersection, and an over-score
line for complementation. (Xenakis 1963 uses the
same logic symbols for intersection and union;
complementation, as a binary operator, is notated
with a “–”.) Transposition is represented by the
variable n and is included with every subscript as
“n+shift” (or “n” when shift is equal to zero). Groups
are notated with parentheses. The following example
(Xenakis 1992, P. 197) demonstrates this notation:
∩ 4n+3)
∩ 4n+1) ∪ (3n+2

∩ 4n+2) ∪ (3¯

∩ 4n) ∪ (3¯

(3¯

n+2

n+1

Xenakis uses two notations for simple sieves. IL

ﬁrst is introduced in the two proofs presented in
“Sieves” (Xenakis 1990). Residual classes are repre-
sented as number pairs delimited by parentheses
and are given with either integers or variables
(where M represents modulus, and I represents
shift). Logic operators are notated as before. Trans-
position, as the variable n or otherwise, is no longer
notated. Groups are notated with braces. The fol-

Ariza

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

lowing example (Xenakis 1992, P. 274) demon-
strates this notation:

{(3,2) ∩ (4,7) ∩ (6,11) ∩ (8,7)} ∪ {(6,9) ∩ (15,18)} ∪
{(15,5) ∩ (8,6) ∩ (4,2)} ∪ {(6,9) ∩ (15,19)}

The second notation for simple sieves, part of the
C-language implementation accompanying Xenakis
(1990), uses an American Standard Code for Infor-
mation Interchange (ASCII) symbol representation.
The use of ASCII ensures the availability of every
character on a computer keyboard. Modulus and
shift are represented as a number pair. Intersection
is represented by the symbol “*,” and union is rep-
resented with the symbol “+.” Incidentally, Xenakis
had used these symbols earlier in “Symbolic Mu-
sic” (1963) and “La voie de la recherche et de la
question” (1965). Complementation is not speci-
ﬁed, and transposition is not notated. Groups are
notated with square brackets, Per esempio:

[(3,2) * (4,7)] + [(6,9) * (15,18)]

The new notation presented here is a “logic
string.” Similar to the notation presented in Xe-
nakis (1990), ASCII characters are used to represent
a sieve formula. To avoid using commas or paren-
theses, a residual class is given as a modulus and a
shift separated by the “@” symbol. This symbol is
chosen primarily for its infrequent use in other no-
tations. (Representing a residual class with two ﬁg-
ures separated by a symbol has a precedent in
Xenakis 1966, where shift and modulus—in that or-
der—are separated by the character “M”.) Logic op-
erators are notated using the pipe (“|") for union, IL
ampersand (“&") for intersection, the circumﬂex
(“^”) for symmetric difference, and the dash (“–”)
for unary complementation. All four logic operators
are permitted, and complementation can be applied
to a single residual class or a group. A group is no-
tated with braces.

This notation has many advantages. It is more
compact and requires fewer characters than Xenakis’s
notations. The use of bitwise logic operator symbols
(pipe, ampersand, and circumﬂex) are transparent in
meaning to those familiar with programming lan-
guages such as C, Java, or Python. The use of a single
set of characters for grouping (braces) reduces visual

complexity. Finalmente, the sieve contains only ASCII
characters, no commas, E (optionally) no spaces,
allowing for easy parsing and isolation when passed
as an argument or included with complex data. Questo
notation, Per esempio, could easily be sent as an
Open Sound Control (OSC) corda; if stored in Hy-
perText Markup Language (HTML) or eXtensible
Markup Language (XML), one character used in this
notation, the ampersand (“&"), must be converted
to a character entity (“&").

Implementations of the Sieve

A software model of the sieve must treat the logic
formula as the primary object, not one of the for-
mula’s possible segments. The logic formula should
be retained as a reusable object such that it can be
represented as conceived, multiple transpositions
and segments can be extracted, and the formula it-
self can be logically combined. Simply combining
ﬁxed sets with logic operators reduces the function-
ality of a sieve to simply an input notation: the in-
formation contained in the design of the formula is
lost only to one of its many output potentials. Of
the handful of implementations available to date,
none has treated the logic formula of the sieve as a
reusable object, allowing the input, maintenance,
representation, and processing of a complex sieve
from a single argument.

Xenakis (1990) provides the ﬁrst published soft-
ware implementation of a sieve. This software con-
sists of two main procedures: the generation of a
sieve segment from a logic formula, and the genera-
tion of a logic formula from an arbitrary set of inte-
gers. Xenakis, in the 1992 edition of Formalized
Music, credits the C code to Gérard Marino, stating
that it is a port of Xenakis’s original BASIC code.
For the version published in Perspectives of New
Music, no authorship is given. Functionally, the two
versions are nearly identical. The version in For-
malized Music (1992), Tuttavia, contains numerous
typographic omissions. Ronald Squibbs has listed
these errors and provides corrected code (1996,
pag. 292–303).

Unfortunately, the implementation Xenakis of-

fered in 1990 cannot process the many complex

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

sieves he had demonstrated since 1965. This soft-
ware, permitting only the calculation of simple
sieves, has other shortcomings. The code lacks
modular design, limiting both ﬂexibility and expan-
sion. The program is intended exclusively for user
rather than programmatic interaction; a general pur-
pose interface, necessary for use in larger systems,
is not provided. A complete sieve cannot be sup-
plied as a single argument: when entering a sieve,
Per esempio, the user must ﬁrst declare the number
of unions, then declare the number of residual
classes in each intersection, then enter a modulus
and shift one at a time. Further, there is no imple-
mentation of transposition and the user cannot
freely designate z.

In 1980, prior to the publication of Xenakis’s
code, Sever Tipei implemented a sieve model in
FORTRAN for use with his computer-assisted com-
position program MP1 (Tipei 1975). In addition to
using sieves for parameter generation, Tipei pro-
duced weighted sieve-segments. If each residual
class is assigned a weight, a sieve can be con-
structed that produces segments encoding com-
bined weights. These techniques and others were
used in his compositions and described in numer-
ous articles (Tipei 1981, 1987, 1989).

Researchers at the Institut de Recherche et Coor-
dination Acoustique/Musique (IRCAM) employed
the sieve in a number of publications. Malherbe et
al. (1985) demonstrate a novel application of sieve
structures to model spectral peaks found in ana-
lyzed sound ﬁles. Amiot et al. (1986) develop upon
this model and provide a more complete descrip-
zione. Here, sieves are employed primarily for ﬁlter-
ing metric patterns. Logic operators are expanded
to include symmetric difference, composition, E
exponentiation. This sieve was implemented by
Gérard Assayag as the “Langage de Cribles” (LC) In
the now-obsolete Le Lisp language. Neither details
of the implementation nor examples of its use are
available. Assayag’s Lisp-based ScoreBoard applica-
zione (1993) may offer a related model.

In 1990, Marcel Mesnage programmed a text-
based system in Macintosh Common Lisp called
“Partitions d’Ensembles de Classes de Résidus”
(PCR; Riotte 1992; Mesnage and Riotte 1993). Questo
system, based on a model by André Riotte, imple-

ments a variety of sieve structures using union,
intersection, and complementation, and produces
sieve segments in integer, binary, and width for-
mats. The system’s sieve notation, Tuttavia, signiﬁ-
cantly deviates from a logic-formula representation.
A more sophisticated sieve model, also written in

Macintosh Common Lisp, was included in Mes-
nage’s “Criblograph,” a graphical user interface en-
vironment for music composition developed from
1989 until 1997, and then merged into Mesnage’s
“Mélusine” system. The sieve implementation in
these systems offered all common logic operators,
the creation and modiﬁcation of reusable sieve seg-
menti, and a unique graphical sieve segment editor.
Some of these tools have been subsequently incor-
porated into Mesnage’s “Morphoscope” (1993). De-
spite the broad functionality of these systems, IL
sieve is not given a practical notation, and a com-
plex sieve cannot be provided as a single argument.
Within Paul Berg’s AC Toolbox (available online
at www.koncon.nl/ACToolbox), a Lisp-based soft-
ware system for algorithmic composition running
on MacOS X are four sieve-related objects: Sieve,
Sieve-Union, Sieve-Filter, and Interpret-
Sieve. The Sieve object here can be better thought
of as a residual class: the user provides a modulus, UN
shift (as start value) and a z (as minimum and maxi-
mum). Evaluation returns an integer segment. IL
object Sieve-Union is a union operator that com-
bines any number of lists (generated by Sieve or
otherwise) and returns a new list. Sieve-Filter
employs a list (generated by Sieve or otherwise) A
select values from another list. Interpret-Sieve is
designed for the production of rhythms: a list of val-
ues, interpreted as either a binary or a width sieve
segment, is used to process a list of rhythm durations
into note (positive) or rest (negative) values. The user
provides a list of durations, the sieve segment, and a
control variable. Although providing useful tools for
the deployment of combined residual class segments,
this model does not allow the input or maintenance
of a complex sieve as a complete logic formula.

Jones (2001), following the limits and notation of

Xenakis (1990), models only simple sieves (called
RCsets) as residual classes combined under union.
Jones is primarily interested in deriving a maxi-
mally simple sieve from an arbitrary set for the pur-

Ariza

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

pose of analysis. A new method of compression by
segment is proposed. He rejects Xenakis’s algorithm
for only accepting residual classes with perfect cor-
respondence to the source set. Because Xenakis of-
ten varied the realization of a sieve in its musical
deployment, Jones proposes an algorithm that pro-
vides a “statistically optimal” (2001, P. 225) match
to the source set, weighted toward fewer residual
classes with lower moduli, even if this requires pro-
ducing sieve segments that do not match the source.
Candidate residual classes, Per esempio, must match
at least three points within the source set. Although
this model suggests an interesting method of lossy
sieve compression, the deviation Jones allows be-
tween source set and resulting sieve is so high as to
suggest a transformation beyond mere compression.
In his analysis of Tetora, Jones offers simple sieves
to replace source sets that, in one case, cover as few
COME 10 out of 37 original points. Jones (2001) includes
an implementation, programmed in BASIC, provid-
ing an interface similar to Xenakis (1990).

Some, perhaps owing to the absence of a complete

software implementation, have calculated sieves
with a numeric table (Squibbs 1996, pag. 304–306;
Gibson 2001). If a sieve uses only two moduli, UN
table can be constructed with each modulus as-
signed to an axis. Each axis has rows or columns for
every shift in the modulus (0 to M–1), thus repre-
senting every residual class of each modulus. Values
in the table are ﬁlled by wrapping a z (from zero to
one less than the product of the moduli) diagonally
through the table. The resulting values, for any two
residual classes, provide the intersection point
found within a single-period sieve segment. Though
Squibbs has demonstrated the use of multiple tables
to handle sieves employing more than two moduli,
this technique is very limited.

The predecessor of the sieve model presented here
(Ariza 2004) introduced the logic string notation and
modeled the logic formula as a reusable object. Sieve
objects, Tuttavia, were limited to simple sieves.

Object-Oriented Implementation

An object-oriented Python implementation has been
developed based on the new model and notation

presented above. This implementation is portable,
modular, and offers the easy creation and deployment
of sieve segments and transpositions. The model
combines Xenakis’s two models into a bi-faceted
object: a sieve can contain both complex and simple
representations simultaneously. The ﬁle sieve.py,
part of the athenaCL library libATH, implements
this model as the Residual and Sieve objects.

The Residual Object

The Residual object is a representation of the
residual class. A Residual contains data attributes
for modulus (M), shift (shift), complement (neg),
and integer range (z). Modulus and shift are integer
values as deﬁned above. As complementation of a
single residual object is a unary operation, comple-
mentation is a Boolean value (neg) stored as an at-
tribute of the Residual object. Each Residual
instance contains a reference to a ﬁnite list of con-
tiguous integers (z) from which sieve segments are
ﬁltered. The attribute segFmt determines segment
output format, where format strings for integer, bi-
nary, unit, and width are notated int, bin, unit,
and wid, rispettivamente. The default segFmt is int.
Object initialization requires a modulus (M) value.
Optional arguments can be provided for shift, neg,
and z. If no z is given, a default range is provided.

The segment() method of a Residual instance

returns a transposed sieve segment in one of four
formats. This method has three optional arguments:
an integer value for transposition (N), by default
zero; a list of integers (z), by default the z set at ini-
tialization; and a format string. Arguments passed
to the segment method do not change attributes of
the object: they are used only in the calculation of
the desired segment. If changes to these attributes
are desired, the method zAssign() can be used to
set z, and the method segFmtSet() can be used to
set segFmt. The method period() provides the pe-
riod of the residual, which in all cases is equal to
the modulus. The repr() method provides a string
representations of the residual class, and the
copy() method returns a new object with identical
M, shift, neg, and z attributes.

Additional functionality is provided through op-

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

erator overloading. The object’s __call__()
method is mapped to the segment() method, E
the __str__() method is mapped to the repr()
method. (In Python, all objects can overload opera-
tors by deﬁning specially named methods. IL
__call__() method is called when an object x is
evaluated as x(). The __str__() method is called
whenever a string representation of an object is
necessario, for example print x.)

The __and__() method, called with the binary &

operator, applies compression by intersection to
two Residual operands and returns the Residual
of the reduced intersection. The z of this new object
is formed from the union of each operand’s z. Com-
pression by intersection is implemented after the al-
gorithm presented in Xenakis (1990). If intersection
of a complemented residual class is attempted, an
error is raised. The __or__() method, evoked with
IL | operator, is not implemented: the union of
two residual classes can only be represented by two
residual classes. The __xor__() method, evoked
with the ^ operator, is likewise not implemented.

The __neg__() method, called with the unary –

operator, changes the neg attribute to its Boolean
opposite. To compare two Residual objects, IL
equal and not-equal operator methods, __eq__()
and __ne__(), are deﬁned by comparing m, shift,
and neg attributes.

A Uniﬁed Modeling Language (UML) class dia-
gram of the Residual, summarizing the public at-
tributes and methods of this object, is provided in
Figura 2. Figura 3 demonstrates the Residual ob-
ject within a Python interactive session. (The Python
prompt >>> precedes user input. Comments are pre-
ceded by #.)

The Sieve Object

The Sieve object is a bi-faceted representation of the
Xenakis sieve. One representation is the expanded
state, which can be any sieve from simple to com-
plex. The other representation is the same sieve com-
pressed; the compressed state is always a maximally
simple sieve. Each state is an independent sieve.

The logic string provided at initialization becomes
the expanded sieve. The type of this sieve (complex

Figura 2. Residual object
class diagram.

Residual
M
shift
neg
z

segFmt
zAssign()
segFmtSet()
__call__(), segment()
period()
copy()
__str__(), repr()
__and__()
__neg__()
__eq__()
__ne__()

or simple) is stored as the expType attribute and is
used to determine the form of compression. Each
state (expanded and compressed) has unique attri-
butes for logic string, residual classes, and period.
Each state generates independent segments. The z
attribute is shared between both states. The object
has an attribute for current state, set at initializa-
tion to expanded. To change states, the compress()
or expand() methods are called.

The Sieve shares aspects of the Residual object
interface. The zAssign() and segFmtSet() meth-
ods set z and segment formats, rispettivamente. IL
segment() method, with the addition of an argu-
ment for state, returns a sieve segment for an optional
shift, z, and format argument. This method, using the
current state, is mapped to the __call__() method.
Segment formats are the same as for Residual ob-
jects: integer, binary, unit, and width. The pe-
riod() method returns the period of the current
state, or the state designated with an optional argu-
ment. The period of each state is calculated by ﬁnd-
ing the lowest common multiple of all residual
periods. The repr() method, also mapped to the
__str__() method, returns a string representation

Ariza

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 3. Python session
demonstrating the Resid-
ual object.

>>> from athenaCL.libATH import sieve
>>> # the built-in Python function “range” can be used to create a z
>>> z = range(0,25) # creates a list of contiguous integers from 0 A 24
>>> a = sieve.Residual(3,2,0,z) # a new Residual object
>>> print a # return a string representation
3@2
>>> a() # calling the Residual returns a sieve segment
[2, 5, 8, 11, 14, 17, 20, 23]
>>> a(2) # the first argument is a transposition
[1, 4, 7, 10, 13, 16, 19, 22]
>>> a(2, range(-20,-10)) # the second argument is z
[-20, -17, -14, -11]
>>> a(0, range(0,13), ‘bin’) # the third argument is segment format
[0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0]
>>> a(0, range(0,13), ‘unit’) # a unit segment
[0.16666666666666666, 0.41666666666666669, 0.66666666666666663,
0.91666666666666663]
>>> a(0, range(0,13), ‘wid’) # a width segment
[3, 3, 3]
>>> a.period() # period, modulus, and width are equal
3
>>> b = sieve.Residual(8,0,1) # a complemented Residual, with a default z
>>> print b
-8@0
>>> b = -b # unary complementation
>>> print b
8@0
>>> b() # calculating a segment with default transposition, z, and format
[0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96]
>>> c = a & B # the intersection of two Residuals
>>> print c
24@8
>>> c()
[8, 32, 56, 80]
>>> c == a # Residuals tested for equality
0
>>> -a != a # Residuals tested for inequality
1

of the logic formula; the copy() method returns a
new Sieve instance with identical attributes.

Many steps are performed at initialization. IL

Sieve object is instantiated with either a logic
string or a list of integers and an optional argument
for z. The sieve given at initialization is set as the
expanded sieve and is parsed.

Parsing consists of translating the formula of the
sieve into a tree string and a collection of Residual
objects stored in a dictionary (resLib). A tree string
is the logic formula of the sieve with residual class
notations replaced by unique string keys. A tree
string is created for each state (expTree and
cmpTree). Each residual class notated in the for-

mula is identiﬁed and replaced by a key, in the form
of “,” where n is an integer index. For each
residual class declared in the logic string, a Resid-
ual object is instantiated in the resLib dictionary.
A Sieve produces a segment by combining resid-

ual class segments with the speciﬁed logic opera-
tori. The combination of segments is facilitated by
Python’s built-in Set object, distributed with
Python 2.3 and found in the module sets.py. IL
Set object offers standard set procedures with oper-
ator overloading of the same symbols used in the
logic string notation; nested structures, ulteriore-
more, are evaluated with the desired precedence.

If a segment is requested from the Sieve, each key

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

in the appropriate tree string is replaced by the string
necessary to instantiate a Set; this Set contains the
integer segment from the corresponding Residual
object. If a residual class is complemented, the seg-
ment returned already reﬂects this complementation.
After all keys are replaced, the entire string is evalu-
ated, causing the instantiation and evaluation of all
Set objects. Evaluation processes Set objects with
the logic operators speciﬁed in the tree string. UN
single Set results and is returned by the Sieve as a
list. If a string representation is requested from the
Sieve, a similar operation is performed: all keys in
the tree string are replaced with the string represen-
tation of the corresponding Residual object.

Sieve objects forbid binary complementation,

but allow unary complementation of Residuals
and groups. Python Set objects, Tuttavia, employ
only binary complementation. This difference is
handled in two ways: (1) A single Residual class,
under complementation, internalizes its comple-
mented state. A Set is then instantiated from an
already-complemented Residual segment; the re-
sulting Set thus does not require complementation.
(2) In the case that a group of Residual objects is
complemented outside of a delimiter, the comple-
mentation operator, at evaluation, is preceded by a
Set object corresponding to a segment of 1@1 for
the current z. Because binary complementation is
evaluated before intersection, symmetric difference,
and union, this effectively converts unary negation
into binary negation at the time of Set evaluation.
During initialization, and after the expanded
sieve is parsed, compression is performed. Two
methods of compression are available: by intersec-
tion and by segment. The expanded sieve type
(expType) determines which compression is per-
formed. If a sieve is complex, compression by seg-
ment must be performed. If a sieve is simple,
compression by intersection is performed.

If compression by intersection is mandated by
expType, the expTree is divided into intersection
groups. The keys for each group of Residual ob-
jects are collected, and the corresponding objects are
intersected. A new tree string (cmpTree) is con-
structed, joining by union keys for each of the re-
sulting Residual objects. Each Residual is stored
in resLib.

If compression by segment is mandated by exp-

Type, a segment is created at the current z and is
processed. Compression by segment cannot be per-
formed if, owing to the logic formula or the size of
z, an empty segment is retuned. Compression re-
turns a list of Residual objects that, when com-
bined under union, will create a sieve that returns
the source segment for the provided z. The Resid-
ual objects are stored in resLib, and a new tree
corda (cmpTree) is created.

A variation of Xenakis’s algorithm (1990; 1992,
P. 274) for compression by segment is implemented
come segue: (1) Two copies of the source integer set
are stored as src and match lists. (2) A z list, if not
provided, is constructed by taking the range of inte-
gers from the minimum to the maximum of the
match list. (3) A value in the match list is treated as
a shift value. (4) A Residual object is created
with this shift, a modulus of 1, and z. (5) A sieve
segment is created by calling the Residual in-
stance. (6UN) If this sieve segment is a subset of src,
the object is appended to the list residuals and the
shift value, as well as any points on the segment
also found in the match list, are removed from
match. (6B) Otherwise, the shift is retained, IL
modulus is incremented, and the process is repeated
until a subset sieve segment is found. (7) Remaining
values in match are each treated as a shift (repeat-
ing from step 3), until match is empty. (Note that,
because the segment is always compared to src and
not match, found Residual objects may cover re-
dundant points; this addresses a shortcoming of Xe-
nakis’s algorithm mentioned in Jones 2001, P. 233.)
If an integer in a source set is treated as a residual

class shift, a modulus can always be found that,
with this shift, produces a segment that is both a
subset of the source and matches at least the shift.
This segment will always be found before the mod-
ulus is incremented past the number of points in z.
At an extreme, a residual class can be created for
each point in the source set, each residual, for the
current z, contributing only one point to a union. It
follows that any arbitrary set can be represented as a
maximally simple sieve.

Compression occurs at initialization with the pro-
vided or default z. After initialization, compression
can be re-performed if a new z is provided. This new

Ariza

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 4. Sieve object class
diagram.

Sieve
expType
state
z

segFmt
resLib
expTree
cmpTree
compress()
expand()
zAssign()
segFmtSet()
__call__(), segment()
period()
copy()
__str__(), repr()
__and__()
__or__()
__xor__()
__neg__()

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

ding to the major scale for all z. Using the conver-
sion function psToNoteName() from the athenaCL
libATH module pitchTools, each integer can be
converted to a pitch name to verify the accuracy of
the scale over four octaves. (The Python map func-
tion applies a function to each value in a list and re-
turns a new list.) The compressed sieve, after
compression by segment, is a maximally simple
sieve. It also has a period of 12 and produces the ma-
jor scale over four octaves.

Figura 6 hides a potential confusion. Because a
complex sieve is supplied at initialization, compres-
sion must occur by segment. As no z is supplied, UN
default z of 0 A 99 is provided. For some smaller z
ranges, Tuttavia, compression by segment will re-
sult in a different compressed sieve.

If a Sieve object is created from an integer set of
a one-octave major scale (where z is automatically
determined by the minimum and maximum of the

z will be set as the current z and will be used to cre-
ate the segment sampled for compression. Changing
the z value, in the case of compression by segment,
can result in different compressed representations.
If, rather than a logic string, a list of integers is
entered at initialization, compression by segment is
used to create the necessary Residual objects;
these objects are stored in resLib, and a tree string
(expTree) is created. The expanded sieve, in this
case, will always be a maximally simple sieve: fur-
ther compression is not possible. The compressed
sieve representation of the object will be identical
to the expanded sieve.

Sieve objects themselves, through operator over-
loading, can be combined with logic operators to pro-
duce new Sieve objects. The methods __and__(),
__or__(), __xor__(), and __neg__() are deﬁned
to overload operators &, |, ^, and –. A new sieve is
created by instantiating an object with a new logic
string and the union of each operand’s z. This new
logic string encodes the operation on each operand’s
expanded sieve, producing a new object that models
the operation.

A UML class diagram, summarizing the public at-

tributes and methods of this object, is provided in
Figura 4.

The Python session provided in Figure 5 demon-
strates, for a complex sieve, the internal representa-
tion of tree strings for both the expanded and
compressed states. Combining Sieve objects with
logic operators is also demonstrated. Practical ex-
amples of the Sieve object are provided next.

Demonstrating the Sieve

The Sieve object can realize all of Xenakis’s sieves,
both complex and simple. One of Xenakis’s earliest
examples is a complex sieve for the generation of a
major scale. This elegant formula is, Tuttavia, In-
compatible with both his second model and its soft-
ware implementation (Xenakis 1990). This sieve
provides an excellent example of the utility of a
bi-faceted representation of the sieve.

A Sieve object can be created from Xenakis’s for-
mula for the major scale. This expanded sieve has a
period of 12, and it produces a segment correspon-

Computer Music Journal

Figura 5. Python session
demonstrating internal
representation of a logic
formula and the combina-
tion of Sieve objects with
logic operators.

>>> from athenaCL.libATH import sieve
>>> a = sieve.Sieve(‘7@0|{-5@2&-4@3}’) # create a complex sieve
>>> a.expType # the expanded type is automatically identified
‘complex’
>>> a.expTree # the expanded tree string
‘|{&}’
>>> a.period() # the period of the expanded state
140
>>> a.compress() # changing the current state of the Sieve
>>> print a # a maximally simple sieve
7@0|10@0|10@4|10@6|10@8|16@13|20@1|20@5|20@9|20@13
>>> a.cmpTree # the corresponding compressed tree string
‘|||||||||‘
>>> a.period() # the period of the compressed sieve
560
>>> a(0, range(0,20), ‘bin’) # return a binary segment
[1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0]
>>> b = -a # Sieve object complementation returns a new object
>>> print b
-{7@0|{-5@2&-4@3}}
>>> b(0, range(0,20), ‘bin’)
[0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1]
>>> c = sieve.Sieve(‘9@7’)
>>> print c
9@7
>>> d = c | B # Sieve object union returns a new object
>>> print d
{-{7@0|{-5@2&-4@3}}}|{9@7}
>>> d(0, range(0,20), ‘bin’) # return a binary segment
[0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1]
>>> d(0, range(0,20), ‘wid’) # return a width segment
[1, 4, 4, 1, 3, 1, 1, 2]
>>> e = sieve.Sieve(‘5@2|5@3’)
>>> f = d & e # Sieve object intersection returns a new object
>>> print f
{5@2|5@3}&{{-{7@0|{-5@2&-4@3}}}|{9@7}}
>>> f(0, range(0,20), ‘bin’) # the expected binary segment
[0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0]

segment), a logic formula is found. This formula,
Tuttavia, is only valid for the points covered by the
z of one octave. Beyond this, pitches deviate from
the major scale. Figura 7 creates four Sieve objects.
Sieve “a” is initiated with a one octave set of the
major scale; the resulting sieve is shown to have a
period of 210 and deviate from the major scale at
values beyond the z set at initialization. Sieve “b”
extends the source set to two octaves. A different
sieve is found with the same period. Again, z values
beyond the z set at initialization result in a scale
that deviates from the desired major scale. This pro-
cess is repeated with a three-octave set. Given a
four-octave set, the desired maximally simple sieve

is ﬁnally found, having the necessary period of 12
and producing correct segments for all z. Xenakis,
aware of this aspect of compression by segment,
states that “one should take into account as many
points as possible in order to secure a more precise
logical expression” (1990, P. 275). Gibson (2001),
likewise using segments of the major scale, has also
demonstrated this constraint.

Jan Vriend, in his examination of Nomos Alpha,

demonstrates the complex system Xenakis em-
ployed for creating a succession of sieves, all based
on a common formulation (1981, P. 55). The sieve is
provided as an algebraic logic formula (Xenakis
1992, P. 230):

Ariza

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 6. Python session
demonstrating Xenakis’s
sieve for the major scale
and its compressed form.

>>> from athenaCL.libATH import sieve, pitchTools
>>> # Xenakis’s logical formula for the major scale
>>> a = sieve.Sieve(‘{-3@2&4}|{-3@1&4@1}|{3@2&4@2}|{-3@0&4@3}’)
>>> print a
{-3@2&4@0}|{-3@1&4@1}|{3@2&4@2}|{-3@0&4@3}
>>> a.period() # the period of the major scale is 12
12
>>> a(0, range(0,13)) # one octave segment as pitch class
[0, 2, 4, 5, 7, 9, 11, 12]
>>> # four octave segment as note names
>>> map(pitchTools.psToNoteName, UN(0, range(0,49)))
[‘C4’, ‘D4’, ‘E4’, ‘F4’, ‘G4’, ‘A4’, ‘B4’, ‘C5’, ‘D5’, ‘E5’, ‘F5’, ‘G5’, ‘A5’,
‘B5’, ‘C6’, ‘D6’, ‘E6’, ‘F6’, ‘G6’, ‘A6’, ‘B6’, ‘C7’, ‘D7’, ‘E7’, ‘F7’, ‘G7’,
‘A7’, ‘B7’, ‘C8’]
>>> a.compress() # toggle the current sieve state
>>> print a # display the compressed sieve
6@5|12@0|12@2|12@4|12@7|12@9
>>> a.period() # return the compressed period
12
>>> # four octave segment from the compressed sieve
>>> map(pitchTools.psToNoteName, UN(0, range(0,49)))
[‘C4’, ‘D4’, ‘E4’, ‘F4’, ‘G4’, ‘A4’, ‘B4’, ‘C5’, ‘D5’, ‘E5’, ‘F5’, ‘G5’, ‘A5’,
‘B5’, ‘C6’, ‘D6’, ‘E6’, ‘F6’, ‘G6’, ‘A6’, ‘B6’, ‘C7’, ‘D7’, ‘E7’, ‘F7’, ‘G7’,
‘A7’, ‘B7’, ‘C8’]

l (M,N) = {–{N@i | N@j | N@k | N@l} & M@p} | {–{M@q

{8@3 & {11@1 | 11@2 | 11@3 | 11@4 | 11@10}} |

| M@r} & N@s} | {N@t | N@u | N@v}

By algorithmically generating variables for modu-

lus and shift, this structure is used to produce six
unique sieves and their resulting segments. A sieve,
using this formulation and employed in Nomos Al-
pha, is given below (Xenakis 1966; 1992, P. 230):

{–{13@3 | 13@5 | 13@7 | 13@9} & 11@2} | {–{11@4 |

11@8} & 13@9} | {13@0 | 13@1 | 13@6}

Vriend (1981, P. 57), after demonstrating the man-

ual calculation of a segment from this sieve, pro-
vides the resulting sieve segment mapped onto a
quarter-tone ELD pitch scale. This scale is notated
in Figure 8. Figura 9, using the Sieve object to model
Xenakis’s sieve, conﬁrms Vriend’s realization of the
segment.

Squibbs (1996, P. 61) provides the logic formula
for a sieve from Xenakis’s À R. (Hommage à Mau-
rice Ravel):

{8@0 & {11@0 | 11@4 | 11@5 | 11@6 | 11@10}} |

{8@1 & {11@2 | 11@3 | 11@6 | 11@7 | 11@9}} |

{8@2 & {11@0 | 11@1 | 11@2 | 11@3 | 11@5 | 11@10}} |

{8@4 & {11@0 | 11@4 | 11@8}} |

{8@5 & {11@0 | 11@2 | 11@3 | 11@7 | 11@9 | 11@10}} |

{8@6 & {11@1 | 11@3 | 11@5 | 11@7 | 11@8 | 11@9}} |

{8@7 & {11@1 | 11@3 | 11@6 | 11@7 | 11@8 | 11@10}}

Two segments from this sieve are given, at trans-
positions 0 E 10. These are provided in Squibbs’s
notation (1996, P. 61–62):

K = {0, 2, 3, 4, 7, 9, 10, 13, 14, 16, 17, 21, 23, 25, 29,

30, 32, 34, 35, 38, 39, 43, 44, 47, 48, 52, 53, 57, 58,
59, 62, 63, 66, 67, 69, 72, 73, 77, 78, 82, 86, 87}

T10(K)(mod 88) = {0, 4, 8, 9, 10, 12, 13, 14, 17, 19, 20,
23, 24, 26, 27, 31, 33, 35, 39, 40, 42, 44, 45, 48, 49,
53, 54, 57, 58, 62, 63, 67, 68, 69, 72, 73, 76, 77, 79,
82, 83, 87}

Figura 9 demonstrates that the creation of a Sieve

object with this logic formula accurately produces
the desired segments.

Ellen Rennie Flint, in her analysis of Psappha,
demonstrates Xenakis’s use of sieves to generate
rhythms. Flint (1989, P. 228) provides the logic for-

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 7. Python session
demonstrating compres-
sion by segment of a
major scale.

Figura 8. Sieve generated
scale from Nomos Alpha,
with ELD equal to a quar-
ter tone (Vriend 1981).

>>> from athenaCL.libATH import sieve, pitchTools
>>> # one octave of the major scale, entered as a list
>>> a = sieve.Sieve([0,2,4,5,7,9,11])
>>> print a
5@2|5@4|6@5|7@0
>>> # pitches deviate from the major scale, excluding E5
>>> map(pitchTools.psToNoteName, UN(0, range(0,25)))
[‘C4’, ‘D4’, ‘E4’, ‘F4’, ‘G4’, ‘A4’, ‘B4’, ‘C5’, ‘D5’, ‘F5’, ‘G5’, ‘A5’, ‘A#5’,
‘B5’, ‘C6’]
>>> a.period() # expected period of 12 not found
210
>>> # two octaves of the major scale, entered as a list
>>> b = sieve.Sieve([0,2,4,5,7,9,11,12,14,16,17,19,21,23])
>>> print b
5@4|6@5|7@0|7@2|7@5
>>> # pitches deviate from the major scale at F#6
>>> map(pitchTools.psToNoteName, B(0, range(0,37)))
[‘C4’, ‘D4’, ‘E4’, ‘F4’, ‘G4’, ‘A4’, ‘B4’, ‘C5’, ‘D5’, ‘E5’, ‘F5’, ‘G5’, ‘A5’,
‘B5’, ‘C6’, ‘D6’, ‘E6’, ‘F6’, ‘F#6’, ‘A6’, ‘A#6’, ‘B6’]
>>> b.period() # expected period of 12 not found
210
>>> # three octaves of the major scale, entered as a list
>>> c = sieve.Sieve([0,2,4,5,7,9,11,12,14,16,17,19,21,23,24,26,28,29,31,33,35])
>>> print c
6@5|7@0|7@5|10@9|12@0|12@2|12@4|12@7
>>> # pitches deviate from the major scale at D#7
>>> map(pitchTools.psToNoteName, C(0, range(0,48)))
[‘C4’, ‘D4’, ‘E4’, ‘F4’, ‘G4’, ‘A4’, ‘B4’, ‘C5’, ‘D5’, ‘E5’, ‘F5’, ‘G5’, ‘A5’,
‘B5’, ‘C6’, ‘D6’, ‘E6’, ‘F6’, ‘G6’, ‘A6’, ‘B6’, ‘C7’, ‘D7’, ‘D#7’, ‘E7’, ‘F7’,
‘F#7’, ‘G7’, ‘B7’]
>>> c.period() # expected period of 12 not found
420
>>> # four octaves of the major scale, entered as a list
>>> d =
sieve.Sieve([0,2,4,5,7,9,11,12,14,16,17,19,21,23,24,26,28,29,31,33,35,36,38,40,
41,43,45,47])
>>> print d
6@5|12@0|12@2|12@4|12@7|12@9
>>> d.period() # expected period of 12 found
12

mula of the sieve used to create the rhythmic articu-
lations of the ﬁrst 39 time units of the composition:

{{8@0 | 8@1 | 8@7} & {5@1 | 5@3}} | {{8@0 | 8@1 | 8@2}

& 5@0} |

{8@3 & {5@0 | 5@1 | 5@2 | 5@3 | 5@4}} | {8@4 & {5@0 |

5@1 | 5@2 | 5@3 | 5@4}} |

{{8@5 | 8@6} & {5@2 | 5@3 | 5@4}} | {8@1&5@2} |

{8@6&5@1}

The resulting sieve segment, as attack points,
can be transcribed from the score; the second voice

of group B provides a clear statement of this sieve
(Harley 2004, P. 96). These points, notated and
expressed as an integer segment, are provided in
Figura 10.

Using the Sieve object, this sieve can be recre-
ated from its logic formula. In Figure 9 integer and
binary segments, over a z from 0 A 38, are created.

Ariza

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 9. Python session
demonstrating Xenakis’s
sieves from Nomos Alpha,
À R. (Hommage à Maurice
Ravel) and Psappha.

>>> from athenaCL.libATH import sieve
>>> # sieve from Xenakis’s Nomos Alpha
>>> x = sieve.Sieve(‘{-{13@3|13@5|13@7|13@9}&11@2}|{-
{11@4|11@8}&13@9}|{13@0|13@1|13@6}’)
>>> print x
{-{13@3|13@5|13@7|13@9}&11@2}|{-{11@4|11@8}&13@9}|{13@0|13@1|13@6}
>>> x() # segment notated in Vriend (1981)
[0, 1, 2, 6, 9, 13, 14, 19, 22, 24, 26, 27, 32, 35, 39, 40, 45, 52, 53, 58, 61,
65, 66, 71, 78, 79, 84, 87, 90, 91, 92, 97]

>>> # sieve from Xenakis’s À R. (Hommage à Maurice Ravel)
>>> a =
sieve.Sieve(‘{8@0&{11@0|11@4|11@5|11@6|11@10}}|{8@1&{11@2|11@3|11@6|11@7|11@9}}
|{8@2&{11@0|11@1|11@2|11@3|11@5|11@10}}|{8@3&{11@1|11@2|11@3|11@4|11@10}}|{8@4&
{11@0|11@4|11@8}}|{8@5&{11@0|11@2|11@3|11@7|11@9|11@10}}|{8@6&{11@1|11@3|11@5|1
1@7|11@8|11@9}}|{8@7&{11@1|11@3|11@6|11@7|11@8|11@10}}’)
>>> a.period() # as modulus values of only 8 E 11 are used, the period is 88
88
>>> a(0, range(0,88)) # segments that correspond with Squibbs (1996)
[0, 2, 3, 4, 7, 9, 10, 13, 14, 16, 17, 21, 23, 25, 29, 30, 32, 34, 35, 38, 39,
43, 44, 47, 48, 52, 53, 57, 58, 59, 62, 63, 66, 67, 69, 72, 73, 77, 78, 82, 86,
87]
>>> a(10, range(0,88)) # transposition at 10
[0, 4, 8, 9, 10, 12, 13, 14, 17, 19, 20, 23, 24, 26, 27, 31, 33, 35, 39, 40,
42, 44, 45, 48, 49, 53, 54, 57, 58, 62, 63, 67, 68, 69, 72, 73, 76, 77, 79, 82,
83, 87]

>>> # sieve from Xenakis’s Psappha (Flint 1989)
>>> x =
sieve.Sieve(‘{{8@0|8@1|8@7}&{5@1|5@3}}|{{8@0|8@1|8@2}&5@0}|{8@3&{5@0|5@1|5@2|5@
3|5@4}}|{8@4&{5@0|5@1|5@2|5@3|5@4}}|{{8@5|8@6}&{5@2|5@3|5@4}}|{8@1&5@2}|{8@6&5@
1}’)
>>> segment corresponds to opening rhythm in group B, voice 2
>>> x(0, range(0,39))
[0, 1, 3, 4, 6, 8, 10, 11, 12, 13, 14, 16, 17, 19, 20, 22, 23, 25, 27, 28, 29,
31, 33, 35, 36, 37, 38]
>>> x.segFmtSet(‘bin’) # change the segment format
>>> x(0, range(0,39))
[1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1,
0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1]

The binary segment provides a clear representa-
tion of a sieve as a sequence of points (notes) E
slots (rests).

Xenakis discussed many methods of transforming

sieve structures. One method, demonstrated above
with the sieve system from Nomos Alpha, includes
the algorithmic generation of sieve moduli and
shifts; other methods employ permutations of shift
values or logic operators, transpositions, or ELD
transformations. Xenakis called these operations
métabolae. Although space does not permit demon-
stration here, métabolae of any complexity can be

programmed in Python by using dynamically gener-
ated Sieve objects.

Integration in athenaCL

The objects provided in sieve.py can be used in iso-
lation or in cooperation with other software. Within
athenaCL (Ariza 2002, 2003, 2004), high-level, prac-
tical object interfaces have been developed to pro-
vide access to sieve functionality. These interfaces
provide sieve-based tools for the algorithmic com-

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 10. Psappha, open-
ing passage, group B, voice
2. Complex sieve with a
period of 40.

Figura 11. Three sieve-
generated simultaneities:
(1) 5@1 | 7@1,C2,C5,C4; (2)
6@2 | 7@3,C4,C7; E (3)
10@4 | 7@4,C3,C6,C4.

position of pitches, rhythms, and general parameter
values. Complete demonstration is beyond the
scope of this article; basic functionality of a selec-
tion of these tools, Tuttavia, will be summarized.

Sieve Pitch Generation

The athenaCL system features specialized objects
for pitch structures, including Pitch, Multiset
(collections of Pitch objects), and Path (ordered
Multiset objects). When using athenaCL for com-
position, a Path deﬁnes reusable pitch collections.
The actual use of a Path is dependent on interpreta-
tion by a Texture, to be described below. The Mul-
tiset objects of a Path can be provided by the user
in many representations, including pitch-class (per esempio.,
0, 5, 6), pitch names (per esempio., C2, F6, F#4), and Forte
(1973) set-class names (per esempio., 3–5B). The Sieve object
enables users to enter a Multiset as a sieve.

When using a sieve in athenaCL to create a Path,
the sieve segment is constructed upon a chromatic
pitch range. When entering a sieve, the logic string
can be followed by two comma-delimited argu-
ments for lower- and upper-bounding pitches. These
pitches are notated with pitch names, where middle
C is denoted by C4. Rather than deﬁning z with
integers, z is derived from the range given by the
bounding pitches. An optional third argument is
the pitch of origin, or the location where the zero
of the sieve is placed within the pitch scale. Questo
value, if treated as an integer, is the same as trans-
position. If no argument is provided, the origin is
automatically set to the lower-bounding pitch.

Commands in athenaCL can be executed with
single command-line arguments or through a series
of interactive, text-based prompts. The following
command-line argument, using the PathInstance
New command (PIn), creates a new Path named “a”
from three simple sieves:

:: PIn a 5@1|7@1,C2,C5,C4 6@2|7@3,C4,C7 10@4|7@4,C3,C6,C4

Each sieve has a cycle of ﬁfths (a residual class with
modulus 7), and all share a common origin (C4).

This Path, notated in Figure 11 as a succession of

un-transposed, sustained simultaneities, demon-
strates the ease with which sieves can be used to
create diverse pitch structures. A Texture in
athenaCL can employ these pitch structures in a va-
riety of fashions: as a scale from which melodies are
created, as a collection from which subset chords
are derived, or as a pointillistic cloud of pitches.

Sieve Rhythm Generation

A Texture in athenaCL is a model of an algorithmic
music layer employing two levels of algorithmic de-
sign. The lower level of algorithmic design is con-
trolled by ParameterObject objects, objects that
provide values for every parameter of an event. IL
number of parameters in a Texture, as well as their
function and interaction, is determined by the parent
type and instrument model of the Texture. The up-
per level of algorithmic design is controlled by the
TextureModule, the parent class of each Texture
instance. The TextureModule manages the deploy-
ment and interaction of lower-level ParameterOb-
ject objects, as well as offering linear or non-linear
event processing. TextureModule objects can gener-
ate either monophonic or polyphonic musical parts,
and they are capable of algorithmic procedures not
possible by parameter generation alone, such as al-
gorithmically generated ornamentation (Ariza 2003).
A ParameterObject is entered by the user as a
list of arguments. Arguments can be strings, num-
bers, lists, or arguments for nested ParameterOb-
ject objects. The ﬁrst argument is always the
name of the ParameterObject.

Ariza

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Rhythms are generated using specialized Param-

eterObject objects. Pulse objects, the rhythm
primitive in athenaCL, are measures of duration rel-
ative to a beat. These objects are notated with three
values: a divisor, a multiplier, and an accent. The di-
visor designates a fraction of the beat; the multiplier
scales this fractional division, and the accent can
code for notes (value of 1) or rests (a value of 0).
Così, at a quarter-note beat equal to 120 BPM, UN
Pulse object of (2,1,1) would be an eighth-note du-
ration equal to 0.25 seconds. A Pulse object of
(4,3,1) would produce a dotted eighth-note duration
equal to 0.375 seconds.

Two sieve-based rhythm ParameterObject ob-
jects, pulseSieve and rhythmSieve, are deployed
within athenaCL. Xenakis (1990; 1992, P. 269)
demonstrates converting a binary sieve segment to
a rhythm by setting the ELD to a duration, segment
points to notes, and segment slots to rests. IL
athenaCL pulseSieve object extends this applica-
zione. The arguments for pulseSieve are as follows:
name; sieve logic string; length; pulse; a selection
string randomChoice, randomWalk, randomPer-
mutate, orderedCyclic, or orderedOscillate;
and an articulation string attack or sustain. IL
length value creates a z from 0 to length–1; pulse
deﬁnes the durational ELD as a Pulse object; IL
selection string determines the method of read-
ing values from the sieve segment; and articula-
tion selects whether the rhythm is created from a
binary segment (an attack articulation, in which
intervening slots become rests) or from a width seg-
ment (a sustain articulation, in which intervening
slots are sustained).

The pulseSieve object can be thought of as ﬁl-
tering a z of equal-valued pulses. For more rhythmic
variety, the ParameterObject called rhythm-
Sieve allows z to be supplied by any non-rest pulse
list. This pulse list is then ﬁltered by the sieve:
points on the sieve segment remain notes, and slots
on the sieve segment become rests. The pulse list,
or z, can be dynamically generated by any other
rhythm ParameterObject. A ParameterObject
for generating rhythmic variants with genetic algo-
rithms (Ariza 2002), for instance, could be used to
generate the z ﬁltered by the sieve. The arguments

for the rhythmSieve ParameterObject are as fol-
lows: name, sieve logic string, length, selection
corda, and rhythm ParameterObject. The rhythm
ParameterObject is given as a list of arguments
for the desired rhythm generator.

All sieves, when interpreted as rhythms, can be

thought of as composite polyrhythms. As each
Residual object produces a periodic stream of
pulses, so the sieve is a periodic stream of composite
pulses. The sieve, used as such, provides a compact
and precise notation for composite polyrhythms. In
athenaCL, Per esempio, numerous independent
Texture objects, each with related sieves, could be
used to create dense polyrhythmic structures.

Sieve Parameter Generation

With the exclusion of rhythm, all event values in
athenaCL can be controlled by generator Parame-
terObject objects. Event values include tempo,
amplitude, panning, microtonal pitch transposition,
E, depending on instrument model, values for
synthesis parameters. Xenakis describes the utility
of controlling many attributes of a note event with
a sieve: “[S]ieve theory is very general and conse-
quently is applicable to any other sound characteris-
tic that may be provided with a totally ordered
structure, such as intensity, instants, density, Di-
grees of order, speed, etc.” (1966; 1992, P. 199).

The athenaCL ParameterObject called value-

Sieve facilitates ﬂexible generation of masked,
ﬂoating point values applicable to a wide range of
parameters. The arguments for valueSieve are as
follows: name, sieve logic string, length, minimum,
maximum, and selection string. Sieve logic strings,
length values, and selection strings function as in
the pulseSieve and rhythmSieve objects. How-
ever, where pulseSieve and rhythmSieve use bi-
nary or width sieve segments, valueSieve uses a
unit segment. Segment points, as ﬂoating-point val-
ues within the unit interval, are read from the unit
segment (as dictated by the selection string) E
then scaled within dynamic minimum and maxi-
mum values. Varying the maximum and minimum
with nested ParameterObject objects provides dy-

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

namic scaling of the sieve segment’s proportions.
The sieve is thus bound by what G. M. Koenig called
a tendency mask (1970). Although with such a mask
absolute values of the sieve are not maintained, IL
proportional distribution of values between points
remains intact. Within athenaCL, such a generator
could be used to control tempo values, panning po-
sitions, amplitudes, or microtonal transpositions;
in combination with a Csound instrument, sieve-
derived values could be used for selecting ﬁlter cut-
off frequencies or start times of an audio ﬁle.

Conclusione

With the sieve, Xenakis sought to “add to our arse-
nal sharper tools”—tools of “trenchant axiomatics
and formalization” (1967; 1992, P. 194). The sieve
model presented here shares the elegance and power
of Xenakis’s original theory while providing an open-
source, portable, modular, and complete implemen-
tazione. With this new model, rigorous exploration of
the sieve is possible, including applications in algo-
rithmic composition, algorithmic synthesis, music
analysis, and music theory. In 1996, Xenakis stated
“the basic problem for the originator of computer
music is how to distribute points on a line” (1996,
P. 150); the sieve is one solution. The Python mod-
ule sieve.py is distributed under the General Public
License (GPL) as part of athenaCL, and it can be
downloaded online at www.athenacl.org.

Ringraziamenti

I particularly thank Elizabeth Hoffman, who, Sopra
the course of this project, provided advice and guid-
ance. I am grateful to Paul Berg, Sean H. Carson,
Robert Rowe, and the Editors and anonymous re-
viewers for providing valuable comments and sug-
gestions on earlier versions of this article. Thanks
also to the following people for discussing and shar-
ing their research: Emmanuel Amiot, Gerard As-
sayag, Anne-Sylvie Barthel-Calvet, Ellen Flint,
Benoît Gibson, James Harley, Evan Jones, Marcel
Mesnage, André Riotte, and Sever Tipei.

Riferimenti

Amiot, E., et al. 1986. “Duration Structure Generation
and Recognition in Musical Writing.” Proceedings of
the International Computer Music Conference. San
Francesco, California: International Computer Music
Association, pag. 185–192.

Andreatta, M. 2003. “Méthodes algébriques en musique
et musicologie du XXe siècle: aspects théoriques, ana-
lytiques et compositionnels.” Dissertation. École des
Hautes Etudes en Sciences Sociales.

Ariza, C. 2002. “Prokaryotic Groove: Rhythmic Cycles as
Real-Value Encoded Genetic Algorithms.” Proceedings
of the International Computer Music Conference. San
Francesco, California: International Computer Music
Association, pag. 561–567.

Ariza, C. 2003. “Ornament as Data Structure: An Algo-
rithmic Model based on Micro-Rhythms of Csángó
Laments and Funeral Music.” Proceedings of the Inter-
national Computer Music Conference. San Francisco,
California: International Computer Music Association,
pag. 187–193.

Ariza, C. 2004. “An Object-Oriented Model of the Xe-

nakis Sieve for Algorithmic Pitch, Rhythm, and Para-
meter Generation.” Proceedings of the International
Computer Music Conference. San Francisco, Califor-
nia: International Computer Music Association,
pag. 63–70.

Assayag, Gérard. 1993. “Cao: vers la partition potentielle.”
Les Cahiers de l’Ircam: La composition assistée par or-
dinateur 1(3). Available at mediatheque.ircam.fr/arti-
cles/textes/Assayag93b/.

Barthel-Calvet, UN. S. 2000. “Le Rythme dans l’Oeuvre et
la Pensée de Iannis Xenakis,” Dissertation. L’Ecole des
Hautes Etudes en Sciences Sociales.

Barthel-Calvet, UN. S. 2001. “Chronologie.” In F. B. Mache,
ed. Portrait(S) de Iannis Xenakis. Paris: Bibliotheque
nationale de France, pag. 133–142.

Emmerson, S. 1976. “Xenakis Talks to Simon Emmer-

son.” Music and Musicians 24:24–26.

Flint, E. R. 1989. “An Investigation of Real Time as Evi-
denced by the Structural and Formal Multiplicities in
Iannis Xenakis’ Psappha.” Dissertation. Graduate
School of the University of Maryland.

Forte, UN. 1973. The Structure of Atonal Music. Nuovo

porto, Connecticut: Stampa dell'Università di Yale.

Gibson, B. 2001. “Théorie des cribles.” In M. Solomos, ed.
Presences of / Présences de Iannis Xenakis. Paris: Cen-
tre de Documentation de la Musique Contemporaine,
pag. 85–92.

Ariza

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Harley, J. 2004. Xenakis: His Life in Music. Oxford: Rout-

Tipei, S. 1975. “MP1—A Computer Program for Music

ledge.

Hawkins, D. 1958. “Mathematical Sieves.” Scientiﬁc

American 199:105–112.

Horsley, S. 1772. “The Sieve of Eratosthenes. Being an
Account of His Method of Finding All the Prime
Numbers.” Philosophical Transactions (1683–1775)
62:327–347.

Jones, E. 2001. “Residue-Class Sets in the Music of Iannis
Xenakis: An Analytical Algorithm and a General Inter-
vallic Expression.” Perspectives of New Music
39(2):229–261.

Koenig, G. M. 1970. “Project Two—A Programme for
Musical Composition.” Electronic Music Reports 3.
Utrecht: Institute of Sonology.

Malherbe, C., G. Assayag, and M. Castellengo. 1985.
“Functional Integration of Complex Instrumental
Sounds in Musical Writing.” Proceedings of the Inter-
national Computer Music Conference San Francisco,
California: International Computer Music Association:
pag. 185–192.

Composition.” Proceedings of the Second Music Com-
putation Conference. Urbana: University of Illinois at
Urbana-Champaign, pag. 68–82.

Tipei, S. 1981. “Solving Speciﬁc Compositional Problems
with MP1.” Proceedings of the International Com-
puter Music Conference. San Francisco, California:
Computer Music Association, pag. 68–82.

Tipei, S. 1987. “Maiden Voyages: A Score Produced with

MP1.” Computer Music Journal 11(2):49–64.

Tipei, S. 1989. “The Computer: A Composer’s Collabora-

tor.” Leonardo Journal 22(2):189–195.

Varga, B. UN. 1996. Conversations with Iannis Xenakis.

London: Faber and Faber.

Vriend, J. 1981. “Nomos Alpha for Violoncello Solo (Xe-
nakis 1966): Analysis and Comments.” Interface
10:15–82.

Xenakis, IO. 1963. Musiques Formelles. Paris: Editions

Richard-Masse.

Xenakis, IO. 1965. “La voie de la recherche et de la ques-

tion.” Preuve 177:33–36.

Mesnage, M. 1993. “Mophoscope, a Computer System for

Xenakis, IO. 1966. “Vers une philosophie de la Musique.”

Music Analysis.” Interface 22(2):119–131.

Gravesaner Blätter 29:39–52.

Mesnage, M., e A. Riotte. 1993. “Modélisation infor-

Xenakis, IO. 1967. “Vers une métamusique.” La Nef

matique de partitions, analyse et composition assistées.”
Les Cahiers de l’Ircam: La composition assistée par
ordinateur 1(3). Available at mediatheque.ircam.fr/
articles/textes/Mesnage93a/.

Riotte, UN. 1979. Formalisation de structures musicales.
Paris: Université de Paris 8, Département d’Informa-
tique.

Riotte, UN. 1992. “Formalisation des échelles de hauteurs
en analyse et en composition.” Actes du Colloque
“Musique et Assistance Informatique.” Marseille:
Musique et Informatique de Marseille.

29:117–140.

Xenakis, IO. 1968. “Vers une philosophie de la musique.”

Revue d’Esthétique 21(2–4):173–210.

Xenakis, IO. 1970. “Towards a Metamusic.” Tempo 93:2–19.
Xenakis, IO. 1971. Formalized Music. Bloomington: Indi-

ana University Press.

Xenakis, IO. 1976. Musique, Architecture. Paris: Casterman.
Xenakis, IO. 1988. “Sur le Temps.” In Redécouvrir le Temps.
Bruxelles: Editions de l’Université de Bruxelles 193–200.

Xenakis, IO. 1989. “Concerning Time.” Perspectives of

New Music 27(1):84–92.

Solomos, M. 1996. Iannis Xenakis (Echos du XXe siècle).

Xenakis, IO. 1990. “Sieves.” Perspectives of New Music

Mercuès: P.O. Editions.

28(1):58–78.

Solomos, M. 2002. “Xenakis’ Early Works: From ‘Bar-

Xenakis, IO. 1992. Formalized Music. Hillsdale, New York:

tokian Project’ to ‘Abstraction’.” Contemporary Music
Review 21(2–3):21–34.

Squibbs, R. 1996. “An Analytical Approach to the Music
of Iannis Xenakis: Studies of Recent Works.” Disserta-
zione. Yale University.

Squibbs, R. 2002. “Some Observations on Pitch, Texture,
and Form in Xenakis’ Mists.” Contemporary Music Re-
view 21(2–3):91–108.

Pendragon Press.

Xenakis, IO. 1994. Kéleütha. Paris: L’Arche.
Xenakis, IO. 1996. “Determinacy and Indeterminacy.”

Organised Sound 1(3):143–155.

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

2
9
2
4
0
1
8
5
4
3
0
7
0
1
4
8
9
2
6
0
5
4
0
9
4
3
9
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3 Christopher Ariza image

Scarica il pdf