ARTICLE
Communicated by Shun-ichi Amari
Center Manifold Analysis of Plateau Phenomena Caused
by Degeneration of Three-Layer Perceptron
Daiji Tsutsui
d-tsutsui@cr.math.sci.osaka-u.ac.jp
Osaka University, Toyonaka-shi, Osaka 560-0043, Japan
A hierarchical neural network usually has many singular regions in the
parameter space due to the degeneration of hidden units. Here, we fo-
cus on a three-layer perceptron, which has one-dimensional singular
regions comprising both attractive and repulsive parts. Such a singu-
lar region is often called a Milnor-like attractor. It is empirically known
that in the vicinity of a Milnor-like attractor, several parameters converge
much faster than the rest and that the dynamics can be reduced to smaller-
dimensional ones. Here we give a rigorous proof for this phenomenon
based on a center manifold theory. As an application, we analyze the re-
duced dynamics near the Milnor-like attractor and study the stochastic
effects of the online learning.
1 introduzione
A three-layer perceptron is one of the simplest hierarchical learning ma-
chines. Mathematically, it is defined by the function
D(cid:2)
F (D)(X; θ) =
v
io
ϕ (w
io
· x + bi) ,
x ∈ Rn,
i=1
, . . . , w
θ = (w
1
, b1
, . . . , bd
D
, v
1
, . . . , v
D ),
(1.1)
1
D
D
, . . . , v
, . . . , w
, . . . , bd
where θ is a system parameter with w
∈ Rn being the weight
∈ R the bias terms for the second,
vectors for the second layer, b1
v
∈ Rm the weight vectors for the third, and ϕ an activation func-
1
zione. Throughout this article, we assume that the activation function is twice
differentiable. Figura 1 is a schematic diagram of the three-layer perceptron.
We shall call the function 1.1 an (n-d-m)-perceptron. The numbers n and m
are fixed at the outset as the sizes of input and output vectors, while the
number d of hidden units can be varied in our analysis. For notational sim-
plicity, we incorporate the bias b in the weight w as w = (B, w1, . . . , wn), E
accordingly, we enlarge x as x = (1, x1
, . . . , xn). By using these conventions,
we obtain the abridged presentation of the three-layer perceptron as
Calcolo neurale 32, 683–710 (2020)
https://doi.org/10.1162/neco_a_01268
© 2020 Istituto di Tecnologia del Massachussetts
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
684
D. Tsutsui
Figura 1: A schematic diagram of a three-layer perceptron presented in equa-
zione 1.1.
F (D)(X; θ) =
D(cid:2)
i=1
v
io
ϕ (w
io
· x) .
(1.2)
In questo articolo, we treat the supervised learning. The goal of the super-
vised learning is to find an optimal parameter θ so that f (D)(X; θ) approxi-
mates a given target function T(X). Such a problem is based on the universal
approximation property of the three-layer perceptron. For a suitable activa-
tion function ϕ (per esempio., sigmoidal or ReLU), the model, equation 1.2, can ap-
proximate quite a wide range of functions as the number d of hidden units
tends to infinity (Cybenko, 1989; Funahashi, 1989; Sonoda & Murata, 2017).
IL (averaged) gradient descent method is a standard method for find-
ing an optimal value of θ numerically. Suppose that a loss function (cid:3)(X, sì)
is nonnegative and is equal to zero if and only if y = T(X) (per esempio., the squared
error ||y − T(X)||2). In the gradient descent method, we aim at minimizing
l(D)(θ) := Ex
(cid:4)
(cid:3)
(cid:3)(X, F (D)(X; θ))
by changing the parameter θ iteratively as
θt+1
= θt − ε
∂L(D)
∂θ (θt ),
(1.3)
(1.4)
where ε > 0 is a learning constant. Here, we assume that the input vector x is
a random variable drawn according to an unknown probability distribution
and Ex denotes the expectation with respect to x. In order for the differential
∂L(D)
/∂θ to make sense, we also assume that (cid:3)(X, sì) is differentiable with
respect to y and that we can interchange the order of the differentiation ∂/∂θ
and the expectation Ex. We study the dynamical system, which represents
the averaged gradient descent method with infinitesimal learning constant:
dθ
dt
= −
∂L(D)
∂θ (θ).
(1.5)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Center Manifold Analysis of Plateau
685
The parameter θ descends along the gradient of L(D) into a local minimum.
In practice, the expectation in equation 1.3 is replaced with the arithmetic
mean over a given data set, O, roughly, with a single realization of the
random variable (cid:3)(X, F (D)(X; θ)) for each learning iteration. Such a learning
method involving some stochastic effects is called a stochastic gradient de-
scent method.
Fukumizu and Amari (2000) studied singular regions arising from de-
generation of hidden units of a three-layer perceptron. Here, the degenera-
tion of hidden units means that several weight parameters w
i take the same
value and the effective number of hidden units becomes fewer than d. When
m = 1, they found a novel type of singular region, often called a Milnor-like
attractor. This region has both an attractive part consisting of local minima
of L(D) and a repulsive part consisting of saddle points. In practical learn-
ing, there may be some stochastic effects. Therefore, once the parameter θ
is trapped in the attractive part of this region, it fluctuates in the region by
stochastic effects for a long time, until it reaches the repulsive part. This may
cause serious stagnation of learning, called plateau phenomena. Later, Amari,
Ozeki, Karakida, Yoshida, and Okada (2018) pointed out a notable fact that
a Milnor-like attractor may not cause serious stagnation of learning when
m ≥ 2, which is also treated in this article.
More quantitative analyses for m = 1 have also been carried out by
Coussear, Ozeki, and Amari (2008), Wei, Zhang, Cousseau, Ozeki, E
Amari (2008), and Amari et al. (2018) in the simplest case d = 2. In particu-
lar, Wei et al. (2008) introduced a new coordinate system in the parameter
space by
⎧
⎪⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎪⎩
v
w =
1
w
2
+ v
+ v
2
2
1
w
v
1
+ v
v = v
1
u = w
v
v
z =
1
1
1
2
− w
− v
+ v
2
2
,
2
(1.6)
and claimed, based on evidence observed in numerical simulations, Quello
when the initial point is taken near a Milnor-like attractor, the parameters
(w, v ) quickly converge to equilibrium values (w∗, v ∗
). They hypothesized
that this would always be the case and analyzed only the reduced dynam-
ical system for the subparameters (tu, z), setting the remaining parameters
(w, v ) to be (w∗, v ∗
). Tuttavia, to the best of our knowledge, no mathemat-
ical justification for this hypothesis has been established.
The objective of this article is to provide a solid ground on Amari et al.’s
(2018) point of view. We introduce a new coordinate system that admits
a center manifold structure around a special point on the Milnor-like at-
tractor. By using the coordinate system, we can analyze the Milnor-like
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
686
D. Tsutsui
attractor more rigorously and integrate the reduced dynamical system
explicitly to obtain analytical trajectories. The obtained trajectories are com-
parable to the preceding work. It is confirmed by several settings of numer-
ical simulations that trajectories in actual learning agree with the analytical
ones.
In addition to the averaged gradient descent method, we also address on-
line learning, a stochastic gradient descent method. Around a Milnor-like
attractor, the behavior of sample paths by the online learning seems quali-
tatively different from that of trajectories by the averaged gradient descent.
To investigate why they are different, we divide the dynamics of parame-
ters into fast and slow ones, as is the case in the averaged gradient descent.
In questo caso, we observed in numerical simulations that the fast parameters
fluctuate intensively around the center manifold for the averaged system.
We show that such a deviation of the fast parameter from the center mani-
fold can influence a trend of the slow parameter.
This article is organized as follows. In section 2, we give a quick review
of Amari et al.’s (2018) lavoro. In section 3, after a brief account of the cen-
ter manifold theory, we introduce a new coordinate system in the parameter
space and prove that it admits the center manifold structure. In section 4, we
carry out numerical simulations and observe the center manifold structure
around a Milnor-like attractor. In section 5, we consider the online learning
from the viewpoint of the center manifold theory. Sezione 6 offers conclud-
ing remarks.
2 Singular Region and Milnor-Like Attractor
In this section, we give a quick review of the Milnor-like attractor that Fuku-
mizu and Amari (2000) found, which appears when the number m of output
units is equal to 1. We also mention an interesting insight by Amari et al.
(2018) for the case m ≥ 2.
The parameter space of a perceptron is sometimes called a perceptron
manifold. Tuttavia, in many cases, it is not really a manifold since it usu-
ally contains a subset whose points correspond to the same input-output
relation. Such a subset is usually referred to as a singular region. Generalmente,
there are many singular regions due to the degeneration of hidden units.
Per esempio, let us consider an (n-2-m)-perceptron. Then the subset
R(w, v) := {θ = (w
, w
, v
, v
2)|w
1
1
2
1
= w
2
= w, v
+ v
2
1
= v}
of the parameter space forms a typical singular region. Infatti, on the subset
R(w, v), an (n-2-m)-perceptron f (2)(X; θ) is reduced to the following (n-1-m)-
perceptron:
F (1)(X; w, v) := v ϕ (w · x) .
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Center Manifold Analysis of Plateau
687
On such a singular region, some properties of L(1) are inherited by L(2).
The following lemma implies that a criticality is a hereditary property.
Lemma 1. Let θ∗ = (w∗, v∗
(w
) be a critical point of L(1). Then the parameter θ =
) is a critical point of L(2) for any λ ∈ R.
2) = (w∗, w∗, λv∗, (1 − λ)v∗
, w
, v
, v
1
2
1
Proof.
∂L(2)
∂w
io
∂L(2)
∂v
io
(θ) = E
(cid:9)
(θ) = E
(cid:9)(cid:10)
∂(cid:3)(X, F (1)(X; θ∗
∂y
∂(cid:3)(X, F (1)(X; θ∗))
∂y
(cid:11)
(cid:12)
))
io
ϕ(cid:5)
· v
(w∗ · x) xT
(cid:12)
ϕ(w∗ · x)
=
∂L(1)
∂v (θ∗
= λ
io
∂L(1)
∂w (θ∗
),
),
i = 1, 2,
1 := λ and λ
2 := 1 − λ. Since θ∗
where λ
zero.
is a critical point of L(1), these are all
(cid:2)
When m = 1, in particular, every point θ ∈ R(w∗, v ∗
) is a critical point of
l(2), since the parameter v, as well as the output f (D)(X; θ), is a scalar quantity.
In questo caso, the second-order property of L(1) is also inherited by L(2) to some
extent, and the singular region R(w∗, v ∗
) may have an interesting structure,
which causes serious stagnation of learning.
Proposition 1 (Fukumizu & Amari, 2000). Let m = 1 and θ∗ = (w∗, v ∗
) be a
strict local minimizer of L(1) with v ∗ (cid:6)= 0. Define an (N + 1) × (N + 1) matrix H
by
H := Ex
(cid:9)
∂(cid:3)(X, F(1)(X; θ∗
∂y
))
(cid:12)
v ∗ϕ(cid:5)(cid:5)
(w∗ · x) x xT
,
(2.1)
and for λ ∈ R, let
θλ := (w∗, w∗, λv ∗, (1 − λ)v ∗
).
If the matrix H is positive (resp. negative) definite, then the point θ = θλ is a lo-
cal minimizer (resp. saddle point) of L(2) for any λ ∈ (0, 1) and is a saddle point
(resp. local minimizer) for any λ ∈ R \ [0, 1]. D'altra parte, if the matrix H
is indefinite, then the point θλ is a saddle point of L(2) for all λ ∈ R \ {0, 1}.
This proposition implies that the one-dimensional region R(w∗, v ∗
) =
{θλ | λ ∈ R} may have both attractive parts and repulsive parts in the gradi-
ent descent method. Such a region is referred to as a Milnor-like attractor (Wei
et al., 2008). The parameter θ near the attractive part flows into the Milnor-
like attractor and fluctuates in the region for a long time, until it reaches the
repulsive part.
The original theorem (Fukumizu & Amari, 2000) is for an (n-d-1)-
perceptron that contains (n-(d-1)-1)-perceptron as a subnetwork and that
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
688
D. Tsutsui
the phenomenon itself is universal with respect to the number d of
hidden units. The proposition above for (n-2-1)-perceptron is a minimal
version.
We also remark that the point θλ cannot be a strict local minimizer since
l(2) takes the same value on the singular region {θλ | λ ∈ R} and is flat along
its direction. The proof of proposition 1 is given mainly by a discussion of
the Hessian matrix of L(2); Tuttavia, we need to treat higher-order deriva-
tives of L(2) than the second order, since the Hessian matrix degenerates on
the singular region (see appendix A).
Let us suppose a situation where a three-layer perceptron has some re-
dundant hidden units to represent the target function T(X). Mathematically,
we suppose that a true parameter θtrue exists (T(X) = f(2)(X; θtrue)) and that
it lies in the singular region R(w∗, v ∗
). In questo caso, the function L(2) takes the
same value L(1)(w∗, v ∗
). Therefore, every point of R(w∗, v ∗
)
becomes a global minimizer of L(2), and a Milnor-like attractor does not ap-
pear. Infatti, one can check that the assumption of proposition 1 fails as
follows. For each x ∈ Rn, we obtain
) = 0 on R(w∗, v ∗
∂(cid:3)(X, F(1)(X; w∗, v ∗
))/∂y = 0,
since a loss function (cid:3)(X, sì) takes its minimum 0 at y = T(X) = f(1)(X; w∗, v ∗
).
This implies that the matrix H becomes the zero matrix. Così, H is neither
positive nor negative definite.
We next treat the case when m ≥ 2. There also exists a one-dimensional
region consisting of critical points due to lemma 1. Tuttavia, in this case,
the region becomes simply repulsive and does not have an attractive part,
as the following theorem asserts.
Theorem 1. Let θ∗ = (w∗, v∗
matrix
) be a local minimizer of L(1). If the m × (N + 1)
(cid:9)
Ex
∂(cid:3)(X, F (1)(X; θ∗
∂y
))
(cid:12)
ϕ(cid:5)
(w∗ · x) xT
(2.2)
is nonzero, then θλ = (w∗, w∗, λv∗, (1 − λ)v∗
λ ∈ R, where we regard the derivative ∂(cid:3)/∂y as a column vector.
) is a saddle point of L(2) for any
Amari et al. (2018) stated a prototype of theorem 1, although they did
not give a full proof. Infatti, we found that some additional assumption
was necessary to prove their assertion. In theorem 1, we have added a mild
assumption that the matrix, equation 2.2, is nonzero. Note that since θ∗ =
(w∗, v∗
) is a local minimizer of L(1), it holds that
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Center Manifold Analysis of Plateau
689
0 =
∂L(1)
∂w (θ∗
) = (v∗
)T Ex
(cid:9)
∂(cid:3)(X, F (1)(X; θ∗
∂y
))
(cid:12)
ϕ(cid:5)
(w∗ · x) xT
.
Così, the matrix 2.2 has a kernel whose dimension is greater than or equal
to one. Hence, the assumption automatically fails when m = 1. This is an
underlying mechanism for proposition 1.
3 Center Manifold of Milnor-Like Attractor
In their analysis of an (n-2-1)-perceptron, Wei et al. (2008) introduced a co-
ordinate transformation,
⎧
⎪⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎪⎩
v
w =
1
w
2
+ v
+ v
2
2
1
w
v
1
+ v
v = v
1
u = w
v
v
z =
1
1
1
2
− w
− v
+ v
2
2
,
2
(3.1)
and claimed that the parameters (w, v ) quickly converge to (w∗, v ∗
) Quando
the initial point is taken near a Milnor-like attractor. Amari et al. (2018) men-
tioned that the dynamics in this coordinate system should be analyzed by
using the center manifold theory, and they analyzed only the reduced dy-
namical system for the subparameters (tu, z), setting the remaining parame-
ters (w, v ) to be (w∗, v ∗
). Strictly speaking, Tuttavia, their coordinate system
does not admit any center manifold structure, and their claim is at the stage
of hypothesis.
In this section, we give a rigorous justification for their hypothesis. Noi
first give a quick review of the center manifold theory and then introduce
a new coordinate system under which the center manifold structures arise
near certain points on the Milnor-like attractor.
3.1 Brief Review of Center Manifold. Suppose that we are given a dy-
namical system,
(cid:13)
˙x(T) = Ax(T) + F (X(T), sì(T))
˙y(T) = By(T) + G(X(T), sì(T))
,
(3.2)
for the parameters (X, sì) ∈ Rd1 × Rd2 , where A and B are constant matrices
and f and g are C2 functions such that they, along with their first deriva-
tives, vanish at the origin. We assume that all the eigenvalues of A have
zero real parts, while all the eigenvalues of B have negative real parts. Questo
assumption means that parameter y converges to the origin exponentially
quickly, and the parameter x is driven only by the higher-order terms of f
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
690
D. Tsutsui
and evolves very slowly compared with y. Since f and g are of the second
order with respect to x and y, the assumptions for equation 3.2 imply that
the coefficient matrix of the linearization of the system has the form
(cid:14)
(cid:15)
.
A O
O B
Definition 1. A set S ⊂ Rd1 × Rd2 is said to be a local invariant manifold of
, y0) ∈ S, the solution (X(T), sì(T)) of equation 3.2 con
equation 3.2 if for (x0
(X(0), sì(0)) = (x0
Definition 2. A local invariant manifold represented in the form of y = h(X) È
called a local center manifold (or simply a center manifold) if h is differentiable and
satisfies h(0) = 0 E
, y0) is in S for |T| < T with some T > 0.
(0) = O.
∂h
∂x
The following center manifold theorems give us a method of simplifying
a dynamical system around an equilibrium point.
Proposition 2 (Center manifold theorem 1: Carr, 1981). Equazione 3.2 has a center
manifold y = h(X) for ||X|| < δ, for some δ > 0 and C2 function h.
Proposition 3 (Center manifold theorem 2: Carr, 1981). Suppose that the origin
u = 0 is a stable equilibrium point of the reduced dynamical system
˙u(T) = Au(T) + F (tu(T), H(tu(T))).
(3.3)
, y0). Then
, y0)|| is sufficiently small, there exists a solution u(T) of equation 3.3 come
Let (X(T), sì(T)) be a solution of equation 3.2 with the initial value (x0
if ||(x0
Quello
X(T) = u(T) + O(e
sì(T) = h(tu(T)) + O(e
−γ t ),
−γ t ),
as t → ∞, where γ is a positive constant.
Proposition 3 asserts that the parameter (X, sì) approaches the center
manifold y = h(X) quickly and then evolves along it. Così, the dynamical
system, equation 3.2, around the origin is essentially controlled by the slow
parameter x and reduced to the lower-dimensional system.
3.2 Main Results. Let us return to the analysis of an (n-2-1)-perceptron.
In a column vector representation, the dynamical system, equation 1.5, for
IL (n-2-1)-perceptron is written as
˙θ = −
(cid:10)
(cid:11)
∂L(2)
∂θ (θ)
T
.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Center Manifold Analysis of Plateau
691
We consider another coordinate system ξ = ξ(θ) and investigate the dynam-
ical system in it. By the coordinate transformation, the dynamical system
above is transformed to
˙ξ = −
(cid:10)
∂ξ
∂θ
∂ξ
∂θ
(cid:11)
T
(cid:10)
(cid:11)
∂L(2)
∂ξ (ξ)
T
.
(3.4)
Così, the coefficient matrix of its linearization at a critical point ξ = ξ∗
È
∂ ˙ξ
∂ξ (ξ∗
) = −
(cid:13)
(cid:10)
∂ξ
∂θ
∂ξ
∂θ
∂
∂ξ
(cid:11)
T
(cid:10)
(cid:11)
∂L(2)
∂ξ (ξ)
T
(cid:16)(cid:17)
(cid:17)
(cid:17)
(cid:17)
(cid:17)
ξ=ξ∗
(cid:11)
(cid:10)
∂ξ
∂θ
∂ξ
∂θ
T ∂ 2L(2)
∂ξ∂ξ (ξ∗
),
= −
/∂ξ)(ξ∗) = 0. This relation implies that the coefficient
where we used (∂L(2)
/∂ξ∂ξ)(ξ∗). In partic-
matrix has the same rank as the Hessian matrix (∂ 2L(2)
ular, the rank of the coefficient matrix of the linearization does not depend
on the choice of a coordinate system.
0
, θ
We focus on the dynamics of the learning process around the two points,
θ = θ
1, which are boundaries of the repulsive and attractive parts of
a Milnor-like attractor {θλ|λ ∈ R}. Concretely, they are denoted as θ
=
(w∗, w∗, 0, v ∗) and θ
= (w∗, w∗, v ∗, 0), Dove (w∗, v ∗) is a minimizer of the
loss L(1) for the (n-1-1)-perceptron as mentioned in proposition 1. This is be-
cause the rank of the Hessian matrix at θλ degenerates by one dimension for
λ (cid:6)= 0, 1 and by n + 2 dimension for λ = 0, 1, which is shown in appendix A.
0
1
We introduce a new coordinate system ξ = (w, v, tu, z) by
⎧
⎪⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎪⎩
v
1 (w
1
− w∗
w =
) + v
v ∗
2 (w
2
− w∗
)
+ w∗
v = v
+ v
2
1
2 (w
v
− w∗
1
u =
z = v
− v
2
1
1 (w
2
− w∗
)
) − v
v ∗
(3.5)
This formula defines a coordinate system on the region {v 2
1
the coordinate system, equation 3.5, the critical points θλ are denoted as
(cid:6)= 0}. Under
+ v 2
2
ξλ = (w∗, v ∗, 0, (2λ − 1)v ∗
).
= (w∗, v ∗, 0, −v ∗
In particular, ξ
the main theorem of this article:
0
) and ξ
1
= (w∗, v ∗, 0, v ∗
). Now we arrive at
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
692
D. Tsutsui
Theorem 2. In the coordinate system ξ = (w, v, tu, z), the dynamical system,
equation 1.5, admits a center manifold structure around the critical points θ =
θ
0
1 in which (w, v ) converge exponentially fast.
, θ
To prove the theorem, we make use of the following lemma.
Lemma 2. If the matrix X is positive definite and Y is positive semidefinite, Tutto
the eigenvalues of the matrix XY are nonnegative.
Proof. The matrix XY is rewritten as
XY = X
1
2 (X
1
2 Y X
1
2 )X
− 1
2 ,
1
2 is a unique positive-definite matrix such that (X
where X
matrix Z := X
of Z, the vector X
ing eigenvalue is nonnegative.
2 )2 = X. Here, IL
2 is positive semidefinite. Hence, for each eigenvector a
2 a is an eigenvector of the matrix XY, and the correspond-
(cid:2)
1
2 Y X
1
1
1
Proof of Theorem 2. The proof is essentially based on a straightforward
calculation. The coefficient matrix of the linearization of the dynamical sys-
tem, equation 3.4, under the coordinate system, equation 3.5, splits into
(w, v ) part and (tu, z) part for λ = 0, 1. Infatti, for λ ∈ R, the negative of the
coefficient matrix is written as
˜Aλ =
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
w, v
⎧
⎨
⎩
(cid:22)
tu
z {
w, v
(cid:18)
(cid:19)(cid:20)
1+2kλ H (1 + 2kλ)P − (−1+2λ)kλ
(1 + 2kλ)Q + 1+3kλ
tu
(cid:19)(cid:20)
(cid:21)
(cid:18)
1+2kλ H 0
z(cid:18)(cid:19)(cid:20)(cid:21)
(cid:21)
2PT
− (−1+2λ)kλ
1+2kλ H
0
2R
0
0
0
− kλ
1+2kλ H
0
0
0
0
⎞
⎟
⎟
⎟
⎟
,
⎟
⎟
⎠
and the system is written as
˙ξ = − ˜Aλ(ξ − ξλ) + ˜gλ(ξ),
where ˜gλ is the higher-order term, which vanish at the ξ = ξλ together with
its first derivative. Here,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
(cid:3)
kλ := (1 − λ)λ,
P := Ex
Q := Ex
R := Ex
(∂ 2(cid:3)) v ∗ ϕ(w∗ · x) ϕ(cid:5)
(∂ 2(cid:3)) (v ∗
)2 ϕ(cid:5)
(∂ 2(cid:3)) ϕ(w∗ · x)2
(cid:3)
(cid:3)
(cid:4)
,
(w∗ · x) X
(cid:4)
,
(w∗ · x)2 x xT
(cid:4)
,
Center Manifold Analysis of Plateau
693
∂(cid:3) :=
∂ 2(cid:3) :=
,
))
∂(cid:3)(X, F(1)(X; θ∗
∂y
∂ 2(cid:3)(X, F(1)(X; θ∗))
∂y2
,
and H is the matrix defined by equation 2.1. H and Q are matrices, P is a
column vector, and R is a scalar. For λ = 0 O 1, the negative of the coefficient
matrix is of the form
tu(cid:18)(cid:19)(cid:20)(cid:21)
z(cid:18)(cid:19)(cid:20)(cid:21)
˜A0
= ˜A1
=
⎛
(cid:29)
w, v
⎜
⎜
⎜
(cid:30)
⎜
⎝
tu
z{
w, v
(cid:18)
(cid:21)
(cid:19)(cid:20)
Q + H P
2PT
0
2R 0
0
0
0
0
0
0
0
0
0
0
⎞
⎟
⎟
⎟
.
⎟
⎠
(3.6)
We show that all the eigenvalues of (w, v )-block of the coefficient matrix
− ˜A0 are strictly negative. Recall that the coefficient matrix at a critical point
ξ∗ of the dynamical system, equation 1.5, is given by
−
∂ξ
∂θ
(cid:11)
(cid:10)
∂ξ
∂θ
T ∂ 2L(2)
∂ξ∂ξ (ξ∗
).
/∂ξ∂ξ)(ξ
Applying lemma 2 to X = (∂ξ/∂θ)(∂ξ/∂θ)T and Y = (∂ 2L(2)
0), all the
eigenvalues of the coefficient matrix − ˜A0 are nonpositive. One can see that
the Hessian matrix is positive semidefinite and degenerates by n + 2 di-
mension at θ = θ
1 in appendix A. Since a coordinate transformation pre-
serves the rank of the coefficient matrix of linearization, ˜A0 degenerates by
N + 2 dimension, which is equal to the size of (tu, z)-block. This implies that
IL (w, v )-block is of full rank, and thus all the eigenvalues of (w, v )-block
are strictly negative. It is proved similarly for ξ = ξ
, θ
0
Due to proposition 2, there are center manifolds parametrized by (tu, z)
(cid:2)
, θ
1.
around θ = θ
0
1 rispettivamente.
3.3 Reduced Dynamical System. By virtue of proposition 3 and theo-
rem 2, we can assume that the dynamics of the gradient descent is on the
center manifold near the points θ = θ
1. Così, we can reduce the dynam-
0
ical system into that of (tu, z). Recalling the coefficient matrix, equation 3.6,
we can see that ˙u and ˙z have no first-order terms. In more detail, calculat-
ing the Taylor expansion of ( ˙u, ˙z) up to the second order around ξ = ξ
1, we
obtain
, θ
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
694
D. Tsutsui
(cid:22)
−(P · (w − w∗
˙u = 1
v ∗
))(tu + (w − w∗
))
− (v − v ∗
)(R I + 1
2
H)(tu + (w − w∗
))
+ 1
2
(z − v ∗
)H(tu + (w − w∗
(cid:31)
))
+ O(||ξ − ξ
||3),
1
(3.7)
(cid:22)
−(w − w∗
˙z = 1
v ∗
)T Q(tu + (w − w∗
))
)(P · (tu + (w − w∗
)))
) + 1
2
− (v − v ∗
− 1
2
(w − w∗
)T H(w − w∗
(cid:31)
+ O(||ξ − ξ
||3),
1
(3.8)
uT Hu
where I denotes the (N + 1) × (N + 1) identity matrix. Now we consider the
reduced dynamical system on the center manifold. Here, the center mani-
fold (w, v ) = h(tu, z) satisfies that
H(tu, z) =
!
=
!
w∗
v ∗
w(tu, z)
v (tu, z)
+ O((cid:10)tu, z − v ∗(cid:10)2),
by definition. This gives an approximation of the dynamics on the center
manifold near ξ = ξ
1 COME
˙u = 1
˙z = 1
)Eh + O((cid:10)tu, z − v ∗(cid:10)3),
2v ∗ (z − v ∗
2v ∗ uT Hu + O((cid:10)tu, z − v ∗(cid:10)3).
(3.9)
Neglecting the higher-order terms, we can integrate this equation to obtain
(cid:10)tu(cid:10)2 = (z − v ∗
)2 + C,
(3.10)
where C is an integral constant.
Around the point ξ = ξ
0, we obtain the similar dynamics,
˙u = − 1
˙z = − 1
)Eh + O((cid:10)tu, z + v ∗(cid:10)3),
2v ∗ (z + v ∗
2v ∗ uT Hu + O((cid:10)tu, z + v ∗(cid:10)3),
and the relation,
(cid:10)tu(cid:10)2 = (z + v ∗
)2 + C.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Center Manifold Analysis of Plateau
695
We remark that theorem 2 is valid even when there exists a true param-
eter in the singular region R(w∗, v ∗
); Tuttavia, in this case, such a simple
form of the reduced dynamical system as equation 3.9 is not obtained. As
mentioned above, this case implies that H becomes the zero matrix. Then,
the second-order terms of the reduced dynamical system, equation 3.9, van-
ish, and the third-order terms become dominant. Così, we have to take into
account the cross terms between (w − w∗, v − v ∗
). It needs to
calculate the center manifold (w, v ) = h(tu, z) up to the second order, Quale
makes the analysis complicated.
) E (tu, z − v ∗
Finalmente, we remark on a difference between our analysis and previous
lavoro. Wei et al. (2008) have studied a reduced dynamical system in the
vicinity of the whole part of a Milnor-like attractor. D'altra parte, UN
center manifold is defined locally, and center manifolds around each of two
points cannot be connected at a midpoint in general. Così, one cannot dis-
cuss a center manifold defined around the entire region of a Milnor-like
attractor.
3.4 More General Models. Our results can be extended to a more
general model including multilayer perceptrons whose output is one-
dimensional. In this section, we consider a parameterized family of func-
tions that can be written as
F (X; θ) := g(X, τ ) + v
θ = (w
, v
, w
1
2
φ(X; w
1
, τ ),
, v
2
1
, τ ) + v
2
φ(X; w
, τ ),
2
1
(3.11)
where we assume that g(X; τ ) and φ(X; w, τ ) are twice differentiable with
respect to τ and (w, τ ), rispettivamente.
A multilayer perceptron ˜α(l)(X; θ) with L layers defined recursively as
, . . . , xn0 )T ,
α(0)(X; θ) := (1, x1
˜α((cid:3))(X; θ) := W ((cid:3))α((cid:3)−1)(X; θ),
”
1, ϕ( ˜α((cid:3))
α((cid:3))(X; θ) :=
1 (X; θ)), . . . , ϕ( ˜α((cid:3))
#
N(cid:3) (X; θ))
T
,
1 ≤ (cid:3) ≤ L,
θ = (W (1), . . . , W (l)),
, . . . , xn0 )T ∈ Rn0 , where W ((cid:3)) is an n(cid:3) × (N(cid:3)−1
+ 1) matrix,
, . . . , nL ∈ N, and ϕ is a twice-differentiable activation function. As-
for each x = (x1
n0
suming that the dimension nL of the output is equal to 1 and denoting
, n1
W (L−1) =
(cid:3)
W (l) =
(cid:3)
w
1
w
2
v
v
1
v
2
0
· · · wnL−1
vnL−1
· · ·
(cid:4)
T ,
(cid:4)
,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
696
D. Tsutsui
a multilayer perceptron is represented as model 3.11 by letting
φ(X; w, τ ) := ϕ(w · α(L−2)(X; τ )),
nL−1(cid:2)
G(X; τ ) :=
v
io
ϕ(w
io
· α(L−2)(X; τ )),
i=3
τ := (W (1), . . . , W (L−2), w
, . . . , wnL−1
3
, v
, v
, . . . , vnL−1 ).
3
0
Our main result is extended to the model, equation 3.11 come segue. Let
) be a strict local minimizer of an averaged loss function for
θ∗ = (w∗, v ∗, τ∗
the degenerate model:
F(1)(X; ˜w, ˜v, τ ) = g(X; τ ) + ˜v φ(X; ˜w, τ ).
Then the coordinate system ξ = (w, v, τ, tu, z), given by formula 3.5, admits
a center manifold structure around the two points θ = (w∗, w∗, 0, v ∗, τ∗),
(w∗, w∗, v ∗, 0, τ∗), and the dynamical system is reduced to that of (tu, z). Questo
is confirmed by the argument of the coefficient matrix of the linearization,
similar to theorem 2.
4 Numerical Simulations
In the previous section, we showed that the dynamics of (w, v ) are fast and
those of (tu, z) are slow under the coordinate system, equation 3.5. In this
section, we verify this fact by numerical simulations.
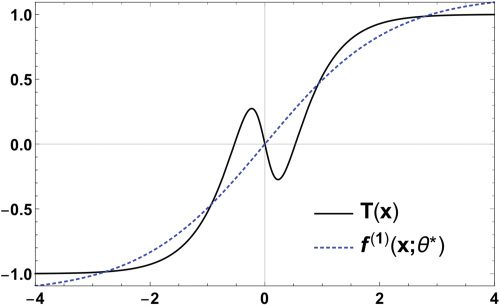
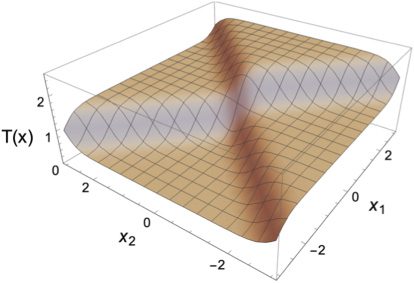
4.1 Esempio 1. As the first example, we set the input dimension to be
n = 1 and choose the teacher function T : R → R defined by
T(X) := 2 di pesce(X) − tanh(4X),
where tanh is the hyperbolic tangent function. The shape of T is shown in
Figura 2 by the solid black line. We set the activation function ϕ as tanh.
Così, the target function T can be represented by the (1-2-1)-perceptron
with no bias terms:
F(2)(X; θ) = v
1
ϕ(w
1X) + v
2
ϕ(w
2X),
and the true parameter is (w
2) = (1, 4, 2, −1). We also discard
1
the bias terms w0
2 of the student perceptron. This makes the ma-
trix H scalar valued, and hence the assumption of proposition 1 holds
trivially.
1 and w0
, w
, v
, v
1
2
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Center Manifold Analysis of Plateau
697
Figura 2: The target function T(X) and the (1-1-1)-perceptron f(1)(X; θ∗), Quale
corresponds to the local minimizer θ∗.
We assume that the data set {xs}S
s=1 is given and that the probability distri-
bution of x is the empirical distribution on that data set. Then the transition
formula, equation 1.4, of the parameter θ is rewritten as
θ(t+1) = θ(T) − ε 1
S
∂(cid:3)(xs, F(2)(xs; θ))
∂θ
(cid:17)
(cid:17)
(cid:17)
(cid:17)
.
θ=θ(T)
S(cid:2)
s=1
In this simulation, we set the size S of the data set to be 1000, and data
{xs}S
s=1 are drawn identical and independenty distributed (i.i.d.) according
to N(0, 22). Here, N(μ, P 2) denotes the gaussian distribution with mean μ
and variance σ 2.
For a data set given as above, we obtained a local minimizer θ∗ =
(w∗, v ∗
) = (0.459, 1.15) of L(1). The shape of the function that corresponds
to the local minimizer is shown by the dashed blue line in Figure 2. IL
value of H is approximately 0.0472. Since H > 0, the attractive region is
{θλ | λ ∈ (0, 1)}, due to proposition 1.
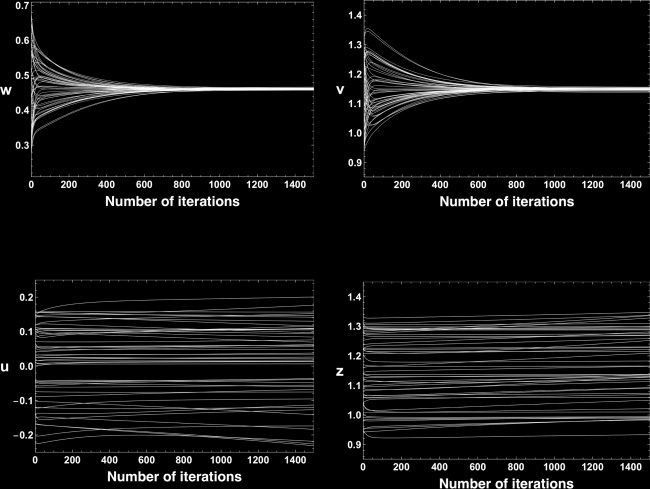
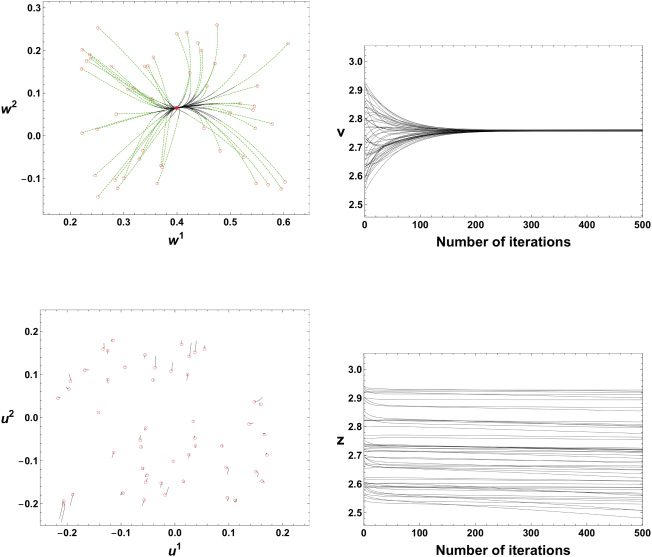
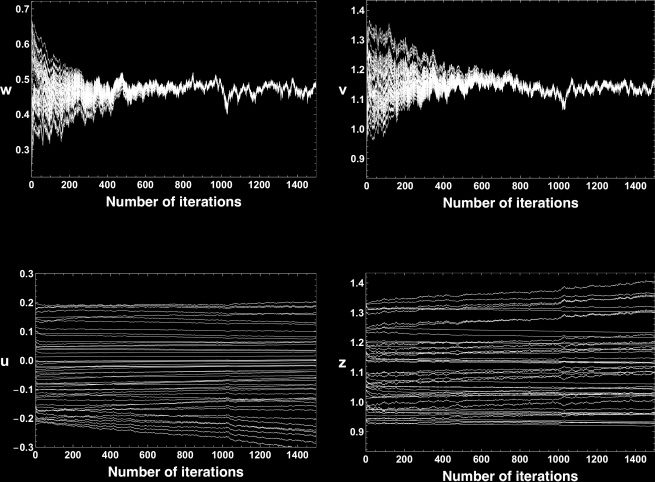
Figura 3 displays time evolutions of each parameter in the first 1500
iterations from 50 different initial points. We chose an initial parameter
θ(0) = (w(0)
1
2 ) by
, w(0)
2
, v (0)
1
, v (0)
w(0)
1
= w∗ + ζ
1
, w(0)
2
= w∗ + ζ
2
,
+ ζ
(ζ
3
v (0)
1
= 1
2
so that v = v ∗ + ζ
∼
4, where ζ
1
U(−0.2, 0.2). Here, U(UN, B) denotes the uniform distribution on the interval
= v ∗ + 1
2
3 and z = v ∗ + ζ
∼ U(−0.2, 0.2), and ζ
3
v (0)
2
, ζ
4
, ζ
2
(ζ
3
4),
4),
− ζ
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
698
D. Tsutsui
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 3: Time evolutions of each parameter for the first 1500 iterations. Each
trajectory of w or v quickly converges to the equilibrium point w∗ = 0.459, v ∗ =
1.15, rispettivamente. Trajectories of u and z evolve very slowly compared with w
and v.
[UN, B] ⊂ R. We set the learning rate ε to be 0.05 and the number of iterations
to be 20,000. We can see that the parameters w and v converge to their equi-
libriums exponentially fast (see Figures 3a and 3b), while u and z evolve
slowly (see Figures 3c and 3d).
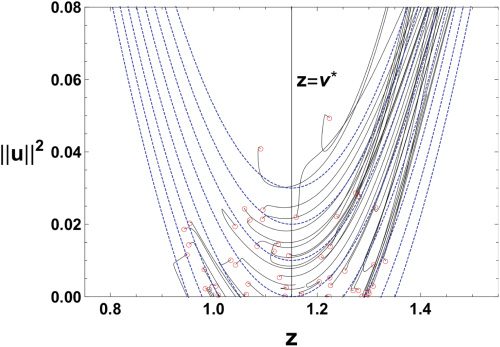
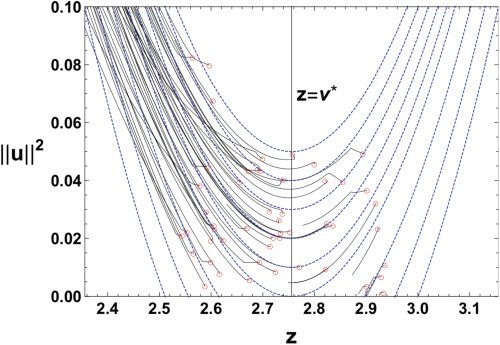
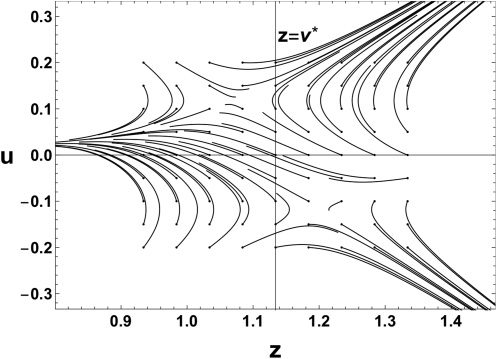
Figura 4 shows evolutions on the (z, ||tu||2)-plane. The red circles in the
and v = v ∗
figure represent initial points. When w = w∗
, the z-axis is a
Milnor-like attractor, and the region |z| < v ∗
is the attractive part of it.
We can check that parameters near the attractive region are trapped and
those near the repulsive region are escaping. The intersection point of the
line z = v ∗
1, the boundary of the
attractive and repulsive parts of the Milnor-like attractor. The analytical
trajectories, equation 3.10, are plotted as dashed blue curves. Numerical
evolutions of the parameter follow the analytical trajectories considerably
well around θ = θ
1. We see in the figure that some instances of time evo-
lutions change their direction sharply. This is because the fast dynamics of
w and v are the main dynamics at the beginning of the learning, while the
and z-axis corresponds to the point θ = θ
Center Manifold Analysis of Plateau
699
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Figure 4: Trajectories on the (z, ||u||2)-plane obtained by learning for 20,000 iter-
ations (solid black curves) and analytical trajectories (dashed blue curves) near
θ = θ
= (w∗, w∗, v ∗, 0). Red circles represent initial points.
1
slow dynamics of u and z become dominant after w and v converge to the
center manifold.
4.2 Example 2. As the second example, we consider a three-layer per-
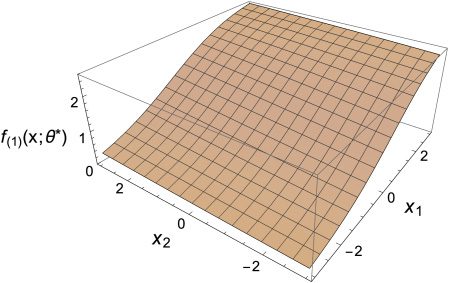
ceptron whose input dimension is n = 2. Let the teacher function T : R2 →
R be given by
T(x1
, x2) := 0.75 Sgm(2.5x1
− 2.5x2) + Sgm(2.5x1
+ 2.5x2) + 0.5,
where Sgm is the logistic sigmoidal function, which is defined by
Sgm(x) :=
1
1 + e−2x
= 1
2
(1 + tanh(x)).
Figure 5 shows the shape of the teacher function T(x). We use a perceptron
with no bias terms also in this simulation and choose Sgm as the activa-
tion function. Note that a (2-2-1)-perceptron is unable to represent the target
function in this case.
Also in this simulation, we assume that the probability distribution of
x is the empirical distribution on a fixed data set {xs}S
s=1. We set the num-
ber S of the data set to be 1000, and draw a data set {xs}S
s=1 i.i.d. according
to N(0, I2), where I2 denotes the 2 × 2 identity matrix. We chose a realiza-
s=1 as above and obtained a local minimizer θ∗ = (w∗, v ∗
tion {xs}S
) of L(1),
where w∗ = (0.399, 0.0652) and v ∗ = 2.76. Figure 6 shows the shape of the
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
n
e
c
o
_
a
_
0
1
2
6
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
700
D. Tsutsui
Figure 5: The target teacher function T(x).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
n
e
c
o
_
a
_
0
1
2
6
8
p
d
.
/
Figure 6: The (2-1-1)-perceptron f(1)(x; θ∗) that corresponds to the local mini-
mizer θ∗.
(2-1-1)-perceptron corresponding to the local minimizer. The matrix H is
numerically computed as
(cid:14)
−0.044 −0.026
−0.026 −0.20
(cid:15)
.
Since this H is negative definite, the attractive region is {θλ | λ ∈ R \ [0, 1]}
due to proposition 1.
Figures 7a to 7d show time evolutions of each parameter in the first 500
iterations from 50 different initial points. We chose initial parameters of the
(2-2-1)-perceptron as
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Center Manifold Analysis of Plateau
701
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
n
e
c
o
_
a
_
0
1
2
6
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7: Time evolutions of each parameter for the first 500 iterations.
Each trajectory of w or v quickly converges to the equilibrium point w∗ =
(0.399, 0.0652), v ∗ = 2.76 respectively. However, trajectories of u and z evolve
very slowly compared with w and v. In panel a, the first 30 iterations are dashed
in green to display the speed of convergence, and the red point at the center rep-
resents w = w∗. Red circles in panels a and c represent initial points.
w(0)
1
v (0)
1
= w∗ + ζ
, w(0)
2
1
= w∗ + ζ
,
2
= v ∗ + 1
2
(ζ
3
+ ζ
4),
v (0)
2
= 1
2
(ζ
3
− ζ
4),
1
2
, ζ
∼ U(−0.2, 0.2)2 and ζ
3
∼ U(−0.2, 0.2). We set the learning
, ζ
where ζ
4
rate ε to be 0.05 and the number of iterations to be 20,000. In this simulation,
since w and u are two-dimensional, their evolutions are not displayed as
time series but as trajectories on each plane. The red circles in Figures 7a
and 7c represent initial values of w and u, respectively. Figures 7a and 7b
show that the parameters w and v converge to their equilibrium w∗
and v ∗
very quickly. To display how quick the convergence is, the first 30 iterations
702
D. Tsutsui
Figure 8: Trajectories on the (z, ||u||2)-plane obtained by learning for 20,000 it-
erations (solid black curves) and analytical trajectories near θ = θ
1 (dashed blue
curves). Red circles represent the initial points.
are dashed in green in Figure 7a. In contrast, Figures 7c and 7d show that
the parameters u and z evolve very slowly.
Figure 8 plots time evolutions of the parameter θ on the (z, ||u||2)-plane,
which means the plane whose axes indicate the values of z and (cid:10)u(cid:10)2. We
can check that parameters near the attractive part {|z| > v ∗, ||tu||2 = 0} Di
the Milnor-like attractor are trapped and that those near the repulsive part
{|z| < v ∗, ||u||2 = 0} are escaping. The numerical evolutions follow the ana-
lytical flows (dashed blue curves) well also in this case.
5 Aspects of Online Learning
In this section, we discuss stochastic effects in the learning process. Thus far,
we have analyzed the dynamical system, equation 1.5, driven by the aver-
aged gradient. In practice, the averaged gradient is estimated by the arith-
metic mean of the instantaneous gradient ∂(cid:3)(x, f(d)(x; θ))/∂θ over a large
number of input data. However, taking the arithmetic mean for each update
of the parameter demands high computational cost. In order to reduce the
cost, the expectation is often replaced by a single realization of the instanta-
neous gradient. Such a method is called online learning, a typical stochastic
gradient descent method. Mathematically, it is given by
θ(t+1) = θ(t) − ε
(cid:17)
(cid:17)
(cid:17)
(cid:3)(xt, f(d)(xt; θ))
(cid:17)
∂
∂θ
,
θ=θ(t)
(5.1)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
n
e
c
o
_
a
_
0
1
2
6
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Center Manifold Analysis of Plateau
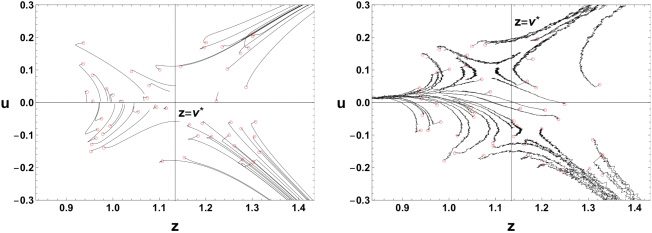
703
Figure 9: Trajectories on the (z, u)-plane obtained by the averaged gradient de-
scent method, equation 1.5, and the online learning, equation 5.1, for 20,000 it-
erations. Red circles represent initial values.
where {xt}t are i.i.d. realizations of the input data x. Unlike the deterministic
dynamical system, equation 1.5, the system 5.1 is a randomized dynamical
system.
In numerical simulations, we found that sample paths of the online
learning seem quite different from trajectories obtained in the averaged
gradient descent method. We set the distribution over which the loss func-
tion L(1) is averaged to be N(0, 22) and obtained a local minimizer of L(1) as
θ∗ = (w∗, v ∗
) ≈ (0.472, 1.13). We carried out numerical simulations of the
online learning in the same setting as example 1 in section 4. Figure 9a
shows numerical trajectories of the averaged gradient descent on the (z, u)-
plane around θ = θ
1. In order to approximate the averaged gradient descent
sufficiently, we used the empirical distribution on a data set of 10,000 data
drawn i.i.d. according to N(0, 22). Figure 9b shows sample paths of the on-
line learning for a common input data sequence {xt}t. In contrast to the av-
eraged gradient descent, in the online learning, some sample paths move
from region {|z| > v ∗} A {|z| < v ∗}. Such sample paths are observed even
when we use another realization of the input data sequence, and its dy-
namics seems qualitatively different from the averaged one.
In order to investigate this phenomenon, we observe the evolution of
the parameters, again in the coordinate system, equation 3.5. Figures 10a to
10d show time evolutions of each parameter in the first 1500 iterations of
the online learning. The parameters (w, v ) evolve very fast compared with
(u, z) also in this case. However, in this case, (w, v ) does not converge to
its equilibrium point (w∗, v ∗
) ≈ (0.472, 1.13), but fluctuates stochastically
around (w∗, v ∗
).
Based on these observations, we suppose that w and v run over a suf-
ficiently wide range of their values to be integrated, while u and z move
in a small range. Then we assume that the dynamics of (u, z) is integrated
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
n
e
c
o
_
a
_
0
1
2
6
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
704
D. Tsutsui
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
n
e
c
o
_
a
_
0
1
2
6
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 10: Time evolutions of each parameter for the first 1500 iterations of the
online learning. Each trajectory of w or v fluctuates intensively around the equi-
librium point w∗ ≈ 0.472, v ∗ ≈ 1.134, respectively. Trajectories of u and z evolve
very slowly compared with w and v in this case.
with respect to (w, v ) according to some stationary distribution. We further
assume that (w, v ) are distributed around (w∗, v ∗
) with finite variance. By
integrating the Taylor expansions, equations 3.7 and 3.8, with (w, v ), we ob-
tain the following dynamical system near θ = θ
1:
˙u = 1
2
˙z = 1
2
(z − v ∗
)Hu + C1
,
uT Hu + C2
.
(5.2)
Here, C1 and C2 are constants resulting from the variance and covari-
ance of (w, v ). Figure 11 shows the analytical trajectories of the dynamical
−4 are de-
= 1.71 × 10
system, equation 5.2, where C1
termined heuristically. One can find that the deterministic dynamical sys-
tem, equation 5.2, gives similar trajectories to sample paths of the online
learning presented in Figure 9b.
= −3.06 × 10
−4 and C2
Center Manifold Analysis of Plateau
705
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Figure 11: Analytical trajectories on the (z, u)-plane given by the dynamical sys-
tem 5.2 with C1
= 1.71 × 10−4 and C2
= −3.06 × 10−4.
We deduce that a fluctuation of the parameter around a center manifold
causes constants C1 and C2 working as drift terms and that it makes the
dynamics of the online learning qualitatively different from those of the
averaged gradient descent. This example suggests that stochastic effects can
influence a macroscopic flow of the learning process via a center manifold
structure.
6 Conclusion
In this article, we first gave a quick review of a mechanism that causes
plateau phenomena in a three-layer perceptron—in particular, how degen-
eration of hidden units gives rise to a Milnor-like attractor consisting of
both attractive and repulsive parts. We next investigated the dynamics of
learning around special points on a Milnor-like attractor and proved the ex-
istence of the center manifold. We also succeeded in integrating the reduced
dynamical system to obtain an analytical form of a trajectory. We performed
several numerical simulations to demonstrate the accuracy of our results.
As an application of the center manifold structure, we gave an explanation
for a characteristic behavior of the online learning.
Unfortunately, the two examples presented in section 4 were the only
ones that we could find in which the assumptions of proposition 1 are
fulfilled. This might suggest that the appearance of a Milnor-like attrac-
tor would be a rather rare situation in a perceptron that has bias terms.
In fact, just by replacing the activation function Sgm with tanh in exam-
ple 2, the matrix H becomes indefinite and the assumption of proposition 1
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
n
e
c
o
_
a
_
0
1
2
6
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
706
D. Tsutsui
is violated. Finding more suggestive examples that shed light on the com-
plex behavior of the dynamics of learning is an important subject for future
study.
In section 5, we investigated stochastic effects of the online learning from
an intermediate viewpoint between fully stochastic and averaged dynam-
ics. We made use of the center manifold of the averaged dynamics and dis-
cussed an integration with quickly fluctuating parameters. There have been
many reports of qualitative differences between stochastic and determin-
istic methods; however, there are few general theories for analyzing such
dissimilarities. We expect that the intermediate viewpoint in this article can
be a clue to clarify stochastic effects in learning.
Appendix: Proofs of Proposition 1 and Theorem 1
This appendix gives proofs of proposition 1 and Theorem 1. The proof of
proposition 1 is based on the analysis of the Hessian matrix of L(2). However,
the Hessian at the point θλ becomes singular, since L(2)(θλ) is constant along
λ ∈ R. Thus, we need to take into account higher-order derivatives of L(2),
which is overlooked in the Fukumizu and Amari (2000). The prototype of
theorem 1 was given by Amari et al. (2018); however, they proved it only
for a special case. Here, we give a rigorous proof with an additional mild
assumption.
Proof of Proposition 1. We introduce a new coordinate system ξ = (w, v,
u, z) by
⎧
⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎩
v
w =
1
w
2
+ v
+ v
2
2
1
w
v
1
+ v
v = v
1
u = w
z = v
1
1
− v
2
2
− w
,
2
(A.1)
1
+ v
where v
2
ξλ = (w∗, v ∗, 0, (2λ − 1)v ∗
L(2)(ξ) by lemma 1. The inverse transformation is given as
(cid:6)= 0. Under this coordinate system, the point θλ is denoted as
). Note that each point ξ = ξλ is a critical point of
v − z
2v u
v + z
2v u
⎧
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩
w
1
w
2
v
1
v
2
= w +
=
= w −
v + z
2
v − z
2
=
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
n
e
c
o
_
a
_
0
1
2
6
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Center Manifold Analysis of Plateau
707
We observe the Hessian matrix Hess(ξλ) of L(2)(ξ) at ξλ for each λ ∈ R.
2), using the inverse trans-
For all ξ such that u = 0 (or, equivalently, w
formation formula above,
= w
1
∂L(2)
∂u
∂L(2)
∂z
(cid:9)
(ξ) = Ex
∂(cid:3)(x, f(2)(x; ξ))
∂y
v 2 − z2
4v
(ϕ(cid:5)
(w
1
· x) − ϕ(cid:5)
(w
2
· x))x
(cid:12)
= 0,
(cid:9)
(ξ) = −Ex
+Ex
= 0.
∂(cid:3)(x, f(2)(x; ξ))
∂y
(cid:9)
(cid:10)
v + z
4v
ϕ(cid:5)
(w
1
· x) −
v − z
4v
(cid:11)
ϕ(cid:5)
(w
2
· x)
(cid:12)
(u · x)
∂(cid:3)(x, f(2)(x; ξ))
∂y
1
2
(ϕ(w
1
· x) − ϕ(w
2
(cid:12)
· x))
Here, we left w
1 and w
2 for notational simplicity. We then have
∂ 2L(2)
∂γ ∂z
∂ 2L(2)
∂γ ∂u
(ξλ) = 0,
(ξλ) = 0,
where γ = w, v, z. Hence, the matrix Hess(ξλ) has the form
⎛
(cid:29)
w, v
⎜
⎜
⎜
(cid:30)
⎜
⎝
u
z{
w, v
(cid:18) (cid:19)(cid:20) (cid:21)
∗ ∗
∗ ∗
0
0
0
0
u(cid:18)(cid:19)(cid:20)(cid:21)
0
z(cid:18)(cid:19)(cid:20)(cid:21)
0
0
∗
0
0
0
0
⎞
⎟
⎟
⎟
.
⎟
⎠
The (w, v )-block is equal to the Hessian matrix of L(1) at θ∗
itive definite. In fact, for any ξ such that u = 0, noting that
f(1)(x; w, v ),
and is pos-
f(2)(x; ξ) ≡
(cid:9)
(cid:9)
∂L(2)
∂w (ξ) = Ex
∂L(2)
∂v (ξ) = Ex
∂(cid:3)(x, f(1)(x; w, v ))
∂y
∂(cid:3)(x, f(1)(x; w, v ))
∂y
v ϕ(cid:5)
(w · x)x
(cid:12)
ϕ(w · x)
=
(cid:12)
=
∂L(1)
∂w
(1)
(w, v ),
∂L(1)
∂v
(1)
(w, v ).
The (w, v )-block of Hess(ξλ) is given by differentiating the equations above
(1))(θ∗
with (w, v ) and thus equal to the Hessian matrix (∂ 2L(1)
),
which is positive definite since θ
is a strict local minimizer of
L(1)(θ
= θ∗
(1)).
/∂θ
∂θ
(1)
(1)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
n
e
c
o
_
a
_
0
1
2
6
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
708
D. Tsutsui
On the other hand, we have
∂ 2L(2)
∂u∂u
(ξλ) = Ex
(cid:9)
∂(cid:3)(x, f(2)(x; ξλ))
∂y
λ(1 − λ) v ∗ϕ(cid:5)(cid:5)
(w∗ · x) x xT
(cid:12)
= λ(1 − λ)H,
where H is the matrix defined in equation 2.1. Thus, when H is positive
definite, the Hessian matrix Hess(ξλ) is positive semidefinite if and only if
λ ∈ [0, 1]. This proves that ξλ is a saddle point of L(2)(ξ) for λ ∈ R \ [0, 1].
Similarly, when H is negative definite, ξλ is a saddle point of L(2)(ξ) for λ ∈
(0, 1). When H is indefinite, so is Hess(ξλ) for every λ ∈ R \ {0, 1}.
We show that the point ξ = ξλ is a local minimizer of L(2)(ξ) for λ ∈ (0, 1)
when the matrix H is positive definite. For λ ∈ (0, 1), since the matrix
Hess(ξλ) is positive semidefinite, the Taylor series of (L(2)(ξ) − L(2)(ξλ)) up
to the second order is nonnegative in a neighborhood of ξ = ξλ. However,
higher-order terms may influence the sign of the Taylor series, since the co-
efficients of the terms of z2 and γ z are zero for γ = w, v, u. Since the terms
of γ kz(cid:3)
with k ≥ 2 are dominated by the term γ 2 near ξ = ξλ, we check if the
coefficients of the terms of z(cid:3)
are equal to zero for all (cid:3) ≥ 1. For all
ξ such that u = 0, f(2)(x; ξ) = vϕ(w · x) is a constant as a function of z, and
so is L(2)(ξ). Hence, we obtain
and γ z(cid:3)
(ξλ) = 0,
∂ (cid:3)L(2)
∂z(cid:3)
∂ (cid:3)+1L(2)
∂γ ∂z(cid:3) (ξλ) = 0,
(cid:3) ≥ 1,
for γ = w, v. Therefore, it suffices to check if
∂ (cid:3)+1L(2)
∂u∂z(cid:3) (ξλ) = 0,
(cid:3) ≥ 1.
/∂u)(ξ) = 0 for all ξ such that u = 0,
Since we have already seen that (∂L(2)
this equality is confirmed. Finally, we have shown that the coefficients of
higher-order terms are all zero, and that they do not influence the sign of the
Taylor series. This shows that (L(2)(ξ) − L(2)(ξλ)) is nonnegative near ξ = ξλ,
and hence the proof is complete. In the case that the matrix H is negative, it
(cid:2)
is proved similarly.
Proof of Theorem 1. Since v
2 are no longer scalars, we cannot use
the coordinate system, given by equation A.1. Therefore, in order to analyze
1 and v
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
n
e
c
o
_
a
_
0
1
2
6
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Center Manifold Analysis of Plateau
709
the Hessian matrix, we introduce another coordinate system ξ = (w, v, u, z)
as
⎧
⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎩
w =
v = v
1
w
u =
z = v
w
1
+ w
2
2
+ v
2
− w
1
2
.
2
− v
2
1
In this coordinate system, the point θλ is denoted as ξλ = (w∗, v∗, 0,
(2λ − 1)v∗).
Fix λ ∈ R arbitrarily. We show that the Hessian matrix Hess(ξλ) of L(2)(ξ)
at ξ = ξλ has both positive and negative eigenvalues. It suffices to show that
the (w, v)-part of the Hessian is positive definite and that the (u, z)-part is
not positive semidefinite. They imply that the full Hessian matrix Hess(ξλ)
is neither negative semidefinite nor positive semidefinite, and hence that
Hess(ξλ) is indefinite.
One can check that the (w, v)-part of Hess(ξλ) is equal to the Hessian
matrix of L(1) at θ∗ by direct calculation. Since θ∗ is a strict local minimizer
of L(1), this is positive definite.
On the other hand, we have
(cid:9)
∂(cid:3)(x, f (2)(x; ξλ))
∂y
(cid:12)
ϕ(cid:5)
(w∗ · x) xT
,
∂ 2L(2)
∂z∂u
∂ 2L(2)
∂z∂z
(ξλ) = Ex
(ξλ) = O,
and thus the (u, z)-part B of Hess(ξλ) is written as
⎛
⎜
⎜
⎝
B =
∂ 2L(2)
∂u∂u (ξλ)
$ Ex ∂(cid:3)(x, f (2) (x;ξλ )) ∂y ϕ(cid:5) (w∗ · x) xT $
Ex
%
∂(cid:3)(x, f (2) (x;ξλ ))
∂y
ϕ(cid:5)(w∗ · x) xT
O
(A.2)
(A.3)
%
T
⎞
⎟
⎟
⎠,
where we treat ∂(cid:3)/∂y as a column vector. Here, since f (2)(x; ξλ) ≡ f (1)(x; θ∗
),
the nondiagonal block, equation A.2, is equal to the matrix, equation 2.2,
and thus is nonzero by assumption. Hence, the (u, z)-part above is not pos-
itive semidifinite. In fact, choosing vectors a ∈ Rm and b ∈ Rn+1 such that
(cid:9)
aT Ex
∂(cid:3)(x, f (2)(x; ξλ))
∂y
(cid:12)
ϕ(cid:5)
(w∗ · x)xT
b < 0,
the vector cε := (εbT , aT )T satisfies cT
Such vectors (a, b) always exist—for instance, by letting ai
ε B cε < 0 for sufficiently small ε > 0.
= 1,
= −ρ, b j
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
710
D. Tsutsui
and other entries be 0, Dove (io, j) is an index such that (io, j)-entry ρ of the
(cid:2)
matrix A.2 is nonzero.
Ringraziamenti
I express my gratitude to Akio Fujiwara for his helpful guidance, discus-
sions, and advice. I thank as well Yuzuru Sato for many discussions and
helpful comments. And I thank the anonymous referees for their insightful
suggestions to improve this article.
Riferimenti
Amari, S.-I., Ozeki, T., Karakida, R., Yoshida, Y., & Okada, M. (2018). Dynamics of
learning in MLP: Natural gradient and singularity revisited. Calcolo neurale,
30(1), 1–33.
Carr, J. (1981). Applications of centre manifold theory. New York: Springer.
Cousseau, F., Ozeki, T., & Amari, S.-I. (2008). Dynamics of learning in multilayer
perceptrons near singularities. IEEE Transactions on Neural Networks, 19(8), 1313–
1328.
Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Math-
ematics of Control, Signals, and Systems, 2(4), 303–314.
Fukumizu, K., & Amari, S.-I. (2000). Local minima and plateaus in hierarchical struc-
tures of multilayer perceptrons. Neural Networks, 13(3), 317–327.
Funahashi, K. (1989). On the approximate realization of continuous mappings by
neural networks. Neural Networks, 2(3), 183–192.
Sonoda, S., & Murata, N. (2017). Neural network with unbounded activation func-
tions is universal approximator. Applied and Computational Harmonic Analysis,
43(2), 233–268.
Wei, H., Zhang, J., Cousseau, F., Ozeki, T., & Amari, S.-I. (2008). Dynamics of learning
near singularities in layered networks. Calcolo neurale, 20(3), 813–843.
Received July 26, 2019; accepted November 26, 2019.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
4
6
8
3
1
8
6
4
7
3
0
N
e
C
o
_
UN
_
0
1
2
6
8
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3