ARTICLE
Communicated by Joel Zylberberg
Optimal Burstiness in Populations of Spiking Neurons
Facilitates Decoding of Decreases in Tonic Firing
Sylvia C. l. Durian
sdurian@uchicago.edu
Departments of Ophthalmology and Neuroscience, Feinberg School of Medicine,
Northwestern University, Chicago, IL, U.S.A.
Mark Agrios
mark.agrios@northwestern.edu
Northwestern Interdepartmental Neuroscience Graduate Program,
Northwestern University, Evanston, IL, U.S.A.
Gregory W. Schwartz
greg.schwartz@northwestern.edu
Departments of Ophthalmology and Neuroscience, Feinberg School of Medicine,
Northwestern University, Chicago, IL, U.S.A.; Northwestern Interdepartmental
Neuroscience Graduate Program, Northwestern University, Evanston, IL, U.S.A.;
Department of Neurobiology, Weinberg College of Arts and Sciences,
Northwestern University, Evanston, IL, U.S.A.
A stimulus can be encoded in a population of spiking neurons through
any change in the statistics of the joint spike pattern, yet we commonly
summarize single-trial population activity by the summed spike rate
across cells: the population peristimulus time histogram (pPSTH). For
neurons with a low baseline spike rate that encode a stimulus with a
rate increase, this simplified representation works well, but for popula-
tions with high baseline rates and heterogeneous response patterns, IL
pPSTH can obscure the response. We introduce a different representation
of the population spike pattern, which we call an “information train,"
that is well suited to conditions of sparse responses, especially those that
involve decreases rather than increases in firing. We use this tool to study
populations with varying levels of burstiness in their spiking statistics
to determine how burstiness affects the representation of spike decreases
(firing “gaps”). Our simulated populations of spiking neurons varied in
size, baseline rate, burst statistics, and correlation. Using the information
train decoder, we find that there is an optimal level of burstiness for gap
detection that is robust to several other parameters of the population. Noi
consider this theoretical result in the context of experimental data from
different types of retinal ganglion cells and determine that the baseline
spike statistics of a recently identified type support nearly optimal detec-
tion of both the onset and strength of a contrast step.
Calcolo neurale 35, 1363–1403 (2023)
https://doi.org/10.1162/neco_a_01595
© 2023 Istituto di Tecnologia del Massachussetts
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1364
S. Durian, M. Agrios, and G. Schwartz
1 introduzione
Most neurons communicate using sequences of action potentials called
spike trains. Decoding information from spike trains involves extracting a
signal in the face of noise, but which features of the spike train represent
signal versus noise and how to represent joint spike patterns across neu-
rons is not always clear (Rieke et al., 1999; Cessac et al., 2010). Neurons may
differ both in the way they respond to a stimulus as well as in their baseline
spike patterns in the absence of a stimulus, and spike trains among a pop-
ulation of neurons can vary in their patterns of correlation. Many papers
have examined the role of first-order statistics (mean firing rate) and cor-
relations on the efficiency of information transmission by spike trains (da
Silveira & Rieke, 2021; Panzeri et al., 1999; Ainsworth et al., 2012; Ratté et al.,
2013; de la Rocha et al., 2007). Higher-order statistics beyond the mean and
variance of the spike rate, such as temporal coding and burst coding, Avere
also been investigated, especially in the auditory cortex (Bowman et al.,
1995; King et al., 2007). Previous work has focused on the effect of higher-
order statistics as a stimulus response feature but has not examined the role
of higher-order baseline spike statistics in the way neural populations en-
code decreases in firing rate. Here, we develop a new analysis to represent
a population response and reveal how the burstiness of spike trains affects
transmission of information about firing gaps—periods of silence in spiking
activity caused by a decreased firing rate.
The spike pattern of even a relatively small neural population is a dis-
tribution in high-dimensional space that is typically infeasible to sample
experimentally and is likely undersampled by any downstream decoder
in the brain. Così, finding a way to approximate this distribution and dis-
covering which of its features are most important for a particular task are
fundamental goals in understanding neural population codes. Any change
in the joint spike distribution could theoretically provide information. Sen-
sory neurons change their firing patterns in the presence of an external stim-
ulus, so we can measure information with respect to a known experimental
variable.
Many neurons have low or zero spontaneous spike rates (Tripathy &
Gerkin, 2016), so rate increases in the presence of a stimulus are the most
common and well-studied type of information transmission (Romo & Sali-
nas, 2001; Britten et al., 1992; Gold & Shadlen, 2007). Tuttavia, the central
nervous system (CNS) also contains a wide variety of tonically firing neu-
rons, which are well suited to transmit information by decreasing their tonic
spike rate. Examples include Purkinje cells (Kase et al., 1980; Ohtsuka &
Noda, 1995), lateral geniculate relay neurons (McCormick & Feeser, 1990),
spinal cord neurons (Legendre et al., 1985), hippocampal CA1 (Azouz et al.,
1996) and CA3 (Raus Balind et al., 2019) cells, and cortical pyramidal cells
(Harris et al., 2001). Tonic firing in neurons results from a combination of
the influence of synaptic networks and intrinsic electrical properties (Llinas,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Optimal Burstiness in Spiking Neurons
1365
2014; Destexhe & Paré, 1999). Both factors can affect the higher-order statis-
tics of tonic spike trains. Higher-order spatial correlations between neurons
have been well studied, including in the retina (Pillow et al., 2008; Zylber-
berg et al., 2016; Ruda et al., 2020), but we focus here on higher-order single-
neuron temporal statistics. Different neurons at the same mean rate can
have spike trains that vary along the spectrum from the perfectly periodic
clock-like transmission of single spikes to highly irregular bouts of bursting
and silence (Zeldenrust et al., 2018; de Zeeuw et al., 2011). The goal of the
theoretical part of this study was to determine how higher-order temporal
statistics affect the encoding capacity of a neural population. Specifically, È
there an optimal level of burstiness for representing firing gaps?
Retinal ganglion cells (RGCs), the projection neurons of the retina, offerta
a tractable system for both experimental and theoretical studies of informa-
tion transmission in spike trains. As the sole retinal outputs, RGCs must
carry all the visual information used by an animal to their downstream tar-
gets in the brain. RGC classification is more complete, particularly in mice
(Goetz et al., 2022), than the classification of virtually any other class of neu-
rons in the CNS. Finalmente, RGCs of each type form mosaics that evenly sam-
ple visual space, creating a clear relationship between the size of a visual
stimulus and the number of neurons used to represent it (Rodieck, 1998).
Inspired by the recent discoveries of how different types of tonically fir-
ing RGCs encode contrast (Jacoby & Schwartz, 2018; Wienbar & Schwartz,
2022), here we develop a theoretical framework for representing informa-
tion changes in a neural population under the assumption that a given
stimulus causes the spiking statistics to strongly deviate from the statistics
during spontaneous activity. We apply this framework to measure the role
of burstiness in a population’s ability to encode the time and duration of a
gap in firing. We propose a continuous, lossless readout of a spike train into
an “information train” that tracks Shannon information (Shannon, 2001)
over time. Critically, we show that information trains can be summed in a
population in a way that is more robust to response heterogeneity and bet-
ter at representing gaps than the population peristimulus-time-histogram
(pPSTH). We first develop a model to generate spike trains with varying
levels of burstiness and correlation, then establish metrics to decode the
start time and duration of a firing gap from the spike trains, and finally
measure decoding performance when we vary the simulation parameters’
burstiness, correlation, firing rate, and population size. We assume a stimu-
lus that depresses the firing rate in proportion to its strength; così, measur-
ing these two characteristics of the resulting firing gap reveals both when
the stimulus is presented and its strength. The goal of these simulations is to
understand how each of the model parameters affects a neural population’s
ability to represent a gap in spiking.
Our principal result is a theoretical justification for why burstiness exists
in some cell types. Under the assumptions of our information train decoder,
we find an optimal level of burstiness for identifying the time of stimulus
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1366
S. Durian, M. Agrios, and G. Schwartz
presentation and an asymptotic optimum for identifying stimulus strength.
This result could help explain the variability in burstiness between differ-
ent types of neurons. Finalmente, we compare our theoretical results to spike
trains from recorded mouse RGCs to measure how close each type lies to
optimality for each decoding task.
2 Results
2.1 A Parameterized Simulation of Populations of Tonic and Bursty
Neurons. To study the role of higher-than-first-order statistics in the en-
coding of spike gaps by populations of neurons, first we needed a pa-
rameterized method to generate spike trains with systematic variation in
these statistics that could accurately model experimental data. Two RGC
types that our lab has studied extensively represent cases near the edges
of the burstiness range. These RGC types have fairly similar mean tonic
firing rates (between 40 E 80 Hz). Tuttavia, while bursty suppressed-by-
contrasto (bSbC) RGCs fire in bursts of rapid activity interspersed with pe-
riods of silence, OFF sustained alpha (OFFsA) RGCs spike in more regular
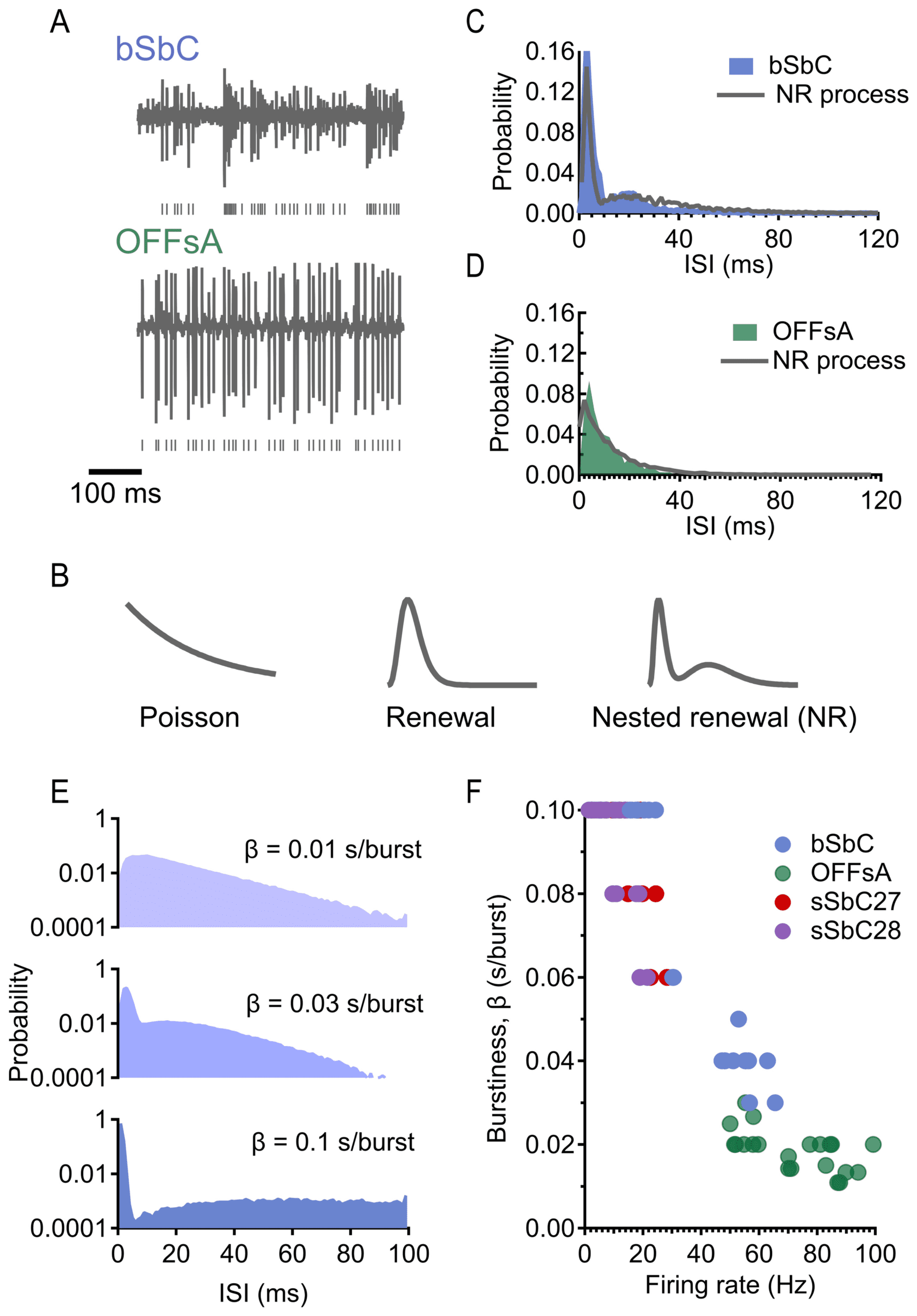
patterns (see Figure 1A) (Wienbar & Schwartz, 2022).
A nested renewal process is a doubly stochastic point process that can
simulate both bursty and tonic firing patterns with only four parameters
(see section 4). This process builds on one of the most commonly used meth-
ods to generate spike trains: the Poisson process. The Poisson model of
spike generation assumes that the generation of spikes depends only on
the instantaneous firing rate (van Vreeswijk, 2010). Using a Poisson process
to generate spikes leads to exponentially distributed interspike intervals
(ISIs; see Figure 1B, left). One obvious limitation of Poisson spike genera-
zione, Tuttavia, is its inability to model refractoriness, the period of time after
a neuron spikes during which it cannot spike again. A renewal process ex-
tends the Poisson process to account for the refractory period by allowing
the probability of spiking to depend on the time since the last spike, anche
as the instantaneous firing rate (van Vreeswijk, 2010; Heeger, 2000). The re-
sulting spike train has gamma-distributed ISIs (see Figure 1B, middle) since
refractoriness does not allow for extremely short intervals between spikes.
Although a renewal process is more physiologically accurate than a
Poisson process, it still fails to model burstiness. Therefore, we extended
the renewal process again by nesting one renewal process inside another
(Yannaros, 1988), similar to how others have previously constructed doubly
stochastic (although nonrenewal) processes to model spike trains (Bingmer
et al., 2011). The outer renewal process parameterized by κ
1 (a shape pa-
rameter) and λ
1 (a rate parameter) determines the number and placement
of events that we will call “burst windows” (opportunities for a burst to oc-
cur), while the inner renewal process with parameters κ
2 determines the
number and placement of spikes within each burst window (see section 4).
Both the number of burst windows and the number of spikes are randomly
2, λ
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Optimal Burstiness in Spiking Neurons
1367
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
= 6, λ
1
= 180 bursts/s, κ
2
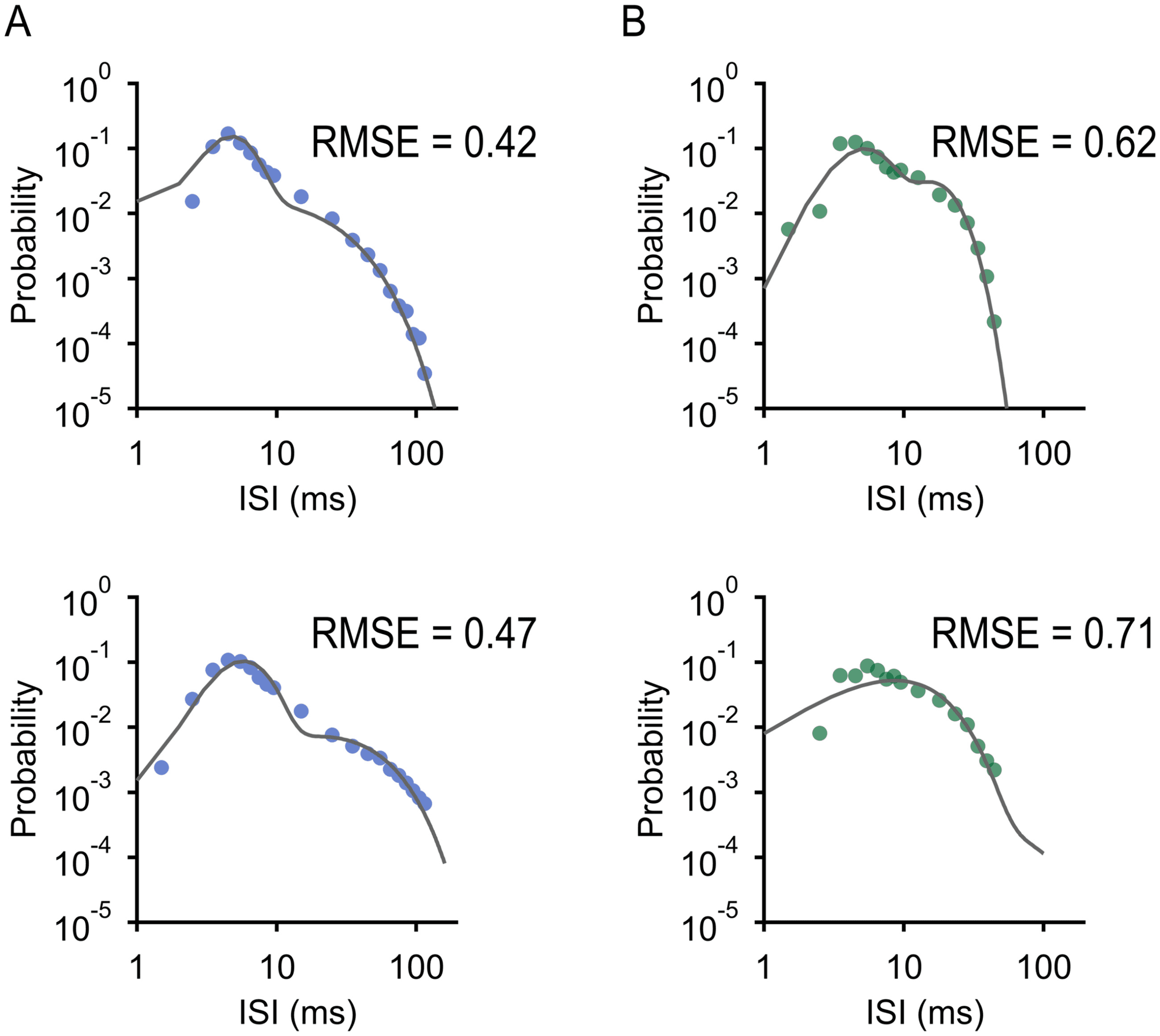
Figura 1: A nested renewal process can simulate bursty and tonic firing patterns
with only four parameters. (UN) Raw traces from bSbC (top) and OFFsA (bottom)
in the absence of a stimulus. (B, da sinistra a destra) ISI distributions resulting from
a Poisson process (exponential), renewal process (gamma) and nested renewal
processi (NR; well fit by sum of gammas). (C) ISI distribution of bSbC and closest
NR process match in the simulated data (as determined by Kullback-Leibler di-
= 600 spikes/s.
vergence) with parameters κ
1
(D) ISI distribution of OFFsA and closest NR process match (as determined
= 500
by KL divergence) with parameters κ
1
spikes/s. (E) ISI distributions resulting from NR processes with the same firing
= 300 bursts/s,
rate of 100 Hz, ranging from regular to bursty. Top: κ = 3, λ
1
= 100 bursts/s, κ
= 3, λ
= 300 spikes/s. Middle: κ
= 1500
= 5, λ
= 3, λ
κ
1
1
2
2
2
2
= 3000 spikes/s. Bottom
= 3, λ
= 30 bursts/s, κ
= 3, λ
spikes/s. Bottom: κ
2
2
1
1
ISI distribution extends out to 500 ms (not shown). Note: ISI distributions are
shown on a semilog scale to emphasize differences in their tails. (F) Range of fir-
ing rates and burstiness in four RGC types: bSbC and OFFsA as defined in the
testo, sSbC27 (sustained suppressed-by-contrast type EW27), and sSbC28 (sus-
tained suppressed-by-contrast type EW28). Details of RGC classification are in
Goetz et al. (2022).
= 150 bursts/s, κ
2
= 3, λ
2
= 3, λ
1
= 3, λ
2
1368
S. Durian, M. Agrios, and G. Schwartz
generated within our model, so it is important to note that a burst window
can contain as few as zero spikes by chance. Therefore, a nested renewal pro-
cess can flexibly simulate both regular (1 spike/burst window, as in a stan-
dard renewal process) and bursty (many spikes per burst window) firing
patterns. The spike trains generated by a nested renewal process have ISIs
that are well fit by a sum of gammas distribution (see Figure 1B, right, E
Figura 9), where the tall, narrow left mode of the distribution corresponds
to the intervals between spikes within burst windows, and the short, wide
right mode of the distribution corresponds to the intervals between burst
windows. Finalmente, a nested renewal process models activity of bSbCs and
OFFsAs well; tuning its parameters results in good approximations to ISI
distributions of experimentally measured bSbC and OFFsA RGCs (see Fig-
ures 1C, 1D, E 10).
Note also that all spikes necessarily occur within burst windows via
this method of spike generation. This makes the analysis more manage-
able in some ways but is mechanistically unrealistic; Per esempio, pyrami-
dal neurons generate isolated spikes and bursts using different mechanisms
(Larkum et al., 2004). We certainly do not believe that a nested renewal pro-
cess is faithful to how real neurons generate spikes; we only claim that it
produces distributions of spikes that are well matched to the specific RGCs
that we are interested in modeling. Because we do not analyze the spike
mechanisms in our model further and simply use the output spikes in our
analysis, this failure of realism in our model of spike generation does not
affect our core results.
Our next goal was to quantify burstiness by a single measure. Because
our method of generating spike trains necessarily places every spike within
a burst window, we could not use a standard definition of burstiness, come
as the number of spikes contained within bursts (as defined by some thresh-
old) divided by the total number of spikes (Oswald et al., 2004). Invece, we
reasoned that a cell should be classified as more bursty if it contains, on av-
erage, more spikes within its burst windows. Tuttavia, increasing the firing
rate will automatically increase the number of spikes per burst window, so
we normalized by the mean firing rate. Therefore, we defined the burstiness
factor, β, as the average number of spikes per burst window divided by the
firing rate (measured in seconds/burst window). Figure 1E illustrates the
effect of different levels of burstiness on the ISI distribution for a fixed firing
rate. We prefer this definition to one that thresholds the number of spikes
within a certain period of time, since our definition of burstiness is easily
computed from the model parameters and eliminates the need to threshold,
thus reducing both the number of parameters and arbitrariness of choosing
a threshold.
Our quantification of burstiness is dependent on the parameters of the
nested renewal process and cannot be applied directly to experimental data.
We overcame this issue by using a procedure that matched experimental ISI
distributions to simulated ones. Whereas previous work has typically used
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Optimal Burstiness in Spiking Neurons
1369
a time threshold to define burstiness, the large range of spiking statistics
we simulated allowed us to take a different approach with our experimen-
tal data. We matched ISI distributions from recorded RGCs with simulated
dati (see Figures 1C and 1D) using Kullback-Leibler (KL) divergence in or-
der to measure burstiness in our recorded RGCs (see Figure 1F). Using KL
divergence allowed us to find the simulated spike train with the most sim-
ilar ISI distribution, out of all the simulated data, to a given recorded RGC.
In addition to variable burstiness, the nested renewal process allowed us
to independently modulate the firing rate and simulate neural populations
of any desired size with different levels of pairwise correlation among the
spike trains (see Figure 2A; see also section 4). For simplicity, we consid-
ered only homogeneous populations in this study: all neurons in a given
population were simulated with the same model parameters (firing rate,
burstiness, and pairwise correlation level). In other words, the model pa-
rameters were varied only on the population level, not on the cell level.
While the statistics of heterogeneous populations of neurons can sometimes
lead to surprising decoding effects (Ecker et al., 2011; Zylberberg et al.,
2016), our choice of homogeneous populations was motivated by the re-
markably homogeneous response characteristics of RGCs within a func-
tional type (Goetz et al., 2022). Extensions of this work could investigate
populations with heterogeneous spike statistics.
We modeled a stimulus-dependent drop in firing as an instantaneous
drop to a firing rate of zero followed by an exponential rise back to the base-
line firing rate, controlled by a variable time constant of recovery (see Fig-
ure 2B). This stimulus model was chosen because it is consistent with how
both bSbC and OFFsA RGCs respond to positive contrast; longer time con-
stants of firing recovery correspond to higher contrast stimuli (Wienbar &
Schwartz, 2022; Jacoby et al., 2015). Although this stimulus model was cho-
sen with bSbCs and OFFsAs in mind, it generalizes to any type of neuron
that decreases its spontaneous firing rate in a stereotyped way to a stimulus.
We also introduced heterogeneity into the population of neurons by vary-
ing responsivity to the stimulus, or the proportion of the population that
responds to the stimulus, since this is often less than 100% in experimen-
tal studies. In other words, we made a subset of the neurons unresponsive
to the stimulus by allowing them to continue spiking with baseline statis-
tics after stimulus onset (see Figure 2C). Analogous to models for detection
of the onset and duration of an increase in firing, this stimulus allowed us
to measure performance in decoding the onset and duration of the gap in
firing for each simulated population of neurons.
2.2 The Information Train Is Useful for Aggregating Heterogeneous
Spike Trains. By aggregating the spike trains of the population of neurons
into a one-dimensional signal over time, decoding the onset and duration
of a gap in firing can be formulated as a threshold detection task. The choice
of threshold determines when the decoder reports that the population is in
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1370
S. Durian, M. Agrios, and G. Schwartz
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 2: A nested renewal process can simulate populations of varying firing
rate, burstiness, size, correlation, and responsivity. (UN) Populations of varying
pairwise (neuron to neuron) correlation simulated using a nested renewal (NR)
processi. Rows in the rasters correspond to different neurons, not different trials.
(B) Population response to varying levels of stimulus strength, modeled with a
drop and subsequent rise in firing rate. The green “rate” line refers to firing
rate. Population peristimulus time histogram (PSTH) is shown in black. Every
neuron in each population has the same recovery time constant, but that varies
from top to bottom (shortest for the top population and longest for the bottom)
(C) Populations of varying responsivity to the stimulus. Here the recovery time
constant is the same for each population, and only the responsivity is varied.
Population PSTH is shown in black.
the baseline state versus the stimulus (or gap detected) state (see Figure 3A),
and it naturally implies a trade-off between reaction time (see Figure 3A),
the delay from stimulus onset until the threshold is crossed, and false de-
tection rate, the rate at which the threshold is crossed in the absence of the
stimulus. To simplify our analysis, we chose a decoder threshold for each
population that achieved a fixed low error rate of 0.1 false detections per
second (we do show, Tuttavia, that our results are robust to the choice of
threshold in Figure 13). Così, for the detection task, reaction time, δ, era
Optimal Burstiness in Spiking Neurons
1371
the sole performance metric for the decoder. The performance metric for
the duration task was more complex and is considered in the subsequent
section.
Prossimo, we considered the choice of the aggregation method used to com-
bine spike trains across cells. The method most commonly used in such
situations is to compute the pPSTH by simply collecting all spikes in the
population and filtering to create a continuous rate signal (see Figure 3F
left). Tuttavia, there are many properties of population activity that can
carry information besides the average firing rate (Tiesinga et al., 2008;
Kumbhani et al., 2007). The pPSTH loses some of the information about
the higher-order statistics of each individual spike train that could, in prin-
ciple, be useful to the decoder. Therefore, we developed a new aggregation
method based on the information content of the spike trains. We called the
resulting signal the “information train.” (See Figure 11 for more compar-
isons between the information train and pPSTH.)
The information train method was inspired by neural self-information
analysis (Li & Tsien, 2017). In order to build a continuous signal of the in-
formation content in a single cell over time, we started by computing a self-
informazione (SI) curve from the ISI distribution using Shannon’s definition
(Shannon, 2001): SI = − log2(P), where p is the ISI probability. The SI curve
gives the information contained in every observed ISI (see Figure 3B). SI
can be thought of as a measure of surprise; very probable ISIs correspond to
small SI, while very improbable ISIs correspond to large SI. A spike train can
be equally well described by its ISIs as its spike times; for each ISI observed
in the spike train, we may use the SI curve to find the amount of informa-
tion it contains. Neural self-information analysis then replaces each ISI in a
spike train with the corresponding SI value (Li & Tsien, 2017), but this cre-
ates a discrete signal. Invece, our threshold detection paradigm requires a
continuous signal that can be aggregated across cells.
Così, we developed a new analysis to translate a spike train into a con-
tinuous self-information train (see Figure 3C, top). We separate ISIs into
three cases. In the first case, the current ISI is of the same length as the most
probable, or most commonly observed, ISI for the cell. Therefore, this ISI
contains the lowest possible SI, which we call the “baseline information.”
The SI train always begins at baseline information, and in this case, it re-
mains there for the duration of the ISI. In the second case, the current ISI
is longer than the most probable one. Tuttavia, we do not know that it is
longer until the time when it has passed the length of the most probable
ISI and the cell has not yet spiked. The SI train reflects this by beginning
at baseline information and staying constant for the duration of the most
probable ISI, then rising according to the SI curve and stopping at the SI
value indicated by the total current ISI (blue sections in Figure 3C, bottom).
Finalmente, in the third case, the current ISI is shorter than the most probable
one. In questo caso, we know that it is shorter as soon as it ends, so the SI
train stays at baseline information until the very end of the ISI, then rises
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1372
S. Durian, M. Agrios, and G. Schwartz
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
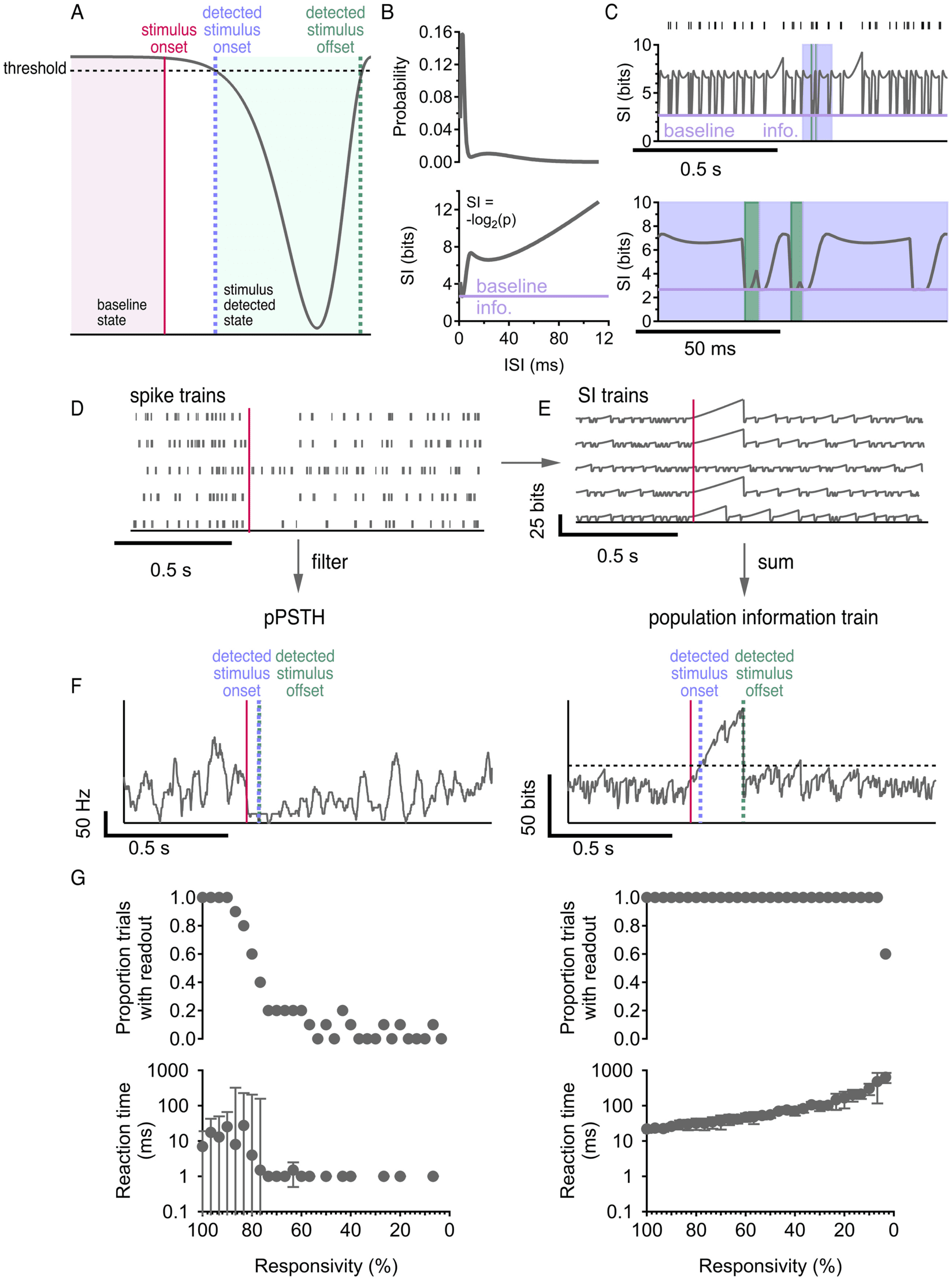
Figura 3: Population firing rate and population information are two plausi-
ble readout mechanisms. (UN) Detecting onset and duration of a stimulus (pink)
from the signal is a threshold detection task: stimulus onset (blue) is detected
when the signal crosses the threshold the first time; stimulus offset (green) È
detected when the signal crosses the threshold the second time. (B) ISI distri-
bution (top) and corresponding self-information (SI) curve (bottom). (C) Top:
raster and corresponding single cell information train. Bottom: inset showing
long ISIs (blue) and short ISIs (green). (D) Population response to a stimulus
Optimal Burstiness in Spiking Neurons
1373
instantaneously to the value indicated by the SI curve (green sections in
Figure 3C, bottom). At the start of each ISI, the SI train resets to baseline
informazione, meaning that it has no memory of its history and considers
subsequent ISIs independently.
For a single cell, the ISI distribution contains all the information in the
spike train, so the self-information train is a lossless representation. Questo
can be seen in Figure 3C, top; the self-information train returns to base-
line immediately upon registering a spike, so the original spike train is
time-aligned with the vertical drops in the information train. Tuttavia, for
multiple cells, there are joint ISI distributions to consider. Assuming inde-
pendence between cells, the information contained in the population is the
sum of the SI trains of each cell (see section 4). Independence is usually not
a reasonable assumption, but our experimental data from RGCs measured
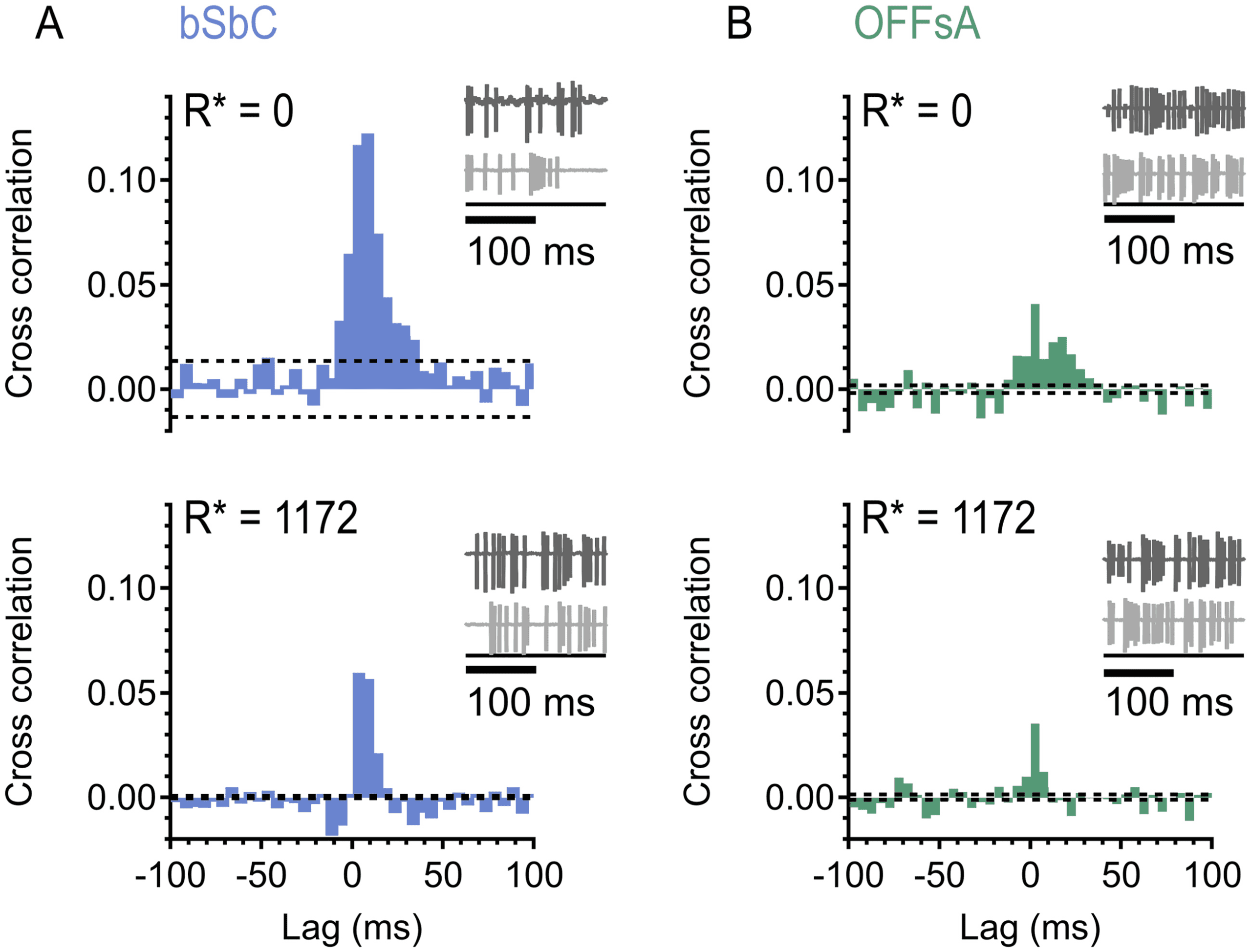
in the conditions simulated here show low pairwise noise correlations (Vedere
Figura 12). Other work has shown that noise correlations in RGC popula-
tions can depend on luminance (Ala-Laurila et al., 2011; Ruda et al., 2020)
and on the stimulus (Zylberberg et al., 2016), sometimes leading to large
possible effects on decoding performance. Correlations can also be induced
by a stimulus, and stimulus correlations in populations of neurons are typ-
ically larger than noise correlations (Schwartz et al., 2012; Cafaro & Rieke,
2010; Josic et al., 2009; Ponce-Alvarez et al., 2013). Our goal, Tuttavia, era
to study the optimal baseline spike statistics for a task in which all respon-
sive neurons were suppressed by the stimulus simultaneously. Così, non-
independence in our population before stimulus onset and after stimulus
offset was only due to noise correlations. Not only are pairwise noise corre-
lations low in different RGC types, but several studies (Petersen et al., 2001;
Averbeck & Lee, 2003; Oram et al., 2001), including in the retina (Niren-
berg et al., 2001; Schwartz et al., 2012; Soo et al., 2011), have shown that
(pink) con 80% responsivity. (E) SI trains constructed from spiking activity in
panel D. (F) Population PSTH (left) and population information train (right)
readout from activity in (D). pPSTH detected stimulus onset 50 ms after stimu-
lus presentation; stimulus offset was detected 2 ms after stimulus onset. Infor-
mation train detected stimulus onset 40 ms after stimulus presentation; stimulus
offset was detected 175 ms after stimulus onset. The filter on the pPSTH and the
threshold on the information train were both chosen so that there was one false
detection in the prestimulus time (the pPSTH touched 0 once and the informa-
tion train crossed the threshold once in the prestimulus time). (G) pPSTH (left)
and population information train (right) readout on stimulus onset detection
task as responsivity decreases in a population of 30 neurons. Top: Proportion of
trials with readout versus responsivity, where readout does not exist whenever
the signal fails to cross the threshold after stimulus onset. Bottom: Reaction time
versus responsivity, where reaction time is the time between stimulus onset and
stimulus onset detection. Error bars are interquartile range across 10 trials.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1374
S. Durian, M. Agrios, and G. Schwartz
only a small amount of information is lost when neural responses are de-
coded using algorithms that ignore noise correlations—on the order of 10%
of the total information (but see Ruda et al., 2020, where larger noise cor-
relations caused a 50% reduction in information). Therefore, we have con-
structed population information trains by summing the SI trains of each cell
in the population (see Figure 3F, right) while recognizing that it is a lower
bound on the total information present in the full joint distribution of the
spike trains. We consider the biological plausibility of such a representation
in section 3, but for now it is worth noting that as a one-dimensional sig-
nal, the aggregated information train is not as straightforward to compute
with neural hardware as a pPSTH but is considerably less complex than a
multidimensional manifold aimed at capturing the joint ISI distribution
within the population.
Although this choice of construction is justifiable at the low end of corre-
lation, where real RGC types lie, we consider correlations that go up to unity
in our simulations. In the case that the population is 100% correlated, IL
spike trains from all the neurons will be identical, as shown in Figure 2A,
and therefore the SI trains from individual neurons will all be exactly the
same as well. Intuitively, the population information train should simply be
equal to that of a single neuron since additional neurons offer only redun-
dant information, but we have suggested a population information train
constructed by summing all the SI trains. Infatti, this is not an issue; sum-
ming identical SI trains will result in a population information train that is
a scaled version of the SI train from any given individual neuron. Since we
use the population information train to detect change via a threshold that is
based on the false detection rate (rather than measuring the absolute value
of the population information train), scaling the information train does not
affect the reaction time that we measure from it. This way of constructing
the population information train could break down for populations with
medium pairwise correlations, but any choice of construction would have
a trade-off between accuracy and ease of use, and we are satisfied that this
choice is easy to implement, motivated by mathematical reasoning, E,
most important, works for low correlations (which is what is actually rele-
vant to the brain) and high correlations.
A critical benefit of the population information train over the pPSTH is
that it should automatically amplify the contribution of responsive cells
(which will have large SI) in a population relative to unresponsive cells
(which will have small SI) without the need to define a cell selection crite-
rion or weighting strategy. To test this intuition, we simulated populations
Di 30 neurons and varied their responsivity to the stimulus. We decoded
the gap onset time for all of these populations using both the pPSTH and
the population information train. The pPSTH decoder was extremely sen-
sitive to responsivity, often failing to even reach the detection threshold,
and therefore failing to have a readout for reaction time, when fewer than
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Optimal Burstiness in Spiking Neurons
1375
80% of cells were responsive (see Figure 3G, left). Nel frattempo, the popula-
tion information train decoder approach was robust to very large fractions
of unresponsive cells (see Figure 3G, right). Subsequent analyses used the
population information train decoder and 100% responsivity, but our con-
clusions are robust to lower responsivity (Guarda la figura 14).
2.3 There Exists Optimal Burstiness for Minimizing Reaction Time.
Having developed a readout mechanism—the population information
train—we then used it to decode the onset of a gap in firing by measur-
ing reaction time. We were interested in the effects of multiple parameters
on reaction time: burstiness, firing rate, population size, and correlation.
For three of these parameters, we had an intuition for how they should af-
fect performance based on one key insight: when trying to decode the time
of a gap onset, temporal precision is key to getting accurate estimates. In-
creasing the firing rate of a population increases temporal precision, so we
expected that increasing the firing rate would improve performance (cioè.,
decrease reaction time). Another way to gain temporal precision is to in-
crease the size of a population; Perciò, we also expected population size
to have a positive effect on performance. A population that has very low
pairwise correlations is unlikely to have many overlapping spikes from
different cells, while a population with high correlation is likely to have
substantial overlap. This implies that temporal precision, and thus perfor-
mance, should decrease with correlation. In contrast to the other parame-
ters, the intuition for how burstiness affects performance is not simple and
was our central question in this part of the study.
We isolated the effect of burstiness on reaction time by holding firing
rate, population size, and correlation constant and found a nonmonotonic
relationship (see Figure 4A), suggesting that for each combination of param-
eters, there may be a different level of burstiness that minimizes reaction
time. We could continue in this way to isolate the effects of each parameter
by holding the other parameters constant at different values, but the num-
ber of parameters, and their ranges, makes this impractical. A more elegant
approach is to try to find a unifying principle that can collapse the data. Di-
mensional analysis gives us the tools to identify such a unifying principle.
Dimensional analysis uncovers the relationships between variables by
tracking their physical dimensions over calculations. Since we held respon-
sivity constant at 100%, there are only five relevant quantities altogether:
reaction time δ, burstiness β, firing rate λ, population size N, and correla-
tion α. Instead of using our simulation parameters λ
2 in the
analysis, we deliberately chose to use only the firing rates and burstiness
that arose from these parameters, because firing rate and burstiness can be
measured from experimental data, while our simulation parameters cannot,
and the results of our analysis should generalize to any simulation choice
and should not depend on our particular nested renewal process.
1, and κ
1, λ
2, κ
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1376
S. Durian, M. Agrios, and G. Schwartz
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
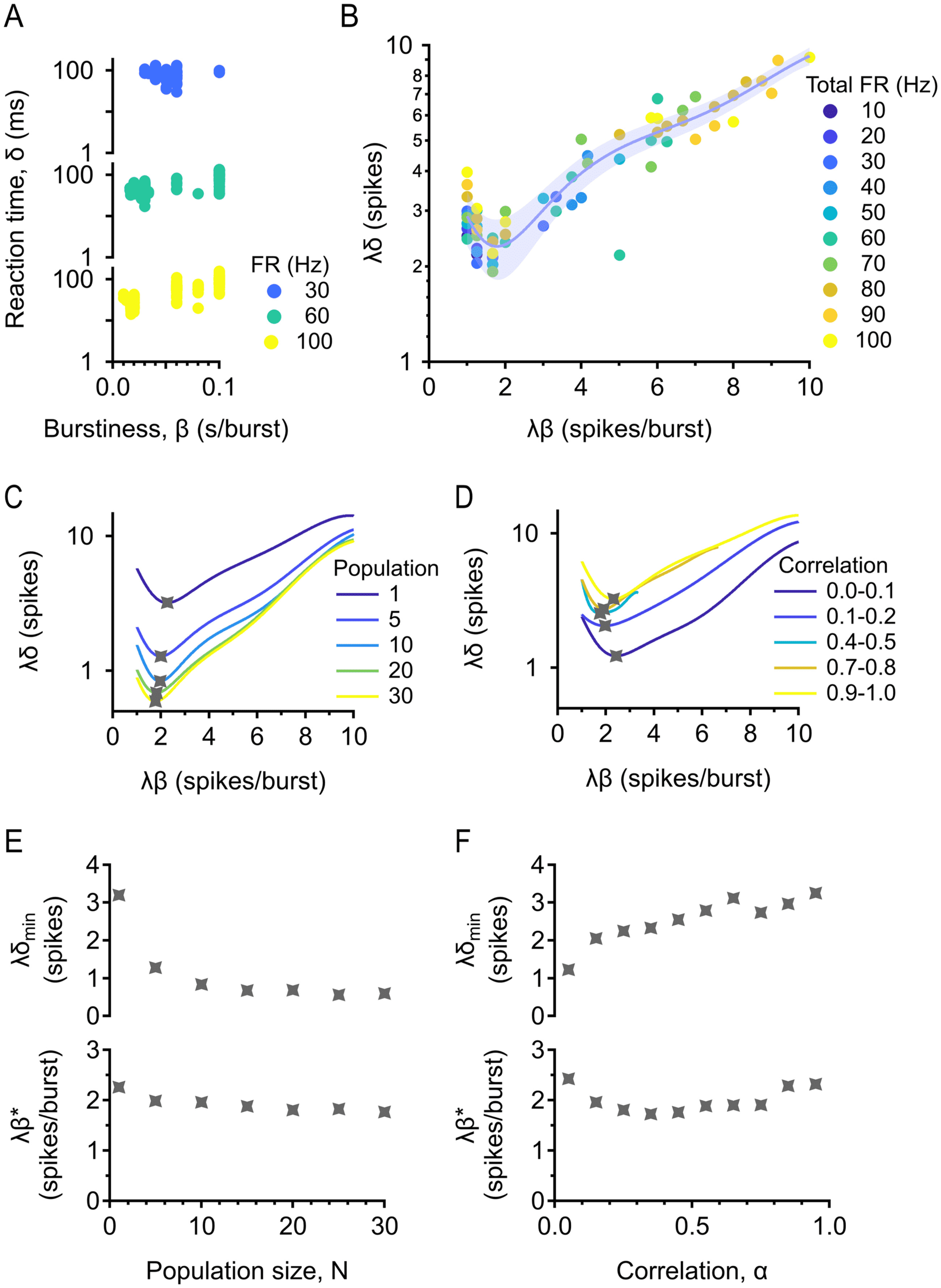
Figura 4: Optimal burstiness for minimizing reaction time. (UN) Reaction time δ
versus burstiness β with information train readout. Population is fixed at 5 cells,
correlation is fixed between 0 E 0.2, and total firing rate is fixed at 30, 60, E
100 Hz. (B) Dimensional analysis collapses the data for different firing rates.
Dimensionless reaction time is plotted against dimensionless burstiness. Popu-
lation is fixed at 5 cells, and correlation is fixed between 0 E 0.2. Trial-averaged
(median) data are shown. Error bar = standard error estimate of the data around
the fit. (C) Existence of a minimum is robust across population sizes. Correla-
tion is fixed between 0 E 0.2. (D) Existence of a minimum is robust across
correlations. Population is fixed at 5 cells. (E) Top: Minimum (dimensionless)
reaction time against population size. Bottom: Optimal (dimensionless) bursti-
ness against population size. (F) Same as in panel E, but correlation is varied.
Optimal Burstiness in Spiking Neurons
1377
The variables in our problem are all either dimensionless or some trans-
formation of the physical dimension “time,” so there is only one relevant di-
mension in this problem. A fundamental theorem in dimensional analysis,
the Buckingham pi theorem (Buckingham, 1914), says that it is possible to
construct exactly 5 − 1 = 4 independent dimensionless groups out of these
five variables, and those dimensionless groups are functionally related. Noi
chose to make reaction time and burstiness dimensionless by multiplying
by firing rate (brackets denote the dimension of the quantity inside and a
dimensionless quantity is said to have dimension 1), so we obtain the fol-
lowing four dimensionless groups:
[λδ] = [λβ] = [N] = [α] = 1.
(2.1)
We may write any one of these dimensionless quantities as a function of
il riposo, but it is difficult to fit functions of three variables, so we fix popu-
lation size and correlation so that the function no longer depends on them,
and then we have
λδ = f (λβ ).
(2.2)
Equazione 2.2 immediately reveals that both reaction time and burstiness
are inversely proportional to the firing rate. While burstiness was defined
in such a way that it must be inversely proportional to firing rate (see sec-
zione 4), it is illuminating that reaction time is inversely proportional as well.
This basic theoretical result of dimensional analysis gives us much more in-
formation than our intuition, which simply told us that reaction time should
decrease with firing rate.
The practical implication of the Buckingham pi theorem is that we may
collapse all the data for different firing rates together, with no pattern, so
we can analyze them together. The functional form of f (see equation 2.2) È
now possible to find by fitting (see Figure 4B). There is a clear minimum in
the data, demonstrating a level of (dimensionless) burstiness that is optimal
for minimizing reaction time across all firing rates. We chose a polynomial
fit of degree 5 to describe the data, since that is a reliable way to find the
minimum. We want to emphasize here that we are not claiming that the
data have a polynomial form; we are only concerned with finding the min-
imum, and any other good fit would give the same minimum. Now we
may separately vary population size and correlation (see Figures 4C and
4D), illustrating that the existence of optimal burstiness for minimizing re-
action time is robust for both parameters. The x and y values of the minima
of these curves completely describe how optimal burstiness and minimum
reaction time depend on population size and correlation. Simply dividing
the x and y values of the minimum by the firing rate of the population, we
obtain the exact (dimensionful) optimal burstiness and minimum reaction
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1378
S. Durian, M. Agrios, and G. Schwartz
time. Minimum reaction time decreases with population size and increases
with correlation (as predicted by our intuition), while optimal burstiness is
relatively constant with both parameters, indicating that there is one level
of burstiness optimal for detecting stimulus onset at any population size
and correlation.
1, and κ
Note that if we were to include the internal simulation parameters λ
1,
λ
/λ
2 in the analysis, we should also control for κ
2, κ
1
(as well as controlling for population size and correlation) when we inves-
tigate the relationship between dimensionless burstiness and reaction time
in equation 2.2. Our choice not to include these parameters results in more
noise in Figure 4B, but also makes our analysis much more generalizable,
as discussed previously, and allows us to draw conclusions with the confi-
dence that they apply to any simulation choice and, more important, to real
neurons.
2, and λ
2
1, κ
2.4 There Exists an Asymptotic Optimal Burstiness for Discriminat-
ing Stimulus Strength. Besides “when,” another fundamental question to
ask about a stimulus is: How strong is it? In our model, stimulus strength
corresponds to the duration of the gap in spiking because we varied stimu-
lus strength by changing the recovery time of the firing rate (see Figure 2B).
We measured the gap length in the information train, or the duration of
time between stimulus onset and offset detection (see Figure 3F, right), In
order to make deductions about how the length of the gap in spiking is af-
fected by the suppressed firing rate (see Figure 5A). The performance metric
here—the measure of how well a population can discriminate the stimulus
strength—is essentially the accuracy with which the time constant of re-
covery (which we varied from 50 A 3000 ms) is captured by the gap length
measurement. Therefore, the performance metric should be the error in the
relationship between gap length and the time constant. Tuttavia, it is not
immediately obvious what the relationship between these two variables
actually is, much less how much scatter there is around it. Dimensional
analysis is again a useful tool here. There are six relevant quantities to this
problem: gap length γ , recovery time constant τ , burstiness β, firing rate
λ, population size N, and correlation α. Applying the Buckingham pi the-
orem and setting all but two of the dimensionless groups (see section 4) A
be constant (so that we obtain a function of one variable that relates the gap
length and time constant of recovery), we have
λγ = f (λτ ).
(2.3)
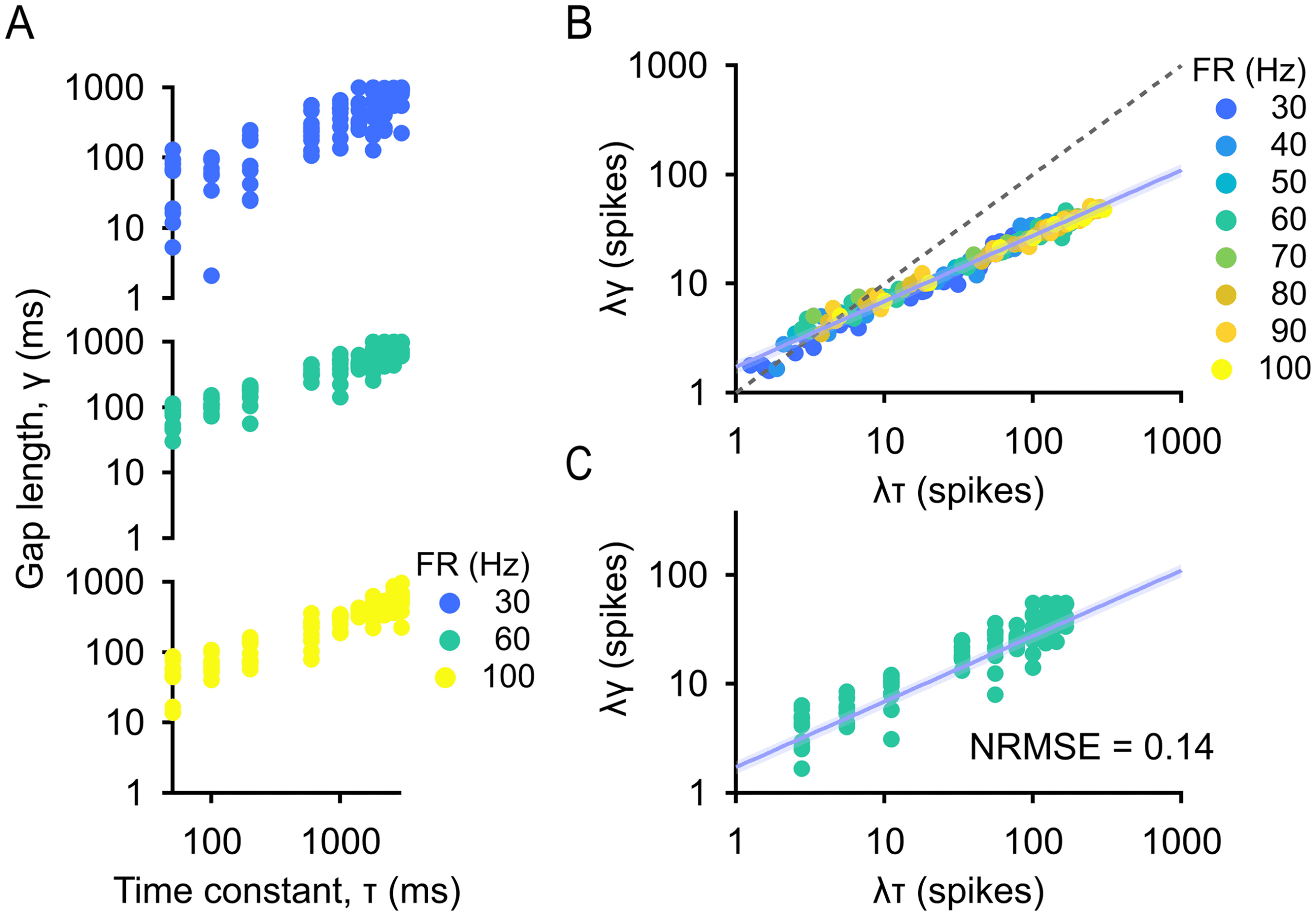
By fitting, it is clear that there is a power law relationship between these
variables (see Figure 5B). Now, for each combination of parameters for
which we have several trials of gap length measurements, we chose the per-
formance metric to be the scatter in the data around the power law function
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Optimal Burstiness in Spiking Neurons
1379
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 5: Gap length is related to the recovery time constant by a power law.
(UN) Gap length γ vs. time constant of recovery τ . Population is fixed at 5 cells,
correlation is fixed between 0 E 0.2, dimensionless burstiness (λβ) is fixed at 3
spikes/burst, and total firing rate is fixed at 30, 60, E 100 Hz. (B) Dimension-
less gap length versus dimensionless time constant. Population is 5 cells, corre-
lation is 0 A 0.2, and dimensionless burstiness is 3 spikes/burst. Trial-averaged
(median) data are shown. Dashed line is y = x, and exponent of power law fit
È 0.6. Error bar = standard error estimate of the data around the fit. (C) Per-
formance metric is the scatter in the data measured with normalized root mean
square error (NRMSE). Population is 5 cells, correlation is 0 A 0.2, dimension-
less burstiness is 3 spikes/burst, and firing rate is 60 Hz. Error bar = standard
error estimate of the data around the fit.
suggested by dimensional analysis (see Figure 5C), which we quantified
with normalized root mean square error (NRMSE; see section 4).
Now that we have a performance metric, we wanted to see how it de-
pended on burstiness in particular, as well as firing rate, population size,
and correlation. Once again, we could isolate the effects of each of these
parameters by holding all the others constant (see Figure 6A), but using
dimensional analysis simplifies the problem by collapsing data. The rele-
vant quantities are the performance metric NRMSE (cid:9), burstiness β, firing
rate λ, population size N, and correlation α, so setting population size and
correlation to be constant, we have
(cid:9) = f (λβ ).
(2.4)
1380
S. Durian, M. Agrios, and G. Schwartz
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
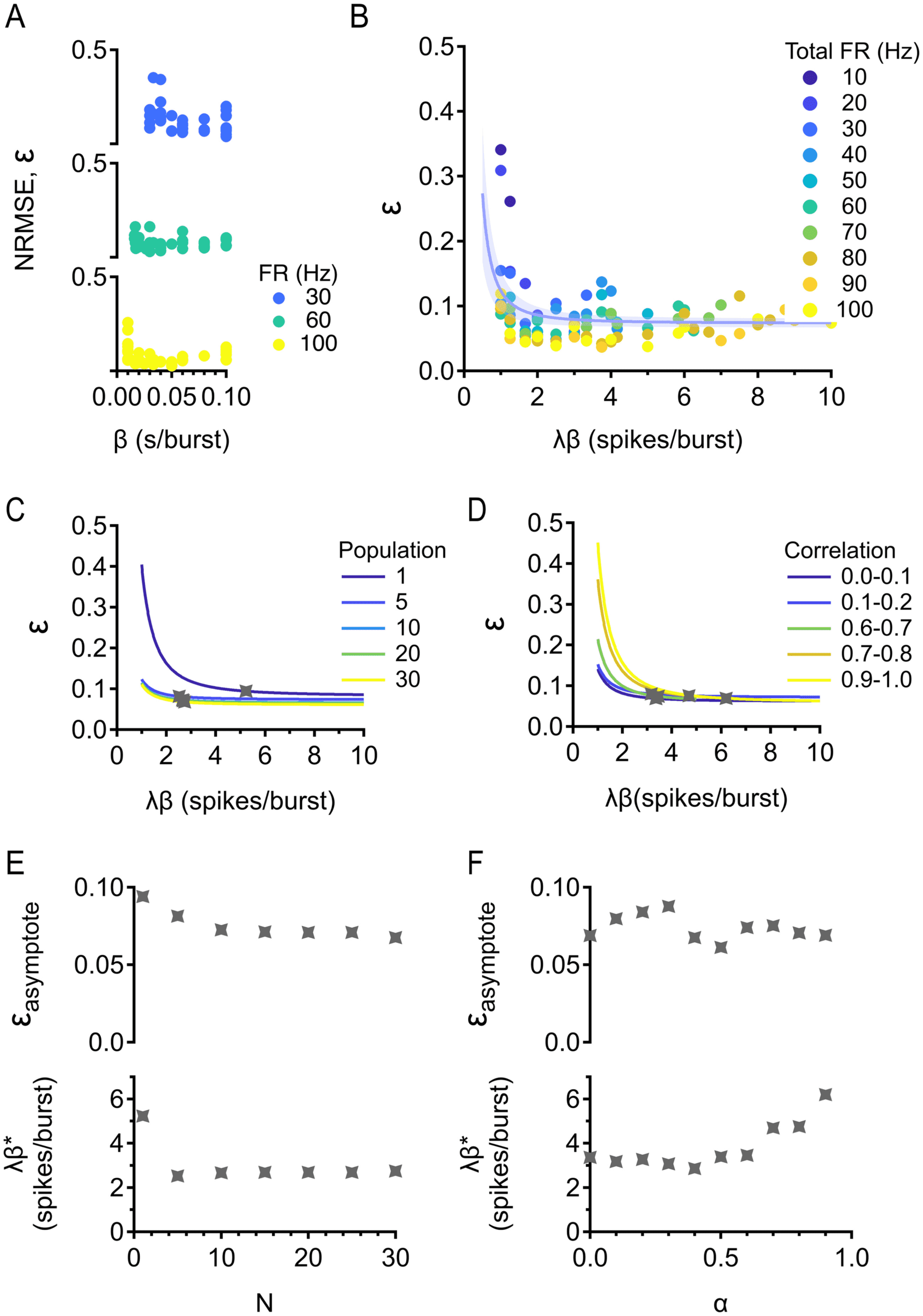
Figura 6: Optimal burstiness for discriminating stimulus strength. (UN) NRMSE
(cid:9) versus burstiness β. Population is fixed at 5 cells, correlation is fixed between
0 E 0.2, and total firing rate is fixed at 30, 60, E 100 Hz. (B) NRMSE versus
dimensionless burstiness. Population is 5 cells, and correlation is 0 E 0.2. Trial-
averaged (median) data are shown. Error bar = standard error estimate of the
data around the fit. (C) Existence of an asymptote is robust across population
sizes. Correlation is fixed between 0 E 0.2. (D) Existence of an asymptote is
robust across correlations. Population is fixed at 5 cells. (E) Top: Asymptotic
NRMSE against population size. Bottom: Optimal (dimensionless) burstiness
against population size. (F) Same as in panel E but correlation is varied.
Optimal Burstiness in Spiking Neurons
1381
While burstiness is still inversely proportional to the firing rate, equa-
zione 2.4 reveals that NRMSE is constant with firing rate. In other words, IL
ability to decode the duration of a gap in firing rate does not depend on the
spontaneous firing rate. Intuitively, this may be because if a downstream
neuron “knows” the spontaneous firing rate of its inputs, it can use that
to deduce how many times they should have fired during a gap but did
non, therefore giving the length of the firing gap. We expect that this may
not hold true in the limit of very low spontaneous rates, where the gap is
barely detectable, but we did not simulate spontaneous rates below 10 Hz
because OFFsAs and bSbCs do not generally have spontaneous rates below
Quello.
Plotting reveals that NRMSE decays to a nonzero constant (see Fig-
ure 6B). È interessante notare, there is a large range of burstiness that optimizes
NRMSE, in contrast to how there was a single optimal value of burstiness
for minimizing reaction time. We chose to fit an asymptotic decay func-
tion to the data (see section 4) in order to characterize the optimal value of
NRMSE. By the nature of an asymptotic function, the fitting function con-
tinues to decay very slightly where the data had already become constant.
We chose to study the point at which the fit reached 90% of the asymptote
because any burstiness larger than this is essentially optimal.
Next we separately varied population size and correlation (see Fig-
ures 6C and 6D), which showed us that the existence of asymptotic NRMSE
and a large range of burstiness resulting in this optimal performance was
robust for both parameters. Asymptotic NRMSE decreases with population
size and is relatively constant with correlation, while optimal burstiness is
constant with population size and increases with correlation, implying that
the level(S) of burstiness optimal for discriminating stimulus strength is not
affected by population size for populations larger than five cells.
2.5 bSbC RGCs Have Close to Optimal Burstiness for Gap Detection.
Having established that optimal burstiness exists for decoding the onset
and duration of a gap in firing, our next question was how the baseline
spike statistics of the RGC types we studied relate to this optimum. Re-
call that we fit functions that describe how reaction time (Guarda la figura 4) E
NRMSE (Guarda la figura 6) depend on dimensionless burstiness. Dimensionless
burstiness is simply burstiness multiplied by firing rate, so another way to
represent the information in Figures 4 E 6 is in three dimensions instead
of two: the dependence of reaction time (and NRMSE) on burstiness and
firing rate is shown in Figure 7. We chose to represent this information with
dimensionful burstiness and firing rate instead of dimensionless burstiness
because we measured those parameters directly from the data and because
different cell types could potentially achieve the same dimensionless bursti-
ness value with different combinations of firing rates and burstiness. Noi
compared the performance of different types of experimentally recorded
cells by using their firing rate and burstiness to predict how quickly they
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1382
S. Durian, M. Agrios, and G. Schwartz
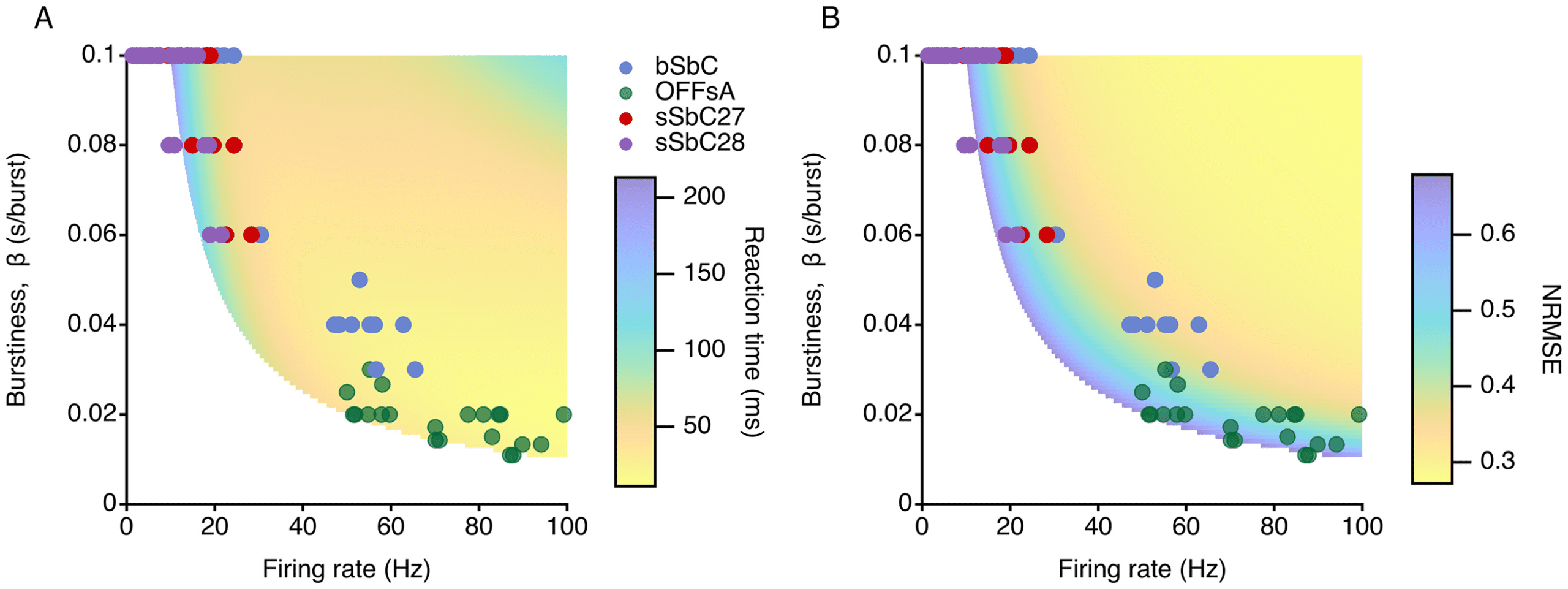
Figura 7: bSbCs RGCs have close to optimal burstiness. (UN) False color plot
showing reaction time predicted from firing rate and burstiness, as described
by the function in Figure 4B. The position of four RGC types on the surface is
shown. Population size is 5 cells, and correlation is 0 A 0.2. (B) False color plot
showing NRMSE predicted from firing rate and burstiness, as described by the
function in Figure 6B. The position of four RGC types on the surface is shown.
Population size is 5 cells, and correlation is 0 A 0.2.
would detect stimulus onset (see Figure 7A) and how accurately they would
discriminate stimulus strength (see Figure 7B) according to our model. Noi
set the population size at five cells and the correlation in the physiological
range of 0 A 0.2, but as we saw earlier, optimal burstiness is negligibly af-
fected by the population size so these results apply to any population size.
Both bSbCs and OFFsAs are quite good at detecting a stimulus quickly, al-
though bSbCs are closer to optimal reaction time, while both types of sus-
tained suppressed-by-contrast RGCs are much worse at this task. Tuttavia,
Figure 7B suggests that bSbCs are by far the best at discriminating stimu-
lus strength, since their burstiness puts them right on the lower bound of
optimal burstiness; OFFsA RGCs do not perform nearly as well. Therefore,
bSbC RGCs have spiking patterns that enable them to both react to a stimu-
lus coming on as quickly as possible and detect the strength of that stimulus
with great accuracy.
3 Discussion
To investigate the role of burstiness in population decoding of firing gaps,
we simulated spike trains for populations of neurons using a nested re-
newal process. This strategy allowed us to capture the statistics of recorded
spike trains from RGCs and also to vary burstiness parametrically (see Fig-
ures 1 E 2). We then developed a new analysis to combine spike trains
across a population into an information train and demonstrated that this
method is more robust to unresponsive cells than a population PSTH (Vedere
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Optimal Burstiness in Spiking Neurons
1383
Figura 3). Using the information trains of different simulated populations,
we discovered that there is an optimal level of burstiness for detecting the
onset of a firing gap that is inversely proportional to firing rate and rela-
tively independent of population size and correlation (Guarda la figura 4). There
is also an optimal range of burstiness for detecting gap duration that is rel-
atively independent of all of these other parameters (see Figures 5 E 6).
Finalmente, we considered the baseline spike statistics of four RGC types in the
context of these theoretical results and revealed that the burst patterns of
bSbC RGCs make them nearly optimal for detecting both the onset and the
strength of a contrast step (Guarda la figura 7).
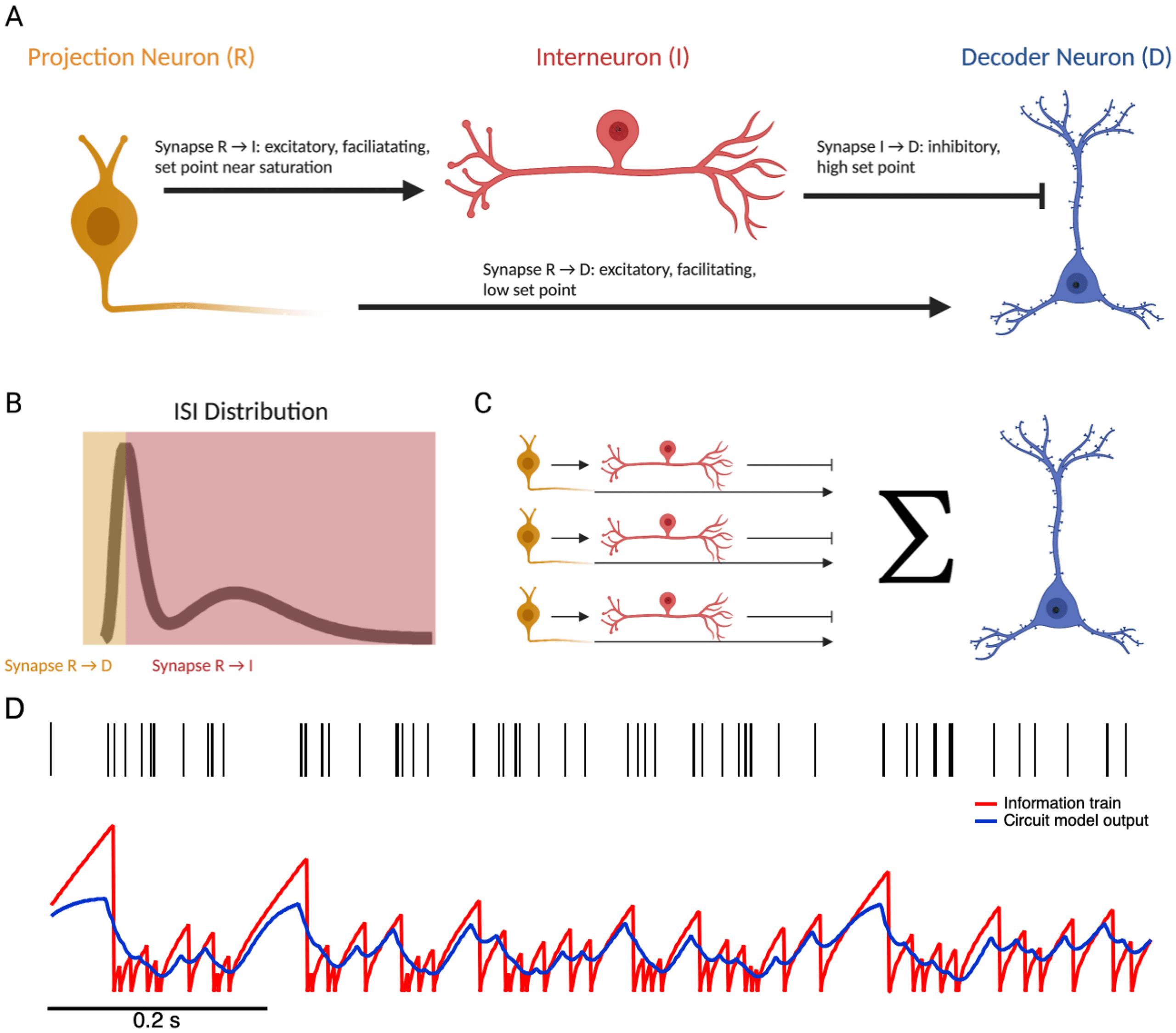
3.1 Could a Biological Circuit Represent the Information Train? For
a single neuron’s spike train, self-information could, in principle, be repre-
sented by a relatively simple three-neuron, three-synapse circuit (see Fig-
ure 8A). Let us first consider ISIs longer than the mode of the distribution.
Our circuit needs to represent these periods of silence with an increasing,
positive signal (see Figure 8B, red-shaded region). A disinhibition circuit
with facilitation at the first synapse achieves this pattern. Imagine a circuit
in which decoder neuron D is tonically inhibited by interneuron I, and I is
excited by RGC R. Decreases in the baseline spike rate of R will lead to a
decreased spike rate in I and, così, disinhibition of D. If the synapse from
R to I is facilitating and near saturation at baseline, then small decreases in
the spike rate of R will have a modest effect on I (and therefore on D), Ma
larger gaps will cause more profound firing rate reductions in I and corre-
spondingly larger activations of D. For ISIs shorter than the mode of the
distribution (see Figure 8B, yellow shaded region), this disinhibition circuit
could be counterbalanced with a direct excitatory connection from R to D.
This synapse would increase the activation of D for short ISIs, questo è, In-
creases in the firing rate of R. We implemented this circuit in a toy model
and found that indeed, it is able to capture the basic shape of information
trains (see Figure 8D). This is not the result of overfitting because we used
separate spike trains in the training set for fitting the model parameters
and the testing set. Importantly, this circuit could easily scale to represent
the full information train in a population of neurons. Since the information
trains of individual neurons sum to the population train in our framework,
a decoder neuron for the population could integrate parallel copies of the
circuit (see Figure 8C).
While this proposed circuit could capture the general shape of the in-
formation train—increased activation in D for either increases or decreases
in the spike rate of R—the degree to which its activation is proportional
to self-information depends on the circuit’s ability to learn the ISI distribu-
tion of R. This learning would presumably take place through plasticity at
each of the three synapses in the circuit. There is certainly evidence that neu-
ral circuits can represent probability distributions and perform probabilistic
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1384
S. Durian, M. Agrios, and G. Schwartz
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 8: Biologically plausible circuit for representing the information train.
(UN) Circuit model for self-information of a spike train from neuron R.
(B) Schematic of the parts of the ISI distribution of neuron R that could be
learned by different synapses in the circuit. (C) Schematic of population in-
formation train circuit comprising parallel circuits for the self-information of
each individual neuron. (D) Example showing a spike train (black ticks) E
the corresponding normalized information train (red) and output of the de-
coder neuron from this model circuit. The circuit model was a simplified version
without synaptic plasticity (see section 4). The fit parameters were as follows:
= 0.47,
τ
RI
SlopeID
= 19.7 ms, HalfMaxID
= 8.80 ms, HalfMaxRI
= 0.001, HalfMaxRD
= 2.66, SlopeRD
= 8.52, SlopeRI
ID
= 0.02.
= 89.4, τ
inference (Pouget et al., 2013; Dabagia et al., 2022). While the baseline spike
statistics of RGCs might be dynamically altered with environmental fac-
tori, like mean luminance, they also may adapt to these factors as light
adaptation in retinal circuits is especially robust (Schwartz, 2021). It is also
unclear to what degree of accuracy the circuit needs to capture the ISI dis-
tribution to be effective as a decoder of gaps in firing in populations of R
neurons. Modeling such biologically plausible circuits in the context of the
Optimal Burstiness in Spiking Neurons
1385
information train is a rich area for future investigations of synaptic learning
rules and their ability to represent probability distributions.
3.2 Baseline Spike Statistics Can Be Optimized for Different Tasks.
The result that some burstiness higher than minimum is optimal for iden-
tifying the time of stimulus presentation and stimulus strength leads us to
a principle that has a long history in population spike analysis (Kepecs &
Lisman, 2003; Oswald et al., 2004; Palmer et al., 2021): different spiking
patterns are optimal for encoding different stimulus features. We extended
these results by demonstrating two concrete examples of how optimal en-
coding of different stimulus features depends on baseline spiking statistics.
The theoretical implication of this is that different cell types may display
different baseline spiking statistics depending on the stimulus features they
encode.
Earlier we provided intuition about the effects of firing rate, population
size, and correlation on reaction time. The same intuition holds for perfor-
mance on decoding the duration of a gap in firing, since it is also depen-
dent on temporal precision. Now we will lay out our intuition for why
there exists optimal burstiness for both tasks, which will explain why it
makes sense that specific spiking patterns are optimal for encoding differ-
ent stimulus features. We again attribute increased performance on these
tasks to increased temporal precision. As explained earlier, a population
could theoretically increase its temporal precision by increasing its firing
rate or its size or decreasing its cell correlations; Tuttavia, there are physi-
ological limits to a population’s firing rate and correlation, and the size of
the population of visual neurons activated by a stimulus is related to the
size of the stimulus (Rodieck, 1998). In contrasto, rearranging the pattern
of spikes without changing the number of spikes generated is something
that a cell could do without expending extra energy, and if it rearranges its
spiking pattern so that it has long periods of silence and short periods of
rapid activity, or bursts, then it has great temporal precision within those
bursts. Now imagine that that cell is part of a population with low pairwise
cell correlations (Guarda la figura 11); then the bursts from different cells would
be staggered in time, allowing the population as a whole to have excellent
temporal precision. Therefore, it is clear that increasing burstiness can im-
prove performance. Following this line of thinking, it is also easy to see why
too much burstiness would be harmful: if the population is trying to detect
stimulus onset, the periods of silence between bursts could become so long
that even with many cells, it is very possible that the population would
entirely miss the stimulus simply because no cell was in the middle of a
burst when the stimulus was presented. Inoltre, the fact that firing rate,
population size, and correlation had effects on performance that were pre-
dictable from this intuition lends further credibility to our result that there
is an optimal level of burstiness for identifying the timing and strength of a
stimulus.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1386
S. Durian, M. Agrios, and G. Schwartz
An intriguing part of our result was that the optimal amount of bursti-
ness for gap detection is very close to two spikes per burst window (Vedere
Figura 4). Our intuition about temporal precision and sampling is relevant
to the location of this minimum as well. Two spikes in a burst window rep-
resent a single, short ISI. It seems that the most efficient way to gain tempo-
ral precision for gap detection at a fixed firing rate is to group spikes into
pairs where the short ISIs are used to encode time at high precision. Adding
more spikes to the burst is counter productive because at a fixed firing rate,
it would necessitate longer intervals between bursts where neurons are un-
able to represent a rate decrease.
We found that the baseline firing statistics of bSbC RGCs lie close to the
optimum for performance on two gap detection tasks (Guarda la figura 7), Ma
what about the other three high-baseline-rate RGC types we analyzed and
the many lower baseline rate ones we did not analyze? It is important to
consider (1) that the gap detection tasks we defined are only two out of
many decoding tasks that must be performed simultaneously across the
population of RGCs, E (2) that biological constraints, including the en-
ergy expenditure of maintaining a high spike rate, also likely drove the
evolution of the different RGC types. Like bSbC RGCs, sustained (S)SbC
RGCs also signal exclusively with gaps in firing, but they do so at a substan-
tially longer timescale (Jacoby & Schwartz, 2018; Schwartz, 2021). Forse
for these RGCs, the energetic benefit of maintaining a lower baseline firing
rate is worth the cost of lower temporal resolution in gap detection because
they represent time more coarsely than bSbC RGCs. The OFF alpha RGCs
(OFFsA and OFFtA) respond to different stimuli with either increases or de-
creases in baseline firing (Homann & Freed, 2017; Van Wyk et al., 2009), E
OFFtA RGCs have been implicated in the detection of several specific visual
caratteristiche (Munch et al., 2009; Krishnamoorthy et al., 2017; Wang et al., 2021),
so for these RGC types, performance in representing spike gaps needs to be
balanced against metrics for their other functions.
3.3 The Information Train as a Way to Track Population-Level
Changes in Spike Patterns. Our work has practical as well as theoretical
implications: we proposed the information train readout, which tracks the
information in a population over time and is more comprehensive and ro-
bust than a standard pPSTH readout. Per esempio, when using a pPSTH
to analyze a population of direction selective cells without first finding the
preferred directions of every single cell in the population, the responses
from cells preferring opposite directions will cancel each other out, leading
to a pPSTH that fails to reflect change due to the stimulus. The same effect
will be observed if a light-dark edge is presented to a population of ON or
OFF cells. Ovviamente, it is possible to remove this effect by classifying each
cell’s response to the stimulus first, but that can be time-consuming if the
population size is large and it requires an (often arbitrary) supervised clas-
sification step. The information train will reflect a stimulus change in both
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Optimal Burstiness in Spiking Neurons
1387
of these cases even when the whole population is analyzed together. This is
because any ISI length out of the ordinary (cioè., different from the most prob-
able one) causes a positive deflection in the information train, so no matter
whether a cell’s firing rate increases or decreases in response to a stimulus,
the population information rises. Therefore, the information train is a con-
venient readout mechanism to use because it does not require any assump-
tions to cluster cells, even when the population recording is heterogeneous.
It is also easy to implement by simply fitting the observed ISI distributions
in the absence of a stimulus to a gamma (many neural circuits have ISI pat-
terns well fit by a gamma distribution; Li et al., 2017) or sum of gammas
distribution (depending on whether the cells in question are bursty).
3.4 Limitations and Future Directions. We have shown that the infor-
mation train can capture more and different information than the pPSTH.
Future work could use this analytical tool for discovery of how popula-
tions of neurons represent stimulus features by computing the filter be-
tween stimulus variables and SI, like continuous-signal generalization of
an SI-triggered average.
The information train, Tuttavia, is not a complete description of the full
mutual information in the population since it assumes independence. IL
natural extension of SI to a population is pointwise mutual information
(PMI) (Shannon, 2001), which measures the association of single events.
Much like entropy is the expected value of SI, mutual information is the
expected value of PMI. In the future, a more accurate way to construct the
population information train would be to use PMI: the value of the infor-
mation train at time t is given by measuring the time since the last spike for
each cell in the population and then calculating the PMI in the coincidence
of those events. This is quite difficult to implement because it requires de-
scribing the joint ISI distributions. Not only is it necessary to estimate the
joint ISI probabilities in the absence of a stimulus, when we can generate a
lot of data but it is still difficult to estimate the joint probabilities; it is also
necessary to be able to accurately extrapolate those joint ISI distributions
in order to deduce the stimulus response. Namely, we need to be able to
accurately estimate the very tails of the joint ISI distributions if we still as-
sume a stimulus that depresses firing rate. We were able to do this in our
study by fitting our observed ISI distributions with a sum of gammas dis-
tribution (Guarda la figura 10), but it could be dangerous to first estimate the joint
ISI distributions and then estimate their tail values. Even small errors in
the density estimation would lead to drastically different results, since PMI
(much like SI) amplifies the significance of extremely improbable events. In
other words, small differences in p lead to large differences in log2(P) for
low p. Calculating the true PMI of the population over time is an important
future direction, and it will be needed to extend this analysis to popula-
tions with high noise correlations (Ruda et al., 2020), but it has to be done
carefully.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
N
e
C
o
_
UN
_
0
1
5
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1388
S. Durian, M. Agrios, and G. Schwartz
Another limitation of this study is that we have not formally seen how
sensitive the information train readout is to more complex tasks and stimuli.
We posit that the information train should be able to flexibly reflect any
change in spiking patterns at the population level since every observed ISI
different from the most common one registers a change. Tuttavia, we only
compared the information train to the standard pPSTH for one task; it might
be illuminating to compare readouts from the information train and pPSTH
on more complex stimuli in the future.
Not only is there potential follow-up research stemming directly from
this study, such as constructing the population information train using PMI
and exploring more complicated stimuli, but in addition, the information
train will, we hope, be used to investigate more complex statistics of spiking
outside the retina, such as statistics exhibited by Purkinje cells (Kase et al.,
1980; Ohtsuka & Noda, 1995) and other variables that affect information
transmission. The power of the information train is not limited to applica-
tions in neural spiking; it can be used to study any change detection task.
Per esempio, it could be applied to the problem of detecting auditory fre-
quency change, where gaps are similarly important. The theoretical frame-
work of the information train is general enough to aid research in a wide
variety of directions.
4 Methods
4.1 Model of Spike Generation. In the Poisson model of spike gener-
ation, the instantaneous firing rate is the only force that generates spikes.
Assuming a constant firing rate λ over time, the number of spikes within
UN (piccolo) interval of time (cid:10)t is a Poisson distributed random variable with
parameter λ. Using the Poisson probability density function,
P(1 spike during (cid:10)T) = λ(cid:10)T.
(4.1)
One can therefore generate a sequence of uniformly distributed random
numbers {xn} in order to determine when to generate a spike: if xi
< λ(cid:10)t,
generate a spike in time bin i. Since the number of spikes within any inter-
val of time is a Poisson random variable with parameter λ, the exponential
distribution Exp(λ) describes the time between spikes (i.e., the interspike
interval distribution).
A renewal process extends the Poisson process to depend on both the
instantaneous firing rate and the time since the previous spike. One way
to model this is to simply generate a Poisson spike train with rate parame-
ter λ and delete all but every κth spike. A gamma distribution predicts the
wait time until the κth Poisson process event, so the ISI distribution of a
renewal process generated in this way is described by Gamma(κ, λ). This is
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Optimal Burstiness in Spiking Neurons
1389
a natural extension of the Poisson process since when κ is 1, the ISI distri-
κ
bution is Gamma(1, λ) = Exp(λ). The average ISI length is
λ , and therefore
the average firing rate is
λ
κ .
1
1, λ
We extended the renewal process again, nesting one renewal process in-
side another. The outer renewal process with parameters κ
1 determines
λ
the number and placement of burst windows, with an average of
burst
κ
1
windows per second. We allowed λ
1 to vary between 30 and 600 bursts per
second, and κ
1 to vary between 3 and 6 in order to obtain a range of 10 to 100
burst windows per second. The inner renewal process with parameters κ
2,
λ
2 determines the number and placement of spikes within each burst win-
dow, with an average of
spikes per second within each burst window.
We let λ
2 range from 3 to
6. Thus, the average spiking rate within a burst window ranged from 100
to 1000 spikes per second. We inserted spikes generated by the inside pro-
cess into the burst windows by setting a burst window length τ
b, which we
chose to be 10 ms. This results in an average of
spikes per burst window,
with a range of 1 to 10 spikes per burst window, and therefore an average
firing rate,
2 range from 300 to 6000 spikes per second, and κ
λ
2
κ
2
λ
κ
2
τ
2
b
λ =
τ
b
λ
1
κ
1
λ
2
κ
2
,
(4.2)
with a range of 10 to 100 Hz.
As a note, the burst window length τ
b was chosen based on anecdotal
observations of the typical length of burst periods in experimental record-
ings of bSbCs, but it is actually arbitrary. Changing the burst length would
not change the ISI distributions we simulated or affect our results, be-
cause the other nested renewal process parameters can simply be changed
in proportion to the burst length in order to generate the same spike
train.
We varied pairwise correlations between nested renewal process spike
trains by using a shared versus random seed strategy. Just as for a Poisson
process, we needed two sequences (for the inner and outer renewal pro-
cesses) of uniformly distributed random numbers, {xn} and {yn}, to deter-
mine when to generate spikes (see above). We first generated two shared
sequences of uniform random numbers, {xnshared
}, then for each
cell in the population generated new independent sequences of uniformly
distributed numbers, {xnindependent
}. For each cell, {xn} was con-
} and {ynindependent
structed by drawing from {xnshared
} with
probability 1 − αx. The other sequence of uniform numbers, {yn}, was con-
structed similarly with weight αy. The choices of αx and αy control the
pairwise correlations of the inner and outer renewal processes; thus, vary-
ing them separately varies the correlation between burst windows or the
} with probability αx and {xnindependent
} and {ynshared
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1390
S. Durian, M. Agrios, and G. Schwartz
correlation between spikes within burst windows. We measured cross-
correlations between all pairs of spike trains in the population and averaged
to obtain the overall correlation reported.
4.2 Burstiness. Burstiness β is the average number of spikes per burst
τ
. Using equation 4.2, the formula
2
λκ
2
. The range of burstiness is 0.01 to
1
λ
window normalized by firing rate: β = λ
for burstiness can be simplified to β = κ
0.1 seconds per burst window.
1
b
4.3 Population Readout Mechanisms. Self-information is defined as
SI = − log2(p) (Shannon, 2001), where p is the ISI probability. We con-
structed a population information train by summing individual SI trains.
This implicitly assumes that cells are independent since if independence
holds, then
− log2(p(x, y)) = − log2(p(x)p(y)) = − log2(p(x)) − log2(p(y)).
(4.3)
In order to measure reaction time and gap length in the information train,
we set a threshold on the information train such that the error rate was
0.1 false crossings per second. We set the threshold for the pPSTH readout
mechanism at 0 and set the filter length such that the pPSTH reached 0 with
a rate of 0.1 errors per second during the prestimulus time.
Population information train options B and C considered in Figure 15
were constructed as follows:
• Option B: The population information train is the SI train constructed
from the ensemble spike train or the spike train obtained by overlay-
ing all the spike trains in the population.
• Option C: The population information train is constructed by sum-
ming the SI trains for each cell in the population, but we let ISIs
shorter than the most probable one have negative deflections in each
SI train, while longer ISIs still have positive deflections.
The analogous threshold (resulting in 0.1 errors/s) was placed on the
information trains in options B and C.
4.4 Dimensional Analysis. We used dimensional analysis to find the
relationship between gap length and the time constant of recovery (see Fig-
ures 5A and 5B). There are six relevant quantities to this problem: gap length
γ , recovery time constant τ , burstiness β, firing rate λ, population size N,
and correlation α. These are all either dimensionless or some transformation
of the physical dimension “time,” so we can construct 6 − 1 = 5 indepen-
dent dimensionless groups related by an unknown function. We chose to
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Optimal Burstiness in Spiking Neurons
1391
make gap length, the recovery time constant, and burstiness dimensionless
by multiplying by firing rate, so we have
[λγ ] = [λτ ] = [λβ] = [N] = [α] = 1.
(4.4)
In order to obtain a function of one variable, which relates gap length
and the time constant, we set dimensionless burstiness, population size,
and correlation to be constant and obtained equation 2.3.
Once we defined a performance metric (NRMSE) for the gap length de-
coding task (see Figure 5C), we used dimensional analysis again to find
its dependence on burstiness and the other model parameters (see Fig-
ures 6A and 6B). The relevant quantities are the performance metric NRMSE
(cid:9), burstiness β, firing rate λ, population size N, and correlation α, so we may
construct 5 − 1 = 4 independent dimensionless groups related by a func-
tion. We again chose to make burstiness dimensionless by multiplying by
firing rate, so we have
[(cid:9)] = [λβ] = [N] = [α] = 1.
(4.5)
Fixing population size and correlation so that the function no longer de-
pends on them, we obtain equation 2.4.
4.5 Circuit Model. A circuit model with three synapses is described in
Figure 8 and associated text in section 3. Each synapse was modeled as in-
tegrating over time as an exponential with one parameter followed by a
sigmoidal nonlinearity with two parameters (HalfMax and Slope) accord-
ing to
f (x) =
1
1 + e−(x−Hal f Max)
Slope
.
(4.6)
We used Matlab’s nonlinear function minimizer fmincon to minimize
the mean squared error between the model output and the information
train using separate training and testing sets. The fmincon function was run
100 times using a different initial point in parameter space each time. The
initial point was made by sampling from a bounded uniform distribution
specific to each parameter: τRI ∈ [10, 30], Hal fMaxRI
∈
[0.05, 0.4], Hal fMaxID
∈ [0.001, 0.01], τID ∈ [0.5, 4],
∈ [0.1, 1.5]. All parameters were constrained
Hal fMaxRI
to be strictly positive during the optimization.
∈ [0.1, 0.5], SlopeID
∈ [0.1, 0.6], SlopeRI
∈ [0.5, 3], SlopeRD
4.6 Fitting Routines. From dimensional analysis, we obtained equa-
tion 2.4. Plotting λβ against (cid:9) revealed that f is an asymptotically decaying
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1392
S. Durian, M. Agrios, and G. Schwartz
function (see Figure 6B). We therefore let f be of the form
f (x) = a + b
xn
.
(4.7)
The range of n obtained from this fitting routine was 0.5 to 4 with no
systematic trends, so n was taken as 2, which results in essentially the same
good fits and reduces the number of fitting parameters to two. We also con-
sidered an exponential fit, but ultimately rejected it because the fit was not
as good as the fit given by equation 4.7 with fixed n, and it requires three
fitting parameters instead of two. Goodness of fit of equation 4.7 with vari-
able n as well as fixed n, and the exponential fit, were all assessed with root
mean square error (RMSE) returned by the fitting routine.
We fit the power law relationship between the dimensionless time con-
stant and the dimensionless gap length (see Figures 5B and 5C) by fitting
a linear relationship of their logarithms. Goodness of fit was assessed with
normalized root mean square error (NRMSE). The NRMSE of an estimator
ˆy with respect to n observed values of a parameter y is the square root of
the mean squared error, normalized by the mean of the measured data, ¯y:
NRMSE = 1
¯y
− ˆyi)2.
(cid:2)(cid:3)
1
n (yi
n
i=1
We fit ISI distributions of simulated (see Figure 9) and experimentally
recorded (see Figure 10) data by minimizing the mean square error of the
log of the data and log of a sum of gammas distribution, since there was a
large dynamic range in the data. This effectively minimizes the percentage
difference between the data and the fitting function. Goodness of fit was
assessed with RMSE returned by the fitting routine.
4.7 RGC Spike Recordings. RGCs were recorded in cell-attached con-
figuration in whole-mount preparations of mouse retina as described pre-
viously (Wienbar & Schwartz, 2022; Jacoby et al., 2015). Animals were
C57/Bl6 mice of both sexes obtained from Jackson Labs (strain 000664) or
bred in our lab. Animals were between 4 and 12 weeks of age. All animal
procedures were performed under the registered protocols approved by
Institutional Animal Care and Use Committee (IACUC) of Northwestern
University. Cell typology was determined using the methods described in
Goetz et al. (2022). Baseline spiking was recorded at a mean luminance of 0
and 1000 isomerizations (R*) per rod per second.
4.8 Data and Code Availability. All simulated data reported in
this paper are publicly available at https://gin.g-node.org/sdurian/Gap
-Detection.git. Experimental data reported are available at https://
data.mendeley.com/datasets/2pdwp5xnmv/1. All code written in sup-
port of this publication is available at https://github.com/sdurian/Gap
-Detection.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Optimal Burstiness in Spiking Neurons
1393
Appendix: Supplementary Information
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
= 4, λ
2
= 200 bursts/s, κ
2
Figure 9: Nested renewal process ISI histograms are well fit by a sum of gamma
= 4,
distribution. (A) ISI distribution from NR process with parameters κ
1
= 400 spikes/s. Firing rate λ = 50 Hz, burstiness
λ
1
β = 0.02 s/burst. Goodness of fit of the sum of gammas distribution is reported
as root mean square error (RMSE). (B) ISI distribution from NR process with
= 1000 spikes/s. λ = 50 Hz,
parameters κ
1
= 6,
β = 0.04 s/burst. (C) ISI distribution from NR process with parameters κ
1
= 1500 spikes/s. λ = 80 Hz, β = 0.06 s/burst. (D) ISI
= 3, λ
λ
1
= 6,
= 5, λ
distribution from NR process with parameters κ
1
1
= 6000 spikes/s. λ = 100 Hz, β = 0.1 s/burst.
λ
2
= 100 bursts/s, κ
2
= 50 bursts/s, κ
2
= 96 bursts/s, κ
2
= 4, λ
1
= 5, λ
2
2
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1394
S. Durian, M. Agrios, and G. Schwartz
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 10: RGC ISI histograms are well fit by a sum of gamma distribution.
(A) ISI distributions of experimentally recorded bSbCs with sum of gammas
fits. Top is the same cell as in Figure 1C. Goodness of fit is reported as RMSE.
(B) ISI distributions of experimentally recorded OFFsAs with sum of gammas
fits. Top is the same cell as in Figure 1D.
Figure 11: More information train and PSTH comparisons. (A) Example spike
train (top), PSTH (middle), and self-information train (bottom) for one neuron,
which increases firing rate to stimulus 1 and suppresses firing rate to stimulus
2. (B) pPSTH (middle) and population information train (bottom) readouts for a
population of two neurons, one of which increases firing rate to a stimulus and
the other of which suppresses firing rate.
Optimal Burstiness in Spiking Neurons
1395
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Figure 12: Noise correlations are low. (A) Cross-correlation histograms from a
pair of bSbCs. Dashed lines are null (epoch-shuffled) correlation. Paired activity
was recorded at a mean luminance of 0 and 1000 isomerizations (R*) per rod per
second. (B) Cross-correlation histograms from a pair of OFFsAs. Dashed lines
are null correlation. Paired activity was recorded at a mean luminance of 0 and
1000 isomerizations (R*) per rod per second.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1396
S. Durian, M. Agrios, and G. Schwartz
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 13: Results are robust to different thresholds on the information train.
(A, B) Dimensionless reaction time measured using threshold 2 (left, 0.2 er-
rors/s) and 3 (right, 0.4 errors/s) versus dimensionless burstiness. Population
is fixed at 5 cells and correlation is fixed between 0 and 0.2. Trial-averaged (me-
dian) data are shown. Error bars = standard error estimate of the data around
the fits. (C, D) Existence of a minimum is robust across population sizes. Cor-
relation is fixed between 0 and 0.2. (E) Top: minimum (dimensionless) reaction
time against population size for thresholds 1 (0.1 errors/s), 2, and 3. Bottom:
optimal (dimensionless) burstiness against population size.
Optimal Burstiness in Spiking Neurons
1397
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
Figure 14: Results are robust to different levels of responsivity. (A) Reaction
time δ versus burstiness β with information train readout. Responsivity is fixed
at 60%, population is fixed at 5 cells, correlation is fixed between 0 and 0.2, and
total firing rate is fixed at 30, 60, and 100 Hz. (B) Dimensional analysis collapses
the data for different firing rates. Dimensionless reaction time is plotted against
dimensionless burstiness. Responsivity is fixed at 60%, population is fixed at
5 cells, and correlation is fixed between 0 and 0.2. Trial-averaged (median)
data are shown. Error bar = standard error estimate of the data around the fit.
(C) Existence of a minimum is robust across population sizes. Responsivity is
fixed at 60%, and correlation is fixed between 0 and 0.2. (D) Top: Minimum (di-
mensionless) reaction time against population size. Bottom: Optimal (dimen-
sionless) burstiness against population size. Responsivity is fixed at 60% and
correlation is fixed between 0 and 0.2.
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1398
S. Durian, M. Agrios, and G. Schwartz
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 15: Results are robust to different ways of constructing the population
information train. (A, B) Dimensionless reaction time measured using aggrega-
tion options B (left) and C (right) versus dimensionless burstiness. Population
is fixed at 5 cells, and correlation is fixed between 0 and 0.2. Trial-averaged (me-
dian) data are shown. Error bars = standard error estimate of the data around
the fits. (C, D) Existence of a minimum is robust across population sizes. Cor-
relation is fixed between 0 and 0.2. (E) Top: Minimum (dimensionless) reaction
time against population size for aggregation options A, B, and C. Bottom: Op-
timal (dimensionless) burstiness against population size.
Optimal Burstiness in Spiking Neurons
1399
Acknowledgments
We are grateful to all members of the Schwartz Lab for their feedback and
support on this project. We thank Stephanie Palmer and Sophia Weinbar for
their comments on the manuscript, as well as Sara Solla and Ann Kennedy
for their feedback on the project.
Competing Interests
We have no competing interests to disclose.
References
Ainsworth, M., Lee, S., Cunningham, M. O., Traub, R. D., Kopell, N. J., & Whitting-
ton, M. A. (2012). Rates and rhythms: A synergistic view of frequency and tem-
poral coding in neuronal networks. Neuron, 75, 572–583. 10.1016/j.neuron.2012
.08.004
Ala-Laurila, P., Greschner, M., Chichilnisky, E. J., & Rieke, F. (2011). Cone photore-
ceptor contributions to noise and correlations in the retinal output. Nature Neu-
roscience, 9, 1309–1316. 10.1038/nn.2927
Averbeck, B. B., & Lee, D. (2003). Neural noise and movement-related codes in
the macaque supplementary motor area. Journal of Neuroscience, 23, 7630–7641.
10.1523/JNEUROSCI.23-20-07630.2003
Azouz, R., Jensen, M. S., & Yaari, Y. (1996). Ionic basis of spike after-depolarization
and burst generation in adult rat hippocampal CA1 pyramidal cells. Journal of
Physiology, 492, 211–223. 10.1113/jphysiol.1996.sp021302
Bingmer, M., Schiemann, J., Roeper, J., & Schneider, G. (2011). Measuring burstiness
and regularity in oscillatory spike trains. Journal of Neuroscience Methods, 201, 426–
437. 10.1016/j.jneumeth.2011.08.013
Bowman, D. M., Eggermont, J. J., & Smith, G. M. (1995). Effect of stimulation on
burst firing in cat primary auditory cortex. Journal of Neurophysiology, 74, 1841–
1855. 10.1152/jn.1995.74.5.1841
Britten, K. H., Shadlen, M. N., Newsome, W. T., & Movshon, J. A. (1992). The analysis
of visual motion: A comparison of neuronal and psychophysical performance.
Journal of Neuroscience, 12, 4745–4765. 10.1523/JNEUROSCI.12-12-04745.1992
Buckingham, E. (1914). On physically similar systems: Illustrations of the use of di-
mensional equations. Physical Review, 4, 345–376. 10.1103/PhysRev.4.345
Cafaro, J., & Rieke, F. (2010). Noise correlations improve response fidelity and stim-
ulus encoding. Nature, 468, 964–967. 10.1038/nature09570
Cessac, B., Paugam-Moisy, H., & Viéville, T. (2010). Overview of facts and issues
about neural coding by spikes. Journal of Physiology, Paris, 104, 5–18. 10.1016/
j.jphysparis.2009.11.002
Dabagia, M., Vempala, S. S., & Papadimitriou, C. (2022). Assemblies of neurons learn
to classify well-separated distributions. In Proceedings of Machine Learning Re-
search, 178, 3685–3717.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1400
S. Durian, M. Agrios, and G. Schwartz
da Silveira, R. A., & Rieke, F. (2021). The geometry of information coding in correlated
neural populations. http://arxiv.org/abs/2102.00772
de la Rocha, J., Doiron, B., Shea-Brown, E., Josié, K., & Reyes, A. (2007). Correla-
tion between neural spike trains increases with firing rate. Nature, 448, 802–806.
10.1038/nature06028
de Zeeuw, C. I., Hoebeek, F. E., Bosman, L. W. J., Schonewille, M., Witter, L., &
Koekkoek, S. K. (2011). Spatiotemporal firing patterns in the cerebellum. Nature
Review Neuroscience, 12, 327–344. 10.1038/nrn3011
Destexhe, A., & Paré, D. (1999). Impact of network activity on the integrative proper-
ties of neocortical pyramidal neurons in vivo. Journal of Neurophysiology, 81, 1531–
1547. 10.1152/jn.1999.81.4.1531
Ecker, A. S., Berens, P., Tolias, A. S., & Bethge, M. (2011). The effect of noise cor-
relations in populations of diversely tuned neurons. Journal of Neuroscience, 31,
14272–14283. 10.1523/JNEUROSCI.2539-11.2011.768
Goetz, J., Jessen, Z. F., Jacobi, A., Mani, A., Cooler, S., Greer, D., . . . Schwartz,
G. W. (2022). Unified classification of mouse retinal ganglion cells using
function, morphology, and gene expression. Cell Reports, 40, 111040. 10.1016/
j.celrep.2022.111040
Gold, J. I., & Shadlen, M. N. (2007). The neural basis of decision making.
Annual Review of Neuroscience, 30, 535–574. 10.1146/annurev.neuro.29.051605
.113038
Harris, K. D., Hirase, H., Leinekugel, X., Henze, D. A., & Buzsáki, G. (2001). Tempo-
ral interaction between single spikes and complex spike bursts in hippocampal
pyramidal cells. Neuron, 32, 141–149. 10.1016/S0896-6273(01)00447-0
Heeger, D. (2000). Poisson model of spike generation. Stanford University handout.
Homann, J., & Freed, M. A. (2017). A mammalian retinal ganglion cell implements a
neuronal computation that maximizes the SNR of its postsynaptic currents. Jour-
nal of Neuroscience, 37, 1468–1478. 10.1523/JNEUROSCI.2814-16.2016
Jacoby, J., & Schwartz, G. W. (2018). Typology and circuitry of suppressed-by-
contrast retinal ganglion cells. Annual Review of Neuroscience, 12, 269.
Jacoby, J., Zhu, Y., DeVries, S. H., & Schwartz, G. W. (2015). An amacrine cell cir-
cuit for signaling steady illumination in the retina. Cell Reports, 13, 2663–2670.
10.1016/j.celrep.2015.11.062
Josi´c, K., Shea-Brown, E., Doiron, B., & de la Rocha, J. (2009). Stimulus-dependent
correlations and population codes. Neural Computation, 21, 2774–2804.
Kase, M., Miller, D. C., & Noda, H. (1980). Discharges of Purkinje cells and
mossy fibres in the cerebellar vermis of the monkey during saccadic eye move-
ments and fixation. Journal of Physiology, 300, 539–555. 10.1113/jphysiol.1980
.sp013178
Kepecs, A., & Lisman, J. (2003). Information encoding and computation with spikes
and bursts. Network, 14, 103–118. 10.1080/net.14.1.103.118
King, A., Bajo, V., Bizley, J., Campbell, R., Nodal, F., Schulz, A., & Schnupp, J. (2007).
Physiological and behavioral studies of spatial coding in the auditory cortex.
Hearing Research, 229, 106–115. 10.1016/j.heares.2007.01.001
Krishnamoorthy, V., Weick, M., & Gollisch, T. (2017). Sensitivity to image recurrence
across eye-movement-like image transitions through local serial inhibition in the
retina. eLife, 6, 22431. 10.7554/eLife.22431
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Optimal Burstiness in Spiking Neurons
1401
Kumbhani, R. D., Nolt, M. J., & Palmer, L. A. (2007). Precision, reliability, and
information-theoretic analysis of visual thalamocortical neurons. Journal of Neu-
rophysiology, 95, 2647–2663. 10.1152/jn.00900.2006
Larkum, M. E., Senn, W., & Lüscher, H. (2004). Top-down dendritic input increases
the gain of layer 5 pyramidal neurons. Cerebral Cortex, 14, 1059–1070. 10.1093/
cercor/bhh065
Legendre, P., McKenzie, J. S., Dupouy, B., & Vincent, J. D. (1985). Evidence for burst-
ing pacemaker neurones in cultured spinal cord cells. Neuroscience, 16, 753–767.
10.1016/0306-4522(85)90092-2
Li, M., Xie, K., Kuang, H., Liu, J., Wang, D., & Fox, G. (2017). Spike-timing pat-
terns conform to gamma distribution with regional and cell type–specific characteristics.
bioXiv:145813.
Li, M., & Tsien, J. Z. (2017). Neural code-neural self-information theory on how cell-
assembly code rises from spike time and neuronal variability. Frontiers in Cellular
Neuroscience, 11, 236.
Llinás, R. R. (2014). Intrinsic electrical properties of mammalian neurons and CNS
function: A historical perspective. Frontiers in Cellular Neuroscience, 8, 320.
McCormick, D. A., & Feeser, H. R. (1990). Functional implications of burst firing and
single spike activity in lateral geniculate relay neurons. Neuroscience, 39, 103–113.
10.1016/0306-4522(90)90225-S
Münch, T. A., Da Silveira, R. A., Siegert, S., Viney, T. J., Awatramani, G. B., & Roska,
B. (2009). Approach sensitivity in the retina processed by a multifunctional neural
circuit. Nature Neuroscience, 12, 1308–1316.
Nirenberg, S., Carcieri, S. M., Jacobs, A. L., & Latham, P. E. (2001). Retinal ganglion
cells act largely as independent encoders. Nature, 411, 698–701. 10.1038/35079612
Ohtsuka, K., & Noda, H. (1995). Discharge properties of Purkinje cells in the oculo-
motor vermis during visually guided saccades in the macaque monkey. Journal of
Neurophysiology, 74, 1828–1840. 10.1152/jn.1995.74.5.1828
Oram, M. W., Hatsopoulos, N. G., Richmond, B. J., & Donoghue, J. P. (2001). Excess
synchrony in motor cortical neurons provides redundant direction information
with that from coarse temporal measures. Journal of Neurophysiology, 86, 1700–716.
10.1152/jn.2001.86.4.1700
Oswald, A-M. M., Chacron, M. J., Doiron, B., Bastian, J., & Maler, L. (2004). Parallel
processing of sensory input by bursts and isolated spikes. Journal of Neuroscience,
24, 4351–4362. 10.1523/JNEUROSCI.0459-04.2004
Palmer, S. E., Wright, B., Doupe, A. J., & Kao, M. (2021). Variable but not random:
Temporal pattern coding in a songbird brain area necessary for song modifica-
tion. Journal of Neurophysiology, 125, 540–555. 10.1152/jn.00034.2019
Panzeri, S., Schultz, S. R., Treves, A., & Rolls, E. T. (1999). Correlations and the en-
coding of information in the nervous system. In Proceedings of the Royal Society B:
Biological Sciences, 266, 1001–1012. 10.1098/rspb.1999.0736
Petersen, R. S., Panzeri, S., & Diamond, M. E. (2001). Population coding of
stimulus location in rat somatosensory cortex. Neuron, 32, 503–514. 10.1016/
S0896-6273(01)00481-0
Pillow, J. W., Shlens, J., Paninski, L., Sher, A., Litke, A. M., Chichilnisky, E. J., & Si-
moncelli, E. P. (2008). Spatio-temporal correlations and visual signalling in a com-
plete neuronal population. Nature, 8, 995–999. 10.1038/nature07140
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1402
S. Durian, M. Agrios, and G. Schwartz
Ponce-Alvarez, A., Thiele, A., Albright, T. D., Stoner, G. R., & Deco, G. (2013).
Stimulus-dependent variability and noise correlations in cortical MT neurons. In
Proceedings of the National Academy of Sciences U.S.A., 110, 13162–13167. 10.1073/
pnas.1300098110
Pouget, A., Beck, J. M., Ma, W. J., & Latham, P. E. (2013). Probabilistic brains: Knowns
and unknown. Nature Neuroscience, 16, 1170–1178. 10.1038/nn.3495
Ratté, S., Hong, S., De Schutter, E., & Prescott, S. A. (2013). Impact of neuronal proper-
ties on network coding: Roles of spike initiation dynamics and robust synchrony
transfer. Neuron, 78, 758–772.
Raus Balind, S., Magó, Á., Ahmadi, M., Kis, N., Varga-Németh, Z., L˝orincz, A., &
Makara, J. (2019). Diverse synaptic and dendritic mechanisms of complex spike
burst generation in hippocampal CA3 pyramidal cells. Nature Communications,
10, 1859. 10.1038/s41467-019-09767-w
Rieke, F., Warland, D., Van Steveninck, R de R., & Bialek, W. (1999). Spikes: Exploring
the neural code. MIT Press.
Rodieck, R. W. (1998). The first steps in seeing. Sinauer Associates.
Romo, R., & Salinas, E. (2001). Touch and go: Decision-making mechanisms in
somatosensation. Annual Review of Neuroscience, 24, 107–137. 10.1146/annurev
.neuro.24.1.107
Ruda, K., Zylberberg, J., & Field, G. (2020). Ignoring correlated activity causes a fail-
ure of retinal population codes. Nature Communications, 1, 4605.
Schwartz, G. (2021). Retinal computation. Academic Press.
Schwartz, G., Macke, J., Amodei, D., Tang, H., & Berry, M. J. (2012). Low error dis-
crimination using a correlated population code. Journal of Neurophysiology, 108,
1069–1088. 10.1152/jn.00564.2011
Shannon, C. E. (2001). A mathematical theory of communication. SIGMOBILE Mobile
Computing and Communications Review, 5, 3–55. 10.1145/584091.584093
Soo, F. S., Schwartz, G. W., Sadeghi, K., & Berry, M. J. (2011). Fine spatial information
represented in a population of retinal ganglion cells. Journal of Neuroscience, 31,
2145–2155. 10.1523/JNEUROSCI.5129-10.2011
Tiesinga, P., Fellous, J.-M., & Sejnowski, T. J. (2008). Regulation of spike timing in
visual cortical circuits. Nature Review Neuroscience, 9, 97–107. 10.1038/nrn2315
Tripathy, S., & Gerkin, R. (2016). Spontaneous firing rate. https://neuroelectro.org/
ephys_prop/18/
Van Wyk, M., Wässle, H., & Taylor, W. R. (2009). Receptive field properties of ON-
and OFF-ganglion cells in the mouse retina. Visual Neuroscience, 26, 297–308.
10.1017/S0952523809990137
van Vreeswijk, C. (2010). Stochastic models of spike trains. In S. Grün & S. Rotter
(Eds.), Analysis of parallel spike trains (pp. 3–20). Springer US.
Wang, F., Li, E., De, L., Wu, Q., & Zhang, Y. (2021). OFF-transient alpha RGCs me-
diate looming triggered innate defensive response. Current Biology, 31, 2262–
2273.
Wienbar, S., & Schwartz, G. W. (2022). Differences in spike generation instead of
synaptic inputs determine the feature selectivity of two retinal cell types. Neuron,
110, 2110–2123. 10.1016/j.neuron.2022.04.012
Yannaros, N. (1988). On Cox processes and gamma renewal processes. Journal of Ap-
plied Probability, 25, 423–427. 10.2307/3214451
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Optimal Burstiness in Spiking Neurons
1403
Zeldenrust, F., Wadman, W. J., & Englitz, B. (2018). Neural coding with bursts—
Current state and future perspectives. Frontiers in Computational Neuroscience, 12.
10.3389/fncom.2018.00048
Zylberberg, J., Cafaro, J., Turner, M. H., Shea-Brown, E., & Rieke, F. (2016). Direction-
selective circuits shape noise to ensure a precise population code. Neuron, 89, 369–
383. 10.1016/j.neuron.2015.11.019
Received November 30, 2022; accepted March 23, 2023.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
8
1
3
6
3
2
1
4
3
2
3
2
n
e
c
o
_
a
_
0
1
5
9
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3