ARTICLE
Communicated by Ian Stevenson
Scalable Variational Inference for Low-Rank Spatiotemporal
Receptive Fields
Lea Duncker
lduncker@stanford.edu
Wu Tsai Neurosciences Institute and Howard Hughes Medical Institute,
Stanford University, Stanford, CA 94302, U.S.A.
Kiersten M. Ruda
kruda@bidmc.harvard.edu
Beth Israel Deaconess Medical Center, Harvard University,
Boston, MA 02115, U.S.A.
Greg D. Field
field@neuro.duke.edu
Department of Neurobiology, Duke University, Durham, NC 27708, U.S.A.
Jonathan W. Pillow
pillow@princeton.edu
Princeton Neuroscience Institute, Princeton University, Princeton, NJ 08544, U.S.A.
An important problem in systems neuroscience is to characterize how a
neuron integrates sensory inputs across space and time. The linear re-
ceptive field provides a mathematical characterization of this weighting
function and is commonly used to quantify neural response properties
and classify cell types. Tuttavia, estimating receptive fields is difficult in
settings with limited data and correlated or high-dimensional stimuli. A
overcome these difficulties, we propose a hierarchical model designed to
flexibly parameterize low-rank receptive fields. The model includes gaus-
sian process priors over spatial and temporal components of the receptive
field, encouraging smoothness in space and time. We also propose a new
temporal prior, temporal relevance determination, which imposes a vari-
able degree of smoothness as a function of time lag. We derive a scalable
algorithm for variational Bayesian inference for both spatial and tempo-
ral receptive field components and hyperparameters. The resulting esti-
mator scales to high-dimensional settings in which full-rank maximum
likelihood or a posteriori estimates are intractable. We evaluate our ap-
proach on neural data from rat retina and primate cortex and show that
it substantially outperforms a variety of existing estimators. Our mod-
eling approach will have useful extensions to a variety of other high-
dimensional inference problems with smooth or low-rank structure.
Calcolo neurale 35, 995–1027 (2023)
https://doi.org/10.1162/neco_a_01584
© 2023 Istituto di Tecnologia del Massachussetts
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
996
l. Duncker, K. Ruda, G. Field, and J. Pillow
1 introduzione
A key problem in computational and systems neuroscience is to under-
stand the information carried by neurons in the sensory pathways (Jones
& Palmer, 1987; Ringach et al., 1997). A common approach to this problem
is to estimate the linear receptive field (RF), which provides a simple char-
acterization of a neuron’s stimulus-response properties. The RF consists of
a set of linear weights that describe how a neuron integrates a sensory stim-
ulus over space and time (Chichilnisky, 2001; deBoer & Kuyper, 1968; Jones
& Palmer, 1987; Lee & Schetzen, 1965; Meyer et al., 2017; Ringach, 2004;
Schwartz et al., 2006; Sharpee et al., 2004; Simoncelli et al., 2004; Theunis-
sen et al., 2001). Estimating the RF from imaging or electrophysiological
recordings can thus be seen as a straightforward regression problem. How-
ever, characterizing RFs in realistic settings poses a number of important
challenges.
One major challenge for RF estimation is the high dimensionality of the
inference problem. The number of RF coefficients is equal to the product
of the number of spatial stimulus elements (per esempio., pixels in an image) E
number of time lags in the temporal filter. In realistic settings, this can
easily surpass thousands of coefficients. Classic RF estimators such as
the least-squares regression suffer from high computational cost and low
statistical power in high-dimensional settings. The computational cost of
the regression estimate scales cubically with the number of RF coefficients,
while memory cost scales quadratically. Inoltre, the standard regression
estimate does not exist unless there are more samples than dimensions
and typically requires large amounts of data to achieve a high level of
accuracy. High dimensionality is thus a limiting factor in terms of both
computational resources and statistical power.
Past efforts to improve statistical power, and thereby reduce data re-
quirements, have relied on various forms of regularization. Regularization
reduces the number of degrees of freedom in the RF by biasing the estima-
tor toward solutions that are more likely a priori and can thus provide for
better estimates from less data. Common forms of regularization involve
smoothness or sparsity assumptions and have been shown to outperform
maximum likelihood (ML) estimation in settings of limited data or corre-
lated stimuli (Aoi & Pillow, 2017; Calabrese et al., 2011; David & Gallant,
2005; Gerwinn et al., 2010; Linden et al., 2003; Park & Pillow, 2011; Smyth
et al., 2003). Tuttavia, the computational cost of such estimators is gener-
ally no better than that of classical estimators, and may be worse due to the
need to optimize hyperparameters governing the strength of regularization.
These poor scaling properties make it difficult to apply such estimators to
settings involving high-dimensional stimulus ensembles.
In questo articolo, we propose to overcome these difficulties using a model
that parameterizes the RF as smooth and low rank. A low-rank recep-
tive field can be described as a sum of a small number of space-time
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
997
separable filters (Linden et al., 2003; Park & Pillow, 2013; Pillow et al., 2008;
Pillow & Simoncelli, 2006; Qiu et al., 2003). This choice of parameteriza-
tion significantly reduces the number of parameters in the model and is the
key to the scalability of our method. To achieve smoothness, we use gaus-
sian process (GP) priors over both the spatial and temporal filters compos-
ing the low-rank RF. For the temporal filters, we introduce the temporal
relevance determination (TRD) prior, which uses a novel covariance func-
tion that allows for increasing smoothness as a function of time lag. To fit
the model, we develop a scalable algorithm for variational Bayesian infer-
ence for both receptive field components and hyperparameters governing
shrinkage and smoothness. The resulting estimator achieves excellent per-
formance in settings with correlated stimuli and scales to high-dimensional
settings in which full-rank estimators are intractable.
The article is organized as follows. Sezioni 2 E 3 review relevant back-
ground and the literature: section 2 introduces the linear encoding model
and low-rank linear receptive fields; section 3 reviews previously proposed
priors for receptive fields. In section 4, we introduce TRD, a new prior for
temporal receptive fields, while in section 5 we introduce our variational
low-rank (VLR) receptive field estimator. Sezione 6 shows applications to
simulated as well as real neural data sets, and section 7 provides discussion
of our results and suggests directions for future work.
2 The Linear-Gaussian Encoding Model
A classic approach to neural encoding is to formulate a parameteric statis-
tical model that describes the mapping from stimulus input to neural re-
sponse (Efron & Morris, 1973; James & Stein, 1961; Jones & Palmer, 1987;
Park & Pillow, 2011; Ringach et al., 1997). Here we focus on linear models,
where the neural response is described as a linear or affine function of the
stimulus plus gaussian noise (Park & Pillow, 2011; Sahani & Linden, 2003)
(Guarda la figura 1). Formalmente, the model can be written as
yt = k
(cid:2)
xt + B + (cid:2)T,
(cid:2)t ∼ N (0, P 2),
(2.1)
where yt is the neuron’s scalar response at the tth time bin, k is the vector re-
ceptive field, xt is the vectorized stimulus at the tth time bin, b is an additive
constant or bias, E (cid:2)t denotes zero-mean gaussian noise with variance σ 2.
2.1 The Receptive Field Tensor. This model description neglects the
fact that the stimulus and receptive field are often more naturally described
as multidimensional tensors. In vision experiments, Per esempio, the stim-
ulus and receptive field are typically third-order tensors, with two dimen-
sions of space and one dimension of time. In questo caso, the full stimulus
movie shown during an entire experiment can be represented by a tensor
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
998
l. Duncker, K. Ruda, G. Field, and J. Pillow
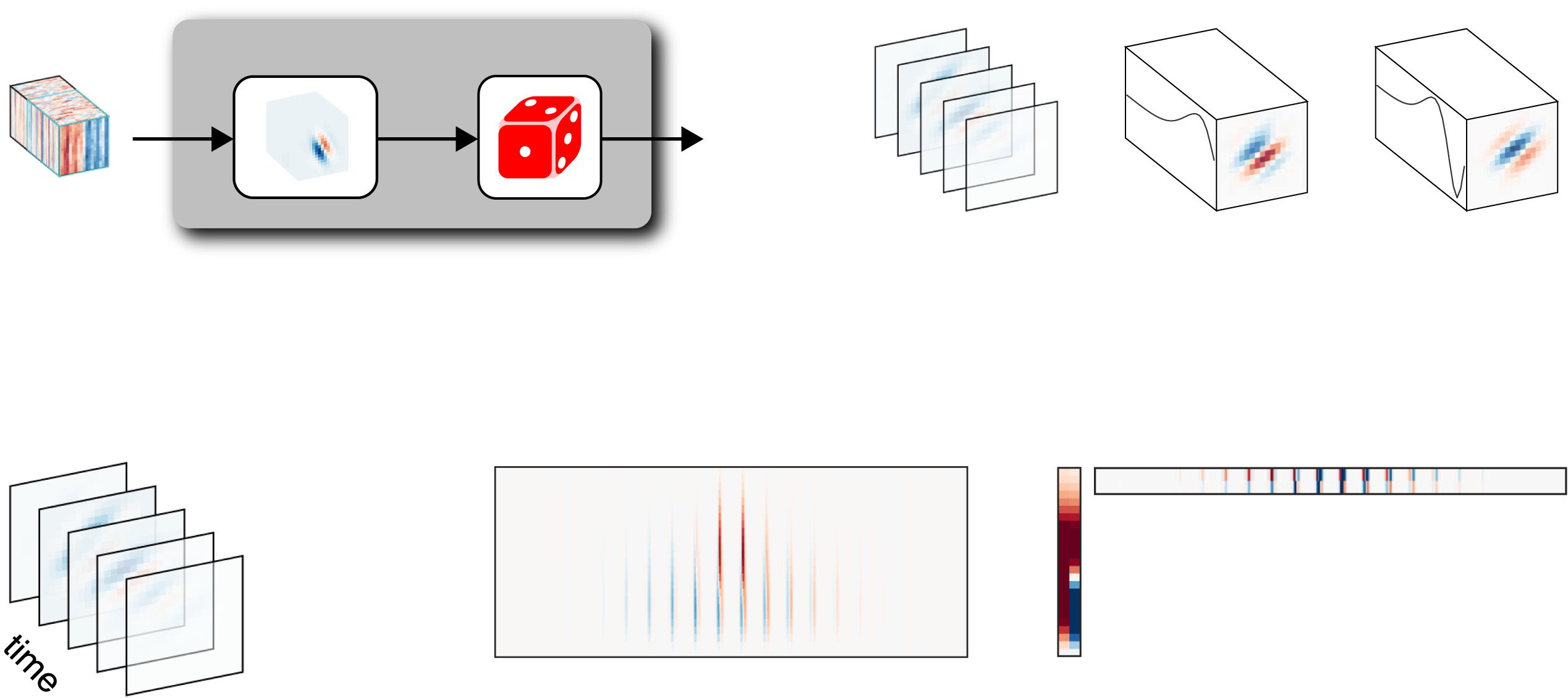
Figura 1: (UN) The linear-gaussian encoding model is a two-stage model consist-
ing of a linear stage followed by a noise stage. Primo, the high-dimensional spa-
tiotemporal stimulus is filtered with the linear receptive field, which describes
how the neuron integrates the stimulus values over space and time. The output
of this filter is a scalar that gives the expected response at a single time bin. Noi
then add noise to obtain the neural response for the given time bin. (B) A low-
rank spatiotemporal receptive field can be described as a sum of two space-time-
separable (rank 1) filters. (C, D) Illustration of different STRF representations as
a third order tensor (C), matrix (D), or in terms of low-rank factors (E).
× nx2
× T, consisting of nx1
× nx2 pixel images over T total time
of size nx1
bins or frames. In questo caso, a given element Xi, j,t in the stimulus tensor could
represent the light intensity in a gray-scale image at time t at spatial location
(io, j) in the image.
×nx2
In such settings, the spatiotemporal receptive field is also naturally de-
×nt , with weights that determine how the neu-
fined as a tensor, K ∈ Rnx1
× nx2 spatial pixels and the nt preceding
ron integrates light over the nx1
time bins (see Figure 1C). Così, the dot product between the receptive field
k and vector stimulus xt in equation 2.1 is equal to the following linear func-
tion defined by summing over the product of all corresponding elements
of the RF tensor K and corresponding portion of the stimulus tensor X at
time t,
(cid:2)
k
xt =
nx1(cid:2)
nx2(cid:2)
nt −1(cid:2)
i=1
j=1
τ =0
Ki, j,τ Xi, j,t−τ ,
(2.2)
× nt. The vectorized RF
where K and Xt are both tensors of size nx1
and stimulus are thus given by k = vec(K), and xt = vec(Xi, j,t−τ ) for i ∈
{1, . . . , nx1
} and τ ∈ {1, . . . , nt}.
}, j ∈ {1, . . . , nx2
× nx2
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
999
2.2 Low-Rank Receptive Fields. A key feature of neural receptive fields
is that they can typically be described by a relatively small number of spa-
tial and temporal components (Adelson & Bergen, 1985; Linden et al., 2003;
Park & Pillow, 2013; Pillow et al., 2008; Pillow & Simoncelli, 2006; Qiu et al.,
× nt in-
2003). This means that we do not need to use a full set of nx1
dependent parameters to represent the coefficients in K. Invece, we can
accurately describe K with a small number of spatial components, each
× nx2 coefficients, and a correspond-
corresponding to an image with nx1
ing number of temporal components, each with nt coefficients. The number
of paired spatial and temporal components needed to represent K is known
as the rank of the tensor, which we denote r.
× nx2
Figure 1B illustrates a scenario with r = 2, in which the tensor K is the
sum of two rank 1 components, each defined as a single spatial and tempo-
ral weighting function. These rank 1 components are commonly referred
to as ”space-time separable” filters. Note that a rank r tensor has only
+ nt ) parameters, which generally represents a significant savings
R(nx1 nx2
over the (nx1 nx2 nt ) parameters needed to parameterize the full-rank tensor.
Inoltre, having an explicit description of the temporal and spatial fil-
ters composing K increases the interpretability of the RF.
For modeling low-rank filters of this form, it is convenient to unfold the
third-order receptive field tensor K into a matrix. Let K ∈ Rnt ×(nx1
· nx2 ) denote
the matrix unfolding of the receptive field, where the two spatial dimen-
sions have been concatenated (see Figures 1C and 1D). This representation
makes it possible to represent low-rank receptive fields with a product of
matrices,
K = KtKx,
(2.3)
where Kt ∈ Rnt ×r is a matrix whose columns are temporal filters and Kx ∈
×r is a matrix whose columns are (reshaped) spatial filters (see Fig-
R(nx1 nn2 )
ure 1E). In section 5, we will develop a Bayesian hierarchical model for ef-
ficient estimation of low-rank receptive fields using this parameterization.
3 Existing Receptive Field Priors
In high-dimensional settings, or settings with highly correlated stimuli, re-
ceptive field estimation can be substantially improved by regularization.
Here we review previously proposed prior distributions for regularizing re-
ceptive field estimates. The general family of priors that we consider takes
the form of a zero-mean multivariate gaussian distribution,
k ∼ N (0, Cθ ) ,
(3.1)
where Cθ denotes a covariance matrix that depends on a set of hyperpa-
rameters θ . Different choices of prior arise by selecting different functional
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1000
l. Duncker, K. Ruda, G. Field, and J. Pillow
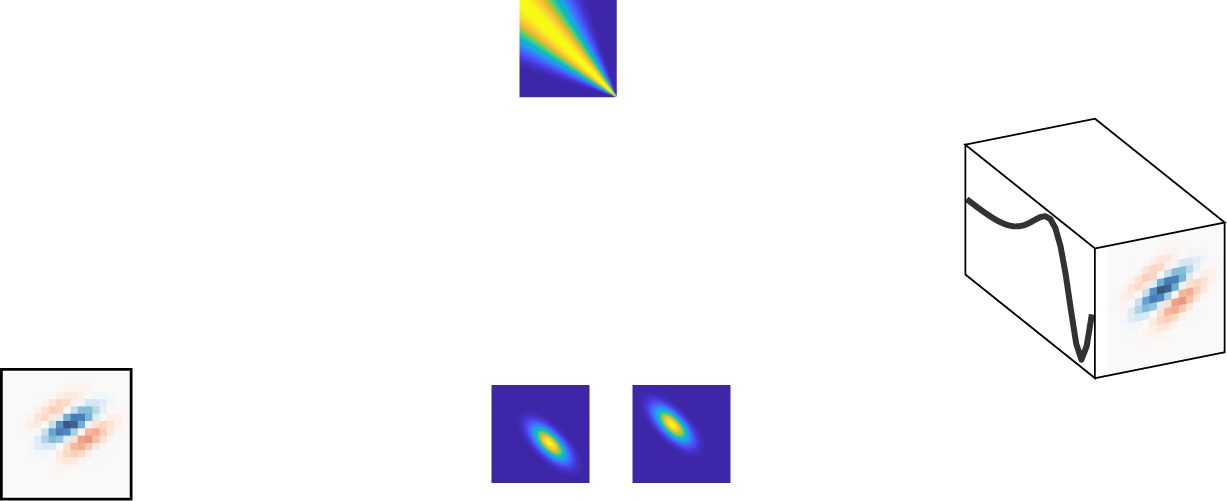
Figura 2: Illustration of different priors for use in receptive field estimation.
(Top) Prior covariance matrices Cθ under different choices of covariance func-
zione. Under the ridge prior, all off-diagonal elements of the covariance ma-
trix are zero, and receptive field coefficients are independent. In the ASD prior
covariance, neighboring coefficients are highly correlated, and the correlation
decreases with increasing distance between coefficient locations in the RF. IL
ALD prior covariance contains high correlations for neighboring coefficients
within a local region and sets the prior covariance of the RF coefficient to zero
outside of this local region, a form of structured sparsity. Finalmente, in the TRD
covariance matrix, the correlation of neighboring RF coefficients increases as
a function of the coefficient location. (Bottom) Four samples from a multivari-
ate gaussian distribution with zero mean and covariance matrix shown above,
illustrating the kinds of receptive fields that are typical under each choice of
prior.
forms for the covariance matrix Cθ . We will review several popular choices
of covariance (Guarda la figura 2) before introducing a novel prior covariance in
section 4.
3.1 Ridge Prior. Ridge regression (Hoerl & Kennard, 1970) is classically
viewed as an added L2 norm penalty on the receptive field weights in the
context of least-squares regression. Tuttavia, it also has a Bayesian interpre-
tation as resulting from a zero-mean gaussian prior with covariance given
by,
Cridge
θ
= 1
λ I,
(3.2)
where the hyperparameter θ = {λ} is known as the ridge parameter and I
denotes the identity matrix. This prior has the effect of biasing the estimate
toward zero, a phenomenon also known as L2 shrinkage.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1001
3.2 Automatic Smoothness Determination. The automatic smoothness
determination (ASD) prior (Sahani & Linden, 2003) goes beyond shrinkage
to incorporate the assumption that the receptive field changes smoothly in
time and/or space. The ASD prior covariance matrix relies on the radial
basis function (RBF) or “gaussian” covariance function that is well known
in the gaussian process literature (Rasmussen & Williams, 2006). IL (io, j)th
element of this covariance matrix is given by
(cid:3)
(cid:4)
[CASD
θ
]i j
= ρ exp
(χ
io
− χ
(cid:2)(cid:9)−1(χ
j )
io
− χ
j )
,
(3.3)
− 1
2
} is a 3D vector containing the locations of RF pixels in space-
Dove {χ
io
time, thus indicating both the 2D spatial locations of the RF coefficients and
the 1D temporal locations (or lags). E (cid:9) = diag((cid:10)S
, (cid:10)T ) is a diagonal
1
matrix containing length-scale parameters. The covariance matrix is thus
controlled by four hyperparameters: θ = {ρ, (cid:10)S
, (cid:10)T}. ρ is the marginal
1
variance (and equivalent to 1/λ in the ridge prior above), and the length-
scale parameters (cid:10)S
1,2 E (cid:10)t determine the degree of smoothness in space
and time, rispettivamente. Recent work has exploited the Kronecker and
Toeplitz structure of the ASD covariance matrix to show that it has an exact
diagonal representation in the Fourier domain, which allows for dramatic
improvements in computational efficiency (Aoi & Pillow, 2017).
, (cid:10)S
2
, (cid:10)S
2
3.3 Automatic Locality Determination. The automatic locality deter-
mination (ALD) prior (Park & Pillow, 2011) goes beyond the smoothness of
the ASD prior by encouraging RF coefficients to be localized in space-time
and spatiotemporal frequency.
It relies on a covariance function that encourages both the space-time
coefficients and the spatiotemporal frequency components of the RF to be
zero outside of some localized region, resulting in a form of structured spar-
sity (Wu et al., 2014). This prior includes the ASD smoothness prior as a
special case, namely, when the region of nonzero spatiotemporal frequency
components is centered at zero, and there is no locality in space or time.
Tuttavia, the ALD prior also allows for bandpass filters in which the RF is
composed primarily of intermediate frequencies.
The ALD covariance matrix can be written in terms of a pair of diagonal
matrices and a discrete Fourier transform matrix,
CALD
θ
= ρ Cs
θ
(cid:2)
1
2 B
Cf
θ BCs
θ
1
2 ,
(3.4)
θ and C f
where Cs
θ are diagonal matrices that specify a region of nonzero
coefficients in space-time and the Fourier domain, rispettivamente, and B is the
discrete-time Fourier transform matrix.
The space-time locality matrix is a diagonal matrix with diagonal ele-
ments given by
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1002
l. Duncker, K. Ruda, G. Field, and J. Pillow
[Cs
θ ]ii
= exp
(cid:3)
− 1
2
(χ
io
− m)
(cid:2)(cid:11) −1(χ
io
− m)
,
(cid:4)
(3.5)
} are the locations of RF pixels in space-time, and m and (cid:11) Di-
Dove {χ
io
note the mean and covariance of the region where the RF coefficients are
nonzero. The Fourier-domain locality matrix takes a similar form,
[C f
θ ]ii
= exp
(cid:3)
− 1
2
( ˜χ
io
− ˜m)
(cid:2) ˜(cid:11) −1( ˜χ
io
− m)
,
(cid:4)
(3.6)
} are the spatiotemporal frequencies for each Fourier coefficient,
Dove { ˜χ
io
and ˜m and ˜(cid:11) denote the mean and covariance of the region in Fourier space
where RF Fourier coefficients are nonzero. The hyperparameters govern-
ing the ALD prior are thus θ = {ρ, M, ˜m, (cid:11), ˜(cid:11)}. As before, ρ governs the
marginal variance of the RF coefficients, analogous to the ridge parameter.
For a 3D tensor receptive field, m and ˜m are both 3-vectors, E (cid:11) and ˜(cid:11)
are both 3 × 3 positive semidefinite covariance matrices.
The full ALD covariance matrix (see equation 3.4), which multiplies to-
θ and C f
gether the diagonal matrices Cs
θ with a discrete Fourier domain
operator in between, has the effect of simultaneously imposing locality in
both space-time and frequency. It is identical to ASD under the setting that
θ = I, ˜m = 0, and ˜(cid:11) is diagonal (Aoi & Pillow, 2017). Empirically, ALD has
Cs
been shown to outperform both the ridge and ASD priors, as well as other
sparsity-inducing priors, in applications to neural data in the early visual
system (Park & Pillow, 2011).
4 A New Prior for Temporal Receptive Fields
Our first contribution is to propose a new prior for temporal receptive fields.
The priors in ASD and ALD both assume a constant degree of smoothness
across the receptive field. Tuttavia, an assumption of stationary smooth-
ness is less appropriate for temporal receptive fields, which are typically
sharper at short time lags and smoother at longer time lags. In order to
incorporate this variable form of smoothness, we introduce the temporal
recency determination (TRD) prior. This prior uses a smoothing covariance
function that is stationary in log-scaled time and is therefore nonstationary
in linear time.
The TRD covariance function can be described as a time-warped version
of the ASD covariance. Specifically, IL (io, j)th element of the prior covari-
ance is given by
[CTRD
θ
]i j
= ρ exp
(cid:3)
− 1
2(cid:10)2
(cid:4)
(cid:5)τα (ti) − τα (t j )(cid:5)2
.
(4.1)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1003
As was the case for the ASD covariance function, ρ describes the marginal
variance of the RF prior and (cid:10) is a length-scale parameter determining the
smoothness of the RF. Additionally, τα (T) is a nonlinear warping function
given by
τα (T) =
T
log(1 + esp(α) ∗ T )
log(1 + esp(α)T).
(4.2)
Here, T is the length of the temporal RF (in seconds), ti is the time lag for
temporal RF coefficient i, and α is a parameter determining how quickly the
RF smoothness increases with time. In summary, the TDR covariance func-
tion is determined through a set of three hyperparameters, θ = {ρ, (cid:10), α} E
can incorporate the prior structure that temporal receptive fields become
smoother for increasing time lags. Figura 2 shows an illustration of the TRD
prior, alongside the other RF priors discussed in section 3.
5 A Probabilistic Model for Low-Rank Receptive Fields
Our second contribution is a model and inference method for smooth, low-
rank receptive field fields. As noted in section 2.2, a low-rank parameteri-
zation for spatiotemporal receptive fields can offer a dramatic reduction in
dimensionality without loss of accuracy. In particular, a rank r spatiotempo-
ral filter requires only r · (nx1
· nt
for a full-rank filter.
+ nt ) coefficients versus N = nx1
· nx2
· nx2
To place our model on a solid probabilistic footing, we place indepen-
dent zero-mean gaussian priors over the r temporal (1D) and r spatial (2D)
components of the receptive field (see Figure 3A). If we use a TRD prior
for the temporal components and an ALD prior for the spatial components,
then the prior over the ith spatial and temporal receptive field components
can be written as
kt i
∼ N (0, CTRD
θt
),
kxi
∼ N (0, CALD
θx
),
(5.1)
(5.2)
θt
θx
where CTRD
denotes the TRD covariance (see equation 4.1), CALD
is the ALD
covariance (see equation 3.4), which we apply here to a 2D spatial receptive
field. Although we selected these covariance functions because of their suit-
ability for the structure of neural receptive fields, our modeling framework
is general and could easily accommodate other choices.
(cid:2) + · · · + kt rkxr
Under this modeling choice,
=
kt 1kx1
represents the product of two gaussian random
variables. This effective prior over K is thus non gaussian. This entails
that posterior inference is not analytically tractable due to the fact that the
prior is not conjugate to the gaussian likelihood of the encoding model (Vedere
the full receptive field K = KtK(cid:2)
(cid:2)
X
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1004
l. Duncker, K. Ruda, G. Field, and J. Pillow
Figura 3: Graphical model representation of the low-rank STRF model. (UN) Noi
combine a multivariate normal temporal relevance determination (TRD) prior
over temporal components (above) and a matrix normal prior over spatial com-
ponents (below), where row and column covariances have an automatic local-
ity determination (ALD) parameterization, to obtain a prior over each rank-1
component or space-time separable filter making up a low-rank filter. (B) IL
graphical model for the full model can be represented in terms of linear trans-
formations Bt
θx , which parameterize the transformation from whitened
θ
temporal and spatial receptive fields wt and wx, which are combined to form
t and θ
the STRF k. The linear transformations depend on hyperparameters θ
X.
The spatial and temporal components are combined to form a low-rank STRF
k, which acts to integrate a stimulus xτ over space and time to generate a neural
response yτ , with constant offset b.
t and Bx
equation 2.1). We therefore develop a scalable variational inference algo-
rithm for setting the hyperparameters θ governing the prior covariance
matrices and inferring the receptive field coefficients Kx and Kt, which we
describe in sections 5.1 E 5.2. We introduce additional modeling choices
that facilitate scalable estimation through a further reduction in the total
number of receptive field coefficients in section 5.1 and describe the result-
ing algorithm in detail in section 5.2.
5.1 Scalability via Sparse Spectral Representations of Covariance Ma-
trices. Performing inference in the model we have already introduced still
requires building and inverting large covariance matrices. To reduce the di-
mensionality of the spatial and temporal receptive field inference further
and to achieve scalability to high-dimensional settings, we make use of
sparse spectral representations of the prior covariance matrices.
This sparse spectral representation involves expressing the prior covari-
ance of k as Cθ ≈ Bθ B(cid:2)
θ . When Bθ contains the eigenvectors of Cθ , scaled
by their square-rooted associated eigenvalues, then this approximation is
exact. Tuttavia, we might be able to incur only a small approximation er-
ror by retaining only the leading eigenvectors of Cθ in Bθ . Per esempio, for
larger length-scale parameters (high degree of smoothness), the covariance
matrix associated with the ASD covariance function has eigenvalues that
quickly decay toward zero (Rasmussen & Williams, 2006). By truncating its
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1005
eigenvalues near zero, it is possible to find a low-rank approximation to the
covariance matrix Cθ that is exact to machine precision. For all choices of
prior covariance matrices we discussed in section 3, it is possible to obtain
an analytic expression for Bθ (Aoi & Pillow, 2017).
Given Bθ , we can express the prior distribution over the receptive field
in terms of a linear transformation of a multivariate standard normal, O
“whitened” random variable: k = Bθ w, with w ∼ N (0, IO). The resulting
prior covariance of k is equal to Cθ = Bθ B(cid:2)
θ and thus unchanged from before.
Tuttavia, performing inference over w instead of k allows us to circumvent
costly inversions of Cθ . Inoltre, if Cθ is represented to sufficient accu-
racy using fewer dimensions in Bθ , then w will contain fewer dimensions
than k, leading to additional improvements in scalability.
To incorporate low-rank receptive field structure into this approach, we
define our model in the transformed, “whitened” space. The receptive field
priors are described by multivariate standard normal distributions over the
whitened temporal receptive field wt and whitened spatial receptive field
wx:
wt ∼ N (0, Ipt ·r),
wx ∼ N (0, Ipx·r),
(5.3)
(5.4)
where wt and wx are vectors containing the concatenated temporal and spa-
tial components, rispettivamente, and are of dimensions pt · r and px · r, Dove
px,t depend on the number of dimensions needed to approximate the re-
spective covariance matrices to sufficient accuracy and r corresponds to the
STRF rank. We define the matrix reshaping of these vectors as
wt = vec(Wt ), wx = vec(Wx
(cid:2)
),
(5.5)
where Wt ∈ Rpt ×r and Wx ∈ Rpx×r. The full STRF can then be represented as
k = vec(Bt
θtWtWx
(cid:2)
θx ),
Bx
(5.6)
where the analytic decompositions of the prior covariances are denoted as
(cid:2) for the temporal and the spatial receptive
(cid:2) and Cx
θ = Bt
Ct
θt
field prior covariances, rispettivamente.
θ = Bx
θx
Bx
θx
Bt
θt
Given this representation of the STRF, the rest of the model remains
unchanged. This model description is illustrated as a graphical model in
Figure 3B.
5.2 Variational Inference and Hyperparameter Learning for Low-
Rank STRFs (VLR). Fitting our low-rank model to data involves perform-
ing posterior inference over the receptive field components wx and wt
and learning the hyperparameters θ that determine the shape of the basis
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1006
l. Duncker, K. Ruda, G. Field, and J. Pillow
functions in Bθ . To do this, we derive a variational optimization framework,
similar to the classic empirical Bayes approach reviewed in appendix A.2.
We rely on a variational approach here, since the effective non gaussian
prior over k makes obtaining an exact expression for the marginal log-
likelihood intractable.
A lower bound to the marginal log-likelihood can be obtained by apply-
ing Jensen’s inequality,
(cid:5)
log P(Y|(cid:13), θ ) = log
P(Y, peso, wx|(cid:13), θ )dwtdwx
(5.7)
(cid:5)
≥
q(peso, wx) log
P(Y, peso, wx|(cid:13), θ )
q(peso, wx)
dwtdwx
def= F (q, θ ),
(5.8)
where q(peso, wx) is a distribution over the whitened temporal and spatial
receptive field parameters wt and wx. F (q, θ ) is often called the variational
“free energy” or “evidence lower bound” (ELBO). Y denotes the recorded
neural responses, while (cid:13) is the stimulus design matrix (see appendix A.1
for details).
Instead of computing and optimizing the model evidence directly, we
can instead perform coordinate ascent and alternatingly maximize F with
respect to the distribution q(peso, wx) and with respect to the parameters θ
as part of the expectation maximization (EM) (Dempster et al., 1977) al-
gorithm. The optimization over q(peso, wx) can either be performed exactly
(which amounts to setting q equal to the posterior joint distribution over
wt and wx) or under additional constraints on q, such as restricting it to a
particular family of variational distribution.
The free energy can be written in two equivalent ways:
F (q(peso, wx), θ ) = log P(Y|(cid:13), θ ) − KL[q(peso, wx)(cid:5)P(peso, wx|Y, (cid:13), θ )],
F (q(peso, wx), θ ) = (cid:9)log P(Y, peso, wx|(cid:13), θ )(cid:10)
+ H[q(peso, wx)],
q(peso ,wx )
(5.9)
(5.10)
where H[q] is the entropy of q. The EM algorithm involves iteratively max-
imizing this lower bound with respect to a distribution over wt and wx
(E-step) and with respect to the hyperparameters θ (M-step). From equa-
zione 5.9, it is apparent that the free energy is maximized when q(peso, wx) È
equal to the posterior distribution,
P(peso, wx|Y, (cid:13), θ ) = P(Y, peso, wx|(cid:13), θ )
P(Y|(cid:13), θ )
,
(5.11)
at which the Kullback-Leibler divergence in equation 5.9 vanishes and the
free energy provides a tight lower bound to the marginal log-likelihood.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1007
Performing this computation exactly is intractable in our model. We there-
fore choose a variational approximation of the form
q(peso, wx) = q(peso )q(wx),
(5.12)
where we assume that the approximate posterior distribution factorizes
over the spatial and temporal receptive field. We now seek to find the dis-
tribution q(peso, wx) that lies within the family of distributions that factorize
over wt and wx and maximizes the free energy. Taking variational deriva-
tives of the free energy, the variational updates for our approximating dis-
tributions are found to be of the general form
q(peso ) ∝ exp(cid:9)log P(Y, peso, wx|(cid:13), θ )(cid:10)
q(wx) ∝ exp(cid:9)log P(Y, peso, wx|(cid:13), θ )(cid:10)
,
q(wx )
,
q(peso )
(5.13)
(5.14)
where angled brackets denote expectations. Evaluating the above in our
modello, we obtain multivariate gaussian distributions of the form q(peso ) =
N (peso|μt, (cid:14)T ) and q(wx) = N (wx|μx, (cid:14)X). The variational updates for the
posterior means μt, μx, and covariances (cid:14)T, (cid:14)x are available in closed
form. Detailed derivations and the exact update equations are given in
appendix B.
The M-step in our variational EM algorithm involves maximizing the
free energy with respect to the model parameters b, σ and hyperparameters
θ = {θt, θx} and requires solving
θ ∗, B
∗, σ ∗ ← arg max(cid:9)log P(Y, peso, wx|(cid:13), θ )(cid:10)
q(peso ,wx )
(5.15)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
using gradient-based optimization. We update the hyperparameters in Bt
θt
, and the model parameters b and σ in separate conditional M-steps.
and Bx
θx
Performing conditional M-steps allows one to project the high-dimensional
stimulus onto either the temporal or spatial basis and never requires build-
ing or inverting the full stimulus design matrix (cid:13). Così, this strategy fur-
ther exploits the lower-dimensional decomposition of the full receptive
field and provides an efficient algorithm, even for high-dimensional data.
Further details are provided in appendix C.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
6 Results
6.1 Data Efficient Estimation under Correlated Stimulus Distribu-
zioni. We first tested the VLR estimator using synthetic data. We simulated
data from a linear-gaussian encoding model with a rank-2 receptive field
that was stimulated with correlated stimuli.
1008
l. Duncker, K. Ruda, G. Field, and J. Pillow
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
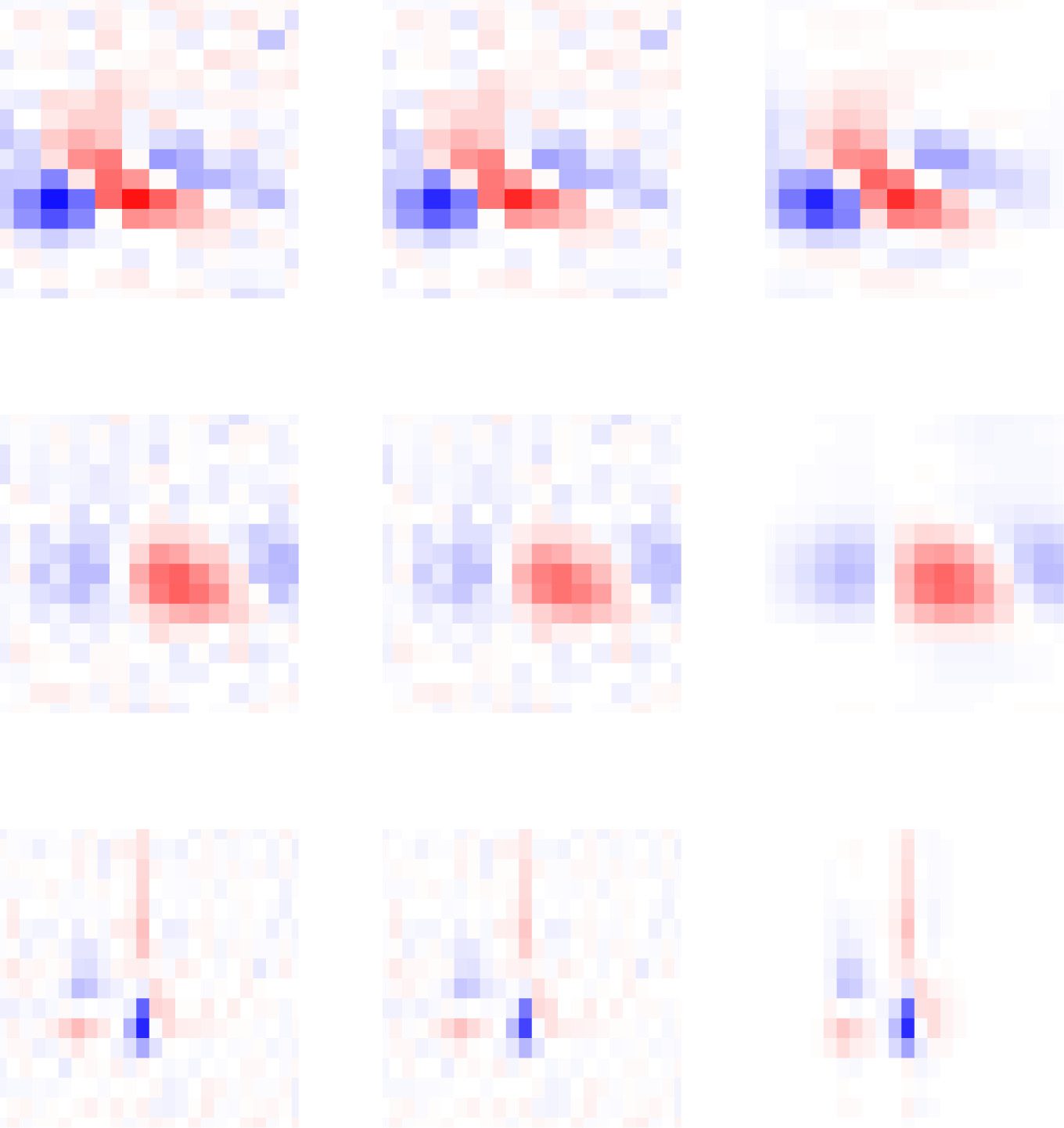
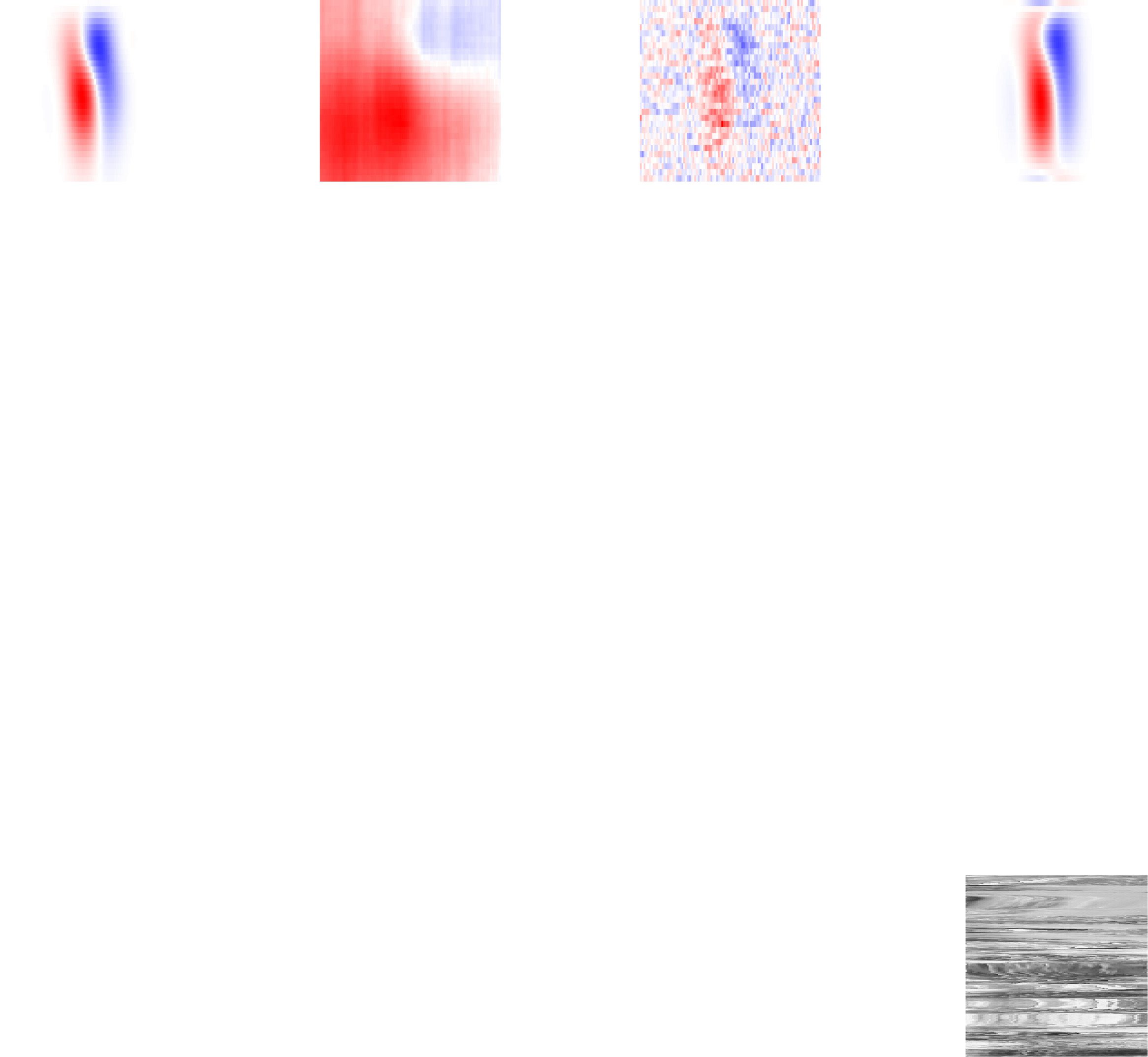
Figura 4: Synthetic data example. (UN) True STRF used for generating synthetic
responses and recovered estimates using STA, RR, and VLR (rank 2), with ALD
priors for the 2D spatial and the TRD prior for the temporal components. Shown
estimates are obtained using 1e4 training samples. (B, C) The top two spatial (B)
and temporal (C) components of the true and recovered STRF estimates. Dashed
lines show components of the true STRF for reference. For STA and RR, spatial
and temporal STRF components were obtained by taking the leading left and
right singular vectors of the STRF in matrix form and rescaling by the size of the
true STRF. (D) Correlation between the true and estimated STRF for different
numbers of STRF coefficients and amounts of training data. Lines represent the
average correlation across 20 repeated simulations with different random seeds;
shaded regions represent ± 1 standard error.
Figura 4 shows results under exponentially filtered gaussian stimuli. A
assess performance, we computed the STRF estimates using different num-
bers of receptive field coefficients and different amounts of simulated train-
ing data. We compared VLR to the classic spike-triggered average (STA)
and Bayesian ridge regression (RR). Figure 4A and 4B show that the STA
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1009
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 5: Application to V1 simple cells (UN, D, G) Example STRF estimates us-
ing MLE, RR, and our VLR approach. Shown estimates are obtained using 5
minutes of training data. (B, E, H) Mean squared error on 10 minutes of held-
out test data using different ranks and amounts of training data for the VLR
approach. (C, F, IO) Mean squared error on 10 minutes of held-out test data when
using different amounts of training data for MLE, RR, and an example rank for
VLR.
estimate suffers from severe bias due to the correlated stimulus distribution.
The RR estimate provides an improvement in terms of the bias but exhibits
a high level of variability. Our proposed VLR estimator, in contrast, yields
accurate estimates under correlated stimulus distributions, even when us-
ing only small amounts of training data. We obtained similar results using
stimuli extracted from natural movies (see Figure D.1).
6.2 Application to Macaque V1 Simple Cells. Prossimo, we examined
recordings from V1 simple cells in response to random binary “bar” stim-
uli, previously published in Rust et al. (2005). The stimulus contained 12
A 24 1D spatial bars on each frame that were aligned with each cell’s pre-
ferred orientation. We used 16 time bins (160 ms) of stimulus history to de-
fine the temporal receptive field, so the entire STRF had between 12 × 16
E 24 × 16 total coefficients. We examined the performance of the estima-
tor for different ranks and different amounts of training data, and evalu-
ated the mean squared error on held-out test data. For comparison, we also
computed the RR estimate and the maximum likelihood estimate (MLE),
which in this setting corresponds to the ordinary least squares regression
estimate (Guarda la figura 5). We found that VLR outperformed the MLE and RR
1010
l. Duncker, K. Ruda, G. Field, and J. Pillow
estimators, achieving lower prediction errors on held-out test data under
varying amounts of training data (see Figures 5C, 5F, and 5I). These results
illustrate the heterogeneity of STRF ranks in the V1 simple cell population,
as the three example STRFs shown in Figures 5A, 5D, and 5G achieved min-
imal prediction error for different choices of STRF rank (see Figures 5B, 5E,
and 5H).
6.3 Application to Rat Retinal Ganglion Cells. Previous work has
identified multiple cell types of retinal ganglion cells (RGCs; Baden et al.,
2016). Functional cell-type distinctions are usually based on receptive field
properties such as ON/OFF regions, temporal filtering properties, or other
structures that can be extracted from STRFs (Chichilnisky & Kalmar, 2002;
Field et al., 2007; Frechette et al., 2005). Other differences in response prop-
erties, such as STRF rank, may prove valuable for further distinguishing
functional cell types.
To further illustrate the power of the VLR estimator, we examined a data
set consisting of electrophysiological recordings from rat RGCs in response
to binary white noise stimuli. We selected a region of 25 × 25 pixels in space
based on the center of the RF (as estimated by the STA) from the 80 × 40
overall stimulus, and we considered 30 time lags (0.5 seconds) of stimu-
lus history. This yielded a total of N = 18,750 STRF coefficients. Standard
regression estimators like the MLE require large amounts of training data
for STRFs of this size. Bayesian estimators like ASD and ALD are compu-
tationally intractable in high-dimensional settings due to the need to store
and invert matrices of size N2. Così, we compare the VLR estimator with
the STA, which can readily be computed even for large STRF sizes such as
those considered here.
Figura 6 shows the performance of STA and VLR for different receptive
field ranks. VLR achieved lower prediction errors on held-out test data,
even when using only small amounts of training data. Figure 6A shows that
VLR outperformed the STA estimate computed on 83 minutes of training
data using as little as 4.2 minutes of training data and under all assumed
STRF ranks (see Figure 6B). Comparing the STA and VLR estimates in the
top panels of Figures 6D and 6E, VLR managed to more successfully extract
signal from the data and reduce speckle noise in the estimate. The temporal
and spatial components of the STRF can be extracted as the leading left
and right singular vectors of the matrix unfolding of the STRF tensor, each
weighted by the square root of the associated singular value. The STA esti-
mate was dominated by noise and provided much poorer estimates of the
spatial and temporal components of the STRF, as demonstrated in the bot-
tom panels of Figures 6D and 6E. The second spatial component of the STA
estimate is dominated almost exclusively by speckle noise (see Figure 6D,
lower left), while it is structured in the VLR estimate (see Figure 6E, inferiore
left). The rank of the receptive field indicates how many rank-1 space-time
components are required to reconstruct the STRF. The singular values of the
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1011
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
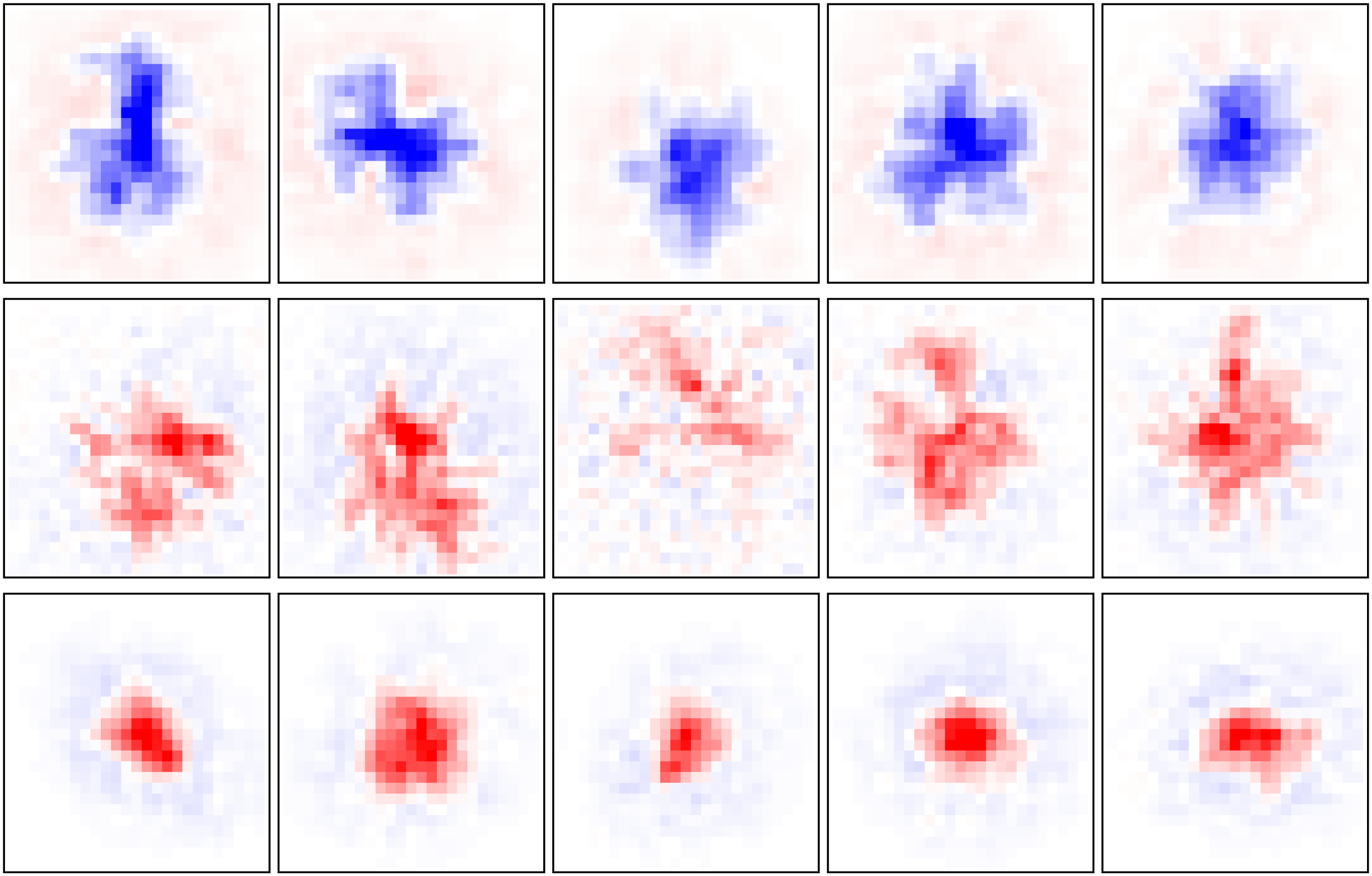
Figura 6: Application to rat retinal ganglion cell (RGC) responses. (UN) Mean
squared error on 27.66 minutes of held-out test data using different ranks and
amounts of training data. Dashed gray line indicates prediction error of the STA
using the maximum amount of training data. (B) Same as panel A but plotting
the prediction error against ranks for the VLR approach. (C) The top singular
values computed on the STRF estimate using STA or the VLR approach under
different assumed ranks and using the maximum amount (83 minutes) of train-
ing data. (D) STRF estimate computed using STA on 13.83 minutes of training
data together with the top two spatial and top four temporal components, Di-
termined as the leading left and right singular vectors of the STRF, scaled by the
square root of the corresponding singular value. (E) Same as panel D but using
the VLR approach with an assumed rank of 4.
STRF indicate the associated weight of each rank-1 space-time component
in this reconstruction. As the assumed rank of the VLR estimate grows,
our model has the capacity to fit more complex structures in the STRF.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1012
l. Duncker, K. Ruda, G. Field, and J. Pillow
Figure 6C shows the singular values of the STA and and VLR STRF esti-
mates under different assumed ranks. As the assumed rank of the VLR
estimate grows, the associated singular values decay to zero. This demon-
strates that the VLR estimator is able to successfully prune out space-time
components that do not reflect signal in the training data and thus prevent
overfitting to noise. This feature can be attributed to the non gaussian
prior distribution over the effective STRF weights of our model and is a
favorable regularization property. Di conseguenza, the prediction error plateaus
after a sufficient rank has been reached, demonstrating that even estimates
obtained under a higher assumed rank generalize well to unseen data (Vedere
Figure 6B).
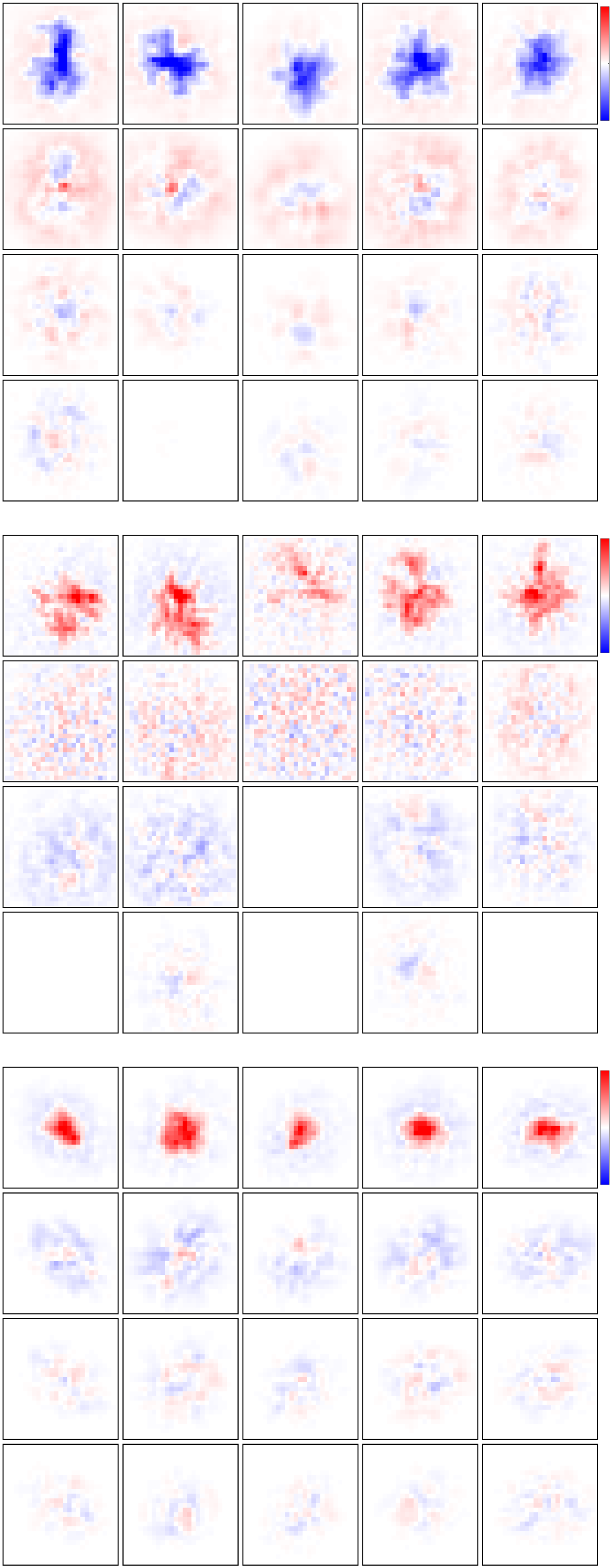
Finalmente, in Figure 7 we show summary statistics across a population
Di 15 RGCs, which can be grouped into three cell types depending on
STRF properties such as ON/OFF regions or STRF shape. Figure 7A
shows that VLR robustly outperforms the STA, while Figure 7B shows that
STRF ranks are diverse across the assigned cell types, adding to previous
reports on diverse response properties within ON/OFF pathways in mam-
malian RGCs (Ravi et al., 2018). Figure 7C shows the leading spatial com-
ponent of the inferred STRFs across different cells and cell types. Further
examples along with the temporal receptive field components are shown in
Figure D.2.
7 Discussion
In questo articolo, we have introduced a novel method for inferring low-rank
STRFs from neural recordings and have shown a substantial improvement
over previous methods for STRF estimation. Previous approaches like the
STA have low computational complexity and are hence applicable to STRFs
with large sizes but provide biased estimates under correlated stimulus dis-
tributions and classically require large amounts of training data to arrive at
accurate estimates. Previous Bayesian approaches have been shown to be
more data efficient and can provide more accurate STRF estimates, even un-
der correlated stimulus distributions. Tuttavia, they require matrix inver-
sions that are computationally costly. Così, applying Bayesian approaches
to large stimulus ensembles remains challenging. Inoltre, all of these
approaches parameterize the full STRF and do not explicitly make use of
potential low-rank structure in the STRF. These methods are therefore gen-
eral but require estimation of large numbers of parameters, which prohibits
their application to large-scale problems.
The VLR estimator we have introduced in this article addresses lim-
itations of previous approaches to STRF estimation in linear encoding
models. We have shown that our method provides accurate estimates in
settings when stimuli are correlated, the receptive field dimensionality
is high, or training data are limited. We developed a new prior covari-
ance function that captures the nonstationary smoothness that is typical of
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1013
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
Figura 7: Application to a population of rat retinal ganglion cells. (UN) Mean
squared error on 27.66 minutes of held-out test data using different ranks and
amounts of training data, averaged across 15 cells. (B) Mean and ± 1 standard
deviation of the singular values for the rank 4 VLR estimate, separated by cell
type. Singular values are normalized to sum to one. Cell types have been clas-
sified by hand by the experimenters based on STRF properties. (C) Leading
spatial STRF component for five example cells of each of three different cell
types.
temporal receptive fields. In combination with previous priors capturing
localized smooth structure for spatial receptive fields, our probabilistic
model provided a powerful framework for low-rank STRF estimation.
While we have focused on these modeling choices in this article, our mod-
eling framework is general and can easily accommodate other choices of
prior covariance functions.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1014
l. Duncker, K. Ruda, G. Field, and J. Pillow
The ability to accurately estimate STRFs from limited amounts of data
will be important for quantifying changes of receptive field properties
over time or during learning. Inoltre, it will open up possibilities for
closed-loop experiments, where stimuli are selected actively on each frame
to reduce uncertainty about the STRF. Inoltre, being able to use high-
dimensional stimuli and correlated stimulus distributions will be important
for studying population responses. In this setting, VLR will be useful for es-
timating the receptive fields of many cells in parallel. Finalmente, VLR allows
for cross-validated estimates of the STRF rank, which may prove important
for quantifying single-cell response properties and categorizing cells into
specific functional classes.
While we have presented our method in the context of gaussian lin-
ear encoding models, it is also possible to extend the variational inference
algorithm we presented here to non gaussian observation models in a gen-
eralized linear encoding model (GLM). Here, the ability to perform closed-
form updates for the posterior means and covariances will be lost and will
instead require direct optimization of the variational free energy. Previous
approaches have made use of basis functions to improve the scalability of
RF estimation in Poisson GLMs (Pillow et al., 2008). Tuttavia, this typi-
cally requires setting parameters like the number, location, and shape of
basis functions by hand. Recent work has started to consider circumvent-
ing this cumbersome by-hand selection of basis functions by using sparse
variational gaussian process approximations instead (Dowling et al., 2020).
This approach relies on inducing point methods that have recently gained
popularity in improving the scalability of gaussian process methods more
generally (Hensman et al., 2013; Titsias, 2009). The framework we presented
here is closely related to the basis function approach for GLMs and can be
used to determine parameters such as the number, location, and shape of
basis functions automatically. The improvements in scalability we achieve
due to whitened representations of the receptive field also apply in the con-
text of GLMs. In definitiva, algorithms that can automatically determine such
hyperparameters and do not require user-dependent input will contribute
to the robustness and reproducability of modeling results.
Appendix A: Bayesian Receptive Field Estimation
Here we review the standard approaches for estimating receptive fields
from data under the linear-gaussian encoding model (section 2) using Gaus-
sian priors (section 3).
A.1 Maximum A Posteriori (MAP) Estimation. Given a fixed setting
of the hyperparameters θ , it is straightforward to compute the maximum a
posteriori (MAP) estimate, which is simply the maximum of the posterior
distribution over k given the data. The posterior can be computed using
Bayes’ rule:
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1015
P(k | sì, X, P 2, θ ) = p(sì | X, k, P 2)P(k | θ )
P(sì | X, θ , P 2)
.
(A.1)
The numerator consists of the likelihood times the prior, where the likeli-
hood term comes from the gaussian encoding model,
P(sì | X, k, P 2) =
T(cid:6)
t=1
and the prior is
N (yt | k
(cid:2)
xt + B, P 2) =
T(cid:6)
t=1
1√
2πσ 2
− (yt
e
xt )2
(cid:2)
−k
2P 2
,
(A.2)
P(k|θ ) = N (k | 0, Cθ ) =
1
|2πCθ | 1
2
2 k(cid:2)C
−1
θ k.
− 1
e
(A.3)
The denominator term, P(sì | X, θ ), is known as the evidence or marginal
likelihood, and represents a normalizing constant that we can ignore when
computing the MAP estimate.
In this setting, where the likelihood and prior are both gaussian in k,
the posterior is also gaussian. The posterior mean, which is also the MAP
estimate, has a closed-form solution,
ˆkmap = ((cid:13)(cid:2)(cid:13) + σ 2C
−1
θ
−1(cid:13)(cid:2)
)
sì,
(A.4)
where y denotes the vector of responses and (cid:13) is the design matrix, Quale
contains the corresponding stimulus vectors along its rows:
y =
⎤
⎥
⎦
⎡
⎢
⎣
y1
…
yT
(cid:13) =
⎤
⎥
⎦ .
⎡
⎢
⎣
− x1
…
− xT
(cid:2)−
(cid:2)−
If needed, the posterior covariance is equal to
(cid:16) =
(cid:3)
1
P 2
−1
(cid:13)(cid:2)(cid:13) + C
θ
(cid:4)−1
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
(A.5)
(A.6)
A.2 Evidence Optimization and Empirical Bayes. A critical question
we have not yet discussed is how to set the noise variance σ 2 and the hy-
perparameters θ governing the prior. A common approach for selecting
hyperparameter values is cross-validation over a grid of candidate values.
Tuttavia, this approach is unwieldy for models with more than one or two
hyperparameters.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
1016
l. Duncker, K. Ruda, G. Field, and J. Pillow
A popular alternative in Bayesian settings is evidence optimization, also
known as type II maximum likelihood estimation (Bishop & Nasrabadi,
2006; MacKay, 1992; Park & Pillow, 2011; Sahani & Linden, 2003). The idea is
to compute maximum likelihood estimates for σ 2 and θ using the marginal
likelihood, or evidence, which is obtained by marginalizing over the model
parameters k. Incidentally, the marginal likelihood is also the denominator
in Bayes’ rule (see equation A.1). In the current setting, the marginal likeli-
hood is given by
(cid:5)
P(sì|X, P 2, θ ) =
P(sì|X, k, P 2)P(k|θ ) dk
=
|(cid:16)| 1
2
(2π )
T
2 |Cθ | 1
2
(cid:3)
esp
− 1
2P 2
(cid:2)
sì
sì + 1
2
(cid:4)
ˆkmap
(cid:2)(cid:16)−1 ˆkmap
,
(A.7)
where ˆkmap and (cid:16) are the posterior mean and covariance defined above.
In practice, one performs inference for σ 2 and θ by numerically optimiz-
ing the log of the marginal likelihood:
ˆσ 2, ˆθ = argmax
log p(sì|X, P 2, θ ),
σ 2,θ
(A.8)
although there are also fixed-point methods available for the ridge regres-
sion case (MacKay, 1992; Park & Pillow, 2011).
Once this numerical optimization is complete, we can compute the MAP
estimate for the receptive field k conditioned on these point estimates. Questo
two-step estimation procedure (evidence optimization followed by MAP
estimation) is known as empirical Bayes:
ˆkEB = argmax
k
−1
P(k|sì, X, ˆσ 2, ˆθ ) = ((cid:13)(cid:2)(cid:13) + ˆσ 2C
ˆθ
−1(cid:13)(cid:2)
)
sì.
(A.9)
This approach has been shown to obtain substantially improved receptive
field estimates in settings with limited data and correlated stimulus distri-
butions, particularly using ASD or ALD priors (see Park & Pillow, 2011; Sa-
hani & Linden, 2003). Tuttavia, computing the evidence (see equation A.7)
or even the simple MAP estimate (see equation A.4) requires storing and
inverting a matrix of size N × N, where N = nx1
· nt is the total number
of coefficients in k. The storage costs thus scale as O(N2), while the compu-
tational costs scale as O(N3), cubically in the number of receptive field coef-
ficients. This severely limits the feasibility of MAP and empirical Bayesian
estimators in high-dimensional settings.
· nx2
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1017
Appendix B: Variational Updates for Low-Rank STRF Inference
The variational updates require computing
q(peso ) ∝ exp(cid:9)log P(Y, peso, wx|(cid:13), θ )(cid:10)
q(wx) ∝ exp(cid:9)log P(Y, peso, wx|(cid:13), θ )(cid:10)
, E
q(wx )
.
q(peso )
Both of these distribution will turn out to be gaussians, such that the
variational update, or E-step, reduces to computing means and covari-
ances that fully specify the distributions q(peso ) = N (peso|μt, (cid:14)T ) and q(wx) =
N (wx|μx, (cid:14)X).
To find the variational update for q(peso ), we evaluate the expected log-
joint distribution of the response and receptive field with respect to q(wx).
The log-joint distribution can be expressed as
log P(Y, peso, wx|(cid:13), θ ) = log P(Y|peso, wx, (cid:13), θ ) + log P(peso ) + C,
(B.1)
where c absorbs all terms that are constant with respect to wt. The log-
likelihood of the response can be expressed as
log P(Y|peso, wx, (cid:13), θ ) = − 1
(cid:2)
2P 2 (Y − b − (cid:13)k)
2P 2 (Y − b − (cid:13)Bθ w)
= − 1
(Y − b − (cid:13)k) + C,
(B.2)
(cid:2)
(Y − b − (cid:13)Bθ w). (B.3)
Using properties of the Kronecker product, we can note that w can be
rewritten in two ways:
w = vec(WtWx
(cid:2)
) = (Ipx
⊗ Wt )wx = (Wx ⊗ Ipt )peso,
with wt = vec(Wt ) and wx = vec(Wx
). Substituting this into the expression
for the log-joint distribution and taking expectations (denoted by angled
brackets), we have
(cid:2)
(cid:9)log P(Y, peso, wx|θ , X )(cid:10)
q(wx )
(B.4)
= − 1
2P 2
(cid:2)
(cid:9)(Y − b − (cid:13)Bθ (Wx ⊗ Ipt )peso )
(Y − b − (cid:13)Bθ (Wx ⊗ Ipt )peso )(cid:10)
q(wx )
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
(cid:2)
peso
peso + C
− 1
2
= − 1
2P 2 (Tr[(cid:9)(Wx ⊗ Ipt )
(cid:2)
− 2wt
(Mx ⊗ Ipt )
B
(cid:2)
(cid:2)
(cid:2)
θ (cid:13)(cid:2)(cid:13)Bθ (Wx ⊗ Ipt )(cid:10)
B
q(wx )wtwt
(cid:2)
]
θ (cid:13)(cid:2)
(cid:2)
(Y − b)) − 1
2
(cid:2)
peso + C
peso
(B.5)
(B.6)
(B.7)
1018
l. Duncker, K. Ruda, G. Field, and J. Pillow
= − 1
2
[peso
(cid:2)
(Ipt r + 1
P 2
(cid:13)
N(cid:2)
n=1
(Ir ⊗ Sn)P((cid:14)X + μxμx
(cid:2)
(cid:2)
(cid:2)
(Ir ⊗ Sn)
)P
peso
(B.8)
(cid:14)
− 2
P 2
peso
(cid:2)
(cid:2)
(Mx ⊗ Ipt )
θ (cid:13)(cid:2)
(cid:2)
B
(Y − b)] + C,
(B.9)
(cid:2)(cid:10)
where μx = vec(Mx(cid:2)
) = vec((cid:9)Wx
q(wx )), P is a commutation matrix (Mag-
nus & Neudecker, 1979) such that vec(Mx) = Pvec(Mx(cid:2)
) = Pμx, and Sn =
reshape( ˜φn, [pt, px]) and ˜φn is the nth row of (cid:13)Bθ . The above can be brought
into a multivariate gaussian form by completing the square, yielding the
variational updates:
(cid:13)
(cid:14)t ←
Ipt r + 1
P 2
(cid:13)
N(cid:2)
n=1
(Ir ⊗ Sn)P((cid:14)X + μxμx
(cid:2)
(cid:2)
(cid:2)
(Ir ⊗ Sn)
)P
(B.10)
(cid:14)(cid:14)−1
μt ← 1
P 2
(cid:2)
(cid:14)T (Mx ⊗ Ipt )
θ (cid:13)(cid:2)
(cid:2)
B
(Y − b).
(B.11)
Allo stesso modo, to evaluate the expectation with respect to q(peso ),
(cid:9)log P(Y, peso, wx|θ , X )(cid:10)
q(peso )
= − 1
2P 2
(cid:2)
(cid:9)(Y − b − (cid:13)Bθ (Wx ⊗ Ipt )peso )
(Y − b − (cid:13)Bθ (Wx ⊗ Ipt )peso )(cid:10)
q(peso )
(cid:2)
wx
wx + C
− 1
2
= − 1
2P 2 (Tr[(Wx ⊗ Ipt )
(cid:2)
− 2μt
(Wx ⊗ Ipt )
B
(cid:2)
= − 1
2P 2 (Tr[(Wx ⊗ Ipt )
(cid:2)
⊗ Mt )
− 2wx
(cid:13)
(cid:13)
(Ipx
(cid:2)
N(cid:2)
= − 1
2P 2
(cid:2)
(cid:2)
P
wx
(cid:2)
(cid:2)
θ (cid:13)(cid:2)(cid:13)Bθ (Wx ⊗ Ipt )(cid:9)wtwt
B
(cid:2)(cid:10)
q(peso )]
θ (cid:13)(cid:2)
(cid:2)
(cid:2)
wx
(Y − b)) − 1
2
θ (cid:13)(cid:2)(cid:13)Bθ (Wx ⊗ Ipt )((cid:14)T + μtμt
wx + C
(cid:2)
(cid:2)
B
(cid:2)
)]
B
θ (cid:13)(cid:2)
(cid:2)
(Y − b)) − 1
2
wx
(cid:2)
wx + C
(cid:14)
(Ir ⊗ S
(cid:2)
N )((cid:14)T + μtμt
(cid:2)
)(Ir ⊗ Sn)
Pwx
n=1
(cid:14)
(cid:2)
− wx
(Ipx
(cid:2)
⊗ Mt )
θ (cid:13)(cid:2)
(cid:2)
B
(Y − b)
− 1
2
wx
(cid:2)
wx + C,
where μt = vec(Mt ) = vec((cid:9)Wt(cid:10)
q(peso )), and Sn and P are the same as before.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
N
e
C
o
_
UN
_
0
1
5
8
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1019
We can again complete the square to obtain a gaussian form in wx, Guida-
ing to the variational updates:
(cid:13)
(cid:14)x ←
(cid:2)
P
(cid:13)
Ipxr + 1
P 2
N(cid:2)
n=1
((Ir ⊗ S
(cid:2)
N )((cid:14)T + μtμt
(cid:2)
)(Ir ⊗ Sn)
P
(cid:14)
(cid:14)−1
μx ← 1
P 2
(cid:14)X(Ipx
(cid:2)
⊗ Mt )
θ (cid:13)(cid:2)
(cid:2)
B
(Y − b).
Appendix C: M-Step Updates for Low-Rank STRF Inference
The M-step updates for the hyperparameters θ = {θx, θt} can be carried out
most efficiently by performing conditional M-steps for either the spatial or
temporal parameters while holding the other set of parameters fixed.
Dropping all terms that do not depend on the hyperparamaters θ from
the free energy,
F = − 1
2P 2
= − 1
2P 2
(cid:15)
N(cid:2)
(cid:15)
n=1
N(cid:2)
n=1
(yn − Tr(Wt
(cid:2)
Bt
θt
(cid:2)(cid:13)nBx
θxWx))2
(cid:16)
Tr(Wt
(cid:2)
Bt
θt
(cid:2)(cid:13)nBx
θxWx)2 − 2ynTr(Wt
(cid:2)
Bt
θt
(cid:2)(cid:13)nBx
θxWx)
(cid:16)
= − 1
2P 2
N(cid:2)
(cid:9)Tr(Wt
(cid:2)
Bt
θt
n=1
(cid:2)(cid:13)nBx
θxWx)2(cid:10) + 1
P 2 Tr(M
(cid:2)
t Bt
θt
(cid:13)
N(cid:2)
(cid:2)
n=1
(cid:14)
yn(cid:13)N)Bx
θx PMx)
.
Here, (cid:13)n is the nth row of (cid:13) (which is equal to xn), reshaped to have the
same size as the STRF.
To evaluate the first term efficiently, it can be rewritten as follows:
(cid:17)
Tr(Wt
(cid:15)(cid:13)
R(cid:2)
(cid:18)
(cid:2)
Bt
θt
(cid:2)(cid:13)nBx
θxWx)2
Wt
(cid:2)
:,iBt
θt
(cid:2)(cid:13)nBx
θxWx:,io
(cid:16)
(cid:14)
2
(cid:15)
i=1
R(cid:2)
(cid:19)
Bt
θt
Tr
(cid:2)(cid:13)nBx
θxWx:,iWx
(cid:2)
:,iBx
θx
=
=
(cid:2)(cid:13)(cid:2)
n Bt
θtWt :,iWt
(cid:16)
(cid:20)
(cid:2)
:,io
i=1
(cid:15)
+ 2
(cid:19)
Bt
θt
Tr
R(cid:2)
(cid:2)
i=1
io< j
(cid:2)(cid:13)nBx
θxWx:,iWx
(cid:2)
:, jBx
θx
(cid:2)(cid:13)(cid:2)
n Bt
θtWt :, jWt
(cid:16)
(cid:20)
(cid:2)
:,i
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
n
e
c
o
_
a
_
0
1
5
8
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1020
L. Duncker, K. Ruda, G. Field, and J. Pillow
=
r(cid:2)
i=1
+ 2
(cid:19)
Bt
θt
Tr
(cid:2)(cid:13)nBx
θx
(cid:16)x
iiBx
θx
(cid:2)(cid:13)(cid:2)
n Bt
θt
(cid:16)t
ii
(cid:20)
(cid:19)
Bt
θt
Tr
r(cid:2)
(cid:2)
i=1
i< j
(cid:2)(cid:13)nBx
θx
(cid:16)x
i jBx
θx
(cid:2)(cid:13)(cid:2)
n Bt
θt
(cid:16)t
ji
(cid:20)
.
Here, the blocks of the second moment of the vectorized STRF are expressed
as
(cid:16)x = P(cid:9)wxwx
(cid:2)(cid:10)P
(cid:2) = P((cid:14)x + μxμ(cid:2)
x )P
(cid:2) =
(cid:16)t = (cid:9)wtwt
(cid:2)(cid:10) = (cid:14)t + μtμt
(cid:2) =
⎡
⎢
⎢
⎣
⎡
⎢
⎢
⎣
(cid:16)x
11
...
(cid:16)x
r1
(cid:16)t
11
...
(cid:16)t
r1
⎤
⎥
⎥
⎦
⎤
⎥
⎥
⎦ .
. . . (cid:16)x
1r
...
. . .
. . . (cid:16)x
rr
. . . (cid:16)t
1r
...
. . .
. . . (cid:16)t
rr
It is apparent from the above expression that the conditional M-steps
will rely on statistics of the stimulus projected onto the basis we are not
optimizing over. In order to evaluate each M-step update as efficiently as
possible, these statistics can be precomputed and stored throughout the M-
step update. Below, we provide further details for each conditional M-step.
C.1 Spatial Parameter Updates.
Fx = − 1
2σ 2
r(cid:2)
i=1
(cid:13)
Tr
(cid:2)
Bx
θx
(cid:13)
N(cid:2)
n=1
(cid:14)
(cid:14)
(cid:13)(cid:2)
n Bt
θt
(cid:16)t
iiBt
θt
(cid:2)(cid:13)n
Bx
θx
(cid:16)x
ii
(cid:14)
(cid:14)
(cid:13)(cid:2)
n Bt
θt
(cid:16)t
jiBt
θt
(cid:2)(cid:13)n
Bx
θx
(cid:16)x
i jBx
θx
(cid:2)
(cid:13)(cid:13)
Tr
N(cid:2)
n=1
− 1
σ 2
r(cid:2)
(cid:2)
i< j
i=1
(cid:13)
+ 1
σ 2 Tr
Mt (cid:2)
(cid:14)
(cid:14)
ynBt
θt
(cid:2)(cid:13)n
θx Mx
Bx
.
(cid:13)
N(cid:2)
n=1
Now, before computing the parameter updates for the spatial parameters,
we can precompute:
=
St
1 ji
(cid:13)
N(cid:2)
n=1
(cid:14)
(cid:13)(cid:2)
n Bt
θt
(cid:16)t
jiBt
θt
(cid:2)(cid:13)n
=
St
2
(cid:14)
ynBt
θt
(cid:2)(cid:13)n
.
(cid:13)
N(cid:2)
n=1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
n
e
c
o
_
a
_
0
1
5
8
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1021
(cid:22)
(cid:21)
r+1
r−1
matrices of size px × px. While building this matrix is
This involves
expensive, the size of px is pruned using ALD. This cost is incurred only
once before performing repeated updates to the spatial hyperparameters.
C.2 Temporal Parameter Updates.
N(cid:2)
r(cid:2)
(cid:19)
Bt
θt
Tr
(cid:2)(cid:13)nBx
θx
(cid:16)x
iiBx
θx
(cid:2)(cid:13)(cid:2)
n Bt
θt
(cid:16)t
ii
(cid:20)
(cid:19)
Bt
θt
Tr
(cid:2)(cid:13)nBx
θx
(cid:16)x
i jBx
θx
(cid:2)(cid:13)(cid:2)
n Bt
θt
(cid:16)t
ji
(cid:20)
Ft = − 1
2σ 2
− 1
σ 2
n=1
i=1
N(cid:2)
r(cid:2)
(cid:2)
i=1
i< j
n=1
(cid:13)
+ 1
σ 2 Tr
(cid:2)
Mt (cid:2)
Bt
θt
(cid:14)
(cid:14)
yn(cid:13)n
θx Mx
Bx
.
(cid:13)
N(cid:2)
n=1
Now, before computing the parameter updates for the spatial parameters,
we can precompute:
=
Sx
1i j
(cid:13)
N(cid:2)
n=1
(cid:14)
(cid:13)nBx
θx
(cid:16)x
i jBx
θx
(cid:2)(cid:13)(cid:2)
n
=
Sx
2
(cid:14)
yn(cid:13)nBx
θx
.
(cid:13)
N(cid:2)
n=1
Analogous to the spatial parameter updates, this involves precomputing
and storing
matrices of size pt × pt.
(cid:21)
(cid:22)
r+1
r−1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
n
e
c
o
_
a
_
0
1
5
8
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1022
L. Duncker, K. Ruda, G. Field, and J. Pillow
Appendix D
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
n
e
c
o
_
a
_
0
1
5
8
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure D.1: Simulated responses using natural movie stimulus. Stimuli were
extracted as a single row of pixels from a movie in the CatCam data set in Betsch
et al. (2004) and used to simulate responses using the same low-rank STRF as
in Figure 4. (A) The true STRF that was used for generating synthetic responses
and recovered estimates using STA, RR, and our VLR approach with a rank of
2, with ALD for the 2D spatial and TRD for the temporal component. Shown
estimates are obtained using 1e4 training samples. (B, C) Same as panel A but
plotting the top two spatial (B) and temporal (C) components of the true and
recovered STRF estimates. Dashed lines show the spatial and temporal compo-
nents of the true STRF for reference. Spatial and temporal components of the
STA and RR were not accessible by estimation; they were obtained by taking
the leading left and right singular vectors of the STRF in matrix form and rescal-
ing by the size of the true STRF. (D) Correlation of the STRF estimate and the
true STRF used to generate data for different amounts of training data. Lines
represent the average correlation across 15 repeated simulations with different
natural movie stimuli; shaded regions represent ± 1 standard error. (E) Tem-
poral autocorrelation of the natural stimulus. (F) Spatial autocorrelation of the
natural stimulus. (G) Five hundred example frames of the natural stimulus.
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1023
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
n
e
c
o
_
a
_
0
1
5
8
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure D.2: Inferred spatial and temporal components using VLR for different
cell types and example cells. Each panel shows the four spatial (A, C, E) and
temporal (B, D, F) low-rank receptive field components for five example cells
that have been classified as OFF brisk sustained (A, B), ON brisk sustained (C, D),
or ON transient (E, F).
1024
L. Duncker, K. Ruda, G. Field, and J. Pillow
Code Availability
We provide Matlab code for fitting low-rank STRFs under flexible choices of
prior covariance functions at https://github.com/pillowlab/VLR-STRF.
Author Contributions
L.D. and J.W.P. conceived of this project. L.D. developed the presented
methods and performed analyses under the supervision of J.W.P. K.M.R.
and G.D.F. collected the retinal ganglion cell experimental data and assisted
in the retinal ganglion cell analyses. L.D. and J.W.P. wrote the manuscript
with input from K.M.R. and G.D.F.
Acknowledgments
We thank Sneha Ravi for sharing the RGC data, and Nicole Rust and Tony
Movshon for providing access to V1 simple cell data. L.D. was supported by
the Gatsby Charitable Foundation. J.W.P. was supported by grants from the
McKnight Foundation, the Simons Collaboration on the Global Brain (SCGB
AWD543027), the NIH BRAIN initiative (NS104899 and R01EB026946), and
a U19 NIH-NINDS BRAIN Initiative Award (5U19NS104648).
References
Adelson, E. H., & Bergen, J. R. (1985). Spatiotemporal energy models for the percep-
tion of motion. J. Opt. Soc. Am. A, 2, 284–299. 10.1364/JOSAA.2.000284
Aoi, M. C., & Pillow, J. W. (2017). Scalable Bayesian inference for high-dimensional neural
receptive fields. bioRxiv:212217.
Baden, T., Berens, P., Franke, K., Román Rosón, M., Bethge, M., & Euler, T. (2016).
The functional diversity of retinal ganglion cells in the mouse. Nature, 529(7586),
345–350. 10.1038/nature16468
Betsch, B. Y., Einhäuser, W., Körding, K. P., & König, P. (2004). The world from a
cat’s perspective: Statistics of natural videos. Biological Cybernetics, 90(1), 41–50.
10.1007/s00422-003-0434-6
Bishop, C. M., & Nasrabadi, N. M. (2006). Pattern recognition and machine learning.
Springer.
Calabrese, A., Schumacher, J. W., Schneider, D. M., Paninski, L., & Woolley, S. M.
N. (2011). A generalized linear model for estimating spectrotemporal receptive
fields from responses to natural sounds. PLOS One, 6(1), e16104.
Chichilnisky, E. (2001). A simple white noise analysis of neuronal light responses.
Network: Computation in Neural Systems, 12(2), 199–213. 10.1080/713663221
Chichilnisky, E., & Kalmar, R. S. (2002). Functional asymmetries in on and off gan-
glion cells of primate retina. Journal of Neuroscience, 22(7), 2737–2747. 10.1523/
JNEUROSCI.22-07-02737.2002
David, S. V., & Gallant, J. L. (2005). Predicting neuronal responses during natural
vision. Network: Computation in Neural Systems, 16(2), 239–260.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
n
e
c
o
_
a
_
0
1
5
8
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1025
deBoer, E., & Kuyper, P. (1968). Triggered correlation. IEEE Transact. Biomed. Eng.,
15, 169–179. 10.1109/TBME.1968.4502561
Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from in-
complete data via the EM algorithm. Journal of the Royal Statistical Society Series B,
39(1), 1–38.
Dowling, M., Zhao, Y., & Park, I. M. (2020). Non-parameteric generalized linear model.
arXiv:2009.01362.
Efron, B., & Morris, C. (1973). Stein’s estimation rule and its competitors—an empiri-
cal Bayes approach. Journal of the American Statistical Association, 68(341), 117–130.
Field, G. D., Sher, A., Gauthier, J. L., Greschner, M., Shlens, J., Litke, A. M., &
Chichilnisky, E. (2007). Spatial properties and functional organization of small
bistratified ganglion cells in primate retina. Journal of Neuroscience, 27(48), 13261–
13272. 10.1523/JNEUROSCI.3437-07.2007
Frechette, E. S., Sher, A., Grivich, M. I., Petrusca, D., Litke, A. M., & Chichilnisky, E.
(2005). Fidelity of the ensemble code for visual motion in primate retina. Journal
of Neurophysiology, 94(1), 119–135. 10.1152/jn.01175.2004
Gerwinn, S., Macke, J. H., & Bethge, M. (2010). Bayesian inference for generalized
linear models for spiking neurons. Frontiers in Computational Neuroscience, 4(Jan-
uary). 10.3389/fncom.2010.00012
Hensman, J., Fusi, N., & Lawrence, N. D. (2013). Gaussian processes for big data. In
Proceedings of the 29th Conference on Uncertainty in Artificial Intelligence (pp. 282–
290).
Hoerl, A. E., & Kennard, R. W. (1970). Ridge regression: Biased estimation for
nonorthogonal problems. Technometrics, 12(1), 55–67. 10.1080/00401706.1970
.10488634
James, W., & Stein, C. (1961). Estimation with quadratic loss. In Proceedings of the
Fourth Berkeley Symposium on Mathematical Statistics and Probability (vol. 1, pp. 361–
379).
Jones, J. P., & Palmer, L. A. (1987). The two-dimensional spatial structure of simple
receptive fields in cat striate cortex. Journal of Neurophysiology, 58(6), 1187–1211.
10.1152/jn.1987.58.6.1187
Lee, Y., & Schetzen, M. (1965). Measurement of the Wiener kernels of a non-linear
system by cross-correlation. International Journal of Control, 2(3), 237–254. 10.1080/
00207176508905543
Linden, J. F., Liu, R. C., Sahani, M., Schreiner, C. E., & Merzenich, M. M. (2003). Spec-
trotemporal structure of receptive fields in areas AI and AAF of mouse auditory
cortex. Journal of Neurophysiology, 90(4), 2660–2675. 10.1152/jn.00751.2002
MacKay, D. J. C. (1992). Bayesian interpolation. Neural Computation, 4(3), 415–447.
10.1162/neco.1992.4.3.415
Magnus, J. R., & Neudecker, H. (1979). The commutation matrix: Some properties
and applications. Annals of Statistics, 7(2), 381–394. 10.1214/aos/1176344621
Meyer, A. F., Williamson, R. S., Linden, J. F., & Sahani, M. (2017). Models of neuronal
stimulus-response functions: Elaboration, estimation, and evaluation. Frontiers in
Systems Neuroscience, 10, 109. 10.3389/fnsys.2016.00109
Park, M., & Pillow, J. W. (2011). Receptive field inference with localized priors. PLOS
Comput Biol., 7(10), e1002219. 10.1371/journal.pcbi.1002219
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
n
e
c
o
_
a
_
0
1
5
8
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1026
L. Duncker, K. Ruda, G. Field, and J. Pillow
Park, M., & Pillow, J. W. (2013). Bayesian inference for low rank spatiotemporal neu-
ral receptive fields. In C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani,
& K. Q. Weinberger (Eds.), Advances in neural information processing systems, 26
(pp. 2688–2696). Curran.
Pillow, J. W., Shlens, J., Paninski, L., Sher, A., Litke, A. M., Chichilnisky, E.,
& Simoncelli, E. P. (2008). Spatio-temporal correlations and visual signalling
in a complete neuronal population. Nature, 454(7207), 995–999. 10.1038/
nature07140
Pillow, J. W., & Simoncelli, E. P. (2006). Dimensionality reduction in neural models:
An information-theoretic generalization of spike-triggered average and covari-
ance analysis. Journal of Vision, 6(4), 9–9. 10.1167/6.4.9
Qiu, A., Schreiner, C. E., & Escabí, M. A. (2003). Gabor analysis of auditory mid-
brain receptive fields: Spectro-temporal and binaural composition. Journal of Neu-
rophysiology, 90(1), 456–476. 10.1152/jn.00851.2002
Rasmussen, C. E., & Williams, C. K. (2006). Gaussian processes for machine learning.
MIT Press.
Ravi, S., Ahn, D., Greschner, M., Chichilnisky, E., & Field, G. D. (2018). Pathway-
specific asymmetries between on and off visual signals. Journal of Neuroscience,
38(45), 9728–9740. 10.1523/JNEUROSCI.2008-18.2018
Ringach, D. L. (2004). Mapping receptive fields in primary visual cortex. J. Physiol.,
558(Pt. 3), 717–728. 10.1113/jphysiol.2004.065771
Ringach, D. L., Sapiro, G., & Shapley, R. (1997). A subspace reverse-correlation
technique for the study of visual neurons. Vision Research, 37(17), 2455–2464.
10.1016/S0042-6989(96)00247-7
Rust, N. C., Schwartz, O., Movshon, J. A., & Simoncelli, E. P. (2005). Spatiotempo-
ral elements of macaque V1 receptive fields. Neuron, 46(6), 945–956. 10.1016/
j.neuron.2005.05.021
Sahani, M., & Linden, J. F. (2003). Evidence optimization techniques for estimating
stimulus- response functions. In S. Becker, S. Thrun, & K. Overmayer (Eds.), Ad-
vances in neural information processing systems, 15 (p. 317). MIT Press.
Schwartz, O., Pillow, J. W., Rust, N. C., & Simoncelli, E. P. (2006). Spike-triggered
neural characterization. Journal of Vision, 6(4), 484–507. 10.1167/6.4.13
Sharpee, T., Rust, N. C., & Bialek, W. (2004). Analyzing neural responses to natural
signals: Maximally informative dimensions. Neural Computation, 16(2), 223–250.
10.1162/089976604322742010
Simoncelli, E. P., Pillow, J. W., Paninski, L., & Schwartz, O. (2004). Characterization
of neural responses with stochastic stimuli. In M. Gazzaniga (Ed.), The cognitive
neurosciences, III (pp. 327–338). MIT Press.
Smyth, D., Willmore, B., Baker, G., Thompson, I., & Tolhurst, D. (2003). The
receptive-field organization of simple cells in primary visual cortex of ferrets
under natural scene stimulation. Journal of Neuroscience, 23, 4746–4759. 10.1523/
JNEUROSCI.23-11-04746.2003
Theunissen, F., David, S., Singh, N., Hsu, A., Vinje, W., & Gallant, J. (2001). Esti-
mating spatiotemporal receptive fields of auditory and visual neurons from their
responses to natural stimuli. Network: Computation in Neural Systems, 12, 289–316.
10.1080/net.12.3.289.316
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
n
e
c
o
_
a
_
0
1
5
8
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Scalable Variational Inference for Low-Rank Spatiotemporal RFs
1027
Titsias, M. (2009). Variational learning of inducing variables in sparse gaussian pro-
cesses. In Proceedings of the 12th International Conference on Artificial Intelligence and
Statistics (pp. 567–574).
Wu, A., Park, M., Koyejo, O. O., & Pillow, J. W. (2014). Sparse Bayesian structure
learning with “dependent relevance determination” priors. In Z. Ghahramani,
M. Welling, C. Cortes, N. Lawrence, & K. Q. Weinberger (Eds.), Advances in neural
information processing systems, 27 (pp. 1628–1636). Curran.
Received August 4, 2022; accepted January 4, 2023.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
6
9
9
5
2
0
8
6
3
3
6
n
e
c
o
_
a
_
0
1
5
8
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3