ARTICLE - Ricerca sull'intelligenza artificiale specializzata al MIT

ARTICLE

Communicated by Sarah Schwoebel

Bayesian Brains and the Rényi Divergence

Noor Sajid
noor.sajid.18@ucl.ac.uk
Wellcome Centre for Human Neuroimaging, University College London,
London WC1N 3AR, U.K.

Francesco Faccio
francesco@idsia.ch
The Swiss AI Lab IDSIA, USI, SUPSI, 6962, Viganello, Lugano, Svizzera

Lancelot Da Costa
l.da-costa@imperial.ac.uk
Wellcome Centre for Human Neuroimaging, University College London,
London WC1N 3AR, U.K., and Department of Mathematics, Imperial College
London, London SW7 2AZ, U.K.

Thomas Parr
thomas.parr.12@ucl.ac.uk
Wellcome Centre for Human Neuroimaging, University College London,
London WC1N 3AR, U.K.

Jürgen Schmidhuber
juergen@idsia.ch
The Swiss AI Lab IDSIA, USI, SUPSI, 6962, Viganello, Lugano, Svizzera

Karl Friston
k.friston@ucl.ac.uk
Wellcome Centre for Human Neuroimaging, University College London,
London WC1N 3AR, U.K.

Under the Bayesian brain hypothesis, behavioral variations can be at-
tributed to different priors over generative model parameters. Questo
provides a formal explanation for why individuals exhibit inconsistent
behavioral preferences when confronted with similar choices. For ex-
ample, greedy preferences are a consequence of confident (or precise)
beliefs over certain outcomes. Here, we offer an alternative account of
behavioral variability using Rényi divergences and their associated vari-
ational bounds. Rényi bounds are analogous to the variational free

Noor Sajid and Francesco Faccio contributed equally to this article.

Calcolo neurale 34, 829–855 (2022)
https://doi.org/10.1162/neco_a_01484

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

830

N. Sajid et al.

energy (or evidence lower bound) and can be derived under the same as-
sumptions. Importantly, these bounds provide a formal way to establish
behavioral differences through an α parameter, given fixed priors. Questo
rests on changes in α that alter the bound (on a continuous scale), induc-
ing different posterior estimates and consequent variations in behavior.
Così, it looks as if individuals have different priors and have reached
+ optimization constrains
different conclusions. More specifically, α → 0
the variational posterior to be positive whenever the true posterior is
positive. This leads to mass-covering variational estimates and increased
variability in choice behavior. Inoltre, α → +∞ optimization con-
strains the variational posterior to be zero whenever the true posterior
is zero. This leads to mass-seeking variational posteriors and greedy
preferences. We exemplify this formulation through simulations of the
multiarmed bandit task. We note that these α parameterizations may be
especially relevant (cioè., shape preferences) when the true posterior is not
in the same family of distributions as the assumed (simpler) approximate
density, which may be the case in many real-world scenarios. The ensu-
ing departure from vanilla variational inference provides a potentially
useful explanation for differences in behavioral preferences of biolog-
ical (or artificial) agents under the assumption that the brain performs
variational Bayesian inference.

1 introduzione

The notion that the brain is Bayesian—or, more appropriately, Laplacian
(Stigler, 1986) and performs some form of inference has attracted enormous
attention in neuroscience (Doya, Ishii, Pouget, & Rao, 2007; Knill & Pouget,
2004). It takes the view that the brain embodies a model about causes of
sensation that allows for predictions about observations (Dayan, Hinton,
Neal, & Zemel, 1995; Hohwy, 2012; Schmidhuber, 1992; Schmidhuber &
Heil, 1995) and future behavior (Friston, FitzGerald, Rigoli, Schwarten-
beck, & Pezzulo, 2017; Schmidhuber, 1990). Practically, this involves the
optimization of a free energy functional (or evidence lower bound; Bo-
gacz, 2017UN; Friston et al., 2017; Penny, 2012), using variational inference
(Blei, Kucukelbir, & McAuliffe, 2017; Wainwright & Jordan, 2008), to make
appropriate predictions. The free energy functional can be derived from
the Kullback-Leibler (KL) divergence (Kullback & Leibler, 1951), Quale
measures the dissimilarity between true and approximate posterior den-
sities. Under this formulation, behavioral variations can be attributed to al-
tered priors over the (hyper-)parameters of a generative model, given the
same (variational) free energy functional (Friston et al., 2014; Schwarten-
beck et al., 2015). This has been used to simulate variations in choice behav-
ior (FitzGerald, Schwartenbeck, Moutoussis, Dolan, & Friston, 2015; Friston
et al., 2014, 2015; Storck, Hochreiter, & Schmidhuber, 1995) and behavioral

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Bayesian Brains and the Rényi Divergence

831

deficits (Sajid, Parr, Gajardo-Vidal, Price, & Friston, 2020; Smith, Lane, Parr,
& Friston, 2019).

Conversely, distinct behavioral profiles could be attributed to differences
in the variational objective, given the same priors. In questo articolo, we con-
sider this alternative account of phenotypic variations in choice behav-
ior using Rényi divergences (Amari, 2012; Amari & Cichocki, 2010; Phan,
Abbasi-Yadkori, & Domke, 2019; Rényi, 1961; Van Erven & Harremos, 2014).
These are a general class of divergences, indexed by an α parameter, Di
which the KL-divergence is a special case. It is perfectly reasonable to di-
verge from this special case since variational inference does not commit
to the KL-divergence (Wainwright & Jordan, 2008) (Infatti, previous work
has developed divergence-based lower bounds that give tighter bounds—
Barber & van de Laar, 1999), yet these may be more difficult to optimize de-
spite being better approximations). Broadly speaking, variational inference
is the process of approximating a posterior probability through application
of variational methods. This means finding the function (here, an approx-
imate posterior), out of a predefined family of functions, that extremizes
an objective functional. In variational inference, the key is choosing the ob-
jective such that the extreme value corresponds to the best approximation.
Rényi divergences can be used to derive a (generalized) variational infer-
ence objective called the Rényi bound (Li & Turner, 2017). The Rényi bound
is analogous to the variational free energy functional and provides a for-
mal way to establish phenotypic differences despite consistent priors. Questo
is accomplished by changes, on a continuous scale, that give rise to differ-
ent posterior estimates and consequent behavioral variations (Minka, 2005).
Così, changing the functional form of the bound will make it look as if indi-
viduals have different priors that is, they have reached different conclusions
from the same observations due to the distinct optimization objective.

It is important to determine whether this formulation introduces funda-
mentally new differences in behavior that cannot be accounted for by al-
tering priors under a standard variational objective. Conversely, it may be
possible to relate changes in prior beliefs to changes in the variational ob-
jective. We investigate this for a simple gaussian system by examining the
relationship between different parameterizations of the Rényi bound under
fixed priors and the variational free energy under different hyperpriors. It
turns out that there is no clear correspondence in most cases. This suggests
that differences in behavior caused by changes in the divergence supple-
ment standard accounts of behavioral differences under changes of priors.
The Rényi divergences depend on an α parameter that controls the
strength of the bound1 and induces different posterior estimates. Conse-
quently, the resulting system behavior may vary and point toward different

Here, strength of bound refers the closeness with which the variational functional

bounds the (negative) log evidence.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

832

N. Sajid et al.

priors that could have altered the variational posterior form. For this, we
assume that systems (or agents) sample their actions based on posterior be-
liefs, and those posterior beliefs depend on the form of the Rényi bound
α parameter. This furnishes a natural explanation for observed behavioral
variation. To make the link to behavior, we assume actions are selected,
based on variational estimates, that maximize the Sharpe ratio (Sharpe,
1994), a variance-adjusted return. Accordingly, evaluation of behavioral
differences rests on a separation between estimation of posterior beliefs
over particular (hidden) states and the action selection criterion. Questo è,
actions are selected given posterior estimates about states. This is contrary
to other Bayesian sequential decision-making schemes, such as active infer-
ence (Da Costa et al., 2020; Friston et al., 2017), where actions are sampled
from posterior beliefs about action sequences (cioè., policies). This effectively
separates action and perception into state estimation and planning as in-
ference.2 However, we will use a simplification of action selection, using
the Sharpe ratio, to focus on inferences about hidden states under different
values. We reserve further details for later sections.

Intuitively, under the Rényi bound, high α values lead to mass-seeking
approximate3 posteriors that is, greedy preferences for a particular out-
come. This happens because the variational posterior is constrained to be
+
zero whenever the true posterior is zero. Conversely, α → 0
can result in
mass-covering approximate posteriors, resulting in a greater range of ac-
tions for which there are plausible outcomes consistent with prior prefer-
enze. In questo caso, the variational posterior is constrained to be positive
whenever the true posterior is positive. Hence, variable individual pref-
erences could be attributed to differences in the variational optimization
objective. This contrasts with standard accounts of behavioral differences,
where the precision of some fixed priors is used to explain divergent be-
havior profiles under the same variational objective. In what follows, we
present, and validate, this generalized kind of variational inference that can
explain the implicit preferences of biological and artificial agents, under the
assumption that the brain performs variational Bayesian inference.

The article is structured as follows. Primo, we provide a primer on stan-
dard variational inference using the KL-divergence (section 2). Sezione 3
introduces Rényi divergences and the derivation for the Rényi bound us-
ing the same assumptions as the standard variational objective. We then
consider what (if any) sort of correspondence exists between the Rényi
bound and the variational free energy functional (cioè., the evidence lower
bound) under different priors (section 4). In section 5, we validate the

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Note that heuristics like the Sharpe ratio are unnecessary in active inference (Da Costa
et al., 2020; Friston et al., 2017), which automatically accommodates uncertainty of this
sort; Tuttavia, it is a useful heuristic because it foregrounds the role of posterior uncer-
tainty in action selection.

We use approximate and variational posterior interchangeably throughout.

Bayesian Brains and the Rényi Divergence

833

approach through numerical simulations of the multiarmed bandit (Auer,
Cesa-Bianchi, & Fischer, 2002; Lattimore & Szepesvári, 2020) paradigm with
multimodal observation distribution. Our simulations demonstrate that
variational Bayesian agents, optimizing a generalized variational bound
(cioè., Rényi bound) can naturally account for variations in choice behavior.
We conclude with a brief discussion of future directions and the implica-
tions of our work for understanding behavioral variations.

2 Variational Inference

Variational inference is an inference scheme based on variational calculus
(Parisi, 1988). It identifies the posterior distribution as the solution to an op-
timization problem, allowing otherwise intractable probability densities to
be approximated (Jordan, Ghahramani, Jaakkola, & Saul, 1999; Wainwright
& Jordan, 2008). For this, we define a family of approximate densities over
the hidden variables of the generative model (Beal, 2003; Blei et al., 2017).
From this, we can use gradient descent to find the member of that vari-
ational family that minimizes a divergence to the true conditional poste-
rior. This variational density then serves as a proxy for the true density.
This formulation underwrites practical applications that characterize the
brain as performing Bayesian inference including predictive coding (Mil-
lidge, Tschantz, & Buckley, 2020; Perrykkad & Hohwy, 2020; Schmidhuber
& Heil, 1995; Spratling, 2017; Whittington & Bogacz, 2017), and active in-
ference (Da Costa et al., 2020; Friston et al., 2017; Sajid, Ball, Parr, & Friston,
2021; Storck et al., 1995; Tschantz, Seth, & Buckley, 2020).

2.1 KL-Divergence and the Standard Variational Objective. To derive
the standard variational objective, known as the variational free energy, O
negative evidence lower bound (ELBO), we consider a simple system with
two random variables. These are s ∈ S denoting hidden states of the system
(per esempio., it rained last night) and o ∈ O the observations (per esempio., the grass is wet).
The joint density over these variables,

P(S, o) = p(o|S)P(S),

(2.1)

where p(S) is the prior density over states and p(o|S) is the likelihood, È
called the generative model. Then the inference problem is to compute the
posterior (cioè., the conditional density) of the states given the outcomes:

P(S|o) = p(o, S)
P(o)

(2.2)

This quantity contains the evidence, P(o), that can be calculated by
marginalizing out the states from the joint density. Tuttavia, the evidence

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

834

N. Sajid et al.

is notoriously difficult to compute, which makes the posterior intractable
in practical applications. This problem can be finessed with variational in-
ference.4 For this, we introduce a variational density, q(·) that can be easily
integrated. The following equations illustrate how we can derive the quan-
tities of interest. We assume that both p(S|o) and q(S) are nonzero:

(cid:2)

log p(o) = log p(o) +
(cid:2)

log

P(S|o)
P(S|o)
(cid:2)

q(S) log

P(S|o)
P(S|o)

ds =

q(S) log p(S, o) ds +

q(S) log p(o) ds +

q(S) log

q(S)
q(S)

ds +

(cid:2)

(cid:3)

q(S) log

1
q(S)

q(S) log p(S, o) ds
(cid:6)

(cid:3)

ds +
(cid:4)(cid:5)
ELBO

(cid:2)

(2.3)

q(S) log

P(S, o)
P(S|o)

(2.4)

q(S) log

1
P(S|o)

(2.5)

q(S)
P(S|o)

q(S) log
(cid:4)(cid:5)
KL Divergence

ds
(cid:6)

(2.6)

The first two summands of the last equality are the evidence lower bound
(Welbourne, Woollams, Crisp, & Lambon-Ralph, 2011), and the last sum-
mand presents the KL-divergence between the approximate and true pos-
terior. If q(·) and p(·) are of the same exponential family, then their KL
divergence can be computed using the formula provided in Huzurbazar
(1955). Our variational objective of interest is the free energy functional (F),
which upper-bounds the negative log evidence. Therefore, we rewrite the
last equality:

− log p(o) = −

(cid:7) (cid:2)

q(S) log

1
q(S)

ds +

(cid:2)

q(S) log p(S, o) ds

(cid:2)

q(S) log

(cid:8)

q(S)
P(S|o)
(cid:2)

(cid:2)

q(S) log q(S) ds −

q(S) log p(S, o) ds −

(2.7)

(cid:2)

q(S) log

q(S)
P(S|o)

(2.8)

There are other methods to estimate the posterior that include sampling-based or
hybrid approaches (per esempio., Markov chain Monte Carlo, MCMC). Tuttavia, variational in-
ference is considerably faster than sampling by employing simpler variational posteriors,
which lead to a simpler optimization procedure (Wainwright & Jordan, 2008).

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Bayesian Brains and the Rényi Divergence

(cid:2)

≤

S
= −E

= DKL
(cid:3)

q(S) log q(S) ds −

(cid:2)

q(S) log p(S, o) ds

q(S)[log p(S, o)] − H[q(S)]
(cid:10)
(cid:9)
q(S)||P(S)
(cid:6)
(cid:4)(cid:5)

− E
(cid:3)

q(S)

(cid:9)

(cid:10)
log p(o|S)
(cid:6)
(cid:4)(cid:5)
accuracy

complexity

= −DKL[q(S)||P(S, o)] = F.

835

(2.9)

(2.10)

(2.11)

(2.12)

The second-to-last line is the commonly presented decomposition of the
variational free energy summands: complexity and accuracy (Friston et al.,
2017; Sajid et al., 2021). The accuracy term represents how well observed
data can be predicted, while complexity is a regularization term. The varia-
tional free energy objective favors accurate explanations for sensory obser-
vations that are maximally consistent with prior beliefs. Additionally, IL
last equality defines the variational free energy in terms of a KL-divergence
between q(S) and p(o, S). This may seem different to those used to dealing
with variational free energy to see it defined in terms of a KL-divergence
since this notation is usually reserved for arguments that are both normal-
ized (Bishop, 2006). Tuttavia, here the normalization factors over p(·) be-
come an additive constant in the KL-divergence, which has no effect on the
gradients used in optimization or inference. Contrariwise, the normalizing
constant of q(·) needs to be the same across the variational family.

In this setting, illustrations of behavioral variations (cioè., differences in
variational posterior estimations) can result from different priors over the
(hyper-)parameters5 of the generative model (Storck et al., 1995), ad esempio
change in precision over the likelihood function (Friston et al., 2014). Noi
reserve description of hyperpriors and their impact on belief updating for
section 4.

3 Rényi Divergences and Their Variational Bound

We are interested in defining a (general) variational objective that can ac-
count for behavioral variations alternate to a change of priors. For this,
we can replace the KL divergence by a general divergence objective, Quello
È, a nonnegative function D[·||·] that satisfies D[q(S)||P(S|o)] = 0 if and
only if q(S) = p(S|o) for all s ∈ S.6 For our purposes, we focus on Rényi

Note that introducing hyperpriors (or precision priors) is standard part of the
Bayesian machinery (Gelman, Carlin, Stern, & Rubin, 1995). Intuitively, this involves scal-
ing the variance over the distribution of interest to make it more or less precise (or con-
fident). Per esempio, a gaussian distribution can become relatively flat (cioè., less precise)
or a Dirac delta function (cioè., infinitely precise) in the limits of high and low variance,
rispettivamente.

Technically, this equality holds up to a set of measure zero.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

836

N. Sajid et al.

divergences, a general class of divergences that includes the KL-divergence.
Explicitly, we can derive the KL-divergence from the Rényi divergence as
α → 1, Per esempio, using L’Hôpital’s rule, or the minimum description
length as α → ∞ (Vedi la tabella 1). This has the advantage of being compu-
tationally tractable and satisfies many additional properties (Amari, 2012;
Rényi, 1961; Van Erven & Harremos, 2014). Rényi divergences are defined
COME (Li & Turner, 2017; Rényi, 1961)

(cid:9)

(cid:10)
q(S)||P(S|o)

Dα

:= 1

α − 1

log

(cid:2)

α
q(S)

P(S|o)1−α

ds,

(3.1)

where α ∈ R+ \ {1}. An analogous definition holds for the discrete case by
replacing the densities with probabilities and the integral by a sum (Rényi,
1961). This family of divergences can provide different posterior estimates
as the minimum of the divergence with respect to q varies smoothly with
α. These differences are possible only when the true posterior (per esempio., some
multimodal distribution) is not in the same family of distributions as the ap-
proximate posterior, such as a gaussian distribution. Note that other (non-
Rényi) divergences in the literature are also parameterized by α, which can
lead to confusion: the I divergence, Amari’s α-divergence, and the Tsallis
divergence. All of these divergences are equivalent in that their values are
related by simple formulas (see appendix A). This allows the results pre-
sented in this article to be generalized to these divergence families using
the relationships in appendix A.

3.1 Rényi Bound. The accompanying variational bound for Rényi di-
vergences can be derived using the same procedures as for deriving the
evidence lower bound (see equation 2.3). This gives us the Rényi bound
introduced in Li & Turner (2017):

(cid:6)⇒

P(o) = p(o, S)
P(S|o)
P(S|o)1−α = p(o, S)1−α

P(o)1−α
(cid:2)

P(o)1−α

P(S|o)1−α

ds =

α
q(S)
(cid:2)

(cid:2)

α
q(S)

P(o, S)1−α
(cid:2)

log

α
q(S)

P(o)1−α
(cid:2)

P(S|o)1−α

ds = log

P(o, S)1−α

α
q(S)
(cid:2)

log p(o)1−α + log

log p(o)1−α = log

S
(cid:2)

α
q(S)

P(S|o)1−α

ds = log

α
q(S)

P(o, S)1−α

ds − log

α
q(S)

P(o, S)1−α

α
q(S)

P(S|o)1−α

S
(cid:2)

(3.2)

(3.3)

(3.4)

(3.5)

(3.6)

(3.7)

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Bayesian Brains and the Rényi Divergence

837

T
N
e
R
e
F
F
io

D
R
o
F

)
4
1
0
2
,
S
o
M
e
R
R
UN
H
&
N
e
v
R
E
N
UN
V

;
5
0
0
2
,
UN
k
N
io
M

;
7
1
0
2
,
R
e
N
R
tu
T
&

l
(

S
e
C
N
e
G
R
e
v
io
D

io
sì
N
é
R

)
D
e
z
io
l
UN
M
R
o
N

(

F
o
S
e
l
P
M
UN
X
E

:
1
e
l
B
UN
T

.
S
D
N
tu
o
B

io
sì
N
é
R
G
N
io
sì
N
UN
P
M
o
C
C
UN
e
H
T
D
N
UN
,

F
o
S
e
tu
l
UN
V

]
P

|
|

q
[
l
K
D

:
e
C
N
e
G
R
e
v
io
D
)
l
K

(

R
e
l
B
io
e
l
–
k
C
UN
B
l
l

tu
K

)
S

o
(
P
G
o
l

)
S
(
q

E
+

]
)
S
(
P

|
|

)
S
(
q
[
l
K
D
−

S
D

]
q

|
|

P
[
l
K
D
R
o

)
S
(
q
G
o
l

)
o

S
(
P

E
+

]
)
o

S
(
P
[

H
−

)
S
(
q

)
o

S
(
P

G
o
l

)
S
(
q

(cid:11)

T
N
e
M
M
o
C

]
)
o

D
N
tu
o
B

io
sì
N
é
R

S
(
P

|
|

)
S
(
q
[
α
D
−

e
C
N
e
G
R
e
v
io
D

io
sì
N
é
R

]
)
o

S
(
P

|
|

)
S
(
q
[
α
D

R
o
e
C
N
UN
T
S
io
D
R
e
G
N
io
l
l
e
H
e
H
T

F
o
N
o
io
T
C
N
tu
F

.
e
C
N
e
G
R
e
v
io
D
UN
sì
sì
R
UN
H
C
UN
T
T
UN
H
B
e
H
T

S
T
N
e
M
tu
G
R
UN
R
io
e
H
T
N
io

C
io
R
T
e
M
M
sì
S

e
R
UN
H
T
o
B

:
e
C
N
e
G
R
e
v
io
D
–
2
χ
o
T

1
−
D

2 P
q

(cid:11)

)
P

q
(
2
χ

l
UN
N
o
io
T
R
o
P
o
R
P

(cid:10)

]
)
o

S
(
P

|
|

)
S
(
q
[
2
χ
+
1

(cid:9)

G
o
l

−

(cid:10)

]
)
o

S
(
P

(cid:12)

)
)
)
S
(
q

)
o

S
(
P
(
2
l
e

H
(
G
o
l
2

)
)
)
S
(
q

)
o

S
(
P
(
2
l
e
H
−
1
(
G
o
l
2
−

S
D
)
S
(
q
)
o

S
(
P

G
o
l
2

S
D
)
S
(
q
)
o

S
(
P

G
o
l
2
−

(cid:12)

|
|

)
S
(
q
[
2
χ
+
1

(cid:9)

G
o
l

2
=
α

)
S
(
q

)
o

S
(
P

S
∈
S
X
UN
M
G
o
l

∞
→
α

≤

)
P

q
(
2
l
e

:
R
e
D
R
o

G
N
io
S
UN
e
R
C
e
D
N
o
N

e
v
UN
H

S
e
C
N
e
G
R
e
v
io
D

e
S
e
H
T

.
e
C
N
e
G
R
e
v
io
D
UN

T
o
N

S
io

H
T
G
N
e
l
N
o
io
T
P
io
R
C
S
e
D
M
tu
M
io
N
io
M

)
S
(
q

)
o

S
(
P

S
∈
S
X
UN
M
G
o
l

−

.
)
4
1
0
2
,
S
o
M
e
R
R
UN
H
&
N
e
v
R
E
N
UN
V

(

)
P

q
(
2
χ
≤

]
P

|
|

q
[
2

D
≤

]
P

|
|

q
[
1

D
≤

]
P

|
|

T
io

io
l

e
H
T

e
S
tu
UN
C
e
B

T
io

M
o

:
S
e
T
o
N

→
α

q
[

→
α

0
=
α

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

838

log p(o) = 1

1 − α log
(cid:3)

(cid:2)

P(o, S)1−α

α
q(S)
(cid:4)(cid:5)

Rényi Bound

+ 1
α − 1
(cid:3)

ds
(cid:6)

log p(o) = −Dα[q(S)||P(o, S)] + Dα[q(S)||P(S|o)].

N. Sajid et al.

(cid:2)

P(S|o)1−α

log

α
q(S)
(cid:4)(cid:5)
Rényi Divergence

ds
(cid:6)

(3.8)

(3.9)

We assume that q(S) and p(S|o) are nonzero and α ∈ R+ \ {1}. Addition-
alleato, we are licensed to make the move from equations 3.5 A 3.6 because
P(o) does not depend on s. The negative Rényi bound can be regarded as
being analogous to the variational free energy objective (F) by providing
an upper bound to the negative log evidence (see equation 2.7):

− log p(o) = 1

α − 1

log

≤ 1

α − 1

log

(cid:2)

α
q(S)

P(o, S)1−α

ds − 1

α − 1

log

(cid:2)

α
q(S)

P(S|o)1−α

α
q(S)

P(o, S)1−α

ds = Dα[q(S)||P(o, S)].

(3.10)

(3.11)

Similar to the Rényi divergence, we expect variations in the estimation of
the approximate posterior with α under the Rényi bound. Explicitly, Quando
α < 1, the variational posterior will aim to cover the entire true posterior; + this is known as exclusivity (or zero-avoiding) property. Thus, α → 0 op- timization constrains the variational posterior to be positive whenever the true posterior is positive. Formally, for all s : p(s, o) > 0 ⇒ q(S) > 0. Questo
leads to mass-covering variational estimates and increased variability. Fur-
thermore, α → +∞ optimization constrains the variational posterior to be
zero whenever the true posterior is zero. Here, the variational posterior will
seek to fit the true posterior at its mode; this is known as inclusivity (O
zero-forcing) mode-seeking behavior (Li & Turner, 2017). In questo caso, for
all s : P(S, o) = 0 ⇒ q(S) = 0. This leads to mass-seeking variational posteri-
ors. Hence, the Rényi bound should provide a formal account of behavioral
differences through changes in the α parameter. Questo è, we would expect
a natural shift in behavioral preferences as we move from small values to
large, positive α values, given fixed priors. Sezione 5 demonstrates this shift
in preferences in a multiarmed bandit setting.

4 Variational Bounds, Precision, and Posteriors

It is important to determine whether this formulation of behavior intro-
duces fundamentally new differences that cannot be accounted for by al-
tering the priors under a standard variational objective. Così, we compare
the Rényi bound and the variational free energy on a simple system to see
whether the same kinds of inferences can be produced through the Rényi

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Bayesian Brains and the Rényi Divergence

839

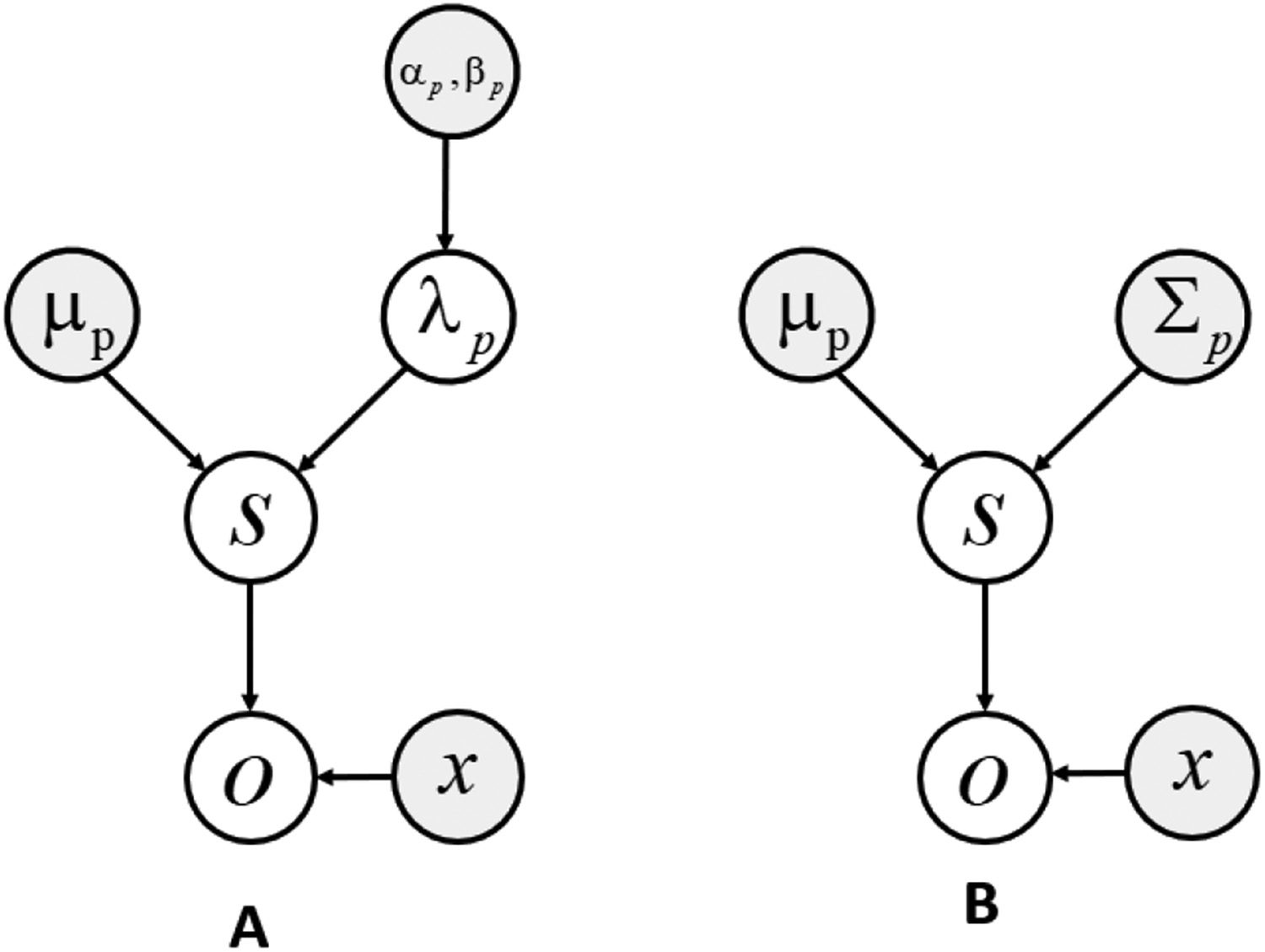
Figura 1: Graphical model for the gaussian-gamma (UN) and gaussian (B) sys-
tem. White circles represent random variables, gray circles represent priors, E
x is the parameter governing the mean. The difference between these models is
that in model A, the precision parameters over hidden states λ
p are random vari-
, β
ables that follow a gamma distribution with parameters α
P, while in model
B, the precision is held fixed. Here, the scalar parameter σ
p has been deliberately
omitted from the figure.

bound (see equation 3.3) with fixed prior beliefs but altered α value and
through the standard variational objective (see equation 2.3) with altered
prior beliefs. If this were to be the case, we would be able to rewrite the
variational free energy under different precision hyperpriors as the Rényi
bound, where hyperparameters now play the role of the α parameter. If
this correspondence holds true, the two variational bounds (cioè., Rényi and
variational free energy) would share similar optimization landscapes (cioè.,
inflection or extrema), with respect to the posterior under some different
priors or α value.

Variations in these hyperpriors speak to different priors, under which
agents can exhibit conservative or greedy choice behavior. Practically, Questo
may be a result of either lending one contribution more precision through
weighting the log probability under the standard variational objective or
altering the priors by taking the log of the probability to the power of α.
To illustrate this equivalence, we consider the following systems (see Fig-
ure 1). Primo, we formulate a gaussian-gamma system to derive the analyti-
cal (exact) form of the variational free energy. Here, the system is gaussian
with gamma priors over the variance that allows us to alter prior beliefs. UN
gamma prior is necessary to model an unknown variance. Prossimo, we intro-
duce a system with a simple gaussian parameterization to derive the analyt-
ical form of the Rényi bound. The difference in parameterization is required
to establish whether changes in prior beliefs (or precision) are equivalent to
the α parameter. In other words, this formulation allows us to ask whether

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

840

N. Sajid et al.

one can either alter the precision prior or the α value to evince behavioral
differences. If this were the case, we would expect equivalences between
the two analytical bounds, given the different parameterizations.

Though the problem setting is simple, it provides an intuition of what (if
any) sort of correspondence exists between the Rényi bound and the varia-
tional free energy functional using different priors.

4.1 Variational Free Energy for a Gaussian-Gamma System. To derive
the variational free energy, we consider a simple system with two random
variables: s ∈ S denoting (hidden) states of the system and o ∈ O the obser-
vations (see Figure 1A). λ
k is the covariance,
and x the parameter governing the mean. The variational family is param-
eterized as a gaussian. This is formalized as

k is the precision parameter, (cid:7)

P(S, λp) = N (S; 0, (λpσp)

−1)Gam(λp; αp, βp),

P(o|S) = N (sx, (cid:7)

l ),
q(S) = N (μq, (cid:7)q),

(4.1)

(4.2)

(4.3)

−1, s are scalars, o has dimension n, and x has dimension-
Dove (cid:7)p = (λpσp)
ality n × 1. Here, (cid:7)
l represents the covariance over the likelihood and (cid:7)
k the
covariance where k ∈ (P, l, q). In equation 4.1, μp = 0 and has been written
as such. Additionally, equation 4.1 denotes the joint probability distribution
over p(S, λp) = p(S|λp)P(λp) (Bishop, 2006; Murphy, 2007).

We use these quantities to derive the variational free energy (see ap-

pendix B for the derivation):

−DKL[q(S)||P(S, o)]

(cid:13)

= 1
2

log

|(cid:7)q|
(2π )N|(cid:7)P||(cid:7)
l

(cid:14)

(cid:16)
l x − 2μqxT (cid:7)−1
l o

l o + μ2

(cid:7)−1
P

+ μ2

(cid:15)
oT (cid:7)−1
(cid:15)
(cid:7)qxT (cid:7)−1

− 1
2
− 1
2

l x + (cid:7)q(cid:7)−1
λαp−1
β αp
P
P
(cid:9)(αp)

− λpβp.

− log

qxT (cid:7)−1
(cid:16)

− 1

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

(4.4)

(4.5)

(4.6)

(4.7)

For additional terms introduced via the gamma prior, see equation 4.7.

4.2 Rényi Bound for a Gaussian System. Prossimo, we consider a similar
system for deriving the Rényi bound. Unlike for the system in section 4.1

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

Bayesian Brains and the Rényi Divergence

841

the densities are parameterized as a gaussian distribution (see Figure 1B),

P(o|S) = N (sx, (cid:7)

P(S) = N (0, (cid:7)P),
l ),
q(S) = N (μq, (cid:7)q),

(4.8)

(4.9)

(4.10)

where s is a scalar, o has dimension n, and x has dimensionality n × 1. Ad-
ditionally, μp = 0 and has been written as such. We use these quantities to
derive the Rényi bound (see appendix B for the derivation):

= 1
2

(cid:13)

log

−Dα[q(S)||P(S, o)]
|(cid:7)q|
(2π )N|(cid:7)P||(cid:7)
l
(cid:15)
α
oT (cid:7)−1
2((cid:7)q(cid:7)−1
α )

−

(cid:14)

l o + μ2

(cid:7)−1
P

+ μ2

qxT (cid:7)−1

(cid:16)
l x − 2μqxT (cid:7)−1
l o
(cid:16)(cid:16)

l x + (cid:7)q(cid:7)−1

− 1

−

1
2(1 − α)
(cid:15)

− 1

2(cid:7)−1
α

(cid:15)
1 + (1 − α)

(cid:15)

log

(cid:7)qxT (cid:7)−1
(cid:16)
p oT (cid:7)−1
l o

(1 − α)(cid:7)−1

(4.11)

(4.12)

(4.13)

(4.14)

(cid:15)

(cid:16)

(cid:16)−1

(cid:7)−1
P

+ α(cid:7)−1

(1 − α)

+ xT (cid:7)−1
Dove, (cid:7)α :=
l x
, under the assumption
Quello (cid:7)α is positive-definite. Since (cid:7)α is a scalar, this is equivalent to satisfy-
(cid:7)q < α. ing the following condition: (cid:7)α (cid:8) 0 ⇐⇒ (α − 1) Importantly, if α ≤ 1, the condition is always true for any choice of (cid:7)q. (cid:7)p However, for α > 1, we must impose (cid:7)q < α α−1 Cov(p(s|o)) α−1 1+(cid:7)pxT (cid:7)−1 l x (Burbea, 1984; Metelli, Papini, Faccio, & Restelli, 2018). + xT (cid:7)−1 l x (cid:7)−1 p = α (cid:15) (cid:16) q 4.3 Correspondence between Variational Free Energy and the Rényi Bound. Using the derived bounds above, we examine the correspondence between the variational free energy and the Rényi bound. First, we consider the case when α → 1. Here, we expect to find an exact correspondence between the variational free energy and the Rényi bound as the Rényi divergence tends toward the KL-divergence as α → 1. Our derivations confirm this, upon comparison of the equivalent terms for each objective. The first terms in each objective, equations 4.4 and 4.11, are the same. Interestingly, the second term in the Rényi bound, equation 4.12, is a scalar multiple of the second term in variational free energy (see equa- α tends to 1 for α → 1. The third term tion 4.5), where the scalar quantity (cid:7)q(cid:7)−1α in equation 4.13, for α → 1, is a limit of the form limx→0 x log(1 + xw) = w, 1 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 4 8 2 9 2 0 0 3 0 7 7 n e c o _ a _ 0 1 4 8 4 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 842 N. Sajid et al. resulting exactly in equation 4.6. Finally, the last term in the Rényi bound tends to zero as α → 1, equation 4.14. Next, we evaluate the correspondence between the variational free en- ergy and Rényi bound when α ∈ R+ \ {1}. Now, the α values scale the terms in the Rényi bound with equation 4.14 having an influence on the final bound estimate. For comparability, we introduced the gamma prior to a simple gaussian system. As shown in equation 4.7, this introduces addi- tional terms that scale the free energy F. We expect the scaling from the α parameter to have some correspondence to the precision priors in the gaussian-gamma system. To assess this, we plot the variational objectives as a function of their estimated sufficient statistics for this simple system (see Figure 2). The numerical simulation illustrates that optimization of these objectives, for appropriate priors (αp, βp) or the α value, can lead to (ex- tremely) different variational densities. Interestingly, the two variational objectives exhibit a similar optimiza- tion landscape under specific parameterizations. For example, a striking (local) minimum of −33.14 nats is observed when αp is approximately 1, βp is greater than 0.8, and α < 5. However, this is constrained to a small space of posterior μq estimates. Outside these posterior parameters, the optimization landscape differs. Importantly, this difference becomes more acute when considering σq. Here, σq represents 1-dimensional (cid:7)q. This sug- gests hyperpriors may be particularly important in shaping the correspon- dence between the two variational objectives. However, the optimization profile can differ under inappropriate priors (i.e., a misalignment between prior beliefs and α value) and lead to divergences in the estimated varia- tional density (see Figure 2). Briefly, we do not observe a direct correspondence in the optimization landscapes (and the variational posterior) for certain priors or α value. These numerical analyses demonstrate that the Rényi divergences account for behavioral differences in a way that is formally distinct from a change in priors, through manipulation of the α parameter. Conversely the stan- dard variational objective could require multiple alterations to the (hyper- )parameters to exhibit a similar functional form in some cases. Further investigation in more complex systems is required to quantify the corre- spondence (if any) between the two variational objectives. 5 Multiarmed Bandit Simulation In this section, we illustrate the differential preferences that arise natu- rally under the Rényi bound. For this, we simulated the multiarmed bandit (MAB) paradigm (Auer et al., 2002; Lattimore & Szepesvári, 2020) using three arms. The MAB environment was formulated as a one-state Markov decision process (MDP) that is, the environment remains in the same state independent of agents’ actions. At each time step t, the agent could pull one arm and a corresponding outcome (i.e., score) Rt was observed. The agent’s l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 4 8 2 9 2 0 0 3 0 7 7 n e c o _ a _ 0 1 4 8 4 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Bayesian Brains and the Rényi Divergence 843 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 4 8 2 9 2 0 0 3 0 7 7 n e c o _ a _ 0 1 4 8 4 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 q (a) and σ q (b). Here, σ p (center column) or β q represents 1-dimensional (cid:7) Figure 2: Heat map of variational bounds as a function of estimated sufficient statistics: μ q. These graph- ics plot the optimization landscape for changing priors or α values. The first column plots the Rényi bound, as a function of α on the x-axis and μ q (a) or σ q (b) on the y-axis. Similarly, the next two columns plot the free energy, as a q (a) or σ function of α q (b) on the y-axis. The variational bound ranges from −33 (yellow) to −47 nats (blue). The empty region in panel b for different α values in the Renyi bound is q for α > 1
a consequence of the (positive-definiteness) constraint imposed on (cid:7)
(cid:7)P
restricting the possible values to be < α . When not varying, hy- 1+(cid:7)pxT (cid:7)−1 α−1 l x = 0.8, = 0.8, λ = 0.8, β = 1e − 4, α perparameters are fixed with μ q p = I x = {r : r = 1.1 × n, n ∈ {0, 1, . . . 19}}, y = 0.4 × x, (cid:7) 20. l p (right column) on the x-axis and μ = 0.4, σ q p p objective was to identify, and select, the arm with the highest Sharpe ratio (Sharpe, 1994) through its interactions with the environment across X trials. The Sharpe ratio is a well-known financial measure for risk-adjusted re- turn. It is an appropriate heuristic for action selection because it measures the expected return after adjusting for the variance of return distribution (i.e., return to variability ratio). In particular, given the expected return of an arm R = E[Rt], the Sharpe ratio is defined as SR := E[Rt ] V[Rt ] , where V[Rt] is the variance of return distribution for a specific arm. This heuristic was chosen because it nicely illustrates how changes in α influence the sufficient 844 N. Sajid et al. statistics of the variational posterior and ensuing behavior. Practically, this means we sample from the posterior distribution for each state (i.e., arm) and select actions that maximize the Sharpe ratio. The Sharpe ratio affords an action selection criterion that accommodates posterior uncertainty about hidden states, which underwrites choice behavior. For example, posterior estimates for some (suboptimal) arms may have high variance, meaning the expected reward is obtained with less certainty. If actions were selected to sample from the arm with the highest reward, then suboptimal arms with uncertain payoff may be selected with unduly high probability. The Sharpe ratio precludes this, penalizing arms with high posterior uncertainty. We modeled each arm with a fixed multimodal distribution (a mixture of gaussians) unknown to the agent, characterizing this as stationary stochas- tic bandit setting. Explicitly, this entailed the following parameterization for each arm: 2(cid:17) p(s) = ω N (μ i i , (cid:7) i), i p(o|s) = N (s, 1.0), q(s) = N(μq, (cid:7)q), 2(cid:17) i ω i = 1, ω i > 0,

(5.1)

(5.2)

(5.3)

(5.4)

Dove, s denotes the hidden state over the arm distribution and o the ob-
served return (R) from an arm. The variational density q(S) was constrained
as a gaussian with an arbitrary mean and variance, under a mean-field as-
sumption.7 However, due to the multimodal prior, the true posterior could
take a complex form that might not be in the variational family of distribu-
zioni. This introduces differences in posteriors that are evident under differ-
ent Rényi bounds. In Figure 3, we show the true distribution for each arm
that is unknown to the agent. The Sharpe ratio for arm 1 was SR = 2.03;
arm 2 was SR = 1.76; and arm 3 was SR = 6.20. Così, arm 3 was the best
choice in our paradigm as the arm with the maximal Sharpe ratio. Accord-
ingly, we measured performance using accumulated regret, R, defined as
R =
is the maximal Sharpe ratio from arm 3
and SRt the Sharpe ratio for the arm pulled at iteration t.

t=1(SR∗ − SRt ). Here, SR∗

Optimizing the Rényi bound under different α values led to varying pos-
terior estimates and accompanying behavioral differences manifested by
distinct arm choices. To show this, we simulated six agents optimizing the
Rényi bound for distinct α values: → +∞, 10, 2, → 1
– across

−, 0.5, → 0

(cid:18)

Questo è, a fully factorized variational distribution. For further details see Minka (2005),

Parr, Sajid, and Friston (2020), and Sajid, Convertino, and Friston (2021).

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Bayesian Brains and the Rényi Divergence

845

Figura 3: Score distribution for each arm. The panels plot the score distributions
for each arm. The x-axis is the s ∼ q(S) and y-axis the score density. Arm 1 ha
=
a multimodal distribution of μ1
1
=
0.97 and ω1
2
= 1) E
16 ((cid:7)2
1
μ3
2

= 1) with ω1
1
= 0.03, rispettivamente. Arm 2 has a gaussian distribution with μ2
1

= 3), and arm 3 has a multimodal distribution of μ3
1
= 0.03, rispettivamente.
= 0.97 and ω3
2

= 1) with ω3
1

= 1) and μ1
2

= 18 ((cid:7)3
1

= 10 ((cid:7)3
2

= 10 ((cid:7)1
1

= 22 ((cid:7)1
2

4000 iterations, repeated 20 times for each agent. Throughout, the agents
selected an arm according to the following strategy. At each iteration, IL
Sharpe ratio (Sharpe, 1994) was calculated for each arm by dividing a sam-
pled point from the estimated posterior with its variance. The arm with the
, (cid:7)io
highest Sharpe ratio was pulled. Formalmente, we sample one si
q)
for each arm i and pull arm,

∼ q(·|μi
q

∗ = argmax
io

si
(cid:7)io
q

(5.5)

Dove (cid:7)io
q is the variance of the variational posterior for arm i. In this set-
ting, we sampled from the posterior to calculate the Sharpe ratio instead of
using the parameter μq optimized under each bound. This avoided prema-
ture convergence to suboptimal policies that selected the greedy arm and
therefore encouraged exploration.

In contrast with section 4.2, for these simulations, we do not compute
the analytical expression for the Rényi bound. Invece, at each iteration,
we used 300 Monte Carlo samples to estimate the gradient of the bound,
which would otherwise be intractable for a multimodal distribution. Prac-
tically, we employed sampling to estimate the gradient updates. This ne-
cessitates a stochastic gradient descent method, Dove, at each iteration,
the Monte Carlo samples were used to calculate the posterior estimate (COME
introduced in Li & Turner, 2017). For this, we used ADAM, as implemented
in Pytorch (Paszke et al., 2019) as the optimizer because it is known to
adequately escape local minima during optimization. Tuttavia, other op-
timization strategies could be used here (per esempio., Momentum or RMSProp;
Soydaner, 2020). Additionally, for each arm, there was a separate memory
buffer and optimization process. The agent learned the score distribution

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

846

N. Sajid et al.

Figura 4: Regret (UN) and Sharpe ratio (B) under the Rényi bound. (UN) The line
plot illustrates the cumulative regret across the 4000 iterations for each agent
optimizing a particular Rényi bound. The x-axis denotes the iteration and y-
axis the accompanying cumulative regret. (B) The line plot illustrates the aver-
age achieved Sharpe ratio of an agent across the 4000 iterations, for each partic-
ular Rényi bound. The x-axis denotes the iteration and y-axis the Sharpe ratio.
Here, blue is for agents optimizing Rényi bound for α → +∞, orange for α = 10,
green for α = 2, red for α → +1−, purple for α = 0.5, and brown for α → 0+.
Dashed black line represents regret under a random policy (cioè., any arm). Each
agent was simulated 20 times (95% confidence interval). In our simulations, IL
agents with α → +1− and α = 2 obtained the best performance.

through the memory buffer that stored the previous 1000 observations. A
each iteration, the observations in memory were used to optimize the varia-
tional posterior estimate. We then selected the appropriate arm by sampling
the variational posterior estimate, at each iteration for each arm and using
it to compute a sample estimate of the Sharpe ratio. This provided an ade-
quate trade-off between exploration and exploitation. Appendix C provides
further experimental details.

The only variable varying across simulations was the α parameter. A
assess the performance of each α, we plot the accumulated regret and
the accompanying Sharpe ratio in Figure 4. We observe that optimizing
−; 2 leads to the lowest cumulative regret and a high Sharpe ratio.
α → +1
+; → +∞ leads to the highest cumulative re-
Conversely, optimizing α → 0
gret and lowest Sharpe ratio.

To investigate this further, we plot the variational bounds for arm 1 un-
der different α parameters (Guarda la figura 5). Recall from Figure 3 that if the
variational posterior fits the right-hand-side mode, this results in subopti-
mal arm selection and the highest regret. This is because the agent would
wrongly infer a high Sharpe ratio for this particular arm, while it is in fact
low, increasing the probability that it was selected. We can explain the high
+
regret of agents with α → +∞; → 0
from the property of their variational
bound. For agents optimizing α → +∞, the approximate posterior fit the
right-hand-side mode of the distribution due to its lower variance (cioè.,
+
mode-seeking behavior). Conversely, agents with α → 0
would exhibit

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Bayesian Brains and the Rényi Divergence

847

Figura 5: The Rényi bound as a function of the variational posterior. Here, P
q
represents 1-dimensional (cid:7)
q. The contour plots show the optimization land-
scape for each α. For α = 1e9, we observe two optima; for small α (1e − 6), IL
optimal solution exhibits high variance.

mass-covering, high-variance posterior estimates. In contrasto, agents opti-
−; 0.5 covered the left-hand-side mode and thus estimated a
mizing α → 1
lower Sharpe ratio for this particular arm, which decreased the probability
of it being selected (Guarda la figura 5).

These numerical experiments suggest that if agents sample their actions
from posterior beliefs about what they are sampling and those posterior be-
liefs depend on the form of the Rényi bound α parameterization, then there
is a natural space and explanation for behavioral variations. In short, IL
shape of the posterior that underwrites ensuing behavior depends sensi-
tively on the functional form of the variational bound.

6 Discussion

This article accounts for behavioral variations among agents using Rényi
divergences and their associated variational bounds. These divergences are
Rényi relative entropies8 and satisfy similar properties as the KL diver-
gence (Rényi, 1961; Van Erven & Harremos, 2014). Rényi divergences de-
pend on an α parameter that controls the strength of the bound and induces
different posterior estimates about the state of the world. In turn, differ-
ent beliefs about the world lead to differences in behavior. This provides a

The Rényi entropy provides a parametric family of measures of information (Rényi,

1961).

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

848

N. Sajid et al.

natural explanation as to why some people are more risk averse than oth-
ers. For this alternative account to hold, we assumed throughout that agents
sample their actions from posterior beliefs about the world, and those pos-
terior beliefs depend on the form of the Rényi bound’s α parameter. Yet
note that a similar account is possible if actions depended on an expected
free energy functional (Friston et al., 2017; Han, Doya, & Tani, 2021; Parr
& Friston, 2019; van de Laar, Senoz, Özçelikkale, & Wymeersch, 2021), In-
trinsic reward (Schmidhuber, 1991, 2006; Storck et al., 1995; Sun, Gomez,
& Schmidhuber, 2011) or any class of objective functions that incorporates
beliefs about the environment.

This space of Rényi bounds can provide different posterior estimates
(and consequent behavioral variations) that vary smoothly with α. As il-
lustrated, in the bimodal scenario under our Rényi divergence definition,
large, positive α values will approximate the mode with the largest mass.
This happens because α ≥ 1 forces the approximate posterior to be small
(cioè., q(·) = 0), whenever the true posterior is small (cioè., zero-forcing). Questo
causes parts of the true posterior (the parts with the small total mass) A
be excluded. Così, the estimated variational posterior might be underesti-
mated. Conversely, with small α values, the approximation tries to cover
the entire distribution, eventually forming an upper bound when α → 1
(Vedi la tabella 1). This happens because α → 1 forces the approximate poste-
rior to be positive (cioè., q(·) > 0) whenever the true posterior is positive (cioè.,
zero-avoiding). This implies that all parts of the true posterior are included,
and the variational posterior may be overestimated.

Crucially, Rényi divergences account for posterior differences in a way
that is formally distinct from a change in prior beliefs. This stems from the
ability to disentangle different preference modes by varying the bound’s α
parameter. Explicitly, we demonstrate that the Rényi bounds influences the
posterior estimate over particular states (cioè., inference procedure). How-
ever, by selecting actions based on these inferences, the Rényi parame-
terization shapes the preferences of the model. We observe this in our
simple multiarmed bandit setting where large α values seek to fit the pos-
terior modes that lead to greater consistency in preferences over which arm
to select. Conversely, small α values try to cover the posterior distribution
that led to greater flexibility over the choice of arm.

This contrasts with formal explanations based on adjusting the precision
or form of the prior under a variational bound based on the KL-divergence
(cioè., α = 1). Under active inference (Da Costa et al., 2020; Friston et al., 2017),
multiple behavioral deficits have been illustrated by manipulation of the
precision over the priors (Parr & Friston, 2017; Sajid et al., 2020). Although
there has been some focus on priors and on the form of the variational pos-
terior (Schwöbel, Kiebel, & Markovi´c, 2018), relatively little attention has
been paid to the nature of the bound itself in determining behavior.

6.1 Implications for the Bayesian Brain Hypothesis. Our work is pred-
icated on the idea that the brain is Bayesian and performs some sort of

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Bayesian Brains and the Rényi Divergence

849

variational inference to infer its environment from its sensations. Practi-
cally, this entails the optimization of a variational functional to make ap-
propriate predictions. Tuttavia, there are no unique functional forms for
implementing such systems and what variables account for differences in
observed behavior. On the basis of the above, we appeal to Rényi bounds,
in addition to altered priors, to model behavioral variations. By commit-
ting to the Rényi bound, we provide an alternative perspective on how
variant (or suboptimal) behavior can be modeled. This leads to a concep-
tual reversal of the standard variational free energy schemes, including pre-
dictive processing (Bogacz, 2017B; Buckley, Kim, McGregor, & Seth, 2017).
Questo è, we can illustrate behavioral variations to be due to different vari-
ational objectives given particular priors instead of different priors given
the variational free energy. This has implications for how we model im-
plementations of variational inference in the brain. Questo è, do we model
suboptimal inferences using altered generative models or alternative vari-
ational bounds? This turns out to be significant in light of our numerical
analysis (see section 4.3) that show no formal correspondence between these
formulations.

In a deep temporal system like the brain, one might ask if different cor-
tical hierarchies might be performing inference under different variational
objectives. It might be possible for variational objectives for lower levels to
be modulated by higher levels through priors over α values, a procedure of
meta-inference. This is analogous to including precision priors over model
parameters that have been associated with different neuromodulatory sys-
tems, such as state transition precision with noradrenergic and sensory pre-
cision with cholinergic systems (Fountas, Sajid, Mediano, & Friston, 2020;
Parr & Friston, 2017). Consequently, this temporal separation of α parame-
terizations may provide an interesting research avenue for understanding
the role of neuromodulatory systems and how they facilitate particular be-
haviors (Angela & Dayan, 2002, 2005).

6.2 Generalized Variational Inference. The Rényi bound provides a
generalized variational inference objective derived from the Rényi diver-
gence. This is because Rényi divergences comprise the KL divergence as
a special case (Minka, 2005). These divergences allow us to naturally ac-
count for multiple behavioral preferences, directly via the optimization ob-
jective, without changing prior beliefs. Other variational objectives can be
derived from other general families of divergences such as f-divergences
and Wasserstein distances (Ambrogioni et al., 2018; Dieng, Tran, Ranganath,
Paisley, & Blei, 2016; Regli & Silva, 2018), which can improve the statistical
properties of the variational bounds for particular applications (Wan, Li, &
Hovakimyan, 2020; Zhang, Bird, Habib, Xu, & Barber, 2019). Future work
could generalize the arguments presented here and examine how these dif-
ferent divergences shape behavior when planning as inference.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

850

N. Sajid et al.

6.3 Limitations and Future Directions. We do not observe a direct cor-
respondence between the Rényi bound and the variational free energy un-
der particular priors. Tuttavia, our evaluations are based on a restricted
gaussian system. Therefore, future work should investigate this in more
complex systems to show what sorts of prior modifications are critical in es-
tablishing similar optimization landscapes for different variational bounds
in order to understand the relationship between the two. This will entail
further exploring the association between the variational posterior and β
or α value.

Implementations of the Rényi bound are constrained by sampling biases
and interesting differences in optimization landscape. Infatti, when α is ex-
tremely large, even if the approximate posterior distribution belongs to the
same family as the true posterior, the optimization becomes very difficult,
causing the bound to be too conservative and introduce convergence issues.
Tuttavia, it must be noted that instances of this are due to the numerics of
optimizing the Rényi bound rather than a failure of the bound itself. Prac-
tically, this means that careful consideration needs to be given to both the
learning rate and stopping procedures during the optimization of the Rényi
bound.

Our work includes implicit constraints on the form of the variational
posterior. We have assumed a mean-field approximation in our simula-
zioni. Tuttavia, this does not necessarily have to be the case. È interessante notare,
richer parameterizations of the variational posterior might negate the im-
pact of the α values. Specifically, we noted that if the true posterior is in the
same family of distributions as the variational posterior, then changing the
α value does not have an impact on the shape of the variational posterior
E, consequently, the system’s behavior. Tuttavia, complex parameteriza-
tions are computationally expensive and can still be inappropriate. There-
fore, this departure from vanilla variational inference provides a useful
explanation for different behaviors that biological (or artificial) agents
might adopt, under the assumption that the brain performs variational
Bayesian inference. Orthogonal to this, an interesting future direction is in-
vestigating the connections between the variational posterior form and how
it may affect the variational bound. This has direct consequences for the
types of message passing schemes that might be implemented in the brain
(Minka, 2005; Parr, Markovic, Kiebel, & Friston, 2019).

We illustrate that the Rényi divergences, and their associated bounds,
provide a complementary (but alternate) formulation to manipulation of
priors for evaluating behavioral variations. Empirically, this poses an inter-
esting question: Are observed differences in choice behavior a consequence
of α values (cioè., optimization objective difference) or specific priors—when
the variational family is not in the same family of distributions as the
true posterior? Formalmente, Rényi bound with α → 0 values provide a more
graceful way of accounting for uncertainty or keeping options open while

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

F
/

3
4
4
8
2
9
2
0
0
3
0
7
7
N
e
C
o
_
UN
_
0
1
4
8
4
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Bayesian Brains and the Rényi Divergence

851

making inferences about hidden states. We leave further links to human
choice behavior for future work.

7 Conclusione

We offer an account of behavioral variations using Rényi divergences and
their associated variational bounds that complement usual formulations in
terms of different prior beliefs. We show how different Rényi bounds induce
behavioral differences for a fixed generative model that are formally distinct
from a change of priors. This is accomplished by changes in an α parameter
that alters the bound’s strength, inducing different inferences and conse-
quent behavioral variations. Crucially, the inferences produced in this way
do not seem to be accounted for by a change in priors under the standard
variational objective. We emphasize that the Rényi bounds are analogous to
the variational free energy (or evidence lower bound) and can be derived
using the same assumptions. This formulation is illustrated through numer-
ical analysis and demonstrates that α > 1 values give rise to mode-seeking
behaviors and α < 1 values to mode-covering behaviors when priors are held constant. Software Note The code required to reproduce the simulations and figures is available at https://github.com/ucbtns/renyibounds. Acknowledgments N.S. is funded by Medical Research Council (MR/S502522/1). F.F. is funded by the ERC Advanced Grant (742870) and the Swiss National Super- computing Centre (CSCS, project s1090). L.D. is supported by the Fonds National de la Recherche, Luxembourg (project code 13568875). This publi- cation is based on work partially supported by the EPSRC Centre for Doc- toral Training in Mathematics of Random Systems: Analysis, Modelling and Simulation (EP/S023925/1). K.J.F. is funded by the Wellcome Trust (203147/Z/16/Z and 205103/Z/16/Z). Conflicts of Interest The authors declare no conflict of interest. References Amari, S.-i. (2012). Differential-geometrical methods in statistic. Berlin: Springer Science & Business Media. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 4 8 2 9 2 0 0 3 0 7 7 n e c o _ a _ 0 1 4 8 4 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 852 N. Sajid et al. Amari, S.-i., & Cichocki, A. (2010). Information geometry of divergence functions. Bulletin of the Polish Academy of Sciences. Technical Sciences, 58(1), 183–195. 10.2478/ v10175-010-0019-1 Ambrogioni, L., Güçlü, U., Güçlütürk, Y., Hinne, M., Maris, E., & van Gerven, M. A. (2018). Wasserstein variational inference. arXiv:1805.11284. Angela, J. Y., & Dayan, P. (2002). Acetylcholine in cortical inference. Neural Networks, 15(4–6), 719–730. 10.1016/S0893-6080(02)00058-8, PubMed: 12371522 Angela, J. Y., & Dayan, P. (2005). Uncertainty, neuromodulation, and attention. Neu- ron, 46(4), 681–692. 10.1016/j.neuron.2005.04.026, PubMed: 15944135 Auer, P., Cesa-Bianchi, N., & Fischer, P. (2002). Finite-time analysis of the multiarmed bandit problem. Machine L, 47(2), 235–256. 10.1023/A:1013689704352 Barber, D., & van de Laar, P. (1999). Variational cumulant expansions for intractable distributions. Journal of Artificial Intelligence Research, 10, 435–455. 10.1613/jair.567 Beal, M. J. (2003). Variational algorithms for approximate Bayesian inference. PhD diss., University College London. Bishop, C. M. (2006). Pattern recognition and machine learning. Berlin: Springer. Blei, D. M., Kucukelbir, A., & McAuliffe, J. D. (2017). Variational inference: A review for statisticians. Journal of the American Statistical Association, 112(518), 859–877. 10.1080/01621459.2017.1285773 Bogacz, R. (2017a). A tutorial on the free-energy framework for modelling per- ception and learning. Journal of Mathematical Psychology, 76, 198–211. 10.1016/ j.jmp.2015.11.003 Bogacz, R. (2017b). A tutorial on the free-energy framework for modelling per- ception and learning. Journal of Mathematical Psychology, 76, 198–211. 10.1016/ j.jmp.2015.11.003. Buckley, C. L., Kim, C. S., McGregor, S., & Seth, A. K. (2017). The free energy prin- ciple for action and perception: A mathematical review. Journal of Mathematical Psychology, 81, 55–79. 10.1016/j.jmp.2017.09.004 Burbea, J. (1984). Informative geometry of probability spaces (Tech. Rep.). Pittsburgh: University of Pittsburgh, Pennsylvania Center for Multivariate Analysis. Da Costa, L., Parr, T., Sajid, N., Veselic, S., Neacsu, V., & Friston, K. (2020). Active inference on discrete state-spaces: A synthesis. arXiv:2001.07203. Dayan, P., Hinton, G. E., Neal, R. M., & Zemel, R. S. (1995). The Helmholtz machine. Neural Computation, 7(5), 889–904. 10.1162/neco.1995.7.5.889, PubMed: 7584891 Dieng, A. B., Tran, D., Ranganath, R., Paisley, J., & Blei, D. M. (2016). Variational in- ference via χ-upper bound minimization. arXiv:1611.00328. Doya, K., Ishii, S., Pouget, A., & Rao, R. P. (2007). Bayesian brain: Probabilistic ap- proaches to neural coding. Cambridge, MA: MIT Press. FitzGerald, T. H., Schwartenbeck, P., Moutoussis, M., Dolan, R. J., & Friston, K. (2015). Active inference, evidence accumulation, and the urn task. Neural Com- put., 27(2), 306–328. 10.1162/NECO_a_00699 Fountas, Z., Sajid, N., Mediano, P. A., & Friston, K. (2020). Deep active inference agents using Monte-Carlo methods. arXiv:2006.04176. Friston, K., FitzGerald, T., Rigoli, F., Schwartenbeck, P., & Pezzulo, G. (2017). Active inference: A process theory. Neural Comput., 29(1), 1–49. 10.1162/NECO_a_00912 Friston, K. J., Rigoli, F., Ognibene, D., Mathys, C., Fitzgerald, T., & Pezzulo, G. (2015). Active inference and epistemic value. Cognitive Neuroscience, 6(4), 187–224. 10.1080/17588928.2015.1020053, PubMed: 25689102 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 4 8 2 9 2 0 0 3 0 7 7 n e c o _ a _ 0 1 4 8 4 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Bayesian Brains and the Rényi Divergence 853 Friston, K., Schwartenbeck, P., FitzGerald, T., Moutoussis, M., Behrens, T., & Dolan, R. J. (2014). The anatomy of choice: Dopamine and decision-making. Philos. Trans. R. Soc. Lond. B. Biol. Sci., 369(1655). 10.1098/rstb.2013.0481, PubMed: 25267823 Gelman, A., Carlin, J. B., Stern, H. S., & Rubin, D. B. (1995). Bayesian data analysis. London: Chapman and Hall/CRC. Han, D., Doya, K., & Tani, J. (2021). Goal-directed planning by reinforcement learning and active inference. arXiv:2106.09938. Hohwy, J. (2012). Attention and conscious perception in the hypothesis test- ing brain. Frontiers in Psychology, 3(2012), 1–14. 10.3389/fpsyg.2012.00096, PubMed: 22279440 Huzurbazar, V. S. (1955). Exact forms of some invariants for distributions admitting sufficient statistics. Biometrika, 42(3/4), 533–537. 10.2307/2333405 Jordan, M. I., Ghahramani, Z., Jaakkola, T. S., & Saul, L. K. (1999). An introduction to variational methods for graphical models. Machine Learning, 37(2), 183–233. 10.1023/A:1007665907178 Knill, D. C., & Pouget, A. (2004). The Bayesian brain: The role of uncertainty in neu- ral coding and computation. Trends in Neurosciences, 27(12), 712–719. 10.1016/ j.tins.2004.10.007, PubMed: 15541511 Kullback, S., & Leibler, R. A. (1951). On information and sufficiency. Annals of Math- ematical Statistics, 22, 79–86. 10.1214/aoms/1177729694 Lattimore, T., & Szepesvári, C. (2020). Bandit algorithms. Cambridge: Cambridge Uni- versity Press. Li, Y., & Turner, R. E. (2017). Rényi divergence variational inference. In I. Guyon, Y. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, & R. Garnett (Eds.), Advances in neural information processing systems, 30 (pp. 1073–1081). Red Hook, NY: Curran. Metelli, A. M., Papini, M., Faccio, F., & Restelli, M. (2018). Policy optimization via im- portance sampling. arXiv:1809.06098. Millidge, B., Tschantz, A., & Buckley, C. L. (2020). Predictive coding approximates back- prop along arbitrary computation graphs. arXiv:2006.04182. Minka, T. (2005). Divergence measures and message passing. Microsoft Research report UK MSR-TR-2005-173. Murphy, K. P. (2007). Conjugate Bayesian analysis of the gaussian distribution. http:// citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.126.4603 Parisi, G. (1988). Statistical field theory. New York: Basic Books. Parr, T., & Friston, K. J. (2017). Uncertainty, epistemics and active inference. Journal of the Royal Society Interface, 14(136), 20170376. 10.1098/rsif.2017.0376 Parr, T., & Friston, K. J. (2019). Generalised free energy and active inference. Biological Cybernetics, 113(5–6), 495–513. 10.1007/s00422-019-00805-w Parr, T., Markovic, D., Kiebel, S. J., & Friston, K. J. (2019). Neuronal message pass- ing using mean-field, Bethe, and marginal approximations. Scientific Reports, 9(1), 1889. 10.1038/s41598-018-38246-3 Parr, T., Sajid, N., & Friston, K. J. (2020). Modules or mean-fields? Entropy, 22(5), 552. Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., . . . Chintala, S. (2019). Pytorch: An imperative style, high-performance deep learning library. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, & R. Garnett (Eds.), Advances in neural information processing systems, 32 (pp. 8024–8035). Red Hook, NY: Curran. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 4 8 2 9 2 0 0 3 0 7 7 n e c o _ a _ 0 1 4 8 4 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 854 N. Sajid et al. Penny, W. (2012). Bayesian models of brain and behavior. ISRN Biomathematics, 2012, 785791. 10.5402/2012/78579110.5402/2012/785791 Perrykkad, K., & Hohwy, J. (2020). Fidgeting as self-evidencing: A predictive pro- cessing account of non-goal-directed action. New Ideas in Psychology, 56, 100750. 10.1016/j.newideapsych.2019.100750 Phan, M., Abbasi- Yadkori, Y., & Domke, J. (2019). Thompson sampling with approximate inference. arXiv:1908.04970. J.-B., & Silva, R. Regli, (2018). Alpha-beta divergence for variational inference. arXiv:1805.01045. Rényi, A. (1961). On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, vol. 1: Contributions to the theory of statistics. Regents of the University of California. Sajid, N., Convertino, L., & Friston, K. (2021). Cancer niches and their kikuchi free energy. Entropy, 23(5), 609. 10.3390/e23050609, PubMed: 34069097 Sajid, N., Ball, P. J., Parr, T., & Friston, K. J. (2021). Active inference: demys- tified and compared. Neural Computation, 33, 674–712. 10.1162/neco_a_01357, PubMed: 33400903 Sajid, N., Parr, T., Gajardo-Vidal, A., Price, C. J., & Friston, K. J. (2020). Paradoxical lesions, plasticity and active inference. Brain Communications, 2, fcaa164. 10.1093/ braincomms/fcaa164, PubMed: 33376985 Schmidhuber, J. (1990). Making the world differentiable: On using fully recurrent self- supervised neural networks for dynamic reinforcement learning and planning in non- stationary environments (Tech. Rep. FKI-126-90). Institut für Informatik, Technis- che Universität München. https://people.idsia.ch/∼juergen/FKI-126-90ocr.pdf Schmidhuber, J. (1991). Curious model-building control systems. In Proc. Interna- tional Joint Conference on Neural Networks (vol. 2, pp. 1458–1463). Piscataway, NJ: IEEE. Schmidhuber, J. (1992). Learning complex, extended sequences using the prin- ciple of history compression. Neural Computation, 4(2), 234–242. 10.1162/ neco.1992.4.2.234 Schmidhuber, J. (2006). Developmental robotics, optimal artificial curiosity, cre- ativity, music, and the fine arts. Connection Science, 18(2), 173–187. 10.1080/ 09540090600768658 Schmidhuber, J., & Heil, S. (1995). Predictive coding with neural nets: Application to text compression. In D. S. Touretzky, M. C. Mozer, & M. E. Hasselmo (Eds.), Advances in neural information processing systems (pp. 1047–1054). Cambridge, MA: MIT Press. Schwartenbeck, P., FitzGerald, T. H., Mathys, C., Dolan, R., Wurst, F., Kronbich- ler, M., & Friston, K. (2015). Optimal inference with suboptimal models: Ad- diction and active Bayesian inference. Med. Hypotheses, 84(2), 109–117. 10.1016/ j.mehy.2014.12.007, PubMed: 25561321 Schwöbel, S., Kiebel, S., & Markovi´c, D. (2018). Active inference, belief propagation, and the Bethe approximation. Neural Computation, 30(2) 1–38. Sharpe, W. F. (1994). The Sharpe ratio. Journal of Portfolio Management, 21(1), 49–58. 10.3905/jpm.1994.409501 Smith, R., Lane, R. D., Parr, T., & Friston, K. J. (2019). Neurocomputational mechanisms underlying emotional awareness: Insights afforded by deep active l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 4 8 2 9 2 0 0 3 0 7 7 n e c o _ a _ 0 1 4 8 4 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Bayesian Brains and the Rényi Divergence 855 inference and their potential clinical relevance. Neuroscience and Biobehavioral Re- views, 107, 473–491. 10.1016/j.neubiorev.2019.09.002, PubMed: 31518636 Soydaner, D. (2020). A comparison of optimization algorithms for deep learning. International Journal of Pattern Recognition and Artificial Intelligence, 34(13), 2052013. 10.1142/S0218001420520138, PubMed: 34267412 Spratling, M. W. (2017). A review of predictive coding algorithms. Brain and Cogni- tion, 112, 92–97. 10.1016/j.bandc.2015.11.003, PubMed: 26809759 Stigler, S. M. (1986). The history of statistics: The measurement of uncertainty before 1900. Cambridge, MA: Harvard University Press. Storck, J., Hochreiter, S., & Schmidhuber, J. (1995). Reinforcement driven information acquisition in non-deterministic environments. In Proceedings of the International Conference on Artificial Neural Networks (vol. 2, pp. 159–164). Sun, Y., Gomez, F., & Schmidhuber, J. (2011). Planning to be surprised: Optimal Bayesian exploration in dynamic environments. In J. Schmidhuber, K. R. Thóris- son, & M. Looks (Eds.), Proceedings of the 4th International Conference on Artificial General Intelligence (pp. 41–51). Berlin: Springer. 10.1007/978-3-642-22887-2_5 Tschantz, A., Seth, A. K., & Buckley, C. L. (2020). Learning action-oriented models through active inference. PLOS Computational Biology, 16(4), e1007805. 10.1371/ journal.pcbi.1007805, PubMed: 32324758 van de Laar, T., Senoz, I., Özçelikkale, A., & Wymeersch, H. (2021). Chance-constrained active inference. arXiv:2102.08792. Van Erven, T., & Harremos, P. (2014). Rényi divergence and Kullback-Leibler di- vergence. IEEE Transactions on Information Theory, 60(7), 3797–3820. 10.1109/ TIT.2014.2320500 Wainwright, M. J., & Jordan, M. I. (2008). Graphical models, exponential families, and variational inference. Foundations and Trends in Machine Learning, 1(1–2), 1– 305. 10.1561/2200000001 Wan, N., Li, D., & Hovakimyan, N. (2020). f-divergence variational inference. In H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan, & H. Lin (Eds.), Advances in neural information processing systems, 33. Red Hook, NY: Curran. Welbourne, S. R., Woollams, A. M., Crisp, J., & Lambon-Ralph, M. A. (2011). The role of plasticity-related functional reorganization in the explanation of central dyslexias. Cognitive Neuropsychology, 28, 65–108. 10.1080/02643294.2011.621937, PubMed: 22122115 Whittington, J. C. R., & Bogacz, R. (2017). An approximation of the error backprop- agation algorithm in a predictive coding network with local Hebbian synaptic plasticity. Neural Comput., 29(5), 1229–1262. 10.1162/NECO_a_00949 Zhang, M., Bird, T., Habib, R., Xu, T., & Barber, D. (2019). Variational f-divergence min- imization. arXiv:1907.11891. Received July 12, 2021; accepted November 29, 2021. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 4 4 8 2 9 2 0 0 3 0 7 7 n e c o _ a _ 0 1 4 8 4 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3

Scarica il pdf