ARTICLE
Communicated by Luke Prince
A Biologically Plausible Neural Network for Multichannel
Canonical Correlation Analysis
David Lipshutz
dlipshutz@flatironinstitute.org
Yanis Bahroun
ybahroun@flatironinstitute.org
Siavash Golkar
sgolkar@flatironinstitute.org
Center for Computational Neuroscience, Flatiron Institute,
New York, NY 10010, U.S.A.
Anirvan M. Sengupta
anirvans@physics.rutgers.edu
Center for Computational Neuroscience, Flatiron Institute, New York,
NY 10010, U.S.A., and Department of Physics and Astronomy,
Rutgers University, Piscataway, NJ 08854 U.S.A.
Dmitri B. Chklovskii
dchklovskii@flatironinstitute.org
Center for Computational Neuroscience, Flatiron Institute, New York,
NY 10010, U.S.A., and Neuroscience Institute, NYU Medical Center,
New York, NY 10016, U.S.A.
Cortical pyramidal neurons receive inputs from multiple distinct neu-
ral populations and integrate these inputs in separate dendritic compart-
menti. We explore the possibility that cortical microcircuits implement
canonical correlation analysis (CCA), an unsupervised learning method
that projects the inputs onto a common subspace so as to maximize the
correlations between the projections. A tal fine, we seek a multichan-
nel CCA algorithm that can be implemented in a biologically plausible
neural network. For biological plausibility, we require that the network
operates in the online setting and its synaptic update rules are local.
Starting from a novel CCA objective function, we derive an online op-
timization algorithm whose optimization steps can be implemented in a
single-layer neural network with multicompartmental neurons and lo-
cal non-Hebbian learning rules. We also derive an extension of our on-
line CCA algorithm with adaptive output rank and output whitening.
È interessante notare, the extension maps onto a neural network whose neural
D.L., Y.B., and S.G. contributed equally.
Calcolo neurale 33, 2309–2352 (2021) © 2021 Istituto di Tecnologia del Massachussetts
https://doi.org/10.1162/neco_a_01414
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2310
D. Lipshutz et al.
architecture and synaptic updates resemble neural circuitry and non-
Hebbian plasticity observed in the cortex.
1 introduzione
Our brains can effortlessly extract a latent source contributing to two syn-
chronous data streams, often from different sensory modalities. Consider,
Per esempio, following an actor while watching a movie with a soundtrack.
We can easily pay attention to the actor’s gesticulation and voice while fil-
tering out irrelevant visual and auditory signals. How can biological neu-
rons accomplish such multisensory integration?
In questo articolo, we explore an algorithm for solving a linear version of this
problem known as canonical correlation analysis (CCA; Hotelling, 1936). In
CCA, the two synchronous data sets, known as views, are projected onto
a common lower-dimensional subspace so that the projections are maxi-
mally correlated. For simple generative models, the sum of these projec-
tions yields an optimal estimate of the latent source (Bach & Jordan, 2005).
CCA is a popular method because it has a closed-form exact solution in
terms of the singular value decomposition (SVD) of the correlation matrix.
Therefore, the projections can be computed using fast and well-understood
spectral numerical methods.
To serve as a viable model of a neuronal circuit, the CCA algorithm must
map onto a neural network consistent with basic biological facts. For our
purposes, we say that a network is “biologically plausible” if it satisfies the
following two minimal requirements: (1) the network operates in the on-
line setting, questo è, upon receiving an input, it computes the corresponding
output without relying on the storage of any significant fraction of the full
insieme di dati, E (2) the learning rules are local in the sense that each synap-
tic update depends only on the variables that are available as biophysical
quantities represented in the pre- or postsynaptic neurons.
There are a number of neural network implementations of CCA (Lai &
Fyfe, 1999; Pezeshki, Azimi-Sadjadi, & Scharf, 2003; Gou & Fyfe, 2004; Vía,
Santamaría, & Pérez, 2007); Tuttavia, most of these networks use nonlo-
cal learning rules and are therefore not biologically plausible. One excep-
tion is the normative neural network model derived by Pehlevan, Zhao,
Sengupta, and Chklovskii (2020). They start with formulating an objective
for single-(produzione) channel CCA and derive an online optimization algo-
rithm (previously proposed in Lai and Fyfe, 1999) that maps onto a pyra-
midal neuron with three electrotonic compartments: soma, as well as apical
and basal dendrites. The apical and basal synaptic inputs represent the two
views, the two dendritic compartments extract highly correlated CCA pro-
jections of the inputs, and the soma computes the sum of projections and
outputs it downstream as action potentials. The communication between
the compartments is implemented by calcium plateaus that also mediate
non-Hebbian but local synaptic plasticity.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
2311
Whereas Pehlevan et al. (2020) also propose circuits of pyramidal neu-
rons for multichannel CCA, their implementations lack biological plau-
sibility. In one implementation, they resort to deflation where the circuit
sequentially finds projections of the two views. Implementing this algo-
rithm in a neural network requires a centralized mechanism to facilitate
the sequential updates, and there is no experimental evidence of such a
biological mechanism. In another implementation that does not require a
centralized mechanism, the neural network has asymmetric lateral connec-
tions among pyramidal neurons. Tuttavia, that algorithm is not derived
from a principled objective for CCA and the network architecture does not
match the neuronal circuitry observed in cortical microcircuits.
In this work, starting with a novel similarity-based CCA objective func-
zione, we derive a novel offline CCA algorithm, algorithm 1, and an online
multichannel CCA algorithm, algorithm 2, which can be implemented in
a single-layer network composed of three-compartment neurons and with
local non-Hebbian synaptic update rules (Guarda la figura 1). While our neural
network implementation of CCA captures salient features of cortical micro-
circuits, the network includes direct lateral connections between the prin-
cipal neurons (Guarda la figura 1), which is in contrast to cortical microcircuits
where lateral influence between cortical pyramidal neurons is often indi-
rect and mediated by interneurons. With this in mind, we derive an exten-
sion of our online CCA algorithm, algorithm 3, which adaptively chooses
the rank of the output based on the level of correlation captured and also
whitens the output. This extension is especially relevant for online unsuper-
vised learning algorithms, which are often confronted with the challenge of
adapting to nonstationary input streams. Inoltre, the algorithm natu-
rally maps onto a neural network with multicompartmental principal neu-
rons and without direct lateral connections between the principal neurons
(Guarda la figura 3 in section 5). È interessante notare, both the neural architecture and lo-
cal, non-Hebbian plasticity resemble neural circuitry and synaptic plasticity
in cortical microcircuits.
There are a number of existing consequential models of cortical mi-
crocircuits with multicompartmental neurons and non-Hebbian plasticity
(Körding & König, 2001; Urbanczik & Senn, 2014; Guerguiev, Lillicrap, &
Richards, 2017; Sacramento, Costa, Bengio, & Senn, 2018; Haga & Fukai,
2018; Richards & Lillicrap, 2019; Milstein et al., 2020). These models provide
mechanistic descriptions of the neural dynamics and synaptic plasticity and
account for many experimental observations, including the nonlinearity of
neural outputs and the layered organization of the cortex. While our neural
network model is single-layered and linear, it is derived from a principled
CCA objective function, which has several advantages. Primo, since biologi-
cal neural networks evolved to adaptively perform behaviorally relevant
computations, it is natural to view them as optimizing a relevant objec-
tive function. Secondo, our approach clarifies which features of the network
(per esempio., multicompartmental neurons and non-Hebbian synaptic updates) are
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2312
D. Lipshutz et al.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 1: Single-layer network architecture with k multicompartmental neu-
rons for outputting the sum of the canonical correlation subspace projec-
, . . . , zk). See algorithm 2. Here a = Wxx and b = Wyy are
zioni (CCSPs) z = (z1
, . . . , yn) onto a common
projections of the views x = (x1
k-dimensional subspace. The output, z = M−1(UN + B), is the sum of the CCSPs
and is computed using recurrent lateral connections. The components of a, B,
and z are represented in three separate compartments of the neurons. Filled
circles denote non-Hebbian synapses, and empty circles denote anti-Hebbian
synapses. Importantly, each synaptic update depends only on variables repre-
sented locally.
, . . . , xm) and y = (y1
central to computing correlations. Finalmente, since the optimization algorithm
is derived from a CCA objective that can be solved offline, the neural ac-
tivities and synaptic weights can be analytically predicted for any input
without resorting to numerical simulation. In this way, our neural network
model is interpretable and analytically tractable, and it provides a useful
complement to nonlinear, layered neural network models.
The remainder of this work is organized as follows. We state the CCA
problem in section 2. In section 3, we introduce a novel objective for the
CCA problem and derive offline and online CCA algorithms. In section 4,
we derive an extension of our CCA algorithm, and in section 5, we map
the extension onto a simplified cortical microcircuit. We provide results of
numerical simulations in section 6.
Notation. For positive integers p, q,
let Rp denote p-dimensional
Euclidean space, and let Rp×q denote the set of p × q real-valued matrices
equipped with the Frobenius norm (cid:2) · (cid:2)
F. We use boldface lowercase letters
A Biologically Plausible Neural Network for CCA
2313
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
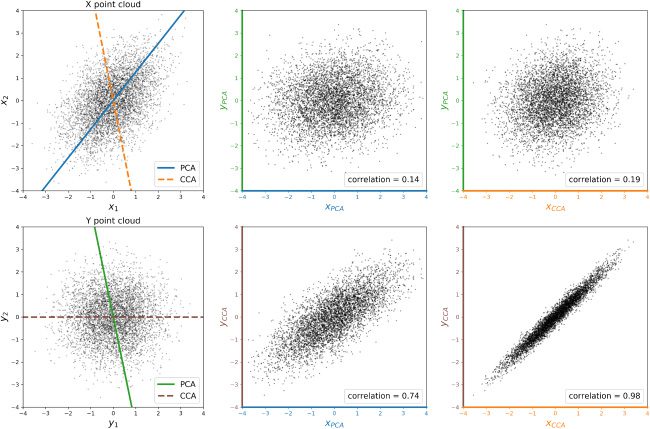
Figura 2: Illustration of CCA. The left column depicts point clouds of two-
dimensional views X and Y with lines indicating the span of the top principal
component and top canonical correlation basis vector for each view (labeled
“PCA” and “CCA,” respectively). The center and right columns depict point
clouds of joint one-dimensional projections of X and Y onto their top principal
component or top canonical correlation basis vector, with the correlations be-
tween the two projections listed. As illustrated in the lower right plot, the cor-
relation between the projected views is maximized when each view is projected
onto its top canonical correlation basis vector.
(per esempio., v) to denote vectors and boldface uppercase letters (per esempio., M) to denote
matrices. We let O(P) denote the set of p × p orthogonal matrices and S p
++
denote the set of p × p positive definite matrices. We let Ip denote the p × p
identity matrix.
2 Canonical Correlation Analysis
, y1), . . . , (xT , yT )
Given T pairs of full-rank, centered input data samples (x1
∈ Rm × Rn and k ≤ min(M, N), the CCA problem is to find k-dimensional
, . . . , yT that are maximally
linear projections of the views x1
correlated (Guarda la figura 2). To be precise, consider the CCA objective,
, . . . , xT and y1
arg max
Vx∈Rm×k,Vy∈Rn×k
Tr
(cid:2)
V
(cid:5)
x CxyVy
(cid:3)
,
(2.1)
2314
D. Lipshutz et al.
subject to the whitening constraint,1
(cid:5)
V
x CxxVx + V
y CyyVy = Ik
(cid:5)
,
(2.2)
where we have defined the sample covariance matrices
Cxx := 1
T
T(cid:4)
t=1
(cid:5)
xtx
T
, Cxy := 1
T
T(cid:4)
t=1
(cid:5)
xty
T
, Cyy := 1
T
T(cid:4)
t=1
(cid:5)
yty
T
.
(2.3)
To compute the solution of the CCA objective equations 2.1 E 2.2, Di-
fine the m × n correlation matrix,
Rxy := C
−1/2
xx CxyC
−1/2
yy
.
(2.4)
≥ · · · ≥ ρ
−1/2
xx Ux and C
min(M,N) denote the singular values, and let Ux ∈ O(M) E
Let ρ
1
Uy ∈ O(N) denote the matrices whose column vectors are respectively the
left- and right-singular vectors of the correlation matrix. The ith singular
value ρ
i is referred to as the ith canonical correlation, and the ith column
−1/2
vectors of C
yy Uy are jointly referred to as the ith pair of
canonical correlation basis vectors, for i = 1, . . . , min(M, N). The maximal
value of the trace in equation 2.1 is the normalized sum of canonical correla-
zioni: (ρ
k+1 so the subspace
1
spanned by the first k canonical correlation basis vectors is unique. In this
case, every solution of the CCA objective, equations 2.1 E 2.2, denoted
(Vx, Vy), is of the form
k)/2. For simplicity, we assume ρ
k
+ · · · + ρ
> ρ
Vx = C
−1/2
xx U(k)
x Q, Vy = C
−1/2
yy U(k)
y Q,
(2.5)
(resp. U(k)
where U(k)
sì ) is the m × k (resp. n × k) matrix whose ith column
X
vector is equal to the ith column vector of Ux (resp. Uy) for i = 1, . . . , k, E
Q ∈ O(k) is any orthogonal matrix. Since the column vectors of any solution
(Vx, Vy) span the same subspaces as the first k pairs of canonical correlation
basis vectors, we refer to the column vectors of Vx and Vy as basis vectors.
(cid:5)
(cid:5)
y yt as canonical cor-
We refer to the k-dimensional projections V
x xt and V
relation subspace projections (CCSPs).
The focus of this work is to derive a single-layer, biologically plausible
network whose input at each time t is the pair (xt, yt ) and the output is the
following sum of the CCSPs:
1
(cid:5)
x CxxVx =
This constraint differs slightly from the usual CCA whitening constraint V
(cid:5)
y CyyVy = Ik; Tuttavia, the constraints are equivalent up to a scaling factor of 2.
V
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
(cid:5)
zt := V
x xt + V
y yt,
(cid:5)
2315
(2.6)
Quale, as mentioned in section 1, is a highly relevant statistic (see also sec-
zione 6.1). This is in contrast to many existing CCA networks that output one
or both CCSPs (Lai & Fyfe, 1999; Pezeshki et al., 2003; Gou & Fyfe, 2004; Vía
et al., 2007; Golkar, Lipshutz, Bahroun, Sengupta, & Chklovskii, 2020). IL
components of the two input vectors xt and yt are represented by the ac-
tivity of upstream neurons belonging to two different populations, Quale
are integrated in separate compartments of the principal neurons in our
rete. The components of the output vector zt are represented by the
activity of the principal neurons in our network (Guarda la figura 1).
While CCA is typically viewed as an unsupervised learning method, Esso
can also be interpreted as a special case of the supervised learning method
reduced-rank regression, in which case one input is the feature vector and
the other input is the label (Vedere, per esempio., Velu & Reinsel, 2013). With this super-
vised learning view of CCA, the natural output of a CCA network is the
CCSP of the feature vector. In separate work (Golkar et al., 2020), we de-
rive an algorithm for the general reduced-rank regression problem, Quale
includes CCA as a special case, for outputting the projection of the feature
vector. The algorithm derived in Golkar et al. (2020) resembles the adap-
tive CCA with output whitening algorithm that we derive in section 4 Di
this work (see algorithm 3 as well as appendix B.2 for a detailed compar-
ison of the two algorithms); Tuttavia, there are significant advantages to
the algorithm derived here. Primo, our network outputs the (whitened) sum
of the CCSPs, which is a relevant statistic in applications. The algorithm in
Golkar et al. (2020) only outputs the CCSP of the feature vector, che è
natural when viewing CCA as a supervised learning method, but not when
viewing CCA as an unsupervised learning method for integrating multi-
view inputs. Secondo, in contrast to the algorithm derived in Golkar et al.
(2020), our adaptive CCA with output whitening algorithm allows for adap-
tive output rank. This is particularly important for analyzing nonstationary
input streams, a challenge that brains regularly face.
3 A Biologically Plausible CCA Algorithm
To derive a network that computes the sums of CCSPs for arbitrary in-
put data sets, we adopt a normative approach in which we identify an ap-
propriate cost function whose optimization leads to an online algorithm
that can be implemented by a network with local learning rules. Previ-
ously, such an approach was taken to derive a biologically plausible PCA
network from a similarity matching objective function (Pehlevan, Eh, &
Chklovskii, 2015). We leverage this work by reformulating a CCA problem
in terms of PCA of a modified data set and then solving it using similarity
matching.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2316
D. Lipshutz et al.
3.1 A Similarity Matching Objective. Primo, we note that the sums of
, . . . , zT are equal to the principal subspace projections of the data
, . . . , ξT , where ξt is the following d-dimensional vector of concatenated
CCSPs z1
ξ
1
whitened inputs (recall d := m + N):
(cid:5)
ξt :=
−1/2
xx xt
−1/2
yy yt
C
C
(cid:6)
.
(3.1)
(See appendix A for a detailed justification.) Prossimo, we use the fact that the
principal subspace projections can be expressed in terms of solutions of
similarity matching objectives. A tal fine, we define the matrices (cid:3) :=
, . . . , zT ] ∈ Rk×T , so that Z is a linear pro-
[ξ
jection of (cid:3) onto its k-dimensional principal subspace. As shown in Cox
and Cox (2000) and Williams (2001), the principal subspace projection Z is
a solution of the following similarity matching objective:
, . . . , ξT ] ∈ Rd×T and Z := [z1
1
arg min
Z∈Rk×T
1
2T 2
(cid:7)
(cid:7)
(cid:5)
Z
Z − (cid:3)(cid:5)(cid:3)
(cid:7)
(cid:7)2
F
.
(3.2)
The objective, equations 3.2, which comes from classical multidimensional
scaling (Cox & Cox, 2000), minimizes the difference between the similar-
ity of output pairs, z(cid:5)
ξt(cid:7) , Dove
similarity is measured in terms of inner products. Finalmente, defining X :=
, . . . , yT ] ∈ Rn×T , we use the definition of
[x1
ξt in equation 3.1, to rewrite the objective, equations 3.2, come segue:
t zt(cid:7) , and the similarity of input pairs, ξ(cid:5)
, . . . , xT ] ∈ Rm×T and Y := [y1
T
arg min
Z∈Rk×T
1
2T 2
(cid:7)
(cid:7)
(cid:5)
(cid:7)Z
(cid:5)
Z − X
−1
xx X − Y
C
(cid:5)
(cid:7)
(cid:7)
−1
(cid:7)
yy Y
C
.
2
F
(3.3)
In the remainder of this section, we derive our online CCA algorithm. Then,
in sections 4 E 5, we derive an extension of our CCA algorithm and map
it onto the cortical microcircuit. Readers who are primarily interested in the
derivation of the extension and its relation to the cortical microcircuit can
safely skip to section 4.
3.2 A Min-Max Objective. While the similarity matching objective,
equations 3.3, can be minimized by taking gradient descent steps with
respect to Z, this would not lead to an online algorithm because such com-
putation requires combining data from different time steps. Piuttosto, we in-
troduce auxiliary matrix variables, which store sufficient statistics allowing
for the CCA computation using solely contemporary inputs and will corre-
spond to synaptic weights in the network implementation, and rewrite the
minimization problem 3.3 as a min-max problem.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
2317
Expanding the square in equation 3.3 and dropping terms that do not
depend on Z yields the minimization problem:
min
Z∈Rk×T
− 1
T 2 Tr
(cid:2)
Z
(cid:5)
(cid:5)
ZX
(cid:3)
−1
xx X
C
− 1
T 2 Tr
(cid:8)
(cid:5)
Z
(cid:5)
ZY
(cid:9)
−1
yy Y
C
+ 1
2T 2 Tr
(cid:2)
(cid:5)
Z
(cid:5)
ZZ
(cid:3)
Z
.
Prossimo, we introduce dynamic matrix variables Wx, Wy, and M in place of
T ZZ(cid:5), rispettivamente, and rewrite the
the matrices 1
yy and 1
xx , 1
minimization problem as a min-max problem,
T ZX(cid:5)C−1
T ZY(cid:5)C−1
min
Z∈Rk×T
min
Wx∈Rk×m
min
Wy∈Rk×n
max
M∈S k
++
l(Wx, Wy, M, Z),
Dove
l(Wx, Wy, M, Z) := 1
T
Tr
(cid:2)
(cid:5)
−2Z
(cid:10)
(cid:5)
WxX − 2Z
(cid:5)
WyY + Z
(cid:3)
MZ
+ Tr
WxCxxW
(cid:5)
X
+ WyCyyW
(cid:11)
M2
.
(cid:5)
sì
− 1
2
(3.4)
To verify the above substitutions are valid, it suffices to optimize over the
matrices Wx, Wy, and M—for example, by differentiating L(Wx, Wy, M, Z)
with respect to Wx, Wy, or M, setting the derivative equal to zero, and solv-
ing for Wx, Wy, or M. Finalmente, we interchange the order of minimization
with respect to Z and (Wx, Wy), as well as the order of minimization with
respect to Z and maximization with respect to M:
min
Wx∈Rk×m
min
Wy∈Rk×n
max
M∈S k
++
min
Z∈Rk×T
l(Wx, Wy, M, Z).
(3.5)
The second interchange is justified by the fact that L(Wx, Wy, M, Z) satisfies
the saddle point property with respect to Z and M, which follows from its
strict convexity in Z (since M is positive definite) and strict concavity in M.
Given an optimal quadruple of the min-max problem, equation 3.5, we
can compute the basis vectors as follows. Primo, minimizing the objective
l(Wx, Wy, M, Z) over Z yields the relation
Z := arg min
Z∈Rk×T
l(Wx, Wy, M, Z) = M
−1WxX + M
−1WyY.
(3.6)
Therefore, if (Wx, Wy, M, Z) is an optimal quadruple of the min-max prob-
lem, 3.5, it follows from equation 2.6 that the corresponding basis vectors
satisfy
(cid:5)
V
X
−1
= M
Wx
(cid:5)
and V
sì
−1
= M
Wy.
(3.7)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2318
D. Lipshutz et al.
3.3 An Offline CCA Algorithm. Before deriving our online CCA algo-
rithm, we first demonstrate how the objective, equations 3.5, can be opti-
mized in the offline setting, where one has access to the data matrices X
and Y in their entirety. In questo caso, the algorithm solves the min-max prob-
lem 3.5 by alternating minimization and maximization steps. Primo, for fixed
Wx, Wy, and M, we minimize the objective function L(Wx, Wy, M, Z) Sopra
Z to obtain the minimum Z defined in equation 3.6. Then, with Z fixed, we
perform a gradient descent-ascent step with respect to (Wx, Wy) and M:
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
Wx ← Wx − η
Wx ← Wy − η
M ← M +
η
τ
∂L(Wx, Wy, M, Z)
∂Wx
∂L(Wx, Wy, M, Z)
∂Wy
∂L(Wx, Wy, M, Z)
∂M
,
,
.
Here η > 0 is the learning rate for Wx and Wy, which may depend on the
iteration, and τ > 0 is the ratio of the learning rates for Wx (or Wy) E
M. Substituting in the explicit expressions for the partial derivatives of
l(Wx, Wy, M, Z) yields our offline CCA algorithm (algorithm 1), which we
refer to as Offline-CCA.
Recall that M is optimized over the set of positive-definite matrices S k
++.
To ensure that M remains positive definite after each update, note that
the update rule for M can be rewritten as the following convex combina-
zione (provided η ≤ τ ): M ← (1 − η
τ )M + η
is positive
semidefinite, to guarantee that M remains positive definite given a positive-
definite initialization, it suffices to assume that η < τ .
). Since 1
T ZZ(cid:5)
T ZZ(cid:5)
τ ( 1
3.4 An Online CCA Algorithm. In the online setting, the input data
(xt, yt ) are streamed one at a time, and the algorithm must compute its out-
put zt without accessing any significant fraction of X and Y. To derive an
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Biologically Plausible Neural Network for CCA
2319
online algorithm, it is useful to write the cost function as an average over
time-separable terms:
L(Wx, Wy, M, Z) = 1
T
T(cid:4)
t=1
lt (Wx, Wy, M, zt ),
where
lt (Wx, Wy, M, zt ) := −2z
(cid:5)
t Wxxt − 2z
(cid:10)
(cid:5)
t Wyyt + z
(cid:5)
t Mzt
+ Tr
Wxxtx
(cid:5)
t W
(cid:5)
x
+ Wyyty
(cid:5)
t W
(cid:5)
y
(cid:11)
M2
.
(3.8)
− 1
2
At iteration t, to compute the output zt, we minimize the cost function
lt (Wx, Wy, M, zt ) with respect to zt by running the following gradient de-
scent dynamics to equilibrium:
dzt (γ )
dγ
= at + bt − Mzt (γ ),
(3.9)
where we have defined the following k-dimensional projections of the in-
puts: at := Wxxt and bt := Wyyt. These dynamics, which will correspond to
recurrent neural dynamics in our network implementation, are assumed to
occur on a fast timescale, allowing zt (γ ) to equilibrate at zt := M−1(at + bt )
before the algorithm outputs its value. After zt (γ ) equilibrates, we update
the matrices (Wx, Wy, M) by taking a stochastic gradient descent-ascent
step of the cost function lt (Wx, Wy, M, zt ) with respect to (Wx, Wy) and M:
Wx ← Wx − η
Wx ← Wy − η
M ← M +
η
τ
∂lt (Wx, Wy, M, zt )
∂Wx
∂lt (Wx, Wy, M, zt )
∂Wy
∂lt (Wx, Wy, M, zt )
∂M
,
,
.
Substituting in the explicit expressions for the partial derivatives of
lt (Wx, Wy, M, zt ) yields our online CCA algorithm (algorithm 2), which we
refer to as Bio-CCA.
Algorithm 2 can be implemented in a biologically plausible single-layer
network with k neurons that each consist of three separate compartments
(see Figure 1). At each time step, the inputs xt and yt are multiplied by the
respective feedforward synapses Wx and Wy to yield the k-dimensional vec-
tors at and bt, which are represented in the first two compartments of the k
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2320
D. Lipshutz et al.
neurons. Lateral synapses, −M, connect the k neurons. The vector of neu-
ronal outputs, zt, equals the normalized sum of the CCSPs and is computed
locally using recurrent dynamics in equation 3.9. The synaptic updates can
be written elementwise as follows:
Wx,i j
Wy,i j
← Wx,i j
← Wy,i j
− at,i)xt, j
− bt,i)yt, j
,
,
1 ≤ i ≤ k, 1 ≤ j ≤ m,
1 ≤ i ≤ k, 1 ≤ j ≤ n,
Mi j
← Mi j
+
− Mi j ),
1 ≤ i, j ≤ k.
+ η(zt,i
+ η(zt,i
η
τ (zt,izt, j
As shown above, the update to synapse Wx,i j (resp. Wy,i j), which connects
the jth input xt, j (resp. yt, j) to the ith output neuron, depends only on the
quantities zt,i, at,i (resp. bt,i), and xt, j (resp. yt, j), which are represented in the
pre- and postsynaptic neurons, so the updates are local but non-Hebbian
due to the contribution from the at,i (resp. bt,i) term. Similarly, the update
to synapse −Mi j, which connects the jth output neuron to the ith output
neuron, is inversely proportional to zt,izt, j, the product of the outputs of the
pre- and postsynaptic neurons, so the updates are local and anti-Hebbian.
4 Online Adaptive CCA with Output Whitening
We now introduce an extension of Bio-CCA that addresses two biologically
relevant issues. First, Bio-CCA a priori sets the output rank at k; however,
it may be advantageous for a neural circuit to instead adaptively set the
output rank depending on the level of correlation captured. In particular,
this can be achieved by projecting each view onto the subspace spanned by
the canonical correlation basis vectors, which correspond to canonical cor-
relations that exceed a threshold. Second, it is useful from an information-
theoretic perspective for neural circuits to whiten their outputs (Plumbley,
1993), and there is experimental evidence that neural outputs in the cor-
tex are decorrelated (Ecker et al., 2010; Miura, Mainen, & Uchida, 2012).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Biologically Plausible Neural Network for CCA
2321
Both adaptive output rank and output whitening modifications were im-
plemented for a PCA network by Pehlevan and Chklovskii (2015) and can
be adapted to the CCA setting. Here we present the modifications without
providing detailed proofs, which can be found in the supplement of Pehle-
van and Chklovskii (2015).
In order to implement these extensions, we need to appropriately modify
the similarity matching objective function equations 3.3. First, to adaptively
choose the output rank, we add a quadratic penalty Tr(Z(cid:5)Z) to the objective
function 3.3:
arg min
Z∈Rk×T
1
2T 2
(cid:7)
(cid:7)
(cid:5)
(cid:7)Z
(cid:5)
Z − X
−1
xx X − Y
C
(cid:5)
(cid:7)
(cid:7)
−1
(cid:7)
yy Y
C
2
F
+
α
T
(cid:2)
(cid:3)
Z
.
(cid:5)
Z
Tr
(4.1)
The effect of the quadratic penalty is to rank-constrain the output, with α ≥
0 acting as a threshold parameter on the eigenvalues values of the output
covariance.
Next, to whiten the output, we expand the square in equation 4.1 and
replace the quartic term Tr(Z(cid:5)ZZ(cid:5)Z) by a Lagrange constraint enforcing
Z(cid:5)Z (cid:9) TIT (i.e., TIT − Z(cid:5)Z is positive semidefinite):
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
arg min
Z∈Rk×T
max
N∈Rk×T
(cid:5)
1
T 2 Tr(−Z
+ 1
T 2 Tr[N
(cid:5)
ZX
−1
xx X − Z
C
(cid:5)
(cid:5)
ZY
−1
yy Y + αTZ
C
(cid:5)
Z)
(cid:5)
(cid:5)
N(Z
Z − TIT )].
(4.2)
The effect of the Lagrange constraint in equation 4.2 is to enforce that all
nonzero eigenvalues of the output covariance are set to one.
Solutions of the objective, equations 4.2, can be expressed in terms
ξ , where
, 0, . . . , 0) is
> 0 are the
of the eigendecomposition of the Gram matrix (cid:3)(cid:5)(cid:3) = TUξ (cid:4)ξ U(cid:5)
Uξ ∈ O(T ) is a matrix of eigenvectors and (cid:4)ξ = diag(λ
1
the T × T diagonal matrix whose nonzero entries λ
1
eigenvalues of the d × d covariance matrix:
, . . . , λ
D
≥ · · · ≥ λ
D
Cξ ξ := 1
T
T(cid:4)
t=1
ξtξ(cid:5)
T
=
(cid:5)
(cid:6)
.
Im Rxy
R(cid:5)
xy
In
(4.3)
Assume, for technical purposes, that α (cid:10)∈ {λ
1
Pehlevan et al. (2015, theorem 3), every solution
form
}. Then, as shown in
, . . . , λ
(cid:12)
Z of objective 4.2 is of the
D
(cid:13)
(cid:12)
Z = Q
(cid:12)(cid:4)(k)
ξ U(k)
ξ
T
(cid:5)
, (cid:12)(cid:4)(k)
ξ = diag(H(λ
1
− α), . . . , H(λ
k
− α)),
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2322
D. Lipshutz et al.
ξ ∈ RT×k is the T × k matrix
where Q ∈ O(k) is any orthogonal matrix, U(k)
whose ith column vector is equal to the ith column vector of Uξ , for i =
1, . . . , k, and H is the Heaviside step function defined by H(R) = 1 if r > 0
and H(R) = 0 otherwise. Finalmente, we note that in view of equation 4.3 E
the SVD of Rxy, the top min(M, N) eigenvalues of Cξ ξ satisfy
λ
io
= 1 + ρ
io
,
i = 1, . . . , min(M, N),
, . . . , ρ
where we recall that ρ
min(M,N) are the canonical correlations. Così,
1
H(λ
− (α − 1)), for i = 1, . . . , k. In other words, the objec-
− α) = H(ρ
io
io
tive 4.2 outputs the sum of the projections of the inputs xt and yt onto the
canonical correlation subspace spanned by the (at most k) pairs of canonical
correlation basis vectors associated with canonical correlations exceeding
the threshold max(α − 1, 0), and sets the nonzero output covariance eigen-
values to one, thus implementing both the adaptive output rank and output
whitening modifications.
With the modified objective, equations 4.2, in hand, the next step is to
derive an online algorithm. Similar to section 3.2, we introduce dynamic
T ZN(cid:5)
matrix variables Wx, Wy, and P in place of 1
to rewrite the objective 4.2 come segue:
T ZY(cid:5)C−1
T ZX(cid:5)C−1
yy and 1
xx , 1
arg min
Z∈Rk×T
max
N∈Rk×T
min
Wx∈Rk×m
min
Wy∈Rk×n
max
P∈Rk×k
(cid:14)
l(Wx, Wy, P, Z, N),
(4.4)
Dove
Tr
l(Wx, Wy, P, Z, N) := 1
(cid:14)
T
+ 1
T
+ Tr
(cid:2)
(cid:5)
−2Z
(cid:5)
WxX − 2Z
(cid:5)
WyY + αZ
(cid:3)
Z
(cid:5)
(cid:5)
(cid:5)
Z − N
N
P
(cid:3)
(cid:2)
2N
Tr
(cid:8)
WxCxxW
(cid:5)
X
+ WyCyyW
(cid:5)
sì
(cid:5)
− PP
(cid:9)
.
After interchanging the order of optimization, we solve the min-max opti-
mization problem by taking online gradient descent-ascent steps, with de-
η
scent step size η and ascent step size
τ . Since the remaining steps are similar
to those taken in section 3 to derive Bio-CCA, we defer the details to section
B.1 and simply state the online algorithm (algorithm 3), which we refer to
as Adaptive Bio-CCA with output whitening.
5 Relation to Cortical Microcircuits
We now show that Adaptive Bio-CCA with output whitening (algorithm 3)
maps onto a neural network with local, non-Hebbian synaptic update rules
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
2323
that emulate salient aspects of synaptic plasticity found experimentally in
cortical microcircuits (in both the neocortex and the hippocampus).
Cortical microcircuits contain two classes of neurons: excitatory pyrami-
dal neurons and inhibitory interneurons. Pyramidal neurons receive exci-
tatory synaptic inputs from two distinct sources via their apical and basal
dendrites. The apical dendrites are all oriented in a single direction, and the
basal dendrites branch from the cell body in the opposite direction (Taka-
hashi & Magee, 2009; Larkum, 2013); Guarda la figura 3. The excitatory synaptic
currents in the apical and basal dendrites are first integrated separately in
their respective compartments (Takahashi & Magee, 2009; Larkum, 2013).
If the integrated excitatory current in the apical compartment exceeds the
corresponding inhibitory input (the source of which is explained below)
it produces a calcium plateau potential that propagates through the basal
dendrites, driving plasticity (Takahashi & Magee, 2009; Larkum, 2013; Bit-
tner et al., 2015). When the apical calcium plateau potential and basal den-
dritic current coincidentally arrive in the soma, they generate a burst in
spiking output (Larkum, Zhu, & Sakmann, 1999; Larkum, 2013; Bittner
et al., 2015). Inhibitory interneurons integrate pyramidal outputs and recip-
rocally inhibit the apical dendrites of pyramidal neurons, thus closing the
loop.
We propose that a network of k pyramidal neurons implements CCA on
the inputs received by apical and basal dendrites and outputs the whitened
sum of CCSPs (algorithm 3). In our model, each pyramidal neuron has three
compartments: two compartments for the apical and basal dendritic cur-
rents and one compartment for the somatic output. The two data sets X and
Y are represented as activity vectors xt and yt streamed onto the apical and
basal dendrites respectively (Guarda la figura 3). At each time step, the activity
vectors are multiplied by the corresponding synaptic weights to yield lo-
calized apical and basal dendritic currents, at = Wxxt and bt = Wyyt, così
implementing projection onto the common subspace. This is followed by
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2324
D. Lipshutz et al.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 3: Cortical microcircuit implementation of Adaptive Bio-CCA with out-
put whitening (algorithm 3). The black cell bodies denote pyramidal neurons,
with the apical tufts pointing upward. The red and blue lines denote the ax-
ons respectively transmitting the apical input x and basal input y. The black
lines originating from the bases of the pyramidal neurons are their axons, Quale
transmit their output z. The green cell bodies denote the interneurons, and the
green lines are their axons, which transmit their output n. Filled circles denote
non-Hebbian synapses whose updates are proportional to the input (cioè., x or y)
and the weighted sum of the calcium plateau potential plus backpropagating
somatic output [cioè., cb + (1 − α)z or ca + (1 − α)z]. The directions of travel of
these weighted sums are depicted using dashed lines with arrows. Empty cir-
cles denote Hebbian or anti-Hebbian synapses whose updates are proportional
or inversely proportional to the pre- and postsynaptic activities.
the following linear recurrent neural dynamics:
dzt (γ )
dγ
dnt (γ )
dγ
= at + bt − Pnt (γ ) − αzt (γ ),
(cid:5)
= P
zt (γ ) − nt (γ ),
(5.1)
(5.2)
where the components of zt are represented by the spiking activity of pyra-
midal neurons, the components of nt are represented by the activity of in-
hibitory interneurons, the components of P are represented by the synaptic
weights from the interneurons to the pyramidal neurons, the components
of P(cid:5)
are represented by the synaptic weights from the pyramidal neurons
A Biologically Plausible Neural Network for CCA
2325
to the interneurons, and α is the threshold parameter of the adaptive algo-
rithm. These dynamics equilibrate at nt = P(cid:5)zt and
zt = (PP
(cid:5) + αIk)
−1(at + bt ).
(5.3)
Provided α > 0, we can rearrange equation 5.3 to write the output as
zt = α−1(bt + ca
T ),
T := at − Pnt are represented by the apical cal-
where the components of ca
cium plateau potentials within each pyramidal neuron. In other words, IL
output is proportional to the sum of the basal dendritic current and the api-
cal calcium plateau potential, which is consistent with experimental evi-
dence showing that the output depends on both the basal inputs and apical
calcium plateau potential (Bittner et al., 2015; Bittner, Milstein, Grienberger,
Romani, & Magee, 2017; Magee & Grienberger, 2020).
Prossimo, we compare the synaptic update rules with experimental evidence.
Rearranging equation 5.3 and substituting into the synaptic update rules in
algorithm 3, we can rewrite the synaptic updates as follows:
(cid:2)
Wx ← Wx + η
cb
T
Wy ← Wy + η (ca
T
(cid:3)
(cid:5)
+ (1 − α)zt
X
T
(cid:5)
+ (1 − α)zt ) sì
T
,
,
P ← P +
η
τ (ztn
(cid:5)
T
− P),
T := bt − Pnt are represented by basal calcium
where the components of cb
plateau potentials within each pyramidal neuron. The learning signal for
the basal (resp. apical) synaptic updates of this circuit is the correlation be-
tween the sum of the apical (resp. basal) calcium plateau potentials plus
+ (1 − α)zt [resp.
the scaled spiking activity of the pyramidal neurons, cb
T
+ (1 − α)zt], and the synaptic inputs to the basal (resp. apical) dendrites,
ca
T
xt (resp. yt). When α = 1 the spiking (action potentials) of the postsynap-
tic neuron is not required for synaptic plasticity, whereas when α (cid:10)= 1, IL
spiking of the postsynaptic neuron affects synaptic plasticity along with the
calcium plateau. Therefore, our model can account for a range of exper-
imental observations that have demonstrated that spiking in the postsy-
naptic neuron contributes to plasticity in some contexts (Golding, Staff, &
Spruston, 2002; Gambino et al., 2014; Bittner et al., 2017; Magee & Grien-
berger, 2020), but does not appear to affect plasticity in other contexts
(Tigaret, Olivo, Sadowski, Ashby, & Mellor, 2016; Sjöström & Häusser,
2006). Unlike Hebbian learning rules, which depend only on the correlation
of the spiking output of the postsynaptic neuron with the presynaptic spik-
ing, the mechanisms involving the calcium plateau potential represented
internally in a neuron are called non-Hebbian. Because synapses have
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2326
D. Lipshutz et al.
access to both the corresponding presynaptic activity and the calcium
plateau potential, the learning rule remains local.
Note that the update rule for the synapses in the apical dendrites, Wx,
depends on the basal calcium plateau potentials cb
T . Experimental evidence
is focused on apical calcium plateau potentials, and it is not clear whether
differences between basal inputs and inhibitory signals generate calcium
signals for driving plasticity in the apical dendrites. Alternatively, the learn-
ing rule for Wx coincides with the learning rule for the apical dendrites in
Golkar et al. (2020), where a biological implementation in terms of local de-
polarization and backpropagating spikes was proposed. Due to the incon-
clusive evidence pertaining to plasticity in the apical tuft, we find it useful
to put forth both interpretations.
Multicompartmental models of pyramidal neurons have been invoked
previously in the context of biological implementation of the backpropaga-
tion algorithm (Körding & König, 2001; Urbanczik & Senn, 2014; Guerguiev
et al., 2017; Haga & Fukai, 2018; Sacramento et al., 2018; Richards & Lilli-
crap, 2019). Under this interpretation, the apical compartment represents
the target output, the basal compartment represents the algorithm predic-
zione, and calcium plateau potentials communicate the error from the apical
to the basal compartment, which is used for synaptic weight updates. IL
difference between these models and ours is that we use a normative ap-
proach to derive not only the learning rules but also the neural dynamics
of the CCA algorithm, ensuring that the output of the network is known
for any input. D'altra parte, the linearity of neural dynamics in our
network means that stacking our networks will not lead to any nontriv-
ial results expected of a deep learning architecture. We leave introducing
nonlinearities into neural dynamics and stacking our network to future
lavoro.
We conclude this section with comments on the interneuron-to-
pyramidal neuron synaptic weight matrix P and pyramidal neuron-to-
interneuron synaptic weight matrix P(cid:5)
, as well as the computational
role of the interneurons in this network. Primo, the algorithm appears to
require a weight-sharing mechanism between the two sets of synapses
to ensure the symmetry between the weight matrices, which is biologi-
cally unrealistic and commonly referred to as the weight transport problem.
Tuttavia, even without any initial symmetry between these feedforward
and feedback synaptic weights, because of the symmetry of the local learn-
ing rules, the difference between the two will decay exponentially with-
out requiring weight transport (see section B.3). Secondo, in equations 5.1
E 5.2, the interneuron-to-pyramidal neuron synaptic weight matrix P
is preceded by a negative sign, and the pyramidal neuron-to-interneuron
synaptic weight matrix P(cid:5)
is preceded by a positive sign, which is consis-
tent with the fact that in simplified cortical microcircuits, interneuron-to-
pyramidal neuron synapses are inhibitory, whereas the pyramidal neuron-
to-interneuron synapses are excitatory. That being said, this interpretation
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
2327
is superficial because the weight matrices are not constrained to be nonneg-
ative, which is due to the fact that we are implementing a linear statistical
method. Imposing nonnegativity constraints on the weights P and P(cid:5)
may
be useful for implementing nonlinear statistical methods; Tuttavia, this re-
quires further investigation. Finalmente, the activities of the interneurons N
were introduced in equation 4.2 to decorrelate the output. This is consistent
with previous models of the cortex (King, Zylberberg, & DeWeese, 2013;
Wanner & Friedrich, 2020), which have introduced inhibitory interneurons
to decorrelate excitatory outputs; Tuttavia, in contrast to the current work,
the models proposed in King et al. (2013) and Wanner and Friedrich (2020)
are not normative.
6 Numerical Experiments
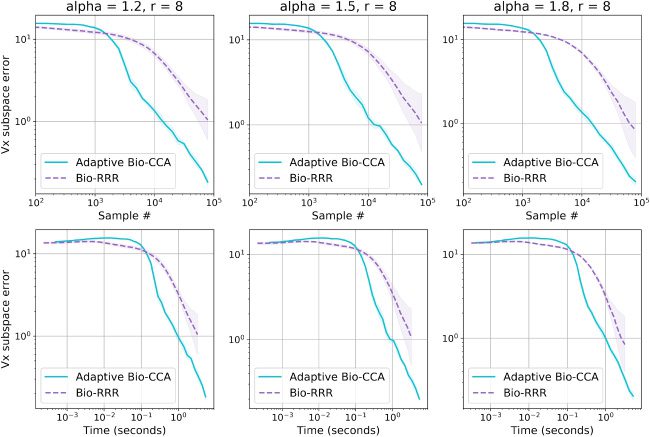
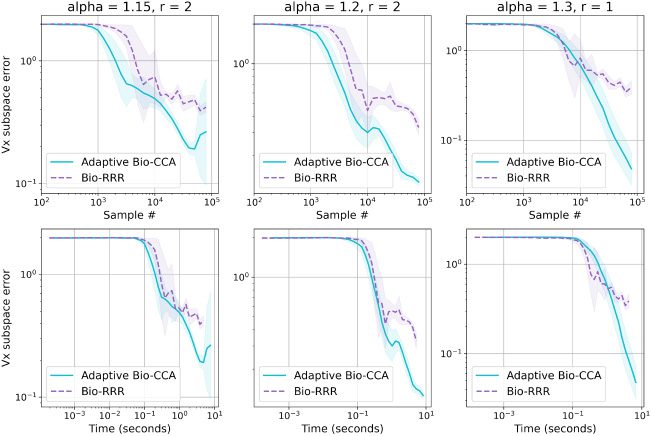
We now evaluate the performance of the online algorithms, Bio-CCA and
Adaptive Bio-CCA with output whitening. In each plot, the lines and
shaded regions respectively denote the means and 90% confidence inter-
vals over five runs. Detailed descriptions of the implementations are given
in section C.1. All experiments were performed in Python on an iMac Pro
equipped with a 3.2 GHz 8-Core Intel Xeon W CPU. The evaluation code is
available at https://github.com/flatironinstitute/bio-cca.
6.1 Data Sets. We first describe the evaluation data sets.
6.1.1 Synthetic. We generated a synthetic data set with T = 100,000 sam-
ples according to the probabilistic model for CCA introduced by Bach and
, . . . , sT be independent and identically
Jordan (2005). In particular, let s1
distributed (i.i.d.) 8-dimensional latent mean-zero gaussian vectors with
identity covariance. Let Tx ∈ R50×8, Ty ∈ R30×8, (cid:5)x ∈ S 50
++ be
randomly generated matrices and define the 50-dimensional observations
x1
, . . . , xT and 30-dimensional observations y1
++, E (cid:5)y ∈ S 30
, . . . , yT by
xt := Txst + φt,
yt := Tyst + ψt,
t = 1, . . . , T,
1
1
, . . . , φT (resp. ψ
where φ
, . . . , ψT ) are i.i.d. 50-dimensional (resp. 30-
dimensional) mean-zero gaussian vectors with covariance (cid:5)X (resp. (cid:5)sì).
Così, conditioned on the latent random variable s, the observation x (resp.
sì) has a gaussian distribution with mean Txs (resp. Tys) with covariance (cid:5)X
(resp. (cid:5)sì):
xt|st ∼ N (Txst, (cid:5)X),
yt|st ∼ N (Tyst, (cid:5)sì).
For this generative model, Bach and Jordan (2005) showed that the pos-
terior expectation of the latent vector st given the observation (xt, yt ) is a
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2328
D. Lipshutz et al.
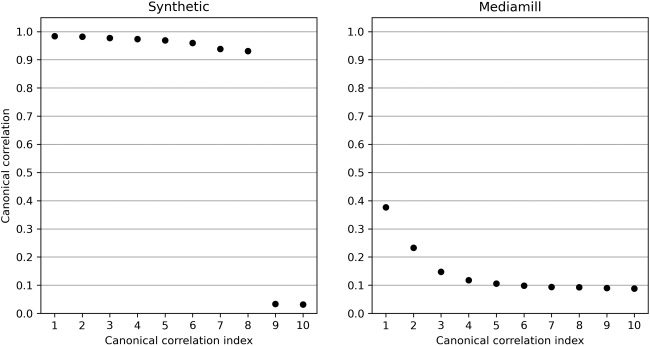
Figura 4: Top 10 canonical correlations ρ
1
and Mediamill (right).
, . . . , ρ
10 of the synthetic data set (left)
(cid:15)
(cid:16)
st|(xt, yt )
linear transformation of the sum of the 8-dimensional CCSPs zt; questo è,
= P1/2
E
= Lzt for some 8 × 8 matrix L. (To see this, set M1
in the paragraph following Bach & Jordan, 2005, theorem 2). The first 10
canonical correlations are plotted in Figure 4 (left). Observe that the first 8
canonical correlations are close to 1, and the remaining canonical correla-
tions are approximately 0. This sharp drop in the canonical correlations is a
consequence of the linear generative model and is generally not the case in
real data (Vedere, per esempio., the right panel in Figure 4). Ancora, we find it useful to test
our algorithms on this synthetic data set since the generative model is well
studied and relevant to CCA (Bach & Jordan, 2005).
= M2
D
6.1.2 Mediamill. The data set Mediamill (Snoek, Worring, Van Gemert,
Geusebroek, & Smeulders, 2006) consists of T = 43,907 samples (includ-
ing training and testing sets) of video data and text annotations, E
has been previously used to evaluate CCA algorithms (Arora, Marinov,
Mianjy, & Srebro, 2017; Pehlevan et al., 2020). The first view consists of 120-
dimensional visual features extracted from representative video frames.
The second view consists of 101-dimensional vectors whose components
correspond to manually labeled semantic concepts associated with the
video frames (per esempio., “basketball” or “tree”). To ensure that the problem is
well conditioned, we add gaussian noise with covariance matrix εI120 (resp.
εI101), for ε = 0.1, to the first (resp. second) view to generate the data ma-
trix X (resp. Y). The first 10 canonical correlations are plotted in Figure 4
(right).
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
2329
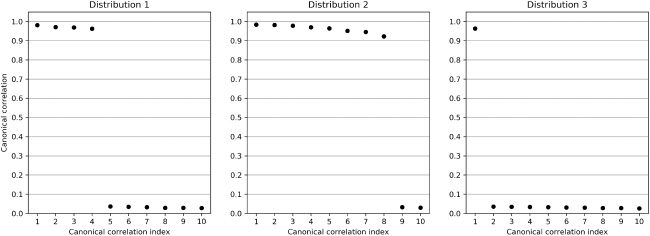
Figura 5: Top 10 canonical correlations ρ
1
contribute to the nonstationary synthetic data set.
, . . . , ρ
10 of the three distributions that
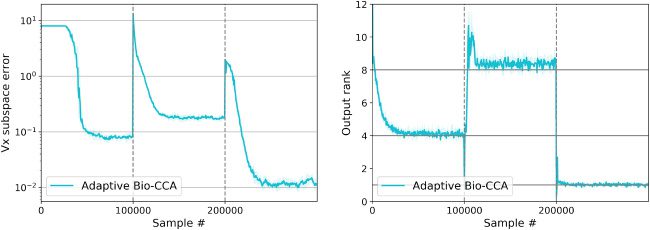
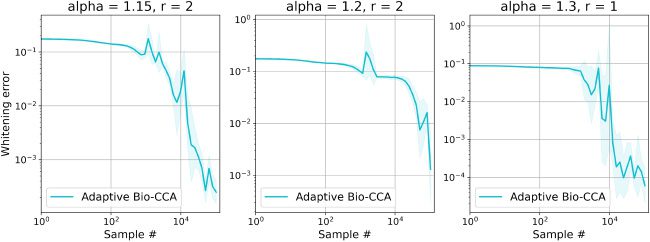
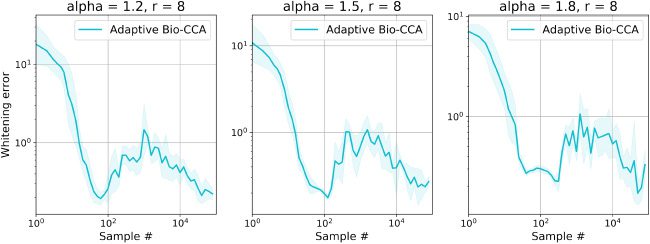
6.1.3 Nonstationary. To evaluate Adaptive Bio-CCA with output whiten-
ing, we generated a nonstationary synthetic data set with T = 300,000
samples, which are streamed from three distinct distributions that are
generated according to the probabilistic model in Bach and Jordan (2005). In
this case, the first N = 100,000 samples are generated from a 4-dimensional
latent source, the second N samples are generated from an 8-dimensional
latent source, and the final N samples are generated from a 1-dimensional
latent source.
Specifically, we let s1
, . . . , s2N and s2N+1
, . . . , sN (resp. sN+1
, . . . , sT ) be
i.i.d. 4-dimensional (resp. 8-dimensional and 1-dimensional) mean-zero
∈
gaussian vectors with identity covariance. We then let T(1)
X
R50×8, T(3)
∈ R30×4, T(2)
sì
X
(cid:5)y ∈ S 30
observations x1
∈ R50×4, T(2)
X
++, E
++ be randomly generated matrices and define the 50-dimensional
, . . . , xT and 30-dimensional observations y1
∈ R30×1, (cid:5)x ∈ S 50
∈ R50×1, T(1)
sì
∈ R30×8, T(3)
sì
, . . . , yT by
xt := T(1)
xt := T(2)
xt := T(3)
x st + φt,
x st + φt,
x st + φt,
yt := T(1)
yt := T(2)
yt := T(3)
y st + ψt,
y st + ψt,
y st + ψt,
t = 1, . . . , N,
t = N + 1, . . . , 2N,
t = 2N + 1, . . . , T,
, . . . , φT (resp. ψ
, . . . , ψT ) are i.i.d. 50-dimensional
Dove, as before, φ
(resp. 30-dimensional) mean-zero gaussian vectors with covariance (cid:5)X
(resp. (cid:5)sì). In Figure 5, we plot the first 10 canonical correlations for each
of the three distributions.
1
1
6.2 Bio-CCA. We now evaluate the performance of Bio-CCA (see algo-
rithm 2) on the synthetic dataset and Mediamill.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2330
D. Lipshutz et al.
6.2.1 Competing Algorithms. We compare the performance of Bio-CCA
with the following state-of-the-art online CCA algorithms:
• A two-timescale algorithm for computing the top canonical correla-
tion basis vectors (cioè., k = 1) introduced by Bhatia et al. (2018). IL
algorithm is abbreviated “Gen-Oja” due to its resemblance to Oja’s
method (Oja, 1982).
• An inexact matrix stochastic gradient method for solving CCA, ab-
breviated “MSG-CCA,” which was derived by Arora et al. (2017).
• The asymmetric neural network proposed by Pehlevan et al. (2020),
which we abbreviate as “Asym-NN.”
• The biologically plausible reduced-rank regression algorithm de-
rived by Golkar et al. (2020), abbreviated “Bio-RRR,” which imple-
ments a supervised version of CCA when s = 1 (see algorithm 4 In
section B.2).
Detailed descriptions of the implementations of each algorithm are pro-
vided in section C.1.
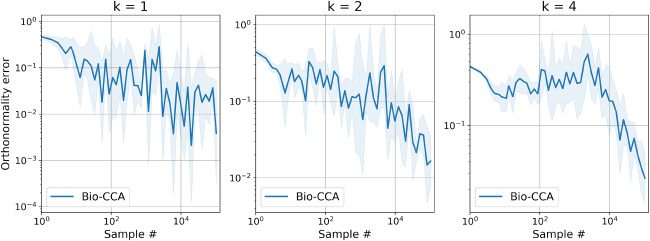
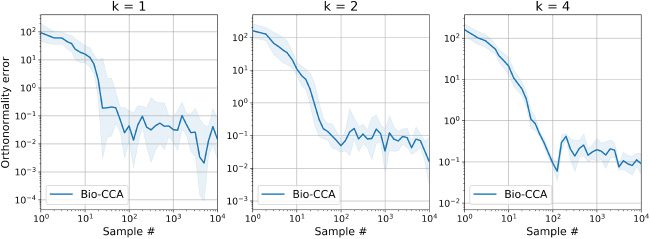
6.2.2 Performance Metrics. To evaluate the performance of Bio-CCA, we
use two performance metrics. The first performance metric is the following
[0,2]-valued normalized objective error function:
Normalized objective error(T) :=
ρ
max
X,tCxyVy,T )
− Tr(V(cid:5)
ρ
max
.
(6.1)
+ · · · + ρ
max := (ρ
1
Here ρ
k)/2 is the optimal value of the CCA objective,
equations 2.1 E 2.2, E (Vx,T, Vy,T ) are the basis vectors reported by the
respective algorithm after iteration t, normalized to ensure they satisfy the
orthonormality constraint, equation 2.2. (We do not evaluate Bio-RRR using
this metric because the algorithm only outputs one set of basis vectors.)
The second performance metric is the (x−)subspace error function de-
fined by
Subspace error(T) :=
(cid:7)
(cid:7)
(cid:5)
(cid:7)Vx,T (V
X,tVx,T )
(cid:5)
−1V
X,T
(cid:5)
− Vx(V
x Vx)
(cid:5)
−1V
X
(cid:7)
(cid:7)
2
(cid:7)
F
,
(6.2)
where Vx is the matrix of optimal basis vectors defined as in equation 2.5.
(We do not evaluate MSG-CCA using this metric because the algorithm out-
puts the product Vx,tV(cid:5)
sì,t rather than outputting the basis vectors Vx,t and
Vy,t separately.)
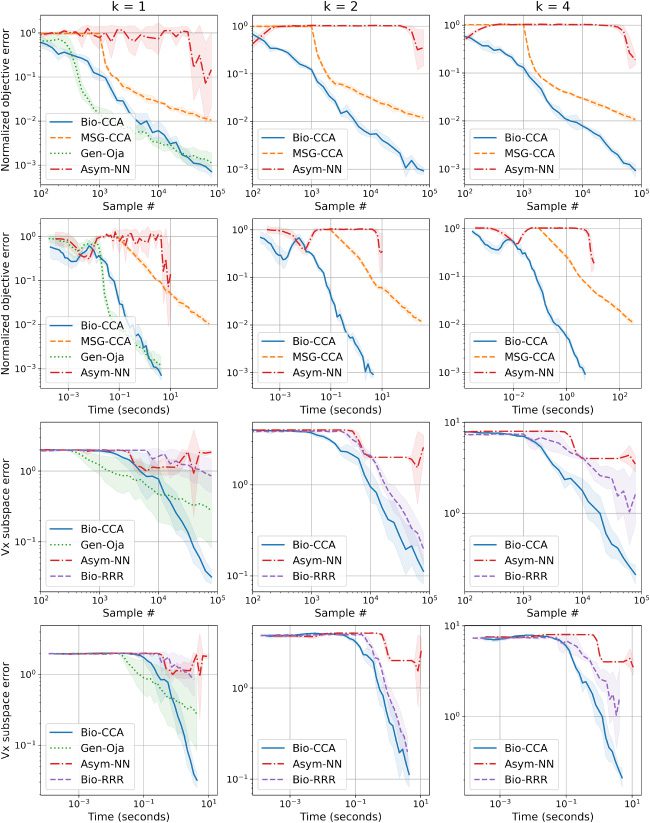
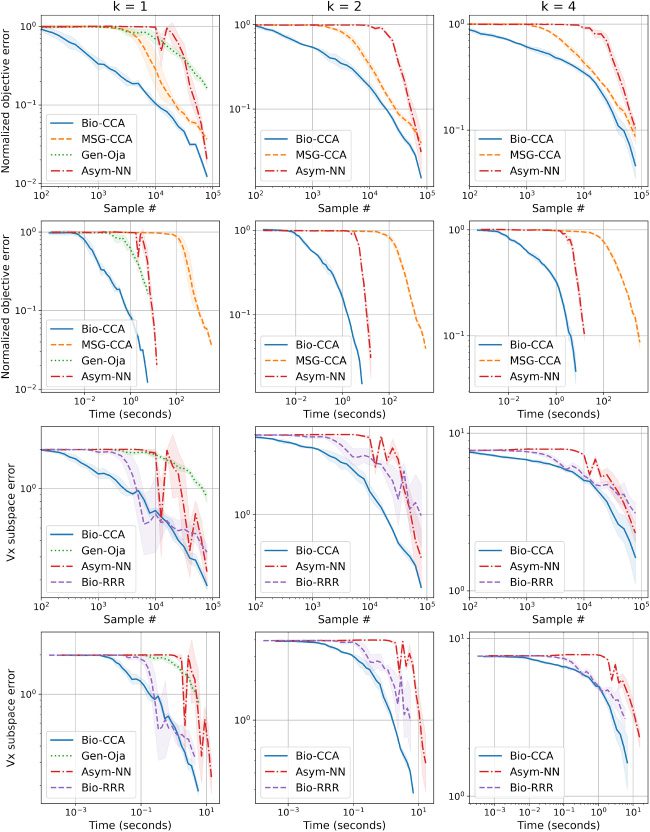
6.2.3 Evaluation on the Synthetic Data Set. In Figure 6 we plot the per-
formance of Bio-CCA in terms of both sample and run-time efficiency,
against the competing algorithms for target dimensions k = 1, 2, 4 on the
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
2331
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 6: Comparisons of Bio-CCA (algorithm 2) with the competing algo-
rithms on the synthetic data set, for k = 1, 2, 4, in terms of the normalized objec-
tive error defined in equation 6.1 as a function of sample number and run time
(top two rows), and in terms of the subspace error defined in equation 6.2 as a
function of sample number and run time (bottom two rows).
synthetic data set, presented once in a randomly permuted order. For k = 1,
Gen-Oja initially outperforms Bio-CCA in sample and run-time efficiency;
Tuttavia, Bio-CCA eventually performs comparable to Gen-Oja when given
2332
D. Lipshutz et al.
sufficiently many samples (and outperforms Gen-Oja in terms of subspace
error). For k = 2, 4, the sample and run-time efficiency of Bio-CCA outper-
forms the other competing algorithms. The MSG-CCA error does not begin
to decay until the 103 iteration because the first 103 samples are used to ob-
tain initial estimates of the covariance matrices Cxx and Cyy. The poor per-
formance of the asymmetric network (Pehlevan et al., 2020) is due in part
to the fact that the algorithm depends on the gaps between the canonical
correlations, which are small for the synthetic data set. In Figure 11 in sec-
tion C.2, we verify that the Bio-CCA basis vectors asymptotically satisfy the
orthonormality constraint equation 2.2.
6.2.4 Evaluation on Mediamill. In Figure 7 we plot the performance of
Bio-CCA, in terms of both sample and run-time efficiency, against the com-
peting algorithms for target dimensions k = 1, 2, 4 on Mediamill, presented
three times with a randomly permuted order in each presentation. When
tested on Mediamill, the sample and run time efficiency of Bio-CCA outper-
form the competing algorithms (for k = 1, Bio-RRR performs comparable to
Bio-CCA). In Figure 12 in section C.2, we verify that the Bio-CCA basis vec-
tors asymptotically satisfy the orthonormality constraint, equation 2.2.
6.3 Adaptive Bio-CCA with Output Whitening. Prossimo, we evaluate the
performance of Adaptive Bio-CCA with output whitening (see algorithm 3)
on all three data sets. Since we are unaware of competing online algorithms
for adaptive CCA with output whitening, to compare the performance of
algorithm 3 to existing methods, we also plot the performance of Bio-RRR
Golkar et al. (2020) with respect to subspace error, where we a priori select
the target dimension. We chose Bio-RRR because the algorithm also maps
onto a neural network that resembles the cortical microcircuit and because
it performs relatively well on the synthetic data set and Mediamill.
6.3.1 Performance Metric. To evaluate the performance of Adaptive
Bio-CCA with output whitening, we use a subspace error metric. Recall that
the target output rank of algorithm 3, denoted r, is equal to the number of
canonical correlations ρ
1
k that exceed max(α − 1, 0), questo è,
, . . . , ρ
R := max{1 ≤ i ≤ k : ρ
io
> max(α − 1, 0)}.
(6.3)
Since the target dimension is often less than k, the subspace error defined
in equation 6.2 is not an appropriate metric because the projection matrices
are rank k. Piuttosto, we evaluate Adaptive Bio-CCA with output whitening
using the adaptive subspace error function defined by
Adaptive subspace error(T) :=
(cid:7)
(cid:7)(cid:14)
Ux,T
(cid:14)
U
(cid:5)
X,T
− (cid:14)
Vx(
(cid:14)
(cid:5)
V
X
(cid:14)
Vx)
−1(cid:14)
(cid:5)
V
X
(cid:7)
(cid:7)2
F
,
(6.4)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
2333
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 7: Comparisons of Bio-CCA (algorithm 2) with the competing algo-
rithms on Mediamill, for k = 1, 2, 4, in terms of the normalized objective error
defined in equation 6.1 as a function of sample number and run time (top two
rows), and in terms of the subspace error defined in equation 6.2 as a function
of sample number and run time (bottom two rows).
(cid:14)
Ux,t is the m × r matrix whose column vectors are the top r right-
Dove
(cid:14)
Vx is the m × r matrix whose ith column vector
singular vectors of Wx,T, E
is equal to the ith column vector of the matrix Vx defined in equation 2.5,
2334
D. Lipshutz et al.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
Figura 8: Comparisons of Adaptive Bio-CCA with output whitening (see algo-
rithm 3) and Bio-RRR on the synthetic data set, for α = 1.2, 1.5, 1.8, in terms
of the subspace error as a function of sample number (top row) and run time
(bottom row). For each α, r is the target output rank defined as in equation 6.3.
for i = 1, . . . , R. (The covariance matrices used in the definition for Vx are
those associated with the distribution that is being streamed at iteration t.)
If r = k, then the error aligns with the subspace error defined in equation 6.2.
Since the output dimension of Bio-RRR is a priori set to r, the performance
of Bio-RRR is evaluated using the subspace error defined in equation 6.2.
6.3.2 Evaluation on the Synthetic Data Set. From Figure 4 (left) we see
that the first eight canonical correlations are close to one, and the remain-
ing canonical correlations are approximately zero. Therefore, for k ≥ 8 E
α ∈ (1.1, 1.9), algorithm 3 should project the inputs xt and yt onto the 8-
dimensional subspace spanned by the top eight pairs of canonical corre-
lation basis vectors, and set the nonzero output covariance eigenvalues to
one. In Figure 8 we plot the performance of algorithm 3 with k = 10 for
α = 1.2, 1.5, 1.8 on the synthetic data set (presented once with a randomly
permuted order). We see that Adaptive Bio-CCA with output whitening
outperforms Bio-RRR, even though the target output dimension of Bio-RRR
was set a priori. In Figure 13 in section C.2, we verify that the Adaptive
Bio-CCA with output whitening basis vectors asymptotically satisfies the
whitenening constraint.
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
2335
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 9: Comparisons of Adaptive Bio-CCA with output whitening (see algo-
rithm 3) with Bio-RRR on the data set Mediamill, for α = 1.2, 1.5, 1.8, in terms
of the subspace error as a function of sample number (top row) and run time
(bottom row). For each α, r is the target output rank defined as in equation 6.3.
6.3.3 Evaluation on Mediamill. From Figure 4 (right) we see that the
canonical correlations of the data set Mediamill exhibit a more gradual de-
cay than the canonical correlations of the synthetic data set. As we increase
the threshold α in the interval (1.1,1.4), the rank of the output of algorithm
3 decreases. In Figure 9 we plot the performance of algorithm 3 with k = 10
for α = 1.15, 1.2, 1.3 on Mediamill (presented three times with a randomly
permuted order in each presentation). As with the synthetic data set, we
find that Adaptive Bio-CCA with output whitening outperforms Bio-RRR.
In Figure 14 in section C.2, we verify that the Adaptive Bio-CCA with output
whitening basis vectors asymptotically satisfy the whitenening constraint.
6.3.4 Evaluation on the Nonstationary Data Set. From Figure 5, we see
that the distributions that contribute to the nonstationary data set all have
canonical correlations that are close to zero or one. The first distribution
has four canonical correlations close to one, the second distribution has
eight canonical correlations close to one and the third distribution has one
canonical correlation close to one. Therefore, for k ≥ 8 and α ∈ (1.1, 1.9), al-
gorithm 3 should initially (for the first 100,000 inputs) project the inputs xt
and yt onto a 4-dimensional subspace, Poi (for the second 100,000 inputs)
project the inputs onto an 8-dimensional subspace, and finally (for the final
2336
D. Lipshutz et al.
Figura 10: On the left, we plot the performance of Adaptive Bio-CCA with out-
put whitening (with α = 1.5) on the nonstationary synthetic data set in terms of
the subspace error defined in equation 6.4. On the right we plot the output rank
defined in equation 6.5.
100,000 inputs) project the inputs onto a 1-dimensional subspaces In Figure
10 (left) we plot the performance of algorithm 3 with k = 10 and α = 1.5 SU
the nonstationary data set in terms of the adaptive subspace error.2 Note
that the adaptive subspace error spikes each time the algorithm is streamed
inputs from a new distribution (these epochs are denoted by the gray ver-
tical dashed lines) before decaying. In Figure 10 (right) we plot the output
rank of Adaptive Bio-CCA with output whitening defined by
(cid:5)
Output rank(T) = Tr(V
(cid:5)
X,tCxyVy,T + V
(cid:5)
(cid:5)
xyVx,T
sì,tC
X,tCxxVx,T + V
sì,tCyyVy,T ),
(cid:5)
+ V
(6.5)
Dove, at each iteration t, the covariance matrices correspond to the dis-
tribution from which (xt, yt ) is streamed. Note that the output rank adapts
each time the algorithm is streamed inputs from a new distribution to match
the dimension of the latent variable generating the distribution. In particu-
lar, we see that the algorithm is able to quickly adapt its output rank to new
distributions.
7 Discussion
In this work, we derived an online algorithm for CCA that can be imple-
mented in a neural network with multicompartmental neurons and local,
non-Hebbian learning rules. We also derived an extension that adaptively
chooses the output rank and whitens the output. Remarkably, the neural
architecture and non-Hebbian learning rules of our extension resembled
2
Since the competing algorithms are not adaptive and need to have their output di-
mension set by hand, we do not include a competing algorithm for comparison.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
2337
neural circuitry and non-Hebbian plasticity in cortical pyramidal neu-
rons. Così, our neural network model may be useful for understanding
the computational role of multicompartmental neurons with non-Hebbian
plasticity.
While our neural network model captures salient features of cortical
microcircuits, there are important biophysical properties that are not ex-
plained by our model. Primo, our model uses linear neurons to solve the
linear CCA problem, which substantially limits its computational capabil-
ities and is a major simplification of cortical pyramidal neurons that can
perform nonlinear operations (Gidon et al., 2020). Tuttavia, studying the
analytically tractable and interpretable linear neural network model is use-
ful for understanding more complex nonlinear models. Such an approach
has proven successful for studying deep networks in the machine learning
literature (Arora, Cohen, Golowich, & Eh, 2019). In future work, we plan
to incorporate nonlinear neurons in our model.
Secondo, our neural network implementation requires the same num-
ber of interneurons and principal neurons, whereas in the cortex, there
are approximately four times more pyramidal neurons than interneurons
(Larkum et al., 1999). In our model, the interneurons decorrelate the output,
E, in practice, the optimal fixed points of the algorithm can destabilize
when there are fewer interneurons than principal neurons (see remark 3A
in the supplementary material of Pehlevan & Chklovskii, 2015). In biologi-
cal circuits, these instabilities could be mitigated by other biophysical con-
straints; Tuttavia, a theoretical justification would require additional work.
Third, the output of our neural network is the equally weighted sum of
the basal and apical projections. Tuttavia, experimental evidence suggests
that the pyramidal neurons integrate their apical and basal inputs asym-
metrically (Larkum, Nevian, Sandler, Polsky, & Schiller, 2009; Larkum, 2013;
Major, Larkum, & Schiller, 2013). Inoltre, in our model, the apical learn-
ing rule is non-Hebbian and depends on a calcium plateau potential that
travels from the basal dendrites to the apical tuft. Experimental evidence
for calcium plateau potential dependent plasticity is focused on the basal
dendrites, with inconclusive evidence on the plasticity rules for the apical
dendrites (Golding et al., 2002; Sjöström & Häusser, 2006).
To provide an alternative explanation of cortical computation, in a sepa-
rate work (Golkar et al., 2020), we derive an online algorithm for the general
supervised learning method reduced-rank regression, which includes CCA
as a special case (see section B.2 for a detailed comparison of the two al-
gorithms). The algorithm also maps onto a neural network with multicom-
partmental neurons and non-Hebbian plasticity in the basal dendrites. Both
models adopt a normative approach in which the algorithms are derived
from principled objective functions. This approach is highly instructive as
the differences between the models highlight which features of the network
that are central to implementing an unsupervised learning method versus
a supervised learning method.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2338
D. Lipshutz et al.
There are three main differences between the biological interpretation of
the two algorithms. Primo, the output of the network in Golkar et al. (2020)
is the projection of the basal inputs, with no apical contribution. Secondo,
the network in Golkar et al. (2020) allows for a range of apical synaptic up-
date rules, including Hebbian updates. Third, the adaptive network derived
here includes a threshold parameter α, which adaptively sets the output di-
mension and is not included in Golkar et al. (2020). In our model, this pa-
rameter corresponds to the contribution of the somatic output to plasticity
in the basal dendrites. These differences can be compared to experimental
outcomes to provide evidence that cortical microcircuits implement unsu-
pervised algorithms, supervised algorithms, or mixtures of both. Così, we
find it informative to put forth and contrast the two models.
Finalmente, we did not prove theoretical guarantees that our algorithms
converge. As we show in appendix D, Offline-CCA and Bio-CCA can be
viewed as gradient descent-ascent and stochastic gradient descent-ascent
algorithms for solving a nonconvex-concave min-max problem. While gra-
dient descent-ascent algorithms are natural methods for solving such min-
max problems, they are not always guaranteed to converge to a desired
solution. Infatti, when the gradient descent step size is not sufficiently
small relative to the gradient ascent step size (cioè., when τ is not suffi-
ciently small), gradient descent-ascent algorithms for solving nonconvex-
concave min-max problems can converge to limit cycles (Hommes & Ochea,
2012; Mertikopoulos, Papadimitriou, & Piliouras, 2018). Establishing local
or global convergence and convergence rate guarantees that for general
gradient descent-ascent algorithms is an active area of research, and even
recent advances (Lin, Jin, & Jordan, 2020) impose assumptions that are not
satisfied in our setting. In appendix D, we discuss these challenges and
place our algorithms within the broader context of gradient descent-ascent
algorithms for solving nonconvex-concave min-max problems.
Appendix A: Sums of CCSPs as Principal Subspace Projections
, . . . , zT can be ex-
In this section, we show that the sums of the CCPSs z1
pressed as the principal subspace projection of the whitened concatenated
data ξ
, . . . , ξT , defined by
1
(cid:5)
ξt :=
−1/2
xx xt
−1/2
yy yt
C
C
(cid:6)
.
(A.1)
A tal fine, recall the CCA objective,
arg max
Vx∈Rm×k,Vy∈Rn×k
Tr
(cid:2)
V
(cid:5)
x CxyVy
(cid:3)
,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
2339
subject to the whitening constraint V(cid:5)
rewrite the CCA objective as a generalized eigenproblem,
x CxxVx + V(cid:5)
y CyyVy = Ik. We can
arg max
Vx∈Rm×k,Vy∈Rn×k
Tr
(cid:6)(cid:5) (cid:5)
(cid:5)
Vx
Vy
C(cid:5)
xy
Cxy
(cid:6) (cid:5)
(cid:6)
Vx
Vy
,
subject to the whitening constraint
(cid:6)(cid:5) (cid:5)
Cxx
(cid:5)
Vx
Vy
(cid:6) (cid:5)
(cid:6)
Vx
Vy
= Ik
.
Cyy
(A.2)
(A.3)
The equivalence can be readily verified by expanding the matrix products
in equations A.2 and A.3.
Prossimo, we transform this generalized eigenproblem formulation, equa-
tions A.2 and A.3, into a standard eigenproblem formulation. Since the trace
of the left-hand side of equation A.3 is constrained to equal k, we can add it
to the trace in equation A.2, without affecting the output of the argmax, A
arrive at the CCA objective:
arg max
Vx∈Rm×k,Vy∈Rn×k
Tr
(cid:5)
Vx
Vy
(cid:6)(cid:5) (cid:5)
(cid:6) (cid:5)
(cid:6)
Cxx Cxy
C(cid:5)
xy Cyy
Vx
Vy
,
(A.4)
subject to the whitening constraint in equation A.3.
Our final step is a substitution of variables. Define the d × k matrix
Vξ :=
(cid:5)
(cid:6)
.
C1/2
xx Vx
C1/2
yy Vy
(A.5)
After substituting into equations A.4 and A.3, we see that (Vx, Vy) is a so-
lution of the CCA objective if and only if Vξ is a solution of
TrV
(cid:5)
ξ Cξ ξ Vξ
subject to
(cid:5)
ξ Vξ = Ik
V
,
(A.6)
arg max
Vξ ∈Rd×k
(cid:17)
T
t=1
ξtξ(cid:5)
is the covariance matrix defined by Cξ ξ :=
where we recall that Cξ ξ
1
T . Importantly, equation A.6 is the variance maximization objec-
T
tive for the standard PCA eigenproblem, which is optimized when the col-
umn vectors of Vξ form an orthonormal basis spanning the k-dimensional
principal subspace of the data ξ
, . . . , ξT . Therefore, by equations A.1 and
1
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2340
D. Lipshutz et al.
A.5, the projection of the vector ξt onto its principal subspace is precisely
the desired sum of CCSPs:
(cid:5)
zt := V
x xt + V
y yt = V
(cid:5)
(cid:5)
ξ ξt.
Appendix B: Adaptive Bio-CCA with Output Whitening
B.1 Detailed Derivation of Algorithm 3. Recall the min-max objective
given in equation 4.4:
arg min
Z∈Rk×T
max
N∈Rk×T
min
Wx∈Rk×m
min
Wy∈Rk×n
max
P∈Rk×k
(cid:14)
l(Wx, Wy, P, Z, N),
(B.1)
Dove
Tr
l(Wx, Wy, P, Z, N) := 1
(cid:14)
T
+ 1
T
+ Tr
(cid:2)
(cid:5)
−2Z
(cid:5)
WxX − 2Z
(cid:5)
WyY + αZ
(cid:3)
Z
(cid:5)
(cid:5)
(cid:5)
Z − N
N
P
(cid:3)
(cid:2)
2N
Tr
(cid:8)
WxCxxW
(cid:5)
X
+ WyCyyW
(cid:5)
sì
(cid:5)
− PP
(cid:9)
.
(cid:14)
l(Wx, Wy, P, Z, N) is strictly convex in Wx, Wy, and Z, and strictly
Since
concave in P and N, we can interchange the order of optimization to obtain
min
Wx∈Rk×m
min
Wy∈Rk×n
max
P∈Rk×k
min
Z∈Rk×T
max
N∈Rk×T
(cid:14)
l(Wx, Wy, P, Z, N).
(B.2)
The interchange of the maximization with respect to N and the minimiza-
tion with respect to Wx and Wy is justified by the fact that for fixed Z and
(cid:14)
l(Wx, Wy, P, Z, N) is strictly convex in (Wx, Wy) and strictly concave in
P,
N. Allo stesso modo, the interchange of the minimization with respect to Z and the
maximization with respect to P is justified by the fact that for fixed N, Wx,
(cid:14)
l(Wx, Wy, P, Z, N) is convex in Z and strictly concave in P. In or-
and Wy,
der to derive an online algorithm, we write the objective in terms of time-
separable terms,
l(Wx, Wy, P, Z, N) = 1
(cid:14)
T
T(cid:4)
t=1
(cid:14)
lt (Wx, Wy, P, zt, nt ),
Dove
(cid:14)
lt (Wx, Wy, P, zt, nt ) := −2z
(cid:5)
t Wxxt − 2z
(cid:8)
(cid:5)
t Wyyt + αz
t zt + 2N
(cid:5)
+ Tr
Wxxtx
(cid:5)
t W
(cid:5)
X
+ Wyyty
(cid:5)
t W
(cid:5)
sì
(cid:5)
− PP
(cid:5)
(cid:5)
t P
(cid:9)
zt − n
(cid:5)
t nt
.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Biologically Plausible Neural Network for CCA
2341
At each time step t, for fixed Wx, Wy, and M, we first simultaneously
(cid:14)
lt (Wx, Wy, P, zt, nt ) over nt and minimize
maximize the objective function
over zt by running the fast gradient descent-ascent dynamics in equa-
(cid:14)
lt (Wx, Wy, P, zt, nt ) is convex in zt
zioni 5.1 E 5.2 to equilibrium. Since
and concave in nt, these fast dynamics equilibriate at the saddle point where
zt = (PP(cid:5) + αIk)
−1(at + bt ) and nt = P(cid:5)zt. Then, con (nt, zt ) fixed, we per-
form a gradient descent-ascent step of the objective function with respect to
(Wx, Wy) and P:
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
Wx ← Wx −
Wx ← Wy −
P ← P +
η
η
2
∂(cid:14)
lt (Wx, Wy, P, zt, nt )
∂Wx
∂(cid:14)
lt (Wx, Wy, P, zt, nt )
∂Wy
2
∂(cid:14)
lt (Wx, Wy, P, zt, nt )
∂P
.
η
2τ
,
,
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
Substituting in with the partial derivatives yields algorithm 3.
B.2 Comparison with Bio-RRR. In this section, we compare Adaptive
Bio-CCA with output whitening (see algorithm 3) and Bio-RRR (Golkar
et al., 2020, algorithm 2). We first state the Bio-RRR algorithm.3
Bio-RRR implements a supervised learning method for minimizing re-
construction error, with the parameter 0 ≤ s ≤ 1 specifying the norm under
which the error is measured (see Golkar et al., 2020, section 3, for details).
Importantly, when s = 1, algorithm 4 implements a supervised version of
CCA. Setting α = 1 in algorithm 3 and s = 1 in algorithm 4, the algorithms
have identical network architectures and synaptic update rules, namely:
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
3
In Golkar et al. (2020) the inputs xt are the basal inputs and the inputs yt are the apical
inputs. Here we switch the inputs to be consistent with algorithm 3.
2342
D. Lipshutz et al.
Tavolo 1: Comparison of Adaptive Bio-CCA with Output Whitening and Bio-
RRR.
Adaptive Bio-CCA
Bio-RRR
Unsupervised/supervised
Whitened outputs
Adaptive output rank
unsupervised
√
√
supervised
√
×
(cid:5)
Wx ← Wx + ηx(zt − at )X
T
(cid:5)
Wy ← Wy + ηyca
t y
T
(cid:5)
P ← P + ηp(ztn
T
− P),
,
,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T := at − Pnt. For this parameter choice, the main
where we recall that ca
difference between the algorithms is that Adaptive Bio-CCA with output
whitening is an unsupervised learning algorithm, whereas Bio-RRR is a su-
pervised learning algorithm, which is reflected in their outputs zt: the out-
put of algorithm 3 is the whitened sum of the basal dendritic currents and
the apical calcium plateau potential, questo è, zt = bt + ca
T , whereas the out-
put of (Golkar et al., 2020, algorithm 2) is the (whitened) CCSP of the basal
inputs, zt = bt. In other words, the apical inputs do not directly contribute
to the output of the network in Golkar et al. (2020), only indirectly via plas-
ticity in the basal dendrites. Experimental evidence suggests that apical cal-
cium plateau potentials contribute significantly to the outputs of pyramidal
cells, which supports the model derived here. Inoltre, the model in
this work allows one to adjust the parameter α to adaptively set the out-
put rank, which is important for analyzing non-stationary input streams.
In Table 1 we summarize the differences between the two algorithms.
B.3 Decoupling the Interneuron Synapses. The neural network for
Adaptive Bio-CCA with output whitening derived in section 4 requires
the pyramidal neuron-to-interneuron synaptic weight matrix P(cid:5)
to be the
the transpose of the interneuron-to-pyramidal neuron synaptic weight ma-
trix P. Enforcing this symmetry via a centralized mechanism is not biologi-
cally plausible. Piuttosto, following (Golkar et al., 2020, appendix D), we show
that the symmetry between these two sets of weights naturally follows from
the local learning rules.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
N
e
C
o
_
UN
_
0
1
4
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
To begin, we replace the pyramidal neuron-to-interneuron weight ma-
trix P(cid:5)
by a new weight matrix R with Hebbian learning rules:
R ← R +
η
τ (ntz
(cid:5)
T
− R).
(B.3)
A Biologically Plausible Neural Network for CCA
2343
Tavolo 2: Optimal Time-Dependent Learning Rates.
Bio-CCA (η
, γ , τ )
0
Gen-Oja (β
, γ )
0
Asym-NN (η
, α)
0
Bio-RRR (η
, γ , μ)
0
Adaptive Bio-CCA (η
0
, γ , τ )
Synthetic
−4, 0.1)
−3, 10
−2 )
(1, 10
−4, 5 × 10
−4, 10)
−4, 0.1)
−3, 10
−3, 10
−6 )
(10
(2 × 10
(10
(10
(10
Mediamill
−2, 10
(10
(2 × 10
(10
(10
−4, 0.1)
−2, 10
−3 )
−3, 5 × 10
−5, 10)
−4, 0.5)
−2, 10
−2, 10
−6 )
Let P0 and R0 denote the initial values of P and R. Then, in view of the
updates rule for P in and R in algorithm 3 and equation B.3, rispettivamente,
the difference P(cid:5) − R after T updates is given by
(cid:5) − R =
P
(cid:8)
1 −
(cid:9)
T
η
τ
(P
(cid:5)
0
− R0).
In particular, the difference decays exponentially (recall that η < τ by
assumption).
Appendix C: Numerics
C.1 Experimental Details.
C.1.1 Bio-CCA. We implemented algorithm 2. We initialized Wx (resp.
Wy) to be a random matrix with i.i.d. mean-zero normal entries with
variance 1/m (resp. 1/n). We initialized M to be the identity matrix Ik.
We used the time-dependent learning rate of the form ηt = η
/(1 + γ t).
To find the optimal hyperparameters, we performed a grid search over
∈ {10−2, 10−3, 10−4}, γ ∈ {10−3, 10−4, 10−5}, and τ ∈ {1, 0.5, 0.1}. The best-
η
performing parameters are reported in Table 2. Finally, to ensure the re-
ported basis vectors satisfy the orthonormality constraints equation 2.2, we
report the following normalized basis vectors:
0
0
V
(cid:5)
x :=
V
(cid:5)
y :=
(cid:18)
M
(cid:18)
M
−1(WxCxxW
(cid:5)
x
+ WyCyyW
−1
(cid:5)
y )M
−1(WxCxxW
(cid:5)
x
+ WyCyyW
−1
(cid:5)
y )M
(cid:19)−1/2
(cid:19)−1/2
M
−1Wx,
M
−1Wy.
(C.1)
(C.2)
C.1.2 MSG-CCA. We implemented the online algorithm stated in Arora
et al. (2017). MSG-CCA requires a training set to estimate the covariance
matrices Cxx and Cyy. We provided the algorithm with 1000 samples to ini-
tially estimate the covariance matrix. Following Arora et al. (2017), we use
the time-dependent learning rate ηt = 0.1/
√
t.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2344
D. Lipshutz et al.
C.1.3 Gen-Oja. We implemented the online algorithm stated in Bhatia
et al. (2018). The algorithm includes two learning rates: αt and βt. As stated
in Bhatia et al. (2018), the Gen-Oja’s performance is robust to changes in
the learning rate αt but sensitive to changes in the learning rate βt. Follow-
ing Bhatia et al. (2018), we set αt to be constant and equal to 1/R2 where
R2 := Tr(Cxx) + Tr(Cyy). To optimize over βt, we used a time-dependent
learning rate of the form βt = β
/(1 + γ t) and performed a grid search over
0
−3}. The best-performing param-
−1, 10
−2} and γ ∈ {10
−1, 10
β
0
eters are reported in Table 2.
∈ {1, 10
−2, 10
C.1.4 Asymmetric CCA Network. We implemented the online multi-
channel CCA algorithm derived in Pehlevan et al. (2020). Following Pehle-
van et al. (2020), we use the linearly decaying learning rate ηt = η
×
max(1 − αt, 0.1). To optimize the performance of the algorithm, we per-
−3} and α ∈ {5 ×
−2, 2 × 10
formed a grid search over η
0
−6}. The best-performing parameters are reported in
−5, 5 × 10
−5, 10
10
Table 2.
∈ {2 × 10
−6, 10
−3, 10
−2, 10
0
C.1.5 Bio-RRR. We implemented the online CCA algorithm derived in
Golkar et al. (2020) with s = 1 (see algorithm 4). The algorithm includes
learning rates ηx, ηy, and ηp. Following Golkar et al. (2020), we set ηy = ηt
and ηx = ηp = ηy/μ and use the time-dependent learning rate of the form
−4},
ηt = η
0
−5} and μ ∈ {1, 10, 100} and list best-performing param-
γ ∈ {10
eters in Table 2.
/(1 + γ t). We performed a grid search over η
0
−3, 10
−3, 10
−4, 10
−2, 10
∈ {10
C.1.6 Adaptive Bio-CCA with Output Whitening. We implemented algo-
rithm 3. We initialized Wx, Wy, and P to be random matrices with i.i.d. stan-
dard normal entries. To find the optimal hyperparameters, we performed
∈ {10−2, 10−3, 10−4}, γ ∈ {10−3, 10−4, 10−5}, and τ ∈
a grid search over η
0
{1, 0.5, 0.1}. The best-performing parameters are reported in Table 2.
C.2 Orthonormality Constraints.
C.2.1 Bio-CCA. To verify that the Bio-CCA basis vectors asymptotically
satisfy the orthonormality constraint, equation 2.2, we use the following
orthonormality error function:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Orthonormality Error(t)
−1
(Wx,tCxxW(cid:5)
(cid:2)M
x,t
t
+ Wy,tCyyW(cid:5)
−1
y,t )M
t
k
:=
− Ik
(cid:2)2
F
.
(C.3)
In Figure 11 (resp. Figure 12) we demonstrate that Bio-CCA asymptotically
satisfies the CCA orthonormality constraints, equation 2.2 on the synthetic
data set (resp. Mediamill).
A Biologically Plausible Neural Network for CCA
2345
Figure 11: The deviation of the Bio-CCA solution from the CCA orthonormality
constraint, in terms of the orthonormality error defined in equation C.3 on the
synthetic data set.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 12: The deviation of the Bio-CCA solution from the CCA orthonormality
constraint, in terms of the orthonormality error defined in equation C.3, on the
data set Mediamill.
C.2.2 Adaptive Bio-CCA with Output Whitening. To verify that the top
r eigenvalues of the output covariance asymptotically approach 1, we let
λ
1(t) ≥ · · · ≥ λ
k(t) denote the ordered eigenvalues of the matrix,
(cid:5)
Czz(t) := V
x,tCxxVx,t + V
x,tCxyVy,t + V
(cid:5)
(cid:5)
(cid:5)
y,tC
xyVx,t + V
(cid:5)
y,tCyyVy,t,
and define the whitening error by
Whitening Error(t) :=
(cid:17)
r
i=1
|λ
i(t) − 1|2 +
k
(cid:17)
k
i=r+1
|λ
i(t)|2
.
(C.4)
In Figure 13 (resp. Figure 14) we demonstrate that Bio-CCA asymptotically
satisfies the CCA orthonormality constraints equation 2.2, on the synthetic
data set (resp. Mediamill).
2346
D. Lipshutz et al.
Figure 13: The deviation of the Bio-CCA solution from the CCA orthonormality
constraint, in terms of the orthonormality error defined in equation C.3, on the
synthetic data set.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 14: The deviation of the Adaptive Bio-CCA with output whitening so-
lution from the whitening constraint, in terms of the whitening error defined in
equation C.4, on the data set Mediamill.
Appendix D: On Convergence of the CCA Algorithms
To interpret our offline and online CCA algorithms (see algorithms 1 and 2)
mathematically, we first make the following observation. Both algorithms
optimize the min-max objective, equation 3.5, which includes optimization
over the neural outputs Z. In this way, the neural activities can be viewed
as optimization steps, which is useful for a biological interpretation of the
algorithms. However, since we assume a separation of timescales in which
the neural outputs equilibrate at their optimal values before the synaptic
weight matrices are updated, the neural dynamics are superfluous when
analyzing the algorithms from a mathematical perspective. Therefore, we
set Z equal to its equilibrium value Z = M−1(WxX + WyY) in the cost
A Biologically Plausible Neural Network for CCA
2347
function L(Wx, Wy, M, Z) to obtain a min-max problem in terms of the
synaptic weights:
min
W∈Rk×d
max
M∈S k
++
F(W, M),
(D.1)
where W := [Wx Wy] is the matrix of concatenated weights and F(W, M) :=
L(Wx, Wy, M, Z). After substitution, we see that F : Rk×d × S k
++ → R is the
nonconvex-concave function,
(cid:10)
F(W, M) = Tr
−M
−1WAW
(cid:5) + WBW
(cid:11)
M2
,
(cid:5) − 1
2
with partial derivatives
−
∂F(W, M)
∂W
∂F(W, M)
∂M
= 2M
−1WA − 2WB,
= M
−1WAW
(cid:5)
−1 − M,
M
where we have defined
(cid:6)
(cid:5)
A :=
Cxx Cxy
C(cid:5)
xy Cyy
, B :=
(cid:5)
Cxx
(cid:6)
.
Cyy
(D.2)
Similar objectives, with different values of A and B, arise in the analysis
of online principal subspace projection (Pehlevan, Sengupta, & Chklovskii,
2018) and slow feature analysis (Lipshutz et al., 2020) algorithms.
The synaptic updates in both our offline and online algorithms can be
viewed as (stochastic) gradient descent-ascent algorithms for solving the
noncovex-concave min-max problem, equation D.1. To make the compari-
son with our offline algorithm, we substitute the optimal value Z into the
synaptic weight updates in algorithm 1 to obtain
W ← W + 2η(M
M ← M +
η
τ (M
−1WA − WB),
(cid:5)
−1WAW
M
−1 − M),
(D.3)
(D.4)
Comparing these updates to the partial derivatives of F, we see that Offline-
CCA is naturally interpreted as a gradient descent-ascent algorithm for
solving the min-max problem, equation D.1, with descent step size η and
η
ascent step size
τ . Similarly, to make the comparison with our online al-
gorithm, we substitute the explicit expression for the equilibrium value
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2348
D. Lipshutz et al.
zt = M−1(at + bt ), where at = Wxxt and bt = Wyyt, into the synaptic weight
updates in algorithm 2 to rewrite the updates:
W ← W + 2η(M
M ← M +
η
τ (M
−1WAt − WBt ),
−1WAtW
M
(cid:5)
−1 − M),
where
(cid:5)
At :=
t
xtx(cid:5)
ytx(cid:5)
t
(cid:6)
, Bt :=
(cid:5)
xtx(cid:5)
t
(cid:6)
.
yty(cid:5)
t
t
xty(cid:5)
yty(cid:5)
t
Comparing these updates to the partial derivatives of F, we see that our
online algorithm is naturally interpreted as a stochastic gradient descent-
ascent algorithm for solving the min-max problem, equation D.1, using the
time t rank-1 approximations At and Bt in place of A and B, respectively.
Establishing theoretical guarantees for solving nonconvex-concave min-
max problems of the form, equation D.1 via stochastic gradient descent-
ascent is an active area of research (Razaviyayn et al., 2020). Borkar (1997,
2009) proved asymptotic convergence to the solution of the min-max prob-
lem for a two timescale stochastic gradient descent-ascent algorithm, where
the ratio between the learning rates for the minimization step and the maxi-
mization step, τ , depends on the iteration and converges to zero in the limit
as the iteration number approaches infinity. Lin et al. (2020) established con-
vergence rate guarantees for a stochastic gradient descent-ascent algorithm
to an equilibrium point (not necessarily a solution of the min-max prob-
lem). Both results, however, impose assumptions that do not hold in our
setting: the partial derivatives of F are Lipschitz continuous and M is re-
stricted to a bounded convex set. Therefore, establishing global stability
with convergence rate guarantees for our offline and online CCA algorithms
requires new mathematical techniques that are beyond the scope of this
work.
Even proving local convergence properties is nontrivial. In the special
case that B = Id, Pehlevan et al. (2018) carefully analyzed the continuous
dynamical system obtained by formally taking the step size η to zero in
equations D.3 and D.4. They computed an explicit value τ
≥ 1/2, in terms
0
the eigenvalues of A such that if τ ≤ τ
0, then solutions of the min-max prob-
lem, equation D.1, are the only linearly stable fixed points of the continu-
ous dynamics. The case that B (cid:10)= Id is more complicated and the approach
in Pehlevan et al. (2018) is not readily extended. In ongoing work, we take
a step toward understanding the asymptotics of our algorithms by analyz-
ing local stability properties for a general class of gradient descent-ascent
algorithms, which includes Offline-CCA and Bio-CCA as special cases.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Biologically Plausible Neural Network for CCA
2349
Acknowledgments
We thank Nati Srebro for drawing our attention to CCA, and we thank
Tiberiu Tesileanu and Charles Windolf for their helpful feedback on an ear-
lier draft of this manuscript.
References
Arora, R., Marinov, T. V., Mianjy, P., & Srebro, N. (2017). Stochastic approximation for
canonical correlation analysis. In I. Guyon, Y. V. Luxburg, S. Bengio, H. Wallach,
R. Fergus, S. Vishwanathan, & R. Garnett (Eds.), Advances in neural information
processing systems, 30 (pp. 4775–4784). Red Hook, NY: Curran.
Arora, S., Cohen, N., Golowich, N., & Hu, W. (2019). A convergence analysis of gra-
dient descent for deep linear neural networks. In Proceedings of the International
Conference on Learning Representations.
Bach, F. R., & Jordan, M. I. (2005). A probabilistic interpretation of canonical correlation
analysis (Technical Report). University of California, Berkeley.
Bhatia, K., Pacchiano, A., Flammarion, N., Bartlett, P. L., & Jordan, M. I. (2018). Gen-
Oja: Simple and efficient algorithm for streaming generalized eigenvector com-
putation. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi,
& R. Garnett (Eds.), Advances in neural information processing systems, 31 (pp. 7016–
7025). Red Hook, NY: Curran.
Bittner, K. C., Grienberger, C., Vaidya, S. P., Milstein, A. D., Macklin, J. J., Suh, J.,
. . . Magee, J. C. (2015). Conjunctive input processing drives feature selectivity in
hippocampal CA1 neurons. Nature Neuroscience, 18(8), 1133.
Bittner, K. C., Milstein, A. D., Grienberger, C., Romani, S., & Magee, J. C. (2017).
Behavioral time scale synaptic plasticity underlies CA1 place fields. Science,
357(6355), 1033–1036.
Borkar, V. S. (1997). Stochastic approximation with two time scales. Systems and Con-
trol Letters, 29(5), 291–294.
Borkar, V. S. (2009). Stochastic approximation: A dynamical systems viewpoint. Berlin:
Springer.
Cox, T. F., & Cox, M. A. (2000). Multidimensional scaling. London: Chapman and
Hall/CRC.
Ecker, A. S., Berens, P., Keliris, G. A., Bethge, M., Logothetis, N. K., & Tolias, A. S.
(2010). Decorrelated neuronal firing in cortical microcircuits. Science, 327(5965),
584–587.
Gambino, F., Pagès, S., Kehayas, V., Baptista, D., Tatti, R., Carleton, A., & Holtmaat,
A. (2014). Sensory-evoked LTP driven by dendritic plateau potentials in vivo.
Nature, 515(7525), 116–119.
Gidon, A., Zolnik, T. A., Fidzinski, P., Bolduan, F., Papoutsi, A., Poirazi, P., . . .
Larkum, M. E. (2020). Dendritic action potentials and computation in human
layer 2/3 cortical neurons. Science, 367(6473), 83–87.
Golding, N. L., Staff, N. P., & Spruston, N. (2002). Dendritic spikes as a mechanism
for cooperative long-term potentiation. Nature, 418(6895), 326–331.
Golkar, S., Lipshutz, D., Bahroun, Y., Sengupta, A. M., & Chklovskii, D. B. (2020).
A simple normative network approximates local non-Hebbian learning in the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2350
D. Lipshutz et al.
cortex. In H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan, & H. Lin (Eds.),
Advances in neural information processing systems, 33 (pp. 7283–7295). Red Hook,
NY: Curran.
Gou, Z., & Fyfe, C. (2004). A canonical correlation neural network for multicollinear-
ity and functional data. Neural Networks, 17(2), 285–293.
Guerguiev, J., Lillicrap, T. P., & Richards, B. A. (2017). Towards deep learning with
segregated dendrites. eLife, 6, e22901.
Haga, T., & Fukai, T. (2018). Dendritic processing of spontaneous neuronal sequences
for single-trial learning. Scientific Reports, 8(1), 1–22.
Hommes, C. H., & Ochea, M. I. (2012). Multiple equilibria and limit cycles in evolu-
tionary games with logit dynamics. Games and Economic Behavior, 74(1), 434–441.
Hotelling, H. (1936). Relations between two sets of variates. Biometrika, 28(3–4), 321–
377.
King, P. D., Zylberberg, J., & DeWeese, M. R. (2013). Inhibitory interneurons decor-
relate excitatory cells to drive sparse code formation in a spiking model of V1.
Journal of Neuroscience, 33(13), 5475–5485.
Körding, K. P., & König, P. (2001). Supervised and unsupervised learning with two
sites of synaptic integration. Journal of Computational Neuroscience, 11(3), 207–215.
Lai, P. L., & Fyfe, C. (1999). A neural implementation of canonical correlation analy-
sis. Neural Networks, 12(10), 1391–1397.
Larkum, M. (2013). A cellular mechanism for cortical associations: An organizing
principle for the cerebral cortex. Trends in Neurosciences, 36(3), 141–151.
Larkum, M. E., Nevian, T., Sandler, M., Polsky, A., & Schiller, J. (2009). Synaptic inte-
gration in tuft dendrites of layer 5 pyramidal neurons: A new unifying principle.
Science, 325(5941), 756–760.
Larkum, M. E., Zhu, J. J., & Sakmann, B. (1999). A new cellular mechanism for cou-
pling inputs arriving at different cortical layers. Nature, 398(6725), 338–341.
Lin, T., Jin, C., & Jordan, M. I. (2020). On gradient descent ascent for nonconvex-
concave minimax problems. In Proceedings of the International Conference on Ma-
chine Learning.
Lipshutz, D., Windolf, C., Golkar, S., & Chklovskii, D. B. (2020). A biologically plau-
sible neural network for slow feature analysis. In H. Larochelle, M. Ranzato, R.
Hadsell, M. F. Balcan, & H. Lin (Eds.), Advances in neural information processing
systems, 33 (pp. 14986–14996). Red Hook, NY: Curran.
Magee, J. C., & Grienberger, C. (2020). Synaptic plasticity forms and functions. An-
nual Review of Neuroscience, 43, 95–117.
Major, G., Larkum, M. E., & Schiller, J. (2013). Active properties of neocortical pyra-
midal neuron dendrites. Annual Review of Neuroscience, 36, 1–24.
Mertikopoulos, P., Papadimitriou, C., & Piliouras, G. (2018). Cycles in adversarial
regularized learning. In Proceedings of the Twenty-Ninth Annual ACM-SIAM Sym-
posium on Discrete Algorithms (pp. 2703–2717). Philadelphia: SIAM.
Milstein, A. D., Li, Y., Bittner, K. C., Grienberger, C., Soltesz, I., Magee, J. C., & Ro-
mani, S. (2020). Bidirectional synaptic plasticity rapidly modifies hippocampal represen-
tations independent of correlated activity. bioRxiv.
Miura, K., Mainen, Z. F., & Uchida, N. (2012). Odor representations in olfactory cor-
tex: Distributed rate coding and decorrelated population activity. Neuron, 74(6),
1087–1098.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Biologically Plausible Neural Network for CCA
2351
Oja, E. (1982). Simplified neuron model as a principal component analyzer. Journal
of Mathematical Biology, 15(3), 267–273.
Pehlevan, C., & Chklovskii, D. B. (2015). A normative theory of adaptive dimen-
sionality reduction in neural networks. In C. Cortes, N. Lawrence, D. Lee, M.
Sugiyama, & R. Garnett (Eds.), Advances in neural information processing systems
(pp. 2269–2277). Red Hook, NY: Curran: Red Hook.
Pehlevan, C., Hu, T., & Chklovskii, D. B. (2015). A Hebbian/anti-Hebbian neural net-
work for linear subspace learning: A derivation from multidimensional scaling
of streaming data. Neural Computation, 27(7), 1461–1495.
Pehlevan, C., Sengupta, A. M., & Chklovskii, D. B. (2018). Why do similarity
matching objectives lead to Hebbian/anti-Hebbian networks? Neural Computa-
tion, 30(1), 84–124.
Pehlevan, C., Zhao, X., Sengupta, A. M., & Chklovskii, D. B. (2020). Neurons as
canonical correlation analyzers. Frontiers in Computational Neuroscience, 15(55).
Pezeshki, A., Azimi-Sadjadi, M. R., & Scharf, L. L. (2003). A network for recursive
extraction of canonical coordinates. Neural Networks, 16(5–6), 801–808.
Plumbley, M. D. (1993). A Hebbian/anti-Hebbian network which optimizes infor-
mation capacity by orthonormalizing the principal subspace. In Proceedings of the
1993 Third International Conference on Artificial Neural Networks (pp. 86–90).
Razaviyayn, M., Huang, T., Lu, S., Nouiehed, M., Sanjabi, M., & Hong, M. (2020).
Nonconvex min-max optimization: Applications, challenges, and recent theoret-
ical advances. IEEE Signal Processing Magazine, 37(5), 55–66.
Richards, B. A., & Lillicrap, T. P. (2019). Dendritic solutions to the credit assignment
problem. Current Opinion in Neurobiology, 54, 28–36.
Sacramento, J., Costa, R. P., Bengio, Y., & Senn, W. (2018). Dendritic cortical mi-
crocircuits approximate the backpropagation algorithm. In S. Bengio, H. Wal-
lach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, & R. Garnett (Eds.), Ad-
vances in neural information processing systems, 31 (pp. 8721–8732). Red Hook, NY:
Curran.
Sjöström, P J., & Haüsser, M. (2006). A cooperative switch determines the sign of
synaptic plasticity in distal dendrites of neocortical pyramidal neurons. Neuron,
51(2), 227–238.
Snoek, C. G., Worring, M., Van Gemert, J. C., Geusebroek, J.-M., & Smeulders, A. W.
(2006). The challenge problem for automated detection of 101 semantic concepts
in multimedia. In Proceedings of the 14th ACM International Conference on Multime-
dia (pp. 421–430). New York: ACM.
Takahashi, H., & Magee, J. C. (2009). Pathway interactions and synaptic plasticity in
the dendritic tuft regions of CA1 pyramidal neurons. Neuron, 62(1), 102–111.
Tigaret, C. M., Olivo, V., Sadowski, J. H., Ashby, M. C., & Mellor, J. R. (2016). Coordi-
nated activation of distinct Ca2+ sources and metabotropic glutamate receptors
encodes Hebbian synaptic plasticity. Nature Communications, 7(1), 1–14.
Urbanczik, R., & Senn, W. (2014). Learning by the dendritic prediction of somatic
spiking. Neuron, 81(3), 521–528.
Velu, R., & Reinsel, G. C. (2013). Multivariate reduced-rank regression: Theory and appli-
cations. Berlin: Springer.
Vía, J., Santamaría, I., & Pérez, J. (2007). A learning algorithm for adaptive canonical
correlation analysis of several data sets. Neural Networks, 20(1), 139–152.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2352
D. Lipshutz et al.
Wanner, A. A., & Friedrich, R. W. (2020). Whitening of odor representations by the
wiring diagram of the olfactory bulb. Nature Neuroscience, 23(3), 433–442.
Williams, C. K. (2001). On a connection between kernel PCA and metric multidi-
mensional scaling. In T. Leen, T. Dietterich, & V. Tresp (Eds.), Advances in neural
information processing systems, 13 (pp. 675–681). Cambridge, MA: MIT Press.
Received November 13, 2020; accepted March 23, 2021.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
9
2
3
0
9
1
9
7
8
1
5
2
n
e
c
o
_
a
_
0
1
4
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3