ARTICLE
Communicated by Joel Zylberberg
Nonlinear Decoding of Natural Images From Large-Scale
Primate Retinal Ganglion Recordings
Young Joon Kim
yjkimnada@gmail.com
Università della Columbia, New York, NY 10027, U.S.A.
Nora Brackbill
nbrack@stanford.edu
Stanford University, Stanford, CA 94305, U.S.A.
Eleanor Batty
erb2180@columbia.edu
JinHyung Lee
jl4303@columbia.edu
Catalin Mitelut
mitelutco@gmail.com
William Tong
wlt2115@columbia.edu
Università della Columbia, New York, NY 10027, U.S.A.
E. J. Chichilnisky
ej@stanford.edu
Stanford University, Stanford, CA U.S.A.
Liam Paninski
liam@stat.columbia.edu
Università della Columbia, New York, NY 10027, U.S.A.
Decoding sensory stimuli from neural activity can provide insight into
how the nervous system might interpret the physical environment, E
facilitates the development of brain-machine interfaces. Nevertheless,
the neural decoding problem remains a significant open challenge. Here,
we present an efficient nonlinear decoding approach for inferring natural
scene stimuli from the spiking activities of retinal ganglion cells (RGCs).
Our approach uses neural networks to improve on existing decoders in
both accuracy and scalability. Trained and validated on real retinal spike
data from more than 1000 simultaneously recorded macaque RGC units,
the decoder demonstrates the necessity of nonlinear computations for
accurate decoding of the fine structures of visual stimuli. Specifically,
high-pass spatial features of natural images can only be decoded using
Calcolo neurale 33, 1719–1750 (2021) © 2021 Istituto di Tecnologia del Massachussetts
https://doi.org/10.1162/neco_a_01395
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1720
Kim et al.
nonlinear techniques, while low-pass features can be extracted equally
well by linear and nonlinear methods. Together, these results advance
the state of the art in decoding natural stimuli from large populations of
neurons.
1 introduzione
What is the relationship between stimuli and neural activity? While this crit-
ical neural coding problem has often been approached from the perspective
of developing and testing encoding models, the inverse task of decoding—
the mapping from neural signals to stimuli—can provide insight into un-
derstanding neural coding. Inoltre, efficient decoding is crucial for
the development of brain-computer interfaces and neuroprosthetic devices
(Cheng, Greenberg, & Borton, 2017; Cottaris & Elfar, 2009; Jarosiewicz et al.,
2015; Liu et al., 2000; Moxon & Foffani, 2015; Nirenberg & Pandarinath,
2012; Schwemmer et al., 2018; Warland, Reinagel, & Meister, 1997; Weiland
et al., 2004; Bialek, de Ruyter van Steveninck, Rieke, & Warland, 1997).
The retina has long provided a useful test bed for decoding methods,
since mapping retinal ganglion cell (RGC) responses into a decoded im-
age provides a direct visualization of decoding model performance. Most
approaches to decoding images from retinal ganglion cells (RGCs) have de-
pended on linear methods due to their interpretability and computational
efficiency (Brackbill et al., 2020; Marre et al., 2015; Warland et al., 1997). Al-
though linear methods successfully decoded spatially uniform white noise
stimuli (Warland et al., 1997) and the coarse structure of natural scene stim-
uli from RGC population responses (Brackbill et al., 2020), they largely fail
to recover final visual details of naturalistic images.
More recent decoders incorporate nonlinear methods for more accurate
decoding of complex visual stimuli. Some have leveraged optimal Bayesian
decoding for white noise stimuli but exhibited limited scalability to large
neural populations (Pillow et al., 2008). Others have attempted to incorpo-
rate key prior information for natural scene image structures and perform
computationally expensive approximations to Bayesian inference (Nase-
laris, Prenger, Kay, Oliver, & Gallant, 2009; Nishimoto et al., 2011). E-
fortunately, computational complexity and difficulties in formulating an
accurate prior for natural scenery have hindered these methods. Other
studies have constructed decoders that explicitly model the correlations
between spike trains of different cells, Per esempio, by using the relative
timings of first spikes as the measure of neural response (Portelli et al.,
2016). Parallel endeavors into decoding calcium imaging recordings from
the visual cortex have produced coarse reconstructions of naturalistic stim-
uli through both linear and nonlinear approaches (Ellis & Michaelides, 2018;
Garasto, Bharath, & Schultz, 2018; Garasto, Nicola, Bharath, & Schultz, 2019;
Yoshida & Ohki, 2020).
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nonlinear Natural Images Decoding
1721
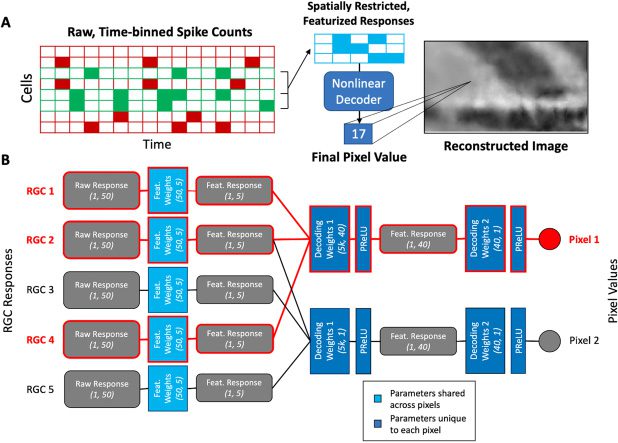
Figura 1: Outline of the decoding method. RGC responses to image stimuli are
passed through both linear and nonlinear decoders to decode the low-pass and
high-pass components of the original stimuli, rispettivamente, before the combined
decoded images are deblurred and denoised by a separate deblurring neural
rete.
In parallel, some recent decoders have relied on neural networks as ef-
ficient Bayesian inference approximators. Tuttavia, established neural net-
work decoders have either only been validated on artificial spike data sets
(McCann, Hayhoe, & Geisler, 2011; Parthasarathy et al., 2017; Zhang, Jia
et al., 2020) or on limited real-world data sets with modest numbers of
simultaneously recorded cells (Botella-Soler et al., 2018; Ryu et al., 2011;
Zhang, Jia et al., 2020). No nonlinear decoder has been developed and eval-
uated with the ultimate goal of efficiently decoding natural scenes from
large populations (per esempio., thousands) of neurons. Because the crux of the neu-
ral coding problem is to understand how the brain encodes and decodes
naturalistic stimuli in through large neuronal populations, it is crucial to
address this gap.
Therefore in this work we developed a multistage decoding approach
that exhibits improved accuracy over linear methods and greater efficiency
over existing nonlinear methods, and applied this decoder to decode nat-
ural images from large-scale multielectrode recordings from the primate
retina.
2 Results
2.1 Overview. All decoding results were obtained on retinal data sets
consisting of macaque RGC spike responses to natural scene images (Brack-
bill et al., 2020). Two identically prepared data sets, each containing re-
sponses to 10,000 images, were used for independent validation of our
decoding methods. The electrophysiological recordings were spike sorted
using YASS (Yet Another Spike Sorter; Lee et al., 2020) to identify 2094 E
1897 natural scene RGC units for the two data sets. We also recorded the
responses to white noise visual stimulation and estimated receptive fields
to classify these units into retinal ganglion cell types, to allow for analyses
of cell-type specific natural scene decoding. (See section 3 for full details.)
Our decoding approach addresses accuracy and scalability by seg-
menting the decoding task into three subtasks (see Figures 1 E 2 E
Tavolo 1):
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1722
Kim et al.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
Figura 2: Outline of the nonlinear decoder. (UN) The first part of the nonlinear
decoder featurizes the RGC units’ time-binned spike responses (50-dimensional
vector for each RGC) to a lower dimension ( f = 5). Afterward, each pixel’s k =
25 most relevant units’ featurized vectors are gathered and passed through
a spatially restricted neural network, where each pixel is assigned its own
nonlinear decoder to produce the final pixel value. (B) A miniaturized schematic
of the spatially restricted neural network. Parameters that are shared across pix-
els versus those that are unique to each pixel are color-coded in different shades
of blue. Inoltre, all the input values and weights that feed into a single
pixel value are outlined in red to indicate the spatially restricted nature of the
rete. The vector dimensions of the weights and inputs are written in ital-
icized parentheses; k represents the number of top units per pixel chosen for
decoding.
• We use linear ridge regression to map the spike-sorted, time-binned
RGC spikes to “low-pass,” gaussian-smoothed versions of the target
images. The smoothing filter size approximates the receptive fields of
ON and OFF midget RGCs, the cell types with the highest densities
in the primate retina.
• A spatially restricted neural network decoder is trained to capture the
nonlinear relationship between the RGC spikes and the “high-pass”
images, which are the residuals between the true and the low-pass
images from the first step. The high-pass and low-pass outputs are
summed to produce combined decoded images (Guarda la figura 2).
• A deblurring network is trained and applied to improve the com-
bined decoder outputs by enforcing natural image priors.
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nonlinear Natural Images Decoding
1723
Tavolo 1: Pixel-Wise Test Correlations of All Decoder Outputs (99% Confidence
Interval Values in Parentheses).
LP ridge (2-bin)
Versus True
LP
0.975
(0.00016)
Versus True
HP
HP NN
0.360
(0.0032)
HP Ridge
0.282
(0.0028)
Whole ridge
LP NN
LP ridge (50-bin)
LP LASSO
0.963
(0.00021)
0.960
(0.00033)
0.979
(0.00015)
0.978
(0.00015)
LP Ridge:
2-bin
HP NN + LP
ridge (2-bin)
Combined-
deblurred
Ridge-
deblurred
Whole
RIDGE
Whole NN
Versus True
0.887
(0.00062)
0.901
(0.00059)
0.912
(0.00055)
0.903
(0.00057)
0.890
(0.00061)
0.874
(0.00076)
Notes: The best results are in bold.
The 2-bin and 50-bin LP ridge labels represent the two linear ridge decoders trained on
the low-pass images. The whole ridge decoder is the 2-bin ridge decoder trained on the
true whole images themselves, while the HP ridge decoder is the same decoder trained
on the high-pass images only. The LP, HP, and whole NN labels denote the spatially
restricted neural network decoder trained on low-pass, high-pass, and whole images,
rispettivamente. LP LASSO represents the 2-bin LASSO regression decoder trained on low-
pass images. Finalmente, the combined-deblurred images are the deblurred versions of the
sum of the HP NN and LP Ridge (2-bin) decoded images, while the ridge-deblurred im-
ages are the deblurred versions of the whole ridge decoder outputs. These final three—
combined-deblurred, ridge-deblurred, and HP NN + LP Ridge (2-bin)—are in bold
because they produced best results. The second, fourth, and sixth columns represent pixel-
wise test correlations of each decoder’s output versus the true low-pass, high-pass, E
whole images, rispettivamente.
The division of visual decoding into low-pass and high-pass decoding
subtasks allowed us to leverage linear regression, which is simple and
quick, for obtaining the target images’ global features, while having the
neural network decoder focus its statistical power on the addition of finer
visual details. As discussed below, this strategy yielded better results than
applying the neural network decoder to either the low-pass or the whole
test images (Vedi la tabella 1).
2.2 Linear Decoding Efficiently Decodes Low-Pass Spatial Features.
We used two penalized linear regression approaches, ridge and LASSO re-
gression (Friedman, Hastie, & Tibshirani, 2001), for linearly decoding the
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1724
Kim et al.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
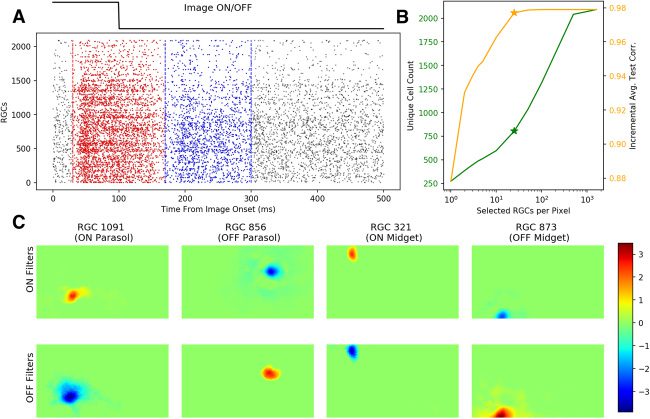
Figura 3: LASSO regression establishes a sparse mapping between RGC units
and pixels. (UN) Schematic of the ON (red; 30–170 ms) and OFF (blue; 170–300 ms)
responses derived from RGC spikes. Each RGC’s ON and OFF filter weights
were multiplied to the summed spike counts within these windows. The spikes
in these bins represent the cells’ responses to stimuli onsets and offsets, respec-
tively. The raster density (each dot represents a spike from a single RGC unit on
a single trial) indicates that most of the RGC units’ spikes were found in these
two bins, which came slightly after the stimuli onsets and offsets themselves,
as shown by the top line. (B) Total unique selected RGC unit count (green) E
mean pixel-wise test correlations of partial LASSO decoded images (orange) COME
functions of the number of units chosen per pixel. For each pixel, {1, 2, 3, 4, 5,
10, 25, 50, 100, 500, 1000, 1600}, top units were chosen. Asterisks mark the top 25
units per pixel (805 unique units and 0.978 test correlation), the hyperparame-
ter setting chosen for the nonlinear decoder below. (C) Representative ON and
OFF spatial weights estimated by LASSO regression for four RGC units. Over-
Tutto, LASSO regression successfully established a sparse mapping between RGC
units and individual pixels by zeroing each cells’ uninformative spatial weights,
which comprise the majorities of the ON and OFF filters.
low-pass images. Both decoders considered only the neural responses dur-
ing the image onset (30–170 ms) and offset (170–300 ms) time frames (Vedere
Figure 3A). While using the spikes from just the onset time bin produced re-
constructions that were nearly as accurate as two bins, spikes from both bins
were included to maximize accuracy with a minimal increase to computa-
tional workload (Guarda la figura 12). For reference, LASSO regression is a form of
linear regression whose regularization method enforces sparsity such that
Nonlinear Natural Images Decoding
1725
the uninformative input variables are assigned zero weights while the in-
formative inputs are assigned nonzero weights (Friedman et al., 2001). In
the process, LASSO successfully identified each RGC unit’s relevant linear
spatial weights for both the image onset and offset time bins while zeroing
out the insignificant spatial weights (see Figure 3C).
The LASSO spatial filters were roughly similar in appearance to the cor-
responding RGC unit receptive fields calculated from spike-triggered aver-
ages of white noise recordings (data not shown; see Brackbill et al., 2020).
These linear filters eventually allowed for a sparse mapping between RGC
units and image pixels so that only the most informative units for each
pixel would be used as inputs for the nonlinear decoder (Botella-Soler et al.,
2018). Partial LASSO-based decoding using smaller subsets of informative
units demonstrated that these few hundred units were responsible for most
of the decoding accuracy observed (see Figure 3B). In definitiva, 25 top units
per pixel, corresponding to 805 total unique RGC units and a mean low-pass
test correlation of 0.978 (±0.0002; this and all following error bars corre-
spond to 99% CI values), were chosen. Choosing fewer than 25 informative
RGC units per pixel resulted in lower LASSO regression test correlations,
while choosing more units per pixel increased computational load without
concomitant improvements in test correlation.
Consistent with previous findings (Brackbill et al., 2020), both linear de-
coders successfully decoded the global features of the stimuli by accurately
modeling the low-pass images (Guarda la figura 4). When evaluated by mean
pixel-wise correlation against the true low-pass images, the decoded out-
puts from the ridge and LASSO decoders registered test correlations of
0.975 (±0.0002) E 0.978 (±0.0002), rispettivamente (Guarda la figura 4 and Table 1).1
Increasing the temporal resolution of linear decoding beyond the two
onset and offset time bins did not yield significant improvements in
accuracy.
How different are decoding results if the linear decoder is instead ap-
plied to the true whole images rather than the low-pass images or if a
nonlinear decoder is used for the low-pass targets? Notably, a ridge regres-
sion decoder trained on true images exhibited performance no better than
the low-pass-specific linear decoders. Specifically, it registered a test corre-
lation of 0.963 (±0.0002) versus true low-pass images and 0.890 (±0.0006)
versus true images, suggesting that linear decoding can recover only low-
pass details regardless of whether the decoding target contains high-pass
details (Vedi la tabella 1). The ridge low-pass decoded images registered a
test correlation of 0.887 (±0.0006) against the whole test images. On the
other hand, applying our neural network decoder to the low-pass targets
1
Note that these correlation values are much higher than the subsequent correlation
values in this manuscript as these low-pass decoded images were evaluated against the
true low-pass images, which are much easier decoding targets than the true whole images
themselves.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1726
Kim et al.
Figura 4: Linear decoding efficiently decodes low-pass spatial features. Rep-
resentative true and true low-pass images along with their decoded low-pass
counterparts produced via ridge (2-time-bin and 50-time-bin) and LASSO re-
gression. Mean pixel-wise test correlations (evaluated against the true low-pass
images, not the true images) are indicated within the top labels. The 50-bin de-
coder considers spike counts from the entire 500 ms stimulus window organized
into 10 ms bins; this decoder achieved similar accuracy as the 2-bin decoder. Tutto
three linear regression techniques produce highly accurate decoding of the true
low-pass images, suggesting that linear methods are sufficient for extracting the
global features of natural scene image stimuli.
demonstrates that linear decoding is slightly more accurate (likely due to
slight overfitting by the neural network) and vastly more efficient for low-
pass decoding, as the former exhibited a lower test correlation of 0.960
(±0.0003) versus the low-pass targets (Vedi la tabella 1). In sum, linear decod-
ing is both the most accurate and appropriate approach for extracting the
global features of natural scenes.
2.3 Nonlinear Methods Improve Decoding of High-Pass Details and
Use Spike Temporal Correlations. Despite the high accuracy of low-pass
linear decoding, the low-pass images and their decoded counterparts are
(by construction) lacking the finer spatial details of the original stimuli.
Therefore, we turned our attention next to decoding the spatially high-
pass images formed as the differences of the low-pass and original images.
Again, we compared linear and nonlinear decoders; unlike in the low-pass
setting, we found that nonlinear decoders were able to extract significantly
more information about the high-pass images than linear decoders. Specif-
ically, a neural network decoder that used the nonzero LASSO regression
weights to select its inputs (see Figure 3B) achieved a test correlation of
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nonlinear Natural Images Decoding
1727
0.360 (±0.003) when evaluated against the high-pass stimuli, compared to
ridge regression’s test correlation of 0.282 (±0.003; see Figure 5B). While the
high-pass reconstructions exhibited a greater spread in quality compared to
their low-pass counterparts, nonlinear decoding consistently outperformed
linear decoding even for the stimuli that both decoders struggled to decode
(Guarda la figura 13).
Inoltre, the combined decoder output (summing the linearly decoded
low-pass and nonlinearly decoded high-pass images) consistently pro-
duced higher test correlations compared to a simple linear decoder. Relative
to the true images, ridge regression (for the whole images) and combined
decoding yielded mean correlations of 0.890 (±0.0006) E 0.901 (±0.0006),
rispettivamente (see Figure 5A). In comparison, the linear low-pass decoded
images alone yielded 0.887 (±0.0006). In other words, linear decoding of
the whole image is almost no better than simply aiming for the low-pass
Immagine, and nonlinear decoding is necessary to recover significantly more
detail beyond the low-pass target. Additionally, a neural network decoder
that targets the whole true images falls short of the combined decoder with
a mean test correlation of 0.874 (±0.0008) versus true images (Vedi la tabella 1). In
conjunction with the previous section’s finding that the neural network de-
coder is not as successful with low-pass decoding as linear decoders, these
results further justify our approach to reserve nonlinear decoding for the
high-pass and linear decoding for the low-pass targets.
We then sought to analyze what characteristics of the RGC spike re-
sponses allowed for the superior performance of the combined decoding
method. Previous studies have reported that nonlinear decoding better in-
corporates spike train temporal structure, which leads to its improvement
over linear methods (Botella-Soler et al., 2018; Field & Chichilnisky, 2007;
Passaglia & Troy, 2004). Tuttavia, these studies were conducted with sim-
plified random or white noise stimuli, and it is unclear how these findings
translate to natural scene decoding. Così, we hoped to shed light on how
spike train correlations, both cross-neuronal and temporal, contribute to lin-
ear and nonlinear decoding. In previous literature, the former have been
referred to as “noise correlations” and the latter as “history correlations”
(Botella-Soler et al., 2018).
On a separate data set of 150 test images, each repeated 10 times, we cre-
ated two modified neural responses to remove the two types of spike train
correlations. As before, we binned each cell’s spike counts into 10 ms bins
so that for a single presented image, each cell exhibited a 50-bin response.
Then, to remove cross-neuronal correlations, we swapped each cell’s 50-bin
response to an image randomly across the 10 repeat trials. Since each cell’s
response was independently swapped of the other cells’ responses, corre-
lations between RGCs within a trial were removed. Nel frattempo, to remove
history correlations, the individual spike counts within each cell’s 50-bin re-
sponse were randomly and independently exchanged with those from the
other repeat trials.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1728
Kim et al.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 5: Nonlinear decoding extracts high-pass features more accurately than
linear decoding. (UN) Representative true images with their linearly decoded and
combined decoder outputs; note that the linear decoder here decodes the true
images (not just the true low-pass images) and was included for overall com-
parison. The correlation values here compare the decoded outputs against the
true images. (B) Representative high-pass images with corresponding nonlinear
and linear decoded versions. The correlation values here compare the high-pass
decoded outputs against the true high-pass images. (C) Pixel-wise test correla-
tion comparisons of linear and nonlinear decoding performance for the true
and high-pass images. Linear decoding, either for the whole or low-pass im-
ages, is distinctly insufficient, and nonlinear methods are necessary for accurate
decoding.
Nonlinear Natural Images Decoding
1729
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
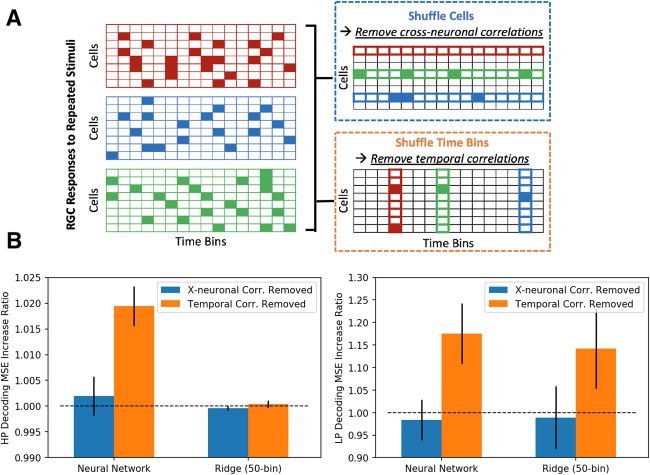
Figura 6: Spike temporal correlations are useful for high-pass nonlinear decod-
ing and low-pass decoding. (UN) Schematic of the shuffling of time bins and units’
responses across repeated stimuli trials. (B) Ratio increases in MSE for neural
network and linear decoders for high-pass and low-pass images before and af-
ter removing spike train correlations. While temporal correlations are impor-
tant for both decoders in low-pass decoding, only the neural network decoder
is reliant on temporal correlations in high-pass decoding. Cross-neuronal cor-
relations are not crucial for both decoders in either decoding scheme.
For high-pass decoding, the neural network decoder exhibited a 1.9%
(±0.4) increase in pixel-wise MSE when temporal correlations were re-
moved, while the ridge decoder experienced a 0.04% (±0.07) increase in
MSE (see Figure 6B); questo è, nonlinear high-pass decoding is dependent
on temporal correlations while linear high-pass decoding is not. Removing
cross-neuronal correlations yielded no significant changes in either decoder,
consistent with Brackbill et al. (2020). Nel frattempo, for low-pass decoding,
both decoders were equally and significantly affected by removing tempo-
ral correlations, as indicated by the 17.5% (±6.7) E 14.2% (±8.9) increases
in MSE for the neural network and linear decoders, rispettivamente (Guarda la figura
6B). For the above comparisons, the ridge linear decoder for 50 time bins
was used to maintain the same temporal resolution as the neural network
decoder. In short, spike temporal correlations are important, specifically for
the low-pass linear and all nonlinear decoders for optimal performance,
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1730
Kim et al.
while cross-neuronal correlations are not influential in any decoding setup
analyzed here (Botella-Soler et al., 2018).
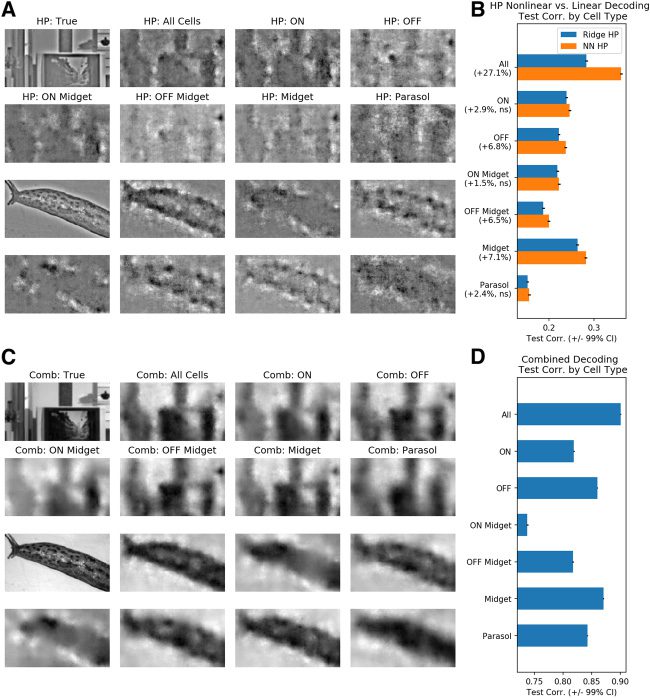
2.4 OFF Midget RGC Units Drive Improvements in High-Pass Decod-
ing when Using Nonlinear Methods. Prossimo, we sought to investigate the
differential contributions of each major RGC type toward visual decoding.
Previous work has revealed that in the context of linear decoding, midget
cells convey more high-frequency visual information, while parasol cells
tend to encode more low-frequency information, consistent with the differ-
ences in density and receptive field size of these cell classes (Brackbill et al.,
2020). Here we focused on the ON/OFF parasol/midget cells, the four nu-
merically dominant RGC types, and their roles in linear versus nonlinear
decoding. We classified the RGCs recorded during natural scene stimula-
tion by first identifying units recorded during white noise stimulation and
then using a conservative matching scheme that ensured one-to-one match-
ing between recorded units in the two conditions. In total, 1033 units were
matched, within which there were 72 ON parasol, 87 OFF parasol, 175 ON
midget, E 195 OFF midget units (see section 4).
We performed standard ridge regression decoding for whole and low-
pass images using spikes from the above four cell types and compared
these decoded outputs to those derived from all 2094 RGC units, Quale
include those not belonging to the four main types (Guarda la figura 7). Consis-
tent with previous results (Brackbill et al., 2020), midget decoding recovers
more high-frequency visual information than parasol decoding, while ON
and OFF units yield decoded images of similar quality. Nel frattempo, differ-
ences between parasol and midget cell decoding are reduced for low-pass
filtered images, as this task is not asking either cell population to decode
high-frequency visual information.
We then investigated cell type contributions in the context of high-pass
decoding (Guarda la figura 8). Specifically, we investigated which cell type con-
tributed most to the advantage of nonlinear over linear high-pass decoding
and thus explained the improved performance of our decoding scheme.
The advantages of nonlinear decoding were most prominent for midget
and OFF units, with mean increases in test correlation of 7.1% E 6.8%,
rispettivamente (see Figure 8B). Parasol and ON units, meanwhile, saw a statis-
tically insignificant change in test correlation. More finely grained analyses
showed that only the OFF midget units enjoyed a statistically significant
increase of 6.5% in mean test correlation in high-pass decoding. While ON
midget units did indeed contribute meaningfully to high-pass decoding (COME
shown by their relatively high test correlations), they enjoyed no improve-
ments with nonlinear over linear decoding. Therefore, one can conclude
that the improvements in decoding for midget and OFF units via nonlinear
methods can both be primarily attributed to the OFF midget subpopula-
zione, which are also better encoders of high-pass details than their parasol
counterparts. Previous studies have indeed indicated that midget units may
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nonlinear Natural Images Decoding
1731
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
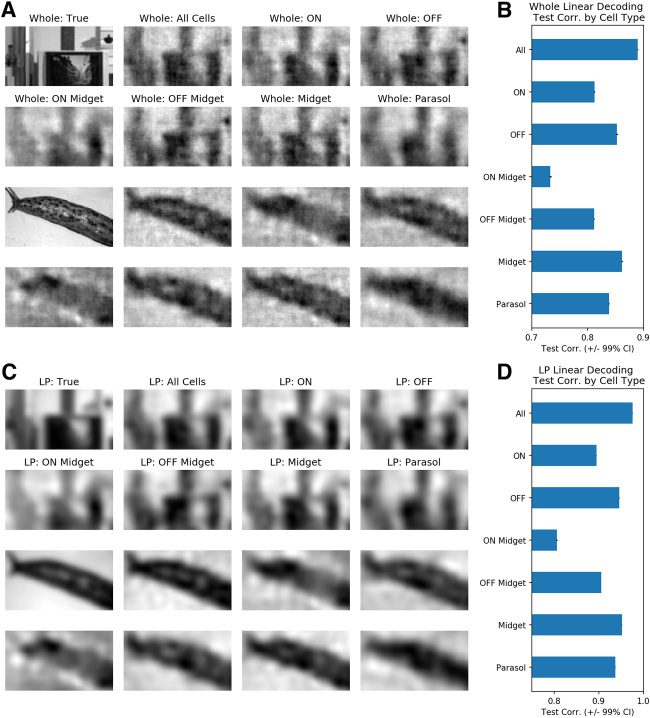
Figura 7: All major RGC types meaningfully contribute to low-pass linear de-
coding. (UN) Representative whole images with their corresponding linearly de-
coded outputs using all, ON, OFF, ON Midget, OFF midget, midget, and parasol
units, rispettivamente. (B) Whole test correlations as functions of RGC type used for
linear decoding. (C) Representative low-pass images with their corresponding
linearly decoded outputs using all, ON, OFF, ON Midget, OFF midget, midget,
and parasol units, rispettivamente. (D) Low-pass test correlations as functions of
RGC type used for linear decoding. Overall, all RGC types contribute meaning-
fully to low-pass, linear decoding.
encode more high-frequency visual information and that OFF midget units,
in particular, exhibit nonlinear encoding properties (Brackbill et al., 2020;
Chichilnisky & Kalmar, 2002; Freeman et al., 2015).
1732
Kim et al.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
Figura 8: Midget and OFF units contribute most to high-pass, nonlinear decod-
ing. (UN) Representative high-pass images with their corresponding nonlinear
decoded versions using all, ON, OFF, ON Midget, OFF midget, midget, E
parasol units, rispettivamente. (B) Comparison of test correlations between linear
and nonlinear high-pass decoding versus cell type. (C) Representative true im-
ages with their corresponding combined decoder outputs using all, ON, OFF,
ON Midget, OFF midget, midget, and parasol units, rispettivamente. (D) Compari-
son of test correlations for the combined decoded images per cell type. Nonlin-
ear decoding most significantly improves midget and OFF cell high-pass and
combined decoding but does not bring any significant benefit to parasol and
ON cell decoding of high-pass details.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nonlinear Natural Images Decoding
1733
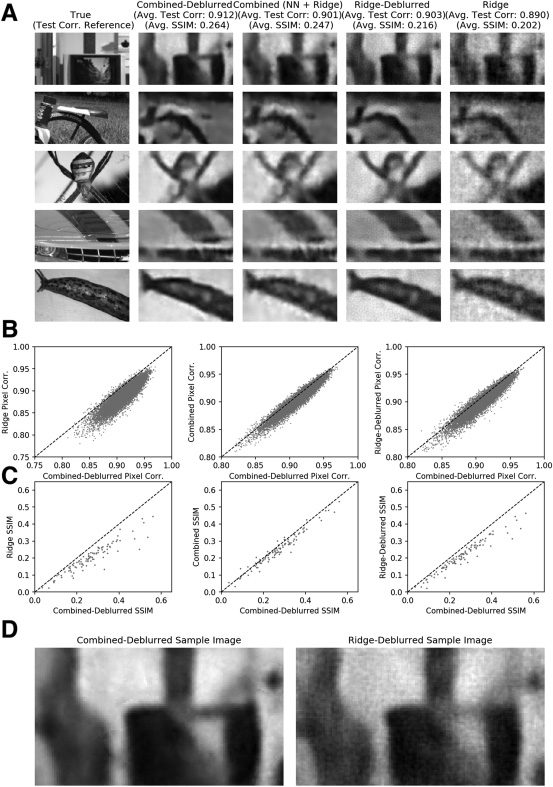
2.5 A Final “Deblurring” Neural Network Further Improves Accuracy,
but Only in Conjunction with Nonlinear High-Pass Decoding. Despite
the success of the neural network decoder in extracting more spatial de-
tail than the linear decoder, the combined decoder output still exhibited
the blurriness near edges that is characteristic of low-pass image decoding.
Therefore we trained a final convolutional “deblurring” network and found
that this network was indeed qualitatively able to sharpen object edges
present in the decoder output images (see Figure 9A; see Parthasarathy
et al., 2017, for a related approach applied to simulated data). Quantita-
tively, the test pixel-wise correlation improved from 0.890 (±0.0006) E
0.901 (±0.0006) in the linear and combined decoder images, rispettivamente,
A 0.912 (±0.0006) in the combined-deblurred images (see Figure 9B and
Tavolo 1). Comparison by SSIM, a more perceptually oriented measure
(Wang, Bovik, Sheikh, & Simoncelli, 2004), also revealed similar advantages
in deblurring in combination with nonlinear decoding over other methods
(see Figure 9C). In short, this final addition to the decoding scheme brought
both subjective and objective improvements to the quality of the final de-
coder outputs.
The deblurring network is trained to map noisy, blurry decoded images
back to the original true natural image—and therefore implicitly takes ad-
vantage of statistical regularities in natural images. (See Parthasarathy et al.,
2017, for further discussion on this point.) Hypothetically, applying the de-
blurring network to linear decoder outputs could be sufficient for improved
decoding. We therefore investigated the necessity of nonlinear decoding in
the context of the deblurring network. Retraining and applying the deblur-
ring network on the simple ridge decoder outputs (with the result denoted
“ridge-deblurred” images) produced a final mean pixel-wise test correla-
tion of 0.903 (±0.0006), which is lower than that of the combined-deblurred
images (Guarda la figura 9 and Table 1). Comparison by SSIM also yielded iden-
tical findings. We note that the deblurring network brought significant
perceptual image quality improvements with or without the nonlinear de-
coder, as can be seen in the sample pipeline outputs. Tuttavia, applying the
deblurring network on the ridge decoder outputs did not fully remove the
grainy, salt-and-pepper noise that is the product of the noisy linear attempt
toward recovering the high-pass details (Guarda la figura 5). This noise is not seen
in the full pipeline (combined-deblurred) outputs, suggesting that one of
the nonlinear decoder’s unique roles is to remove noise during high-pass
decoding that neither the linear decoder nor the deblurring network can ac-
complish. Così, to obtain maximal results, the nonlinear decoder must be
included alongside all the other components.
3 Discussion
The approach we have presented combines recent innovations in image
restoration with prior knowledge of neuronal receptive fields to yield a
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1734
Kim et al.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 9: Neural network deblurring further improves nonlinear decoding
quality. (UN) Representative true images and their corresponding combined-
deblurred, combined, ridge-deblurred, and ridge decoder outputs. Compar-
isons of pixel-wise test correlation (B) and SSIM (C) of the combined-deblurred
versus ridge, combined, and ridge-deblurred decoder outputs, rispettivamente.
The combined-deblurred images had the highest mean SSIM at 0.265 (±0.018,
90% CI). The ridge-deblurred images had an SSIM of 0.216 (±0.015), che è
lower than that of the combined-deblurred images. (D) Sample outputs from the
combined-deblurred and ridge-deblurred pipelines. The deblurring network,
specifically in combination with nonlinear decoding, brings quantitative and
qualitative improvements to the decoded images. See Figure 10 for a similar
analysis on a second data set.
Nonlinear Natural Images Decoding
1735
decoder that is both more accurate and scalable than the previous state of
the art. A comparison of linear and nonlinear decoding reveals that linear
methods are just as effective as nonlinear approaches for low-pass decod-
ing, while nonlinear methods are necessary for accurate decoding of high-
pass image details. The nonlinear decoder was able to take advantage of
spike temporal correlations in high-pass decoding while the linear decoder
was not; both decoders used temporal correlations in low-pass decoding.
Inoltre, much of the advantage that nonlinear decoding brings can be
attributed to the fact that OFF midget units best encode high-pass visual
details in a manner that is more nonlinear than the other RGC types, Quale
aligns with previous findings about the nonlinear encoding properties of
this RGC sub-class (Freeman et al., 2015).
These results differ from previous findings (using non-natural stimuli)
that linear decoders are unaffected by spike temporal correlations (Botella-
Soler et al., 2018; Passaglia & Troy, 2004) COME, evidently, the low-pass linear
decoder is just as reliant on such correlations as the nonlinear decoder for
low-pass decoding. D'altra parte, they also seem to support prior work
indicating that nonlinear decoders are able to extract temporally coded in-
formation that linear decoders cannot (Field & Chichilnisky, 2007; Passaglia
& Troy, 2004). Infatti, previous studies have noted that retinal cells can en-
code some characteristics of visual stimuli linearly and others nonlinearly
(Gollisch, 2013; Passaglia & Troy, 2004; Schreyer & Gollisch, 2020; Schwartz
& Rieke, 2011), which corresponds with our findings that temporally en-
coded low-pass stimuli information can be recovered linearly while tempo-
rally encoded high-pass information cannot. The above may help explain
why linear and neural network decoders perform equally well for low-pass
images but exhibit significantly different efficacies for high-pass details. Noi
note that different experimental and recording conditions may yield alter-
native conclusions on the role of correlations in RGC population behav-
ior. For instance, it has been suggested that different luminance conditions
can affect the degree to which RGC populations rely on spike train correla-
tions to encode visual information (Ruda, Zylberberg, & Field, 2020). Nostro
recorded data set exhibited relatively low trial-to-trial variability, and this
may have influenced the spike train correlation results. Infatti, for data sets
with greater trial-to-trial noise, such as in low-light settings, different find-
ings could have been made.
Nevertheless, several key questions remain. While our nonlinear de-
coder demonstrated state-of-the-art performance in decoding the high-
pass images, the neural networks still missed many spatial details from
the true image. Although it is unclear how much of these missing details
can theoretically be decoded from spikes from the peripheral retina, we
suspect that improvements in nonlinear decoding methods are possible.
It is entirely possible that our spatially restricted parameterization of the
nonlinear decoding may result
information during the
dimentionality-reduction process even though close analysis of architecture
in loss of
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1736
Kim et al.
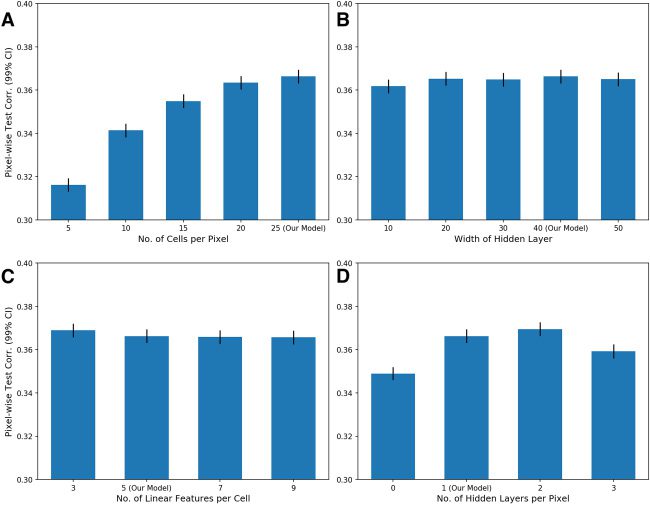
choice on decoding performance does not suggest so (Guarda la figura 14). Noi
found that nonlinear high-pass decoding performance did not improve be-
yond 20 A 25 unique RGCs per pixel and actually decreased when using
more than two nonlinear layers. Nevertheless, we do not rule out the pos-
sibility of other architecture choices producing better decoding results.
The deblurring of the combined decoder outputs is a challenging prob-
lem that current image restoration methods in computer vision likely
cannot fully capture. Specifically, this step represents an unknown com-
bination of superresolution, deblurring, denoising, and inpainting. Con
ongoing advances in image restoration networks that can handle more
complex blur kernels and noise, it is likely that further improvements in per-
formance are possible (Kupyn, Martyniuk, Wu, & Wang, 2019; Ledig et al.,
2017; Maeda, 2020; Wang et al., 2018; Wang, Chen, & Hoi, 2020; Zhang, Zuo,
& Zhang, 2019; Zhang, Zuo, Gu, & Zhang, 2017; Zhang, Tian et al., 2020;
Zhou & Susstrunk, 2019).
Finalmente, while our decoding approach helped shed some light on the
importance of nonlinear spike temporal correlations and OFF midget cell
signals on accurate, high-pass decoding, the specific mechanisms of visual
decoding have yet to be fully investigated. Infatti, many other sources
of nonlinearity, including nonlinear spatial interactions within RGCs or
nonlinear interactions between RGCs or RGC types, are all factors that
could help justify nonlinear decoding that we did not explore (Gollisch,
2013; Odermatt, Nikolaev, & Lagnado, 2012; Pitkow & Meister, 2012;
Schreyer & Gollisch, 2020; Schwartz & Rieke, 2011; Turner, Schwartz, &
Rieke, 2018; Turner & Rieke, 2016). Per esempio, it has been suggested that
nonlinear interactions between jointly activated, neighboring ON and OFF
cells may signal edges in natural scenes (Brackbill et al., 2020). We hope to
investigate these issues further in future work.
4 Materials and Methods
The nonlinear decoder and deblurring network codes can be found at https:
//github.com/yjkimnada/ns_decoding.
4.1 RGC Data Sets. See Brackbill et al. (2020) for full experimental
procedures. Briefly, retinas were obtained from terminally anesthetized
macaques used by other researchers in accordance with animal ethics
guidelines (see the Ethics Statement). After the eyes were enucleated, only
the eye cup was placed in a bicarbonate-buffered Ames’ solution. In a dark
setting, retinal patches, roughly 3 mm in diameter, were placed with the
RGC side facing down on a planar array of 512 extracellular microelectrodes
covering a 1.8 mm-by-0.9 mm region. For the duration of the recording, IL
ex vivo preparation was perfused with Ames’ solution (30–34C
, pH 7.4)
bubbled with 95% O2, 5% CO2 and the raw voltage traces were bandpass
◦
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nonlinear Natural Images Decoding
1737
filtered, amplified, and digitized at 20 kHz (Chichilnisky & Kalmar, 2002;
Field et al., 2010; Frechette et al., 2005; Litke et al., 2004).
In total, 10,000 natural scene images were displayed, with each image be-
ing displayed for 100 ms before and after 400 ms intervals of a blank, gray
screen. For training, 9900 images were chosen and the remaining 100 for
testing. The recorded neural spikes were spike-sorted using the YASS spike
sorter to obtain the spiking activities of 2094 RGC units (Lee et al., 2020),
which is significantly more units than previous decoders were trained to de-
code (Botella-Soler et al., 2018; Brackbill et al., 2020; Ryu et al., 2011; Zhang,
Jia et al., 2020). Due to spike sorting errors, some of these 2094 units may be
either oversplit (partial-cell) or overmerged (multicell). Nevertheless, Sopra-
split and overmerged units can still provide decoding information (Deng,
Liu, Kay, K., Frank, & Eden, 2015), and we therefore chose to include all
spike-sorted units in the analyses here in an effort to maximize decoding
accuracy. In the LASSO regression analysis (described below), we perform
feature selection to choose the most informative subset of units, riducendo
the selected population roughly by a factor of two. Finalmente, to incorporate
temporal spike train information, the binary spike responses were time-
binned into 10 ms bins (50 bins per displayed image). A second retinal
data set prepared in an identical manner was used to validate our decoding
method and accompanying findings (Guarda la figura 10).
While the displayed images were 160-by-256 in pixel dimensions, we re-
stricted the images to a center portion of size 80-by-144 that corresponded
to the placement of the multielectrode array. To facilitate low-pass and high-
pass decoding, each of the train and test images was blurred with a gaussian
blur of σ = 4 pixels and radius 3σ to produce the low-pass images. The fil-
ter size approximates the average size of the midget RGC. The high-pass
images were subsequently produced by subtracting the low-pass images
from their corresponding whole images.
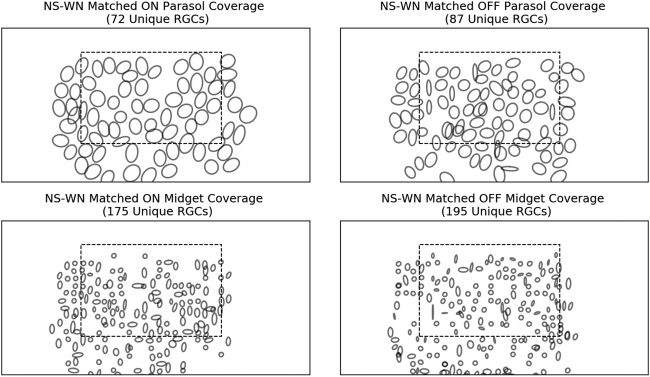
4.2 RGC Unit Matching and Classification. To begin, we obtained spa-
tiotemporal spike-triggered averages (STAs) of the RGC units from their re-
sponses to a separate white noise stimulus movie and classified them based
on their relative spatial receptive field sizes and the first principal compo-
nent of their temporal STAs (Chichilnisky & Kalmar, 2002). Afterward, both
MSE and cosine similarity between electrical spike waveforms were used
to identify each white noise RGC unit’s best natural scene unit match and
vice versa. Specifically, for each identified white noise unit, we chose the
natural scene unit with the closest electrical spike waveform using both
measures and kept only the white noise units that had the same top nat-
ural scene candidate found by both metrics. Then we performed the same
procedure on all natural scene units, keeping only the units that had the
same top white noise match using both metrics. Finalmente, we kept only the
white noise-natural scene RGC unit pairs where each member of the pair
chose each other as the top match via both MSE and cosine similarity. Questo
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1738
Kim et al.
ensured one-to-one matching and that no white noise or natural scene RGC
was represented more than once in the final matched pairs. In total, 1033
RGC units were matched in this one-to-one fashion, within which there
were 72 ON parasol, 87 OFF parasol, 175 ON midget, E 195 OFF midget
units. Several other cell types, such as small bistratified and ON/OFF large
RGC units, were also found in smaller numbers. We also confirmed that the
top 25 units chosen per pixel by LASSO, which comprise the 805 unique
units feeding into the nonlinear decoder, also represented the four main
RGC classes proportionally.
We chose a very conservative matching strategy to ensure one-to-one
representation and maximize the confidence in the classification of the nat-
ural scene units. Naturally, such a matching scheme produced many un-
matched natural scene units and a smaller number of unmatched white
noise units. On average, the unmatched natural scene units had similar
firing rates to the matched units while having smaller maximum chan-
nel spike waveform peak-to-peak magnitudes. While it is likely that a re-
laxation of matching requirements would yield more matched pairs, we
confirmed that our matching strategy still resulted in full coverage of the
stimulus area by each of the four RGC types (Guarda la figura 11).
4.3 Low-Pass Linear Decoding. To perform efficient linear decoding on
a large neural spike matrix without overfitting, for each RGC, we summed
spikes within the 30 A 170 ms and 170 A 300 ms time bins, which corre-
spond to the image onset and offset response windows. Così, with n, T, X
indexing the RGC units, training images, and pixels, rispettivamente, the RGC
spikes were organized into matrix X ∈ Rt×2n and the training images into
Y ∈ Rt×x. To initially solve the linear equation Y = Xβ, the weights were
inferred through the expression ˆβ = (XT X + λI)
XTY, in which the regu-
larization parameter λ = 4833 was selected via three-fold cross-validation
on the training set (Friedman et al., 2001). Although we reduced the num-
ber of per-image time bins from 50 A 2, we confirmed that performing ridge
regression on the augmented ˜X = Rt×mn with m indexing the 50 time bins
yielded essentially identical low-pass decoding performance, as discussed
in the section 2.
−1
Additionally, to perform pixel-specific feature selection for high-pass de-
coding, we performed LASSO regression (Friedman et al., 2001), which was
proven to successfully select for relevant units, on the same neural bin ma-
trix X from above (Botella-Soler et al., 2018). Due to the enormity of the neu-
ral bin matrix, Celer, a recently developed accelerated L1 solver, was used to
individually set each pixel’s L1 regularization parameter, as decoding each
pixel represents an independent regression subtask (Massias, Gramfort, &
Salmon, 2018).
4.4 High-Pass Nonlinear Decoding. To maximize high-pass decoding
efficacy with the nonlinear decoder, the augmented ˜X = Rt×mn was chosen
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nonlinear Natural Images Decoding
1739
as the training neural bin matrix. As noted, nonlinear methods, including
kernel ridge regression and feedforward neural networks, have been suc-
cessfully applied to decode both the locations of black disks on white back-
grounds (Botella-Soler et al., 2018) and natural scene images (Zhang, Jia
et al., 2020). Notably the former study used L1 sparsification of the neural
response matrix so that only a handful of RGC responses contributed to
each pixel before applying kernel ridge regression. We borrow this idea of
using L1 regression to create a sparse mapping between RGC units and pix-
els before applying our own neural network decoding, as explained below.
Tuttavia, the successful applications of feedforward decoding networks
above crucially depended on the fact that they used a small number of RGCs
(91 RGCs with 5460 input values and 90 RGCs with 90 input values, Rif-
spectively). For reference, constructing a feedforward network for our spike
data of 2094 RGC units and 104,700 inputs would yield an infeasibly large
number of parameters in the first feedforward layer alone. Allo stesso modo, kernel
ridge regression, which is more time-consuming than a feedforward net-
lavoro, would be even more impractical for large neural data sets.
Therefore, we constructed a spatially restricted network based on the
fact that each RGC’s receptive field encodes a small subset of the pixels
E, conversely, each pixel is represented by a small number of RGCs.
Specifically, each unit’s image-specific response m-vector is featurized to a
reduced f -vector so that each unit is assigned its own featurization map-
ping that is preserved across all pixels. Afterward, for each pixel, the fea-
turized response vectors of the k most relevant units are gathered into a
f k-vector and further processed by nonlinear layers to produce a final pixel
intensity value. The k relevant units are derived from the L1 weight ma-
trix β ∈ R2n×x from above. Within each pixel’s weight vector βx ∈ R2n×1 and
an individual unit’s pixel-specific weights (βn,x ∈ R2×1), we calculate the
L1-norm λx,n = |βn,X|
1 and select the units corresponding to the k largest
norms for each pixel. The resulting high-pass decoded images are added
to the low-pass decoded images to produce the combined decoder output.
Note that while the RGC featurization weights are shared across all pixels,
each pixel has its own optimized set of nonlinear decoding weights (Vedere
Figura 2).
The hyperparameters f = 5, k = 25 were chosen from an exhaustive grid
search spanning f ∈ {5, 10, 15, 20}k ∈ {5, 10, 15, 20, 25} so that the values at
which no further performance gains were observed were selected. The neu-
ral network itself was trained with a variant of the traditional stochastic
gradient descent (SGD) optimizer that includes a momentum term to speed
up training (Qian, 1999) (momentum hyperparameter of 0.9, learning rate
Di 0.1, and weight regularization of 5.0 × 10−6 used for training the network
Sopra 32 epochs).
4.5 Deblurring Network. To further improve the quality of the de-
coded images, we sought to borrow image restoration techniques from
the ever-growing domain of neural network–based deblurring. Specifically,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1740
Kim et al.
a deblurring network leveraging natural image priors would take in the
combined decoder outputs and produce sharpened versions of the inputs.
Tuttavia, these networks usually come with high requirements for train-
ing data set size; using only the 100 decoded images corresponding to the
originally held out test images would be insufficient.
Di conseguenza, we sought to virtually augment our decoder training data set
Di 9,900 spikes-image pairs for use as training examples in the deblurring
scheme. IL 9900 training spikes-image pairs were subdivided into 10 sub-
sets of 990 pairs. Then each subset was held out and decoded (both linearly
and nonlinearly) with the other 9 subsets used as the decoders’ training
examples. Rotating and repeating through each of the 10 subsets allowed
for all 9900 training examples to be transformed into test-quality decoder
outputs, which could be used to train the deblurring network. (To be clear,
100 of the original 10,000 spikes-images pairs were held out for final eval-
uation of the deblurring network, with no data leakage between these 100
test pairs and the 9900 training pairs obtained through the above data set
augmentation.) An existing alternative method would be to craft and use a
generative model for artificial neural spikes corresponding to any arbitrary
input image (Parthasarathy et al., 2017; Zhang, Jia et al., 2020). Tuttavia, IL
search for a solution for the encoding problem is still a topic of active inves-
tigation in neuroscience; our method circumvents this need for a forward
generative model.
With a sufficiently large set of decoder outputs, we could adopt well-
established neural network methods for image deblurring and super-
resolution (Kupyn et al., 2019; Ledig et al., 2017; Maeda, 2020; X. Wang et al.,
2018; Wang et al., 2020; Zhang et al., 2019; Zhang et al., 2017; Zhang, Tian
et al., 2020; Zhou & Susstrunk, 2019). Specifically, we chose the convolu-
tional generator of DeblurGANv2, an improvement of the widely adopted
DeblurGAN with superior deblurring capabilities (Kupyn et al., 2019). Af-
ter performing a grid search of the generator ResNet block number hy-
perparameter ranging {1, 2, . . . , 7, 8}, the 6-block generator was chosen for
training under the Adam optimizer (Kingma & Ba, 2017) for 32 epochs at
an initial learning rate of 1 × 10−5 that was reduced by half every 8 epochs.
We do not expect that the decoded images will be near-perfect replicas of
the original image. Recordings here were taken from the peripheral retina,
where spatial acuity is lower; as a result, one would expect the neural de-
coding of the stimuli to miss some of the fine details of the original image.
Therefore, while the original DeblurGANv2 paper includes pixel-wise L1
loss, a VGG discriminator-based content/perceptual loss, and an additional
adversarial loss during training, we excluded the final adversarial loss term
due to the fact that the deblurred images of the decoder would not be per-
fect (or near-perfect) look-alikes of the raw stimuli images. Invece, we fo-
cus on improving the perceptual qualities of the output image, including
edge sharpness and contrast, for more facile visual identification. We use
both pixel-wise L1 loss and L1 loss between the features extracted from the
true images and from the reconstructions in the third convolutional layer
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nonlinear Natural Images Decoding
1741
of the pretrained VGG-19 network before the corresponding pooling layer
(Johnson, Alahi, & Fei-Fei, 2016; Wang et al., 2018).
Appendix: Supplemental Information
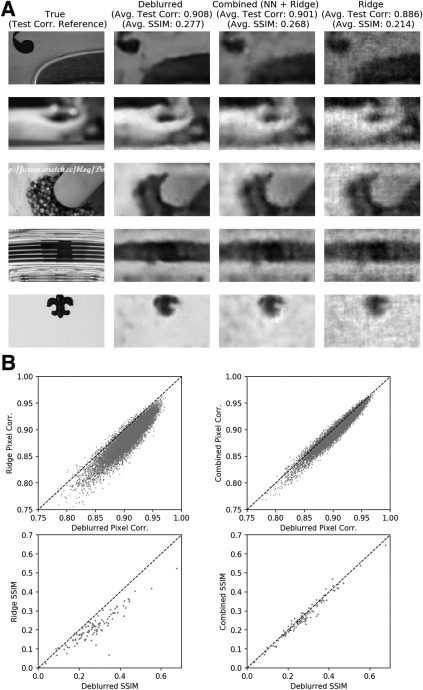
A.1 Validation of Decoding Methods on Second RGC Data Set (Figura
10).
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 10: Decoding method results corroborated on a second RGC data set. (UN)
Representative outputs from the decoding algorithm compared to those from a
simple linear decoder. (B) Comparison of pixel-wise test correlations and SSIM
values between deblurred and linear decoder outputs and against combined
decoder outputs, rispettivamente. The second data set consisted of the responses of
1987 RGC units to 10,000 images, prepared in an identical manner as the first
insieme di dati. The superiority of nonlinear decoding with deblurring is apparent.
1742
Kim et al.
Figura 11: Coverage of image area by matched RGC cells. All four cell types,
ON/OFF parasol/midget, sufficiently cover the image area (marked in dashed
rectangle) with the receptive fields of their constituent white noise-natural scene
matched units.
A.2 Matching of White Noise and Natural Scene RGC Units (Figura
11). Because hundreds of white noise and more than a thousand natural
scene RGC units were discarded during the matching process, these un-
matched units were analyzed to see whether they exhibited any distin-
guishing properties from the matched units. Comparing the mean firing
rates of the matched and unmatched units revealed no clear differences:
10.53 Hz versus 11.46 Hz for matched and unmatched natural scene units
E 6.56 Hz versus 7.03 Hz for matched and unmatched white noise units.
Tuttavia, the mean maximum channel peak-to-peak values (PTPs) were
markedly different between matched and unmatched units within both ex-
perimental settings: 22.06 versus. 10.21 for matched and unmatched natural
scene units and 24.93 versus 18.48 for matched and unmatched white noise
units.
Nonmatching of units is likely caused by several factors. To begin, MSE
and cosine similarity are not perfect measures of template similarity. Many
close candidates were quite similar in shape to the reference templates but
had either a slightly different amplitude or peaks and troughs at different
temporal locations. Indeed it is possible that using a more flexible similar-
ity metric would recover more matching units. Nel frattempo, it is also likely
that some of the unmatched units in either experimental setting are simply
inactive units. Specifically, it could be the case that some units are inactive
during white noise stimulation but more active for natural scene input, E
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nonlinear Natural Images Decoding
1743
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 12: Comparison of ridge regression decoding using both onset (30–
170 ms) and offset (170–300 ms) time bins versus using only one time bin.
(UN) Ridge decoding on one versus two time bins for whole image and (B) low-
pass image reconstruction. Using the onset but not the offset time bin gives re-
constructions of nearly the same quality as using both time bins.
vice versa. Finalmente, difficulties with spike-sorting smaller units could also
lead to mismatches. Nevertheless, despite the above issues, we were able
to recover full coverage of the stimulus region for each cell type, come mostrato
in Figure 11.
A.3 Linear Decoding Using Spikes from Only Either Onset or Off-
set Time Bins (Figura 12). While our standard ridge regression decoder
used spikes from both the onset (30–170 ms) and offset (170–300 ms) time
bins, we investigated how much the onset and offset spikes, rispettivamente,
contributed to linear decoding. Whole and low-pass image reconstructions
using just the onset spikes resulted in test correlations of 0.885 (±0.0006)
E 0.968 (±0.000) versus true whole and low-pass images, rispettivamente.
1744
Kim et al.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 13: The eight best (UN) and worst (B) high-pass images and their linear
and nonlinear reconstructions. Both decoders performed best for stimuli with
clear edges marked by high contrast and performed worst for low-contrast stim-
uli with either too few or too many edges.
Nel frattempo, using just offset spikes yielded 0.0837 (±0.0008) E 0.936
(±0.0004) against true whole and low-pass images. For reference, using both
time bins results in 0.890 (±0.0006) E 0.975 (±0.0002) against the same tar-
gets, rispettivamente. In short, while it is possible to use just the onset spikes
to give reconstructions that were nearly as good as those produced from
two time bins, using both onset and offset spikes produced the best ridge
decoding results.
A.4 High-Pass Decoding Benefits from Stimuli with High Contrast
Edges (Figura 13). Because high-pass decoding via both the linear and
nonlinear decoders exhibited greater spread in the quality of reconstruc-
tions compared to low-pass decoding, we investigated which high-pass im-
ages yielded the best and worst reconstructions, rispettivamente. IL 20 best
high-pass images (measured by nonlinear decoder outputs’ test correlation
versus their respective true high-pass images) resulted in mean image cor-
relations of 0.519 (±0.029) E 0.380 (±0.031) via the nonlinear and linear
Nonlinear Natural Images Decoding
1745
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 14: Comparison of pixel-wise high-pass test correlation for variants of
the neural network decoder. Comparisons included architectures with (UN) dif-
ferent cell numbers used per pixel, (B) width of the pixel-specific hidden layer,
(C) linear features extracted per cell, E (D) number of pixel-specific hidden
layers.
decoders, rispettivamente. Meanwhile the 20 worst high-pass images produced
mean image correlations of 0.232 (±0.030) E 0.152 (±0.029) via nonlinear
and linear decoding, rispettivamente. Note that these values represent corre-
lations between individual images and not the pixel-wise test correlations
used throughout the study.
A closer analysis of the best and worst high-pass images suggests that
both linear and nonlinear high-pass decoding performed the best when the
target stimuli had clear edges marked by high contrast. Nel frattempo, both
high-pass decoders struggled to reconstruct stimuli with too few or too
many object edges combined with low color contrast. Nevertheless, as indi-
cated by the above image correlations, nonlinear decoding still significantly
outperforms linear decoding in both best and worst case scenarios.
A.5 Influence of Cell Number and Architecture on High-Pass Decod-
ing (Figura 14). The high-pass neural network decoder takes in cell num-
ber used, number and width of pixel-specific layers, and number of linear
1746
Kim et al.
features per cell as its hyperparameters. Naturally, we sought to investigate
how these values affect the performance of high-pass decoding. We remind
readers that our chosen model takes in 25 cells per pixel, transforms each
cell’s 50-bin response into 5 linear features, and uses 1 hidden layer that is
40 units wide.
To begin, we compared performance when using 5, 10, 15, 20, E 25
cells per pixel, which corresponds to 512, 597, 676, 746, E 805 unique cells
incorporated. Unsurprisingly, this was the hyperparameter with the great-
est influence on high-pass decoding with significant gains in performance
being observed up until at least 20 cells per pixel are used. We note that we
could not go much below using 512 unique cells as our sparse cell-to-pixel
feature selection process zeroes out each cell’s influence on pixels outside
of its receptive field.
Prossimo, we noted that at least one nonlinear hidden layer per pixel was re-
quired for optimal decoding performance. Tuttavia, using more than two
hidden layers resulted in lower performance, suggesting that using more
parameters than necessary results in either overfitting or difficulties in the
optimization process. This conclusion is reinforced by the fact that increas-
ing the number of linear features per cell and width of each pixel-specific
hidden layer did not further improve decoding performance. Since our neu-
ral network decoder does not seem to improve indefinitely with increasing
number of parameters and layers, our choice of a spatially restricted neural
network decoder still stands as a reasonable one over much more massive,
intractable fully connected architectures.
Ethics Statement
Eyes were removed from terminally anesthetized macaque monkeys
(Macaca mulatta, Macaca fascicularis) used by other laboratories in the course
of their experiments, in accordance with the Institutional Animal Care and
Use Committee guidelines. All of the animals were handled according to
approved institutional animal care and use committee (IACUC) protocols
(28860) of the Stanford University. The protocol was approved by the Ad-
ministrative Panel on Laboratory Animal Care of the Stanford University
(Assurance Number: A3213-01).
Ringraziamenti
We thank Eric Wu and Nishal Shah for helpful discussions.
Riferimenti
Bialek, W., de Ruyter van Steveninck, R., Rieke, F., & Warland, D. (1997). Spikes: Ex-
ploring the neural code. Cambridge, MA: CON Premere.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nonlinear Natural Images Decoding
1747
Botella-Soler, V., Deny, S., Martius, G., Marre, O., & Tkaˇcik, G. (2018). Nonlinear
decoding of a complex movie from the mammalian retina. PLOS Computational
Biology, 14(5), e1006057. https://doi.org/10.1371/journal.pcbi.1006057.
Brackbill, N., Rhoades, C., Kling, A., Shah, N. P., Sher, A., Litke, UN. M., &
Chichilnisky, E. J. (2020). Reconstruction of natural images from responses of
primate retinal ganglion cells. Neuroscience. https://doi.org/10.1101/2020.05.04.
077693.
Cheng, D. L., Greenberg, P. B., & Borton, D. UN. (2017). Advances in retinal prosthetic
research: A systematic review of engineering and clinical characteristics of cur-
rent prosthetic initiatives. Current Eye Research, 42(3), 334–347. https://doi.org/
10.1080/02713683.2016.1270326.
Chichilnisky, E. J., & Kalmar, R. S. (2002). Functional asymmetries in ON and OFF
ganglion cells of primate retina. Journal of Neuroscience, 22(7), 2737–2747. https:
//doi.org/10.1523/JNEUROSCI.22-07-02737.2002.
Cottaris, N. P., & Elfar, S. D. (2009). Assessing the efficacy of visual prostheses by
decoding ms-LFPs: Application to retinal implants. Journal of Neural Engineering,
6(2), 026007. https://doi.org/10.1088/1741-2560/6/2/026007.
Deng, X., Liu, D. F., Kay, K., Frank, l. M., & Eden, U. T. (2015). Clusterless decoding
of position from multiunit activity using a marked point process filter. Neural
Computation, 27(7), 1438–1460. https://doi.org/10.1162/NECO_a_00744.
Ellis, R. J., & Michaelides, M. (2018). High-accuracy decoding of complex visual
scenes from neuronal calcium responses. Neuroscience. https://doi.org/10.1101/
271296.
Field, G. D., & Chichilnisky, E. J. (2007). Information processing in the primate retina:
Circuitry and coding. Annual Review of Neuroscience, 30(1), 1–30. https://doi.org/
10.1146/annurev.neuro.30.051606.094252.
Field, Greg D., Gauthier, J. L., Sher, A., Greschner, M., Machado, T. A., Jepson, l.
H., . . . Chichilnisky, E. J. (2010). Functional connectivity in the retina at the res-
olution of photoreceptors. Nature, 467(7316), 673–677. https://doi.org/10.1038/
nature09424.
Frechette, E. S., Sher, A., Grivich, M. I., Petrusca, D., Litke, UN. M., & Chichilnisky, E.
J. (2005). Fidelity of the ensemble code for visual motion in primate retina. Journal
of Neurophysiology, 94(1), 119–135. https://doi.org/10.1152/jn.01175.2004.
Freeman, J., Field, G. D., Li, P. H., Greschner, M., Gunning, D. E., Mathieson, K.,
. . . Chichilnisky, E. (2015). Mapping nonlinear receptive field structure in primate
retina at single cone resolution. ELife, 4, e05241. https://doi.org/10.7554/eLife.
05241.
Friedman, J., Hastie, T., & Tibshirani, R. (2001). The elements of statistical learning. Nuovo
York: Springer.
Garasto, S., Bharath, UN. A., & Schultz, S. R. (2018). Visual reconstruction from 2-photon
calcium imaging suggests linear readout properties of neurons in mouse primary visual
cortex. bioRxiv:300392. https://doi.org/10.1101/300392.
Garasto, S., Nicola, W., Bharath, UN. A., & Schultz, S. R. (2019). Neural sampling strate-
gies for visual stimulus reconstruction from two-photon imaging of mouse pri-
mary visual cortex. In Proceedings of the 9th International IEEE/EMBS Conference on
Neural Engineering (pag. 566–570). Piscataway, NJ: IEEE. https://doi.org/10.1109/
NER.2019.8716934.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1748
Kim et al.
Gollisch, T. (2013). Features and functions of nonlinear spatial integration by reti-
nal ganglion cells. Journal of Physiology–Paris, 107(5), 338–348. https://doi.org/
10.1016/j.jphysparis.2012.12.001.
Jarosiewicz, B., Sarma, UN. A., Bacher, D., Masse, N. Y., Simeral, J. D., Sorice, B., . . .
Hochberg, l. R. (2015). Virtual typing by people with tetraplegia using a self-
calibrating intracortical brain-computer interface. Science Translational Medicine,
7(313), 313ra179-313ra179. https://doi.org/10.1126/scitranslmed.aac7328.
Johnson, J., Alahi, A., & Fei-Fei, l. (2016). Perceptual losses for real-time style transfer
and super-resolution. arXiv:1603.08155 [Cs]. http://arxiv.org/abs/1603.08155.
Kingma, D. P., & Ba,
J.
(2017). Adam: A method for stochastic optimization.
arXiv:1412.6980 [Cs]. http://arxiv.org/abs/1412.6980.
Kupyn, O., Martyniuk, T., Wu, J., & Wang, Z. (2019). DeblurGAN-v2: Deblurring
(orders-of-magnitude) faster and better. arXiv:1908.03826 [Cs]. http://arxiv.org/
abs/1908.03826.
Ledig, C., Theis, L., Huszar, F., Caballero, J., Cunningham, A., Acosta, A., . . . Shi,
W. (2017). Photo-realistic single image super-resolution using a generative adversarial
rete. arXiv:1609.04802 [Cs, Stat].
Lee, J., Mitelut, C., Shokri, H., Kinsella, I., Dethe, N., Wu, S., . . . Paninski, l. (2020).
YASS: Yet another spike sorter applied to large-scale multi-electrode array record-
ings in primate retina. Neuroscience. https://doi.org/10.1101/2020.03.18.997924.
Litke, UN. M., Bezayiff, N., Chichilnisky, E. J., Cunningham, W., Dabrowski, W., Grillo,
UN. A., . . . Sher, UN. (2004). What does the eye tell the brain?: Development of a
system for the large-scale recording of retinal output activity. IEEE Transactions
on Nuclear Science, 51(4), 1434–1440. https://doi.org/10.1109/TNS.2004.832706.
Liu, W., Vichienchom, K., Clements, M., DeMarco, S. C., Hughes, C., McGucken, E.,
Humayun, M. S., De Juan, E., Weiland, J. D., & Greenberg, R. (2000). A neuro-
stimulus chip with telemetry unit for retinal prosthetic device. IEEE Journal of
Solid-State Circuits, 35(10), 1487–1497. https://doi.org/10.1109/4.871327.
Maeda, S.
(2020). Unpaired image
super-resolution using pseudo-supervision.
arXiv:2002.11397 [Cs, Eess].
Marre, O., Botella-Soler, V., Simmons, K. D., Mora, T., Tkaˇcik, G., & Berry, M. J.
(2015). High accuracy decoding of dynamical motion from a large retinal pop-
ulation. PLOS Computational Biology, 11(7), e1004304. https://doi.org/10.1371/
journal.pcbi.1004304.
Massias, M., Gramfort, A., & Salmon, J. (2018). Celer: A fast solver for the lasso with dual
extrapolation. arXiv:1802.07481 [Stat].
McCann, B. C., Hayhoe, M. M., & Geisler, W. S. (2011). Decoding natural signals from
the peripheral retina. Journal of Vision, 11(10), 1–11. https://doi.org/10.1167/11.
10.19.
Moxon, K. A., & Foffani, G. (2015). Brain-machine interfaces beyond neuroprosthet-
ics. Neuron, 86(1), 55–67. https://doi.org/10.1016/j.neuron.2015.03.036.
Naselaris, T., Prenger, R. J., Kay, K. N., Oliver, M., & Gallant, J. l. (2009). Bayesian
reconstruction of natural images from human brain activity. Neuron, 63(6), 902–
915. https://doi.org/10.1016/j.neuron.2009.09.006.
Nirenberg, S., & Pandarinath, C. (2012). Retinal prosthetic strategy with the capacity
to restore normal vision. In Proceedings of the National Academy of Sciences, 109(37),
15012–15017. https://doi.org/10.1073/pnas.1207035109.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Nonlinear Natural Images Decoding
1749
Nishimoto, S., Vu, UN. T., Naselaris, T., Benjamini, Y., Yu, B., & Gallant, J. l. (2011).
Reconstructing visual experiences from brain activity evoked by natural movies.
Current Biology, 21(19), 1641–1646. https://doi.org/10.1016/j.cub.2011.08.031.
Odermatt, B., Nikolaev, A., & Lagnado, l. (2012). Encoding of luminance and con-
trast by linear and nonlinear synapses in the retina. Neuron, 73(4), 758–773. https:
//doi.org/10.1016/j.neuron.2011.12.023.
Parthasarathy, N., Batty, E., Falcon, W., Rutten, T., Rajpal, M., Chichilnisky, E. J., &
Paninski, l. (2017). Neural networks for efficient Bayesian decoding of natural
images from retinal neurons [Preprint]. Neuroscience. https://doi.org/10.1101/
153759.
Passaglia, C. L., & Troy, J. B. (2004). Information transmission rates of cat retinal
ganglion cells. Journal of Neurophysiology, 91(3), 1217–1229. https://doi.org/10.
1152/jn.00796.2003.
Pillow, J. W., Shlens, J., Paninski, L., Sher, A., Litke, UN. M., Chichilnisky, E. J., & Si-
moncelli, E. P. (2008). Spatio-temporal correlations and visual signalling in a com-
plete neuronal population. Nature, 454(7207), 995–999. https://doi.org/10.1038/
nature07140.
Pitkow, X., & Meister, M. (2012). Decorrelation and efficient coding by retinal gan-
glion cells. Nature Neuroscience, 15(4), 628–635. https://doi.org/10.1038/nn.3064.
Portelli, G., Barrett, J. M., Hilgen, G., Masquelier, T., Maccione, A., Di Marco, S., . . .
Sernagor, E. (2016). Rank order coding: A retinal information decoding strategy
revealed by large-scale multielectrode array retinal recordings. Eneuro, 3(3). https:
//doi.org/10.1523/ENEURO.0134-15.2016.
Qian, N. (1999). On the momentum term in gradient descent learning algo-
rithms. Neural Networks, 12(1), 145–151. https://doi.org/10.1016/S0893-6080(98)
00116-6.
Ruda, K., Zylberberg, J., & Field, G. D. (2020). Ignoring correlated activity causes
a failure of retinal population codes. Nature Communications, 11(1), 4605. https:
//doi.org/10.1038/s41467-020-18436-2.
Ryu, S. B., Ye, J. H., Goo, Y. S., Kim, C. H., & Kim, K. H. (2011). Decoding of tempo-
ral visual information from electrically evoked retinal ganglion cell activities in
photoreceptor-degenerated retinas. Investigative Opthalmology and Visual Science,
52(9), 6271. https://doi.org/10.1167/iovs.11-7597.
Schreyer, H. M., & Gollisch, T. (2020). Nonlinearities in retinal bipolar cells shape the
encoding of artificial and natural stimuli. bioRxiv:2020.06.10.144576.
Schwartz, G., & Rieke, F. (2011). Nonlinear spatial encoding by retinal ganglion cells:
When 1 + 1 (cid:4)= 2. Journal of General Physiology, 138(3), 283–290. https://doi.org/
10.1085/jgp.201110629.
Schwemmer, M. A., Skomrock, N. D., Sederberg, P. B., Ting, J. E., Sharma, G., Bock-
brader, M. A., & Friedenberg, D. UN. (2018). Meeting brain–computer interface user
performance expectations using a deep neural network decoding framework. Na-
ture Medicine, 24(11), 1669–1676. https://doi.org/10.1038/s41591-018-0171-y.
Turner, M. H., & Rieke, F. (2016). Synaptic rectification controls nonlinear spatial
integration of natural visual inputs. Neuron, 90(6), 1257–1271. https://doi.org/
10.1016/j.neuron.2016.05.006.
Turner, M. H., Schwartz, G. W., & Rieke, F. (2018). Receptive field center-surround
interactions mediate context-dependent spatial contrast encoding in the retina.
eLife, 7, e38841. https://doi.org/10.7554/eLife.38841.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1750
Kim et al.
Wang, X., Yu, K., Wu, S., Gu, J., Liu, Y., Dong, C., Loy, C. C., Qiao, Y., &
Tang, X. (2018). ESRGAN: Enhanced super-resolution generative adversarial networks.
arXiv:1809.00219 [Cs].
Wang, Z., Bovik, UN. C., Sheikh, H. R., & Simoncelli, E. P. (2004). Image quality as-
sessment: From error visibility to structural similarity. IEEE Transactions on Image
in lavorazione, 13(4), 600–612. https://doi.org/10.1109/TIP.2003.819861.
Wang, Z., Chen, J., & Hoi, S. C. H. (2020). Deep learning for image super-resolution: UN
survey. arXiv:1902.06068 [Cs].
Warland, D. K., Reinagel, P., & Meister, M. (1997). Decoding visual information from
a population of retinal ganglion cells. Journal of Neurophysiology, 78(5), 2336–2350.
https://doi.org/10.1152/jn.1997.78.5.2336.
Weiland, J. D., Yanai, D., Mahadevappa, M., Williamson, R., Mech, B. V., Fujii, G. Y.,
. . . Humayun, M. S. (2004). Visual task performance in blind humans with retinal
prosthetic implants. In Proceedings of the 26th Annual International Conference of the
IEEE Engineering in Medicine and Biology Society (p.p. 4172–4173). Piscataway, NJ:
IEEE.
Yoshida, T., & Ohki, K. (2020). Natural images are reliably represented by sparse and
variable populations of neurons in visual cortex. Nature Communications, 11(1),
872. https://doi.org/10.1038/s41467-020-14645-x.
Zhang, K., Zuo, W., Gu, S., & Zhang, l. (2017). Learning deep CNN denoiser prior
for image restoration. Negli Atti del 2017 IEEE Conference on Computer Vision
and Pattern Recognition (pag. 2808–2817). Piscataway, NJ: IEEE. https://doi.org/
10.1109/CVPR.2017.300.
Zhang, K., Zuo, W., & Zhang, l. (2019). Deep plug-and-play super-resolution for arbitrary
blur kernels. arXiv:1903.12529 [Cs].
Zhang, Y., Jia, S., Zheng, Y., Yu, Z., Tian, Y., Mamma, S., . . . Liu, J. K. (2020). Reconstruction
of natural visual scenes from neural spikes with deep neural networks. Neural
Networks, 125, 19–30. https://doi.org/10.1016/j.neunet.2020.01.033.
Zhang, Y., Tian, Y., Kong, Y., Zhong, B., & Fu, Y. (2020). Residual dense network for
image restoration. IEEE Transactions on Pattern Analysis and Machine Intelligence,
Gennaio. https://doi.org/10.1109/TPAMI.2020.2968521.
Zhou, R., & Susstrunk, S. (2019). Kernel modeling super-resolution on real low-
resolution images. In Proceedings of the IEEE/CVF International Conference on Com-
puter Vision (pag. 2433–2443). https://doi.org/10.1109/ICCV.2019.00252.
Received September 15, 2020; accepted January 25, 2021.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
3
7
1
7
1
9
1
9
2
5
3
5
5
N
e
C
o
_
UN
_
0
1
3
9
5
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3