ARTICLE
Communicated by Adam Kampff
High-Dimensional Cluster Analysis with the Masked
EM Algorithm
Shabnam N. Kadir
s.kadir@ucl.ac.uk
UCL Institute of Neurology and UCL Department of Neuroscience, Physiology,
and Pharmacology, University College London, London WC1E 6DE, U.K.
Dan F. M. Goodman
Dan_Goodman@meei.harvard.edu
Eaton-Peabody Laboratories, Massachusetts Eye and Ear Infirmary, Department
of Otology and Laryngology, Harvard Medical School, Boston, MA 02114, U.S.A.
Kenneth D. Harris
kenneth.harris@ucl.ac.uk
UCL Institute of Neurology and UCL Department of Neuroscience, Physiology,
and Pharmacology, University College London, London WC1E 6DE, U.K.
Cluster analysis faces two problems in high dimensions: the “curse of
dimensionality” that can lead to overfitting and poor generalization per-
formance and the sheer time taken for conventional algorithms to pro-
cess large amounts of high-dimensional data. We describe a solution to
these problems, designed for the application of spike sorting for next-
generation, high-channel-count neural probes. In this problem, only a
small subset of features provides information about the cluster mem-
bership of any one data vector, but this informative feature subset is
not the same for all data points, rendering classical feature selection
ineffective. We introduce a “masked EM” algorithm that allows accurate
and time-efficient clustering of up to millions of points in thousands of
dimensions. We demonstrate its applicability to synthetic data and to
real-world high-channel-count spike sorting data.
1 introduzione
Cluster analysis is a widely used technique for unsupervised classifica-
tion of data. A popular method for clustering is fitting a mixture of gaus-
sians, often achieved using the expectation-maximization (EM) algorithm
(Dempster, Laird, & Rubin, 1977) and variants thereof (Fraley & Raftery,
D.F.M.G. is now with the Department of Electrical and Electronic Engineering, Impe-
rial College London, London U.K.
Calcolo neurale 26, 2379–2394 (2014)
doi:10.1162/NECO_a_00661
C(cid:2) 2014 Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 3.0 Unported (CC BY 3.0) licenza
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2380
S. Kadir, D. Goodman, and K. Harris
2002). In high dimensions, Tuttavia, this method faces two challenges
(Bouveyron & Brunet-Saumard, 2012). First is the “curse of dimensional-
ità,” which leads to poor classification, particularly in the presence of a large
number of uninformative features; second, for large and high-dimensional
set di dati, the computational cost of many algorithms can be impractical.
This is particularly the case where covariance matrices must be estimated,
leading to computations of order O(p2), where p is the number of features;
furthermore, even a cost of O(P) can render a clustering method impractical
for applications in which large high-dimensional data sets must be analyzed
daily. In many cases, Tuttavia, the dimensionality problem is solvable, at
least in principle, as the features sufficient for classification of any particular
data point are a small subset of the total available.
A number of approaches have been suggested for the problem of high-
dimensional cluster analysis. One approach consists of modifying the
generative model underlying the mixture of gaussians fit to enforce
low-dimensional models. For example the mixture of factor analyzers
(Ghahramani & Hinton, 1996; McLachlan, Peel, & Bean, 2003) models the
covariance matrix of each cluster as a low-rank matrix added to a fixed
diagonal matrix forming an approximate model of observation noise. Questo
approach can reduce the number of parameters for each cluster from O(p2)
to O(P) and may thus provide a substantial improvement in both compu-
tational cost and performance. An alternative approach, which offers the
opportunity to reduce both the number of parameters and computational
cost substantially below O(P), is feature selection, whereby a small subset
of informative features is selected and other noninformative features are
discarded (Raftery & Dean, 2006). A limitation of global feature selection
metodi, Tuttavia, is that they cannot deal with the case where different
data points are defined by different sets of features. One proposed solution
to this consists of assigning each cluster a unique distribution of weights
over all features, which has been applied to the case of hierarchical cluster-
ing (Friedman & Meulman, 2004).
The algorithm described below was developed to solve the problems of
high-dimensional cluster analysis for a particular application: spike sort-
ing of neurophysiological recordings using newly developed high-count
silicon microelectrodes (Einevoll, Franke, Hagen, Pouzat, & Harris, 2012).
Spike sorting is the problem of identifying the firing times of neurons from
electric field signatures recorded using multisite microfabricated neural
electrodes (Lewicki, 1998). In low-noise systems, such as retinal explants ex
vivo, it has been possible to decompose the raw recorded signal into a sum of
waveforms, each corresponding to a single action potential (Pillow, Shlens,
Chichilnisky, & Simoncelli, 2013; Marre et al., 2012; Prentice et al., 2011).
For recordings in the living brain, noise levels are considerably higher, E
an approach based on cluster analysis is more often taken. In a typical ex-
periment, this will involve clustering millions of data points, each of which
reflects a single action potential waveform that could have been produced
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
High-Dimensional Cluster Analysis with the Masked EM Algorithm
2381
by one of many neurons. Historically, neural probes used in vivo have had
only a small number of channels (usually four), typically resulting in fea-
ture vectors of 12 dimensions, which required sorting into 10 A 15 clusters.
Analysis of “ground truth” shows that the data are quite well approximated
by a mixture of gaussians with different covariance matrices between clus-
ters (Harris, Henze, Csicsvari, Hirase, & Buzs´aki, 2000). Accordingly, in this
low-dimensional case, traditional EM-derived algorithms work close to op-
timally, although specialized rapid implementation software is required to
cluster the millions of spikes recorded on a daily basis (Harris, Kadir, &
Goodman, 2000–2013). More recent neural probes, Tuttavia, contain tens to
hundreds of channels, spread over large spatial volumes, and probes with
thousands are under development. Because different neurons have differ-
ent spatial locations relative to the electrode array, each action potential is
detected on only a small fraction of the total number of channels, ma il
subset differs between neurons, ruling out a simple global feature selection
approach. Inoltre, because spikes produced by simultaneous firing of
neurons at different locations must be clustered independently, most fea-
tures for any one data point are not simply noise, but must be regarded
as missing data. Finalmente, due to the large volumes of data produced by
these methods, we require a solution that is capable of clustering millions
of data points in reasonably short running time. Although numerous ex-
tensions and alternatives to the simple cluster sorting method have been
proposed: (Takahashi, Anzai, & Sakurai, 2003; Quian Quiroga, Nadasdy, &
Ben-Shaul, 2004; Legna & Black, 2008; Sahani, 1999; Lewicki, 1998; Gasthaus,
Legna, Gorur, & Teh, 2008; Calabrese & Paninski, 2011; Ekanadham,
Tranchina, & Simoncelli, 2013; Shoham, Fellows, & Normann, 2003; Franke,
Natora, Boucsein, Munk, & Obermayer, 2010; Carin et al. 2013), none
have been shown to solve the problems created by high-count electrode
arrays.
Here we introduce a “masked EM” algorithm to solve the problem of
high-dimensional cluster analysis, as found in the spike-sorting context.
The algorithm works in two stages. In the first stage, a “mask vector” is
computed for each data point via a heuristic algorithm, encoding a weight-
ing of each feature for every data point. This stage may take advantage of
domain-specific knowledge, such as the topological constraint that action
potentials occupy a spatially contiguous set of recording channels. Nel
case that the majority of masks can be set to zero, both the number of pa-
rameters per cluster and running time can be substantially below O(P). Noi
note that the masks are assigned to data points rather than clusters and need
be computed only once at the start of the algorithm. The second stage con-
sists of cluster analysis. This is implemented using a mixture-of-gaussians
EM algorithm, but with every data point replaced by a virtual mixture
of the original feature value and the fixed subthreshold noise distribution
weighted by the masks. The use of this virtual mixture distribution avoids
the splitting of clusters due to arbitrary threshold crossings. At no point is it
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2382
S. Kadir, D. Goodman, and K. Harris
Tavolo 1: Mathematical Notation.
Dimensions (number of features)
Data
Masks
Cluster label
Total number of clusters
Mixture weight, cluster mean, covariance
Probability density function of the multivariate gaussian
distribution
Total number of data points
Number of points for which feature i is masked
Noise mean for feature i
Noise variance for feature i
Virtual features (random variable)
Mean of virtual feature
zn,io
Variance of virtual feature
Log likelihood of ˜xn in cluster k
Set of data points assigned to cluster k
Subset of C
k for which feature i is fully masked
P
xn,io, point n, feature i
mn,io
∈ [0, 1]
k
K
w
, (cid:2)
, μ
k
k
, (cid:2)
φ(X|μ
k
k
)
k
Nmask
io
= 0}|
N
= |{N : mn,io
ν
io
σ 2
io
˜xn,io
= E[ ˜xn,io]
)2]
yn,io
E[( ˜xn,io
N,io := Var( ˜xn,io
η
π
nk
C
k
M
ik
)
required to generate samples from the virtual distribution, as expectations
over it can be computed analytically.
2 The Masked EM Algorithm
The mathematical notation used in this article can be found in Table 1.
2.1 Stage 1: Mask Generation. The first stage of the algorithm consists
of computing a set of mask vectors indicating which features should be used
to classify which data points. Specifically, the outcome of this algorithm is a
∈ [0, 1]. A value of 1 indicates that
set of vectors mn with components, mn,io
feature i is to be used in classifying data point xn, a value of 0 indicating it is
to be ignored, and intermediate values corresponding to partial weighting.
We refer to features being used for classification as unmasked and features
being ignored as masked (cioè., concealed). Masked features are not simply
set to zero, but are ignored by replacing them with a virtual ensemble of
points, drawn from a distribution of subthreshold noise.
The use of masks provides two major advantages over a standard mix-
ture of gaussians classification: it overcomes the curse of dimensionality,
because assignment of points to classes is no longer overwhelmed by the
noise on the large number of masked channels, and it allows the algo-
rithm to run in time proportional to O(unmasked features2) piuttosto che
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
High-Dimensional Cluster Analysis with the Masked EM Algorithm
2383
O(features2). Because a small number of features may be unmasked for
each data point, this can allow computational costs substantially below
O(P). The way masks are chosen can depend on the application domain
and typically follows a heuristic method. A simple approach that can work
in general is to compute masks based on a standard deviation of each
feature:
=
mn,io
⎧
⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎩
0
1
|xn,io
βSDi
| − αSDi
− αSDi
|xn,io
|xn,io
| < αSDi | > βSDi
αSDi
< |xn,i | < βSDi . (2.1) This strategy smoothly interpolates between a mask of zero for fea- tures below a lower threshold and a mask of 1 for features above a higher threshold; such smooth interpolation avoids the artificial creation of dis- crete clusters when variables cross a fixed boundary. In the case of spike sorting, a slightly more complex procedure is used to derive the masks, which takes advantage of the topological constraint that spikes must be dis- tributed across continuous groups of recording channels (see section 3.2). In practice, we have found that good performance can be obtained for a range of masking parameters, provided the majority of noninformative fea- tures have a mask of 0 and that features that are clearly suprathreshold are given a mask of 1 (see section 3.1). Once the masks have been computed, an additional set of quantities is precomputed before the main EM loop starts. Specifically, the subthreshold noise mean for feature i, ν i, is obtained by taking the mean of feature i when- = 0, and analogously, the ever that particular feature is masked, that is, mn,i noise variance for feature i, σ 2 i : i := 1 ν Nmask i (cid:6) n:mn,i =0 , xn,i σ 2 i := 1 Nmask i (cid:6) n:mn,i =0 (xn,i − ν i )2, where Nmask i = |{n : mn,i = 0}|. 2.2 Stage 2: Clustering. The second stage consists of a maximum- likelihood mixture-of-gaussians fit, with both the E and M steps modified by replacing each data point xn with a virtual ensemble of points ˜xn distributed as (cid:7) ˜xn,i = xn,i N(ν i , σ 2 i prob mn,i ) prob 1 − mn,i , (2.2) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 2 6 1 1 2 3 7 9 2 0 1 7 3 2 6 n e c o _ a _ 0 0 6 6 1 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 2384 S. Kadir, D. Goodman, and K. Harris ∈ [0, 1] is the mask vector component associated with xn,i for the where mn,i nth spike. Intuitively, any feature below a noise threshold is replaced by a virtual ensemble of the entire noise distribution. The noise on each feature will be modeled as independent univariate gaussian distributions N(ν ) , σ 2 i i for each i, which we shall refer to as the noise distribution for feature i. This is, of course, a simplification, as the noise may be correlated. However, for tractability, ease of implementation, and, as we shall later show, efficacy, this approximation suffices. The algorithm maximizes the expectation of the usual log likelihood over the virtual distribution: L(w k , μ k , (cid:2) k ) := (cid:8) (cid:9) K(cid:6) E˜x log (cid:10) exp − 1 2 w k k=1 N(cid:6) n=1 (˜xn − μ k (2π )d/2(cid:4)(cid:2) k )T (cid:2)−1 k (cid:4)1/2 (˜xn − μ k (cid:12)(cid:13) (cid:11) ) . The masked EM algorithm therefore acts as if it were passed an ensemble of points, with each data point replaced by an infinite sample, correspond- ing to different possibilities for the noisy masked variables. This solves the curse of dimensionality by “disenfranchising” each data point’s masked features, disregarding the value that was actually measured and replacing it by a virtual ensemble that is the same in all cases and thus does not contribute to cluster assignment. Before we run the EM algorithm, we also compute the following quan- tities, which will greatly speed up computation of the modified M- and E-steps: yn,i := E[ ˜xn,i] = mn,ixn,i zn,i := E[( ˜xn,i )2] = mn,i n,i := Var[ ˜xn,i] = zn,i η + (1 − mn,i (xn,i − (yn,i )2 + (1 − mn,i )2. , )ν i (cid:10) ) ν2 i + σ 2 i (cid:11) , 2.3 M-Step. For the M-step, replacing x with the virtual ensemble ˜x requires computing the expectation with respect to ˜xn,i of the mean and the covariance of each cluster. For simplicity, we henceforth focus on a “hard” EM algorithm in which each data point xn is fully assigned to a single cluster, although a “soft” version can be easily derived. We denote by C k the set of data point indices assigned to the cluster with index k. It is straightforward to show that (μ ) i k = 1 |C k | (cid:6) n∈C , yn,i ((cid:2) k ) i j = E[( ˜(cid:2) k i j] = 1 ) |C k (cid:6) (cid:10) | n∈C (yn,i − (μ ) i )(yn, j k − (μ k ) j ) + η δ i, j n,i (2.3) (cid:11) . (2.4) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 2 6 1 1 2 3 7 9 2 0 1 7 3 2 6 n e c o _ a _ 0 0 6 6 1 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 High-Dimensional Cluster Analysis with the Masked EM Algorithm 2385 Note that this is the same formula as the classical M-step, but with xn,i replaced by the expected value yn,i of the virtual distribution ˜x, plus a n,i of ˜x. correction term to (cid:10) Computation of these quantities can be carried out very efficiently as we ) can decompose (μ i j as follows: ⎞ i, j corresponding to the covariance matrix η i and ((cid:2) ) k ⎛ k (μ ) i k ((cid:2) k ) i j = 1 |C k = 1 |C k | | (cid:6) ⎝ n∈C k \M k,i (cid:6) yn,i + |M ⎠ , |ν i k,i (2.5) (yn,i − (μ ) i )(yn, j k − (μ k ) i ) n∈C k \(M k,i ∩ M k, j ) |M ∩ M | k, j k,i + | |C ⎛ k (cid:6) ⎝ n∈C k \M k,i + 1 |C k | (ν i − (μ )(ν ) i k j − (μ ) ) j k ⎞ η n,i + |M |σ 2 i k,i ⎠ δ i, j , k,i |mn,i = {n ∈ C k where M k denotes the set of points within cluster k for which feature i is fully masked. Note that if all data points in a cluster have feature i masked, then (μ i , the noise variance. i, the noise mean, and ((cid:2) = 0} ⊆ C = σ 2 = ν ) ii ) i k k 2.4 E-Step. In the E-step, we compute the responsibility of each cluster for each point, defined as the probability that point n came from cluster k, conditional on its feature values. The responsibility is computed via Bayes theorem from π nk, the log likelihood of point n under the gaussian model for cluster k. In the masked EM algorithm, we compute π nk as its expected value over the virtual distribution ˜xn. Thus, the algorithm acts as if each data point is replaced by an infinite ensemble of points drawn from the distribution of ˜xn, which must all be assigned the same cluster label. Explicitly, π nk = E ˜xn (cid:18) − d 2 log 2π − 1 2 log det (cid:2) k − 1 2 (˜xn − μ k )T ((cid:2) k )−1(˜xn − μ k (cid:19) ) . The final term of equation 2.6 corresponds to the expectation of the Mahalanobis distance of ˜xn,i from cluster k. It can be shown that (2.6) π nk = − d 2 − 1 2 log 2π − 1 2 (cid:9) log det (cid:2) k (cid:12) − 1 2 (yn − (μ ))T ((cid:2) k k )−1(yn − (μ )) k (cid:6) i η ((cid:2) k )−1 ii n,i . l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 2 6 1 1 2 3 7 9 2 0 1 7 3 2 6 n e c o _ a _ 0 0 6 6 1 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 2386 S. Kadir, D. Goodman, and K. Harris This leads to the original E-step for the EM algorithm, but with yn,i substi- tuted for xn,i, plus a diagonal correction term − 1 )−1 ii ((cid:2) (cid:20) n,i η . k i 2 2.5 Penalties. Automatically determining the number of clusters in a mixture of gaussians requires a penalty function that penalizes overfitting by discouraging models with a large number of parameters. Commonly used penalization methods include the Akaike information criterion (AIC) (Akaike, 1974) and Bayes information criterion (BIC) (Schwarz, 1978): AIC = 2κ − 2 ln(L), BIC = κ ln(N) − 2 ln(L), where κ is the number of free parameters in the statistical model and L is the maximum of the likelihood for the estimated model and N is the number of data points. For the classical mixture-of-gaussians fit, the number of parameters κ is equal to K( p(p+1) + p + 1) − 1, where K is the number of clusters and p is number of features. The elements of the first term in κ correspond to the number of free parameters in a p × p covariance matrix, a p-dimensional mean vector, and a single weight for each cluster. Finally, 1 is subtracted from the total because of the constraint that the weights must sum to 1 for a mixture model. 2 For masked data, the estimation of the number of parameters in the model is more subtle. Because masked features are replaced by a fixed distribution that does not vary between data points, the effective degrees of freedom per cluster are much smaller than p(p+1) + p + 1. We therefore define a cluster penalty for each cluster C that depends only on the average number of unmasked features corresponding to that cluster. Specifically, let p rn := j=1 mn, j be the effective number of unmasked features for data point n (i.e., sum of the weights over the features). Define F(r) := r(r+1) + r + 1, where the three terms correspond to the number of free parameters in an r × r covariance matrix, mean vector of length r, and a mixture weight, respectively. (cid:20) 2 2 Our estimate of the effective number of parameters is thus ˆκ = ⎛ ⎝ 1 |C k | K(cid:6) k=1 |C |(cid:6) k n=1 ⎞ F(rn ⎠ − 1 . ) (2.7) 2.6 Implementation. The algorithm was implemented in custom C++ code, based on previously released open-source software for fast mixture- of-gaussians fitting termed KlustaKwik (Harris et al., 2000–2013). Because we require the algorithm to run in reasonable time on large numbers of high- dimensional data points, several approximations are made to give faster running times without significantly affecting performance. These include l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 2 6 1 1 2 3 7 9 2 0 1 7 3 2 6 n e c o _ a _ 0 0 6 6 1 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 High-Dimensional Cluster Analysis with the Masked EM Algorithm 2387 not only hard classification but also a heuristic that eliminates the great majority of E-step iterations, a split-and-merge feature that changes the number of clusters dynamically if this increases the penalized likelihood, and an additional uniform distributed mixture component to catch outliers. The software can be downloaded from https://github.com/klusta-team/ klustakwik (Harris, Kadir, & Goodman, 2013) . 3 Evaluation 3.1 Mixture of Gaussians. We first demonstrate the efficacy of the masked EM algorithm using a simple data set synthesized from a high- dimensional mixture of gaussians. The data set consisted of 20,000 points in 1000 dimensions, drawn from seven separate clusters. The means were chosen by centering probability density functions of gamma distributions on certain chosen features. All covariance matrices were identical: a Toeplitz matrix with all the diagonal entries 1 and off-diagonal entries that decayed exponentially with distance from the diagonal. Figure 1A shows this data set in pseudocolor format. Figure 1B shows a confusion matrix generated by the masked EM algo- rithm on this data, with the modified BIC penalty and masks defined by equation 2.1, indicating perfect performance. By contrast, Figure 1C shows the result of classical EM, in which many clusters have been erroneously merged; the results for AIC penalty are shown since using a BIC penalty yielded only a single cluster. To verify that this is not simply due to an inap- propriate choice of penalty, we reran with the penalty term linearly scaled by various factors. Figure 1D shows the results of a penalty 0.5 × AIC that gave more clusters than the ground-truth data. Even in this case, however, the clusters produced by classical EM contained points from a mixture of the original clusters and could not be corrected even by manual post hoc cluster merging. To systematically evaluate the effectiveness of both algo- rithms, we measured performance using the variation of information (VI) metric (Meil˘a, 2003), for which a value of 0 indicates a perfect clustering. Both algorithms were tested for a variety of different penalties measured in multiples of AIC (see Figures 1E and 1F). Whereas the masked EM algo- rithm was able to achieve a perfect clustering for a large range of penalties around BIC, the classical EM algorithm produced a poorer value of 1.83 (corresponding to the poor result of merging all the points into a single cluster). Figure 2 shows how clustering performance depends on the precise choice of masking parameters α and β defined in equation 2.1, using BIC penalty. Good performance did not require a single precise parameter set- ting but could be obtained with a range of parameters with α ≈ 2 and 3 ≤ β ≤ 7. The results illustrate the benefits of using a double-threshold approach in preference to a single threshold: performance when α = β is markedly worse than when β > α.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2388
S. Kadir, D. Goodman, and K. Harris
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
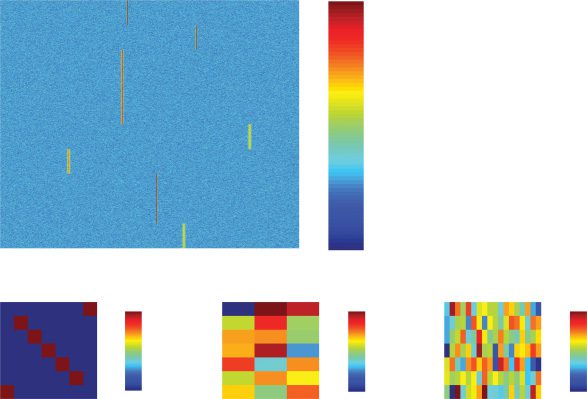
Figura 1: Simulated data. (UN) Subsampled raw data. (B) Confusion matrix in
percentages for masked EM with α = 2, β = 3, and BIC penalty (equivalent to
10 × AIC for 20,000 points). (C) Confusion matrix in percentages for classical EM
for an AIC penalty. (D) Confusion matrix in percentages for classical EM for a
penalty of 0.5 × AIC. (E) VI metric measure of performance of both algorithms
using various values for penalty, where the black vertical line indicates BIC.
(F) The number of clusters obtained for various values of penalty, dove il
black vertical line indicates BIC.
Finalmente, in order to explore in more detail how the classical and masked
EM algorithm deal with increasing dimensionality, we varied the number
of features input to the algorithms. Primo, we sorted the features in rough
order of relevance, according to the mean value of that feature over all input
patterns. Both algorithms were then run on subsets of the most relevant p
features for varying values of p. Performance was quantified with the VI
metric (Guarda la figura 3); in order to ensure differences between algorithms
were not simply due to differences in penalty strategy, we also permitted
post hoc manual merging of clusters that were overspilt. With fewer than
17 caratteristiche, both algorithms performed badly. For 17 A 22 caratteristiche, both
algorithms perform perfectly; Tuttavia, as more uninformative features
were added, the performance of the classical, but not masked, EM algorithm
started deteriorating. The performance of the masked algorithm remained
good for all dimensionalities tested.
F
/
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
High-Dimensional Cluster Analysis with the Masked EM Algorithm
2389
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
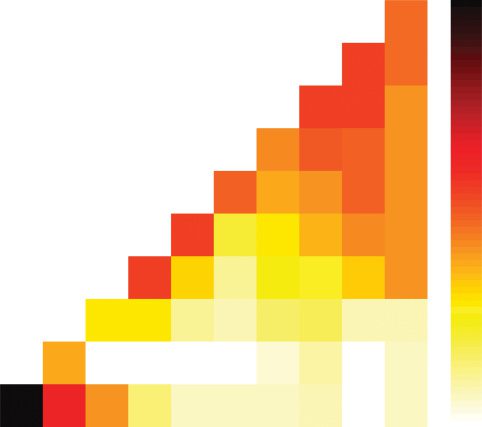
Figura 2: The effect of varying α and β in equation 2.1 for the simulated 1000-
dimensional data set with seven clusters. The plot shows a pseudocolor repre-
sentation of performance measured using the Meila VI metric for various values
of α and β using BIC penalty.
3.2 Spike Sorting. To test the performance of the masked EM algorithm
on our target application of high-channel-count spike sorting requires a
ground-truth data set. Previous work established the performance of the
classical EM algorithm for low-channel spike sorting with ground truth
obtained by simultaneous recordings of a neuron using not only the extra-
cellular array, but also an intracellular method using a glass pipette that
unequivocally determined firing times (Harris et al., 2000). Because such
dual recordings are not yet available for high-count electrodes, we created
a simulated ground truth we term “hybrid data sets.” In this approach, IL
mean spike waveform on all channels of a single neuron taken from one
recording (the donor) is digitally added onto a second recording (the accep-
tor) made with the same electrode in a different brain. Because the hybrid
spikes are linearly added to the acceptor traces, this simulates the linear
addition of neuronal electric fields and recreates many of the challenges of
spike sorting, such as the variability of amplitudes and waveforms of the
hybrid spike between channels, and overlap between the digitally added
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2390
S. Kadir, D. Goodman, and K. Harris
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
Figura 3: The effect of increasing the number of dimensions on the quality of
cluster analysis. The dimensions are added in order of relevance relative to the
seven ground-truth clusters of the simulated mixture of gaussians data set.
hybrid with spikes of other neurons in the acceptor data set (Harris et al.,
2000). Inoltre, to simulate the common difficulty caused by of ampli-
tude variability in bursting neurons, the amplitude of the hybrid spike was
varied randomly between 50% E 100% of its original value. The hybrid
data sets we consider were constructed from recordings in rat cortex kindly
provided by Mariano Belluscio and Gy ¨orgy Buzs´aki, using a 32-channel
probe with a zig-zag arrangement of electrodes and minimum 20 μm spac-
ing between neighboring contacts. Three principal components were taken
from each channel, resulting in 96-dimensional feature vectors.
For the spike data, masks were generated using a generalization of
equation 2.1 that took into account the topology of the electrode array.
Data were first high-pass-filtered (500 Hz cutoff); then spikes were detected
and masks were generated using a two-threshold flood-fill algorithm. IL
flood-fill algorithm finds spatiotemporally connected sets S of samples (T, C)
(where t is time and c is channel number), for which the filtered signal ex-
ceeds a lower threshold α for every point in each set and each set contains
at least one sample where the filtered signal exceeds an upper threshold
β. The values of α and β were set as 2 E 4.5 times the standard devia-
tion of the filtered signal, which was estimated robustly as a scaled median
absolute deviation. For each spike, a mask for channel c was defined as
F
/
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
High-Dimensional Cluster Analysis with the Masked EM Algorithm
2391
β−α
(cid:20)
(cid:20)
(T,C)∈S tθ
T,C
θ
T,C
(T,C)∈S
θ (T, C), where θ (T, C) = min( V (T,C)−α
, 1). Spikes were resampled
. Finalmente, fea-
maxt:(T,C)∈S
and aligned to a mean spike time estimated as ¯t =
ture vectors were extracted from the resampled filtered spike waveforms
by principal component analysis channel by channel. For each channel,
the first three principal components were used to create the feature vector;
hence for a C-channel data set, each spike was given a 3C-dimensional
feature vector. The component of the mask vector corresponding to
θ (T, C) computed on the chan-
each feature was obtained by taking as maxt
nel from which the feature was derived. The data set contained 138,572
points of 96 dimensions; running 1500 iterations of the clustering algorithm
on it took 10 hours on a single core of a 2.4 GHz Intel Xeon L5620 computer
running Scientific Linux 5.5. (The data we analyzed are publicly available
at https://github.com/klusta-team/hybrid_analysis.)
FP
TP
To evaluate the performance of the masked EM algorithm on this data set,
we first identified the cluster with the highest number of true positive spikes
and used it to compute a false discovery rate,
FP+TP , and a true positive rate,
FN+TP , where FP denotes the number of false-positive, TP the number of
true-positive, and FN the number of false-negative spikes. This performance
was compared against a theoretical upper bound obtained by supervised
apprendimento. The upper bound was obtained by using a quadratic support
vector machine (SVM) (Cortes & Vapnik, 1995) trained using the ground-
truth data, with performance evaluated by 20-fold cross-validation. In order
to ensure we estimated maximal performance, the SVM was run over a large
range of parameters such as margin and class weights, as well as including
runs in which only features relevant to hybrid cells were included. IL
theoretical optimum performance was estimated as a receiver operating
characteristic (ROC) curve by computing the convex hull of false discovery
and true positive rates for all SVM runs.
Figura 4 shows the performance of the masked EM algorithm and classi-
cal EM algorithm on the hybrid data set, set against the theoretical optimum
estimated by the SVM. While the masked EM algorithm performs at close to
the estimated upper bound, the classical EM algorithm is much poorer. A
verify that this poorer performance indeed resulted from a curse of dimen-
sionality, we reran the classical EM algorithm on only the subset of features
that were unmasked for the hybrid spike (9 out of 96 caratteristiche). As expected,
the upper-bound performance was poorer in this case, but the classical EM
algorithm performed close to the theoretical upper bound. This indicates
that the classical algorithm fails in high-dimensional settings, whereas the
masked EM algorithm performs well.
4 Discussion and Conclusion
We have introduced a method for high-dimensional cluster analysis, ap-
plicable to the case where a small subset of the features is informative for
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2392
S. Kadir, D. Goodman, and K. Harris
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 4: Performance of the masked and classical EM algorithms for a spike
sorting data. Blue and red points indicate performance of multiple runs of the
masked and classical EM algorithms with different penalty parameter settings.
The cyan curve indicates optimal possible performance, estimated as the convex
hull of supervised learning results obtained from a support vector machine with
quadric kernel.
any data point. Unlike global feature selection methods, both the number
and the precise set of unmasked features can vary between different data
points. Both the number of free parameters and computational cost scale
with the number of unmasked features per data point, rather than the total
number of features. This approach was found to give good performance
on simulated high-dimensional data and in our target application of neu-
rophysiological spike sorting for large electrode arrays.
A potential caveat of allowing different features to define different clus-
ters is the danger of artificial cluster splitting. If simply a hard threshold
were used to decide whether a particular feature should be used for a
particular cluster or data point, this could lead to a single cluster being
erroneously split in two, according to whether the threshold was exceeded
by noisy data. The masked EM algorithm overcomes this problem with
two approaches. Primo, because the masks are not binary but real valued,
crossing a threshold such as that in equation 2.1 leads to smooth rather than
discontinuous changes in responsibilities; second, because masked features
are replaced by a virtual distribution of empirically measured subthresh-
old data, the assignment of points with masked features is close to that
High-Dimensional Cluster Analysis with the Masked EM Algorithm
2393
expected for the original subthreshold features. With these approaches in
place, we found that erroneous cluster splitting was not a problem in sim-
ulation or in our target application.
In this study, we have applied the masking strategy to a single application
of unsupervised classification using a hard EM algorithm for a mixture-of-
gaussians fitting. Tuttavia, the same approach may apply more generally
whenever only a subset of features is informative for any data point and
when the expectation of required quantities over the modeled subthresh-
old distribution can be analytically computed. Other domains in which
this approach may work therefore include not only cluster analysis with
soft EM algorithms or different probabilistic models but also model-based
supervised classification.
Riferimenti
Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions
on Automatic Control, 19(6), 716–723.
Bouveyron, C., & Brunet-Saumard, C. (2012). Model-based clustering of high-
dimensional data: A review. Computational Statistics and Data Analysis, 71, 52–78.
Calabrese, A., & Paninski, l. (2011). Kalman filter mixture model for spike sorting
of non-stationary data. Journal of Neuroscience Methods, 196(1), 159–169.
Carin, L., Wu, Q., Carlson, D., Lian, W., Stoetzner, C., Kipke, D., . . . Dunson, D. (2013).
Sorting electrophysiological data via dictionary learning and mixture modeling.
IEEE Transactions on Biomedical Engineering, 61, 41–54.
Cortes, C., & Vapnik, V. (1995). Support-vector networks. Apprendimento automatico, 20(3),
273–297.
Dempster, UN. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from
incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series
B (Methodological), 39, 1–38.
Einevoll, G. T., Franke, F., Hagen, E., Pouzat, C., & Harris, K. D. (2012). Towards
reliable spike-train recordings from thousands of neurons with multielectrodes.
Current Opinion in Neurobiology, 22(1), 11–17.
Ekanadham, C., Tranchina, D., & Simoncelli, E. P. (2013). A unified framework and
method for automatic neural spike identification. Journal of Neuroscience Methods,
22, 47–55.
Fraley, C., & Raftery, UN. E. (2002). Model-based clustering, discriminant analysis, E
density estimation. Journal of the American Statistical Association, 97(458), 611–631.
Franke, F., Natora, M., Boucsein, C., Munk, M. H. J., & Obermayer, K. (2010). An
online spike detection and spike classification algorithm capable of instantaneous
resolution of overlapping spikes. Journal of Computational Neuroscience, 29(1–2),
127–148.
Friedman, J. H., & Meulman, J. J. (2004). Clustering objects on subsets of attributes
(with discussion). Journal of the Royal Statistical Society: Series B (Statistical Method-
ology), 66(4), 815–849.
Gasthaus, J., Legna, F., Gorur, D., & Teh, Y. W. (2008). Dependent Dirichlet process
spike sorting. In D. Koller, D. Schuurmans, Y. Bengio, & l. Bottou (Eds.), Advances
in neural information processing systems (pag. 497–504). Cambridge, MA: CON Premere.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2394
S. Kadir, D. Goodman, and K. Harris
Ghahramani, Z., & Hinton, G. E. (1996). The EM algorithm for mixtures of factor analyzers
(Tech. Rep. CRG-TR-96-1). Toronto: University of Toronto.
Harris, K. D., Henze, D. A., Csicsvari, J., Hirase, H., & Buzs´aki, G. (2000). Accu-
racy of tetrode spike separation as determined by simultaneous intracellular and
extracellular measurements. Journal of Neurophysiology, 84(1), 401–414.
Harris, K. D., Kadir, S. N., & Goodman, D. F. M. (2000–2013). KlustaKwik. https://
sourceforge.net/projects/klustakwik/files/.
Harris, K. D., Kadir, S. N., & Goodman, D. F. M. (2013). Masked KlustaKwik.
https://klusta-team.github.com/klustakwik.
Lewicki, M. S. (1998). A review of methods for spike sorting: the detection and
classification of neural action potentials. Network: Computation in Neural Systems,
9(4), R53–R78.
Marre, O., Amodei, D., Deshmukh, N., Sadeghi, K., Soo, F., Holy, T. E., & Berry,
M. J. (2012). Mapping a complete neural population in the retina. Journal of Neu-
roscience, 32(43), 14859–14873.
McLachlan, G. J., Peel, D., & Bean, R. W. (2003). Modelling high-dimensional data
by mixtures of factor analyzers. Computational Statistics and Data Analysis, 41(3),
379–388.
Meil˘a, M. (2003). Comparing clusterings by the variation of information. In B.
Sch ¨olkopf & M. K. Warmuth (Eds.), Learning theory and kernel machines (pag. 173–
187). New York: Springer.
Pillow, J. W., Shlens, J., Chichilnisky, E. J., & Simoncelli, E. P. (2013). A model-
based spike sorting algorithm for removing correlation artifacts in multi-neuron
recordings. PLoS ONE, 8(5), e62123.
Prentice, J. S., Homann, J., Simmons, K. D., Tkaˇcik, G., Balasubramanian, V., &
Nelson, P. C. (2011). Fast, scalable, Bayesian spike identification for multi-
electrode arrays. PLoS ONE, 6(7), e19884.
Quian Quiroga, R., Nadasdy, Z., & Ben-Shaul, Y. (2004). Unsupervised spike detec-
tion and sorting with wavelets and superparamagnetic clustering. Neural Com-
putation, 16(8), 1661–1687.
Raftery, UN. E., & Dean, N. (2006). Variable selection for model-based clustering.
Journal of the American Statistical Association, 101(473), 168–178.
Sahani, M. (1999). Latent variable models for neural data analysis. Doctoral dissertation,
California Institute of Technology.
Schwarz, G. (1978). Estimating the dimension of a model. Annals of Statistics, 6(2),
461–464.
Shoham, S., Fellows, M. R., & Normann, R. UN. (2003). Robust, automatic spike sorting
using mixtures of multivariate t-distributions. Journal of Neuroscience Methods,
127(2), 111–122.
Takahashi, S., Anzai, Y., & Sakurai, Y. (2003). Automatic sorting for multi-neuronal
activity recorded with tetrodes in the presence of overlapping spikes. Journal of
Neurophysiology, 89(4), 2245–2258.
Legna, F., & Black, M. J. (2008). A nonparametric Bayesian alternative to spike sorting.
Journal of Neuroscience Methods, 173(1), 1–12.
Received November 29, 2013; accepted May 23, 2014.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
6
1
1
2
3
7
9
2
0
1
7
3
2
6
N
e
C
o
_
UN
_
0
0
6
6
1
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3