Andrew Robertson and Mark D. Plumbley - Ricerca sull'intelligenza artificiale specializzata al MIT

Andrew Robertson and Mark D. Plumbley
School of Electronic Engineering and
Computer Science
Queen Mary University of London
Mile End Road
London E1 4NS, UK
{andrew.robertson, mark.plumbley}
@eecs.qmul.ac.uk

Synchronizing Sequencing
Software to a Live Drummer

Astratto: This article presents a method of adjusting the tempo of a music software sequencer so that it remains
synchronized with a drummer’s musical pulse. This allows music sequencer technology to be integrated into a band
scenario without the compromise of using click tracks or triggering loops with a fixed tempo. Our design implements
real-time mechanisms for both underlying tempo and phase adjustment using adaptable parameters that control its
behavior. The aim is to create a system that responds to timing variations in the drummer’s playing but is also stable
during passages of syncopation and fills. We present an evaluation of the system using a stochastic drum machine that
incorporates a level of noise in the underlying tempo and phase of the beat. We measure synchronization error between
the output of the system and the underlying pulse of the drum machine and contrast this with other real-time beat
trackers. The software, B-Keeper, has been released as a Max for Live device, available online at www.b-keeper.org.

Introduction and Motivation

One challenge currently faced by rock and pop bands
is how to incorporate electronic and pre-recorded
musical parts when playing live. In the studio,
bands typically use multi-track tape and Digital
Audio Workstation (DAW) software to overdub
extra parts and combine these together in an offline
editing process. In the digital sequencer, audio
effects, panning, and volume changes can all be
automated when crafting the mix of a song, con
the result that listeners are increasingly used to
hearing an idealized and transformed representation
of sound. These processes contribute to making such
performances difficult to recreate live. Di conseguenza,
bands often make use of pre-recorded audio, either
through triggering samples or by playing along to
backing tracks.

The problem with this is that the pre-recorded
material does not respond to timing fluctuations
of the band in the way that musicians do, so
that often the musicians are forced to follow the
timing dictated by the backing track via a click
track. In the studio, there has been an increasing
prevalence for the use of click tracks on recordings
(Lamere 2009). Often bands record digitally onto
DAW software, also referred to as sequencers,
which control the playback of audio tracks and

Computer Music Journal, 37:2, pag. 46–60, Estate 2013
doi:10.1162/COMJ a 00178
C(cid:2) 2013 Istituto di Tecnologia del Massachussetts.

MIDI messages. Commercial sequencers include
Ableton Live, Pro Tools, Logic Studio, Nuendo, E
others. These programs provide an optional click
track when recording, thereby providing audible
feedback to the drummer and other musicians when
recording to ensure that they stay “in time.” This
means the resulting performance has very accurate
timing. When a fixed tempo is used, it simplifies
the offline editing procedure, because when sections
of audio are moved between different locations of
the song they are still at the correct tempo. It also
allows timing “quantization,” whereby the timing
of events is corrected to align more closely with the
underlying grid.

Although in the studio these restrictions may
also have some advantages, in live performance the
backing track restricts the freedom of musicians to
make changes in timing and isolates the drummer
through the required wearing of headphones. Nel
situation where musicians want technology to be
incorporated into their live shows, there is a need
for an accurate synchronization system that keeps
the sequencer in time with the band rather than
forcing the musicians to play to a click track. In
Questo articolo, we present an algorithm to control the
tempo of sequencer, thereby allowing recorded parts
or backing tracks to respond to subtle changes in
tempo in the way that musicians would naturally
respond when playing together.

We first present relevant background material to
explain our design methodology. In the subsequent
section, we explain our design of the algorithm
and then describe two approaches to evaluating the

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

system. In order to successfully track the timing
variations of a drummer, we first need to look at the
nature of drum signals and how drummers behave.

Drumming, Rhythm, and Beat Tracking

In popular music, performers generally take their
cue from the drummer and it therefore makes sense
to align the sequencer as accurately as possible to
the drum beat.

Rhythmic Features of Drumming

In rock and pop music, an interlocking pattern
is created by the kick drum (also called the bass
drum), the snare drum, and the cymbal pattern,
played on the hi-hat or ride. Jeff Pressing (2002)
characterizes the qualities associated with what he
terms “Black Atlantic Rhythm,” the rhythms shared
culturally between America and Africa, Quale
have given rise to most forms of popular music:
blues, jazz, rock, reggae, hip-hop, eccetera. The devices
used by these rhythms all rely on the “support
of a firmly structured temporal matrix,” defined
as a “groove,” characterized by the perception
of a regular pulse with a subdivision structure
and of a longer repeating time cycle. Rhythmic
devices enumerated by Pressing that “build on the
groove” include syncopation, displacement, off-beat
phrasing, polyrhythm, hocketing (an interlocking
pattern shared between multiple instruments),
and swing. There is a conflict between a fixed
pulse and various timing accents played against
Esso (Waadeland 2001), and individual drum events
can display microtime deviation from the regular
beat that defines the groove (Iyer 1998; Freeman
and Lacey 2002). Meter can then be defined as the
hierarchical structure emerging from the occurrence
of alternating strong and weak beats as proposed
in The General Theory of Tonal Music (GTTM; cf.
Lerdahl and Jackendorff 1983). Drum patterns are
built around a regular metric structure. Klapuri,
Eronen, and Astola (2006) identify the tactus or beat
level as the regular pulse at which trained humans
tap in time with music.

Music Perception of Musical Beats and Rhythm

To successfully follow a beat, we need to solve
two problems: updating the underlying tempo, E
making phase updates so that we remain precisely
aligned (Gouyon and Dixon 2005). There are indi-
cations from music psychology that humans solve
these problems separately. The two-level timing
modello, first suggested by Wing and Kristofferson
(1973), also found in Mates (1994) and in Vorberg and
Wing (1996), posits separate mechanisms for period
(cioè., tempo) and phase, leading to the implication
that changes in phase can be made independently
of changes in period. Repp (2005) proposed a similar
two-process model to explain how humans tap in
time, featuring a fast phase-synchronization process
and a slower process that measures the underlying
tempo.

Automatic Beat Tracking

Computer-based beat trackers aim to accept a
musical signal as input and to produce as output a
pulse at intervals where humans would naturally
tap “in time” to the music (Hainsworth 2006).
Beat trackers tend fall into two categories: event-
based and audio-based. Event-based beat-tracking
algorithms process symbolic input, such as a list of
discrete onset times generated by an onset detector.
Audio-based beat trackers process features derived
from the audio signal, such as an onset detection
function’s output that represents the degree to
which the corresponding audio frame contains the
onset of a new musical event.

Event-based multiple-agent approaches were
used by Dixon (2007) and Goto and Muraoka
(1996), the latter exploiting the regular kick- E
snare-drum pattern found in pop and rock music.
McAuley (1995), Large (1995), Large and Kolen
(1994), Toiviaienen (1998), and Eck (2002) Avere
investigated the use of adaptive oscillators for
symbolic beat tracking, whereby the oscillators
adjust their tempo and phase only when observing
onsets at certain points during their cycle. For
audio-based analysis, Bello et al. (2005) describe
methods for the generation of the onset detection

Robertson and Plumbley

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

function, which include changes in energy and
spectral change. Audio-based approaches to beat
tracking often make use of comb filtering (Scheirer
1998) and autocorrelation (Eck 2007; Davies and
Plumbley 2007; Stark, Davies, and Plumbley 2008)
to subsequently process the output of the onset
detection function.

One major difficulty for the live beat-tracking
problem is that many previous algorithms for beat
tracking have been designed to analyze audio files
offline, such as for the Music Information Retrieval
eXchange (MIREX) annual competition. Di conseguenza,
many algorithms addressing this task are designed to
be as flexible as possible, giving the highest average
performance on a wide variety of songs. They cannot
be depended on to always track the beats correctly in
any given musical signal, Tuttavia. Common errors
are switching to tapping on the off-beat, difficulties
in following complex rhythmic sequences such as
syncopation, and shifting to a wrong but related
tempo (Dannenberg 2005).

Design of the Drum-Tracking Algorithm

We want to design a robust algorithm for tracking
drums that will always remain in time for most rock
and pop music. Because traditional beat-tracking
algorithms experience difficulties at correctly
tracking some types of signals, we shall make three
reasonable assumptions according to the kind of
situation where we envisage the algorithm will be
used. This will enable us to simplify the problem
and to design a robust beat-tracker for this kind of
situation.

1. Event-based input: To use accurate onset
timing information as input to our beat
tracker, we should take advantage of the fact
that the input to the system is a drum signal.
Dedicated microphones (usually dynamic,
using electromagnetic induction) are often
placed on each drum in both the studio
and live environments. This microphone ar-
rangement means that we have a reasonable
separation, both acoustically and physically,
between the kick drum and snare, although

there may be some “bleed” between them.
In rock and pop music, these signals tend to
have fast transients and high sound pressure
created by drum events. Onset detection
can then provide event times for the kick
and snare drum. Real-time onset detectors
include the bonk∼ object for Max/MSP by
Puckette, Apel, and Zicarelli (1998) and the
C++ aubio library by Brossier, Bello, E
Plumbley (2004).

2. Initial tempo estimate: We will assume that
an initial tempo estimate is available, per esempio.,
by tapping the drum sticks as a “count-
In,” a well-known technique often used by
musicians in performance.

3. Known meter: To know the position of each
event within the bar, we will assume a
constant known metrical rhythm, ad esempio
4/4. Where this changes, an operator might
inform the algorithm by intervention, for
instance by sending a message in the soft-
ware, or the message could be automatically
sequenced. This allows us to place more em-
phasis on events that have more significance
in the metrical hierarchy.

The output of the algorithm controls the tempo
of a sequencer in order to synchronize the musical
events with a live performance. A click track sent
from the sequencer is used to communicate its
beat position. For the beat tracker, we follow the
two-process model, similar to that of Repp (2005),
consisting of a tempo process that updates the
underlying tempo, and a phase-synchronization
process that aims to align the beat locations of the
sequencer with the drum onsets that occur on a
beat. In our implementation we make use of the
sequencer Ableton Live.

An overview of the algorithm is shown in
Figura 1. We will now describe in more detail the
design of the two components for tempo and phase
synchronization.

Phase Synchronization Process

We have seen from experiments in music psychology
that humans tapping to an isochronous pulse

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figura 1. Overview of the
algorithm with
components for tempo and
phase update.

will quickly respond to minimize the timing
discrepancy between their taps and the pulse
(Repp 2005). The onset event list may also include
musically expressive events and off-beat events from
syncopated rhythms, Tuttavia. From the observation
that human tappers tend to synchronize with the
main beats in the bar (Klapuri, Eronen, and Astola
2006), we prioritize synchronization to drum events
at the metrical level of the beat. In a regular meter,
these would consist of the “one,” “two,” “three,"
and “four” as opposed to the eighth notes between
them (the “and”s). The snare drum can exhibit
complex rhythms and expressive timing relative to
the kick drum (Iyer 1998; Freeman and Lacey 2002),
and thus we choose to prioritize synchronization to
the latter over the snare. These two preferences can
be considered as two “rules” that guide our design of
the synchronization process. In order to implement
these rules, we will quantify certain attributes of
events such as the accuracy of the beat (relative to
the sequencer’s position given by an internal click
track) or the importance of a particular metrical
location.

The system uses the click track of the audio

sequencer to provide an approximation of the
current beat location. Whereas other beat-tracking
algorithms infer the beat position directly from
the audio signal, we assume that the click track is
close to that of the underlying beat from the drums.
This allows us to interpret events relative to their
position in the bar and removes the necessity for
an additional stage for phase correction. Often, IL
sequencer is playing musical parts, and thus there is
audible feedback confirming that the representation
of the beat position used by the system is correct.

We make use of an accuracy function that
quantifies how close the new onset at time tn is to
the predicted beat time provided by the click track
at time E[tn] by using a non-normalized Gaussian
window around the predicted time:

UN(tn) = g(tn − E[tn], σsync)

(1)

where g is the non-normalized Gaussian function:

G (T, P ) = exp

(cid:3)

(cid:2)
− t2
2P 2

(2)

The width of the Gaussian window is param-
eterized by σsync, the standard deviation, Quale
reflects our current uncertainty about the beat
position. When σsync is large, the Gaussian window
is wider, and so the value of the accuracy function
remains high for larger time differences between
the observed onset and the expected beat location.
This results in more response to timing variation.
When the Gaussian window’s standard deviation
is smaller, the accuracy function is focused around
the expected beat and we are more likely to ignore
events that are not close to the metrical divisions of
the bar.

We rate the metrical importance of incoming
events by quantizing to the closest eighth note.
We use a weighting measure, Lsync(k), which gives
preference to events on the main beats. We set
(cid:4)

Lsync (k) =

if k is even

lodd

if k is odd

(3)

where kis the quantized metrical position of the beat
in eighth notes from the beginning of the bar, E

Robertson and Plumbley

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figura 2. Overview of the
phase synchronization
component of the
algorithm.

lodd is the weight given to the eighth notes between
the main beats. We used the value lodd = 0.4 so that
events on the beat are given more weight and are
therefore more likely to be used for synchronization.
To prioritize the main beats of the bar for
synchronization, we use an update rule that states:

IF a drum onset event is accurate AND on a

metrically important beat,
THEN synchronize to that event.

To implement this rule, we have derived two
measures from the timing data: accuracy of the
drum event relative to the current beat estimate
given in Equation 1, and metrical importance given
in Equation 3. We combine these using the algebraic
Prodotto (multiplication) into a single measure
between zero and one that quantifies the extent to
which an event is both accurate and on a metrically
important beat. Our combined function, reflecting
our belief that the event is accurately timed and on
a metrically important beat, È

F (tn) = a(tn)Lsync( pn)

(4)

where pn is the quantized bar position of the onset
at time tn in eighth notes.

The decision about whether an event requires
synchronization is made by evaluating the combined
function relative to a threshold. Così, if f (tn) > θsync,
the current threshold, then we synchronize to this
event. We introduce a control parameter 0 ≤ β ≤
1 that determines the extent to which the system
will make a corresponding phase adjustment for
observations above the threshold but away from the
expected beat location. Then our synchronization
adjustment is:
(cid:2)

(cid:3)

(cid:5)Tsync =

Lsync ( pn) (tn − E [tn])

(5)

F (tn) + β
1 + β

By setting β close to its maximum value of
one, the value of the fractional term is increased
for any given value of f (tn) less than one, thereby
tending towards full phase synchronization for all
observations over the threshold. The design for the
phase synchronization component of the algorithm
is shown in Figure 2.

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Automatic Adjustment of Control Parameters

In early versions of the system, where we used static
windows around the beat locations (Robertson and
Plumbley 2007), we found that it was difficult to
achieve the right balance of responsiveness and
reliability in the drum tracker. Syncopated rhythms,
drum fills, and passages featuring complex rhyth-
mic information commonly present difficulties for
beat trackers (Dannenberg 2005). We experienced
similar problems when the threshold and window

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

Figura 3. Illustration of the
different regions for decisions
taken by the synchronization
algorithm for a standard
deviation of 30 msec. The zones
that cause adjustment are
labeled “Accurate” and “Outside.”

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

parameters were set by hand. Events such as
sixteenth notes or eighth-note triplets could be
mistaken for the main quarter notes, which denote
the beat, thereby causing an erroneous synchroniza-
zione. Ideally, we would like the receptive window
around the beat locations to be as narrow as possible
so that these other syncopated events will happen
outside and be ignored. We also want the tracker
to be responsive to events that do fall on the beat,
Tuttavia, and so we require the window to be wide
enough that these are correctly identified.

To find a balance between these criteria, we
automatically adjust the threshold and the standard
deviation of the Gaussian window. As illustrated
in Figure 3, there are three zones into which the
beat can fall, two of which cause alteration to these
control parameters. When the accuracy is above
θsync + H, where h is an extra amount of “headroom,"
the threshold is raised and the window narrowed.
Allo stesso modo, when the accuracy is below the threshold,
we decrease the threshold and widen the window.

For details of how this adjustment is performed see
Robertson (2009).

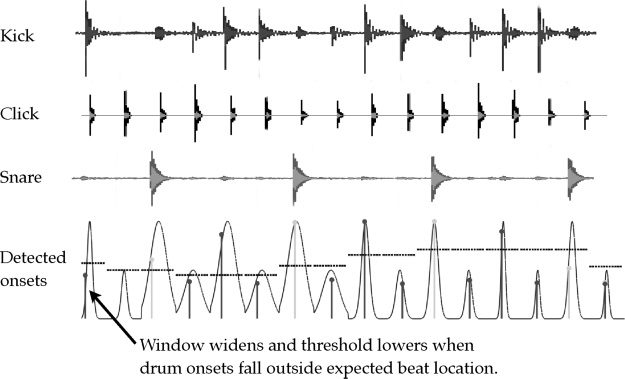
The drum tracker continually adapts its behavior

to achieve a balance between being responsive to
subtle timing shifts and ensuring the reliability
of the system in handling complex rhythms and
fills. This can be seen in Figure 4, where the first
kick-drum onset has a combined accuracy measure
that is beneath the threshold. There is an automatic
adjustment of the width of the Gaussian windows
around the subsequent expected beat locations to
maintain synchronization.

Layer Function

Interpretation of rhythm takes place through a
“layer function,” which labels the onsets according
to their metrical position and restricts the automatic
adjustment to occur only upon the main beat events.
If a recent onset has higher metrical position,

Robertson and Plumbley

Figura 4. Illustration of the
synchronization process
responding to kick and
snare events.

according to the GTTM hierarchy (Lerdahl and
Jackendorff 1983), and it was accurate, then neither
widening nor adjustment of the threshold for events
of a lesser metrical position will take place. Where
the rhythm is syncopated, or during drum fills
where there is rapid playing on subdivisions of
the beat, the layer function maintains the same
system parameters. These parameters are sufficient
to correctly identify and synchronize with the main
beats.

We have seen in the section on “Rhythmic Fea-

tures of Drumming” how drum beats are built
around the structure of the groove, with individual
hits exhibiting microtime delay that characterizes
the “feel” of what is being played. When encounter-
ing expressive timing and swing, the layer function
will prioritize the main downbeat. Phase synchro-
nization will only take place on the lesser metrical
level of “two” and “four” if the onset event is
more accurate with respect to the sequencer’s click
track. Phase synchronization parameters are still
automatically adapted for main drum events that
have lower accuracy than the threshold, in order to
maintain the responsiveness of the drum tracker.

Tempo Process

To make the system robust for live performance, we
seek to make the smallest possible change to the

tempo that agrees with the observed timing data.
To do so, we look at all recent inter-onset intervals
(IOIs) between the new onset event at time tn and
any recent event within the last two measures (O
16 eighth notes). Out of the IOIs corresponding to
musically regular durations (such as an eighth note,
quarter note, half note, or whole note), we find that
which most closely matches the current tempo. Noi
adapt the tempo estimate if these two values are
sufficiently close. We embody this heuristic in the
following rule:

IF the closest IOI matches the current tempo

AND is of regular duration

THEN adapt the tempo towards the beat period

suggested by the IOI.

The IOI between the new event and another
recent event at time tk has duration tk − tn. Then
the closest corresponding integer multiple of eighth
note durations at the current tempo is

νn,k = r ound

(cid:2)

(cid:3)

tn − tk
τ

(6)

where τ is the duration of an eighth note at the
current tempo and round(X) gives the closest integer
to x. Then the error between the observed interval
and that predicted by the current tempo estimate is

εn,k = (tn − tk) − νn,kτ

(7)

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

We quantify how well this accords to the current

tempo estimate by using a Gaussian function
that is also weighted to favor regular intervals.
Our combined weighting for the interval between
current onset n at time tn and previous onset k at
time tk is

M(N, k) = g (εn,k, σtempo) W (νn,k)

(8)

where g(εn,k, σtempo) is the non-normalized Gaussian
function defined in Equation 2, and W(νn,k) are
the interval weights. To favor only intervals that
correspond to the eighth note, quarter note, half
note, and whole note durations, which we expect
to observe in a regular drum pattern, we used
heuristically determined values of W(1) = 0.9, W(2)
= 1, W(4) = 1, W(8) = 0.8, and W(16) = 0.8, E
we set W(k) to zero for other k. We evaluate this
measure for all intervals between the new event
and events that have happened in the most recent
two bars. The winning measure is the interval,
between the current onset and the “best” onset k∗,
that exhibits the best combination of agreeing with
the current tempo hypothesis and corresponding to
these preferred durations. Then

k∗ = arg max

M(N, k)

(9)

where k∗ is the index of the onset time with the
highest weighting. We decide whether to use the
winning interval to update the underlying tempo
by evaluating the highest measure relative to a
threshold. If m(N, k∗) > θtempo, then the tempo is
updated, so that we assign

τ ← τ + αm(N, k∗

)

εn,k∗
ν
N,k∗

(10)

As in the case of the synchronization process,
we dynamically adjust the threshold, θtempo, E
standard deviation, σtempo. So, if m(N, k∗) < θtempo, the threshold θtempo is decreased and σtempo, in Equation 8, is increased, and vice versa if m(n, k∗) > θtempo.

Implementation

The algorithm has been coded as a Java external
within Max/MSP (Puckette 2002). The onset times

for kick and snare events are provided by the bonk∼
onset detector object (Puckette, Apel, and Zicarelli
1998) for percussive signals. For real-time adjust-
ment of the tempo, we have used the audio sequencer
Ableton Live 9, which uses zplane’s “ ´elastique” al-
gorithm for time stretching (www.zplane.de). In
order to avoid latency problems due to soundcard
buffering and the onset detection process, we send
the audio click track that communicates the beat
position of the sequencer through the same process
as the drum signals by sending it out and back
in through the soundcard, then through the onset
detector.

System Evaluation

Traditionally, offline beat-tracking algorithms are
tested against a database of songs from many genres.
There is no database that can be used for such
a specialized drum tracker, Tuttavia. In earlier
lavoro (Robertson, Bryan-Kinns, and Plumbley 2008;
Stowell et al. 2009) we performed an interactive
evaluation of a version of B-Keeper using a “musical
Turing test” with human drummers. We concluded
that B-Keeper is perceived as behaving closer to
a human tapper than to a steady state (per esempio., UN
metronome).

To perform an automatic evaluation, allowing us

to assess the range of timing variability that can
be accommodated by the system, we constructed
a “Stochastic Drum Machine” and performed a
comparative evaluation with other real-time beat-
tracking systems.

Evaluation with a Stochastic Drum Machine

The Stochastic Drum Machine simulates a simple
drummer. It exhibits controllable randomness in
the pattern that it plays and incorporates a level
of variability (“noise”) in the underlying tempo
and phase of the beat. Using this, we can quantify
the error between the underlying beat and the
predicted beats of a beat-tracking algorithm under
test. For each “noise” setting, the drum machine is
initialized at 120 beats per minute (BPM), typically

Robertson and Plumbley

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figura 5. Design for the
stochastic drum machine.
For each eighth note of the
bar, there is a possible
event type and associated
probability that this event
will play.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

used in the DAW Logic Pro and the preferred tempo
of the beat-tracking system designed by Davies and
Plumbley (2007). The drum machine proceeds in
eighth-note steps. On any given step, rather than a
pre-determined pattern, there is a probability that
a kick or snare event will play. These patterns of
possible kick and snare events and their associated
probabilities, are shown in Figure 5. These were set
heuristically so that it plays a regular rhythm with
occasional syncopated events at the eighth note
level.

At every quarter note, Gaussian noise of zero

mean and a set standard deviation is added to
both the beat period and to the phase offset, IL
latter corresponding to a local tempo shift in the

terminology of Gouyon and Dixon (2005). IL
standard deviation of the underlying “tempo noise”
was varied between 0 E 16 msec per quarter note
(Dove 16 msec is approximately 3.2 percent of
the beat period), and the standard deviation of the
“phase-offset noise” varied between 0 E 64 msec,
added at every eighth note.

Evaluation Results

We first looked at a qualitative evaluation of three
different beat trackers: our proposed B-Keeper;
the btrack∼ external object for Max/MSP devel-
oped by Stark, Davies, and Plumbley (2009); E

Computer Music Journal

Figura 6. Diagram of the
BPM plots (top) and the
three beat trackers’ errors
(in msec) at two different
values of standard
deviation for Gaussian
noise introduced into

the underlying beat period:
2 msec per quarter note
(left) E 8 msec per quar-
ter note (right). The phase-
offset noise has a standard
deviation of 8 msec
per eighth note in both.

G
N
io
sì
l
R
e
D
N
U

M
P
B

)
C
e
S
M

(

R
o
R
R
e

R
e
P
e
e
K
−
B

)
C
e
S
M

(

R
o
R
R
e

~
k
C
UN
R
T
B

~
R
e
B
M
o
C
T
UN
e
B

)
C
e
S
M

(

R
o
R
R
e

140
130
120
110
0

100

−100
0

100

−100
0

100

−100
0

2 msec

8 msec

140
130
120
110
0

100

−100
0

100

−100
0

100

−100
0

128

32
96
64
Quarter−note beats

128

32
96
64
Quarter−note beats

128

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

beatcomber∼, an external object that uses a comb
filter matrix, developed by Robertson, Stark, E
Plumbley (2011), and which resembles the approach
of Eck (2007). The larger values in either process
(adding tempo noise or phase-offset noise) resulted in
rather “unmusical” drum patterns where the rhythm
sounds jerky and unpleasant. We conducted an infor-
mal analysis of ten recordings by The Beatles which
featured a strong drum component using a method
to find the optimal phase and tempo variations for a
set of beat annotations (Robertson 2012). These had
mean standard deviations between 2.3 E 4.5 msec
for the tempo variations and 5.5 E 9.1 msec for the
phase variations, suggesting that the bounds of noise
we are testing would approximate those present in
the steady sections of real-world recordings.

Figura 6 shows the tempo output for standard
deviations of 2 msec and 8 msec. In the left-hand
plots, we can observe how all beat-trackers respond

successfully to the lesser degree of noise. IL
higher degree of noise, Tuttavia, gives rise to sudden
variations in tempo, which can be problematic. In
this case it has caused the btrack∼ algorithm to
skip a beat and misalign.

We then quantitatively measured and compared
the beat times that the three different beat trackers
produced as output. We ran the experiment a total
Di 25 times for each possible combination of noise
settings. Each trial had a duration of 32 bars, O 128
beats. The performance error between the beat times
for the drum machine and the predicted beat times
for each beat tracker were measured as the standard
deviation in both Gaussian noise processes was
increased. The other two beat trackers, btrack∼
and beatcomber∼, do not have the same latency
compensation as B-Keeper, so we corrected for
latency in those two cases by passing the output of
the drum machine through an onset detector that has

Robertson and Plumbley

Tavolo 1. Median Error for Beat Trackers Synchronizing to Stochastic Drum Machine

Tempo
noise

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

14 26

13 26

16 26

14 26

12 25

15 25

12 24

13 24

12 24

13 25

14 24

14 25

15 25

13 25

15 24

13 25

14 25

13 24

14 25

15 25

Phase noise

13 26

13 25

15 25

16 25

15 25

16 25

15 25

13 26

15 26

16 26

16 25

17 25

18 26

17 26

17 25

17 26

19 27

18 27

19 26

19 27

19 26

19 27

19 28

19 27

20 28

20 29

21 27

13 25

14 25

16 25

18 26

20 27

22 27

Median error between the beat output times of the stochastic machine and the beat trackers at the lower levels of noise, specified
by the standard deviation for the Gaussian noise added (in msec). The median error times for different controllers are all shown:
B-Keeper in the top-center of each cell, BeatComber in the lower left corner, and btrack∼ in the lower right corner. The beat
tracker with least error is indicated in bold for each noise setting.

the effect of lowering their error by approximately
12 msec.

In live performance, the discrepancy between
the drum tracker’s beat location and the underlying
beat will play a crucial role in how well the backing
track fits with the drums. Discussing the problem
of latency with respect to music performance, Lago
and Kon (2004) consider that a delay of between 20
E 30 msec can be tolerated. There is thus a need
to minimize any delay between the perceived beat
and the output of the system. To quantify this, we
calculated the median of the errors between each
beat tracker and the drum-machine event times over
all trials in which synchronization was maintained
for the full 32 bars. Tavolo 1 shows the median error
for each beat tracker over all the 25 trials at the
lower levels of noise.

Surface plots showing these median timing errors

for each beat tracker over the full range of noise
parameters tested are shown in Figure 7.

We find that, even with the adjustment for
additional latency that other beat trackers introduce,
for the lowest levels of noise B-Keeper synchronizes
more closely with the drum events than the other
beat trackers do. In this zone, the difference between
the drum-machine beat times and the click time
of B-Keeper tends to be between 10 E 20 msec,
a difference that is small enough for this not to be
problematic in performance.

Looking at the surface plots in Figure 7, Esso
appears that B-Keeper is slightly less tolerant of high
quantities of noise than the other two trackers are.
This might be expected as the other beat trackers are
designed to be more responsive to strong changes in

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figura 7. Surface plots
showing the median error
between the beat output
times of the stochastic
machine for each beat
tracker over the full range
of noise parameters that
were tested.

)
C
e
S
M

(

R
o
R
R
e
N
UN
io
D
e
M

B−Keeper

btrack~

)
C
e
S
M

(

R
o
R
R
e
N
UN
io
D
e
M

Tempo noise (msec)

Phase noise (msec)

Tempo noise (msec)

Phase noise (msec)

beatcomber~

)
C
e
S
M

(

R
o
R
R
e
N
UN
io
D
e
M

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Tempo noise (msec)

Phase noise (msec)

tempo, whereas B-Keeper is designed to be consistent
through passages of syncopation. Nevertheless, Esso
will consistently handle tempo deviations with
a standard deviation of 7 msec per quarter note
(approximately 1.4 percent of the period) and phase
deviation of 20 msec per eighth note (4.0 percent of
the beat period).

Figura 8 shows how consistent the synchroniza-

tion is across all trials. The limits of what noise
can be accommodated by each tracker are the areas
mapped out by the white rectangles where there is
consistent synchronization across all 25 runs. These
results suggest that there may be a trade-off between
low synchronization error and tolerance to noise.

A repository with the files to reproduce the
evaluation results is hosted at the SoundSoftware
project website (https://code.soundsoftware.ac.uk/
projects/b-keeper-stochastic-drum-evaluation/).

Live Performance Experience

By synchronizing a sequencer with a drummer,
there are several applications for which B-Keeper
può essere utilizzata. The first is to provide accurately
synchronized backing tracks, where audio and MIDI
parts play in time with drums in a responsive
maniera. Over the last two years, the band Higamos

Robertson and Plumbley

Figura 8. Consistency of
synchronization across all
beat trackers at various
levels of noise introduced.
White areas denote 100
percent consistency; IL
black areas denote 0
percent consistency.

B−Keeper

)
e
T
o
N
H
T
H
G
io
e

R
e
P
C
e
S
M

(
N
o
io
T
UN
io
v
e
D
D
R
UN
D
N
UN
T
S

e
S
io
o
N
o
P
M
e
T

32
Comb Filter Matrix Beat Tracker (beatcomber~)

32
btrack~

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

32
Phase noise standard deviation (msec per eighth note)

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Hogamos (www.higamoshogamos.com) has been
experimenting with the system to perform their
live set of seven songs. Their performances feature
synthesized bass lines and other electronic sounds
that would be hard to play live, so the system offers
a way to use the original studio parts without the
compromise of click tracks and headphones.

The consensus in the band is that the live shows

would have changed considerably in character
without B-Keeper. Steve Webster, keyboard-player
and vocalist, describes the experience by saying it
“felt like suddenly having another member of the
band, band members that groove and flow with you.”
The system has also been used for live looping
and improvisation in several sessions with James
Sedwards (www.noughtmusic.com), and drummer
Jem Doulton (www.jemdoulton.com). Audio parts
from guitar and bass were successfully recorded
and looped in real time, using a foot pedal to allow
the musician to determine which instruments are
playing and when they are recorded. This differs
from the usual looping set-up, where the loop
remains fixed.

Finalmente, we developed a performance with a
robotic glockenspiel (Meckin 2010) to demon-
strate how the system brings about possibil-
ities for new musical collaborations. Videos
of these two performances can be seen on
the B-Keeper–dedicated YouTube channel
(www.youtube.com/bkeepersystem).

Conclusions

In questo articolo, we presented a novel system for
live drum tracking, designed around a two-process
model for tempo and phase tracking, in which a rule-
based approach is used to respond to drum events.
This is one of the first adaptive sequencer systems
for steady-beat music. In order to optimize the
system for a variety of playing styles and rhythmic
caratteristiche, such as syncopation and fills, the model’s
parameters dynamically adapt so that the behavior
of the algorithm continually adjusts to the input. Noi
have presented a new evaluation method that tests
the quantity of “tempo noise” and “phase-offset

Computer Music Journal

noise” that can be tolerated by the system using a
stochastic drum machine.

Our evaluation results indicate that our system
is capable of synchronizing more closely to the beat
at low levels of “noise” than do two other real-
time beat trackers. This is desirable in performance
because, when drummers play accurately, we require
as close a synchrony between the accompaniment
and the musicians as possible.

Future work will address the problem of tempo
and phase initialization and error recovery. Alter-
native beat-tracking algorithms, such as btrack∼
and beatcomber∼, might be used for such tasks
because they are more suited to sudden changes in
the musical signal and perform continual tempo
estimation across multiple hypotheses. We will ex-
tend our investigation of how the system interprets
drum events with the aim of improving the range
of timing “noise” and rhythmic patterns that the
system is capable of following.

The system is available to download at www
.b-keeper.org, both for Max/MSP and as a Max for
Live device for Ableton Live, allowing musicians
to use it as a plug-in over a stereo channel with
microphone input from the drums.

Ringraziamenti

Andrew Robertson is supported by a Research Fel-
lowship from the Royal Academy of Engineering
and the Engineering and Physical Sciences Re-
search Council. Mark D. Plumbley is supported
by a Leadership Fellowship (EP/G007144/1) from
the Engineering and Physical Sciences Research
Council. The authors would like to thank the mu-
sicians who took part in testing the software and
are grateful to David Nock, James Sedwards, Jem
Doulton, Steve Webster, Whetham Allpress, Marcus
Efstratiou, Matthew Davies, and Adam Stark for
their contributions to the project.

Riferimenti

Bello, J. P., et al. 2005. “A Tutorial on Onset Detection
in Music Signals.” IEEE Transactions on Speech and
Audio Processing 13(5, Part 2):1035–1047.

Brossier, P. M., J. P. Bello, and M. D. Plumbley. 2004.
“Fast Labelling of Notes in Music Signals.” In
Proceedings of the Fifth International Conference
on Music Information Retrieval, pag. 331–336.

Dannenberg, R. B. 2005. “Toward Automated Holistic

Beat Tracking, Music Analysis and Understanding.” In
Proceedings of the Fourth International Conference on
Music Information Retrieval, pag. 366–373.

Davies, M. E. P., and M. D. Plumbley. 2007. “Context-
Dependent Beat Tracking of Musical Audio.” IEEE
Transazioni su audio, Speech and Language Process-
ing 15(3):1009–1020.

Dixon, S. 2007. “Evaluation of the Audio Beat Tracking
System BeatRoot.” Journal of New Music Research
36(1):39–50.

Eck, D. 2002. “Finding Downbeats with a Relaxation
Oscillator.” Psychological Research 66(1):18–25.

Eck, D. 2007. “Beat Tracking Using an Autocorrelation

Phase Matrix.” In Proceedings of the International Con-
ference on Acoustics, Speech, and Signal Processing,
pag. 1313–1316.

Freeman, P., and L. Lacey. 2002. “Swing and Groove:

Contextual Rhythmic Nuance in Live Performance.” In
Proceedings of the Seventh International Conference
on Music Perception and Cognition, pag. 548–550.
Goto, M., and Y. Muraoka. 1996. “Beat Tracking Based
on Multiple-Agent Architecture—A Real-Time Beat
Tracking System for Audio Signals.” In Proceedings of
the Second International Conference on Multiagent
Sistemi, pag. 103–110.

Gouyon, F., and S. Dixon. 2005. “A Review of Automatic
Rhythm Description Systems.” Computer Music
Journal 29(1):34–54.

Hainsworth, S. 2006. “Beat Tracking and Musical Metre
Analysis.” In A. Klapuri and M. Davy, eds. Signal
Processing Methods for Music Transcription. Nuovo
York: Springer Science and Business Media, pag. 101–
129.

Iyer, V. 1998. “Microstructures of Feel, Macrostructures
of Sound: Embodied Cognition in West African and
African-American Musics.” PhD thesis, University of
California, Berkeley.

Klapuri, UN. P., UN. J. Eronen, and J. T. Astola. 2006.

“Analysis of the Meter of Acoustic Musical Signals.”
IEEE Transactions on Audio, Speech and Language
in lavorazione, pag. 342–355.

Lago, N. P., and F. Kon. 2004. “The Quest for Low Latency.”
In Proceedings of the International Computer Music
Conferenza, pag. 33–36.

Lamere, P. 2009. “In Search of the Click Track.” Available
online at musicmachinery.com/2009/03/02/in-search
-of-the-click-track/. Accessed 22 agosto 2011.

Robertson and Plumbley

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Large, E. W. 1995. “Beat Tracking with a Nonlinear

Oscillator.” In Working Notes of the IJCAI-95 Workshop
on Artiﬁcial Intelligence and Music, pag. 24–31.

Large, E. W., and J. F. Kolen. 1994. “Resonance and the
Perception of Musical Meter.” Connection Science
6(2):177–208.

Lerdahl, J., and R. Jackendorff. 1983. A Generative Theory
of Tonal Music. Cambridge, Massachusetts: CON Premere.

Mates, J. 1994. “A Model of Synchronization of Motor

Acts to a Stimulus.” Biological Cybernetics 70(5):463–
473.

McAuley, J. D. 1995. “Perception of Time as Phase:
Toward an Adaptive Oscillator Model of Rhythmic
Pattern Processing.” PhD thesis, Indiana University.

Meckin D. 2010. “SMARTLab Advanced Placement

Project.” Master’s Thesis, Queen Mary University of
London.

Pressing, J. 2002. “Black Atlantic Rhythm: Its Com-
putational and Transcultural Foundations.” Music
Perception 19(3):285–310.

Puckette, M. 2002. “Max at Seventeen.” Computer Music

Journal 26(4):31–43.

Puckette, M., T. Apel, and D. Zicarelli. 1998. “Real-Time
Audio Analysis Tools for Pd and MSP.” In Proceedings
of the International Computer Music Conference,
pag. 109–112.

Repp, B. H. 2005. “Sensorimotor Synchronization: UN
Review of the Tapping Literature.” Psychonomic
Bulletin and Review 12(6):969–992.

Robertson, UN. 2009. “Interactive Real-Time Musical
Systems.” Ph.D. thesis, Queen Mary University of
London.

Robertson, UN. 2012. “Decoding Tempo and Timing Vari-
ations in Music Recordings from Beat Annotations.”
In Proceedings of the 13th International Society for
Music Information Retrieval Conference, pag. 475–
480.

Robertson, A., N. Bryan-Kinns, and M. D. Plumbley.
2008. “A Turing Test for B-Keeper: Evaluating an

Interactive Real-Time Beat Tracker.” In Proceedings of
the Eighth International Conference on New Interfaces
for Musical Expression, pag. 319–324.

Robertson, A., and M. D. Plumbley. 2007. “B-Keeper: UN
Beat Tracker for Live Performance.” In Proceedings
of the Seventh International Conference on New
Interfaces for Musical Expression, pag. 234–237.

Robertson, A., UN. M. Stark, and M. D. Plumbley. 2011.
“Real-Time Visual Beat Tracking using a Comb Filter
Matrix.” In Proceedings of the International Computer
Music Conference, pag. 617–620.

Scheirer, E. D. 1998. “Tempo and Beat Analysis of Acoustic
Musical Signals.” Journal of the Acoustical Society of
America 103(1):588–560.

Stark, UN. M., M. E. P. Davies, and M. D. Plumbley. 2008.
“Rhythmic Analysis for Real-Time Audio Effects.”
In Proceedings of the International Computer Music
Conferenza, pag. 144–147.

Stark, UN. M., M. E. P. Davies, and M. D. Plumbley. 2009.
“Real-Time Beat-Synchronous Analysis of Musical
Audio” In Proceedings of the Twelfth Conference on
Digital Audio Effects, pag. 299–304.

Stowell, D., et al. 2009. “Evaluation of Live Human-

Computer Music-Making: Quantitative and Qualita-
tive Approaches.” International Journal of Human-
Computer Studies 67(11):960–975.

Toiviainen, P. 1998. “An Interactive MIDI Accompanist.”

Computer Music Journal 22(4):63–75.

Vorberg, D., e A. Wing. 1996. “Modeling Variability and
Dependence in Timing.” In H. Heuer and S. Keele, eds.
Handbook of Perception and Action, Vol. 2. London:
Academic Press, pag. 181–262.

Waadeland, C. H. 2001. “‘It Don’t Mean a Thing If It

Ain’t Got That Swing’—Simulating Expressive Timing
by Modulated Movements.” Journal of New Music
Research 30(1):23–37.

Wing, UN. M., e A. B. Kristofferson. 1973. “Response

Delays and the Timing of Discrete Motor Responses.”
Perception and Psychophysics 14(1):5–12.

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

3
7
2
4
6
1
8
5
5
8
9
9
/
C
o
M
_
UN
_
0
0
1
7
8
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3 Andrew Robertson and Mark D. Plumbley image

Scarica il pdf