An Empirical Study on Robustness to Spurious Correlations using
Pre-trained Language Models
Lifu Tu1 ∗ Garima Lalwani2 Spandana Gella2 He He3 ∗
1Toyota Technological Institute at Chicago 2Amazon AI
3New York University
lifu@ttic.edu, {glalwani, sgella}@amazon.com, hehe@cs.nyu.edu
Astratto
Recent work has shown that pre-trained lan-
guage models such as BERT improve robust-
ness to spurious correlations in the dataset.
Intrigued by these results, we find that the
key to their success is generalization from a
small amount of counterexamples where the
spurious correlations do not hold. When such
minority examples are scarce, pre-trained mod-
els perform as poorly as models trained from
scratch. In the case of extreme minority, we
propose to use multi-task learning (MTL) A
improve generalization. Our experiments on
natural
language inference and paraphrase
identification show that MTL with the right
auxiliary tasks significantly improves perfor-
mance on challenging examples without hurt-
ing the in-distribution performance. Further,
we show that the gain from MTL mainly comes
from improved generalization from the minor-
ity examples. Our results highlight the impor-
tance of data diversity for overcoming spurious
correlations.1
1 introduzione
A key challenge in building robust NLP models
is the gap between limited linguistic variations in
the training data and the diversity in real-world
languages. Thus models trained on a specific
dataset are likely to rely on spurious correlations:
prediction rules that work for
the majority
examples but do not hold in general. Per esempio,
in natural language inference (NLI) compiti, previous
work has found that models learned on notable
benchmarks achieve high accuracy by associating
∗Most work was done during first author’s internship and
last author’s work at Amazon AI.
high word overlap between the premise and the
hypothesis with entailment (Dasgupta et al., 2018;
McCoy et al., 2019). Consequently, these models
perform poorly on the so-called challenging or
adversarial datasets, where such correlations no
longer hold (Glockner et al., 2018; McCoy et al.,
2019; Nie et al., 2019; Zhang et al., 2019). Questo
issue has also been referred to as annotation arti-
facts (Gururangan et al., 2018), dataset bias (Lui
et al., 2019; Clark et al., 2019), and group shift
(Oren et al., 2019; Sagawa et al., 2020) in the
literature.
Most current methods rely on prior knowledge
of spurious correlations in the dataset and tend to
suffer from a trade-off between in-distribution
accuracy on the independent and identically
distributed (i.i.d.) test set and robust accuracy2 on
the challenging dataset. Nevertheless, recent em-
pirical results have suggested that self-supervised
pre-training improves robust accuracy, while not
using any task-specific knowledge nor incurring
in-distribution accuracy drop (Hendrycks et al.,
2019, 2020).
in questo documento, we aim to investigate how and
when pre-trained language models such as BERT
improve performance on challenging datasets. Nostro
key finding is that pre-trained models are more
robust to spurious correlations because they can gen-
eralize from a minority of training examples that
counter the spurious pattern, per esempio., non-entailment
examples with high premise-hypothesis word
sovrapposizione. Specifically, removing these counterex-
amples from the training set significantly hurts
their performance on the challenging datasets.
Inoltre, larger model size, more pre-training
dati, and longer fine-tuning further improve robust
accuracy. Nevertheless, pre-trained models still
suffer from spurious correlations when there are
too few counterexamples. In the case of extreme
1Code is available at https://github.com/lifu-
2We use the term ‘‘robust accuracy’’ from now on to refer
tu/Study-NLP-Robustness.
to the accuracy on challenging datasets.
621
Operazioni dell'Associazione per la Linguistica Computazionale, vol. 8, pag. 621–633, 2020. https://doi.org/10.1162/tacl a 00335
Redattore di azioni: Yoav Goldberg. Lotto di invio: 2/2020; Lotto di revisione: 6/2020; Pubblicato 10/2020.
C(cid:13) 2020 Associazione per la Linguistica Computazionale. Distribuito sotto CC-BY 4.0 licenza.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
T
l
UN
C
_
UN
_
0
0
3
3
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
Dataset
Size
Heuristic
Input
Label
Natural language inference
Train MNLI
Test
HANS
393k
high word overlap
⇒ entailment
high word overlap
30k ; entailment
P: The doctor mentioned the manager who ran.
H: The doctor mentioned the manager.
P: The actors who advised the manager saw the tourists.
H: The manager saw the tourists.
entailment
non-entailment
Paraphrase Identification
Train QQP
Test
PAWSQQP
364k
same bag-of-words S1: Bangkok vs Shanghai?
⇒ paraphrase
S2: Shanghai vs Bangkok?
same bag-of-words S1: Are all dogs smart or can some be dumb?
677 ; paraphrase
S2: Are all dogs dumb or can some be smart?
paraphrase
non-paraphrase
Tavolo 1: Representative examples from the training datasets (MNLI and QQP) and the challenging/test datasets
(HANS and PAWSQQP). Overlaping text spans are highlighted for NLI examples and swapped words are
highlighted for paraphrase identification examples. The word overlap-based heuristic that works for typical
training examples fails on the test data.
minority, we empirically show that multi-task
apprendimento (MTL) improves robust accuracy by
improving generalization from the minority exam-
ples, even though preivous work has suggested
that MTL has limited advantage in i.i.d. settings
(Søgaard and Goldberg, 2016; Hashimoto et al.,
2017).
This work sheds light on the effectiveness of
pre-training on robustness to spurious correlations.
Our results highlight
the importance of data
diversity (even if the variations are imbalanced).
The improvement from MTL also suggests that
traditional techniques that improve generalization
in the i.i.d. setting can also improve out-of-
distribution generalization through the minority
examples.
2 Challenging Datasets
In a typical supervised learning setting, we test
the model on held-out examples drawn from the
same distribution as the training data, cioè., the in-
distribution or i.i.d. test set. To evaluate if the
model latches onto known spurious correlations,
challenging examples are drawn from a different
distribution where such correlations do not hold. In
practice, these examples are usually adapted from
the in-distribution examples to counter known
spurious correlations on notable benchmarks.
Poor performance on the challenging dataset is
considered an indicator of a problematic model
that relies on spurious correlations between inputs
and labels. Our goal is to develop robust models
that have good performance on both the i.i.d. test
set and the challenging test set.
2.1 Datasets
We focus on two natural language understanding
compiti, NLI and paraphrase identification (PI).
Both have large-scale benchmarking datasets with
around 400k examples. Although recent models
have achieved near-human performance on these
benchmarks,3 the challenging datasets exploiting
spurious correlations bring down the performance
of state-of-the-art models below random guessing.
We summarize the datasets used for our analysis
in Table 1.
NLI. Given a premise sentence and a hypothesis
sentence, the task is to predict whether the hy-
pothesis is entailed by, neutral with, or contradicts
the premise. MultiNLI (MNLI) (Williams et al.,
2017) is the most widely used benchmark for NLI,
and it is also the most thoroughly studied in terms
of spurious correlations. It was collected using the
same crowdsourcing protocol as its predecessor
SNLI (Bowman et al., 2015) but covers more
domini. Recentemente, McCoy et al. (2019) exploit
high word overlap between the premise and the
hypothesis for entailment examples to construct
a challenging dataset called HANS. They use
syntactic rules to generate non-entailment (neutro
or contradicting) examples with high premise-
hypothesis overlap. The dataset is further split
into three categories depending on the rules
used: lexical overlap, subsequence,
and constituent.
3See the leaderboard at https://gluebenchmark.
com.
622
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
T
l
UN
C
_
UN
_
0
0
3
3
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
Model
Non pre-trained baselines
BERTscratch
ESIM
pre-trained models
BERTBASE(prior)
BERTBASE(ours)
BERTLARGE
RoBERTaBASE
RoBERTaLARGE
Trained on MNLI
Trained on QQP
In-distribution
MNLI-m
Challenging
HANS
In-distribution
QQP
Challenging
PAWSQQP
67.9 (0.5)
78.1UN
84.0C
84.5 (0.1)
86.2 (0.2)
87.4 (0.2)
89.1 (0.1)
49.9 (0.2)
49.1UN
53.8C
62.5 (3.4)
71.4 (0.6)
74.1 (0.9)
77.1 (1.6)
83.0 (0.7)
85.3B
90.5D
90.8 (0.3)
91.3 (0.3)
91.5 (0.2)
89.0 (3.1)
40.6 (1.9)
38.9B
33.5D
36.1 (0.8)
40.1 (1.8)
42.6 (1.9)
39.5 (4.8)
Tavolo 2: Accuracies (with standard deviation) on the in-distribution datasets, MNLI-matched (MNLI-m)
and QQP dev sets, as well as the challenging datasets, HANS and PAWSQQP. Pre-trained transformers
improve accuracies on both the in-distribution and challenging datasets over non pre-trained models,
except on PAWSQQP. Our models, fine-tuned for more epochs, further improve prior results on the
challenging data. Results taken from prior work: a He et al. (2019), b Zhang et al. (2019), c McCoy
et al. (2019), d Zhang et al. (2019).
PI. Given two sentences, the task is to predict
whether they are paraphrases or not. On Quora
Question Pairs (QQP) (Iyer et al., 2017), one of
the largest PI dataset, Zhang et al. (2019) show
that very few non-paraphrase pairs have high word
sovrapposizione. They then created a challenging datasets
called PAWS that contains sentence pairs with
high word overlap but different meanings through
word swapping and back-translation. Inoltre
to PAWSQQP, which is created from sentences in
QQP, they also released PAWSWiki, created from
Wikipedia sentences.
3 Pre-training Improve Robust Accuracy
Recent results have shown that pre-trained models
appear to improve performance on challenging
examples over models trained from scratch
(Yaghoobzadeh et al., 2019; He et al., 2019;
Kaushik et al., 2020). In this section, we confirm
this observation by thorough experiments on
different pre-trained models and motivate our
inquiries.
Modelli. We compare pre-trained models of
different sizes and using different amounts of pre-
training data. Specifically, we use the BERTBASE
(340M
(110M parameters) and BERTLARGE
parameters) models implemented in GluonNLP
(Guo et al., 2020) pre-trained on 16GB of text
(Devlin et al., 2019).4 To investigate the effect
of size of the pre-training data, we also experiment
with the RoBERTaBASE and RoBERTaLARGE
models (Liu et al., 2019D),5 which have the same
architecture as BERT but were trained on ten
times as much text (about 160GB). To ablate the
effect of pre-training, we also include a BERTBASE
model with random initialization, BERTscratch.
Fine-Tuning. We fine-tuned all models for 20
epochs and selected the best model based on
the in-distribution dev set. We used the Adam
optimizer with a learning rate of 2e-5, L2 weight
decay of 0.01, and batch sizes of 32 E 16 for
base and large models, rispettivamente. Weights
of BERTscratch and the last layer (classifier) Di
pre-trained models are initialized from a normal
distribution with zero mean and 0.02 variance.
All experiments are run with 5 random seeds and
the average values are reported.
Observations and Inquiries.
In Table 2, we
show results for NLI and PI, rispettivamente. As
4 The book corpus wiki en uncased model from
https://gluon-nlp.mxnet.io/model zoo/bert/
index.html.
5The openwebtext ccnews stories books
cased model from https://gluon-nlp.mxnet.io/
model zoo/bert/index.html.
623
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
T
l
UN
C
_
UN
_
0
0
3
3
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
T
l
UN
C
_
UN
_
0
0
3
3
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
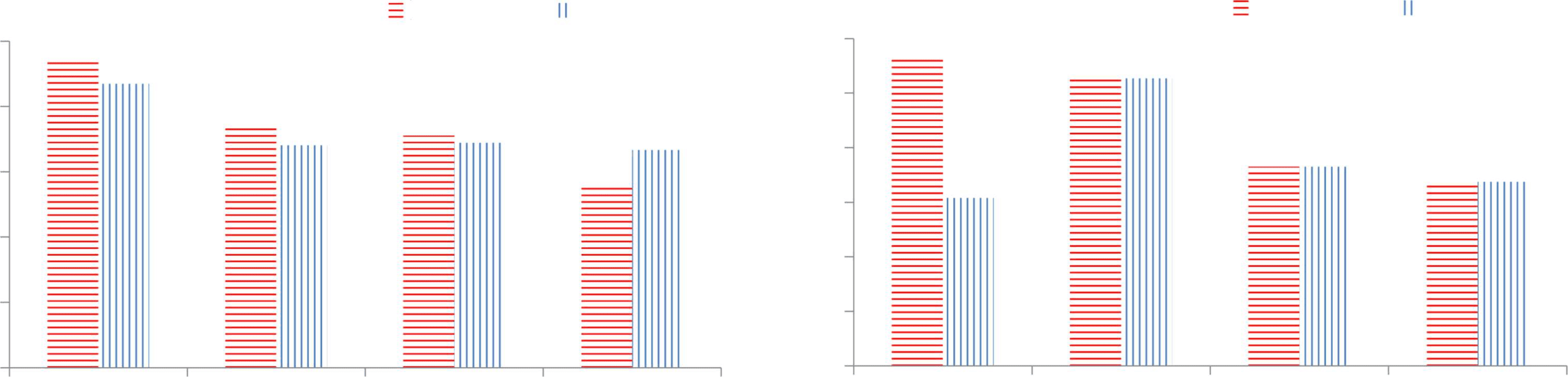
Figura 1: Accuracy on the in-distribution data (MNLI dev and QQP dev) and the challenging data (HANS and
PAWSQQP) after each fine-tuning epoch using BERTBASE. The performance plateaus on the in-distribution data
quickly around epoch 3, although, accuracy on the challenging data keeps increasing.
expected,
they improve performance on in-
distribution test sets significantly.6 On the chal-
lenging datasets, we make two key observations.
Primo, although pre-trained models improve
the performance on challenging datasets,
IL
improvement is not consistent across datasets.
Specifically, the improvement on PAWSQQP are
less promising than HANS. Whereas larger
models (large vs. base) and more training
dati (RoBERTa vs. BERT) yield a further im-
provement of 5 A 10 accuracy points on HANS,
the improvement on PAWSQQP is marginal.
Secondo, even though three to four epochs of
fine-tuning is typically sufficient for in-distribu-
longer fine-tuning
tion data, we observe that
improves results on challenging examples signi-
ficantly (see BERTBASE ours vs. prior in Table 2).
Come mostrato in figura 1, although the accuracy
on MNLI and QQP dev sets saturate after three
epochs, the performance on the corresponding
challenging datasets keeps increasing until around
the tenth epoch, with more than 30% improvement.
The above observations motivate us to ask the
following questions:
1. How do pre-trained models generalize to
out-of-distribution data?
2. When do they generalize well given the
inconsistent improvements?
3. What role does longer fine-tuning play?
We provide empirical answers to these questions
in the next section and show that the answers are
all related to a small number of counterexamples
in the training data.
4 Generalization from Minority
Esempi
4.1 Pre-training Improves Robustness to
Data Imbalance
One common impression is that the diversity in
large amounts of pre-training data allows pre-
trained models to generalize better to out-of-
distribution data. Here we show that although
pre-training improves generalization, they do not
enable extrapolation to unseen patterns. Invece,
they generalize better from minority patterns in
the training set.
Importantly, we notice that examples in HANS
and PAWS are not completely uncovered by the
training data, but belong to the minority groups.7
Per esempio, in MNLI, there are 727 HANS-like
non-entailment examples where all words in the
hypothesis also occur in the premise; in QQP, there
are 247 PAWS-like non-paraphrase examples
where the two sentences have the same bag of
parole. We refer to these examples that counter
the spurious correlations as minority examples.
We hypothesize that pre-trained models are more
robust to group imbalance, thus generalizing well
from the minority groups.
6 The lower performance of RoBERTaLARGE compared
with RoBERTaBASE is partly due with its high variance in
our experiments.
7Following Sagawa et al. (2020), we loosely define group
as a distribution of examples with similar patterns, per esempio., high
premise-hypothesis overlap and non-entailment.
624
Figura 2: Accuracy on HANS when a small fraction of training data is removed. Removing non-entailment
examples with high premise-hypothesis overlap significantly hurt performance compared with removing examples
uniformly at random.
To verify our hypothesis, we remove minority
examples during training and observe their effect
on robust accuracy. Specifically, for NLI we
sort non-entailment (contradiction and neutral)
examples in MNLI by their premise-hypothesis
sovrapposizione, which is defined as the percentage of
hypothesis words that also appear in the premise.
We then remove increasing amounts of these
examples in the sorted order.
Come mostrato in figura 2, all models have
significantly worse accuracy on HANS as more
counterexamples are removed, while maintaining
the original accuracy when the same amounts
of random training examples are removed. Con
6.4% of counterexamples removed, the perfor-
mance of most pretrained models is near-random,
as poor as non-pretrained models. È interessante notare,
larger models with more pre-training data
(RoBERTaLARGE) appear to be slightly more
robust with increased level of imbalance.
Takeaway. These results reveal that pre-training
improves robust accuracy by improving the i.i.d.
accuracy on minority groups, highlighting the
importance of increasing data diversity when
creating benchmarks. Further, pre-trained models
still suffer from suprious correlations when the
minority examples are scarce. To enable extra-
polation, we might need additional inductive bias
(Nye et al., 2019) or new learning algorithms
(Arjovsky et al., 2019).
4.2 Minority Patterns Require Varying
Amounts of Training Data
Given that pre-trained models generalize better
from minority examples, why do we not see similar
improvement on PAWSQQP even though QQP
also contains counterexamples? Unlike HANS
examples that are generated from a handful of
625
Figura 3: Learning curves of models trained on HANS
and PAWSQQP. Accuracy on PAWSQQP increases
slowly, whereas all models quickly reach 100% accu-
racy on HANS.
templates, PAWS examples are generated by
swapping words in a sentence followed by human
inspection. They often require recognizing nuance
syntactic differences between two sentences with
a small edit distance. Per esempio, compare
‘‘What’s classy if you’re poor, but trashy if you’re
ricco?’’ and ‘‘What’s classy if you’re rich, Ma
trashy if you’re poor?’.’ Therefore, we posit
that more samples are needed to reach good
performance on PAWS-like examples.
To test the hypothesis, we plot learning curves
by fine-tuning pre-trained models on the challeng-
ing datasets directly (Liu et al., 2019B). Specifi-
cally, we take 11,990 training examples from
PAWSQQP, and randomly sample the same number
of training examples from HANS;8 the rest is used
as dev/test set for evaluation. In Figure 3, we see
that all models reach 100% accuracy rapidly on
HANS. Tuttavia, on PAWS, accuracy increases
slowly and the models struggle to reach around
90% accuracy even with the full training set. Questo
suggests that the amount of minority examples in
QQP might not be sufficient for reliably estimating
the model parameters.
8HANS has more examples in total (30,000), Perciò
we sub-sample it to control for the data size.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
T
l
UN
C
_
UN
_
0
0
3
3
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
Figura 4: Accuracy of BERTBASE and RoBERTaBASE on PAWSQQP decreases with increasing sentence length and
parse tree height.
Figura 5: The average losses and accuracies of the examples in the training and dev set when fine-tuning BERTBASE
on MNLI. We show plots for the whole training set and the minority examples separately. The minority examples
are non-entailment examples with at least 80% premise-hypothesis overlap. Accuracy of minority examples takes
longer to plateau.
To have a qualitative understanding of why
PAWS examples are difficult to learn, we compare
sentence length and constituency parse tree height
of examples in HANS and PAWS.9 We find that
PAWS contains longer and syntactically more
complex sentences, with an average length of 20.7
words and parse tree height of 11.4, compared
A 9.2 E 7.5 on HANS. Figura 4 shows that
the accuracy of BERTBASE and RoBERTaBASE on
PAWSQQP decreases as the example length and
the parse tree height increase.
Takeaway. We have shown that the inconsistent
improvement on different challenging datasets
result from the same mechanism: Pre-trained
models improve robust accuracy by generalizing
from minority examples, although, perhaps unsur-
9We use the off-the-shelf constituency parser
from
Stanford CoreNLP (Manning et al., 2014). For each example,
we compute the maximum length (number of words) E
parse tree height of the two sentences.
prisingly, different minority patterns may require
varying amounts of training data. This also poses
a potential challenge in using data augmentation
to tackle spurious correlations.
4.3 Minority Examples Require Longer
Fine-Tuning
In the previous section, we have shown in
Figura 1 that longer fine-tuning improves accuracy
on challenging examples, even though the in-
distribution accuracy saturates pretty quickly. A
understand the result from the perspective of
minority examples, we compare the loss on all
examples and the minority examples during fine-
tuning. Figura 5 shows the loss and accuracy
at each epoch on all examples and HANS-like
examples in MNLI separately.
Primo, we see that the training loss of minority
examples decreases more slowly than the average
626
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
T
l
UN
C
_
UN
_
0
0
3
3
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
loss, taking more than 15 epochs to reach near-
zero loss. Secondo, the dev accuracy curves show
that the accuracy of minority examples plateaus
Dopo, around epoch 10, whereas the average
accuracy stops increasing around epoch 5. In
aggiunta, it appears that BERT does not overfit
with additional fine-tuning based on the accuracy
curves.10 Similary, a concurrent work (Zhang
et al., 2020) has found that longer fine-tuning
improves few-sample performance.
Takeaway. Although longer fine-tuning does
not help in-distribution accuracy, we find that it
improves performance on the minority groups.
This suggests that selecting models or early
stopping based on the i.i.d. dev set performance
is insufficient, and we need new model selection
criteria for robustness.
5 Improve Generalization Through
Multi-task Learning
Our results on minority examples show that
increasing the number of counterexamples to
spurious correlations helps to improve model
robustness. Then, an obvious solution is data
augmentation; Infatti, both McCoy et al. (2019)
and Zhang et al. (2019) show that adding a
small number of challenging examples to the
training set significantly improves performance
on HANS and PAWS. Tuttavia, these methods
often require task-specific knowledge on spurious
correlations and heavy use of rules to generate
the counterexamples. Instead of adding examples
with specific patterns, we investigate the effect of
aggregating generic data from various sources
through MTL. It has been shown that MTL
reduces the sample complexity of individual tasks
compared to single-task learning (Caruana, 1997;
Baxter, 2000; Maurer et al., 2016), thus it may
further improve the generalization capability of
pre-trained models, especially on the minority
groups.
5.1 Multi-task Learning
We learn from datasets from different sources
jointly, where one is the target dataset to be
10 We find that the average accuracy stays almost the
same while the dev loss is increasing. Guo et al. (2017) had
similar observations. One possible explanation is that the
model prediction becomes less confident (hence larger log
loss), but the argmax prediction is correct.
evaluated on, and the rest are auxiliary datasets.
The target dataset and the auxiliary dataset can
belong to either the same task, per esempio., MNLI and
SNLI, or different but related tasks, per esempio., MNLI
and QQP.
All datasets share the representation given
by the pre-trained model, and we use separate
linear classification layers for each dataset. IL
learning objective is a weighted sum of average
losses on each dataset. We set the weight to be
1 for all datasets, equivalent to sampling examples
from each dataset proportional to its size.11 During
training, we sample mini-batches from each data-
set sequentially and use the same optimization
hyperparameters as in single-task fine-tuning
(Sezione 3) except for smaller batch sizes due
to memory constraints.12
Auxiliary Datasets. We consider NLI and PI
as related tasks because they both require under-
standing and comparing the meaning of two
sentences. Therefore, we use both benchmark
datasets and challenging datasets for NLI and PI
as our auxiliary datasets. The hope is that bench-
mark data from related tasks help transfer
useful knowledge across tasks, thus improving
generalization on minority examples, and the
challenging datasets countering specific spurious
correlations further improve generalization on the
corresponding minority examples. We analyze the
contribution of the two types of auxiliary data in
Sezione 5.2. The MTL training set up is shown
in Table 4.13 Details on the auxiliary datasets are
described in Section 2.1.
5.2 Results
MTL Improves Robust Accuracy. Our main
MTL results are shown in Table 3. MTL increases
accuracies on the challenging datasets across tasks
without hurting the in-distribution performance,
11 Prior work has shown that the mixing weights may
impact the final results in MTL, especially when there is a
risk of overfitting to low-resource tasks (Raffel et al., 2019).
Given the relatively large dataset sizes in our experiments
(Tavolo 4), we did not see significant change in the results
when varying the mixing weights.
12The minibatch size of the target dataset is 16. For the
auxiliary dataset, it is proportional to the dataset size and not
larger than 16, such that the total number of examples in a
batch is at most 32.
13 For MNLI, we did not include other PI datasets such as
STS-B (Cer et al., 2017) and MPRC (Dolan and Brockett,
2005) because their sizes (3.7k and 7k) are too small compared
with QQP and other auxiliary tasks.
627
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
T
l
UN
C
_
UN
_
0
0
3
3
5
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
Task = MNLI
Task = QQP
Model
BERTBASE
RoBERTaBASE
In-distribution Challenging In-distribution Challenging Challenging
PAWSQQP PAWSWiki
QQP
HANS
Algo. MNLI-m
STL
MTL
STL
MTL
84.5 (0.1)
83.7 (0.3)
87.4 (0.2)
86.4 (0.2)
62.5 (0.2)
68.2 (1.8)
74.1 (0.9)
72.8 (2.4)
90.8 (0.3)
91.3 (.07)
91.5 (0.2)
91.7 (.04)
36.1 (0.8)
45.9 (2.1)
42.6 (1.9)
51.7 (1.2)
46.9 (0.3)
52.0 (1.9)
49.6 (1.9)
57.7 (1.5)
Tavolo 3: Comparison between models fine-tuned with multi-task (MTL) and single-task (STL)
apprendimento. MTL improves robust accuracy on challenging datasets. We ran t-tests for the mean
accuracies of STL and MTL on five runs and the larger number is bolded when they differ
significantly with a p < 0.001.
Target
Model
Algo. HANS-O HANS-C HANS-S
Auxiliary Datasets
MNLI
SNLI
QQP
PAWSQQP+Wiki
HANS
Size
393k
549k
364k
60k
30k
NLI
X
X
X
PI
X
X
X
the
Table 4: Auxiliary dataset sizes for
different target datasets from two tasks: NLI
and PI.
75.8 (4.9) 59.1 (4.8) 52.7 (1.2)
STL
BERTBASE
MTL 89.5 (1.9) 61.9 (2.3) 53.1 (1.1)
BERTBASE
RoBERTaBASE STL
88.5 (2.0) 70.0 (2.3) 63.9 (1.4)
RoBERTaBASE MTL 90.3 (1.2) 64.8 (3.1) 63.5 (4.9)
Table 5: MTL Results on different categories
on HANS: lexical overlap (O), con-
stituent (C), and subsequence (S). Both
auxiliary data (MTL) and larger pre-training
data (RoBERTa) improve accuracies mainly on
lexical overlap.
especially when the minority examples in the
target dataset is scarce (e.g., PAWS). Whereas
prior work has shown limited success of MTL
when tested on in-distribution data (Søgaard and
Goldberg, 2016; Hashimoto et al., 2017; Raffel
et al., 2019), our results demonstrate its value for
out-of-distribution generalization.
On HANS, MTL improves the accuracy signif-
icantly for BERTBASE but not for RoBERTaBASE.
To confirm the result, we additionally experi-
mented with RoBERTaLARGE and obtained consis-
tent results: MTL achieves an accuracy of 75.7 (2.1)
on HANS, similar to the STL result, 77.1 (1.6).
One potential explanation is that RoBERTa is
already sufficient for providing good generaliza-
tion from minority examples in MNLI.
In addition, both MTL and RoBERTaBASE yield
the biggest improvement on lexical overlap,
as shown in the results on HANS by category
(Table 5), We believe the reason is that lexi-
cal overlap is the most representative pattern
among high-overlap and non-entailment training
examples. In fact, 85% of the 727 HANS-like
examples belong to lexical overlap. This
suggests that further improvement on HANS may
require better data coverage on other categories.
On PAWS, MTL consistently yields large im-
provement across pre-trained models. Given that
QQP has fewer minority examples resembling the
patterns in PAWS, which is also harder to learn
(Section 4.2), the results show that MTL is an
effective way to improve generalization when the
minority examples are scarce. Next, we investigate
why MTL is helpful.
Improved Generalization
from Minority
Examples. We are interested in finding how
MTL helps generalization from minority exam-
ples. One possible explanation is that the chal-
lenging data in the auxiliary datasets prevent the
model from learning suprious patterns. However,
the ablation studies on auxiliary datasets in Table 6
and Table 7 show that the challenging datasets are
not much more helpful than benchmark datasets.
The other possible explanation is that MTL
reduces sample complexity for learning from the
minority examples in the target dataset. To verify
this, we remove minority examples from both the
628
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
t
l
a
c
_
a
_
0
0
3
3
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Removed
MNLI-m HANS
∆
Removed
QQP
PAWSQQP ∆
None
PAWSQQP+Wiki
QQP
SNLI
83.7 (0.3)
83.5 (0.3)
83.2 (0.3)
84.3 (0.2)
68.2 (1.8)
−
64.6 (3.5) −3.6
63.2 (3.7) −5.0
66.9 (1.5) −1.3
Table 6: Results of the ablation study on auxiliary
datasets using BERTBASE on MNLI (the target
task). While the in-distribution performance is
hardly affected when a specific auxiliary dataset
is excluded, performance on the challenging data
varies (difference shown in ∆).
Removed
QQP
PAWSQQP
∆
None
HANS
MNLI
SNLI
91.3 (.07)
91.5 (.06)
91.2 (.11)
91.3 (.09)
45.9 (2.1)
−
45.3 (1.8) −0.6
42.3 (1.8) −3.6
44.2 (1.3) −1.7
Table 7: Results of the ablation study on auxiliary
datasets using BERTBASE on QQP (the target
task). While the in-distribution performance is
hardly affected when a specific auxiliary dataset
is excluded, performance on the challenging data
varies (difference shown in ∆).
auxiliary and the target datasets, and compare their
effect on the robust accuracy.
We focus on PI because MTL shows the largest
improvement there. In Table 8, we show the results
after removing minority examples in the target
dataset, QQP, and the auxiliary dataset, MNLI,
respectively. We also add a control baseline
where the same amounts of randomly sampled
examples are removed. The results confirm our
hypothesis: Without the minority examples in the
target dataset, MTL is only marginally better than
STL on PAWSQQP. In contrast, removing minority
examples in the auxiliary dataset has a similar
effect to removing random examples; both do not
cause significant performance drop. Therefore, we
conclude that MTL improves robust accuracy by
improving generalization from minority examples
in the target dataset.
Takeaway. These results suggest that both pre-
training and MTL do not enable extrapolation;
instead, they improve generalization from minor-
ity examples in the (target) training set. Thus it is
important to increase coverage of diverse patterns
None
91.3 (.07)
45.9 (2.1)
−
random examples
QQP
MNLI
minority examples
QQP
MNLI
91.3 (.03) 44.3 (.31 ) −1.6
91.4 (.02) 45.0 (1.5 ) −0.9
91.3 (.09)
91.3 (.08)
38.2 (.73) −7.7
44.3 (2.0) −1.6
Table 8: Ablation study on the effect of minority
examples in the auxiliary (MNLI) and the target
(QQP) datasets in MTL with BERTBASE. For
MNLI, we removed 727 non-entailment examples
with 100% overlap. For QQP, we removed 228
non-paraphrase examples with 100% overlap. We
also removed equal amounts of random examples
in the control experiments. We ran t-tests for
the mean accuracies after minority removal and
random removal based on five runs, and numbers
with a significant difference (p < 0.001) are
bolded. The improvement from MTL mainly
comes from better generalization from minority
examples in the target dataset.
in the data to improve robustness to spurious
correlations.
6 Related Work
Pre-training and Robustness. Recently, there
has been an increasing amount of interest
in
studying the effect of pre-training on robustness.
Hendrycks et al. (2019, 2020) show that pre-
training improves model robustness to label noise,
class imbalance, and out-of-distribution detection.
In cross-domain question-answering, Li et al.
(2019) show that the ensemble of different pre-
trained models significantly improves perfor-
mance on out-of-domain data. In this work, we
answer why pre-trained models appear to improve
out-of-distribution robustness and point out the
importance of minority examples in the training
data.
Data Augmentation. The most straightforward
way to improve model robustness to out-of-
distribution data is to augment the training set
with examples from the target distribution. Recent
work has shown that augmenting syntactically
rich examples improves robust accuracy on NLI
(Min et al., 2020). Similarly, counterfactual
629
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
t
l
a
c
_
a
_
0
0
3
3
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
augmentation aims to identify parts of the input
that impact the label when intervened upon, thus
avoiding learning spurious features (Goyal et al.,
2019; Kaushik et al., 2020). Finally, data recom-
bination has been used to achieve compositional
generalization (Jia and Liang, 2016; Andreas,
2020). However, data augmentation techniques
largely rely on prior knowledge of the spurious
correlations or human efforts. In addition, as
shown in Section 4.2 and a concurrent work
(Jha et al., 2020), it is often unclear how much
augmented data is needed for learning a pattern.
Our work shows promise in adding generic pre-
training data or related auxiliary data (through
MTL) without
target
distribution.
assumptions on the
Robust Learning Algorithms. Serveral recent
papers propose new learning algorithms that are
robust to spurious correlations in NLI datasets
(He et al., 2019; Clark et al., 2019; Yaghoobzadeh
et al., 2019; Zhou and Bansal, 2020; Sagawa
et al., 2020; Mahabadi et al., 2020). They rely on
prior knowledge to focus on ‘‘harder’’ examples
that do not enable shortcuts during training. One
weakness of these methods is their arguably strong
assumption on knowing the spurious correlations
a priori. Our work provides evidence that large
amounts of generic data can be used to improve
out-of-distribution generalization. Similarly, re-
cent work has shown that semi-supervised learning
with generic auxiliary data improves model ro-
bustness to adversarial examples (Schmidt et al.,
2018; Carmon et al., 2019).
Transfer Learning. Robust
learning is also
related to domain adaptation or transfer learning
because both aim to learn from one distribution
and achieve good performance on a different
but related target distribution. Data selection
and reweighting are common techniques used in
domain adaptation. Similar to our findings on
minority examples, source examples similar to
the target data have been found to be helpful
to transfer (Ruder and Plank, 2017; Liu et al.,
2019a). In addition, much work has shown that
MTL improves model performance on out-of-
domain datasets (Ruder, 2017; Li et al., 2019;
Liu et al., 2019c). A concurrent work (Akula
et al., 2020) shows that MTL improves robustness
on advesarial examples in visual grounding. In
this work, we further connect the effectiveness of
MTL to generalization from minority examples.
7 Discussion and Conclusion
Our study is motivated by recent observations on
the robustness of large-scale pre-trained trans-
formers. Specifically, we focus on robust accuracy
on challenging datasets, which are designed to
expose spurious correlations learned by the model.
Our analysis reveals that pre-training improves
robustness by better generalizing from a minority
of examples that counter dominant spurious pat-
terns in the training set. In addition, we show
that more pre-training data, larger model size,
and additional auxiliary data through MTL further
improve robustness, especially when the amount
of minority examples is scarce.
Our work suggests that it is possible to go
beyond the robustness–accuracy trade-off with
more data. However, the amount of improvement
is still limited by the coverage of the training
data because current models do not extrapolate to
unseen patterns. Thus, an important future direc-
tion is to increase data diversity through new
crowdsourcing protocols or efficient human-in-
the-loop augmentation.
Although our work provides new perspectives
on pre-training and robustness, it only scratches
the surface of the effectiveness of pre-trained
models and leaves many questions open, for
example: why pre-trained models do not overfit to
the minority examples; how different initialization
(from different pre-trained models) influences
optimization and generalization. Understanding
these questions are key to designing better pre-
training methods for robust models.
Finally,
the difference between results on
HANS and PAWS calls for more careful thinking
on the formulation and evaluation of out-of-
distribution generalization. Semi-manually con-
structed challenging data often cover only a
specific type of distribution shift, thus the results
may not generalize to other types. A more com-
prehensive evaluation will drive the develop-
ment of principled methods for out-of-distribution
generalization.
Acknowledgments
We would like to thank the Lex and Comprehend
groups at Amazon Web Services AI for helpful
630
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
t
l
a
c
_
a
_
0
0
3
3
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
discussions, and the reviewers for their insightful
comments. We would also like to thank the
GluonNLP team for the infrastructure support.
Evaluating compositionality in sentence em-
beddings. In Annual Meeting of the Cognitive
Science Society, CogSci 2018.
References
Arjun R. Akula, Spandana Gella, Yaser Al-
Onaizan, Song-Chun Zhu, and Siva Reddy.
2020. Words aren’t enough, their order matters:
On the robustness of grounding visual referring
expressions. In Association for Computational
Linguistics (ACL).
J. Andreas. 2020. Good-enough compositional
data augmentation. In Association for Com-
putational Linguistics (ACL).
M. Arjovsky, L. Bottou, I. Gulrajani, and D.
Lopez-Paz. 2019. Invariant risk minimization.
arXiv preprint arXiv:1907.02893v2.
J. Baxter. 2000. A model of inductive bias
learning. Journal of Artificial Intelligence Re-
search (JAIR), 12:149–198.
S. Bowman, G. Angeli, C. Potts, and C. D.
Manning. 2015. A large annotated corpus for
learning natural language inference. In Empi-
rical Methods in Natural Language Processing
(EMNLP).
Y. Carmon, A. Raghunathan, L. Schmidt, P. Liang,
and J. C. Duchi. 2019. Unlabeled data improves
adversarial robustness. In Advances in Neural
Information Processing Systems (NeurIPS).
Rich Caruana. 1997. Multitask learning. Machine
Learning, 28(1):41–75.
D. Cer, M. Diab, E. Agirre, I. Lopez-Gazpio, and
L. Specia. 2017. SemEval-2017 task 1: Seman-
tic textual similarity - multilingual and cross-
lingual focused evaluation. In Proceedings of
the Eleventh International Workshop on Se-
mantic Evaluations.
C. Clark, M. Yatskar, and L. Zettlemoyer. 2019.
Don’t take the easy way out: Ensemble based
methods for avoiding known dataset biases.
In Empirical Methods in Natural Language
Processing (EMNLP).
Ishita Dasgupta, Demi Guo, Andreas Stuhlm¨uller,
Samuel Gershman, and Noah Goodman. 2018.
J. Devlin, M. Chang, K. Lee, and K. Toutanova.
2019. Bert: Pre-training of deep bidirectional
transformers for language understanding. In
North American Association for Computational
Linguistics (NAACL).
W. B. Dolan and C. Brockett. 2005. Automatically
constructing a corpus of sentential paraphrases.
In Proceedings of the International Workshop
on Paraphrasing.
M. Glockner, V. Shwartz, and Y. Goldberg.
2018. Breaking NLI systems with sentences that
require simple lexical inferences. In Association
for Computational Linguistics (ACL).
Y. Goyal, Z. Wu, J. Ernst, D. Batra, D. Parikh, and
S. Lee. 2019. Counterfactual visual explana-
tions. In International Conference on Machine
Learning (ICML).
C. Guo, G. Pleiss, Y. Sun, and K. Q. Weinberger.
2017. On calibration of modern neural net-
works. In International Conference on Machine
Learning (ICML).
J. Guo, H. He, T. He, L. Lausen, M. Li, H. Lin,
X. Shi, C. Wang, J. Xie, S. Zha, A. Zhang, H.
Zhang, Z. Zhang, Z. Zhang, S. Zheng, and
Y. Zhu. 2020. Gluoncv and gluonnlp: Deep
learning in computer vision and natural lan-
guage processing. Journal of Machine Learning
Research (JMLR), 21:1–7.
S. Gururangan, S. Swayamdipta, O. Levy, R.
Schwartz, S. R. Bowman, and N. A. Smith.
2018. Annotation artifacts in natural language
inference data. In North American Association
for Computational Linguistics (NAACL).
K. Hashimoto, C. Xiong, Y. Tsuruoka, and
R. Socher. 2017. A joint many-task model:
Growing a neural network for multiple NLP
tasks. In Empirical Methods in Natural Lan-
guage Processing (EMNLP).
H. He, S. Zha, and H. Wang. 2019. Unlearn dataset
bias for natural language inference by fitting
the residual. In Proceedings of the EMNLP
Workshop on Deep Learning for Low-Resource
NLP.
631
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
t
l
a
c
_
a
_
0
0
3
3
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
D. Hendrycks, K. Lee, and M. Mazeika.
2019. Using pre-training can improve model
robustness and uncertainty. In International
Conference on Machine Learning (ICML).
D. Hendrycks, X. Liu, E. Wallace, A. Dziedzic,
R. Krishnan, and D. Song. 2020. Pretrained
transformers
out-of-distribution
robustness. In Association for Computational
Linguistics (ACL).
improve
S. Iyer, N. Dandekar, and K. Csernai. 2017.
First quora dataset release: Question pairs.
Accessed online at. https://www.quora.
com/q/quoradata/First-Quora-
Dataset-Release-Question-Pairs
R. Jha, C. Lovering, and E. Pavlick. 2020. When
does data augmentation help generalization
in NLP? In Association for Computational
Linguistics (ACL).
R. Jia and P. Liang. 2016. Data recombination
for neural semantic parsing. In Association for
Computational Linguistics (ACL).
D. Kaushik, E. Hovy, and Z. C. Lipton. 2020.
Learning the difference that makes a difference
with counterfactually-augmented data. In Inter-
national Conference on Learning Representa-
tions (ICLR).
Hongyu Li, Xiyuan Zhang, Yibing Liu, Yiming
Zhang, Quan Wang, Xiangyang Zhou, Jing Liu,
Hua Wu, and Haifeng Wang. 2019. D-net:
A pre-training and fine-tuning framework for
improving the generalization of machine read-
ing comprehension. In Proceedings of the 2nd
Workshop on Machine Reading for Question
Answering, pages 212–219.
Miaofeng Liu, Yan Song, Hongbin Zou, and
Tong Zhang. 2019a. Reinforced training data
selection for domain adaptation. In Proceedings
of the 57th Annual Meeting of the Association
for Computational Linguistics, pages 1957–1968.
N. F. Liu, R. Schwartz, and N. A. Smith. 2019b.
Inoculation by fine-tuning: A method for an-
alyzing challenge datasets. In North American
Association for Computational Linguistics
(NAACL).
Xiaodong Liu, Pengcheng He, Weizhu Chen, and
Jianfeng Gao. 2019c. Multi-task deep neural
632
networks for natural language understanding.
In Association for Computational Linguistics
(ACL).
Y. Liu, M. Ott, N. Goyal, J. Du, M. Joshi,
D. Chen, O. Levy, M. Lewis, L. Zettlemoyer,
and V. Stoyanov. 2019d. RoBERTa: A robustly
optimized BERT pretraining approach. arXiv
preprint arXiv:1907.11692.
R. K. Mahabadi, Y. Belinkov, and J. Henderson.
2020. End-to-end bias mitigation by modelling
biases in corpora. In Association for Compu-
tational Linguistics (ACL).
Christopher D. Manning, Mihai Surdeanu, John
Bauer, Jenny Finkel, Steven J. Bethard, and
David McClosky. 2014. The Stanford CoreNLP
natural language processing toolkit. In Associa-
tion for Computational Linguistics
(ACL)
System Demonstrations.
A. Maurer, M. Pontil, and B. Romera-Paredes.
2016. The benefit of multitask representation
learning. Journal of Machine Learning Re-
search (JMLR), 17:1–32.
R. T. McCoy, E. Pavlick, and T. Linzen. 2019.
the wrong reasons: Diagnosing
language
heuristics
Right
syntactic
inference. arXiv preprint arXiv:1902.01007.
natural
for
in
J. Min, R. T. McCoy, D. Das, E. Pitler, and
T. Linzen. 2020. Syntactic data augmentation
increases robustness to inference heuristics.
In Association for Computational Linguistics
(ACL).
Yixin Nie, Yicheng Wang, and Mohit Bansal.
2019. Analyzing compositionality-sensitivity
of NLI models. In Proceedings of the AAAI
Conference on Artificial Intelligence, volume 33,
pages 6867–6874.
M. I. Nye, A. Solar-Lezama, J. B. Tenenbaum,
and B. M. Lake. 2019. Learning compositional
rules via neural program synthesis. In Advances
Information Processing Systems
in Neural
(NeurIPS).
Y. Oren, S. Sagawa, T. B. Hashimoto, and
P. Liang. 2019. Distributionally robust language
modeling. In Empirical Methods in Natural
Language Processing (EMNLP).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
t
l
a
c
_
a
_
0
0
3
3
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
C. Raffel, N. Shazeer, A. Roberts, K. Lee,
S. Narang, M. Matena, Y. Zhou, W. Li, and
P. J. Liu. 2019. Exploring the limits of transfer
learning with a unified text-to-text transformer.
arXiv preprint arXiv:1910.10683.
Sebastian Ruder and Barbara Plank. 2017.
Learning to select data for transfer learning
with bayesian optimization. arXiv preprint
arXiv:1707.05246.
S. Ruder. 2017. An overview of multi-task learn-
ing in deep neural networks. arXiv preprint
arXiv:1706.05098.
S. Sagawa, P. W. Koh, T. B. Hashimoto, and
P. Liang. 2020. Distributionally robust neural
networks for group shifts: On the importance
of regularization for worst-case generalization.
In International Conference on Learning
Representations (ICLR).
L. Schmidt, S. Santurkar, D. Tsipras, K. Talwar,
and A. Madry. 2018. Adversarially robust gen-
eralization requires more data. In Advances
in Neural
Information Processing Systems
(NeurIPS), pages 5014–5026.
A. Søgaard and Y. Goldberg. 2016. Deep multi-
task learning with low level tasks supervised at
lower layers. In Association for Computational
Linguistics (ACL).
A. Williams, N. Nangia, and S. R. Bowman. 2017.
A broad-coverage challenge corpus for sentence
understanding through inference. arXiv preprint
arXiv:1704.05426.
Yadollah Yaghoobzadeh, Remi Tachet des
Combes, Timothy J. Hazen, and Alessandro
Sordoni. 2019. Robust natural language infe-
rence models with example forgetting. CoRR,
abs/1911.03861.
T. Zhang, F. Wu, A. Katiyar, K. Q. Weinberger,
and Y. Artzi. 2020. Revisiting few-sample
BERT fine-tuning. arXiv preprint arXiv:2006.
05987.
Y. Zhang, J. Baldridge, and L. He. 2019.
PAWS: Paraphrase adversaries from word
scrambling. In North American Association for
Computational Linguistics (NAACL).
X. Zhou and M. Bansal. 2020. Towards robust-
ifying NLI models against lexical dataset biases.
In Association for Computational Linguistics
(ACL).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
5
1
9
2
3
5
0
6
/
/
t
l
a
c
_
a
_
0
0
3
3
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
633