Adolescents Adapt More Slowly than Adults to
Varying Reward Contingencies
Amir Homayoun Javadi1,2*, Dirk H. K. Schmidt1*,
and Michael N. Smolka1
Astratto
■ It has been suggested that adolescents process rewards dif-
ferently from adults, both cognitively and affectively. In an fMRI
study we recorded brain BOLD activity of adolescents (age
range = 14–15 years) and adults (age range = 20–39 years) A
investigate the developmental changes in reward processing
and decision-making. In a probabilistic reversal learning task, ad-
olescents and adults adapted to changes in reward contingencies.
We used a reinforcement learning model with an adaptive learn-
ing rate for each trial to model the adolescentsʼ and adultsʼ be-
havior. Results showed that adolescents possessed a shallower
slope in the sigmoid curve governing the relation between
expected value (the value of the expected feedback, +1 E
−1 representing rewarding and punishing feedback, rispettivamente)
and probability of stay (selecting the same option as in the previ-
ous trial). Trial-by-trial change in expected values after being cor-
rect or wrong was significantly different between adolescents
and adults. These values were closer to certainty for adults. Addi-
tionally, absolute value of model-derived prediction error for
adolescents was significantly higher after a correct response but
a punishing feedback. At the neural level, BOLD correlates of
learning rate, expected value, and prediction error did not sig-
nificantly differ between adolescents and adults. Nor did we see
group differences in the prediction error-related BOLD signal for
different trial types. Our results indicate that adults seem to be-
haviorally integrate punishing feedback better than adolescents
in their estimation of the current state of the contingencies. On
the basis of these results, we argue that adolescents made de-
cisions with less certainty when compared with adults and spec-
ulate that adolescents acquired a less accurate knowledge of
their current state, questo è, of being correct or wrong. ■
INTRODUCTION
A basic function of the brain is to evaluate the motiva-
tional and emotional importance of events and to adapt
behavior accordingly ( Jocham, Klein, & Ullsperger, 2011;
Pessiglione, Seymour, Flandin, Dolan, & Frith, 2006;
Schultz, 2006). On the basis of behavioral decision theo-
ries, decisions are guided by the value assigned to each
potential option (Luce, 1959). Reward prediction error
signals are used to reflect the difference between the
expected value and the actual outcome of an action
(OʼDoherty, Dayan, Friston, Critchley, & Dolan, 2003;
Schultz, Dayan, & Montague, 1997). “Expected value” is
defined as the value of the expected outcome. Positive
values indicate expectation of a rewarding feedback and
negative values expectation of punishment or loss. A
behave adaptively in a changing world, these values must
be continuously updated based on experience (Montague,
2006; Montague, Hyman, & Cohen, 2004).
Maturation of the human brain and reorganization of
the neuronal structures related to emotional, motiva-
tional, and cognitive processes are essential for the estab-
lishment of behavioral control, cognitive flexibility, E
1Technische Universität Dresden, 2University College London
*These authors contributed equally to the study.
efficient brain function. Differences in the pattern of devel-
opment of various brain areas and circuits have been pro-
posed to lead to an “imbalance” in the adolescent brain
(Casey, Jones, & Hare, 2008; Gogtay et al., 2004). Speci-
fically, the subcortical brain circuitries and the frontal,
cortical circuitries show a lead-lag gradient of maturation
(Casey, Jones, et al., 2008; Steinberg, 2005), with subcorti-
cal processes developing earlier and reaching maturation
already in adolescence, whereas the development of cor-
tical frontal processes is much more protracted and reach
maturation only in emerging adulthood.
One consequence of this is that adolescents engage in
increased risky decision-making compared with other
age groups, because they place greater value on the poten-
tial positive (as opposed to negative) consequences of
risk-taking (Steinberg, 2010; Casey, Getz, & Galvan,
2008; Ernst, Pine, & Hardin, 2006). Brain imaging studies
that focused on the developmental aspects of reward pro-
cessing offered different explanations for risky adolescent
behavior. On the one hand, it was hypothesized that lower
activation (cioè., hyposensitivity) in the reward system of
adolescents (compared with adults) may lead to more
extensive reward seeking (Spear, 2000). On the other
hand, higher activation (cioè., hypersensitivity) in the reward
system has been hypothesized to lead to an increase in risk
taking behavior (van Leijenhorst, Moor, et al., 2010; Galvan,
© 2014 Massachusetts Institute of Technology Published under a
Creative Commons Attribution 3.0 Unported (CC BY 3.0) licenza
Journal of Cognitive Neuroscience 26:12, pag. 2670–2681
doi:10.1162/jocn_a_00677
D
o
w
N
l
o
UN
D
e
D
F
R
o
M
l
l
/
/
/
/
j
F
/
T
T
io
T
.
:
/
/
H
T
T
P
:
/
D
/
o
M
w
io
N
T
o
P
UN
R
D
C
e
.
D
S
F
io
R
o
l
M
v
e
H
R
C
P
H
UN
D
io
io
R
R
e
.
C
C
T
.
o
M
M
/
j
e
o
D
tu
C
N
o
/
C
UN
N
R
UN
T
R
io
T
io
C
C
l
e
e
–
P
–
D
P
D
2
F
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
C
4
N
8
_
6
UN
/
_
j
0
o
0
C
6
N
7
7
_
UN
P
_
D
0
0
B
6
sì
7
G
7
tu
.
e
P
S
T
D
o
F
N
B
0
sì
8
S
M
e
IO
P
T
e
M
l
io
B
B
e
R
R
UN
2
R
0
2
io
3
e
S
/
j
T
F
.
/
tu
S
e
R
o
N
1
7
M
UN
sì
2
0
2
1
Hare, Voss, Glover, & Casey, 2007). Bjork, Smith, Chen,
and Hommer (2010) and Bjork et al. (2004) found the
adolescentsʼ reward system (especially the ventral striatum
[VS]) to be hyposensitive compared with adults. Others
found hypersensitivity of the VS (Galvan & McGlennen,
2013; Cohen et al., 2010; van Leijenhorst, Zanolie, et al.,
2010; Galvan et al., 2006; Ernst et al., 2005). As for adults, Esso
has been shown that they are not only adequately sensitive
but also able to exert control over impulsive tendencies
(Ripke et al., 2012; Cohen et al., 2010). Using a determin-
istic reversal learning task, van der Schaaf, Warmerdam,
Crone, and Cools (2011) found that overall performance
increases from age 10 A 25. È interessante notare, punishment-
based learning was best for the youngest age group,
whereas reward-based learning was best in young adults.
The goal of this study was to investigate age-related dif-
ferences in the behavioral effect and neural processing of
rewarding and punishing feedback. Efficient processing of
feedback is necessary for decision-making and, more impor-
tantly, for adaptive behavior in a changing environment.
We used a probabilistic reversal learning task to study how
adolescents adapt to changes of reward contingencies, anche
as how they deal with uncertainty in the system. We mod-
eled adolescentsʼ and adultsʼ behavior, using a reinforcement
learning method to compare their modeling parameters to
achieve a better understanding of the underlying mecha-
nisms of possible behavioral differences both groups.
In our model each decision is governed by a sigmoid
curve, which relates reward expectation (expected value)
and likelihood of behavioral stay ( pstay, selecting the
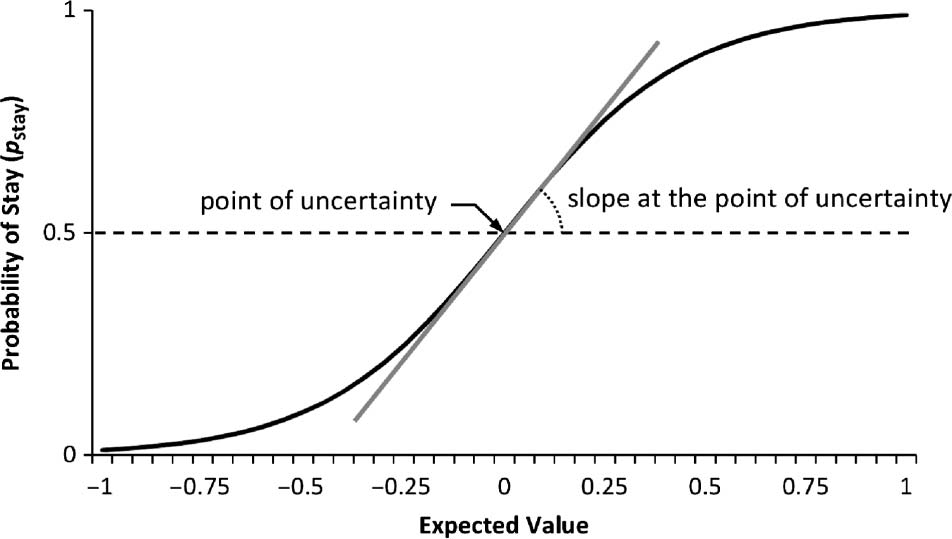
same option in the subsequent trial). Figura 1 shows this
curve with expected value spanning over [−1…+1], rep-
resenting 100% punishment and 100% reward for the
option chosen before in the two ends of the plot. Indiffer-
ence or the uncertainty point is the point at which there is
no difference between options, where pstay = 0.5. IL
slope at this point indicates how one integrates expected
values to make decisions with more certainty in sub-
sequent trials, questo è, making decisions with pstay values
smaller or greater than 0.5. In other words, the slope shows
Figura 1. Sigmoid curve that relates expected value and likelihood of
behavioral stay, showing the point of uncertainty and slope at that
point.
how fast one crosses the uncertainty point (toward either
pstay = 1 or pstay = 0), questo è, a higher slope corresponds to
a faster passage of the uncertainty point and vice versa.
Regarding the neural correlates of parameters derived
from such reinforcement learning algorithms, it has pre-
viously been shown that BOLD activity of the dorsal ACC
(dACC) is correlated with learning rate (Krugel, Biele,
Mohr, Li, & Heekeren, 2009; Behrens, Woolrich, Walton,
& Rushworth, 2007; Klein et al., 2007), the VS with pre-
diction error (Gläscher, Hampton, & OʼDoherty, 2009;
Hampton, Bossaerts, & OʼDoherty, 2006), and the ventro-
medial pFC (vmPFC) with expected value (Gläscher et al.,
2009; Hampton et al., 2006). Although it has to be
acknowledged that other brain areas, such as the lateral
orbital frontal cortex, the dorsolateral pFC, and the ante-
rior insula are involved in reversal learning (Xue et al.,
2013; Remijnse, Nielen, Uylings, & Veltman, 2005), we
focused on VS, dACC, and vmPFC, as combined signals
from these three regions are reported to be predictive
of behavior (Hampton & OʼDoherty, 2007), which we
expect to be different across age groups.
Given the work of van der Schaaf et al. (2011), we hypoth-
esized that adolescents would show a lower performance
during the task and a higher sensitivity to punishments,
compared with adults. Regarding the applied reinforce-
ment learning algorithm, we expected lower certainty
E, consequently, a shallower slope in their decision curve.
Further to this, we investigated the correlation of model-
ing parameters with BOLD brain activity and explored
whether age related differences can be observed.
METHODS
Participants
The data set used in this study was part of the “Adoles-
cent Brain” project, funded by the German Federal Min-
istry of Education and Research (BMBF). This project is
a longitudinal study investigating the relationship be-
tween brain development and susceptibility to substance
use disorders, involving two assessments over 4 years
(Ripke et al., 2012).
Two hundred sixty adolescents were recruited from
local secondary schools. We had to exclude 42 adolescents
from the analysis because of excessive head movements
(movements greater than 3 mm in any one direction),
interruptions in scanning, faults in data transfer, or missing
dati. The remaining 218 adolescents (115 boys (52.75%),
age range = 14–15 years, mean age = 14.61 years (SD =
0.32)) were included in the analysis. As a control group,
we recruited 29 adult participants by board and Internet an-
nouncements (17 men (58.62%), age range = 20–39 years,
mean age = 25.24 years (SD = 6.34)). Adolescents were
screened with a structured, diagnostic interview “devel-
opment and well-being assessment” (Goodman, Ford,
Richards, Gatward, & Meltzer, 2000) according to the
fourth edition of the Diagnostic and Statistical Manual
Javadi, Schmidt, and Smolka
2671
D
o
w
N
l
o
UN
D
e
D
F
R
o
M
l
l
/
/
/
/
j
F
/
T
T
io
T
.
:
/
/
H
T
T
P
:
/
D
/
o
M
w
io
N
T
o
P
UN
R
D
C
e
.
D
S
F
io
R
o
l
M
v
e
H
R
C
P
H
UN
D
io
io
R
R
e
.
C
C
T
.
o
M
M
/
j
e
o
D
tu
C
N
o
/
C
UN
N
R
UN
T
R
io
T
io
C
C
l
e
e
–
P
–
D
P
D
2
F
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
C
4
N
8
_
6
UN
/
_
j
0
o
0
C
6
N
7
7
_
UN
P
_
D
0
0
B
6
sì
7
G
7
tu
.
e
P
S
T
D
o
F
N
B
0
sì
8
S
M
e
IO
P
T
e
M
l
io
B
B
e
R
R
UN
2
R
0
2
io
3
e
S
/
j
.
F
/
T
tu
S
e
R
o
N
1
7
M
UN
sì
2
0
2
1
(DSM-IV), and adults were screened with the Composite
International Diagnostic Interview ( Wittchen & Pfister,
1997; Robins et al., 1988) to control for homogeneity
among the two groups and to exclude participants with a
history of psychiatric or neurological diseases, including
substance use disorder. All participants were compensated
for their expenses.
All participants in the adult and adolescent groups and
at least one legal guardian per adolescent gave their
written informed consent to participate in the study, after
receiving a comprehensive description of the study pro-
tocol. The study was carried out in accordance with the
Declaration of Helsinki and was approved by the local
research ethics committee.
Apparatus
The stimuli were presented via a head-coil-mounted dis-
play system, based on LCD technology (NordicNeuroLab
AS, Bergen, Norway). Participants responded using a
ResponseGrip (NordicNeuroLab AS, Bergen, Norway).
Stimuli were presented using Presentation (v11.1 Neuro-
behavioral Systems, Inc., Albany, CA). Computational
modeling was done using MATLAB (v7.5; MathWorks
Company, Natick, MA). We used constrained, nonlinear
optimization from the MATLAB optimization toolbox
(v5.1). Statistical data analysis was performed using SPSS
(v17.0; LEAD Technologies, Inc., Charlotte, NC).
Task Description
We used a probabilistic reversal learning task, similar to
that used by Hampton et al. (2006). Participants carried
out a decision-making task in which the feedback was
probabilistic. In each trial, one of the options was associ-
ated with a greater probability of reward. We refer to this
as the correct option and the other as the wrong option.
The correct option changed from time to time, depend-
ing on the performance of the participant. We subse-
quently refer to this as system change. Participants had
to adapt to these changes. Contingencies reversed with
a probability of .25 after at least four consecutive correct
responses. Participants were informed before the exper-
iment that reversals would occur at random intervals
throughout the experiment.
The main task performed in the scanner consisted of
120 trials. In each of the trials, participants were shown a
circle and a square (appearing at random on the left- O
right-hand side of the screen). They were asked to
choose one of the options by pressing the left or right
button. The correct stimulus led to a monetary reward
(+20 cents) 70% of the time and a monetary loss (−20 cents)
30% of the time. The wrong stimulus led to a reward
(+20 cents) 40% of the time and a punishment (−20 cents)
60% of the time. Additionally, on the feedback screen,
participants were provided with the total amount of money
they had collected. This paradigm has been used in pre-
vious probabilistic reversal learning studies (Hampton
et al., 2006; Hornak et al., 2004; OʼDoherty, Kringelbach,
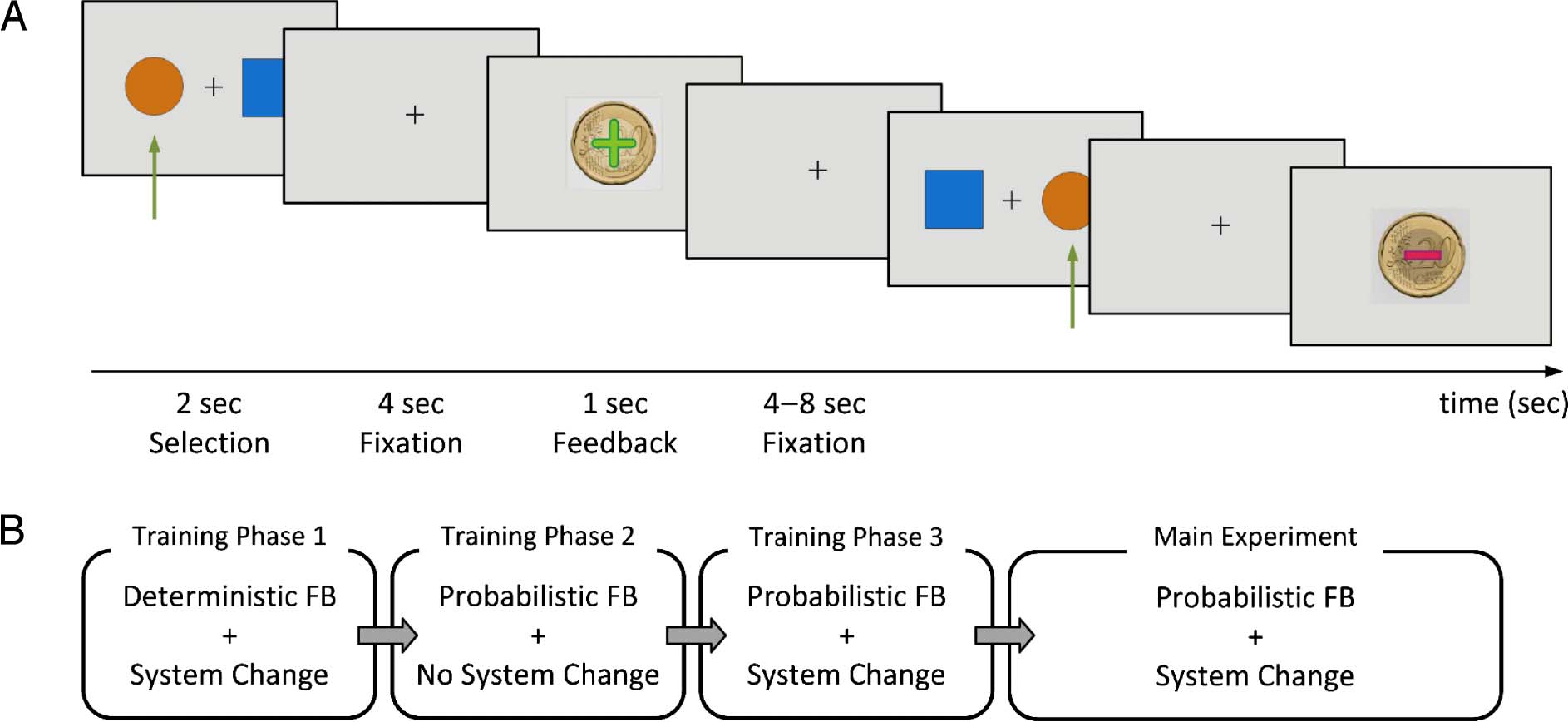
Rolls, Hornak, & Andrews, 2001). See Figure 2A for the
procedure of the experiment and for two examples of
response and feedback.
Participants performed a three-phase training session
of the task before entering the scanner to become ac-
quainted with the task and to ensure that both adoles-
cents and adults entered the main experiment with a
D
o
w
N
l
o
UN
D
e
D
F
R
o
M
l
l
/
/
/
/
j
T
T
F
/
io
T
.
:
/
/
H
T
T
P
:
/
D
/
o
M
w
io
N
T
o
P
UN
R
D
C
e
.
D
S
F
io
R
o
l
M
v
e
H
R
C
P
H
UN
D
io
io
R
R
e
.
C
C
T
.
o
M
M
/
j
e
o
D
tu
C
N
o
/
C
UN
N
R
UN
T
R
io
T
io
C
C
l
e
e
–
P
–
D
P
D
2
F
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
C
4
N
8
_
6
UN
/
_
j
0
o
0
C
6
N
7
7
_
UN
P
_
D
0
0
B
6
sì
7
G
7
tu
.
e
P
S
T
D
o
F
N
B
0
sì
8
S
M
e
IO
P
T
e
M
l
io
B
B
e
R
R
UN
2
R
0
2
io
3
e
S
/
j
/
T
.
F
tu
S
e
R
o
N
1
7
M
UN
sì
2
0
2
1
Figura 2. Overview of the experiment. (UN) Procedure of the probabilistic reversal learning task. Two sample trials are shown. The participantʼs
selection is highlighted with a green arrow. The first trial is rewarded, and the second trial is punished, reflecting the probabilistic nature of the task.
(B) Structure of the session. System change refers to change of contingencies. FB = feedback.
2672
Journal of Cognitive Neuroscience
Volume 26, Numero 12
similar level of understanding. In the first phase of the
training session, the rule for system change was imple-
mented, but participants were provided with determinis-
tic feedback. This means that they were always rewarded
after correct responses and punished after wrong re-
sponsorizzato. The criterion to finish this phase was three system
i cambiamenti. In the second phase, participants were intro-
duced to probabilistic feedback, without system changes.
The criterion to finish this phase was to select the better
option 10 times consecutively. The third phase combined
probabilistic feedback with system changes. This phase was
similar to the main task in the scanner. The criterion to
finish this phase was to achieve three system changes.
See Figure 2B for the procedure of the session.
Participants were instructed to maximize their gains.
They were informed that, in addition to a fixed amount
of A5, they would receive any extra money they accu-
mulated at the end of the study. The duration of the task
era 26 min.
Computational Modeling
We used a similar model as described in Krugel et al.
(2009) to model participantsʼ behavioral choices. Noi
considered a sigmoid curve (Equazione 6), indicating the
relation between difference of expected values for the
two options, va(T) and vb(T) for options a and b, respec-
tively, to calculate the probability of the selection of each
option, pa(T + 1) and pb(T + 1). On the basis of these
probabilities, we defined probability of behavioral stay
( pstay), questo è, selecting the same option in the current
trial as the previous trial (Equazione 8). We constructed
the sigmoid curve based on the difference of expected
values, va(T) − vb(T), and pstay. We chose difference of
expected values instead of expected value for each option,
va and vb, and pstay instead of the probability of selection of
that option ( pa and pb). Difference of expected values and
pstay combine va and vb into a uniform parameter that is
indifferent to the options per se.
(cid:1)
vselectedðtÞ ¼ vaðtÞ
vbðtÞ
if option a is selected
if option b is selected
ð1Þ
the expected value for the two options were updated
come segue:
8
>><
>>:
vaðt þ 1Þ ¼ vselectedðt þ 1Þ
vbðt þ 1Þ ¼ vselectedðt þ 1Þ
if option a is selected
if option b is selected
vbðt þ 1Þ ¼ vbðtÞ
vaðt þ 1Þ ¼ vaðtÞ
ð5Þ
Subsequently the probability of selecting options a and
b were calculated as follows:
paðt þ 1Þ ¼
1
1 þ expð−γ (cid:2) ðvaðtÞ − vbðtÞÞÞ
pbðt þ 1Þ ¼ 1 − paðt þ 1Þ
ð6Þ
ð7Þ
where γ is the slope of the sigmoid curve, considered as
the sensitivity parameter determining the influence of
reward expectations on choice probabilities.
pstay(T + 1) and pswitch(T + 1) were calculated as
follows:
(cid:1)
pstayðt þ 1Þ ¼ paðt þ 1Þ
pstayðt þ 1Þ ¼ pbðt þ 1Þ
E
if option a is selected
if option b is selected
ð8Þ
pswitchðt þ 1Þ ¼ 1 − pstayðt þ 1Þ
ð9Þ
Because traditional approaches using constant learning
rate do not allow for fast adaptation after the occurrence
of a reversal, nor do they allow for stabilization of behav-
ior once the best option is found, we used an adaptive
learning rate (Krugel et al., 2009). α(T) was updated as
follows, where f(M) is a mapping function to ensure that
α(T) values are maintained in the range of ]0..1[ , M(T) È
the normalized value of first derivation of δ(T) and δabs(T)
is the smoothed, unsigned value of δ(T).
δabsðtÞ ¼ δabsðt − 1Þ (cid:2) ð1 − αðtÞÞ þ jδðtÞj (cid:2) αð1Þ
ð10Þ
D
o
w
N
l
o
UN
D
e
D
F
R
o
M
l
l
/
/
/
/
j
F
/
T
T
io
T
.
:
/
/
H
T
T
P
:
/
D
/
o
M
w
io
N
T
o
P
UN
R
D
C
e
.
D
S
F
io
R
o
l
M
v
e
H
R
C
P
H
UN
D
io
io
R
R
e
.
C
C
T
.
o
M
M
/
j
e
o
D
tu
C
N
o
/
C
UN
N
R
UN
T
R
io
T
io
C
C
l
e
e
–
P
–
D
P
D
2
F
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
C
4
N
8
_
6
UN
/
_
j
0
o
0
C
6
N
7
7
_
UN
P
_
D
0
0
B
6
sì
7
G
7
tu
.
e
P
S
T
D
o
F
N
B
0
sì
8
S
M
e
IO
P
T
e
M
l
io
B
B
e
R
R
UN
2
R
0
2
io
3
e
S
/
j
T
F
/
.
in which va(T) and vb(T) show expected value on trial t for
the two options a and b, namely circle and square.
mðtÞ ¼
δabsðtÞ − δabsðt − 1Þ
ðδabsðtÞ þ δabsðt − 1ÞÞ=2
δðtÞ ¼ rewardðtÞ − vselectedðtÞ
ð2Þ
(cid:3)
f ðmðtÞÞ ¼ signðmðtÞÞ (cid:2) 1 − exp −ðmðtÞ=βÞ2
(cid:3)
(cid:4)
(cid:4)
ð11Þ
ð12Þ
in which δ(T) shows the prediction error and reward(T)
shows reward, for trial t.
(cid:1)
α(t+1) ¼
αðtÞ þ f ðmðtÞÞ (cid:2) ð1 − αðtÞÞ
αðtÞ þ f ðmðtÞÞ (cid:2) αðtÞ
if mðtÞ > 0
if mðtÞ < 0
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
dvðtÞ ¼ αðtÞ (cid:2) δðtÞ
vselectedðt þ 1Þ ¼ vselectedðtÞ þ dvðtÞ
ð3Þ
ð4Þ
where β is a modulatory factor to which the derivation of
δ(t) affects α(t + 1).
ð13Þ
in which α(t) is the adaptive learning rate (see below). dv(t)
represents change of expectation. After each decision
Finally γ, α(1) and β were the three parameters that
needed to be optimized using the logarithm of likelihood
Javadi, Schmidt, and Smolka
2673
of fit (log L ). L represents how accurately the model can
predict participantsʼ behavior in a subsequent trial. We
used the following formula to calculate L, where i repre-
sents trial number and n represents total number of trials
(n = 120).
L ¼
þ
Xn
i¼2
Xn
i¼2
Bi;switchPi;switch=
Xn
i¼2
Bi;switch
Bi;stayPi;stay=
Xn
i¼2
Bi;stay:
ð14Þ
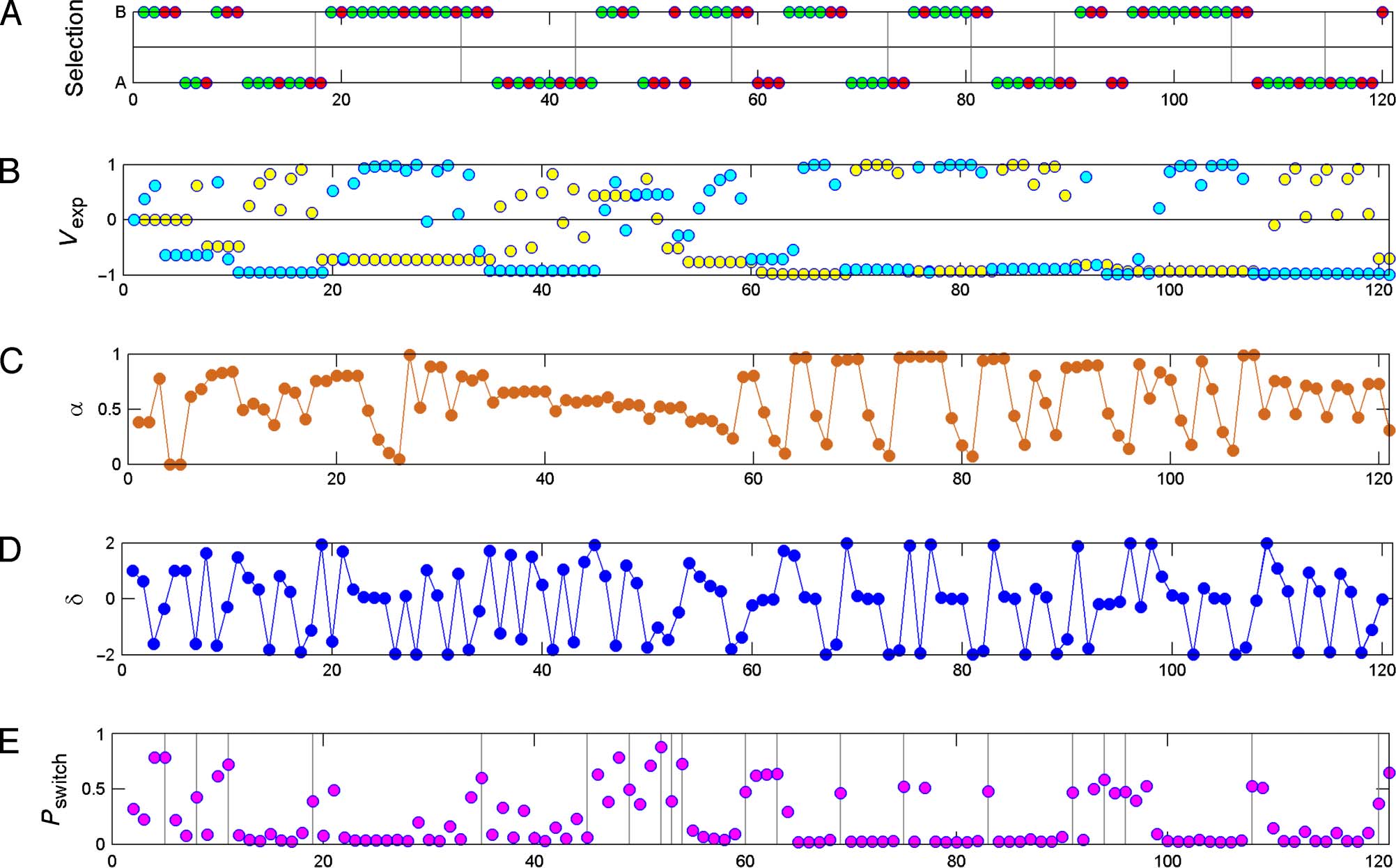
Figure 3 shows modeling of a sample session for
choices, reward, and modeling parameters.
Statistical Analysis
Behavioral Measures
We compared the ratio of correct responses using an
independent sample t test and the difference in the
number of system changes between adolescents and
adults using non-parametric Mann–Whitney U test. We
also analyzed effects on the switching rate, using a 2 ×
2 × 2 mixed-factorial ANOVA with Response (correct/
wrong) and Feedback (reward/punishment) as within-
subject factors and Group (adults/adolescents) as between-
subject factor. Subsequently, we compared switching rates
of adolescents and adults in all four types of trials using
independent sample t tests.
Modeling Measures
Two sets of parameters were estimated in our models:
the ones that model the behavior as a whole (learning
rate for the first trial α(1), modulatory factor β, logarithm
of the slope of the sigmoid curve γ, and logarithm of like-
lihood of fit L) and the ones that model the behavior on
each trial (learning rate α, change of expected value dv,
and prediction error δ). The former set of parameters
(α(1), β, logγ, and logL) was subjected to independent
sample t tests with group as the independent factor.
The latter set of parameters (α, dv, and δ) was subjected
to three 2 × 2 × 2 mixed-factorial ANOVAs with Response
(correct/wrong) and Feedback (reward/punishment) as
within-subject factors and Group (adults/adolescents) as
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
c
4
n
8
_
6
a
/
_
j
0
o
0
c
6
n
7
7
_
a
p
_
d
0
0
b
6
y
7
g
7
u
.
e
p
s
t
d
o
f
n
b
0
y
8
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
f
/
.
t
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
Figure 3. (A) Selected task option. A and B represent the two options, square and circle, respectively. Red color indicates punishment, and green
indicates reward. Vertical lines indicate trials in which a system change has occurred. As it is clear from the figure, each system change was preceded
with at least four consecutive selections of the correct option, regardless of possible negative feedback. (B) Expected value for option A, yellow
circles, and B, cyan circles. As shown, expected value for an option changes only when that option is selected. Its value increased with positive
feedbacks. (C) Adaptive learning rate (α). (D) Prediction error is defined as the difference between reward and expected value, δ(t) = reward(t) − vselected(t).
(E) Probability of switch as calculated by the model. Vertical lines indicate trials in which a behavioral switch has occurred.
2674
Journal of Cognitive Neuroscience
Volume 26, Number 12
between-subject factor. Subsequently, Bonferroni-corrected
independent sample t tests were used for post hoc com-
parisons. Data were checked for normality of distribution
using the Kolmogorov–Smirnov test.
It should be mentioned that SPSS controls for highly
imbalanced group sizes in independent two-sample t tests.
The standard two-sample t test allows the sample sizes to
be different (Press, Teukolsky, Vetterling, & Flannery,
2007). The sample variance is estimated by combining
the sample variances from each group. Importantly, each
is weighted by the number of samples in the group. So,
in this sense, the standard t test already accommodates
differences in sample size. A similar argument applies to
ANOVAs. Variances were different between adolescents
and adults; therefore, we report the result of tests with
the assumption of inequality of variance. The distributions
of p values for post hoc tests for each group of analyses
were corrected for multiple comparisons according to
the false discovery rate (FDR) procedure (Benjamini &
Hochberg, 1995). We computed a q threshold for four
comparisons per group that set the expected rate of false
discoveries to 0.025 for q* = 0.050.
Image Acquisition
All MRI data were acquired at the Neuroimaging Centre at
the Technische Universität Dresden, using a 3.0-T scanner
(Magnetom Tim Trio, Siemens, Erlangen, Germany). Series
of T2*-weighted, EPIs with 42 transverse slices, tilted
approximately 30° toward the coronal beyond the anterior
and posterior commissure lines, with a 3-mm in-plane reso-
lution and a slice thickness of 2 mm (1-mm gap resulting
in a voxel size of 3 × 3 × 3 mm3), a field of view of 192 ×
192 mm2, a flip angle of 80°, a repetition time of 2410 msec,
a bandwidth of 2112 Hz/pixel, and an echo time of 25 msec,
were acquired. The first 3 volumes were discarded to allow
the magnetization to reach equilibrium. High-resolution
three-dimensional anatomical images were acquired using
a T1-weighted, magnetization-prepared, rapid acquisi-
tion gradient-echo sequence with a field of view of 256 ×
224 mm2, 176 slices, a voxel size of 1 × 1 × 1 mm3, a rep-
etition time of 1900 msec, an echo time of 2.26 mm, and a
flip angle of 9°.
Imaging Data Analysis
Imaging data analysis was done using SPM5 ( Wellcome
Trust, London, UK). Data were preprocessed to correct
for slice timing and head motion, spatially normalized
to a standard EPI template in MNI space and smoothed
(8 mm FWHM isotropic Gaussian kernel). Templates
were based on the MNI305 stereotaxic space (Cocosco,
Kollokian, Remi, Pike, & Evans, 1997), an approximation
of Talairach space (Talairach & Tournoux, 1988).
Following Gläscher et al. (2009) and Krugel et al.
(2009), three binary and three parametric regressors of
interest were specified. Binary regressors were convolved
with a canonical hemodynamic response function and
modulated by respective parameters (α, v, and δ). Spe-
cifically we specified regressors for the response event
(1 sec before the response until button press) modulated
with the expected value (v), the learning event (1 sec after
onset of feedback for 1 sec) modulated with learning rate
(α; Krugel et al., 2009), and the feedback event (from
onset of feedback for 1 sec) modulated with prediction
error (δ; Gläscher et al., 2009). Please note, however, that
we did not split up the positive and negative prediction
errors as in Krugel et al. (2009).
Additionally, we also conducted a similar first-level
model with 12 regressors. These regressors were combi-
nations of 3 parameters (learning rate/expected value/
prediction error) × 2 response (correct/wrong) × 2 feed-
back (rewarded/punished). All these regressors were
modulated by respective parameters (α, v, and δ) and
convolved with a canonical hemodynamic response func-
tion. The parametric modulators were all corrected to
achieve zero mean. This resulted into two sets of beta
images, with slope representing correlation and the inter-
ception representing mean. In addition, the six scan-to-
scan motion parameters produced during realignment
were included to account for residual motion effects.
These were fitted to each voxel individually using a stan-
dard general linear model (GLM).
To explore the neural correlates of changes in rein-
forcement learning parameters at the second level, we
ran three 1-sample t tests using the respective first-level
contrasts, condition against baseline, capturing the cor-
relation of α, v, and δ with brain activity. To compare
adolescentsʼ and adultsʼ brain BOLD activity, we ran
three independent sample t tests, using the same first-
level contrasts and Group (adults/adolescents) as between-
subject factors. Finally, we ran six 2 (Group: adolescents/
adults) × 2 (Response: correct/wrong) × 2 (Feedback:
rewarded/punished) mixed factorial ANOVAs, with the
contrast reflecting the correlation (slope) and mean (inter-
cept) of α, v, and δ for the respective trial type. We report
activations in the corresponding ROI when p < .05 (small
volume-corrected FDR) and with a minimum number of
k = 10 voxels in a cluster.
For small volume correction, three ROIs were specified
based on probabilistic maps that are freely available online
(Nielsen & Hansen, 2002). We made three binary images
using a threshold value of 0.5 on the dorsal part of ACC
(referred to as dACC), the VS, and the ventromedial part
of the pFC (referred to as vmPFC).
RESULTS
Behavioral and Modeling
An independent sample t test showed no significant differ-
ences in task performance between groups, according to the
ratio of correct responses (adolescents mean (SD) =
0.59 (0.07), adults 0.61 (0.06), t(42.653) = 1.292, p = .203).
Javadi, Schmidt, and Smolka
2675
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
c
4
n
8
_
6
a
/
_
j
0
o
0
c
6
n
7
7
_
a
p
_
d
0
0
b
6
y
7
g
7
u
.
e
p
s
t
d
o
f
n
b
0
y
8
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
.
t
f
/
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
On the other hand, a nonparametric Mann–Whitney U test
revealed that the number of system changes for adults was
significantly higher compared with adolescents (median
adolescents 6, adults 7, Z = −2.04, p = .04).
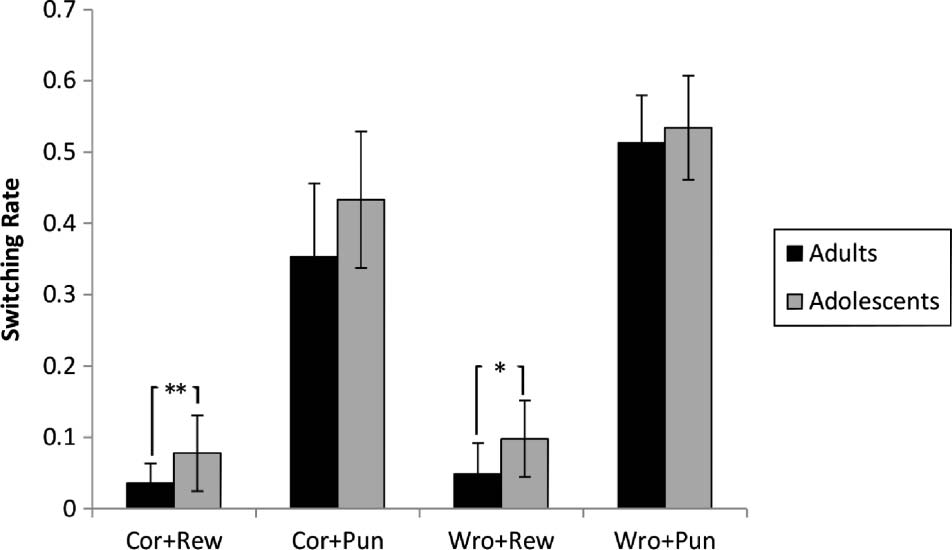
The 2 × 2 × 2 mixed-factor ANOVA revealed that
adolescents switched choices from one trial to the next
more frequently compared with adults (significant main
effect of Group; adolescents 0.28 (0.10), adults 0.23
(0.10), F(1, 245) = 5.729, p = .017). This test showed
significant three-way interaction of Group, Feedback, and
Response, F(1, 245) = 4.169, p = .042. Post hoc t tests
comparing switching rates of adolescents and adults in
all four conditions of Response × Feedback showed a
significant higher switching rates in the case of correct-
rewarded, t(59.591) = 3.328, p = .002, and wrong-
rewarded trials in adolescents, t(40.592) = 2.569, p = .014,
and nonsignificant differences in the case of correct-
punished, t(34.824) = 1.983, p = .055, and wrong-punished,
t(37.598) = 0.812, p = .422 (Figure 4).
Independent sample t tests showed no significant dif-
ference for α(1) (adolescents 0.307 (0.251), adults 0.286
(0.179), t(44.228) = 0.578, p = .567) and no significant
difference for β (adolescents 1.654 (1.177), adults 1.825
(1.337), t(34.026) = 0.654, p = .518). Similar t tests showed
a highly significant difference in logγ between the two
groups, with adults achieving a higher value (adolescents
0.137 (0.311), adults 0.330 (0.342), t(34.456) = 2.847,
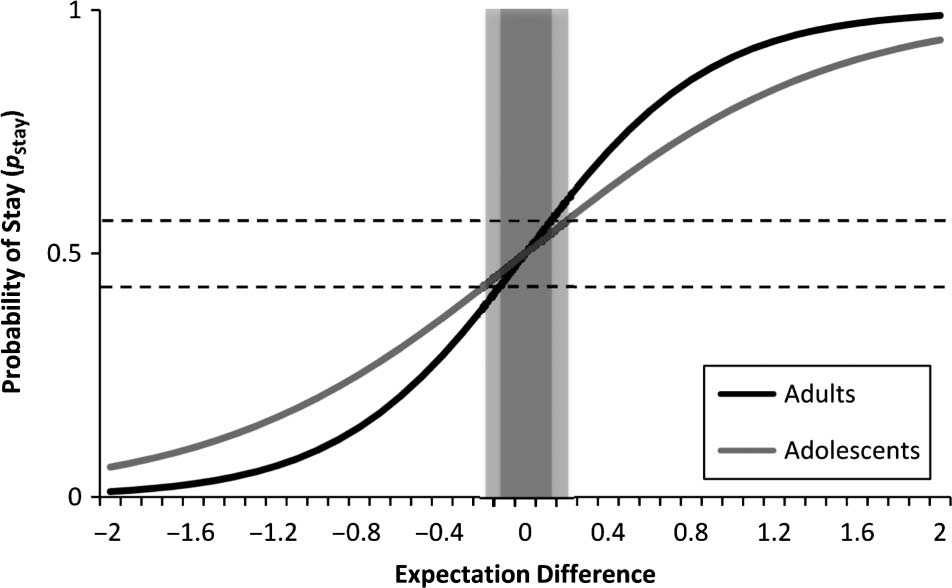
p = .007). Figure 5 shows the decision curve for ado-
lescents and adults. We should emphasize that, contrary
to Figure 1, which shows reward expectation, Figure 5
shows expectation difference: the difference between
the expected reward of the selected and unselected
options. Expectation difference spans over [−2…+2],
with 100% expectation of receiving reward for one
option and 100% expectation of receiving punishment
for the other option placed at either end of the curve.
Logarithm of likelihood of fit (logL) was significantly dif-
ferent between adults and adolescents, t(33.667) = 3.031,
Figure 4. Switching rates for adolescents and adults for different trial
and response conditions. Switching rate reflects the ratio of behavioral
switch to the total number of trials. Error bars reflect one standard
deviation (SD). Cor = Correct; Wro = Wrong; Rew = Rewarded;
Pun = Punished. *p = .014, **p = .002.
Figure 5. Decision curve used in the computational modeling showing
shallower slope at pstay = 0.5 for adolescents when compared with
adults. Shaded areas show uncertainty area for adolescents (lighter) and
adults (darker). See Discussion for further explanation. Expectation
difference shows the difference between the expected value of the
selected and unselected options in any given trial. Upper and lower
dashed lines show puncertainty, upper and puncertainty, lower, respectively.
p = .005, with a better fit for adults (−0.481 (0.085)) com-
pared with adolescents (−0.531 (0.071)).
A 2 × 2 × 2 mixed-factorial ANOVA with Response and
Feedback as within-subject factors and Group as a between-
subject factor on α showed no significant difference for any
of the comparisons (F < 1). In contrast, two 2 × 2 × 2 mixed-
factorial ANOVAs on dv and δ showed a significant effect of
Response and Feedback, two-way interaction of Response
and Group, and three-way interaction of Response, Feed-
back, and Group for both dv and δ, as well as a significant
two-way interaction of Response and Feedback for dv. The
results of these ANOVAs are summarized in Table 1.
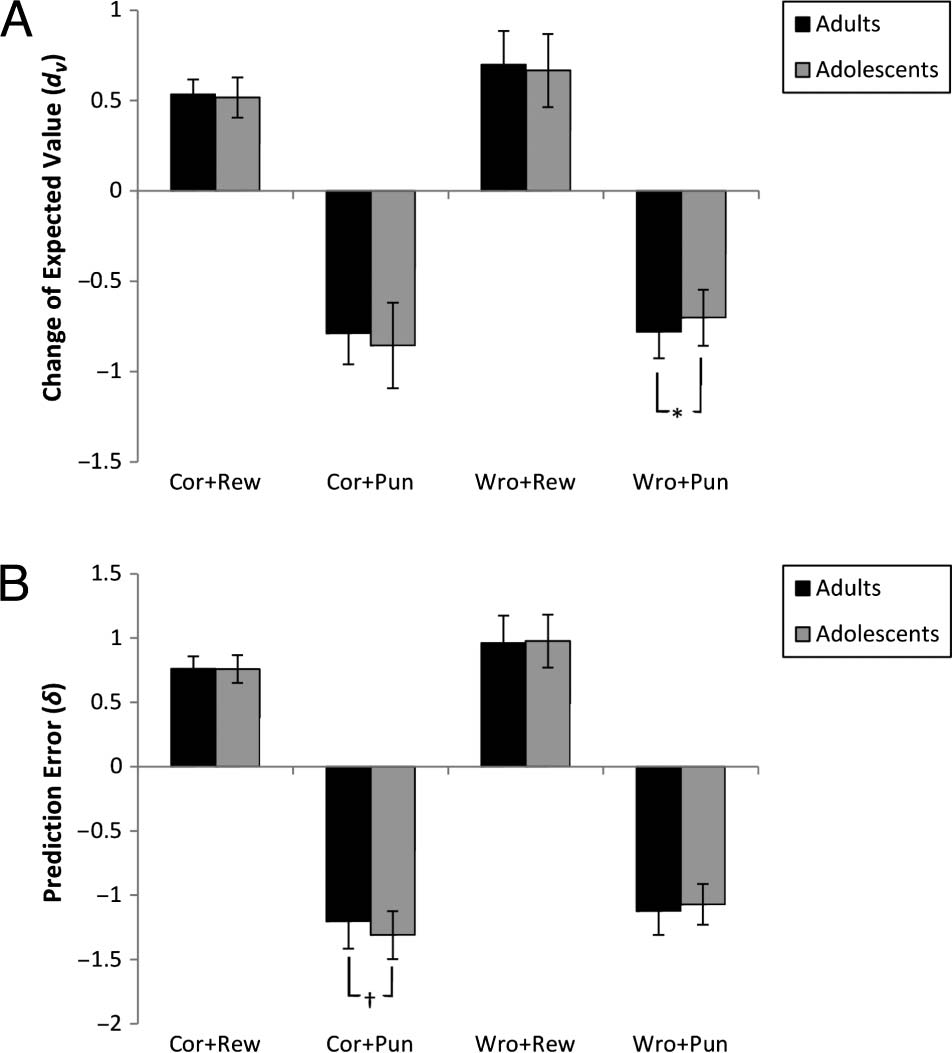
Independent sample t tests on the interaction of re-
sponse, feedback, and group showed a significant difference
between adolescents and adults for the wrong-punished
condition, with adults having a smaller dv(t(36.483) =
2.333, p = .025). No other comparison was significant
( p > .145). Figure 6A shows the change of expected values
for all the post hoc comparisons.
Post hoc independent sample t tests on the interaction
of response, feedback, and group showed a near-to-
significant difference between adolescents and adults for
the correct-punished condition, with adolescents having a
smaller δ (T(33.821) = 2.284, p = .029). No other compar-
ison was significant ( p > .225). Figure 6B shows δ values
for all the post hoc comparisons.
Brain Imaging
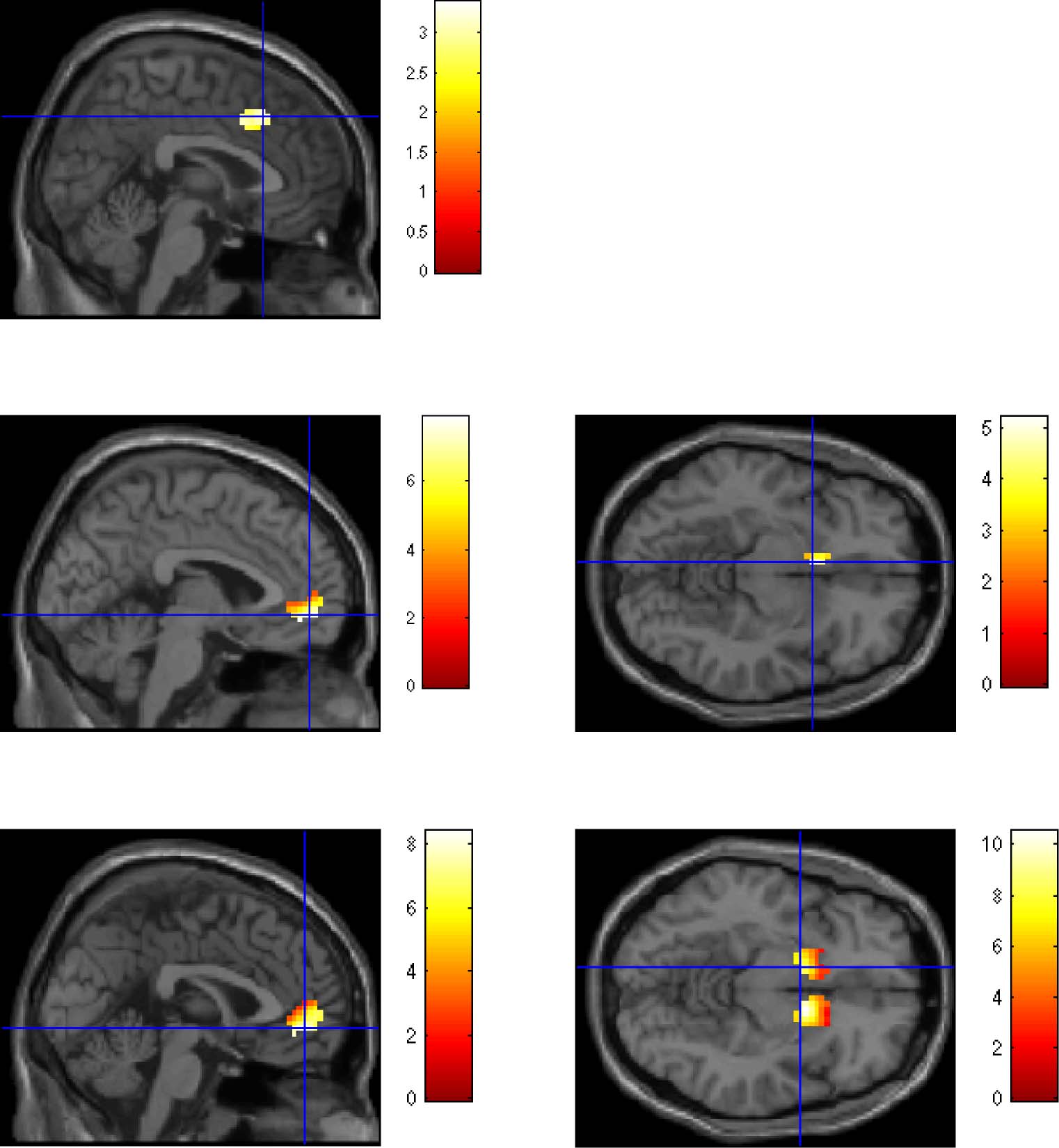
For the whole sample, we found that the trial-by-trial
time course of α was correlated with the BOLD response
of the dACC, v was correlated with activity of the vmPFC,
and activity of the VS reflected δ (Figura 7; Krugel et al.,
2009; Hampton et al., 2006). Independent sample t tests
on the trial-wise correlation of α, v, and δ with BOLD data
2676
Journal of Cognitive Neuroscience
Volume 26, Numero 12
D
o
w
N
l
o
UN
D
e
D
F
R
o
M
l
l
/
/
/
/
j
T
T
F
/
io
T
.
:
/
/
H
T
T
P
:
/
D
/
o
M
w
io
N
T
o
P
UN
R
D
C
e
.
D
S
F
io
R
o
l
M
v
e
H
R
C
P
H
UN
D
io
io
R
R
e
.
C
C
T
.
o
M
M
/
j
e
o
D
tu
C
N
o
/
C
UN
N
R
UN
T
R
io
T
io
C
C
l
e
e
–
P
–
D
P
D
2
F
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
C
4
N
8
_
6
UN
/
_
j
0
o
0
C
6
N
7
7
_
UN
P
_
D
0
0
B
6
sì
7
G
7
tu
.
e
P
S
T
D
o
F
N
B
0
sì
8
S
M
e
IO
P
T
e
M
l
io
B
B
e
R
R
UN
2
R
0
2
io
3
e
S
/
j
F
T
.
/
tu
S
e
R
o
N
1
7
M
UN
sì
2
0
2
1
Tavolo 1. Summary of 2 × 2 × 2 Mixed-factorial ANOVA with Response and Feedback as Within-subject Factors and Group as
Between-subject Factor on Change of Expectation (dv) and Prediction Error (δ)
Effect
Main effect of Response
Main effect of Feedback
Main effect of Group
Interaction of Response and Feedback
Interaction of Feedback and Group
Interaction of Response and Group
dv
δ
F(1, 245) = 76.667
P < .001
F(1, 245) = 89.886
p < .001
F(1, 245) = 2330.9
p < .001
F(1, 245) = 18179
p < .001
F(1, 245) = 1.054
F(1, 245) = 8.512
F(1, 245) = 0.378
F(1, 245) = 3.508
p = .306
p = .004
p = .539
p = .062
p = .002
F(1, 245) = 0.476
F(1, 245) = 2.338
F(1, 245) = 1.144
F(1, 245) = 3.135
F(1, 245) = 5.083
p = .491
p = .128
p = .286
p = .078
p = .025
Interaction of Response, Feedback, and Group
F(1, 245) = 9.366
showed nonsignificant differences between adults and
adolescents.
between both groups (adults/adolescents) in correct-
punished trials.
Three full-factorial GLM (with group as a between-
subject factor and feedback and response as within-subject
factors) on the correlation of α, v, and δ with brain re-
sponse did not show any significant main effect of Group
or three-way interaction of Group × Feedback × Response.
Three complimentary full-factorial GLM on the mean brain
response (intercepts) of α, v, and δ during the different
trial types also showed no significant main effect of group
or three-way interaction. Furthermore, a post hoc t test on
the mean δ in the VS showed nonsignificant differences
Figure 6. (A) shows change of expected value (dv) and (B) shows
prediction error (δ) for the three-way interaction of group, response,
and punishment (rewarded/punished). Error bars reflect one standard
deviation (SD). Cor = Correct; Wro = Wrong; Rew = Rewarded;
Pun = Punished. *p = .025, †
p = .029.
DISCUSSION
Reinforcement learning modeling has been used to investi-
gate the underlying brain areas in decision-making (Krugel
et al., 2009; Hampton et al., 2006). In contrast, we used it to
achieve a better understanding of the contributing factors
underlying behavioral differences in decision-making
between adolescents and adults. On the basis of behavioral
data that showed that adolescents switched more often
than adults ( p = .02) and achieved a lower number of sys-
tem changes (change of contingencies; p = .04), we hypoth-
esized that adolescents performed the task with lower
certainty and consequently possessed a shallower slope
in their decision-making curve.
Our results are in line with our hypothesis. We defined
pstay = 0.5 as the uncertainty point and considered slope
at this point as the rate of transition from the uncertainty
point toward a more certain area ( pstay = 1 or pstay = 0).
An alternative way is to define an uncertainty area. We
can define the uncertainty area as the range of expecta-
tion difference values that correspond to pstay values as
puncertainty, lower < pstay < puncertainty, upper. This range is
shown as shaded bars in Figure 5. Because adolescents
showed a shallower slope in their decision curve, they
achieve a wider uncertainty range (lighter shading). This
wider range of uncertainty can be interpreted as reduced
decisiveness, that is, adolescents made decisions with
lower certainty, compared with adults.
We investigated the correlation of BOLD activity with
modeling parameters α, v, and δ. In line with previous
literature (Krugel et al., 2009; Hampton et al., 2006),
our results showed that BOLD activity in the VS, dACC,
and vmPFC is correlated with learning rate, expected value,
and prediction error, respectively. Comparing the cor-
relation of the three model parameters with BOLD signal
between adolescents and adults showed no difference in
the VS, dACC, and vmPFC. Moreover, no differences were
found regarding the neural correlates of these parameters
Javadi, Schmidt, and Smolka
2677
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
c
4
n
8
_
6
a
/
_
j
0
o
0
c
6
n
7
7
_
a
p
_
d
0
0
b
6
y
7
g
7
u
.
e
p
s
t
d
o
f
n
b
0
y
8
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
f
t
.
/
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
c
4
n
8
_
6
a
/
_
j
0
o
0
c
6
n
7
7
_
a
p
_
d
0
0
b
6
y
7
g
7
u
.
e
p
s
t
d
o
f
n
b
0
y
8
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
.
/
f
t
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
Figure 7. Masked brain images showing the correlation of the BOLD activity of the adult and adolescent groups ( p < .05 small volume-corrected
FDR with minimum number of k = 10 voxels in a cluster) with (A) dynamic learning rate (α), (B and C) expected value (v), and (D and E) prediction
error (δ). kE represents the number of voxels in a cluster. Coordinates refer to the peak voxel for each cluster.
during the four different trial types (correct-rewarded/
correct-punished/wrong-rewarded/wrong-punished). Taken
together, these results indicate that task-related brain activ-
ity does not or only slightly differs between adolescents
and adults and that learning mechanisms in adolescents
and adults are quite similar and therefore recruit similar
brain regions.
In addition to our predictions, correlation of BOLD
activity with prediction error was not limited to VS but
was also found in the vmPFC. This is in line with the find-
ings of Hampton et al. (2006). We also found a weak cor-
relation in the VS with expected value. Correlation of BOLD
activity with expected value is also reportedly not limited to
the vmPFC. Gläscher (2009) and Hampton et al. (2006)
showed that the amygdalaʼs BOLD activity is correlated
with expected value. We argue that finding prediction error
and expected value parameters to be correlated with BOLD
activity in identical brain regions might either be because
of an intercorrelation of dependent model parameters or
because of correlations in regressors caused by the rela-
tively rapid timing of events in our design.
The modeling fit, as measured by logL, was signifi-
cantly worse for adolescents than for adults. One might
speculate that the differences in modeling parameters
are merely the result of difference in model fit. We argue
that although the degree of fit was different, the three
modeling parameters were calculated with equal accu-
racy, as shown by the similarity of adolescentsʼ and adultsʼ
correlation analysis of brain BOLD activity. Therefore, the
difference in model fit can be interpreted as a result of the
difference in predictability of adolescentsʼ and adultsʼ
behavior, demonstrated by a higher rate of behavioral
2678
Journal of Cognitive Neuroscience
Volume 26, Number 12
switch in adolescents and a lower number of system
changes, which we interpret as a higher level of uncertainty
in adolescents. This behavioral difference is captured by
the difference in slope of decision curves.
There is a strong agreement that dramatic behavioral
changes during adolescence are driven by differences in
reward processing and sensitivity (Somerville, Jones, &
Casey, 2010; Steinberg, 2005; Dahl, 2004; for a review,
see Blakemore & Robbins, 2012; Galvan, 2010). Although
the interaction effect of feedback and group was not sig-
nificant, the three-way interaction effect of response,
feedback, and group was significant. Post hoc tests on
this three-way interaction showed interesting results:
first, adults achieved a smaller absolute value of pre-
diction error for being punished after trials which they
responded correctly to, and second, they achieved a
higher absolute value of change in expectation for being
punished after trials which they responded wrongly to.
The former finding shows that adults were more capable
of interpreting negative feedback as either leading or
misleading and therefore had more accurate expecta-
tions. The latter finding, on the other hand, shows that
they incorporated punishment when updating their state
to a greater extent when they felt like they were mis-
taken. Has to be noted that the sample sizes were differ-
ent, as was the variance of the two samples; hence, the
adult group results are likely less stable than the adoles-
cent group results.
Galvan et al. (2006) and Ernst et al. (2005) showed that
adolescents are hypersensitive to reward, whereas Bjork
et al. (2004) showed a hyposensitivity. Inconsistency in
the findings might be because of task design and the
developmental stage of the adolescents recruited. Cohen
et al. (2010) argued that enhanced prediction error signal
leads to adolescentsʼ reward-seeking behavior. Our
modeling results showed no difference between the
two groups in response to rewarding feedback (no dif-
ferences in post hoc comparisons on rewarding feedback
on the interaction of feedback, response, and group). In
contrast, we found significant differences in the response
to punishing feedback after being wrong (difference in
the change of expected value) and after being correct
(difference in prediction error). Another reason for this
inconsistency might be our choice of age range for
adults. This range is not always consistent between stud-
ies (Blakemore & Robbins, 2012). For example, in some
studies, the adult group is within our selected range (20–
39 years old), and in other studies this range is higher.
For instance, the adult age range for Chein, Albert,
OʼBrien, Uckert, and Steinberg (2011) was 24–29 years,
for Jarcho et al. (2012) it was 23–40 years, and for Vaidya,
Knutson, OʼLeary, Block, and Magnotta (2013) it was
26–30 years old. To further investigate the effect of age in
the adults group, we ran similar three full-factorial GLM
(with Group as a between-subject factor and Feedback
and Response as within-subject factors) on the correlation
of α, v, and δ with brain response in adults older than
24 years (n = 14) and adolescents. These analyses showed
no significant three-way interaction of the three factors of
Group, Response, and Feedback, even with p < .01 uncor-
rected and k = 5. These results, however, might be because
of the small number of participants in the adults group.
Appropriate weighting and interpretation of both re-
wards and punishments are crucial for effective decision-
making. Numerous studies have shown that rewards and
punishments are processed and weighted differently in
adults than in adolescents (Tversky & Kahneman, 1991;
Kahneman & Tversky, 1979). Regardless of clear differ-
ences in the processing of reward and punishment, most
of the attention in the developmental differences between
adults and adolescents is focused on reward processing
(Penolazzi, Gremigni, & Russo, 2012; Padmanabhan, Geier,
Ordaz, Teslovich, & Luna, 2011; van Leijenhorst, Moor,
et al., 2010; for review, see Blakemore & Robbins, 2012;
Steinberg, 2005). Only recently has the developmental dif-
ferences in the processing of punishment between adoles-
cents and adults been studied (Galvan & McGlennen, 2013;
Aïte et al., 2012; Barkley-Levenson, van Leijenhorst, &
Galvan, 2012; van der Schaaf et al., 2011). In a recent study,
Galvan and McGlennen (2013) showed that adolescents
are hypersensitive to punishments when compared with
adults. In line with their findings, our results showed that
adolescents possessed significantly higher absolute pre-
diction error in response to punishments in correct trials.
Behavioral data showed that adolescents switched
more often than adults in several conditions, even after
receiving rewarding feedback. This fact is perfectly in line
with this idea. Here, we argue that rewards possibly do
not affect the change of expectation strongly enough to
pass the uncertainty area, as seen by shallower slope, and
thus, this leaves adolescents at a higher probability of
switching because of a higher state of uncertainty.
In conclusion, from a developmental perspective, we
showed that behavioral differences between groups are
reflected in the slope, change of expected value, and pre-
diction error parameters. We showed that (1) adults up-
dated their expected value to a greater extent toward
higher certainty and (2) they were adequately sensitive
to negative feedback on correct and wrong trials. On
the basis of these findings, we argued that adolescents
performed the task with lower certainty, reflected by
the shallower slope in their decision curves. Further-
more, we speculated about the possibility that adults
acquired more accurate knowledge about their current
status. Additionally, our approach shows that com-
putational modeling can be effectively used to better
understand the mechanisms of decision-making in devel-
opmental studies.
Acknowledgments
We would like to thank Fraser Merchant and Ying Lee for
proofreading the document. We would also like to thank the
two anonymous reviewers for their constructive comments as
Javadi, Schmidt, and Smolka
2679
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
c
4
n
8
_
6
a
/
_
j
0
o
0
c
6
n
7
7
_
a
p
_
d
0
0
b
6
y
7
g
7
u
.
e
p
s
t
d
o
f
n
b
0
y
8
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
/
f
.
t
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
well as Thomas Hübner, Michael Marxen, Eva Mennigen,
Kathrin U. Müller, Stephan Ripke, and Sarah Rodehacke for their
help in the different stages of the project. This research was sup-
ported the Deutsche Forsungsgemeinschaft (grants SM 80/7-1
and SFB 940) and the German Ministry of Education and Research
(BMBF grant 01EV0711). A. H. J. was supported by Wellcome
Trust.
Reprint requests should be sent to Amir Homayoun Javadi,
Institute of Behavioral Neuroscience, University College London,
26 Bedford Way, WC1H 0AP, London, United Kingdom, or via
e-mail: a.h.javadi@gmail.com or Michael N. Smolka, Section
of Systems Neuroscience, Technische Universität Dresden,
Würzburger Str. 35, 01187, Dresden, Germany, or via e-mail:
michael.smolka@tu-dresden.de.
REFERENCES
Aïte, A., Cassotti, M., Rossi, S., Poirel, N., Lubin, A., Houdé, O.,
et al. (2012). Is human decision-making under ambiguity
guided by loss frequency regardless of the costs? A
developmental study using the Soochow Gambling
Task. Journal of Experimental Child Psychology, 113,
286–294.
Barkley-Levenson, E. E., van Leijenhorst, L., & Galvan, A. (2012).
Behavioral and neural correlates of loss aversion and risk
avoidance in adolescents and adults. Developmental Cognitive
Neuroscience, 3, 72–83.
Behrens, T. E. J., Woolrich, M. W., Walton, M. E., & Rushworth,
M. F. S. (2007). Learning the value of information in an
uncertain world. Nature Neuroscience, 10, 1214–1221.
Benjamini, Y., & Hochberg, Y. (1995). Controlling the false
discovery rate: A practical and powerful approach to multiple
testing. Journal of the Royal Statistical Society, Series B,
Methodological, 57, 289–300.
Bjork, J. M., Knutson, B., Fong, G. W., Caggiano, D. M., Bennett,
S. M., & Hommer, D. W. (2004). Incentive-elicited brain
activation in adolescents: Similarities and differences from
young adults. The Journal of Neuroscience, 24, 1793–1802.
Bjork, J. M., Smith, A. R., Chen, G., & Hommer, D. W. (2010).
Adolescents, adults and rewards: Comparing motivational
neurocircuitry recruitment using fMRI. PloS One, 5, e11440.
Blakemore, S.-J., & Robbins, T. W. (2012). Decision-making in
the adolescent brain. Nature Neuroscience, 15, 1184–1191.
Casey, B. J., Getz, S., & Galvan, A. (2008). The adolescent brain.
Developmental Review, 28, 62–77.
Casey, B. J., Jones, R. M., & Hare, T. A. (2008). The adolescent
brain. Annals of the New York Academy of Sciences, 1124,
111–126.
Chein, J., Albert, D., OʼBrien, L., Uckert, K., & Steinberg, L.
(2011). Peers increase adolescent risk taking by enhancing
activity in the brainʼs reward circuitry. Developmental
Science, 14, F1–F10.
Cocosco, C. A., Kollokian, V., Remi, K. S. K., Pike, G. B., &
Evans, A. C. (1997). Brainweb: Online interface to a 3D MRI
simulated brain database. Neuroimage, 5, S425.
Cohen, J. R., Asarnow, R. F., Sabb, F. W., Bilder, R. M.,
Bookheimer, S. Y., Knowlton, B. J., et al. (2010). A unique
adolescent response to reward prediction errors. Nature
Neuroscience, 13, 669–671.
Dahl, R. E. (2004). Adolescent brain development: A period of
vulnerabilities and opportunities. Keynote address. Annals of
the New York Academy of Sciences, 1021, 1–22.
Ernst, M., Nelson, E. E., Jazbec, S., McClure, E. B., Monk, C. S.,
Leibenluft, E., et al. (2005). Amygdala and nucleus
accumbens in responses to receipt and omission of gains in
adults and adolescents. Neuroimage, 25, 1279–1291.
Ernst, M., Pine, D. S., & Hardin, M. (2006). Triadic model of the
neurobiology of motivated behavior in adolescence.
Psychological Medicine, 36, 299–312.
Galvan, A. (2010). Adolescent development of the reward
system. Frontiers in Human Neuroscience, 4, 6.
Galvan, A., Hare, T. A., Parra, C. E., Penn, J., Voss, H., Glover, G.,
et al. (2006). Earlier development of the accumbens
relative to orbitofrontal cortex might underlie risk-taking
behavior in adolescents. The Journal of Neuroscience, 26,
6885–6892.
Galvan, A., Hare, T. A., Voss, H., Glover, G., & Casey, B. J.
(2007). Risk taking and the adolescent brain: Who is at risk?
Developmental Science, 10, F8–F14.
Galvan, A., & McGlennen, K. M. (2013). Enhanced striatal
sensitivity to aversive reinforcement in adolescents versus
adults. Journal of Cognitive Neuroscience, 25, 284–296.
Gläscher, J. (2009). Visualization of group inference data in
functional neuroimaging. Neuroinformatics, 7, 73–82.
Gläscher, J., Hampton, A. N., & OʼDoherty, J. P. (2009).
Determining a role for ventromedial prefrontal cortex in
encoding action-based value signals during reward-related
decision making. Cerebral Cortex, 19, 483–495.
Gogtay, N., Giedd, J. N., Lusk, L., Hayashi, K. M., Greenstein, D.,
Vaituzis, A. C., et al. (2004). Dynamic mapping of human
cortical development during childhood through early adulthood.
Proceedings of the National Academy of Sciences, U.S.A., 101,
8174–8179.
Goodman, R., Ford, T., Richards, H., Gatward, R., & Meltzer, H.
(2000). The development and well-being assessment:
Description and initial validation of an integrated assessment
of child and adolescent psychopathology. Journal of Child
Psychology and Psychiatry, 41, 645–655.
Hampton, A. N., Bossaerts, P., & OʼDoherty, J. P. (2006).
The role of the ventromedial prefrontal cortex in abstract
state-based inference during decision making in humans.
The Journal of Neuroscience, 26, 8360–8367.
Hampton, A. N., & OʼDoherty, J. P. (2007). Decoding the neural
substrates of reward-related decision making with functional
MRI. Proceedings of the National Academy of Sciences,
U.S.A., 104, 1377–1382.
Hornak, J., OʼDoherty, J. P., Bramham, J., Rolls, E., Morris, R.,
Bullock, P., et al. (2004). Reward-related reversal learning
after surgical excisions in orbito-frontal or dorsolateral
prefrontal cortex in humans. Journal of Cognitive Neuroscience,
16, 463–478.
Jarcho, J. M., Benson, B. E., Plate, R. C., Guyer, A. E., Detloff,
A. M., Pine, D. S., et al. (2012). Developmental effects of
decision-making on sensitivity to reward: An fMRI study.
Developmental Cognitive Neuroscience, 2, 437–447.
Jocham, G., Klein, T. A., & Ullsperger, M. (2011). Dopamine-
mediated reinforcement learning signals in the striatum and
ventromedial prefrontal cortex underlie value-based choices.
The Journal of Neuroscience, 31, 1606–1613.
Kahneman, D., & Tversky, A. (1979). Prospect theory:
An analysis of decision under risk. Econometrica, 47,
263–291.
Klein, T. A., Neumann, J., Reuter, M., Hennig, J., von Cramon,
D. Y., & Ullsperger, M. (2007). Genetically determined
differences in learning from errors. Science, 318, 1642–1645.
Krugel, L. K., Biele, G., Mohr, P. N. C., Li, S., & Heekeren, H. R.
(2009). Genetic variation in dopaminergic neuromodulation
influences the ability to rapidly and flexibly adapt decisions.
Proceedings of the National Academy of Sciences, U.S.A.,
106, 17951–17956.
Luce, R. D. (1959). Individual choice behavior: A theoretical
analysis. New York, 115, 191–243.
Montague, P. R. (2006). Why choose this book? How we make
decisions. New York: EP Dutton.
2680
Journal of Cognitive Neuroscience
Volume 26, Number 12
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
c
4
n
8
_
6
a
/
_
j
0
o
0
c
6
n
7
7
_
a
p
_
d
0
0
b
6
y
7
g
7
u
.
e
p
s
t
d
o
f
n
b
0
y
8
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
t
f
.
/
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
Montague, P. R., Hyman, S. E., & Cohen, J. D. (2004).
Computational roles for dopamine in behavioural control.
Nature, 431, 760–767.
Nielsen, F. A., & Hansen, L. K. (2002). Automatic anatomical
labeling of Talairach coordinates and generation of volumes
of interest via the BrainMap database. Neuroimage, 16, 2–6.
OʼDoherty, J. P., Dayan, P., Friston, K., Critchley, H., & Dolan,
R. J. (2003). Temporal difference models and reward-related
learning in the human brain. Neuron, 38, 329–337.
OʼDoherty, J. P., Kringelbach, M. L., Rolls, E. T., Hornak, J., &
Andrews, C. (2001). Abstract reward and punishment
representations in the human orbitofrontal cortex. Nature
Neuroscience, 4, 95–102.
Padmanabhan, A., Geier, C. F., Ordaz, S. J., Teslovich, T., &
Luna, B. (2011). Developmental changes in brain function
underlying the influence of reward processing on inhibitory
control. Developmental Cognitive Neuroscience, 1, 517–529.
Penolazzi, B., Gremigni, P., & Russo, P. M. (2012). Impulsivity
and reward sensitivity differentially influence affective and
deliberative risky decision making. Personality and
Individual Differences, 53, 655–659.
Pessiglione, M., Seymour, B., Flandin, G., Dolan, R. J., & Frith,
C. D. (2006). Dopamine-dependent prediction errors underpin
reward-seeking behaviour in humans. Nature, 442, 1042–1045.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery,
B. P. (2007). Numerical recipes in C: The art of scientific
computing (pp. 727–729). Cambridge: Cambridge
University Press.
Remijnse, P. L., Nielen, M., Uylings, H., & Veltman, D. J. (2005).
Neural correlates of a reversal learning task with an affectively
neutral baseline: An event-related fMRI study. Neuroimage,
26, 609–618.
Ripke, S., Hübner, T., Mennigen, E., Müller, K. U., Rodehacke,
S., Schmidt, D., et al. (2012). Reward processing and inter-
temporal decision making in adults and adolescents: The role
of impulsivity and decision consistency. Brain Research,
1478, 36–47.
Robins, L. N., Wing, J., Wittchen, H. U., Helzer, J. E., Babor,
T. F., Burke, J., et al. (1988). The composite international
diagnostic interview: An epidemiologic instrument suitable
for use in conjunction with different diagnostic systems and
in different cultures. Archives of General Psychiatry, 45, 1069.
Schultz, W. (2006). Behavioral theories and the neurophysiology
of reward. Annual Review of Psychology, 57, 87–115.
Schultz, W., Dayan, P., & Montague, P. R. (1997). A neural
substrate of prediction and reward. Science, 275, 1593–1599.
Somerville, L. H., Jones, R. M., & Casey, B. (2010). A time of
change: Behavioral and neural correlates of adolescent
sensitivity to appetitive and aversive environmental cues.
Brain and Cognition, 72, 124–133.
Spear, L. P. (2000). The adolescent brain and age-related
behavioral manifestations. Neuroscience & Biobehavioral
Reviews, 24, 417–463.
Steinberg, L. (2005). Cognitive and affective development in
adolescence. Trends in Cognitive Sciences, 9, 69–74.
Steinberg, L. (2010). A dual systems model of adolescent
risk-taking. Developmental Psychobiology, 52, 216–224.
Talairach, J., & Tournoux, P. (1988). Co-planar stereotaxic
atlas of the human brain ( Vol. 147). New York: Thieme.
Tversky, A., & Kahneman, D. (1991). Loss aversion in riskless
choice: A reference-dependent model. The Quarterly
Journal of Economics, 106, 1039–1061.
Vaidya, J. G., Knutson, B., OʼLeary, D. S., Block, R. I., &
Magnotta, V. (2013). Neural sensitivity to absolute and relative
anticipated reward in adolescents. PloS One, 8, e58708.
van der Schaaf, M. E., Warmerdam, E., Crone, E. A., & Cools, R.
(2011). Distinct linear and non-linear trajectories of reward
and punishment reversal learning during development:
Relevance for dopamineʼs role in adolescent decision
making. Developmental Cognitive Neuroscience, 1, 578–590.
van Leijenhorst, L., Moor, B. G., Op de Macks, Z. A., Rombouts,
S. A. R. B., Westenberg, P. M., & Crone, E. A. (2010). Adolescent
risky decision-making: Neurocognitive development of reward
and control regions. Neuroimage, 51, 345–355.
van Leijenhorst, L., Zanolie, K., Van Meel, C. S., Westenberg,
P. M., Rombouts, S. A. R. B., & Crone, E. A. (2010). What
motivates the adolescent? Brain regions mediating reward
sensitivity across adolescence. Cerebral Cortex, 20, 61–69.
Wittchen, H. U., & Pfister, H. (1997). DIA-X-Interview.
Instruktionsmanual zur Durchführung von DIA-X-
Interviews. Frankfurt: Swets & Zeitlinger.
Xue, G., Xue, F., Droutman, V., Lu, Z.-L., Bechara, A., & Read, S.
(2013). Common neural mechanisms underlying reversal
learning by reward and punishment. PloS One, 8, e82169.
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
6
/
1
2
2
6
/
2
1
6
2
7
/
0
2
1
6
9
7
4
0
8
/
2
1
2
1
7
8
o
2
c
4
n
8
_
6
a
/
_
j
0
o
0
c
6
n
7
7
_
a
p
_
d
0
0
b
6
y
7
g
7
u
.
e
p
s
t
d
o
f
n
b
0
y
8
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
.
/
f
t
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
Javadi, Schmidt, and Smolka
2681