Word Acquisition in Neural Language Models

Tyler A. Chang1,2, Benjamin K. Bergen1
1Department of Cognitive Science
2Halıcıo˘glu Data Science Institute
Université de Californie, San Diego, Etats-Unis
{tachang, bkbergen}@ucsd.edu

Abstrait

We investigate how neural language mod-
els acquire individual words during training,
extracting learning curves and ages of acqui-
sition for over 600 words on the MacArthur-
Bates Communicative Development Inventory
(Fenson et al., 2007). Drawing on studies of
word acquisition in children, we evaluate mul-
tiple predictors for words’ ages of acquisition
in LSTMs, BERT, and GPT-2. We find that
the effects of concreteness, word length, et
lexical class are pointedly different in children
and language models, reinforcing the impor-
tance of interaction and sensorimotor experi-
ence in child language acquisition. Language
models rely far more on word frequency than
enfants, mais, like children, they exhibit slower
learning of words in longer utterances. Inter-
estingly, models follow consistent patterns
during training for both unidirectional and bidi-
rectional models, and for both LSTM and
Transformer architectures. Models predict
based on unigram token frequencies early in
entraînement, before transitioning loosely to bigram
probabilities, eventually converging on more
nuanced predictions. These results shed light
on the role of distributional learning mecha-
nisms in children, while also providing insights
for more human-like language acquisition in
language models.

1

Introduction

Language modeling, predicting words
depuis
contexte, has grown increasingly popular as a pre-
training task in NLP in recent years; neural lan-
guage models such as BERT (Devlin et al., 2019),
ELMo (Peters et al., 2018), and GPT (Brown et al.,
2020) have produced state-of-the-art performance
on a wide range of NLP tasks. There is now a sub-
stantial amount of work assessing the linguistic
information encoded by language models (Rogers
et coll., 2020); in particular, behavioral approaches
from psycholinguistics and cognitive science have

1

been applied to study language model predictions
(Futrell et al., 2019; Ettinger, 2020). From a
cognitive perspective, language models are of
theoretical interest as distributional models of lan-
guage, agents that learn exclusively from statistics
over language (Boleda, 2020; Lenci, 2018).

Cependant, previous psycholinguistic studies of
language models have nearly always focused on
fully-trained models, precluding comparisons to
the wealth of literature on human language acqui-
sition. There are limited exceptions. Rumelhart
and McClelland (1986) famously studied past
tense verb form learning in phoneme-level neural
networks during training, a study which was repli-
cated in more modern character-level recurrent
neural networks (Kirov and Cotterell, 2018). Comment-
jamais, these studies focused only on sub-word fea-
photos. There remains a lack of research on language
acquisition in contemporary language models,
which encode higher level features such as syntax
and semantics.

As an initial step towards bridging the gap
between language acquisition and language mod-
eling, we present an empirical study of word
acquisition during training in contemporary lan-
guage models,
including LSTMs, GPT-2, et
BERT. We consider how variables such as word
frequency, concreteness, and lexical class con-
tribute to words’ ages of acquisition in language
models. Each of our selected variables has effects
on words’ ages of acquisition in children; our lan-
guage model results allow us to identify the extent
to which each effect in children can or cannot
be attributed in principle to distributional learn-
ing mechanisms.

Enfin, to better understand how computational
models acquire language, we identify consistent
patterns in language model training across archi-
tectures. Our results suggest that language models
may acquire traditional distributional statistics
such as unigram and bigram probabilities in a

Transactions of the Association for Computational Linguistics, vol. 10, pp. 1–16, 2022. https://doi.org/10.1162/tacl a 00444
Action Editor: Micha Elsner. Submission batch: 5/2021; Revision batch: 8/2021; Published 1/2022.
c(cid:2) 2022 Association for Computational Linguistics. Distributed under a CC-BY 4.0 Licence.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
4
4
4
1
9
8
6
5
8
9

/

/
t

je

un
c
_
un
_
0
0
4
4
4
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

systematic way. Understanding how language
models acquire language can lead to better archi-
tectures and task designs for future models, alors que
also providing insights into distributional learning
mechanisms in people.

2 Related Work

Our work draws on methodologies from word ac-
quisition studies in children and psycholinguistic
evaluations of language models. Dans cette section,
we briefly outline both lines of research.

2.1 Child Word Acquisition

Child development researchers have previously
studied word acquisition in children, identifying
variables that help predict words’ ages of ac-
quisition in children. In Wordbank, Frank et al.
(2017) compiled reports from parents reporting
when their child produced each word on the
MacArthur-Bates Communicative Development
Inventory (CDI; Fenson et al., 2007). For each
word w, Braginsky et al. (2016) fitted a logistic
curve predicting the proportion of children that
produce w at different ages; they defined a word’s
age of acquisition as the age at which 50% of chil-
dren produce w. Variables such as word frequency,
word length, lexical class, and concreteness were
found to influence words’ ages of acquisition in
children across languages. Recently, it was shown
that fully trained LSTM language model surprisals
are also predictive of words’ ages of acquisition
in children (Portelance et al., 2020). Cependant,
no studies have evaluated ages of acquisition in
language models themselves.

2.2 Evaluating Language Models

Recently, there has been substantial research eval-
uating language models using psycholinguistic
approaches, reflecting a broader goal of interpret-
ing language models (BERTology; Rogers et al.,
2020). Par exemple, Ettinger (2020) used the out-
put token probabilities from BERT in carefully
constructed sentences, finding that BERT learns
commonsense and semantic relations to some degree,
although it struggles with negation. Gulordava
et autres. (2018) found that LSTM language models
recognize long distance syntactic dependencies;
cependant, they still struggle with more complicated
constructions (Marvin and Linzen, 2018).

These psycholinguistic methodologies do not
rely on specific language model architectures or

fine-tuning on a probe task. Notably, because these
approaches rely only on output token probabilities
from a given language model, they are well suited
to evaluations early in training, when fine-tuning
on downstream tasks is unfruitful. That said, pre-
vious language model evaluation studies have fo-
cused on fully-trained models, progressing largely
independently from human language acquisition
literature. Our work seeks to bridge this gap.

3 Method

We trained unidirectional and bidirectional lan-
guage models with LSTM and Transformer ar-
chitectures. We quantified each language model’s
age of acquisition for each word in the CDI
(Fenson et al., 2007). Similar to word acquisition
studies in children, we identified predictors for
words’ ages of acquisition in language models.1

3.1 Language Models

Datasets and Training Language models were
trained on a combined corpus containing the
BookCorpus (Zhu et al., 2015) and WikiText-103
datasets (Merity et al., 2017). Following Devlin
et autres. (2019), each input sequence was a sentence
pair; the training dataset consisted of 25.6M sen-
tence pairs. The remaining sentences (5.8M pairs)
were used for evaluation and to generate word
learning curves. Sentences were tokenized using
the unigram language model
tokenizer imple-
mented in SentencePiece (Kudo and Richardson,
2018). Models were trained for 1M steps, avec
batch size 128 and learning rate 0.0001. As a
metric for overall language model performance,
we report evaluation perplexity scores in Table 1.
We include evaluation loss curves, full training
details, and hyperparameters in Appendix A.1.

Transformers The two Transformer models
followed the designs of GPT-2 (Radford et al.,
2019) and BERT (Devlin et al., 2019), allowing us
to evaluate both a unidirectional and bidirectional
Transformer language model. GPT-2 was trained
with the causal
language modeling objective,
where each token representation is used to predict
the next token; the masked self-attention mech-
anism allows tokens to attend only to previous
tokens in the input sequence. In contrast, BERT
used the masked language modeling objective,

1Code and data are available at https://github.com

/tylerachang/word-acquisition-language-models.

2

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
4
4
4
1
9
8
6
5
8
9

/

/
t

je

un
c
_
un
_
0
0
4
4
4
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

# Parameters

Perplexity

LSTM
GPT-2
BiLSTM
BERT

37M.
108M.
51M.
109M.

54.8
30.2
9.0
7.2

Tableau 1: Parameter counts and evaluation per-
plexities for the trained language models. Pour
reference, the pre-trained BERT base model from
Huggingface reached a perplexity of 9.4 on our
evaluation set. Additional perplexity comparisons
with comparable models are included in Ap-
pendix A.1.

where masked tokens are predicted from sur-
rounding tokens in both directions.

Our BERT model used the base size model from
Devlin et al. (2019). Our GPT-2 model used the
similar-sized model from Radford et al. (2019),
equal in size to the original GPT model. Parameter
counts are listed in Table 1. Transformer models
were trained using the Huggingface Transformers
library (Wolf et al., 2020).

LSTMs We also trained both a unidirectional
and bidirectional LSTM language model, chaque
with three stacked LSTM layers. Similar to GPT-2,
the unidirectional LSTM predicted the token at
time t from the hidden state at time t − 1. Le
bidirectional LSTM (BiLSTM) predicted the to-
ken at time t from the sum of the hidden states at
times t − 1 and t + 1 (Aina et al., 2019).

3.2 Learning Curves and Ages of Acquisition

We sought to quantify each language model’s
ability to predict individual words over the course
of training. We considered all words in the CDI
that were considered one token by the language
models (611 out of 651 words).

For each such token w, we identified up to
512 occurrences of w in the held-out portion of
the language modeling dataset.2 To evaluate a
language model at training step s, we fed each
sentence pair into the model, attempting to predict
the masked token w. We computed the surprisal:

2We only selected sentence pairs with at least eight tokens
of context, unidirectionally or bidirectionally depending on
model architecture. Ainsi, the unidirectional and bidirectional
samples differed slightly. Most tokens (92.3%) had the max-
imum of 512 samples both unidirectionally and bidirection-
ally, and all tokens had at least 100 samples in both cases.

Chiffre 1: Learning curves for the word ‘‘walk’’ in a
BERT language model and human children. Blue hori-
zontal lines indicate age of acquisition cutoffs. The blue
curve represents the fitted sigmoid function based on
the language model surprisals during training (black).
Child data obtained from Frank et al. (2017).

− log2(P. (w)) averaged over all occurrences of w
to quantify the quality of the models’ predictions
for word w at step s (Levy, 2008; Goodkind and
Bicknell 2018).

We computed this average surprisal for each
target word at approximately 200 different steps
during language model training, sampling more
heavily from earlier training steps, prior to model
convergence. The selected steps are listed in Ap-
pendix A.1. By plotting surprisals over the course
of training, we obtained a learning curve for each
word, generally moving from high surprisal to
low surprisal. The surprisal axis in our plots is
reversed to reflect increased understanding over
the course of training, consistent with plots show-
ing increased proportions of children producing a
given word over time (Frank et al., 2017).

For each learning curve (4 language model
architectures × 611 words), we fitted a sigmoid
function to model the smoothed acquisition of
word w. Sample learning curves are shown in
Figures 1 et 2.

Age of Acquisition To extract age of acquisi-
tion from a learning curve, we established a cut-
off surprisal where we considered a given word
‘‘learned.’’ In child word acquisition studies, un
analogous cutoff is established when 50% of chil-
dren produce a word (Braginsky et al., 2016).

Following this precedent, we determined our
cutoff to be 50% between a baseline surprisal
(predicting words based on random chance) et
the minimum surprisal attained by the model for
word w. We selected the random chance baseline
to best reflect a language model’s ability to predict
a word with no access to any training data, similar

3

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
4
4
4
1
9
8
6
5
8
9

/

/
t

je

un
c
_
un
_
0
0
4
4
4
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 2: Learning curves for the word ‘‘eat’’ for all four language model architectures. Blue horizontal lines
indicate age of acquisition cutoffs, and blue curves represent fitted sigmoid functions.

to an infant’s language-specific knowledge prior
to any linguistic exposure. We selected minimum
surprisal as our other bound to reflect how well
a particular word can eventually be learned by a
particular language model, analogous to an adult’s
understanding of a given word.

For each learning curve, we found the inter-
section between the fitted sigmoid and the cutoff
surprisal value. We defined age of acquisition for
a language model as the corresponding training
step, on a log10 scale. Sample cutoffs and ages of
acquisition are shown in Figures 1 et 2.

3.3 Predictors for Age of Acquisition

As potential predictors for words’ ages of acqui-
sition in language models, we selected variables
that are predictive of age of acquisition in children
(Braginsky et al., 2016). When predicting ages
of acquisition in language models, we computed
word frequencies and utterance lengths over the
language model training corpus. Our five selected
predictors were:

• Log-frequency: The natural log of the word’s

per-1000 token frequency.

• MLU: We computed the mean length of
utterance as the mean length of sequences
containing a given word.3 MLU has been
used as a metric for the complexity of syn-
tactic contexts in which a word appears (Roy
et coll., 2015).

• n-chars: As in Braginsky et al. (2016), nous
used the number of characters in a word as a
coarse proxy for the length of a word.

3We also considered a unidirectional MLU metric (count-
ing only previous tokens) for the unidirectional models,
finding that it produced similar results.

• Concreteness: We used human-generated
concreteness norms from Brysbaert et al.
(2014), rated on a five-point scale. We im-
puted missing values (3% of words) en utilisant
the mean concreteness score.

• Lexical class: We used the lexical classes an-
notated in Wordbank. Possible lexical classes
were Noun, Verb, Adjective, Function Word,
and Other.

We ran linear regressions with linear terms for
each predictor. To determine statistical signifi-
cance for each predictor, we ran likelihood ratio
tests, comparing the overall regression (y compris
the target predictor) with a regression including
all predictors except the target. To determine the
direction of effect for each continuous predictor,
we used the sign of the coefficient in the overall
regression.

As a potential concern for interpreting regres-
sion coefficient signs, we assessed collinearities
between predictors by computing the variance in-
flation factor (VIF) for each predictor. No VIF
exceeded 5.0,4 although we did observe moderate
correlations between log-frequency and n-chars
(r = −0.49), and between log-frequency and
concreteness (r = −0.64). These correlations
are consistent with those identified for child-
directed speech in Braginsky et al. (2016). À
ease collinearity concerns, we considered single-
predictor regressions for each predictor, en utilisant
adjusted predictor values after accounting for log-
frequency (residuals after regressing the predictor
over log-frequency). In all cases, the coefficient
sign in the adjusted single predictor regression
was consistent with the sign of the coefficient in
the overall regression.

4Common VIF cutoff values are 5.0 et 10.0.

4

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
4
4
4
1
9
8
6
5
8
9

/

/
t

je

un
c
_
un
_
0
0
4
4
4
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Log-frequency
MLU
n-chars
Concreteness
Lexical class

R2

LSTM
∗∗∗(−)

∗∗∗(−)

GPT-2
∗∗∗(−)
∗∗(+)
∗∗∗(−)

BiLSTM
∗∗∗(−)
∗∗∗(+)
∗∗∗(−)

BERT
∗∗∗(−)
∗∗∗(+)
∗∗∗(−)

∗∗∗

∗∗∗

Children
∗∗∗(−)
∗∗∗(+)
∗∗(+)
∗∗∗(−)
∗∗∗

0.93

0.92

0.95

0.94

0.43

Tableau 2: Significant predictors for a word’s age of acquisition are marked by aste-
risks (p < 0.05∗; p < 0.01∗∗; p < 0.001∗∗∗). Signs of coefficients are notated in parentheses. The R2 denotes the adjusted R2 in a regression using all five predictors. When lexical class (the sole categorical predic- tor) reached significance based on the likelihood ratio test, we ran a one-way analysis of covariance (ANCOVA) with log-frequency as a covariate. The ANCOVA ran a standard ANOVA on the age of acquisition residuals after regressing over log-frequency. We used Tukey’s honestly sig- nificant difference (HSD) test to assess pairwise differences between lexical classes. 3.4 Age of Acquisition in Children For comparison, we used the same variables to predict words’ ages of acquisition in chil- dren, as in Braginsky et al. (2016). We obtained smoothed ages of acquisition for children from the Wordbank dataset (Frank et al., 2017). When predicting ages of acquisition in children, we com- puted word frequencies and utterance lengths over the North American English CHILDES corpus of child-directed speech (MacWhinney, 2000). Notably, CHILDES contained much shorter sentences on average than the language model training corpus (mean sentence length 4.50 to- kens compared to 15.14 tokens). CDI word log-frequencies were only moderately correlated between the two corpora (r = 0.78). This aligns with previous work finding that child-directed speech contains on average fewer words per utter- ance, smaller vocabularies, and simpler syntactic structures than adult-directed speech (Soderstrom, 2007). These differences were likely compounded by differences between spoken language in the CHILDES corpus and written language in the language model corpus. We computed word fre- quencies and MLUs separately over the two corpora to ensure that our predictors accurately reflected the learning environments of children and the language models. We also note that the language model training corpus was much larger overall than the CHILDES corpus. CHILDES contained 7.5M tokens, while the language model corpus contained 852.1M to- kens. Children are estimated to hear approximately 13K words per day (Gilkerson et al., 2017), for a total of roughly 19.0M words during their first four years of life. Because contemporary language models require much more data than children hear, the models do not necessarily reflect how children would learn if restricted solely to linguis- tic input. Instead, the models serve as examples of relatively successful distributional learners, establishing how one might expect word acquisi- tion to progress according to effective distribu- tional mechanisms. 4 Results Significant predictors of age of acquisition are shown in Table 2, comparing children and each of the four language model architectures. 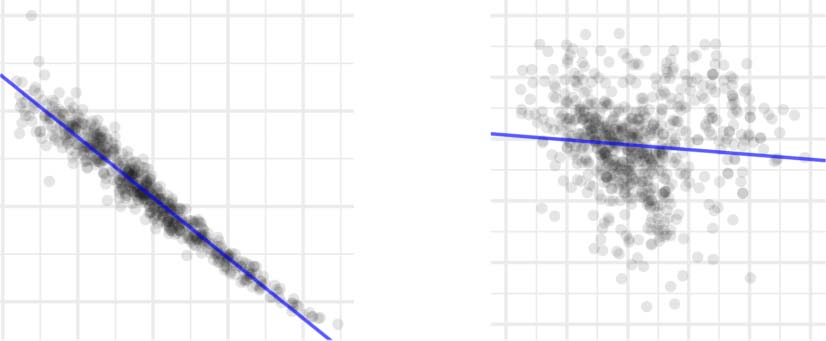Log-frequency In children and all four lan- guage models, more frequent words were learned earlier (a negative effect on age of acquisition). As shown in Figure 3, this effect was much more pro- nounced in language models (adjusted R2 = 0.91 to 0.94) than in children (adjusted R2 = 0.01).5 5Because function words are frequent but acquired later by children, a quadratic model of log-frequency on age of acqui- sition in children provided a slightly better fit (R2 = 0.03) if not accounting for lexical class. A quadratic model of log-frequency also provided a slightly better fit for unidirec- tional language models (R2 = 0.93 to 0.94), particularly for high-frequency words; in language models, this could be due either to a floor effect on age of acquisition for high-frequency words or to slower learning of function words. Regardless, significant effects of other predictors remained the same when using a quadratic model for log-frequency. 5 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Concreteness Although children overall learn more concrete words earlier, the language models showed no significant effects of concreteness on age of acquisition. This entails that the effects in children cannot be explained by correlations between concrete words and easier distributional learning contexts. Again, this highlights the im- portance of sensorimotor experience and concep- tual development in explaining the course of child language acquisition. Lexical Class The bidirectional language mod- els showed no significant effects of lexical class on age of acquisition. In other words, the differ- ences between lexical classes were sufficiently ac- counted for by the other predictors for BERT and the BiLSTM. However, in the unidirectional lan- guage models (GPT-2 and the LSTM), nouns and function words were acquired later than adjectives and verbs.6 This contrasts with children learning English, who on average acquired nouns ear- lier than adjectives and verbs, acquiring function words last.7 Thus, children’s early acquisition of nouns cannot be explained by distributional properties of English nouns, which are acquired later by uni- directional language models. This result is com- patible with the hypothesis that nouns are acquired earlier because they often map to real world objects; function words might be acquired later because their meanings are less grounded in sen- sorimotor experience. It has also been argued that children might have an innate bias to learn ob- jects earlier than relations and traits (Markman, 1994). Lastly, it is possible that the increased sa- lience of sentence-final positions (which are more likely to contain nouns in English and related lan- guages) facilitates early acquisition of nouns in children (Caselli et al., 1995). Consistent with these hypotheses, our results suggest that English verbs and adjectives may be easier to learn from a purely distributional perspective, but children ac- quire nouns earlier based on sensorimotor, social, or cognitive factors. 6Significant pairwise comparisons between lexical classes are listed in Appendix A.2. 7There is ongoing debate around the existence of a uni- versal ‘‘noun bias’’ in early word acquisition. For instance, Korean and Mandarin-speaking children have been found to acquire verbs earlier than nouns, although this effect appears sensitive to context and the measure of vocabulary acquisition (Choi and Gopnik, 1995; Tardif et al., 1999). Figure 3: Effects of log-frequency on words’ ages of acquisition (AoA) in the BiLSTM and children. The BiLSTM was the language model architecture with the largest effect of log-frequency (adjusted R2 = 0.94). The sizeable difference in log-frequency predic- tivity emphasizes the fact that language models learn exclusively from distributional statistics over words, while children have access to additional social and sensorimotor cues. MLU Except in unidirectional LSTMs, MLU had a positive effect on a word’s age of acquisition in language models. Interestingly, we might have expected the opposite effect (particularly in Trans- formers) if additional context (longer utterances) facilitated word learning. Instead, our results are consistent with effects of MLU in children; words in longer utterances are learned later, even after accounting for other variables. The lack of effect in unidirectional LSTMs could simply be due to LSTMs being the least sensitive to contextual in- formation of the models under consideration. The positive effect of MLU in other models suggests that complex syntactic contexts may be more diffi- cult to learn through distributional learning alone, which might partly explain why children learn words in longer utterances more slowly. n-chars There was a negative effect of n-chars on age of acquisition in all four language models; longer words were learned earlier. This contrasts with children, who acquire shorter words earlier. This result is particularly interesting because the language models we used have no information about word length. We hypothesize that the ef- fect of n-chars in language models may be driven by polysemy, which is not accounted for in our regressions. Shorter words tend to be more pol- ysemous (a greater diversity of meanings; Casas et al., 2019), which could lead to slower learning in language models. In children, this effect may be overpowered by the fact that shorter words are easier to parse and produce. 6 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Language models Children First a, and, for, he, her, baby, ball, bye, his, I, it, my, of, on, daddy, dog, hi, she, that, the, to, was, with, you Last bee, bib, choo, cracker, crayon, mommy, moo, no, shoe, uh, woof, yum above, basement, beside, country, giraffe, glue, kitty, downtown, each, moose, pancake, popsicle, quack, hate, if, poor, walker, which, would, rooster, slipper, tuna, yourself yum, zebra Table 3: First and last words acquired by the lan- guage models and children. For language models, we identified words that were in the top or bot- tom 5% of ages of acquisition for all models. For children, we identified words in the top or bottom 2% of ages of acquisition. 4.1 First and Last Learned Words As a qualitative analysis, we compared the first and last words acquired by the language models and children, as shown in Table 3. In line with our previous results, the first and last words learned by the language models were largely determined by word frequencies. The first words acquired by the models were all in the top 3% of frequent words, and the last acquired words were all in the bottom 15%. Driven by this effect, many of the first words learned by the language models were function words or pronouns. In contrast, many of the first words produced by children were single-word expressions, such as greetings, exclamations, and sounds. Children acquired several highly frequent words late, such as ‘‘if,’’ which is in the 90th frequency percentile of the CHILDES corpus. Of course, direct comparisons between the first and last words acquired by the children and language models are confounded by differing datasets and learning environments, as detailed in Section 3.4. 4.2 Age of Acquisition vs. Minimum Surprisal Next, we assessed whether a word’s age of ac- quisition in a language model could be predicted from how well that word was learned in the fully trained model. To do this, we considered the min- imum surprisal attained by each language model for each word. We found a significant effect of minimum surprisal on age of acquisition in all four language models, even after accounting for all five other predictors (using likelihood ratio tests; p < 0.001). In part, this is likely because the acquisition cutoff for each word’s fitted sigmoid was dependent on the word’s minimum surprisal. It could then be tempting to treat minimum sur- prisal as a substitute for age of acquisition in lan- guage models; this approach would require only publicly available fully trained language mod- els. Indeed, the correlation between minimum surprisal and age of acquisition was substantial (Pearson’s r = 0.88 to 0.92). However, this cor- relation was driven largely by effects of log- frequency, which had a large negative effect on both metrics. When adjusting minimum surprisal and age of acquisition for log-frequency (using residuals after linear regressions), the correlation decreased dramatically (Pearson’s r = 0.22 to 0.46). While minimum surprisal accounts for a sig- nificant amount of variance in words’ ages of ac- quisition, the two metrics are not interchangeable. 4.3 Alternative Age of Acquisition Definitions Finally, we considered alternative operationaliza- tions of words’ ages of acquisition in language models. For instance, instead of defining an acqui- sition cutoff at 50% between random chance and the minimum surprisal for each word, we could consider the midpoint of each fitted sigmoid curve. This method would be equivalent to defining up- per and lower surprisal baselines at the upper and lower asymptotes of the fitted sigmoid, relying on the assumption that these asymptotes roughly ap- proximate surprisal values before and after train- ing. However, this assumption fails in cases where the majority of a word’s learning curve is mod- eled by only a sub-portion of the fitted sigmoid. For example, for the word ‘‘for’’ in Figure 4, the high surprisal asymptote is at 156753.5, com- pared to a random chance surprisal of 14.9 and a minimum surprisal of 4.4. Using the midpoint age of acquisition in this case would result in an age of acquisition of −9.6 steps (log10). We also considered alternative cutoff propor- tions (replacing 50%) in our original age of acquisition definition. We considered cutoffs at each possible increment of 10%. The signs of nearly all significant coefficients in the overall 7 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 4: LSTM learning curves for the words ‘‘for,’’ ‘‘eat,’’ ‘‘drop,’’ and ‘‘lollipop.’’ Blue horizontal lines indicate age of acquisition cutoffs, and blue curves represent fitted sigmoid functions. Green dashed lines indicate the surprisal if predicting solely based on unigram probabilities (raw token frequencies). Early in training, language model surprisals tended to shift towards the unigram frequency-based surprisals. regressions (see Table 2) remained the same for all language models regardless of cutoff proportion.8 5 Language Model Learning Curves The previous sections identified factors that pre- dict words’ ages of acquisition in language mod- els. We now proceed with a qualitative analysis of the learning curves themselves. We found that language models learn traditional distributional statistics in a systematic way. 5.1 Unigram Probabilities First, we observed a common pattern in word learning curves across model architectures. As ex- pected, each curve began at the surprisal value corresponding to random chance predictions. Then, as shown in Figure 4, many curves shifted towards the surprisal value corresponding to raw unigram probabilities (i.e., based on raw token frequencies). This pattern was particularly pronounced in LSTM-based language models, although it appeared in all architectures. Inter- estingly, the shift occurred even if the unigram surprisal was higher (or ‘‘worse’’) than random- chance surprisal, as demonstrated by the word ‘‘lollipop’’ in Figure 4. Thus, we posited that lan- guage models pass through an early stage of train- ing where they approximate unigram probabilities. To test this hypothesis, we aggregated each model’s predictions for randomly masked tokens in the evaluation dataset (16K sequences), includ- ing tokens not on the CDI. For each saved training step, we computed the average Kullback-Leibler 8The only exception was a non-significant positive co- efficient for n-chars in BERT with a 90% acquisition cutoff. (KL) divergence between the model predictions and the unigram frequency distribution. For com- parison, we also computed the KL divergence with a uniform distribution (random chance) and with the one-hot true token distribution. We note that the KL divergence with the one-hot true token distribution is equivalent to the cross-entropy loss function using log base two.9 As shown in Figure 5, we plotted the KL diver- gences between each reference distribution and the model predictions over the course of training. As expected, all four language models converged towards the true token distribution (minimizing the loss function) throughout training, diverg- ing from the uniform distribution. Divergence from the uniform distribution could also reflect that the models became more confident in their predictions during training, leading to lower en- tropy predictions. As hypothesized, we also found that all four language models exhibited an early stage of train- ing in which their predictions approached the unigram distribution, before diverging to reflect other information. This suggests that the mod- els overfitted to raw token frequencies early in training, an effect which was particularly pro- nounced in the LSTM-based models. Importantly, because the models eventually diverged from the unigram distribution, the initial unigram phase cannot be explained solely by mutual informa- tion between the true token distribution and uni- gram frequencies. 9All KL divergences were computed using log base two. KL divergences were computed as KL(yref , ˆy), where ˆy was the model’s predicted probability distribution and yref was the reference distribution. 8 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 5: KL divergences between reference distributions and model predictions over the course of training. The KL divergence with the one-hot true token distribution is equivalent to the base two cross-entropy loss. Early in training, the models temporarily overfitted to unigram then bigram probabilities. 5.2 Bigram Probabilities We then ran a similar analysis using bigram probabilities, where each token probability was dependent only on the previous token. A bi- gram distribution Pb was computed for each masked token in the evaluation dataset, based on bigram counts in the training corpus. As dictated by the bigram model definition, we de- fined Pb(wi) = P (wi|wi−1) for unidirectional models, and Pb(wi) = Pb(wi|wi−1, wi+1) ∝ P (wi|wi−1)P (wi+1|wi) for bidirectional models. We computed the average KL divergence be- tween the bigram probability distributions and the language model predictions. As shown in Figure 5, during the unigram learn- ing phase, the bigram KL divergence decreased for all language models. This is likely caused by mu- tual information between the unigram and bigram distributions; as the models approached the uni- gram distribution, their divergences with the bigram distributions roughly approximated the average KL divergence between the bigram and unigram distributions themselves (average KL = 3.86 between unidirectional bigrams and uni- grams; average KL = 5.88 between bidirectional bigrams and unigrams). In other words, the mod- els’ initial decreases in bigram KL divergences can be explained predominantly by unigram fre- quency learning. However, when the models began to diverge from the unigram distribution, they continued to approach the bigram distributions. Each model then hit a local minimum in average bigram KL divergence before diverging from the bigram dis- tributions. This suggests that the models overfitted to bigram probabilities after the unigram learning phase. Thus, it appears that early in training, lan- guage models make predictions based on unigram frequencies, then bigram probabilities, eventually learning to make more nuanced predictions. Of course, this result may not be surprising for LSTM-based language models. Because tokens are fed into LSTMs sequentially, it is intuitive that they would make use of bigram probabilities. Our results confirm this intuition, and they further show that Transformer language models follow a similar pattern. Because BERT and GPT-2 only encode token position information through learned absolute position embeddings before the first self- attention layer, they have no architectural reason to overfit to bigram probabilities based on adja- cent tokens.10 Instead, unigram and bigram learn- ing may be a natural consequence of the language modeling task, or even distributional learning more generally. 6 Discussion We found that language models are highly sen- sitive to basic statistics such as frequency and 10Absolute position embeddings in the Transformers were randomly initialized at the beginning of training. 9 bigram probabilities during training. Their acqui- sition of words is also sensitive to features such as sentence length and (for unidirectional models) lexical class. Importantly, the language models exhibited notable differences with children in the effects of lexical class, word lengths, and con- creteness, highlighting the importance of social, cognitive, and sensorimotor experience in child language development. 6.1 Distributional Learning, Language Modeling, and NLU In this section, we address the broader relationship between distributional language acquisition and contemporary language models. Distributional Learning in People There is on- going work assessing distributional mechanisms in human language learning (Aslin and Newport, 2014). For instance, adults can learn syntactic categories using distributional information alone (Reeder et al., 2017). Adults also show effects of distributional probabilities in reading times (Goodkind and Bicknell, 2018) and neural re- sponses (Frank et al., 2015). In early language acquisition, there is evidence that children are sensitive to transition (bigram) probabilities be- tween phonemes and between words (Romberg and Saffran, 2010), but it remains an open ques- tion to what extent distributional mechanisms can explain effects of other factors (e.g., utterance lengths and lexical classes) known to influence naturalistic language learning. To shed light on this question, we considered neural language models as distributional language learners. If analogous distributional learning mech- anisms were involved in children and language models, then we would observe similar word ac- quisition patterns in children and the models. Our results demonstrate that a purely distributional learner would be far more reliant on frequency than children are. Furthermore, while the effects of utterance length on words’ ages of acquisition in children can potentially be explained by distri- butional mechanisms, the effects of word length, concreteness, and lexical class cannot. Distributional Models Studying language ac- quisition in distributional models also has implica- tions for core NLP research. Pre-trained language models trained only on text data have become central to state-of-the-art NLP systems. Language 10 models even outperform humans on some tasks (He et al., 2021), making it difficult to pinpoint why they perform poorly in other areas. In this work, we isolated ways that language models differ from children in how they acquire words, emphasizing the importance of sensorimotor expe- rience and cognitive development for human-like language acquisition. Future work could inves- tigate the acquisition of syntactic structures or semantic information in language models. Non-distributional Learning We showed that language models acquire words distributional in very different ways from children. Notably, children’s linguistic experience is grounded in sensorimotor and cognitive experience. Children as young as ten months old learn word-object pairings, mapping novel words onto perceptually salient objects (Pruden et al., 2006). By the age of two, they are able to integrate social cues such as eye gaze, pointing, and joint attention (C¸ etinc¸elik et al., 2021). Neural network models of one-word child utterances exhibit vocabulary acquisition trajectories similar to children when only using features from conceptual categories and relations (Nyamapfene and Ahmad, 2007). Our work shows that these grounded and interactive features im- pact child word acquisition in ways that cannot be explained solely by intra-linguistic signals. That said, there is a growing body of work grounding language models using multimodal in- formation and world knowledge. Language mod- els trained on visual and linguistic inputs have achieved state-of-the-art performance on visual question answering tasks (Antol et al., 2015; Lu et al., 2019; Zellers et al., 2021b), and models equipped with physical dynamics modules are more accurate than standard language models at modeling world dynamics (Zellers et al., 2021a). There has also been work building models di- rectly for non-distributional tasks; reinforcement learning can be used for navigation and multi- agent communication tasks involving language (Chevalier-Boisvert et al., 2019; Lazaridou et al., 2017; Zhu et al., 2020). These models highlight the grounded, interactive, and communicative na- ture of language. Indeed, these non-distributional properties may be essential to more human-like natural language understanding (Bender and Koller, 2020; Emerson, 2020). Based on our results for word acquisition in language mod- these multimodal and els, is possible that it l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 non-distributional models could also exhibit more human-like language acquisition. 7 Conclusion In this work, we identified factors that predict words’ ages of acquisition in contemporary lan- guage models. We found contrasting effects of lexical class, word length, and concreteness in children and language models, and we observed much larger effects of frequency in the models than in children. Furthermore, we identified ways that language models aquire unigram and bi- gram statistics early in training. This work paves the way for future research integrating language acquisition and natural language understanding. Acknowledgments We would like to thank the anonymous reviewers for their helpful suggestions, and the Language and Cognition Lab (Sean Trott, James Michaelov, and Cameron Jones) for valuable discussion. We are also grateful to Zhuowen Tu and the Ma- chine Learning, Perception, and Cognition Lab for computing resources. Tyler Chang is par- tially supported by the UCSD HDSI graduate fellowship. References Laura Aina, Kristina Gulordava, and Gemma Boleda. 2019. Putting words in context: LSTM language models and lexical ambiguity. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 3342–3348, Florence, Italy. Association for Computational Linguistics. https://doi .org/10.18653/v1/P19-1324 Stanislaw Antol, Aishwarya Agrawal, Jiasen Lu, Margaret Mitchell, Dhruv Batra, Lawrence Zitnick, and Devi Parikh. 2015. VQA: Visual question answering. In International Confer- ence on Computer Vision. https://doi .org/10.1109/ICCV.2015.279 Richard Aslin and Elissa Newport. 2014. Distribu- tional language learning: Mechanisms and mod- els of category formation. Language Learning, 64:86–105. https://doi.org/10.1111 /lang.12074, PubMed: 26855443 Emily M. Bender and Alexander Koller. 2020. Climbing towards NLU: On meaning, form, and understanding in the age of data. In Pro- ceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 5185–5198, Online. Association for Computational Linguistics. https://doi .org/10.18653/v1/2020.acl-main.463 Gemma Boleda. 2020. Distributional semantics and linguistic theory. Annual Review of Lin- guistics, 6(1):213–234. https://doi.org/10 .1146/annurev-linguistics-011619 -030303 Mika Braginsky, Daniel Yurovsky, Virginia Marchman, and Michael Frank. 2016. From uh-oh to tomorrow: Predicting age of acqui- sition for early words across languages. In the Proceedings of Cognitive Science Society. the Annual Meeting of Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D. Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, Tom Henighan, Rewon Child, Aditya Ramesh, Daniel Ziegler, Jeffrey Wu, Clemens Winter, Chris Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever, and Dario Amodei. 2020. Language models are few-shot learners. In Conference on Neural Information Processing Systems. Marc Brysbaert, Amy Warriner, and Victor Kuperman. 2014. Concreteness ratings for 40 thousand generally known English word lemmas. Behavior Research Methods, 46. https://doi.org/10.3758/s13428-013 -0403-5, PubMed: 24142837 Bernardino Casas, Antoni Hern´andez-Fern´andez, Neus Catal`a, Ramon Ferrer-i-Cancho, and Jaume Baixeries. 2019. Polysemy and brevity versus frequency in language. Computer Speech & Language, 58:19–50. https://doi.org /10.1016/j.csl.2019.03.007 Maria Cristina Caselli, Elizabeth Bates, Paola Casadio, Judi Fenson, Larry Fenson, Lisa Sanderl, and Judy Weir. 1995. A cross- linguistic study of early lexical develop- ment. Cognitive Development, 10(2):159–199. https://doi.org/10.1016/0885-2014 (95)90008-X 11 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Maxime Chevalier-Boisvert, Dzmitry Bahdanau, Salem Lahlou, Lucas Willems, Chitwan Saharia, Thien Huu Nguyen, and Yoshua Bengio. 2019. BabyAI: A platform to study the efficiency of grounded lan- guage learning. In International Conference on Learning Representations. https://doi .org/10.1017/S0305000900009934 sample Soonja Choi and Alison Gopnik. 1995. Early acquisition of verbs in Korean: A cross- linguistic study. Journal of Child Language, 22(3):497–529. Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of deep bidirectional transformers for language the 2019 understanding. In Proceedings of Conference of the North American Chapter of the Association for Computational Linguis- tics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 4171–4186, Minneapolis, Minnesota. Association for Com- putational Linguistics. Guy Emerson. 2020. What are the goals of dis- tributional semantics? In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 7436–7453, Online. Association for Computational Linguis- tics. https://doi.org/10.18653/v1 /2020.acl-main.663 Allyson Ettinger. 2020. What BERT is not: Lessons from a new suite of psycholinguistic diagnostics for language models. Transactions of the Association for Computational Lin- guistics, 8:34–48. https://doi.org/10 .1162/tacl_a_00298 Larry Fenson, Virginia Marchman, Donna Thal, Phillip Dale, Steven Reznick, and Elizabeth Bates. 2007. MacArthur-Bates communicative development inventories. Paul H. Brookes Pub- lishing Company, Baltimore, MD. https:// doi.org/10.1037/t11538-000 Michael Frank, Mika Braginsky, Daniel Yurovsky, and Virginia Marchman. 2017. Wordbank: An open repository for develop- mental vocabulary data. Journal of Child Lan- guage, 44(3):677–694. https://doi.org /10.1017/S0305000916000209, PubMed: 27189114 Stefan Frank, Leun Otten, Giulia Galli, and Gabriella Vigliocco. 2015. The ERP response to the amount of information conveyed by words in sentences. Brain and Language, 140:1–11. https://doi.org/10.1016/j .bandl.2014.10.006, PubMed: 25461915 Richard Futrell, Ethan Wilcox, Takashi Morita, Peng Qian, Miguel Ballesteros, and Roger Levy. 2019. Neural language models as psycho- linguistic subjects: Representations of syntactic the 2019 Confer- state. In Proceedings of ence of the North American Chapter of the Association for Computational Linguistics: Hu- man Language Technologies, Volume 1 (Long and Short Papers), pages 32–42, Minneapolis, Minnesota. Association for Computational Lin- guistics. https://doi.org/10.18653 /v1/N19-1004 Jill Gilkerson, Jeffrey Richards, Steven Warren, Judith Montgomery, Charles Greenwood, D. Kimbrough Oller, John Hansen, and Terrance Paul. 2017. Mapping the early language environment using all-day recordings and au- tomated analysis. American Journal of Speech- LanguagePathology, 26(2):248–265. https:// doi.org/10.1044/2016 AJSLP-15-0169, PubMed: 28418456 Adam Goodkind and Klinton Bicknell. 2018. Pre- dictive power of word surprisal for reading times is a linear function of language model quality. In Proceedings of the 8th Workshop on Cognitive Modeling and Computational Linguistics (CMCL 2018), pages 10–18, Salt Lake City, Utah. Association for Computa- tional Linguistics. https://doi.org/10 .18653/v1/W18-0102 Kristina Gulordava, Piotr Bojanowski, Edouard Grave, Tal Linzen, and Marco Baroni. 2018. Colorless green recurrent networks dream hierarchically. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguis- tics: Human Language Technologies, Volume 1 (Long Papers), pages 1195–1205, New Orleans, Louisiana. Association for Computational Lin- guistics. https://doi.org/10.18653 /v1/N18-1108 Pengcheng He, Xiaodong Liu, Jianfeng Gao, and Weizhu Chen. 2021. DeBERTa: Decoding- enhanced BERT with disentangled attention. In International Conference on Learning Representations. 12 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Christo Kirov and Ryan Cotterell. 2018. Re- current neural networks in linguistic theory: Revisiting pinker and prince (1988) and the the past Association for Computational Linguistics, 6:651–665. https://doi.org/10.1162 /tacl_a_00247 tense debate. Transactions of Taku Kudo and John Richardson. 2018. Sen- tencePiece: A simple and language indepen- dent subword tokenizer and detokenizer for neural text processing. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing: System Demon- strations, pages 66–71, Brussels, Belgium. Association for Computational Linguistics. https://doi.org/10.18653/v1/D18 -2012 Angeliki Lazaridou, Alexander Peysakhovich, and Marco Baroni. 2017. Multi-agent coopera- tion and the emergence of (natural) language. In International Conference on Learning Representations. Alessandro Lenci. 2018. Distributional models of word meaning. Annual Review of Linguis- tics, 4(1):151–171. https://doi.org/10 .1146/annurev-linguistics-030514 -125254 Roger Levy. 2008. Expectation-based syntactic comprehension. Cognition, 106(3):1126–1177. https://doi.org/10.1016/j.cognition .2007.05.006, PubMed: 17662975 Jiasen Lu, Dhruv Batra, Devi Parikh, and Stefan Lee. 2019. ViLBERT: Pretraining task-agnostic visiolinguistic representations for vision-and- language tasks. In Conference on Neural In- formation Processing Systems. Brian MacWhinney. 2000. The CHILDES project: Tools for analyzing talk. Lawrence Erlbaum Associates, Mahwah, NJ. Ellen Markman. 1994. Constraints on word meaning in early language acquisition. Lin- gua, 92:199–227. https://doi.org/10 .1016/0024-3841(94)90342-5 Rebecca Marvin and Tal Linzen. 2018. Targeted syntactic evaluation of language models. In Proceedings of the 2018 Conference on Empir- ical Methods in Natural Language Processing, pages 1192–1202, Brussels, Belgium. Associ- ation for Computational Linguistics. https:// doi.org/10.18653/v1/D18-1151 Stephen Merity, Caiming Xiong, James Bradbury, sen- and Richard Socher. 2017. Pointer tinel mixture models. In Proceedings of the Fifth International Conference on Learning Representations. Abel Nyamapfene and Khurshid Ahmad. 2007. A multimodal model of child language ac- quisition at the one-word stage. In Interna- tional Joint Conference on Neural Networks, 783–788. https://doi.org/10 pages .1109/IJCNN.2007.4371057 Matthew Peters, Mark Neumann, Mohit Iyyer, Matt Gardner, Christopher Clark, Kenton Lee, and Luke Zettlemoyer. 2018. Deep contextu- alized word representations. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers), pages 2227–2237, New Orleans, Louisiana. Association for Com- putational Linguistics. https://doi.org /10.18653/v1/N18-1202 Eva Portelance, Judith Degen, and Michael Frank. 2020. Predicting age of acquisition in early word learning using recurrent neural networks. In Proceedings of CogSci 2020. Shannon M. Pruden, Kathy Hirsh-Pasek, Roberta Michnick Golinkoff, and Elizabeth Hennon. 2006. The birth of words: Ten-month-olds learn words through perceptual salience. Child Devel- opment, 77(2):266–280. https://doi.org /10.1111/j.1467-8624.2006.00869.x, PubMed: 16611171 Alec Radford, Jeff Wu, Rewon Child, David Luan, Dario Amodei, and Ilya Sutskever. 2019. Language models are unsupervised multitask learners. OpenAI Technical Report. Patricia Reeder, Elissa Newport, and Richard Aslin. 2017. Distributional learning of sub- categories in an artificial grammar: Category generalization and subcategory restrictions. Journal of Memory and Language, 97:17–29. https://doi.org/10.1016/j.jml.2017 .07.006, PubMed: 29456288 Anna Rogers, Olga Kovaleva, and Anna Rumshisky. 2020. A primer in BERTology: What we know about how BERT works. Trans- actions of the Association for Computational Linguistics, 8:842–866. https://doi.org /10.1162/tacl_a_00349 13 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Alexa Romberg and Jenny Saffran. 2010. Sta- learning and language acquisition. tistical Wiley Interdisciplinary Reviews in Cognitive Science, 1(6):906–914. https://doi.org /10.1002/wcs.78, PubMed: 21666883 Brandon Roy, Michael Frank, Philip DeCamp, Matthew Miller, and Deb Roy. 2015. Pre- dicting the birth of a spoken word. Proceed- the National Academy of Sciences, ings of 112(41):12663–12668. https://doi.org /10.1073/pnas.1419773112, PubMed: 26392523 David Rumelhart and James McClelland. 1986. On learning the past tenses of English verbs. Parallel Distributed Processing: Explorations in the Microstructure of Cognition, 2. https:// doi.org/10.7551/mitpress/5236.001 .0001 Melanie Soderstrom. 2007. Beyond babytalk: Re-evaluating the nature and content of speech input to preverbal infants. Developmental Re- view, 27(4):501–532. https://doi.org /10.1016/j.dr.2007.06.002 Twila Tardif, Susan Gelman, and Fan Xu. 1999. Putting the ‘‘noun bias’’ in context: A comparison of English and Mandarin. Child Development, 70(3):620–635. https://doi .org/10.1111/1467-8624.00045 Thomas Wolf, Lysandre Debut, Victor Sanh, Julien Chaumond, Clement Delangue, Anthony Moi, Pierric Cistac, Tim Rault, Remi Louf, Morgan Funtowicz, Joe Davison, Sam Shleifer, Patrick von Platen, Clara Ma, Yacine Jernite, Julien Plu, Canwen Xu, Teven Le Scao, Sylvain Gugger, Mariama Drame, Quentin Lhoest, and Alexander Rush. 2020. Transformers: State-of- the-art natural language processing. In Pro- ceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, pages 38–45, On- line. Association for Computational Linguis- tics. https://doi.org/10.18653/v1 /2020.emnlp-demos.6 Rowan Zellers, Ari Holtzman, Matthew Peters, Roozbeh Mottaghi, Aniruddha Kembhavi, Ali Farhadi, and Yejin Choi. 2021a. PIGLeT: Language grounding through neuro-symbolic interaction in a 3D world. In Proceedings the Asso- of the 59th Annual Meeting of ciation for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), pages 2040–2050, Online. Association for Computational Linguistics. https://doi .org/10.18653/v1/2021.acl-long.159 Rowan Zellers, Ximing Lu, Jack Hessel, Youngjae Yu, Jae Sung Park, Jize Cao, Ali Farhadi, and Yejin Choi. 2021b. MERLOT: Multimodal neu- ral script knowledge models. arXiv preprint arXiv:2106.02636v2. Wang Zhu, Hexiang Hu, Jiacheng Chen, Zhiwei Deng, Vihan Jain, Eugene Ie, and Fei Sha. 2020. BabyWalk: Going farther in vision-and- language navigation by taking baby steps. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguis- tics, pages 2539–2556, Online. Association for Computational Linguistics. https://doi .org/10.18653/v1/2020.acl-main.229 Yukun Zhu, Ryan Kiros, Rich Zemel, Ruslan Salakhutdinov, Raquel Urtasun, Antonio Torralba, and Sanja Fidler. 2015. Aligning books and movies: Towards story-like visual explanations by watching movies and reading books. In 2015 IEEE International Conference on Computer Vision, pages 19–27. https:// doi.org/10.1109/ICCV.2015.11 Melis C¸ etinc¸elik, Caroline Rowland, and Tineke Snijders. 2021. Do the eyes have it? A system- atic review on the role of eye gaze in infant lan- guage development. Frontiers in Psychology, 11. https://doi.org/10.3389/fpsyg .2020.589096, PubMed: 33584424 A Appendix A.1 Language Model Training Details Language model training hyperparameters are listed in Table 4. Input and output token em- beddings were tied in all models. Each model was trained using four Titan Xp GPUs. The LSTM, BiLSTM, BERT, and GPT-2 models took four, five, seven, and eleven days to train, respectively. To verify language model convergence, we plotted evaluation loss curves, as in Figure 6. To ensure that our language models reached performance levels comparable to contemporary language models, in Table 6 we report perplexity 14 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Hyperparameter Hidden size Embedding size Vocab size Max sequence length Batch size Train steps Learning rate decay Warmup steps Learning rate Adam (cid:2) Adam β1 Adam β2 Dropout Value 768 768 30004 128 128 1M Linear 10000 1e-4 1e-6 0.9 0.999 0.1 Transformer hyperparameter Value Transformer layers Intermediate hidden size Attention heads Attention head size Attention dropout BERT mask proportion LSTM hyperparameter LSTM layers Context size 12 3072 12 64 0.1 0.15 Value 3 768 Table 4: Language model training hyperparameters. comparisons between our trained models and mod- els with the same architectures in previous work. For BERT, we evaluated the perplexity of Hug- gingface’s pre-trained BERT base uncased model on our evaluation dataset (Wolf et al., 2020). For the remaining models, we used the evalua- tion perplexities reported in the original papers: Gulordava et al. (2018) for the LSTM,11 Radford et al. (2019) for GPT-2 (using the comparably- sized model evaluated on the WikiText-103 dataset), and Aina et al. (2019) for the BiLSTM. Because these last three models were cased, we could not evaluate them directly on our uncased evaluation set. Due to differing vocabularies, 11The large parameter count for the LSTM in Gulordava et al. (2018) is primarily due to its large vocabulary without a decreased embedding size. 15 Figure 6: Evaluation loss during training for all four language models. Note that perplexity is equal to exp(loss). hyperparameters, and datasets, our perplexity comparisons are not definitive; however, they show that our models perform similarly to contemporary language models. Finally, we evaluated each of our models for word acquisition at 208 checkpoint steps during training, sampling more heavily from earlier steps. We evaluated checkpoints at the following steps: • Every 100 steps during the first 1000 steps. • Every 500 steps during the first 10,000 steps. • Every 1000 steps during the first 100,000 steps. • Every 10,000 steps for the remainder of training (ending at 1M steps). A.2 Lexical Class Comparisons We assessed the effect of lexical class on age of acquisition in children and each language model. As described in the text, when lexical class reached significance based on the likelihood ratio test (accounting for log-frequency, MLU, n-chars, and concreteness), we ran a one-way analysis of covariance (ANCOVA) with log-frequency as a covariate. There was a significant effect of lexical class in children and the unidirectional language models (the LSTM and GPT-2; p < 0.001). Pairwise differences between lexical classes were assessed using Tukey’s honestly signifi- cant difference (HSD) test. Significant pairwise differences are listed in Table 5. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 LSTM Adj < Function ∗∗∗ Adj < Nouns ∗∗ Adj < Other ∗∗ Verbs < Function ∗∗∗ Verbs < Nouns ∗∗ Verbs < Other ∗ GPT-2 Adj < Function ∗∗∗ Adj < Other ∗ Verbs < Function ∗∗∗ Verbs < Nouns ∗ Verbs < Other ∗∗ Nouns < Function ∗∗∗ Children Nouns < Adj ∗∗∗ Nouns < Verbs ∗∗∗ Nouns < Function ∗∗∗ Function > Adj ∗∗∗
Function > Verbs ∗∗∗
Function > Other ∗∗∗
Other < Adj ∗∗ Other < Verbs ∗∗ Table 5: Significant pairwise differences between lexical classes when predicting words’ ages of acquisition in language models and children (adjusted p < 0.05∗; p < 0.01∗∗; p < 0.001∗∗∗). A higher value indicates that a lexical class is acquired later on average. The five possible lexical classes were Noun, Verb, Adjective (Adj), Function Word (Function), and Other. Ours Previous work # Params Perplexity # Params Perplexity 37M LSTM GPT-2 108M BiLSTM 51M 109M BERT 54.8 30.2 9.0 7.2 72M a 117M b 42M c 110M d 52.1 37.5 18.1 9.4 Table 6: Rough perplexity comparisons between our trained language models and models with the same architectures in previous work (aGulordava et al., 2018; bRadford et al., 2019; cAina et al., 2019; dWolf et al., 2020). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 4 4 4 1 9 8 6 5 8 9 / / t l a c _ a _ 0 0 4 4 4 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 16

Télécharger le PDF