WHERE YOU COME FROM OR - Recherche en IA spécialisée au MIT

WHERE YOU COME FROM OR

WHERE YOU GO? DISTINGUISHING

BETWEEN SCHOOL QUALITY

AND THE EFFECTIVENESS OF

TEACHER PREPARATION

PROGRAM GRADUATES

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly

(corresponding author)

RAND Corporation

Arlington, VA 22202

kmihaly@rand.org

Daniel McCaffrey

RAND Corporation
Pittsburgh, Pennsylvanie 15213

danielm@rand.org

Tim R. Sass

Department of Economics

Georgia State University

Atlanta, GA 30303

tsass@gsu.edu

J.. R.. Lockwood

RAND Corporation
Pittsburgh, Pennsylvanie 15213

lockwood@rand.org

Abstrait
We consider the challenges and implications of control-
ling for school contextual bias when modeling teacher
preparation program effects. Because teachers are not
randomly distributed across schools, failing to account
for contextual factors in achievement models could bias
preparation program estimates. Including school ﬁxed
effects controls for school environment by relying on
differences among student outcomes within the same
schools to identify the program effects, but this speciﬁ-
cation may be unidentiﬁed. Using statewide data from
Florida, we examine whether the inclusion of school
ﬁxed effects is feasible, compare the sensitivity of the
estimates to assumptions underlying for ﬁxed effects,
and determine what their inclusion implies about the
precision of the preparation program estimates. We dis-
cuss the implications of our results on the feasibility,
precision, and ranking of programs using the school
ﬁxed effect model for policy makers designing teacher
preparation program evaluation systems.

est ce que je:10.1162/EDFP_a_00110
© 2013 Association pour le financement et la politique de l'éducation

459

WHERE YOU COME FROM OR WHERE YOU GO?

INTRODUCTION

1.
Sur 17 Février 2009, President Obama signed into law the American Recov-
ery and Reinvestment Act of 2009. This historic legislation included $4.35 billion for the Race to the Top Fund (RTTT), a competitive grant program designed to reward states that are demonstrating success in raising student achievement scores and developing effective teachers and principals. The se- lection criteria included a provision on improving the effectiveness of teacher and principal preparation programs. Speciﬁcally, it awarded points to states based on “[t]he extent to which the State has a high-quality plan and ambitious yet achievable annual targets to link student achievement and student growth data to the students’ teachers and principals, to link this information to the in-State programs where those teachers and principals were prepared for cre- dentialing, and to publicly report the data for each credentialing program in the State” (USDOE 2009, p. 10). Following the announcement of RTTT winners, in September 2011 the Department of Education released the Obama Administration’s plan for teacher education reform and improvement (USDOE 2011). This compre- hensive agenda describes the disbursement of federal money in three areas: institutional reporting and state accountability, reform ﬁnancing of students preparing to become teachers, and targeted support to institutions that prepare teachers from a diverse background. States will be provided funds to identify top-tier and low performing teacher preparation programs based on three out- come measures: student learning growth, job placement and retention, and customer satisfaction survey results. In highlighting the goals of the new ini- tiative, Secretary Arne Duncan indicated in remarks at the Education Sector Forum that “[un] good feedback loop and accountability system would reward high-performing teacher preparation programs and scale them up. It would help programs in the middle of the spectrum to self-correct and improve. And it would support states to reshape low-performing programs or eliminate low-performers that fail to improve over time, even after receiving help.”1 A persistent and unresolved concern with the value-added models (VAMs) that are proposed for evaluating teacher preparation programs is the existence of contextual effects of the schools where the teachers teach.2 Because teach- ers from any one preparation program are hired in more than one school, the growth in student achievement associated with the preparation program will come from various sources (Boyd et coll.. 2009). En outre, new teachers are not randomly distributed across schools within the state. Par exemple, là 1. See www.ed.gov/news/speeches/new-approach-teacher-education-reform-and-improvement. 2. For the remainder of this article we refer to “preparation programs” as the institutions that train (and certify) teachers, and “schools” as the institutions where they teach after graduation. 460 l Téléchargé à partir du site Web : / / direct . m je t . / / f edu ed p a r t i c e – pdlf / / / / / 8 4 4 5 9 1 6 8 9 5 0 5 e d p _ a _ 0 0 1 1 0 pdf . f par invité 0 7 Septembre 2 0 2 3 Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood is anecdotal evidence from other states that schools tend to hire teachers from local preparation programs, suggesting there is a geographic clustering of pro- gram graduates. Si, in addition to geographic preferences in hiring decisions, student ability is not evenly distributed across schools, then failing to account for school contextual factors could bias preparation program estimates. In this paper we focus on the feasibility and implications of controlling for school contextual factors when comparing teacher preparation programs.3 Policy makers may wish to remove the differences in schools when com- paring teacher preparation programs using student growth measures. One method to overcome observed differences in schools is to include school char- acteristics in the VAM. An alternative speciﬁcation of the VAMs that overcomes unobserved differences in school context includes school ﬁxed effects. With school ﬁxed effects, comparisons among teachers from different programs are made within schools. School ﬁxed effects may be desirable in preparation program models because they control for unobserved factors that are poten- tially correlated with school quality. It is important to understand, cependant, whether the inclusion of school ﬁxed effects is feasible in this setting, what the sensitivity of the estimates to underlying assumptions for ﬁxed effects are, and what their inclusion implies about the precision of the preparation program estimates and the resulting rankings of preparation program effectiveness. When ﬁxed effects are included in a regression, a primary concern is whether these coefﬁcients are identiﬁed. Preparation programs not directly sharing teachers in schools can still be compared indirectly, as long as there is some linkage with teachers from other programs that teach in the same school. Cependant, if preparation program graduates are not sufﬁciently mixed across schools, this type of estimation is not feasible. Identiﬁcation depends on the time horizon of the data being used to esti- mate program effects. In the simplest case, a cross-section of recent graduates and the schools in which they end up teaching may be used, which could pro- vide single-year estimates of program effects. This ensures that programs are being compared based on graduates teaching in the same school at the same point in time. This also limits the ties between programs, cependant, as many schools may not have recent graduates from multiple programs teaching there during any one school year. Alternativement, one can use a multi-year window of successive cohorts of graduates and estimate average program effects over a longer time horizon. Increasing the length of the window increases both 3. An implicit assumption in this exercise is that teacher preparation programs can be validly com- pared based on the performance of the teachers they train. There are numerous concerns with this type of comparison, including selection of teachers into and out of programs, selection of program graduates into teaching positions within the state, and how teacher performance is measured. These issues are addressed in the Discussion section below. l Téléchargé à partir du site Web : / / direct . m je t . / / f edu ed p a r t i c e – pdlf / / / / / 8 4 4 5 9 1 6 8 9 5 0 5 e d p _ a _ 0 0 1 1 0 pd . f f par invité 0 7 Septembre 2 0 2 3 461 WHERE YOU COME FROM OR WHERE YOU GO? connectivity of preparation programs and the power to discern among them, but requires time invariance of model parameters. Even when the time horizon of the data permits the inclusion of school ﬁxed effects in the model, the extent to which the estimation relies on the indi- rect linkages of preparation programs needs to be considered. The inclusion of school ﬁxed effects assumes homogeneity of effects, namely, that the teachers and schools that create ties among the preparation programs do not have differ- ent effects than other teachers or schools in the state. The larger the reliance on indirect linkages, the more sensitive are the assumptions regarding the homogeneity of effects. En outre, indirect linkages can make estimates im- precise, with the potential for signiﬁcant variance inﬂation. To understand the implications of the homogeneity assumption we use tools from social network analysis to identify the key teachers and schools creating direct links in our preparation program/school network and we consider whether these teachers and schools are representative of teachers and schools throughout the state. Another consideration for evaluating preparation program effectiveness is the sample of teachers to include in the analysis. In order to separate the effect of the preparation program from other factors, it may be desirable to restrict the sample to recent graduates of the preparation program. Including school ﬁxed effects with only inexperienced teachers can greatly reduce the sample used to estimate the program effects, cependant, which can result in variance inﬂation of program effects. Although including experienced teachers in the modeling can help make the analysis feasible and may be more desirable from a policy perspective, this speciﬁcation may falsely imply that the preparation program effect is constant for all levels of teacher experience. This paper uses a case study of elementary school teachers and their prepa- ration programs from the state of Florida in 2000–04 to explore the feasibility, underlying assumptions, variance inﬂation, and sampling choice implications of controlling for school context in the estimation of preparation program ef- fects. We examine whether the school ﬁxed effect parameters are identiﬁed and the difference in the precision of the program estimates under different modeling choices. We also consider whether program estimates with school ﬁxed effects are biased due to violations of the assumptions underlying the ﬁxed effect speciﬁcation and the implications of restricting the teacher sam- ple to inexperienced teachers. We then estimate three speciﬁcations of student achievement growth models: no school controls, school covariates (such as per- cent black and percent free lunch), and school ﬁxed effects. Using the estimated program effects, we rank the preparation programs in order of effectiveness, and examine the sensitivity of the rankings to the modeling choices. Our ﬁndings indicate that although there is some regional clustering of program graduates, new teachers from many programs are hired by schools 462 l Téléchargé à partir du site Web : / / direct . m je t . F / / e du e d p a r t i c e – pdlf / / / / / 8 4 4 5 9 1 6 8 9 5 0 5 e d p _ a _ 0 0 1 1 0 pdf . f par invité 0 7 Septembre 2 0 2 3 Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood across the state of Florida. Donc, school ﬁxed effects can be included in the student achievement model as long as three or more years of data are used in the estimation. Cependant, we ﬁnd evidence that schools and teachers inte- gral to connecting preparation programs are different from the average within the state, with disproportionately larger Hispanic and immigrant populations in schools and more Hispanic teachers. These differences in the schools and teachers that identify the estimates challenge the plausibility of the homogene- ity assumption required by the ﬁxed effects estimation. Importantly for policy makers, we ﬁnd that the rankings of preparation programs’ effectiveness are sensitive to the inclusion of school ﬁxed effects. When comparing the ranking quartiles of preparation programs with and without school ﬁxed effects, we ﬁnd signiﬁcant changes to the programs that are ranked in the top and bottom quartiles under different speciﬁcations. Par exemple, regardless of our sample restrictions, we ﬁnd at least one preparation program that is ranked in the bottom quartile of rankings without school ﬁxed effects and the top quartile of rankings with school ﬁxed effects. The quartile rankings of preparation programs are more stable across the speciﬁcations for low performing programs as compared to top-tier programs. Enfin, we ﬁnd that including school ﬁxed effects results in less precise preparation program estimates. Even with a ﬁve-year window there is signiﬁ- cant variance inﬂation due to the inclusion of school ﬁxed effects. The variance inﬂation grows rapidly as we shorten the window for estimation to one or two years, primarily because many more graduates teach in schools with gradu- ates from a single program and thus do not contribute to program estimates in models with school ﬁxed effects. Including experienced teachers in the es- timation sample has an effect on the variance inﬂation for some preparation programs. Based on these results, we argue that states will need to choose among three options for modeling preparation program effectiveness, each with its own drawbacks. The ﬁrst option is to estimate models without school ﬁxed effects and make conclusions about preparation programs that may be sen- sitive to the model’s untestable assumption of no school contextual effects. Alternativement, if school covariate data are available, states should consider an approach that controls for observable school characteristics. This may mitigate bias from nonrandom assignment of program graduates to schools but does not account for unmeasured school conditions that can impact job placements and estimates of the productivity of program graduates. Enfin, states could choose to estimate models with school ﬁxed effects that take into account both measured and unobserved time-invariant school characteristics. This may re- quire relying on a small and atypical set of schools and teachers to identify the models which yield much less precise estimates. It is unclear which of these l D o w n o a d e d f r o m h t t p : / / direct . m je t . / F / e du e d p a r t i c e – pdlf / / / / / 8 4 4 5 9 1 6 8 9 5 0 5 e d p _ a _ 0 0 1 1 0 pdf . f par invité 0 7 Septembre 2 0 2 3 463 WHERE YOU COME FROM OR WHERE YOU GO? three approaches will yield estimates with the smallest mean square errors and the least bias. States may need to describe the uncertainty of the model they use but this could weaken the utility of estimates. Without clear evidence for or against contextual effects and the sensitivity of conclusions about programs like we found in Florida, states may need to reconsider if this approach alone can provide useful information about preparation programs. The remainder of the paper is organized as follows. D'abord, we review pre- vious studies that have compared teacher preparation programs on the basis of the outcomes of the public elementary and secondary students taught by their graduates. Deuxième, we present the VAM and the exploration of the data regarding the feasibility and suitability of the school ﬁxed effect estimation. Suivant, we present the preparation program effectiveness estimates under al- ternative model speciﬁcations and, ﬁnally, we conclude with a summary and discussion of our ﬁndings. 2. REVIEW OF PREVIOUS STUDIES OF PREPARATION PROGRAMS AND STUDENT OUTCOMES Due in large measure to extensive data requirements, there are only a handful of existing studies that have attempted to link value-added measures of teacher performance to the preparation programs from which the teachers graduated. These include studies of teachers in seven states: New York, Florida, Louisiana, Kentucky, Texas, Missouri, and Washington. These studies have dealt with the problem of school contextual effects in different ways. In their study of New York City public school teachers, Boyd et coll.. (2009) include school ﬁxed effects in their model. They do not discuss the implications of this choice in terms of the overlap of program graduates in schools or the impact of school ﬁxed effects on the precision of their estimated program effects. They ﬁnd considerable variation in teacher value-added across preparation programs but do not provide standard errors of these effects. Sass (2008) and Kukla-Acevedo, Streams, and Toma (2009) also include school ﬁxed effects in the achievement models they use to estimate preparation program effects in Florida and Kentucky, respectivement. Sass estimates models with and without school ﬁxed effects and ﬁnds that the magnitude and signif- icance of estimated program effects are very sensitive to this choice. Although speciﬁc estimates are quite variable, in general the effect sizes of programs tend to be larger in absolute value and standard errors smaller when school effects are not included in the model. This suggests that either differences exist among program graduates teaching in different schools or that school indicators are correlated with program indicators, and including school effects increases the variance of estimates. 464 l Téléchargé à partir du site Web : / / direct . m je t . / / f edu ed p a r t i c e – pdlf / / / / / 8 4 4 5 9 1 6 8 9 5 0 5 e d p _ a _ 0 0 1 1 0 pd . f f par invité 0 7 Septembre 2 0 2 3 Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood The work of Kukla-Acevedo, Streams, and Toma (2009) illustrates many of the practical difﬁculties in conducting a value-added based assessment of teacher preparation programs. Because of data limitations, their analysis focuses on three preparation programs (UN, B, and C), and eleventh grade math teachers in just three of Kentucky’s 125 school districts. In one district, two-thirds of eleventh grade math teachers were graduates of institution A, and none had received a degree from institution C. In the second district, a plurality of teachers came from institution C and none from A, whereas the third district hires most of its teachers from institution B, and none from A. This extreme geographic clustering of teachers means there is little chance that teachers from some program pairs will be teaching in the same schools and great potential for contextual effects bias to exist. The lack of overlap among graduates also increases the variance inﬂation due to the inclusion of school effects. Perhaps as a result, the authors found no signiﬁcant program effects. Noell and co-authors, in their studies of teacher preparation program ef- fects in Louisiana (Noell et al. 2009; Gansle et al. 2010) take a different course when faced with the possibility of regional separation of graduates from dif- ferent preparation programs. These authors exclude school ﬁxed effects and include school-level aggregate student demographics and prior achievement in the models instead. They ﬁnd few signiﬁcant differences among programs. If these aggregates proxy for all the school contextual effects, then they have found an efﬁcient way to remove potential bias from contextual effects; oth- erwise, their estimates may be biased. Mellor et al. (2010), in their study of University of Texas teacher training programs, also excluded school ﬁxed ef- fects from the models and included a school effectiveness measure (based on school-wide test performance growth) and district indicators instead of school ﬁxed effects because of limited overlap of program graduates in schools. Koedel et al. (2012) examine teacher preparation programs in Missouri, and present results for models with school ﬁxed effects, school covariates, and without school ﬁxed effects. Across model speciﬁcations they consistently ﬁnd small to no differences in teacher preparation program effectiveness. They note that existing studies overstate the signiﬁcance of teacher training effects by not appropriately accounting for the clustering of teachers within program. Enfin, Goldhaber and Liddle (2012) use district and school covariates and ﬁxed effects to examine the impact of teacher preparation programs in Washington state on the effectiveness of teachers trained within the state. Compared with out-of-state trained teachers, the effectiveness of within-state programs is relatively stable across the model speciﬁcations. Clairement, controlling for school contextual effects is a concern when using VAMs to assess teacher training programs. Understanding the implications l D o w n o a d e d f r o m h t t p : / / direct . m je t . F / / e du e d p a r t i c e – pdlf / / / / / 8 4 4 5 9 1 6 8 9 5 0 5 e d p _ a _ 0 0 1 1 0 pdf . f par invité 0 7 Septembre 2 0 2 3 465 WHERE YOU COME FROM OR WHERE YOU GO? of including controls for school contexts will be useful in future attempts at such modeling, such as those to be conducted by the Race to the Top winners. 3. DATA FOR THE CURRENT STUDY Eleven states and the District of Columbia were announced as winners of RTTT funds on 24 Août 2010. As one of the winners of the competition, the state of Florida will receive $700 million, impacting over 2.6 million students and
over 180,000 teachers in 4,250 schools.4 To meet the requirements of RTTT,
Florida will be linking student achievement growth to the preparation program
where the students’ teachers were trained for the purpose of evaluating these
programs.5

En plus, with rich administrative data on teachers and student out-
comes and information about school and preparation programs for teachers,
Florida is well suited for this study. Data for our analysis come from three
sources. The Florida Education Data Warehouse (FL-EDW) provides longitu-
dinal data on all public school teachers, including demographic information,
expérience, educational attainment, and certiﬁcation status. Each classroom
has a unique identiﬁer, so we can reliably link teachers and students to speciﬁc
classrooms at each grade level.

The determination of whether a teacher obtained initial certiﬁcation by
graduating from a teacher preparation program or by an alternative route, et
the institution of preparation program completers, is accomplished by linking
data ﬁles from the Florida Department of Education’s Ofﬁce of Teacher Certiﬁ-
cation with the FL-EDW data. The addresses of schools come from the Florida
Department of Education’s Master School ID ﬁle. Preparation institution ad-
dresses come from the Web sites of the individual colleges and universities.
These address data are then geocoded with latitudes and longitudes for map-
ping teacher preparation institutions and the schools in which preparation
program graduates teach.

Until recently, the state administered two sets of reading and math tests
to all third through tenth graders in Florida. The Sunshine State Standards
Florida Comprehensive Achievement Test (FCAT-SSS) is a criterion-based
exam designed to test for the skills that students are expected to master at each
grade level. It is a high-stakes test used to determine school grades and student
retention in some grades. The second test is the FCAT Norm-Referenced Test
(FCAT-NRT), a version of the Stanford Achievement Test used throughout the
country. No accountability measures are tied to student performance on the
NRT.

4. See http://nces.ed.gov/nationsreportcard/states/.
5. See www.ﬂdoe.org/committees/pdf/RTTT-TLP.pdf for details.

466

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

The focus of our analysis is on elementary schools and elementary prepa-
ration programs. We deﬁne an elementary school preparation program as one
with a graduate teaching in self-contained regular education classrooms in
grades 4 ou 5 in a Florida public school during our study period (2000–04).
Elementary education is by far the largest program offered by the training
programs. Preparation programs offer varying mixes of programs of study
and within an institution, the training of teachers can vary among them. Fur-
ther, as Sass (2008) shows, the pre-college ability of future teachers differs
signiﬁcantly across certiﬁcation areas within an institution.

Due to both population growth and a constitutionally mandated class-size
restriction, Florida was a net importer of teachers during our period of study
(2000/01–2004/05). In addition to signiﬁcant numbers of teachers trained in
other states, Florida had alternative certiﬁcation programs in place that served
as pathways into teaching for many teachers. En fait, less than half of newly cer-
tiﬁed elementary education teachers in Florida obtained their certiﬁcation as a
result of graduating from an approved Florida preparation program.6 Among
teachers obtaining certiﬁcation by completing a Florida preparation program,
about three-fourths were graduates of public universities and the remainder
graduated from private universities or four-year public colleges (Yecke 2006).
Out-of-state and alternatively certiﬁed teachers are included in the value-added
analysis of teacher quality, but we only present comparisons between the av-
erage performance of teachers from different Florida preparation programs.7
There are thirty-three preparation programs with at least one graduate
teaching fourth- or ﬁfth-grade mathematics or English language arts in a
Florida public school during the 2000–01 to 2004–05 school years.8 To be
included in the analysis, a teacher must be teaching in an elementary school
in grades 4 et 5 at some point during our ﬁve-year data window.9 For some
analyses we restrict the sample to teachers who have two or fewer years of
expérience (c'est à dire., in their ﬁrst, second, or third year of teaching). As shown in
table 1, the majority of the elementary school teachers are teachers with more

6. For more details on teacher certiﬁcation in Florida see Sass (2011).
7. A detailed analysis of the attributes and relative performance of teachers who obtain certiﬁcation
from pathways other than graduating from a Florida preparation program is provided in Sass
(2011).

8. There are forty colleges and universities that certify teachers in the state of Florida. Four of these
programs are excluded because they are part of the “Educator Preparation Institute” program,
which is a type of alternative certiﬁcation program. One program is excluded because all graduates
were “business education” teachers, and are not certiﬁed to teach in elementary schools. Enfin,
two additional elementary teacher preparation programs do not appear in the analysis. Ceux-ci sont
small programs, with one or two recent graduates between 2000 et 2004 who are not teaching
a fourth or ﬁfth grade class during the analysis time period.

9. We exclude teachers who teach in charter schools, as well as teachers in classrooms with less than
10 or more than 50 students (loss of 112 teachers). Teachers are not included if all of their students
are missing gain scores or demographic covariates (loss of 459 teachers).

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

467

WHERE YOU COME FROM OR WHERE YOU GO?

Tableau 1. Number of Teachers by Experience and Certiﬁcation Status

Program ID

Experienced Teachers

Inexperienced, Alternative Cert.

Inexperienced, Out of State Cert.

Inexperienced, Cert. in Prep Program 25

Inexperienced, Cert. in Prep Program 1

Inexperienced, Cert. in Prep Program 5

Inexperienced, Cert. in Prep Program 2

Inexperienced, Cert. in Prep Program 4

Inexperienced, Cert. in Prep Program 8

Inexperienced, Cert. in Prep Program 7

Inexperienced, Cert. in Prep Program 3

Inexperienced, Cert. in Prep Program 10

Inexperienced, Cert. in Prep Program 6

Inexperienced, Cert. in Prep Program 9

Inexperienced, Cert. in Prep Program 11

Inexperienced, Cert. in Prep Program 14

Inexperienced, Cert. in Prep Program 13

Inexperienced, Cert. in Prep Program 12

Inexperienced, Cert. in Prep Program 16

Inexperienced, Cert. in Prep Program 15

Inexperienced, Cert. in Prep Program 21

Inexperienced, Cert. in Prep Program 18

Inexperienced, Cert. in Prep Program 22

Inexperienced, Cert. in Prep Program 23

Inexperienced, Cert. in Prep Program 24

Inexperienced, Cert. in Prep Program 20

Inexperienced, Cert. in Prep Program 19

Inexperienced, Cert. in Prep Program 17

Inexperienced, Cert. in Prep Program 28

Inexperienced, Cert. in Prep Program 27

Inexperienced, Cert. in Prep Program 26

Inexperienced, Cert. in Prep Program 29

Inexperienced, Cert. in Prep Program 33

Inexperienced, Cert. in Prep Program 30

Inexperienced, Cert. in Prep Program 32

Inexperienced, Cert. in Prep Program 31

Number of Teachers

6,688

1,594

1,231

496

304

293

286

279

201

174

163

148

140

124

104

Remarques: Inexperienced teachers deﬁned as having less than two years of experience. Program identi-
ties masked.

468

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

than two years of experience. Inexperienced teachers who were certiﬁed out
of state or through alternative pathways in Florida make up a large percent-
age of the remaining teachers. Enfin, for inexperienced teachers certiﬁed in
Florida, the preparation programs range in number of employed elementary
mathematics or English language arts teachers (in grades 4 et 5) depuis 496
all the way down to just one graduate during the ﬁve-year window.

In addition to information on the graduates and the schools where they
are working, the data include summary statistics on schools, such as student
gender and racial ethnic distribution, achievement levels, average test scores
and gains in achievement, student mobility measures, disciplinary incidents,
grade repeaters, free or reduced price lunch status, limited English proﬁciency
status (LEP), immigrant status, home language, parents’ language, special
education status, and enrollment. The data also include characteristics of the
preparation program graduates including gender, race/ethnicity, Scholastic
Aptitude Test (SAT) scores (for teachers who began their college career at a
four-year public university in Florida), whether they passed each of the general-
knowledge licensure exams on the ﬁrst try, and their score the last time they
took the exam.

The explanatory variables used in our analysis are summarized in table 2.
Over a quarter of the students in the sample are black, and one quarter are His-
panic. De la même manière, one quarter of students and parents of students do not speak
English at home. Sur 50 percent of students receive free or reduced-price
lunches. Almost one-third of teachers constitute our sample of inexperienced
teachers because they have fewer than two years of experience.10

4. VALUE-ADDED MODEL
Our value-added framework relates achievement for student i in year t(Yit )
to time varying student demographic characteristics (Xit ), prior year student
achievement scores (Faire,t−1), experience indicators for teacher k in year t(Zkt ),
grade and year indicators (γit and τt , respectivement), and preparation program
ﬁxed effects (ρk), as expressed in equation 1:

Yit = X

(cid:2)
il

β1 + Oui

(cid:2)

je,t−1β2 + Z

(cid:2)
kt

β3 + γit + τt + ρk + (cid:6)il .

(1)

One option to control for school contextual factors is to include observable

school characteristics Ss , as shown in equation 2:

Yit = X

(cid:2)
il

β1 + Oui

(cid:2)

je,t−1β2 + Z

(cid:2)
kt

(cid:2)
β3 + S
s

β4 + γit + τt + ρk + (cid:6)il .

(2)

10. These summary statistics are based on a sample of all teachers. Because in some model spec-
iﬁcations many of these teachers are excluded, we examined whether the student and teacher
characteristics of the estimation sample differ from the full sample, and found few statistically
signiﬁcant differences.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

469

Mean

Std. Dev.

Panel (UN) – Student and Teacher Characteristics

WHERE YOU COME FROM OR WHERE YOU GO?

Tableau 2. Summary Statistics of Explanatory Variables

Variable

Femelle

Noir

Hispanic

Asian

Change School

Student No English @ Home

Parent No English @ Home

Free Lunch

Reduced Lunch

LEP

0.5022

0.2457

0.2489

0.0181

0.1403

0.2427

0.2588

0.4491

0.1038

0.0642

Lag # Days in School

95.84

Lag # Days Suspended

Teacher Experience 1–2 Yrs

Teacher Experience 6–12 Yrs

Teacher Experience 13–20 Yrs

Teacher Experience 21–27 Yrs

Teacher Experience 28+ Yrs

Proportion Free Lunch

Proportion Black

Proportion Hispanic

Proportion Gifted

Proportion Special Ed

Proportion LEP

Proportion Change School

0.1627

0.3052

0.2011

0.0833

0.0326

0.0169

Panel (B) – School Characteristics

0.5674

0.2416

0.2630

0.0470

0.1579

0.1347

0.1502

0.5000

0.4305

0.4324

0.1333

0.3473

0.4287

0.4380

0.4974

0.3059

0.2452

4.05

1.2200

0.4605

0.4009

0.2764

0.1776

0.1288

0.2608

0.2416

0.2694

0.0653

0.0574

0.1418

0.0959

371,624

371,621

371,638

371,624

371,604

371,638

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Alternativement, school ﬁxed effects (θs ) can be included in the model to

capture unobserved school characteristics:

Yit = X

(cid:2)
il

(cid:2)
β1 + Z
kt

(cid:2)

β2 + Oui

je,t−1β3 + γit + τt + ρk + θs + (cid:6)il.

(3)

We compare the preparation program coefﬁcients (ρk) and precision of the
estimates across the three models. In some speciﬁcations we restrict the sam-
ple to only inexperienced teachers. This restriction has implications for the
identiﬁcation of the school ﬁxed effects (as discussed subsequently) ainsi que
the size of the analysis sample. In all speciﬁcations we estimate preparation

470

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

program effects for the recent graduates relative to the average Florida prepa-
ration program.11

5. SCHOOL FIXED EFFECTS SPECIFICATION—FEASIBILITY
AND SUITABILITY
To identify school ﬁxed effects in the model requires all the preparation pro-
grams to be connected to the network through at least one graduate teaching
in a school with graduates of other programs. Estimation of program effects
controlling for school effects cannot occur if programs can be partitioned into
distinct groups or strata such that programs in any one stratum are not con-
nected to programs in any of the other strata.12 A feature of the preparation
program/school network that will allow us to compare preparation programs
with school ﬁxed effects is that all of the preparation programs are connected
in a single stratum.

Regional Clustering of Program Graduates

One feature of teacher hiring decisions that could result in stratiﬁcation is the
regional clustering of graduates. To examine the evidence for this phenomenon
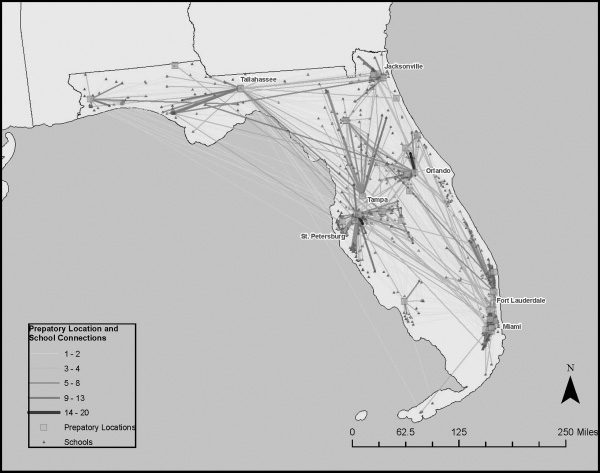
in Florida, ﬁrst we mapped the location of the preparation programs and
schools with connections showing programs that sent graduates to a particular
school. Chiffre 1 depicts programs and schools in Florida, where lines indicate
that a new teacher was hired from a preparation program to a particular
school. The shade of the line connecting schools and programs represents the
strength of this connection, with darker lines indicating that more teachers
were hired from the preparation program at the school. It is evident in ﬁgure
1 that although the stronger connections are regional, there are many teachers
who end up teaching far away from their preparation program.

Suivant, we veriﬁed the tendency for stronger regional connections by mod-
eling the number of teachers from a particular program teaching in a school
with at least one recent graduate from any of the programs as a function of the
distance from the preparation program to the school using a generalized ad-
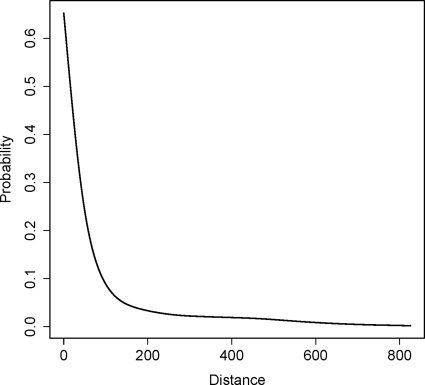
ditive Poisson regression with a smooth function for distance. Chiffre 2 shows
the estimated probability of one or more graduates teaching in a school as a

11. We use the Stata command felsdvregdm to estimate the program effects. For cases where the
estimation sample includes all four groups of teachers, we specify two reference collections: one for
inexperienced teachers certiﬁed in Florida preparation programs, and the second for the remaining
teachers. This allows us to compare recent graduates relative to the average Florida preparation
program even when teachers with more experience and other forms of certiﬁcation are included
in the data set.

12. A stratum or connected component is a maximal subset of the network in which all nodes are
reachable from every other. Maximal means that it is the largest possible subgraph: You could not
ﬁnd another node anywhere in the graph such that it could be added to the subgraph and all the
nodes in the subgraph would still be connected.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

471

WHERE YOU COME FROM OR WHERE YOU GO?

Chiffre 1. Preparation Program and School Connections

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 2. Estimated Probability of Preparation Program Graduate Teaching at School with at Least
One Graduate from Any Program as a Function of Distance from Program to School

function of distance from the preparation program. The clearly negative rela-
tionship is statistically signiﬁcant, indicating that, en effet, graduates are more
likely to teach in schools closer to where they graduated. This is consistent
with evidence reported by other researchers working on this issue in other
states (Boyd et coll.. 2009).

472

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

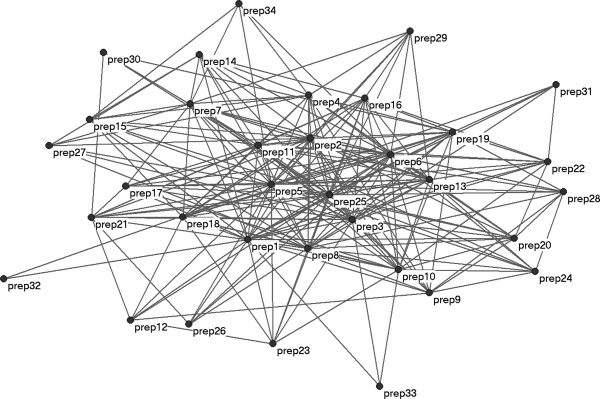
Chiffre 3. Elementary Preparation Program Network

Connectivity of Preparation Programs

Using social network visualization, we are able to show that school ﬁxed effects
estimation is feasible in Florida using a ﬁve-year window. Chiffre 3 depicts the
preparation program network for elementary schools, where a connection be-
tween two programs is deﬁned to exist if the graduates of the program teach at
the same school. All preparation programs have at least one graduate teaching
in an elementary school with a graduate of at least one other program. Plus-
over, the ties among programs are sufﬁcient for all programs to be connected
with all other programs at least indirectly when using a ﬁve-year window.

Suivant, we consider how the number of years of student achievement data
used to estimate program effects inﬂuence our ability to identify school ﬁxed
effects. Our data have teachers and school links for a ﬁve-year window. If we
use all ﬁve years of data, two programs will have a link through a school if both
have a graduate teaching in the school sometime during the ﬁve-year window.
They do not need to be teaching in the school during the same year, juste
during the same window. Clairement, as we lengthen the window, more programs
will have links. Cependant, lengthening the window requires the assumption
that both school and program effects are constant over the entire window.
A longer window increases the potential for this assumption to be violated,
as school-level factors such as school leadership, instructional resources, et
community support can change during the window, possibly changing the
school effect. Ainsi, shorter windows are desirable because they require less
stringent assumptions but they could break links and network connectivity,
making estimates less stable, or even infeasible.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

473

WHERE YOU COME FROM OR WHERE YOU GO?

We examined the stratiﬁcation in the Florida preparation program network
as the window size creating links is reduced from ﬁve years to one year.13 With
just a three-year window, the network of preparation programs remains fully
connected, even with the regional clustering and some very small programs
included in the sample. Restricting the sample to a two-year window, cependant,
with just the 2003–04 and 2004–05 school years, results in two very small
preparation programs having no graduates working in Florida elementary
schools. Aussi, when we restrict to just these two school years, the network
of programs with graduates teaching in schools is no longer fully connected
because one very small program is disconnected from all other programs. Le
disconnected program has a single graduate working in a school with no other
recent graduates during the 2004–05 school year.

The calculations for the connectivity of the preparation program network
presented here were based on the sample of inexperienced teachers trained
in Florida. Alternativement, we could include experienced teachers and allow for
a common school effect for all teachers in Florida. Because this new sam-
ple would include more teachers, the resulting preparation program network
would be more connected. Donc, the results for inexperienced teachers
represent a “lower bound” on the connectivity of the teacher preparation pro-
gram network that could be achieved if assuming common school effects for
experience and inexperienced teachers was justiﬁed.

Schools in the Preparation Program Network

Although all preparation programs are connected with a ﬁve-year window,
as shown in ﬁgure 1, graduates from different programs often do not teach
in the same schools. This is reﬂected in ﬁgure 3. Many programs do not
connect directly with other programs but they are connected indirectly. Pour
instance, graduates from Program 32 teach in schools with graduates from
only two other programs (Program 1 and Program 18), but these programs
then connect to the rest of the network.

Indirect connections are fostered by schools that hire many recent gradu-
ates from multiple programs. Par exemple, a few schools have graduates from
ﬁve or even six programs. Such schools create links for ﬁve or six programs
which can then link back to other programs, creating the connected network.
As shown in table 3, schools with graduates from many preparation programs
tend to be large schools, with relatively large proportions of black and Hispanic
students who are English language learners with parents who do not speak
English. The students in these schools also tend to be somewhat more likely
to be eligible for free school meals.

13. Figures available upon request.

474

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

Tableau 3. Testing Homogeneity of School Characteristics for Schools by Number of Preparation Program
Connections

School Characteristic

1 Prep

2 Prep

3 Prep

4 à 6 Prep Difference

School Size

Femelle

Noir

Hispanic

Parent No English @ Home

LEP

Free or Reduced Lunch

Math Gain Score

712.23
(266.68)

741.71
(271.35)

855.22
(300.51)

878.47
(343.50)

164.85∗

0.4782
(0.0416)

0.2646
(0.2496)

0.1695
(0.1990)

0.1728
(0.2022)

0.0882
(0.1143)

0.5496

0.4792
(0.0350)

0.3089
(0.2875)

0.2337
(0.2532)

0.2411
(0.2447)

0.1231
(0.1389)

0.6306

0.4825
(0.0218)

0.2982
(0.2991)

0.3429
(0.3003)

0.3446
(0.2804)

0.1627
(0.1461)

0.6533

(119.13)

(104.85)

(112.47)

155.84
(57.49)

163.88
(45.38)

160.61
(34.86)

0.4806
(0.0181)

0.3813
(0.3180)

0.3144
(0.3104)

0.3448
(0.3003)

0.1689
(0.1545)

0.7054

(98.87)

166.12
(37.65)

0.0024

0.1140∗

0.1472∗

0.1682∗

0.0817∗

0.1557∗

9.65∗

657

348

159

Remarques: Standard deviations in parentheses. “Difference” is taken between “1 Prep” and “4 to 6
Prep” values.
∗Statistically signiﬁcant at the 5% level.

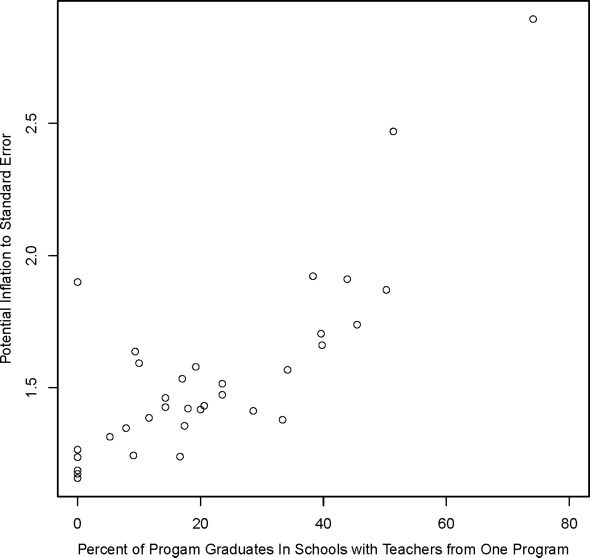
Some schools with fewer new hires can also be central to the connectivity
of the network if they support connections that do not otherwise exist and
link programs that then have many indirect links. The data from students in
these schools may be necessary for identifying many of the program effects
in our models, et par conséquent, these schools may have undue inﬂuence on
the estimates of program effects (Belsley, Kuh, and Welsch 1980). Cependant,
because these schools can be difﬁcult to identify, we use the betweenness
centrality index, a tool from social network analysis, to identify pivotal schools
within the network.14

If central schools are unusual in some ways, then their teachers may also
be unrepresentative of typical program graduates, potentially resulting in bias.

14. This is based on the idea of communication ﬂow, and the measure counts the number of shortest
paths between all other nodes that pass through each node (Borgatti and Everett 2006). We use a
version of the betweenness centrality index that takes into account the bimodal nature of our data,
namely, that the network contains two types of entities, preparation programs and schools, et
connections exist only between the two types of entities (preparation programs are only connected
to one another through the schools where the teachers are employed) (Everett and Borgatti 2005).
The two-mode centrality of the network is calculated using the social network analysis program
UCINET, developed by Steve Borgatti, Martin Everett, and Lin Freeman, and available for download
at www.analytictech.com/ucinet/.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

475

WHERE YOU COME FROM OR WHERE YOU GO?

Tableau 4. Testing Homogeneity of School Characteristics for Central and Non-Central Schools

Teacher Characteristic

Non-Central

School Size

Femelle

Noir

Hispanic

Parent No English @ Home

LEP

Free or Red. Lunch

Math Gain Score

738.54
(279.02)

0.4788
(0.0382)

0.2890
(0.2739)

0.2125
(0.2419)

0.2215
(0.2381)

0.1080
(0.1289)

0.5922
(0.2523)

159.37
(52.46)

1,109

Central

835.50
(299.58)

0.4821
(0.0192)

0.2782
(0.2643)

0.2684
(0.2649)

0.2731
(0.2520)

0.1487
(0.1491)

0.6160
(0.2418)

159.14
(32.72)

124

Différence

96.96∗

0.0033

−0.0108

0.0560∗

0.0516∗

0.0406∗

0.0238

−0.23

1,233

Remarques: Standard deviations in parentheses. Central schools are in the 90th percentile of between-
ness centrality.
∗Statistically signiﬁcant at the 5% level.

Schools that rank high on the betweenness centrality index (c'est à dire., above 90th
percentile of all schools on this index) are often in urban centers around the
state, but they are distributed across much of the state. As shown in table 4, comme
schools with graduates from many different programs, highly central schools
tend be large and serve high percentages of Hispanic, immigrant, and LEP
students. The proportion of program graduates teaching in these highly central
schools varies from zero to 100 percent in one very small school. Dans l'ensemble, less
than a quarter of graduates from 70 percent of programs teach in these central
schools.

Given that the schools central to identiﬁcation are distinctly different from
other schools and have relatively few graduates from most programs, là
is a signiﬁcant risk that modeling with school ﬁxed effects could actually
introduce bias rather than remove it. Par exemple, if program graduates who
are drawn to teach in large, highly Hispanic schools are different from other
program graduates, then ﬁxed effects could create biased contrasts among the
preparation programs within the central schools, and the bias could ripple
through all of the estimates via the indirect connections shown in ﬁgure 3.

Tableau 3 also shows the majority of schools hired teachers from only a sin-
gle preparation program. These schools tend to be smaller and serve smaller

476

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

percentages of minority (black and Hispanic), LEP, and free or reduced-price
lunch–eligible students as compared with schools with multiple program grad-
uates. The schools with graduates from a single program also tend to serve
smaller percentages of students whose parents do not speak English and make
smaller gains in math achievement.

The differences between schools with graduates from a single program
and those with graduates from multiple programs present challenges for es-
timating program effects. If the context of the schools with graduates from
one program is not removed by the covariates in Model 1 then the context
could confound our estimates of program effects. Modeling with school ﬁxed
effects will eliminate the outcomes of students whose teachers are from a
single program in the estimation of preparation program effects. This could
be problematic. If teachers drawn to these schools are different from others
in their programs or if programs have different effects on these teachers, alors
our program effects could be biased. Model 2 is the natural choice, but we
must capture all the contextual variables—and we can never be certain we
have.

Plausibility of Homogeneity Assumption

Implementing school ﬁxed effects in the preparation program VAMs requires
a homogeneity of effects assumption. C'est, the analysis assumes no sys-
tematic differences among teachers and schools that create the connections
among programs. If program effects differ for teachers that connect programs
and those that do not, then ﬁxed effects will yield biased estimates of the
program effects. De la même manière, if the teachers or schools that connect programs
are systematically different from other teachers or schools then differences
among programs will be confounded. Par exemple, if only the best graduates
of program A teach in schools that connect program A to program B, then the
estimate of the relative effects of program A and B will be biased in favor of
program A. If many graduates connect programs, this sort of selection is less
likely than if few graduates support the connection, as these rare cases can be
more extreme than the majority of the sample.

Tableau 5 shows the average characteristics of program graduates by the
number of program graduates in the schools where they teach. Graduates
who teach in schools with graduates from multiple programs are more likely
to be minorities when compared with other graduates from their programs.
They also tend to score lower on the mathematics certiﬁcation exam than
other graduates from their programs and have somewhat lower SAT scores.
Our models do not control for these teacher attributes. To the extent that
these attributes affect student achievement they will result in a correlation
between the error term and the school indicators in Model 3 and thus bias the

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

477

WHERE YOU COME FROM OR WHERE YOU GO?

Tableau 5. Testing Homogeneity of Teacher Characteristics by Number of Preparation Program Connections

Teacher Characteristic

1 Prep

2 Prep

3 Prep

4 à 6 Prep

Différence

Male

Blanc

Noir

Hispanic

First Pass Math

First Pass Reading

First Pass Essay

Math Test

Reading Test

Essay Test

SAT

0.1223
(0.3278)

0.8002
(0.4000)

0.0994
(0.2994)

0.0845
(0.2783)

0.6415
(0.4800)

0.8074
(0.3947)

0.9358
(0.2453)

0.1179
(0.3226)

0.6626
(0.4731)

0.1636
(0.3701)

0.5733
(0.4950)

0.7440
(0.4368)

0.9007
(0.2993)

0.0997
(0.2998)

0.5396
(0.4988)

0.1584
(0.3653)

0.2859
(0.4522)

0.5320
(0.4996)

0.7252
(0.4470)

0.8930
(0.3096)

0.1250
(0.3311)

0.4814
(0.5003)

0.2394
(0.4273)

0.2660
(0.4424)

0.5248
(0.5006)

0.7225
(0.4489)

0.8691
(0.3382)

306.04
(26.91)

315.60
(25.59)

7.57
(1.60)

954.27
(146.71)

301.75
(26.62)

308.85
(25.40)

7.26
(1.59)

926.67
(156.71)

297.57
(24.79)

309.17
(24.93)

7.33
(1.60)

916.27
(156.76)

300.05
(25.61)

309.61
(27.76)

7.13
(1.68)

910.22
(154.87)

1,006

984

682

376

0.0027

−0.3188∗

−0.1400∗

0.1815∗

−0.1167∗

−0.0849∗

−0.0667∗

−5.98∗

−5.99∗

0.44∗

−44.04∗

Remarques: Standard deviations in parentheses. “Difference” is taken between “1 Prep” and “4 to 6
Prep” values.
∗Statistically signiﬁcant at the 5% level.

program effect estimates. Expanding our models to include these attributes
could remove bias due to the observables, but given the differences in teachers
on observables, we have remaining concerns that unobservable differences also
exist among the teachers choosing to teach in schools that are the backbone of
the ﬁxed-effects analysis.

Homogeneity could also be violated if a school tended to hire similar quality
teachers regardless of the preparation program quality. Par exemple, schools
with many resources and serving highly afﬂuent students may be able to at-
tract top-performing teachers regardless of where they were trained. This may
mean such schools would hire the top graduates from average programs, le
average graduates from top programs, and no graduates from the weakest pro-
grams. In these schools all teachers would be about equal quality regardless
of the quality of their preparation programs because selection offsets the pro-
gram differences. The error terms would be strongly negatively correlated with

478

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

program effects and associated indicators, violating the model assumptions
and yielding biased estimates. We cannot fully test this possibility but we
found a notable range in teacher licensure and SAT test scores in most schools
with ﬁve or more recent graduates on staff during the study period.15 Hence,
the available data do not support the conjecture of such restricted hiring based
on information available to school administrators when they hire teachers.
Cependant, we do not have data on many other potential variables that may
affect hiring, such as personality, student teaching reports, or transcripts, pour
exemple.

6. PREPARATION PROGRAM ESTIMATES AND RANKINGS
Value-Added Models

Inexperienced Teachers

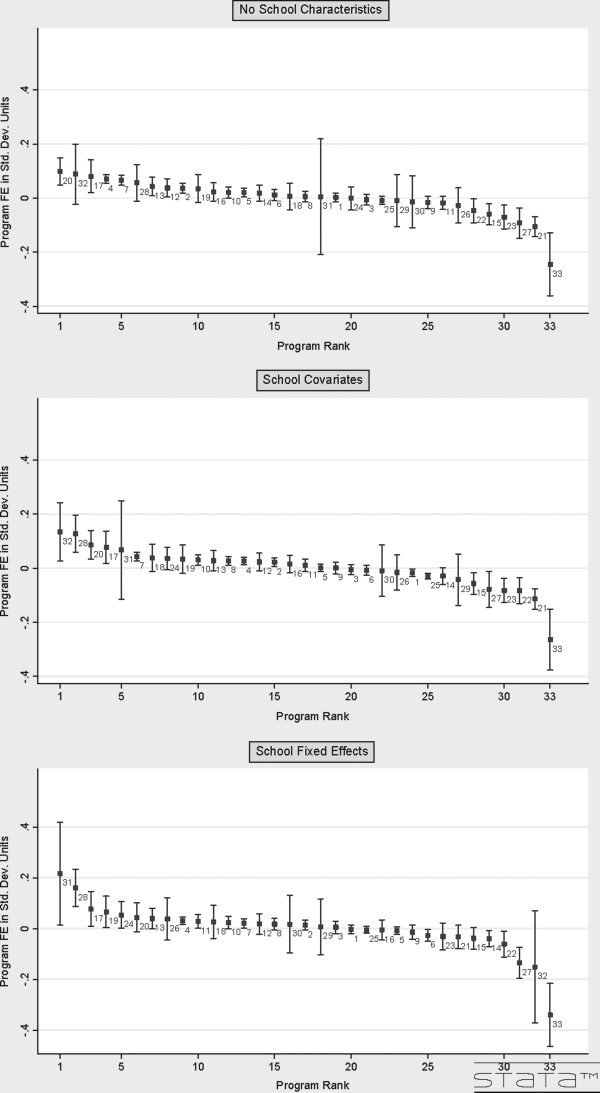
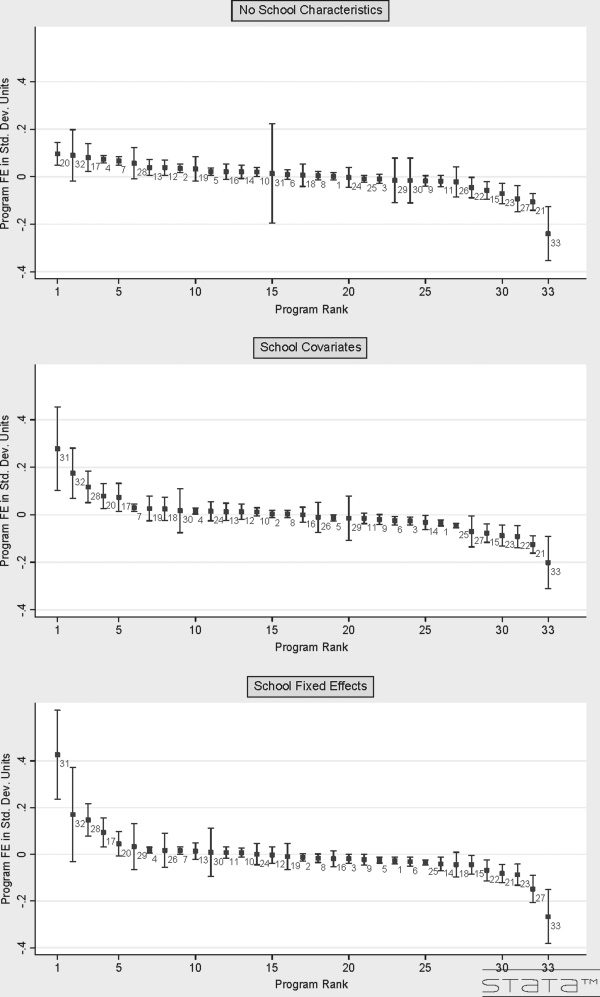
Chiffre 4 shows the preparation program effects relative to the average program
in Florida as well as the 95 percent conﬁdence intervals for the estimates for
three models: (1) no school controls, (2) with controls for school characteristics,
et (3) with controls for school ﬁxed effects.16 These results correspond to the
preparation program coefﬁcients (ρk) from equations 1, 2, et 3, respectivement.
The sample in these regressions is restricted to inexperienced teachers, et
the outcome variable is the high-stakes SSS achievement test. The regression
models include controls for student characteristics, teacher experience, aussi
as grade and year indicators. The preparation programs are ranked based on
effectiveness according to the results from each estimation model.17

There are a number of conclusions that can be drawn from these ﬁgures.
D'abord, although a large proportion of the preparation program estimates are
statistically signiﬁcantly different from zero from any one model, the preci-
sion of the estimates differs widely across models. En fait, of the thirty-three
preparation programs, eight programs are signiﬁcantly different (à la 95
percent conﬁdence level) from the average in all three speciﬁcations, eight are
signiﬁcantly different from the mean in two of the three speciﬁcations, ten pro-
grams are signiﬁcantly different from the mean in one speciﬁcation, and seven

15. We have two available measures of observed teacher quality in the data set: an indicator for whether
the teacher passed the state licensure test on the ﬁrst try and SAT test scores. We examined the
frequency of ﬁrst pass rates by subject, and found considerable variation in ﬁrst pass rates within
schools, with average school level ﬁrst pass rates of 55 percent in math and 71 percent in reading.
De la même manière, there is considerable school-level variation in the SAT test scores. The average school-
level range for test scores is 308 points on the 1200 scale SAT, et 80 percent of schools hired
teachers who scored below 760 as well as above 995 on the SAT.

16. The average preparation program in Florida is normalized to zero in these regressions.
17. We also estimated these models using the low-stakes NRT exam as the outcome variable. Quand
comparing across outcome variables for a speciﬁcation, we found large differences in the results
for the no-school-covariates model, but small changes in the coefﬁceints and resulting rankings in
the school-ﬁxed-effect model.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

479

WHERE YOU COME FROM OR WHERE YOU GO?

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 4. Preparation Program Fixed Effects Regression Coeffcients and 95 Percent Conﬁdence
Intervals: Inexperienced Teachers

480

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

programs are insigniﬁcantly different from the mean in all speciﬁcations.18
Deuxième, the preparation program coefﬁcient estimates vary to a large degree
for some programs with the model speciﬁcation. And ﬁnally, as more restric-
tive school controls are included in the models, the distribution of program
effect estimates and conﬁdence intervals increases.

Using table 6 we explore the changes in program rankings. The table
displays the rankings of each preparation program based on the estimated
coefﬁecient and the quartile of the rankings for each speciﬁcation. The prepa-
ration program rankings are sorted by the rankings from the speciﬁcation
without school characteristics.

Policy makers may be interested in identifying the top-ranked preparation
programs to scale up operations. To that effect, we consider the stability of the
top quartile of preparation programs. There are three programs ranked in the
top quartile under all three speciﬁcations. Of the remaining eleven programs
in the top quartile under any speciﬁcations, seven preparation program change
rankings from the top to at worst the second quartile, two preparation programs
change rankings from the top to at worst the third quartile, and signiﬁcantly,
two programs change rankings from the top to at worst the bottom quartile.

Next we considered a similar exercise for a policy that targets the lowest
quartile schools. Par exemple, policy makers could wish to modify or terminate
poor performing programs as suggested in the Department of Education’s
plan for teacher education reform. Six preparation programs are ranked in the
bottom quartile in all speciﬁcations. Of the remaining ﬁve programs ranked
in the bottom quartile for any speciﬁcation, one program changes rankings to
at best the third quartile, two preparation programs change rankings to at best
the second quartile, and as mentioned earlier, two programs change rankings
from the bottom to at best the top quartile.

Whereas so far we have focused on the preparation program effects, le
sample used to estimate these effects includes all inexperienced elementary
school teachers in the state, such as teachers who were certiﬁed out of state or
obtained certiﬁcations through alternative pathways in Florida. The estimation
model allows for comparisons of these two groups of teachers to one another.
Teachers certiﬁed in Florida through alternative pathways are slightly more ef-
fective than teachers certiﬁed out of state in the no school effects speciﬁcation.
These coefﬁcients are no longer signiﬁcantly different from zero once school
controls are included in the model, however.19

18. See Appendix table A.1 for preparation program effect coefﬁcients and standard errors.
19. See Appendix table A.1 for coefﬁcient estimates and standard errors.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

481

WHERE YOU COME FROM OR WHERE YOU GO?

Tableau 6. Preparation Program Rankings and Ranking Quartiles: Inexperienced Teachers

No Schl Vars

Schl Covars

Schl FE

Program ID

Rank

Rank Quartile

Rank

Rank Quartile

Rank

Rank Quartile

Remarques: Rankings based on program estimates in Appendix table A.1. Programs ordered by “No Schl
Covars” rankings.

482

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

Chiffre 5. Preparation Program Fixed Effects Regression Coefﬁcients and 95 Percent Conﬁdence
Intervals: All Teachers

Teachers with All Levels of Experience

Chiffre 5 shows the preparation program effects for the three speciﬁcations on
a sample that includes experienced elementary school teachers. Experienced

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

483

WHERE YOU COME FROM OR WHERE YOU GO?

teachers were excluded from the preparation program estimates in ﬁgure 4,
but these teachers could affect estimates for the with-school-ﬁxed-effects spec-
iﬁcation because they could have aided in identifying school effects. This is
because non-recent graduates could provide a link between preparation pro-
grams that otherwise would not be linked in the preparation program/school
réseau. Aussi, the school ﬁxed effects are restricted to be the same for all teach-
ers working at a given school, and this restriction could alter the parameter
estimates in the model.

The general conclusions about the three model speciﬁcations using the
larger sample are very similar to earlier results. D'abord, we note that under
all speciﬁcations experienced teachers are more effective than inexperienced
teachers who received out of state or alternative certiﬁcation.20 When consid-
ering preparation program effects based on inexperienced teachers trained in
Florida, a large number of programs are statistically different from the average
program in Florida, but there is a signiﬁcant change in the distribution of
preparation program effects, the precision of the estimates, and the program
rankings when comparing the three models.

Tableau 7 displays the rankings and ranking quartiles of preparation pro-
grams using all elementary school teachers in the Florida data set. Five prepa-
ration programs are ranked in the top quartile in all speciﬁcations. De la
remaining ten programs in the top quartile under any speciﬁcations, six pro-
grams change rankings from the top to at worst the second quartile, deux
programs change rankings from the top to at worst the third quartile, and two
programs change rankings from the top to at worst the fourth quartile. Regarder-
ing at the stability of the rankings across speciﬁcations in the bottom quartile,
six programs are ranked in the bottom quartile under all speciﬁcations, deux
preparation programs are ranked in the second quartile at worst in another
speciﬁcation, two programs are ranked at worst in the third quartile in another
speciﬁcation, and two programs are ranked in the fourth quartile at worst in
another speciﬁcation.

When comparing the results from the two samples of teachers in ﬁgures
4 et 5, there are no differences in the model with no school characteristics.
The program effects with school covariates vary more in the sample with
all teachers, and in the school ﬁxed effects speciﬁcations the rankings vary
signiﬁcantly across the two samples. This provides evidence that restricting
the school effects to be the same for all teachers working at a given school
regardless of experience does affect preparation program estimates. Twelve of
the thirty-three preparation programs are ranked in different quartiles when
comparing the estimation using only inexperienced teachers to the full sample

20. See Appendix table A.2 for these results.

484

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

Tableau 7. Preparation Program Rankings and Ranking Quartiles: All Teachers

NoSchlVars

SchlCovars

SchlFE

ProgramID

Rank

RankQuartile

Rank

RankQuartile

Rank

RankQuartile

Remarques: Rankings based on program estimates in Appendix table A.2. Programs ordered by “No Schl
Covar” rankings.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

485

WHERE YOU COME FROM OR WHERE YOU GO?

for the school covariates model, and thirteen programs are ranked in different
quartiles for the school ﬁxed effect model.

Variance Inﬂation

Variance inﬂation is a concern with models involving multiple sets of ﬁxed
effects such as preparation programs and schools.21 School ﬁxed effects can
be collinear with the program effects in the model when graduates of some
programs never teach with graduates of other programs and groups of pro-
grams have many connections within the groups but few outside the group.
Such multicollinearity can make the estimates of the program effects for some
programs highly unstable and dependent on the students of very few teachers
teaching in small numbers of schools.

Comparing the standard errors of the models with and without school
ﬁxed effects, the standard errors of twenty-eight out of thirty-three preparation
programs are inﬂated in the with-school-ﬁxed-effect estimation. This is partly
because approximately 32 percent of the program graduates in the data teach
in schools that employ only teachers from a single preparation program. These
teachers do not contribute to the estimation of program effects in models with
school ﬁxed effects, although they would contribute in models with no school
controls or with school covariates.

As shown in ﬁgure 6, the loss of these teachers can greatly inﬂate the
standard errors of the estimated program effects for some programs. Le
ﬁgure plots the square root of the variance inﬂation factor for the estimated
program effects against the percent of program graduates teaching in a school
with graduates from only one program—that is, graduates lost in the school
ﬁxed effects analysis.22 The relationship is very strong with the percentage of
graduates lost by including ﬁxed effects explaining 63 percent of the variability
in the variance inﬂation factor. De plus, variance inﬂation from adding school
ﬁxed effects can be as large as 2.9, ou 190 pour cent, and is over 1.5 for over 40
percent of the programs. Ainsi, the potential bias reduction from including
school ﬁxed effects comes at a very high price for a large percentage of the
programs.

The years of data used to estimate the program effects also has an impact
on the variance inﬂation from including school ﬁxed effects. Using a one- ou
two-year window results in an increase in the variance inﬂation factor to 3.7 pour

21. Other applications with multiple sets of ﬁxed effects include students and teachers, workers and

ﬁrms, or treatments and incomplete blocks.

22. Variance inﬂation equals the ratio of the variances of the estimators (program effects and contrasts)
from a model with school ﬁxed effects to the variances of the corresponding parameters from models
without school ﬁxed effects. The ratio is scaled by the ratio of the residual variances. Ainsi, variance
inﬂation is a measure of the collinearity of the variables in the models and it is consistent with the
traditional variance inﬂation factor (Belsley, Kuh, and Welsch 1980).

486

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

Chiffre 6. Variance Inﬂation from Including School Fixed Effects

a one-year window, a nearly 50 percent increase over median variance inﬂa-
tion when we use a ﬁve-year window. Variance inﬂation for contrasts between
programs increases similarly with reductions in the window length. The weak-
ening of the network and the consequent increase in variance inﬂation from
shortening the window is due to the decrease in the number of graduates in
the programs where the medians fall from 25.5 à 10, the smaller number of
schools where graduates are working, and the large increase in the proportion
of graduates teaching in schools with graduates from a single program. With a
one-year window, 50 percent of graduates from the median program are teach-
ing at schools with graduates from a single program and will not contribute to
program estimates from models with school ﬁxed effects.

7. DISCUSSION
States like Florida that won the RTTT competition must provide measures
of the performance of degree-granting teacher preparation programs in their
states. One of the major concerns with such analyses is that program grad-
uates may be teaching in very different contexts and those differences could
be confounded with measures of the programs’ relative efﬁcacy. This concern

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

487

WHERE YOU COME FROM OR WHERE YOU GO?

is exacerbated by the strong tendency for preparation program graduates to
take jobs geographically close to the programs where they trained, potentiellement
creating regional clusters of graduates. Models with school ﬁxed effects would
typically be seen as the best approach to removing potential confounding
of context differences, because program estimates would rely on differences
among student outcomes within the same schools to identify the program ef-
fects. Such estimates may not be feasible, cependant, if the training programs are
not connected to each other. En outre, ﬁxed effects estimates are consistent
only under the assumption of homogeneity of effects, which may not hold if
program effects differ in schools with teachers from multiple programs. Ce
could occur if those schools are distinct from other schools or the program
graduates drawn to work in them are distinct from the other graduates in their
programs. Even if all the requirements for consistent ﬁxed effects estimation
hold, including school ﬁxed effects in the models could inﬂate the variance of
the estimates of program effects and contrasts between different programs.
All the results are also likely to be sensitive to the number of school years for
which school and program effects are assumed constant. Shortening the win-
dow will decrease the opportunities for graduates from different programs to
be teaching in the same school and increase the challenges with using school
ﬁxed effects estimation to control for contextual differences among the work-
ing conditions for different program graduates. Enfin, restricting the sample
to only inexperienced teachers can also inﬂuence the preparation program
coefﬁcients and standard errors.

We used panel data from the 2000–01 to the 2004–05 school years linking
teachers in Florida to their training programs and the schools where they teach
to explore the potential for contextual bias and the feasibility of using school
ﬁxed effects when modeling teacher preparation program effects. We found
strong evidence of regional clustering with program graduates signiﬁcantly
more likely to be working in schools geographically close to their training
programs than ones far away. Il y avait, cependant, enough graduates going
far away and enough programs close together so that the network of programs
was fully connected, provided we combined at least three years of data. Même
with just one year of data the network of programs is fully connected, sauf
for a few very small programs with one or two graduates each year. Ainsi, si
desirable, school ﬁxed effects would be feasible with a modest window or by
restricting attention away from very small programs.

We also found that schools with graduates from a single program dif-
fered from other schools in terms of the demographics and achievement of
their students. They tended to be smaller and to enroll smaller proportions
of minority students, immigrant students, and students whose parents do not
speak English. Students from schools with graduates from one program also
tended to be higher achieving, but make smaller achievement gains. If these

488

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

differences are not fully accounted for or unobserved differences in these dis-
tinct schools remain in the model, then program effects could be confounded,
making models with school ﬁxed effects highly desirable for protection against
biases.

We found that the rankings of preparation programs based on relative
effectiveness were signiﬁcantly affected by the model speciﬁcation for school
contexte. Regardless of the sample we used in the analysis (all teachers or
only inexperienced teachers), we found that at least one preparation program
switched rankings from the top quartile to at worst the bottom quartile when
school ﬁxed effects were used. We observed that the rankings were more stable
across speciﬁcations at the bottom of the ranking distribution than at the top,
indicating the use of student growth models may be more effective at capturing
low-performing programs than top tier programs.

We also found that the variance of the estimated program effects could
be strongly inﬂated by including school effects in the model. Removing the
potential for bias from the contextual effects of the schools with graduates
from a single program is the primary motivation for using school ﬁxed effects,
but it will come at a cost. The cost is relatively insensitive to the window length
provided three or more years of data are used for the analysis.

The modeling discussed in this paper only addresses issues of potential
confounding of differences among programs due to the context where their
graduates teach. It does not address the challenges to attributing those differ-
ences to the quality of the training the graduates received. Numerous factors
other than the actual quality of the program training could be the sources of
differences even if we have removed the potential bias of context. Par exemple,
programs may select more or less capable pre-service teachers, or the skills of
the graduates from different programs who do or do not get jobs in Florida
may differ. Plus loin, the value-added framework only measures the produc-
tivity of program graduates in tested grades and subjects. Including school
ﬁxed effects in achievement models would not address any of these issues.
Cependant, they can improve the comparisons of graduates working in tested
grades and subjects within schools in the state.

Our analyses suggest that if school ﬁxed effects are desirable, a window of
three years might provide an acceptable compromise between adding collinear
variables and trying to protect against potential biases due to unobserved
differences in the schools where graduates from different programs teach.
With three years of data, variance inﬂation is not substantially larger than with
the ﬁve-year window and school and program effects are assumed constant
for three years rather than ﬁve. Given the tendency for schools and graduates
that are inﬂuential for model identiﬁcation to differ from other schools and
graduates, it would be valuable to test for interactions between those observable
differences and program effects.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

489

WHERE YOU COME FROM OR WHERE YOU GO?

There is no clean empirical method, cependant, to identify a model with no
bias or a model that yields program effect estimates with the smallest mean
squared error. States will need to make a choice on how to specify the student
achievement growth model knowing that the choice may affect preparation
program rankings and might be yielding a biased estimate unless untestable
assumptions hold. In light of this evidence, states may need to consider if
value-added modeling alone can provide useful information about preparation
program effectiveness.

At the time of publication Daniel McCaffrey and J. R.. Lockwood were employed by
the Educational Testing Service, Princeton, New Jersey. This research was supported by an IES
grant through a supplement to the National Center on Performance Incentives. Le
authors are grateful to the Florida Department of Education for providing the data. Le
views expressed are those of the authors and should not be attributed to the RAND
Corporation, its trustees, or any of the funders or supporting organizations mentioned
herein. Any errors are attributable to the authors.

RÉFÉRENCES
Belsley, David A., Edwin Kuh, and Roy E. Welsch. 1980. Regression diagnostics: Identifying
inﬂuential data and sources of collinearity, 1st ed. New York: John Wiley and Sons, Inc.
est ce que je:10.1002/0471725153

Borgatti, Stephen P., and Martin G. Everett. 2006. A graph-theoretic perspective on
centrality. Social Networks 28(4): 466–84. est ce que je:10.1016/j.socnet.2005.11.005

Boyd, Donald, Pamela Grossman, Hamilton Lankford, Susanna Loeb, and James Wyck-
off. 2009. Teacher preparation and student achievement. Educational Evaluation and
Policy Analysis 31(4): 416–40. est ce que je:10.3102/0162373709353129

Everett, Martin G., and Stephen P. Borgatti. 2005. Extending centrality. In Mod-
els and methods in social network analysis, edited by P. Carrington, J.. Scott, et S.
Wasserman, pp. 57–76. Cambridge, MA: la presse de l'Universite de Cambridge. est ce que je:10.1017/
CBO9780511811395.004

Gansle, Kristin A., George H. Noell, R.. Maria Knox, and Michael J. Schafer. 2010. Value
added assessment of teacher preparation in Louisiana: 2005–2006 to 2008–2009. Technique
Report, Louisiana State University.

Goldhaber, Dan, and Stephanie Liddle. 2012. The gateway to the profession: Assessing
teacher preparation programs based on student achievement. CALDER Working Paper
Non. 65, American Institutes for Research.

Koedel, Cory, Eric Parsons, Michael Podgursky, and Mark Ehlert. 2012. Teacher prepa-
ration programs and teacher quality: Are there real differences across programs? Travail-
ing Paper No. WP 12–04, University of Missouri, Columbia.

Kukla-Acevedo, Sharon, Megan Streams, and Eugenia F. Toma. 2009. Evaluation of
teacher preparation programs: A reality show in Kentucky. IFIR Working Paper No.
2009–09, University of Kentucky.

490

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

Mellor, L., M.. Lummus-Robinson, Veronica Brinson, and C. Dougherty. 2010. Linking
teacher preparation programs to student achievement in Texas. In Preparing Texas
teachers: A study of the University of Texas system teacher preparation programs,
edited by the Institute for Public School Initiatives and the University of Texas System,
pp. 5–42. Austin: University of Texas.

Noell, George H., Kristin A. Gansle, R.. Maria Patt, and Michael J. Schafer. 2009. Value
added assessment of teacher preparation in Louisiana: 2005–2006 to 2007–2008 (année 4).
Baton Rouge: Louisiana State University.

Sass, Tim R. 2008. Teacher preparation pathways, institutions and programs in Florida
(paper prepared for the Committee on Teacher Preparation Programs). Washington, CC:
Division of Behavioral and Social Sciences and Education, National Research Council.

Sass, Tim R. 2011. Certiﬁcation requirements and teacher quality: A comparison of
alternative routes to teaching. CALDER Working Paper No. 64, American Institutes
for Research.

U.S. département d'éducation (USDOE). 2009. Race to the top program: Executive
summary. Available www2.ed.gov/programs/racetothetop/executive-summary.pdf. Ac-
cessed 30 Août 2012.

U.S. département d'éducation (USDOE). 2011. Our future, our teachers: The Obama ad-
ministration’s plan for teacher education reform and improvement. Available www.ed.gov/
teaching/documents/our-future-our-teachers.pdf. Accessed 30 Août 2012.

Yecke, Cheri Pierson. 2006. The state of teacher quality and supply in Florida. Power-
Point presentation, State Board of Education Workshop, 17 Octobre 2006.

APPENDIX

Table A.1. Preparation Program Estimates and Standard Errors: Inexperienced Teachers

No Schl Vars

Schl Covars

Schl FE

Program ID

Coef

s.e.

Coef

s.e.

Coef

s.e.

0.0018

0.0367∗

−0.0064

0.0707∗

0.0207∗

0.0116

0.0655∗

0.0051

−0.0157

0.0210∗

−0.0180

0.0083

0.0091

0.0101

0.0080

0.0083

0.0107

0.0094

0.0095

0.0115

0.0103

0.0124

−0.0165∗

0.0223∗

−0.0051

0.0271∗

0.0014

−0.0075

0.0437∗

0.0275∗

0.0010

0.0305∗

0.0102

0.0066

0.0077

0.0091

0.0068

0.0069

0.0096

0.0084

0.0083

0.0111

0.0094

0.0117

−0.0036

0.0139

0.0050

0.0299∗

−0.0088

−0.0269∗

0.0201∗

0.0174

−0.0146

0.0233∗

0.0283∗

0.0089

0.0102

0.0125

0.0076

0.0120

0.0095

0.0114

0.0147

0.0126

0.0142

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

491

WHERE YOU COME FROM OR WHERE YOU GO?

Table A.1. Continued.

No Schl Vars

Schl Covars

Schl FE

Program ID

Coef

s.e.

Coef

s.e.

Coef

s.e.

InexpOutofStateCert.

InexpAlternativeCert.

0.0374∗

0.0422∗

0.0181

−0.0592∗

0.0228

0.0801∗

0.0059

0.0348

0.0984∗

−0.1053∗

−0.0466∗

−0.0705∗

−0.0012

−0.0089

−0.0272

−0.0928∗

0.0560∗

−0.0104

−0.0140

0.0046

0.0880

−0.2454∗

−0.0055∗

0.0055∗

0.0169

0.0175

0.0149

0.0198

0.0171

0.0308

0.0248

0.0266

0.0254

0.0186

0.0225

0.0226

0.0215

0.0074

0.0332

0.0288

0.0345

0.0492

0.0493

0.1093

0.0565

0.0593

0.0021

0.0233

0.0280

−0.0287∗

−0.0568∗

0.0156

0.0772∗

0.0379

0.0340

0.0858∗

−0.1136∗

−0.0836∗

−0.0823∗

0.0359∗

−0.0286∗

−0.0156

−0.0776∗

0.1277∗

−0.0418

−0.0092

0.0673

0.1341∗

−0.2638∗

−0.0031

0.0031

0.0167

0.0188

0.0157

0.0204

0.0167

0.0307

0.0258

0.0271

0.0270

0.0193

0.0243

0.0230

0.0212

0.0053

0.0331

0.0339

0.0345

0.0485

0.0487

0.0927

0.0552

0.0576

0.0022

0.0176

0.0393∗

−0.0400∗

−0.0390∗

−0.0056

0.0764∗

0.0259

0.0656∗

0.0438

−0.0330

−0.0616∗

−0.0314

0.0533∗

−0.0053

0.0377

−0.1358∗

0.1602∗

0.0070

0.0166

0.2165∗

−0.1514

−0.3409∗

−0.0022

0.0209

0.0207

0.0163

0.0221

0.0202

0.0348

0.0332

0.0315

0.0293

0.0234

0.0260

0.0268

0.0267

0.0070

0.0427

0.0312

0.0375

0.0559

0.0578

0.1032

0.1129

0.0634

0.0026

0.0022

0.0026

Note: Models include student characteristics, teacher experience measures, as well as grade and
year indicators.
∗Statistically signiﬁcant at the 5% level.

Table A.2. Preparation Program Estimates and Standard Errors: All Teachers

No Schl Vars

Schl Covars

Schl FE

Program ID

Coef

s.e.

Coef

s.e.

Coef

s.e.

0.0014

0.0353∗

−0.0095

0.0732∗

0.0216∗

0.0081

0.0088

0.0099

0.0078

0.0081

−0.0342∗

0.0032

−0.0261∗

0.0156∗

−0.0131∗

0.0064

0.0075

0.0087

0.0063

0.0066

−0.0268∗

−0.0127

−0.0186∗

0.0179∗

−0.0245∗

0.0071

0.0080

0.0101

0.0064

0.0066

492

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Kata Mihaly, Daniel McCaffrey, Tim R. Sass, and J. R.. Lockwood

Table A.2. Continued.

No Schl Vars

Schl Covars

Schl FE

Program ID

Coef

s.e.

Coef

s.e.

Coef

s.e.

InexpOutofStateCert.

InexpAlternativeCert.

ExperiencedTeachers

0.0092

0.0659∗

0.0037

−0.0177

0.0201∗

−0.0190

0.0383∗

0.0388∗

0.0208

−0.0577∗

0.0211

0.0807∗

0.0066

0.0327

0.0963∗

−0.1061∗

−0.0459∗

−0.0709∗

−0.0031

−0.0087

−0.0219

−0.0931∗

0.0568∗

−0.0155

−0.0160

0.0130

0.0899

−0.2403∗

−0.0298∗

−0.0152∗

0.0450∗

0.0104

0.0092

0.0093

0.0112

0.0101

0.0121

0.0165

0.0171

0.0146

0.0193

0.0167

0.0301

0.0243

0.0260

0.0248

0.0182

0.0220

0.0210

0.0072

0.0325

0.0281

0.0337

0.0480

0.0482

0.1067

0.0552

0.0579

0.0023

0.0025

0.0023

−0.0252∗

0.0296∗

0.0026

−0.0199∗

0.0118

−0.0154

0.0123

0.0125

−0.0319∗

−0.0776∗

−0.0002

0.0734∗

0.0244

0.0262

0.0785∗

−0.1249∗

−0.0921∗

−0.0878∗

0.0150

−0.0456∗

−0.0106

−0.0709∗

0.1170∗

−0.0144

0.0172

0.2775∗

0.1749∗

−0.2015∗

−0.0270∗

−0.0153∗

0.0423∗

0.0093

0.0079

0.0080

0.0106

0.0090

0.0113

0.0162

0.0183

0.0152

0.0198

0.0162

0.0300

0.0251

0.0264

0.0188

0.0237

0.0224

0.0207

0.0050

0.0323

0.0330

0.0336

0.0473

0.0475

0.0898

0.0538

0.0562

0.0023

0.0025

0.0024

−0.0313∗

0.0158∗

−0.0168∗

−0.0226∗

0.0070

0.0077

−0.0026

0.0135

−0.0409∗

−0.0444∗

−0.0186

0.0935∗

−0.0442∗

−0.0092

0.0445∗

−0.0818∗

−0.0689∗

−0.0870∗

0.0006

−0.0354∗

0.0170

−0.1487∗

0.1468∗

0.0327

0.0080

0.4262∗

0.1705∗

−0.2668∗

−0.0243∗

−0.0174∗

0.0101

0.0082

0.0093

0.0121

0.0100

0.0122

0.0180

0.0177

0.0147

0.0203

0.0175

0.0318

0.0269

0.0282

0.0265

0.0198

0.0233

0.0230

0.0232

0.0056

0.0368

0.0297

0.0353

0.0500

0.0525

0.0971

0.1029

0.0590

0.0025

0.0026

0.0416∗

0.0024

Note: Models include student characteristics, teacher experience measures, as well as grade and
year indicators.
∗Statistically signiﬁcant at the 5% level.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d

F
/

8
4
4
5
9
1
6
8
9
5
0
5
e
d
p
_
un
_
0
0
1
1
0
p
d