Transactions of the Association for Computational Linguistics, vol. 4, pp. 507–519, 2016. Action Editor: Jason Eisner.
Submission batch: 3/2016; Revision batch: 5/2016; Published 11/2016.
2016 Association for Computational Linguistics. Distributed under a CC-BY 4.0 Licence.
c
(cid:13)
MinimallySupervisedNumberNormalizationKyleGormanandRichardSproatGoogle,Inc.1118thAve.,NewYork,New York,USAAbstractWeproposetwomodelsforverbalizingnum-bers,akeycomponentinspeechrecognitionandsynthesissystems.Thefirstmodelusesanend-to-endrecurrentneuralnetwork.Thesec-ondmodel,drawinginspirationfromthelin-guisticsliterature,usesfinite-statetransducersconstructedwithaminimalamountoftrainingdata.Whilebothmodelsachievenear-perfectperformance,thelattermodelcanbetrainedusingseveralordersofmagnitudelessdatathantheformer,makingitparticularlyusefulforlow-resourcelanguages.1IntroductionManyspeechandlanguageapplicationsrequiretexttokenstobeconvertedfromoneformtoanother.Forexample,intext-to-speechsynthesis,onemustcon-vertdigitsequences(32)intonumbernames(thirty-two),andappropriatelyverbalizedateandtimeex-pressions(12:47→twelveforty-seven)andabbre-viations(kg→kilograms)whilehandlingallomor-phyandmorphologicalconcord(e.g.,Sproat,1996).QuiteabitofrecentworkonSMS(e.g.,Beaufortetal.,2010)andtextfromsocialmediasites(e.g.,YangandEisenstein,2013)hasfocusedondetect-ingandexpandingnovelabbreviations(e.g.,cnuplzhlp).Collectively,suchconversionsallfallundertherubricoftextnormalization(Sproatetal.,2001),butthistermmeansradicallydifferentthingsindiffer-entapplications.Forinstance,itisnotnecessarytodetectandverbalizedatesandtimeswhenpreparingsocialmediatextfordownstreaminformationextrac-tion,butthisisessentialforspeechapplications.Whileexpandingnovelabbreviationsisalsoim-portantforspeech(RoarkandSproat,2014),num-bers,fois,dates,measurephrasesandthelikearefarmorecommoninawidevarietyoftextgenres.FollowingTaylor(2009),werefertocate-goriessuchascardinalnumbers,fois,anddates—eachofwhichissemanticallywell-circumscribed—assemioticclasses.Somepreviousworkontextnor-malizationproposesminimally-supervisedmachinelearningtechniquesfornormalizingspecificsemi-oticclasses,suchasabbreviations(e.g.,Changetal.,2002;PennellandLiu,2011;RoarkandSproat,2014).Thispapercontinuesthistraditionbycon-tributingminimally-supervisedmodelsfornormal-izationofcardinalnumberexpressions(e.g.,ninety-seven).PreviousworkonthissemioticclassincludeformallinguisticstudiesbyCorstius(1968)andHur-ford(1975)andcomputationalmodelsproposedbySproat(1996;2010)andKanisetal.(2005).Ofallsemioticclasses,numbersarebyfarthemostim-portantforspeech,ascardinal(andordinal)num-bersarenotonlysemioticclassesintheirownright,butknowinghowtoverbalizenumbersisimportantformostoftheotherclasses:onecannotverbalizetimes,dates,measures,orcurrencyexpressionswith-outknowinghowtoverbalizethatlanguage’snum-bersaswell.Onecomputationalapproachtonumbernamever-balization(Sproat,1996;Kanisetal.,2005)employsacascadeoftwofinite-statetransducers(FSTs).ThefirstFSTfactorstheinteger,expressedasadigitse-quence,intosumsofproductsofpowersoften(i.e.,inthecaseofabase-tennumbersystem).ThisiscomposedwithasecondFSTthatdefineshowthe
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
1
1
4
1
5
6
7
4
1
4
/
/
t
je
un
c
_
un
_
0
0
1
1
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
508
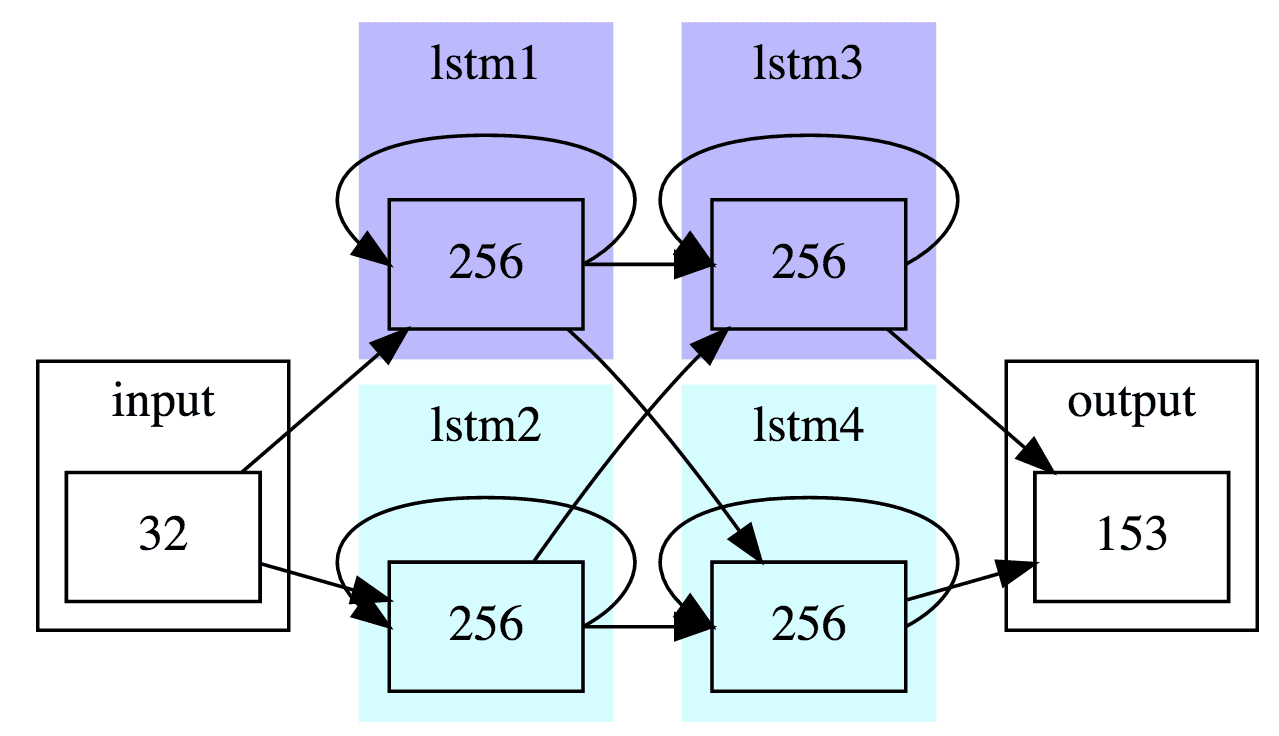
numericfactorsareverbalized,andmayalsohandleallomorphyormorphologicalconcordinlanguagesthatrequireit.Numbernamescanberelativelyeasy(asinEnglish)orcomplex(asinRussian;Sproat,2010)andthustheseFSTsmayberelativelyeasyorquitedifficulttodevelop.WhiletheGoogletext-to-speech(TTS)(seeEbdenandSproat,2014)andau-tomaticspeechrecognition(ASR)systemsdependonhand-builtnumbernamegrammarsforabout70languages,developingthesegrammarsfornewlan-guagesrequiresextensiveresearchandlabor.Forsomelanguages,aprofessionallinguistcandevelopanewgrammarinaslittleasaday,butotherlan-guagesmayrequiredaysorweeksofeffort.Wehavealsofoundthatitisverycommonforthesehand-writtengrammarstocontaindifficult-to-detecter-rors;en effet,thecomputationalmodelsusedinthisstudyrevealedseverallong-standingbugsinhand-writtennumbergrammars.Theamountoftime,effort,andexpertiserequiredtoproduceerror-freenumbergrammarsleadsustoconsidermachinelearningsolutions.Yetitisim-portanttonotethatnumberverbalizationposesadauntinglyhighstandardofaccuracycomparedtonearlyallotherspeechandlanguagetasks.WhileonemightforgiveaTTSsystemthatreadstheam-biguousabbreviationplzasplazaratherthanthein-tendedplease,itwouldbeinexcusableforthesamesystemtoeverread72asfourhundredseventytwo,evenifitrenderedthevastmajorityofnumberscor-rectly.Tosetthestageforthiswork,wefirst(§2–3)brieflydescribeseveralexperimentswithapower-fulandpopularmachinelearningtechnique,namelyrecurrentneuralnetworks(RNNs).Whenprovidedwithalargecorpusofparalleldata,thesesystemsarehighlyaccurate,butmaystillproduceoccasionaler-rors,renderingitunusableforapplicationslikeTTS.Inordertogivethereadersomebackgroundontherelevantlinguisticissues,wethenreviewsomecross-linguisticpropertiesofcardinalnumberexpressionsandproposeafinite-stateapproachtonumbernor-malizationinformedbytheselinguisticproperties(§4).Thecoreoftheapproachisanalgorithmforin-ducinglanguage-specificnumbergrammarrules.Weevaluatethistechniqueondatafromfourlanguages.Figure1:TheneuralnetarchitectureforthepreliminaryRussiancardinalnumberexperiments.PurpleLSTMlay-ersperformforwardstransitionsandgreenLSTMlayersperformbackwardstransitions.TheoutputisproducedbyaCTClayerwithasoftmaxactivationfunction.Inputto-kensarecharactersandoutputtokensarewords.2PreliminaryexperimentwithrecurrentneuralnetworksAspartofaseparatestrandofresearch,wehavebeenexperimentingwithvariousrecurrentneuralnetwork(RNN)architecturesforproblemsintextnormaliza-tion.Inonesetofexperiments,wetrainedRNNstolearnamappingfromdigitsequencesmarkedwithmorphosyntactic(caseandgender)information,andtheirexpressionasRussiancardinalnumbernames.ThemotivationforchoosingRussianisthatthenum-bernamesystemofthislanguage,likethatofmanySlaviclanguages,isquitecomplicated,andthereforeservesasagoodtestoftheabilitiesofanytextnor-malizationsystem.ThearchitectureusedwassimilartoanetworkemployedbyRaoetal.(2015)forgrapheme-to-phonemeconversion,asuperficiallysimilarsequence-to-sequencemappingproblem.Weusedarecurrentnetworkwithaninputlayer,fourhiddenfeed-forwardLSTMlayers(HochreiterandSchmid-huber,1997),andaconnectionisttemporalclassi-fication(CTC)outputlayerwithasoftmaxactiva-tionfunction(Gravesetal.,2006).1Twoofthehiddenlayersmodeledforwardsequencesandtheothertwobackwardsequences.Therewere32in-putnodes—correspondingtocharacters—and153outputnodes—correspondingtopredictednumbernamewords.Eachofthehiddenlayershad256nodes.ThefullarchitectureisdepictedinFigure1.Thesystemwastrainedon22Muniquedigitse-1Experimentswithanon-CTCsoftmaxoutputlayeryieldedconsistentlypoorresults,andwedonotreportthemhere.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
1
1
4
1
5
6
7
4
1
4
/
/
t
je
un
c
_
un
_
0
0
1
1
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
509
quencesrangingfromonetoonemillion;thesewerecollectedbyapplyinganexistingTTStextnormal-izationsystemtoseveralterabytesofwebtext.Eachtrainingexampleconsistedofadigitsequence,gen-derandcasefeatures,andtheRussiancardinalnum-berverbalizationofthatnumber.Thus,forexample,thesystemhastolearntoproducethefemininein-strumentalformof60.ExamplesofthesemappingsareshowninTable1,andthevariousinflectedformsofasinglecardinalnumberaregiveninTable2.Inpreliminaryexperiments,itwasdiscoveredthatshortdigitsequenceswerepoorlymodeledduetounder-sampling,soanadditional240,000shortsequencesamples(ofthreeorfewerdigits)wereaddedtocom-pensate.2.2Mexamples(10%)wereheldoutasadevelopmentset.Thesystemwastrainedforoneday,afterwhichithada0%labelerrorrate(LER)onthedevelopmentdataset.Whendecoding240,000tokensofheld-outtestdatawiththismodel,weachievedveryhighac-curacy(LER<.0001).Thefewremainingerrors,however,areaseriousobstacletousingthissystemforTTS.Themodelappearstomakenomistakesap-plyinginflectionalsuffixestounseendata.Plausibly,thistaskwasmadeeasierbyourpositioningofthemorphologicalfeaturestringattheendoftheinput,makingitlocaltotheoutputinflectionalsuffix(atleastforthelastwordinthenumberexpression).Butitdoesmakeerrorswithrespecttothenumericvalueoftheexpression.Forexample,for9801plu.ins.(девятьютысячамивосьмьюстамиодними),thesystemproducedдевятьютысячамисемьюстамиодними(9701plu.ins.):themorphologyiscor-rect,butthenumericvalueiswrong.2Thispatternoferrorswasexactlytheoppositeofwhatwewantforspeechapplications.OnemightforgiveaTTSsystemthatreads9801withthecor-rectnumericvaluebutinthewrongcaseform:alis-tenerwouldlikelynoticetheerrorbutwouldusuallynotbemisledaboutthemessagebeingconveyed.Incontrast,readingitasninethousandsevenhundredandoneiscompletelyunacceptable,asthiswouldactivelymisleadthelistener.Itisworthpointingoutthatthetrainingsetusedhere—22Mexamples—wasquitelarge,andwewere2Theexactnumberoferrorsandtheirparticulardetailsvar-iedfromruntorun.onlyabletoobtainsuchalargeamountoflabeleddatabecausewealreadyhadahigh-qualityhand-builtgrammardesignedtodoexactlythistransduc-tion.Itissimplyunreasonabletoexpectthatonecouldobtainthisamountofparalleldataforanewlanguage(e.g.,fromnaturally-occurringexamples,orfromspeechtranscriptions).Thisproblemises-peciallyacuteforlow-resourcelanguages(i.e.,mostoftheworld’slanguages),wheredataisbydefini-tionscarce,butwhereitisalsohardtofindhigh-qualitylinguisticresourcesorexpertise,andwhereamachinelearningapproachisthusmostneeded.Inconclusion,thesystemdoesnotperformaswellaswedemand,norisitinanycaseapracticalsolu-tionduetothelargeamountoftrainingdataneeded.TheRNNappearstohavedoneanimpressivejoboflearningthecomplexinflectionalmorphologyofRussian,butitoccasionallychoosesthewrongnum-bernamesaltogether.3NumbernormalizationwithRNNsForthepurposeofmoredirectlycomparingtheper-formanceofRNNswiththemethodswereportonbelow,wechosetoignoretheissueofallomorphyandmorphologicalconcord,whichappearstobe“easy”forgenericsequencemodelslikeRNNs,andfocusinsteadonverbalizingnumberexpressionsinwhatevermorphologicalcategoryrepresentsthelan-guage’scitationform.3.1DataandgeneralapproachForourexperimentsweusedthreeparalleldatasetswherethetargetnumbernamewasincitationform(inRussian,nominativecase):•Alargesetconsistingof28,000examplesex-tractedfromseveralterabytesofwebtextusinganexistingTTStextnormalizationsystem•Amediumsetof9,000randomly-generatedex-amples(fordetails,seeAppendixA)•Aminimalsetof300examples,consistingofthecountingnumbersupto200,and100carefully-chosenexamplesengineeredtocoverawidevarietyofphenomenaAseparatesetof1,000randomly-generatedexam-pleswereheldoutforevaluation.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
1
1
4
1
5
6
7
4
1
4
/
/
t
l
a
c
_
a
_
0
0
1
1
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
510
5neu.gen.→пятиfive24mas.acc.→двадцатьчетыреtwenty-four99plu.ins.→девяностадевятьюninety-nine11fem.nom.→одиннадцатьeleven81fem.gen.→восьмидесятиоднойeighty-one60fem.ins.→шестьюдесятьюsixty91neu.ins.→девяностаоднимninety-one3mas.gen.→трёхthreeTable1:Exampleinputandoutputdata(andglosses)fortheRussianRNNexperiments.шестьдесятnominative(nom.)шестидесятиgenitive(gen.)шестидесятиdative(dat.)шестьдесятaccusative(acc.)шестьюдесятьюinstrumental(ins.)шестидесятиprepositional(pre.)Table2:Inflectionalformsofthecardinalnumbernumber“60”inRussian.Theminimalsetwasintendedtoberepresentativeofthesortofdataonemightobtainfromanative-speakerwhenaskedtoprovidealltheessentialinfor-mationaboutnumbernamesintheirlanguage.3IntheseexperimentsweusedtwodifferentRNNmodels.ThefirstwasthesameLSTMarchitectureasabove(henceforthreferredtoas“LSTM”),exceptthatthenumbersofinputandoutputnodeswere13and53,respectively,duetothesmallerinputandout-putvocabularies.ThesecondwasaTensorFlow-basedRNNwithanattentionmechanism(Mnihetal.,2014),usinganoverallarchitecturesimilartothatusedinasystemforend-to-endspeechrecognition(Chanetal.,2016).Specifically,weuseda4-layerpyramidalbidirec-tionalLSTMreaderthatreadsinputcharacters,alayerof256attentionalunits,anda2-layerdecoderthatproduceswordsequences.ThereaderisreferredtoChanetal.,2016forfurtherdetails.Henceforthwerefertothismodelas“Attention”.Allmodelsweretrainedfor24hours,atwhichpointtheyweredeterminedtohaveconverged.3Notethatthenativespeakerinquestionmerelyneedstobeabletoanswerquestionsoftheform“howdoyousay‘23’inyourlanguage?”;theydonotneedtobelinguisticallytrained.Incontrast,hand-builtgrammarsrequireatleastsomelinguisticsophisticationonthepartofthegrammarian.3.2ResultsanddiscussionResultsfortheseexperimentsonatestcorpusof1,000randomexamplesaregiveninTable3.TheRNNwithattentionclearlyoutperformedtheLSTMinthatitperformedperfectlywithboththemediumandlargetrainingsets,whereastheLSTMmadeasmallpercentageoferrors.Notethatsincethenumberswereincitationform,therewaslittleroomfortheLSTMtomakeinflectionalerrors,andtheer-rorsitmadewereallofthe“silly”variety,inwhichtheoutputsimplydenotesthewrongnumber.Butneithersystemwascapableoflearningvalidtrans-ductionsgivenjust300trainingexamples.4Wedrawtwoconclusionsfromtheseresults.First,evenapowerfulmachinelearningmodelknowntobeapplicabletoawidevarietyofproblemsmaynotbeappropriateforallsuperficially-similarprob-lems.Second,itremainstobeseenwhetheranyRNNcouldbedesignedtolearneffectivelyfromanamountofdataassmallasoursmallesttrainingset.Learningfromminimaldatasetsisofgreatpracticalconcern,andwewillproceedtoprovideaplausiblesolutiontothisproblembelow.Wenoteagainthatverylowerrorratesdonotensurethatasystemis4ThefailureoftheRNNstogeneralizefromtheminimaltrainingsetsuggeststheyareevidentlynotexpressiveenoughforthesortof“clever”inferencethatisneededtogeneralizefromsolittledata.ItisplausiblethatanalternativeRNNarchi-tecturecouldlearnwithsuchasmallamountofdata,thoughweleaveittofutureresearchtodiscoverjustwhatsuchanar-chitecturemightbe.InanattempttoprovidetheRNNswithadditionalsupport,wealsoperformedanevaluationwiththeminimaltrainingsetinwhichinputswereencodedsothateachdecimalpositionabove0wasrepresentedwithaletter(Afor10,Bfor100,andsoforth).Thus2034wasrepresentedas2C3A4.Inprinciple,thisoughttohavepreventederrorswhichfailtotakepositionalinformationintoaccount.Unfortunately,thismadenodifferencewhatsoever.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
1
1
4
1
5
6
7
4
1
4
/
/
t
l
a
c
_
a
_
0
0
1
1
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
511
TrainingsizeLSTMAcc.AttentionAcc.Overlap28,0000.9991.00056%9,0000.9941.0000%300<0.001<0.001<1%Table3:Accuraciesonatestcorpusof1,000randomRussiancitation-formnumber-nameexamplesforthetwoRNNarchitectures.“Overlap”indicatesthepercentageofthetestexamplesthatarealsofoundinthetrainingdata.usable,sincenotallerrorsareequallyforgivable.4Numbernormalizationwithfinite-statetransducersTheproblemofnumbernormalizationnaturallyde-composesintotwosubproblems:factorizationandverbalizationofthenumericfactors.Wefirstcon-siderthelatterproblem,thesimplerofthetwo.Letλbethesetofnumbernamesinthetargetlan-guage,andletνbethesetofnumerals,theintegersdenotedbyanumbername.ThenletL:ν∗→λ∗beatransducerwhichreplacesasequenceofnu-meralswithasequenceofnumbernames.Forin-stance,forEnglish,Lwillmap907toninetyseven.Inlanguageswheretherearemultipleallomorphsorcaseformsforanumeral,Lwillbenon-functional(i.e.,one-to-many);wereturntothisissueshortly.Innearlyallcases,however,therearenomorethanafewdozennumeralsinν,5andnomorethanafewnamesinλfortheequivalentnumeralinν.There-fore,weassumeitispossibletoconstructLwithmin-imaleffortandminimalknowledgeofthelanguage.Indeed,alltheinformationneededtoconstructLfortheexperimentsconductedinthispapercanbefoundinEnglish-languageWikipediaarticles.Theremainingsubproblem,factorization,isre-sponsibleforconvertingdigitsequencestonumeralfactors.InEnglish,forexample,97000isfactoredas9071000.Factorizationisalsolanguage-specific.InStandardFrench,forexample,thereisnosim-plexnumbernamefor‘90’;insteadthisisrealizedasquatre-vingt-dix“fourtwentyten”,andthus97000(quatre-vingt-dix-septmille)isfactoredas4201071000.Itisnotaprioriobvioushowonemightgoaboutlearninglanguage-specificfactorizations.For5Atworst,asmallnumberoflanguages,suchasseveralIndiclanguagesofNorthIndia,effectivelyuseuniquenumeralsforallcountingnumbersupto100.inspiration,weturntoalesser-knownbodyoflin-guisticsresearchfocusingonnumbergrammars.Hurford(1975)surveyscross-linguisticpropertiesofnumbernamingandproposesasyntacticrepre-sentationwhichdirectlyrelatesverbalizednumbernamestothecorrespondingintegers.Hurfordinter-pretscomplexnumberconstructionsasarithmeticexpressionsinwhichoperators(andtheparenthe-sesindicatingassociativity)havebeenelided.Byfarthetwomostcommonarithmeticoperationsaremultiplicationandaddition.6InFrench,forexam-ple,theexpressiondix-sept,literally‘tenseven’,de-notes17,thesumofitsterms,andquatre-vingt(s),literally‘fourtwenty’,refersto80,theproductofitsterms.Thesemaybecombined,inquatre-vingt-dix-sept.Tovisualizearithmeticoperationsandas-sociativities,wehenceforthwritefactorizationsus-ings-expressions—pre-orderserializationsofk-arytrees—withnumeralterminalsandarithmeticoper-atornon-terminals.Forexample,quatre-vingt-dix-septiswritten(+(*420)107).Withinanylanguagetherearecuestothiselidedarithmeticstructure.Insomelanguages,someoralladdendsareseparatedbyawordtranslatedasand.Inotherlanguagesitispossibletodeterminewhethertermsaretobemultipliedorsummeddependingontheirrelativemagnitudes.InFrench(asinEnglish),forinstance,anexpressionXYusuallyisinterpretedasaproductifX
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
1
1
4
1
5
6
7
4
1
4
/
/
t
je
un
c
_
un
_
0
0
1
1
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
512
theirdenotations(e.g.,Kwiatkowskietal.,2011).4.1FSTmodelThecompletemodelconsistsoffourcomponents:1.Alanguage-independentcoveringgrammarF,transducingfromintegersexpressedasdigitse-quencestothesetofpossiblefactorizationsforthatinteger2.Alanguage-specificnumeralmapM,transduc-ingfromdigitsequencestonumerals3.Alanguage-specificverbalizationgrammarG,acceptingonlythosefactorizationswhicharelicitinthetargetlanguage4.Alanguage-specificlexicalmapL,transducingfromsequencesofnumerals(e.g.,20)tonum-bernames(alreadydefined)Asthefinalcomponent,thelexicalmapL,hasal-readybeendescribed,weproceedtodescribethere-mainingthreecomponentsofthesystem.4.1.1Finite-statetransduceralgorithmsWhileweassumethereaderhassomefamiliaritywithFSTs,wefirstprovideabriefreviewofafewkeyalgorithmsweemploybelow.OurFSTmodelisconstructedusingcomposition,denotedbythe◦operator.Whenbothargumentstocompositionaretransducers,compositionisequiva-lenttochainingthetworelationsdescribed.Forex-ample,ifAtransducesstringxtostringy,andBtrans-ducesytoz,thenA◦Btransducesfromstringxtostringz.Whentheleft-handsideofcompositionisatransducerandtheright-handsideisanaccep-tor,thentheircompositionproducesatransducerinwhichtherangeoftheleft-handsiderelationisinter-sectedwiththesetofstringsacceptedbytheright-handsideargument.ThusifAtransducesstringxtostrings{oui,z},andBacceptsythenA◦Btransducesfromxtoy.Wemakeuseoftwootherfundamentaloperations,namelyinversionandprojection.EverytransducerAhasaninversedenotedbyA−1,whichisthetrans-ducersuchthatA−1(oui)→xifandonlyifA(X)→y.AnytransducerAalsohasinputandoutputprojec-tionsdenotedbyπi(UN)andπo(UN),respectively.IfthetransducerAhasthedomainα∗andtherangeβ∗,thenπi(UN)istheacceptoroverα∗whichacceptsxifandonlyifA(X)→yforsomey∈β∗;outputpro-jectionisdefinedsimilarly.Theinverse,inputpro-jection,andoutputprojectionofanFST(orapush-downtransducer)arecomputedbyswappingand/orcopyingtheinputoroutputlabelsofeacharcinthemachine.SeeMohrietal.,2002formoredetailsontheseandotherfinite-statetransduceralgorithms.4.1.2CoveringgrammarLetAbeanFSTwhich,whenrepeatedlyappliedtoanarithmetics-expressionstring,producesthes-expression’svalue.Forexample,oneapplicationofAto(+(*420)107)produces(+80107),andasecondapplicationproduces97.Letμbethesetofs-expressionmarkupsymbols{‘(',‘)',‘+’,‘*’}andΔbetheset{0,1,2,…,9}.Alors,F:Δ∗→(μ∪Δ)∗=A−1◦A−1◦A−1…(1)isanFSTwhichtransducesanintegerexpressedasadigitstringtoallitscandidatefactorizationsexpressedass-expressionstrings.7LetC(d)=πo(d◦F),whichmapsfromadigitsequencedtothesetofallpossiblefactorizations—inanylanguage—ofthatdigitsequence,encodedass-expressions.Forexample,C(97)containsstringssuchas:(+907)(+80107)(+(*420)107)…4.1.3GrammarinferenceLetM:(μ∪Δ)∗→ν∗beatransducerwhichdeletesallmarkupsymbolsinμandreplacesse-quencesofintegersexpressedasdigitsequenceswiththeappropriatenumeralsinν.LetD(je)=πi(M◦L◦l),whichmapsfromaverbalizationltothesetofalls-expressionswhichcontainlaster-minals.Forexample,D(420107)contains:7Inpractice,ours-expressionsneverhaveadepthexceedingfive,soweassumeF=A−1◦A−1◦A−1◦A−1◦A−1.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
1
1
4
1
5
6
7
4
1
4
/
/
t
je
un
c
_
un
_
0
0
1
1
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
513
S→(7|90|*|+)∗→(7|90|+)1000+→907Table4:AfragmentofanEnglishnumbergrammarwhichacceptsfactorizationsofthenumbers{7,90,97,7000,90000,and97000}.Srepresentsthestartsymbol,and‘|’denotesdisjunction.Notethatthisfragmentisregularratherthancontext-free,thoughthisisrarelythecaseforcompletegrammars.(+420107)(+420(*107))(+(*420)107)…Then,given(d,je)whered∈Δ∗isanintegerex-pressedasadigitsequence,andl∈λ∗isd’sverbal-ization,theirintersectionE(d,je)=C(d)◦D(je)(2)willcontainthefactorization(s)ofdthatverbalizesasl.Inmostcases,Ewillcontainexactlyonepathforagiven(d,je)pair.Forinstance,ifdis97000andlisninetyseventhousand,E(d,je)est(*(+907)10000).WecanuseEtoinduceacontext-freegrammar(CFG)whichacceptsonlythosenumberverbaliza-tionspresentinthetargetlanguage.Thesimplestpos-siblesuchCFGuses‘*’and‘+’asnon-terminalla-bels,andtheelementsinthedomainofL(e.g.,20)asterminals.Thegrammarwillthenconsistofbinaryproductionsextractedfromthes-expressionderiva-tionsproducedbyE.Table4providesafragmentofsuchagrammar.Withthisapproach,wefacethefamiliarissuesofambiguityandsparsity.Concerningtheformer,theoutputofEisnotuniqueforalloutputs.Weaddressthiseitherbyapplyingnormalformconstraintsonthesetofpermissibleproductions,orignoringam-biguousexamplesduringinduction.Onecaseofam-biguityinvolvesexpressionsinvolvingadditionwith0ormultiplicationby1,bothidentityoperationsthatleavetheidentityelement(i.e.,0or1)freetoasso-ciateeithertotheleftortotheright.Fromourper-spective,thisambiguityisspurious,sowestipulatethatidentityelementsmayonlybesiblingsto(i.e.,ontheright-handsideofaproductionwith)anotherdigit→(2|3|4|…9)teen→(11|12|13|…19)decade→(20|30|40|…90)century→(200|300|400|…900)power_of_ten→(1000|10000|…)Table5:Optionalpreterminalrules.terminal.Thusanexpressionlikeonethousandonehundredcanonlybeparsedas(+(*11000)(*1100)).Butnotallambiguitiescanbehandledbynormalformconstraints.Someexpressionsaream-biguousduetothepresenceof“palindromes”intheverbalizationstring.Forinstance,twohundredtwocaneitherbeparsedas(+2(*1002))ou(+(*2100)).Thelatterderivationis“correct”insofarasitfollowsthesyntacticpatternsofotherEnglishnumberexpressions,butthereisnowaytodeter-minethisexceptwithreferencetotheverylanguage-specificpatternsweareattemptingtolearn.There-foreweignoresuchexpressionsduringgrammarin-duction,forcingtherelevantrulestobeinducedfromunambiguousexpressions.Similarly,multiplicationandadditionareassociativesoexpressionslikethreehundredthousandcanbebinarizedeitheras(*(*3100)10000)ou(*3(*1001000)),thoughbothderivationsareequally“correct”.Onceagainweig-noresuchambiguousexpressions,insteadextractingtherelevantrulesfromunambiguousexpressions.Sinceweonlyadmittwonon-terminallabels,thevastmajorityofourrulescontainnumeralterminalsontheirright-handsides,andasaresult,thenum-berofrulestendstoberoughlyproportionaltothesizeoftheterminalvocabulary.Thusitiscommonthatwehaveobserved,forinstance,thirteenthou-sandandfourteenmillionbutnotfourteenthousandorthirteenmillion,andasaresult,theCFGmaybedeficientsimplyduetosparsityinthetrainingdata,particularlyinlanguageswithlargeterminalvocab-ularies.Toenhanceourabilitytogeneralizefromasmallnumberofexamples,weoptionallyinsertpreterminallabelsduringgrammarinductiontoformclassesofterminalsassumedtopatterntogetherinallproductions.Forinstance,byintroducing‘teen’and‘power_of_ten’preterminals,allfourofthepreviousexpressionsaregeneratedbythesametop-levelpro-duction.ThefullsetofpreterminallabelsweusehereareshowninTable5.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
1
1
4
1
5
6
7
4
1
4
/
/
t
je
un
c
_
un
_
0
0
1
1
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
514
Inpractice,obtainingproductionsusingEisinef-ficient:itisroughlyequivalenttoanaïvealgorithmwhichgeneratesallpossiblederivationsforthenu-meralsgiven,thenfiltersoutallofthosewhichdonotevaluatetotheexpectedtotal,violatetheafore-mentionednormalformconstraints,orareotherwiseambiguous.Thisfailstotakeadvantageoftop-downconstraintsderivedfromtheparticularstructureoftheproblem.Forexample,thenaïvealgorithmen-tertainsmanycandidateparsesforquatre-vingt-dix-sept‘97’wheretherootis‘*’andthefirstchildis‘4’,despitethefactthatnosuchhypothesisisviableas4isnotadivisorof97.Weinjectarithmeticconstraintsintothegram-marinductionprocedure,asfollows.Theinputstothemodifiedalgorithmaretuplesoftheform(T,ν0,…,νn)whereTisthenumericvalueoftheexpressionandν0,…,νnarethen+1numeralsintheverbalization.Considerahypothesizednumericvalueoftheleftmostchildoftheroot,T0…je,whichdominatesν0,…,νiwherei
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
u
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
1
1
4
1
5
6
7
4
1
4
/
/
t
je
un
c
_
un
_
0
0
1
1
4
p
d
.
F
b
oui
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
520