Transactions of the Association for Computational Linguistics, 1 (2013) 279–290. Action Editor: Lillian Lee.
Submitted 11/2012; Revised 1/2013; Published 7/2013. c
(cid:13)

2013 Association for Computational Linguistics.

Good,Great,Excellent:GlobalInferenceofSemanticIntensitiesGerarddeMeloICSI,Berkeleydemelo@icsi.berkeley.eduMohitBansalCSDivision,UCBerkeleymbansal@cs.berkeley.eduAbstractAdjectiveslikegood,great,andexcellentaresimilarinmeaning,butdifferinintensity.In-tensityorderinformationisveryusefulforlanguagelearnersaswellasinseveralNLPtasks,butismissinginmostlexicalresources(dictionaries,WordNet,andthesauri).Inthispaper,wepresentaprimarilyunsupervisedapproachthatusessemanticsfromWeb-scaledata(e.g.,phraseslikegoodbutnotexcel-lent)torankwordsbyassigningthemposi-tionsonacontinuousscale.WerelyonMixedIntegerLinearProgrammingtojointlydeter-minetheranks,suchthatindividualdecisionsbenefitfromglobalinformation.Whenrank-ingEnglishadjectives,ourglobalalgorithmachievessubstantialimprovementsoverpre-viousworkonbothpairwiseandrankcorre-lationmetrics(specifically,70%pairwiseac-curacyascomparedtoonly56%bypreviouswork).De plus,ourapproachcanincorpo-rateexternalsynonymyinformation(increas-ingitspairwiseaccuracyto78%)andextendseasilytonewlanguages.Wealsomakeourcodeanddatafreelyavailable.11IntroductionCurrentlexicalresourcessuchasdictionariesandthesauridonotprovideinformationaboutthein-tensityorderofwords.Forexample,bothWordNet(Miller,1995)andRoget’s21stCenturyThesaurus(thesaurus.com)presentacceptable,great,andsu-perbassynonymsoftheadjectivegood.However,anativespeakerknowsthatthesewordsrepresentvaryingintensityandcaninfactgenerallyberankedbyintensityasacceptabledemelo.org/gdm/intensity/however,iscrucialbecauseitallowsustodifferen-tiatee.g.betweenvariousintensitiesofanemotion,andishenceveryusefulforhumanswhenlearningalanguageorjudgingproductreviews,aswellasforautomatictextunderstandingandgenerationtaskssuchassentimentandsubjectivityanalysis,recog-nizingtextualentailment,questionanswering,sum-marization,andcoreferenceanddiscourseanalysis.Inthiswork,weattempttoautomaticallyranksetsofrelatedwordsbyintensity,focusinginpar-ticularonadjectives.Thisismadepossiblebythevastamountsofworldknowledgethatarenowavail-able.Weuselexico-semanticinformationextractedfromaWeb-scalecorpusinconjunctionwithanal-gorithmbasedonaMixedIntegerLinearProgram(MILP).Linguisticanalyseshaveidentifiedphrasessuchasgoodbutnotgreatorhotandalmostscorch-inginatextcorpusassourcesofevidenceabouttherelativeintensitiesofwords.However,pureinfor-mationextractionapproachesoftenfailtoprovideenoughcoverageforreal-worlddownstreamappli-cations(TandonanddeMelo,2010),unlesssomeformofadvancedinferenceisused(Snowetal.,2006;Suchaneketal.,2009).Inourwork,weaddressthissparsityproblembyrelyingonWeb-scaledataandusinganMILPmodelthatextendsthepairwisescorestoamorecom-pletejointrankingofwordsonacontinuousscale,whilemaintainingglobalconstraintssuchastransi-tivityandgivingmoreweighttotheorderofwordpairswithhighercorpusevidencescores.Insteadofconsideringintensityrankingasapairwisedeci-sionprocess,wethusexploitthefactthatindividualdecisionsmaybenefitfromglobalinformation,e.g.abouthowtwowordsrelatetosomethirdword.Previouswork(SheinmanandTokunaga,2009;SchulamandFellbaum,2010;Sheinmanetal.,2012)hasalsousedlexico-semanticpatternstoor- l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 2 2 7 1 5 6 6 6 7 1 / / t l a c _ a _ 0 0 2 2 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 280 deradjectives.Theymainlyevaluatetheiralgorithmonasetofpairwisedecisions,butalsopresentapar-titioningapproachthatattemptstoformscalesbyplacingeachadjectivetotheleftorrightofpivotwords.Unfortunately,thisapproachoftenfailsbe-causemanypairslackorder-basedevidenceevenontheWeb,asexplainedinmoredetailinSection3.Incontrast,ourMILPjointlyusesinformationfromallrelevantwordpairsandcapturescom-plexinteractionsandinferencestoproduceinten-sityscales.Wecanthusobtainanorderbetweentwoadjectivesevenwhenthereisnoexplicitevi-denceinthecorpus(usingevidenceforrelatedpairsandtransitiveinference).OurglobalMILPisflex-ibleandcanalsoincorporateadditionalsynonymyinformationifavailable(whichhelpstheMILPfindanevenbetterrankingsolution).Ourapproachalsoextendseasilytonewlanguages.Wedescribetwoapproachesforthismultilingualextension:patternprojectionandcross-lingualMILPs.Weevaluateourpredictedintensityrankingsus-ingbothpairwiseclassificationaccuracyandrank-ingcorrelationcoefficients,achievingstrongresults,significantlybetterthanthepreviousapproachbySheinman&Tokunaga(32%relativeerrorreduc-tion)andquiteclosetohuman-levelperformance.2MethodInthissection,wedescribeeachstepofourap-proachtoorderingadjectivesonasingle,relativescale.OurmethodcanalsobeappliedtootherwordclassesandtolanguagesotherthanEnglish.2.1Web-basedScoringModel2.1.1IntensityScalesNear-synonymsmaydifferinintensity,e.g.joyvs.euphoria,ordrizzlevs.rain.Thisisparticu-larlytrueofadjectives,whichcanrepresentdifferentdegreesofagivenqualityorattributesuchassizeorage.Manyadjectivesaregradableandthusal-lowforgradingadverbialmodifierstoexpresssuchintensitydegrees,e.g.,ahousecanbeverybigorextremelybig.Often,cependant,completelydiffer-entadjectivesrefertovaryingdegreesonthesamescale,e.g.,huge,gigantic,gargantuan.Evenadjec-tiveslikeenormous(orsuperb,impossible)thatareconsiderednon-gradablefromasyntacticperspec-tivecanbeplacedonasuchascale.Weak-StrongPatternsStrong-WeakPatterns?(,)butnot?pas?(,)juste??(,)ifnot?pas?(,)butjust??(,)althoughnot?pas?(,)still??(,)thoughnot?pas?(,)butstill??(,)(and/or)même?pas?(,)althoughstill??(,)(and/or)presque?pas?(,)thoughstill?notonly?mais??(,)orvery?notjust?mais?Table1:Rankingpatternsusedinthiswork.Amongthepatternsrepresentedbytheregularexpressionsabove,weuseonlythosethatcapturelessthanorequaltofivewords(tofitintheGooglen-grams,seeSection2.1.2).Articles(un,un,le)areallowedtoappearbeforethewildcardswhereverpossible.2.1.2IntensityPatternsLinguisticstudieshavefoundlexicalpatternslike‘?butnot?'(e.g.goodbutnotgreat)torevealorderinformationbetweenapairofadjectives(SheinmanandTokunaga,2009).Weassumethatwehavetwosetsoflexicalpatternsthatallowustoinferthemostlikelyorderingbetweentwowordswhenencoun-teredinacorpus.Afirstpatternset,Pws,containspatternsthatreflectaweak-strongorderbetweenapairofword(thefirstwordisweakerthanthesec-ond),andasecondpatternset,Psw,capturesthestrong-weakorder.SeeTable1fortheadjectivepat-ternsthatweusedinthiswork(andseeSection4.1forimplementationdetailsregardingourpatterncol-lection).Manyofthesepatternsalsoapplytootherpartsofspeech(e.g.‘drizzlebutnotrain’,‘runningorevensprinting’),withsignificantdiscriminationontheWebintherightdirection.2.1.3PairwiseScoresGivenaninputsetofwordstobeplacedonascale,wefirstcollectevidenceoftheirintensityor-derbyusingtheabove-mentionedintensitypatternsandalarge,Web-scaletextcorpus.Previousworkoninformationextractionfromlimited-sizedrawtextcorporarevealedthatcover-ageisoftenlimited(Hearst,1992;HatzivassiloglouandMcKeown,1993).Somestudies(ChklovskiandPantel,2004;SheinmanandTokunaga,2009)usedhitcountsfromanonlinesearchengine,butthisisunstableandirreproducible(Kilgarriff,2007).Toavoidtheseissues,weusethelargestavailable l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 2 2 7 1 5 6 6 6 7 1 / / t l a c _ a _ 0 0 2 2 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 281 (good,great)(great,good)(petit,minute)good,butnotgreat→24492.0notgreat,justgood→248.0small,almostminute→97.0good,ifnotgreat→1912.0greatorverygood→89.0small,evenminute→41.0good,thoughnotgreat→504.0notgreatbutstillgood→47.0good,orevengreat→338.0notjustgoodbutgreat→181.0good,almostgreat→156.0Table2:SomeexamplesfromtheWeb-scalecorpusofusefulintensity-basedphrasesonadjectivepairs.staticcorpusofcounts,theGooglen-gramscorpus(BrantsandFranz,2006),whichcontainsEnglishn-grams(n=1to5)andtheirobservedfrequencycounts,generatedfromnearly1trillionwordtokensand95billionsentences.Weconsidereachpairofwords(a1,a2)inthein-putsetinturn.Foreachpatternpinthetwopatternsets(weak-strongPwsandstrong-weakPsw),wein-sertthewordpairintothepatternasp(a1,a2)togetaphrasalquerylike“bigbutnothuge”.Thisisdonebyreplacingthetwowildcardsinthepatternbythetwowordsinorder.Finally,wescantheWebn-gramscorpusinabatchapproachsimilartoBansalandKlein(2011)andcollectfrequenciesofallourphrasequeries.Table2depictssomeexamplesofusefulintensity-basedphrasequeriesandtheirfre-quenciesintheWeb-scalecorpus.Wealsocollectfrequenciesfortheinputwordunigramsandthepat-ternsfornormalizationpurposes.Givenawordpair(a1,a2)andacorpuscountfunctioncnt,wedefineW1=1P1Xp1∈Pwscnt(p1(a1,a2))S1=1P2Xp2∈Pswcnt(p2(a1,a2))W2=1P1Xp1∈Pwscnt(p1(a2,a1))S2=1P2Xp2∈Pswcnt(p2(a2,a1))(1)withP1=Xp1∈Pwscnt(p1)P2=Xp2∈Pswcnt(p2),(2)suchthatthefinaloverallweak-strongscoreisscore(a1,a2)=(W1−S1)−(W2−S2)cnt(a1)·cnt(a2).(3)HereW1andS1representWebevidenceofa1anda2beingintheweak-strongandstrong-weakrelation,respectively.W2andS2fitthereversepair(a2,a1)inthepatternsandhencerepresentthestrong-weakandweak-strongrelations,respec-tively,intheoppositedirection.Hence,overall,(W1−S1)−(W2−S2)representsthetotalweak-strongscoreofthepair(a1,a2),i.e.thescoreofa1beingontheleftofa2onarelativeintensityscale,suchthatscore(a1,a2)=−score(a2,a1).Therawfrequenciesinthescorearedividedbycountsofthepatternsandbyindividualwordunigramcountstoobtainapointwisemutualinformation(PMI)stylenormalizationandhenceavoidanybiasinthescoreduetohigh-frequencypatternsorwordunigrams.22.2GlobalOrderingwithanMILP2.2.1ObjectiveandConstraintsGivenpairwisescores,wenowaimatproducingaglobalrankingoftheinputwordsthatismuchmoreinformativethantheoriginalpairwisescores.Jointinferencefrommultiplewordpairsallowsustoben-efitfromglobalinformation:Duetothesparsityofthepatternevidence,determininghowtwoadjec-tivesrelatetoeachothercansometimese.g.onlybeinferredbyobservinghoweachofthemrelatetosomethirdadjective.WeassumethatwearegivenNinputwordsA=a1,...,aNthatwewishtoplaceonalinearscale,say[0,1].Thuseachwordaiistobeassignedapositionxi∈[0,1]basedonthepairwiseweak-strongweightsscore(ai,aj).Apositivevaluefor2Inpreliminaryexperimentsonadevelopmentset,wealsoevaluatedotherintuitiveformsofnormalization. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 2 2 7 1 5 6 6 6 7 1 / / t l a c _ a _ 0 0 2 2 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 282 Figure1:Theinputweak-strongdatamaycontainoneormorecycles,e.g.duetonoisypatterns,sothefinalrankingwillhavetochoosewhichinputscorestohonorandwhichtoremove.score(ai,aj)meansthataiissupposedlyweakerthanajandhencewewouldliketoobtainxixj.Therefore,intuitively,ourgoalcorrespondstomaximizingtheobjectiveXi,jsgn(xj−xi)·score(ai,aj)(4)Notethatitisimportanttousethesignumfunc-tionsgn()ici,becauseweonlycareabouttherel-ativeorderofxiandxj.MaximizingPij(xj−xi)·score(ai,aj)wouldleadtoallwordsbeingplacedattheedgesofthescale,becausethehighestscoreswoulddominateoverallotherones.Wedoincludethescoremagnitudesintheobjective,becausetheyhelpresolvecontradictionsinthepairwisescores(e.g.,seeFigure1).Thisisdiscussedinmorede-tailinSection2.2.2.Inordertomaximizethisnon-differentiableob-jective,weuseMixedIntegerLinearProgramming(MILP),avariantoflinearprogramminginwhichsomebutnotallofthevariablesareconstrainedtobeintegers.UsinganMILPformalization,wecanfindagloballyoptimalsolutioninthejointdeci-sionspace,andunlikepreviouswork,wejointlyex-ploitglobalinformationratherthanjustindividuallocal(pairwise)scores.ToencodetheobjectiveinaMILP,weneedtointroduceadditionalvariablesdij,wij,sijtocapturetheeffectofthesignumfunction,asexplainedbelow.WeadditionallyalsoenableourMILPtomakeuseofanyexternalequivalence(synonymy)infor-mationE⊆{1,…,N}×{1,…,N}thatmaybeavailable.Inthiscontext,twowordsareconsideredsynonymousiftheyarecloseenoughinmeaningtobeplacedon(presque)thesamepositionintheinten-sityscale.If(je,j)∈E,wecansafelyassumethatai,ajhavenear-equivalentintensity,soweshouldencouragexi,xjtoremainclosetoeachother.TheMILPisdefinedasfollows:maximizeX(je,j)6∈E(wij−sij)·score(ai,aj)−X(je,j)∈E(wij+sij)Csubjecttodij=xj−xi∀i,j∈{1,…,N}dij−wijC≤0∀i,j∈{1,…,N}dij+(1−wij)C>0∀i,j∈{1,…,N}dij+sijC≥0∀i,j∈{1,…,N}dij−(1−sij)C<0∀i,j∈{1,...,N}xi∈[0,1]∀i∈{1,...,N}wij∈{0,1}∀i,j∈{1,...,N}sij∈{0,1}∀i,j∈{1,...,N}Thedifferencevariablesdijsimplycapturediffer-encesbetweenxi,xj.CisanyverylargeconstantgreaterthanPi,j|score(ai,aj)|;theexactvalueisirrelevant.Theindicatorvariableswijandsijarejointlyusedtodeterminethevalueofthesignumfunctionsgn(dij)=sgn(xj−xi).Variableswijbecome1ifandonlyifdij>0andhenceserveasindicatorvariablesforweak-strongrelationshipsintheoutput.Variablessijbecome1ifandonlyifdij<0andhenceserveasindicatorvariablesforastrong-weakrelationshipintheoutput.Theob-jectiveencourageswij=1forscore(ai,aj)>0andsij=1forscore(ai,aj)<0.3Whenequiva-lence(synonymy)informationisavailable,thenfor(i,j)∈Ebothsij=0andwij=0areencouraged.2.2.2DiscussionOurMILPusesintensityevidenceofallinputpairstogetherandassimilatesallthescoresviaglobaltransitivityconstraintstodeterminetheposi-tionsoftheinputwordsonacontinuousreal-valuedscale.Hence,ourapproachaddressesdrawbacks3Inordertoavoidnumericinstabilityissuesduetoverysmallscore(ai,aj)valuesafterfrequencynormalization,inpracticewehavefounditnecessarytorescalethembyafac-torof1overthesmallest|score(ai,aj)|>0.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
2
2
7
1
5
6
6
6
7
1

/

/
t

je

un
c
_
un
_
0
0
2
2
7
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

283

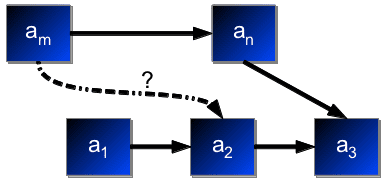
Figure2:EquivalenceInformation:Knowingthatam,a2aresynonymsgivestheMILPanindicationofwheretoplaceanonthescalewithrespecttoa1,a2,a3oflocalordivide-and-conquerapproaches,whereadjectivesarescoredwithrespecttoselectedpivotwords,andhencemanyadjectivesthatlackpairwiseevidencewiththepivotsarenotproperlyclassified,althoughtheymayhaveorderevidencewithsomethirdadjectivethatcouldhelpestablishtheranking.Optionalsynonymyinformationcanfurtherhelp,asshowninFigure2.Moreover,ourMILPalsogiveshigherweighttopairswithhigherscores,whichisusefulwhenbreakingglobalconstraintcyclesasinthesimpleexampleinFigure1.Ifweneedtobreakacon-straintviolatingtriangleorcycle,wewouldhavetomakearbitrarychoicesifwewererankingbasedonsgn(score(un,b))alone.Instead,wecanchooseabetterrankingbasedonthemagnitudeofthepair-wisescores.Astrongerscorebetweenanadjectivepairdoesn’tnecessarilymeanthattheyshouldbefurtherapartintheranking.ItmeansthatthesetwowordsareattestedtogetherontheWebwithrespecttotheintensitypatternsmorethanwithothercandi-datewords.Therefore,wetrytorespecttheorderofsuchwordpairsmoreinthefinalrankingwhenwearebreakingconstraint-violatingcycles.3RelatedWorkHatzivassiloglouandMcKeown(1993)presentedthefirststeptowardsautomaticidentificationofad-jectivescales,thoroughlydiscussingthebackgroundofadjectivesemanticsandameansofdiscoveringclustersofadjectivesthatbelongonthesamescale,thusprovidingonewayofcreatingtheinputforourrankingalgorithm.InkpenandHirst(2006)studynear-synonymsandnuancesofmeaningdifferentiation(suchasstylistic,attitudinal,etc.).Theyattempttoautomaticallyac-quireaknowledgebaseofnear-synonymdifferencesviaanunsuperviseddecision-listalgorithm.How-ever,theirmethoddependsonaspecialdictionaryofsynonymdifferencestolearntheextractionpat-terns,whileweuseonlyarawWeb-scalecorpus.Mohammadetal.(2013)proposedamethodofidentifyingwhethertwoadjectivesareantonymous.Thisproblemisrelatedbutdistinct,becausethede-greeofantonymydoesnotnecessarilydeterminetheirpositiononanintensityscale.Antonyms(e.g.,little,big)arenotnecessarilyontheextremeendsofscales.SheinmanandTokunaga(2009)andSheinmanetal.(2012)presentthemostcloselyrelatedpreviousworkonadjectiveintensities.Theycollectlexico-semanticpatternsviabootstrappingfromseedadjec-tivepairstoobtainpairwiseintensities,albeitusingsearchengine‘hits’,whichareunstableandprob-lematic(Kilgarriff,2007).Whiletheirapproachisprimarilyevaluatedintermsofalocalpairwiseclassificationtask,theyalsosuggestthepossibil-ityoforderingadjectivesonascaleusingapivot-basedpartitioningapproach.Althoughintuitiveintheory,theextractedpairwisescoresarefrequentlytoosparseforthistowork.Thus,manyadjec-tiveshavenoscorewithaparticularheadword.Inourexperiments,wereimplementedthisapproachandshowthatourMILPmethodimprovesoveritbyallowingindividualpairwisedecisionstobenefitmorefromglobalinformation.SchulamandFell-baum(2010)applytheapproachofSheinmanandTokunaga(2009)toGermanadjectives.Ourmethodextendseasilytovariousforeignlanguagesasde-scribedinSection5.Anotherrelatedtaskistheextractionoflexico-syntacticandlexico-semanticintensity-orderpat-ternsfromlargetextcorpora(Hearst,1992;ChklovskiandPantel,2004;TandonanddeMelo,2010).SheinmanandTokunaga(2009)followsDavidovandRappoport(2008)toautomaticallybootstrapadjectivescalingpatternsusingseedad-jectivesandWebhits.Thesemethodsthuscanbeusedtoprovidetheinputpatternsforouralgorithm.VerbOceanbyChklovskiandPantel(2004)ex-tractsvariousfine-grainedsemanticrelations(in-cludingthestronger-thanrelation)betweenpairsofverbs,usinglexico-syntacticpatternsovertheWeb.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
2
2
7
1
5
6
6
6
7
1

/

/
t

je

un
c
_
un
_
0
0
2
2
7
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

284

OurapproachofjointlyrankingasetofwordsusingpairwiseevidenceisalsoapplicabletotheVerbO-ceanpairs,andshouldhelpaddresssimilarsparsityissuesoflocalpairwisedecisions.Suchscaleswillagainbequiteusefulforlanguagelearnersandlan-guageunderstandingtools.deMarneffeetal.(2010)inferyes-or-noanswerstoquestionswithresponsesinvolvingscalaradjec-tivesinadialoguecorpus.Theycorrelateadjectiveswithratingsinamoviereviewcorpustofindthatgoodappearsinlower-ratedreviewsthanexcellent.Finally,therehasbeenalotofworkonmeasuringthegeneralsentimentpolarityofwords(Hatzivas-siloglouandMcKeown,1997;HatzivassiloglouandWiebe,2000;TurneyandLittman,2003;LiuandSeneff,2009;Taboadaetal.,2011;YessenalinaandCardie,2011;PangandLee,2008).Ourworkin-steadaimsatproducingalarge,unrestrictednumberofindividualintensityscalesfordifferentqualitiesandhencecanhelpinfine-grainedsentimentanaly-siswithrespecttoveryparticularcontentaspects.4Experiments4.1DataInputClustersInordertoobtaininputclustersforevaluation,westartedoutwiththesatelliteclusteror‘dumbbell’structureofadjectivesinWordNet3.0,whichconsistsoftwodirectantonymsasthepolesandanumberofothersatelliteadjectivesthatarese-manticallysimilartoeachofthepoles(GrossandMiller,1990).Foreachantonymypair,wedeter-minedanextendeddumbbellsetbylookingupsyn-onymsandwordsinrelated(satelliteadjectiveand‘see-also’)synonymsets.Wecutsuchanextendeddumbbellintotwoantonymoushalvesandtreatedeachofthesehalvesasapotentialinputadjectivecluster.MostoftheseWordNetclustersarenoisyforthepurposeofourtask,i.e.theycontainadjectivesthatappearunrelatableonasinglescaleduetopolysemyandsemanticdrift,e.g.violentwithrespecttosuper-naturalandaffected.MotivatedbySheinmanandTokunaga(2009),wesplitsuchhard-to-relatead-jectivesintosmallerscale-specificsubgroupsusingthecorpusevidence4.Forthis,weconsideranundi-4NotethatwedonotusetheWordNetdatasetofSheinmanandTokunaga(2009)forevaluation,asitdoesnotprovidefull438 115 60 35 19 12 14 5 4 3 0 100 200 300 400 500 2 3 4 5 6 7 8 9 10-14 15-17 # of chains Length of chain Figure3:Thehistogramofclustersizesafterpartitioning.41 27 12 3 3 2 0 10 20 30 40 50 3 4 5 6 7 8 # of chains Length of chain Figure4:Thehistogramofclustersizesinthetestset.rectededgebetweeneachpairofadjectivesthathasanon-zerointensityscore(basedontheWeb-scalescoringproceduredescribedinSection2.1.3).Theresultinggraphisthenpartitionedintoconnectedcomponentssuchthatanyadjectivesinasubgraphareatleastindirectlyconnectedviasomepathandthusmuchmorelikelytobelongtothesameinten-sityscale.Whilethisdoesbreakuppartitionswhen-everthereisnocorpusevidenceconnectingthem,orderingtheadjectiveswithineachsuchpartitionre-mainsachallengingtask.ThisisbecausetheWebevidencewillstillnotnecessarilydirectlyrelatealladjectives(inapartition)toeachother.Addition-ally,theWebevidencemaystillindicatethewrongdirection.Figure3showsthesizedistributionoftheresultingpartitions.PatternsToconstructourintensitypatternset,westartedwithacoupleofcommonrankableadjectiveseedpairssuchas(good,great)et(hot,boiling)andusedtheWeb-scalen-gramscorpus(BrantsandFranz,2006)tocollectthefewmostfrequentpat-ternsbetweenandaroundtheseseed-pairs(inbothdirections).Amongthese,wemanuallychoseascales.Instead,theirannotatorsonlymadepairwisecompar-isonswithselectwords,usinga5-wayclassificationscheme(neutral,mild,verymild,intense,veryintense).

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
2
2
7
1
5
6
6
6
7
1

/

/
t

je

un
c
_
un
_
0
0
2
2
7
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

285

smallsetofintuitivepatternsthatarelinguisticallyusefulfororderingadjectives,severalofwhichhadnotbeendiscoveredinpreviouswork.TheseareshowninTable1.Notethatweonlycollectedpat-ternsthatwerenotambiguousinthetwoorders,forexamplethepattern’?,pas?’isambiguousbe-causeitcanbeusedasboth’good,notgreat’and’great,notgood’.Alternatively,onecaneasilyalsousefully-automaticbootstrappingtechniquesbasedonseedwordpairs(Hearst,1992;ChklovskiandPantel,2004;YangandSu,2007;Turney,2008;DavidovandRappoport,2008).Cependant,oursemi-automaticapproachisasimpleandfastprocessthatextractsasmallsetofhigh-qualityandverygen-eraladjective-scalingpatterns.Thisprocesscanquicklyberepeatedfromscratchinanyotherlan-guage.Moreover,asdescribedinSection5.1,theEnglishpatternscanalsobeprojectedautomaticallytopatternsinotherlanguages.DevelopmentandTestSetsSection2.1describesthemethodforcollectingtheintensityscoresforad-jectivepairs,usingWeb-scalen-grams(BrantsandFranz,2006).WereliedonasmalldevelopmentsettotesttheMILPstructureandthepairwisescoresetup.Forthis,wemanuallychose5representativeadjectiveclustersfromthefullsetofclusters.Thefinaltestset,distinctfromthisdevelopmentset,consistsof569wordpairsin88clusters,eachannotatedbytwonativespeakersofEnglish.Boththegoldtestdata(andourcode)arefreelyavail-able.5Toarriveatthisdata,werandomlydrew30clusterseachforclustersizes3,4,and5+fromthehistogramofpartitionedadjectiveclustersinFig-ure3.Whilelabelingacluster,annotatorscouldex-cludewordsthattheydeemedunsuitabletofitonasinglesharedintensityscalewiththerestofthecluster.Fortunately,thepartitioningdescribedear-lierhadalreadyseparatedmostsuchcasesintodis-tinctclusters.Theannotatorsorderedtheremainingwordsonascale.Wordsthatseemedindistinguish-ableinstrengthcouldsharepositionsintheiranno-tation.Asourgoalistocomparescaleformationalgo-rithms,wedidnotincludetrivialclustersofsize2.Onsuchtrivialclusters,theWebevidencealonede-terminestheoutputandhenceallalgorithms,includ-5http://demelo.org/gdm/intensity/ingthebaseline,obtainthesamepairwiseaccuracy(definedbelow)of93.3%onaseparatesetof30ran-domclustersofsize2.Figure4showsthedistributionofclustersizesinourmaingoldset.Theinter-annotatoragreementintermsofCohen’sκ(Cohen,1960)onthepairwiseclassificationtaskwith3labels(weaker,stronger,orequal/unknown)was0.64.Intermsofpairwiseaccuracy,theagreementwas78.0%.4.2MetricsInordertothoroughlyevaluatetheperformanceofouradjectiveorderingprocedure,werelyonbothpairwiseandranking-correlationevaluationmetrics.ConsiderasetofinputwordsA={a1,a2,…,un}andtworankingsforthisset–agold-standardrank-ingrG(UN)andapredictedrankingrP(UN).4.2.1PairwiseAccuracyForapairofwordsai,aj,wemayconsidertheclassificationtaskofchoosingoneofthreelabels(<,>,=?)forthecaseofaibeingweaker,stronger,andequal(orunknown)inintensity,respectivement,com-paredtoa2:L(a1,a2)=>ifr(ai)>r(aj)=?ifr(ai)=r(aj)Foreachpair(a1,a2),wecomputegold-standardlabelsLG(a1,a2)andpredictedlabelsLP(a1,a2)asabove,andthenthepairwiseaccuracyPW(UN)foraparticularorderingonAissimplythefractionofpairsthatarecorrectlyclassified,i.e.forwhichthepredictedlabelissameasthegold-standardlabel:PW(UN)=Pil D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 2 2 7 1 5 6 6 6 7 1 / / t l a c _ a _ 0 0 2 2 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 286 Kendall’staucorrelationcoefficientWeusetheτbversionofKendall’scorrelationmetric,asitin-corporatesacorrectionforties(Kruskal,1958;Douetal.,2008):τb=P−Qp(P+Q+X0)·(P+Q+Y0)wherePisthenumberofconcordantpairs,Qisthenumberofdiscordantpairs,X0isthenumberofpairstiedinthefirstranking,Y0isthenumberofpairstiedinthesecondranking.Giventhetworank-ingsofanadjectivesetA,thegold-standardrankingrG(UN)andthepredictedrankingrP(UN),twowordsai,ajare:•concordantiffbothrankingshavethesamestrictorderofthetwoelements,i.e.,rG(ai)>rG(aj)andrP(ai)>rP(aj),orrG(ai)>rG(aj)andrP(ai)>rP(aj).•tiediffrG(ai)=rG(aj)orrP(ai)=rP(aj).Spearman’srhocorrelationcoefficientFortwon-sizedrankedlists{xi}et{yi},theSpearmancorrelationcoefficientisdefinedasthePearsoncor-relationcoefficientbetweentheranksofvariables:ρ=Pi(xi−¯x)·(yi−¯y)rPi(xi−¯x)2·Pi(yi−¯y)2Ici,¯xand¯ydenotethemeansofthevaluesintherespectivelists.Weusethestandardprocedureforhandlingtiescorrectly.Tiedvaluesareassignedtheaverageofallranksofitemssharingthesamevalueintherankedlistsortedinascendingorderofthevalues.HandlingInversionsWhileannotating,wesome-timesobservedthattheorderingitselfwasveryclearbuttheannotatorsdisagreedaboutwhichendofaparticularscalewastocountasthestrongone,e.g.whentransitioningfromsofttohardorfromalphatobeta.Wethusalsoreportaverageabsolutevaluesofbothcorrelationcoefficients,astheseproperlyac-countforanticorrelations.Ourtestsetonlycontainsclustersofsize3orlarger,sothereisnoneedtoaccountforinversionsinclustersofsize2.4.3ResultsInTable3,weusetheevaluationmetricsmentionedabovetocompareseveraldifferentapproaches.WebBaselineThefirstbaselinesimplyreflectstheoriginalpairwiseWeb-basedintensityscores.Weclassify(withoneof3labels)agivenpairofadjectivesusingtheWeb-basedintensityscores(asdescribedinSection2.1.3)asfollows:Lbaseline(a1,a2)=0>ifscore(ai,aj)<0=?ifscore(ai,aj)=0Sincescore(ai,aj)representstheweak-strongscoreofthetwoadjectives,amorepositivevaluemeansahigherlikelihoodofaibeingweaker(<,ontheleft)inintensitythanaj.InTable3,weobservethatthe(micro-averaged)pairwiseaccuracy,asdefinedearlier,fortheorigi-nalWebbaselineis48.2%,whiletherankingmea-suresareundefinedbecausetheindividualpairsdonotleadtoacoherentscale.Divide-and-ConquerThedivide-and-conquerbaselinerecursivelysplitsasetofwordsintothreesubgroups,placedtotheleft(weaker),onthesameposition(noevidence),ortotheright(stronger)ofagivenrandomlychosenpivotword.Whilethisapproachshowsonlyaminorimprove-mentintermsofthepairwiseaccuracy(50.6%),itsmainbenefitisthatoneobtainswell-definedinten-sityscalesratherthanjustacollectionofpairwisescores.SheinmanandTokunagaTheapproachbySheinmanandTokunaga(2009)involvesasimi-lardivide-and-conquerbasedpartitioninginthefirstphase,exceptthattheirmethodmakesuseofsyn-onymyinformationfromWordNetandusesallsyn-onymsinWordNet’ssynsetfortheheadwordasneutralpivotelements(iftheheadwordisnotinWordNet,thenthewordwiththemaximalunigramfrequencyischosen).Inthesecondphase,theirmethodperformspairwisecomparisonswithinthemoreintenseandlessintensesubgroups.Wereim-plementtheirapproachhere,usingtheGoogleN-GramsdatasetinsteadofonlineWebsearchenginehits.WeobserveasmallimprovementovertheWebbaselineintermsofpairwiseaccuracy.Notethatthe l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 2 2 7 1 5 6 6 6 7 1 / / t l a c _ a _ 0 0 2 2 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 287 MethodPairwiseAccuracyAvg.τAvg.|τ|Avg.ρAvg.|r|WebBaseline48.2%N/AN/AN/AN/ADivide-and-Conquer50.6%0.450.530.520.62SheinmanandTokunaga(2009)55.5%N/AN/AN/AN/AMILP69.6%0.570.650.640.73MILPwithsynonymy78.2%0.570.660.670.80Inter-AnnotatorAgreement78.0%0.670.760.750.86Table3:MaintestresultsPredictedClassWeakerTieStrongerTrueClassWeaker11712715Tie54215Stronger11122115Table4:Confusionmatrix(Webbaseline)rankcorrelationmeasurescoresareundefinedfortheirapproach.Thisisbecauseinsomecasestheirmethodplacedallwordsonthesamepositioninthescale,whichthesemeasurescannothandleevenintheirtie-correctedversions.Overall,theSheinmanandTokunagaapproachdoesnotaggregateinforma-tionsufficientlywellatthegloballevelandoftenfailstomakeuseoftransitiveinference.MILPOurMILPexploitsthesamepairwisescorestoinducesignificantlymoreaccuratepair-wiselabelswith69.6%accuracy,a41%relativeerrorreductionovertheWebbaseline,38%overDivide-and-Conquer,and32%overSheinmanandTokunaga(2009).WefurtherseethatourMILPmethodisabletoexploitexternalsynonymy(equiv-alence)information(usingsynonymsmarkedbytheannotators).Theaccuracyofthepairwisescoresaswellasthequalityoftheoverallrankingincreaseevenfurtherto78.2%,approachingthehumaninter-annotatoragreement.Intermsofaveragecorrelationcoefficients,weobservesimilarimprovementtrendsfromtheMILP,butofdifferentmagnitudes,becausetheseaveragesgivesmallclustersthesameweightaslargerones.4.4AnalysisConfusionMatricesForagivenapproach,wecanstudytheconfusionmatrixobtainedbycross-tabulatingthegoldclassificationwiththepredictedPredictedClassWeakerTieStrongerTrueClassWeaker1772953Tie92429Stronger1538195Table5:Confusionmatrix(MILP)classificationofeveryuniquepairofadjectivesinthegroundtruthdata.Table4showstheconfusionmatrixfortheWebbaseline.Weobservethatduetothesparsityofpairwiseintensityorderevidence,thebaselinemethodpredictstoomanyties.Table5providestheconfusionmatrixfortheMILP(withoutexternalequivalenceinformation)forcomparison.AlthoughthemiddlecolumnstillshowsthattheMILPpredictsmoretiesthanhumansannotators,wefindthataclearmajorityofalluniquepairsarenowcorrectlyplacedalongthediagonal.ThisconfirmsthatourMILPsuccessfullyinfersneworderingdecisions,althoughitusesthesameinput(corpusevidence)asthebaseline.TheremainingtiesaremostlyjusttheresultofpairsforwhichtheresimplyisnoevidenceatallintheinputWebcounts.Notethatthisproblemcouldforinstancebecircum-ventedbyrelyingonacrowdsourcingapproach:Afewdispersedtie-breakersareenoughtoallowourMILPtocorrectmanyotherpredictions.PredictedExamplesFinally,inTable6,wepro-videaselectionofrealresultsobtainedbyouralgo-rithm.Forinstance,itcorrectlyinferredthatterri-fyingismoreintensethancreepyorscary,althoughtheWebpatterncountsdidnotprovideanyexplicitinformationaboutthesewordspairs.Insomecases,cependant,theWebevidencedidnotsufficetodrawtherightconclusions,oritwasmisleadingduetois-sueslikepolysemy(asforthewordfunny). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 2 2 7 1 5 6 6 6 7 1 / / t l a c _ a _ 0 0 2 2 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 288 AccuracyPredictionGoldStandardGoodhardd/excellentresultsin‘goodbutnotexcellent’.Thisphraseisthentrans-latedintothetargetlanguageusingthetranslationsystem,sayintoGerman‘gutabernichtausgezeich-net’.Finally,putbackthewildcardsintheplaceofthetranslationsoftheadjectivewords,heregutandausgezeichnet,togetthecorrespondingGermanpat-tern‘?abernicht?’.Table7showsvariousGermanintensitypatternsthatweobtainbyprojectingfromtheEnglishpatternsasdescribed.Theprocessisre-peatedwithmultipleadjectivepairsincasedifferentvariantsarereturned,e.g.duetomorphology.Mostofthesetranslationsdeliverusefulresults.Nowthatwehavethetargetlanguageadjectivesandtherankingpatterns,wecancomputethepair-wiseintensityscoresusinglarge-scaledatainthatlanguage.WecanusetheGooglen-gramscor-porafor10Europeanlanguages(BrantsandFranz,2009),andalsoforChinese(LDC2010T02)andJapanese(LDC2009T08).Forotherlanguages,onecanuseavailablelargeraw-textcorporaorWebcrawlingtools.5.2CrosslingualMILPToimprovetherankingsforlesser-resourcedlan-guages,wecanfurtheruseajointMILPapproachforthenewlanguagewewanttotransferthispro-cessto.AdditionalconstraintsbetweentheEnglish l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e - p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 2 2 7 1 5 6 6 6 7 1 / / t l a c _ a _ 0 0 2 2 7 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 289 Weak-StrongPatternsStrong-WeakPatternsEnglishGermanEnglishGerman?butnot??abernicht?pas?juste?nicht?gerade??ifnot??wennnicht?pas?butjust?nicht?abernur??andalmost??undfast?pas?thoughstill?nicht?aberimmernoch?notjust?mais?nichtnur?sondern??orvery??odersehr?Table7:ExamplesofGermanintensitypatternsprojected(translated)directlyfromtheEnglishpatterns.wordsandtheircorrespondingtargetlanguagetrans-lations,incombinationwiththeEnglishrankingin-formation,allowthealgorithmtoobtainbetterrank-ingsforthetargetwordswheneverthenon-Englishtargetlanguagecorpusdoesnotprovidesufficientintensityorderevidence.Inthiscase,theinputsetAcontainswordsinmultiplelanguages.TheWebintensityscoresscore(ai,aj)shouldbesettozerowhencomparingwordsacrosslanguages.WeinsteadlinkthemusingatranslationtableT⊆{1,...,N}×{1,...,N}fromatranslationdictionaryorphrasetable.Here,(je,j)∈Tsignifiesthataiisatranslationofaj.Wedonotrequireabijectiverelationshipbetweenthem(i.e.,translationsneedn’tbeunique).TheobjectivefunctionisaugmentedbyaddingthenewtermX(je,j)∈T(w0ij+s0ij)CT(5)foraconstantCT>0thatdetermineshowmuchweightweassigntotranslationsasopposedtothecorpuscountscores.TheMILPisextendedbyaddingthefollowingextraconstraints.dij−w0ijCT<−dmax∀i,j∈{1,...,N}dij+(1−w0ij)CT≥−dmax∀i,j∈{1,...,N}dij+s0ijCT>dmax∀i,j∈{1,…,N}dij−(1−s0ij)CT≤dmax∀i,j∈{1,…,N}w0ij∈{0,1}∀i,j∈Ts0ij∈{0,1}∀i,j∈TThevariablesdi,j,asbefore,encodedistancesbe-tweenpositionsofwordsonthescale,butnowalsoincludecross-lingualpairsofwordsindifferentlan-guages.Thenewconstraintsencouragetranslationalequivalentstoremainclosetoeachother,preferablywithinadesired(butnotstrictlyenforced)maximumdistancedmax.Thenewvariablesw0ij,s0ijaresim-ilartowij,sijinthestandardMILP.However,thew0ijbecome1ifandonlyifdij≥−dmaxandthes0ijbecome1ifandonlyifdij≤dmax.Ifbothw0ijands0ijare1,thenthetwowordshaveasmalldistance−dmax≤dij≤dmax.Theaugmentedobjectivefunctionexplicitlyencouragesthisfortranslationalequivalents.Overall,thisapproachthusallowsevi-dencefromalanguagewithmoreWebevidencetoimprovetheprocessofadjectiveorderinginlesser-resourcedlanguages.6ConclusionInthiswork,wehavepresentedanapproachtothechallengingandlittle-studiedtaskofrankingwordsintermsoftheirintensityonacontinuousscale.Weaddresstheissueofsparsityoftheintensityorderev-idenceintwoways.First,pairwiseintensityscoresarecomputedusinglinguisticallyintuitivepatternsinaverylarge,Web-scalecorpus.Next,aMixedIntegerLinearProgram(MILP)expandsonthisfur-therbyinferringnewrelativerelationships.Insteadofmakingorderingdecisionsaboutwordpairsin-dependently,ourMILPconsidersthejointdecisionspaceandfactorsine.g.howtwoadjectivesrelatetosomethirdadjective,thusenforcingglobalcon-straintssuchastransitivity.Ourapproachisgeneralenoughtoallowaddi-tionalevidencesuchassynonymyintheMILP,andcanstraightforwardlybeappliedtootherwordclasses(suchasverbs),andtootherlanguages(monolinguallyaswellascross-lingually).Theoverallresultsacrossmultiplemetricsaresubstan-tiallybetterthanpreviousapproaches,andfairlyclosetohumanagreementonthischallengingtask.AcknowledgmentsWewouldliketothanktheeditorandtheanony-mousreviewersfortheirhelpfulfeedback.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

e
d
toi

/
t

un
c
je
/

je

un
r
t
je
c
e
–
p
d

F
/

d
o

je
/

.

1
0
1
1
6
2

/
t

je

un
c
_
un
_
0
0
2
2
7
1
5
6
6
6
7
1

/

/
t

je

un
c
_
un
_
0
0
2
2
7
p
d

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

290

ReferencesMohitBansalandDanKlein.2011.Web-scalefeaturesforfull-scaleparsing.InProceedingsofACL2011.ThorstenBrantsandAlexFranz.2006.TheGoogleWeb1T5-gramcorpusversion1.1.LDC2006T13.ThorstenBrantsandAlexFranz.2009.Web1T5-gram,10Europeanlanguages,version1.LDC2009T25.TimothyChklovskiandPatrickPantel.2004.VerbO-cean:Miningthewebforfine-grainedsemanticverbrelations.InProceedingsofEMNLP2004.JacobCohen.1960.Acoefficientofagreementfornom-inalscales.EducationalandPsychologicalMeasure-ment,20(1):37–46.DmitryDavidovandAriRappoport.2008.Unsuper-viseddiscoveryofgenericrelationshipsusingpatternclustersanditsevaluationbyautomaticallygeneratedsatanalogyquestions.InProceedingsofACL2008.Marie-CatherinedeMarneffe,ChristopherD.Manning,andChristopherPotts.2010.Wasitgood?itwasprovocative.learningthemeaningofscalaradjectives.InProceedingsofACL2010.GerarddeMeloandGerhardWeikum.2009.Towardsauniversalwordnetbylearningfromcombinedevi-dence.InProceedingsofCIKM2009.ZhichengDou,RuihuaSong,XiaojieYuan,andJi-RongWen.2008.Areclick-throughdataadequateforlearn-ingwebsearchrankings?InProc.ofCIKM2008.DerekGrossandKatherineJ.Miller.1990.AdjectivesinWordNet.InternationalJournalofLexicography,3(4):265–277.VasileiosHatzivassiloglouandKathleenR.McKeown.1993.Towardstheautomaticidentificationofadjecti-valscales:Clusteringadjectivesaccordingtomeaning.InProceedingsofACL1993.VasileiosHatzivassiloglouandKathleenR.McKeown.1997.Predictingthesemanticorientationofadjec-tives.InProceedingsofACL1997.VasileiosHatzivassiloglouandJanyceM.Wiebe.2000.Effectsofadjectiveorientationandgradabilityonsen-tencesubjectivity.InProceedingsofCOLING2000.MartiHearst.1992.Automaticacquisitionofhyponymsfromlargetextcorpora.InProceedingsofCOLING1992.DianaInkpenandGraemeHirst.2006.Buildingandusingalexicalknowledgebaseofnear-synonymdif-ferences.ComputationalLinguistics,32(2):223–262.MauriceG.Kendall.1938.Anewmeasureofrankcor-relation.Biometrika,30(1/2):81–93.AdamKilgarriff.2007.Googleologyisbadscience.ComputationalLinguistics,33(1).WilliamH.Kruskal.1958.Ordinalmeasuresofassocia-tion.JournaloftheAmericanStatisticalAssociation,53(284):814–861.JingjingLiuandStephanieSeneff.2009.Reviewsenti-mentscoringviaaparse-and-paraphraseparadigm.InProceedingsofEMNLP2009.GeorgeA.Miller.1995.WordNet:Alexicaldatabaseforenglish.CommunicationsoftheACM,38(11):39–41.SaidM.Mohammad,BonnieJ.Dorr,GraemeHirst,andPeterD.Turney.2013.Computinglexicalcontrast.ComputationalLinguistics.BoPangandLillianLee.2008.Opinionminingandsentimentanalysis.FoundationsandTrendsinInfor-mationRetrieval,2(1-2):1–135,January.PeterF.SchulamandChristianeFellbaum.2010.Au-tomaticallydeterminingthesemanticgradationofger-manadjectives.InProceedingsofKONVENS2010.VeraSheinmanandTakenobuTokunaga.2009.AdjS-cales:Visualizingdifferencesbetweenadjectivesforlanguagelearners.IEICETransactionsonInformationandSystems,92(8):1542–1550.VeraSheinman,TakenobuTokunaga,I.Julien,P.Schu-lam,andC.Fellbaum.2012.RefiningWordNetadjec-tivedumbbellsusingintensityrelations.InProceed-ingsofGlobalWordNetConference2012.RionSnow,DanielJurafsky,andAndrewY.Ng.2006.Semantictaxonomyinductionfromheterogenousevi-dence.InProceedingsofCOLING/ACL2006.CharlesSpearman.1904.Theproofandmeasurementofassociationbetweentwothings.TheAmericanjournalofpsychology,15(1):72–101.FabianM.Suchanek,MauroSozio,andGerhardWeikum.2009.SOFIE:aself-organizingframeworkforinformationextraction.InProceedingsofWWW2009.MaiteTaboada,JulianBrooke,MilanTofiloskiy,andKimberlyVollz.2011.Lexicon-basedmethodsforsentimentanalysis.ComputationalLinguistics.NiketTandonandGerarddeMelo.2010.Informationextractionfromweb-scalen-gramdata.InProceed-ingsoftheSIGIR2010WebN-gramWorkshop.PeterD.TurneyandMichaelL.Littman.2003.Mea-suringpraiseandcriticism:Inferenceofsemanticorientationfromassociation.ACMTrans.Inf.Syst.,21(4):315–346,October.PeterD.Turney.2008.Auniformapproachtoanalogies,synonyms,antonyms,andassociations.InProceed-ingsofCOLING2008.XiaofengYangandJianSu.2007.Coreferenceresolu-tionusingsemanticrelatednessinformationfromauto-maticallydiscoveredpatterns.InProceedingsofACL2007.AinurYessenalinaandClaireCardie.2011.Composi-tionalmatrix-spacemodelsforsentimentanalysis.InProceedingsofEMNLP2011.

Télécharger le PDF