THE EFFECTS OF DEMOGRAPHIC MISMATCH
IN AN ELITE PROFESSIONAL SCHOOL
SETTING
Chris Birdsall
School of Public Service
Boise State University
Boise, ID 83725
chrisbirdsall@boisestate.edu
Seth Gershenson
(corresponding author)
American University and IZA
Washington, CC 20016
gershens@american.edu
Raymond Zuniga
Center for Public
Administration and Policy
Virginia Tech University
Blacksburg, VA 24061
raymondz@vt.edu
Abstrait
Ten years of administrative data from a diverse, private, top-100
law school are used to examine the ways in which female and non-
white students benefit from exposure to demographically sim-
ilar faculty in first-year, required law courses. Arguably, causal
impacts of exposure to same-sex and same-race instructors on
course-specific outcomes such as course grades are identified by
leveraging quasi-random classroom assignments and a two-way
(student and classroom) fixed effects strategy. Having an other-
sex instructor reduces the likelihood of receiving a good grade
(A or A–) par 1 percentage point (3 pour cent) and having an other-
race instructor reduces the likelihood of receiving a good grade by
3 percentage points (10 pour cent). The effects of student–instructor
demographic mismatch are particularly salient for nonwhite and
female students. These results provide novel evidence of the per-
vasiveness of demographic-match effects and of the graduate
school education production function.
https://doi.org/10.1162/edfp_a_00280
© 2018 Association pour le financement et la politique de l'éducation
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
F
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
un
_
0
0
2
8
0
p
d
.
/
F
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
457
Effects of Demographic Mismatch
INTRODUCTION
1 .
A robust literature in the economics of education documents wide-ranging impacts
of student–teacher demographic match on both students and teachers. In K–12 class-
rooms, assignment to an other-race or other-sex teacher has been shown to harm
student achievement (Dee 2004, 2007) and increase student absences (Holt and Ger-
shenson 2019).1 De la même manière, racial mismatch lowers teachers’ perceptions of student
behavior (Dee 2005) and their expectations for students’ educational attainment (Ger-
shenson, Holt, and Papageorge 2016). The impact of faculty representation has also
been studied in the postsecondary context, particularly among first-year undergradu-
ates (Bettinger and Long 2005; Hoffmann and Oreopoulos 2009; Carrell, Page, et
West 2010; Fairlie, Hoffmann, et Oréopoulos 2014). These studies typically find mod-
est effects of having a same-sex or same-race instructor on course grades, the likelihood
of dropping a class, and choice of major. Lusher, Campbell, and Carrell (2015) show sim-
ilar effects of having a same-race teaching assistant (recitation section leader) on course
grades and office-hour and course attendance. Even in online environments, instruc-
tors, particularly white instructors, are more likely to respond to white male students’
comments (Baker et al. 2018).
Cependant, the extant literature has yet to investigate the extent of student–instructor
demographic mismatch effects in the postgraduate or professional school setting.2 The
current study contributes to this gap in the literature by showing that the consequences
of student–instructor demographic mismatch are just as pronounced in an elite, pro-
fessional school setting as they are in K–12, community college, and first-year under-
graduate classrooms. Doing so is important for at least three reasons.
D'abord, this study enhances our understanding of the production of graduate degrees.
Remarkably little is known about the nature of the law school education production
fonction, or that for graduate school more generally.3 This is troubling, as graduate
students comprise a nontrivial segment of the U.S. postsecondary student population:
à propos 15 percent of postsecondary students are graduate students and about 40 pour cent
of outstanding student loan debt was accumulated to finance graduate degrees (Delisle
2014). Graduate degrees themselves facilitate entrance into many high-status and high-
paying professions central to the modern economy. The legal profession is one promi-
nent example: Nearly all states require that lawyers hold a Juris Doctor (JD) from an
American Bar Association (ABA)-accredited law school, lawyers constitute about 1 par-
cent of the U.S. labor force, and law firm revenues constitute about 1 percent of U.S.
gross domestic product (Azmat and Ferrer 2017). The current study provides evidence
on some of the educational inputs and environments that affect law school students’
achievement, skill development, choice of specialization, and persistence.
1. Mismatch is not universally harmful, cependant, as Antecol, Eren, and Ozbeklik (2015) find that less-prepared
female math teachers reduce female students’ achievement but have no such effect on male students.
2. There is a litany of qualitative and anecdotal evidence of such demographic biases in legal education (Banks
1988; Guinier et al. 1994; Darling-Hammong and Holmquist 2015), but to our knowledge there is no credi-
bly identified, quantitative evidence on the impact of law student–instructor demographic match on student
résultats.
3. Exceptions include recent natural experiments involving first-year law students at Stanford, who were randomly
assigned to small classes (Ho and Kelman 2014) and at Minnesota, where students were randomly assigned to
receive individualized feedback (Schwarcz and Farganis 2017). Neumark and Gardecki (1998) find that increas-
ing female faculty members in economics departments improved time to completion and completion rates for
female graduate students.
458
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
F
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
un
_
0
0
2
8
0
p
d
.
/
F
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
Deuxième, the current study sheds light on the role that institutions play in per-
petuating demographic wage, skill, and partnership gaps in the legal profession. Pour
example, female lawyers earn lower salaries and are less likely to be promoted to part-
ner than their male counterparts, even after conditioning on basic employee and firm
characteristics (Wood, Corcoran, and Courant 1993; Dinovitzer, Reichman, and Sterling
2009; Azmat and Ferrer 2017).4Azmat and Ferrer (2017) show that performance gaps
explain much of the previously unexplained sex gap in lawyers’ earnings, though the
exact sources of gaps in performance and specialization among practicing lawyers re-
main unclear. Law school environments and mentoring practices might contribute to
this divergence in post–law school productivity, even when male and female students
enter law school with similar skills (Bertrand 2011; Ho and Kelman 2014). We test this
hypothesis by examining whether the demographic match between law students and
instructors affects student outcomes. Doing so will inform law school policy and prac-
tice by identifying the malleable factors that influence the success of underrepresented
graduate school students and our understanding of the importance that faculty play in
the production of graduate education more generally. En effet, law schools are repre-
sentative of a broad class of professional graduate schools and programs from which
professional service providers are recruited directly into the labor market (par exemple., busi-
ness, engineering; Oyer and Schaefer 2015).
Enfin, there are social consequences of demographic gaps in the receipt of law
degrees and in the career paths of law school graduates (Holder 2001). Par exemple,
the underrepresentation of racial and ethnic minorities in the U.S. judiciary likely con-
tributes to documented demographic disparities in sentencing (Mustard 2001). En effet,
implicit association tests show that white judges often hold implicit (unconscious)
biases against nonwhite defendants (Rachlinski and Johnson 2009). In the field,
emotional shocks associated with the outcomes of football games have been shown to
increase the sentences assigned by judges, particularly for black defendants (Eren and
Mocan 2016). And regarding the demographic pay gaps discussed above, a lack of rep-
resentation among law school faculty and/or how law school faculty interact with and
mentor women and students of color can cause sorting into specializations and other
behavioral responses that affect prestige, pay, and upward mobility. Finalement, biases
against women and people of color can produce self-fulfilling prophecies in which
members of stereotyped groups ultimately conform to what were initially incorrect be-
liefs (Steele 1997; Loury 2009; Papageorge, Gershenson, and Kang 2016). Institutional
factors, such as faculty composition, can therefore perpetuate the underrepresentation
of certain demographic groups in the legal profession (Wilkins and Gulati 1996).
Specifically, we use rich administrative data from a top-100 law school in which first-
year students are at least quasi-randomly assigned to course sections in conjunction
with an array of arguably causal fixed-effects identification strategies to show that hav-
ing a demographically mismatched first-year law instructor significantly reduces the
probability of receiving a “good grade” (A/A–) in the course. Surtout, we find no
such effects on the likelihood of dropping a course, which suggests the course-grade
4. This is consistent with “glass ceilings” and pay gaps in top management positions (Bertrand and Hallock 2001),
as well as in the labor force more generally (Altonji and Blank 1999).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
F
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
un
_
0
0
2
8
0
p
d
F
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
459
Effects of Demographic Mismatch
analyses are not biased by missing grades for courses that students dropped, and is
likely due to the relatively rigid first-year requirements for progressing in the program.
Other-race effects tend to be larger in magnitude than other-sex effects, particularly
among nonwhite and nonwhite female students, though both are statistically and
economically significant. There are cumulative effects of exposure to demographically
mismatched first-semester instructors on second-semester course grades in two-
course sequences, suggesting that such effects persist, though we find no evidence of
contemporaneous spillover effects of exposure to demographically matched faculty on
performance in unrelated courses.5 Classroom environments such as class size and
class composition moderate the impact of student–instructor demographic mismatch
in ways that hint at the mechanisms through which such effects operate. That we find
such effects in an elite professional school setting suggests that the phenomena of im-
plicit bias, stereotype threat, and role-model effects are broad, societal phenomena that
permeate beyond relatively vulnerable populations of schoolchildren and community
college students, and have implications for all social interactions, even those involving
high-achieving individuals. En effet, a recent field experiment finds that black men
are more likely to select preventive services and talk to the doctor about their health
problems when the doctor is of the same race (Alsan, Garrick, and Graziani 2018).
The paper proceeds as follows: Section 2 describes the administrative data and in-
stitutional details. Section 3 introduces the identification strategy. Section 4 presents
the results. Section 5 concludes.
2 . DATA A N D I N S T I T U T I O N A L D E TA I L S
This section describes the administrative data analyzed in the current study. We first
describe the institutional context and the formation of the analytic sample, then we
summarize the analytic sample.
Administrative Data
All analyses use longitudinal administrative data from a private, top-100 law school
(LS) located in a major urban center. The LS enrolls approximately 1,000 students per
année, on average, and employs approximately 200 full-time and part-time faculty. C'est
one of the most demographically and geographically diverse top-ranked law schools.
The most recent U.S. News & World Report (U.S. News) rankings rank the LS in the
top 100.6 Demographically, LS ranks in the top 50 ABA-approved law schools for both
racial/ethnic minority and female JD-student enrollment.7 Thus, although LS is one of
the more demographically diverse law schools in the United States, it is not an outlier
and is comparable to other highly ranked, national law schools in this regard.
The main analytic sample is restricted to students’ first-year required courses for
three reasons. D'abord, entering students take the same set of courses during their first
two semesters of law school. Most courses are semester-specific, meaning that course
A is usually taken in the fall semester and course B is taken in the spring semester.
5. See Appendix table A.1.
6. See http://grad-schools.usnews.rankingsandreviews.com/best-graduate-schools/top-law-schools/law-rankin
gs/page+4.
7. Rankings calculated as average percent enrollment from 2009 à 2013 using data obtained from the American
Bar Association (www.americanbar.org/groups/legal_education/resources/statistics.html).
460
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
F
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
un
_
0
0
2
8
0
p
d
.
F
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
Deuxième, the majority of first-year courses are assessed using a blind grading system.8
This speaks to the mechanisms through which observed mismatch effects operate, comme
it precludes explicit grading biases of the type documented by Lavy (2008) from being
the primary mechanism. Enfin, at least in some years, student assignments to specific
class sections, made by LS advisors and administrators, were quasi-random.9 Similarly,
the courses taken in each semester of the first year are randomly assigned by school
administrators. About three to four sections of each course are offered in a semester in
which the course is offered, with the exception of one writing course that has smaller
class sizes and thus has about twenty-five sections per semester. We verify, and exploit,
this random assignment in the empirical analysis.
The administrative data include detailed information on course-specific outcomes,
such as grades, dropout behavior, and taking an elective course in the same concentra-
tion in the second year or beyond, as well as student-level outcomes such as persistence,
graduation, and engagement with the LS’s Law Journals, for every student who entered
the JD program between fall 2000 and fall 2011. En plus, we observe student de-
mographic characteristics, such as sex, âge, and race/ethnicity, as well as Law School
Admission Test (LSAT) scores, undergraduate grade point average (GPA), and home
ZIP Code.10 We use home ZIP Codes to construct measures of distance from LS and to
collect the median income and fraction of adults who have a college degree in each ZIP
Code from the 2000 et 2010 U.S. censuses, which proxy for students’ socioeconomic
status. Administrative data on instructors include rank (par exemple., tenure line, tenured, ad-
junct) and years at LS. Demographic information (c'est à dire., race/ethnicity and sex) and rank
of faculty members’ JD-granting institutions were determined by reviewing public re-
sumes, curriculum vitae, and Web sites.11
Sample and Summary Statistics
Our aim is to estimate the impact of student–instructor demographic match in first-year
required courses. The primary unit of analysis is therefore the student-course level.
There are ten required courses in the first year, which cover subjects such as proce-
dure, constitutional law, and property law. The main analytic sample includes 36,560
student-course observations from more than 1,000 unique course sections.12 Panel A
of table 1 summarizes the student-course data, separately by students’ race and sex. Sur
average, white students have higher first-year course grades than nonwhite students.
There is no appreciable sex gap in first-year course grades. Dropping first-year required
courses is exceedingly rare, likely because they are required and students are gener-
ally forbidden from switching sections. White students and nonwhite students have
8. Malheureusement, the data do not identify which, if any, courses were subject to non-blind grading. Another com-
plication is that students may challenge their grades in some circumstances, at which point the grading is no
longer blind, and more advantaged students may feel more confident in challenging grades. Malheureusement, nous
do not observe which grades were challenged.
9. The assignment protocol changed about midway through the period of study, though both processes were ar-
guably conditionally random. That said, we do not assume or rely on random assignment in the main analysis
and instead rely on a quasi-experimental two-way fixed-effects identification strategy. Cependant, a series of bal-
ance and Hausman-style tests suggests that assignments were, in fact, as good as random.
10. Malheureusement, LSAT and undergraduate GPA data are missing for a large, nonrandom subset. Accordingly, nous
rely on these data sparingly and do not report demographic group means for these variables.
11. The rank of instructors’ JD programs comes from the usual U.S. News Rankings.
12. We report all sample sizes rounded to the nearest ten.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
F
/
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
un
_
0
0
2
8
0
p
d
F
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
461
Effects of Demographic Mismatch
Tableau 1. Sample Statistics for First-Year Required Courses
Blanc
Nonwhite
Male
Femelle
Mean
SD
Mean
SD
Mean
SD
Mean
SD
Panel A: Student-Course Level
0.49
3.36
0.80
0.003
0.40
0.56
0.04
0.51
0.18
0.93
0.46
3.14
0.81
0.003
0.23
0.67
0.10
0.53
0.95
0.92
0.51
3.27
0.80
0.003
0.33
0.61
0.07
0.42
0.41
0.93
0.50
3.29
0.81
0.003
0.34
0.60
0.06
0.58
0.50
0.92
23,200
13,360
15,250
21,320
Panel B: Student Level
Course grade (0-4)
Take another course
Dropped course
Grade: UN
Grade: B
Grade: C, D, F
Other-sex instructor
Other-race instructor
Same instructor
Observations
Age (first semester)
25.5
2.6
25.4
2.4
25.7
2.7
25.3
2.5
Female student
Black student
Latinx student
Asian student
White student
Other race student
Persist to second year
Joined top law review at LS
Graduated in 5 années
Observations
Nonwhite instructor
Black instructor
Latinx instructor
Asian instructor
White instructor
Female instructor
Years of experience at LS
Has JD
0.54
0.00
0.00
0.00
1.00
0.00
0.89
0.14
0.82
0.66
0.21
0.37
0.34
0.00
0.08
0.91
0.06
0.82
0.00
0.05
0.12
0.10
0.70
0.03
0.88
0.12
0.81
1.00
0.10
0.14
0.14
0.59
0.03
0.90
0.11
0.82
2,890
1,680
1,910
2,660
Panel C: Instructor Level
1.00
0.47
0.23
0.30
0.00
0.57
3.00
0.97
0.15
0.08
0.02
0.05
0.85
0.00
7.37
0.94
5.89
9.64
0.00
0.00
0.00
0.00
1.00
0.47
5.76
0.95
0.20
0.08
0.06
0.06
0.80
1.00
3.15
0.96
10.90
6.24
Rank of JD school
37.6
36.1
42.4
44.1
36.1
39.9
40.6
34.5
Has PhD
Has master of laws degree
Has bachelor of laws degree
0.10
0.09
0.04
0.03
0.21
0.00
0.08
0.13
0.05
0.10
0.09
0.01
Observations
140
30
90
90
Remarques: The Dropped course descriptive statistics are based on slightly larger samples (23,300 for white students, 13,430
for nonwhite students, 15,320 for male students, et 21,400 for female students) because including dropped courses
increases the number of student-course level observations for students who drop classes. There are no Other race instructors
in the analytic sample. Same instructor in panel A is a binary variable indicating the student had the same instructor in
the previous course. JD = Juris Doctor; SD = standard deviation; LSAT = Law School Admission Test; LS = Law School.
462
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
un
_
0
0
2
8
0
p
d
F
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
Tableau 2. Sample Statistics for First-Year Required Courses
Course Level Characteristics
Mean
SD
Course Name
Percent
Class size
Female student
Age (first semester)
Black student
Latinx student
Asian student
White student
Other student
Female instructor
Black instructor
Asian instructor
Latinx instructor
White instructor
More than one instructor race choice in term
More than one instructor race choice in academic year
More than one instructor sex choice in term
More than one instructor sex choice in academic year
5.76
2.30
6.14
6.14
5.47
28.60
31.29
5.85
1.92
6.53
1,040
41.60
34.00
Civil Procedure
Civil Procedure II
Constitutional Law
Contracts
Torts
Legal Writing I
Legal Writing II
Property
Property II
Criminal Law
Observations
0.59
25.90
0.08
0.13
0.13
0.63
0.03
0.45
0.08
0.02
0.04
0.87
0.74
0.75
0.94
0.95
0.14
2.33
0.07
0.10
0.10
0.13
0.05
0.50
0.26
0.15
0.19
0.34
0.44
0.43
0.24
0.21
Observations
1,040
Remarques: Classroom level demographics are presented as proportions. SD = standard deviation.
near-equal likelihoods of having an other-sex instructor, whereas female students are
more likely than male students to have an other-sex instructor. Nonwhite students are
much more likely to have an other-race instructor than are white students, as the ma-
jority of instructors are white.
Panel B of table 1 reports descriptive statistics at the student level. The average age
of first-year JD students is about 25 years for all demographic groups. Whereas female
students form a majority of both white and nonwhite students, the representation of fe-
male students is greater among nonwhite students than among white students. Parmi
nonwhite students, 21 percent are black, 37 percent are Latinx, et 34 percent are Asian.
Graduation rates are similar across demographic groups, which for students are coded
as White, Noir, Latinx, Asian, or Other.
Enfin, panel C of table 1 reports descriptive statistics at the instructor level, for in-
structors who taught at least one first-year required course between 2000 et 2012. Sur
average, white instructors have more experience at LS than nonwhite instructors, et
male instructors have more experience than female instructors. About 47 percent of
white instructors are female, alors que 57 percent of nonwhite instructors are female. Al-
most half of nonwhite faculty are black, 23 percent are Latinx, et 30 percent are Asian;
unlike for students, there is no “Other race” category for instructors. In the empirical
models, same-race is coded as an exact racial group match, as opposed to an indica-
tor for both student and teacher being nonwhite. The average instructor attended a
JD program ranked in the top 50 by U.S. News. White and male instructors attended
slightly higher-ranked programs, on average, than did nonwhite and female instructors,
respectivement.
Tableau 2 reports descriptive statistics at the classroom (c'est à dire., course-section) level.
Il y a 1,040 unique first-year required course offerings in the analytic sample. Le
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
F
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
un
_
0
0
2
8
0
p
d
.
/
F
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
463
Effects of Demographic Mismatch
average class contained about 42 students, 59 percent of whom were female. The ma-
jority (87 pour cent) of courses were taught by white faculty, 8 percent were taught by
black instructors, 4 percent by Latinx instructors, et 2 percent by Asian instructors.
Tableau 2 also reports the frequency of the ten courses that constitute the analytic sam-
ple. Some courses appear less often either because they had smaller average class sizes,
were merged into a single course, or ceased to be required between 2000 et 2012. Toujours,
outliers here are the legal writing classes, which are overrepresented because of their
smaller class size. Subject-specific summary statistics are provided in table A.2, lequel
shows that the average writing class has fifteen students whereas the other classes av-
erage fifty to eighty students. Because of the notably smaller class size and the different
structure of writing classes, as a sensitivity analysis, we reestimate the baseline model
on a sample that excludes the writing classes in table A.3 and confirm the main results
are not driven by student outcomes in these unique classes.
I D E N T I F I C AT I O N S T R AT E G Y
3 .
This section describes the main identification strategy used to estimate the causal ef-
fects of student–instructor demographic match on course-specific outcomes. We first
introduce the preferred two-way fixed effects (FE) specification. We then discuss the key
identifying assumptions and present a test of the “endogenous sorting” threat to iden-
tification. Enfin, we describe a three-way FE specification used to identify the effect
of mismatch in the first course of two-course sequences on performance in the second
cours.
Baseline Model
Our primary interest is in how student–instructor demographic match affects outcomes
(oui) at the student-course level. Specifically, we are interested in δ in the linear regression
model:
yi jcst = β0 + β1Xi + β2Wj + β3Zcst + δOtheri j + (cid:4)i jcst,
(1)
where X, W, and Z are vectors of observed student (je), instructor (j), and course-section
(cs) characteristics, respectivement; t indexes semesters; Other is a vector of variables that
measure the degree of demographic similarity between student and instructor; et
(cid:4) represents the unobserved determinants of y.13 We operationalize Other in various
ways, such as a set of four mutually exclusive race-by-sex indicators (c'est à dire., same race
and other sex, same sex and other race, same race and same sex, other race and other
sex) and simpler definitions that include binary indicators for other sex and/or other
course. Cependant, in all specifications, race matches are coded as specific matches such as
black-black, Latinx-Latinx, and so forth, as opposed to “minority-minority.”
Given that course-section assignments are allegedly conditionally (on X) random,
ordinary least squares (OLS) estimates of equation 1 might well be unbiased and
13. We consider models that allow the effect of Other to vary by subject, but find no systematic evidence of differ-
ential effects by subject, perhaps because we are under-powered to do so. Accordingly, we report estimates of
the average effect of student-instructor demographic match that are averages across subjects.
464
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
un
_
0
0
2
8
0
p
d
/
.
F
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
have a causal interpretation. Cependant, if the quasi-random assignment rule is im-
perfectly followed, these estimates might be biased. Par exemple, unobserved student
characteristics might jointly predict outcomes and assignment to an other-race teacher.
De la même manière, equation 1 fails to control for unobserved instructor attributes, such as grad-
ing policies or teaching style. Accordingly, we follow Fairlie, Hoffmann, et Oréopoulos
(2014) and augment equation 1 to condition on both student and classroom FE, lequel
yields our preferred specification:
yik = θi + ωk + δOtherik + (cid:4)ik.
(2)
Several aspects of equation 2 merit attention. D'abord, the vectors X, W, and Z fall out of
the model because they are colinear with the FE. Deuxième, we collapse the subscripts jcst
into a single k subscript because identification now comes from within-classroom varia-
tion in Other and classrooms are instructor-, course-, section-, and semester-specific: le
classroom FE (ω) subsumes instructor, cours, semester, and year FE. Specifically, le
classroom FE uniquely identify each course section taught in a given semester and thus
control for the course’s location (classroom) qualité, meeting day(s) and time, class size,
and class composition. Thus the classroom FE also ensure that identification comes
from students who experienced the same lectures, assignments, and grading prac-
tices. Troisième, equation 2 is only identified for outcomes that vary within students across
courses, such as course grades, due to the student FE (je ). Enfin, there is a possible
sample selection issue for the analyses of course grades, since grades are only observed
for students who complete the course, and it is possible that student–instructor demo-
graphic mismatch affects the likelihood that students complete the course. This turns
out to be a practically unimportant concern, as dropping courses is quite rare (occurs
in only 0.6 percent of cases) and we find no evidence that demographic mismatch af-
fects course dropouts.14 We estimate equation 2 using the estimation routine proposed
by Correia (2016) and compute two-way cluster-robust standard errors, which allows
for correlation both within instructors across semesters, and within students across
courses (Cameron, Gelbach, and Miller 2012).15
Sorting Test
Although the two-way FE in equation 2 address many threats to validity, one poten-
tial threat remains: differential sorting by student race or sex (Fairlie, Hoffmann and
Oreopoulos 2014). Par exemple, the student FE control for scenarios in which high-
ability students sort into female-taught courses, but does not adequately control for
sex-specific sorting processes in which high-ability female students sort into female-
taught courses and high-ability male students sort into male-taught courses. To discern
the extent to which differential sorting on unobservables occurs, we follow Fairlie, Hoff-
mann, et Oréopoulos (2014) in implementing a formal test for differential sorting
on observables. The test relies on the intuition of difference-in-differences estimators
14. This is perhaps unsurprising, as we are investigating required first-year courses.
15. Clustering along only one dimension and/or at lower levels yields nearly identical inferences and slightly
smaller standard errors for the main course-grade results. Accordingly, we report the more conservative two-way
clustered standard errors in the main text. This is motivated by the guidance in Angrist and Pischke (2009),
which suggests clustering at the highest level.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
un
_
0
0
2
8
0
p
d
/
.
F
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
465
Effects of Demographic Mismatch
and the bounding procedure of Altonji, Elder, and Taber (2005). It is best illustrated
via an example. Suppose we want to test for differential sorting by sex. We would first
compute the mean of observed student characteristic L (par exemple., LSAT score) in classroom
k for each sex g: ¯Lg
k . Then estimate the linear regression
Female = g
(cid:2)
(cid:3)
+ γ3Femalek × 1
= γ0 + γ1Femalek + γ21
(cid:2)
Female = g
(cid:3)
,
(3)
¯Lg
k
where Female is a binary indicator equal to 1 if the section-k teacher is female, and zero
otherwise; 1{·} is the indicator function; and γ 3 is the parameter of interest. Specifi-
cally, c 3 represents “the difference-in-differences estimate” of the average difference in
observed characteristics between female and male students in female- and male-taught
courses. If γ 3 is significantly different from zero, there are differences by student sex in
sorting into courses on observables that systematically vary with the sex of the instruc-
tor. Alternativement, if the OLS estimate of γ 3 in equation 3 is statistically indistinguishable
from zero, there is no evidence of differential sorting on observables, and thus differ-
ential sorting on unobservables in a way that would bias the two-way FE estimates of
equation 2 is unlikely.
Cross-Semester Effects in Two-Course Sequences
Enfin, we consider whether exposure to an other-race or other-sex instructor in the first
course of a two-course sequence affects performance in the second course. Naturellement,
this analysis can only be conducted for the subset of first-year courses that are part
of a required two-course sequence.16 While this question can be addressed using the
baseline two-way FE model given in equation 2, it is also possible to further increase the
estimates’ validity by augmenting equation 2 to condition on a second-semester course
FE (ϕ).17 Specifically, we estimate three-way FE models of the form
yis2 = θi + ω(je)
s1
+ ϕ(je)
s2
+ δOtheris1 + (cid:4)est,
(4)
où 1 et 2 index semesters and s indexes subjects. Estimates of δ in equation 4
are robust to excluding the second-semester course FE, which is reassuring because it
suggests the demographic background of the first-semester instructor does not affect
second-semester classroom assignments. Estimates of equation 4 report standard er-
rors clustered along three dimensions: étudiant, semester 1 instructor, and semester 2
instructor.
4 . R E S U LT S
This section presents the empirical results. We first present estimates of the sort-
ing test characterized by equation 3. We then present the baseline two-way FE esti-
mates, followed by tests for heterogeneous impacts of student–instructor demographic
mismatch.
16. There are three such sequences: Civil Procedure I & II, Legal Writing I & II, and Property Law I & II.
17. This is similar to the identification strategy used by Figlio, Schapiro, and Soter (2015) to identify the impact of
adjunct instructors, though in that case the first-semester course FE were not included because adjunct status
varies only at the classroom level.
466
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
F
/
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
un
_
0
0
2
8
0
p
d
/
F
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
Tableau 3. Sorting Test Estimates
Résultat
LSAT
UGPA
Median Income (ZIP)
% Adult w/BA (ZIP)
In/Nearby State
Student Age
Nonwhite instructor
Nonwhite student
−0.025
(0.058)
0.078
(0.248)
−4.848*** −0.149***
(0.107)
Nonwhite instructor
* Nonwhite student
Constant
0.376
(0.263)
160.790***
(0.091)
(0.033)
−0.067
(0.104)
3.460***
(0.023)
Panel A: Sorting by Race
−3,874.264***
(1,268.960)
−32,14.724***
(577.044)
49.169
(1,210.234)
78,674.542***
(529.096)
Observations
1,820
490
2,010
Panel B: Sorting by Sex
Female instructor
Female student
Female instructor
* Female student
Constant
0.255
(0.167)
−1.048***
(0.115)
−0.036
(0.181)
159.560***
(0.115)
−0.059
(0.060)
0.132***
(0.046)
0.013
(0.073)
3.337***
(0.038)
−623.512
(1,124.828)
−1,477.353**
(727.315)
−1,359.981
(1,149.638)
78,731.551***
(760.778)
Observations
1,860
480
2,090
4.051***
(1.361)
−2.406***
(0.288)
−1.867**
(0.813)
37.980***
(0.455)
2,010
1.168
(0.814)
0.495
(0.317)
−0.809
(0.513)
36.831***
(0.550)
2,090
−0.019
(0.015)
−0.027***
(0.010)
0.025
(0.025)
0.530***
(0.006)
2,020
0.008
(0.013)
0.040***
(0.012)
−0.010
(0.017)
0.492***
(0.009)
2,090
0.004
(0.068)
−0.181***
(0.049)
0.104
(0.104)
25.560***
(0.033)
2,020
−0.093
(0.066)
−0.369***
(0.057)
0.001
(0.081)
25.738***
(0.046)
2,090
Remarques: Each column represents tests for sorting on a different student background characteristic. In/Nearby State is a binary variable indicating
the student’s home address is within the same state as the institution or a bordering state. Standard errors in parentheses are clustered by
cours. LSAT = Law School Admission Test; UGPA = undergraduate grade point average; BA = Bachelor of Arts degree.
**p < 0.05; ***p < 0.01.
Sorting Test Estimates
Table 3 presents estimates of the sorting test characterized by equation 3.18 Panel A
reports estimates for differential sorting by race, comparing the average characteristics
of white and nonwhite students. Panel B does the same for differential sorting by sex,
comparing the average characteristics of male and female students.
We perform the sorting test for six outcomes: LSAT score, undergraduate GPA,
median income in student’s home ZIP Code, percent of population with college de-
gree in student’s home ZIP Code, a binary indicator equal to one if the student came
from the surrounding tristate area, and student age.19 The LSAT and undergraduate
GPA variables likely measure a combination of students’ cognitive and noncognitive
skills (Heckman and Kautz 2012). The ZIP Code information proxies for the student’s
socioeconomic background, which is an important predictor of undergraduate college
success (Bailey and Dynarski 2011). The “In/Nearby State” indicator provides a crude
measure of students’ distances from home, which is known to predict undergraduate
enrollments (Alm and Winters 2009; Cooke and Boyle 2011).
Only one of the twelve estimates of γ 3 in table 3 is statistically significant, which
suggests little differential sorting on observables by sex or race. Given the multiple hy-
potheses tested, it is possible that the significant result in panel A is spurious: Indeed,
18. The sorting test estimates remain essentially unchanged when course name and year FE are added to the re-
gression.
19. Data on LSAT and undergraduate GPA are missing for many students, so these results should be interpreted
with caution.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
467
Effects of Demographic Mismatch
Table 4.
Impact of Demographic Mismatch on First-Year Required Course Outcomes
Other-sex
Other-race
Differences in coefficients (P)
Observations
Course fixed effects
Student fixed effects
Continuous Grade
A Grade
A/A- Grade
C, D, F Grade
Take Another
Dropped Course
(1)
−0.016**
(0.007)
−0.037**
(0.016)
0.214
36,560
Yes
Yes
(2)
(3)
−0.008**
(0.004)
−0.015**
(0.007)
0.455
36,560
Yes
Yes
−0.013**
(0.007)
−0.028***
(0.011)
0.186
36,560
Yes
Yes
(4)
0.001
(0.003)
0.009
(0.007)
0.256
36,560
Yes
Yes
(5)
0.016
(0.010)
−0.000
(0.008)
0.197
18,620
Yes
Yes
(6)
−0.000
(0.000)
0.001
(0.001)
0.867
36,730
Yes
Yes
Notes: Each column represents a different model specification. The outcomes are measured as follows: Continuous Grade measures a student’s
received grade on a 0—4 scale (F—A); A Grade is a binary indicator for whether a student received an A grade; A or A— Grade is a binary
indicator for whether a student received an A or A— grade; C, D, or F Grade is a binary indicator for whether a student received a C, D, or F grade;
Take Another is a binary indicator for whether a student takes a subsequent elective course in the same field after his first year; and Dropped
Course is a binary indicator for whether a student drops the course before the end of the semester. Column 5 has fewer observations because
not all required courses correspond to elective course subjects. Difference in coefficients compares the other-sex effect to the other-race effect.
Standard errors in parentheses are clustered by student and instructor.
**p < 0.05; ***p < 0.01.
it loses its statistical significance after adjusting for multiple comparisons (Schochet
2009). Moreover, this result suggests sorting in the “wrong” direction, in the sense that
nonwhite students assigned to nonwhite faculty are from lower socioeconomic back-
grounds, which would bias against finding a positive impact of demographic match on
student outcomes. In sum, the general lack of sorting on observables observed in table 3
suggests differential sorting on unobservables is unlikely to bias two-way FE estimates
of equation 2. The lack of endogenous sorting is unsurprising given LS’s claims that
students were at least quasi-randomly assigned to classrooms. We further test this claim
below by examining the sensitivity of the baseline estimates to controlling for student
FEs.
Main Results
Table 4 reports two-way FE estimates of equation 2 using a simple definition of Other:
binary indicators for whether or not the student had an other-sex and other-race in-
structor. The first four columns of table 4 use different definitions of the course grade
as the outcome. Column 1 uses a continuous measure of the course grade, which is
measured on a 0 to 4 scale. Having an other-sex and other-race teacher significantly
reduced the student’s course grade by 0.02 and 0.04, respectively, though these esti-
mates are not significantly different from one another. These effects represent small
((cid:2)1 percent) changes from the average course grade of 3.36. Although small in mag-
nitude, recall that these are course-specific effects that might add up to nontrivial dif-
ferences in cumulative GPA that preclude underrepresented students from prestigious
internships after the first year or alter class rankings in ways that affect initial job place-
ments and starting salaries.
Additionally, these small effects could be due to the effect of student–instructor de-
mographic mismatch operating on particular margins of the course-grade distribution.
Accordingly, in columns 2 and 3 we estimate linear probability models in which the out-
comes are binary indicators for “good” grades, defining a good grade as an A or an A
468
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
or A−, respectively. Consistent with the results in column 1, columns 2 and 3 show
significant, negative effects of demographic mismatch on the probability that students
receive a good grade regardless of how good grade is coded. That the effect on having
an A is smaller than that on the more inclusive definition of good grade suggests that
demographic match effects operate on both the A/A− and A−/B+ margins. Column 4
shows that there is no effect of student–instructor demographic mismatch on the like-
lihood of receiving a “bad grade” (less than B−). These results show that demographic
mismatch affects grades, primarily by affecting the likelihood of receiving top grades (A
or A−). Racial mismatch effects tend to be larger than sex mismatch effects, but these
differences are not statistically significant. These effects are arguably economically sig-
nificant, as the other-race effect of 0.03 constitutes 9 percent of the sample average
“good-grade” rate and might add up to have a nontrivial effect on cumulative GPA. The
remaining columns of table 4 show that there are neither effects of mismatch on the
likelihood that the student takes an elective course in the subject in the second year or
beyond nor on the likelihood the student drops the course.20 The latter null result is im-
portant, as it suggests that the sample selection inherent in the course-grade analyses
is negligible.
Because an important contribution of the current paper is the identification of
causal effects of same-race and same-sex instructors on course outcomes, we now
leverage the alleged quasi-random assignment of students to course sections to cross-
validate the baseline two-way FE estimates. The intuition of the Hausman test (Haus-
man 1978) suggests that if student assignments to course sections were conditionally
random, then the estimates should be robust to the inclusion of student FE, as the claim
is that students are randomly assigned to course sections (classrooms). Similar intu-
ition motivates the common practice of verifying that experimental estimates of causal
effects are robust to conditioning on predetermined characteristics in treatment-effect
regressions (Angrist and Pischke 2009).
In table 5, we show that the baseline estimates are quite robust to the inclusion of
student and/or classroom FE. This lends additional support to a causal interpretation
of the baseline estimates and to the claim that students were randomly assigned to first-
year courses.21 Specifically, column 2 shows that the “naive OLS” mismatch effects in
column 1 are robust to controlling for observed student characteristics such as LSAT
score, undergraduate GPA, socioeconomic status, and distance to the law school. This
suggests students were, in fact, randomly assigned to course sections.22 Columns 3
and 4 compare student random effects and student FE estimators, in the spirit of the
original Hausman test, and again find the point estimates are robust to controlling
for unobserved student heterogeneity. Finally, columns 5 and 6 show the results are
robust to conditioning on classroom FE, which means that the mismatch effects are not
driven by differential teacher or classroom characteristics, such as teaching or grading
20. The sample size for subsequent course taking is smaller because there are not subsequent courses in all required
first-year courses.
21. Because table 5 shows the pooled OLS estimates can be given a causal interpretation, we can also estimate pooled
logit models to verify that the baseline linear model provides reasonable approximations of the partial effects
of interest. Accordingly, table A.4 reports logit average partial effects (APE) that are comparable to the linear
estimates reported in table 4. The logit APE are quite similar to the linear coefficient estimates, suggesting that
the main results are robust to the functional form choice.
22. We include missing-data dummies to allow use of the full sample.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
f
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
469
Effects of Demographic Mismatch
Table 5.
Impact of Demographic Mismatch on First-Year Required Course Outcomes
Other-sex
Other-race
Female instructor
Nonwhite instructor
Nonwhite student
Female student
A/A— Grade
(1)
(2)
(3)
(4)
(5)
(6)
−0.012**
(0.005)
−0.024**
(0.009)
0.041***
(0.005)
0.009
(0.008)
−0.152***
(0.011)
0.038***
(0.008)
−0.011**
(0.005)
−0.027***
(0.009)
0.029***
(0.005)
0.021***
(0.008)
−0.088***
(0.011)
0.044***
(0.008)
−0.012***
(0.005)
−0.031***
(0.009)
0.031***
(0.005)
0.017**
(0.008)
−0.085***
(0.011)
0.042***
(0.008)
−0.013*
(0.007)
−0.033***
(0.012)
0.031*
(0.018)
0.015
(0.016)
−0.012*
(0.007)
−0.023*
(0.013)
−0.013**
(0.007)
−0.028***
(0.011)
−0.088***
(0.013)
0.042***
(0.009)
Observations
Cohort class dummies
Course subject type dummies
Student characteristics
Course FE
Student RE
Student FE
36,560
36,560
36,560
36,560
36,560
36,560
Yes
No
No
No
No
No
Yes
Yes
Yes
No
No
No
Yes
Yes
Yes
No
Yes
No
No
Yes
No
No
No
Yes
No
No
Yes
Yes
No
No
No
No
No
Yes
No
Yes
Notes: Each column represents a different model specification. The outcome A/A— Grade is a binary indicator for whether a
student received an A or A— grade. Course Subject Types are Civil Procedure, Constitutional, Contracts, Criminal, Legal Writing,
Property, and Torts. Student Characteristics are age, Law School Admission Test, undergraduate grade point average, median
income, and percent of adults with Bachelor of Arts degree in home ZIP Code, in/nearby state, and missing data indicators for
each. Standard errors in parentheses are clustered by student in columns 1—4 and by student and instructor in columns 5 and
6. FE = fixed effects; RE = random effects.
*p < 0.1, **p < 0.05, ***p < 0.01.
practices, or the physical location or condition of the classroom. Column 6 replicates
the baseline two-way FE estimates of equation 2.
Heterogeneity
Having established arguably causal impacts of student–instructor demographic mis-
match on course grades, we now test for possible heterogeneity in such effects. First, we
investigate possible heterogeneity by student background and by the precise type of de-
mographic mismatch, because understanding the determinants of success for students
from historically underrepresented groups is of paramount policy interest.23 Second,
we investigate whether these demographic mismatch effects are moderated by the de-
mographic composition or the size of specific classrooms, as classroom environments
might moderate the impact of mismatch (Inzlicht and Ben-Zeev 2000; Ho and Kelman
2014).24
23. We find no evidence of heterogeneity along other observable student dimensions, such as students’ ability
(LSAT score), age, home region, and ZIP Code socioeconomic status. Nor do we find evidence of heterogeneity
by observable instructor characteristics, such as experience, rank of JD program, or faculty rank (i.e., adjunct,
teaching-track, tenure-line, tenured). These null results are not reported in tabular form in the interest of brevity.
24. A relevant question here is whether class characteristics vary by subject. Table A.2 reports mean course char-
acteristics by subject. The primary outlier is leal writing, which has significantly smaller classes than the other
470
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
Table 6.
Impact of Demographic Mismatch on First-Year Required Course Outcomes
All Students
Female Students
Nonwhite Students
Nonwhite Female Students
(1)
(2)
(3)
(4)
Other-sex
Other-race
Female faculty
Nonwhite faculty
Same race, Mismatch sex (1)
Mismatch race, Same sex (2)
Mismatch race, Mismatch sex (3)
Female faculty
Nonwhite faculty
Difference in Coefficients (P)
1 = 2
1 = 3
2 = 3
Observations
Course fixed effects
Student fixed effects
−0.013*
(0.007)
−0.033***
(0.012)
0.031*
(0.018)
0.015
(0.016)
−0.013
(0.008)
−0.033**
(0.013)
−0.046***
(0.015)
0.031*
(0.018)
0.015
(0.016)
0.111
0.018**
0.155
36,560
No
Yes
Panel A
−0.035*
(0.019)
−0.031**
(0.013)
0.028
(0.018)
Panel B
−0.038
(0.023)
−0.034**
(0.017)
−0.066***
(0.024)
0.028
(0.018)
0.876
0.048**
0.083*
21,320
No
Yes
−0.017*
(0.009)
−0.046*
(0.024)
0.033*
(0.017)
0.011
(0.016)
−0.093***
(0.032)
−0.083**
(0.032)
−0.096***
(0.033)
0.033*
(0.017)
0.012
(0.016)
0.666
0.931
0.176
13,360
No
Yes
−0.041**
(0.019)
−0.052*
(0.028)
0.020
(0.019)
−0.094*
(0.049)
−0.078*
(0.043)
−0.116**
(0.045)
0.021
(0.019)
0.599
0.473
0.052*
8,790
No
Yes
Notes: Each column in each panel represents a different model specification. The outcome A or A— Grade is a binary indicator for
whether a student received an A or A— grade. The omitted category in panel B is Same Race, Same Sex. Estimates are not shown
for course subject dummies. In some samples, estimates are not shown for certain instructor effects because they are perfectly
colinear with other-sex or other-race parameters. Standard errors in parentheses are clustered by student and instructor.
*p < 0.1; **p < 0.05; ***p < 0.01.
Panel A of table 6 estimates the baseline student-FE specification, sans classroom
FE, to enable identification of mismatch effects for specific demographic subgroups of
the sample. We feel comfortable making this trade-off because table 5 shows that the
full-sample estimates are robust to omitting the classroom FE. Column 1 of table 6 re-
peats the estimates shown in column 4 of table 5 to facilitate comparisons. Columns 2
and 3 estimate this specification separately for female and nonwhite students, respec-
tively. We might expect these groups to be particularly affected by faculty representa-
tion, given the general overrepresentation of white men in the legal profession. These
models yield two key findings. First, as expected, the other-sex effect is driven by fe-
male students’ grades and the other-race effect is driven by nonwhite students’ grades.
Specifically, for female students, the likelihood of receiving an A/A– increases by 3.5
percentage points (10 percent) when taught by a female instructor, compared with an
subjects. However, we find no evidence of systematic differences between legal writing and other subjects in
tests for subject heterogeneity.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
471
Effects of Demographic Mismatch
overall sex-match effect of 1.3 percentage points (3 percent) in the full sample. Similarly,
the race-match advantage for nonwhite students is 4.6 percentage points (20 percent),
compared with 3.3 percentage points (9 percent) in the full sample.25 Second, the other-
sex effect is similar for both white and nonwhite students, and the other-race effect is
similar for both male and female students. This lack of heterogeneity is also interesting.
Finally, column 4 shows that the harmful effects of demographic mismatch are most
pronounced for nonwhite female students, although these differences are not signif-
icantly different from the overall effects of sex representation for women or of racial
representation for nonwhite students.
Panel B of table 6 generalizes the models estimated in panel A by allowing for
multiplicative effects of having both an other-race and other-sex instructor. Here,
Other is specified as a set of four mutually exclusive categorical indicators, with
same-sex and same-race serving as the omitted reference category. Column 1 shows
that overall, relative to students whose instructors are of the same race and sex, any
type of demographic mismatch leads to a lower likelihood of receiving a good grade.
However, having a different-race and different-sex instructor is significantly worse
than instances in which demographic mismatch occurs along only one dimension.
Column 2 shows that this is true for the female subsample as well, which is consistent
with the results presented in panel A, and shows the effect of having a different-race
and different-sex instructor is more pronounced for female students than for male
students. However, column 3 shows that nonwhite students are similarly harmed by
any type of student–instructor demographic mismatch. Finally, and again consistent
with the results presented in panel A, column 4 of panel B shows that nonwhite female
students benefit the most from intersectional demographic representation (i.e., having
both a same-race and same-sex instructor).
Next, we test for heterogeneity in the impact of student–instructor demographic
mismatch by classroom characteristics, such as class size and class composition.
Whether larger classrooms magnify or dampen the mismatch effects documented pre-
viously is theoretically ambiguous, as smaller classrooms could either shine a spotlight
on implicit biases or facilitate relationships that supersede stereotypes. We also allow
the effect of mismatch to vary with the demographic composition of classrooms, as the
impact of an other-race or other-sex instructor might be more pronounced in less di-
verse settings in which female or nonwhite students feel isolated. Given the exploratory
nature of this analysis, we model the heterogeneity using quadratics in class size and
percent female (nonwhite). The quadratics are at least marginally jointly significant in
both cases.26
Appendix table A.5 reports the coefficient estimates for these models, though for
ease of interpretation we plot the marginal effects as functions of class size and percent
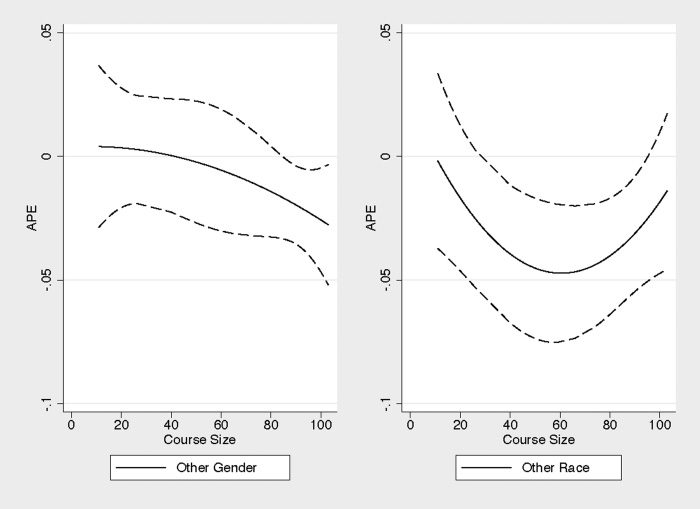
female (nonwhite). Figure 1 plots the marginal effects (and corresponding 95 percent
confidence intervals) on the probability of receiving an A/A– of having an other-race
or other-sex instructor as a function of class size for the range of class sizes observed
in the analytic sample. Interestingly, there is essentially no effect of mismatch in the
25. The nonwhite effect itself is almost entirely driven by black students’ responses to black instructors, which is
consistent with Fairlie, Hoffmann, and Oreopoulos (2014), although we focus on the aggregate nonwhite effect
because the race-specific analysis is underpowered due to the small share of Asian and Latinx instructors.
26. Cubic and nonparametric specifications yield qualitatively similar results.
472
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
/
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
Notes: Good Grade is defined as an A or A–. Each graph represents a different model specification.
Figure 1. Average Partial Effects (APE) of Student—Instructor Mismatch on the Probability of Receiving a Good Grade as a Function of Class
Size
smallest classes. The other-sex effect monotonically increases in magnitude with class
size, though at a relatively slow pace, and only becomes statistically significant in rela-
tively large classes. The other-race effect, meanwhile, exhibits a U-shaped pattern. The
deleterious effect of having an other-race instructor is largest in classrooms of about
sixty students. One possible interpretation of this pattern is that the personal connec-
tions and relative anonymity in very small and very large classes, respectively, mitigate
the harm associated with having an other-race instructor.
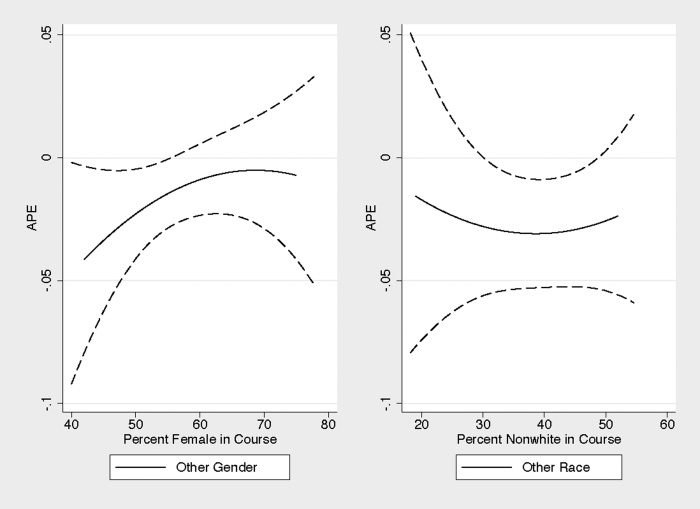
Similarly, figure 2 plots the marginal effects on the probability of receiving an A/A–
of having an other-race (other-sex) instructor as a function of the fraction of the class-
room that is nonwhite (female). The other-race effect is fairly constant at about −0.03
or −0.04, regardless of the proportion of nonwhite students in the class. However, the
other-sex effect is less linear. Intuitively, it is most pronounced when female students
make up less than half the class. The other-sex effect approaches zero when 60 to 70
percent of the class is female. This is suggestive of stereotype threat,27 whereby females
disengage with law school when they perceive themselves as outsiders, and consistent
with experimental evidence that shows the sex ratio of a classroom affects a female
student’s test performance but not a male student’s (Inzlicht and Ben-Zeev 2000).
27. Stereotype threat occurs when the presence of a white or male instructor triggers historically underrepresented
students’ recognition of their outgroup status, which in turn causes emotional responses that hinder their
academic performance and ultimately lessens their engagement with school (Steele 1997).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
473
Effects of Demographic Mismatch
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Notes: Good Grade is defined as an A or A–. Each graph represents a different model specification.
Figure 2. Average Partial Effects (APE) of Student—Instructor Mismatch on the Probability of Receiving a Good Grade as a Function of Class
Composition
Cross Semester Effects
Finally, table 7 reports estimates of equation 4, which show the impact on performance
in the second course of having an other-sex or other-race instructor in the first course
of a required two-course sequence. These are all required first-year courses that take
place in the fall and spring semesters of the first year. The model is estimated for three
outcomes: course grade, a binary indicator for “good grade” (i.e., A or A−), and a binary
indicator for “bad grade” (i.e., < B−). These models can only be estimated for the subset
of courses that are part of a two-course sequence.
Panel A of table 7 shows results that are broadly similar to the baseline two-way
FE estimates reported in table 4: There are negative effects of student–instructor mis-
match in the first course on grades, and on the probability of receiving a good grade in
the second course. Once again, the other-race effect is about twice as large as the other-
sex effect, though here only the other-sex effect is statistically significant at traditional
confidence levels; this is due to the larger standard errors associated with the smaller
sample of courses that constitute two-course sequences and the fact that there are more
female faculty than nonwhite faculty in two-course sequences. That these estimates are
qualitatively similar to the baseline estimates reported in table 4 lends further credence
to a causal interpretation of the relationship between student–instructor demographic
mismatch and course grades. Moreover, this similarity sheds some light on the mech-
anisms at work, as the cross-semester effects documented in table 7 suggest increased
subject-specific learning that persists into the subsequent semester.
474
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
Table 7. Cross-Semester Effects of Demographic Mismatch in Two-Course
Sequences
Continuous Grade
A/A— Grade
C, D, F Grade
(1)
(2)
(3)
Panel A: Cross-Semester Effects
Panel B: Cross-Semester Effects — Same Instructor
Other-sex (OS)
Other-race (OR)
Course 1 FE
Course 2 FE
Student FE
Other-sex
Other-race
OS * Same instructor
OR * Same instructor
Course 1 Fixed Effects
Course 2 Fixed Effects
Student Fixed Effects
−0.032**
(0.012)
−0.077
(0.050)
Yes
Yes
Yes
−0.034**
(0.016)
−0.072
(0.048)
Yes
Yes
Yes
−0.074
(0.063)
−0.206***
(0.063)
0.047
(0.065)
0.145***
(0.054)
Yes
Yes
Yes
−0.120**
(0.060)
−0.046
(0.070)
0.095*
(0.057)
−0.029
(0.060)
Yes
Yes
Yes
0.004
(0.008)
0.016
(0.021)
Yes
Yes
Yes
0.005
(0.031)
0.073*
(0.043)
−0.001
(0.030)
−0.064
(0.039)
Yes
Yes
Yes
Notes: N = 4,340. Each column represents a different model specification. The
outcomes are measured as follows: Continuous Grade measures a student’s re-
ceived grade on a 0—4 scale (F—A). A/A— Grade is a binary indicator for whether a
student received an A or A— grade. C, D, F Grade is a binary indicator for whether a
student received a C, D, or F grade. Same Instructor indicates the student had the
same instructor for both Courses 1 and 2 in two-course sequences. Estimates are
not shown for Same Instructor in even numbered columns because it is perfectly
correlated with the Courses 1 and 2 fixed effects. Standard errors in parentheses
are clustered three ways: by student, first instructor, and second instructor.
*p < 0.1, **p < 0.05, ***p < 0.01.
Panel B of table 7 augments equation 4 to allow the cross-semester demographic
match effects to vary by student–instructor familiarity. Specifically, we interact the de-
mographic mismatch indicators with indicators for whether the student had the same
instructor in both semesters.28 This idea is motivated by recent research by Hill and
Jones (2018) in the primary school setting, who show that students, particularly non-
white students, benefit from having the same classroom teacher in consecutive years.
Intuitively, having the same instructor in consecutive semesters would foster a stronger
relationship and better understanding of expectations and learning styles, which in
turn might mitigate the harmful effects of demographic mismatch. Indeed, this is
precisely what the interaction terms in panel B of table 7 show: The other-sex mismatch
effects on good grades are significantly smaller, and indistinguishable from zero, for
students who had the same instructor in both courses of the two-course sequence.
28. The familiarity indicator itself is subsumed by the “Course-2 FE.”
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
f
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
475
Effects of Demographic Mismatch
5 . C O N C L U S I O N
We use rich student–instructor matched administrative data from a large, private,
top-100 law school to provide novel evidence on the causal relationship between
student–instructor demographic match and student outcomes in the law school
context. Two-way student and course fixed-effects models provide arguably causal
estimates of the impact of such mismatch on short-run (course-specific) outcomes,
such as course grades. Sorting and balance tests provide no evidence of endogenous
sorting on observables into classrooms, which is consistent with at least quasi-random
assignment of students to course sections in the law school, buttressing a causal
interpretation of these results.
The baseline estimates suggest that having an other-race or other-sex instructor in
a first-year required course significantly reduces the likelihood of earning a good grade
(i.e., A or A−) in the course. Specifically, having an other-sex instructor reduces the
likelihood of receiving a good grade by 1 percentage point (3 percent) and having an
other-race instructor reduces the likelihood of receiving a good grade by 3 percentage
points (10 percent). The most comparable estimate in the extant literature comes from
Fairlie, Hoffmann, and Oreopoulos (2014), who find that having a same-race commu-
nity college instructor increases the probability of having a good grade ((cid:3) B) in first-year
undergraduate courses by about 3 percentage points (5 percent).29 That we document
similarly sized effects in first-year courses at a top-100 law school suggests that even
high-achieving college graduates’ graduate and professional school outcomes are influ-
enced by the demographic representation of their instructors.
This result has the potential to contribute to pay gaps, as Oyer and Schaefer (2019)
provide descriptive evidence of a wage-class rank gradient in law schools outside the
top ten.30 However, we find no effects of student–instructor demographic mismatch
on dropping courses or taking subsequent courses in the same field, nor do we find
effects at other points of the grade distribution. Consistent with previous research in
the K–12 context, these effects are stronger for underrepresented groups such as female
and nonwhite students. The effects are most pronounced for nonwhite female students.
What behaviors drive these results? Unfortunately, the mechanisms at work cannot
be precisely identified with these administrative data.31 However, we can make some
informed speculation and perhaps rule out some possible channels. For example, the
importance of blindly graded written exams in determining course grades suggests that
instructors’ grading biases, conscious or not, are not driving these results (Lavy 2008;
Hanna and Linden 2012). Of course, this does not rule out the possibility that implicit
biases affect how instructors interact with students, which could in turn affect student
engagement, and ultimately academic performance. That racial mismatch effects are
observed in medium-sized but not in small or large classes suggests that stereotype
threat is not the sole explanation, as such effects should not vanish in classrooms of a
29. Grade inflation in graduate school accounts for the different definitions of “good grade,” as a C is often consid-
ered failing in graduate and professional schools.
30. Our own analyses of the publicly available After the JD survey data confirm the positive association between law
school GPA and earnings both overall, and for specific demographic groups, for lawyers who attended non-top
ten law schools. See Appendix B for details.
31. Dee (2004), Ferguson (2003), Gershenson, Holt, and Papageorge (2016), Papageorge, Gershenson, and Kang
(2016), and Dee and Gershenson (2017) provide rich discussions of the channels through which demographic
representation might affect student outcomes.
476
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
certain size. Similarly, because sex mismatch effects primarily exist in classrooms with
fewer female students suggests, whatever the channel, they are more salient in less
representative classroom environments. Moving forward, it is important that future re-
search, in all academic environments, seeks to better understand the specific channels
through which student–instructor demographic match effects operate and to use this
information to better design instructor-facing interventions and instructor training.
Finally, these results suggest that diversity in the legal profession, and the status
of women and people of color in the legal profession, would be improved by increas-
ing the diversity of law school faculty. However, whether and how these results would
generalize to other law schools, particularly those with less diverse student and fac-
ulty populations, remains an open question worthy of future exploration. There are
also questions regarding the general equilibrium responses to the hiring of a more
diverse faculty, particularly in the law context, which might exacerbate demographic
gaps in law offices and the judiciary. There are also potential supply-side limitations
of such faculty in the short run. For these reasons, another potential policy response
is to provide law school (and university) faculty with theoretically informed implicit
bias training, which has proven to be effective in some early pilots (Carnes et al. 2015).
Similarly, Darling-Hammong and Holmquist (2015) provide suggestions to law school
faculty on how to better serve historically underrepresented students, many of which
echo the theoretically-informed, “WISE” interventions and strategies advocated by so-
cial psychologists (Walton 2014; Okonofua, Paunesku, and Walton 2016).
ACKNOWLEDGMENTS
Scott Carrell, Stephen B. Holt, Michal Kurlaender, Nicholas Papageorge, and participants at
the 2016 APPAM Fall Conference, 2016 Access Group Legal Education Research Symposium,
2017 Royal Economic Society Symposium for Junior Researchers, and 2017 Society of Labor
Economists Annual Meeting provided many helpful comments. The authors are thankful for
financial support from the Research Grant Program of the AccessLex Institute/Association for
Institutional Research (AIR). Opinions reflect those of the authors and not necessarily those of
the granting agency. We also thank Stephanie Cellini and three anonymous referees for their
helpful comments and suggestions. Kimberly Trocha provided excellent research assistance. An
earlier draft of this paper was circulated as IZA Discussion Paper No. 10459, “Stereotype Threat,
Role Models, and Demographic Mismatch in an Elite Professional School Setting.”
REFERENCES
Alm, James, and John V. Winters. 2009. Distance and intrastate college student migration. Eco-
nomics of Education Review 28(6): 728–738.
Alsan, Marcella, Owen Garrick, and Grant C. Graziani. 2018. Does diversity matter for health?
Experimental evidence from Oakland. NBER Working Paper No. 24787.
Altonji, Joseph G., and Rebecca M. Blank. 1999. Race and gender in the labor market. In Hand-
book of labor economics, Vol. 3, edited by Orley Ashenfelter and David Card, pp. 3143–3259. New
York: Elsevier.
Altonji, Joseph G., Todd E. Elder, and Christopher R. Taber. 2005. Selection on observed and
unobserved variables: Assessing the effectiveness of Catholic schools. Journal of Political Economy
113(1): 151–184.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
477
Effects of Demographic Mismatch
Angrist, Joshua, and Jorn-Steffen Pischke. 2009. Mostly harmless econometrics: An empiricist’s com-
panion. Princeton, NJ: Princeton University Press.
Antecol, Heather, Ozkan Eren, and Serkan Ozbeklik. 2015. The effect of teacher gender on stu-
dent achievement in primary school. Journal of Labor Economics 33(1): 63–89.
Azmat, Ghazala, and Rosa Ferrer. 2017. Gender gaps in performance: Evidence from young
lawyers. Journal of Political Economy 125(5): 1306–1355.
Bailey, Martha J., and Susan M. Dynarski. 2011. Gains and gaps: Changing inequality in U.S.
college entry and completion. NBER Working Paper No. 17633.
Baker, Rachel, Thomas Dee, Brent Evans, and June John. 2018. Bias in online classes: Evidence
from a field experiment. Stanford, CA: CEPA Working Paper No. 18-03.
Banks, Taunya Lovell. 1988. Gender bias in the classroom. Journal of Legal Education 38(1/2):
137–146.
Bertrand, Marianne. 2011. New perspectives on gender. In Handbook of labor economics, Vol. 4,
edited by David Card and Orley Ashenfelter, pp. 1543–1590. New York: Elsevier.
Bertrand, Marianne, and Kevin F. Hallock. 2001. The gender gap in top corporate jobs. ILR Review
55(1): 3–21.
Bettinger, Eric P., and Bridget Terry Long. 2005. Do faculty serve as role models? The impact of
instructor gender on female students. American Economic Review 95(2): 152–157.
Cameron, A. Colin, Jonah B. Gelbach, and Douglas L. Miller. 2012. Robust inference with multi-
way clustering. Journal of Business & Economic Statistics 29(2): 238–249.
Carnes, Molly, Patricia G. Devine, Linda Baier Manwell, Angela Byars-Winston, Eve Fine,
Cecilia E. Ford, Patrick Forscher, Carol Isaac, Anna Kaatz, Wairimu Magua, Mari Palta, and
Jennifer Sheridan. 2015. Effect of an intervention to break the gender bias habit for fac-
ulty at one institution: A cluster randomized, controlled trial. Academic Medicine 90(2): 221–
230.
Carrell, Scott E., Marianne E. Page, and James E. West. 2010. Sex and science: How professor
gender perpetuates the gender gap. Quarterly Journal of Economics 125(3): 1101–1144.
Cooke, Thomas J., and Paul Boyle. 2011. The migration of high school graduates to college. Edu-
cational Evaluation and Policy Analysis 33(2): 202–213.
Correia, Sergio. 2016. A feasible estimator for linear models with multi-way fixed effects. Available
from http://scorreia.com/research/hdfe.pdf . Accessed 22 May 2020.
Darling-Hammong, Sean, and Kristen Holmquist. 2015. Creating wise classrooms to empower
diverse law students: Lessons in pedagogy from transformative law professors. Berkeley La Raza
Law Journal 25(1): 1–67.
Dee, Thomas S. 2004. Teachers, race, and student achievement in a randomized experiment.
Review of Economics and Statistics 86(1): 195–210.
Dee, Thomas S. 2005. A teacher like me: Does race, ethnicity, or gender matter? American Eco-
nomic Review 95(2): 158–165.
Dee, Thomas S. 2007. Teachers and the gender gaps in student achievement. Journal of Human
Resources 42(3): 528–554.
478
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
/
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
Dee, Thomas S., and Seth Gershenson. 2017. Unconscious bias in the classroom: Evidence
and opportunities. Available http://services.google.com/fh/files/misc/unconscious-bias-in-the
-classroom-report.pdf . Accessed 9 December 2019.
Delisle, Jason. 2014. The graduate student debt review: The state of graduate student borrowing.
Washington, DC: New America Education Policy Program.
Dinovitzer, Ronit, Nancy Reichman, and Joyce Sterling. 2009. The differential valuation of
women’s work: A new look at the gender gap in lawyers’ incomes. Social Forces 88(2): 819–
864.
Eren, Ozkan, and Naci Mocan. 2016. Emotional judges and unlucky juveniles. NBER Working
Paper No. 2261.
Fairlie, Robert W., Florian Hoffmann, and Philip Oreopoulos. 2014. A community college instruc-
tor like me: Race and ethnicity interactions in the classroom. American Economic Review 104(8):
2567–2591.
Ferguson, Ronald F. 2003. Teachers’ perceptions and expectations and the black–white test score
gap. Urban Education 38(4): 460–507.
Figlio, David N., Morton O. Schapiro, and Kevin B. Soter. 2015. Are tenure track professors better
teachers? Review of Economics and Statistics 97(4): 715–724.
Gershenson, Seth, Stephen B. Holt, and Nicholas W. Papageorge. 2016. Who believes in me? The
effect of student–teacher demographic match on teacher expectations. Economics of Education
Review 52:209–224.
Guinier, Lani, Michelle Fine, Jane Balin, Ann Bartow, and Deborah Lee Stachel. 1994. Becoming
gentlemen: Women’s experiences at one ivy league law school. University of Pennsylvania Law
Review 143(1): 1–110.
Hanna, Rema N., and Leigh L. Linden. 2012. Discrimination in grading. American Economic Jour-
nal: Economic Policy 4(4): 146–168.
Hausman, Jerry A. 1978. Specification tests in econometrics. Econometrica 46(6): 1251–1271.
Heckman, James J., and Tim Kautz. 2012. Hard evidence on soft skills. Labour Economics 19(4):
451–464.
Hill, Andrew J., and Daniel B. Jones. 2018. A teacher who knows me: The academic benefits of
repeat student-teacher matches. Economics of Education Review 64: 1–12.
Ho, Daniel E., and Mark G. Kelman. 2014. Does class size affect the gender gap? A natural ex-
periment in law. Journal of Legal Studies 43(2): 291–321.
Hoffmann, Florian, and Philip Oreopoulos. 2009. A professor like me: The influence of instruc-
tor gender on college achievement. Journal of Human Resources 44(2): 479–494.
Holder, Eric H. 2001. The importance of diversity in the legal profession. Cardozo Law Review
23(6): 2241–2251.
Holt, Stephen B., and Seth Gershenson. 2019. The impact of demographic representation on
absences and suspensions. Policy Studies Journal 47(4): 1069–1099.
Inzlicht, Michael, and Talia Ben-Zeev. 2000. A threatening intellectual environment: Why fe-
males are susceptible to experiencing problem-solving deficits in the presence of males. Psycho-
logical Science 11(5): 365–371.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
479
Effects of Demographic Mismatch
Lavy, Victor. 2008. Do gender stereotypes reduce girls’ or boys’ human capital outcomes? Evi-
dence from a natural experiment. Journal of Public Economics 92(10): 2083–2105.
Loury, Glenn C. 2009. The anatomy of racial inequality. Cambridge, MA: Harvard University
Press.
Lusher, Lester, Doug Campbell, and Scott Carrell. 2015. TAs like me: Racial interactions between
graduate teaching assistants and undergraduates. NBER Working Paper No. 21568.
Mustard, David B. 2001. Racial, ethnic, and gender disparities in sentencing: Evidence from the
U.S. federal courts. Journal of Law and Economics 44(1): 285–314.
Neumark, David, and Rosella Gardecki. 1998. Women helping women? Role model and mentor-
ing effects on female Ph.D. students in economics. Journal of Human Resources 33(1): 220–246.
Okonofua, Jason A., David Paunesku, and Gregory M. Walton. 2016. Brief intervention to en-
courage empathic discipline cuts suspension rates in half among adolescents. Proceedings of the
National Academy of Sciences U.S.A. 113(19): 5221–5226.
Oyer, Paul, and Scott Schaefer. 2015. Firm/employee matching: An industry study of U.S. lawyers.
ILR Review 69(2): 378–404.
Oyer, Paul, and Scott Schaefer. 2019. The returns to elite degrees: The case of American lawyers.
ILR Review 72(2): 446–479.
Papageorge, Nicholas W., Seth Gershenson, and Kyungmin Kang. 2016. Teacher expectations
matter. IZA Discussion Paper No. 10165.
Rachlinski, Jeffrey J., Sheri Lynn Johnson. 2009. Does unconscious racial bias affect trial judges?
Notre Dame Law Review 84(3): 1195–1246.
Schochet, Peter Z. 2009. An approach for addressing the multiple testing problem in social
policy impact evaluations. Evaluation Review 33(6): 539–567.
Schwarcz, Daniel, and Dion Farganis. 2017. The impact of individualized feedback on law student
performance. Journal of Legal Education 67(1): 139–175.
Steele, Claude M. 1997. A threat in the air: How stereotypes shape intellectual identity and per-
formance. American Psychologist 52(6): 613–629.
Walton, Gregory M. 2014. The new science of wise psychological interventions. Current Directions
in Psychological Science 23(1): 73–82.
Wilkins, David B., and G. Mitu Gulati. 1996. Why are there so few black lawyers in corporate law
firms? An institutional analysis. California Law Review 84(3): 493–625.
Wood, Robert G., Mary E. Corcoran, and Paul N. Courant. 1993. Pay differences among the highly
paid: The male–female earnings gap in lawyers’ salaries. Journal of Labor Economics 11(3): 417–441.
480
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
f
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
A P P E N D I X A
Table A.1. Baseline Model Allowing for Contemporaneous Spillovers
Continuous Grade
A/A— Grade
(1)
(2)
(3)
(4)
−0.017**
(0.007)
−0.003
(0.013)
−0.037**
(0.016)
−0.003
(0.011)
Other-sex (OS)
Another OS
Other-race (OR)
Another OR
OS * Another OS
OR * Another OR
Observations
36,560
Course fixed effects
Student fixed effects
Yes
Yes
0.017
(0.029)
0.033
(0.025)
−0.053***
(0.019)
−0.010
(0.014)
−0.048*
(0.028)
0.023
(0.022)
36,560
Yes
Yes
−0.012*
(0.007)
0.009
(0.011)
−0.028***
(0.011)
−0.001
(0.010)
36,560
Yes
Yes
−0.004
(0.028)
0.021
(0.019)
−0.028
(0.019)
−0.001
(0.011)
−0.016
(0.028)
−0.000
(0.022)
36,560
Yes
Yes
Notes: Each column represents a different model specification. The outcomes are
measured as follows: Continuous Grade measures a student’s received grade on a
0—4 scale (F—A). A/A— Grade is a binary indicator for whether a student received
an A or A— grade. Standard errors in parentheses are clustered by student and
instructor.
*p < 0.1; **p < 0.05; ***p < 0.01.
Table A.2. Mean Course Characteristics by Subject
Subject
Civil Procedure
Constitutional
Contracts
Criminal Law
Legal Writing
Property
Torts
N
80
60
60
70
620
80
60
Course Size
Female Students
White Students
Female Faculty
White Faculty
83.1
83.1
75.0
76.8
15.5
85.0
79.2
0.60
0.58
0.59
0.59
0.59
0.59
0.58
0.65
0.63
0.62
0.65
0.63
0.64
0.63
0.21
0.14
0.31
0.57
0.50
0.60
0.42
0.82
0.69
0.84
0.62
0.92
0.79
1.00
Notes: The unit of analysis is course sections. Each statistic reported is the average across course sections: average size,
percent female students in class, percent white students in class, percent of course sections taught by female faculty, and
percent of course sections taught by white faculty.
Table A.3.
Impact of Demographic Mismatch on Non-Writing First-Year Required Course Outcomes
Other-sex
Other-race
Differences in coefficients (P)
Observations
Continuous Grade
A Grade
A/A— Grade
C, D, F Grade
Take Another
Dropped Course
(1)
−0.011
(0.008)
−0.042**
(0.017)
0.071*
28,290
(2)
(3)
−0.005
(0.004)
−0.017**
(0.007)
0.151
28,290
−0.012
(0.008)
−0.034***
(0.011)
0.061*
28,290
(4)
−0.001
(0.003)
0.011
(0.008)
0.119
28,290
(5)
0.016
(0.010)
0.000
(0.008)
0.198
18,620
(5)
0.000
(0.000)
0.001
(0.001)
0.271
28,400
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
f
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
481
Effects of Demographic Mismatch
Table A.3. Continued.
Continuous Grade
A Grade
A/A— Grade
C, D, F Grade
Take Another
Dropped Course
Course fixed effects
Student fixed effects
(1)
Yes
Yes
(2)
Yes
Yes
(3)
Yes
Yes
(4)
Yes
Yes
(5)
Yes
Yes
(5)
Yes
Yes
Notes: Each column represents a different model specification. The outcomes are measured as follows: Continuous Grade measures a student’s
received grade on a 0—4 scale (F—A); A Grade is a binary indicator for whether a student received an A grade; A or A— Grade is a binary
indicator for whether a student received an A or A— grade; C, D, F Grade is a binary indicator for whether a student received a C, D, or F grade;
Take Another is a binary indicator for whether a student takes a subsequent elective course in the same field after his first year; and Dropped
Course is a binary indicator for whether a student drops the course before the end of the semester. Column 5 has fewer observations because
not all required courses correspond to elective course subjects. Difference in coefficients compares Other-sex effect against Other-race effect.
Standard errors in parentheses are clustered by student and instructor.
*p < 0.1; **p < 0.05; ***p < 0.01.
Table A.4.
Average Partial Effects)
Impact of Demographic Mismatch on First-Year Required Course Outcomes (Logit
A/A— Grade
C, D, F Grade
Take Another
Dropped Course
Other-sex
Other-race
Female instructor
Nonwhite instructor
Nonwhite student
Female student
(1)
−0.011**
(0.005)
−0.029***
(0.010)
0.029***
(0.005)
0.025***
(0.009)
−0.088***
(0.012)
0.044***
(0.008)
(2)
0.002
(0.002)
0.007
(0.004)
−0.001
(0.003)
−0.002
(0.003)
0.030***
(0.005)
−0.019***
(0.004)
Observations
36,560
36,560
(3)
0.012**
(0.006)
−0.008
(0.010)
0.002
(0.007)
−0.009
(0.009)
0.038***
(0.013)
0.000
(0.009)
18,540
(4)
0.001
(0.000)
0.001
(0.001)
−0.000
(0.001)
0.001
(0.001)
−0.001
(0.001)
−0.000
(0.001)
36,730
Notes: Each column represents a different model specification. The outcomes are measured
as follows: A/A— Grade is a binary indicator for whether a student received an A or A— grade.
C, D, F Grade is a binary indicator for whether a student received a C, D, or F grade. Take
Another is a binary indicator for whether a student takes a subsequent course in the same
field. Dropped Course is a binary indicator for whether a student drops the course before
the end of the semester. Column 3 has fewer observations because not all required courses
correspond to elective course subjects. Standard errors in parentheses are clustered by student
and instructor.
**p < 0.05; ***p < 0.01.
Table A.5. Heterogeneity by Course Size and Percent Female (Nonwhite) in Course
Course Size
Percent Female (Nonwhite) in Course
(1)
(2)
(3)
(4)
Other-sex (OS)
OS * Course size
OS * Course size (Sq)
0.003828
(0.024974)
0.000052
(0.001052)
−0.000003
(0.000009)
−0.245622
(0.176855)
482
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
Table A.5. Continued.
OS * Percent female
OS * Percent female (Sq)
Other-race (OR)
OR * Course size
OR * Course size (Sq)
OR * Percent nonwhite
Course Size
Percent Female (Nonwhite) in Course
(1)
(2)
(3)
(4)
0.007005
(0.005837)
−0.000051
(0.000048)
0.020580
(0.024309)
−0.002240**
(0.000928)
0.000018**
(0.000008)
0.028642
(0.094617)
−0.003086
(0.004580)
0.00004
(0.000056)
0.052*
36,560
Yes
Yes
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
OR * Percent nonwhite (Sq)
p value for joint significance tests
Observations
Course fixed effects
Student fixed effects
0.076*
36,560
Yes
Yes
0.005***
36,560
Yes
Yes
0.088*
36,560
Yes
Yes
Notes: The covariates are defined as follows: Other-sex is a binary indicator for whether the student’s sex is
different from the instructor. Other-race is a binary indicator for whether the student’s race is different from
the instructor. Course size measures the total number of students in the classroom. Percent Female measures
the percentage of female students in the classroom. Percent Nonwhite measures the percentage of nonwhite
students in the classroom. Sq indicates quadratic term. Standard errors in parentheses.
*p < 0.1; **p < 0.05; ***p < 0.01.
A P P E N D I X B
This appendix uses publicly available data from After the JD (AJD) to document the
descriptive relationship between law school grades and early-career salaries for individ-
uals who earned JDs from non–top 10 law schools.32 The motivation for this appendix
is to show the impacts of student–instructor mismatch on course grades documented
in the current study likely translate into demographic pay gaps among early-career law
professionals.
The public-use AJD data report annual earnings in eight bins: <$40,000, $40,000-
$49,999, $50,000-$59,999, $60,000-$74,999, $75,000-$99,999, $100,000-
$124,999, $125,000-$149,999, and >$150,000. Accordingly, we estimate descriptive
ordered-logit models in which this categorical annual-earnings variable is the de-
pendent variable. Appendix table B.1 reports the ordered-logit coefficients for the full
sample. The parsimonious specifications in columns 1 et 2 document the uncon-
ditional female pay gap and wage-GPA gradient, respectivement. The omitted reference
category for the GPA variable is <3.0. Column 4 shows that these patterns are robust
to controlling for law school quality.
Because the ordered-logit coefficients are not directly interpretable, table B.2 re-
ports the average partial effects (APE) of these covariates on the probability of being in
each earnings band for the fully-specified, full-sample estimates reported in column 4
32. The AJD is a representative survey of new law-school graduates, conducted by the American Bar Foundation,
in 2002, 2007, and 2010. See www.americanbarfoundation.org/research/project/118 for further information.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
483
Effects of Demographic Mismatch
Table B.1. Descriptive Ordered-Logit Earnings Regressions: Coefficient Estimates
(1)
(2)
(3)
(4)
−0.45***
(0.07)
−0.02
(0.11)
−0.10
(0.11)
0.62***
(0.13)
0.06
(0.19)
−0.49***
(0.07)
0.11
(0.12)
0.04
(0.12)
0.63***
(0.14)
0.10
(0.19)
1.90***
(0.16)
1.65***
(0.13)
1.09***
(0.13)
0.59***
(0.12)
1.35***
(0.10)
1.82***
(0.16)
1.59***
(0.13)
1.04***
(0.13)
0.56***
(0.12)
1.34***
(0.10)
Female
Black
Latinx
Asian
Other race
> 3.75 grade point average (GPA)
3.5—3.74 GPA
3.25—3.49 GPA
3.0—3.24 GPA
Missing GPA
Top 10 law school
11—20 law school
21—100 law school
Observations
3,785
3,892
3,785
−0.49***
(0.07)
0.02
(0.11)
−0.01
(0.12)
0.42***
(0.13)
0.06
(0.20)
1.68***
(0.18)
1.42***
(0.14)
0.87***
(0.13)
0.48***
(0.12)
1.16***
(0.10)
2.21***
(0.15)
1.45***
(0.13)
0.38***
(0.07)
3,755
Remarques: Each column represents a different model specification. Cut points not shown. Standard
errors in parentheses.
***p < 0.01.
Table B.2. Descriptive Ordered-Logit Earnings Regressions: Average Partial Effects
0—39K
40—49K
50—59K
60—74K
75—99K
100—124K
125—149K
(1)
(2)
(3)
(4)
(5)
(6)
(7)
Female
Black
Latinx
Asian
Other race
> 3.75 GPA
3.5—3.74 GPA
3.25—3.49 GPA
3.0—3.24 GPA
Missing GPA
0.04***
(0.01)
−0.00
(0.01)
0.00
(0.01)
−0.03***
(0.01)
−0.00
(0.02)
−0.13***
(0.02)
−0.11***
(0.01)
−0.07***
(0.01)
−0.04***
(0.01)
−0.09***
(0.01)
0.04***
(0.01)
−0.00
(0.01)
0.00
(0.01)
−0.04***
(0.01)
−0.00
(0.02)
−0.15***
(0.02)
−0.13***
(0.01)
−0.08***
(0.01)
−0.04***
(0.01)
−0.10***
(0.01)
0.02***
(0.00)
−0.00
(0.00)
0.00
(0.00)
−0.02***
(0.01)
−0.00
(0.01)
−0.07***
(0.01)
−0.06***
(0.01)
−0.03***
(0.01)
−0.02***
(0.01)
−0.05***
(0.00)
0.00**
(0.00)
−0.00
(0.00)
0.00
(0.00)
−0.00*
(0.00)
−0.00
(0.00)
−0.01**
(0.00)
−0.01**
(0.00)
−0.00**
(0.00)
−0.00*
(0.00)
−0.01**
(0.00)
−0.02***
(0.00)
0.00
(0.00)
−0.00
(0.00)
0.02***
(0.01)
0.00
(0.01)
0.06***
(0.01)
0.05***
(0.01)
0.03***
(0.01)
0.02***
(0.00)
0.04***
(0.00)
−0.02***
(0.00)
0.00
(0.00)
−0.00
(0.01)
0.02***
(0.01)
0.00
(0.01)
0.07***
(0.01)
0.06***
(0.01)
0.04***
(0.01)
0.02***
(0.01)
0.05***
(0.00)
−0.02***
(0.00)
0.00
(0.01)
−0.00
(0.01)
0.02***
(0.01)
0.00
(0.01)
0.08***
(0.01)
0.07***
(0.01)
0.04***
(0.01)
0.02***
(0.01)
0.06***
(0.01)
>150K)
(8)
−0.04***
(0.01)
0.00
(0.01)
−0.00
(0.01)
0.03***
(0.01)
0.00
(0.02)
0.13***
(0.01)
0.11***
(0.01)
0.07***
(0.01)
0.04***
(0.01)
0.09***
(0.01)
484
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
F
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
un
_
0
0
2
8
0
p
d
.
F
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chris Birdsall, Seth Gershenson, and Raymond Zuniga
Table B.2. Continued.
0—39K
40—49K
50—59K
60—74K
75—99K
100—124K
125—149K
(1)
(2)
(3)
(4)
(5)
(6)
(7)
Top 10 law school
11-20 law school
21-100 law school
−0.17***
(0.01)
−0.11***
(0.01)
−0.03***
(0.01)
−0.20***
(0.02)
−0.13***
(0.01)
−0.03***
(0.01)
−0.09***
(0.01)
−0.06***
(0.01)
−0.02***
(0.00)
Observations
3,755
3,755
3,755
−0.01**
(0.00)
−0.01**
(0.00)
−0.00**
(0.00)
3,755
0.08***
(0.01)
0.06***
(0.01)
0.01***
(0.00)
3,755
0.09***
(0.01)
0.06***
(0.01)
0.02***
(0.00)
3,755
0.11***
(0.01)
0.07***
(0.01)
0.02***
(0.00)
3,755
>150K)
(8)
0.18***
(0.01)
0.12***
(0.01)
0.03***
(0.01)
3,755
Remarques: Standard errors in parentheses.
*p < 0.1; **p < 0.05; ***p < 0.01.
Table B.3. Descriptive Ordered-Logit Earnings Regressions by Demographic Background: Coefficient
Estimates
Male
(1)
Female
(2)
White
(3)
Black
(4)
Latinx
(5)
−0.49***
(0.08)
−0.97***
(0.23)
−0.65**
(0.27)
Asian
(6)
−0.28
(0.25)
0.15
(0.16)
0.04
(0.17)
0.27
(0.20)
0.13
(0.28)
1.62***
(0.29)
1.54***
(0.19)
0.92***
(0.18)
0.43**
(0.17)
1.15***
(0.14)
2.26***
(0.20)
1.47***
(0.17)
0.34***
(0.10)
1,995
−0.09
(0.16)
−0.09
(0.18)
0.53***
(0.18)
−0.03
(0.29)
1.70***
(0.22)
1.31***
(0.20)
0.83***
(0.19)
0.53***
(0.17)
1.18***
(0.15)
2.15***
(0.24)
1.43***
(0.20)
0.41***
(0.11)
1,760
1.69***
(0.19)
1.48***
(0.16)
0.87***
(0.15)
0.51***
(0.14)
1.27***
(0.12)
2.15***
(0.18)
1.51***
(0.16)
0.42***
(0.08)
2,703
17.99***
(1.07)
3.34***
(0.68)
2.41***
(0.64)
0.83**
(0.39)
1.00***
(0.29)
2.49***
(0.41)
1.53***
(0.38)
0.36
(0.28)
330
0.61
(0.84)
2.86***
(0.81)
0.40
(0.53)
0.42
(0.43)
0.71**
(0.33)
3.02***
(0.50)
0.85
(0.54)
0.33
(0.30)
312
1.44**
(0.59)
0.62
(0.56)
0.48
(0.35)
−0.10
(0.41)
2.08***
(0.45)
1.03***
(0.34)
0.13
(0.30)
341
Female
Black
Latinx
Asian
Other Race
> 3.75 GPA
3.5—3.74 GPA
3.25—3.49 GPA
3.0—3.24 GPA
Missing GPA
Top 10 law school
11—20 law school
21—100 law school
Observations
Remarques: Each column represents a different model specification. Cut points not shown. Standard errors in
parentheses.
**p < 0.05; ***p < 0.01.
of table B.1. Here we see that female lawyers are 2 to 4 percentage points more likely
than male lawyers to be in the lowest-earning categories and 2 to 4 percentage points
less likely than male lawyers to be in the highest-earning categories. The APE for the
categorical GPA indicators show that each 0.25 increase in GPA is associated with a 2
to 4 percentage point increase in the probability of being in one of the high-earnings
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
/
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
485
Effects of Demographic Mismatch
Table B.4. Descriptive Ordered-Logit Earnings Regressions by Law School
Rank: Coefficient Estimates
Top 10
(1)
−0.55**
(0.24)
0.07
(0.33)
0.42
(0.37)
0.57
(0.37)
1.13*
(0.64)
−0.12
(1.02)
0.80
(0.85)
0.97
(0.82)
0.42
(0.81)
0.52
(0.78)
370
11-20
(2)
−0.44**
(0.20)
0.11
(0.28)
−0.60
(0.37)
0.23
(0.30)
−0.36
(0.46)
2.72***
(0.43)
2.15***
(0.38)
1.50***
(0.42)
1.99***
(0.41)
2.40***
(0.33)
467
21-100
Outside 100
(3)
(4)
−0.44***
(0.10)
−0.07
(0.17)
−0.00
(0.17)
0.33*
(0.20)
−0.28
(0.26)
1.98***
(0.26)
1.62***
(0.21)
1.07***
(0.20)
0.42**
(0.19)
1.33***
(0.16)
1,737
−0.60***
(0.12)
0.06
(0.23)
0.10
(0.27)
0.72***
(0.27)
0.67
(0.41)
1.54***
(0.31)
1.33***
(0.26)
0.50**
(0.21)
0.41**
(0.18)
0.90***
(0.16)
1,181
Female
Black
Latinx
Asian
Other race
> 3.75 GPA
3.5—3.74 GPA
3.25—3.49 GPA
3.0—3.24 GPA
Missing GPA
Observations
Remarques: Each column represents a different model specification. Cut points not
shown. Standard errors in parentheses.
*p < 0.1; **p < 0.05; ***p < 0.01.
brackets, and a symmetric decrease in the probability of being in a low-earning bracket.
Importantly, this suggests that even a relatively small change in GPA attributable to
student–instructor demographic mismatch in first-year law courses might substan-
tively affect early-career earnings.
Table B.3 estimates the fully specified ordered-logit model separately by sex and race.
The key results here are: (1) the sex pay gap exists for white, black, and Latinx lawyers
and (2) the wage-GPA gradient exists in the male, female, white, and black subsamples.
Table B.4 similarly shows that the wage–GPA gradient exists for graduates of all law
schools outside the U.S. News Top 10. This is consistent with results reported in Oyer
and Schaefer (2019). The U.S. News rank of the law school studied in the current paper
falls in the 21–100 range (column 3), for which grades are quite important.
486
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
5
3
4
5
7
1
8
9
3
7
4
5
e
d
p
_
a
_
0
0
2
8
0
p
d
/
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3