RESOURCE NEEDS OF
CALIFORNIA PUBLIC SCHOOLS:
RESULTS FROM A SURVEY OF
TEACHERS, PRINCIPALS, AND
SUPERINTENDENTS
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
F
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
.
.
.
.
F
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jon Sonstelie
Department of Economics
Université de Californie,
Santa Barbara
Santa Barbara, Californie 93106-2150
jon@econ.ucsb.edu
Abstrait
This article reports the results of school budget sim-
ulations with 568 randomly selected California public
school teachers, principals, and superintendents. Simu-
lation participants were presented with the budget for a
hypothetical school and asked to use that budget to em-
ploy the resources that would maximize the academic
achievement of the school’s students. Their responses
were used to estimate the resources that professional
educators believe their schools need to meet state aca-
demic achievement standards.
58
c(cid:1) 2008 American Education Finance Association
Jon Sonstelie
INTRODUCTION
1.
California has established an ambitious goal for its public schools. En effet,
the state expects 70 percent of students in each school to exceed the national
median on standardized tests. As of 2007, eight years after the goal was estab-
léché, less than 30 percent of schools have achieved it. Virtually all of these
successful schools are in relatively affluent communities. Partly in response
to this unsatisfactory outcome, state policy makers requested a number of
studies of California’s public school system (Loeb, Bryk, and Hanushek 2007).
Because the teacher-student ratio in California public schools is approximately
70 percent of the ratio in the rest of the country, it is only natural that one
focus of these studies was the adequacy of school resources. Imazeki (2007)
addressed this issue through an econometric study of the relationship between
school district expenditures and student achievement. Chambers, Lévine, et
DeLancey (2007) convened two groups of professional educators to determine
the resources schools need to meet the state’s goal. The present study is a third
attempt to address this issue.
The study’s objectives are to learn what resources teachers, principals, et
superintendents believe their schools need to achieve the state’s goal and to
communicate those beliefs to policy makers. These objectives are addressed
through a series of budget simulations conducted with 568 randomly selected
public school teachers, principals, and superintendents. The simulations
describe a hypothetical school—the characteristics of its students, the cost of
its resources, and its total budget. Participants select the quantities of each
resource that would maximize the academic achievement of the school’s
students subject to the school’s budget constraint. They then predict that
achievement. Budget scenarios and student characteristics vary among
participants, revealing how educational practitioners would spend additional
funds and how they believe those funds would affect student achievement.
Those responses are used to estimate a relationship between school budgets
and student achievement.
These budget simulations build on the work of Rose, Sonstelie, et
Richardson (2004) and were inspired by the professional judgment panels
convened in a number of states to “cost out” an adequate education (Taylor,
Boulanger, and Vedlitz 2005). In the typical professional judgment panel, a group
of educators is brought together to design an instructional program that would
achieve a specified objective. Researchers then determine the cost of the re-
sources involved in that program.
The budget simulations differ from the professional judgment panels in
two notable ways. D'abord, the budget simulations present participants with a
fixed budget and the costs of resources, forcing participants to trade one re-
source off against another. In the professional judgment panels, participants
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
F
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
59
RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS
are typically instructed to design a program that is the least costly method of
meeting the objective, but they are not given the costs of resources or a budget.
Deuxième, the budget simulations produce responses from hundreds of indi-
vidual participants, revealing differences in opinion among educators in the
value they place on various resources. While the process of reaching consensus
in professional judgment panels is valuable because it forces participants to
defend their views against those of others, it does blur differences of opinion
among participants.
The simulations have two key shortcomings. The first is that many pro-
fessional educators have little actual experience with allocating budgets at the
school level. This is particularly true for teachers, but it is also true for many
principals. Deuxième, in many cases, participants are asked to predict student
achievement for hypothetical schools with more resources than any school
they have experienced. Those predictions cannot be based on hard evidence
of what actual schools were able to achieve with equivalent resources. Ce
problem is not unique to this study, cependant. Particularly for schools with
many low-income students, the state’s current standards ask schools to ac-
complish something that very few, if any, in similar circumstances have ever
accomplished. In addressing the question of what resources schools need to
meet state standards, any method is essentially an out-of-sample prediction.
The simulations do not include all of the resources employed by school dis-
tricts. Special education, maintenance, pupil transportation, utilities, district
administration, and other costs not explicitly included in the simulations are es-
timated using data on the expenditures of California school districts in 2003–4.
These costs are added to the cost of the school resources that simulation par-
ticipants believe to be necessary to meet the state’s achievement goal. Le
result is a total that is 40 percent more than California school districts spent
in 2003–4. Even with that large increase, schools serving low-income students
would not meet the state’s goal. En fait, for those schools, the highest budget
in the simulations would not be high enough, in the view of participants.
2. AN OVERVIEW OF THE BUDGET SIMULATIONS
Sonstelie (2007) describes these simulations in detail; this section provides a
brief overview. Simulation participants are asked to consider the budget of a
hypothetical school. The budget is presented as a spreadsheet on which each
line specifies a resource and the cost of a unit of that resource. The spreadsheet
also specifies a total budget, and participants are asked to choose the units of
each resource that would maximize the academic achievement of the school’s
students subject to their school’s budget constraint. As participants enter their
choices, the spreadsheet calculates the cost of those choices and the amount
60
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
F
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jon Sonstelie
of the budget remaining. The simulations have three different versions: un
for an elementary school (grades K–5), one for a middle school (grades 6–8),
and one for a high school (grades 9–12). Tableau 1 shows the resources used in
each version.
When the budget is spent, participants are asked to predict the school’s
academic performance index (API), the measure of school performance in
California’s accountability system. The API is essentially a weighted average
of students’ scores on a battery of statewide achievement tests. The state’s
goal for each school is an API of 800, which is equivalent to 70 percent of a
school’s students exceeding the median performance of students throughout
the country (Rose et al. 2003).
The decisions about what resources to include in the simulations were
based on visits to forty-nine randomly selected school sites in California,
visits summarized in Rose, Sonstelie, and Richardson (2004). The simulation
spreadsheets are intended to include every school district employee directly
involved either in general instruction at the school level or in the support
or administration of that instruction. Included are teachers, principals,
assistant principals, clerical office staff, aides, counselors, nurses, librarians,
security officers, technology support staff, tutors, and academic coaches. Le
simulations also include instructional computers. They exclude resources
associated with the following areas: instructional materials, special education,
maintenance and operations, pupil transportation, district administration,
and extracurricular activities.
Naturally teachers play a prominent role in all three versions of the spread-
sheets. Cependant, the elementary spreadsheet has a different classification
of teachers than the middle and high school spreadsheets. The elementary
spreadsheet has kindergarten teachers, teachers in grades 1–3, teachers in
grades 4–5, and specialty teachers (reading specialists and art and music teach-
ers). In contrast, the middle and high school spreadsheets have core teachers,
non-core teachers, and physical education teachers. Core teachers teach re-
quired subjects such as English, math, science, and history. Non-core teachers
teach elective subjects such as music and art. Based on this classification of
teachers, the spreadsheets calculate the average class size for various types
of classes. Underlying this calculation is an assumed distribution of students
through grades and a distribution of students among core, non-core, et
physical education classes.
Adding more teachers reduces class sizes, which may improve instruction
and student achievement. As recent research has shown, cependant, a more
important factor may be the effectiveness of teachers (Hanushek, Rivkin, et
Kain 2005; Hanushek et al. 2005). The simulations deal with teacher effective-
ness in two ways. D'abord, participants are instructed to assume that all teachers
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
F
/
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
F
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
61
RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS
Tableau 1. School Resources Spreadsheet
Resource
Teachers
Kindergarten
Grades 1–3E
Grades 4 and 5E
SpecialtyE
CoreM,H
Non-coreM,H
Physical educationM,H
Administration
Principals
Assistant principals
Clerical office staff
Support staff
Instructional aides
Counselors
Nurses
Librarians
Security officers
Technology support staff
Community liaisons
Professional development
Academic coaches
Collaborative time
Student programs
PreschoolE
Unit of Measure
Cost per Unit ($ per year) FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE 66,000 66,000 66,000 66,000 66,000 66,000 66,000 112,000 100,000 41,000 32,000 87,000 87,000 75,000 41,000 86,000 40,000 75,000 Hours per year per Number of teachers × hourly teacher teacher wage Students 4,900 Full-day kindergartenE 1 = yes 0 = no Number of K teachers × annual teacher wage After-school tutoring program Teacher hours per week 1,845 Longer school day Hours per day Number of teachers × hourly teacher wage × instructional days per year Summer school Students 359 Longer school year Days per year Number of teachers × daily teacher wage Computers for instruction Computers 400 Other Other expenditures $ thousands
1,000
E = elementary schools.
M = middle schools.
H = high schools.
62
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
.
F
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jon Sonstelie
are fully credentialed with an average of eleven years of experience. Deuxième,
participants are provided with two methods for improving the quality of in-
struction. They may hire academic coaches to work with teachers to improve
instruction, help with curriculum design, and analyze results from student as-
sessments. They may also purchase collaborative time for their teachers, temps
for teachers to work together on curriculum, pacing calendars, and student as-
sessments. This collaborative time may also be used to work with instructional
consultants on effective pedagogy. Collaborative time is assumed to be in addi-
tion to the standard work day and year, requiring that teachers be appropriately
compensated for participating.
In addition to these staff positions, participants may allocate their budgets
for certain other programs. Par exemple, in the elementary school spreadsheet,
participants may decide to allocate some of their budget to send a specified
number of their students to preschool. The preschool is assumed to have
classes of twenty students staffed by one teacher and one aide. The compen-
sation of that teacher and aide divided by twenty is the unit cost of preschool,
c'est, the cost of sending one student to preschool. Participants may also
decide to make their kindergarten classes five hours per day instead of three,
the cost of which is compensating kindergarten teachers for an additional two
hours per day.
In all versions of the spreadsheet, participants may choose to allocate some
of their budget to an after-school tutoring program to assist students who are
struggling. The cost of this program is the salary of teachers who would be
hired to conduct this program. Participants may also decide how many of their
students to send to a summer school, which runs for four weeks and has class
sizes of twenty students. The cost is the compensation of teachers who would
be hired in this program.
Participants may also choose to lengthen the school day and school year,
the cost of which is the additional compensation for teachers. These costs
and those of collaborative time raise issues about how the unit cost of teach-
ers is defined. Par exemple, if the hourly salary of teachers is $50, a one- hour increase in collaborative time increases the unit cost of teachers by $50. Sonstelie (2007) describes how these interactions are represented in the
simulations.
All of these unit costs depend on an hourly compensation for teachers,
which is derived by dividing the annual cost of teachers by the number of hours
a teacher is employed per year under the standard contract. According to the
standard contract, teachers are employed seven hours per day for 184 days per
year—180 days of instruction plus 2 days of professional development and 2
teacher work days. Ainsi, under the standard contract, teachers are employed
pour 1,288 hours per year.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
.
F
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
63
RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS
In addition to budgets and unit costs, the simulations describe the students
in each participant’s hypothetical school. This description varied among partic-
ipants, revealing how student characteristics affect resource choices and API
prédictions. To ensure that participants had hypothetical schools like those
they had experienced, the description of each hypothetical school was taken
from the participant’s actual school. The variety of school descriptions was
thus determined by the selection of participants.
Participants were selected by first choosing schools by stratified random
sampling. Schools were stratified into twenty-seven groups, and twenty-one
schools were randomly selected from each group. The stratifications were
based on three factors: grade span, enrollment, and percent of students partic-
ipating in a school’s free or reduced price lunch program, referred to below as
socioeconomic status (SES). There were nine groups of elementary schools,
nine groups of middle schools, and nine groups of high schools. Within each
grade span, there were three groups of small schools, three groups of medium-
sized schools, and three groups of large schools. For each grade span and size,
one group of schools had students with low SES, one group had students with
average SES, and one group had students with high SES.
Once a school was chosen, a person associated with that school was selected
to participate in the simulations. That person was either the school’s principal,
a teacher in the school, or the superintendent of the school’s district. Pour
the twenty-one schools in a group, seven schools were randomly selected
to be represented by the school’s principal, seven by one of its teachers, et
seven by its superintendent. This sampling strategy yields 567 participants: 189
associated with an elementary school, 189 associated with a middle school, et
189 associated with a high school. It also yields 189 teachers, 189 principals,
et 189 superintendents.
The description of schools follows the format of the API reports for schools
produced by the California Department of Education. It includes enrollment,
percentage of students participating in the free or reduced price lunch pro-
gram, percentage of English learners (ELs), race and ethnicity of students,
and education of their parents. En outre, the middle and high school sim-
ulations provide a description of the average API of the hypothetical school’s
feeder schools. Unlike the student characteristics for which variations were
determined through the selection of participants, the average API of feeder
schools was selected randomly, as described below.
Each participant completed a budget simulation under each of two dif-
ferent scenarios. A scenario specifies the school’s budget and the unit costs
of its certificated personnel. En outre, for participants in the middle and
high school simulations, it also specifies the average API of feeder schools.
Budgets and personnel costs are expressed as percentages of a baseline. Le
64
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
F
/
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
.
.
.
.
F
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jon Sonstelie
Tableau 2. Treatments for Elementary Schools of Medium SES
Percent of Baseline
First Scenario
Second Scenario
Scenario
Expenditures
per Student
Certificated
Salaries
Expenditures
per Student
Certificated
Salaries
Participant
Type
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
0
20
10
30
20
40
30
50
40
60
50
70
60
80
40
40
40
40
60
60
60
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
15
15
30
0
15
30
20
0
30
10
40
20
50
30
60
40
70
50
80
60
40
40
40
40
60
60
60
0
0
0
0
0
0
0
0
0
0
0
0
0
0
15
0
30
15
15
0
15
Superintendent
Principal
Teacher
Superintendent
Principal
Teacher
Superintendent
Principal
Teacher
Superintendent
Principal
Teacher
Superintendent
Principal
Teacher
Superintendent
Principal
Teacher
Superintendent
Principal
Teacher
baseline budget is $4,000 per pupil, which is approximately 9 percent less than California school districts spent in 2003–4 for the resources covered in the simulations. The unit costs for the baseline are listed in table 1. The costs are those used in Rose, Sonstelie, and Richardson (2004), updated to 2003–4. The two scenarios faced by any one participant are referred to as the par- ticipant’s treatment. Tableau 2 lists the twenty-one treatments for participants from elementary schools of medium SES. Par exemple, in treatment 12, a participant first completes the simulation with a budget of $6,800 per pupil
(70 percent more than $4,000 per pupil) and personnel costs equal to the baseline. In the second scenario, the budget is $6,000 per pupil (50 pour cent
plus que $4,000 per pupil) and the personnel costs are the same. In treat- ment 20, a participant first faces a budget of $6,400 per pupil and personnel
costs for certificated staff that are 15 percent above the baseline. In the second
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
.
.
.
.
F
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
65
RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS
scénario, the budget is the same, but personnel costs are equal to the baseline
frais.
Each treatment is associated with a certain type of participant: teacher,
principal, or superintendent. Aussi, the treatments vary with the SES of the
participant’s schools. For high SES schools, the budgets in each treatment were
reduced by 10 percentage points. Ainsi, Par exemple, the budget in the first
scenario of treatment 2 est 10 percent above the baseline. De la même manière, for low SES
schools, the budgets in each treatment were increased by 10 percentage points.
The budget in the first scenario of treatment 2 est 30 percent above the baseline.
The treatments have two notable features. D'abord, only one parameter
changes between scenarios: either the budget or the unit costs of certificated
staff. Deuxième, each treatment except the last has a mirror image. In treatment
1, Par exemple, the budget is $4,000 per pupil in the first scenario and $4,800
in the second. Its mirror image is scenario 2, in which the budget is $4,800 per pupil in the first scenario and $4,000 per pupil in the second. En conséquence-
quence, half of the participants see an increase in resources between the first
and second scenarios and half see a decrease.
In addition to budgets and unit costs, the middle and high school scenarios
also include the average API of feeder schools. This API is the same in both
scenarios of a treatment. One-third of the treatments had an average API of
650, one-third had 750, and one-third had 850. As table 3 shows, as the average
API was increased from 650 à 750 or from 750 à 850, the budget percentages
were decreased by 10 percentage points. Par exemple, compare treatments 1
et 8. Treatment 1 has the lowest budgets for treatments with an API of 650,
and treatment 8 has the lowest budgets for treatments with an API of 750. Pour
the former treatment, the budgets are 20 et 40 percentage points above the
baseline; for the latter, ils sont 10 et 30 percentage points above the baseline.
As in the case of the elementary school simulations, the budget percentages
varied with the SES of a participant’s school. For participants from a low
SES school, budget percentages were reduced by 5 percentage points in every
treatment. For those from a high SES school, percentages were increased by 5
percentage points in every treatment.
Invitations to complete the simulations were issues in six rounds. In the
first, 567 individuals were identified by randomly selecting twenty-one schools
from each group. Each individual was randomly assigned one of the treat-
ments associated with his or her type. The invitation to participate specified a
Web site and log-in information that directed individuals to their simulations.
Individuals were given three weeks to complete their simulations and were
paid $250 for doing so. After the deadline, a second group of individuals was chosen in the same way to complete any treatments not completed in the first round. Three more 66 l Téléchargé à partir du site Web : / / direct . m je t . / / f edu ed p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pd . . . F . . f par invité 0 7 Septembre 2 0 2 3 Jon Sonstelie Table 3. Treatments for Middle and High Schools of Medium SES Percent of Baseline First Scenario Second Scenario Feeder School Expenditures Certificated Expenditures Certificated Participant API per Student per Pupil Salaries Salaries Type 650 650 650 650 650 650 650 750 750 750 750 750 750 750 850 850 850 850 850 850 850 20 40 40 60 60 60 60 10 30 30 50 50 50 50 0 20 20 40 40 40 40 0 0 0 0 0 15 15 0 0 0 0 0 15 15 0 0 0 0 0 15 15 40 20 60 40 60 60 60 30 10 50 30 50 50 50 20 0 40 20 40 40 40 0 0 0 0 15 0 30 0 0 0 0 15 0 30 0 0 0 0 15 0 30 Teacher Superintendent Principal Teacher Superintendent Principal Teacher Superintendent Principal Teacher Superintendent Principal Teacher Superintendent Principal Teacher Superintendent Principal Teacher Superintendent Principal Scenario 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 rounds were conducted in the same way, one invitation being issued for each treatment that had not been completed. In the sixth and final round, multiple invitations were issued for the few remaining treatments. The response rate to these invitations varied by type of participant. It was highest among teachers; 86.7 percent of those invited completed the simulations. For principals and superintendents, the response rate was 43 percent and 41.5 pour cent, respectivement. The high response rate from teachers is somewhat misleading, cependant. Principals of 1,214 schools were first asked to identify a teacher at their school who would be willing to participate in the simulations. This request yielded the names of 465 teachers. Invitations to participate were then sent to randomly selected teachers from this group. Because they had already expressed an interest in participating, they would be highly likely to do so if invited. l Téléchargé à partir du site Web : / / direct . m je t . / / f edu ed p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pdf . . . . . f par invité 0 7 Septembre 2 0 2 3 67 RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS This recruitment process resulted in 568 complete simulations, one more than the goal. For teachers, all treatments were completed, and none were duplicated, for a total of 189 réponses. All treatments were also completed for principals, and one was duplicated, for a total of 190 réponses. For super- intendents, 189 treatments were completed, et 4 were duplicated, leaving 4 treatments uncompleted. The uncompleted treatments were spread among grade spans, cependant. In total, there were 190 complete treatments for ele- mentary schools, 189 complete treatments for middle schools, et 189 com- plete treatments for high schools. As shown in Sonstelie (2007), the schools associated with simulation participants are representative of the universe of California public schools. 3. BUDGET ALLOCATIONS The statistical analysis aggregates these data into a relationship expressing the average response of participants as a function of budget scenarios. The relationship has the general form of the linear expenditure system described in Pollak and Wales (1992). Expenditures per pupil on resource i in observation t of the simulation is represented by the function eit = cit bit + mi yt − n(cid:3) j =1 c j t b j t + εit ; i = 1, . . . , n; t = 1, . . . , T. (1) In this formulation, n is the number of resource categories, T is the number of observations in the simulation, cit is the unit cost of resource i for observation t, yt is the per pupil budget for the simulation, and εit is an error term. The parameters bit are functions of other variables: bit = ai + fi zt , where zt is a k by 1 vector of variables describing the participant and his or her school. For each resource category i, there are k + 2 parameters: mi , ai , et le 1 by k vector fi . Intuitively, b j t represents a baseline amount for resource j, and c j t b j t is the cost of that amount. The amount (yt − c j t b j t ) is the revenue left after those n(cid:6) j =1 baseline expenditures are made, and the parameter mi is the fraction of that remaining revenue that is spent on resource i. This fraction does not depend on the characteristics of individuals or schools, but the baseline amounts do. The vector of descriptive variables (zt ) has seven elements. Four describe the school’s students: enrollment, percentage of students in the school’s free and reduced price lunch program, percentage of students who are classified as ELs, and average API of the feeder schools (for middle and high school simulations). En outre, the description includes an index variable indicating whether the participant is a teacher and an index variable for principals. It also 68 l Téléchargé à partir du site Web : / / direct . m je t . / F / e du e d p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pdf . . . . . f par invité 0 7 Septembre 2 0 2 3 Jon Sonstelie includes the similar school ranking for the participant’s school. The similar schools rank, which is produced by the California Department of Education, is the rank of a school’s API among the APIs of one hundred other schools with similar student characteristics. A rank of one means the school’s API is in the top 10 percent of those one hundred APIs; a rank of ten means it is in the bottom 10 pour cent. Sonstelie (2007) gives coefficient estimates for each equation in the lin- ear expenditure system. Rather than report those estimates here, this article reports estimated resource choices for a school with characteristics that are average for the simulation participants. Autrement dit, it reports the average resource choice for the average school and the average participant. To reflect the range of opinion around this average, the article also reports the residual standard error for each resource choice. Tableau 4 presents the estimated choices for the average elementary school, which has 583 students, 52 percent of whom participate in the school’s subsi- dized lunch program and 26 percent of whom are ELs. Choices are presented for two levels of total expenditures: $4,000 per pupil, which approximates
the average budget of a California school in 2003–4, et $6,000 per pupil, a budget 50 percent larger. The estimates are an average of those for teachers, principals, and superintendents, and they assume that the participants come from a school with a similar schools rank of five. The residual standard errors are relatively small for the choice of teachers and administrators, suggérer- ing widespread agreement about staffing levels for these positions. Cependant, for support staff, professional development, and student programs, standard errors are quite large. The higher budget funds increases in all spending areas. The teaching staff increases from 25.6 full-time equivalent (FTE) à 29.3 FTE, an increase of 15 pour cent. Administrative staff increases from 3.4 FTE to 4.3 FTE, an increase of 27 pour cent. While the percentage increases in the teaching and administrative staffs are substantial, both are much less than the 50 percent increase in total expenditures. Necessarily, other areas increase much more in percentage terms. Support staff triples from 3.2 FTE to 9.9 FTE. Expenditures on professional development also rise substantially. With the larger budget, an academic coach is added, and the time that teachers work together on curriculum, assessment, and pedagogy increases from forty-one to fifty-nine hours per year. With the larger budget, hours of instruction also increase. The school day is lengthened by eighteen minutes and the school year by four days. Participants also add individualized instructional time for students who are falling behind. The after-school tutoring program increases from eighteen teacher hours per week to forty-one. The number of students in summer school doubles to 120. l Téléchargé à partir du site Web : / / direct . m je t . / / f edu ed p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pdf . . . . . f par invité 0 7 Septembre 2 0 2 3 69 RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS Table 4. Resource Choices for the Average Elementary School: Estimates (Est.) and Standard Errors (S.E.) Resource Teachers Kindergarten Grades 1–3 Grades 4 et 5 Specialty Administration Principals Assistant principals Clerical office staff Support staff Instructional aides Counselors Nurses Librarians Security officers Technology support staff Community liaisons Professional development Academic coaches Expenditures per Student $4,000 $6,000 Unit of Measure Est. S.E. Est. S.E. FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE 4.6 13.1 6.6 1.3 1.2 0.2 2.1 1.3 0.4 0.3 0.4 0.1 0.4 0.3 1.0 2.2 1.4 1.4 0.4 0.4 1.2 4.4 0.5 0.4 0.5 0.6 0.6 0.6 5.2 14.1 7.8 2.2 1.2 0.5 2.7 5.9 0.7 0.6 0.9 0.2 1.0 0.6 1.0 2.2 1.4 1.4 0.4 0.4 1.2 4.4 0.5 0.4 0.5 0.6 0.6 0.6 0.2 1.0 1.4 1.0 Collaborative time Hours per year per teacher 40.5 76.1 59.0 66.8 Student programs Preschool Students Full-day kindergarten 1 = yes 0 = no 0.4 0.4 1.5 0.7 1.6 0.7 1.5 0.6 After-school tutoring program Teacher hours per week 18.5 46.2 40.7 46.4 Longer school day Hours per day 0.0 0.5 0.3 0.4 Summer school Students 59.9 103.9 119.8 104.6 Longer school year Days per year −0.2 14.4 4.3 12.6 Computers for instruction Computers 65.1 106.9 151.2 107.6 Other Other expenditures $ thousands
−14.4
127.4
52.2
128.2
Class size
Kindergarten
Grades 1–3
Grades 4 et 5
21.4
22.2
29.3
18.7
20.7
24.8
70
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
.
.
F
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jon Sonstelie
The simulations suggest some modest economies of scale. Moving from a
school with 357 students (one standard deviation below the average) to a school
de 809 students (one standard deviation above the average), administrative
expenditures per pupil decrease by 36 pour cent, and support staff expenditures
per pupil decrease by 18 pour cent.
Expenditures by area also change as the SES of students changes. Mov-
ing from a school in which no students participate in the free or reduced
price lunch program to a school in which all students participate, expenditures
on student programs increase by 20 percent and administrative expenditures
increase by 27 pour cent. Expenditures on support staff also increase, par 10
pour cent. These increases are financed by a decrease of 8 percent in teacher ex-
penditures, 20 percent in professional development, et 30 percent in other
expenditures. Though the percentage of ELs in a school is highly correlated
with participation in the subsidized lunch program, an increase in the per-
centage of ELs has a different effect on predicted expenditures. As students
classified as ELs increase from zero to 82 pour cent (the highest percentage in
the sample), expenditures on professional development increase by 83 par-
cent. This increase is financed by decreases of 9–16 percent in every other area
except teacher expenditures, which remain essentially unchanged.
Tableau 5 presents estimated resource choices for the average middle school,
which has 950 students, 44 percent of whom participate in the school’s sub-
sidized lunch program, et 18 percent of whom are ELs. The estimates are
an average of those for teachers, principals, and superintendents, et ils
assume that the participants come from a school with a similar schools rank of
five. En outre, the estimates assume that the average API of feeder schools is
750. As with elementary schools, residual standard errors are relatively small
for teachers and administrators. Unlike the elementary schools simulations,
they are also relatively small for support staff.
An increase in the budget from $4,000 per pupil to $6,000 per pupil is
spread across the six resource areas. The teaching staff increases from 38.3
FTE to 48.8 FTE, an increase of 27 pour cent. As in the case of elementary
schools, the administrative staff also increases less than proportionally to the
expansion in the budget. Administrative FTEs increase from 6.8 à 8.2, un 20
percent rise.
The percentage increases were much larger for professional development
and student programs. With the larger budget, 1.5 academic coaches are
added, doubling the total, and the time each teacher spends collaborating
with other teachers rises from 45 hours per year to 122 hours per year. Le
after-school tutoring program nearly triples in size, the school year is length-
ened by four days, and the school day is lengthened by thirty-six minutes. Le
number of computers also rises from fifteen for every one hundred students
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
F
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
F
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
71
RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS
Tableau 5. Resource Choices for the Average Middle School: Estimates (Est.) and Standard Errors (S.E.)
Resource
Teachers
Core
Non-core
Physical education
Administration
Principals
Assistant principals
Clerical office staff
Support staff
Instructional aides
Counselors
Nurses
Librarians
Security officers
Technology support staff
Community liaisons
Professional development
Academic coaches
Expenditures per Student
$4,000 $6,000
Unit of Measure
Est.
S.E.
Est.
S.E.
FTE
FTE
FTE
FTE
FTE
FTE
FTE
FTE
FTE
FTE
FTE
FTE
FTE
FTE
28.1
5.9
4.3
1.2
1.5
4.1
5.8
2.0
0.6
1.0
1.3
0.9
0.8
0.7
0.3
0.3
0.1
0.1
0.2
0.6
0.1
0.1
0.1
0.2
0.1
0.1
34.6
8.0
6.2
1.3
1.9
5.0
7.7
2.8
0.9
1.3
1.7
1.5
1.2
0.8
0.3
0.3
0.1
0.1
0.2
0.7
0.1
0.1
0.1
0.2
0.1
0.1
1.5
0.2
3.1
0.3
Collaborative time
Hours per year per teacher
44.7
15.5
122.1
13.1
Student programs
After-school tutoring program
Teacher hours per week
55.6
16.6
133.1
17.9
Longer school day
Hours per day
0.0
0.1
0.6
0.1
Summer school
Students
204.5
27.2
271.2
29.3
Longer school year
Days per year
0.6
1.0
4.9
0.8
Computers for instruction
Computers
149.5
25.5
322.2
27.5
Other
Other expenditures
$ thousands 18.7 12.5 74.0 13.5 Class size Core Non-core Physical education 27.0 32.4 44.4 22.0 23.8 30.6 to thirty-four for every one hundred students. With the lower budget, partici- pants allocated only $19 per student to expenditures not explicitly enumerated
in the spreadsheet. With the higher budget, these expenditures rise to $74 per student. 72 l Téléchargé à partir du site Web : / / direct . m je t . F / / e du e d p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pd . . . . F . f par invité 0 7 Septembre 2 0 2 3 Jon Sonstelie As with the elementary simulations, there is some evidence of economies of scale in school administration. As enrollment increases from 555 students to 1,345 students, per pupil expenditures for administration decrease by 29 pour cent, and per pupil expenditures for support staff decrease by 13 pour cent. Student SES has a notable effect on the allocation of expenditures. Com- pared with a school in which no students participate in the subsidized lunch program, expenditures on teachers are 14 percent less in a school in which every student participates. These lower expenditures finance increased ex- penditures on support staff (18 pour cent), student programs (27 pour cent), and professional development (61 pour cent). As in the elementary school simula- tion, the pattern is almost reversed for increases in the percentage of ELs. As that percentage increases from zero to 68 pour cent, expenditures on teachers rise by 12 pour cent, expenditures on professional development decline by 16 pour cent, and expenditures on student programs fall by 37 pour cent. The average resource choices of participants in the high school simulations are presented in table 6. The estimated averages are for a high school with 1,759 students, 32 percent of whom participate in the subsidized lunch pro- gram and 13 percent of whom are ELs. The estimates are an equally weighted average of the estimated choices of teachers, principals, and superintendents. They also assume a similar schools ranking of five for all participants and an average API of 750 for the school’s feeder middle schools. Residual stan- dard errors follow the same pattern as for middle schools—relatively small for teachers, administrators, and support staff and relatively large for other areas. With the 50 percent increase in the budget, the number of teachers in- creases by 24 percent and the number of administrators increases by 50 par- cent. In contrast, support staff doubles, the number of academic coaches increases from 1.5 à 4.1, and collaborative time more than doubles. Hours in the after-school tutoring program are nearly tripled, and nearly twice as many students attend summer school. Participants also extend the school year by two days and add twenty-four minutes to the school day. The number of com- puters increases from nineteen per one hundred students to thirty-four per one hundred students. With the budget of $6,000 per student, participants
would spend an average of $206 per student on items not explicitly covered in the simulation spreadsheet. As with the elementary and middle school simulations, participant choices are consistent with economies of scale in administration and support staff. As enrollment increases from 767 students (one standard deviation below the average) à 2,751 students (one standard deviation above the average), administrative expenditures per pupil fall by 44 pour cent, and support staff expenditures per pupil decline by 21 pour cent. l Téléchargé à partir du site Web : / / direct . m je t . F / / e du e d p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pd . . F . . . f par invité 0 7 Septembre 2 0 2 3 73 RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS Table 6. Resource Choices for the Average High School: Estimates (Est.) and Standard Errors (S.E.) Resource Teachers Core Non-core Physical education Administration Principals Assistant principals Clerical office staff Support staff Instructional aides Counselors Nurses Librarians Security officers Technology support staff Community liaisons Professional development Academic coaches Expenditures per Student $4,000 $6,000 Unit of Measure Est. S.E. Est. S.E. FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE FTE 43.6 26.3 4.5 2.0 2.2 7.3 5.2 4.0 0.7 1.2 2.2 1.7 0.6 1.3 1.0 0.3 0.3 0.2 0.5 1.0 0.2 0.1 0.2 0.3 0.2 0.1 52.4 34.3 5.7 2.1 3.2 11.4 13.8 5.6 1.1 1.9 3.9 2.6 1.7 1.3 1.1 0.3 0.3 0.2 0.6 1.0 0.3 0.1 0.2 0.3 0.2 0.1 1.5 0.4 4.1 0.4 Collaborative time Hours per year per teacher 42.5 13.2 100.1 11.4 Student programs After-school tutoring program Teacher hours per week 63.2 19.9 153.9 21.3 Longer school day Hours per day 0.4 0.1 0.8 0.1 Summer school Students 346.1 43.8 598.9 47.0 Longer school year Days per year 2.4 1.0 4.4 0.9 Computers for instruction Computers 328.4 54.8 606.1 58.8 Other Other expenditures $ thousands
39.5
32.8
205.7
35.2
Class size
Core
Non-core
Physical education
24.2
33.4
38.9
20.2
25.7
30.6
With an increase in student poverty, participants allocate more of their
budget to teachers and administration and less to professional development.
With an increase in the percent on subsidized lunch from zero to 100 pour cent,
expenditures on teachers and administrators increase by 4 et 28 pour cent,
74
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
F
/
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
.
.
.
.
F
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jon Sonstelie
respectivement, and expenditures on professional development decline by more
que 50 pour cent. Expenditures on student programs also decline by 5 pour cent.
As was the case in the elementary and middle school simulations, an increase
in the percentage of ELs has an effect on the allocation of expenditures that
is opposite to the effect of an increase in student poverty. With an increase in
ELs from zero to 52 pour cent, expenditures on teachers decline by 7 pour cent,
expenditures on administrators fall by 15 pour cent, and other expenditures
decrease by 80 pour cent. These declines are offset by a 45 percent increase in
professional development and a 20 percent increase in student programs.
4. ACADEMIC ACHIEVEMENT
Tableau 7 reports estimates of the relationship between the APIs predicted by
participants in the elementary school simulations and several important vari-
ables conditioning each simulation. These conditioning variables are either
assumptions that participants were instructed to take as conditions defining
the simulation (budget, unit costs, enrollment, student characteristics) or char-
acteristics of the participants themselves (superintendent, principal, teacher,
similar schools’ rank). At the 5 percent level, only three coefficients are sig-
nificantly different from zero: the coefficients for expenditures per pupil, free
or reduced price lunch, and the similar schools’ rank. According to the par-
ticipants in the elementary simulations, increased expenditures do increase
achievement, but the effect is relatively modest. An expenditure increase of
$1,000 per pupil increases the API prediction by thirteen points. In contrast, poverty has a relatively large effect. An increase of ten points in the percent of students in a school’s subsidized lunch program decreases a school’s API by fifteen points. Tableau 7. Coefficient Estimates for Relationship between API and Conditioning Variables, Elementary School Simulations Conditioning Variables Coefficient S.E. l Téléchargé à partir du site Web : / / direct . m je t . F / / e du e d p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pd . . F . . . f par invité 0 7 Septembre 2 0 2 3 Expenditures per pupil Unit cost of teachers Teacher index (1 if teacher, 0 otherwise) 0.0130 −0.0004 −2.4584 Principal index (1 if principal, 0 otherwise) 10.9474 0.0039 0.0005 7.6614 7.6443 0.0152 0.1523 0.2332 1.2248 0.0099 −1.4522 0.0100 3.8082 Enrollment Percent in subsidized lunch Percent English learners Similar school rank Constant R2 787.3 40.6 0.35 75 RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS One test of the reliability of these predictions is to compare them with the actual achievement of California schools. A regression of the APIs of elementary schools in 2003–4 on the percentage of their students in subsidized lunch (Lunch) and the percentage who are English learners (English) yields the following result: API = 876 − 2.3 ∗ Lunch − 0.4 ∗ English. (2) In comparison, for a school budget of $4,300 per pupil (about average in 2003–
4), a unit cost for teachers of $66,000 (also about average), a similar school’s rank of five, and a weighted average of teacher, principal, and superintendent responses, the coefficients in table 7 yield this equation: API = 847 − 1.5 ∗ Lunch + 0.1 ∗ English. (3) Relative to actual APIs, simulation participants tend to predict slightly lower APIs for schools with few students who participate in subsidized lunch and who are ELs than those schools actually achieve on average. For schools with none of those students, the average API is 876, while the average prediction of simulation participants is 847. Cependant, participants tend to predict higher APIs of schools with many poor students and many ELs than those schools achieve. For schools in which every student participates in subsidized lunch and half of the students are English learners, the average API is 626. The regression in table 7 would predict 702. Another test of the API predictions is to compare them with recent research on the relationship between school resources and academic achievement. One standard for comparison is Krueger’s (1999) analysis of the Tennessee class size experiment. In the experiment, elementary school students and their teachers were randomly assigned to either small classes (13–17 students) or large classes (22–25 students). The assignments lasted from kindergarten through grade 3, and students were assessed at the end of each year using the Stanford Achievement Test (SAT). By the end of the third year, students in the smaller classes were scoring 5 percentile points higher on average on the math and reading tests than did students in larger classes. As shown in Sonstelie (2007), these results are equivalent to the following effect in the simulations: an expenditure of $1,600 per pupil on reducing class sizes would increase a
school’s API by forty-one points. In comparison, the simulation participants
predicted a much smaller effect of increased resources on academic achieve-
ment. According to the estimates, an increase of $1,600 would increase the predicted API by twenty-one points, half of the increase found by Krueger. A second standard for comparison is the analysis of Texas achievement data by Rivkin, Hanushek, and Kain (2005). Though the class sizes in this 76 l Téléchargé à partir du site Web : / / direct . m je t . F / / e du e d p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pd . F . . . . f par invité 0 7 Septembre 2 0 2 3 Jon Sonstelie study were not randomly assigned, the study does have two important ad- vantages over other studies of class size. D'abord, it uses test results for over 1 million students, making precise estimates more likely. Deuxième, the records of students can be linked across time, revealing the gain in achievement in each grade. Rivkin and his coauthors find that class size has a statistically significant effect on gains in reading and mathematics in grades 4, 5, 6, et 7. Translating those results into the terms of the simulation exercise (Sonstelie 2007), a reduction in class size comparable to that studied by Krueger (1999) implies an API increase of thirty-one points, halfway between the twenty-one points predicted by simulation participants and the forty-one points found by Krueger. In interpreting these comparisons, it is important to bear in mind that participants would not allocate all of their increased budgets to reducing class sizes. En moyenne, only about 20 percent of any budget increase is allocated to this purpose. Presumably, cependant, the portion allocated to other areas, such as professional development and after-school tutoring, would have an even larger effect on student achievement than if it were allocated to increasing class sizes. Under that presumption, if an increase of $1,600 per pupil were
allocated solely to reducing class sizes, the average API gain predicted by
simulation participants would be no greater than twenty-one points, which is
considerably smaller than the achievement gains found by either of the two
comparison studies.
The API predictions for middle schools are presented in table 8. As in
the elementary simulations, participants with higher budgets predict higher
Apis. Again the effect is modest, cependant. An increase of $1,000 per pupil increases the average API prediction by 11.5 API points. In contrast, the aca- demic preparation of students has a large effect on the average API prediction. If the average API of a school’s feeder schools increases by 100 API points, the average API prediction for the school increases by 39 points. Student SES also has a large effect. If the percentage of students in a school’s subsidized lunch program increases by 10 pour cent, the average API prediction for the school decreases by 10.4 points. These API predictions are consistently higher than the APIs achieved by California schools in 2003–4. A regression of actual APIs on the percentage of students in the subsidized lunch program (Lunch) and the percentage of English learners (English) yields API = 837 − 2.6 ∗ Lunch − 0.7 ∗ English. (4) A comparable equation for the API prediction is formed in the same way as for the elementary schools, except that the middle school counterpart requires l D o w n o a d e d f r o m h t t p : / / direct . m je t . F / / e du e d p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pd . . . . F . f par invité 0 7 Septembre 2 0 2 3 77 RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS Table 8. Coefficient Estimates for Relationship between API and Conditioning Variables, Middle School Simulations Conditioning Variables Coefficient S.E. Expenditures per pupil Unit cost of teachers Teacher index (1 if teacher, 0 otherwise) Principal index (1 if principal, 0 otherwise) Enrollment Percent in subsidized lunch Percent English learners Similar school rank Average API of feeder schools Constant R2 0.0115 −0.0013 −7.8768 −4.4131 −0.0096 −1.0440 0.1688 1.1759 0.3916 0.0061 0.0006 8.1100 7.9033 0.0084 0.1828 0.3233 1.3867 0.0464 563.4 58.2 0.30 an assumption about the average API of feeder schools. Équation 2 is used to estimate that average API. The result is API = 859 − 1.9 ∗ Lunch − 0.2 ∗ English. (5) For schools in which no students participate in the subsidized lunch program and no students are ELs, the average API is 837. In comparison, the simulation participants predict an API of 859. For schools in which all students participate in the subsidized lunch program and half are ELs, the average API is 542 and the predicted API is 659. Studies of the effect of resources on achievement are rare for middle schools. The best study is Rivkin, Hanushek, and Kain (2005), which finds that class size has significant effects for reading and math scores of Texas seventh and eighth graders, although the effects are quite small. Sonstelie (2007) transforms those results into the following API effects: an expenditure of $1,000 on reducing middle school class sizes would increase a school’s
API by no more than four points. In contrast, participants in the simulation
predicted a much larger effect. In the API prediction equation, the coefficient
on expenditures per pupil is 0.0115, indicating that a $1,000 increase in ex- penditures per pupil is predicted to increase a school’s API by 11.5 points. Part of this difference may be explained by the allocation of additional revenues. The simulation participants would allocate only about one-third of the addi- tional revenue to hiring more teachers. The additional two-thirds is allocated to professional development, after-school tutoring, and other areas, which partic- ipants believe to be more effective uses of resources than reducing class sizes. 78 l Téléchargé à partir du site Web : / / direct . m je t . / F / e du e d p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pd . . F . . . f par invité 0 7 Septembre 2 0 2 3 Jon Sonstelie Table 9. Coefficient Estimates for Relationship between API and Conditioning Variables, High School Simulations Conditioning Variables Coefficient S.E. Expenditures per pupil Unit cost of teachers Teacher index (1 if teacher, 0 otherwise) Principal index (1 if principal, 0 otherwise) Enrollment Percent in subsidized lunch Percent English learners Similar school rank Average API of feeder schools Constant R2 0.0102 −0.0005 −4.2569 −13.2359 0.0090 −0.5055 −0.4400 1.5888 0.4545 0.0055 0.0005 7.0706 7.0663 0.0033 0.1768 0.3201 1.1650 0.0414 413.6 51.1 0.32 Tableau 9 presents the API predictions from the high school simulations, predictions that follow the same general pattern as those for participants in the elementary and middle school simulations. Resources have a positive, but modest, effect on achievement, student poverty has a strong negative effect, and the average API of feeder schools has a large, positive effect. An increase of $1,000 per pupil increases the API prediction by ten points. In contrast,
a one-hundred point increase in the average API of feeder schools increases
the average API prediction by forty-five points, and a ten-point increase in
the percentage of students participating in the subsidized lunch program
decreases the average API prediction by five points.
As was the case with the middle schools, the API predictions are con-
sistently higher than the APIs achieved by California schools in 2003–4. UN
regression of actual APIs on the percentage of students in the subsidized
lunch program (Lunch) and the percentage of English learners (English) yields
API = 764 − 2.1 ∗ Lunch − 1.1 ∗ English.
(6)
Following the same procedure as for middle schools and using equation 4 à
predict the average API of feeder schools, the coefficients in table 9 imply the
equation
API = 813 − 1.7 ∗ Lunch − 0.8 ∗ English.
(7)
For a school in which no students are in the subsidized lunch program or are
ELs, the predicted API is 813 as opposed to the actual average of 764. For a
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
F
/
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
F
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
79
RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS
school with all students in the subsidized lunch program and half ELs, le
equivalent figures are 603 et 499.
5. THE COST OF ADEQUATE SCHOOL RESOURCES
The estimated relationship between school budgets and achievement can be
used to address the ultimate question for this analysis: given the characteristics
of a school’s students, what budget do practitioners believe a school needs to
achieve an 800 API, the API goal for all schools?
Because simulation participants were asked to assume that none of the
students in their hypothetical schools require special education services, que
goal must be adjusted slightly for the reality that schools do include special
education students and that those students score lower, on average, on stan-
dardized tests than do other students. As explained in Sonstelie (2007), le
adjustment is based on two simplifying assumptions. The first is that the
percentage of special education students in each school equals the statewide
average for schools with its grade span. The second assumption is that the
average scores of special education students in each school are proportional to
the average scores of other students in the school. Under those assumptions,
students who do not require special education services would need to achieve
an API higher than 800 for the school as a whole to achieve an 800 API. Dans
particular, for elementary schools, students not requiring special education
services would need to achieve an API of 813. For middle schools, the target is
822. For high schools, it is 816.
In determining the budget a school needs to achieve those target APIs,
the same targets are assumed for the average feeder school APIs. Ainsi, pour
middle schools, the average API of feeder elementary schools is assumed to
être 813. For high schools, the average is assumed to be 822. The budgets
are determined using an equally weighted average of the API predictions of
teachers, principals, and superintendents and assuming a score of five for the
participant’s similar schools rank. With those assumptions and conditions,
the API prediction equations yield the following equations for the dollars per
pupil needed to reach an 800 API:1
Elementary schools:
Budget = 2, 103 − 0.75 ∗ Enrollment + 111 ∗ Lunch − 0.76 ∗ English
(8)
1.
The coefficients in these equations are the ratio of estimated coefficients from the API prediction re-
gressions, specifically the estimated coefficient for each variable divided by the estimated coefficient
for expenditures per pupil. Because the ratio of the expected values of two random variables does
not equal the expected value of the ratio of those variables, the coefficients in the three equations
are biased estimates.
80
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
F
/
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
.
F
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jon Sonstelie
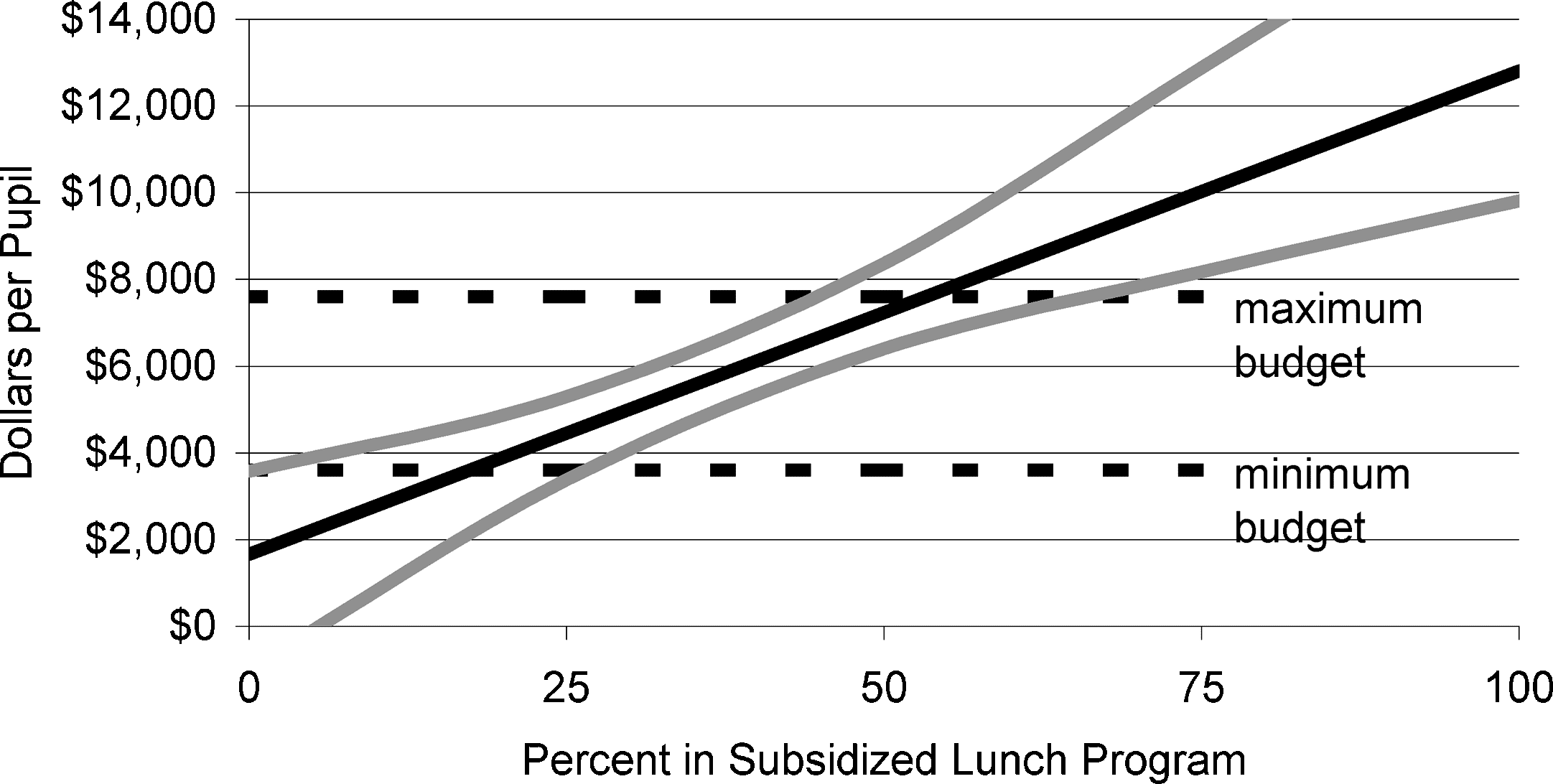
Chiffre 1. Estimates and Confidence Intervals for Budget Required for 813 API, Average Elementary
School with No Special Education Students
Middle schools:
Budget = 1, 936 + 0.83 ∗ Enrollment + 91 ∗ Lunch − 15 ∗ English
(9)
High schools:
Budget = 6, 080 − 0.89 ∗ Enrollment + 49 ∗ Lunch + 43 ∗ English
(10)
In these equations, Budget is dollars per pupil required for the target API,
Enrollment is the enrollment of the school, Lunch is the percent of the school’s
students who participate in the subsidized lunch program, and English is the
percent of the school’s students who are classified as English learners.
The budget required for the target API depends critically on the percent-
age of a school’s students in its subsidized lunch program. This relationship
is represented by the dark line in figure 1. The other variables in equation 8,
Enrollment and English, are fixed at their averages for the sample of hypothet-
ical schools. The gray lines in the figure are the boundaries of a 90 pour cent
confidence interval for the Budget variable.2 To be precise about this interval,
consider a particular level of the Lunch variable and the predictions of the entire
universe of educational practitioners about the budget necessary for a school
with these characteristics to achieve the target API. Now take the average of
those budget predictions. With a probability of 90 pour cent, that average lies
within the confidence interval portrayed in the figure. As the figure shows, le
confidence interval is wide. For the average elementary school, the school in
lequel 52 percent of students participate in the subsidized lunch program, le
estimated budget required to reach an 813 API is $7,430 et le 90 percent confidence interval runs from $6,403 à $8,368 per pupil. 2. The confidence intervals were formed by the bootstrap method. From the empirical distribution resulting from that method, the smallest 90 percent interval was chosen as the confidence interval for the estimate. l Téléchargé à partir du site Web : / / direct . m je t . F / / e du e d p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pd . . . F . . f par invité 0 7 Septembre 2 0 2 3 81 RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS Figure 2. Estimates and Confidence Intervals for Budget Required for 822 API, Average Middle School with No Special Education Students For schools at the extremes of subsidized lunch participation, the budget estimates are an out-of-sample prediction. For schools with no students in the subsidized lunch program, the estimated budget is less than $3,600 per pupil,
the minimum budget in the simulations. For schools in which all students
participate in the subsidized lunch program, the estimated budget is greater
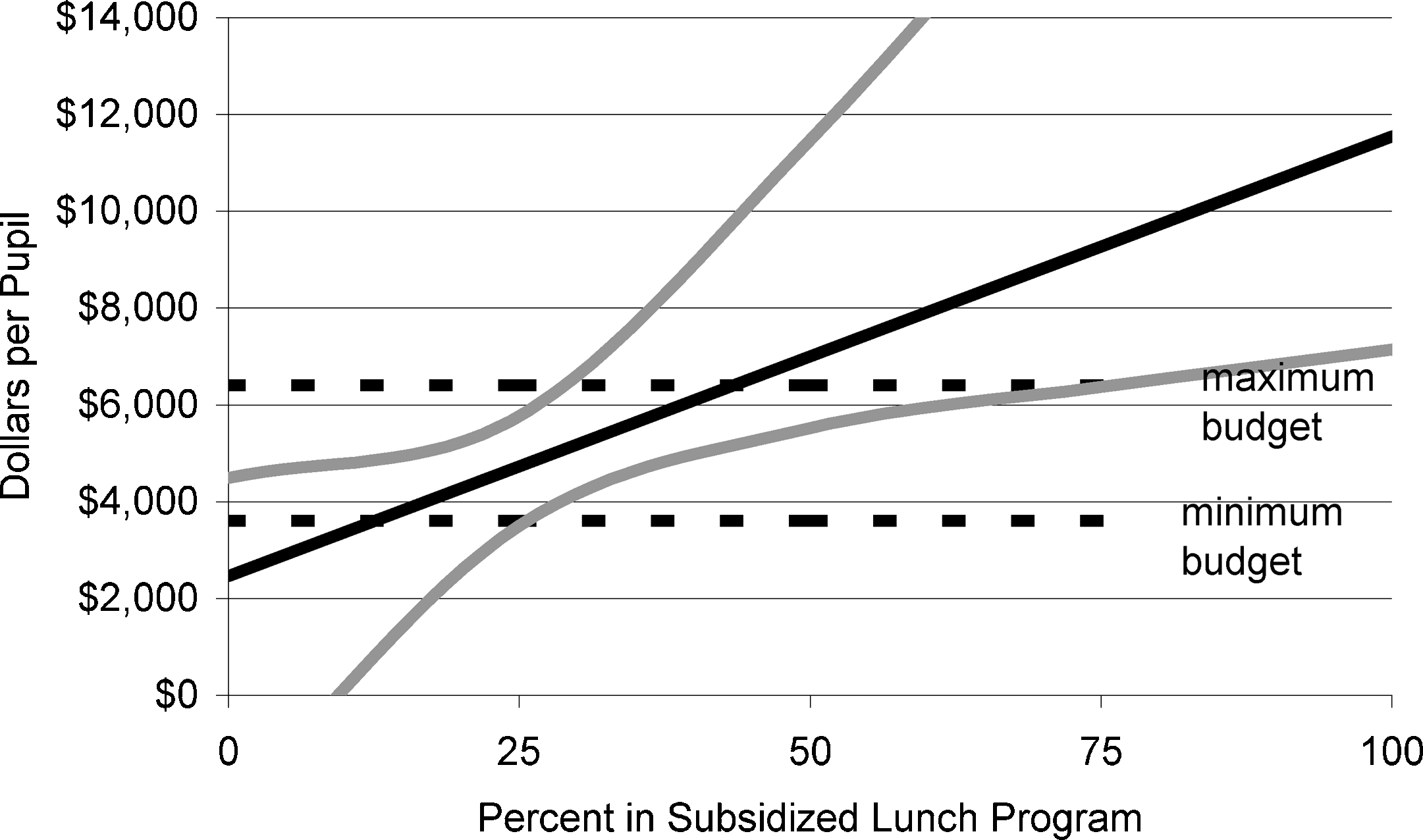
que $7,600 per pupil, the maximum budget. The dashed lines in figure 1 represent the minimum and maximum budgets. Chiffre 2 portrays the equivalent estimates and confidence intervals for middle schools. For the average middle school (42 percent of students partic- ipating in subsidized lunch), the estimated budget for an 822 API is $6,458
per pupil. Le 90 percent confidence interval for that estimate lies between
$4,874 et $9,649 per pupil. As with the elementary school simulations,
the estimated budget is an out-of-sample prediction when participation in the
subsidized lunch program is either very low or very high.
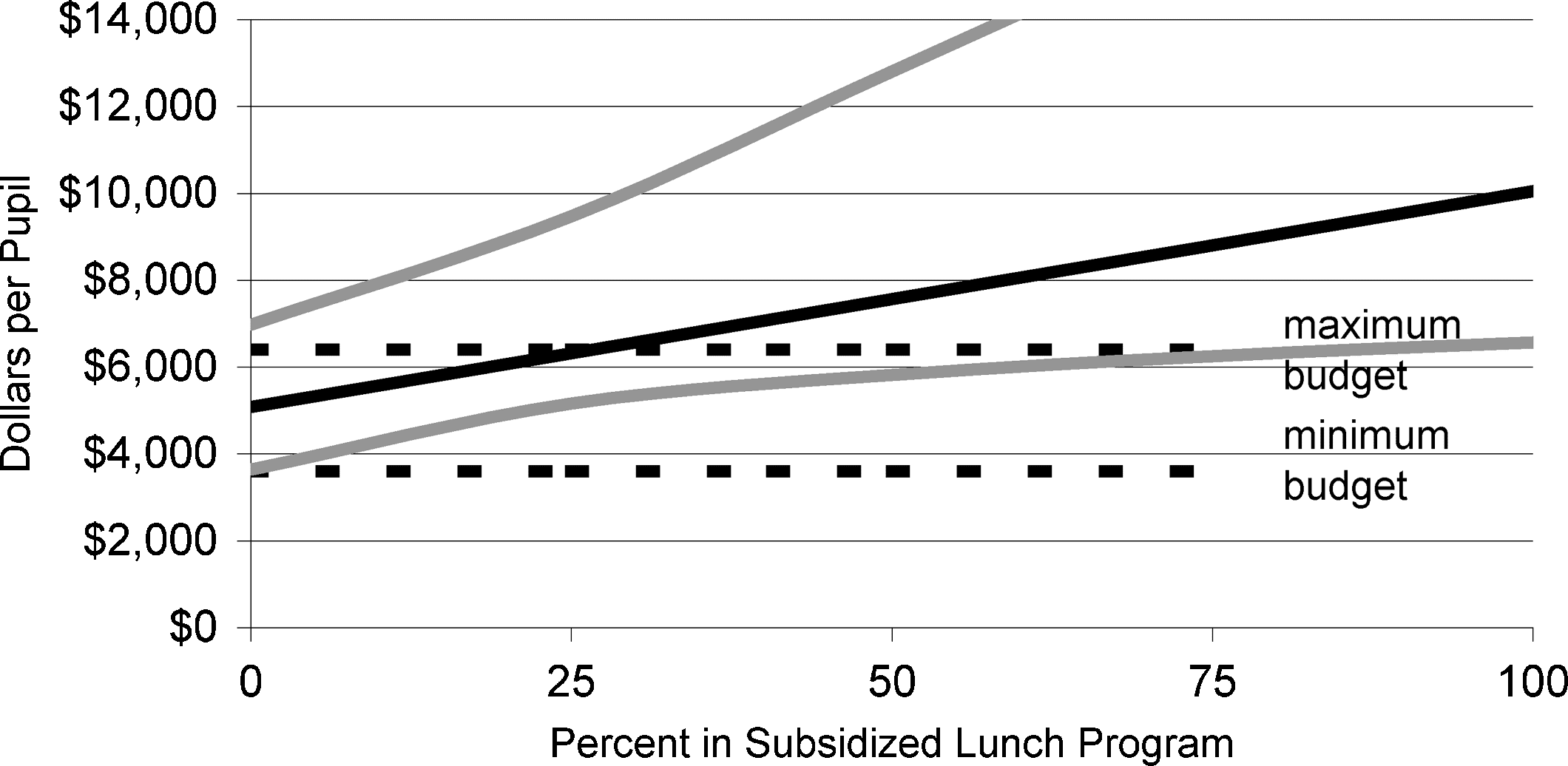
The same general patterns hold for budget estimates from the high school
simulations (figure 3). For the average high school (subsidized lunch partic-
ipation of 32 pour cent), the estimated budget to achieve the target API of 816
est $6,672 per pupil. Le 90 percent confidence interval surrounding that estimate is $5,340 per pupil to $10,406 per pupil. The next step in the analysis is to use the budget equations to estimate the budget required for each California school to achieve the state’s API standard. For each school, this prediction entails substituting that school’s values for the Enrollment, Lunch, and English variables into either equations 8, 9, ou 10. Because the budget equations yield out-of-sample predictions for many schools, the estimates were truncated at the minimum and maximum budgets in the simulations. 82 l Téléchargé à partir du site Web : / / direct . m je t . / / f edu ed p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pd . . . . F . f par invité 0 7 Septembre 2 0 2 3 Jon Sonstelie Figure 3. Estimates and Confidence Intervals for Budget Required for 816 API, Average High School with No Special Education Students Table 10. Predicted APIs with Budgets Truncated at Simulation Minimum and Maximum Percentile Elementary Schools Middle Schools High Schools 5th 25th 50th 75th 95th 736 761 796 800 819 750 776 797 800 804 758 783 797 800 800 The significance of these truncations is demonstrated by the range of predicted APIs for schools given the budget assigned to them. For schools without truncated budgets, the predicted API is 800. For schools with budgets truncated at the maximum budget, the predicted API is calculated assuming that budget. For schools with budgets truncated at the minimum, the predicted API is calculated assuming the minimum budget. The range of predicted APIs is displayed in table 10. Approximately half of schools have predicted APIs of 800 ou plus. For middle and high schools, the median predicted API is 797. For elementary schools, it is 796. Cependant, many schools have predicted APIs considerably below 800. Twenty percent of elementary schools have APIs between 736 et 761. For middle and high schools, the equivalent ranges are 750–776 and 758–783. The estimated budgets for each school are then aggregated to the school district level. This aggregate is a weighted average of the budget estimates for each school in a district where the weight for a school is its enrollment divided by the district’s enrollment. l Téléchargé à partir du site Web : / / direct . m je t . F / / e du e d p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pdf . . . . . f par invité 0 7 Septembre 2 0 2 3 83 RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS 6. THE COST OF OTHER RESOURCES The budget simulations encompass resources constituting approximately 60 percent of school district expenditures. This section summarizes estimates of resource needs in remaining areas, such as district administration, pupil transportation, and maintenance and operations. The approach is to use ac- tual expenditures of California school districts in 2003–4 to estimate a linear expenditure function for expenditures in each area as a function of factors external to districts. The estimates are then used to predict what the average school district would spend in each area. In this prediction, the average school district is the school district with average revenue per pupil, average resource costs, and average values for all external factors. These expenditure predictions are then adjusted for the actual factors external to each district and for differ- ences in resource costs. The adjusted expenditures provide each district with resources equivalent to those of the average district, accounting for factors external to the district. To understand these adjustments, consider the example of population density. A particular district has a lower population density than that of the average district. Its students have farther to travel to school each day, which means that the district must spend more on pupil transportation than the average district. If it had the same total expenditures per pupil as the average district, its higher expenditures on pupil transportation would imply lower expenditures in other areas. To offset the cost of its lower population density, the district would require more revenue than the average district. How much additional revenue would offset that cost? Enough so that the district could spend as much as the average district in areas other than pupil transportation. The estimated expenditure function is used to calculate this additional revenue. Sonstelie (2007) describes this adjustment in detail. In addition to external factors such as population density, expenditures in each expenditure area are also adjusted for local labor market conditions. To accommodate this adjustment, expenditures in each area are partitioned into expenditures on employee compensation and expenditures on other re- sources. The cost of personnel in each expenditure area is assumed to be affected by local labor market conditions, but the costs of noncompensation resources are assumed to be the same across districts. In estimating the linear expenditure system, expenditures on employee compensation in an expendi- ture area are treated as a different expenditure category from expenditures on other resources in that area. The estimated coefficients thus yield estimates of expenditures of both employee compensation and other resources in each expenditure area. Four external factors are incorporated in this analysis. The first is pop- ulation density, which affects expenditures on pupil transportation. Ce 84 l Téléchargé à partir du site Web : / / direct . m je t . / / f edu ed p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pd . . . F . . f par invité 0 7 Septembre 2 0 2 3 Jon Sonstelie factor is measured by first calculating the land area of each district using block-level census data based on the 2002 TIGER line files. Blocks within school district boundaries were excluded if they were designated as water or had no population between the ages of five and seventeen. These ex- clusions reduce the land area of districts with large bodies of water, na- tional or state parks, and uninhabited areas such as deserts or mountains. Density is measured by school district enrollment in 2003–4 divided by land area in square kilometers. Land area could not be determined for four small districts, so those districts were excluded from the statistical analysis.3 The second external factor is district enrollment. Several studies have identified economies of scale for school districts, economies often associ- ated with district administration (Andrés, Duncombe, and Yinger 2002; Duncombe, Miner, and Ruggiero 1995). Accordingly, the natural logarithm of district enrollment is included as an external factor affecting district administration. The third factor is special education cost, which is the weighted aver- age of the cost of various special education disabilities. The weights for each disability are the percentages of students in a district with that disability. The cost estimates were taken from Parrish et al. (2004). The external fac- tor for special education costs is these prorated amounts divided by district enrollment. The last factor is a regional salary index. The index plays the role of the resource cost for expenditure areas involving employee compensation. The index, compiled by Rose and Sengupta (2007), is computed for each of thirty regions of California. For each region, the index is based on the average salary of workers with a college degree who are not employed by public school districts. As a consequence, the index represents local labor market conditions external to each district. 7. TOTAL COST A district’s cost of meeting the state’s achievement standards is the sum of three elements. The first is the cost of school resources derived from the simulations. The second is the cost of other resources not included in the simu- lations. This second element does not include special education cost, cependant, which is treated separately. Special education costs are based on the recent re- port by Parrish et al. (2004). Appendix H of that report lists the thirteen student 3. The districts are Pacifica Elementary (3,169 students), Casmalia Elementary (30 students), Pleasant Valley Elementary (7,455 students), and Big Oak Flat-Grove Unified (552 students). l Téléchargé à partir du site Web : / / direct . m je t . F / / e du e d p a r t i c e – pdlf / / / / / 3 1 5 8 1 6 8 9 0 7 2 e d p 2 0 0 8 3 1 5 8 pd . . . . F . f par invité 0 7 Septembre 2 0 2 3 85 RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS disabilities delineated in the California Special Education Management Infor- mation System and provides the average cost per student for each disability. The costs are additional: the total cost of educating a student with a particular disability minus the cost of educating a student with no disability. These additional costs for each disability were then multiplied by the number of students in California with each disability in 2003–4, and the products summed over disability categories to yield a total cost for special education. The total was $5.4 milliard. Dividing by the total number of students in 2003–4
(6.2 million) yields a special education cost of $870 per student. These three elements are calculated for each district and then summed. The total is then adjusted for regional salary differences using the index compiled by Rose and Sengupta (2007). For the 950 districts with complete data, the sum of this total across districts is $60.5 milliard, $9,912 per pupil.4 In contrast, these districts spent a total of $43 billion in 2003–4 for a per pupil average of $7,055. Thus the estimated cost of meeting the state’s achievement standards is 40 percent more than those districts spent in 2003–4. Even with that large increase, about half of schools would be short of the 800 API goal. This estimated cost varies widely across districts. For the district in the 5th percentile of the distribution of this variable, the estimated total cost is $7,379 per pupil. For the district in the 95th
percentile, the estimate is $11,490 per pupil.
Ce 40 percent estimate lies between estimates produced by two other
études. The professional judgment panels convened by Chambers, Lévine, et
DeLancey (2007) arrived at higher costs. One panel believed that a 53 pour cent
increase would be necessary; the other found that a 70 percent increase would
be required. Using the cost function approach, Imazeki (2007) estimated that
it would cost 4–13 percent more for California school districts to attain the
state’s API goal.
In the present study, each district’s estimated cost is a complex function of
many factors. Cependant, per pupil costs can be reasonably approximated by just
two factors: the regional salary index and the percentage of poor students. UN
regression of costs per pupil on those two factors yields the following equation:
Dollars per Pupil = 9, 533.31 + 58.62 ∗ Salary + 11.99 ∗ Poverty
(11)
4. The data for expenditures are from California’s standardized account code structure. For 2003–4,
there was expenditure data for 973 districts. The school-level estimates require data on percentage
of students participating in the subsidized lunch program and percentage of students classified as
ELs. For these variables, there is complete data for only 950 districts. The districts with missing
data are primarily small, one-school elementary districts. Le 950 districts included comprise 98
percent of all students.
86
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
F
/
/
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
.
F
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jon Sonstelie
where Salary is the region’s salary index and Poverty is the percentage of
children in a district between the ages of five and seventeen who lived in
families below the poverty line in the 2000 census. Both factors are measured
as percentage deviations from their state averages.
8. CONCLUSION
The objective of this research is to learn what resources educators believe
their schools need and to communicate those beliefs to policy makers. Having
carried out that research, the question is obviously this: should policy makers
take these beliefs seriously? Plus généralement, viewing the present research as
just one variant of the professional judgment approach that has now been
used many times in many states, how seriously should policy makers take the
results of this type of research?
By asking that question, I am not suggesting that policy makers should
ignore the views of professional educators. In the new world of standards and
accountability, policy makers are asking educators to accomplish quite a lot.
If this mission is to succeed, it must have the active support of those charged
with carrying it out, support that is unlikely to come if policy makers ignore
the beliefs of educators about the resources they need to carry out the mission
assigned to them.
That does not mean, cependant, that policy makers must take those beliefs
without question. They will certainly consider the possibility that the views
expressed to them may be self-serving, that they may not be the true beliefs
about what resources are necessary but rather a plea for additional and perhaps
unnecessary support. One way to evaluate that possibility is to compare the
expressed beliefs of educators against the best social science research on the
relationship between resources and outcomes, a comparison implemented
au-dessus de. The difficulty, bien sûr, is that there is not much good research for
comparison.
Short of that, we can also study the nature of professional beliefs. Comment
much consensus is there among educators on the relationship between re-
sources and outcomes? Does how we ask about beliefs affect the answer
we receive? These are questions that research can address, with the an-
swers likely to affect the weight policy makers place on professional judg-
ments. This research agenda is described more fully in Rose and Sonstelie
(2008).
I am grateful for the superb research assistance of Irene Altman, Sarah Battersby,
Cynthia Benelli, Elizabeth Dhuey, and Stephen Lipscomb. Henry Levin, Susanna Loeb,
and two anonymous referees provided valuable comments on an earlier draft of this
article.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
F
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
87
RESOURCE NEEDS OF CALIFORNIA PUBLIC SCHOOLS
RÉFÉRENCES
Andrés, Matthew, William Duncombe, and John Yinger. 2002. Revisiting economies
of size in American education: Are we any closer to a consensus? Economics of
Education Review 21: 245–62.
Chambers, Jay, Jesse Levin, and Danielle DeLancey. 2007. Efficiency and adequacy in
California school finance: A professional judgment approach. In Getting down to facts:
A research project examining California’s school governance and finance systems, édité par
S. Loeb, UN. Bryk, and E. Hanushek. Stanford, Californie: Université de Stanford, Institute for Re-
search on Education Policy and Practice. Available http://irepp.stanford.edu/projects/
cafinance-studies.htm. Accessed 13 Décembre 2007.
Duncombe, William D., Jerry Miner, and John Ruggiero. 1995. Potential cost savings
from school district consolidation: A case study of New York. Economics of Education
Review 14: 265–84.
Hanushek, Eric A., John F. Kain, Daniel M. O’Brien, and Steven G. Rivkin. 2005. Le
market for teacher quality. NBER Working Paper No. 11154.
Hanushek, Eric A., Steven G. Rivkin, and John F. Kain. 2005. Teachers, schools, et
academic achievement. Econometrica 19: 417–58.
Imazeki, Jennifer. 2007. Assessing the costs of K–12 education in California
public schools. In Getting down to facts: A research project examining California’s
school governance and finance systems, edited by S. Loeb, UN. Bryk, and E. Hanushek.
Stanford, Californie: Université de Stanford, Institute for Research on Education Policy and
Practice.
Krueger, Alan B. 1999. Experimental estimates of education production functions.
Quarterly Journal of Economics 114: 497–532.
Loeb, Susanna, Anthony Bryk, and Erick Hanushek. 2007. Getting down to facts: UN
research project examining California’s school governance and finance systems. Stanford,
Californie: Université de Stanford, Institute for Research on Education Policy and Practice.
Parrish, Tom, Jenifer Harr, Yael Kidron, Leslie Brock, and Priyanka Anand. 2004.
Study of the incidence adjustment in the special education funding model. Palo
Alto, Californie: American Institutes of Research. Available www.csef-air.org/publications/
related/Incidence03.pdf. Accessed 15 Septembre 2007.
Pollak, Robert A., and Terence J. Wales. 1992. Demand system specification and
estimation. New York: Presse universitaire d'Oxford.
Rivkin, Steven G., Eric A. Hanushek, and John F. Kain. 2005. Teachers, schools, et
academic achievement. Econometrica 73 (2): 417–58.
Rose, Heather, and Ria Sengupta. 2007. Teacher compensation and local labor market
conditions in California: Implications for school funding. Sacramento, Californie: Governor’s
Committee on Education Excellence.
Rose, Heather, and Jon Sonstelie. 2008. An analysis of professional judgments.
Education Finance and Policy. In press.
88
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
F
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jon Sonstelie
Rose, Heather, Jon Sonstelie, Ray Reinhard, and Sharmaine Heng. 2003. High
expectations, modest means: The challenge facing California’s public schools. San Francisco,
Californie: Public Policy Institute of California.
Rose, Heather, Jon Sonstelie, and Peter Richardson. 2004. School budgets and student
achievement in California: The principal’s perspective. San Francisco, Californie: Public Policy
Institute of California.
Sonstelie, Jon. 2007. Aligning school finance with academic standards: A weighted-student
formula based on a survey of practitioners. San Francisco, Californie: Public Policy Institute of
California.
Taylor, Lori L., Bruce D. Boulanger, and Arnold Vedlitz. 2005. Measuring educational
adequacy in public schools. Working Paper No. 580, Texas A&M University. Available
http://bush.tamu.edu/research/working papers. Accessed 15 Septembre 2007.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
F
e
d
toi
e
d
p
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
1
5
8
1
6
8
9
0
7
2
e
d
p
2
0
0
8
3
1
5
8
p
d
.
.
.
F
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
89