ARTICLE DE RECHERCHE
Know thy tools! Limits of popular algorithms
used for topic reconstruction
Matthias Held
Social Studies of Science and Technology, TU Berlin, Berlin, Allemagne
un accès ouvert
journal
Mots clés: algorithms, concept definitions, qualitative and quantitative approaches, science
mapping
Citation: Détenu, M.. (2022). Know thy
tools! Limits of popular algorithms
used for topic reconstruction.
Études scientifiques quantitatives, 3(4),
1054–1078. https://est ce que je.org/10.1162
/qss_a_00217
EST CE QUE JE:
https://doi.org/10.1162/qss_a_00217
Peer Review:
https://publons.com/publon/10.1162
/qss_a_00217
Reçu: 4 Novembre 2021
Accepté: 15 Septembre 2022
Auteur correspondant:
Matthias Held
matthias.held@tu-berlin.de
Éditeur de manipulation:
Vincent Larivière
droits d'auteur: © 2022 Matthias Held.
Publié sous Creative Commons
Attribution 4.0 International (CC PAR 4.0)
Licence.
La presse du MIT
ABSTRAIT
To reconstruct topics in bibliometric networks, one must use algorithms. Spécifiquement,
researchers often apply algorithms from the class of network community detection algorithms
(such as the Louvain algorithm) that are general-purpose algorithms not intentionally
programmed for a bibliometric task. Each algorithm has specific properties “inscribed,” which
distinguish it from the others. It can thus be assumed that different algorithms are more or less
suitable for a given bibliometric task. Cependant, the suitability of a specific algorithm when it
is applied for topic reconstruction is rarely reflected upon. Why choose this algorithm and
not another? Dans cette étude, I assess the suitability of four community detection algorithms for
topic reconstruction, by first deriving the properties of the phenomenon to be reconstructed—
topics—and comparing if these match with the properties of the algorithms. The results suggest
that the previous use of these algorithms for bibliometric purposes cannot be justified by their
specific suitability for this task.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1.
INTRODUCTION
Ever since the advent of larger and larger networks that can be created from bibliometric data,
researchers have been confronted with different tasks to find structures in these data. These
tasks include the reconstruction of entities on a higher aggregation level, such as scientific
specialties (Petit & Griffith, 1974) or fields (Klavans & Boyack, 2011); ou, at a lower aggrega-
tion level, research fronts (Boyack & Klavans, 2010) and topics (Sjögårde & Ahlgren, 2018).
Over the last 50 années, the methods for these reconstruction tasks have changed, yet the basic
principle for finding thematic structures in the researchers’ artifacts, the publications, a
remained the same: “A set of publications is delineated and its intellectual structure analyzed
with algorithms that utilize properties of these publications” (Gläser, Glänzel, & Scharnhorst,
2017, p. 984). Algorithms are necessary to analyze these large amounts of data, and the results
obtained are meant to represent certain intellectual structures.
For the algorithmically detected structures to be useful for science studies and other prac-
tical applications, cependant, one needs to be able to relate them to a conceptualization of the
structure/phenomenon in question. To engender the relation between algorithmic structures
and concepts, a theoretical definition of the concept is needed, from which certain properties
(in my case: properties of topics) can then be derived. Only by having these properties of the
concept is it possible to assess the algorithms according to the degree to which the algorithms’
properties are suitable for the task.
Know thy tools!
The community detection algorithms used for the bibliometric task of science mapping
have not been developed to perform this specific task, and each one has specific (algorithmic)
properties “inscribed.” Thus, it can be assumed that different algorithms are more or less suit-
able for a given bibliometric task. This suitability, alors, can and must be evaluated.
In many bibliometric studies, cependant, the algorithms chosen are usually not subject to discus-
sion. The data model and the algorithm are usually considered together, where their performance
is assessed by comparing their outcomes to an external standard. Studies provide arguments con-
cerning data models (Boyack & Klavans, 2010), but in the scientometric literature I have not found
work performing a separate analysis of reasons why algorithms may be more or less suitable. Là
is only the study by Šubelj, Van Eck, and Waltman (2016) who do systematically compare a large
set of commonly used algorithms and apply them to bibliometric networks, but we do not learn
why the results differ and why a certain algorithm would be suitable for a particular bibliometric
application. Ainsi, certain algorithms are applied, and no argument is provided that links their
choice to the purpose of the analysis (only arguments related to efficiency or performance). Ainsi,
it is of utmost importance to learn more about the tools that we as bibliometricians are using.
With the research in this paper, I suggest an approach to the assessment of the suitability of
community detection algorithms for the task of topic reconstruction. The four algorithms ana-
lyzed here have all been “successfully” applied to find thematic structures, including studies
applying the Louvain algorithm (Glänzel & Thijs, 2017), the Leiden algorithm (Colavizza,
Costas et al., 2021), Infomap (Velden, Yan, & Lagoze, 2017) and OSLOM (Šubelj et al.,
2016). My results suggest that the previous use of these algorithms for bibliometric purposes
cannot be justified by their specific suitability for this task.
The next section will introduce my approach, followed by the derivation of topic properties
from the definition, together with the criteria to analyze the algorithms which I consider rel-
evant for the topic reconstruction task. Enfin, the results of the analysis of each algorithm are
provided and some implications are discussed.
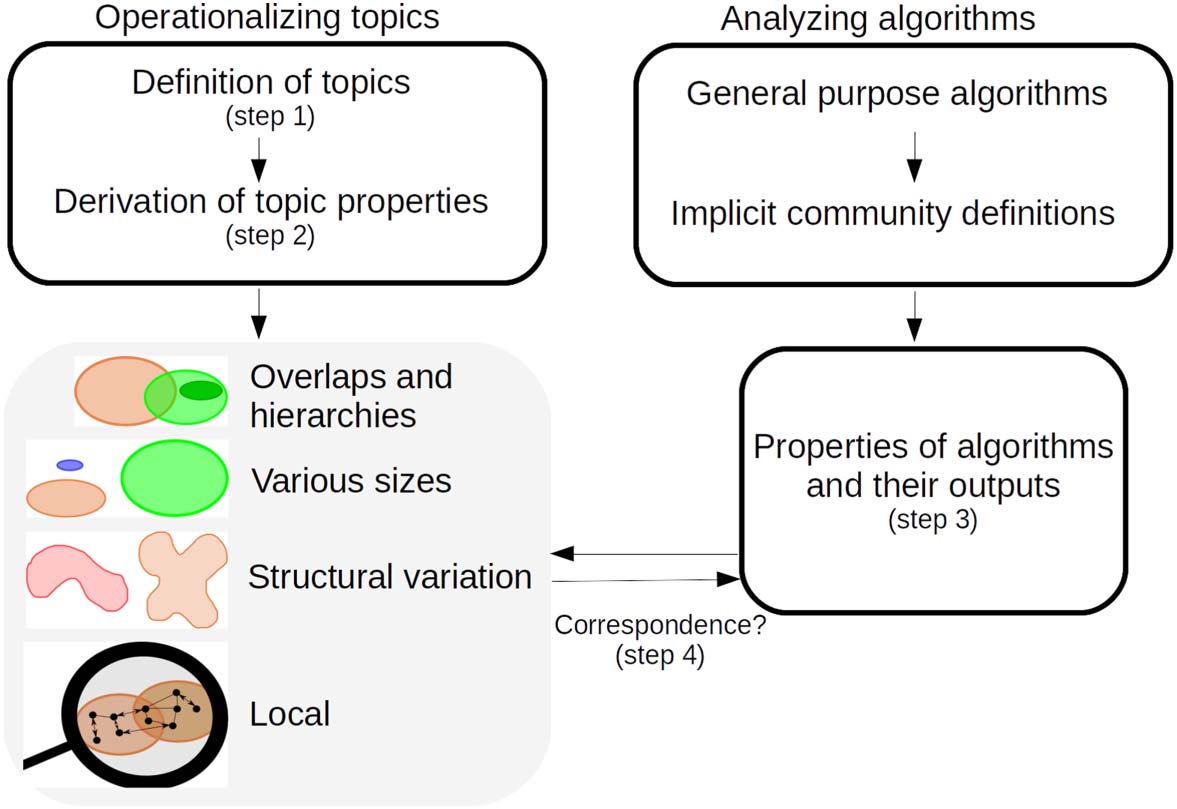
2. APPROACH
The approach used here to assess different algorithms for their suitability for topic reconstruc-
tion can be described as follows. At first, I need to make clear what exactly I intend to achieve
with the help of algorithms applied to bibliometric networks. In my case, I want to reconstruct
topics. This goal requires a match between what I consider a topic to be (Chiffre 1, left side)
and what the algorithm constructs (Chiffre 1, lower right side). Autrement dit, I need to oper-
ationalize my concept of “topic” and compare the result of this operationalization to the out-
comes of algorithms. It is possible to define the concept “topic” in different ways, and different
operationalizations of each concept are possible. Drawing on knowledge from the sociology
of science, I first provide a definition for topics, and from this definition, I derive properties
that topics have to have (steps 1 et 2; see Section 3). Alors, algorithms with their properties
(step 3) have to be confronted with these properties if we want to use them for measurement.
The properties that characterize each algorithm and their outputs are assessed if they corres-
pond with the properties of topics (step 4, “correspondence”).
3. DEFINITION OF TOPICS AND DERIVED PROPERTIES
3.1. Definitions of Topics in Bibliometrics
Studies attempting to reconstruct topics in scientific papers have approached the problem from
various angles, using different approaches. Despite the variety of directions from which
Études scientifiques quantitatives
1055
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
Chiffre 1. Workflow to be able to compare algorithms on the basis of their suitability for topic
reconstruction.
researchers have come, all these attempts to reconstruct topics share that some kind of defi-
nition of topic is involved, be it implicit or explicit.
Most approaches work with implicit definitions—usually with an everyday understanding
of the topic and/or simply equating topics with the outcome of the chosen algorithmic
approach—such as sets of publications at the lowest level of aggregation of a (hierarchical)
mapping exercise (van den Besselaar & Heimeriks, 2006). Other approaches either equate a
topic with the occurrence of one specific term (Kiss, Broom et al., 2010) ou, in the case of topic
modeling, define a topic using the probability distribution of several words across publica-
tion, where specific words in these publications do represent the topic (Griffiths & Steyvers,
2004; Yau, Porter et al., 2014). Sometimes a patchwork of implicit and explicit definitions with
not much regard to theory is provided, and the actual operationalization is at odds with (à
least parts of ) this definition (as in Sjögårde and Ahlgren (2018), Par exemple, who recognize
topics to overlap, but reconstruct disjunct clusters)—a phenomenon already well observed in
scientometrics when concepts (par exemple., “discipline”) are to be measured (Sugimoto & Weingart,
2015, p. 785). This neglect of basing the analysis on theoretical knowledge precludes the
findings from being linked to theory.
Ainsi, topics have either been implicitly defined while performing the reconstruction
attempts, or explicit definitions have been given that are not based on theory, either. To be
able to make clear what the algorithms used for topic reconstruction are to operationalize
and to be able to assess their suitability for the reconstruction task, I provide below one explicit
definition of topics which is based on knowledge from the sociology of science, lequel, à son tour,
allows me to derive the properties of topics.
3.2. Understanding of Topics in the Sociology of Science
The sociology of science has a long tradition of discussing conceptual units that allow us to
best understand the development of science. Cozzens (1985, p. 440) highlights the enduring
desirability to find a “diagnostic tool to describe and compare differences among the sciences
in their process of knowledge growth.” Over the course of time, several different “diagnostic
tools” have been in focus.
Études scientifiques quantitatives
1056
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
Much research done since the 1960s and 1970s has built on Kuhn’s important idea of the
interplay of researchers organizing knowledge, and knowledge that organizes the researchers
(Kuhn, 2012/1962). This interplay leads to the formation of scientific communities, où
researchers collectively orient themselves to a knowledge base and contribute to it, lequel
is characterized by increased communication among themselves (Kuhn, 2012/1962, p. 176).
In the quest to empirically demonstrate Kuhn’s idea of an interplay, Whitley (1974) devel-
oped this idea further and ended up with hierarchical relationships between scientific units.
He contrasted different levels of aggregation of specific sociocognitive units, namely special-
ties and research areas. According to Whitley (1974, pp. 77–78), a research area can emerge
“around” a phenomenon, a material, or a new instrument, Par exemple. “‘Research areas,’” he
states, “are collectivities based on some degree of commitment to a set of research practices
and techniques” (Whitley, 1976, p. 472). Par exemple, after the introduction of the electron
microscope, a research area may form when researchers collectively intend to accumulate
knowledge on how to analyze biological tissue with this electron microscope, et, plus tard, quand
practice with this instrument has become commonplace, new research areas based on specific
phenomena or materials to be investigated could emerge. Specialties, on the other hand, il
considers partly different in scope and partly different in kind. They are “more general in scope
than research areas” (Whitley, 1974, p. 79) and are built around a set of cognitive structures
(“models”) that order and interpret a particular, restricted aspect of reality (Whitley, 1974).
Since Whitley set out to spot the relevant social units in which science is taking place, le
task has continued to be pursued and is still under way today.
Building on the idea of Kuhn, in the subsequent literature we find indications that different
structures exist in science. Zuckerman and Merton (1973, p. 507) highlight differences in the
organization of “different sciences and specialties” and introduce the degree of codification of
connaissance. How I could actually measure codification, cependant, remains unclear. Regarding
more codified “fields,” for example, they only state that the “comprehensive and more precise
theoretical [connaissance] structures […] not only allow empirical particulars to be derived from
them but also provide more clearly defined criteria for assessing the importance of new prob-
lems, new data, and newly proposed solutions” (Zuckermann & Merton, 1973). Contributions in
this direction are also provided by Chubin’s (1976, p. 449) review on specialties, who recog-
nizes that “intellectual, cognitive, or problem content can generate different kinds of
structure.” And further by the hypothesis of a “hierarchy of the sciences” (Cole, 1983), distin-
guishing different “sciences” according to their ability to achieve consensus and accumulate
connaissance (Fanelli & Glänzel, 2013), or the urban or rural organization of science (Colavizza,
Franssen et al., 2019).
Edge and Mulkay (1976, p. 374) contributed to what is known about shared commitments
to knowledge by tracing the entanglement of “scientific and technical development” with the
“evolution of social relationships” in their analysis of researchers forming and changing their
collective orientation during the emergence and development of the specialty of radio astron-
omy (their study also analyzes several other specialties). Ici, et ailleurs, l'un des
researchers’ overarching topics for some time might have been the phenomenon of emissions
of radio wavelengths from sources in space (par exemple., Edge & Mulkay, 1976, pp. 374–376), et
several groups from different established specialties interpreted this with their own theoretical
and methodological background, creating different topics depending on their collective
interpretation.
It can be concluded that, even though the literature offers no precise method to measure
relevant units of science, the idea of knowledge with the corresponding social structures has
Études scientifiques quantitatives
1057
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
been established and relevant since then. En outre, evidence can be found of researchers
having a shared commitment to a body of knowledge that orients their work, and that struc-
tural differences among scientific units can be expected.
The exact conceptualization of “topic” used in this paper stands in the tradition sketched
au-dessus de, building on the idea of shared commitments to knowledge, indicating that scientific
communities form along with topics. This concept of topic is similar to Whitley’s concept
of a research area but abandons the idea of a hierarchy of research areas and specialties.
In contrast, I consider research areas and specialties as not qualitatively different but only
different in size. Topics, alors, can be part of specialties, and also span several specialties, ren-
dering them a relevant unit in science. En outre, I consider topics not just to represent
(fixed) bodies of knowledge that are unambiguously structured—an idea that is more related
to information retrieval—but to represent collective interpretations of knowledge that have a
scope that can be situated somewhere between the very elementary level of individual knowl-
edge claims and the much broader level of a scientific field or specialty.
In contrast to the abovementioned definitions of topic in bibliometrics, where they are con-
sidered to be somehow fixed in publications and/or equivalent to specific sets of terms therein, je
regard topics as things that are actively constructed by researchers, which can eventually leave
traces in the resulting publications (which could, among other traces, be terms or citations).
Spécifiquement, I consider topics to emerge from coinciding interpretations and uses of some
scientific knowledge by researchers, using the definition of topics provided by Havemann,
Gläser, and Heinz (2017, p. 1091):
a focus on theoretical, methodological or empirical knowledge that is shared by a number
of researchers and thereby provides these researchers with a joint frame of reference for the
formulation of problems, the selection of methods or objects, the organisation of empirical
data, or the interpretation of data1.
Ainsi, a topic is a cognitive phenomenon relevant to researchers, and to which researchers
contribute. From the definition it can be derived that thematic similarity and dense communi-
cation characterize topics. The latter is in line with Kuhn’s observation of scientific commu-
nities to be characterized by “relatively full” communication (Kuhn, 2012/1962, p. 176). Et
bibliometric data models are in line with this definition because data models such as a direct
citation network or a bibliographic coupling network operationalize communication or
thematic similarity, respectivement, whereas the typically applied algorithms are used to find
the dense structures in these data models2.
Using an explicit sociological definition of topics makes it possible to establish a link between
the rich accumulated knowledge of the sociology of science, with bibliometrics. The procedure
of a precise definition and operationalization for measurement represents a standard procedure
en sciences. Without such a definition and a coherent operationalization, bibliometrics decou-
ples itself completely from science studies, precluding the results of bibliometric studies from
being interpreted using the knowledge existing in science studies, or from accumulating knowl-
edge in science studies with the use of bibliometrics (see also Held, Laudel, & Gläser, 2021:
1 Other definitions of topics could also be given, but these still would have to be developed.
2 It shall not be forgotten here that only focusing on the bibliometric structures, such as citations, neglects
important aspects of science. Lievrouw (1989, p. 616) highlights that there are communication processes
relevant for the researchers “behind” the bibliometric (structural) réseau, and these communication pro-
cesses should not be neglected in our studies (see also Edge, 1979).
Études scientifiques quantitatives
1058
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
4513–4515). En outre, the definition and its derived properties (Section 4) enable me then
to compare the algorithms based on their suitability for this particular application.
For whatever purpose the concept of “topic” is used (whatever the specific application in
question might be, be it science policy or science studies), the algorithms’ inner workings and
their properties must correspond to the purpose of the topic reconstruction exercise. Other-
wise, their outcomes are of no use.
The abovementioned definition, cependant, cannot overcome the inherent vagueness of the
phenomenon in question (c'est à dire., topics being based on researchers’ perceptions of knowledge).
Even if a precise definition is given, and it has been plausibly operationalized as dense com-
munication or thematic similarity, these phenomena remain empirically difficult to identify.
Nevertheless, clearly defined and operationalizable properties of topics can be derived,
et, with my analysis, I ask whether the algorithms can reconstruct these properties.
3.3. Properties of Topics
To operationalize this definition of topics, I derive several properties from the definition, lequel
in turn shape the demands placed on algorithms aiming to reconstruct topics. Even though I
am confronted with the difficulty of transforming the topic definition into instructions for how
to bibliometrically measure it, the derived properties themselves are precise, and it is each
property’s specific expression of the various topics “out there” that varies greatly3.
1. Topics are local because they are being defined as products of the participating
chercheurs. Outsiders perceive the topic but do not construct it (Havemann et al.,
2017, p. 1091).
2. Topics can differ in their size, from a few researchers working on them up to many,
many more. Because the degree of engagement will vary, the size of a topic will always
be difficult to measure.
3. A researcher can contribute to several topics simultaneously. Publications may address
several topics (Sullivan, Blanc, & Barboni, 1977, p. 235; Amsterdamska & Leydesdorff,
1989, p. 461). Topics are overlapping, which I define as the phenomenon that one and
the same bibliometric entity (author or publication) can contribute to several topics.
4. Topics as shared frames of reference with intensified communication between
researchers are cohesive, defined as dense communication between researchers or
thematic similarity between publications. Separation from other topics is only a by-
product of cohesiveness (Havemann et al. (2017, p. 1091).
5. Because topics can connect knowledge in many different ways (Section 3.2), it follows
also that topics can have various communication or thematic structures. Ainsi, topics
are defined as structurally variable, which makes it likely that they are represented
by various structural forms in bibliometric networks.
The organizational unit of a specialty I consider to be similar to a topic in that it also rep-
resents a shared knowledge base of researchers that orients their research actions and towards
which they contribute. Fondamentalement, delineating topics and delineating specialties constitute
the same task: finding thematic structures in sets of publications. Ainsi, most considerations
made in this paper about topics should also hold for specialties.
3 Note that some properties are on a binary scale (par exemple., local/global) and algorithms’ properties might agree or
pas, while other topic properties are fuzzier and the degree of alignment has to be assessed (par exemple., variability
in structural forms).
Études scientifiques quantitatives
1059
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
4. PROPERTIES OF ALGORITHMS
One frequently applied set of approaches in scientometrics to find thematic structures consists
of using optimization algorithms, specifically algorithms that intend to find “communities”4 in
bibliometric networks, where the found communities are often directly interpreted as topics
(Sjögårde & Ahlgren, 2018; Šubelj et al., 2016). These algorithmically delineated communities
are structures with dense links in the network and, depending on the bibliometric network
used, can correspond to two aspects of topics that are included in my definition. D'abord, if the
links represent thematic similarity between the nodes (publications), then the communities
reflect a shared knowledge base (bibliographic coupling creates these kinds of links). And sec-
ond, if the links represent communication relations, then the communities represent dense
communication in the sense of Kuhn (direct citations create these kinds of links). Ainsi, biblio-
metric studies always implicitly operationalize the idea of a shared commitment to knowledge
when they search for dense structures in networks.
When looking closer at the properties and assumptions of different community detection
algorithms in this context, it appears worthwhile to differentiate between global algorithms
and local algorithms, due to their difference in the general underlying idea. By local algo-
rithms, I mean specifically those solving the cohesion/separation problem for an individual
community by evaluating only its immediate neighborhood and ignoring statistics of the rest
of the network (Fortunato, 2010, p. 84). Global algorithms are those that solve the
cohesion/separation problem by using statistics from the entire network to form a partition
(Fortunato, 2010, p. 85). In bibliometrics, so far, global approaches have taken precedence
over local algorithms which, on the other hand, have not gained much attention.
The general assumptions behind both groups of optimization algorithms are (un) that the
sought network communities (however different they may be) represent the structures of inter-
est, and typically (b) that one single function that gets optimized can best detect these struc-
tures5. Dans cette étude, I will take assumption (un) as given because, as mentioned above, a topic is
likely characterized by intensified communication, lequel, à son tour, would engender more
dense citation patterns, which might be represented as network communities. Assumption
(b) I also accept at this moment, and this point will be taken up later in the discussion.
As the definition of community inscribed in an algorithm (plus optimization function) est
different and very characteristic in each of the analyzed algorithms (and in their optimization
fonction), and this should be relevant for the evaluation of topic structures, I will first take a
closer look at community definitions in algorithms. This will then be followed by the list of the
abovementioned further evaluation criteria for the four community detection algorithms in
order to evaluate if these agree with the properties of the topics.
4.1. General Considerations About Algorithms’ Community Definitions
Each of the analyzed algorithms as optimization algorithms for community detection optimizes
a predefined function (“optimization function”). Once the algorithm has finished (c'est à dire., a
achieved its optimization goal), the output represents the algorithm’s specific way of achieving
a partition into communities where the optimization function cannot be optimized further
4 “Community” is a specific term in network science, referring to specific, yet not uniquely specified, struc-
tural entities in networks. Equipped with a completely different meaning is “scientific community,” which
stands for researchers focusing on and contributing to a knowledge base.
5 Note that not all relevant larger structures in networks need to be communities (Newman, 2012), and some
community detection algorithms use multiple optimization functions (Wu & Pan, 2015).
Études scientifiques quantitatives
1060
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
with this algorithm. The idea of what a community “is” is not provided by an “a priori def-
inition” (Fortunato, 2010, p. 84), and no “definition is universally accepted” (Fortunato, 2010,
p. 83). The definition is to a large degree inscribed into this optimization function, et le
algorithm is usually “built around” the idea inscribed into the optimization function6, lequel
also contributes to the (implicit) community definition. As different algorithms represent
unique approaches to optimize these functions, and these differences also influence the
algorithms’ implicit definitions of communities, I will in this paper differentiate between
algorithms and optimization functions, but structure the paper with the algorithms, acknowl-
edging that each combination of the two leads to unique (implicit) community definitions.
The very basic notion underlying many community definitions in the literature is that “there
must be more edges ‘inside’ the community than edges linking vertices of the community with
the rest of the graph” (Fortunato, 2010, p. 84). Fortunato and Hric (2016, p. 6) state that “[F]or a
proper community definition, one should take into account both the internal cohesion of the
candidate subgraph and its separation from the rest of the network.” Because maximally cohe-
sive components that are well separated from their environment (in the extreme: isolated
cliques) in the network are rarely found in networks (Havemann, Gläser, & Heinz, 2019), un
multicriteria optimization problem to empirically detect communities is created. Each com-
munity detection algorithm must therefore find a compromise between the separation of the
communities and the internal cohesion of the same.
The question as to how a highly cohesive structure in network communities could be iden-
tified has various answers (Havemann et al., 2019), including searching for a high internal
conductance value (communities should be hard to split), a high-density region (many links
between nodes), a region with a high clustering coefficient (number of links in nodes’ neigh-
borhoods divided by possible links) (Lequel & Leskovec, 2014) or a high value of the second
eigenvalue of the community’s Laplacian matrix (Tibély, 2012), which can be a measure of
cohesion because a higher second eigenvalue indicates graphs being hard to split. There is
not only no agreed-upon answer to this question of cohesion measures, but one can also find
that this question is hardly ever discussed (Tibély, 2012, p. 1832), and the definition of cohe-
sion (as is the case for community definitions) typically remains implicit.
What separation means, on the other hand, seems more agreed upon, namely the minimum
links to other communities. Cependant, because networks do not have clear-cut structures
when an algorithm maximizes cohesion for a structure, it will not maximize separation and
vice versa.
Another issue that should also be considered is the idea of each algorithm to optimize one
function for the entire network7. This might collide with the expectation that these will recon-
struct sufficient variability of structural forms in the network.
4.2. Criteria for Algorithm Analysis
For the assessment of the properties of the algorithms (step 3, Chiffre 1), and their correspon-
dence (step 4) with the topic properties, I select criteria for the algorithm analysis. The algo-
rithms need to fulfil these criteria to obtain results that have the properties of topics (Tableau 1).
6 Par exemple, the Louvain algorithm has, first and foremost, been programmed to optimize the modularity of
a partition. The Leiden algorithm is programmed mainly to optimize CPM (explained in Section 5) and mod-
ularity, and Infomap is built to find the optimum for the map equation (see Section 5). Cependant, one could,
Par exemple, also use the Louvain or Leiden algorithm to optimize the map equation.
7 An example of research in other directions can, Par exemple, be found in Wu and Pan (2015).
Études scientifiques quantitatives
1061
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
Tableau 1.
Topic properties with definitions and relevant criteria of bibliometric mapping algorithms
Properties of topics
Cohesion
Definition
Dense communication/Thematic
similarité
Criteria for algorithm analysis
Structures searched for
(community definition)
Cohesion-separation trade-off
Various structural forms
Knowledge connected in different ways
Structures searched for
Local
Overlapping
Variable size
Researchers define topics
User’s degrees of freedom
Use of local information
One bibliometric entity belongs to
Finding overlaps and hierarchies
several topics
Extent and degree of researchers’
engagement with a topic
Flexible size distribution
4.2.1. Definition of community/separation and cohesion
With this criterion, I attempt to elucidate a better understanding of what can be said about the
community definitions that are implicit in the approaches and how the necessary trade-off
between separation and cohesion in the network has been dealt with. From the various pos-
sible definitions of cohesion mentioned above (Havemann et al., 2019), which all share a ref-
erence to a high density of connections, I define a cohesive community as a subgraph with a
structural form that is hard to split (Tibély, 2012) (c'est à dire., a high number of links need to be
removed to split the subgraph). I define structural forms as topological classes, as differentiated
by Estrada (2007)—see examples in Figure 2.
4.2.2. Use of local information
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
I define a local algorithm as one that solves the cohesion/separation problem for one commu-
nity by only assessing its immediate neighborhood (examples can be found in Fagnan, Zaiane,
and Barbosa (2014) or Hamann, Röhrs, and Wagner (2017)). As a global algorithm, on the
other hand, I define one that uses information about the whole graph to partition it into com-
munities. It has to make compromises to decide on a partition, considering more parts of the
network beyond a community’s immediate neighborhood to make the node assignments (c'est à dire.,
the decision for the assignment of a node to a community depends also on more distant parts
of the network). Because of the many algorithms that combine both local and global elements,
I consider this property to be fluid.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2.
Selected topological classes of subgraphs, taken from Estrada (2007).
Études scientifiques quantitatives
1062
Know thy tools!
4.2.3.
Finding overlaps and hierarchies
Can the algorithm be used to construct communities that overlap in their boundaries or even
pervasively, and how does the algorithm achieve this? Are hierarchies in the network detected
(or even poly-hierarchies, c'est à dire., complex hierarchies) and how can the algorithm be used to
obtain these?
4.2.4.
Flexible size distribution
Does the algorithm force a certain community size distribution, or is the size distribution deter-
mined by the structure of the network?
4.2.5. Users’ degrees of freedom
Généralement, the users of algorithms need to set some parameters to specify the behavior of the
algorithme. Which decisions does the algorithm require from the user and to which degree does
this contribute to the constructedness8 of the result? More degrees of freedom can be helpful if
they support tuning an algorithm to the bibliometric task or finding various structural forms.
Fewer degrees of freedom may prevent exploring the “sample space.” At the same time, many
degrees of freedom may make the link between parameters and the outcomes nontransparent.
Some important parameters are briefly analyzed, as a deeper investigation would comprise a
separate study.
The abovementioned properties of topics and the corresponding criteria for the algorithms
are shown in Table 1. To my knowledge, both have never been considered and applied before
in the context of mapping.
5. ANALYSIS OF ALGORITHMS
Tableau 2 briefly lists the results of the analysis of the algorithms’ properties. Dans ce qui suit,
each algorithm is analyzed individually.
5.1. Louvain Algorithm/Leiden Algorithm
5.1.1. Background: How does it work?
Developed in 2008, the Louvain algorithm (Blondel, Guillaume et al., 2008) represented a novel
heuristic to optimize a network partition quality function and efficiently determine this partition.
In an agglomerative manner, two steps are repeated several times. After starting with each node
in its own community, individual nodes are moved between communities, which induces the
maximum (mondial) increase of the optimization function. Once this cannot be improved further,
a new network is constructed with the previously created communities as nodes, and then the
previous local moving phase is repeated, which eventually leads to a hierarchical result.
It turned out that the greedy optimization performed by the Louvain algorithm can create
some problems in the results with respect to the quality of individual communities, among
them completely internally disconnected communities. The Leiden algorithm was developed
to improve this (Traag, Waltman, & Van Eck, 2019). It generally builds on the idea of the Lou-
vain algorithm but includes refining steps in the aggregation process, where communities in
the found partition are again checked to see if they can be split. Nodes are here moved
between the communities not necessarily greedily (c'est à dire., such that the global optimization func-
tion gets the highest increase), but with a random factor (ibid., 5).
8 Through the various decisions a researcher has to make for a bibliometric mapping task, they have to engage
with several steps of a construction process. Finalement, the goal is to minimize the degree of distortion created
through the decisions made. At least the awareness of the construction process should be present.
Études scientifiques quantitatives
1063
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Q
toi
un
n
t
je
t
un
je
t
je
v
e
S
c
e
n
c
e
S
toi
d
e
s
t
je
Tableau 2.
Brief overview of the four algorithms’ properties relevant for topic reconstruction.
Community definition/
separation-cohesion
Louvain
Dense community,
focus on separation
Degree of local and
global information usage
Mainly global
Hierarchies
Not directly
Overlapping
Non
Preference
of size
Non
Leiden
Dense community,
Global and partly local
Not directly
Non
focus on separation
and slightly cohesion
OSLOM
Statistically significant
Local and partly global
Oui
Pervasive
Non
Non
community, cohesion
likely, separation not
an issue
Users’ degrees of freedom
Resolution parameter,
optimization function,
random seed
Resolution parameter,
optimization function,
random seed
Coverage parameter,
p-value, random seed,
singletons
Infomap
Nodes’ closeness,
Mainly global
Oui
In boundaries
Non
Deux- or multilevel
focus on separation
solution, detection of
overlaps, random seed
1
0
6
4
K
n
o
w
t
h
oui
t
o
o
je
s
!
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
5.1.2. Definition of community/separation and cohesion
Both algorithms take up the general idea of the functions they seek to optimize, which is to
find an optimal partition of the network via community structure. The focus is thus more on
finding a community (modulaire) structure in the network, rather than defining individual com-
munities. Donc, the definition of a (individual) community remains implicit. Typical opti-
mization functions for these algorithms are modularity or the Constant Potts Model (CPM), mais
other optimization functions can be used as well.
(cid:129) Optimization functions
The community definition of the CPM may be explained as follows: A community is a set
of members where the most connections between the members are realized, compared to
the possible connections that could be there9. Only members in the considered commu-
nity determine how many connections can possibly be realized, and thereby if a new
member will be part of the community. Modularity’s community definition, on the other
main, is oriented more globally, in that a community is considered a set of members where
more connections are realized than would be expected from counting the global number
of connections existing in the network, and then determining the expected number of
internal connections. Ici, the other parts of the network thus also influence whether a
new member will be part of the community. Both optimization functions can include a
resolution parameter, which changes, as in the case of CPM, if all the possibly realizable
connections are counted (resolution value of 1), or if a higher or lower resolution value
changes this calculation. This resolution parameter can be considered a slight modifica-
tion to the implicit community definition of the optimization function.
(cid:129) Algorithms
Once the algorithms terminate, their result will represent their best way to have optimized
the quality function10. Regardless of the optimization function used, both algorithms show
differences in the implicit community definition due to their different workflows. In the case
of Louvain, while moving the nodes in between communities, the resulting communities
could eventually be internally disconnected (communities have low or no cohesion),
which cannot happen with the Leiden algorithm. Obviously, the greedy, agglomerative
approach of the Louvain algorithm for achieving the optimal result neglects internal cohe-
sion, even though the abovementioned optimization functions are actually used to find
dense edge structures. The Leiden algorithm, on the other hand, gives slightly more impor-
tance to internal cohesion, due to the refinement phases, but also here creating structures
with high internal cohesion is not the main objective of the algorithm.
Both algorithms focus more on good separation in the partition they create through their
local reassignment of nodes until the function is optimized, even though the actual focus
is not on maximizing separation.
Chiffre 3 shows four selected structures of communities from the results of both algorithms,
which were applied to a typical citation network taken from my previous project11, after the
9 Note that I am only talking about counting the connections (edges) between members here. The same can be
said and calculated in the same way using the optimization functions for using weights on each edge that are
pas 1 (only counting the connections means using edge weights of 1, but these weights can take any real-
valued number).
10 Finding the “best” partition using modularity or CPM as optimization function cannot efficiently be solved
(NP-hard).
11 A direct citation network used in Held and Velden (2019).
Études scientifiques quantitatives
1065
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
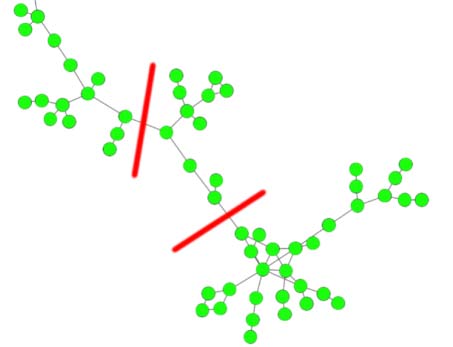
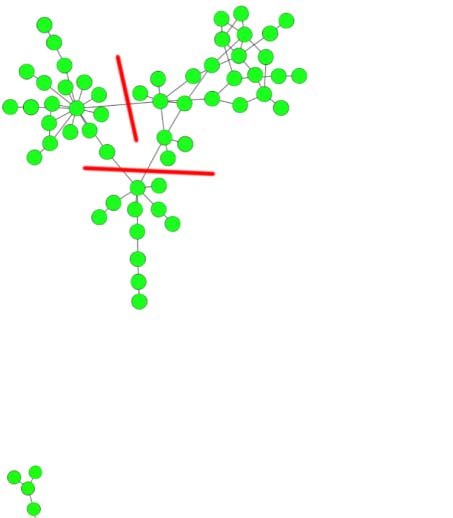
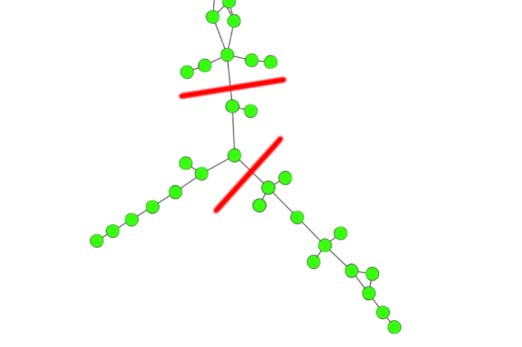
Chiffre 3. Some selective communities (“clusters”) from clustering results of the Louvain and Leiden
algorithms. Possible cuts that easily split the community are highlighted.
optimization of modularity (top row, both with resolution 3) and CPM (bottom row, resolution
5 × 10−4). The nodes represent publications, (unweighted) edges represent citations, et le
layout was created with ForceAtlas2. These kinds of (“drawn-out”) structures are not hard to
split, and thus cannot be considered cohesive. The selection shown here is not representative,
cependant, but shows communities that can easily occur across a wide range of resolution
valeurs. The examples here were found by ranking the communities of a solution according
to the second eigenvalue of their subgraph’s Laplacian (Tibély, 2012). Lower values indicate
communities that are easy to split.
5.1.3. Use of local information
As each of the two algorithms represents a method that uses statistics from the entire network
to find a (globally optimal) partition, both represent global algorithms. Cependant, the degree of
consideration of local information differs slightly between the algorithms, et, furthermore, comme
mentioned above, different optimization functions chosen for the algorithm also differ in the
relative importance they assign to local information. Because the Leiden algorithm makes
much more use of local statistics (considering local edge weights), it can be considered to
some degree to be more “local” than Louvain. The same holds for the modularity and CPM
optimization functions, where the CPM is an optimization function that can be calculated for
one community solely with local statistics (but in the case of the Leiden and Louvain algo-
rithms it is calculated for all communities to find a global partition), compared to the
completely global orientation of modularity.
5.1.4.
Finding overlaps
Both algorithms produce disjoint communities in a partition and thus do not reconstruct over-
lapping structures.
Études scientifiques quantitatives
1066
Know thy tools!
5.1.5.
Finding hierarchies
Hierarchies are not directly provided with the (default) résultats. This is because partitions pro-
duced in the intermediate steps are suboptimal solutions according to the optimization func-
tion (c'est à dire., a more aggregated result will be created if it improves the optimization function). Le
optimum for each given resolution parameter is a nonhierarchical solution, and solutions with
different resolution parameters cannot be matched to each other. Nevertheless, one could also
view the solutions at different resolution levels as a possibility to examine a poly-hierarchy. Or
the clusters of one solution could be aggregated (par exemple., based on the citation relations between
the clusters, as has been done in Waltman and van Eck (2012)) to obtain a strict hierarchy.
5.1.6.
Flexible size distribution
Through the resolution parameter included in the two optimization functions, more coarse-
grained or more fine-grained results allow for a lot of flexibility in the sizes of the communities.
Using the CPM avoids the resolution limit of modularity (Traag, Van Dooren, & Nesterov,
2011), thus making it possible to also detect very small clusters in very large networks. Expe-
rience shows that in bibliometric networks the cluster size distribution of more coarse-grained
solutions (low resolution value) follows a power law distribution, with a few very large clusters
and many smaller ones, while increasing the resolution more and more leads to a more bal-
anced cluster size distribution, for both CPM and modularity12.
5.1.7. Degrees of freedom as a user
Next to the already mentioned resolution parameter (-r), which one must specify beforehand
and will have an influence on the cluster sizes, the seed (–seed) for the random number gen-
erator can be fixed to allow for the reproduction of results. The quality function (optimization
fonction, -q) can be chosen, either modularity or CPM. En outre, if there are edge weights
provided with the network, these can be chosen to be included in the calculations of the opti-
mization function (-w) ou non (then each edge gets a value of 1). Par exemple, in the case of
CPM, because it is working with local edge weights, this will create not only edge-dense struc-
photos (as in the case of edge value 1), but specifically areas with higher edge weights will be
considered denser than areas with lower edge weights. Both the option for a choice of opti-
mization function and the inclusion of edge weights allow for some degree of variability in the
structures detected.
5.2. Order Statistics Local Optimization Method (OSLOM)
5.2.1. Background: How does it work?
This algorithm has been developed by Lancichinetti, Radicchi et al. (2011). It is based on the
idea to optimize a function that assesses the statistical significance of each community (c'est à dire., le
probability that nodes with their edges to this community could also have been found there
randomly). Ici, it is not the quality of the whole partition of the network that is evaluated, mais
the quality of individual communities. OSLOM starts with a random selection of single nodes
as seeds for communities and repeatedly adds significant neighbors to nodes to let the com-
munities grow. Significance is determined here via a comparison to an edge configuration that
is based on a null model (c'est à dire., a network without community structure, similar to what is used
in the modularity calculation). In cases where parts of the network are close to structures of
12 Note that, in contrast to OSLOM, both the Louvain and Leiden algorithms assign every node to a community,
irrespective of the community structure of the network (as does Infomap). This means that nodes that are
barely linked in the network will still end up in a community.
Études scientifiques quantitatives
1067
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
random networks, they might end up unassigned, being part of no community. Each of the
neighbors (nodes) of the existing community is evaluated for inclusion, and it is included if
the number of links to the community is much more than expected randomly. Next to the
evaluation for inclusion, it is also repeatedly evaluated if internal nodes can be “pruned” (dis-
carded), which is also done by significance evaluation. The algorithm is repeated several times
from the start with different seed sets, and when communities (with a certain overlap over the
runs) are repeatedly found, the algorithm will converge. Considering the results of several rep-
etitions, the algorithm searches for the minimum significant communities (c'est à dire., communautés
that cannot be combined with neighboring ones because they do not “overlap” sufficiently
with others over the runs).
5.2.2. Definition of community/separation and cohesion
By comparing the grown communities to a null model (random network) (c'est à dire., assessing the
likelihood for the found structures to have occurred randomly), OSLOM defines a community
statistically, by qualifying communities as structures found “unexpectedly unlikely.” Eventu-
ally, ce, again, means that more internal edges are there than expected, here compared to
a null model. The perspective of a community is constructed locally (c'est à dire., a community is con-
sidered a community from the very perspective of this random-seed-grown community with
respect to its direct surrounding). Ainsi, some nodes of one community might be considered
part of another community from another “neighboring” perspective (community).
The trade-off between cohesion and separation is here again approached through the
actions of the algorithm and its application of the optimization function. The optimization
function is based on statistical significance and includes nodes that connect well to the
community—which is likely to lead to good cohesion, but the comparison with the global null
model indicates that local cohesion is not the sole focus. Another aspect that can contribute to
generating cohesive structures is that the algorithm checks for the minimum significant struc-
tures and decides whether to merge or split communities. En général, OSLOM does not take
much effort to increase the separation, as only finding a cover of the network is the aim, not an
entire partition.
5.2.3. Use of local information
The OSLOM algorithm can be considered more a local than a global approach. Quand
OSLOM considers the significance of a community, it considers the surrounding of each
seed-grown community to add significant nodes from the perspective of each community,
which is one aspect in which it can be considered a local approach. Toujours, as all parts of the
network are “touched” several times for finding communities in the entire network, it can be
considered not a fully local approach.
5.2.4.
Finding overlaps
Exploring the significance of structures from several seed nodes can create parts of the network
where nodes are considered to be significant additions to more than one community. Thereby,
even pervasive overlaps can be created by OSLOM.
5.2.5.
Finding hierarchies
En principe, OSLOM is able to detect a poly-hierarchy in a network. After finding the smallest
significant communities, it then builds a new network from these communities by using these
as new nodes, where again each node addition is assessed for significance. In this way, it is
Études scientifiques quantitatives
1068
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
continued until no more significant communities are found in the next coarser level, et
potentially several levels of a hierarchy are found.
5.2.6.
Flexible size distribution
Very small communities can be found in these minimum significant structures, et, through
repeated aggregation, also very large significant communities can be found (the largest in the
highest hierarchical level). Ainsi, it allows a lot of flexibility in community sizes.
5.2.7. Degrees of freedom as a user
One major decision that has to be made is about the significance level P (which decides
whether a found community is significant). This influences the size of the communities found,
with lower values leading to larger communities (fewer communities) and higher values to
smaller ones (more communities). Aussi, here the -seed for the random number generator
can be set. Other relevant parameters include the coverage parameter (-cp) to change the
size of the communities, and to ignore “homeless” nodes -singlet can be used.
5.3.
Infomap
5.3.1. Background: How does it work?
Infomap is the name of a search algorithm that seeks to optimize an information-theoretic
quantity in a network (called the map equation). It was developed by Rosvall, Axelsson,
and Bergstrom (2009) and utilizes the generalized principle known from information theory
that regularities in data can be used to compress the data (in the style of Shannon and Weaver,
who introduced this way of thinking in 1948). Ainsi, pattern recognition and information com-
pression are combined. The regularities in the network are detected by random walks (used as
proxies for “real” flow in the network), which “walk” through the network by jumping from
node to node and counting the frequencies of visits to each node. If the network contains
régions (“modules”), the random walker visits these nodes more frequently. To find the shape
of this frequently visited region, the goal is defined to code each step of the random walker
with the least amount of information (to most efficiently code the entire walk of the random
walker). This goal is best achieved when frequently visited nodes get a shorter (more efficient)
code (the specific code used is based on Huffman coding, explained in Rosvall and Bergstrom
(2008, p. 1118)).
The efficient coding scheme also reuses (at least parts of ) the coding scheme within one
module (“module codebook”) when the random walker visits another module (Bohlin, Edler
et coll., 2014, p. 6). To complete the encoding of the random walk and be able to reuse the
codes of the node visits in each module, the leaving and entering of a module is recorded
by the “index codebook.” Thus, the “map equation gauges how successful different network
partitions are at finding regularities in the flow on the network” (Esquivel & Rosvall, 2011, p. 2).
The abovementioned quantity (the random walker description length), called the map
equation, is minimized with a procedure that the Louvain algorithm also uses. Initially, chaque
node is in its own community (“module”). Alors, in a random sequential order, neighboring
communities are joined, resulting in the largest decrease in the map equation. If this is finished,
the same process now repeats with the previously resulting communities as nodes, represent-
ing a hierarchical rebuilding of the network. Similar to the Leiden algorithm, a refining pro-
cedure looks again at the modules and checks for possible single node and submodule
movements to further improve the result (Bohlin et al., 2014, p. 9). This whole procedure
Études scientifiques quantitatives
1069
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
has been generalized to detect hierarchical and overlapping structures as well, which I will
analyze in the respective section below.
5.3.2. Definition of community/separation and cohesion
From the above, it follows that a community (“module”) can be considered as a set of nodes
where nodes inside the community can visit each other more easily (with fewer steps) que
nodes outside the community. It is a region in the network where (theoretical) flow between
the nodes is more easily “trapped” in the community, whereas the random walker represents
le (possible) flow. This means that the random walker has a higher persistence probability in
this region. The aspect of being trapped represents the general focus of Infomap on separation.
On the other hand, the refining step, when each module is checked again for submodules,
allows for the detection of smaller and smaller structures (submodules), and also represents
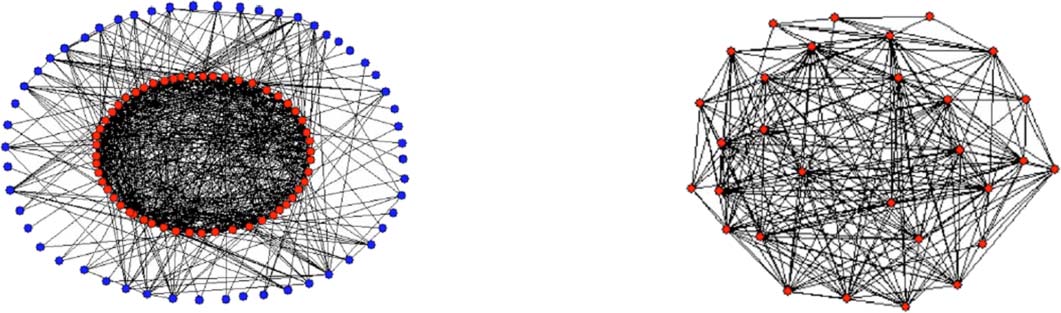
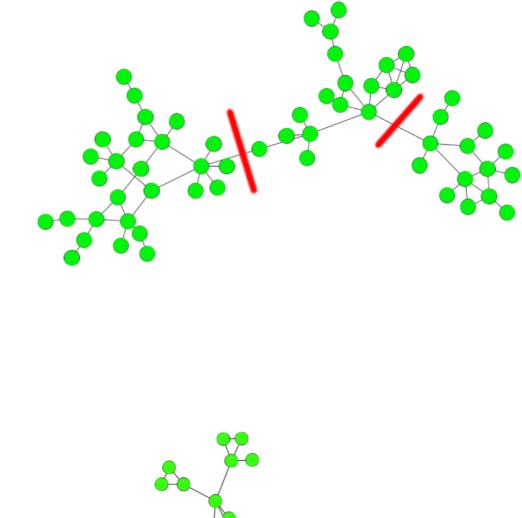
a consideration for cohesion. In Figure 4, an example is given of a (star-like) community that
Infomap has constructed in a citation network (cf. footnote 11). These kinds of structures are
preferentially treated by Infomap, because, with a high-degree node included, clearly every
node can be reached easily from everywhere. Encore, this is not a representative sample, either,
but it illustrates a problem.
5.3.3. Use of local information
For the creation of the modules to find the minimum description length of a random walker,
information from the entire network is used, and thus Infomap must be considered a global
algorithme. Especially when perturbing the number of intermodule links in one place of the
réseau, this then can affect the optimal partitioning of the whole network (Tibély, 2011,
pp. 103–104).
5.3.4.
Finding overlaps
An extension of Infomap has been provided by Esquivel and Rosvall to allow for “border
nodes” to belong to more than one module. This can be the case if two modules belong to
“separate flow systems with shared nodes” (Esquivel & Rosvall, 2011, p. 2). Ici, after the
creation of modules such that the description length is minimal, it is checked if the assignment
of boundary nodes to several modules could further decrease the value of the map equation.
Chiffre 4. One selected community (“cluster”) from a clustering result of Infomap applied on a
citation network. Nodes represent publications and (unweighted) edges represent citations.
Études scientifiques quantitatives
1070
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
5.3.5.
Finding hierarchies
Infomap is also able to detect modules at different levels of a hierarchy (Rosvall & Bergstrom,
2011). The “standard” two-level compression does not detect hierarchies, but the multilevel
compression option does. Ici, the algorithm checks if the introduction of additional (hierar-
chically nested) index codebooks at a coarser level can further reduce the description length.
Ainsi, two or several levels of hierarchy can possibly be detected. In this hierarchy, like in a
typical dendrogram, one node belongs to exactly one branch (no poly-hierarchy).
5.3.6.
Flexible size distribution
The multilevel option in particular allows for flexibility in the detection of very small modules
at the lowest level of the hierarchy, as well as very coarse modules at the highest level. Le
resolution limit (when small modules are undetectable) known from modularity does not seem
a relevant issue (Kawamoto & Rosvall, 2015).
5.3.7. Degrees of freedom as a user
Relevant options for the user concern the already mentioned options to detect overlapping and
multilevel structures. By default, Infomap uses multilevel compression, and thus can possibly
automatically detect several levels in the hierarchy (the parameter –two-level disables this),
and also by default does not include the search for overlapping nodes (–overlapping
enables this). Another option regards the seed for the random number generator (–seed n)
which makes it possible to reproduce the results13.
6. DISCUSSION
In this paper, the correspondence of the properties of a set of algorithms with the properties of
sociologically defined topics was assessed. The properties of topics were derived from a
definition of “topic” that builds on the established idea of a topic as an object of the shared
commitment of researchers. To evaluate and compare whether algorithms are suitable to
reconstruct a certain phenomenon from data, the conditio sine qua non here is to have a clear
conceptualization of the phenomenon in question, including an explicit theoretical definition
that explicates the properties that are to be reconstructed. This is what I started with.
My results indicate that the algorithms that are commonly applied for the task of recon-
structing topics are, one the one hand—due to their properties—prone to creating various arti-
facts in the results, mais, on the other hand, each algorithm and its accompanying optimization
function produces communities that more or less match some of the properties of topics.
6.1. Do Communities in Networks Represent Communities in Science?
According to the topic definition used here, every topic should “have” a scientific community
(in the Kuhnian sense). And topics and scientific communities have certain characteristics. Sci-
entific communities are, according to Kuhn (2012/1962, p. 176), characterized by “relatively
full” communication and do exist on “various levels.” It can thus be assumed that dense com-
munication is something to search for to find scientific communities and topics. But are the
algorithms optimizing for density? After all, finding dense structures in networks is what “com-
munity detection” algorithms are built to achieve (Fortunato & Hric, 2016, p. 7) and what
makes them a plausible choice for analyzing networks. This is also what all four analyzed
13 For the details, see https://www.mapequation.org/infomap/ (accessed May 18, 2021).
Études scientifiques quantitatives
1071
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
algorithms aim for, finding subgraphs that are particularly dense—yet each one in a different
way with diverging ideas behind how to (concernant)construct communities.
6.1.1. Considerations of cohesion and local character of communities
The Leiden and Louvain algorithms search for dense structures by their specific approach to
optimize modularity or CPM (two functions with different ideas of density), yet they also
“accept” communities that are only mildly cohesive or even disconnected (c'est à dire., not cohesive
at all: voir la figure 3). Infomap uses the map equation to find density by creating modules that
keep a random walker trapped, which ensures that each node in the module can be reached
facilement. This can, in the extreme, also be a community with a (réseau) star in the middle
(c'est à dire., one high-degree node/highly cited publication with the others attached only to this one
(in the case of direct citations)), and this does not necessarily represent a dense communication
contexte. OSLOM’s focus on the statistical significance of the new nodes with respect to the
current (single) grown community represents a focus on cohesion, and OSLOM is the only
algorithm that ignores surrounding nodes if they do not fulfill this criterion of significance.
Ainsi, not sufficiently well-connected nodes are then not added to the community.
Ideally, a topic reconstruction algorithm focuses on the cohesion in the construction of the
communautés, and the separation of communities would only be a secondary result of that.
The globally oriented algorithms of my analysis (Louvain, Leiden, Infomap) cannot maximize
the cohesion of all communities, as they have to optimize an entire partition, and cohesion
may be ignored, and in some cases be “sacrificed” in the compromise with good separation
between the communities (voir la figure 3). Reid, McDaid, and Hurley (2013) demonstrated that
modularity optimizing algorithms disregard cohesion to the extent that they cut through
cliques. The focus of Infomap is only partially on individual communities by focusing on
the flow in local structures, but the main focus is on optimizing the partition such that infor-
mation can flow efficiently. Ainsi, the local structures found are always affected by the entire
réseau, which is not in line with the local character of topics. OSLOM assesses the quality of
single communities rather than the quality of a partition of the whole network (advantages of
this approach are discussed in Fortunato and Hric (2016, p. 33)). Ainsi, it does not need to find
a global compromise and can ensure a higher degree of cohesion compared to the other
algorithms. Encore, OSLOM also does not focus mainly on cohesion, and even though it is called
a local algorithm by the authors, its requirement of statistics from the entire network to assess
the significance of the communities found makes it not entirely local.
Donc, none of the global algorithms optimizes the cohesion of individual communities.
They mainly optimize the partition and mainly focus on separation. The Leiden algorithm has
a mild focus on cohesion, while Louvain almost none. Infomap’s focus on the smallest mod-
ules ensures some cohesion, as is the case for OSLOM. It is thus difficult to provide a detailed
ranking of the algorithms with respect to the cohesion property. For a more specific compar-
ison, this would have to be shown empirically in future work.
6.1.2. Tolerance of algorithms for variations in size and structures of communities
That science shows itself in different kinds of communication or thematic structures is indi-
cated by the literature mentioned in Section 3.2. From that, it can be inferred that different
types of topics must exist and each “topic type”14 is characterized by distinct communication
14 A typification of specialties has been tried in the last decades, but an agreed-upon framework for character-
izing and comparing types of specialties does not seem to exist.
Études scientifiques quantitatives
1072
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
structures with differences in scope. These topic types, alors, are likely to correspond to differ-
ent kinds of structural types in bibliometric networks (cf. topological types in Estrada (2007)).
The task is then to be able to reconstruct these distinct communication structures represented
by distinct structural types in networks. Which types of topics the four algorithms with their
optimization functions are able to reconstruct is currently difficult to answer. D'abord, we lack
knowledge about the types of topics and about their representation in bibliometric networks.
Deuxième, the partition-oriented algorithms create “specific” individual communities only as a
by-product due to their global focus on the partition.
A certain tolerance for various structures of communities is found in every algorithm. Comment-
jamais, the focus of each algorithm on optimizing one function for the entire network is likely to
limit the discovery of different subgraph structures, because the boundaries of these structures
are not taken into account. In the case of the Leiden and Louvain algorithms, Par exemple, les deux
make the assumption that all (algorithmic) communities in the network form along the same
“rules” (which manifest as a certain density pattern). In the case of Infomap, this means that all
(algorithmic) communities are characterized by an efficient flow pattern. Further analyses,
cependant, would depend on knowing to which degree these assumptions agree with which
topic types (and some topic types might be reconstructed by some rules for formation made
by the algorithms, or topic types that are characterized by efficient flow). What we know so far
est, cependant, que (dense) communication structures are very different in different scientific
fields (Colavizza et al., 2019) and that relevant differences exist in the knowledge production
of the various sciences (Nagi & Corwin, 1972, pp. 6–7; Whitley, 1977).
Regarding the flexibility in size distribution, all four algorithms are flexible and produce
community sizes across the whole range. No relevant differences need to be discussed
between the four algorithms.
6.1.3. Overlaps and hierarchies
Different topics can overlap in their boundaries, or pervasively, with the possibility of even
forming poly-hierarchical relationships between them. Algorithms for topic reconstruction
should account for that. The three global algorithms optimize the partition to obtain a disjunct
partition, contradicting the overlapping character of topics and communication structures.
Even though there is also a variation of Infomap for overlapping “modules,” the general think-
ing behind these algorithms is to take a global “partition perspective,” and a local phenome-
non such as a topic, which stays local, is not in the focus. OSLOM, on the other hand, allows
for overlaps and can be considered closer to topic properties in this case.
For the possibilities of each of the four algorithms to extract hierarchies in networks, it
should be noted that what hierarchy means is specific to each algorithm. The different solu-
tions of the Louvain and Leiden algorithms that can be obtained with an added resolution
parameter to the optimization functions make it possible to extract different levels of aggrega-
tion, but there are already indications that algorithmic resolution does not mean that by tuning
the resolution one can extract scientific community structures at different levels of aggregation
(Held et al., 2021). Infomap detects, when using the multilevel solution, in the coarser solu-
tions those partitions where information can flow even more efficiently. When topics are con-
sidered as entities where information can flow efficiently—as Infomap assumes—then these
higher level partitions might provide interesting insights. Nevertheless, as I have mentioned
earlier, the focus of Infomap to optimize a partition is not in line with the local character of
topics, and each node cannot be part of a poly-hierarchy. Ainsi, the meaning of these hierar-
chical levels also has to be taken with caution in the context of topic reconstruction. OSLOM,
Études scientifiques quantitatives
1073
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
on the other hand, intends to build significant hierarchical levels from its local orientation. Il
allows also for poly-hierarchies, which can be considered more in accordance with this topic
property.
Havemann et al. (2019) highlight the general difficulty of the best trade-off between sepa-
ration and cohesion when communities are assumed to comprise core–periphery structures
and communities are included in other communities. This further complicates the search for
suitable algorithms, even though there are many algorithms available that can detect overlap-
ping structures (next to OSLOM and Infomap included here). Par exemple, some of them are
based on clustering links instead of nodes (Ahn, Bagrow, & Lehmann, 2010; Evans &
Lambiotte, 2009; Havemann et al., 2017), or based on locally grown communities (related
to the idea of OSLOM) which naturally overlap (Huang, Sun et al., 2011; Whang, Gleich,
& Dhillon, 2013) and generative models such as stochastic block models (Peixoto, 2019).
6.2. Applying General-Purpose Algorithms for Bibliometric Tasks?
The algorithms analyzed here are general-purpose algorithms, requiring only nodes and edges
as input (c'est à dire., they can be used for various tasks). Aldecoa and Marín (2013) have shown that
no algorithm is suitable to cluster all kinds of networks, and Dao, Bothorel, and Lenca (2020,
p. 3) provide good reasons why “choosing the community detection method that corresponds
well to a particular scenario or to an expectation of quality is not straightforward.” This raises
the question of whether the four are particularly suitable for the bibliometric task of topic
reconstruction. My analysis has shown that this is not necessarily the case. The ideas of each
algorithm’s developers are not necessarily applicable for this task. Next to the very general-
purpose algorithms (Leiden, Louvain, and OSLOM), Infomap could perhaps be considered an
algorithm with slightly more specific application orientation compared to the others, where it
might be easier to determine if this is a suitable algorithm for the specific application. Le
specific assumption on the input network that Infomap makes is that there is (directed) flow
present in the network, made possible by the interconnections. The developers imagine poten-
tial fields of application (where patterns of flow play a role), and even mention the (potential)
suitability of their algorithm for “bibliometric analysis” (Bohlin et al., 2014, p. 3), because their
random walker could be considered a model for researchers navigating the publications.
While it is our task to reflect on the idea of what moving a random walker on citations means,
it becomes more difficult to imagine to what degree the (potential) benefits of the goal to “trap”
the flow in the network via the creation of “modules” for our bibliometric task are impacted.
The other basic assumption that all three global algorithms (in contrast to OSLOM) make is
that all nodes in the network are members of communities (c'est à dire., that every publication contrib-
utes to a topic that is represented in the network). Ce, certainly, is something that can be
questioned in the topic reconstruction context. Il a, Par exemple, been shown by Boyack
and Klavans (2014) and by Held and Velden (2022) that every graph has its relevant environ-
ment that might be unduly excluded in an analysis. Ainsi, publications in a network might
belong to a community that is located largely outside that network.
Even though my analysis did not consider the role of the data model (direct citation model
vs. bibliographic coupling model, etc.) that one has to choose in conjunction with an algo-
rithm for a topic reconstruction exercise, which I believe is important and should be analyzed
by researchers conducting empirical bibliometric analysis using an algorithm and a data
model (as done by Boyack and Klavans (2010), Par exemple), the analysis, cependant, indicates
that several deficits, among them the assumption that all nodes are part of (scientific) commu-
nités, cannot be overcome by choosing (plus) appropriate data models.
Études scientifiques quantitatives
1074
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
7. CONCLUSIONS
None of the four analyzed algorithms is able to reconstruct topics as defined in the context of
the sociology of science. One or more properties of each algorithm do not match the proper-
ties of topics derived from my definition. As the criteria cannot be weighted, I cannot conclude
a ranking of the algorithms’ suitability for topic reconstruction. Plutôt, I could provide a frame-
work on which future research can build to accumulate knowledge on what a particular
choice of algorithm means for a bibliometric application. For the task of topic reconstruction,
this analysis helps to guide the further search for the most suitable algorithms. Encore, a lot of work
is still ahead of us, such that we can expect to reconstruct meaningful representations of topics.
On the technical side, we need algorithms that are specifically developed to better match the
properties of topics and where community definitions are inscribed that are related to actual
scientific communities associated with topics, which brings me to necessary knowledge from
the sociology of science. I would like to use the argument of Lievrouw of coming back to the
communication processes behind the bibliometric networks and the definition of topics as
shared frames of reference. If we, Par exemple, understood the communication processes of
researchers who focus on a method topic in a field, we could learn something from contrasting
these with communication processes associated with a different topic type. Knowledge about
these topic types can only be acquired by analyzing the research and communication behav-
ior of the researchers themselves. Only then can the bibliometric traces of these topics in the
publications be identified and more suitable algorithms found or developed to reconstruct
these traces.
What could be learned from this analysis of the four algorithms is that each represents a
general-purpose algorithm that makes certain assumptions on the input and optimizes a spe-
cific mathematical quantity. These are developed independently of specific applications.
Translating the assumptions of the algorithms and the optimization functions seems to be a
difficult task, yet an absolutely necessary one for scientific work. It is our job in a field of appli-
cation to do the “translation task” from the “world of algorithms,” where often algorithms are
(only) tested for performance (speed) and a certain (mathematical) quality measure, into the
world of application, with its specific necessities. When we as bibliometricians apply an algo-
rithm to a network with the goal to reconstruct topics, the in-built definitions of communities of
the algorithms need to be understood, as well as the intricacies of the chosen data model and
its interaction with the algorithm (such as the role of review papers in the network and influ-
ence on the communities searched for).
I have shown that each algorithm comes from a different tradition and uses different
(implicit) definitions of a community in a network. None of these definitions appears to fit
the diversity of dense communication structures occurring in science. This diversity can only
be reconstructed with a more differentiated approach, accounting for the different topic types
that form in science and the associated communication.
Thinking in terms of analyzing algorithms before using them, which has been done here,
helped to learn about the assumptions and properties of algorithms, as using a tool without
knowing how it is working and what it is for will very likely create biased results.
Future work could also start exploring other local algorithms which explore the network
entirely (or mostly) locally, as this has been largely neglected so far. These local algorithms,
like OSLOM, focus on finding network communities around specified seed nodes, thus natu-
rally capturing the “perspectives” of individual nodes and yielding overlapping structures.
Jeub, Balachandran et al. (2015) provide a general argument for that (see also Schaub,
Delvenne et al. (2017, p. 5)), which might be in line with the local nature of topics.
Études scientifiques quantitatives
1075
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
REMERCIEMENTS
I am grateful for the fruitful comments of two anonymous reviewers. En outre, I acknowl-
edge support by the German Research Foundation and the Open Access Publication Fund of
TU Berlin.
COMPETING INTERESTS
The author has no competing interests.
INFORMATIONS SUR LE FINANCEMENT
The work of MH was supported by the German Ministry of Education and Research (Grant
16PU17003).
DATA AVAILABILITY
This study did not use any data.
RÉFÉRENCES
Ahn, Y.-Y., Bagrow, J.. P., & Lehmann, S. (2010). Link communities reveal
multiscale complexity in networks. Nature, 466(7307), 761–764.
https://doi.org/10.1038/nature09182, PubMed: 20562860
Aldecoa, R., & Marín, je. (2013). Exploring the limits of community
detection strategies in complex networks. Rapports scientifiques, 3(1),
2216. https://doi.org/10.1038/srep02216, PubMed: 23860510
Amsterdamska, O., & Leydesdorff, L. (1989). Citations: Indicators of
significance? Scientometrics, 15(5–6), 449–471. https://doi.org
/10.1007/BF02017065
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E.
(2008). Fast unfolding of communities in large networks. Journal
of Statistical Mechanics: Theory and Experiment, 2008(10),
P10008. https://doi.org/10.1088/1742-5468/2008/10/P10008
Bohlin, L., Edler, D., Lancichinetti, UN., & Rosvall, M.. (2014). Com-
munity detection and visualization of networks with the map
equation framework. In Y. Ding, R.. Rousseau, & D. Wolfram
(Éd.), Measuring scholarly impact (pp. 3–34). Springer Interna-
tional Publishing. https://doi.org/10.1007/978-3-319-10377-8_1
Boyack, K. W., & Klavans, R.. (2010). Co-citation analysis, biblio-
graphic coupling, and direct citation: Which citation approach
represents the research front most accurately? Journal of the
American Society for Information Science and Technology, 61(12),
2389–2404. https://doi.org/10.1002/asi.21419
Boyack, K. W., & Klavans, R.. (2014). Including cited non-source
items in a large-scale map of science: What difference does it
make? Journal of Informetrics, 8(3), 569–580. https://est ce que je.org/10
.1016/j.joi.2014.04.001
Chubin, D. E. (1976). The conceptualization of scientific speciali-
liens. Sociological Quarterly, 17(4), 448–476. https://est ce que je.org/10
.1111/j.1533-8525.1976.tb01715.x
Colavizza, G., Costas, R., Traag, V. UN., Van Eck, N. J., van Leeuwen,
T., & Waltman, L. (2021). A scientometric overview of CORD-19.
PLOS ONE, 16(1), e0244839. https://doi.org/10.1371/journal
.pone.0244839, PubMed: 33411846
Colavizza, G., Franssen, T., & van Leeuwen, T. (2019). An empiri-
cal investigation of the tribes and their territories: Are research
specialisms rural and urban? Journal of Informetrics, 13(1),
105–117. https://doi.org/10.1016/j.joi.2018.11.006
Cole, S. (1983). The hierarchy of the sciences? American Journal of
Sociology, 89(1), 111–139. https://doi.org/10.1086/227835
Cozzens, S. E. (1985). Using the archive: Derek Price’s theory of
differences among the sciences. Scientometrics, 7(3), 431–441.
https://doi.org/10.1007/BF02017159
Dao, V.-L., Bothorel, C., & Lenca, P.. (2020). Community structure:
A comparative evaluation of community detection methods. Net-
work Science, 8(1), 1–41. https://doi.org/10.1017/nws.2019.59
Edge, D. (1979). Quantitative measures of communication in science:
A critical review. History of Science, 17(2), 102–134. https://doi.org
/10.1177/007327537901700202, PubMed: 11610633
Edge, D., & Mulkay, M.. J.. (1976). Astronomy transformed: Le
emergence of radio astronomy in Britain. John Wiley & Fils, Inc.
Esquivel, UN. V., & Rosvall, M.. (2011). Compression of flow can reveal
overlapping-module organization in networks. Physical Review X,
1(2), 021025. https://doi.org/10.1103/PhysRevX.1.021025
Estrada, E. (2007). Topological structural classes of complex net-
travaux. Physical Review E, 75(1), 016103. https://est ce que je.org/10
.1103/PhysRevE.75.016103, PubMed: 17358220
Evans, T. S., & Lambiotte, R.. (2009). Line graphs, link partitions, et
overlapping communities. Physical Review E, 80(1), 016105.
https://doi.org/10.1103/ PhysRevE.80.016105, PubMed:
19658772
Fagnan, J., Zaiane, O., & Barbosa, D. (2014). Using triads to iden-
tify local community structure in social networks. Dans 2014
IEEE/ACM International Conference on Advances in Social Net-
works Analysis and Mining (ASONAM 2014) (pp. 108–112).
https://doi.org/10.1109/ASONAM.2014.6921568
Fanelli, D., & Glänzel, W. (2013). Bibliometric evidence for a hier-
archy of the sciences. PLOS ONE, 8(6), e66938. https://doi.org
/10.1371/journal.pone.0066938, PubMed: 23840557
Fortunato, S. (2010). Community detection in graphs. Physics Reports,
486(3), 75–174. https://doi.org/10.1016/j.physrep.2009.11.002
Fortunato, S., & Hric, D. (2016). Community detection in networks:
A user guide. Physics Reports, 659, 1–44. https://est ce que je.org/10.1016
/j.physrep.2016.09.002
Glänzel, W., & Thijs, B. (2017). Using hybrid methods and “core
documents” for the representation of clusters and topics: Le
astronomy dataset. Scientometrics, 111(2), 1071–1087. https://
doi.org/10.1007/s11192-017-2301-6
Gläser, J., Glänzel, W., & Scharnhorst, UN. (2017). Same
data—Different results? Towards a comparative approach to the
Études scientifiques quantitatives
1076
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
identification of thematic structures in science. Scientometrics,
111(2), 981–998. https://doi.org/10.1007/s11192-017-2296-z
Griffiths, T. L., & Steyvers, M.. (2004). Finding scientific topics. Proceed-
ings of the National Academy of Sciences, 101(Supplement 1),
5228–5235. https://doi.org/10.1073/pnas.0307752101, PubMed:
14872004
Hamann, M., Röhrs, E., & Wagner, D. (2017). Local community
detection based on small cliques. Algorithms, 10(3), 90. https://
doi.org/10.3390/a10030090
Havemann, F., Gläser, J., & Heinz, M.. (2017). Memetic search
for overlapping topics based on a local evaluation of link com-
munities. Scientometrics, 111(2), 1089–1118. https://est ce que je.org/10
.1007/s11192-017-2302-5
Havemann, F., Gläser, J., & Heinz, M.. (2019). Communities as
well separated subgraphs with cohesive cores: Identification
of core-periphery structures in link communities. In L. Aiello,
C. Cherifi, H. Cherifi, R.. Lambiotte, P.. Lió, & L. Rocha (Éd.),
Complex networks and their applications VII. COMPLEX
NETWORKS 2018. Studies in Computational Intelligence,
vol. 812. Springer, Cham. https://doi.org/10.1007/978-3-030
-05411-3_18
Détenu, M., Laudel, G., & Gläser, J.. (2021). Challenges to the validity
of topic reconstruction. Scientometrics, 126, 4511–4536. https://
doi.org/10.1007/s11192-021-03920-3
Détenu, M., & Velden, T. (2019). How to interpret algorithmically
constructed topical structures of research specialties? A case
study comparing an internal and an external mapping of the
topical structure of invasion biology. In Proceedings of the
International Conference on Scientometrics and Informetrics
(pp. 1933–1939).
Détenu, M., & Velden, T. (2022). How to interpret algorithmically
constructed topical structures of scientific fields? A case study
of citation-based mappings of the research specialty of invasion
biology. Études scientifiques quantitatives, 1–21. https://est ce que je.org/10
.1162/qss_a_00194
Huang, J., Sun, H., Liu, Y., Song, Q., & Weninger, T. (2011).
Towards online multiresolution community detection in large-
scale networks. PLOS ONE, 6(8), e23829. https://est ce que je.org/10
.1371/journal.pone.0023829, PubMed: 21887325
Jeub, L. G. S., Balachandran, P., Porter, M.. UN., Mucha, P.. J., &
Mahoney, M.. W. (2015). Think locally, act locally: Detection
of small, medium-sized, and large communities in large net-
travaux. Physical Review E, 91(1), 012821. https://est ce que je.org/10
.1103/PhysRevE.91.012821, PubMed: 25679670
Kawamoto, T., & Rosvall, M.. (2015). Estimating the resolution limit
of the map equation in community detection. Physical Review E,
91(1), 012809. https://doi.org/10.1103/ PhysRevE.91.012809,
PubMed: 25679659
Kiss, je. Z., Broom, M., Craze, P.. G., & Rafols, je. (2010). Can epi-
demic models describe the diffusion of topics across disciplines?
Journal of Informetrics, 4(1), 74–82. https://doi.org/10.1016/j.joi
.2009.08.002
Klavans, R., & Boyack, K. W. (2011). Using global mapping to
create more accurate document-level maps of research fields.
Journal of the American Society for Information Science and
Technologie, 62(1), 1–18. https://doi.org/10.1002/asi.21444
Kuhn, T. (2012). The structure of scientific revolutions. Université de
Chicago Press. (Original work published 1962). https://est ce que je.org/10
.7208/chicago/9780226458144.001.0001
Lancichinetti, UN., Radicchi, F., Ramasco, J.. J., & Fortunato, S.
(2011). Finding statistically significant communities in networks.
PLOS ONE, 6(4), e18961. https://doi.org/10.1371/journal.pone
.0018961, PubMed: 21559480
Lievrouw, L. UN. (1989). The invisible college reconsidered: Biblio-
metrics and the development of scientific communication theory.
Communication Research, 16(5), 615–628. https://est ce que je.org/10
.1177/009365089016005004
Nagi, S. Z., & Corwin, R.. G. (1972). The research enterprise: Un
overview. In The social contexts of research (pp. 1–27). Londres:
Wiley-Interscience.
Newman, M.. E. J.. (2012). Communities, modules and large-scale
structure in networks. Nature Physics, 8(1), 25–31. https://est ce que je
.org/10.1038/nphys2162
Peixoto, T. P.. (2019). Bayesian stochastic blockmodeling. In P.
Doreian, V. Batagelj, & UN. Ferligoj (Éd.), Advances in network
clustering and blockmodeling (pp. 289–332). John Wiley & Fils,
Inc. https://doi.org/10.1002/9781119483298.ch11
Reid, F., McDaid, UN., & Hurley, N. (2013). Partitioning breaks
communautés. In Mining social networks and security informatics
(pp. 79–105). Springer. https://doi.org/10.1007/978-94-007
-6359-3_5
Rosvall, M., Axelsson, D., & Bergstrom, C. T. (2009). The map
equation. The European Physical Journal Special Topics, 178(1),
13–23. https://doi.org/10.1140/epjst/e2010-01179-1
Rosvall, M., & Bergstrom, C. T. (2008). Maps of random walks on
complex networks reveal community structure. Proceedings of
the National Academy of Sciences, 105(4), 1118–1123. https://
doi.org/10.1073/pnas.0706851105, PubMed: 18216267
Rosvall, M., & Bergstrom, C. T. (2011). Multilevel compression of
random walks on networks reveals hierarchical organization in
large integrated systems. PLOS ONE, 6(4), e18209. https://est ce que je
.org/10.1371/journal.pone.0018209, PubMed: 21494658
Schaub, M.. T., Delvenne, J.-C., Rosvall, M., & Lambiotte, R.. (2017).
The many facets of community detection in complex networks.
Applied Network Science, 2(1), 1–13. https://doi.org/10.1007
/s41109-017-0023-6, PubMed: 30533512
Sjögårde, P., & Ahlgren, P.. (2018). Granularity of algorithmically
constructed publication-level classifications of research publi-
cations: Identification of topics. Journal of Informetrics, 12(1),
133–152. https://doi.org/10.1016/j.joi.2017.12.006
Petit, H., & Griffith, B. C. (1974). The structure of scientific litera-
tures I: Identifying and graphing specialties. Science Studies, 4(1),
17–40. https://doi.org/10.1177/030631277400400102
Šubelj, L., Van Eck, N. J., & Waltman, L. (2016). Clustering scien-
tific publications based on citation relations: A systematic com-
parison of different methods. PLOS ONE, 11(4), e0154404.
https://doi.org/10.1371/journal.pone.0154404, PubMed:
27124610
Sugimoto, C. R., & Weingart, S. (2015). The kaleidoscope of disci-
plinarity. Journal of Documentation, 71(4), 775–794. https://est ce que je
.org/10.1108/JD-06-2014-0082
Sullivan, D., Blanc, D. H., & Barboni, E. J.. (1977). Co-citation anal-
yses of science: An evaluation. Social Studies of Science, 7(2),
223–240. https://doi.org/10.1177/030631277700700205
Tibély, G. (2011). Mesoscopic structure of complex networks.
https://repozitorium.omikk.bme.hu/ bitstream/ handle/10890
/1094/ertekezes.pdf
Tibély, G. (2012). Criterions for locally dense subgraphs. Physica A:
Statistical Mechanics and Its Applications, 391(4), 1831–1847.
https://doi.org/10.1016/j.physa.2011.09.040
Traag, V. UN., Van Dooren, P., & Nesterov, Oui. (2011). Narrow scope
for resolution-limit-free community detection. Physical Review E,
84(1), 016114. https://doi.org/10.1103/ PhysRevE.84.016114,
PubMed: 21867264
Traag, V. UN., Waltman, L., & Van Eck, N. J.. (2019). From Louvain to
Leiden: Guaranteeing well-connected communities. Scientific
Études scientifiques quantitatives
1077
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Know thy tools!
Reports, 9(1), 5233. https://doi.org/10.1038/s41598-019-41695-z,
PubMed: 30914743
van den Besselaar, P., & Heimeriks, G. (2006). Mapping research
topics using word-reference co-occurrences: A method and an
exploratory case study. Scientometrics, 68(3), 377–393. https://
doi.org/10.1007/s11192-006-0118-9
Velden, T., Yan, S., & Lagoze, C. (2017). Mapping the cognitive
structure of astrophysics by infomap clustering of the citation
network and topic affinity analysis. Scientometrics, 111(2),
1033–1051. https://doi.org/10.1007/s11192-017-2299-9
Waltman, L., & Van Eck, N. J.. (2012). A new methodology for con-
structing a publication-level classification system of science.
Journal of the American Society for Information Science and
Technologie, 63(12), 2378–2392. https://doi.org/10.1002/asi
.22748
Whang, J.. J., Gleich, D. F., & Dhillon, je. S. (2013). Overlapping
community detection using seed set expansion. In Proceedings of
the 22nd ACM International Conference on Conference on Informa-
tion & Knowledge Management – CIKM ’13 (pp. 2099–2108).
https://doi.org/10.1145/2505515.2505535
Whitley, R.. (1974). Cognitive and social institutionalization of sci-
entific specialties and research areas. In R. Whitley (Ed.), Social
processes of scientific development (pp. 69–95). Routledge &
Kegan Paul.
Whitley, R.. (1976). Umbrella and polytheistic scientific disciplines
and their elites. Social Studies of Science, 6(3–4), 471–497.
https://doi.org/10.1177/030631277600600309
Whitley, R.. (1977). Changes in the social and intellectual organisa-
tion of the sciences: Professionalisation and the arithmetic ideal.
In The social production of scientific knowledge (pp. 143–169).
Springer. https://doi.org/10.1007/978-94-010-1186-0_7
Wu, P., & Pan, L. (2015). Multi-objective community detection based
on memetic algorithm. PLOS ONE, 10(5), e0126845. https://est ce que je
.org/10.1371/journal.pone.0126845, PubMed: 25932646
Lequel, J., & Leskovec, J.. (2014). Structure and overlaps of ground-
truth communities in networks. ACM Transactions on Intelligent
Systems and Technology, 5(2), 1–35. https://doi.org/10.1145
/2594454
Yau, C.-K., Porter, UN., Newman, N., & Suominen, UN. (2014). Clus-
tering scientific documents with topic modeling. Scientometrics,
100(3), 767–786. https://doi.org/10.1007/s11192-014-1321-8
Zuckermann, H., & Merton, R.. K. (1973). Age, aging and age
structure in science. In N. Storer (Ed.), The sociology of science
(pp. 497–559). University of Chicago Press.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
5
4
2
0
7
0
7
5
1
q
s
s
_
un
_
0
0
2
1
7
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Études scientifiques quantitatives
1078