ARTICLE DE RECHERCHE - Recherche en IA spécialisée au MIT

ARTICLE DE RECHERCHE

Further improvements on estimating the
popularity of recently published papers

Serafeim Chatzopoulos1,2

, Thanasis Vergoulis2

, Ilias Kanellos2

Theodore Dalamagas2

, and Christos Tryfonopoulos1

1Department of Informatics and Telecommunications, University of the Peloponnese, Tripolis, Grèce
2Information Management Systems Institute (IMSI), “Athena” Research Center, Athens, Grèce

Mots clés: scientific impact assessment, scholarly knowledge graphs

ABSTRAIT

As the number of published scientific papers continually increases, the ability to assess their
impact becomes more valuable than ever. In this work, we focus on the problem of estimating
the expected citation-based popularity (or short-term impact) of papers. State-of-the-art
methods for this problem attempt to leverage the current citation data of each paper. Cependant,
these methods are prone to inaccuracies for recently published papers, which have a limited
citation history. In this context, we previously introduced ArtSim, an approach that can
be applied on top of any popularity estimation method to improve its accuracy. Its power
originates from providing more accurate estimations for the most recently published papers
by considering the popularity of similar, older ones. In this work, we present ArtSim+,
an improved ArtSim adaptation that considers an additional type of paper similarity and
incorporates a faster configuration procedure, resulting in improved effectiveness and
configuration efficiency.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

INTRODUCTION

With the growth rate of scientific articles (also known as papers) continually increasing (Larsen
& von Ins, 2010), the reliable assessment of their scientific impact is now more valuable than
jamais. Par conséquent, a variety of impact measures have been proposed, aiming to quantify
scientific impact at the paper level. Such measures have various practical applications:
par exemple, they can be used to rank the results of keyword-based searches (par exemple., Vergoulis,
Chatzopoulos et al., 2019), facilitating literature exploration and reading prioritization, or to
assist the comparison and monitoring of the impact of different research projects, institutions,
or researchers (par exemple., Papastefanatos, Papadopoulou et al., 2020).

Because scientific impact can be defined in many, diverse ways (Bollen, Van de Sompel
et coll., 2009), the proposed measures vary in terms of the approach they follow (par exemple.,
citation-based, altmetrics), as well as in the aspect of scientific impact they attempt to capture
(par exemple., impact in academia, social media attention). In this work, we focus on citation-based
measures that attempt to estimate the expected scientific impact of each paper in the near
avenir (c'est à dire., its current popularity). Providing accurate estimations of paper popularity is an
open problem, as indicated by a recent extensive experimental evaluation (Kanellos, Vergoulis
et coll., 2021un). En outre, popularity distinctly differs from the overall (long terme) impact of a
paper that is usually captured by traditional citation-based measures (par exemple., citation count).

un accès ouvert

journal

Citation: Chatzopoulos, S., Vergoulis,
T., Kanellos, JE., Dalamagas, T., &
Tryfonopoulos, C. (2021). Plus loin
improvements on estimating the
popularity of recently published
papers. Études scientifiques quantitatives,
2(4), 1529–1550. https://est ce que je.org/10.1162
/qss_a_00165

EST CE QUE JE:
https://doi.org/10.1162/qss_a_00165

Auteur correspondant:
Serafeim Chatzopoulos
schatzop@uop.gr

droits d'auteur: © 2021 Serafeim
Chatzopoulos, Thanasis Vergoulis, Ilias
Kanellos, Theodore Dalamagas, et
Christos Tryfonopoulos. Published
under a Creative Commons Attribution
4.0 International (CC PAR 4.0) Licence.

La presse du MIT

Further improvements on estimating the popularity of recently published papers

One important issue in estimating paper popularity is to provide accurate estimations for
the most recently published papers. The estimations of most popularity measures rely on the
existing citation history of each paper. Cependant, as very limited citation history data are avail-
able for recent papers, their impact estimation based on these data is prone to inaccuracies.
Ainsi, these measures fail to provide accurate estimations for recent papers. To alleviate this
issue, in Chatzopoulos, Vergoulis et al. (2020) we introduced ArtSim, an approach that can be
applied on top of any existing popularity estimation method to improve its accuracy. ArtSim
does not only rely on each paper’s citation history data but also considers the history of older,
similar papers, for which these data are more complete. The intuition behind the approach is that
similar papers (par exemple., having similar topics and/or author lists) are likely to have similar popularity
dynamics. To quantify paper similarity, ArtSim exploits author lists and the involved topics,
based on data that can be easily found in scholarly knowledge graphs, a large variety of which
has been made available in recent years (par exemple., AMiner’s DBLP-based data sets (Tang, Zhang
et coll., 2008), the Open Research Knowledge Graph (Jaradeh, Oelen et al., 2019), the OpenAIRE
Research Graph (Manghi, Atzori et al., 2019un; Manghi, Bardi et al., 2019b)).

Our experiments showed that ArtSim effectively enhances the performance of traditional
methods in estimating article popularity. Cependant, at the same time, we found that there was
room for further improvements. In this context, we extended ArtSim and produced an
improved version called ArtSim+. This new approach maintains all the benefits of ArtSim
and introduces two main improvements: (un) it takes into consideration an additional type of
paper similarities, based on their publication venues, et (b) it leverages a more efficient and
more effective configuration procedure based on the technique of generalized simulated
annealing. To evaluate ArtSim+’s performance, we reproduce the most important of our pre-
vious experiments and we extend them by investigating the effect on an additional popularity
estimation method. En outre, we conduct thorough experiments to showcase the effects of
the new configuration procedure. Enfin, we provide both ArtSim and ArtSim+ implemen-
tations as open source code under a GNU/GPL license1.

2. BACKGROUND

2.1. Preliminaries

In this work, we focus on approaches that aim at estimating the citation-based popularity of
scientific papers. En général, citation-based measures are defined and calculated on top of the
citation network, c'est, the directed graph of all papers (nodes) along with their citations
(edges); each directed edge i → j, with i and j being nodes of the graph, denotes that paper
i cites paper j. This information is usually encoded in the citation network’s adjacency matrix
UN, where A[je, j] = 1 if a paper j cites paper i and A[je, j] = 0, otherwise.

For popularity, we adopt the definition given in Kanellos et al. (2021un). According to this,
popularity at current time tc can only be accurately quantified a posteriori, when papers
receive citations as a result of being currently studied. Because citation networks evolve over
temps, we define the adjacency matrix at time tc as A(tc). Given a parameter T, which denotes a
future time window, we can define adjacency matrix A(tc + T ) − A(tc), which describes the
citation network containing only the citations made in the time span [tc, tc + T]. The popularity
of papers is then given by the citation count based on A(tc + T ) − A(tc). It is worth mentioning
that T is a problem parameter, which depends on various factors, such as the publication life
cycle in a particular scientific discipline (manuscript writing, peer-review, publication).

1 https://github.com/schatzopoulos/ArtSim

Études scientifiques quantitatives

1530

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

Chiffre 1. A scholarly knowledge graph including papers, authors, venues, and topics.

Our proposed approach to estimate popularity is based on exploiting path-based similarities of
papers that can be calculated using scholarly knowledge graphs. Knowledge graphs, also known
as heterogeneous information networks (Shi, Li et al., 2017), are graphs that encode rich domain-
specific information about various types of entities, represented as nodes, and the relationships
between them, represented as edges. Chiffre 1 presents an example of such a knowledge graph,
consisting of nodes representing papers (P.), authors (UN), venues (V), and topics (T). Three types of
(bidirectional) edges are present in this example network: edges between authors and papers,
denoted as AP or PA, edges between papers and topics, denoted as PT or TP, and edges between
papers and venues, denoted as PVor VP. The first edge type captures the authorship of papers, le
second one encodes the information that a particular paper is written on a particular topic, alors que
the last one captures the fact that a paper has been published in a particular venue.

Various semantics are implicitly encoded in the paths (c'est à dire., edge/node sequences) of knowl-
edge graphs. En fait, all paths that correspond to the same sequence of node and edge types
(c'est à dire., the same metapath (Sun, Han et al., 2011b)) encode latent relationships of the same inter-
pretation between the starting and ending nodes. Metapaths can be represented by the
sequence of the respective node and edge types but, for the sake of simplifying the notation,
it is usually assumed (Shi, Li et al., 2016un; Sun et al., 2011b) that there is at most one type of
edges between any pair of node types in the HIN, thus each metapath is denoted by the
sequence of the respective node types. Par exemple, in the graph of Figure 1, the metapath
Author – Paper – Topic – Paper – Author, or APTPA for brevity, relates two authors that
have published works in the same topic (par exemple., both ‘John Doe’ and ‘Henry Jekyll’ have
papers about ‘DL’). Metapaths are useful for many graph analysis and exploration applica-
tion. Par exemple, in our approach, we use them to calculate metapath-based similarities: le
similarity between two nodes of the same type, based on the semantics of a given metapath,
can be captured by considering the number of instances of this metapath connecting these
nodes (par exemple., Sun et al., 2011b; Xiong, Zhu, & Yu, 2015).

2.2. Related Work

2.2.1. Methods to estimate scientific impact

There is a lot of work in the areas of bibliometrics and scientometrics to quantify the impact of
scientific articles. Much focus was been on methods to calculate variations of the citation

Études scientifiques quantitatives

1531

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

counts and PageRank. The latter algorithm, although originally introduced to evaluate the
importance of Web pages, has been successfully adapted and applied to citation networks
providing insights about the scientific impact of papers (Chen, Xie et al., 2007). En outre,
it has additionally spawned a separate line of work that aims at improving it when applied on
citation networks (Mariani, Medo, & Zhang, 2016; Su, Pan et al., 2011; Vaccario, Medo et al.,
2017; Zhou, Zheng et al., 2016). However these works focus on capturing the overall impact
of papers, instead of their expected short-term impact (or popularity) (Ghosh, Kuo et al., 2011;
Sayyadi & Getoor, 2009; Walker, Xie et al., 2007). This is an interesting problem, as on the one
hand this problem has been shown to have a more pronounced improvement margin (Kanellos
et coll., 2021un), and on the other hand it corresponds to important real application scenarios:
Researchers using search engines to find papers in their scientific fields would benefit from a
popularity-based ranking to find the current and most recent research trends. In-depth exam-
inations of various impact measures that have been proposed in the relevant literature can be
found in Kanellos et al. (2021un) and Bai, Liu et al. (2017). In contrast to these methods, ArtSim
and ArtSim+, our approaches, do not aim to introduce a new popularity measure but rather aim
to improve the accuracy of existing ones.

2.2.2. ArtSim

In previous work (Chatzopoulos et al., 2020), we introduced ArtSim, an approach that can be
applied on top of any popularity estimation method to improve its accuracy. Its power origi-
nates from providing better estimations for most of the recently published papers by finding
older papers that are similar to them, and considering their average popularity. The intuition is
that older papers have a more complete citation track and that similar papers are likely to
follow a similar trajectory in terms of popularity. To quantify paper similarity, ArtSim exploits
the corresponding author lists and the involved topics. This information is available in schol-
arly knowledge graphs, a large variety of which have been made available in recent years.

2.2.3.

Entity similarity in HINs

Both ArtSim+ and its predecessor are built upon recent work on entity similarity in the area of
heterogeneous information networks. Some of the first entity similarity approaches for such
réseaux (par exemple., PopRank (Nie, Zhang et al., 2005) and ObjectRank (Balmin, Hristidis, &
Papakonstantinou, 2004)) are based on random walks. Later works, such as PathSim (Sun
et coll., 2011b), focus on providing more meaningful results by calculating node similarity mea-
sures based on user-defined semantics. Our work is based on JoinSim (Xiong et al., 2015), which is
more efficient compared to PathSim, making it more suitable for analyses on large-scale networks.

3. ARTSIM+

3.1. Basic Approach
Like its predecessor, ArtSim+ can be applied on top of any popularity measure to increase
the accuracy of its estimations. En tant que tel, ArtSim+ takes the scores calculated by any popu-
larity method as input, applies transformations on them, and produces a new set of improved
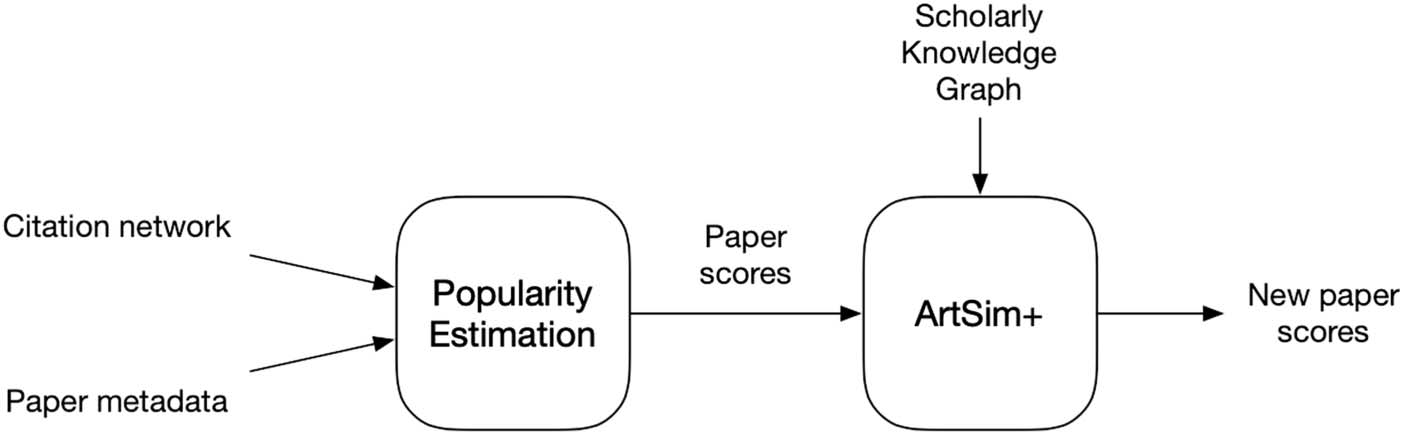
popularity scores. This process is illustrated in Figure 2.

The transformations applied on popularity scores by ArtSim+, rely on the assumption that
similar articles are expected to share similar popularity dynamics. To calculate the similarity
between different papers, ArtSim+ relies on a scholarly knowledge graph that contains infor-
mation about papers, authors, venues, and topics, as well as connections between them (like
the one presented in Figure 1). On a knowledge graph of such a schema, it is possible to define

Études scientifiques quantitatives

1532

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

Chiffre 2. Our proposed approach.

paper similarity according to various semantics using the JoinSim (Xiong et al., 2015) similarité
measure calculated on different metapaths (see Section 2.1 for details). ArtSim+ considers
paper similarity according to the Paper – Author – Paper (PAP), Paper – Topic –
Paper (PTP), and Paper – Venue – Paper (PVP) metapaths. The PAP metapath defines
the similarity of papers according to their common authors, the PTP metapath defines similar-
ity based on their common topics, and the PVP metapath is based on their venue. ArtSim+
uses the calculated similarity scores to provide improved popularity estimates (scores),
focusing, in particular, on recent papers that have a limited citation history (c'est à dire., those that
are going through their cold start period ). The calculation of ArtSim+ scores is based on
the following formula:

(cid:1)

S pð Þ ¼

un (cid:2) SPAP pð Þ þ β (cid:2) SPTP pð Þ þ γ (cid:2) SPVP þ δ (cid:2) Si pð Þ; p:year > tc −y
Si pð Þ;

otherwise

where SPAP, SPTP, and SPVP are the average popularity scores of all the articles that are similar to
p, based on metapaths PAP, PTP, and PVP respectively. Si is the initial popularity score of
paper p based on the original popularity measure and tc denotes the current year. Enfin,
our method applies transformations on popularity scores for those papers published in years
that range in the time span (tc − y, tc], where y > 0.

3.2.

Improving Method Configuration

ArtSim+ depends on parameters α, β, c, d 2 [0, 1], the values of which are set so that α + β +
c + δ = 1. Varying these parameters in the range [0, 1] has the following effects: As α increases,
ArtSim+ score mostly depends on similar articles based on common authors. De la même manière, as β
and γ increase, the score is mainly based on similar articles based on common topics and
venues, respectivement. Enfin, as δ approaches 1 the popularity scores remain identical to those
calculated by the original popularity measure.

To determine the best configuration of our approach, an exhaustive “grid” search of the
parameter space can be performed. The original version of ArtSim (Chatzopoulos et al.,
2020) follows this approach, but the same technique can be applied on any possible ArtSim
adaptation incorporating different types of metapaths. Cependant, grid search can be highly
inefficient; in practice, the efficiency of such a search depends on the number of parameters
to be determined and the granularity of the examined grid. Ainsi, in the case of a method with
a large number of parameters (such as ArtSim+) the corresponding search grid could be
really large, resulting in a time-consuming process. To counterbalance this problem a
coarse-grained grid search could be performed. Cependant, this would run the risk of missing
the optimal configuration.

Études scientifiques quantitatives

1533

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

To alleviate this issue, we propose the use of the Generalized Simulated Annealing (GSA) (Tsallis
& Stariolo, 1996; Xiang, Sun et al., 1997) algorithm to search the parameter space for the optimal
configuration instead of performing a full grid search. GSA is a search algorithm that can be used to
approximate the optimal parameter values for an optimization problem (par exemple., to find the parame-
ters of ArtSim+ that achieve the best accuracy). It combines the approach of Simulated Annealing
(SA) (Kirkpatrick, Gelatt, & Vecchi, 1983) with that of Fast Simulated Annealing (FSA) (Szu &
Hartley, 1987). SA is a traditional search algorithm that combines hill climbing with a random
search mechanism, accepting not only changes that improve the objective function but also
underperforming ones with a certain probability. Cependant, SA employs a local visiting distribution
(Gaussian) so that the majority of the search is confined in certain regions of the search space. Pour
this reason, Fast Simulated Annealing (FSA) was introduced. FSA utilizes a semilocal distribution
(Cauchy-Lorentz) traversing the search space more efficiently, but it can still be trapped in local
optima (Xiang & Gong, 2000). GSA achieves faster convergence and higher probability to find the
global optimal (Xiang & Gong, 2000), outperforming SA and FSA. It utilizes a distorted Cauchy-
Lorentz distribution controlled by parameter qv, while its acceptance probability depends on the
acceptance parameter qα (Xiang, Gubian et al., 2013). GSA searches the space more uniformly
than its competitors, with the difference in performance being more prominent as the number
of variables of the objective function increases (Xiang & Gong, 2000).

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

4. EVALUATION

Dans cette section, we discuss the experiments conducted to assess the effectiveness of our
method. En particulier, we first elaborate on the experimental setup (Section 4.1). Alors, dans
Section 4.2, we provide our findings regarding the effectiveness of ArtSim+ in improving
the accuracy of various state-of-the-art popularity estimation methods. During this experiment
we also compare ArtSim+ to ArtSim (Chatzopoulos et al., 2020), its predecessor, show-
casing the superior performance of the current approach. Enfin, in Section 4.3 we discuss
the efficiency and effectiveness gains introduced to ArtSim+ due to the improved config-
uration process described in Section 3.2.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

4.1. Experimental Setup

4.1.1. Data sets

For our experiments, we used the following data sets:

(cid:129) DBLP Scholarly Knowledge Graph (DSKG) data set. This contains data for 3,079,008 com-
puter science papers, 1,766,548 authors, 5,079 venues and 3,294 topics from DBLP. C'est
based on AMiner’s citation network data set (Tang et al., 2008) enriched with topics from the
CSO Ontology (Salatino, Thanapalasingam et al., 2018). The topics have been assigned to
each paper by applying the CSO Classifier (Salatino, Osborne et al., 2019) to its abstract.
(cid:129) DBLP Article Similarities (DBLP-ArtSim) data set. This contains similarities among papers in
the previous network based on different metapaths. En particulier, we calculated paper sim-
ilarities based on (un) their author list using the Paper – Author – Paper (PAP) metapath,
(b) their common topics, captured by the Paper – Topic – Paper (PTP) metapath, et
(c) their venue, according to the Paper – Venue – Paper (PVP) metapath2. This data set
is openly available on Zenodo3 (Chatzopoulos, Vergoulis et al., 2021) under CC BY 4.0

2 For PAP and PTP all paper pairs with similarities less than 0.2 were dropped; for PVP all pairs with zero

similarity were dropped.

3 https://doi.org/10.5281/zenodo.3778915

Études scientifiques quantitatives

1534

Further improvements on estimating the popularity of recently published papers

license and contains approximately 31 million PAP, 207 million PTP, et 11 billion PVP
metapath instances. It should be noted that the first version of this data set was a contri-
bution of our previous work (Chatzopoulos et al., 2020); the current version of the data set
has been updated to also include the Paper to Venue relationships.

4.1.2.

Evaluation methodology

To assess the accuracy of methods in estimating paper popularity, we follow the experimental
framework proposed in Kanellos et al. (2021un). As discussed in Sections 1 et 2, a paper’s pop-
ularity, by definition, is reflected in the citations it receives in the near future. The aforementioned
framework splits a given citation network data set C into two parts, Cold and Cfuture, according to a
given split time point ts and uses Cold (containing all papers published no later than ts) as input to
the estimation methods, while Cfuture (all papers published between ts and a second given time
point ts + T, with T > 0) is taken as a ground truth. The ground truth is used to calculate, for each
paper published no later than ts, all citations it received during the (ts, ts + T ] period. Alors, the total
orderings (the rankings) of these papers based on these citations are compared with the rankings
provided by each popularity estimation method. The method that produced the most similar
ranking to the ground truth ranking is the one with the most accurate estimations. The ranking
similarities are usually measured using both an overall similarity measure (par exemple., the ranked list
correlation according to Spearman’s ρ or Kendall’s τ), and a top-k similarity measure (par exemple.,
nDCG@k); each type of similarity better fits the need of different applications.

À ce point, it should be highlighted that each popularity estimation method produces its own
measure value for each paper (c'est à dire., its own score), and thus a direct comparison of these scores for
the same paper is not possible; donc, comparing the similarities of the methods’ ranking to the
ground truth ranking to measure each method’s accuracy is an adequate alternative, especially as
most applications only require popularity/impact measures for partial comparisons.

In our experiments, we configured the framework so that ts splits the used citation network
data set into two equally sized (in terms of nodes) réseaux, while T is selected so that Cfuture
contains 30% more papers than Cold. Regarding ranked list similarities, we use Kendall’s τ
(Kendall, 1948) to capture their overall similarity, while we use nDCG@k to capture their
top-k similarity. Kendall’s τ is an overall correlation measure, having values in the [−1, 1]
range, avec 1 and −1 corresponding to a perfect agreement and disagreement, respectivement,
alors que 0 reflects no correlation. nDCG@k, on the other hand, is a measure of ranking quality
that has values in the range [0, 1], avec 1 corresponding to ideal ranking of the top-k elements.

4.1.3. Popularity estimation methods

As mentioned, our approaches (ArtSim and ArtSim+) are used on top of other popularity
estimation methods, resulting in improvements in their estimation accuracy. Ainsi, any exper-
iments should involve at least one popularity method, on top of which ArtSim and ArtSim+
will be applied. In this work, we selected to use four popularity estimation methods that were
found to perform well according to a recent experimental study (Kanellos et al., 2021un). Dans
addition, we have also included AttRank (Kanellos, Vergoulis et al., 2021b), which was found
to outperform the best popularity estimation methods in later experiments. Cependant, this is just
an indicative set of methods: ArtSim and ArtSim+ can be easily applied on top of any other
un. The configurations used for each method (presented in Tables 1 et 2) have been
selected after examining various configurations and selecting the one that achieved the best
result according to the similarity measure (Kendall’s τ or nDCG@k, see also Section 4.1.2)
under consideration.

Études scientifiques quantitatives

1535

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

Tableau 1.

Parameter configuration for each popularity measure for Kendall’s τ

Method
AttRank

ECM

RAM

Configuration

α = 0.2, β = 0.4, c = 0.4, y = 3

α = 0.2, c = 0.4

c = 0.4

α = 0.4, τdir = 10

α = 0.5, β = 0.2, c = 0.3, ρ = −0.42

De plus, for convenience, we briefly describe the intuition behind each method below:

(cid:129) AttRank (Kanellos et al., 2021b) is a PageRank variation that modifies PageRank’s so-
called random jump probability. In AttRank, this probability is not uniform, but results
as a combination of an age-based weight, and a recent attention-based weight. The latter
is determined based on the fraction of total citations received by each paper in recent
années. It uses parameters α, β, c 2 (0, 1), r 2 (−∞, 0), and y. Parameter y denotes the
starting year, onward from which the recent attention is determined. Parameter ρ is
the coefficient of the publication age-based weights, which decrease exponentially
based on age. Parameters α, β, γ are the coefficients of the PageRank calculation, ran-
dom jump probability based on recent attention, and random jump probability based on
publication age, respectivement.

(cid:129) Retained Adjacency Matrix (RAM ) (Ghosh et al., 2011) estimates popularity using a time-
aware adjacency matrix to capture the recency of cited papers. The parameter γ 2 (0, 1)
is used as the basis of an exponential function to scale down the value of a citation link
according to its age.

(cid:129) Effective Contagion Matrix (ECM ) (Ghosh et al., 2011) is an extension of RAM that also
considers the temporal order of citation chains apart from direct links. It uses two param-
eters α, c 2 (0, 1) where α is used to adjust the weight of citation chains based on their
length and γ is the same as in RAM.

(cid:129) CiteRank (CR) (Walker et al., 2007) estimates popularity by simulating the behavior of
researchers searching for new articles. It uses two parameters, un 2 (0, 1) and τdir 2 (0, ∞)
to model the traffic to a given paper. A paper is randomly selected with an exponentially
discounted probability according to its age with τdir being the decay factor. Parameter α

Chiffre 3. Effectiveness of our approach (Kendall’s τ) for each popularity method.

Études scientifiques quantitatives

1536

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

is the probability that a researcher stops her search, avec 1 − α being the probability that
she continues with a reference of the paper she just read.

(cid:129) FutureRank (FR) (Sayyadi & Getoor, 2009) scores are calculated by combining PageRank
with calculations on a bipartite graph with authors and papers, while also promoting
recently published articles with time-based weights. It uses parameters α, β, c 2 (0, 1)
and ρ 2 (−∞, 0); α is the coefficient of the PageRank scores, β is the coefficient of the
authorship scores and γ is the coefficient of time-based weights which decrease expo-
nentially based on the exponent ρ.

4.2. Evaluating the Effectiveness of ArtSim+

In this experiment, we examine the gains introduced by applying ArtSim+ on top of various
popularity estimation methods in terms of their improved estimation accuracy. Based on the
evaluation framework used (see Section 4.1.2), we first evaluate the estimation accuracy in
terms of Kendall’s τ (Section 4.2.1) and then in terms of nDCG@k (Section 4.2.2).

4.2.1.

Improvements in terms of Kendall’s τ

In this experiment, we examine the accuracy of each of the examined popularity estimation
méthodes (AttRank, ECM, RAM, CR, and FR) with and without the assistance of ArtSim and
ArtSim+, in terms of Kendall’s τ, for y 2 {1, 3, 5}. Recall that y is the parameter that deter-
mines which papers are in their “cold start” phase (par exemple., if y = 3, then all papers published
between ts − 2 and ts are considered to be in their cold start phase). All methods were con-
figured based on the parameter settings included in Table 1, ArtSim was configured exactly
as it was in Chatzopoulos et al. (2020), and ArtSim+ was configured based on the outputs of
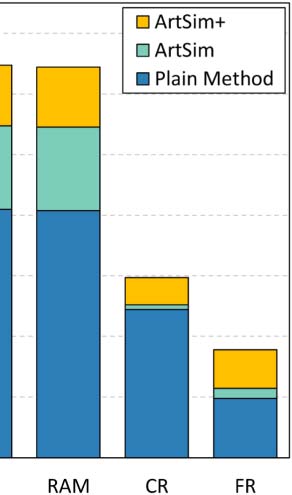
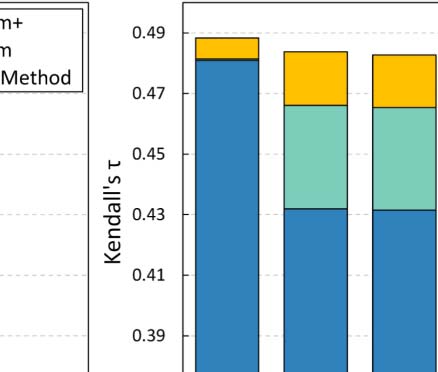
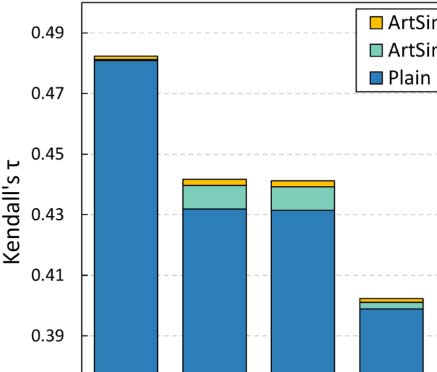
the experiments in Section 4.3. Chiffre 3 summarizes our findings.

Dans l'ensemble, both ArtSim and ArtSim+ introduce accuracy improvements to all popularity
estimation methods. In all cases, ArtSim+ achieves a larger improvement than ArtSim,
something that indicates that considering the venue-based paper similarities (captured by
the PVP metapath) indeed results in improving accuracy. The most significant improvements,
for both ArtSim and ArtSim+, are observed when they are applied on ECM and RAM. Dans
particular, ECM and RAM are improved by 10–12% when applying ArtSim+ over the plain
methods and by 4–5% over ArtSim for y 2 {3, 5}. AttRank, on the other hand, appears to have
significantly smaller gains. The larger gains achieved for RAM and ECM can be explained by
the fact that these methods rely heavily on each paper’s current citations. Ainsi, a large num-
ber of recent papers without any citations, lequel, cependant, are likely to gather citations in the
near future, are ranked at the bottom based on these methods. In contrast, AttRank, CR, and FR
give ranking advantages to papers based on their publication age. Hence the papers that can
benefit from ArtSim/ArtSim+ are already advantaged in part by these methods. It should be
noted that, as expected, smaller gains for all methods are achieved for y = 1. In that case, comme
previously mentioned, our approach affects the popularity score of the papers published only
in the last year, affecting only a small fraction of the overall papers.

4.2.2.

Improvements in terms of nDCG@k

We also examine the accuracy of all estimation methods (with and without the ArtSim/
ArtSim+ assistance) in terms of nDCG@k, for y 2 {1, 3, 5} and k 2 {5, 50, 500 000}. De la même manière
to the experiment in Section 4.2.1, the best configurations for the examined accuracy measure4

4 It should be noted that the corresponding experiments in Chatzopoulos et al. (2020) were conducted using
the best configurations according to Kendall’s τ (c'est à dire., the popularity estimation methods had not been opti-
mized for the nDCG@k experiment).

Études scientifiques quantitatives

1537

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

Method
AttRank

ECM

RAM

Tableau 2.

Parameter configuration for each popularity estimation measure for nDCG@k

k = 5

α = 0.2, β = 0.8, c = 0, y = 1

k = 500
α = 0.2, β = 0.8, c = 0, y = 1

k = 500,000

α = 0, β = 0.7, c = 0.3, y = 1

α = 0.3, c = 0.1

c = 0.1

α = 0.1, τdir = 1

α = 0.3, c = 0.1

c = 0.1

α = 0.2, τdir = 1

α = 1, c = 0.3

c = 0.3

α = 0.4, τdir = 0.8

α = 0.1, β = 0, c = 0.9, ρ = −0.82

α = 1, β = 0, c = 0.9, ρ = −0.62

α = 0.5, β = 0.1, c = 0.4, ρ = −0.42

were selected for ArtSim, ArtSim+, and each estimation method (see also Table 2). Our find-
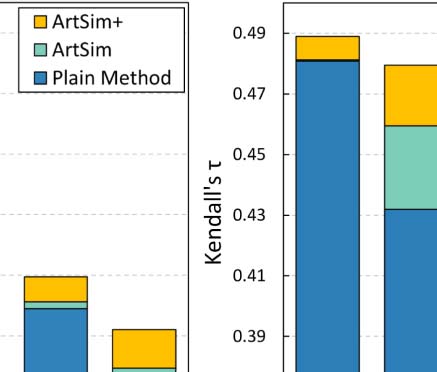
ings are depicted in Figure 4.

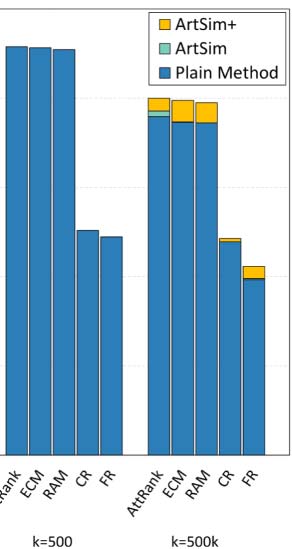
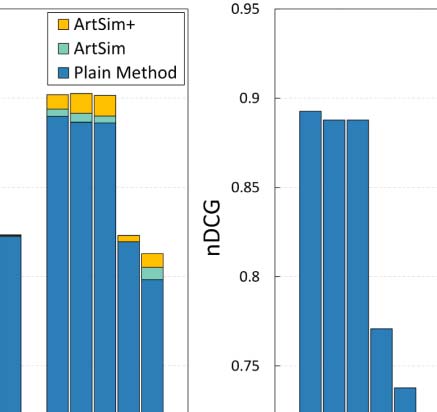
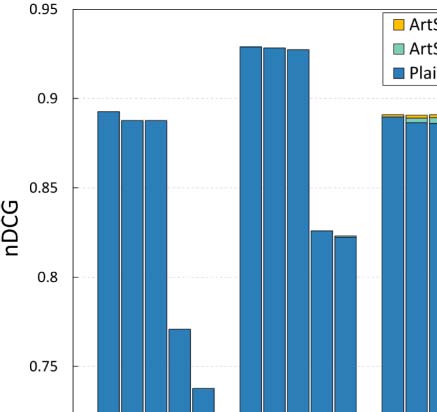
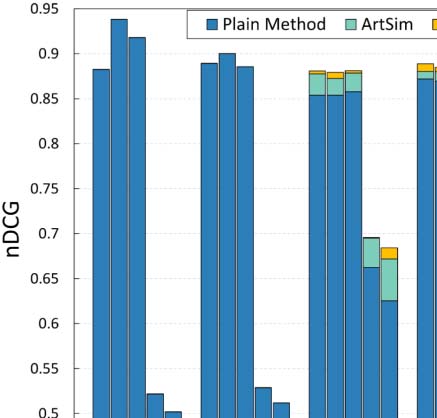
Fait intéressant, for small values of k, our approach performs equally well as the plain popu-
larity estimation methods. This behavior indicates that, at least to some extent, the existing
state-of-the-art methods accurately identify the top popular papers. Another apparent explana-
tion is that, in the case of a small k the set of top-k popular papers at the level of the whole data
ensemble, mainly consists of widely known, fundamental papers that already have a significant
citation trajectory. To put it differently, the percentage of the top-k popular papers that are
going through their cold start period is significantly smaller for small k values (see Table 3).
This characteristic of the small k values was the motivation to also examine the k = 500,000
valeur, apart from k = 5 and k = 500. Going back to our experimental results, it is evident
that the accuracy gains for all popularity estimation methods are indeed more apparent for
k = 500,000.

It may be tempting to think that, although ArtSim+ brings evident accuracy improvements
in terms of Kendall’s τ, it can provide apparent improvements in terms of nDCG@k only for
extremely large k values, which are not relevant to any practical scenario. Although this seems
to be intuitively correct, this rationale does not reflect the truth, because, in practice, the over-
all top-ranking papers may be dominated by particular subfields that are characterized by a
higher citation density, or which gather citations quicker (par exemple., due to large numbers of fre-
quent conferences in the field). Ainsi, the accuracy gains that ArtSim+ brings may be useful
in various real applications involving searches on particular subfields/keywords. To showcase
ce, we also conducted an experiment that replicates a real-world application scenario, that of
literature exploration by a researcher in an academic search engine.

The concept is the following: the users of such search engines usually refine their searches
based on multiple keywords and filters (par exemple., based on the venues of interest or the publication
années) to reduce the number of papers they have to examine. Cependant, even in this case, usu-
ally at least hundreds of papers are contained in the results. Ainsi, effective popularity-based
ranking is crucial to facilitate the reading prioritization. Our experiment involves three indi-
vidual search scenarios. In the first scenario we used the query “expert finding.” This keyword
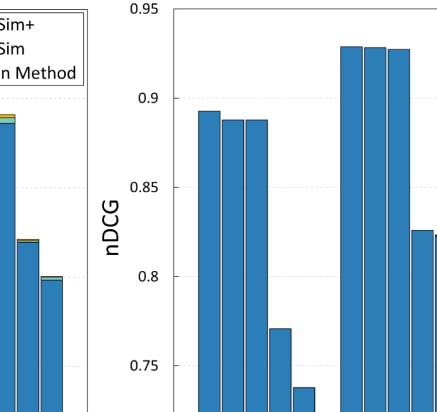
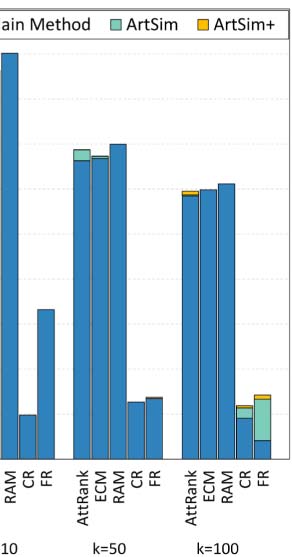
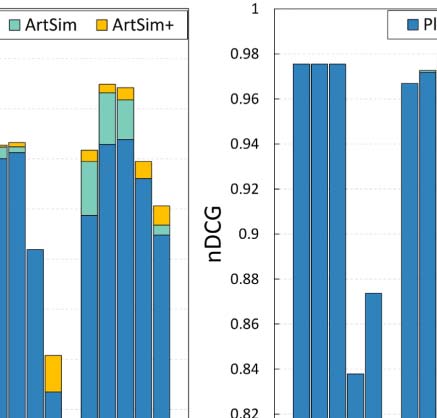
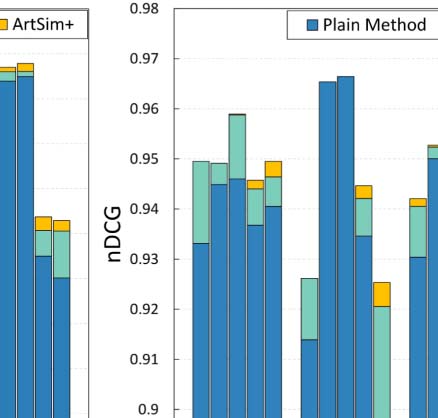
search resulted in a set of 549 articles. Chiffre 5(un) presents the nDCG values for this search, par
popularity estimation method5, along with the gains of ArtSim and ArtSim+ for y = 3. Nous

5 All popularity estimation methods have been configured based on their parameters that achieve the best

nDCG@k values with k = 500,000 for the whole data set.

Études scientifiques quantitatives

1538

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

Chiffre 4. Effectiveness of our approach (nDCG@k) for each popularity estimation method.

observe that ArtSim+ improves the nDCG values for k = 50 and k = 100. In our second sce-
nario, we tried a constrained query. En particulier, we used “recommender systems” as the
search keywords keeping only papers published in well-known venues of data management
and recommender systems, namely VLDB, SIGMOD, TKDE, ICDE, EDBT, RecSym, and ICDM.
The result set includes 318 articles. Chiffre 5(b) presents the nDCG results. We observe that
ArtSim+ boosts nDCG scores for all measures, starting from the smallest value of k = 5.
Enfin, we tried a keyword search with the phrase “digital libraries” that yielded 3,793 articles;
the results are presented in Figure 5(c). Dans ce cas, the benefits are smaller than in the previous
two search scenarios; cependant, we do note that ArtSim and ArtSim+ add improvements to
the nDCG scores at k = 50 and k = 100.

Dans l'ensemble, the results of these keyword search scenarios indicate that in addition to improving
the overall correlation, our approach also offers improvements in the case of practical,
keyword-search based queries with regard to the top returned results. For all the aforemen-
tioned scenarios, the best parameter configuration of ArtSim and ArtSim+ are presented
in Table A3 of the Appendix.

4.3. ArtSim+ Configuration

ArtSim+ has a wide range of configuration parameters. This is why a new, GSA-based config-
uration process was introduced to easily and efficiently configure most of them (see Section 3.2).
Dans cette section, we present a series of experiments that evaluates the efficiency and accuracy
gains introduced by this process.

Before proceeding with the experiments, it is worth mentioning that ArtSim+ has a parameter
oui, the values of which are manually selected. The reason for not including y in the automatic

Tableau 3. Number of articles in cold start period in top-k most popular

k = 5

k = 500

k = 500,000

y = 1
0

9,701

y = 3

154,140

y = 5

129

262,454

1539

Études scientifiques quantitatives

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

Chiffre 5. Effectiveness of our approach (nDCG@k) for various keyword search scenarios ( y = 3, varying k).

configuration process is that it gets discrete integer values from a narrow domain, and thus it is
easy to configured manually. En particulier, y is the parameter that determines which are the
papers that are going through their “cold start” phase. The best y value for a given data set relies
on the disciplines of the papers contained in it. Par exemple, papers from life sciences are
expected to receive citations at a faster rate than papers from theoretical mathematics; hence,
a smaller y value should be selected to configure ArtSim+ for a data set with papers from the
former discipline than for another with papers from the latter one. The data set we are using for
our experiments contains computer science papers; based on previous experience, we decided
to use (for all of our experiments) y values that are not greater than 5. En particulier, we examined
three different configurations of this parameter (namely, y = 1, y = 3, and y = 5) to investigate the
effect that different values of y have on the popularity estimation accuracy and to the gains intro-
duced by ArtSim+.

Donc, the GSA-based automatic configuration process (here denoted as GSA) est
focused on finding the best values for ArtSim+’s α, β, c, et δ. In our experiment, we used
GSA6 to find the best configuration of ArtSim+ in terms of accuracy (Kendall’s τ) for y = 3.
We also used two alternative configuration processes: un (full) grid search that examines all
distinct α, β, c, δ values in [0, 1] with a step of size 0.1 (GS1) and a grid search using a step
of size 0.01 (GS2). En outre, because ArtSim can also be configured in a similar way
(cependant, having only three instead of four parameters), we included it in the experiment,
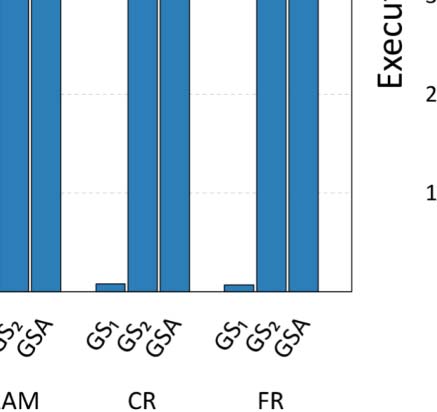
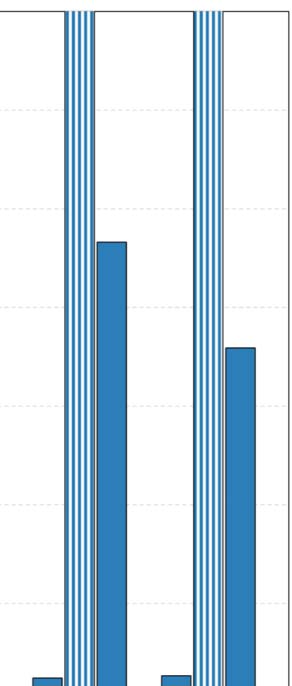
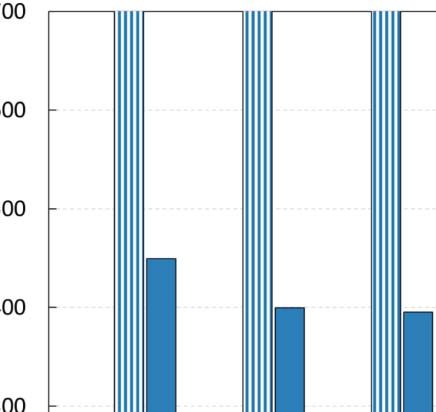
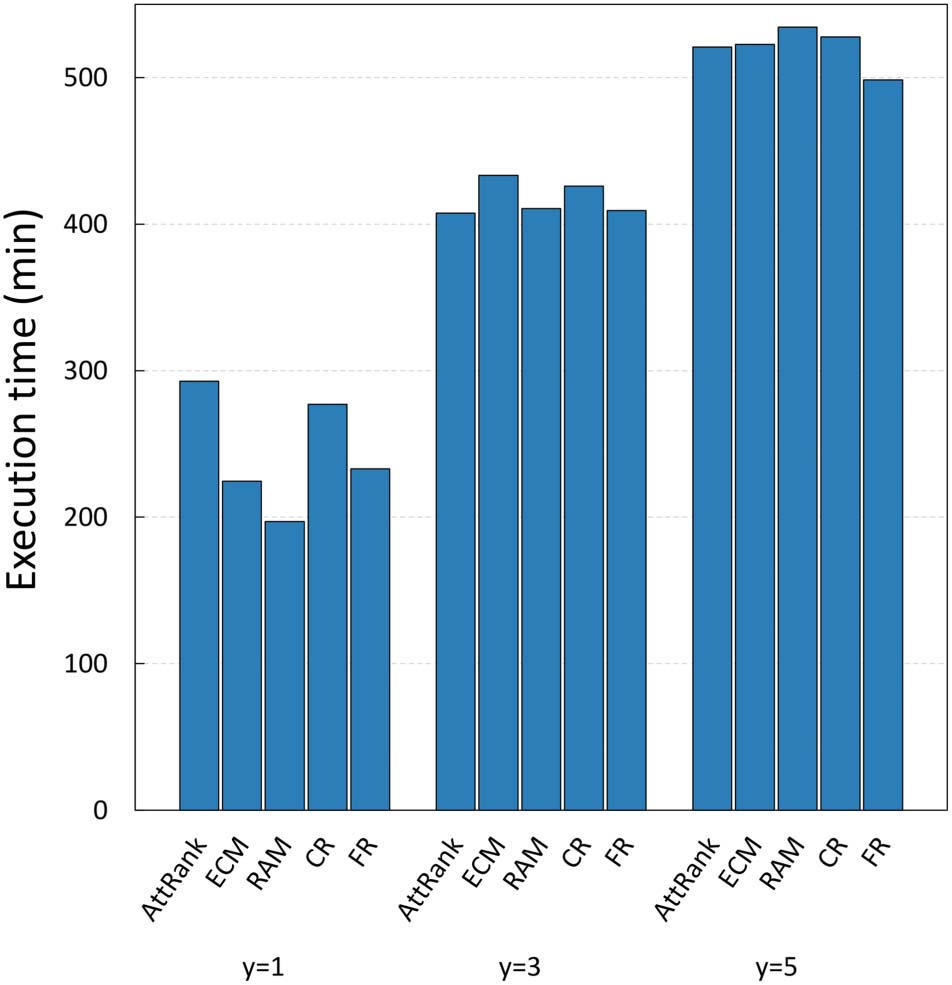
aussi. The execution times for all configuration approaches are depicted in Figure 6, alors que
the achieved accuracy of each revealed configuration is presented in Table 4 (best accuracy
highlighted in bold).

First of all, it is apparent from Table 4 que, in almost all cases, GS2 and GSA identify con-
figurations that result in improved accuracy, compared to the best configuration identified by
GS1. Bien sûr, the main benefit of the latter configuration processes is that it is significantly
faster than the other two, having the shortcoming of not finding the optimal configuration.
Although GS2 can identify configurations that achieve improved accuracy, the computational
cost of a full search in such a grid is very large. En particulier, in the case of ArtSim, GS2 was
found to be 35–40% slower than GSA, while in the case of ArtSim+ (which has one extra

6 For all our experiments, we used the implementation of GSA in SciPy9 assuming Kendall’s τ or nDCG@k as

our objective function, setting qv = 2.62, qα = −5, and initial temperature T0 = 5,230.

Études scientifiques quantitatives

1540

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

Chiffre 6. Execution times for different ArtSim/ArtSim+ configuration methods ( y = 3).

parameter that needs to be tuned) GS2 was so large that it did not finish execution after 5,000
minutes, with GSA finishing in less than 500 minutes.

As an additional remark, our experiments reveal that considering the venue-based paper
similarité (c'est à dire., exploiting the PV-P metapath) is a valid addition to our approach. The first clue
to this is based on the fact that ArtSim+ outperforms ArtSim (see Table 4); a second clue is
that for most of our experiments (presented in both the current and the previous section) le
best ArtSim+ accuracy was achieved using a configuration for which γ > α, β (see Tables A1
and A2 of the Appendix).

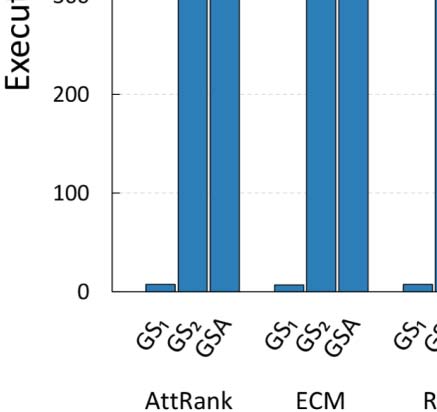
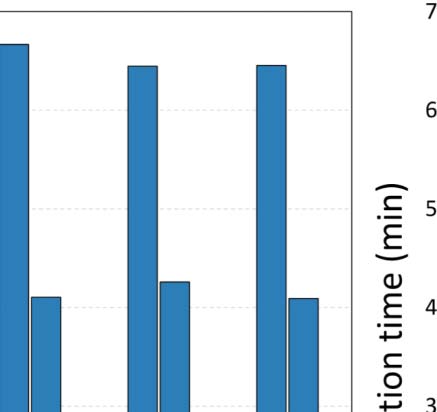
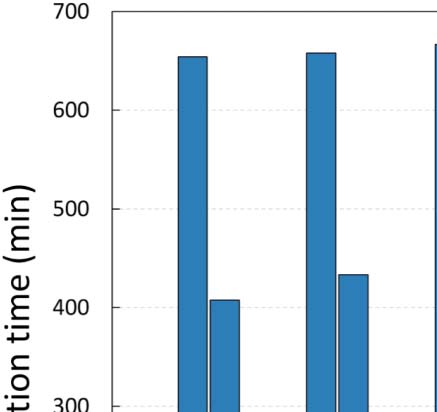
As a final experiment, we investigated the effect of different values of parameter y in the
efficiency of the GSA configuration process for ArtSim+. The results are presented in
Chiffre 7. It is apparent that an increase in the value of y results in larger configuration times.
This is due to the fact that as parameter y increases, the number of papers that are going
through their cold start period increases; thus ArtSim+ needs to perform calculations for more
papers.

Tableau 4.
the best configuration ( y = 3)

ArtSim/ArtSim+’s accuracy (in terms of Kendall’s τ) for the examined methods, en utilisant

AttRank

ECM

RAM

GS1
0.4814

0.4661

0.4653

0.4011

0.3793

ArtSim

GS2
0.4814

0.4664

0.4656

0.4012

0.3794

GSA
0.4814

0.4664

0.4656

0.4012

0.3794

ArtSim+

GS2
–

–

GS1
0.4880

0.4832

0.4823

0.4093

0.3917

GSA
0.4883

0.4837

0.4827

0.4094

0.3919

1541

Études scientifiques quantitatives

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

Chiffre 7. GSA execution times for ArtSim+ configuration for different y values.

4.4. Discussion

Previous sections outlined the improvements in estimation accuracy that ArtSim+ introduces
when applied on top of existing popularity estimation methods in terms of Kendall’s τ and
nDCG@k. Despite the fact that ArtSim+ exhibits gains in estimation accuracy in all consid-
ered popularity estimation methods, in the configuration we examined, we make some partic-
ular limiting assumptions.

First of all, as already mentioned, the impact of papers has multiple aspects; some of them
may be captured (to an extent) by particular types of citation analysis, others can only be quan-
tified by altmetrics, while there are also aspects that are very difficult to quantify. ArtSim+
focuses on estimating citation-based short-term impact, which is more formally described in
Section 2.1, hence it is not examined whether it is useful in estimating other scientific impact
aspects. It is also really important to mention that, although related, impact and scientific merit
are not completely (or even highly) correlated.

De plus, ArtSim+ considers similarity between papers based on three specific dimen-
sions (c'est à dire., authors, topics and publication venues captured by metapaths PAP, PTP, et
PVP respectively). Bien sûr, the choice of the actual metapaths is not an inherent limitation
of ArtSim+ as it can be adapted accordingly to also incorporate other metapaths. Cependant, it
is important to highlight that the currently tested version of ArtSim+ makes the aforemen-
tioned assumption regarding paper similarity. An additional limitation with regard to the meta-
paths we chose to implement is that they are unconstrained, c'est, they do not limit the paths
to be considered according to the values of the attributes of the involved nodes or edges. Con-
strained metapaths (par exemple., used in Shi et al. (2016un)) could be used to tighten the focus of the
similarities to be considered. Par exemple, for a recent paper, it may be useful to consider its
similarité, based on metapath PAP, but only to papers published in the last 10 années, as intu-
itively, a paper in its cold start period is more likely to share similar popularity dynamics with
the recent papers of a given author than with its older ones.

Études scientifiques quantitatives

1542

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

En outre, the scholarly knowledge graph that ArtSim+ utilizes is based on AMiner’s
citation network data set (Tang et al., 2008) (see Section 4.1.1 for details). Although this is a
popular data source used by many works (par exemple., Dong, Chawla, & Swami, 2017; Shi, Li et al.,
2016b; Sun, Barber et al., 2011un), it comprises a limited number of node types. Knowledge
graphs with a richer schema, such as the Open Research Knowledge Graph (Jaradeh et al.,
2019) and the OpenAIRE Research Graph (Manghi et al., 2019un, 2019b), would allow additional,
more complex metapaths to be used when considering paper similarity. En outre, contrary to
AMiner’s graph, which focuses on computer science papers (because it is based on papers
included in DBLP), the aforementioned knowledge graphs incorporate publications from various
disciplines, paving the way for the investigation of domains with possibly distinct characteristics.
In these cases, the importance of the examined similarity dimensions may be different, while even
alternative, nonexamined dimensions may be of large importance.

Last but not least, for recently published papers, ArtSim+ assigns the average of the pop-
ularity scores of their similar papers. Although using the average as an aggregation function is a
logical choice, other options can be examined as a future work, especially considering that the
popularity scores follow a power law distribution. It can also be useful to consider a weighted
scheme that incorporates the similarity score between papers in the aggregation process, as a
paper may have significantly higher similarity scores with some papers than with others.

5. CONCLUSIONS
In this work, we presented ArtSim+, an approach that can be applied on top of an existing
popularity estimation method to increase the accuracy of its results. The main intuition of our
approach is that the popularity of papers in their cold start period can be better estimated
based on the characteristics of older, similar papers. For our purposes, paper similarity is cal-
culated exploiting information stored in scholarly knowledge graphs. More particularly, le
proposed approach considers similarities based on the authors, the venues, and the topics
of the papers under consideration. Our experimental evaluation showcases the effectiveness
of ArtSim+, yielding noteworthy improvements in terms of Kendall’s τ correlation and nDCG
when applied on five state-of-the-art popularity measures, also outperforming ArtSim, its pre-
decessor, which had been introduced in Chatzopoulos et al. (2020).

Future work could address ArtSim+’s current limitations, or apply its underlying ideas in
different contexts (see Section 4.4). Par exemple, it may be interesting to examine different
types of (more complex) metapaths on HINs to calculate paper similarity. This could in turn
reveal new semantics on what constitutes “more similar” papers, based on the underlying
metapaths. De plus, although ArtSim+ focuses on improving the estimation of paper pop-
ularity for cold start papers, similarity based on HINs could be used to improve the estimation
of different types of paper impact, such as long-term impact or social media attention.

REMERCIEMENTS

Chiffre 1 was designed using resources from www.flaticon.com.

CONTRIBUTIONS DES AUTEURS

Serafeim Chatzopoulos: Conceptualisation, Conservation des données, Méthodologie, Logiciel, Validation,
Writing—original draft, Writing—review & édition. Thanasis Vergoulis: Conceptualisation, Pro-
ject administration, Méthodologie, Validation, Writing—original draft, Writing—review & édition.

Études scientifiques quantitatives

1543

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

Ilias Kanellos: Conceptualisation, Conservation des données, Writing—original draft, Writing—review &
édition. Theodore Dalamagas: Surveillance, Writing—original draft, Writing—review & édition.
Christos Tryfonopoulos: Surveillance, Writing—original draft, Writing—review & édition.

COMPETING INTERESTS

The authors have no competing interests.

INFORMATIONS SUR LE FINANCEMENT
We acknowledge support of this work by the project “Moving from Big Data Management to
Data Science” (MIS 5002437/3) which is implemented under the Action “Re-inforcement of
the Research and Innovation Infrastructure,” funded by the Operational Programme “Compet-
itiveness, Entrepreneurship and Innovation” (NSRF 2014-2020) and cofinanced by Greece and
the European Union (European Regional Development Fund).

DATA AVAILABILITY

Article similarities used in our experimental evaluation are openly available on Zenodo (https://
doi.org/10.5281/zenodo.3778915) under CC BY 4.0 Licence.

RÉFÉRENCES

Bai, X., Liu, H., Zhang, F., Ning, Z., Kong, X., … Xia, F. (2017). Un
overview on evaluating and predicting scholarly article impact.
Information, 8(3), 73. https://doi.org/10.3390/info8030073

Balmin, UN., Hristidis, V., & Papakonstantinou, Oui. (2004). Objec-
trank: Authority-based keyword search in databases. Procédure
of the 30th International Conference on Very Large Data Bases.
https://doi.org/10.1016/B978-012088469-8/50051-6

Bollen, J., Van de Sompel, H., Hagberg, UN., & Chute, R.. (2009). UN
principal component analysis of 39 scientific impact measures.
PLOS ONE, 4(6), e6022. https://doi.org/10.1371/journal.pone
.0006022, PubMed: 19562078

Chatzopoulos, S., Vergoulis, T., Kanellos, JE., Dalamagas, T., &
Tryfonopoulos, C. (2020). Artsim: Improved estimation of current
impact for recent articles. ADBIS, TPDL and EDA 2020 Common
Workshops and Doctoral Consortium (pp. 323–334). https://est ce que je
.org/10.1007/978-3-030-55814-7_27

Chatzopoulos, S., Vergoulis, T., Kanellos, JE., Dalamagas, T., &
Tryfonopoulos, C. (2021). DBLP article similarities (DBLP-ArtSim)
data set ( Version 2). Zenodo. https://doi.org/10.5281/zenodo
.4567527

Chen, P., Xie, H., Maslov, S., & Redner, S. (2007). Finding scientific
gems with Google’s PageRank algorithm. Journal of Informetrics,
1(1), 8–15. https://doi.org/10.1016/j.joi.2006.06.001

Dong, Y., Chawla, N. V., & Swami, UN. (2017). Metapath2vec:
Scalable representation learning for heterogeneous networks.
Proceedings of the 23rd ACM SIGKDD International Conference
on Knowledge Discovery and Data Mining (pp. 135–144). https://
doi.org/10.1145/3097983.3098036

Ghosh, R., Kuo, T., Hsu, C., Lin, S., & Lerman, K. (2011). Time-
aware ranking in dynamic citation networks. Proceedings of
the International Conference on Data Mining Workshops
(pp. 373–380). https://doi.org/10.1109/ICDMW.2011.183

Jaradeh, M.. Y., Oelen, UN., Farfar, K. E., Prinz, M., D’Souza, J., …
Auer, S. (2019). Open research knowledge graph: Suivant

generation infrastructure for semantic scholarly knowledge. Pro-
ceedings of the International Conference on Knowledge Capture.
https://doi.org/10.1145/3360901.3364435

Kanellos, JE., Vergoulis, T., Sacharidis, D., Dalamagas, T., &
Vassiliou, Oui. (2021un). Impact-based ranking of scientific publica-
tion: A survey and experimental evaluation. IEEE Transactions
on Knowledge and Data Engineering, 33(4), 1567–1584. https://
doi.org/10.1109/TKDE.2019.2941206

Kanellos, JE., Vergoulis, T., Sacharidis, D., Dalamagas, T., &
Vassiliou, Oui. (2021b). Ranking papers by their short-term scien-
tific impact. 37th IEEE International Conference on Data Engi-
neering, ICDE 2021 (pp. 1997–2002). https://doi.org/10.1109
/ICDE51399.2021.00190

Kendall, M.. G. (1948). Rank correlation methods. Londres: C. Griffin.
Kirkpatrick, S., Gelatt, C. D., & Vecchi, M.. P.. (1983). Optimization
by simulated annealing. Science, 220(4598), 671–680. https://
doi.org/10.1126/science.220.4598.671, PubMed: 17813860
Larsen, P.. O., & von Ins, M.. (2010). The rate of growth in scientific
publication and the decline in coverage provided by science
citation index. Scientometrics, 84(3), 575–603. https://doi.org
/10.1007/s11192-010-0202-z, PubMed: 20700371

Manghi, P., Atzori, C., Bardi, UN., Shirrwagen, J., Dimitropoulos,
H., … Summan, F. (2019un). OpenAIRE research graph dump
( Version 1.0.0-beta). Zenodo. https://doi.org/10.5281/zenodo
.3516918

Manghi, P., Bardi, UN., Atzori, C., Baglioni, M., Manola, N., …
Principe, P.. (2019b). The OpenAIRE research graph data model.
Zenodo. https://doi.org/10.5281/zenodo.2643199

Mariani, M.. S., Medo, M., & Zhang, Y.-C. (2016). Identification of
milestone papers through time-balanced network centrality.
Journal of Informetrics, 10(4), 1207–1223. https://est ce que je.org/10
.1016/j.joi.2016.10.005

Nie, Z., Zhang, Y., Wen, J.-R., & Ma, W.-Y. (2005). Object-level
ranking: Bringing order to web objects. Proceedings of the 14th

Études scientifiques quantitatives

1544

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

International Conference on World Wide Web (pp. 567–574).
https://doi.org/10.1145/1060745.1060828

Papastefanatos, G., Papadopoulou, E., Meimaris, M., Lempesis, UN.,
Martziou, S., … Manola, N. (2020). Open science observatory:
Monitoring open science in Europe. ADBIS, TPDL and EDA 2020
Common Workshops and Doctoral Consortium (pp. 341–346).
https://doi.org/10.1007/978-3-030-55814-7_29

Salatino, UN., Osborne, F., Thanapalasingam, T., & Motta, E. (2019).
The CSO classifier: Ontology-driven detection of research topics
in scholarly articles. ArXiv, arxiv.2104.00948. https://est ce que je.org/10
.1007/978-3-030-30760-8_26

Salatino, UN. UN., Thanapalasingam, T., Mannocci, UN., Osborne, F., &
Motta, E. (2018). The computer science ontology: A large-scale
taxonomy of research areas. In The Semantic Web – ISWC 2018
(pp. 187–205). Cham: Springer. https://doi.org/10.1007/978-3
-030-00668-6_12

Sayyadi, H., & Getoor, L. (2009). FutureRank: Ranking scientific
articles by predicting their future PageRank. Actes du
2009 SIAM International Conference on Data Mining. https://
doi.org/10.1137/1.9781611972795.46

Shi, C., Li, Y., Philip, S. Y., & Wu, B. (2016un). Constrained-meta-
path-based ranking in heterogeneous information network.
Knowledge and Information Systems, 49(2), 719–747. https://
doi.org/10.1007/s10115-016-0916-1

Shi, C., Li, Y., Zhang, J., Sun, Y., & Philip, S. Oui. (2016b). A survey of
heterogeneous information network analysis. IEEE Transactions
on Knowledge and Data Engineering, 29(1), 17–37. https://est ce que je
.org/10.1109/TKDE.2016.2598561

Shi, C., Li, Y., Zhang, J., Sun, Y., & Yu, P.. S. (2017). A survey of het-
erogeneous information network analysis. IEEE Transactions on
Knowledge and Data Engineering, 29(1), 17–37. https://doi.org
/10.1109/TKDE.2016.2598561

Su, C., Pan, Y., Zhen, Y., Ma, Z., Yuan, J., … Wu, Oui. (2011).
PrestigeRank: A new evaluation method for papers and journals.
Journal of Informetrics, 5(1), 1–13. https://doi.org/10.1016/j.joi
.2010.03.011

Sun, Y., Barber, R., Gupta, M., Aggarwal, C. C., & Han, J.. (2011un).
Co-author relationship prediction in heterogeneous biblio-
graphic networks. 2011 International Conference on Advances
in Social Networks Analysis and Mining (pp. 121–128). https://
doi.org/10.1109/ASONAM.2011.112

Sun, Y., Han, J., Yan, X., Yu, P.. S., & Wu, T. (2011b). PathSim: Meta
path-based top-K similarity search in heterogeneous information

réseaux. Proceedings of the VLDB Endowment, Vol. 4, Non. 11
(pp. 992–1003). https://doi.org/10.14778/3402707.3402736
Szu, H., & Hartley, R.. (1987). Fast simulated annealing. Physics Letters
UN, 122(3), 157–162. https://doi.org/10.1016/0375-9601(87)90796-1
Tang, J., Zhang, J., Yao, L., Li, J., Zhang, L., & Su, Z. (2008). Arnet-
Miner: Extraction and mining of academic social networks. Pro-
ceedings of the 14th ACM SIGKDD International Conference on
Knowledge Discovery and Data Mining (pp. 990–998). https://est ce que je
.org/10.1145/1401890.1402008

Tsallis, C., & Stariolo, D. UN. (1996). Generalized simulated anneal-
ing. Physica A: Statistical Mechanics and its Applications, 233(1),
395–406. https://doi.org/10.1016/S0378-4371(96)00271-3

Vaccario, G., Medo, M., Wider, N., & Mariani, M.. S. (2017). Quan-
tifying and suppressing ranking bias in a large citation network.
Journal of Informetrics, 11(3), 766–782. https://est ce que je.org/10.1016/j
.joi.2017.05.014

Vergoulis, T., Chatzopoulos, S., Kanellos, JE., Deligiannis, P.,
Tryfonopoulos, C., & Dalamagas, T. (2019). BIP! finder: Facilitating
scientific literature search by exploiting impact-based ranking. Pro-
ceedings of the 28th ACM International Conference on Information
and Knowledge Management (pp. 2937–2940). https://est ce que je.org/10
.1145/3357384.3357850

Walker, D., Xie, H., Yan, K., & Maslov, S. (2007). Ranking scientific
publications using a model of network traffic. Journal of Statisti-
cal Mechanics: Theory and Experiment, P06010. https://doi.org
/10.1088/1742-5468/2007/06/P06010

Xiang, Y., & Gong, X. (2000). Efficiency of generalized simulated
annealing. Physical Review E, 62(3), 4473. https://est ce que je.org/10
.1103/PhysRevE.62.4473, PubMed: 11088992

Xiang, Y., Sun, D., Fan, W., & Gong, X. (1997). Generalized simu-
lated annealing algorithm and its application to the Thomson
model. Physics Letters A, 233(3), 216–220. https://est ce que je.org/10
.1016/S0375-9601(97)00474-X

Xiang, Y., Gubian, S., Suomela, B., & Hoeng, J.. (2013). Generalized
simulated annealing for global optimization: The GenSA pack-
âge. R Journal, 5(1). https://doi.org/10.32614/RJ-2013-002

Xiong, Y., Zhu, Y., & Yu, P.. S. (2015). Top-k similarity join in hetero-
geneous information networks. IEEE Transactions on Knowledge
and Data Engineering, 27(6), 1710–1723. https://doi.org/10.1109
/TKDE.2014.2373385

Zhou, J., Zeng, UN., Fan, Y., & Di, Z. (2016). Ranking scientific pub-
lications with similarity-preferential mechanism. Scientometrics,
106(2), 805–816. https://doi.org/10.1007/s11192-015-1805-1

Études scientifiques quantitatives

1545

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

APPENDIX: DETAILED CONFIGURATIONS

In this section we present the exact parameter configurations that found, according to our
experiments, to perform best in terms of Kendall’s τ (Table A1) and nDCG@k (Table A2 and
Table A3).

Table A1.

Best parameter configuration for ArtSim and ArtSim+ in terms of Kendall’s τ per year for each popularity method

Year
1

Method
AttRank

ECM

RAM

AttRank

ECM

RAM

AttRank

ECM

RAM

ArtSim
β

0.4

0.2

0.3

0.2

0.1

0.2

0.6

0.2

0.5

0.1

0.3

0.1

0.4

0.1

0.2

0.1

0.2

0.8

0.6

0.2

0.9

0.5

0.6

0.9

0.6

0.9

0.7

0.9

0.8

ArtSim+

0.145277031

0.005990299

0.392695704

0.456036966

0.166595965

0.051491999

0.78170659

0.000205446

0.174886077

0.084557577

0.739320582

0.001235764

0.141299869

0.052432926

0.342913579

0.463353626

0.299168329

0.066391927

0.525240422

0.109199321

0.071201881

0.000441011

0.232924271

0.695432837

0.124719079

0.033437058

0.453243798

0.388600065

0.121034883

0.029444383

0.457015556

0.392505178

0.096200844

0.003343715

0.178251376

0.722204064

0.253654548

0.001748901

0.412244396

0.332352156

0.057220357

0.000289696

0.19245648

0.750033468

0.09662166

0.018328432

0.376102089

0.508947819

0.098584522

0.015406401

0.378614784

0.507394293

0.073013872

0.000202049

0.14995334

0.776830739

0.130730497

8.27 × 10−6

0.316954706

0.552306527

Études scientifiques quantitatives

1546

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

Table A2.

Best parameter configuration for ArtSim and ArtSim+ in terms of nDCG@k per year for each popularity method

Year
1

k
5

Method
AttRank

ECM

RAM

ArtSim
β

ArtSim+

0.043625002

0.760936801

0.172958251

0.022479946

0.30321382

0.139308721

0.085667133

0.471810326

0.078200724

0.209446825

0.523403316

0.188949135

0.322596419

0.145074983

0.296640004

0.235688594

0.558044348

0.230585542

0.033053398

0.178316712

500

AttRank

0.2

0.1

0.7

0.050379753

0.160489046

0.390471383

0.398659818

ECM

RAM

500,000

AttRank

ECM

RAM

AttRank

ECM

RAM

500

AttRank

ECM

RAM

500,000

AttRank

ECM

RAM

0.4

0.5

0.1

0.3

0.1

0.2

0.3

0.4

0.1

0.5

0.2

0.1

0.2

0.9

0.6

0.7

0.5

0.9

0.7

0.5

0.4

0.6

0.071599655

0.622626528

0.276073605

0.029700212

0.207121894

0.206278636

0.28684085

0.29975862

0.074572398

0.004112483

0.761882122

0.159432997

0.002971828

0.298428552

0.356929537

0.341670083

0.101250724

0.018056559

0.588413691

0.292279026

0.080106949

0.017726557

0.43321531

0.468951184

0.057742507

0.309127443

0.506898549

0.126231501

0.065828375

0.146518413

0.144194363

0.643458849

0.214986246

0.114349369

0.276839755

0.39382463

0.099902043

0.292021176

0.600068405

0.008008376

0.072232038

0.070181228

0.767059885

0.090526849

0.562914654

0.196196764

0.115728874

0.125159707

0.475429667

0.093437465

0.29715535

0.133977517

0.602712266

0.151896879

0.180489376

0.064901479

0.000912722

0.005481492

0.011619274

0.981986512

0.003226199

0.00406899

0.001153354

0.991551457

0.000194946

0.000278283

3.09 × 10−5

0.999495919

0.000270543

0.000836071

0.000764652

0.998128735

0.035743025

0.002154389

4.56 × 10−5

0.962057036

0.061192937

0.015727155

0.274961586

0.648118322

0.110264084

0.034738339

0.452098454

0.402899123

0.140312586

0.060003571

0.487685497

0.311998346

0.139931046

0.048694312

0.159261233

0.652113409

0.289656061

0.002568592

0.421741717

0.28603363

Études scientifiques quantitatives

1547

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Further improvements on estimating the popularity of recently published papers

Year
5

k
5

Method
AttRank

ECM

RAM

500

AttRank

ECM

RAM

500,000

AttRank

ECM

RAM

Table A2.

(a continué )

ArtSim
β

0.2

0.1

0.8

0.9

ArtSim+

0.254735149

0.400572483

0.093551236

0.251141133

0.144458279

0.644575879

0.096725866

0.114239976

8.60 × 10−5

0.059359795

0.115967461

0.824586774

0.507882291

0.115380129

0.292696901

0.084040679

0.266829708

0.383419901

0.1309652

0.218785191

0.001514395

0.000303422

0.000478885

0.997703298

0.000244054

7.66 × 10−6

0.000220143

0.999528147

0.000115121

0.000152117

0.00030992

0.999422842

0.000156193

0.000286387

0.0001181

0.999439321

0.007912242

0.009869723

0.014731817

0.967486219

0.052416259

0.000443834

0.22470206

0.722437847

0.085897883

0.001210377

0.348135752

0.564755987

0.057993087

0.003274152

0.433195616

0.505537146

0.025359166

0.004514882

0.122811346

0.847314606

0.064196382

0.001714464

0.349049967

0.585039187

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Études scientifiques quantitatives

1548

Further improvements on estimating the popularity of recently published papers

Table A3.

Best parameter configuration for ArtSim and ArtSim+ in terms of nDCG@k for each examined topic

ArtSim
β

Topic
Expert finding

k
5

Method
AttRank

ECM

RAM

AttRank

ECM

RAM

AttRank

ECM

RAM

100

AttRank

ECM

RAM

Recommender

AttRank

systèmes

ECM

RAM

0.2

0.3

0.5

0.3

0.1

0.3

0.1

AttRank

0.1

ECM

RAM

0.1

0.4

0.1

0.2

0.5

0.3

0.4

0.3

0.1

0.4

0.8

0.7

0.6

0.1

0.4

0.6

0.9

0.5

0.2

0.6

0.7

0.6

0.9

0.5

ArtSim+

0.318945527

0.387600347

0.263146218

0.030307908

0.263209321

0.011831591

0.467087611

0.257871478

0.076321143

0.278387096

0.148059788

0.497231972

0.674347997

0.01595822

0.211572856

0.098120928

0.434464085

0.154521517

0.288870201

0.122144197

0.355738938

0.157116685

0.177619562

0.309524816

0.760536872

0.002808183

0.065108165

0.17154678

0.072857969

0.551987126

0.048909731

0.326245174

0.082820579

0.298510738

0.30785628

0.310812403

0.552667305

0.195999026

0.16464645

0.086687218

0.29709521

0.029676421

0.009150453

0.664077915

0.35230451

0.005913817

0.004136306

0.637645367

0.292722728

0.009505206

0.060268797

0.637503269

0.223996634

0.327760944

0.049808818

0.398433604

0.273877432

0.485109295

0.07477427

0.166239003

0.067818375

0.157541287

0.155592109

0.619048229

0.105135398

0.199013155

0.156840822

0.539010625

0.158085551

0.002543293

0.226640395

0.612730761

0.236667123

0.046077763

0.134524079

0.582731035

0.23351202

0.170436426

0.289606127

0.306445427

0.49503607

0.242641224

0.170978719

0.091343988

0.072749272

0.420233212

0.156097919

0.350919597

0.316198223

0.386945436

0.228266676

0.068589665

0.183461457

0.075922995

0.375714561

0.364900986

0.043971889

0.072296798

0.648212135

0.235519178

0.224575087

0.242631659

0.094701089

0.438092165

0.097994186

0.058254115

0.00967669

0.834075009

0.039734593

0.034851974

0.031039131

0.894374302

0.060285992

0.081740805

0.001095072

0.85687813

0.046729717

0.262857787

0.246810331

0.443602165

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Études scientifiques quantitatives

1549

Further improvements on estimating the popularity of recently published papers

Table A3.

(a continué )

ArtSim
β

Topic

k
50

Method
AttRank

ECM

RAM

100

AttRank

ECM

RAM

Digital libraries

AttRank

ECM

RAM

AttRank

ECM

RAM

AttRank

ECM

RAM

0.1

100

AttRank

0.4

ECM

RAM

0.1

0.4

ArtSim+

0.8

0.9

0.7

0.8

0.039846102

0.200974421

0.022942085

0.736237393

1.37 × 10−5

0.106821757

0.082604612

0.810559951

0.011877

0.063374774

0.002079611

0.922668615

0.022298246

0.046676171

0.136956699

0.794068884

0.001793162

0.070989721

0.230536328

0.69668079

0.022545982

0.241902737

0.154471291

0.58107999

0.108727851

0.0682923

0.005589207

0.817390642

0.091769576

0.067962699

0.042434178

0.797833546

0.037544838

0.04777025

0.041397125

0.873287787

0.2

0.1

0.2

0.1

0.3

0.7

0.000163269

0.057215872

0.00626263

0.936358229

0.440890055

0.440788373

0.050406601

0.06791497

0.035452394

0.323090417

0.375018593

0.266438596

0.123127252

0.076995268

0.670160726

0.129716754

0.005766049

0.324871898

0.534817755

0.134544298

0.392114952

0.095157534

0.398464507

0.114263007

0.004026815

0.080299776

0.249444719

0.666228689

0.2

0.8

0.265280902

0.008267418

0.705189019

0.021262661

0.1

0.9

0.8

0.022408143

0.466746345

0.047284402

0.46356111

0.343271628

0.136936739

0.073675163

0.44611647

0.385045044

0.063966699

0.095219605

0.455768652

0.015545828

0.049709792

0.01338067

0.92136371

0.162153267

0.00126089

0.051704516

0.784881327

0.02970865

0.004979305

0.016878103

0.948433942

0.153234527

0.079760894

0.291113428

0.475891151

0.005373266

0.009087298

0.104202454

0.881336982

0.6

0.223751459

0.019836748

0.277374635

0.479037158

0.9

0.6

0.009969812

0.003605646

0.007221275

0.979203266

0.014382594

0.005526553

0.004064104

0.976026749

0.04975274

0.018105728

0.02802847

0.904113062

0.280155701

0.017660161

0.126081608

0.57610253

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
4
1
5
2
9
2
0
0
7
8
5
6
q
s
s
_
un
_
0
0
1
6
5
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Études scientifiques quantitatives

1550 RESEARCH ARTICLE image

Télécharger le PDF