ARTICLE DE RECHERCHE - Recherche en IA spécialisée au MIT

ARTICLE DE RECHERCHE

A Bayesian hurdle quantile regression model for
citation analysis with mass points at lower values

Marzieh Shahmandi

, Paul Wilson

, and Mike Thelwall

Statistical Cybermetrics Research Group, School of Mathematics and Computer Science, University of Wolverhampton,
Wulfruna Street, Wolverhampton WV1 1LY, ROYAUME-UNI

Mots clés: Bayesian method, citation analysis, excess zeros, hurdle model, Markov Chain Monte
Carlo, quantile regression

ABSTRAIT

Quantile regression presents a complete picture of the effects on the location, scale, and shape
of the dependent variable at all points, not just the mean. We focus on two challenges for
citation count analysis by quantile regression: discontinuity and substantial mass points at
lower counts. A Bayesian hurdle quantile regression model for count data with a substantial
mass point at zero was proposed by King and Song (2019). It uses quantile regression for
modeling the nonzero data and logistic regression for modeling the probability of zeros versus
nonzeros. We show that substantial mass points for low citation counts will almost certainly
also affect parameter estimation in the quantile regression part of the model, similar to a mass
point at zero. We update the King and Song model by shifting the hurdle point past the main
mass points. This model delivers more accurate quantile regression for moderately to highly
cited articles, especially at quantiles corresponding to values just beyond the mass points, et
enables estimates of the extent to which factors influence the chances that an article will be low
cited. To illustrate the potential of this method, it is applied to simulated citation counts and
data from Scopus.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

INTRODUCTION

Citation analysis can help to estimate the relative importance or impact of articles by counting
the number of times that they have been cited by other works. Nonspecialists in governments
and funding bodies or even researchers in different scientific disciplines sometimes use citation
counts to help judge the importance of a piece of scientific research (Meho, 2007). Citation
analysis has statistical challenges due to the characteristics of citation counts (a substantial
mass point at zero, high right skewness, and heteroskedasticity). Various statistical models have
been proposed for citation counts (par exemple., Brzezinski, 2015; Eom & Fortunato, 2011; Garanina &
Romanovsky, 2016; Low, Wilson, & Thelwall, 2016; Redner, 1998; Seglen, 1992; Shahmandi,
Wilson, & Thelwall, 2020; Thelwall, 2016; Thelwall & Wilson, 2014), but most have sought to
model the conditional mean of citation counts from independent variables. Autrement dit, ils
generate a formula for the expected number of citations for given values of research-related
parameters, such as article age, topic, and the number of authors.

Quantile regression (QR) is a statistical method proposed by Koenker and Bassett (1978) à
complement classical linear regression analysis (par exemple., Coad & Rao, 2008; Koenker & Hallock,

un accès ouvert

journal

Citation: Shahmandi, M., Wilson, P., &
Thelwall, M.. (2021). A Bayesian hurdle
quantile regression model for citation
analysis with mass points at lower
valeurs. Études scientifiques quantitatives,
2(3), 912–931. https://est ce que je.org/10.1162
/qss_a_00147

EST CE QUE JE:
https://doi.org/10.1162/qss_a_00147

Peer Review:
https://publons.com/publon/10.1162
/qss_a_00147

Reçu: 7 Février 2021
Accepté: 11 Juin 2021

Auteur correspondant:
Marzieh Shahmandi
m.shahmandihounejani@wlv.ac.uk

Éditeur de manipulation:
Ludo Waltman

droits d'auteur: © 2021 Marzieh Shahmandi,
Paul Wilson, and Mike Thelwall.
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence.

La presse du MIT

A Bayesian hurdle quantile regression model

2001). Unlike a linear regression, where the conditional mean of a dependent variable is
modeled, in QR the different conditional quantiles of the dependent variable, such as the
median, are modeled based on a set of independent variables. In QR the entire distribution
of the dependent variable is related to the set of independent variables. In scientometrics,
Danell (2011) used QR to investigate whether the future citation rate of an article can be pre-
dicted from the author’s publication count and previous citation rate. In the study of nanotech-
nology publications, QR was used to investigate whether funding acknowledgments influence
journal impact factors and citation counts as two dependent variables in two separate models
(Wang & Shapira, 2015). Stegehuis, Litvak, and Waltman (2015) proposed a QR-based model
to estimate a probability distribution for the future number of citations of a publication in
relation to variables such as the publishing journal’s impact factor. Anauati, Galiani, et
Gálvez (2016) assessed the life cycle of articles across fields of economic research through
QR. Ahlgren, Colliander, and Sjögårde (2018) used QR to show how some factors, tel que
the number of cited references, affect the field normalized citation rate across all disciplines.
Dans une autre étude, Wang (2018) used QR models to explore the relationship between SCI
(Index des citations scientifiques) editorial board representation and research output of universities
(measured by indicators such as the number of articles, total number of citations) in the field
of computer science, Mäntylä and Garousi (2019) applied QR at the 0.50 quantile to indicate
how factors such as publication venue and author team past citations influence the number of
citations of software engineering papers. Galiani and Gálvez (2019) proposed identifying
citation aging by combining QR with a nonparametric specification to capture citation infla-
tion. Despite this extensive use of QR for citation analysis, the problem of the influence of
point masses (low citation counts having high frequencies in a set of articles) has not been
fully resolved, undermining the value of the results.

The continuity of the dependent variable is important for minimization of the objective
function in QR. A discrete dependent variable leads to nondifferentiability of the objective
fonction, resulting in problems deriving the asymptotic distribution of the conditional quan-
tiles. A substantial mass point at zero in the data results in all conditional quantiles less than
the proportion of the zeros being equal to zero. In some of the articles cited above, the dis-
continuity of citation counts was ignored, leading to biased and misspecified estimates for pa-
rameters in the model. In other articles, citation counts were normalized by different methods,
or a random positive value was added to each citation count to account for the discontinuity.
En général, for the case of a discrete variable, jittering proposed by Machado and Silva (2005)
is used. In jittering, random noise in the interval (0, 1) is added to each data point to make the
data continuous. In the situation of the substantial mass point at zero, researchers frequently
focus on the interpretation of the upper quantiles of the dependent variable because the ap-
parent variation in the lower tail might be a consequence of random noise produced by the
jittering process. In practice, some important parts of the analysis can be lost. Par exemple, dans
the case of the citation counts as a dependent variable, we can lose the information about the
effects of factors (as independent variables in the model) on zero or very low cited articles.
Donc, a new methodology related to QR should be considered to tackle these challenges.
The approach proposed in this article is an extension of the Bayesian two-part hurdle QR
model of King and Song (2019). Having a two-part structure is a fundamental aspect of this
model. The two-part model of King and Song (2019) allows zero and nonzero citations to be
modeled separately. The QR part of the model is for modeling the nonzeros, and logistic re-
gression is used for modeling the probability of zeros versus nonzeros. The Bayesian structure
of the model assists the estimation of model parameters. En outre, King and Song (2019)
showed another advantage of the application of the Bayesian technique for this model. Par
simulation, it was shown that the estimates of parameters based on the Bayesian method

Études scientifiques quantitatives

913

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A Bayesian hurdle quantile regression model

Field
Literature and

Literary Theory

Arts and

Sciences humaines

Visual Arts and

Performing Arts

Architecture

Religious Studies

1,460

1,799

2,215

2,176

Emergency Nursing

1,299

Media Technology

1,889

Tableau 1. Details of the citation count data for the seven fields from 2010 analyzed

Nombre
of articles
3,126

Percentage
of zeros
51

Percentage
of ones
18

Percentage
of twos
11

Percentage
of threes
5

Percentage of
substantial mass
points in 1 ≤ y ≤ 3
34

Total percentage
of substantial
mass points
85

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

are more precise in comparison to their classical counterparts, even for small sample sizes and
when the prior information of the parameters in the model is noninformative. In the case of
citation count data, there are frequently substantial mass points at one, deux, and three (et
possibly also at greater values) that influence the estimates of parameters in the QR part of
the model in a similar manner to the substantial mass point at zero, so a new update of the
model will be proposed to reduce the effect of the substantial mass points on the estimation of
the model. We take “substantial” to mean greater than about 6%, as mass points less than this
appear to have little effect on subsequent estimation (see Table 1). This paper, based on sim-
ulations of log-normal continuous data with substantial mass points at zero, un, deux, et
three (approximating a common distribution of citation counts), will assess, by considering
the mean squared error of the estimates of the coefficients corresponding to the independent
variables in the model, whether the QR part of the two-part model with a hurdle at three results
in more accurate estimates than are obtained by the other models. We also assess prediction
errors and credible intervals for the estimates.

2. DEFINITIONS AND CONCEPTS

2.1. QR
Gilchrist (2000) describes a quantile as “the value that corresponds to a specified proportion of
un (ordered) sample of a population.” The quantiles are the values that divide the distribution
such that there is a given proportion of observations below the quantile. Thus the τth quantile
splits the area under the density curve into two parts: one with area τ below the τth quantile
and the other with area 1 − τ above it. The best-known quantile is the median, which is the
0.50 quantile. The median is a measure of the central tendency of the distribution: Half the
data are less than or equal to it and half are greater than or equal to it. En général, for any τ in
the interval (0, 1) and any continuous random variable Y with the probability distribution func-
tion F, the τth quantile of Y can be defined as

FY yτð

Þ ¼ P Y ≤ yτ
ð

Þ ¼ τ

Études scientifiques quantitatives

914

A Bayesian hurdle quantile regression model

and the empirical quantile distribution function can be defined as

−1
yτ ¼ F
Oui

τð Þ ¼ inf yjFY yð Þ ≥ τ
F

The regression model for the conditional quantile level τ of Y is (Koenker & Bassett, 1978)

where xi is the ith vector of p independent variables, and βτ is estimated by minimization of the
sample objective function or the weighted absolute sum:

QYi

τjxi
ð

Þ ¼ xi

Tβτ

(1)

(cid:2)

ρτ yi − xi

min
βτ

i¼1

(cid:3)

Tβτ

(2)

where n is the number of observations and ρτ(r) = τ max(r, 0) + (1 − τ) maximum(−r, 0) is the check loss
fonction. The solution of Eq. 2 can be obtained by linear programming techniques such as the
simplex method (Dantzig, 1963), the interior-point method (Portnoy & Koenker, 1997), et le
smoothing method (Clark & Osborne, 1986; Madsen & Nielsen, 1993). QR preserves QY(τ|X)
under transformation. Suppose that (cid:2)(·) is a nondecreasing (monotone) function on R; alors

Qη Yð Þ τjxð

Þ ¼ η QY τjxð
ð

Þ:
Þ

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

This is important because in the following, transformations need to be used for citation

analyse.

2.2. The Asymmetric Laplace Distribution in Bayesian QR

Here we define the (three-parameter) asymmetric Laplace distribution. Because of the
distribution-free characteristic of QR, the minimization of Eq. 2 can be considered as a non-
parametric problem. This can cause a challenge for defining the Bayesian version of QR be-
cause the Bayesian framework needs the likelihood function of the model. Different
approaches have been suggested for this issue, but the ALD method proposed by Yu and
Moyeed (2001) is the simplest and most understandable method. The ALD has density prob-
ability function

f yijμ; p; τ
ð

Þ ¼

τ 1 − τ
ð
p

n
exp ρτ

(cid:4)
yi − μ
p

(cid:5)

(3)

where μ 2 R., σ > 0, and τ 2 [0, 1] are respectively location, scale, and skewness parameters.

For a random variable W, where W (cid:2) ALD( m, p, τ), there is a location-scale mixture repre-
sentation following a normal distribution with specific parameters (par exemple., Kozumi & Kobayashi,
2011; Lee & Neocleous, 2010). En fait
p

(cid:3)

ﬃﬃﬃﬃﬃﬃ
σv

(cid:2)
toi; Wjv (cid:2) N μ þ θv; ψ2σv

W ¼ θv þ ψ

(4)

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

où

θ ¼

1 − 2τ
τ 1 − τ
Þ
ð

; ψ2 ¼

2
τ 1 − τ
ð

Two variables u and v are independent. u follows a standard normal distribution, and v is
exponentially distributed with mean σ. This valuable feature of ALD enables the use of QR in
the Bayesian framework.

By considering the location parameter in ALD as a linear function of the independent vari-
T βτ, the maximum likelihood estimate of the β in Eq. 3 is equivalent to the estimate

ables, m

i = xi

Études scientifiques quantitatives

915

A Bayesian hurdle quantile regression model

obtained from the minimization of Eq. 2, for every fixed τ. QR may be regarded as linear
regression where the error term has been replaced by the ALD distribution. ALD provides a
likelihood base for data in the Bayesian framework which holds the data fixed, and treats the
parameters as random variables, which are explained probabilistically by prior knowledge.
The combination of the evidence extracted from the data (likelihood) and the prior beliefs is
a posterior distribution corresponding to the parameters. A Gibbs sampler of the Markov chain
Monte Carlo (MCMC) method is used for the approximation of the posterior distribution.

3. BAYESIAN TWO-PART HURDLE QR

Santos and Bolfarine (2015) proposed a Bayesian two-part QR methodology for a continuous
response variable with a substantial mass point at zero or one. King and Song (2019) intro-
duced a Bayesian two-part QR model with a hurdle at zero for the case of count data with
a substantial mass point at zero. Dans ce qui suit, a new version of this model for the case
of a hurdle at a specific value of c is introduced. To fit this model, for the first step, the count
data should be transformed by

(cid:7)

oui(cid:3)
i ¼

0
ln yi − c − ui

yi ≤ c
yi > c

(5)

to provide a semicontinuous variable. By this transformation, all substantial mass points less
than or equal to c are mapped to zero and the rest of the data are converted to a real number in
the domain of the ALD distribution. By considering c = 0 in the relationship (5), the original
transformation used by King and Song (2019) is obtained.

The two-part probability function has the form

(cid:2)
f y(cid:3)

i jγ; βτ; p; vi; τ

(cid:3)

¼ ωið

(cid:2)
Þ : I y(cid:3)

i ¼ 0

(cid:3)

þ 1 − ωi
ð

(cid:2)

Þ : N xi

Tβτ þ θvi; ψ2σvi

(cid:3)

(cid:2)
I y(cid:3)
je

(cid:3)
6¼ 0

(6)

i = P(oui(cid:3)

where ω
i = 0) and I is the indicator function. In the literature the parameter ω has been
used both to denote the probability of observing a nonzero (par exemple., King and Song, 2019) and a
zero (par exemple., Ospina & Ferrari, 2012; Santos & Bolfarine, 2015). Previous research in the area of
citation count analysis, for example Didegah, Thelwall, and Wilson (2013), has used ω to
denote the probability of observing a zero; thus we shall follow this precedent here.

A logit link is usually applied to model ω

i based on a linear combination of the independent

variables so that

logit ωið

Þ ¼ zi

Tγ

(7)

where zi is a vector of independent variables. The variables used to model ω
be the same as those used to model the nonzero data.

i may or may not

The two-part model is a mixture model that is a linear combination of a continuous normal
distribution (corresponding to QR for modeling the jittered nonzero citation counts) and a
point distribution at zero. ωi and 1 − ωi are respectively the contributions of the point distri-
bution and the continuous distribution in this mixture. This is a hurdle model because the
zeros and nonzeros are modeled separately.

Études scientifiques quantitatives

916

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A Bayesian hurdle quantile regression model

From Eq. 7, Eq. 6 can be rewritten as

(cid:3)
(cid:2)
i j:
f y(cid:3)

¼ ω

Þ
i ¼0

I y(cid:3)
ð
je

(cid:8)
ð

1 − ωi

(cid:3)

(cid:9)I y(cid:3)
ð

Þ
i 6¼0

(cid:2)

Þ: N xi
Tβτ þ θvi; ψ2σvi
(cid:8)
(cid:2)
Þ N xi
(cid:10)
Þ

Tβτ þ θvi; ψ2σvi
(cid:11)I y(cid:3)
ð

i 6¼0
(cid:11)I y(cid:3)
ð

i ¼0

I y(cid:3)
ð
Þ

(cid:3)

(cid:9)I y(cid:3)
ð

i 6¼0

(8)

i 6¼0

i ¼0

I y(cid:3)
ð
¼ ω
je
(cid:10)

1 − ωi
ð

1
ð

1 þ exp −zi
(cid:8)
(cid:2)

Tγ

(cid:4) N xi

Tβτ þ θvi; ψ2σvi

Tγ

1 þ exp zi
(cid:9)I y(cid:3)
(cid:3)
ð

Þ
i 6¼0

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Suppose noninformative priors are

(cid:5)

(cid:4)
e
b; e
B

π βτð
Þ (cid:2) N
π við Þ (cid:2) E σð Þ
π σð Þ (cid:2) IG en;es
Þ
ð
(cid:5)
(cid:4)
π γð Þ (cid:2) N eg; e
G

where E denotes the exponential distribution with mean σ and I G denotes an inverse gamma
distribution with the hyperparameters ñ and ~s. The posterior distribution of the model is

π βτ; c; p; vijy(cid:3)
ð

Þ / L y(cid:3)

i jβτ; p; vi; τ

π βτð

Þπ γð Þπ σð Þπ vijσð
Þ

(9)

(cid:2)

(cid:3)

where L(oui(cid:3)
je |.) is the likelihood function of f(oui(cid:3)
Gibbs sampler of the MCMC method will be used.

je |.). To approximate the posterior distribution, le

4. SIMULATION STUDY

Dans cette section, samples with sizes 500, 1,000, et 3,000 are simulated from continuous log-
normal distribution (LN ) with mean (2 − 0.2 * x1 + 0 * x2 + (cid:3)) and standard deviation 0.4 où
x1 (cid:2) LN(2, 2), x2 (cid:2) N(0.5, 0.5), et (cid:3) (cid:2) N(0, 1). The log-normal distribution was chosen because
it approximates the typical distribution of citation counts. The floor function was used for sim-
ulated values less than 4 to simulate substantial mass points at 0, 1, 2, et 3. The intercept value
de 2 and the coefficient −0.2 of x1 were chosen so that approximately 45% of the data will be
zeros and 75% of the data less than 3, similar to much citation count data. The coefficient of x2
was chosen as zero to enable comparison of the proposed models when one of the variables is
nonsignificant. Bayesian QR and Bayesian two-part QR models with a hurdle at 0 and with a
hurdle at 3 will be fitted. The objective is to compare Bayesian QR with the QR parts of the two-
part models with hurdles at 0 et 3. For each sample size and for each quantile level, le
Bayesian QR model is fitted to the whole data. Then the quantile level of the corresponding
quantile value is found in the data in which the zeros are excluded and the Bayesian QR model
is fitted (c'est à dire., the QR part of the two-part model with a hurdle at 0). Suivant, the quantile value cor-
responding to the quantile level is found in the data in which all substantial mass points (inclure-
ing 0, 1, 2, et 3) are removed and the Bayesian QR model is fitted for the corresponding
quantile (this model is the QR part of the two-part model with a hurdle at 3). For more clarifica-
tion, suppose the specific quantile level is 0.85, and the Bayesian QR model is fitted to the whole
data at this quantile. Say the value corresponding to this quantile is 7.640. Now the quantile
corresponding to 7.640 for the data with zeros removed is computed; say it is 0.70. Then the
Bayesian QR model is fitted to this data (> 0) for the 0.70 quantile. This model is the QR part
of the two-part model with a hurdle at 0. Suivant, the quantile level corresponding to 7.640 is found
in the data with substantial mass points at 0, 1, 2, et 3 removed. Say this is 0.40. The Bayesian

Études scientifiques quantitatives

917

A Bayesian hurdle quantile regression model

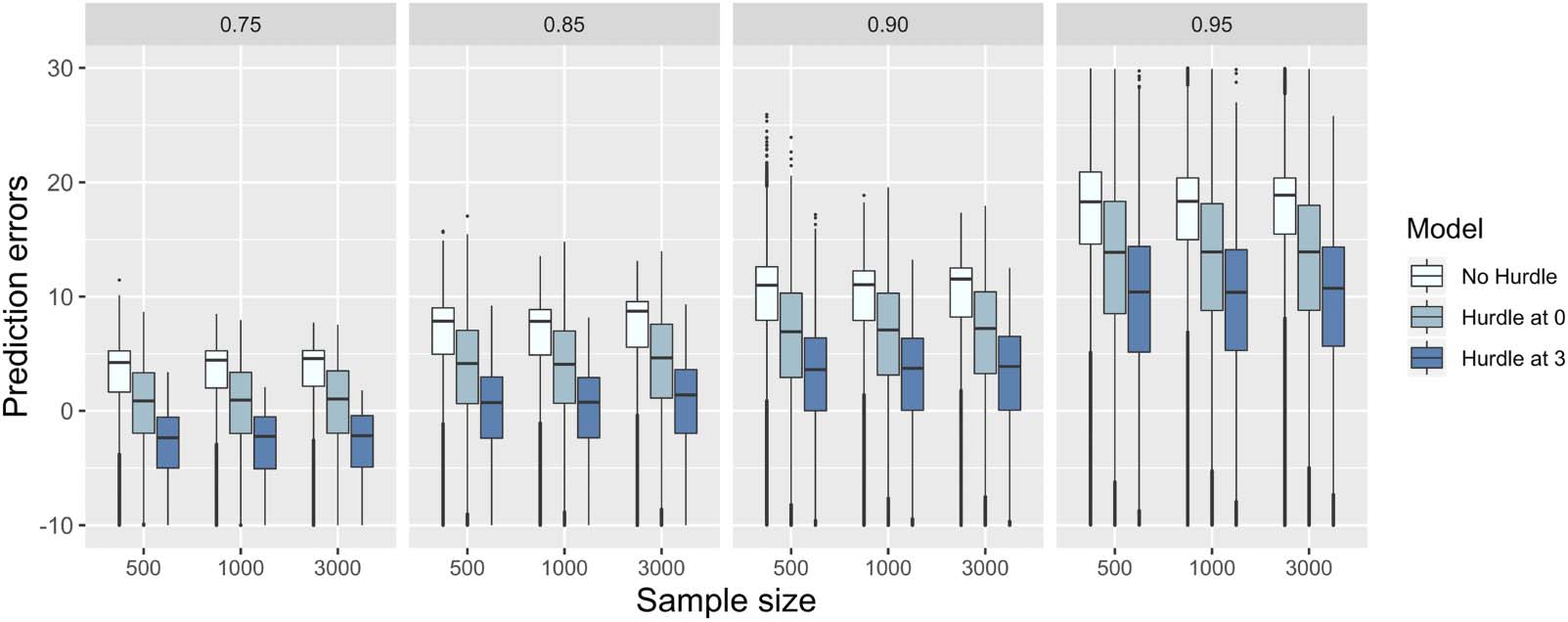
Chiffre 1. Prediction errors based on different models and sample sizes.

QR model is fitted to this data (≥ 3) at this quantile. The estimates of parameters based on this
model are the QR part of the two-part model with a hurdle at 3. This process is repeated 100
times for each sample size, and for four specific quantiles of 0.75, 0.85, 0.90, et 0.95 (of the
whole data) separately. For each combination, the prediction error of each model, the mean
squared error of the parameters’ estimates (intercept excluded), and the width of the credible
intervals for both independent variables x1 and x2 are computed. The function jags from the
R-library R2jags, which is based on the Gibbs sampler, was used for MCMC computation cor-
responding to the Bayesian QR models. In this function, three chains will run. For each chain,
10,000 iterations with burn-in 1,000 and thinning number of 90 were considered. The quality of
the obtained MCMC samples was assessed based on both qualitative (graphical) and quantita-
tive diagnostics. Par exemple, autocorrelation plots showed that by increasing the lag number
the correlation between the samples decreases sharply and approaches zero, indicating the in-
dependence among the samples. En outre, the Gelman-Rubin potential scale-reduction factor
(PSRF) diagnostic and its values near 1 showed achieving convergence in the MCMC chains.
The effective sample size diagnostic revealed the reasonable number of independent samples
for the parameters of each model. R code related to the simulations is available online1. Enfin,
for each model, the boxplots of the prediction errors, the mean squared errors of the parameters’
estimates, and the width of the credible intervals are compared. The results are reported in
Figures 1–4.

Chiffre 1 shows the prediction errors (y − y^) where y^ is calculated for each fitted model for
each quantile and sample size. It shows that the prediction error for the QR part of the two-part
model with a hurdle at 3 is least, followed by the model with a hurdle at 0, and then followed
by the Bayesian QR (no hurdle model).

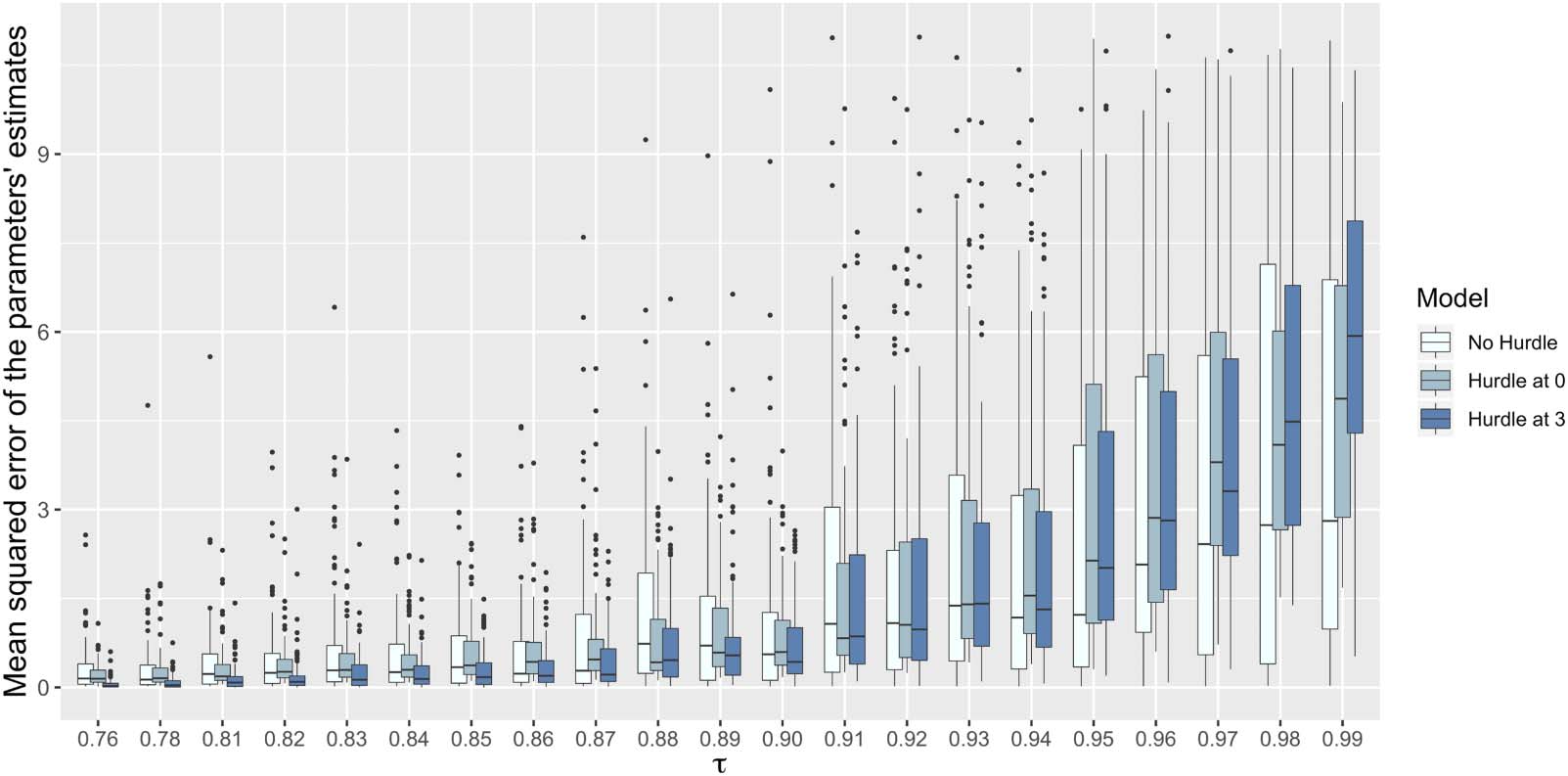
Chiffre 2 displays the mean squared errors of the parameters’ estimates computed based on

the formula:

MSE ¼

1
p

Xp
(cid:2)

(cid:3)2

− ^β

i¼1

where p is the number of independent variables, not including the intercept, in the model. All
calculations were based on a sample size of 1,000 and quantile levels of 0.76, 0.78, and a

1 https://doi.org/10.6084/m9.figshare.13726198.v1

Études scientifiques quantitatives

918

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A Bayesian hurdle quantile regression model

Chiffre 2. Mean squared errors for the parameter estimates (excluding intercept) for different models with a sample size of 1,000.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

sequence from 0.81 à 0.99 (of the whole data). The first quantile was chosen as 0.76 because
its corresponding value is just greater than three. This set of quantile levels is considered to
present a complete picture of the trend of the mean squared errors corresponding to all three
models. Smaller values (near zero) of the mean squared errors are desirable. The results show
que, in general, for quantile levels lower than 0.93, the model with a hurdle at 3 outperformed
the model with a hurdle at 0. En outre, the hurdle models present more precise estimates in
comparison to the no hurdle model. Cependant, for the cases of quantile levels greater than
0.93, there are examples that the model with a hurdle at 0 has the poorest estimates in com-
parison to the other two models. Just for one quantile level (0.99), the model with a hurdle at 3
shows the bigger mean squared errors. It can be deduced that influence of the mass points is
greatest at the quantiles shortly after the mass points (where the hurdle models, particularly the
hurdle model at 3, show more accurate estimates), but by the time we reach the extreme upper
quantiles the influence has waned and the no hurdle model returns better estimates as it is
based upon a larger sample size. En général, by increasing the quantile, the estimates of the
mean squared errors become larger for all three models.

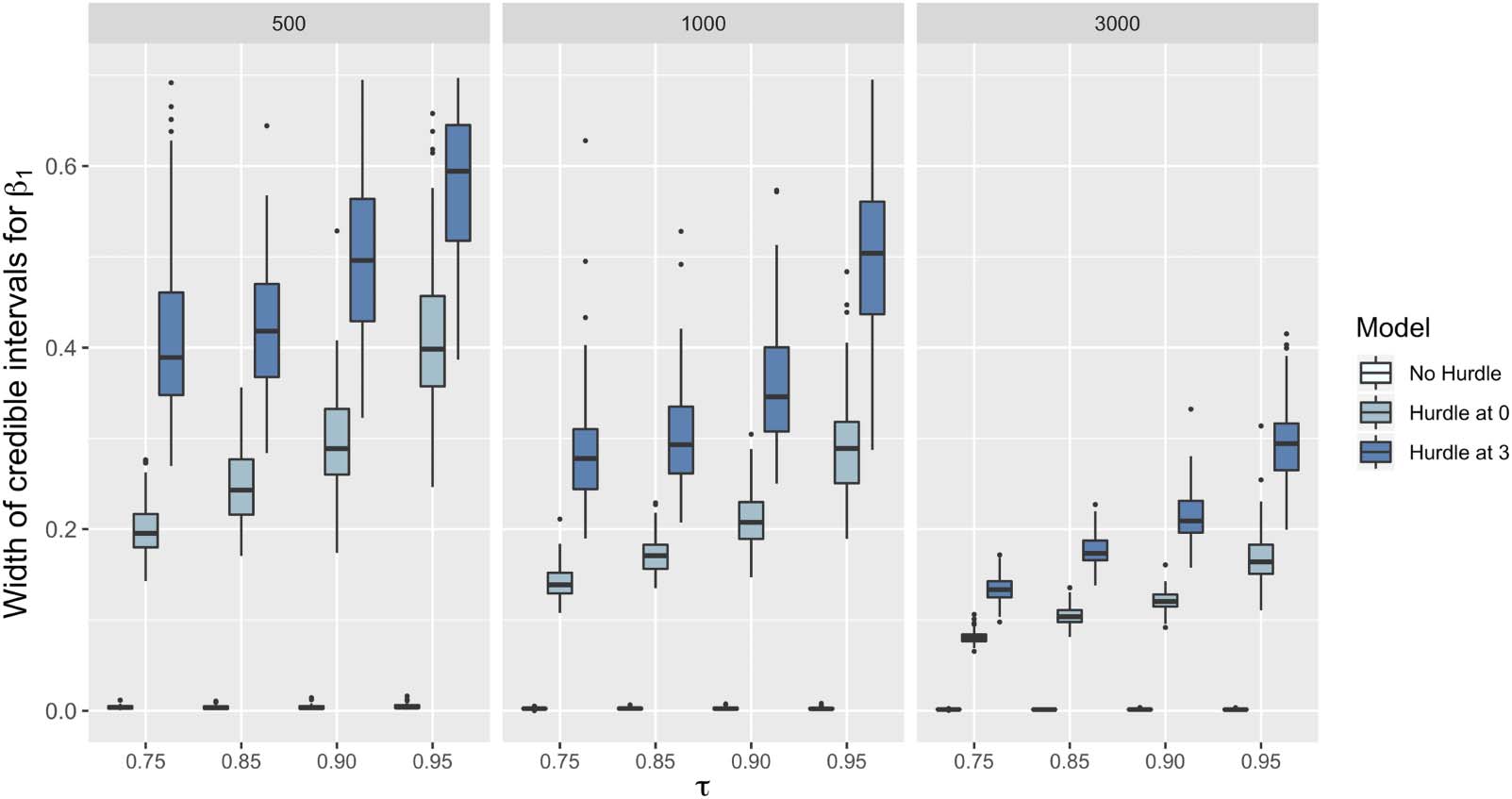
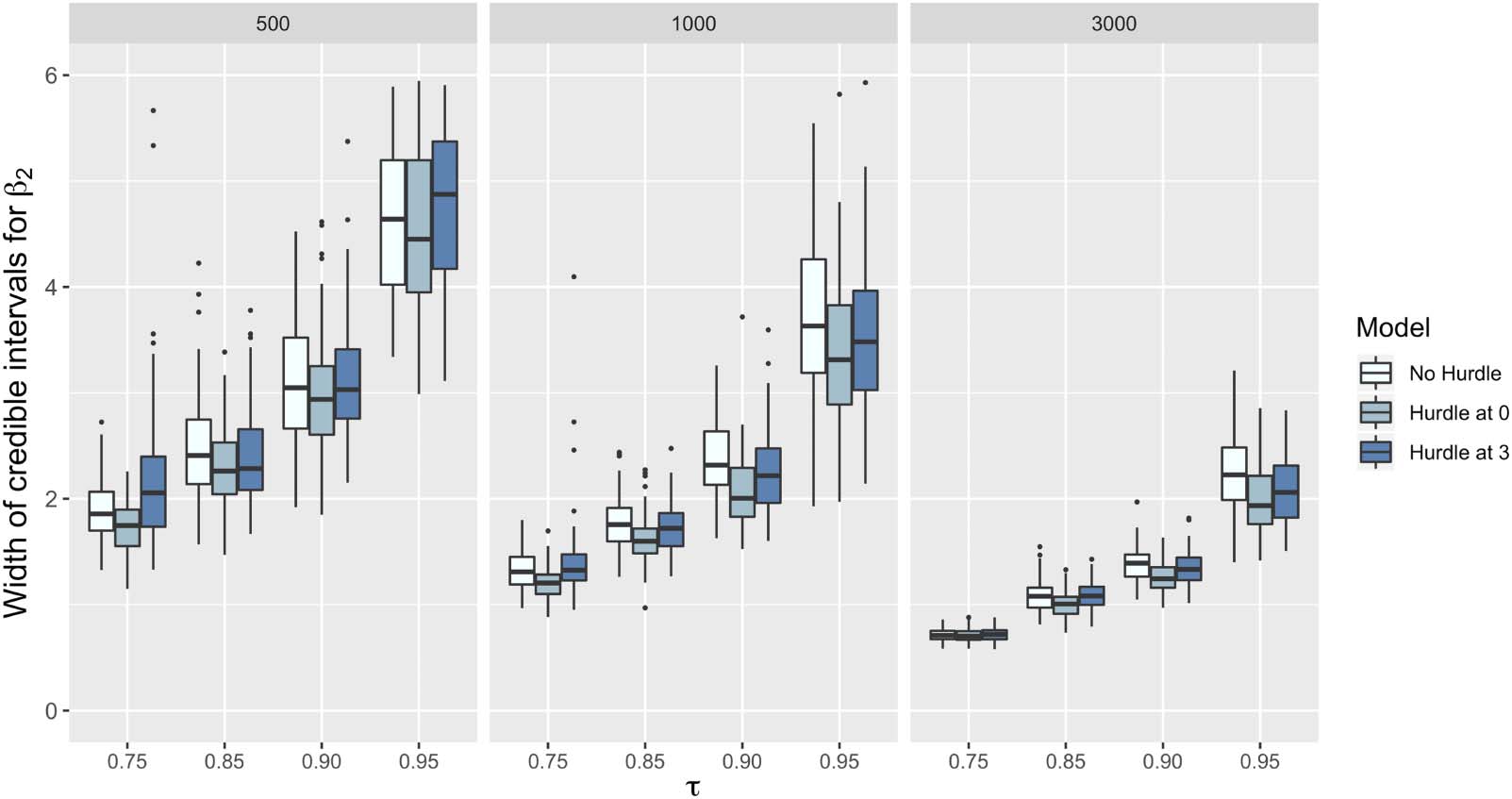
Chiffre 3 illustrates the width of credible intervals for the estimates of the coefficients of x1
based on the different models and sample sizes. The credible intervals provided are based on
the percentiles of the posterior probability distribution. Credible intervals are the Bayesian
counterparts of confidence intervals in classical statistics. We see that, as is to be expected,
by increasing the sample size from 500 à 3,000, the width of the credible interval decreases
considerably. De plus, the model with a hurdle at 3 has the largest width for all the quantiles,
followed by the model with a hurdle at 0, followed with the no hurdle model. Encore, this is as
would be expected as less data is available for the hurdle at 3 model than for the hurdle at 0
and then for the no hurdle model.

Chiffre 4 shows the widths of the credible intervals for the estimates of the coefficients of x2
based on the different models and sample sizes. The coefficient of x2 in the model from which
the data was simulated was 0. C'est, x2 is not significant. The figure shows that for most of the
quantiles and sample sizes, the widths of the credible intervals based on the three models are
approximately the same. This approximate equality of widths of credible intervals across the

Études scientifiques quantitatives

919

A Bayesian hurdle quantile regression model

Chiffre 3. Width of credible intervals for the estimates of x1.

models is surprising given that the models all have different amounts of data available to them.
It is unclear whether this phenomenon is universal, or whether it only applies to specific data.
This approximate equality of the widths of credible intervals has also occurred in other simu-
lations performed by the authors, cependant, and is worthy of further investigation.

The results of the simulation show that the model with a hurdle at 3 in general returns more
accurate estimates based on the mean squared errors of the estimates of parameters (excluding
the intercept) at quantiles just beyond the hurdle. The hurdle models mostly can present the

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 4. Width of credible intervals for the estimates of x2.

Études scientifiques quantitatives

920

A Bayesian hurdle quantile regression model

more precise estimates for the parameters for moderate and high levels of quantiles, while for
the extreme high quantiles, the no hurdle model has better estimates due to waning of the
biasing influence of the mass points by this point, and the fact that the no hurdle model works
off a greater amount of data. En outre, the model with a hurdle at 3 results in smaller pre-
diction errors at the cost of wider credible intervals. This is followed by the model with a hur-
dle at 0, and then by the no hurdle model. De plus, a larger sample size also decreases the
differences between models for the width of their credible intervals (particularly when the in-
dependent variable is not significant in the model).

5. CITATION COUNT EXAMPLE

The data used in this article consists of citation counts for standard journal articles (excluding
reviews) published in the following seven Scopus fields: Arts and Humanities (tous), Literature
and Literary Theory, Religious Studies, Visual Arts and Performing Arts, Media Technology,
Architecture, and Emergency Nursing. The articles were published in 2010 and their informa-
tion was extracted at the end of 2019, giving the citation counts time to mature. These seven
fields were selected because after discarding the records with missing cells for computation of
the dependent and possible independent variables, they have the highest proportions of zeros
and also have a maximum of around 3,000 records. The effect of sample size on computation
time is a method limitation because MCMC is time consuming. The number of citations of
each article is the dependent variable. The independent variables available were the number
of keywords, the number of pages, title length, abstract length, collaboration (the number of
authors of an article), international collaboration, abstract readability, and journal internation-
ality. Collaboration, length of title, and journal internationality were selected as independent
variables because with this selection fewer records with missing data had to be discarded and
the percentage of zeros in the data remained high. The selected variables have a reasonably
strong correlation with the corresponding citation counts for most of the seven fields.

The highest proportions of zeros are related to both Literature and Literary Theory and Arts
and Humanities respectively (Tableau 1). The portions of ones, twos, and threes in comparison to
the portion of zeros are not huge but they are still noticeable. There are no substantial mass
points greater than 3 for the fields. The percentage of substantial mass points greater than zero
in the fields varies from approximately 20% for Media Technology up to 37% for Religious
Études. The total percentages of substantial mass points for the fields of Literature and
Literary Theory and Media Technology are the largest (85%) and smallest (47%) respectivement.

Collaboration, title length, and journal internationality were included in the models as in-
dependent variables. Collaboration and title length are discrete variables. The log function of
collaboration was used in the models to provide a closer to linear relationship with the citation
compte. Journal internationality is a continuous variable on the interval [0, 1]. Journal interna-
tionality was computed with the Gini coefficient (Gini, 1997). A value of 0 shows the highest
level of internationality of the journal related to the article, and a value of 1 shows the least
internationality. A sequence of quantiles from 0.05 à 0.95 is considered. Ordinary Bayesian
QR, Bayesian two-part QR with a hurdle at 0 and Bayesian two-part QR with a hurdle at 3
were fitted to the data sets. MCMC was calculated again with the jags function by considering
three chains. For each chain, 100,000 iterations with burn-in 50,000 and thinning size of 160
were used. Based on a pretest, the autocorrelation plots for the parameters corresponding to
the journal internationality in both parts of the model showed a slow decreasing pattern, dans-
dicating slow mixing in the chain. To fix this, the large number of iterations, burn-in, and thin-
ning size were selected. The qualitative (graphical) and quantitative convergence diagnostics,

Études scientifiques quantitatives

921

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A Bayesian hurdle quantile regression model

the same as those used for simulation section, were applied to check the quality of the MCMC
samples. The autocorrelation plots decreased and approached zero by increasing the lag num-
ber, showing convergence in the chains. There are also reasonable values for the effective
sample size and also PSRFs near 1 for all parameters in the models. R code related to the
MCMC computation is available online2.

5.1. Comparison of the QR Part of the Two-Part Models with the Bayesian QR Model

Dans ce qui suit, the results related to the QR parts of the Bayesian two-part QR models with
hurdles at 0 et 3 are compared to the results of the Bayesian QR.

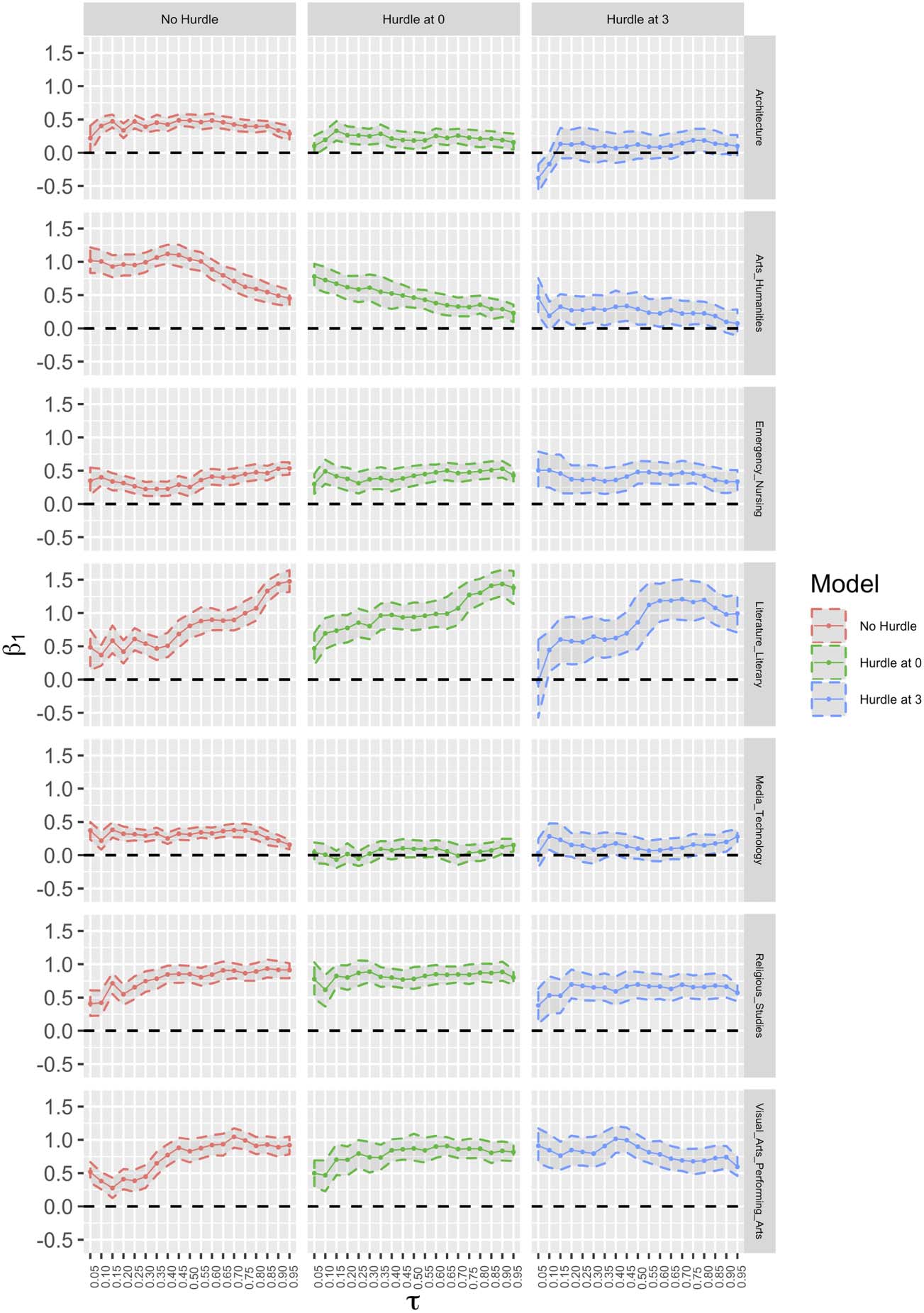
In Figure 5, the linear effect of collaboration and its 95% credible intervals over all the
quantiles of the citation counts in different fields are shown. The credible intervals provided
based on the percentiles of the posterior probability distribution in Bayesian statistics are coun-
terparts of confidence intervals in classical statistics. The upper and lower boundaries of the
95% credible intervals are represented by dashed lines. A narrower band illustrates a smaller
variance for the estimated parameter. When a band includes zero, it indicates a nonsignificant
effect related to the variable.

The effects of collaboration on citation counts in Bayesian QR are significantly positive at
all quantiles for all fields. In comparison with two-part models with hurdles at 0 et 3, dans le
Bayesian QR model, the impact size of the collaboration for Literature and Literary Theory and
Emergency Nursing was the smallest over the quantiles, while for Architecture, Médias
Technologie, Religious Studies, and Arts and Humanities, the effect size is the largest. Au pair-
particulier, for the field of Arts and Humanities, which has substantial mass points at lower counts,
the difference in impact size based on the Bayesian QR model against the hurdle models is
considerable. For the field of Visual Arts and Performing Arts, for the first half of the quantiles
the effect size of collaboration for the Bayesian QR model is the smallest, but for the second
half of the quantiles it is the greatest. By discarding the substantial mass points of the citation
counts and fitting the models with hurdles at 0 et 3, the collaboration effect stabilizes over
the quantiles for most of the fields (except Literature and Literary Theory and Arts and
Sciences humaines), indicating that collaboration equally influences the moderately cited and highly
cited articles. For Literature and Literary Theory, the effect still follows an increasing trend
based on the hurdle models, the same as in the no hurdle model, showing the benefit of col-
laboration for the highly cited articles. Cependant, for Arts and Humanities, based on all three
models, collaboration experiences a downward trend. In previous studies, collaboration has
sometimes (but not always) been shown to be related to citation counts. Previous research has
used different data sets and statistical methods to assess the relationship between citation
counts and collaboration with differing results. Par exemple, Bornmann, Schier et al. (2012)
used a negative binomial regression model (with a log link) for approximately 2,000 manu-
scripts that were submitted to the journal Angewandte Chemie International Edition (AC-IE).
The estimated coefficient of collaboration was 0.023 (c'est à dire., for each unit increase in collabora-
tion, the log of the citation count increases by 0.023 on average) with a p-value greater than
0.05. Cependant, Borsuk, Budden et al. (2009) used ordinary least squares (OLS) regression to
analyze data from six journals in ecology from 1997 à 2004 and estimated that the effect size
and p-value were 0. 196 et 0.005 respectivement. By applying the negative binomial hurdle

2 https://doi.org/10.6084/m9.figshare.14742939.v4

Études scientifiques quantitatives

922

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A Bayesian hurdle quantile regression model

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 5. Parameter estimates for collaboration (β

1) over the quantiles of the citation count distribution separated by the types of models.

model, Didegah (2014) also showed that the collaboration has a significant positive impact on
citation counts for all subjects of the Web of Science except Physics.

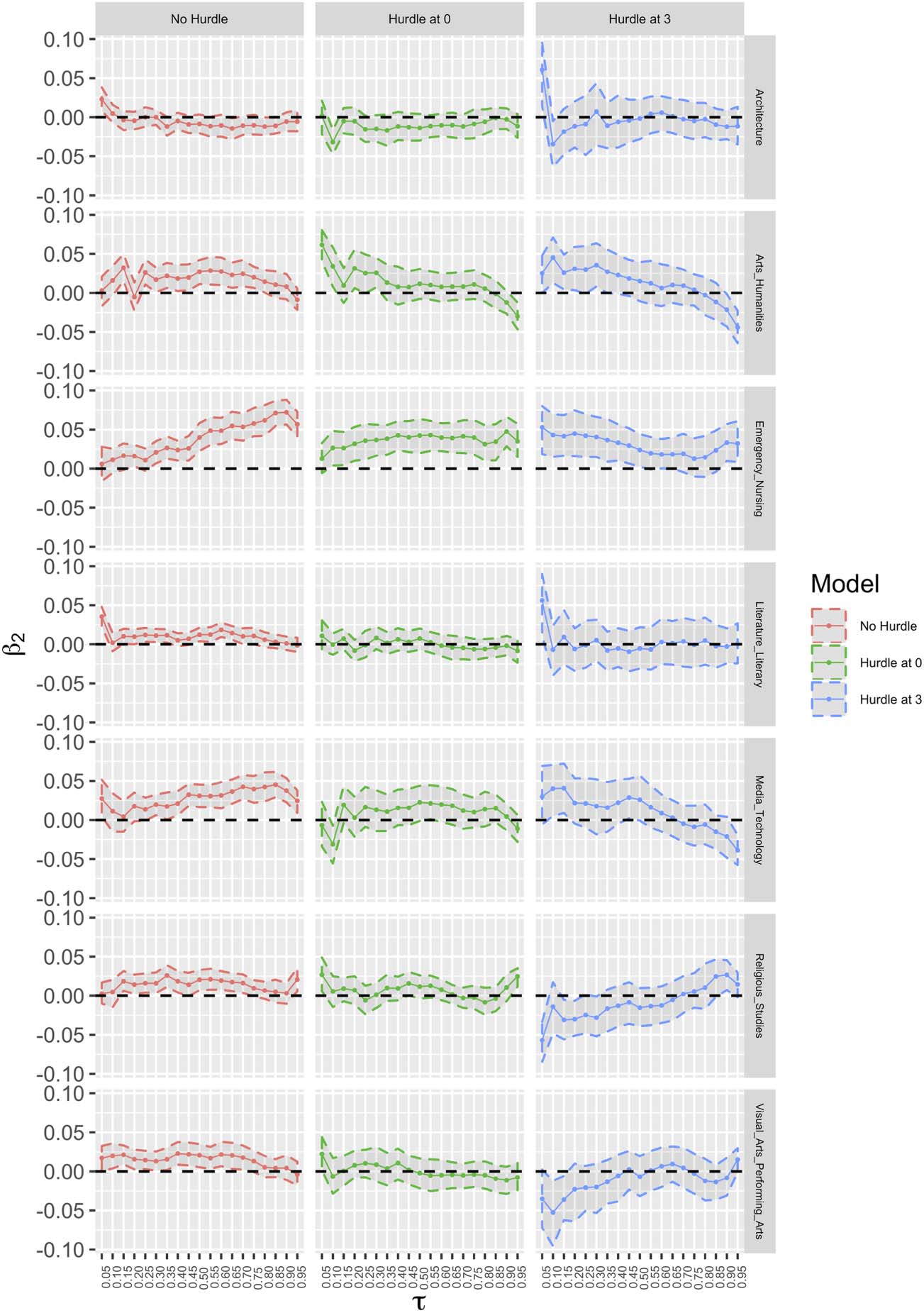
Chiffre 6 displays the linear impact of the length of title on the citation count distribution
across the quantiles in the various fields. Based on the Bayesian QR model, in general, the effect
is mostly positive but very small in size and just statistically significant for some quantiles in
some fields. According to this model, this effect fluctuated gradually over the quantiles, illus-
trating that low, moderately, and highly cited articles are equally influenced by this effect. Le
impact size of the length of title based on the Bayesian QR is greatest for most of the fields and
quantile levels in comparison to the two-part QR models with hurdles at 0 et 3. This effect is a
significant factor for just a few numbers of fields and quantiles based on the two-part models

Études scientifiques quantitatives

923

A Bayesian hurdle quantile regression model

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 6. Parameter estimates for title length (β

2) over the quantiles of the citation count distribution separated by the types of models.

with hurdle points of 0 et 3. By skipping the zero mass point and fitting the Bayesian two-part
QR model with a hurdle at 0, the effect shows a flatter pattern in comparison to the Bayesian QR
model, particularly for the fields of Emergency Nursing and Media Technology. The effect
based on the two-part model with a hurdle at 3 shows a slightly different pattern but still with
small size for some quantiles in some fields. Par exemple, it shows the least effect size for lower
quantiles of the citation counts for the fields of Visual Arts and Performing Arts and Religious
Studies that have high percentages of mass points in 1 ≤ y ≤ 3. When interpreting the various
diagrams of Figure 6, comments made elsewhere in this paper concerning the relative suit-
ability of the various models at the various quantiles should be considered, different models
being more suitable depending upon the quantile under consideration. According to

Études scientifiques quantitatives

924

A Bayesian hurdle quantile regression model

Haslam, Ban et al. (2008) and using correlations tests and regression analyses, longer title
lengths displayed a negative impact on citation counts in psychology. En outre, by applying
negative binomial hurdle models in different subjects of Web of Science, Didegah (2014)
showed that the mean length of title associated negatively with nonzero citation counts in some
fields of Web of Science, such as Economics & Business, Computer Science, and Chemistry, mais
nonsignificantly in the fields of Clinical Medicine, Multidisciplinary and Physics.

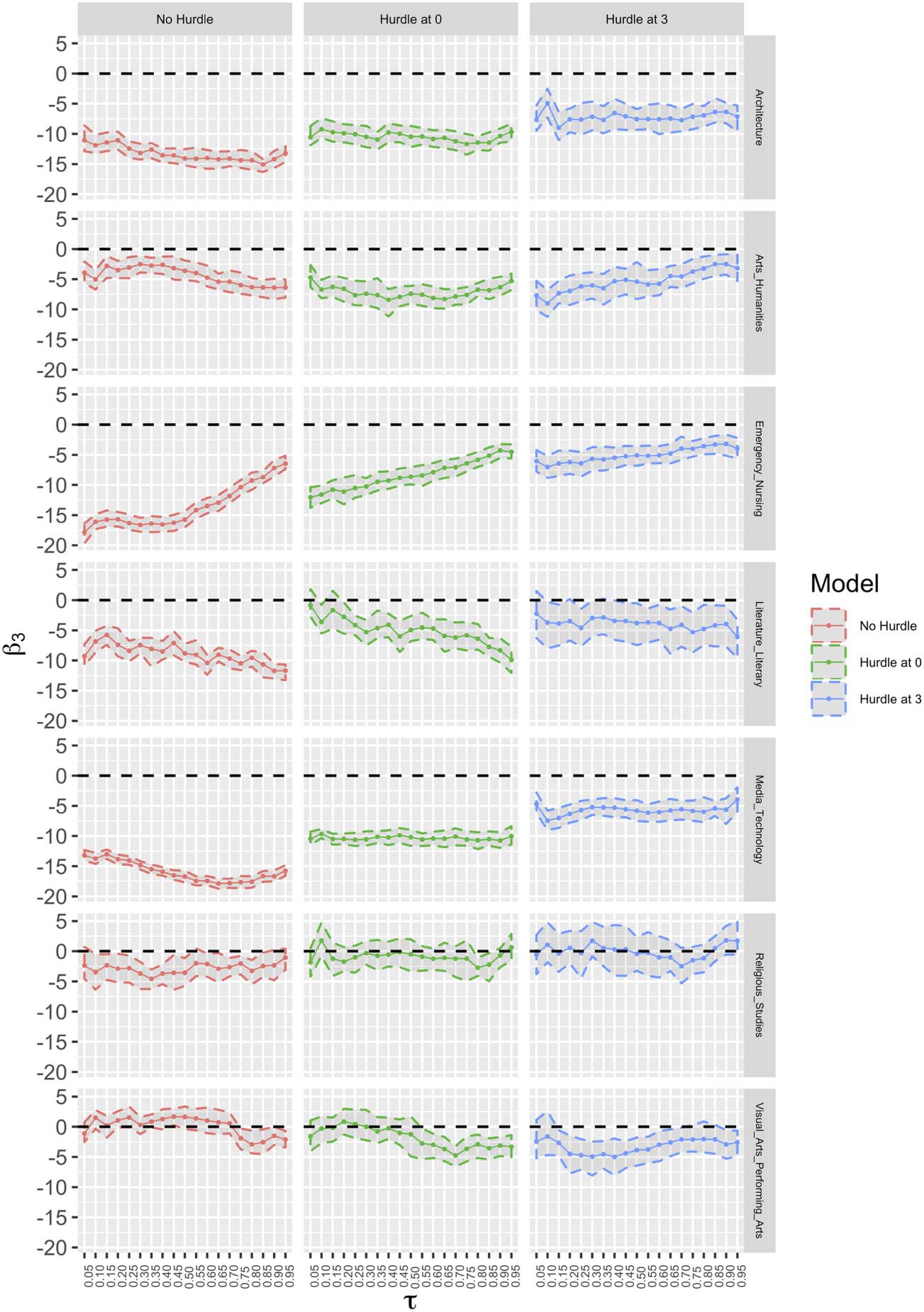
Chiffre 7 illustrates how journal internationality influences the citation counts at all quan-
tiles in the different fields. As was mentioned, a lesser value for the Gini coefficient corre-
sponds to greater journal internationality, indicating that the journals in this field published

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 7. Parameter estimates for journal internationality (β
models.

3) over the quantiles of the citation count distribution separated by the types of

Études scientifiques quantitatives

925

A Bayesian hurdle quantile regression model

articles from a broad range of countries. Based on the Bayesian QR, the effect of the Gini co-
efficient significantly negatively influences the citation counts over all the quantiles for all the
fields except Visual Arts and Performing Arts, where its impact is not significant for the majority
of the quantiles. The negativity of the effect reflects the direct relationship between journal
internationality and citation counts. Fitting the Bayesian two-part QR models with hurdles
à 0 et 3 results in the trend of the effect becoming smoother and of noticeably smaller mag-
nitude, especially for the model with a hurdle at 3, for the quantiles in all fields except Visual
Arts and Performing Arts and Arts and Humanities, where the estimates based on the various
models intersect. Perhaps it refers to the existence of the high portions of mass points in these
two fields that influenced the estimates of the effect in the Bayesian QR model. En fait, for the
case of Visual Arts and Performing Arts, the Bayesian QR model shows that journal

Tableau 2.
hurdles at 0 et 3. c
the models

Estimates of the vector and credible intervals and standard deviations from the logistic part of the Bayesian two-part QR model with
3 are parameters corresponding respectively to intercept, collaboration, title length, and journal internationality in

2, c

0, c

1, c

Field
Literature and

Literary Theory

Arts and

Sciences humaines

Emergency Nursing

Visual Arts and

Performing Arts

Architecture

Religious Studies

Media Technology

BTPQR with hurdle at 0

BTPQR with hurdle at 3

Lower
band
6.465
0.460
0.001
−11.563

−1.703
0.884
0.003
−2.931

11.437
0.158
0.020
−18.095

−3.712
0.399
0.010
−0.881

10.485
0.433
−0.027
−15.367

1.500
0.457
0.004
−6.772

Mean

8.918
0.716
0.016
−9.527

0.519
1.160
0.027
−0.835

14.064
0.345
0.048
−15.235

−1.421
0.622
0.029
1.490

12.687
0.595
−0.009
−13.068

4.112
0.711
0.027
−3.945

Upper
band
10.875
0.992
0.030
−7.007

2.574
1.412
0.051
1.484

16.804
0.533
0.078
−12.592

0.833
0.854
0.050
3.900

14.943
0.774
0.010
−10.704

6.813
0.963
0.045
−1.183

19.359
0.499
0.029
−25.749

21.461
0.685
0.062
−23.635

23.415
0.867
0.097
−21.471

Standard
deviation
1.072
0.134
0.008
1.105

1.100
0.133
0.012
1.137

1.399
0.095
0.014
1.425

1.177
0.115
0.010
1.245

1.149
0.088
0.010
1.211

1.366
0.127
0.011
1.423

1.033
0.098
0.017
1.089

Lower
band
4.444
1.185
−0.017
−12.844

3.821
0.940
−0.009
−10.108

10.035
0.446
0.026
−17.345

−2.207
0.837
−0.018
−3.822

11.566
0.309
−0.034
−17.418

−2.269
0.984
−0.015
−5.328

14.719
0.099
0.010
−20.710

Mean

7.265
1.485
0.006
−9.908

5.628
1.187
0.019
−8.030

12.087
0.674
0.057
−15.120

−0.113
1.056
0.005
−1.506

13.424
0.472
−0.012
−15.538

0.746
1.210
0.006
−2.314

Upper
band
10.082
1.766
0.026
−6.922

7.635
1.422
0.048
−6.167

14.206
0.902
0.087
−13.115

2.056
1.287
0.028
0.655

15.209
0.664
0.012
−13.524

3.664
1.410
0.028
0.809

16.389
0.297
0.043
−19.177

17.779
0.488
0.074
−17.353

Parameters
c
0
c
1
c
2
c
3

c
0
c
1
c
2
c
3

Études scientifiques quantitatives

Standard
deviation
1.457
0.150
0.011
1.511

0.965
0.123
0.015
1.011

1.081
0.115
0.015
1.094

1.133
0.111
0.010
1.198

0.947
0.092
0.011
1.024

1.497
0.111
0.011
1.556

0.791
0.096
0.016
0.867

926

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A Bayesian hurdle quantile regression model

internationality is not significant at most quantiles, whereas the model with a hurdle at 3 indi-
cates that it is, the model with a hurdle at 0 being somewhere in-between. This is a good ex-
ample that shows the importance of using the appropriate model. Based on the Bayesian QR
model, the effect follows mostly a decreasing trend by increasing the quantiles for most of the
fields, indicating higher impact size on highly cited articles, but mostly a stabilized trend for the
two-part models, showing the equal importance of the effect on moderately and highly cited
articles. Previous literature has also found a significant positive association between journal
internationality and citation impact, with the application of Structural Equation Modeling
and a simple correlation coefficient by Yue (2004) and Kim (2010) respectivement. Didegah
(2014) applied the negative binomial hurdle model to show both negative and positive relation-
ships between journal internationality and nonzero citation counts in different fields. For exam-
ple, a positive association in Psychiatry/Psychology but a negative one in Social Sciences were
reported.

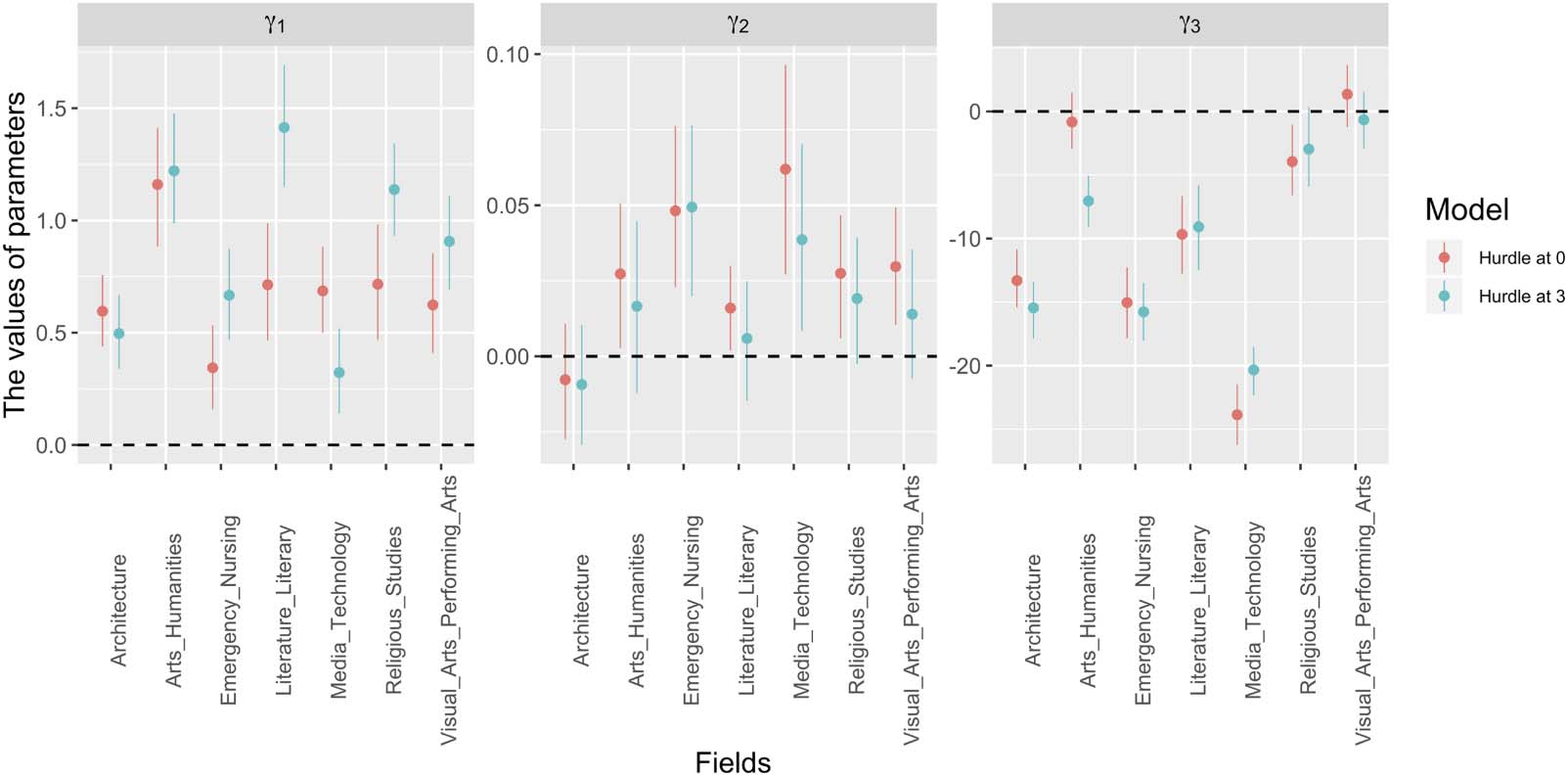
5.2. Analyzing the Logistic Parts of the Two-Part Models with Hurdles at 0 et 3

The estimates in the logistic part, their credible intervals, and standard errors are reported in
Tableau 2 and illustrated in Figure 8. It is seen that shifting the hurdle from 0 à 3 can influence
the significance status and mostly the size of the effects corresponding to the independent var-
iables for the fields with high substantial mass points at 1, 2, et 3. Par exemple, for the fields
of Literature and Literary Theory, Religious Studies, and Visual Arts and Performing Arts, le
absolute effect size of the collaboration gets larger and title length ceases to be significant. Dans
général, in all fields except Architecture and Media Technology, collaboration shows smaller
absolute impact size on zero citation in comparison to its impact on low citation (par exemple., 0–3
citations). For title length, this trend is inverse over the fields except for Emergency Nursing.
The absolute impact size of the longer title on zero citation is slightly larger than on low ci-
tation. En outre, for some of the fields, the influence of journal internationality on zero ci-
tation is a little larger than on low citation, but for other fields it is a little smaller.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 8. Parameter estimates from the logistic part of the two-part QR models. c
intercept, collaboration, title length, and journal internationality in the models.

0, c

1, c

2, c

3 are parameters corresponding respectively to

Études scientifiques quantitatives

927

A Bayesian hurdle quantile regression model

Collaboration has a significant positive impact on both zero and low cited articles. For ex-
ample for Emergency Nursing, based on the model with a hurdle at 0, with greater collabo-
ration, the odds of zero citations increases on average by 41% (plus de détails: (exp(0.345) − 1) ×
100 = 41%). In the same field but for the model with a hurdle at 3, the odds of low citation
increases on average by 96% (plus de détails: (exp(0.674) − 1) × 100 = 96%). Collaboration has
its absolute largest impact in the field of Arts and Humanities based on the model with a hurdle
à 0, while it occurs in the field of Literature and Literary Theory for the model with a hurdle at
3. Based on the previous studies, Par exemple, Didegah (2014) used the negative binomial
hurdle model and showed that collaboration negatively impacts zero citation in most Web
of Science subjects.

Title length in comparison to collaboration and journal internationality has the smallest ab-
solute impact size in all the fields. This effect also shows wider credible intervals for all models
with hurdles at 0 et 3 compared to the effects of collaboration and journal internationality.
The cases of nonsignificant status related to this effect are more in comparison to other factors,
particularly for the hurdle model at 3. For both hurdle models, the title length has a negative
impact on zero citation and also on low citation for the field of Architecture, while for other
fields this effect is positive with the small size of the impact. The negativity means that a longer
title decreases the odds of zero citations based on the model with a hurdle at 0 and decreases
the odds of low citation in the model with a hurdle at 3. En outre, the positivity means that a
longer title increases zero or low citations. The largest and smallest impact sizes for title length
are in Media Technology and Architecture, respectivement, for the model with a hurdle at 0, alors que
for the models with a hurdle at 3 they are Emergency Nursing and Architecture. Didegah (2014)
showed that title length is a nonsignificant factor for zero citation for most Web of Science sub-
projets, but for Agricultural Sciences, Geosciences, Materials Science, Mathematics, and Physics,
title length has a significant positive impact on the odds of zero citations.

Journal internationality has the largest absolute impact on both zero citation and low cita-
tion, and also has shorter credible intervals in comparison with collaboration and title length
for all models with hurdles at 0 et 3 for all fields. The impact of a greater Gini coefficient
(smaller journal internationality) has a significant negative effect on the odds of zero citation
and low citation for most of the fields, indicating the direct relationship between journal in-
ternationality and zero or low citation. Didegah (2014) showed that greater journal interna-
tionality increases the odds of zero citation for most of the subjects in Web of Science, except
in Space Science, for which the effect has a decreasing pattern.

6. DISCUSSION AND CONCLUSION

QR enables a deep description of the relationship between independent variables and a de-
pendent variable. It is a useful technique for analyzing the entire citation count distribution
corresponding to low, moderately, and highly cited articles. Discontinuity and the presence
of substantial mass points at lower counts are characteristics of citation counts that make the
application of the “usual” QR inappropriate. In this research, an update of a Bayesian two-part
hurdle QR model was introduced to scientometrics to address these problems. The original
Bayesian two-part hurdle QR model was introduced for the case of count data with a substan-
tial mass point at zero. It allows the zeros and nonzeros data to be modeled separately but
simultaneously. For citation count data, as well as a substantial mass point at zero in some
fields, there can be substantial mass points at lower counts, such as ones, twos, and threes,
that influence the estimation of the model. Donc, we introduce a method to shift the hur-
dle forward to discard the effect of the substantial mass points on the estimation of the model

Études scientifiques quantitatives

928

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A Bayesian hurdle quantile regression model

for fields with many low cited articles. Articles without more citations than the hurdle are re-
garded as “low cited articles.” In this new update, the model enables analyses of the citation
counts of low cited articles simultaneously but separately from those of the moderately and
highly cited articles. It uses jittering for citation counts greater than the hurdle to render such
data continuous. The model benefits from the power of its QR portion for modeling the differ-
ent quantiles of the jittered citation counts, and its logistic portion for analyzing the influence
of factors such as collaboration, title length, and journal internationality on the chances of an
article receiving few citations. The usefulness and applicability of the method were illustrated
based on both simulated and real citation count data. The simulation showed that the QR part
of the two-part model with a hurdle point past the substantial mass points in the data gives
more accurate estimates at quantiles just beyond the hurdle based on the indicator of the mean
squared error of the estimates of the coefficients corresponding to the independent variables in
the model. De plus, the QR part of the two-part QR models provides smaller prediction
errors at the cost of slightly wider credible intervals for the parameter estimates in comparison
to the Bayesian QR model. Citation data from seven Scopus fields were also considered and
three models including Bayesian QR, Bayesian two-part QR with a hurdle at 0, and Bayesian
two-part QR with a hurdle at 3 were fitted to the data. The results of the Bayesian QR model
based on the whole data shows a pattern with more fluctuations for the independent variables
over the quantiles. Cependant, the two-part models with hurdles at 0 et 3 generally show a
smoother trend of the estimates over the quantiles for most of the fields. Shifting the hurdle
depuis 0 to a larger point and passing the substantial mass points in the data influence the impact
size, the significance status, and the width of the credible intervals, illustrating the importance
of choosing the hurdle appropriately.

En résumé, we have shown that the proposed hurdle-at-three model has many advantages
over the hurdle-at-zero model of King and Song (2019) for the modeling of citation count data
for fields with large percentages of articles with few citations.

REMERCIEMENTS

The authors would like to thank Clay King for his helpful comments.

CONTRIBUTIONS DES AUTEURS
Marzieh Shahmandi: Conservation des données, Enquête, Méthodologie, Writing—original draft,
Validation, Logiciel. Paul Wilson: Surveillance, Writing—review & édition. Mike Thelwall:
Surveillance, Writing—review & édition.

COMPETING INTERESTS

The authors have no competing interests.

INFORMATIONS SUR LE FINANCEMENT

No funding was received for this study.

DATA AVAILABILITY

The processed data used to produce the tables and figures for the section of citation count
examples are available in the supplementary material (https://doi.org/10.6084/m9.figshare
.14742939.v4).

Études scientifiques quantitatives

929

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

A Bayesian hurdle quantile regression model

RÉFÉRENCES

Ahlgren, P., Colliander, C., & Sjögårde, P.. (2018). Exploring the relation
between referencing practices and citation impact: A large-scale
study based on web of science data. Journal of the Association for
Information Science and Technology, 69, 728–743. https://doi.org
/10.1002/asi.23986

Anauati, V., Galiani, S., & Gálvez, R.. H. (2016). Quantifying the
life cycle of scholarly articles across fields of economic research.
Economic Inquiry, 54(2), 1339–1355. https://doi.org/10.1111
/ecin.12292

Bornmann, L., Schier, H., Marx, W., & Daniel, H.-D. (2012). What
factors determine citation counts of publications in chemistry
besides their quality? Journal of Informetrics, 6(1), 11–18.
https://doi.org/10.1016/j.joi.2011.10.002

Borsuk, R., Budden, UN., Leimu, R., Aarssen, L., & Lortie, C. (2009).
The influence of author gender, national language and number
of authors on citation rate in ecology. Open Ecology Journal, 2,
25–28. https://doi.org/10.2174/1874213000902010025

Brzezinski, M.. (2015). Power laws in citation distributions:
Evidence from Scopus. Scientometrics, 103(1), 213–228.
https://doi.org/10.1007/s11192-014-1524-z, PubMed: 25821280
Clark, D. JE., & Osborne, M.. R.. (1986). Finite algorithms for Huber’s
M-estimator. SIAM Journal on Scientific and Statistical
Computing, 7(1), 72–85. https://doi.org/10.1137/0907005

Coad, UN., & Rao, R.. (2008). Innovation and firm growth in high-
tech sectors: A quantile regression approach. Research Policy,
37(4), 633–648. https://doi.org/10.1016/j.respol.2008.01.003
Danell, R.. (2011). Can the quality of scientific work be predicted
using information on the author’s track record? Journal of the
American Society for Information Science and Technology, 62(1),
50–60. https://doi.org/10.1002/asi.21454

Dantzig, G. (1963). Linear programming and extensions. Rand
Corporation Research Study. Princeton University Press. https://
doi.org/10.7249/R366

Didegah, F. (2014). Factors associating with the future citation
impact of published articles: A statistical modelling approach.
PhD Thesis.

Didegah, F., Thelwall, M., & Wilson, P.. (2013). Which factors help
to produce high impact research? A combined statistical modelling
approche. Proceedings of ISSI 2013 – 14th International Society of
Scientometrics and Informetrics Conference, 2, 1830–1844.
Eom, Y.-H., & Fortunato, S. (2011). Characterizing and modeling
citation dynamics. PLOS ONE, 6(9), 1–7. https://est ce que je.org/10
.1371/journal.pone.0024926, PubMed: 21966387

Galiani, S., & Gálvez, R.. H. (2019). An empirical approach based on
quantile regression for estimating citation ageing. Journal de
Informetrics, 13(2), 738–750. https://doi.org/10.1016/j.joi.2019
.03.014

Garanina, O., & Romanovsky, M.. (2016). Citation distribution of
individual scientist: Approximations of stretch exponential distri-
bution with power law tails. Proceedings of ISSI 2015. Istanbul,
Turkey: Bogaziçi University Printhouse (pp. 272–277).

Gilchrist, W. (2000). Statistical modeling with quantile functions.
Chapman and Hall/CRC. https://doi.org/10.1201/9781420035919
Gini, C. (1997). Concentration and dependency ratios. Rivista di

politica economica, 87(8–9), 769–790.

Haslam, N., Ban, L., Kaufmann, L., Loughnan, S., Peters, K., …
Wilson, S. (2008). What makes an article influential? Predicting
impact in social and personality psychology. Scientometrics, 76,
169–185. https://doi.org/10.1007/s11192-007-1892-8

Kim, M.-J. (2010). Visibility of Korean science journals: An analysis
between citation measures among international composition of

editorial board and foreign authorship. Scientometrics, 84,
505–522. https://doi.org/10.1007/s11192-010-0168-x

King, C., & Song, J.. J.. (2019). A Bayesian two-part quantile regression
model for count data with excess zeros. Statistical Modelling,
19(6), 653–673. https://doi.org/10.1177/1471082X18799919
Koenker, R., & Bassett, G. (1978). Regression quantiles.
Econometrica, 46(1), 33–50. https://doi.org/10.2307/1913643
Koenker, R., & Hallock, K. F. (2001). Quantile regression. Journal de
Economic Perspectives, 15(4), 143–156. https://doi.org/10.1257
/jep.15.4.143

Kozumi, H., & Kobayashi, G. (2011). Gibbs sampling methods for
Bayesian quantile regression. Journal of Statistical Computation
and Simulation, 81(11), 1565–1578. https://est ce que je.org/10.1080
/00949655.2010.496117

Lee, D., & Neocleous, T. (2010). Bayesian quantile regression for
count data with application to environmental epidemiology.
Journal of the Royal Statistical Society: Series C (Applied
Statistics), 59(5), 905–920. https://doi.org/10.1111/j.1467-9876
.2010.00725.X

Low, W. J., Wilson, P., & Thelwall, M.. (2016). Stopped sum models
and proposed variants for citation data. Scientometrics, 107(2),
369–384. https://doi.org/10.1007/s11192-016-1847-z

Machado, J.. UN. F., & Silva, J.. M.. C. S. (2005). Quantiles for
compte. Journal of the American Statistical Association, 100(472),
1226–1237. https://doi.org/10.1198/016214505000000330
Madsen, K., & Nielsen, H. B. (1993). A finite smoothing algorithm
for linear l1 estimation. SIAM Journal on Optimization, 3, 223–235.
https://doi.org/10.1137/0803010

Mäntylä, M., & Garousi, V. (2019). Citations in software engineer-
ing – paper-related, journal-related, and author-related factors.
ArXiv. https://arxiv.org/abs/1908.04122v2

Meho, L. (2007). The rise and rise of citation analysis. Physics
Monde, 20, 32–36. https://doi.org/10.1088/2058-7058/20/1/33
Ospina, R., & Ferrari, S. L. (2012). A general class of zero-or-one
inflated beta regression models. Computational Statistics & Données
Analysis, 56(6), 1609–1623. https://doi.org/10.1016/j.csda.2011
.10.005

Portnoy, S., & Koenker, R.. (1997). The Gaussian hare and the
Laplacian tortoise: Computability of squared-error versus
absolute-error estimators. Statistical Science, 12(4), 279–300.
https://doi.org/10.1214/ss/1030037960

Redner, S. (1998). How popular is your paper? An empirical study
of the citation distribution. European Physical Journal B –
Condensed Matter and Complex Systems, 4, 131–134. https://
doi.org/10.1007/s100510050359

Santos, B., & Bolfarine, H. (2015). Bayesian analysis for zero-or-one
inflated proportion data using quantile regression. Journal de
Statistical Computation and Simulation, 85(17), 3579–3593.
https://doi.org/10.1080/00949655.2014.986733

Seglen, P.. Ô. (1992). The skewness of science. Journal of the
American Society for Information Science, 43(9), 628–638.
https://doi.org/10.1002/(SICI)1097-4571(199210)43:9<628::AID -ASI5>3.0.CO;2-0

Shahmandi, M., Wilson, P., & Thelwall, M.. (2020). A new algo-
rithm for zero-modified models applied to citation counts.
Scientometrics, 125(2), 993–1010. https://doi.org/10.1007
/s11192-020-03654-8

Stegehuis, C., Litvak, N., & Waltman, L. (2015). Predicting the
long-term citation impact of recent publications. Journal de
Informetrics, 9(3), 642–657. https://doi.org/10.1016/j.joi.2015
.06.005

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d

F
/

2
3
9
1
2
1
9
7
0
8
0
3
q
s
s
_
un
_
0
0
1
4
7
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Études scientifiques quantitatives

930

A Bayesian hurdle quantile regression model

Thelwall, M.. (2016). Are there too many uncited articles? Zero in-
flated variants of the discretised lognormal and hooked power
law distributions. Journal of Informetrics, 10(2), 622–633.
https://doi.org/10.1016/j.joi.2016.04.014

Thelwall, M., & Wilson, P.. (2014). Regression for citation data: Un
evaluation of different methods. Journal of Informetrics, 8(4),
963–971. https://doi.org/10.1016/j.joi.2014.09.011

Wang, J., & Shapira, P.. (2015). Is there a relationship between research
sponsorship and publication impact? An analysis of funding ac-
knowledgments in nanotechnology papers. PLOS ONE, 10(2), 1–19.
https://doi.org/10.1371/journal.pone.0117727, PubMed: 25695739

Wang, X. (2018). The relationship between SCI editorial board
representation and university research output in the field of
computer science: A quantile regression approach. Malaysian
Journal of Library & Information Science, 23, 67–84. https://
doi.org/10.22452/mjlis.vol23no1.5

Yu, K., & Moyeed, R.. UN. (2001). Bayesian quantile regression.
Statistics & Probability Letters, 54(4), 437–447. https://doi.org
/10.1016/S0167-7152(01)00124-9

Yue, W. (2004). Predicting the citation impact of clinical neurology
journals using structural equation modeling with partial least
squares. PhD Thesis.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
q
s
s
/
un
r
t
je
c
e
–
p
d