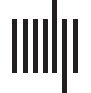RECHERCHE - Recherche en IA spécialisée au MIT

RECHERCHE

Directed functional and structural connectivity
in a large-scale model for the mouse cortex

Ronaldo V. Nunes1

, Marcelo B. Reyes1

, Jorge F. Mejias2

, and Raphael Y. de Camargo1

1Center for Mathematics, Computing, et cognitif, Universidade Federal do ABC, São Bernardo do Campo, Brazil
2Swammerdam Institute for Life Sciences, University of Amsterdam, Amsterdam, The Netherlands

Mots clés: Large-scale brain models, Directed functional connectivity, Causality, Generalized par-
tial directed coherence

un accès ouvert

journal

ABSTRAIT

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

Inferring the structural connectivity from electrophysiological measurements is a fundamental
challenge in systems neuroscience. Directed functional connectivity measures, such as the
generalized partial directed coherence (GPDC), provide estimates of the causal influence
between areas. Cependant, the relation between causality estimates and structural connectivity is
still not clear. We analyzed this problem by evaluating the effectiveness of GPDC to estimate the
connectivity of a ground-truth, data-constrained computational model of a large-scale network
model of the mouse cortex. The model contains 19 cortical areas composed of spiking neurons,
with areas connected by long-range projections with weights obtained from a tract-tracing cortical
connectome. We show that GPDC values provide a reasonable estimate of structural connectivity,
with an average Pearson correlation over simulations of 0.74. De plus, even in a typical
electrophysiological recording scenario containing five areas, the mean correlation was above
0.6. These results suggest that it may be possible to empirically estimate structural connectivity
from functional connectivity even when detailed whole-brain recordings are not achievable.

RÉSUMÉ DE L'AUTEUR

We analyzed the relationship between structural and directed functional connectivity by
evaluating the effectiveness of generalized partial directed coherence (GPDC) to estimate the
connectivity of a ground-truth, data-constrained computational model of a large-scale network
model of the mouse cortex. We show that GPDC values provide a reasonable estimate of
structural connectivity even in a typical electrophysiological recording scenario containing few
domaines. These results suggest that it may be possible to empirically estimate structural connectivity
from functional connectivity even when detailed whole-brain recordings are not achievable.

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

INTRODUCTION

The communication between brain regions is often analyzed using structural and functional
connectivité (Avena-Koenigsberger, Misic, & Sporns, 2018). The former refers to anatomical
connections between brain regions generally quantified using tracer injections or diffusion
magnetic resonance imaging (Ambrosen et al., 2020). The map of these connections is called
“connectome” (Sporns, Tononi, & Kötter, 2005). Network measures are usually used to analyze
the connectome, whereas nodes represent brain regions and edges refer to axonal projections

Citation: Nunes, R.. V., Reyes, M.. B.,
Mejias, J.. F., & de Camargo, R.. Oui.
(2021). Directed functional and
structural connectivity in a large-scale
model for the mouse cortex. Réseau
Neurosciences, 5(4), 874–889. https://est ce que je
.org/10.1162/netn_a_00206

EST CE QUE JE:
https://doi.org/10.1162/netn_a_00206

Informations complémentaires:
https://doi.org/10.1162/netn_a_00206

Reçu: 12 Mars 2021
Accepté: 9 Août 2021

Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.

Auteur correspondant:
Ronaldo V. Nunes
ronaldovnunes@gmail.com

Éditeur de manipulation:
Olaf Sporns

droits d'auteur: © 2021
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence

La presse du MIT

Directed functional connectivity from mouse cortex simulated dynamics

(Bassett & Sporns, 2017; Bassett, Zurn, & Gold, 2018). Functional connectivity estimates brain
communication from statistical relations between recorded brain signals (Avena-Koenigsberger
et coll., 2018; Reid et al., 2019). Particularly, directed functional connectivity methods use the
concept of causality to infer both the intensity and the direction of the connections between
brain regions (Bastos & Schoffelen, 2016). Even though there is some association between
structural and functional connectivity, the relationship between them is not straightforward
(Avena-Koenigsberger et al., 2018). While the former is practically static and composes the
map of possible pathways for information flow between brain regions, the latter changes
continuously and depends, Par exemple, on the dynamical states of brain regions, bruit, et
strength of structural connections (Nunes, Reyes, & De Camargo, 2019).

During electrophysiological procedures, researchers typically record brain signals using
electrodes positioned in different depths of brain regions. Even with the improvement in tech-
nologies for recording signals, it is usually possible to record signals only from a few areas
compared with the number of sources of activity in the brain (Harris, Quiroga, Freeman, &
Forgeron, 2016; Hong & Lieber, 2019; Schölvinck, Leopold, Brookes, & Khader, 2013). Ainsi,
the functional connectivity analysis presents a problem because many unrecorded regions
may indirectly influence other regions as common inputs (Bastos & Schoffelen, 2016; Reid
et coll., 2019; Sanchez-Romero & Cole, 2019). Donc, the comparison between structural
and functional connectivity becomes more complicated since spurious inferred causality re-
lations can lead to misinterpretations of electrophysiological data.

Previous simulation studies evaluated the relation between directed functional connectivity
and structural connections (Baccalá & Sameshima, 2001; Barnett & Seth, 2014; Mi, Cheng, &
Zhang, 2014; Nunes et al., 2019). Cependant, most of these studies used either autoregressive
(Novelli, Wollstadt, Mediano, Wibral, & Lizier, 2019) or rate-based models (Mi et al., 2014)
for the dynamics of each cortical area. These studies provided essential steps towards evaluating
the reliability of causality measures. Cependant, the time series obtained from autoregressive and
rate models are distant from electrophysiological signals obtained in experimental laboratory
conditions. Using spiking models, we can capture the dynamic of neuronal networks while
generating simulated local field potential (LFP) signals from the synaptic currents. Aussi, most
studies do not consider the impact of accessing only part of the activity in the brain.

In this work, we investigate the relationship between directed functional connectivity and
structural connectivity in a large-scale network model of the cortex, derived from a cortical
connectome of the mouse obtained using tracer injections (Ga(cid:1)ma(cid:1)nut¸ et al., 2018). Nous avons utilisé
generalized partial directed coherence (GPDC), a frequency-domain method based on multi-
variate vector autoregressive (MVAR) models, which provides estimates of directed functional
connectivité (Baccalá, Sameshima, & Takahashi, 2007; Sameshima & Baccalá, 2014). Le
mean correlation between the fraction of labeled neurons (FLN) and GPDC remained high
(r > 0.6) even when only a few cortical areas were considered in the GPDC calculation, dans-
dicating that this causality measure provides reliable results in typical experimental conditions
in which only recordings from a subset of areas are available.

MÉTHODES

Neuron Model
We modeled the neurons using a single-compartment Hodgkin–Huxley-type model, où
the membrane potential of the i-th neuron described by,

Spiking models:
A network model composed of
spiking neurons (nodes) connected
by synapses (edges). A spiking
neuron is a simplified neuron model,
which generates discrete spike
events. It is also referred to as a
spiking neuronal population model.

Local field potential (LFP):
A transient electrical activity in the
extracellular medium resulting from
ionic flows in multiple neurons.

Multivariate vector autoregressive
(MVAR) model:
Autoregressive models permit
predicting future values in time series
from past values. Multivariate vector
models extend them to work with
multiple interdependent time series.

dVi
dt

¼ −gNam3

i hi V − ENa

Þ − gKn4

ð
i V − Ek

ð
Þ − gL V − EL

Þ þ I ext;i þ Isyn;je;

(1)

Neurosciences en réseau

875

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Directed functional connectivity from mouse cortex simulated dynamics

the membrane capacitance Cm is 0.50 nF (0.25 nF) for excitatory (inhibitory) neurons. Le
maximal conductances values were gNa = 12.5 μS, gK = 4.74 μS, and gL = 0.025 μS. The re-
versal potentials ENa = 40 mV, EK = −80 mV, and EL = −65 mV correspond to the sodium,
potassium, and leakage channel, respectivement (Gutfreund, Yarom, & Segev, 1995). The dynam-
ics of the voltage-gated ion channels are described by activation and inactivation variables m,
n, and h, where m and n account for the dynamics of Na channels and h for K channels. Le
probability that an ion channel is open evolves according to a set of ordinary differential
equations (Sancristóbal, Vicente, & Garcia-Ojalvo, 2014),

dm
dt

dh
dt

dn
dt

¼ αm Vð Þ 1 − mð

Þ − β

m Vð Þm;

¼ α

ð
h Vð Þ 1 − h

Þ − β

h Vð Þh;

¼ αn Vð Þ 1 − mð

Þ − β

n Vð Þn;

αm Vð Þ ¼ 0:1

V þ 16
ð
Þ
ð
ð
1 − exp − V þ 16

Þ
Þ=10

;

où

m Vð Þ ¼ 4 exp − V þ 41

Þ=18

Þ;

h Vð Þ ¼ 0:07 exp − V þ 30

Þ=20

Þ;

(cid:2)−1;
Þ
h Vð Þ ¼ 1 þ exp −V=10

αn Vð Þ ¼ 0:01

V þ 20
ð
Þ
ð
ð
1 − exp − V þ 20

Þ
Þ=10

;

h Vð Þ ¼ 0:125 exp − V þ 30

Þ=80

Þ:

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

The parameters used in this neuron model were previously reported and applied in some
studies that modeled cortical neuronal populations (Barardi, Sancristóbal, & Garcia-Ojalvo,
2014; De Sancristóbal, Vicente, Sancho, & Garcia-Ojalvo, 2013; Sancristóbal et al., 2014).

Spiking Neuronal Population Model

Each spiking neuronal population was composed of 2,000 neurons, 1,600 excitatory and 400
inhibitory. Connections between neurons within each spiking neuronal population are

Neurosciences en réseau

876

Directed functional connectivity from mouse cortex simulated dynamics

Tableau 1.
deviation (cid:2)
neurons, and external input, respectivement. The arrow indicates the direction of the connection.

Synaptic weights for intra-areal connections. Mean synaptic weight w and standard
w for all possible synapses. E, je, and input represent excitatory neurons, inhibitory

Synapses
E ! E

E ! je

je ! E

je ! je

Input ! E

Input ! je

(cid:3)w (nS)
2.5

2.5

240

3.2

(cid:2)w (nS)
1.0

1.0

random with connection probability pintra = 10%. The synaptic current Isyn that arrives to post-
synaptic neuron i is modeled by

Isyn;i tð Þ ¼

(cid:3)
(cid:2)
gsyn;je;j tð Þ Esyn − Vi tð Þ

;

(11)

j2presyn

where the index j represents a presynaptic neuron connected to neuron i, and the sum over j
accounts for all the synapses that impinge on neuron i. Esyn is the synaptic reversal potential,
which is 0 mV for excitatory and −70 mV for inhibitory synapses. The dynamics of synaptic
conductance gsyn,je,j is described by an exponential function as follows (Tomov, Pena, Zaks, &
Roque, 2014):

gsyn;je;j tð Þ ¼ we− t−tj−d

Þ=τ:

(12)

The characteristic decay time τ is 2 ms and 8 ms for excitatory and inhibitory synapses,
respectivement. When a presynaptic neuron j fires a spike at time tj, gsyn,je,j is incremented by a
synaptic weight w after the axonal delay d, which was set as 1 ms for all intra-areal connec-
tion (Sancristóbal et al., 2014). The value of w depends on the excitatory/inhibitory nature of
the presynaptic and postsynaptic neurons. En outre, all neurons receive a background in-
put given by a heterogeneous Poisson-process spiking activity with a rate of 7.3 kHz
(Sancristóbal et al., 2014). The background input acts as an excitatory synaptic current. À
add heterogeneity in our model, all synaptic weights w for recurrent connections and back-
ground input were taken from a Gaussian distribution (Tableau 1).

Mouse Large-Scale Cortical Network
The mouse cortex’s large-scale network model is composed of 19 areas where a spiking neu-
ronal population models each area with long-range and recurrent synapses. Parameters related
to recurrent synapses were described in the previous session. Neurons from different areas are
randomly connected with probability pinter = 5%. The synaptic weights between cortical areas
are based on the previously published anatomical connectivity dataset for the mouse cortex
(Ga(cid:1)ma(cid:1)nut¸ et al., 2018) obtained by retrograde tracer injections (Markov et al., 2014).

This technique consists of injecting a tracer that flows from the target synapses to the cell
bodies, allowing us to identify neurons projecting to the target area. The fraction of labeled
neurons (FLN) was measured as the ratio of the number of labeled neurons in a source area to
the total quantity of labeled neurons in all source areas, where labeled neurons considered are

Neurosciences en réseau

877

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Directed functional connectivity from mouse cortex simulated dynamics

extrinsic to the injected area (Markov et al., 2014; Theodoni et al., 2020; Vezoli et al., 2020).
We defined the edge measure FLNij as the number of neurons projecting from area j to area i,
divided by the number of neurons projecting to area i from all the areas except i (de Lange,
Ardesch, & van den Heuvel, 2019; Joglekar, Mejias, Lequel, & Wang, 2018). The synaptic
weights for directed long-range connections are the FLNs scaled by the global scaling param-
eters μ

E = 50 and μ

I = 25,

lr;E

¼ μ
E

FLNij;

j¼1

lr;je

¼ μ
je

FLNij:

j¼1

(13)

(14)

lr;E, and wi

Long-range connections are excitatory, targeting either excitatory or inhibitory neurons
with synaptic weight, wi
lr;je, respectivement. The index j represents the source area, je
represents the target area, and N is the total number of simulated cortical areas. The axonal
delay for long-range connections is given by the ratio between the inter-areal anatomical dis-
tance estimates between cortical areas and the conduction speed set as 3.5 m/s (Choi &
Mihalas, 2019).

LFP Signal
We computed the local field potential (LFP) signal as a sum of the currents’ absolute values
acting upon excitatory neurons in a spiking neuronal population (Mazzoni et al., 2015;
Mazzoni, Panzeri, Logothetis, & Brunel, 2008). Ainsi, for a cortical area in our model, le
LFP signal will be given by

(cid:5)

NE
je

LFP ¼ R

(cid:4)
(cid:4)

IE;je

(cid:4)
(cid:4)
(cid:4)
(cid:4) þ II;je
NE

(cid:4)
(cid:4)
(cid:4)
(cid:4) þ Ibkg;je

(cid:4)
(cid:4)

(cid:6)

(15)

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

IE,i accounts for both the local (within population) and global (inter-areal projections) excit-
atory synaptic currents, while II,i corresponds to the local inhibitory current. Ibkg,i is the synap-
tic current related to the background Poisson input. R represents the resistance of a typical
electrode used for extracellular measurements, here chosen to be 1 MΩ (Sancristóbal et al.,
2014). NE is the number of excitatory neurons in each neuronal population.

The mean was subtracted from the simulated LFP signal. The resultant signal was filtered

using a 1 kHz low-pass filter to avoid aliasing and downsampled to 1 kHz.

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Generalized Partial Directed Coherence

Generalized partial directed coherence (GPDC) is a frequency-domain method of directed
functional connectivity established on a multivariate vector autoregressive (MVAR) model
(Baccalá et al., 2007). The MVAR model for a set x(t) = [x1(t) (cid:3) (cid:3) (cid:3) xN(t)]T of simultaneously ob-
served time series is defined as

x tð Þ ¼

k¼1

ð
x t − k

Þ þ ε tð Þ;

(16)

where p is the MVAR model order. Ak are coefficient matrices in which the element Aij,k define
the effect of xj(t − k) on xi(t), where k is the time lag. The term ε tð Þ is a vector of N white noises

Neurosciences en réseau

878

Directed functional connectivity from mouse cortex simulated dynamics

with covariance matrix (cid:4). The GPDC from the time series xj to the time series xi at frequency (cid:3)
is defined as

GPDCij λð Þ ¼

(cid:4)
(cid:4)
(cid:4)
(cid:4)
q
(cid:4)
(cid:4)
(cid:4)

(cid:4)
(cid:4)
2
(cid:4)
(cid:3)
Aij λð Þ
(cid:4)
ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
(cid:4)
P.
(cid:4)
(cid:3)
Akj* λð Þ
(cid:4)
Akj

λð Þ(cid:3)

N
k¼1

1
σi
1
σ2
k

;

où

(

Aij λð Þ ¼ 1−
(cid:3)
P.
−

P.
p

k¼1 Aij;ke−2π
k¼1 Aij;ke−2π

ﬃﬃﬃﬃ
−1

p
ﬃﬃﬃﬃ
−1

λk;
λk;

si
si

i ¼ j
i ≠ j;

(17)

(18)

i refers to the variance of white noise (cid:4)

and σ2
je(t) (Baccalá et al., 2007). (cid:3) is a normalized fre-
quency where |(cid:3)| ≤ 0.5 so that (cid:3) = 0.5 means one-half of the sampling rate fs (Sameshima &
Baccalá, 2014).

The MVAR model was estimated by the method of ordinary least squares (OLS; Hamilton,
1994). We used Akaike’s information criterion (AIC) to select model order (Supplementary
Equation S1), choosing the order p ≤ 50 that had the minimum AIC (Supplementary Figure S6)
valeur.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

GPDC has values in the range from 0 à 1 and is invariant to scale, so the normalization of
time series is unnecessary (Baccalá et al., 2007; Sameshima & Baccalá, 2014). Similar to other
(directed) functional connectivity measures, unrecorded time series can lead to spurious esti-
mates. Donc, the reliability of estimates depends on the number of time series included in
the estimates. For all analysis we used the peak GPDC value over all frequencies [0, fs

2].

Estimated Activity

The activity flow mapping measures the propagation of neural activity by estimating the acti-
vation of a target region. It is defined as the sum of the activity in each source region multiplied
by the functional connectivity with the target region (Cole, Ito, Bassett, & Schultz, 2016). Nous
adapted the idea of activity flow by defining two measures of estimated activity arriving in a
cortical area i mediated by pathways of structural connectivity (FLNs) and directed functional
connectivité (GPDC peak),

PFLN
je

PGPDC
je

FLNijrj;

j≠i2N

GPDCijrj;

j≠i2N

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(19)

(20)

where FLNij is the FLN from area j to area i, rj is the firing rate for area j, GPDCij is the peak of
GPDC from area j to area i, and N is the total number of simulated cortical areas.

Centrality Measure

We computed the nodal in-strength for the mouse cortical connectome. The nodal in-strength
for a node i is given by

si ¼

FLNij;

(21)

where j is the source area, i is the target area, and N is the total number of simulated cortical
domaines (Fornito, Zalesky, & Bullmore, 2016).

j≠i2N

Neurosciences en réseau

879

Directed functional connectivity from mouse cortex simulated dynamics

Power spectral density (PSD):
Description of the distribution of the
power of a signal in terms of its
frequencies.

Numerical Simulations

All simulations were performed using the simulator Brian2 (Stimberg, Brette, & Homme bon,
2019) applying the exponential Euler method (Bower & Beeman, 2012) to integrate the differ-
ential equations with an integration step of 0.1 ms. Each simulation was 30 s long, generating
sufficient data points to apply GPDC on the simulated LFP signals (Sommariva, Sorrentino,
Piana, Pizzella, & Marzetti, 2019).

RÉSULTATS

The large-scale network model of the mouse cortex contains 19 spiking neural populations
with recurrent connections and excitatory long-range connections between populations, con-
strained by the directed and weighted structural connectome (Figure 1A and Figure 1B). Le
dynamical behavior of each simulated cortical area is predominantly asynchronous with tran-
sient spike synchronization (Palmigiano, Geisel, Loup, & Battaglia, 2017; Uhlhaas et al., 2009)
(Figure 1C), with the typical power spectral density (PSD) of LFP signals displaying a peak in
the gamma band (Figures 1D and 1E) (Buzsáki & Wang, 2012). The firing rate of inhibitory
neurons is 4.74 ± 0.11, higher than the excitatory neurons’ rate of 3.64 ± 0.42 (Figure 1F).
Differences in population behavior are mostly due to inputs from other areas since we sample
their parameters from the same distributions.

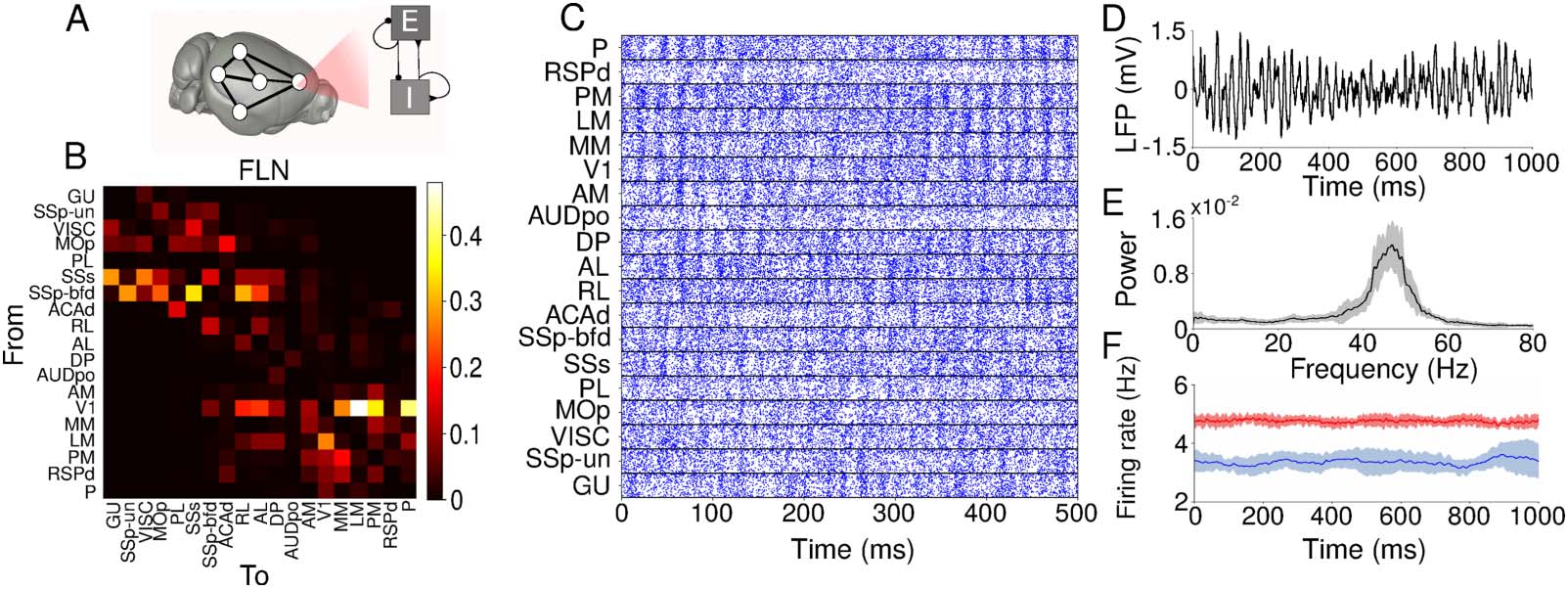
We first compared the FLN values with the average GPDC over 10 simulations of the model.
Most medium to strong connections from the structural connectome were also captured by the
directed functional connectivity (Figure 2A and Figure 2B). We used the GPDC largest value
(peak), but other approaches such as the average of GPDC over frequencies and area under
the GPDC curve (Supplementary Figure S1) produced similar results.

Although the graph density of the structural connectome is 97% (Ga(cid:1)ma(cid:1)nut¸ et al., 2018),
most structural connections are weak, which leads to a prevalence of weak average GPDC
valeurs. Weak structural connections is a characteristic shared by connectomes from different
mammals, with FLNs varying by several orders of magnitude, log-normally distributed (Buzsáki

Chiffre 1.
Large-scale cortical network. (UN) Local neuronal population where E and I are populations of spiking neurons (Bakker, Tiesinga, &
Kötter, 2015; Lein et al., 2007). (B) Map of structural connectivity given by the FLNs. These values define the strength of long-range projections
in the large-scale network model. (C) Raster plot of 500 ms of activity for each cortical area. (D) Simulated LFP signal for an area in the
large-scale network model. (E) Power spectral density for simulated LFP signal for one area. The continuous black line corresponds to the
average over 10 simulations, and the gray shaded area delimits its standard deviation. (F) Firing rate for excitatory (blue) and inhibitory (red)
populations computed using a sliding window of 100 ms. The continuous line corresponds to an average firing rate over 10 simulations, et
the shaded area is the standard deviation. To exemplify, we used data from area MOp in (D), (E), et (F).

Neurosciences en réseau

880

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Directed functional connectivity from mouse cortex simulated dynamics

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

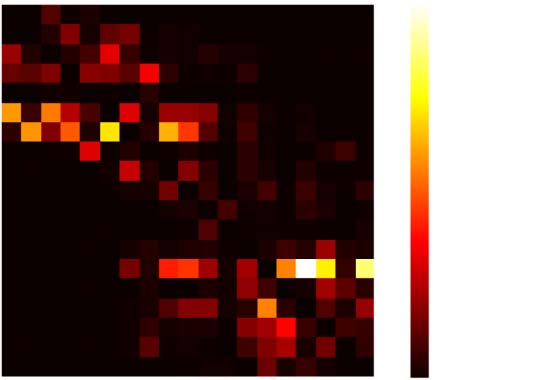
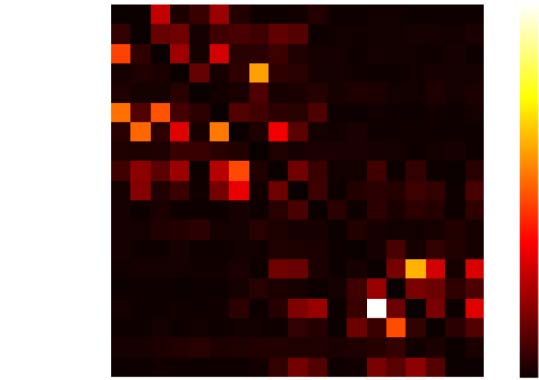
Chiffre 2. Relation between structural and directed functional connectivity. (UN) Map of structural
connectivity given by the FLNs. (B) Map of directed functional connectivity given by GPDC peaks
for one simulation. GPDC from a cortical area to itself was set as 0. (C) Scatterplot of FLNs versus
GPDC peak for one simulation. The red line corresponds to the linear fit. The Pearson correlation
between FLNs and GPDC is 0.74. (D) Box plot showing the distribution of Pearson correlation be-
tween FLN and GPDC for 10 simulations. The white circle represents the average Pearson correla-
tion over 10 simulations, which is (cid:3)r = 0.74.

& Mizuseki, 2014; Ga(cid:1)ma(cid:1)nut¸ et al., 2018; Markov et al., 2014; Theodoni et al., 2020). To eval-
uate the relation between structural and directed functional connectivity, we plotted GPDC
values from 10 simulations against FLNs and fitted a linear model, obtaining the Pearson
correlation r (Figure 2C). The scatterplot presents most points close to the origin due to the pre-
dominance of small values for the GPDC and FLN. The average Pearson correlation between FLN
and GPDC is 0.74 (Figure 2D). We also verified that the average correlation between GPDC and
FLN over bootstrap samples of 80 randomly chosen edges is 0.74 (Supplementary Figure S2). Ce
correlation level is close to those obtained by other works that analyzed different structural
connectomes using functional connectivity applied to empirical data (r ≈ 0.79; Hagmann et al.,
2008) or firing rate models (r ≈ 0.73; Chaudhuri, Knoblauch, Gariel, Kennedy, & Wang, 2015).

The centrality of the cortical area seems to influence the variability of GPDC estimates over
simulations. The variability of directed functional connectivity was measured by the coefficient
of variation of GPDC (Figure 3A). The centrality, measured by the nodal in-strength (c'est à dire., the sum
of inward FLNs to a cortical area; Figure 3B), is positively correlated (r = 0.64) to the sum of the
coefficients of variation (CVs) of the connections emerging from that area (source; Figure 3C).
When the cortical area is considered the target of directed functional connectivity, the correlation
with nodal in-strength is negative (r = −0.52) (Figure 3D). We performed the same analysis corre-
latingthe sum of coefficient ofvariation with eigenvector centrality (Supplementary Figure S3), et
we obtained the same relationship, but with smaller Pearson correlation coefficients (r = 0.59
and r = −0.44). We should note that in both cases (source and target), the actual variability
(standard deviation) increases with larger nodal in-strength values (Supplementary Figure S4).

Coefficient of variation (CV):
The ratio between the standard
deviation and the mean. It measures
the relative dispersion around the
mean.

Neurosciences en réseau

881

Directed functional connectivity from mouse cortex simulated dynamics

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 3. Relationship between nodal in-strength and variability of GPDC. (UN) Coefficient of variation for GPDC (CVGPDC). (B) Nodal
in-strength for all cortical areas. (C) Sum of CVGPDC for a source (sum of columns in A) versus nodal in-strength. (D) Sum of CVGPDC for a target
(sum of rows in A) versus nodal in-strength.

We also investigated the relationship between the firing rate in a cortical area and the esti-
mated activity that is arriving at this cortical area mediated by structural or directed functional
connectivity pathways. The propagation of activity in the cortex is constrained by direct anatom-
ical connections between areas and indirect paths (Vézquez-Rodríguez, Liu, Hagmann, & Misic,
2020), with the propagation of activity occurring mainly through the strongest long-range pro-
jections (Joglekar et al., 2018). The estimated activity mediated by FLNs is strongly correlated to
the target areas’ firing rate (Figure 4A), while the correlation of estimated activity mediated by
GPDCs and firing rates was 0.54 (Figure 4B). This indicates that GPDC estimates can be used to
infer the propagation pathways, although less reliably than when using FLN values directly.

We analyzed the behavior of GPDC estimates when considering a reduced number of
domaines, reproducing typical experimental setups. We considered a visual and a frontoparietal
cluster, each containing seven cortical areas (Ga(cid:1)ma(cid:1)nut¸ et al., 2018) (Figure 5A). We evaluated
the distribution of correlation between FLN and GPDC when GPDC estimates between all
areas of each cluster are conditioned on the whole connectome, conditioned on the areas
in each cluster, and using only pairwise (bivariate) estimates (Figures 5B and 5C). This analysis
simulates the situations where an electrophysiologist has information only from a single cluster
of cortical areas or a pair of areas. The highest correlations between the GPDC and FLN
occurred when we conditioned GPDC to the whole connectome, followed by GPDC condi-
tioned to the cluster area, and pairwise GPDC. Aussi, the correlation for the frontoparietal clus-
ter was higher than for the visual cluster in all scenarios.

Neurosciences en réseau

882

Directed functional connectivity from mouse cortex simulated dynamics

Chiffre 4.
Estimated activity through structural and directed functional pathways. (UN) Estimated ac-
tivity mediated by structural connectivity versus firing rate for target areas (r = 0.94). (B) Estimated
activity mediated by directed functional connectivity versus firing rate for target areas (r = 0.54). Red
lines are linear fits.

We extended the analysis to evaluate the effect of cluster size on GPDC correlation to FLN.
We used cluster sizes ranging from 3 à 15 domaines. We created 150 random clusters sampled
from all areas in the connectome for each cluster size and computed the Pearson correlation
for the GPDC (un) conditioned on the whole connectome, (b) conditioned on the cluster areas,
et (c) evaluated using pairwise data. For cases (un) et (b), the Pearson correlation increases,
and the standard variation decreases as we increase the cluster size (Chiffre 6), showing that it
is advantageous to include more areas in the GPDC calculation. Surprisingly, the correlation
between structural and directed functional connectivity when using simulated signals from a
few cortical areas (blue dots) is similar to using signals from the whole cortex (black dots), avec
most points showing statistically different results. The bivariate GPDC (Chiffre 6) had a statis-
tically significant lower average Pearson correlation for all cluster sizes with four or more
domaines, indicating that these measures are affected by interference from ignored signals.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 5. Correlation between FLN and GPDC for the visual and frontoparietal clusters. (UN) Graph
representing the mouse cortical connectome. Nodes represent cortical areas and edges, directed
long-range projections between them. Green nodes are cortical areas belonging to the frontopar-
ietal cluster. Red nodes are cortical areas belonging to the visual cluster. Each cluster contains seven
cortical areas. Box plot of Pearson correlation between FLN and GPDC for the visual cluster (B) et
frontoparietal cluster (C). GPDC was computed considering the whole connectome (blue box), only
the cluster (orange box), and pairwise (green box).

Neurosciences en réseau

883

Directed functional connectivity from mouse cortex simulated dynamics

Chiffre 6. Pearson correlations between FLN and GPDC for the different cluster sizes with ran-
domly chosen areas. The graph shows the average (dots) and error bars of the GPDC conditioned
to the whole connectome (in black), to areas in the cluster (in blue), and to pairwise signals (dans
red). The error bar is the standard deviation of Pearson correlation considering values for all ran-
domly chosen areas and all simulations. Stars represent statistically different averages when com-
pared with the whole connectome (Holm-Bonferroni corrected Welch t test).

DISCUSSION

Our results shed light on the relationship between structural and directed functional connec-
tivity in circumstances similar to those faced by electrophysiologists. They indicate that the
reliability of directed functional connectivity estimates and their relationship with structural
connectivity depends on the number of areas considered. Nevertheless, the GPDC condi-
tioned on few cortical areas had similar results to the GPDC conditioned on all areas, provid-
ing evidence that it is possible to obtain a reasonable relationship between structural and
directed functional connectivity in electrophysiological experiments even with signals from
few areas.

Previous studies evaluated the relationship between structural and functional network con-
nectivity strength on electrophysiological data (Straathof, Sinke, Dijkhuizen, & Otte, 2019),
with some using undirected functional connectivity measures (Grandjean, Zerbi, Balsters,
Wenderoth, & Rudin, 2017; Stafford et al., 2014). But in electrophysiology studies, chercheurs
do not have access to signals from unrecorded areas and have only estimates of structural
strengths from tracers. Using large-scale network models solves this problem, as the researcher
has access to all variables in the system, allowing a better understanding of the obtained func-
tional connectivity results.

The relationships between structural and functional connectivity have been largely unex-
plored through large-scale network models (Bansal, Nakuci, & Muldon, 2018), and the exist-
ing models use neural mass descriptions (rate models) to describe each area’s activity (Honey
et coll., 2009; Novelli & Lizier, 2021). Cependant, information propagated between brain regions
can be characterized not only by the rate code but also by the temporal code (Bieler et al.,
2017; Hahn, Ponce-Alvarez, Deco, Aertsen, & Kumar, 2019; Kumar, Rotter, & Aertsen,
2010; Luczak, McNaughton, & Harris, 2015; Seth, 2015), and hypotheses are pointing to
spike-timing and spike coherence as essential components of cortical communication
(Hahn, Bujan, Frégnac, Aertsen, & Kumar, 2014; Palmigiano et al., 2017; Tiesinga &
Sejnowski, 2010). Spiking neuronal populations have richer dynamical behaviors than rate
models and better resemble cortical activity; through spiking neuronal networks it is possible

Neurosciences en réseau

884

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Directed functional connectivity from mouse cortex simulated dynamics

to investigate the consequences of spike synchronization (Palmigiano et al., 2017), model dif-
ferent approaches for the propagation of information (Hahn et al., 2019; Joglekar et al., 2018),
and generate simulated LFP signals from the synaptic currents, which better resemble biological
LFP signals (Mazzoni et al., 2015). De plus, our obtained correlations are in the same range as
the studies using more complex electrophysiological data (Straathof et al., 2019).

The centrality of a cortical area affects the variability of GPDC estimates in different ways
when such area is examined as the target or source of functional connections. Strong functional
connectivity generally occurs between areas with direct structural connections (Honey et al.,
2009), and network measures applied to structural connections can help predict the resting-state
functional connectivity (Goñi et al., 2014). Cependant, as far as we know, no previous work has
indicated that the variability of directed functional connections could be partially explained by
centrality measures applied to structural connectivity. We also noticed that synchronization is
strongly correlated to the centrality of the node (Supplementary Figure S5). So it is likely that
stronger long-range connections targeting an area increase the synchronization of spikes in this
area, and the increased synchronization changes the variability in directed functional connec-
tivité. En effet, it was observed in previous work that synchronization has an important role in
directed functional connectivity (Palmigiano et al., 2017).

The firing rate of cortical areas is explained by the estimated activity flow, as proposed by
Cole et al. (2016). When using GPDC as an estimate of structural connections, the correlation
between actual and estimated activity in the target area decreases to 0.54. This indicates that
directed functional connectivity can be used to estimate the activity flow. Although it is less
reliable than when using the actual structural connection strengths, researchers may only have
access to directed functional measures.

The relationship between structural and directed functional connectivity is the largest when
GPDC is conditioned to all areas in the connectome and decreases as we reduce the number
of areas. Ga(cid:1)ma(cid:1)nut¸ et al. (2018) identified six clusters in the mouse connectome (prefrontal,
frontal, pariétal, cingulate, temporal, and visual) based on the same approach used to inves-
tigate the macaque cortex (Ercsey-Ravasz et al., 2013). We evaluated the relationship between
GPDC and FLNs in the visual cluster and in a combination of the prefrontal, frontal, and pa-
rietal clusters, which we called frontoparietal. We did not use the other clusters, which had a
small number of regions. The average correlation was in the range of correlation obtained for
random clusters, with r = 0.76 for the frontoparietal and r = 0.50 for the visual cortex. Ce
indicates that within anatomical clusters the relationship between GPDC and FLNs does not
change in relation to randomly selected areas. These results also show that GPDC estimates
provide statistical information on structural connections even when considering only a few
domaines. Cependant, when considering individual connections, there can be large differences be-
tween GPDC estimates and actual structural connection strengths.

Our large-scale network model has some limitations. D'abord, modeled neuronal population
parameters are drawn from the same distributions with activity in the gamma band range
(Chiffre 1). The activity of cortical areas in mice occurs in multiple frequency ranges
(Sherman et al., 2016; Tsurugizawa, Djemai, & Zalesky, 2019) and the relationship between
structural and functional connectivity depends on the frequency (Vezoli et al., 2020). A sec-
ond limitation is that we do not model changes in network states, which are known to influ-
ence functional connectivity (Stitt et al., 2017). Some studies in computational neuroscience
have already explored multistability and temporal patterns of functional connectivity (Deco &
Jirsa, 2012; Golos, Jirsa, & Daucé, 2015; Orio et al., 2018). Enfin, we considered only cor-
tical areas in our large-scale network model, excluding subcortical areas, which have a more

Neurosciences en réseau

885

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Directed functional connectivity from mouse cortex simulated dynamics

complex dynamic (Erö, Gewaltig, Keller, & Markram, 2018; Knox et al., 2018). Future studies
can overcome these limitations by creating richer spiking network models, with different op-
erating frequencies and evolving neuronal dynamics. These models are difficult to create but
would allow one to compare functional connectivity values with structural connection
strength in more dynamic settings.

INFORMATIONS À L'APPUI

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00206.

CONTRIBUTIONS DES AUTEURS

Ronaldo V. Nunes: Conceptualisation; Enquête; Méthodologie; Gestion de projet;
Logiciel; Validation; Visualisation; Rédaction – ébauche originale. Marcelo B. Reyes:
Conceptualisation; Méthodologie; Surveillance; Rédaction – révision & édition. Jorge F. Mejias:
Conceptualisation; Méthodologie; Surveillance; Rédaction – révision & édition. Raphael Y. de
Camargo: Conceptualisation; Méthodologie; Surveillance; Rédaction – révision & édition.

INFORMATIONS SUR LE FINANCEMENT

Ronaldo V. Nunes, Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (https://dx
.doi.org/10.13039/501100002322), Award ID: Finance Code 001.

RÉFÉRENCES

Ambrosen, K. S., Eskildsen, S. F., Hinne, M., Krug, K., Lundell, H.,
Schmidt, M.. N., … Dyrby, T. B. (2020). Validation of structural
brain connectivity networks: The impact of scanning parameters.
NeuroImage, 204, 116207. https://doi.org/10.1016/j.neuroimage
.2019.116207, PubMed: 31539592

Avena-Koenigsberger, UN., Misic, B., & Sporns, Ô. (2018).
Communication dynamics in complex brain networks. Nature
Reviews Neuroscience, 19(1), 17. https://doi.org/10.1038/nrn
.2017.149, PubMed: 29238085

Baccalá, L. UN., & Sameshima, K. (2001). Partial directed coherence:
A new concept in neural structure determination. Biological
Cybernetics, 84(6), 463–474. https://doi.org/10.1007
/PL00007990, PubMed: 11417058

Baccalá, L. UN., Sameshima, K., & Takahashi, D. (2007).
Generalized partial directed coherence. Dans 2007 15th interna-
tional conference on digital signal processing (pp. 163–166).
https://doi.org/10.1109/ICDSP.2007.4288544

Bakker, R., Tiesinga, P., & Kötter, R.. (2015). The scalable brain at-
las: Instant web-based access to public brain atlases and related
content. Neuroinformatics, 13(3), 353–366. https://est ce que je.org/10
.1007/s12021-014-9258-x, PubMed: 25682754

Bansal, K., Nakuci, J., & Muldon, S. F. (2018). Personalized brain
network models for assessing structure–function relationships.
Opinion actuelle en neurobiologie, 52, 42–47. https://est ce que je.org/10
.1016/j.conb.2018.04.014, PubMed: 29704749

Barardi, UN., Sancristóbal, B., & Garcia-Ojalvo, J.. (2014). Phase-
coherence transitions and communication in the gamma range
b e t w e e n d e l a y – c o u p l e d n e u r o n a l p o p u l a t i o n s . P L o S

Computational Biology, 10(7), e1003723. https://est ce que je.org/10
.1371/journal.pcbi.1003723, PubMed: 25058021

Barnett, L., & Seth, UN. K. (2014). The MVGC multivariate Granger
causality toolbox: A new approach to Granger-causal inference.
Journal of Neuroscience Methods, 223, 50–68. https://est ce que je.org/10
.1016/j.jneumeth.2013.10.018, PubMed: 24200508

Bassett, D. S., & Sporns, Ô. (2017). Network neuroscience. Nature
Neurosciences, 20(3), 353–364. https://doi.org/10.1038/nn.4502,
PubMed: 28230844

Bassett, D. S., Zurn, P., & Gold, J.. je. (2018). On the nature and use
of mod els in network neu roscien ce. Nature Reviews
Neurosciences, 19(9), 566–578. https://doi.org/10.1038/s41583
-018-0038-8, PubMed: 30002509

Bastos, UN. M., & Schoffelen, J.-M. (2016). A tutorial review of func-
tional connectivity analysis methods and their interpretational
pitfalls. Frontiers in Systems Neuroscience, 9, 175. https://est ce que je
.org/10.3389/fnsys.2015.00175, PubMed: 26778976

Bieler, M., Sieben, K., Cichon, N., Schildt, S., Röder, B., & Hanganu-
Opatz, je. L. (2017). Rate and temporal coding convey multisensory
information in primary sensory cortices. eNeuro, 4(2). https://est ce que je
.org/10.1523/ENEURO.0037-17.2017, PubMed: 28374008

Bower, J.. M., & Beeman, D. (2012). The book of GENESIS:
Exploring realistic neural models with the general neural simula-
tion system. Springer Science & Business Media.

Buzsáki, G., & Mizuseki, K. (2014). The log-dynamic brain: Comment
skewed distributions affect network operations. Nature Reviews
Neurosciences, 15(4), 264–278. https://doi.org/10.1038/nrn3687,
PubMed: 24569488

Neurosciences en réseau

886

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Directed functional connectivity from mouse cortex simulated dynamics

Buzsáki, G., & Wang, X.-J. (2012). Mechanisms of gamma oscilla-
tion. Revue annuelle des neurosciences, 35, 203–225. https://est ce que je
.org/10.1146/annurev-neuro-062111-150444, PubMed:
22443509

Chaudhuri, R., Knoblauch, K., Gariel, M.-A., Kennedy, H., &
Wang, X.-J. (2015). A large-scale circuit mechanism for hierar-
chical dynamical processing in the primate cortex. Neurone, 88(2),
419–431. https://doi.org/10.1016/j.neuron.2015.09.008, PubMed:
26439530

Choi, H., & Mihalas, S. (2019). Synchronization dependent on spa-
tial structures of a mesoscopic whole-brain network. PLoS
Computational Biology, 15(4), e1006978. https://est ce que je.org/10
.1371/journal.pcbi.1006978, PubMed: 31013267

Cole, M.. W., Ito, T., Bassett, D. S., & Schultz, D. H. (2016). Activity
flow over resting-state networks shapes cognitive task activa-
tion. Neurosciences naturelles, 19(12), 1718–1726. https://doi.org
/10.1038/nn.4406, PubMed: 27723746

Deco, G., & Jirsa, V. K. (2012). Ongoing cortical activity at rest:
Criticality, multistability, and ghost attractors. Journal de
Neurosciences, 32(10), 3366–3375. https://est ce que je.org/10.1523
/JNEUROSCI.2523-11.2012, PubMed: 22399758

de Lange, S. C., Ardesch, D. J., & van den Heuvel, M.. P.. (2019).
Connection strength of the macaque connectome augments
topological and functional network attributes. Réseau
Neurosciences, 3(4), 1051–1069. https://doi.org/10.1162/netn_a
_00101, PubMed: 31637338

De Sancristóbal, B., Vicente, R., Sancho, J.. M., & Garcia-Ojalvo, J..
(2013). Emergent bimodal firing patterns implement different en-
coding strategies during gamma-band oscillations. Frontiers in
Computational Neuroscience, 7, 18. https://doi.org/10.3389
/fncom.2013.00018, PubMed: 23532173

Ercsey-Ravasz, M., Markov, N. T., Lamie, C., Van Essen, D. C.,
Knoblauch, K., Toroczkai, Z., & Kennedy, H. (2013). A predic-
tive network model of cerebral cortical connectivity based on a
distance rule. Neurone, 80(1), 184–197. https://est ce que je.org/10.1016/j
.neuron.2013.07.036, PubMed: 24094111

Erö, C., Gewaltig, M.-O., Keller, D., & Markram, H. (2018). A cell
atlas for the mouse brain. Frontiers in Neuroinformatics, 12, 84.
https://doi.org/10.3389/fninf.2018.00084, PubMed: 30546301
Fornito, UN., Zalesky, UN., & Bullmore, E. (2016). Fundamentals of

brain network analysis. Academic Press.

Ga(cid:1)ma(cid:1)nut¸, R., Kennedy, H., Toroczkai, Z., Ercsey-Ravasz, M., Van
Essen, D. C., Knoblauch, K., & Burkhalter, UN. (2018). The mouse
cortical connectome, characterized by an ultra-dense cortical
graph, maintains specificity by distinct connectivity profiles.
Neurone, 97(3), 698–715. https://doi.org/10.1016/j.neuron.2017
.12.037, PubMed: 29420935

Golos, M., Jirsa, V., & Daucé, E. (2015). Multistability in large scale
models of brain activity. Biologie computationnelle PLoS, 11(12),
e1004644. https://doi.org/10.1371/journal.pcbi.1004644,
PubMed: 26709852

Goñi, J., van den Heuvel, M.. P., Avena-Koenigsberger, UN., De
Mendizabal, N. V., Betzel, R.. F., Griffa, UN., … Sporns, Ô.
(2014). Resting-brain functional connectivity predicted by ana-
lytic measures of network communication. Actes du
Académie nationale des sciences, 111(2), 833–838. https://doi.org
/10.1073/pnas.1315529111, PubMed: 24379387

Grandjean, J., Zerbi, V., Balsters, J.. H., Wenderoth, N., & Rudin, M..
(2017). Structural basis of large-scale functional connectivity in
the mouse. Journal des neurosciences, 37(34), 8092–8101.
https://doi.org/10.1523/ JNEUROSCI.0438-17.2017, PubMed:
28716961

Gutfreund, Y., Yarom, Y., & Segev, je. (1995). Subthreshold oscilla-
tions and resonant frequency in guinea-pig cortical neurons:
Physiology and modelling. Journal of Physiology, 483(3), 621–640.
https://doi.org/10.1113/jphysiol.1995.sp020611, PubMed:
7776248

Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Sporns, Ô. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6(7), e159. https://est ce que je
.org/10.1371/journal.pbio.0060159, PubMed: 18597554

Hahn, G., Bujan, UN. F., Frégnac, Y., Aertsen, UN., & Kumar, UN.
(2014). Communication through resonance in spiking neuronal
réseaux. Biologie computationnelle PLoS, 10(8), e1003811.
https://doi.org/10.1371/journal.pcbi.1003811, PubMed:
25165853

Hahn, G., Ponce-Alvarez, UN., Deco, G., Aertsen, UN., & Kumar, UN.
(2019). Portraits of communication in neuronal networks. Nature
Reviews Neuroscience, 20(2), 117–127. https://est ce que je.org/10.1038
/s41583-018-0094-0, PubMed: 30552403

Hamilton, J.. (1994). Times series analysis. Princeton University

Presse. https://doi.org/10.1515/9780691218632

Harris, K. D., Quiroga, R.. Q., Freeman, J., & Forgeron, S. L. (2016).
Improving data quality in neuronal population recordings.
Neurosciences naturelles, 19(9), 1165–1174. https://est ce que je.org/10
.1038/nn.4365, PubMed: 27571195

Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J.-P.,
Meuli, R., & Hagmann, P.. (2009). Predicting human resting-
state functional connectivity from structural connectivity.
Actes de l'Académie nationale des sciences, 106(6),
2035–2040. https://doi.org/10.1073/pnas.0811168106,
PubMed: 19188601

Hong, G., & Lieber, C. M.. (2019). Novel electrode technologies
for neural recordings. Nature Revues Neurosciences, 20(6),
330–345. https://doi.org/10.1038/s41583-019-0140-6,
PubMed: 30833706

Joglekar, M.. R., Mejias, J.. F., Lequel, G. R., & Wang, X.-J. (2018).
Inter-areal balanced amplification enhances signal propagation
in a large-scale circuit model of the primate cortex. Neurone,
98(1), 222–234. https://doi.org/10.1016/j.neuron.2018.02.031,
PubMed: 29576389

Knox, J.. E., Harris, K. D., Graddis, N., Whitesell, J.. D., Zeng, H.,
Harris, J.. UN., … Mihalas, S. (2018). High-resolution data-driven
model of the mouse connectome. Neurosciences en réseau, 3(1),
217–236. https://doi.org/10.1162/netn_a_00066, PubMed:
30793081

Kumar, UN., Rotter, S., & Aertsen, UN. (2010). Spiking activity propaga-
tion in neuronal networks: Reconciling different perspectives on
neural coding. Nature Revues Neurosciences, 11(9), 615–627.
https://doi.org/10.1038/nrn2886, PubMed: 20725095

Lein, E. S., Hawrylycz, M.. J., Ao, N., Ayres, M., Bensinger, UN.,
Bernard, UN., … Jones, UN. R.. (2007). Genome-wide atlas of gene ex-
pression in the adult mouse brain. Nature, 445(7124), 168–176.
https://doi.org/10.1038/nature05453, PubMed: 17151600

Neurosciences en réseau

887

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Directed functional connectivity from mouse cortex simulated dynamics

Luczak, UN., McNaughton, B. L., & Harris, K. D. (2015). Packet-
based communication in the cortex. Nature Reviews
Neurosciences, 16(12), 745–755. https://est ce que je.org/10.1038
/nrn4026, PubMed: 26507295

Markov, N. T., Ercsey-Ravasz, M., Ribeiro Gomes, UN., Lamie, C.,
Magrou, L., Vezoli, J., … Kennedy, H. (2014). A weighted and
directed interareal connectivity matrix for macaque cerebral cor-
tex. Cortex cérébral, 24(1), 17–36. https://doi.org/10.1093/cercor
/bhs270, PubMed: 23010748

Mazzoni, UN., Linden, H., Cuntz, H., Lansner, UN., Panzeri, S., &
Einevoll, G. T. (2015). Computing the local field potential (LFP)
from integrate-and-fire network models. PLoS Computational
Biology, 11(12). https://doi.org/10.1371/journal.pcbi.1004584,
PubMed: 26657024

Mazzoni, UN., Panzeri, S., Logothetis, N. K., & Brunel, N. (2008).
Encoding of naturalistic stimuli by local field potential spectra
in networks of excitatory and inhibitory neurons. PLoS
Computational Biology, 4(12), e1000239. https://est ce que je.org/10
.1371/journal.pcbi.1000239, PubMed: 19079571

Mi, X., Cheng, N., & Zhang, T. (2014). Performance comparison
between GPDC and PCMI for measuring directionality of neural
information flow. Journal of Neuroscience Methods, 227, 57–64.
https://doi.org/10.1016/j.jneumeth.2014.02.006, PubMed:
24548795

Novelli, L., & Lizier, J.. T. (2021). Inferring network properties from
time series using transfer entropy and mutual information: Choisir-
tion of multivariate versus bivariate approaches. Réseau
Neurosciences, 5(2), 373–404. https://doi.org/10.1162/netn_a
_00178, PubMed: 34189370

Novelli, L., Wollstadt, P., Mediano, P., Wibral, M., & Lizier, J.. T.
(2019). Large-scale directed network inference with multivariate
transfer entropy and hierarchical statistical testing. Réseau
Neurosciences, 3(3), 827–847. https://doi.org/10.1162/netn_a
_00092, PubMed: 31410382

Nunes, R.. V., Reyes, M.. B., & De Camargo, R.. Oui. (2019). Evaluation
of connectivity estimates using spiking neuronal network models.
Biological Cybernetics, 113(3), 309–320. https://doi.org/10.1007
/s00422-019-00796-8, PubMed: 30783758

Orio, P., Gatica, M., Herzog, R., Maidana, J.. P., Castro, S., & Xu, K.
(2018). Chaos versus noise as drivers of multistability in neural
réseaux. Chaos: An Interdisciplinary Journal of Nonlinear
Science, 28(10), 106321. https://doi.org/10.1063/1.5043447,
PubMed: 30384618

Palmigiano, UN., Geisel, T., Loup, F., & Battaglia, D. (2017). Flexible
i n f o r m a t i o n r o u t i n g b y t r a n s i e n t s y n c h r o n y . N a t u r e
Neurosciences, 20(7), 1014. https://doi.org/10.1038/nn.4569,
PubMed: 28530664

Reid, UN. T., Headley, D. B., Mill, R.. D., Sanchez-Romero, R.,
Uddin, L. Q., Marinazzo, D., … Cole, M.. W.
(2019).
Advancing functional connectivity research from association to
causation. Neurosciences naturelles, 22(11), 1751–1760. https://
doi.org/10.1038/s41593-019-0510-4, PubMed: 31611705

Sameshima, K., & Baccalá, L. UN. (2014). Methods in brain connec-
tivity inference through multivariate time series analysis. CRC
Presse.

Sanchez-Romero, R., & Cole, M.. W. (2019). Combining multiple
functional connectivity methods to improve causal inferences.

Journal des neurosciences cognitives, 1–15. https://est ce que je.org/10
.1162/jocn_a_01580, PubMed: 32427070

Sancristóbal, B., Vicente, R., & Garcia-Ojalvo, J.. (2014). Role of fre-
quency mismatch in neuronal communication through coher-
ence. Journal of Computational Neuroscience, 37(2), 193–208.
https://doi.org/10.1007/s10827-014-0495-7, PubMed: 24519733
Schölvinck, M.. L., Leopold, D. UN., Brookes, M.. J., & Khader, P.. H.
(2013). The contribution of electrophysiology to functional con-
nectivity mapping. NeuroImage, 80, 297–306. https://est ce que je.org/10
.1016/j.neuroimage.2013.04.010, PubMed: 23587686

Seth, UN. K. (2015). Neural coding: Rate and time codes work to-
gether. Biologie actuelle, 25(3), R110–R113. https://est ce que je.org/10
.1016/j.cub.2014.12.043, PubMed: 25649819

Sherman, M.. UN., Lee, S., Loi, R., Haegens, S., Thorn, C. UN.,
Hämäläinen, M.. S., … Jones, S. R.. (2016). Neural mechanisms
of transient neocortical beta rhythms: Converging evidence from
humans, computational modeling, monkeys, and mice.
Actes de l'Académie nationale des sciences, 113(33),
E4885–E4894. https://doi.org/10.1073/pnas.1604135113,
PubMed: 27469163

Sommariva, S., Sorrentino, UN., Piana, M., Pizzella, V., & Marzetti, L.
(2019). A comparative study of the robustness of frequency-
domain connectivity measures to finite data length. Cerveau
Topography, 32(4), 675–695. https://doi.org/10.1007/s10548
-017-0609-4, PubMed: 29168017

Sporns, O., Tononi, G., & Kötter, R.. (2005). The human connec-
tome: A structural description of the human brain. PLoS
Computational Biology, 1(4), e42. https://doi.org/10.1371
/journal.pcbi.0010042, PubMed: 16201007

Stafford, J.. M., Jarrett, B. R., Miranda-Dominguez, O., Mills, B. D.,
Cain, N., Mihalas, S., … Fair, D. UN. (2014). Large-scale topology
and the default mode network in the mouse connectome.
Actes de l'Académie nationale des sciences, 111(52),
18745–18750. https://doi.org/10.1073/pnas.1404346111,
PubMed: 25512496

Stimberg, M., Brette, R., & Homme bon, D. F. (2019). Brian 2, an in-
tuitive and efficient neural simulator. eLife, 8, e47314. https://est ce que je
.org/10.7554/eLife.47314, PubMed: 31429824

Stitt, JE., Hollensteiner, K. J., Galindo-Leon, E., Pieper, F., Fiedler, E.,
Stieglitz, T., … Engel, UN. K. (2017). Dynamic reconfiguration
of cortical
functional connectivity across brain states.
Rapports scientifiques, 7(1), 1–14. https://doi.org/10.1038/s41598
-017-08050-6, PubMed: 28821753

Straathof, M., Sinke, M.. R., Dijkhuizen, R.. M., & Otte, W. M..
(2019). A systematic review on the quantitative relationship be-
tween structural and functional network connectivity strength in
mammalian brains. Journal of Cerebral Blood Flow and
Metabolism , 39(2), 189–20 9. https://doi .org/10.1177
/0271678X18809547, PubMed: 30375267

Theodoni, P., Majka, P., Reser, D. H., Wójcik, D. K., Rose, M.. G., &
Wang, X.-J. (2020). Structural attributes and principles of the neo-
cortical connectome in the marmoset monkey. bioRxiv. https://
doi.org/10.1101/2020.02.28.969824

Tiesinga, P.. H., & Sejnowski, T. J.. (2010). Mechanisms for phase
shifting in cortical networks and their role in communication
through coherence. Frontiers in Human Neuroscience, 4, 196.
https://doi.org/10.3389/fnhum.2010.00196, PubMed: 21103013

Neurosciences en réseau

888

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Directed functional connectivity from mouse cortex simulated dynamics

Tomov, P., Pena, R.. F., Zaks, M.. UN., & Roque, UN. C. (2014).
Sustained oscillations, irregular firing, and chaotic dynamics in
hierarchical modular networks with mixtures of electrophysio-
logical cell types. Frontiers in Computational Neuroscience, 8,
103. https://doi.org/10.3389/fncom.2014.00103, PubMed:
25228879

Tsurugizawa, T., Djemai, B., & Zalesky, UN. (2019). The impact of
fasting on resting state brain networks in mice. Rapports scientifiques,
9(1), 1–12. https://doi.org/10.1038/s41598-019-39851-6,
PubMed: 30814613

Uhlhaas, P., Pipa, G., Lima, B., Melloni, L., Neuenschwander, S.,
Nikolic(cid:5), D., & Chanteur, W. (2009). Neural synchrony in cortical

réseaux: Histoire, concept and current status. Frontiers in
Integrative Neuroscience, 3, 17. https://doi.org/10.3389/neuro
.07.017.2009, PubMed: 19668703

Vezoli, J., Vinck, M., Bosman, C. UN., Bastos, UN. M., Lewis, C. M.,
Kennedy, H., & Fries, P.. (2020). The role of anatomical connec-
tion strength for interareal communication in macaque cortex.
Available at SSRN 3751057. https://doi.org/10.2139/ssrn
.3751057

Vézquez-Rodríguez, B., Liu, Z.-Q., Hagmann, P., & Misic, B.
(2020). Signal propagation via cortical hierarchies. Réseau
Neurosciences, 4(4), 1072–1090. https://doi.org/10.1162/netn_a
_00153, PubMed: 33195949

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

5
4
8
7
4
1
9
7
5
1
8
1
n
e
n
_
un
_
0
0
2
0
6
p
d