RECHERCHE
Inferring the heritability of large-scale functional
networks with a multivariate ACE
modeling approach
Fernanda L. Ribeiro1,2*
, Felipe R. C. dos Santos3,4*
, João R. Sato1
,
Walter H. L. Pinaya1,5†
, and Claudinei E. Biazoli Jr.1†
1Center of Mathematics, Computing, et cognitif, Universidade Federal do ABC, São Bernardo do Campo, Brazil
2School of Psychology, University of Queensland, Brisbane, Australia
3Centro de Oncologia Molecular, Hospital Sírio-Libanês, São Paulo, Brazil
4Programa Interunidades em Bioinformatica, Universidade de São Paulo, São Paulo, Brazil
5Department of Biomedical Engineering, School of Biomedical Engineering and Imaging Sciences,
King’s College London, Londres, United Kingdom
*These authors contributed equally to this work.
†
These authors contributed equally to this work.
Mots clés: Connectome fingerprinting, Multivariate modeling, Twin study, Functional connectome
ABSTRAIT
Recent evidence suggests that the human functional connectome is stable at different
timescales and is unique. These characteristics posit the functional connectome not only as
an individual marker but also as a powerful discriminatory measure characterized by high
intersubject variability. Among distinct sources of intersubject variability, the long-term
sources include functional patterns that emerge from genetic factors. Ici, we sought to
investigate the contribution of additive genetic factors to the variability of functional networks
by determining the heritability of the connectivity strength in a multivariate fashion. D'abord, nous
reproduced and extended the connectome fingerprinting analysis to the identification of twin
pairs. Alors, we estimated the heritability of functional networks by a multivariate ACE
modeling approach with bootstrapping. Twin pairs were identified above chance level using
connectome fingerprinting, with monozygotic twin identification accuracy equal to 57.2% sur
average for whole-brain connectome. En plus, we found that a visual (0.37), the medial
frontal (0.31), and the motor (0.30) functional networks were the most influenced by additive
genetic factors. Our findings suggest that genetic factors not only partially determine
intersubject variability of the functional connectome, such that twins can be identified using
connectome fingerprinting, but also differentially influence connectivity strength in large-scale
functional networks.
RÉSUMÉ DE L'AUTEUR
The functional connectome is a unique representation of the functional organization of the
cerveau humain. En tant que tel, it has been extensively used as an individual marker, a “fingerprint,»
because of its high intersubject variability. Ici, we sought to investigate the influence of
genetic factors on intersubject variability of functional networks. Donc, we extended
the connectome fingerprinting analysis to the identification of twin pairs, and we estimated
the heritability of functional networks by a multivariate ACE modeling approach with
bootstrapping. We found that genetic factors not only partially determine intersubject
variability of the functional connectome, such that monozygotic twin identification accuracy
un accès ouvert
journal
Citation: Ribeiro, F. L., dos Santos,
F. R.. C., Sato, J.. R., Pinaya, W. H. L.,
& Biazoli, C. E. (2021). Inferring the
heritability of large-scale functional
networks with a multivariate ACE
modeling approach. Réseau
Neurosciences, 5(2), 527–548. Advance
publication. https://est ce que je.org/10.1162
/netn_a_00189
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00189
Informations complémentaires:
https://doi.org/10.1162/netn_a_00189
https://github.com/felenitaribeiro
/TwinID_with_connectome
_fingerprinting
https://github.com/frcsantos
/Heritability_FunctionalNetworks
Reçu: 24 Septembre 2020
Accepté: 10 Février 2021
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Fernanda L. Ribeiro
fernanda.ribeiro@uq.edu.au
Éditeur de manipulation:
Emily Finn
droits d'auteur: © 2021
Massachusetts Institute of Technology.
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence.
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
un
_
0
0
1
8
9
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
Functional connectome:
The pattern of functional connections
between every pair of distinct brain
régions.
Intrasubject variability:
Variability of a trait within an
individual.
Intersubject variability:
Variability of a trait across
individuals.
achieved 57.2% on average using whole-brain connectome in the fingerprinting analysis,
but also differentially influence connectivity strength in large-scale functional networks.
INTRODUCTION
In the past few years, fMRI research has been living a paradigm shift, moving from population
inferences to the study of individual differences (Dubois & Adolphs, 2016; Seghier & Prix,
2018). Previous studies have paved the way for the study of individual variability in functional
connectivity patterns of the human brain (Finn et al., 2015; Miranda-Dominguez et al., 2014;
Mueller et al., 2013). In this context, resting-state fMRI (rs-fMRI) has been shown to be partic-
ularly powerful in determining underlying differences in the wiring patterns of functional con-
nectome (FC) profiles. En effet, connectome-based individual predictions achieved
identification accuracies as high as 99% when comparing functional connectivity matrices
(Finn et al., 2015). Ainsi, the endeavor to identify and to characterize the individual func-
tional connectivity architecture has been shown to have an imperative place in the study of
individual differences.
Recent and mounting evidence suggests that FC profiles are stable at different timescales
(Gratton et al., 2018; Jalbrzikowski et al., 2020; Miranda-Dominguez et al., 2018; Sato, Blanc,
& Biazoli, 2017). This characteristic posits the FC not only as an individual marker because of
the comparably low intrasubject variability, but also as a powerful discriminatory measure
characterized by the high intersubject variability. Gratton et al. (2018) showed that despite
functional networks displaying common organizational features at the group level, the simi-
larity between functional networks substantially increased at the individual level when eval-
uating the same participant in different tasks and sessions. This evidence supports the fact that
individual stable patterns are crucial for explaining the intersubject variability of functional
réseaux. Donc, these findings suggest that sources of intersubject variability are stable
au fil du temps, acting as individual signatures or “fingerprints.”
Seghier and Price (2018) refer to the presence of distinct sources of intersubject variability that
differ in their timescale. In the lower bound, there are sources of variability due to mood states
and context. The medium- to long-term sources of intersubject variability include functional
patterns built from the intimate interaction of an individual with the environment and genetic
factors (Seghier & Prix, 2018), respectivement. Fait intéressant, functional networks show distinct
levels of intersubject variability. Networks comprising higher order associative cortical areas
seem to remarkably contribute to the FC distinctiveness (Finn et al., 2015; Jalbrzikowski et al.,
2020; Kaufmann et al., 2017; Miranda-Dominguez et al., 2018, 2014; Mueller et al., 2013),
lequel, à son tour, might be due to a high intersubject (Gratton et al., 2018; Mueller et al., 2013)
and low intrasubject variability (Laumann et al., 2015; Poldrack et al., 2015). On the other hand,
functional connectivity within networks that comprises primary sensory and motor regions
showed high intrasubject and low intersubject variability (Gratton et al., 2018; Laumann
et coll., 2015; Mueller et al., 2013; Poldrack et al., 2015). The importance of genetic factors to
these different levels of intersubject variability, cependant, is yet to be further investigated.
Recent reports suggest that genetic factors crucially influence the intersubject variability in
the functional connectome (Colclough et al., 2017; Demeter et al., 2020; Elliott et al., 2019;
Ge, Holmes, Buckner, Smoller, & Sabuncu, 2017; Miranda-Dominguez et al., 2018; Lequel
et coll., 2016). Connectome-based identification analyses were extended to the identification
Neurosciences en réseau
528
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
un
_
0
0
1
8
9
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
Heritability:
The proportion of the intersubject
variability that is due to variability in
genetic factors.
Connectivity strength:
The degree to which the functional
activity of two distinct brain regions
is coordinated, typically given by the
correlation coefficient.
Narrow-sense heritability (h2):
The proportion of the intersubject
variability that is solely due to
additive genetic factors, lequel
represent the contribution of genes
transmitted by parents to the
offspring’s phenotype.
of twin pairs, suggesting that part of the intersubject variability is due to genetic factors
(Demeter et al., 2020; Miranda-Dominguez et al., 2018). Accordingly, studies indicate that
the average heritability of the connectivity strength of the whole-brain connectome is between
15% et 25% within the Human Connectome Project dataset (Adhikari et al., 2018;
Colclough et al., 2017; Elliott et al., 2019). On the other hand, the heritability of the connec-
tivity strength within some functional networks seems to be much higher (Ge et al., 2017;
Teeuw et al., 2019) than in the whole-brain connectome.
Cependant, substantial differences in brain parcellation schemas (Arslan et al., 2018; Eickhoff,
Yeo, & Genon, 2018; Salehi et al., 2020) undermine the effort to determine the relationship
between heritability and the different levels of intersubject variability. Ici, nous (un) reproduced
and extended the identification analysis introduced by Finn et al. (2015) to determine the
functional networks that best uncovered individual uniqueness and intersubject similarity
among matched twin pairs, et (b) investigated how the different levels of intersubject vari-
ability of functional networks relate to their heritability by using a multivariate ACE modeling
approach with bootstrapping. In our approach, 10 functional connections (edges) were ran-
domly drawn from the pool of connections and were used as variables in a multivariate
ACE model. This model decomposes the variance of each variable (c'est à dire., each edge) et le
covariance between variables into additive genetic influences (UN, or narrow-sense heritability;
Mayhew & Meyre, 2017), shared environment (C), and external sources of variability (E). Ici,
we only focused on the partitioning of variance to estimate network heritability, doing so by
averaging the decomposition of variances into A, C, and E components across variables (c'est à dire.,
across edges) for each model fit. This process was repeated for many iterations, which results
in the distributions of means for each component (UN, C, and E). En plus, cette approche
allows one to easily generate null distributions for statistical testing by randomly shuffling
monozygotic and dizygotic twin statuses at each iteration (Colclough et al., 2017).
RÉSULTATS
Functional Connectivity-Based Identification Analyses
Individual identification. Whole-brain functional connectivity matrices were determined by
using two distinct parcellation schemas: “Shen” (Shen, Tokoglu, Papademetris, & Constable,
2013; 268 nodes, 71,824 edges) and “Gordon” (Gordon et al., 2014; 333 nodes, 110,889
edges). For brevity, we report the results using only Shen parcels with appropriate reference
to equivalent results using Gordon parcels in the Supporting Information. Connectivity-based
identifications were performed comparing pairs of resting-state functional connectivity matri-
ces (Finn et al., 2015). Resting-state data were acquired in two different days for every partic-
ipant included in this study, resulting in two distinct functional connectivity matrices per
participant. These pairs of connectivity matrices were separated into a “target” and a “data-
base” set. Individual identification was determined by computing the Pearson’s correlation
score of a target connectivity matrix from the target set (n = 380) with all connectivity ma-
trices from the database set (n = 380). Following that, the maximum correlation score among
all comparisons between the target matrix and each of the FC matrices from the database set
should correspond to the correlation of the functional connectivity matrices of the same par-
ticipant in different sessions. This process was repeated for all functional connectivity matrices
within the target set (Figure 1A). The accuracy of the method was defined by the proportion of
correct predicted participants.
Individual identification analyses were determined with whole-brain functional connec-
tome and individual functional networks (Supplementary Table 1). The resulting accuracy
Neurosciences en réseau
529
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
un
_
0
0
1
8
9
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
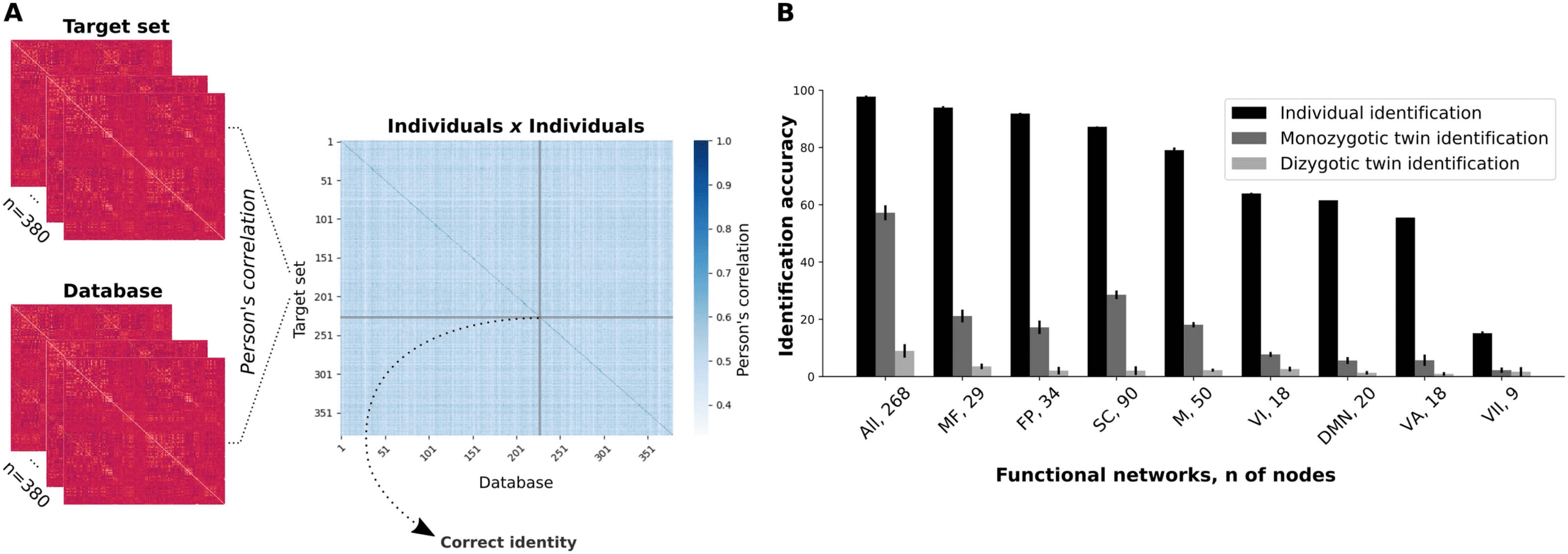
Chiffre 1. Connectome-based identifications. (UN) Functional connectivity matrices from different sessions were grouped into two datasets,
which could be either the “target” set or the “database.” Following that, we computed the Pearson’s correlation of each individual connectivity
matrix from a target set with each connectivity matrix from the database. Donc, each row within the individuals × individuals matrix
contains the correlation scores between a target’s FC and all functional connectivity matrices of the database. (B) Mean identification accu-
racies for individual and twin identification analyses for all functional networks (whole brain included). Mean identification for individual
prediction was determined from two combinations of database and target sets (RESTX × RESTY, where X and Y 2 {1, 2} and X ≠ Y ), alors que
the mean twin identification was determined from four combinations (RESTX × RESTY, where X and Y 2 {1, 2}). Error bars represent the
standard deviation. All, whole brain; MF, medial frontal; FP, frontoparietal; SC, subcortical-cerebellum; M., moteur; VI, visual I; DMN, default
mode network; VA, visual association; VII, visual II. We also present the number of nodes in each network.
of whole-brain connectome-based individual predictions was 97.8% (SD = 0.4%), in agree-
ment with previous studies (Finn et al., 2015; Waller et al., 2017). We also investigated the
relevance of individual functional networks for individual predictions by sectioning the whole-
brain functional connectome into submatrices of single networks. From the eight functional
networks previously defined (Finn et al., 2015), the most successful networks were the medial
frontal (93.9 ± 0.5%) and frontoparietal (91.8 ± 0.3%) réseaux (Figure 1B and Supplementary
Tableau 1). Note that the visual networks and the default mode network were the ones with the
worst individual identification accuracy.
Twin identification. Previous studies indicate that functional connectivity among higher order
associative brain regions greatly varies across individuals (Gratton et al., 2018; Mueller et al.,
2013), even though they are comparably more stable within an individual across sessions
(Laumann et al., 2015; Poldrack et al., 2015). Ainsi, we hypothesized that genetic factors gov-
erned sources of high intersubject and low intrasubject variability in the functional connec-
tome. In order to test this hypothesis, we sought to determine whether the FC profiles from
pairs of twins were more similar compared with the ones from pairs of unrelated individuals
by using connectome-based predictions.
D'abord, we evaluated monozygotic twin identification by computing the correlation coeffi-
cients of the functional connectivity matrices of monozygotic individuals (n = 246) within
the target set with all matrices in the database (246 × 380 = 93,480 comparisons). Our pre-
diction was based on the selection of the highest correlation score (excluding the correlation
scores between functional connectivity matrices of the same individual) for each target partic-
ipant versus database iteration. The mean whole-brain-based prediction accuracy was 57.2%
(SD = 2.6%). This result indicates that the idiosyncratic FC profiles might be genetically
Neurosciences en réseau
530
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
un
_
0
0
1
8
9
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
determined and they are sufficiently stable so one could identify monozygotic twins well
above chance. En effet, we have performed a permutation test, by exchanging twin pairs’ iden-
tities 1,000 times, such that for each identification iteration, a new twin pair identity was as-
signed. The maximum identification accuracy found through these 1,000 permutations was
1.6%, indicating that the whole-brain-based identification performance is significantly differ-
ent from the chance level ( p value < 0.001).
Later on, we investigated the ability of specific functional networks in discriminating a twin
pair from pairs of unrelated individuals (Figure 1B). At this stage, the most successful functional
networks were the subcortical-cerebellum (28.6 ± 1.5%) and medial frontal (21.1 ± 2.2%)
networks. Noteworthy, the most successful functional networks on twin identification were
among the ones that best performed on individual identifications. Nonetheless, a substantial
decrease in the successful twin identification rates was observed for functional networks when
compared with the whole-brain connectome, and these results were particularly affected by
the number of nodes within each network. The least successful functional networks on twin
identification were the ones with the least number of nodes, while the networks with a larger
number of nodes tended to present higher accuracies. The Pearson’s correlation score be-
tween the number of nodes of each network and its ability to correctly identify monozygotic
twins was r = 0.95 ( p value = 6.3E-5; Supplementary Table 2), as opposed to a nonsignificant
correlation between the number of nodes and individual identification accuracy (r = 0.52,
p value = 0.15). This implies that the ability of a priori–defined functional networks to capture
similarities in the FC profiles of monozygotic twins differentially relies on the amount of infor-
mation provided (i.e., by the number of nodes).
Finally, we performed all the previous analyses for the identification of dizygotic twins. At
this time, we selected only the dizygotic individuals (n = 134) within the target set, giving 134 ×
380 = 50,920 comparisons. For the whole-brain-based identification, the mean prediction
accuracy was 8.9% (SD = 2.3%; p value < 0.001). This abrupt change in twin identification
accuracy indicates that the functional connectivity patterns of monozygotic twins are strictly
more similar in comparison to dizygotic twins, which indicates the relevance of shared genetic
background. At the level of individual functional networks, identification accuracies dropped
even further (Figure 1B), and they were also correlated with the number of nodes of the net-
works (r = 0.92, p value < 0.001).
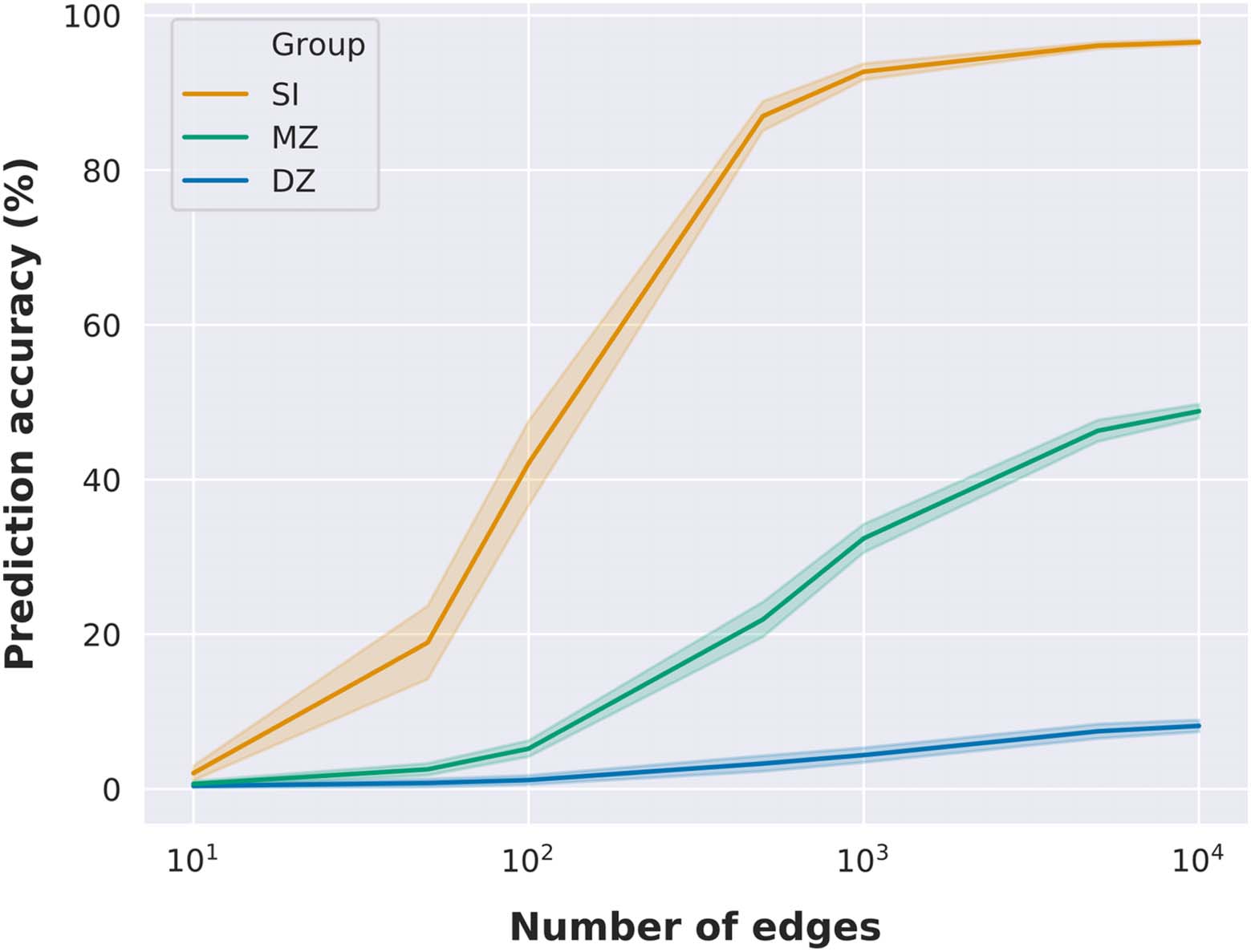
Fingerprinting as a Function of the Number of Edges
The previous results indicated that twin identification accuracy was correlated with the num-
ber of nodes of functional networks, and hence with the number of edges. To further investi-
gate the relationship between the number of edges in connectome fingerprinting and twin
identification accuracy, we performed identification analyses using randomly selected subsets
of edges, with 100 random selections per subset size (Byrge & Kennedy, 2018). Our results
show that it is possible to identify an individual with high accuracy using a random subset
of edges (Figure 2), with accuracy above 80% using only 500 random edges (a similar finding
is reported at Byrge & Kennedy, 2018). However, monozygotic twin identification reaches
only near 50% accuracy using 10,000 random edges, while dizygotic twin identification ac-
curacy is equal to 8% on average with the same subset size. Noteworthy, monozygotic twin
identification accuracy with 500 random edges was on average equal to approximately 20%,
similar to the prediction accuracy using the medial frontal network (29 nodes and 406 unique
edges). On the other hand, prediction accuracy reached 32% with 1,000 random edges and
46% with 5,000 random edges. At a similar level, the prediction accuracy of the subcortical-
cerebellum network (90 nodes and 4,005 unique edges) was 28.6%.
Connectome fingerprinting:
Technique used for individual
identification based on the similarity
between pairs of functional
connectome matrices.
Network Neuroscience
531
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2.
Identification accuracy as a function of the number of edges. Identification accuracy as a
function of subsets of randomly selected edges. Mean identification accuracy and standard devia-
tion are illustrated as a function of the number of edges (we evaluated only 7 different subset sizes:
10, 50, 100, 500, 1,000, 5,000, and 10,000 edges). Mean and standard deviation were determined
across 100 random edge selections per subset size.
Therefore, our findings suggest that while it is possible to identify twin pairs above chance,
differences seen across functional networks in twin pair identification may be mostly driven by
differences in the number of nodes/edges. However, the fact that twin identification accuracy
with subsets of random edges could outperform functional networks with a similar amount of
edges suggests that edges might be differently influenced by genetic factors.
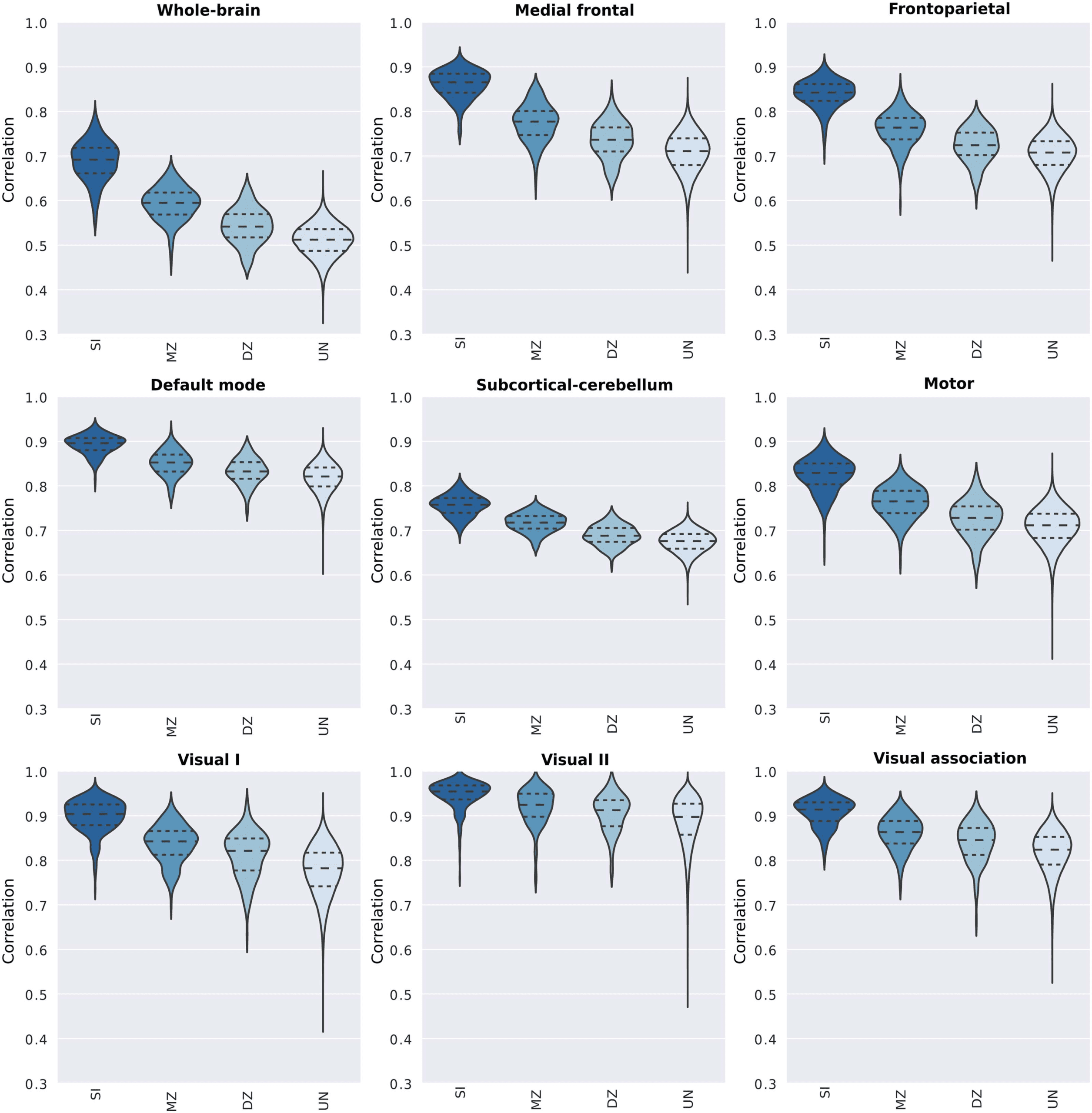
Intra- and Intersubject Variability in the Functional Connectome
In order to characterize the intra- and intersubject variabilities (i.e., among unrelated indi-
viduals, monozygotic and dizygotic twin pairs) for the whole-brain connectome and each
functional network, we arranged the correlation coefficients in four groups according to their
relationship: (a) same individual, SI (n = 380); (b) monozygotic twins, MZ (n = 246); (c)
dizygotic twins, DZ (n = 134), and (d) unrelated individuals, UN (n = 143,640). The distri-
butions of correlations across all these pairs for the whole-brain and functional networks are
illustrated in Figure 3 (Supplementary Figure 1).
As one could expect, the mean of the distributions of correlation scores from the SI group is
notably higher than the ones from the remaining groups. This is observed not only for the
whole-brain connectome but also for most of the functional networks, especially for the medial
frontal and frontoparietal functional networks. In order to characterize the importance of the
distance between these distributions—that is, the effect size—to identification analyses, we
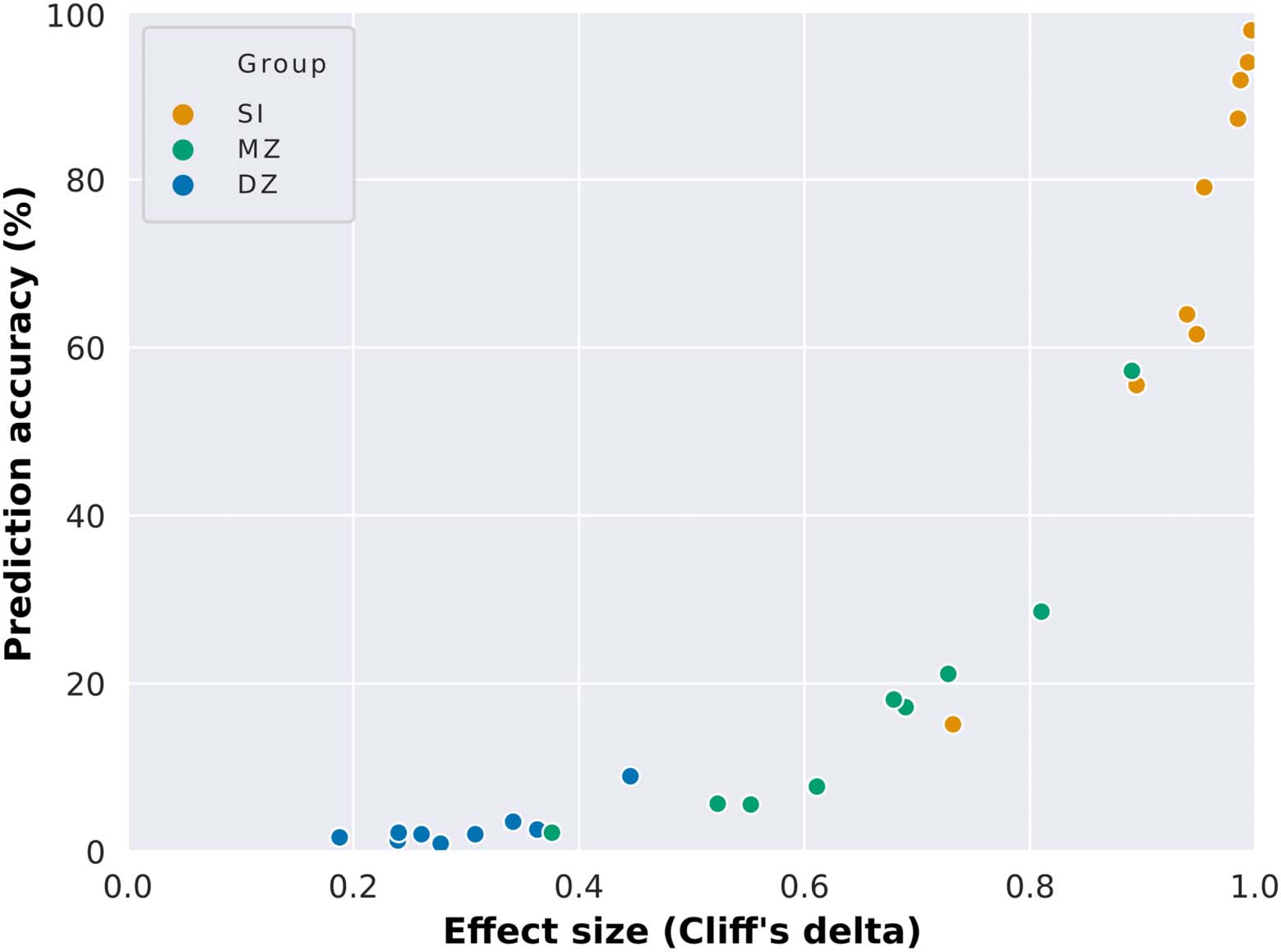
determined identification accuracy as a function of effect size, Cliff’s delta (Cliff, 1993;
Network Neuroscience
532
Heritability of large-scale functional networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Distribution of correlation coefficients between pairs of functional connectivity matrices for the whole brain and individual func-
tional networks. Pearson’s correlation scores were determined from pairs of connectivity matrices (REST1 × REST2), and they were grouped
based on individuals’ genetic relationship. Hence, violin plots show the distribution of the correlation scores between pairs of matrices of the
same individual (SI), monozygotic twin (MZ), dizygotic twin (DZ), and unrelated individuals (UN).
Network Neuroscience
533
Heritability of large-scale functional networks
Figure 4, Supplementary Figure 2, and Supplementary Table 3). In Figure 4, we observe that
high prediction accuracy is associated with high effect size, while low prediction accuracy is
associated with low effect size. This suggests that high intersubject variability (which is related
to low correlation between unrelated individuals’ connectivity matrices) and low intrasubject
variability (high correlation between the connectivity matrices of the same individual in different
sessions) are crucial for high prediction accuracy. Additionally, the higher similarity between
monozygotic twins in comparison to unrelated individuals (medium to high effect sizes) suggests
that a portion of this intersubject variability is heritable and differs across functional networks.
Narrow-Sense Heritability of Functional Connections
To further investigate these functional networks, we performed heritability analyses using a
multivariate ACE modeling approach with bootstrapping. High dimensionality is a common
hurdle when multivariate processing is considered for regression or inference methods.
Hence, univariate analyses are usually preferred to avoid the necessity of increasing computa-
tional resources and time because of high-dimensional multivariate analyses trade-off, despite
the fact that multivariate analyses tend to be more suitable for complex data that include several
thousand covariates. In neuroscience, the heritability of functional networks is usually deter-
mined as the average heritability of individual functional connections (edges) over their con-
stituent brain regions (nodes; Colclough et al., 2017; Elliott et al., 2019; Ge et al., 2017). Here,
we propose a lower dimensional multivariate ACE modeling approach with bootstrapping
that allows one to generate a distribution of means for each variance component (Figure 5).
ACE model:
Model typically used for the
decomposition of intersubject
variability into variance due to
additive genetic factors (A), shared
environment (C), and external
sources of variability (E).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Dependence of connectome-based predictions on effect size. Mean prediction accuracies
from all functional networks (whole brain included) as a function of the effect size of the difference
between the group of interest (same individual, SI; monozygotic twins, MZ; or dizygotic twins, DZ)
and unrelated individuals.
Network Neuroscience
534
Heritability of large-scale functional networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
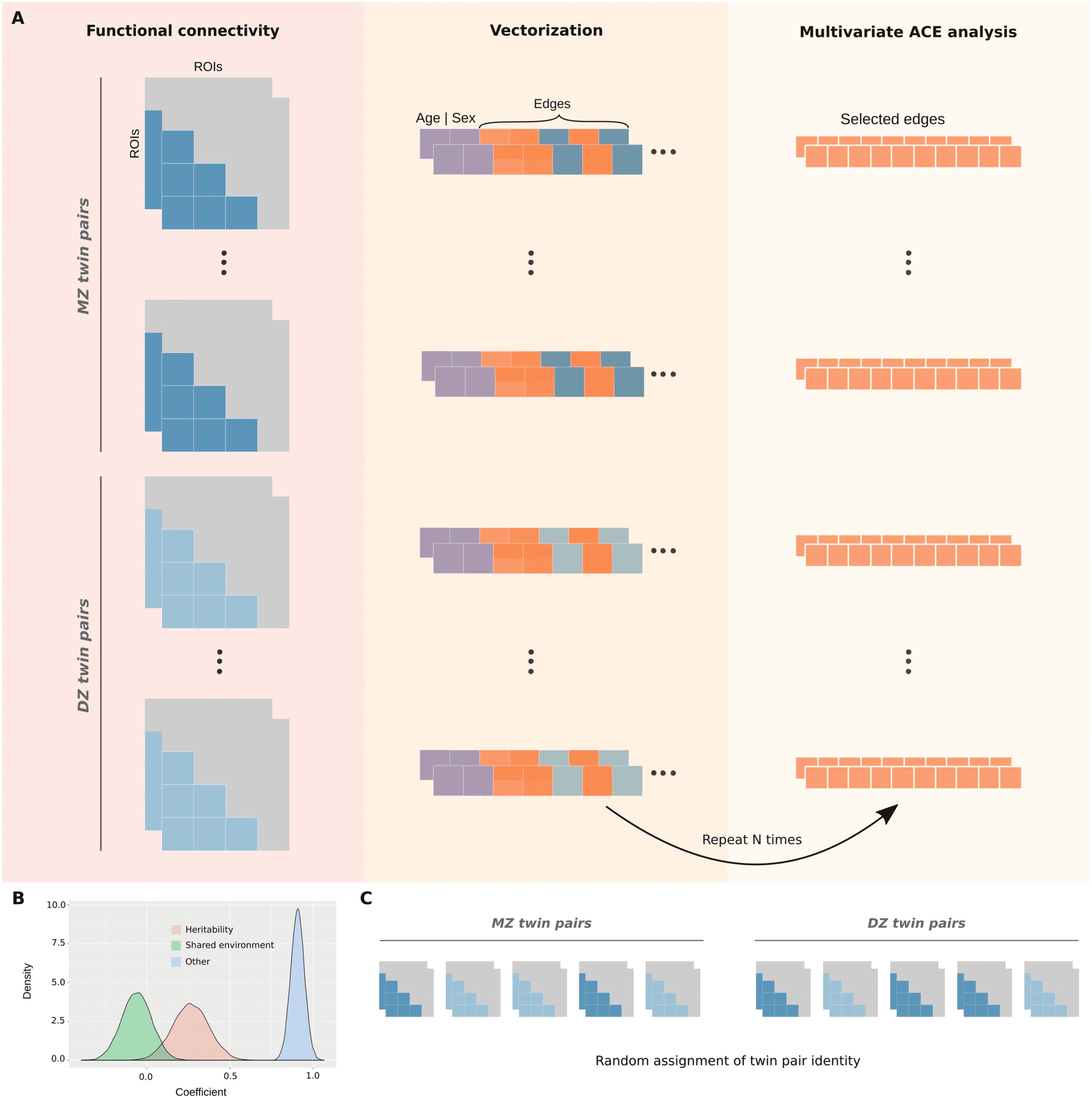
Figure 5. Multivariate ACE model with bootstrapping. (A) The lower triangles of mean functional connectivity matrices were vectorized, and
the effect of age and sex were regressed out from each edge. In an iterative process, 10 edges were randomly selected and used as variables to
fit a multivariate ACE model. This procedure was repeated with reposition for 8,000 times for the whole-brain network (or 1,000 times for each
functional network). (B) This approach provides distributions of means for each variance component (A, C, and E) by taking the average of their
estimates across edges at each iteration. (C) Null distributions were similarly obtained by randomly shuffling monozygotic and dizygotic twin
statuses at each iteration.
Network Neuroscience
535
Heritability of large-scale functional networks
This multivariate approach involved the random selection of 10 edges (within the functional
network of interest) that were used as variables to fit a multivariate ACE model (Figure 5A). The
multivariate ACE model decomposes the variance of each edge into additive genetic
influences (A, or arrow-sense heritability; (Mayhew & Meyre, 2017), shared environment
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
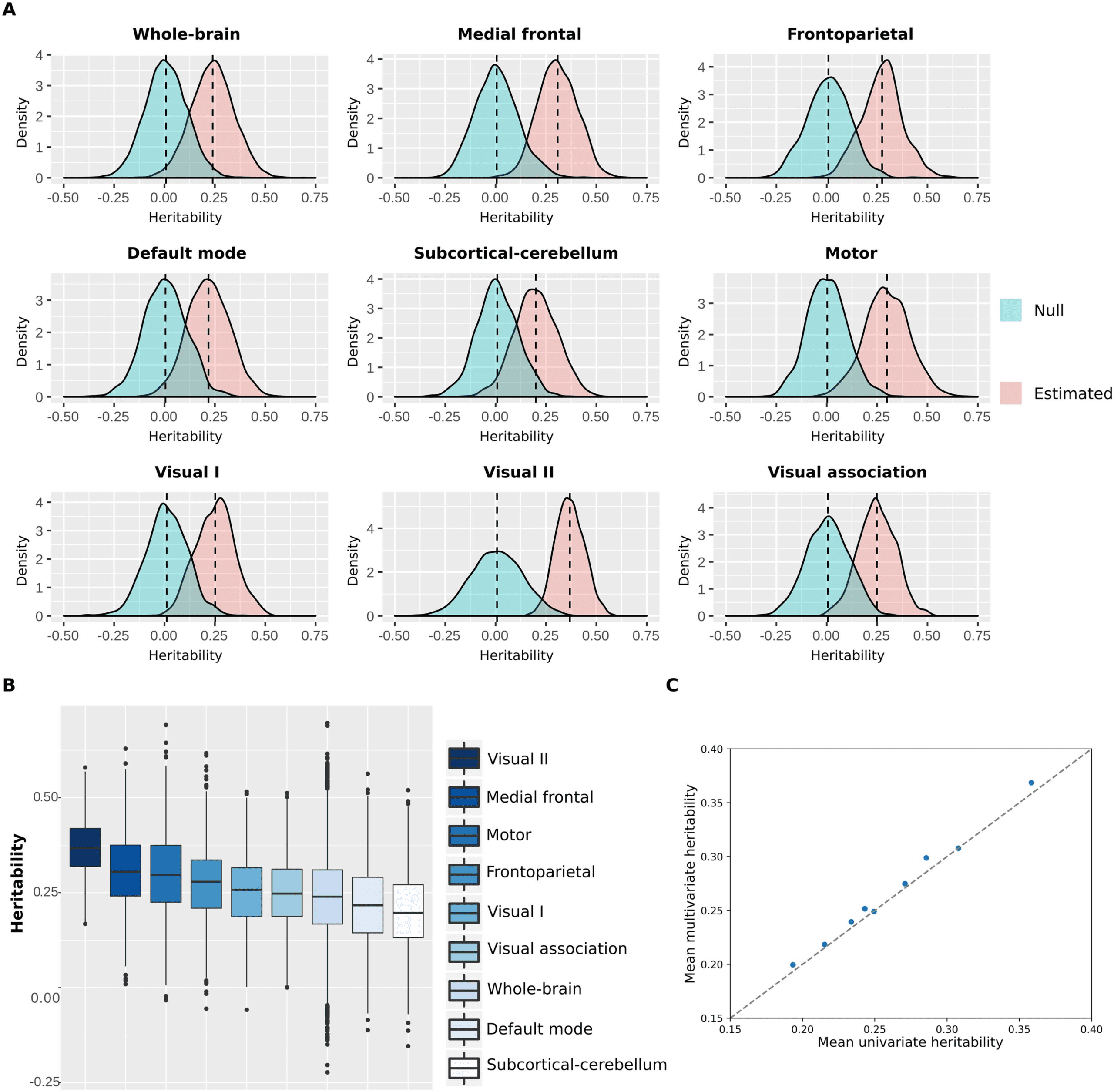
Figure 6. Heritability distributions for each functional network. (A) Heritability estimates and null distributions for each functional network.
(B) Heritability estimates distributions displayed from the most heritable (visual II) to the least heritable (subcortical-cerebellum). (C)
Comparison of the mean heritability found with multivariate ACE models versus univariate ACE models for all functional networks.
Network Neuroscience
536
Heritability of large-scale functional networks
(C), and external sources of variability (E). Then, we determined the mean of A, C, and E com-
ponents across edges. This procedure was repeated with reposition for 8,000 times for the
whole-brain network and 1,000 times for each functional network, which resulted in the final
distributions of means for each component (A, C, and E; Figure 5B). Finally, null distributions
were similarly obtained by randomly shuffling monozygotic and dizygotic twin statuses at each
iteration (Figure 5C).
The heritability distributions with their respective null distributions for all functional net-
works are illustrated in Figure 6A (Supplementary Figure 3). As expected, the mean heritability
of all null distributions was virtually equal to 0. Apart from that, all heritability estimate distri-
butions were significantly different from their respective null distributions (independent t test,
p < 0.001). Among all functional networks, the visual II has shown to be the most heritable
with mean heritability of 0.37 (37% of the variance of the phenotype is attributed to additive
shared genetics; Supplementary Table 4), while the subcortical-cerebellum was the least
heritable with mean heritability of 0.20 (Figure 6B and Supplementary Tables 4, 5, and 6).
Additionally, we compared the mean heritability found for all functional networks using our
approach with the mean estimates based on univariate models (Figure 6C). As expected, the
mean heritability found using our approach is nearly equal to the classic univariate heritability
(Supplementary Table 7), which is based on averaging estimates across all functional connec-
tions within each functional network. Finally, heritability estimates were not significantly
correlated with number of nodes (r = −0.34, p value = 0.38) or monozygotic twin identifica-
tion accuracy (r = −0.33, p value = 0.39).
DISCUSSION
Here, we found that the functional connectivity profiles of twin pairs were more similar than of
unrelated individuals, although the degree of similarity varied across functional networks.
Indeed, we demonstrated that functional networks have distinct discriminatory power in con-
nectome fingerprinting analyses, in both individual and twin identifications, although in the
latter differences in identification performances may be mostly driven by differences in the
number of nodes/edges. We also found that high intersubject variability (i.e., variability of a
trait between individuals) is crucial for connectome fingerprinting. Finally, our multivariate
ACE modeling approach suggests that the heritability of functional networks is consistent
throughout the brain, although our findings suggest that functional networks are differentially
influenced by additive genetic factors. Altogether, we were able to establish the influence of
genetic factors to intersubject variability of functional networks by leveraging a multivariate
ACE model in addition to the multivariate connectome fingerprinting approach.
Intra- and Intersubject Variability Trade-Off in Connectome Fingerprinting
Evidence suggests that the different levels of inter- and intrasubject variability in functional
networks contribute to their distinctiveness, such that high intersubject (Gratton et al., 2018;
Mueller et al., 2013) and low intrasubject (Laumann et al., 2015; Poldrack et al., 2015)
variability in higher order associative networks are often related to their high discriminability
(Finn et al., 2015; Jalbrzikowski et al., 2020; Kaufmann et al., 2017; Miranda-Dominguez
et al., 2018, 2014; Mueller et al., 2013) and the opposite pattern to the low discriminability
of primary sensory and motor networks (Gratton et al., 2018; Laumann et al., 2015; Mueller
et al., 2013; Poldrack et al., 2015). We confirmed that higher order associative networks were
the most discriminatory, while visual networks were the least discriminatory, although they
showed similar levels of intrasubject variability. This finding was similarly seen in twin pair
Network Neuroscience
537
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
identifications, although in the latter the prediction accuracy was positively correlated with the
number of nodes defining each functional network. To further investigate the inter- and intra-
subject variability trade-off in connectome fingerprinting, we determined the prediction accu-
racy as a function of the difference between the similarity scores of functional networks
derived from the same individual—in different resting-state sessions—and unrelated indi-
viduals. We found that high identification accuracy requires high intersubject variability, sug-
gesting that although the stability of idiosyncratic functional connectivity patterns is relevant
and seen across all functional networks, fingerprinting seems to rely prominently on high
intersubject variability.
Genetic Influence on Functional Networks
To investigate the impact of additive genetic factors in determining stable patterns of intersub-
ject variability, we performed an alternative approach to the univariate ACE model. In our
multivariate ACE model, a fixed number of edges were randomly and iteratively selected to
fit the model, and the mean heritability estimate was determined by averaging individual edge
heritability at each of those iterations. Therefore, 8,000 models were fitted to estimate the
heritability of the whole-brain network, as opposed to fitting 35,778 univariate models. In
addition to that, 1,000 models were generated for each functional network, totaling 16,000
models (8,000 models for the whole-brain network + 8 × 1,000 models), which is still far less
than fitting 35,778 univariate models. We also observed a gain in statistical power with our
approach (this is illustrated by the narrower confidence intervals of the multivariate model—
Supplementary Table 4—as opposed to the univariate version—Supplementary Table 7).
Additionally, our modeling approach provides a straightforward way for building null distribu-
tions by randomly shuffling twin statuses at each iteration as the final step before heritability
estimation. Therefore, we believe that the contribution of this method is twofold: It reduces the
number of models to be fitted for the estimation of the heritability of functional networks, and it
also provides a straightforward way for building null distributions.
We found that the functional networks that were the most influenced by additive genetic
factors were not the ones that best performed on twin identifications. This is particularly prom-
inent for the visual II and subcortical-cerebellum functional networks. The first has shown to
be highly influenced by additive genetic factors, but it had a poor performance on monozy-
gotic twin identification and individual identification. This indicates that the intersubject
variability was low, thus being difficult to discriminate between pairs of connectomes from
UN/twin/SI groups. However, a great portion of this low intersubject variability might be
due to additive genetic factors. On the other hand, the subcortical-cerebellum network has
shown lower heritability but the best performance on twin identification (after whole-brain
network). A possible explanation for this finding is that a high intersubject variability allowed
a better discrimination between unrelated individuals versus twin pairs, even though a smaller
portion of its intersubject variability was due to additive genetic factors. Nonetheless, our
findings also suggest that twin identification accuracy of functional networks varies with the
number of edges, indicating that the inconsistency seen between twin identification accuracy
and heritability is perhaps an artifact associated with the confounding effect of number of
edges on twin identification.
Finally, heritable patterns of functional connectivity strength of individual edges may
emerge from underlying brain anatomy. Anatomical features of the brain have been shown
to be highly heritable (Panizzon et al., 2009; Roshchupkin et al., 2016; Strike et al., 2015;
Thompson et al., 2001). This suggests that the similarity of brain anatomy in twins might lead
Network Neuroscience
538
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
to better alignment of their brain structure to a template space as opposed to unrelated
individuals. Therefore, when functional units of the brain are determined by a group-based
parcellation, variability in functional connectivity strength partly reflects how well a template
parcel matches the actual functional unit of a given individual. For example, a given region A
in a group-based parcellation could not only overlap with distinct regions across unrelated
individuals, but also consistently overlap with a similar area in twins (Anderson et al.,
2020). This could lead to the greater similarity of individual edges between twins and higher
intersubject variability across unrelated individuals just because regions being selected are
ultimately different. We believe that assessing heritability of functional connectivity patterns
using individualized parcellations (Glasser et al., 2016; Kong et al., 2019) might shed some
light into this issue.
Parcellation Schema
The individual and twin identification analyses resulted in high prediction accuracy using both
parcellation schemas, Shen and Gordon. Notably, individual identification accuracies using
Shen parcellation schema is about the same as in previous studies (Finn et al., 2015; Waller
et al., 2017), even though we have a more homogenous sample. At the network level, higher
order associative networks were particularly better at discriminations. This result further
supports that associative networks accommodate higher intersubject variability in comparison
to sensorimotor networks (Gratton et al., 2018). Despite that, we observed that the default
mode network (DMN) defined by both parcellation schemas differed in performance during
identification analyses. For Gordon parcels, the DMN figured among the most distinctive net-
works, similarly to other associative networks. However, this pattern was not observed using
Shen parcels, in which the defined DMN figured among the worst functional networks on indi-
vidual predictions. This distinction could be due to the different number of nodes attributed to
DMN in both schemas. Another finding is that the heritability level of functional networks
differed between parcellations, although the mean heritability of the whole-brain functional
network was 0.18 using Gordon parcels and 0.24 using Shen parcels (Supplementary Table 4).
This suggests that different brain areas definition greatly impacts heritability estimates, which
is a potential topic for further investigation.
Using Gordon parcellation, we found that the cingulo parietal and retrosplenial temporal
networks were the most influenced by additive genetic factors, while the somatosensory
mouth and salience networks were the least ones. On the other hand, Miranda-Dominguez
et al. (2018) found that the retrosplenial temporal and somatosensory mouth were the most
heritable, and the visual and salience networks the least heritable. Additionally, their herita-
bility estimates ranged from 0.11 to 0.14, with the heritability of the whole-brain network
being equal to 0.20 (Miranda-Dominguez et al., 2018), while our estimates ranged from
0.47 to 0.12. These differences are likely due to differences in heritability estimation
approaches; while we used the conventional ACE modeling approach, they used three-way
repeated-measures ANOVAs. Although the heritability estimates we obtained using Shen par-
cels were more homogeneous, we were still able to capture the different levels of heritability of
functional networks, suggesting that our approach is suitable for capturing such differences.
Additionally, using a similar methodology, Colclough et al. (2017) found that the heritability
of the connectivity strength averaged over parcels was 0.17 for the whole-brain network, and
Elliott et al. (2019) found a value of about 0.20. This suggests that, although heritability
estimates of functional networks vary depending on the parcellation being used, the whole-
brain functional network heritability seems to be reasonably consistent across studies using
different methodologies and parcellations.
Network Neuroscience
539
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
Limitations
The effect of head motion on rs-fMRI functional connectivity has been assessed over the last
decade, and evidence suggests that head motion parameters systematically affect functional
connectivity estimates. Van Dijk, Sabuncu, and Buckner (2012) found that increasing mean
motion was significantly associated with decreased functional correlation strength among
regions in the DMN and the frontoparietal control network, even after regressing out six
parameters from the rigid body head motion correction at the preprocessing stage. On the
other hand, high levels of head motion were associated with increased local functional con-
nectivity. Finally, their findings suggested that aspects of head motion may behave as trait,
which was further investigated by Couvy-Duchesne and colleagues. In Couvy-Duchesne
et al. (2014), the influence of additive genetics and environment factors on three head motion
parameters have been estimated, and their findings suggest that head motion is partially
heritable. These findings effectively suggest not only that head motion systematically affects
functional connectivity but that it is also partially heritable, indicating that head motion may
bias heritability estimates of functional connectivity strength.
The effect of additional preprocessing steps on the confounding effect of head motion in func-
tional connectivity has been systematically investigated (Siegel et al., 2017). Researchers found
that extra preprocessing steps to the HCP minimally preprocessed dataset have substantially
reduced the correlation of head motion with functional connectivity. Here, we have similarly
added extra preprocessing steps, which included CompCor, temporal band-pass filtering, and
regressing out the linear components of participants’ movement parameters from the BOLD time
series. However, it is important to note that complete removal of the spurious effect of motion
through regression is difficult (if not impossible). Thus, we believe that the field would benefit
from more studies that systematically assess the effect of removing motion parameters at different
stages on heritability estimates of functional connectivity.
Future Directions
Our multivariate ACE model suggests that part of the intersubject variability seen in functional
networks is due to genetic factors. Transcriptomics and genomics approaches have indicated
that many brain disorders are, at least partly, determined by the genetic background (Gandal
et al., 2018; Kasten et al., 2018; Prata, Costa-Neves, Cosme, & Vassos, 2019; Sims, Hill, &
Williams, 2020). Additionally, disruptions in the human functional and structural connectomes
have been associated with neurological conditions, such as amyotrophic lateral sclerosis (ALS;
Chenji et al., 2016), Parkinson’s disease (Gratton et al., 2019; Hall et al., 2019), and epilepsy
(Lee et al., 2018). Specifically, neurotoxic accumulation of amyloid plaques in Alzheimer’s
disease has been located in areas consistent with cortical hubs, indicating that while cortical
hubs are fundamental for information processing, they also bring vulnerability to the human
brain (Buckner et al., 2009). Also, many compelling studies have linked psychiatric disorders
to fundamental connectome disruptions (van den Heuvel & Sporns, 2019). Despite their unique
functional and structural connectivity patterns, these conditions also exhibit some shared
patterns that differ from healthy connectomes. The common features of many of these disorders
make it difficult to diagnose them and to determine the mechanisms behind their onset, partic-
ularly for psychiatric disorders. Thus, detailed scrutiny of the human connectome and genome
may lead to a promising new era for precision medicine in psychiatry and neurology.
Connectome fingerprinting in addition to heritability analyses may allow for the search of
connectome features that bring general and specific vulnerabilities to the human brain, which
may be highly heritable, and are central factors among brain disorders (van den Heuvel &
Sporns, 2019).
Network Neuroscience
540
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
Finally, it is important to acknowledge that although we found differences in heritability
estimates across functional networks, such estimates of heritability could be susceptible to
different models of heritability. For example, heritability could be better explained with an AE
model, in which variance is decomposed into additive genetic factors (A) and external sources of
variability (E) only. Additionally, the low reliability of individual edges’ connectivity strength
(Noble, Scheinost, & Constable, 2019; Noble et al., 2017) and higher reliability of the connec-
tome as a whole suggests that common (shared among edges) and specific (nonshared) sources
of genetic variance may differ. The multivariate ACE model used here has been used before to
estimate the genetic correlation between two traits, cortical surface area and cortical thickness
(Panizzon et al., 2009). However, we believe that a common pathway model would be the most
suitable model to study common sources of genetic variance of many edges (Couvy-Duchesne
et al., 2014). Therefore, although we found differences in how additive genetic factors may be
influencing intersubject variability of functional networks, such estimates are not definite.
Critically, different models’ assumptions may potently lead to inconsistent findings of heritability
estimates for large-scale functional networks, and future refinements of such estimates (using
meta-analysis, for instance) should consider them.
MATERIALS AND METHODS
Database and Participant Information
In this study, we used the dataset from the 1,200 subjects data release of the Human
Connectome Project (HCP; Van Essen et al., 2013). We restricted our analysis to monozygotic
(MZ) and dizygotic (DZ) individuals as indicated by genotyping information. So, we initially
selected all MZ and DZ individuals from the original sample. From this subsample, we ex-
cluded the participants who did not have resting-state fMRI sessions (ICA-FIX versions) avail-
able, and who did not have the twin within the group. Therefore, our final sample size was
n = 380. Table 1 summarizes the demographic data.
Data Acquisition
The acquisition protocol has been previously described (Van Essen et al., 2013). In summary,
functional and structural data were acquired in a 3T Siemens Skyra scanner using a 32-channel
head coil. Resting-state data were collected in two separated sessions (REST1 and REST2) in
different days, each session containing two runs of 15 min. In this protocol, participants had
to keep their eyes open with a relaxed fixation on a projected bright crosshair in a dark back-
ground. Each run within a session is distinguished by the oblique axial acquisition, of which
Table 1. Demographic information
Monozygotic (n = 246)
Dizygotic (n = 134)
Age, y
Mean ± SD
Range (min–max)
Sex, n (%)
Female
Male
29.4 ± 3.3
22–36
144 (58.5)
102 (41.5)
29.1 ± 3.5
22–35
78 (58.2)
56 (41.8)
541
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
one run used phase encoding in a right-to-left (RL) direction and the other used phase encoding
in a left-to-right (LR) direction.
Data Preprocessing
Preprocessing pipeline. For this study, we used the spatial and temporal preprocessed rs-fMRI
time courses (Glasser et al., 2013; Smith et al., 2013), which have undergone the steps of ar-
tifact removal, motion correction, and registration to standard space. Furthermore, we applied
additional preprocessing steps by using the CONN toolbox (v.17.f; Whitfield-Gabrieli & Nieto-
Castanon, 2012), which included structural segmentation, functional outlier detection (inter-
mediate setting: 5 for z-score scan-to-scan global signal changes and 0.9 mm for scan-to-scan
head motion composite changes), and functional smoothing. Following that, a component-
based noise correction method (CompCor; Behzadi, Restom, Liau, & Liu, 2007) and a tempo-
ral band-pass filtering (preserving frequencies between 0.01 and 0.10 Hz) were applied. For
spatial smoothing, a Gaussian with the full width at half maximum (FWHM) equal to 6 mm
was used. We also included participant movement parameters as first-level covariates to re-
gress out their linear components from the BOLD time series.
Parcellations and functional networks. Time courses were calculated as the mean signal within
the regions of interest (ROIs) defined by different parcellation schemas used: Gordon (Gordon
et al., 2014) and Shen (Shen et al., 2013). Both Gordon and Shen schemas are data-driven par-
cellation schemas. The first defines 333 ROIs clustered in 12 functional networks (Supplementary
Table 1), in addition to 47 ROIs not assigned to any specific network. The latter defines 268
ROIs clustered in 8 networks (Supplementary Table 1).
Functional connectivity matrices. Finally, for the two resting-state sessions, data from both the
left-right (LR) and right-left (RL) phase-encoding runs were used to calculate the connectivity
matrices. To obtain the connectivity matrices, ROI-to-ROI bivariate correlation connectivity
measures were computed for all ROIs defined by both parcellation methods, obtaining two
symmetric connectivity matrices for each session for each participant.
Individual Identification
The identification analysis was based on previous work (Finn et al., 2015) with few alterations.
Initially, two databases were created containing the functional connectivity matrices for each
session (REST1 and REST2). The individual identification was determined by computing the
Pearson’s correlation of each individual connectivity matrix from one database with all the
other connectivity matrices from the second database (RESTX × RESTY, where X and Y 2
{1, 2} and X ≠ Y ). For a pair of functional connectivity matrices linearly transformed in a col-
umn vector (vectorization), Ti and Dn, where Ti is the connectivity matrix of a target participant
i, and Dn is the connectivity matrix of a participant (n = 1, …, 380) from the other database, the
Pearson’s correlation coefficient r is
ri;N ¼
r
(cid:3)
(cid:3)
(cid:2)
(cid:2)
P
−
e
(cid:1)Ti
j ¼ 1 Tij
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r
(cid:3)2
(cid:2)
P
e
j ¼ 1 Tij
−
(cid:1)Ti
DNj
−
(cid:1)DN
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
(cid:3)2
(cid:2)
P
e
j ¼ 1 DNj
−
(cid:1)DN
;
(1)
where e is the number of edges. In order to predict the identity of the target participant, the
maximal Pearson’s correlation coefficient was selected (Figure 1A). Additionally, we also inves-
tigated the contribution of single networks to identification accuracy by subsectioning the
functional connectivity matrices into submatrices of single networks. To perform this, we
Network Neuroscience
542
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
selected only connections within a specified network. Then, we calculated the Pearson’s corre-
lation coefficients, similarly to the previous approach. Results are reported as mean ± SD.
Twin Identification
The twin pair identification algorithm was based on the previous individual identification
analysis. At this stage, we removed the correlations corresponding to the same individual in
different sessions, that is, the diagonal of individuals × individuals matrices, and then performed
a new set of identification analyses. In this condition, if the chosen maximum correlation value
belonged to the target subject’s twin, the prediction was considered correct. Monozygotic and
dizygotic twins were analyzed separately, and all conditions (RESTX × RESTY, where X and
Y 2 {1, 2}) were tested. Results are reported as mean ± SD.
Statistical Significance Assessment
To assess the statistical significance of twin identification analyses, we performed a permuta-
tion testing. To ensure the independence of the dataset, we permuted the twin pairs’ identities,
such that for each row of the individuals × individuals matrix (Figure 1A) a new twin pair
identity was assigned. The permutation process was repeated 1,000 times for each functional
network.
Effect Size
The distribution of correlation scores between pairs of connectivity matrices (i.e., correlation
among the vectorized form of the connectivity matrices) was determined by grouping these
scores based on familial relationship: (a) same individual, SI; (b) monozygotic twins, MZ;
(c) dizygotic twins, DZ; and (d) unrelated individuals, UN. Following that, the effect size of
the differences between the distributions of correlation values was measured through the
calculation of Cliff’s delta. This is a nonparametric effect size measure based on all pairwise
differences (Cliff, 1993), which gives how often values from one distribution are larger than the
ones from a second distribution (Equation 2).
Delta dð Þ ¼ Sum x1 > x2
ð
ð
Þ − Sum x1 < x2
n1n2
Þ
:
(2)
Therefore, the number of times that values from one group are higher than the ones from a
second group is calculated for all possible combinations of values between the two groups
(n1n2, where n1 and n2 are the number of values within the distribution 1 and 2, respectively).
The final Cliff’s delta value is the difference between the previous calculations divided by all
possible combinations. Thus, a positive and high value of d (dmaximum = 1) means that values
within distribution 1 are mostly higher than the ones within distribution 2; a negative and high
absolute value of d (dminimum = −1) means the opposite, that values within distribution 1 are
mostly lower than the ones within distribution 2; and d = 0 means that distributions 1 and 2 are
equal.
Heritability Analyses
Functional connectivity measures from two different days (REST1 and REST2) were averaged,
giving a functional connectivity matrix per participant. As mentioned before, whole-brain
functional connectivity matrices were determined by using two distinct parcellation schemas:
Shen (Shen et al., 2013; 268 nodes, 71,824 edges) and Gordon (Gordon et al., 2014; 333
nodes, 110,889 edges). The first step involved the vectorization of functional connectivity
Network Neuroscience
543
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
matrices’ lower triangle (Shen: 35,778 edges; Gordon: 55,278 edges). The heritability analyses
were performed using the umx package (Bates, Maes, & Neale, 2019), after regressing out the
effect of age and sex using umx_residualize.
Heritability of functional networks was estimated using a multivariate ACE model,
umxACEv from umx package (Bates et al., 2019), with bootstrapping. Specifically, umxACEv
model allocates observed phenotypic variability of each variable and between variables
(variance/covariance matrix) into three latent factors: A (additive genetic factors – h2),
C (shared environment – c2), and E (measurement error or external sources of variability –
e2; Neale & Cardon, 1992; Panizzon et al., 2009). This model outputs a variance/covariance
load matrix for each component (A, C, and E). In each component matrix, the diagonal
represents the proportion of variance that that factor explains of each variable’s phenotypic
variability, while off-diagonal terms give the proportion of the covariance between variables.
Here, we only focused on the partitioning of variance for the estimation of network heritability,
doing so by averaging the estimates in the diagonal of each component matrix for each model fit.
In each iteration of model fitting, a subset of 10 edges was randomly selected and used to fit
the previously described ACE model. This procedure was repeated with reposition for 8,000
times (or 12,000 times when Gordon parcels were used) for whole brain, and 1,000 times for
each functional network. The number of iterations was determined such that every edge would
be selected at least twice (i.e., 8,000 iterations × 10 edges = 80,000). This approach provides
distributions of means of each component (A, C, and E) for each functional network. Finally,
null distributions were similarly obtained by randomly shuffling monozygotic and dizygotic
twin statuses at each iteration (Colclough et al., 2017). Independent t student tests were
performed separately to evaluate whether each functional network’s heritability distribution
significantly differed from their respective null distribution.
CITATION DIVERSITY STATEMENT
Recent work in neuroscience and other fields identified a bias in citation practices such that
papers from women and other minorities are under-cited relative to the number of such papers
in the field (Caplar, Tacchella, & Birrer, 2017; Dion, Sumner, & Mitchell, 2018; Dworkin et al.,
2020; Maliniak, Powers, & Walter, 2013; Mitchell, Lange, & Brus, 2013). Here we sought to
proactively consider choosing references that reflect the diversity of the field in thought, form
of contribution, gender, and other factors. Gender of the first and last author of each reference
was predicted by using databases that store the probability of a name being carried by a man
or a woman (Dworkin et al., 2020). By this measure (and excluding self-citations to the first
and last authors of our current paper), our references contain 10.31% woman(first)/woman
(last), 18.36% man/woman, 21.55% woman/man, and 49.78% man/man. We look forward
to future work that could help us to better understand how to support equitable practices in
science.
ACKNOWLEDGMENTS
This work was supported by the Universidade Federal do ABC (UFABC) and Coordination of
Improvement of Higher Education Personnel (CAPES). JRS and CEB are grateful to Sao Paulo
Research Foundation (FAPESP) grant (2018/21934-5). Data were provided by the Human
Connectome Project, WU-Minn Consortium (principal investigators: David Van Essen and
Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support
the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems
Neuroscience at Washington University.
Network Neuroscience
544
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
CODE AVAILABILITY
All source codes are available at https://github.com/felenitaribeiro/TwinID_with_connectome
_fingerprinting (Ribeiro, 2021) and https://github.com/frcsantos/Heritability_FunctionalNetworks
(Santos, 2021).
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00189,
https://github.com/felenitaribeiro/TwinID_with_connectome_fingerprinting, https://github
.com/frcsantos/Heritability_FunctionalNetworks.
AUTHOR CONTRIBUTIONS
Fernanda Lenita Ribeiro: Conceptualization; Data curation; Formal analysis; Funding acquisition;
Investigation; Methodology; Project administration; Software; Validation; Visualization; Writing –
original draft; Writing – review & editing. Felipe R. C. dos Santos: Conceptualization; Data cura-
tion; Formal analysis; Investigation; Methodology; Software; Validation; Visualization; Writing –
review & editing. João Ricardo Sato: Conceptualization; Methodology; Writing – review & editing.
Walter H. L. Pinaya: Conceptualization; Data curation; Methodology; Software; Supervision;
Writing – review & editing. Claudinei Eduardo Biazoli: Conceptualization; Methodology;
Project administration; Resources; Supervision; Writing – review & editing.
FUNDING INFORMATION
Fernanda Lenita Ribeiro, Coordenação de Aperfeiçoamento de Pessoal de Nível Superior
(https://dx.doi.org/10.13039/501100002322).
REFERENCES
Adhikari, B. M., Jahanshad, N., Shukla, D., Glahn, D. C., Blangero,
J., Fox, P. T., Reynolds, R. C., Cox, R. W., Fieremans, E., Veraart,
J., Novikov, D. S., Nichols, T. E., Hong, L. E., Thompson, P. M., &
Kochunov, P. (2018). Comparison of heritability estimates on
resting state fMRI connectivity phenotypes using the ENIGMA
analysis pipeline. Human Brain Mapping, 39(12), 4893–4902.
https://doi.org/10.1002/hbm.24331, PubMed: 30052318
Anderson, K. M., Ge, T., Kong, R., Patrick, L. M., Spreng, R. N.,
Sabuncu, M. R., Yeo, B. T. T., & Holmes, A. J. (2020).
Heritability of individualized cortical network topography.
bioRxiv. https://doi.org/10.1101/2020.07.30.229427
Arslan, S., Ktena, S. I., Makropoulos, A., Robinson, E. C., Rueckert,
D., & Parisot, S. (2018). Human brain mapping: A systematic
comparison of parcellation methods for the human cerebral cortex.
NeuroImage, 170, 5–30. https://doi.org/10.1016/j.neuroimage
.2017.04.014, PubMed: 28412442
Bates, T. C., Maes, H., & Neale, M. C. (2019). Umx: Twin and path-
based structural equation modeling in R. Twin Research and Human
Genetics, 22(1), 27–41. https://doi.org/10.1017/thg.2019.2,
PubMed: 30944056
Behzadi, Y., Restom, K., Liau, J., & Liu, T. T. (2007). A component
based noise correction method (CompCor) for BOLD and perfu-
sion based fMRI. NeuroImage, 37(1), 90–101. https://doi.org/10
.1016/j.neuroimage.2007.04.042, PubMed: 17560126
Buckner, R. L., Sepulcre, J., Talukdar, T., Krienen, F. M., Liu, H.,
Hedden, T., Andrews-Hanna, J. R., Sperling, R. A., & Johnson,
K. A. (2009). Cortical hubs revealed by intrinsic functional
connectivity: Mapping, assessment of stability, and relation
to Alzheimer’s disease.
Journal of Neuroscience, 29(6),
1860–1873. https://doi.org/10.1523/ JNEUROSCI.5062-08
.2009, PubMed: 19211893
Byrge, L., & Kennedy, D. P. (2018). High-accuracy individual identi-
fication using a “thin slice” of the functional connectome. Network
Neuroscience, 1–48. https://doi.org/10.1162/netn_a_00068,
PubMed: 30793087
Caplar, N., Tacchella, S., & Birrer, S. (2017). Quantitative evaluation
of gender bias in astronomical publications from citation counts.
Nature Astronomy, 1. https://doi.org/10.1038/s41550-017-0141
Chenji, S., Jha, S., Lee, D., Brown, M., Seres, P., Mah, D., & Kalra, S.
(2016). Investigating default mode and sensorimotor network con-
nectivity in amyotrophic lateral sclerosis. PLoS ONE, 11(6). https://
doi.org/10.1371/journal.pone.0157443, PubMed: 27322194
Cliff, N. (1993). Dominance statistics: Ordinal analyses to answer
ordinal questions. Psychological Bulletin, 114(3), 494–509.
https://doi.org/10.1037/0033-2909.114.3.494
Colclough, G. L., Smith, S. M., Nichols, T. E., Winkler, A. M.,
Sotiropoulos, S. N., Glasser, M. F., Van Essen, D. C., & Woolrich,
M. W. (2017). The heritability of multi-modal connectivity in
Network Neuroscience
545
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
human brain activity. eLife, 6. https://doi.org/10.7554/eLife.20178,
PubMed: 28745584
Couvy-Duchesne, B., Blokland, G. A. M., Hickie, I. B., Thompson,
P. M., Martin, N. G., de Zubicaray, G. I., McMahon, K. L., &
Wright, M. J. (2014). Heritability of head motion during resting
state functional MRI in 462 healthy twins. NeuroImage, 102(2),
424–434. https://doi.org/10.1016/j.neuroimage.2014.08.010,
PubMed: 25132021
Demeter, D. V., Engelhardt, L. E., Mallett, R., Gordon, E. M.,
Nugiel, T., Harden, K. P., Tucker-Drob, E. M., Lewis-Peacock,
J. A., & Church, J. A. (2020). Functional connectivity fingerprints
at rest are similar across youths and adults and vary with genetic
similarity. iScience, 23(1), 100801. https://doi.org/10.1016/j.isci
.2019.100801, PubMed: 31958758
Dion, M. L., Sumner, J. L., & Mitchell, S. M. (2018). Gendered
citation patterns across political science and social science
methodology fields. Political Analysis, 26(3), 312–327. https://
doi.org/10.1017/pan.2018.12
Dubois, J., & Adolphs, R. (2016). Building a science of individual dif-
ferences from fMRI. Trends in Cognitive Sciences, 20(6), 425–443.
https://doi.org/10.1016/j.tics.2016.03.014, PubMed: 27138646
Dworkin, J. D., Linn, K. A., Teich, E. G., Zurn, P., Shinohara, R. T., &
Bassett, D. S. (2020). The extent and drivers of gender imbalance in
neuroscience reference lists. Nature Neuroscience, 23(8), 918–926.
https://doi.org/10.1038/s41593-020-0658-y, PubMed: 32561883
Eickhoff, S. B., Yeo, B. T. T., & Genon, S. (2018). Imaging-based
parcellations of the human brain. Nature Reviews Neuroscience,
19(11), 672–686. https://doi.org/10.1038/s41583-018-0071-7,
PubMed: 30305712
Elliott, M. L., Knodt, A. R., Cooke, M., Kim, M. J., Melzer, T. R.,
Keenan, R., Ireland, D., Ramrakha, S., Poulton, R., Caspi, A.,
Moffitt, T. E., & Hariri, A. R. (2019). General functional connec-
tivity: Shared features of resting-state and task fMRI drive reliable
and heritable individual differences in functional brain networks.
NeuroImage, 189, 516–532. https://doi.org/10.1016/j.neuroimage
.2019.01.068, PubMed: 30708106
Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M. D., Huang, J.,
Chun, M. M., Papademetris, X., & Constable, R. T. (2015).
Functional connectome fingerprinting: Identifying individuals
using patterns of brain connectivity. Nature Neuroscience, 18(11),
1664–1671. https://doi.org/10.1038/nn.4135, PubMed: 26457551
Gandal, M. J., Haney, J. R., Parikshak, N. N., Leppa, V.,
Ramaswami, G., Hartl, C., Schork, A. J., Appadurai, V., Buil,
A., Werge, T. M., Liu, C., White, K. P., CommonMind
Consortium, PsychENCODE Consortium, iPSYCH-BROAD
Working Group, Horvath, S., & Geschwind, D. H. (2018).
Shared molecular neuropathology across major psychiatric disor-
ders parallels polygenic overlap. Science, 359(6376), 693–697.
https://doi.org/10.1126/science.aad6469, PubMed: 29439242
Ge, T., Holmes, A. J., Buckner, R. L., Smoller, J. W., & Sabuncu, M. R.
(2017). Heritability analysis with repeat measurements and its
application to resting-state functional connectivity. Proceedings
of the National Academy of Sciences, 114(21), 5521–5526.
https://doi.org/10.1073/pnas.1700765114, PubMed: 28484032
Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D.,
Harwell, J., & Yacoub, E. (2016). A multi-modal parcellation of
human cerebral cortex. Nature, 536(7615), 171–178. https://doi
.org/10.1038/nature18933, PubMed: 27437579
Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,
Fischl, B., Andersson, J. L., Xu, J., Jbabdi, S., Webster, M.,
Polimeni, J. R., Van Essen, D. C., & Jenkinson, M. (2013). The
minimal preprocessing pipelines for the Human Connectome
Project. NeuroImage, 80, 105–124. https://doi.org/10.1016/j
.neuroimage.2013.04.127, PubMed: 23668970
Gordon, E. M., Laumann, T. O., Adeyemo, B., Huckins, J. F.,
Kelley, W. M., & Petersen, S. E. (2014). Generation and evalua-
tion of a cortical area parcellation from resting-state correlations.
Cerebral Cortex, 26(1), 288–303. https://doi.org/10.1093/cercor
/bhu239, PubMed: 25316338
Gratton, C., Koller, J. M., Shannon, W., Greene, D. J., Maiti, B.,
Snyder, A. Z., Petersen, S. E., Perlmutter, J. S., & Campbell,
M. C. (2019). Emergent functional network effects in Parkinson
disease. Cerebral Cortex, 29(6), 2509–2523. https://doi.org/10
.1093/cercor/bhy121, PubMed: 29878081
Gratton, C., Laumann, T. O., Nielsen, A. N., Greene, D. J., Gordon,
E. M., Gilmore, A. W., Nelson, S. M., Coalson, R. S., Snyder, A. Z.,
Schlaggar, B. L., Dosenbach, N. U. F., & Petersen, S. E. (2018).
Functional brain networks are dominated by stable group and
individual factors, not cognitive or daily variation. Neuron, 98(2),
439–452. https://doi.org/10.1016/j.neuron.2018.03.035, PubMed:
29673485
Hall, J. M., O’Callaghan, C., Muller, A. J., Martens, K. A. E., Phillips, J. E.,
Moustafa, A. A., Lewis, S. J. G., & Shine, J. M. (2019). Changes in
structural network topology correlate with severity of hallucina-
tory behavior in Parkinson’s disease. Network Neuroscience, 3(2),
521–538. https://doi.org/10.1162/netn_a_00078, PubMed:
30984905
Jalbrzikowski, M., Liu, F., Foran, W., Klei, L., Calabro, F. J., Roeder,
K., Devlin, B., & Luna, B. (2020). Functional connectome finger-
printing accuracy in youths and adults is similar when examined
on the same day and 1.5-years apart. Human Brain Mapping, 41(15),
4187–4199. https://doi.org/10.1002/ hbm.25118, PubMed:
32652852
Kasten, M., Hartmann, C., Hampf, J., Schaake, S., Westenberger, A.,
Vollstedt, E. J., Balck, A., Domingo, A., Vulinovic, F., Dulovic, M.,
Zorn, I., Madoev, H., Zehnle, H., Lembeck, C. M., Schawe, L.,
Reginold, J., Huang, J., König, I. R., Bertram, L., … Klein, C.
(2018). Genotype-phenotype relations for the Parkinson’s disease
genes Parkin, PINK1, DJ1: MDSGene systematic review.
Movement Disorders, 33(5), 730–741. https://doi.org/10.1002
/mds.27352, PubMed: 29644727
Kaufmann, T., Alnæs, D., Doan, N. T., Brandt, C. L., Andreassen,
O. A., & Westlye, L. T. (2017). Delayed stabilization and individ-
ualization in connectome development are related to psychiatric
disorders. Nature Neuroscience, 20(4), 513–515. https://doi.org
/10.1038/nn.4511, PubMed: 28218917
Kong, R., Li, J., Orban, C., Sabuncu, M. R., Liu, H., Schaefer, A.,
Sun, N., Zuo, X.-N., Holmes, A. J., Eickhoff, S. B., & Yeo, B. T. T.
(2019). Spatial topography of individual-specific cortical networks
predicts human cognition, personality, and emotion. Cerebral
Cortex, 29(6), 2533–2551. https://doi.org/10.1093/cercor/bhy123,
PubMed: 29878084
Laumann, T. O., Gordon, E. M., Adeyemo, B., Snyder, A. Z., Joo, S. J.,
Chen, M. Y., Gilmore, A. W., McDermott, K. B., Nelson, S. M.,
Dosenbach, N. U. F., Schlaggar, B. L., Mumford, J. A., Poldrack,
R. A., & Petersen, S. E. (2015). Functional system and areal
Network Neuroscience
546
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
organization of a highly sampled individual human brain.
Neuron, 87(3), 658–671. https://doi.org/10.1016/j.neuron.2015
.06.037, PubMed: 26212711
Lee, K., Khoo, H. M., Lina, J. M., Dubeau, F., Gotman, J., & Grova,
C. (2018). Disruption, emergence and lateralization of brain
network hubs in mesial temporal lobe epilepsy. NeuroImage:
Clinical, 20, 71–84. https://doi.org/10.1016/j.nicl.2018.06.029,
PubMed: 30094158
Maliniak, D., Powers, R., & Walter, B. F. (2013). The gender citation
gap in international relations. International Organization, 67(4),
889–922. https://doi.org/10.1017/S0020818313000209
Mayhew, A. J., & Meyre, D. (2017). Assessing the heritability of
complex traits in humans: Methodological challenges and
opportunities. Current Genomics, 18(4), 332–340. https://doi.org
/10.2174/1389202918666170307161450, PubMed: 29081689
Miranda-Dominguez, O., Feczko, E., Grayson, D. S., Walum, H., Nigg,
J. T., & Fair, D. A. (2018). Heritability of the human connectome: A
connectotyping study. Network Neuroscience, 2(2), 175–199.
https://doi.org/10.1162/netn_a_00029, PubMed: 30215032
Miranda-Dominguez, O., Mills, B. D., Carpenter, S. D., Grant, K. A.,
Kroenke, C. D., Nigg, J. T., & Fair, D. A. (2014). Connectotyping:
Model based fingerprinting of the functional connectome. PLoS
ONE, 9(11). https://doi.org/10.1371/journal.pone.0111048,
PubMed: 25386919
Mitchell, S. M., Lange, S., & Brus, H. (2013). Gendered citation
patterns in international relations journals. International Studies
Perspectives, 14(4), 485–492. https://doi.org/10.1111/insp.12026
Mueller, S., Wang, D., Fox, M. D., Yeo, B. T. T., Sepulcre, J.,
Sabuncu, M. R., Shafee, R., Lu, J., & Liu, H. (2013). Individual
variability in functional connectivity architecture of the human
brain. Neuron, 77(3), 586–595. https://doi.org/10.1016/j.neuron
.2012.12.028, PubMed: 23395382
Neale, M. C., & Cardon, L. R. (1992). Methodology for genetic studies
of twins and families. Kluwer Academic Publishers. https://doi.org
/10.1007/978-94-015-8018-2
Noble, S., Scheinost, D., & Constable, R. T. (2019). A decade of
test-retest reliability of functional connectivity: A systematic
review and meta-analysis. NeuroImage, 203, 116157. https://doi
.org/10.1016/j.neuroimage.2019.116157, PubMed: 31494250
Noble, S., Spann, M. N., Tokoglu, F., Shen, X., Constable, R. T., &
Scheinost, D. (2017). Influences on the test-retest reliability of
functional connectivity MRI and its relationship with behavioral
utility. Cerebral Cortex, 27(11), 5415–5429. https://doi.org/10
.1093/cercor/bhx230, PubMed: 28968754
Panizzon, M. S., Fennema-Notestine, C., Eyler, L. T., Jernigan, T. L.,
Prom-Wormley, E., Neale, M., Jacobson, K., Lyons, M. J., Grant,
M. D., Franz, C. E., Xian, H., Tsuang, M., Fischl, B., Seidman, L.,
Dale, A., & Kremen, W. S. (2009). Distinct genetic influences on
cortical surface area and cortical thickness. Cerebral Cortex, 19(11),
2728–2735. https://doi.org/10.1093/cercor/ bhp026, PubMed:
19299253
Poldrack, R. A., Laumann, T. O., Koyejo, O., Gregory, B., Hover,
A., Chen, M. Y., Gorgolewski, K. J., Luci, J., Joo, S. J., Boyd, R. L.,
Hunicke-Smith, S., Simpson, Z. B., Caven, T., Sochat, V., Shine,
J. M., Gordon, E., Snyder, A. Z., Adeyemo, B., Petersen, S. E., …
Mumford, J. A. (2015). Long-term neural and physiological phe-
notyping of a single human. Nature Communications, 6. https://
doi.org/10.1038/ncomms9885, PubMed: 26648521
Prata, D. P., Costa-Neves, B., Cosme, G., & Vassos, E. (2019).
Unravelling the genetic basis of schizophrenia and bipolar disorder
with GWAS: A systematic review. Journal of Psychiatric Research,
114, 178–207. https://doi.org/10.1016/j.jpsychires.2019.04.007,
PubMed: 31096178
Ribeiro, F. L. (2021). Twin identification with connectome finger-
printing, GitHub, https://github.com/felenitaribeiro/ TwinID_with
_connectome_fingerprinting
Roshchupkin, G. V., Gutman, B. A., Vernooij, M. W., Jahanshad,
N., Martin, N. G., Hofman, A., McMahon, K. L., van der Lee,
S. J., van Duijn, C. M., de Zubicaray, G. I., Uitterlinden, A. G.,
Wright, M. J., Niessen, W. J., Thompson, P. M., Ikram, M. A., &
Adams, H. H. H. (2016). Heritability of the shape of subcortical brain
structures in the general population. Nature Communications, 7,
Article 13738. https://doi.org/10.1038/ncomms13738, PubMed:
27976715
Salehi, M., Greene, A. S., Karbasi, A., Shen, X., Scheinost, D., &
Constable, R. T. (2020). There is no single functional atlas even
for a single individual: Functional parcel definitions change with
task. NeuroImage, 208, 116366. https://doi.org/10.1016/j
.neuroimage.2019.116366, PubMed: 31740342
Santos, F. R. C. (2021). Heritability of functional networks, GitHub,
https://github.com/frcsantos/Heritability_FunctionalNetworks
Sato, J. R., White, T. P., & Biazoli, C. E. (2017). Commentary: A
test-retest dataset for assessing long-term reliability of brain
morphology and resting-state brain activity. Frontiers in
Neuroscience, 11. https://doi.org/10.3389/fnins.2017.00085,
PubMed: 28275335
Seghier, M. L., & Price, C. J. (2018). Interpreting and utilising intersub-
ject variability in brain function. Trends in Cognitive Sciences, 22(6),
517–530. https://doi.org/10.1016/j.tics.2018.03.003, PubMed:
29609894
Shen, X., Tokoglu, F., Papademetris, X., & Constable, R. T. (2013).
Groupwise whole-brain parcellation from resting-state fMRI data
for network node identification. NeuroImage, 82, 403–415.
https://doi.org/10.1016/j.neuroimage.2013.05.081, PubMed:
23747961
Siegel, J. S., Mitra, A., Laumann, T. O., Seitzman, B. A., Raichle,
M., Corbetta, M., & Snyder, A. Z. (2017). Data quality influences
observed links between functional connectivity and behavior.
Cerebral Cortex, 27(9), 4492–4502. https://doi.org/10.1093/cercor
/bhw253, PubMed: 27550863
Sims, R., Hill, M., & Williams, J. (2020). The multiplex model of the
genetics of Alzheimer’s disease. Nature Neuroscience, 23(3),
311–322. https://doi.org/10.1038/s41593-020-0599-5, PubMed:
32112059
Smith, S. M., Andersson, J., Auerbach, E. J., Beckmann, C. F.,
Bijsterbosch, J., Douaud, G., Duff, E., Feinberg, D. A., Griffanti,
L., Harms, M. P., Kelly, M., Laumann, T., Miller, K. L., Moeller,
S., Petersen, S., Power, J., Salimi-Khorshidi, G., Snyder, A. Z., Vu,
A. T., … WU-Minn HCP Consortium. (2013). Resting-state fMRI in
the Human Connectome Project. NeuroImage, 80, 144–168.
https://doi.org/10.1016/j.neuroimage.2013.05.039, PubMed:
23702415
Strike, L. T., Couvy-Duchesne, B., Hansell, N. K., Cuellar-Partida,
G., Medland, S. E., & Wright, M. J. (2015). Genetics and brain
morphology. Neuropsychology Review, 25, 63–96. https://doi
.org/10.1007/s11065-015-9281-1, PubMed: 25773500
Network Neuroscience
547
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heritability of large-scale functional networks
Teeuw, J., Brouwer, R. M., Guimarães, J. P. O. F. T., Brandner, P.,
Koenis, M. M. G., Swagerman, S. C., Verwoert, M., Boomsma,
D. I., & Hulshoff Pol, H. E. (2019). Genetic and environmental in-
fluences on functional connectivity within and between canonical
cortical resting-state networks throughout adolescent develop-
ment in boys and girls. NeuroImage, 202. https://doi.org/10
.1016/j.neuroimage.2019.116073, PubMed: 31386921
Thompson, P. M., Cannon, T. D., Narr, K. L., Van Erp, T., Poutanen,
V. P., Huttunen, M., Lönnqvist, J., Standertskjöld-Nordenstam,
C.-G., Kaprio, J., Khaledy, M., Dail, R., Zoumalan, C. I., &
Toga, A. W. (2001). Genetic influences on brain structure.
Nature Neuroscience, 4(12), 1253–1258. https://doi.org/10
.1038/nn758, PubMed: 11694885
van den Heuvel, M. P., & Sporns, O. (2019). A cross-disorder con-
nectome landscape of brain dysconnectivity. Nature Reviews
Neuroscience, 20(7), 435–446. https://doi.org/10.1038/s41583
-019-0177-6, PubMed: 31127193
van Dijk, K. R. A., Sabuncu, M. R., & Buckner, R. L. (2012). The
influence of head motion on intrinsic functional connectivity
MRI. NeuroImage, 59(1), 431–438. https://doi.org/10.1016/j
.neuroimage.2011.07.044, PubMed: 21810475
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E. J.,
Yacoub, E., & Ugurbil, K. (2013). The WU-Minn Human
Connectome Project: An overview. NeuroImage, 80, 62–79.
https://doi.org/10.1016/j.neuroimage.2013.05.041, PubMed:
23684880
Waller, L., Walter, H., Kruschwitz, J. D., Reuter, L., Müller, S., Erk,
S., & Veer, I. M. (2017). Evaluating the replicability, specificity,
and generalizability of connectome fingerprints. NeuroImage,
158, 371–377. https://doi.org/10.1016/j.neuroimage.2017.07
.016, PubMed: 28710040
Whitfield-Gabrieli, S., & Nieto-Castanon, A. (2012). Conn: A func-
tional connectivity toolbox for correlated and anticorrelated
brain networks. Brain Connectivity, 2(3), 125–141. https://doi
.org/10.1089/brain.2012.0073, PubMed: 22642651
Yang, Z., Zuo, X.-N., McMahon, K. L., Craddock, R. C., Kelly,
C., de Zubicaray, G.
I., Bandettini, P. A.,
I., Hickie,
Castellanos, F. X., Milham, M. P., & Wright, M. J. (2016).
Genetic and environmental contributions to functional con-
nectivity architecture of the human brain. Cerebral Cortex,
26(5), 2341–2352. https://doi.org/10.1093/cercor/ bhw027,
PubMed: 26891986
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
5
2
7
1
9
2
5
2
2
5
n
e
n
_
a
_
0
0
1
8
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
548