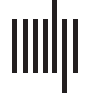RECHERCHE

Long-term stability of avalanche scaling
and integrative network organization
in prefrontal and premotor cortex

Stephanie R. Miller1, Shan Yu1,2, Sinisa Pajevic3, and Dietmar Plenz1

1Section on Critical Brain Dynamics, National Institute of Mental Health, Béthesda, MARYLAND, Etats-Unis
2Brainnetome Center, Institute of Automation, Chinese Academy of Sciences, Chine
3Section on Quantitative Imaging and Tissue Sciences, National Institute of Child Health and Development,
NIH, Béthesda, MARYLAND, Etats-Unis

un accès ouvert

journal

Mots clés: Nonhuman primate, Resting activity, Criticality, Brain dynamics, Neuronal avalanches,
Integrative network organization

ABSTRAIT

Ongoing neuronal activity in the brain establishes functional networks that reflect normal and
pathological brain function. Most estimates of these functional networks suffer from low
spatiotemporal resolution and indirect measures of neuronal population activity, limiting the
accuracy and reliability in their reconstruction over time. Ici, we studied the stability of
neuronal avalanche dynamics and corresponding reconstructed functional networks in the
adult brain. Using chronically implanted high-density microelectrode arrays, the local field
potential (LFP) of resting-state activity was recorded in prefrontal and premotor cortex of awake
nonhuman primates. Avalanche dynamics revealed stable scaling exhibiting an inverted
parabolic profile and collapse exponent of 2 in line with a critical branching process over
many days and weeks. Functional networks were based on a Bayesian-derived estimator and
demonstrated stable integrative properties characterized by nontrivial high neighborhood
overlap between strongly connected nodes and robustness to weak-link pruning. Entropy-
based mixing analysis revealed significant changes in strong link weights over weeks. Le
long-term stability in avalanche scaling and integrative network organization in the face of
individual link weight changes should support the development of noninvasive biomarkers to
characterize normal and abnormal brain states in the adult brain.

RÉSUMÉ DE L'AUTEUR

The brain is spontaneously active even in the absence of specific sensations or movements.
This ongoing activity arises from the interactions among hundreds of thousands of neurons,
which has been captured by a variety of distinct functional networks predictive of healthy
and pathological brain functions. The global dynamical states and overarching network
principles that underlie such ongoing brain activity are not well understood. Here we
identify avalanche dynamics and “friendship” networks as two major features of ongoing
activity in the frontal cortex of nonhuman primates. We demonstrate their stability over
weeks in the face of local network changes. Deviation from avalanche dynamics and
“friendship” organization might provide robust biomarkers to identify normal and
pathological brain states.

Citation: Miller, S. R., Yu, S., Pajevic, S.,
& Plenz, D. (2021). Long-term stability
of avalanche scaling and integrative
network organization in prefrontal and
premotor cortex. Neurosciences en réseau,
5(2), 505–526. https://est ce que je.org/10.1162
/netn_a_00188

EST CE QUE JE:
https://doi.org/10.1162/netn_a_00188

Reçu: 17 Novembre 2020
Accepté: 11 Février 2021

Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.

Auteur correspondant:
Dietmar Plenz
plenz@mail.nih.gov

Éditeur de manipulation:
Gustavo Deco

droits d'auteur: © 2021
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence

La presse du MIT

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Long-term stability in avalanches and integrative networks

INTRODUCTION

Ongoing neuronal activity in the mammalian brain gives rise to distinct functional networks
that reflect normal and pathological brain function (Bullmore & Sporns, 2009; Fox & Raichle,
2007; Raichle, 2015). Empirical measures of these networks, cependant, are often limited in the
precision with which they reflect the organization of neuronal population activity and a lack of
longitudinal follow-up. Networks are reconstructed either from indirect nonneuronal activity
at low temporal resolution using functional magnetic resonance imaging (IRMf), or via more
direct neuronal activity measures such as magnetoencephalography (MEG) and electroen-
cephalography (EEG), which suffer predominantly from low spatial resolution (Bassett &
Sporns, 2017). Accordingly, there is limited knowledge about the stability and nature of the
spatiotemporal dynamics and corresponding functional connectivity of local neuronal popu-
lations that give rise to fluctuations in ongoing cortical activity.

In contrast to macroscopic and indirect methods, neuronal activity measured at single-
cell resolution could in principle allow for precise and robust spatiotemporal reconstruction
of functional networks in cortex. Par exemple, in macaque cortex single-unit activity can be
recorded over many weeks (Nicolelis et al., 2003) and identifies firing statistics of neurons
over days (Dickey et al., 2009; Jackson & Fetz, 2007). Advanced approaches may involve
tetrodes, automated classifiers (Tolias et al., 2007), or second-order statistics as classifiers
(Fraser & Schwartz, 2011). Even advanced single-unit approaches, cependant, limit robust
tracking of activity to small groups of individual neurons. Chronic expression of genetically
encoded calcium indicators can increase the neuronal count and identify orientation-
selective neurons over months (Li et al., 2017), yet at low temporal resolution. The local
field potential (LFP), alternativement, provides access to an intermediate spatial resolution of
cortical activity that is between the macroscopic scale of fMRI, MEG and EEG, and single-
cell accuracy. It robustly measures local neuronal population activity with high temporal
and reasonable spatial resolution of several hundred micrometers (par exemple., Bellay et al.,
2021; Katzner et al., 2009) over many weeks. In nonhuman primates (NHPs), the LFP has
been shown to correlate well with local unit-activity (Donoghue et al., 1998; Petermann
et coll., 2009; Rasch et al., 2008) and offers robust brain-machine interface performance
(Mehring et al., 2003).

It is now well established that the ongoing LFP in superficial layers of nonhuman primates
organizes into spatiotemporal activity clusters whose sizes and durations distribute according
to power laws (Miller et al., 2019; Shew et al., 2009; Yu et al., 2017), the hallmark of neuronal
avalanches (Beggs & Plenz, 2003). The spatiotemporal correlations underlying neuronal ava-
lanches give rise to functional “integrative” networks, in which the topology and weights of
links organize such that end nodes of strong links are more likely to have many common
neighbors, as quantified by a high correlation between the link weight and the link clustering
coefficient (Pajevic & Plenz, 2012; cf. edge-clustering coefficient in Radicchi et al., 2004),
while being robust to the loss of weak links, in terms of maintaining the advantages of a
small-world topology (Watts & Strogatz, 1998). This specific arrangement describes many
complex networks ranging from genetic networks to social, c'est, “friendship,” networks
(Pajevic & Plenz, 2012). Surtout, integrative networks can form using local plasticity rules
that operate on neuronal avalanches (Alstott et al., 2015) in which weak links provide a large
basin for plastic changes as they can be removed or rewired, permitting flexibility, while pre-
serving the small-world network property. The stability over days and weeks of cortical ava-
lanche dynamics and corresponding integrative networks has not been explored for cortex.
Size and duration distributions of avalanches do not consider the spatiotemporal organization
of avalanches, thus multiple functional connectivities could give rise to similar power law

Functional connectivity:
The activity between nodes can be
positively or negatively correlated,
resulting in a corresponding
functional connectivity link that is
either positive or negative. Souvent
noted as link strength or link weight.

Local field potential:
A neuronal signal that typically
reflects the summed activity within a
local neighborhood. It allows for
robust tracking of local neuronal
population activity, yet the origins of
the contributing neural elements are
ambiguous.

Neuronal avalanches:
Scale-invariant spatiotemporal
activity in ongoing and evoked
activity of cortex. Sizes and durations
of avalanches follow a power law
and the mean size scales with
avalanche duration according to
a power law with slope of 2.

Small-world topology:
A network organization where the
local clustering between nodes is
high while the average number of
links to reach between nodes
remains low, typically maintained by
a low number of long-range links.

Neurosciences en réseau

506

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Long-term stability in avalanches and integrative networks

High-density microelectrode array:
An array of microelectrodes that
samples neuronal activity at discrete,
spatial sampling points in
accordance to the layout of the array.

Critical branching process:
A dynamical process that describes
the evolution of descendants from
ancêtres. In its simplest form, it is
expressed in discrete generations (que
est, discrete time steps), with no
mémoire (in other words, ancêtres
contribute only to the next
generation), and is stationary (c'est,
the average number of descendants
per generation is constant). In a critical
branching process, one ancestor on
average leads to exactly one
descendant. The resulting branched
chains of ancestors/descendants over
generations exhibit scale-invariant
properties as found for neuronal
avalanches in the brain tissue.

Entropy of mixing:
An entropy measure to quantify the
mixing over time of members that
were initially separated into different
catégories.

Integrative network organization:
A network with small-world topology
in which nodes connected by strong
links also exhibit a relatively large
common neighbor node overlap. Ce
organization of strong links is also
found in so-called friendship networks,
in which agents with a high percentage
of common friends communicate often.

Ongoing activity:
The brain is spontaneously active
even in the absence of specific sensory
inputs or motor outputs. The specific
organization of spontaneous activity
might arise from numerous internal
processes, such as posture
maintenance, as well as internal
cognitive processes, such as attention.

Neurosciences en réseau

statistics. De même, integrative networks allow for the reorganization of individual links while
maintaining global integrative properties (Pajevic & Plenz, 2012).

Here we recorded ongoing LFP activity in prefrontal and premotor cortex of NHPs over
weeks using chronically implanted high-density microelectrode arrays. We demonstrate stable
avalanche dynamics with power law statistics, the temporal avalanche profile of an inverted
parabola and corresponding scaling exponent of 2, which is the expected value for critical
branching process dynamics (di Santo et al., 2017; Miller et al., 2019; Sethna et al., 2001).
We further demonstrate that these avalanches give rise to nontrivial integrative functional net-
works despite progressive reorganization of the link strengths as identified using normalized
count (Caroline du Nord) estimators (Pajevic & Plenz, 2009) and the “entropy of mixing” analysis (voir
Material and Methods). Our results suggest that avalanche dynamics and corresponding inte-
grative network organization identify a robust cortical state in the adult brain, which should
inform dynamical models of brain function and might allow for the early identification of path-
ological brain states.

RÉSULTATS

The spatiotemporal organization of the ongoing LFP (1–100 Hz) was monitored with chroni-
cally implanted high-density microelectrode arrays (~10 × 10 électrodes; interelectrode dis-
tance 400 μm) in premotor (MP, n = 2 arrays) and prefrontal cortex (PF, n = 4 arrays) de
three macaque monkeys (Macaca mulatta; K, V, N; Figure 1A, 1B). The animals were awake
and seated in a monkey chair during the recording sessions but were not given any specific
stimulus or task.

On average about 4 ± 2 hr of LFP activity during 9 ± 7 recording sessions over the course of

5 ± 4 weeks were analyzed per monkey (85 ± 8 electrodes/array; Figure 1C).

Stability of Average Pairwise Correlation and Avalanche Dynamics in Prefrontal and Premotor Cortex
The pairwise Pearson’s correlation, R., is a standard measure to quantify the correlation in neu-
ronal activity between distant cortical sites. We found that for the continuous LFP, the distri-
bution of R, obtained from ~5,000 electrode comparisons per array, was broad yet similar
across days (Figure 1D, 1E). The average correlation, , while different between arrays,
was constant over many days and weeks (Figure 1F, 1G; linear regression fit of 0.4 ± 0.7 ×
10

−2 for all arrays; see Table 1 for individual arrays).

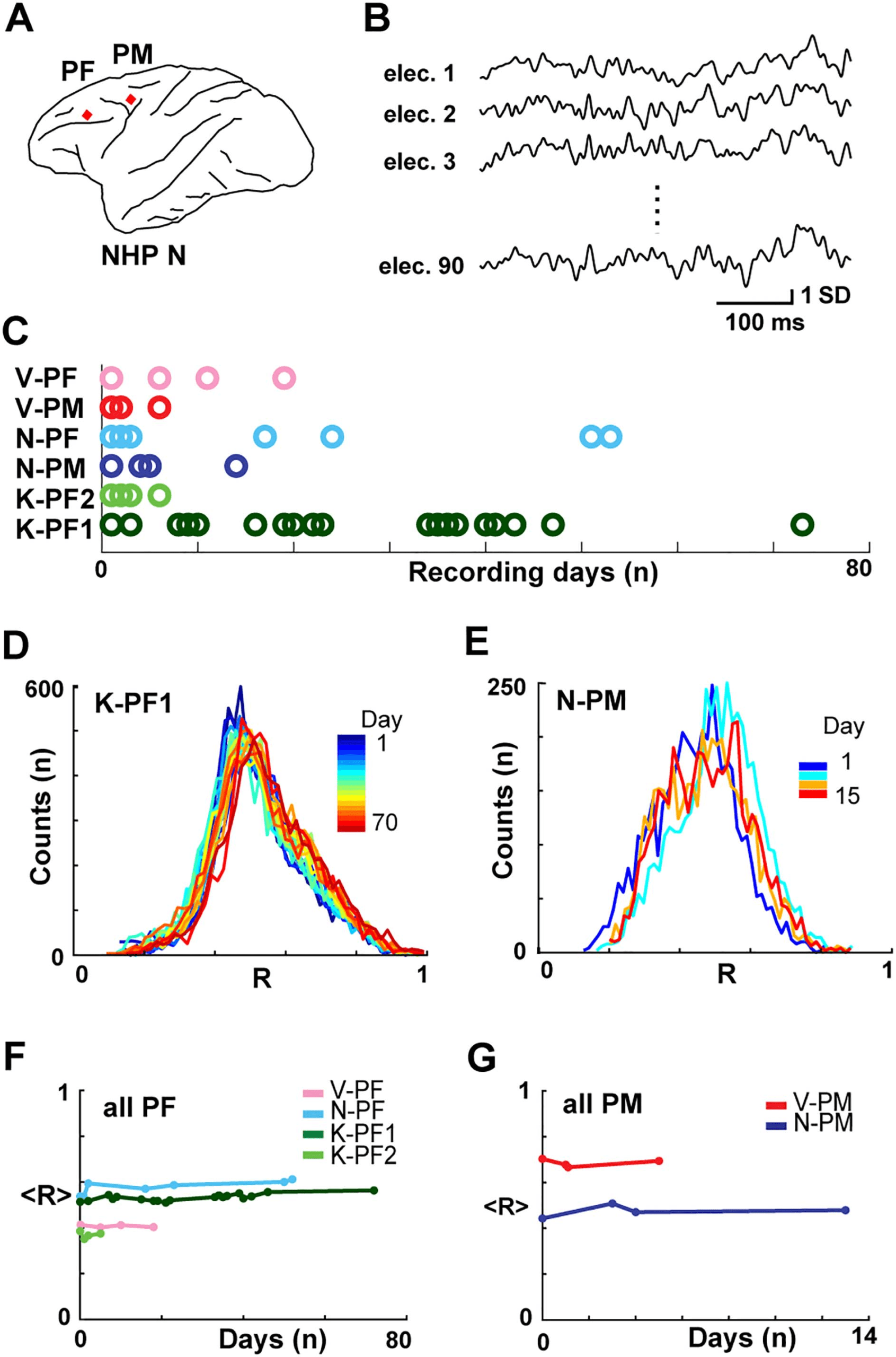
We next explored the stability of neuronal avalanche dynamics by discretizing the LFP from
ongoing activity in the NHPs (Petermann et al., 2009; Yu et al., 2017). We previously dem-
onstrated that negative deflections in the continuous LFP signal (nLFPs) track the local neuro-
nal population activity and correlate with extracellular unit firing (Bellay et al., 2021;
Petermann et al., 2009). Accordingly, discrete nLFPs were defined by crossing a threshold
of −2 SD and extracting their peak times (Figure 2A). The nLFPs were then grouped into av-
alanches at temporal resolution Δt of the mean time interval of successive nLFPs on the full
array, , which ranged between 3 et 4 ms (Figure 2B; see Material and Methods). Nous
found that the probability density distribution of avalanche size, which typically ranges from
size 1 to the number of electrodes for each array (Yu et al., 2011), exhibited power laws for
each day of recording (Figure 2C, 2D; Δt = , truncated power law vs. exponential, LLR (cid:1)
1, p < 0.005; or vs. log-normal, LLR (cid:1) 1, p < 0.005; constant across all recording days). The stability of the power law in size was associated with an average slope α = 1.32 ± 0.05 for all arrays (Table 1), which is close to the expectations for the size exponent of a critical branching 507 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 2 5 0 5 1 9 2 5 1 9 7 n e n _ a _ 0 0 1 8 8 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Long-term stability in avalanches and integrative networks l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 2 5 0 5 1 9 2 5 1 9 7 n e n _ a _ 0 0 1 8 8 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 1. Ongoing cortical dynamics are stable over weeks in superficial layers assessed by pair- wise correlations in the LFP. (A) Sketch of chronic prefrontal (PF) and premotor (PM) cortical im- plantation sites (red diamonds) for high-density microelectrode arrays. (B) Example of simultaneously recorded ongoing LFP (1–100 Hz) at single electrodes with correlated activity. (C) Overview of ~30-min recording sessions per day (color-coded circles) over several weeks for each NHP. (D, E) Pairwise correlations of the continuous LFP distribute similarly over time. Normalized histogram of pairwise correlations between all functioning channels for each recording day (color bar) in two NHPs (left: prefrontal recording in K; right: premotor recordings in N). (F, G) The average correlation, (from D, E ), was constant over weeks in PF (gauche) and PM (droite) arrays.

Neurosciences en réseau

508

Long-term stability in avalanches and integrative networks

Summary of average estimates for the mean Pearson’s pairwise correlation coefficient, , the exponent α of avalanche size

Tableau 1.
distributions for each nonhuman primate, and array at temporal resolutions of Δt = 1 ms and Δt = 30 ms, respectivement. Exponents were derived
from maximum likelihood estimates. Stability of α over all recording days was quantified by the linear regression slope within 95% confidence
limits (CfL)

Avalanche size
distribution
(Δt = 1 ms)

Exponent α
(± SD)
1.71 ± 0.00

Slope α
stability
(Δt = 1 ms)
Regression
slope
(95% CfL)
−3)
(× 10
0 (−1, 0)

Avalanche size
distribution
(Δt = )

Exponent α
(± SD)
1.26 ± 0.01

Slope α
stability
(Δt = )
Regression
slope
(95% CfL)
−3)
(× 10
−2 (−3, 3)

Avalanche size
distribution
(Δt = 30 ms)

Exponent α
(± SD)
0.65 ± 0.03

Slope α
stability
(Δt = 30 ms)
Regression
slope
(95% CfL)
−3)
(× 10
−3 (−9, 2)

Stability
Regression
slope
(95% CfL)
−3)
(× 10
−1 (−3, 2)

0 (−62, 62)

1.64 ± 0.02

6 (−40, 51)

1.29 ± 0.04

16 (−28, 60)

1.12 ± 0.05

20 (−2, 43)

1 (0, 2)

1.71 ± 0.02

1 (−13, 15)

1.73 ± 0.02

1 (0, 1)

1.65 ± 0.02

0 (−20, 20)

1.77 ± 0.03

−1 (−1, 0)

2 (−8, 12)

−1 (−1, 0)

5 (−33, 43)

1.41 ± 0.01

1.31 ± 0.02

1.29 ± 0.01

0 (−1, 0)

0 (−1, 1)

0 (−1, 0)

0.97 ± 0.02

0.75 ± 0.02

0 (−1, 1)

3 (−6, 12)

0.90 ± 0.02

0 (0, 1)

1.36 ± 0.02

1 (−27, 29)

0.74 ± 0.03

10 (−16, 35)

V-PF

V-PM

N-PF

N-PM

K-PF1

K-PF2

Mean ± SD

0 ± 1

1.70 ± 0.05

2 ± 3

1.32 ± 0.05

3 ± 7

0.86 ± 0.17

5 ± 9

processus (Figure 2E, 2F; Harris, 1963). These results demonstrate the presence of avalanche
dynamics in all NHPs for up to 2 weeks in PM and up to 10 weeks in PF.

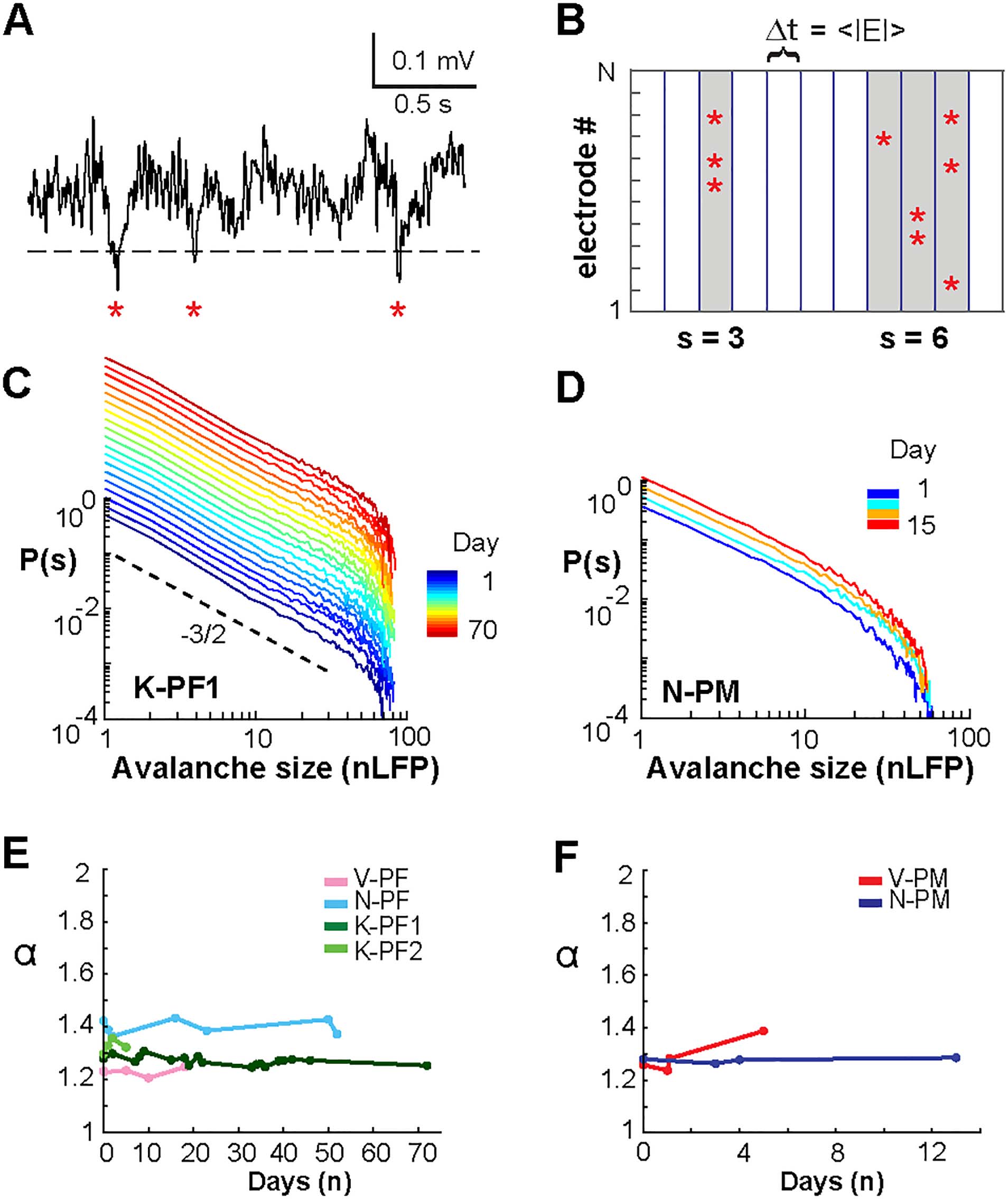
Long-Term Stability in the Temporal Profile of Avalanches and Corresponding Scaling Collapse

The temporal profile of a neuronal avalanche describes how avalanches unfold in time by ini-
tiating locally, growing in magnitude, and eventually contracting spatially before ending.
Recent work (Miller et al., 2019) confirmed the prediction that the temporal profile of neuronal
avalanches obeys the characteristic motif of an inverted parabola and that empirically observed
mean avalanche profiles collapse onto this scale-invariant motif regardless of avalanche dura-
tion. For this analysis, the temporal resolutions were set to Δt = 1 ms and Δt = 30 ms respec-
tivement, which demonstrated stable power law size distributions and expected change in slope α
(Tableau 1; 1 ms: all LLR > 104, all p (cid:3) 0.005; 30 ms: all LLR > 10, all p (cid:3) 0.005) as reported
previously (Beggs & Plenz, 2003; Petermann et al., 2009). These resolutions allow for the col-
lapse of temporal avalanche profiles in the presence of transient (cid:1)-oscillations in ongoing PF
and PM activity of NHPs (Miller et al., 2019).

We explored the stability of these scaling predictions over time, finding that the character-
istic motif for mean profiles of avalanche lifetime, L, with L = 3Δt − 5Δt did trace inverted
parabolas for fine (Δt = 1 ms, Figure 3A, 3B) and coarse (Δt = 30 ms, Figure 3C, 3D) temporal
resolutions (for statistical comparison see Table 2 for individual arrays). Surtout, the scal-
ing exponent χ producing these parabolic, collapsed motifs was close to the value of 2 expected
for a critical branching process (di Santo et al., 2017; Miller et al., 2019; Sethna et al., 2001)
and did not change over time (Figure 3B, 3D; for Δt = 1 ms, χ = 1.93 ± 0.14, linear regression
−2 ± 0.04;
−2 ± 0.2; for Δt = 30 ms, χ = 2.01 ± 0.24, linear regression slope of 2 ×10
fit of 1 × 10
see Table 3 for individual arrays). In contrast, time-shuffled data reliably produced flattened
motifs (Figure 3E, 3F) with a scaling exponent close to 1, as found for noncritical dynamics, dans
which sizes grow linearly with duration (Villegas et al., 2019).

Neurosciences en réseau

509

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Long-term stability in avalanches and integrative networks

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

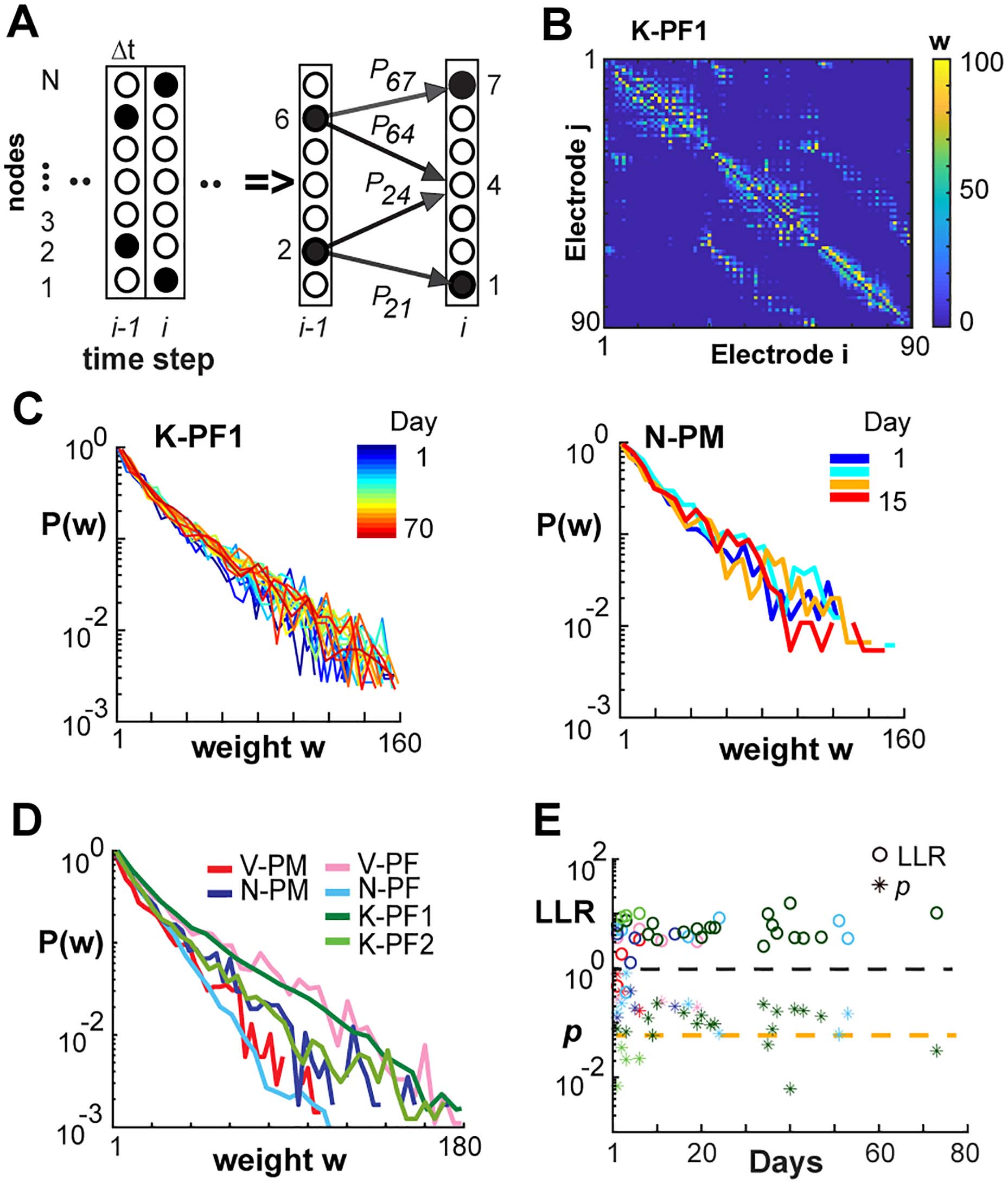
Chiffre 2. Neuronal avalanche dynamics is stable over weeks in frontal cortex of NHPs. (UN) Sample
ongoing LFP at single electrode. A negative threshold (dashed line) is applied to identify significant
negative deflections from the mean (nLFPs, red asterisks). (B) Schematic nLFP raster at Δt = hIEIi
showing neuronal avalanches identified as concurrent or consecutive nLFPs on the array separated
by at least one empty time bin. Two avalanches (gray) of size 3 et 6 are identified. (C, D) Power
law in size S for nLFP avalanches for all recordings (color bar) in two NHP (Δt = hIEIi). Broken line:
power law with slope −3/2 as visual guide. Distributions for following days have been shifted vertically
for ease of visualization. Size distributions remain power laws for all days (LLR values > 0 significant;
vs. exponential distribution; see also Table 1). (E, F) Stability of slope α as a function of time (color
coded).

Persistence of Integrative Global Network Properties

In order to quantify in more detail the spatiotemporal correlations underlying persistent ava-
lanche activity, we reconstructed functional networks from neuronal avalanches using the NC

Neurosciences en réseau

510

Long-term stability in avalanches and integrative networks

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

Chiffre 3. Collapse in the temporal profiles of neuronal avalanches and corresponding scaling exponent χ = 2 are stable over weeks in frontal
cortex. (UN) Collapse in the temporal profile of avalanches at Δt = 1 ms. Best collapse per recording day (color bar) for K-PF1 (gauche) and N-PM
(middle). Rightmost column summarizes the normalized collapse motif (norm.) averaged across days for each NHP and cortical area. Shaded
region indicates mean ± standard error per array within line thickness. (B) The scaling exponent χ at which the best temporal profile collapse is
obtained remains close to the theoretical value of 2 predicted for a critical branching process for all recording sessions. (C, D) Same as in A and
B but at Δt = 30 ms, demonstrating the characteristic parabolic profile for coarse-grained temporal scale. (E) Same as in A–D, but nLFP events
have been shuffled in time to remove spatial and temporal correlations. Note that the characteristic profile no longer traces a parabola as
expected for critical dynamics. (F) The scaling exponent χ is close to 1 when correlations are destroyed.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

reconstruction (Pajevic & Plenz, 2009). This method uses a shortcut to Bayesian estimation of
network connections, making it approximate, but also computationally efficient, and hence
applicable to reconstructing relatively large networks from lengthy event train recordings
(Figure 4A). It also reduces the influence of indirect common input correlations and has been
found in simulations to accurately and efficiently reconstruct the directed networks and
weights from simulated point-process dynamics (Pajevic & Plenz, 2009). An example of the
directed connectivity matrix for a single recording session derived from spontaneous ava-
lanche activity is shown in Figure 4B. We found that for all arrays and recording sessions,
the weights of the directed functional connections were not particularly heavy-tailed and dis-
tributed between an exponential and log-normal function over more than 3 orders of magni-
tude (Figure 4C–4E).

Neurosciences en réseau

511

Long-term stability in avalanches and integrative networks

Tableau 2.
semicircle fit (Δ
phase-randomized profile (random) at Δt = 1 ms

Summary of scaling function estimate for the temporal profile of neuronal avalanches. A parabolic fit (Δ

parab) is compared with a

semi) at temporal resolutions Δt = 1 ms and Δt = 30 ms for each nonhuman primate and array and its corresponding

Temporal profile fit:
Parabola vs. semicircle
RMSE (Δt = 1 ms)

Temporal profile fit:
Parabola vs. semicircle
RMSE (Δt = 30 ms)

Random profile fit:
Parabola vs. semicircle
RMSE (Δt = 1 ms)

Paired t test
( p value)
4.36E-05

3.87E-04

6.12E-11

6.81E-08

2.76E-22

2.60E-06

ANOVA
(F )
110.44

121.17

460.49

991.66

472.20

290.68

Paired t test
( p value)
2.00E-04

3.40E-05

2.66E-13

3.15E-06

2.41E-25

9.64E-06

ANOVA
(F )
62.26

417.07

1156.15

272.38

715.09

186.09

Paired t test
( p value)
5.96E-10

7.82E-07

3.74E-14

2.41E-10

1.98E-50

1.91E-09

ANOVA
(F )
4,832.54

2,776.65

1,607.96

6,533.12

18,530.05

3,277.87

V-PF

V-PM

N-PF

N-PM

K-PF1

K-PF2

Fit Error Δ

Δ

parab < Δ semi Δ parab < Δ semi Δ parab < Δ semi Δ parab < Δ semi Δ parab > Δ

semi

Δ

parab > Δ

semi

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

Having reconstructed the directed, weighted links in our avalanche-derived functional net-
travaux, we proceeded to calculate several graph-theoretical properties. Integrative networks
are characterized by a positive correlation, RCL, between the link cluster coefficient, CL, et
the corresponding link weight, w, between two nodes (Figure 5A; Pajevic & Plenz, 2012). Ce
positive correlation demonstrates that strongly connected nodes have more common neigh-
bors compared with weakly connected nodes (Figure 5B). We employed degree-sequence
preserved randomization to subtract potential contributions to link clustering from the node
degree distribution and report here the resulting excess link clustering, ΔCL (see Material and

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

Summary of estimates for the scaling exponent χ to optimally collapse temporal avalanche profiles at temporal resolutions Δt = 1 ms
Tableau 3.
and Δt = 30 ms for each nonhuman primate and array. The stability of χ across all recording days was quantified by the linear regression slope
reported and 95% confidence limits. Random: Phase-randomized control of temporal avalanche profile

Scaling
exponent χ
(Δt = 1 ms)
Mean χ
(± SD)
1.78 ± 0.05

χ Stability
(Δt = 1 ms)
Regression slope
(95% CfL)
0.002 (−0.019, 0.022)

Scaling
exponent χ
(Δt = 30 ms)
Mean χ
(± SD)
1.61 ± 0.09

χ Stability
(Δt = 30 ms)
Regression slope
(95% CfL)
−0.01 (−0,02, 0.01)

Scaling
exponent χ
Random
(Δt = 1 ms)
Mean χ
(± SD)
1.15 ± 0.01

χ Stability
Random
(Δt = 1 ms)
Regression slope
(95% CfL)
0.001 (−0.001, 0.003)

1.93 ± 0.15

0.051 (−0.3, 0.4)

2.25 ± 0.20

0.06 (−0.6, 0.7)

1.15 ± 0.00

0.000 (−0.001, 0.002)

2.10 ± 0.06

0.002 (−0.000, 0.004)

2.15 ± 0.15

−0.00 (−0.01, 0.00)

1.14 ± 0.03

0.000 (−0.001, 0.002)

2.05 ± 0.13

0.011 (−0.053, 0.075)

1.85 ± 0.05

0.005 (−0.016, 0.027)

1.14 ± 0.01

0.002 (−0.005, 0.008)

1.92 ± 0.03

0.000 (−0.001, 0.001)

2.11 ± 0.10

−0.000 (−0.003, 0.003)

1.15 ± 0.01

0.000 (−0.000, 0.000)

1.76 ± 0.02

0.007 (−0.004, 0.018)

2.12 ± 0.20

0.086 (−0.029, 0.200)

1.15 ± 0.00

0.000 (−0.004, 0.005)

V-PF

V-PM

N-PF

N-PM

K-PF1

K-PF2

Mean ± SD 1.93 ± 0.14

0.012 ± 0.19

2.01 ± 0.24

0.02 ± 0.04

1.15 ± 0.01

0.001 ± 0.001

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neurosciences en réseau

512

Long-term stability in avalanches and integrative networks

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 4. NC reconstruction of directed functional connectivity from ongoing LFPs reveals stable
exponential distributions in link weights across time for all NHPs. (UN) Sketch of the NC algorithm.
Active nodes (filled circles) at time Δti−1 are evaluated regarding all existing prior probabilities (solid
arrows) to obtain the pattern of active and inactive nodes at the next time step Δti (for details, voir
Pajevic & Plenz, 2009). (B) NC-reconstructed network based on 15 min of nLFP activity at Δt = 1 ms
from K-PF1 produces an adjacency matrix of weights wij showing sparse and mostly local functional
connectivité. (C) Normalized distributions in directed link strength for all recording days (gauche,
K-PF1; droite, N-PM). Color bar: recording day. (D) Normalized probability distribution trends were
consistent across areas and NHPs. Average distribution over all recording days. Color coded: NHP
area. (E) LLR (open circles) and p values (asterisks) for exponential vs. log-normal comparison of
daily weight distributions (par exemple., C ) for all arrays and days (color coded as in D).

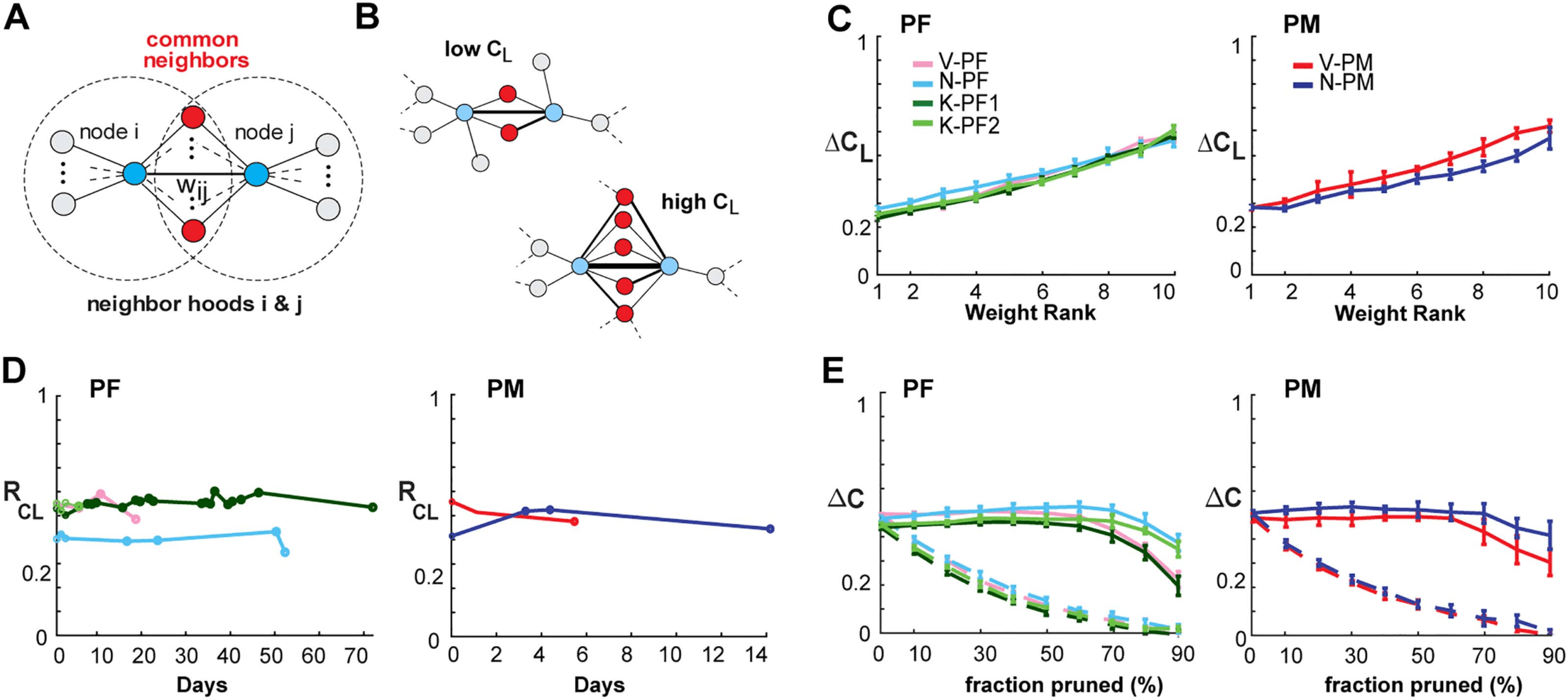
Methods). The monotonic increase in ΔCL with lowest-to-highest weight rank (Figure 5C)
clearly identifies integrative functional network organization in both PM and PF that was
stable over time (Figure 5D; linear regression slope of 0.005 +/− 0.01; 95% confidence limit;
see Table 4 for individual arrays).

Neurosciences en réseau

513

Long-term stability in avalanches and integrative networks

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

Chiffre 5. Link clustering analysis reveals that integrative global network properties are stable over time. (UN) Schematic clustering diagram
depicting two nodes (blue) connected by a link with weight wij. In an integrative network, the proportion of common neighbors (red) is ex-
pected to positively correlate with wij. (B) Sketch of two subnetworks with low and high link clustering CL respectively. (C) The excess link
clustering ΔCL (see Material and Methods) increases with link strength in all prefrontal (gauche) and premotor (droite) cortical arrays. Color coded:
NHP area. (D) Analysis of cortical networks showed strongly positive RCL over all recording sessions for up to 73 jours. (E) Link-pruning analysis
of excess node clustering ΔC calculated via degree-sequence preserved randomization (Pajevic & Plenz, 2012) showed that integrative clus-
tering motif was robust to weak-link pruning (solid lines; error bars denote mean ± SD over all recordings for an array), while the clustering
“backbone” of the network quickly degraded when strong links were pruned first (dotted lines: color coded as in D). C − E, Δt = 1 ms.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Functional network stability based on NC reconstruction algorithm at Δt = 1. Shown is
Tableau 4.
the stability of RCL over time (see also Figure 5D). HM p values given for top 50% and bottom 50%
for significant trend in mixing observed.

RCL
stability
(Δt = 1 ms)
Regression slope
−3)
(95% CfL) (× 10
−1 (−28, 18)

0 (−62, 62)

1 (0, 0.002)

14 (−13, 15)

1 (0, 1)

0 (−20, 21)

5 ± 10

V-PF

V-PM

N-PF

N-PM

K-PF1

K-PF2

Mean ± SD

Top 50%
p
0.46

0.007

−5

<10 0.08 0.003 0.27 HM trend (Δt = 1 ms) Bottom 50% p 0.34 0.05 0.03 0.54 0.2 0.35 514 Network Neuroscience Long-term stability in avalanches and integrative networks Pruning analysis: The systematic change network properties when links or nodes are removed systematically. This is contrasted by a perturbation analysis where network components randomly to study something such as failures. Pruning analysis is an efficient approach study the weight organization of networks (Onnela et al., 2007; Pajevic & Plenz, 2009). We found that pruning from bottom, that is, weakest progressively, had negligible effect on clustering prop- erties. was evidenced near constant value excess node clustering, ΔC, until the vast majority (80–90%, Figure 5E; solid lines) were removed. In contrast, from the top, is, removing strongest first, rapidly decreased result consistently found for all NHPs (Figure 5E). conclude property arises “back- bone” strong robust weak-link pruning, yet quickly degrades strong links are removed. Entropy Mixing Identifies Link Progression Over Many Weeks Given observed over weeks global dynamics, , un, χ, et
integrative network organization, c'est, RCL, we next sought to analyze in more detail the
stability at the local level of individual link weights. Spécifiquement, we examined whether the
stability identified at the global level simply arises from stability at the local level. To quantify
changes at the local level, we categorize the links, such as weak, moyen, and strong, et
analyze whether links switch between categories over time, for example from weak to medium

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

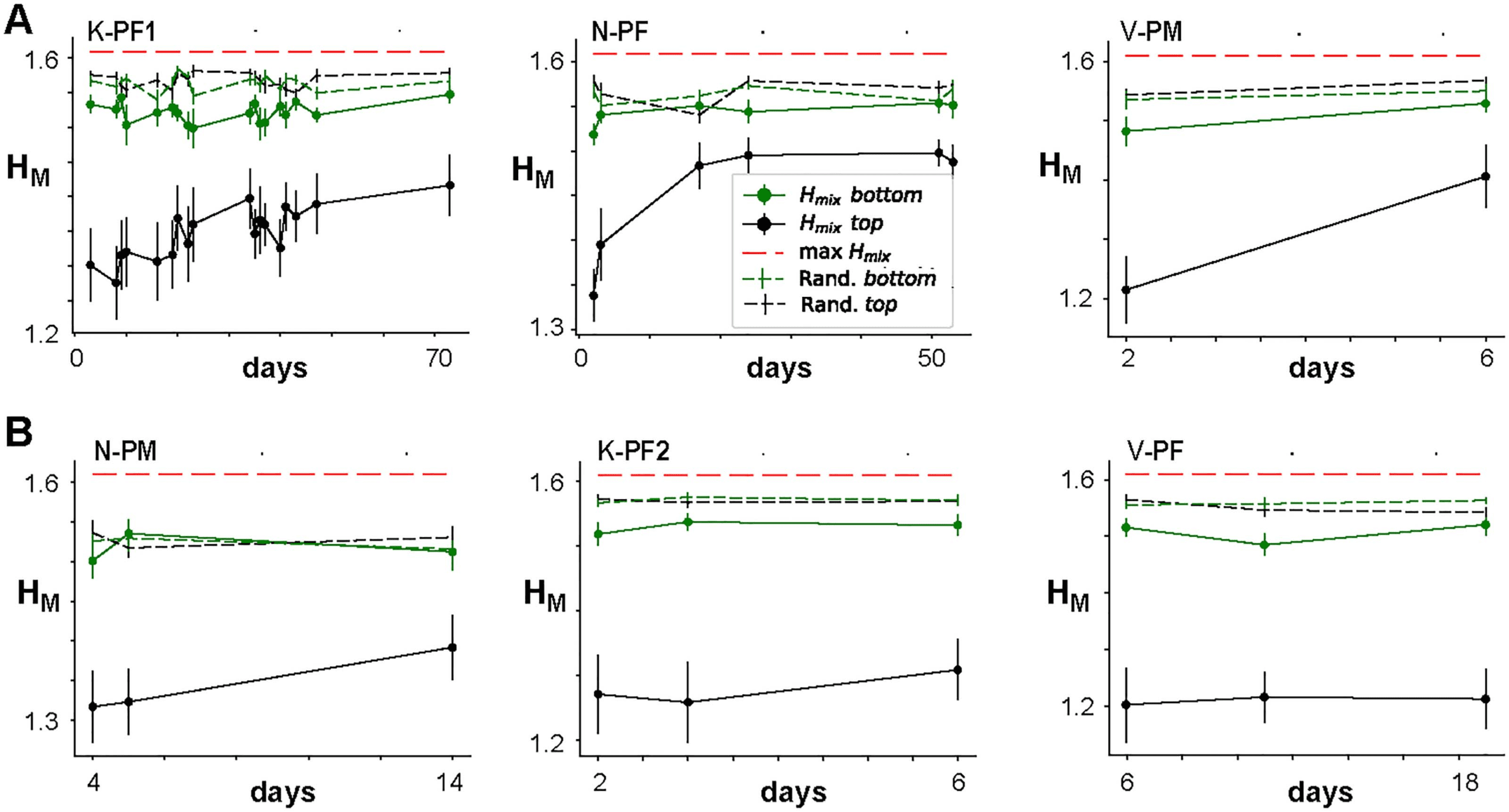
Chiffre 6. Entropy of mixing analysis demonstrates progressive changes in strong links over time for some networks. Entropy of mixing (HM)
analysis of the link weights obtained with NC reconstructions from Δt = 1 ms raster recordings. HM is plotted for the “top” half (strongest 50%
of links; black curves) and “bottom” half (weakest 50% of links; green curves) versus the days after the initial recording. The black and green
dashed lines indicate corresponding HM obtained when the labels were fully randomized, while the red dashed line indicates the theoretical
maximum of HM. The six panels represent six different arrays from the three monkeys shown in two rows. (UN) Arrays for which statistically
significant progression of mixing was obtained for “top” links. (B) Arrays for which no statistically significant progression was observed. Le
“top” half of the links consistently showed lower HM than the “bottom” half of the links, which is mainly due to the smaller reconstruction
error. The Day 1 points are not plotted because, by default of our labeling, the initial value for HM is 0.

Neurosciences en réseau

515

Long-term stability in avalanches and integrative networks

or vice versa. As a measure of mixing, we calculate the entropy of mixing, HM (see Material
and Methods). Two main factors contribute to potential changes in HM, which originate from
changes in link categories in a network from one day to another. D'abord, independent random
changes on each day will result in increased mixing and HM, but not progressively over time.
Par exemple, errors in network reconstruction alone will result in a constant HM over many
days if the underlying network is not changing. Deuxième, link weights could gradually evolve
over days and weeks, and potentially change their categories, which is now progressively
mixed and therefore is expected to lead to a monotonic increase in HM until the maximum
in mixing is reached. Because reconstruction errors are higher for weak links compared with
strong links, we quantified potential changes in link weight from NC-reconstructed networks
separately for the strongest (top 50%) and weakest (bottom 50%) links. This separation is also
motivated by our results for top- versus bottom-pruning, which demonstrated that networks are
less robust to link changes in the top half of the link weight distribution. For each half, nous
partitioned link weights further into strength quintiles, yielding five categories, and then studied
whether members from different categories will mix over time. In Figure 6, we show the data for
the top half and bottom half and compare those curves to HM obtained if the category labels
were fully randomized at each step and also present the theoretical maximum for HM (see also
Material and Methods). Because all successive distributions used the link labels derived from
Day 1 (making HM = 0), the average entropy of mixing was plotted beginning from the second
recording for each NHP.

For all arrays, we found that HM for the bottom half of links reaches close to the maximal
entropy by the following day, demonstrating that weak links fluctuate randomly. On the other
main, we found progressive and statistically significant increases of HM over subsequent days
for strong links in three out of six arrays (Figure 6A, 6B; see also Table 4). These findings dem-
onstrate stability in avalanche dynamics and integrative network organization even though the
network undergoes significant weight reorganization at the individual link level.

DISCUSSION

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Fluctuations in ongoing neuronal activity give rise to functional networks that allow for the cat-
egorization of healthy and pathological brain states (Bullmore & Sporns, 2009; Fox & Raichle,
2007; Raichle, 2015), yet the dynamical and graph-theoretical markers underlying these ongo-
ing fluctuations have been challenging to identify. By recording the LFP in prefrontal and pre-
motor cortex of NHPs over weeks at high spatiotemporal resolution, we established two robust
markers of ongoing activity: the dynamical category of neuronal avalanches and the graph-
theoretical category of integrative networks. Avalanche dynamics revealed power law statistics,
parabolic temporal profiles and a scaling exponent of 2 in support of critical branching process
dynamics (di Santo et al., 2017; Miller et al., 2019; Sethna et al., 2001). We further demonstrate
that avalanches form integrative networks despite reorganization of individual link weights as
identified using NC estimators and an entropy of mixing approach (Onnela et al., 2007;
Pajevic & Plenz, 2009, 2012). Our results suggest that avalanche dynamics and corresponding
integrative networks identify a robust state of the awake frontal cortex. This work should be im-
pactful for computational studies of cortex function and for translational research into the iden-
tification of brain dynamics in healthy subjects and corresponding deviation in brain disorders.

Recent analysis of evoked cortical activity in nonhuman primates during behavior demon-
strated the preservation of neuronal avalanche dynamics in the face of transient activity changes,
specifically the nLFP rate (Yu et al., 2017). Given the robustness of integrative network properties
observed in combination with avalanche dynamics in vitro (Pajevic & Plenz, 2009, 2012) aussi

Neurosciences en réseau

516

Long-term stability in avalanches and integrative networks

as in vivo (the present study), we would expect integrative network properties to also persist
during behavioral tasks.

Stability of LFP-Based Avalanches and Relation to Neuronal Activity

Technical advances in identifying long-term robustness in neuronal activity using cellular res-
olution approaches (Dickey et al., 2009; Fraser & Schwartz, 2011; Jackson & Fetz, 2007; Li
et coll., 2017; Nicolelis et al., 2003; Tolias et al., 2007) typically suffer from spatial and temporal
subsampling (Levina & Priesemann, 2017; Petermann et al., 2009; Ribeiro et al., 2010; Ribeiro
et coll., 2014) limiting proper identification of avalanche dynamics and corresponding recon-
struction of functional connectivity. The LFP, on the other hand, is a robust neuronal population
signal, less prone to spatial subsampling and at high temporal resolution contains local spike
information particularly when recorded from superficial layers (Donoghue et al., 1998;
Mehring et al., 2003; Petermann et al., 2009; Rasch et al., 2008). En effet, we recently demon-
strated in nonhuman primates and in vitro slices that single neurons selectively participate in
expansive, repeated LFP avalanches (Bellay et al., 2021), which suggest that the stability ob-
served in the present study for LFP-based avalanches might extend to the single neuron level.

Experimental manipulations support a homeostatic regulation of avalanche dynamics in
cortex. Transient pharmacological perturbation in vitro (Plenz, 2012) or sensory deprivation
in vivo (Ma et al., 2019) initially abolishes avalanche dynamics, which is followed by a recov-
ery over several days. Developmental findings further support an autonomous regulation of
neuronal avalanches in isolated cortex in vitro in the absence of sensory input (Pasquale
et coll., 2008; Stewart & Plenz, 2007; Tetzlaff et al., 2010). Identifying the homeostatic regula-
tion of avalanche dynamics and integrative networks will require precise perturbation ap-
proaches (Chialvo et al., 2020) in combination with advanced cellular techniques suitable
for long-term monitoring such as ratiometric genetically encoded calcium indicators, lequel
naturally compensate for cell-intrinsic expression variability (Lutcke et al., 2013).

NC Reconstruction of Integrative Networks

Reconstruction of our directed, weighted functional networks utilized a Bayesian-derived NC
approche, which is easily scalable to large networks (Pajevic & Plenz, 2009, 2012) and re-
duces correlations from common input. Network simulations demonstrated ground-truth re-
construction for various small-world topologies from subcritical, supercritical, and critical
dynamics, the latter in line with reconstructions from observed avalanche activity (Pajevic
& Plenz, 2009).

Here we used significant events in LFP fluctuations, c'est, nLFPs, for the reconstruction of
functional connectivity, which differs from the more common ansatz based on continuous
time series. Accordingly, our approach, which selectively reconstructs synchronization dy-
namics in the form of avalanches, introduces a timescale Δt to which the NC reconstruction
is sensitive. In order to identify the spatiotemporal spread of avalanches, the use of a micro-
electrode array introduces a spatial discretization, which consequently enforces a discretiza-
tion Δt in time. It was found empirically that Δt should be linked to the average propagation
velocity of neuronal activity in the network, allowing Δt to be approximated by (Beggs &
Plenz, 2003; Petermann et al., 2009). For Δt smaller than , errors of prematurely termi-
nating avalanches increase, whereas errors of concatenating successive avalanches increase
for Δt larger than . An approximate balance regarding these two errors is struck for Δt =
IEI. With respect to NC reconstruction, increasing Δt will increase the count in nLFP occur-
rences on the array per time step, resulting in an increase in the computational load and

Neurosciences en réseau

517

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Long-term stability in avalanches and integrative networks

increased error in estimating priors for potentially activated links. Accordingly, we chose a Δt
slightly smaller than IEI for a conservative and balanced estimate of the functional connectivity
based on avalanche propagation.

Integrative networks differ from networks in which the weight is positively correlated with
the node degree (Barrat et al., 2004; Bianconi, 2005; Pajevic & Plenz, 2012). Our shuffling
correction further demonstrates that the organization of weighted links in integrative networks
cannot be simply explained by the link-degree distribution and in which strong links are part of
a continuous, in our case near exponential, distribution (cf. Figure 4D). Integrated networks are
also not a simple consequence of critical branching processes generating avalanches, lequel
can be realized in many topologies and architectures (Pajevic & Plenz, 2009, 2012).

Robust Avalanche Scaling of χ = 2 Over Many Weeks

Heterogeneous activity in the form of neuronal avalanches has been the hallmark of ongoing
(Beggs & Plenz, 2003; Bellay et al., 2015) and evoked (Yu et al., 2017) brain activity in super-
ficial layers of the cerebral cortex. The scale-invariant hallmark of avalanches has been found
to capture ongoing neuronal activity in nonhuman primates at the mesoscopic level in the LFP
(Klaus et al., 2011; Petermann et al., 2009; Yu et al. 2014; Yu et al. 2017; Yu et al., 2011) et
macroscopic activity measured with EEG (Meisel et al., 2013), MEG (Shriki et al., 2013), et
IRMf (Fraiman & Chialvo, 2012; Tagliazucchi et al., 2012). The observed power law distribu-
tions in cluster size and duration support the idea that the cortex operates close to a critical
state at which networks gain numerous advantages in information processing (Beggs & Plenz,
2003; Gautam et al., 2015; Kinouchi & Copelli, 2006; Shew et al., 2009, Shew et al., 2011;
Yang et al., 2012).

Our present demonstration of an inverted-parabolic avalanche shape, collapse exponent of
2, and size distribution slope >−2 is in line with predictions that the unfolding of avalanches in
the adult brain is governed by a critical branching process (for details, see Miller et al., 2019).
This profile demonstrates that the initial spatial unfolding of an avalanche in time is truly ex-
pansive and should not be viewed as being dominated by a few strong links. Recently, ava-
lanches with a scaling factor of 2 have been described for whole-brain neuronal activity in the
zebra fish larvae (Ponce-Alvarez et al., 2018); cependant, the corresponding size and duration
exponent were significantly steeper compared with reports for the mammalian cortex, suggérer-
ing a different dynamical model for the zebra fish.

Connectome analyses on a timescale of seconds have identified transient fluctuations in
functional connectivity reflecting distinct states (Hutchison et al., 2013; Liu & Duyn, 2013;
Zalesky et al., 2014), which based on computational modeling were found to be intermittent,
a signature of metastability (Deco et al., 2017; Hansen et al., 2015). Because our analysis was
based on nLFPs and not on continuous time signals, we were unable to obtain NC-
reconstructed networks for shorter time periods than 15–30 min. En fait, our entropy of mixing
analysis allowed for an assessment of link weight progression in the face of reconstruction
errors due to limited data availability. Transient fluctuations in functional connectivity esti-
mates are not in contrast to the reorganization of links reported in our study. Short-term fluc-
tuations in the face of long-term stability are hallmarks of critical dynamics (Fraiman &
Chialvo, 2012; Tagliazucchi et al., 2012).

Potential Advantages of Avalanche Dynamics and Integrative Networks for Cortex Function

Anatomically, the mammalian cortex is a sheet of local, functional modules that dynamically
combine to support complex brain functions (Braitenberg & Schüz, 1991; Honey et al., 2007).

Neurosciences en réseau

518

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Long-term stability in avalanches and integrative networks

Local connectivity ensures diverse local operations, whereas long-range connections support
global coordination (par exemple., Bullmore & Sporns, 2009; Kirst et al., 2016). These structural hall-
marks are dynamically realized in neuronal avalanches, which support a scale-free and selec-
tive organization of neuronal synchronization over all distances. They are graph-theoretically
embedded in integrative networks, which maintain a high level of node clustering until about
90% of the weakest links are pruned, c'est, à propos 10% of strong links are used for long-range
relations. Intriguingly, simulations identified a particular local learning rule that operates
on activity cascades such as avalanches to build integrative networks from random networks
(Pajevic & Plenz, 2012). The rule increases link weights at locations of recent cascade failure,
thereby facilitating the unfolding of future avalanches (Alstott et al., 2015). This mechanism
opens bottlenecks in the network and further supports activity propagation over long dis-
tances. We therefore hypothesize that avalanche dynamics in combination with integrative
network organization are beneficial for local operational diversity while supporting long-
range, selective propagation of information.

MATERIAL AND METHODS

Animal Procedures

All animal procedures were conducted in accordance with National Institutes of Health guide-
lines and were approved by the Animal Care and Use Committee of the National Institute of
Mental Health. Three adult NHPs (Macaca mulatta; 1 male, 2 females; 7–8 years old) received
two chronic implantations of high-density 96-microelectrode arrays each (Blackrock
Microsystems; 4 × 4 mm2; 400 μm interelectrode distance; 10 × 10 grid with corner grounds).
To direct recordings towards superficial cortical layers II/III, electrode shanks of 0.6-mm length
were used in prefrontal cortex (PF; n = 4), and shanks of 1-mm length were used for premotor
cortex (MP; n = 2). During recording sessions, monkeys sat head-fixed and alert in a monkey
chair with no behavioral task given. Portions of this dataset have been analyzed previously
(Bellay et al., 2021; Meisel et al., 2013; Miller et al., 2019; Yang et al., 2012; Yu et al., 2014).

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

.

t

Local Field Potential Recordings in Awake Monkeys
Simultaneous and continuous extracellular recordings were obtained for 12–60 min per re-
cording session (2 kHz sampling frequency), band-pass filtered between 1 et 100 Hz
(sixth-order Butterworth filter) to obtain the local field potential (LFP), and notch-filtered
(60 Hz) to remove line noise. About 2 ± 1% of time periods were removed from functional
electrodes because of artifacts introduced by vocalization, chewing, sudden movements, et
the like. These artifacts were identified by threshold crossing (SD > 7) and excised (± 0.25 s).
Arrays on average contained 86 ± 8 functional electrodes that exhibited 64 ± 50 μV of spon-
taneous LFP fluctuations (SD). Channels that had been removed from an array at any recording
day were discounted for all recording days. Electrode LFPs were z-transformed and recording
sessions for each array were analyzed individually. The current study represents a combined
26 hr of ongoing cortical LFP activity.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neuronal Avalanche Definition and Temporal Resolution

For each electrode in the array, peak amplitude and time of negative LFP (nLFP) threshold
crossings (−2 SD) were extracted at the temporal resolution of Δt = 0.5 ms given our sampling
taux de 2 kHz. We note that the negative peak amplitude of the LFP correlates with the prob-
ability of extracellular unit firing and synchrony in nonhuman primates (Bellay et al., 2021;
Petermann et al., 2009). The mean inter-event interval, , defined as the average time

Neurosciences en réseau

519

Long-term stability in avalanches and integrative networks

between consecutive nLFPs among all functional electrodes on the array, was calculated. Nous
then binned nLFP times in steps of Δt = for each electrode, which ranged between 3 et
4 ms across NHPs and arrays. All nLFP events from all electrodes were combined into a matrix,
c'est, raster, with rows representing electrodes and columns representing time steps. A pop-
ulation time vector was obtained by summing nLFPs in the raster for each time step.
Avalanches were defined as spatiotemporal continuous activity in the population vector
bracketed on each side by at least one time bin of duration Δt with no nLFP. The size of an
avalanche, S, was defined as the number of nLFPs participating. Multiple nLFPs at an electrode
during an avalanche are rare (Yu et al., 2014) and were counted in size estimates. Scale-
invariance of S was visualized by plotting probability distributions P(S) in double-log coordi-
nates. We previously showed that analyzing nLFP at Δt = results in a distribution of
avalanches with a slope close to −3/2 in line with expectations for a critical branching process
(par exemple., Beggs & Plenz, 2003).

The maximum log-likelihood ratio (LLR) was calculated to test potential power law distri-
butions in avalanche size S against the alternatives of exponential or log-normal distribution
models (Clauset et al., 2009; Klaus et al., 2011). When tested positive for power law, the LLR
estimate for best slope α was reported. Here we used the range of S = 1 à 40, which excludes
the distribution cutoff (Klaus et al., 2011) close to the total number of functional electrodes on
the array (n > 70). We note that analyzing avalanche dynamics at different temporal resolu-
tion, such as at shorter Δt or longer Δt compared with the , increases or decreases the
slope α respectively, but not the power law form itself (see also Table 1; Beggs & Plenz, 2003;
Petermann et al., 2009).

Avalanche Temporal Profile Collapse and Scaling Exponent

Given the difficulty of obtaining robust lifetime distributions in the presence of ongoing oscil-
lations, the stability analysis for avalanches in the present work focused mainly on the calcu-
lation of size distributions and temporal profile collapse (for details, see Miller et al., 2019).
The temporal profile, S(t), was described by the number of participating electrodes at each
time step t = 1 up to the avalanche lifetime, L, which was defined by the number of time steps
Δt that the avalanche persisted. In line with our previous results, profile analysis was carried
out at Δt = 1 ms and Δt = 30 ms to avoid profile modulation by ongoing (cid:1)-oscillations (Miller
et coll., 2019). Avalanches were grouped by L in multiples of Δt and averaged to obtain the
mean temporal profile for a given lifetime, hSi(t, L). After normalizing to dimensionless time
units, c'est, the relative lifetime, t/L, amplitudes were then rescaled via Equation 1.

(cid:1) (cid:3)
t
L

(cid:1) (cid:3)
e L(cid:3) − 1FFFF t
L

Sh i

:

(1)

The profile collapse function, shown in Equation 1, relates the mean profile for each lifetime L,
χ−1, which is indepen-
hSi(t/L), with a characteristic temporal motif FFFF (t/L), and scaling factor, L
dent of L according to Equation 1. To perform a shape collapse, we plotted hSi(t, L) from L − 1
through L + 1 for Lmin = 4Δt (to reduce finite size effects in shape caused by too few data
points). The collapse error, Δ
F, was quantified via a normalized mean squared error of
height-normalized individual profiles to the combined normalized average of all collapsed
profiles, FFFF (t/L). Minimized collapse error was calculated by scanning through χ = 0.5 à 3
at resolution of 0.001 to find the collapse in avalanche waveform associated with the smallest
Δ
F via χ

F > 1 was considered a failure in collapse.

collapse. A value of Δ

We note that for fractal objects such as spatiotemporal avalanches, changing the temporal
resolution also partitions avalanches differently. For a Δt = 1 ms, avalanche durations in

Neurosciences en réseau

520

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Long-term stability in avalanches and integrative networks

multiples of Δt will exhibit a power law as well as for Δt = 30 ms (voir, par exemple., Miller et al., 2019).
Accordingly, the temporal profile of avalanches must be examined in multiples of generations
of duration Δt. A comparison between timescales in absolute times may not be possible. In the
present study, an avalanche of duration 150 ms encompasses L = 5 generations at Δt = 30 mais
would require L = 150 generations at Δt = 1, which is highly unlikely to occur.

Fit of the Average Temporal Profile of Avalanches

For the parabolic fit we used the approach by Laurson et al. (2013) as follows:

y ¼ A : t
T

(cid:1)

1 − t
T

(cid:3)γ−0:5

:

(2)

The parabolic fit error, Δ
parab, was quantified via a normalized mean squared error of individual
profiles to an amplitude-matched parabola that was coarse-grained to match L. Comparison to
a semicircle fit was conducted in the same manner to obtain Δ

semi using

y ¼ A :

(cid:5)q
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
T= Þ2:
1 − t

(3)

Correlation-Based Network Reconstruction

Networks were reconstructed for each recording session individually and the links with low
pairwise correlations were removed before subsequent network analysis. Rather than applying
a strict minimum correlation threshold for removing the links, which would leave our analysis
vulnerable to inter-NHP differences in electrode impedances and so on, we instead sequen-
tially removed the weakest links in 0.01 increments of the correlation threshold until a prede-
fined sparsity of approximately 40% was achieved. Weight bins were divided into deciles for
pruning analysis (Chiffre 4).

Normalized Count Reconstruction of Network

To remove the influence of common input to electrodes on the array, which inflates the
Pearson’s pairwise correlation, we conducted a network reconstruction. This nonparametric
method, called the NC approach, is used for the network reconstruction because its compu-
tational efficiency is comparable to the correlation analysis yet with much lower reconstruc-
tion error, which are important considerations for analysis of long LFP time series collected in
awake in vivo preparations. For this reconstruction, the time window within which active
nodes can influence each other was examined for 0.5, 1, , et 30 ms. For each node
activation (spike), all nodes that were active within Δt, prior to the spike, were deemed to
be potential causes. Results were very similar for Δt = 0.5 et 1 ms (data not shown). Pour
longer Δt, the precision of the algorithm decreases rapidly because of (un) the increase in am-
biguous potential associations between the number of active nodes in successive frames and
(b) a decrease in the number of transition time steps to estimate link weights (Pajevic & Plenz,
2009). Here we show results for Δt = 1 ms, which matches our avalanche scaling analysis.

Integrative Networks and Pruning Analysis

Once the networks were defined, we studied their integrative properties (Pajevic & Plenz,
2012). The link clustering coefficient, CL, was defined for each link as the ratio of the number
of common neighbors of its end nodes to the number of all neighbors (see Figure 4A). In an
integrative network, there is a positive correlation RCL between CL and the weight of the link,
indicating that strongly connected nodes are likely to share more common neighbors. À

Neurosciences en réseau

521

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Long-term stability in avalanches and integrative networks

visualize this correlation, we divide links based on their weight into equally sized 10 blocks
ranging from the weakest block (rank 1) to the highest rank. For each block, we obtain the
average CL and subtract the equivalent value that is obtained from the degree-sequence pre-
served randomized network, yielding the excess link clustering, ΔCL. We also conducted a
“pruning analysis” in which we studied the robustness of the excess node clustering ΔC upon
the progressive removal of the weakest (bottom pruning) or strongest (top pruning) links.
De la même manière, the excess node clustering, ΔC, was defined as the difference of the mean clustering
coefficient of the original network and the corresponding randomized network after the
degree-sequence preserved randomization.

Entropy of Mixing Analysis

The estimated link weights fluctuated over time both in pairwise correlation and in directed
networks obtained with the NC reconstruction algorithm. We sought to explore whether these
fluctuations predominantly represent an error in the network reconstruction or arise from a
genuine and progressive change in the underlying network weights. To answer this question,
we developed a novel method that utilizes the entropy of mixing to quantify the progression of
these fluctuations in individual link strengths from one day to another. The entropy of mixing is
a concept from thermodynamics and describes the increase in total entropy when partitioned
(pure and equilibrated) subsystems are allowed to mix. It is quantified using the Shannon en-
tropy in which probabilities are replaced by the fractions of each of the original species found
at different partitions. Ainsi, to conduct our entropy of mixing analysis, we need to partition
the links into different categories. Labels are assigned according to the magnitude of their
weights obtained from the Day 1 data, and partitioning them into a finite set of categories,
Nc, ranging from the weakest links to the strongest links. In our case, we used Nc = 5, so that
the label c = 1 marked the weakest 20% of the sorted links and incrementally, c = 5 marked
the strongest 20% of the links.

We conducted the entropy of mixing analysis on two different and complementary subnet-
travaux. The first is the “top” network, consisting of the 50% of the strongest links, and the sec-
ond is the “bottom” network, consisting of the weakest 50% percent of links. This was done
mainly to have some test of the performance of the entropy of mixing analysis, as we expect
that the “bottom” half is more dominated by the reconstruction errors of the NC algorithm than
the “top” half. Note that with this two-stage stratification of the links, the strongest 20% links in
the “top” network are effectively representing the 10% of strongest links in the full network,
while the weakest 20% of the “top” network links have still greater magnitude than the stron-
gest quintile of the “bottom” networks, et, vice versa, the weakest 20% of the links in the
“bottom” represent the 10% of weakest links in the full network. Once the chosen links were
labeled, we then monitored the changes of their weights over subsequent days. Spécifiquement,
we sort them again based on their new weights, but now partition them over a potentially
larger number of weight groups, Ng = k Nc, where k is an integer, in order to make all groups
contain a single category label for the Day 1 stratification (we use k = 3 and Ng = 15, meaning
that the links in groups 1 through 3 will all initially carry the label c = 1, the groups g = 4–6 will
be labeled c = 2, etc.). À cause de (un) reconstruction errors and (b) potential actual network
weight changes from one day to another, each of the groups will on the subsequent days con-
tain a mixture of the original labels, although it is expected that the low group indices, g, will
early on predominantly carry the labels of the weak links, and vice versa. For each group, nous
calculate a fraction, fc, of the links that carry label c, which by definition are normalized to 1,
Nc
c¼1 fc = 1. For each group g we then calculate the Shannon entropy of such mixture
c'est,

P.

Neurosciences en réseau

522

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Long-term stability in avalanches and integrative networks

P.

according to Hg = −
Nc
c¼1 fc log fc. Enfin, we report the average and the standard error over all
non-edge Hg values, c'est, excluding the extreme groups, g = 1 and g = 15, as those have
only unidirectional mixing (n = Ng − 2 = 13). Ainsi, the average entropy of mixing reported in
our results is HM = 1
Ng−2

g¼2 Hg.

PNg−1

To evaluate whether we have seen a progression in the weight evolution, we test it against
the null hypothesis that there was no significant linear trend across the subsequent days. To do
so we use a Monte Carlo (MC) procedure, in which we generate one million normally distrib-
uted replicates, N(0,p
G are the standard deviations of the means
obtained using the non-edge groups described in the previous paragraph. For each of the
NMC = 1,000,000 replicates we perform a linear regression and count the number of times
the MC slopes were greater than the slope we obtained using the mean values for HM.
From this count, Npos, our estimate of the p values is p = (Npos + 1)/(NMC + 1) (see Table 4).

G) for each point, where σ

REMERCIEMENTS

We thank members of the Plenz lab and attendees of the Critical Brain Dynamics: 5ème
International Workshop on Criticality and the Brain, 2016, NIH, Etats-Unis, for their support and
useful discussions. This research utilized the computational resources of the NIH HPC
Biowulf cluster (https://hpc.nih.gov).

CONTRIBUTIONS DES AUTEURS

Stephanie R. Miller: Enquête; Méthodologie; Logiciel; Rédaction – ébauche originale. Sinisa
Pajevic: Conceptualisation; Analyse formelle; Enquête; Méthodologie; Logiciel; En écrivant -
brouillon original. Shan Yu: Conceptualisation; Analyse formelle; Enquête; Méthodologie;
Logiciel; Rédaction – ébauche originale. Dietmar Plenz: Conceptualisation; Enquête;
Méthodologie; Surveillance; Rédaction – ébauche originale.

INFORMATIONS SUR LE FINANCEMENT

Dietmar Plenz, National Institute of Mental Health, Division of the Intramural Research
Program, Award ID: ZIAMH002797. Sinisa Pajevic, National Institute of Child Health and
Développement, Division of the Intramural Research Program.

RÉFÉRENCES

Alstott, J., Pajevic, S., Bullmore, E., & Plenz, D. (2015). Opening
bottlenecks on weighted networks by local adaptation to cascade
failures. Journal of Complex Networks, 3, 552–565. https://est ce que je
.org/10.1093/comnet/cnv002, PubMed: 28890788

Barrat, UN., Barthelemy, M., Pastor-Satorras, R., & Vespignani, UN. (2004).
The architecture of complex weighted networks. Proceedings of
the National Academy of Sciences, 101, 3747–3752. https://est ce que je
.org/10.1073/pnas.0400087101, PubMed: 15007165

Bassett, D. S., & Sporns, Ô. (2017). Network neuroscience. Nature
Neurosciences, 20, 353–364. https://doi.org/10.1038/nn.4502,
PubMed: 28230844

Beggs, J.. M., & Plenz, D. (2003). Neuronal avalanches in neocortical
circuits. Journal des neurosciences, 23, 11167–11177. https://doi.org
/10.1523/JNEUROSCI.23-35-11167.2003, PubMed: 14657176
Bellay, T., Klaus, UN., Seshadri, S., & Plenz, D. (2015). Irregular spik-
ing of pyramidal neurons organizes as scale-invariant neuronal
avalanches in the awake state. eLife, 4, Article e07224. https://
doi.org/10.7554/eLife.07224, PubMed: 26151674

Bellay, T., Shew, W. L., Yu, S., Falco-Walter, J.. J., & Plenz, D. (2021).
Selective participation of single cortical neurons in neuronal
avalanches. Frontiers in Neural Circuits, 14. https://est ce que je.org/10
.3389/fncir.2020.620052, PubMed: 33551757

Neurosciences en réseau

523

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Long-term stability in avalanches and integrative networks

Bianconi, G. (2005). Emergence of weight-topology correlations in
complex scale-free networks. Europhysics Letters, 71, 1029–1035.
https://doi.org/10.1209/epl/i2005-10167-2

Braitenberg, V., & Schüz, UN. (1991). Anatomy of the cortex:
Statistics and geometry. Springer-Verlag. https://doi.org//10
.1007/978-3-662-02728-8

Bullmore, E., & Sporns, Ô. (2009). Complex brain networks:
Graph theoretical analysis of structural and functional systems.
Nature Revues Neurosciences, 10, 186–198. https://est ce que je.org/10
.1038/nrn2575, PubMed: 19190637

Chialvo, D. R., Cannas, S. UN., Grigera, T. S., Martine, D. UN., & Plenz, D.
(2020). Controlling a complex system near its critical point via
temporal correlations. Rapports scientifiques, 10, Article 12145.
https://doi.org/10.1038/s41598-020-69154-0, PubMed: 32699316
Clauset, UN., Shalizi, C. R., & Newman, M.. E. J.. (2009). Power-law
distributions in empirical data. SIAM Review, 51, 661–703.
https://doi.org/10.1137/070710111

Deco, G., Kringelbach, M.. L., Jirsa, V. K., & Ritter, P.. (2017). Le
dynamics of resting fluctuations in the brain: Metastability and its
dynamical cortical core. Rapports scientifiques, 7, Article 3095.
https://doi.org/10.1038/s41598-017-03073-5, PubMed: 28596608
Dickey, UN. S., Suminski, UN., Amit, Y., & Hatsopoulos, N. G. (2009).
Single-unit stability using chronically implanted multielectrode
arrays. Journal de neurophysiologie, 102, 1331–1339. https://est ce que je
.org/10.1152/jn.90920.2008, PubMed: 19535480

di Santo, S., Villegas, P., Burioni, R., & Muñoz, M.. UN. (2017).
Simple unified view of branching process statistics: Random
walks in balanced logarithmic potentials. Physical Review E,
95, 032115. https://doi.org/10.1103/ PhysRevE.95.032115,
PubMed: 28415350

Donoghue, J.. P., Sanes, J.. N., Hatsopoulos, N. G., & Gaál, G. N.
(1998). Neural discharge and local field potential oscillations
in primate motor cortex during voluntary movements. Journal
of Neurophysiology, 79, 159–173. https://est ce que je.org/10.1152/jn
.1998.79.1.159, PubMed: 9425187

Fox, M.. D., & Raichle, M.. E. (2007). Spontaneous fluctuations in
brain activity observed with functional magnetic resonance im-
aging. Nature Revues Neurosciences, 8, 700–711. https://doi.org
/10.1038/nrn2201, PubMed: 17704812

Fraiman, D., & Chialvo, D. R.. (2012). What kind of noise is brain
bruit: Anomalous scaling behavior of the resting brain activity
fluctuations. Frontiers in Physiology, 3, 307. https://est ce que je.org/10
.3389/fphys.2012.00307, PubMed: 22934058

Fraser, G. W., & Schwartz, UN. B. (2011). Recording from the same
neurons chronically in motor cortex. Journal de neurophysiologie,
107, 1970–1978. https://est ce que je.org/10.1152/jn.01012.2010,
PubMed: 22190623

Gautam, H., Hoang, T. T., McClanahan, K., Grady, S. K., & Shew, W. L.
(2015). Maximizing sensory dynamic range by tuning the cortical
state to criticality. Biologie computationnelle PLoS, 11, Article
e1004576. https://doi.org/10.1371/journal.pcbi.1004576,
PubMed: 26623645

Hansen, E. C. UN., Battaglia, D., Spiegler, UN., Deco, G., & Jirsa, V. K.
(2015). Functional connectivity dynamics: Modeling the switching
behavior of the resting state. NeuroImage, 105, 525–535. https://est ce que je
.org/10.1016/j.neuroimage.2014.11.001, PubMed: 25462790
Harris, T. E. (1963). The theory of branching processes. Springer-

Verlag. https://doi.org/10.1007/978-3-642-51866-9

Honey, C. J., Kotter, R., Breakspear, M., & Sporns, Ô. (2007).
Network structure of cerebral cortex shapes functional connec-
tivity on multiple time scales. Actes de la Nationale
Académie des Sciences, 104, 10240–10245. https://est ce que je.org/10
.1073/pnas.0701519104, PubMed: 17548818

Hutchison, R.. M., Womelsdorf, T., Allen, E. UN., Bandettini, P.. UN.,
Calhoun, V. D., Corbetta, M., Della Penna, S., Duyn, J.. H., Glover,
G. H., Gonzalez-Castillo, J., Handwerker, D. UN., Keilholz, S.,
Kiviniemi, V., Leopold, D. UN., de Pasquale, F., Sporns, O., Walter,
M., & Chang, C. (2013). Dynamic functional connectivity: Promise,
issues, and interpretations. NeuroImage, 80, 360–378. https://doi.org
/10.1016/j.neuroimage.2013.05.079, PubMed: 23707587

Jackson, UN., & Fetz, E. E. (2007). Compact movable microwire array
for long-term chronic unit recording in cerebral cortex of pri-
mates. Journal de neurophysiologie, 98, 3109–3118. https://est ce que je
.org/10.1152/jn.00569.2007, PubMed: 17855584

Katzner, S., Nauhaus, JE., Benucci, UN., Bonin, V., Ringach, D. L., &
Carandini, M.. (2009). Local origin of field potentials in visual
cortex. Neurone, 61, 35–41. https://est ce que je.org/10.1016/j.neuron
.2008.11.016, PubMed: 19146811

Kinouchi, O., & Copelli, M.. (2006). Optimal dynamical range of
excitable networks at criticality. Nature Physics, 2, 348–351.
https://doi.org/10.1038/nphys289

Kirst, C., Timme, M., & Battaglia, D. (2016). Dynamic information
routing in complex networks. Communications naturelles, 7, Article
11061. https://doi.org/10.1038/ncomms11061, PubMed: 27067257
Klaus, UN., Yu, S., & Plenz, D. (2011). Statistical analyses support power
law distributions found in neuronal avalanches. PLoS ONE, 6,
Article e19779. https://doi.org/10.1371/journal.pone.0019779,
PubMed: 21720544

Laurson, L., Illa, X., Santucci, S., Tore Tallakstad, K., Måløy, K. J., &
Alava, M.. J.. (2013). Evolution of the average avalanche shape with
the universality class. Communications naturelles, 4, Article 2927.
https://doi.org/10.1038/ncomms3927, PubMed: 24352571

Levina, UN., & Priesemann, V. (2017). Subsampling scaling. Nature
Communications, 8, Article 15140. https://est ce que je.org/10.1038
/ncomms15140, PubMed: 28469176

Li, M., Liu, F., Jiang, H., Lee, T. S., & Tang, S. (2017). Long-term
two-photon imaging in awake macaque monkey. Neurone, 93,
1049–1057. https://doi.org/10.1016/j.neuron.2017.01.027,
PubMed: 28215557

Liu, X., & Duyn, J.. H. (2013). Time-varying functional network
information extracted from brief instances of spontaneous brain
activité. Actes de l'Académie nationale des sciences, 110,
4392–4397. https://doi.org/10.1073/pnas.1216856110,
PubMed: 23440216

Lutcke, H., Margolis, D. J., & Helmchen, F. (2013). Steady or
changing? Long-term monitoring of neuronal population activity.
Trends in Neurosciences, 36, 375–384. https://est ce que je.org/10.1016/j
.tins.2013.03.008, PubMed: 23608298

Ma, Z., Turrigiano, G. G., Wessel, R., & Hengen, K. B. (2019).
Cortical circuit dynamics are homeostatically tuned to criticality
in vivo. Neurone, 104, 655–664. https://est ce que je.org/10.1016/j.neuron
.2019.08.031, PubMed: 31601510

Mehring, C., Rickert, J., Vaadia, E., Cardoso de Oliveira, S., Aertsen,
UN., & Rotter, S. (2003). Inference of hand movements from local
field potentials in monkey motor cortex. Neurosciences naturelles, 6,
1253–1254. https://doi.org/10.1038/nn1158, PubMed: 14634657

Neurosciences en réseau

524

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Long-term stability in avalanches and integrative networks

Meisel, C., Olbrich, E., Shriki, O., & Achermann, P.. (2013). Fading
signatures of critical brain dynamics during sustained wakeful-
ness in humans. Journal des neurosciences, 33, 17363–17372.
https://doi.org/10.1523/ JNEUROSCI.1516-13.2013, PubMed:
24174669

Miller, S. R., Yu, S., & Plenz, D. (2019). The scale-invariant, tem-
poral profile of neuronal avalanches in relation to cortical
(cid:1)-oscillations. Rapports scientifiques, 9, Article 16403. https://est ce que je
.org/10.1038/s41598-019-52326-y, PubMed: 31712632

Nicolelis, M.. UN., Dimitrov, D., Carmena, J.. M., Crist, R., Lehew, G.,
Kralik, J.. D., & Sage, S. P.. (2003). Chronic, multisite, multielec-
trode recordings in macaque monkeys. Actes du
Académie nationale des sciences, 100, 11041–11046. https://est ce que je
.org/10.1073/pnas.1934665100, PubMed: 12960378

Onnela, J.. P., Saramaki, J., Hyvonen, J., Szabo, G., Lazer, D., Kaski, K.,
Kertesz, J., & Barabási, UN. L. (2007). Structure and tie strengths in
mobile communication networks. Actes de la Nationale
Académie des Sciences, 104, 7332–7336. https://doi.org/10.1073
/pnas.0610245104, PubMed: 17456605

Pajevic, S., & Plenz, D. (2009). Efficient network reconstruction
from dynamical cascades identifies small-world topology from
neuronal avalanches. Biologie computationnelle PLoS, 5, Article
e1000271. https://doi.org/10.1371/journal.pcbi.1000271,
PubMed: 19180180

Pajevic, S., & Plenz, D. (2012). The organization of strong links in
complex networks. Nature Physics, 8, 429–436. https://doi.org
/10.1038/nphys2257, PubMed: 28890731

Pasquale, V., Massobrio, P., Bologna, L. L., Chiappalone, M., &
Martinoia, S. (2008). Self-organization and neuronal avalanches
in networks of dissociated cortical neurons. Neurosciences, 153,
1354–1369. https://doi.org/10.1016/j.neuroscience.2008.03
.050, PubMed: 18448256

Petermann, T., Thiagarajan, T., Lébédev, M.. UN., Nicolelis, M.. UN.,
Chialvo, D. R., & Plenz, D. (2009). Spontaneous cortical activity
in awake monkeys composed of neuronal avalanches.
Actes de l'Académie nationale des sciences, 106,
15921–15926. https://doi.org/10.1073/pnas.0904089106,
PubMed: 19717463

Plenz, D. (2012). Neuronal avalanches and coherence potentials.
European Physical Journal Special Topics, 205, 259–301. https://
doi.org/10.1140/epjst/e2012-01575-5

Ponce-Alvarez, UN., Jouary, UN., Privat, M., Deco, G., & Sumbre, G.
(2018). Whole-brain neuronal activtity displays crackling noise
dynamics. Neurone, 100, 1446–1459. https://est ce que je.org/10.1016/j
.neuron.2018.10.045, PubMed: 30449656

Radicchi, F., Castellano, C., Cecconi, F., Loreto, V., & Parisi, D. (2004).
Defining and identifying communities in networks. Proceedings of
the National Academy of Sciences, 101, 2658–2663. https://doi.org
/10.1073/pnas.0400054101, PubMed: 14981240

Raichle, M.. E. (2015). The brain’s default mode network. Annual
Review of Neuroscience, 38, 433–447. https://doi.org/10.1146
/annurev-neuro-071013-014030, PubMed: 25938726

Rasch, M.. J., Gretton, UN., Murayama, Y., Maass, W., & Logothetis,
N. K. (2008). Inferring spike trains from local field potentials.
Journal de neurophysiologie, 99, 1461–1476. https://est ce que je.org/10
.1152/jn.00919.2007, PubMed: 18160425

Ribeiro, T. L., Copelli, M., Caixeta, F., Belchior, H., Chialvo, D.
R., Nicolelis, M.. UN., & Ribeiro, S. (2010). Spike avalanches

exhibit universal dynamics across the sleep-wake cycle. PLoS
ONE, 5, Article e14129. https://doi.org/10.1371/journal.pone
.0014129, PubMed: 21152422

Ribeiro, T. L., Ribeiro, S., Belchior, H., Caixeta, F., & Copelli, M..
(2014). Undersampled critical branching processes on small-
world and random networks fail to reproduce the statistics of
spike avalanches. PLoS ONE, 9, Article e94992. https://doi.org
/10.1371/journal.pone.0094992, PubMed: 24751599

Sethna, J.. P., Dahmen, K. UN., & Myers, C.R. (2001). Crackling noise.
Nature, 410, 242–250. https://doi.org/10.1038/35065675,
PubMed: 11258379

Shew, W. L., Lequel, H., Petermann, T., Roy, R., & Plenz, D. (2009).
Neuronal avalanches imply maximum dynamic range in cortical
networks at criticality. Journal des neurosciences, 29, 15595–15600.
https://doi.org/10.1523/ JNEUROSCI.3864-09.2009, PubMed:
20007483

Shew, W. L., Lequel, H., Yu, S., Roy, R., & Plenz, D. (2011).
Information capacity is maximized in balanced cortical networks
with neuronal avalanches. Journal des neurosciences, 5, 55–63.
https://doi.org/10.1523/ JNEUROSCI.4637-10.2011, PubMed:
21209189

Shriki, O., Alstott, J., Carver, F., Holroyd, T., Henson, R.. N., Forgeron,
M.. L., Coppola, R., Bullmore, E., & Plenz, D. (2013). Neuronal
avalanches in the resting MEG of the human brain. Journal de
Neurosciences, 33, 7079–7090. https://doi.org/10.1523/JNEUROSCI
.4286-12.2013, PubMed: 23595765

Stewart, C. V., & Plenz, D. (2007). Homeostasis of neuronal ava-
lanches during postnatal cortex development in vitro. Journal
of Neuroscience Methods, 169, 405–416. https://est ce que je.org/10
.1016/j.jneumeth.2007.10.021, PubMed: 18082894

Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R..
(2012). Criticality in large-scale brain fMRI dynamics unveiled
by a novel point process analysis. Frontiers in Physiology, 3.
https://doi.org/10.3389/fphys.2012.00015, PubMed: 22347863
Tetzlaff, C., Okujeni, S., Egert, U., Wörgötter, F., & Butz, M.. (2010).
Self-organized criticality in developing neuronal networks. PLoS
Computational Biology, 6, Article e1001013. https://est ce que je.org/10
.1371/journal.pcbi.1001013, PubMed: 21152008

Tolias, UN. S., Ecker, UN. S., Siapas, UN. G., Hoenselaar, UN., Keliris, G. UN.,
& Logothetis, N. K. (2007). Recording chronically from the
same neurons in awake, behaving primates. Journal de
Neurophysiologie, 98, 3780–3790. https://est ce que je.org/10.1152/jn
.00260.2007, PubMed: 17942615

Villegas, P., Di Santo, S., Burioni, R., & Muñoz, M.. UN. (2019). Time-
series thresholding and the definition of avalanche size. Physical
Review E, 100. https://doi.org/10.1103/PhysRevE.100.012133,
PubMed: 31499802

Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of
“small-world” networks. Nature, 393, 440–442. https://doi.org
/10.1038/30918, PubMed: 9623998

Lequel, H., Shew, W. L., Roy, R., & Plenz, D. (2012). Maximal variabil-
ity of phase synchrony in cortical networks with neuronal ava-
lanches. Journal des neurosciences, 32, 1061–1072. https://est ce que je
.org/10.1523/JNEUROSCI.2771-11.2012, PubMed: 22262904
Yu, S., Klaus, UN., Lequel, H., & Plenz, D. (2014). Scale-invariant
neuronal avalanche dynamics and the cut-off in size distribu-
tion. PLoS ONE, 9, Article e99761. https://doi.org/10.1371
/journal.pone.0099761, PubMed: 24927158

Neurosciences en réseau

525

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Long-term stability in avalanches and integrative networks

Yu, S., Ribeiro, T. L., Meisel, C., Chou, S., Mitz, UN., Saunders, R., &
Plenz, D. (2017). Maintained avalanche dynamics during task-
induced changes of neuronal activity in nonhuman primates.
eLife, 6, Article e27119. https://doi.org/10.7554/eLife.27119,
PubMed: 29115213

Yu, S., Lequel, H., Nakahara, H., Santos, G. S., Nikolic, D., & Plenz,
D. (2011). Higher-order interactions characterized in cortical ac-

tivité. Journal des neurosciences, 31, 17514–17526. https://doi.org
/10.1523/JNEUROSCI.3127-11.2011, PubMed: 22131413

Zalesky, UN., Fornito, UN., Cocchi, L., Gollo, L. L., & Breakspear,
(2014). Time-resolved resting-state brain networks.
M..
Actes de l'Académie nationale des sciences, 111,
10341–10346. https://doi.org/10.1073/pnas.1400181111,
PubMed: 24982140

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

5
2
5
0
5
1
9
2
5
1
9
7
n
e
n
_
un
_
0
0
1
8
8
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Neurosciences en réseau

526

Télécharger le PDF