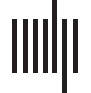RECHERCHE
Spontaneous eye movements during eyes-open
rest reduce resting-state-network modularity by
increasing visual-sensorimotor connectivity
Cemal Koba1, Giuseppe Notaro2
Gustav Nilsonne3,4
, and Uri Hasson2
, Sandra Tamm3,4,5
,
1MoMiLab Research Unit, IMT School for Advanced Studies Lucca, Lucca, Italy
2Center for Mind/ Brain Sciences (CIMeC), The University of Trento, Trento, Italy
3Department of Clinical Neuroscience, Karolinska Institutet, Solna, Sweden
4Département de psychologie, Stockholm University, Stockholm, Sweden
5Département de psychiatrie, Oxford University, Oxford, ROYAUME-UNI
un accès ouvert
journal
Mots clés: Eye-movements, Resting-state, Networks, Modularity, Eye-orbit
ABSTRAIT
During wakeful rest, individuals make small eye movements during fixation. We examined
how these endogenously driven oculomotor patterns impact topography and topology of
functional brain networks. We used a dataset consisting of eyes-open resting-state (RS) IRMf
data with simultaneous eye tracking. The eye-tracking data indicated minor movements during
repos, which correlated modestly with RS BOLD data. Cependant, eye-tracking data correlated
well with echo-planar imaging time series sampled from the area of the eye-orbit (EO-EPI),
which is a signal previously used to identify eye movements during exogenous saccades and
movie viewing. Further analyses showed that EO-EPI data were correlated with activity in an
extensive motor and sensorimotor network, including components of the dorsal attention
network and the frontal eye fields. Partialling out variance related to EO-EPI from RS data
reduced connectivity, primarily between sensorimotor and visual areas. It also produced
networks with higher modularity, lower mean connectivity strength, and lower mean clustering
coefficient. Our results highlight new aspects of endogenous eye movement control during
wakeful rest. They show that oculomotor-related contributions form an important component of
RS network topology, and that those should be considered in interpreting differences in network
structure between populations or as a function of different experimental conditions.
RÉSUMÉ DE L'AUTEUR
We studied how subtle eye movements made during fixation, in absence of any other task, sont
related to resting-state connectivity measured using fMRI. We used a dataset for which eye tracking
and BOLD resting-state were acquired simultaneously. We correlated brain activity with both
eye-tracking metrics as well as time series sampled from the area of the eye orbits (EO-EPI).
Eye-tracking data correlated well with the EO-EPI data. En outre, EO-EPI correlated with BOLD
signal in sensorimotor and visual brain systems. Removing variance related to EO-EPI reduced
connectivity between sensorimotor and visual areas and resulted in more modular resting-state
réseaux. Our findings show that oculomotor-related contributions are an important component of
resting-state network topology, and that they can be studied using EPI data from the eye orbits.
Citation: Koba, C., Notaro, G., Tamm,
S., Nilsonne, G., & Hasson, U. (2021).
Spontaneous eye movements during
eyes-open rest reduce resting-state-
network modularity by increasing
visual-sensorimotor connectivity.
Neurosciences en réseau, 5(2), 451–476.
https://doi.org/10.1162/netn_a_00186
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00186
Informations complémentaires:
https://doi.org/10.1162/netn_a_00186
Reçu: 7 Juin 2020
Accepté: 28 Janvier 2021
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Uri Hasson
uri.hasson@unitn.it
Éditeur de manipulation:
Olaf Sporns
droits d'auteur: © 2021
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
un
_
0
0
1
8
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
INTRODUCTION
The study of human brain activity during resting state (RS) is of considerable interest in both
basic and clinical brain research. For mechanistically oriented perspectives, RS activity patterns
identify constraints that may govern task-evoked activity as seen by relations between RS con-
nectivity and interindividual differences in various cognitive tasks (par exemple., Kelly, Uddin, Biswal,
Castellanos, & Milham, 2008; Rosenberg, Hsu, Scheinost, Constable, & Chun, 2018). And be-
cause RS connectivity is related to structural connectivity (par exemple., Honey et al., 2009; Mišic(cid:1) et coll.,
2016), it is considered an important mediator between anatomical organization and task-
evoked activity. From the perspective of predictive models of interindividual differences in
healthy and clinical populations, the quantification of RS features (using time-domain,
network-based analyses, spatiotemporal clustering, or control-based approaches, to name a
few) is used for machine learning or statistical learning. This has proved promising in contexts
such as prediction of IQ (par exemple., Dubois, Galdi, Paul, & Adolphs, 2018), personality (par exemple., Nostro
et coll., 2018), or the likelihood of developing clinical conditions (par exemple., de Vos et al., 2018).
Resting-state data measured via fMRI reflect endogenous neural activity, but also additional
sources that introduce fluctuations in the signal. Some of these are physiological artifacts (par exemple.,
cardiac and respiratory effects, Birn, 2012; J.. Chen et al., 2020), or head and body motion (par exemple.,
Parkes, Fulcher, Yücel, & Fornito, 2018). For machine learning, these nonneural effects on the
BOLD signal may be informative; Par exemple, motion-related patterns could differ across
populations (par exemple., Zacà, Hasson, Minati, & Jovicich, 2018). Cependant, motion and physiological
effects complicate drawing conclusions about brain systems mediating endogenous information-
computation during wakeful rest. For this reason, researchers often remove effects of motion and
physiology from RS data prior to analysis, even though some effects of physiology could be mean-
ingfully related to central neural systems involved in control of autonomic activity (par exemple., Iacovella,
Faes, & Hasson, 2018; Iacovella & Hasson, 2011).
Here we examined how RS connectivity is related to a distinct factor, which is eye move-
ment during rest (while fixating with eyes open). For purposes of understanding endogenous
computations, spontaneous eye movement at rest straddles the boundary between an interest-
ing neurobiological phenomenon reflecting the output of endogenous activity and a nuisance
factor reflecting motor activity. On one hand, eye movement can be considered a truly integral
component of wakeful rest, because at minimum, retinal input is continuously refreshed to min-
imize adaptation (for review, see Rucci & Poletti, 2015). On the other hand, oculomotor control
differs from prototypical covert, nonmotor processes exactly because motor control involves
planning, execution, efference copy, feedback, and correction (par exemple., West, Welsh, & Pratt,
2009). Oculomotor control during rest may therefore require coordination between brain sys-
tems that otherwise present modest levels of connectivity.
Statistically, eye movements during rest could therefore produce stronger connectivity
between regions. Perhaps more importantly, it could produce a more integrated (less-modular)
view of RS connectivity networks, because eye movement is supported by a widely distributed
fronto-parietal network and occipital regions (par exemple., Balslev, Albert, & Miall, 2011; Mort et al.,
2003). From a theoretical perspective, identifying neural systems controlling eye movement
during rest could allow better partitioning between relatively more ‘active,' (oculo)motor-related
aspect of RS as opposed to other more covert, nonmotor-related aspects of RS. Enfin, eye move-
ments themselves could be a possible confounder when studying healthy and clinical popula-
tions that differ in oculomotor control, including autism (par exemple., Takarae, Minshew, Luna, Krisky, &
Sweeney, 2004), Parkinson’s disease (par exemple., Pretegiani & Optican, 2017; Zhang et al., 2018), ou
schizophrenia (par exemple., Dowiasch et al., 2016; Morita, Miura, Kasai, & Hashimoto, 2020).
Neurosciences en réseau
452
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
un
_
0
0
1
8
6
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
Current Knowledge
There is relatively little prior work on the relationship between eye movements and RS activity.
Using fMRI, Fransson, Flodin, Seimyr, and Pansell (2014) studied neural correlates of horizontal
or vertical guided fixations, as well as spontaneous fixations during RS. Guided fixations pro-
duced activity in systems typically involved in oculomotor movement, including visual cortex,
frontal eye fields (FEF), supplementary motor area (SMA), cerebellum, and a few other regions.
To quantify correlates of spontaneous eye movement during RS, they derived a gaze-velocity
time series from the eye tracking data, reduced its dimensionality using PCA, convolved the
resulting time series with a hemodynamic response function, and used the result as a regressor
in a whole-brain analysis. Fait intéressant, this latter analysis identified fewer regions, which fur-
thermore did not overlap with those found for guided saccades, and which were all associated
with the default mode network (DMN): the posterior cingulate cortex (PCC) and dorsomedial
prefrontal cortex (dmPFC). As the authors noted, “at first glance it would seem more likely to
expect the neuronal control for slow changes in eye position during fixation to be localized to
visual cortices and attention-related cortical networks” (Fransson et al., 2014, p. 3833). C'est
unclear how slow fluctuations in the DMN impact eye movement.
Electrooculography (EOG):
A technique for measuring eye
position using two electrodes that
record the variation in electric
potential generated by the eye
displacement.
McAvoy et al. (2012) used electrooculography (EOG) to monitor eye movement during fix-
ation, in an analysis based on a relatively small sample of nine participants. Using EOG, ils
separated blinks from other eye movement during eyes-open RS. In the analysis of EOG during
RS fixation they identified brain systems correlated with blinks, but no brain systems where
activity correlated with other types of eye movements.
Pupil size:
A measure of the dilation of a
participant’s pupil. Usually expressed
as the length of the major axis of the
ellipse that best approximates the
pupil, normalized to the camera’s
sensor size.
Yellin, Berkovich-Ohana, and Malach (2015) examined correlations between fMRI BOLD
fluctuations during rest and pupil size. They identified widespread negative correlations in sen-
sorimotor areas and temporal areas, and positive correlations in the DMN. The study did not
evaluate BOLD correlates of gaze location or velocity. Cependant, it is possibly related to under-
standing systems related to spontaneous eye movement, because pupil size measurements are
known to be confounded with the deviation of the pupil from the center of camera view. C'est,
eye trackers will misreport systematically decreasing pupil size values—for the exact same pu-
pil size—as the pupil deviates from the camera axis (Hayes & Petrov, 2016). This mismeasure-
ment is known as the pupil foreshortening error (PFE). Spécifiquement, Hayes and Petrov (2016)
showed that deviations from center of camera view produce systematic PFEs that can reach
12% at typical viewing distances. Significant PFEs were produced even with movements as
small as 4° from center.
Ramot et al. (2011) used EOG to determine BOLD correlates of spontaneous eye movements
during an eyes-closed condition. The relation to eyes-open oculomotor control is unclear, comme
eyes-closed RS conditions produce different patterns of brain activity (par exemple., Marx et al., 2003)
and connectivity (par exemple., McAvoy et al., 2012). En outre, saccades made under closed eye lids
have different trajectories than those made with eyes open in complete darkness (Becker &
Fuchs, 1969). For this reason we consider prior studies examining RS activity during eyes-open
condition as more relevant for the current study.
En outre, numerous neuroimaging studies have used various types of tasks, y compris
visually-guided saccades, memory-guided saccades, antisaccades, and so-called “voluntary”
saccades (either precued [endogenous control] or freely initiated). Cependant, these studies used
explicit tasks rather than study naturally occurring oculomotor control during eyes-open RS.
Perhaps the essential difference is that controlled studies oftentimes orient the saccade toward
or away from a presented target (pro- vs. antisaccade). For this reason the brain systems iden-
tified could mediate visual detection and attention processes that have no parallel during rest. Dans
Neurosciences en réseau
453
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
un
_
0
0
1
8
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
Global network metrics:
Network metrics that derive from the
entire (mondial) network structure.
Local network metrics:
Network metrics quantifying
characteristics defined by relations
between local units in the network.
a neuroimaging study demonstrating this point (Brun, Goltz, Vilis, Ford, & Everling, 2006),
participants were required to saccade either toward a stimulus (prosaccade), away from a stim-
ulus (antisaccade), or maintain fixation while inhibiting an orienting saccade (no-go). They doc-
umented numerous regions, including FEF, IPS, cingulate cortex, and precuneus, all showing
highly similar activation patterns for both prosaccade and no-go trials. The authors interpreted
this as suggesting that “BOLD signal in cortical saccade regions might predominantly reflect
visual detection and attention processes rather than saccade generation or inhibition…” For
this reason, it is unclear to what extent brain systems identified in typical studies of saccades
are strongly involved in saccade control during the resting state.
Specific Aims
The two aims of our current study were: (un) to identify brain systems associated with endoge-
nously driven eye movements during rest, and conjointly, (b) to determine how removal of eye
movement–related activity impacts resting-state connectivity. We quantified eye movement
during rest using both eye tracking and EPI data extracted from the eye orbit area. We validated
the relationship between different features of eye movement (pupil size, gaze velocity, gaze
location) and eye orbit EPI time series (EO-EPI) during rest. We then evaluated how removal
of eye-related activity, as manifested in EO-EPI, impacts the topography and topology of RS
réseaux. Ce faisant, we examine how EO-EPI removal impacts global metrics of network
connectivity including modularity, number of modules, and properties of the degree distribu-
tion because these speak to large-scale, holistic changes to brain networks. En outre, nous
quantify the impact of EO-EPI removal on other, local metrics of connectivity (par exemple., mean
degree) in order to allow relating past and future results to our results.
MÉTHODES
Dataset
We used resting-state data from the Sleepy Brain study (Nilsonne et al., 2016). All data are available
online from OpenNeuro, Dataset ds000201 (https://www.openneuro.org/datasets/ds000201/).
Full details of the dataset and imaging parameters are given in Nilsonne et al. (2016), and here
we provide only the main details. Les données ont été collectées auprès de 86 participants on a 3T MRI scanner
(Découverte 750, General Electric) using an 8-channel head coil. Each participant was scanned on
two different days. In each scanning session, a T1 structural image, two resting-state functional EPI
scans, and three task-related functional scans (emotional mimicry, empathy for pain, emotional
reappraisal) were acquired. Our analyses rely only on the structural and resting-state scans.
For the structural (T1) images, the relevant properties were as follows: slice thickness 1 mm,
sagittal orientation, whole-brain acquisition; for the resting state EPI images: slice thickness
3 mm no gap, axial orientation, 49 slices covering the entire brain, interleaved acquisition
inferior to superior, TE ¼ 30, TR ¼ 2.5 sec, flip angle 75°.
Four resting-state datasets were acquired for each participant; two runs on each of two scan-
ning days. In one of the two days, data were collected when participants were sleep deprived,
and we did not analyze these data. Of the remaining two RS runs, one was typical, where par-
ticipants were asked to fixate on a white cross presented a gray background for 8 minutes. Le
second run was quasirest in that in addition to fixation, it included self-rated sleepiness probes
every 2 minutes. We only analyzed data from the typical RS session. To summarize, nous
processed one RS run per participant, which was a typical RS scan acquired in absence of sleep
deprivation. Three participants did not provide these runs so 83 participants were included
in our initial sample. Participants belonged to two age groups: 20–30 years of age (n ¼ 45,
Neurosciences en réseau
454
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
un
_
0
0
1
8
6
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
Median ¼ 23) and 65–75 years of age (n ¼ 38, Median ¼ 68). We did not have specific hypoth-
eses about how age may mediate correlations between eye movement and BOLD. Donc, dans
investigating potential age effects, our main intention was to understand whether this factor
confounded any of the reported analyses. Because of the large difference between the age dis-
tributions, we treated age as a categorical variable (age group) rather than as a continuous one.
Pre-Processing of Eye Tracking Data
Eye tracking data were available for 77 of the 83 participants for which we analyzed the RS
data. Participants were required to maintain their gaze on a central fixation cross for the dura-
tion of the 8-min scan. Right-eye movement and pupil size were recorded using a ViewPoint
EyeTracker (Arrington Research, Etats-Unis) integrated into head-mounted goggles. Eye data were
sampled at 60 Hz. Participants were monitored during the experiment to ensure that they
did not have prolonged eye closures (>5 sec).
When analyzing these data we observed a substantial proportion of missing values, likely
due to loss of pupil tracking during the task. We therefore implemented a quality assurance
procedure as detailed below. We constructed a histogram of the standard deviations of the gaze
norm (defined as
); see Supporting Information Figure S1. On the basis of the
q
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
þ gaze2
gaze2
oui
X
distribution of these values and visual inspection of the data, we set the upper bound to SDgaze
0.32 and excluded participants with SDgaze above this threshold. We chose this threshold in
order to maintain time series with relatively low proportion of potential artifact peaks, because
the adaptive threshold algorithm we use for peak detection (décrit ci-dessous) is applicable if
peaks are relatively rare as compared to baseline. This step resulted in exclusion of 43 of the
77 datasets.
¼
Manufacturer guidelines define artifacts as measurements where one of the pupil dimen-
sions is outside the range of 0.1–0.5. Based on this definition, we removed an additional two
participants for whom more than 50% of measurements were outside this range. For the remain-
ing 32 subjects we performed the following analysis to detect eye blinks and nonblink artifacts,
based on estimations of the artifact duration. We first defined an artifact function as the sum of
the following three functions (Equations 1–3, each normalized to its maximum value). Dans ces
equations, f1 is the pupil aspect ratio, whereas f2 and f3 diverge when one pupil dimension
approach the boundaries of the validity range 0.1–0.5.
f1 ¼ pupilwidth=pupilheight
(cid:3)
f2 ¼ 1= pupilwidth
(cid:4)
2
(cid:3)
þ 1= pupilheight
(cid:4)
2
(cid:3)
f3 ¼ 1= pupilwidth − :6
ð
(cid:4)
Þ2
(cid:3)
þ 1= pupilheight − :6
ð
Þ2
(1)
(2)
(3)
(cid:4)
To individuate the artifacts’ start and end points, we applied an adaptive algorithm proposed
by Nyström and Holmqvist (2010). This algorithm was originally developed for saccade detec-
tion using gaze speed as input, and we adapted it to use the absolute value of the artifact function
as input. In brief, this method consists of first detecting the peaks of the input through a locally
adaptive threshold, which is then followed by detecting the artifact onset and offset as the closest
point of minimum below that threshold. Supporting Information Figure S2 shows an example of
detected peaks of the artifact function. These peaks correspond to intervals of pupil size mea-
surements outside the validity range.
Neurosciences en réseau
455
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
un
_
0
0
1
8
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
En résumé, we analyzed data from 32 (de 77) participants (25 from the younger participants
group, 7 from the older). For these, the proportion of artifacts was on average 18 ± 2%. Blinks
occurred with an average period of 2.36 ± 0.21 sec.
Pre-Processing of fMRI Data and Creation of Eye Orbit EPI Regressors
We include the analysis workflow described below as Supporting Information, also available
online via a GitHub repository (Koba, 2021).
D'abord, we applied brain extraction and tissue segmentation (gray matter, white matter, CSF) to the
structural T1 images using the antsBrainExtraction function of ANTs software (Avants, Tustison, &
Song, 2011). We used ANTs for all registration routines in our pipeline. We registered each par-
ticipant’s structural image to standard space using non-linear registration (ICBM 2009 nonlinear
asymetric template; Fonov, Evans, McKinstry, Almli, & Collins, 2009) and saved the inverse of the
warps. We also registered the structural and functional images using affine transformation. Nous
used the combination of these two transformations to align data from each participant’s original
space to common space, or vice versa, in a single step.
To delineate each participants “eye orbit” area, we first marked this area on the common space
template. We then transformed this mask to each participant’s original space and made any ad-
ditional modifications therein, if required. Spécifiquement, we delineated anatomical masks of the
“eye orbit” area in common space using MRICRON (Rorden, Karnath, & Bonilha, 2007), Pour qui
we used an MNI template provided with FSL (Jenkinson, Beckmann, Behrens, Woolrich, & Forgeron,
2012). Both eye orbits were included in the mask. The masks’ location was transformed to each
participant’s individual space using the combination of the MNI!T1 and T1!subject space
alignment matrices mentioned above. We also created cerebral spinal fluid (CSF) and white matter
masks in MNI space and transformed them to individual space, where they were eroded by one
voxel from their outer boundaries to be more conservative. We then extracted the mean time series
from these white matter and CSF masks. These were used as nuisance regressors in an initial
regression (details below).
We used AFNI (Cox, 1996) for analyzing the functional RS images. We implemented the
following steps: slice time correction, motion correction (base image: first volume of the run),
and band-pass filtering (0.01–0.1 Hz). To remove other nuisance sources of variance from the
functional times series, we implemented preliminary data-cleaning using regression with the
following regressors: (un) motion parameters estimated during motion correction, (b) mean white
matter and CSF time series, et (c) frame-wise displacement values. We considered the residuals
of this regression as a “cleaned” time series that was the entry point for further analyses.
To improve signal to noise of the subsequent regression models that were of primary interest,
we then spatially smoothed the cleaned time series with a 6-mm FWHM kernel. From this time
series we also derived an Eye-Orbit EPI regressor, which was defined as the mean time series
from both eye orbit masks, after spatial smoothing, which we refer to as EYEraw. We convolved
the EYEraw with an HRF basis function (using AFNI’s waver command), producing an EYEconv
time series. In separate analyses we used either EYEraw or EYEconv as “seed” regressors to identify
EO-EPI-correlated brain areas.
Determining Correlation Between Eye-Tracking Measures and EO-EPI Time Series
We were interested in the relationship between several measures of eye movement and the EPI
time series sampled from the eye orbit regions (EO-EPI series). We derived 12 time series from
the eye-tracking data: the measured gaze location, GazeX and GazeY (mean normalized for
Neurosciences en réseau
456
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
un
_
0
0
1
8
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
horizontal center per participant), their squared values, their temporal derivatives (vel_GazeX,
vel_GazeY), gaze amplitude: GazeX2 + GazeY2, gaze power: vel_GazeX2 + vel_GazeY2,
Pupil_size (de-meaned), its first derivative vel_Pupil_size, and squared value Pupil_size2. Nous
were also interested in the blink function (coding for 1 whenever a blink was present; 0 other-
wise), but we determined the relation between blinks and EO-EPI in a different manner as
detailed below. Pupil_size was defined as ( pupil_width + pupil_height)/2. We note that with
our instrumentation, as well as many other eye trackers, the pupil size measure may be confounded
with gaze position (Hayes & Petrov, 2016), resulting in significant correlations between pupil_size
and gaze location in both x and y directions ( p < .01 for 30 of the 32 participants in the current
study).
For each of the 12 eye-tracking quantities mentioned above (with the exception of blinks),
we performed the following procedure: we first downsampled the time series to the fMRI
frequency rate (0.4 Hz). Rather than assume that the relation between the eye tracker data
and EO-EPI is mediated by a typical hemodynamic response function, we used a simple statis-
tical learning approach to estimate and validate this relationship. Specifically, we calculated a
kernel function to describe the relation between the eye tracking quantity and the EO-EPI en-
velope. We computed a kernel as follows. First, for each oculomotor time series we considered
as meaningful oculomotor ‘events’ the top 10% of the peak values in the given series. Second,
we calculated the mean EO-EPI signal in the interval [−10, 10] seconds around those peak
events. For each participant, the triggered mean was normalized to that participant’s absolute
maximum value, in this way producing the participant’s event-triggered average (ETA). To
maintain independence between estimation and testing, the kernels linking an eye-tracking
measure to the EO-EPI signal were calculated using a leave-one-participant-out procedure.
That is, for each participant the kernel was derived as the mean of the ETAs calculated from
all other participants. This kernel was convolved with the (left-out) participant’s eye-tracking
time series, and a correlation with EO-EPI computed. The resulting correlation values (32 in
all) were then Fisher-Z transformed and analyzed on the group level using a t test.
We used a different approach to evaluate the relation between blinks and EO-EPI dynamics.
The blink time series was sparse and binary, with ‘1’ coding blink presence. We downsampled
this time series to consecutive 2.5-sec windows, assigning to each window the value 1 if at least
one blink was coded in the original series. For each participant we computed a blink-related
event-triggered average by averaging the EO-EPI data around each blink (as described above).
To determine the statistical significance of blinks and EO-EPI, we evaluated the reliability of the
ETAs across participants: we calculated for each participant the correlation between his/or own
ETA and the average of the ETAs of all the other subjects. We then tested the distribution of
these (Fisher-Z transformed) correlation values at the group level using a t test.
Statistical Inference for fMRI Analyses
Correlates of eye-tracking metrics: We examined whole-brain correlations between RS activity
and several eye tracking measures: GazeX, GazeX2, vel_GazeX, vel_GazeX2, Pupil_size, and
blink function. The BOLD data modeled were the “cleaned” time series from which only typical
artifact sources were removed. We implemented two modeling approaches: in the first, we re-
sampled each eye-tracking measure of interest to the sampling resolution of the MR acquisition
(0.4 Hz) and convolved the result with canonical HRF via AFNI’s waver function to construct a
regressor. In the second, we used a finite impulse response (FIR) function modeling approach
where the BOLD impulse response was estimated using six tent functions (using AFNI’s tent
basis function). This approach does not assume a fixed shape. From these estimates, we averaged
Network Neuroscience
457
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
Wilcoxon signed-rank test:
A nonparametric statistical test
that can be applied to repeated-
measurement designs.
tSNR map:
A parameter map showing tSNR
values for each brain area, defined
as the ratio of the mean of a signal
divided by its standard deviation.
the first three beta coefficients (corresponding to 0–7.5 sec post eye-tracker dynamics) and propa-
gated the value to a group-level analysis. Family wise error correction was implemented using FSL’s
TFCE implementation.
Correlates of EO-EPI regressors: Beta values associated with EYEconv or EYEraw were transformed
to MNI space. To identify clusters where these beta values were significantly positive or signif-
icantly negative, we computed voxel-wise statistics using a Wilcoxon signed-rank test, and then
implemented cluster-level control for family-wise error using permutations as described below.
We used a nonparametric test because the relevant beta values data did not satisfy typical para-
metric assumptions.
We defined statistically significant clusters as ones where the statistical significance (uncorrected)
at the single voxel level was below p = .01, and where the cluster size (volume) passed a value
determined from the sampling distribution we derived using the following permutation procedure.
In each of 10,000 permutations, we reversed the signs of 42 of the 83 datasets, and we implemented
a Wilcoxon signed-rank test (Siegel & Castellan, 1956) to identify all clusters consisting of voxels
where the statistical significance of the difference from chance (zero; 0) exceeded p < .01 and where
all values were positive (we limited to positive values so that the resulting clusters could not com-
bine both negative and positive values, as our main analysis also probed for clusters where all
values were either positive or negative). We saved the largest cluster size from each permutation,
and the resulting set of 10,000 values of largest cluster sizes defined the sampling distribution. The
95% percentile rank entry of the sampling distribution served as the critical value. This value was
used to define statistically significant clusters in the experimental data. In addition, in those clus-
ters defined as statistically significant, we computed the voxel-level effect size of the test (see
Poldrack et al., 2008). We used the effect size (r) definition for the Wilcoxon test, quantified as
r = Z/√(N), where N is the number of participants (data pairs). To determine whether the clusters
identified by the EO-EPI/BOLD analyses were differentially driven by the young or older partic-
ipant groups, for each of the statistically significant clusters we compared the mean beta value per
cluster between the two groups. For each participant, we extracted the mean beta from the
EO-EPI/BOLD regression, per cluster. We then evaluated whether these values differed for older
and younger participants (Mann-Whitney between groups nonparametric test).
To evaluate whether significant EO-EPI correlates were found in areas dominated by artifacts,
we calculated voxel-level temporal signal-to-noise ratio (tSNR) for each participant. To create a
tSNR map for each participant, we used the raw functional images (before applying any signal
processing steps), but after removal of the initial 10 stabilization images. We divided the absolute
mean value of each voxel by its standard deviation. We then applied the statistically significant
clusters found for EYEraw and EYEconv series as masks to determine mean ± standard deviation of
the tSNR in each statistically significant spatial cluster. The motivation for this analysis was a prior
report (W. Chen & Zhu, 1997) showing that Nyquist ghosting artifacts can propagate eye signals
into midbrain areas (in the case of axial acquisition). Two MR physicists examined the QA reports
produced by the scanner and did not find evidence for ghosting. However, we still wanted to
evaluate if any EO-EPI whole-brain correlates were found in regions with low tSNR.
To evaluate the specificity of our findings to the eye-orbit region, we defined a control region
of interest (ROI) in the maxillary sinus cavity below the eye, and analyzed the mean time series
of that region identically to how we analyzed the data from the eye orbit region. Given the axial
acquisition, ghosting is not likely to be propagated to this more inferior region.
In addition, we evaluated the relation between the EO-EPI regressor and the framewise-
displacement regressor to understand the contribution of the latter to the EO-EPI data. We
Network Neuroscience
458
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
computed the correlation between the FD regressor and EYEraw regressor per person, normal-
ized the correlation values (Fisher-Z) and conducted a statistical test at the group level. We
conducted a similar analysis to evaluate the relationship between EO-EPI and the global signal
(GS). We defined GS as the mean whole-brain time series of all gray matter voxels, following
removal of the motion artifacts, WM/CSF contributions, and subsequent to spatial smoothing.
Because GS also contains neural information (e.g., Liu, Nalci, & Falahpour, 2017) we did not
partial out GS, but evaluated its relationship to EO-EPI. We used the same approach we applied
to framewise displacement.
To study the relation between EO-EPI activity and regions previously linked to oculomotor
control, we defined the frontal eye fields (FEF) and supplementary eye fields (SEF) as indepen-
dent ROIs and for each we examined correlations with the EO-EPI regressor. To create FEF and
SEF ROIs, we used the NeuroSynth database (Yarkoni, Poldrack, Nichols, Van Essen, & Wager,
2011). The probability mask corresponding to the keyword eye was saved and thresholded by
z-score of 7 (max Z = 9.1, generated from 417 studies). From the thresholded image, regions
around the intersection of precentral sulcus and superior frontal sulcus were marked as FEF, and a
region around the medial frontal gyrus was marked as SEF (see Supporting Information Figure S6).
Those masks were spatially translated to the individual-subject space and mean activation of
those two ROIs extracted from the cleaned and smoothed data. We constructed a regression
model to predict the FEF and SEF ROIS’ activity from the EO-EPI series, per participant.
Coefficients were analyzed using a Wilcoxon rank sum test.
Functional connectivity maps and derived network metrics: To create functional connectivity net-
works, we used a resting-state functional connectivity parcellation based on 500 ROIs (Schaefer
et al., 2018). We spatially translated this parcellation into each participant’s individual space,
where they were further limited to gray matter by multiplying all ROIs with the participant-
specific gray matter mask (to limit the influence of data from nongray matter areas). We extracted
the mean time series from each ROI, for the two types of spatially smoothed resting-state data we
derived (one typical, and the other with EO-EPI EYEconv regressed). We examined the network
features after thresholding the connectivity matrices at 12 sparsity levels: 30%, 20%, and
1–10%. In all, from each participant’s resting-state network we derived the following metrics:
node degree, strength, cluster coefficient, transitivity, assortativity, efficiency, number of commu-
nities, betweenness centrality, and modularity. Subsequent to thresholding, the feature values
were processed as follows. We generally used nonbinarized connections maintaining the
original weights, with the following exceptions: (a) for node degree we used binarized values;
(b) for clustering coefficient, transitivity and betweenness centrality we used normalized values,
per participant, per condition; (c) for betweenness centrality we used connection-length matrices
as inputs. We calculated these using the Brain Connectivity Toolbox (Rubinov & Sporns, 2010)
(see Supporting Information for description of the metrics as described in the Brain Connectivity
Toolbox). We calculated these parameters for the original and “clean” networks as defined
above. We then tested which of these parameters differed as a result of the EO-EPI removal pro-
cedure using paired-sample t tests. We defined a robust result as one that was statistically signif-
icant across all 12 levels of sparsity thresholding. We report the results for all network metrics for
completeness so that they could be cross-referenced again prior and future work. Because subsets
of those features are expected to be correlated, we constructed correlation matrices (using across-
participant variance) to identify positive and negative correlations between features in order to
inform our discussion of changes to modularity.
We also probed for changes in global topology by quantifying the impact of EO-EPI removal
on the shape of the entire degree distribution (for the largest three sparsity levels: 10%, 20%,
Network Neuroscience
459
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
Exponentially truncated power law:
A distribution that follows a power
law multiplied by an exponential
decay.
Dual regression:
An ICA-based technique that allows
creating participant-specific
connectivity maps from network
templates defined in standard space
or group template.
30%). Following prior work (e.g., Fornito, Zalesky, & Bullmore, 2010) we fit an exponentially
truncated power law function to each participant’s degree distribution. The function was Y ¼ a ×
Xb × e(x×c), where Y is the cumulative probability of the distribution and X is node degree. From
this equation, we derived the coefficient (a), power law exponent (b), and degree cutoff point
(c). A paired-sample t test was applied to each parameter to evaluate the impact of partialling
out EO-EPI.
We wanted to know whether fronto-parietal systems that mediate exogenous attention become
less hub-like when EO-EPI is removed. To evaluate this, we used previously defined criteria
(Xu et al., 2014) in order to detect network hubs, separately for each of the three largest sparsity
thresholds. These criteria required that the value of a node be higher than 1 SD above the mean
value for each of these empirical distributions: node strength, node degree, and node betweenness
centrality. Nodes matching all three criteria were considered hubs. The chance probability of a
node being a hub (assuming a normal distribution) is (cid:2)0.343 ¼ .04. To evaluate whether removal
of EO-EPI variance impacted whether a region satisfied hub criteria, for each region we counted the
number of participants for which the region was classified as a hub, with our without EO-EPI
removal. On a binomial, a difference would need to consist of at least seven or more participants
(binomial test parameters: N ¼ 83; K ¼ 7; p ¼ .04).
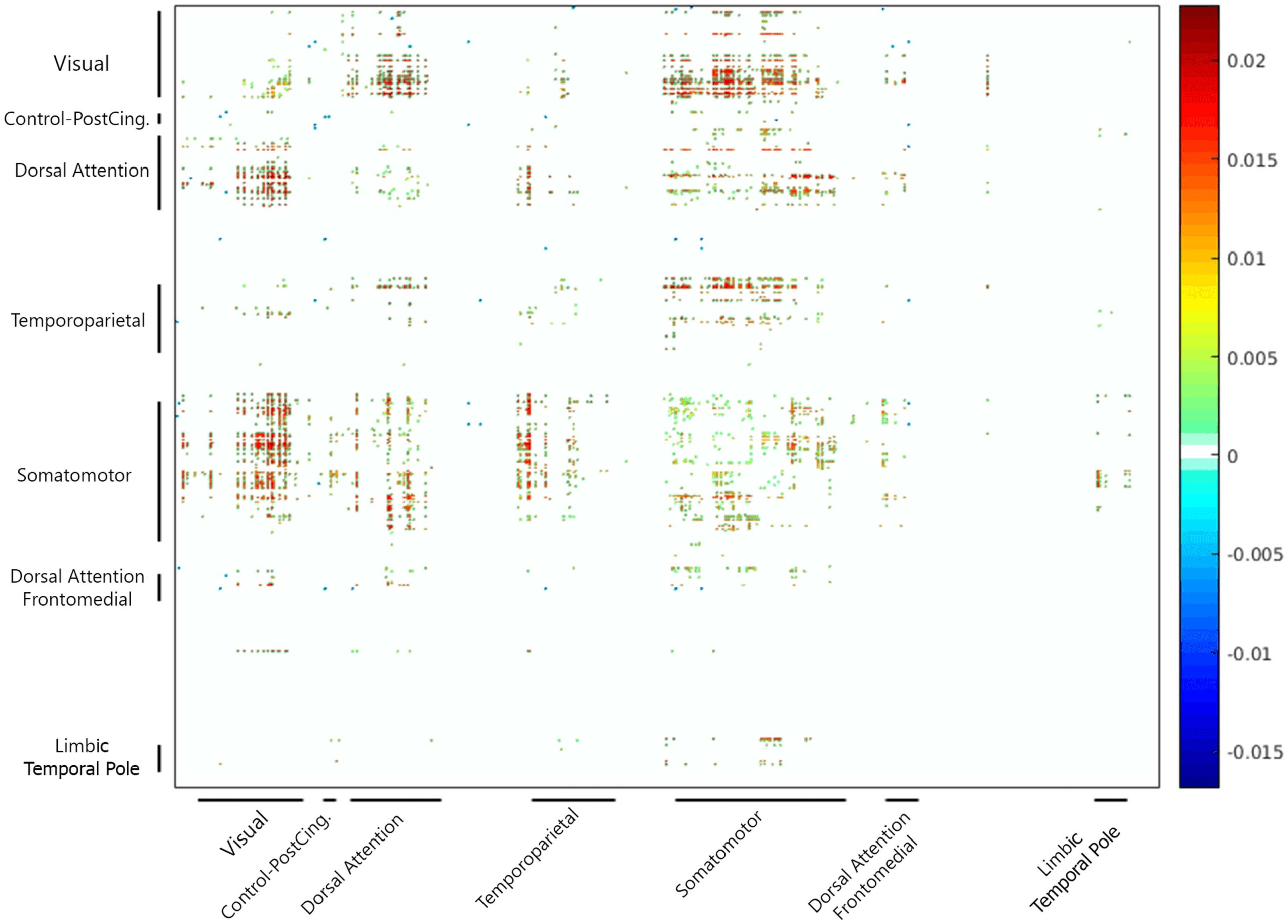
We also identified any specific pair-wise differences in regional connectivity for the raw and
cleaned matrices. After applying Fisher’s Z transformation, pair-wise correlation values were
subjected to paired-sample t tests. We used false discovery rate (FDR) to correct for multiple
comparisons.
Dual regression: We used dual regression to determine how removal of activity associated with
the EO-EPI regressor impacted connectivity in previously defined resting-state networks. The pro-
cedure was implemented in AFNI and followed workflows described previously (Beckmann,
Mackay, Filippini, & Smith, 2009; Nickerson, Smith, Öngür, & Beckmann, 2017). In the first step
we used 14 predefined resting-state network spatial masks (Shirer, Ryali, Rykhlevskaia, Menon, &
Greicius, 2012) to extract ‘seed’ time series for each of the networks. The 14 resting-state network
masks were spatially transposed to individual space and multiplied by the gray matter mask of
each participant to reduce contribution from nongray matter areas. For each participant we then
produced two seed time series for each of the 14 networks: one from the functional data from
which the EO-EPI variance was not removed, and one from the functional data from which this
variance was removed using the EYEconv regressor.
To determine whole-brain connectivity of the seed regions, we inserted all 14 time series into a
single multiple regression. In effect, we conducted two separate regression models: Model #1 was
a “typical” model where the mask-derived seed time series produced from the original (typically
processed) functional data served as regressors to predict whole-brain resting-state data. This
process reproduces the typical dual regression procedure. Model #2 was an “EO-EPI-removed”
model. Here, the dataset analyzed was the EO-EPI-removed BOLD data. From that point on, the
dual regression was carried out as usual, with seed time series (one per network) used conjointly to
predict whole-brain activity.
The produced beta weights were analyzed using group level repeated-measures test to iden-
tify seed time series whose connectivity differed between the two data sets; that is, whose con-
nectivity was impacted by the EO-EPI removal procedure. We used FSL’s randomise function
(Jenkinson et al., 2012). A within group t test with 10,000 permutations and threshold-free cluster
enhancement was applied. Because our interest was in evaluating the impact EO-EPI regressor
we adopted a liberal approach of not correcting for multiple comparisons across the 14 networks
Network Neuroscience
460
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
tested in the dual regression procedure. We also note that the 14 time series used for dual re-
gression were relatively weakly correlated in this data set: to determine collinearity, on the single
participant level we computed the 14 × 14 cross-correlation matrix and then averaged these
across participants. The highest mean correlation was 0.55, which licensed separate analyses
for each network regressor.
Relation between analyses and control for multiple comparisons: Taken together, we report two
core independent analyses: (a) the first uses the EO-EPI regressor for whole-brain analyses,
using a convolved or nonconvolved regressor. Its findings constrain the findings from the pair-
wise functional connectivity analysis based on the 500-region parcellation, because regions
identified by EO-EPI/BOLD are more likely to show reduced connectivity after removing the
EO-EPI contribution; (b) the second analysis is the network-metric analyses: some of its findings
(e.g., modularity, clustering) are independent of other analyses. The whole-brain analysis is cor-
rected for family-wise error, whereas the network metric is not corrected for multiple tests in
order to allow cross-referencing our network-level findings against prior and future literature. In
addition, we report several analyses in order to offer insight into mechanisms, or for compati-
bility with prior studies. Specifically, the analyses of the relation between EO-EPI and eye-
tracking data are meant to elucidate the sources of the EO-EPI signal, rather than to provide
further information on the relationship between eye movement and brain activity. This analysis
is internally corrected for family-wise error. The analysis relating eye tracking to BOLD/fMRI is
presented as a contrast to the EO-EPI and for consistency with prior work.
RESULTS
Eye-tracking Data: Quality and Correlation with Whole-brain BOLD
Based on our artifact rejection criteria, usable eye-tracking data were available for 32 of 77
participants for which eye tracking data were collected. A power-spectra analysis of the eye
tracking data (Supporting Information Figure S3) indicated higher broadband power in all fre-
quencies in the rejected data, including those approaching the Nyquist frequency of the eye-
tracking data in the current study ( f ¼ 30 Hz). Participants largely avoided making large eye
movements during the resting-state session. To quantify these movements, we calculated the
maximal displacement of gaze position in nonoverlapping 2-sec windows. The resulting em-
pirical cumulative distribution functions (see Figure 1A) indicated modest movement, with
around 50% of analysis windows showing displacement values below 1° and only around
10% of windows showing displacement values above 3°.
Figure 1. Relation between eye-tracking measures and EO-EPI regressor from eye orbits. (A) modest eye movements in 2-sec nonoverlapping
time windows. (B) and (C) whole brain correlates of resting-state BOLD with blink events and GazeX2. No other areas showed statistically
significant effects. Each analysis is corrected for multiple comparisons using FSL’s implementation of TFCE Family-wise error control.
Network Neuroscience
461
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
Whole-brain correlations with eye-tracking metrics were found for the blink function and
GazeX2 regressors and presented in Figure 1B, C ( p < .05, corrected for multiple comparisons
with family-wise error; see Supporting Information Table S1 for coordinates). We note these
findings were identified via a finite impulse response (FIR) analysis (see Methods) which esti-
mated the HRF shape per regressor. Regressions based on canonical HRF-convolved regressors
produced results that were not statistically significant.
Eye-tracking Data: Correlation with Eye Orbit EPI Data
We evaluated the correlation between each of the 12 types of eye tracking time series (see
Methods) and the EO-EPI data. We controlled for the 12 tests using Bonferroni correction, because
some of the eye-tracking measures were highly correlated (see Supporting Information Figure S4).
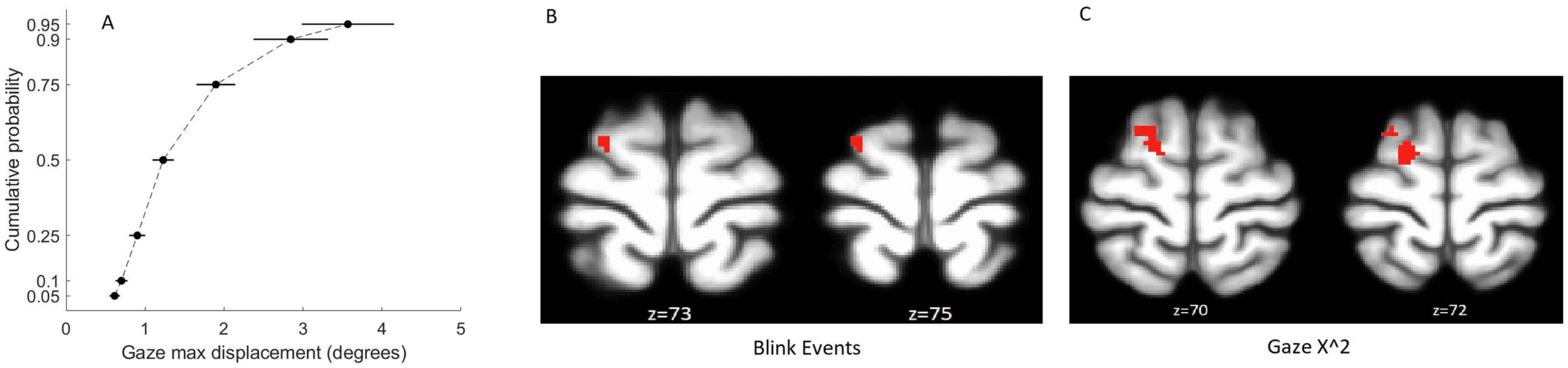
We identified three eye-tracking regressors that significantly predicted the EO-EPI envelope
(Bonferroni corrected for 12 tests): the gaze power (vel_GazeX2 + vel_GazeY2), square of pupil
size PupilSize2, and the gaze velocity in the vertical (Y ) direction. The pupil size was evaluated
as deviation from the subject’s mean value, so its squared value indicated absolute deviations from
mean value. We used squared deviation rather than absolute value as the derivative of the expo-
nent is better behaved than that of the absolute function. Figure 2A shows sample time series re-
flecting raw EO-EPI, its envelope, and eye-tracking regressors, and Figure 2B shows the estimated
Kernels for gaze power and square of pupil size.
Pupil size squared explained 7 ± 2% of the variance of the EO-EPI envelope and presented a
significant positive correlation: (cid:2) ¼ 0.17 ± 0.05, t(30) ¼ 3.45, p ¼ .0017, d ¼ 0.62. Gaze power
explained 5.4 ± 1.6% of the variance of the EO-EPI envelope and had a significant negative
correlation: (cid:2) ¼ −0.17 ± 0.03, t(30) ¼ 5.18, p < .001, d ¼ 0.93. These two variables jointly
explained the 11 ± 3% of EO-EPI envelope’s variance, a significant improvement in model per-
formance with respect to the single variable cases (ΔBIC < −2). Gaze velocity in the Y direction
had a weaker impact; it explained 3.7 ± 1.0% of the EO-EPI’s envelope variance and had a
significant positive correlation: (cid:2) ¼ 0.11 ± 0.03, t(30) ¼ 3.67, p < .001, d ¼ 0.66. Adding this
variable to the preceding regression model did not significantly increase explained variance
(ΔBIC ¼ −0.5). The exact numeric values corresponding to these kernels is given in
Supporting Information Table S2. Blinks were not significantly correlated with EO-EPI.
Figure 2. Relation between eye-tracking measures and EPI Orbit (EO-EPI) regressor. (A) sample time window showing relationship between
raw EO-EPI signal, EO-EPI Envelope used for Kernel computation, and pupil size and gaze power measures derived from simultaneously
acquired eye tracking data. (B) two Kernels estimated as relating the relationship between the EO-EPI envelope and pupil size (gray) or gaze
power (green). Note that peaks in eye-tracking gaze power (time ¼ 0) precede a peak in EO-EPI envelope by around 2 sec.
Network Neuroscience
462
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
Connectivity of EO-EPI regressors
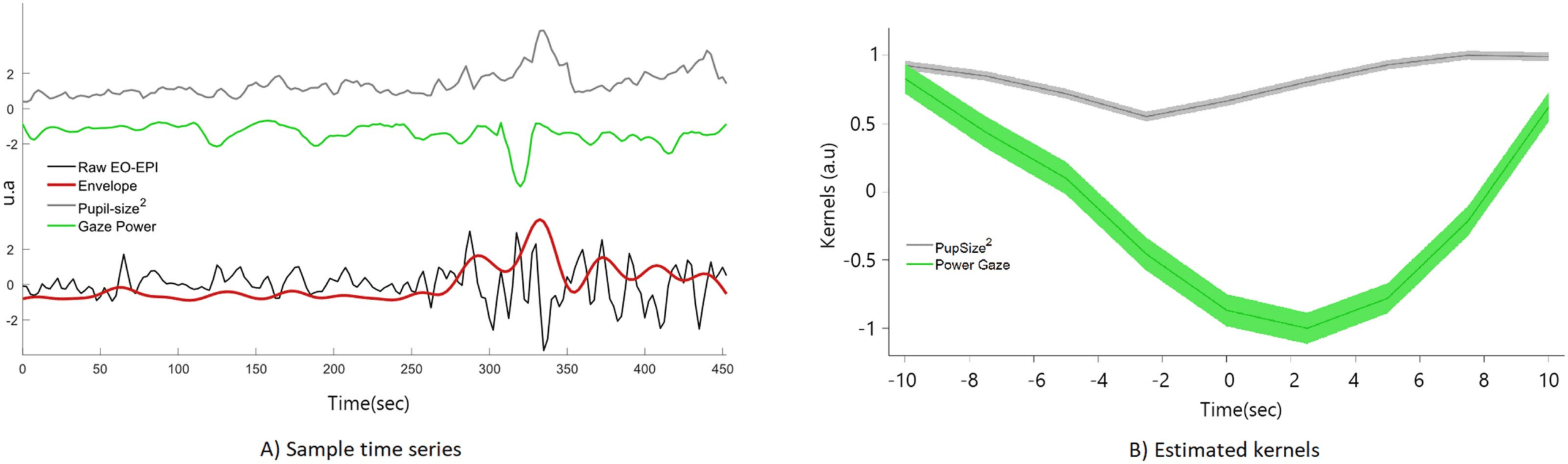
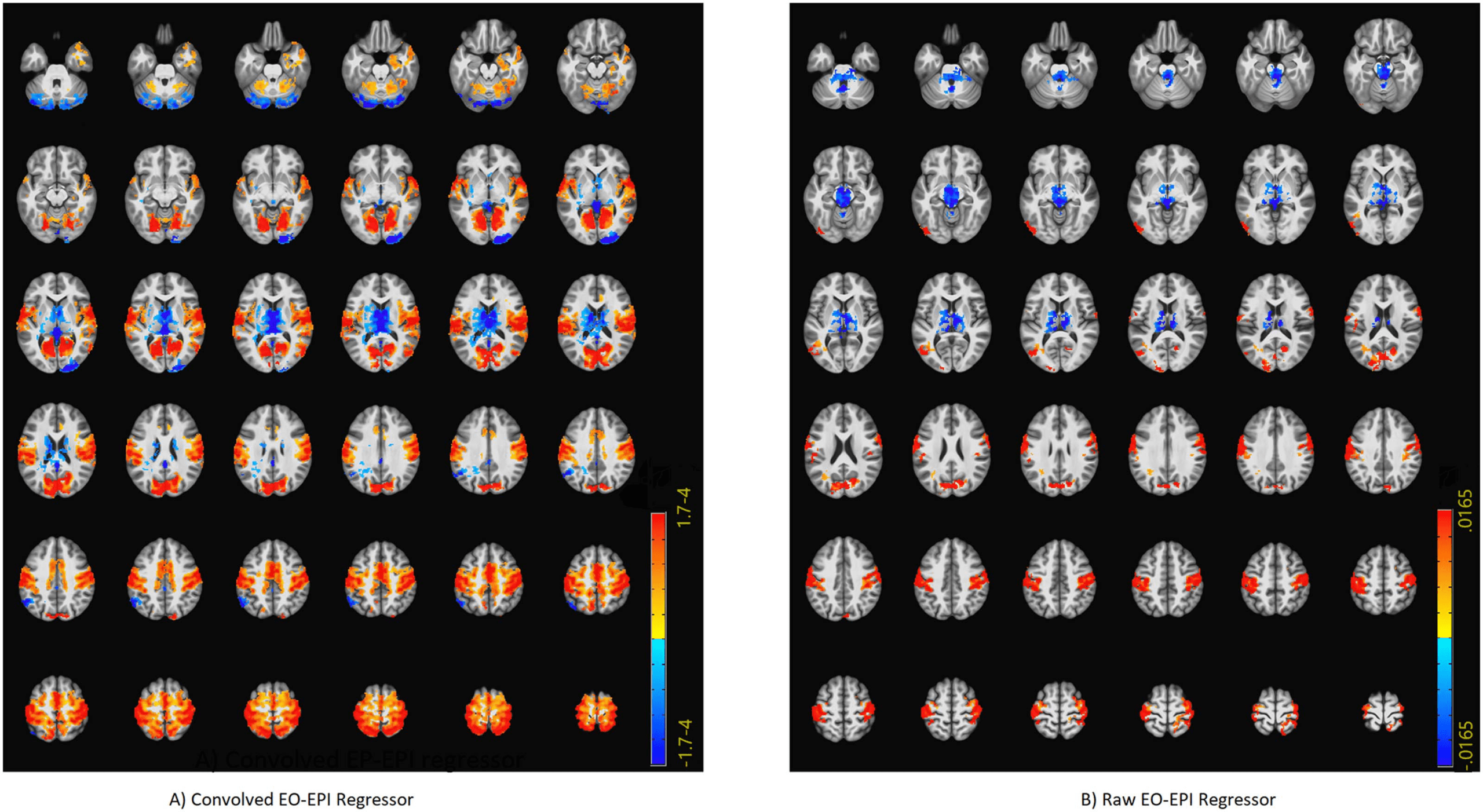
We identified an extensive system that correlated with the EO-EPI regressor. For the convolved
version of the EO-EPI regressor (EYEconv), we found correlations in pre- and postcentral gyri
bilaterally, parts of the superior temporal gyrus and visual cortex (Figure 3A). We also identified
strong correlations (of opposite sign) in the thalamus (Figure 4A). In addition, we identified
whole-brain correlations for the nonconvolved versions of the EO-EPI regressor (EYEraw).
These were qualitatively similar, but reduced in extent (see Figures 3B and 4B). Whole-brain
clusters in MNI space for the EYEraw and EYEconv regressors are reported in Supporting
Information Tables S3 and S4. We examined the effect size of the test for each voxel within
these statistically significant clusters. As shown in Supporting Information Figure S7, effect-size
values peaked at around 0.5 in sensorimotor and visual cortices. In addition, for each statisti-
cally significant cluster we evaluated whether correlations differed for younger and older par-
ticipants, but no cluster showed a statistically significant result. A region of interest analysis
indicated statistically significant correlations with EO-EPI in FEF ( Wilcoxon z ¼ 6.15, p <
.001) but not in SEF (z ¼ −1.28, p > .05).
An identical analysis that used time series from the maxillary sinus cavity rather than the eye
orbit area produced a different pattern of results: the distribution of clusters was mainly limited
to the sinus and eye areas with some ghosting presented along the Z-direction, as expected. Le
distribution does not resemble that found for the (nearby) eye orbit area (see Supporting
Information Figure S9).
En général, the tSNR of the raw time series was quite good across the cortex (see Supporting
Information Figure S8), with typical drop-off in low-signal areas and those susceptible to
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
un
_
0
0
1
8
6
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 3. Whole-brain connectivity maps for the EYEconv (UN) and EYEraw regressors (B). These were produced by deriving a mean time series
from each participant’s eye orbit, correlating it with each voxel’s time series, and then producing family-wise error-corrected group-level maps
using a single-voxel threshold of p < .01, and cluster correction based on permutations. ’Convolved’ refers to an analyses where the orbital
time series was convolved with an HRF basis function, whereas ’Raw’ refers to nonconvolved regressors.
Network Neuroscience
463
Eye movements during rest reduce resting-state network modularity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Axial slices showing whole-brain connectivity for the EYEconv (A) and EYEraw regressors (B). The figure reports the results of the same
analysis depicted in Figure 3, but overlaid on axial slices.
motion. Values were similar to the those reported by the Human Connectome Project for 2-mm
and 3-mm noncleaned data (Smith et al., 2013). We treated each cluster where BOLD activity
correlated with EO-EPI (raw or convolved) as a functional ROI and calculated the mean and
standard deviation of tSNR in each cluster across participants. Most of these areas were asso-
ciated with adequate tSNR, including the thalamus. This held for all statistically significant clus-
ters picked up by the EYEraw regressor (see Supporting Information Table S5). For EYEconv the
clusters found in the left and right cerebellum were associated with low tSNR (and relatively
systematically across participants, see Supporting Information Table S6), as was a cluster in the
mid occipital gyrus bilaterally (potentially as it includes time series from the field of view be-
tween the two hemisphere).
EO-EPI Regressor: Variance, Power Spectra, and Relation to Motion Parameters and Global Signal
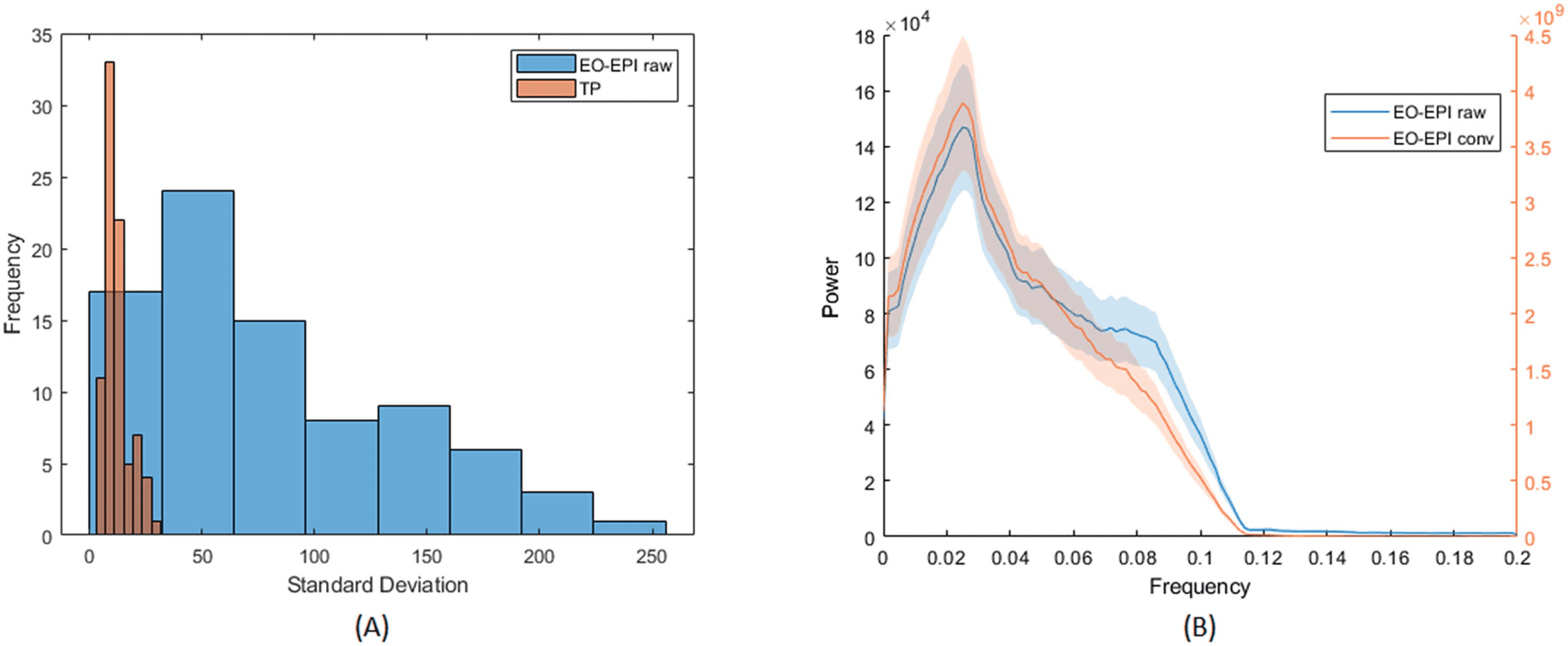
Across participants, the time series of the EO-EPI regressor presented a larger range of standard
deviation values than found in other ROIs. Figure 5A presents a histogram of the standard
deviation values for EYEraw in the participant group and comparative values from the temporo
parietal junction (TPJ). The standard deviation values for TP were relatively low and tightly
clustered in the range of 5–45, with a mode of 10. In contrast, for the EO-EPI regressor, there
was much less systematicity in the spread of values across participants: the distribution of stan-
dard deviation values was relatively more uniform and showed much larger values, some with
SD > 200. The mean number of voxels in these regions was 1,270 for TPJ and 406 for EYEraw.
Neurosciences en réseau
464
Eye movements during rest reduce resting-state network modularity
Chiffre 5. Spectral and spread properties of EO-EPI regressor. (UN) Across-participant distribution of standard deviations of EO-EPI time series
et (for comparison) average time series from temporoparietal junction ROI. (B) Frequency distribution of convolved and raw EO-EPI series.
Differences in order of magnitude are due to convolution with HRF basis function.
Convolution:
Mathematical transformation of
a function through the weights
provided by a second function that
is referred to as a ‘kernel.’ This
operation can be conducted both
in time, espace, or both.
The reason for these differences across participants is unclear. Cependant, a byproduct is that
when the EO-EPI regressor is correlated with brain activity in the context of regression, the re-
sulting beta values for this regressor have a very broad distribution with significant differences
across participants and outliers. For this reason, using a parametric test on the group level can
produce false negatives or positives. To illustrate, in this current study, when nonparametric
tests are used for group-level analysis, then both the Sign test and the Wilcoxon test produce
group-level significance maps as reported here. AFNI’s multilevel analysis 3DMEMA (G. Chen,
Saad, Nath, Beauchamp, & Cox, 2012), which downweights beta values from participants with
noisier beta estimates, produces similar results, though statistically weaker. Cependant, a typical
group-level t test of beta values against zero produced a null result.
The large standard deviation of the EO-EPI regressor was related to peaks in that signal. Comme
indicated in the Methods section, applying a ‘despiking’ procedure reduced the sensitivity of
the whole-brain correlation analysis: its most extreme effect was flattening several time series
from the eye orbit area, and in other cases it impacted a large number of time points in that area
(see Supporting Information Figure S5 for illustration). An analyses of the spectral features of
EO-EPI (Figure 5B) showed a strong peak in those time series at 0.04 Hz, c'est, a cycle of
25 sec. This is consistent with slow fluctuations sometimes observed in cortical regions. À
summarize, the EO-EPI regressor, as would be expected, presented some time domain features
(spikes and strong interindividual differences in spread) that differ from BOLD time series
acquired in the brain, and these need to be considered during preprocessing and group-level
analyses. That said, its spectral power presented a strong peak at low frequencies of the sort
seen for cortical BOLD time series.
With rare exceptions, EYEraw was not correlated with the estimated head motion parameters.
Significant correlations with any of the six motion parameters were found for 3 of the 83 par-
ticipants: in the first case there was correlation with L/R displacement; in the second case there
was correlation with L/R displacement and rotation; in the third case five of the six parameters
Neurosciences en réseau
465
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
un
_
0
0
1
8
6
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
were correlated. In all cases, correlation values were below 0.2. This lack of correlation sug-
gests that variance in EYEraw signal is not related to head motion, though an extreme case of
movement may be picked up in this signal as well. We also examined if the EYEraw EO-EPI
regressor reflected framewise displacement, as well as its relation to the global signal (defined
as mean gray matter signal after removal of motion, WM, and CSF regressors; see Methods). Pour
framewise displacement the group-level test on Fisher-Z normalized correlation values indicated
mean (and mode) value very close to zero (M ¼ 0.006, SD ¼ 0.14) producing a result that was not
statistically significant at the group level, t(82) ¼ 1.75, p > .05. For global signal the mean
(Z-normalized) correlation was statistically significant at the group level, t(82) ¼ 2.61, p < .01,
but the absolute mean Fisher-Z value was still close to zero (M ¼ 0.04, SD ¼ 0.14), which
corresponds to a mean Pearson’s R value of around 0.04.
Functional Connectivity Networks
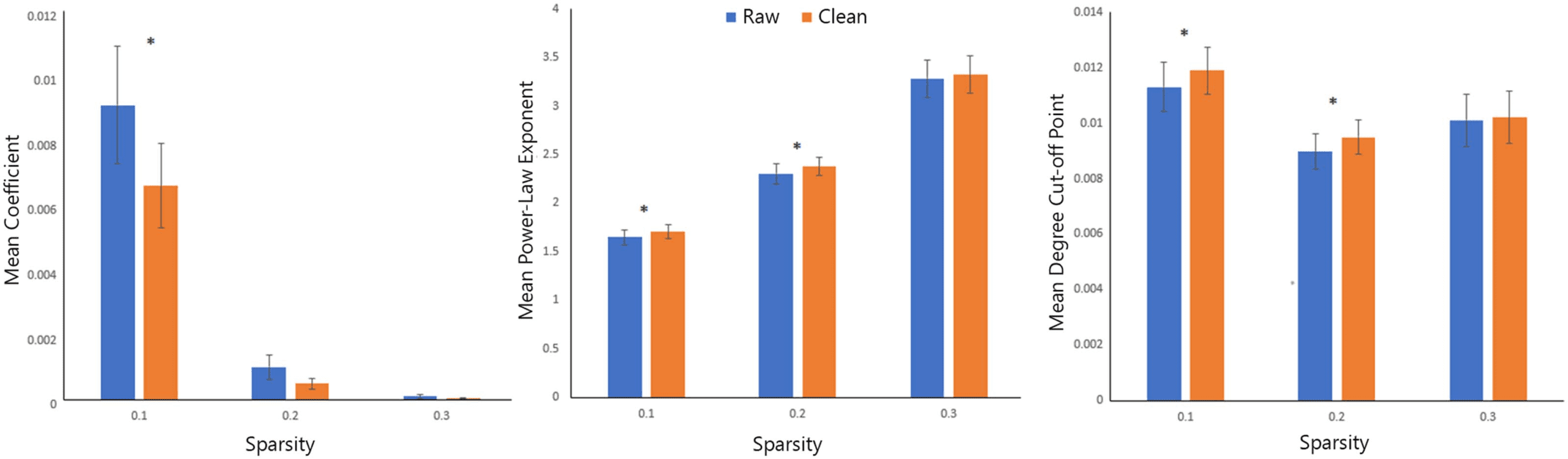
An analysis of the network metrics revealed that several were significantly impacted by EO-EPI
removal, across all sparsity thresholds. The raw connectivity matrices presented higher values
for node strength (both maximum and mean), and mean cluster coefficient (and transitivity).
Conversely, maximized modularity was greater for the clean (EO-EPI-removed) matrices.
Difference values, effect sizes, and results of statistical tests are reported in Table 1 and in
Supporting Information File 1. As shown in the Tables, statistically significant results were
Table 1. Difference of network metrics between Raw and Clean (EO-EPI-removed) functional connectivity matrices.
Sparsity == 0.1
Preserved nodes == 1,248
Sparsity == 0.2
Preserved nodes == 2,495
Difference Cohen’s D T-stat Difference Cohen’s D T-stat Difference Cohen’s D T-stat
−0.22
Sparsity == 0.3
Preserved nodes == 3,743
−0.04
3.40**
3.33**
0.37
1.23
0.38
0.74
0.02
Max Degree
Min Degree
Max Strength
Min Strength
Mean Strength
Max Cluster Coefficient
Min Cluster Coefficient
Mean Cluster Coefficient
Transitivity
Assortativity
Efficiency
Max Number of Community
3.45
2.45
8.03
0.99
0.50
6.05
1.08
1.92
0.31
0.12
0.02
Maximized modularity
Max betweenness centrality
−0.007
−0.21
Mean betweenness centrality
0.86
0.04
0.49
0.10
0.49
0.12
0.02
0.46
0.46
0.06
0.18
0.01
0.44
0.02
0.41
0.38
−2.58
4.41***
2.11
0.86
4.36***
1.06
0.14
−4.59
1.22
1.21
−3.52
4.11***
1.65
4.11***
0.54
1.60
0.10
2.39
1.44
0.58
−0.02
−3.95***
−0.005
−0.16
3.70***
0.12
0.76
0.08
0.46
0.16
0.46
0.26
0.08
0.47
0.46
0.22
0.49
0.05
0.38
0.01
0.39
−0.76
−1.90
4.13***
1.91
−1.47
−2.51
4.14***
2.32*
1.38
1.87
−0.70
−1.43
4.22***
1.84
4.14***
1.95
4.39***
2.49
2.12
0.80
−0.42
−0.02
−3.36**
−0.003
0.10
3.50***
0.65
0.25
0.10
0.42
0.14
0.44
0.32
0.07
0.44
0.45
0.28
0.46
0.05
0.34
0.07
0.14
−0.92
3.79***
−1.26
3.94***
2.90**
−0.61
3.94***
3.99***
2.46*
4.07***
−0.44
−3.03**
0.63
1.29
Note. Differences shown are in units of percentage apart from the number of communities and maximized modularity which maintain the original scale; *p < .05,
**p < .005, ***p < .001.
Network Neuroscience
466
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
associated with medium effect sizes in the range of 0.4–0.5. These results maintained almost
without exception for networks at sparsity levels of 0.01 to 0.09 (see Supporting Information
File 1). Supporting Information Table S7 reports the raw values for each metric, for the sparsity
levels of 10%, 20%, 30%. In addition, we determined if age modulated the impact of EO-EPI
removal on network metrics. We computed for each person the impact of EO-EPI removal for
each network property and then tested if these values differ between age groups. None of the
tests were significant. An across-participant correlation analysis indicated that modularity was
generally negatively correlated with measures that load on stronger connectivity, including
degree, strength and clustering coefficient (see Discussion).
Fitting the degree distributions using an exponentially truncated power law showed that the
EO-EPI removed networks differed in the degree distribution (see Figure 6). As shown in
Figure 6, for 10% sparsity networks, EO-EPI removal impacted all three coefficients of the trun-
cated power-law fit: power law coefficient: t(82) ¼ 3.33, p < .01, d ¼ 0.37, power law expo-
nent, t(82) ¼ −3.70, p < .001, d ¼ 0.41, and degree cutoff point, t(82) ¼ 3.59, p < .001, d ¼ 0.4.
For the 20% sparsity networks, differences were found for power law exponent, t(82) ¼ −3.13,
p < .01, d ¼ 0.37, and degree cutoff point, t(82) ¼ 2.59, p < .01, d ¼ 0.33. No statistically
significant differences were found for 30% sparsity networks. Supporting Information Figure
S10 presents mean degree distributions for Raw and Clean networks for these sparsity levels.
We determined which areas tended to show changes in connectivity as a function of EO-EPI
removal. In general, this analysis is not independent of the whole-brain correlation with the EO-
EPI time series used as a regressor, but it is more sensitive in identifying strongest pairwise dif-
ferences. For each of the 124,500 pairwise correlations we conducted a t test to determine
whether the pairwise correlations differed for raw and EO-EPI-removed connectivity matrices.
The results (FDR corrected; Figure 7) showed that connectivity matrices constructed from the
raw matrices presented stronger connectivity between sensorimotor areas and temporoparietal,
dorsal attention, visual cortex, and other sensorimotor regions. There were relatively few re-
gions that showed stronger connectivity in the EO-EPI-removed condition, notably the posterior
cingulate, which showed stronger connectivity with multiple other brain areas.
The dual regression analysis did not identify any predefined RS network for which connec-
tivity changed significantly. A hub-focused analysis that examined whether there were regions
Figure 6. Analysis of degree distributions. Degree distributions were fit using an exponentially-truncated power law with three parameters:
coefficient, power law exponent, power law cutoff point. The three bar plots show the mean values of these parameters across the three largest
sparsity levels. Bar pairs for which a difference was significant are marked with a star (*). For sparsity of 0.1, all three parameters differed
between raw and clean (EO-EPI removed) connectivity matrices.
Network Neuroscience
467
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7.
Impact of EO-EPI removal on pairwise connectivity. For each participant, 500-region connectivity matrices were produced from
time series from which the variance attributable to EO-EPI was either removed (‘clean’) or not (‘raw’). Pairwise connectivity differences were
then computed at group level to identify region pairs where EO-EPI removal produced a change in connectivity strength. Family-wise control:
Raw − Clean, p < .05 two tailed, for each single connection, corrected for multiple comparisons using FDR.
more frequently identified as hubs in the raw or EO-EPI-removed series also produced a null
result: the most extreme example was a region defined as hub for 20 participants in one case
and 25 in another (a nonsignificant difference on a binomial). While the location of these hubs
was not a central point of the current study, broadly speaking, for the 10% sparsity threshold
(raw) matrices, hubs were localized to motor and sensorimotor areas (9 regions) Dorsal atten-
tion (6 regions), DMN (4 regions), temporal-parietal areas (4 regions), and ventral attention
(2 areas). Only one visual extrastriate area was identified as a hub.
DISCUSSION
Neuroimaging is continuously expanding our understanding of the principles that determine
organized patterns of RS connectivity. Our findings demonstrate that endogenous eye move-
ments during RS contribute significantly to structured patterns of RS connectivity. Our main
finding is that eye movements, measured via EPI time series recorded from the eye orbits,
Network Neuroscience
468
Eye movements during rest reduce resting-state network modularity
identified a sensorimotor system that appeared to be linked to oculomotor activity. Removal of
activity accounted for by eye movements had systematic impact on whole-brain connectivity.
We first address issues related to oculomotor measurement during the resting state that emerged
in the study and then discuss the implications of the results for basic and applied research.
Probing Resting-state Networks with Eye Tracking and Eye Orbit EPI Data
As reviewed in the Introduction, few studies have studied brain activity patterns that are corre-
lated with oculomotor activity during the resting state, and those have produced inconsistent
and sometimes puzzling results. The most relevant is Fransson et al. (2014, N ¼ 18): It derived
gaze velocity data from eye tracking during a resting-state scan, finding correlation with DMN
activity. Also related is McAvoy et al. (2012, N ¼ 9), which examined Brain/EOG correlations
and reported a null result. In our own analyses of eye tracking data (N ¼ 32), we found corre-
lation between BOLD-RS and only two eye tracking metrics: horizontal eye displacement and
blinks. These relatively modest correlations could be the result of noise in the eye tracking data,
which presented itself in higher power across all frequencies for rejected data as compared to
analyzed data. We also note that participant exclusion for the eye tracking data was more ex-
tensive in the older age group, and so future studies of related topics could prefer to collect data
from younger participants unless there is a specific interest in the older population.
We found correlations between the eye tracking metrics and EPI data recorded from the eye
orbit area (EO-EPI), Bonferroni corrected for 12 correlation tests. These were found for gaze
power, pupil size (squared), and gaze velocity in the Y (horizontal) direction. These data are
consistent with several prior reports. Beauchamp (2003) showed that peaks in the EO-EPI time
series occur when an MR acquisition coincides with a rapid saccadic eye movement. Brodoehl,
Witte, and Klingner (2016) and Son et al. (2019) showed that EO-EPI data can be used to esti-
mate gaze location (when nonaveraged; i.e., used in a multivariate context). In addition,
Beauchamp’s observations suggest that for our interleaved acquisition, eye movements occur-
ring either during odd- (up direction) or even-numbered (down direction) slice acquisition
could be picked up in the analysis, because we treated the entire eye orbit as a single ROI.
Consequently, while the volume acquisition time was 2.5 sec, our effective temporal resolution
for the eye orbit ROI could have been higher, as we could identify eye movement during both
the up- or down-acquisition direction. EO-EPI fluctuations are likely mainly driven by signal
disturbances due to air/tissue motion, but we cannot exclude the possibility that the signal also
contains a BOLD component, due to the metabolic activity in nearby muscles. In particular, Law
(1998) used PET rCBF to study brain systems involved in generation of voluntary saccades and
reported active areas in the eye orbit, “primarily located close to the apex of the pyramidal
shaped orbital cavity.” Our finding of a systematic delayed coupling in which changes in gaze
power preceded local minima in EO-EPI fluctuations (the latter delayed by (cid:2)2 sec), and of a
strong peak frequency of 0.04 Hz for EO-EPI are both consistent with the possibility that EO-EPI
also reflects metabolic activity. We also found little independent evidence to suggest a strong
contribution of motion artifacts to EO-EPI: beyond one participant for which five of six motion
parameters correlated with EO-EPI, we only found two additional correlations with motion
elements, for two additional participants. In addition, regarding framewise displacement (FD),
this regressor too was removed prior to the EO-EPI analysis, and separately, we found no
systematic relation between FD and EO-EPI on the single-participant level. With respect to
relation to Global Signal (derived here from gray matter), we found a statistically significant
relation with EO-EPI, but the absolute magnitude of correlation was modest with mean
Pearsons’s R value of around 0.04. A modest component of GS could therefore be related to eye
movements.
Network Neuroscience
469
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
Note that task compliance during this RS study was good. First, participants were continuously
monitored and experimenters verified participants did not drift off to sleep during the scan.
Second, the eye tracking data indicated compliance with the task instructions in that the eye
movements that were made during fixation were modest in magnitude (see Figure 1A). When eval-
uating average eye movement between successive 2 sec epochs, we found that in 75% of the
cases, the magnitude was below 2°, which corresponds to a small displacement. For this reason,
we consider these data to be representative of typical compliant behavior during wakeful rest.
Given these findings, it can still be asked whether, practically, one should control for ocu-
lomotor influences measured by EO-EPI in future work. On the basis of these findings we sug-
gest that EO-EPI should not be treated as a nuisance factor with the exception of very specific
circumstances. In contrast to factors such as head motion that are a nuisance factor that com-
plicate studying BOLD functions related to neural activity, EO-EPI/BOLD correlates do not ap-
pear to be spurious or necessarily linked to nonneural causes. For this reason, EO-EPI
covariance should be maintained in the data, unless one has a very specific interest in those
facets of brain connectivity (or dynamics) that are completely unrelated to the function of the
brain’s motor systems. Otherwise, EO-EPI should be treated as an identifiable independent fac-
tor that is informative with respect to the natural function of oculomotor systems.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Brain Systems Identified by Eye Orbit EPI (EO-EPI) Regressor
When used as a whole-brain regressor, the EO-EPI time series correlated with an extensive bi-
lateral sensorimotor system. In addition, activity was found in superior parietal lobule, the dor-
sal part of the superior frontal gyrus, supplementary motor areas, and the extrastriate cortex in
occipital lobe (excluding striate cortex). There was no indication for differences between youn-
ger and older participants in these areas. ROI analyses indicated activity in frontal eye fields.
The topography of this system does not match either the ventral or dorsal attention networks as
usually defined, but it is quite similar to the frontal-eye-field connectivity map reported by Fox,
Corbetta, Snyder, Vincent, and Raichle (2006). It is also highly similar to activity maps reported
for simple eye movements in absence of attention, which have identified extensive activity in
motor and premotor areas (e.g., Balslev et al., 2011) with little fronto-parietal involvement. A
subset of these regions was also picked up by a nonconvolved (‘Raw’) version of the EO-EPI
regressor which may indicate that activity in these areas does not precede eye movements, but
is relatively contemporaneous with them (to the extent that can be inferred from fMRI), or even
that the eye movements reflected in the EO-EPI time series follow activity in those areas.
The brain areas we identify using EO-EPI (or eye tracking regressors) depart from ones fre-
quently mentioned in studies of saccadic mechanisms, which prototypically reveal involve-
ment of FEF/SEF and IPS. There are several possible explanations for this, which are not
mutually exclusive. First, neuroimaging studies of saccades study saccade execution under ex-
ogenously determined conditions. Specifically, a distinction is made between two saccade cat-
egories, both externally controlled: ‘reflexive’ saccades that orient to peripheral (typically
sudden) target appearance, and ‘voluntary’ saccades that are not oriented toward a target in
an unmediated manner but rather require a cognitive judgment prior to eye movement (for re-
view, see Mort et al., 2003). These voluntary saccades are studied by paradigms such as anti-
saccades (saccading to the opposite screen side of a target), memory-guided saccades
(saccading to a location maintained in memory), or saccading to a location precued by an ar-
row. Note that both reflexive and voluntary saccades are associated with few degrees of free-
dom with respect to the actual saccade target, which constitutes a fundamental difference from
the resting-state case. In addition, as indicated by Brown et al.’s study (reviewed in the
Network Neuroscience
470
Eye movements during rest reduce resting-state network modularity
Introduction), activity in FEF/SEF/IPS may not be related to oculomotor control per se, but to the
paradigm demands that require attention and detection of visual cues. In support of this possi-
bility, a recent study (Agtzidis, Meyhöfer, Dorr, & Lencer, 2020) examining eye movements
during naturalistic movie viewing similarly failed to identify a frontal parietal system related
to saccades (neither dorsal nor ventral attention systems; see their Table 2), but instead docu-
mented saccade-related activity in visual cortex, and smooth-pursuit activity in precuneus, cin-
gulate, and occipital cortices. The authors attribute this failure to differences in paradigm,
suggesting that natural viewing is associated with constant engagement rather than phasic shifts
between fixation and saccades. This is also corroborated by a report by Son et al. (2019, N ¼ 5)
showing that during naturalistic viewing, data acquired from the eye orbits correlates with brain
activity in areas that do not resemble the topography of attentional networks (see their Figure 5).
Another possibility, which does not assume substantial differences between RS and active
tasks, is technical in nature. It is possible that endogenous oculomotor-linked sensory motor
activity during resting state is simply not often reported just because fixation is frequently used
as an implicit baseline in many oculomotor studies. If the network we identify is correlated
with oculomotor activity both during fixation and saccade-to-target epochs (either reflexive
or voluntary), then it will not be identifiable in analyses against baseline because it is partialled
out in the contrast.
The Impact of Removal of EO-EPI Properties from BOLD Activity
We examined the impact of removing the variance related to EO-EPI from brain activity using a
few well-defined topographical and topological properties. For topography we found that
removal did not have a statistically significant impact on connectivity in any of the 14 well-
defined resting-state networks. We also examined the impact of removal on pair-wise regional
connectivity using a 500-ROI parcellation (Schaefer et al., 2018). We grouped these 500 re-
gions into 7 main clusters for purposes of graphical presentation (see Figure 7). The analysis
produced statistically significant effects (FDR corrected), mainly showing that EO-EPI-removal
was associated with reduced connectivity between the somatomotor regions and visual, tem-
poroparietal, and also few dorsal-attention network areas. Also as shown in Figure 7, connec-
tivity within each system was weakly impacted by EO-EPI removal if at all (i.e., few changes
along the diagonal), which is consistent with the dual-regression results. To conclude, EO-EPI-
removal appeared to primarily impact cross-network connectivity rather than within-network
connectivity. Finally, we did not find evidence that EO-EPI removal impacted the distribution of
network hubs in the brain.
However, robust results were found for both global and local topological metrics identified
by a network analysis, and we found no evidence that these differed for the younger and older
participants. Here we address findings that were consistent across the three largest sparsity
thresholds: 10%, 20%, and 30% of connections. For global properties, we find that modularity
(Q) was higher for the clean matrices. We note that, across participants, modularity negatively
correlated with local properties including degree, strength. and clustering coefficient. It may be
that the finding of reduced modularity for clean matrices owes to its relation to certain other
connectivity measures. One specific possibility is that weaker connectivity necessarily pro-
duces lower modularity. This, however, seems not to be the case, as it has been shown that
periods of high modularity can be found for epochs of both very high and very low connectivity
(Betzel, Fukushima, He, Zuo, & Sporns, 2016).
For local properties, we found that the raw matrices were associated with greater node-
strength values (indicating sum of connectivity linked to each node). For max strength, the
Network Neuroscience
471
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
difference was 2.45% (effect size ¼ 0.49). The mean cluster coefficient (and strongly related,
transitivity) were also impacted, showing reduced values (approaching 2.5% difference; effect
size ¼ 0.49) for the cleaned time series.
These changes are consistent with our other findings. EO-EPI is correlated with occipital,
sensorimotor and few fronto-parietal areas, and as shown, EO-EPI removal predominantly
impacts interregional/interinternetwork connections rather than intranetwork connections.
For this reason, its removal serves to increase the modularity of resting-state networks.
Implications for Network Studies of Typical and Apecial Populations
Graph theoretical approaches are increasingly applied in the context of resting-state fMRI stud-
ies of clinical disorders (Hallquist & Hillary, 2018). In some cases, these features are deployed
clinically to define new clinical subtypes, and in other cases, they are used to advance under-
standing of the brain systems that may be associated with the clinical deficit. Being able to link
differences in graph-theoretic metrics to the oculomotor systems can increase the specificity of
the explanations provided by RS analyses, by linking differences to a specific behavior. It could
also allow determining to what extent differences in RS connectivity between populations can
be attributed to differences in oculomotor activity during resting-state acquisition.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A number of examples present the logic of this approach. For example, Parkinson’s disease
(PD) is associated with changes to functional connectivity when analyzed both from dynamic
and static perspectives (Kim et al., 2017). Neurophysiologically, it is associated with abnormal-
ity in eye movement control, including the generation of voluntary saccades. Anomalies are
more evident for voluntary saccades, in early stages of disease (for review, see Pretegiani &
Optican, 2017). A behavioral study (Zhang et al., 2018) showed that PD is linked to reduced
fixation stability when fixation is required. Conversely, during free viewing of single images, PD
patients make fewer saccadic eye movements, and within a more narrow range. Differences in
network modularity for clinical populations have been documented in the case of autism,
which present lower modularity (Rudie et al., 2013) and traumatic brain injury (Han et al.,
2014), which has been associated with higher modularity and lower participation coefficient
of sensorimotor systems (i.e., these areas are more weakly involved in between-module con-
nectivity). In addition, schizophrenia (e.g., Alexander-Bloch et al., 2012) has been linked to
changes in RS connectivity. Alexander-Bloch et al. showed that schizophrenia is associated
with reduced modularity in functional networks, with motor areas bilaterally linked to different
partitions. Individuals diagnosed with schizophrenia show lower mean saccade frequency dur-
ing free gaze (Dowiasch et al., 2016) and during free viewing of photos, their gaze is limited to
smaller areas of the photo (e.g., Morita et al., 2020; Silberg et al., 2019).
Our findings could also have implications for the study of dynamic, time-varying connec-
tivity in healthy and clinical populations. Knowing that some dynamic changes are associated
with phasic states of eye movements would allow better interpretation of the drivers of time-
varying dynamics. An early study of time-varying dynamics (Hutchison, Womelsdorf, Gati,
Everling, & Menon, 2013) is consistent with this possibility. It documented time points present-
ing phasic, strong connectivity between frontal eye fields, sensorimotor regions and occipital
regions, whereas such connectivity was completely absent at other time points. This suggests
temporary synchronization of multiple brain networks in relation to eye movement.
Conclusions
We found that oculomotor movement provides a systematic contribution to RS connectivity in
the human brain. It is correlated with activity in a brain network that largely involves
Time-varying connectivity:
An approach for studying time-
varying aspects of functional
connectivity.
Network Neuroscience
472
Eye movements during rest reduce resting-state network modularity
sensorimotor and visual cortex, as well as the frontal eye fields. Removal of oculomotor con-
tribution, as quantified via EPI time series sampled from the eye orbit area, produces changes to
global topological features of RS networks. Isolating this contribution can produce a better un-
derstanding of activity sources that organize RS networks in health and disease, and could im-
prove the use of RS network features in the context of machine learning.
ACKNOWLEDGMENTS
The authors are grateful to the Sleepy Brain project team for openly sharing the data, to staff
physicist Rouslan Sitnikov for technical advice, and to Jorge Jovicich for assistance in assess-
ment of ghosting artifacts.
SUPPORTING INFORMATION
Supporting information for this article is available at https://www.doi.org/10.1162/netn_a
_00186.
AUTHOR CONTRIBUTIONS
Cemal Koba: Formal analysis; Investigation; Methodology; Visualization; Writing – original draft;
Writing – review & editing. Giuseppe Notaro: Formal analysis; Methodology; Visualization;
Writing – original draft; Writing – review & editing. Sandra Tamm: Data curation; Investigation;
Resources; Writing – review & editing. Gustav Nilsonne: Data curation; Investigation; Resources;
Writing – review & editing. Uri Hasson: Conceptualization; Investigation; Methodology;
Supervision; Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
Gustav Nilsonne, Riksbankens Jubileumsfond (https://dx.doi.org/10.13039/501100004472),
Award ID: P15-0310:1. Gustav Nilsonne, Fredrik och Ingrid Thurings Stiftelse (https://dx.doi
.org/10.13039/501100003186), Award ID: 2014-00037, 2015-00170.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
REFERENCES
Agtzidis, I., Meyhöfer, I., Dorr, M., & Lencer, R. (2020). Following
Forrest Gump: Smooth pursuit related brain activation during free
movie viewing. NeuroImage, 116491. https://doi.org/10.1016/j
.neuroimage.2019.116491, PubMed: 31923604
Alexander-Bloch, A., Lambiotte, R., Roberts, B., Giedd, J., Gogtay,
N., & Bullmore, E. (2012). The discovery of population differences
in network community structure: New methods and applications
to brain functional networks in schizophrenia. NeuroImage, 59(4),
3889–3900. https://doi.org/10.1016/j.neuroimage.2011.11.035,
PubMed: 22119652
Avants, B. B., Tustison, N., & Song, G. (2011). Advanced Normalization
Tools (ANTS) Brian B. Avants, Nick Tustison and Gang Song, 1–35.
Retrieved from www.picsl.upenn.edu/ANTS.
Balslev, D., Albert, N. B., & Miall, C. (2011). Eye muscle proprio-
ception is represented bilaterally in the sensorimotor cortex.
Human Brain Mapping, 32(4), 624–631. https://doi.org/10.1002
/hbm.21050, PubMed: 21391252
Beauchamp, M. S. (2003). Detection of eye movements from fMRI
data. Magnetic Resonance in Medicine, 49(2), 376–380. https://
doi.org/10.1002/mrm.10345, PubMed: 12541259
Becker, W., & Fuchs, A. (1969). Further properties of the human sac-
cadic system: Eye movements and correction saccades with and
without visual fixation points. Vision Research, 9(10), 1247–1258.
https://doi.org/10.1016/0042-6989(69)90112-6, PubMed:
5360604
Beckmann, C., Mackay, C., Filippini, N., & Smith, S. (2009). Group
comparison of resting-state fMRI data using multi-subject ICA
and dual regression. NeuroImage. https://doi.org/10.1016/s1053
-8119(09)71511-3
Betzel, R. F., Fukushima, M., He, Y., Zuo, X.-N., & Sporns, O. (2016).
Dynamic fluctuations coincide with periods of high and low
modularity in resting-state functional brain networks. NeuroImage,
127, 287–297. https://doi.org/10.1016/j.neuroimage.2015.12.001,
PubMed: 26687667
Birn, R. M. (2012). The role of physiological noise in resting-state
functional connectivity. NeuroImage, 62(2), 864–870. https://doi
.org/10.1016/j.neuroimage.2012.01.016, PubMed: 22245341
Brodoehl, S., Witte, O. W., & Klingner, C. M. (2016). Measuring eye
states in functional MRI. BMC Neuroscience, 17(1). https://doi.org
/10.1186/s12868-016-0282-7, PubMed: 27411785
Network Neuroscience
473
Eye movements during rest reduce resting-state network modularity
Brown, M. R., Goltz, H. C., Vilis, T., Ford, K. A., & Everling, S. (2006).
Inhibition and generation of saccades: Rapid event-related fMRI of
prosaccades, antisaccades, and no go trials. NeuroImage, 33(2),
644–659. https://doi.org/10.1016/j.neuroimage.2006.07.002,
PubMed: 16949303
Chen, G., Saad, Z. S., Nath, A. R., Beauchamp, M. S., & Cox, R. W.
(2012). fMRI group analysis combining effect estimates and their
variances. NeuroImage, 60(1), 747–765. https://doi.org/10.1016
/j.neuroimage.2011.12.060, PubMed: 22245637
Chen, J., Lewis, L., Chang, C., Tian, Q., Fultz, N., Ohringer, N., …
Polimeni, J. (2020). Resting-state “physiological networks.”
NeuroImage, 116707. https://doi.org/10.1016/j.neuroimage.2020
.116707, PubMed: 32145437
Chen, W., & Zhu, X.-H. (1997). Suppression of physiological eye
movement artifacts in functional MRI using slab presaturation.
Magnetic Resonance in Medicine, 38(4), 546–550. https://doi
.org/10.1002/mrm.1910380407, PubMed: 9324320
Cox, R. W. (1996). AFNI: Software for analysis and visualization of
functional magnetic resonance neuroimages. Computers and
Biomedical Research, 29(3), 162–173. https://doi.org/10.1006
/cbmr.1996.0014, PubMed: 8812068
de Vos, F., Koini, M., Schouten, T. M., Seiler, S., van der Grond, J.,
Lechner, A., … Rombouts, S. A. (2018). A comprehensive anal-
ysis of resting state fMRI measures to classify individual patients
with Alzheimer’s disease. NeuroImage, 167, 62–72. https://doi
.org/10.1016/j.neuroimage.2017.11.025, PubMed: 29155080
Dowiasch, S., Backasch, B., Einhäuser, W., Leube, D., Kircher, T.,
& Bremmer, F. (2016). Eye movements of patients with schizo-
phrenia in a natural environment. European Archives of
Psychiatry and Clinical Neuroscience, 266(1), 43–54. https://doi
.org/10.1007/s00406-014-0567-8, PubMed: 25472882
Dubois, J., Galdi, P., Paul, L. K., & Adolphs, R. (2018). A distributed
brain network predicts general intelligence from resting-state hu-
man neuroimaging data. Philosophical Transactions of the Royal
Society B: Biological Sciences, 373(1756), 20170284. https://doi
.org/10.1098/rstb.2017.0284, PubMed: 30104429
Fonov, V., Evans, A., McKinstry, R., Almli, C., & Collins, D. (2009).
Unbiased nonlinear average age-appropriate brain templates
from birth to adulthood. NeuroImage. https://doi.org/10.1016
/s1053-8119(09)70884-5
Fornito, A., Zalesky, A., & Bullmore, E. T. (2010). Network scaling
effects in graph analytic studies of human resting-state fMRI data.
Frontiers in Systems Neuroscience, 4, 22. https://doi.org/10.3389
/fnsys.2010.00022, PubMed: 20592949
Fox, M. D., Corbetta, M., Snyder, A. Z., Vincent, J. L., & Raichle, M. E.
(2006). Spontaneous neuronal activity distinguishes human
dorsal and ventral attention systems. Proceedings of the National
Academy of Sciences, 103(26), 10046–10051. https://doi.org/10
.1073/pnas.0604187103, PubMed: 16788060
Fransson, P., Flodin, P., Seimyr, G., & Pansell, T. (2014). Slow fluctu-
ations in eye position and resting-state functional magnetic reso-
nance imaging brain activity during visual fixation. European
Journal of Neuroscience, 40(12), 3828–3835. https://doi.org/10
.1111/ejn.12745, PubMed: 25302817
Hallquist, M. N., & Hillary, F. G. (2018). Graph theory approaches
to functional network organization in brain disorders: A critique
for a brave new small-world. Network Neuroscience, 3(1), 1–26.
https://doi.org/10.1162/netn_a_00054, PubMed: 30793071
Han, K., Mac Donald, C. L., Johnson, A. M., Barnes, Y., Wierzechowski,
L., Zonies, D., … Brody, D. L. (2014). Disrupted modular orga-
nization of resting-state cortical functional connectivity in US mil-
itary personnel following concussive ‘mild’ blast-related
traumatic brain injury. NeuroImage, 84, 76–96. https://doi.org
/10.1016/j.neuroimage.2013.08.017, PubMed: 23968735
Hayes, T. R., & Petrov, A. A. (2016). Mapping and correcting the
influence of gaze position on pupil size measurements. Behavior
Research Methods, 48(2), 510–527. https://doi.org/10.3758
/s13428-015-0588-x, PubMed: 25953668
Honey, C., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J.-P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Proceedings
of the National Academy of Sciences, 106(6), 2035–2040. https://
doi.org/10.1073/pnas.0811168106, PubMed: 19188601
Hutchison, R. M., Womelsdorf, T., Gati, J. S., Everling, S., & Menon,
R. S. (2013). Resting-state networks show dynamic functional con-
nectivity in awake humans and anesthetized macaques. Human
Brain Mapping, 34(9), 2154–2177. https://doi.org/10.1002/hbm
.22058, PubMed: 22438275
Iacovella, V., Faes, L., & Hasson, U. (2018). Task-induced deacti-
vation in diverse brain systems correlates with interindividual dif-
ferences in distinct autonomic indices. Neuropsychologia, 113,
29–42. https://doi.org/10.1016/j.neuropsychologia.2018.03.005,
PubMed: 29530799
Iacovella, V., & Hasson, U. (2011). The relationship between bold
signal and autonomic nervous system functions: Implications for
processing of “physiological noise.” Magnetic Resonance
Imaging, 29(10), 1338–1345. https://doi.org/10.1016/j.mri.2011
.03.006, PubMed: 21543181
Jenkinson, M., Beckmann, C. F., Behrens, T. E., Woolrich, M. W., &
Smith, S. M. (2012). FSL. Neuroimage, 62(2), 782–790. https://doi
.org/10.1016/j.neuroimage.2011.09.015, PubMed: 21979382
Kelly, A. C., Uddin, L. Q., Biswal, B. B., Castellanos, F. X., &
Milham, M. P. (2008). Competition between functional brain
networks mediates behavioral variability. NeuroImage, 39(1),
527–537. https://doi.org/10.1016/j.neuroimage.2007.08.008,
PubMed: 17919929
Kim, J., Criaud, M., Cho, S. S., Díez-Cirarda, M., Mihaescu, A.,
Coakeley, S., … Strafella, A. P. (2017). Abnormal intrinsic brain
functional network dynamics in Parkinson’s disease. Brain, 140(11),
2955–2967. https://doi.org/10.1093/ brain/awx233, PubMed:
29053835
Koba, C. (2021). NetNeuroSleepyBrain, GitHub, https://github.com
/KobaCemal/SleepyBrain
Law, I. (1998). Parieto-occipital cortex activation during self-generated
eye movements in the dark. Brain, 121(11), 2189–2200. https://doi
.org/10.1093/brain/121.11.2189, PubMed: 9827777
Liu, T. T., Nalci, A., & Falahpour, M. (2017). The global signal in fMRI:
Nuisance or information? NeuroImage, 150, 213–229. https://doi
.org/10.1016/j.neuroimage.2017.02.036, PubMed: 28213118
Marx, E., Stephan, T., Nolte, A., Deutschländer, A., Seelos, K. C.,
Dieterich, M., & Brandt, T. (2003). Eye closure in darkness animates
sensory systems. NeuroImage, 19(3), 924–934. https://doi.org/10
.1016/S1053-8119(03)00150-2, PubMed: 12880821
McAvoy, M., Larson-Prior, L., Ludwikow, M., Zhang, D., Snyder,
A. Z., Gusnard, D. L., … d’Avossa, G. (2012). Dissociated mean
and functional connectivity bold signals in visual cortex during
Network Neuroscience
474
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
eyes closed and fixation. Journal of Neurophysiology, 108(9),
2363–2372. https://doi.org/10.1152/jn.00900.2011, PubMed:
22875902
Mišic(cid:1), B., Betzel, R. F., De Reus, M. A., Van Den Heuvel, M. P.,
Berman, M. G., McIntosh, A. R., & Sporns, O. (2016). Network-
level structure-function relationships in human neocortex.
Cerebral Cortex, 26(7), 3285–3296. https://doi.org/10.1093
/cercor/bhw089, PubMed: 27102654
Morita, K., Miura, K., Kasai, K., & Hashimoto, R. (2020). Eye move-
ment characteristics in schizophrenia: A recent update with clinical
implications. Neuropsychopharmacology Reports, 40(1), 2–9.
https://doi.org/10.1002/npr2.12087, PubMed: 31774633
Mort, D. J., Perry, R. J., Mannan, S. K., Hodgson, T. L., Anderson, E.,
Quest, R., … Kennard, C. (2003). Differential cortical activation
during voluntary and reflexive saccades in man. NeuroImage, 18(2),
231–246. https://doi.org/10.1016/S1053-8119(02)00028-9,
PubMed: 12595178
Nickerson, L. D., Smith, S. M., Öngür, D., & Beckmann, C. F. (2017).
Using dual regression to investigate network shape and amplitude
in functional connectivity analyses. Frontiers in Neuroscience.
https://doi.org/10.3389/fnins.2017.00115, PubMed: 28348512
Nilsonne, G., Tamm, S., D’Onofrio, P., Thuné, H. Å., Schwarz, J.,
Lavebratt, C., … Åkerstedt, T. (2016). A multimodal brain imaging
dataset on sleep deprivation in young and old humans. 1–27.
Retrieved from https://openarchive.ki.se/xmlui/ handle/10616
/45181
Nostro, A. D., Müller, V. I., Varikuti, D. P., Pläschke, R. N.,
Hoffstaedter, F., Langner, R., … Eickhoff, S. B. (2018). Predicting
personality from network-based resting-state functional connec-
tivity. Brain Structure and Function, 223(6), 2699–2719. https://
doi.org/10.1007/s00429-018-1651-z, PubMed: 29572625
Nyström, M., & Holmqvist, K. (2010). An adaptive algorithm for
fixation, saccade, and glissade detection in eyetracking data.
Behavior Research Methods, 42(1), 188–204. https://doi.org/10
.3758/BRM.42.1.188, PubMed: 20160299
Parkes, L., Fulcher, B., Yücel, M., & Fornito, A. (2018). An evalua-
tion of the efficacy, reliability, and sensitivity of motion correc-
tion strategies for resting-state functional MRI. NeuroImage, 171,
415–436. https://doi.org/10.1016/j.neuroimage.2017.12.073,
PubMed: 29278773
Poldrack, R. A., Fletcher, P. C., Henson, R. N., Worsley, K. J., Brett, M., &
Nichols, T. E. (2008). Guidelines for reporting an fMRI study.
NeuroImage, 40(2), 409–414. https://doi.org/10.1016/j.neuroimage
.2007.11.048, PubMed: 18191585
Pretegiani, E., & Optican, L. M. (2017). Eye movements in Parkinson’s
disease and inherited Parkinsonian syndromes. Frontiers in
Neurology, 8, 592. https://doi.org/10.3389/fneur.2017.00592,
PubMed: 29170650
Ramot, M., Wilf, M., Goldberg, H., Weiss, T., Deouell, L. Y., &
Malach, R. (2011). Coupling between spontaneous (resting state)
fMRI fluctuations and human oculo-motor activity. NeuroImage,
58, 213–225. https://doi.org/10.1016/j.neuroimage.2011.06
.015, PubMed: 21703354
Rorden, C., Karnath, H. O., & Bonilha, L. (2007). Improving lesion-
symptom mapping. Journal of Cognitive Neuroscience. https://
doi.org/10.1162/jocn.2007.19.7.1081, PubMed: 17583985
Rosenberg, M. D., Hsu, W.-T., Scheinost, D., Constable, T. R., &
Chun, M. M. (2018). Connectome-based models predict
separable components of attention in novel individuals. Journal
of Cognitive Neuroscience, 30(2), 160–173. https://doi.org/10
.1162/jocn_a_01197, PubMed: 29040013
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage. https://
doi.org/10.1016/j.neuroimage.2009.10.003, PubMed: 19819337
Rucci, M., & Poletti, M. (2015). Control and functions of fixational
eye movements. Annual Review of Vision Science, 1, 499–518.
https://doi.org/10.1146/annurev-vision-082114-035742,
PubMed: 27795997
Rudie, J. D., Brown, J., Beck-Pancer, D., Hernandez, L., Dennis, E.,
Thompson, P., … Dapretto, M. (2013). Altered functional and
structural brain network organization in autism. NeuroImage:
Clinical, 2, 79–94. https://doi.org/10.1016/j.nicl.2012.11.006,
PubMed: 24179761
Schaefer, A., Kong, R., Gordon, E. M., Laumann, T. O., Zuo, X.-N.,
Holmes, A. J., … Yeo, B. T. T. (2018). Local-global parcellation
of the human cerebral cortex from intrinsic functional connectiv-
ity MRI. Cerebral Cortex. https://doi.org/10.1093/cercor/bhx179,
PubMed: 28981612
Shirer, W. R., Ryali, S., Rykhlevskaia, E., Menon, V., & Greicius, M. D.
(2012). Decoding subject-driven cognitive states with whole-brain
connectivity patterns. Cerebral Cortex. https://doi.org/10.1093
/cercor/bhr099, PubMed: 21616982
Siegel, S., & Castellan, N. J. (1956). Nonparametric statistics for the
behavioral sciences (Vol. 7). New York: McGraw-Hill.
Silberg, J. E., Agtzidis, I., Startsev, M., Fasshauer, T., Silling, K.,
Sprenger, A., … Lencer, R. (2019). Free visual exploration of nat-
ural movies in schizophrenia. European Archives of Psychiatry
and Clinical Neuroscience, 269(4), 407–418. https://doi.org/10
.1007/s00406-017-0863-1, PubMed: 29305645
Smith, S. M., Beckmann, C. F., Andersson, J., Auerbach, E. J.,
Bijsterbosch, J., Douaud, G., … WU-Minn HCP Consortium.
(2013). Resting-state fMRI in the human connectome project.
NeuroImage, 80, 144–168. https://doi.org/10.1016/j.neuroimage
.2013.05.039, PubMed: 23702415
Son, J., Ai, L., Lim, R., Xu, T., Colcombe, S., Franco, A. R., …
Milham, M. (2019). Evaluating fMRI-based estimation of eye
gaze during naturalistic viewing. Cerebral Cortex. https://doi
.org/10.1093/cercor/bhz157, PubMed: 31595961
Takarae, Y., Minshew, N. J., Luna, B., Krisky, C. M., & Sweeney, J. A.
(2004). Pursuit eye movement deficits in autism. Brain, 127(12),
2584–2594. https://doi.org/10.1093/ brain/awh307, PubMed:
15509622
West, G. L., Welsh, T. N., & Pratt, J. (2009). Saccadic trajectories
receive online correction: Evidence for a feedback-based sys-
tem of oculomotor control. Journal of Motor Behavior, 41(2),
117–127. https://doi.org/10.3200/JMBR.41.2.117-127, PubMed:
19201682
Xu, P., Huang, R., Wang, J., Van Dam, N. T., Xie, T., Dong, Z., …
Luo, Y.-J. (2014). Different topological organization of human
brain functional networks with eyes open versus eyes closed.
N e u r o I m a g e , 9 0 , 2 4 6 – 2 5 5 . h t t p s : / / d o i . o r g / 1 0 . 1 0 1 6 / j
.neuroimage.2013.12.060, PubMed: 24434242
Yarkoni, T., Poldrack, R. A., Nichols, T. E., Van Essen, D. C., &
Wager, T. D. (2011). Large-scale automated synthesis of human
functional neuroimaging data. Nature Methods. https://doi.org
/10.1038/nmeth.1635, PubMed: 21706013
Network Neuroscience
475
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Eye movements during rest reduce resting-state network modularity
Yellin, D., Berkovich-Ohana, A., & Malach, R. (2015). Coupling
between pupil fluctuations and resting-state fMRI uncovers a
slow build-up of antagonistic responses in the human cortex.
NeuroImage, 106, 414–427. https://doi.org/10.1016/j
.neuroimage.2014.11.034, PubMed: 25463449
Zacà, D., Hasson, U., Minati, L., & Jovicich, J. (2018). Method for ret-
rospective estimation of natural head movement during structural
MRI. Journal of Magnetic Resonance Imaging, 48(4), 927–937.
https://doi.org/10.1002/jmri.25959, PubMed: 29393987
Zhang, Y., Yan, A., Liu, B., Wan, Y., Zhao, Y., Liu, Y., … Liu, Z. (2018).
Oculomotor performances are associated with motor and non-
motor symptoms in Parkinson’s disease. Frontiers in Neurology, 9,
960. https://doi.org/10.3389/fneur.2018.00960, PubMed:
30546341
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
4
5
1
1
9
2
5
2
1
4
n
e
n
_
a
_
0
0
1
8
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
476