RECHERCHE
Network topology of symbolic and nonsymbolic
number comparison
Benjamin N. Conrad 1,2, Eric D. Wilkey
1,2,3, Darren J. Yeo 1,2,4, and Gavin R. Price1,2
1Psychology and Human Development, Vanderbilt University, Nashville, TN, Etats-Unis
2Vanderbilt Brain Institute, Vanderbilt University, Nashville, TN, Etats-Unis
3Cerveau & Mind Institute, Western University, Londres, ON, Canada
4Division of Psychology, School of Social Sciences, Nanyang Technological University, Singapore
Mots clés: Numerical cognition, Functional connectivity, Modularity, Community allegiance, Beta-
series correlation
un accès ouvert
journal
ABSTRAIT
Studies of brain activity during number processing suggest symbolic and nonsymbolic
numerical stimuli (par exemple., Arabic digits and dot arrays) engage both shared and distinct neural
mechanisms. Cependant, the extent to which number format influences large-scale functional
network organization is unknown. Dans cette étude, en utilisant 7 Tesla MRI, we adopted a network
neuroscience approach to characterize the whole-brain functional architecture supporting
symbolic and nonsymbolic number comparison in 33 adultes. Results showed the degree of
global modularity was similar for both formats. The symbolic format, cependant, elicited
stronger community membership among auditory regions, whereas for nonsymbolic, stronger
membership was observed within and between cingulo-opercular/salience network and
basal ganglia communities. The right posterior inferior temporal gyrus, left intraparietal
sulcus, and two regions in the right ventromedial occipital cortex demonstrated robust
differences between formats in terms of their community membership, supporting prior
findings that these areas are differentially engaged based on number format. En outre,
a unified fronto-parietal/dorsal attention community in the nonsymbolic condition was
fractionated into two components in the symbolic condition. Taken together, these results
reveal a pattern of overlapping and distinct network architectures for symbolic and
nonsymbolic number processing.
RÉSUMÉ DE L'AUTEUR
Previous studies of local activity levels suggest that both shared and distinct neural
mechanisms support the processing of symbolic (Arabic digits) and nonsymbolic (dot sets)
number stimuli, involving regions distributed across frontal, temporal, and parietal cortices.
Network-level characterizations of functional connectivity patterns underlying number
processing have gone unexplored, cependant. In this study we examined the whole-brain
functional architecture of symbolic and nonsymbolic number comparison. Stronger
community membership was observed among auditory regions during symbolic processing,
and among cingulo-opercular/salience and basal ganglia networks for nonsymbolic. A dual
versus unified fronto-parietal/dorsal attention community organization was observed for
symbolic and nonsymbolic formats, respectivement. Enfin, the inferior temporal gyrus and left
intraparietal sulcus, both thought to be preferentially involved in processing number
symbols, demonstrated robust differences in community membership between formats.
Citation: Conrad, B. N., Wilkey, E. D.,
Yeo, D. J., & Prix, G. R.. (2020).
Network topology of symbolic and
nonsymbolic number comparison.
Neurosciences en réseau, 4(3), 714–745.
https://doi.org/10.1162/netn_a_00144
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00144
Informations complémentaires:
https://doi.org/10.1162/netn_a_00144
https://osf.io/sb5v2/
https://github.com/conradbn/
CR7T_Connectivity
Reçu: 27 Septembre 2019
Accepté: 8 May 2020
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Gavin R. Prix
gavinprice@gmail.com
Éditeur de manipulation:
Lucina Uddin
droits d'auteur: © 2020
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
Symbolic number processing:
Operating on numerical information
derived from a learned notation
système, par exemple., Arabic numerals or
number words.
Nonsymbolic number processing:
Operating on numerical information
derived from sets of perceptual
elements, par exemple., dot arrays or tone
sequences.
INTRODUCTION
The representation and manipulation of numerical information in the brain has received con-
siderable attention over the last 20 années. A longstanding debate in the field regards the extent
to which symbolic (par exemple., Arabic digits) and nonsymbolic (par exemple., dot arrays) number formats en-
gage shared versus distinct neural mechanisms (Cohen Kadosh & Walsh, 2009; Knops, 2017;
Leibovich & Ansari, 2016; Reynvoet & Sasanguie, 2016). Regions of the bilateral intraparietal
sulcus (IPS) have been found to be involved in symbolic (Ansari et al., 2005; Eger, Sterzer, Russ,
Giraud, & Kleinschmidt, 2003; Holloway, Battista, Vogel, & Ansari, 2013; Kaufmannet al.,
2005; Pinel, Dehaene, Riviére, & LeBihan, 2001) and nonsymbolic (Ansari & Dhital, 2006;
Cantlon, Brannon, Carter, & Pelphrey, 2006; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004)
numerical processing during both adaptation and number comparison paradigms, support-
ing proposals that the IPS provides a substrate for quantity encoding shared between formats
(Dehaene & Cohen, 1995; Dehaene, Piazza, Pinel, & Cohen, 2003). A recent meta-analysis
of the extant functional magnetic resonance imaging (IRMf) literature supports the notion that
the parietal lobe subserves a shared representation of numerical magnitude across nonsym-
bolic and symbolic formats, detecting convergence of activation foci between symbolic and
nonsymbolic number processing in several bilateral parietal areas, as well as medial superior
frontal gyrus (Sokolowski, Fias, Mousa, & Ansari, 2016). Such findings suggest shared neural
resources for numerical processing across formats.
In addition to evidence for shared neural substrates across numerical formats, there is also
considerable evidence for distinct mechanisms between formats. Symbolic number compar-
ison has been shown, par exemple, to engage left superior temporal gyrus (STG) (Holloway,
Prix, & Ansari, 2010) as well as bilateral angular gyri, to a greater extent than nonsymbolic
number comparison, potentially reflecting increased reliance on verbal mechanisms during
number symbol processing (Ansari, Lyons, van Eimeren, & Xu, 2007; Dehaene et al., 2003;
Il, Zuo, Chen, & Humphreys, 2014; Holloway et al., 2010). A meta-analytic contrast between
formats suggests a general asymmetry in parietal activations, such that Arabic digits preferen-
tially engage left inferior parietal cortex, whereas nonsymbolic stimuli more strongly engage
distributed areas of right superior parietal, right frontal, and insular cortices (Sokolowski et al.,
2016). Symbolic number processing has also been shown to engage ventral occipitotemporal
(vOT) areas involved in the decoding of visual symbols (Dehaene & Cohen, 1995), tel que
during active processing of Arabic digits (Grotheer, Herrmann, et coll., 2016; Pollack & Prix,
2019; Shum et al., 2013; Yeo, Wilkey, & Prix, 2017). Cependant, it is unclear the extent to
which vOT areas are differentially engaged between symbolic and nonsymbolic number for-
mats. Par exemple, the meta-analytic contrast performed by Sokolowski et al. (2016) found no
clusters in the vOT. En résumé, the current state of evidence suggests that symbolic and non-
symbolic number processing share neural resources in frontal and parietal regions, mais aussi
engage distinct mechanisms distributed across the frontal, pariétal, and temporal cortices.
While prior work has focused on the extent to which brain regions are similarly or differ-
entially activated across number formats, complementary questions remain in regards to how
these regions interact and participate in functional networks during number processing. Since
the earliest theories of numerical cognition, there has been an implicit understanding that
multiple brain systems and subnetworks are involved in extracting and operating on numeri-
cal information (Campbell, 1994; Dehaene, 1992; McCloskey, 1992; McCloskey, Caramazza,
& Basili, 1985), yet to date, whole-brain network-level descriptions have gone unexplored.
We propose that description of symbolic and nonsymbolic number processing mechanisms in
terms of their widespread functional interactions among multiple brain areas and systems, tel
Neurosciences en réseau
715
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
Beta-series correlation:
A method for measuring functional
connectivity in event-related fMRI
data that assesses how similarly two
regions respond to trials of a given
condition.
Community:
A subnetwork of nodes (par exemple., régions)
that are more densely connected to
each than to other nodes of the
réseau.
as those implicated in visual perception, attention, and cognitive control, will shed new light
on the format-dependent versus format-independent processing debate, and provide comple-
mentary insights into how numerical cognition is accomplished in the human brain.
Graph theory provides a methodological framework for characterizing complex networks,
such as those derived from whole-brain functional connectivity data (Bassett & Gazzaniga,
2011; Bassett & Sporns, 2017). One application that has been particularly fruitful in cogni-
tive neuroscience has been the use of graph topology–based clustering techniques to group
brain regions into functional subnetworks, which can then be associated with various cognitive
and behavioral functions (Garcia, Ashourvan, Muldon, Vettel, & Bassett, 2018; Power et al.,
2011; Sporns & Betzel, 2016). In the present study, we collected 7 Tesla fMRI data in adults who
performed a numerical magnitude comparison task involving symbolic and nonsymbolic stim-
uli. We employed task-evoked functional connectivity (c'est à dire., beta-series correlation; Rissman,
Gazzaley, & DEsposito, 2004) and modularity maximization–based clustering (Lancichinetti
& Fortunato, 2012) to assess the network topology, or organization, of symbolic and nonsym-
bolic number comparison. We contrasted topologies between formats first at the macroscale
(c'est à dire., global level involving all regions), then the community level (c'est à dire., involving groups of re-
gions), and finally the individual region level. Specifically, we asked the following questions:
(1) Is there a difference in the whole-brain functional connectivity structure (c'est à dire., global mod-
ularity) between the symbolic and nonsymbolic formats? (2) What is the topographic layout
of functional communities in response to each format? (3) To what extent is the connectiv-
ity within and between each community significantly different between formats? (4) Do any
regions demonstrate a significant change in their whole-brain connectivity profile between
formats?
Given that the same task was performed across all trials, we expected that multiple task-
level processes would be shared between formats, Par exemple, involving cognitive control
and response selection mechanisms. We thus predicted a similar macroscale network archi-
tecture would be observed for each format (Krienen, Yeo, & Buckner, 2014), indicated by
an equivalent degree of global modularity, and the inclusion of a fronto-parietal network in-
volving IPS and prefrontal regions. We hypothesized, cependant, that differences would arise
among regional communities, with the symbolic format differentially engaging ventral visual
and temporoparietal pathways involved in object recognition and orthographic decoding, et
the nonsymbolic format engaging an occipitoparietal pathway involved in object location,
individuation, and summation coding. En outre, if the posterior inferior temporal gyrus
(pITG) is preferentially involved in the recognition of Arabic numerals, we expected this region
to show increased interaction with parietal regions. Cependant, if the pITG plays a nonspecific
role in number processing more generally, we expected a similar pattern between formats in
the functional interactions of this region.
RÉSULTATS
Behavioral Results
Descriptive statistics of behavioral performance are provided in Table 1. Mean reaction times
were computed from correctly answered trials only. Symbolic comparison trials elicited a sig-
nificantly lower error rate than nonsymbolic trials using paired tests (t(32) = 2.20, p = 0.035).
A significant difference in mean reaction time was also observed, whereby nonsymbolic trials
required approximately 45 ms more time to complete than symbolic trials (t(32) =
6.27, p =
7). In sum, participants were both faster and more accurate when solving symbolic
5.02
versus nonsymbolic comparisons.
10−
−
×
Neurosciences en réseau
716
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
Tableau 1. Scanner task performance.
Standard
Mean deviation Minimum Maximum
Symbolic condition accuracy (%)
Nonsymbolic condition accuracy (%)
Symbolic condition reaction time (ms)
Nonsymbolic condition reaction time (ms)
97.1
94.9
774.2
818.8
3.7
7.0
142.6
129.0
85.0
71.3
550.9
627.1
100.0
100.0
1,133.6
1,130.2
Modularity (Q):
Indexes the quality ofa network
partition relative to a null model
et, when maximized, summarizes
the extent of segregation versus
integration among a network’s
communautés.
Structural resolution parameter (c):
A free variable in the modularity
quality function that affects the
number and size of communities
detected.
Global Modularity Across Topological Scales
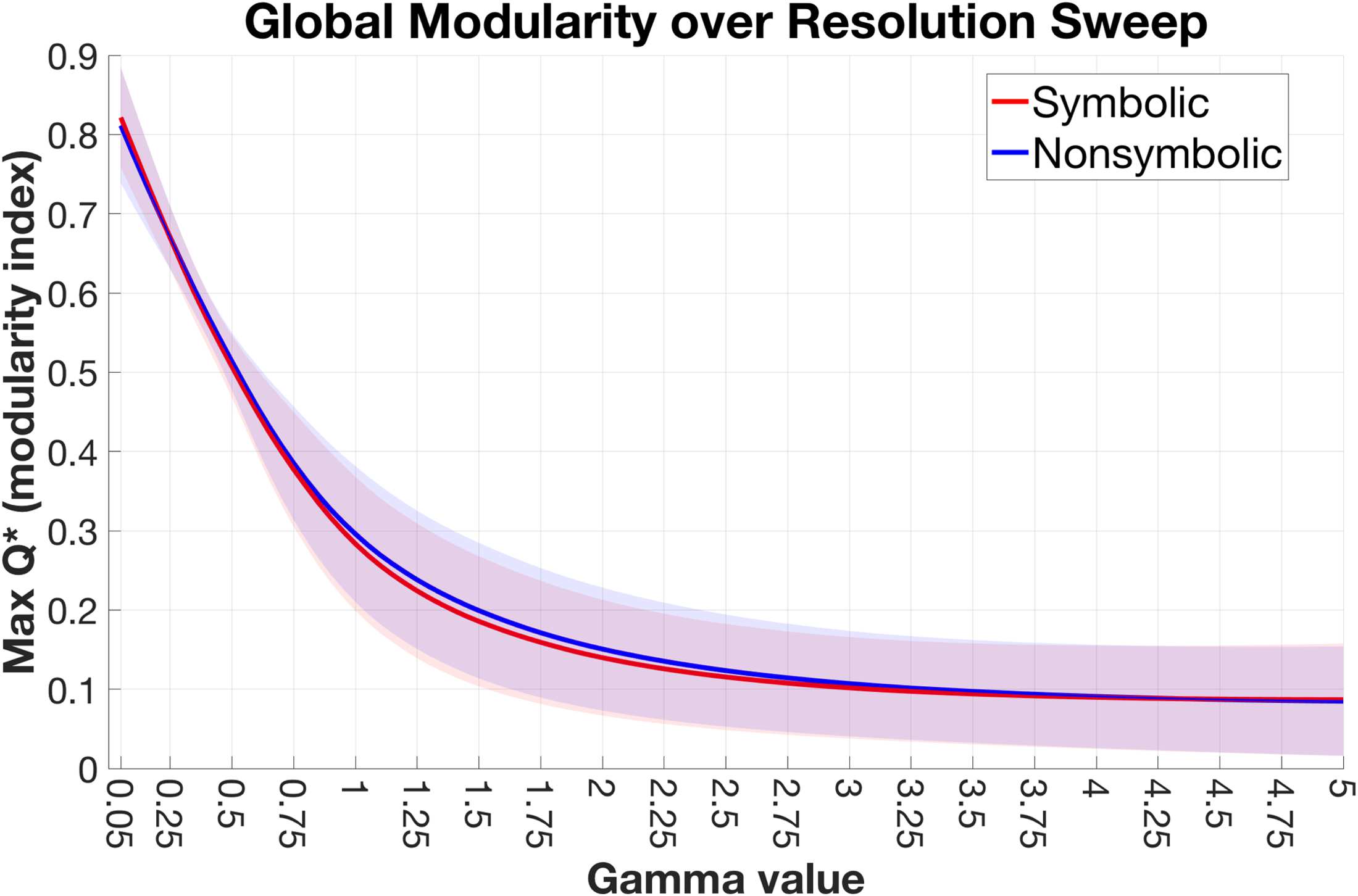
Our first question was, is there a difference in overall modular organization between formats?
The modularity of a network is indexed by the statistic, Q*, and provides a summary measure of
the extent to which a network can be decomposed into nonoverlapping communities when
each node (c'est à dire., region) is assigned to only one community (see Methods for algorithmic defini-
tion). A positive Q* value indicates that intracommunity connections are stronger than chance
Et ainsi, Q* summarizes the modular topology of a network in regards to the relative bal-
ance of segregated versus integrated connectivity structure (high versus low Q*, respectivement)
(Newman, 2006). Pour chaque sujet, we extracted the max Q* observed over 100 iterations
for the symbolic and nonsymbolic networks separately, and performed this procedure at each
step of the structural resolution parameter (c) over the resolution range of interest (Chiffre 1;
see Methods for more details on this range). A paired t test was performed at each step and
revealed no significant difference between the max Q* in the symbolic versus nonsymbolic
conditions (p > 0.05 uncorrected). This result indicates that there was no consistent difference
between formats at any topological scale in the degree of global segregation/integration across
the brain.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 1. No format differences in global modularity. The maximum global modularity (Q*) valeur
for each participant/format was extracted at every step along the resolution sweep (γ = 0.05–5.0,
with steps of 0.05). The mean lines are plotted along with shaded bars representing the standard
deviation across participants.
Neurosciences en réseau
717
Network topology of symbolic and nonsymbolic number comparison
Community Topology
While our first analysis indicated a similar modular structure between formats at the global
level, similar macroscale characteristics can arise from differing underlying topologies, mak-
ing it important to supplement global metrics with more fine-grained assessment of specific
network elements (Sporns, 2014). Donc, we investigated the subnetwork organization of
functional communities, looking at community topography for each format separately and dif-
ferences between formats in the degree of community allegiance.
The graph-theoretical concept of allegiance refers to the
Functional communities within format
probability of two regions being assigned to the same community across multiple partitions of
a network, and has been used extensively to study community organization during task perfor-
mance (Bassett, Lequel, Wymbs, & Grafton, 2015; Bertolero, Thomas Yeo, & D'Esposito, 2015;
Braun et al., 2015; Chaï, Mattar, Blank, Fedorenko, & Bassett, 2016; Mattar, Cole, Thompson-
Schill, & Bassett, 2015; Rizkallah et al., 2018; Telesford et al., 2016). The allegiance matrix
contains the probability for every region pair, c'est, the tendency for two brain regions to be
part of the same functional community, and thus describes region-to-region associations with
respect to shared community membership. Where functional connectivity asks of two regions,
“How much do they communicate?,” allegiance asks, “Do they belong to the same group?»
While the two metrics are related (and especially so in functional connectivity matrices due to
the transitive nature of time series correlations), they can in principle diverge in a number of
scenarios. Par exemple, two regions may exhibit relatively low connectivity to each other but,
due to stronger association with other members of the same community, demonstrate high
allegiance. In another case, a hub region with strong connectivity to two communities may
demonstrate relatively low allegiance to any one region, due to inconsistency in its commu-
nity assignment (c'est à dire., it belongs equally to two communities). From these examples, one can
appreciate that allegiance and connectivity provide complementary information about rela-
tionships among nodes of a network. Surtout, cependant, an allegiance-based approach has
some advantages. As an allegiance matrix is derived from network partitions (which reduce
connectivity information down to singular community assignments), allegiance values are ro-
bust to (1) noise inherent in connectivity measurements, ainsi que (2) differences in raw con-
nectivity strengths and/or distributions across conditions or subjects, making them appealing
for studying functional reconfiguration across task states (Bassett et al., 2015). Autrement dit,
the allegiance matrix serves as a pure representation of a network’s modular topology. En effet,
an allegiance-based approach was shown to be more sensitive to differences in functional net-
work architecture compared with connectivity information alone (Bassett et al., 2015). Dans ce
study we used group-level allegiance measures to assess community and region-level topology
during symbolic and nonsymbolic number comparison (see Methods).
To evaluate community-level organization, one must first define the topological “resolution”
of interest, which relates to the size of communities detected via modularity maximization and
is modulated by the resolution parameter γ (Reichardt & Bornholdt, 2006). Since our goal was
to compare topologies between the symbolic and nonsymbolic networks, we sought a reso-
lution at which there was a maximal balance between similarities and differences in group-
level community structure between formats (Mattar et al., 2015). Based on this heuristic, nous
found an optimal resolution at γ = 2.45 and used this value for subsequent community-level
analyses (see Methods for details on this procedure). Our group-level consensus clustering
procedure delineated 44 communities for symbolic (25 nonsingleton and 19 singleton, où
singleton refers to a community of just one region) et 36 communities for nonsymbolic (23
718
Allegiance:
The extent to which two regions
belong to the same community,
measured by the probability of
shared community membership
across multiple partitions.
Network partition:
A decomposition of network (c'est à dire.,
clustering solution) in which each
node is assigned to exactly one
community.
Modularity maximization:
An algorithmic process to determine
a partition that maximizes the
modularity quality index (Q), c'est à dire., le
optimal clustering solution.
Consensus clustering:
An algorithm for determining a
representative network partition from
many partitions of the same network
or from multiple subjects.
Neurosciences en réseau
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
nonsingleton, 13 singleton). We reduced the set of communities to only those that demon-
strated a strong modularity contribution (Q*c) at the subject level, ensuring that the commu-
nities of interest were (1) not driven by noise, et (2) not solely a feature of the group-level
réseaux, but biologically meaningful in individuals (Bassett, Owens, Daniels, & Porter, 2012;
Betzel et al., 2017; Guimerà, Sales-Pardo, & Amaral, 2004). Briefly, we computed the Q*c for
each community in the subject-level connectivity matrices and compared against null models,
selecting for further analyses only those that exceeded the 99th percentile of the null distribu-
tion (see Supporting Information Methods and Supporting Information Results Figure S1), in an
approach adapted from Betzel et al. (2017). This procedure resulted in 10 de 25 communautés
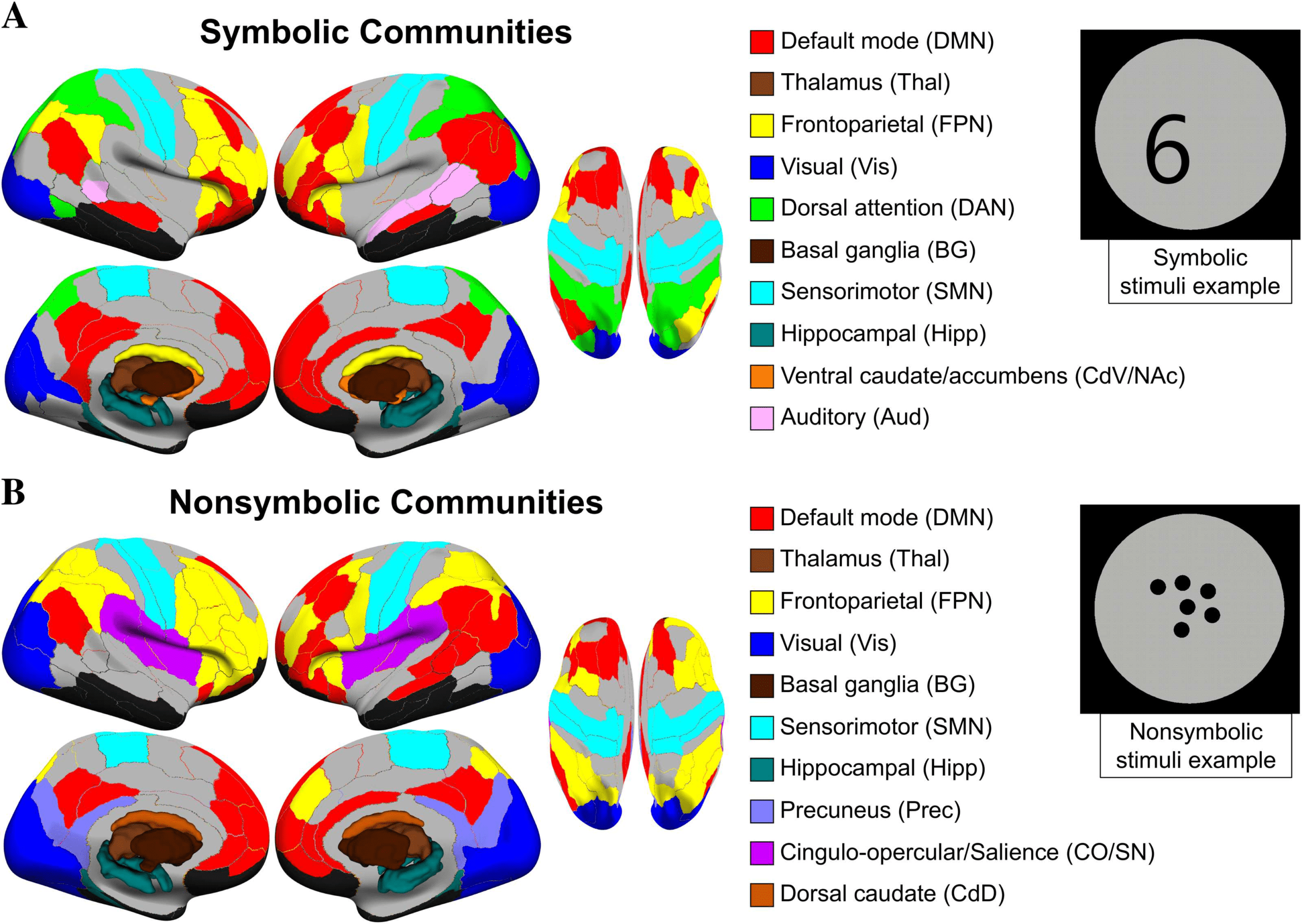
selected for symbolic and 10 de 23 communities selected for nonsymbolic (Chiffre 2).
One challenge in interpreting functional brain network results based on data-driven cluster-
ing solutions is the assignment of labels to the resulting communities (Yeo et al., 2011). Using
the widely adopted Power et al. (2011) network definitions, we took a quantitative approach in
which we calculated the voxel-wise overlap of our final community assignments with the con-
sensus assignments from Power et al. (acquired from https://www.jonathanpower.net/2011-
neuron-bigbrain.html). In almost all cases where an analogous community existed in the Power
et autres. partition, a clear “winner” was determined based on the relative percentage overlap ver-
sus other communities, including the default mode network (DMN), fronto-parietal task con-
trol network (FPN), dorsal attention network (DAN), sensorimotor network (SMN), visuel (Vis),
auditory (Aud), hippocampus (Hipp), thalamus (Thal), and basal ganglia (BG) communautés.
In the case of our smaller communities, involving the dorsal caudate (CdD), ventral caudate
and nucleus accumbens (CdV/NAc), and precuneus (Prec), there was not a corresponding
Power et al. assignment, so we labeled these according to their anatomical description in the
Brainnetome atlas (see Methods and Supporting Information Table S1) (Fan et al., 2016). Un
nonsymbolic community, involving primarily bilateral insular regions, was composed equally
of voxels within the cingulo-opercular task control (CO, 40.1%) and salience network (SN,
39.9%) communities from Power et al. Given that a clear distinction could not be made in this
case, we refer to this community by using the combined label CO/SN.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
Qualitative differences were observed between formats in the existence and topography of
individual communities (Chiffre 2). The FPN community, par exemple, was more distributed in
the nonsymbolic condition, including bilateral superior and inferior parietal regions as well as
a majority of prefrontal regions in the right hemisphere. For symbolic, the regions making up
the FPN in nonsymbolic were largely divided into a more ventral FPN and a DAN community,
with the DAN including superior parietal lobule (SPL) regions and a region of right pITG (voir
next section and Supporting Information Figure S2 for further investigation of the dual versus
unified FPN/DAN network architecture between formats). En outre, a left-lateralized audi-
tory (Aud) community, including left STG and bilateral superior temporal sulcus regions, était
only detected in the symbolic condition, and a CO/SN community, involving primarily bilat-
eral insular regions, was only detected in the nonsymbolic condition. On the other hand, le
visuel, sensorimotor, default mode, and subcortical communities were topographically com-
parable between formats. Supporting Information Table S1 includes labels and community
assignments for all regions of the Brainnetome Atlas.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
As a final analysis of community topography, we sought to determine whether the observed
dual versus unified FPN/DAN network architecture in the symbolic and nonsymbolic con-
ditions, respectivement, was specific to the particular γ value employed in these analyses (c'est à dire.,
c = 2.45), or was robust across γ values. The dual FPN/DAN network architecture in the sym-
bolic condition persisted across a relatively large range of γ (Supporting Information Figure S2),
Neurosciences en réseau
719
Network topology of symbolic and nonsymbolic number comparison
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
Chiffre 2. Functional communities by format. Group-level communities were determined for symbolic and nonsymbolic formats separately.
The depicted communities represent the reduced set that passed our selection criterion of showing strong modularity in subject-level con-
nectivity matrices (see Supporting Information Methods and Supporting Information Figure S1 for details on the selection procedure). Cortical
regions are plotted to a surface representation and subcortical regions are presented as 3D volumes. Community labels were determined
based on voxel-wise overlap with the networks delineated in Power et al. (2011), ou, when an analogous network did not exist in Power et al.,
based on the anatomical region(s). Colors were chosen to match those networks where possible. Gray indicates regions that did not belong to
a selected community; black indicates regions excluded based on signal dropout (see Supporting Information Methods).
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
whereas these communities were not consistently distinguished in the nonsymbolic condition,
suggesting that the observed difference in FPN/DAN integration between formats is robust
across γ values.
Differences in the degree of within- and between-community allegiance between formats While the
previous analysis delineated the functional communities present within each condition sep-
arately, the detection of a community is driven in part by the organization of the rest of the
réseau. En tant que tel, the existence of a community in one condition but not the other does not
necessarily indicate that allegiance among these regions (c'est à dire., within-community allegiance) est
stronger in that condition per se. En outre, even if community assignments are similar be-
tween conditions, differences may exist in the hierarchical organization of the network and/or
Neurosciences en réseau
720
Network topology of symbolic and nonsymbolic number comparison
Monte Carlo permutation:
A technique used for nonparametric
hypothesis testing in which a null
distribution is constructed by
randomly resampling observed data.
the degree of integration across communities, properties that can be captured by the strength
of between-community allegiance. Allegiance values within or between communities provide
an indication of how strongly connected, or “allegiant,” the members of a given community
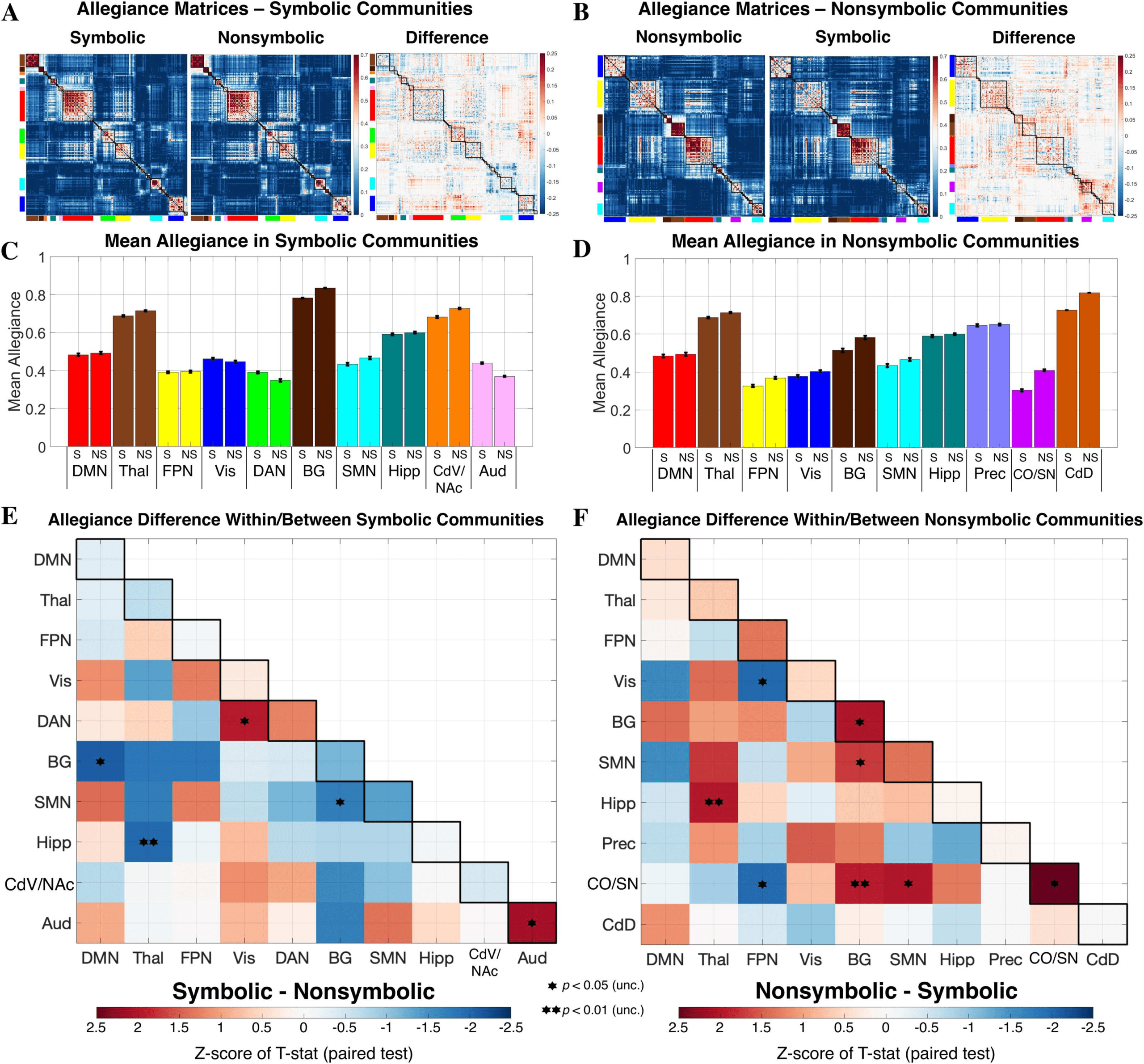
are to each other across subjects. A mean allegiance of 0.8 within a community (Figure 3C
and D), Par exemple, specifies that the regions of this community were members of the same
community in 80% of participants (on average across region pairs). To quantitatively assess
whether statistically significant differences existed at the community level, we extracted the
vector of region-to-region connections (allegiance values below the diagonal) from the two
group-level matrices (Figure 3A and B), for each pair of communities identified in the sym-
bolic and nonsymbolic conditions. To assess the difference between formats, a paired t test
was then performed on the vectors of allegiance values (par exemple., allegiance across regions of the
symbolic DAN community in the symbolic matrix versus the same regions in the nonsymbolic
matrice). A Monte Carlo permutation procedure with 50,000 iterations was used to determine
the significance of the observed t statistics, whereby subject-level partitions from each con-
dition were randomly relabeled, null group-level allegiance matrices were constructed, et
allegiance values were compared for each community, constructing a null distribution for each
t statistic of interest. This represents a nonparametric approach to significance testing that is
appropriate for repeated measures (Nichols & Holmes, 2004). Z scores for the true (c'est à dire., ob-
µTnull )/σTnull, and p values were assigned based
served) t statistics were computed as (Ttrue −
on the position of the value t statistic within the null distribution (Figure 3E and F). No com-
munity pairs survived FDR correction for multiple comparison across the 55 tests of within-
and between-community allegiance conducted for each set of communities (Figure 3E and F)
(Benjamini & Hochberg, 1995). Cependant, given the data-driven, exploratory approach em-
ployed here assessing all pairwise associations, we did not expect effect sizes to be strong
enough to pass such a stringent criterion. The goal here was rather to look for underlying
patterns in the data that could then generate hypotheses for future research. In line with rec-
ommendations for exploratory research, we report the outcome of our multiple comparison
correction procedure but also present the observed effect sizes (z scores) as well as the uncor-
rected p values, with a strong caution that these findings must be confirmed in future studies
(Althouse, 2016; Feise, 2002; Rothman, 1990; Streiner, 2015; Thompson, Wright, & Bissett,
2020).
Several differences were observed between formats in regards to within- and/or between-
community allegiance based on an uncorrected threshold of p < 0.05 (two-tailed) (Figure 3E
and F). Of the communities identified in the symbolic condition, stronger allegiance was
found for symbolic versus nonsymbolic among regions of the auditory (Aud) community (Aud:
z score = 2.11, p = 0.019). This suggests that not only was an auditory community identi-
fied in the symbolic condition and not the nonsymbolic condition, but that the regions of this
community are significantly more functionally coupled to each other during symbolic trials.
Furthermore, allegiance between the dorsal attention (DAN) and visual (Vis) communities was
stronger in the symbolic condition (DAN–Vis: z score = 1.97, p = 0.015). Weaker allegiance
was observed in the symbolic condition between basal ganglia (BG) and both the default mode
2.09, p = 0.010; BG–
(DMN) and sensorimotor (SMN) communities (BG–DMN: z score =
1.70, p = 0.016), and between the hippocampal (Hipp) and thalamic (Thal)
SMN: z score =
−
1.97, p = 0.004). Of the communities identified in the
communities (Hipp–Thal: z score =
nonsymbolic condition, stronger allegiance (nonsymbolic > symbolic) was found among re-
gions of BG and cingulo-opercular/salience network (CO/SN) community (BG: z score = 2.02,
p = 0.021; CO/SN: z score = 2.50, p = 0.005). In nonsymbolic condition, the CO/SN and BG
communities were also more allegiant to each other (CO/SN–BG: z score = 1.94, p = 0.004),
−
−
Neurosciences en réseau
721
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 3. Comparison of community allegiance between formats. (A and B) Group-level allegiance matrices are presented, indicating at
each cell in the matrix the proportion of subjects in which two regions were assigned to the same community. Matrix cells are reordered based
on the community composition of the symbolic (UN) and nonsymbolic (B) formats, respectivement, but the values are identical within each format.
(C and D) Mean allegiance across region pairs is depicted for each format and was computed using communities as defined for symbolic
and nonsymbolic, respectivement. Black bars represent standard error of the mean across region pairs. (E and F) Allegiance difference within and
between communities detected in each format. No p values survived correction for multiple comparisons (p < 0.05, FDR corrected for 55
tests along + below the diagonal). The CdD community was composed of two regions (right/left dorsal caudate) and thus contained only one
region-to-region connection. In this case, since a paired t test was not possible, the z score for CdD represents that of the simple difference
between formats. DMN = default mode network; Thal = thalamus; FPN = fronto-parietal network; Vis = visual; DAN = dorsal attention network;
BG = basal ganglia; SMN = sensorimotor network; Hipp = hippocampus; CdV/NAc = ventral caudate/nucleus accumbens; Aud = auditory;
Prec = precuneus; CO/SN = cingulo-opercular/salience network; CdD = dorsal caudate.
Network Neuroscience
722
Network topology of symbolic and nonsymbolic number comparison
and both more allegiant to the SMN community (CO/SN–SMN: z score = 2.00, p = 0.014;
BG–SMN: z score = 1.73, p = 0.016). Additionally, greater allegiance between the Hipp and
Thal communities was observed in the nonsymbolic condition (Hipp–Thal: z score = 1.98,
p = 0.004). Weaker allegiance in the nonsymbolic condition was observed between the FPN
1.98, p = 0.022; FPN–
and both the Vis and and CO/SN communities (FPN–Vis: z score =
CO/SN: z score =
1.96, p = 0.021).
−
−
×
We additionally asked whether the differences between formats we observed in commu-
nity allegiance could have been captured by a simpler analysis of raw connectivity strengths.
We therefore assessed the relation between allegiance and connectivity values for each format
separately, and then critically, whether connectivity information provided a similar pattern of
statistically significant differences between formats. These analyses were performed using the
median group-level connectivity matrices, group-level allegiance matrices, and the commu-
nities as defined at γ = 2.45. We first constructed two 10
10 matrices representing the
mean allegiance and mean connectivity within/between the 10 communities, for each format
separately. We then computed the correlation between these matrices, excluding the mirrored
values above the diagonal. In other words, we asked, “before taking the difference between
formats, are community-level allegiance and connectivity values related?” We found that (as
expected) these values were highly related (Pearson r = 0.64, p < 0.001 in the symbolic
data; Pearson r = 0.55, p < 0.001 in the nonsymbolic data). Next, to determine whether a
similar pattern of statistically significant differences could be observed using the connectiv-
ity data, we correlated the values depicted in the matrices of Figure 3E and F with those in
Supporting Information Figure S3 (excluding values above the diagonal). Neither set of re-
sults were significantly correlated (Pearson r = 0.07, p = 0.60 using symbolic communities;
Pearson r = 0.23, p = 0.08 using nonsymbolic communities), though a marginal positive ef-
fect was observed using the nonsymbolic communities. We found the effect sizes of the values
within these matrices (i.e., z scores of difference between formats, determined via our Monte
Carlo procedure) were relatively smaller in the connectivity data (Supporting Information
Figure S3) compared with the allegiance data (Figure 3E and F). This analysis highlights the di-
vergence between connectivity and allegiance metrics, and suggests that an allegiance-based
approach is sensitive to changes in community topology that are not captured by simple con-
nectivity differences.
Region-level Allegiance Profiles Across Topological Scales
To provide insights into how the functional roles of particular regions may differ based on
number format, we investigated the extent to which node-level allegiance profiles changed
between the symbolic and nonsymbolic conditions. In the community-level analysis, we used
modularity maximization to define communities of interest and followed this up with quan-
titative analysis of allegiance differences between formats. This process necessitated a partic-
ular setting of the resolution parameter (γ = 2.45). Regions, on the other hand, make up the
fundamental units of the network and were predetermined by the atlas parcellation, so region-
level analyses need not be constrained to a particular topological scale. We reasoned that a
more comprehensive assessment of regional allegiance profiles would be to summarize differ-
ences between formats across a large range of resolutions (Betzel & Bassett, 2016). We thus
performed the following analysis of allegiance profile (dis)similarity for every resolution step
across our range of interest, γ = 0.05–5, with steps of 0.05 (see Methods for more details on
this range).
Network Neuroscience
723
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
a
_
0
0
1
4
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
The allegiance profile of a region was defined as the vector of group-level allegiance val-
ues from one region to all others, which characterizes a region’s position in the network in
relation to the network’s community structure. We computed the (dis)similarity of a region’s
allegiance profile between the symbolic and nonsymbolic conditions using Pearson correlation
coefficient converted to Fisher Z values, with lower values indicating greater dissimilarity. The
significance of dissimilarity was assessed using a similar Monte Carlo permutation approach
as before, involving 10,000 random reshufflings of the subject-level partitions to construct a
null distribution of group-level allegiance matrices (Nichols & Holmes, 2004). From these null
matrices, a z score and p value for the observed dissimilarity coefficient (inverse of Fisher Z)
was computed for every region. To characterize the overall robustness of allegiance profile
differences across the resolution sweep, we counted the number of steps in which a region
demonstrated a significant dissimilarity in its allegiance profile between formats (p < 0.05
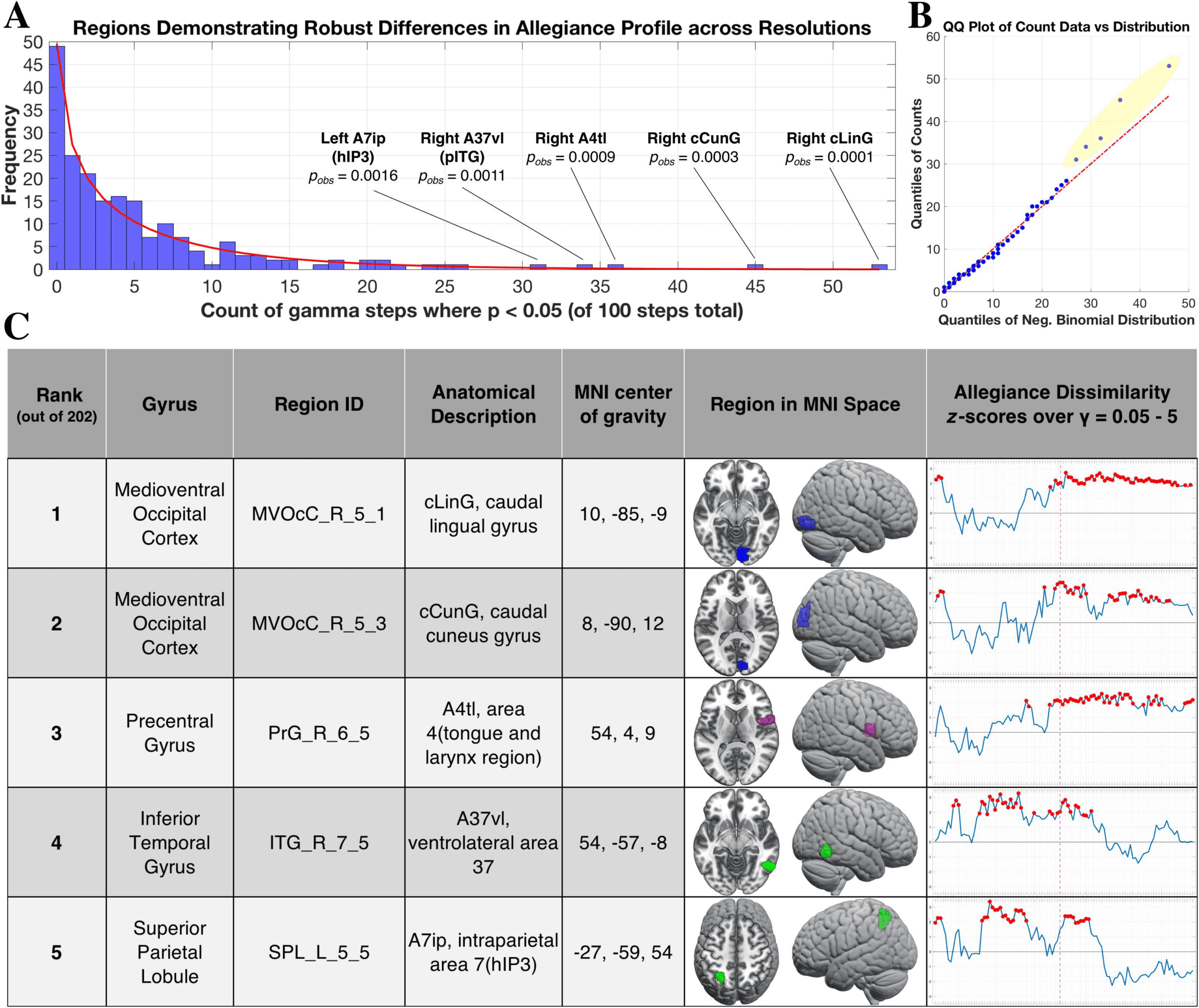
one-tailed, uncorrected), and the counts are depicted as a histogram in Figure 4A. In order to
reduce the set of regions to those that showed the greatest total count, we first fit a negative
binomial curve to the observed distribution, which is commonly used to model overdispersed
count data (Bliss & Fisher, 1953; Hartley, 1958; White & Bennetts, 1996). We then assessed the
goodness of fit of this theoretical distribution to the observed counts using a quantile-quantile
plot (Figure 4B). In general, there was high overlap in the observed versus fitted distribution,
with the exception of five outlying regions (highlighted in yellow, Figure 4B): the (1) right
caudal lingual gyrus, (2) right caudal cuneus gyrus, (3) right area 4 in precentral gyrus, (4)
right ventrolateral area 37 in pITG, and (5) left intraparietal area 7 (hIP3). These five regions
demonstrated higher counts than expected given the observed pattern, indicating that, relative
to other regions, they showed robust differences in community allegiance between formats
across a wide range of organizational scales. We highlight these regions in Figure 4C, includ-
ing their anatomical description and location, as well as plots of their dissimilarity z scores
across the full resolution sweep.
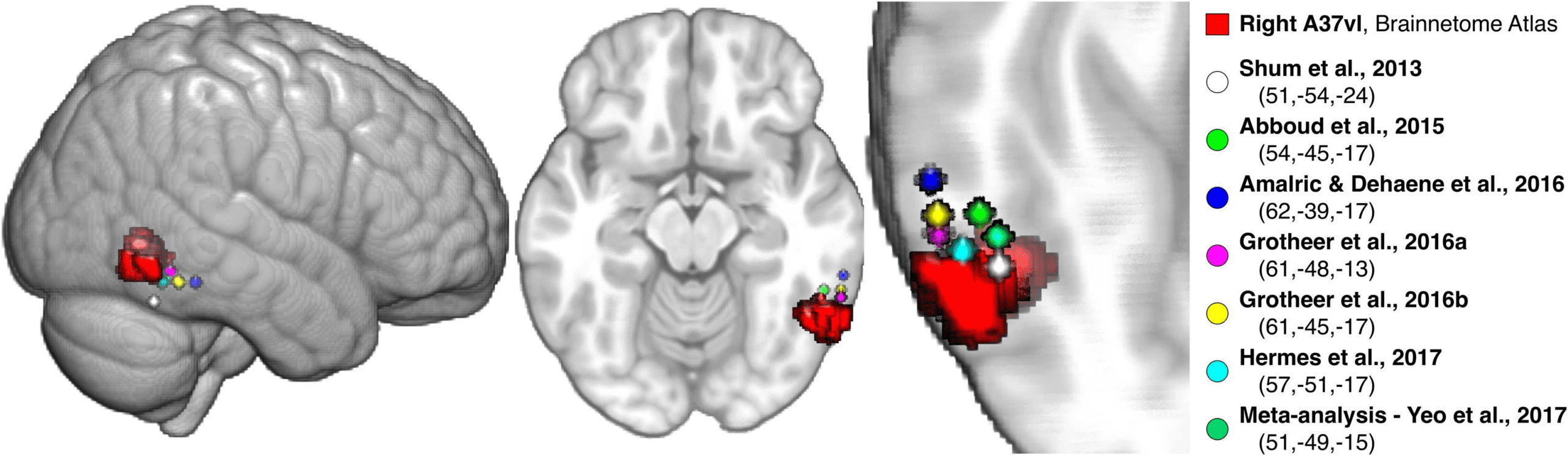
The right pITG region sits posterior but immediately adjacent to the putative “Number Form
Area” as described in recent literature. The volumetric location of this region relative to the
peak coordinates reported across multiple studies, including an fMRI meta-analysis, is depicted
in Figure 5 (Abboud, Maidenbaum, Dehaene, & Amedi, 2015; Amalric & Dehaene, 2016;
Grotheer, Ambrus, et al. , 2016; Grotheer, Herrmann, et al., 2016; Hermes et al., 2017; Shum
et al., 2013; Yeo et al., 2017). Both the right pITG and left intraparietal hIP3 regions were
part of the DAN community—one part of the dual fronto-parietal networks identified in the
symbolic condition (Figures 2 and 3; Supporting Information Table S1).
As a supplementary analysis, we investigated the extent to which the observed differences
in regional allegiance profiles related to differences in the raw connectivity profiles of each
region, using the median group-level connectivity matrices in place of the group-level alle-
giance matrices (Supporting Information Figure S4). We found that the count of significant
steps over the resolution sweep was positively related to the degree of connectivity dissim-
ilarity (Spearman’s rho = 0.202, p = 0.004), indicating that, albeit a modest relation, there
is overlap between allegiance and connectivity at the region level. However, the specific re-
gions showing the greatest counts versus connectivity dissimilarity differed. For instance, three
regions showing a high count from the allegiance analysis (right caudal lingual gyrus, right
area 4, and left intraparietal hIP3) demonstrated connectivity dissimilarity z scores near 0.
Along with Supporting Information Figure S3, this indicates that allegiance and connectivity
information are largely independent and that allegiance-based analyses can detect changes in
regional community membership regardless of strong and/or consistent changes in the region’s
raw connectivity profile.
Network Neuroscience
724
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
a
_
0
0
1
4
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
a
_
0
0
1
4
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Regions showing robust differences in allegiance profile between formats. (A) Histogram plot showing counts of significant steps
over the resolution sweep from all 202 regions, in terms of a significant dissimilarity in allegiance profile between the symbolic and nonsym-
bolic conditions (p < 0.05, uncorrected). The red line indicates the fitted negative binomial distribution, and pobs indicates the probability of
the selected count, given the distribution of all counts observed. (B) Quantile-quantile (QQ) of the fitted distribution (x-axis) with respect to the
sample distribution (y-axis). Note the five regions highlighted in yellow that show considerable deviation from what was expected given the
counts demonstrated by the rest of the regions. (C) Table of the five regions showing the most robust differences in allegiance, with z scores
over the resolution sweep plotted in the rightmost column. The dashed magenta line indicates γ = 2.45, the setting for the community-level
analysis (Figure 3) and the red dot indicates p < 0.05 at that step. Both occipital regions were members of the visual community in the symbolic
and nonsymbolic conditions (at γ = 2.45), so are presented as blue. The precentral gyrus region was a part of the CO/SN community (magenta)
in the nonsymbolic community (and not selected in the symbolic condition). The pITG and hIP3 regions were part of the DAN community in
the symbolic condition (green). In the nonsymbolic condition, the hIP3 region was part of the FPN community while the pITG region was not
selected (see Supporting Information Table S1 for the community assignments of all regions).
Network Neuroscience
725
Network topology of symbolic and nonsymbolic number comparison
Figure 5. Posterior ITG region (ventrolateral area 37) relative to reported “Number Form Area” coordinates. The ventrolateral area 37
(A37vl) Brainnetome region in the posterior ITG showed significant differences in its allegiance profile between the symbolic and nonsym-
bolic conditions (see the region-level allegiance analysis in Figure 4). This region is depicted (red) along with spheres centered at the peak
MNI coordinates (x,y,z) from several recent studies demonstrating Arabic numeral-selectivity versus other stimuli, using either fMRI or electro-
corticography measurements, as well as from an fMRI meta-analysis of numeral versus other symbol processing (Abboud et al., 2015; Amalric
& Dehaene, 2016; Fan et al., 2016; Grotheer, Ambrus, et al., 2016; Grotheer, Herrmann, et al., 2016; Hermes et al., 2017; Shum et al.,
2013; Yeo et al., 2017). Where coordinates were reported in Talairach space, the tal2mni.m function was used to convert to MNI space via
the Brett transform (http://imaging.mrc-cbu.cam.ac.uk/downloads/MNI2tal/tal2mni.m). The A37vl region sits immediately posterior to these
coordinates, and was the only ITG region in the Brainnetome Atlas that survived our signal dropout threshold (the others are more anterior).
DISCUSSION
Little is currently known regarding the network architecture of brain systems supporting numer-
ical cognition. While region-based analyses have provided important insights into the neural
mechanisms of numerical cognition, a growing body of work outside the numerical cognition
field suggests that understanding the network topology of those mechanisms, as well as how
this topology is reconfigured across task states, can provide additional meaningful insights
(e.g., Braun et al., 2015; Cohen & D’Esposito, 2016; Cole, Bassett, Power, Braver, & Petersen,
2014; Hearne, Cocchi, Zalesky, & Mattingley, 2017; Shine et al., 2019). In this study, we used
measurements of task-evoked functional connectivity and network-based analysis to assess the
similarities and differences between symbolic and nonsymbolic numerical magnitude process-
ing. Our findings provide evidence for a similar global topology across formats, but selective
differences in community and region-level organization.
No Difference in Global Modularity Between Formats
In regards to functional connectivity networks, the modularity index has been considered as a
measure of segregated versus integrated information processing among functional subsystems,
with lower modularity indicating greater integration across the brain (Bertolero, Yeo, Bassett,
& D’Esposito, 2018; Godwin, Barry, & Marois, 2015; Shine et al., 2016). Our results showed
no evidence of a difference in global modularity in subject-level connectivity networks at any
topological scale (Figure 1), suggesting that the balance of segregated versus integrated in-
formation processing among subnetworks of the brain is similar between formats. It is worth
noting, however, that the task employed here involved comparison of each stimulus to the ref-
erence number 5, with symbolic and nonsymbolic trials intermixed across the experiment. We
speculate that global topological differences between formats may be more pronounced when
more than one stimulus must be processed, as is the case in tasks using simultaneous or se-
quential presentation of two stimuli to be compared, and/or if comparison tasks are performed
Network Neuroscience
726
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
a
_
0
0
1
4
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
separately for each format. For instance, in separate tasks, global topological differences may
emerge from the adoption of different strategies or attentional states (Bertolero et al., 2018;
Cocchi et al., 2014; Cohen & D’Esposito, 2016; Heinzle, Wenzel, & Haynes, 2012), rather
than a difference in symbolic versus nonsymbolic processing per se. Our use of intermixed
stimuli prevented participants from anticipating one format versus another, thus our results
are likely to reflect format-dependent processing differences, rather than strategic differences
related to task context.
Community Allegiance Versus Functional Connectivity
The remaining analyses focused on a comparison of network architectures between number
formats at the subnetwork (i.e., community) and region levels. Our approach leveraged the
concept of community allegiance, which characterizes region-to-region associations in terms
of shared membership among functional subnetworks (see Results section for a more thorough
introduction). Intuitively, functional connectivity indexes the extent to which two regions di-
rectly interact, whereas allegiance indexes the tendency for two regions to be associated with
the same community. Compared with connectivity, allegiance-based analysis is in principle
more robust to noise and intersubject variance, and has been shown to be particularly sen-
sitive to reconfigurations in brain network architectures (Bassett et al., 2015). We found that
while connectivity and allegiance measures were related (which is expected, given that al-
legiance is derived from partitions of connectivity matrices), they also diverged considerably
(see Results, as well as Supporting Information Figures S3 and S4). The present study indicates
that an allegiance-based approach offers a unique and complimentary perspective on network
organization, and suggests that future research assessing functional brain networks may benefit
from the methodology described herein.
Fronto-parietal Unification and Fractionation Between Formats
In contrast to the global level, our community-level results revealed that the topography of
fronto-parietal control systems differed considerably between formats. Specifically, during non-
symbolic trials, the fronto-parietal network (FPN) was a unitary community composed of 33
regions, while during symbolic trials, these regions were largely fractionated into two distinct
communities, a dorsal attention (DAN) community and more ventrally/anteriorly positioned
FPN (Figure 2A and B). Distinctions have previously been made between dorsal and ventral
attention systems (Corbetta & Shulman, 2002). Previous literature suggests the DAN is involved
in the voluntary deployment of attentional control based on goals and expectations as well as
ultimately linking stimuli to responses, whereas the ventral network is involved in reorienting
of attention to relevant stimuli (Corbetta, Patel, & Shulman, 2008; Ptak, Schnider, & Fellrath,
2017). Through top-down signaling, the DAN in particular is thought to bias sensory areas to
be responsive to appropriate features of inputs, and is often found to be functionally connected
to visual areas in the ventral occipitotemporal (vOT) cortex (in line with the inclusion of the
right pITG region in the symbolic DAN community in the current data; see further discussion
below and Figure 2A) (Corbetta et al., 2008; Fox, Corbetta, Snyder, Vincent, & Raichle, 2006;
Ptak, 2012; A. C. Vogel, Miezin, Petersen, & Schlaggar, 2012). While both formats may engage
the DAN, we speculate that nonsymbolic dot arrays place greater demand on the (ventral) at-
tentional reorienting system by containing multiple objects organized randomly across space.
While we did vary the location of the digits across trials (e.g., see Figure 2), it may be that the
perceptual regularity of the symbolic stimuli leads to reduced interactions between the DAN
and more ventral/anterior components of the FPN during task performance (Vossel, Geng, &
Fink, 2014). A potentially related finding came from a recent study by Dixon et al. (2018),
Network Neuroscience
727
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
a
_
0
0
1
4
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
who showed that an FPN subsystem (“FPCNB”), which has a qualitatively similar spatial pro-
file to our symbolic FPN community, was integrated with the DAN across a range of task states
involving externally directed attention and perception. The other component of the FPN, the
“FPCNA,” was more integrated with the default mode network (DMN) and recruited during
internally directed thought (Dixon et al., 2018). The authors suggest that the FPCNB represents
task-relevant information (e.g., rules and response mappings) and exerts moment-to-moment,
top-down control of the DAN, allowing the DAN to deploy this information in the guidance of
spatial attention (e.g., saccades) and ultimately action initiation (Baldauf & Desimone, 2014;
Bichot, Heard, DeGennaro, & Desimone, 2015; Dixon et al., 2018). The unified FPN/DAN
community we observed in the nonsymbolic condition supports this account, possibly reflect-
ing a stronger engagement of this distributed, visuospatial attentional control system when
processing dot sets compared to single digits.
It is important to note that while Power et al. (2011) and Yeo et al. (2011) distinguish sep-
arate dorsal attention, ventral attention, and fronto-parietal networks, their boundaries (along
with the cingulo-opercular network; Dosenbach, Fair, Cohen, Schlaggar, & Petersen, 2008)
are not completely consistent across the literature, nor with our own data-driven community
assignments. During task performance, multiple components of these networks are recruited
and likely integrated to form a so-called “task-positive” network (Dwyer et al., 2014; Fox et al.,
2005). The extent to which each of these putative systems separately contribute to cognitive
and attentional control is an ongoing area of research (Petersen & Posner, 2012). In general,
our findings indicate that symbolic and nonsymbolic comparison differentially engage large-
scale association networks, and further, suggest that assessment of community-level topology
may help to incorporate canonical mechanisms of cognitive control and attention into our
understanding of number processing.
Cingulo-Opercular/Salience Network and Basal Ganglia Allegiance Increases During
Nonsymbolic Processing
A second pattern of results at the community level involved stronger allegiance, that is, shared
community membership, within and between the cingulo-opercular/salience (CO/SN) and
basal ganglia (BG) communities in the nonsymbolic condition (Figure 3F). The CO network
has been implicated in tonic alertness and task-set maintenance, and demonstrates sustained
activity across trials of a cognitive task (Dosenbach et al., 2007; Sadaghiani & D’Esposito,
2015). As part of the dual control network architecture proposed by Dosenbach et al. (2008),
the CO operates in parallel to the FPN, which is instead thought to be involved in phasic
alertness and adaptive control on a trial-level basis. Our beta-series approach specifically fo-
cused on coupling in trial-level responses, and thus is expected to be less sensitive to cou-
pling extending across multiple trials. And even so, the same “task-set” should have been
engaged regardless of format, given the trials were intermixed and the same comparison oper-
ation was required. Thus, it is difficult to interpret the difference we observed between formats
involving CO/SN allegiance within the context of the dual control network framework. On
the other hand, this community was a hybrid between the CO and SN communities in the
Power et al. (2011) parcellation. The SN is involved in the detection of relevant stimuli, in-
cluding both internal and external cues, and, for instance, is particularly engaged during odd-
ball paradigms in response to surprising or deviant cues (Menon, 2015). It is implicated in a
broad range of goal-directed cognitive functions and is thought to integrate processing among
disparate functional subnetworks, potentially filtering input to the ventral attention system
(Chang, Yarkoni, Khaw, & Sanfey, 2013; Corbetta et al., 2008). The increased allegiance during
nonsymbolic comparison within the CO/SN community in our data may be due to the fact that
Network Neuroscience
728
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
a
_
0
0
1
4
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
dot arrays simply involve more visual objects to detect and process, requiring stronger com-
munication among regions in this network. However, this interpretation is highly speculative
and further empirical investigation is clearly required to elucidate the mechanisms underlying
this finding.
We also observed significantly increased allegiance among regions of the basal ganglia
(BG) community, including bilateral putamen, globus pallidus, ventral caudate, and nucleus
accumbens (Figure 2B) in the nonsymbolic versus symbolic condition (Figure 3F). BG struc-
tures are generally implicated in motor initiation and control, including eye movements, but
are also known to participate in multiple cognitive processes such as inhibition, working
memory, decision-making, and learning (Helie, Chakravarthy, & Moustafa, 2013; Leisman,
Braun-Benjamin, & Melillo, 2014; Middleton & Strick, 2000; Packard & Knowlton, 2002;
Wei & Wang, 2016). Multiple parallel cortico-basal ganglia loops are thought to be required
during a stimulus-response task, where some cognitive operation is performed (e.g., < or > 5)
and then linked to a motor output (par exemple., press left or right) (Guthrie, Leblois, Garenne, & Boraud,
2013). Since symbolic and nonsymbolic trials required the same motor responses, our finding
of increased integration among BG for nonsymbolic trials may relate to the longer response
times in the nonsymbolic condition (Yarkoni, Barch, Gray, Conturo, & Plus courageux, 2009). Intérêt-
franchement, BG regions are often shown to coactivate with the SN, and our observation of greater
BG–CO/SN allegiance in the nonsymbolic condition (Figure 3F) further suggests a mechanistic
link between these findings (Menon, 2015). Given the diverse roles of the BG, CO, and SN
systems in cognition, cependant, the pattern of increased allegiance among these communities
is difficult to interpret and requires future investigation.
Symbolic Processing Engages an Auditory Community
A final result of interest from the community-level analysis was the observation of the auditory
(Aud) community for symbolic trials (Figures 2 and 3E). The Aud community was left lateralized
and extended along the left superior and middle temporal gyri (STG/MTG; c'est à dire., Brodmann area
22), involving a set of auditory cortex regions involved in the representation of phonemes and
phonological retrieval (Binder, 2015; Liebenthal, Binder, Spitzer, Possing, & Medler, 2005). Gauche
temporal regions overlapping with the Aud community found here have been both theoreti-
cally (Dehaene & Cohen, 1997) and empirically (Prado, Mutreja, & Booth, 2014) implicated
in verbal arithmetic fact retrieval, but their role in symbolic quantity processing has been less
well appreciated. The comparison task we employed here does not explicitly require a digit
to be mapped to its phonological representation, and thus we did not predict a priori the en-
gagement of a superior temporal network. Cependant, our analysis indicates this system forms a
coherent functional community during only the symbolic condition, potentially indicating the
implicit binding of number symbols to their spoken word forms. These results are in line with
previous studies showing increased functional activation in the superior/middle temporal cor-
tex during symbolic compared with nonsymbolic number comparison (Holloway et al., 2010;
Castaldi, Vignaud, & Eger, 2019) and addition (Van Der Ven, Takashima, Segers, Fernández,
& Verhoeven, 2016). Our analysis suggests a functional network involving bilateral superior
temporal cortex regions is engaged during symbolic but not nonsymbolic number comparison.
Robust Differences in Community Allegiance of Visual Regions Between Formats
In our region-level analysis we asked, at each step across the resolution range, whether a
region showed a difference between formats in its profile of community membership. À
identify those regions that showed a robust effect (c'est à dire., regardless of topological scale), nous
counted the number of steps in which a significant difference was observed. The two regions
Neurosciences en réseau
729
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
showing the highest count were located in the right ventromedial occipital cortex (Chiffre 4).
While we controlled for total occupied area and luminance across formats, it is possible that
the visual processing streams engaged by the symbolic and nonsymbolic stimuli quickly di-
verge, and that this is reflected in differential patterns of community affiliation for primary
visual cortex as well as higher level visual regions, specifically observed here in the caudal
cuneus and lingual gyri, respectivement. In a study of symbolic and nonsymbolic processing by
Holloway et al. (2010), a univariate contrast between formats found multiple occipital areas
more engaged by nonsymbolic stimuli, and this was after subtracting out activation associated
with control conditions that were matched in terms of total pixels. Our findings of allegiance
differences involving visual regions seem convergent, and could reflect engagement of ob-
ject location, individuation, and summation mechanisms thought to underlie nonsymbolic
number processing (Verguts & Fias, 2004). En effet, these stages are proposed to serve as the
inputs necessary for numerical magnitude representation in parietal cortex, and have been
shown to involve an occipitoparietal pathway including the inferior and middle occipital gyri
(Roggeman, Santens, Fias, & Verguts, 2011). Symbolic numerals may take an alternative route to
their associated magnitude representations, bypassing the multi-object normalization and ac-
cumulation mechanisms required to process dot sets (Bulthé et al., 2019; Santens, Roggeman,
Fias, & Verguts, 2010), and instead engage a ventral stream object-recognition pathway ex-
tending into the ITG (Hannagan, Amedi, Cohen, Dehaene-Lambertz, & Dehaene, 2015; Harel,
2016; Prix & Devlin, 2011). We hesitate to make any mechanistic interpretations, but our data
at least indicate that the “position” of these visual regions with respect to community topology
is significantly altered between formats. Taken together with the trend of greater allegiance
during symbolic trials between the Visual and DAN as well as FPN communities (Figure 3E
and F), our results build on prior univariate work, suggesting that number format influences
not only local activity but also the distributed interactions of occipital regions.
Robust Differences in Community Allegiance of the pITG and hIP3 Between Formats
A growing body of evidence suggests that number symbol processing engages a region in pos-
terior inferior temporal gyrus (pITG) that preferentially responds to digits compared to other
symbols (Grotheer, Herrmann, et coll., 2016; Hermes et al., 2017; Pollack & Prix, 2019; Shum
et coll., 2013). Given this literature, we hypothesized that if this region is preferentially engaged
during the recognition of Arabic numerals, it would show a greater tendency to join a func-
tional community involving parietal areas during the symbolic trials. Among the 202 régions
analyzed here, the right pITG (Chiffre 5) was one of only five regions demonstrating robust dif-
ferences in its allegiance profile between conditions (Chiffre 4). Its affiliation with the symbolic
DAN community (Chiffre 2 and Supporting Information Table S1) provides evidence that inter-
actions between the right pITG and superior parietal cortex and intraparietal sulcus (IPS) sont
particularly relevant for processing number symbols. This is in line with recent electrocorticog-
raphy and fMRI work showing coupling between lateral vOT and parietal areas during numeral
recognition and arithmetic tasks, including behavioral relevance of task-evoked coupling for
math ability and developmental increases over adolescence (Battista et al., 2018; Daitch et al.,
2016). Even at rest a similar pattern of robust connectivity is observed, specifically involving
pITG to IPS regions (Abboud et al., 2015; Nemmi, Schel, & Klingberg, 2018). Building on this
literature, we found that connectivity patterns of the pITG are differentiated in a task context,
and that selective coupling of the pITG with parietal regions during symbolic processing occurs
even while performing a simple magnitude comparison task. Our analysis further indicates that
the topological position of the pITG with respect to large-scale community organization is a
distinguishing feature between formats, suggesting the pITG plays a pivotal role in the sym-
bolic number processing network. The pITG to parietal coupling we observed here may reflect
Neurosciences en réseau
730
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
a mechanism by which visual number forms are “mapped” to magnitude representations in the
IPS. Alternativement, though not mutually exclusive, this interaction may represent a more general
process of recurrent exchange between neural populations in the vOT (tuned to learned sets
of visual features) and the DAN (involved in feature-based, attentional control), whereby pre-
sentation of a preferred stimulus (par exemple., a number symbol) elicits efficient attentional capture,
allowing for identification and further task-level processing. Such an argument has been made
for the role of the visual word form area in reading and why it shows similarly strong connec-
tivity to the DAN (UN. C. Vogel et al., 2012; note the visual word form area is near the pITG
region described here, albeit in left vOT). Whatever the case, the present results, together with
other recent findings, suggest work looking into the mechanistic contributions of the pITG and
its functional interactions will be a fruitful avenue for future research in numerical cognition.
Enfin, we found that a region in the hIP3 subdivision of the left IPS demonstrated robust
differences in its allegiance profile between formats. The IPS has been extensively implicated
in number processing tasks and thought to be involved in the representation of both sym-
bolic and nonsymbolic magnitude information (Ashkenazi, Henik, Ifergane, & Shelef, 2008;
Dehaene et al., 2003; Fias, Lammertyn, Reynvoet, Dupont, & Orban, 2003; Piazza et al.,
2004). Compared with the right IPS, the left IPS has been shown to be more sharply tuned to
Arabic numerals than to nonsymbolic arrays (Piazza, Pinel, Le Bihan, & Dehaene, 2007) et
is also thought to be more affected by the ontogenetic process of learning number symbols
(Ansari, 2008; Cantlon et al., 2006; Rivera, Reiss, Eckert, & Menon, 2005; S. E. Vogel, Goffin,
& Ansari, 2015). Fait intéressant, Santens et al. (2010) reported a differential connectivity profile
of the left IPS between symbolic and nonsymbolic processing, despite this region being equally
activated by both formats. Our findings are convergent, demonstrating that the left hIP3 takes
on a distinct pattern of community membership between formats, and that this distinction is
pronounced relative to other brain regions. This line of evidence indicates that, while both
formats may engage the left IPS, the functional pathways to and from this region are divergent
between symbolic and nonsymbolic processing, and highlights the additional level of insight
afforded by connectivity-based approaches. It is important to note that the analysis we have
performed here does not directly speak to the question of whether symbolic and nonsymbolic
number engage shared representations in the IPS, as has been a topic of intense study in recent
années (par exemple., Bulthé, De Smedt, & Sur le Beeck, 2015, 2018; Lyons, Ansari, & Beilock, 2015).
Our results instead provide complementary evidence that the whole-brain functional architec-
tures involving left hIP3 are different between formats, and suggest that a more comprehensive
understanding of hIP3 function during number processing will require a characterization of this
region’s role with respect to functional network dynamics. En outre, given previous reports
that symbolic processing in the left IPS changes over development, longitudinal studies look-
ing at the trajectory of this region’s connectivity profile over learning may provide mechanistic
insights into the acquisition of symbolic number abilities.
Limitations
One limitation of this work is that our community-level analyses were conducted at a partic-
ular setting of the structural resolution parameter (c = 2.45), which influences the size and
composition of the detected communities (par exemple., see Methods) (Fortunato & Hric, 2016). Nous
determined this setting based on the heuristic of maximizing the balance across regions of
community stability and change between conditions (Mattar et al., 2015). The goal here was
to be sensitive to differences in community organization while avoiding an unrealistic scenario
in which a majority of regions change their community affiliation (c'est à dire., assuming that there is
Neurosciences en réseau
731
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
some common functional architecture between formats). For other questions, such as “What
is the shared community structure across task states?,” using a heuristic where partitions are
maximally consistent between conditions may be more appropriate. At other settings of γ, le
number of communities as well as regional allegiance profiles will change (par exemple., see Methods),
and thus additional patterns of community-level differences between formats may have been
observed.
Another limitation to note is that the Brainnetome Atlas we used to define our nodes repre-
sents a parcellation of the brain at particular spatial scale (n = 246 régions) and was derived
based on structural-connectivity patterns. We chose this atlas because it has been shown to
capture areas with relatively homogenous functional connectivity profiles (Fan et al., 2016).
Cependant, node definitions at different spatial scales or based on different properties, for ex-
ample, anatomical, architectonic, or random subdivisions, may demonstrate different patterns
from what we observed (Fornito, Zalesky, & Breakspear, 2013; Sporns, 2014; Zalesky et al.,
2010).
Conclusions
En résumé, in this study we adopted a data-driven, network neuroscience approach to charac-
terize the whole-brain functional architecture supporting symbolic and nonsymbolic number
comparison. Our findings provide several novel insights. A unified fronto-parietal control
network in the nonsymbolic condition was fractionated into FPN and DAN communities during
symbolic number processing. We found evidence for stronger allegiance among a left-lateralized
Auditory network in the symbolic condition, potentially reflecting access to phonological rep-
resentations of number word forms. The right pITG, proximal to the putative “Number Form
Area,” joined the DAN system in the symbolic condition only, supporting its proposed role in
the processing of number symbols. Both the right pITG and the hIP3 subdivision of the left
IPS demonstrated robust differences in their community allegiance profiles between formats.
Taken together, these results reveal a pattern of overlapping and distinct network architectures
for symbolic and nonsymbolic number processing, and highlight the additional level of insight
provided by analysis of functional network topology.
MÉTHODES
Participants
Forty neurologically healthy, right-handed subjects participated in the study for undergraduate
course credit. Of those recruited, 6 participants were excluded from analyses due to high levels
of motion and 1 was excluded for significant signal dropout (exclusion criteria detailed below),
resulting in a final sample of 33 participants (19.5
0.9 années, 20 females). All subjects had
normal or corrected-to-normal vision. Informed consent was obtained from each subject in
accordance with the Vanderbilt University Institutional Review Board policy.
±
fMRI Tasks
Participants completed two consecutive runs of an event-related number comparison paradigm.
For each trial, participants judged whether an Arabic digit (symbolic) or dot array (nonsym-
bolic) was less or more than five by pressing a button with either their right index or right
middle finger, respectivement, as quickly and accurately as possible. A total of 160 trials were
présenté, composed of 80 symbolic trials and 80 nonsymbolic trials that were intermixed and
pseudo-randomly ordered (c'est à dire., no more than 3 consecutive trials were of the same number
or format). Stimulus numerosity was either 2, 4, 6, ou 8, which occurred at equal probability
and was counterbalanced across formats. Stimuli were created using the MATLAB package
Neurosciences en réseau
732
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
first described by Piazza et al. (2004). Nonsymbolic stimuli were controlled for total surface
area across numerosities by reducing dot size with increasing numerosity. En plus, stim-
uli were controlled for total occupied area and luminance across formats (c'est à dire., on average, dot
sets contained the same number of pixels as numerals) in an effort to control for nonnumerical
visual parameters across trials. Stimulus duration was 500 ms and interstimulus intervals (ISI)
ranged from 3,300–7,300 ms, in 1,000-ms increments, with an average of 5,300 ms. ISI was
counterbalanced across numerosities and formats.
Imagerie
×
240
Imaging was performed using a 7 Tesla (7T) Philips Achieva scanner with a 32-channel head
coil. An MP2RAGE (Marques et al., 2010) image was acquired for anatomical reference,
aligned to the anterior/posterior commissures, with the following parameters: TR = 4.315 ms,
LE = 1.92 ms, flip angle = 7, 240 coronal slices, voxel size = 1 mm3, imaging matrix = 240
192, acquisition time = 1,010 s. These images were corrected for B1-field inhomo-
×
geneities, as well as proton density and T2* effects according to the procedure described by
Marques et al. (2010). For the event-related experiment, functional T2*-weighted images were
acquired over two runs of 243 volumes each, with the following parameters: TR = 2, 000 ms,
LE = 25 ms, flip angle = 63, 46 tranches axiales (with no interslice gap), voxel size = 2.5 mm3,
46, acquisition time = 500 s per run (16 m 40 s of functional data
imaging matrix = 96
total).
96
×
×
Preprocessing
fMRI data was preprocessed in AFNI (Cox, 1996) using the afni_proc.py program. Preprocess-
ing involved slice-time and motion correction, coregistration, normalization to the MNI152
2009c template using affine registration, smoothing with a 4-mm kernel, and scaling. All trans-
formations of the raw functional data were concatenated and applied in one step to reduce
multiple resampling and interpolation errors. Head-motion/outlier censoring was performed by
removing volumes from the activation model (décrit ci-dessous) that demonstrated between-
volume movement of >0.3-mm Euclidean norm distance or if >5% of voxels in a volume
(within a brain mask) were determined to be outliers. Across our final sample, the percentage
of censored volumes was 4.0
4.1%.
±
Beta-Series Estimation
To assess task-related functional connectivity, we used a beta-series correlation method (BSC)
(Rissman et al., 2004). This method allows for estimation of condition-specific, task-evoked
connectivity by looking at correlated fluctuations in coactivity patterns across multiple stim-
ulus events. Compared with an alternative, commonly used methodology of standard or gen-
eralized psychophysiological interaction analysis (PPI/gPPI) (Friston et al., 1997; McLaren,
Ries, Xu, & Johnson, 2012), BSC has been shown to be more powerful for detecting task-
evoked connectivity in event-related designs that feature many trials, short stimulus durations,
and short ISIs, such as we have implemented here (Cisler, Bush, & Steele, 2014). To com-
pute trial-wise beta (c'est à dire., activation) maps, we employed the “least-squares separate” (LS-S)
method proposed by Mumford et al. (2012) using AFNI’s 3dLSS function (Geib, Stanley,
Dennis, Woldorff, & Cabeza, 2017; Mumford Turner, Ashby, & Poldrack, 2012). Compared
with the original implementation of BSC in which each trial is included as a separate regressor
in a single general linear model (GLM), the LS-S method includes a regressor for the trial of inter-
est and then a nuisance regressor with all other trials of interest combined. This method is more
computationally efficient and, importantly, was found to produce more accurate estimates of
Neurosciences en réseau
733
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
trial-specific activations in simulations (Mumford Turner, Ashby, & Poldrack, 2012). Also in-
cluded in these subject-level GLMs were the following nuisance regressors: 6 motion param-
eters, 6 motion derivatives, 0ème- to 4th-order Legendre polynomials to model low-frequency
drifts (per run), the first five principal components in white matter voxels, and first five princi-
pal components in the lateral ventricles. Tissue masks were created using the Computational
in SPM12 (https://www.fil.ion.ucl.ac.uk/spm/software/spm12/)
Anatomy Toolbox (CAT12)
(Gaser & Dahnke, 2016). The ventricle region of interest (ROI) was created by masking the
cerebrospinal fluid segmentation with the lateral ventricle regions from the Neuromorphome-
tric Atlas included in CAT12. The inclusion of these tissue-based principal component regres-
sors, known as the aCompCor method, was intended to account for nonneural physiological
fluctuations as well as residual motion-related noise and has been shown to improve con-
nectivity estimates in resting-state studies (Caballero-Gaudes & Reynolds, 2017; Ciric et al.,
2017; Muschelli et al., 2014). The preprocessed 4D functional data (after smoothing and scal-
ing) served as the inputs into the 3dLSS function for beta-series estimation. Censoring was
32 volumes (c'est à dire., obser-
performed at this stage and resulted in GLMs with a mean of 933
vations) out of 972 collected volumes. These models included trials/volumes from a separate
identification task (not analyzed here) performed at the beginning of the scanning session. Le
inclusion of all acquired data into one model ensured more accurate estimates of nuisance
effects. For each trial a separate GLM was constructed that included a total of 42 nuisance
regressors plus a regressor for the trial of interest and one for the sum of all other trial re-
sponses. The output of this process involved 3D beta maps for every trial indicating the model
coefficient at each voxel, serving as trial-level activation maps that could then be sorted by
formats.
±
Within-Format Normalization
To ensure that differences in voxel-wise activity levels and/or variance between formats did
not confound our estimates of connectivity, prior to extraction of average beta series from
ROI, we implemented a within-format normalization procedure in which the beta maps were
first separated by format and concatenated, then each voxel-wise beta series was normalized
by subtracting the voxel-wise mean and dividing by the voxel-wise standard deviation. Ce
procedure was adapted from the multivariate pattern analysis literature, in which normalization
of beta values is commonly employed prior to classifier training (Misaki, Kim, Bandettini, &
Corps de guerre, 2010). With this procedure, we could be more certain our connectivity estimates
were derived from covariance in the pattern of trial-level activation, rather than biased by the
magnitude of activations, per se.
Beta-Series Extraction and Scrubbing
We extracted the average beta series in each of 202 cortical and subcortical ROIs from the
Brainnetome Atlas (Fan et al., 2016), which represented the reduced set of ROIs (originally
246) after accounting for signal dropout (Chiffre 6; see Supporting Information Methods). Nous
chose the Brainnetome Atlas as it a connectivity-based parcellation which provides a bio-
logically plausible set of fine-grained regions in both cortex and subcortex (Fan et al., 2016).
Since censoring (c'est à dire., exclusion of high-motion/outlier volumes) was performed in subject-level
GLMs, some trials’ convolved response contained fewer volumes in the final model. Note that
the hemodynamic response to a single trial lasted approximately 13.1 s and spanned either
six or seven volumes of data at our 2-s sampling rate (TR). We expected less reliable beta
estimates for trials in which the response profile contained censored volumes. Donc, nous
implemented a “beta-scrubbing” approach similar to Ray et al. (2017), in which we excluded
trials during which two or more volumes were censored (c'est à dire., the associated beta was removed
Neurosciences en réseau
734
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
Chiffre 6. Functional connectivity and consensus clustering pipeline. The data processing pipeline is depicted, starting from trial-level beta
map estimation to final group-level allegiance matrices and community assignments. Gray arrows indicate the stepwise progression from one
stage of processing to the next. All plots portray representative data from the analysis.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
from the series before running correlations). Across the original sample of 40 sujets, le
median number of retained trials was 147 (91.9%). We determined six subjects were outliers
in the number of retained trials based on a threshold of 3.5
the median absolute deviation
(MAD), a metric for robust outlier detection (Leys, Ley, Klein, Bernard, & Licata, 2013). These
subjects thus demonstrated a significant degree of motion compared with the rest of the sample
and were excluded from further analyses, along with one additional subject who demonstrated
significant signal dropout (see Supporting Information Methods). In the final sample of 33 sub-
projets, out of 80 trials presented for each format, there was an average of 74.2
±
7.3%) trials used for symbolic and 74.6
6.4%) used for nonsymbolic. A paired
5.2 (93.2
t test indicated the number of retained trials was not significantly different between formats
(t(32) =
1.08, p = 0.29)
5.8 (92.8
±
±
±
×
−
Neurosciences en réseau
735
Network topology of symbolic and nonsymbolic number comparison
Functional Connectivity
×
To construct subject-level connectivity matrices, we computed the Pearson correlation be-
tween all region pairs by using the average beta-series vector from each region, yielding a
202 matrix that was symmetric about the diagonal (Chiffre 6). Matrices were constructed
202
for symbolic and nonsymbolic trials separately. Correlation coefficients were Fisher Z trans-
3 ), where N is the
formed and converted to z scores via dividing by the standard error (
number of observations (c'est à dire., betas) retained after the scrubbing procedure (Pêcheur, 1915). Le
z-score matrices served as the final subject-level matrices for network analyses.
1
√N
−
Modularity Maximization and Consensus Clustering
To characterize network topology during the symbolic and nonsymbolic conditions, we em-
ployed the graph-theoretical approach of modularity maximization. This data-driven cluster-
ing procedure attempts to partition a network into nonoverlapping communities where each
node is assigned to exactly one community, such that there is high within-community and low
between-community connectivity (Newman, 2006). The modularity quality function quanti-
fies the degree to which this is achieved given a partition of matrix w. Specifically, we em-
ployed a generalized Louvain algorithm (Blondel, Guillaume, Lambiotte, & Lefebvre, 2008)
that maximized a variant of the standard Newman–Girvan quality function, termed Q*, lequel
incorporates an asymmetric treatment of negative weights, as proposed by Rubinov & Sporns
(2011; Dwyer et al., 2014). This modified treatment of negative weights is recommended for
functional networks because of differing neurobiological significance of positive and negative
correlations in BOLD timeseries (for further discussion, see Rubinov & Sporns, 2011) and is
calculated as follows:
Q∗ =
1
v+ ∑ij (w+
ij −
γe+
ij )δMi Mj −
1
v+ + v−
∑ij (w−ij −
γe−ij )δMi Mj
where each brain region i is assigned to community Mi and region j is assigned to community
Mj; δMi Mj = 1 if Mi = Mj and equals 0 otherwise; e±ij is the within-community connection
strength expected by chance for either positive or negative weights; v+ and v− denote the sum
of all positive and negative weights in the network, respectivement; et, γ is the structural resolu-
tion parameter, which influences the size of the detected communities (Reichardt & Bornholdt,
2006) (see below for details of a data-driven approach to choosing a value for this parameter).
The Louvain algorithm uses a two-step procedure in which first every node is assigned to its
own community, and iterative moves are made assigning a node to its neighboring community
until a maximum Q* is reached. In a second step, the resulting communities are combined
into a smaller network that sums the node weights within each community, and this simplified
network gets submitted back to the first step for a second pass, et ainsi de suite, until no changes
can be made in step 1 to improve Q* (Blondel et al., 2008). Critique, the resulting community
structure is dependent on the random order of moves considered at each pass. En principe,
there is some “optimal” partition of the network, c'est, a partition or set of partitions exists that
returns the highest possible Q* for that matrix. In practice, the optimal partition of a given net-
work is unknown and multiple iterations of modularity maximization result in distinct, though
often similar, solutions, referred to as the so-called degeneracy of modular solutions (Good,
De Montjoye, & Clauset, 2010). Degeneracy can be leveraged through the use of consensus
clustering methods, which aggregate across many partitions of the same network to define a
consensus partition (Lancichinetti & Fortunato, 2012). We implemented a multistep approach
that involved modularity maximization and consensus clustering at the subject level, then con-
sensus clustering at the group level (Chiffre 6).
Neurosciences en réseau
736
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
×
Each fully weighted, subject-level matrix was first partitioned using the generalized com-
munity Louvain algorithm (Blondel et al., 2008) (via the community_louvain.m function of the
Brain Connectivity Toolbox (BCT), http://www.brain-connectivity-toolbox.net, with the “neg-
ative_asym” flag). The algorithm was run 103 times, with each iteration resulting in a single
partition of the 202 regions into communities (c'est à dire., a vector of values indicating the commu-
nity assignment for each region). From these partitions, un 202
202 allegiance matrix was
constructed which represents, at each cell, the percentage of iterations in which two regions
were assigned to the same community (Bassett et al., 2015) (via the agreement_weighted.m
function of the BCT). The subject-level allegiance matrix was then further clustered using a
consensus clustering procedure to obtain a final, consensus partition of regional communities
(Lancichinetti & Fortunato, 2012) (via the consensus_und.m function of the BCT; note the “tau”
parameter was set to 0.5 for all analyses herein, which thresholds the allegiance matrix to re-
move elements weaker than 0.5, c'est à dire., when there is less than 50% agreement across partitions).
The final subject-level partitions were then used to create a group-level allegiance matrix that
représentée, at each cell, the percentage of subjects in which two regions were assigned to
the same community. The same consensus clustering procedure was then used to determine
the final group-level community assignments (Chiffre 6). Because assigned community labels
are arbitrary, labels were maximally matched between the final partitions of the symbolic and
nonsymbolic conditions based on community overlap (via the pair_labeling.m function of the
Network Community Toolbox, http://commdetect.weebly.com). As a final step, permutation
testing was performed to reduce the set of communities to only those demonstrating signifi-
cance at the subject level (see Supporting Information Methods).
Defining the Structural Resolution Parameter
When applying modularity maximization, an important consideration is the definition of the
free parameter, c, referred to as the structural resolution parameter. The effect of γ is such
that lower values result in fewer and larger communities, and higher values result in more and
smaller communities, which provides some constraint on the topological scale of the resulting
partitions. We fully sampled this parameter space in Figure 7A and B, varying γ from 0.05 à 15.
At the highest settings, the algorithm discovered as many communities as there were regions
(c'est à dire., all singletons, which refers to regions that are assigned a community unto themselves).
To further refine this space to a range of interest, we determined the point at which there was
relatively little change in community structure. We used a sliding window approach in which
we calculated average normalized variation of information, a measure of partition distance,
over community partitions within a window size of 0.35 (Meilˇa, 2007). This procedure revealed
that at approximately γ = 5, there was little change in community structure, suggesting that a
stable set of strongly connected (nonsingleton) communities existed at this topological scale,
and that beyond this point, nodes from these communities progressively became singletons
and no new community organization was discovered (Figure 7B and C). We therefore adopted
the range from γ = 0.05 à 5 as our resolution range of interest for all subsequent analyses.
With the range of interest defined, we still needed to determine the ideal setting of γ for
the community-level analysis (note that for the global- and region-level analyses, we present
the results across the full range of interest; Figures 1 et 4). Though setting γ to an arbitrary
value of 1 is common practice, this is not necessarily optimal. A more principled approach
involves “sweeping” across parameter space and using some heuristic to determine the op-
timal value, Par exemple, where community definitions are most consistent across repeated
iterations (Betzel & Bassett, 2016; Betzel et al., 2017; Gu et al., 2015). Since we were inter-
ested here in a comparison of network architecture between the symbolic and nonsymbolic
Neurosciences en réseau
737
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
±
Chiffre 7. Resolution parameter sweep. (A and B) Results of a parameter “sweep,” in which the structural resolution parameter (c) was varied
depuis 0 à 15 in increments of 0.05, avec 100 iterations of the multistep consensus clustering approach at each level of γ. The mean for each
format is plotted in red and blue, with shaded regions indicating the SD across iterations. (C) Mean partition distance over sliding window
3 steps (window size = 0.35 c) is plotted for each format, measured using the normalized variation of information (Meilˇa, 2007). Ce
de
plot indexes the change in community structure over incremental steps in γ, highlighting the point in parameter space in which no new scale
5. We used this result to define the range of interest for our analyses of format differences
of community organization is discovered, at γ
across resolutions (c'est à dire., γ = 0.05–5). (D) The red dashed line indicates the γ at which the variability (SD) of flexibility was maximal, avec
flexibility defined as the number of regions that changed their community assignment between the symbolic and nonsymbolic conditions.
The maximum SD would result from half of all regions changing community assignments and the other half maintaining their assignment. Le
distribution at each gamma value represents the result of all pairwise comparisons of the 100 group-level partitions generated for each format
at that step. The mean of this distribution (black circle) was used to determine the optimal gamma setting for further analyses (c'est à dire., c = 2.45).
≈
conditions, we wanted to conduct our investigation at a resolution that would be sensitive
to both similarities and differences between formats. Pour y parvenir, we employed a heuris-
tic, used previously by Mattar et al. (2015), where the optimal γ value is that which maxi-
mizes variability in the flexibility coefficient across regions. Flexibility is defined simply as the
Neurosciences en réseau
738
Network topology of symbolic and nonsymbolic number comparison
proportion of (task) conditions in which a region changes its assigned community (calculated
via the flexibility.m function of the Network Community Toolbox). With only two conditions,
a region’s flexibility can be 1 ou 0, and the variability of flexibility is the standard deviation of
the vector of 1’s and 0’s (one value for each of the 202 region). By maximizing the variability of
flexibility across brain regions, we are looking for a γ at which there is a balance between sta-
ble and changing community assignments between conditions (c'est à dire., is maximal if exactly half
of regions change their assignment between conditions). Surtout, the procedure does not
ensure the differences are significant within subjects (which we assess via permutation testing),
just that some differences and some similarities exist between the final group-level partitions
of each condition. This approach is thus orthogonal to the prospect of finding reliable within-
subject effects. To determine the optimal γ setting for further investigation, we performed the
multistep group partitioning procedure 100 times at each value of γ, ranging from 0.05 à 5
in increments of 0.05 (for this analysis, subject-level matrices were partitioned 100 times with
community_louvain.m). For each iteration, we calculated the flexibility of nodal assignments
between formats in the final group-level partitions (Figure 7D). At low levels of γ there are
fewer communities (Figure 7A) and the region assignments are stable between formats, thus
resulting in many regions with a flexibility of 0, c'est, low variability across regions. At high
levels of γ, there are many communities, including an increasing number of singletons. After
2.8, the number of nonsingleton communities detected drops, due to the fact that
γ values
a few previously detected communities break apart into singleton communities. Finalement,
we found a maximum in the mean variability (SD) of flexibility at an intermediate value of
c = 2.45. The subsequent community-level analyses involved modularity maximization using
this value.
≈
REMERCIEMENTS
We thank all the volunteers who participated in this study.
INFORMATIONS À L'APPUI
Supporting Information for this article is available at https://doi.org/10.1162/netn_a_00144.
Data and code for this project have been made publicly available at https://osf.io/sb5v2/ and
https://github.com/conradbn/CR7T_Connectivity, respectivement (Conrad et al., 2020un, 2020b).
CONTRIBUTIONS DES AUTEURS
Benjamin N Conrad: Conceptualisation; Conservation des données; Analyse formelle; Méthodologie; Soft-
ware; Visualisation; En écrivant – Original Draft; En écrivant – Review & Editing. Eric D Wilkey:
Conceptualisation; Conservation des données; Acquisition de financement; Enquête; Méthodologie; Project
administration; Ressources; En écrivant – Review & Editing. Darren J Yeo: Conceptualisation; Données
curation; Enquête; Méthodologie; En écrivant – Review & Editing. Gavin R Price: Conceptual-
ization; Conservation des données; Acquisition de financement; Méthodologie; Gestion de projet; Ressources;
Surveillance; En écrivant – Review & Editing.
INFORMATIONS SUR LE FINANCEMENT
Gavin R. Prix, Peabody College Small Research Grant. Gavin R. Prix, National Science Foun-
dation (NSF) Division of Research on Learning in Formal and Informal Settings (http://dx.doi.org/
10.13039/100000173), Award ID: 1660816. Gavin R. Prix, National Science Foundation
(NSF) Division of Research on Learning in Formal and Informal Settings (http://dx.doi.org/10.
Neurosciences en réseau
739
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
13039/100000173), Award ID: 1750213. Eric D. Wilkey is the recipient of a BrainsCAN Post-
doctoral Fellowship at Western University, funded by the Canada First Research Excellence
Fund (CFREF) and Banting Postdoctoral Fellowship funded by the Natural Sciences and Engi-
neering Research Council (NSERC) of Canada. Darren J. Yeo is supported by the Humanities,
Arts, and Social Sciences International PhD Scholarship, co-funded by Nanyang Technological
University and the Government of Singapore: Ministry of Education.
RÉFÉRENCES
Abboud, S., Maidenbaum, S., Dehaene, S., & Amedi, UN.
(2015).
A number-form area in the blind. Communications naturelles, 6,
6026. https://doi.org/10.1038/ncomms7026
Althouse, UN. D. (2016). Adjust for multiple comparisons? It’s not that
simple. Annals of Thoracic Surgery, 101(5), 1644–1645. https://
doi.org/10.1016/j.athoracsur.2015.11.024
Amalric, M., & Dehaene, S. (2016). Origins of the brain networks
for advanced mathematics in expert mathematicians. Proceed-
ings of the National Academy of Sciences, 113(18), 4909–4917.
https://doi.org/10.1073/pnas.1603205113
Ansari, D.
(2008). Effects of development and enculturation on
number representation in the brain. Nature Revues Neurosciences,
9(4), 278–291. https://doi.org/10.1038/nrn2334
Ansari, D., & Dhital, B. (2006). Age-related changes in the activation
of the intraparietal sulcus during nonsymbolic magnitude pro-
cessation: An event-related functional magnetic resonance imaging
Journal des neurosciences cognitives, 18(11), 1820–1828.
étude.
https://doi.org/10.1162/jocn.2006.18.11.1820
Ansari, D., Garcia, N., Lucas, E., Hamon, K., Dhital, B., & Dhitalm,
B. (2005). Neural correlates of symbolic number processing in
children and adults. Neuroreport, 16(16), 1769–1773. https://
doi.org/10.1097/01.wnr.0000183905.23396.f1
Ansari, D., Lyons, je. M., van Eimeren, L., & Xu, F. (2007). Linking
visual attention and number processing in the brain: The role of
the temporo-parietal junction in small and large symbolic and
Journal of Cognitive Neuro-
nonsymbolic number comparison.
science, 19(11), 1845–1853. https://doi.org/10.1162/jocn.2007.
19.11.1845
Ashkenazi, S., Henik, UN., Ifergane, G., & Shelef, je.
(2008). Basic
numerical processing in left intraparietal sulcus (IPS) acalculia.
Cortex, 44(4), 439–448. https://doi.org/10.1016/j.cortex.2007.
08.008
Baldauf, D., & Désimone, R.. (2014). Neural mechanisms of object-
based attention. Science, 344(6182), 424–427. https://est ce que je.org/
10.1126/science.1247003
Bassett, D. S., & Gazzaniga, M.. S.
(2011). Understanding com-
plexity in the human brain. Tendances des sciences cognitives, 15(5),
200–209. https://doi.org/10.1016/j.tics.2011.03.006
Bassett, D. S., Owens, E. T., Daniels, K. E., & Porter, M.. UN. (2012).
Influence of network topology on sound propagation in granu-
lar materials. Physical Review E – Statistical, Nonlinear, and Soft
Matter Physics, 86(4), 1–17. https://doi.org/10.1103/PhysRevE.
86.041306
Bassett, D. S., & Sporns, Ô.
(2017). Network neuroscience. Na-
ture Neuroscience, 20(3), 353–364. https://est ce que je.org/10.1038/nn.
4502
Bassett, D. S., Lequel, M., Wymbs, N. F., & Grafton, S. T.
(2015).
Learning-induced autonomy of sensorimotor systems, 18(5).
https://doi.org/10.1038/nn.3993
Battista, C., Evans, T. M., Ngoon, T. J., Chen, T., Chen, L., Kochalka,
J., & Menon, V. (2018). Mechanisms of interactive specialization
and emergence of functional brain circuits supporting cognitive
development in children. Npj Science of Learning, 3(1), 1. https://
doi.org/10.1038/s41539-017-0017-2
Benjamini, Y., & Hochberg, Oui.
(1995). Controlling the false
discovery rate: A practical and powerful approach to multiple
testing. Journal of the Royal Statistical Society: Série B (Method-
ological), 57(1), 289–300. https://doi.org/10.1111/j.2517-6161.
1995.tb02031.x
Bertolero, M.. UN., Thomas Yeo, B. T., & D'Esposito, M..
(2015).
The modular and integrative functional architecture of the hu-
man brain. Proceedings of the National Academy of Sciences of
the United States of America, 112(49), E6798–E6807. https://est ce que je.
org/10.1073/pnas.1510619112
Bertolero, M.. UN., Yeo, B. T. T., Bassett, D. S., & D'Esposito, M..
(2018). A mechanistic model of connector hubs, modularity and
cognition. Nature Human Behaviour, 2(Chiffre 1), 5–7. https://
doi.org/10.1038/s41562-018-0420-6
Betzel, R.. F., & Bassett, D. S.
(2016). Multi-scale brain net-
travaux. NeuroImage, (Novembre), 0–1. https://est ce que je.org/10.1016/
j.neuroimage.2016.11.006
Betzel, R.. F., Medaglia, J.. D., Papadopoulos, L., Baum, G. L., Gur,
R., Gur, R., . . . Bassett, D. S. (2017). The modular organization
of human anatomical brain networks: Accounting for the cost of
wiring. Neurosciences en réseau, 1(1), 42–68. https://est ce que je.org/10.
1162/NETN_a_00002
Bichot, N. P., Heard, M.. T., DeGennaro, E. M., & Désimone, R..
(2015). A source for feature-based attention in the prefrontal Cor-
tex. Neurone, 88(4), 832–844. https://est ce que je.org/10.1016/j.neuron.
2015.10.001
Binder, J.. R..
(2015). The Wernicke area: Modern evidence and a
reinterpretation. Neurologie, 85(24), 2170–2175. https://est ce que je.org/
10.1212/WNL.0000000000002219
Bliss, C. JE., & Pêcheur, R.. UN.
(1953). Fitting the negative binomial
distribution to biological data. Biometrics, 9(2), 176. https://est ce que je.
org/10.2307/3001850
Blondel, V. D., Guillaume, J.. L., Lambiotte, R., & Lefebvre, E.
Jour-
(2008). Fast unfolding of communities in large networks.
nal of Statistical Mechanics: Theory and Experiment, 2008(10),
1–12. https://doi.org/10.1088/1742-5468/2008/10/P10008
Brun, U., Schäfer, UN., Walter, H., Erk, S., Romanczuk-Seiferth, N.,
Haddad, L., . . . Bassett, D. S. (2015). Dynamic reconfiguration
Neurosciences en réseau
740
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
of frontal brain networks during executive cognition in humans.
Proceedings of the National Academy of Sciences of the United
States of America, 112(37), 11678–11683. https://est ce que je.org/10.
1073/pnas.1422487112
Bulthé, J., De Smedt, B., & Sur le Beeck, H. P..
(2015). Visual
number beats abstract numerical magnitude: Format-dependent
representation of arabic digits and dot patterns in human parietal
Journal des neurosciences cognitives, 27(7), 1376–1387.
cortex.
https://doi.org/10.1162/jocn_a_00787
Bulthé, J., De Smedt, B., & Sur le Beeck, H. P..
(2018). Arith-
metic skills correlate negatively with the overlap of symbolic and
non-symbolic number representations in the brain. Cortex, 101,
306–308. https://doi.org/10.1016/j.cortex.2018.01.008
Bulthé, J., Prinsen, J., Vanderauwera, J., Duyck, S., Daniels, N.,
Gillebert, C. R., et autres. (2019). Multi-method brain imaging reveals
impaired representations of number as well as altered connec-
tivity in adults with dyscalculia. NeuroImage, 190(Mars 2017),
289–302. https://doi.org/10.1016/j.neuroimage.2018.06.012
Caballero-Gaudes, C., & Reynolds, R.. C. (2017). Methods for clean-
ing the BOLD fMRI signal. NeuroImage, 154(Décembre 2016),
128–149. https://doi.org/10.1016/j.neuroimage.2016.12.018
Campbell, J.. je. D.
(1994). Architectures for numerical cognition.
Cognition, 53(1), 1–44. https://doi.org/10.1016/0010-0277(94)
90075-2
Cantlon, J.. F., Brannon, E. M., Carter, E. J., & Pelphrey, K. UN. (2006).
A Functional imaging of numerical processing in adults and 4-
y-old children. PLoS Biology, 4(5), 844–854. https://est ce que je.org/10.
1371/journal.pbio.0040125
Castaldi, E., Vignaud, UN., & Eger, E.
(2019). Mapping numerical
perception and operations in relation to functional and anatomi-
cal landmarks of human parietal cortex. bioRxiv. https://est ce que je.org/
10.1101/602599
Chaï, L. R., Mattar, M.. G., Blank, je. UN., Fedorenko, E., & Bassett,
D. S. (2016). Functional network dynamics of the language sys-
tem. Cortex cérébral, 26(11), 4148–4159. https://est ce que je.org/10.
1093/cercor/bhw238
Chang, L. J., Yarkoni, T., Khaw, M.. W., & Sanfey, UN. G.
(2013).
Decoding the role of the insula in human cognition: Functional
parcellation and large-scale reverse inference. Cortex cérébral,
23(3), 739–749. https://doi.org/10.1093/cercor/bhs065
Ciric, R., Loup, D. H., Power, J.. D., Roalf, D. R., Baum, G. L.,
Ruparel, K., . . . Satterthwaite, T. D.
(2017). Benchmarking
of participant-level confound regression strategies for the control
of motion artifact in studies of functional connectivity. Neuro-
Image, 154(Mars), 174–187. https://doi.org/10.1016/j.neuroimage.
2017.03.020
Cisler, J.. M., Bush, K., & Steele, J.. S. (2014). A comparison of sta-
tistical methods for detecting context-modulated functional con-
nectivity in fMRI. NeuroImage, 84, 1042–1052. https://est ce que je.org/
10.1016/j.neuroimage.2013.09.018
Cocchi, L., Halford, G. S., Zalesky, UN., Harding, je. H., Ramm, B. J.,
Cutmore, T., . . . Mattingley, J.. B. (2014). Complexity in relational
processing predicts changes in functional brain network dynam-
ics. Cortex cérébral, 24(9), 2283–2296. https://est ce que je.org/10.1093/
cercor/bht075
Cohen, J.. R., & D'Esposito, M.. (2016). The segregation and integra-
tion of distinct brain networks and their relationship to cognition.
Journal des neurosciences, 36(48), 12083–12094. https://est ce que je.org/
10.1523/JNEUROSCI.2965-15.2016
Cohen, Kadosh, R., & Walsh, V. (2009). Numerical representation
in the parietal lobes: Abstract or not abstract? The Behavioral and
Sciences du cerveau, 32(3–4), 313–328; discussion 328–373. https://
doi.org/10.1017/S0140525X09990938
Cole, M.. W., Bassett, D. S., Power, J.. D., Plus courageux, T. S., & Petersen,
S. E. (2014). Intrinsic and task-evoked network architectures of
the human brain. Neurone, 83(1), 238–251. https://est ce que je.org/10.
1016/j.neuron.2014.05.014
Conrad, B. N., Wilkey, E. D., Yeo, D. J., & Prix, G. R..
(2020un).
GitHub repository for Network topology of symbolic and non-
symbolic number comparison. https://doi.org/10.5281/zenodo.
3974650
Conrad, B. N., Wilkey, E. D., Yeo, D. J., & Prix, G. R..
(2020b).
Network Topology of Symbolic and Nonsymbolic Number Com-
parison. https://doi.org/10.17605/OSF.IO/SB5V2
Corbetta, M., Patel, G., & Shulman, G. L. (2008). The reorienting
system of the human brain: From environment to theory of mind.
Neurone, 58(3), 306–324. https://doi.org/10.1016/j.neuron.2008.
04.017
Corbetta, M., & Shulman, G. L.
(2002). Control of goal-directed
and stimulus-driven attention in the brain. Nature Reviews Neu-
roscience, 3(3), 201–215. https://doi.org/10.1038/nrn755
Cox, R.. W.
(1996). AFNI: Software for analysis and visualization
of functional magnetic resonance neuroimages. Computers and
Biomedical Research, 29(29), 162–173. https://doi.org/10.1006/
cbmr.1996.0014
Daitch, UN. L., Foster, B. L., Schrouff, J., Rangarajan, V., Ka¸sikçi, JE.,
Gattas, S., & Parvizi, J..
(2016). Mapping human temporal and
parietal neuronal population activity and functional coupling
during mathematical cognition. Actes de la Nationale
Academy of Sciences of the United States of America, 113(46),
E7277–E7286. https://doi.org/10.1073/pnas.1608434113
Dehaene, S.
Dehaene, S., & Cohen, L.
(1992). Varieties of numerical abilities. Cognition,
44(1–2), 1–42. https://doi.org/10.1016/0010-0277(92)90049-N
(1995). Towards an anatomical and
functional model of number processing. Mathematical Cogni-
tion. https://doi.org/10.1155/2014/461647
Dehaene, S., & Cohen, L. (1997). Cerebral pathways for calcula-
tion: Double dissociation between rote verbal and quantitative
knowledge of arithmetic. Cortex, 33(2), 219–250. https://est ce que je.
org/10.1016/S0010-9452(08)70002-9
Dehaene, S., Piazza, M., Pinel, P., & Cohen, L. (2003). Three parietal
circuits for number processing. Cognitive Neuropsychology,
20(3–6), 487–506. https://doi.org/10.1080/02643290244000239
Dixon, M.. L., De La Vega, UN., Mills, C., Andrews-Hanna, J., Spreng,
R.. N., Cole, M.. W., & Christoff, K. (2018). Heterogeneity within
the frontoparietal control network and its relationship to the de-
fault and dorsal attention networks. Actes de la Nationale
Academy of Sciences of the United States of America, 115(7),
E1598–E1607. https://doi.org/10.1073/pnas.1715766115
Dosenbach, N. U. F., Fair, D. UN., Cohen, UN. L., Schlaggar, B. L., &
Petersen, S. E. (2008). A dual-networks architecture of top-down
control. Tendances des sciences cognitives, 12(3), 99–105. https://est ce que je.
org/10.1016/j.tics.2008.01.001
Neurosciences en réseau
741
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
Dosenbach, N. U. F., Fair, D. UN., Miezin, F. M., Cohen, UN. L.,
Wenger, K. K., Dosenbach, R.. UN. T., . . . Petersen, S. E.
(2007).
Distinct brain networks for adaptive and stable task control in
humans. Proceedings of the National Academy of Sciences of
the United States of America, 104(26), 11073–11078. https://
doi.org/10.1073/pnas.0704320104
Dwyer, D. B., Harrison, B. J., Yucel, M., Whittle, S., Zalesky, UN.,
Pantelis, C., . . . Fornito, UN.
(2014). A Large-scale brain net-
work dynamics supporting adolescent cognitive control. Journal
of Neuroscience, 34(42), 14096–14107. https://doi.org/10.1523/
JNEUROSCI.1634-14.2014
Eger, E., Sterzer, P., Russ, M.. O., Giraud, A.-L., & Kleinschmidt, UN.
(2003). A supramodal number representation in human intra-
parietal cortex. Neurone, 37(4), 719–725. Extrait de http://
www.ncbi.nlm.nih.gov/pubmed/12597867
Fan, L., Li, H., Zhuo, J., Zhang, Y., Wang, J., Chen, L., . . . Jiang,
(2016). The Human Brainnetome Atlas: A new brain at-
T.
las based on connectional architecture. Cortex cérébral, 26(8),
3508–3526. https://doi.org/10.1093/cercor/bhw157
Feise, R.. J..
(2002). Do multiple outcome measures require p-
value adjustment? BMC Medical Research Methodology, 2(1),
8. https://doi.org/10.1186/1471-2288-2-8
Fias, W., Lammertyn, J., Reynvoet, B., Dupont, P., & Orban, G. UN.
(2003). Parietal representation of symbolic and nonsymbolic
Journal des neurosciences cognitives, 15(1), 47–56.
magnitude.
https://doi.org/10.1162/089892903321107819
Pêcheur, R.. UN. (1915). Frequency distribution of the values of the cor-
relation coefficient in samples from an indefinitely large popula-
tion. Biometrika, 10(4), 507. https://doi.org/10.2307/2331838
Fornito, UN., Zalesky, UN., & Breakspear, M.. (2013). Graph analysis of
the human connectome: Promise, progress, and pitfalls. Neuro-
Image, 80, 426–444. https://doi.org/10.1016/j.neuroimage.2013.
04.087
Fortunato, S., & Hric, D. (2016). Community detection in networks:
A user guide, 1–43. https://doi.org/10.1016/j.physrep.2016.09.
002
Fox, M.. D., Corbetta, M., Snyder, UN. Z., Vincent, J.. L., & Raichle,
M.. E. (2006). Spontaneous neuronal activity distinguishes human
dorsal and ventral attention systems. Actes de la Nationale
Academy of Sciences of the United States of America, 103(26),
10046–10051. https://doi.org/10.1073/pnas.0604187103
Fox, M.. D., Snyder, UN. Z., Vincent, J.. L., Corbetta, M., Van Essen,
D. C., & Raichle, M.. E. (2005). The human brain is intrinsically
organized into dynamic, anticorrelated functional networks. Pro-
ceedings of the National Academy of Sciences of the United
States of America, 102(27), 9673–9678. https://doi.org/10.1073/
pnas.0504136102
Friston, K. J., Buechel, C., Fink, G. R., Morris, J., Rolls, E., & Dolan,
R.. J.. (1997). Psychophysiological and modulatory interactions in
neuroimaging. Neuroimage, 6(3), 218–229. https://est ce que je.org/10.
1006/nimg.1997.0291
Garcia, J.. O., Ashourvan, UN., Muldon, S. F., Vettel, J.. M., & Bassett,
D. S.
(2018). Applications of community detection techniques
to brain graphs: algorithmic considerations and implications for
neural function. Proceedings of the IEEE, 1–22. https://est ce que je.org/
10.1109/JPROC.2017.2786710
Gaser, C., & Dahnke, R..
(2016). CAT-a computational anatomy
toolbox for the analysis of structural MRI data. Organization for
Human Brain Mapping, 2016, 336–348.
Geib, B. R., Stanley, M.. L., Dennis, N. UN., Woldorff, M.. G., &
Cabeza, R.. (2017). From hippocampus to whole-brain: The role
of integrative processing in episodic memory retrieval, 2259,
2242–2259. https://doi.org/10.1002/hbm.23518
Godwin, D., Barry, R.. L., & Marois, R..
(2015). Breakdown of the
brain’s functional network modularity with awareness. Proceed-
ings of the National Academy of Sciences of the United States
of America, 112(12), 3799–3804. https://doi.org/10.1073/pnas.
1414466112
Good, B. H., De Montjoye, Oui. UN., & Clauset, UN.
(2010). Perfor-
mance of modularity maximization in practical contexts. Physical
Review E – Statistical, Nonlinear, and Soft Matter Physics, 81(4),
1–20. https://doi.org/10.1103/PhysRevE.81.046106
Grotheer, M., Ambrus, G. G., & Kovács, G.
(2016). Causal evi-
dence of the involvement of the number form area in the visual
detection of numbers and letters. NeuroImage, 132, 314–319.
https://doi.org/10.1016/j.neuroimage.2016.02.069
Grotheer, M., Herrmann, K.-H., & Kovács, G. (2016). Neuroimag-
ing evidence of a bilateral representation for visually presented
numbers. Journal des neurosciences, 36(1), 88–97. https://est ce que je.org/
10.1523/JNEUROSCI.2129-15.2016
Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Yu, UN. B., Kahn,
UN. E., . . . Bassett, D. S. (2015). Controllability of structural brain
réseaux. Communications naturelles, 6, 1-dix. https://est ce que je.org/10.
1038/ncomms9414
Guimerà, R., & Amaral, L. UN. N.
(2004). Modularity from fluctu-
ations in random graphs and complex networks. Physical, Review
E – Statistical Physics, Plasmas, Fluids, and Related Interdisci-
plinary Topics, 70(2), 4. https://doi.org/10.1103/PhysRevE.70.
025101
Guthrie, M., Leblois, UN., Garenne, UN., & Boraud, T. (2013). Inter-
action between cognitive and motor cortico-basal ganglia loops
during decision making: A computational study. Journal of Neu-
rophysiology, 109(12), 3025–3040. https://est ce que je.org/10.1152/jn.
00026.2013
Hannagan, T., Amedi, UN., Cohen, L., Dehaene-Lambertz, G., &
Dehaene, S.
(2015). Origins of the specialization for letters
and numbers in ventral occipitotemporal cortex. Trends in Cog-
nitive Sciences, 19(7), 374–382. https://doi.org/10.1016/j.tics.
2015.05.006
Harel, UN.
(2016). What is special about expertise? Visual exper-
tise reveals the interactive nature of real-world object recogni-
tion. Neuropsychologie, 83, 88–99. https://est ce que je.org/10.1016/j.
neuropsychologia.2015.06.004
Hartley, H. Ô.
(1958). Maximum likelihood estimation from in-
complete data. Biometrics, 14(2), 174. https://doi.org/10.2307/
2527783
Il, L., Zuo, Z., Chen, L., & Humphreys, G. (2014). Effects of num-
ber magnitude and notation at 7T: Separating the neural response
to small and large, symbolic and nonsymbolic number. Cere-
bral Cortex, 24(8), 2199–2209. https://doi.org/10.1093/cercor/
bht074
Hearne, L. J., Cocchi, L., Zalesky, UN., & Mattingley, J.. B.
(2017).
Reconfiguration of brain network architectures between resting
state and complexity-dependent cognitive reasoning. The Journal
Neurosciences en réseau
742
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
of Neuroscience, 37(35), 0485–17.
JNEUROSCI.0485-17.2017
https://doi.org/10.1523/
Heinzle, J., Wenzel, M.. UN., & Haynes, J.-D.
(2012). Visuomotor
Journal
functional network topology predicts upcoming tasks.
of Neuroscience, 32(29), 9960–9968. https://doi.org/10.1523/
JNEUROSCI.1604-12.2012
Helie, S., Chakravarthy, S., & Moustafa, UN. UN.
(2013). Exploring
the cognitive and motor functions of the basal ganglia: An inte-
grative review of computational cognitive neuroscience models.
Frontiers in Computational Neuroscience, 7(Décembre), 1–16.
https://doi.org/10.3389/fncom.2013.00174
Hermes, D., Rangarajan, V., Foster, B. L., King, J.. R., Kasikci, JE.,
Miller, K. J., & Parvizi, J.. (2017). Electrophysiological responses
in the ventral temporal cortex during reading of numerals and
calculation. Cortex cérébral, 27(1), 567–575. https://est ce que je.org/10.
1093/cercor/bhv250
Holloway, je. D., Battista, C., Vogel, S. E., & Ansari, D. (2013). Se-
mantic and perceptual processing of number symbols: Evidence
from a cross-linguistic fMRI adaptation study. Journal of Cognitive
Neurosciences, 25(3), 388–400. https://doi.org/10.1162/jocn_a_
00323
Holloway, je. D., Prix, G. R., & Ansari, D.
(2010). Common and
segregated neural pathways for the processing of symbolic and
nonsymbolic numerical magnitude: Une étude IRMf. NeuroImage,
49(1), 1006–1017. https://doi.org/10.1016/j.neuroimage.2009.
07.071
Kaufmann, L., Koppelstaetter, F., Delazer, M., Siedentopf, C.,
Rhomberg, P., Golaszewski, S., . . . Ischebeck, UN. (2005). Neural
correlates of distance and congruity effects in a numerical Stroop
task: An event-related fMRI study. NeuroImage, 25(3), 888–898.
https://doi.org/10.1016/j.neuroimage.2004.12.041
Knops, UN. (2017). Probing the neural correlates of number process-
ing. Neuroscientist, 23(3), 264–274. https://doi.org/10.1177/
1073858416650153
Krienen, F. M., Yeo, B. T. T., & Buckner, R.. L.
(2014). Re-
configurable task-dependent functional coupling modes cluster
around a core functional architecture. Philosophical Trans-
actions of the Royal Society B: Sciences biologiques, 369(1653),
20130526–20130526. https://doi.org/10.1098/rstb.2013.0526
Lancichinetti, UN., & Fortunato, S. (2012). Consensus clustering in
complex networks. Scientific Reports, 2. https://doi.org/10.1038/
srep00336
Leibovich, T., & Ansari, D. (2016). The symbol-grounding problem
in numerical cognition: A review of theory, evidence, and out-
standing questions. Canadian Journal of Experimental Psychology/
Revue Canadienne de Psychologie Expérimentale, 70(1), 12–23.
https://doi.org/10.1037/cep0000070
Leisman, G., Braun-Benjamin, O., & Melillo, R.. (2014). Cognitive-
motor interactions of the basal ganglia in development. Frontiers
in Systems Neuroscience, 8(Février), 1–18. https://est ce que je.org/10.
3389/fnsys.2014.00016
Leys, C., Ley, C., Klein, O., Bernard, P., & Licata, L.
(2013). De-
tecting outliers: Do not use standard deviation around the mean,
use absolute deviation around the median. Journal of Experimen-
tal Social Psychology, 49(4), 764–766. https://est ce que je.org/10.1016/j.
jesp.2013.03.013
Liebenthal, E., Binder, J.. R., Spitzer, S. M., Possing, E. T., & Medler,
D. UN. (2005). Neural substrates of phonemic perception. Cere-
bral Cortex, 15(10), 1621–1631. https://doi.org/10.1093/cercor/
bhi040
Lyons, je. M., Ansari, D., & Beilock, S. L. (2015). Qualitatively differ-
ent coding of symbolic and nonsymbolic numbers in the human
brain. Human Brain Mapping, 36(2), 475–488. https://est ce que je.org/
10.1002/hbm.22641
Marques, J.. P., Kober, T., Krueger, G., van der Zwaag, W., Van de
Moortele, P.. F., & Gruetter, R.. (2010). MP2RAGE, a self bias-field
corrected sequence for improved segmentation and T1-mapping
at high field. NeuroImage, 49(2), 1271–1281. https://est ce que je.org/10.
1016/j.neuroimage.2009.10.002
Mattar, M.. G., Cole, M.. W., Thompson-Schill, S. L., & Bassett, D. S.
(2015). A functional cartography of cognitive systems. PLoS Com-
putational Biology, 11(12), 1–26. https://doi.org/10.1371/journal.
pcbi.1004533
McCloskey, M..
(1992). Cognitive mechanisms in numerical pro-
cessation: Evidence from acquired dyscalculia. Cognition, 44(1–2),
107–157. https://doi.org/10.1016/0010-0277(92)90052-J.
McCloskey, M., Caramazza, UN., & Basili, UN.
(1985). Cognitive
mechanisms in number processing and calculation: Evidence
from dyscalculia. Brain and Cognition, 4(2), 171–196. https://
doi.org/10.1016/0278-2626(85)90069-7
McLaren, D. G., Ries, M.. L., Xu, G., & Johnson, S. C. (2012). A gen-
eralized form of context-dependent psychophysiological interac-
tion (gPPI): A comparison to standard approaches. NeuroImage,
61(4), 1277–1286. https://doi.org/10.1016/j.neuroimage.2012.
03.068
Meilˇa, M.. (2007). Comparing clusterings-an information based dis-
Journal of Multivariate Analysis, 98(5), 873–895. https://
tance.
doi.org/10.1016/j.jmva.2006.11.013
Menon, V.
(2015). Brain mapping: An encyclopedic reference
(Vol. 2). Elsevier Inc. https://doi.org/10.1016/B978-0-12-397025
-1.00052-X
Middleton, F. UN., & Strick, P.. L. (2000). Basal ganglia output and
cognition: Evidence from anatomical, behavioral, and clinical
études. Brain and Cognition, 42(2), 183–200. https://est ce que je.org/10.
1006/brcg.1999.1099
Misaki, M., Kim, Y., Bandettini, P.. UN., & Corps de guerre, N.
(2010).
Comparison of multivariate classifiers and response normaliza-
tions for pattern-information fMRI. NeuroImage, 53(1), 103–118.
https://doi.org/10.1016/j.neuroimage.2010.05.051
Mumford, J.. UN., Tourneur, B. O., Ashby, F. G., & Poldrack, R.. UN. (2012).
Deconvolving BOLD activation in event-related designs for
multivoxel pattern classification analyses. NeuroImage, 59(3),
2636–2643. https://doi.org/10.1016/j.neuroimage.2011.08.076
Muschelli, J., Nebel, M.. B., Caffo, B. S., Barber, UN. D., Pekar, J.. J., &
Mostofsky, S. H. (2014). Reduction of motion-related artifacts in
resting state fMRI using aCompCor. NeuroImage, 96(2), 22–35.
https://doi.org/10.1016/j.neuroimage.2014.03.028
Nemmi, F., Schel, M.. UN., & Klingberg, T.
(2018). Connectivity
of the human number form area reveals development of a cor-
Frontiers in Human Neuro-
tical network for mathematics.
science, 12(Novembre), 1–15. https://doi.org/10.3389/fnhum.
2018.00465
Newman, M.. E. J.. (2006). Modularity and community structure in
réseaux. Proceedings of the National Academy of Sciences of
the United States of America, 103(23), 8577–8582. https://est ce que je.
org/10.1073/pnas.0601602103
Neurosciences en réseau
743
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
Nichols, T., & Holmes, UN. (2004). Nonparametric permutation tests
for functional neuroimaging. In Human Brain Function (pp. 887–910).
Elsevier. https://doi.org/10.1016/B978-012264841-0/50048-2
Packard, M.. G., & Knowlton, B. J..
(2002). Learning and memory
functions of the basal ganglia. Revue annuelle des neurosciences, 25(1),
563–593. https://doi.org/10.1146/annurev.neuro.25.112701.142937
Petersen, S. E., & Posner, M.. je. (2012). The attention system of the hum-
an brain: 20 des années après. Revue annuelle des neurosciences, 35(1),
73–89. https://doi.org/10.1146/annurev-neuro-062111-150525
Piazza, M., Izard, V., Pinel, P., Le Bihan, D., & Dehaene, S. (2004).
Tuning curves for approximate numerosity in the human intra-
parietal sulcus. Neurone, 44(3), 547–555. https://est ce que je.org/10.1016/j.
neuron.2004.10.014
Piazza, M., Pinel, P., Le Bihan, D., & Dehaene, S. (2007). A mag-
nitude code common to numerosities and number symbols in
human intraparietal cortex. Neurone, 53(2), 293–305. https://est ce que je.
org/10.1016/j.neuron.2006.11.022
Pinel, P., Dehaene, S., Riviére, D., & LeBihan, D.
(2001). Mod-
ulation of parietal activation by semantic distance in a number
comparison task. NeuroImage, 14(5), 1013–1026. https://est ce que je.
org/10.1006/nimg.2001.0913
Pollack, C., & Prix, G. R.. (2019). Neurocognitive mechanisms of
digit processing and their relationship with mathematics compe-
tence. NeuroImage, 185(May 2018), 245–254. https://est ce que je.org/
10.1016/j.neuroimage.2018.10.047
Power, J.. D., Cohen, UN. L., Nelson, S. M., Wig, G. S., Barnes, K. UN.,
Church, J.. UN., . . . Petersen, S. E. (2011). Functional network or-
ganization of the human brain. Neurone, 72(4), 665–678. https://
doi.org/10.1016/j.neuron.2011.09.006
Prado, J., Mutreja, R., & Booth, J.. R..
(2014). Developmental dis-
sociation in the neural responses to simple multiplication and
subtraction problems. Developmental Science, 17(4), 537–552.
https://doi.org/10.1111/desc.12140
Prix, C. J., & Devlin, J.. T. (2011). The interactive account of ven-
tral occipitotemporal contributions to reading. Trends in Cog-
nitive Sciences, 15(6), 246–253. https://doi.org/10.1016/j.tics.
2011.04.001
Ptak, R.. (2012). The frontoparietal attention network of the human
brain. Le neuroscientifique, 18(5), 502–515. https://doi.org/10.1177/
1073858411409051
Ptak, R., Schnider, UN., & Fellrath, J.. (2017). The dorsal frontoparietal
réseau: A core system for emulated action. Tendances cognitives
les sciences, 21(8), 589–599. https://doi.org/10.1016/j.tics.2017.
05.002
Ray, K. L., Lesh, T. UN., Howell, UN. M., Salo, T. P., Ragland, J.. D.,
MacDonald, UN. W., . . . Carter, C. S. (2017). Functional network
changes and cognitive control in schizophrenia. NeuroImage:
Clinique, 15(May), 161–170. https://doi.org/10.1016/j.nicl.2017.
05.001
Reichardt, J., & Bornholdt, S.
(2006). Statistical mechanics of
community detection. Physical Review E – Statistical, Nonlinear,
and Soft Matter Physics, 74(1), 1–16. https://doi.org/10.1103/
PhysRevE.74.016110
Reynvoet, B., & Sasanguie, D.
The symbol ground-
ing problem revisited: A thorough evaluation of
the ANS
mapping account and the proposal of an alternative account
(2016).
based on symbol–symbol associations. Frontiers in Psychology,
07(Octobre), 1–11. https://doi.org/10.3389/fpsyg.2016.01581
Rissman, J., Gazzaley, UN., & D'Esposito, M.. (2004). Measuring func-
tional connectivity during distinct stages of a cognitive task. Neu-
roImage, 23(2), 752–763. https://doi.org/10.1016/j.neuroimage.
2004.06.035
Rivera, S. M., Reiss, UN. L., Eckert, M.. UN., & Menon, V. (2005). Devel-
opmental changes in mental arithmetic: Evidence for increased
functional specialization in the left inferior parietal cortex. Cere-
bral Cortex, 15(11), 1779–1790. https://doi.org/10.1093/cercor/
bhi055
Rizkallah, J., Benquet, P., Kabbara, UN., Dufor, O., Wendling, F., &
Hassan, M.. (2018). Dynamic reshaping of functional brain net-
Journal of Neural Engi-
works during visual object recognition.
neering, 15(5). https://doi.org/10.1088/1741-2552/aad7b1
Roggeman, C., Santens, S., Fias, W., & Verguts, T. (2011). Stages of
nonsymbolic number processing in occipitoparietal cortex dis-
entangled by fMRI adaptation. Journal des neurosciences, 31(19),
7168–7173. https://doi.org/10.1523/jneurosci.4503-10.2011
Rothman, K. J.. (1990). No adjustments are needed for multiple com-
parisons. Epidemiology, 1(1), 43–46. https://est ce que je.org/10.1097/
00001648-199001000-00010
Rubinov, M., & Sporns, Ô. (2011). Weight-conserving characteriza-
tion of complex functional brain networks. NeuroImage, 56(4),
2068–2079. https://doi.org/10.1016/j.neuroimage.2011.03.069
(2015). Functional characteri-
zation of the cingulo-opercular network in the maintenance of
tonic alertness. Cortex cérébral, 25(9), 2763–2773. https://est ce que je.
org/10.1093/cercor/bhu072
Sadaghiani, S., & D'Esposito, M..
Santens, S., Roggeman, C., Fias, W., & Verguts, T. (2010). Nombre
processing pathways in human parietal cortex. Cortex cérébral,
20(1), 77–88. https://doi.org/10.1093/cercor/bhp080
Shine, J.. M., Bissett, P.. G., Cloche, P.. T., Koyejo, O., Balsters, J.. H.,
Gorgolewski, K. J., . . . Poldrack, R.. UN. (2016). The dynamics of
functional brain networks: Integrated network states during cog-
nitive task performance. Neurone, 92(2), 544–554. https://est ce que je.
org/10.1016/j.neuron.2016.09.018
Shine, J.. M., Breakspear, M., Cloche, P.. T., Ehgoetz Martens, K., Shine,
R., Koyejo, O., . . . Poldrack, R.. UN. (2019). Human cognition in-
volves the dynamic integration of neural activity and neuromod-
ulatory systems. Neurosciences naturelles. https://doi.org/10.1038/
s41593-018-0312-0
Shum, J., Hermes, D., Foster, B. L., Dastjerdi, M., Rangarajan, V.,
Winawer, J., . . . Parvizi, J.. (2013). A brain area for visual numer-
als. Journal des neurosciences, 33(16), 6709–6715. https://est ce que je.org/
10.1523/JNEUROSCI.4558-12.2013
Sokolowski, H. M., Fias, W., Mousa, UN., & Ansari, D.
(2016).
Common and distinct brain regions in both parietal and frontal
cortex support symbolic and nonsymbolic number processing
in humans: A functional neuroimaging meta-analysis. Neu-
roImage, 146(Octobre 2016), 1–73. https://est ce que je.org/10.1016/j.
neuroimage.2016.10.028
Sporns, Ô.
(2014). Contributions and challenges for network
models in cognitive neuroscience. Neurosciences naturelles, 17(5),
652–660. https://doi.org/10.1038/nn.3690
Neurosciences en réseau
744
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network topology of symbolic and nonsymbolic number comparison
Sporns, O., & Betzel, R.. F. (2016). Modular brain networks. Annual
Review of Psychology, 67(1), 613–640. https://doi.org/10.1146/
annurev-psych-122414-033634
Streiner, D. L.
(2015). Best (but oft-forgotten) pratiques: The mul-
tiple problems of multiplicity—whether and how to correct for
many statistical tests. The American Journal of Clinical Nutrition,
102(4), 721–728. https://doi.org/10.3945/ajcn.115.113548
Telesford, Q. K., Lynall, M.. E., Vettel, J., Miller, M.. B., Grafton, S. T.,
& Bassett, D. S. (2016). Detection of functional brain network re-
configuration during task-driven cognitive states. NeuroImage, 142,
198–210. https://doi.org/10.1016/j.neuroimage.2016.05.078
Thompson, W. H., Wright, J., & Bissett, P.. G. (2020). Open explo-
ration. ELife, 9, 1–5. https://doi.org/10.7554/eLife.52157
Van Der Ven, F., Takashima, UN., Segers, E., Fernández, G., &
Verhoeven, L. (2016). Non-symbolic and symbolic notations in
simple arithmetic differentially involve intraparietal sulcus and
angular gyrus activity. Brain Research, 1643, 91–102. https://
doi.org/10.1016/j.brainres.2016.04.050
Verguts, T., & Fias, W. (2004). Representation of number in animals
and humans: A neural model. Journal des neurosciences cognitives,
16(9), 1493–1504. https://doi.org/10.1162/0898929042568497
Vogel, UN. C., Miezin, F. M., Petersen, S. E., & Schlaggar, B. L. (2012).
The putative visual word form area is functionally connected to
the dorsal attention network. Cortex cérébral, 22(3), 537–549.
https://doi.org/10.1093/cercor/bhr100
Vogel, S. E., Goffin, C., & Ansari, D. (2015). Developmental special-
ization of the left parietal cortex for the semantic representation
of Arabic numerals: An fMR-adaptation study. Developmental
Neurosciences cognitives, 12(1), 61–73. https://est ce que je.org/10.1016/
j.dcn.2014.12.001
Vossel, S., Geng, J.. J., & Fink, G. R..
(2014). Dorsal and ven-
tral attention systems: Distinct neural circuits but collaborative
roles. Neuroscientist, 20(2), 150–159. https://doi.org/10.1177/
1073858413494269
Wei, W., & Wang, X. J..
Inhibitory control in the cortico-
(2016).
basal ganglia-thalamocortical
loop: Complex regulation and
interplay with memory and decision processes. Neurone, 92(5),
1093–1105. https://doi.org/10.1016/j.neuron.2016.10.031
Blanc, G. C., & Bennetts, R.. E. (1996). Analysis of frequency count
data using the negative binomial distribution. Ecology, 77(8),
2549–2557. https://doi.org/10.2307/2265753
Yarkoni, T., Barch, D. M., Gray, J.. R., Conturo, T. E., & Plus courageux, T. S.
(2009). BOLD correlates of trial-by-trial reaction time variability
in gray and white matter: A multi-study fMRI analysis. PLoS One,
4(1). https://doi.org/10.1371/journal.pone.0004257
Yeo, B. T., Krienen, F. M., Sepulcre, J., Sabuncu, M.. R., Lashkari, D.,
(2011). The organization
Hollinshead, M., . . . Buckner, R.. L.
of the human cerebral cortex estimated by intrinsic functional
Journal de neurophysiologie, 106(3), 1125–1165.
connectivité.
https://est ce que je.org/10.1152/jn.00338.2011
Yeo, D. J., Wilkey, E. D., & Prix, G. R..
(2017). The search for
the number form area: A functional neuroimaging meta-analysis.
Neurosciences & Biobehavioral Reviews, 78(Avril), 145–160.
https://doi.org/10.1016/j.neubiorev.2017.04.027
Zalesky, UN., Fornito, UN., Harding, je. H., Cocchi, L., Yücel, M.,
Pantelis, C., & Bullmore, E. T. (2010). Whole-brain anatomical
réseaux: Does the choice of nodes matter? NeuroImage, 50(3),
970–983. https://doi.org/10.1016/j.neuroimage.2009.12.027
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
3
7
1
4
1
8
6
7
3
1
1
n
e
n
_
un
_
0
0
1
4
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Neurosciences en réseau
745