Research

Organizing principles of whole-brain functional
connectivity in zebrafish larvae

Richard F. Betzel

1,2,3,4

1Department of Psychological and Brain Sciences, Indiana University, Bloomington, IN, Etats-Unis
2Cognitive Science Program, Indiana University, Bloomington, IN, Etats-Unis
3Program in Neuroscience, Indiana University, Bloomington, IN, Etats-Unis
IU Network Science Institute, Indiana University, Bloomington, IN, Etats-Unis

4

Mots clés: Mesoscale connectomics, Functional connectivity, Modularity, Wiring cost, Flexibility

un accès ouvert

journal

ABSTRAIT

Network science has begun to reveal the fundamental principles by which large-scale brain
networks are organized, including geometric constraints, a balance between segregative and
integrative features, and functionally flexible brain areas. Cependant, it remains unknown
whether whole-brain networks imaged at the cellular level are organized according to similar
principles. Ici, we analyze whole-brain functional networks reconstructed from calcium
imaging data recorded in larval zebrafish. Our analyses reveal that functional connections
are distance-dependent and that networks exhibit hierarchical modular structure and hubs
that span module boundaries. We go on to show that spontaneous network structure places
constraints on stimulus-evoked reconfigurations of connections and that networks are
highly consistent across individuals. Our analyses reveal basic organizing principles of
whole-brain functional brain networks at the mesoscale. Our overarching methodological
framework provides a blueprint for studying correlated activity at the cellular level using
a low-dimensional network representation. Our work forms a conceptual bridge between
macro- and mesoscale network neuroscience and opens myriad paths for future studies
to investigate network structure of nervous systems at the cellular level.

RÉSUMÉ DE L'AUTEUR

Little is known about the principles by which mesoscale functional networks are organized
and whether they parallel the features of macroscale networks. Ici, we used network
science methods to investigate the architecture of functional connectivity in zebrafish larvae.
We find that its architectural features are remarkably similar to that of macroscale functional
brain networks, with connection weights exhibiting clear distance-dependence, evidence of
multiscale and hierarchical community structure, high participation hub regions, and flexible
reconfiguration across a range of tasks.

INTRODUCTION

Nervous systems are collections of functionally and structurally connected neurons, neuronal
populations, and brain areas (Sporns, Tononi, & Kötter, 2005). Coordination of and within
these networks underpins an organism’s ability to process sensory stimuli (Downar, Crawley,
Mikulis, & Davis, 2000; Ko et al., 2011), to successfully navigate its environment (Hartley,
Lever, Bourgeois, & O’Keefe, 2014; Jacobs et al., 2013), and to perform goal-directed action
(Spreng, Stevens, Chamberlain, Gilmore, & Schacter, 2010). Network science provides a
quantitative framework for representing and analyzing the organization of biological neural

Citation: Betzel, R.. F. (2020).
Organizing principles of whole-brain
functional connectivity in zebrafish
larvae. Neurosciences en réseau, 4(1),
234–256. https://est ce que je.org/10.1162/
netn_a_00121

EST CE QUE JE:
https://doi.org/10.1162/netn_a_00121

Informations complémentaires:
https://doi.org/10.1162/netn_a_00121
http://github.com/LJeub/
HierarchicalConsensus

Reçu: 6 Avril 2019
Accepté: 4 Décembre 2019

Intérêts concurrents: The author has
a déclaré qu'aucun intérêt concurrent
exister.

Auteur correspondant:
Richard Betzel
richard.betzel@gmail.com

Éditeur de manipulation:
Marcus Kaiser

droits d'auteur: © 2019
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence

La presse du MIT

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

4
1
2
3
4
1
8
6
6
7
6
9
n
e
n
_
un
_
0
0
1
2
1
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Whole-brain functional connectivity in zebrafish

réseaux (Bassett & Sporns, 2017). Within this framework, neural elements and their pairwise
interactions are modeled as the nodes and edges of a complex network (Bullmore & Sporns,
2009), to which one can apply a growing suite of powerful graph-theoretic tools to assay the
network’s structural (Rubinov & Sporns, 2010), functional (Parc & Friston, 2013), and dynami-
cal (Deco, Jirsa, Robinson, Breakspear, & Friston, 2008) properties.

Though the network model can be applied to nervous systems imaged at virtually any spatial
scale (Betzel & Bassett, 2017b; Craddock et al., 2013; Schröter, Paulsen, & Bullmore, 2017),
the majority of applications thus far have focused on the macroscale, where nodes represent
brain regions and connections represent pairwise statistical associations of recorded activity
(functional connectivity; FC). Though macroscale network analyses have been most successful
in linking variation of network features to cognition (Parc & Friston, 2013), maladie (Fornito,
Zalesky, & Breakspear, 2015), and development (Di Martino et al., 2014), they have also begun
to elucidate the general principles by which biological neural networks are organized (Betzel
et coll., 2016; Rubinov, 2016).

These principles include a balance between network structures that support segregative (lo-
cal and specialized) and integrative (global and generalized) information processing (Cohen &
D'Esposito, 2016; Sporns, Tononi, & Edelman, 2002), such as modules versus hubs (Meunier,
Lambiotte, Fornito, Ersche, & Bullmore, 2009; Power, Schlaggar, Lessov-Schlaggar, & Petersen,
2013; Sporns & Betzel, 2016; van den Heuvel & Sporns, 2013), a strong brain-wide drive to
reduce the material and metabolic cost of wiring (Betzel & Bassett, 2018; Bullmore & Sporns,
2012; B. L. Chen, Hall, & Chklovskii, 2006), and an intrinsic functional architecture that recon-
figures subtly and efficiently in response to tasks or stimulation (Cole, Bassett, Power, Plus courageux,
& Petersen, 2014; Schultz & Cole, 2016).

While these organizing principles have been observed at the macroscale across individu-
als and phylogeny (Rubinov, Ypma, Watson, & Bullmore, 2015; van den Heuvel, Bullmore,
& Sporns, 2016), it remains unclear whether analogous principles shape the architecture of
nervous systems at the mesoscale, where networks represent interactions among collections
of cells and molecules (Humphries, 2017; Schröter et al., 2017). Though the number of studies
investigating mesoscale network structure continues to grow (Betzel, Wood, Angeloni, Geffen,
& Bassett, 2018; Briggman & Kristan, 2006; Bruno, Frost, & Humphries, 2015; Dann, Michaels,
Schaffelhofer, & Scherberger, 2016; Faber, Timme, Beggs, & Newman, 2018; Lee et al., 2016;
Mann, Gallen, & Clandinin, 2017; Orlandi, Soriano, Alvarez-Lacalle, Teller, & Casademunt,
2013; Romano et al., 2017; Rosch, Hunter, Baldeweg, Friston, & Meyer, 2017; Yamamoto et al.,
2018), technological limitations restricting the field of view and an emphasis on neuronal pop-
ulations as the unit of interest (rather than the brain as a whole) have made it difficult to uncover
the general principles by which mesoscale functional networks are organized.

Actuellement, the organizing principles underpinning whole-brain mesoscale networks remain
largely unexplored. Ici, we take advantage of recent technological advances (Ahrens et al.,
2012; Ahrens, Orger, Robson, Li, & Keller, 2013; Keller & Ahrens, 2015; Panier et al., 2013;
Vladimirov et al., 2014) and a publicly available dataset (X. Chen et al., 2018) to investi-
gate spontaneous and stimulus-evoked FC in zebrafish larvae. Our analyses reveal several
putative organizing principles. These include strong geometric constraints on the magnitude
and valence of connection weights, and evidence of hierarchical and multiscale modular
structure balanced by the presence of polyfunctional hubs. We show that spontaneous and
stimulus-evoked networks are highly similar. Néanmoins, we also find evidence of stimulus-
the nodes with the greatest propensity for
driven module reconfiguration.

Fait intéressant,

Functional connectivity:
Statistical associations between
activity recorded at different
locations in the brain.

Hubs:
Nodes whose connections span
modular boundaries, linking
modules to one another.

Mesoscale:
Spatial organization of cell-to-cell
connectivity aggregated into parcels,
régions, or areas.

Hierarchical and multiscale modules:
Smaller modules nested within larger
modules; may span multiple
hierarchical levels.

Neurosciences en réseau

235

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

4
1
2
3
4
1
8
6
6
7
6
9
n
e
n
_
un
_
0
0
1
2
1
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Whole-brain functional connectivity in zebrafish

Geometric organization:
Dependence of functional
connectivity on the spatial
organization of the brain.

reconfiguration overlap with the same polyfunctional hubs uncovered under spontaneous
conditions, linking intrinsic network architecture to behavior. En résumé, our findings link
whole-brain macro- and microscale analyses and highlight network science as a framework
for bridging neuroscientific inquiry across spatial scales and domains.

RÉSULTATS

Ici, we aimed to uncover organizing principles of spontaneous and stimulus-evoked FC
in zebrafish larvae. All details concerning data acquisition and network construction are in-
cluded in the Materials and Methods section. The following subsections are organized as
follows. D'abord, we analyze group-representative spontaneous FC to identify signatures of geo-
metric constraints, hierarchical modular structure, and polyfunctional hubs. Suivant, we extend
these analyses to stimulus-evoked FC and show that it is shaped by the brain’s intrinsic (sponta-
neous) functional organization. Enfin, we present results of single-subject analyses and show
a high level of intersubject consistency.

Geometric Organization of Spontaneous FC

Previous analyses of whole-brain FC have revealed that connection weights and other network
features are shaped by underlying geometric relationships, such as nodes’ locations in space
(Bellec et al., 2006; Stiso & Bassett, 2018; Vértes et al., 2012). These constraints result in net-
works that favor strong, short-range connections and are believed to reflect brain-wide drives
to reduce the metabolic cost of coordinating activity between brain areas over long distances
(Laughlin & Sejnowski, 2003). Cependant, it remains largely unknown whether whole-brain
mesoscale functional networks are subject to similar constraints. To address this question, nous
= 11 zebrafish larvae recorded
analyzed single-cell calcium fluorescence traces from Nsub
in stimulus-free (c'est à dire., spontaneous) conditions. We aggregated cells into N = 256 hemispher-
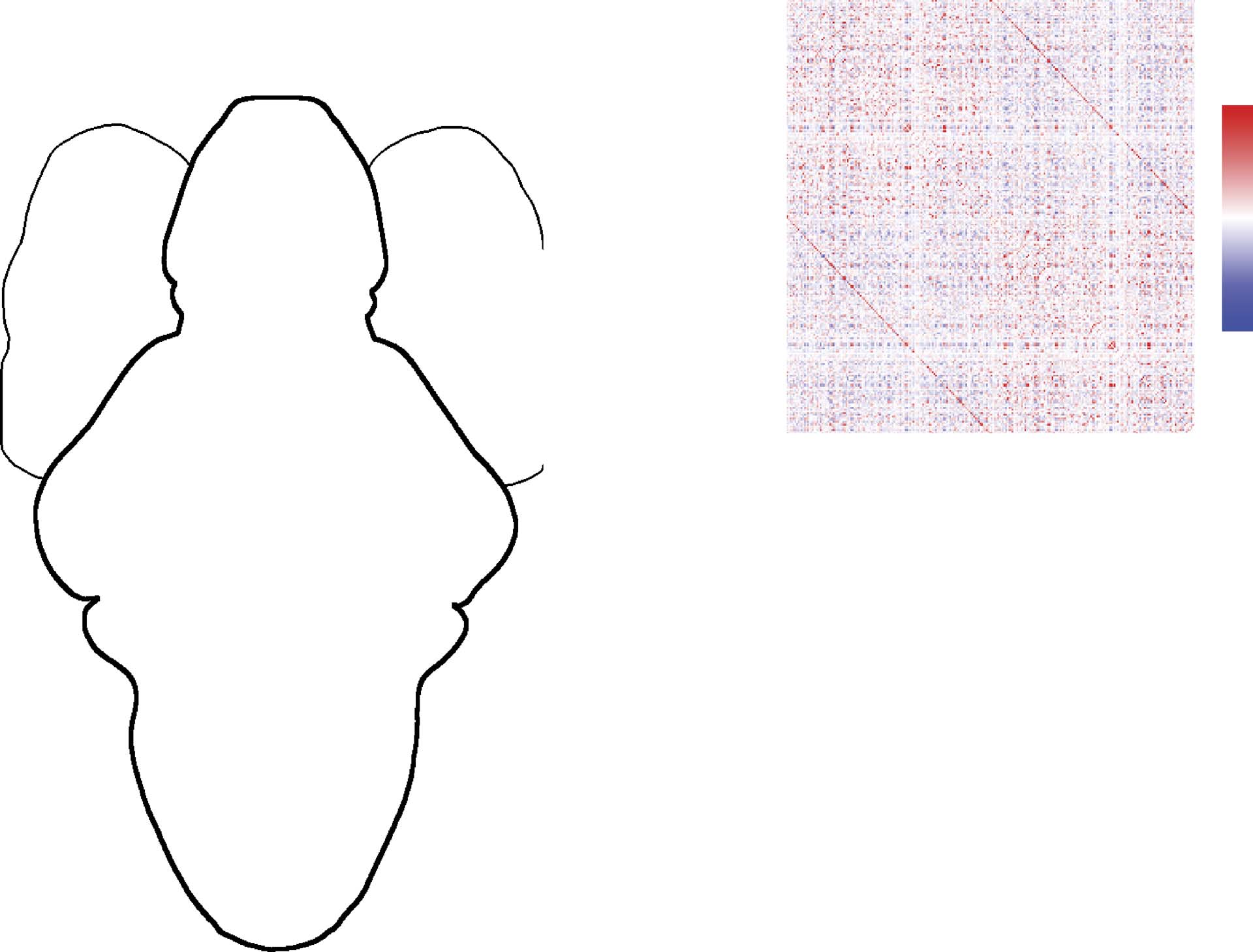
ically symmetric, functionally homogeneous, and spatially localized parcels (Figure 1A; voir
Materials and Methods for details; see Supporting Information Figure S4a for a side projection
of same figure). The number of cells per parcel followed a heavy-tailed distribution, with many
parcels containing a small number of cells and a few parcels containing disproportionately
many (See Supporting Information Figure S1). We then calculated the average fluorescence
trace for each parcel (node), and computed A = {Aij
}, the full matrix of Fisher-transformed
Pearson correlations (Figure 1B; see Materials and Methods for preprocessing details). Unless
otherwise noted, all subsequent analyses were carried out on this group-averaged matrix A,
which we regarded as a fully weighted and signed connectivity matrix.

D'abord, to assess whether FC exhibited hemispheric symmetries, we calculated the similar-
ity of all left and right within-hemisphere connections (Figure 1C). We observed that within-
hemisphere connectivity patterns were highly correlated (r = 0.88; p < 0.05). To further assess the relationship of network architecture with geometry, we then plotted connection weight as a function of the Euclidean distance between parcel centroids. We found that, on average, connection weight decayed monotonically as a function of distance. However, we also ob- served a small subset of interhemispheric connections that were unexpectedly strong given their length (Figure 1D). We provide an additional analysis of these stronger-than-expected connections as they relate to homotopy in Supporting Information Figure S2. A similar pat- tern was observed when we classified connections according to their valence and magnitude, and examined the proportion of each class within a fixed set of distance bins (Figure 1E). In general, nodes separated by short distances tended to be linked by strong, positive correla- tions. At longer distances, however, the proportion of positive correlations decreased and was Network Neuroscience 236 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Whole-brain functional connectivity in zebrafish l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 1. Spatial features of zebrafish whole-brain functional connectivity. (A) Thresholded network in anatomical space. Nodes represent parcels with size proportional to average absolute correlation. Red and blue lines represent top 400 positive and negative correlations/ anticorrelations according to magnitude. (B) Correlation matrix, A, ordered by hemisphere. (C) Scatterplot of left versus right within- hemisphere connectivity (D) Scatterplot of straight-line distance between parcel centroids and their correlation magnitude. Within- and between-hemisphere connections are plotted separately. Note that in both cases, connection weight decays as a function of distance. However, there nonetheless exists a small fraction of long-distance interhemispheric connections. (E) Breakdown of connection types by distance bins. Note that in general, the proportion of positive (strong or weak) correlations decreases with distance, while the prevalence of anticorrelations increases with over longer distances. In this panel, the term “neutral” is used to refer to correlations whose magnitude was close to 0. overtaken by an increase in neutral (i.e., weak correlations whose magnitude was near zero) to strong anticorrelations. These observations confirm that geometric relationships serve as powerful determinants of connections’ strengths and valences. Despite the fact that connection weight (on average) decreases monotonically with distance, the presence of strong, long-distance correlations sug- gests that geometry insufficiently explains brain-wide patterns of FC, and that coordination of activity over long distances may act as an additional functional constraint on network archi- tecture. Collectively, these findings are analogous to those observed at the macroscale (Bellec et al., 2006; Stiso & Bassett, 2018) and draw a clear conceptual link between the organization of biological neural networks at the macro- and mesoscales. Modular Organization of Spontaneous FC In the previous section, and in agreement with observations made at the macroscale, we suggested that a monotonically decaying relationship of connection weight with distance may serve as a key organizing principle responsible for shaping the architecture of biological Network Neuroscience 237 Whole-brain functional connectivity in zebrafish Modules: Cohesive groups of nodes that are segregated from the rest of the brain. neural networks. Here and in the next section, we explore another putative organizing prin- ciple. Namely, the requirement that biological neural networks balance features that support both segregated (localized) and integrated (global) brain function, that is, network modules and hubs, respectively (Cohen & D’Esposito, 2016; Sporns et al., 2002). Modules are groups of nodes that are densely connected to one another, but weakly con- nected between groups (Meunier et al., 2009; Sporns & Betzel, 2016). Because of modules’ near-autonomy from one another, they are thought to represent groups of nodes that perform the same or similar brain function and are believed to engender specialized information pro- cessing. In general, modules are not restricted to a single topological scale and can be arranged hierarchically, with deeper levels of the hierarchy reflecting increasing functional specializa- tion (Betzel & Bassett, 2017b; Betzel, Bertolero, Gordon, et al., 2018; Betzel et al., 2013). While modular organization has been frequently observed in whole-brain macroscale net- works (Bertolero, Yeo, & D’Esposito, 2015; Power et al., 2011; Sporns & Betzel, 2016), little is known about the modular structure of whole-brain networks at the mesoscale (Bruno et al., 2015; Lee et al., 2016; Vanni, Chan, Balbi, Silasi, & Murphy, 2017). Here, we leverage re- cent advances in modularity maximization, a data-driven method for uncovering a network’s modules, to uncover the hierarchical modular structure of spontaneous FC (Jeub, Sporns, & Fortunato, 2018; see Materials and Methods for more details). Modularity maximization returns hierarchically related partitions of nodes into modules, where the hierarchical levels are determined using a statistical criterion (Jeub et al., 2018). 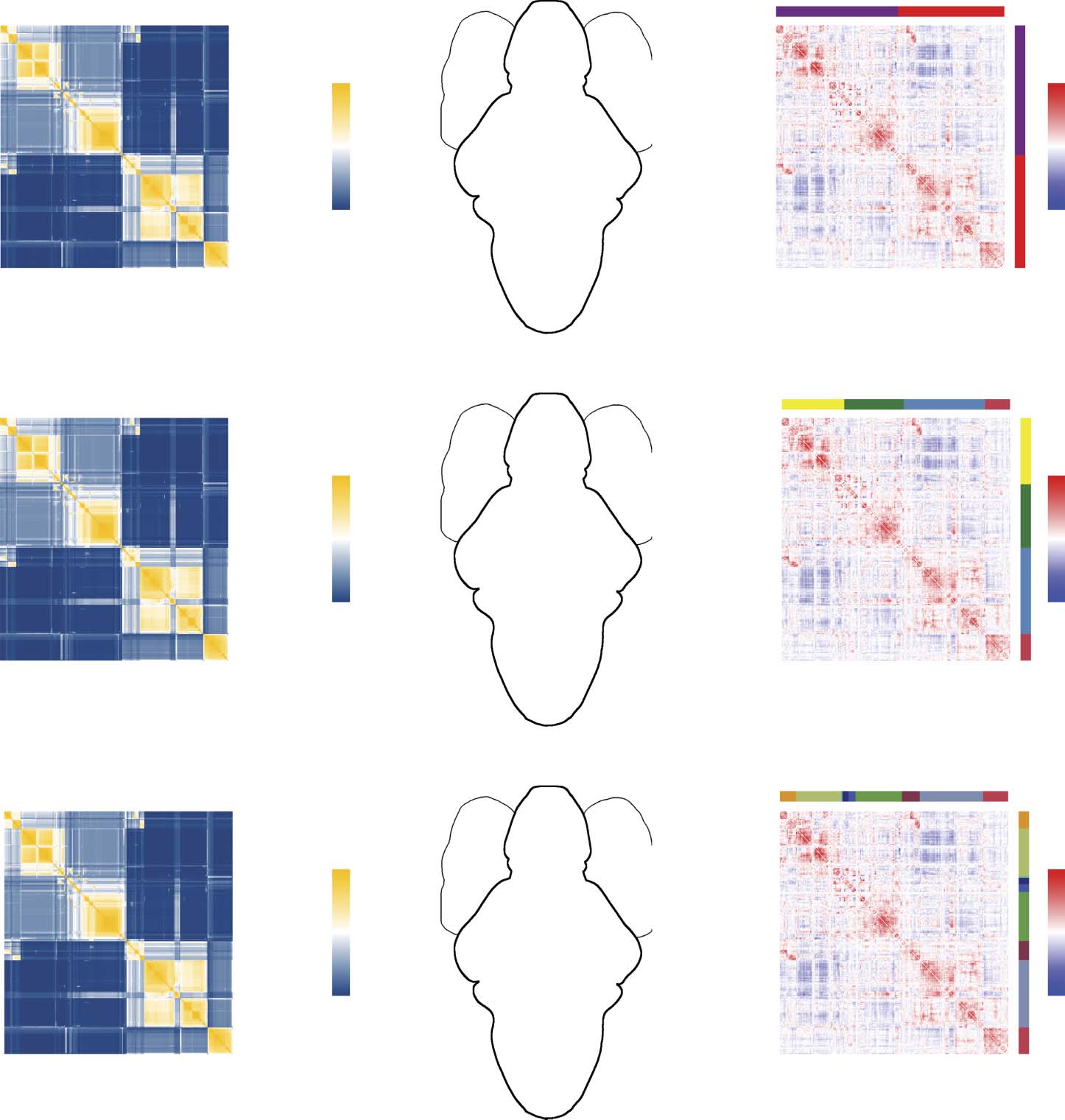We found evidence of a hierarchy comprising 24 distinct levels, with the number of modules at any level ranging from 2 to 25 (Figure 2A). For the sake of brevity, we show partitions of nodes into c = 2 (Figure 2A–C), 4 (Figure 2D–F), and 9 (Figure 2G–I) modules (see Supporting Information Figure S4b–d for side projections of the same modules). We note that the quality of detected partitions, as indexed by the modularity index, Q (Newman & Girvan, 2004), was significantly greater in the empirical networks compared with the partitions of networks estimated from phase-randomized surrogate time series (p < 0.05, Bonferroni-corrected; see Supporting Information Figure S3). Many of the modules recapitulate known functional and anatomical divisions of zebrafish. For instance, the red module (labeled 4 in Figure 2E and 9 in Figure 2H) overlaps closely the telencephalnon. Interestingly, this module isolates itself early within the hierarchy, and exhibits no clear subdivisions at deeper levels. Similarly, module 2 in Figure 2E and modules 4, 5, 6, and 8 in Figure 2H depict coarse and fine approximations of the mesencephalon. Unlike the telencephalic cluster, we identify multiple mesencephalic subdivisions, suggesting that these areas have the capacity to subtend varying levels of functional specialization. Collectively, these findings suggest that spontaneous FC is organized hierarchically into modules that exhibit clear mappings to known neuroanatomy. These findings are in close agreement with analogous investigations of whole-brain networks at the macroscale (Meunier et al., 2009) and suggest that modular organization may be a unifying principle by which brain networks at all scales are structured (Taylor, Wang, & Kaiser, 2017). Hub Organization of Spontaneous FC In the previous section we presented evidence that zebrafish spontaneous FC exhibits hier- archical modular structure. While segregated modules may be useful for the development of specialized brain function, complex behavior also requires network features that support the Network Neuroscience 238 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Whole-brain functional connectivity in zebrafish l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d . 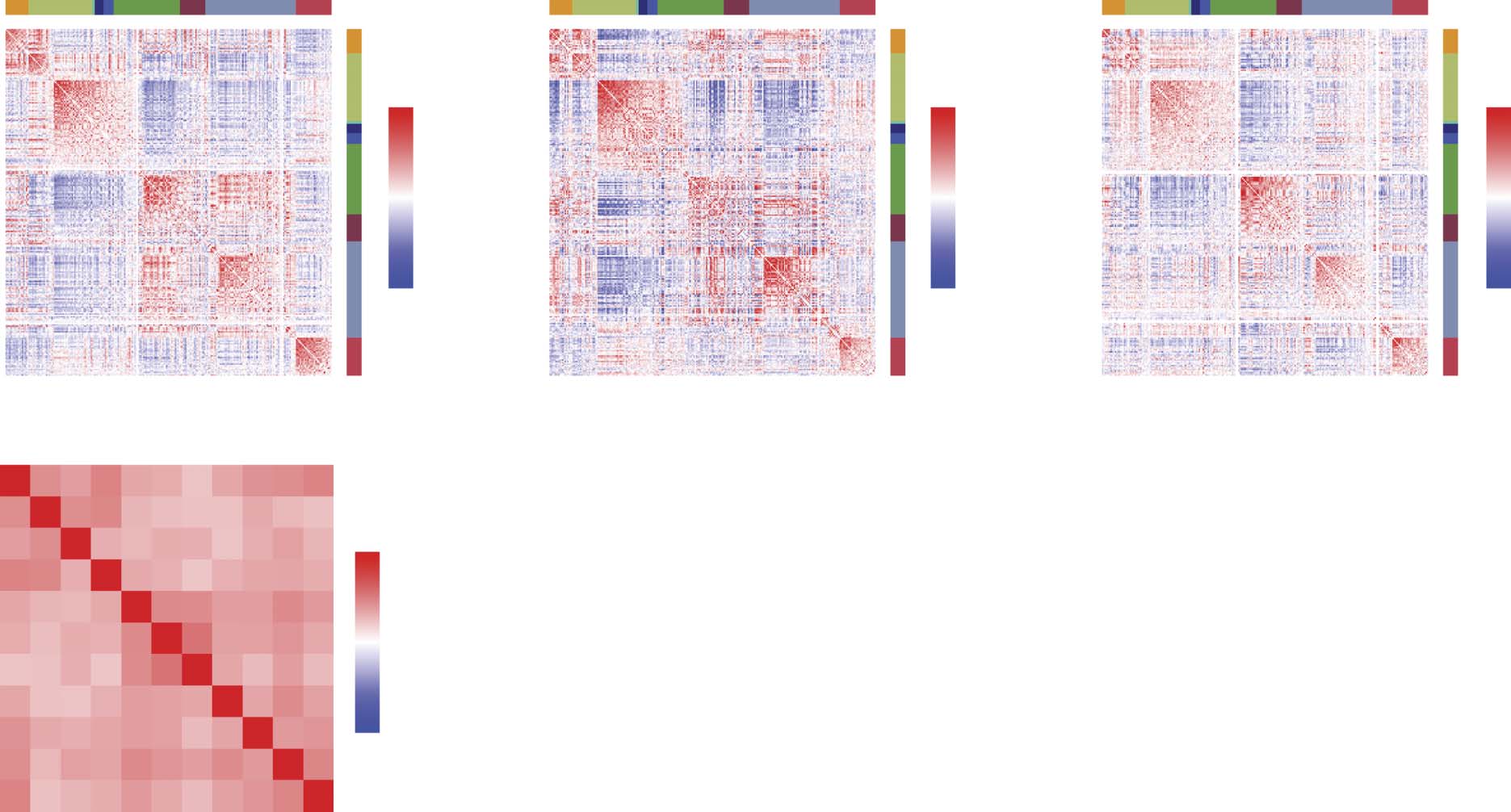t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 2. Hierarchical and multiresolution modular structure. (A) Coassignment matrix with hier- archy cut to highlight a two-module division (red blocks). (B) Modules plotted in anatomical space. Nodes are colored according to their module assignment, and within-module connections are col- ored similarly. (C) Correlation matrix ordered and blocked to highlight modular structure. Panels D–F and G–I show similar figures but with the number of modules equal to four and nine, respectively. integration of information across different modules (Cohen & D’Esposito, 2016; Deco, Tononi, Boly, & Kringelbach, 2015; Sporns, 2013). One class of network feature that supports precisely this type of processing is hubs, nodes whose connections straddle the boundaries of modules. Here, we identify hubs in spontaneous FC using the network measure participation coefficient (Guimera & Amaral, 2005). 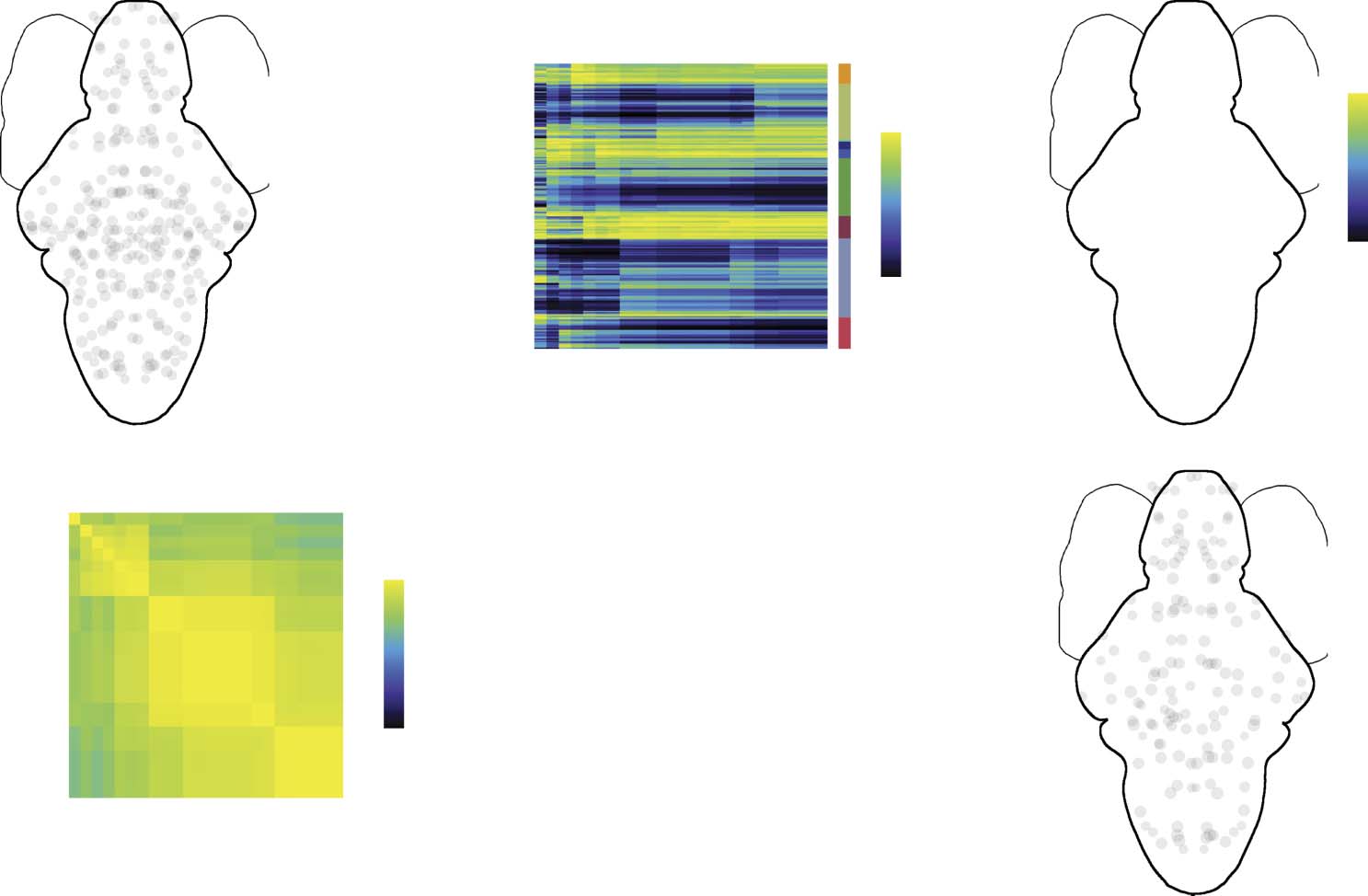Participation coefficient measures the uniformity with which a node’s connections are distributed across modules; values close to 1 or 0 indicate nodes that connect to many dif- ferent modules or are concentrated within a small number of modules, respectively. We illus- trate this concept schematically in Figure 3A, where we show examples of two nodes—one with low (top) and another with high (bottom) participation. We calculated each node’s par- ticipation coefficient at every hierarchical level and averaged these values over the entire hi- erarchy. In Figure 3B we show these coefficients after a rank transformation. On average, we find marked heterogeneity in the spatial locations of high-participation hubs, with the greatest Network Neuroscience 239 Whole-brain functional connectivity in zebrafish l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 3. Participation coefficient and hub classification. (A) Schematic illustration of low- and high-participation nodes. Connections made by nodes with low participation (nonhubs) are con- centrated within those nodes’ modules; connections made by nodes with high participation (hubs) are distributed across many modules. (B) Mean participation coefficient (ranked) as a function of the number of detected modules. (C) Average participation coefficient when the number of mod- ules ranges from 2 to 25. (D) Correlation of brain-wide participation coefficient maps for different numbers of modules. While the changes in participation coefficient maps are subtle, there nonethe- less appear to be three “regimes” (based on visual inspection) corresponding to distinct patterns of participation. (E) Participation coefficient and signed strength, z-scored and plotted against one another. Both measures serve as indices of “hubness” but are, on average, only weakly correlated. (F) Nodes in the top 25th percentile by participation and absolute strength. On average, there is little overlap. concentration appearing within the rhombencephalon (Figure 3C). Though brain-wide patterns of participation coefficient are largely stable as we vary the number of modules, we nonethe- less observe subtle scale dependencies (Figure 3D), suggesting that small subsets of nodes may be uniquely configured to act as hubs at one particular scale but less so at another. To better contextualize these findings, we compared nodes’ participation coefficients with their absolute strength (total weight of functional connections), another measure sometimes used for identifying hubs (Figure 3E). In general, we find that these two metrics are only weakly correlated (r = 0.16; p < 0.05), that is, the most hub-like nodes according to participation coefficient and strength are not necessarily overlapping. Indeed, when we examine the top 25% of hubs according to each measure, we find little overlap between the two hub measures (Figure 3F). These findings, combined with those from the previous section, suggest that spontaneous FC at the mesoscale strikes a precarious balance between features that promote segregated (i.e., local) brain function and those that promote integrative (i.e., global) brain function. These find- ings mirror those reported in macroscale networks (Cohen & D’Esposito, 2016), where the ex- pression of hub areas has been linked to both genetics and cognitive performance (Bertolero, Yeo, Bassett, & D’Esposito, 2018). An important caveat here is that, typically, a node’s “hubness” Network Neuroscience 240 Whole-brain functional connectivity in zebrafish is defined based on how it is situated with respect to a network’s modules (participation) and its capacity to exert influence over the network (degree/strength; Guimera & Amaral, 2005). Here, we study fully weighted and signed networks in which nodes have uniform degree and both positive and negative strengths (both of which are biased by community size; Power et al., 2013). Rather than risk misinterpreting a node’s capacity for influence, we focus entirely on the participation measure. Correspondence of Spontaneous and Stimulus-Evoked FC In the previous sections, we focused on organizing principles of spontaneous (i.e., stimulus- free) FC. Spontaneous FC represents an intrinsic, baseline state in which functional connections are shaped primarily by an underlying network of physical pathways, projections, and fiber tracts rather than the functional demands of a task or stimulus (Goñi et al., 2014; Honey et al., 2009; Lin, Okun, Carandini, & Harris, 2015; Park & Friston, 2013). Nonetheless, nervous sys- tems must be flexible and capable of reconfiguring in order meet those demands should they arise (Betzel, Bertolero, & Bassett, 2018; Cole et al., 2014). What features character- ize stimulus-induced reconfiguration? Is it a wholesale reorganization of the network? Is it restricted to a small subset of connections or nodes? In this section, we explore the effect of different stimuli on FC organization. To study stimulus-evoked changes in functional network organization, we estimated FC dur- ing the presentation of different visual stimuli. In addition to spontaneous activity, we consid- ered phototaxis (PT), optomotor response (OMR), looming response (Looming), and dark-flash response (DF; see Materials and Methods for more details). First we estimated a FC matrix separately for each stimulus condition (Figure 4A). To as- sess the similarity of these matrices, we extracted their upper triangle elements, computed pairwise interstimulus correlations (Figure 4B), and also generated a scatterplot of these ele- ments against one another (Figure 4C). Overall, we found that the stimulus-evoked connectivity matrices were highly similar (mean correlation of r = 0.72; p < 0.05, Bonferroni-corrected). Additionally, we statistically assessed the correspondence of spontaneous and stimulus-evoked correlation structure using the Mantel test (Mantel, 1967). For all combinations, we found that the correspondence was statistically significant (p < 0.05, Bonferroni-corrected; see Supporting Information Figure S9). These results support the hypothesis that the differences between spontaneous and stimulus-evoked connectivity is characterized by subtle shifts in connection weights and not by a wholesale reorganization of FC. In the next section, we explore these subtleties in greater detail. Hub Nodes Reconfigure in Response to Stimuli In the previous section we found that stimulus-evoked and spontaneous FC were highly cor- related with one another across different stimulus conditions. In this section, we tease apart those differences. To address this question, we adapted a multilayer modularity maximization procedure (see Materials and Methods for more details; Mucha, Richardson, Macon, Porter, & Onnela, 2010), which has been used to study time-varying FC (Bassett et al., 2011) and interindividual differences at the macroscale (Betzel, Bertolero, Gordon, et al., 2018). This procedure entails treating each spontaneous and stimulus-evoked FC matrix as a “layer” in a multilayer network ensemble. Layers are coupled to one another and the entire ensemble used as input for modularity maximization, thereby estimating modules in all layers simultaneously. As a result, this procedure allows us to effortlessly map modules across stimulus conditions Network Neuroscience 241 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Whole-brain functional connectivity in zebrafish l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 4. Comparing spontaneous and stimulus-evoked network architecture. (A) Functional connectivity matrices for four different stim- ulus conditions: dark-flash (DF), looming, optomotor response (OMR), and phototaxis (PT). (B) Upper triangle correlation for four stimulus conditions + spontaneous. (C) Scatterplot of all stimulus conditions plotted against one another. Size and color of each point indicate density of points at that location. Examples of (D) low-flexibility and (E) high-flexibility modules. In D and E, modules have been recolored to match the nine-module partition detected using the spontaneous network alone. Nodes with gray colors have module assignments that cannot be easily mapped to one of the nine modules. (F) Similarity (z-score of the Rand index) of stimulus-evoked and spontaneous modular structure as a function of the interlayer coupling parameter, ω. When ω is small, detected modules reflect specific stimuli; when ω is larger, detected modules are more similar to spontaneous modular structure. (G) Node-level flexibility grouped according to modules. Note: high levels of heterogeneity across modules. (H) Node-level flexibility plotted in anatomical space. (I) Correlation of stimulus-evoked flexibility and par- ticipation coefficient estimated from spontaneous network data alone (J) Variation of flexibility patterns as the number of detected modules changes. and to identify flexible and inflexible nodes, that is, those whose module assignments are consistently variable versus those that are stable. The multilayer modularity maximization framework includes an additional free parameter, ω, that can be tuned to different values so that the detected modules emphasize either the unique modular structure for each stimulus condition or the shared modular structure across conditions. When ω is large (emphasizing common modular structure), the detected multi- layer modules are highly similar to those detected in the previous section using the sponta- neous networks, alone (Figure 4D). This result is expected given the high correlation between stimulus-evoked and spontaneous FC. Here, we show as an example the module assignments Network Neuroscience 242 Whole-brain functional connectivity in zebrafish Flexibility: Nodes whose module assignment frequently changes (here, this change is across different stimulus conditions). that best match the nine-module partition shown in Figure 2G. When ω is set to smaller val- ues, however, the algorithm detects modules that are uniquely suited to each layer and there- fore more variable (Figure 4E). We see this more clearly when we compare stimulus-evoked and spontaneous modular structure as a function of ω (Figure 4F). The average similarity of stimulus-evoked and spontaneous modular structure, as measured by the z-score of the Rand index (Traud, Kelsic, Mucha, & Porter, 2011), increases monotonically as a function of ω. Because the multilayer modularity maximization framework preserves module labels across layers, it facilitates straightforward comparisons of modules from one stimulus condition with modules from another. This allows us to calculate each node’s “flexibility” (Bassett et al., 2013, 2011), a measure of its network variability across stimuli (see Materials and Methods). Intu- itively, nodes with high flexibility are those that frequently switch module allegiance in re- sponse to a stimulus, whereas low-flexibility nodes are invariant and serve as stable anchors of network organization across different conditions. Here, we calculated the average flexibility for each node across all sets of multilayer modules for which the mean number of modules was between 2 and 25. Interestingly, we found that flexible nodes were not uniformly distributed across modules, but exhibited high levels of heterogeneity (Figure 4F, G). Perhaps most sur- prising, when we compared participation coefficient (estimated from spontaneous FC alone) with flexibility, we found a strong positive correlation (r = 0.57; p < 0.05), indicating that spontaneous network structure may play a role in shaping network responses to stimuli. Collectively, these findings suggest that spontaneous, intrinsic network architecture repre- sents a powerful constraint on FC during stimulus-evoked conditions, in terms of both con- nectivity patterns as well as modular structure. More specifically, we find a common, stable modular core around which a flexible periphery of nodes reconfigure their connections as they adapt and respond to ongoing stimuli (Oram, 2010). More importantly, the nodes that appear most capable of reconfiguration under task conditions are the same nodes that occupy posi- tions of influence with respect to the spontaneous modular structure. These findings further validate observations made at the macroscale, wherein high participation areas overlap with polyfunctional association cortex (Cole et al., 2013; Power et al., 2013; Zanto & Gazzaley, 2013). We note, however, that while the link between participation at rest and flexibility across tasks is not without precedent, for example, control networks having high task flexibility (Cole et al., 2013) and participation (Power et al., 2013), this relationship is not a mathematical ne- cessity. The observations used to estimate spontaneous and task FC were independent from one another. Accordingly, there is no mathematical reason to expect that participation and flexibility should be related to one another. Stability of Network Architecture Across Individuals In the previous sections, we demonstrated that spontaneous FC is organized by geometry, ex- hibits hierarchical modules and hubs, and constrains stimulus-evoked FC. In this final section, we conclude by showing that the network structure of spontaneous FC appears to be con- served and similar across individual subjects. To compare network structure across subjects, we estimated spontaneous FC networks separately for subjects 8–18. We note that the deci- sion to focus on this subset of subjects was motivated practically; at the time of data accession, only data from fish 8–18 were fully annotated. For subjects 1–7, we were unable to determine experimental state, such as spontaneous versus stimulus, from the data descriptors. Nodes and connections were defined exactly as before. In Figure 5A–C we show example FC matrices for subjects 8, 11, and 17. Network Neuroscience 243 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Whole-brain functional connectivity in zebrafish l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Intersubject similarity of spontaneous FC. Panels A, B, and C depict single-subject spontaneous FC matrices ordered according to Figure 5. the nine-module partition shown in Figure 2G. (D) Correlation (similarity) matrix of upper triangle elements in subject-specific spontaneous FC matrices. (E) Distribution of elements in upper triangle of correlation matrix shown in panel D. (F) Scatterplot of functional connections for subjects s and t. Upon visual inspection alone, the similarity of these matrices is apparent. Nonetheless, we quantified their similarity precisely by computing the correlation of their upper triangle elements with one another (Figure 5D). We found that the mean correlation was r = 0.35 ± 0.08, indicating that while the correspondence of network architecture across subjects was imperfect, it was nonetheless robustly similar. We visualize these findings in two different ways: In Figure 5E we plot the distribution of intersubject similarity and in Figure 5F we show the two-dimensional histogram of connections plotted against one another. We also report a robust correspondence of spontaneous and task-evoked connectivity (mean correlation of rest to all tasks of r = 0.45 ± 0.10) and evidence that, averaged across tasks, subjects are more similar to themselves than to other subjects (mean self-similarity of r = 0.46 ± 0.08 and intersubject similarity of r = 0.34 ± 0.04; Finn et al., 2015; Supporting Information Figure S8). In summary, these findings indicate that network structure of spontaneous FC is reproducible and conserved across individuals. Further, they suggest the presence of a neuro-functional blueprint shared across individuals. These findings contribute to the growing literature on un- covering sources of intersubject variability in FC (Gordon et al., 2017; Seghier & Price, 2018) and extend this research domain from the macro- to the mesoscale. DISCUSSION Nervous systems are fundamentally complex networks of interacting neurons, neuronal pop- ulations, and brain areas. Current research into the structure of these networks has begun to reveal their basic organizing principles. Despite this, little is known about the architecture of Network Neuroscience 244 Whole-brain functional connectivity in zebrafish biological neural networks at the mesoscale (at the level of groups or clusters of individual neurons). Here, we use network science methods to investigate the organization of mesoscale networks in larval zebrafish during spontaneous and stimulus conditions. Our analyses reveal the effect of geometry on network structure, a modular architecture and the hubs that span module boundaries, and the constraint of intrinsic network structure on stimulus-evoked con- nectivity. These features are analogous to those observed in whole-brain networks constructed at the macroscale; our findings and methods therefore serve as conceptual bridges, linking investigations of nervous system structure and function across organizational scales. The work presented here serves as a methodological blueprint for future mesoscale network analyses and highlights several outstanding neuroscientific questions to be addressed with additional experiments and modeling. Bridging Scales Nervous systems exhibit meaningful organization and behavior across a wide range of spa- tial scales—from the level of cells and molecules up to brain areas (Betzel & Bassett, 2017b). However, different spatial scales are imaged using different technologies, resulting in data that are often modeled and analyzed using different statistical and mathematical methods. These distinctions in how spatial scales are researched can give rise to sometimes competing or con- tradictory accounts of nervous system organization and behavior; this is especially true when the neural phenomenon being studied is not clearly restricted to a single scale. Accordingly, there is a growing need for theoretical frameworks capable of explaining and modeling obser- vations simultaneously at many scales. In the present work, we use network science methodology to model and characterize whole- brain mesoscale networks. Though these methods have been widely used at the macroscale (Bullmore & Sporns, 2009; He & Evans, 2010; Rubinov & Sporns, 2010), they are only begin- ning to be applied to mesoscale functional datasets and have been restricted to network re- constructions at the population level (Bruno et al., 2015; Faber et al., 2018; Muldoon, Soltesz, & Cossart, 2013; Orlandi et al., 2013; Yamamoto et al., 2018) or at the level of entire brains but without cellular resolution (Barson et al., 2018; Lake et al., 2018; Vanni et al., 2017). In extending the network approach to the whole-brain level and for networks reconstructed from single-cell observations, we provide a powerful demonstration of the utility of network science for gaining insight into nervous system architecture. Moreover, our work showcases network science as a framework with the ability to form bridges across spatial scales and, potentially, help reconcile disparate findings (Bassett & Sporns, 2017). Universal Organizational Principles One of the goals of network neuroscience is not simply to describe a network, but to iden- tify the principles by which nervous systems are organized (Bassett & Sporns, 2017). In other words, what are the rules by which a network’s structure is shaped (Betzel & Bassett, 2017a; Ercsey-Ravasz et al., 2013; Goulas, Betzel, & Hilgetag, 2018; Vértes et al., 2012) and are those rules universally true or do they apply only to particular organism and scale (van den Heuvel et al., 2016)? This goal is challenging to address, as most research that constitutes network neuroscience has focused on a single scale (macro) for a single organism (human), limiting the possibility of discovering scale- and species-invariant organizing principles. Here, because of recent advances in cellular-level imaging (Ahrens et al., 2012; Vladimirov et al., 2014), we constructed whole-brain mesoscale functional networks and found, surpris- ingly, that these networks express analogous features as macroscale networks, suggesting that Network Neuroscience 245 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Whole-brain functional connectivity in zebrafish similar rules and principles are responsible for their organization. These features include con- nection weights with a strong geometric dependence, a balance between segregated and in- tegrated brain function, and subtle stimulus-induced reconfigurations of network architecture. These findings indicate that functional networks reconstructed at the mesoscale may be orga- nized according to an analogous set of rules and principles, suggesting that these rules may be approximately scale-invariant. Moreover, these findings also suggest that, despite increases in dimensionality at the mesoscale, network organization can be succinctly described by a low-dimensional set of principles. Future Directions There are several ways that the work presented here could be extended in the future. First, although the network science methods we used provided novel insight into network structure at the mesoscale, those methods are relatively established in the network neuroscience litera- ture (Guimera & Amaral, 2005; Newman & Girvan, 2004; Rubinov & Sporns, 2010). Recently, increasingly novel methods have been developed that assay more nuanced aspects of net- work structure; in the long term, it would be useful to test whether these new (but more com- plex) approaches based on algebraic topology (Saggar et al., 2018), control theory (Gu et al., 2015), blockmodeling (Betzel, Medaglia, & Bassett, 2018), and graph signal processing (W. Huang et al., 2018) can give novel insights into mesoscale network structure and function. In the near term, a potentially more fruitful approach could involve estimating time-varying FC to track fluctuations in network structure over short timescales and thereby gain insight into network dynamics (Hutchison et al., 2013). Second, though networks analyzed here were reconstructed from single-cell recordings, we aggregated cells into parcels that we regarded as nodes. Though the parcels were defined to be both spatially and functionally homogeneous, each parcel-averaged fluorescence trace likely does not perfectly explain the variance of traces for every cell assigned to that parcel. In future work, it is critical to explore the effect of alternative parcellations on network statistics (Wang et al., 2009). Additionally, it would be useful to explore parcellation-free approaches, wherein connections are estimated between individual cells (though this approach will likely scale poorly as the number of recorded cells increases; Kim et al., 2016). Additionally, our work sets the stage for future studies to form much stronger bridges be- tween observation and theory. In network neuroscience, specifically, there is no shortage of theories concerning the functional roles of particular classes of network structures. For exam- ple, it remains unclear exactly what role connections play in shaping communication patterns between neural elements, and whether this process is selective, for example, biased towards the utilization of specific pathways, or unguided, as in a random walk or diffusion process (Avena-Koenigsberger, Misic, & Sporns, 2018). Testing hypotheses like these is challenging, largely because the experimental perturbations necessary, such as ablating cells or pathways, are invasive and because most macroscale networks are constructed noninvasively in human subjects, where invasive perturbations are, in general, not possible (with some notable ex- ceptions; Solomon et al., 2018). Extending network analysis to the mesoscale and to model organisms like zebrafish makes it possible to leverage focused perturbations (Yamamoto et al., 2018) and novel neuroscientific techniques (Vladimirov et al., 2018), to confront, test, and disambiguate network-level hypotheses about brain function. Another important direction for future work involves the comparison of the functional imag- ing data analyzed in this study and made available via (X. Chen et al., 2018), with additional Network Neuroscience 246 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Whole-brain functional connectivity in zebrafish biological data collected and disseminated as part of other neuroinformatics studies. For in- stance, paralleling structure-function work carried out at the macroscale (Betzel et al., 2019), future studies could establish an anatomical basis for correlated activity at the mesoscale and cellular levels through detailed comparisons against physical connections (Kunst et al., 2019). Similarly, and by virtue of working with model organisms, the genetic mechanisms that un- derlie patterns of correlated activity can be probed in much greater detail than is possible at the macroscale by, for example, taking advantage of publicly available gene expression atlases (Sprague, Doerry, Douglas, & Westerfield, 2001). While this work includes analysis of functional brain networks reconstructed from cellular- level recordings, to facilitate intersubject comparisons it was nonetheless necessary to cluster cells into a set of parcels. This aggregation step resulted in a consistent set of network nodes across all individuals. Future work should explore granular approaches for analyzing these networks that do not sacrifice the single-cell resolution of these data, such as by embedding subject-level networks in the same space (Simas, Chavez, Rodriguez, & Diaz-Guilera, 2015). Though this work helps clarify the organizational features and constraints of biological neural networks at the mesoscale, future studies of single-cell organization will provide even greater clarity (Ponce-Alvarez, Jouary, Privat, Deco, & Sumbre, 2018). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Limitations Despite contributing to our understanding of the organizing principles underpinning mesoscale biological neural networks, this study has a number of important limitations. First, it is critical to note that our measure of connectivity is a linear correlation. Though this particular measure has been used extensively to model functional connectivity of slowly evolving fMRI BOLD data (David, Cosmelli, & Friston, 2004) and performs well in recovering underlying network structure when applied to synthetic time series data (Smith et al., 2011), it is not a direct mea- sure of structural connections (axonal projections), it is not equivalent to the coupling matrix in a dynamical systems model, does not indicate directedness of a connection, and is in no way a measure of causality or mechanism. Consequently, the results of all analyses are descriptive in nature. In future work, perturbational experiments and novel network reconstruction tech- niques will help clarify the causal role of network organization (L. Huang et al., 2018; Lansdell & Kording, 2018). Second, we infer connection weights based on zero-lag correlations of calcium fluores- cence, which serves as an indirect measurement of a neuron’s activity. This indirectness, coupled with lack of temporal precision (two volumes acquired per second), opens to the pos- sibility that reconstructed networks are not fully recapitulating the “true” correlation structure of neurons’ activities. Advances in electrophysiological methods that enable recording from a large number of neurons (Jun et al., 2017) and optical techniques for accelerating acquisition times (Sadovsky et al., 2011) will prove useful in addressing these and related issues in future work. Finally, another limitation concerns the methodology used for parcel (node) definition. Here, we combined data from all subjects and all stimulus conditions to generate spatially contiguous and functionally homogeneous parcels, which is common in the large-scale imag- ing literature (Eickhoff, Yeo, & Genon, 2018). In principle, these parcels would be validated in an independently acquired dataset to ensure their robustness and reduce the risk of overfit- ting. However, because of the uniqueness of the present dataset, finding a second comparable and independent dataset was not possible. Relatedly, parcels were defined to be similar across Network Neuroscience 247 Whole-brain functional connectivity in zebrafish subjects and stimulus conditions. However, recent large-scale imaging work has shown that parcel boundaries fluctuate with both individuals and task (Salehi et al., 2019). As sim- ilar datasets become available in the future, the validity and robustness of parcels should be investigated further using cross-validation procedures. Similarly, future work should explore alternative parcellations that may better reflect subject-level and stimulus-specific network organization. MATERIALS AND METHODS Data Acquisition Activity from a majority of neurons was recorded in larval zebrafish using light-sheet mi- croscopy (Vladimirov et al., 2014). Activity was recorded under spontaneous conditions and also while subjects were presented with a series of visual stimuli. As reported in X. Chen et al. (2018), calcium imaging data were recorded at ≈ 2 volumes/second for ≈ 50 min (or ≈ 6, 800 volumes). As in Vladimirov et al. (2014), the calcium indicator GCaMP6f (T.-W. Chen et al., 2013), was expressed pan-neuronally and fused to cell nuclei, allowing for the automatic seg- mentation of cells (Kawashima, Zwart, Yang, Mensh, & Ahrens, 2016). The result was contin- uous fluorescence traces for ≈ 80,000 cells per subject. As noted in X. Chen et al. (2018), this number accounts for the majority of neurons in the brain, excluding extremely ventral areas. For complete details of data acquisition, see X. Chen et al. (2018). Spontaneous Activity and Visual Stimuli Most of our analyses focused on networks reconstructed from spontaneous activity, that is, in the absence of any visual stimuli. During this condition, which lasted on average 419.0 ± 131.4 s, the fish engage in fictive swimming through a series of alternating left- and right-turn sequences (X. Chen et al., 2018; Dunn et al., 2016). In addition to spontaneous activity, subjects were imaged concurrent with the presenta- tion of visual stimuli, the precise timing of which varied from subject to subject (see X. Chen et al., 2018, for complete details). Briefly, these stimuli included the following: 1. Phototaxis: Subjects were presented with half-field black and white visual stimuli on either side. Presentations were followed by a whole-field black stimulus. On average, the half-field black and white stimuli were presented for 17.9 ± 5.2 s, interspersed by the whole-field black stimulus, lasting for 7.04 ± 3.6 seconds. This repeated motif of whole-field black to half-field white to whole-field black to half-field black lasted for 759.7 ± 331.7 s. 2. Optomotor response: Whole-field stripes moving in different directions. Here, some sub- jects were presented with three different movement directions and others with four, the precise timing of which was variable. Presentation lasted 8 ± 3.9 s, between which were blank stimuli lasting approximately 9.6 ± 4.3 s. The total duration of this stimulus was, on average, 631.5 ± 303.1 s. 3. Looming response: Expanding discs on either left or right side interspersed by long peri- ods of no stimulus. The disc periods alternated and lasted, on average, 3.6 ± 1.3 s, while the nonstimulus periods lasted 18.1 ± 6.6 s. This stimulus lasted 350.0 ± 158.7 s. 4. Dark-flash response: Sudden darkening of environment lasting, on average, 15.2 ± 6.7 s, followed by lightening, lasting almost an equal amount of time, 16.1 ± 7.2 s. This stimulus lasted, on average, 335.2 ± 109.3 s. Network Neuroscience 248 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 1 2 3 4 1 8 6 6 7 6 9 n e n _ a _ 0 0 1 2 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Whole-brain functional connectivity in zebrafish Node Definition Rather than analyze networks where nodes correspond to individual cells, we focused on networks where the nodes represented clusters of cells, effectively reducing computational burden and facilitating straightforward interpretation. We developed a data-driven approach to assign cells to clusters that possessed three distinct properties: (a) spatial contiguity, (b) functional homogeneity, and (c) intersubject consistency. To generate clusters with this set of properties, we designed a multistage clustering algo- rithm. First, we aggregated normalized spatial coordinates of cells in the left hemisphere across all subjects and clustered them using k-means into k = 2, 500 contiguous spatial clusters (distance metric = Euclidean; number of replicates = 10). This aggregation step was possible because cells had previously been aligned across subjects (X. Chen et al., 2018). We then mir- rored the centroids about the midline and assigned cells in the right hemisphere to the nearest spatial cluster centroid (5,000 hemispherically symmetric clusters; mean spatial cluster size of 280 ± 73 cells). Because this procedure defines spatial clusters based on cells’ spatial loca- tions, the resulting spatial clusters were also spatially contiguous. Moreover, because spatial clusters were defined using aggregated coordinates, spatial clusters contained cells from mul- tiple subjects. Of the 5,000 spatial clusters, 82.6% contained cells from all subjects and 92.5% contained cells from at least 75% of subjects. Next, we concatenated spontaneous and stimulus-evoked activity and regressed the global signal from each cell’s fluorescence trace (Power et al., 2014). This procedure ensured that any observed fluctuations in fluorescence were not driven by changes in baseline fluores- cence. (Note: We also carried out select sets of analyses on data in which the global signal regression step was omitted and found generally similar results, but with baseline correlation increased and more clear monotonic decay of connection weight as a function of distance; see Supporting Information Figure S5.) Then for each spatial cluster and each subject, we ex- tracted a cluster-averaged fluorescence trace, and computed pairwise correlations for all spa- tial clusters. This correlation structure reflects both spontaneous and stimulus-evoked activity and effectively helps mitigate the possibility that subsequent clusters are overfit and biased towards the correlation structure of one condition or another. We repeated this algorithm sep- arately for both each hemisphere before averaging over subjects and hemispheres, resulting in a single 2,500 × 2,500 matrix of group- and hemisphere-averaged correlations (we were able to average over hemispheres because spatial clusters were defined to be hemispherically symmetric and so each spatial cluster had a homotopic partner). Next, we used this matrix to identify functional clusters with high average functional homogeneity by clustering its rows using k-means. We asked the algorithm to generate k = 100 functional clusters (distance = correlation; number of replicates = 10). However, the resulting functional clusters were, in general, no longer spatially contiguous (i.e., functional clusters could include spatial clusters whose fluorescence traces were similar, but not necessarily proximal to one another). Accord- ingly, we extracted all spatial clusters assigned to each functional cluster and further divided them according to their spatial coordinates until the maximum diameter was <200 pixels and each spatial cluster in a functional was no fewer than 60 from any other spatial cluster assigned to the same cluster. In end, this procedure resulted N =256 parcels, each of which represented node our network. We note that clustering necessarily sacrifices some resolution at which the original data were recorded. That is, by consolidating single cells into clusters, unique identities those (and information carried fluctuations their activity over time) Network Neuroscience 249 l D o w n o a d e d f r o m h t t p : >r

d(gi,r

, gi,s

).

(3)

In the context of the current study, high-flexibility nodes represent nodes whose community
assignment varies from one stimulus condition to another. Low-flexibility nodes, on the other
main, refer to nodes whose community assignment is invariant across conditions.

For both the hierarchical and multilayer variants of modularity maximiza-
Louvain algorithm.
tion, we used the generalized Louvain toolbox to optimize Q (Jutla, Jeub, & Mucha, 2011).
In both cases, we sampled 10,000 values of γ within the range [−0.05, 1.285]. The value of
γ = −0.05 was determined by experimentation and represented the approximate smallest
value of γ for which the network was partitioned into two or more communities. The second
value of γ = 1.285 represented a theoretical upper limit, above which the optimal partition
was always to assign each node to a singleton community. Donc, this range bounds all “in-
teresting” partitions—below which all nodes were assigned to one big community and above
which all nodes were assigned to singleton communities. We sampled γ values within this
range to approximate the distribution of connection weights in the network. Specifically, nous
sampled 10,000 times with replacement from the set of connection weights that fell within
the acceptable range. We relied on a similar approach for sampling γ values when we used
multilayer modularity maximization.

The ω parameter enters into modularity maximization only in the multilayer case and con-
trols the heterogeneity of communities across layers (conditions). When ω is small, commu-
nities reflect organization unique to each layer; when ω is large, they reflect organization that
is shared across layers. Ici, we sampled ω from logarithmic distribution. C'est, we first

Neurosciences en réseau

251

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

4
1
2
3
4
1
8
6
6
7
6
9
n
e
n
_
un
_
0
0
1
2
1
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Whole-brain functional connectivity in zebrafish

selected 10,000 exponents between the values of [−3, 1] and obtained ωs by raising the value
de 10 to the power of each sample. Accordingly, the smallest and largest possible values of ω
étaient 0.001 et 10.

As described in a recent paper (Betzel, Bertolero, Gordon, et coll., 2018), we found that
variation in ω effectively changed the baseline level of community variability (flexibility) mais
had little influence on the overall pattern of flexibility. So when we remove the effect of baseline
differences in flexibility by rank transforming flexibility (as we do in Figure 4), the flexibility
patterns over which we average tend to be homogeneous.

To compare two modular partitions, we used the z-score of the
Comparing modular structure.
Rand index (Traud et al., 2011), a similarity measure that, intuitively, corrects the more com-
mon Rand index for the number and size of communities in the partitions. For two partitions,
X and Y, we calculate their similarity as

Zr(X, Oui) =

1
σwXY

wXY

− WXWY
W

.

(4)

Ici, W is the total number of node pairs in the network, WX and WY are the number of pairs
in the same modules in partitions X and Y, respectivement, wXY is the number of pairs assigned
to the same module in both X and Y, and σwXY is the standard deviation of wXY. The value
of Zr(X, Oui) can be interpreted as how great, beyond chance, is the similarity of partitions X
and Y.

Defining Network Hubs

Hubs are considered nodes of disproportional importance to a network. We use three mea-
sures to identify hubs. The first measure is the flexibility metric. Nodes with high flexibility are
those whose module affiliation changes across stimulus conditions and are therefore able to
reconfigure in response to different stimuli or tasks.

The second metric used for hub classification is a node’s absolute strength—that is, the total

weight of all of its connections:

si

= ∑
j

|Aij

|.

(5)

Intuitively, nodes with stronger connection weights, either positive or negative, may occupy
positions of influence within the network.

Enfin, we also defined hubs to be nodes with large participation coefficient (Guimera &
Amaral, 2005). A participation coefficient measures how uniformly a node’s connections (pos-
itive, in this case) are distributed across modules. A node that makes positive connections to
many different modules will have a high participation coefficient, while a node whose con-
nections are restricted to a small number of modules will have a low participation coefficient.
More specifically, participation is calculated as

= 1 −

p+
je

(

Nc∑
c=1

κ+
ic
k+
je

)2.

(6)

Ici, Nc is the number of modules, κ+
ic is the total weight of positive connections from node i
to module c, and k+
i is the total weight of positive connections incident upon node i. Intuitively,
nodes whose connections are distributed uniformly across modules have values of p+
i close
à 1, while nodes whose connections are concentrated within a small number modules have

Neurosciences en réseau

252

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

4
1
2
3
4
1
8
6
6
7
6
9
n
e
n
_
un
_
0
0
1
2
1
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Whole-brain functional connectivity in zebrafish

values of p+
Connectivity Toolbox (Rubinov & Sporns, 2010).

i closer to 0. Participation coefficient was computed using functions from the Brain

ACKNOWLEGMENTS

RFB is grateful to M. Ahrens and X. Chen for sharing zebrafish imaging data. RFB thanks Olaf
Sporns and Joshua Faskowitz for reading an early draft and providing invaluable feedback. RFB
acknowledges support from that National Institute of Biomedical Imaging and Bioengineering
(1R01EB029272-01). This research was supported by Indiana University Office of the Vice
President for Research Emerging Area of Research Initiative, Apprentissage: Brains, Machines and
Children.

DATA AVAILABILITY

All imaging data are available courtesy of M. Ahrens and X. Chen (https://github.com/xiuyechen/
fishexplorer) (Jeub, Sporns, & Fortunato, 2018). All analysis scripts used in this manuscript are
available from the authors upon request.

INFORMATIONS À L'APPUI

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00121.

CONTRIBUTIONS DES AUTEURS

Richard Betzel: Conceptualisation; Analyse formelle; Enquête; Méthodologie; Logiciel; Vi-
sualization; En écrivant – Original Draft; En écrivant – Review & Editing.

INFORMATIONS SUR LE FINANCEMENT

Richard Betzel, National Institute of Biomedical Imaging and Bioengineering (NOUS), Award ID:
1R01EB029272-01.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

4
1
2
3
4
1
8
6
6
7
6
9
n
e
n
_
un
_
0
0
1
2
1
p
d

.

t

RÉFÉRENCES

Ahrens, M.. B., Li, J.. M., Orger, M.. B., Robson, D. N., Schier, UN. F.,
Engert, F., & Portugues, R.. (2012). Brain-wide neuronal dynamics
during motor adaptation in zebrafish. Nature, 485(7399), 471.
Ahrens, M.. B., Orger, M.. B., Robson, D. N., Li, J.. M., & Keller, P.. J..
(2013). Whole-brain functional imaging at cellular resolution us-
ing light-sheet microscopy. Nature Methods, 10(5), 413.

Avena-Koenigsberger, UN., Misic, B., & Sporns, Ô. (2018). Commu-
nication dynamics in complex brain networks. Nature Reviews
Neurosciences, 19(1), 17.

Barson, D., Hamodi, UN. S., Shen, X., Lur, G., Constable, R.. T.,
Cardin, J., . . . Higley, M.. (2018). Simultaneous mesoscopic
and two-photon imaging of neuronal activity in cortical circuits.
bioRxiv:468348.

Bassett, D. S., Porter, M.. UN., Wymbs, N. F., Grafton, S. T., Carlson,
J.. M., & Mucha, P.. J.. (2013). Robust detection of dynamic com-
munity structure in networks. Chaos: An Interdisciplinary Journal
of Nonlinear Science, 23(1), 013142.

Bassett, D. S., & Sporns, Ô. (2017). Network neuroscience. Nature

Neurosciences, 20(3), 353.

Bassett, D. S., Wymbs, N. F., Porter, M.. UN., Mucha, P.. J., Carlson,
J.. M., & Grafton, S. T. (2011). Dynamic reconfiguration of hu-

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

man brain networks during learning. Actes de la Nationale
Académie des Sciences, 108(18), 7641–7646.

Bazzi, M., Porter, M.. UN., Williams, S., McDonald's, M., Fenn, D. J., &
Howison, S. D. (2016). Community detection in temporal mul-
tilayer networks, with an application to correlation networks.
Multiscale Modeling and Simulation, 14(1), 1–41.

Bellec, P., Perlbarg, V., Jbabdi, S., Pélégrini-Issac, M., Anton, J.-L.,
Doyon, J., & Benali, H. (2006). Identification of large-scale net-
works in the brain using fMRI. NeuroImage, 29(4), 1231–1243.
Bertolero, M.. UN., Yeo, B., Bassett, D. S., & D'Esposito, M.. (2018).
A mechanistic model of connector hubs, modularity, and cogni-
tion. arXiv:1803.08109

Bertolero, M.. UN., Yeo, B. T., & D'Esposito, M.. (2015). The modu-
lar and integrative functional architecture of the human brain.
Actes de l'Académie nationale des sciences, 112(49),
E6798–E6807.

Betzel, R.. F., Avena-Koenigsberger, UN., Goñi, J., Il, Y., De Reus,
M.. UN., Griffa, UN., . . . Sporns, Ô. (2016). Generative models of
the human connectome. NeuroImage, 124, 1054–1064.

Betzel, R.. F., & Bassett, D. S. (2017un). Generative models for net-
work neuroscience: Prospects and promise. Journal of the Royal
Society Interface, 14(136), 20170623.

Neurosciences en réseau

253

Whole-brain functional connectivity in zebrafish

Betzel, R.. F., & Bassett, D. S. (2017b). Multi-scale brain networks.

NeuroImage, 160, 73–83.

Betzel, R.. F., & Bassett, D. S. (2018). Specificity and robustness of
long-distance connections in weighted, interareal connectomes.
Actes de l'Académie nationale des sciences, 201720186.
Betzel, R.. F., Bertolero, M.. UN., & Bassett, D. S. (2018). Non-
assortative community structure in resting and task-evoked func-
tional brain networks. bioRxiv:355016

Betzel, R.. F., Bertolero, M.. UN., Gordon, E. M., Gratton, C., Dosenbach,
N. U., & Bassett, D. S. (2018). The community structure of func-
tional brain networks exhibits scale-specific patterns of variability
across individuals and time. bioRxiv:413278.

Betzel, R.. F., Griffa, UN., Avena-Koenigsberger, UN., Goñi, J., Thiran,
J.-P., Hagmann, P., & Sporns, Ô. (2013). Multi-scale community
organization of the human structural connectome and its rela-
tionship with resting-state functional connectivity. Network Sci-
ence, 1(3), 353–373.

Betzel, R.. F., Medaglia, J.. D., & Bassett, D. S. (2018). Diversity of
meso-scale architecture in human and non-human connectomes.
Communications naturelles, 9(1), 346.

Betzel, R.. F., Medaglia, J.. D., Kahn, UN. E., Soffer, J., Schonhaut, D. R.,
& Bassett, D. S.
(2019). Structural, geometric and genetic fac-
tors predict interregional brain connectivity patterns probed by
electrocorticography. Nature Biomedical Engineering, 1.

Betzel, R.. F., Wood, K. C., Angeloni, C., Geffen, M.. N., & Bassett,
D. S. (2018). Stability of spontaneous, correlated activity in mouse
auditory cortex. arXiv:1812.03796

Briggman, K. L., & Kristan, W. B.

Imaging dedicated
and multifunctional neural circuits generating distinct behaviors.
Journal des neurosciences, 26(42), 10925–10933.

(2006).

Bruno, UN. M., Frost, W. N., & Humphries, M.. D. (2015). Modular de-
construction reveals the dynamical and physical building blocks
of a locomotion motor program. Neurone, 86(1), 304–318.

Bullmore, E., & Sporns, Ô. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186.

Bullmore, E., & Sporns, Ô. (2012). The economy of brain network

organization. Nature Revues Neurosciences, 13(5), 336.

Chen, B. L., Hall, D. H., & Chklovskii, D. B. (2006). Wiring opti-
mization can relate neuronal structure and function. Procédure
of the National Academy of Sciences, 103(12), 4723–4728.
Chen, T.-W., Wardill, T. J., Sun, Y., Pulver, S. R., Renninger, S. L.,
Baohan, UN., . . . Kim, D. S. (2013). Ultrasensitive fluorescent pro-
teins for imaging neuronal activity. Nature, 499(7458), 295.
Chen, X., Mu, Y., Hu, Y., Kuan, UN. T., Nikitchenko, M., Randlett, O.,
. . . Ahrens, M.. B. (2018). Brainwide organization of neuronal
activity and convergent sensorimotor transformations in larval
zebrafish. Neurone, 100, 876–890.

Cohen, J.. R., & D'Esposito, M.. (2016). The segregation and integra-
tion of distinct brain networks and their relationship to cognition.
Journal des neurosciences, 36(48), 12083–12094.

Cole, M.. W., Bassett, D. S., Power, J.. D., Plus courageux, T. S., & Petersen,
S. E. (2014). Intrinsic and task-evoked network architectures of
the human brain. Neurone, 83(1), 238–251.

Cole, M.. W., Reynolds, J.. R., Power, J.. D., Repovs, G., Anticevic, UN.,
& Plus courageux, T. S. (2013). Multi-task connectivity reveals flexible

hubs for adaptive task control. Neurosciences naturelles, 16(9), 1348.
Craddock, R.. C., Jbabdi, S., Yan, C.-G., Vogelstein, J.. T., Castellanos,
F. X., Di Martino, UN., . . . Milham, M.. P.. (2013). Imaging human
connectomes at the macroscale. Nature Methods, 10(6), 524.
Dann, B., Michaels, J.. UN., Schaffelhofer, S., & Scherberger, H.
(2016). Uniting functional network topology and oscillations
in the fronto-parietal single unit network of behaving primates.
eLife, 5, e15719.

David, O., Cosmelli, D., & Friston, K. J.. (2004). Evaluation of dif-
ferent measures of functional connectivity using a neural mass
model. Neuroimage, 21(2), 659–673.

Deco, G.,

Jirsa, V. K., Robinson, P.. UN., Breakspear, M., &
Friston, K. (2008). The dynamic brain: From spiking neurons to
neural masses and cortical fields. Biologie computationnelle PLoS,
4(8), e1000092.

Deco, G., Tononi, G., Boly, M., & Kringelbach, M.. L. (2015). Re-
thinking segregation and integration: contributions of whole-
brain modelling. Nature Revues Neurosciences, 16(7), 430.
Di Martino, UN., Fair, D. UN., Kelly, C., Satterthwaite, T. D.,
Castellanos, F. X., Thomason, M.. E., . . . Milham, M.. P.. (2014).
Unraveling the miswired connectome: A developmental perspec-
tive. Neurone, 83(6), 1335–1353.

Downar, J., Crawley, UN. P., Mikulis, D. J., & Davis, K. D. (2000). UN
multimodal cortical network for the detection of changes in the
sensory environment. Neurosciences naturelles, 3(3), 277.

Dunn, T. W., Mu, Y., Narayan, S., Randlett, O., Naumann, E. UN.,
Lequel, C.-T., . . . Ahrens, M.. B. (2016). Brain-wide mapping of
neural activity controlling zebrafish exploratory locomotion.
eLife, 5, e12741.

Eickhoff, S. B., Yeo, B. T., & Genon, S. (2018). Imaging-based par-
cellations of the human brain. Nature Revues Neurosciences, 1.
Ercsey-Ravasz, M., Markov, N. T., Lamie, C., Van Essen, D. C.,
Knoblauch, K., Toroczkai, Z., & Kennedy, H. (2013). A predic-
tive network model of cerebral cortical connectivity based on a
distance rule. Neurone, 80(1), 184–197.

Faber, S. P., Timme, N. M., Beggs, J.. M., & Newman, E. L. (2018).
Computation is concentrated in rich clubs of local cortical net-
travail. Neurosciences en réseau, 1–21.

Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M.. D., Huang, J.,
Chun, M.. M., . . . Constable, R.. T. (2015). Functional connectome
fingerprinting: Identifying individuals using patterns of brain con-
nectivity. Neurosciences naturelles, 18(11), 1664.

Fornito, UN., Zalesky, UN., & Breakspear, M..

(2015). The con-
nectomics of brain disorders. Nature Revues Neurosciences,
16(3), 159.

Goñi,

J., van den Heuvel, M.. P., Avena-Koenigsberger, UN.,
de Mendizabal, N. V., Betzel, R.. F., Griffa, UN., . . . Sporns, Ô.
(2014). Resting-brain functional connectivity predicted by ana-
lytic measures of network communication. Actes du
Académie nationale des sciences, 111(2), 833–838.

Gordon, E. M., Laumann, T. O., Gilmore, UN. W., Newbold, D. J.,
Vert, D. J., Berger, J.. J., . . . Dosenbach, N. U. F. (2017). Pre-
cision functional mapping of individual human brains. Neurone,
95(4), 791–807.

Goulas, UN., Betzel, R.. F., & Hilgetag, C. C. (2018). Spatiotemporal

ontogeny of brain wiring. bioRxiv:385369

Neurosciences en réseau

254

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

4
1
2
3
4
1
8
6
6
7
6
9
n
e
n
_
un
_
0
0
1
2
1
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Whole-brain functional connectivity in zebrafish

Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Alfred, B. Y.,
Kahn, UN. E., . . . Bassett, D. S. (2015). Controllability of structural
brain networks. Communications naturelles, 6, 8414.

Guimera, R., & Amaral, L. UN. N. (2005). Functional cartography of

complex metabolic networks. Nature, 433(7028), 895.

Hartley, T., Lever, C., Bourgeois, N., & O’Keefe, J.. (2014). Space in
the brain: How the hippocampal formation supports spatial cog-
nition. Philosiphical Transactions of the Royal Society of London
B: Sciences biologiques, 369(1635), 20120510.

Il, Y., & Evans, UN. (2010). Graph theoretical modeling of brain con-

nectivity. Opinion actuelle en neurologie, 23(4), 341–350.

Honey, C., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J.-P.,
Meuli, R., & Hagmann, P.. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Procédure
of the National Academy of Sciences, 106(6), 2035–2040.

Huang, L., Kebschull, J., Furth, D., Musall, S., Kaufman, M.. T.,
Churchland, UN. K., & Zador, UN. (2018). High-throughput mapping
of mesoscale connectomes in individual mice. bioRxiv:422477
Huang, W., Bolton, T. UN., Medaglia, J.. D., Bassett, D. S., Ribeiro, UN.,
& Van De Ville, D. (2018). A graph signal processing perspective
on functional brain imaging. Proceedings of the IEEE, 106(5).
Humphries, M.. D. (2017). Dynamical networks: Finding, measur-
ing, and tracking neural population activity using network sci-
ence. Neurosciences en réseau, 1(4), 324–338.

Hutchison, R.. M., Womelsdorf, T., Allen, E. UN., Bandettini, P.. UN.,
Calhoun, V. D., Corbetta, M., . . . Chang, C. (2013). Dynamic
functional connectivity: Promise, issues, and interpretations. Neuro-
Image, 80, 360–378.

Jacobs, J., Weidemann, C. T., Miller, J.. F., Solway, UN., Burke, J.. F.,
Wei, X.-X., . . . Kahana, M.. J.. (2013). Direct recordings of grid-
like neuronal activity in human spatial navigation. Nature Neuro-
science, 16(9), 1188.

Jeub, L. G., Sporns, O., & Fortunato, S. (2018). Multiresolution con-
sensus clustering in networks. Scientific Reports, 8(1), 3259.
Jun, J.. J., Steinmetz, N. UN., Siegle, J.. H., Denman, D. J., Bauza,
M., Barbarits, B., . . . Harris, T. D. (2017). Fully integrated sili-
con probes for high-density recording of neural activity. Nature,
551(7679), 232.

Jutla, je. S., Jeub, L. G., & Mucha, P.. J.. (2011). A generalized lou-
vain method for community detection implemented in MATLAB.
Extrait de http://netwiki.amath.unc.edu/GenLouvain

Kawashima, T., Zwart, M.. F., Lequel, C.-T., Mensh, B. D., & Ahrens,
M.. B. (2016). The serotonergic system tracks the outcomes of actions
to mediate short-term motor learning. Cell, 167(4), 933–946.
Keller, P.. J., & Ahrens, M.. B. (2015). Visualizing whole-brain ac-
tivity and development at the single-cell level using light-sheet
microscopy. Neurone, 85(3), 462–483.

Kim, T. H., Zhang, Y., Lecoq, J., Jung, J.. C., Li, J., Zeng, H., . . .
Schnitzer, M.. J.. (2016). Long-term optical access to an esti-
mated one million neurons in the live mouse cortex. Cell Reports,
17(12), 3385–3394.

Ko, H., Hofer, S. B., Pichler, B., Buchanan, K. UN., Sjöström, P.. J., &
Mrsic-Flogel, T. D. (2011). Functional specificity of local synap-
tic connections in neocortical networks. Nature, 473(7345), 87.
Kunst, M., Laurell, E., Mokayes, N., Kramer, UN., Kubo, F., Fernandes,
UN. M., . . . Baier, H. (2019). A cellular-resolution atlas of the larval
zebrafish brain. Neurone, 103(1), 21–38.e5.

Lake, E. M., Ge, X., Shen, X., Herman, P., Hyder, F., Cardin, J.. UN.,
. . . Constable, R.. T. (2018). Spanning spatiotemporal scales with
2+
simultaneous mesoscopic Ca
imaging and functional MRI.
bioRxiv:464305

Lansdell, B., & Kording, K. (2018). Spiking allows neurons to esti-

mate their causal effect. bioRxiv:253351

Laughlin, S. B., & Sejnowski, T. J.. (2003). Communication in neu-

ronal networks. Science, 301(5641), 1870–1874.

Lee, W.-C. UN., Bonin, V., Reed, M., Graham, B. J., Hood, G.,
Glattfelder, K., & Reid, R.. C. (2016). Anatomy and function of an
excitatory network in the visual cortex. Nature, 532(7599), 370.
Lin, I.-C., Okun, M., Carandini, M., & Harris, K. D. (2015). The na-

ture of shared cortical variability. Neurone, 87(3), 644–656.

Mann, K., Gallen, C. L., & Clandinin, T. R..

(2017). Whole-
brain calcium imaging reveals an intrinsic functional network in
Drosophila. Biologie actuelle, 27(15), 2389–2396.

Mantel, N. (1967). The detection of disease clustering and a general-
ized regression approach. Cancer Research, 27(2 Pt. 1), 209–220.
Meunier, D., Lambiotte, R., Fornito, UN., Ersche, K., & Bullmore, E. T.
(2009). Hierarchical modularity in human brain functional net-
travaux. Frontiers in Neuroinformatics, 3, 37.

Mucha, P.. J., Richardson, T., Macon, K., Porter, M.. UN., & Onnela,
J.-P. (2010). Community structure in time-dependent, multiscale,
and multiplex networks. Science, 328(5980), 876–878.

Muldon, S. F., Soltesz, JE., & Cossart, R.. (2013). Spatially clustered
neuronal assemblies comprise the microstructure of synchrony
in chronically epileptic networks. Actes de la Nationale
Académie des Sciences, 110(9), 3567–3572.

Newman, M.. E., & Girvan, M.. (2004). Finding and evaluating com-
munity structure in networks. Physical Review E, 69(2), 026113.
Oram, M.. W. (2010). Visual stimulation decorrelates neuronal
activité. American Journal of Physiology-Heart and Circulatory
Physiology.

Orlandi, J.. G., Soriano, J., Alvarez-Lacalle, E., Teller, S., & Casademunt,
J.. (2013). Noise focusing and the emergence of coherent activity
in neuronal cultures. Nature Physics, 9(9), 582.

Panier, T., Romano, S., Olive, R., Pietri, T., Sumbre, G., Candelier,
R., & Debrégeas, G. (2013). Fast functional imaging of multiple
brain regions in intact zebrafish larvae using selective plane illu-
mination microscopy. Frontiers in Neural Circuits, 7, 65.

Parc, H.-J., & Friston, K. (2013). Structural and functional brain net-
travaux: From connections to cognition. Science, 342(6158), 1238411.
Ponce-Alvarez, UN., Jouary, UN., Privat, M., Deco, G., & Sumbre, G.
(2018). Whole-brain neuronal activity displays crackling noise
dynamics. Neurone, 100(6), 1446–1459.

Power, J.. D., Cohen, UN. L., Nelson, S. M., Wig, G. S., Barnes, K. UN.,
Church, J.. UN., . . . Petersen, S. E. (2011). Functional network or-
ganization of the human brain. Neurone, 72(4), 665–678.

Power, J.. D., Mitra, UN., Laumann, T. O., Snyder, UN. Z., Schlaggar,
B. L., & Petersen, S. E. (2014). Methods to detect, characterize,
and remove motion artifact in resting state fmri. NeuroImage, 84,
320–341.

Power, J.. D., Schlaggar, B. L., Lessov-Schlaggar, C. N., & Petersen,
S. E. (2013). Evidence for hubs in human functional brain net-
travaux. Neurone, 79(4), 798–813.

Romano, S. UN., Pérez-Schuster, V., Jouary, UN., Boulanger-Weill,
J., Candeo, UN., Pietri, T., & Sumbre, G. (2017). An integrated

Neurosciences en réseau

255

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

4
1
2
3
4
1
8
6
6
7
6
9
n
e
n
_
un
_
0
0
1
2
1
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Whole-brain functional connectivity in zebrafish

calcium imaging processing toolbox for the analysis of neu-
ronal population dynamics. Biologie computationnelle PLoS, 13(6),
e1005526.

Rosch, R.. E., Hunter, P., Baldeweg, T., Friston, K., & Meyer, M..
(2017). Imaging and dynamic causal modelling reveal brain-wide
changes in effective connectivity and synaptic dynamics during
epileptic seizures. bioRxiv:160259

Rubinov, M.. (2016). Constraints and spandrels of interareal connec-

tomes. Communications naturelles, 7, 13812.

Rubinov, M., & Sporns, Ô. (2010). Complex network measures of
brain connectivity: uses and interpretations. NeuroImage, 52(3),
1059–1069. https://sites.google.com/site/bctnet/Home

Rubinov, M., Ypma, R.. J., Watson, C., & Bullmore, E. T. (2015).
Wiring cost and topological participation of the mouse brain
connectome. Actes de l'Académie nationale des sciences,
112(32), 10032–10037.

Sadovsky, UN.

J., Kruskal, P.. B., Kimmel,

J.,
Neubauer, F. B., & MacLean, J.. N. (2011). Heuristically optimal
path scanning for high-speed multiphoton circuit imaging. Jour-
nal of Neurophysiology, 106(3), 1591–1598.

J.. M., Ostmeyer,

Saggar, M., Sporns, O., Gonzalez-Castillo, J., Bandettini, P.. UN.,
Carlsson, G., Glover, G., & Reiss, UN. L. (2018). Towards a new
approach to reveal dynamical organization of the brain using
topological data analysis. Communications naturelles, 9(1), 1399.
Salehi, M., Vert, UN. S., Karbasi, UN., Shen, X., Scheinost, D., &
Constable, R.. T. (2019). There is no single functional atlas even
for a single individual: Functional parcel definitions change with
task. NeuroImage, 116366.

Schröter, M., Paulsen, O., & Bullmore, E. T.

(2017). Micro-
connectomics: Probing the organization of neuronal networks at
the cellular scale. Nature Revues Neurosciences, 18(3), 131.
Schultz, D. H., & Cole, M.. W. (2016). Higher intelligence is associ-
ated with less task-related brain network reconfiguration. Journal
of Neuroscience, 36(33), 8551–8561.

Seghier, M.. L., & Prix, C. J.. (2018). Interpreting and utilising inter-
subject variability in brain function. Tendances des sciences cognitives,
22(6), 517–530.

Simas, T., Chavez, M., Rodriguez, P.. R., & Diaz-Guilera, UN. (2015).
An algebraic topological method for multimodal brain networks
comparisons. Frontiers in Psychology, 6, 904.

Forgeron, S. M., Miller, K. L., Salimi-Khorshidi, G., Webster, M.,
Beckmann, C. F., Nichols, T. E., . . . Woolrich, M.. W. (2011). Net-
work modelling methods for fMRI. NeuroImage, 54(2), 875–891.
Solomon, E., Kragel, J., Gross, R., Lega, B., Sperling, M., Worrell, G.,
. . . Kahana, M.. J.. (2018). Medial temporal lobe functional con-
nectivity predicts stimulation-induced theta power. Nature Com-
munications, 9(1), 4437.

Sporns, Ô. (2013). Network attributes for segregation and integra-
tion in the human brain. Opinion actuelle en neurobiologie, 23(2),
162–171.

Sporns, O., & Betzel, R.. F. (2016). Modular brain networks. Annual

Review of Psychology, 67, 613–640.

Sporns, O., Tononi, G., & Kötter, R.. (2005). The human connectome:
A structural description of the human brain. PLoS Computational
Biology, 1(4), e42.

Sprague, J., Doerry, E., Douglas, S., & Westerfield, M.. (2001). Le
Zebrafish Information Network (ZFIN): A resource for genetic,
genomic and developmental research. Nucleic Acids Research,
29(1), 87–90.

Spreng, R.. N., Stevens, W. D., Chamberlain, J.. P., Gilmore, UN. W., &
Schacter, D. L. (2010). Default network activity, coupled with the
frontoparietal control network, supports goal-directed cognition.
Neuroimage, 53(1), 303–317.

Stiso, J., & Bassett, D. (2018). Spatial embedding imposes constraints
on the network architectures of neural systems. arXiv:1807.04691
Taylor, P.. N., Wang, Y., & kaiser, M.. (2017). Within brain area trac-
tography suggests local modularity using high resolution connec-
tomics. Scientific Reports, 7, 39859.

Theiler, J., Eubank, S., Longtin, UN., Galdrikian, B., & Farmer, J.. D.
(1992). Testing for nonlinearity in time series: The method of sur-
rogate data. Physica D: Nonlinear Phenomena, 58(1–4), 77–94.
Traag, V. UN., Van Dooren, P., & Nesterov, Oui. (2011). Narrow scope
for resolution-limit-free community detection. Physical Review E,
84(1), 016114.

Traud, UN. L., Kelsic, E. D., Mucha, P.. J., & Porter, M.. UN. (2011). Com-
paring community structure to characteristics in online collegiate
social networks. SIAM Review, 53(3), 526–543.

van den Heuvel, M.. P., Bullmore, E. T., & Sporns, Ô. (2016). Compar-
ative connectomics. Tendances des sciences cognitives, 20(5), 345–361.
van den Heuvel, M.. P., & Sporns, Ô. (2013). Network hubs in the
cerveau humain. Tendances des sciences cognitives, 17(12), 683–696.
Vanni, M.. P., Chan, UN. W., Balbi, M., Silasi, G., & Murphy, T. H.
(2017). Mesoscale mapping of mouse cortex reveals frequency-
dependent cycling between distinct macroscale functional mod-
ules. Journal des neurosciences, 37(31), 7513–7533.

Vértes, P.. E., Alexander-Bloch, UN. F., Gogtay, N., Giedd, J.. N.,
Rapoport, J.. L., & Bullmore, E. T. (2012). Simple models of human
brain functional networks. Proceedings of the National Academy
of Sciences, 201111738.

Vladimirov, N., Mu, Y., Kawashima, T., Bennett, D. V., Lequel, C.-T.,
Looger, L. L., . . . Ahrens, M.. B. (2014). Light-sheet functional imag-
ing in fictively behaving zebrafish. Nature Methods, 11(9), 883.
Vladimirov, N., Wang, C., Hockendorf, B., Pujala, UN., Tanimoto, M.,
Mu, Y., . . . Ahrens, M.. (2018). Brain-wide circuit interrogation at
the cellular level guided by online analysis of neuronal function.
Nature Methods, 15, 1117–1125.

Wang, J., Wang, L., Zang, Y., Lequel, H., Tang, H., Gong, Q., . . . Il, Oui.
(2009). Parcellation-dependent small-world brain functional net-
travaux: A resting-state fMRI study. Human Brain Mapping, 30(5),
1511–1523.

Yamamoto, H., Moriya, S., Ide, K., Hayakawa, T., Akima, H., Sato,
S., . . . Hirano-Iwata, UN. (2018). Impact of modular organization
on dynamical richness in cortical networks. Science Advances,
4(11), eaau4914.

Sporns, O., Tononi, G., & Edelman, G. (2002). Theoretical neuro-
anatomy and the connectivity of the cerebral cortex. Behavioural
Brain Research, 135(1–2), 69–74.

Zanto, T. P., & Gazzaley, UN. (2013). Fronto-parietal network: Flexi-
ble hub of cognitive control. Tendances des sciences cognitives, 17(12),
602–603.

Neurosciences en réseau

256

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

4
1
2
3
4
1
8
6
6
7
6
9
n
e
n
_
un
_
0
0
1
2
1
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Télécharger le PDF