RECHERCHE
Clinically feasible brain morphometric similarity
network construction approaches with restricted
magnetic resonance imaging acquisitions
Daniel J. King
1 and Amanda G. Wood 1,2
1School of Life and Health Sciences and Aston Neuroscience Institute, Aston University, Birmingham, United Kingdom
2School of Psychology, Faculty of Health, Melbourne Burwood Campus, Deakin University, Geelong, Victoria, Australia
Mots clés: Morphometric similarity networks, Structural MRI, Morphology, Connectome, Cognition
un accès ouvert
journal
ABSTRAIT
Morphometric similarity networks (MSNs) estimate organization of the cortex as a
biologically meaningful set of similarities between anatomical features at the macro- et
microstructural level, derived from multiple structural MRI (sMRI) sequences. These networks
are clinically relevant, predicting 40% variance in IQ. Cependant, the sequences required
(T1w, T2w, DWI) to produce these networks are longer acquisitions, less feasible in some
populations. Ainsi, estimating MSNs using features from T1w sMRI is attractive to clinical and
developmental neuroscience. We studied whether reduced-feature approaches approximate
the original MSN model as a potential tool to investigate brain structure. In a large,
homogenous dataset of healthy young adults (from the Human Connectome Project, HCP),
we extended previous investigations of reduced-feature MSNs by comparing not only
T1w-derived networks, but also additional MSNs generated with fewer MR sequences, à
their full acquisition counterparts. We produce MSNs that are highly similar at the edge level
to those generated with multimodal imaging; cependant, the nodal topology of the networks
differed. These networks had limited predictive validity of generalized cognitive ability.
Dans l'ensemble, when multimodal imaging is not available or appropriate, T1w-restricted MSN
construction is feasible, provides an appropriate estimate of the MSN, and could be a useful
approach to examine outcomes in future studies.
RÉSUMÉ DE L'AUTEUR
We can estimate the higher order organization of cortical gray matter as a connectome
using structural MRI. Cependant, this methodology, termed morphometric similarity, requires
multiple advanced neuroimaging protocols that are unsuitable, unavailable, or intolerable to
certain populations, including children and some clinical groups. In a large, homogenous
dataset of healthy young adults, we estimated these connectomes using three different feature
sets, each extracted from fewer MRI sequences. Even when produced using only T1-weighted
structural MRI scans, these connectomes were broadly similar to those produced with
more complex or numerous MRI sequences. We did not replicate previous findings linking
variation in the morphometric similarity networks (MSNs) to individual differences in
cognitive abilities. We highlight potential reasons for this, including the developmental stage
of the young adult imaging cohort in which our hypotheses were tested, and conclude that
this study provides putative evidence that, in those populations where advanced imaging is
not plausible, MSNs generated from T1-weighted structural MRIs are a promising alternative.
Citation: King, D. J., & Wood, UN. G.
(2020). Clinically feasible brain
morphometric similarity network
construction approaches with
restricted magnetic resonance imaging
acquisitions. Neurosciences en réseau,
4(1), 274–291. https://est ce que je.org/
10.1162/netn_a_00123
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00123
Informations complémentaires:
https://doi.org/10.1162/netn_a_00123
Reçu: 2 Septembre 2019
Accepté: 16 Décembre 2019
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Amanda G. Wood
a.wood4@aston.ac.uk
Éditeur de manipulation:
Olaf Sporns
droits d'auteur: © 2019
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MSN construction with restricted MR acquisitions
Cortical thickness:
Distance between the inner (blanc
matter/gray matter boundary) et
outer (gray matter/dura boundary)
cortical surfaces at each vertex.
INTRODUCTION
Cortical gray matter structural covariance networks (SCNs) model the degree to which the
morphology of cortical regions (par exemple., cortical thickness or volume) statistically covaries across
all possible pairs of regions (Alexander-Bloch, Giedd, & Bullmore, 2013; Evans, 2013). These
whole-brain network approaches to morphometry, within a graph theoretic framework, allow
us to investigate additional information beyond univariate approaches to neuroanatomy
(Pagani, Bifone, & Gozzi, 2016). Disruption to the SCN has been explored in a range of
neurological and neuropsychiatric conditions. Cependant, this methodology necessarily gener-
ates group-level networks indexing population-level covariance in neuroanatomy (Alexander-
Bloch, Raznahan, Bullmore, & Giedd, 2013). This limits the ability to quantify system-level
abnormalities within individual patients, who could benefit from stratified diagnosis and prog-
nosis (Zheng, Yao, Xie, Fan, & Hu, 2018).
An alternative approach to investigate the regional covariance structure between multi-
ple morphometric features at an individual level is morphometric similarity networks (MSNs;
Seidlitz et al., 2018). This approach estimates mesoscale organization of the cortex as a bi-
ologically meaningful set of similarities between anatomical features at both the macro- et
the microstructural level (Morgan et coll., 2018), including mesoscale morphometry, tissue dif-
fusion properties, and myelination indices. MSNs have been shown to be clinically useful,
predicting ∼40% variance in IQ, as well as biologically meaningful, with edges of the MSN
highly aligned with regional gene coexpression in human data and axonal tract tracing in the
rhesus macaque (Seidlitz et al., 2018). These findings reflect the fact that cortical regions that
are more anatomically similar are likely to be anatomically connected (Goulas, Uylings, &
Hilgetag, 2017; Wei, Scholtens, Turk, & van den Heuvel, 2019). The MSN represents a new
neuroimaging phenotype, which may provide additional, biologically relevant information be-
yond existing network approaches.
MSNs have already been utilized in a small number of clinical studies (characteristics of
these studies, including neuroanatomical features extracted, are listed below in Table 1). Pour
example, previous studies identified a robust, replicable pattern of differences in morphome-
tric similarity between patients with psychosis compared with controls (Morgan et coll., 2018)
and detected dysmaturation of the brain in preterm infants (Galdi et al., 2018). Dans l'ensemble, ces
findings suggest that MSNs represent a useful and clinically relevant phenotype.
Multimodal, high-quality MRI sequences are required for these approaches. These may not
be feasible or tolerable for all research settings and/or populations. Existing (héritage) clinical
cohorts often lack advanced imaging. Longer acquisition times for advanced sequences may
reduce image quality, especially in pediatric or clinical applications where noncompliance
and movement are more likely as acquisition time increases (Rosen et al., 2018).
Estimating MSNs using a single T1w 3-D anatomical MRI is appealing for clinical and de-
velopmental neuroscience (Batalle, Edwards, & O’Muircheartaigh, 2018). Seidlitz et al. (2018)
and Li et al. (2017) estimated morphometric similarity in this way and found that network edge
weights were similar to multimodal MSNs (r = 0.68; Seidlitz et al., 2018), with good test-retest
reliability in terms of network topology (ICC = 0.60; Li et al., 2017). Using only T1w MRI it
is possible to identify patterns of morphometric similarity that classify autism spectrum disor-
der (Zheng et al., 2019), Alzheimer’s disease, and mild cognitive impairment (Zheng et al.,
2018) from controls, albeit with reduced estimation precision, and greater standard deviation
of edge-level weights across participants (Seidlitz et al., 2018). This method also identified
a spatial pattern of anatomical disruptions associated with regional gene expression, résultats
Neurosciences en réseau
275
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MSN construction with restricted MR acquisitions
Tableau 1. Characteristics of previous studies utilizing morphometric similarity networks to investi-
gate cortical organization
Étude
Seidlitz et al. (2018)
Population
Typically developing
adolescents
Morgan et al. (2018)
Galdi et al. (2018)
Schizophrenia or nonaffective
psychotic disorders
Term and preterm neonates
Seidlitz et al. (2019)
Neurodevelopmental
disorders of known
genetic origin
Healthy adults
MRI acquisitions
Multiparametric
mapping sequence
and DWI
T1w MRI and DWI
T1w MRI, T2w MRI,
and DWI
T1w MRI
MSN feature set
FA, MARYLAND, MT, GM, SA,
CT, GC, MC, CI, FI
(Reduced-feature MSN;
CT, SA, GM, GC, MC)
GM, SA, CT, GC, MC,
FA, MARYLAND
GM, T1/T2 ratio, FA,
MARYLAND, RD, AD, VISO,
IVF, ODI
CT, SA, GM, MC, GC
T1w MRI
T1w MRI
Li et al. (2017)
Zheng et al. (2018)
Zheng et al. (2019)
Mild cognitive impairment
and Alzheimer’s disease
Autism spectrum disorders
Vertices, GM, SA, CT,
SD-CT, MC, GC, CI, FI
CT, SA, GM, LGI, sulcul
depth, gyrus height
CT, SA, GM, LGI, sulcul
depth, gyrus height, MC
Note. FA = fractional anisotropy, MD = mean diffusivity, MT = magnetization transfer, GM = gray
matter volume, SA = surface area, CT = cortical thickness, GC = Gaussian curvature, MC = mean
curvature, CI = curvature index, FI = folding index, RD = radial diffusivity, AD = axial diffusivity,
VISO = isotropic volume fraction, IVF = intracellular volume fraction, ODI = orientation dispersion
index, vertices = number of vertices, SD-CT = standard deviation of cortical thickness, LGI = local
gyrification index.
T1w MRI
consistent with a transcriptional vulnerability model of neurodevelopmental disorders (Seidlitz
et coll., 2019). Characteristics of these studies, including neuroanatomical features extracted,
are listed below in Table 1. Cependant, existing studies provide limited assessment of reliability,
consistency with group networks, biological validity, and predictive ability.
The current study aimed to determine whether reduced-feature approaches approximate
the original MSN model. We extended previous investigations of reduced-feature MSNs by
comparing not only T1w-derived networks, but also additional MSN models, each using fewer
metrics from a reduced number of MRI acquisitions.
We predicted that for each measure of reliability/replicability, performance would be
ordered hierarchically with MSNs generated with the greatest number of features outperform-
ing those generated with fewer. We also predicted that between-model comparisons would
suggest that the models themselves were highly similar. In line with previous work (Seidlitz
et coll., 2018), we predicted that there would be an association between cognition and MSN
organization and that this would generalize to a novel cognitive domain, specifically executive
functioning.
MÉTHODES
Participants: HCP Data
The current study uses open-access, 3T MRI data provided by the Human Connectome Project
(Van Essen et al., 2013), shared via ConnectomeDB (https://db.humanconnectome.org) sous
the HCP 1200 and HCP test-retest release. Favorable ethical approval for the secondary analysis
of this data was granted by the Aston University ethics panel.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Fractional anisotropy:
Scalar measuring the degree of
directional restriction of water
molecule diffusion.
Mean diffusivity:
Average diffusion motion of water
molecules independent of
directionality.
Gaussian curvature:
The product of the two principal
curvatures at every vertex of the
surface, indicating local curvature.
Mean curvature:
The mean of the two principal
curvatures at every vertex, indicating
local folding.
Curvature index:
Integrating across all regions of
positive Gaussian curvature and
dividing by 4π.
Folding index:
Integral of the product of the
maximum principal curvature and
the difference between maximum
and minimum curvature.
Executive functions:
A collection of top-down control
processes that allow an individual to
be adaptive to novel situations in their
environment.
Neurosciences en réseau
276
MSN construction with restricted MR acquisitions
The HCP 1200 release contains data from n = 1, 206 sujets (550 males,
HCP 1200 release.
656 females). Subjects are grouped into age bins from 22–25 to 36+ (median age = 26–30).
While n = 1, 206 subjects provided behavioral data, only 1,113 subjects had MRI data avail-
capable. These were the subjects for which data were accessed and downloaded from Connec-
tomeDB for the current study.
Pour 46 subjects from the HCP 1200 release, a second retest dataset is
HCP test-retest release.
available to assess test-retest reliability of analyses. These second MRI visits occurred within
time bins from 1–2 months to 11 months post initial scanning session. The median retest-
interval bin was 5 mois. Of these subjects, 45 had available MRI data, and these were the
subjects used for subsequent analyses.
Methods
Subjects were selected for inclusion if, in the 1,200-subject HCP release,
Data quality control.
they had T1w (0.7 mm isotropic), T2w (0.7 mm isotropic), and diffusion data uploaded. Ce
led to exclusion of n = 76 cases.
Aussi, utilizing QC data shared by the Human Connectome Project, any data labeled with
QC issue code B (which flags cases as having focal segmentation and surface errors when the
corresponding FreeSurfer outputs were checked) were further excluded from the current study
(n = 33). The final dataset consisted of n = 1, 004 sujets. In the test-retest cohort, only one
subject was excluded as flagged with QC issue code B by the Human Connectome Project.
The current study utilizes data shared in preprocessed format, including the
MRI processing.
output of the HCP FreeSurfer pipeline (Fischl et al., 2002; Glasser et al., 2013; Jenkinson,
Bannister, Brady, & Forgeron, 2002; Jenkinson, Beckmann, Behrens, Woolrich, & Forgeron, 2012),
processed DWI (gradient nonlinearity, eddy current, and EPI distortion corrected; Andersson,
Skare, & Ashburner, 2003; Andersson & Sotiropoulos, 2015, 2016), and calculated T1/T2w
ratio myelin maps (Glasser & Van Essen, 2011). For further details of HCP processing pipelines
see Glasser et al. (2013).
Once cases were selected, measures indexing the underlying neuroanatomical structure
were derived from multiple imaging modalities (see Table 2). Seidlitz et al. (2018) leverage
near-identical MRI-derived metrics for the construction of the MSN network. Cependant, we are
using the T1/T2 ratio as a proxy for myelin content, rather than the magnetization transfer scan
used by Seidlitz et al. (2018). The rationale for this modification was both pragmatic and clin-
ically driven; (un) the T1/T2w ratio maps are already implemented by the Human Connectome
Project and thus these data are available for use with the rest of the high-quality HCP acquisi-
tion data; et (b) in clinical populations, for which the methods may provide greatest benefit,
multiparameter mapping MRI sequences may not be acquired as part of a clinical protocol,
whereas T1w and T2w sequences are.
Preprocessed DWI (1.25 mm isotropic, b = 1, 000) in T1w space were fitted to a tensor
model using FMRIB’s “dtifit” function, and the subsequent FA and MD maps were mapped to
the individual subject’s FreeSurfer-generated surface model in MNI space, using the connec-
tome workbench (Marcus et al., 2011) function “volume-to-surface-mapping.” These, and the Tw1/
T2w ratio myelin maps, were parcellated based on the Desikan-Killiany atlas (Desikan et al.,
2006), by generating a dense-cifti (using the “cifti-create-dense-from-template” function) et
parcellating the output (using “cifti-parcellate”). FreeSurfer metrics were also extracted for each
parcellated region using the “aparcstats2table” function.
Neurosciences en réseau
277
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MSN construction with restricted MR acquisitions
Folding index:
Integral of the product of the
maximum principal curvature and
the difference between maximum
and minimum curvature.
Tableau 2. Morphometric measures and the modality of MRI from which they were derived
Modality
T1w
T2w
DWI
Metrics
Cortical thickness (CT), surface area (SA), mean (extrinsic) curvature
(MC), Gaussian (intrinsic) curvature (GC), folding index (FI), curvature
index (CI), and gray matter volume (GM)
Myelination (T1/T2w ratio)
Fractional anisotropy (FA), mean diffusivity (MARYLAND)
To generate MSNs we apply the methods of Seidlitz et al. (2018) to the
MSN construction.
HCP data. The Desikan-Killiany atlas was mapped to the individual subjects with a surface-
based registration, using the FreeSurfer pipeline. The Desikan-Killiany atlas regions of interest
(ROI) were used as the nodes for all network construction.
Morphometric features (parcellated to the Desikan-Killiany atlas) for each participant can
be expressed as a set of n vectors of length 10, with each vector as a different anatomical region
(n = 68), and each element of the vector a different morphometric measure. Cependant, ces
features are not all measured at the same magnitude of scale. Par exemple, volume (mm3) est
measured at the order of 103, whereas folding index is measured to the order of 101. Ainsi,
to normalize within this length 10 vector, each of these morphometric features is normalized
across the 68 régions, using Z-scores (demeaned and SD scaled). This brings the measures
across the feature vector into a comparable range.
Using the normalized features, a correlation matrix is generated for each participant, où
each element of the matrix is the correlation between the feature vectors for every possible
pairwise combinations of regions. Because each feature is zero-centered, the resultant distri-
bution of correlation coefficients is normally distributed about zero. This correlation matrix
represents the MSN-estimated connectivity for each participant.
We constructed these networks across three different MSN models. These models were
hierarchically organized, with reduced acquisition complexity from Models A to C below:
(UN) MSN (T1w + T1w/T2w ratio + DWI; 10 features (MSN10-feat.)),
(B) MSN (T1w + T1w/T2w ratio; eight features (MSN8-feat.)),
(C) MSN (T1w; seven features (MSN7-feat.))
Model A, hereto referred to as MSN10-feat., is the best approximation of the Seidlitz et al.
(2018) approche, with magnetization transfer replaced with T1w/T2w ratio mapping (Glasser
& Van Essen, 2011) in the current study. Ainsi, pour chaque participant, three MSNs (one per model)
were estimated.
Demographic and Behavioral Data
Demographic variables were selected from the unrestricted data table accessed via Connec-
tomeDB. These included age bin, sex recorded at birth, and recorded quality control issues.
Behavioral data were also extracted to assess the relationship between the MSNs and both
general cognitive ability (measured with both fluid and crystallized intelligence measures) et
executive functioning. These neuropsychological assessments were conducted contempora-
neously in relation to the MRI scans. Further details of the tasks and measures acquired in the
HCP dataset can be found in Barch et al. (2013).
Neurosciences en réseau
278
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MSN construction with restricted MR acquisitions
General cognitive ability. General cognitive functioning is measured with the Cognitive Func-
tion Composite (CogComp) score (Heaton et al., 2014), derived from the average of the nor-
malized, scaled scores of Fluid and Crystallized cognition measures, then subsequently age
adjusted, and scaled. The Fluid Cognition Composite score is derived by averaging the nor-
malized scores of each of the fluid ability measures in the NIH Toolbox (Flanker, Dimensional
Change Card Sort, Picture Sequence Memory, List Sorting, and Pattern Comparison), alors que
the Crystallized Cognition Composite score is derived by averaging the normalized scores of
each of the crystallized measures in the NIH Toolbox (Picture Vocabulary and Reading Tests).
Higher Cognitive Function Composite scores indicate higher levels of cognitive functioning.
Behavioral executive function (EF) measures were selected based on an
Executive functioning.
evidence-based, three-factor model of executive function (Karr et al., 2018); measures selected
from the HCP cognitive battery to model EF were the same as previous studies of EF utilizing
the HCP data (Lerman-Sinkoff et al., 2017; Nomi et al., 2017). These tests assessed multiple
cognitive aspects of executive functioning, including cognitive flexibility/shifting (Dimensional
Change Card Sort Test; Zelazo, 2006; Zelazo et al., 2014), inhibition (Flanker Inhibitory Control
and Attention Task; Zelazo et al., 2014), and working memory (List Sorting Task; Tulsky et al.,
2013). Age-adjusted scores were used for all behavioral data.
Since we have only one neuropsychological measure per subdomain of EF and there is
therefore potential risk of measurement error, a principal component analysis (using the
“prcomp” function in the R stats base package; R Core Team, 2016) was used to find a common
EF component across all three EF measures. This produced a single principal component with
an eigenvalue above 1, upon which all measures positively loaded onto, and thus this com-
ponent was used as a summary score of EF (see the Supporting Information for further details).
Higher summary EF scores reflect greater EF functioning.
Statistical Comparison
When comparing weighted networks produced by each model, we use multiple metrics to
assess the (dis)similarity of the subsequent covariance matrices.
To reduce the number of comparisons and, based on our premise that the MSN10-feat. is the
most precise estimation of the MSN network (as shown by Seidlitz et al., 2018), all intermodel
comparisons were done in a hierarchical fashion in comparison to this “gold-standard” net-
travail. That is to say that model MSN10-feat. was compared with the MSN8-feat. and then the
MSN10-feat. was subsequently compared with the MSN7-feat..
To test differences in the topological organization of the networks produced by each model,
we calculate average nodal strength for each graph. Nodal strength is the magnitude of struc-
tural covariance for each node; c'est, the sum of the connectivity weights of all edges con-
nected to node i (Fornito, Zalesky, & Bullmore, 2016). We did not normalize this measure
based on number of edges as we averaged the nodal measures over the graph, where the num-
ber of edges was consistent across models because of density thresholding. This metric was
calculated per subject, per density for each MSN model. For each comparison, we calculate
the difference in distributions of graph strength using a paired t test. Because of the large num-
ber of comparisons (across densities, and contrasts) we do not report p values, but instead
report the effect sizes for comparisons.
We also calculate the Pearson correlation coefficient between all edge weights for both
models (as per Seidlitz et al., 2018), and also specifically between all nonzero edge weights
Neurosciences en réseau
279
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MSN construction with restricted MR acquisitions
(those elements where a zero is present in the correlation matrix for each model are excluded).
Cependant, because of the symmetric, undirected nature of the correlation matrix, this correla-
tion coefficient may inflate/bias the supposed similarity between the sets of edge weights. Ainsi
we also employed the Mantel test, which calculates the Pearson correlation on either half of
the off-diagonal elements of the correlation matrix (Mantel, 1967).
To compare the binary networks produced by each model at each density (where edges
retained after thresholding are set to 1 and those excluded are set to 0), we assessed the number
of edges in the reduced model that replicated as a proportion of the fuller model, as per the
following formula:
∑ (xi 6= 0 & yi 6= 0)
∑ (xi 6= 0)
,
where xi and yi represent the correlation matrices estimated from two of the MSN models for
a given subject i.
Deuxième, we calculate these similarity measures between the subject-level network and the
group average network, across all densities and models. This allows the assessment of the inter-
subject reliability of the networks being constructed by each model. Troisième, we similarly test the
intrasubject reliability of the produced networks, based on test-retest data from a subset of the
overall dataset. Because of the categorical and inaccurate nature of the binned measurement
of time between initial and retest scan, this was not controlled for in this analysis.
In order to assess the functional relevance of these networks, we assess their ability to predict
CogComp and EF scores using a supervised-learning approach, namely partial least squares
(PLS) regression (similar to Seidlitz et al., 2018) using the “plsRglm” package in R (Bertrand &
Maumy-Bertrand, 2018). This multivariate approach finds the optimal low-dimensional rela-
tionship between a high-dimensional set of predictors (in this case the MSN networks) and a
univariate predictor variable (either CogComp or EF). This approach is commonly used when
the number of predictors exceeds the number of observations (Krishnan, Williams, McIntosh,
& Abdi, 2011).
A PLS regression was used to find the maximal low-dimensional covariance between com-
ponents derived from the MSN and cognitive outcomes. The PLS regression was used to de-
compose the predictor variables into latent variables (components) that simultaneously model
the predictors and predict the response variable (Krishnan et al., 2011). The predictor matrix
consisted of either the degree or the strength of each node of the MSN, pour chaque participant.
Using a linear model, the potential confounding effect of age, genre, and age × gender in-
teraction was regressed out of values for nodal degree/strength (but not our cognitive outcome
variable as these were already age-adjusted within the HCP dataset). For each model (at each
threshold), a PLS regression model was fitted between principal components derived from the
resultant predictor matrix (68 × 991) and the outcome variable. This was repeated across 100
instances of ninefold cross-validation.
Cross-validated R2 (R2
CV), otherwise known as the Q2 statistic (Consonni, Ballabio, &
Todeschini, 2010; Stone, 1974), was used to select the number of components to retain in the
predictor matrix. Q2 was defined as the following:
Q2 = R2
CV = 1 −
PRESS
TSS
= 1 −
je = 1 ( ˆyi − yi)2
∑n
je = 1 (yi − ¯y)2 ,
∑n
where PRESS is the predictive residual error sum of squares and TSS is the total sum of squares.
Neurosciences en réseau
280
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MSN construction with restricted MR acquisitions
The number of components to retain in the predictive model was selected as the number of
components that resulted in the greatest Q2 value. This was repeated over the cross-validations
and resulted in a count measure of the number of times a model with a given number of com-
ponents was selected. Hence the final model was the given number of components that were
most commonly selected as having the greatest Q2 statistic. Given the model with the retained
number of components, we report the variance explained by the model and the bias corrected
and accelerated bootstrapped (Bastien, Vinzi, & Tenenhaus, 2005) weightings of each predic-
tor. This allows us to assess which brain regions are contributing most to the prediction.
Because of the normal distribution of the cognitive measures (CogComp and EF) data,
there may be an issue of class imbalance for more extreme cases (Torgo, Branco, Ribeiro, &
Pfahringer, 2015). As there are fewer subjects who fall within the tails of the continuous distri-
bution on our cognition measures, the cross-validation approach may lead to training samples
where there are too few extreme cases (those with particularly high/low cognitive abilities) à
learn from. This may result in a model where there is accurate prediction around the mean but
not at the tail ends of the distribution. To ensure the training samples contain subjects from a
stratified sampling approach, we repeated the analyses discretizing the performance on cog-
nitive measures into four discrete bins across the distribution and training a model based on
equally sized, random samples from each bin.
RÉSULTATS
Intermodel Comparisons
In terms of the topology of the net-
Magnitude of morphometric similarity: Graph-level strength.
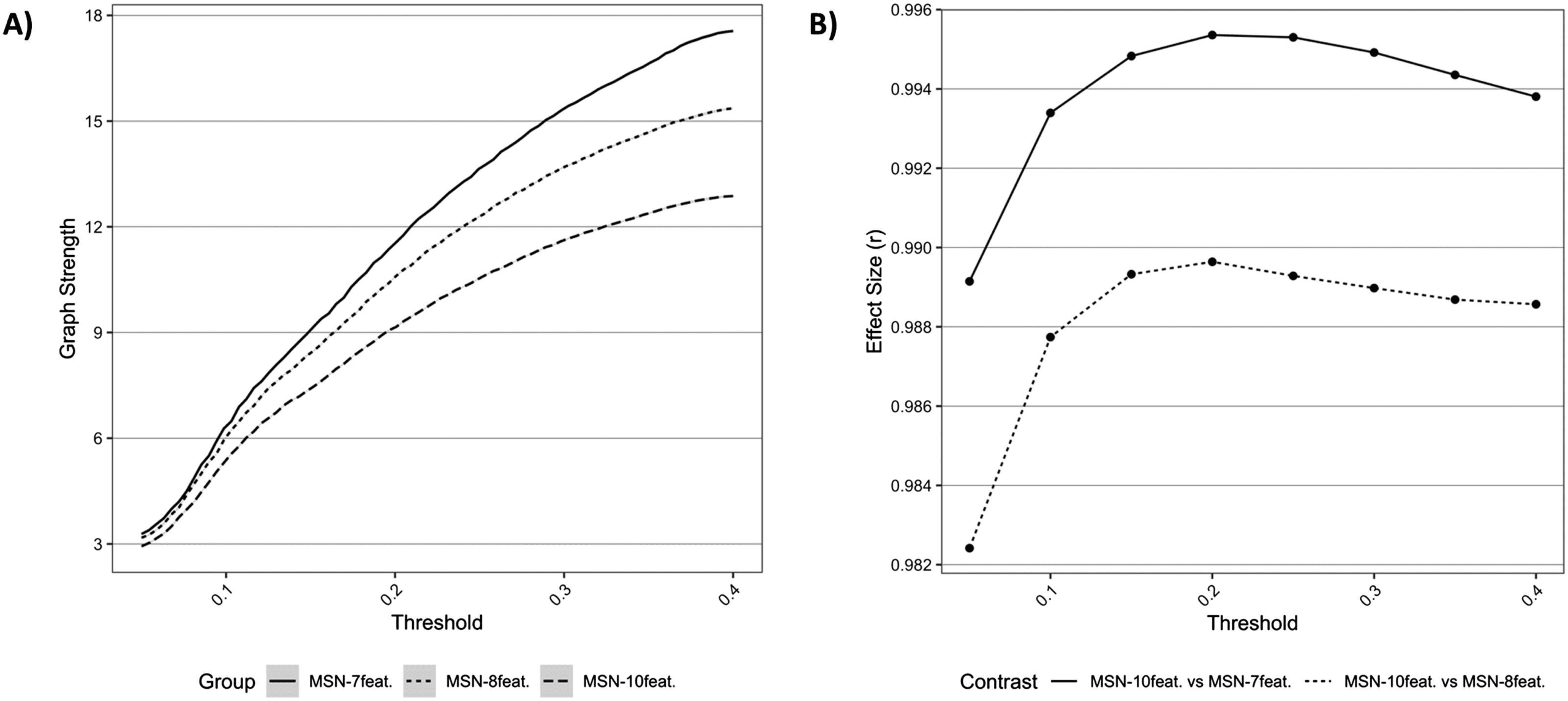
travaux, global graph strength for each model, across densities, can be seen in Figure 1. Ce
plot shows the similar trajectories across densities for all models tested; cependant, the observed
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 1. Comparisons of network topology. (UN) Graph metrics describing average network strength for each MSN model, across all densities.
(B) Effect sizes of differences between (un) MSN10-feat. versus MSN8-feat. et (b) MSN10-feat. versus MSN7-feat. for differing graph metrics, across
densities.
Neurosciences en réseau
281
MSN construction with restricted MR acquisitions
average graph strength was different between models, with lower strength seen in the MSN
models with greater features. The effect size of differences (estimated with a paired t test) être-
tween MSN10-feat. versus MSN8-feat. and MSN10-feat. versus MSN7-feat. can be also be seen in
Chiffre 1. Effect sizes (r) were extremely large, especially between MSN10-feat. versus MSN7-feat.
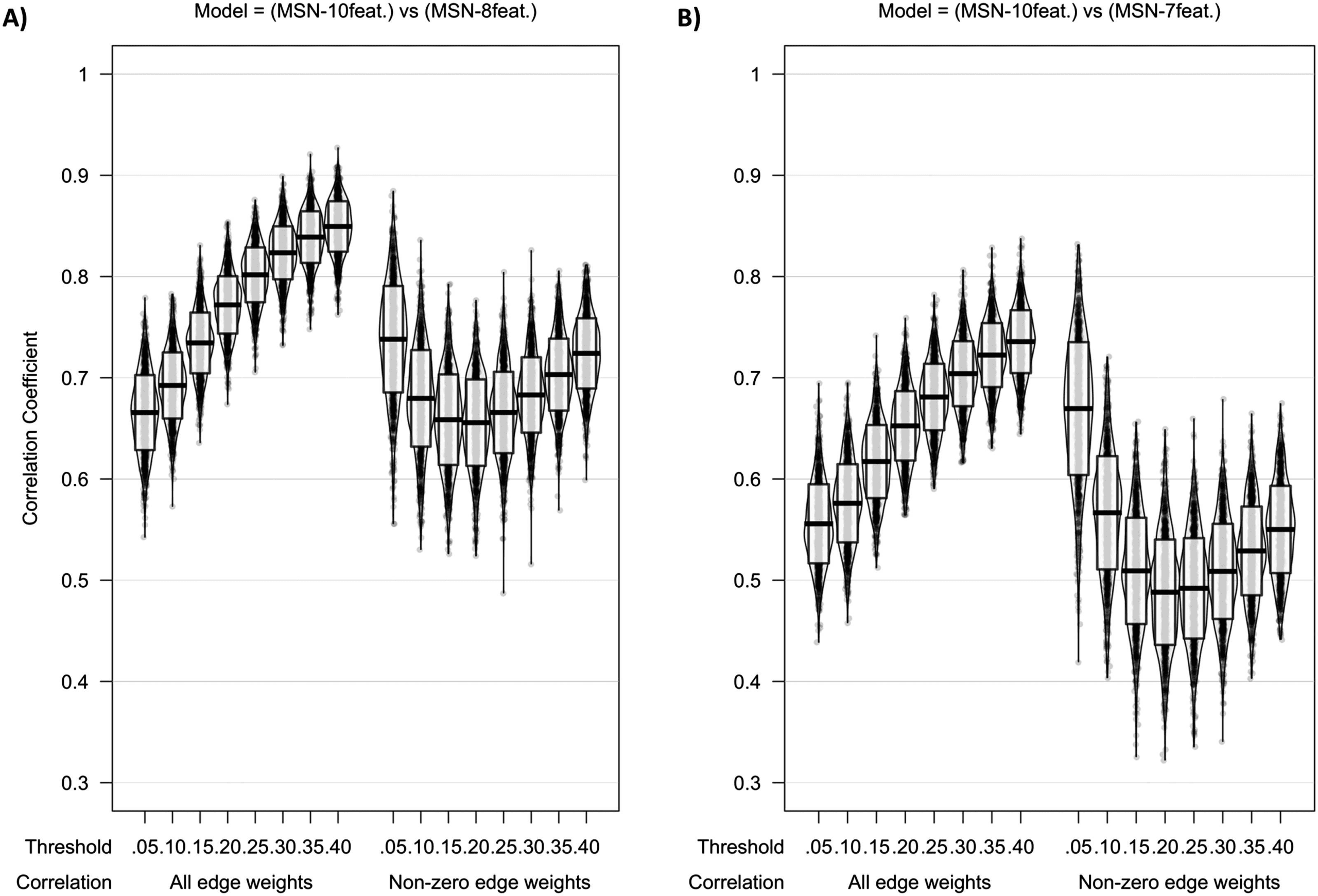
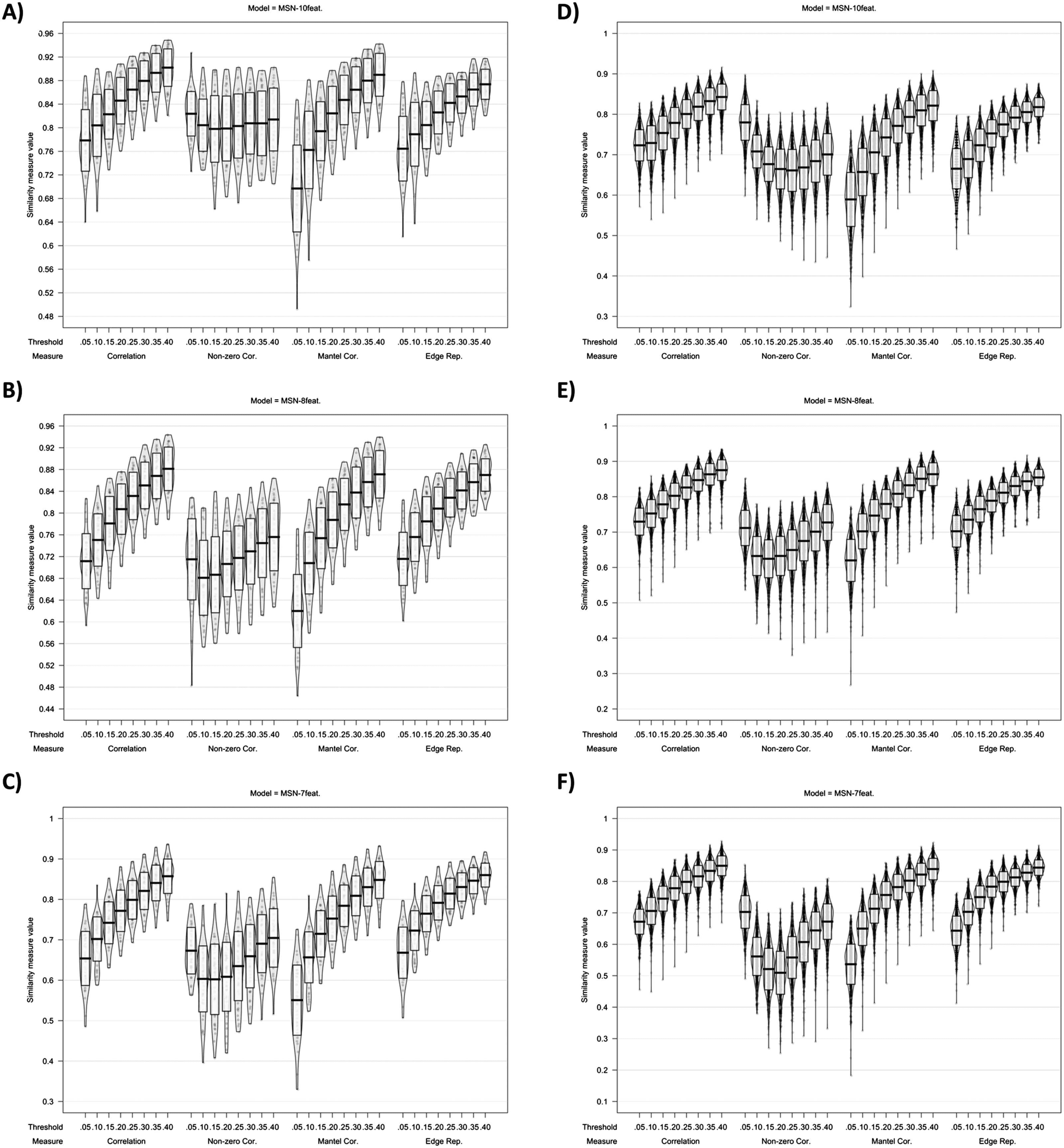
Chiffre 2 shows the intermodel comparisons between MSN10-feat. and MSN8-feat.,
Edge weights.
and between MSN10-feat. and MSN7-feat.. There is a gradual increase in correlation of edge
weights across densities with the peak mean correlation being found between MSN10-feat.
and MSN8-feat. at a 40% threshold (r(M ± SD) = 0.849 (± 0.025)), with slightly weaker
correlations found between MSN10-feat. and MSN7-feat. (r(M ± SD) = 0.736 (± 0.031)). Quand
considering only the nonzero edge weights (only edge weights remaining after thresholding),
a slightly weaker peak correlation was found for both contrasts at 5% threshold (MSN10-feat.
versus MSN8-feat. r(M ± SD) = 0.738 (± 0.053); MSN10-feat. versus MSN7-feat. r(M ± SD) =
0.670 (± 0.066)). Cependant, as the threshold increased, the dispersion of individual-level non-
zero edge correlation decreases, especially in the MSN10-feat. versus MSN7-feat. contraste.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2. Violin plot of correlation of edge weights between (UN) MSN10-feat. versus MSN8-feat. et (B) MSN10-feat. versus MSN7-feat. Midline
of the box plot component of the violin represents the mean of all correlation coefficients, with the box itself representing the SD of this mean.
Individual data points are also plotted.
Neurosciences en réseau
282
MSN construction with restricted MR acquisitions
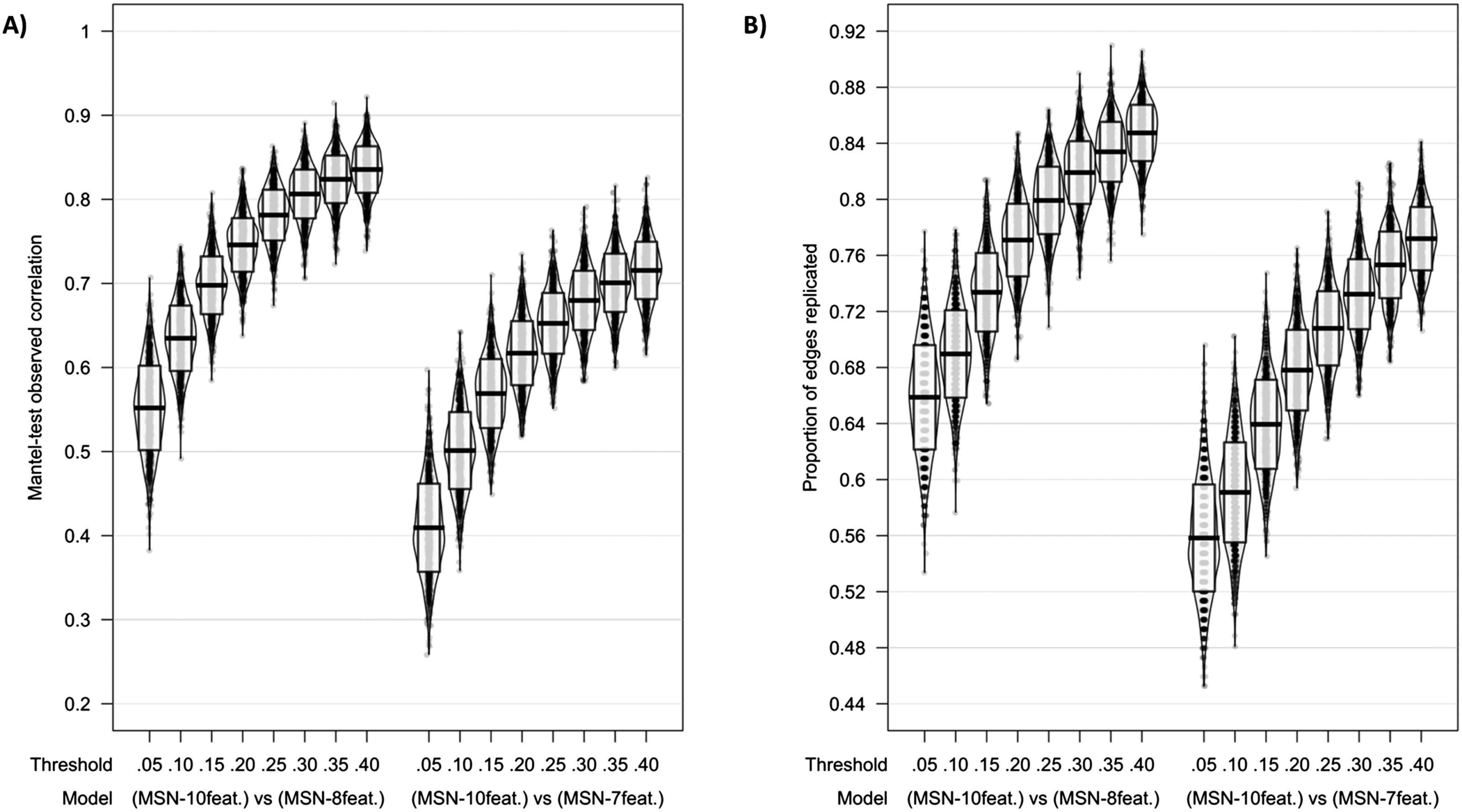
When considering correlation coefficients calculated using the Mantel test, similarly strong
correlations were found between edge weights across all models; cependant, as predicted, le
MSN10-feat. versus MSN8-feat. were most similar. À 40% threshold: MSN10-feat. versus MSN8-feat.
Mantel r(M ± SD) = 0.835 (± 0.028); MSN10-feat. versus MSN7-feat. Mantel r(M ± SD) =
0.715 (± 0.034). For the binarized networks, the proportion of edges replicated also peaked
à 40% threshold (MSN10-feat. versus MSN8-feat. proportion of replicated edges = 85%(± 2%);
MSN10-feat. versus MSN7-feat. proportion of replicated edges = 77%(± 2%; Chiffre 3)).
Intramodel Comparisons
Test-retest reliability of MSN models. We compared the MSN models at the initial scan with
those calculated from test-retest scans acquired between 1 et 11 months after the initial MRI.
All models showed high test-retest reliability of the MSN (correlation of all edge weights at 40%
threshold: MSN10-feat. r(M ± SD) = 0.902 (± .032); MSN8-feat. r(M ± SD) = 0.881 (± 0.040);
MSN7-feat. r(M ± SD) = 0.857 (± .043)). This high test-retest reliability of networks held
even when networks were binarized. À 40% threshold: MSN10-feat. proportion of replicated
edges = 87%(± 3%); MSN8-feat. proportion of replicated edges = 87%(± 3%); MSN7-feat.
proportion of replicated edges = 86%(± 3%). Voir la figure 3 for plots.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
For each model, at each threshold, a group-level network was
Similarity with average MSN.
produced as the mean of the correlation matrices for all subjects. Example correlation matrices
are found in Figure 4. Across all models (MSN10-feat., MSN8-feat., and MSN7-feat.), regardless
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 3. Model comparisons across thresholds using (UN) Mantel test correlation coefficient and (B) proportion of edges replicated
as measures of model similarities. Midline of the box plot component of the violin represents the mean, while the box itself represents
the SD.
Neurosciences en réseau
283
MSN construction with restricted MR acquisitions
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
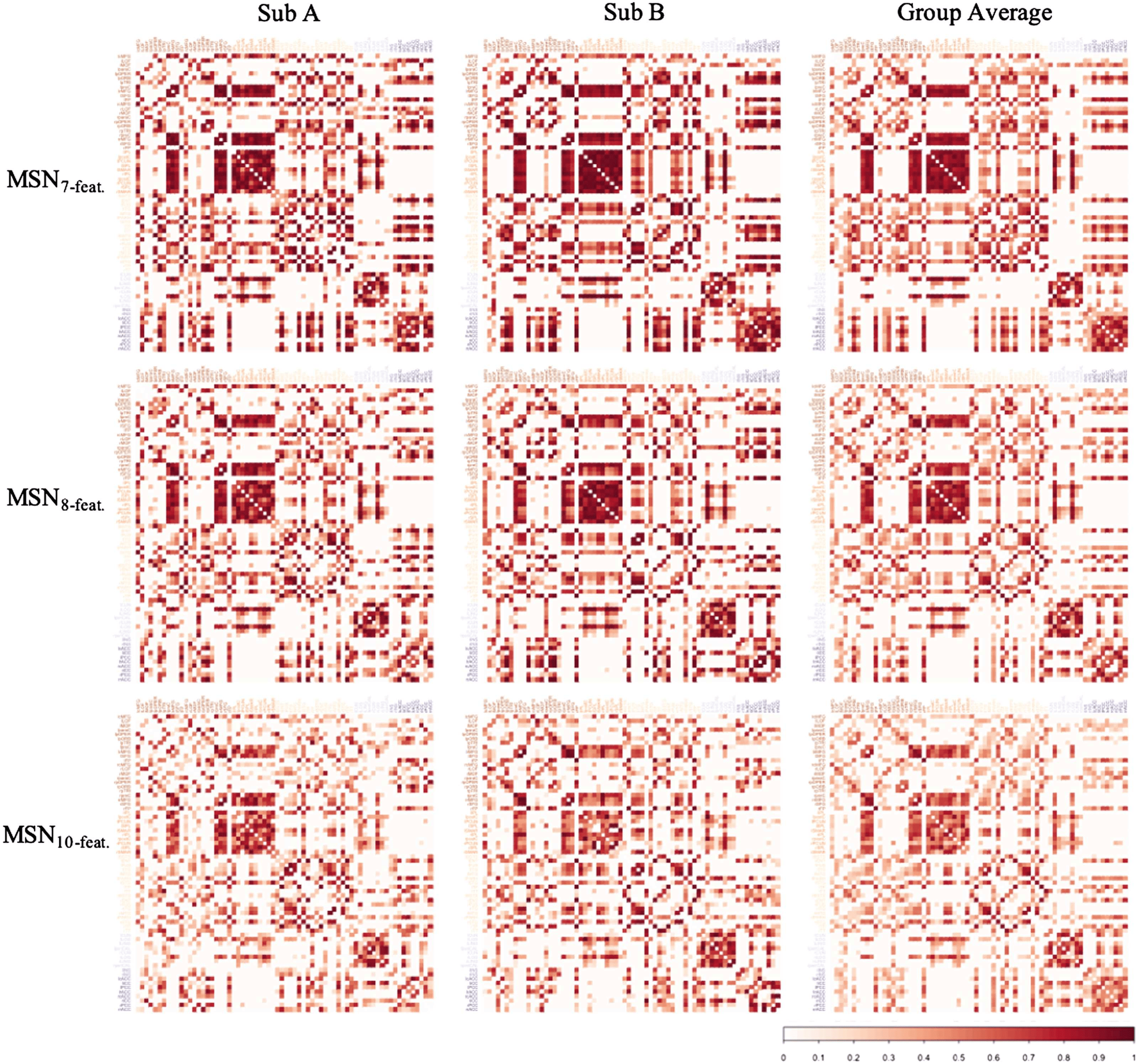
Chiffre 4. Examples of the correlation matrices generated with each MSN model. Columns A and B represent MSNs from two random subjects
from the HCP dataset, while the final column represents the group average MSN for each MSN model. All correlation matrices visualized
here represent the MSN thresholded at a density of 40% and are sorted by lobe assignment as defined by the Desikan-Killiany atlas (frontal,
pariétal, temporal, occipital, insula, cingulate).
of similarity metric used, the individual-level MSNs were highly similar to the group-mean
réseau (voir la figure 5). Fait intéressant, the MSN8-feat. model showed greatest correlation between
edge weights. À 40% threshold: MSN10-feat. r(M ± SD) = 0.843 (± 0.032); MSN8-feat. r(M ±
SD) = 0.875 (± 0.029); MSN7-feat. r(M ± SD) = 0.850, (± 0.031). Similar to the intermodel
analyses, correlation peaked at the highest threshold tested (40%) for all models.
Neurosciences en réseau
284
MSN construction with restricted MR acquisitions
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5. Plots showing MSN similarity (across thresholds, with multiple similarity measures) entre (A–C) individual MSNs generated
with test-retest MRI scans and (D–F) individual-level MSNs and the group average MSN network.
Neurosciences en réseau
285
MSN construction with restricted MR acquisitions
Relationship With Cognitive Scores
Only participants who had available a full dataset comprising the three EF subtests and the
CogComp measure were included in the following analyses (n = 991). For both cognitive
variables, en utilisant 100 instances of ninefold cross-validation, the greatest Q2 was found most
frequently when zero components were retained and thus no models were built.
This suggests that no PLS-derived components of nodal degree, strength, or normalized
strength of the MSN provided greater explanation than the intercept alone. After the stratified
sampling of the training cohort, there was no improvement in the result outlined above; cross-
validation still recommended retention of zero components for all MSN models.
DISCUSSION
The current study is the first to formally investigate the potential for generation of MSNs based
upon a reduced number of neuroanatomical features, dependent on the complexity of the MRI
acquisition sequence. We found that the weighted networks generated from these models are
highly congruent, across a number of similarity measures. We expanded previous assessments
(par exemple., Seidlitz et al., 2018, compared five morphometric features to their full MSN10-feat.model)
to include multiple MSN models. Irrespective of the statistical assessments used here, le
between-model similarity was nearly always hierarchical, with greater similarity seen between
MSN10-feat. and MSN8-feat. compared with that between MSN10-feat. and MSN7-feat. Weaker sim-
ilarity was found for sparser networks at a much lower density (c'est à dire., 0.05). When edges were
binarized, replication rates remained relatively high, suggesting that the models are sensitive
to the specific edges within the network. Each model displayed high levels of congruence with
the group average network, suggesting that these methods index individual differences from a
relatively consistent mesoscale phenotype of brain structure. Li et al. (2017) found high levels
of test-retest reliability of the T1w MSN, and we replicated this with each of the reduced-feature
MSNs, which seemingly had similar reproducibility in terms of test-retest MRI. This is maybe
unsurprising given that the HCP scan acquisitions are designed for high within-subject repro-
ducibility (Van Essen et al., 2013). Cependant, in terms of average nodal strength, a measure of
the magnitude of morphometric similarity, significant between-model differences with large
effect sizes were found. Specifically, as myelo-architectural features were added to the MSN
model (T1w/T2w ratio, FA, MARYLAND), the magnitude of morphometric similarity was reduced and
regions appeared less similar and more differentiated, hence the lower average nodal strength.
This suggests that, despite edge-level congruence, the weighted topology of individual nodes
is different between models. Given that the current and previous studies (c'est à dire., Seidlitz et al.,
2018) utilize these nodal-level metrics to predict functional outcomes, this difference in topol-
ogy means that between-study comparisons of these predictive models, when generated from
different feature sets, is not justified. These differences were investigated with only a single
metric of network topology. Additional metrics (c'est à dire., efficiency/clustering) were less attractive
candidates given that the MSNs do not adhere to typical assumptions of networks (tel que
edges representing definitive real connections). Ainsi, by using strength as a simpler metric
we made fewer assumptions about the underlying neurophysiology of the network.
Fait intéressant, none of the models tested here showed perfect or even near-perfect concor-
dance across the statistical measures employed. This may be because these models were gen-
erated with fewer features, rather than being specific to the modality of feature being dropped.
Future research could examine this systematically by generating MSNs with 10, 8, et 7 ran-
domly selected features, irrespective of modality of MRI sequence used to derive said feature.
Neurosciences en réseau
286
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MSN construction with restricted MR acquisitions
Each model may also index a different network phenotype. Each MRI acquisition assesses
different neuroanatomical features (par exemple., T1w/T2w ratio and DWI specifically index myelo-
architecture of regions while the T1w MRI assesses macroscopic morphology of the cortex).
Ainsi, when features are systematically removed in this way by removing an imaging modality,
the resultant MSN is likely to represent a different imaging phenotype. Donc, although each
MSN may be substantially statistically similar, in cases where multimodal imaging is available
or is feasible, the most appropriate MSN model may depend on the research question to be
answered or the clinical population/pathological mechanism under investigation.
The main benefit of reduced MR-acquisition approaches (specifically the MSN7-feat. model)
is the applicability to those populations where multiple MR sequence acquisition is more chal-
lenging or difficult (Batalle et al., 2018). Par exemple, in clinical populations where research
MRI scans are acquired alongside routine examinations and therefore time is limited, or in de-
velopmental populations where acquisition time needs to be kept at a tolerable level for chil-
dren to ensure compliance with the full MRI protocol and reduce the likelihood of movement
across each of the scans. Another potential application of these models is in legacy clinical
imaging. Routine clinical imaging generates vast quantities of MR data that are not typically
assessed using quantitative methods. Although expert reporting yields the information needed
to inform acute diagnostic requirements, the ability of those scans to predict later outcomes
is largely untested or unsatisfactory. The majority of hospital settings will not have access to
high-resolution, so-called advanced, MRI sequences, or the expertise to analyze such data
quantitatively. Dans l'ensemble, this therefore positions MSNs as a useful in vivo imaging phenotype
for studying both clinical and developmental populations, with the T1w-only model holding
greatest potential to become a widely adopted, automated approach in clinical neurosciences.
A common assumption is that the topological organization of the brain networks (across
multiple MR modalities), as quantified within a graph theoretic framework, captures physi-
ological information relevant to individual differences in cognitive functioning (Bullmore &
Sporns, 2009; Fornito, Zalesky, & Breakspear, 2013; Hahn, Lanzenberger, & Kasper, 2019).
We assessed the brain-behavior relationships using the MSN models by comparing the pre-
dictive validity of the three MSN models in relation to general intelligence, with previous re-
search showing that the organization of the MSN network (modeled similarly to the MSN10-feat.)
predicted ∼40% variance in WASI (Wechsler Abbreviated Scale of Intelligence) IQ (Seidlitz
et coll., 2018). The current study did not find a relationship with either a measure of general
cognitive functioning or a previously untested domain, executive functioning. Using ninefold
cross-validation, no model (at any density) recommended retention of any PLS components.
An important strength of the current study is our quantitative approach to cross-validation to
confirm the retained number of components; previous studies retained either the single or two
components that explained the greatest amount of variance (Seidlitz et al., 2019; Seidlitz et al.,
2018). This may mean that previous findings are less generalizable to new datasets, explaining
our inability to replicate findings of Seidlitz et al. (2018).
A number of other factors may explain our results. Developmental differences between
our sample (healthy young adult population between the third and fourth decades of life)
and that of Seidlitz et al. (2018) may account for the lack of predictive ability in our work.
Adolescence is a peak period for brain maturation (Gogtay et al., 2004; Sowell et al., 2004),
including establishment of cognitive skills such as executive functions, as studied here. This is
reflected in data from the NIH Toolbox, in which the total cognition composite highlights shows
a greater magnitude of age effects in childhood compared with adulthood (Akshoomoff et al.,
2013; Heaton et al., 2014). Throughout childhood, the regions subsuming these functions are
Neurosciences en réseau
287
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MSN construction with restricted MR acquisitions
reaching structural maturity. Donc, it is reasonable to believe that it is within the child/
adolescent period where the most variance in these neurocognitive skills can be explained
by structural networks (as seen by the ∼40% variance in IQ explained by the MSN in Seidlitz
et coll., 2018).
In the age range that the current study has sampled, the brain should have reached structural
maturity (with only subtle age-related effects) and so there is likely less between-individual
variance in the MSN. Greater congruence between individual MSNs and the group average
MSN in the current study compared with previous adolescent MSNs (correlation of all edge
weights: mean r = 0.60; Seidlitz et al., 2018) supports this contention. Donc, the limited
variance in the MSN within the age group we studied may mean that there is not enough
variance to relate to cognitive functioning.
While we were not able to replicate previous brain-behavior relationships with the MSN,
given the evidence above, there is an open hypothesis as to whether the MSN is a valuable
tool in independent populations. We therefore propose that the MSN may in fact be a use-
ful phenotype for assessing neuropsychological functioning, but only in populations where
there is sufficient variation in the structure of the brain. This may be populations in the in-
fant/child/adolescent period where structural networks are likely to see greatest variability due
to developmentally mediated change (such as Galdi et al., 2018; and Seidlitz et al., 2018) ou
clinical populations where atypical brain structure is seen in the pathophysiology of the disor-
der (such as Seidlitz et al., 2019; Morgan et coll., 2018; and Zheng et al., 2019). It may be the
case that these networks hold utility in populations such as these, rather than healthy, matured
populations (where measures of brain structure are likely to heavily regress to the mean).
Our analytic approach may also explain the different findings. Seidlitz et al. (2018) used the
Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999), whereas we used the NIH
Toolbox Cognition Composite scores (Heaton et al., 2014). The composite score shows high
convergent validity with other Wechsler assessments of general intelligence (with the Wechsler
Adult Intelligence Scale [WAIS-IV; Wechsler, 2008] r = 0.89; Heaton et al., 2014; and with
the Wechsler Intelligence Scale for Children [WISC-IV; Wechsler, 2003] r = 0.88; Akshoomoff
et coll., 2013), and therefore core data elements will enable future studies to clarify whether the
application of MSNs is relevant to specific measures. We also calculated the MSN at a much
lower spatial scale (68 ROI) compared with previous work (308 ROI). This lower spatial res-
olution may result in more regionally specific effects being difficult to detect; cependant, it may
also have allowed us to detect more subtle effects because of increased power. Yet it is impor-
tant to note that the 308 ROIs are derived by subdividing the 68 ROI atlas used in the current
study into equally sized patches and thus still respect the anatomy of the brain in the same
chemin. Donc, it is highly unlikely that this would explain why we did not replicate previous
résultats. Future research should replicate the current findings in independent datasets, across
different atlases and at different spatial resolutions.
CONCLUSION
We have demonstrated that when we generate the MSN based on a reduced/limited num-
ber of MR features, we produce correlation matrices that are highly similar to those gen-
erated with multimodal imaging. Cependant, the nodal-level topology differed based on the
number of features. In contrast to previous research, we found that regardless of the num-
ber of features, these networks have limited predictive validity of generalized cognitive ability
scores, although this may be specific to the current age range under study. Dans l'ensemble, this study
provides tentative evidence that in situations where multimodal imaging is not available or
Neurosciences en réseau
288
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MSN construction with restricted MR acquisitions
clinically/developmentally inappropriate, T1w-restricted MSN construction may be an appro-
priate proxy for multimodal MSNs. Cependant, nodal-level topology is likely to be biased based
upon the neuroanatomical feature sets utilized to construct these networks, limiting general-
izability across studies.
REMERCIEMENTS
Data were provided (in part) by the Human Connectome Project, WU-Minn Consortium (prin-
cipal investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657), funded by the 16
NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by
the McDonnell Center for Systems Neuroscience at Washington University.
INFORMATIONS À L'APPUI
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00123.
CONTRIBUTIONS DES AUTEURS
Dan King: Conceptualisation; Conservation des données; Analyse formelle; Méthodologie; En écrivant – Original
Draft; En écrivant – Review & Editing. Amanda Wood: Conceptualisation; Enquête; Supervi-
sion; En écrivant – Review & Editing.
INFORMATIONS SUR LE FINANCEMENT
Amanda Wood, Conseil européen de la recherche
Award ID: 682734.
(http://dx.doi.org/10.13039/501100000781),
RÉFÉRENCES
Akshoomoff, N., Beaumont, J.. L., Bauer, P.. J., Dikmen, S. S.,
Gershon, R.. C., Mungas, D., . . . Heaton, R.. K. (2013). VIII. NIH
Toolbox Cognition Battery (CB): Composite scores of crystallized,
fluid, and overall cognition. Monographs of the Society for Re-
search in Child Development, 78(4), 119–132. https://est ce que je.org/10.
1111/mono.12038
Alexander-Bloch, UN., Giedd, J.. N., & Bullmore, E. (2013). Imag-
ing structural co-variance between human brain regions. Nature
Reviews Neuroscience, 14(5), 322–336. https://doi.org/10.1038/
nrn3465
Alexander-Bloch, UN., Raznahan, UN., Bullmore, E., & Giedd,
J..
(2013). The convergence of maturational change and structural
covariance in human cortical networks. Journal des neurosciences,
33(7), 2889–2899. https://doi.org/10.1523/jneurosci.3554-12.
2013
Andersson, J.. L. R., Skare, S., & Ashburner, J.. (2003). How to correct
susceptibility distortions in spin-echo echo-planar images: Appli-
cation to diffusion tensor imaging. NeuroImage, 20(2), 870–888.
https://doi.org/10.1016/S1053-8119(03)00336-7
Andersson, J.. L. R., & Sotiropoulos, S. N. (2015). Non-parametric
representation and prediction of single- and multi-shell diffusion-
weighted MRI data using Gaussian processes. NeuroImage, 122,
166–176. https://doi.org/10.1016/j.neuroimage.2015.07.067
Andersson, J.. L. R., & Sotiropoulos, S. N. (2016). An integrated
approach to correction for off-resonance effects and subject
movement in diffusion MR imaging. NeuroImage, 125, 1063–
1078. https://doi.org/10.1016/j.neuroimage.2015.10.019
Barch, D. M., Bourgeois, G. C., Harms, M.. P., Petersen, S. E., Schlaggar,
B. L., Corbetta, M., . . . Van Essen, D. C. (2013). Function in
the human connectome: Task-fMRI and individual differences in
behavior. NeuroImage, 80, 169–189. https://est ce que je.org/10.1016/j.
neuroimage.2013.05.033
Bastien, P., Vinzi, V. E., & Tenenhaus, M.. (2005). PLS generalised
linear regression. Computational Statistics & Data Analysis, 48(1),
17–46. https://doi.org/10.1016/j.csda.2004.02.005
Batalle, D., Edwards, UN. D., & O’Muircheartaigh, J.. (2018). Un-
nual Research Review: Not just a small adult brain: Understand-
ing later neurodevelopment through imaging the neonatal brain.
Journal of Child Psychology and Psychiatry, 59(4), 350–371.
https://doi.org/10.1111/jcpp.12838
Bertrand, F., & Maumy-Bertrand, M.. (2018). plsRglm: Partial least
squares linear and generalized linear regression for processing
incomplete datasets by cross-validation and bootstrap techniques
with R. arXiv:1810.01005
Bullmore, E., & Sporns, Ô. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038/
nrn2575
Consonni, V., Ballabio, D., & Todeschini, R.. (2010). Evaluation
of model predictive ability by external validation techniques.
Neurosciences en réseau
289
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MSN construction with restricted MR acquisitions
Journal of Chemometrics, 24(3–4), 194–201. https://est ce que je.org/10.
1002/cem.1290
Desikan, R.. S., Segonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C.,
Blacker, D., . . . Killiany, R.. J.. (2006). An automated labeling
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. NeuroImage, 31(3), 968–980.
https://doi.org/10.1016/j.neuroimage.2006.01.021
Evans, UN. C. (2013). Networks of anatomical covariance. Neuro-
Image, 80, 489–504. https://doi.org/10.1016/j.neuroimage.2013.
05.054
Fischl, B., Salat, D. H., Busa, E., Albert, M., Dieterich, M.,
Haselgrove, C., . . . Dale, UN. M.. (2002). Whole brain segmen-
tation: Automated labeling of neuroanatomical structures in the
cerveau humain. Neurone, 33(3), 341–355.
Fornito, UN., Zalesky, UN., & Breakspear, M.. (2013). Graph analy-
sis of the human connectome: Promise, progress, and pitfalls.
NeuroImage, 80, 426–444. https://doi.org/10.1016/j.neuroimage.
2013.04.087
Fornito, UN., Zalesky, UN., & Bullmore, E. (2016). Fundamentals of brain
network analysis. Amsterdam, The Netherlands: Academic Press.
Galdi, P., Blesa, M., Sullivan, G., Lamb, G. J., Stoye, D. Q., Quigley,
UN. J., . . . Boardman, J.. P.. (2018). Neonatal morphometric similar-
ity networks predict atypical brain development associated with
preterm birth. In G. Wu, je. Rekik, M.. Schirmer, UN. Chung, & B.
Munsell (Éd.), Connectomics in NeuroImaging. CNI 2018. Lec-
ture Notes in Computer Science 10842 (pp. 47–57). https://est ce que je.
org/10.1007/978-3-030-00755-3_6
Glasser, M.. F., Sotiropoulos, S. N., Wilson, J.. UN., Coalson, T. S.,
Fischl, B., & Andersson, J.. L., . . . WU-598 Minn HCP Consortium.
(2013). The minimal preprocessing pipelines for the Human Con-
nectome Project. NeuroImage, 80, 105–124. https://est ce que je.org/10.
1016/j.neuroimage.2013.04.127
Glasser, M.. F., & Van Essen, D. C. (2011). Mapping human cortical
areas in vivo based on myelin content as revealed by T1- and T2-
weighted MRI. Journal des neurosciences, 31(32), 11597–11616.
https://doi.org/10.1523/jneurosci.2180-11.2011
Gogtay, N., Giedd, J.. N., Lusk, L., Hayashi, K. M., Greenstein,
D., Vaituzis, UN. C., . . . Thompson, P.. M.. (2004). Dynamic
mapping of human cortical development during childhood
through early adulthood. Proceedings of the National Academy
of Sciences, 101(21), 8174–8179. https://doi.org/10.1073/pnas.
0402680101
Goulas, UN., Uylings, H. B., & Hilgetag, C. C. (2017). Principles of
ipsilateral and contralateral cortico-cortical connectivity in the
mouse. Structure et fonction du cerveau, 222(3), 1281–1295. https://
doi.org/10.1007/s00429-016-1277-y
Hahn, UN., Lanzenberger, R., & Kasper, S. (2019). Making sense
of connectivity. International Journal of Neuropsychopharmacol-
ogy, 22(3), 194–207. https://doi.org/10.1093/ijnp/pyy100
Heaton, R.. K., Akshoomoff, N., Tulsky, D., Mungas, D., Weintraub,
S., Dikmen, S., . . . Gershon, R.. (2014). Reliability and validity
of composite scores from the NIH Toolbox Cognition Battery in
adultes. Journal of the International Neuropsychological Society,
20(6), 588–598. https://doi.org/10.1017/S1355617714000241
Jenkinson, M., Bannister, P., Brady, M., & Forgeron, S. (2002). Improved
optimization for the robust and accurate linear registration and
motion correction of brain images. NeuroImage, 17(2), 825–841.
https://doi.org/10.1006/nimg.2002.1132
Jenkinson, M., Beckmann, C. F., Behrens, T. E., Woolrich, M.. W., &
Forgeron, S. M.. (2012). FSL. NeuroImage, 62(2), 782–790. https://
doi.org/10.1016/j.neuroimage.2011.09.015
Karr, J.. E., Areshenkoff, C. N., Rast, P., Hofer, S. M., Iverson, G. L., &
Garcia-Barrera, M.. UN. (2018). The unity and diversity of executive
les fonctions: A systematic review and re-analysis of latent variable
études. Psychological Bulletin, 144(11), 1147–1185. https://est ce que je.
org/10.1037/bul0000160
Krishnan, UN., Williams, L. J., McIntosh, UN. R., & Abdi, H. (2011). Par-
tial least squares (PLS) methods for neuroimaging: A tutorial and
revoir. NeuroImage, 56(2), 455–475. https://est ce que je.org/10.1016/j.
neuroimage.2010.07.034
Lerman-Sinkoff, D. B., Sui, J., Rachakonda, S., Kandala, S., Calhoun,
V. D., & Barch, D. M.. (2017). Multimodal neural correlates of
cognitive control in the Human Connectome Project. Neuro-
Image, 163, 41–54. https://doi.org/10.1016/j.neuroimage.2017.
08.081
Li, W., Lequel, C., Shi, F., Wu, S., Wang, Q., Nie, Y., et autres. (2017). Con-
struction of individual morphological brain networks with mul-
tiple morphometric features. Frontiers in Neuroanatomy, 11, 34.
https://doi.org/10.3389/fnana.2017.00034
Mantel, N.
(1967). The detection of disease clustering and a
generalized regression approach. Cancer Research, 27(2 Pt. 1),
209–220.
Marcus, D. S., Harwell, J., Olsen, T., Hodge, M., Glasser, M.. F.,
Prior, F., . . . Van Essen, D. C. (2011). Informatics and data
mining tools and strategies for the Human Connectome Project.
Frontiers in Neuroinformatics, 5, 4. https://doi.org/10.3389/fninf.
2011.00004
Morgan, S. E., Seidlitz, J., Whitaker, K., Romero-Garcia, R., Clifton,
N. E., Scarpazza, C., . . . Bullmore, E. T. (2018). Cortical pat-
terning of abnormal morphometric similarity in psychosis is as-
sociated with brain expression of schizophrenia related genes.
bioRxiv:501494. https://doi.org/10.1101/501494
Nomi, J.. S., Vij, S. G., Dajani, D. R., Steimke, R., Damaraju,
E., Rachakonda, S., . . . Uddin, L. Q. (2017). Chronnectomic pat-
terns and neural flexibility underlie executive function. Neuro-
Image, 147, 861–871.https://doi.org/10.1016/j.neuroimage.2016.
10.026
Pagani, M., Bifone, UN., & Gozzi, UN. (2016). Structural covariance
networks in the mouse brain. NeuroImage, 129, 55–63. https://
doi.org/10.1016/j.neuroimage.2016.01.025
R Core Team. (2016). R.: A language and environment for statisti-
cal computing (Version 3.3.2). Vienna, Austria: R Foundation for
Statistical Computing. Retrieved from https://www.R-project.org/
Rosen, UN. F. G., Roalf, D. R., Ruparel, K., Blake, J., Seelaus, K., Villa,
L. P., . . . Satterthwaite, T. D. (2018). Quantitative assessment of
structural image quality. NeuroImage, 169, 407–418. https://est ce que je.
org/10.1016/j.neuroimage.2017.12.059
Seidlitz, J., Nadig, UN., Liu, S., Bethlehem, R.. UN. JE., Vértes, P.. E., Morgan,
S. E., . . . Raznahan, UN. (2019). Transcriptomic and cellular de-
coding of regional brain vulnerability to neurodevelopmental dis-
ordres. bioRxiv. https://doi.org/10.1101/573279
Seidlitz, J., Vasa, F., Shinn, M., Romero-Garcia, R., Whitaker, K. J.,
Vertes, P.. E., . . . Bullmore, E. T. (2018). Morphometric similarity
Neurosciences en réseau
290
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MSN construction with restricted MR acquisitions
networks detect microscale cortical organization and predict inter-
individual cognitive variation. Neurone, 97(1), 231–247. (e237)
https://doi.org/10.1016/j.neuron.2017.11.039
Sowell, E. R., Thompson, P.. M., Leonard, C. M., Welcome, S. E.,
Kan, E., & Toga, UN. W. (2004). Longitudinal mapping of cortical
thickness and brain growth in normal children. Journal of Neuro-
science, 24(38), 8223–8231. https://doi.org/10.1523/jneurosci.
1798-04.2004
Stone, M.. (1974). Cross-validatory choice and assessment of statis-
tical predictions. Journal of the Royal Statistical Society: Série B
(Statistical Methodology), 36(2), 111–147.
Torgo, L., Branco, P., Ribeiro, R.. P., & Pfahringer, B. (2015). Resam-
pling strategies for regression. Expert Systems, 32(3), 465–476.
https://doi.org/10.1111/exsy.12081
Tulsky, D. S., Carlozzi, N. E., Chevalier, N., Espy, K. UN., Beaumont,
J.. L., & Mungas, D. (2013). V. NIH toolbox cognition battery (CB):
Measuring working memory. Monographs of the Society for Re-
search in Child Development, 78(4), 70–87. https://est ce que je.org/10.
1111/mono.12035
Van Essen, D. C., Forgeron, S. M., Barch, D. M., Behrens, T. E., Yacoub,
E., Voiture d'Ugur, K., & WU-Minn HCP Consortium (2013). The WU-
Minn Human Connectome Project: An overview. NeuroImage,
80, 62–79. https://doi.org/10.1016/j.neuroimage.2013.05.041
Wechsler, D. (1999). Manual for the wechsler abbreviated scale of in-
telligence (WASI). San Antonio, TX: The Psychological Corporation.
Wechsler, D. (2008). Wechsler Adult Intelligence Scale. (4th ed.).
San Antonio, TX: NCS Pearson.
Wechsler, D.
(2003). Wechsler Intelligence Scale for Children.
(4th ed.) San Antonio: TX: The Psychological Corporation.
Wei, Oui. B., Scholtens, L. H., Turk, E., & van den Heuvel, M.. P.. (2019).
Multiscale examination of cytoarchitectonic similarity and hu-
man brain connectivity. Neurosciences en réseau, 3(1), 124–137.
https://doi.org/10.1162/netn_a_00057
Zelazo, P.. D. (2006). The Dimensional Change Card Sort (DCCS): UN
method of assessing executive function in children. Nature Pro-
tocols, 1(1), 297–301. https://doi.org/10.1038/nprot.2006.46
Zelazo, P.. D., Anderson,
J.. E., Richler,
J., Wallner-Allen, K.,
Beaumont, J.. L., Conway, K. P., . . . Weintraub, S. (2014). IH
toolbox cognition battery (CB): Validation of executive func-
tion measures in adults. Journal of the International Neuro-
psychological Society, 20(6), 620–629. https://doi.org/10.1017/
S1355617714000472
Zheng, W., Eilamstock, T., Wu, T., Spagna, UN., Chen, C., Hu, B., &
Fan, J.. (2019). Multi-feature based network revealing the struc-
tural abnormalities in autism spectrum disorder. IEEE Transac-
tions on Affective Computing, 1–1. https://doi.org/10.1109/taffc.
2018.2890597
Zheng, W., Yao, Z., Xie, Y., Fan, J., & Hu, B. (2018). Identifie-
tion of Alzheimer’s disease and mild cognitive impairment using
networks constructed based on multiple morphological brain
features. Biological Psychiatry: Cognitive Neuroscience and
Neuroimaging, 3(10), 887–897. https://doi.org/10.1016/j.bpsc.
2018.06.004
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
2
7
4
2
0
3
9
4
0
4
n
e
n
_
un
_
0
0
1
2
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Neurosciences en réseau
291