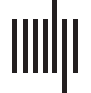Research
Alpha oscillation, criticality, and responsiveness
in complex brain networks
MinKyung Kim 1,2 and UnCheol Lee1,2
1Department of Anesthesiology, University of Michigan Medical School, Ann-Arbor, MI, Etats-Unis
2Center for Consciousness Science, University of Michigan Medical School, Domino’s Farms, Ann-Arbor, MI, Etats-Unis
Mots clés: Alpha oscillation, Criticality, Responsiveness, Brain network, Coupled oscillator, Periodic
perception
un accès ouvert
journal
ABSTRAIT
Brains in unconsciousness are characterized by significantly limited responsiveness to
stimuli. Even during conscious wakefulness, responsiveness is highly dependent on ongoing
brain activity, specifically, of alpha oscillations (∼10 Hz). We hypothesized that the variety of
brain responses to external stimuli result from the interaction between state-specific and
transient alpha oscillations and stimuli. To justify this hypothesis, we simulated various alpha
oscillations in the human brain network, modulating criticality (a balanced state between
order and disorder), and investigated specific alpha oscillation properties (instantaneous
amplitude, phase, and global synchronization) that induce a large or small response. As a
result, we found that the alpha oscillations near a critical state show a more complex and
long-lasting response, which is more prominent when stimuli are given to globally
desynchronized and low-amplitude oscillations. We also found specific phases of alpha
oscillation that barely respond to stimuli, which implies the presence of temporal windows in
the alpha cycle for a large or small response. The results explain why brain responses are so
variable across conscious and unconscious states and across time windows even during
conscious wakefulness, and emphasize the importance of considering ongoing alpha
oscillations for effective brain stimulation.
RÉSUMÉ DE L'AUTEUR
Responsiveness of the brain varies depending on the brain states (wakefulness, dormir,
anesthesia, and traumatic injuries) and even during wakefulness, resulting in various
responses to the same stimulus. What makes those different responses across brain states and
even across time windows in conscious state? What is an effective way to obtain the largest
response to external stimulus? To answer those questions, we simulated various alpha
oscillations (∼10 Hz) in a large-scale brain network and found state-specific alpha oscillation
properties that show large or small responsiveness. Notably, the results suggest the presence
of temporal windows in alpha cycle that inhibit external information integration and
emphasize considering the large/small responsiveness conditions for effective brain
stimulation.
INTRODUCTION
The brain’s responsiveness to external stimuli is significantly dependent on its state. Previous
studies with transcranial magnetic stimulation (TMS) have demonstrated that stimulation effects
during sleep (NREM), anesthesia, and vegetative states are simple and constrained to local ar-
eas, whereas they are more complex and diffuse in the conscious state (Casali et al., 2013;
Citation: Kim, M., & Lee, U. (2020).
Alpha oscillation, criticality, et
responsiveness in complex brain
réseaux. Neurosciences en réseau, 4(1),
155–173. https://doi.org/10.1162/netn_
a_00113
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00113
Informations complémentaires:
https://doi.org/10.1162/netn_a_00113
Reçu: 29 Juin 2019
Accepté: 29 Octobre 2019
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
UnCheol Lee
uclee@umich.edu
Éditeur de manipulation:
Gustavo Deco
droits d'auteur: © 2019
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
un
_
0
0
1
1
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Specific alpha oscillations that evoke small or large response
Responsiveness:
Here it is defined as responsivity and
complexity of perturbed response
(magnitude and complexity of
synchronization and amplitude
changes) after stimulation.
Ongoing brain activity:
Spontaneous brain activity without
any explicit tasks. Dans
electroencephalography (EEG), it is
referred to as the signal components
that are not induced by external
stimuli or other events.
Alpha oscillation:
Neural oscillations in the frequency
range of 8–13 Hz in brain.
Criticality:
In physics, a system at criticality
exhibits a state between ordered and
disordered with the largest
fluctuations it its dynamics. Emerging
evidence shows that human brain in
conscious wakefulness operates near
criticality.
Global synchronization:
A global quantity measuring
consistent phase relationship among
the population of oscillators.
Ferrarelli et al., 2010; Sarasso et al., 2015, 2014). In the conscious state, perceptual responses
to sensory stimuli are associated with ongoing brain activity at the moment when the stimulus
is applied. In visual perception tasks, Par exemple, target detectability is dependent on the
power and phase of ongoing alpha oscillations (∼10 Hz) (Benedetto, Lozano-Soldevilla, &
VanRullen, 2018; Busch, Dubois, & VanRullen, 2009; Dugue, Marque, & VanRullen, 2011;
Ergenoglu et al., 2004; Mathewson, Gratton, Fabiani, Beck, & Ro, 2009; Mathewson, Lleras,
Beck, Fabiani, Ro, & Gratton, 2011; Milton & Pleydell-Pearce, 2016; Nunn & Osselton, 1974;
Romei et al., 2008; van Dijk, Schoffelen, Oostenveld, & Jensen, 2008). Recent repetitive TMS
(SMTr) studies have suggested that the instantaneous phase of the sensorimotor µ-rhythm
in the alpha band (8–12 Hz) is an important factor in determining the stimulation effect
(Schaworonkow, Triesch, Ziemann, & Zrenner, 2018; Zrenner, Desideri, Belardinelli, & Ziemann,
2017).
Cependant, despite many relevant experimental studies, researchers have not elucidated how
external stimulation interacts with specific amplitudes and phases of alpha oscillation in ways
that result in a large or small perceptual response. Dans cette étude, we hypothesized that percep-
tual binding associates with the brain’s network response, and the network response largely
depends on the ongoing coupled oscillation properties at stimulus onset. Recent studies have
revealed that alpha oscillations transfer information through traveling waves in the cortex,
and the global functional connectivity of alpha oscillations reflect conscious and unconscious
states (Deco et al., 2018; Deco, Woolrich, Stevner, van Hartevelt, & Kringelbach, 2017un; Jobst
et coll., 2017; H. Kim, Moon, Mashour, & Lee, 2018; M.. Kim, Kim, Mashour, & Lee, 2017;
Moon et al., 2017; Moon, Lee, Blain-Moraes, & Mashour, 2015; Zhang, Watrous, Patel, &
Jacobs, 2018). Donc, we assumed that the propagation and complexity of perturbed re-
sponses in the brain network may be determined by the alpha oscillations at stimulus onset.
In this modeling study, we examined the specific amplitude, phase, and synchronization level
of alpha oscillations that evoke a large or small network response.
To identify such a condition, we constructed a large-scale human brain network model with
the Stuart-Landau oscillators of the alpha band frequencies (∼10 Hz) that are coupled with
each other in an anatomically informed human brain connection structure. We tested three
dynamic brain states, modulating criticality (below, près, and above critical state). The three
brain states produced various transient alpha oscillations in terms of global synchronization,
amplitude, and phase. The critical state was defined with the largest pair correlation func-
tion (PCF), measuring the variance of global synchronization fluctuation across time (Yoon,
Sorbaro Sindaci, Goltsev, & Mendes, 2015), which is equivalent to susceptibility in statistical
physics models. Theoretically, near the critical point, a large dynamic fluctuation would be
expected. (Chialvo, 2010; Cocchi, Gollo, Zalesky, & Breakspear, 2017). Empirically, the brain
during conscious wakefulness presents a large dynamic fluctuation, especially in synchroniza-
tion (Haimovici, Tagliazucchi, Balenzuela, & Chialvo, 2013; Kitzbichler, Forgeron, Christensen,
& Bullmore, 2009); cependant, various brain perturbations (par exemple., dormir, anesthesia, traumatic
injuries) mitigate this fluctuation, which implies that the brain deviates from criticality (Hutt,
Lefebvre, Hight, & Sleigh, 2018).
The various alpha oscillations of the three brain states were decomposed into basic oscil-
lation properties: instantaneous global synchronization, amplitude, and phase. We applied a
pulsatile stimulus to the brain network in order to investigate the relationship between these
alpha oscillation properties at stimulus onset and brain network responsiveness. We found spe-
cific phases of alpha oscillation that barely respond to the pulsatile stimulus, which suggests
the presence of periodic temporal windows in the alpha frequency cycle for a large/small re-
sponsiveness, and which is consistent with the empirical studies (Callaway & Alexander, 1960;
Neurosciences en réseau
156
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
un
_
0
0
1
1
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Specific alpha oscillations that evoke small or large response
Ergenoglu et al., 2004; Nunn & Osselton, 1974; VanRullen, 2016, 2018; VanRullen & Koch,
2003). A schematic diagram of the study design is presented in Figure 1.
RÉSULTATS
Alpha Oscillations Near and Far from a Critical State
Various alpha oscillations in the human brain network were simulated in three brain states,
Cb, Cp, and Ca (below, près, and above a critical state, see Materials and Methods for details).
To simplify our model, we applied a simple form of stimulus (a pulsatile stimulus) to all nodes
pour 50 ms. In total, 600 stimulation trials were performed for each state. D'abord, we examined the
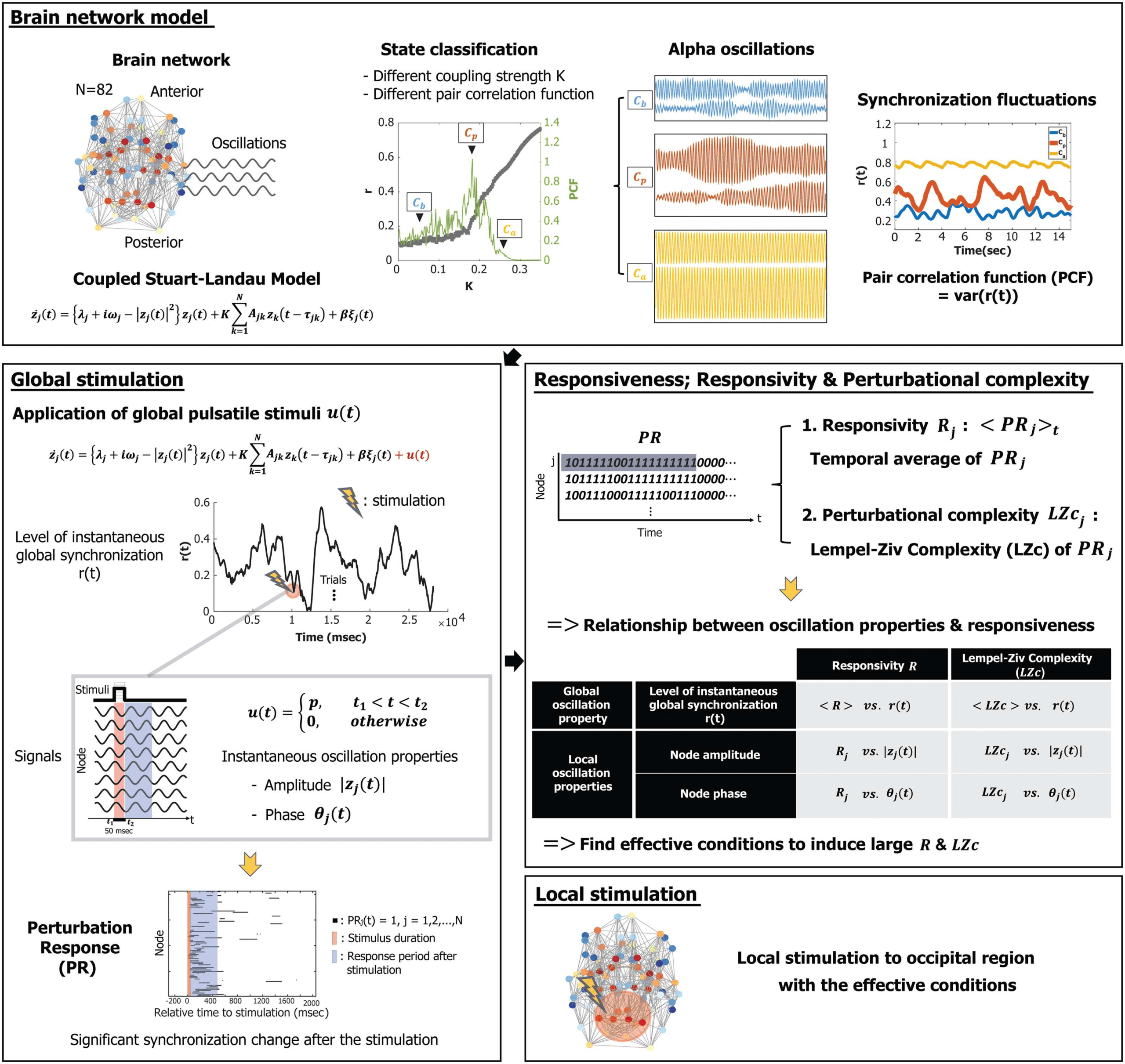
characteristics of alpha oscillations near and far from a critical state. Figure 2A provides exam-
ples of distinct global synchronization fluctuations for the three states. Synchronization fluc-
tuation was measured with the PCF. Figure 2B presents the average synchronization < r(t) >
and PCF of the alpha oscillations at Cb, Cp, and Ca. Twenty different frequency configurations
of the brain network were tested. The average levels of synchronization at Cp (orange trian-
gle) are widely distributed between the small and large average levels of synchronization at Cb
(blue circle) and Ca (yellow square). The alpha oscillations at Cp (orange triangle) show a larger
PCF (mean ± SD = 1.39 ± 0.68) than those of Cb (blue circle) and Ca (yellow square), lequel
suggests a large variance of brain network dynamics at Cp. Figure 2C and 2D demonstrate the
instantaneous synchronization rs and instantaneous amplitude
of the alpha oscillations
at stimulus onset (s = 1, 2, . . . , 600, and j = 1, 2, . . . , 82). At Cp (orange), both the instantaneous
à la 600 stimulus onsets are variable between
synchronization levels rs and amplitudes
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
Z
Z
j
s
j
s
j
s
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
Z
the two small and large rs and
of Cb (blue) and Ca (yellow), respectivement (in Figure 2C,
median ± SD, 0.11 ± 0.04 for Cb, 0.32 ± 0.14 for Cp, et 0.78 ± 0.05 for Ca; in Figure 2D,
0.21 ± 0.04 for Cb, 0.48 ± 0.57 for Cp, et 1.75 ± 1.65 for Ca). In the next sections, we will
show how these state-specific alpha oscillations respond to the same stimulus and identify
specific conditions of alpha oscillations that produce a large or small response in the brain
réseau.
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
Distinct Responses of the Alpha Oscillations Near and Far from a Critical State
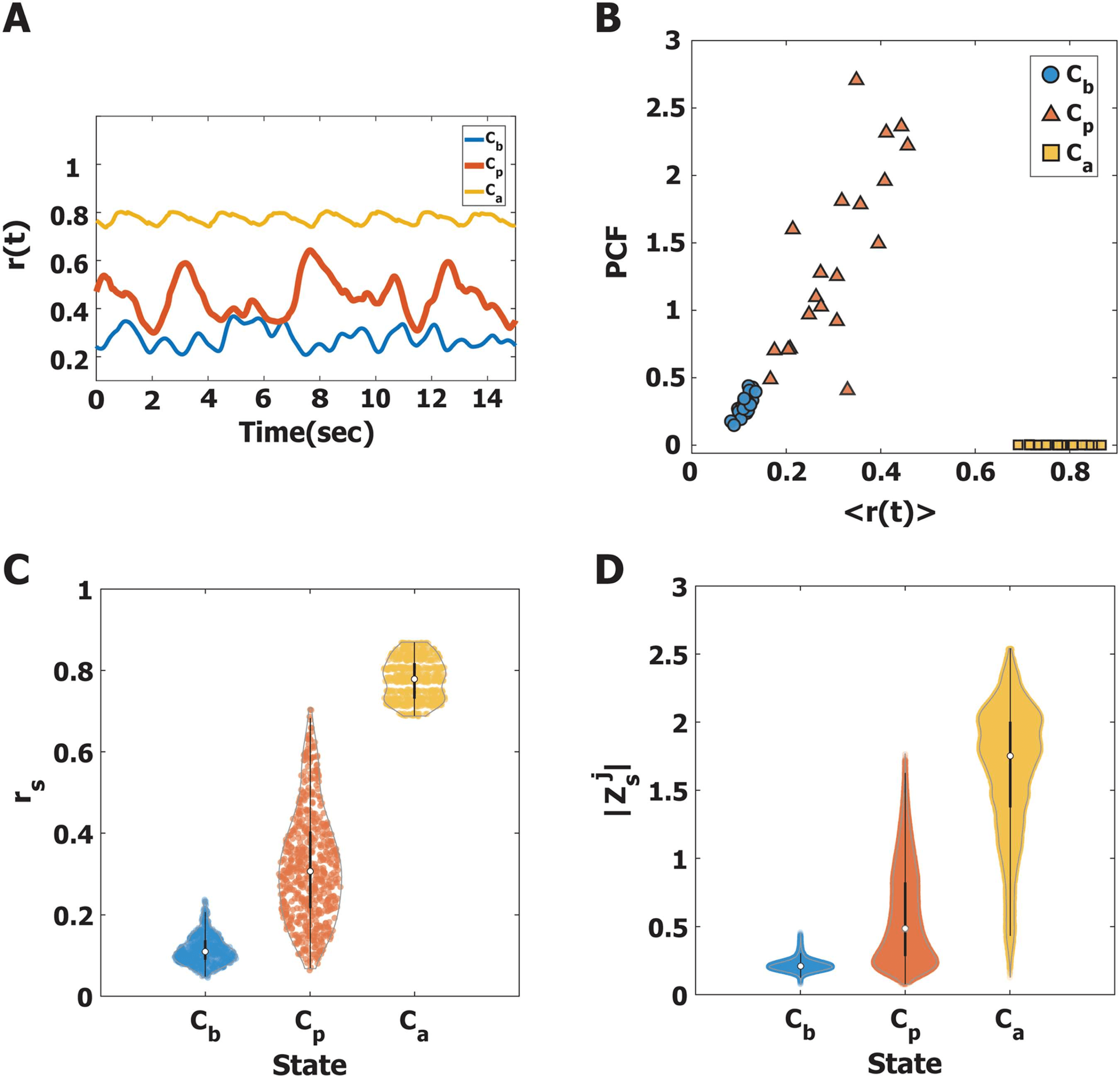
Alpha oscillations at diverse states of criticality show distinct responses to the stimulus. Chiffre 3
shows examples of the instantaneous global synchronization level r(t) at Cb, Cp, and Ca. Chaque
triangle indicates a discrete application of the stimulus. One pulsatile stimulus was applied
at random per simulation; a total of 600 such simulations were performed for each state. À
calculate the responsiveness of each stimulation trial, we first defined a perturbation response
(PR) of phase synchronization (PRj(t)) for node j ( j = 1, 2, …, 82) at time t, setting PRj(t) comme 1,
if the synchronization value of node j was significantly increased from the prestimulus period
(1 s); otherwise PRj(t) was set as 0 (see Materials and Methods for details). Figure 3B presents
examples of PR. The black dot represents PRj(t) equals 1 and the red and blue shaded areas
indicate the pulsatile stimulus of 50 ms and the response period, respectivement. La moyenne
PRj(t) was calculated over 600 stimulation trials. Figure 3C shows the temporal changes of
the median (thick line) and of the 25% et 75% quantiles (thin lines) of the average PR for the
three states. The results show that the PR at Cp persists longer than the PRs at Cb and Ca (sign
test, p < 0.05 after 190 ms, Figure 2C). We used the PRs during the first 500 ms to quantify
responsiveness for further analysis. In addition to the PR of phase synchronization, we also
calculated the PR of the amplitudes of the alpha oscillations. These results are presented in the
Supporting Information.
Network Neuroscience
157
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Specific alpha oscillations that evoke small or large response
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Schematic diagram of the study design. In this study, we simulated alpha oscillations, applying a coupled Stuart-Landau model
to a human brain network structure consisting of 82 brain regions. Brain states were classified as below, near, or above a critical state based
on the pair correlation function (PCF, the variance of the instantaneous global synchronization level). The critical state Cp was defined with
the largest PCF. Global pulsatile stimuli u were applied to the 82 alpha oscillation nodes in three brain states, and the following perturbation
responses of phase synchronization (PRj(t)) for node j were binarized by comparing them to the prestimulus period. Using PRj, we first
defined a responsivity Rj, an average of PRj during certain epochs after stimulation, to measure the magnitude of the response. Second,
the Lempel-Ziv complexity (LZc) of PRj was calculated to measure the perturbational complexity of the response. Then we investigated the
relationship between the ongoing alpha oscillation properties (global synchronization, amplitude, and phase) at stimulus onset and brain
network responsiveness to find specific alpha oscillation conditions that induce large (or small) responsiveness. Finally, we stimulated the
occipital region and compared effective, random, and less effective stimulation conditions.
Network Neuroscience
158
Specific alpha oscillations that evoke small or large response
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Characteristics of alpha oscillations near and far from a critical state, Cb, Cp, and Ca.
(A) Examples of global synchronization fluctuations at Cb (blue), Cp (red), and Ca (yellow) for one
initial frequency configuration in the brain network. (B) The average instantaneous global synchro-
nization r(t) and the pair correlation functions (PCF) for Cb (blue), Cp (red), and Ca (yellow) for 20
different initial frequency configurations in the brain network. Without a stimulus, the critical state
Cp is characterized by the largest PCF (mean±SD = 1.39 ± 0.68), compared with the PCF of Cb and
Ca. (C) The estimated density distributions of instantaneous global synchronization (rs) at the 600
stimulus onsets for Cb (blue), Cp (red), and Ca (yellow). The small white circles indicate the median
of rs, and the thick black lines indicate standard deviation. The estimated Gaussian density distri-
bution for the 600 stimuli is plotted with a gray line. The alpha oscillations at Cp have a broad and
balanced distribution (median ±SD = 0.32 ± 0.14). (D) The estimated density distributions of the
j
s| values at
alpha oscillation amplitudes |Z
Cb and Ca are biased with small and large amplitudes, respectively, while the |Zj
s| at Cp is relatively
balanced between the others. The distinct alpha oscillation properties at stimulus onset may result
in different responses of the brain network to the stimulus.
j
s| at the 600 stimulus onsets for Cb, Cp, and Ca. The |Z
Magnitude and Complexity of Perturbation Responses
In this study, we defined two responsiveness indexes to quantify the PRs. First, we defined the
responsivity Rj of a node j, counting the total amount of 1s in PRj (significantly changed phase
synchronization) during the first 500 ms after the stimulus (see Materials and Methods for de-
tails), which measures the magnitude of PRs. We also defined the Lempel-Ziv complexity (LZc)
Network Neuroscience
159
Specific alpha oscillations that evoke small or large response
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Quantifying the perturbation responses (PRs). (A) Examples of the global synchronization level r(t) for the three brain states, Cb
(left), Cp (middle), and Ca (right). A triangle indicates the timing of a stimulus. The response to a single pulsatile stimulus was stimulated
repeatedly 600 times with random stimulus timings. (B) The PR of a pulsatile stimulus is presented for the three brain states. The red and blue
shaded areas indicate the stimulus period (50 ms) and response period (500 ms), respectively. The black dot at each node indicates the time
point at which phase synchronization significantly increased after the stimulus compared with the prestimulus period; PRj = 1. (C) The average
PR(t) was calculated over 600 stimulation trials, using a new time axis in which the timing of the stimulus coincides with zero. The thick
lines indicate the median of the average PR, and the shaded areas cover the 25% to 75% quantiles. The PR persists longer at Cp than at Cb
and Ca (sign test, p < 0.05 after 190 ms).
(Lempel & Ziv, 1976) of the PRj for a node j, which measures the perturbational complexity
(see Materials and Methods for details). The LZc measures the amount of information con-
tained in the spatiotemporal pattern of PR, which is similar to the perturbational complexity
index (PCI) that has been successfully applied to quantify the level of consciousness in sleep,
anesthesia, and pathologic unconsciousness (Casali et al., 2013; Sarasso et al., 2015).
Network Neuroscience
160
Specific alpha oscillations that evoke small or large response
Correlation Between Responsiveness and Synchronization of Alpha Oscillations
First, we investigated the relationship between instantaneous synchronization at stimulus on-
set (rs, s = 1, 2, . . . , 600) and the responsiveness indexes. The average responsivity < R > était
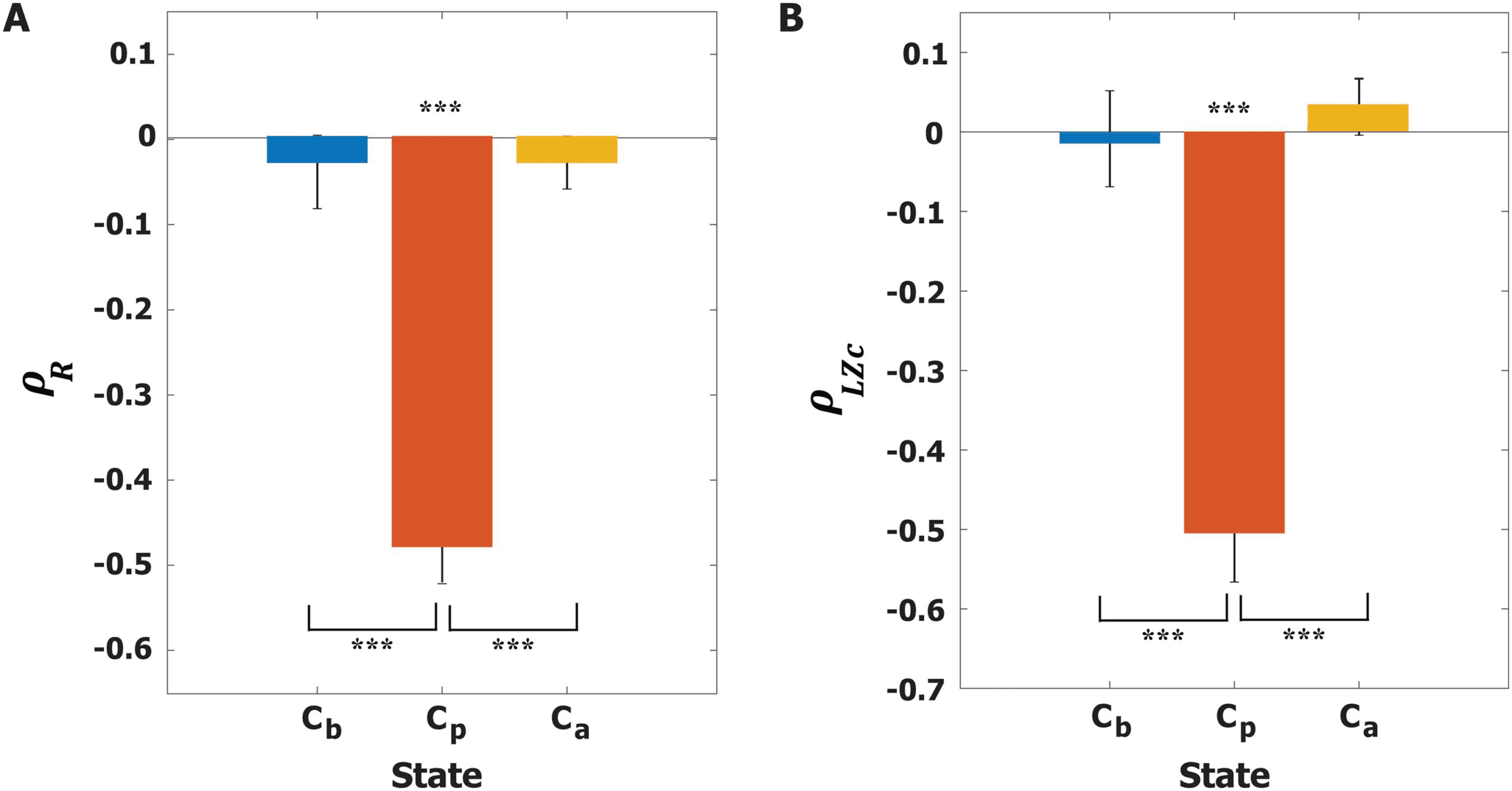
calculated by taking the average of Rj over all nodes. Chiffre 4 presents the Spearman corre-
lation coefficients of the three states (Cb, Cp, and Ca) entre
synchronization rs for 600 stimulation trials. Only at Cp does < R > show a significant neg-
ative correlation with rs (Spearman correlation ρR = −0.48, p < 0.001 for Cp), suggesting a
more desynchronized alpha oscillation induces a larger magnitude of PR at Cp.
Next, we calculated the LZc at each time point and averaged it over 500 ms, defining
< LZc > (see Materials and Methods for details). Figure 4B presents the Spearman correlation
coefficients between rs and < LZc > for the three brain states. Only at Cp is < LZc >
significantly correlated with rs (Spearman correlation ρLZc = −0.52, p < 0.001 for Cp). At Cp
a more desynchronized alpha oscillation induces a larger complexity of PR, and the complexity
itself is the largest among the three states (Supporting Information Figure S1, mean ± SD =
0.57 ± 0.05, 0.67 ± 0.17, and 0.39 ± 0.18 for Cb, Cp, and Ca).
We found that near a critical state, stimulating a globally more desynchronized alpha os-
cillation (small rs) gave rise to greater brain responsiveness in terms of both magnitude and
complexity of PR, whereas far from a critical state, responsiveness was not correlated with the
global synchronization of alpha oscillations.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Correlations between instantaneous synchronization (rs) at stimulus onset and the re-
sponsiveness of the brain network. (A) Spearman correlation coefficient ρR between rs and the
average responsivity < R > et (B) Spearman correlation coefficient ρLZc between rs and the av-
erage complexity of perturbation response < LZc > for Cb (blue), Cp (red), and Ca (yellow). Le
Spearman correlations were calculated across 600 stimulation trials. The average Spearman correla-
tion coefficients at Cp for both responsiveness indexes are −0.49 and −0.51, respectivement, avec le
significance level ***p < 0.001. At Cp, applying a stimulus at a lower level of global synchroniza-
tion induces a larger magnitude and complexity of perturbation response. A Kruskal-Wallis test with
a Tuckey-Kramer multiple comparison test was performed to compare the correlation coefficients
across the three states (***p < 0.001).
Network Neuroscience
161
Specific alpha oscillations that evoke small or large response
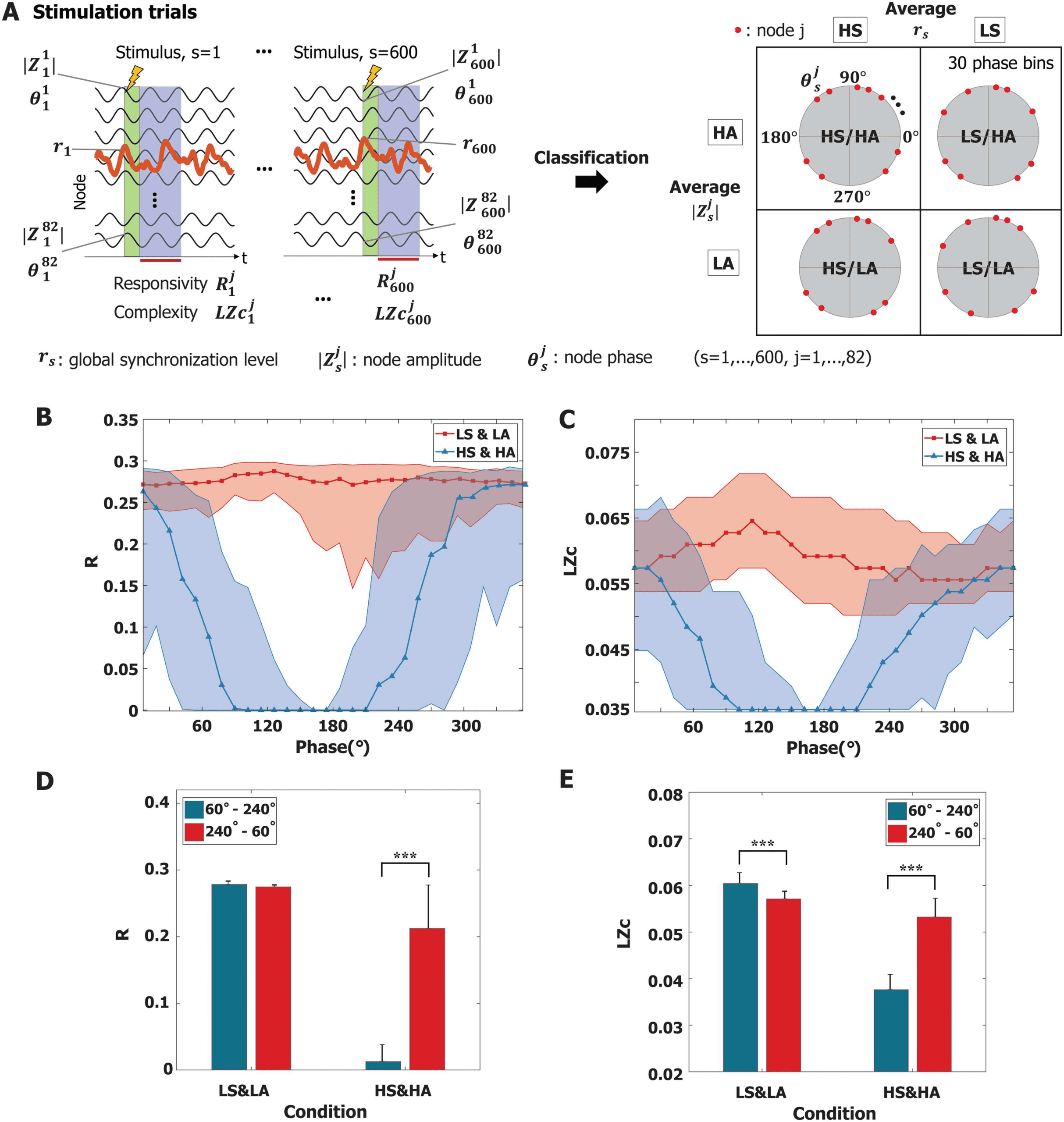
Specific Phases of Alpha Oscillation Unresponsive to Stimulus
s| (HA/LA) by comparing them to the average rs and |Zj
In the previous section, we found a significant correlation between the synchronization of
alpha oscillations and responsiveness. In this section, we focus on the critical state Cp and ex-
plore whether the amplitude and phase of alpha oscillation also play a role in responsiveness.
Interestingly, we found specific phases of alpha oscillation that barely respond to stimuli. We
first classified all nodes into two groups according to their oscillation properties—rs (instanta-
neous global synchronization level, s = 1, 2, . . . , 600) and |Zj
s| (instantaneous node amplitude,
j = 1, 2, . . . , 82)—at stimulus onset. These nodes were classified into high/low rs (HS/LS) and
high/low |Zj
s|, respectively. We further
j
s in each group into 30 phase bins of 12◦ intervals. The graphi-
separated the phases of node θ
cal description of classification is presented in Figure 5A. Therefore, responses were classified
by phase groups with intersections of ongoing oscillation properties (global synchronization
level, node amplitude, and phase). Figure 5B and 5C present responsiveness (R and LZc) in each
phase bin for the low synchronization and low amplitude (LS and LA) group and high synchro-
nization and high amplitude (HS and HA) group. The thick lines indicate the median value of
responsiveness for each phase bin, and the shaded area covers the 25% to 75% quantiles of the
values of each phase bin for each group. We found that the average responsiveness of LS and
LA is larger than that of HS and HA (p < 0.001; Kruskal-Wallis test). Notably, the HS and HA
group showed significant phase dependence. For the purpose of statistical evaluation, we sep-
arated these phases into two phase regimes, 60◦ to 240◦ and 240◦ to 60◦. The HS and HA group
showed significant phase dependence in both responsiveness measures (R and LZc) (Wilcoxon
rank sum test, Figure 5D and 5E); in particular, stimuli applied to specific phases from 60◦ to
240◦ failed to evoke significant brain response (***p < 0.001). These results suggest the exis-
tence of a periodic temporal window that does not significantly respond to external stimuli. We
also tested various other conditions: LS and HA, HS and LA, different stimulus strengths, the
two other states, Cb and Ca, and different model parameter λ = −1 (see Supporting Information
Figure S2 for LS and HA and HS and LA; Supporting Information Figures S3–S7 for the responses
to different stimulus strengths; Supporting Information Figures S8 and S9 for the two other
states, Cb and Ca; and Supporting Information Figures S10 for the different model parameter).
An excessively small stimulus failed to evoke a response, whereas an excessively strong stimulus
produced large responses that eliminated the difference between LS and LA and HS and HA. Phase
dependence was also observed in Cb and Ca; however, in this study we focused on the response
behavior at critical state Cp to interpret the empirical results during conscious wakefulness.
Testing Global Stimulus Conditions with a Local Stimulus
In the previous sections, we examined the various degrees of responsiveness of alpha oscilla-
tions to a global stimulus. For this section, we tested if stimulation conditions for large/small
responsiveness to the global stimulus also held for a local stimulus. Here we applied a pul-
satile stimulus to nodes within a radius of 50 mm centered on the left cuneus in the occipital
region to roughly simulate stimulation of the visual area (13 regions; (left) cuneus, inferior
parietal, isthmus cingulate, lateral occipital, lingual, pericalcarine, precuneus, superior pari-
etal, (right) cuneus, isthmus cingulate, lingual, pericalcarine, precuneus). We considered three
stimulation conditions: effective, noneffective, and random stimulation. The effective stimula-
tion condition was defined as the phases from 240◦ to 60◦ of LS and LA (red bar in LS and LA of
Figure 5D and 5E) that induce a large degree of responsiveness. The noneffective stimulation
conditions were defined as the phases from 60◦ to 240◦ of HS and HA (green bar in HS and HA
of Figure 5D and 5E) that induce a small degree of responsiveness. For the random stimulation
condition, we randomly selected the stimulus onset, which may correspond to conventional
Network Neuroscience
162
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Specific alpha oscillations that evoke small or large response
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
j
s
Z
, and θ
j
s and complexity LZc
j
Figure 5. Phase dependence of responsiveness at Cp. (A) For each stimulation trial, the responsivity R
s (the number
of trials, s = 1, . . . , 600, the number of nodes, j = 1, . . . , 82) were calculated for each trial and each node; each node has the instantaneous
j
alpha oscillation properties at stimulus onset: rs,
s. These oscillation properties were separated into four groups. In the main text,
we show the results of two groups: low synchronization and low amplitude (LS and LA) and high synchronization and high amplitude (HS and
HA). The phases of alpha oscillation were segmented into 30 phase bins of 12◦ intervals for each group. Results for other groups are presented
in Supporting Information Figure S2. (B) The responsivity R and (C) the complexity LZc of perturbation responses for the HS and HA group
significantly depend on the phase of alpha oscillation. The R and LZc of specific phases (around 180◦) show a lower responsiveness to stimuli.
A thick red (blue) line indicates the median value; the shaded areas cover the 25% to 75% quantiles. (D and E) For statistical evaluation, the
phases of alpha oscillation were separated into two regimes (60◦ − 240◦ and 240◦ − 60◦). In the LS and LA group, stimulation induced greater
responsiveness than that in the HS and HA group for both (D) R and (E) LZc (p < 0.001, multiple comparison test using the Tukey-Kramer
method). Phase dependence is more prominent in the HS and HA condition than the LS and LA condition, showing larger responsiveness
(R and LZc) in the 60◦ − 240◦ regime (***p < 0.001, Wilcoxon rank sum test). In the case of high-amplitude, highly synchronized alpha
oscillations, the results imply the existence of temporal windows (with an alpha frequency cycle) that barely respond to external stimuli. The
error bar indicates the standard deviation.
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
Network Neuroscience
163
Specific alpha oscillations that evoke small or large response
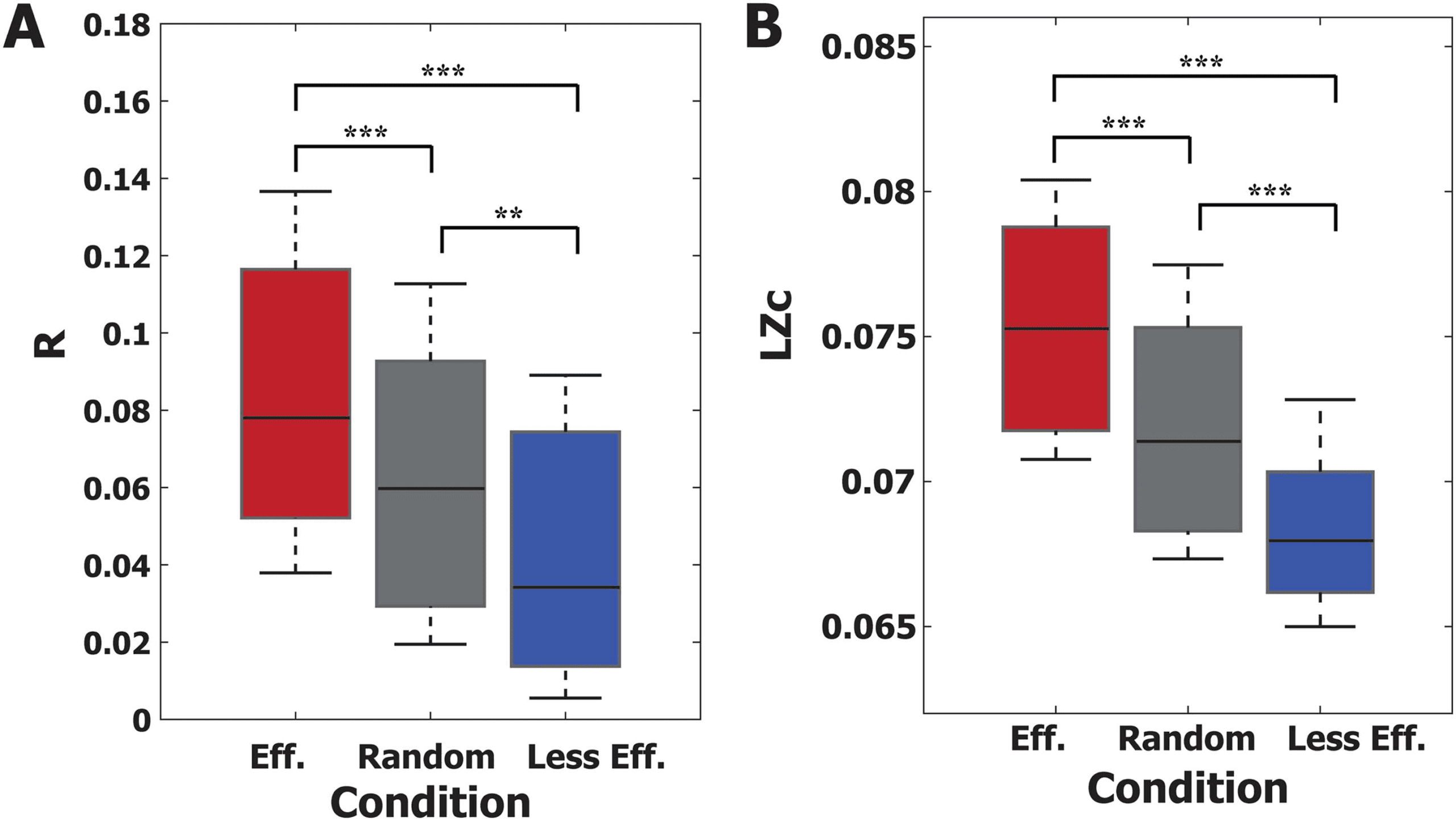
Figure 6. Testing the responsiveness of a local stimulus under (effective, random, and less effective)
global stimulation conditions. Three global stimulation conditions were tested to see if they also hold
for local stimulation in the brain network. (A) R and (B) Lempel-Ziv complexity (LZc) of the occipital
region stimulation were compared under three global stimulation conditions. Under the effective
stimulation condition, specific phases of alpha oscillation (240◦ to 60◦) were stimulated with low
synchronization and low amplitude (red). Under the random stimulation condition, stimulation of
alpha oscillations was random (gray). In the less effective stimulation condition, specific phases of
alpha oscillation (60◦ − 240◦) were stimulated with high synchronization and high amplitude (blue).
For occipital region stimulation, the effective (less effective) stimulation conditions produce larger
(smaller) responsiveness. The responsiveness of the three conditions is significantly different in both
R and LZc (Kruskal-Wallis test, p < 0.001). Multiple comparison tests were performed with the
Tukey-Kramer method (**p < 0.005 and ***p < 0.001). The results showed that the effective and
less effective stimulation conditions of global stimulation also hold for local stimulation.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
.
t
stimulation methods. In comparisons of responsiveness (R and LZc), we found that the ef-
fective (less effective) stimulation condition induces larger (smaller) responsiveness (Figure 6A
and 6B), while the responsiveness of the random stimulation condition fell in the middle. The
R and LZc of the PRs were significantly different across the three conditions (Kruskal-Wallis
test, p < 0.001; in addition, a multicomparison test was performed using the Tukey-Kramer
method for R and LZc, respectively; **p < 0.005 and ***p < 0.001). The results demonstrated
that the effective and less effective stimulation conditions we identified for global stimulation
can be also applied to local stimulation.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
DISCUSSION
Empirical studies have suggested that brain responsiveness is associated with ongoing brain
activities at specific frequencies (e.g., alpha oscillation, ∼10 Hz) when a stimulus is applied.
In this study, we hypothesized that brain responsiveness is determined by the interaction be-
tween a stimulus and coupled alpha oscillations in the brain network. We simulated various
alpha oscillations for three brain states (Cb, Cp, and Ca) and investigated the conditions of
alpha oscillation that facilitate large and small responses to a stimulus. Each brain state pre-
sented characteristic alpha oscillation features: below the critical state (Cb), low amplitude was
associated with an incoherent state; near the critical point (Cp), high and low amplitudes were
balanced with a large degree of synchronization fluctuation; above the critical point (Ca), high
Network Neuroscience
164
Specific alpha oscillations that evoke small or large response
amplitude was associated with a highly synchronized state. The alpha oscillation response
was the most complex and persisted longer at critical state; in this state, responses were larger
and more complex when global pulsatile stimuli were applied to a globally desynchronized,
low-amplitude state. Importantly, we found there are specific phases of high-amplitude, highly
synchronized alpha oscillations that barely respond to stimuli.
Dependence on Network Criticality
Empirical and computational model studies have proposed that the brain in conscious wake-
fulness resides near a critical state, whereas brain states under significant alterations such as
anesthesia and traumatic injury are distant from a critical state (Fekete et al., 2018; Haimovici
et al., 2013; Hutt et al., 2018; Kitzbichler et al., 2009). In this model study, we observed that
the responsivity (the magnitude of the significant response) at Cb and Ca was larger than that
at Cp (Figure 3D). However, the persistence of responsivity is longer at Cp, which implies re-
stricted propagation at the states far from criticality, Cb and Ca (Figure 3D). The brain network
at Cp also exhibited the most complex response when we measured perturbational complexity
(Supporting Information Figure S1). These characteristics are consistent with TMS outcomes in
empirical studies. TMS-evoked activities during unconsciousness show large but short-lasting
simple response patterns (Ferrarelli et al., 2010; Sarasso et al., 2014), whereas EEG responses
induced by TMS during conscious wakefulness show more complex perturbational patterns
compared with anesthesia and NREM sleep (Casali et al., 2013; Ferrarelli et al., 2010; Sarasso
et al., 2015, 2014). The similarity between the results of our model study and empirical results
from previous studies suggests that state-dependent responses of the human brain to TMS may
be due to the distinct response behaviors of the characteristic states (synchronous/incoherent
or high/low amplitude) of networked oscillators below, near, and above a critical state.
Dependence on Instantaneous Global Synchronization
In our modeling study, we found that brain network responsiveness correlates with the level
of instantaneous global synchronization at the critical state (Figure 4). Stimulation at lower
levels of instantaneous global synchronization produced larger responses for both amplitude
and phase synchronization, whereas higher levels of instantaneous global synchronization in-
duced smaller responses (Supporting Information Figures S12 and S13). Therefore, considering
the large synchronization fluctuation at a critical state, it might be important to stimulate the
brain network at appropriate times in order to induce large network perturbation. Not con-
sidering the timing of stimulation may produce greater variability in outcomes. In addition,
synchronization dependence provides novel insight into the role of synchronization fluctua-
tion in brain information processing. In an epoch of lower levels of synchronization, the brain
might not be able to integrate distributed information within the brain network, but may be
highly susceptible to external stimuli. In contrast, in an epoch of higher levels of synchro-
nization, the brain might easily integrate distributed information within the brain network, but
may not be able to respond to external stimuli. Regarding the typical large synchronization
fluctuation at a critical state, the response behaviors of a network at high and low levels of
instantaneous synchronization seem to create temporal windows that can integrate internal
and external information, respectively, while systematically separating internal and external
information processing in the brain network.
Dependence on the Amplitude and Phase of Ongoing Oscillations
In our modeling study, we found that responsiveness also associates with the amplitude and
phase of the ongoing alpha oscillations. We decomposed the alpha oscillations into high and
Network Neuroscience
165
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Specific alpha oscillations that evoke small or large response
low instantaneous synchronization levels, amplitudes, and phases from 0◦ to 360◦. The av-
erage responsiveness of lower instantaneous synchronization and low amplitude (LS and LA)
was larger than that of higher instantaneous synchronization and high amplitude (HS and HA)
(Figure 5). Importantly, considering the alpha oscillations of high synchronization and high am-
plitude, we found that there are specific phases (60◦ to 240◦) that exhibit significantly smaller
responsiveness in both responsiveness indexes. The results suggest periodic temporal windows
(phases from 60◦ to 240◦ in each cycle of an alpha wave) in which the responsiveness of the
brain network was largely inhibited.
The amplitude and phase of alpha waves (8–13 Hz) are associated with sensory stimuli pro-
cessing, especially in regard to visual perception (Benedetto et al., 2018; Busch et al., 2009;
Dugue et al., 2011; Ergenoglu et al., 2004; Mathewson et al., 2009, 2011; Milton & Pleydell-
Pearce, 2016; Nunn & Osselton, 1974; Romei et al., 2008; van Dijk et al., 2008). Stimulation
at lower amplitudes and at a phase near the trough of an alpha wave show increased target de-
tectability (Brüers & VanRullen, 2018; Busch et al., 2009; Ergenoglu et al., 2004; Mathewson
et al., 2009, 2011; Milton & Pleydell-Pearce, 2016; van Dijk et al., 2008). Phosphenes arti-
ficially induced by TMS are more detectable in lower prestimulus alpha power and specific
alpha phase ranges (Dugue et al., 2011; Romei et al., 2008; Samaha, Gosseries, & Postle,
2017). Recent TMS studies have also shown that motor-evoked potential (MEP) amplitude is
dependent on the prestimulus cortical µ-rhythm phase (Schaworonkow et al., 2018; Zrenner
et al., 2017). The established dependence of the brain’s responsiveness on the amplitude and
specific phase of alpha waves is consistent regardless of stimulus type. Our human brain net-
work model showed that stimuli applied at specific phases of alpha oscillation resulted in
larger responsivity and perturbational complexity at the critical state. Interestingly, phase de-
pendence was more pronounced when the stimulus was given at higher amplitudes of alpha
oscillation (Figure 5C and 5D), which is consistent with the visual target detectability experi-
ments (Mathewson et al., 2009). This result emphasizes the importance of considering effec-
tive stimulation conditions, especially when the stimulus is applied to alpha oscillations with
high amplitudes and high levels of synchronization. We also note that phase-dependent re-
sponses are diminished when stimulus strength is too small or too large (Supporting Information
Figures S3–S7).
We also tested if the conditions identified under global stimulation would still hold for local
stimulation. We applied the same stimulus to the occipital region across three different condi-
tions: effective (low instantaneous synchronization, low amplitude, and phases of 240◦ − 60◦),
less effective (high instantaneous synchronization, high amplitude, and phases of 60◦ − 240◦),
and random (conventional stimulation method without considering ongoing brain activity).
Relative to the random condition, the effective and less effective conditions produced signifi-
cantly larger and smaller brain responsiveness. These results may explain why the outcomes of
conventional brain stimulation studies show such large intrasubject variability (Huang et al.,
2017), which degrades the reliability of brain stimulation studies. In addition, finding the spe-
cific phases of alpha oscillations for large or small responsiveness reilluminates the histori-
cal concept of the “neuronic shutter” described in the 1960s (Callaway & Alexander, 1960),
which implies the existence of temporal windows that periodically prohibit sensory informa-
tion processing during conscious states (Callaway & Alexander, 1960; Cecere, Rees, & Romei,
2015; Harris & Thiele, 2011; Nunn & Osselton, 1974; VanRullen, 2016, 2018; VanRullen &
Koch, 2003). Further study is required to identify the relevance of temporal windows of sensory
information processing to the response behavior of networked alpha oscillations to external
stimuli.
Network Neuroscience
166
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Specific alpha oscillations that evoke small or large response
Multi-Scale Mechanisms of Large and Small Responsiveness
A desynchronized EEG, as characterized by low amplitude, noise, and fast-frequency activity,
is associated with arousal and increased awareness (Zerlaut & Destexhe, 2017). This desyn-
chronized state emerges as the product of highly recurrent and stochastic interactions within,
and between, the excitatory-inhibitory neuronal populations at both the cellular and network
level (Zerlaut & Destexhe, 2017). At the cellular level, the stochastic interplay of excitatory and
inhibitory conductance sets neurons into a high-conductance state with enhanced responsive-
ness. At the population level, neuronal ensembles also become highly responsive to afferent
inputs (Zerlaut & Destexhe, 2017). At the large-scale brain network level, responsiveness is
determined by the characteristics of ongoing networked oscillators. However, it remains to be
answered how the specific oscillation properties induce such large or small responsiveness.
One of the potential mechanisms is the phase response curve (PRC) that has been studied
in physics. The PRC characterizes the way that a system with a collective periodic behavior
responds to external stimuli. The response of a periodically driven oscillating system is mea-
sured by the phase shift from the original phase, and the phase shift (advancing or delaying the
original phase) is an inherent characteristic of any oscillatory system. This method has been
applied to many rhythmic biological systems such as circadian rhythms, cardiac rhythms, and
spiking neurons to study how external stimuli perturb the original rhythms (Granada, Hennig,
Ronacher, Kramer, & Herzel, 2009; Hannay, Booth, & Forger, 2015; Ko & Ermentrout, 2008).
The previous analytic studies discovered influential factors causing phase shift and phase syn-
chronization perturbation: a low (high) phase coherence induces a large (small) phase shift
(Hannay et al., 2015). Dynamically, stimulation to the phases around a stable fixed point of
the PRC increases phase coherence, whereas stimulation to the phases around an unstable
fixed point decreases phase coherence. These properties also hold for networks with differ-
ent coupling functions, network structure, connectivity, and even for the amplitude dynamics
of Stuart-Landau oscillators (Levnaji´c & Pikovsky, 2010). If the alpha oscillations are glob-
ally coupled in the human brain network (Zhang et al., 2018), the response behavior may be
governed by the same mechanism of PRC. Furthermore, future study needs to answer how
responsiveness across multiple scales, including cellular, neural population, and large-scale
brain networks, are related to each other.
Conclusion
In summary, this modeling study demonstrated for the first time a relationship between brain
network responsiveness and the ongoing alpha oscillations at different states (below, near, and
above a critical state). We found properties of alpha oscillation that induce a large or small
responsiveness with the same stimulus. The results explain why brain responsiveness is so vari-
able across brain states in consciousness and unconsciousness and across time windows even
during conscious wakefulness. They will also provide a theoretical foundation for developing
an effective brain stimulation method that considers state-specific and transient brain activity.
Limitations
This modeling study has several limitations. First, despite the potential contribution of other
frequency bands to periodic brain responsiveness (Fiebelkorn, Pinsk, & Kastner, 2018; Helfrich
et al., 2018), our model simulated only alpha oscillations. Further studies are required to con-
firm periodic responsiveness for other frequency bands. Our modeling results suggested that
the periodic prohibition of sensory information processing in the human brain is due to the
general response behavior of networked oscillations. However, to justify this argument, the
Network Neuroscience
167
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Specific alpha oscillations that evoke small or large response
Stuart-Landau model:
A mathematical model to describe a
nonlinear oscillating system near the
Hopf bifurcation. It shows noisy to
oscillating system with changes of
parameters of the model.
association of the global synchronization of alpha oscillations (HS and HA and LS and LA) with
responsiveness, which our modeling study discovered, needs to be tested empirically. Second,
we only studied a pulsatile stimulus, which is similar to the stimulus type applied in previous
experiments (Brüers & VanRullen, 2018; Busch et al., 2009; Ergenoglu et al., 2004; Mathewson
et al., 2009, 2011; Milton & Pleydell-Pearce, 2016; van Dijk et al., 2008). Even though we
tested various stimulus strengths, we cannot assure that other types of stimulus, for instance,
a continuous sinusoidal stimulus, would give the same result. Third, in this study, we mainly
focused on the effect of a global stimulus and in addition, tested a local stimulus targeting the
occipital region. However, considering the significant influence of network topology on local
brain dynamics, further study is required to identify the effects of other regional stimuli.
MATERIALS AND METHODS
Simulation of Networked Alpha Oscillations in a Human Brain Network Structure
We constructed a large-scale functional brain network using coupled Stuart-Landau models on
the human anatomical brain structure to generate spontaneous oscillations. The Stuart-Landau
model with brain topology has been used to replicate the oscillatory dynamics of different types
of electromagnetic brain signals such as electroencephalography (EEG), magnetoencephalog-
raphy (MEG), and functional magnetic resonance imaging (fMRI) (Deco et al., 2018, 2017a;
Deco, Kringelbach, Jirsa, & Ritter, 2017b; H. Kim et al., 2018; Moon et al., 2015). The coupled
Stuart-Landau model is defined as the following:
˙zj (t) =
λj + iωj −
zj (t)
2
zj (t) + ∑N
k=1 AjkKjkzk
t − τjk
+ βξ j(t)
(1)
n
(cid:12)
(cid:12)
o
(cid:12)
(cid:12)
(cid:16)
(cid:17)
Here, the state of the jth oscillator, j = 1, 2, . . . , N, is determined by a complex variable
zj(t) at time t. N is the total number of brain regions acquired from group-averaged diffusion
tensor imaging (DTI) with 82 nodes (van den Heuvel & Sporns, 2011). The Ajk = 1 if there is a
connection between the jth and kth oscillators, and Ajk = 0 if there is not, based on the struc-
tural brain network. Each node undergoes supercritical Hopf bifurcation, and the dynamics of
the oscillator settle on a limit cycle if λj > 0 and on a stable focus if λj < 0. Here, we fixed
all λj as 1. The ωj = 2π f j and is an initial angular natural frequency of each jth oscillator.
We used a Gaussian distribution for natural frequency with a mean frequency of 10 Hz and
standard deviation of 0.5 Hz to simulate the alpha bandwidth of human EEG activity (H. Kim
et al., 2018; M. Kim et al., 2017; Lee et al., 2018; Moon et al., 2017, 2015). We also used
the homogeneous coupling term Kjk = K between the jth and kth oscillators from 0 to 0.4
with δK = 0.002, which determines the global connection strength among brain regions. The
time delay between oscillators, τjk = Djk/s, was introduced with the average speed of axons
in brain areas, s = 7 ms (Caminiti et al., 2013), and the distance Djk between brain regions.
The node j received input from connected node k after the time delay τjk. The time delays
are various, but as long as the time delay is smaller than a quarter of the period of oscillation,
here τjk <∼ 25ms, results are not qualitatively different (Moon et al., 2015). A Gaussian white
noise ξ j(t) for each node was added with the standard deviation β = 0.05. We numerically
solved the differential equations of the Stuart-Landau model by using the Stratonovich-Heun
method with 1,000 discretization steps. We also tested the Runge-Kutta fourth-order method
and the results were qualitatively same. The first 10 s of time series were discarded and last
25 s were used for the analysis of each simulation. Therefore, each brain region generates its
own spontaneous oscillatory dynamics within the alpha bandwidth at each coupling strength
K for one simulation.
Network Neuroscience
168
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Specific alpha oscillations that evoke small or large response
Three Brain States: Below, Near, and Above Critical State
We selected three representative brain states at different coupling strengths based on the level
of global synchronization and the pair correlation function (PCF) to understand the responsive-
ness of different systems. We first calculated an instantaneous global synchronization level r(t)
at time t using phase difference ∆θjk(t) = θj(t) − θk(t) at each coupling strength K.
r(t) = h
1
N
∑N
k=1 ei∆θjk(t)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
i
(2)
Here r(t) = 1 if all phases are equal, but r(t) is nearly zero if all phases are randomly dis-
tributed. Then we calculated the variance of r(t) for each coupling strength as a PCF to define
the critical state Cp (Shanahan, 2010). The PCF is equivalent to susceptibility in statistical
physics models. Coupled phase oscillators in complex networks showed the largest suscepti-
bility and PCF at critical state (Yoon et al., 2015). We considered generated signals at certain
coupling strengths with the largest PCF to be equivalent to spontaneous alpha oscillations
in conscious wakefulness. There has been emerging evidence in computational model studies
that brain dynamics at critical point show the largest spatiotemporal diversity (Haimovici et al.,
2013; Hudetz, Humphries, & Binder, 2014). Notably, a large repertoire of metastable states
exists in brain dynamics during the conscious state (Deco et al., 2017b). With the critical state,
we selected two other representative states, one below (Cb) and one above (Ca) critical state.
We defined Cb and Ca as the states at the 10th and 90th percentiles of the averaged order
parameters over all coupling strengths, respectively. These states are the representative states
far from the critical states that show small PCF. Generated signals in these three states were
used for the analysis. We used 20 different initial frequency distributions and selected three
representative states for each frequency distribution.
Brain Network Stimulation Procedure
Global pulsatile stimuli were induced as a stimulation with u(t) as the following:
˙zj (t) =
λj + iωj −
zj (t)
2
zj (t) + ∑N
k=1 AjkK
zk
jk
t − τjk
+ βξ j (t) + u(t)
(3)
n
(cid:12)
(cid:12)
o
(cid:12)
(cid:12)
u(t) =
(
t1 < t < t2
p,
0, otherwise
(cid:16)
(cid:17)
(4)
Here p is the strength of the stimulus during a period T = t2 − t1. We fixed the p = 10
for the analysis after testing the effects of various stimulus strengths (Supporting Information
Figure S11). We also fixed the duration of the stimulus, T = 50 ms, which is about half of the
period of the alpha frequency range cycle. We first gave the same stimulus to the whole-brain
network to understand the dependence of the brain’s response derived only from the network
dynamics of the system (as opposed to its network structure). The stimuli were induced at
randomly selected timing t1 for one trial. In total, 30 different timings, each with 10 itera-
tions, were selected for 20 different frequency distributions. Therefore, Cb, Cp, and Ca each
underwent 600 stimulation trials of pulsatile stimuli. Each stimulus was applied at a unique
instantaneous brain state (i.e., a different one was used for each trial). We decomposed the
instantaneous brain states into the level of instantaneous global synchronization and the am-
plitude and phase of alpha waves to identify the relationship of each of these separate factors
with responsiveness.
Network Neuroscience
169
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Specific alpha oscillations that evoke small or large response
Calculation of Significant Response After Stimulation
First, we calculated the instantaneous phase synchronization of the jth node,
, for each
trial. The |Sj (t) | was obtained by taking the average of the pairwise synchronization between
node j and node k at time t,
(cid:12)
(cid:12)
(cid:12)
(cid:12)
Sj(t)
Sj(t) =
1
Nj
∑N
k=1 Ajkei∆θjk(t)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(5)
Here Nj is the number of connections of the jth node. The instantaneous synchronization value
for the jth node of one trial was normalized by the mean and standard deviation of the baseline
synchronization values of the jth node. Baseline values were obtained by using a total of 10 s,
consisting of 10 iterations of a 1-s prestimulus segment for each trial. We considered the one
tail (1 − α) ∗ 100th quantile with α = 0.05 as a significantly increased synchronization after
stimulus onset. A perturbation response (PR) of the jth node at time t was defined in a binary
fashion: PRj(t) = 1, for the significantly increased synchronization of node j, and PRj(t) = 0,
otherwise.
Responsiveness Measures: Responsivity and Perturbational Complexity
We defined two different measures to quantify the responsiveness of stimulation at different
instantaneous brain states. First, a responsivity Rj was defined by taking the average PRj during
a specific epoch after stimulation. It quantifies the total amount of significant responses after
stimulation. Here we used t = 500 ms, which covers the maximum response changes after
stimulation.
Second, we also calculated the Lempel-Ziv complexity (LZc) of the PR to understand how
complex the response was. The LZc of the PRj was defined as the following:
LZcj =
cj
t/log2t
(6)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
.
t
Here (cj) is the nonnormalized Lempel-Ziv complexity of PRj calculated by a LZ76-algorithm
(Lempel & Ziv, 1976), that is, the number of unique patterns in the PRj during time t. We
defined a perturbational complexity, LZcj, as the normalized cj.
We first investigated the relationships between the level of instantaneous global synchro-
nization at the stimulus onset rs, s = 1, 2, . . . , 600, and the average R and LZc over all nodes at
Cb, Cp, and Ca (Figure 4). Here we calculated spatial LZc, which is LZct =
N/log2 N , N = 82,
to see the global effect of the stimulation. Spearman correlations with p value were calculated
between rs and the average R and LZc at Cb, Cp, and Ca. A Kruskal-Wallis test with a multi-
ple comparison test using the Tukey-Kramer method was used to see the statistical differences
across brain states (***p < 0.001).
ct
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
We also examined the instantaneous alpha amplitude/phase dependences of responsiveness
(R and LZc) to the stimuli (Figure 5). Here we found the certain oscillatory conditions of alpha
oscillations that can induce large or small responsiveness at Cp. We considered the oscillation
properties with certain levels of instantaneous global synchronization, amplitudes, and phases
that induce large (small) responsiveness as effective (less effective) stimulation conditions and
applied these conditions to stimulate the local areas described below.
The same procedures were performed for the amplitude response; these results are shown
in the supplementary materials (Supporting Information Figures S11–S13).
Network Neuroscience
170
Specific alpha oscillations that evoke small or large response
Local Stimulation Effect
At Cp, we induced stimuli to 13 regions in the occipital area within a 50-mm radius of the left
cuneus to confirm that the specific stimulation conditions we found from global stimulation
could be applied to local stimulation (Figure 6). On the left and right hemispheres of the brain,
respectively, the stimulated regions included: (left) cuneus, inferior parietal, isthmus cingulate,
lateral occipital, lingual, pericalcarine, precuneus, superior parietal; (right) cuneus, isthmus
cingulate, lingual, pericalcarine, precuneus. We selected the occipital region because abun-
dant previous sensory stimulation studies mostly targeted the occipital region for visual tasks
within the alpha frequency band. We compared the responsiveness measures with effective,
less effective, and random stimulation conditions. For the effective (less effective) stimulation,
we applied the stimulus to the alpha phases from 240◦ to 60◦ (60◦ to 240◦) with low (high) levels
of instantaneous global synchronization and low (high) amplitude. The stimuli were applied
to the random instantaneous brain states of the occipital region for the random stimulation
condition. The number of nodes for random stimulation was determined by a mean value of
the number of nodes for effective and noneffective conditions. We performed 600 different
trials at Cp, in which each trial consisted of stimuli with p = 30 for 50 ms, and classified the
target nodes with specific conditions. We used a Kruskal-Wallis test to compare the signifi-
cant differences in responsiveness for three conditions. A multiple comparison test was also
performed using the Tukey-Kramer method (**p < 0.005 and ***p < 0.001).
SUPPORTING INFORMATION
Supporting Information for this article is available at https://doi.org/10.1162/netn_a_00113.
ROLE INFORMATION
Minkyung Kim: Conceptualization; Formal Analysis; Investigation; Methodology; Visualiza-
tion; Writing - Original Draft; Writing - Review & Editing. Uncheol Lee: Conceptualization;
Funding Acquisition; Project Administration; Supervision; Writing - Original Draft; Writing -
Review & Editing.
FUNDING INFORMATION
Uncheol Lee, Foundation for the National Institutes of Health (http://dx.doi.org/10.13039/
100000009), Award ID: R01 GM098578.
REFERENCES
Benedetto, A., Lozano-Soldevilla, D., & VanRullen, R.
(2018).
Different responses of spontaneous and stimulus-related alpha ac-
tivity to ambient luminance changes. European Journal of Neuro-
science, 48(7), 2599–2608. https://doi.org/10.1111/ejn.13791
Brüers, S., & VanRullen, R. (2018). Alpha power modulates per-
ception independently of endogenous factors. Frontiers in Neuro-
science, 12, 1–8. https://doi.org/10.3389/fnins.2018.00279
Busch, N. A., Dubois, J., & VanRullen, R.
(2009). The phase
of ongoing EEG oscillations predicts visual perception. Journal
of Neuroscience, 29(24), 7869–7876. https://doi.org/10.1523/
JNEUROSCI.0113-09.2009
Callaway, E., & Alexander, J. D. (1960). The temporal coding of sen-
sory data: An investigation of two theories. Journal of General
Psychology, 62(2), 293–309. https://doi.org/10.1080/00221309.
1960.9920419
Caminiti, R., Carducci, F., Piervincenzi, C., Battaglia-Mayer, A.,
Confalone, G., Visco-Comandini, F., . . . Innocenti, G. M. (2013).
Diameter, length, speed, and conduction delay of callosal axons
in Macaque monkeys and humans: Comparing data from his-
tology and magnetic resonance imaging diffusion tractography.
Journal of Neuroscience, 33(36), 14501–14511. https://doi.org/
10.1523/JNEUROSCI.0761-13.2013
Casali, A. G., Gosseries, O., Rosanova, M., Boly, M., Sarasso, S.,
Casali, K. R., . . . Massimini, M.
(2013). A theoretically based
index of consciousness independent of sensory processing and
behavior. Science Translational Medicine, 5(198). https://doi.
org/10.1126/scitranslmed.3006294
Cecere, R., Rees, G., & Romei, V. (2015). Individual differences in
alpha frequency drive crossmodal illusory perception. Current Biol-
ogy, 25(2), 231–235. https://doi.org/10.1016/j.cub.2014.11.034
Network Neuroscience
171
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Specific alpha oscillations that evoke small or large response
Chialvo, D. R. (2010). Emergent complex neural dynamics. Nature
Physics, 6(10), 744–750. https://doi.org/10.1038/nphys1803
Cocchi, L., Gollo, L. L., Zalesky, A., & Breakspear, M. (2017). Criti-
cality in the brain: A synthesis of neurobiology, models and cog-
nition. Progress in Neurobiology, 158, 132–152. https://doi.org/
10.1016/j.pneurobio.2017.07.002
Deco, G., Cabral, J., Saenger, V. M., Boly, M., Tagliazucchi, E.,
Laufs, H., . . . Kringelbach, M. L. (2018). Perturbation of whole-
brain dynamics in silico reveals mechanistic differences between
brain states. NeuroImage, 169, 46–56. https://doi.org/10.1016/j.
neuroimage.2017.12.009
Deco, G., Cabral, J., Woolrich, M. W., Stevner, A. B. A., van
Hartevelt, T. J., & Kringelbach, M. L. (2017a). Single or multiple
frequency generators in on-going brain activity: A mechanistic
whole-brain model of empirical MEG data. NeuroImage, 152,
538–550. https://doi.org/10.1016/j.neuroimage.2017.03.023
Deco, G., Kringelbach, M. L., Jirsa, V. K., & Ritter, P. (2017b).
The dynamics of resting fluctuations in the brain: Metastability
and its dynamical cortical core. Scientific Reports, 7(1), 1–14.
https://doi.org/10.1038/s41598-017-03073-5
Dugue, L., Marque, P., & VanRullen, R. (2011). The phase of ongoing
oscillations mediates the causal relation between brain excitation
and visual perception. Journal of Neuroscience,31(33), 11889–11893.
https://doi.org/10.1523/JNEUROSCI.1161-11.2011
Ergenoglu, T., Demiralp, T., Bayraktaroglu, Z., Ergen, M., Beydagi,
H., & Uresin, Y. (2004). Alpha rhythm of the EEG modulates
visual detection performance in humans. Cognitive Brain Re-
search, 20(3), 376–383. https://doi.org/10.1016/j.cogbrainres.
2004.03.009
Fekete, T., Omer, D. B., O’Hashi, K., Grinvald, A., van Leeuwen, C.,
& Shriki, O. (2018). Critical dynamics, anesthesia and informa-
tion integration: Lessons from multi-scale criticality analysis of
voltage imaging data. NeuroImage, 183, 919–933. https://doi.
org/10.1016/j.neuroimage.2018.08.026
Ferrarelli, F., Massimini, M., Sarasso, S., Casali, A., Riedner, B. A.,
Angelini, G., . . . Pearce, R. A. (2010). Breakdown in cortical
effective connectivity during midazolam-induced loss of con-
sciousness. Proceedings of the National Academy of Sciences,
107(6), 2681–2686. https://doi.org/10.1073/pnas.0913008107
Fiebelkorn, I. C., Pinsk, M. A., & Kastner, S. (2018). A dynamic inter-
play within the frontoparietal network underlies rhythmic spatial
attention. Neuron, 99(4), 842–853.e38. https://doi.org/10.1016/
j.neuron.2018.07.038
Granada, A., Hennig, R. M., Ronacher, B., Kramer, A., & Herzel, H.
(2009). Phase response curves elucidating the dynamics of cou-
pled oscillators. Methods in Enzymology, 454, 1–27. https://doi.
org/10.1016/S0076-6879(08)03801-9
Haimovici, A., Tagliazucchi, E., Balenzuela, P., & Chialvo, D. R.
(2013). Brain organization into resting state networks emerges at
criticality on a model of the human connectome. Physical Re-
view Letters, 110(17), 1–4. https://doi.org/10.1103/PhysRevLett.
110.178101
Hannay, K. M., Booth, V., & Forger, D. B. (2015). Collective phase
response curves for heterogeneous coupled oscillators. Physical
Review E - Statistical, Nonlinear, and Soft Matter Physics, 92(2),
1–9. https://doi.org/10.1103/PhysRevE.92.022923
Harris, K. D., & Thiele, A. (2011). Cortical state and attention.
Nature Reviews Neuroscience, 12(9), 509–523. https://doi.org/
10.1038/nrn3084
Helfrich, R. F., Fiebelkorn, I. C., Szczepanski, S. M., Lin, J. J., Parvizi,
J., Knight, R. T., & Kastner, S. (2018). Neural mechanisms of
sustained attention are rhythmic. Neuron, 99(4), 854–865.e5.
https://doi.org/10.1016/j.neuron.2018.07.032
Huang, Z., Zhang, J., Longtin, A., Dumont, G., Duncan, N. W.,
Pokorny, J., . . . Northoff, G. (2017). Is there a nonadditive
interaction between spontaneous and evoked activity? Phase-
dependence and its relation to the temporal structure of scale-free
brain activity. Cerebral Cortex, 27(2), 1037–1059. https://doi.org/
10.1093/cercor/bhv288
Hudetz, A. G., Humphries, C. J., & Binder, J. R. (2014). Spin-glass
model predicts metastable brain states that diminish in anesthe-
sia. Frontiers in Systems Neuroscience, 8, 1–9. https://doi.org/10.
3389/fnsys.2014.00234
Hutt, A., Lefebvre, J., Hight, D., & Sleigh, J. (2018). Suppression
of underlying neuronal fluctuations mediates EEG slowing dur-
ing general anaesthesia. NeuroImage, 179, 414–428. https://doi.
org/10.1016/j.neuroimage.2018.06.043
Jobst, B. M., Hindriks, R., Laufs, H., Tagliazucchi, E., Hahn, G.,
Ponce-Alvarez, A., . . . Deco, G. (2017). Increased stability
and breakdown of brain effective connectivity during slow-
wave sleep: Mechanistic insights from whole-brain computa-
tional modelling. Scientific Reports, 7(1), 1–16. https://doi.org/
10.1038/s41598-017-04522-x
Kim, H., Moon, J., Mashour, G. A., & Lee, U. (2018). Mechanisms
of hysteresis in human brain networks during transitions of con-
sciousness and unconsciousness: Theoretical principles and em-
pirical evidence. PLoS Computational Biology. https://doi.org/10.
1371/journal.pcbi.1006424
Kim, M., Kim, S., Mashour, G. A., & Lee, U. (2017). Relationship
of topology, multiscale phase synchronization, and state transi-
tions in human brain networks. Frontiers in Computational Neu-
roscience, 11, 1–12. https://doi.org/10.3389/fncom.2017.00055
Kitzbichler, M. G., Smith, M. L., Christensen, S. R., & Bullmore, E.
(2009). Broadband criticality of human brain network synchro-
nization. PLoS Computational Biology, 5(3). https://doi.org/10.
1371/journal.pcbi.1000314
Ko, T.-W., & Ermentrout, B. (2008). Phase response curves of
coupled oscillators. Physical Review E. https://doi.org/10.1103/
PhysRevE.79.016211
Lee, U., Kim, M., Lee, K., Kaplan, C. M., Clauw, D. J., Kim, S., . . .
Harris, R. E. (2018). Functional brain network mechanism of hy-
persensitivity in chronic pain. Scientific Reports. https://doi.org/
10.1038/s41598-017-18657-4
Lempel, A., & Ziv, J. (1976). On the complexity of finite sequences
IEEE transactions on information theory vol IT22. IEEE Transac-
tions on Information Theory1, 22(1), 75–81. https://doi.org/10.
1109/TIT.1976.1055501
Levnaji´c, Z., & Pikovsky, A.
(2010). Phase resetting of collective
rhythm in ensembles of oscillators. Physical Review E - Statisti-
cal, Nonlinear, and Soft Matter Physics, 82(5), 1–10. https://doi.
org/10.1103/PhysRevE.82.056202
Mathewson, K. E., Gratton, G., Fabiani, M., Beck, D. M., & Ro, T.
(2009). To see or not to see: Prestimulus phase predicts visual
Network Neuroscience
172
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Specific alpha oscillations that evoke small or large response
awareness. Journal of Neuroscience, 29(9), 2725–2732. https://
doi.org/10.1523/JNEUROSCI.3963-08.2009
EEG and Neuroscience, 45(1), 40–49. https://doi.org/10.1177/
1550059413513723
Mathewson, K. E., Lleras, A., Beck, D. M., Fabiani, M., Ro, T., &
Gratton, G. (2011). Pulsed out of awareness: EEG alpha oscilla-
tions represent a pulsed-inhibition of ongoing cortical process-
ing. Frontiers in Psychology, 2, 1–15. https://doi.org/10.3389/
fpsyg.2011.00099
Milton, A., & Pleydell-Pearce, C. W. (2016). The phase of pre-
stimulus alpha oscillations influences the visual perception of
stimulus timing. NeuroImage, 133, 53–61. https://doi.org/10.
1016/j.neuroimage.2016.02.065
Moon, J. Y., Kim, J., Ko, T. W., Kim, M., Iturria-Medina, Y., Choi,
J. H., . . . Lee, U. C. (2017). Structure shapes dynamics and di-
rectionality in diverse brain networks: Mathematical principles
and empirical confirmation in three species. Scientific Reports.
https://doi.org/10.1038/srep46606
Moon, J. Y., Lee, U. C., Blain-Moraes, S., & Mashour, G. A.
(2015). General relationship of global topology, local dynamics,
and directionality in large-scale brain networks. PLoS Computa-
tional Biology, 11(4), 1–21. https://doi.org/10.1371/journal.pcbi.
1004225
Nunn, C. M., & Osselton, J. W. (1974). The influence of the EEG
alpha rhythm on the perception of visual stimuli. Psychophysiol-
ogy. https://doi.org/10.1111/j.1469-8986.1974.tb00547.x
Romei, V., Brodbeck, V., Michel, C., Amedi, A., Pascual-Leone, A.,
& Thut, G. (2008). Spontaneous fluctuations in posterior α-band
EEG activity reflect variability in excitability of human visual
areas. Cerebral Cortex, 18(9), 2010–2018. https://doi.org/10.1093/
cercor/bhm229
Samaha, J., Gosseries, O., & Postle, B. R. (2017). Distinct oscillatory
frequencies underlie excitability of human occipital and parietal
cortex. The Journal of Neuroscience, 37(11), 2824–2833. https://
doi.org/10.1523/JNEUROSCI.3413-16.2017
Sarasso, S., Boly, M., Napolitani, M., Gosseries, O., Charland-
Verville, V., Casarotto, S., .
. . Massimini, M. (2015). Con-
sciousness and complexity during unresponsiveness induced
by propofol, xenon, and ketamine. Current Biology, 25(23),
3099–3105. https://doi.org/10.1016/j.cub.2015.10.014
Sarasso, S., Rosanova, M., Casali, A. G., Casarotto, S., Fecchio,
M., Boly, M.,
(2014). Quantifying cor-
tical EEG responses to TMS in (Un)consciousness. Clinical
. Massimini, M.
.
.
Schaworonkow, N., Triesch, J., Ziemann, U., & Zrenner, C. (2018).
EEG-triggered TMS reveals stronger brain state-dependent mod-
ulation of motor evoked potentials at weaker stimulation inten-
sities. BioRxiv. https://doi.org/10.1101/251363
Shanahan, M. (2010). Metastable chimera states in community-
structured oscillator networks. Chaos, 20(1). https://doi.org/10.
1063/1.3305451
van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organization
of the human connectome. Journal of Neuroscience, 31(44),
15775–15786. https://doi.org/10.1523/JNEUROSCI.3539-11.2011
van Dijk, H., Schoffelen, J. M., Oostenveld, R., & Jensen, O. (2008).
Prestimulus oscillatory activity in the alpha band predicts visual
discrimination ability. Journal of Neuroscience, 28(8), 1816–1823.
https://doi.org/10.1523/JNEUROSCI.1853-07.2008
VanRullen, R. (2016). Perceptual cycles. Trends in Cognitive Sciences,
20(10), 723–735. https://doi.org/10.1016/j.tics.2016.07.006
VanRullen, R. (2018). Attention cycles. Neuron, 99(4), 632–634.
https://doi.org/10.1016/j.neuron.2018.08.006
VanRullen, R., & Koch, C. (2003). Is perception discrete or continu-
ous? Trends in Cognitive Sciences, 7(5), 207–213. https://doi.org/
10.1016/S1364-6613(03)00095-0
Yoon, S., Sorbaro Sindaci, M., Goltsev, A. V., & Mendes, J. F. F.
(2015). Critical behavior of the relaxation rate, the susceptibility,
and a pair correlation function in the kuramoto model on scale-
free networks. Physical Review E - Statistical, Nonlinear, and Soft
Matter Physics, 91(3), 1–10. https://doi.org/10.1103/PhysRevE.
91.032814
Zerlaut, Y., & Destexhe, A. (2017). Enhanced responsiveness and
low-level awareness in stochastic network states. Neuron, 94(5),
1002–1009. https://doi.org/10.1016/j.neuron.2017.04.001
Zhang, H., Watrous, A. J., Patel, A., & Jacobs, J. (2018). Theta and
alpha oscillations are traveling waves in the human neocortex.
Neuron, 98(6), 1269–1281.e4. https://doi.org/10.1016/j.neuron.
2018.05.019
Zrenner, C., Desideri, D., Belardinelli, P., & Ziemann, U. (2017).
Real-time EEG-defined excitability states determine efficacy of
TMS-induced plasticity in human motor cortex. Brain Stimula-
tion, 11(2), 374–389. https://doi.org/10.1016/j.brs.2017.11.016
Network Neuroscience
173
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
1
5
5
1
8
6
6
7
3
3
n
e
n
_
a
_
0
0
1
1
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3