RECHERCHE
Comparison between diffusion MRI tractography
and histological tract-tracing of cortico-cortical
structural connectivity in the ferret brain
Céline Delettre1,2,3, Arnaud Messé2, Leigh-Anne Dell2, Ophélie Foubet1,
Katja Heuer1,4, Benoit Larrat5, Sebastien Meriaux5, Jean-Francois Mangin5,
Isabel Reillo6, Camino de Juan Romero6, Victor Borrell6,
Roberto Toro1,7, and Claus C. Hilgetag
2,8
1Unité de Génétique Humaine et Fonctions Cognitives, Institut Pasteur, UMR 3571, CNRS, Paris, France
2Institute of Computational Neuroscience, University Medical Center Eppendorf, Hamburg University, Hamburg, Allemagne
3Université Paris Diderot, Sorbonne Paris Cité, Paris, France
4Department of Neuropsychology, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Allemagne
5NeuroSpin, CEA, Paris-Saclay University, Gif-sur-Yvette, France
6Developmental Neurobiology Unit, Instituto de Neurociencias, Consejo Superior de Investigaciones Científicas,
Universidad Miguel Hernández, Sant Joan d’Alacant, Espagne
7Center for Research and Interdisciplinarity (CRI), Université Paris Descartes, Paris, France
8Department of Health Sciences, Université de Boston, Boston, MA, Etats-Unis
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
un
_
0
0
0
9
8
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mots clés: Validation, Diffusion MRI, Tractography, Tract-tracing, Structural connectivity, Ferret
ABSTRAIT
The anatomical wiring of the brain is a central focus in network neuroscience. Diffusion MRI
tractography offers the unique opportunity to investigate the brain fiber architecture in vivo
and noninvasively. Cependant, its reliability is still highly debated. Ici, we explored the
ability of diffusion MRI tractography to match invasive anatomical tract-tracing connectivity
data of the ferret brain. We also investigated the influence of several state-of-the-art
tractography algorithms on this match to ground truth connectivity data. Tract-tracing
connectivity data were obtained from retrograde tracer injections into the occipital, pariétal,
and temporal cortices of adult ferrets. We found that the relative densities of projections
identified from the anatomical experiments were highly correlated with the estimates from all
the studied diffusion tractography algorithms (Spearman’s rho ranging from 0.67 à 0.91),
while only small, nonsignificant variations appeared across the tractography algorithms.
These results are comparable to findings reported in mouse and monkey, increasing the
confidence in diffusion MRI tractography results. De plus, our results provide insights into
the variations of sensitivity and specificity of the tractography algorithms, and hence into the
influence of choosing one algorithm over another.
RÉSUMÉ DE L'AUTEUR
In this article we used tract-tracing data as a gold standard to validate the use of diffusion MRI
tractography for inferring structural connectivity in the ferret brain as well as for assessing the
influence of several state-of-the-art tractography algorithms on the inferred connections. Nous
found high correspondence between diffusion MRI tractography and tract-tracing with little
differences between the explored algorithms. We conclude that diffusion MRI tractography
provides a worthwhile whole-brain estimate of structural connectivity that can be employed
in further anatomical, developmental, and computational studies of the ferret brain.
un accès ouvert
journal
Citation: Delettre, C., Messé, UN., Dell,
L-A., Foubet, O., Heuer, K., Larrat, B.,
. . . Hilgetag, C. C. (2019). Comparaison
between diffusion MRI tractography
and histological tract-tracing of
cortico-cortical structural connectivity
in the ferret brain. Réseau
Neurosciences, 3(4), 1038–1050.
https://doi.org/10.1162/netn_a_00098
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00098
Informations complémentaires:
https://doi.org/10.1162/netn_a_00098
https://github.com/neuroanatomy/
FerretDiffusionTractTracingComparison
Reçu: 22 Janvier 2019
Accepté: 23 May 2019
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Claus C. Hilgetag
c.hilgetag@uke.de
Éditeur de manipulation:
Olaf Sporns
droits d'auteur: © 2019
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
Comparing tractography and tract-tracing in the ferret brain
Structural connectivity:
A network of physical or anatomical
connections linking neuronal
ensembles often referred to as the
brain connectome.
Diffusion MRI:
MRI sequence quantifying the
orientation of water molecule
diffusion.
Tractography:
A technique used to reconstruct
brain white matter connections
based on diffusion MRI.
INTRODUCTION
Brain function emerges from the communication of spatially distributed large-scale networks via the
underlying structural connectivity architecture (Ange, Gerloff, Hilgetag, & Nolte, 2013; Kandel,
Schwartz, Jessell, Siegelbaum, & Hudspeth, 2012; Parc & Friston, 2013; Varela, Lachaux,
Rodriguez, & Martinerie, 2001). Systematic analysis of structural connectivity has revealed
characteristic features of brain networks, including the presence of modules, hubs, and higher
order topological properties, thought to support efficient information processing (Sporns, 2010).
De plus, structural connectivity is considered as a neural substrate that is affected in various
pathological conditions, such as Alzheimer’s disease and schizophrenia spectrum disorders
(Fornito & Bullmore, 2015). Donc, reliable estimates of brain structural connectivity are
essential for advancing our understanding of the network basis of brain function.
Diffusion MRI tractography is an indirect approach for inferring brain structural connectivity
from the Brownian motion of water molecules constrained by the axonal fiber architecture
(Jeurissen, Descoteaux, Mori, & Leemans, 2017). Ainsi, it provides the unique opportunity to
investigate, in vivo and noninvasively, the structural connectivity of intact or altered brains,
such as in the case of stroke (Visser et coll., 2018), in longitudinal analysis of brain development
(Hagmann et al., 2010), or in utero acquisitions of prenatal brain structure (Kasprian et al.,
2008). Cependant, the reliability of diffusion MRI tractography for properly mapping structural
connections remains highly debated (Jones, Knösche, & Tourneur, 2013; Thomas et al., 2014).
Donc, validation appears as a key step in evaluating current methodologies and identifying
new perspectives of improvement (Dyrby, Innocenti, Bech, & Lundell, 2018).
A small number of studies designed benchmarks in order to explore the reliability of diffu-
sion MRI tractography (Schilling et al., 2018). Par exemple, using a phantom dataset composed
of known tracts reconstructed by diffusion MRI tractography as ground truth, the accuracy of a
large number of state-of-the-art tractography algorithms was assessed in humans (Maier-Hein
et coll., 2017). The results showed, for all the algorithms, their ability to recover most of the exist-
ing bundles, but also revealed a variable, but substantial, number of false positives. De la même manière
Sarwar, Ramamohanarao, & Zalesky (2018) compared deterministic and probabilistic tracto-
graphy algorithms with a numerically generated phantom and concluded on a trade-off to be
made between sensitivity and specificity depending on the type of tractography algorithm.
While these studies provided a first estimate of the specificity and sensitivity of a wide range
of tractography algorithms, the ground truths used were based on diffusion MRI tractography
or numerically generated and thus, one can debate their realism.
Tract-tracing:
An invasive neuroscience technique
used to determine the pathway
between neuronal entities by
injecting a dye into a brain region.
Anterograde tracing:
A technique to map the neural
connections from the injection site
(cell bodies) to the projection targets,
labeling the synaptic terminals.
Retrograde tracing:
A technique to map the neural
connections by labeling the sources
(cell bodies) of neurons projecting to
the injection site (synapse).
À ce jour, the gold standard for assessing structural brain connectivity is provided by tract-
tracing experiments, which physically investigate, at the cellular level, the relative number of
connections of an area to the rest of the brain using viral, bacterial, or biotinylated dextran
agents (Bizley, Bajo, Nodal, & King, 2015; Bota, Sporns, & Swanson, 2015; Markov et al.,
2014; Zingg et al., 2015). These agents act as either anterograde or retrograde tracers. Tel
histological tracing of anatomical connections provides directional as well as laminar infor-
In the case of retrograde tracing, histological tracing also quantifies
mation on projections.
the number of axons in a projection, since each labeled projection neuron provides one axon.
Studies performed in macaque (Azadbakht et al., 2015; Donahue et al., 2016; Schilling, Nath,
et coll., 2019; Zhang et al., 2018), squirrel monkey (Gao et al., 2013; Schilling, Gao, et coll.,
2019), pig (Knösche, Anwander, Liptrot, & Dyrby, 2015), mouse (Calabrese, Badea, Cofer,
Qi, & Johnson, 2015), and rat (Sinke et al., 2018) have explored the relationship between
tract-tracing experiments and tractography. Dans l'ensemble, these studies have shown that diffusion
MRI tractography provides a good estimate of structural brain connectivity. Few explorations
Neurosciences en réseau
1039
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
un
_
0
0
0
9
8
p
d
t
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Comparing tractography and tract-tracing in the ferret brain
have been made on the ability of the different tractography approaches available to estimate
structural connectivity weights (Gao et al., 2013). Previous studies have mainly focused on
the ability of tractography algorithms to properly estimate white matter pathways by means
of voxelwise overlap (Knösche et al., 2015), or on the detectability (presence or absence) de
relations (Sinke et al., 2018), or both (Schilling, Gao, et coll., 2019; Schilling, Nath, et coll.,
2019).
The ferret brain starts to fold after birth, and reaches the adult folding pattern at about one
month of age. Donc, the ferret is a widely used animal model for studying brain fold-
ing (Barnette et al., 2009; Feng, Clayton, Chang, Okamoto, & Bayly, 2013). En outre,
these mammals display complex behavior, are inexpensive to house, and have a short gesta-
tion period as well as a limited lifetime, making them an attractive “whole lifespan model”
(Fox, 1998). Recently established extensive tract-tracing connectivity data of the ferret (voir
Dell, Innocenti, Hilgetag, & Manger, 2019un, 2019b, 2019c) have made it possible to compare
anatomical cortical connectivity with that reported by tractography methods. Ainsi, the present
study aimed to use the ferret as an animal model to assess the performance of six diffusion trac-
tography algorithms compared with histological tract-tracing data from the occipital, pariétal,
and temporal cortices in the ferret. Dans l'ensemble, our results showed that diffusion MRI tractography
provides statistically significant estimates of ferret brain structural connectivity, although the
different tractography algorithms presented variations in terms of sensitivity and specificity.
MATERIALS AND METHODS
Ferret Brain Atlas
We used a parcellation based on the atlas of the posterior cortex by Bizley & King (2009). Le
parcellation scheme was manually drawn on the left hemisphere in the diffusion MRI space us-
ing the online tool BrainBox (Heuer, Ghosh, Sterling, & Toro, 2016, http://brainbox.pasteur.fr/).
Tract-tracing data were available for areas 17, 18, 19, 21 (occipital visual areas); 20a and 20b
combined (temporal visual areas); and PPr and PPc (parietal visual areas). See Figure 1A.
Diffusion MRI Data
High-resolution MRI were acquired ex vivo using a small animal 7 Tesla Bruker MRI scanner
(Neurospin, Saclay, France). The acquisitions were performed postmortem in order to reduce
movement artefacts and improve sensitivity (Holmes et al., 2017). The brain was obtained
from a 2-month-old ferret. The ferret was euthanized by an overdose of pentobarbital and
perfused transcardially with 0.9% saline solution and post-fixed with phosphate-buffered 4%
paraformaldehyde (PFA). After extraction, the brain was stored at 4
C in a 4% PFA solution
until the MRI acquisition. All procedures were approved by the Institutional Animal Care
and Use Committee of the Universidad Miguel Hernández and CSIC (Consejo Superior de
Investigaciones Científicas), Alicante, Espagne.
◦
The brain was transferred to a 0.01 M phosphate-buffered saline (PBS) solution for
rehydration 24 hr before MRI acquisition. Shortly before MRI acquisition, the brain sample
was transferred to a plastic tube filled with nonprotonic liquid (fluorinert) in order to avoid
air-tissue interfaces that may induce susceptibility artefacts, as well as to avoid foldover MRI
artefacts due to a proton signal coming from a protonic liquid outside the imaging field of
voir (McRobbie, Moore, & Graves, 2017). The tube was then placed in a dedicated holder in
the middle of the transmit/receive MRI volume radiofrequency coil. Temperature stability was
ensured by a regulated room temperature as well as the cooling of the gradient coils, by water
Neurosciences en réseau
1040
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
un
_
0
0
0
9
8
p
d
t
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Comparing tractography and tract-tracing in the ferret brain
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
un
_
0
0
0
9
8
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
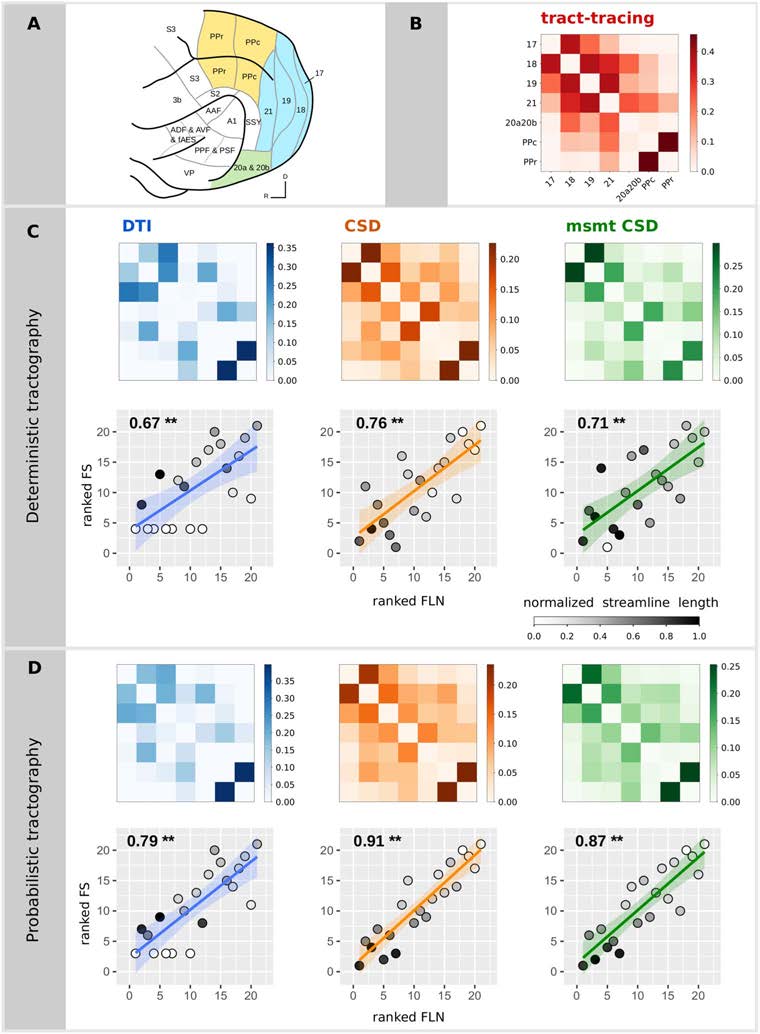
Chiffre 1. Relationship between diffusion MRI tractography and tract-tracing experiments.
(UN)
Ferret brain atlas according to the parcellation of Bizley and King (figure adapted from Bizley &
King, 2009). The regions of interest for the comparative study are those colored. Colors code for
the different visual brain areas: posterior parietal (yellow), occipital (blue), and temporal cortices
(vert).
(B) Structural connectivity matrix based on tract-tracing experiments, where the weights
represent the fraction of labeled neurons (FLN). Structural connectivity matrices estimated from the
deterministic (C) and the probabilistic (D) tractography algorithms and the associated scatterplots of
the ranked FLN vs. the ranked FS. Each point in the scatterplot corresponds to a connection between
a pair of areas for the tract-tracing results (abscissa) and the diffusion results (ordinate). The ranked
weights of the connections allow visualization of the Spearman’s rho as the slope of the fitted curve.
Gray colors code for the average streamline length (values normalized by the maximum streamline
length of all the algorithms). P values smaller than 0.001 are indicated by **.
Neurosciences en réseau
1041
Comparing tractography and tract-tracing in the ferret brain
C that was constantly flowing inside the innermost part of the magnet. The equilibrium
◦
à 16
temperature at the sample was 20
◦
C.
High-resolution T2-weighted MRI data were acquired using a multislice multiecho (MSME)
sequence with 18 echo times and 0.12 mm isotropic voxels. Diffusion MRI data were acquired
using a multislice 2-D spin-echo segmented DTI-EPI sequence (4 segments) and the following
parameters: TR = 40 s; LE = 32 ms; matrix size = 160 × 120 × 80; 0.24 mm isotropic voxels;
200 diffusion-weighted directions with b = 4,000 s/mm2; et 10 b0 at the beginning of the se-
quence, diffusion gradient duration = 5 ms and diffusion gradient separation = 17 ms. Thanks
to strong gradients compared with clinical scanners, the b-value could reach 4,000 s/mm2, dans-
suring a strong diffusion weighting and therefore an improved sensitivity to anisotropy while
keeping the echo time low enough to save signal-to-noise ratio (SNR) and limit EPI distor-
tion. A b-value of 4,000 s/mm2 has been previously shown to be a good compromise for
disentangling crossing fibers for ex vivo imaging (Dyrby et al., 2011). The noise introduced by
the high diffusion weighting was balanced by a high angular resolution. Le 200 instructions
were generated as noncollinear directions uniformly distributed over a sphere (Hasan, Parker,
& Alexander, 2001). The spatial resolution was chosen as the highest resolution available on
the scanner in order to achieve a good SNR while keeping a reasonable acquisition time. Nous
obtained an SNR of 4.2, measured as the ratio between the mean of our signal in the brain
and the standard deviation of the signal in the background. The total acquisition time of the
diffusion MRI sequences was about 37 hr.
Preprocessing
D'abord, MRI data were converted from the 2dseq Bruker format to the standard NIFTI format using
a modified version of the bruker2nifti script (original version: https://github.com/SebastianoF/
bruker2nifti; modified version: https://github.com/neuroanatomy/bruker2nifti). For a limited
number of volumes, EPI trajectories were poorly corrected by the Bruker routine image re-
constructor, which resulted in noisy volumes. In order to exclude these volumes, diffusion-
weighted directions for which their mean signal was 2 standard deviations away from the
global average across all the volumes were visually inspected and removed. Three out of 200
volumes were removed following this criterion. The preprocessing steps were mainly done
using MRtrix3 functions and included a local principal component analysis (LPCA) denois-
ing (Veraart et al., 2016), Gibbs ringing correction (Kellner, Dhital, Kiselev, & Reisert, 2016),
FSL-based eddy current correction (Andersson & Sotiropoulos, 2016; Jenkinson, Beckmann,
Behrens, Woolrich, & Forgeron, 2012), and B1 field inhomogeneity correction (Tustison et al.,
2010). A brain mask was manually segmented from the high-resolution T2 image, pour
obtain a precise delineation of the sulci and gyri. Spatial normalization using a linear transfor-
mation between the high-resolution T2 volume and diffusion MRI data was computed using
FLIRT tools (Jenkinson, Bannister, Brady, & Forgeron, 2002), and the brain mask was registered to
the diffusion space.
Tractography
We evaluated the ability of different tractography approaches to reliably reconstruct structural
connectivity provided by the tract-tracing experiments. We considered three local models:
(un) the diffusion tensor (DT) model; (b) fiber orientation distribution (FOD) estimated with a
constrained spherical deconvolution (CSD) using the tournier algorithm (Tournier, Calamante,
& Connelly, 2013); et (c) FOD estimated with the multishell multitissue CSD (msmt CSD) us-
ing the dhollander algorithm, which provides an unsupervised estimation of tissue-specific
1042
Diffusion tensor model (DT):
A mathematical model representing
the orientation of the diffusion of
water molecules as an ellipsoid
(or cigar).
Fiber orientation distribution (FOD):
A complex mathematical model
representing the orientation of fiber
populations that may contain
multiple orientations.
Constrained spherical deconvolution
(CSD):
A high-order mathematical model
that allows inference of the fiber
orientation distribution.
Neurosciences en réseau
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
un
_
0
0
0
9
8
p
d
t
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Comparing tractography and tract-tracing in the ferret brain
response functions. The msmt CSD was performed using a WM/CSF compartment model
(Jeurissen, Tournier, Dhollander, Connelly, & Sijbers, 2014). Each of the three tractography
models was then paired with a deterministic and a probabilistic tracking algorithm. Determin-
istic DT-based tracking was performed using Euler integration (Tensor_Det; Basser, Pajevic,
Pierpaoli, Duda, & Aldroubi, 2000), while DT-based probabilistic tracking used bootstrapping
(Tensor_Prob; Jones, 2008). CSD-based tractography was performed according to FOD peaks
either deterministically (SD_STREAM; Tournier, Calamante, & Connelly, 2012) or probabilis-
tically (iFOD2; Tournier, Calamante, & Connelly, 2010). A spherical harmonic order of 8 était
used for CSD-based estimations. One million streamlines were tracked over the full brain with
the parameters recommended by MRtrix3: stepsize 0.024 mm (0.12 mm for iFOD2), angle
90
for iFOD2), minimal streamline length 1.2 mm, maximal length 2.4 cm.
Streamline seeds were produced at random locations within the brain mask until the defined
number of streamlines was reached. To prevent streamlines from going across sulci, the brain
mask was used as a stopping criterion.
per voxel (45
◦
◦
Tractography-Based Connectivity Matrices
Structural connectivity matrices were extracted from the tractography results using the num-
ber of streamlines connecting pairs of regions. The connectivity matrices are available in the
Informations complémentaires. Matrices reporting the averaged fiber lengths between regions were
also computed. Alors, structural connectivity matrices were normalized using fractional scal-
ing, such that the number of streamlines between pairs of regions were divided by the sum of
the streamline counts connected to each of the regions, excluding self-connections (Donahue
et coll., 2016). The weights then represent the fraction of streamlines (FS).
All MRI data analysis was performed using the MRtrix3 software (http://www.mrtrix.org/),
and custom scripts for Python (http://www.python.org), including Python packages Nipype
(Gorgolewski et al., 2011), NiBabel (Brett et al., 2018), and NumPy (Oliphant, 2015). All the
scripts and data are available on the following GitHub repository: Delettre & Toro (2019).
Anatomical Tract-Tracing Data
Structural connectivity data from anatomical tract-tracing experiments in adult ferrets (de
2 years of age) were obtained from Dell et al. (2019un, 2019b, 2019c). The experiments exam-
ined the cortico-cortical and cortico-thalamic connectivity of areas 17, 18, 19, et 21 (occip-
ital visual cortex), PPc and PPr (posterior parietal visual cortex), and 20a and 20b (temporal
visual cortex) in adult ferrets by means of retrograde biotinylated dextran amine tracer (BDA).
By retrograde tract-tracing, neuronal projections were traced from the axon terminations lo-
cated in areas 17, 18, 19, 21, PPc, PPr, 20un, and 20b (injection sites) of one hemisphere to
the neurons’ cell bodies, located in different brain regions and across both brain hemispheres.
Ainsi, the injected brain regions were defined as the target regions, and the brain regions with
cell bodies that were labeled positive for BDA were defined as the source regions. The con-
nections were then quantified by obtaining a fraction of labeled neuron (FLN) valeur; refer to
Dell et al. (2019un, 2019b, 2019c) for a detailed explanation on the experimental procedures.
En outre, for the purpose of this study, we considered only ipsilateral projections and ad-
justed the connectivity matrix and FLN values to exclude contralateral projections, pour
focus on the edge-complete subnetwork.
Tract-Tracing-Based Connectivity Matrix
A structural connectivity matrix was assembled from the left hemisphere such that the weights
represent the number of retrograde labeled neurons between pairs of regions. This provided
Neurosciences en réseau
1043
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
un
_
0
0
0
9
8
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Comparing tractography and tract-tracing in the ferret brain
us with an asymmetric (directed) matrix indicating projections to the tracer injection sites.
The weights were normalized using the fraction of labeled neurons (FLN), the number of la-
beled neurons in a source region divided by the total number of labeled neurons from the
injected region (Markov et al., 2014). Considering that diffusion MRI tractography does not
provide information on the directionality of the connections, the tract-tracing matrix was also
symmetrized by averaging FLN values in both directions.
Statistical Analyses
Correlation coefficients were used to quantify the degree to which diffusion MRI tractography
matched tract-tracing data. Thereafter, in order to characterize the ability of tractography to
map structural weights, the strongest connections in the tract-tracing data were progressively
removed from both sources (tractography and tract-tracing), and correlation coefficients were
then computed on the remaining connections.
In the same way, we also computed corre-
lation coefficients when excluding the weakest tract-tracing connections. Such exploration
allowed us to probe whether the correlation coefficient values were mainly driven by strong
relations, which correlate with short-range connections and are statistically more likely to
be detected. Par contre, weak or longer range connections are more likely to be spurious (false
positives). In order to deal with the lognormal distribution of structural connectivity values in
both diffusion MRI tractography and tract-tracing experiments, we computed either the non-
parametric Spearman’s correlation coefficient or the Pearson’s correlation coefficient on the
values logarithmically transformed (both FLN and FS). In order to cope with absent connec-
tions when performing the logarithmic transformation, for the Pearson’s correlations, all raw
counts of streamlines and labeled neurons (before the normalizations) were incremented by
1. Confidence intervals were computed using bootstrapping at a confidence level of 95%. Dans
addition, we computed the partial Spearman correlations when regressing out the Euclidean
distance between the centroids of our cortical areas. We first modeled the relationship be-
tween the logarithm of the FLN and FS values with the Euclidean distance between each pair
of cortical areas and extracted its residuals. The residuals from the FLN and the FS were then
correlated using Spearman’s correlation.
To quantify the ability of tractography to correctly detect existing tract-tracing connections,
we computed basic classification performance measures: sensitivity, specificity, and precision.
Sensitivity quantifies how good a measure is at detecting true connections, while specificity
estimates how good a quantity is at avoiding false detections. Average precision quantifies how
many of the positively detected connections were relevant. Tract-tracing structural connectivity
matrix was progressively thresholded and binarized keeping a given proportion of the strongest
weights, depuis 0.1 à 0.9 by step of 0.1 (Rubinov & Sporns, 2010) in order to build a series of
receiver operating characteristic and precision and recall curves. The performance measures
were then averaged for each threshold as summary statistics.
The statistical analyses were performed using R (https://www.R-project.org/) et Python
with the scikit-learn package (Garreta & Moncecchi, 2013).
RÉSULTATS
Structural connectivity estimates from diffusion MRI tractography were all highly positively
−3;
correlated with the tract-tracing data (Spearman’s rho ranging from 0.67 à 0.91, all p < 10
see Table 1 and Figure 1). Probabilistic tractography algorithms increased the correlation val-
ues obtained with deterministic tractography. The DT model was not able to recover all the
connections found in tract-tracing data for both deterministic (7 connections) and probabilistic
Network Neuroscience
1044
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
a
_
0
0
0
9
8
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Comparing tractography and tract-tracing in the ferret brain
Table 1. Correlations between diffusion MRI tractography and tract-tracing experiments.
Undirected tract-tracing matrix
Directed tract-tracing matrix
Spearman
Pearson
Spearman
Pearson
Deterministic
DTI
CSD
0.67 ** [0.44–0.94]
0.69 ** [0.37–0.86]
0.50 * [0.22–0.82]
0.48 * [0.07–0.75]
0.76 ** [0.56–1.00]
0.68 ** [0.36–0.86]
0.62 * [0.36–0.93]
0.53 * [0.13–0.78]
msmt CSD
0.71 ** [0.50–0.98]
0.71 ** [0.40–0.87]
0.57 * [0.22–0.94]
0.55 ** [0.16–0.79]
Probabilistic
DTI
CSD
0.79 ** [0.65–0.99]
0.78 ** [0.53–0.90]
0.67 ** [0.49–0.91]
0.63 ** [0.27–0.83]
0.91 ** [0.83–1.00]
0.88 ** [0.73–0.95]
0.77 ** [0.56–1.00]
0.69 ** [0.38–0.86]
msmt CSD
0.87 ** [0.76–1.00]
0.89 ** [0.76–0.95]
0.70 ** [0.46–0.98]
0.67 ** [0.33–0.85]
P values smaller than 0.001 are indicated by ** and p values inferior to 0.05 by *.
(5 connections) tractography, as shown by the white circles that correspond to connections that
were not found by the diffusion MRI tractography (lowest rank), and hence the average stream-
line length of these connections is 0 (white circles; Figures 1C and 1D). The 95% confidence
intervals for the relative predictive power of the different tractography algorithms overlapped,
suggesting an absence of statistically significant differences. Consistent results were observed
when using the Pearson correlation coefficient (Table 1; and Supplementary Figure 1, Support-
ing Information).
Spearman correlations were decreased after regressing out the Euclidean distance. Partial
Spearman correlation values were no longer statistically significant for deterministic tractogra-
phy (DTI: r = 0.36, p = 0.10; CSD: r = 0.39, p = 0.09; msmt CSD: r = 0.40, p = 0.07). How-
ever, for probabilistic tractography correlations remained statistically significant (DTI: r = 0.54,
p < 0.05; CSD: r = 0.66, p < 0.05; msmt CSD: r = 0.77, p < 0.05); see Supplementary Figure
8 (Supporting Information). Consistent results were observed when using the Pearson correla-
tion coefficient (Supplementary Table 1, Supporting Information).
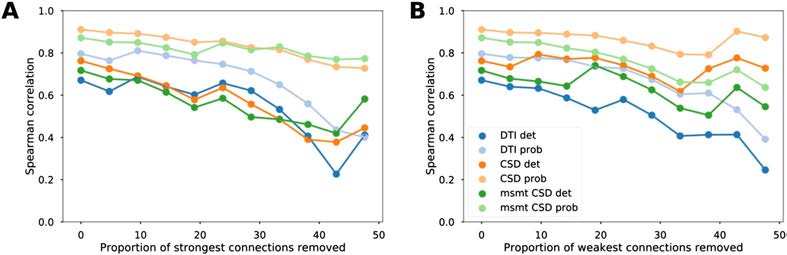
We then tested the influence of strong and weak connections on the relationship be-
tween diffusion MRI tractography and tract-tracing data. Structural connectivity estimates
from diffusion MRI tractography remained highly positively correlated to tract-tracing data
after progressive removal of 25% of the strongest connections and similarly after removal of
the weakest connections (Figure 2 and Supplementary Figure 2, Supporting Information, for
Figure 2. Reliability of the association between diffusion MRI tractography and tract-tracing data.
Evolution of the Spearman correlation values between tract-tracing and diffusion MRI tractography
data as a function of the proportion of strongest (A) and weakest (B) connections removed for the
different tractography algorithms.
Network Neuroscience
1045
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
a
_
0
0
0
9
8
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Comparing tractography and tract-tracing in the ferret brain
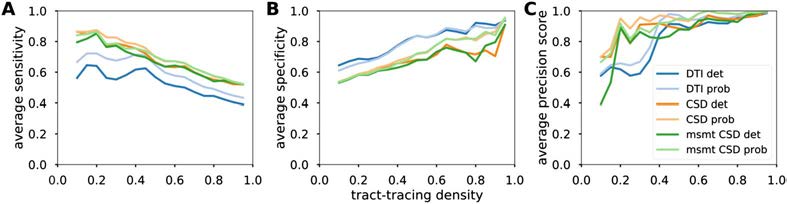
Figure 3. Detection performance of diffusion MRI tractography algorithms. Averaged sensitivity
(A), specificity (B), and precision (C) as a function of the tract-tracing density.
Pearson correlations). These results show that the correlations between diffusion tractography
and tract-tracing were not primarily driven by connections most likely to be recovered by dif-
fusion tractography because of their topographic proximity or their strength (strong weights).
Similarly, we observed that the correlations were not affected by the weakest connections,
which are generally more sensitive to noise (leading to false positives); otherwise there would
have been an increase in correlation values.
Measures of sensitivity/specificity/precision give an indication of the detectability of the con-
nections. Our results were averaged and plotted as a function of the proportion of tract-tracing
connections (Figure 3). CSD-based algorithms had generally higher sensitivity and precision
compared with the diffusion tensor model, while tensor-based tractography had slightly higher
specificity.
All analyses were also performed comparing tractography with the directed structural con-
nectivity from tract-tracing. We found decreased yet still statistically significant associations
(see Table 1; Supplementary Figures 3 to 7, Supporting Information).
DISCUSSION
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
a
_
0
0
0
9
8
p
d
.
/
t
In the present study, we investigated the ability of different diffusion MRI tractography algo-
rithms to reliably map ferret brain structural connectivity as retrieved from invasive tract-tracing
experiments. We found that structural connectivity estimates from tractography were highly
correlated with tract-tracing data. The different algorithms presented small, nonsignificant
variations. Our findings in the ferret results from previous studies in the monkey (Donahue
et al., 2016) and the mouse (Calabrese et al., 2015) as well as results using manganese tracing
in the pig (Knösche et al., 2015). Overall, these findings enhance our confidence in diffusion
MRI tractography as a powerful tool for exploring the structural connectional architecture of
the brain.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
We obtained estimates of the reliability of six different tractography algorithms with regard
to tract-tracing data for the same cortical areas of the ferret brain. CSD-based algorithms pre-
sented the highest degree of concordance with tract-tracing data, and DT-based algorithms the
least. However, the differences in correlation values did not appear to be statistically signifi-
cant, as suggested by the overlapping 95% confidence intervals. High concordance with no
particular algorithm outperforming the others was also reported when matching tract pathways
from tractography and manganese tracing for a set of tractography algorithms (Knösche et al.,
2015). Comparable overall correlations of the weighted connections have been obtained in
the macaque brain, with a Spearman’s correlation of 0.59 (Donahue et al., 2016). However,
here we report little effect of the strongest/weakest connections in the correlation values. The
Network Neuroscience
1046
Comparing tractography and tract-tracing in the ferret brain
gradual decrease of our correlations indicated that our correlations were not amplified by the
weight of strong connections or underestimated by a high amount of false positives stemming
from weak connections.
In addition, we showed high detection performance values across
algorithms. Consistent with the correlation analysis, we observed higher performances for
CSD-based algorithms in terms of precision. Also consistent with prior studies, DT-based re-
sults appeared to give slightly higher specificity than CSD-based algorithms, to the detriment
of their sensitivity (Knösche et al., 2015; Sarwar et al., 2018). Such results are likely due to the
lower ability of diffusion tensor models to resolve complex fiber geometries (Maier-Hein et al.,
2017; Zalesky et al., 2016).
Our correlations were decreased and no longer statistically significant after regressing out
distance, for deterministic tractography. Similar results have been reported in the macaque,
where correlations decreased from r = 0.59 to r = 0.22 after regressing out the distance
effects (Donahue et al., 2016). Tractography’s ability to recover tracts is expected to decrease
as a function of the distance because of technical biases (e.g., in probabilistic tractography, the
probability to follow a given path drops exponentially with distance). Thus, it has been shown
that structural connectivity estimates from diffusion MRI tractography are highly related to their
lengths (Liptrot, Sidaros, & Dyrby, 2014; Roberts et al., 2016). On the other hand, distance
is a biological principle for the preferential connection between two brain areas (Hilgetag,
Medalla, Beul, & Barbas, 2016). As such, it remains challenging to disentangle these two
factors from tractography outputs. Our regions can also be considered as neighbors relative to
the whole-brain size as they are all located in the occipital, parietal, and temporal lobes of one
hemisphere. This proximity could have inflated our correlations benefiting from the ability of
tractography and tract-tracing to more accurately recover connections from neighboring areas.
In any case, the correlations in which distance was regressed out, which corrects for both
effects of distance (proximity and remoteness), maintain statistically significant correlations
for all probabilistic tractography algorithms (especially based on CSD).
Our results showed a high correlation between diffusion MRI tractography and tract-tracing
data; however, we note the limitations in our methodology. First, the two datasets had different
origins (i.e., the tract-tracing and tractography were not performed in the same animal) and the
sample sizes were very small. Although the ferrets could all be considered mature in terms of
brain development (Jackson, Peduzzi, & Hickey, 1989; Neal et al., 2007), the ferret used for
the MR imaging was only 2 months old, while the animals used in tract-tracing were around 2
years old. This may have increased interindividual variability and induced a bias in our cortical
parcellations: Although the sulcal and gyral patterns (used for cortical parcellation of MRI data,
in relation to Bizley & King, 2009) are unchanged after postnatal week 4, the ferret brain is
still undergoing maturation and growth in all brain structures. The ferret brain growth reaches
a plateau at postnatal week 24; however, the differences due to age should be only minor
because the cortical architecture at 2 months of age resembles that at adult age (Jackson et al.,
1989; Neal et al., 2007). Similarly, the cortex continues to undergo rostrocaudal expansion
until postnatal week 24, after which the ferret brain reaches its adult size; however, previous
studies have showed no significant changes of MRI-measured indices (Barnette et al., 2009;
Neal et al., 2007). Although the brain of a 2-month-old ferret is structurally similar to that of
an adult brain, it still undergoes functional differentiation and pruning of connections, which
could result in a minor shift in the placement of our cortical cytoarchitectonic parcellations,
and such parcellations can be observed only in histological sections and not in MRI scans.
Second, tract-tracing experiments, despite considered as ground truth, are not exempted
from limitations, such as the creation of false positives and false negatives, specificity of tracer
Network Neuroscience
1047
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
a
_
0
0
0
9
8
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Comparing tractography and tract-tracing in the ferret brain
and antibody used, spillage of tracer, and passive diffusion (Heimer & Robards, 2013; Köbbert
et al., 2000; Zaborszky, Wouterlood, & Lanciego, 2006). In addition, in this study we con-
sidered only the retrograde connections that are easier to quantify and neglected anterograde
tracing results.
In sum, this study allowed us to validate structural connectivity estimates from diffusion
MRI tractography by comparison with tract-tracing data in the ferret brain, and it provided an
estimation of the performance of three diffusion tractography algorithms, namely DT, CSD,
and msmt CSD, using both deterministic and probabilistic tracking. Generally, the currently
available connectivity data for the ferret are quite limited; therefore, whole-brain tractography
based on diffusion imaging can provide an initial, worthwhile estimate of structural connectiv-
ity that can be used for further anatomical, developmental, and computational studies of the
ferret brain.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00098.
AUTHOR CONTRIBUTIONS
Céline Delettre: Conceptualization; Data curation; Formal analysis; Methodology; Software;
Writing – Original Draft; Writing – Review & Editing. Arnaud Messé: Conceptualization; Data
curation; Formal analysis; Investigation; Methodology; Validation; Writing – Original Draft;
Writing – Review & Editing. Leigh-Anne Dell: Data curation; Investigation; Methodology;
Writing – Original Draft; Writing – Review & Editing. Ophélie Foubet: Data curation; Re-
sources. Katja Heuer: Software. Benoit Larrat: Investigation; Resources; Writing – Review
& Editing. Sebastien Meriaux:
Jean-Francois Mangin: Concep-
Investigation; Resources.
Isabel Reillo: Project administration; Resources. Camino de Juan
tualization; Resources.
Romero: Project administration; Resources. Victor Borrell: Project administration; Resources.
Roberto Toro: Conceptualization; Funding acquisition; Investigation; Project administration;
Resources; Software; Supervision; Writing – Original Draft; Writing – Review & Editing. Claus
C. Hilgetag: Conceptualization; Funding acquisition; Investigation; Project administration; Re-
sources; Supervision; Writing – Original Draft; Writing – Review & Editing.
FUNDING INFORMATION
Claus C. Hilgetag, Deutsche Forschungsgemeinschaft (http://dx.doi.org/10.13039/501100001659),
Award ID: SFB 936/A1/Z3 and SPP 2041 / HI 1286/6-1. Claus C. Hilgetag, Human Brain
Project, Award ID: HBP-SGA2 (785907)/ SGA2. Roberto Toro, Agence Nationale de la
Recherche (http://dx.doi.org/10.13039/501100001665), Award ID: ANR-15-HBPR-0005.
REFERENCES
Andersson, J. L. R., & Sotiropoulos, S. N. (2016). An integrated ap-
proach to correction for off-resonance effects and subject move-
ment in diffusion MR imaging. NeuroImage, 125, 1063–1078.
Azadbakht, H., Parkes, L. M., Haroon, H. A., Augath, M.,
Logothetis, N. K., de Crespigny, A.,
J. M.
(2015). Validation of high-resolution tractography against in vivo
tracing in the macaque visual cortex. Cerebral Cortex, 25(11),
4299–4309.
. Parker, G.
.
.
Barnette, A. R., Neil, J. J., Kroenke, C. D., Griffith, J. L., Epstein,
A. A., Bayly, P. V., . . . Inder, T. E. (2009). Characterization of brain
development in the ferret via MRI. Pediatric Research, 66(1),
80–84.
Basser, P. J., Pajevic, S., Pierpaoli, C., Duda, J., & Aldroubi, A.
(2000). In vivo fiber tractography using DT-MRI data. Magnetic
Resonance in Medicine, 44(4), 625–632.
Bizley, J. K., Bajo, V. M., Nodal, F. R., & King, A. J. (2015). Cortico-
Journal of
cortical connectivity within ferret auditory cortex.
Comparative Neurology, 523(15), 2187–2210.
Bizley, J. K., & King, A. J. (2009). Visual influences on ferret auditory
cortex. Hearing Research, 258(1–2), 55–63.
Network Neuroscience
1048
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
a
_
0
0
0
9
8
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Comparing tractography and tract-tracing in the ferret brain
Bota, M., Sporns, O., & Swanson, L. W. (2015). Architecture of
the cerebral cortical association connectome underlying cogni-
tion. Proceedings of the National Academy of Sciences, 112(16),
E2093–E2101.
Brett, M., Hanke, M., Markiewicz, C., Côté, M. -A., McCarthy, P.,
Ghosh, S., . . . Basile. (2018). Nipy/nibabel: 2.3.0. https://doi.
org/10.5281/zenodo.1287921
Calabrese, E., Badea, A., Cofer, G., Qi, Y., & Johnson, G. A. (2015).
A diffusion MRI tractography connectome of the mouse brain and
comparison with neuronal tracer data. Cerebral Cortex, 25(11),
4628–4637.
Delettre, C., & Toro, R. (2019). A comparison between diffusion
tractography and tract tracing in ferrets. GitHub. https://github.
com/neuroanatomy/FerretDiffusionTractTracingComparison
Dell, L.-A., Innocenti, G. M., Hilgetag, C. C., & Manger, P. R.
(2019a). Cortical and thalamic connectivity of occipital visual
cortical areas 17, 18, 19 and 21 of the domestic ferret (Mustela
putorius furo). Journal of Comparative Neurology. https://doi.org/
10.1002/cne.24631
Dell, L.-A., Innocenti, G. M., Hilgetag, C. C., & Manger, P. R.
(2019b). Cortical and thalamic connectivity of posterior parietal
visual cortical areas PPc and PPr of the domestic ferret (Mustela
putorius furo). Journal of Comparative Neurology. https://doi.org/
10.1002/cne.24630
Dell, L.-A., Innocenti, G. M., Hilgetag, C. C., & Manger, P. R.
(2019c). Cortical and thalamic connectivity of temporal visual
cortical areas 20a and 20b of the domestic ferret (Mustela puto-
rius furo). Journal of Comparative Neurology. https://doi.org/10.
1101/492728
Donahue, C.
J., Sotiropoulos, S. N.,
Jbabdi, S., Hernandez-
Fernandez, M., Behrens, T. E., Dyrby, T. B., . . . Glasser, M. F.
(2016). Using diffusion tractography to predict cortical connec-
tion strength and distance: A quantitative comparison with trac-
ers in the monkey. Journal of Neuroscience, 36(25), 6758–6770.
Dyrby, T. B., Baaré, W. F. C., Alexander, D. C., Jelsing, J., Garde, E.,
& Søgaard, L. V. (2011). An ex vivo imaging pipeline for produc-
ing high-quality and high-resolution diffusion-weighted imaging
datasets. Human Brain Mapping, 32(4), 544–563.
Dyrby, T. B., Innocenti, G. M., Bech, M., & Lundell, H. (2018). Val-
idation strategies for the interpretation of microstructure imag-
ing using diffusion MRI. NeuroImage. https://doi.org/10.1016/j.
neuroimage.2018.06.049
Engel, A. K., Gerloff, C., Hilgetag, C. C., & Nolte, G. (2013). In-
trinsic coupling modes: Multiscale interactions in ongoing brain
activity. Neuron, 80(4), 867–886.
Feng, Y., Clayton, E. H., Chang, Y., Okamoto, R. J., & Bayly, P. V.
(2013). Viscoelastic properties of the ferret brain measured in
vivo at multiple frequencies by magnetic resonance elastography.
Journal of Biomechanics, 46(5), 863–870.
Fornito, A., & Bullmore, E. T.
(2015). Connectomics: A new
paradigm for understanding brain disease. European Neuropsy-
chopharmacology, 25(5), 733–748.
Fox,
J. G.
Blackwell.
(1998). Biology and diseases of
the ferret. Wiley-
Gao, Y., Choe, A. S., Stepniewska, I., Li, X., Avison, M. J., &
Anderson, A. W. (2013). Validation of DTI tractography-based
measures of primary motor area connectivity in the squirrel
monkey brain. PLoS ONE. https://doi.org/10.1371/journal.pone.
0075065
Garreta, R., & Moncecchi, G. (2013). Learning scikit-learn: Machine
learning in python. Packt Publishing.
Gorgolewski, K., Burns, C. D., Madison, C., Clark, D., Halchenko,
Y. O., Waskom, M. L., & Ghosh, S. S. (2011). Nipype: A flexible,
lightweight and extensible neuroimaging data processing frame-
work in Python. Frontiers in Neuroinformatics, 5, 13.
Hagmann, P., Sporns, O., Madan, N., Cammoun, L., Pienaar, R.,
Wedeen, V. J., . . . Grant, P. E. (2010). White matter matura-
tion reshapes structural connectivity in the late developing hu-
man brain. Proceedings of the National Academy of Sciences,
107(44), 19067–19072.
Hasan, K. M., Parker, D. L., & Alexander, A. L. (2001). Comparison
of gradient encoding schemes for diffusion-tensor MRI. Journal
of Magnetic Resonance Imaging, 13(5), 769–780.
Heimer, L., & Robards, M. J. (2013). Neuroanatomical tract-tracing
methods. Springer Science & Business Media.
Heuer, K., Ghosh, S., Sterling, A. R., & Toro, R. (2016). Open neu-
roimaging laboratory. Research Ideas and Outcomes, 2, e9113.
Hilgetag, C. C., Medalla, M., Beul, S. F., & Barbas, H. (2016). The
primate connectome in context: Principles of connections of the
cortical visual system. NeuroImage, 134, 685–702.
Holmes, H. E., Powell, N. M., Ma, D., Ismail, O., Harrison, I. F.,
Wells, J. A., . . . Lythgoe, M. F. (2017). Comparison of in vivo
and ex vivo MRI for the detection of structural abnormalities in
a mouse model of tauopathy. Frontiers in Neuroinformatics, 11,
20.
Jackson, C. A., Peduzzi, J. D., & Hickey, T. L. (1989). Visual cor-
tex development in the ferret. I. Genesis and migration of visual
cortical neurons. Journal of Neuroscience, 9(4), 1242–1253.
Jenkinson, M., Bannister, P., Brady, M., & Smith, S. (2002). Im-
proved optimization for the robust and accurate linear registra-
tion and motion correction of brain images. NeuroImage, 17(2),
825–841.
Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W.,
& Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790.
Jeurissen, B., Descoteaux, M., Mori, S., & Leemans, A. (2017). Dif-
fusion MRI fiber tractography of the brain. NMR in Biomedicine.
https://doi.org/10.1002/nbm.3785
Jeurissen, B., Tournier,
J.-D., Dhollander, T., Connelly, A., &
Sijbers, J. (2014). Multi-tissue constrained spherical deconvo-
lution for improved analysis of multi-shell diffusion MRI data.
NeuroImage, 103, 411–426.
Jones, D. K. (2008). Tractography gone wild: Probabilistic fibre
tracking using the wild bootstrap with diffusion tensor MRI. IEEE
Transactions on Medical Imaging, 27(9), 1268–1274.
Jones, D. K., Knösche, T. R., & Turner, R. (2013). White matter in-
tegrity, fiber count, and other fallacies: The do’s and don’ts of
diffusion MRI. NeuroImage, 73, 239–254.
Kandel, E., Schwartz, J., Jessell, T., Siegelbaum, S., & Hudspeth,
A. J. (2012). Principles of neural science (5th ed.). McGraw-Hill
Professional.
Kasprian, G., Brugger, P. C., Weber, M., Krssák, M., Krampl, E.,
Herold, C., & Prayer, D. (2008). In utero tractography of fetal
white matter development. NeuroImage, 43(2), 213–224.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
a
_
0
0
0
9
8
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
1049
Comparing tractography and tract-tracing in the ferret brain
Kellner, E., Dhital, B., Kiselev, V. G., & Reisert, M. (2016). Gibbs-
ringing artifact removal based on local subvoxel-shifts. Magnetic
Resonance in Medicine, 76(5), 1574–1581.
Knösche, T. R., Anwander, A., Liptrot, M., & Dyrby, T. B. (2015).
Validation of tractography: Comparison with manganese tracing.
Human Brain Mapping, 36(10), 4116–4134.
Köbbert, C., Apps, R., Bechmann, I., Lanciego, J. L., Mey, J., &
Thanos, S. (2000). Current concepts in neuroanatomical tracing.
Progress in Neurobiology, 62(4), 327–351.
Liptrot, M. G., Sidaros, K., & Dyrby, T. B. (2014). Addressing the
path-length-dependency confound in white matter tract segmen-
tation. PLoS ONE, 9(5), e96247.
Maier-Hein, K. H., Neher, P. F., Houde,
J.-C., Côté, M.-A.,
Garyfallidis, E., Zhong, J., . . . Descoteaux, M. (2017). The chal-
lenge of mapping the human connectome based on diffusion
tractography. Nature Communications, 8(1), 1349.
Markov, N. T., Vezoli, J., Chameau, P., Falchier, A., Quilodran, R.,
Huissoud, C., . . . Kennedy, H.(2014). Anatomy of hierarchy:
Feedforward and feedback pathways in macaque visual cortex.
Journal of Comparative Neurology, 522(1), 225–259.
McRobbie, D. W., Moore, E. A., & Graves, M. J. (2017). MRI from
picture to proton. https://doi.org/10.1017/9781107706958
Neal, J., Takahashi, M., Silva, M., Tiao, G., Walsh, C. A., & Sheen,
V. L. (2007). Insights into the gyrification of developing fer-
ret brain by magnetic resonance imaging. Journal of Anatomy,
210(1), 66–77.
Oliphant, T. (2015). Guide to NumPy (2nd ed.). CreateSpace.
Park, H.-J., & Friston, K. (2013). Structural and functional brain
networks: From connections to cognition. Science, 342(6158),
1238411.
Roberts, J. A., Perry, A., Lord, A. R., Roberts, G., Mitchell, P. B.,
Smith, R. E., . . . Breakspear, M. (2016). The contribution of
geometry to the human connectome. NeuroImage, 124(Pt. A),
379–393.
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069.
Sarwar, T., Ramamohanarao, K., & Zalesky, A. (2018). Mapping
connectomes with diffusion MRI: Deterministic or probabilistic
tractography? Magnetic Resonance in Medicine. https://doi.org/
10.1002/mrm.27471
Schilling, K. G., Daducci, A., Maier-Hein, K., Poupon, C.,
Houde, J. C., Nath, V., . . . Descoteaux, M. (2018). Challenges
in diffusion MRI tractography: Lessons learned from interna-
tional benchmark competitions. Magnetic Resonance Imaging,
57, 194–209.
Schilling, K. G., Gao, Y., Stepniewska, I., Janve, V., Landman, B. A.,
& Anderson, A. W. (2019). Anatomical accuracy of standard-
practice tractography algorithms in the motor system: A histolog-
ical validation in the squirrel monkey brain. Magnetic Resonance
Imaging, 55, 7–25.
Schilling, K. G., Nath, V., Hansen, C., Parvathaneni, P., Blaber, J.,
Gao, Y., . . . Landman, B. A. (2019). Limits to anatomical accuracy
of diffusion tractography using modern approaches. NeuroImage,
185, 1–11.
Sinke, M. R. T., Otte, W. M., Christiaens, D., Schmitt, O., Leemans,
A., van der Toorn, A., . . . Dijkhuizen, R. M. (2018). Diffusion
MRI-based cortical connectome reconstruction: Dependency
on tractography procedures and neuroanatomical characteristics.
Brain Structure and Function, 223(5), 2269–2285.
Sporns, O. (2010). Networks of the brain. MIT Press.
Thomas, C., Ye, F. Q., Irfanoglu, M. O., Modi, P., Saleem, K. S.,
Leopold, D. A., & Pierpaoli, C. (2014). Anatomical accuracy
of brain connections derived from diffusion MRI tractography is
inherently limited. Proceedings of the National Academy of Sci-
ences, 111(46), 16574–16579.
Tournier, J.-D., Calamante, F., & Connelly, A. (2010). Improved
probabilistic streamlines tractography by 2nd order integra-
tion over fibre orientation distributions. Paper presented at the
ISMRM, Proceedings of the International Society for Magnetic
Resonance in Medicine.
Tournier, J.-D., Calamante, F., & Connelly, A. (2012). MRtrix: Diffu-
sion tractography in crossing fiber regions. International Journal
of Imaging Systems and Technology, 22(1), 53–66.
Tournier, J.-D., Calamante, F., & Connelly, A. (2013). Determina-
tion of the appropriate b value and number of gradient directions
for high-angular-resolution diffusion-weighted imaging. NMR in
Biomedicine, 26(12), 1775–1786.
Tustison, N. J., Avants, B. B., Cook, P. A., Zheng, Y., Egan, A.,
Yushkevich, P. A., & Gee, J. C. (2010). N4ITK: Improved N3
bias correction. IEEE Transactions on Medical Imaging, 29(6),
1310–1320.
Varela, F., Lachaux, J. P., Rodriguez, E., & Martinerie, J. (2001).
The brainweb: Phase synchronization and large-scale integra-
tion. Nature Reviews Neuroscience, 2(4), 229–239.
Veraart, J., Novikov, D. S., Christiaens, D., Ades-Aron, B., Sijbers, J.,
& Fieremans, E. (2016). Denoising of diffusion MRI using random
matrix theory. NeuroImage, 142, 394–406.
Visser, M. M., Yassi, N., Campbell, B. C. V., Desmond, P. M., Davis,
S. M., Spratt, N., . . . Bivard, A. (2018). White matter degenera-
tion after ischemic stroke: A longitudinal diffusion tensor imag-
ing study. Journal of Neuroimaging. https://doi.org/10.1111/jon.
12556
Zaborszky, L., Wouterlood, F. G., & Lanciego, J. L. (2006). Neu-
roanatomical tract-tracing: Molecules, neurons, and systems.
Springer Science & Business Media.
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., van den Heuvel,
M. P., & Breakspear, M. (2016). Connectome sensitivity or speci-
ficity: Which is more important? NeuroImage, 142, 407–420.
Zhang, T., Kong, J., Jing, K., Chen, H., Jiang, X., Li, L., . . . Liu,
T. (2018). Optimization of macaque brain DMRI connectome
by neuron tracing and myelin stain data. Computerized Medical
Imaging and Graphics, 69, 9–20.
Zingg, B., Hintiryan, H., Gou, L., Song, M. Y., Bay, M., Bienkowski,
M. S., . . .Dong, H.-W. (2015). Neural networks of the mouse
neocortex. Annals of Neurosciences, 22(4), . https://doi.org/10.
5214/ans.0972.7531.220409
Network Neuroscience
1050
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
3
8
1
8
6
6
7
6
1
n
e
n
_
a
_
0
0
0
9
8
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3