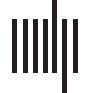RECHERCHE
High-accuracy individual identification using a
“thin slice” of the functional connectome
Lisa Byrge and Daniel P. Kennedy
Department of Psychological and Brain Sciences, Indiana University, Bloomington, IN, Etats-Unis
Mots clés: Functional connectivity MRI, Individual differences, Single-subject fMRI, Resting state,
Within-subject reliability
ABSTRAIT
Connectome fingerprinting—a method that uses many thousands of functional connections
in aggregate to identify individuals—holds promise for individualized neuroimaging. A better
characterization of the features underlying successful fingerprinting performance—how many
and which functional connections are necessary and/or sufficient for high accuracy—will
further inform our understanding of uniqueness in brain functioning. Ainsi, here we
examine the limits of high-accuracy individual identification from functional connectomes.
Using ∼ 3, 300 scans from the Human Connectome Project in a split-half design and
an independent replication sample, we find that a remarkably small “thin slice” of the
connectome—as few as 40 out of 64,620 functional connections—was sufficient to uniquely
identify individuals. Encore, we find that no specific connections or even specific networks
were necessary for identification, as even small random samples of the connectome
were sufficient. These results have important conceptual and practical implications for
the manifestation and detection of uniqueness in the brain.
RÉSUMÉ DE L'AUTEUR
Patterns of functional connectivity are so distinct between different people that they can be
used to predict individual identity with high accuracy. Ici, we show that a strikingly small
fraction of the functional connectome is actually needed to predict individual identity
(as few as 40 functional connections from 64,620). We further show that although certain
functional connections may be most informative, even small fractions of the connectome
selected at random can be used to identify individuals, and that no specific connections or
even networks are actually necessary. The results indicate that uniquely identifying signatures
of brain functioning are widely distributed throughout the brain and can be detected in a
much more compact manner than previously appreciated.
INTRODUCTION
Efforts toward accurately detecting, parsing, and understanding individual differences in func-
tional imaging data have grown tremendously in recent years. One key advance toward these
goals is the recent finding that individuals can be identified using fMRI data (Finn et al., 2015,
2017; Miranda-Dominguez et al., 2014, 2017; Vanderwal et al., 2017; Waller et al., 2017;
Peña-Gómez et al., 2017; Horien et al., 2018; Amico & Goñi, 2018). Because functional con-
nectomes, which quantify coordination between different regions spanning the entire brain,
are consistently more similar within individuals than across individuals (par exemple., Birn et al., 2013;
Laumann et al., 2015; Noble et al., 2017un; Gratton et al., 2018), it is possible to predict with
un accès ouvert
journal
Citation: Byrge, L., & Kennedy, D. P..
(2019). High-accuracy individual
identification using a “thin slice” of the
functional connectome. Réseau
Neurosciences, 3(2), 363–383.
https://doi.org/10.1162/netn_a_00068
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00068
Informations complémentaires:
https://doi.org/10.1162/netn_a_00068
Reçu: 8 Juin 2018
Accepté: 22 Août 2018
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Lisa Byrge
lbyrge@indiana.edu
Éditeur de manipulation:
Alex Fornito
droits d'auteur: © 2018
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
Functional connectome:
The set of all functional connections
associated with a given fMRI scan
and a given parcellation.
Functional connection (bord):
The extent to which the measured
activity of two different brain regions
is coordinated, as assessed via
correlation.
Fingerprinting algorithm:
Predicting which participant
contributed an fMRI scan based on
relative similarity across functional
connectomes.
Functional network:
Distributed brain regions whose
activity is coordinated.
Thin-slicing:
Making inferences from minimal
amounts of information (often from
brief experiences) that can be highly
accurate.
Parcellation:
Subdivision of the brain (typically
based on neuroanatomy or function)
into regions of interest within which
brain activity is measured.
extremely high accuracy which individual contributed a particular fMRI scan simply on the
basis of maximal similarity to functional connectomes from different scans.
Characterizing the specific features underlying the success of the fingerprinting algorithm—
how many or how few, and which, functional connections are needed to differentiate
individuals—will contribute to our understanding of
the expression of neurobiological
uniqueness. Cependant, thus far there have been only a few studies of the connectome features
underlying these successful identifications: we now know that fingerprinting accuracy is par-
ticularly high when using a subset of functional connections located within specific high-level
functional networks (Finn et al., 2015; Peña-Gómez et al., 2017) or between specific regions
of interest (Peña-Gómez et al., 2017), and that high identification accuracy can also be ob-
tained when connectomes are reconstructed using a procedure that effectively compresses
each connectome in a way that maximizes uniqueness (Amico & Goñi, 2018). But the lower
limits are as yet unknown: we do not yet know how many functional connections are neces-
sary for uniquely identifying individuals and how many are sufficient, and whether there are
any specific functional connections or high-level functional networks that are necessary for
high accuracy.
Ainsi, here we examine the limits of high-accuracy individual identification from functional
connectomes. We find that a strikingly small number of functional connections (edges)—as
few as 40 out of 64,620—is sufficient for high fingerprinting accuracy when those edges are
selected on the basis of their individual distinctness in an independent partition of the data.
Cependant, none of those edges—and indeed no specific edges and no specific networks at
all—are necessary for near-perfect identification accuracy. En effet, random selections of hun-
dreds of edges are also sufficient for high accuracy, suggesting that uniqueness in the functional
connectome, although particularly concentrated in certain areas, is diffusely distributed. Just as
identity can be predicted using a fraction of all possible individually diagnostic information in
many other domains—from a partial fingerprint or DNA segment or from a brief glimpse at
an occluded face—individuals can be identified using only a “thin slice” of the functional
connectome.
RÉSULTATS
Here we examine 3,333 functional connectomes constructed from 835 sujets (∼ 4 scans
chaque) from the Human Connectome project (Van Essen et al., 2013) in a split-half design.
D'abord, we seek to learn how small a subset (or “thin slice”) of the connectome can provide high
identification accuracy by including only those functional connections (edges) most likely to
distinguish individuals. To determine individually diagnostic value, we ranked edges according
to their ratio of mean across-subject variability and mean within-subject variability by using
an independent half of the dataset. Using the other half of the dataset, we then attempted to
predict individual identity by using a subset of the connectome containing only those most
individually distinct edges, using numerous different parcellations.
Identity Can Be Predicted Using a Very Small “Thin Slice” of the Connectome
The results, presented in Figure 1A, indicate that a remarkably small fraction of the full con-
nectome under most parcellations examined is needed to identify individuals with near-perfect
accuracy, with under 0.3% of all functional connections sufficient to provide effectively per-
fect accuracy (au-dessus de 98%) for all but the three coarsest parcellation granularities. (See also
Supporting Information Figure S1 for the same analysis conducted using a more stringent
test of accuracy, in which the pattern of results is effectively the same despite slightly lower
Neurosciences en réseau
364
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 1.
Individual identification accuracy as a function of how many of the most individually distinct edges in the functional connectome
are used for identification. (UN) Accuracy across different parcellations, expressed in terms of the percentage of the complete connectome
used. Par exemple, x = 1 denotes using a subset of only the most distinct 1% of edges to identify individuals. Percentages are cumulative
(par exemple., the most distinct 2% includes the most distinct 1%) such that subset size changes as percent increases. The insets depict the same data
rescaled to reveal very small x-axis values, with the left inset expressed in terms of the percentage of the complete connectome included
(as in the main figure) and the right inset expressed in terms of the number of edges included in each subset. Note that the total number of
edges varies across parcellations as indicated in the legend. (B) Accuracy across different contiguous temporal subsets of each scan, ranging
from approximately 1 to approximately 13 min of data, using the HCP_MMP1.0 parcellation only. (The line for ∼ 14 min includes the entire
scan rather than a temporal subset, and is a duplicate of the black line in Figure 1A presented for comparison.) Temporal subsets were
taken from randomly selected initial TRs for each length examined (100 starting locations for temporal lengths up to 12 min; 18 starting
locations, the maximum possible, pour 13 min). Individual distinctness (c'est à dire., individually diagnostic value) was independently computed using
the corresponding temporal subset of the training partition (c'est à dire., using the same number of TRs). The inset depicts the main figure rescaled to
reveal very small x-axis values, and is expressed in terms of the number of edges rather than percentages. All plots depict 99% confidence
intervals based on a bootstrap estimate of the mean across (un) five randomly selected parcellations of the same size or (b) five randomly selected
initial TRs for the same temporal length.
Neurosciences en réseau
365
“Thin slice” connectome fingerprinting
accuracy; Byrge & Kennedy, 2019.) Note also that neither head motion nor family structure is
driving the pattern of results, which are the same when the analysis is conducted using different
data quality thresholds (Supporting Information Figure S2, Byrge & Kennedy, 2019) and using
a subset of only unrelated participants (Supporting Information Figure S3, Byrge & Kennedy,
2019). Figure 1A (inset, droite) presents the same analysis rescaled as a function of the num-
ber of most distinct edges included in each connectome subset. Fait intéressant, despite the large
range of connectome sizes examined (depuis 1,225 à 124,750 edges), accuracy appears to con-
verge more across parcellations when similar numbers of edges rather than similar fractions of
edges are used for prediction, with around 40–60 edges sufficient in most parcellations.
We replicate this same finding in a second independently collected dataset (coarsely par-
cellated; 114 regions of interests [ROI]) composed of rest and video-watching scans from
48 individuals, using the same split-half design (half the subjects’ data for determining in-
dividually diagnostic value; half for prediction, with the ranking and prediction procedure
conducted separately for rest and for video scans): 98% identification accuracy is achieved
with a subset comprised of under 0.3% of the connectome for the rest scans (Supporting Infor-
mation Figure S4, purple line, Byrge & Kennedy, 2019) and for the video scans (Supporting
Information Figure S4, orange line, Byrge & Kennedy, 2019).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
HCP_MMP1.0 parcellation:
State-of-the-art neuroanatomically
and neurofunctionally informed
group-level 360-ROI parcellation
of the cortex.
We also conducted this same primary thin-slice analysis while varying the temporal extent
of the data included (c'est à dire., the number of contiguous TRs), rather than parcellation size, par
using the HCP_MMP1.0 parcellation only (Glasser et al., 2016) and using the HCP dataset
here and for all subsequent analyses unless noted. These analyses were conducted separately
within each temporal length (par exemple., connectomes constructed using X TRs were used both for
ranking and for prediction). The results, presented in Figure 1B, show a similar pattern: dans
most cases examined (for all but very short epochs), very high accuracy can be achieved using
a very small fraction of the connectome (sous 60/64,620 edges, ou 0.09% of connectome,
when at least 7 min of data are included, et sous 194 edges, ou 0.3%, for at least 3 min of
data). Both Figure 1A and 1B also demonstrate that identification accuracy using connectome
subsets can exceed accuracy for using the complete connectome (consistent with Finn et al.,
2015), sometimes negligibly so, especially when near-ceiling performance is achieved, mais
considerably for coarse parcellations or short temporal extents.
Dans l'ensemble, very high fingerprinting accuracy can be achieved with a tiny subset of the most diag-
nostic connectome edges. The structure driving these successful identifications (c'est à dire., “finger-
prints”) can be observed at a glance. Chiffre 2 presents the values for the most distinct 40 edges
(from the HCP_MMP1.0 parcellation) for all scans from several example subjects (for even more
sujets, see also Supporting Information Figure S5, Byrge & Kennedy, 2019). It is apparent
that functional connectivity patterns across these edges are consistent within individuals and
distinct from other individuals (see also Supporting Information Figure S6, Byrge & Kennedy,
2019, which separately examines within-individual similarity [or self-similarity] et à travers-
individual similarity [or other-similarity] following Amico & Goñi, 2018; the gap between with-
in and across- individual similarity is apparent and especially pronounced for high-ranked edges).
Individually Distinct Information Is Widespread Throughout the Cortex and Concentrated
in Fronto-Parietal Regions
Figure 3A depicts the individually diagnostic values computed to capture the distinctness
of each functional connection (bord) in the HCP_MMP1.0 parcellation, calculated as the
ratio of mean across-subject variability and mean within-subject variability in an indepen-
dent partition of the dataset. (The data used to create this plot has been made available at
Neurosciences en réseau
366
“Thin slice” connectome fingerprinting
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2.
Examples of distinct patterns (c'est à dire., fingerprints) of functional connectivity within indi-
vidual subjects. Each plot presents data from one randomly selected subject, with data from their
four different scans plotted in different colors. All plots depict functional connectivity values (Pêcheur
z-transformed correlations) for the 40 edges with highest individual distinctness. To allow for visu-
alization of negative correlation values, the radius extends from −0.5 at center to a maximum of
1.2; grid lines indicate 0, 0.5, et 1. See also Supporting Information Figure S5 (Byrge & Kennedy,
2019) for data from many other randomly selected subjects.
brainlab.psych.indiana.edu/resources/hcpmmp10_diagnostic_values.mat). Figure 3B depicts
the most distinct 1% of edges and least distinct 1% of edges in this parcellation. Consis-
tent with other reports (Miranda-Dominguez et al., 2014; Finn et al., 2015; Laumann et al.,
2015; Airan et al., 2016; Peña-Gómez et al., 2017; Gratton et al., 2018), edges that fall within
Neurosciences en réseau
367
“Thin slice” connectome fingerprinting
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
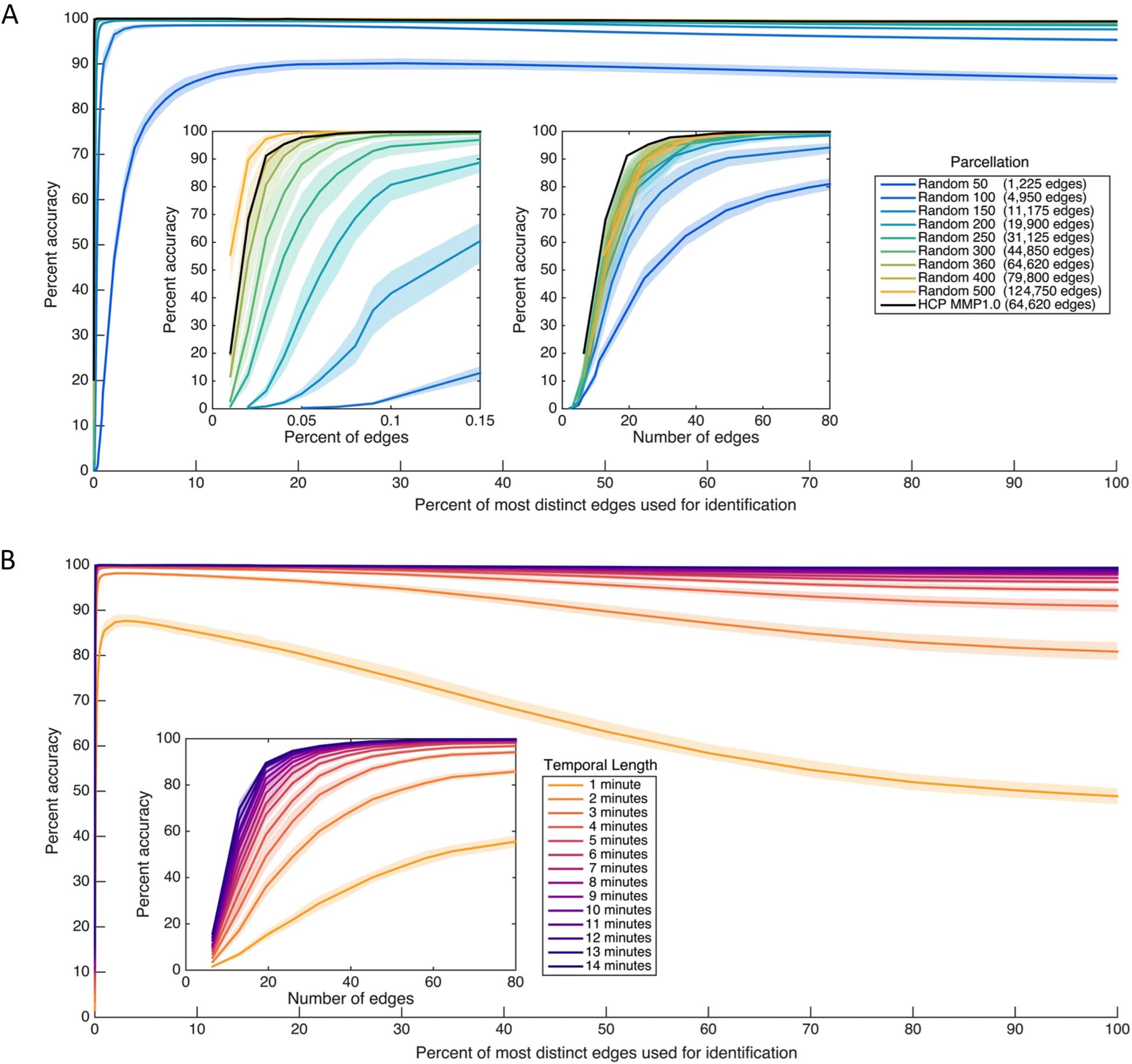
Chiffre 3.
Individually diagnostic values for the HCP_MMP1.0 (Glasser et al., 2016) parcellation established using an independent partition
of the dataset. Individually diagnostic value is computed here as the ratio of mean variability across subjects and mean variability within
sujets, such that values above 1 indicate some individually distinct information (par exemple., greater variability across than within subjects).
(UN) Individually diagnostic values for each edge, ordered to indicate large-scale functional membership (Yeo et al., 2011). As ratios, ces
values are unitless and indicate the magnitude with which across-subject variability exceeds within-subject variability (or vice versa); the high
values indicate edges that are considerably more variable across subjects than within them. (B) Circle plots visualizing the 1% of edges with
the highest (top) and the lowest (bottom) individually diagnostic value. Nodes and within-network edges are in color; across-network edges
are in gray. (C) Histogram of all diagnostic values. Gray vertical lines indicate, de gauche à droite, 1, the bottom 1%, and the top 1%. Note that
nearly all edges exceed 1, indicating some individually distinct information. See also Supporting Information Figure S9 (Byrge & Kennedy,
2019) for similar information for the replication dataset.
fronto-parietal and default networks are particularly individually distinct. The most distinct
edges tend to be intrahemispheric (Figure 3B) and within-network (purple edges in Figure 3A).
Less-distinct edges appear concentrated in the limbic regions, which are located in areas with
high artifact susceptibility near sinuses and subcortical structures and have a lower signal-
to-noise ratio (Yeo et al., 2011). Supporting Information Figure S7 (Byrge & Kennedy, 2019)
depicts the most and least distinct edges across several random parcellations; as is clear,
these edges largely converge across parcellations, with the same networks consistently im-
plicated as more informative or as less informative. Supporting Information Figure S8 (Byrge &
Kennedy, 2019) presents the top-ranked edges for the primary dataset and for the replication
rest dataset together for visual comparison, as well as the mean individually diagnostic values
within and between each pair of high-level functional networks; although individual edges
are not compared directly across these datasets because of data format differences (surface-
based vs. volumetric), similarities are apparent and mean individually diagnostic values for
high-level functional networks are highly correlated across datasets (r = 0.89, p << 0.001). See
also Supporting Information Figure S9 (Byrge & Kennedy, 2019) for a comparison of the
Network Neuroscience
368
“Thin slice” connectome fingerprinting
individually diagnostic values computed in the replication rest and replication movie data-
set using the same selection of training partition subjects: rankings were generally similar
(r = 0.74, p << 0.001) despite some modulation by task context (cf. visual and somatomotor
network among top-ranked edges in movie but not rest data).
Finally, the distribution of individual diagnostic values (Figure 3C) reveals that the vast ma-
jority of edges—throughout the cortex—exceed 1 (median = 1.45 with 99.98% > 1 dans le
primary dataset; median = 1.57 avec 99.97% > 1 in the replication rest dataset; median 1.63
avec 99.8% >1 in the replication video dataset), indicating some individual distinctness (par exemple.,
more across-subject variability than within-subject variability, on average). This suggests that
many connections (and not only the maximally ranked edges) might contribute to the identi-
fication of individuals.
Identity Can Be Predicted Without Highly Distinct Functional Connections
To examine this possibility, we attempted to predict individual identity using the reverse of
the first analysis: connectome subsets that exclude the most diagnostic edges. Donc, par exemple,
instead of predicting individual identity by using a subset of the most distinct 1% of edges (as in
Figure 1A), here we predict individual identity by using a subset of all functional connections
except the most distinct 1% (in other words, using the least distinct 99% of edges; see also
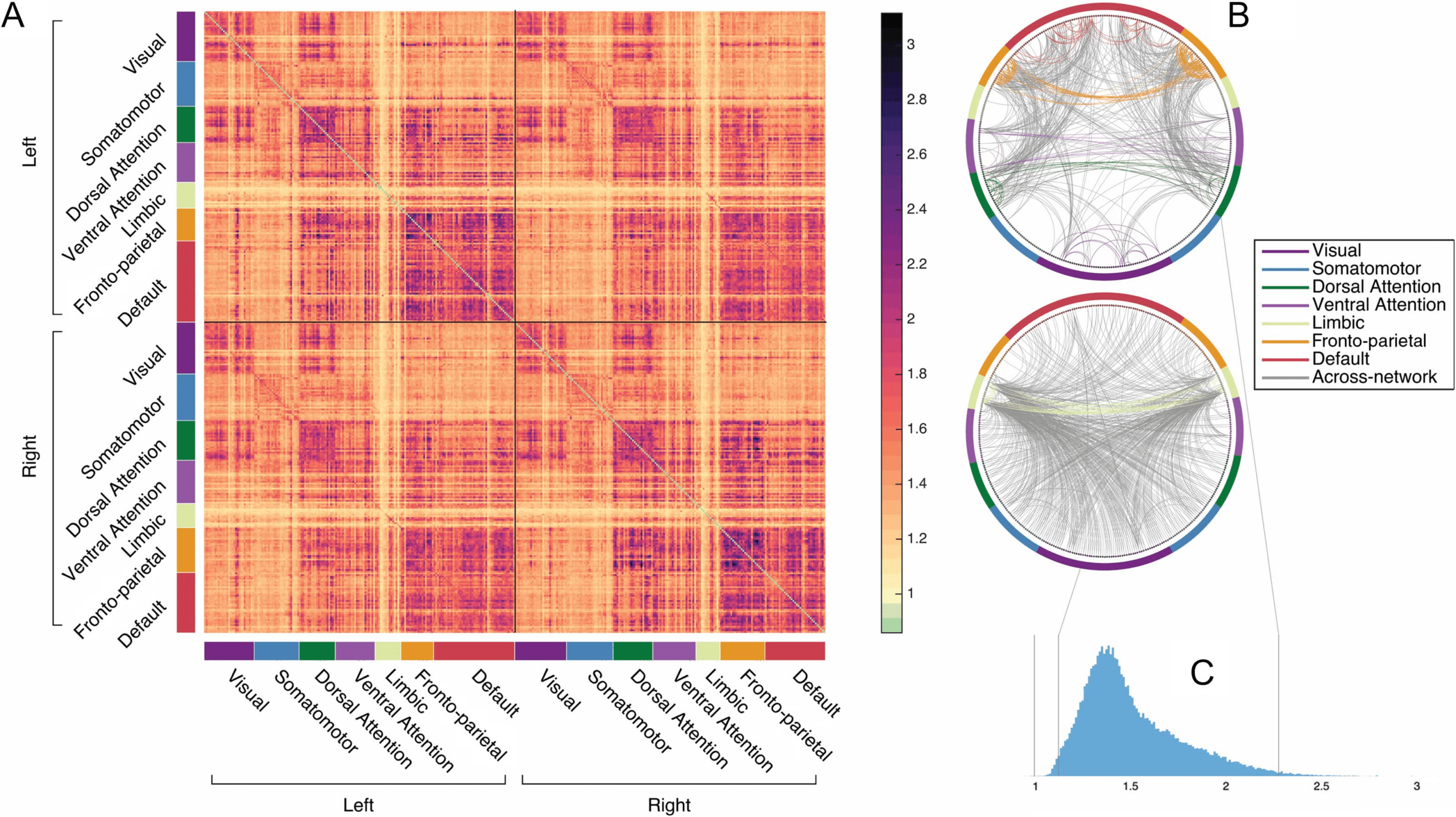
Vanderwal et al., 2017, for a similar approach). The results, depicted in Figure 4A, indicate that
although accuracy decreases as the most distinct edges are eliminated (as would be expected),
the edges with the highest distinctness are not required for high identification accuracy. For the
most fine-grained parcellations, successful fingerprinting can still be achieved even when the
most distinct 15% of the connectome is omitted, using the least distinct 85% of the connectome
to identify individuals.
In the previous analyses, the size of the connectome subset used for prediction has covaried
with the distinctness of the edges included in that subset. To decouple these two dimensions,
next, using the HCP_MMP1.0 parcellation only for this and subsequent analyses, we attempted
to predict individual identity by using connectome subsets composed of quantiles of ranked
edges, across several quantile sizes. Donc, more concretely, for percentiles (the coarsest quantile
size examined), we first predicted identity using the 646 most distinct edges (the first 1%),
and then using the 646 next most distinct edges (the second 1%), et ainsi de suite. In this way the
individually diagnostic value of edges within a subset is varied but the size of the subset remains
fixed. The results, presented in Figure 4B, indicate again that the most distinct edges are not
required for high identification accuracy, and furthermore that large connectome subsets are
not required nor are any specific edges. Individual identity can be predicted with above 98%
accuracy by using many different subsets composed of ∼ 400−650 functional connections
(0.7%–1% of the connectome) even without using the most distinct 25% of the connectome.
Identity Can Be Predicted Using Randomly-Selected “Thin Slices”
These results indicate that no specific functional connection is required for high identification
accuracy. The next question that arises is whether any sufficiently large subset of the functional
connectome—with functional connections selected at random—might also provide high iden-
tification accuracy. The previous results hint at this possibility: virtually any random selection
of edges from a distribution like Figure 3C will contain edges with some individual distinct-
ness, and a sufficiently large selection will contain some of the more highly distinct edges that
especially facilitate high accuracy (see Figure 1A). We thus attempt to identify individuals by
Neurosciences en réseau
369
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4.
Identification accuracy when the most distinct connectome edges are not used for identification. (UN) Accuracy as a function of how
many of the most distinct edges in the functional connectome are excluded in each subset, across different parcellations, expressed in terms of
the percentage of the complete connectome excluded in each subset. Par exemple, x = 1 denotes using a subset that excludes the most distinct
1% of edges to identify individuals (and instead includes the remaining, least distinct, 99% of edges). Percentages are cumulative, and subset
size changes as percent increases. Confidence intervals of 99% based on a bootstrap estimate of the mean across five random parcellations
of the same resolution are depicted for each random parcellation resolution. (B) Accuracy as a function of the quantile of most distinct edges
used for identification, for different quantile sizes, using the HCP_MMP1.0 parcellation only. Quantiles are not cumulative (par exemple., neighboring
quantiles contain different edges) and are plotted on a scale of 0–100 for comparability even though most are smaller than percentiles.
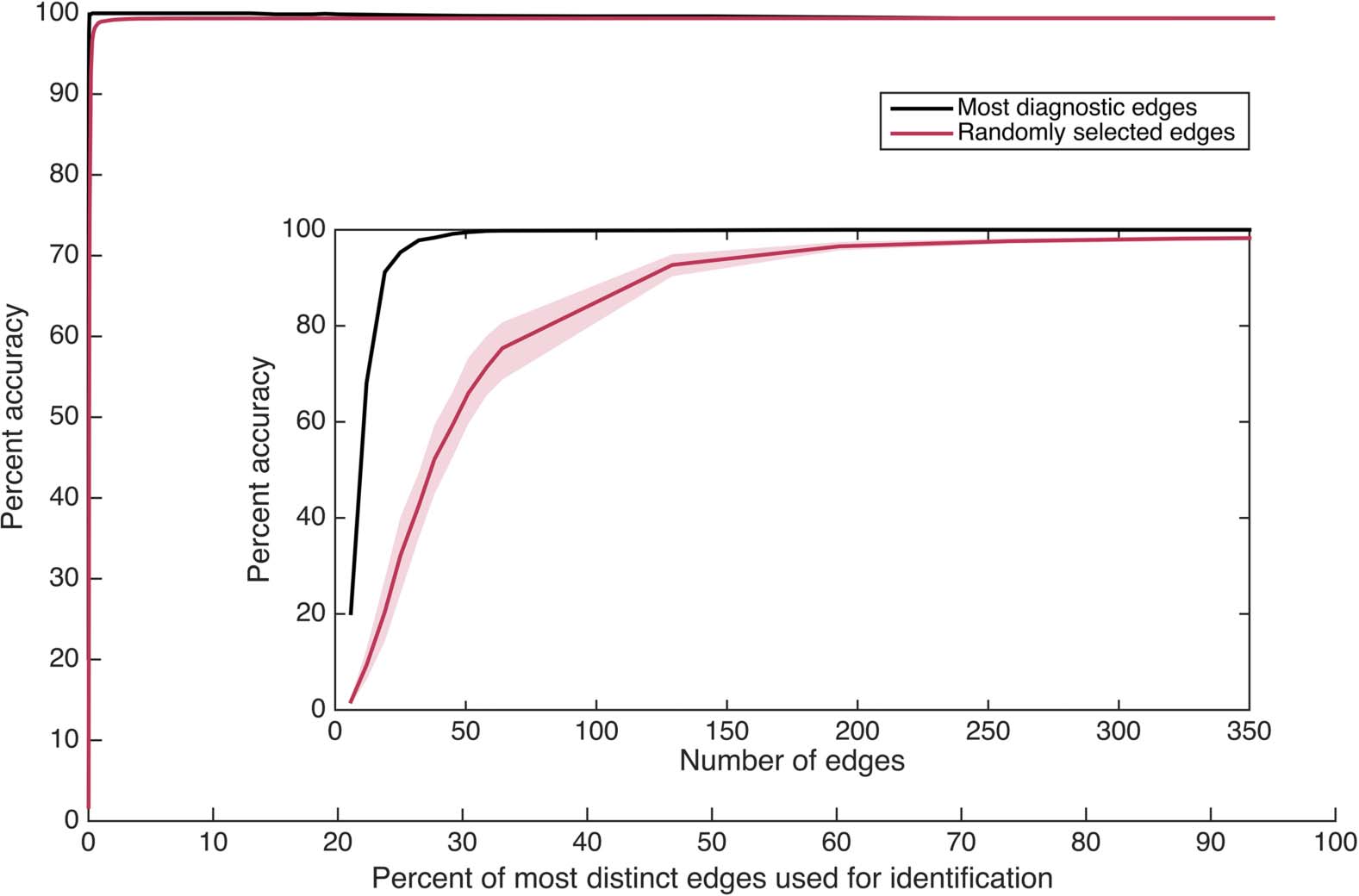
using randomly selected subsets of the same sizes examined in Figure 1A, avec 100 random
selections per subset size. The results are presented in Figure 5 (along with the corresponding
original results from Figure 1A, using the most distinct edges, re-presented for comparison).
They indicate that although random edge selection underperforms ranked edge selection for
very small subset sizes, the two selection methods quickly converge, and a random subset
Neurosciences en réseau
370
“Thin slice” connectome fingerprinting
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5.
Identification accuracy as a function of how many randomly selected edges are in-
cluded in each subset, using the HCP_MMP1.0 parcellation only. Percentages are cumulative (par exemple.,
2% contains twice as many edges as 1%). Confidence intervals of 99% based on a bootstrap esti-
mate of the mean across five (out of 100) random edge selections for each percentage examined
are displayed. The inset depicts the main figure rescaled to reveal very small x-axis values. Voir
also Supporting Information Figure S6 (Byrge & Kennedy, 2019), which presents mean within-
individual and across-individual similarity for these random connectome subsets.
composed of 0.5% of the connectome (323 edges) achieves individual identification accuracy
exceeding 98% on average.
No Specific Functional Network, Functional Connection, or Set of Functional Connections Is Required
for Identity Prediction
That randomly-selected subsets of edges considerably smaller than large-scale functional net-
works can identify individuals raises the possibility that perhaps no specific functional network
is required for identifying individuals. We thus examined individual identification accuracy by
using connectome subsets defined at the network level (using a data-driven parcellation of the
cortex into 7 functional networks; Yeo et al., 2011). For each network, we examined identifi-
cation accuracy by using subsets composed of only the edges associated with that network,
and then, taking a virtual lesion approach, using subsets composed of the entire connectome
except the edges associated with that network. In both cases, we repeated this analysis by
using within-network edges exclusively, as well as within- and across-network edges for the
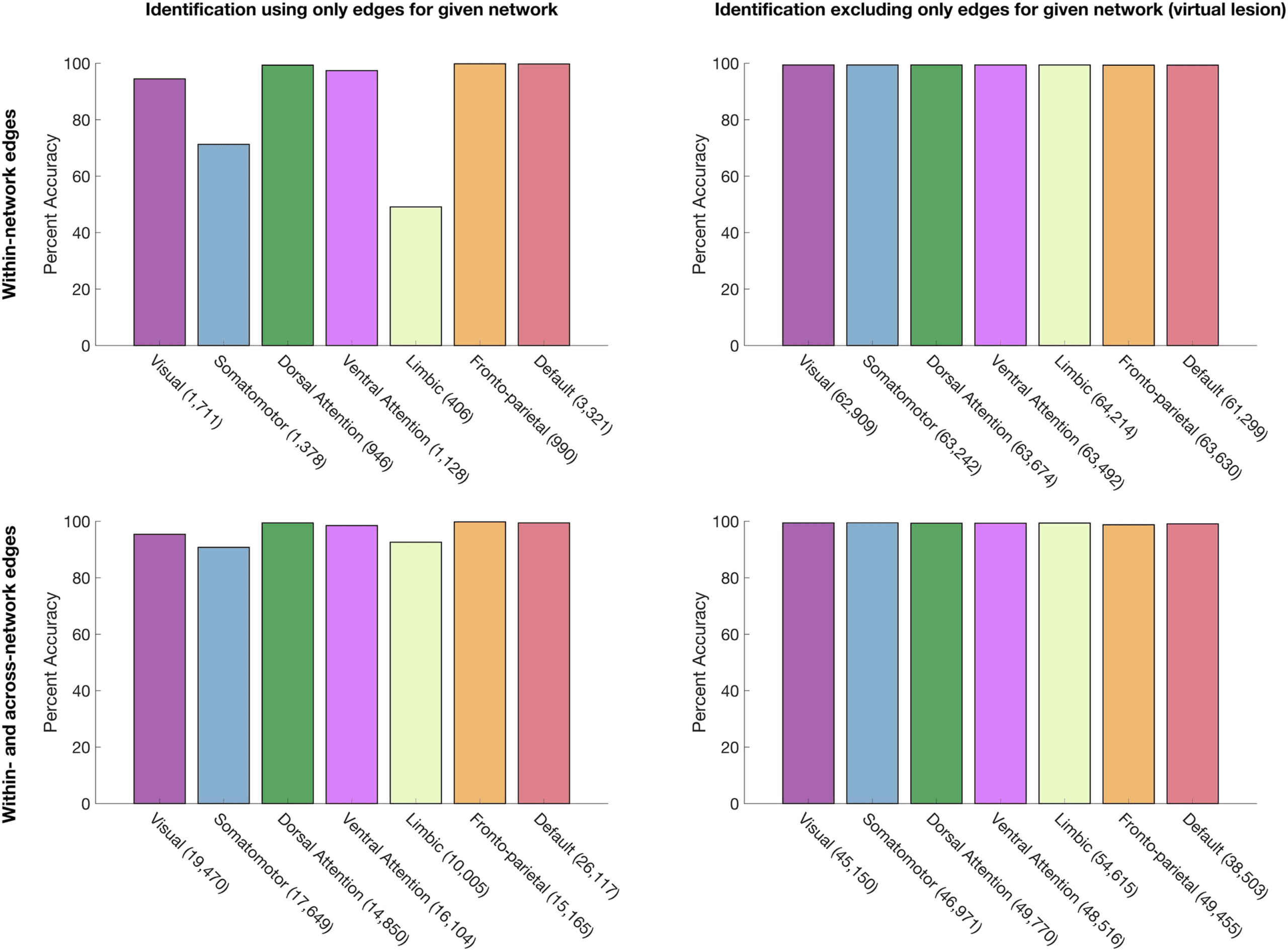
given network. The results, presented in Figure 6, replicate previous findings (Finn et al., 2015;
Peña-Gómez et al., 2017) of a gradient of identification accuracy when each network is used
for identification in isolation (Chiffre 6, top), but provide a complementary perspective on those
findings by showing that although several networks are sufficient for identification, no one
network is necessary (Chiffre 6, bottom); even the fronto-parietal network can be explicitly
excluded with high accuracy maintained. Altogether, these findings indicate that while signa-
tures of individual variability may be particularly concentrated in some networks, régions, et
edges, signatures of individual uniqueness can be detected throughout the cortex.
Neurosciences en réseau
371
“Thin slice” connectome fingerprinting
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
.
t
Chiffre 6.
Identification accuracy using network-level connectome subsets. The number of edges included in each subset is listed in paren-
theses. Left column: identification using subsets composed of (top row) only within-network edges and (bottom row) only within- et à travers-
network edges for each network. Right column: virtual lesion approach, with identification using subsets comprised of (top row) all connectome
edges except within-network edges, et (bottom row) all connectome edges except within- and across-network edges for each network.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
DISCUSSION
Here we find that in this large and high-resolution fMRI dataset, individual identity can be
predicted using a surprisingly tiny fraction—a “thin slice”—of the full functional connectome.
High accuracy with the smallest possible connectome subset can be obtained using specifi-
cally those edges that were determined to be highly individually distinct in an independent
partition of the data, and those highly distinct edges were largely located within fronto-parietal
regions consistent with prior work (Miranda-Dominguez et al., 2014; Finn et al., 2015; Airan
et coll., 2016; Peña-Gómez et al., 2017; Gratton et al., 2018; Amico & Goñi, 2018). Cependant,
nearly all edges in the connectome contain some individually diagnostic information, et
no specific edges or specific functional networks are necessary for predicting identity in this
dataset. Effectively perfect accuracy can be obtained without the most distinct 10–15% of the
Neurosciences en réseau
372
“Thin slice” connectome fingerprinting
connectome (when the remainder of the connectome is used for prediction) and even without
the most distinct 25% of the connectome (when a small subset of moderately diagnostic edges
is used for prediction). Perhaps most strikingly, a randomly selected subset smaller than 1% de
the functional connectome can also provide effectively perfect identification. Individuals can
thus be identified by not just one but many “thin slices” of the connectome.
Together these findings suggest that although individual variability in brain function may be
particularly concentrated in fronto-parietal regions in accord with previous literature (Mueller
et coll., 2013; Miranda-Dominguez et al., 2014; Finn et al., 2015; Airan et al., 2016; Peña-
Gómez et al., 2017; Gratton et al., 2018; Amico & Goñi, 2018), uniqueness in functional
coupling patterns is far more diffusely distributed throughout the brain than previously ap-
preciated. Less highlighted findings in earlier work hint at this possibility: identification accu-
racy using networks outside fronto-parietal regions (Finn et al., 2015), using random selections
of ROIs (Peña-Gómez et al., 2017), and using the least informative edges in the connectome
(Vanderwal et al., 2017), while below ceiling accuracy, far exceeded what would be expected
by chance. Ainsi, just as time-locked task-based fMRI responses are revealed as far less local-
ized and more diffusely distributed than previously appreciated when sampled in a different
chemin (Gonzalez-Castillo et al., 2012), detecting individual uniqueness in fMRI data appears
to be not exclusively a question of sampling from specific locations but also a question of
sampling from enough functional interactions. Autrement dit, we need to cast a net that can
capture diffusely distributed individually diagnostic information, rather than a net that must
land on specific locations.
Because we show here that individually diagnostic information from one independent group
of subjects (from the training partition) contributes to identification accuracy in a different
group of subjects (from the test partition), this implies that relative distinctness of connectome
edges is similar across different groups of individuals, which is itself noteworthy. We also con-
firmed this post hoc and found highly correlated individually diagnostic values across training
and test sets across the entire cortex (r = 0.972, p << 0.001) and within each individual net-
work (mean r = 0.942 [SD = 0.031], all p << 0.001). This did not necessarily have to be the
case: an alternative model for why connectome fingerprinting works is that if enough edges are
sampled (either from the whole connectome or from large-scale distributed networks, like the
fronto-parietal network), then enough individually distinctive patterns are obtained that can be
used in aggregate to differentiate individuals. For example, edges 1–40 might be highly pre-
dictive of individual A, whereas edges 41–80 are highly predictive of individual B and edges
81–120 are predictive of individual C. And so, by sampling from edges 1–120 and beyond,
we obtain enough information to differentiate all these individuals from one another. How-
ever, our results indicate that although such broad sampling is certainly sufficient to identify
individuals (Figure 5), it is not necessary. Rather, although we find that individually distinc-
tive information is widely distributed throughout the brain (see Figure 3A and 3C), the specific
edges with the most or the least individually distinct edges are consistent across independent
groups of subjects. Furthermore, although edges from the primary and replication datasets
were not directly compared because of different data formats (surface-based vs. volumetric),
a visual comparison of the top-ranked edges in the different datasets (Supporting Information
Figure S8, Byrge & Kennedy, 2019) and of the mean ranking of within- and across-network
edges (Supporting Information Figure S9, Byrge & Kennedy, 2019) are suggestive of consid-
erable similarities in the relative distinctness of edges across the two datasets. Altogether these
findings indicate that there may be a consistent, reproducible gradient of uniqueness across
the connectome, such that some edges can play an outsized role in individual identification
while others play a more minimal (and even detrimental; see below) role. We have made
Network Neuroscience
373
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
a
_
0
0
0
6
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
available the individually diagnostic values of edges using the HCP_MMP1.0 (Glasser) parcel-
lation at brainlab.psych.indiana.edu/resources/hcpmmp10_diagnostic_values.mat.
Not only was the individually diagnostic information for different edges consistent between
two groups of subjects, it was consistent within the training partition across 900 random parcel-
lations of nine different granularities. As Supporting Information Figure S7 (Byrge & Kennedy,
2019) demonstrates, we observed a high degree of convergence across parcellations in the
networks implicated in the most and least distinct edges. We also observed that same-sized
connectome subsets obtain similar accuracy across different parcellations of the same granular-
ity (cf. narrow confidence intervals in Figures 1A and 4A; also cf. black line for HCP_MMP1.0
parcellation and yellow-green line for random parcellations of the same size). Together these
results indicate that precise boundaries between regions are not driving the pattern of results; in
other words, individual distinctness of connectome edges arises broadly not as a result of how
the data are aggregated but rather as a property of the underlying signals. (We note, however,
that only group-level parcellations were employed in this study and that individually defined
parcellations as described by Bijsterbosch et al. [ 2018] may be expected to further enhance
accuracy, potentially with even smaller connectome subsets.)
Across training and test partitions, across random parcellations, and within the replication
dataset, neuroanatomical locations of the nodes involved in the more distinct and in the less-
distinct edges accord with the existing literature: more distinct edges involve locations with
higher interindividual variability (Mueller et al., 2013; Laumann et al., 2015; Airan et al., 2016;
Bijsterbosch et al., 2018; Gratton et al., 2018); less-distinct edges originate near sinuses and
brainstem with their susceptibility to fMRI signal dropout and other artifacts (Yeo et al., 2011;
Peña-Gómez et al., 2017). That the least informative edges may consistently contain increased
fMRI noise is likely to explain the decrement in accuracy we observe when identifying individ-
uals by using the complete connectome (see also Finn et al., 2015, who found that accuracy
using combined fronto-parietal networks exceeds that of the whole connectome). Although
this accuracy deficit is negligible for higher granularity parcellations and longer scans, it may
have real practical consequences in applications where scan duration is limited or parcella-
tions must be coarse (see also Airan et al., 2016; Waller et al., 2017; Horien et al., 2018).
Amico and Goñi ( 2018) have pointed out the importance of going beyond accuracy metrics
and understanding the underlying similarity among connectomes in fingerprinting analyses—
in principle, high identification accuracy could be obtained in datasets where scans are gen-
erally highly dissimilar and within-individual scans are also dissimilar, just slightly less so,
potentially changing the interpretation of the results. Figure 2 (see also Supporting Informa-
tion Figure S5, Byrge & Kennedy, 2019) demonstrates that such a scenario is unlikely in
this dataset, given the visually evident similarity among connectome subsets from an individ-
ual and dissimilarity across individuals; Supporting Information Figure S6 (Byrge & Kennedy,
2019) shows that not only is within-individual similarity higher than across-individual sim-
ilarity, within-individual similarity is itself very high. These similarity measures also speak to
an apparent tension between our findings that individuals can be identified using mere min-
utes of data (Figure 1B) and other work showing that hours of data is necessary for a stable
estimate of functional connectivity within an individual (Laumann et al., 2015): for the con-
nectome subset sizes achieving high accuracy, the gap between within-individual similarity
and across-individual similarity is substantial. Even though within-individual similarity would
be expected to continue to increase given longer scan times, it would still be expected to be
high after several minutes of data (cf. Figure 4 in Laumann et al., 2015), and sufficiently higher
than across-individual similarity to permit identification. We note that it could also be the case
Network Neuroscience
374
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
a
_
0
0
0
6
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
that the within-individual similarity for the maximally distinct connectome subsets analyzed
here might stabilize more quickly (i.e., requiring fewer hours of data), because the influence
of less-distinct noisy edges would be eliminated.
That small connectome subsets selected at random can accurately identify individuals is
likely to arise from a combination of two factors: sampling (random selections of 1% of all
edges are likely to include some edges within the top tier of individually diagnostic value)
and more widespread individual distinctness than previously appreciated. For instance, iden-
tity prediction using a small subset of connectome edges in the 70th percentile of indi-
vidually diagnostic values can achieve accuracy exceeding 80% (Figure 4B)—dramatically
higher than expected by chance—indicating considerable individually diagnostic informa-
tion is present even in those relatively less distinct edges. An important question for future
studies is whether it might be possible to better harness the individually diagnostic informa-
tion present in edges with moderate-to-low distinctness. Perhaps with some modifications to
the fingerprinting algorithm (potentially combining information across scans or changes to
scan acquisition parameters), ceiling accuracy might be achievable using only those relatively
less distinct edges as well. Alternatively—just as identification from actual fingerprints (from
fingers) preferentially uses the most informative points or features—weighting connectome
edges according to their (independently determined) distinctness prior to prediction might
improve identification accuracy. Indeed, preliminary results with no attempt at optimization
indicate that linearly weighting connectome edges can improve accuracy by around 5% for
the coarsest parcellation examined (Supporting Information Figure S10, Byrge & Kennedy,
2019). Such an improvement may be particularly important for identification in extremely
large datasets, for which accuracy might be expected to fall below ceiling level.
Whether these results have implications for biomarker development and other approaches
for linking individual difference measures with their neural correlates is thus far an open ques-
tion. These results do provide a reason for optimism—signals at the level of individual edges
can be highly and precisely measured within approximately 15 min of scanning (an important
feature for potential biomarkers)—and combining dozens of such edges are uniquely identi-
fying. Thus, if there are signals that differentiate two groups reliably (e.g., clinical groups), or
continuously track well-measured behavioral or cognitive traits, we should be able to detect
them. However, it is also likely to be the case that identifying individuals from connectomes
may be a less difficult task than identifying behavioral or clinical links. For example, individual
neuroanatomy is more consistent across scans for the same individual compared with differ-
ent individuals. Similarly, the identity of an individual is known with 100% certainty, whereas
clinical group membership, for instance, is not. These, and other factors, including the com-
plex mapping between brain and behavior whereby distinct neurobiological presentations can
underlie similar behaviors and vice versa (Seghier & Price, 2018), make the challenge even
more daunting when extending this and related approaches to studies of individual differences.
Future studies will be needed to address these issues.
It is important to make it clear that we do not know to what extent, if at all, the specific
connectome edges we identified, as maximally individually distinct might also be associated
with individual differences in behavior. Further study of the minimal connectome subsets asso-
ciated with behavioral variability rather than individual identity could reveal that the specific
edges that maximally distinguish a particular behavioral measure may not be the same as those
edges identified here as individually distinct. For instance, Noble et al. ( 2017b) have shown
that the reliability of an edge (which is related to individual distinctness) is not linked with
its usefulness in predicting one particular behavioral measure (IQ). More generally, the goals
Network Neuroscience
375
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
a
_
0
0
0
6
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
of predicting individual identity and predicting behavioral measures or groups can sometimes
be at odds. The edges most effective at predicting group membership, for instance, will be
maximally distinct between groups but must be similar within groups. There could thus be
minimal overlap between the edges that distinguish groups and the edges that distinguish in-
dividuals, because the latter, by virtue of being individually distinct, may not be similar within
group members. A characterization of the relationship between individually distinct and be-
haviorally distinct connectome edges—how many are needed for high-accuracy prediction,
how diffusely they are distributed, and how many span different behavioral measures and how
many are specific—will be important questions for future work.
We note that our general pattern of results is robust across our primary and replication
datasets, numerous parcellations, temporal subsets of data, and across both resting-state and
naturalistic viewing conditions. How minimal connectome subset sizes might change as a
function of differing sample sizes and lower resolution data (Airan et al., 2016; Waller et al.,
2017; Horien et al., 2018) is a question for future work. Furthermore, although a full explo-
ration of thin-slice fingerprinting across different task conditions is beyond the current scope,
a comparison between two different task conditions (rest and video-watching) in the replica-
tion dataset (Supporting Information Figure S4, Byrge & Kennedy, 2019) indicates that sim-
ilarly high identification accuracy can be obtained in two task contexts by using similarly
small numbers of edges, and that the individually diagnostic values of edges computed sep-
arately for each task context were broadly similar but not identical (Supporting Information
Figure S9, Byrge & Kennedy, 2019). This is consistent with other work indicating similar but
not the same patterns of functional connectivity across task contexts (e.g., Cole et al., 2014),
and work showing largely similar numbers of principal components achieve optimal accu-
racy across different task conditions (Amico & Goñi, 2018; see also Finn et al., 2017, for a
discussion of some of these issues).
In sum, we find that not only is a complete functional connectome not required for individ-
ual identification (see also Finn et al., 2015; Peña-Gómez et al., 2017; Amico & Goñi, 2018),
but also that a remarkably small “thin slice” of the connectome is sufficient to identify indi-
viduals. Predicting identity on the basis of a targeted selection of the most individually distinct
functional connections permits identification with the smallest subset possible (under 0.3% of
connectome and fewer than 100 edges). However, many different connectome subsets permit
high identification accuracy—including quite small randomly selected subsets (under 1% of
connectome)—in part because individually distinct information is widespread across the cor-
tex. Individualized brain signatures in high-dimensional fMRI datasets can thus be detected
in a much more compact manner than previously appreciated, with potential implications for
the underlying sources of that uniqueness as well. These results may also have implications for
how one might approach developing brain-based measures that link to individual differences
(see also Dubois & Adolphs, 2016), including the construction of biomarkers for psychiatric
conditions.
METHODS
Participants
We primarily analyzed resting-state fMRI scans from the “S900 subjects release” of the Human
Connectome Project (http://www.humanconnectome.org). Participant recruitment and consent
is described in (Van Essen et al., 2013); briefly, informed consent was obtained from each par-
ticipant, and the study protocol was approved by the institutional review board at Washington
University in St. Louis, MO. We excluded participants with less than three resting-state scans
Network Neuroscience
376
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
a
_
0
0
0
6
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
available, leaving a final sample of N = 835 and 3,333 scans (828 participants with 4 scans;
7 with 3 scans). This dataset includes participants who are relatives; we also repeated the pri-
mary analysis using a randomly selected subsample of 282 unrelated individuals (1,125 scans;
279 subjects with 4 scans and 3 subjects with 3 scans).
As a replication dataset, we also examined a dataset collected at Indiana University and
described in Byrge and Kennedy (2018) in which 54 adults (25 diagnosed with autism spectrum
disorder [ASD]; 29 controls) participated. Informed consent was obtained from all participants;
the local institutional review board at Indiana University approved the study protocol. This
dataset consisted of resting-state scans and video-watching (i.e., naturalistic viewing) scans;
we analyzed these scan types separately, treating them as different subdatasets. In the video-
watching scans, participants watched sequences of movie trailers, which were different for
each scan. After excluding participants with fewer than three rest or three video scans, the final
sample consisted of scans from 48 participants (19 ASD), with 251 scans in the rest replication
dataset (30 participants with 6 scans; 1 with 5; 15 with 4; 3 with 2) and 183 scans in the video
replication dataset (42 participants with 4 scans; 3 with 3). No individuals in this sample were
relatives.
Data Acquisition and Preprocessing
MRI data acquisition and preprocessing is detailed in Smith et al. (2013) and Glasser et al.
(2013) and briefly summarized here. Subjects participated in four resting-state scans across two
sessions (2 scans per session, with opposite phase encoding directions, each approximately
14 minutes long [1,200 TRs]). Participants were instructed to remain awake with eyes open.
MRI images were acquired using a customized 3 Tesla Siemens Skyra with 32-channel head
coil. Parameters for T2*-weighted resting-state scans were as follows: TR/TE = 720/33.1 ms;
1,200 volumes; flip angle = 52
; 2-mm isotropic voxels; 72 slices; multiband acceleration fac-
tor of 8. High-resolution T1-weighted images of the whole brain were also acquired (MPRAGE,
.7-mm isotropic voxel size; TR/TE/TI = 2,400/2.14/1,000 ms) as anatomical references.
◦
We analyzed the “Resting State fMRI FIX-Denoised” release with preprocessing detailed
in Smith et al. (2013) and Glasser et al. (2013); weak high-pass temporal filtering (>2,000 s
FWHM) to remove slow drifts was performed. We regressed out the mean cortical signal
(and its derivative) from the FIX-denoised BOLD data in a second step (Burgess et al., 2016;
Byrge & Kennedy, 2018), and the residuals were analyzed as the cleaned data. Framewise dis-
placement traces based on the movement parameters distributed with the data were computed
via in-house MATLAB scripts following Power et al. (2012). We finally extracted BOLD time
courses from the cleaned data as the mean signal across individual ROIs taken from numerous
cortical parcellations.
Data acquisition and preprocessing for the replication dataset is described in Byrge and
Kennedy (2018) and was designed to be similar to the HCP dataset. Briefly, four to six ∼16-min
multiband resting-state scans per subject (TR = 813 ms; 1,200 TRs) and four video-watching
scans (TR = 813 ms; 1,000, 952, 1,026, et 977 TRs) were acquired across two to three dif-
ferent days. Data was preprocessed using ICA-FIX followed by mean cortical signal regression,
as described above. Weak high-pass temporal filtering was used for linear detrending.
Cortical Parcellations
The primary parcellation examined was the 360-ROI HCP_MMP1.0 parcellation introduced
by Glasser et al. (2016). We also examined symmetrical random parcellations of the cortical
Neurosciences en réseau
377
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
surface across numerous granularities (50, 100, 150, 200, 250, 300, 360, 400, et 500 ROI).
To create each random parcellation with granularity g, we used ft_read_cifti to import the
HCP_MMP1.0 parcellation into MATLAB 2014b and then submitted the cortical surface co-
ordinates or vertices (.pos data structure of imported cifti file) for the left hemisphere to the
k-means algorithm (kmeans command in MATLAB 2014b), using a squared Euclidean dis-
tance measure, to obtain solutions with k = 1/2g clusters, which we then mirrored to the right
hemisphere. We created 100 random parcellations for each granularity by using this method.
We also estimated higher level functional network membership for each ROI by using the
Yeo 7-network parcellation (Yeo et al., 2011). In brief, we defined the network assignment for
a given ROI as the mode of the Yeo network assignments for each of the grayordinates compris-
ing that ROI. More concretely, we used a mapping of resting-state networks to the cifti file for-
mat (RSN-networks.32k_fs_LR.dlabel.nii from https://balsa.wustl.edu/study/show/WG33) et
used the HCP wb_command utility (wb_command -cifti-all-labels-to-rois) to convert the Yeo 7
network parcellation to a format that could be compared with the distributed HCP_MMP1.0
parcellation. The result was two assignments for each grayordinate, one assignment to one of
le 360 HCP_MMP1.0 parcellation ROIs, and another to one of the Yeo 7 réseaux. Suivant, pour
each of the HCP_MMP1.0 parcellation ROIs, we extracted the Yeo 7 network assignment for
each of the grayordinates assigned to that ROI and computed the mode, c'est, the most fre-
quently occurring Yeo 7 network across all the grayordinates in the given HCP_MMP1.0 ROI.
This modal network was taken as the Yeo 7 network for the given HCP_MMP1.0 ROI. Ce
mapping is available at brainlab.psych.indiana.edu/resources/hcp_mmp10_yeo7_modes.pdf
for the interested reader.
For the replication dataset, the only parcellation examined was a 114-ROI cortical parcella-
tion anatomically subdividing the Yeo 17 functional networks (Yeo et al., 2011) and described
more fully in Betzel et al. (2014). For some visualizations, we assigned each of these ROIs to
their best corresponding Yeo 7 functional network by using the following mapping from Yeo
17 network numbers to Yeo 7 network names (numbers): 1–2 to Visual (1); 3–4 to Somatomo-
tor (2); 5–6 to Dorsal Attention (3); 7–8 to Ventral Attention (4); 9–10 to Limbic (5); 11–14 to
Contrôle (6); 15–17 to Default (7).
Functional Connectome Construction
For each scan, we created functional connectivity (FC) matrices (“functional connectomes”)
for each of the 901 parcellations examined.
Motion censoring/scrubbing prior to connectome construction was performed in all analy-
ses. For all analyses unless stated otherwise, all TRs with FD >= 0.39 mm were censored, et
all the remaining (uncensored) TRs were used to construct the connectivity matrices. Note that
this means that the number of TRs used for constructing connectivity matrices varied across
scans. We also conducted two Supporting Information analyses (Byrge & Kennedy, 2019) dans
which we altered the censoring procedure. In one, we constructed connectivity matrices after
using a stricter censoring threshold (FD >= 0.2 mm) to examine whether the quality of in-
cluded TRs might be influencing the pattern of results. In the other, we equated the number of
TRs across scans to examine whether the quantity of included frames might be influencing the
modèle de résultats. Pour faire ça, we excluded scans in which more than 30% of TRs (360) étaient
censored (106 scans), and then for each remaining scan we randomly selected 840 “good”
(uncensored) TRs to be used for connectome construction, ensuring that the same number of
TRs was included for all scans. We repeated this random selection of 840 TRs 100 times. These
alternate censoring procedures did not influence the pattern of results.
Neurosciences en réseau
378
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
In all cases, using only the remaining TRs, we generated functional connectivity matrices
by computing the Fisher z-transformed pairwise correlations among all ROI time series in the
given parcellation. In contrast to other approaches (Finn et al., 2015, 2017), we analyzed one
FC matrix for each scan, for a total of four matrices per subject, rather than averaging FC
matrices acquired on the same day.
For the HCP_MMP1.0 parcellation only, we also examined FC matrices based on various
fractions of the duration of the entire scan. We constructed FC matrices in the same manner
as described above, except we did not include the entire length of the scan (1,200 TRs). Dans-
stead, we constructed FC matrices from contiguous fragments of the scan with the following
durations, each increasing by approximately 1 min: 83, 167, 250, 333, 417, 500, 583, 667,
750, 833, 917, 1,000, et 1,083 TRs. For each such duration, we randomly varied the starting
location 100 times or as many times as possible (18 times for 1,083 TRs; 100 times for all other
durations), resulting in 1,218 temporally limited FC matrices for each scan.
Symmetric g × g FC matrices, for each parcellation granularity g (c'est à dire., the number of ROIs)
were reduced to 1/2 ∗ g∗ (g − 1) ×1 FC vectors for use in subsequent analyses.
General “Connectome Fingerprinting” Algorithm
We predicted individual subject identity from functional connectomes by using an approach
based on the method originally introduced by Finn et al. ( 2015; 2017) and adapted for compar-
ing four scans in one pass (vs. 2 scans as in Finn et al., 2015, 2017). In brief, we first computed
the similarity between all pairs of scans as the correlation between the corresponding pair of
FC vectors. Suivant, we predicted subject identity for a given scan by (un) identifying the scan with
maximal similarity to the given scan, et (b) taking the subject identity corresponding to the
maximally similar scan as the predicted subject identity for the given scan. Accuracy was com-
puted as the percentage of scans for which the predicted subject identity was equal to the actual
subject identity. We also conducted an even more stringent version of this same procedure in
which we excluded scans from the same subject that were acquired on the same day (given that
same-day scans would be expected to be more similar than different-day scans for a given sub-
ject; Birn et al., 2013), while retaining all available scans from other subjects (both same-day
and different-day acquisitions). This across-day accuracy metric is presented in the Supporting
Information (Byrge & Kennedy, 2019); highly similar results were obtained.
Accurate identification requires higher similarity of FC within individuals than across in-
dividuals; following Amico and Goñi (2018) we also separately examined within-individual
similarité (c'est à dire., the mean correlation among FC vectors from the same subject, or Iself ) et
across-individual similarity (c'est à dire., the mean correlation between FC vectors from different sub-
projets, or Iother).
In all the HCP dataset analyses presented, we employed a split-half design in which the 883
available subjects were randomly divided into a training partition and a test partition that were
held fixed for all analyses. Exclusions based on data quality and available scans occurred after
dividing the dataset, resulting in a training dataset with data from 421 sujets (418 avec 4 scans
et 3 avec 3 scans for a total of 1,681 scans) and a test dataset with data from 414 sujets (410
avec 4 scans and 4 avec 3 scans for a total of 1,652 scans). Data from the 421 training partition
subjects were used to rank the FC edges on the basis of individually diagnostic information
(décrit ci-dessous) but never used in the fingerprinting procedure itself. Data from the 414 test
partition subjects were used in the fingerprinting procedure, such that for each scan, là
were three possible true positive subject identifications (par exemple., 3 other scans from the same
Neurosciences en réseau
379
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
un
_
0
0
0
6
8
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
sujet, ou 2 scans using the across-day metric) and up to 1,649 possible false positive subject
identifications. Because some of the 883 available subjects were relatives and might have
more similar functional connectomes (Miranda-Dominguez et al., 2017), we also repeated the
primary analysis by using a randomly selected subset of 282 unrelated subjects, avec 143 de
the original training subjects (572 scans; 4 scans per subject) retained in the unrelated training
partition and 139 of the original test subjects (553 scans; 136 subjects with 4 scans; 3 sujets
avec 3 scans) and retained in the unrelated test partition; results were unchanged.
For the replication dataset, a split-half design was also used, and the training partition and
test partition contained equivalent proportions of ASD participants. The same participants were
assigned to the same partitions in the rest and video analyses.
The fingerprinting procedure was always carried out separately within each parcellation or
temporal duration or dataset, never comparing similarity of FC vectors across different parcel-
lations or durations or datasets.
Computing Individually Diagnostic Information (or Distinctness) for Each Functional Connection
We independently ranked functional connections (edges of the vectorized FC matrices) accord-
ing to individually diagnostic information (or distinctness). Edges that are more diagnostic of
individuals should have two properties: low within-subject variability and high across-subject
variability. Ainsi, using FC vectors for the 414 training partition subjects only, we used a ra-
tio of across-subject and within-subject variability to capture individually diagnostic value for
each edge. We computed across-subject variability as the mean (across 4 scan sessions) of the
standard deviation of the FC value for that edge across subjects within a given session, et
within-subject variability as the mean (across subjects) of the standard deviation of the FC value
for that edge across all sessions within each subject. We then ranked each edge according to
this variability ratio from most to least individually diagnostic.
We note that the existing literature (Finn et al., 2015; Vanderwal et al., 2017) employs a
different “differential power” ranking approach designed for comparing pairs of scan sessions;
our approach is simpler and ranks multiple scans in one pass. The correlations between the
differential power metric for different scan pairs and our variability ratio metric range from
r = .63 to r = .66 for the HCP_MMP1.0 parcellation. Another alternative metric for evaluating
the individual distinctness of FC edges is intraclass correlation (Shrout & Fleiss, 1979; Noble
et coll., 2017un, b; Amico & Goñi, 2018), a measurement highly correlated with ours (r = 0.96,
p << 0.001).
Individually diagnostic values were independently computed for each analysis conducted
using parallel data (e.g., using the same parcellation, or the same temporal duration).
“Thin-Slice” Connectome Fingerprinting Algorithm
To examine how much of the available information in the connectome is needed to accurately
identify individuals, we conducted the general fingerprinting algorithm using various restricted
subsets, or “thin slices,” of the vectorized FC matrix.
First, we attempted to identify individuals by using a subset of the connectome consisting
of only the most individually distinct FC edges (as ranked by an independent partition of the
data; see above). As a concrete example, we masked 99% of each vectorized FC matrix so that
only the most individually diagnostic 1% of edges remained, producing a most distinct FC sub-
set. Then, using these FC subsets from the test subjects only, we conducted the fingerprinting
Network Neuroscience
380
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
a
_
0
0
0
6
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
algorithm, predicting which individual contributed a given FC subset, based on maximal simi-
larity with all other such FC subsets. We explored a complete range of percentages of the con-
nectome, ranging from the top 0.01% of edges (where nearly the entire FC matrix is masked/not
considered) to 95% (where only the least distinct 5% of edges is masked), sampling the per-
centage range more densely where needed to ascertain inflection points. This procedure is
cumulative, such that when we predict identity by using the most distinct 2% of edges, the
most distinct 1% of edges is also included; thus, both the number of edges included and the
individually diagnostic value of edges included changes as the percentage is varied. We con-
ducted this “thin-slice” fingerprinting procedure for each parcellation and temporal duration.
Next, we reversed this procedure, predicting individual identity by using connectome sub-
sets that omit the most distinct edges. For instance, we predicted individual identity without
using the most distinct 1% of edges, using instead a subset composed of the least distinct 99%
of edges (see also Vanderwal et al., 2017, for a similar approach). We examined the same
range of percentages as before, excluding the same percentage of the connectome that was
included in the previous analysis.
In both of the preceding analyses, the size of the connectome subset used for prediction
and the individually diagnostic value of the edges included in that subset covary. To decouple
these factors, next, for the HCP_MMP1.0 parcellation only, we conducted a variant of this
same procedure in which we kept the number of edges constant in each use of the algorithm
while still varying the ranking of edges included from most to least distinct. To do this, we
repeated the “thin-slice” fingerprinting algorithm by using one quantile of the independently
ranked edges at a time. In contrast to the previous analyses, this procedure is not cumulative,
such that the second quantile does not include edges that fall within the first quantile. We
explored a range of q-quantile sizes corresponding to 0.02% of the connectome (subsets of
13 edges; q = 5, 000) to 1% of the connectome (subsets of 646 edges; q = 100) and then
scaled all quantiles to a maximum of 100 for comparability (although, note that most quantiles
examined were smaller than percentiles).
We next examined “thin-slice” fingerprinting accuracy when the connectome subset con-
tains randomly-selected edges, ignoring the ranking of individually diagnostic value. Here,
for each of the percentages explored in the first “thin-slice” analysis, we randomly selected
the same number of edges without considering individually diagnostic value, and obtained
fingerprinting accuracy by using the connectome subset corresponding to those edges. We
conducted 100 random selections for each connectome percentage examined.
Finally, we predicted individual identity by using connectome subsets defined at the net-
work level using the mapping between the 360 HCP_MMP1.0 parcellation ROIs and seven
functional networks (Yeo et al., 2011) described previously. For each network, we predicted
individual identity by using subsets composed of only within-network edges as well as using
only within- and across-network edges. Then, taking a virtual lesion approach, for each net-
work, we predicted identity by using the entire connectome except within-network edges for
that network, as well as using the entire connectome except within- and across-network edges
for that network.
ACKNOWLEDGMENTS
This work was supported by the NIH (R01MH110630 and R00MH094409 to DPK), and NICHD
(T32HD007475 Postdoctoral Traineeship to LB). For supercomputing resources, this work was
supported in part by Lilly Endowment, Inc., through its support for the Indiana University
Network Neuroscience
381
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
a
_
0
0
0
6
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
Pervasive Technology Institute, and in part by the Indiana METACyt Initiative. The Indiana
METACyt Initiative at IU was also supported in part by Lilly Endowment, Inc. We thank the
Human Connectome Project for making their data available. Data were provided in part by the
Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen
and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that sup-
port the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems
Neuroscience at Washington University. For the replication dataset collection and analysis, we
thank Hu Cheng for MRI protocol development, Soyoung Park for training the FIX classifier,
and Brad Caron and Susannah Burkholder for data collection. We also thank Olaf Sporns for
helpful discussions.
AUTHOR CONTRIBUTIONS
Lisa Byrge: Conceptualization; Formal analysis; Visualization; Writing – original draft; Writing –
review & editing. Daniel P. Kennedy: Conceptualization; Funding acquisition; Supervision;
Writing – review & editing.
FUNDING INFORMATION
Daniel P. Kennedy, National Institutes of Health (http://dx.doi.org/10.13039/100000002),
Award ID: R01MH110630. Daniel P. Kennedy, National Institutes of Health (http://dx.doi.
org/10.13039/100000002), Award ID: R00MH094409. Linda B. Smith, National Institute of
Child Health and Human Development (http://dx.doi.org/10.13039/100000071), Award ID:
T32HD007475, postdoctoral traineeship to Lisa Byrge.
REFERENCES
Airan, R. D., Pillai, J. J., Caffo, B., Pekar, J. J., & Sair, H. I. (2016). Fac-
tors affecting characterization and localization of interindividual
differences in functional connectivity using MRI. Human Brain
Mapping, 37, 1986–1997.
Amico, E., & Goñi, J. (2018). The quest for identifiability in human
functional connectomes. Scientific Reports, 8(1), 8254.
Betzel, R. F., Byrge, L., He, Y., Goñi, J., Zuo, X. N., & Sporns, O.
(2014). Changes in structural and functional connectivity among
resting-state networks across the human lifespan. NeuroImage,
102, 345–357.
Bijsterbosch, J. D., Woolrich, M. W., Glasser, M. F., Robinson, E. C.,
Beckmann, C. F., Van Essen, D. C., . . . Smith, S. M. (2018). The
relationship between spatial configuration and functional con-
nectivity of brain regions. eLife, 7, e32992.
Birn, R. M., Molloy, E. K., Patriat, R., Parker, T., Meier, T. B., Kirk,
G. R., . . . Prabhakaran, V. (2013). The effect of scan length on
the reliability of resting-state fMRI connectivity estimates. Neuro-
Image, 83, 550–558.
Burgess, G. C., Kandala, S., Nolan, D., Laumann, T. O., Power, J. D.,
Adeyemo, B., . . . Barch, D. M. (2016). Evaluation of denoising
strategies to address motion-correlated artifacts in resting-state
functional magnetic resonance imaging data from the human
connectome project. Brain Connectivity, 6(9), 669–680.
Byrge, L., & Kennedy, D. P. (2018). Identifying and characterizing syste-
matic temporally-lagged BOLD artifacts. NeuroImage, 171, 376–392.
Byrge, L., & Kennedy, D. P. (2019). Supporting Information for
identification using a “thin slice”
“High-accuracy individual
of the functional connectome.” Network Neuroscience, 3(2),
363–383. https://doi.org/10.1162/netn_a_00068
Cole, M. W., Bassett, D. S., Power, J. D., Braver, T. S., & Petersen,
S. E. (2014). Intrinsic and task-evoked network architectures of
the human brain. Neuron, 83(1), 238–251.
Di Martino, A., O’Connor, D., Chen, B., Alaerts, K., Anderson,
J. S., Assaf, M., . . . Blanken, L. M. (2017). Enhancing studies
of the connectome in autism using the autism brain imaging data
exchange II. Scientific Data, 4, 170010.
Dubois, J., & Adolphs, R. (2016). Building a science of individ-
ual differences from fMRI. Trends in Cognitive Sciences, 20(6),
425–443.
Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M. D., Huang, J.,
Chun, M. M., . . . Constable, R. T. (2015). Functional connectome
fingerprinting: Identifying individuals using patterns of brain con-
nectivity. Nature Neuroscience, 18(11), 1664.
Finn, E. S., Scheinost, D., Finn, D. M., Shen, X., Papademetris, X.,
& Constable, R. T. (2017). Can brain state be manipulated to
emphasize individual differences in functional connectivity?
NeuroImage, 160, 140–151.
Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D., Harwell,
J., Yacoub, E., . . . Smith, S. M. (2016). A multi-modal parcellation
of human cerebral cortex. Nature, 536(7615), 171–178.
Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,
Fischl, B., Andersson, J. L., . . . Van Essen, D. C. (2013). The mini-
mal preprocessing pipelines for the Human Connectome Project.
Neuroimage, 80, 105–124.
Network Neuroscience
382
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
a
_
0
0
0
6
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
“Thin slice” connectome fingerprinting
Gonzalez-Castillo, J., Saad, Z. S., Handwerker, D. A., Inati, S. J.,
Brenowitz, N., & Bandettini, P. A. (2012). Whole-brain, time-
locked activation with simple tasks revealed using massive
averaging and model-free analysis. Proceedings of the National
Academy of Sciences of the United States of America, 109(14),
5487–5492.
Gratton, C., Laumann, T. O., Nielsen, A. N., Greene, D. J., Gordon,
E. M., Gilmore, A. W., . . . Dosenbach, N. U. (2018). Functional
brain networks are dominated by stable group and individual fac-
tors, not cognitive or daily variation. Neuron, 98(2), 439–452.
Horien, C., Noble, S., Finn, E. S., Shen, X., Scheinost, D., & Constable,
R. T.
(2018). Considering factors affecting the connectome-
based identification process: Comment on Waller et al. Neuro-
Image, 169, 172–175.
Laumann, T. O., Gordon, E. M., Adeyemo, B., Snyder, A. Z., Joo,
S. J., Chen, M. Y., . . . Schlaggar, B. L. (2015). Functional sys-
tem and areal organization of a highly sampled individual human
brain. Neuron, 87(3), 657–670.
Miranda-Dominguez, O., Mills, B. D., Carpenter, S. D., Grant, K. A.,
Kroenke, C. D., Nigg, J. T., & Fair, D. A. (2014). Connectotyping:
model based fingerprinting of the functional connectome. PloS
One, 9(11), e111048.
Miranda-Dominguez, O., Feczko, E., Grayson, D. S., Walum, H.,
Nigg, J. T., & Fair, D. A. (2017). Heritability of the human con-
nectome: A connectotyping study. Network Neuroscience, 2(2),
175–199, 1–25.
Mueller, S., Wang, D., Fox, M. D., Yeo, B. T., Sepulcre, J., Sabuncu,
M. R., . . . Liu, H. (2013). Individual variability in functional connec-
tivity architecture of the human brain. Neuron, 77(3), 586–595.
Noble, S., Scheinost, D., Finn, E. S., Shen, X., Papademetris, X.,
(2017a). Multisite reli-
McEwen, S. C., . . . Mirzakhanian, H.
ability of MR-based functional connectivity. NeuroImage, 146,
959–970.
Noble, S., Spann, M. N., Tokoglu, F., Shen, X., Constable, R. T., &
Scheinost, D. (2017b). Influences on the test–retest reliability of
functional connectivity MRI and its relationship with behavioral
utility. Cerebral Cortex, 27(11), 5415–5429.
Peña-Gómez, C., Avena-Koenigsberger, A., Sepulcre, J., & Sporns,
O. (2017). Spatiotemporal network markers of individual vari-
ability in the human functional connectome. Cerebral Cortex,
28(8), 2922–2934.
Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., & Petersen,
S. E. (2012). Spurious but systematic correlations in functional
connectivity MRI networks arise from subject motion. Neuro-
Image, 59(3), 2142–2154.
Seghier, M. L., & Price, C. J. (2018). Interpreting and utilising inter-
subject variability in brain function. Trends in Cognitive Sciences,
22(6), 517–530.
Shrout, P. E., & Fleiss, J. L. (1979). Intraclass correlations: Uses in
assessing rater reliability. Psychological Bulletin, 86(2), 420.
Smith, S. M., Beckmann, C. F., Andersson, J., Auerbach, E. J.,
Bijsterbosch, J., Douaud, G., . . . Kelly, M. (2013). Resting-
state fMRI in the human connectome project. NeuroImage, 80,
144–168.
Vanderwal, T., Eilbott, J., Finn, E. S., Craddock, R. C., Turnbull,
A., & Castellanos, F. X.
Individual differences in func-
tional connectivity during naturalistic viewing conditions. Neuro-
Image, 157, 521–530.
(2017).
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E.,
Yacoub, E., Ugurbil, K., & Wu-Minn HCP Consortium. (2013).
The WU-minn human connectome project: An overview. Neuro-
Image, 80, 62–79.
Waller, L., Walter, H., Kruschwitz, J. D., Reuter, L., Müller, S., Erk,
S., & Veer, I. M. (2017). Evaluating the replicability, specificity,
and generalizability of connectome fingerprints. NeuroImage,
158, 371–377.
Yeo, B. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D.,
Hollinshead, M., . . . Fischl, B. (2011). The organization of the
human cerebral cortex estimated by intrinsic functional connec-
tivity. Journal of neurophysiology, 106(3), 1125–1165.
Network Neuroscience
383
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
6
3
1
0
9
2
5
9
1
n
e
n
_
a
_
0
0
0
6
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3