RECHERCHE
Differential contributions of static and
time-varying functional connectivity
to human behavior
Adam Eichenbaum 1∗, Ioannis Pappas
1∗, Daniel Lurie
2,
Jessica R. Cohen3†, and Mark D’Esposito1,2†
1Helen Wills Neuroscience Institute, Université de Californie, Berkeley
2Département de psychologie, Université de Californie, Berkeley
3Department of Psychology and Neuroscience, University of North Carolina at Chapel Hill
∗These authors contributed equally to this work.
†These senior authors contributed equally to this work.
un accès ouvert
journal
Mots clés: Functional connectivity, Static functional connectivity, Time-varying functional connec-
tivité, Canonical correlation analysis
ABSTRAIT
Measures of human brain functional connectivity acquired during the resting-state track
critical aspects of behavior. Recently, fluctuations in resting-state functional connectivity
patterns—typically averaged across in traditional analyses—have been considered for their
potential neuroscientific relevance. There exists a lack of research on the differences between
traditional “static” measures of functional connectivity and newly considered “time-varying”
measures as they relate to human behavior. Using functional magnetic resonance imagining
(IRMf) data collected at rest, and a battery of behavioral measures collected outside the
scanner, we determined the degree to which each modality captures aspects of personality
and cognitive ability. Measures of time-varying functional connectivity were derived by fitting
a hidden Markov model. To determine behavioral relationships, static and time-varying
connectivity measures were submitted separately to canonical correlation analysis. A single
relationship between static functional connectivity and behavior existed, defined by
measures of personality and stable behavioral features. Cependant, two relationships were
found when using time-varying measures. The first relationship was similar to the static case.
The second relationship was unique, defined by measures reflecting trialwise behavioral
variability. Our findings suggest that time-varying measures of functional connectivity are
capable of capturing unique aspects of behavior to which static measures are insensitive.
RÉSUMÉ DE L'AUTEUR
Correlated patterns of brain activity measured in the absence of any prescribed task show
meaningful temporal fluctuations. Cependant, the manner by which such fluctuations track
aspects of human behavior remains unresolved. The current report takes a data-driven
approach to characterize how time-varying patterns of human brain functional connectivity
differ from traditional static measures in their ability to track aspects of personality and
cognitive ability. We determine that time-varying patterns of functional connectivity not only
track similar aspects of behavior as do static measures, but also unique behavioral qualities
aussi, specifically those that reflect behavioral variability. These results highlight the
importance and relevance of examining time-varying measures of functional connectivity.
Citation: Eichenbaum, UN., Pappas, JE.,
Lurie, D., Cohen, J.. R., & D'Esposito, M..
(2021). Differential contributions of
static and time-varying functional
connectivity to human behavior.
Neurosciences en réseau, 5(1), 145–165.
https://doi.org/10.1162/netn_a_00172
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00172
Informations complémentaires:
https://doi.org/10.1162/netn_a_00172
Reçu: 25 Juin 2020
Accepté: 5 Octobre 2020
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Adam Eichenbaum
eichenbaum@berkeley.edu
Éditeur de manipulation:
Olaf Sporns
droits d'auteur: © 2020
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
un
_
0
0
1
7
2
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
INTRODUCTION
Measuring activity in the human brain during a task-free “resting state” has become common
as this activity is known to be spatially and temporally organized (Biswal et al., 1995). These
patterns of resting-state functional connectivity (rsFC) are sensitive to numerous aspects of
behavior, including cognitive performance (Stevens et al., 2012; Chan et coll., 2014), âge
(Chan et coll., 2014), and the extent of cognitive impairments (Alexander-Bloch et al., 2010;
Rudie et al., 2013). Using rsFC data from the Human Connectome Project (Van Essen et al.,
2013), a recent report utilized canonical correlation analysis (CCA) to reveal that rsFC and nu-
merous behavioral measures were linked via a single mode of population covariation, provid-
ing a single inextricable link between stable functional brain organization and interindividual
behavioral differences (Smith et al., 2015).
The majority of neuroimaging studies have investigated rsFC by assuming that it is stable
across the measurement period. Cependant, a recent emphasis has been placed on determin-
ing whether, and to what degree, rsFC systematically varies in time (Calhoun et al., 2014).
While some measurable fluctuations are likely due to noise or nonneural physiological sig-
nals (Hutchison et al., 2013; Lindquist et al., 2014; Hindriks et al., 2016; Duff et al., 2018;
Lurie et al., 2019), there is evidence that these rapidly evolving changes have a neuronal basis
(Chang & Glover, 2010; de Pasquale et al., 2010; Brookes et al., 2014; Thompson, 2018).
De plus, analysis of time-varying FC might reveal new relationships to behavior unobtain-
able by static analyses (Cohen, 2018; Kucyi et al., 2018). There is recent evidence that fluctua-
tions of task-based FC track aspects of cognitive control (Khambhati et coll., 2018) and attention
(Sadaghiani et al., 2015), suggesting that flexible network reconfiguration indexes trial-by-trial
performance.
It is important to consider ways in which static and time-varying FC differ, and how these
differences impact the way each modality encodes aspects of behavior. Whereas static mea-
sures provide a snapshot of the stable organization of the brain, time-varying measures in-
dex higher order relationships between brain regions. Such measures include the degree to
which functional networks vary their interconnectivity with other networks, the change in
global organizational structure, and how the global FC profile transitions between different
functional substates (Vidaurre et al., 2017; Shine & Breakspear, 2018). Ainsi, it is likely that
measures of static and time-varying FC encode different behavioral features; cependant, a pre-
cise characterization of this relationship is missing. Studies have focused on either one type
of connectivity (static: Smith et al., 2015; time-varying: Casorso et al., 2019), or on specific
behaviors (Rosenberg et al., 2016), but only two studies attempted to simultaneously disen-
tangle static and time-varying FC’s behavioral relevance (Jia et al., 2014; Liégeois et al., 2019).
Jia and colleagues (2014) found that time-varying measures of FC explained more variance in
behaviors tracking alertness, cognition, emotion, and personality than did static FC. Liégeois
and colleagues (2019) found that measures of time-varying FC tracked both task-based be-
havior and self-reported personality traits, whereas static measures only captured self-reported
traits. Although leveraging the power of the Human Connectome Project, these studies only
had access to basic measures of human behavior, lacking access to measures typically em-
ployed by cognitive neuroscientists studying working memory, cognitive control, and execu-
tive function.
To directly address the behavioral differences captured by static and time-varying FC, nous
utilized resting-state blood oxygen level–dependent (AUDACIEUX) data collected alongside a bat-
tery of complex behavior and personality measures. These measures ranged across working
mémoire, executive functioning, processing speed, affect, and impulsivity. Building off Smith
146
Canonical correlation analysis:
Statistical model that finds the
maximal correlation between two
datasets using cross-covariance
matrices.
Cognitive control:
The ability to adapt one’s behavior
in a dynamic environment where
multiple sources of information must
be processed.
Working memory:
The active short-term retention of
information no longer present in the
current environment.
Executive function:
The management and awareness of
multiple sources of information in
order to attain goals of varying
urgency.
Neurosciences en réseau
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
un
_
0
0
1
7
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
Hidden Markov model:
Statistical model that infers the
current state of a system based only
on the state immediately preceding it
in time.
and colleagues (2015), we leveraged CCA to determine whether there exist modes of co-
variation between behavior and static, as compared to time-varying, rsFC. Static rsFC was
estimated by computing a node-node correlation matrix across all regions of the brain. Time-
varying rsFC was estimated by fitting a hidden Markov model (HMM) to the data. The HMM
allowed for the characterization of, and transition likelihood between, multiple latent “states”
in a data-driven fashion as fast as the modality allowed, overcoming limitations imposed by
sliding window methods (Hutchison et al., 2013). The HMM has been used to character-
ize brain dynamics across multiple neuroimaging modalities during rest (Baker et al., 2014;
Vidaurre et al., 2017) and task (Vidaurre et al., 2018).
Using static FC, CCA revealed a single relationship primarily defined by variance in mea-
sures of personality and affect, as well as task-general behavioral features. With time-varying
FC, CCA instead revealed two (orthogonal) relationships. The first was highly similar to that
found using static FC. Cependant, the second was specific to time-varying FC and was defined by
variance in trialwise measures of reaction time to processing speed and working memory tasks,
as well as measures tapping into overall processing accuracy. These results suggest that there
exists meaningful information in the temporal fluctuations of rsFC patterns that can explain
aspects of human behavior to which previous analytic methods have been insensitive.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
un
_
0
0
1
7
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MÉTHODES
Participants
Twenty-three healthy, young adult participants (âge moyen = 28.26 années, SD = 4.52 années, 10
females) were recruited for a repeated measures study to participate in two or three sessions.
Five participants were unable to attend the third study session as a result of having moved away
from the state of California. Par conséquent, only 18 participants were included in the third session
(âge moyen = 27.67 années, SD = 4.64 années, 8 females). All participants were native English
speakers, had normal or corrected-to-normal vision, and had normal hearing. Participants
were excluded for any history of neurological or psychiatric disorders, use of psychotropic
drugs, a history of substance abuse, or MRI contraindications. All participants provided writ-
ten, informed consent according to the procedures of the University of California Berkeley
Comité d'examen institutionnel.
Experimental Design and Procedure
Participants underwent one practice session approximately 1 week (mean = 6 jours, SD = 2.37
jours) before their first testing session. They then completed two or three identical testing ses-
sions. Testing sessions 1 et 2 were separated by approximately 1 week (mean = 8 jours, SD =
1.47 jours), while testing sessions 2 et 3 were separated by approximately 1 année (mean =
399 jours, SD = 28.73 jours).
Each session began with two 6-minute resting-state scans in the MRI machine, dans lequel
participants were instructed to stay awake with their eyes open and fixate on a crosshair. Dur-
ing the first session, the resting-state scans were followed by a structural scan. Immediately
after the MRI scan, participants completed two self-report questionnaires and a task outside
of the scanner: a visual analog scale (VAS; McCormack et al., 1988), the Barratt Impulsive-
ness Scale (BIS; Patton et al., 1995), and a box completion task (Salthouse, 1996). Immedi-
ately following completion of the questionnaires and task, participants then completed four
computerized cognitive tasks in counterbalanced order (different orders across participants
and for each session): a Stroop task (Stroop, 1935), a digit symbol substitution task (DSST;
Rypma et al., 2006), a spatial working memory (WM) task (Kuo et al., 2011), and a Color
Neurosciences en réseau
147
Behavioral significance of time-varying functional connectivity
WM task (Zhang & Luck, 2008). Visual depiction of the four computerized task paradigms are
shown in Supporting Information Figure S1.
The BIS is a survey that determines measures of impulsivity along a set of three subtraits:
“Attentional,” “Motor,” and “Non-planning.” The VAS has participants make a mark along
a line segment in which one side represents “Not” and the other side “Extremely” for the
following items: “Anxious,” “Happy,” “Sad,” “Nauseous,” “Drowsy,” “Jittery,” “Fatigued," et
“Dizzy.” Participant responses are measured as the distance (in centimeters) away from the
“Not” end of the line. The box completion task requires that participants use a pencil to fill in
the fourth side of an open-ended square as rapidly as possible. The measure of interest is the
duration of time it takes to complete 100 squares.
In the Stroop task, color words (blue, red, vert, yellow) or animal names (horse, bird, cat,
dog) printed in different colors (blue, red, vert, yellow) were presented on the left side of the
computer screen. Participants had to indicate the font color by pressing one of four buttons.
For ease of task performance color-to-button mappings were presented at the bottom part of
the screen throughout the duration of the experiment. Participants used the four fingers of
their right hand for responding with color-to-button mappings randomly assigned to partici-
pants. Compatible, neutral, and incompatible trials were presented with equal probability. Dans
compatible trials, color and word were the same. In neutral trials, the task-irrelevant dimen-
sion (par exemple., word meaning) was not related to the task (par exemple., animal names). In incompatible
trials, color and word differed. Each Stroop session was 10 minutes long and comprised eight
blocks of 36 trials each. The stimuli were presented for 300 ms with an interstimulus interval
de 1,700 ms. The measures of interest included the difference score, in milliseconds, entre
the median response time of correct responses to trials in which there was an incongruity be-
tween the word and color (incongruent trials: c'est à dire., the word “RED” in blue text) and the median
response time of correct responses to a trial in which the color of the text matched the word
(congruent trials: c'est à dire., the word “RED” in red text). De plus, we also focused on the standard
deviation of this response time difference, as well as the accuracy on incongruent trials. Nous
chose not to compute a difference score for accuracy as individual differences for accuracy on
congruent trials was likely to be minimal.
The DSST required that participants indicated via button press whether a presented symbol-
number pair correctly matched an on-screen answer key. Nine symbols were paired with
numbers 1 through 9, and the answer key was shown at the top of the screen on every trial;
140 pairs were presented in which the symbol-number pair either matched (50%), or did not
match (50%), the provided answer key. Pairs were presented on screen for 4,000 ms, pendant
which the participant could indicate their response. Participants were instructed to respond
as rapidly and as accurately as possible. Measures of interest included the overall accuracy,
median reaction time, and standard deviation of reaction time, for match and nonmatch trials
separately.
The Spatial WM task (“Spatial WM”) required that participants initially encode and retain
the color of a rapidly presented set of colored squares. The task followed a 2 (load: 2 vs. 4)
× 2 (cue onset: early vs. late) conception. Participants viewed an array of 2 ou 4 colored squares
pour 180 ms prior to retaining this information over a 900-ms delay period.
In the early-cue
condition, a cue appeared in the location of where one of the squares had previously been
after 200 ms (and stayed on screen for the remaining 700 ms). In the late-cue condition, le
cue appeared after 800 ms (and stayed on screen for the remaining 100 ms). Suivant, participants
had to indicate whether a newly presented colored square, among an array of 2 ou 4 colored
Neurosciences en réseau
148
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
un
_
0
0
1
7
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
squares, matched the color of the spatially cued square prior to the delay. The new array
remained on screen for 1,920 ms. Participants were instructed to respond as accurately and
as quickly as possible. In total, participants completed 240 trials, avec 60 trials coming from
each condition. Measures of interest included percent accuracy, median reaction time, et
the standard deviation of reaction time, across both cognitive loads, for match and nonmatch
trials separately.
The color working memory task (“Color WM”) required that participants initially encode the
colors of three squares rapidly presented on screen for 1,000 ms. Following a delay of 500 ms,
a visual cue to the location of one of the squares appeared for 500 ms. After a 1,250 ms delay,
a distractor color appeared on screen for 500 ms. Following another delay of 1,250 ms, le
participants were then presented with a colorwheel for 3,000 ms and were instructed to move
the cursor along the wheel in a continuous fashion until the selected color matched the color
of the cued square being held in memory. Participants completed 40 trials in total and were
provided a 5-second break after the end of the 20th trial. Measures of interest included the
median and standard deviation of reaction time and error angle (calculated as the difference
in degrees along the colorwheel between the correct answer and the response provided by the
participant) across all responses.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
un
_
0
0
1
7
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
During the practice session, participants completed the four cognitive tasks so as to famil-
iarize themselves with the tasks before the testing sessions. The purpose of this session was
to minimize practice effects. The testing sessions were all identical. The final testing session
was conducted on the same MRI machine as the previous sessions, but in a different location.
Reliability tests ensured that MRI effects (such as signal-to-noise ratio and artifacts) were not
different across the two locations.
Behavioral measures for each subject at each session were considered as separate yet de-
pendent datapoints, and therefore no averaging across sessions occurred. Given the depen-
dent nature of these data points, we utilize the analytic methodology from Smith et al. (2015),
which accounted for familial relationships between specific subjects in the Human Connec-
tome Project. Specifically, we performed all statistics such that permuted null distributions
never shuffled labels across sessions for subjects. Autrement dit, all sessions from any partic-
ular subject were always grouped together so as to appropriately account for within-subject
variability.
Factor Analysis of the Behavioral Data
All 31 behavioral measures were included in the analyses and subjected to a factor analysis.
Six measures each came from the Spatial WM task and the DSST: percent accuracy, median
reaction time, and the standard deviation of reaction times for match and nonmatch trials.
Three measures came from the Stroop task: percent accuracy on incongruent trials, median
reaction time difference between congruent and incongruent trials, and the standard deviation
of the reaction time difference between congruent and incongruent trials. Four measures came
from the Color WM task: median and standard deviation of response error, as well as median
and standard deviation of reaction times. All eight measures from the VAS were included, comme
well as the scores of the three subtraits of the BIS. Last, the time to complete all 100 squares
for the box completion task was included.
We clustered the behavioral data into eight factors using MATLAB’s factoran function and
allowed for promax oblique rotation (Supporting Information Figure S2). We labeled these fac-
tors qualitatively by observing which behavioral measures loaded highest on each factor. Nous
Neurosciences en réseau
149
Behavioral significance of time-varying functional connectivity
chose eight factors as it most cleanly separated tasks from one another and grouped together
correlated measures.
fMRI Data Acquisition
Imaging data were collected on a 3-Tesla Siemens MAGNETOM Trio whole-body MR scan-
ner using a 12-channel head coil at the University of California, Berkeley, Henry H. Wheeler
Jr.. Brain Imaging Center. Whole-brain functional data were acquired in two runs using a
T2*-weighted echo planar imaging pulse sequence (180 volumes/run, 37 interleaved axial
slices parallel to the AC-PC line, slice thickness 3.5 mm, interslice distance = 0.7 mm, TR =
2,000 ms, LE = 24 ms, FA = 60◦, matrice 64 × 64, field of view 224 mm). A high-resolution
T1-weighted structural 3D MP-RAGE was also acquired (160 slices, slice thickness 1 mm, TR =
2,300 ms, LE = 2.98 ms, FA = 9◦, matrice 256 × 256, field of view 256 mm). An LCD pro-
jector back projected a fixation cross for the resting-state scan onto a screen mounted to the
radiofrequency (RF) coil.
fMRI Data Processing
Preprocessing of the imaging data were performed using fMRIPrep 1.1.4 (Esteban, Markiewicz,
et autres. 2018; Esteban, Blair, et coll., 2018), which is based on Nipype 1.1.1 (Gorgolewski et al.,
2011). The T1-weighted (T1w) image was corrected for intensity nonuniformity (INU) en utilisant
N4BiasFieldCorrection (ANTs 2.2.0; Tustison et al., 2010, and used as T1w-reference through-
out the workflow. The T1w-reference was then skull stripped using ANTs BrainExtraction (ANTs
2.2.0), using OASIS as target template. Brain surfaces were reconstructed using recon-all
(FreeSurfer 6.0.1; Dale, Fischl, & Séréno, 1999), and the brain mask estimated previously
was refined with a custom variation of the method to reconcile ANTs-derived and FreeSurfer-
derived segmentations of the cortical gray matter of Mindboggle (Klein et al., 2017). Spatial
normalization to the ICBM 152 Nonlinear Asymmetrical template version 2009c (MNI152NLin
2009cAsym; Fonov et al., 2009) was performed through nonlinear registration with ANTs Reg-
istration (ANTs 2.2.0; Avants et al., 2008), using brain-extracted versions of both T1w vol-
ume and template. Brain tissue segmentation of cerebrospinal fluid (CSF), white matter, et
gray matter was performed on the brain-extracted T1w using fast (FSL 5.0.9; Zhang, Brandy,
& Forgeron, 2001).
For each of the BOLD runs found per participant (across all sessions), the following prepro-
cessing was performed. D'abord, a reference volume and its skull-stripped version were generated
using a custom methodology of fMRIPrep. Head-motion parameters with respect to the BOLD
reference (transformation matrices, and six corresponding rotation and translation parameters)
were estimated before any spatiotemporal filtering using mcflirt (FSL 5.0.9; Jenkinson et al.,
2002). BOLD runs were slice-time corrected using 3dTshift from AFNI. The BOLD time series
(including slice-timing correction when applied) were resampled onto their original, native
space by applying a single, composite transform to correct for head motion and susceptibil-
ity distortions. These resampled BOLD time series will be referred to as preprocessed BOLD
in original space, or just preprocessed BOLD. The BOLD reference was then co-registered
to the T1w reference using bbregister (FreeSurfer), which implements boundary-based regis-
tration (Greve & Fischl, 2009). Co-registration was configured with nine degrees of freedom
to account for distortions remaining in the BOLD reference. The BOLD time series were re-
sampled to MNI152NLin2009cAsym standard space, generating a preprocessed BOLD run in
MNI152NLin2009cAsym space. Several confounding time series were calculated based on
the preprocessed BOLD: framewise displacement (FD), DVARS, and three region-wise global
signals. FD and DVARS were calculated for each functional run, both using their implemen-
tations in Nipype (following the definitions by Power et al., 2014). The three global signals
Neurosciences en réseau
150
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
un
_
0
0
1
7
2
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
Static functional connectivity:
Statistical similarity of recorded time
series between two brain regions
assessed across the entire recording
period, producing one value.
were extracted within the CSF, the white matter, and the whole-brain masks (c'est à dire., global sig-
nal). The head-motion estimates calculated in the correction step were also placed within the
corresponding confounds file. All resamplings were performed with a single interpolation step
by composing all the pertinent transformations (c'est à dire., head-motion transform matrices, suscep-
tibility distortion correction when available, and co-registrations to anatomical and template
les espaces). Gridded (volumetric) resamplings were performed using ANTs ApplyTransforms, con-
figured with Lanczos interpolation to minimize the smoothing effects of other kernels (Lanczos,
1964).
Further postprocessing included removal of artifactual signals from the time series data. Nous
used recommended nuisance regression approaches based on recent processing comparisons
(Ciric et al., 2017; Parkes et al., 2018). We regressed out the six head-motion estimates, le
mean white matter signal, the mean cerebral spinal fluid signal, their temporal derivatives and
quadratic expansions, and the quadratic expansions of the temporal derivatives. We chose to
avoid global signal regression due to (1) the known effect of introducing artifactual negative
correlations into the data and (2) the increase in distance-dependent motion effects. As tempo-
ral contiguity is necessary to accurately estimate changes in FC across time, we did not apply
any scrubbing techniques to our data. Last, we applied a bandpass filter from 0.01 à 0.1 Hz
to the data. Mean framewise displacement of our sample was relatively low (mean FD = 0.14,
range = 0.06–0.37) and aligned with previously analyzed samples (Power et al., 2014).
Static Functional Connectivity
To obtain measures of FC, we first measured the mean BOLD signal across all voxels con-
tained within each node of our brain atlases. Cortical nodes were taken from the 400-node
Local-Global atlas (Schaeffer et al., 2018). Twenty-one subcortical nodes were taken from the
Harvard-Oxford atlas (Makris et al., 2006). Twenty-two cerebellar nodes were taken from the
AAL atlas (Tzourio-Mazoyer et al., 2002). Four cortical nodes in bilateral anterior temporal
pole regions had to be removed from all analyses due to insufficient coverage (less than 25%
of voxels contained data) in one or more participants in one or more scans. This left data from
439 nodes distributed across the entire brain.
Scans were concatenated within session, per participant, in order to increase reliability
of the measured FC profile for each session. To remove spurious data differences between
sessions, each session’s data was standardized. FC was measured as the Pearson correlation
coefficient between every node and all other nodes for which there was sufficient coverage.
Hidden Markov Model
Setup
The HMM derives brain dynamics based on BOLD time series parcellation data. The HMM
assumes that the time series data are characterized by a number of states that the brain cycles
through at different times throughout the scanning period (Baker et al., 2014).
At each time point t of brain activity, the observed time series data was modeled as a mixture
of multivariate Gaussian distributions. Each one of these Gaussian distributions corresponded
to a different state k and was described by first-order and second-order statistics (activité [µk]
and FC [Σ
k], respectivement) that can be interpreted as the activity and FC of each state. Using
notation, if xt describes the BOLD data at each time point t, then the probability of being in
state k is assumed to follow a multivariate Gaussian distribution:
P.(xt|st = k) ∼ multivariate Gaussian(µk, Σ
k)
Neurosciences en réseau
151
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
un
_
0
0
1
7
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
À son tour, we modeled how transitions between states took place. The basic Markovian prin-
ciple that describes the transition between states assumes that the probability of the data being
in state k at time t relates only to the probability of being in state l at time t − 1. This can be
described by the following equation:
P.(st = k) = Σ
je
Ème
je,kP(st−1 = l)
where Θ
je,k is the transition probability from state l to state k. Taken together, the HMM infers
the P(st = k) probabilities for each state k and time t (state time courses) as well as the
transition probabilities Θ
k) that best describe the data.
To make inference tractable, a variational Bayes algorithm was used that works by minimizing
the Kullback–Leibler divergence between the real and the modeled data (Wainwright & Jordan,
2007).
je,k and the statistics of each state (µk, Σ
The input time series data for the HMM was the total time series data for all participants and
all sessions (for the last session there were only 18 participants). Specifically, across the three
sessions and for all participants we concatenated the processed functional time series and ob-
tained a matrix of dimensions: (360 × 23 + 360 × 23 + 360 × 18) × number of regions
of interest (439) (Vidaurre et al., 2017). Data were standardized for each participant prior to
running the HMM. To control the dimensionality in the final data matrix, a principal compo-
nent analysis (APC) dimensionality reduction technique was applied on the concatenated time
courses using 25 components (Stevner et al., 2019). Enfin, the number of states for the HMM
was chosen as 12. Both of these settings were similar to the previous work that introduced the
use of the HMM on fMRI data (Vidaurre et al., 2017).
Inference
Running the HMM with these parameters resulted in a data matrix of dimensions (Non. temps
points × no. participants) × no. states. Each row represented the probability of each state
being active at each timepoint for each participant. Additional quantities related to the tempo-
ral characteristics of each state could then be obtained. D'abord, we quantified the proportion of
time that an individual resided in the state during the scan acquisition (fractional occupancy,
FO). En plus, the switching rate was defined as the difference between the probability of
activating a state at time t and activating a state at time t+1 summed over all states and over
all time points and divided by the number of time points. The HMM also provided each state’s
mean activity and connectivity µk and Σ
k, respectivement. Enfin, the HMM also provided the
state transition probability matrix of dimensions (Non. states × no. states) where each matrix
entry (k, je) quantified the transition probability of going from state k to state l.
An agglomerative hierarchical clustering algorithm was applied to the transition probability
matrix in order to determine whether there existed a temporal structure in the data, as had pre-
viously been shown with resting-state FC data from the Human Connectome Project (Vidaurre
et coll., 2017). This analysis starts by classifying each data point as a separate cluster and pro-
gressively combines clusters of data at different hierarchical levels: similar data are clustered at
a low level of hierarchy and less similar data are clustered at a higher level of hierarchy (Hastie,
Friedman, & Tibshirani, 2009). We used the linkage function as implemented in MATLAB with
default settings (method = ‘single,’ distance = ‘euclidean’). We regarded each identified cluster
as one metastate. À son tour, the metastate time courses were considered as the sum of the time
courses of the individual states that comprised them. Fractional occupancy and switching rate
of the metastates were calculated as in the case for single states.
Neurosciences en réseau
152
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
un
_
0
0
1
7
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
To assess whether there existed any relationship between the derived HMM time-varying
FC measures and in-scanner head motion, we first computed the mean FD across both runs
for each subject in each session. There existed no difference in mean FD across sessions (tous
t’s < 1.19, adjusted p’s = 0.679). Next, we correlated these session-specific mean FD values
with each of the 17 measures derived from the HMM (i.e., fractional occupancy of each of the
12 states, fractional occupancy of each of the 3 metastates, mean switching rate across the 12
states, and mean switching rate across the 3 metastates). Given the number of statistical tests
performed (17 × 3 = 51) and the related nature of the data being assessed, we applied false
discovery rate (FDR) correction to our results to account for multiple comparisons. Two of the
51 tests survived multiple comparisons correction: Fractional Occupancy of State 1 in Session
2 (r = 0.847, adjusted p < 0.001), and Fractional Occupancy of State 11 in Session 3 (r = 0.734,
adjusted p = 0.026). Given the lack of any consistent relationship between in-scanner head
motion and our HMM measures across sessions, it is likely that our preprocessing strategy of
the fMRI BOLD data appropriately corrected for motion artifact for the current study’s analyses
of time-varying FC.
Spatial Characterization of States
To spatially characterize the derived states, we thresholded the activity maps of each state to
include the top 40% of both positive and negative activations. We then spatially overlapped
each state with the 10 resting-state networks described in Smith et al. (2009) to obtain an
overlap index for each network. The index was calculated by counting the number of voxels
that were included in the thresholded map and then dividing these by the size of the resting-
state network under consideration in order to account for size bias.
Canonical Correlation Analysis
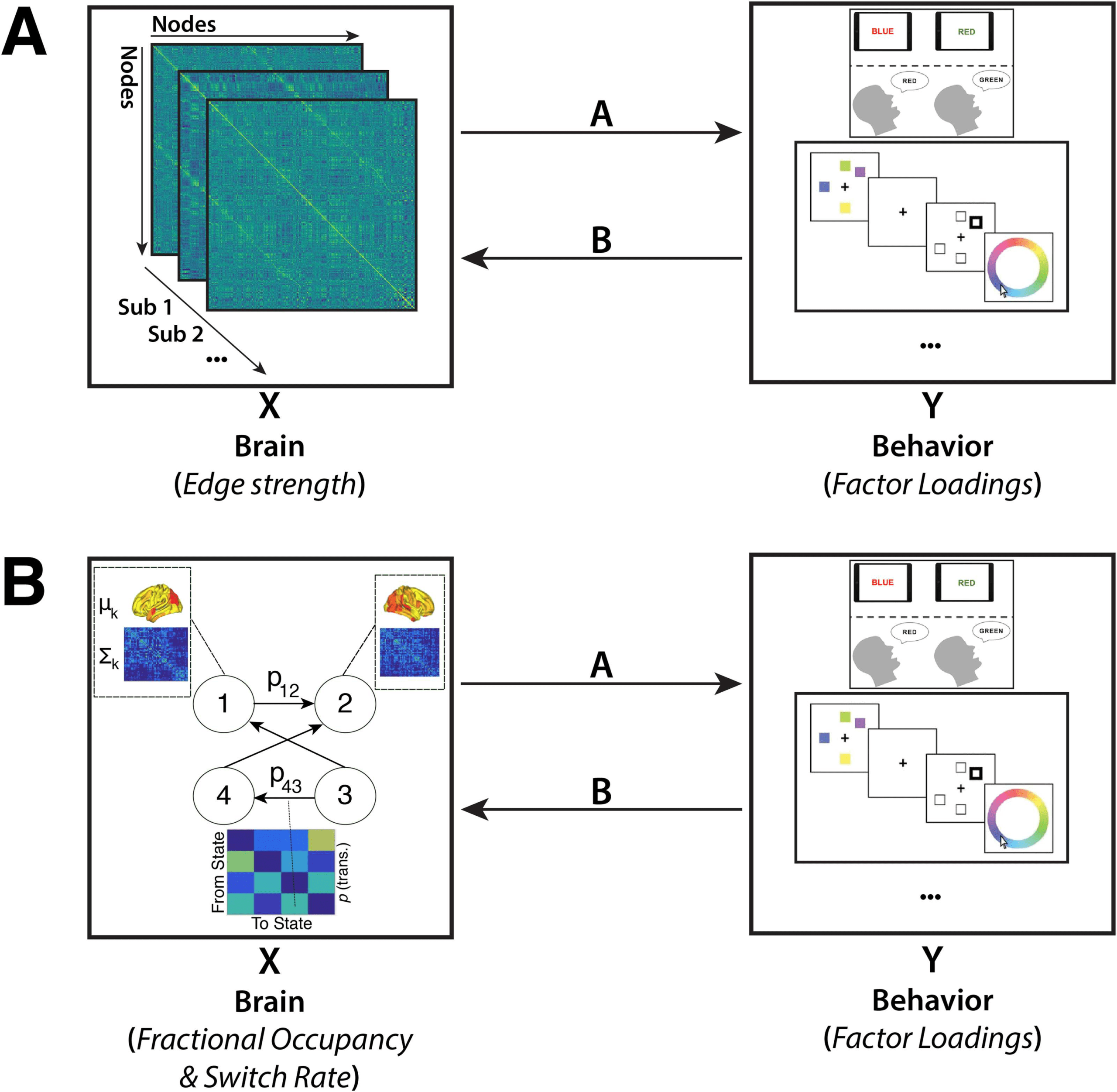
To relate the behavioral measures to static and time-varying FC we used CCA (Figure 1).
CCA finds correlations between multidimensional data wherein potential relationships may
be present (Hotelling, 1936). This is a more principled approach compared to conducting all
potential correlations and correcting for multiple comparisons. Specifically, this analysis finds
maximal correlations between two sets of variables, X (n × d1) and Y (n × d2), where d1 and
d2 are the number of variables used in X and Y respectively, and n is the number of obser-
vations for each variable. It produces two matrices, A and B, such that the variables U = AX
and V = BY are maximally related. CCA values were obtained from the MATLAB canoncorr
function. It is worth noting that like the PCA, this function can produce more than one mode,
with each mode ranked by the covariance that can be explained between X and Y.
We conducted two separate CCAs. First, we designated the factors of the behavioral data
In a second CCA, Y remained
as Y, and the edgewise static FC strength as X (n = 96,141).
the same, but we varied X. Specifically, we designated X as the fractional occupancy of each
HMM state (n = 12) and temporally defined metastate (n = 3), as well as the mean switching
rate across states (n = 1) and metastates (n = 1) separately. As a final preprocessing step, the
dimensionality of the static FC data was reduced using PCA as described in Smith et al. (2015),
retaining the top 13 components. No dimensionality reduction was required for the HMM
data as the number of variables was low. However, we performed an analysis of the HMM
data by using PCA and reported the results in the Supporting Information (Figure S4) where it
can be seen that the results are highly similar to the case in which PCA is not employed.
Statistical significance of the CCA analyses was estimated as follows. We calculated 10,000
permutations of the rows of X relative to Y, respecting the within-participant structure of the
Network Neuroscience
153
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
a
_
0
0
1
7
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
a
_
0
0
1
7
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mode of covariation:
A statistical relationship between two
weighted datasets that represents the
bidirectional association between
each set.
Figure 1. Methodology Overview. Canonical correlation analysis (CCA) was performed on two
different datasets, which were matched for measures of behavior but differed with regard to the
resting-state functional connectivity (rsFC) data included. The first CCA (A) included measures of
static FC (i.e., the node-to-node connectivity strength), while the second CCA (B) included measures
of time-varying FC. Measures of time-varying FC were derived by fitting a hidden Markov model to
the BOLD time series.
data, and recalculated the CCA mode for each permutation in order to build a distribution of
canonical variate pair correlation values (i.e.,
CCA of the true data to the shuffled data, we found that each mode of covariation discovered
with the true data was highly significant (p < 1/10,000). In addition, a cross-validation ap-
proach was adopted in order to assess the robustness of the discovered mode(s) (as described
in Smith et al., 2015). Across 1,000 runs, we ran CCA on a randomly selected set of 80% of
the data, respecting the within-participant nature of the data, and stored the resultant U and V.
We then estimated the mode on the heldout 20% of data and determined the significance of
the estimated mode employing the same permutation significance testing procedure as before.
These estimated modes were found to be highly significant, with the correlation between the
derived canonical weight vectors in the test dataset being very robust (replicating the results
from Smith et al., 2015).
Post hoc correlations of the values of X (Y-respective) with the columns of the significant
mode U (V-respective) were used to quantify the contributions (positively or negatively) of each
Network Neuroscience
154
Behavioral significance of time-varying functional connectivity
behavioral measure with the CCA mode. In other words, we quantified the extent to which
the Y variables were loaded/weighted on the CCA mode. There is no clear cutoff at which one
finds a significant correlation value and thus correlation values are reported in isolation.
Validation of CCA Analysis
We validated the identified CCA modes by comparing outcomes across a range of behavioral
factors (behavior) and FC principal components (static FC, time-varying FC). The number of
behavioral factors ranged from 1 to 9, while the number of static FC principal components
ranged from 1 to 20 and the number of time-varying FC principal components ranged from
1 to 17 (see Supporting Information). For the static case, we ran CCA on each combination
and stored the resulting post hoc correlations for each behavioral measure (i.e., with respect to
FC), and computed the Pearson correlation between these values across all 180 combinations
(Supporting Information Figures S3 and S4). For combinations that included two or more be-
havioral factors, we found that the discovered canonical covariate modes were highly similar,
with Pearson correlations tending to be very highly positive (i.e., greater than r = 0.90) as well
as very highly negative (i.e., less than r = −0.90). This bimodal distribution at the extremes of
the correlation range indicates that the discovered modes were highly preserved in structure
(i.e., the same behavioral measures loaded highly). We determined the optimal combination
(i.e., 8 behavioral factors, 13 FC PCs) by selecting either (A) the most significant canonical co-
variate pair (i.e., U × V), or (B) in cases where multiple pairs had the same maximal 1/10,000
permutation significance value, determining if combinations were highly similar after a cer-
tain number of factors or components were included, and then taking the smallest number of
factors and components that produced this outcome, restricted by those that had a significant
permutation value.
RESULTS
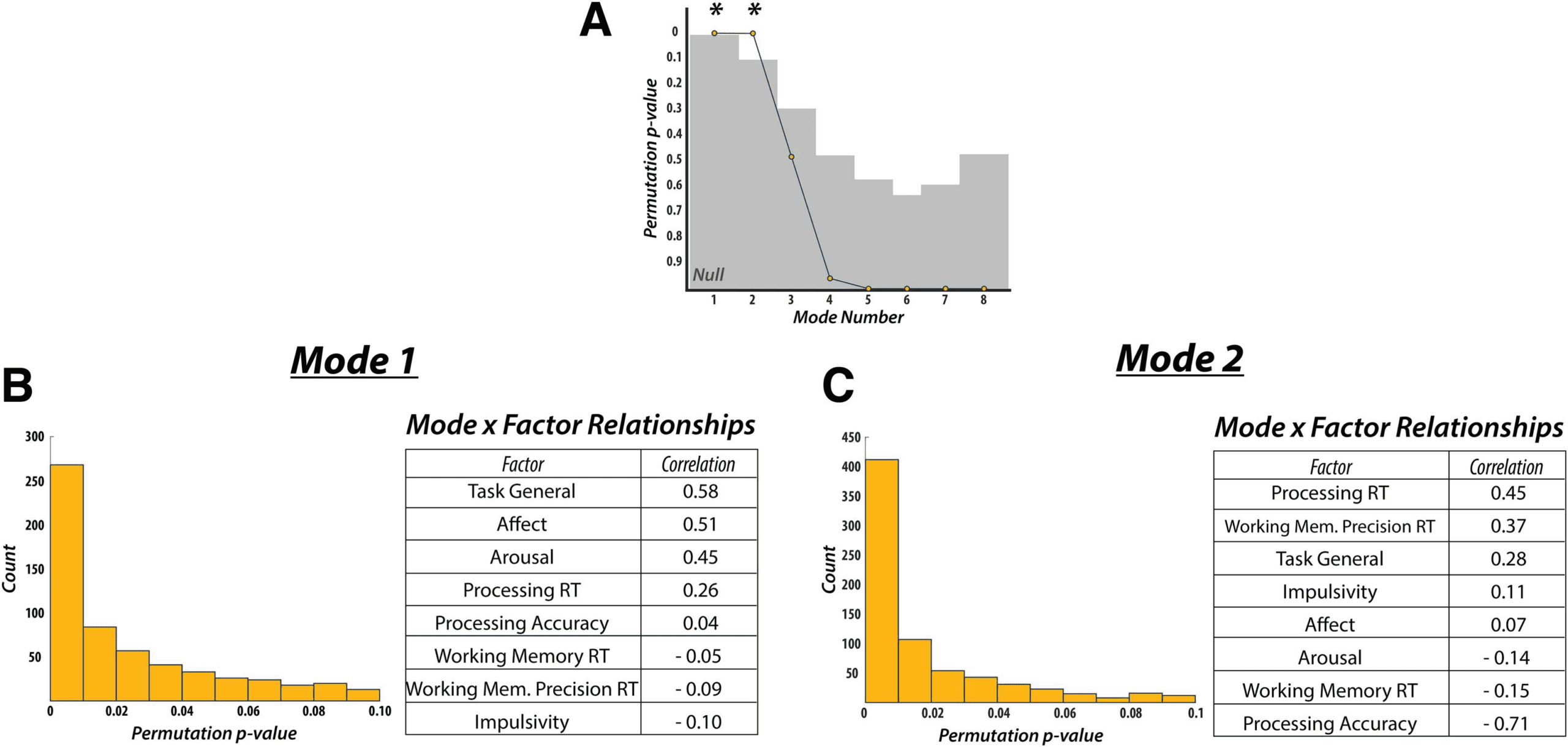
Factor Analysis
Brain and behavioral data were obtained as described in the Methods. We used factor analysis
to reduce the 31 behavioral measures to 8 factors (Supporting Information Figure S2). The first
factor, referred to as “Processing Reaction Time,” had DSST median and standard deviation
reaction time measures for both match and nonmatch trials loading highly positively. The
second factor was referred to as “Task General” because it contained a mixture of measures
across multiple tasks, with positive loadings from the Spatial WM task percent accuracy (match
trials), the Stroop task percent accuracy, and “Anxious” on the VAS, and negative loadings
on the Stroop task median reaction time and the DSST percent accuracy (both match and
nonmatch trials). The third factor, referred to as “Working Memory Reaction Time,” had the
Spatial WM task median and standard deviation reaction time measures, for both match and
nonmatch trials, loading highly positively. The fourth factor, referred to as ”Working Memory
Precision Reaction Time,” had two Color WM task measures loading highly positively: median
and standard deviation of reaction time. The fifth factor, referred to as “Affect,” had the VAS
measures “Sad” and “Happy” loading highly positively and negatively, respectively. The sixth
factor, referred to as “Processing Accuracy,” had only the DSST percent accuracy on match
trials loading highly positively. The seventh factor, referred to as “Arousal,” had high positive
loadings for both the “Drowsy” and “Jittery” VAS measures. Finally, the eighth factor, referred
to as “Impulsivity,” included high positive loadings of all three BIS measures.
The first (“Processing Reaction Time”), third (“Working Memory Reaction Time”), and fourth
(“Working Memory Precision Reaction Time”) factors all contain measures of both the median
Network Neuroscience
155
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
a
_
0
0
1
7
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
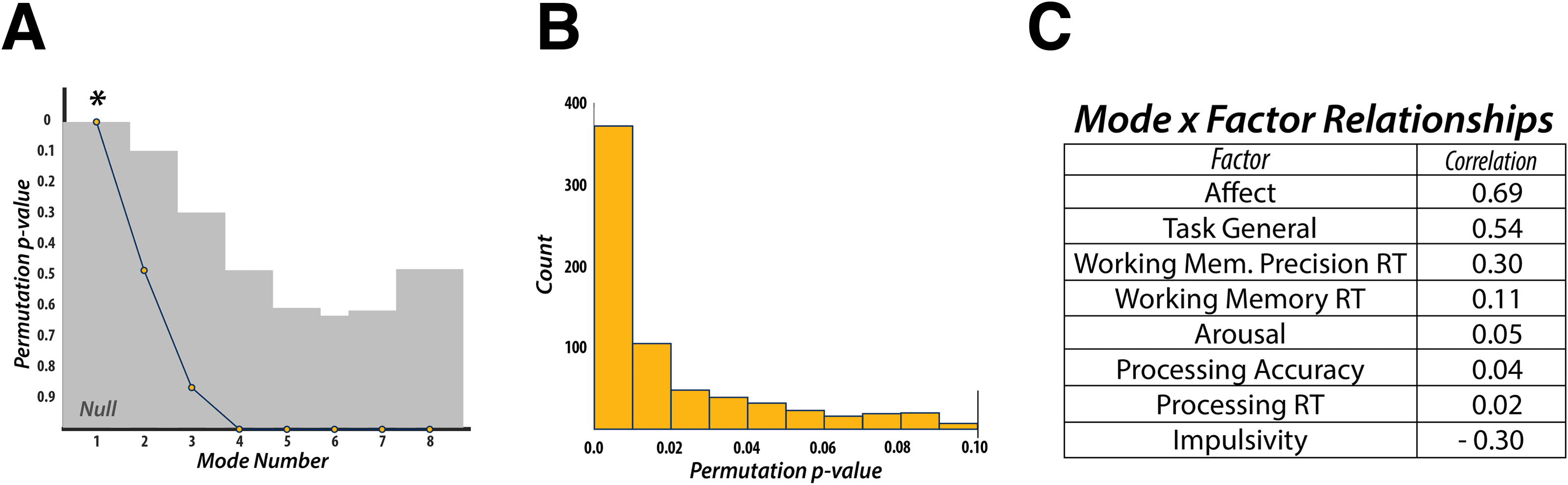
Figure 2. Canonical Correlation Analysis—Static Functional Connectivity. (A) CCA can discover as many modes of covariation as the lowest
rank of each dataset (i.e., 8 behavioral factors). Statistical significance was found only for the first discovered mode. (B) Additional cross-
validation of the discovered mode revealed that the first mode was statistically robust across the majority of the 1,000 folds. (C) Post hoc
correlations for the discovered mode and the 8 behavioral factors revealed that measures of “Affect” and “Impulsivity,” as well as a “Task
General” factor, dictated the structure of the mode. RT, reaction time.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
a
_
0
0
1
7
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
and standard deviation of reaction time across the DSST, Spatial WM, and Color WM tasks,
respectively, and therefore reflect aspects of within-task stability (median reaction time) and
within-task variability (standard deviation of reaction time).
In contrast, the second (“Task
General”) and sixth (“Processing Accuracy”) factors only contain task measures of accuracy
and/or median reaction time, and thus only reflect aspects of within-task stability. Last, the
fifth (“Affect”), seventh (“Arousal”), and eighth (“Impulsivity”) factors all contain measures that
reflect the personality and mood of the participant.
Canonical Correlation Analysis: Static Functional Connectivity
CCA was used to find a mode of population covariation between behavior and static FC. The
CCA included the behavioral data in 8-factor space, as well the static rsFC data in 13-principal
component space, based on the validation we performed (see the “Validation of CCA Analysis”
section of the Methods for details). The CCA revealed a single mode of covariation between
these two datasets (Figure 2). To assess the statistical significance of the discovered modes
of covariation, we followed the permutation and cross-validation procedure as outlined in
Smith and colleagues (2015; also see “Canonical Correlation Analysis” section in Methods
and Figure 2A and Figure 2B in this article).
We used post hoc correlations between the discovered mode and the behavioral factors
to evaluate the contribution of each factor to the mode, with respect to the static FC data.
This mode was defined by highly positive weights for the “Affect” (r = 0.69), “Task General”
(r = 0.54), and “Working Memory Precision Reaction Time” (r = 0.30) factors, and a highly
negative weight for the “Impulsivity” (r = −0.30) factor. All other factors had correlation values
below an absolute value of 0.11. These results indicate that static connectivity might encode
more general behavioral and personality features rather than information that may relate more
to task, or trial-specific, behavior.
Canonical Correlation Analysis: Time-Varying Functional Connectivity
We next assessed whether any relationships existed between time-varying FC and behavior.
To quantify the time-varying FC profile in each participant we fit the resting-state BOLD data
156
Time-varying functional connectivity:
Statistical similarity of recorded time
series between two brain regions
assessed continuously throughout the
recording period, producing multiple
values.
Network Neuroscience
Behavioral significance of time-varying functional connectivity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
a
_
0
0
1
7
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
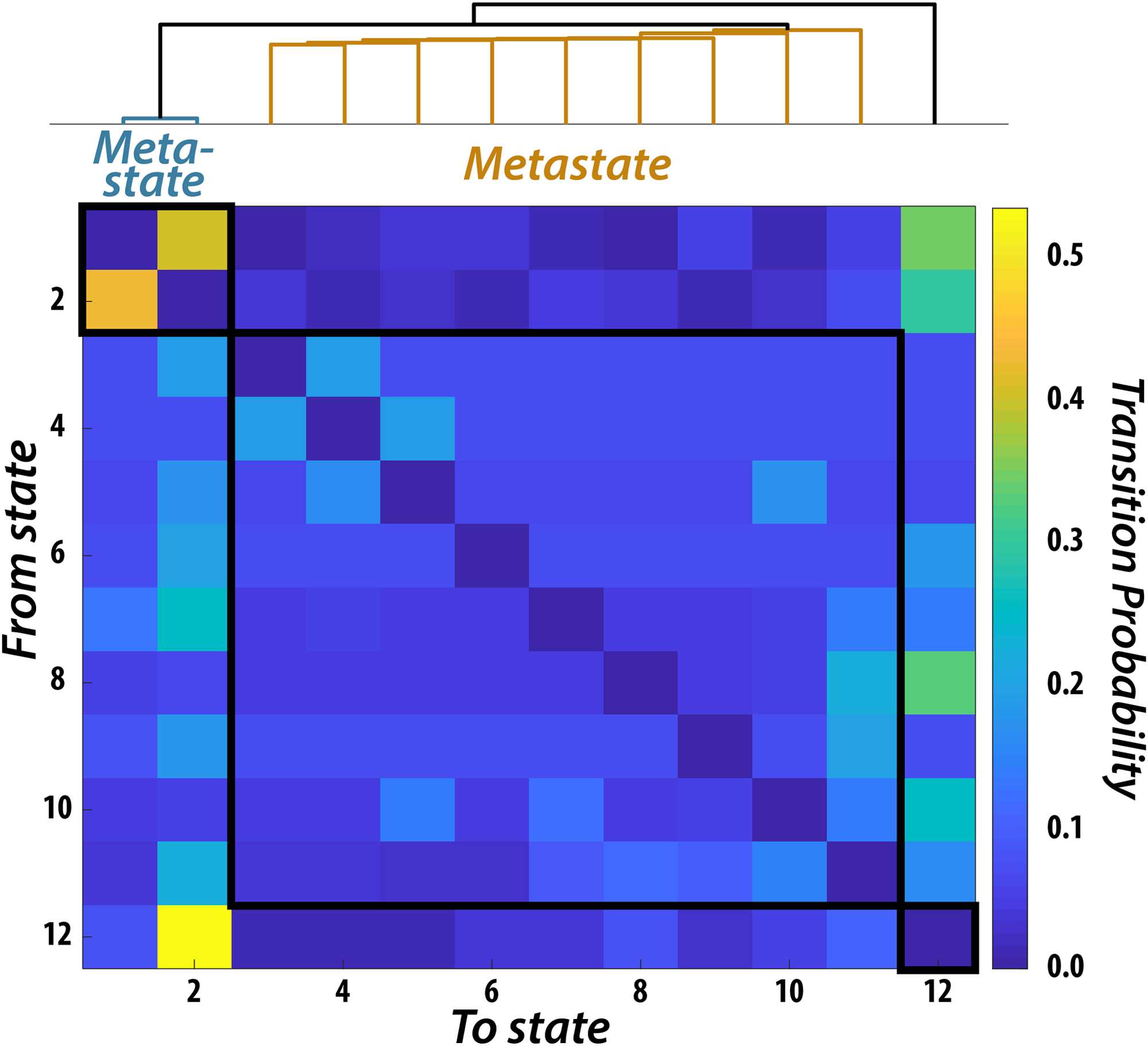
Figure 3. Metastates Resulting from the Temporal Clustering of Brain Dynamics. Probability, across
all participants, of transitioning from one state to another. Clustering of the 12-state transition prob-
ability matrix revealed a temporal hierarchy wherein groups of states preferentially transitioned
within groupings compared to across groupings. Two groupings contained multiple states (i.e.,
“metastates”), while one state was clustered only with itself.
with a HMM. This model works by finding relevant states and their associated spatial (activity,
connectivity) and temporal (fractional occupancy, switching rate) characteristics (see the “Hid-
den Markov Model” section in the Methods). After fitting the HMM, we identified 12 states
that were representative of brain dynamics across all participants (Figure 3). Previous work has
shown that the transition probabilities between HMM states derived from resting-state data is
structured (Vidaurre et al., 2017). Specifically, there are certain sets of states, or “metastates,”
that are more temporally coherent than others. In other words, if a participant visits a state
within one metastate they are more likely to stay within that metastate compared to transition-
ing to another metastate. Hierarchically clustering the transition probability matrix resulted
in three main clusters. One included two states, another included nine states, and the third
included a single state. These results are similar to those found previously with the Human
Connectome Project dataset (Vidaurre et al., 2017), indicating that even with our compara-
tively small sample size, we could reliably estimate brain dynamics. For completeness, we
included all 12 states in our analysis; however, our results remained unchanged when we
excluded the state that failed to cluster with the other states.
Next, we used the fractional occupancy (i.e., time spent in each state) of each state and
metastate, as well as the mean switching rate between states and metastates (n = 17 in total), as
input into a CCA to determine the relationship between time-varying FC characteristics and the
behavioral factors (n = 8; see Methods for description of selection and validation process). We
found two significant CCA modes by using the same permutation testing and cross-validation
procedure as employed for static FC (Figure 4A).
Network Neuroscience
157
Behavioral significance of time-varying functional connectivity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
a
_
0
0
1
7
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Canonical correlation analysis: time-varying functional connectivity. (A) CCA performed on measures of time-varying FC revealed
two significant modes of covariation. Results of the cross-validation procedure and post hoc correlations between (B) mode 1 and (C) mode 2
revealed that both modes were highly robust (assessed across 1,000 folds) and were sensitive to different sets of behavioral features. Whereas
mode 1 largely matched the mode discovered with static measures of FC, mode 2 was instead sensitive to task- and trial-specific measures of
behavior. RT, reaction time.
The first mode was defined by positive weights for “Task General” (r = 0.58), “Affect”
(r = 0.51), “Arousal” (r = 0.45), and “Processing Reaction Time” (r = 0.26) factors, showing a
similar pattern to the mode obtained from static FC (Figure 4B). Specifically, “Task General”
and “Affect” loaded highest, while “Impulsivity” (r = −0.10) loaded most negatively (although
its loading was greatly reduced compared to the previously discovered static mode). All other
loadings fell below an absolute value of 0.09.
The second mode exhibited different behavioral weights when compared to the first time-
varying mode. Here, “Task General” (r = 0.28), “Affect” (r = 0.07), and “Arousal” (r = −0.14)
factors had substantially lower weights. Instead, “Processing Reaction Time” (r = 0.45) and
“Working Memory Precision Reaction Time” (r = 0.37) factors loaded most highly on the
positive end, while the “Processing Accuracy” (r = −0.71) factor loaded most negatively
(Figure 4C). All remaining factors had weights below an absolute value of 0.15.
Similar to a previous analysis on the differentiable contributions of static and time-varying
FC (Liégeois et al., 2019), we found that time-varying FC, while showing some similar rela-
tionships to behavior as static FC, could also distinguish relationships with more task-based
measures of behavior. However, by using more specific measures of working memory (i.e.,
match-to-sample vs. free recall, accuracy vs. reaction time), task processing, and cognitive
control, we were additionally able to determine that the second time-varying CCA mode dis-
tinguished unique behaviors associated with task performance. Specifically, the mode was
defined by a separation (i.e., a positive-negative split in post hoc correlations) between re-
action time and accuracy, thus revealing within-task effects that previously had not been
Network Neuroscience
158
Behavioral significance of time-varying functional connectivity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
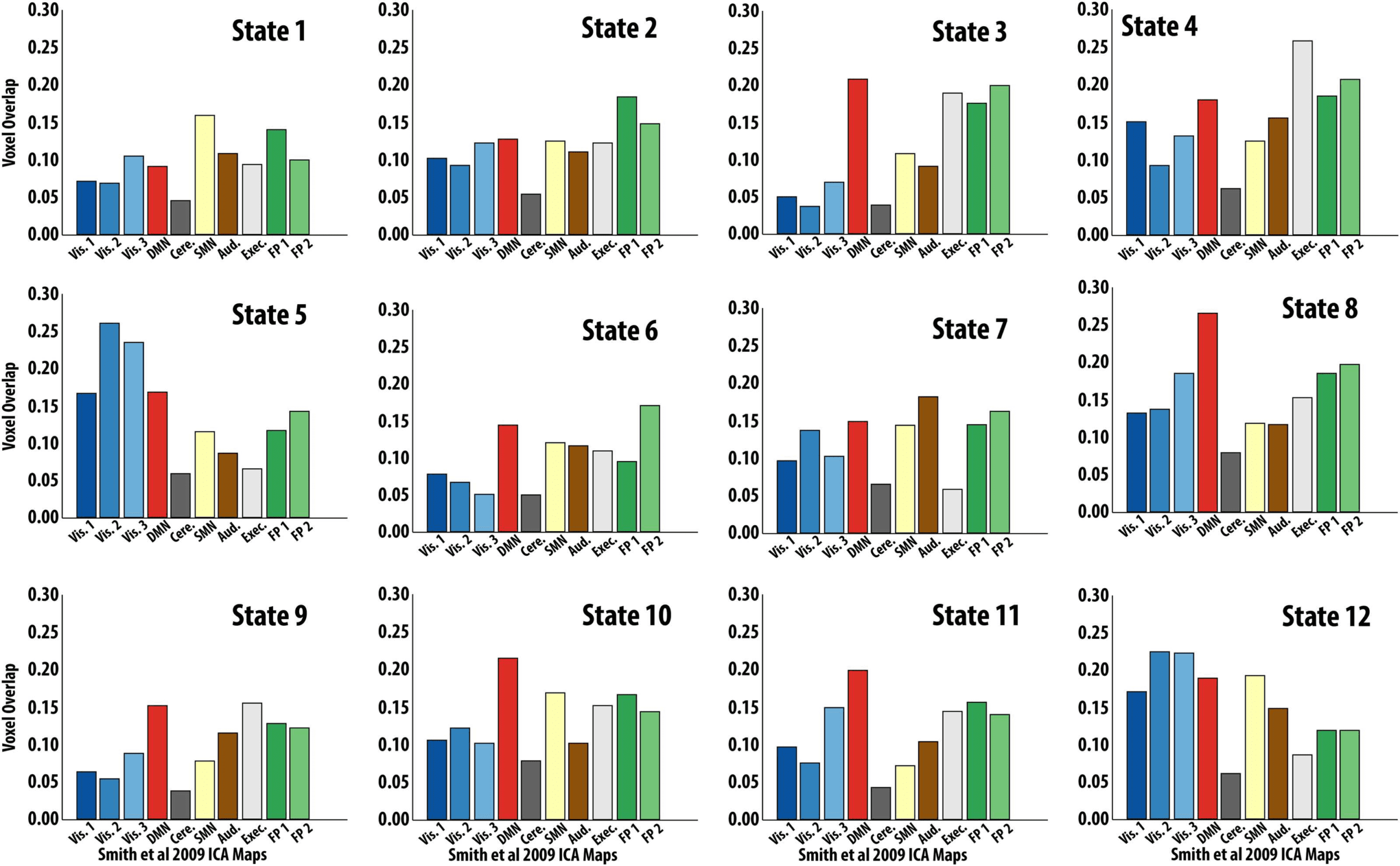
Figure 5. Hidden Markov Model (HMM) State Activation Map Overlap with Resting-State Networks Voxel overlap proportion for each
HMM-derived state to the 10 resting-state independent component analysis (ICA) maps from Smith et al. (2009). Ordering of states matches
that of Figure 3. Specifically, states 1 and 2 clustered together in one metastate, states 3–11 in another metastate, and state 12 clustered alone.
f
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
a
_
0
0
1
7
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
interrogated. The robustness of these time-varying FC results are largely confirmed when com-
pared to a phase-randomized surrogate analysis (see Supporting Information).
To further characterize each state obtained from the HMM, we overlapped their spatial pro-
files with those of canonical rsFC networks (Smith et al., 2009). Qualitatively, we found that
the two-state metastate overlapped with two distinct task-positive networks (i.e., fronto-parietal
and somatomotor networks; Figure 5). The nine-state metastate overlapped with a larger
variety of networks, including the default-mode, executive, and visual networks (Figure 5).
Unthresholded spatial maps of each of
the 12 states can be found in the Supporting
Information (Figure S5).
DISCUSSION
Using CCA, we investigated the relationship between complex measures of human behavior
and both static and time-varying rsFC. We found a single CCA mode between the behavioral
measures and static FC. In contrast, we found two CCA modes relating behavior and time-
varying FC. Of these two modes, the first one resembled its static counterpart, while the other
appeared to be distinct in that it was more sensitive to measures of task-specific behavioral
Network Neuroscience
159
Behavioral significance of time-varying functional connectivity
variability. We thus argue that time-varying FC describes nuanced brain–behavior relationships
distinctly from that which is captured by static FC.
Measures of static FC typically consider average FC over a prolonged period of time (e.g.,
several minutes of an fMRI scan) and have been used extensively to study the functional organ-
ization of the brain during rest and task performance (Cole et al., 2014; Cohen & D’Esposito,
2016). We used nodal bidirectional FC edge strength quantified across the entire scan in a
CCA to relate the brain’s intrinsic static functional organization to behavior. The CCA revealed
a significant relationship between these measures and our behavioral factors. Measures of
affect and impulsivity determined the main positive and negative directions of this mode, re-
spectively. To a lesser extent, the positive direction of this mode was also characterized by a
“Task General” factor. This factor represents accuracy measures derived from tasks sensitive to
working memory (Spatial WM), cognitive control (Stroop), and processing speed (DSST). This
factor also contains a high loading for the median reaction time measure from the Stroop task.
The “Task General” factor is thus most similar to previous analyses that have used data from
the Human Connectome Project in which behavioral measures include median reaction times
either in isolation or multiplexed with task-specific performance values. These results indicate
that static FC likely tracks participant-level personality measures present during the scanning
session (e.g., affective state). Unsurprisingly, static connectivity is also sensitive to measures
of task performance that likely characterize stable behavioral features of the individual (i.e.,
general, multitask performance, including working memory). As such, these results largely
confirm the findings of previous studies on static rsFC’s predictive power in regard to certain
measures of human behavior.
However, it has been shown that FC, including measures from resting-state protocols, is
likely a dynamic process whereby fluctuations in regional connectivity occur rapidly (Lurie
et al., 2019). Given the rate at which they occur, these fluctuations might better encode be-
havioral information reflecting ongoing cognitive demands, as compared to a general char-
acteristic which would remain stable over the span of minutes, hours, or days. Previously,
Casorso et al. (2019) assessed a similar, albeit broader, hypothesis by extracting time-varying
rsFC components and submitting these to a CCA along with behavioral measures collected in
the Human Connectome Project. Two modes of covariation were found between their time-
varying components and behavior; however, no analysis of static FC was made against which
to compare. One mode was largely defined by positive post hoc correlation values for vo-
cabulary comprehension and working memory, and negative values for prosocial behaviors.
The second mode was defined by positive post hoc correlation values for visuospatial orient-
ing and emotional processing, and negative values for inter- and intrapersonal processing and
well-being. Although a critical step forward in the analysis and validation of time-varying FC’s
relevance to human behavior, this study did not address the nature of how time-varying FC
relates to behavior in a unique manner compared to static FC measures. Specifically, the Hu-
man Connectome Project behavioral measures used preclude the ability to measure processes
that likely vary from trial to trial, as task-specific measures of reaction time only reflect the me-
dian, and not trialwise variability. In our experiment, we recorded behavioral measures that
separately tracked processes related to stable (e.g., accuracy) vs. time-varying (e.g., reaction
time) aspects of behavior to better assess our hypothesis. Although reaction time variability
and accuracy measures never loaded highly together on any factor, it should be noted that our
two measures of reaction time (i.e., median and standard deviation) loaded together on the
three factors representing working memory and processing speed reaction times. Even so, the
high loading of reaction time variability measures in these factors represents a novel behavioral
measure compared to previous reports using publicly available datasets.
Network Neuroscience
160
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
a
_
0
0
1
7
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
Using measures of time-varying FC calculated from fitting an HMM to our rsFC data, we
investigated whether CCA would reveal modes of population covariation sensitive to measures
of behavioral variability. Our analysis resulted in two significant modes. One mode largely
resembled the mode discovered with static measures of FC. The primary difference between
these modes is that this time-varying FC mode carried a highly positive weight for measures
of drowsiness and fatigue, potentially reflecting a sensitivity of time-varying FC to neural and
physiological correlates of arousal (Patanaik et al., 2018).
Whereas one of the time-varying modes reflected a largely similar, but not identical, be-
havioral profile as the static FC mode, the other time-varying mode reflected a more unique
behavioral profile. High positive weights were associated with response time measures for
tasks that assessed working memory and processing speed, while a strong negative weight
was found for the measure of accuracy on the processing speed task. Characterized in part
by measures of trial-by-trial response variability, this mode’s positive end potentially reflects a
greater sensitivity to behavioral dynamics that occur on a more rapid timescale compared to
what static FC is likely sensitive. In addition, the separation of measures of response variability
and overall response accuracy, especially within the same task, reveals that time-varying FC is
likely capable of disentangling unique behavioral components within the same task. Although
our static FC mode did show some sensitivity to a measure that captures response variability,
the distinction between stable and time-varying components of behavior was not present as
is seen in our second time-varying mode. Overall, it is possible that this time-varying mode
captures the relationship between brain dynamics and the measures of trial-by-trial behavioral
variability within complex measures of human behavior.
The manner by which time-varying fluctuations in rsFC relate to independent measures of
human behavior remains unresolved. It is known that the spatial organization of functional
connections changes in response to different tasks compared to rest (Cole et al., 2014; Cohen
& D’Esposito, 2016). Specifically, internetwork connectivity is more predominant during tasks
that require flexible cognition (i.e., working memory) compared to more rudimentary tasks
such as finger tapping. Moreover, a previous report found that measures of global network
integration and within-network connectivity (i.e., participation coefficient and module degree,
respectively), when assessed in a time-varying manner, varied throughout the performance of
tasks and tracked the cognitive complexity of the task demands (Shine et al., 2016). Thus, one
hypothesis as to how resting dynamics relate to behavior is that the dynamic interactions within
and between these networks observed during tasks can be recapitulated during periods of
wakeful rest. However, it should be noted that the dynamic interactions that occur during task
performance are likely more constrained than during rest due to the confined cognitive context
required by task performance. Resting-state dynamics can serve as a “baseline” repertoire
that can potentially index the extent to which FC reconfigures during task and, in turn, track
behavioral performance (Liégeois et al., 2019).
It will be crucial for future studies on the
behavioral relevance of time-varying FC to assess this possibility.
It is also important to emphasize the spatiotemporal signature of these time-varying net-
work interactions and what it means for behavioral performance. Methods such as the HMM
investigate brain dynamics with high temporal resolution, thus extending previous methods
showing reconfiguration of connectivity between different task blocks (Cohen, 2018). For ex-
ample, Vidaurre et al. (2018) used an HMM to show how a motor task drives reconfiguration of
large-scale networks on a timepoint-by-timepoint basis showing that task execution happens
at faster timescales that had been previously undetected when interrogated using sliding win-
dow methods (Vidaurre et al., 2018). Regarding the spatial profile of the current HMM states,
Network Neuroscience
161
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
a
_
0
0
1
7
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
a visual and quantitative assessment of their overlap with canonical rsFC networks (Smith
et al., 2009) suggested that our metastates had distinct spatial profiles. We identified a nine-
state metastate spanning multiple networks including fronto-parietal, executive, default-mode,
and visual networks. Integration of the “task-positive” and “task-negative” networks has been
observed during motor tapping and autobiographical planning, suggesting a more mutually
compatible role than previously believed (Fox et al., 2005), one that can facilitate goal-directed
cognition (Spreng et al., 2010; Braga et al., 2013; Vatansever et al., 2015). On the other hand,
the two-state metastate we identified, characterized by a more constrained spatial profile of
fronto-parietal and somatomotor networks, potentially reflects networks specific to task exe-
cution. The differences in spatial topography of the two-state versus nine-state metastates may
provide insight regarding the different behavioral relationships we found with static versus
time-varying FC. The flexible interaction of activity across each metastate’s respective individ-
ual states might allow for the encoding of information to which static measures are insensitive.
Although static measures are capable of reflecting multinetwork interactions, they are inca-
pable of tapping into the specific temporal patterns through which these network interactions
occur. Further investigation of the spatial patterns of these states is needed.
In conclusion, the current study demonstrates that static and time-varying FC are differ-
entially associated with behavior. We argue that via integration across multiple networks at
different temporal scales, time-varying FC is associated with both trial-by-trial and stable be-
havioral measures, while static FC is associated with participant-level personality measures and
measures of stable task-general performance. These results demonstrate that it is important for
future studies to look at both the static and temporal aspects of FC to more fully delineate the
behavioral contributions of each.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00172.
AUTHOR CONTRIBUTIONS
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
a
_
0
0
1
7
2
p
d
.
t
Investigation; Methodology;
Adam Eichenbaum: Conceptualization; Formal analysis;
Visualization; Writing - Original Draft; Writing - Review & Editing. Ioannis Pappas: Concep-
tualization; Formal analysis; Investigation; Methodology; Supervision; Visualization; Writing -
Original Draft; Writing - Review & Editing. Daniel Lurie: Methodology.
Jessica R Cohen:
Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Project ad-
ministration; Software; Supervision; Validation; Writing - Review & Editing. Mark D’Esposito:
Conceptualization; Funding acquisition; Project administration; Writing - Review & Editing.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
FUNDING INFORMATION
Mark D’Esposito, National Institutes of Health (http://dx.doi.org/10.13039/100000002), Award
ID: MH63901.
REFERENCES
Alexander-Bloch, A. F., Gogtay, N., Meunier, D., Birn, R., Clasen,
L., Lalonde, F., . . . Bullmore, E. T.
(2010). Disrupted modu-
larity and local connectivity of brain functional networks in
childhood-onset schizophrenia. Frontiers in Systems Neuro-
science, 4(October), 1–16. DOI: https://doi.org/10.3389/fnsys
.2010.00147, PMID: 21031030, PMCID: PMC2965020
Avants, B. B., Epstein, C. L., Grossman, M., & Gee,
J. G.
(2008). Symmetric diffeomorphic image registration with cross-
correlation: Evaluating automated labeling of elderly and neu-
rodegenerative brain. Medical Image Analysis, 12(1), 26–41.
DOI: https://doi.org/10.1016/j.media.2007.06.004, PMID:
17659998, PMCID: PMC2276735
Network Neuroscience
162
Behavioral significance of time-varying functional connectivity
Baker, A. P., Brookes, M. J., Rezek, I. A., Smith, S. M., Behrens, T.,
Smith, P. J. P., & Woolrich, M. (2014). Fast transient networks in
spontaneous human brain activity. ELife, 2014(3), 1–18. DOI:
https://doi.org/10.7554/eLife.01867, PMID: 24668169, PMCID:
PMC3965210
Biswal, B., Yetkin, F. Z., Haughton, V. M., & Hyde, J. S.
(1995).
Functional connectivity in the motor cortex of resting human
brain using echo-planar MRI. Magnetic Resonance in Medicine,
34(4), 537–541. DOI: https://doi.org/10.1002/mrm.1910340409,
PMID: 8524021
Braga, R. M., Sharp, D. J., Leeson, C., Wise, R. J. S., & Leech, R.
(2013). Echoes of the brain within default mode, association,
Journal of Neuroscience, 33(35),
and heteromodal cortices.
14031–14039. DOI: https://doi.org/10.1523/jneurosci.0570-13
.2013, PMID: 23986239, PMCID: PMC3810536
Brookes, M. J., O’Neill, G. C., Hall, E. L., Woolrich, M. W., Baker,
A., Palazzo Corner, S., . . . Barnes, G. R.
(2014). Measuring
temporal, spectral and spatial changes in electrophysiological
brain network connectivity. NeuroImage, 91, 282–299. DOI:
https://doi.org/10.1016/j.neuroimage.2013.12.066, PMID:
24418505
Calhoun, V. D., Miller, R., Pearlson, G., & Adali, T.
(2014). The
chronnectome: Time-varying connectivity networks as the next
frontier in fMRI data discovery. Neuron, 84(2), 262–274. DOI:
https://doi.org/10.1016/j.neuron.2014.10.015, PMID: 25374354,
PMCID: PMC4372723
Casorso, J., Kong, X., Chi, W., Van De Ville, D., Yeo, B. T. T., &
Liégeois, R. (2019). Dynamic mode decomposition of resting-
state and task fMRI. NeuroImage, 194(February), 42–54. DOI:
https://doi.org/10.1016/j.neuroimage.2019.03.019,
PMID:
30904469
Chan, M. Y., Park, D. C., Savalia, N. K., Petersen, S. E., &
Wig, G. S.
(2014). Decreased segregation of brain systems
across the healthy adult lifespan. Proceedings of the National
Academy of Sciences of the United States of America, 111(46),
E4997–5006. DOI: https://doi.org/10.1073/pnas.1415122111,
PMID: 25368199, PMCID: PMC4246293
Chang, C., & Glover, G. H.
(2010). Time–frequency dynamics of
resting-state brain connectivity measured with fMRI. NeuroIm-
age, 50(1), 81–98. DOI: https://doi.org/10.1016/j.neuroimage
.2009.12.011, PMID: 20006716, PMCID: PMC2827259
Ciric, R., Wolf, D. H., Power, J. D., Roalf, D. R., Baum, G. L.,
Ruparel, K., . . . Satterthwaite, T. D.
(2017). Benchmarking of
participant-level confound regression strategies for the control
of motion artifact in studies of functional connectivity. Neuro-
Image, 154, 174–187. DOI: https://doi.org/10.1016/j.neuroimage
.2017.03.020
Cohen, J. R.
(2018). The behavioral and cognitive relevance of
time-varying, dynamic changes in functional connectivity.
NeuroImage, 180(April 2017), 515–525. DOI: https://doi.org/10
.1016/j.neuroimage.2017.09.036, PMID: 28942061, PMCID:
PMC6056319
Cohen, J. R., & D’Esposito, M. (2016). The segregation and integra-
tion of distinct brain networks and their relationship to cognition.
Journal of Neuroscience, 36(48), 12083–12094. DOI: https://
doi.org/10.1523/JNEUROSCI.2965-15.2016, PMID: 27903719,
PMCID: PMC5148214
Cole, M. W., Bassett, D. S., Power,
J. D., Braver, T. S., &
Petersen, S. E. (2014). Intrinsic and task-evoked network architec-
tures of the human brain. Neuron, 83(1), 238–251. DOI: https://
doi.org/10.1016/j.neuron.2014.05.014, PMID: 24991964, PMCID:
PMC4082806
Dale, A. M., Fischl, B., & Sereno, M. I.
(1999). Cortical surface-
based analysis. NeuroImage, 9(2), 179–194. DOI: https://doi.org
/10.1006/nimg.1998.0395, PMID: 9931268
de Pasquale, F., Della Penna, S., Snyder, A. Z., Lewis, C., Mantini,
D., Marzetti, L., . . . Corbetta, M.
(2010). Temporal dynamics
of spontaneous MEG activity in brain networks. Proceedings of
the National Academy of Sciences of the United States of
America, 107(13), 6040–6045. DOI: https://doi.org/10.1073/pnas
.0913863107, PMID: 20304792, PMCID: PMC2851876
Duff, E. P., Makin, T., Cottaar, M., Smith, S. M., & Woolrich, W. M.
(2018). Disambiguating brain functional connectivity. Neuro-
Image, 173, 540–550. DOI: https://doi.org/10.1016/j.neuroimage
.2018.01.053, PMID: 29476911, PMCID: PMC5929905
Esteban, O., Blair, R., Markiewicz, C. J., Berleant, S. L., Moodie,
C., Ma, F., . . . Gorgolewski, K. J. (2018). poldracklab/fmriprep:
1.0.10. DOI: https://doi.org/10.5281/zenodo.1219187
Esteban, O., Markiewicz, C. J., Blair, R. W., Moodie, C. A., Isik,
A. I., Erramuzpe, A., . . . Gorgolewski, K. J. (2018). fMRIPrep: A
robust preprocessing pipeline for functional MRI. Nature Meth-
ods, 16(1), 111–116. DOI: https://doi.org/10.1038/s41592-018
-0235-4, PMID: 30532080, PMCID: PMC6319393
Fonov, V., Evans, A., McKinstry, R., Almli, C., & Collins, D.
(2009). Unbiased nonlinear average age-appropriate brain tem-
plates from birth to adulthood. NeuroImage, 47(S102). DOI:
https://doi.org/10.1016/S1053-8119(09)70884-5
Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen,
D. C., & Raichle, M. E.
(2005). From the cover: The human
brain is intrinsically organized into dynamic, anticorrelated func-
tional networks. Proceedings of the National Academy of Sci-
ences of the United States of America, 102(27), 9673–9678.
DOI:
PMID:
https://doi.org/10.1073/pnas.0504136102,
15976020, PMCID: PMC1157105
Gorgolewski, K., Burns, C. D., Madison, C., Clark, D., &
Halchenko, Y. O.
(2011). Nipype: A flexible, lightweight and
extensible neuroimaging data processing framework in Python.
Frontiers in Neuroinformatics, 5(August). DOI: https://doi.org
/10.3389/fninf.2011.00013,
PMCID:
PMC3159964
21897815,
PMID:
Greve, D. N., & Fischl, B. (2009). Accurate and robust brain image
alignment using boundary-based registration. NeuroImage,
48(1), 63–72. DOI: https://doi.org/10.1016/j.neuroimage.2009
.06.060, PMID: 19573611, PMCID: PMC2733527
Hastie, T., Friedman, J. H., & Tibshirani, R. (2009). The elements of
statistical learning. New York City, New York: Springer US. DOI:
https://doi.org/10.1007/978-0-387-84858-7
Hindriks, R., Adhikari, M. H., Murayama, Y., Ganzetti, M., Mantini,
D., Logothetis, N. K., & Deco, G. (2016). Can sliding-window
correlations reveal dynamic functional connectivity in resting-
state fMRI? NeuroImage, 127, 242–256. DOI: https://doi.org/10
.1016/j.neuroimage.2015.11.055, PMID: 26631813, PMCID:
PMC4758830
Hotelling, H. (1936). Relations between two sets of variates. Bio-
metrika, 28(3–4), 321–377. DOI: https://doi.org/10.1093/biomet
/28.3-4.321
Network Neuroscience
163
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
a
_
0
0
1
7
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A.,
Calhoun, V. D., Corbetta, M., . . . Chang, C. (2013). Neuro-
Image dynamic functional connectivity: Promise, issues, and
interpretations. NeuroImage, 80, 360–378. DOI: https://doi.org
/10.1016/j.neuroimage.2013.05.079, PMID: 23707587, PMCID:
PMC3807588
(2002).
Jenkinson, M., Bannister, P., Brady, M., & Smith, S.
Im-
proved optimization for the robust and accurate linear registra-
tion and motion correction of brain images. NeuroImage, 17(2),
825–841. DOI: https://doi.org/10.1016/S1053-8119(02)91132-8
Jia, H., Hu, X., & Deshpande, G. (2014). Behavioral relevance of
the dynamics of the functional brain connectome. Brain Connec-
tivity, 4(9), 741–759. DOI: https://doi.org/10.1089/brain.2014
.0300, PMID: 25163490, PMCID: PMC4238311
J. D., Karuza, E. A., Thompson-
Khambhati, A. N., Medaglia,
Schill, S. L., & Bassett, D. S.
(2018). Subgraphs of functional
brain networks identify dynamical constraints of cognitive con-
trol. PLoS Computational Biology, 14. DOI: https://doi.org/10.org
/10.1371/journal.pcbi.1006234, PMID: 29979673, PMCID:
PMC6056061
. . . Keshavan, A.
Klein, A., Ghosh, S. S., Bao, F. S., Giard, J., Häme, Y., Stavsky,
E.,
(2017). Mindboggling morphometry of
human brains. PLOS Computational Biology, 13(2), e1005350.
DOI: https://doi.org/10.1371/journal.pcbi.1005350, PMID:
28231282, PMCID: PMC5322885
Kucyi, A., Tambini, A., Sadaghiani, S., Keilholz, S., & Cohen, J. R.
(2018). Spontaneous cognitive processes and the behavioral
validation of time-varying brain connectivity. Network Neuro-
science, 2(4), 397–417. DOI: https://doi.org/10.1162/netn_a_00037,
PMID: 30465033, PMCID: PMC6195165
Lanczos, C.
Kuo, B.-C., Yeh, Y.-Y., Chen, A. J.-W., & D’Esposito, M. (2011).
Functional connectivity during top-down modulation of visual
short-term memory representations. Neuropsychologia, 49(6),
1589–1596. DOI: https://doi.org/10.1016/j.neuropsychologia
.2010.12.043, PMID: 21241721, PMCID: PMC3085092
(1964). Evaluation of noisy data.
Journal of the So-
ciety for Industrial and Applied Mathematics Series B Numerical
Analysis, 1(1), 76–85. DOI: https://doi.org/10.1137/0701007
Liégeois, R., Li, J., Kong, R., Orban, C., Van De Ville, D., Ge, T., . . .
Yeo, B. T. T. (2019). Resting brain dynamics at different timescales
capture distinct aspects of human behavior. Nature Communica-
tions, 10(1). DOI: https://doi.org/10.1038/s41467-019-10317-7,
PMID: 31127095, PMCID: PMC6534566
Lindquist, M. A., Xu, Y., Nebel, M. B., & Caffo, B. S. (2014). Evalu-
ating dynamic bivariate correlations in resting-state fMRI: A com-
parison study and a new approach. NeuroImage, 101, 531–546.
DOI: https://doi.org/10.1016/j.neuroimage.2014.06.052, PMID:
24993894, PMCID: PMC4165690
Lurie, D. J., Kessler, D., Bassett, D. S., Betzel, R. F., Breakspear, M.,
Keilholz, S., . . . Calhoun, V. D.
(2019). Questions and contro-
versies in the study of time-varying functional connectivity in
resting fMRI. Network Neuroscience, 4(1), 30–69. DOI: https:
//doi.org/10.1162/netn_a_00116,
PMCID:
PMC7006871
PMID: 32043043,
Makris, N., Goldstein, J. M., Kennedy, D., Hodge, S. M., Caviness,
V. S., Faraone, S. V., . . . Seidman, L. J.
(2006). Decreased vol-
ume of left and total anterior insular lobule in schizophrenia.
Schizophrenia Research, 83(2–3), 155–171. DOI: https://doi.org
/10.1016/j.schres.2005.11.020, PMID: 16448806
McCormack, H. M., Horne, D. J., & Sheather, S.
(1988). Clinical
applications of visual analogue scales: A critical review. Psycho-
logical Medicine, 18(4), 1007–1019. DOI: https://doi.org/10.1017
/s0033291700009934, PMID: 3078045
Parkes, L., Fulcher, B., Yücel, M., & Fornito, A. (2018). An evalua-
tion of the efficacy, reliability, and sensitivity of motion correction
strategies for resting-state functional MRI. NeuroImage, 171,
415–436. DOI: https://doi.org/10.1016/j.neuroimage.2017.12
.073
Patanaik, A., Tandi, J., Ong, J. L., Wang, C., Zhou, J., & Chee,
M. W. L.
(2018). Dynamic functional connectivity and its be-
havioral correlates beyond vigilance. NeuroImage, 177, 1–10.
DOI: https://doi.org/10.1016/j.neuroimage.2018.04.049, PMID:
29704612
Patton, J. H., Stanford, M. S., & Barratt, E. S. (1995). Factor structure
of the barratt impulsiveness scale. Journal of Clinical Psychology,
51(6), 768–774. DOI: https://doi.org/10.1002/1097-4679(199511)
51:6<768::AID-JCLP2270510607>3.0.CO;2-1
Power, J.. D., Mitra, UN., Laumann, T. O., Snyder, UN. Z., Schlaggar,
B. L., & Petersen, S. E. (2014). Methods to detect, characterize,
and remove motion artifact in resting state fMRI. NeuroImage,
84, 320–341. EST CE QUE JE: https://doi.org/10.1016/j.neuroimage.2013
.08.048, PMID: 23994314, PMCID: PMC3849338
Prichard, D., & Theiler, J.. (1994). Generating surrogate data for time
series with several simultaneously measured variables. Physical
Review Letters, 73(7), 951–954. EST CE QUE JE: https://doi.org/10.1103
/PhysRevLett.73.951, PMID: 10057582
Rosenberg, M.. D., Finn, E. S., Scheinost, D., Papademetris, X.,
Shen, X., Constable, R.. T., & Chun, M.. M..
(2016). A neuro-
marker of sustained attention from whole-brain functional con-
nectivity. Neurosciences naturelles, 19(1), 165–171. EST CE QUE JE: https://
PMCID:
doi.org/10.1038/nn.4179,
PMC4696892
26595653,
PMID:
Rudie, J.. D., Brun, J.. UN., Beck-Pancer, D., Hernandez, L. M.,
Dennis, E. L., Thompson, P.. M., . . . Dapretto, M.. (2013). Altered
functional and structural brain network organization in autism.
NeuroImage: Clinique, 2(1), 79–94. EST CE QUE JE: https://est ce que je.org/10.1016
/j.nicl.2012.11.006, PMID: 24179761, PMCID: PMC3777708
Rypma, B., Berger, J.. S., Prabhakaran, V., Bly, B. M., Kimberg, D. Y.,
Biswal, B. B., & D'Esposito, M.. (2006). Neural correlates of
cognitive efficiency. NeuroImage, 33(3), 969–979. EST CE QUE JE: https://
doi.org/10.1016/j.neuroimage.2006.05.065, PMID: 17010646
Sadaghiani, S., Poline, J.-B., Kleinschmidt, UN., & D'Esposito, M..
(2015). Ongoing dynamics in large-scale functional connectiv-
ity predict perception. Proceedings of the National Academy of
Sciences of the United States of America, 112(27), 8463–8468.
EST CE QUE JE:
PMID:
https://doi.org/10.1073/pnas.1420687112,
26106164, PMCID: PMC4500238
Salthouse, T. UN. (1996). The processing-speed theory of adult age
differences in cognition. Psychological Review, 103(3), 403–428.
EST CE QUE JE: https://doi.org/10.1037/0033-295X.103.3.403, PMID:
8759042
Schaefer, UN., Kong, R., Gordon, E. M., Laumann, T. O., Zuo, X.-N.,
. . . Yeo, B. T. T. (2018). Local-global parcel-
Holmes, UN. J.,
lation of the human cerebral cortex from intrinsic functional
connectivity MRI. Cortex cérébral, 28(9), 3095–3114. EST CE QUE JE:
https://doi.org/10.1093/cercor/bhx179, PMID: 28981612, PMCID:
PMC6095216
Neurosciences en réseau
164
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
un
_
0
0
1
7
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Behavioral significance of time-varying functional connectivity
Schultz, D. H., & Cole, M.. W. (2016). Higher intelligence is associ-
ated with less task-related brain network reconfiguration. Journal
of Neuroscience, 36(33), 8551–8561. EST CE QUE JE: https://est ce que je.org/10
.1523/JNEUROSCI.0358-16.2016, PMID: 27535904, PMCID:
PMC4987432
Shine, J.. M., Bissett, P.. G., Cloche, P.. T., Koyejo, O., Balsters, J.. H.,
Gorgolewski, K. J., . . . Poldrack, R.. UN.
(2016). The dynamics
of functional brain networks:
Integrated network states during
cognitive task performance. Neurone, 92(2), 544–554. EST CE QUE JE: https://
doi.org/10.1016/j.neuron.2016.09.018, PMID: 27693256,
PMCID: PMC5073034
Shine, J.. M., & Breakspear, M.. (2016). Understanding the brain, par
default. Trends in Neurosciences, 41(5), 244–247. EST CE QUE JE: https://
doi.org/10.1016/j.tins.2018.03.004, PMID: 29703375
Forgeron, S. M., Fox, P.. T., Miller, K. L., Glahn, D. C., Fox, P.. M.,
Mackay, C. E., . . . Beckmann, C. F. (2009). Correspondence of
the brain’s functional architecture during activation and rest. Pro-
ceedings of the National Academy of Sciences of the United
States of America, 106(31), 13040–13045. EST CE QUE JE: https://est ce que je
.org/10.1073/pnas.0905267106, PMID: 19620724, PMCID:
PMC2722273
Forgeron, S. M., Nichols, T. E., Vidaurre, D., Winkler, UN. M., Behrens,
. . . Miller, K. L. (2015). A positive-
T. E. J., Glasser, M.. F.,
negative mode of population covariation links brain connectiv-
ville, demographics and behavior. Neurosciences naturelles, 18(11),
1565–1567. EST CE QUE JE: https://doi.org/10.1038/nn.4125, PMID:
26414616, PMCID: PMC4625579
Spreng, R.. N., Stevens, W. D., Chamberlain, J.. P., Gilmore, UN. W.,
& Schacter, D. L. (2010). Default network activity, coupled with
the frontoparietal control network, supports goal-directed cogni-
tion. NeuroImage, 53(1), 303–317. EST CE QUE JE: https://est ce que je.org/10.1016
/j.neuroimage.2010.06.016, PMID: 20600998, PMCID:
PMC2914129
Stevens, UN. UN., Tappon, S. C., Garg, UN., & Fair, D. UN. (2012). Func-
tional brain network modularity captures inter- and intra-
individual variation in working memory capacity. PLoS One, 7(1).
EST CE QUE JE: https://doi.org/10.1371/journal.pone.0030468, PMID:
22276205, PMCID: PMC3262818
Stevner, UN. B. UN., Vidaurre, D., Cabral, J., Rapuano, K., Nielsen,
S. F. V., Tagliazucchi, E., . . . Kringelbach, M.. L.
(2019). Dis-
covery of key whole-brain transitions and dynamics during
human wakefulness and non-REM sleep. Nature Communica-
tion, 10(1). EST CE QUE JE: https://doi.org/10.1038/s41467-019-08934-3,
PMID: 30833560, PMCID: PMC6399232
Stroop, J.. R..
(1935). Studies of interference in serial verbal reac-
tion. Journal de psychologie expérimentale, 18(6), 643–662. EST CE QUE JE:
https://doi.org/10.1037/h0054651
Thompson, G. J..
(2018). Neural and metabolic basis of dyna-
mic resting state fMRI. NeuroImage, 180, 448–462. EST CE QUE JE: https://
doi.org/10.1016/j.neuroimage.2017.09.010, PMID: 28899744,
PMCID: PMC5844792
Tustison, N. J., Avants, B. B., Cook, P.. UN., Zheng, Y., Egan, UN.,
(2010). N4ITK: Improved N3
Yushkevich, P.. UN., & Gee, J.. C.
bias correction. IEEE Transactions on Medical Imaging, 29(6),
1310–1320. EST CE QUE JE: https://doi.org/10.1109/TMI.2010.2046908,
PMID: 20378467, PMCID: PMC3071855
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello,
F., Etard, O., Delcroix, N., . . . Joliot, M.. (2002). Automated ana-
tomical labeling of activations in SPM using a macroscopic
anatomical parcellation of the MNI MRI single-subject brain.
NeuroImage, 15(1), 273–289. EST CE QUE JE: https://doi.org/10.1006/nimg
.2001.0978, PMID: 11771995
Van Essen, D. C., Forgeron, S. M., Barch, D. M., Behrens, T. E. J.,
Yacoub, E., & Voiture d'Ugur, K. (2013). The WU-Minn Human Con-
nectome Project: An overview. NeuroImage, 80, 62–79. EST CE QUE JE:
PMID:
https://doi.org/10.1016/j.neuroimage.2013.05.041,
23684880, PMCID: PMC3724347
Vatansever, D., Menon, D. K., Manktelow, UN. E., Sahakian,
B. J., & Stamatakis, E. UN. (2015). A Default mode dynamics for
Journal des neurosciences, 35(46),
global functional integration.
15254–15262. EST CE QUE JE: https://doi.org/10.1523/JNEUROSCI.2135
-15.2015, PMID: 26586814, PMCID: PMC4649001
Vidaurre, D., Abeysuriya, R., Becker, R., Quinn, UN. J., Alfaro-
Almagro, F., Forgeron, S. M., & Woolrich, M.. W. (2018). Discovering
dynamic brain networks from big data in rest and task. Neuro-
Image, 180, 646–656. EST CE QUE JE: https://doi.org/10.1016/j.neuroimage
.2017.06.077, PMID: 28669905, PMCID: PMC6138951
Vidaurre, D., Forgeron, S. M., & Woolrich, M.. W. (2017). Brain net-
work dynamics are hierarchically organized in time. Procédure
of the National Academy of Sciences of the United States of
America, 114(48), 201705120. EST CE QUE JE: https://doi.org/10.1073
/pnas.1705120114, PMID: 29087305, PMCID: PMC5715736
Wainwright, M.. J., & Jordan, M.. je. (2007). Graphical models,
exponential families, and variational inference. Foundations and
Trends in Machine Learning, 1(1–2), 1–305. EST CE QUE JE: https://doi.org
/10.1561/2200000001
Zhang, W., & Luck, S. J.. (2008). Discrete fixed-resolution represen-
tations in visual working memory. Nature, 453(7192), 233–235.
EST CE QUE JE: https://doi.org/10.1038/nature06860, PMID: 18385672,
PMCID: PMC2588137
Zhang, Y., Brady, M., & Forgeron, S.
(2001). Segmentation of brain
MR images through a hidden Markov random field model and
IEEE Transactions on
the expectation-maximization algorithm.
Medical Imaging, 20(1), 45–57. EST CE QUE JE: https://doi.org/10.1109/42
.906424, PMID: 11293691
Neurosciences en réseau
165
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
5
1
1
4
5
1
8
8
9
6
7
0
n
e
n
_
un
_
0
0
1
7
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3