RECHERCHE
Resolving inter-regional communication
capacity in the human connectome
Filip Milisav
, Vincent Bazinet, Yasser Iturria-Medina, and Bratislav Misic
McConnell Brain Imaging Centre, Montréal Neurological Institute, Université McGill, Montréal, Canada
Mots clés: Connectome, Communication, Polysynaptic, Null model, Structure-function
relationship, Segregation-Integration
un accès ouvert
journal
ABSTRAIT
Applications of graph theory to the connectome have inspired several models of how neural
signaling unfolds atop its structure. Analytic measures derived from these communication
models have mainly been used to extract global characteristics of brain networks, obscuring
potentially informative inter-regional relationships. Here we develop a simple standardization
method to investigate polysynaptic communication pathways between pairs of cortical regions.
This procedure allows us to determine which pairs of nodes are topologically closer and which
are further than expected on the basis of their degree. We find that communication pathways
delineate canonical functional systems. Relating nodal communication capacity to meta-
analytic probabilistic patterns of functional specialization, we also show that areas that are most
closely integrated within the network are associated with higher order cognitive functions. Nous
find that these regions’ proclivity towards functional integration could naturally arise from the
brain’s anatomical configuration through evenly distributed connections among multiple
specialized communities. Throughout, we consider two increasingly constrained null models
to disentangle the effects of the network’s topology from those passively endowed by spatial
embedding. Altogether, the present findings uncover relationships between polysynaptic
communication pathways and the brain’s functional organization across multiple topological
levels of analysis and demonstrate that network integration facilitates cognitive integration.
RÉSUMÉ DE L'AUTEUR
Several mathematical models describe how neural signaling unfolds atop the structure of the
brain. These communication models have mainly been used to characterize brain networks at
a global scale. Ici, using a simple standardization procedure, we benchmark inter-regional
measures of communication capacity to determine which pairs of brain regions show a higher
or lower propensity to communicate than expected by chance. We identify relationships
between communication pathways and the brain’s functional organization across multiple
network levels and show that network integration facilitates cognitive integration. Throughout,
we consider the effect of spatial proximity on inter-regional communication relationships.
INTRODUCTION
The anatomical connectivity of neural circuits supports signal propagation between neuronal
populations (Bargmann & Marder, 2013). Signals, in the form of electrical impulses, are relayed
via axonal projections (monosynaptic communication). Wiring among multiple populations
Citation: Milisav, F., Bazinet, V.,
Iturria-Medina, Y., & Misic, B.
(2023). Resolving inter-regional
communication capacity in the human
connectome. Neurosciences en réseau,
7(3), 1051–1079. https://est ce que je.org/10.1162
/netn_a_00318
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00318
Informations complémentaires:
https://doi.org/10.1162/netn_a_00318;
https://github.com/fmilisav/milisav
_dyadic_communication
Reçu: 11 Octobre 2022
Accepté: 3 Avril 2023
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Bratislav Misic
bratislav.misic@mcgill.ca
Éditeur de manipulation:
Claus C. Hilgetag
droits d'auteur: © 2023
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
un
_
0
0
3
1
8
p
d
t
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
Connectome:
Comprehensive catalogue of all
neural elements and their
relations.
Communication model:
Mathematical model describing how
neural signaling takes place in a
brain network.
Communication capacity:
Measure of the propensity for neural
signaling between two brain regions
as derived from a communication
model.
Shortest path:
Minimum sequence of unique
consecutive connections between
two brain regions.
Functional connectivity:
Map of statistical relationships
between regional neural activity time
courses.
forms circuits in which signals can also be relayed between populations that do not share a
direct projection, but can be reached via multiple synapses (polysynaptic communication)
(Marder, Gutiérrez, & Nusbaum, 2017). Ainsi, the architecture of the brain’s connectome
shapes communication patterns and integration among specialized brain regions (Avena-
Koenigsberger, Misic, & Sporns, 2018; Vézquez-Rodríguez, Liu, Hagmann, & Misic, 2020).
The conventional approach to studying communication in brain networks is to model the
global capacity of the network. Broadly, this paradigm involves estimating communication
efficiency between all pairs of regional nodes and then taking the average to summarize
communication efficiency with a scalar value (Achard & Bullmore, 2007; Goñi et al., 2013;
Iturria-Medina, Sotero, Canales-Rodríguez, Alemán-Gómez, & Melie-García, 2008; van den
Heuvel, Stam, Kahn, & Hulshoff Pol, 2009). Par exemple, the oft-studied global efficiency sta-
tistic is defined as the inverse of the mean shortest path length among all pairs of nodes in a
réseau (Boccaletti, Latora, Moreno, Chavez, & Hwang, 2006; Latora & Marchiori, 2001).
Cependant, this broad, globally focused approach obscures potentially informative heterogene-
ity of communication between specific pairs of regions. Encore, there is increasing appreciation
for local heterogeneity in the brain, including spatial patterning of micro-architecture (Burt
et coll., 2018; Fulcher, Murray, Zerbi, & Wang, 2019; Hansen et al., 2022; Huntenburg, Bazin,
& Margulies, 2018; Wagstyl, Ronan, Goodyer, & Fletcher, 2015), dynamics (Shafiei et al.,
2020; Wang, 2020), and functional specialization (Hansen et al., 2021; Yarkoni, Poldrack,
Nichols, Van Essen, & Wager, 2011). Surtout, numerous studies have reported evidence
of regional heterogeneity in connection profiles or fingerprints of regions (Mars, Passingham, &
Jbabdi, 2018), as well as patterns of structure-function coupling (Baum et al., 2020; Liu et al.,
2022; Preti & Van De Ville, 2019; Vázquez-Rodríguez et al., 2019; Zamani Esfahlani,
Faskowitz, Slack, Mišić, & Betzel, 2022) and electromagnetic-haemodynamic coupling
(Shafiei, Baillet, & Misic, 2022).
Previous studies have also considered inter-regional communication capacity in specific
settings. Most efforts have been focused on the predictive utility of pairwise communication
measures, relating them to functional connectivity or behavior (Goñi et al., 2014; Grayson
et coll., 2016; Kahn et al., 2017; Seguin, Tian, & Zalesky, 2020; Vázquez-Rodríguez et al.,
2019; Zamani Esfahlani et al., 2022). Other studies have investigated its potential in distin-
guishing between patients with neurological disorders and healthy controls (Crofts & Higham,
2009; Crofts et al., 2011; Lella, Amoroso, Diacono, et coll., 2019; Lella, Amoroso, Lombardi,
et coll., 2019). The most widely studied communication mechanism is the topological shortest
chemin (Avena-Koenigsberger et al., 2018), but numerous other models have been proposed,
involving both routing protocols relaying signals through specific paths and diffusive processes
in which neural signaling is driven by local network features (Avena-Koenigsberger et al.,
2017; Crofts & Higham, 2009; Goñi et al., 2014; Mišić et al., 2015; Mišić, Goñi, Betzel,
Sporns, & McIntosh, 2014; Mišić, Sporns, & McIntosh, 2014; Seguin, van den Heuvel, &
Zalesky, 2018). Par exemple, communicability, a communication measure integrating all pos-
sible walks on a network (Crofts & Higham, 2009; Estrada & Hatano, 2008), has been used to
cluster patients (Crofts & Higham, 2009; Crofts et al., 2011; Lella, Amoroso, Diacono, et coll.,
2019; Lella, Amoroso, Lombardi, et coll., 2019), characterize regional lesion effects (Andreotti
et coll., 2014; Crofts et al., 2011; Lella, Amoroso, Lombardi, et coll., 2019), and even compensa-
tory inter-regional responses to Alzheimer’s disease (Lella, Amoroso, Diacono, et coll., 2019).
Nevertheless, global aggregated accounts of the brain’s communication capacity remain the
norm and are often used even for diffusive processes, such as mean navigation time/efficiency
(Imms et al., 2021, 2023; Kuceyeski, Jamison, Owen, Raj, & Mukherjee, 2019; Seguin et al.,
2018), diffusion efficiency (Avena-Koenigsberger et al., 2014; Chari et al., 2022; Goñi et al.,
Neurosciences en réseau
1052
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
un
_
0
0
3
1
8
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
2013; Goulas, Betzel, & Hilgetag, 2019), and average communicability (Shine, Aburn,
Breakspear, & Poldrack, 2018). En outre, while it is commonplace to provide a null frame
of reference when evaluating the prominence of global network attributes (Váša & Mišić,
2022), this procedure is not applied at the inter-regional level. En résumé, how inter-regional
and regional communication preferences are organized remains poorly understood but
methodologically accessible.
Here we develop a simple method to study the capacity for pairs of brain regions (dyads)
to communicate with each other. We deconstruct the conventional global approach and esti-
mate communication capacity without averaging over pairs of regions. En outre, we intro-
duce a procedure to standardize the communication capacity between pairs of regions by
their communication capacity in a population of rewired null networks, allowing us to iden-
tify pairs of regions with greater or less than expected communication capacity. An important
advantage of this method is that it can be used in combination with any null network model.
Increasingly constrained surrogates constitute increasingly conservative benchmarks that
more closely resemble the empirical network under study (Váša & Mišić, 2022). Using them
in parallel can simultaneously allow us to control for a covariate or disentangle its effect
from those of other unconstrained features in a more liberal null model (Váša & Mišić,
2022). Degree-preserving null models are the most commonly used for network statistic nor-
malization (Humphries, Gurney, & Prescott, 2006; Maslov & Sneppen, 2002; Newman &
Girvan, 2004; van den Heuvel & Sporns, 2011; van Wijk, Stam, & Daffertshofer, 2010). Ils
allow us to mitigate the effect of this simple, but influential, graph feature to assess to what
extent a network attribute is unexpected in contrast to a random graph that only preserves
the empirical network’s degree sequence. Ce faisant, they highlight the effect of more subtle
topological properties on a given statistic. Ici, the main null model under consideration
further constrains the empirical network’s weighted degree sequence using a simulated
annealing procedure (Cimini et al., 2019; Khachaturyan, Semenovskaya, & Vainstein,
1979; Kirkpatrick, Gelatt, & Vecchi, 1983; Mišić et al., 2015). In parallel, we additionally
consider the effect of the human connectome’s geometry with a null model that approxi-
mately preserves the edge length distribution of the empirical network, in addition to its
degree sequence, allowing us to strictly attribute the remaining effects to topology (R.. F. Betzel
& Bassett, 2018).
We initially focus on the topological shortest path (hereafter referred to as a “path”),
because (un) it is a simple and fundamental method to infer communication, et (b) in many
classes of networks, including brain networks, alternative communication mechanisms never-
theless take advantage of shortest paths without any knowledge of the global topology, inclure-
ing diffusion (Goñi et al., 2013, 2014; Mišić et al., 2015) and navigation (Seguin, Razi, &
Zalesky, 2019; Seguin, Mansour, Sporns, Zalesky, & Calamante, 2022; Seguin et al., 2018,
2020; Vézquez-Rodríguez et al., 2020). We then investigate inter-regional communication
capacity, mapping it onto large-scale cognitive systems and patterns of functional specializa-
tion. Enfin, we also consider the relationship between spatial proximity/geometric embed-
ding and communication capacity, as well as alternative communication mechanisms.
RÉSULTATS
The results are organized as follows. D'abord, we develop a method to standardize communica-
tion capacity between pairs of brain regions. We then relate inter-regional communication to
the brain’s spatial embedding, canonical functional systems, and patterns of functional spe-
cialization. All analyses were conducted in a sample of N = 69 healthy participants (source:
1053
Dyad:
Pair of brain regions.
Null models:
Models used to produce random
surrogate brain networks under
specific constraints to benchmark the
statistical unexpectedness of an
observed brain feature.
Degree sequence:
Ordered list of degrees of all nodes in
a network.
Spatial embedding:
Physical space in which a brain
network is defined.
Neurosciences en réseau
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
un
_
0
0
3
1
8
p
d
/
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
Structural connectivity:
Map of the anatomical connections
among neural elements.
Lausanne University Hospital; https://doi.org/10.5281/zenodo.2872624; Griffa, Alemán-
Gómez, & Hagmann, 2019) see Methods for detailed procedures):
▪
▪
Structural connectivity. Structural connectivity was reconstructed from individual par-
ticipants’ diffusion spectrum imaging data using deterministic streamline tractography.
A distance-dependent consensus-based thresholding procedure was then used to
assemble a group-representative weighted structural connectivity matrix of streamline
density (R.. F. Betzel, Griffa, Hagmann, & Mišić, 2019; Mišić et al., 2015, 2018).
Functional connectivity. Functional connectivity was estimated from the same individ-
uals’ resting-state functional MRI (rs-fMRI) data using pairwise Pearson correlations
among regional time courses. Fisher’s r-to-z transformation was applied to individual
functional connectivity matrices. A group-average functional connectivity matrix was
then computed as the mean across individuals, which was back-transformed to corre-
lation values.
The sample was randomly divided into Discovery (n = 34) and Validation (n = 35) subsets.
Analyses were conducted in a high-resolution (1,000 nodes) and low-resolution (219 nodes)
parcellation using the Cammoun atlas (Cammoun et al., 2012), a subdivision of the Desikan-
Killiany anatomical atlas (Desikan et al., 2006). See Sensitivity Analyses for details.
Benchmarking Dyadic Communication Capacity
To quantify polysynaptic communication capacity between pairs of brain regions, we first
compute the topological weighted shortest path lengths on the unthresholded structural con-
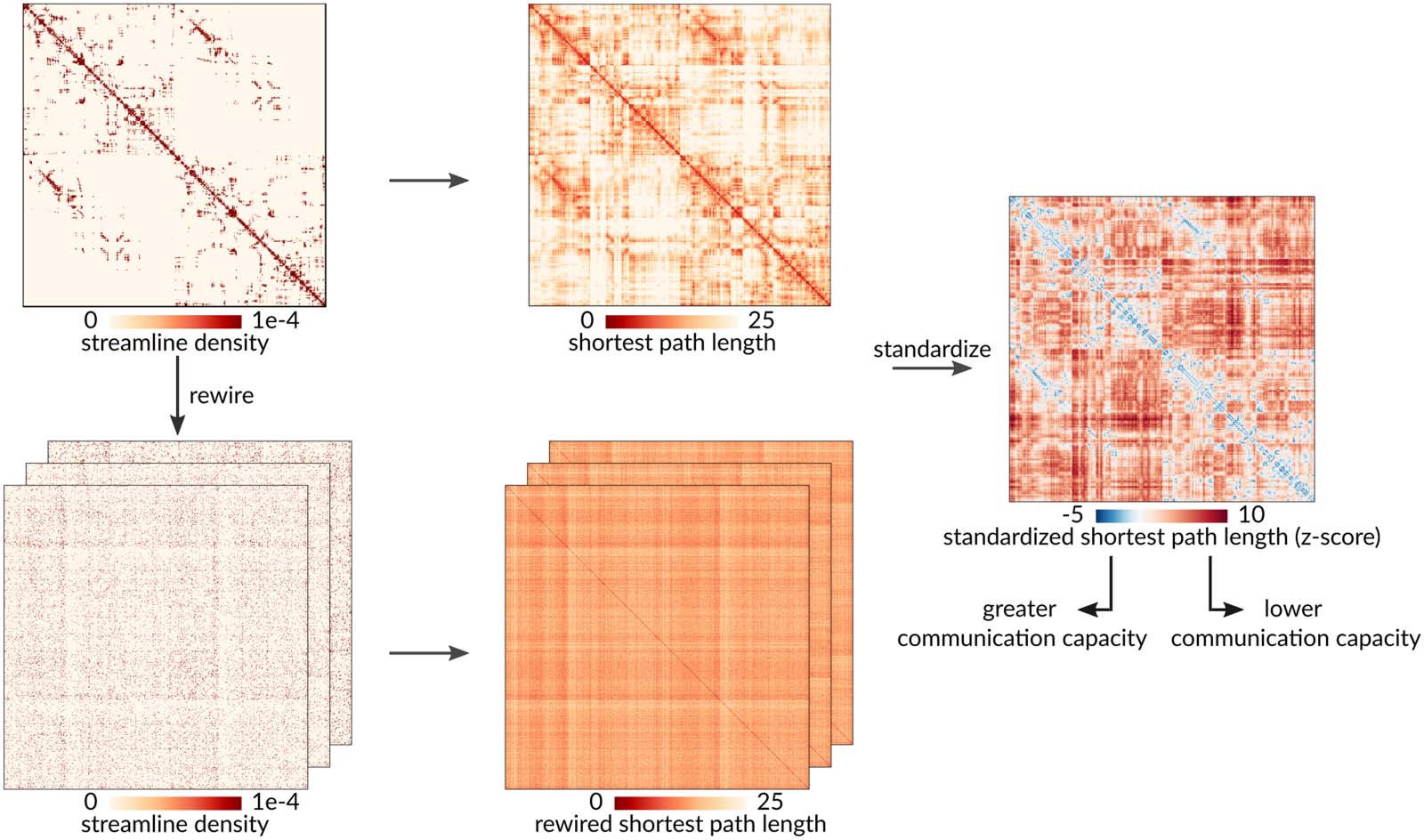
nectome (Chiffre 1) (Dijkstra, 1959). Shorter weighted path length between a pair of regions
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
un
_
0
0
3
1
8
p
d
.
t
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Standardization procedure. A population of null structural connectivity matrices that preserve the size, density, and weighted
Chiffre 1.
degree sequence of the empirical group-consensus network was generated by randomly rewiring pairs of edges. Weighted shortest path lengths
were then computed between every pair of brain regions for the empirical structural brain network and each rewired null. Enfin, the path
lengths of the empirical network were standardized element-wise against the null population of path lengths from the rewired networks. Lower
standardized shortest path length indicates greater communication capacity.
Neurosciences en réseau
1054
Communication capacity in the human connectome
indicates greater communication capacity (Avena-Koenigsberger et al., 2017, 2018; Rubinov
& Sporns, 2010). We simultaneously construct a population of rewired networks that preserve
the density and weighted degree sequence of the empirical network (Mišić et al., 2015; Váša &
Mišić, 2022). We then compute the path lengths for each rewired network, indicating the
communication capacity between pairs of brain regions under the null hypothesis that
inter-regional relationships depend only on weighted degree and density (Chiffre 1). Enfin,
we standardize element-wise the empirical path lengths against the population of path lengths
in the rewired null networks. The resulting standardized shortest path length matrix quantifies
in terms of z-scores how unexpectedly short (<0) or unexpectedly long (>0) communication
pathways are between any given pair of brain regions.
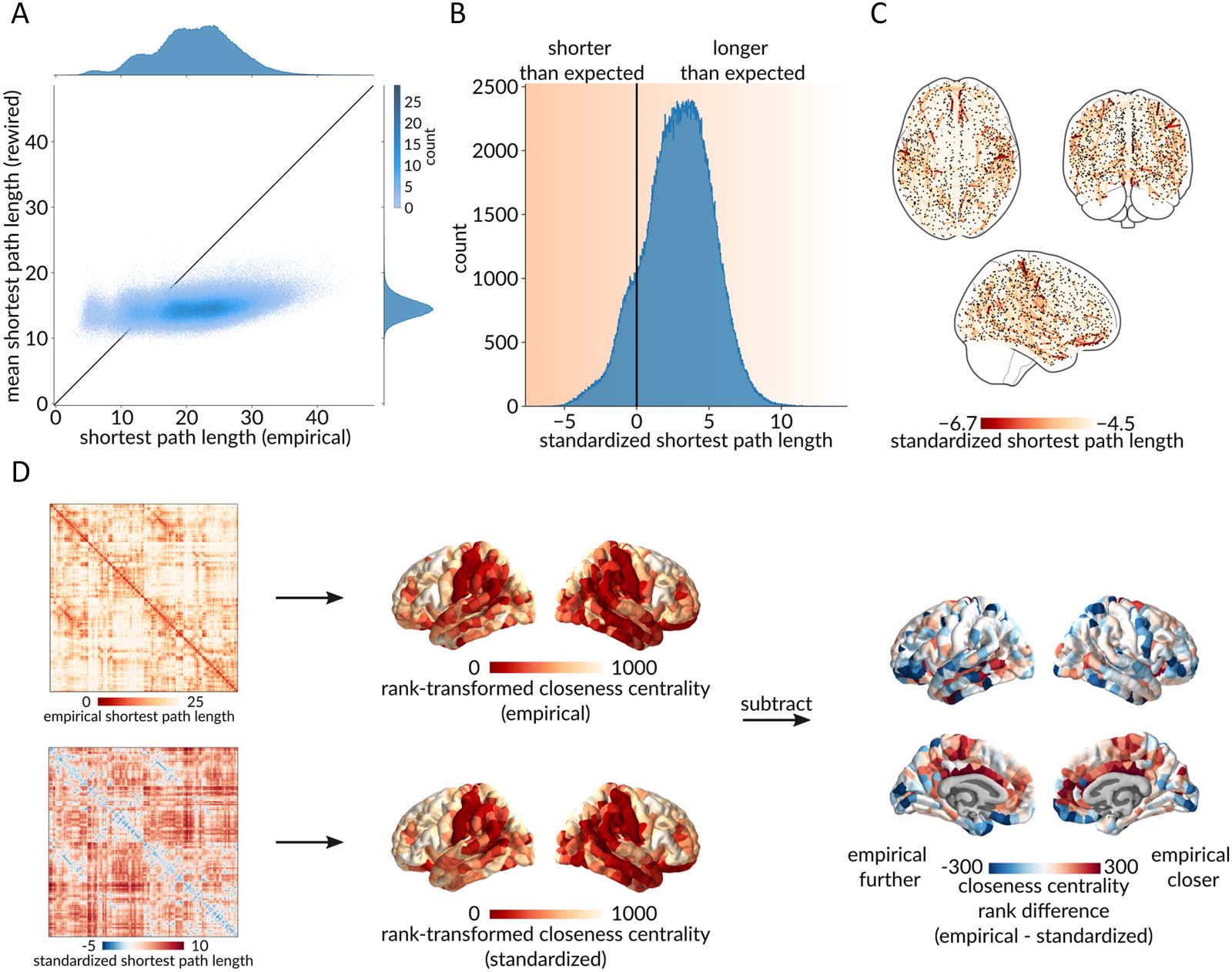
Figure 2A shows a scatterplot between empirical (abscissa) and rewired (ordinate) chemin
lengths, where each point represents a pair of regions. As expected, the majority of points fall
below the identity line (87.15%), suggesting that most path lengths in rewired networks are
shorter than in the empirical structural brain network (Watts & Strogatz, 1998). This is in line
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
un
_
0
0
3
1
8
p
d
t
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2. Benchmarking dyadic communication capacity. (UN) Scatterplot between empirical (abscissa) and rewired (ordinate) shortest path
lengths, where each point represents a pair of brain regions. Marginal distribution histograms are shown on the top and right axes. Points that
appear below the identity line correspond to paths with a shorter length in the rewired networks than in the empirical network, and vice versa
for points above the identity line. (B) Distribution of standardized shortest path lengths (z-scores) for all pairs of brain regions. Values less than 0
indicate greater-than-expected communication capacity, and values greater than 0 indicate lower-than-expected communication capacity. (C)
Spatial distribution of the top 1% unexpectedly short path lengths. (D) Using the empirical and the standardized path length matrices, close-
ness centrality (inverse mean path length to the rest of the network) was computed and rank-transformed for every brain region. The two
resulting brain maps were then subtracted, resulting in a brain map of the region-wise differences between closeness centrality ranks in the
empirical and the standardized networks. Red regions are more integrated in the empirical network, and blue regions are more integrated in
the standardized network.
Neurosciences en réseau
1055
Communication capacity in the human connectome
with numerous global accounts of the shortest path length of random networks and their com-
parison with characteristic path lengths of empirical brain networks (Albert & Barabási, 2002;
Bassett & Bullmore, 2006; Hilgetag & kaiser, 2004; Sporns & Zwi, 2004; Watts & Strogatz,
1998). Fait intéressant, a number of points reside above identity (12.85%), suggesting that these
region pairs enjoy greater-than-expected capacity for communication. Figure 2B further dem-
onstrates this result, showing the distribution of standardized path lengths for all pairs of regions.
Negative values indicate dyads with greater-than-expected communication capacity, and posi-
tive values indicate dyads with lower-than-expected communication capacity.
To get a sense of how the centrality or “hub-ness” of each brain region changes when path
lengths are standardized, we compute the closeness centrality (inverse mean path length to the
rest of the network) of each brain region using the empirical and the standardized path length
matrices. Figure 2D shows the difference between rank-transformed closeness computed using
empirical and standardized path lengths. The figure suggests that the inferred importance of a
brain region changes considerably when the procedure is applied. Namely, red regions (par exemple.,
cingulate cortex) are more central in the empirical shortest path length network, and blue
régions (par exemple., orbitofrontal cortex) are more central in the standardized shortest path length
réseau.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
un
_
0
0
3
1
8
p
d
t
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Intrinsic networks:
Networks of functionally related
brain regions with synchronous
spontaneous activity.
Communication Pathways Delineate Functional Systems
We next consider how communication paths can be contextualized with respect to canonical
features of brain networks, including spatial embedding, structure-function coupling, et
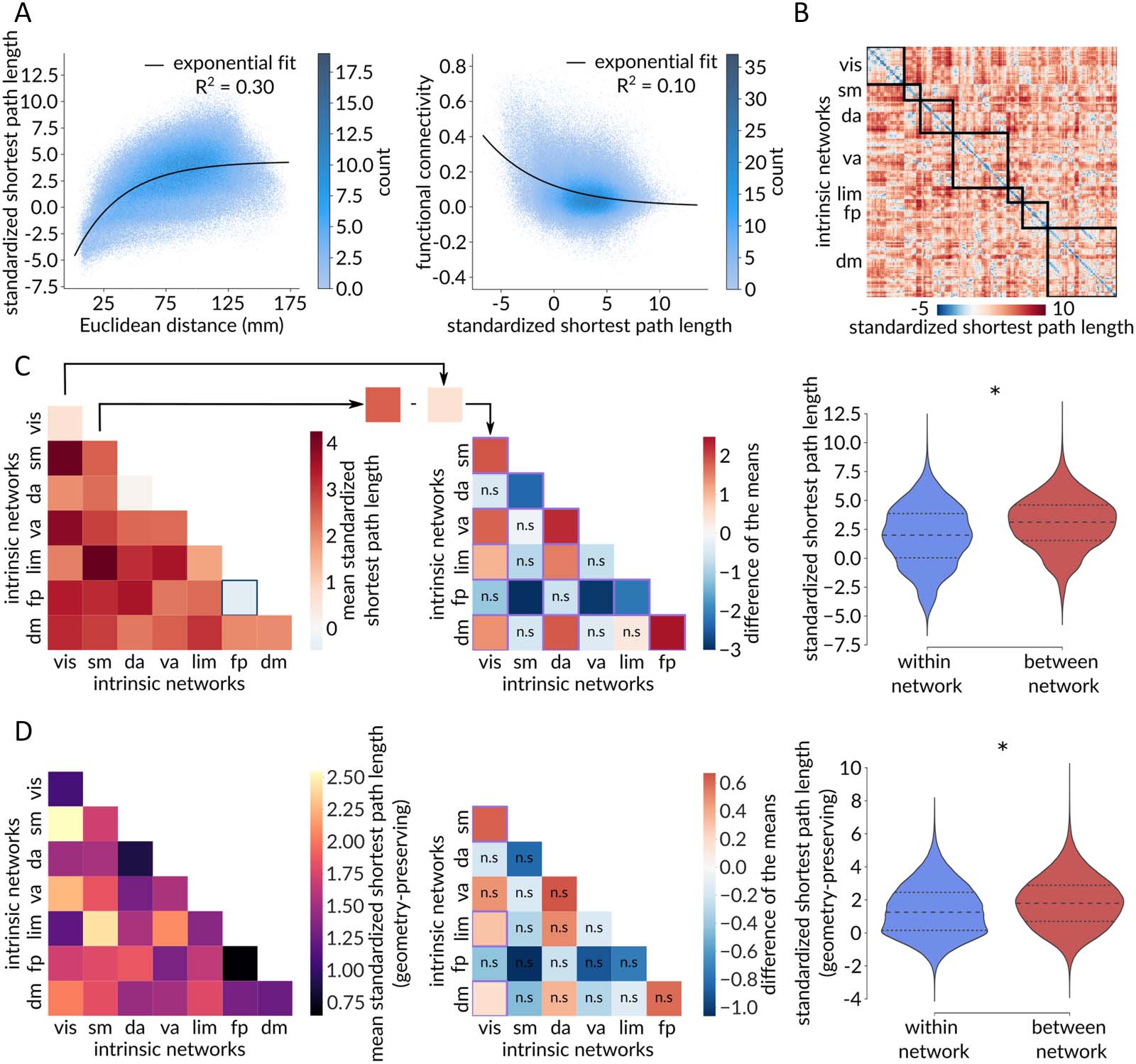
macroscale intrinsic network organization. Figure 3A shows the relationship between stan-
dardized path length and pairwise inter-regional physical distance (gauche) and pairwise inter-
regional functional connectivity (droite). There is a positive association between physical
distance and standardized path length, consistent with the notion that areas that are physically
further apart have lower communication capacity (Roberts et al., 2016; Seguin et al., 2018;
Stiso & Bassett, 2018). There is also a negative association between standardized path length
and functional connectivity, consistent with the notion that pairs of areas that are topologically
closer have more coherent time courses (Goñi et al., 2014; Honey et al., 2009). Collectively,
these results show that standardized path length recapitulates well-known and expected rela-
tionships between the topology, geometry, and functional connectivity of the brain (Suárez,
Markello, Betzel, & Misic, 2020).
How are communication pathways organized among the canonical macroscale intrinsic
réseaux? Resting-state functional connectivity networks are communities of functionally
related areas with coherent time courses that are thought to be putative building blocks of
higher cognition (Bellec, Rosa-Neto, Lyttelton, Benali, & Evans, 2010; Damoiseaux et al.,
2006; Power et al., 2011; Yeo et al., 2011), but how these networks map onto the underlying
communication pathways is not completely understood (Avena-Koenigsberger et al., 2018;
Suárez et al., 2020). To address this question, we first stratify brain regions according to their
membership in the intrinsic networks derived by Yeo, Krienen and colleagues (Yeo et al., 2011)
(Figure 3B). Figure 3C (gauche) shows the mean standardized path length within each intrinsic
réseau (diagonal) and between all pairs of intrinsic networks (off-diagonal). We generally
observe shorter path lengths within networks compared with between networks; Figure 3C
(droite) confirms this intuition, showing that the mean within-network path length is significantly
shorter than the mean between-network path length (pspin < 0.001).
Next, we quantify and compare the internal communication capacities of pairs of intrinsic
networks by computing the difference between their respective within-network mean
Network Neuroscience
1056
Communication capacity in the human connectome
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Communication pathways delineate functional systems. (A) Standardized shortest path length (y) between two brain regions grows
as a function of the Euclidean distance (x) between them (left). The black line corresponds to the fitted exponential y = −9.31e−0.03x + 4.33.
Functional connectivity (y) between two brain regions decays as a function of the standardized shortest path length (x) between them (right).
The black line corresponds to the fitted exponential y = 0.12e−0.18x. (B) Standardized shortest path length matrix with brain regions ordered
based on their affiliations to the Yeo intrinsic networks. (C) Left: Heatmap of the mean standardized path lengths across node pairs belonging to
the same intrinsic network (diagonal) and to different intrinsic networks (off-diagonal). A blue square identifies a negative mean standardized
path length, indicative of shorter-than-expected communication pathways with greater-than-expected communication capacity. Middle: Heat-
map of the pairwise differences of the means among Yeo intrinsic networks, calculated as the mean value of the network on the y-axis minus
the mean value of the network on the x-axis, with the mean value corresponding to the mean standardized path length across node pairs
belonging to the same network (diagonal elements of the left heatmap). A purple square indicates significant difference of the means based on
network label permutation using spatial autocorrelation-preserving null models (Bonferroni corrected, α = 0.05), whereas “n.s.” denotes not
significant differences. The frontoparietal network displays a consistently shorter mean standardized path length (i.e., higher internal commu-
nication capacity) compared with other networks, whereas the somatomotor network exhibits a consistently greater mean standardized path
length (i.e., lower internal communication capacity) in comparison to other networks. Right: The mean within-network standardized path
length is significantly shorter than the mean between-network standardized path length (pspin < 0.001). (D) Same as panel C but for shortest
path lengths standardized using a geometry-preserving null model. Intrinsic networks: vis = visual, sm = somatomotor, da = dorsal attention,
va = ventral attention, lim = limbic, fp = frontoparietal, dm = default mode.
standardized path length (Figure 3C, middle). We find that the frontoparietal network has
consistently greater internal communication capacity compared with other networks, while
the somatomotor network has consistently lower internal communication capacity compared
with other networks. Interestingly, Figure 3C (left) also indicates that communication path-
ways internal to the frontoparietal network are the only ones to exhibit a greater-than-
Network Neuroscience
1057
Communication capacity in the human connectome
expected communication capacity, characterized by a negative mean standardized path
length.
Moreover, we reproduce this analysis using a geometry-preserving null model (Figure 3D).
Once again, we find significantly shorter path lengths within Yeo networks (pspin < 0.001;
Figure 3D, right) and identify the frontoparietal network and the somatomotor networks as
consistently exhibiting the highest and lowest internal communication capacity, respectively
(Figure 3D, middle). However, most pairwise comparisons between intrinsic networks are now
not significant as assessed by spatial autocorrelation-preserving nulls (Bonferroni corrected,
α = 0.05). Furthermore, the frontoparietal network does not present a negative mean stan-
dardized path length anymore, indicating that its greater-than-expected communication
capacity can be partly attributed to its spatial embedding (Figure 3D, left).
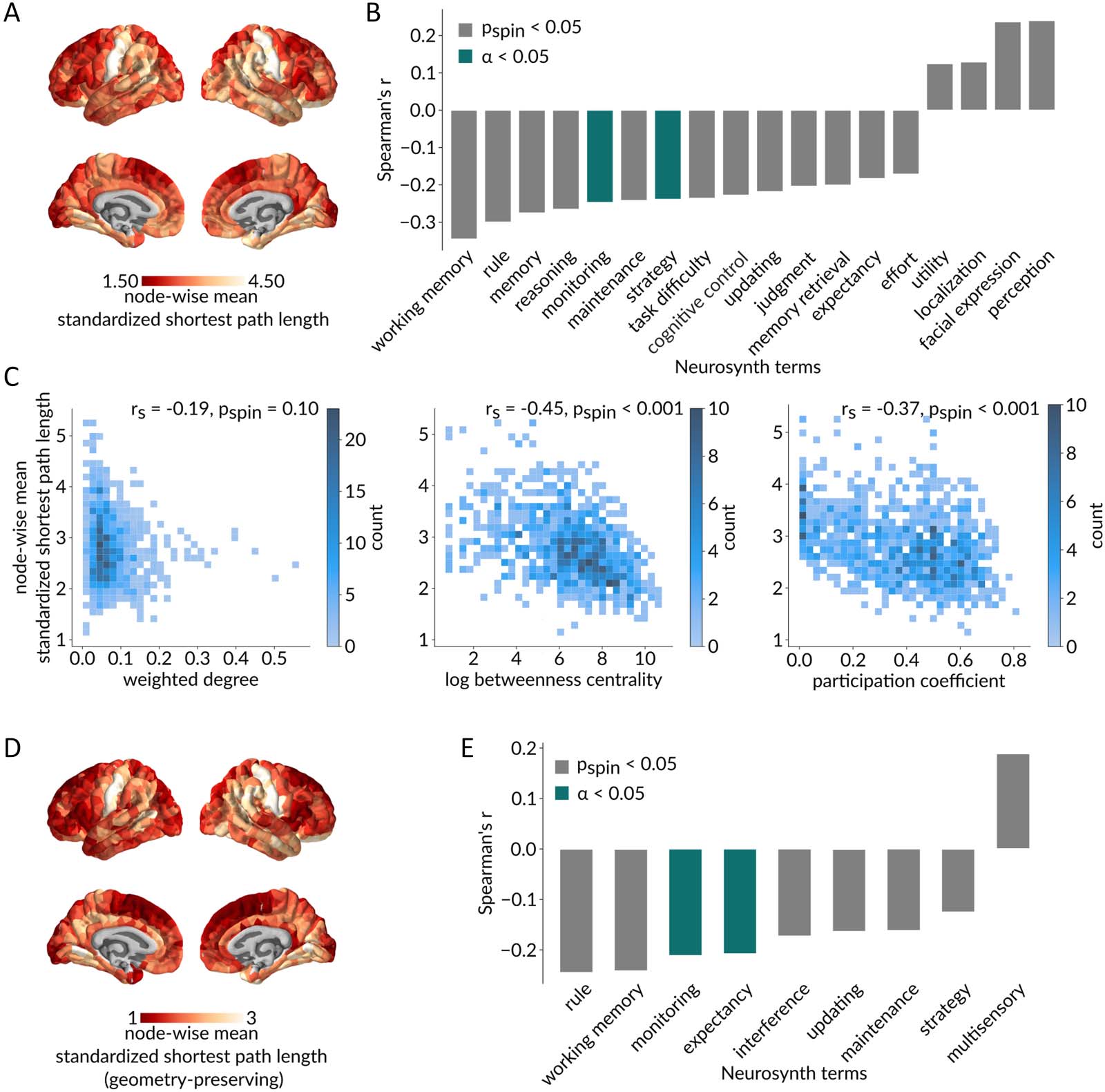
Communication Capacity and Functional Specialization
Given that communication capacity is regionally heterogeneous and maps onto intrinsic net-
works, we ask whether regional communication capacity is related to functional specializa-
tion. Figure 4A shows the mean standardized path length from each region to the rest of the
network, with red indicating greater integration with the network and yellow indicating lower
integration.
We statistically compare this map with a library of meta-analytic task-based fMRI activation
maps from the Neurosynth repository (Hansen et al., 2021; Yarkoni et al., 2011). Each of the
Neurosynth brain maps consists of region-wise measures of the probability that a particular term
is reported in a study if an activation was observed in a given region. In this analysis, we only
consider the intersection of terms from the Neurosynth database and the Cognitive atlas
(Poldrack et al., 2011), comprising a total of 123 cognitive and behavioral terms. Figure 4B
shows statistically significant spatial correlations between the node-wise standardized path length
map and each of the Neurosynth term maps, as assessed using spatial autocorrelation-preserving
null models (Alexander-Bloch et al., 2018; Markello & Misic, 2021; pspin < 0.05 in gray;
Bonferroni corrected, α = 0.05 in green). We find anticorrelations with higher order cognitive
terms (e.g., “monitoring,” “strategy”). This suggests that areas that communicate closely with
many other areas in the connectome are associated with higher order cognitive function. In other
words, cognitive integration appears to be supported by network integration.
To better understand why lower standardized path length is associated with higher order
cognitive function, we compare the regional map of standardized path length with maps of
weighted degree (sum of edge weights incident on a node; strength), betweenness (proportion
of shortest paths that traverse a node), and participation (distribution of node links among func-
tional network communities) (Figure 4C). All three topological features were computed on the
empirical weighted structural network. As expected due to the standardization procedure,
there is no significant correlation with weighted degree (rs = −0.19, pspin = 0.10). However,
standardized path length is significantly negatively correlated with betweenness (rs = −0.45,
pspin < 0.001) and participation (rs = −0.37, pspin < 0.001), suggesting that regions that are
closely integrated into the connectome can better sample information from multiple special-
ized communities.
Furthermore, we replicate this analysis using a geometry-preserving null model (Figure 4D–E).
Once again, we find significant anticorrelations between node-wise standardized path lengths
and higher order cognitive terms (e.g., “monitoring”, “expectancy”). This suggests that the
observed association between cognitive and network integration is not passively endowed by
the brain’s physical embedding, but rather driven by its topological organization.
Network Neuroscience
1058
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
.
t
Figure 4. Communication capacity and functional specialization. (A) Brain map of mean standardized path length from each node to the rest
of the network, with red denoting a greater integration of the node within the network and yellow denoting a lower integration. (B) Statistically
significant spatial correlations based on spatial autocorrelation-preserving nulls (pspin < 0.05 in gray; Bonferroni corrected, α = 0.05 in green)
between node-wise mean standardized path lengths and meta-analytic probabilistic functional activation maps from the Neurosynth platform,
associated with 123 terms overlapping the Neurosynth database and the Cognitive atlas. An important set of anticorrelations suggests that
highly integrated nodes are associated with higher order cognitive functions. (C) Relationships between node-wise mean standardized path
length and topological features of the empirical weighted structural network. As expected due to the standardization procedure, node-wise
mean standardized path length is not significantly correlated with weighted degree (rs = −0.19, pspin = 0.10; left), while it is significantly
negatively correlated with betweenness (rs = −0.45, pspin < 0.001; middle) and participation (rs = −0.37, pspin < 0.001; right), suggesting that
regions that are more topologically integrated also have a more diverse connection profile among functionally specialized intrinsic networks.
(D–E) Same as panel C but for shortest path lengths standardized using a geometry-preserving null model.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Extending to Multiple Communication Models
So far, we have only considered path length as a proxy for communication. However, there
exist numerous other models of communication in the connectome (Avena-Koenigsberger
et al., 2018). Here we extend the framework developed in the previous sections to additional
measures of communication proximity that have been proposed for brain networks, including
search information (Goñi et al., 2014; Rosvall, Grönlund, Minnhagen, & Sneppen, 2005), path
transitivity (Goñi et al., 2014), communicability (Crofts & Higham, 2009; Estrada & Hatano,
Network Neuroscience
1059
Communication capacity in the human connectome
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
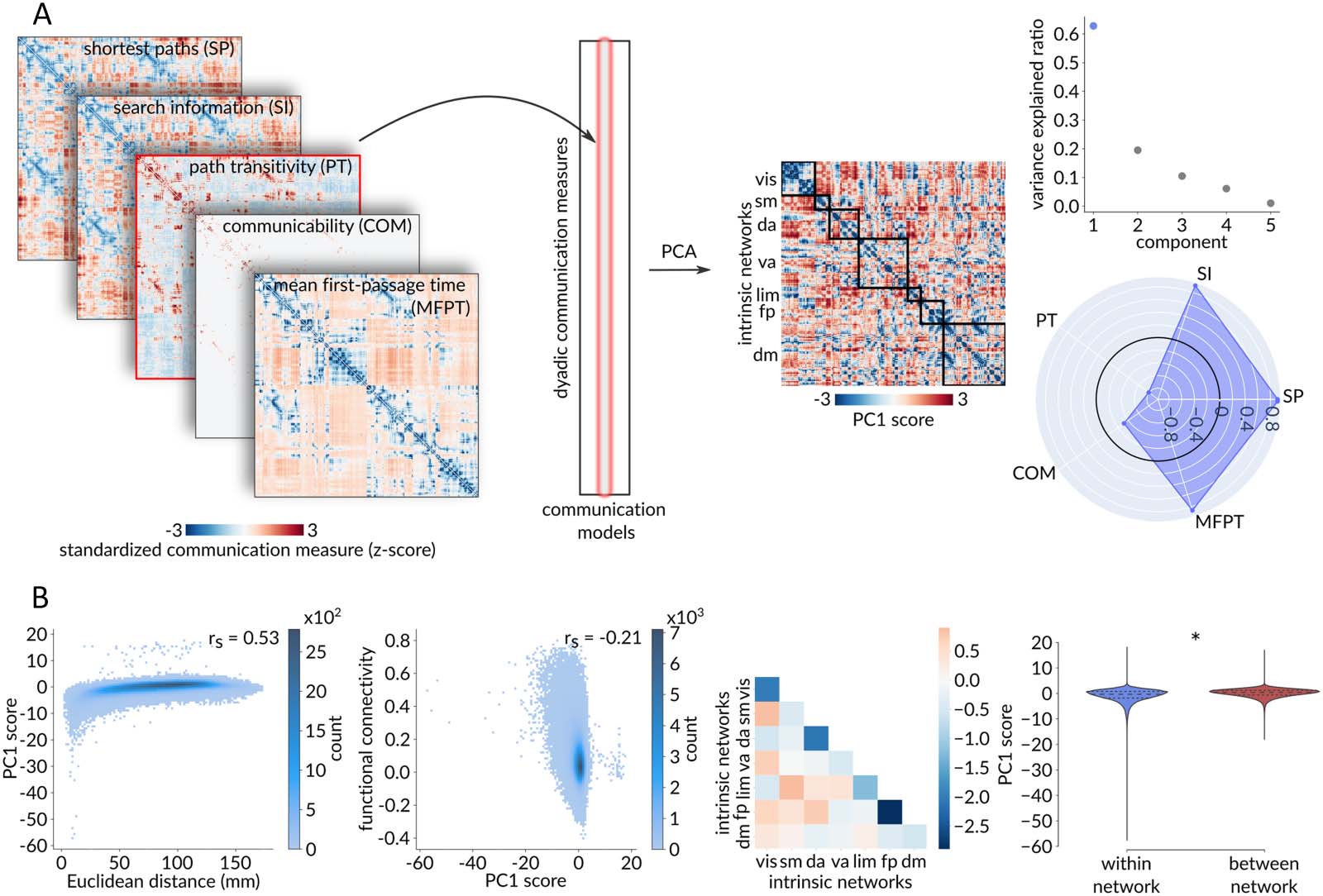
Figure 5. Extending to multiple communication models—Dyad-level. (A) Standardized dyadic communication measures across five com-
munication models were assembled into the columns of a dyads × communication models matrix. Principal component analysis, applied to
this matrix, identified a single dominant component that accounts for 62.79% of the dyadic-level variance in communication capacity. The
radar chart represents the first component’s loadings (i.e., correlations with the five communication models under consideration), with the
greatest contribution to the aggregated communication measure coming from search information, path length, and mean first-passage time,
with only a minor contribution from communicability. (B) The aggregate communication measure yields similar results to the standardized
shortest path length. From left to right: Positive Spearman correlation between PC1 score and Euclidean distance (rs = 0.53, p ≈ 0), negative
Spearman correlation between functional connectivity and PC1 score (rs = −0.21, p ≈ 0), and significantly lower within-network than
between-network PC1 score (pspin < 0.001).
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2008), and mean first-passage time (Goñi et al., 2013; Noh & Rieger, 2004). As before, we first
standardize each communication matrix using a population of rewired networks (Figure 5A).
We then extract all dyadic (i, j ) elements from each communication matrix and assemble them
into the columns of a dyads × communication models matrix.
Applying principal component analysis (PCA) to this matrix identifies a single dominant
component that accounts for 62.79% of the dyad-level variance in communication. The result-
ing PC1 scores are then used to constitute an “aggregated” communication matrix that shows
the capacity for communication among all pairs of brain areas across multiple communication
models. The greatest contribution to the aggregated communication measure is from search
information, path length, and mean first-passage time, with modest contribution from commu-
nicability. Note that, unlike the original communication measures, this aggregated communi-
cation measure is not necessarily transitive.
Overall, we observe similar results using the aggregated multicommunication measure
(Figure 5). Namely, we find a positive relationship between standardized communication dis-
tance and physical distance (rs = 0.53, p ≈ 0; Figure 5B), a negative relationship between stan-
dardized communication distance and functional connectivity (rs = −0.21, p ≈ 0; Figure 5B),
and significantly shorter communication distance within canonical intrinsic networks than
between networks ( pspin < 0.001; Figure 5B).
Network Neuroscience
1060
Communication capacity in the human connectome
Rewiring:
Randomly swapping pairs of
connections under specific
constraints.
Figure S1A in the Supporting Information shows the same procedure applied at the node
level. As before, we find consistent results, showing that areas that are closer in communica-
tion distance to other areas in the connectome tend to be associated with higher order
cognitive function (Figure S1C) and greater participation in network communities (rs =
−0.40, pspin < 0.001; Figure S1D; right).
Disentangling the Contributions of Topology and Geometry
Physical proximity is an important predictor of connection probability and connection weight
(R. F. Betzel & Bassett, 2018; Roberts et al., 2016), and therefore by extension, communication
capacity between areas. We therefore seek to disentangle the contribution of geometry from
the contribution of topology to the results reported so far. Initially, we utilized degree-
preserving rewiring to construct populations of null networks and standardize path length
(Maslov & Sneppen, 2002; Mišić et al., 2015). To additionally control for the role of geometry,
we repeat the experiments using a more conservative null model that approximately preserves
the edge length distribution and the edge length-to-weight mapping, in addition to degree
sequence (R. F. Betzel & Bassett, 2018).
Supporting Information Figure S2 shows the results when applying the geometry-preserving
null model. As for the degree-preserving null model, Figure S2A shows that the majority of
path lengths are shorter in the rewired networks than in the empirical network (86.04%). How-
ever, the majority of points (region pairs) now lie closer to the identity line, suggesting that the
physical embedding of the structural brain network contributes in pulling its regions apart
topologically. Furthermore, controlling for geometry in the standardization procedure accen-
tuates the integration and segregation of certain regions, providing a clearer, more homoge-
neous picture of changes in closeness centrality (Figure S2B). The orbitofrontal cortex becomes
more integrated and the cingulate cortex and precuneus become more segregated when
strictly considering the empirical network’s topology. Interestingly, the paracentral lobule
and the motor cortex now move in directions opposite to those observed when using the null
model that did not preserve the connectome’s geometry. Indeed, the geometry-preserving
standardization procedure moved the paracentral lobule topologically closer to the rest of
the network and the motor cortex further. This suggests that the physical distance of these
regions to the rest of the brain interacts with its topology to centralize the motor cortex and
segregate the paracentral lobule.
As expected, controlling for edge length considerably attenuates the relationship between
standardized path length and Euclidean distance (Supporting Information Figure S2C, left).
Importantly, most of the other results are largely preserved, including shorter standardized path
lengths within compared with between networks (pspin < 0.001; Figure 3D, right) and a rela-
tionship between node-wise communication and integrative function (Figure 4E). Collectively,
this control experiment suggests that most of the results reported previously—except the rela-
tionship with Euclidean distance—are mainly driven by the topological organization of the
connectome rather than spatial embedding and geometric relationships. An important excep-
tion is the higher-than-expected internal communication capacity of the frontoparietal net-
work, which seems to have been partly driven by the brain’s geometry.
Sensitivity Analyses
We test the replicability of the findings in the Validation sample (Supporting Information Figure
S3) and seek to assess the sensitivity of the results to a variety of processing choices. We repeat
Network Neuroscience
1061
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
all analyses using a lower parcellation resolution of 219 nodes (Figure S4) and binary (non-
weighted) structural networks (Figure S5).
We find consistent results across all sensitivity analyses. This includes significantly shorter
communication pathways between cortical regions belonging to the same intrinsic functional
network than between regions belonging to different intrinsic networks, as well as significant
relationships between a region’s topological integration and its association with higher order
executive functions (Supporting Information Figures S3, S4, S5). The frontoparietal network is
consistently identified as exhibiting the highest internal communication capacity. Communi-
cation pathways internal to the frontoparietal network also have a negative mean standard-
ized path length, indicative of a greater-than-expected communication capacity (Figures S3,
S4, S5).
Next, we seek to test the extent to which the results are influenced by the inclusion of direct
monosynaptic pathways (i.e., paths between directly anatomically connected nodes; Support-
ing Information Figure S6). We therefore repeat the analyses in strictly polysynaptic commu-
nication pathways (i.e., paths between pairs of nodes that are separated by two or more
anatomical connections; Supporting Information Figures S6C, S7, S8, S9). Again, we find con-
sistent results with the notable exception of the communication capacity of the frontoparietal
network (Figure S7; original result in Figure 3C). This indicates that the greater-than-expected
communication capacity of this network is partly driven by monosynaptic connections.
Recently, there has been a growing interest to relate patterns of brain communication with
the higher order connectivity of brain networks (Battiston et al., 2021; Crofts, Forrester, &
O’Dea, 2016; Griffa et al., 2022; Sizemore et al., 2018). In alignment with this new line of
inquiry, and to demonstrate the flexibility of our standardization procedure, we apply it to a
recently introduced higher order multimodal communication measure: structure-function
bandwidth (Parsons et al., 2022). Based on a multilayer framework in which structural and
functional connectivity are considered simultaneously, bandwidth between two brain regions
in the functional connectivity layer is defined according to the minimum edge weight of a path
connecting these nodes in the structural connectivity layer. The maximum bandwidth is then
selected across all paths of a given length. Here, we consider triangles composed of two-hop
structural paths closed by a functional edge. We weigh structure-function bandwidth by the
functional edge weights to provide a generalized communication measure taking into account
all functional connections enclosing triangles. This yields a structure-function bandwidth
matrix that we concurrently standardize using the same procedure previously described, with
structure-function bandwidth being recomputed in a population of rewired structural networks
while the functional network is left intact. We then consider how our generalized structure-
function bandwidth measure is organized among intrinsic functional networks. We observe
distinct patterns of intra- and inter-network structure-function bandwidth when comparing
the empirical and the standardized measures (Supporting Information Figure S10). This anal-
ysis demonstrates how the standardization procedure can be readily extended to accommo-
date questions about higher order brain network architecture.
DISCUSSION
In the present report, we introduce a simple method to standardize communication path
lengths in brain networks. These results showcase how dyadic relationships can be resolved
and studied while accounting for more basic topological and geometric features of the net-
work. Building on hierarchically constrained null models, this rigorous standardization proce-
dure enables specific quantification and localization of the degree of unexpectedness of
Network Neuroscience
1062
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
communication measures. In contrast to classical approaches, considering communication
capacity at a finer granularity allows us to revisit previous investigations of brain hubs, reca-
pitulate well-known geometric and functional attributes of inter-regional communication, and
uncover new relationships between the human connectome’s topological and functional
architectures across multiple topological levels of analysis in a nuanced and principled way.
Classical studies focused on global path length or efficiency of brain networks. These
reports found evidence of near-minimal path length characteristic of small-world architecture
across multiple species and reconstruction methods (Bassett & Bullmore, 2017; Hilgetag &
Kaiser, 2004; Kaiser & Hilgetag, 2006; Sporns & Zwi, 2004; Watts & Strogatz, 1998). In addi-
tion, empirical studies found that low characteristic path length or high global efficiency is
associated with greater cognitive performance (Li et al., 2009; van den Heuvel, Stam, et al.,
2009) and is concomitant with healthy neurodevelopment (Baum et al., 2017; Fan et al., 2011;
Hagmann et al., 2010; Khundrakpam, Lewis, Zhao, Chouinard-Decorte, & Evans, 2016;
Khundrakpam et al., 2013). Altogether, these findings speak to the behavioral and biological
relevance of global accounts of communication capacity.
However, global communication measures such as characteristic path length or global effi-
ciency are effectively summary statistics of a myriad of complex inter-regional communication
relationships. In the present study, we focus specifically on dyadic communication while
statistically controlling for fundamental topological and geometric features (i.e., degree and
spatial position). We find that most communication pathways between brain regions are longer
than expected on the basis of their degree and/or spatial position. Despite the standardization
procedure, we still recapitulate fundamental features of inter-regional communication, such as
positive relationships with spatial proximity (Roberts et al., 2016; Seguin et al., 2018; Stiso &
Bassett, 2018) and negative relationships with resting-state functional connectivity (Goñi et al.,
2014; Honey et al., 2009; Seguin et al., 2020; Vázquez-Rodríguez et al., 2019; Zamani
Esfahlani et al., 2022).
We note that the procedure used here is similar to what is typically done when considering
global communication statistics, such as characteristic path length. Namely, characteristic
path length is often normalized by the mean characteristic path length across a population
of null networks, such as when estimating the small-world coefficient (Humphries et al.,
2006; Watts & Strogatz, 1998). We build on this general approach by finely resolving dyadic
communication relationships. In addition, by standardizing each dyadic path length as
opposed to normalizing by the mean, we implicitly take into account variance across the null
population (Bassett et al., 2008).
The standardization procedure alters the centrality rankings of brain regions, suggesting that
taking the constraints of degree into account can lead to different inferences about the func-
tional importance of brain regions. For instance, we find that the orbitofrontal cortex is more
integrated in the standardized network than the empirical network, and that parts of the medial
prefrontal cortex, cingulate cortex, and precuneus are less integrated in the standardized net-
work. These results run counter to numerous classical investigations of brain hubs that did not
explicitly control for degree when estimating different centrality measures based on path
length, such as betweenness and closeness (Hagmann et al., 2008; van den Heuvel & Sporns,
2011, 2013b).
A large body of neuroimaging studies has highlighted the existence of a number of macro-
scale communities of functionally related brain regions with correlated resting-state fMRI sig-
nals (Damoiseaux et al., 2006; Power et al., 2011; Uddin, Yeo, & Spreng, 2019; Yeo et al.,
2011). Previous efforts were made to relate these patterns of synchronized spontaneous
Network Neuroscience
1063
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
activity to the underlying anatomical scaffolding of the brain (van den Heuvel & Hulshoff Pol,
2010). Specifically, some studies have investigated the structural underpinnings of the func-
tional links within and between resting-state networks by identifying specific white matter
tracts that could mediate these relationships (Greicius, Supekar, Menon, & Dougherty,
2009; van den Heuvel, Mandl, Kahn, & Hulshoff Pol, 2009). More recently, a growing interest
in the functional predictive utility of communication measures based on structural connectiv-
ity has led to investigations into the relationships between functional brain networks and
underlying patterns of polysynaptic communication. It has been shown that the intrinsic
functional hierarchy of the brain guides communication trajectories and allows for signal
diversification (Vézquez-Rodríguez et al., 2020). Furthermore, it was found that the modular
boundaries of resting-state functional connectivity were approximated by modules of polysyn-
aptic communication distance (Seguin et al., 2022). In line with these studies, we map com-
munication pathways among canonical intrinsic functional networks (Yeo et al., 2011). We
find that standardized path lengths are significantly shorter within than between intrinsic net-
works, suggesting that the topological organization of the human connectome contributes in
giving rise to macroscale intrinsic patterns of functional interactions.
Moreover, by organizing communication pathways within individual intrinsic networks and
between pairs of networks, we identify the frontoparietal network as exhibiting the highest
internal communication capacity. Previous findings had associated a greater structural global
efficiency of a frontoparietal network (mean closeness centrality across nodes of the network
to all brain regions) with a higher working memory capacity (Pineda-Pardo, Martínez, Román,
& Colom, 2016). The present result suggests that, in addition to global integration of frontopar-
ietal nodes, the higher order executive control functions that have been widely attributed to
frontoparietal networks (Dosenbach et al., 2007; Fedorenko, Duncan, & Kanwisher, 2013;
Laird et al., 2011; Niendam et al., 2012; Power & Petersen, 2013; Vincent, Kahn, Snyder,
Raichle, & Buckner, 2008; Yeo et al., 2015) might also benefit from an unexpectedly high level
of internal communication capacity.
What are the functional consequences of lower or greater communication capacity? Com-
parison with meta-analytic maps of functional specialization suggests that regions that are
topologically closer to others tend to be associated with higher order cognitive functions such
as monitoring and strategy. In other words, we find that greater network integration is associ-
ated with cognitive integration (Cole, Yarkoni, Repovš, Anticevic, & Braver, 2012; Mišić et al.,
2015; Sporns, 2013; Worrell, Rumschlag, Betzel, Sporns, & Mišić, 2017). This is consistent
with numerous theories that posit that patterns of regional specialization arise from connectiv-
ity profiles (Bressler & Menon, 2010; Mars et al., 2016, 2018; McIntosh, 2000; Passingham,
Stephan, & Kötter, 2002) and topological embedding of brain regions (Petersen & Sporns,
2015; Sporns, 2011, 2013; Wig, 2017). Moreover, we find that nodal topological integration
is positively associated with the number of shortest paths traversing it and the diversity of a
region’s connections among intrinsic functional communities. This is in line with previous
accounts of hub characteristics (Hagmann et al., 2008; van den Heuvel, Kahn, Goñi, & Sporns,
2012; van den Heuvel & Sporns, 2011, 2013a, 2013b). Here, we further show these features to
be related even when controlling for the effects of degree and strength. Previous reports have
also shown positive associations between a node’s involvement in complex tasks and the
diversity and flexibility of its functional links to the rest of the brain, especially in frontoparietal
regions (Bertolero, Yeo, & D’Esposito, 2015; Cole et al., 2013; Power et al., 2011). Altogether,
the present results complement these findings, suggesting that brain regions that subserve
higher order cognition also benefit from a structural substrate for the diversification and inte-
gration of information.
Network Neuroscience
1064
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
This work is part of a wider trend in the field to infer and quantify the potential for communi-
cation among brain regions based on their wiring patterns (Avena-Koenigsberger et al., 2018;
Graham, Avena-Koenigsberger, & Mišić, 2020; Graham & Rockmore, 2011; Srivastava et al., 2020;
Zhou et al., 2022). Although we mainly focus on shortest paths, multiple alternative communica-
tion protocols have been proposed (Avena-Koenigsberger et al., 2017; R. F. Betzel, Faskowitz,
Mišić, Sporns, & Seguin, 2022; Crofts & Higham, 2009; Goñi et al., 2014; Mišić et al., 2015; Mišić,
Sporns, & McIntosh, 2014; Seguin et al., 2018; Zhou et al., 2022). The present standardization
procedure can be readily applied to any dyadic communication measure. Combining additional
measures of decentralized communication such as search information and path transitivity, we
find results consistent with those derived using path length. As the field moves towards more
biologically realistic and validated communication protocols, future studies could adapt this stan-
dardization procedure to accommodate emerging measures of communication capacity. As an
example, we show that it can be readily adapted to a higher order multimodal communication
measure defined in a multiplex brain network combining structural and functional connectivity.
In addition, the present procedure standardizes communication measures using two com-
mon types of rewiring null models. Here we focus on disentangling the contribution of the
structural brain network’s topology from the background effect of spatial embedding. We
therefore apply one null model that preserves the (weighted) degree sequence and another
that additionally preserves wiring length (R. F. Betzel & Bassett, 2018). Interestingly, most
effects are preserved when applying the geometric null model, suggesting that they are driven
by topology rather than by spatial embedding. More generally, this highlights the fact that any
null model—embodying a specific null hypothesis—could be used for the standardization pro-
cedure to selectively tease apart features that shape communication in brain networks (Váša &
Mišić, 2022; Zamora-López & Brasselet, 2019).
The present findings should be viewed in light of multiple methodological limitations. First,
all networks were reconstructed using diffusion-weighted MRI, a method known to be subject
to false positives and false negatives (de Reus & van den Heuvel, 2013; Maier-Hein et al.,
2017; Thomas et al., 2014). Although we attempt to mitigate this limitation by splitting the
sample and repeating all analyses, future work is necessary to improve the quality of connec-
tome reconstruction. Second, networks reconstructed from diffusion-weighted MRI are
undirected, limiting the biological plausibility of these networks and our capacity to fit
communication models to them. Third, we focus on several well-studied and mathematically
fundamental communication protocols, including centralized (e.g., shortest paths) and decen-
tralized (e.g., search information) measures, but this selection is non-exhaustive and alterna-
tive communication measures could be considered in future work.
In summary, we present a simple method to resolve communication capacity in brain net-
works. The method is based on conventional procedures already commonplace in connec-
tomics, but allows researchers to focus on dyadic communication. This procedure is inherently
flexible, being able to accommodate emerging communication measures and null models. As
the field develops increasingly sophisticated and biologically realistic generative models of
inter-regional communication, this procedure will allow greater insight into features that shape
signaling patterns in brain networks.
METHODS
Data Acquisition
A total of n = 69 healthy participants (25 females, age 28.8 ± 8.9 years old) were scanned at
the Lausanne University Hospital in a 3-Tesla MRI Scanner (Trio, Siemens Medical, Germany)
Network Neuroscience
1065
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
using a 32-channel head coil (Griffa et al., 2019). The protocol included (a) a magnetization-
prepared rapid acquisition gradient echo (MPRAGE) sequence sensitive to white/gray matter
contrast (1 mm in-plane resolution, 1.2 mm slice thickness), (b) a diffusion spectrum imaging
(DSI) sequence (128 diffusion-weighted volumes and a single b0 volume, maximum b-value
8,000 s/mm2, 2.2 × 2.2 × 3.0 mm voxel size), and (c) a gradient echo-planar imaging (EPI)
sequence sensitive to blood oxygen level–dependent (BOLD) contrast (3.3 mm in-plane reso-
lution and slice thickness with a 0.3 mm gap, TR 1,920 ms, resulting in 280 images per par-
ticipant). The last sequence was used as part of an eyes-open resting-state fMRI (rs-fMRI) scan
in which the participants were not overtly engaged in a task. Informed written consent was
obtained for all participants in accordance with institutional guidelines and the protocol
was approved by the Ethics Committee of Clinical Research of the Faculty of Biology and
Medicine, University of Lausanne, Switzerland.
Network Reconstruction
Structural connectomes were reconstructed for individual participants using deterministic
streamline tractography and divided according to a gray matter parcellation of 1,000 cortical
nodes (Cammoun et al., 2012). The analyses were also repeated at a coarser 219 cortical-
region resolution. White matter and gray matter were segmented from the MPRAGE volumes
using the FreeSurfer version 5.0.0 open-source package, whereas DSI data preprocessing was
implemented with tools from the Connectome Mapper open-source software (Daducci et al.,
2012), initiating 32 streamline propagations per diffusion direction for each white matter voxel
(Wedeen et al., 2008). Structural connectivity was defined as streamline density between node
pairs, that is, the number of streamlines between two regions normalized by the mean length
of the streamlines and the mean surface area of the regions (Hagmann et al., 2008). The fMRI
data underwent regression of physiological variables, including white matter, cerebrospinal
fluid, and motion (estimated via rigid body coregistration). BOLD time series were subse-
quently subjected to a lowpass temporal Gaussian filter with 1.92 s full width half maximum,
and motion “scrubbing” (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012) was performed
after excluding the first four time points for the time series to stabilize. Functional connectivity
was then computed as the Pearson correlation coefficient between the fMRI BOLD time series
of each node pair.
The data were randomly split into Discovery (n = 34) and Validation (n = 35) subsets. We
then generated group-representative brain networks for each subset to amplify signal-to-noise
ratio using functions from the netneurotools open-source package (https://netneurotools
.readthedocs.io/en/latest/index.html). A consensus approach that preserves (a) the mean
density across participants and (b) the participant-level edge length distributions was adopted
for the structural connectomes (R. F. Betzel et al., 2019). First, the cumulative edge length
distribution across individual participants’ structural connectivity matrices is divided into
M bins, M corresponding to the average number of edges across participants. The edge
occurring most frequently across participants is then selected within each bin, breaking ties
by selecting the higher weighted edge on average. This procedure was applied separately for
intra- and interhemispheric edges to ensure that the latter are not underrepresented. The
selected edges constitute the distance-dependent group-consensus structural brain network.
Finally, the weight of each edge is computed as the mean across participants. The group-
representative functional connectivity matrix was defined as the group average following
Fisher’s r-to-z transformation. The final group-consensus matrix was back-transformed to cor-
relation values.
Network Neuroscience
1066
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
Communication Models
In this section, we define the analytic communication measures associated with the network
communication models considered in the present study and provide their implementation
details. All the communication measures, with the exception of path transitivity, were com-
puted using functions from the open-access Python version of the Brain Connectivity Toolbox
(https://github.com/aestrivex/bctpy; Rubinov & Sporns, 2010). Path transitivity was imple-
mented in Python based on a MATLAB script openly available in the Brain Connectivity
Toolbox.
Shortest paths. Let A denote a weighted adjacency matrix. To identify the sequence of unique
edges πu→v = {Aui, …, Ajv} spanning the minimum length between nodes u and v (i.e., shortest
path), we first defined a monotonic transformation from edge weights, namely streamline den-
sity in the present case, to edge lengths L, which can be more intuitively considered as the cost
of traversing this edge. We used the negative natural logarithm: Lui = −log(Aui), mapping
greater streamline density to lower cost of signal propagation. Dijkstra’s algorithm (Dijkstra,
1959) was used to identify shortest paths, and their length was computed as the sum Luv =
Lui + … + Ljv of traversed edges’ lengths.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Search information. Search information quantifies the amount of information required by a
naïve random walker to travel along a specific path in a network (Goñi et al., 2014; Rosvall
et al., 2005). More specifically, here we consider shortest paths πu→v, capturing the accessi-
bility of these optimal routes in network topology. This analytic measure is derived from the
probability that a random walker starting at u follows Ωu→v = {u, …, v}, the sequence of nodes
visited along πu→v to reach v. This probability depends on the strength of the nodes comprised
in Ωu→v and can be expressed as follows:
P πu→v
ð
Þ ¼ pui (cid:2) … (cid:2) pjv ; where pui ¼ AuiP
iAui
:
Search information can then be defined as
ð
S πu→v
ð
Þ ¼ − log2 P πu→v
ð
Þ:
Þ
(1)
(2)
Note that this definition assumes that the random walker has no memory of its previous
step, which would reduce the information needed to determine the next. Importantly, this
measure is not symmetric. That is, S(πu→v) ≠ S(πv→u). Search information is contingent on
the assignment of the path’s source and target nodes.
Path transitivity. Path transitivity is a measure of transitivity based on the shortest path between
a pair of nodes. It quantifies the density of one-step detours (triangles) available along the path
(Goñi et al., 2014). Intuitively, it can be considered to be the accessibility of the shortest path
or its robustness to a deviation of the signal traversing it. Path transitivity can be computed as
the average pairwise matching index of the nodes comprising the path.
The matching index between two nodes is a measure of the similarity of their connectivity
profiles, excluding edges incident on both nodes (Hilgetag, Burns, O’Neill, Scannell, & Young,
2000). The matching index M between nodes s and t is defined as
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
P
Mst ¼
Network Neuroscience
ð
P
i≠s;t Asi þ Ati
i≠t Asi þ
ÞΘ Asi
ð
P
ð
ÞΘ Ati
Þ
i≠sAti
;
(3)
1067
Communication capacity in the human connectome
where Θ is the Heaviside step function.
Building on this definition, the path transitivity P of the shortest path πu→v can be defined as
ð
P πu→v
Þ ¼
P
P
Mst
2
Þ
jΩu→v j jΩu→v j − 1
s2Ωu→v
ð
t2Ωu→v
:
(4)
Communicability. Communicability between two nodes is defined as the length-weighted sum
of all walks between them, with longer walks being more penalized (Estrada & Hatano, 2008).
The communicability matrix C of pairwise communicability estimates between all nodes in the
network is calculated as the matrix exponential of the adjacency matrix: C = eA. Following
Crofts and Higham (2009), in the case of a weighted structural connectivity matrix, we first
normalize the adjacency matrix as D1/2AD1/2, where D is the diagonal weighted degree matrix.
The objective of this procedure is to reduce the undue influence of nodes with large strength.
Mean first-passage time. The mean first-passage time from node u to node v is the expected
number of hops in a random walk evolved by a random walker starting at node u before arriv-
ing for the first time at node v (Noh & Rieger, 2004). Considering nodes of an undirected con-
nected network as the states of an ergodic Markov chain allowed Goñi et al. (2013) to derive
the mean first-passage time T between nodes u and v as
Tuv ¼ Zvv − Zuv
wv
; u ≠ v;
(5)
where w is the steady-state vector of the underlying Markov process and Z is the fundamental
matrix calculated as (I − P + W )−1. P is the transition probability matrix computed as D−1A,
where D is the diagonal weighted degree matrix. W is a square matrix whose columns corre-
spond to w. In the present study, following Zamani Esfahlani et al. (2022), we standardize as
z-scores the columns of the matrix of pairwise mean first-passage time among all nodes in the
network to remove nodal bias.
Structure-function bandwidth. Structure-function bandwidth quantifies how well structural con-
nectivity throughput mediates functional connectivity in a multiplex network composed of a
structural connectivity layer and a functional connectivity layer. Bandwidth between two
nodes in the functional connectivity layer is defined according to the minimum edge weight
of a path connecting these nodes in the structural connectivity layer. The maximum bandwidth
is then selected across all paths of a given length. Here, we consider triangles composed of
two-hop structural paths closed by a functional edge. We weigh structure-function bandwidths
by the functional edge weights to provide a generalized communication measure taking into
account all node pairs in the functional connectivity layer. The functional connectivity-
weighted bandwidth B between nodes u and v is computed as follows:
Buv ¼ Fuv 1 − Suv
ð
Þ max
i
ð
min Aui; Aiv
ð
Þ
Þ;
(6)
where F is the weighted functional connectivity matrix, and S is the binary structural connec-
tivity matrix. The (1 − Suv) term excludes all cases where a direct structural edge also connects
nodes u and v. Every possible intermediary node i in the structural connectivity layer is
considered to complete the triangle.
Null Models
Standardization. Network features are interrelated, with many complex network properties
depending on basic features (Váša & Mišić, 2022). To mitigate the effect of differences in
Network Neuroscience
1068
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
simple features on the topological relationships under study, we provide a frame of reference
to communication measures. First, we built a population of 100 null structural connectivity
matrices by randomly rewiring pairs of edges of the empirical group-consensus networks,
systematically disrupting their topology while maintaining basic network features. Next,
communication measures were computed for every node pair of the empirical structural brain
networks and all 100 surrogate graphs. Finally, the empirical communication matrices were
demeaned and standardized to unit variance elementwise using the null population. This pro-
cedure yielded, in units of standard deviation, an approximate communication measure in
relation to what would be expected by chance in a similar network.
Two null models were considered as part of this procedure, resulting in a hierarchy of pre-
served network features. Both surrogate models guarantee the connectedness of the produced
rewired network, that is, no node is disconnected from the rest of the network.
The first method randomly swaps pairs of edges (approximately 10 swaps per edge) while
maintaining network size (i.e., number of nodes), density (i.e., proportion of possible edges
expressed), and degree sequence (i.e., number of edges incident to each node) (Maslov &
Sneppen, 2002). We applied an implementation of this technique openly available in the
Python version of the Brain Connectivity Toolbox (https://github.com/aestrivex/bctpy; Rubinov
& Sporns, 2010). To extend this procedure to weighted structural connectivity matrices, we
then used simulated annealing to further preserve the empirical network’s strength sequence
(sum of edge weights incident to each node) (Mišić et al., 2015). Simulated annealing is a
stochastic search method used to approximate the global optimum of a given function
(Kirkpatrick et al., 1983). This is achieved through the Metropolis procedure (Metropolis,
Rosenbluth, Rosenbluth, Teller, & Teller, 1953), controlled by the temperature parameter T.
The simulated annealing process is initiated at a high temperature that allows the exploration
of costly system configurations, preventing the algorithm from getting stuck in local minima.
Throughout the process, the system is slowly cooled down while descending along the opti-
mization landscape, with increasingly limited uphill rearrangements and smaller, fine-tuned
changes in the system cost. Here, we minimize the cost function E defined as the sum of
squares between the strength sequence vectors of the empirical and the randomized networks:
E ¼
i are the strengths of node i in the empirical and the null net-
works, respectively. To optimize this function, weights were randomly permuted among edges.
Rearrangements were only accepted if they lowered the cost of the system or followed the
probabilistic Metropolis acceptance criterion: r < exp(−(E 0 − E )/T ), where r ∼ U(0, 1). We used
an annealing schedule composed of 100 stages of 10,000 permutations with an initial temper-
ature of 1,000, halved after each stage.
2, where si and s0
(cid:2)
i s0
− si
P
(cid:3)
i
A limitation of this rewiring procedure is that, on average, randomly flipping pairs of edges
will result in unrealistically large distances between nodes (Váša & Mišić, 2022). To address
this issue, we use a Python implementation of an approach proposed in R. F. Betzel and Bassett
(2018), openly available as a function in the netneurotools package (https://netneurotools
.readthedocs.io/en/latest/index.html). This method applies the same iterative rewiring proce-
dure as the first, but with additional constraints. Edges are binned according to the Euclidean
distance between the centroids of their associated parcel pair. The number of bins was deter-
mined heuristically as the square root of the number of edges in the empirical group-consensus
network. Swapping is then performed within each bin to approximately preserve the edge
length distribution, in addition to exactly reproducing the network’s size, density, and degree
sequence like the first method. The maximum total number of edge swaps to perform was set
to the network size times 20. In maintaining the geometry of the empirical network, this
Network Neuroscience
1069
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
rewiring model provides a more representative surrogate, resulting in a more conservative null
model.
Collectively, the two null models used for the standardization of the structural connectivity
matrices express a hierarchy of constraints. When considered in parallel, they allow us to distin-
guish the contribution of the structural brain network’s topology from effects passively endowed
by its spatial embedding when studying the connectome’s architecture (Roberts et al., 2016).
Significance testing. To assess the significance of statistics based on node-level communication
measures, we relied on spatial permutation null models (Markello & Misic, 2021). We gener-
ated null distributions of statistical estimates derived from permuted brain maps, while preserv-
ing the spatial autocorrelation of the original data to respect the assumption of exchangeability.
First, we parcellated the FreeSurfer fsaverage surface according to the Cammoun atlas
(Cammoun et al., 2012) using tools from the Connectome Mapper (Daducci et al., 2012). A
spherical projection of the fsaverage surface was then used to assign spherical coordinates to
each parcel; centroids were defined as the vertices closest (in terms of Euclidean distance) to
the center-of-mass (i.e., arithmetic mean across all the vertices’ coordinates) of each parcel.
Random rotations were then applied to one hemisphere of this spherical representation of the
atlas to disrupt its topography. Rotations were then mirrored to the other hemisphere. Finally,
each parcel in the original brain map was reassigned a rotated parcel using the Hungarian
algorithm (Kuhn, 1955). In contrast to other reassignment heuristics, this method attempts to
reassign each rotated parcel to a unique original parcel, that is, to retain the exact original data
distribution. This is particularly important when testing network-based statistics as in the pres-
ent study (Markello & Misic, 2021). Overall, this procedure was repeated 1,000 times using an
openly accessible function from the netneurotools package (https://netneurotools.readthedocs
.io/en/latest/index.html) to generate null statistical distributions.
For the correlational analyses, brain maps of communication measures were subjected to
this spatial autocorrelation-preserving permutation procedure. For each 1,000 rotated nulls, a
correlation coefficient was computed between the surrogate brain map and the statistical map
under study (i.e., maps of topological features or Neurosynth functional activation maps),
yielding a null distribution of 1,000 coefficients. The original rho was then compared against
this null distribution to assess its significance by computing a two-sided p value (pspin) as the
proportion of more extreme null coefficients.
For the partition of the communication measures within and between Yeo intrinsic networks
(Yeo et al., 2011), network labels were first permuted according to the spatially constrained
Hungarian method (Markello & Misic, 2021). Dyadic communication measures associated
with a node pair belonging to the same intrinsic network, as identified by the permuted labels,
were considered within-network, whereas measures associated with a node pair belonging to
different intrinsic networks were considered between-networks. The difference between the
mean values of the distributions associated with these two categories was then computed
for each 1,000 permutation, once again generating a null distribution of this statistical estimate
against which the empirical difference was compared to produce a two-sided p value.
A similar method was employed to assess the significance of the differences between mean
internal standardized path lengths for pairs of Yeo intrinsic networks.
Yeo Intrinsic Networks
When stratifying brain regions according to their membership in canonical macroscale func-
tional systems, we used the seven intrinsic networks derived by Yeo et al. (2011) via clustering
Network Neuroscience
1070
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
of resting-state fMRI data from 1,000 subjects. A parcellation of the seven resting-state net-
works in the FreeSurfer fsaverage5 surface space was downloaded from https://github.com
/ThomasYeoLab/CBIG/. Nodes of the Cammoun parcellations were then labeled using a
winner-take-all approach in which each parcel was attributed the most common intrinsic net-
work assignment across its vertices.
Neurosynth
Functional activation maps synthesizing more than 15,000 published fMRI studies into prob-
abilistic measures of the association between individual voxels and cognitive terms of interest
were obtained from the Neurosynth platform (https://github.com/neurosynth/neurosynth;
Yarkoni et al., 2011). This association measure quantifies the probability that a particular term
is reported in a study if an activation was observed in a given region. The probabilistic maps
were extracted from Neurosynth using 123 cognitive terms overlapping the set of keywords
from the Neurosynth database and the Cognitive atlas (Poldrack et al., 2011), a public knowl-
edge base of cognitive science. The list of cognitive and behavioral terms ranges from generic
concepts (e.g., “attention”, “emotion”) to specific cognitive processes (“visual attention”, “epi-
sodic memory”), behaviors (“eating”, “sleeping”), and emotions (“fear”, “anxiety”).
For each of the 123 terms, volumetric reverse inference maps were generated from Neurosynth
and projected to the FreeSurfer fsaverage5 mid-gray surface with nearest neighbor interpolation
using FreeSurfer’s mri_vol2surf function (v6.0.0; https://surfer.nmr.mgh.harvard.edu/). The resulting
surface maps were then parcellated according the both the 219 and 1,000 cortical node resolutions
of the Cammoun atlas (Cammoun et al., 2012) to obtain node-wise mean probabilistic measures.
Topological Features
In this section, we define the topological features examined in this study and provide their
implementation details. All the graph measures, with the exception of closeness centrality,
were computed using functions from the open-access Python version of the Brain Connectivity
Toolbox (https://github.com/aestrivex/bctpy; Rubinov & Sporns, 2010).
▪ Degree. Binary degree corresponds to the number of edges incident on a node, whereas
weighted degree (strength) corresponds to the sum of edge weights incident on a node.
▪ Closeness centrality. The closeness centrality of a node is the inverse of the mean short-
est path length between this node and all the other nodes in the network (Rubinov &
Sporns, 2010). The closeness centrality C of a node u is defined as
Cu ¼ n − 1P
v Luv
;
(7)
where n is the number of nodes in the network and Luv corresponds to the shortest path
length between nodes u and v.
Note that this measure can be problematic when standardizing shortest path lengths,
because of negative contributions to the mean. Nevertheless, we maintain this conven-
tional definition, because all node-wise mean standardized shortest path lengths
obtained were positive.
Betweenness centrality. The betweenness centrality of a node is the fraction of shortest
paths between all pairs of nodes in the network that contain this node (Freeman, 1977).
The betweenness centrality B of a node i is defined as
▪
Bi ¼
X
uv:u≠i≠v
λuv ið Þ
λuv
;
(8)
1071
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
where λuv is the total number of shortest paths from node u to node v and λuv(i) is the
number of these paths that include node i. Brandes’ algorithm (Brandes, 2001) was used
to compute the betweenness centrality of each individual node of the structural connec-
tivity matrices under study.
Participation coefficient. The participation coefficient is a measure of the diversity of a
node’s connection profile among the communities of the network (Guimera & Nunes
Amaral, 2005). The participation coefficient P of a node i is defined as
▪
Pi ¼ 1 −
(cid:4) (cid:5)
2
si;c
si
;
XC
c¼1
(9)
where si,c corresponds to the sum of the weights of all edges incident on node i and
nodes in community c, si is the strength of node i, and C represents the number of com-
munities. A participation coefficient of 0 indicates that the totality of a node’s edges are
connected to other nodes within its community. The closer the participation coefficient
is to 1, the more evenly distributed are its edges among the communities. Note that this
measure presumes an established community structure. Here, we used the functional
networks derived by Yeo et al. (2011) as communities to compute participation coeffi-
cients for each individual node of the structural connectomes under study.
Principal Component Analysis
To take into account a range of models of communication in the brain in addition to shortest
path routing, we generated an aggregate measure of the capacity for communication using
principal component analysis. First, the standardized communication matrices derived follow-
ing the procedures detailed above were z-scored across all elements. For each communication
matrix, we then extracted all pairwise measures of communication distance, with the excep-
tion of undefined diagonal entries, and assembled them into the columns of a matrix X of size
d × c, where d is the number of dyads and c is the number of communication models. PCA was
then applied to this matrix using the PCA function from the scikit-learn package for machine
learning in Python (Pedregosa et al., 2011). First, X was mean centered, that is, demeaned
column-wise to obtain Xc. Then, a full singular value decomposition (SVD) was applied to
Xc such that
Xc ¼ USV 0;
(10)
where U and V are orthonormal matrices of sizes d × c and c × c, consisting of the left and right
singular vectors, respectively, and S is a diagonal matrix of singular values of size c × c (Eckart
& Young, 1936).
In this analysis, we kept only the first component, corresponding to U1, the first column of
U, which accounted for 62.79% of the total variance in dyadic communication capacity
across models. The matrix multiplication U1S yielded the principal component scores used
in this study.
The same analysis was then reproduced at the node level with standardized node-wise
mean vectors of communication distance directly constituting the columns of X. Note that
before computing the row averages of the communication matrices, we enforced symmetry
of the search information and mean first-passage time matrices by replacing them with (C +
CT)/2, where C is the communication matrix and CT is its transpose. In doing so, we consider
both the incoming and the outgoing nodal communication capacity. The same procedure was
Network Neuroscience
1072
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
also applied to the matrix of principle component scores prior to the partition of its elements
within and between Yeo intrinsic networks.
ACKNOWLEDGMENTS
We thank Mark Nelson, Justine Hansen, Zhen-Qi Liu, Andrea Luppi, Golia Shafiei, and Estefany
Suarez for helpful comments. FM acknowledges support from the Fonds de Recherche du
Québec - Nature et Technologies (FRQNT). BM acknowledges support from the Natural Sci-
ences and Engineering Research Council of Canada (NSERC), the Canadian Institutes of Health
Research (CIHR), the Brain Canada Foundation Future Leaders Fund, the Canada Research
Chairs Program, the Michael J. Fox Foundation, and the Healthy Brains for Healthy Lives
initiative.
DATA AVAILABILITY
Code and data used to perform the analyses can be found at https://github.com/fmilisav
/milisav_dyadic_communication (Milisav, 2023).
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00318.
AUTHOR CONTRIBUTIONS
Filip Milisav: Formal analysis; Methodology; Visualization; Writing – original draft. Vincent
Bazinet: Methodology; Writing – review & editing. Yasser Iturria-Medina: Methodology;
Writing – review & editing. Bratislav Misic: Conceptualization; Methodology; Supervision;
Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
Filip Milisav, Fonds de recherche du Québec - Nature et technologies (FRQNT). Bratislav
Misic, Natural Sciences and Engineering Research Council of Canada (NSERC). Bratislav
Misic, Canadian Institutes of Health Research (CIHR). Bratislav Misic, Brain Canada Founda-
tion Future Leaders Fund. Bratislav Misic, Canada Research Chairs Program. Bratislav Misic,
Michael J. Fox Foundation. Bratislav Misic, Healthy Brains, Healthy Lives Initiative.
REFERENCES
Achard, S., & Bullmore, E. (2007). Efficiency and cost of econom-
ical brain functional networks. PLOS Computational Biology,
3(2), e17. https://doi.org/10.1371/journal.pcbi.0030017,
PubMed: 17274684
Albert, R., & Barabási, A.-L. (2002). Statistical mechanics of com-
plex networks. Reviews of Modern Physics, 74(1), 47–97. https://
doi.org/10.1103/RevModPhys.74.47
Alexander-Bloch, A. F., Shou, H., Liu, S., Satterthwaite, T. D.,
Glahn, D. C., Shinohara, R. T., … Raznahan, A. (2018). On
testing for spatial correspondence between maps of human
brain structure and function. NeuroImage, 178, 540–551.
https://doi.org/10.1016/j.neuroimage.2018.05.070, PubMed:
29860082
Andreotti, J., Jann, K., Melie-Garcia, L., Giezendanner, S., Abela, E.,
Wiest, R., … Federspiel, A. (2014). Validation of network commu-
nicability metrics for the analysis of brain structural networks.
PLOS ONE, 9(12), e115503. https://doi.org/10.1371/journal
.pone.0115503, PubMed: 25549088
Avena-Koenigsberger, A., Goñi, J., Betzel, R. F., van den Heuvel,
M. P., Griffa, A., Hagmann, P., … Sporns, O. (2014). Using pareto
optimality to explore the topology and dynamics of the human
connectome. Philosophical Transactions of the Royal Society B:
Biological Sciences, 369(1653), 20130530. https://doi.org/10
.1098/rstb.2013.0530, PubMed: 25180308
Avena-Koenigsberger, A., Mišić, B., Hawkins, R. X. D., Griffa, A.,
Hagmann, P., Goñi, J., & Sporns, O. (2017). Path ensembles
Network Neuroscience
1073
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
and a tradeoff between communication efficiency and resilience
in the human connectome. Brain Structure and Function, 222(1),
603–618. https://doi.org/10.1007/s00429-016-1238-5, PubMed:
27334341
Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018). Commu-
nication dynamics in complex brain networks. Nature Reviews
Neuroscience, 19(1), 17–33. https://doi.org/10.1038/nrn.2017
.149, PubMed: 29238085
Bargmann, C. I., & Marder, E. (2013). From the connectome to
brain function. Nature Methods, 10(6), 483–490. https://doi.org
/10.1038/nmeth.2451, PubMed: 23866325
Bassett, D. S., & Bullmore, E. T. (2006). Small-world brain networks.
Neuroscientist, 12(6), 512–523. https://doi.org/10.1177
/1073858406293182, PubMed: 17079517
Bassett, D. S., & Bullmore, E. T. (2017). Small-world brain networks
revisited. Neuroscientist, 23(5), 499–516. https://doi.org/10.1177
/1073858416667720, PubMed: 27655008
Bassett, D. S., Bullmore, E. T., Verchinski, B. A., Mattay, V. S.,
Weinberger, D. R., & Meyer-Lindenberg, A. (2008). Hierarchical
organization of human cortical networks in health and schizo-
phrenia. Journal of Neuroscience, 28(37), 9239–9248. https://doi
.org/10.1523/JNEUROSCI.1929-08.2008, PubMed: 18784304
Battiston, F., Amico, E., Barrat, A., Bianconi, G., Ferraz de Arruda,
G., Franceschiello, B., … Petri, G. (2021). The physics of
higher-order interactions in complex systems. Nature Physics,
17(10), 1093–1098. https://doi.org/10.1038/s41567-021-01371-4
Baum, G. L., Ciric, R., Roalf, D. R., Betzel, R. F., Moore, T. M.,
Shinohara, R. T., … Satterthwaite, T. D. (2017). Modular segre-
gation of structural brain networks supports the development
of executive function in youth. Current Biology, 27(11),
1561–1572. https://doi.org/10.1016/j.cub.2017.04.051,
PubMed: 28552358
Baum, G. L., Cui, Z., Roalf, D. R., Ciric, R., Betzel, R. F., Larsen, B., …
Satterthwaite, T. D. (2020). Development of structure–function
coupling in human brain networks during youth. Proceedings of
the National Academy of Sciences, 117(1), 771–778. https://doi
.org/10.1073/pnas.1912034117, PubMed: 31874926
Bellec, P., Rosa-Neto, P., Lyttelton, O. C., Benali, H., & Evans, A. C.
(2010). Multi-level bootstrap analysis of stable clusters in
resting-state fMRI. NeuroImage, 51(3), 1126–1139. https://doi
.org/10.1016/j.neuroimage.2010.02.082, PubMed: 20226257
Bertolero, M. A., Yeo, B. T. T., & D’Esposito, M. (2015). The modular
and integrative functional architecture of the human brain.
Proceedings of the National Academy of Sciences, 112(49),
E6798–E6807. https://doi.org/10.1073/pnas.1510619112,
PubMed: 26598686
Betzel, R. F., & Bassett, D. S. (2018). Specificity and robustness of
long-distance connections in weighted, interareal connectomes.
Proceedings of the National Academy of Sciences, 115(21),
E4880–E4889. https://doi.org/10.1073/pnas.1720186115,
PubMed: 29739890
Betzel, R. F., Faskowitz, J., Mišić, B., Sporns, O., & Seguin, C.
(2022). Multi-policy models of interregional communication in
the human connectome. bioRxiv. https://doi.org/10.1101/2022
.05.08.490752
Betzel, R. F., Griffa, A., Hagmann, P., & Mišić, B. (2019). Distance-
dependent consensus thresholds for generating group-represen-
tative structural brain networks. Network Neuroscience, 3(2),
475–496. https://doi.org/10.1162/netn_a_00075, PubMed:
30984903
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., & Hwang, D.-U.
(2006). Complex networks: Structure and dynamics. Physics
Reports, 424(4–5), 175–308. https://doi.org/10.1016/j.physrep
.2005.10.009
Brandes, U. (2001). A faster algorithm for betweenness centrality.
Journal of Mathematical Sociology, 25(2), 163–177. https://doi
.org/10.1080/0022250X.2001.9990249
Bressler, S. L., & Menon, V. (2010). Large-scale brain networks in
cognition: emerging methods and principles. Trends in Cognitive
Sciences, 14(6), 277–290. https://doi.org/10.1016/j.tics.2010.04
.004, PubMed: 20493761
Burt, J. B., Demirtaş, M., Eckner, W. J., Navejar, N. M., Ji, J. L.,
Martin, W. J., … Murray, J. D. (2018). Hierarchy of transcriptomic
specialization across human cortex captured by structural neuro-
imaging topography. Nature Neuroscience, 21(9), 1251–1259.
https://doi.org/10.1038/s41593-018-0195-0, PubMed:
30082915
Cammoun, L., Gigandet, X., Meskaldji, D., Thiran, J. P., Sporns, O.,
Do, K. Q., … Hagmann, P. (2012). Mapping the human connec-
tome at multiple scales with diffusion spectrum MRI. Journal of
Neuroscience Methods, 203(2), 386–397. https://doi.org/10.1016
/j.jneumeth.2011.09.031, PubMed: 22001222
Chari, A., Seunarine, K. K., He, X., Tisdall, M. M., Clark, C. A.,
Bassett, D. S., … Rosch, R. E. (2022). Drug-resistant focal epilepsy
in children is associated with increased modal controllability of
the whole brain and epileptogenic regions. Communications
Biology, 5(1), 394. https://doi.org/10.1038/s42003-022-03342
-8, PubMed: 35484213
Cimini, G., Squartini, T., Saracco, F., Garlaschelli, D., Gabrielli, A.,
& Caldarelli, G. (2019). The statistical physics of real-world net-
works. Nature Reviews Physics, 1(1) 58–71. https://doi.org/10
.1038/s42254-018-0002-6
Cole, M. W., Reynolds, J. R., Power, J. D., Repovs, G., Anticevic,
A., & Braver, T. S. (2013). Multi-task connectivity reveals flexible
hubs for adaptive task control. Nature Neuroscience, 16(9),
1348–1355. https://doi.org/10.1038/nn.3470, PubMed:
23892552
Cole, M. W., Yarkoni, T., Repovš, G., Anticevic, A., & Braver, T. S.
(2012). Global connectivity of prefrontal cortex predicts cogni-
tive control and intelligence. Journal of Neuroscience, 32(26),
8988–8999. https://doi.org/10.1523/JNEUROSCI.0536-12.2012,
PubMed: 22745498
Crofts, J. J., Forrester, M., & O’Dea, R. D. (2016). Structure-function
clustering in multiplex brain networks. Europhysics Letters,
116(1), 18003. https://doi.org/10.1209/0295-5075/116/18003
Crofts, J. J., & Higham, D. J. (2009). A weighted communicability
measure applied to complex brain networks. Journal of the Royal
Society Interface, 6(33), 411–414. https://doi.org/10.1098/rsif
.2008.0484, PubMed: 19141429
Crofts, J. J., Higham, D. J., Bosnell, R., Jbabdi, S., Matthews, P. M.,
Behrens, T., & Johansen-Berg, H. (2011). Network analysis
detects changes in the contralesional hemisphere following
stroke. NeuroImage, 54(1), 161–169. https://doi.org/10.1016/j
.neuroimage.2010.08.032, PubMed: 20728543
Daducci, A., Gerhard, S., Griffa, A., Lemkaddem, A., Cammoun, L.,
Gigandet, X., … Thiran, J.-P. (2012). The connectome mapper: An
Network Neuroscience
1074
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
open-source processing pipeline to map connectomes with MRI.
PLOS ONE, 7(12), e48121. https://doi.org/10.1371/journal.pone
.0048121, PubMed: 23272041
Damoiseaux, J. S., Rombouts, S., Barkhof, F., Scheltens, P., Stam,
C. J., Smith, S. M., & Beckmann, C. F. (2006). Consistent
resting-state networks across healthy subjects. Proceedings of
the National Academy of Sciences, 103(37), 13848–13853.
https://doi.org/10.1073/pnas.0601417103, PubMed: 16945915
de Reus, M. A., & van den Heuvel, M. P. (2013). Estimating false
positives and negatives in brain networks. NeuroImage, 70,
402–409. https://doi.org/10.1016/j.neuroimage.2012.12.066,
PubMed: 23296185
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson,
B. C., Blacker, D., … Killiany, R. J. (2006). An automated labeling
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. NeuroImage, 31(3), 968–980.
https://doi.org/10.1016/j.neuroimage.2006.01.021, PubMed:
16530430
Dijkstra, E. W. (1959). A note on two problems in connexion with
graphs. Numerische Mathematik, 1(1), 269–271. https://doi.org
/10.1007/BF01386390
Dosenbach, N. U. F., Fair, D. A., Miezin, F. M., Cohen, A. L., Wenger,
K. K., Dosenbach, R. A. T., … Petersen, S. E. (2007). Distinct brain
networks for adaptive and stable task control in humans. Proceed-
ings of the National Academy of Sciences, 104(26), 11073–11078.
https://doi.org/10.1073/pnas.0704320104, PubMed: 17576922
Eckart, C., & Young, G. (1936). The approximation of one matrix by
another of lower rank. Psychometrika, 1(3), 211–218. https://doi
.org/10.1007/BF02288367
Estrada, E., & Hatano, N. (2008). Communicability in complex net-
works. Physical Review E, 77(3), 036111. https://doi.org/10.1103
/PhysRevE.77.036111, PubMed: 18517465
Fan, Y., Shi, F., Smith, J. K., Lin, W., Gilmore, J. H., & Shen, D.
(2011). Brain anatomical networks in early human brain devel-
opment. NeuroImage, 54(3), 1862–1871. https://doi.org/10
.1016/j.neuroimage.2010.07.025, PubMed: 20650319
Fedorenko, E., Duncan, J., & Kanwisher, N. (2013). Broad domain
generality in focal regions of frontal and parietal cortex. Proceed-
ings of the National Academy of Sciences, 110(41), 16616–16621.
https://doi.org/10.1073/pnas.1315235110, PubMed: 24062451
Freeman, L. C. (1977). A set of measures of centrality based on
betweenness. Sociometry, 40(1), 35–41. https://doi.org/10.2307
/3033543
Fulcher, B. D., Murray, J. D., Zerbi, V., & Wang, X.-J. (2019).
Multimodal gradients across mouse cortex. Proceedings of the
National Academy of Sciences, 116(10), 4689–4695. https://doi
.org/10.1073/pnas.1814144116, PubMed: 30782826
Goñi, J., Avena-Koenigsberger, A., Velez de Mendizabal, N., van
den Heuvel, M. P., Betzel, R. F., & Sporns, O. (2013). Exploring
the morphospace of communication efficiency in complex net-
works. PLOS ONE, 8(3), e58070. https://doi.org/10.1371
/journal.pone.0058070, PubMed: 23505455
Goñi, J., van den Heuvel, M. P., Avena-Koenigsberger, A., Velez de
Mendizabal, N., Betzel, R. F., Griffa, A., … Sporns, O. (2014).
Resting-brain functional connectivity predicted by analytic mea-
sures of network communication. Proceedings of the National
Academy of Sciences, 111(2), 833–838. https://doi.org/10.1073
/pnas.1315529111, PubMed: 24379387
Goulas, A., Betzel, R. F., & Hilgetag, C. C. (2019). Spatiotemporal
ontogeny of brain wiring. Science Advances, 5(6), eaav9694.
https://doi.org/10.1126/sciadv.aav9694, PubMed: 31206020
Graham, D., Avena-Koenigsberger, A., & Mišić, B. (2020). Network
communication in the brain. Network Neuroscience, 4(4), 976–979.
https://doi.org/10.1162/netn_e_00167, PubMed: 33195944
Graham, D., & Rockmore, D. (2011). The packet switching brain.
Journal of Cognitive Neuroscience, 23(2), 267–276. https://doi
.org/10.1162/jocn.2010.21477, PubMed: 20350173
Grayson, D. S., Bliss-Moreau, E., Machado, C. J., Bennett, J., Shen,
K., Grant, K. A., … Amaral, D. G. (2016). The rhesus monkey
connectome predicts disrupted functional networks resulting
from pharmacogenetic inactivation of the amygdala. Neuron,
91(2), 453–466. https://doi.org/10.1016/j.neuron.2016.06.005,
PubMed: 27477019
Greicius, M. D., Supekar, K., Menon, V., & Dougherty, R. F. (2009).
Resting-state functional connectivity reflects structural connectiv-
ity in the default mode network. Cerebral Cortex, 19(1), 72–78.
https://doi.org/10.1093/cercor/bhn059, PubMed: 18403396
Griffa, A., Alemán-Gómez, Y., & Hagmann, P. (2019). Structural and
functional connectome from 70 young healthy adults [Data set].
Zenodo. https://doi.org/10.5281/zenodo.2872624
Griffa, A., Mach, M., Dedelley, J., Gutierrez-Barragan, D., Gozzi,
A., Allali, G., … Amico, E. (2022). The evolution of information
transmission in mammalian brain networks. bioRxiv. https://doi
.org/10.1101/2022.05.09.491115
Guimera, R., & Nunes Amaral, L. A. (2005). Functional cartography
of complex metabolic networks. Nature, 433(7028), 895–900.
https://doi.org/10.1038/nature03288, PubMed: 15729348
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6(7), e159. https://doi
.org/10.1371/journal.pbio.0060159, PubMed: 18597554
Hagmann, P., Sporns, O., Madan, N., Cammoun, L., Pienaar, R.,
Wedeen, V. J., … Grant, P. (2010). White matter maturation
reshapes structural connectivity in the late developing human
brain. Proceedings of the National Academy of Sciences,
1 07 ( 4 4 ) , 1 9 06 7 –1 9 07 2 . h t t p s : / / d o i . o rg/ 1 0 . 1 0 7 3 / p n a s
.1009073107, PubMed: 20956328
Hansen, J. Y., Markello, R. D., Vogel, J. W., Seidlitz, J., Bzdok, D.,
& Misic, B. (2021). Mapping gene transcription and neurocog-
nition across human neocortex. Nature Human Behaviour, 5(9),
1240–1250. https://doi.org/10.1038/s41562-021-01082-z,
PubMed: 33767429
Hansen, J. Y., Shafiei, G., Markello, R. D., Smart, K., Cox, S. M. L.,
Nørgaard, M., … Misic, B. (2022). Mapping neurotransmitter sys-
tems to the structural and functional organization of the human
neocortex. Nature Neuroscience, 25(11), 1569–1581. https://doi
.org/10.1038/s41593-022-01186-3, PubMed: 36303070
Hilgetag, C.-C., Burns, G. A., O’Neill, M. A., Scannell, J. W., &
Young, M. P. (2000). Anatomical connectivity defines the organi-
zation of clusters of cortical areas in the macaque and the cat.
Philosophical Transactions of the Royal Society of London, Series
B: Biological Sciences, 355(1393), 91–110. https://doi.org/10
.1098/rstb.2000.0551, PubMed: 10703046
Hilgetag, C. C., & Kaiser, M. (2004). Clustered organization of cor-
tical connectivity. Neuroinformatics, 2(3), 353–360. https://doi
.org/10.1385/NI:2:3:353, PubMed: 15365196
Network Neuroscience
1075
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J.-P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Proceedings
of the National Academy of Sciences, 106(6), 2035–2040. https://
doi.org/10.1073/pnas.0811168106, PubMed: 19188601
Humphries, M. D., Gurney, K., & Prescott, T. J. (2006). The brain-
stem reticular formation is a small-world, not scale-free, network.
Proceedings of the Royal Society B: Biological Sciences,
273(1585): 503–511. https://doi.org/10.1098/rspb.2005.3354,
PubMed: 16615219
Huntenburg, J. M., Bazin, P.-L., & Margulies, D. S. (2018). Large-
scale gradients in human cortical organization. Trends in Cogni-
tive Sciences, 22(1), 21–31. https://doi.org/10.1016/j.tics.2017
.11.002, PubMed: 29203085
Imms, P., Clemente, A., Deutscher, E., Radwan, A. M., Akhlaghi,
H., Beech, P., … Caeyenberghs, K. (2023). Exploring personalised
structural connectomics for moderate to severe traumatic brain
injury. Network Neuroscience, 7(1), 160–183. https://doi.org/10
.1162/netn_a_00277, PubMed: 37334004
Imms, P., Domínguez Duque, J. F., Burmester, A., Seguin, C.,
Clemente, A., Dhollander, T., … Caeyenberghs, K. (2021).
Navigating the link between processing speed and network com-
munication in the human brain. Brain Structure and Function,
226(4), 1281–1302. https://doi.org/10.1007/s00429-021-02241-8,
PubMed: 33704578
Iturria-Medina, Y., Sotero, R. C., Canales-Rodríguez, E. J., Alemán-
Gómez, Y., & Melie-García, L. (2008). Studying the human brain
anatomical network via diffusion-weighted MRI and graph the-
ory. NeuroImage, 40(3), 1064–1076. https://doi.org/10.1016/j
.neuroimage.2007.10.060, PubMed: 18272400
Kahn, A. E., Mattar, M. G., Vettel, J. M., Wymbs, N. F., Grafton,
S. T., & Bassett, D. S. (2017). Structural pathways supporting swift
acquisition of new visuomotor skills. Cerebral Cortex, 27(1),
173–184. https://doi.org/10.1093/cercor/ bhw335, PubMed:
27920096
Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component place-
ment, but short processing paths, due to long-distance projec-
tions in neural systems. PLOS Computational Biology, 2(7), e95.
https://doi.org/10.1371/journal.pcbi.0020095, PubMed:
16848638
Khachaturyan, A., Semenovskaya, S., & Vainstein, B. (1979). Statistical-
thermodynamic approach to determination of structure amplitude
phases. Soviet Physics, Crystallography, 24(5), 519–524.
Khundrakpam, B. S., Lewis, J. D., Zhao, L., Chouinard-Decorte, F.,
& Evans, A. C. (2016). Brain connectivity in normally developing
children and adolescents. NeuroImage, 134, 192–203. https://doi
.org/10.1016/j.neuroimage.2016.03.062, PubMed: 27054487
Khundrakpam, B. S., Reid, A., Brauer, J., Carbonell, F., Lewis, J.,
Ameis, S., … Brain Development Cooperative Group. (2013).
Developmental changes in organization of structural brain net-
works. Cerebral Cortex, 23(9), 2072–2085. https://doi.org/10
.1093/cercor/bhs187, PubMed: 22784607
Kirkpatrick, S., Gelatt, C. D., Jr., & Vecchi, M. P. (1983). Optimization
by simulated annealing. Science, 220(4598), 671–680. https://doi
.org/10.1126/science.220.4598.671, PubMed: 17813860
Kuceyeski, A. F., Jamison, K. W., Owen, J. P., Raj, A., & Mukherjee,
P. (2019). Longitudinal increases in structural connectome segre-
gation and functional connectome integration are associated
with better recovery after mild TBI. Human Brain Mapping,
40(15), 4441–4456. https://doi.org/10.1002/ hbm.24713,
PubMed: 31294921
Kuhn, H. W. (1955). The Hungarian method for the assignment
problem. Naval Research Logistics Quarterly, 2(1–2), 83–97.
https://doi.org/10.1002/nav.3800020109
Laird, A. R., Fox, P. M., Eickhoff, S. B., Turner, J. A., Ray, K. L.,
McKay, D. R., … Fox, P. T. (2011). Behavioral interpretations of
intrinsic connectivity networks. Journal of Cognitive Neurosci-
ence, 23(12), 4022–4037. https://doi.org/10.1162/jocn_a
_00077, PubMed: 21671731
Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world
networks. Physical Review Letters, 87(19), 198701. https://doi
.org/10.1103/PhysRevLett.87.198701, PubMed: 11690461
Lella, E., Amoroso, N., Diacono, D., Lombardi, A., Maggipinto, T.,
Monaco, A., … Tangaro, S. (2019). Communicability characteri-
zation of structural DWI subcortical networks in Alzheimer’s dis-
ease. Entropy, 21(5), 475. https://doi.org/10.3390/e21050475,
PubMed: 33267189
Lella, E., Amoroso, N., Lombardi, A., Maggipinto, T., Tangaro, S.,
Bellotti, R., & Alzheimer’s Disease Neuroimaging Initiative.
(2019). Communicability disruption in Alzheimer’s disease con-
nectivity networks. Journal of Complex Networks, 7(1), 83–100.
https://doi.org/10.1093/comnet/cny009
Li, Y., Liu, Y., Li, J., Qin, W., Li, K., Yu, C., & Jiang, T. (2009). Brain
anatomical network and intelligence. PLOS Computational Biol-
ogy, 5(5), e1000395. https://doi.org/10.1371/journal.pcbi
.1000395, PubMed: 19492086
Liu, Z.-Q., Vázquez-Rodríguez, B., Spreng, R. N., Bernhardt, B. C.,
Betzel, R. F., & Misic, B. (2022). Time-resolved structure-function
coupling in brain networks. Communications Biology, 5(1), 532.
https://doi.org/10.1038/s42003-022-03466-x, PubMed:
35654886
Maier-Hein, K. H., Neher, P. F., Houde, J.-C., Côté, M.-A., Garyfallidis,
E., Zhong, J., … Descoteaux, M. (2017). The challenge of mapping
the human connectome based on diffusion tractography. Nature
Communications, 8(1), 1349. https://doi.org/10.1038/s41467-017
-01285-x, PubMed: 29116093
Marder, E., Gutierrez, G. J., & Nusbaum, M. P. (2017). Complicat-
ing connectomes: Electrical coupling creates parallel pathways
and degenerate circuit mechanisms. Developmental Neurobiol-
ogy, 77(5), 597–609. https://doi.org/10.1002/dneu.22410,
PubMed: 27314561
Markello, R. D., & Misic, B. (2021). Comparing spatial null models
for brain maps. NeuroImage, 236, 118052. https://doi.org/10
.1016/j.neuroimage.2021.118052, PubMed: 33857618
Mars, R. B., Passingham, R. E., & Jbabdi, S. (2018). Connectivity
fingerprints: From areal descriptions to abstract spaces. Trends
in Cognitive Sciences, 22(11), 1026–1037. https://doi.org/10
.1016/j.tics.2018.08.009, PubMed: 30241910
Mars, R. B., Verhagen, L., Gladwin, T. E., Neubert, F.-X., Sallet, J., &
Rushworth, M. F. S. (2016). Comparing brains by matching con-
nectivity profiles. Neuroscience and Biobehavioral Reviews, 60,
90–97. https://doi.org/10.1016/j.neubiorev.2015.10.008,
PubMed: 26627865
Maslov, S., & Sneppen, K. (2002). Specificity and stability in topol-
ogy of protein networks. Science, 296(5569), 910–913. https://
doi.org/10.1126/science.1065103, PubMed: 11988575
Network Neuroscience
1076
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
McIntosh, A. R. (2000). Towards a network theory of cognition.
Neural Networks, 13(8–9), 861–870. https://doi.org/10.1016
/S0893-6080(00)00059-9, PubMed: 11156197
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., &
Teller, E. (1953). Equation of state calculations by fast computing
machines. Journal of Chemical Physics, 21(6), 1087–1092.
https://doi.org/10.1063/1.1699114
Milisav, F. (2023). Dyadic communication, GitHub. https://github
.com/fmilisav/milisav_dyadic_communication
Mišić, B., Betzel, R. F., Griffa, A., de Reus, M. A., He, Y., Zuo, X.-N., …
Zatorre, R. J. (2018). Network-based asymmetry of the human
auditory system. Cerebral Cortex, 28(7), 2655–2664. https://doi
.org/10.1093/cercor/bhy101, PubMed: 29722805
Mišić, B., Betzel, R. F., Nematzadeh, A., Goni, J., Griffa, A.,
Hagmann, P., … Sporns, O. (2015). Cooperative and competitive
spreading dynamics on the human connectome. Neuron, 86(6),
1518–1529. https://doi.org/10.1016/j.neuron.2015.05.035,
PubMed: 26087168
Mišić, B., Goñi, J., Betzel, R. F., Sporns, O., & McIntosh, A. R.
(2014). A network convergence zone in the hippocampus. PLOS
Computational Biology, 10(12), e1003982. https://doi.org/10
.1371/journal.pcbi.1003982, PubMed: 25474350
Mišić, B., Sporns, O., & McIntosh, A. R. (2014). Communication
efficiency and congestion of signal traffic in large-scale brain net-
works. PLOS Computational Biology, 10(1), e1003427. https://
doi.org/10.1371/journal.pcbi.1003427, PubMed: 24415931
Newman, M. E. J., & Girvan, M. (2004). Finding and evaluating
community structure in networks. Physical Review E, 69(2),
026113. https://doi.org/10.1103/PhysRevE.69.026113, PubMed:
14995526
Niendam, T. A., Laird, A. R., Ray, K. L., Dean, Y. M., Glahn, D. C.,
& Carter, C. S. (2012). Meta-analytic evidence for a superordi-
nate cognitive control network subserving diverse executive
functions. Cognitive, Affective, and Behavioral Neuroscience,
12(2), 241–268. https://doi.org/10.3758/s13415-011-0083-5,
PubMed: 22282036
Noh, J. D., & Rieger, H. (2004). Random walks on complex net-
works. Physical Review Letters, 92(11), 118701. https://doi.org
/10.1103/PhysRevLett.92.118701, PubMed: 15089179
Parsons, N., Ugon, J., Morgan, K., Shelyag, S., Hocking, A., Chan,
S. Y., … Caeyenberghs, K. (2022). Structural-functional connec-
tivity bandwidth of the human brain. NeuroImage, 263, 119659.
https://doi.org/10.1016/j.neuroimage.2022.119659, PubMed:
36191756
Passingham, R. E., Stephan, K. E., & Kötter, R. (2002). The anatom-
ical basis of functional localization in the cortex. Nature Reviews
Neuroscience, 3(8), 606–616. https://doi.org/10.1038/nrn893,
PubMed: 12154362
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B.,
Grisel, O., … Duchesnay, É. (2011). Scikit-learn: Machine learning
in Python. Journal of Machine Learning Research, 12, 2825–2830.
Petersen, S. E., & Sporns, O. (2015). Brain networks and cognitive
architectures. Neuron, 88(1), 207–219. https://doi.org/10.1016/j
.neuron.2015.09.027, PubMed: 26447582
Pineda-Pardo, J. A., Martínez, K., Román, F. J., & Colom, R. (2016).
Structural efficiency within a parieto-frontal network and cogni-
tive differences. Intelligence, 54, 105–116. https://doi.org/10
.1016/j.intell.2015.12.002
Poldrack, R. A., Kittur, A., Kalar, D., Miller, E., Seppa, C., Gil, Y., …
Bilder, R. M. (2011). The cognitive atlas: Toward a knowledge
foundation for cognitive neuroscience. Frontiers in Neuroinfor-
matics, 5, 17. https://doi.org/10.3389/fninf.2011.00017,
PubMed: 21922006
Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., &
Petersen, S. E. (2012). Spurious but systematic correlations in
functional connectivity MRI networks arise from subject motion.
NeuroImage, 59(3), 2142–2154. https://doi.org/10.1016/j
.neuroimage.2011.10.018, PubMed: 22019881
Power, J. D., Cohen, A. L., Nelson, S. M., Wig, G. S., Barnes, K. A.,
Church, J. A., … Petersen, S. E.. (2011). Functional network orga-
nization of the human brain. Neuron, 72(4), 665–678. https://doi
.org/10.1016/j.neuron.2011.09.006, PubMed: 22099467
Power, J. D., & Petersen, S. E. (2013). Control-related systems in the
human brain. Current Opinion in Neurobiology, 23(2), 223–228.
https://doi.org/10.1016/j.conb.2012.12.009, PubMed: 23347645
Preti, M. G., & Van De Ville, D. (2019). Decoupling of brain func-
tion from structure reveals regional behavioral specialization in
humans. Nature Communications, 10(1), 4747. https://doi.org/10
.1038/s41467-019-12765-7, PubMed: 31628329
Roberts, J. A., Perry, A., Lord, A. R., Roberts, G., Mitchell, P. B.,
Smith, R. E., … Breakspear, M. (2016). The contribution of
geometry to the human connectome. NeuroImage, 124, 379–393.
https://doi.org/10.1016/j.neuroimage.2015.09.009, PubMed:
26364864
Rosvall, M., Grönlund, A., Minnhagen, P., & Sneppen, K. (2005).
Searchability of networks. Physical Review E, 72(4), 046117.
https://doi.org/10.1103/PhysRevE.72.046117, PubMed: 16383478
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Seguin, C., Razi, A., & Zalesky, A. (2019). Inferring neural signalling
directionality from undirected structural connectomes. Nature
Communications, 10(1), 4289. https://doi.org/10.1038/s41467
-019-12201-w, PubMed: 31537787
Seguin, C., Mansour, S., Sporns, O., Zalesky, A., & Calamante, F.
(2022). Network communication models narrow the gap
between the modular organization of structural and functional
brain networks. NeuroImage, 257, 119323. https://doi.org/10
.1016/j.neuroimage.2022.119323, PubMed: 35605765
Seguin, C., Tian, Y., & Zalesky, A. (2020). Network communication
models improve the behavioral and functional predictive utility
of the human structural connectome. Network Neuroscience,
4(4), 980–1006. https://doi.org/10.1162/netn_a_00161,
PubMed: 33195945
Seguin, C., van den Heuvel, M. P., & Zalesky, A. (2018). Navigation
of brain networks. Proceedings of the National Academy of
Sciences, 115(24), 6297–6302. https://doi.org/10.1073/pnas
.1801351115, PubMed: 29848631
Shafiei, G., Baillet, S., & Misic, B. (2022). Human electromagnetic
and haemodynamic networks systematically converge in unimo-
dal cortex and diverge in transmodal cortex. PLOS Biology,
20(8), e3001735. https://doi.org/10.1371/journal.pbio.3001735,
PubMed: 35914002
Shafiei, G., Markello, R. D., Vos de Wael, R., Bernhardt, B. C.,
Fulcher, B. D., & Misic, B. (2020). Topographic gradients of
Network Neuroscience
1077
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
intrinsic dynamics across neocortex. eLife, 9, e62116. https://doi
.org/10.7554/eLife.62116, PubMed: 33331819
Shine, J. M., Aburn, M. J., Breakspear, M., & Poldrack, R. A. (2018).
The modulation of neural gain facilitates a transition between
functional segregation and integration in the brain. eLife, 7,
e31130. https://doi.org/10.7554/eLife.31130, PubMed:
29376825
Sizemore, A. E., Giusti, C., Kahn, A., Vettel, J. M., Betzel, R. F., &
Bassett, D. S. (2018). Cliques and cavities in the human connec-
tome. Journal of Computational Neuroscience, 44(1), 115–145.
https://doi.org/10.1007/s10827-017-0672-6 , PubMed:
29143250
Sporns, O. (2011). The non-random brain: Efficiency, economy,
and complex dynamics. Frontiers in Computational Neurosci-
ence, 5, 5. https://doi.org/10.3389/fncom.2011.00005,
PubMed: 21369354
Sporns, O. (2013). Network attributes for segregation and integra-
tion in the human brain. Current Opinion in Neurobiology, 23(2),
162–171. https://doi.org/10.1016/j.conb.2012.11.015, PubMed:
23294553
Sporns, O., & Zwi, J. D. (2004). The small world of the cerebral
cortex. Neuroinformatics, 2(2), 145–162. https://doi.org/10
.1385/NI:2:2:145, PubMed: 15319512
Srivastava, P., Nozari, E., Kim, J. Z., Ju, H., Zhou, D., Becker, C., …
Bassett, D. S. (2020). Models of communication and control for
brain networks: distinctions, convergence, and future outlook.
Network Neuroscience, 4(4), 1122–1159. https://doi.org/10
.1162/netn_a_00158, PubMed: 33195951
Stiso, J., & Bassett, D. S. (2018). Spatial embedding imposes con-
straints on neuronal network architectures. Trends in Cognitive
Sciences, 22(12), 1127–1142. https://doi.org/10.1016/j.tics.2018
.09.007, PubMed: 30449318
Suárez, L. E., Markello, R. D., Betzel, R. F., & Misic, B. (2020). Link-
ing structure and function in macroscale brain networks. Trends
in Cognitive Sciences, 24(4), 302–315. https://doi.org/10.1016/j
.tics.2020.01.008, PubMed: 32160567
Thomas, C., Ye, F. Q., Irfanoglu, M. O., Modi, P., Saleem, K. S.,
Leopold, D. A., & Pierpaoli, C. (2014). Anatomical accuracy of
brain connections derived from diffusion MRI tractography is
inherently limited. Proceedings of the National Academy of
Sciences, 111(46), 16574–16579. https://doi.org/10.1073/pnas
.1405672111, PubMed: 25368179
Uddin, L. Q., Yeo, B., & Spreng, R. N. (2019). Towards a universal
taxonomy of macro-scale functional human brain networks.
Brain Topography, 32(6), 926–942. https://doi.org/10.1007
/s10548-019-00744-6, PubMed: 31707621
van den Heuvel, M. P., Kahn, R. S., Goñi, J., & Sporns, O. (2012).
High-cost, high-capacity backbone for global brain communica-
tion. Proceedings of the National Academy of Sciences, 109(28),
11372–11377. https://doi.org/10.1073/pnas.1203593109,
PubMed: 22711833
van den Heuvel, M. P., Mandl, R. C., Kahn, R. S., & Hulshoff Pol,
H. E. (2009). Functionally linked resting-state networks reflect the
underlying structural connectivity architecture of the human
brain. Human Brain Mapping, 30(10), 3127–3141. https://doi
.org/10.1002/hbm.20737, PubMed: 19235882
van den Heuvel, M. P., & Hulshoff Pol, H. E. (2010). Exploring the
brain network: A review on resting-state fMRI functional
connectivity. European Neuropsychopharmacology, 20(8),
519–534. https://doi.org/10.1016/j.euroneuro.2010.03.008,
PubMed: 20471808
van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organization
of the human connectome. Journal of Neuroscience, 31(44),
15775–15786. https://doi.org/10.1523/ JNEUROSCI.3539-11
.2011, PubMed: 22049421
van den Heuvel, M. P., & Sporns, O. (2013a). An anatomical sub-
strate for integration among functional networks in human cortex.
Journal of Neuroscience, 33(36), 14489–14500. https://doi.org/10
.1523/JNEUROSCI.2128-13.2013, PubMed: 24005300
van den Heuvel, M. P., & Sporns, O. (2013b). Network hubs in the
human brain. Trends in Cognitive Sciences, 17(12), 683–696.
https://doi.org/10.1016/j.tics.2013.09.012, PubMed: 24231140
van den Heuvel, M. P., Stam, C. J., Kahn, R. S., & Hulshoff Pol, H. E.
(2009). Efficiency of functional brain networks and intellectual
performance. Journal of Neuroscience, 29(23), 7619–7624. https://
doi.org/10.1523/JNEUROSCI.1443-09.2009, PubMed: 19515930
van Wijk, B. C., Stam, C. J., & Daffertshofer, A. (2010). Comparing
brain networks of different size and connectivity density using
graph theory. PLOS ONE, 5(10), e13701. https://doi.org/10
.1371/journal.pone.0013701, PubMed: 21060892
Váša, F., & Mišić, B. (2022). Null models in network neuroscience.
Nature Reviews Neuroscience, 23(8), 493–504. https://doi.org/10
.1038/s41583-022-00601-9, PubMed: 35641793
Vázquez-Rodríguez, B., Suárez, L. E., Markello, R. D., Shafiei, G.,
Paquola, C., Hagmann, P., … Misic, B. (2019). Gradients of
structure–function tethering across neocortex. Proceedings of
the National Academy of Sciences, 116(42), 21219–21227.
https://doi.org/10.1073/pnas.1903403116, PubMed: 31570622
Vézquez-Rodríguez, B., Liu, Z.-Q., Hagmann, P., & Misic, B.
(2020). Signal propagation via cortical hierarchies. Network
Neuroscience, 4(4), 1072–1090. https://doi.org/10.1162/netn_a
_00153, PubMed: 33195949
Vincent, J. L., Kahn, I., Snyder, A. Z., Raichle, M. E., & Buckner,
R. L. (2008). Evidence for a frontoparietal control system
revealed by intrinsic functional connectivity. Journal of Neuro-
physiology, 100(6), 3328–3342. https://doi.org/10.1152/jn
.90355.2008, PubMed: 18799601
Wagstyl, K., Ronan, L., Goodyer, I. M., & Fletcher, P. C. (2015).
Cortical thickness gradients in structural hierarchies. Neuro-
Image, 111, 241–250. https://doi.org/10.1016/j.neuroimage
.2015.02.036, PubMed: 25725468
Wang, X.-J. (2020). Macroscopic gradients of synaptic excitation
and inhibition in the neocortex. Nature Reviews Neuroscience,
21(3), 169–178. https://doi.org/10.1038/s41583-020-0262-x,
PubMed: 32029928
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of
‘small-world’ networks. Nature, 393(6684), 440–442. https://doi
.org/10.1038/30918, PubMed: 9623998
Wedeen, V. J., Wang, R. P., Schmahmann, J. D., Benner, T., Tseng,
W.-Y. I., Dai, G., … de Crespigny, A. J. (2008). Diffusion spectrum
magnetic resonance imaging (DSI) tractography of crossing
fibers. NeuroImage, 41(4), 1267–1277. https://doi.org/10.1016/j
.neuroimage.2008.03.036, PubMed: 18495497
Wig, G. S. (2017). Segregated systems of human brain networks.
Trends in Cognitive Sciences, 21(12), 981–996. https://doi.org
/10.1016/j.tics.2017.09.006, PubMed: 29100737
Network Neuroscience
1078
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Communication capacity in the human connectome
Worrell, J. C., Rumschlag, J., Betzel, R. F., Sporns, O., & Mišić, B.
(2017). Optimized connectome architecture for sensory-motor
integration. Network Neuroscience, 1(4), 415–430. https://doi
.org/10.1162/NETN_a_00022, PubMed: 30090872
Yarkoni, T., Poldrack, R. A., Nichols, T. E., Van Essen, D. C., &
Wager, T. D. (2011). Large-scale automated synthesis of human
functional neuroimaging data. Nature Methods, 8(8), 665–670.
https://doi.org/10.1038/nmeth.1635, PubMed: 21706013
Yeo, B. T. T., Krienen, F. M., Eickhoff, S. B., Yaakub, S. N., Fox, P. T.,
Buckner, R. L., … Chee, M. W. L. (2015). Functional specializa-
tion and flexibility in human association cortex. Cerebral Cortex,
25(10), 3654–3672. https://doi.org/10.1093/cercor/ bhu217,
PubMed: 25249407
Yeo, B. T. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari,
D., Hollinshead, M., … Buckner, R. L. (2011). The organization of
the human cerebral cortex estimated by intrinsic functional con-
nectivity. Journal of Neurophysiology, 106(3), 1125–1165.
https://doi.org/10.1152/jn.00338.2011, PubMed: 21653723
Zamani Esfahlani, F., Faskowitz, J., Slack, J., Mišić, B., & Betzel,
R. F. (2022). Local structure-function relationships in human
brain networks across the lifespan. Nature Communications,
13(1), 2053. https://doi.org/10.1038/s41467-022-29770-y,
PubMed: 35440659
Zamora-López, G., & Brasselet, R. (2019). Sizing complex net-
works. Communications Physics, 2(1), 144. https://doi.org/10
.1038/s42005-019-0239-0
Zhou, D., Lynn, C. W., Cui, Z., Ciric, R., Baum, G. L., Moore, T. M., …
Bassett, D. S. (2022). Efficient coding in the economics of human
brain connectomics. Network Neuroscience, 6(1), 234–274.
https://doi.org/10.1162/netn_a_00223, PubMed: 36605887
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
0
5
1
2
1
5
4
8
5
3
n
e
n
_
a
_
0
0
3
1
8
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
1079