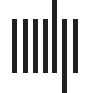RECHERCHE
Description length guided nonlinear unified
Granger causality analysis
Fei Li1, Qiang Lin1, Xiaohu Zhao2, and Zhenghui Hu1
1Key Laboratory of Quantum Precision Measurement, College of Science, Zhejiang University of Technology, Hangzhou, Chine
2Department of Radiology, Shanghai Fifth People’s Hospital, Fudan University, Shanghai, Chine
Mots clés: Nonlinear modeling, Description length, Unified Granger causality analysis, Functional
IRM
un accès ouvert
journal
ABSTRAIT
Most Granger causality analysis (GCA) methods still remain a two-stage scheme guided by
different mathematical theories; both can actually be viewed as the same generalized model
selection issues. Adhering to Occam’s razor, we present a unified GCA (uGCA) based on the
minimum description length principle. In this research, considering the common existence of
nonlinearity in functional brain networks, we incorporated the nonlinear modeling procedure
into the proposed uGCA method, in which an approximate representation of Taylor’s
expansion was adopted. Through synthetic data experiments, we revealed that nonlinear
uGCA was obviously superior to its linear representation and the conventional GCA.
Entre-temps, the nonlinear characteristics of high-order terms and cross-terms would be
successively drowned out as noise levels increased. Alors, in real fMRI data involving mental
arithmetic tasks, we further illustrated that these nonlinear characteristics in fMRI data may
indeed be drowned out at a high noise level, and hence a linear causal analysis procedure
may be sufficient. Suivant, involving autism spectrum disorder patients data, compared with
conventional GCA, the network property of causal connections obtained by uGCA methods
appeared to be more consistent with clinical symptoms.
Citation: Li, F., Lin, Q., Zhao, X., & Hu, Z.
(2023). Description length guided
nonlinear unified Granger causality
analyse. Neurosciences en réseau, 7(3),
1109–1128. https://doi.org/10.1162/netn
_a_00316
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00316
RÉSUMÉ DE L'AUTEUR
In previous studies on functional brain networks, we have proposed a linear unified Granger
causality analysis (uGCA) method based on description length. Considering that functional
brain image data is characterized by nonlinear nonstationary signals with complex long- et
short-range correlations, we thus proposed a nonlinear uGCA method. Alors, à travers
simulated data experiments and logical self-consistent fMRI experiments, its causality
identification performance was demonstrated to be superior to that of conventional GCA. À
en même temps, we further revealed the phenomenon that nonlinear high-order characteristics
and nonlinear cross-characteristics were submerged successively at high noise levels,
indicating that linear modeling procedures might be sufficient to cope with causality studies
based on fMRI data.
Reçu: 5 Février 2023
Accepté: 22 Mars 2023
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Corresponding Authors:
Xiaohu Zhao
xhzhao999@263.net
Zhenghui Hu
zhenghui@zjut.edu.cn
Éditeur de manipulation:
Alex Fornito
droits d'auteur: © 2023
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
u
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
un
_
0
0
3
1
6
p
d
.
/
t
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
Granger causality analysis:
Determines whether the historical
information of exogenous variables is
helpful in predicting the information
of endogenous variables.
Model selection:
Using a model selection strategy to
select an optimal descriptive model
among the candidate models.
F-test:
A statistical inference that compares
the variances of two datasets to
determine whether there is a
significant difference between them.
Unified Granger causality analysis:
The proposed method based on the
minimum description principle, un
unified description length guided
Granger causality analysis.
Minimum description length
principle:
A general model selection strategy,
rooted in coding theory and
stochastic complexity.
Neurosciences en réseau
INTRODUCTION
Granger causality analysis (GCA), as a data-driven test, is one of the most established methods
to identify causal connections of brain networks. Spécifiquement, GCA requires statistical signifi-
cance to determine whether the unrestricted model provides a better prediction than the
restricted model (C. Granger & Newbold, 1974; C. W. J.. Granger, 1969). En général, à travers
model selection technique, its optimal model basically is selected by balancing fitting error
term and penalized term, then it uses F statistics to evaluate significance predictability. Là-
fore, most of the extensions of GCA are based on improvements in model selection tech-
niques, F test, and modeling procedure (Shojaie & Renard, 2022). Par exemple, since F test only
involves bivariate variance comparison, numerous efforts have been made to scale from a
small network with several nodes to a large-scale complex network (D’Souza, Abidin, Leistritz,
& Wismüller, 2017; Marinazzo, Pellicoro, & Stramaglia, 2008; Wang et al., 2020; Zou,
Ladroue, Guo, & Feng, 2010). Et, to differentiate the causal effects of positive from negative,
an asymmetric causality test was proposed (Hatemi-J, 2012). De plus, causal investigation of
GCA has been also generalized in other function spaces, Par exemple, Fourier space (Geweke,
1982; Ning & Rathi, 2017; Stokes & Purdon, 2017). En outre, considering asymptotic noise
distribution data, several forms of extensions, which are especially suitable in task-related fMRI
études, have been developed (Hacker & Hatemi-J, 2006; Kaminski, 2007). These extensions
are essential since the causal effects between neuronal populations have complicated statisti-
cal interference due to various sources of uncertainties. Jusqu'à présent, these methods have provided
lots of profound insights for functional brain studies.
Néanmoins, most of these extensions are still in a conventional two-stage scheme: (1)
specify model time-lag through Bayesian information criterion or Akaike information criterion
(BIC/AIC), et puis (2) identify causal effect by F test (S. Li, Xiao, Zhou, & Cai, 2018;
Marinazzo et al., 2008; Tank, Covert, Foti, Shojaie, & Renard, 2018; Wismüller, Dsouza, Vosoughi,
& Abidin, 2021; Lequel, Wang, & Wang, 2017). This conventional scheme of GCA will lead to
inconsistency in mathematical theories, subjective selection in confidence level, and repeated
comparison of nested models, which will bring some performance issues. Spécifiquement, differ-
ent mathematical theories (BIC/AIC technique and F test) have different selection benchmark,
which would bring some inconsistency in determining the optimal model. And selection
results by pairwise F statistics sometimes depend on initially selected model and search path
heavily. Entre-temps, it is worth noting that selecting and using F statistics have become very
careful in current scientific researches, and its statistical significance has also caused extensive
discussion (Amrhein, Greenland, & McShane, 2019; Benjamin et al., 2018; Wasserstein &
Lazar, 2016). Another problem brought about by F test needs to be compared with each other
through an intermediate model, which will increase algorithm complexity, especially in large-
scale networks. Alors, we referred to all these conventional two-stage GCA methods as the
conventional GCA; in the comparison of different methods, the conditional GCA was used
to deal with multivariate time series. But for as a matter of convenience, we named the con-
ventional conditional GCA as conventional GCA in the following.
Adhering to Occam’s razor, we proposed a novel unified GCA (uGCA) (Hu, Li, Wang, &
Lin, 2021; Li, Wang, Lin, & Hu, 2020); it rises above conventional GCA, in which the
two-stage scheme can actually be viewed as the same generalized model selection issue.
Spécifiquement, with help of minimum description length (MDL) principle, uGCA unifies these
two generalized model selection issues into a description length (or code length) guided
framework. This means that it can integrate all candidate models into a unified framework with
the same selection benchmark. Autrement dit, the uGCA method integrates the whole causal
investigation procedure together and straightway returns to the most suitable descriptive
1110
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
u
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
un
_
0
0
3
1
6
p
d
.
t
/
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
model by the description length. Alors, through synthetic data and real fMRI data, nous avons
verified and illustrated the superiority of uGCA method over conventional GCA in our previ-
ous study (Li et al., 2020).
Further on, based on different coding schemes, we present three different uGCA forms,
uGCA-TP, uGCA-MIX, and uGCA-NML (Hu et al., 2021), and their large-scale network exten-
sion and dynamic network extension also have been developed (Hu, Li, Cheng, & Lin, 2022; F.
Li et al., 2023). En général, we found that uGCA methods can identify true connections with a
high accuracy, while eliminate false connections to a large extent. Entre-temps, we illustrated
that uGCA-NML is the most recommended form (Hu et al., 2021). On the contrary, conven-
tional GCA would cause lots of false positives whatever its confidence level, and it cannot
guarantee a stable performance in true connection identifications, soit.
D'autre part, it is well known that the nonlinear coupling phenomena commonly
exist in complex brain networks (Bullmore & De la Sporn, 2009; Friston, 2000). But conventional
GCA is performed in the context of linear autoregressive models for stationary time series.
Donc, nonlinear extensions of GCA have been paid lots of effort ( Oui. Chen, Rangarajan,
Feng, & Ding, 2004; Farokhzadi, Hossein-Zadeh, & Soltanian-Zadeh, 2018; Oui. Li, Wei,
Facturations, & Liao, 2012; Marinazzo et al., 2008; Tank et al., 2018), and two of the main
approaches are the neural network–based extensions (Shojaie & Renard, 2022; Talebi, Nasrabadi,
Mohammad-Rezazadeh, & Coben, 2019) and kernel-based extensions (Z. T. Chen, Zhang,
Chan, & Schölkopf, 2014; Guo, Zeng, Shi, Deng, & Zhao, 2020; Liao, Marinazzo, Pan, Gong,
& Chen, 2009). These nonlinear extensions have provided remarkable insights into functional
brain networks, but they are essentially a conventional two-stage scheme, even though it
improvements modeling procedure. De plus, the prior knowledge about real connection
networks of brain regions (neuronal populations) is insufficient, so their substantive coupling
patterns are often difficult to capture due to the lack of ground truth. This means it may be
harder to model the nonlinear characteristics of functional brain networks.
Immediately, we considered that a descriptive modeling procedure can be adopted, c'est,
using an approximate prediction model to approach the ground truth, which does not need the
prior knowledge of nonlinear coupling function. Spécifiquement, inspired by the idea of Taylor’s
expansion, we decomposed nonlinear characteristics into two terms: high-order nonlinear
term and cross-nonlinear term. Ainsi, we incorporated this nonlinear modeling procedure
into our proposed unified method, which will be more available for causal investigating on
nonlinear coupling networks. More significantly, we consider that some nonlinear character-
istics of acquired brain imaging data may be easily drowned in high-noise environments.
Donc, through synthetic data and real fMRI data, we hope to demonstrate the superiority
of nonlinear uGCA method over its linear representation and conventional two-stage GCA,
while further verifying and illustrating these submerged phenomena.
UNIFIED GRANGER CAUSALITY ANALYSIS
Inspired by coding theory, we proposed a novel causal investigation method based on coding
candidate models, which to describe data models succinctly. This proposal unifies the two-
stage scheme of conventional GCA into a description length guided framework by a single
mathematical theory (Li et al., 2020), which can avoid some inherent issues in conventional
GCA, such as the inconsistency of applying several mathematical theories, the subjective
selection of confidence levels, and pairwise comparison of nested models, and so forth. Asso-
ciating with the MDL principle, it provides a generic solution for model selection issues as a
mathematical theory (Bryant & Cordero-Brana, 2000; Grünwald, Myung, & Pitt, 2005; Hansen
Ground truth:
Truth value, true valid value, ou
standard answer, physically true
existence.
Taylor’s expansion:
An approximate expression using
polynomials to approach the real
physical model.
Neurosciences en réseau
1111
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
u
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
un
_
0
0
3
1
6
p
d
/
t
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
& Yu, 2001), which regards probability distribution as a descriptive standpoint to choose a
model with the shortest coding length scheme.
Description Length Guided Linear Causal Modeling
Firstly, given two variables, XN and YN, the linear presentations about XN
(
Xt ¼ A1Xt−i þ (cid:1)1t
Xt ¼ A2Xt−j þ B2Yt−k þ (cid:1)2t
(1)
où (cid:1)1t, (cid:1)2t are noise terms. A1, A2, and B2 are coefficient matrices. Xt denotes predicted
vector (n * 1) at time t, Xt−j is explanatory vector, a n * m state matrix of variable X with
time-lag i(i = 1, 2, …, m), same as Yt−k. Distilling the sense of Granger causality, if the joint
historical information of Y and X can provide a better prediction to X than only using the his-
torical information of X itself, then Y has Granger-cause to X. Ainsi, causal effect under the
uGCA can be defined by
FY →X ¼ LX − LXþY
(2)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
u
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
un
_
0
0
3
1
6
p
d
/
.
t
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
where LX denotes the shortest description length of restricted model in Equation 1, and LX+Y
denotes the shortest length of unrestricted model after adding YN. Causal effect from Y to X
existed when FY→X > 0, or else there is no causal effect.
Conditional Granger Causality Concept
In order to remove spurious connections caused by indirect causal effects between nodes
(L. Barnett, UN. B. Barrett, & Seth, 2018; L. Barnett & Seth, 2014; Oui. Chen, Bressler, & Ding,
2006), GCA also provides a measure of conditional causal connection by introducing another
variable ZN into Equation 1:
(
Xt ¼ A3Xt−i þ C3Zt−j þ (cid:1)3t
Xt ¼ A4Xt−k þ C4Zt−p þ B4Yt−q þ (cid:1)4t
(3)
where A, B, C are coefficient matrices, le (cid:1)t are noise terms. Alors, for conventional con-
ditional GCA used for comparisons, the causal effect from Y to X, conditional on Z, est
defined as
FY →XjZ ¼ ln
var (cid:1)3tð
var (cid:1)4tð
Þ
Þ
:
(4)
Accessing conditional GCA notion, the effect from Y to X can also be identified while con-
trolling the influence from another mediate node Z to X, in uGCA method (Li et al., 2020).
C'est, if FY→X > 0 existed, causal effect from Y to X conditioned Z is defined
FY →XjZ ¼ LXþZ − LXþY þZ :
(5)
Thus in uGCA method, all candidate models can be compared freely in the context of their
description length. Different from the conventional conditional GCA, the causal effects
between multiple variables are obtained through repeated comparisons of nested models;
uGCA can unified all candidate models into the same model space, the description length
Neurosciences en réseau
1112
Nonlinear unified Granger causality analysis
guided framework, and to obtain the conditional causal effect directly. Par exemple, if both
FY→X > 0 and FZ→X > 0 existed,
FY ;Z →X ¼ min LXþY ; LXþZ
ð
Þ − LXþY þZ :
(6)
If FY,Z→X > 0, it means that both Y and Z have direct influence on X. But if FY,Z→X < 0, there will be two cases. One is FY,Z→X = (LX+Y − LX+Y+Z) < 0; it indicates only Y has direct influence on X. The other is FY,Z→X = (LX+Z − LX+Y+Z) < 0; it indicates that Z impacts X directly (Li et al., 2020). In the unified model selection space of uGCA, multiple selected models can be directly compared by their description lengths, which can release the algorithm complexity. In this way, the proposed uGCA is more in line with Occam’s razor, or the principle of parsimony. Description Length Models in uGCA In our previous studies, we have present three different uGCA forms based on different coding schemes (Hu et al., 2021), further illustrating that uGCA-NML method is the most recommended choice (Hu et al., 2021). Thus, the following are generalized model selection strategies by description length in uGCA-NML. With the MDL principle, the shortest length of parametric model (that is, the L in Equation 2) is carried out. Variable υn = {υ1,…,υn} is given, υt ¼ β1υt−1 þ β2υt−2 þ … þ βk υt−k þ (cid:1)t (7) where t = 1, …, m, and m is more than k to keep the solution determined. In earlier two- part coding scheme, it divided the descriptive model into a fitting error term (L1) and a parameter literal coding term (L2) ( J. Rissanen, 1978), and its generalized description length is given by Ltwo−part ¼ L1 υnjF ð Þ þ L2 Fð Þ (8) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 7 3 1 1 0 9 2 1 5 4 8 6 1 n e n _ a _ 0 0 3 1 6 p d . t / where F denotes a probability distribution for the data set υn. The parameter vector in Equa- tion 7 consists of θ = (k, ξ) and ξ = (σ2,β1,…,βk), where σ2 = ξ0 is the variance parameter of zero-mean Gaussian distribution for (cid:1)t. In order to describe υn, turn to describe (cid:1)t, thus it arrives at ð f (cid:1)t jυt ; β; τ Þ ¼ 1 Þm=2 ð 2πτ ð − 1=2τ e P P Þ ð υt − t βk υt −k k Þ: (9) f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 And the description length of two-part coding scheme for describing variable υn is ð L υ; θ Þ ¼ ln f (cid:1)t jυt ; β; τ ð ð Þ Þ þ Xk i¼0 j jξ i δ ln Þ þ ln k þ 1 ð (10) where δ is the precision, it’s optimal to choose 1= p ffiffiffi . Specially, n jξ j δ < 1 should be ignored. i uGCA-NML-Minimax Solution for Inherent Redundancy To remove some inherent redundancy in earlier two-part coding scheme, a sharper description length with stochastic complexity and universal process, combining Fisher information, is derived for a class of parametric processes ( J. J. Rissanen, 1996), the so-called normalized Network Neuroscience 1113 Nonlinear unified Granger causality analysis maximum-likelihood (NML) coding scheme. In short, it applies an exponentiated asymptotic complexity instead of the parameter space complexity (the second part in two-part coding scheme, L2), LNML ¼ − ln f υnj^θ υnð (cid:3) (cid:7) þ ln (cid:4) Þ k=2 (cid:5) (cid:6) n 2π Z : p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi detI θð Þ (cid:8) dθ : (11) This form is motivated by the maximum likelihood estimate (MLE) that requires satis- fying the Central Limit Theorem (Barron, Rissanen, & Yu, 1998; J. Rissanen, 2000). Then, the nonintegrability of MLE is a key issue to be solved. Firstly, Fisher information is given by ð jI β; τ (cid:3) Þj ¼ jSj= 2τ kþ2 (cid:4) ; and the integral of its square root dealt by Barron et al. (1998), J. Rissanen (2000), and J. J. Rissanen (1996) is Z Z ∞ βSβ≤R τ 0 j ð I β; τ j1=2dτdβ ¼ 2jSj Þ ð (cid:9) (cid:10) Þ1=2 R τ 0 k=2 Ck k : (12) (cid:5) Þk 2= k p ffiffiffiffiffiffi jSj (cid:3) (cid:4) Γ k 2 (cid:6) 2 ¼ 2 πRð Where Ck Rk is the volume of a k-dimensional ball B = {β’Sβ ≤ R}. Lower bound τ 0 is determined by precision of data written, ^τ 0 ¼ RSS=m and ^R ¼ (cid:3) ^β’Vt−k’ Vt−k =m are given by MLE. Finally, the description length in uGCA-NML arrives at ^β (cid:4) LuGCA−NML ¼ m ln p ffiffiffiffiffiffiffiffi 2πτ þ RSS 2τ þ k 2 ln (cid:9) (cid:10) − log Γ k 2 m 2 þ k 2 log ^R τ 0 − 2 logk: (13) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 7 3 1 1 0 9 2 1 5 4 8 6 1 n e n _ a _ 0 0 3 1 6 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Nonlinear Characteristic Modeling Procedure As stated above, most of modeling procedures fail to capture the nonlinear characteristics of neural coupling, which means that underlying functional brain networks may not be well uncovered. Thus, linear representation in Equation 1 should be described in nonlinear cou- pling form, ( ð (cid:3) Xt ¼ f1 Xt−i Xt ¼ f2 Xt−j Þ þ (cid:1)1t (cid:4) (cid:3) þ g2 Yt−j (cid:4) (cid:3) þ h2 Xt−qYt−r (cid:4) þ (cid:1)2t (14) where f, g, and h denote underlying nonlinear coupling functions, and Xt−iYt−j is the instanta- neous cross-term. It is well known that the current prior knowledge of real functional brain network is far from insufficient. And, in fact, from a methodological perspective, adopting an accurate and careful description model of causal effect may be more essential and urgent than searching a ground truth model. As a result, in this study, we used an approximate modeling procedure to characterize the neural response, f, g, and h. Specifically, with the help of the idea of Taylor’s approximation Network Neuroscience 1114 Nonlinear unified Granger causality analysis expansion, their nonlinear characteristics can be decomposed into superpositions of high- order terms and cross-terms. That is, 2 2 3 3 Xt ¼ 6 6 6 6 4 X 2 Xt;i t;i Xt;iþ1 X 2 t;iþ1 ::: ::: Xt;iþn X 2 t;iþn ::: X s t;i ::: X s t;iþ1 ::: ::: ::: X s t;iþn 7 7 7 7 5 ; Yt ¼ 6 6 6 6 4 Y 2 Yt;j t;j Yt;jþ1 Y 2 t;jþ1 ::: ::: Yt;jþn Y 2 t;jþn ::: Y s t;j ::: Y s t;jþ1 ::: ::: ::: Y s t;jþn 7 7 7 7 5 (15) (16) h Zt ¼ β; X t; Y t; X 1ð Þ t Y 1ð Þ t i where Xt,i is descriptive vector (xt−1, xt−2, …, xt−i) at time t, the same as Yt,j. And s is the poly- nomial order, i and j denote their time-lag. Xt and Yt are the nonlinear representation matrices; Zt is the joint nonlinear representation matrix, where β denotes model coefficient vector. X t (1) (1) are the first column of Yt and Yt, respectively. Actually, this nonlinear representation and Y t can be concluded as follow: Zt ¼ linearity term þ high(cid:2)order term þ cross term: (17) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 7 3 1 1 0 9 2 1 5 4 8 6 1 n e n _ a _ 0 0 3 1 6 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 In this representation, we applied an approximate representation of Taylor’s expansion. The measured signal was decomposed into linear term and nonlinear terms, in which the nonlinear term was approximated by the high-order polynomial term and the cross-term. By the way, both conventional GCA and uGCA use the same nonlinear modeling procedure. In contrast to the linear modeling procedure, the nonlinear modeling procedure is essentially establishing a mixture descriptive model, in which it integrates nonlinear high-order terms and nonlinear cross-terms into a linear regression model. In general, in the course of practical application, we used the least square method (LSQ) to estimate the model parameter of candidate models for both conventional GCA and uGCA methods. And different time delay orders in the model will get a different estimated model parameter. Then, for conventional GCA, it evaluates models with different estimation param- eters according to BIC/AIC to obtain the optimal model, and then determines whether there is a causal relationship between variables through statistical inference. As for uGCA method, it is based on MDL principle, that is, by selecting the shortest description length among candidate models with different estimated parameters (e.g., in Equation 1) to determine the optimal models, and then by comparing the description length of selected optimal restricted model (in Equation 1) and the description length of selected optimal unrestricted model (in Equation 1) to establish the causal relationship. Therefore, their model estimations are consistent for both conventional GCA and uGCA (Barnett et al., 2018). Furthermore, in uGCA method, its model selection process and causal connection model construction were also under the same mathematical theory, which will obtain more consistent causal connection results. EXPERIMENTS AND RESULTS Synthetic Data Experiments Nonlinear characteristics of high-order terms and cross terms may be easily drowned out by background noise. Therefore, through the synthetic data experiments, we hoped to demon- strated the priority of uGCA methods to conventional GCA within the nonlinear modeling procedure, and then attempted to illustrate that high-order terms and cross-terms in nonlinear systems were indeed drowned out successively with the increase of noise level. Network Neuroscience 1115 Nonlinear unified Granger causality analysis l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . Figure 1. The obtained causal connections. Data length was 300, simulation number was 1,000. ‘Low’ denoted a low noise level (variance = 0.2), the noise variance in ‘Mid’ (‘high’) was 0.6 (1.2). 3-node network. To ensure that the linear terms are the same and will not be affected by the added random noise term, we synthesize nonlinear data containing higher order terms and cross-terms, respectively, given by / t / e d u n e n a r t i c e - p d l f / / / / 7 3 1 1 0 9 2 1 5 4 8 6 1 n e n _ a _ 0 0 3 1 6 p d / . t (18) f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 8 >>>>>>>>>>>>>>>>>>< >>>>>>>>>>>>>>>>>>:
1;i−1
2;i−1
X1;i ¼ 0:35X1;i−1 þ 0:34X2;i−1 þ (cid:1)1
− 0:14X 2
¼ X1;i − 0:14X 2
X h
1;je
¼ X1;i − 0:14X1;i−1X2;i−1
X c
1;je
X2;i ¼ 0:39X2;i−1 − 0:36X1;i−1 þ (cid:1)2
þ 0:24X 2
X h
2;je
X c
2;je
X3;i ¼ −0:37X3;i−1 þ 0:34X1;i−1 þ 0:35X2;i−1 þ (cid:1)3
X h
3;je
X c
3;je
¼ X3;i þ 0:22X 2
− 0:20X 2
2;i−1
¼ X3;i þ 0:21X1;i−1X3;i−1 − 0:20X2;i−1X3;i−1
¼ X2;i − 0:24X 2
¼ X2;i − 0:24X1;i−1X2;i−1
− 0:21X 2
1;i−1
1;i−1
2;i−1
3;i−1
where Xh represents variable X after adding high-order terms, and Xc is after adding cross-
termes, ϵi is the noise terms. To ensure the effectiveness, synthetic data performed stationarity
analysis and passed before being allowed to be further used.
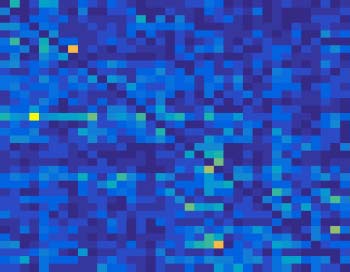
Firstly, for nonlinear data containing high-order terms, the results were shown in the left
panel of Figure 1. Spécifiquement, in terms of identifying true connections, the accuracy of linear
uGCA-NML decreased significantly with the increase of noise level, especially in 2→3 and
1→3. Alors, nonlinear uGCA-NML guaranteed a stable accuracy performance on the identifi-
cation of 1→2 and 1→3 connections, but their accuracies in 2→1 and 2→3 had some descents.
For the linear conventional GCA, their true prositive rates (TPRs) showed a descent of about
3% (un 7% descent in the high confidence level). After using nonlinear modeling, all accuracies
TPR:
True positive rate, the number of
obtained true connections divided by
the number of all true connection in
real existed system.
Neurosciences en réseau
1116
Nonlinear unified Granger causality analysis
Chiffre 2. The comparison between linear data and nonlinear data with the high-order term (cross-term).
TNR:
True negative rate, the percentage of
non-existent connections that are
correctly judged to be non-existent.
of its four true connections had some descents, especially in 2→1. D'autre part, for these
false connections, whether using nonlinear or linear modeling, uGCA-NML achieved more
stable and accurate identification even at high noise levels. But for conventional GCA, its true
negative rates (TNRs) were affected by noise terms to some extent, especially after using
nonlinear modeling. Even if the confidence level was changed, the false connections iden-
tification performance of conventional GCA did not improve. Ainsi, as the noise level
increased, the performance of all methods in identifying true connections decreased to
some extent, whether using linear or nonlinear modeling. Autrement dit, as the noise level
increased, their high-order nonlinear characteristics would gradually be drowned out.
Alors, for nonlinear data containing cross terms, the right panel of Figure 1 showed the cumulative
result of all connection edges. Spécifiquement, uGCA-NML behaved with superior identification perfor-
mance in true connection whether using the linear or nonlinear modeling, and its accuracies were
always maintained above 98%. Bien que, the accuracy of GCA-NML had a 2% decrease in 2→3
with the increase in noise level. Entre-temps, whether using linear or nonlinear modeling, uGCA-
NML eliminated false connections to a large extent. D'autre part, conventional GCA had a
good performance in identifying true connections, especially after using linear modeling. Cependant,
with the increase in noise level, its identification accuracy of some true connections had slight
decreases, while the accuracy of false connections also fluctuated to some extent. With a high con-
fidence level of the F test, conventional GCA eliminated false connections to a certain extent, mais
there would be more misjudgments in true connections. Donc, with the increase in noise level,
nonlinear characteristics with cross-terms will be also drowned to a certain extent.
Donc, as the noise level increased, more false negatives were made. And the high-order
terms were significantly more affected by the increase in noise level than the cross-terms.
Donc, we considered that the nonlinear characteristics of high-order terms and cross-terms
will be drowned out successively with the increase in noise level. And actually, these phenom-
ena can be inferred in the time series diagram between linear data and nonlinear data,
because they overlapped to a large extent, as seen in Figure 2. Cependant, previous studies
(Hu et al., 2021; Li et al., 2020) showed that identifying linear coupling would hold a stable
level at the above noise ranges. In view of the fact that these obtained false negatives actually
contained linear coupling characteristics, we considered that the disorder of nonlinear char-
acteristics due to the increasing noise level may further cause the loss of linear characteristics.
D'autre part, we found that uGCA-NML can ensure stable and superior performance in
all identified connections, regardless of using linear or nonlinear modeling, while conven-
tional GCA only obtains good identification in true connections.
Neurosciences en réseau
1117
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
u
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
un
_
0
0
3
1
6
p
d
.
/
t
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
Chiffre 3. The relationships of simulation data sets in the six-node network.
6-node network. The above results seemed to indicate that these methods have similar perfor-
mance in causal connection identification through the linear or nonlinear modeling. Ainsi, un
six-node network was further synthesized as follow, as shown in Figure 3,
8
>>>>>>>>>< >>>>>>>>>:
1;i−1 − 0:34Y1;i−2 þ 0:35Y2;i−2 þ (cid:1)1
2;i−1 − 0:34Y2;i−2 þ 0:86Y1;i−1 þ (cid:1)2
Y1;i ¼ 0:85Y1;i−1e−Y 2
Y2;i ¼ 0:96Y2;i−1e−Y 2
Y3;i ¼ 0:82Y3;i−1 − 0:36Y3;i−2 þ 0:81Y1;i−1 − 0:32Y1;i−2 þ (cid:1)3
−Y 2
Y4;i ¼ 0:88Y4;i−1e
Y5;i ¼ 0:82Y5;i−1e−Y 2
−Y 2
Y6;i ¼ 0:85Y6;i−1e
4;i−1 þ 0:32Y4;i−2 þ 0:89tanhðY2;i−1Þ − 0:84tanhðY5;i−1Þ þ (cid:1)4
5;i−1 − 0:59Y5;i−2 − 0:48Y2;i−1Y4;i−1 þ 0:43Y2;i−1Y5;i−1 þ 0:45Y4;i−1Y5;i−1 þ (cid:1)5
6;i−1 þ 0:26Y6;i−2 þ 0:82Y3;i−1 − 0:55Y5;i−1 þ 0:22Y3;i−1Y5;i−1 þ (cid:1)6
Firstly, data length varied from 300 à 1,000, as shown in Figure 4, we found that both the
uGCA and conventional GCA were affected by changes in data length, regardless of whether
they used linear or nonlinear modeling procedure.
When data length increased, nonlinear conventional GCA obtained more true connections,
but the misjudgment of some false connections increased, as same as using linear modeling. Dans
général, when data length ranged from 300 à 1,000, linear conventional GCA cannot guar-
antee high accuracy in identifying true connections, especially 2→5, 4→5, and its false con-
nections misjudgment was also relatively high. After using the nonlinear modeling, le
identification performance of some true connections was improved, but lots of false negatives
in 2→1, 2→5 still existed. And for false connections, there were also more very obvious mis-
judgments. Plus important encore, its identification performance cannot be improved even if its
Chiffre 4. The obtained causal connections. The L denotes data length, its noise variance variance = 0.4.
Neurosciences en réseau
1118
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
u
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
un
_
0
0
3
1
6
p
d
.
t
/
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
Tableau 1. Comparison between uGCA methods and conventional GCA under different data length
uGCA-NML
GCA(α = 0.05)
GCA(α = 0.01)
Data length
L = 300
Indice
TPR
TNR
non linéaire
98.90%
linear
83.87%
non linéaire
97.14%
99.86%
99.77%
76.89%
Ground truth rate
88.0%
3.6%
L = 500
TPR
TNR
99.97%
86.34%
99.87%
99.79%
Ground truth rate
97.0%
7.6%
L = 1000
TPR
TNR
100.00%
92.33%
99.64%
99.54%
0.3%
98.28%
71.00%
0.0%
99.52%
61.81%
linear
91.41%
85.52%
1.3%
95.48%
81.73%
1.1%
99.44%
75.80%
non linéaire
96.67%
85.95%
2.1%
97.88%
78.89%
0.3%
99.38%
67.35%
linear
88.64%
95.11%
7.1%
93.43%
93.08%
11.4%
99.10%
89.21%
Ground truth rate
92.5%
32.8%
0.0%
0.5%
0.0%
9.4%
Note. The L was data length. The ground-truth rate denoted the total numbers of the obtained individual connection network which was same as the ground
truth network, divided by the sample number (1,000).
confidence level was changed. C'est, when increasing the confidence level, conventional
GCA (α = 0.01) eliminated false connections to some extents, but led to more false negative
in identifying true connections, as seen in Figure 4.
But for nonlinear uGCA-NML, it obtained 100% accuracy of true connections when data
length was 1,000, and the identification accuracy was also close to 100% as data length was
500. For most false connections, nonlinear uGCA-NML had stable and superior performance.
But in some false connections, long data length led to some increases in false positives,
especially in 2→6, 4→6. En général, it can be found that nonlinear uGCA-NML had a high
identification accuracy of true connections, and it also suppressed false positives of false con-
nections at a low level. As for linear uGCA-NML, their false positives were suppressed at a
lower level than when using nonlinear modeling. Cependant, for true connections 2→5, 4→5,
linear uGCA-NML apparently failed to identify them well. Even when data length was 1,000,
these two identification accuracies were significantly lower than that of other connected
edges, especially for 2→5, its accuracy was always lower than 60%.
As shown in Table 1, with data length increased, uGCA-NML obtained a higher accuracy
than conventional GCA, while their nonlinear modeling procedures were significantly better
than linear procedures. En outre, when data length increased to 1,000, using nonlinear
modeling resulted in a little increase in the misjudgment of some false connections, lequel
led to a decrease in the ground truth rate. Even so, nonlinear uGCA-NML also obtained a
much higher ground truth rate than that using linear modeling procedure. En général, non linéaire
uGCA-NML can ensure high identification accuracy, and the possibility of obtaining a ground
truth network is also significantly higher. En revanche, regardless of its confidence level, con-
ventional GCA has a low probability of obtaining ground truth network whether using the non-
linear or linear modeling, and its ground truth rate is basically less than 10%.
By changing noise levels, their accuracies were further directly compared when using non-
linear modeling and linear modeling, respectivement, as shown in Table 2. Obviously, non linéaire
uGCA-NML was basically not affected by noise terms, and it had a more stable and accurate
performance of causal connection identification, especially for ground truth rate. En revanche,
Neurosciences en réseau
1119
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
u
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
un
_
0
0
3
1
6
p
d
/
t
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
Tableau 2. Comparison between uGCA methods and conventional GCA under different noise level
uGCA-NML
GCA(α = 0.01)
GCA(α = 0.01)
Data length
Low
Indice
TPR
TNR
non linéaire
99.99%
99.82%
Ground truth rate
96.3%
Moderate
TPR
TNR
99.97%
99.87%
Ground truth rate
97.0%
High
TPR
TNR
99.94%
99.78%
linear
85.91%
99.77%
9.4%
86.34%
99.79%
7.6%
85.82%
99.70%
non linéaire
99.40%
65.93%
0.0%
98.28%
71.00%
0.0%
99.12%
69.23%
linear
97.24%
75.22%
0.3%
95.48%
81.73%
1.1%
94.34%
81.41%
non linéaire
99.16%
71.60%
0.0%
97.88%
78.89%
0.3%
98.86%
75.64%
linear
94.60%
89.38%
6.9%
93.43%
93.08%
11.4%
92.61%
92.40%
Ground truth rate
95.3%
5.5%
0.0%
1.5%
0.0%
10.4%
Note. ‘Low’ denoted a low noise level (variance = 0.2), the noise variance in ‘Moderate’ (‘High’) était 0.4 (0.6).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
linear uGCA-NML cannot guarantee high identification accuracy, especially in TPR and
ground truth rate. D'autre part, conventional GCA performed poorly whether using non-
linear or linear modeling, especially for the ground truth rate. As with changing the data
length, its TPR had some decreases while the TNR and ground truth rate were improved when
its confidence level was increased, although its ground truth remained at a low level. In gen-
eral, nonlinear uGCA-NML was little affected by noise term, and can identify true connections
with high accuracy while eliminating most false connection to a large extent.
fMRI Data
/
t
/
e
d
u
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
un
_
0
0
3
1
6
p
d
t
/
.
In this experiment, we let nine subjects (five female, 24 ± 1.5 années
Mental arithmetic experiment.
vieux) perform simple one-digit (consisting of 1–10) serial addition (SSA) and complex two-digit
(consisting of 1–5) serial addition (CSA) by visual stimulus and simultaneously measured their
brain activities with fMRI. Immediately following, each subject was asked to perform the same
serial addition arithmetic tasks by an auditory stimulus. Written informed consent was obtained
from all participants. This study was approved by the local ethics committee of Zhejiang
University of Technology.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
It is well known that the obtained fMRI data are bound to be accompanied by highly non-
linear characteristics and often have large background noise. Although some studies have
revealed that some noise of fMRI data may be potential neural activity signals of the brain
(Bright & Murphy, 2015; Faisal, Selen, & Wolpert, 2008; Uddin, 2020), most of the noise is
still objective. Especially for the inherent background imaging noise in fMRI, it is more likely to
exister. Donc, the nonlinear characteristics of coupled systems are likely to be drowned out
in high noise level. Suivant, nonlinear uGCA-NML and nonlinear conventional GCA will be used
to further analyze causal connection of mental arithmetic networks and verify whether non-
linear characteristics in fMRI data will be drowned out.
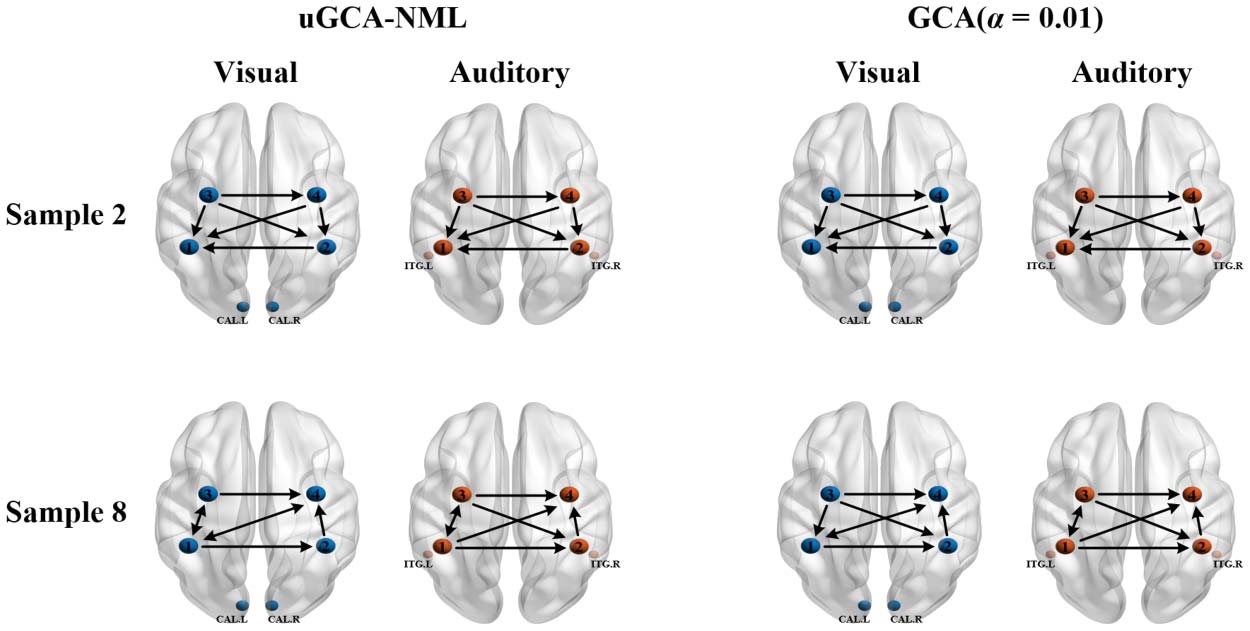
Firstly, from a logical self-consistent view, we considered that mental arithmetic tasks would
activate the same functional brain networks, whether under visual or auditory stimulus. Appar-
ently, as seen in Figure 5, the activation maps under different stimuli overlapped to a large
Neurosciences en réseau
1120
Nonlinear unified Granger causality analysis
Chiffre 5. Mental arithmetic of CSA control state under the two stimuli. The activation regions were processed by SPM12; the control state
meant that the sample was in rest state. (UN) CSA control state under visual stimulus. (B) CSA control state under auditory stimulus ( p < 0.0001,
uncorrected).
extent, which validated the reliability of the above experimental design. Thus, the effective-
ness of these methods can be verified by measuring the similarity of their mental arithmetic
networks under different stimuli.
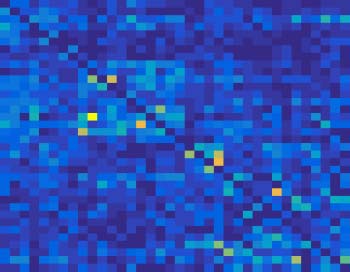
As shown in Figure 6, in subject 2, their obtained mental arithmetic networks under differ-
ent stimuli were completely consistent. In subject 8, only one connection edge in mental arith-
metic network by nonlinear conventional GCA was inconsistent, and two edges were different
for nonlinear uGCA-NML. Thus, using nonlinear modeling procedure could identify a high
similarity of mental arithmetic networks under different stimuli.
Then, the network similarity between using nonlinear modeling and linear modeling was
given by
P P
P P
S ¼
A∩B
ð
ð
A∪B
Þ
Þ
:
(19)
Where S represents the measured similarity, A and B are the connection matrices of mental
arithmetic networks under the same stimulus by nonlinear modeling and linear modeling,
respectively. For the fMRI data under the same stimulus, nonlinear and linear modeling
Figure 6. Mental arithmetic networks under different stimuli obtained by nonlinear uGCA and
nonlinear conventional GCA.
Network Neuroscience
1121
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
a
_
0
0
3
1
6
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
Figure 7. The obtained network similarity under the same stimulus between using nonlinear modeling and linear modeling.
procedures were used to identify the causal connection, respectively, and then the similarities
between them were compared. As shown in Figure 7, for both of methods, the most of causal
connections between nonlinear modeling and linear modeling were exactly the same, except
for the auditory stimulus fMRI data in subject 9.
As a result, due to some background noise terms, nonlinear characteristics in this mental
arithmetic fMRI data seemed to be drowned out. Thus, for fMRI data, causal connections in the
brain network can be well analyzed even using a linear procedure. In essence, linear AR
model is the first-order approximation of a nonlinear system. For datasets with a high noise
level, nonlinear characteristics will be drowned, and maybe only the first-order linear charac-
teristics preserved. Furthermore, for the brain networks obtained by fMRI data, it will also
retain linear causal connections. Using a nonlinear modeling procedure may result in high
algorithm complexity, thus a simple linear modeling procedure is enough in most cases. Of
course, it is necessary to use nonlinear modeling procedures to further analyze the deep char-
acteristics of functional brain networks, such as analyzing and comparing topological proper-
ties of functional brain networks between normal people and patients.
Autism. Autism spectrum disorder (ASD) refers to a group of complex neurodevelopmental
disorders characterized by impairments in social interaction, verbal and nonverbal communi-
cation, and the presence of limited interests and repetitive behaviors (Lord et al., 2020; Lord,
Elsabbagh, Baird, & Veenstra-Vanderweele, 2018; Sicile-Kira & Grandin, 2014). It is well
known that diagnosing ASD is difficult because there is no specific medical diagnostic test,
and the usual diagnosis is based on a doctor’s clinical observation and experience. Recently,
many achievements have been made in revealing functional and anatomical abnormalities in
the brain of ASD patients (Grove et al., 2019; Lord et al., 2020; Sicile-Kira & Grandin, 2014).
The imaging data used involved the resting-state fMRI data of ASD patients and normal
people (NP). The ASD data contained 84 samples (42 female and 42 male) and were all from
a data collection project: ABIDE I (https://ida.loni.usc.edu/) on the IDA website. For normal
control group, we downloaded the datasets from NITRC website (https://www.nitrc.org/) which
provided by V. J. Kiviniemi from the University of Oulu. The dataset included 66 female and
37 male (ages 20–23). Data preprocessing was performed on SPM12. According to previous
studies (Alcalá-López et al., 2018), 36 regions of interest associated with ASD symptoms were
Network Neuroscience
1122
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
a
_
0
0
3
1
6
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
Figure 8. Causal connection matrices of social brain network identified by nonlinear uGCA and nonlinear conventional GCA.
selected. It was called a social brain network, containing four subsystems, limbic system, high-
level cognitive system, visual-sensory system, and intermediate system.
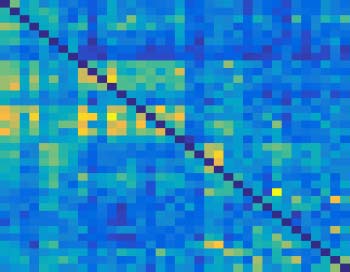
Firstly, their obtained causal connections in social brain networks were shown in Figure 8.
Obviously, there were some intuitive differences between the causal networks of ASDs and NP
obtained using these two nonlinear modeling methods. Specifically, these obtained causal
connections appeared to be haphazard in ASDs. In contrast, the obtained social brain net-
works of NP possessed more regularity and had different functional clusters among some cer-
tain nodes. For example, for the high-level cognitive system, there was a clear internal cluster
of causal connections. But one of the differences was that nonlinear uGCA-NML identified
relatively sparse networks.
To further reveal differences in obtained causal networks between ASDs and NP, out-degree
and in-degree of four subnetworks in the social brain identified by these two methods were
shown in Figure 9. Here, the in-degree represents the sum of (input) causal connections from
other nodes to its own node, and the out-degree represents the sum of (output) causal connec-
tions from its own node to other nodes. For these subnetworks, whether using nonlinear
uGCA-NML or nonlinear conventional GCA, the distributions of in-degree and out-degree
of NP were intuitively more concentrated than that of ASDs. These suggested weaker group
consistency for ASDs and broad overall distribution of social brain network characteristics.
Thus, these results further implied the complexity of ASD symptoms.
On the other hand, the results showed that there were intuitive differences in social brain
network between ASDs and NP, regardless of using nonlinear uGCA-NML or nonlinear con-
ventional GCA. Specifically, for the limbic system and visual-sensory systems, nonlinear
uGCA-NML revealed some differences in the causal networks between ASD and NP, implying
that nonlinear uGCA considered ASD to be inconsistent in external information reception
compared to NP. But nonlinear uGCA found little difference in out-degree between ASDs
and NP for high-level cognitive system, and little difference in in-degree for intermediate sys-
tem, these implying that nonlinear uGCA-NML believed the output of high-level cognitive and
the input of intermediate systems in ASDs was no different from that of NP. In combination
with Figure 8, internal connections of high-level cognitive network were sparser in ASD indi-
viduals than in normal individuals, from which it can be inferred that there may be some dis-
order in causal connections involving the high-level cognitive subnetwork in ASDs, and the
same is true for the intermediate subnetwork. In general, to some extent, the differences in out-
degree and in-degree between ASDs identified by nonlinear conventional GCA and normal
individuals appear to be more pronounced.
Next, the graph shortest paths of their social brain networks were further compared, as
shown in Figure 10. Among them, nonlinear uGCA-NML showed that the distribution of graph
shortest paths in social brain network of ASDs was more concentrated than that of NP. This
implied that the ASD group had a higher consistency in the functional characteristics of their
Network Neuroscience
1123
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
a
_
0
0
3
1
6
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
a
_
0
0
3
1
6
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. The out-degree and in-degree of subnetwork in social brain network within nonlinear uGCA and nonlinear conventional GCA. The
four subnetworks are limbic, high-level, visual-sensory, and intermediate network.
social brain networks when faced with social tasks (i.e., all individuals exhibited symptoms
such as social difficulties). In contrast, nonlinear conventional GCA found some deviation
in the center of the graphs shortest path distribution between ASDs and NP.
This result suggested that social brain network nodes in ASDs had shorter connected path-
ways (i.e., respond quickly to social tasks) than normal population when faced with social
Figure 10. The small-world property of social brain networks obtained by nonlinear uGCA and
nonlinear conventional GCA.
Network Neuroscience
1124
Nonlinear unified Granger causality analysis
tasks, which was distinctly inconsistent with their clinical symptoms. Also, this could explain
the greater difference in network out-degree and in-degree between ASD and normal individ-
uals identified by nonlinear conventional GCA to some extent, which may actually be
misjudged.
DISCUSSIONS
As mentioned above, conventional GCA is still in a two-stage scheme, specifying model order
by BIC/AIC and then determining causal effect by F test, which causes the inconsistency in
selection benchmarks due to different mathematical theories, subjective selection of confi-
dence level due to F test, and the extra algorithm complexity bringing by nested model (Li
et al., 2020). Thus, we proposed a unified model selection approach for GCA based on
MDL principle, named uGCA. Meanwhile, we all know that the nonlinear nature in functional
brain networks is self-evident, but most conventional GCA methods identify causal effects
through linear modeling. Therefore, we further incorporated Taylor’s approximate expansion
technique into the proposed uGCA to identify causal connections in functional brain networks
by nonlinear modeling procedure. It should be noted that the nonlinear uGCA and conven-
tional nonlinear GCA actually used the same nonlinear modeling procedure. And instead of
using BIC/AIC to determine the order of these nonlinear characteristics in conventional GCA,
the order of high-order terms and cross-terms in uGCA method is determined by the descrip-
tion length, which is consistent with its whole modeling procedure. Thus in this sense, the
superiority of nonlinear uGCA compared with nonlinear conventional GCA seems to out-
weigh its theoretical advantage in linear representations, in which its generalized model selec-
tion process is more consistent and simpler.
Through three-node synthetic network (including high-order term and cross-term, respec-
tively), we revealed a noteworthy phenomenon that increasing noise levels in nonlinear sys-
tems will drown out some nonlinear characteristics. That is, with the increase of noise level,
the nonlinear characteristics of high-order terms and cross-terms will be drowned out succes-
sively, and even affect the stability of its corresponding linear causal coupling at the same time.
On the other hand, different from nonlinear conventional GCA, nonlinear uGCA-NML still can
guarantee a relatively superior performance of causal connection identification. But nonlinear
procedure seemed to be worse than linear procedure in the identification of some connec-
tions, as shown in Figure 1. We considered that nonlinear modeling involved incorporating
higher order characteristics of the data into the model estimation process. And nonlinear char-
acteristics in the data fitting might be more affected by the noise terms, which will generate
additional uncertainties. As for linear modeling procedure, it only involved the description of
first-order linear characteristics. Then, through a six-node synthetic network, it was further
revealed that nonlinear uGCA were obviously prior to linear uGCA, which confirmed the
necessity of using a nonlinear procedure to some extent.
Then, in the real fMRI data involving mental arithmetic tasks under different stimuli, the
results showed that causal connections obtained using nonlinear modeling procedure and lin-
ear modeling procedure are largely consistent, which further revealed that nonlinear charac-
teristics (high-order terms and cross-terms) in fMRI data may have been drowned out. In other
words, applying a linear modeling procedure to investigate causal effect for real fMRI data
(usually with a high noise level) may be appropriate enough. By the way, the advantages of
linear uGCA over linear conventional GCA have been previously demonstrated in real fMRI
experiment (Hu et al., 2021; Li et al., 2020). Then refer to the similarity measurement in
Figure 7; the obtained mental networks using nonlinear modeling and linear modeling were
Network Neuroscience
1125
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
a
_
0
0
3
1
6
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
highly similar, whether the uGCA or conventional GCA, so the advantage of nonlinear uGCA
over nonlinear conventional GCA was self-evident. Next, for resting-state fMRI data involving
ASDs and NP, uGCA-NML method revealed that ASDs showed a more consistent and concen-
trated distribution for graph shortest paths of social brain network, as shown in Figure 10. But
for the four subnetworks, the consistency of its out-degree and in-degree distribution was obvi-
ously worse than in NP, as shown in Figure 9. Therefore, it can be concluded that ASDs may
have some common dysfunction symptoms in the integration of social functions, and the
individual differences of ASDs in four social brain subnetworks may be diverse. These are
all consistent with ASD-related symptoms and the complex and extensive pathology may lead
to significant differences in the inner connectivity of these four social brain subnetworks in
ASDs. In this sense, nonlinear uGCA-NML may have certain advantages in distinguishing
ASDs from NP.
CONCLUSION
In this research, we incorporated the unified model selection framework with a nonlinear
modeling procedure, which distilled the idea of Taylor’s approximate expansion, where a non-
linear uGCA approach was proposed. Through synthetic data and fMRI data experiments, the
proposed uGCA methods showed a superior identification performance in nonlinear charac-
teristics compared with conventional two-stage GCA, which will be more available in further
functional brain network investigation. Meanwhile, we found that the nonlinear characteristics
of high-order terms and cross-terms will be successively drowned out by the increasing noise
level. Especially for the real fMRI data, we suggest that a simple linear modeling procedure for
causal investigation may be appropriate enough.
On the other hand, uGCA methods can deal with different kinds of the noise terms auto-
matically due to its model selection strategy involving modeling the noise term. And adopt-
ing a minimax solution for the inherent redundancy in earlier coding scheme, uGCA-NML
method ensures a sharper description length with stochastic complexity and universal pro-
cess, which actually applies a normalized maximum likelihood coding form for the gener-
alized model selection issues. In this sense, uGCA-NML method can provide a more
generic scheme for nonlinear modeling of causal connections. On the contrary, conven-
tional GCA need additional techniques to accommodate different noise sources, which
further bring in the inconsistency of mathematical theories and the subjectivity in model
selection. Specifically, these will lead to more false positives and false negatives in the
causal identification.
AUTHOR CONTRIBUTIONS
Fei Li: Conceptualization; Data curation; Formal analysis; Investigation; Methodology;
Resources; Software; Validation; Visualization; Writing – original draft; writing – review &
editing. Qiang Lin: Funding acquisition; Supervision. Xiaohu Zhao: Funding acquisition;
Project administration; Resources. Zhenghui Hu: Conceptualization; Funding acquisition;
Project administration; Writing – review & editing.
FUNDING INFORMATION
Zhenghui Hu, National Key Research and Development Program of China, Award ID:
2018YFA0701400. Zhenghui Hu, Public Projects of Science Technology Department of
Zhejiang Province, Award ID: LGF20H180015. Xiaohu Zhao, Science and Technology Com-
mission of Shanghai Municipality, Award ID: 201409002200.
Network Neuroscience
1126
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
a
_
0
0
3
1
6
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
REFERENCES
Alcalá-López, D., Smallwood, J., Jefferies, E., Van Overwalle, F.,
Vogeley, K., Mars, R. B., … Bzdok, D. (2018). Computing the
social brain connectome across systems and states. Cerebral Cor-
tex, 28(7), 2207–2232. https://doi.org/10.1093/cercor/bhx121,
PubMed: 28521007
Amrhein, V., Greenland, S., & McShane, B. (2019). Scientists rise
up against statistical significance. Nature, 567(7748), 305–307.
https://doi.org/10.1038/d41586-019-00857-9, PubMed:
30894741
Barnett, L., Barrett, A. B., & Seth, A. K. (2018). Misunderstandings
regarding the application of Granger causality in neuroscience.
Proceedings of the National Academy of Sciences, 115(29),
E6676–E6677. https://doi.org/10.1073/pnas.1714497115,
PubMed: 29991604
Barnett, L., & Seth, A. K. (2014). The MVGC multivariate granger
causality toolbox: A new approach to Granger-causal inference.
Journal of Neuroscience Methods, 223, 50–68. https://doi.org/10
.1016/j.jneumeth.2013.10.018, PubMed: 24200508
Barron, A., Rissanen, J., & Yu, B. (1998). The minimum description
length principle in coding and modeling. IEEE Transactions on
Information Theory, 44(6), 2743–2760. https://doi.org/10.1109
/18.720554
Benjamin, D. J., Berger, J. O., Johannesson, M., Nosek, B. A.,
Wagenmakers, E.-J., Berk, R., … Johnson, V. E. (2018). Redefine
statistical significance. Nature Human Behaviour, 2(1), 6–10.
https://doi.org/10.1038/s41562-017-0189-z, PubMed: 30980045
Bright, M. G., & Murphy, K. (2015). Is fMRI noise really noise? Rest-
ing state nuisance regressors remove variance with network
structure. NeuroImage, 114, 158–169. https://doi.org/10.1016/j
.neuroimage.2015.03.070, PubMed: 25862264
Bryant, P. G., & Cordero-Brana, O. I. (2000). Model selection using the
minimum description length principle. The American Statistician,
54(4), 257–268. https://doi.org/10.1080/00031305.2000.10474558
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038
/nrn2575, PubMed: 19190637
Chen, Y., Bressler, S. L., & Ding, M. (2006). Frequency decomposi-
tion of conditional Granger causality and application to multivar-
iate neural field potential data. Journal of Neuroscience Methods,
150(2), 228–237. https://doi.org/10.1016/j.jneumeth.2005.06
.011, PubMed: 16099512
Chen, Y., Rangarajan, G., Feng, J., & Ding, M. (2004). Analyzing
multiple nonlinear time series with extended Granger causality.
Physics Letters A, 324(1), 26–35. https://doi.org/10.1016/j
.physleta.2004.02.032
Chen, Z. T., Zhang, K., Chan, L. W., & Schölkopf, B. (2014). Causal
discovery via reproducing kernel Hibert space embedding. Neu-
ral Computation, 26(7), 1484–1517. https://doi.org/10.1162
/NECO_a_00599, PubMed: 24708374
D’Souza, A. M., Abidin, A. Z., Leistritz, L., & Wismüller, A. (2017).
Exploring connectivity with large-scale Granger causality on
resting-state functional MRI. Journal of Neuroscience Methods,
287, 68–79. https://doi.org/10.1016/j.jneumeth.2017.06.007,
PubMed: 28629720
Faisal, A. A., Selen, L. P., & Wolpert, D. M. (2008). Noise in the
nervous system. Nature Reviews Neuroscience, 9(4), 292–303.
https://doi.org/10.1038/nrn2258, PubMed: 18319728
Farokhzadi, M., Hossein-Zadeh, G.-A., & Soltanian-Zadeh, H.
(2018). Nonlinear effective connectivity measure based on adap-
tive neuro fuzzy inference system and Granger causality. Neuro-
Image, 181, 382–394. https://doi.org/10.1016/j.neuroimage
.2018.07.024, PubMed: 30010006
Friston, K. J. (2000). The labile brain. I. Neuronal transients and
nonlinear coupling. Philosophical Transactions of the Royal
Society of London. Series B: Biological Sciences, 355(1394),
215–236. https://doi.org/10.1098/rstb.2000.0560, PubMed:
10724457
Geweke, J. (1982). Measurement of linear dependence and feed-
back between multiple time series. Journal of the American
Statistical Association, 77(378), 304–313. https://doi.org/10
.1080/01621459.1982.10477803
Granger, C., & Newbold, P. (1974). Spurious regressions in econo-
metrics. Journal of Econometrics, 2, 111–120. https://doi.org/10
.1016/0304-4076(74)90034-7
Granger, C. W. J. (1969). Investigating causal relations by econo-
metric models and cross-spectral methods. Econometrica,
37(3), 424–438, https://doi.org/10.2307/1912791
Grove, J., Ripke, S., Als, T. D., Mattheisen, M., Walters, R. K., Won,
H., … Børglum, A. D. (2019). Identification of common genetic
risk variants for autism spectrum disorder. Nature Genetics,
51(3), 431–444. https://doi.org/10.1038/s41588-019-0344-8,
PubMed: 30804558
Grünwald, P. D., Myung, I. J., & Pitt, M. A. (2005). Advances in
minimum description length: Theory and applications. Cam-
bridge, MA: MIT Press. https://doi.org/10.7551/mitpress/1114
.001.0001
Guo, H., Zeng, W., Shi, Y., Deng, J., & Zhao, L. (2020). Kernel
Granger causality based on back propagation neural network
fuzzy inference system on FMRI data. IEEE Transactions on Neu-
ral Systems and Rehabilitation Engineering, 28(5), 1049–1058.
https://doi.org/10.1109/ TNSRE.2020.2984519, PubMed:
32248114
Hacker, R. S., & Hatemi-J, A. (2006). Tests for causality between
integrated variables using asymptotic and bootstrap distributions:
Theory and application. Applied Economics, 38(13), 1489–1500.
https://doi.org/10.1080/00036840500405763
Hansen, M. H., & Yu, B. (2001). Model selection and the principle
of minimum description length. Journal of the American Statis-
tical Association, 96(454), 746–774. https://doi.org/10.1198
/016214501753168398
Hatemi-J, A. (2012). Asymmetric causality tests with an application.
Empirical Economics, 43(1), 447–456. https://doi.org/10.1007
/s00181-011-0484-x
Hu, Z., Li, F., Cheng, M., & Lin, Q. (2022). Investigating large-scale
network with unified Granger causality analysis. Computational
and Mathematical Methods in Medicine, 2022, 6962359.
https://doi.org/10.1155/2022/6962359
Hu, Z., Li, F., Cheng, M., Shui, J., Tang, Y., & Lin, Q. (2021). Robust
unified Granger causality analysis: A normalized maximum
Network Neuroscience
1127
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
a
_
0
0
3
1
6
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nonlinear unified Granger causality analysis
likelihood form. Brain Informatics, 8(1), 1–11. https://doi.org/10
.1186/s40708-021-00136-2, PubMed: 34363137
Hu, Z., Li, F., Wang, X., & Lin, Q. (2021). Description length guided
unified Granger causality analysis. IEEE Access, 9, 13704–13716.
https://doi.org/10.1109/ACCESS.2021.3051985
Kaminski, M. (2007). Multichannel data analysis in biomedical
research. (2nd ed.). Pacific Grove, CA: Duxbury Resource Center.
https://doi.org/10.1007/978-3-540-71512-2_11
Li, F., Cheng, M., Chu, L., Zhang, Y., Zhao, X., Lin, Q., & Hu, Z.
(2023). Investigating dynamic causal network with unified
Granger causality analysis. Journal of Neuroscience Methods,
383, 109720. https://doi.org/10.1016/j.jneumeth.2022.109720,
PubMed: 36257377
Li, F., Wang, X., Lin, Q., & Hu, Z. (2020). Unified model selection
approach based on minimum description length principle in
Granger causality analysis. IEEE Access, 8, 68400–68416.
https://doi.org/10.1109/ACCESS.2020.2987033
Li, S., Xiao, Y., Zhou, D., & Cai, D. (2018). Causal inference in non-
linear systems: Granger causality versus time-delayed mutual
information. Physical Review E, 97(5), 052216. https://doi.org
/10.1103/PhysRevE.97.052216, PubMed: 29906860
Li, Y., Wei, H.-L., Billings, S. A., & Liao, X.-F. (2012). Time-varying
linear and nonlinear parametric model for Granger causality
analysis. Physical Review E, 85(4), 041906. https://doi.org/10
.1103/PhysRevE.85.041906, PubMed: 22680497
Liao, W., Marinazzo, D., Pan, Z., Gong, Q., & Chen, H. (2009).
Kernel Granger causality mapping effective connectivity on
fMRI data. IEEE Transactions on Medical Imaging, 28(11),
1825–1835. https://doi.org/10.1109/ TMI.2009.2025126,
PubMed: 19709972
Lord, C., Brugha, T. S., Charman, T., Cusack, J., Dumas, G., Frazier,
T., … Veenstra-VanderWeele, J. (2020). Autism spectrum disorder.
Nature Reviews Disease Primers, 6(1), 1–23. https://doi.org/10
.1038/s41572-019-0138-4, PubMed: 31949163
Lord, C., Elsabbagh, M., Baird, G., & Veenstra-Vanderweele, J.
(2018). Autism spectrum disorder. The Lancet, 392(10146),
508–520. https://doi.org/10.1016/S0140-6736(18)31129-2,
PubMed: 30078460
Marinazzo, D., Pellicoro, M., & Stramaglia, S. (2008). Kernel
method for nonlinear Granger causality. Physical Review Letters,
100(14), 144103. https://doi.org/10.1103/ PhysRevLett.100
.144103, PubMed: 18518037
Ning, L., & Rathi, Y. (2017). A dynamic regression approach for
frequency-domain partial coherence and causality analysis of
functional brain networks. IEEE Transactions on Medical Imaging,
37(9), 1957–1969. https://doi.org/10.1109/TMI.2017.2739740,
PubMed: 28816657
Rissanen, J. (1978). Modeling by shortest data description. Automatica,
14(5), 465–471. https://doi.org/10.1016/0005-1098(78)90005-5
Rissanen, J. (2000). MDL denoising. IEEE Transactions on Informa-
tion Theory, 46(7). 2537–2543. https://doi.org/10.1109/18
.887861
Rissanen, J. J. (1996). Fisher information and stochastic complexity.
IEEE Transactions on Information Theory, 42(1), 40–47. https://doi
.org/10.1109/18.481776
Shojaie, A., & Fox, E. B. (2022). Granger causality: A review and recent
advances. Annual Review of Statistics and Its Application, 9,
289–319. https://doi.org/10.1146/annurev-statistics-040120-010930
Sicile-Kira, C., & Grandin, T. (2014). Autism spectrum disorder
(revised): The complete guide to understanding autism. East Ruth-
erford, NJ: Penguin.
Stokes, P. A., & Purdon, P. L. (2017). A study of problems encoun-
tered in Granger causality analysis from a neuroscience perspec-
tive. Proceedings of the National Academy of Sciences of the
United States of America, 114(34), E7063–E7072. https://doi.org
/10.1073/pnas.1704663114, PubMed: 28778996
Talebi, N., Nasrabadi, A. M., Mohammad-Rezazadeh, I., & Coben, R.
(2019). nCREANN: Nonlinear causal relationship estimation by
artificial neural network; Applied for autism connectivity study.
IEEE Transactions on Medical Imaging, 38(12), 2883–2890.
https://doi.org/10.1109/TMI.2019.2916233, PubMed: 31094685
Tank, A., Covert, I., Foti, N., Shojaie, A., & Fox, E. (2018). Neural
Granger causality for nonlinear time series. arXiv:1802.05842.
https://doi.org/10.48550/arXiv.1802.05842
Uddin, L. Q. (2020). Bring the noise: Reconceptualizing spontane-
ous neural activity. Trends in Cognitive Sciences, 24(9), 734–746.
https://doi.org/10.1016/j.tics.2020.06.003, PubMed: 32600967
Wang, X., Wang, R., Li, F., Lin, Q., Zhao, X., & Hu, Z. (2020). Large-
scale granger causal brain network based on resting-state fMRI
data. Neuroscience, 425, 169–180. https://doi.org/10.1016/j
.neuroscience.2019.11.006, PubMed: 31794821
Wasserstein, R. L., & Lazar, N. A. (2016). The ASA’s statement on
p-values: context, process, and purpose. The American Statistician,
70(2), 129–133. https://doi.org/10.1080/00031305.2016.1154108
Wismüller, A., Dsouza, A. M., Vosoughi, M. A., & Abidin, A.
(2021). Large-scale nonlinear Granger causality for inferring
directed dependence from short multivariate time-series data.
Scientific Reports, 11(1), 1–11. https://doi.org/10.1038/s41598
-021-87316-6, PubMed: 33837245
Yang, G., Wang, L., & Wang, X. (2017). Reconstruction of complex
directional networks with group lasso nonlinear conditional
granger causality. Scientific Reports, 7(1), 1–14. https://doi.org
/10.1038/s41598-017-02762-5, PubMed: 28592807
Zou, C. L., Ladroue, C., Guo, S. X., & Feng, J. F. (2010). Identifying
interactions in the time and frequency domains in local and
global networks—A Granger causality approach. BMC Bioinfor-
matics, 11, 337. https://doi.org/10.1186/1471-2105-11-337,
PubMed: 20565962
Network Neuroscience
1128
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
7
3
1
1
0
9
2
1
5
4
8
6
1
n
e
n
_
a
_
0
0
3
1
6
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3