RECHERCHE - Recherche en IA spécialisée au MIT

RECHERCHE

Fast-local and slow-global neural
ensembles in the mouse brain

Thomas J. Delaney1 and Cian O’Donnell1,2

1School of Computer Science, Electrical and Electronic Engineering, and Engineering Mathematics,
University of Bristol, Bristol, ROYAUME-UNI
2School of Computing, Engineering and Intelligent Systems, Ulster University, Derry/ Londonderry, ROYAUME-UNI

Mots clés: Neural ensembles, Neural correlations, Whole-brain computation, Multi-timescale,
Electrophysiology

un accès ouvert

journal

ABSTRAIT

Ensembles of neurons are thought to be coactive when participating in brain computations.
Cependant, it is unclear what principles determine whether an ensemble remains localised
within a single brain region, or spans multiple brain regions. To address this, we analysed
electrophysiological neural population data from hundreds of neurons recorded
simultaneously across nine brain regions in awake mice. At fast subsecond timescales, spike
count correlations between pairs of neurons in the same brain region were stronger than for
pairs of neurons spread across different brain regions. In contrast at slower timescales, within-
and between-region spike count correlations were similar. Correlations between high-firing-
rate neuron pairs showed a stronger dependence on timescale than low-firing-rate neuron
pairs. We applied an ensemble detection algorithm to the neural correlation data and found
that at fast timescales each ensemble was mostly contained within a single brain region,
whereas at slower timescales ensembles spanned multiple brain regions. These results suggest
that the mouse brain may perform fast-local and slow-global computations in parallel.

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d

Citation: Delaney, T. J., & O’Donnell, C.
(2023). Fast-local and slow-global
neural ensembles in the mouse brain.
Neurosciences en réseau, 7(2), 731–742.
https://doi.org/10.1162/netn_a_00309

EST CE QUE JE:
https://doi.org/10.1162/netn_a_00309

Reçu: 28 Septembre 2022
Accepté: 8 Février 2023

Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.

Auteur correspondant:
Cian O’Donnell
c.odonnell2@ulster.ac.uk

Éditeur de manipulation:
Arvind Kumar

droits d'auteur: © 2023
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence

La presse du MIT

RÉSUMÉ DE L'AUTEUR

In this study we analysed publicly available neural population electrophysiology data from
nine brain regions in awake mice. To discover neural ensembles, we applied community
detection algorithms to the spike count correlation matrices estimated from the data. Nous
repeated the analysis at different timescales, ranging from 10 milliseconds to 3 seconds. Nous
found that at fast timescales < 1 s, neural ensembles tended to be localised within single brain regions. In contrast at slower timescales of > 1 s, ensembles tended to include neurons spread
across multiple brain regions. Most of this effect was due to high-firing-rate neurons.

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

INTRODUCTION

The brain is traditionally parcellated into anatomical regions that perform distinct computa-
tion (Zilles & Amunts, 2010). Cependant, these regions do not operate independently: success-
ful brain function must also involve computations spread over multiple regions (Bassett &
Bullmore, 2009; Power et al., 2011; Sporns & Betzel, 2016). It is unclear how local compu-
tations within a single brain region are coordinated with global computations spread across

Fast-local and slow-global neural ensembles in the mouse brain

Brain region:
Anatomical subpart of the brain,
typically defined by connectivity or
architecture, often assumed to be
semispecialised for particular
cognitive functions.

Timescale:
An approximate length of time over
which some given processes may
typically occur.

many brain regions. Several possibilities have been proposed: synchronous oscillatory activity
may bind together spatially separated neural signals (Berger, Warren, Normann, Arieli, & Grün,
2007; Ange, Schölvinck, & Lewis, 2021; Fries, 2015; Gray, Konig, Ange, & Chanteur, 1989;
Siegel, Donner, & Ange, 2012); travelling waves may propagate signals across the cortex
(Muller, Chavane, Reynolds, & Sejnowski, 2018); or a hierarchy of timescales may separate
low-level sensory processing from higher level cognitive computations in the brain (Murray
et coll., 2014; Siegle et al., 2021; Zeraati et al., 2023).

Here we tested the hypothesis that computations are local to single brain regions at fast

timescales, but spread across multiple regions at slower timescales.

Spike count correlations:
Neurons communicate by emitting
action potentials, or spikes. The rate
of these spikes tends to be correlated
between pairs of neurons. Spike
count correlation is a statistical
measure of the strength of this
correlation.

RÉSULTATS

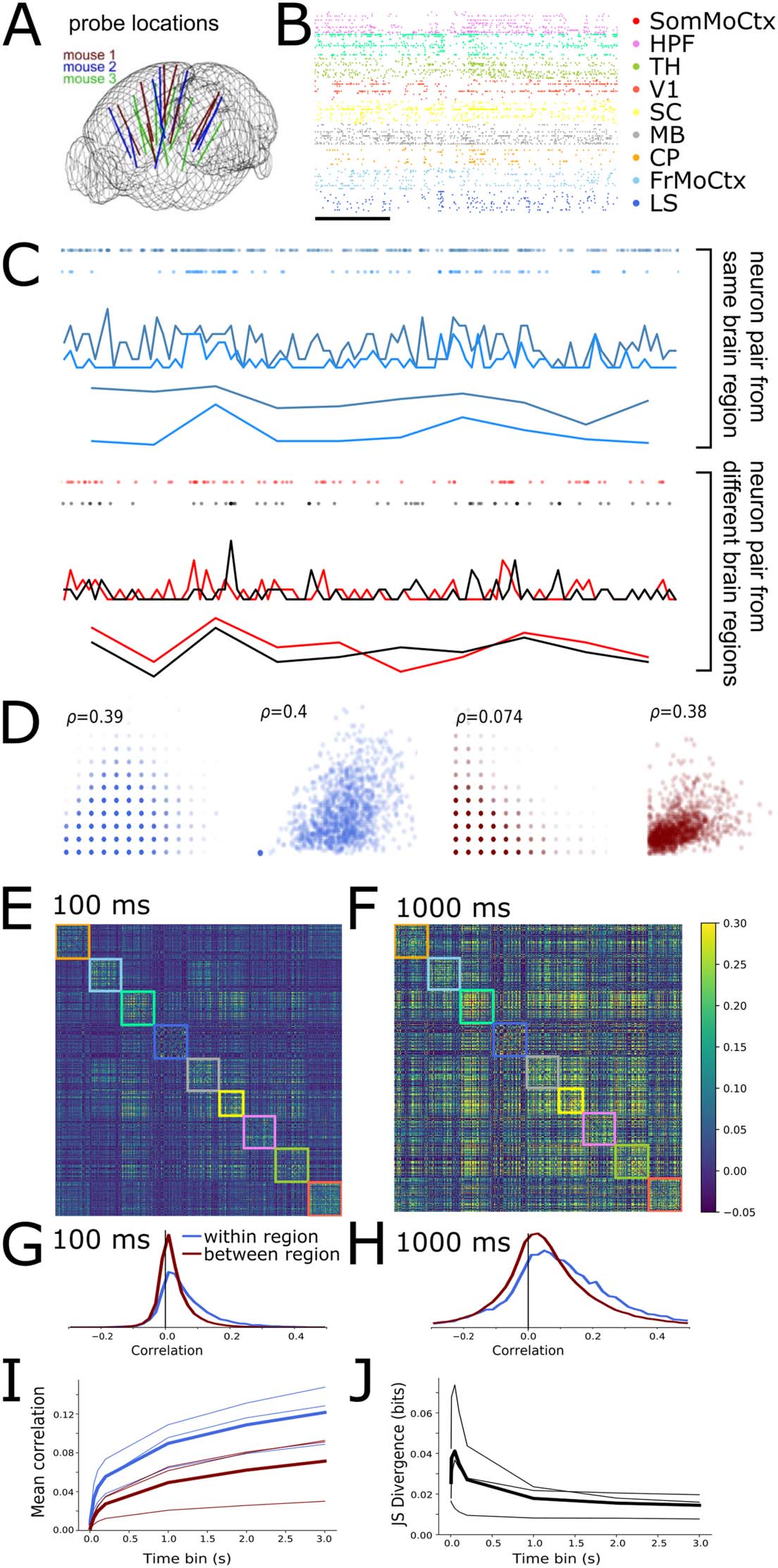
Spatial Extent of Neural Correlations Varies With Timescale

We first characterised the magnitudes of within- and between-region neural spike count correla-
tions by analysing previously published data from ∼500 neurons recorded simultaneously across
nine brain regions (frontal, sensorimotor, visuel, and retrosplenial cortex, hippocampus, striatum,
thalamus, and midbrain) in awake mice (Steinmetz, Pachitariu, Stringer, Carandini, & Harris,
2019; Stringer et al., 2019) (Figure 1A and B). We calculated spike count correlations for each
pair of neurons in the dataset over a range of different time bin widths, depuis 10 ms to 3 s.

Figure 1C shows example 10-s raster plots and corresponding spike count time series from a
pair of neurons within the same brain region (light and dark blue, top) and a pair of neurons
from two different brain regions (red and black, bottom) for both 100-ms and 1-s time bins. Nous
choose these two timescales as representative examples throughout the paper. Figure 1D shows
scatter plots of the spike counts for the same neuron pairs. The within-region cell pair showed
the same high spike count correlation of ρ ≈ 0.4 at both 100-ms and 1-s time bins. In contrast,
the between-region pair showed a low spike count correlation of 0.07 at fast 100-ms time bins,
but a high correlation of 0.4 at slower 1-s time bins. This general pattern held up across the
dataset: Figure 1E shows the pairwise correlation matrices for all 494 neurons analysed from
this animal for both the 100-ms and 1-s time bin sizes. The rows and columns of these matrices
are ordered by brain region, so within-region correlations are inside the coloured boxes along
the main diagonal (each colour represents a different brain region). With 100-ms bins, le
within-region correlations appear stronger than the between-region correlations. Cependant,
with 1-s time bins, the within- and between-region correlations appear visually similar. À
explore this phenomenon, we separately histogrammed the within- and between-region values
from the correlation matrices (Figure 1G and H). Both the mean (Figure 1I) and the width of
correlation histograms increased with time bin size, for both within- and between-region cor-
relations (Bair, Zohary, & Newsome, 2001). Cependant, the within-region correlations had a
heavier positive tail than the between-region correlations at fast timescales, but markedly less
so at slow timescales (Figure 1G and H). To quantify this effect, we calculated the Jensen–
Shannon ( JS) divergence between the two distributions. High divergence values imply greater
differences in the distributions. Indeed the JS divergence decreased as a function of time bin
size, consistently for the data from all three animals (Figure 1J). These results imply that at
fast timescales, correlations are high only between neurons within brain regions, but at slow
timescales within- and between-region neural correlations are similar.

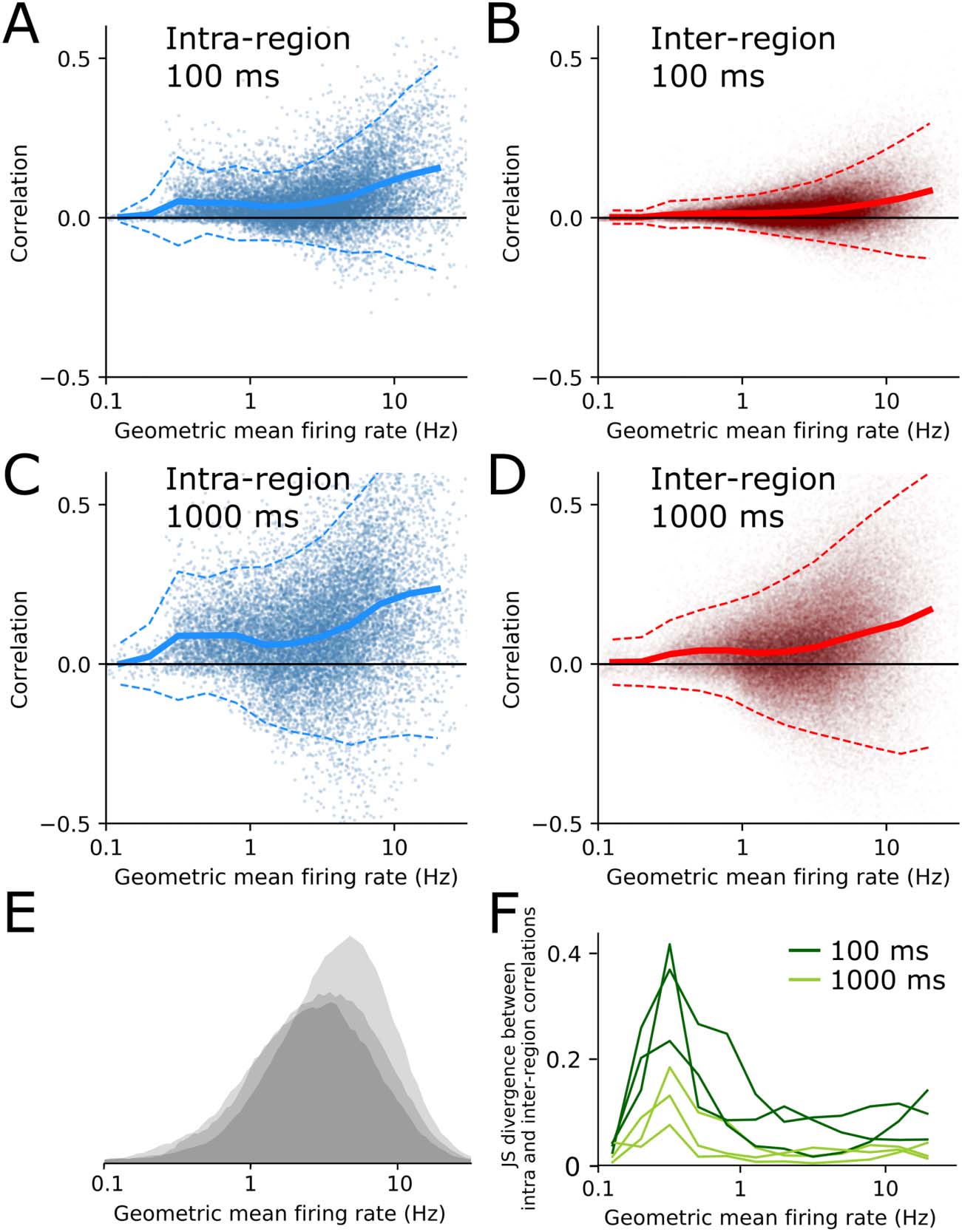
Low-Firing-Rate Neurons Preferentially Correlate Within Brain Region

Low- and high-firing-rate neurons have previously been shown to serve different functions in
neural circuits (Gava et al., 2021; Levenstein, Watson, Rinzel, & Buzsáki, 2017). To test whether

Neurosciences en réseau

732

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Fast-local and slow-global neural ensembles in the mouse brain

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 1. Within- and between-region neural correlations are more similar at slow timescales than fast timescales. (UN) Neuropixels probe loca-
tions in the three mouse brains (adapted from Stringer et al., 2019). (B) Raster plot of spikes from 198 sample units from one mouse. Scale bar
corresponds to 1 s. (C) Spike count time series from a pair of neurons recorded in the same brain region (top) and pair recorded from different
régions (bottom). (D) Scatter plots of all spike counts for same pairs of neurons shown in panel C. The x-axis shows spike count from one neuron,
y-axis spike counts from the other neuron. From left to right: within region pair at 100-ms and 1,000-ms time bins; different-region pair at 100-ms
and 1,000-ms time bins. Inset indicates pairwise spike count correlation coefficient. (E and F) Correlation matrix for spike counts from 494 nouveau-
rons recorded from one animal with a time bin of 100 ms (E) ou 1 s (F). (G and H) Histograms of pairwise correlations from matrices in C and D for
within- and between-region pairs of neurons (colours blue and red respectively) for 100-ms (G) ou 1 s (H) time bins. (je) Mean pairwise correlations
as a function of time bin. ( J.) Jensen–Shannon divergence of within versus between-region correlation distributions as a function of time bin.

Neurosciences en réseau

733

Fast-local and slow-global neural ensembles in the mouse brain

this dissociation is also visible in the within- versus between-region correlation structure, nous
plotted correlation values against geometric mean firing rate for each pair of neurons in the data-
ensemble (Figure 2A–D). Most pairs of neurons had geometric mean firing rates between 1–10 Hz
(Figure 2E). Correlations tended to get stronger as a function of firing rate, for both within- et
between-region pairs (Figure 2A–D) (de la Rocha, Doiron, Shea-Brown, Josić, & Reyes, 2007). Nous
binned pairs by their geometric mean firing rate and calculated the JS divergence between the
within- and between-region correlations as a function of firing rate bin (Figure 2F). At both fast
and slow timescales, low-firing-rate pairs had stronger within-region correlations than between-
region correlations. In contrast, high-firing-rate pairs had moderate divergence at 100-ms time
bins and almost zero divergence at 1-s time bins. This implies that high-firing-rate neurons

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Low-firing-rate neurons preferentially correlate within brain regions. (A–D) Pairwise neu-
Chiffre 2.
ral correlations versus geometric mean of firing rate for many pairs from one animal, for intra (A and
C) and inter (B and D) region neuron pairs, with time bin interval shown in panel insets. Solid line
shows mean correlation, dashed lines are ± 2 SD from mean. (E) Histograms of all pairwise geo-
metric mean firing rates for all three animals. (F) Jensen–Shannon divergence between intra- et
interregion correlations as a function of geometric mean firing rate, for all three animals. Dark green
corresponds to spikes binned at 100-ms intervals, light green is 1,000-ms intervals.

Neurosciences en réseau

734

Fast-local and slow-global neural ensembles in the mouse brain

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

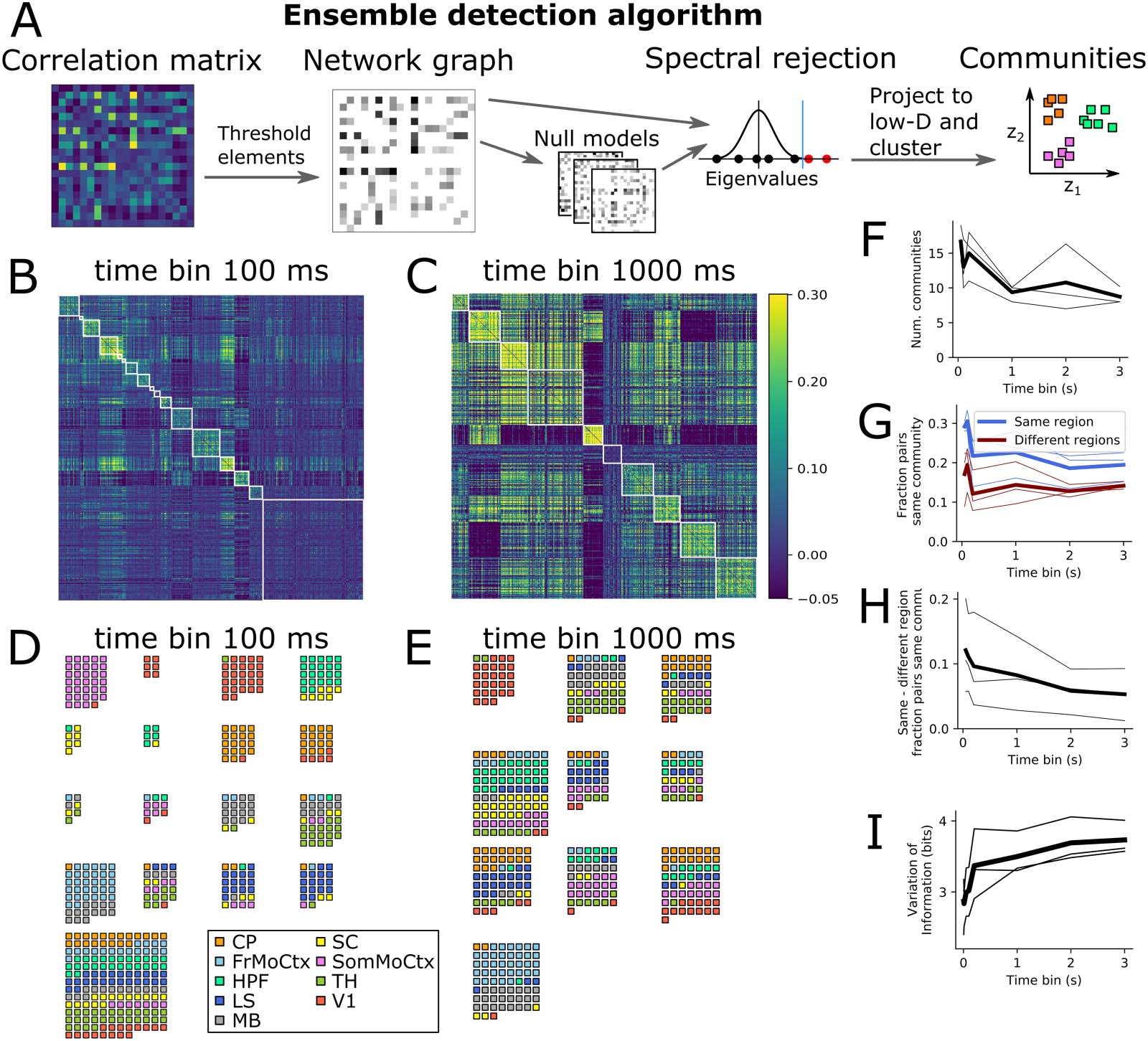
Chiffre 3. Neural ensembles are within-region at fast timescales but multiregion at slow timescales. (UN) Schematic diagram of community
detection algorithm steps. (B, C) Same correlation matrices as Figure 1 sorted by ensemble. (D, E) Example ensembles at short (D) and long (E)
timescales. (F) Number of detected ensembles versus time bin size. (G) Fraction of same and different region neuron pairs being in same
community, versus time bin size. (H) Difference in fraction of same and different region neuron pairs being in same community (same data
as panel G). (je) Variation of information (measure of dissimilarity of anatomical versus ensemble partitions) versus time bin size.

correlate almost equally strongly within- and between-regions, but low-firing-rate pairs have
similarly low within- and between-region correlations at all timescales. Therefore the phenom-
enon seen in Figure 1 is mainly due to high-firing-rate neuron pairs.

Detected Ensembles Align With Anatomical Regions at Short Time Bins, But Not Long Time Bins

To test if neural ensembles also showed different structure at fast and slow timescales, we ran a
community detection algorithm from network science on the correlation matrices to detect
ensembles (Figure 3A) (Humphries, Caballero, Evans, Maggi, & Singh, 2021). The algorithm
splits the neurons into nonoverlapping subsets based on their correlations, trying to discover
ensembles of neurons with strong positive correlations between the members of each ensemble,
but weaker correlations with neurons in other ensembles (Methods). Figure 3B and C shows the
same example correlation matrices from Figure 1E, but with the rows and columns reordered by
ensemble membership. In all three animals we found fewer ensembles at longer time bin sizes
(Figure 3F). Surtout, the ensemble detection algorithm did not know anything about which
brain regions each neuron belonged to. To visualise the brain region membership of each
ensemble, we plotted a small square for each neuron coloured according to its brain region

Neural ensemble:
A group of neurons that are often
active at the same time, likely
participating in a collective
representation or computation.

Community detection algorithm:
An algorithm which tries to split
items into groups such that the
connections between items in a
group tend to be stronger than for
items in different groups.

Neurosciences en réseau

735

Fast-local and slow-global neural ensembles in the mouse brain

(Figure 3D and E). At 100-ms time bins, most ensembles contained neurons from only a small
number of brain regions, whereas at 1-s time bins almost all ensembles contained neurons from
several brain regions. To quantify this effect, we asked the following questions: what is the prob-
ability that any arbitrary neuron pair is in the same ensemble? And does this differ for pairs of
neurons within the same brain region versus pairs across two brain regions? Some 20–30% of
same-region pairs were in the same ensemble, but only 10–20% of different-region pairs were in
the same ensemble (Figure 3G). The difference between these two fractions decreased towards
zero as a function of time bin size (Figure 3H), implying that at fast timescales neurons in the
same brain region had a higher chance of being in the same ensemble than two neurons in
different brain regions, but this distinction got weaker at slower timescales. To further quantify
the effect, we used a distance measure from information theory to ask the following question:
how different are the sets of neuron groups when defined by brain region versus defined by
ensemble? (Methods: Clustering Comparison). This ‘variation of information’ measure increased
as a function of time bin size in all three animals (Figure 3I), again implying that anatomical
regions and neural activity ensembles are more similar at fast timescales than slow timescales.

DISCUSSION

Although previous studies have compared within- and between-region neural correlations, à
our knowledge none have described the fast-local versus slow-global ensembles phenomenon
we presented here. There are a few possible reasons for this gap: most electrophysiological
studies either looked at small numbers of neurons where the phenomenon may not be statis-
tically detectable, or looked at aggregate neural activity measures such as local field potentials
(Engel et al., 2021) that would miss the single-neuron-resolution ensembles we discovered.
Modern large-scale two-photon imaging methods do enable simultaneous recordings from sin-
gle neurons in multiple brain regions, but with poorer signal-to-noise and slow sampling rate,
so also may not be able detect the phenomenon we described. Noninvasive methods for
recording brain activity such as functional magnetic resonance imaging, magneto- and elec-
troencephalography do not have high enough spatial resolution to isolate single neurons, donc
will not be able to resolve these ensembles which are often spatially intermingled.

We examined this phenomenon only for nine particular brain regions, which despite all
exhibiting the effect, differed in their mean firing rates and correlations (Stringer et al.,
2019), and presumably also differ in the computations that they perform for the brain at large.
It would be interesting to try to understand if and how each brain region adapts variations of
the general fast-local, slow-global principle and relate it to its overall function. Par exemple, it
may be the case that region pairs that have strong, direct anatomical connections between
eux (Oh et al., 2014) show stronger correlations, or prefer to correlate on fast timescales.

There are several important limitations to our analysis. D'abord, we used Pearson’s correlation as
our measure of coactivity between neurons. This captures only linear dependencies so may
miss nonlinear interactions, but crucially is also averaged over the entire 1-hour recordings.
Therefore it may miss transient coactivity events such as ripple oscillations, which can synchro-
nize neural activity across multiple brain regions (Jadhav, Rothschild, Roumis, & Frank, 2016).
Deuxième, we defined ensembles as groups of neurons with positively correlated activity, lequel
ignores the fact that negative correlations may also be indicative of an interaction between neu-
rons. Cependant, we found qualitatively consistent results when we ran our ensemble detection
algorithm on graphs defined by absolute values of the correlations. In contrast, running the
algorithm based on only negative-correlation interactions did not reproduce the fast-local ver-
sus slow global effect. Troisième, we assumed for simplicity that ensembles were nonoverlapping.

Neurosciences en réseau

736

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Fast-local and slow-global neural ensembles in the mouse brain

Cependant, the correlation matrices in Figure 3B and C show substantial structure outside the
detected communities, which implies that at least some neurons participate in multiple ensem-
bles. It would be interesting for future studies to explore the fast-local, slow-global phenomenon
in overlapping neuron groups using alternative community detection algorithms (Xie, Kelley, &
Szymanski, 2013). Fourth, we examined neural coactivity only in the time range of 10 ms to 3 s,
but there may well be important coactivity dynamics at both faster and slower timescales. Pour
fast timescales, 1–10 ms, spike count correlations would not be an appropriate measure
because most neurons in this dataset fired at <10 Hz (Figure 2E), so almost all time bins would have zero spike counts and correlations would be very close to 1I). Future studies exploring fast timescales could use alternative measures, such as cross-correlograms (Berger et al., 2007; Cohen & Kohn, 2011). Conversely, there may also interesting cross-brain neural ensemble dynamics at the ‘infraslow’ ∼10–100 s, which has previously been shown have qualitatively different features neural population timescales (Okun, Steinmetz, Lak, Dervinis, Harris, 2019). It is important note that these results do not imply local computations are while all global slow. Indeed, Figure 3D shows some evidence for mixed-region ensembles timescales. There established counter-examples phenomenon, such>1-s cell-intrinsic persistent spiking activity (Egorov, Hamam, Fransén, Hasselmo, &
Alonso, 2002; Lüthi & McCormick, 1999), and >100 Hz fast ripple oscillations that synchronize
distal brain regions (Jadhav et al., 2016). We also did not explore how these effects vary with the
behavioral state of the animal, or the sensory stimuli it is exposed to. Par exemple, behavioral-
state fluctuations have widespread effects on neural activity across the brain at >1-s timescales
(Stringer et al., 2019). Therefore it may be that behavioral-state changes are a major contributor
to the slow-global coordination effects we report—future studies could assess this by manipu-
lating animal behavior or by statistically regressing out the effect of behaviour measures on
neural coactivity. En résumé, we consider the fast-local, slow-global phenomenon we
describe here as only an average tendency for neural activity coordination in the mouse brain,
which may act as a scaffold for other spatiotemporal dynamical structures to rest upon.

Why might the fast-local versus slow-global dissociation exist? From a mechanistic point of
voir, one explanation may be that the energetic and space constraints on brain wiring imply that
long-range, between-region signals can be transmitted only at low bandwidth and with some
latency (Sterling & Laughlin, 2015). There are typically fewer long-range synaptic connections
than local connections, between-region signalling is low-dimensional (Semedo, Zandvakili,
Machens, Byron, & Kohn, 2019), and mammalian axons transmit action potentials between brain
regions with latencies of 10–100 ms (Swadlow & Waxman, 2012). These bandwidth and latency
constraints will limit the speed of any computations that require back-and-forth recurrent
signalling between neurons. This issue is well known in human-made computers, where the
‘von Neumann bottleneck’ for transferring data between memory and CPU via low-bandwidth
and high-latency databuses constrains computation speed (Hennessy & Patterson, 2011). From a
functional point of view, a separation of timescales between local and global computations may
allow for less interference between processes, and allow local neural circuits to complete their
tasks quickly before broadcasting the results to other brain regions (Engel et al., 2021).

MÉTHODES

Original Data Description

All data analysed in this study were sourced from a publicly available dataset (Steinmetz et al.,
2019). The experimental procedures have been described previously (Stringer et al., 2019).

Low-dimensional:
The idea that the signal carried by a
large number of items can be
compressed and represented by a
smaller number of factors without
much loss of information.

Neurosciences en réseau

737

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Fast-local and slow-global neural ensembles in the mouse brain

Briefly, eight Neuropixel probes were used to record electrophysiological activity simulta-
neously from nine brain areas: frontal, sensorimotor, visuel, and retrosplenial cortex, hippo-
campus, striatum, thalamus, and midbrain, in each of three 10-to-16-week-old mice. The mice
were awake but head-fixed; 2,296, 2,668, et 1,462 stable units were isolated from each
mouse, respectivement, across a ∼1-hour recording. Spikes were sorted using the Kilosort2 algo-
rithm (Stringer et al., 2019). The published dataset lists spike times for each of the units.

Code Availability

All analyses were performed using Python, and figures were prepared using Inkscape. Le
computer code we used for calculating neural correlations is available at https://github.com
/thomasjdelaney/Regional_Correlations (Delaney, 2019).

We also implemented the community detection algorithm from Humphries et al. (2021) dans
our own Python code: https://github.com/thomasjdelaney/Network_Noise_Rejection_Python
(Delaney, 2020). Code for calculating the firing rate dependencies of correlations and for gen-
erating the figures is available at https://github.com/odonnellgroup/fast-local-slow-global
-ensembles (O’Donnell, 2023).

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

Conversion to Spike Count Data
We selected a random subset of ∼500 neurons for each mouse, approximately balancing the
number of neurons from each of the nine brain regions so as not to introduces regional biases
into our analyses. We transformed the spike timing data into binned spike count data by divid-
ing the experimental period into time bins, and counting the spikes fired by each unit per time
bin. We varied the time bin size from 10 ms to 3,000 ms.

Correlation Coefficients
We used the python function scipy.stats.pearsonr to calculate Pearson’s sample cor-
relation coefficient for spike counts from each pair of neurons:

rXY ¼

n
i¼1 xi − (cid:1)X
ð
ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
q
P.
Þ2
i¼1 xi − (cid:1)X
ð

Þ yi − (cid:1)oui
Þ
ð
ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
P.
Þ2
n
i¼1 yi − (cid:1)oui
ð

où {(xi, yi)} for i 2 {1, …, n} are the paired samples from neurons X and Y, et (cid:1)x = 1
n
et (cid:1)y = 1
n

n
i¼1 yi are the sample means.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d

(1)

n
i¼1 xi,

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Ensemble Detection Analysis

The correlation matrices can be interpreted as an undirected weighted graph between the neu-
rons, where the weight of each connection is equal to the correlation between each pair of
neurons.

The community detection algorithm we used to detect neural ensembles (Humphries et al.,
2021) is designed for networks with positively weighted connections, but many neuron pairs
were negatively correlated. To adapt the correlation matrices for the algorithm, we rectified the
network by setting all the negative weights to zero.

We also wanted to exclude any correlations that could be judged to exist ‘by chance’. To do
ce, for each neuron pair and time bin width we shuffled the spike count time series, calcu-
lated correlations from many shuffle permutations, then found the 5th and 95th percentiles of
the shuffled correlation distributions. We used these percentiles as detection thresholds for the

Neurosciences en réseau

738

Fast-local and slow-global neural ensembles in the mouse brain

data correlations and set any intermediate correlation values to 0. This excluded any ‘chance’
correlations from our network and created a sparser network.

We now give an overview of the community detection algorithm. Full details are available
in Humphries et al. (2021). Given some network represented by an adjacency matrix A, un
community within that network is defined as a collection of nodes where the number of con-
nections within these nodes is higher than the expected number of connections between these
nodes. In order to quantify the ‘expected’ number of connections, we need a model of random
networks with little or no structure, analogous to a ‘null model’ in traditional hypothesis test-
ing. Since we are working with weighted sparse networks, we used a weighted configuration
model, a canonical null network model for weighted networks. This model preserves the
degree sequence and weight sequence of each node in the data network, but with the edges
distributed randomly (Fosdick, Larremore, Nishimura, & Ugander, 2018). Any structure in the
data-derived network beyond its degree sequence and weight sequence will not be captured
by the weighted configuration model. In practice, we used an extension that also preserves
sparsity, by sampling from a probability distribution for the creation or noncreation of each
possible connection, then distributing the weight of the data network randomly in this sparse
réseau (Humphries et al., 2021). To detect the structure in the data beyond that seen in the
null model we used a spectral rejection procedure, as follows.

Given a data network matrix W and expected network of our null network model hPi, alors
the departure of our data network from the null network can be described by the ‘deviation
matrix’

B ¼ W − Ph i:

(2)

A common choice for hPi in community detection is the ‘configuration model’ (Fosdick et al.,
2018; Humphries et al., 2021).

To test for structure in the network W, we examine the eigenspectrum of B and compare it
to the eigenspectrum of the null model. Since our data model doesn’t allow self loops and is
not directed, the matrix representing the network will be symmetric and positive semidefinite,
and will therefore be invertible with real eigenvalues. We selected a null model with the same
characteristics.

To find the eigenspectrum of the null model, we generated N samples from our null model
P1, …, PN, and we measured their deviation matrices B1, …, BN. We then calculated the eigen-
spectrum of each of those samples. We calculated the upper bound of the null model eigen-
spectrum by taking the mean of the largest eigenvalues of B1, …, BN.

We then calculated the eigenspectrum of B, our data network deviation matrix. Eigenvalues
above the upper bound of the null model eigenspectrum give evidence for community struc-
ture in the data network. If there are d data eigenvalues lying outside of the null network eigen-
spectrum, the d eigenvectors corresponding to these eigenvalues form a vector space. If we
project the nodes of our network into this vector space, by projecting either rows or columns of
the data matrix, we can see how strongly each node contributes to the vector space. Nodes
that contribute strongly to the additional structure will project far away from the origin; nodes
that do not contribute to the additional structure will project close to the origin. We used this
information to discard those nodes that do not contribute.

To detect the neural ensembles, we first project all of the nodes into this d-dimensional
subspace, then perform the clustering. The clustering and community detection procedure
is described in Humphries et al. (2021).

Neurosciences en réseau

739

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Fast-local and slow-global neural ensembles in the mouse brain

In practice, the procedure is carried out n times (we chose n = 100 times); this returns n
clusterings. We resolve these n clusterings to one final clustering using consensus clustering.
We used the consensus clustering method that uses an explicit null model for the consensus
matrice, as outlined in Humphries et al. (2021).

Clustering Comparison
A clustering C is a partition of a set D into sets C1, C2, …, CK, called clusters, that satisfy the
following for all k, je 2 {1, …, K}:

Ck ∩Cl ¼ ;

K
∪
k¼1

Ck ¼ D

(3)

(4)

2, …, C0
If we consider two clusterings, C with clusters C1, C2, …, CK and C0 with clusters C0
K.
There are a number of possible measurements to compare C and C0, we used the ‘variation of
information’ ( VI). This is an information theoretical quantity based on the mutual information,
defined as

1, C0

VI X; Yð

Þ ¼ H Xð Þ þ H Yð Þ−2I X; Yð

We can rewrite this as the summation of two positive quantities

VI X; Yð

Þ ¼ H Xð Þ−I X; Yð

(cid:2) þ H Yð Þ−I X; Yð

(cid:2)
Þ

(5)

(6)

It is the summation of the uncertainty in the random variables X and Y excluding the uncer-
tainty shared by those variables. It forms a metric on the space of clusterings. C'est,

VI C; C0
ð

Þ ≥ 0

VI C; C0
ð

Þ ¼ 0 ⇔ C ¼ C0

VI C; C0
ð

Þ ¼ VI C0; C
ð

(cid:3)
VI C; C″

(cid:4)

≤ VI C; C0
ð

(cid:3)
Þ þ VI C0; C″

(cid:4)

(7)

(8)

(9)

(10)

In order to quantify the difference or similarity between the communities detected in our
correlation network and the anatomical classification of the cells in that network, we consid-
ered the communities and the anatomical regions as two different clusterings, Ccomm and Canat,
respectivement. We measured the distance between the clusterings using the variation of infor-
mation. This quantity is zero if the two clusterings are identical and large if the clusterings are
dissimilar. We calculated this quantity using custom Python code.

REMERCIEMENTS

We thank Michael Ashby for useful discussions and Nick Steinmetz for making the data public.

INFORMATIONS À L'APPUI

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00309.

Neurosciences en réseau

740

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Fast-local and slow-global neural ensembles in the mouse brain

CONTRIBUTIONS DES AUTEURS

Thomas J. Delaney: Conceptualisation; Enquête; Méthodologie; Logiciel; En écrivant -
brouillon original. Cian O’Donnell: Acquisition de financement; Enquête; Méthodologie; Logiciel;
Surveillance; Visualisation; Rédaction – ébauche originale; Rédaction – révision & édition.

INFORMATIONS SUR LE FINANCEMENT

Cian O’Donnell, Medical Research Council (https://dx.doi.org/10.13039/501100000265),
Award ID: MR/S026630/1. Cian O’Donnell, Engineering and Physical Sciences Research
Council, Award ID: EP/N509619/1.

RÉFÉRENCES

Bair, W., Zohary, E., & Newsome, W. T. (2001). Correlated firing in
macaque visual area MT: Time scales and relationship to behav-
ior. Journal des neurosciences, 21(5), 1676–1697. https://doi.org
/10.1523/JNEUROSCI.21-05-01676.2001, PubMed: 11222658
Bassett, D. S., & Bullmore, E. T. (2009). Human brain networks in
health and disease. Opinion actuelle en neurologie, 22(4), 340–347.
https://doi.org/10.1097/ WCO.0b013e32832d93dd, PubMed:
19494774

Berger, D., Warren, D., Normann, R., Arieli, UN., & Grün, S. (2007).
Spatially organized spike correlation in cat visual cortex. Neuro-
computing, 70(10–12), 2112–2116. https://est ce que je.org/10.1016/j
.neucom.2006.10.141

Cohen, M.. R., & Kohn, UN. (2011). Measuring and interpreting neu-
ronal correlations. Neurosciences naturelles, 14(7), 811–819. https://
doi.org/10.1038/nn.2842, PubMed: 21709677

Delaney, T. J.. (2019). Regional_Correlations, GitHub. https://github

.com/thomasjdelaney/Regional_Correlations

Delaney, T. J.. (2020). Network_Noise_Rejection_Python, GitHub.
https://github.com/thomasjdelaney/ Network_Noise_Rejection
_Python

de la Rocha, J., Doiron, B., Shea-Brown, E., Josić, K., & Reyes, UN.
(2007). Correlation between neural spike trains increases with
firing rate. Nature, 448(7155), 802–806. https://est ce que je.org/10.1038
/nature06028, PubMed: 17700699

Egorov, UN. V., Hamam, B. N., Fransén, E., Hasselmo, M.. E., &
Alonso, UN. UN. (2002). Graded persistent activity in entorhinal cor-
tex neurons. Nature, 420(6912), 173–178. https://est ce que je.org/10
.1038/nature01171, PubMed: 12432392

Ange, T. UN., Schölvinck, M.. L., & Lewis, C. M.. (2021). The diversity
and specificity of functional connectivity across spatial and tem-
poral scales. NeuroImage, 245, 118692. https://est ce que je.org/10.1016/j
.neuroimage.2021.118692, PubMed: 34751153

Fosdick, B. K., Larremore, D. B., Nishimura, J., & Ugander, J..
(2018). Configuring random graph models with fixed degree
sequences. Siam Review, 60(2), 315–355. https://est ce que je.org/10
.1137/16M1087175

Fries, P.. (2015). Rhythms for cognition: Communication through
coherence. Neurone, 88(1), 220–235. https://est ce que je.org/10.1016/j
.neuron.2015.09.034, PubMed: 26447583

Gava, G. P., McHugh, S. B., Lefèvre, L., Lopes-dos-Santos, V.,
Trouche, S., El-Gaby, M., … Dupret, D. (2021). Integrating new

memories into the hippocampal network activity space. Nature
Neurosciences, 24(3), 326–330. https://doi.org/10.1038/s41593
-021-00804-w, PubMed: 33603228

Gray, C. M., Konig, P., Ange, UN. K., & Chanteur, W. (1989). Oscillatory
responses in cat visual cortex exhibit inter-columnar synchroniza-
tion which reflects global stimulus properties. Nature, 338(6213),
334–337. https://doi.org/10.1038/338334a0, PubMed: 2922061
Hennessy, J.. L., & Patterson, D. UN. (2011). Computer architecture: UN

quantitative approach. Cambridge, MA: Elsevier.

Humphries, M.. D., Caballero, J.. UN., Evans, M., Maggi, S., & Singh,
UN. (2021). Spectral estimation for detecting low-dimensional
structure in networks using arbitrary null models. PLoS One,
16(7), e0254057. https://doi.org/10.1371/journal.pone
.0254057, PubMed: 34214126

Jadhav, S. P., Rothschild, G., Roumis, D. K., & Frank, L. M.. (2016).
Coordinated excitation and inhibition of prefrontal ensembles
during awake hippocampal sharp-wave ripple events. Neurone,
90(1), 113–127. https://doi.org/10.1016/j.neuron.2016.02.010,
PubMed: 26971950

Levenstein, D., Watson, B. O., Rinzel, J., & Buzsáki, G. (2017).
Sleep regulation of the distribution of cortical firing rates. Actuel
Opinion in Neurobiology, 44, 34–42. https://est ce que je.org/10.1016/j
.conb.2017.02.013, PubMed: 28288386

Lüthi, UN., & McCormick, D. UN. (1999). Modulation of a pacemaker
current through Ca2+-induced stimulation of cAMP production.
Neurosciences naturelles, 2(7), 634–641. https://est ce que je.org/10.1038
/10189, PubMed: 10404196

Muller, L., Chavane, F., Reynolds, J., & Sejnowski, T. J.. (2018).
Cortical travelling waves: Mechanisms and computational prin-
ciples. Nature Revues Neurosciences, 19(5), 255–268. https://est ce que je
.org/10.1038/nrn.2018.20, PubMed: 29563572

Murray, J.. D., Bernacchia, UN., Freedman, D. J., Romo, R., Wallis,
J.. D., Cai, X., … Wang, X.-J. (2014). A hierarchy of intrinsic time-
scales across primate cortex. Neurosciences naturelles, 17(12),
1661–1663. https://doi.org/10.1038/nn.3862, PubMed:
25383900

O’Donnell, C. (2023). Fast-local-slow-global-ensembles, GitHub.
https://github.com/odonnellgroup/fast-local-slow-global
-ensembles

Oh, S. W., Harris, J.. UN., Ng, L., Winslow, B., Cain, N., Mihalas, S., …
Zeng, H. (2014). A mesoscale connectome of the mouse brain.

Neurosciences en réseau

741

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d

b
oui
g
toi
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Fast-local and slow-global neural ensembles in the mouse brain

Nature, 508(7495), 207–214. https://est ce que je.org/10.1038
/nature13186, PubMed: 24695228

Okun, M., Steinmetz, N. UN., Lak, UN., Dervinis, M., & Harris, K. D.
(2019). Distinct structure of cortical population activity on fast
and infraslow timescales. Cortex cérébral, 29(5), 2196–2210.
https://doi.org/10.1093/cercor/bhz023, PubMed: 30796825

Power, J.. D., Cohen, UN. L., Nelson, S. M., Wig, G. S., Barnes, K. UN.,
Church, J.. UN., … Petersen, S. E. (2011). Functional network orga-
nization of the human brain. Neurone, 72(4), 665–678. https://est ce que je
.org/10.1016/j.neuron.2011.09.006, PubMed: 22099467

Semedo, J.. D., Zandvakili, UN., Machens, C. K., Byron, M.. Y., &
Kohn, UN. (2019). Cortical areas interact through a communica-
tion subspace. Neurone, 102(1), 249–259. https://est ce que je.org/10
.1016/j.neuron.2019.01.026, PubMed: 30770252

Siegel, M., Donner, T. H., & Ange, UN. K. (2012). Spectral finger-
prints of large-scale neuronal interactions. Nature Reviews Neu-
roscience, 13(2), 121–134. https://doi.org/10.1038/nrn3137,
PubMed: 22233726

Siegle, J.. H., Jia, X., Durand, S., Coup de vent, S., Bennett, C., Graddis, N., …
Koch, C.(2021). Survey of spiking in the mouse visual system
reveals functional hierarchy. Nature, 592(7852), 86–92. https://
doi.org/10.1038/s41586-020-03171-x, PubMed: 33473216

Sporns, O., & Betzel, R.. F. (2016). Modular brain networks. Annual
Review of Psychology, 67, 613–640. https://doi.org/10.1146
/annurev-psych-122414-033634, PubMed: 26393868

Steinmetz, N., Pachitariu, M., Stringer, C., Carandini, M., & Harris,
K. D. (2019). Eight-probe Neuropixels recordings during sponta-
neous behaviors. https://doi.org/10.25378/janelia.7739750.v4
Sterling, P., & Laughlin, S. (2015). Principles of neural design. Cam-
bridge, MA: AVEC Presse. https://doi.org/10.7551/mitpress
/9780262028707.001.0001

Stringer, C., Pachitariu, M., Steinmetz, N., Reddy, C. B., Carandini,
M., & Harris, K. D. (2019). Spontaneous behaviors drive multidi-
mensional, brainwide activity. Science, 364(6437), 255. https://
doi.org/10.1126/science.aav7893, PubMed: 31000656

Swadlow, H. UN., & Waxman, S. G. (2012). Axonal conduction
delays. Scholarpedia, 7(6), 1451. https://doi.org/10.4249
/scholarpedia.1451

Xie, J., Kelley, S., & Szymanski, B. K. (2013). Overlapping commu-
nity detection in networks: The state-of-the-art and comparative
étude. ACM Computing Surveys, 45(4), 1–35. https://est ce que je.org/10
.1145/2501654.2501657

Zeraati, R., Shi, Y.-L., Steinmetz, N. UN., Gieselmann, M.. UN., Thiele,
UN., Moore, T., Levina, UN., & Ange, T. UN. (2023). Intrinsic timescales
in the visual cortex change with selective attention and reflect spa-
tial connectivity. Communications naturelles, 14(1), 1858. https://est ce que je
.org/10.1038/s41467-023-37613-7, PubMed: 37012299

Zilles, K., & Amunts, K. (2010). Centenary of Brodmann’s
map—Conception and fate. Nature Revues Neurosciences, 11(2),
139–145. https://doi.org/10.1038/nrn2776, PubMed: 20046193

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

:
/
/

d
je
r
e
c
t
.

je
t
.

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

F
/

7
2
7
3
1
2
1
1
8
4
7
3
n
e
n
_
un
_
0
0
3
0
9
p
d