RECHERCHE
Dynamic structure of motor cortical neuron
coactivity carries behaviorally relevant information
Marina Sundiang1
, Nicholas G. Hatsopoulos1,2,3*
, and Jason N. MacLean1,2,4*
1Committee on Computational Neuroscience, University of Chicago, Chicago, IL, Etats-Unis
2University of Chicago Neuroscience Institute, Chicago, IL, Etats-Unis
3Department of Organismal Biology and Anatomy, University of Chicago, Chicago, IL, Etats-Unis
4Department of Neurobiology, University of Chicago, Chicago, IL, Etats-Unis
*Co–senior authors.
un accès ouvert
journal
Mots clés: Functional network, Motor cortex, Temporal network
ABSTRAIT
Skillful, voluntary movements are underpinned by computations performed by networks of
interconnected neurons in the primary motor cortex (M1). Computations are reflected by
patterns of coactivity between neurons. Using pairwise spike time statistics, coactivity can be
summarized as a functional network (FN ). Ici, we show that the structure of FNs constructed
from an instructed-delay reach task in nonhuman primates is behaviorally specific: Low-
dimensional embedding and graph alignment scores show that FNs constructed from closer
target reach directions are also closer in network space. Using short intervals across a trial, nous
constructed temporal FNs and found that temporal FNs traverse a low-dimensional subspace
in a reach-specific trajectory. Alignment scores show that FNs become separable and
correspondingly decodable shortly after the Instruction cue. Enfin, we observe that reciprocal
connections in FNs transiently decrease following the Instruction cue, consistent with the
hypothesis that information external to the recorded population temporarily alters the structure
of the network at this moment.
RÉSUMÉ DE L'AUTEUR
It remains unclear how motor cortical neurons flexibly perform the computations necessary to
generate movement. We hypothesized that neuronal coactivity contains movement information,
and its dynamics can reveal how the population switches computations during a task. Nous
quantified coactivity as a functional network (FN) with single neurons as nodes and population
coactivity as directed weighted edges. We also constructed FNs within short epochs across a trial
to determine when coactivity begins to carry information and to investigate the dynamic structure
of these interactions. Following the Instruction cue, reciprocal connections in FNs transiently
decrease, and shortly after, FNs become maximally decodable for reach direction.
INTRODUCTION
Individual neurons do not function in isolation, but rather as coactive and cooperatively inter-
acting components of spiking networks. The resulting coordinated neuronal coactivity is
reflected in pairwise spike time statistics. Spike time correlations have been implicated in
Citation: Sundiang, M., Hatsopoulos,
N. G., & MacLean, J.. N. (2023). Dynamic
structure of motor cortical neuron
coactivity carries behaviorally relevant
information. Neurosciences en réseau,
7(2), 661–678. https://doi.org
/10.1162/netn_a_00298
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00298
Informations complémentaires:
https://doi.org/10.1162/netn_a_00298;
https://doi.org/10.5061/dryad
.9p8cz8wm6;
https://github.com/ hatsopoulos-lab
/macaque-dynamic_functional
_networks
Reçu: 12 Août 2022
Accepté: 2 Décembre 2022
Intérêts concurrents: See Competing
Interests section
.
Q1
Corresponding Authors:
Nicholas G. Hatsopoulos
nicho@uchicago.edu
Jason N. MacLean
jmaclean@uchicago.edu
Éditeur de manipulation:
Sarah Muldoon
droits d'auteur: © 2023
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
un
_
0
0
2
9
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
the propagation of spiking in networks (Bojanek et al., 2020; Chambers & MacLean, 2016)
making them an intriguing signal when studying the circuit mechanisms and computations
that give rise to behavior. Recent work has shown that spike time correlations provide infor-
mation, in addition to that provided by changes in firing rate, as to the nature of visual stimuli
(Dechery & MacLean, 2018; Kotekal & MacLean, 2020; M.. Levy et al., 2020; Ruda et al.,
2020), auditory stimuli (Betzel et al., 2019; Insanally et al., 2019), and spatial location
(E. R.. J.. Levy et al., 2021; Nardin et al., 2021). In motor cortex (M1) pairwise spike count cor-
relations have similarly been shown to provide information about motor behavior beyond
what is provided by firing rates alone (Maynard et al., 1999), and have also been used to
improve encoding models that predict the activity of neurons (Stevenson et al., 2012). Comment-
jamais, it remains unclear whether pairwise spike time correlations contain behaviorally relevant
information. The temporal dynamics of spike time correlations over the course of a behavioral
trial and the extent of specificity of spike time correlations to kinematic variables are consis-
tently underexplored.
Ici, we represent pairwise spike time statistics as functional networks (FNs) and use tools
from network science (Bassett & Sporns, 2017; Bullmore & Sporns, 2009; Rubinov & Sporns,
2010) to examine the structure and information content of pairwise spike time correlated activ-
ity of active populations in M1. Given that many of the computations needed to carry out a
movement happen in fractions of a second, averaging interactions over long periods of time is
unlikely to capture important dynamic aspects of the network (Pedreschi et al., 2020). Nous
extend the FN framework by constructing temporal FNs (Holme & Saramäki, 2012; Ju &
Bassett, 2020; Thompson et al., 2017) of single trials by computing pairwise spike time statis-
tics across short intervals to elucidate the temporal progression of pairwise correlations among
a population of M1 neurons throughout a trial and to relate single-trial population dynamics to
network structure.
Using temporal FNs, we evaluate whether the dynamics of pairwise correlations carry infor-
mation about the instructed reach, and determine when network structure begins to carry
information relative to behaviorally relevant moments during the trial. We also determine what
types of network interactions are most prevalent relative to different phases of the trial. We find
that temporal FNs evolve during the trial in a way that specifies the instructed reach. Using a
perceptron decoder, we demonstrate that temporal FNs contain information about motor
behavior beyond what is conveyed by firing rate changes alone. We show that the topology
of temporal FNs varies systematically over the time course of a trial, becoming transiently less
reciprocal after the onset of the Instruction cue, coinciding with the increase in decodable
behavioral information from the FNs.
RÉSULTATS
We analyzed single-unit recordings from M1 while two macaques (Monkey Rs and Monkey Rj)
performed a center-out reaching task in the horizontal plane. Subjects were trained to control
a cursor on a screen by moving a handle on a 2D arm exoskeleton (Kinarm, Kingston,
Ontario). The task was to hold the cursor in the center position during an instructed-delay
period while an Instruction cue was presented that indicated one of eight target reach loca-
tions positioned radially around the center. After the end of the delay period (1 s), a Go cue
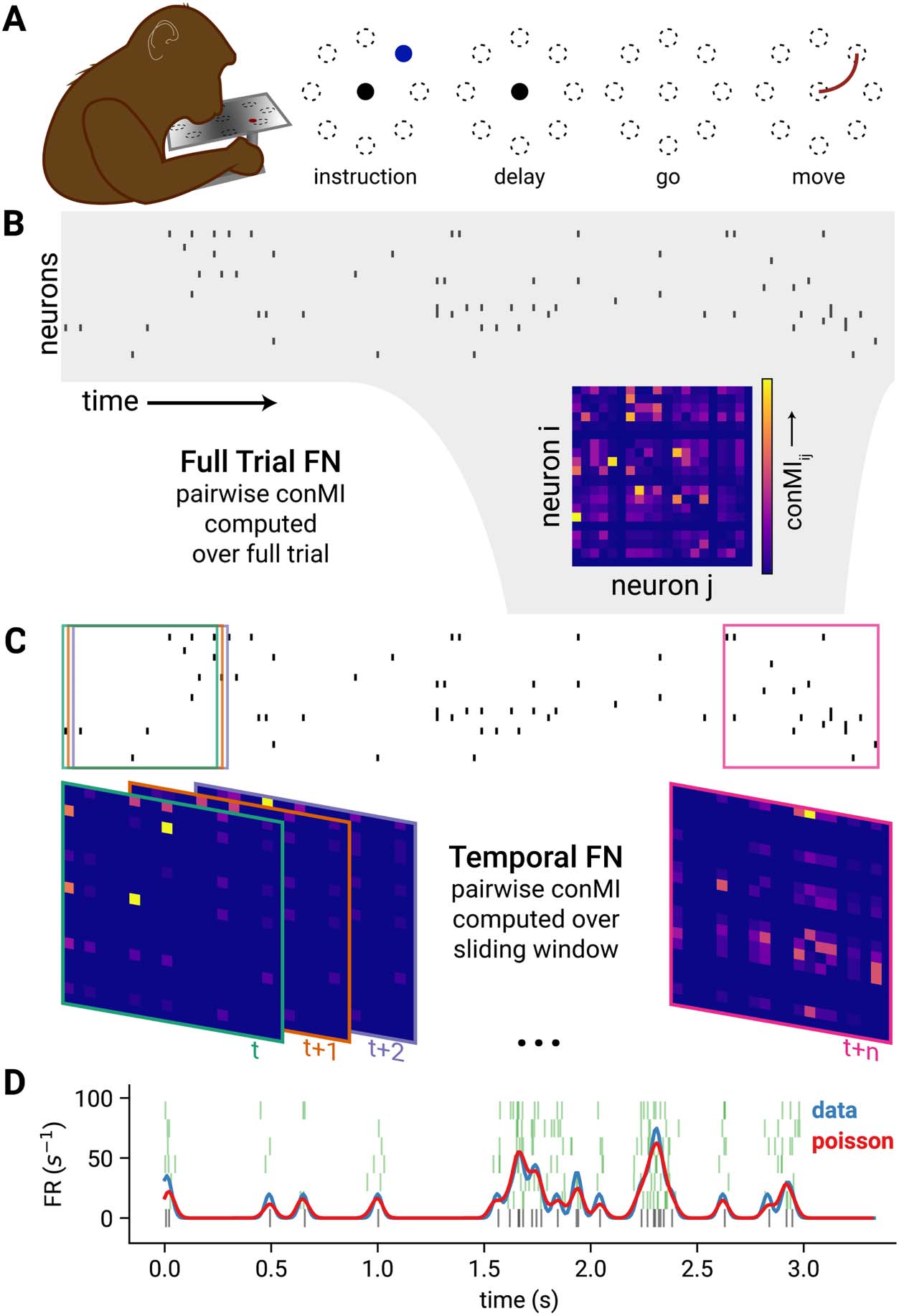
appeared instructing the subjects to initiate a reaching movement (Figure 1A).
We summarized neuronal population activity during the task as a functional network (FN,
Figure 1B–C). The FN is composed of nodes, which are the spiking single units, and edges
between nodes, which correspond to the pairwise spike time statistics and not anatomical
Neurosciences en réseau
662
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
un
_
0
0
2
9
8
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
un
_
0
0
2
9
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 1. Task structure and functional network construction. (UN) Subject using a Kinarm exoskel-
eton to control a cursor on a screen. The subject holds the cursor at the center target (black circle) à
initiate a trial. An Instruction cue (blue) appears in one of eight target locations (indicated by the
circles with broken lines). After the delay period the target cue begins blinking, which indicates that
the subject may move to the instructed target. (B) A raster plot shows the binned spikes of the
recorded neurons across time. The full trial FN is constructed by computing the confluent mutual
information (conMI; see Methods) between the spike train for the full trial for each pair of recorded
neurons. (C) To generate the temporal FN, pairwise conMI were computed within a 200-ms sliding
window across the trial. Boxes on the raster indicate the interval in the spike train that was consid-
ered for the corresponding FN with the same color border. (D) To generate rate-matched nulls, nous
computed the instantaneous firing rate of a unit for each single trial (blue trace) from the raw spikes
(black raster plot, bottom). We used this firing rate profile to generate new spikes from an inhomo-
geneous Poisson process (five example spike trains, green rasters). The mean of the instantaneous
firing rates for 50 iterations of this Poisson process is shown in red.
Neurosciences en réseau
663
Dynamic structure of M1 neural coactivity
Confluent mutual information:
The mutual information between a
source neuron at time t, and a target
neuron at time t and t + 1.
Low-dimensional embedding:
A low-dimensional space that
optimizes distances between
elements to match the original high-
dimensional data.
Graph alignment score:
A metric that quantifies the fraction
of similar edges between two
réseaux.
connectivité (Rs: 142 single units, Rj: 78 single units). Spécifiquement, edges are computed using a
mutual information measure (Chambers et al., 2018). Confluent mutual information (conMI;
see the Methods section) computes the mutual information between the binned activity of neu-
ron i at time t, and of neuron j at time t and the adjacent time bin, t + 1 (where bins are 10 ms),
and it is positive, by definition. The reliability of the coactivity between neuron i and j during a
specified time window resulted in a weight. The resultant FN is both weighted and directed
corresponding to the reliability and the directionality of the pairwise spike time correlation
between units. We assessed whether the conMI between i and j is strongly influenced by their
firing rates (FR). We found that the relationship between conMI and pairwise FR (geometric
mean) is not a simple linear correlation (see Supplementary Figure 1 in the Supporting Infor-
mation). Notably, the relationship between conMI and the FR is similar in both the data and
the rate-matched null.
Correlational Structure in Population Activity Is Specific to Reach Direction
We first determined whether FNs during the entirety of single reach trials are specific to reach
target direction. We did so in two ways: low-dimensional embedding of FNs and a graph
similarity metric. Both approaches showed that FNs constructed from closer reach target
directions are also closer in network space. D'abord, we embedded the FNs in a low-dimensional
manifold that optimizes the distances between data points according to the original high-
dimensional similarity. Par conséquent, FNs that are more similar to each other will lie closer
together on the low-dimensional manifold, and conversely, FNs that are structurally different
will be more distant. Spécifiquement, we used UMAP to project the high-dimensional FNs into a
lower dimensional space (see Methods). We found that networks from reaches to neighboring
directions are close together in the low-dimensional manifold. En fait, the embedding pro-
duced a radial arrangement of data points that reflected the radial arrangement of the target
locations (Figure 2A–D).
To further evaluate the similarities and differences between FNs according to reach direc-
tion as well as control for similarities and differences resulting from firing rates, we compared
FNs and single trial rate-matched FN nulls using graph alignment scores (GAS; see Methods).
GAS allows for a quantitative comparison of FNs by identifying common edges between
graphs (Gemmetto et al., 2016). This metric preserves node identities and reflects the fraction
of similar edges out of all the existing edges between two networks. Donc, a value of 1
means that the two networks are exactly the same. We measured alignment between each pair
of FNs constructed from single trials. We then grouped the measured GAS according to the
degree difference between the respective instructed reach targets: same (Δ0°), neighboring
(Δ45°), and opposite (Δ180°). We observe that pairs of FNs from trials with the same reach
target have higher alignment scores (Δ0° Rs = 0.399 ± 0.014, Rj = 0.393 ± 0.011, mean ± SD)
than those from neighboring reach directions (Δ45°: Rs = 0.388 ± 0.015, Rj = 0.389 ± 0.011;
p ≤ 1.865e−89, Mann-Whitney U (MWU) two-sided test, mean ± SD). Alignment scores were
lowest when computed using FNs from opposite reach targets (Δ180°: Rs = 0.363 ± 0.015,
Rj = 0.385 ± 0.012; p ≤ 1.882e−236, MWU two-sided test, mean ± SD), indicating that the
shared correlational network structure, in this case summarized as FNs, are informative of the
instructed reach (Figure 2E–F). En plus, while the rate-matched networks also exhibited
differences in these distributions, GAS from the data were higher for all three distributions,
suggesting that FNs are more consistent than firing rates trial to trial (Rs = 0.363 ± 0.016,
0.353 ± 0.016, 0.331 ± 0.016; Rj = 0.380 ± 0.012, 0.378 ± 0.012, 0.374 ± 0.014; GAS for
pairs of rate-matched FNs for same, neighboring, and opposite trials, respectivement, p < 0.001,
MWU two-sided test for all data and rate-matched comparisons, mean ± SD). Together both
Network Neuroscience
664
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Correlational structure of full trial FNs are specific to reach target direction. (A, C) Hand trajectories of included trials colored by
reach direction. (B, D) Low-dimensional embedding of full trial FNs preserve reach target direction. Colored the same as panels A, C. Shaded
contour is the bivariate kernel density estimation (see Methods) for the (x, y) positions of the FNs to visualize the boundaries of the projected
FNs of each direction. (E, F) Distribution of alignment scores between each pair of FNs separated by target distance in dark gray and score
distributions for corresponding rate-matched FNs shown in light gray (**** p < 1.00e−04, MWU two-sided test). Dashed lines indicate
quartiles.
measures, UMAP and GAS, demonstrated that there were differences in the pairwise spike
time correlation structure within the recorded population across different reach directions,
and that there was additional structure resulting from pairwise spike time statistics of the pop-
ulations that was not accounted for by firing rate correlations.
Temporal Progression of Pairwise Spike Time Statistics on Single Trials Are Specific to Reach Direction
Correlations between neurons are dynamic (Aertsen et al., 1989) and can vary over a behav-
ioral trial depending on task condition (Vaadia et al., 1995). Thus, we next evaluated the time-
varying spike time correlational structure by constructing FNs from short epochs (200 ms) of
trial time. These “snapshots” of the network across time, temporal FNs, allowed us to evaluate
how the network evolves over the time course of single trials and to determine when, during a
trial, the reach-specific differences in the FNs first occur and are most pronounced. Again, we
examined the differences between FNs in two ways. First, we embedded the FNs into a lower
dimensional subspace using UMAP, as we had done with the full trial FNs. This allowed us to
use the embedding to track the progression of temporal FNs relative to trial structure and reach
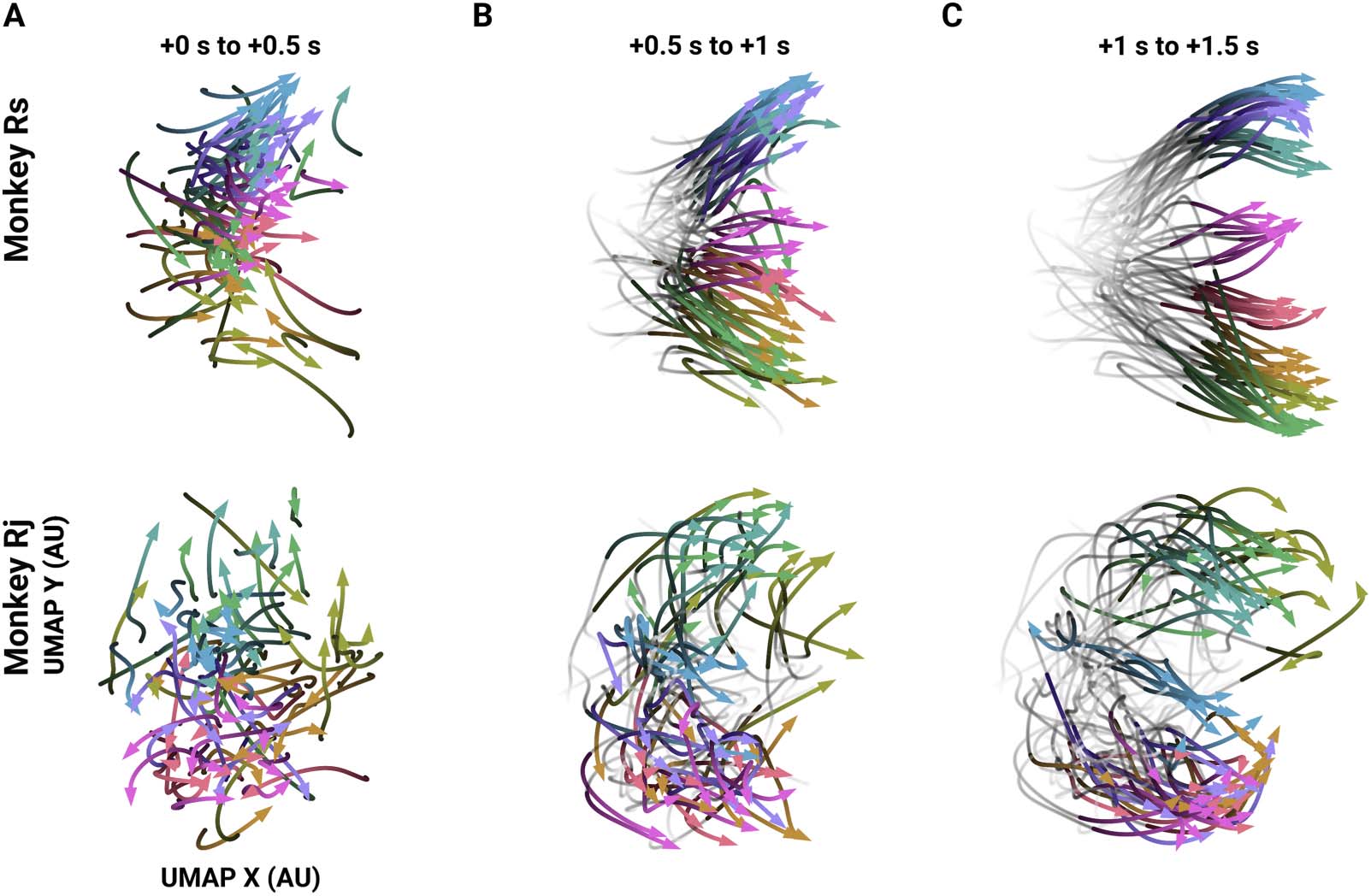
direction. We found that the temporal FNs progressed along trajectories through the subspace
in a reach-specific path (Figure 3). Temporal FNs are initially close together in the computed
subspace (Figure 3A) and then increasingly separate according to the instructed reach direc-
tion as the trial progresses (Figure 3B), separating maximally after the Go cue and during
movement (Figure 3C). Again, we used an unsupervised method of dimensionality reduction
and therefore did not include information about the behavior of the subject in the embedding.
Network Neuroscience
665
Dynamic structure of M1 neural coactivity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Trajectories of single trial temporal FNs through a low-dimensional subspace. Example trajectories of single trial temporal FNs
across a low-dimensional subspace (10 trials per direction). Times (in seconds) indicate the time post-instruction. (A) Trajectories from instruc-
tion (0 s) to 0.5 s after instruction. Trajectory begins with the darkest hue. Color legend is the same as Figure 2A–D. (B) The same trajectories
from panel A later in time: the gray, low-opacity tails show the trajectory from Instruction, and the colored and opaque section shows the
trajectory at 0.5 s post-instruction to Go cue (1 s post-instruction). (C) The same as panel B but for after Go (1 s) and through the end of the trial.
Consequently, any separation in the embedding of the temporal FNs is the result of the
differences in the pairwise spike time statistics of the neural population and not from any
training labels.
As with the full trial FNs, we next computed the extent to which the structure of the tem-
poral FNs indicated the instructed reach and compared the temporal FNs with the rate-
matched FNs. At each time window, we measured the GAS of every pair of FNs and sorted
the scores according to difference in target direction. We then evaluated the distribution of
graph alignment scores for the same, neighboring, and opposite reach directions across the
time course of the trial (Figure 4). Before and shortly after instruction, the FNs are not infor-
mative as to reach direction as indicated by similar GAS values (MWU two-sided test, p ≥
4.045e−3, Bonferroni corrected between all scores from data FNs). The score distributions
of neighboring and opposite reach directions became significantly different from scores of
FNs from the same reach trials after the Instruction cue, consistent with the embedding result
(Figure 4A; Δ0° vs. Δ180°: MWU two-sided test, p ≤ 1.576e−6, Bonferroni corrected from
160 ms post-instruction for Rs, and 180 ms post-instruction for Rj. Δ0° vs Δ45°: MWU
two-sided test, p ≤ 3.106e−4, Bonferroni corrected from 210 ms post-instruction for Rs, and
230 s post-instruction for Rj). The scores remained significantly different for the remainder of
the trial and also at movement onset (Figure 4B–C). Notably, the scores between the same and
the opposite reach directions diverge first before scores from the same and neighboring reach
directions, again suggesting that FNs generated from nearby reach directions are also more
similar in network space. We also note that while the rate-matched FNs exhibited differences
between distributions (Δ0° vs. Δ180°: MWU two-sided test, p ≤ 2.305e−4, Bonferroni
corrected from 160 ms post-instruction for Rs and Rj. Δ0° vs Δ45°: MWU two-sided test,
Network Neuroscience
666
Dynamic structure of M1 neural coactivity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Graph alignment scores between FNs reflect distance of reach targets. (A) Mean alignment scores between pairs of FNs at each
sliding window (solid lines), and corresponding scores for rate-matched FNs (broken lines) aligned to the Instruction cue. The shaded region
indicates the standard error of the GAS distribution, which is very small. Alignment scores are separated based on reach target difference: same
(violet), neighboring (blue), and opposite (green) reach targets. Straight horizontal lines on the lower left of the plot indicate when the score
distributions from neighboring or opposite locations (blue and green, respectively) become significantly different from the score distributions
between FNs of the same direction (p < 0.01, MWU two-sided test, Bonferroni corrected). (B) The same as panel A but aligned to the Go cue.
Differences between distributions are significant throughout the plotted window (p < 0.01, MWU two-sided test, Bonferroni corrected). (C) The
same as panel A but aligned to movement onset. Differences between distributions are significant throughout the plotted window (p < 0.01,
MWU two-sided test, Bonferroni corrected).
p ≤ 8.688e−4, Bonferroni corrected from 220 ms post-instruction for Rs, and 229 ms post-
instruction for Rj), the GAS between pairs of FNs computed from pairwise spike time statistics
from the data are consistently higher, indicating that the structure of pairwise spike timing is
conserved from trial to trial. Additionally, if the temporal evolution in alignment scores are due
to rates alone and if the GAS values for the data are merely offset by some value, we would
expect that the normalized GAS (see Supplementary Figure 2 in the Supporting Information)
would show neither (a) changes across time nor (b) significant differences in the GAS values
between reach directions. We show that when we normalize the GAS we still find that for Rs,
GAS between Δ0 and Δ45 are significantly different at 210 ms (similar to the non-normalized
GAS). For Rj, while the mean normalized GAS for Δ0 is consistently higher than the mean
for Δ45 starting at 110 ms, the scores are significantly different at 380 ms. However, it must
also be noted that the scores were significantly different between Δ0 and Δ90 starting at
220 ms for Rj.
Decoding Behavior From Functional Networks
Temporal FNs became increasingly differentiable during the trial with the differences following
a stereotyped time course relative to trial structure, indicating that there is information about
motor behavior in the temporal FN. We next asked whether this information can be used to
decode reach target direction. Since GAS analysis indicated that the differences in the tempo-
ral FN depended on time, we also measured when the temporal FNs were decodable relative
Network Neuroscience
667
Dynamic structure of M1 neural coactivity
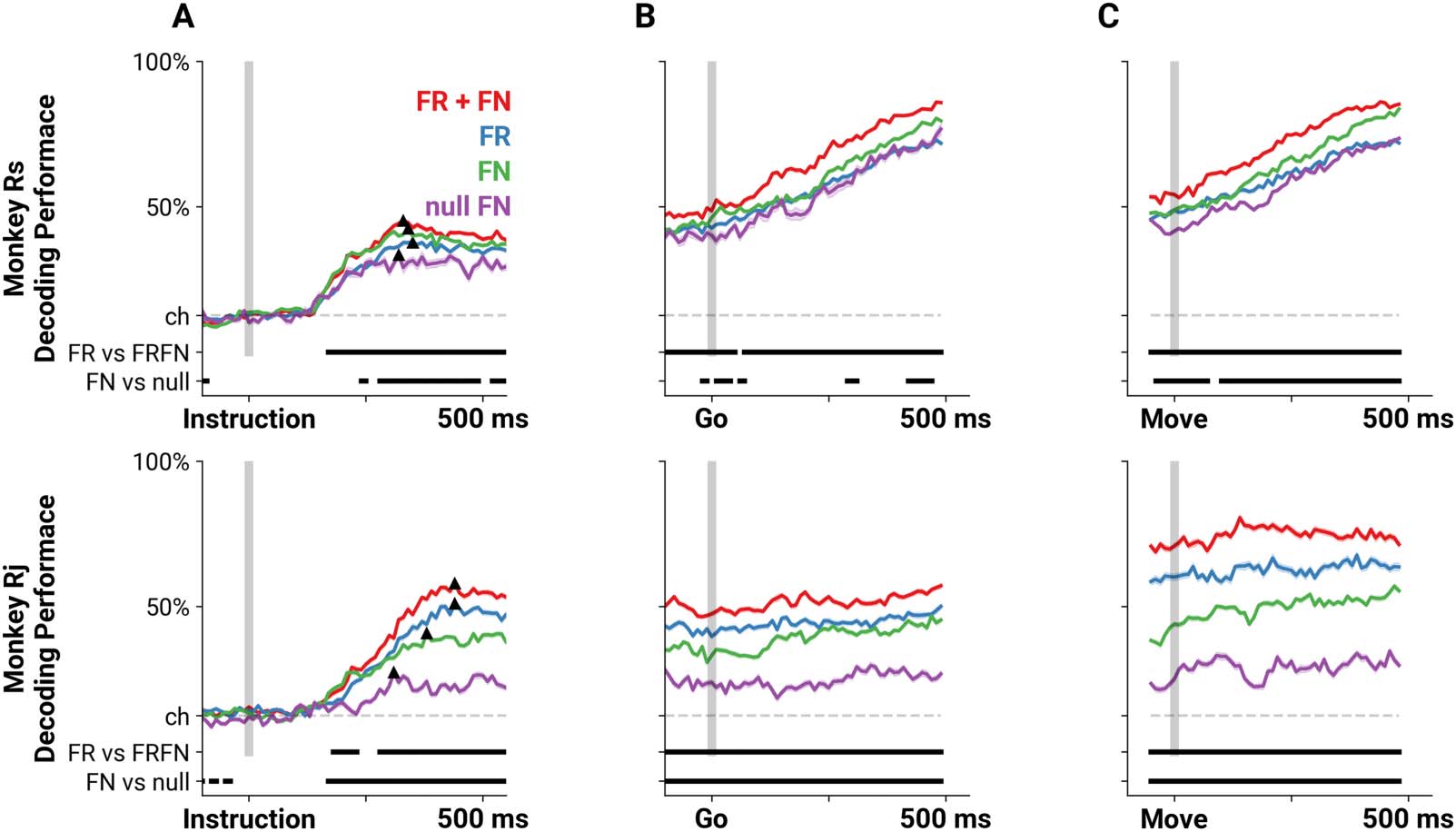
Figure 5. Decoders that incorporate pairwise spike time statistics predict reach direction more accurately. Mean performance perceptron
decoders trained on either firing rates (FR, blue), the set of pairwise correlations as FNs (FN, green), both firing rates and correlations (FR +
FN, red), or correlations from rate-matched nulls (null FN, purple) aligned on Instruction cue (A), Go cue (B), and movement onset (C). Dashed
gray line indicates chance level (one in eight), and the two bars on the bottom of each panel indicate the times during which performance of
the FR and FRFN, or the FN and null FN decoders are significantly different from each other (p < 0.01, MWU two-sided test, Bonferroni
corrected). The triangles in panel A mark the initial peak in performance for the decoders. The shading represents the standard error of the
decoder performance.
to trial structure and movement onset, and when they were maximally decodable. To do so,
we employed multilayer perceptron decoders trained on different features of the data to pre-
dict the reach target of a 200-ms sample window of a single trial (see Methods). We then com-
pared the performance of the decoders based on the features on which they were trained.
Specifically, decoders were trained on either the set of pairwise spike time statistics between
neurons generated in the time window (FN decoder, Figure 5, green), or the firing rates of the
neurons during the window (FR decoder, Figure 5, blue). To determine whether pairwise spike
time statistics carry additional information beyond firing rates, we also examined decoding
performance when both firing rate and the temporal FNs were included in decoder training
(FRFN decoder, Figure 5, red). Comparing the decoding performance of the FN and FR
decoders to the full FRFN decoder allowed us to establish the contribution of each held-out
feature to the overall decoding performance. Finally, in order to rule out the effect of spurious
correlations due to firing rate dynamics, we generated FNs from trial-by-trial Poisson rate-
matched neurons and similarly evaluated decoding performance (null FN decoder, Figure 5,
purple; see Methods).
As expected, before the Instruction cue, all four decoders performed at chance level
(Figure 5A, 12.5% performance indicated by dashed line). At 147 ± 9 ms following the Instruc-
tion cue, decoding performance increased above chance for the FN, FR, and FRFN decoders
(one-sample t test, p ≤ 9.550e−4, Bonferroni corrected, mean ± SD). The null FN decoders
achieved performance above chance about 50 ms later, at 205 ± 44 ms (mean ± SD). All four
decoders reached an initial peak around 364 ± 48 ms (defined as the maximum performance
within 500 ms of the instruction, indicated by the black triangle on every performance trace
in Figure 5). At this peak, the FRFN decoders performed better than the FR decoder (Rs:
Network Neuroscience
668
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
45.10% vs. 37.67%, Rj: 58.03% vs. 51.03%, respectively, p ≤ 6.438e−05, MWU two-sided
test), suggesting that the inclusion of pairwise spike time statistics provides additional infor-
mation about the reach direction. In fact, the FRFN decoder performance was significantly
higher than the performance of the FR decoder beginning at 170 ms for Rs and 180 ms for Rj
and remained significantly higher throughout the rest of the trial, as well as during movement
(MWU two-sided test, p ≤ 9.888e−04, Bonferroni corrected between FRFN and FR perfor-
mance scores). We note that the FR decoder performed better than the FN decoder for Rj
(51.03% vs. 40.85% at their initial peaks, respectively). However, the increase in perfor-
mance in the combined FRFN decoder compared with the FR decoder indicates that precise
spike time correlations contain additional information about the reach target beyond firing
rates alone.
We also observed that at the initial peak, the FN decoders performed significantly better
than the rate-matched FNs (Rs: 42.39% vs. 33.37%, Rj: 40.85% vs. 27.28%, respectively,
p ≤ 3.562e−04, MWU two-sided test). For Rj, this performance difference was significant from
170 ms throughout the rest of the trial (MWU two-sided test, p ≤ 3.3845e−04, Bonferroni
corrected). For Rs, this difference was significant beginning at 240 ms (MWU two-sided test,
p ≤ 8.853e−04, Bonferroni corrected) and sporadically thereafter. This highlights that there is
information about the instructed reach in the pairwise spike time statistics in the data that does
not arise from chance correlations due to firing rates.
Reciprocity in the Network Varies Systematically During the Trial
One of the strengths of representing cortical population activity as a weighted and directed
temporal FN is that not only can we investigate the dynamics of pairwise spike time statistics
across the population (as weighted edges), we can also consider the changes to network archi-
tecture. Doing so has the potential to provide insights into information propagation and com-
putation. Here, we focus on the most reliable reciprocal connections in the temporal FN. We
thresholded the temporal FNs according to weight percentile, in order to isolate the most reli-
able edges, and then measured the normalized reciprocity of the temporal FNs throughout the
trial (see Methods). Reciprocity tells us how likely two units in the temporal FN are mutually
linked (Squartini et al., 2013) as well as the importance of the direction of the interaction
between neurons: A fully reciprocal FN means that units are coactive symmetrically, in con-
trast to a less reciprocal FN where the direction of the interaction is important in characterizing
the network. In the temporal regime, reciprocity may influence the state of the FNs in the next
time point. We investigated whether and when the reciprocity of the temporal FN changes
over the time course of the trial. We compared the mean scores of each trial from instruction
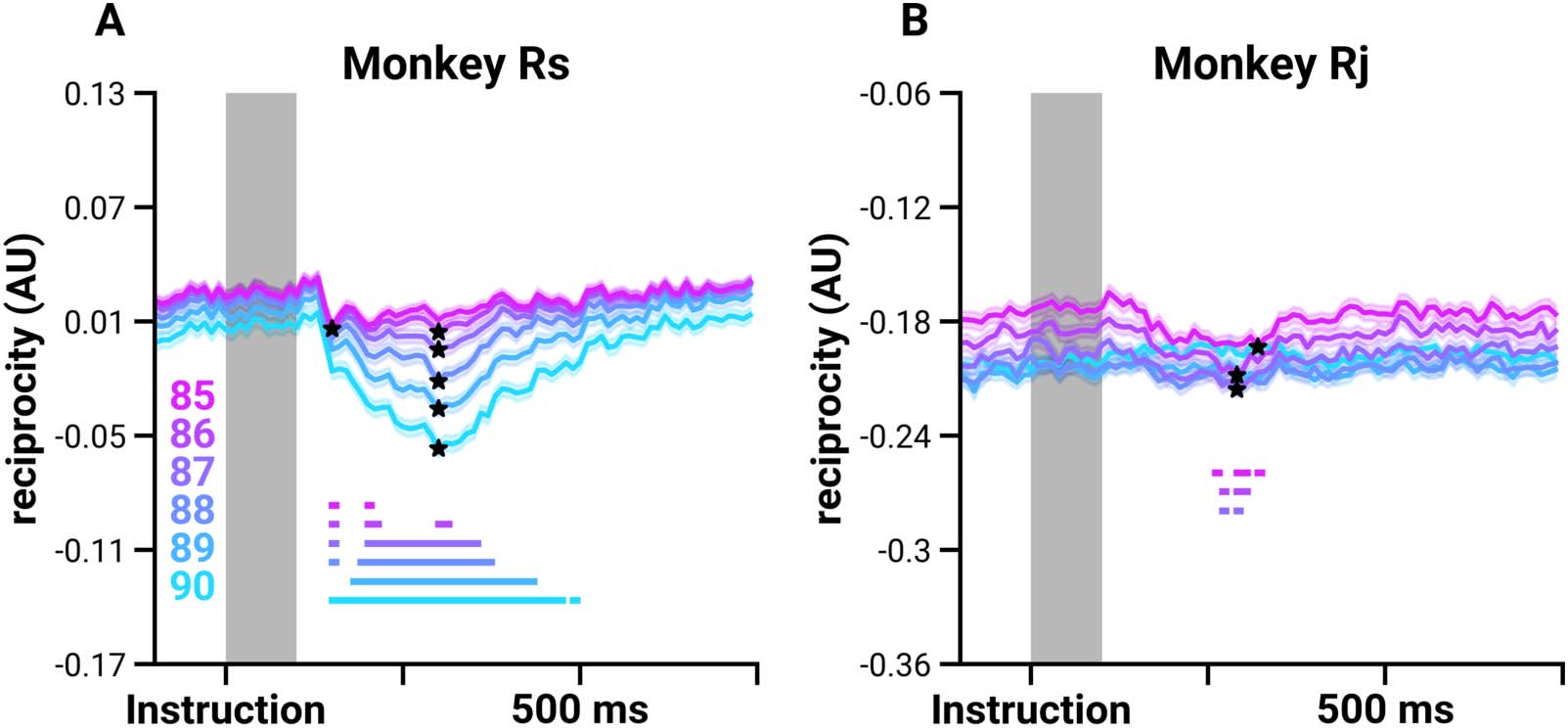
to 100 ms post-instruction (Figure 6, gray shaded region; defined as the baseline, see Methods)
with the mean scores at each time point during the delay period. Reciprocity significantly
decreases at 156 ± 11.1 ms for Rs and 267 ± 4.7 ms for Rj (independent sample t test, p ≤
7.46e−03 and p ≤ 9.83e−03, respectively). The significant decrease in reciprocity lasts until
358 ± 91.4 ms for Rs and 303 ± 12.5 ms for Rj.
We also compared the reciprocity scores at the time when the mean reciprocity over trials
is at its minimum (Figure 6, indicated by ★) with the mean of the baseline distribution. The
minima occurred at 291 ± 31 ms after the Instruction cue (mean ± SD). We found that reci-
procity is significantly decreased at the minima for the networks thresholded at 85th to 87th
percentile for both Rs and Rj (Figure 6, independent sample t test, p ≤ 3.773e−4). There is a
significant decrease in reciprocity with Rs at the higher threshold levels (88th to 90th percen-
tile of edge weights), and a significant decrease in reciprocity scores with Rj at lower
Reciprocity:
The likelihood that two nodes are
mutually connected.
Network Neuroscience
669
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
Figure 6. Reciprocity decreases shortly after instruction. Mean normalized reciprocity scores (lines; the shaded region shows the standard
error) from thresholded FNs based on weight percentile values for Monkey Rs (A) and Monkey Rj (B) indicated by the color legend in the lower
left. The mean reciprocity for the shaded region (Instruction to 100 ms post-instruction) is computed for each trial, resulting in a distribution of
reciprocity scores, which is then compared with the scores at each time point and at the minima to determine whether there is a decrease in
reciprocity. Stars indicate whether the distributions at the minima decrease significantly (p < 0.01, independent sample t test). Solid straight
lines at the bottom of the plot show the times that are significantly different from the baseline (p < 0.01, independent sample t test, Bonferroni
corrected).
thresholds (75th to 85th percentiles; see Supplementary Figure 3 in the Supporting Informa-
tion). The difference in significant threshold levels is due to the differences in the density and
size of the FNs. Nevertheless, this decrease is present in both subjects. At moments when
inputs external to the recorded population would be most likely, the network structure
becomes less reciprocal.
DISCUSSION
We show that pairwise spike time statistics between neurons, summarized as functional net-
works (FNs), are informative of reach direction and are dynamic over the course of a single
task trial. Previous studies have shown that firing rate correlations between neurons provide
additional information about behavior or the environment that is not gleaned from observing
each neuron independently (Maynard et al., 1999). Moreover, the dynamics of pairwise firing
rate correlations are indicative of behavioral conditions that are otherwise unobservable from
individual neuron firing rates or from trial-averaged cross-correlations (Vaadia et al., 1995).
These previous studies measured correlations of spike counts across trials and over broad
timescales. In contrast we focused on spike time correlations over short intervals. Earlier work
has documented fine timescale synchrony between pairs of M1 neurons that emerges predom-
inantly at movement onset and carries information about reach direction (Hatsopoulos et al.,
1998). Our results are consistent with this earlier work but extends it in several ways. First and
foremost, our focus here was on characterizing the FN structure among the entire recorded
neuronal population as opposed to multiple, individual pairwise interactions. Second, by using
conMI, we could distinguish directed functional interactions as opposed to synchronous inter-
actions. This allowed us to analyze the temporal dynamics of reciprocal versus nonreciprocal
interactions across the duration of the reach. Third, we documented the emergence of
information-bearing interactions early during movement preparation in the instructed-delay
period, which was not evident in the earlier work.
Network Neuroscience
670
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
Since movement is the culmination of multiple computations, many of which happen at
short timescales, we hypothesized that task-relevant information must be represented in the
short timescale pairwise spike time statistics. Our work substantiates this hypothesis, since
we find evidence that temporal FNs constructed from short intervals during single trials
carry a representation of the instructed movement. Specifically, we found that the similarity
between pairs of temporal FNs from single trials reflected the distance between their respec-
tive target directions and are correspondingly decodable. The temporal FN framework also
allows us to identify when correlations begin to be indicative of reach direction, which in
turn has the potential to provide insight into corresponding computations. We find that FNs
become decodable above chance 140 ± 10 ms after the Instruction cue appeared. Notably,
an increase in timing precision of spiking in individual neurons across trials has been found
around this time (∼100 ms), and mutual information increases between target location and
spike counts of single neurons at this time (Reimer & Hatsopoulos, 2010). The modulation
of firing rates across the population and the stronger relationship between spike count and
target location suggest that information about the target arrives at M1 at this time lag. Con-
sistently, we find that precise spike timing between neurons in single trials, as reflected in
their correlation, is additionally informative of target direction. Moreover, alignment scores
between temporal FNs constructed from single trials of the same target direction are higher
than alignment between temporal FNs that correspond to neighboring and opposite direc-
tions, suggesting that there is consistent and informative spike timing between neurons on a
trial-to-trial basis that is specific to reach direction.
Local connectivity patterns shape the activity patterns and consequently, the dimension-
ality and behavior of a recurrent network (Recanatesi et al., 2019). In this work, we focused
on measuring reciprocal connections because they serve as building blocks for higher order
(beyond pairwise) structures. When external inputs impinge on local circuitry, they must be
integrated into ongoing activity and processed across the network. A recent study that
inferred single trial M1 dynamics using LFADS (latent factor analysis via dynamical systems)
found that it was necessary to include external inputs in order to maximize model accuracy
(Malonis et al., 2021). They found that large input transients were disproportionately nec-
essary at ∼150 ms after target presentation compared with other times in the trial. Here we
find that reciprocal connections begin to decrease with similar latencies to the target
appearance as the inferred input transients (significantly at 156 ± 11.1 ms for Rs and
267 ± 4.7 ms for Rj). Also at this time, decoding performance improves above chance
(147 ± 9 ms), and GAS values between the same and opposite directions begin to diverge
(170 ± 10 ms). This shift in structure may be an indication of the network integrating and
propagating information about inputs external to the recorded population, such as a visual
stimulus related to the instructed target direction. Interestingly, this topology is transient;
the network returns to its baseline level of reciprocity, but it is important to note that the
information about the reach target is maintained in the FN after this transient topological
shift, since decodability of the FNs remains stable for the remainder of the delay period.
Previous studies have shown that the population activity during the preparatory and the
movement phase are dynamic (Churchland et al., 2012; Shenoy et al., 2013; Vyas et al.,
2020), that they occupy orthogonal subspaces (Kaufman et al., 2014), and that these
subspaces can be linked (Elsayed et al., 2016). Consistent with this work on computation
through population dynamics, we show that the patterns of coordinated activity of the
neural population evolves during the reach trial in a systematic way. Our findings provide
evidence that the network transiently reorganizes to a less reciprocal topology that may
facilitate processing external inputs, setting the state of the population according to the
Network Neuroscience
671
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
instructed movement, and may enable the reported transition from the preparatory subspace
to the movement subspace.
In this study we did not try to classify the single units functionally or into putative cell clas-
ses. Future work would clearly benefit from data in which individual classes of neurons are
considered separately. The FN framework can be extended to include labels on nodes and
edges such as cell type, or functional properties (Faskowitz et al., 2022). Notably, an impres-
sive census of cell types in motor cortex has recently been published by the BRAIN Initiative
Cell Census Network (BICCN, 2021) highlighting the potential for an analytical approach,
such as FNs, that can incorporate both cell information and network dynamics. For example,
in the visual cortex the topology of single trial FNs depends on the visual stimulus, and
untuned neurons act as hubs in the network, serving an integral role in stimulus coding
(M. Levy et al., 2020). A functional network framework revealed that frontoparietal areas in
the grasping motor network have modular organization that is not constrained to anatomical
boundaries, and a rich club of oscillatory neurons that may be key to synchronizing the net-
work and generating grasping behavior (Dann et al., 2016). Previous work has shown that
modeling functional connections can predict neural responses in M1 more accurately than
canonical tuning curves, suggesting that the tuning properties of individual neurons is in part
a result of network interactions (Stevenson et al., 2012). Additionally, tuning properties are not
stationary such that single cortical neurons in M1 encode temporally extensive movement
fragments or trajectories, as opposed to single movement parameters such as direction
(Hatsopoulos et al., 2007). The temporal FN framework that we introduce in this paper has
the potential to link dynamically changing network interactions across the trial to time-varying
preferred movement trajectory tuning.
Aside from containing information about the instructed reach, upon visual inspection of the
low-dimensional embeddings, we found that FNs carry kinematic information. For example, in
the full trial and temporal embeddings of FNs from Rj (Figure 2C–D, Figure 3, bottom row),
overlapping projected FNs show trials that had similar kinematic trajectories despite different
target directions. Rj’s kinematic trajectories towards the lower right targets were not straight
towards the target (pink in Figure 2C and Figure 3 bottom row); Rj moves straight down
and then right. We found that FN embeddings where the target is the lower right (pink) and
the one straight down (violet) are correspondingly overlapping. Additionally, low-dimensional
embeddings of temporal FNs separate into two main branches: temporal paths of the FNs for
reach directions to the lower left targets (hand trajectories shown in Figure 2A and C) tended
to be closer together, forming a “branch” of paths, and the paths for the upper right targets
form another. Specifically, in Rs (Figure 3, top row), the upper branch of paths corresponds
to pulls towards the body. Conversely, the lower branch corresponds to reaches that require
the subject to push away from the body. This suggests that, while we have performed these
analyses on data where the subject is performing an eight-direction center-out task, FNs may
be able to capture a wider range of movement directions and kinematic variability than
explored here.
FNs are a useful tool to achieve insight into M1 network dynamics that correspond to motor
behavior. FNs provide a tractable summary of population activity that is decodable and can
provide insight into how the state of the system changes over the time course of a trial. The
neural interactions summarized by FNs influence spiking activity of the population that can
be, in turn, read out by downstream agents (M. Levy et al., 2020). Our results suggest that FNs
reorganize according to motor goals and argue that a functional network examination of motor
cortical FNs may provide insights into the underlying circuit mechanisms that drive these
cortical population responses and ultimately motor behavior.
Network Neuroscience
672
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
METHODS
Data Collection and Reaching Task
We used previously published datasets from two macaques, Monkey Rs and Monkey Rj, perform-
ing an instructed center-out reaching task (Hatsopoulos et al., 2004; O’Leary & Hatsopoulos,
2006). Subjects were trained to hold a cursor on a center target presented on a video screen
using a 2D arm exoskeleton (Kinarm, Kingston, Ontario). One of eight radially positioned
peripheral targets was then presented and served as an Instruction cue during which time
the subjects were required to keep holding the cursor on the center target. After a 1-s delay
period, the peripheral target began blinking (Go cue), instructing the subjects to move the
cursor to the peripheral target (Figure 1A). Trial start was 0.5 s before the Instruction cue
appeared, and trial termination was 0.5 s after the peripheral target was acquired. Trial inclu-
sion depended upon target acquisition falling within 1.5 s following movement onset. We also
included only correct trials. Movement onset is defined as the time when the hand velocity
reached 5% of the peak velocity of the movement after the Go cue.
Neural data were recorded from 96-channel Utah arrays implanted in the arm/hand area
of primary motor cortex (M1) on the precentral gyrus. Spike waveform snippets sampled at
30 kHz were extracted using a user-defined threshold (Cerebus Blackrock Microsystems, Salt
Lake City, UT) and were sorted into individual units using Offline Sorter (Plexon, Dallas, TX).
The surgical and behavioral procedures involved in this study were approved by the Uni-
versity of Chicago Institutional Animal Care and Use Committee.
Using Pairwise Spike Time Statistics to Construct Functional Networks
To compute pairwise spike time statistics between recorded neurons, we binned the recorded
spike trains into 10-ms bins, assigning a value of 1 if at least one spike occurred in that bin, and
0 otherwise. We then used the confluent mutual information (conMI) between the binned
spike train (Chambers et al., 2018). ConMI tells us how much information we gain from the
firing state of a source neuron i at time t about the firing state of target neuron j in the same
time bin t and the consecutive bin, t + 1:
X
X
conMI ¼
i tð Þ2 0;1f
g
j ^tð Þ2 0;1f
g
(cid:2)
(cid:2) (cid:3)
p i tð Þ; j ^t
(cid:3)
: log2
"
(cid:3)
(cid:2)
(cid:2) (cid:3)
p i tð Þ; j ^t
(cid:3)
(cid:2) (cid:3)
(cid:2)
: p j ^t
p i tð Þ
Þ
ð
#
;
(cid:2) (cid:3)
where j ^t
¼
(cid:4)
1;
0;
if j tð Þ ¼ 1 OR j t þ 1
ð
Þ ¼ 1
otherwise
:
The functional network constructed using this measure is consequently weighted and
directed. We computed functional networks from either the full trial duration or from
200-ms epochs. For the full trial networks, we computed the conMI between the entire spike
train of the source and target neurons for a single trial (Figure 1B). We also computed the
conMI for 200-ms windows that we slid in 10-ms (1-bin) increments across a single trial,
resulting in a temporal FN per trial: a set of FNs each representing the measured coactivity
of the recorded population during the trial at each time window (Figure 1C).
To disambiguate the structure that arises from firing rates alone and that which is the con-
sequence of precise spike timing, we computed FNs from short interval rate-matched Poisson
neurons. Specifically, we computed the instantaneous firing rate of each neuron on a trial-by-
trial basis by convolving each neurons’ spike train (Figure 1D, black raster) with a Gaussian
kernel (σ = 20 ms). This smoothed rate-signal (Figure 1D, blue trace) is then used as the
Network Neuroscience
673
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
probability of observing a spike for that neuron within a sampling period (10 ms) in an inho-
mogeneous Poisson process (Elephant RRID:SCR_003833, Denker 2018), which results in a
spike train with the same rate profile over the time course of a trial as the original data, but
the precise timing, which is crucial to compute pairwise spike time statistics, is jittered within
the width of the Gaussian kernel (Figure 1D, green rasters and mean instantaneous rate in red).
We generate a rate-matched spike train for each neuron for every trial, and then generate the
rate-matched FNs using the methods described above.
Dimensionality Reduction and Visualization
We vectorized each FN adjacency matrix and used the UMAP algorithm to reduce the dimen-
sionality of the FN adjacency matrix from N-by-N (neurons, N: Rs: N = 143, and Rj: N = 78) to
two dimensions (McInnes et al., 2018). For the full trial FNs we used the following UMAP
parameters: n_neighbors = 50, min_dist = 1, metric = ’cosine’. Each sample used to construct
the low-dimensional embedding is a FN computed from an entire trial (total samples: Rs =
391, Rj = 246). We used a bivariate kernel density estimation for the (x, y) positions of the
FNs to visualize the boundaries of the projected FNs for each reach direction. As with the full
trial FN, we embedded all the temporal FNs together, but in this case each sample is a FN
computed from 200 ms in the trial (total samples: Rs = 103,246, Rj = 20,856). For the temporal
FNs, because there are significantly more samples, we used a different set of parameters in
order to balance the local versus global structure of the data accordingly (n_neighbors =
100, min_dist = 0.1, metric = ’cosine’). We then used a spline to interpolate a path through
the set of embedded FNs from a single trial to visualize the trajectory of the temporal FN in the
low-dimensional subspace.
Graph Alignment Score
Similarity between two FNs, M and N with k neurons, was measured using a node-identity
preserving graph alignment score (GAS), as described in M. Levy et al. (2020) and Gemmetto
et al. (2016):
2
GAS ¼
P
P
(cid:2)
k
j¼1 min Mij; Nij
P
k
j¼1 Mij þ Nij
(cid:3)
:
k
i¼1
P
k
i¼1
GAS measures the ratio of overlapping edges over the total number of edges. In the
weighted case, the numerator represents the sum of the minimum edge weight between each
pair of nodes, and the denominator is the total sum of the edge weights. Alignment scores were
grouped according to the degree difference between the instructed target in a trial. Specifically,
we evaluated the GAS distributions for FNs from the same (Δ0°), neighboring (Δ45°), and
opposite (Δ180°) reach directions. For the temporal networks, we computed the alignment
scores between pairs of FNs within the same 200-ms time window aligned to the trial cues
(Instruction and Go), and to movement onset.
Decoding
A multilayer perceptron classifier (MLPC) was trained to decode the trial target direction from
either the FN, the firing rates, both the FNs and firing rates, or the rate-matched Poisson FNs.
The MLPC architecture has one hidden layer with 100 rectified linear activation units, linear
output units, and a constant learning rate (step size = 0.001). The MLPC was trained for 200
iterations or until convergence, whichever happened first. We trained a different decoder for
each time point and feature set (75% of the data are used for training), and tested on held-out
Network Neuroscience
674
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
data (the remaining 25%). We trained and tested 50 decoders for each feature set in order to
get a distribution of performance scores.
Reciprocity
We computed the weighted reciprocity of FNs using a method described in Squartini et al.
(2013). First, we used a range of percentiles, from 85th to 90th (i.e., the top 15% to 10% of
magnitudes), to threshold the FNs in order to isolate the most reliable interactions in the pop-
ulation. In order to measure the overlapping or reciprocal edges, we take the minimum weight
between neuron i and j:
(cid:5)
≡ min wi; wj
(cid:6)
w$ i;j ¼ w$
i;j
:
The reciprocity of a network is the ratio between the sum of the reciprocal edge weights and
the total sum of edge weights:
$ W ≡ W ≡ X X i ; w$
i;j
j≠i
X
X
i
j≠i
wi;j;
r ≡
$
W
W
:
We normalized the value to the average reciprocity of 45 rate-matched networks ((cid:2)r) using
the equation described in Garlaschelli and Loffredo (2004) for binary networks and adapted by
Squartini et al. (2013) for weighted networks:
ρ ¼
r − (cid:2)r
1 − (cid:2)r
:
Thus when the value is positive, the FNs from the data are more reciprocal than what is
expected from chance correlations due to firing rates, and negative when they are less recip-
rocal. The mean reciprocity was computed between the presentation of the Instruction cue to
100 ms post-instruction for every trial. This resulted in a distribution of scores that we defined
as the baseline distribution. We compared the distribution of reciprocity scores at the time
when the mean reciprocity over trials is at its minimum to determine whether the reciprocity
of the FNs significantly changed during the trial relative to the baseline.
ACKNOWLEDGMENTS
We thank Jacob Reimer, Zach Haga, and Dawn Paulsen for collecting the data presented in
this work. We thank Mayaan Levy, Caleb Sponheim, Wei Liang, and Gabriella Wheeler Fox for
their helpful comments on the manuscript.
DATA AND CODE AVAILABILITY
The data used in this work can be found publicly at https://doi.org/10.5061/dryad.9p8cz8wm6
(Sundiang et al., 2022). All code written in support of this publication is publicly available
at https://github.com/hatsopoulos-lab/macaque-dynamic_functional_networks (Hatsopoulos,
2022).
Network Neuroscience
675
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00298.
AUTHOR CONTRIBUTIONS
Marina Sundiang: Conceptualization; Data curation; Formal analysis; Investigation; Method-
ology; Software; Validation; Visualization; Writing – original draft; Writing – review & editing.
Nicholas Hatsopoulos: Conceptualization; Data curation; Funding acquisition; Methodology;
Project administration; Resources; Supervision; Writing – original draft; Writing – review &
editing. Jason Neil MacLean: Conceptualization; Funding acquisition; Methodology; Project
administration; Resources; Supervision; Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
Nicholas G. Hatsopoulos, NIH NINDS, Award ID: R01NS111982. Nicholas G. Hatsopoulos
and Jason N. MacLean, NIH NINDS, Award ID: R01NS104898.
COMPETING INTERESTS
N. G. H. serves as a consultant for Blackrock Microsystems, Inc., the company that sells the
multielectrode arrays and acquisition system used in this study.
REFERENCES
Aertsen, A. M., Gerstein, G. L., Habib, M. K., & Palm, G. (1989).
Dynamics of neuronal firing correlation: Modulation of “effective
connectivity.” Journal of Neurophysiology, 61(5), 900–917.
https://doi.org/10.1152/jn.1989.61.5.900, PubMed: 2723733
Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353–364. https://doi.org/10.1038/nn.4502,
PubMed: 28230844
Betzel, R. F., Wood, K. C., Angeloni, C., Geffen, M. N., & Bassett,
D. S. (2019). Stability of spontaneous, correlated activity in mouse
auditory cortex. PLOS Computational Biology, 15(12),
e1007360. https://doi.org/10.1371/journal.pcbi.1007360,
PubMed: 31815941
BICCN (BRAIN Initiative Cell Census Network). (2021). A multi-
modal cell census and atlas of the mammalian primary motor
cortex. Nature, 598(7879), 86–102. https://doi.org/10.1038
/s41586-021-03950-0, PubMed: 34616075
Bojanek, K., Zhu, Y., & MacLean, J. (2020). Cyclic transitions
between higher order motifs underlie sustained asynchronous
spiking in sparse recurrent networks. PLOS Computational Biol-
ogy, 16(9), e1007409. https://doi.org/10.1371/journal.pcbi
.1007409, PubMed: 32997658
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038
/nrn2575, PubMed: 19190637
Chambers, B., Levy, M., Dechery, J. B., & Maclean, J. N. (2018).
Ensemble stacking mitigates biases in inference of synaptic con-
nectivity. Network Neuroscience, 2(1), 60–85. https://doi.org/10
.1162/NETN_a_00032, PubMed: 29911678
Chambers, B., & MacLean, J. N. (2016). Higher-order synaptic
interactions coordinate dynamics in recurrent networks. PLOS
Computational Biology, 12(8), e1005078. https://doi.org/10
.1371/journal.pcbi.1005078, PubMed: 27542093
Churchland, M. M., Cunningham, J. P., Kaufman, M. T., Foster,
J. D., Nuyujukian, P., Ryu, S. I., & Shenoy, K. V. (2012). Neural
population dynamics during reaching. Nature, 487(7405), 51–56.
https://doi.org/10.1038/nature11129, PubMed: 22722855
Dann, B., Michaels, J. A., Schaffelhofer, S., & Scherberger, H.
(2016). Uniting functional network topology and oscillations in
the fronto-parietal single unit network of behaving primates.
eLife, 5, e15719. https://doi.org/10.7554/eLife.15719, PubMed:
27525488
Dechery, J. B., & MacLean, J. N. (2018). Functional triplet motifs
underlie accurate predictions of single-trial responses in popula-
tions of tuned and untuned V1 neurons. PLOS Computational
Biology, 14(5), e1006153. https://doi.org/10.1371/journal.pcbi
.1006153, PubMed: 29727448
Elsayed, G. F., Lara, A. H., Kaufman, M. T., Churchland, M. M., &
Cunningham, J. P. (2016). Reorganization between preparatory
and movement population responses in motor cortex. Nature
Communications, 7(1), 13239. https://doi.org/10.1038
/ncomms13239, PubMed: 27807345
Faskowitz, J., Betzel, R. F., & Sporns, O. (2022). Edges in brain
networks: Contributions to models of structure and function.
Network Neuroscience, 6(1), 1–28. https://doi.org/10.1162/netn
_a_00204, PubMed: 35350585
Garlaschelli, D., & Loffredo, M. I. (2004). Patterns of link reciproc-
ity in directed networks. Physical Review Letters, 93(26),
Network Neuroscience
676
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
268701. https://doi.org/10.1103/ PhysRevLett.93.268701,
PubMed: 15698035
Gemmetto, V., Squartini, T., Picciolo, F., Ruzzenenti, F., &
Garlaschelli, D. (2016). Multiplexity and multireciprocity
in directed multiplexes. Physical Review E, 94(4), 042316.
https://doi.org/10.1103/ PhysRevE.94.042316, PubMed:
27841559
Hatsopoulos, N. G. (2022). Macaque dynamic functional networks,
GitHub. https://github.com/hatsopoulos-lab/macaque-dynamic
_functional_networks
Hatsopoulos, N. G., Joshi, J., & O’Leary, J. G. (2004). Decoding
continuous and discrete motor behaviors using motor and pre-
motor cortical ensembles. Journal of Neurophysiology, 92(2),
1165–1174. https://doi.org/10.1152/jn.01245.2003, PubMed:
15277601
Hatsopoulos, N. G., Ojakangas, C. L., Paninski, L., & Donoghue,
J. P. (1998). Information about movement direction obtained
from synchronous activity of motor cortical neurons. Proceedings
of the National Academy of Sciences, 95(26), 15706–15711.
https://doi.org/10.1073/pnas.95.26.15706, PubMed: 9861034
Hatsopoulos, N. G., Xu, Q., & Amit, Y. (2007). Encoding of move-
ment fragments in the motor cortex. Journal of Neuroscience,
27(19), 5105–5114. https://doi.org/10.1523/ JNEUROSCI.3570
-06.2007, PubMed: 17494696
Holme, P., & Saramäki, J. (2012). Temporal networks. Physics
Reports, 519(3), 97–125. https://doi.org/10.1016/j.physrep.2012
.03.001
Insanally, M. N., Carcea, I., Field, R. E., Rodgers, C. C., DePasquale,
B., Rajan, K., DeWeese, M. R., Albanna, B. F., & Froemke, R. C.
(2019). Spike-timing-dependent ensemble encoding by non-
classically responsive cortical neurons. eLife, 8, e42409. https://
doi.org/10.7554/eLife.42409, PubMed: 30688649
Ju, H., & Bassett, D. S. (2020). Dynamic representations in net-
worked neural systems. Nature Neuroscience, 23(8), 908–917.
https://doi.org/10.1038/s41593-020-0653-3 , PubMed:
32541963
Kaufman, M. T., Churchland, M. M., Ryu, S. I., & Shenoy, K. V.
(2014). Cortical activity in the null space: Permitting preparation
without movement. Nature Neuroscience, 17(3), 440–448.
https://doi.org/10.1038/nn.3643, PubMed: 24487233
Kotekal, S., & MacLean, J. N. (2020). Recurrent interactions can
explain the variance in single trial responses. PLOS Computa-
tional Biology, 16(1), e1007591. https://doi.org/10.1371/journal
.pcbi.1007591, PubMed: 31999693
Levy, E. R. J., Park, E. H., Redman, W. T., & Fenton, A. A. (2021). A
neuronal code for space in hippocampal coactivity dynamics
independent of place fields. SSRN Electronic Journal. https://doi
.org/10.2139/ssrn.3928087
Levy, M., Sporns, O., & MacLean, J. N. (2020). Network analysis of
murine cortical dynamics implicates untuned neurons in visual
stimulus coding. Cell Reports, 31(2), 107483. https://doi.org/10
.1016/j.celrep.2020.03.047, PubMed: 32294431
Malonis, P. J., Hatsopoulos, N. G., MacLean, J. N., & Kaufman,
M. T. (2021). M1 dynamics share similar inputs for initiating
and correcting movement. bioRxiv. https://doi.org/10.1101
/2021.10.18.464704
Maynard, E. M., Hatsopoulos, N. G., Ojakangas, C. L., Acuna,
B. D., Sanes, J. N., Normann, R. A., & Donoghue, J. P. (1999).
Neuronal interactions improve cortical population coding of
movement direction. Journal of Neuroscience, 19(18),
8083–8093. https://doi.org/10.1523/ JNEUROSCI.19-18-08083
.1999, PubMed: 10479708
McInnes, L., Healy, J., & Melville, J. (2018). UMAP: Uniform
Manifold Approximation and Projection for dimension reduc-
tion. arXiv:1802.03426. https://doi.org/10.48550/arXiv.1802
.03426
Nardin, M., Csicsvari, J., Tkačik, G., Tkačik, T., & Savin, C. (2021).
The structure of hippocampal CA1 interactions optimizes spatial
coding across experience. bioRxiv. https://doi.org/10.1101/2021
.09.28.460602
O’Leary, J. G., & Hatsopoulos, N. G. (2006). Early visuomotor rep-
resentations revealed from evoked local field potentials in motor
and premotor cortical areas. Journal of Neurophysiology, 96(3),
1492–1506. https://doi.org/10.1152/jn.00106.2006, PubMed:
16738219
Pedreschi, N., Bernard, C., Clawson, W., Quilichini, P., Barrat, A.,
& Battaglia, D. (2020). Dynamic core-periphery structure of
information sharing networks in entorhinal cortex and hippo-
campus. Network Neuroscience, 4(3), 946–975. https://doi.org
/10.1162/netn_a_00142, PubMed: 33615098
Recanatesi, S., Ocker, G. K., Buice, M. A., & Shea-Brown, E.
(2019). Dimensionality in recurrent spiking networks: Global
trends in activity and local origins in connectivity. PLOS Compu-
tational Biology, 15(7), e1006446. https://doi.org/10.1371
/journal.pcbi.1006446, PubMed: 31299044
Reimer, J., & Hatsopoulos, N. G. (2010). Periodicity and evoked
responses in motor cortex. Journal of Neuroscience, 30(34),
11506–11515. https://doi.org/10.1523/ JNEUROSCI.5947-09
.2010, PubMed: 20739573
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Ruda, K., Zylberberg, J., & Field, G. D. (2020). Ignoring correlated
activity causes a failure of retinal population codes. Nature Com-
munications, 11(1), 4605. https://doi.org/10.1038/s41467-020
-18436-2, PubMed: 32929073
Shenoy, K. V., Sahani, M., & Churchland, M. M. (2013). Cortical
control of arm movements: A dynamical systems perspective.
Annual Review of Neuroscience, 36(1), 337–359. https://doi
.org/10.1146/annurev-neuro-062111-150509, PubMed:
23725001
Squartini, T., Picciolo, F., Ruzzenenti, F., & Garlaschelli, D. (2013).
Reciprocity of weighted networks. Scientific Reports, 3(1), 2729.
https://doi.org/10.1038/srep02729, PubMed: 24056721
Stevenson, I. H., London, B. M., Oby, E. R., Sachs, N. A., Reimer, J.,
Englitz, B., David, S. V., Shamma, S. A., Blanche, T. J., Mizuseki,
K., Zandvakili, A., Hatsopoulos, N. G., Miller, L. E., & Kording,
K. P. (2012). Functional connectivity and tuning curves in popu-
lations of simultaneously recorded neurons. PLOS Computa-
tional Biology, 8(11), e1002775. https://doi.org/10.1371/journal
.pcbi.1002775, PubMed: 23166484
Sundiang, M., Hatsopoulos, N. G., & MacLean, J. N. (2022).
Dynamic structure of motor cortical neuron co-activity carries
behaviorally relevant information, Dryad, Dataset. https://doi
.org/10.5061/dryad.9p8cz8wm6
Network Neuroscience
677
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic structure of M1 neural coactivity
Thompson, W. H., Brantefors, P., & Fransson, P. (2017). From static
to temporal network theory: Applications to functional brain con-
nectivity. Network Neuroscience, 1(2), 69–99. https://doi.org/10
.1162/NETN_a_00011, PubMed: 29911669
Vaadia, E., Haalman, I., Abeles, M., Bergman, H., Prut, Y., Slovin, H.,
& Aertsen, A. (1995). Dynamics of neuronal interactions in monkey
cortex in relation to behavioural events. Nature, 373(6514),
515–518. https://doi.org/10.1038/373515a0, PubMed: 7845462
Vyas, S., Golub, M. D., Sussillo, D., & Shenoy, K. V. (2020). Com-
putation through neural population dynamics. Annual Review of
Neuroscience, 43(1), 249–275. https://doi.org/10.1146/annurev
-neuro-092619-094115, PubMed: 32640928
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
6
6
1
2
1
1
8
3
4
8
n
e
n
_
a
_
0
0
2
9
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
678