RECHERCHE

Multimodal multilayer network centrality
relates to executive functioning

Lucas C. Breedt1

, Fernando A. N. Santos1,2, Arjan Hillebrand3, Liesbeth Reneman4,

Anne-Fleur van Rootselaar5, Menno M. Schoonheim1, Cornelis J. Stam3,6, Anouk Ticheler1,
Betty M. Tijms7, Dick J. Veltman8, Chris Vriend1,8, Margot J. Wagenmakers8,9,
Guido A. van Wingen10, Jeroen J. G. Geurts1, Anouk Schrantee4, and Linda Douw1

1Department of Anatomy and Neurosciences, Amsterdam UMC, Vrije Universiteit Amsterdam,
Amsterdam Neuroscience, The Netherlands
2Institute of Advanced Studies, University of Amsterdam, The Netherlands
3Department of Clinical Neurophysiology and MEG Center, Amsterdam UMC, Vrije Universiteit Amsterdam,
Amsterdam Neuroscience, The Netherlands
4Department of Radiology and Nuclear Medicine, Amsterdam UMC, University of Amsterdam,
Amsterdam Neuroscience, The Netherlands
5Department of Neurology and Clinical Neurophysiology, Amsterdam UMC, University of Amsterdam,
Amsterdam Neuroscience, The Netherlands
6Department of Neurology, Amsterdam UMC, Vrije Universiteit Amsterdam, Amsterdam Neuroscience, The Netherlands
7Alzheimer Center Amsterdam, Department of Neurology, Amsterdam Neuroscience, Amsterdam UMC,
Vrije Universiteit Amsterdam, The Netherlands
8Département de psychiatrie, Amsterdam UMC, Vrije Universiteit Amsterdam, Amsterdam Neuroscience, The Netherlands
9GGZ in Geest Specialized Mental Health Care, Amsterdam, The Netherlands
10Département de psychiatrie, Amsterdam UMC, University of Amsterdam, Amsterdam Neuroscience, The Netherlands

Mots clés: Cognition, Graph theory, Functional connectivity, Structural connectivity, Multiplex
réseaux, Minimum spanning tree

ABSTRAIT

Executive functioning (EF) is a higher order cognitive process that is thought to depend on a
network organization facilitating integration across subnetworks, in the context of which the
central role of the fronto-parietal network (FPN) has been described across imaging and
neurophysiological modalities. Cependant, the potentially complementary unimodal information
on the relevance of the FPN for EF has not yet been integrated. We employ a multilayer framework
to allow for integration of different modalities into one ‘network of networks.’ We used diffusion
IRM, resting-state functional MRI, MEG, and neuropsychological data obtained from 33 healthy
adults to construct modality-specific single-layer networks as well as a single multilayer network
per participant. We computed single-layer and multilayer eigenvector centrality of the FPN as a
measure of integration in this network and examined their associations with EF. We found that
higher multilayer FPN centrality, but not single-layer FPN centrality, was related to better EF. Nous
did not find a statistically significant change in explained variance in EF when using the multilayer
approach as compared to the single-layer measures. Dans l'ensemble, our results show the importance of
FPN integration for EF and underline the promise of the multilayer framework toward better
understanding cognitive functioning.

RÉSUMÉ DE L'AUTEUR

Until now, the relationship between brain network topology and cognition has mostly been
studied using isolated modal information (par exemple., functional MRI or magnetoencephalography).
Such isolated analyses ignore potentially complementary information. Ici, we use

un accès ouvert

journal

Citation: Breedt, L. C., Santos, F. UN. N.,
Hillebrand, UN., Reneman, L., van
Rootselaar, A.-F., Schoonheim, M.. M.,
Stam, C. J., Ticheler, UN., Tijms, B. M.,
Veltman, D. J., Vriend, C., Wagenmakers,
M.. J., van Wingen, G. UN., Geurts, J.. J.. G.,
Schrantee, UN., & Douw, L. (2023).
Multimodal multilayer network centrality
relates to executive functioning. Réseau
Neurosciences, 7(1), 299–321. https://est ce que je
.org/10.1162/netn_a_00284

EST CE QUE JE:
https://doi.org/10.1162/netn_a_00284

Informations complémentaires:
https://doi.org/10.1162/netn_a_00284;
https://github.com/nkoub/multinetx;
https://github.com/networkx; https://
github.com/multinetlab-amsterdam
/projects/tree/master/mumo_paper_2021

Reçu: 9 Mars 2022
Accepté: 7 Octobre 2022

Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.

Auteur correspondant:
Lucas C. Breedt
l.breedt@amsterdamumc.nl

Éditeur de manipulation:
Olaf Sporns

droits d'auteur: © 2022
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence

La presse du MIT

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Multilayer network centrality relates to executive functioning

multimodal imaging and neuropsychological data collected from healthy adults to demonstrate
that increased centrality of the fronto-parietal network in a multilayer network is related to better
executive functioning. We find no such relation for single-layer networks. These results show
the importance of fronto-parietal network integration for executive functioning, as well as the
value of a multilayer framework in network analyses of the brain.

INTRODUCTION

A thread of network thinking runs through the history of cognition research. Dans 1983, Fodor
introduced the ‘modularity of mind’ theory of cognition and behavior (Fodor, 1983). Il
posited that lower order processes of the mind are modular, with domain-specific modules
operating independently without interacting with other modules. Contrastingly, he argued that
higher order cognitive processes such as executive functioning (EF), which is thought to be the
most complex and evolutionarily special cognitive domain (Ardila, 2008), are global rather
than modular. De même, the evolution of neuroscience has led to a data-driven approach
toward understanding how the brain governs such higher order cognition by studying the brain
as a complex network through the framework of graph theory (Barabási, 2016; Bullmore &
Sporns, 2009). Brain regions are thus represented as nodes, and the interactions between them
as links.

Different modalities can be used to obtain these brain networks. Anatomically, diffusion
magnetic resonance imaging (dMRI) maps the physical connections (c'est à dire., white matter bun-
dles) between the neural elements of the brain, yielding a structural network. Functionally,
multiple imaging techniques can be used to observe brain activity. Resting-state functional
magnetic resonance imaging (rsfMRI) detects variations in blood oxygenation as an indirect
measure of neuronal activity at a high spatial resolution, and magnetoencephalography
(MEG) provides a direct measure of the summed electromagnetic activity generated by groups
of neurons. In both rsfMRI and MEG, statistical interdependencies between levels of activity in
different areas of the brain are used as a measure for functional connectivity (Aertsen et al.,
1989; Friston et al., 1993), yielding functional networks.

The organization of these structural and functional networks appears to be crucial for EF.
Although the exact mechanisms underlying this cognitive function remain unknown (Jurado &
Rosselli, 2007), EF appears to be highly reliant on network integration, c'est, the interplay
between specialized modules (Bullmore & Sporns, 2012). Key in facilitating this integration
is the fronto-parietal network (FPN), a module that plays a crucial central role as a ‘connector’
within the brain network, having diverse connections to other modules of the brain (Bertolero
et coll., 2017). The network integration that is hypothetically happening in the individual brain
regions that form the FPN can be characterized through network measures of centrality. Nodal
centrality reflects the relative importance of a node within the network. Highly central regions
are typically connected to many other regions, implying a pivotal role in the facilitation of
network integration (Bertolero et al., 2017; van den Heuvel & Sporns, 2011). En effet, a more
central role of the FPN has been related to better EF in unimodal network studies that utilized
dMRI (Caeyenberghs et al., 2016), rsfMRI (Cole et al., 2012; Takeuchi et al., 2015), or MEG
(van Dellen et al., 2013).

Cependant, in such unimodal network studies the different aspects of the brain network, pour
example, structural and functional, are only studied in isolation, while we know from other
types of complex networks that network structure and different types of functional dynamics

Unimodal:
Consisting of a single form of
imaging, par exemple., only MRI or only MEG.

Neurosciences en réseau

300

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Multilayer network centrality relates to executive functioning

Multimodal:
Consisting of more than one form of
imaging, par exemple., MRI as well as MEG.

Multilayer network:
Network comprised of multiple
layers whose nodes interact. Chaque
layer contains different information.

occurring on top of it jointly and synergistically determine system behavior (Boccaletti et al.,
2006, 2014; Cardillo et al., 2013; Zanin, 2015). In the brain, it remains unclear exactly how
the integration between these network aspects relates to EF. Nevertheless, the interplay
between structural and functional connectivity has been shown to be nontrivial, suggérant
both should be considered simultaneously (Damoiseaux & Greicius, 2009; Parc & Friston,
2013; Stam et al., 2016). De plus, in the case of networks based on MEG data, the broad-
band signal is often filtered into canonical frequency bands, and network analysis is performed
for each frequency band separately, but the different imaging modalities and frequency bands
each yield unique and even complementary information that should perhaps not be consid-
ered in isolation. Unimodal networks are thus limited representations of the essentially multi-
modal brain network (Garcés et al., 2016; Mandke et al., 2018; Zanin, 2015), but until recently
we lacked the appropriate tools to integrate multiple modalities into a single network
representation.

Multilayer network analysis is a newly developed mathematical framework that enables this
integration and allows for analysis of multimodal data (Boccaletti et al., 2014; De Domenico
et coll., 2013; Kivelä et al., 2014). A multilayer network is a ‘network of networks,’ comprised of
multiple interconnected layers, each characterizing a different aspect of the same system.
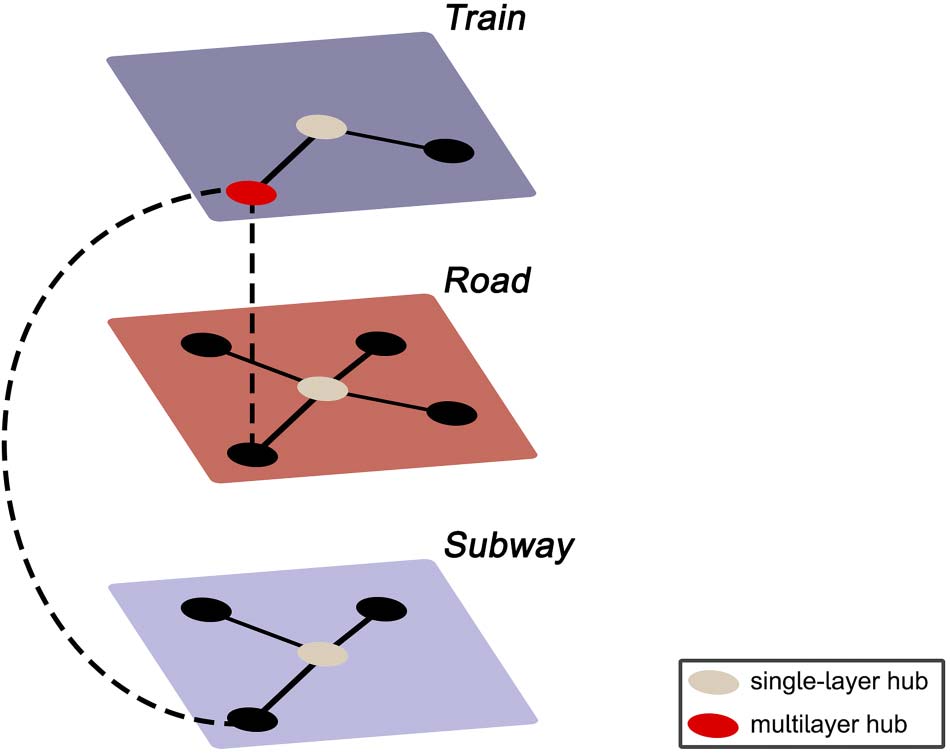
Chiffre 1 illustrates the concept of multilayer networks using the analogy of a commuter net-
travail. Although the framework of multilayer networks is relatively new in the field of neuro-
science, promising results have already been reported. Multilayer analysis of dMRI and fMRI
networks of healthy participants confirmed the synergistic nature of the structure and function
of the brain network (Battiston et al., 2017). Further relevance of multilayer analysis has been

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Example of a multilayer transport network, encoding information about train, subway,
Chiffre 1.
and road connectivity, and the interlayer links between them. Suppose there is a sudden increase in
commuters in the subway network in the absence of any delayed or cancelled subway cars or sus-
pended subway stations. Considering the single-layer subway network in isolation, the observed
spike in commuters would seem inexplicable, as the properties of the subway network (c'est à dire., le
links and nodes) are unaltered. Cependant, observing the entire transport system might reveal severe
delays in the train network, forcing people who usually commute by train to now use the subway,
thus leading to an increase in commuters in the subway network. De même, consider the red node in
the train network. From a single-layer perspective, this is a peripheral station that is of little impor-
tance to the transport system. Cependant, the multilayer perspective reveals this to be the only loca-
tion where all three modes of transport connect, and the seemingly peripheral station thus plays a
significant integrative role in the transportation network—a property that would have remained
unnoticed without incorporating all the layers of the system.

Neurosciences en réseau

301

Multilayer network centrality relates to executive functioning

shown in clinical studies: multilayer connectivity differences were reported between patients
with schizophrenia and healthy controls, and these differences were related to symptom sever-
ville (Brookes et al., 2016). De plus, a study in schizophrenia and another study in Alzheimer’s
disease suggested that multilayer centrality could outperform single-layer measures to distin-
guish cases from healthy controls (De Domenico et al., 2016; Guillon et al., 2017). Addition-
ally, an MEG study used nodal centrality metrics to identify brain regions that were vulnerable
in patients with Alzheimer’s disease compared to healthy controls and found that such regions
could only be detected using a multilayer approach. Even more relevant to our work, ce
vulnerability of central regions in the multilayer network was related to cognitive dysfunction
(Yu et al., 2017). Multilayer network analysis can thus contribute to a better understanding of
the relation between the FPN and EF.

Ici, we used multimodal data to assess the association between FPN centrality and EF in
healthy participants and statistically explored the potential added value of a multilayer frame-
work over a single-layer framework. Nous (un) hypothesized a positive association between FPN
centrality of both the single- and multilayer networks, which could already indicate that the
multilayer approach is useful to integrate multimodal data toward investigating executive func-
tioning. De plus, nous (b) aimed to test whether multilayer centrality supersedes its single-layer
equivalents in explaining individual differences in EF statistically, through a significant change
in explained variance.

MÉTHODES

Participants

This study was preregistered in the International Clinical Trials Registry Platform under trial ID
NTR7510. Thirty-nine (39) healthy participants were prospectively recruited for this specific
study through an online platform, Hersenonderzoek.nl (www.hersenonderzoek.nl), where vol-
unteers can register for participation in neuroscience studies. Participants were selected based
on the following inclusion criteria: (un) age between 20 et 70 ans, (b) native Dutch
conférencier, et (c) able to provide written informed consent. The following exclusion criteria
were used: (un) history of neurological or psychiatric disease, (b) current and regular use of
centrally acting drugs, et (c) presence of contra-indications for MRI or MEG. Participants
were asked not to ingest any caffeine or alcohol on the testing days. Approval was obtained
from the VU University Medical Center Medical Ethical Committee, and all subjects provided
written informed consent prior to participation.

Neuropsychological Evaluation

Participants underwent an extensive customized neuropsychological test battery, consisting of
the Dutch version of Rey’s Auditory Verbal Learning Test (van den Burg et al., 1985), the Con-
cept Shifting Test (CST; van der Elst et al., 2006un), the Memory Comparison Test (van der Elst
et coll., 2007), the Stroop Color-Word Test (SCWT; Hammes, 1978), the Location Learning Test
(LLT; Bucks & Willison, 1997), the Categorical Word Fluency Test (Mulder et al., 2006), et
the Letter-Digit Modalities Test (van der Elst et al., 2006b). Nous avons utilisé (subscores on) three of
these tests to assess EF. The first test we used was the CST, where the participant was shown
16 small circles, grouped in a large circle, containing either digits (CST part A), letters (CST part
B), or both digits and letters (CST part C). These circles needed to be crossed out in ascending
order in part A, in alphabetical order in part B, and in alternating order (digit-letter) in part C.
The participant was asked to perform the test as quickly as possible without making mistakes.
En plus, to correct for motor speed, a null-condition with empty circles (CST zero) était

Neurosciences en réseau

302

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Multilayer network centrality relates to executive functioning

carried out three times. The second test we used was the SCWT, where the participant was
asked to read four different cards. On the first card, names of colors—red, vert, yellow,
and blue—were printed in black ink. On the second card, rectangles were printed in these
same colors. On the third card, the names of the colors were printed in an incongruent color
encre; Par exemple, the word ‘red’ was printed in yellow ink, and the participant was asked to
read the color of the ink and ignore the word. The fourth card was identical to the third card,
but several words were circled. For these circled words, the participant was asked to read the
word itself instead of the color of the ink. The third test we used was the Word Fluency Test,
where the participant was asked to name as many words in the category ‘animals’ as possible
within 60 seconds.

We used validated norms of the CST, SCWT, and Word Fluency Test to transform raw scores
into z-scores relative to a comparable healthy population. Briefly, raw CST scores were
adjusted for age only, as no effects of gender or age squared were present in the normative
sample of 1,794 Dutch adults (van der Elst et al., 2006un). Raw SCWT scores were corrected for
âge, age squared, and education (classified according to the Dutch Verhage system (Verhage,
1964), which ranges from level 1 [less than 6 years of primary education] to level 7 [university
degree]) (Schmand et al., 2012). Raw scores on the Word Fluency Test were corrected for age
and education, as there were no effects of age squared in the normative sample (Schmand
et coll., 2012). EF was defined as the average of z-scores for Word Fluency, Stroop-interference
(time to complete card 3 corrected for the time to complete card 2), and CST-shift (time to
complete card C minus the average time to complete cards A and B, adjusted for time to
complete CST zero).

Magnetic Resonance Imaging

MRI data were obtained using a 3T MRI system (Philips Ingenia CX) with a 32-channel
receive-only head coil at the Spinoza Centre for Neuroimaging in Amsterdam, The Nether-
lands. A high-resolution 3D T1-weighted image was collected with a magnetization-prepared
rapid acquisition with gradient echo (MPRAGE; TR = 8.1 ms, LE = 3.7 ms, flip angle = 8°,
voxel dimensions = 1 mm3 isotropic). This anatomical scan was registered to MNI space
through linear registration with nearest-neighbor interpolation, and was used for
co-registration and normalization of all other modalities (dMRI, IRMf, and MEG) to the same
espace.

Diffusion MRI. Diffusion MRI was collected with diffusion weightings of b = 1,000 et
2,000 s/mm2 applied in 29 et 59 instructions, respectivement, along with 9 nondiffusion weighted
(b = 0 s/mm2) volumes using a multiband sequence (MultiBand SENSE factor = 2, TR = 4.7 s,
LE = 95 ms, flip angle = 90°, voxel dimensions = 2 mm3 isotropic, no interslice gap). In addi-
tion, two scans with opposite phase encoding directions were collected for blip-up blip-down
distortion correction using FSL topup (Andersson et al., 2003). Structural connectomes were
constructed by performing probabilistic anatomically-constrained tractography (ACT) (Forgeron
et coll., 2012) in MRtrix3 (Tournier et al., 2019). A tissue response function was estimated from
the preprocessed and bias field corrected dMRI data using the multishell multitissue five-
tissue-type algorithm (msmt_5tt). Subsequently, the fiber orientation distribution for each voxel
was determined by performing multishell multitissue constrained spherical deconvolution
(MSMT-CSD) (Jeurissen et al., 2014). ACT was performed by randomly seeding 100 million
fibers within the white matter to construct a tractogram, and spherical-deconvolution informed
filtering of tractograms (SIFT, SIFT2 method in MRtrix3) (Smith et al., 2015) was then performed
to improve the accuracy of the reconstructed streamlines and reduce false positives. For every

Neurosciences en réseau

303

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Multilayer network centrality relates to executive functioning

participant, their respective 3D T1-weighted image was used to parcellate the brain into 210
cortical Brainnetome atlas (BNA) (Fan et al., 2016) régions. We then used this parcellation to
convert the tractogram to a structural network, where weighted edges represented the sum of
all streamlines leading to and from all voxels within two brain regions.

Resting-state functional MRI. Resting-state fMRI was collected using a multiband sequence
(MultiBand SENSE factor = 2, TR = 1.52 s, LE = 30 ms, flip angle = 70°, voxel size = 2.5 ×
2.5 × 2.75 mm3, interslice gap = 0.25 mm, 310 volumes, 12-min acquisition). Participants
were instructed to remain awake with their eyes open. Preprocessing was done using FSL 5
(FMRIB 2012, Oxford, United Kingdom, https://www.fmrib.ox.ac.uk/fsl) and included brain
extraction, removal of the first four volumes, motion correction by regressing out six motion
parameters, and spatial smoothing at 5-mm full width half maximum. An independent com-
ponent analysis was performed for automatic removal of motion artifacts (ICA-AROMA) (Pruim
et coll., 2015), followed by regressing out white matter and cerebrospinal fluid signals and high-
pass filtering (100 s cutoff ). Mean absolute motion did not exceed 0.6 mm for any participant;
the median was 0.27 mm (0.08–0.59 mm). The rsfMRI data were registered to native 3D T1
space using boundary-based registration. The BNA atlas was then reverse-registered to each
participant’s functional data using nearest-neighbor interpolation. For every participant, un
mask containing only gray matter voxels with reliable rsfMRI signal was constructed by com-
bining a gray matter mask and an rsfMRI mask, excluding all voxels with a signal intensity in
the lowest quartile of the robust range (for more details, see Eijlers et al., 2017). Time series
were extracted from all atlas regions by averaging time series across all voxels within each
region. Thirteen regions with signal loss (c'est à dire., regions with zeros in the functional connectivity
matrices) due to magnetic field inhomogeneities in these echo-planar imaging sequences were
removed from further analyses across all participants and modalities. Ainsi, 197 atlas regions
remained for all further analyses. Enfin, for every participant, Pearson correlation coefficients
between all pairs of time series were calculated to obtain a functional connectivity matrix.
Correlation coefficients were absolutized, as most network metrics do not take into account
negative values, but inverse correlations may carry relevant information (Chai et al., 2012;
Zhan et al., 2017).

Magnetoencephalography

MEG data were recorded in a magnetically shielded room ( Vacuumschmelze GmbH, Hanau,
Allemagne) using a 306-channel (102 magnetometers and 204 gradiometers) whole-head MEG
système (Elekta Neuromag Oy, Helsinki, Finlande) with a sampling frequency of 1250 Hz during
a no-task, eyes-closed condition for 5 minutes, an eyes-open condition for 2 minutes, and a
final eyes-closed condition for another 5 minutes, with the participant in supine position.
Ici, we used only the first eyes-closed recording for all further analyses. An anti-aliasing filter
de 410 Hz and a high-pass filter of 0.1 Hz were applied online. The cross-validation signal
space separation (xSSS) (van Klink et al., 2017) was applied to aid visual inspection of the data.
We removed channels containing no signal or noisy signal, with a maximum of 12 chaînes
removed per participant. Further noise removal was performed offline using the temporal
extension of signal space separation (tSSS) (Taulu & Simola, 2006) in MaxFilter (version
2.2.15). The head position relative to the MEG sensors was recorded continuously using the
signals from five head-localization coils. Coil positions and the scalp outline were digitized
using a 3D digitizer (Fastrak, Polhemus, Colchester, VT). A surface-matching procedure was
used to achieve co-registration of the participant’s digitized scalp surface and their anatomical
IRM, with an estimated resulting accuracy of 4 mm (Whalen et al., 2008). A single best fitting
sphere was fitted to the outline of the scalp as obtained from the co-registered MRI, ce qui était

Neurosciences en réseau

304

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Multilayer network centrality relates to executive functioning

Phase lag index:
Measure of connectivity in MEG
(or EEG) based on the asymmetry of
the distribution of phase differences
between two signals.

used as a volume conductor model for the beamformer approach described below. The co-
registered MRI was spatially normalized to a template MRI, and the voxels in the normalized
co-registered MRI were again labeled according to the same atlas. We then used a scalar beam-
forming approach (Hillebrand et al., 2012) to reconstruct the source of neurophysiological
activity from the sensor signal. The beamformer weights were based on the lead fields, le
broadband (0.5–48 Hz) data covariance, and noise covariance. The data covariance was based
sur, on average, 298 s of data (range 293–314 s). A unity matrix was used noise covariance.
Broadband data were then projected through the normalized beamformer weights to obtain
time series for each atlas region. Out of all the voxels that constitute an atlas region, the centroid
(Hillebrand et al., 2016) was selected to reconstruct localized MEG activity, resulting in time
series for each of the 197 included cortical regions. For all participants, we included the first
88 epochs of 4,096 samples (3.28 s) of the obtained time series (total length 4 min and ∼48 s).
Fast Fourier transforms were applied to filter the time series into six frequency bands: delta (0.5–
4 Hz), theta (4–8 Hz), lower alpha (8–10 Hz), upper alpha (10–13 Hz), beta (13–30 Hz), et
gamma (30–48 Hz). We then computed the phase lag index (PLI) (Stam et al., 2007) entre
the frequency-filtered time series of all pairs of regions using custom-made scripts in MATLAB
(R2018b, Mathworks, Natick, MA) to obtain weighted functional connectivity matrices.

Single-Layer Network Construction and Analysis
D'abord, we constructed minimum spanning trees (MST) for the six frequency band–specific MEG
networks by applying Kruskal’s algorithm (Kruskal, 1956) to the functional connectivity matri-
ces. The MST is a binarized subgraph of the original graph that connects all the nodes in the
network without forming loops. This represents the backbone of the network (Stam et al.,
2014; Tewarie et al., 2015), lequel, importantly, is not hindered by common methodological
issues such as effects of connection strength or link density on the estimated topological char-
acteristics of networks, while measures calculated on this sparse network are closely related to
measures computed on the original underlying network (Tewarie et al., 2015). Edge weights
were defined as the inverted PLI values (1/PLI) when constructing the minimum spanning tree,
since we were interested in the strongest connections (Tewarie et al., 2014).

While the usage of the MST is ubiquitous in MEG studies (Blomsma et al., 2022), it is only
rarely used in dMRI and rsfMRI studies, where weighted networks are more commonly ana-
lyzed. As we here aimed to compare a relatively new multilayer network approach to the now
often-used single-layer methodology, we primarily opted to remain as close as possible to the
existing literature on single-layer networks. We therefore calculated nodal eigenvector central-
ville (EC) individually for each of the six MEG MSTs, and for the fully connected weighted dMRI
and rsfMRI connectivity matrices, using the brain connectivity toolbox (https://sites.google
.com/site/bctnet/) in MATLAB. EC is a measure of nodal centrality that assumes that a node
is more influential if it is connected to nodes that are highly central themselves, and thus con-
siders both the connections of a node itself as well as the connections of its neighbors. Ce
makes it an interesting measure of centrality that takes the entire network into account. Addi-
tionally, EC is a spectral measure, and may therefore be less sensitive to noise than other
measures of centrality (Kardos et al., 2020), particularly when applied to the backbone of
the network. En outre, EC has been shown to be highly relevant for cognition in studies
using dMRI (Fagerholm et al., 2015), rsfMRI (Eijlers et al., 2017), and MEG (Hardmeier et al.,
2012). For a more detailed explanation of the EC and its mathematical definition, see Fornito
et autres. (2016).

Enfin, we extracted and subsequently averaged the ECs of all nodes belonging to the FPN
to obtain one value per single-layer network per participant (for a total of eight values per

Neurosciences en réseau

305

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

/

t

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Multilayer network centrality relates to executive functioning

Multiplex network:
Special case of multilayer networks,
with interlayer connections present
only between a node’s counterparts
across layers.

Interlayer links:
Connections between two different
layers of a multilayer network.

Intralayer links:
Connections within one layer
(of a multilayer network).

Supra-adjacency matrix:
Matrix representation of a multilayer
réseau. Diagonal blocks contain
connectivity within a layer; off-
diagonal blocks contain connectivity
between layers.

participant), allowing us to assess interindividual differences in the integration of the FPN in
the context of the entire brain network. Regions belonging to the FPN were defined based on
an earlier categorization (Vriend et al., 2018) of the regions of the BNA according to the clas-
sical seven-network parcellation by Yeo et al. (2011).

Multilayer Network Construction and Analysis

A multiplex network is a multilayer network used to describe different interactions between the
same set of nodes (Bianconi, 2018). In this context, each layer is characterized by a different
modality of interaction. Donc, this mathematical framework is useful to encode informa-
tion from brain networks created using different edge weights or imaging modalities as long as
all layers are built using the same atlas. In such a multiplex network, links between different
layers, also known as interlayer links, exclusively connect the same node or brain region
across layers.

There is, as of yet, no established method for determining biologically meaningful weighted
interlayer links between different modalities. En plus, network metrics can potentially be
biased by differences in link density (especially when comparing dMRI networks, which are
inherently sparse, and functional networks) and average connectivity across layers and
between participants (Mandke et al., 2018). Ici, we therefore decided to construct binary
multiplex networks. Par conséquent, in addition to the MEG MSTs described in the section
Single-Layer Network Construction and Analysis, we used Kruskal’s algorithm to construct MSTs
for the dMRI and rsfMRI data. We then integrated these eight MSTs to obtain an interconnected
multiplex network for every participant. Each participant’s multiplex thus consisted of L = 8
layers (one for dMRI, one for rsfMRI, and one for each of the six MEG frequency bands), avec
each layer containing the same set of N = 197 nodes (atlas regions), and each spanning tree
and thus layer having M = N − 1 = 196 intralayer links. The weights of the interlayer connec-
tions were set to 1, identical to the intralayer connections. The resulting multilayer network
was represented as an LxN by LxN supra-adjacency matrix with diagonal blocks encoding
intralayer connectivity for each modality and off-diagonal blocks encoding interlayer connec-
tivité. Supra-adjacency matrices were then exported to Python (version 3.6, Python Software
Fondation, available at https://www.python.org), and multilayer nodal EC was computed
according to earlier work. Briefly, we first computed the leading eigenvector of the supra-
adjacency matrix, and we then aggregated the corresponding eigenvector of size LxN into a
vector of size N, by averaging the entries corresponding to the same nodes, as described in De
Domenico et al. (2013). To do so, we used custom-made scripts that integrate the Python
libraries multiNetX (Solé-Ribalta et al., 2013) and NetworkX (version 2.3) (Hagberg et al.,
2008), which can be found on GitHub (https://github.com/nkoub/multinetx and https://
github.com/networkx, respectivement). To validate our code, we compared, for a subset of our
data, the EC values obtained through the use of our scripts to those obtained using muxViz, un
well-known tool for multilayer analysis (De Domenico et al., 2015b). We then again extracted
and averaged ECs of the FPN nodes, yielding one value for multilayer EC per participant. UN
schematic overview of the methods can be found in Figure 2, and a 3D plot of a multilayer
network can be found in the Supporting Information. All of the custom-made scripts, ainsi que
the data that we used in this study, can be found on this project’s GitHub page (https://github
.com/multinetlab-amsterdam/projects/tree/master/mumo_paper_2021).

Statistical Analyses

Frequentist statistics were used, with a significance threshold of 0.05 set before starting the
analyses, through SPSS (version 26, IBM Corp., Armonk, New York). To assess the relation between

Neurosciences en réseau

306

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Multilayer network centrality relates to executive functioning

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

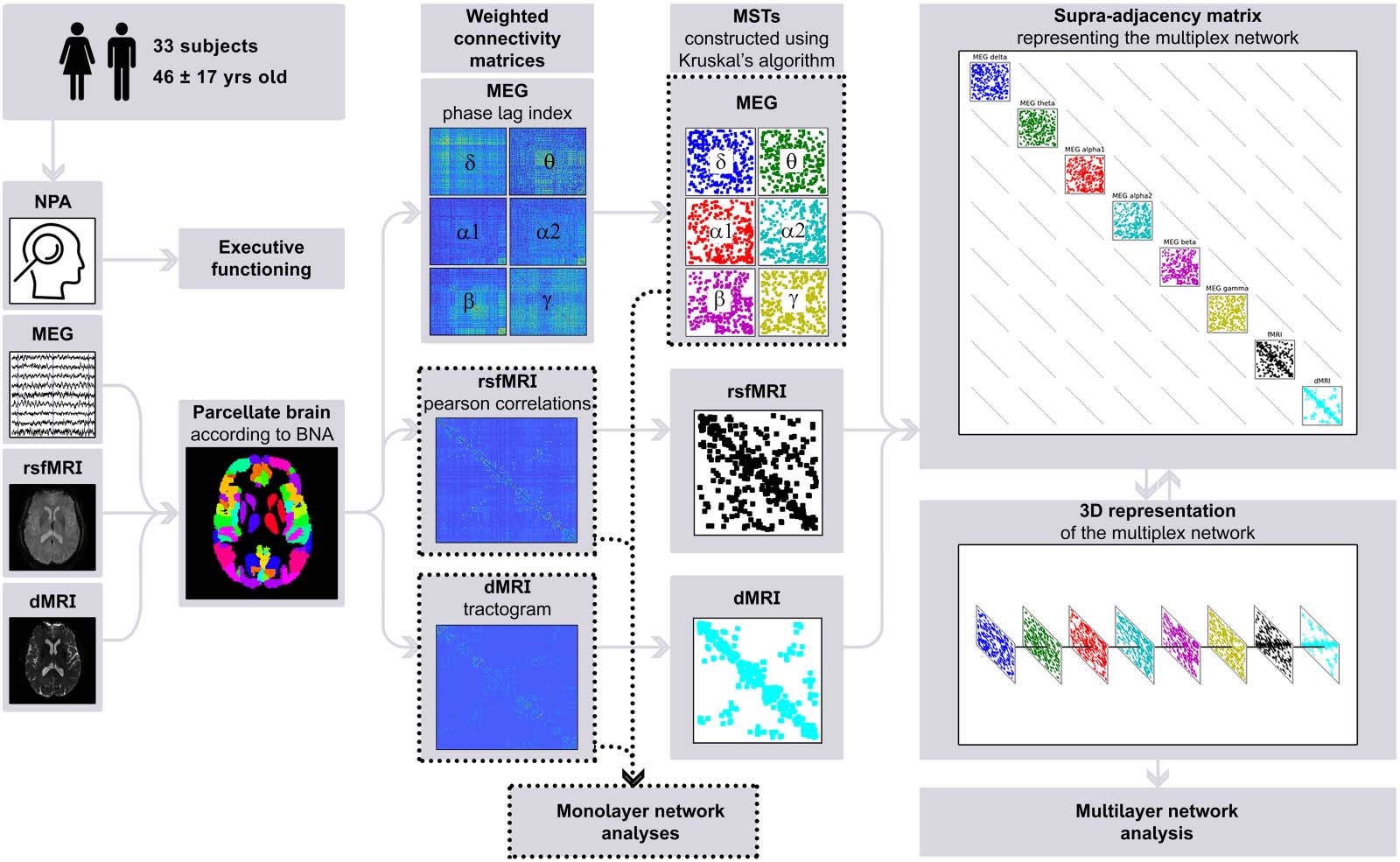
Chiffre 2. Schematic overview of the analysis pipeline. For every participant, neuropsychological data was used to compute cognition scores;
raw imaging data obtained from diffusion MRI, resting-state functional MRI, and magnetoencephalography was preprocessed; the brain was
parcellated according to the Brainnetome Atlas; connectivity was calculated to construct weighted connectivity matrices; minimum spanning
trees of the weighted matrices were constructed using Kruskal’s algorithm; and finally a supra-adjacency matrix representing a multilayer
network was constructed. Note that single-layer network measures were computed on the minimum spanning trees of the magnetoenceph-
alography frequency bands, but weighted data was used for diffusion MRI and resting-state functional MRI. NPA = neuropsychological assess-
ment; MEG = magnetoencephalography; rsfMRI = resting-state functional MRI; dMRI = diffusion MRI; BNA = Brainnetome Atlas; MST =
minimum spanning tree.

single- or multilayer EC of the FPN and age, sex, and education-corrected EF scores, we per-
formed a multiple regression analysis. With EF as the dependent variable, average EC values of
the FPN of each of the eight single-layer networks described in section Single-Layer Network
Construction and Analysis were added in a first block using a backward stepwise procedure
(F probability for removal 0.10), and the average EC of the FPN of the multilayer network was
entered in a second block. To assess whether these data met the assumption of collinearity, nous
ran multicollinearity diagnostics based on the variance inflating factor ( VIF). The VIF of a pre-
dictor is calculated by doing a linear regression of that predictor on all other predictors, after
which the VIF is defined by 1/(1 − R2). A high VIF is thus indicative of the presence of mul-
ticollinearity. Tolerance is the inverse of the VIF, and it is suggested that it should not be below
0.2 (Menard, 1995), which we used as a threshold in our manuscript. Regression models were
checked for normality of residuals using a Q-Q plot.

Post Hoc Analyses

To ensure the validity of our main result, we performed several additional post hoc analyses.
Firstly, we repeated the multiple regression analysis described above with a forward selection
procedure (F probability for entry 0.05). En plus, to explore whether the results were
affected by our decision to compute single-layer network metrics on the MSTs for the MEG
réseaux, but on the fully connected weighted networks for the fMRI and dMRI networks,
we re-ran the same regression using ECs of the FPN calculated on the MSTs of all the
single-layer networks. Aussi, to confirm the relevance of the multilayer framework, nous

Neurosciences en réseau

307

Multilayer network centrality relates to executive functioning

performed a multiple regression relating the average FPN centrality of all single-layer networks
to executive functioning. As before, we added the average FPN centrality values of each of the
eight single-layer networks in a first block by using a backward stepwise procedure; we then
entered the average EC of the FPN across the single-layer networks in a second block. In order
to assess whether EC was, as hypothesized, most sensitive to individual differences in EF, nous
also computed the degree centrality of the multilayer network and performed a linear regres-
sion relating the average multilayer degree centrality of the FPN to executive functioning.
En outre, we performed a leave-one-out cross-validation for the final regression model
of multilayer EC of the FPN and EF to assess whether regression results were not driven by
any single subject, and computed the cross-validated coefficient of determination (R2) en utilisant
the following equation:

R2 ¼ 100 (cid:2) 1 −

P.
n
i¼1 yi − (cid:1)y i
ð
P.
Þ2
n
i¼1 yið

Þ2

!

;

with n being the number of measurements, y the vector of measurements, and ý the vector of
model predictions, as described previously (Yeatman et al., 2014). En outre, we repeated
our analysis using a different parcellation, namely the automated anatomical labeling (AAL)
atlas (Tzourio-Mazoyer et al., 2002), and re-ran the regression model, to compare to the results
that were found using the BNA. Enfin, as a post hoc analysis, we explored the relationship
between multilayer centrality of the FPN and several other cognitive domains, namely, verbal
mémoire ( VM), information processing speed (IPS), working memory ( WM), and attention. À
this end, we performed four separate linear regression analyses with multilayer EC of the FPN
as the independent variable and the cognitive domains as the dependent variables. See the
Supporting Information for a detailed specification of the cognitive domains.

En plus, we performed a post hoc analysis to validate the methodology we used for
network thresholding within each layer, by comparing our chosen method of the MST to a
preliminary analysis inspired by recent developments on network inference (Nakamura
et coll., 2016). Briefly, in the latter, surrogate data is used to assign each edge in a network a
value reflecting its statistical significance, c'est, edges with significance below a chosen level
are more likely to be “true” edges. Ici, we leveraged this methodology as follows: nous (un)
create an ensemble of 100 null models for each single-layer matrix for every subject in our
cohort, by shuffling the edge weights in the original weighted matrix while preserving the
degree, weight, and strength distributions (using the function null_model_und_sign.m of the
Brain Connectivity Toolbox); (b) perform a nonparametric Kolmogorov–Smirnov test to assess
the significance of each original edge in comparison with the correspondent edges in the ran-
domized matrices (using a significance threshold of 0.05); (c) create a new, thresholded matrix,
containing only those edges that were significantly different from their randomized counter-
parties; et (d) compare the edges of the MST matrix with the significance matrix to establish the
fraction of significant edges in the MST matrix.

RÉSULTATS

Participant Characteristics

De la 39 included participants, two participants dropped out before completion of the study,
two were excluded during the study because of contra-indications for MRI, and another two
were excluded after visual inspection of their MRI data revealed artifacts. This resulted in a
total of 33 included participants with complete structural MRI, dMRI, rsfMRI, MEG, and neu-
ropsychological data that were used in the analyses. Of these participants, 18 were female and

Neurosciences en réseau

308

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Multilayer network centrality relates to executive functioning

15 were male. They were well spread out in terms of age, ranging between 22 et 70 années
vieux, with a mean age of 46 ± 17 années. Participants were mainly higher educated.

Network Correlates of Cognition

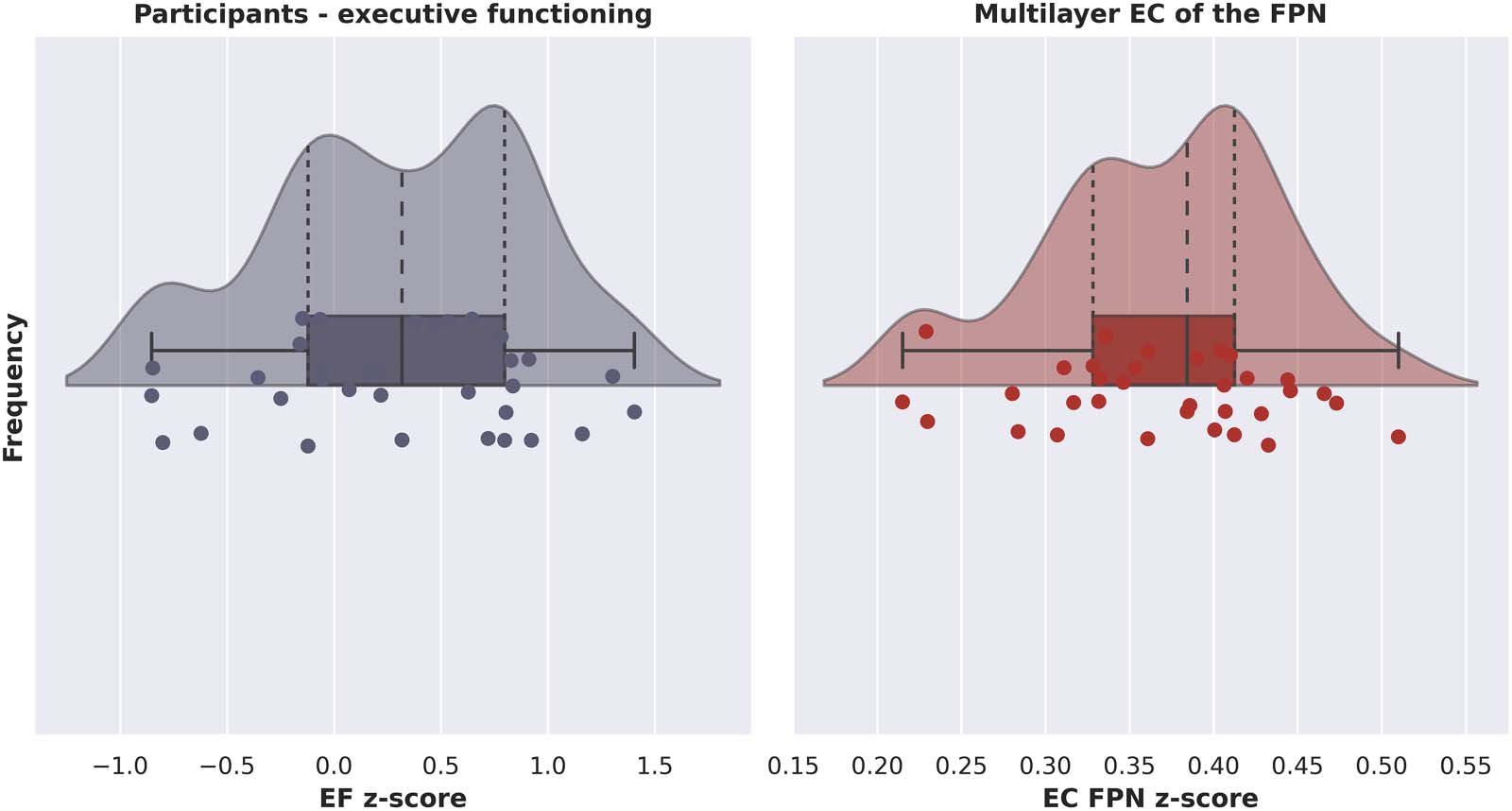
Chiffre 3 shows a raincloud plot with the distribution of EF z-scores for all participants. Impor-
tantly, as indicated by the wide range of normed z-scores, our sample was diverse in terms of
EF performance. There was no evidence of problematic multicollinearity between network
variables as indicated by their tolerance values, which were all greater than 0.2 (Menard,
1995). Chiffre 4 shows exemplar values of EC for the multilayer network as well as all the
single-layer networks, averaged over all subjects.

Testing our hypotheses, none of the single-layer network eigenvector centralities survived
the backward stepwise selection, see Table 1 for the coefficients of the included and excluded
variables. The final regression model, containing only multilayer EC of the FPN as a predictor
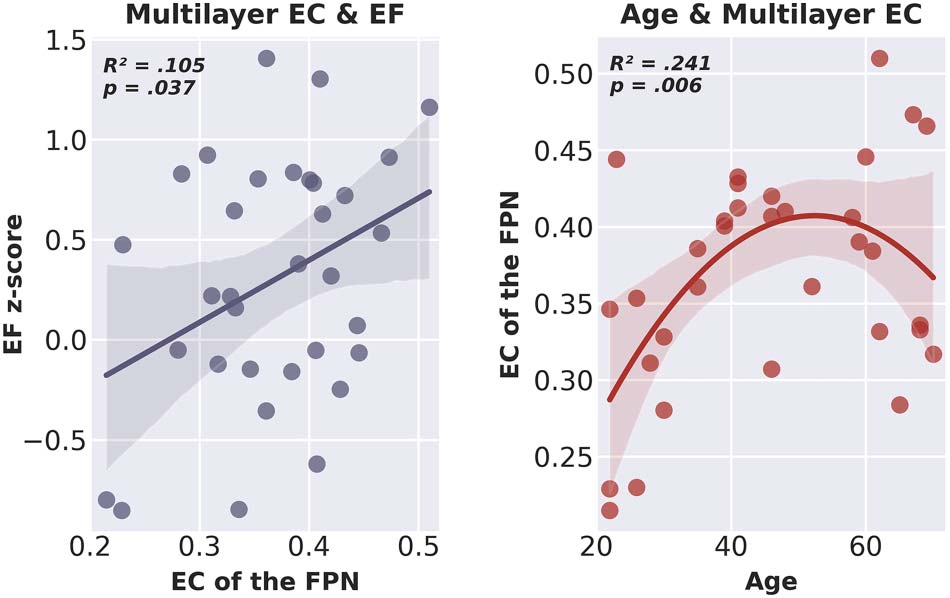
of EF, was statistically significant (R2 = .133, adjusted R2 = .105, F[1, 31] = 4.753, p = .037).
There was no significant increase in R2 from the second-to-last model, containing two predic-
tors (single-layer EC in the lower alpha band and multilayer EC), to this final significant model.
These results suggest that only EC of the FPN of the multilayer network was a significant pre-
dictor of EF, and that a higher multilayer EC of the FPN was related to better EF (voir la figure 5).

Post hoc testing confirmed these results. Repeating the analyses using a forward stepwise
procedure resulted in an identical, significant final model, containing only multilayer EC as a
predictor of EF (R2 = .133, adjusted R2 = .105, F[1, 31] = 4.753, p = .037). The regression using
the ECs of the FPN calculated on the MSTs of all single-layer networks (instead of the full
matrix for dMRI and rsfMRI) likewise yielded comparable results to the regression model
implemented initially, as the final model contained only the multilayer EC of the FPN. Le
multiple regression using the average EC of the single-layer networks instead of the multilayer
EC did not reach significance (p = .328 for the final model containing only the average EC of

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

t

/

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

t

.

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 3. Raincloud plots showing probability density, summary statistics, and individual datapoints of the z-score per participant of exec-
utive functioning (gauche) and multilayer eigenvector centrality of the fronto-parietal network (droite). EF = executive functioning; EC = eigenvector
centrality; FPN = fronto-parietal network.

Neurosciences en réseau

309

Multilayer network centrality relates to executive functioning

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

t

/

e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d

je

F
/

/

/

/

/

7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
un
_
0
0
2
8
4
p
d

.

t

F

b
oui
g
toi
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

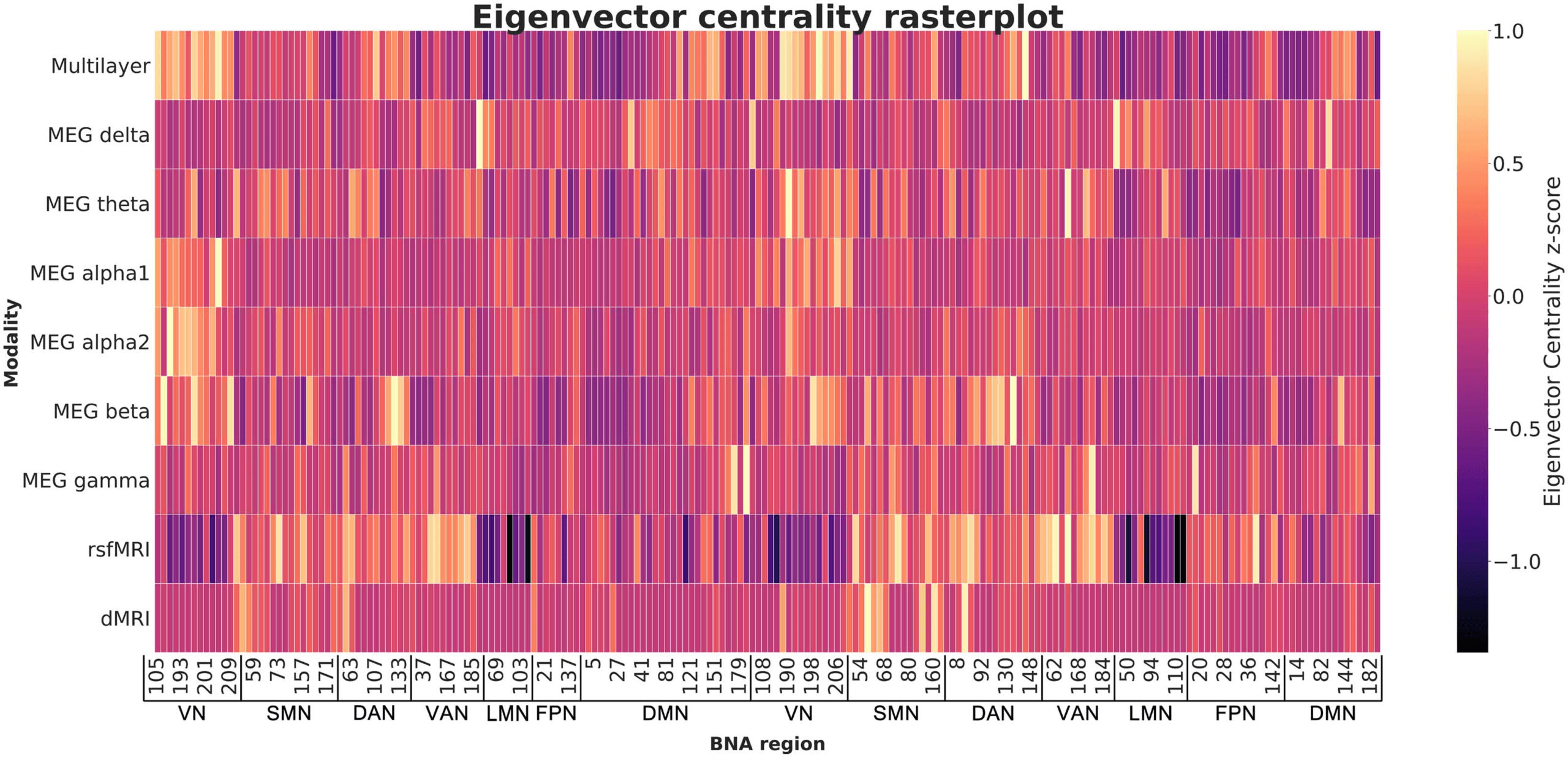
Chiffre 4. Raster plot showing eigenvector centrality in the eight single-layer networks and the multilayer network averaged over all subjects,
ordered by subnetwork (all left-hemisphere regions followed by all right-hemisphere regions). Yellow indicates regions with high EC. This shows
the differences in ‘centrality profiles’ across modalities. BNA region numbers refer to the labels as given in Supporting Information Table S1.
MEG = magnetoencephalography. rsfMRI = resting-state functional MRI; dMRI = diffusion MRI; BNA = Brainnetome Atlas; VN = visual network;
SMN = somatomotor network; DAN = dorsal attention network; VAN = ventral attention network; LMN = limbic network; FPN = fronto-parietal
réseau; DMN = default mode network.

all single-layer networks), indicating that multilayer EC does not simply represent the average
of all single-layer ECs. Multilayer degree centrality of the FPN did not relate significantly to EF
(p = .091), suggesting that, in the context of a multilayer framework, EC is a more sensitive
correlate of EF than degree centrality. The leave-one-out cross-validation resulted in a cross-
validated coefficient of determination of 20.75 as opposed to 30.22 for the full, non-cross-
validated, model. Repeating the analysis using a different atlas resulted in a nonsignificant final
model, albeit with comparable explanatory value to the model based on BNA data (R2 = .177,
adjusted R2 = .122, F[2, 32] = 3.220, p = .054); cependant, single-layer dMRI EC of the FPN was
a significant individual predictor in the final model (p = .021). Enfin, additional post hoc
analyses revealed associations between multilayer EC of the FPN and other cognitive domains.
There were no significant associations between multilayer EC of the FPN and VM (p = .227)
and attention (p = .565); cependant, there were significant associations between multilayer EC
of the FPN and IPS and WM. Higher multilayer EC of the FPN was related to better IPS, R2 =
.395, adjusted R2 = .129, F[1, 31] = 5.744, p = .023; β = .395. De la même manière, higher multilayer
EC of the FPN was related to better WM, R2 = .171, adjusted R2 = .144, F[1, 31] = 6.402,
p = .017; β = .414.

Multilayer Network Correlates of Age

To further validate the relevance of multilayer FPN centrality, we tested its relationship with
âge. Single-layer network studies have revealed that the brain network tends to become more

Neurosciences en réseau

310

Multilayer network centrality relates to executive functioning

Tableau 1.
regression models

Standardized beta coefficients and p values of included and excluded variables of the

Multilayer EC of the FPN and EF

Final model (R2

adj = .105)

Multilayer EC

Excluded variables

EC MEG delta

EC MEG upper alpha

EC dMRI

EC MEG theta

EC rsfMRI

EC MEG beta

EC MEG gamma

EC MEG lower alpha

Age & multilayer EC of the FPN

Final model (R2

adj = .241)

Age

Age squared

β

.365

.047

.056

.074

−.065

.097

.144

−.204

−.238

β

.014

.00013

P.

.037*

.798

.752

.669

.716

.587

.407

.234

.163

P.

.010*

.021*

Note. Top: multilayer eigenvector centrality of the fronto-parietal network and executive functioning. Bottom:
age and multilayer eigenvector centrality of the fronto-parietal network. EC = eigenvector centrality; FPN =
fronto-parietal network; EF = executive functioning; MEG = magnetoencephalography; dMRI = diffusion
IRM; rsfMRI = resting-state functional MRI. Asterisk (*) indicates significance at the p < 0.05 level. Scatter plot including line of best fit of multilayer eigenvector centrality of the fronto- Figure 5. parietal network and executive functioning (left) and age and multilayer eigenvector centrality of the fronto-parietal network (right). EC = eigenvector centrality; EF = executive functioning; FPN = fronto-parietal network. Network Neuroscience 311 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 1 2 9 9 2 0 7 2 1 0 2 n e n _ a _ 0 0 2 8 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multilayer network centrality relates to executive functioning efficiently integrated in early life (Hwang et al., 2013), after which its development plateaus during middle age (Cao et al., 2014) and subsequently regresses to a less integrative topology with older age (Onoda & Yamaguchi, 2013). This relation is also reflected in changes in for example whole-brain (Hedman et al., 2012) and white matter volume (Ge et al., 2002; Walhovd et al., 2005) across the life-span, indicating that the quadratic relationship between brain measures and age may be a general developmental principle. We therefore hypothesized an inverted-U relation between age and multilayer EC of the FPN. We employed a hierarchical multiple regression model with multilayer centrality as the depen- dent variable. Age was entered in a first block, and the square of age was added to the model in a second block. See Figure 3 for a raincloud plot of multilayer centrality, showing the distribution of mul- tilayer network EC of the FPN for all participants. The final model with both age and age squared indicated a statistically significant quadratic relation between age and multilayer EC of the FPN (R2 = .289, adjusted R2 = .241, F[2, 30] = 6.082, p = .006). The square of age added significantly to the model, leading to an increase in R2 of .140 (F[1, 30] = 5.915, p = .021), suggesting that the quadratic model indeed more accurately explained age varia- tions than the simple linear model. The coefficients of the included variables are reported in Table 1; Figure 5 shows the relation between age and multilayer EC of the FPN. Post Hoc: Edge Inference The results of the comparison between the individual edges in the MST networks used in our analyses with its correspondent edges in an ensemble of 100 randomized matrices are detailed in Table 2. On average, over all modalities and all subjects, 74.2% of the edges in the MSTs are statistically significant. In contrast, on average only 3.9% of edges in the fully weighted networks are significant. This preliminary analysis provides evidence that most links in our multilayer network are in fact statistically “true” edges. Table 2. the MST network Edge inference: Comparison between the mean accuracy of the complete network versus Modality MEG delta MEG theta MEG lower alpha MEG upper alpha MEG beta MEG gamma rsfMRI dMRI Average Weighted network 3.8% MST network 73.5% 3.8% 3.8% 3.8% 3.7% 3.9% 4.9% 3.6% 3.9% 73.7% 69.7% 74.1% 68.0% 75.1% 73.5% 85.7% 74.2% Note. Accuracy represents percentage of edges where p < 0.05. For the full weighted network, the mean accu- racy is lower than 5% for all modalities; for the MSTs, the mean accuracy is greater than 67% for all modalities. MST = minimum spanning tree; MEG = magnetoencephalography; rsfMRI = resting-state functional MRI; dMRI = diffusion MRI. Network Neuroscience 312 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 1 2 9 9 2 0 7 2 1 0 2 n e n _ a _ 0 0 2 8 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multilayer network centrality relates to executive functioning DISCUSSION We studied how multilayer centrality of the FPN was related to individual differences in EF, and whether this provided additional information to modality- and frequency-specific single- layer FPN centrality. We found that higher multilayer FPN centrality related to better EF, whereas FPN centrality of single-layer networks did not significantly explain differences in EF between healthy adults. Finally, post hoc analyses established an inverted-U relationship between age and multilayer centrality of the FPN. Firstly, at least for the multilayer network, these results are in line with other studies display- ing the importance of FPN network centrality for EF. The relation between FPN centrality and, by extension, network integration and cognition has been well-established in single-layer net- works, using different neuroimaging and neurophysiological modalities. Increased integration of the FPN within the entire brain network specifically has been related to better EF in studies utilizing dMRI (Caeyenberghs et al., 2016), rsfMRI (Cole et al., 2012; Takeuchi et al., 2015), and MEG (van Dellen et al., 2013). While network segregation is thought to enable fast pro- cessing of lower order information (e.g., analysis of visual inputs) (Clune et al., 2013), highly central nodes like those within the FPN facilitate global communication between these segre- gated communities, presumably enabling higher order cognitive processes and specifically EF (see, e.g., Bertolero et al., 2017; Sporns, 2013). Our significant results for EC, but not degree centrality, may indicate that EC, which is a spectral measure, may be optimally sensitive to individual differences in EF. Moreover, the associations we found between multilayer central- ity of the FPN and several other cognitive domains, namely, IPS and WM, suggest that the importance of FPN integration is not exclusive to EF as defined in this study. IPS, WM, and EF are closely related constructs (see, e.g., McCabe et al., 2010), and the FPN may play a similar integrative role in these aspects of cognition. Secondly, our results demonstrate the relevance of multimodal network analysis through a multilayer network approach in explaining cognitive variance. While FPN centrality of the unimodal networks did not relate significantly to EF, higher FPN centrality of the multilayer networks was indeed associated with better EF. Visual exploration of our data confirmed that the level of integration per node depends on the modality on which the network is based, and that this is again different for the multilayer network. Central nodes (i.e., nodes with high EC) in the multilayer network are thus not the same as central nodes in the single-layer networks (see Figure 4). Other multilayer studies have similarly reported that the precise node that can be considered most central in a single-layer network may not serve as the most central node in a multilayer network, and vice versa (De Domenico et al., 2016; Yu et al., 2017). We build upon these studies by demonstrating that multimodal information captures variance in EF that networks obtained from a single modality do not. Finally, the quadratic relation between age and multilayer centrality possibly reflects the rise and decline of brain network efficiency across the life-span and is in line with findings from studies reporting on other brain-related processes as well as unimodal network data. Whole-brain volume has been shown to increase up to about 35 years of age, and then decline at a slow but steady rate (Hedman et al., 2012). Another study reported that the per- centage of white matter volume (relative to intracranial volume) slowly increases until approx- imately 40 years of age, after which it decreases quickly (Ge et al., 2002). Network measures have likewise been shown to be sensitive to age effects. Single-layer brain networks become more segregated or modular during development (He et al., 2019), and connectivity of highly central regions increases from childhood to adulthood (Hwang et al., 2013), suggesting that the brain network becomes increasingly efficient (i.e., a better balance between segregation Network Neuroscience 313 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 1 2 9 9 2 0 7 2 1 0 2 n e n _ a _ 0 0 2 8 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multilayer network centrality relates to executive functioning and integration emerges) with maturation. However, after a certain age, modularity of the network seems to decrease (Onoda & Yamaguchi, 2013), indicating a degradation of the effi- ciency of the brain network. In our study, a similar plateauing seems to occur at middle age. Together with the literature, these findings indicate that brain characteristics have a universal tendency to develop in a particular manner across the life-span. As such, FPN centrality of the multilayer network may be considered an age-relevant metric in future studies. Note that we corrected EF scores for age, such that the association we find between EF and multilayer cen- trality cannot be ascribed to age effects alone. However, future work is needed to disentangle the exact relationship between age, network centrality, and EF: it is possible that age impacts both EF and network measures, necessitating future studies either investigating the relationship between EF and network centrality in a homogeneously aged sample, or much larger studies able to regress age effects from both EF and network measures. The biological interpretation of the multilayer network used in this work deserves further consideration. Importantly, the spatial definition of nodes is identical across layers: the nodes in each modality represented the same brain regions. The use of the Brainnetome Atlas, which is based on both structural and functional connectivity pattern similarity within and across brain regions, supports the assumption that these nodes can indeed be seen as canonical units across layers. This is further evidenced by the results of repeating the analysis using a different atlas: the final model did not reach statistical significance, although the explanatory value was comparable to the results based on the Brainnetome Atlas, and FPN centrality of the single- layer dMRI network was a significant individual predictor. Indeed, single-layer reviews have shown that network metrics are not necessarily robust across parcellations, especially when the number of regions differs (Arslan et al., 2018; de Reus & van den Heuvel, 2013). The AAL atlas is a purely anatomically driven parcellation that comprises 78 cortical regions as opposed to 210 regions in the Brainnetome Atlas and is based on the single-subject MNI image (Tzourio-Mazoyer et al., 2002), which may thus be less suited to multilayer analyses, espe- cially when using multimodal connectivity data as was the case here. We then used interlayer links between the same brain regions (nodes) across layers to integrate different modalities. The biological assumption here is that structure and function conflate maximally within the same brain region. There is ample evidence that this assumption holds across macroscopic modalities when correlating, for instance, structural and rsfMRI connectivity patterns across the whole brain (Garcés et al., 2016; Honey et al., 2010; Park & Friston, 2013). The spatial variation that exists in nodal correlations between structural and functional connectivity (Honey et al., 2009; Vázquez-Rodríguez et al., 2019), however, may indicate that although this connectivity is highest within the same region instead of between regions, the linkage between layers varies per region. Such variations were not taken into account in the current work, where we used MSTs of the individual layers for the construction of multiplex networks and set the weights of all interlayer connections in the multilayer networks to one. It should be noted that using the MST results in networks of very low density (∼1% for typical brain network sizes). Results may not be the same at different densities, and the effect of thresholding at different densities perhaps warrants future exploration. Nevertheless, our decision to use the MST as the foundation for building the multilayer networks in the present study was well considered. Network thresholding, although well explored in isolated modal- ities, has not yet been studied extensively in multilayer networks. What we do know, however, is that the same methodological issues that apply to single-layer networks (i.e., network measures are influenced by differences in link density and average connectivity) also apply to multilayer networks, and that constructing MSTs of the individual layers of a multilayer net- work can adequately correct for these biases (Mandke et al., 2018). Furthermore, replicability Network Neuroscience 314 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 1 2 9 9 2 0 7 2 1 0 2 n e n _ a _ 0 0 2 8 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multilayer network centrality relates to executive functioning of results across thresholding densities is an inherent issue of all methodologies for network thresholding (e.g., Buchanan et al., 2020; Garrison et al., 2015). The MST has not only been amply used in studies investigating the cognitive relevance of particularly MEG single-layer network topology for cognition, thus providing a logical springboard for more complicated analyses such as the multilayer framework we employed here; it is also considered the backbone of the network (Stam et al., 2014; Tewarie et al., 2015), using mainly the original network’s strongest connections, which are unlikely to be purely driven by noise. Indeed, the initial post hoc analyses we performed give a strong indication that most of the edges included in each network by the MST algorithm are statistically significant. Future work, though, may benefit from a more data-driven approach for network reconstruction based on statistical sampling of network ensembles, to ensure that networks comprise statistically significant edges (Raimondo & De Domenico, 2021). Next, future studies may attempt to incorporate weighted interlayer links to represent the spatial variation in within-region correlations across modalities. Additionally, even when choosing to assign the same weight to all interlayer links, other multilayer work has suggested that an optimal value for the interlayer weight exists (De Domenico et al., 2016), and future implementations of the multilayer framework could benefit from optimization of the interlayer weights. Another potential shortcoming of the binarization of link weights is that it eliminates layer dominance (Sahneh & Scoglio, 2014): some layers may have a stronger influence on multilayer network characteristics than others, but when all layers carry the same importance, this information is lost. However, just as some layers may drive the properties of the multilayer more strongly than other layers, other layers may play a negligible role. This raises the question whether all possible layers should be included, or whether an a priori selection should be made, and, if so, how this selection should be made. A few papers have begun to probe this issue, for example, in brain networks (De Domenico et al., 2015a) and in a dataset of social contacts (Casiraghi, 2017), but the layer selection problem in multimodal brain networks warrants further exploration. Furthermore, although interlayer connectivity may be maximal within brain regions, there is potential connectivity between different regions across different modalities, that is, cross-talk between node A in modality X and node B in modality Y may be relevant to overall functioning of the network. A general multilayer network formulation allows interlayer links between all nodes in all layers (see, e.g., Bianconi, 2018). However, multimodal datasets present considerable challenges when constructing a full multilayer network. Chief among them is determining biologically meaningful interlayer links between different modalities at the individual participant level. Additionally, a recent modeling study revealed that interlayer connectivity is driven mostly by one-to-one (i.e., multiplex) connec- tions (Tewarie et al., 2021), and as evidenced by previous empirical studies (De Domenico et al., 2016; Yu et al., 2017), a multiplex approach is therefore a logical and intuitive first step for analyzing multidimensional data. Lastly, we defined the FPN based on a predefined classification. As such, the FPN was comprised of the same regions across the different single-layers as well as in the multilayer network. However, subnetworks like the FPN and the hubs within them have been found to vary depending on the modality used (Brookes et al., 2011; Garcés et al., 2016), and have also been shown to be different in a multiplex compared to a single-layer network (De Domenico et al., 2016). Additionally, there is a large individual variability in the functional topography of the FPN (Marek & Dosenbach, 2018). A more data-driven approach to the formulation of the FPN may therefore further increase the explanatory power of the multilayer approach. Some additional limitations need to be taken into consideration. In this study, we chose to absolutize negative correlations in the fMRI networks, but it should be noted that there is an Network Neuroscience 315 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 7 1 2 9 9 2 0 7 2 1 0 2 n e n _ a _ 0 0 2 8 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multilayer network centrality relates to executive functioning ongoing debate on what negative correlations indicate and how to best deal with them (Hallquist & Hillary, 2018). However, the relative magnitude of such negative edge weights is low and the MST only incorporates the strongest links, and as such it is unlikely that this decision has impacted our results. Furthermore, there are some inherent drawbacks to the stepwise regression models we employed to answer our research question. Although this approach was the one best suited to answer our research question, it is imperative that our work is replicated in larger samples using our work to establish more straightforward regression models. Indeed, the relatively small sample size of the present study is particularly important to take into account: the absence of any single-layer effects could be due to a lack of statistical power, rather than the true absence of any correlations between single-layer network metrics and cognition. Our sample was powered using previous studies correlating cognition with single-layer network properties (Douw et al., 2016; Hassan et al., 2017; Lord et al., 2017; Ystad et al., 2011), but these may have overestimated the size of the actual effect: there is significant discussion on the minimal sample size needed to establish reliable brain-behavior associations (Marek et al., 2022). Moreover, since the multilayer approach has not been used to explain cognitive variance before, we could not power for significance of change going from single-layer to multilayer correlates of EF. There was no significant increase in R2 from the model containing a nonsignificant single-layer plus the multilayer predictor and the model containing only the significant multilayer predictor. We therefore cannot claim, statistically, that the multilayer network approach is a better predictor of EF than the single-layer network approach. However, the fact that the final model containing only the multilayer predictor was significant, whereas the single-layer predictors were not, suggests that (a) sample size may have contributed to a lack of statistical power to find evidence of significant change between these models and (b) a multilayer approach may require less data points in order to observe significant correlates of EF in the brain. We therefore conclude that the multilayer methodology is a potentially valuable framework for explaining EF, although its statistical superiority over single-layer approaches must be assessed in adequately powered, larger, samples. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 1 2 9 9 2 0 7 2 1 0 2 n e n _ a _ 0 0 2 8 4 p d t . CONCLUSIONS Integration of multimodal brain networks through a multilayer framework relates to EF in healthy adults, and corroborates known brain associations with aging. These findings under- line the relevance of a multimodal view on integration of the brain network as a correlate of EF. Furthermore, the multilayer approach may be of particular interest in populations where net- work alterations differ across modalities. For instance, early neurodegeneration and structural network deterioration of particularly the most central regions in the brain are initially associ- ated with increases in functional communication, after which the functional brain networks seems to collapse (Hillary et al., 2015; Schoonheim et al., 2015). Multilayer network analysis may advance our understanding of the interplay between structural and different functional network aspects in such clinical populations. f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 ACKNOWLEDGMENTS The authors would like to thank the Amsterdam Neuroscience research institute for supporting this study. We would also like to thank Hersenonderzoek.nl, a Dutch online registry that facilitates participant recruitment for neuroscience studies (www.hersenonderzoek.nl). Hersenonderzoek.nl is funded by ZonMw-Memorabel (project no. 73305095003), a project in the context of the Dutch Deltaplan Dementie, Gieskes-Strijbis Foundation, the Alzheimer’s Network Neuroscience 316 Multilayer network centrality relates to executive functioning Society in the Netherlands and Brain Foundation Netherlands. We thank the laboratory tech- nicians of the Amsterdam UMC, Department of Clinical Neurophysiology and MEG Center, as well as the scan assistants of the Spinoza Centre for Neuroimaging, for their help with the data acquisition. Finally, we thank all participants for their participation. SUPPORTING INFORMATION Supporting information for this article is available at https://doi.org/10.1162/netn_a_00284 and https://github.com/multinetlab-amsterdam/projects/tree/master/mumo_paper_2021. Addition- ally, this article made use of scripts available at https://github.com/nkoub/multinetx and https://github.com/networkx. AUTHOR CONTRIBUTIONS Lucas C. Breedt: Data curation; Formal analysis; Investigation; Methodology; Project administration; Software; Visualization; Writing – original draft; Writing – review & editing. Fernando A. N. Santos: Data curation; Formal analysis; Methodology; Software; Supervision; Visualization; Writing – original draft; Writing – review & editing. Arjan Hillebrand: Concep- tualization; Formal analysis; Funding acquisition; Software; Writing – review & editing. Liesbeth Reneman: Conceptualization; Funding acquisition; Writing – review & editing. Anne-Fleur van Rootselaar: Conceptualization; Funding acquisition; Writing – review & editing. Menno M. Schoonheim: Conceptualization; Funding acquisition; Writing – review & editing. Cornelis J. Stam: Conceptualization; Funding acquisition; Writing – review & editing. Anouk Ticheler: Investigation; Project administration; Writing – review & editing. Betty M. Tijms: Conceptualization; Funding acquisition; Writing – review & editing. Dick J. Veltman: Conceptualization; Funding acquisition; Writing – review & editing. Chris Vriend: Conceptualization; Formal analysis; Funding acquisition; Methodology; Writing – review & editing. Margot J. Wagenmakers: Investigation; Project administration; Writing – review & editing. Guido A. van Wingen: Conceptualization; Funding acquisition; Writing – review & editing. Jeroen J. G. Geurts: Conceptualization; Funding acquisition; Supervision; Writing – review & editing. Anouk Schrantee: Conceptualization; Funding acquisition; Methodology; Project administration; Supervision; Writing – review & editing. Linda Douw: Conceptuali- zation; Funding acquisition; Methodology; Project administration; Supervision; Writing – original draft; Writing – review & editing. FUNDING INFORMATION Linda Douw, Amsterdam Neuroscience Alliance Grant. Linda Douw, Netherlands Organiza- tion for Scientific Research (NWO) Vidi grant, Award ID: 198.015. REFERENCES Aertsen, A. M., Gerstein, G. L., Habib, M. K., & Palm, G. (1989). Dynamics of neuronal firing correlation: Modulation of “effective connectivity.” Journal of Neurophysiology, 61(5), 900–917. https://doi.org/10.1152/jn.1989.61.5.900, PubMed: 2723733 Andersson, J. L., Skare, S., & Ashburner, J. (2003). How to correct sus- ceptibility distortions in spin-echo echo-planar images: Application to diffusion tensor imaging. NeuroImage, 20(2), 870–888. https://doi .org/10.1016/S1053-8119(03)00336-7, PubMed: 14568458 Ardila, A. (2008). On the evolutionary origins of executive func- tions. Brain and Cognition, 68(1), 92–99. https://doi.org/10 .1016/j.bandc.2008.03.003, PubMed: 18397818 Arslan, S., Ktena, S. I., Makropoulos, A., Robinson, E. C., Rueckert, D., & Parisot, S. (2018). Human brain mapping: A systematic comparison of parcellation methods for the human cerebral cortex. NeuroImage, 170, 5–30. https://doi.org/10.1016/j.neuroimage .2017.04.014, PubMed: 28412442 Network Neuroscience 317 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 1 2 9 9 2 0 7 2 1 0 2 n e n _ a _ 0 0 2 8 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multilayer network centrality relates to executive functioning Barabási, A.-L. (2016). Network science. Cambridge, UK: Cambridge University Press. Battiston, F., Nicosia, V., Chavez, M., & Latora, V. (2017). Multi- layer motif analysis of brain networks. Chaos: An Interdisciplin- ary Journal of Nonlinear Science, 27(4), 047404. https://doi.org /10.1063/1.4979282, PubMed: 28456158 Bertolero, M. A., Yeo, B. T. T., & D’Esposito, M. (2017). The diverse club. Nature Communications, 8(1), 1277. https://doi.org/10 .1038/s41467-017-01189-w, PubMed: 29097714 Bianconi, G. (2018). Multilayer networks: Structure and function. Oxford, UK: Oxford University Press. https://doi.org/10.1093 /oso/9780198753919.001.0001 Blomsma, N., de Rooy, B., Gerritse, F., van der Spek, R., Tewarie, P., Hillebrand, A., Otte, W. M., Stam, C. J., & van Dellen, E. (2022). Minimum spanning tree analysis of brain networks: A systematic review of network size effects, sensitivity for neuro- psychiatric pathology and disorder specificity. Network Neuro- science, 6(2), 301–319. https://doi.org/10.1162/netn_a_00245, PubMed: 35733422 Boccaletti, S., Bianconi, G., Criado, R., Del Genio, C. I., Gómez- Gardeñes, J., Romance, M., Sendiña-Nadal, I., Wang, Z., & Zanin, M. (2014). The structure and dynamics of multilayer net- works. Physics Reports, 544(1), 1–122. https://doi.org/10.1016/j .physrep.2014.07.001, PubMed: 32834429 Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., & Hwang, D.-U. (2006). Complex networks: Structure and dynamics. Physics Reports, 424(4–5), 175–308. https://doi.org/10.1016/j.physrep.2005.10.009 Brookes, M. J., Tewarie, P. K., Hunt, B. A., Robson, S. E., Gascoyne, L. E., Liddle, E. B., Liddle, P. F., & Morris, P. G. (2016). A multi-layer network approach to MEG connectivity analysis. NeuroImage, 132, 425–438. https://doi.org/10.1016/j .neuroimage.2016.02.045, PubMed: 26908313 Brookes, M. J., Woolrich, M., Luckhoo, H., Price, D., Hale, J. R., Stephenson, M. C., Barnes, G. R., Smith, S. M., & Morris, P. G. (2011). Investigating the electrophysiological basis of resting state networks using magnetoencephalography. Proceedings of the National Academy of Sciences, 108(40), 16783–16788. https://doi.org/10.1073/pnas.1112685108, PubMed: 21930901 Buchanan, C. R., Bastin, M. E., Ritchie, S. J., Liewald, D. C., Madole, J. W., Tucker-Drob, E. M., Deary, I. J., & Cox, S. R. (2020). The effect of network thresholding and weighting on structural brain networks in the UK Biobank. NeuroImage, 211, 116443. https://doi.org/10 .1016/j.neuroimage.2019.116443, PubMed: 31927129 Bucks, R., & Willison, J. R. (1997). Development and validation of the Location Learning Test (LLT): A test of visuo-spatial learning designed for use with older adults and in dementia. The Clinical Neuropsychologist, 11(3), 273–286. https://doi.org/10.1080 /13854049708400456 Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph theoretical analysis of structural and functional systems. Nature Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038 /nrn2575, PubMed: 19190637 Bullmore, E., & Sporns, O. (2012). The economy of brain network organization. Nature Reviews Neuroscience, 13(5), 336–349. https://doi.org/10.1038/nrn3214, PubMed: 22498897 Caeyenberghs, K., Metzler-Baddeley, C., Foley, S., & Jones, D. K. (2016). Dynamics of the human structural connectome underly- ing working memory training. Journal of Neuroscience, 36(14), 4056–4066. https://doi.org/10.1523/JNEUROSCI.1973-15.2016, PubMed: 27053212 Cao, M., Wang, J.-H., Dai, Z.-J., Cao, X.-Y., Jiang, L.-L., Fan, F.-M., Song, X.-W., Xia, M.-R., Shu, N., & Dong, Q. (2014). Topological organization of the human brain functional connectome across the lifespan. Developmental Cognitive Neuroscience, 7, 76–93. https://doi.org/10.1016/j.dcn.2013.11.004, PubMed: 24333927 Cardillo, A., Gómez-Gardeñes, J., Zanin, M., Romance, M., Papo, D., del Pozo, F., & Boccaletti, S. (2013). Emergence of network features from multiplexity. Scientific Reports, 3(1), 1344. https:// doi.org/10.1038/srep01344, PubMed: 23446838 Casiraghi, G. (2017). Multiplex network regression: How do rela- tions drive interactions? arXiv preprint arXiv:1702.02048. https:// doi.org/10.48550/arXiv.1702.02048 Chai, X. J., Castañón, A. N., Öngür, D., & Whitfield-Gabrieli, S. (2012). Anticorrelations in resting state networks without global signal regression. NeuroImage, 59(2), 1420–1428. https://doi.org /10.1016/j.neuroimage.2011.08.048, PubMed: 21889994 Clune, J., Mouret, J.-B., & Lipson, H. (2013). The evolutionary ori- gins of modularity. Proceedings of the Royal Society B: Biological Sciences, 280(1755), 20122863. https://doi.org/10.1098/rspb .2012.2863, PubMed: 23363632 Cole, M. W., Yarkoni, T., Repovš, G., Anticevic, A., & Braver, T. S. (2012). Global connectivity of prefrontal cortex predicts cognitive control and intelligence. Journal of Neuroscience, 32(26), 8988–8999. https:// doi.org/10.1523/JNEUROSCI.0536-12.2012, PubMed: 22745498 Damoiseaux, J. S., & Greicius, M. D. (2009). Greater than the sum of its parts: A review of studies combining structural connectivity and resting-state functional connectivity. Brain Structure and Function, 213(6), 525–533. https://doi.org/10.1007/s00429-009 -0208-6, PubMed: 19565262 De Domenico, M., Nicosia, V., Arenas, A., & Latora, V. (2015a). Structural reducibility of multilayer networks. Nature Communi- cations, 6(1), 6864. https://doi.org/10.1038/ncomms7864, PubMed: 25904309 De Domenico, M., Porter, M. A., & Arenas, A. (2015b). MuxViz: A tool for multilayer analysis and visualization of networks. Journal of Complex Networks, 3(2), 159–176. https://doi.org/10.1093 /comnet/cnu038 De Domenico, M., Sasai, S., & Arenas, A. (2016). Mapping multi- plex hubs in human functional brain networks. Frontiers in Neu- roscience, 10, 326. https://doi.org/10.3389/fnins.2016.00326, PubMed: 27471443 De Domenico, M., Solé-Ribalta, A., Cozzo, E., Kivelä, M., Moreno, Y., Porter, M. A., Gómez, S., & Arenas, A. (2013). Mathematical formulation of multilayer networks. Physical Review X, 3(4), 041022. https://doi.org/10.1103/PhysRevX.3.041022 de Reus, M. A., & van den Heuvel, M. P. (2013). The parcellation- based connectome: Limitations and extensions. NeuroImage, 80, 397–404. https://doi.org/10.1016/j.neuroimage.2013.03.053, PubMed: 23558097 Douw, L., Wakeman, D. G., Tanaka, N., Liu, H., & Stufflebeam, S. M. (2016). State-dependent variability of dynamic functional connectivity between frontoparietal and default networks relates to cognitive flexibility. Neuroscience, 339, 12–21. https://doi.org /10.1016/j.neuroscience.2016.09.034, PubMed: 27687802 Eijlers, A. J. C., Meijer, K. A., Wassenaar, T. M., Steenwijk, M. D., Uitdehaag, B. M. J., Barkhof, F., Wink, A. M., Geurts, J. J. G., & Network Neuroscience 318 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 1 2 9 9 2 0 7 2 1 0 2 n e n _ a _ 0 0 2 8 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multilayer network centrality relates to executive functioning Schoonheim, M. M. (2017). Increased default-mode network centrality in cognitively impaired multiple sclerosis patients. Neurology, 88(10), 952–960. https://doi.org/10.1212/ WNL .0000000000003689, PubMed: 28179464 Fagerholm, E. D., Hellyer, P. J., Scott, G., Leech, R., & Sharp, D. J. (2015). Disconnection of network hubs and cognitive impair- ment after traumatic brain injury. Brain, 138(6), 1696–1709. https://doi.org/10.1093/brain/awv075, PubMed: 25808370 Fan, L., Li, H., Zhuo, J., Zhang, Y., Wang, J., Chen, L., Yang, Z., Chu, C., Xie, S., & Laird, A. R. (2016). The human brainnetome atlas: A new brain atlas based on connectional architecture. Cerebral Cortex, 26(8), 3508–3526. https://doi.org/10.1093/cercor /bhw157, PubMed: 27230218 Fodor, J. A. (1983). The modularity of mind. Cambridge, MA: MIT Press. https://doi.org/10.7551/mitpress/4737.001.0001 Fornito, A., Zalesky, A., & Bullmore, E. (2016). Fundamentals of brain network analysis. Amsterdam, The Netherlands: Academic Press. Friston, K. J., Frith, C. D., Liddle, P. F., & Frackowiak, R. S. (1993). Functional connectivity: The principal-component analysis of large (PET) data sets. Journal of Cerebral Blood Flow & Metabo- lism, 13(1), 5–14. https://doi.org/10.1038/jcbfm.1993.4, PubMed: 8417010 Garcés, P., Pereda, E., Hernández-Tamames, J. A., Del-Pozo, F., Maestú, F., & Ángel Pineda-Pardo, J. (2016). Multimodal descrip- tion of whole brain connectivity: A comparison of resting state MEG, fMRI, and DWI. Human Brain Mapping, 37(1), 20–34. https://doi.org/10.1002/hbm.22995, PubMed: 26503502 Garrison, K. A., Scheinost, D., Finn, E. S., Shen, X., & Constable, R. T. (2015). The (in)stability of functional brain network mea- sures across thresholds. NeuroImage, 118, 651–661. https://doi .org/10.1016/j.neuroimage.2015.05.046, PubMed: 26021218 Ge, Y., Grossman, R. I., Babb, J. S., Rabin, M. L., Mannon, L. J., & Kolson, D. L. (2002). Age-related total gray matter and white matter changes in normal adult brain. Part I: Volumetric MR imaging analysis. American Journal of Neuroradiology, 23(8), 1327–1333. PubMed: 12223373 Guillon, J., Attal, Y., Colliot, O., La Corte, V., Dubois, B., Schwartz, D., Chavez, M., & Fallani, F. D. V. (2017). Loss of brain inter-frequency hubs in Alzheimerʼs disease. Scientific Reports, 7(1), 10879. https://doi.org/10.1038/s41598-017-07846-w, PubMed: 28883408 Hagberg, A., Swart, P., & S Chult, D. (2008). Exploring network structure, dynamics, and function using NetworkX. https://www .osti.gov/biblio/960616 Hallquist, M. N., & Hillary, F. G. (2018). Graph theory approaches to functional network organization in brain disorders: A critique for a brave new small-world. Network Neuroscience, 3(1), 1–26. https://doi.org/10.1162/netn_a_00054, PubMed: 30793071 Hammes, J. G. W. (1978). De Stroop kleur-woord test. San Diego, CA: Harcourt Test Publishing. Hardmeier, M., Schoonheim, M. M., Geurts, J. J., Hillebrand, A., Polman, C. H., Barkhof, F., & Stam, C. J. (2012). Cognitive dys- function in early multiple sclerosis: Altered centrality derived from resting-state functional connectivity using magneto- encephalography. PLoS One, 7(7), e42087. https://doi.org/10 .1371/journal.pone.0042087, PubMed: 22848712 Hassan, M., Chaton, L., Benquet, P., Delval, A., Leroy, C., Plomhause, L., Moonen, A. J. H., Duits, A. A., Leentjens, A. F. G., & van Kranen- Mastenbroek, V. (2017). Functional connectivity disruptions correlate with cognitive phenotypes in Parkinsonʼs disease. NeuroImage: Clinical, 14, 591–601. https://doi.org/10.1016/j .nicl.2017.03.002, PubMed: 28367403 He, W., Sowman, P. F., Brock, J., Etchell, A. C., Stam, C. J., & Hillebrand, A. (2019). Increased segregation of functional networks in developing brains. NeuroImage, 200, 607–620. https://doi.org /10.1016/j.neuroimage.2019.06.055, PubMed: 31271847 Hedman, A. M., van Haren, N. E. M., Schnack, H. G., Kahn, R. S., & Hulshoff Pol, H. E. (2012). Human brain changes across the life span: A review of 56 longitudinal magnetic resonance imaging studies. Human Brain Mapping, 33(8), 1987–2002. https://doi .org/10.1002/hbm.21334, PubMed: 21915942 Hillary, F. G., Roman, C. A., Venkatesan, U., Rajtmajer, S. M., Bajo, R., & Castellanos, N. D. (2015). Hyperconnectivity is a funda- mental response to neurological disruption. Neuropsychology, 29(1), 59–75. https://doi.org/10.1037/neu0000110, PubMed: 24933491 Hillebrand, A., Barnes, G. R., Bosboom, J. L., Berendse, H. W., & Stam, C. J. (2012). Frequency-dependent functional connectivity within resting-state networks: An atlas-based MEG beamformer solution. NeuroImage, 59(4), 3909–3921. https://doi.org/10 .1016/j.neuroimage.2011.11.005, PubMed: 22122866 Hillebrand, A., Tewarie, P., van Dellen, E., Yu, M., Carbo, E. W. S., Douw, L., Gouw, A. A., van Straaten, E. C. W., & Stam, C. J. (2016). Direction of information flow in large-scale resting-state networks is frequency-dependent. Proceedings of the National Academy of Sciences, 113(14), 3867–3872. https://doi.org/10 .1073/pnas.1515657113, PubMed: 27001844 Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J.-P., Meuli, R., & Hagmann, P. (2009). Predicting human resting-state functional connectivity from structural connectivity. Proceedings of the National Academy of Sciences, 106(6), 2035–2040. https:// doi.org/10.1073/pnas.0811168106, PubMed: 19188601 Honey, C. J., Thivierge, J.-P., & Sporns, O. (2010). Can structure pre- dict function in the human brain? NeuroImage, 52(3), 766–776. https://doi.org/10.1016/j.neuroimage.2010.01.071, PubMed: 20116438 Hwang, K., Hallquist, M. N., & Luna, B. (2013). The development of hub architecture in the human functional brain network. Cere- bral Cortex, 23(10), 2380–2393. https://doi.org/10.1093/cercor /bhs227, PubMed: 22875861 Jeurissen, B., Tournier, J.-D., Dhollander, T., Connelly, A., & Sijbers, J. (2014). Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage, 103, 411–426. https://doi.org/10.1016/j.neuroimage.2014.07 .061, PubMed: 25109526 Jurado, M. B., & Rosselli, M. (2007). The elusive nature of executive functions: A review of our current understanding. Neuropsychol- ogy Review, 17(3), 213–233. https://doi.org/10.1007/s11065-007 -9040-z, PubMed: 17786559 Kardos, O., London, A., & Vinkó, T. (2020). Stability of network centrality measures: A numerical study. Social Network Analysis and Mining, 10(1), 1–17. https://doi.org/10.1007/s13278-020 -00693-0 Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., & Porter, M. A. (2014). Multilayer networks. Journal of Complex Net- works, 2(3), 203–271. https://doi.org/10.1093/comnet/cnu016 Network Neuroscience 319 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 7 1 2 9 9 2 0 7 2 1 0 2 n e n _ a _ 0 0 2 8 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multilayer network centrality relates to executive functioning Kruskal, J. B. (1956). On the shortest spanning subtree of a graph and the traveling salesman problem. Proceedings of the Ameri- can Mathematical Society, 7(1), 48–50. https://doi.org/10.1090 /S0002-9939-1956-0078686-7 Lord, A. R., Li, M., Demenescu, L. R., van den Meer, J., Borchardt, V., Krause, A. L., Heinze, H.-J., Breakspear, M., & Walter, M. (2017). Richness in functional connectivity depends on the neu- ronal integrity within the posterior cingulate cortex. Frontiers in Neuroscience, 11, 184. https://doi.org/10.3389/fnins.2017 .00184, PubMed: 28439224 Mandke, K., Meier, J., Brookes, M. J., O’Dea, R. D., Van Mieghem, P., Stam, C. J., Hillebrand, A., & Tewarie, P. (2018). Comparing multilayer brain networks between groups: Introducing graph metrics and recommendations. NeuroImage, 166, 371–384. https://doi.org/10.1016/j.neuroimage.2017.11.016, PubMed: 29138088 Marek, S., & Dosenbach, N. U. F. (2018). The frontoparietal net- work: Function, electrophysiology, and importance of individual precision mapping. Dialogues in Clinical Neuroscience, 20(2), 133–140. https://doi.org/10.31887/ DCNS.2018.20.2/smarek, PubMed: 30250390 Marek, S., Tervo-Clemmens, B., Calabro, F. J., Montez, D. F., Kay, B. P., Hatoum, A. S., Donohue, M. R., Foran, W., Miller, R. L., & Hendrickson, T. J. (2022). Reproducible brain-wide association studies require thousands of individuals. Nature, 603(7902), 654–660. https://doi.org/10.1038/s41586-022-04492-9, PubMed: 35296861 McCabe, D. P., Roediger III, H. L., McDaniel, M. A., Balota, D. A., & Hambrick, D. Z. (2010). The relationship between working mem- ory capacity and executive functioning: Evidence for a common executive attention construct. Neuropsychology, 24(2), 222–243. https://doi.org/10.1037/a0017619, PubMed: 20230116 Menard, S. (1995). An introduction to logistic regression diagnostics. In Applied logistic regression analysis (pp. 58–79). Thousand Oaks, CA: Sage. Mulder, J., Dekker, P., & Dekker, R. (2006). Woord-fluency test/ figuur-fluency test, handleiding. Leiden, The Netherlands: PITS. Nakamura, T., Tanizawa, T., & Small, M. (2016). Constructing net- works from a dynamical system perspective for multivariate non- linear time series. Physical Review E, 93(3), 032323. https://doi .org/10.1103/PhysRevE.93.032323, PubMed: 27078382 Onoda, K., & Yamaguchi, S. (2013). Small-worldness and modular- ity of the resting-state functional brain network decrease with aging. Neuroscience Letters, 556, 104–108. https://doi.org/10 .1016/j.neulet.2013.10.023, PubMed: 24157850 Park, H.-J., & Friston, K. (2013). Structural and functional brain networks: From connections to cognition. Science, 342(6158), 1238411. https://doi.org/10.1126/science.1238411, PubMed: 24179229 Pruim, R. H. R., Mennes, M., van Rooij, D., Llera, A., Buitelaar, J. K., & Beckmann, C. F. (2015). ICA-AROMA: A robust ICA-based strategy for removing motion artifacts from fMRI data. Neuro- Image, 112, 267–277. https://doi.org/10.1016/j.neuroimage .2015.02.064, PubMed: 25770991 Raimondo, S., & De Domenico, M. (2021). Measuring topological descriptors of complex networks under uncertainty. Physical Review E, 103(2), 022311. https://doi.org/10.1103/ PhysRevE .103.022311, PubMed: 33735966 Sahneh, F. D., & Scoglio, C. (2014). Competitive epidemic spread- ing over arbitrary multilayer networks. Physical Review E, 89(6), 062817. https://doi.org/10.1103/PhysRevE.89.062817, PubMed: 25019843 Schmand, B., Houx, P., & De Koning, I. (2012). Normen van psy- chologische tests voor gebruik in de klinische neuropsychologie. Sectie Neuropsychologie Nederlands Instituut van Psychologen. Schoonheim, M. M., Meijer, K. A., & Geurts, J. J. (2015). Network collapse and cognitive impairment in multiple sclerosis. Frontiers in Neurology, 6, 82. https://doi.org/10.3389/fneur.2015.00082, PubMed: 25926813 Smith, R. E., Tournier, J.-D., Calamante, F., & Connelly, A. (2012). Anatomically-constrained tractography: Improved diffusion MRI streamlines tractography through effective use of anatomical information. NeuroImage, 62(3), 1924–1938. https://doi.org/10 .1016/j.neuroimage.2012.06.005, PubMed: 22705374 Smith, R. E., Tournier, J.-D., Calamante, F., & Connelly, A. (2015). SIFT2: Enabling dense quantitative assessment of brain white matter connectivity using streamlines tractography. NeuroImage, 119, 338–351. https://doi.org/10.1016/j.neuroimage.2015.06 .092, PubMed: 26163802 Solé-Ribalta, A., De Domenico, M., Kouvaris, N. E., Díaz-Guilera, A., Gómez, S., & Arenas, A. (2013). Spectral properties of the Laplacian of multiplex networks. Physical Review E, 88(3), 032807. https://doi.org/10.1103/PhysRevE.88.032807, PubMed: 24125312 Sporns, O. (2013). Network attributes for segregation and integra- tion in the human brain. Current Opinion in Neurobiology, 23(2), 162–171. https://doi.org/10.1016/j.conb.2012.11.015, PubMed: 23294553 Stam, C. J., Nolte, G., & Daffertshofer, A. (2007). Phase lag index: Assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources. Human Brain Mapping, 28(11), 1178–1193. https://doi.org/10.1002 /hbm.20346, PubMed: 17266107 Stam, C. J., Tewarie, P., Van Dellen, E., van Straaten, E. C. W., Hillebrand, A., & Van Mieghem, P. (2014). The trees and the for- est: Characterization of complex brain networks with minimum spanning trees. International Journal of Psychophysiology, 92(3), 129–138. https://doi.org/10.1016/j.ijpsycho.2014.04.001, PubMed: 24726900 Stam, C. J., van Straaten, E. C. W., Van Dellen, E., Tewarie, P., Gong, G., Hillebrand, A., Meier, J., & Van Mieghem, P. (2016). The relation between structural and functional connectivity patterns in complex brain networks. International Journal of Psychophys- iology, 103, 149–160. https://doi.org/10.1016/j.ijpsycho.2015.02 .011, PubMed: 25678023 Takeuchi, H., Taki, Y., Nouchi, R., Sekiguchi, A., Hashizume, H., Sassa, Y., Kotozaki, Y., Miyauchi, C. M., Yokoyama, R., & Iizuka, K. (2015). Degree centrality and fractional amplitude of low-frequency oscillations associated with Stroop interference. NeuroImage, 119, 197–209. https://doi.org/10.1016/j .neuroimage.2015.06.058, PubMed: 26123381 Taulu, S., & Simola, J. (2006). Spatiotemporal signal space separa- tion method for rejecting nearby interference in MEG measure- ments. Physics in Medicine & Biology, 51(7), 1759–1768. https:// doi.org/10.1088/0031-9155/51/7/008, PubMed: 16552102 Tewarie, P., Hillebrand, A., Schoonheim, M. M., van Dijk, B. W., Geurts, J. J. G., Barkhof, F., Polman, C. H., & Stam, C. J. (2014). Network Neuroscience 320 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 1 2 9 9 2 0 7 2 1 0 2 n e n _ a _ 0 0 2 8 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multilayer network centrality relates to executive functioning Functional brain network analysis using minimum spanning trees in multiple sclerosis: An MEG source-space study. NeuroImage, 88, 308–318. https://doi.org/10.1016/j.neuroimage.2013.10 .022, PubMed: 24161625 Tewarie, P., Prasse, B., Meier, J., Byrne, Á., De Domenico, M., Stam, C. J., Brookes, M. J., Hillebrand, A., Daffertshofer, A., & Coombes, S. (2021). Interlayer connectivity reconstruction for multilayer brain networks using phase oscillator models. New Journal of Physics, 23, 063065. https://doi.org/10.1088/1367-2630/ac066d Tewarie, P., van Dellen, E., Hillebrand, A., & Stam, C. J. (2015). The minimum spanning tree: An unbiased method for brain network analysis. NeuroImage, 104, 177–188. https://doi.org/10.1016/j .neuroimage.2014.10.015, PubMed: 25451472 Tournier, J.-D., Smith, R., Raffelt, D., Tabbara, R., Dhollander, T., Pietsch, M., Christiaens, D., Jeurissen, B., Yeh, C.-H., & Connelly, A. (2019). MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. NeuroImage, 202, 116137. https://doi.org/10.1016/j.neuroimage.2019 .116137, PubMed: 31473352 Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F., Etard, O., Delcroix, N., Mazoyer, B., & Joliot, M. (2002). Auto- mated anatomical labeling of activations in SPM using a macro- scopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage, 15(1), 273–289. https://doi.org/10.1006 /nimg.2001.0978, PubMed: 11771995 van Dellen, E., de Witt Hamer, P. C., Douw, L., Klein, M., Heimans, J. J., Stam, C. J., Reijneveld, J. C., & Hillebrand, A. (2013). Con- nectivity in MEG resting-state networks increases after resective surgery for low-grade glioma and correlates with improved cog- nitive performance. NeuroImage: Clinical, 2, 1–7. https://doi.org /10.1016/j.nicl.2012.10.007, PubMed: 24179752 van den Burg, W., Saan, R. J., & Dellman, B. G. (1985). 15- woordentest: Provisional manual. Groningen, The Netherlands: University Hospital, Department of Neuropsychology. van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organization of the human connectome. Journal of Neuroscience, 31(44), 15775–15786. https://doi.org/10.1523/ JNEUROSCI.3539-11 .2011, PubMed: 22049421 van der Elst, W., van Boxtel, M. P. J., van Breukelen, G. J. P., & Jolles, J. (2006a). The concept shifting test: Adult normative data. Psychological Assessment, 18(4), 424–432. https://doi.org/10 .1037/1040-3590.18.4.424, PubMed: 17154763 van der Elst, W., van Boxtel, M. P. J., van Breukelen, G. J. P., & Jolles, J. (2006b). The Letter Digit Substitution Test: Normative data for 1,858 healthy participants aged 24–81 from the Maastricht Aging Study (MAAS): Influence of age, education, and sex. Journal of Clinical and Experimental Neuropsychology, 28(6), 998–1009. https://doi.org/10.1080/13803390591004428, PubMed: 16822738 van der Elst, W., van Boxtel, M. P. J., van Breukelen, G. J. P., & Jolles, J. (2007). Assessment of information processing in working memory in applied settings: The paper and pencil memory scan- ning test. Psychological Medicine, 37(9), 1335–1344. https://doi .org/10.1017/S0033291707000360, PubMed: 17376260 van Klink, N., van Rosmalen, F., Nenonen, J., Burnos, S., Helle, L., Taulu, S., Furlong, P. L., Zijlmans, M., & Hillebrand, A. (2017). Automatic detection and visualisation of MEG ripple oscillations in epilepsy. NeuroImage: Clinical, 15, 689–701. https://doi.org /10.1016/j.nicl.2017.06.024, PubMed: 28702346 Vázquez-Rodríguez, B., Suárez, L. E., Markello, R. D., Shafiei, G., Paquola, C., Hagmann, P., van den Heuvel, M. P., Bernhardt, B. C., Spreng, R. N., & Misic, B. (2019). Gradients of structure– function tethering across neocortex. Proceedings of the National Academy of Sciences, 116(42), 21219–21227. https://doi.org/10 .1073/pnas.1903403116, PubMed: 31570622 Verhage, F. (1964). Intelligentie en leeftijd bij volwassenen en bejaarden. Assen, The Netherlands: Van Gorcum. Vriend, C., van den Heuvel, O. A., Berendse, H. W., van der Werf, Y. D., & Douw, L. (2018). Global and subnetwork changes of the structural connectome in de novo Parkinson’s disease. Neurosci- ence, 386, 295–308. https://doi.org/10.1016/j.neuroscience .2018.06.050, PubMed: 30004009 Walhovd, K. B., Fjell, A. M., Reinvang, I., Lundervold, A., Dale, A. M., Eilertsen, D. E., Quinn, B. T., Salat, D., Makris, N., & Fischl, B. (2005). Effects of age on volumes of cortex, white mat- ter and subcortical structures. Neurobiology of Aging, 26(9), 1261–1270. https://doi.org/10.1016/j.neurobiolaging.2005.05 .020, PubMed: 16005549 Whalen, C., Maclin, E. L., Fabiani, M., & Gratton, G. (2008). Valida- tion of a method for coregistering scalp recording locations with 3D structural MR images. Human Brain Mapping, 29(11), 1288–1301. https://doi.org/10.1002/hbm.20465, PubMed: 17894391 Yeatman, J. D., Wandell, B. A., & Mezer, A. A. (2014). Lifespan maturation and degeneration of human brain white matter. Nature Communications, 5(1), 4932. https://doi.org/10.1038 /ncomms5932, PubMed: 25230200 Yeo, B. T. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D., Hollinshead, M., Roffman, J. L., Smoller, J. W., Zöllei, L., & Polimeni, J. R. (2011). The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of Neurophysiology, 106(3), 1125–1165. https://doi.org/10.1152/jn .00338.2011, PubMed: 21653723 Ystad, M., Hodneland, E., Adolfsdottir, S., Haász, J., Lundervold, A. J., Eichele, T., & Lundervold, A. (2011). Cortico-striatal con- nectivity and cognition in normal aging: A combined DTI and resting state fMRI study. NeuroImage, 55(1), 24–31. https://doi .org/10.1016/j.neuroimage.2010.11.016, PubMed: 21073962 Yu, M., Engels, M. M. A., Hillebrand, A., van Straaten, E. C. W., Gouw, A. A., Teunissen, C., van der Flier, W. M., Scheltens, P., & Stam, C. J. (2017). Selective impairment of hippocampus and posterior hub areas in Alzheimer’s disease: An MEG–based mul- tiplex network study. Brain, 140(5), 1466–1485. https://doi.org /10.1093/brain/awx050, PubMed: 28334883 Zanin, M. (2015). Can we neglect the multi-layer structure of func- tional networks? Physica A: Statistical Mechanics and its Applica- tions, 430, 184–192. https://doi.org/10.1016/j.physa.2015.02.099 Zhan, L., Jenkins, L. M., Wolfson, O. E., GadElkarim, J. J., Nocito, K., Thompson, P. M., Ajilore, O. A., Chung, M. K., & Leow, A. D. (2017). The significance of negative correlations in brain connec- tivity. Journal of Comparative Neurology, 525(15), 3251–3265. https://doi.org/10.1002/cne.24274, PubMed: 28675490 Network Neuroscience 321 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 7 1 2 9 9 2 0 7 2 1 0 2 n e n _ a _ 0 0 2 8 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3

Télécharger le PDF