RECHERCHE
H1 persistent features of the resting-state
connectome in healthy subjects
Darwin Eduardo Martínez-Riaño1
, Fabio González1, and Francisco Gómez2
1Departamento de Ingeniería de Sistemas e Industrial, Universidad Nacional de Colombia, Bogotá, Colombia
2Departamento de Matemáticas, Universidad Nacional de Colombia, Bogotá, Colombia
Mots clés: Functional connectivity, Topological data analysis, Persistent homology, Resting state
ABSTRAIT
The analysis of the resting-state functional connectome commonly relies on graph representations.
Cependant, the graph-based approach is restricted to pairwise interactions, not suitable to capture
high-order interactions, c'est, more than two regions. This work investigates the existence of
cycles of synchronization emerging at the individual level in the resting-state fMRI dynamic.
These cycles or loops correspond to more than three regions interacting in pairs surrounding a
closed space in the resting dynamic. We devised a strategy for characterizing these loops on the
fMRI resting state using persistent homology, a data analysis strategy based on topology aimed
to characterize high-order connectivity features robustly. This approach describes the loops
exhibited at the individual level on a population of 198 healthy controls. Results suggest that
these synchronization cycles emerge robustly across different connectivity scales. En outre,
these high-order features seem to be supported by a particular anatomical substrate. These
topological loops constitute evidence of resting-state high-order arrangements of interaction
hidden on classical pairwise models. These cycles may have implications for the synchronization
mechanisms commonly described in the resting state.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
.
t
RÉSUMÉ DE L'AUTEUR
Functional connectivity describes relationships between brain regions that are based on graph
representations. Graph-based approaches are limited to pairwise interactions, which are not
suitable for describing higher order interactions and meaningful topological structures such as
loops and voids. This work uses persistent homology to investigate the existence of synchronization
loops arising at the individual level in resting-state fMRI. These loops correspond to more than
three regions interacting in pairs surrounding a closed space. Our results indicate that these
loops emerge across different scales of connectivity that appear to be supported by a particular
anatomical substrate; moreover, they provide a kind of evidence for higher order arrangements
of interactions that seem to have implications for the described synchronization mechanisms in
the resting state.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
INTRODUCTION
The functional connectome of brain activity acquired in the resting state provides descriptions
of the cerebral function at multiple scales (Biswal, 2012; van den Heuvel & Sporns, 2019).
Graph theory is commonly used for the analysis of this connectome, helping to identify central
un accès ouvert
journal
Citation: Martínez-Riaño, D. E.,
González, F., & Gómez, F. (2023). HHHHH1
persistent features of the resting-state
connectome in healthy subjects.
Neurosciences en réseau, 7(1), 234–253.
https://doi.org/10.1162/netn_a_00280
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00280
Reçu: 30 Avril 2022
Accepté: 26 Septembre 2022
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Darwin Eduardo Martínez-Riaño
demartinezr@unal.edu.co
Éditeur de manipulation:
Olaf Sporns
droits d'auteur: © 2022
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
H
1 persistent features of the resting-state connectome in healthy subjects
Connectome:
Graph of the neural connections
within the brain.
Resting state:
State of spontaneous brain activity,
c'est, activity without stimuli.
Persistent homology:
A collection of cavities that persist
across a sequence of simplicial
complexes.
nodes, critical paths, and communities, among other functional brain components related to
particular synchronization patterns (van den Heuvel & Sporns, 2019). These functional
descriptions characterize various functional network connectivity properties associated with
brain dynamics in healthy subjects and provide biomarkers for several pharmacological and
pathological conditions (Wang et al., 2019; Wig, 2017). Notably, most of these analyses oper-
ate on the graph abstraction, with nodes representing the brain regions and edges the values of
measures of interaction or synchronization between pairs of regions (Rubinov & Sporns, 2010;
Sporns, 2013; van den Heuvel & Sporns, 2019). In FNC, this measure commonly links to the
correlation value between two time courses, which describe commonalities in the activation
of both areas. This approach provides a powerful representation to model a variety of phenom-
ena related to connectivity (van den Heuvel & Sporns, 2019). Cependant, the pairwise interac-
tion assumption underlying the functional graph model oversimplifies brain dynamics by
considering at the very base only cofluctuations on the activity of two brain regions (Battiston
et coll., 2020). This could underestimate how brain function may exhibit high-order interactions
among multiple brain regions, c'est, interactions among more than two areas (Battiston et al.,
2020). This paper investigates the existence of robust high-order functional components on the
resting-state dynamic in healthy subjects at an individual level by using persistent homology
(PH), a data analysis strategy based on topology to characterize high-order connectivity fea-
tures robustly.
Description of high-order interactions in resting state has been previously explored, mainly
through graph measurements based on triangles. In contrast to an edge, a triangle represents
the coexistence of interactions for ensembles of three nodes (Petri et al., 2014; Sporns, 2013).
This high-order interaction representation is the base for different connectome characteriza-
tion, like the clustering coefficient, transitivity, and small-worldness (Rubinov & Sporns,
2010). These approaches aim to describe the resting state as a network of distributed modules
likely performing segregated tasks (Sporns, 2013). Cependant, despite the success of these strat-
egies for the resting-state connectome characterization, other high-order interaction mecha-
nisms are still poorly studied (Battiston et al., 2020). Plus récemment, alternative methods for
exploring these interactions in the fMRI brain functional connectome have emerged, tel
as topological data analysis (TDA; Cassidy, Bowman, Rae, & Solo, 2018; Giusti, Ghrist, &
Bassett, 2016; Lord et al., 2016; Preti, Bolton, & Ville, 2017). TDA encompasses methods
aimed to characterize datasets using techniques from topology. In contrast to graph-based
méthodes, TDA allows the description of high-order interactions (Ghrist, 2008). Par exemple,
Saggar et al. (2018) proposed a TDA description of brain function, identifying the topology of
fMRI acquired in related evoked stimuli by using a combination of dimensionality reduction,
clustering, and graph network techniques (Singh, Memoli, & Carlsson, 2007). They found
cohesive high modularity across different tasks, where each module reflects similarities in task
réponses. Salch et al. (2021) illustrated the use of TDA for characterizing loops in fMRI
acquired during an associative learning paradigm. De la même manière, Ellis and colleagues showed that
TDA could discover cycles in simulated event-related fMRI data (Élise, Lesnick, Henselman-
Petrusek, Keller, & Cohen, 2019), and Billings and colleagues used TDA to segment brain
states that differ across a time series of experimental conditions (Facturations, Saggar, Hlinka,
Keilholz, & Petri, 2021). These approaches confirm the capacity of TDA to identify high-order
structures of interaction over functional datasets (Billings et al., 2021; Ellis et al., 2019; Salch
et coll., 2021). Cependant, in these cases, the emergence of the functional structures was condi-
tioned by an experimental stimulus, absent during resting-state protocols. On the other hand,
Cassidy et al. (2018) used TDA to examine the spatiotemporal consistency of resting state at
different temporal and spatial scales. Cependant, they focused on a description of low-order
Neurosciences en réseau
235
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
R-fMRI:
Functional MRI acquired at resting
state.
Simplicial complex:
A collection of simplices.
k-simplex:
Object of k + 1 elements interacting
simultaneously.
topological features. Petri et al. (2014) also used TDA on resting-state fMRI to investigate the
emergence of loops in the R-fMRI dynamic, showing that the distribution of the complete set of
loops observed for the whole population may help distinguish between two conditions,
namely, placebo and psilocybin. This evidence points to the existence of loops underlying
the resting state. Cependant, these works do not indicate whether these cycles emerge individ-
ually or whether they are persistent enough to be considered functional components.
This work investigates the existence of robust cycles at the individual level in the R-fMRI
dynamic. For this, we devised a strategy for characterizing loops on the R-fMRI dynamic using
PH. We evaluated this strategy at the individual level on a healthy control population. Enfin,
we characterize the brain regions involved in the emergence of these loops. Our main con-
tributions are the description through high-order topological features in R-fMRI applying PH at
an individual level, and the identification of brain regions involved in the emergence of these
features. In contrast, previous studies aimed to characterize loops in the fMRI induced by stim-
uli or focused on the whole set of loops at the population level on R-fMRI.
This paper first provides a motivation to use TDA to describe (R-fMRI) time courses. Deuxième,
it presents some relevant TDA concepts and their use in the brain function description. Troisième, it
describes the TDA method employed to characterize R-fMRI time courses for healthy control
(HC) sujets. Enfin, it reports the high-order features of the HC subjects and the brain
regions implicated in its emergence.
FROM RESTING-STATE CONNECTIVITY TO TOPOLOGY DESCRIPTION
THROUGH BOUNDARIES
Topology provides a straightforward alternative to encode high-order interactions by describ-
ing them as groups of nodes or simplices. Simplices represent the simultaneous interactions of
multiple elements. De plus, simplices can be collected on a simplicial complex, just like
graphs are collections of edges and vertices. Alors, the simplicial complex represents the con-
nectivity among elements from a general perspective not limited by the number of interacting
components. To characterize the properties of the simplicial complex, TDA, or specifically
algebraic topology, provides tools like PH (Edelsbrunner & Harer, 2008). PH is a method to
describe topological features at various resolutions (Berry, Chen, Cisewski-Kehe, & Fasy, 2018;
Edelsbrunner & Harer, 2008; Ghrist, 2008). For this, PH first represents the data, a set of points,
as a simplicial complex, and then computes robust descriptors related to boundaries of the
holes across different scales (Edelsbrunner & Harer, 2008). These descriptors correspond to
the number of loops, voids, and in general, cavities (Carlsson, 2009; Edelsbrunner & Harer,
2010), summarizing the topological properties of data. These topological features may provide
meaningful data insights because they describe robust data organization structures.
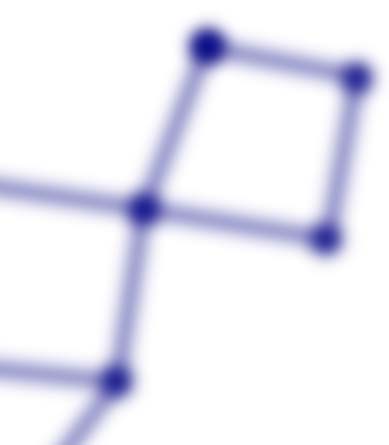
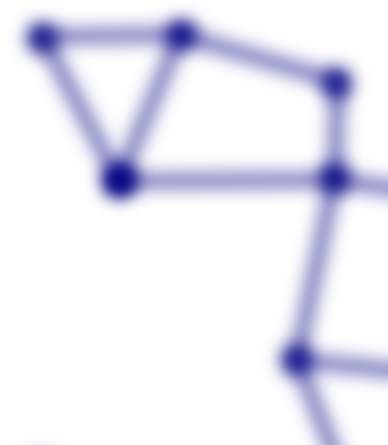
Chiffre 1 illustrates some simplicies and a particular simplicial complex. The figure shows
the first four simplices that describe simultaneous interactions among elements. A simplex of
degree k or k-simplex indicates the structure with k + 1 elements connected simultaneously,
c'est, a 0-simplex refers to points, a 1-simplex refers to an object with two points with a con-
nection (a line), a 2-simplex represents an object with three points with a simultaneous con-
nection among them (a triangle, which is also called a face), a 3-simplex a tetrahedron, and so
on for higher dimensional simplices (Ghrist, 2008; Lord et al., 2016; Figure 1A). Figure 1B
displays a simplicial complex. As observed, a simplicial complex is formed by simplices of
different degrees in configurations that may also include holes. Par exemple, a graph is a sim-
plicial complex with 0-simplices (nodes) and 1-simplices (edges). The simplicial complex
objet (simplices and holes) constitutes a base to describe high-order features in terms of
Neurosciences en réseau
236
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
Illustration of simplices and simplicial complex. (UN) Simplices from 0 à 4 simultaneusly
Chiffre 1.
interacting elements. (B) A simplicial complex with three connected components, two 0-simplex
and a complex composed of simplices of different dimensions, and a set of holes defined by these
simplices. The 0-hole appears at the boundaries of a set of connected simplices (shaded area
surrounded by a dashed line). De la même manière, the 1-hole is a cavity completely bounded by at least
1-simplices. The 2-hole is completely bounded by at least 2-simplices, et ainsi de suite.
cavities. Figure 1B exemplifies three distinct types of cavities: (un) 0-holes, which are cavities in
the space that emerges by the existence of clusters, c'est, a set of points connected by sim-
plices of degree 1 ou plus. Figure 1B shows three different clusters, and the corresponding
three 0-holes, each indicated by the shaded areas surrounded by a dashed line. (b) 1-holes,
cavities completely bounded by at least three 1-simplex, c'est, empty spaces surrounded by
lines. The illustration shows two of these 1-holes. (c) 2-holes, voids enclosed by at least four
2-simplex, c'est, holes surrounded by triangles. Figure 1B illustrates one 2-hole, c'est, un
cavity completely contained by eight 2-simplex.
This differentiation in holes of different dimensions extends the notion of interaction, pro-
viding a complementary perspective beyond the pairwise interactions used on graph theory.
Surtout, holes in dimensions greater than one represent an alternative mechanism of inte-
gration between points because the presence of one of these holes indicates the existence of a
surrounding high-order particular structure of interactions.
To compute this structure, PH starts with a point cloud expressed in some adequate repre-
sentation space, commonly a metric space. From this point cloud, the first step is the construc-
tion of a connectivity structure representing the neighborhood associations between these
points, codifying high-order relationships. According to Ghrist (2008, p. 3), “the more obvious
way to convert a collection of points {xα} in a metric space into a global object is to use the
point cloud as vertices of a combinatorial graph whose edges are determined by proximity (le
vertices within some specified distance (cid:1)).” This construction results in a high-dimensional
objet, a simplicial complex, which is a space built from simple pieces (simplices) identified
combinatorially by faces that codify a proximity representation between points (Ghrist, 2008).
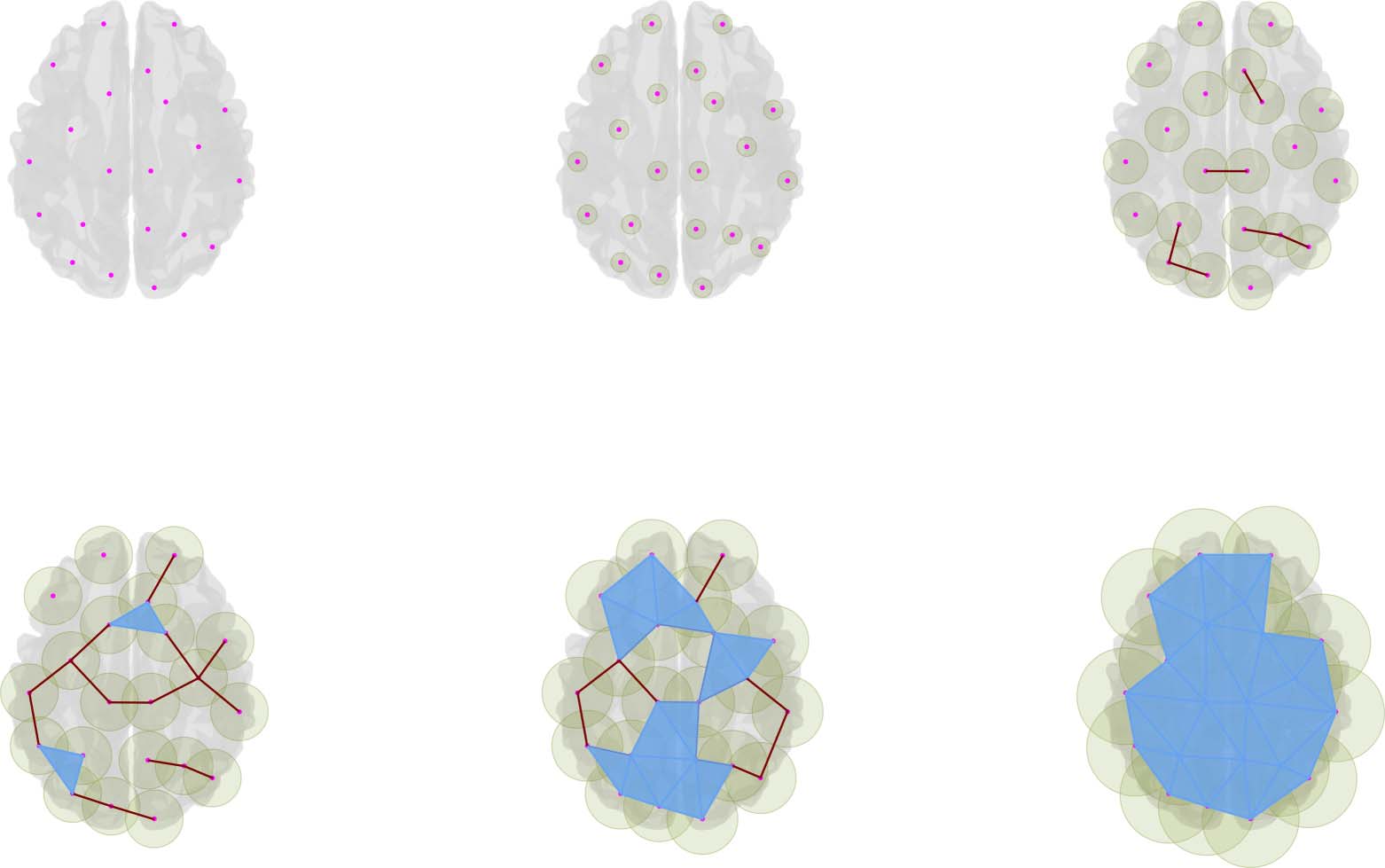
Chiffre 2 illustrates the simplicial-complex computation via the Vietoris-Rips algorithm (fur-
ther details are in Ghrist, 2008). Dans cette approche, the simplicial complex contains k-simplices,
each corresponding to unordered (k + 1)-tuples of points that are pairwise within a distance (cid:1).
Ce (cid:1) is called the filtration value, and it represents the extent of a neighborhood considered
around each point. The term filtration is also used to designate the process of adding simplices
to form a simplicial complex when changing the filtration value up to (cid:1). In this particular
example, the filtration starts with a set of 21 disconnected nodes, (cid:1) = 0. Then while the
237
Filtration value ((cid:1)):
Distance used to compute a filtration,
resulting in a simplicial complex.
Neurosciences en réseau
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2. Simplicial-complex computation. This image is for illustrative purposes. It exposes the simplicial constructions from a set of cloud
points using a Euclidean distance over an anatomical brain reference. The pictures in the image show the simplices for an increasing value (cid:1),
from a to e. Ainsi, as the (cid:1) value grows, different configurations of simplices appear, and with them, Betti numbers count the corresponding
topological features.
filtration value increases, the intersections of the balls with radius (cid:1) centered around points
result in neighborhood relationships (see the green area around points), involving more than
two points, as illustrated with triangles in the figure. These neighborhood relationships are
codified as simplices that together conform the simplicial complex. As observed in Figure 2
for an increasing sequence of (cid:1) valeurs, namely, 0, un, b, c, d, and e, each filtration value results
in a corresponding simplicial complex modeling a particular extent of the neighborhood rela-
tionship. Donc, the filtration and the filtration value are comparable to the network and threshold
in the traditional connectome approach, where the threshold codifies the structure of the net-
travail, as the filtration value codifies the filtration (Battiston et al., 2020).
Once the neighborhood relationships between points, corresponding to particular (cid:1) valeurs,
have been defined and codified as a simplicial complex. It is possible to compute the topo-
logical invariants that describe high-order interactions (Ghrist, 2008). These invariants are
features associated with a topological space that do not change under continuous space defor-
mations, such as the number of holes (Giusti, Pastalkova, Curto, & Itskov, 2015). Alors, le
notion of topological invariant is related to those features that survive across successive
deformations, and a hole can be understood as a structure that prevents an object from being
continuously shrunk to a point. Ainsi, the existence of a hole is an indicator of a particular
connectivity structure around it, c'est, the connectivity configuration that prevents that the
space represented by the simplicial complex collapses under continuous deformations, acting
as a connectivity boundary.
Remarquablement, well-known facts about R-fMRI signal can be interpreted in the PH context. Pour
instance, from the PH perspective, the resting-state connectome can be understood as the
Neurosciences en réseau
238
H
1 persistent features of the resting-state connectome in healthy subjects
k-hole:
A k-dimensional cavity, an empty
space bounded by k-simplices.
complement of the 0-holes, c'est, the connected components at a given threshold. These
connected components are simplicial-complex of degree 1 ou plus (voir la figure 1). Ainsi, it
is possible to macth the graph in the connectome approach with the connected components
that produce the 0-holes described by PH. Nevertheless, it is worthy to recall that the PH
approach accounts for the “holes” that emerge from the data rather than for the connection
lui-même. This way, it provides a view of the interaction among elements complementary to the
view commonly used in R-fMRI brain analysis. En outre, the PH could be understood as a
generalization of the graph approaches where a graph is a fixed instance with degree 1. PH or
specifically algebraic topology provides tools for counting these holes. En particulier, PH relies
on the notion of homology, which allows counting the number of holes of finite simplicial
complexes. The homology or homology group (H) of a simplicial complex is the collection
of k-holes formed by k-simplices (further details are in Ghrist, 2008; Giusti et al., 2016). PH
counts the boundaries surrounding the holes that are persistent for a sequence of filtrations,
c'est, the number of simplicial complex holes of filtrations at different filtration values. Alors,
PH counts the persistent k-holes, c'est, holes in the homology at dimension k (Hk ). Dans ce
contexte, another tool for homology description is the Betti numbers; they are the rank of
features of a particular k-dimension for a complex at a fixed (cid:1) valeur. Betti numbers count
the occurrence of k-holes (a k-hole is a hole bounded by k-simplices): Betti 0 counts the
0-holes; Betti 1 counts 1-holes (the appearance of a hole surrounded by 1-simplex, an empty
area surrounded by pairs of connected objects); Betti 2 counts voids, the emergence of a
2-dimensional hole (a void enclosed by 2-simplices, triangles); et ainsi de suite. Voir la figure 2.
Two distinct approaches are commonly used to represent the emergence and disappear-
ance of the topological features, namely, TDA barcodes (Ghrist, 2008) and persistence dia-
grams (Berry et al., 2018). Voir la figure 3. A barcode is a representation of the homology groups
resulting from different filtration values as a collection of bars (intervals) representing the birth
and death times of the k-dimensional holes (Atienza, Gonzalez-Diaz, & Rucco, 2017; Ghrist,
2008). It allows studying the evolution of these holes along a nested sequence of a simplicial
complexe (Atienza et al., 2017). This nested sequence of a simplicial complex results from
using increased values of filtration. A significant attribute of this representation is that long
barcodes are associated with robust features, c'est, long barcodes link to features that persist
along different filtration values (Islambekov & Gel, 2019). In contrast, short barcodes are com-
monly related to noisy topological features, such as holes that appear during small intervals of
filtration values.
Persistence diagrams provide an alternative way to summarize the topological structure of
data. As in the barcodes, persistence diagrams summarize the topological features for the
Illustration of the barcodes (gauche) and persistence diagrams (droite). Both barcodes and persistence diagrams show the features birth
Chiffre 3.
and death for the homology H0 and H1. Persistent H1 features are labeled with capital letters, in order of appearance (UN, B, and C, respectivement)
in both diagrams. In the barcodes, the length of the horizontal line indicates persistence of a feature, while the number of lines crossed by a
vertical line is the Betti number at a specific (cid:1) valeur. De la même manière, in the persistence diagram, the distance di between each point and the diagonal
indicates persistence, but it is hard to see the Betti number for a given (cid:1).
Neurosciences en réseau
239
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
sequence of filtration values. Officiellement, the persistence diagram is a collection of triplets
(homology degree, birth time, death time) of the filtration sequence (Berry et al., 2018). Le
set of triplets can be represented as points in a two-dimensional plot, with x the birth time and
y the death time. The triplets with short distances between birth and death time correspond to
short barcodes, which can be associated with noise and are represented as points close to the
diagonal line. In contrast, the triplets with long distances correspond to persistent or highly
robust features, c'est, the points far from the diagonal line (voir la figure 3).
Donc, Betti numbers, barcodes, and persistence diagrams allow identification of persis-
tent features. In R-fMRI context, they provide a description of high-order structures that could
be associated with connectivity phenomena from a complementary perspective focus on
holes.
RÉSULTATS
Loops in the fMRI Resting-State Connectivity Dynamic
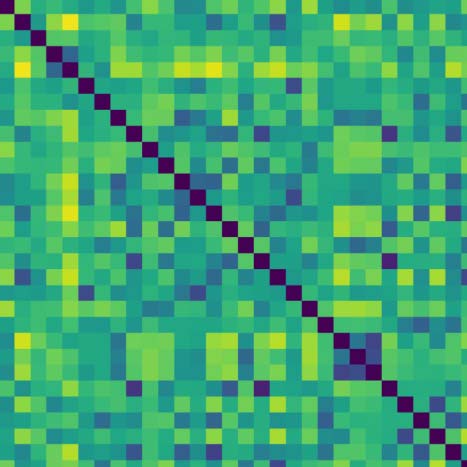
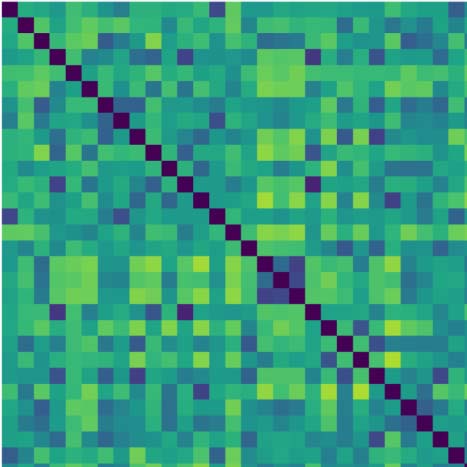
Chiffre 4 shows the topological features exhibited by the fMRI resting-state dynamic summa-
rized as barcodes and the persistence diagrams for the average population. Chiffre 4 aussi
shows the corresponding distance matrix (Figure 4A), computed from the Pearson’s correlation
between the regional time courses, used for the PH calculations. This distance matrix induces
an implicit data space to describe the brain’s time course fMRI dynamic. This space contains
the connectivity relationships or neighborhoods linked to regional R-fMRI regional time course
synchronizations.
Topological holes characterize the connectivity relationships in this fMRI data space,
1-dimensional holes (H1), which refer to loops in the R-fMRI data space, c'est, sets of time
courses weakly synchronized in pairs that together conform cycles. Each line in the barcode
(Figure 4B) represents a particular hole. Large lines refer to persistent holes, c'est, holes that
consistently appear across different filtration values. The persistence diagram (Figure 4C) aussi
shows these persistent topological features as two-dimensional points appearing far from the
diagonal, with different colors representing the dimension of the topological feature. Comme
observed, the fMRI resting-state time courses in this subject show high levels of connectivity,
as evidenced by the 0-holes found in the persistent analysis (blue dots in Figure 4C). Remark-
ably, the time courses are organized around 1-dimensional holes (see Figure 4B), indicating
that the resting state may also exhibit high-order interactions. Surtout, these high-order
interactions seem to be highly robust across different filtration values or scales, as illustrated
for instance by the topological 1-hole feature marked as an orange line in H1 and also shown
in the persistence diagram with a black cross (see Figure 4C).
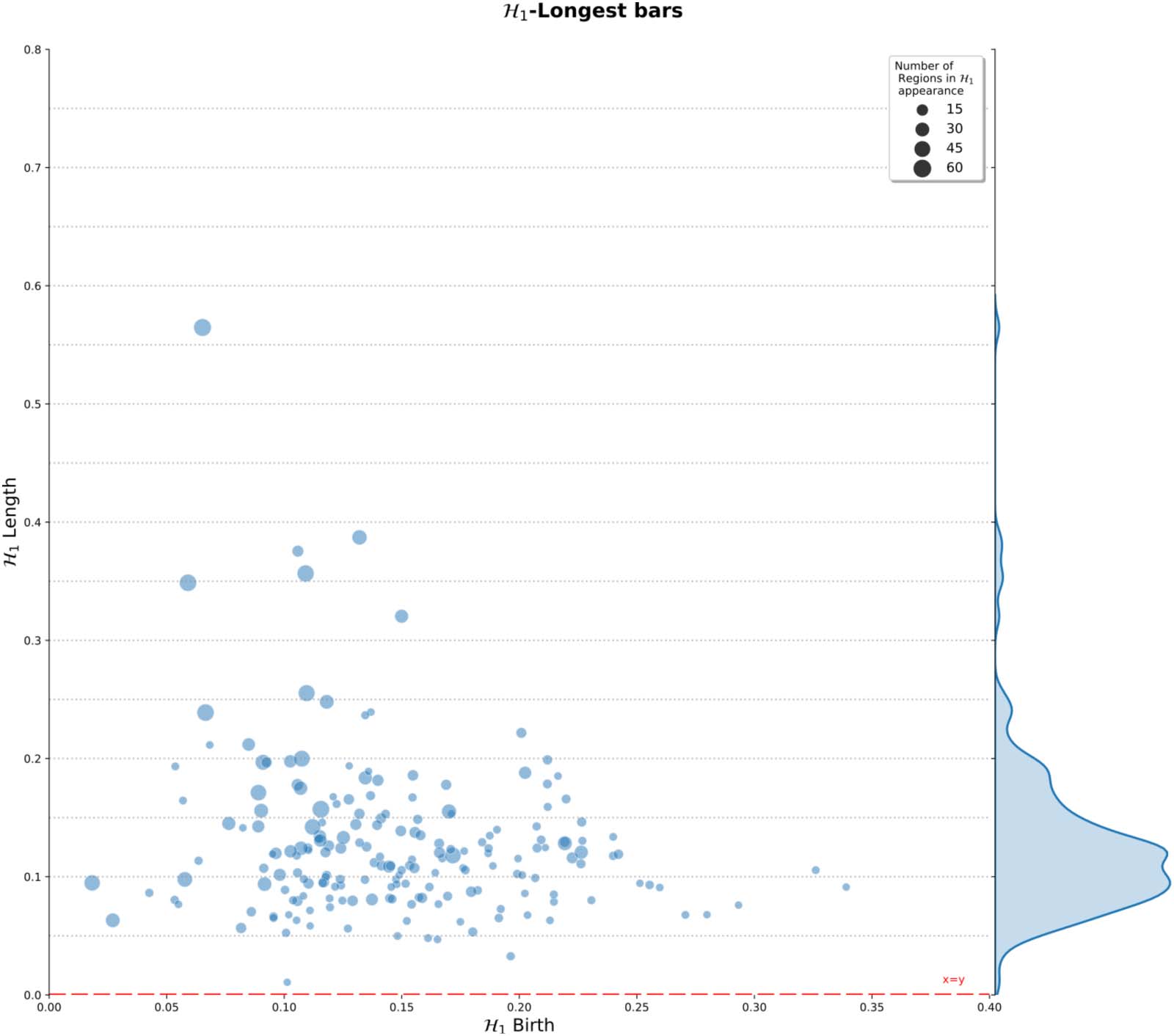
Chiffre 5 shows the distribution of the most persistent H1 feature at the group level. Ce
figure includes a histogram summarizing the length of the largest H1 bars. These lengths indi-
cate the persistence of the 1-holes in the population under study. Surtout, this figure shows
that a large percentage of subjects showed persistent 1-holes, with lengths between 0.05 et
0.24 for most of them (183 de 198). Cependant, the complete range of distances was between
0.02 et 0.51, showing that there are also subjects for which the R-fMRI dynamic exhibited
both highly persistent and noisy loops in connectivity. The higher frequencies ranged between
0.05 à 0.17, indicating that 1-holes consistently emerge for at least 10% of filtration values,
normalized between 0 et 1. En plus, the distribution of points exhibits a wide range of
birth values for the persistent 1-holes, ranging from 0.02 à 0.34, mainly concentrated between
0.05 et 0.25. The distribution presents no apparent relation between the birth and death
times of the largest loop for the population. Aussi, the radius of the circle representing the
Neurosciences en réseau
240
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4. Topological features computed for the average of the population. (UN) The average distance matrix computed from the Pearson’s correlation
between R-fMRI time courses; dark blue indicates lower distances while yellow indicates larger distances. (B) H1 barcodes, orange line, highlight the
most persistent H1 loop. (C) Persistence diagram summarizing H0 and H1 measurements; black contour dot indicates the most persistent H1 loop.
Neurosciences en réseau
241
H
1 persistent features of the resting-state connectome in healthy subjects
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
Chiffre 5. H1 persistent summary of the topological features computed over all subjects. Distribution of the H1 largest loops at left. Droite,
length frequency of the persistent 1-holes. Gray dashed lines are only for reference of distances from the x = y line at the bottom. Aussi, le
circle radius indicates the number of regions involved in the appearance of the longest H1 feature in the corresponding subject.
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H1 feature is an indicator of the number of regions involved in the emergence of the feature.
The figure presents small and big radius at different birth values and lengths, indicating no
apparent relation between the number of regions with the length of the features, or the birth
of it. En fait, most of the H1 features show fewer than 15 brain regions implicated in their
emergence.
1 Topological Persistent Structures
Brain Regions Involved in HHHHH
Once the existence of robust H1 topological features in healthy controls at the individual level
was established, the next section investigates how these features emerge in the brain regions.
But first it is worthy to recall that a boundary, or a sequence of nodes, defines a 1-hole. In our
case, these nodes refer to the brain regions, which compose the boundary of synchronization
loops. These nodes can be recovered from the PH analysis (Bauer, 2018; Tralie, Saul, &
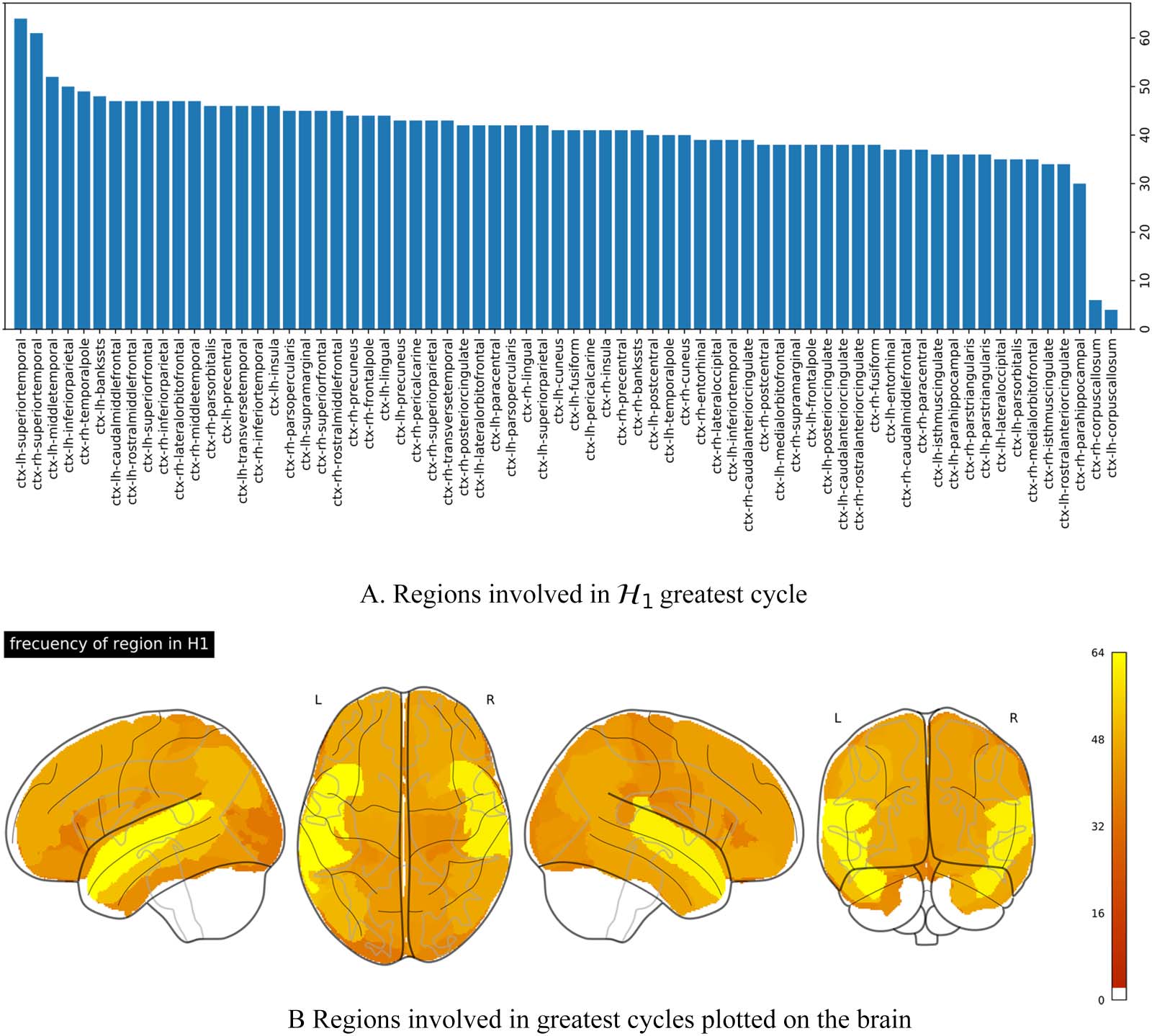
Bar-On, 2018). Figure 6A shows the number of subjects in which each brain region was
involved in the composition of the most persistent H1 loop, c'est, the number of times a
region was involved in highly persistent synchronization loops. These regions are sorted in
increasing order. The region with the highest occurrence in the large synchronization loops
corresponded to the superior-temporal cortical areas in both hemispheres, appearing in more
Neurosciences en réseau
242
H
1 persistent features of the resting-state connectome in healthy subjects
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
Chiffre 6. Regions involved in the most persistent loops. (UN) Frequency of appearance of the cortical region in the emergence of the greatest
cycle. (B) Projection of the frequency onto the brain.
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
t
.
que 30% of the population. The left middle-temporal, left inferior-parietal, the right temporal-
pole, and the left bankssts were involved in more than 22% of the subjects.
Figure 6B shows region occurrences in the most persistent synchronization loops projected
onto the brain. Dark orange values represent a low level of occurrences, while yellow areas
correspond to high occurrence levels. This projection reveals symmetries in the involvement of
the regions in the emergence of the loops, which is more notorious in the temporal lobe, par-
ticularly in the superior, middle, and bankssts cortical regions of both hemispheres.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
DISCUSSION
Dans cette étude, we used TDA to describe the persistence loops in R-fMRI time courses on healthy
sujets. Remarquablement, these topological features emerge robustly across different scales, c'est,
while filtration values change. These features are formed by 1-simplexes surrounding a space,
indicating at least two directions to reach any other element in the simplex structure. These
cycles in the network suggest that information can be delivered using two different redundant
paths and interpreted as redundant connections (Saggar et al., 2018). Surtout, even if
cycles can be computed directly from network approaches, their persistence is not considered
in the analysis because of the threshold selection in the connectome analysis. These topolog-
ical features (cycles or loops) constitute evidence of R-fMRI high-order arrangements hidden
Neurosciences en réseau
243
H
1 persistent features of the resting-state connectome in healthy subjects
on classical pairwise models. En outre, we identified the brain regions most involved in the
emergence of these topological structures. We found that some brain regions frequently appear
in these persistence loops, suggesting a particular anatomical substrate of these regions in the
emergence of these interactions. Together this evidence supports the existence of high-order
structures in functional connectivity in R-fMRI. Nevertheless, their meaning and the specific
roles of the brain regions involved are still unknown.
Initial studies in R-fMRI discovered that the existence of low-level synchronous fluctuations
(<0.1 Hz) in BOLD signal occurred independently of task stimulation (Biswal, 2012; Biswal,
Kylen, & Hyde, 1997). This evidence pointed for the first time to a nontrivial organization of
the resting-state dynamic. Posterior studies robustly identified regions with coherent spatiotem-
poral fluctuations grouped under the so-called resting-state networks (Damoiseaux et al.,
2006). This evidence suggests that the brain function in the resting state organizes in patterns
of coordinated activity related to synchronization mechanisms among brain regions. However,
the true extent and the nature of these patterns of coordination remain poorly understood.
Notably, the characterization of most coordination patterns described for R-fMRI relies on pair-
wise synchronicity descriptions between time courses, neglecting that alternative synchroni-
zation mechanisms may also emerge from multiregional interactions (Battiston et al., 2020;
Cassidy et al., 2018). From the connectivity point of view, the graph approach considers
the correlation as edge value, with or without a threshold, for binary or weighted settings,
respectively. The topological strategy provides a tool that does not depend on a fixed threshold
selection to create a graph. Instead, persistent homology works with all possible networks at
the same time. It focuses on the features that appear and disappear while the (cid:1) value increases.
Then, a graph built from a specific threshold resembles a simplicial complex with only
1-simplices. Moreover, in graph approaches, it could result in more than one connected
component. Therefore, graph measurements such as efficiency result in infinite values. This
situation does not occur with TDA because it analyzes all possible connected components
simultaneously no matter how many they are at a given (cid:1) value; it is just a simplicial complex.
Even in the case where there is no threshold fixed, that is, where the graph measurements were
affected by the weight of the relationship, the focus of TDA is on the occurrence of the struc-
ture rather than on the existence of particular associations; thus, a weak relation from the
graph perspective represents a greater distance between elements in TDA, but in TDA, it
has the same importance once reached. In particular, TDA focuses on those structures that
persist across distinct (cid:1) values, providing a robust set of features at different levels. More
recently, some studies in small populations aimed to overcome this limitation by directly
studying high-order interactions by looking for high-dimensional topological holes, which
indicate surrounding high-order interactions. The proposed analysis confirmed the existence
of H1 topological loops in healthy control R-fMRI, as in Petri et al. (2014). Their work intro-
duces a new approach to assessing the robustness of H1 features based on the persistence of
the feature, and the frequency with which an edge appears in the feature set. In contrast, the
proposed analysis is based on the persistence of the H1 feature by itself, while considering
nodes, or, anatomical regions. Furthermore, it calculates H1 features in a large healthy popu-
lation. Moreover, our results (Figure 5) suggest that the appearance of these 1-holes across the
people is not spurious, that is, these holes robustly emerged across multiple scales in most
subjects for the large population herein studied. Thus, the occurrence of these 1-holes points
to the existence of multiregional synchronization mechanisms of high-order nature underlying
the RS dynamic in healthy controls.
Description of high-dimensional data through algebraic methods such as PH is beginning to
be widely used. For fMRI (resting and evocated) in particular, these methods avoid the arbitrary
Network Neuroscience
244
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
a
_
0
0
2
8
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
collapsing of data in space or time (Cassidy et al., 2018; Saggar et al., 2018). An interesting
approach was developed by Saggar et al. (2018). In their approach they use Mapper to under-
stand the shape of the fMRI dynamic among different activation processes related to instruc-
tions, working memory, video, and math tasks. They found that activation is similar in the
related cognitive tasks. Although they describe the resting-state periods between activation
tasks as peripheric shapes, it is not the focus of the work. Recently Saggar, Shine, Liégeois,
Dosenbach, and Fair (2021) have been focusing on the resting state. They are characterizing
the activation transitions occurring at rest. For this, they use Mapper to distinguish between
discrete or continuous variations associated with activation transitions, mainly to understand
the underlying phenomena of resting-state activations. Finally, they claim that there is a hub
responsible for resting transitions. Another approach that tackles the resting-state fMRI is the
work introduced by Cassidy et al. (2018). They use TDA to overcome the drawbacks related to
the scale and threshold selection in connectome analysis of healthy subjects. They study the
first Betti number, B0, which models the topology of connections, and found that the topology
properties are robust across different scales; however, they do not use the information of high
topological dimensions. Here, we use the second Betti number, B1 to understand the topolog-
ical structures (loops) of R-fMRI. TDA loops studies are not new, and asking for the emergence
of these structures seems to have a sense in biology and other fields. Topological studies have
been introduced to describe different phenomena in various domains, including biological,
medical, physical, and other specialties. In biology, Bhaskar, Zhang, and Wong (2021) incor-
porate the TDA connected loops descriptors to summarize the cell proliferation architectures;
they also use those descriptions to classify particle configurations. Additionally, persistent
cycles of gene network information shown to be robust features appear in the study of different
datasets of glioblastoma (Mao et al., 2019). In physics, topological voids (H2 structures) were
found in the study of the baryon acoustic oscillation related to the galaxy distribution (Kono,
Takeuchi, Cooray, Nishizawa, & Murakami, 2020). Finally, in medicine, Carpio, Bonilla,
Mathews, and Tannenbaum (2019) use the topological descriptors for the two first dimensions,
that is, H0 and H1. They found that different cancer cells have distinct topological values at
these dimensions, indicating the descriptors’ usefulness as biomarkers.
Our approach in R-fMRI analysis allows identifying the most persistent H1 loop structures
for each subject. Also, it determines the brain regions involved in the emergence of the topo-
logical features. Bhaskar et al. (2021) identify the largest loop in the multicellular architecture
of epithelial cells, but they do not inquire about the elements in the cycle. In our approach, we
found that middle temporal gyri, both hemispheres, are the regions that appear more fre-
quently in the most persistent H1 loops in the population considered for this study. These brain
regions are involved in auditory association, multisensory integration, speech processing,
language comprehension (Muñoz-López, Insausti, Mohedano-Moriano, Mishkin, & Saunders,
2015; Turken & Dronkers, 2011), and social cognition (Olson, McCoy, Klobusicky, & Ross,
2013). From the functional perspective, these regions are in the cognition pathway, associated
with the amygdala and the prefrontal cortex (Olson et al., 2013). They are involved in spatial
working memory tasks with the occipital region (Ding et al., 2016). Also, they have been
suggested as part of a separate ventral attention system that acts as a circuit breaker to reorient
attention (Corbetta, Patel, & Shulman, 2008). With this in mind, the appearance of the superior
temporal gyrus (STG) in the persistent cycle might be associated with alert systems, that is, the
process of achieving and maintaining a state of high sensitivity to incoming stimuli. In partic-
ular, the participants are ordered to keep their eyes closed during the acquisition process, but
because of the acquisition condition, they are continuously prepared to follow instructions.
These have been described as an interface between language comprehension and the
Network Neuroscience
245
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
a
_
0
0
2
8
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
attention network (Kristensen, Wang, Petersson, & Hagoort, 2012). Then, in this specific acqui-
sition process, the STG appearance in the persistent cycle might be related to the reorientation
of attention.
The approach developed in this study presents some drawbacks. Beginning with the TDA
process, the selection of the distance to compute the topological properties influences the
appearance of the topological structures (Edelsbrunner & Harer, 2008). In this case, we use
a “distance” built from Pearson’s correlation (Cha, 2007), which limits the range of possible
distances as well as affects the Betti numbers and all other topological features. This distance is
a global measure robust to variations that globally affect the time points of all time courses, as
described above. Then, a working perspective is to consider other types of distances that are
sensitive to some variations such as permutations of points, or translations. Also, Pearson’s-
based distance only captures differences of the similarity assessed as the co-occurrence of
the time courses. Thus, another perspective is to contemplate a distance intended for varia-
tions over time; for instance, a distance based on a measure used to describe dynamic func-
tional connectivity (Hutchison et al., 2013; Zalesky, Fornito, Cocchi, Gollo, & Breakspear,
2014). Moreover, as this approach can not describe nonlinear dependencies between time
courses, the employment of a distance that considers nonlinear dependencies opens a per-
spective to explore. Another TDA consideration is the selection of the coefficients group used.
The presented approach uses ℤ/2ℤ as the coefficient group, which is a 2-order cyclic group
(Giusti et al., 2016). Although it is suitable for loop description, richer structures related to
high-order coefficient groups are out of its scope. The presented approach is limited to H1
features. These features offer advantages for results interpretation and comparability with other
strategies in anatomical space. Although higher order features, that is, H2, H3, and others,
could be computed, they are computationally expensive (Zomorodian & Carlsson, 2005)
and less interpretable at the moment (Molnar, 2022). Nevertheless, the computations of
high-order features are another perspective to develop. Another concern is the focus on only
the most persistent loop. Figure 5 shows the existence of an interesting number of features that
are not spurious. Therefore, extending the analysis of loops to a percentage of the most per-
sistent could provide a new perspective for the analysis, because with more cycles, it is pos-
sible to (a) enrich the R-fMRI topological description of each subject, which can be used in
other developments like classification (Bhaskar et al., 2021; Carpio et al., 2019), and (b) iden-
tify the nodes that are involved in more than one persistent loop because they could be rel-
evant in the study of brain high-order processes. Another concern is the use of the proposed
approach for comparison between population and/or specific brain regions. To this end, the
presented approach could be improved by introducing some statistics that provide a suitable
basis for comparison between populations, such as healthy versus pathological subjects.
Examples include a contrast of the occurrence of the level of loops between the populations,
and comparisons in studies focused on specific brain regions such as the STG. Here we high-
light that this new perspective found the nodes and associations not only that are important by
their connections, as in connectome analysis, but also that are important because there are
some emerging limits, and the properties of these boundaries in brain functions are unknown.
An interesting perspective is to use the approach proposed here in the topological description
of the R-fMRI in pathological conditions where the STG are involved. Then, the topological
features (H1) could be used in research with clinical application, mainly focusing on those
where functional connectivity alterations have been reported, in particular, for the study of
bipolar and unipolar depression (C. Liu, Pu, Wu, Zhao, & Xue, 2019), corneal ulcer (Zhu
et al., 2019), deafness (Ding et al., 2016), depression in Alzheimer disease (X. Liu et al.,
2018), Alzheimer disease (Hafkemeijer et al., 2015), comatose patients (Huang et al.,
Network Neuroscience
246
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
a
_
0
0
2
8
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
2019), tinnitus (Cai et al., 2020; Xu et al., 2019), anxiety disorders (Xiong, Guo, & Shi, 2020),
attention deficit hyperactivity disease (H. Zhang et al., 2020), post-stroke memory (J. Liu et al.,
2017), and internet gaming disorder (J.-T. Zhang et al., 2016), among others. But not only path-
ological conditions alter the functional connectivity of the superior temporal gyri; this topo-
logical approach could also be used for studies of brain function related to chess practice
(Song, Ge, Long, & Dong, 2020), meditation (Jang et al., 2018), and second language learning
(Chai et al., 2016). However, the proposed approach does not consider the effects of head
movements during the R-fMRI acquisition on healthy subjects. They are associated with some
brain diseases such as Parkinson’s and disorders of consciousness. Therefore, the approach
should be updated to include the framewise displacement (Power, Barnes, Snyder, Schlaggar,
& Petersen, 2012; Power et al., 2014) for brain disease studies.
CONCLUSION
The presented PH strategy characterizes the resting-state connectome for healthy control
subjects. Persistent H1-holes were robustly found in healthy people, providing a new set of
features to consider in resting-state studies. These H1-holes indicate the existence of bound-
aries surrounded by 1-simplex (lines), conforming to a loop, that is, a structure providing two
directions of connections for the boundary elements. Additionally, specific brain regions were
linked to the occurrence of these properties, pointing to a functional boundary. Moreover,
these brain regions frequently appear across populations, expressing a sort of symmetry in
the resting-state connectome topology and providing biological insight.
MATERIALS AND METHODS
Figure 7 shows the proposed strategy to characterize the topological features for the resting-
state functional brain activity. The first stage (blue rectangles) encompasses the computations
made on each individual in the dataset. This phase extracts a representative time course per
cortical region using independent component analysis (ICA) followed by the computation of
topological features. This computation includes (a) estimation of the distance matrix summa-
rizing the neighborhoods’ relations among representative time courses, (b) description of H0
and H1 features on the filtrations resulting from the Vietoris-Rips algorithm, and (c) identifica-
tion of the most persistent H1 feature at the individual level. The second stage (orange rectan-
gle) characterizes H1 features emerging at an individual level for the whole population and
consists of two main subprocesses. The first one summarizes the topological features found at
an individual level for the whole population through a 1-hole distribution. The second one
identifies the brain regions most involved in the emergence of the longest H1 feature. This last
process estimates the number of times that a region appears associated with the persistent H1,
the depiction of frequency of occurrence of these regions onto a brain map representation.
Dataset
The Beijing-Zang Center dataset from the 1000 Functional Connectomes Project, consisting of
resting-state functional MRI (R-fMRI) acquisitions and a T1 MRI for anatomical reference, was
used to investigate loops in synchronization. It is composed of 198 subjects (122 females) aged
between 18 and 26 years. The R-fMRI acquisition properties are the following: time resolution
of 2.0 s, 33 slices, and 255 time points. All datasets in the project are anonymous, and the
demographic information is limited to gender, age, and handedness.
Network Neuroscience
247
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
a
_
0
0
2
8
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
a
_
0
0
2
8
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Method to compute the topological features for R-fMRI, starting with the images acquisition, followed by the data preprocessing,
continuing with the topological description, and ending with the summarization of properties on the population. Blue boxes indicate the
process done per individual.
Data Preprocessing
The structural T1 image was segmented into cortical and subcortical regions by the FreeSurfer
standard stream. This segmentation process offers two atlas-based region sets (Desikan-Killiany
and Destrieux). The segmentation is based on a probabilistic information model. The model
was estimated from manually labeled images and uses geometric information from the cortical
model plus the naming convention for the final segmentation (Desikan et al., 2006). In this
approach, the Desikan-Killiany parcellation was selected, which provides a set of 64 cortical
regions and 15 subcortical regions, but only the cortical regions were considered for the func-
tional analysis. The R-fMRI process provides signals linked to neuronal activity. It entails two
stages made by using SPM and AirRepair toolboxes (Mazaika, Hoeft, Glover, & Reiss, 2009).
The first stage includes realignment and adjustments for movement effects for functional
images, as well as coregistration onto structural data, normalized into standard stereotactic
MNI space and spatially smoothed with a Gaussian kernel of 8 mm. These were motion-
corrected (small, large, and rapid motions, noise spikes, and spontaneous deep breaths), as
described previously (Demertzi et al., 2014). Second, the R-fMRI signal was decomposed into
maximally independent spatial maps using spatial ICA. This decomposition used a fixed-point
algorithm implemented in the GroupICA toolbox. The signal was described by 30 independent
components classified by their origin into neuronal or artifactual. The classification employed
a machine learning labeling method, a support vector machine trained on 19 healthy subjects
independently assessed. Then, the signals were reconstructed by combining the independent
components exhibiting neuronal behavior (Demertzi et al., 2014). The preprocess ends with
the computation of the representative signal of each cortical region estimated by averaging the
reconstructed signals that belong to a specific area.
Network Neuroscience
248
H
1 persistent features of the resting-state connectome in healthy subjects
Figure 8. Cloud point representation from n-dimensional signals. For each brain region a representative signal is considered as a point in a
n-dimensional space.
Functional Connectome TDA Description
The topological description was made based on the assembly of simplicial complex per sub-
ject. It was built from the dataset of reconstructed functional signals. These signals constitute a
set of points in an n-dimensional Euclidean space, one point per signal, and one representative
signal per brain region; see Figure 8. The ensemble of points turns into a global object via
simplicial complex computation. Here, proximity is defined as a joint distance, that is, a dis-
tance from a similarity measurement. In this case, Pearson’s correlation (r) is used to compute
the distance matrix (Falcone & Albuquerque, 2004), which is the input of TDA. See Equation 1:
d X; Yð
Þ ¼
1 −
r
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2 r
¼
1 −
(cid:2)
q
v
u
u
t
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
P
i¼1 xiyi − (cid:1)x (cid:1)y
q
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
P
Þ2
i¼1 xi − (cid:1)x
ð
n
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
P
Þ2
n
i¼1 yi − (cid:1)y
ð
1
2
;
(1)
where X = (X1, X2, …, Xn) and Y = (Y1, Y2, …, Yn) are two R-fMRI time courses, and (cid:1)x and (cid:1)y are the
mean of the time course X and Y, respectively. It is important to note that the distance calculated
here is a global measure independent of the order of the time points; that is, the same permuta-
tion of points in all time courses does not affect the distance measured between them. Similarly, it
is not affected by a global translation, an addition or a subtraction of the same quantity for all time
points in all time courses. Thus, calculations as a summary of local differences are robust to these
global variations, such as those that are considered by dynamic approaches (Hutchison et al.,
2013; Zalesky et al., 2014).
Persistent homology computations. Barcode computation was performed on the distance matrix
by using Ripser (Bauer, 2018), through its Python wrapper (PyRipser; Tralie et al., 2018). This
tool provides a simple set of settings to compute homology features. PH computations were
based on the Vietoris-Rips approach, establishing the criteria to compute a simplex based on
the distances. (Py)Ripser allows specifying the homology group and the maximum number of
dimensions to consider in the computation of TDA features. Informally, 0-degree homology
groups (0-hole topological features) capture the connected components, and 1-degree homol-
ogy groups capture regions forming a loop structure (Edelsbrunner & Harer, 2008). The Ripser
process on a distance matrix results in a set of birth and death values per bar at the respective
degree or dimension. It also provides a corresponding set with the list of elements associated
with the feature emergence. The process supplies two lists with corresponding components,
one with the bar description and the other with the elements involved in the appearance of a
topological feature. Once the topological features are computed, the process continues with
the association of the longitude to each H1 bar. Then, all bars in H1 have the birth, death, and
longitude. The set of H1 bars are sorted by the longitude value. The persistent feature is the
1-hole with the largest longitude, the first in the sorted bars. Finally, the selection of regions
Network Neuroscience
249
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
a
_
0
0
2
8
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
related to the persistent 1-hole consists of (a) sorting the list of associated elements based on
the longitude criteria and (b) choosing the first list.
Population Description of Topological Features
The description of the topological features, in this case for H1, was performed from two per-
spectives. The first one summarizes the computed features for the population. The second one
estimates the frequency of the brain region appearance in the persistent 1-holes.
1 topological features. The H1 persistent features at the group level were sum-
Summary of the HHHHH
marized using the length of the most persistent H1 feature per subject. In particular, the longest
bar linked to H1 was selected per subject, and the distribution of these features was calculated.
Following this, the probability of observing particular longitudes for these features was com-
puted, indicating the distribution of these persistent features in the population. Similarly, the
birth values of these features could be different through the group. An enhanced persistence
diagram illustrates the summary of the 1-holes. It depicts the distribution of 1-holes, one point
per subject in the group, and the frequency of longitudes as a histogram at left; see Figure 5.
Brain regions in persistent 1-hole. Brain regions associated with the emergence of H1 were also
characterized. In principle, any brain region can belong to an H1 feature; the 1-holes could be
related to distinct elements. Therefore, the number of times a brain region appears to be
related to the largest H1 emergence was quantified. This quantification results from searching
all the regions in the element list of nodes conforming to the H1 nodes of each subject. The
frequency of brain regions in the emergence of 1-hole in the population is twofold, presented
as a sorted bar diagram and projected onto a brain representation.
ACKNOWLEDGMENTS
We would like to thank José Perea (PhD) for the dialogues and discussion about TDA process
application, Jorge Rudas (PhD) for the interesting discussions about high-order methods apart
from TDA, and Gabriel Castellanos (MD, PhD) for the dialogue about function of brain
regions.
AUTHOR CONTRIBUTIONS
Darwin Eduardo Martínez-Riaño: Conceptualization; Formal analysis; Software; Writing –
original draft; Writing – review & editing. Fabio González: Conceptualization; Supervision;
Writing – review & editing. Francisco Gómez: Conceptualization; Supervision; Writing –
original draft; Writing – review & editing.
REFERENCES
Atienza, N., Gonzalez-Diaz, R., & Rucco, M. (2017). Persistent
entropy for separating topological features from noise in Vietoris-
Rips complexes. arXiv:1701.07857. https://doi.org/10.48550
/arXiv.1701.07857
Battiston, F., Cencetti, G., Iacopini, I., Latora, V., Lucas, M., Patania,
A., … Petri, G. (2020). Networks beyond pairwise interactions:
Structure and dynamics (Vol. 874). Elsevier. https://doi.org/10
.1016/j.physrep.2020.05.004
Bauer, U. (2018). Ripser: A lean C++ code for the computation of
Vietoris-Rips persistence barcodes. https://github.com/ Ripser
/ripser
Berry, E., Chen, Y.-C., Cisewski-Kehe, J., & Fasy, B. T. (2018). Func-
tional summaries of persistence diagrams. arXiv:1804.01618.
https://doi.org/10.48550/arXiv.1804.01618
Bhaskar, D., Zhang, W. Y., & Wong, I. Y. (2021). Topological data
analysis of collective and individual epithelial cells using persis-
tent homology of loops. Soft Matter, 17(17), 4653–4664. https://
doi.org/10.1039/D1SM00072A, PubMed: 33949592
Billings, J., Saggar, M., Hlinka, J., Keilholz, S., & Petri, G. (2021).
Simplicial and topological descriptions of human brain dynam-
ics. Network Neuroscience, 5(2), 549–568. https://doi.org/10
.1162/netn_a_00190, PubMed: 34189377
Network Neuroscience
250
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
a
_
0
0
2
8
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
Biswal, B. B. (2012). Resting state fMRI: A personal history. Neuro-
Image, 62(2), 938–944. https://doi.org/10.1016/j.neuroimage
.2012.01.090, PubMed: 22326802
Biswal, B. B., Kylen, J. V., & Hyde, J. S. (1997). Simultaneous assess-
ment of flow and BOLD signals in resting-state functional con-
nectivity maps. NMR in Biomedicine, 10(4–5), 165–170.
https://doi.org/10.1002/(SICI )1099-1492(199706/08)10:4
/5<165::AID-NBM454>3.0.CO;2-7, PubMed: 9430343
Cai, Y., Xie, M., Su, Y., Tong, Z., Wu, X., Xu, W., … Zheng, Oui. (2020).
Aberrant functional and causal connectivity in acute tinnitus with
sensorineural hearing loss. Frontiers in Neuroscience, 14, 592.
https://doi.org/10.3389/fnins.2020.00592, PubMed: 32714128
Carlsson, G. (2009). Topology and data. Bulletin of the American
Mathematical Society, 46(2), 255–308. https://doi.org/10.1090
/S0273-0979-09-01249-X
Carpio, UN., Bonilla, L. L., Mathews, J.. C., & Tannenbaum, UN. R..
(2019). Fingerprints of cancer by persistent homology. bioRxiv.
https://doi.org/10.1101/777169
Cassidy, B., Bowman, F. D., Rae, C., & Solo, V. (2018). On the reli-
ability of individual brain activity networks. IEEE Transactions on
Medical Imaging, 37(2), 649–662. https://doi.org/10.1109/TMI
.2017.2774364, PubMed: 29408792
Cha, S.-H. (2007). Comprehensive survey on distance/similarity
measures between probability density functions. International
Journal of Mathematical Models and Methods in Applied Sci-
ences, 1, 300–307.
Chaï, X. J., Berken, J.. UN., Barbeau, E. B., Soles, J., Callahan, M.,
Chen, J.-K., & Klein, D. (2016). Intrinsic functional connectivity
in the adult brain and success in second-language learning. Jour-
nal of Neuroscience, 36(3), 755–761. https://est ce que je.org/10.1523
/JNEUROSCI.2234-15.2016, PubMed: 26791206
Corbetta, M., Patel, G., & Shulman, G. L. (2008). The reorienting
system of the human brain: from environment to theory of mind.
Neurone, 58(3), 306–324. https://doi.org/10.1016/j.neuron.2008
.04.017, PubMed: 18466742
Damoiseaux, J.. S., Rombouts, S. UN. R.. B., Barkhof, F., Scheltens, P.,
Stam, C. J., Forgeron, S. M., & Beckmann, C. F. (2006). Consistent
resting-state networks across healthy subjects. Actes du
Académie nationale des sciences, 103(37), 13848–13853. https://
doi.org/10.1073/pnas.0601417103, PubMed: 16945915
Demertzi, UN., Gómez, F., Vieille femme, J.. S., Vanhaudenhuyse, UN.,
Tshibanda, L., Noirhomme, Q., … Soddu, UN. (2014). Multiple
fMRI system-level baseline connectivity is disrupted in patients
with consciousness alterations. Cortex, 52, 35–46. https://est ce que je
.org/10.1016/j.cortex.2013.11.005, PubMed: 24480455
Desikan, R.. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson,
B. C., Blacker, D., … Killiany, R.. J.. (2006). An automated labeling
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. NeuroImage, 31(3), 968–980.
https://doi.org/10.1016/j.neuroimage.2006.01.021, PubMed:
16530430
Ding, H., Ming, D., Wan, B., Li, Q., Qin, W., & Yu, C. (2016).
Enhanced spontaneous functional connectivity of the superior
temporal gyrus in early deafness. Rapports scientifiques, 6(1), 23239.
https://doi.org/10.1038/srep23239, PubMed: 26984611
Edelsbrunner, H., & Harer, J.. (2008). Persistent homology—A
survey. In Surveys on discrete and computational geometry
(Vol. 453). https://doi.org/10.1090/conm/453/08802
Edelsbrunner, H., & Harer, J.. (2010). Computational topology: Un
introduction. American Mathematical Society. https://est ce que je.org/10
.1090/mbk/069
Élise, C. T., Lesnick, M., Henselman-Petrusek, G., Keller, B., &
Cohen, J.. D. (2019). Feasibility of topological data analysis for
event-related fMRI. Neurosciences en réseau, 3(3), 695–706.
https://doi.org/10.1162/netn_a_00095, PubMed: 31410374
Falcone, J.-L., & Albuquerque, P.. (2004). A correlation-based
distance. arXiv:cs/0402061. https://doi.org/10.48550/arXiv.cs
/0402061
Ghrist, R.. (2008). Barcodes: The persistent topology of data. Bulle-
tin of the American Mathematical Society, 45, 61–75. https://est ce que je
.org/10.1090/S0273-0979-07-01191-3
Giusti, C., Ghrist, R., & Bassett, D. S. (2016). Two’s company, three
(ou plus) is a simplex: Algebraic-topological tools for under-
standing higher-order structure in neural data. arXiv:1601.01704.
https://doi.org/10.48550/arXiv.1601.01704
Giusti, C., Pastalkova, E., Curto, C., & Itskov, V. (2015). Clique
topology reveals intrinsic geometric structure in neural correla-
tion. Actes de l'Académie nationale des sciences,
11 2 ( 4 4 ) , 1 3 45 5 – 1 3 4 6 0 . h t t p s : / / d o i . o rg / 1 0 . 1 0 7 3 / p n a s
.1506407112, PubMed: 26487684
Hafkemeijer, UN., Möller, C., Dopper, E., Jiskoot, L., Schouten, T.,
van Swieten, J., … Rombouts, S. (2015). Resting state functional
connectivity differences between behavioral variant frontotem-
poral dementia and Alzheimer’s disease. Frontiers in Human
Neurosciences, 9, 474. https://doi.org/10.3389/fnhum.2015
.00474, PubMed: 26441584
Huang, L., Zheng, Y., Zeng, Z., Li, M., Zhang, L., & Gao, Oui. (2019).
Fractional amplitude of low-frequency fluctuations and func-
tional connectivity in comatose patients subjected to
resting-state functional magnetic resonance imaging. Annales de
Indian Academy of Neurology, 22(2), 203–209. https://doi.org
/10.4103/aian.AIAN_420_17, PubMed: 31007434
Hutchison, R.. M., Womelsdorf, T., Allen, E. UN., Bandettini, P.. UN.,
Calhoun, V. D., Corbetta, M., … Chang, C. (2013). Dynamic
functional connectivity: Promise, issues, and interpretations.
N e u ro I m a g e , 8 0 , 3 6 0 – 3 7 8 . h t t p s : / / d o i . o rg / 1 0 . 1 0 1 6 / j
.neuroimage.2013.05.079, PubMed: 23707587
Islambekov, U., & Gel, Oui. R.. (2019). Unsupervised space-time clus-
tering using persistent homology. Environmetrics, 30(4), e2539.
https://doi.org/10.1002/env.2539
Jang, J.. H., Kim, J.-H., Yun, J.-Y., Choi, S.-H., Un, S. C., & Kang,
D.-H. (2018). Differences in functional connectivity of the insula
between brain wave vibration in meditators and non-meditators.
Mindfulness, 9(6), 1857–1866. https://doi.org/10.1007/s12671
-018-0928-X, PubMed: 30524515
Kono, K. T., Takeuchi, T. T., Cooray, S., Nishizawa, UN. J., &
Murakami, K. (2020). A study on the baryon acoustic oscillation
with topological data analysis. arXiv:2006.02905. https://doi.org
/10.48550/arXiv.2006.02905
Kristensen, L. B., Wang, L., Petersson, K. M., & Hagoort, P.. (2012).
The interface between language and attention: Prosodic focus
marking recruits a general attention network in spoken language
comprehension. Cortex cérébral, 23(8), 1836–1848. https://est ce que je
.org/10.1093/cercor/bhs164, PubMed: 22763170
Liu, C., Pu, W., Wu, G., Zhao, J., & Xue, Z. (2019). Abnormal
resting-state cerebral-limbic functional connectivity in bipolar
Neurosciences en réseau
251
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
depression and unipolar depression. BMC Neuroscience, 20(1),
30. https://doi.org/10.1186/s12868-019-0508-6, PubMed:
31208340
Liu, J., Wang, Q., Liu, F., Song, H., Liang, X., Lin, Z., … Chen, L.-D.
(2017). Altered functional connectivity in patients with
post-stroke memory impairment: A resting fMRI study. Experi-
mental and Therapeutic Medicine, 14(3), 1919–1928. https://
doi.org/10.3892/etm.2017.4751, PubMed: 28962104
Liu, X., Chen, W., Tu, Y., Hou, H., Huang, X., Chen, X., … Chen, W.
(2018). The abnormal functional connectivity between the hypo-
thalamus and the temporal gyrus underlying depression in
Alzheimer’s disease patients. Frontiers in Aging Neuroscience,
10, 37. https://doi.org/10.3389/fnagi.2018.00037, PubMed:
29487521
Lord, L.-D., Expert, P., Fernandes, H. M., Petri, G., Van Hartevelt,
T. J., Vaccarino, F., … Kringelbach, M.. L. (2016). Insights into
brain architectures from the homological scaffolds of functional
connectivity networks. Frontiers in Systems Neuroscience, 10, 85.
https://doi.org/10.3389/fnsys.2016.00085, PubMed: 27877115
Mao, X.-G., Xue, X.-Y., Wang, L., Wang, L., Li, L., & Zhang, X.
(2019). Hypoxia regulated gene network in glioblastoma has spe-
cial algebraic topology structures and revealed communications
involving Warburg effect and immune regulation. Cellular and
Molecular Neurobiology, 39(8), 1093–1114. https://est ce que je.org/10
.1007/s10571-019-00704-5, PubMed: 31203532
Mazaika, P.. K., Hoeft, F., Glover, G. H., & Reiss, UN. L. (2009).
Methods and software for fMRI analysis of clinical subjects. Neu-
roImage, 47(Supplément. 1), S58. https://doi.org/10.1016/S1053-8119
(09)70238-1
Molnar, C. (2022). Interpretable machine learning (2nd ed.).
Retrieved from https://christophm.github.io/interpretable-ml
-livre.
Muñoz-López, M., Insausti, R., Mohedano-Moriano, UN., Mishkin,
M., & Saunders, R.. C. (2015). Anatomical pathways for auditory
memory II: Information from rostral superior temporal gyrus to
dorsolateral temporal pole and medial temporal cortex. Frontiers
in Neuroscience, 9, 158. https://doi.org/10.3389/fnins.2015
.00158, PubMed: 26041980
Olson, je. R., McCoy, D., Klobusicky, E., & Ross, L. UN. (2013). Social
cognition and the anterior temporal lobes: A review and theo-
retical framework. Social Cognitive and Affective Neuroscience,
8(2), 123–133. https://doi.org/10.1093/scan/nss119, PubMed:
23051902
Petri, G., Expert, P., Turkheimer, F., Carhart-Harris, R., Nutt, D.,
Hellyer, P.. J., & Vaccarino, F. (2014). Homological scaffolds of
brain functional networks. Journal of the Royal Society Interface,
11(101), 20140873. https://doi.org/10.1098/rsif.2014.0873,
PubMed: 25401177
Power, J.. D., Barnes, K. UN., Snyder, UN. Z., Schlaggar, B. L., & Petersen,
S. E. (2012). Spurious but systematic correlations in functional
connectivity MRI networks arise from subject motion. Neuro-
Image, 59(3), 2142–2154. https://doi.org/10.1016/j.neuroimage
.2011.10.018, PubMed: 22019881
Power, J.. D., Mitra, UN., Laumann, T. O., Snyder, UN. Z., Schlaggar,
B. L., & Petersen, S. E. (2014). Methods to detect, characterize,
and remove motion artifact in resting state fMRI. NeuroImage,
84, 320–341. https://doi.org/10.1016/j.neuroimage.2013.08
.048, PubMed: 23994314
Preti, M.. G., Bolton, T. UN. W, & Ville, D. V. D. (2017). The dynamic
functional connectome: State-of-the-art and perspectives. Neuro-
Image, 160, 41–54. https://doi.org/10.1016/j.neuroimage.2016
.12.061, PubMed: 28034766
Rubinov, M., & Sporns, Ô. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Saggar, M., Shine, J.. M., Liégeois, R., Dosenbach, N. U. F., & Fair, D.
(2021). Precision dynamical mapping using topological data
analysis reveals a unique hub-like transition state at rest. bioRxiv.
https://doi.org/10.1101/2021.08.05.455149
Saggar, M., Sporns, O., Gonzalez-Castillo, J., Bandettini, P.. UN.,
Carlsson, G., Glover, G., & Reiss, UN. L. (2018). Towards a new
approach to reveal dynamical organization of the brain using
topological data analysis. Communications naturelles, 9(1), 1399.
https://doi.org/10.1038/s41467-018-03664-4, PubMed:
29643350
Salch, UN., Regalski, UN., Abdallah, H., Suryadevara, R., Catanzaro,
M.. J., & Diwadkar, V. UN. (2021). From mathematics to medicine:
A practical primer on topological data analysis (TDA) et le
development of related analytic tools for the functional discovery
of latent structure in fMRI data. PLoS ONE, 16(8), e0255859.
https://doi.org/10.1371/journal.pone.0255859, PubMed:
34383838
Singh, G., Memoli, F., & Carlsson, G. (2007). Topological methods
for the analysis of high dimensional data sets and 3D object rec-
ognition. En M. Botsch, R.. Pajarola, B. Chen, & M.. Zwicker (Éd.),
Eurographics symposium on point-based graphics. Eurographics
Association. https://doi.org/10.2312/SPBG/SPBG07/091-100
Song, L., Ge, Y., Long, J., & Dong, P.. (2020). Altered intrinsic and
casual functional connectivities of the middle temporal visual
motion area subregions in chess experts. Frontiers in Neurosci-
ence, 14, 605986. https://doi.org/10.3389/fnins.2020.605986,
PubMed: 33335474
Sporns, Ô. (2013). Structure and function of complex brain networks.
Dialogues in Clinical Neuroscience, 15(3), 247–262. https://doi.org
/10.31887/DCNS.2013.15.3/osporns, PubMed: 24174898
Tralie, C., Saul, N., & Bar-On, R.. (2018). Ripser.py: A lean persistent
homology library for Python. Journal of Open Source Software,
3(29), 925. https://doi.org/10.21105/joss.00925
Turken, UN. U., & Dronkers, N. F. (2011). The neural architecture of
the language comprehension network: Converging evidence
from lesion and connectivity analyses. Frontiers in Systems Neu-
roscience, 5, 1. https://doi.org/10.3389/fnsys.2011.00001,
PubMed: 21347218
van den Heuvel, M.. P., & Sporns, Ô. (2019). A cross-disorder con-
nectome landscape of brain dysconnectivity. Nature Reviews
Neurosciences, 20(7), 435–446. https://doi.org/10.1038/s41583
-019-0177-6, PubMed: 31127193
Wang, R., Lin, P., Liu, M., Wu, Y., Zhou, T., & Zhou, C. (2019). Hier-
archical connectome modes and critical state jointly maximize
human brain functional diversity. Physical Review Letters, 123(3),
038301. https://doi.org/10.1103/ PhysRevLett.123.038301,
PubMed: 31386449
Wig, G. S. (2017). Segregated systems of human brain networks.
Tendances des sciences cognitives, 21(12), 981–996. https://doi.org
/10.1016/j.tics.2017.09.006, PubMed: 29100737
Neurosciences en réseau
252
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
H
1 persistent features of the resting-state connectome in healthy subjects
Xiong, H., Guo, R.-J., & Shi, H.-W. (2020). Altered default mode
network and salience network functional connectivity in patients
with generalized anxiety disorders: An ICA-based resting-state
fMRI study. Evidence-Based Complementary and Alternative
Medicine, 2020, 4048916. https://doi.org/10.1155/2020
/4048916, PubMed: 32855650
Xu, Y., Shi, Y., Yao, J., Lequel, H., Ding, Z., Chen, Q. Q., … Chen, W.
(2019). Altered brain functional connectivity and correlation
with psychological status in patients with unilateral pulsatile tin-
nitus. Neuroscience Letters, 705, 235–245. https://est ce que je.org/10
.1016/j.neulet.2019.04.046, PubMed: 31042571
Zalesky, UN., Fornito, UN., Cocchi, L., Gollo, L. L., & Breakspear, M..
(2014). Time-resolved resting-state brain networks. Procédure
of the National Academy of Sciences, 111(28), 10341–10346.
https://doi.org/10.1073/pnas.1400181111, PubMed: 24982140
Zhang, H., Zhao, Y., Cao, W., Cui, D., Jiao, Q., Lu, W., … Qiu, J..
(2020). Aberrant functional connectivity in resting state networks
of ADHD patients revealed by independent component analysis.
BMC Neuroscience, 21(1), 39. https://doi.org/10.1186/s12868
-020-00589-X, PubMed: 32948139
Zhang, J.-T., Yao, Y.-W., Li, C.-S. R., Zang, Y.-F., Shen, Z.-J., Liu, L.,
… Fang, X.-Y. (2016). Altered resting-state functional connectivity
of the insula in young adults with internet gaming disorder.
Addiction Biology, 21(3), 743–751. https://doi.org/10.1111/adb
.12247, PubMed: 25899520
Zhu, F., Tang, L., Zhu, P., Lin, Q., Yuan, Q., Shi, W., … Shao, Oui.
(2019). Resting-state functional magnetic resonance imaging
(IRMf) and functional connectivity density mapping in patients
with corneal ulcer. Neuropsychiatric Disease and Treatment,
15, 1833–1844. https://doi.org/10.2147/ NDT.S210658,
PubMed: 31308676
Zomorodian, UN., & Carlsson, G. (2005). Computing persistent
homology. Discrete and Computational Geometry, 33(2),
249–274. https://doi.org/10.1007/s00454-004-1146-y
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
2
3
4
2
0
7
1
9
7
5
n
e
n
_
un
_
0
0
2
8
0
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Neurosciences en réseau
253