RECHERCHE
Graph theoretical approach to brain
remodeling in multiple sclerosis
AmirHussein Abdolalizadeh1,2
, Mohammad Amin Dabbagh Ohadi1,2,
Amir Sasan Bayani Ershadi1,2, and Mohammad Hadi Aarabi3
1Students’ Scientific Research Program, Tehran University of Medical Sciences, Tehran, Iran
2Interdisciplinary Neuroscience Research Program, Tehran University of Medical Sciences, Tehran, Iran
3Department of Neuroscience, Padova Neuroscience Center, University of Padova, Padova, Italy
Mots clés: Multiple sclerosis, Remodeling, Diffusion MRI, Cognition, Graph theory
un accès ouvert
journal
ABSTRAIT
Multiple sclerosis (MS) is a neuroinflammatory disorder damaging structural connectivity.
Natural remodeling processes of the nervous system can, to some extent, restore the damage
caused. Cependant, there is a lack of biomarkers to evaluate remodeling in MS. Our objective is
to evaluate graph theory metrics (especially modularity) as a biomarker of remodeling and
cognition in MS. We recruited 60 relapsing-remitting MS and 26 healthy controls. Structural
and diffusion MRI, plus cognitive and disability evaluations, were done. We calculated
modularity and global efficiency from the tractography-derived connectivity matrices.
Association of graph metrics with T2 lesion load, cognition, and disability was evaluated using
general linear models adjusting for age, genre, and disease duration wherever applicable. Nous
showed that MS subjects had higher modularity and lower global efficiency compared with
controls. In the MS group, modularity was inversely associated with cognitive performance
but positively associated with T2 lesion load. Our results indicate that modularity increase
is due to the disruption of intermodular connections in MS because of the lesions, with no
improvement or preserving of cognitive functions.
RÉSUMÉ DE L'AUTEUR
Network remodeling is an inherent property of the nervous system, diminishing the harm caused
by lesions in multiple sclerosis (MS). Modularity has been proposed previously as a measure of
network remodeling in several disorders. Dans cette étude, we studied modularity of structural
networks in MS, and its associations with clinical and cognitive measures. We showed increased
modularity in the patients that is associated with higher T2 lesion load and poor cognitive
fonction; the latter became nonsignificant after covarying the lesion load. Our results indicate
that modularity increase is due to the disruption of intermodular connections in MS because of
the lesions, rather than a remodeling procedure resulting in a cognitive improvement.
INTRODUCTION
Multiple sclerosis (MS) is a neuroinflammatory disease that causes demyelination in the central
nervous system, seen as white and gray matte plaques (Frohman, Racke, & Raine, 2006).
Although much has been done to comprehend its etiology, there are still some undisclosed
Citation: Abdolalizadeh, UN., Ohadi, M..
UN. D., Ershadi, UN. S. B., & Aarabi, M.. H.
(2023). Graph theoretical approach to
brain remodeling in multiple sclerosis.
Neurosciences en réseau, 7(1), 148–159.
https://doi.org/10.1162/netn_a_00276
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00276
Reçu: 30 May 2021
Accepté: 5 Septembre 2022
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
AmirHussein Abdolalizadeh
amirhussein.a@gmail.com
Éditeur de manipulation:
Alex Fornito
droits d'auteur: © 2022
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
un
_
0
0
2
7
6
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory in MS brain remodeling
Multiple sclerosis (MS):
An autoimmune disorder of the
central nervous system causing
moteur, sensoriel, and cognitive
symptoms.
Demyelination:
Destruction of the myelin sheaths
that surround the axons or dendrites,
resulting in impaired neural impulse
conduction.
Relapsing-remitting multiple sclerosis
(RRMS):
The most common form of MS; it is
marked by periods of remission
divided by attacks (c'est à dire., relapse) de
the disease.
Primary progressive multiple
sclerosis (PPMS):
A form of MS in which the patient’s
status deteriorates from the first
attack, causing severe disability
within a few years.
Secondary progressive multiple
sclerosis (SPMS):
RRMS patients fail to remit to a nearly
healthy status after several years of
attacks, showing severe disability.
areas requiring more attention. It seems that axonal loss in both forms of demyelination or
degeneration disrupts information relay between gray matter areas, causing cognitive and
functional impairments (Rocca et al., 2016).
Various studies indicate that the damaged brain tries to restore its normal functions by neuronal
plasticity and axonal remodeling. Human MRI studies have demonstrated rewiring and activations
in cortical segments of MS patients in both aspects of structural and functional forms, either
because of intrinsic mechanisms or induced by rehabilitation (Prosperini & Di Filippo, 2019).
The expanding field of graph theoretical analysis helps neuroscientists better comprehend
brain networks in health and disease. A graph consists of different nodes that are connected
via pathways (c'est à dire., edges). One of the methods to define a brain graph is to use cortical par-
cellations and subcortical regions as node definition and the wirings connecting these areas as
the edges. Diffusion-weighted imaging (DWI) is a technique that can be used to identify the
wirings (c'est à dire., tracts) and their strength. Several metrics are derived from the resulting graph,
which can be interpreted biologically (Rubinov & Sporns, 2010). Global efficiency is one of
the integration measures that can determine the information flow efficiency of the whole brain.
Along with that are other local segregation measurements, including modularity. Modules are
a group of network nodes with stronger connections within the group and weaker connections
between modules. This parameter can evaluate the optimization of the brain in varying envi-
ronments (Girvan & Newman, 2002).
Various graph theory metrics have been applied in studies with MS patients. In a recent
comprehensive review by Fleischer, Radetz, et autres. (2019), both increase and decrease in global
efficiency in structural and functional connectivity matrices of MS patients, and the presence
or absence of association of such metrics with clinical status were reported. It seems that this
heterogeneity in results arises from different analytic pipelines, confounding factors such as
disease duration, and heterogeneity in the studied samples (including relapsing-remitting
and primary or secondary progressive MS [RRMS, PPMS, and SPMS, respectivement]). For exam-
ple, in another study, lower global efficiency was reported in the MS group (including RRMS,
PPMS, and SPMS) compared with healthy controls; cependant, there were no differences
between RRMS and healthy controls (Charalambous et al., 2019). Fait intéressant, there is much
less debate in the studies investigating modularity in MS. Increased modularity is a common
finding in MS and is believed to represent the underlying network reorganization in response
to lesions (Fleischer, Koirala, et coll., 2019; Gonzalez-Escamilla et al., 2020); cependant, a few
studies have investigated the clinical importance of it. In Fleischer et al. (2017), modularity
was increased during the first year of RRMS diagnosis, without any change in clinical status,
implying the probable protective role of network reorganization.
Our objective was to investigate the association between graph-derived metrics and
cognitive/disability severity in RRMS patients, with a focus on the network remodeling assess-
ment following lesions. To overcome the limitations of previous studies, we included a larger
homogenous RRMS sample, to avoid the variability due to other phenotypes, and various clin-
ical and cognitive measures. We hypothesize that modularity increase may underlie compen-
sation of disease severity.
MÉTHODES
Participants
We recruited our subjects from the Cross-Modal Research Initiative for Multiple Sclerosis and
Optic Neuritis (CRIMSON) étude. This study was conducted at MS Research Center, Sina
Neurosciences en réseau
149
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
un
_
0
0
2
7
6
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory in MS brain remodeling
Corticosteroid:
A drug group that reduces the tissue
damage caused by the immune
système. They are used in multiple
sclerosis attacks.
Hospital, Tehran, Iran, which included RRMS and healthy controls (HC). More information
regarding the inclusion and exclusion criteria and ethical approval of the study are reported
elsewhere (Roostaei et al., 2019). In brief, the subjects had no prior history of head trauma and
no psychiatric or neurologic disorders other than MS. All subjects had Expanded Disability
Status Scale (EDSS) scores less than 6, and they had no history of relapse or corticosteroid
therapy in the past three months. Before inclusion, all subjects signed informed consent,
and this study was confirmed by the Ethical Review Board of Tehran University of Medical
les sciences, Tehran, Iran.
Evaluations
Cognitive scores. All evaluations were done by expert researchers and neurologists in the
CRIMSON study. Three cognitive tests were done: the Symbol Digit Modalities Test (SDMT;
Brochet et al., 2008), California Verbal Learning Test (CVLT; Stegen et al., 2010), and Paced
Auditory Serial Addition Test (PASAT; Rosti, Hämäläinen, Koivisto, & Hokkanen, 2007). These
tests are widely used to evaluate cognitive function in MS patients. The procedure, evaluated
cognitive functions, and evaluations included in the current study are explained in Table 1.
Clinical and disability scores. We used the EDSS, MS Functional Composite (MSFC), and MS
Severity Score (MSSS) as surrogates of disease severity and disability in our subjects. EDSS
is scored by an expert MS clinician and is based on clinical examination and patient-reported
dysfunctions in daily routines. It is widely used in clinical trials and routine patient evaluations
(Kurtzke, 1983). MSFC is the mean of Z-score transformed scores of patients in three tests:
timed 25-foot walk, 9-hole peg test, and PASAT (Fischer, Rudick, Cutter, & Reingold, 1999).
Both MSFC and EDSS are cross-sectional evaluations that cannot address the speed of disabil-
ity progression during disease duration. MSSS addresses this issue by correcting EDSS to dis-
ease duration based on an algorithm (Roxburgh et al., 2005).
Imaging Acquisition
Using a Siemens Avanto 1.5T scanner, the following sequences were acquired: a magnetiza-
tion prepared rapid-acquisition gradient-echo (MPRAGE) T1 sequence (repetition time [TR] =
2,730 ms, echo time [TE] = 2.81 ms, inversion time [TI] = 1,000 ms, field of view [FoV] =
Tableau 1.
Cognitive tests used in this study: The procedure, measures, and evaluated cognitive functions
Test
Symbol Digit
Modalities
Test (SDMT)
California Verbal
Learning Test
(CVLT)
Procedure
A symbol is assigned to each number 1 à 9
and is presented to the subject. Alors, le
subject is asked to pair a list of symbols
to the numbers in 90 s.
A list of 16 nouns (list A) is read by the
examiner to the subject and is recalled
immediately, with a delay, cued or free,
and with an interference (another list of
16 nouns; list B).
Paced Auditory
Serial Addition
Test (PASAT)
A list of numbers is read by the computer,
and the subject must add the last two
numbers read.
Evaluations
Number of correct answers
Cognitive function
Processing speed;
attention
CVLT-TL (Total Learning): Total
correct answers of five trials
of the immediate recall
CVLT-LD (Long Delay):
Number of words recalled
from list A after 20 min
Number of correct answers
Declarative memory
Working memory;
executive function
Neurosciences en réseau
150
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
un
_
0
0
2
7
6
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory in MS brain remodeling
256 mm, voxel size = 1 × 1 × 1 mm); a T2-weighted turbo spin echo with variable flip angle
(TSE-VFL; TR = 3,200 ms, LE = 473 ms, FoV = 256 mm, voxel size = 1 × 1 × 1 mm); a fluid-
attenuated inversion recovery (FLAIR) séquence (TR = 9,400 ms, LE = 83 ms, TI = 2,500 ms,
FoV = 250 mm, voxel size = 1.3 × 1.0 × 3.0 mm); and a DWI sequence (TR = 9,500 ms, LE =
93 ms, voxel size = 2 × 2 × 2.1 mm, b-value = 1,000 s/mm2, dans 64 diffusion directions) avec
three b0 volumes.
Imaging Analysis
Lesion filling and lesion load. We used lesion-filled T1 volumes and individual T2 hyperintense
lesion load provided by the main investigators of the CRIMSON study. In brief, T2 hyper-
intense lesions were manually segmented, and individual lesion load was calculated. T2-to-T1
registration warp was then applied to the lesion mask to bring them into T1 space. Alors,
lesions were filled using the nearby normal-appearing white matter (Roostaei et al., 2019).
In order to preprocess and quality-check the diffusion data, the PreQual
DWI preprocessing.
pipeline was built using the MRtrix3 (Tournier et al., 2019), FSL (Jenkinson, Beckmann,
Behrens, Woolrich, & Forgeron, 2012), and advanced normalization tools (ANTs; Tustison
et coll., 2014) software packages. D'abord, diffusion MR images were denoised using the MP-
PCA function included with MRtrix3 (Cordero-Grande, Christiaens, Hutter, Prix, & Hajnal,
2019; Veraart, Fieremans, & Novikov, 2016; Veraart, Novikov, et coll., 2016). Gibbs ringing arti-
fact reduction was attained by the local subvoxel-shifts method (Kellner, Dhital, Kiselev, &
Reisert, 2016). Rician correction was performed with the moments method (Koay & Basser,
2006). The images were then intensity-normalized to the first image and concatenated for
further processing. No reverse phase-encoded images were acquired, but corresponding
lesion-filled T1 images of the subjects were available. Ainsi, a T1 image was used to generate
a synthetic susceptibility-corrected b0 volume using SYNB0-DISCO, a deep learning frame-
work by Schilling et al. (2019). This synthetic b0 image was used in conjunction with FSL’s
topup to correct for susceptibility-induced artifacts in the diffusion data. FSL’s eddy algorithm
was then used to correct for motion artifacts and eddy currents and to remove outlier slices
(Andersson, Graham, Zsoldos, & Sotiropoulos, 2016; Andersson, Skare, & Ashburner, 2003;
Andersson & Sotiropoulos, 2016; S. M.. Smith et al., 2004). N4 bias field correction was then
performed (Tustison et al., 2010). Dernièrement, the preprocessed data were fitted with a tensor model
using the dwi2tensor function included with MRtrix3 using an iterative reweighted least
squares estimator (Veraart, Sijbers, Sunaert, Leemans, & Jeurissen, 2013). This preprocessing
pipeline’s quality was assessed qualitatively for gross errors and analyzed quantitatively using
a three-step approach. In the first step, the preprocessed data were analyzed in accordance
with the method outlined by Lauzon et al. (2013). The brain parenchyma without cerebrospi-
nal fluid was masked in a restrictive manner by using an eroded brain mask generated on the
average b0 image using the bet2 function included with FSL (S. M.. Forgeron, 2002). Alors, le
tensor fits of the masked data were backpropagated through the diffusion model to reconstruct
the original diffusion signal. The goodness of fit for the tensor model was then assessed using a
modified pixel chi-squared value per slice per volume. In the second step, the tensor fit was
converted to a fractional anisotropy (FA) image (Basser, Mattiello, & LeBihan, 1994). The ICBM
FA MNI atlas with 48 white matter tract labels provided with FSL was then non-rigidly regis-
tered to each subject’s FA image with the ANTs software package (Avants, Epstein, Grossman,
& Gee, 2008; Hua et al., 2008; Mori, Wakana, Van Zijl, & Nagae-Poetscher, 2005; Wakana
et coll., 2007). The average FA of each tract was quantified and assessed for physiologic con-
gruence. Dernièrement, the gradient orientations were visualized and checked using the dwigradcheck
script included with MRtrix (Jeurissen, Leemans, & Sijbers, 2014).
Neurosciences en réseau
151
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
un
_
0
0
2
7
6
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory in MS brain remodeling
DWI tractography. The T1 image is corrected for intensity nonuniformity (Tustison et al., 2010)
and skull-stripped, subcortical structures are segmented with FSL FIRST (Patenaude, Forgeron,
Kennedy, & Jenkinson, 2011), and tissue types (gray matter, white matter, and cerebrospinal
fluid) are labeled with FSL FAST (Zhang, Brady, & Forgeron, 2001). For anatomically constrained
tractography, a nonlinear registration to MNI152 is computed (Tustison & Avants, 2013) and a
five-tissue-type (5TT) image segmentation is derived. Cortical surface segmentations are
derived from lesion-filled T1-weighted scans using FreeSurfer 6.0 (Fischl, 2012). The next step
is to calculate an affine registration from native FreeSurfer space to T1 space. Nous avons utilisé
Desikan-Killiany parcellations provided by FreeSurfer (Desikan et al., 2006). Alors, subcortical
and cerebellar parcellations are nonlinearly registered to native DWI space (Tournier et al.,
2019).
Structural connectomes are generated using MRtrix3. The iFOD2 algorithm and a three-
tissue anatomically constrained tractography are used to create a tractography with 40 million
streamlines (R.. E. Forgeron, Tournier, Calamante, & Connelly, 2012; maximum/minimum tract
length = 400/10 mm, FOD amplitude cutoff = 0.06, step size = 0.5). The resulting tractogra-
phy’s second tract density image (TDI) is calculated for quality control. Alors, full brain stream-
lines weighted by cross-sectional multipliers are rebuilt using spherical deconvolution guided
filtering of tractograms (SIFT2; R.. E. Forgeron, Tournier, Calamante, & Connelly, 2015). Alors, un
parcellation scheme is mapped to the reconstructed cross section weighted streamlines. Addi-
tionally, these are warped to DWI native space. Edge length matrices are also constructed, et
the connection weights between nodes are defined as the weighted streamline count. All pro-
cessing steps were done by the Micapipe pipeline (Cruces et al., 2022; https://micapipe
.readthedocs.io/en/latest/).
Connectivity Matrix
The connectivity matrix was obtained for each participant by dividing the streamline count by
edge lengths, resulting in streamline density. Labels were based on Desikan-Killiany cortical
parcellation plus subcortical structures and cerebellum, which generated 120 × 120 weighted
connectivity matrices. We used Brain Connectivity Toolbox to calculate modularity (Louvain’s
algorithme) and global efficiency for each individual (Rubinov & Sporns, 2010). More informa-
tion regarding the graph metrics, their mathematical formula, and their possible interpretation
in neurological studies can be found in numerous studies such as Rubinov and Sporns (2010).
We used an iterative approach for modularity calculation. The iterations continued until the
difference between the two calculations is less than the tolerance, which is chosen as 0.00001.
Statistical Analysis
We used R statistical package v 4.0.4 (https://www.R-project.org/; R Core Team, 2019) for the
statistical analysis of our data. D'abord, subject demographics were analyzed using the Shapiro-
Wilk statistical test to evaluate the normality of the data. Based on its results, a t test or Mann-
Whitney U test was done to compare group (HC vs. MS) differences in demographics. Nous avons utilisé
analysis of covariance (ANCOVA) to compare group differences in graph metrics. Age and
gender were inserted as covariates. To evaluate the time-dependent changes in graph metrics,
we used Pearson’s or Spearman’s correlation tests based on the normal distribution of our data.
Alors, we confined our analysis to the MS group to analyze possible associations of graph
metrics and markers of disease severity and cognitive tests. A general linear model was used
with age and gender as covariates, with cognitive tests (SDMT, PASAT, CVLT-LD, CVLT-TL) ou
markers of disease severity (MSFC, EDSS, MSSS) included in the model as dependent variables
and graph metrics (modularity and global efficiency) included as the predictor variable. À
Neurosciences en réseau
152
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
un
_
0
0
2
7
6
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory in MS brain remodeling
evaluate the association between T2 lesion load and graph metrics, we calculated normalized
lesion load as total lesion volume divided by whole-brain volume for each individual. Le
normalized lesion load was then inserted into a general linear model with age and gender
as covariates, and graph metrics as dependent variables. We used the Benjamini-Hochberg
method to correct multiple-comparison correction in each category of tests (c'est à dire., cognitive bat-
teries and disease severity). Corrected p values less than 0.05 were considered significant.
RÉSULTATS
Demographics
A total of 60 RRMS patients and 26 HC subjects were included in this study. Age did not follow
a normal distribution (Shapiro-Wilk test p value for age in both groups < 0.001), so the Mann-
Whitney U test was done. There were no significant differences of sex (p = 0.98) and age (p =
0.75) between the two groups. Subject demographics and values of cognitive and clinical
evaluations are presented in Table 2.
Between-Group Differences
Compared with HCs, RRMS subjects had higher modularity (mean (SD); for MS = 0.70 (0.01),
for HC = 0.69 (0.01); p < 0.001) and lower global efficiency (mean (SD) × 1,000; for MS =
0.53 (0.03), for HC = 0.55 (0.04); p = 0.002).
Between-group differences in demographics and cognitive and clinical evaluations. MSFC
Table 2.
is calculated among 55 subjects who have their 9-hole peg test, 25-foot walk, and PASAT completed.
HC = Healthy control. EDSS = Expanded Disability Status Scale. MSFC = Multiple Sclerosis
Functional Composite. MSSS = Multiple Sclerosis Severity Score. SDMT = Symbol Digit Modalities
Test. PASAT = Paced Auditory Serial Addition Test. CVLT = California Verbal Learning Test. CVLT-LD =
CVLT–Long Delay. CVLT-TL = CVLT–Total Learning.
HC n = 26
MS n = 60
p value
Demographics
Gender (male (%))
4 (15.38)
11 (18.33)
Age (mean (SD))
30.65 (7.82)
30.75 (7.07)
0.98
0.75
Clinical evaluations (mean (SD))
EDSS
MSFC
MSSS
–
–
–
Cognitive evaluations (correct responses; mean (SD))
SDMT
PASAT
CVLT-LD
CVLT-TL
–
–
–
–
2.76 (1.34)
0.00 (1.59)
4.37 (2.05)
48.06 (15.94)
43.28 (10.98)
11.53 (2.90)
53.28 (8.21)
Network Neuroscience
153
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
a
_
0
0
2
7
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory in MS brain remodeling
Estimate (std. error) and p values of general linear models applied to identify significant
Table 3.
associations between graph metrics (global efficiency and modularity), and clinical or cognitive
evaluations of multiple sclerosis subjects, with age and gender as covariates. The p values are all
corrected using Benjamini-Hochberg’s method. EDSS = Expanded Disability Status Scale. MSFC =
Multiple Sclerosis Functional Composite. MSSS = Multiple Sclerosis Severity Score. SDMT =
Symbol Digit Modalities Test. PASAT = Paced Auditory Serial Addition Test. CVLT = California
Verbal Learning Test. CVLT-LD = CVLT–Long Delay. CVLT-TL = CVLT–Total Learning.
Global efficiency
Modularity
Estimate (std. error)
p value
Estimate (std. error)
p value
Clinical evaluations
EDSS
MSFC
MSSS
−3,017.185 (5,749.439)
2,951.321 (2,551.787)
92.591 (8,796.878)
T2 lesion load
−19.153 (30.554)
Cognitive evaluations
SDMT
PASAT
61,450.748 (67,305.672)
69,843.475 (49,542.373)
CVLT-LD
3,364.148 (13,358.354)
CVLT-TL
52,578.776 (35,848.396)
* p < 0.05, *** p < 0.001.
Graph Metrics and Disease Severity
0.80
0.67
0.99
0.80
0.41
0.25
0.80
0.25
21.756 (11.828)
−3.395 (5.129)
3.702 (18.592)
0.29
0.80
0.96
0.262 (0.049)
<0.001***
−384.624 (133.871)
0.04*
−167.882 (103.082)
−35.425 (26.507)
−109.18 (72.304)
0.25
0.25
0.25
There were no significant associations between graph metrics and markers of clinical disease
severity, except a negative association between modularity and normalized T2 lesion load. On
the other hand, in the cognitive evaluations and after adjusting for multiple comparisons, mod-
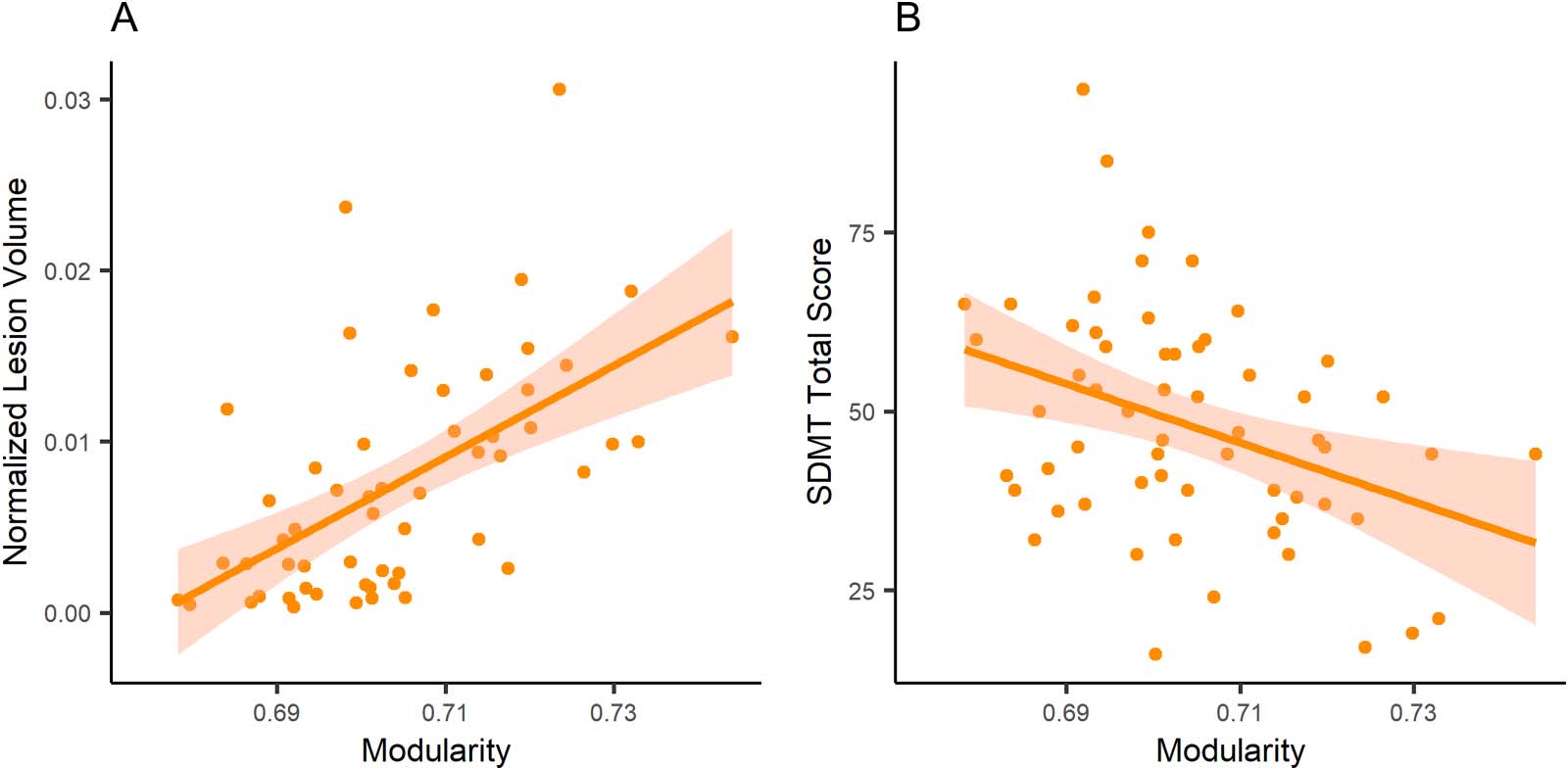
ularity was significantly associated with SDMT (Table 3; Figure 1). Interestingly, there were no
Figure 1. Linear models applied to an association of modularity with (A) normalized lesion volume and (B) correct answers in SDMT (Symbol
Digit Modalities Test).
Network Neuroscience
154
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
a
_
0
0
2
7
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory in MS brain remodeling
significant associations between global efficiency and clinical/cognitive evaluations. We also
added normalized lesion volume as a covariate for associations of cognitive evaluations; there
were no significant findings.
Also, neither global efficiency nor modularity was significantly correlated with disease
duration (Pearson’s r = 0.22 and −0.09; p = 0.08 and 0.48, respectively).
DISCUSSION
We investigated modularity and global efficiency within patients with RRMS and HC subjects,
showing higher modularity and lower global efficiency in patients with RRMS. We also dem-
onstrated that higher modularity is associated with higher T2 lesion load and lower SDMT total
scores. The association between modularity and SDMT disappeared after taking lesion load as
a covariate in the statistical model. Our results indicate that modularity increase is due to the
disruption of intermodular connections in MS because of the lesions, and have not resulted in
preservation or improvement in cognitive functions.
Multiple sclerosis is considered a neuroinflammatory disease, and most of the current
therapies target immune processes. While these treatments reduce disease progression, they
cannot fully return the brain to the former undamaged state (Stampanoni Bassi et al., 2017).
Recently, therapies such as remyelinating agents (Plemel, Liu, & Yong, 2017) have been pro-
posed to try to regain function. These therapies can also be influenced by factors that affect
neuroplasticity, such as immune responses (Golia et al., 2019) and even hormones (such as
thyroid hormones; Remaud, Gothié, Morvan-Dubois, & Demeneix, 2014). Thus, developing
novel biomarkers for plasticity can be of great importance in evaluating regain-of-function
therapies. Modularity is proposed as a promising tool and has shown promising results in brain
injury (Han, Chapman, & Krawczyk, 2020).
Network changes in RRMS have been reported in previous studies conducted using both
structural and functional connectivity measures (Fleischer, Radetz, et al., 2019). Decreased
global efficiency using connectivity matrices derived from fMRI is a common finding in RRMS
and is also associated with disease severity (Rocca et al., 2016; Tommasin et al., 2020). Usu-
ally, in fMRI studies, the Pearson correlation coefficient of time series between each pair of
regions is used as a measure of connectivity between two regions. However, studies based
on DWI-derived connectivity matrices have shown different results. While some studies
reported a decrease in global efficiency in RRMS (Charalambous et al., 2019; Shu et al.,
2011), others have shown no differences between HC and RRMS (Fleischer et al., 2017;
Muthuraman et al., 2016). Our results support the former studies. Interestingly, both global
efficiency and modularity were not correlated with disease duration in our RRMS group, prob-
ably showing no time-dependent changes in these metrics in RRMS.
According to the hierarchical Newman’s equation of modularity or the optimization-based
Louvain’s algorithm, increased modularity can be achieved either by increasing intramodular
connections (i.e., reorganization) or through loss of intermodular connections (i.e., damage
caused by lesions; Blondel, Guillaume, Lambiotte, & Lefebvre, 2008; Newman & Girvan,
2004). In other words, in the former, the brain generates new connections and modules to
regain its function. In the latter, lesions damaging local and global connections result in more
collection of locally connected nodes (i.e., modules). Modularity increase due to remodeling
has been shown in traumatic brain injury (Han et al., 2020), as a developmental process (Chen
& Deem, 2015), and as a marker of improvement in the narrative production of aphasic
patients (Duncan & Small, 2016). However, in another study, higher modularity in the left
Network Neuroscience
155
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
a
_
0
0
2
7
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory in MS brain remodeling
hemisphere in post-stroke patients was associated with poor clinical outcomes (Marebwa
et al., 2017), probably reflecting the lesions damaging the intermodular (rather than intramod-
ular) connections, causing increased modularity. Increased modularity in MS patients
compared with HC has been reported previously. Fleischer et al. (2017) showed that RRMS
subjects had higher modularity than HC, at baseline, and in the follow-up. This increase in
modularity was not associated with disease severity using EDSS. Modularity based on gray
matter covariance matrices was also associated with T2 lesion load and disease duration; how-
ever, no results were reported for such correlation using DWI-based networks (Fleischer et al.,
2017). In another study, modularity was lower in clinically isolated syndrome (CIS), but higher
in RRMS patients compared with HC (Kocevar et al., 2016). In a similar study, Muthuraman
et al. (2016) showed increased modularity in RRMS compared with CIS, and both compared
with HC. A recent study using higher order DWI models also revealed this increase in mod-
ularity. They also reported a negative association between modularity and SDMT (Tur et al.,
2019). In a relevant study using fMRI, higher modularity was evident in early MS patients, but
similar to our findings, it was inversely correlated with a cognitive function (Gamboa et al.,
2014). We report this negative association between modularity and cognitive function of pro-
cessing speed and attention based on SDMT. Of great importance, this association became
nonsignificant after adjusting for T2 lesion load. This indicates that reduced SDMT perfor-
mance can be the result of widespread lesions across the brain. Based on this finding and also
the negative association of modularity with T2 lesion load in our sample, we postulate that
increased modularity based on tractography-based networks reflects the preferable disruption
of intermodular connections in RRMS, which leaves an isolated collection of nodes (i.e., gen-
erating modules) or a failed remodeling, rather than a successful remodeling procedure.
Despite implementing novel graph theoretical approaches to investigate remodeling in MS,
our study is faced with limitations. Our study has a cross-sectional research design that lacks
the power of longitudinal studies to better address the main question of the current study. Trac-
tography in MS has always been problematic because of the random presence of lesions, caus-
ing a sudden stop in tractography or even spurious tracts. Any algorithm applied has its caveats
and benefits, and currently, there is no gold standard algorithm developed for such situations
(Lipp et al., 2020). To overcome this issue, we used the PreQual pipeline, which uses several
applications to improve volumetric segmentation, cortical parcellation, tractography, and con-
nectivity matrix generation. It also has several quality-control checkpoints to ensure the min-
imizing of analytic pitfalls. Adding another imaging method, such as fMRI, and comparing the
graph metrics derived from the fMRI-based with DWI-based networks may add some more
perspective to our findings. Also, since we did not have cognitive evaluations done on the
HC, we do not know for sure whether the observed association between cognitive measures
and modularity is limited to MS or whether it is also applicable to HC. Future studies adding
cognitive measures in HC and applying group × cognition interaction analysis may address
this problem.
In conclusion, our study showed that increased modularity is the result of disrupted inter-
modular connection due to lesions and has not resulted in regaining cognitive function. Future
longitudinal studies using both structural and functional imaging are suggested.
ACKNOWLEDGMENTS
We gratefully thank Dr. Parvin Pasalar, the former director of the Students’ Scientific Research
Center of Tehran University of Medical Sciences, Tehran, Iran, for her role in supporting and
mentoring authors (Namely A. H. A. and A. O.).
Network Neuroscience
156
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
a
_
0
0
2
7
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory in MS brain remodeling
AUTHOR CONTRIBUTIONS
AmirHussein Abdolalizadeh: Conceptualization; Formal analysis; Investigation; Methodology;
Project administration; Writing – original draft; Writing – review & editing. Mohammad Amin
Dabbagh Ohadi: Formal analysis; Writing – original draft. Amir Sasan Bayani Ershadi: Writing –
original draft. Mohammad Hadi Aarabi: Formal analysis; Methodology; Writing – original draft.
FUNDING INFORMATION
Mohammad Hadi Aarabi, euSNN European School of Network Neuroscience, Award ID:
MSCA-ITN-ETN H2020-860563.
REFERENCES
Andersson, J. L. R., Graham, M. S., Zsoldos, E., & Sotiropoulos, S. N.
(2016). Incorporating outlier detection and replacement into a
non-parametric framework for movement and distortion correc-
tion of diffusion MR images. NeuroImage, 141, 556–572. https://
doi.org/10.1016/j.neuroimage.2016.06.058, PubMed:
27393418
Andersson, J. L. R., Skare, S., & Ashburner, J. (2003). How to correct
susceptibility distortions in spin-echo echo-planar images: Appli-
cation to diffusion tensor imaging. NeuroImage, 20(2), 870–888.
https://doi.org/10.1016/S1053-8119(03)00336-7, PubMed:
14568458
Andersson, J. L. R., & Sotiropoulos, S. N. (2016). An integrated
approach to correction for off-resonance effects and subject
movement in diffusion MR imaging. NeuroImage, 125, 1063–1078.
https://doi.org/10.1016/j.neuroimage.2015.10.019, PubMed:
26481672
Avants, B. B., Epstein, C. L., Grossman, M., & Gee, J. C. (2008).
Symmetric diffeomorphic image registration with cross-correlation:
Evaluating automated labeling of elderly and neurodegenerative
brain. Medical Image Analysis, 12(1), 26–41. https://doi.org/10
.1016/j.media.2007.06.004, PubMed: 17659998
Basser, P. J., Mattiello, J., & LeBihan, D. (1994). MR diffusion tensor
spectroscopy and imaging. Biophysical Journal, 66(1), 259–267.
https://doi.org/10.1016/S0006-3495(94)80775-1, PubMed:
8130344
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E.
(2008). Fast unfolding of communities in large networks. Journal
of Statistical Mechanics: Theory and Experiment, 2008(10),
P10008. https://doi.org/10.1088/1742-5468/2008/10/P10008
Brochet, B., Deloire, M. S. A., Bonnet, M., Salort-Campana, E.,
Ouallet, J. C., Petry, K. G., & Dousset, V. (2008). Should SDMT
substitute for PASAT in MSFC? A 5-year longitudinal study. Mul-
tiple Sclerosis Journal, 14(9), 1242–1249. https://doi.org/10.1177
/1352458508094398, PubMed: 18653737
Charalambous, T., Tur, C., Prados, F., Kanber, B., Chard, D. T.,
Ourselin, S., … Toosy, A. T. (2019). Structural network disruption
markers explain disability in multiple sclerosis. Journal of Neuro-
logy, Neurosurgery, and Psychiatry, 90(2), 219–226. https://doi
.org/10.1136/jnnp-2018-318440, PubMed: 30467210
Chen, M., & Deem, M. W. (2015). Development of modularity in
the neural activity of childrenʼs brains. Physical Biology, 12(1),
016009. https://doi.org/10.1088/1478-3975/12/1/016009,
PubMed: 25619207
Cordero-Grande, L., Christiaens, D., Hutter, J., Price, A. N., &
Hajnal, J. V. (2019). Complex diffusion-weighted image estima-
tion via matrix recovery under general noise models. Neuro-
Image, 200, 391–404. https://doi.org/10.1016/j.neuroimage
.2019.06.039, PubMed: 31226495
Cruces, R. R., Royer, J., Herholz, P., Larivière, S., Vos de Wael, R.,
Paquola, C., … Bernhardt, B. C. (2022). Micapipe: A pipeline for
multimodal neuroimaging and connectome analysis. bioRxiv.
https://doi.org/10.1101/2022.01.31.478189
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson,
B. C., Blacker, D., … Killiany, R. J. (2006). An automated labeling
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. NeuroImage, 31(3), 968–980.
https://doi.org/10.1016/j.neuroimage.2006.01.021, PubMed:
16530430
Duncan, E. S., & Small, S. L. (2016). Increased modularity of resting
state networks supports improved narrative production in apha-
sia recovery. Brain Connectivity, 6(7), 524–529. https://doi.org/10
.1089/brain.2016.0437, PubMed: 27345466
Fischer, J. S., Rudick, R. A., Cutter, G. R., & Reingold, S. C. (1999).
The multiple sclerosis functional composite measure (MSFC): An
integrated approach to MS clinical outcome assessment. Multiple
Sclerosis Journal, 5(4), 244–250. https://doi.org/10.1177
/135245859900500409, PubMed: 10467383
Fischl, B. (2012). FreeSurfer. NeuroImage, 62(2), 774–781. https://
doi.org/10.1016/j.neuroimage.2012.01.021, PubMed: 22248573
Fleischer, V., Gröger, A., Koirala, N., Droby, A., Muthuraman, M.,
Kolber, P., … Groppa, S. (2017). Increased structural white and
grey matter network connectivity compensates for functional
decline in early multiple sclerosis. Multiple Sclerosis Journal,
23(3), 432–441. https://doi.org/10.1177/1352458516651503,
PubMed: 27246143
Fleischer, V., Koirala, N., Droby, A., Gracien, R.-M., Deichmann,
R., Ziemann, U., … Groppa, S. (2019). Longitudinal cortical net-
work reorganization in early relapsing-remitting multiple sclero-
sis. Therapeutic Advances in Neurological Disorders, 12. https://
doi.org/10.1177/1756286419838673, PubMed: 31040880
Fleischer, V., Radetz, A., Ciolac, D., Muthuraman, M., Gonzalez-
Escamilla, G., Zipp, F., & Groppa, S. (2019). Graph theoretical
Network Neuroscience
157
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
a
_
0
0
2
7
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory in MS brain remodeling
framework of brain networks in multiple sclerosis: A review of
concepts. Neuroscience, 403, 35–53. https://doi.org/10.1016/j
.neuroscience.2017.10.033, PubMed: 29101079
Frohman, E. M., Racke, M. K., & Raine, C. S. (2006). Multiple
sclerosis—The plaque and its pathogenesis. New England Journal
of Medicine, 354(9), 942–955. https://doi.org/10.1056
/NEJMra052130, PubMed: 16510748
Gamboa, O. L., Tagliazucchi, E., von Wegner, F., Jurcoane, A.,
Wahl, M., Laufs, H., & Ziemann, U. (2014). Working memory
performance of early MS patients correlates inversely with mod-
ularity increases in resting state functional connectivity networks.
NeuroImage, 94, 385–395. https://doi.org/10.1016/j.neuroimage
.2013.12.008, PubMed: 24361662
Girvan, M., & Newman, M. E. (2002). Community structure in
social and biological networks. Proceedings of the National
Academy of Sciences, 99(12), 7821–7826. https://doi.org/10
.1073/pnas.122653799, PubMed: 12060727
Golia, M. T., Poggini, S., Alboni, S., Garofalo, S., Ciano Albanese,
N., Viglione, A., … Maggi, L. (2019). Interplay between inflam-
mation and neural plasticity: Both immune activation and sup-
pression impair LTP and BDNF expression. Brain, Behavior,
and Immunity, 81, 484–494. https://doi.org/10.1016/j.bbi.2019
.07.003, PubMed: 31279682
Gonzalez-Escamilla, G., Ciolac, D., De Santis, S., Radetz, A.,
Fleischer, V., Droby, A., … Groppa, S. (2020). Gray matter net-
work reorganization in multiple sclerosis from 7-Tesla and
3-Tesla MRI data. Annals of Clinical and Translational Neurology,
7(4), 543–553. https://doi.org/10.1002/acn3.51029, PubMed:
32255566
Han, K., Chapman, S. B., & Krawczyk, D. C. (2020). Cognitive
training reorganizes network modularity in traumatic brain
injury. Neurorehabilitation and Neural Repair, 34(1), 26–38.
https://doi.org/10.1177/1545968319868710, PubMed:
31434528
Hua, K., Zhang, J., Wakana, S., Jiang, H., Li, X., Reich, D. S., …
Mori, S. (2008). Tract probability maps in stereotaxic spaces:
Analyses of white matter anatomy and tract-specific quantifica-
tion. NeuroImage, 39(1), 336–347. https://doi.org/10.1016/j
.neuroimage.2007.07.053, PubMed: 17931890
Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W.,
& Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790. https://
doi.org/10.1016/j.neuroimage.2011.09.015, PubMed: 21979382
Jeurissen, B., Leemans, A., & Sijbers, J. (2014). Automated correc-
tion of improperly rotated diffusion gradient orientations in diffu-
sion weighted MRI. Medical Image Analysis, 18(7), 953–962.
https://doi.org/10.1016/j.media.2014.05.012, PubMed:
24968247
Kellner, E., Dhital, B., Kiselev, V. G., & Reisert, M. (2016). Gibbs-
ringing artifact removal based on local subvoxel-shifts. Magnetic
Resonance in Medicine, 76(5), 1574–1581. https://doi.org/10
.1002/mrm.26054, PubMed: 26745823
Koay, C. G., & Basser, P. J. (2006). Analytically exact correction
scheme for signal extraction from noisy magnitude MR signals.
Journal of Magnetic Resonance, 179(2), 317–322. https://doi
.org/10.1016/j.jmr.2006.01.016, PubMed: 16488635
Kocevar, G., Stamile, C., Hannoun, S., Cotton, F., Vukusic, S., Durand-
Dubief, F., & Sappey-Marinier, D. (2016). Graph theory-based brain
connectivity for automatic classification of multiple sclerosis
clinical courses. Frontiers in Neuroscience, 10, 478. https://doi
.org/10.3389/fnins.2016.00478, PubMed: 27826224
Kurtzke, J. F. (1983). Rating neurologic impairment in multiple
sclerosis: An expanded disability status scale (EDSS). Neurology,
33(11), 1444–1452. https://doi.org/10.1212/ WNL.33.11.1444,
PubMed: 6685237
Lauzon, C. B., Asman, A. J., Esparza, M. L., Burns, S. S., Fan, Q.,
Gao, Y., … Landman, B. A. (2013). Simultaneous analysis and
quality assurance for diffusion tensor imaging. PLoS ONE, 8(4),
e61737. https://doi.org/10.1371/journal.pone.0061737,
PubMed: 23637895
Lipp, I., Parker, G. D., Tallantyre, E. C., Goodall, A., Grama, S.,
Patitucci, E., … Jones, D. K. (2020). Tractography in the presence
of multiple sclerosis lesions. NeuroImage, 209, 116471. https://doi
.org/10.1016/j.neuroimage.2019.116471, PubMed: 31877372
Marebwa, B. K., Fridriksson, J., Yourganov, G., Feenaughty, L.,
Rorden, C., & Bonilha, L. (2017). Chronic post-stroke aphasia
severity is determined by fragmentation of residual white matter
networks. Scientific Reports, 7(1), 8188. https://doi.org/10.1038
/s41598-017-07607-9, PubMed: 28811520
Mori, S., Wakana, S., Van Zijl, P. C., & Nagae-Poetscher, L. (2005).
MRI atlas of human white matter. Elsevier.
Muthuraman, M., Fleischer, V., Kolber, P., Luessi, F., Zipp, F., &
Groppa, S. (2016). Structural brain network characteristics can
differentiate CIS from early RRMS. Frontiers in Neuroscience,
10, 14. https://doi.org/10.3389/fnins.2016.00014, PubMed:
26869873
Newman, M. E. J., & Girvan, M. (2004). Finding and evaluating
community structure in networks. Physical Review E, 69(2),
026113. https://doi.org/10.1103/PhysRevE.69.026113, PubMed:
14995526
Patenaude, B., Smith, S. M., Kennedy, D. N., & Jenkinson, M.
(2011). A Bayesian model of shape and appearance for subcor-
tical brain segmentation. NeuroImage, 56(3), 907–922. https://
doi.org/10.1016/j.neuroimage.2011.02.046, PubMed: 21352927
Plemel, J. R., Liu, W.-Q., & Yong, V. W. (2017). Remyelination ther-
apies: A new direction and challenge in multiple sclerosis.
Nature Reviews Drug Discovery, 16(9), 617–634. https://doi.org
/10.1038/nrd.2017.115, PubMed: 28685761
Prosperini, L., & Di Filippo, M. (2019). Beyond clinical changes:
Rehabilitation-induced neuroplasticity in MS. Multiple Sclerosis
J o u r n a l , 2 5 ( 1 0 ) , 1 3 4 8 – 1 3 6 2 . h t t p s : / / d o i . o rg / 1 0 . 11 7 7
/1352458519846096, PubMed: 31469359
R Core Team. (2019). R: A language and environment for statistical
computing. R Foundation for Statistical Computing, Vienna,
Austria.
Remaud, S., Gothié, J.-D., Morvan-Dubois, G., & Demeneix, B. A.
(2014). Thyroid hormone signaling and adult neurogenesis in
mammals. Frontiers in Endocrinolgoy, 5, 62. https://doi.org/10
.3389/fendo.2014.00062, PubMed: 24808891
Rocca, M. A., Valsasina, P., Meani, A., Falini, A., Comi, G., &
Filippi, M. (2016). Impaired functional integration in multiple
sclerosis: A graph theory study. Brain Structure and Function,
221(1), 115–131. https://doi.org/10.1007/s00429-014-0896-4,
PubMed: 25257603
Roostaei, T., Sadaghiani, S., Mashhadi, R., Falahatian, M., Mohamadi,
E., Javadian, N., … Sahraian, M. A. (2019). Convergent effects of a
functional C3 variant on brain atrophy, demyelination, and
Network Neuroscience
158
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
a
_
0
0
2
7
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory in MS brain remodeling
cognitive impairment in multiple sclerosis. Multiple Sclerosis Jour-
nal, 25(4), 532–540. https://doi.org/10.1177/1352458518760715,
PubMed: 29485352
Rosti, E., Hämäläinen, P., Koivisto, K., & Hokkanen, L. (2007).
PASAT in detecting cognitive impairment in relapsing-remitting
MS. Applied Neuropsychology, 14(2), 101–112. https://doi.org
/10.1080/09084280701319938, PubMed: 17523884
Roxburgh, R. H. S. R., Seaman, S. R., Masterman, T., Hensiek, A. E.,
Sawcer, S. J., Vukusic, S., … Compston, D. A. S. (2005). Multiple
sclerosis severity score: Using disability and disease duration to
rate disease severity. Neurology, 64(7), 1144–1151. https://doi
.org/10.1212/01.WNL.0000156155.19270.F8, PubMed:
15824338
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Schilling, K. G., Blaber, J., Huo, Y., Newton, A., Hansen, C., Nath,
V., … Landman, B. A. (2019). Synthesized b0 for diffusion distor-
tion correction (Synb0-DisCo). Magnetic Resonance Imaging, 64,
62–70. https://doi.org/10.1016/j.mri.2019.05.008, PubMed:
31075422
Shu, N., Liu, Y., Li, K., Duan, Y., Wang, J., Yu, C., … He, Y. (2011).
Diffusion tensor tractography reveals disrupted topological effi-
ciency in white matter structural networks in multiple sclerosis.
Cerebral Cortex, 21(11), 2565–2577. https://doi.org/10.1093
/cercor/bhr039, PubMed: 21467209
Smith, R. E., Tournier, J. D., Calamante, F., & Connelly, A. (2012).
Anatomically constrained tractography: Improved diffusion MRI
streamlines tractography through effective use of anatomical
information. NeuroImage, 62(3), 1924–1938. https://doi.org/10
.1016/j.neuroimage.2012.06.005, PubMed: 22705374
Smith, R. E., Tournier, J. D., Calamante, F., & Connelly, A. (2015).
SIFT2: Enabling dense quantitative assessment of brain white
matter connectivity using streamlines tractography. NeuroImage,
119, 338–351. https://doi.org/10.1016/j.neuroimage.2015.06
.092, PubMed: 26163802
Smith, S. M. (2002). Fast robust automated brain extraction. Human
Brain Mapping, 17(3), 143–155. https://doi.org/10.1002/ hbm
.10062, PubMed: 12391568
Smith, S. M., Jenkinson, M., Woolrich, M. W., Beckmann, C. F.,
Behrens, T. E. J., Johansen-Berg, H., … Matthews, P. M. (2004).
Advances in functional and structural MR image analysis and
implementation as FSL. NeuroImage, 23, S208–S219. https://
doi.org/10.1016/j.neuroimage.2004.07.051 , PubMed:
15501092
Stampanoni Bassi, M., Gilio, L., Buttari, F., Maffei, P., Marfia, G. A.,
Restivo, D. A., … Iezzi, E. (2017). Remodeling functional connec-
tivity in multiple sclerosis: A challenging therapeutic approach.
Frontiers in Neuroscience, 11, 710. https://doi.org/10.3389/fnins
.2017.00710, PubMed: 29321723
Stegen, S., Stepanov, I., Cookfair, D., Schwartz, E., Hojnacki, D.,
Weinstock-Guttman, B., & Benedict, R. H. B. (2010). Validity of
the California Verbal Learning Test–II in multiple sclerosis. The
Clinical Neuropsychologist, 24(2), 189–202. https://doi.org/10
.1080/13854040903266910, PubMed: 19953426
Tommasin, S., De Giglio, L., Ruggieri, S., Petsas, N., Giannì, C.,
Pozzilli, C., & Pantano, P. (2020). Multi-scale resting state func-
tional reorganization in response to multiple sclerosis damage.
Neuroradiology, 62(6), 693–704. https://doi.org/10.1007
/s00234-020-02393-0, PubMed: 32189024
Tournier, J. D., Smith, R., Raffelt, D., Tabbara, R., Dhollander, T.,
Pietsch, M., … Connelly, A. (2019). MRtrix3: A fast, flexible
and open software framework for medical image processing
and visualisation. NeuroImage, 202, 116137. https://doi.org/10
.1016/j.neuroimage.2019.116137, PubMed: 31473352
Tur, C., Grussu, F., Prados, F., Charalambous, T., Collorone, S.,
Kanber, B., … Ciccarelli, O. (2019). A multi-shell multi-tissue
diffusion study of brain connectivity in early multiple sclerosis.
Multiple Sclerosis Journal, 26(7), 774–785. https://doi.org/10
.1177/1352458519845105, PubMed: 31074686
Tustison, N. J., & Avants, B. B. (2013). Explicit B-spline regulariza-
tion in diffeomorphic image registration. Frontiers in Neuroinfor-
matics, 7, 39. https://doi.org/10.3389/fninf.2013.00039,
PubMed: 24409140
Tustison, N. J., Avants, B. B., Cook, P. A., Zheng, Y., Egan, A.,
Yushkevich, P. A., & Gee, J. C. (2010). N4ITK: Improved N3
bias correction. IEEE Transactions on Medical Imaging, 29(6),
1310–1320. https://doi.org/10.1109/ TMI.2010.2046908,
PubMed: 20378467
Tustison, N. J., Cook, P. A., Klein, A., Song, G., Das, S. R., Duda,
J. T., … Avants, B. B. (2014). Large-scale evaluation of ANTs and
FreeSurfer cortical thickness measurements. NeuroImage, 99,
166–179. https://doi.org/10.1016/j.neuroimage.2014.05.044,
PubMed: 24879923
Veraart, J., Fieremans, E., & Novikov, D. S. (2016). Diffusion MRI
noise mapping using random matrix theory. Magnetic Resonance
in Medicine, 76(5), 1582–1593. https://doi.org/10.1002/mrm
.26059, PubMed: 26599599
Veraart, J., Novikov, D. S., Christiaens, D., Ades-Aron, B., Sijbers, J.,
& Fieremans, E. (2016). Denoising of diffusion MRI using random
matrix theory. NeuroImage, 142, 394–406. https://doi.org/10
.1016/j.neuroimage.2016.08.016, PubMed: 27523449
Veraart, J., Sijbers, J., Sunaert, S., Leemans, A., & Jeurissen, B.
(2013). Weighted linear least squares estimation of diffusion
MRI parameters: Strengths, limitations, and pitfalls. NeuroImage,
81, 335–346. https://doi.org/10.1016/j.neuroimage.2013.05
.028, PubMed: 23684865
Wakana, S., Caprihan, A., Panzenboeck, M. M., Fallon, J. H., Perry,
M., Gollub, R. L., … Mori, S. (2007). Reproducibility of quantita-
tive tractography methods applied to cerebral white matter. Neu-
roImage, 36(3), 630–644. https://doi.org/10.1016/j.neuroimage
.2007.02.049, PubMed: 17481925
Zhang, Y., Brady, M., & Smith, S. (2001). Segmentation of brain MR
images through a hidden Markov random field model and the
expectation-maximization algorithm. IEEE Transactions on Med-
ical Imaging, 20(1), 45–57. https://doi.org/10.1109/42.906424,
PubMed: 11293691
Network Neuroscience
159
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
1
4
8
2
0
7
1
9
8
5
n
e
n
_
a
_
0
0
2
7
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3