RECHERCHE
Optimized connectome architecture for
sensory-motor integration
Jacob C. Worrell1, Jeffrey Rumschlag2, Richard F. Betzel3, Olaf Sporns1, and Bratislav Miši´c4
1Department of Psychological and Brain Sciences, Indiana University, Bloomington, Indiana, Etats-Unis
2Department of Cell Biology and Neuroscience, University of California Riverside, Riverside, Californie, Etats-Unis
3Department of Bioengineering, University of Pennsylvania, Philadelphia, Pennsylvanie, Etats-Unis
4Montréal Neurological Institute, Université McGill, Montréal, Canada
Mots clés: Connectome, Cerveau, Spreading, Drosophila
un accès ouvert
journal
ABSTRAIT
The intricate connectivity patterns of neural circuits support a wide repertoire of
communication processes and functional interactions. Here we systematically investigate
how neural signaling is constrained by anatomical connectivity in the mesoscale Drosophila
(fruit fly) brain network. We use a spreading model that describes how local perturbations,
such as external stimuli, trigger global signaling cascades that spread through the network.
Through a series of simple biological scenarios we demonstrate that anatomical embedding
potentiates sensory-motor integration. We find that signal spreading is faster from nodes
associated with sensory transduction (sensors) to nodes associated with motor output
(effectors). Signal propagation was accelerated if sensor nodes were activated simultaneously,
suggesting a topologically mediated synergy among sensors. En outre, the organization of
the network increases the likelihood of convergence of multiple cascades towards effector
nodes, thereby facilitating integration prior to motor output. De plus, effector nodes tend to
coactivate more frequently than other pairs of nodes, suggesting an anatomically enhanced
coordination of motor output. Altogether, our results show that the organization of the
mesoscale Drosophila connectome imparts privileged, behaviorally relevant communication
patterns among sensors and effectors, shaping their capacity to collectively integrate
information.
RÉSUMÉ DE L'AUTEUR
The complex network spanned by neurons and their axonal projections promotes a diverse
set of functions. In the present report, we study how the topological organization of the fruit
fly brain supports sensory-motor integration. Using a simple communication model, nous
demonstrate that the topology of this network allows efficient coordination among sensory
and motor neurons. Our results suggest that brain network organization may profoundly
shape the functional repertoire of this simple organism.
INTRODUCTION
Recent advances in imaging of neural circuits have resulted in detailed maps of neural
elements and their connections (Lichtman & Denk, 2011). Topological analysis of these “con-
nectomes” has revealed several organizational features that appear to be conserved across
spatial scales (Betzel & Bassett, 2016; Sporns, 2014) and phylogeny (van den Heuvel,
Bullmore, & Sporns, 2016),
functionally specialized modules
(Rubinov, Ypma, Watson, & Bullmore, 2015; Shih et al., 2015; Varshney, Chen, Paniagua,
including the existence of
Citation: Worrell, J.. C., Rumschlag, J.,
Betzel, R.. F., Sporns, O., & Miši ´c, B.
(2017). Optimized connectome
architecture for sensory-motor
l'intégration. Neurosciences en réseau,
1(4), 415–430. https://est ce que je.org/10.1162/
netn_a_00022
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00022
Reçu: 7 Avril 2017
Accepté: 5 Juillet 2017
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Bratislav Miši ´c
bratislav.misic@mcgill.ca
Éditeur de manipulation:
Dante Chialvo
droits d'auteur: © 2017
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
un
_
0
0
0
2
2
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sensory-motor integration in the Drosophila connectome
Hall, & Chklovskii, 2010) bound together by an integrative core of highly connected hub
nodes (Bota, Sporns, & Swanson, 2015; Towlson, Vértes, Ahnert, Schafer, & Bullmore, 2013;
van den Heuvel, Kahn, Goñi, & Sporns, 2012; Zamora-López, Zhou, & Kurths, 2010). A sig-
nificant remaining challenge is to understand how the organization of neural circuits
interactions and adaptive behavior (Miši´c & Sporns, 2016;
supports emergent
Vogelstein et al., 2014).
functional
Theoretical models that describe the unfolding of communication processes through
anatomical pathways hold great promise to bridge the gap between static anatomical
features and global dynamical interactions. A spectrum of frameworks and models, em-
phasizing communication via shortest paths (van den Heuvel et al., 2012), ensembles
of paths and walks (Avena-Koenigsberger et al., 2017; Crofts & Higham, 2009), diffu-
sion (Abdelnour, Voss, & Raj, 2014; Bacik, Schaub, Beguerisse-Díaz, Billeh, & Barahona,
2016; Miši´c, Goñi, Betzel, Sporns, & McIntosh, 2014; Miši´c, Sporns, & McIntosh, 2014),
and sustained coherent oscillations (Deco, Jirsa, McIntosh, Sporns, & Kötter, 2009; Gollo,
Zalesky, Hutchison, van den Heuvel, & Breakspear, 2015) have begun to link anatomical
connectivity patterns with emergent activity patterns. Par exemple, diffusion models have
been used to predict statistical associations (functional connectivity) between distributed
domaines (Abdelnour et al., 2014; Goñi et al., 2013), as well as the clustering of functional brain
networks into coherent modules (Atasoy, Donnelly, & Pearson, 2016; R.. Betzel et al., 2013).
Altogether, these studies suggest that integrative properties of brain networks and specific
brain regions naturally arise from their anatomical connectivity and topological embedding
(Bacik et al., 2016).
In the present report we investigate the spreading and subsequent integration of neural sig-
nals in the mesoscale Drosophila connectome, previously reconstructed from 12,995 images
of individual neurons (Shih et al., 2015). Neurons are grouped into 49 distinct populations,
termed local processing units (LPUs), that serve as the nodes of the network. We apply a
simple model of collective spreading that describes how local perturbations trigger global
activity cascades that propagate across the network (linear threshold model) (Granovetter,
1978; Miši´c et al., 2015; O’Dea, Crofts, & kaiser, 2013; Watts, 2002). We consider three
biological scenarios: (un) how a single perturbation develops into a single cascade, (b) how two
signals synergistically spread through the network, et (c) how two signals, endowed with
different content, spread and ultimately integrate with one another. To investigate whether
anatomical embedding potentiates integration, we focused on several test cases directly re-
lated to sensory-motor integration. We tested the hypothesis that signals initiated in neuronal
populations associated with sensory transduction (sensors) would spread to populations asso-
ciated with motor output (effectors) more effectively than to other targets. En outre, nous
hypothesized that, in order to produce coordinated action patterns, the architecture of the
Drosophila connectome would potentiate the convergence of signals towards effector nodes.
RÉSULTATS
Modules
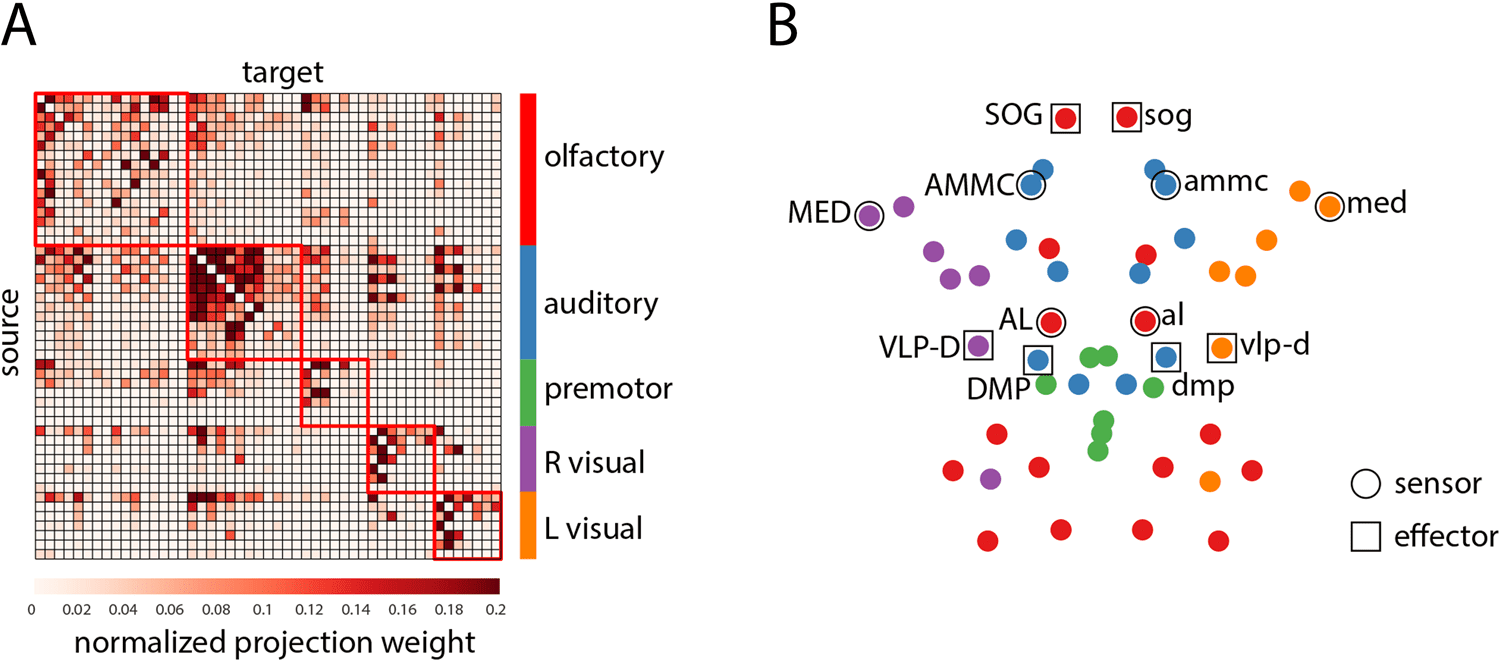
Multiscale community detection revealed five modules: olfactory, auditory or mechano-
sensoriel, premotor, right visual, left visual (Chiffre 1). The recovered communities were identi-
cal to the communities reported by Shih et al. (2015), save for the assignment of the left and
right optic tubercle (optu/OPTU), which were placed in the central auditory/mechanoreceptive
module, rather than the left and right visual modules. To facilitate comparisons with previous
LPU (local processing unit):
Neuronal population with common
morphological and functional
characteristics.
Linear threshold model:
A dynamic model in which
perturbations develop into signaling
cascades and spread through a
network of linked elements.
Sensors:
Neuronal populations involved
in transducing or processing
sensory information.
Effectors:
Neuronal populations involved
in motor execution.
Neurosciences en réseau
416
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
un
_
0
0
0
2
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sensory-motor integration in the Drosophila connectome
Chiffre 1. Modular organization of the Drosophila connectome. (UN) Drosophila connectome adjacency matrix derived from the FlyCircuit 1.1
database. Modules were estimated using multiresolution community detection. The nodes of the adjacency matrix are ordered by community
(B) Axial view of the network’s spatial layout. LPUs involved in sensory signal transduction (sensors) and motor execution
assignment.
(effectors) are outlined with circular and square markers, respectivement.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
un
_
0
0
0
2
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Spread time:
Time required for a cascade initiated
in a given source node to reach a
target node.
reports, the optu and OPTU LPUs were manually reassigned to the left and right visual
modules, yielding the same partition as first reported in Shih et al. (2015).
Sensor-Effector Spreading
We initially consider the scenario where a single perturbation triggers a global cascade that
spreads through the network (Figure 2A). The perturbation may represent the transduction of
an external stimulus or some endogenous event, such as synchronized postsynaptic potentials
in a neuronal ensemble. The spread time is the time (in dimensionless units) that it takes for a
signal initiated at some source node to reach a target node.
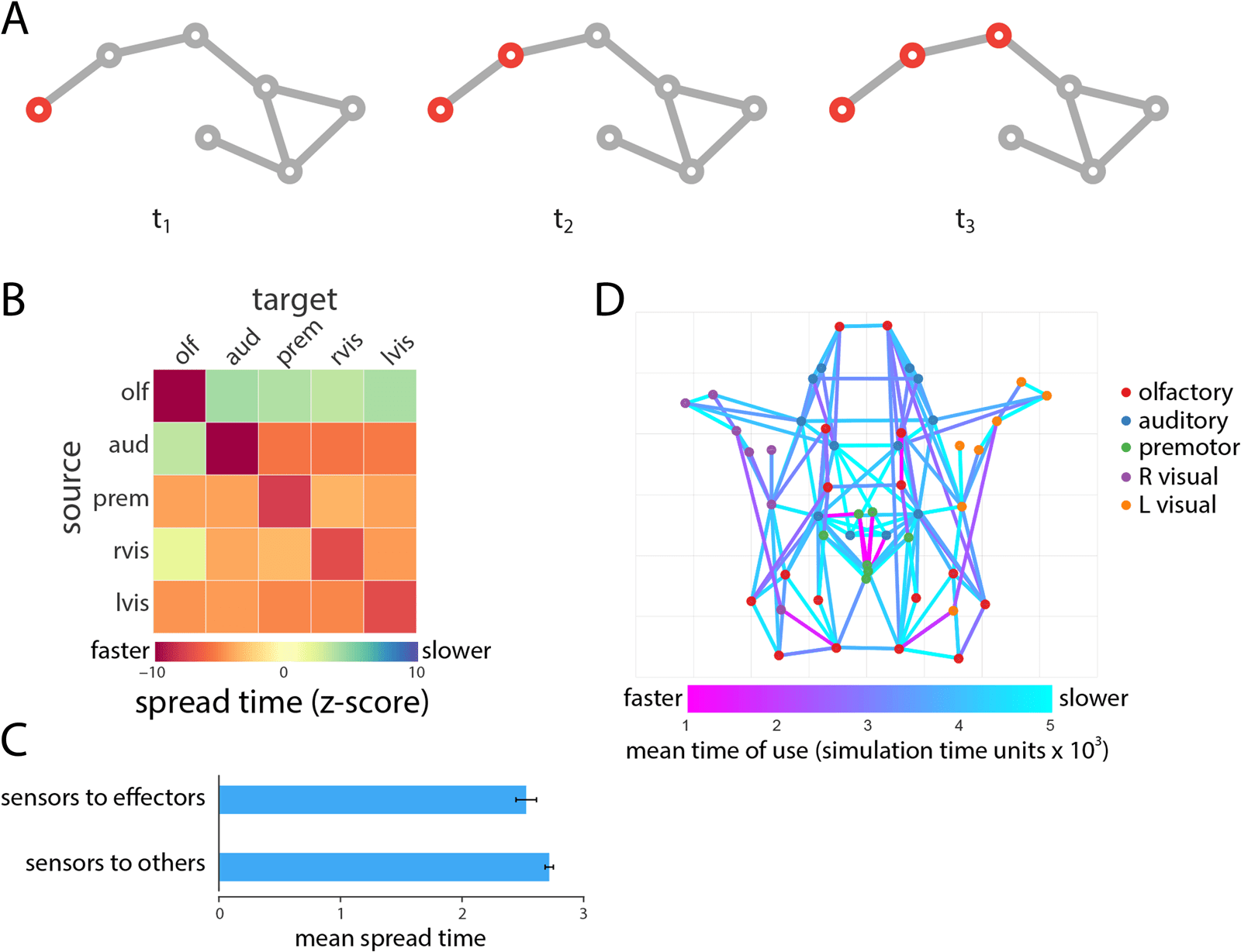
We first seek to build intuition about how spread times and the overall performance of
the spreading model relate to more traditional network measures. Seed node out-strength
was significantly correlated with mean spread time to the rest of the network (r = −0.48, p =
−4), suggesting that perturbations initiated at nodes with stronger outputs spread faster.
5.6 × 10
De la même manière, target node in-strength was significantly correlated with mean spread times across
−11), indicating that target nodes with more inputs
all seed nodes (r = −0.78, p = 3.5 × 10
adopted the active state faster. Enfin, we find that the communicability between seed and
target nodes, corresponding to a weighted sum of all walks between them (Crofts & Higham,
2009; Estrada & Hatano, 2008), was also a significant predictor of spread time between those
nodes (r = −0.42, p ≈ 0). Autrement dit, source-target pairs that have greater communica-
bility (indicating that they are, on average, connected by shorter paths and walks) also have
faster spread times.
We next investigate spreading within and between modules (Figure 2B). For each source
and target module, we first calculate the mean spread time among all constituent nodes.
We then express this quantity as a z-score relative to a null distribution obtained by ran-
domly permuting module labels and recalculating mean spread times. We find that spread
times are generally faster in the empirical network (corresponding to negative z-scores),
suggesting that the modular organization of the Drosophila connectome may be optimized
for rapid communication. Fastest spreading was observed within modules, consistent with
Neurosciences en réseau
417
Sensory-motor integration in the Drosophila connectome
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
un
_
0
0
0
2
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2. Single cascade spreading. (UN) Schematic showing the spread of a single cascade. (B) Mean spread time for all seed-target com-
binations, stratified by module membership. (C) Test case comparing spread times from sensor to effector nodes versus sensor to noneffector
nodes. (D) Projections most commonly used to spread cascades and the average time at which they are used.
the definition of modules as communities of nodes with high mutual connection density
(Nematzadeh, Ferrara, Flammini, & Ahn, 2014).
To address the hypothesis that the organization of the Drosophila connectome should
potentiate information transmission from sensors to effectors, we compared the mean spread
time from sensor nodes to effector nodes with spread time from sensor nodes to noneffector
nodes. Consistent with the hypothesis, we find that spreading from sensors to effectors is sig-
nificantly faster compared with spreading from sensors to noneffectors (Wilcoxon p = 0.0011;
Cohen’s d = 0.35; Figure 2C).
Enfin, we investigate the contribution of individual projections to global spreading pat-
terns (Figure 2D). We define the transit time associated with each projection as the ratio of
the Euclidean distance spanned by that projection and the weight of the projection. We then
use asynchronous updating to infer the contributions of specific projections to the activation
of specific nodes (see Methods section). Figure 2D shows the most commonly used projec-
tions across all n = 49 possible seeding scenarios, as well as the mean time (in dimensionless
simulation time units) at which those projections were used. The projections and subnetworks
they delineate bear a close correspondence to the putative rich club of the Drosophila con-
nectome (bilateral DMP, VMP, VLP-D, SDFP, and FB in the central brain), encompassing many
of the strongest projections and integrative LPUs in the network (Shih et al., 2015). Statisti-
cally, connections between rich club nodes were used earlier and more often compared with
other connections (p = 0.05 and p ≈ 0 for both measures, Cohen’s d = 0.43 et 0.97,
Neurosciences en réseau
418
Sensory-motor integration in the Drosophila connectome
Speedup:
Decrease in spread time
(acceleration) to a target node if a
cascade is initiated in two source
nodes as opposed to just one;
quantifies potential for synergy
between two nodes.
respectivement), suggesting that this central collective of high-strength nodes is disproportion-
ately more involved in signal spreading.
Synergistic Relationships Among Sensors
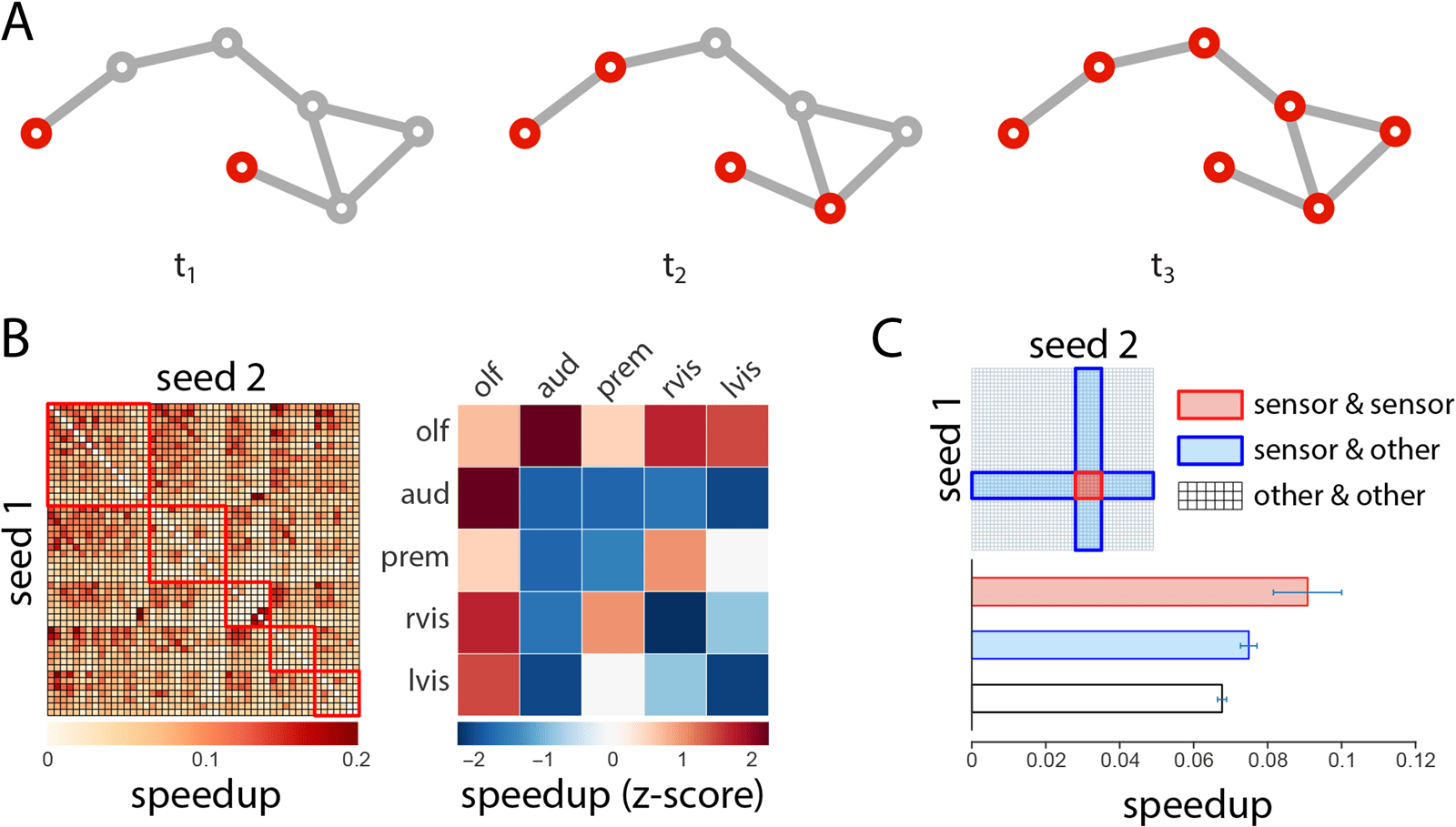
We next investigate the effects of initiating a cascade simultaneously in two seed nodes
(Figure 3A). In certain instances, introducing a perturbation at two seed nodes may theoret-
ically accelerate the spread of the cascade across the network. We operationalize the syn-
ergistic benefit of simultaneous perturbations as the percentage speedup in spread time for
the two-seed scenario compared with the faster of the two individual one-seed scenarios
(see Methods).
The speedups for every two-seed combination are shown in matrix form in Figure 3B (gauche).
The results suggest that simultaneous perturbations are less effective when triggered in the same
−5),
module and more effective when triggered in different modules (Wilcoxon p = 6.69 × 10
consistent with the definition of modules as densely interconnected communities. We then
calculate the mean within- and between-module speedups and express them as z-scores rela-
tive to a null distribution that was constructed by randomly permuting module assignments for
individual nodes (Figure 3B right). Comparison with the null model suggests several greater
than expected cooperative effects, including between the higher-order olfactory and audi-
tory modules (permuted p = 0.016), indicating an enhanced potential for functional coupling
among these two modules.
Figure 3C shows a set of test cases in which we focus on the cooperative effects among
pairs of sensor LPUs. We hypothesize that, if the architecture of the network has evolved to
support multisensory integration, sensor LPUs may show greater synergy with each other than
with other nodes in the network. We thus compare speedups for two-sensor pairs (sensor and
sensor) with speedups for sensor and nonsensor nodes (sensor and other), as well as nonsensor
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
un
_
0
0
0
2
2
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 3. Synergistic spreading.
(UN) Schematic showing the spread a signaling cascade initiated in two seed nodes. (B) The percentage
speedup in spread time for the whole network, shown for all possible two-seed combinations. (C) Test cases comparing speedups for cascades
initiated at two sensor seed nodes, versus cascades initiated at one sensor and one nonsensor node, and two nonsensor nodes.
Neurosciences en réseau
419
Sensory-motor integration in the Drosophila connectome
Diversity:
The entropy of a node’s
neighborhood vector; quantifies the
tendency for multiple cascades to
converge at a particular node.
pairs (other and other). The speedup for sensor pairs is greater than for sensor/nonsensor pairs
(Wilcoxon p = 0.051, Cohen’s d = 0.44) and for nonsensor pairs (p = 0.007, d = 0.62), but is
statistically significant only for the latter comparison.
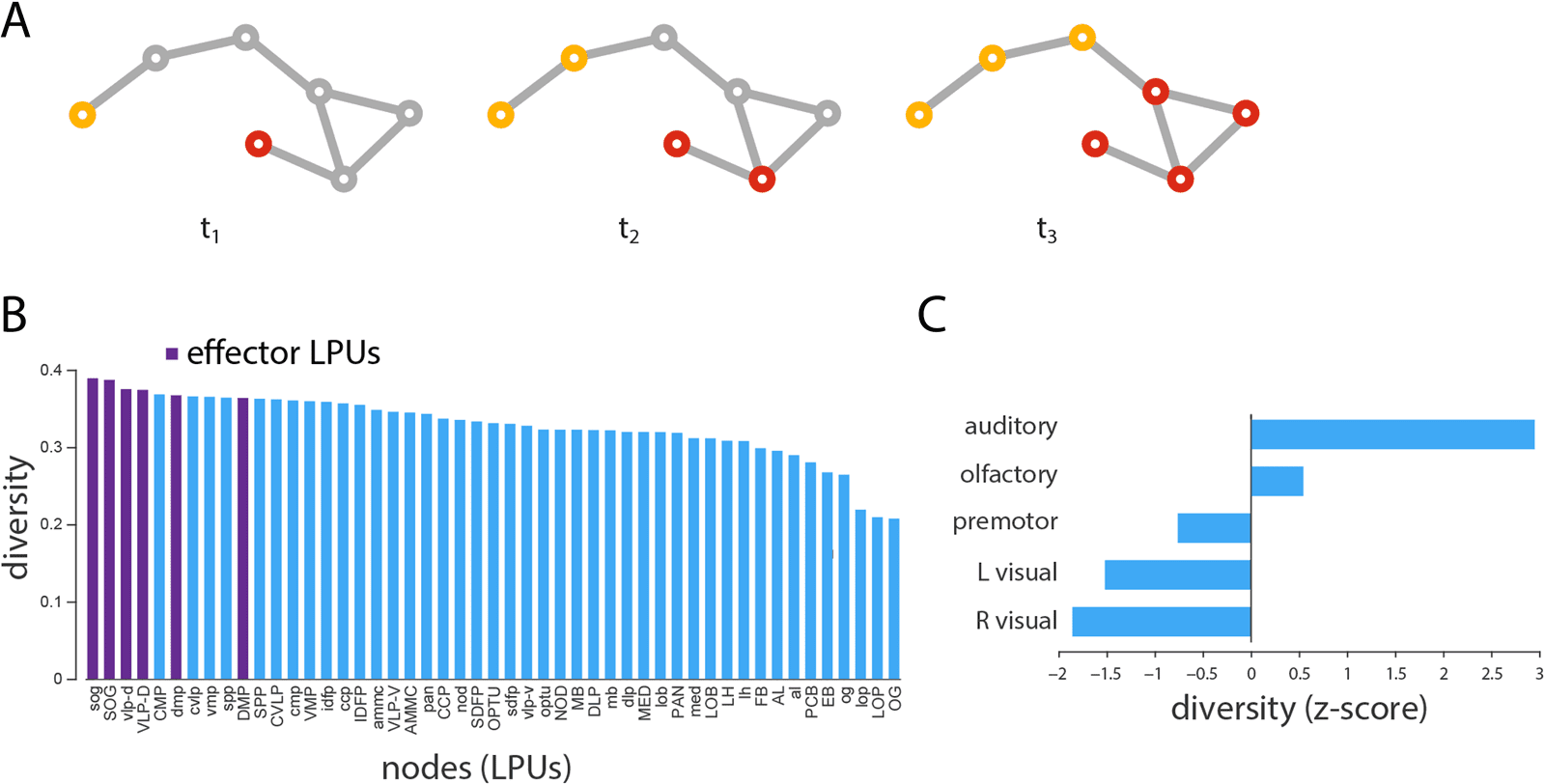
Signal Convergence at Effectors
We next investigate the scenario in which two perturbations, carrying different signals, de-
velop into competing cascades (Figure 4A). This scenario allows us to characterize how sepa-
rate signaling cascades develop and to determine where they converge. To estimate the likely
convergence points between cascades, we define the diversity of individual nodes’ neighbor-
hoods as the entropy of their neighborhood vector (see Methods). Nodes whose neighbors
adopt the same state and are part of the same cascade will have low diversity, while nodes
whose neighbors are distributed among the two cascades will have high diversity.
Across all possible seeding scenarios, we find in-strength to be significantly correlated with
−4), suggesting that highly connected nodes are better posi-
diversity (r = 0.50, p = 2.8 × 10
tioned to mediate the integration of multiple signals. Fait intéressant, the six effector LPUs (sog,
SOG, vlp-d, VLP-D, dmp, and DMP) ranked as the top first, second, troisième, fourth, sixth, et
tenth most diverse nodes (Figure 4B), suggesting that the Drosophila connectome is organized
to maximize the convergence and, presumably, integration of information prior to motor out-
put. At the modular level, we find that modules contributing significantly to the highly cen-
tral rich club, such as the auditory and olfactory modules, have the greatest average diversity
(Figure 4C).
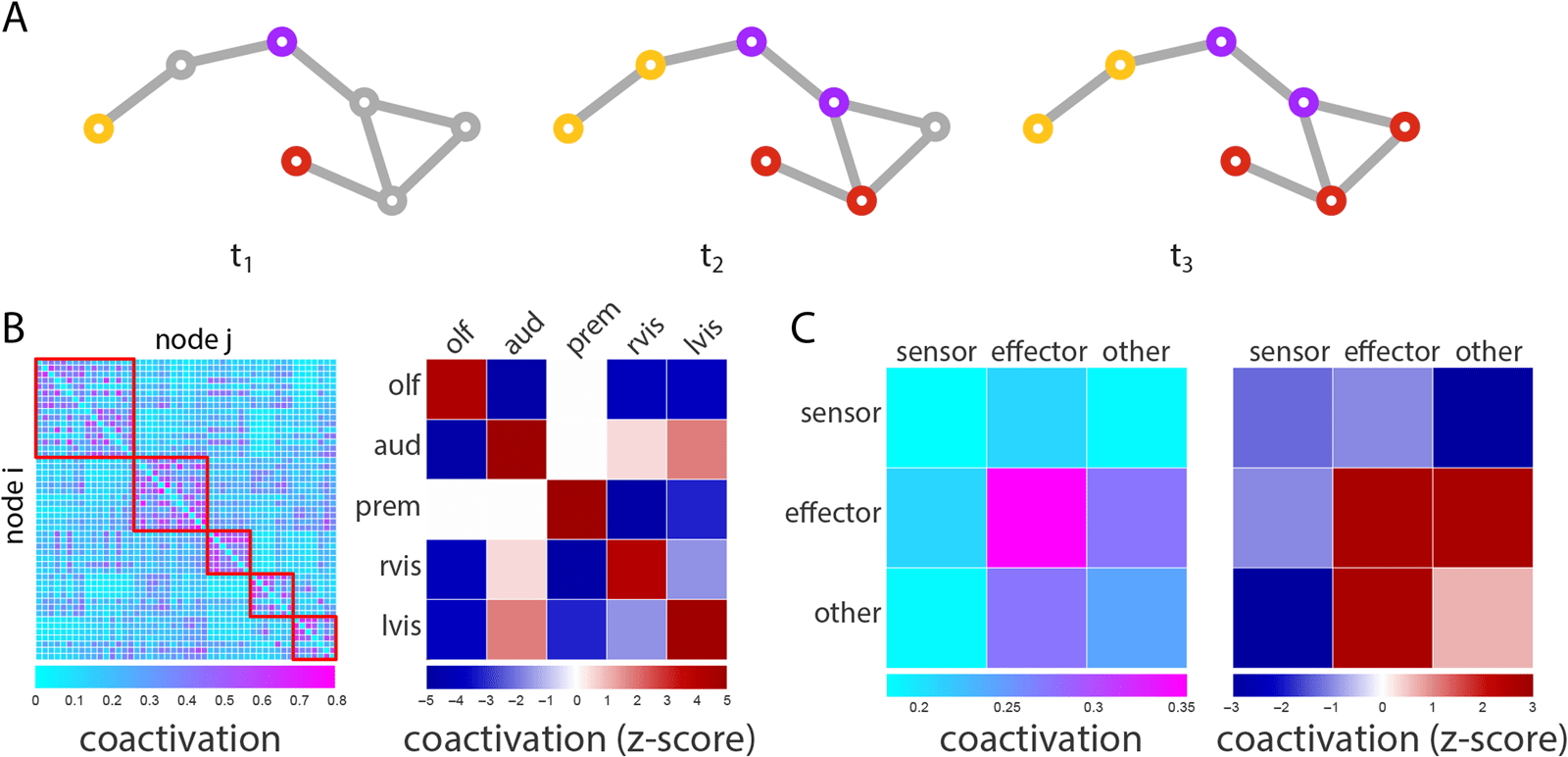
Coactivation of Effectors
Enfin, we investigate the scenario in which more than two perturbations are introduced, chaque
carrying a different signal (par exemple., an auditory and a visual stimulus; Figure 5A). To estimate the
propensity for two nodes to coactivate, we calculate the proportion of time a given node pair
adopts the same signal across all possible seeding scenarios. Node pairs that coactivate often
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
un
_
0
0
0
2
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4. Signal convergence. (UN) Schematic showing the propagation and convergence of two signaling cascades. (B) Mean neighborhood
diversity of all nodes, calculated across all possible two-seed scenarios. (C) Mean neighborhood diversity for each module, expressed as a
z-score relative to a label-permuting null model.
Neurosciences en réseau
420
Sensory-motor integration in the Drosophila connectome
Chiffre 5. Co-activation patterns. (UN) Schematic showing the spread of three competing cascades. (B) Propensity for two nodes to adopt the
same signal (coactivation). Mean coactivations within and between modules are expressed as z-scores relative a label-permuting null model.
(C) Mean coactivation for all combinations of sensor, effector and nonsensor, noneffector (other) nodes. Mean coactivations are also expressed
as z-scores relative to a label-permuting null model.
Coactivation:
Probability for two nodes to be
activated by the same cascade;
quantifies the tendency for
two nodes to engage in similar or
overlapping functions.
are presumably more likely to engage in common or overlapping functions. En effet, pairs of
nodes belonging to the same module tend to display greater coactivation than pairs belonging
to different modules (Figure 5B). Post hoc comparison confirmed that coactivation of nodes
within the same module was greater than coactivation of nodes in different modules (Wilcoxon
p = 9.37 × 10
−50).
Stratifying nodes into sensors and effectors, we find that the greatest coactivation is ob-
served for pairs of effectors, compared with pairs of sensors, pairs of sensors and effectors,
and pairs of sensors and other (nonsensor and noneffector) nodes (p ≈ 0, p = 0.001, p ≈
0; d = 1.21, 1.42, 1.38, respectivement; Figure 5C), suggesting the wiring of the Drosophila connec-
tome potentiates coordination among effectors by allowing common inputs to converge to out-
put LPUs. Comparison with a label-permuting null model further suggests that this enhanced
effector-effector coactivation is driven by topological organization (permuted p = 0.0013;
Figure 5C). Fait intéressant, coactivation among other classes of nodes, such as pairs of sensors,
is lower than expected according to the null model. This suggests that the wiring of the
Drosophila connectome may also minimize some types of functional interactions, effectively
slowing integration or mixing of signals in areas where segregation of function may be more
important, such as sensor nodes.
DISCUSSION
The present study provides further evidence that the anatomical connectivity of brain networks
supports specific modes of neural signaling, giving rise to highly organized spreading patterns.
Using a simple spreading model, we demonstrate that (un) topology potentiates spreading from
sensors to effectors; (b) topology potentiates synergistic relationships among sensors; et (c)
information flow converges towards effectors, facilitating integration and coordination prior to
motor output. The scenarios presented here, while implemented in a formally simple model
of spreading processes in networks, offer a useful framework for testing specific hypotheses
about interactions in neural circuits.
Neurosciences en réseau
421
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
un
_
0
0
0
2
2
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sensory-motor integration in the Drosophila connectome
While the propensity for anatomical pathways to shape functional interactions is well doc-
umented both in computational models (Deco et al., 2009; Goñi et al., 2013; Honey et al.,
2009) and in empirical data (Honey et al., 2009; Miši´c et al., 2016; Shen et al., 2015), a key
question is how topological characteristics shape signal propagation. Our results suggest that
signal spreading is strongly influenced by node strength and by the community structure of the
réseau. Across all spreading scenarios, highly connected nodes and their mutual projections
were disproportionately more involved in signal spreading. This is consistent with the notion
that “hub” nodes promote information transfer and synchronization among remote neuronal
populations, enabling a diverse repertoire of cognitive functions (Bertolero, Yeo, & D'Esposito,
2015; Crossley et al., 2013; Gollo et al., 2015; van den Heuvel & Sporns, 2013; Váša et al.,
2015).
De même, the modular specialization of the network, reflected in its community structure,
imparts a distinct signature on the observed spreading patterns. Two of the central, higher
modules (olfactory and auditory) exhibited a tendency for synergistic interactions, suggérer-
ing a topological predisposition for cooperative function. En outre, LPUs in these modules
were more likely to occupy positions at the border or intersection of multiple cascades, sug-
gesting that their anatomical embedding naturally predisposes them to integrate information
from multiple sources.
Plus généralement, these results highlight how organizational features persist across spatial
scales (Betzel & Bassett, 2016; Lichtman & Denk, 2011). Clear roles have been observed
for rich clubs/cores and for modules, both at the microscopic (Shih et al., 2015; Towlson
et coll., 2013; Varshney et al., 2010) and macroscopic scales (Bota et al., 2015; Hagmann
et coll., 2008; Harriger, van den Heuvel, & Sporns, 2012;
van den
Heuvel et al., 2012; Zamora-López et al., 2010. Our results complement these past studies
by showcasing the possible dynamical importance of these architectural features.
Rubinov et al., 2015;
The importance of anatomical embedding is salient in sensor-effector relationships. Signal
cascades originating from sensor nodes propagated more rapidly to effectors than to other
nodes, suggesting that communication between these classes of nodes may be privileged,
ensuring a rapid transition from perception to action. En outre, signal propagation was
supra-additive (c'est à dire., accelerated) when signals were introduced at pairs of sensors, suggérer-
ing that simultaneous activation of sensors would result in accelerated signaling through the
réseau.
Further downstream, effectors appeared to be the main points of convergence for multiple
cascades. This anatomically driven funneling of information towards motor LPUs suggests that
the Drosophila connectome may be organized to maximize integration prior to motor output,
possibly to allow for sustained control and adjustment. En outre, pairs of effectors displayed
an enhanced potential to coactivate, perhaps reflecting an anatomical organizational principle
to facilitate motor coordination. Fait intéressant, the topological importance of motor neurons has
also been reported in the nematode C. elegans, where synthetic ablations of motor neurons are
associated with the greatest functional disruptions (Bacik et al., 2016). Altogether, these results
demonstrate how simple tractable models can be used to test the effects of focal perturbations
applied to specific regions of interest.
A notable methodological limitation is the choice of threshold parameter. As there is no
external metric by which to evaluate the threshold (par exemple., correspondence with functional con-
nectivity), we employed a heuristic. Namely, we chose the largest possible threshold at which
all perturbations elicit complete cascades, in order to facilitate comparisons among all nodes.
Neurosciences en réseau
422
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
un
_
0
0
0
2
2
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sensory-motor integration in the Drosophila connectome
In the future, we foresee three alternative criteria by which to select the threshold. D'abord, thresh-
olds could be selected with respect to a measure of model fit, such as the correspondence be-
tween spreading patterns and empirical functional connectivity patterns. Deuxième, thresholds
could be selected to favor certain types of dynamics. As we discuss in the Methods section,
at greater thresholds cascades spread via walks outside of shortest paths, akin to a diffusion
processus. Troisième, investigators could allow for the possibility that some cascades do not spread
through the whole network, and instead use the size of the cascade as the dependent variable
in the model, rather than spread velocity. This is commonly done with the linear threshold
model (LTM) (Nematzadeh et al., 2014) and would permit exploration of a wider range of
thresholds.
The present model can offer novel insight into the design principles of neural circuits,
but it does so by sacrificing potentially significant physiological detail. This approach is
similar to other models of naturally occurring complex systems with collective dynam-
ics, such as flocking and swarming behavior in animals (Couzin, Krause, Franks, & Lévine,
2005; Vicsek, Czirók, Ben-Jacob, Cohen, & Shochet, 1995), metropolitan traffic patterns
(Helbing, Farkas, & Vicsek, 2000), disease epidemics (Pastor-Satorras & Vespignani, 2001),
and human social interactions (Schelling, 1971), all of which emphasize the emergent prop-
erties of systems under study at the expense of microscopic detail. This type of approach has
recently been adopted in systems neuroscience as well, where simple models have been used
to gain insight into the emergence of functional interactions (Deco, Senden, & Jirsa, 2012;
Fraiman, Balenzuela, Foss, & Chialvo, 2009; Stramaglia et al., 2017).
it
En particulier,
is worth considering what specific neurobiological phenomena this
model can and cannot represent. The modeled spreading patterns may be thought of as
episodes of synchronized, coherent communication (Beggs & Plenz, 2003; Fries, Reynolds,
Rorie, & Désimone, 2001; Womelsdorf et al., 2007; Zhou, Zemanová, Zamora, Hilgetag, &
Kurths, 2006). Par exemple, if several afferent projections to a neuronal population emanate
from populations that are themselves mutually synchronized, they will act as an external syn-
chronizing force on that population. Ainsi, the model captures how neuronal populations may
generically influence each other via direct and indirect projections. Compared with other types
of neural models (Deco, Jirsa, Robinson, Breakspear, & Friston, 2008), the present spreading
model does not explicitly embody physiological parameters, such as firing rates or membrane
conductance, but serves as a tool to characterize the architecture and dynamic potential of
neural circuits.
Another significant limitation is that the LTM models only the initial spreading pattern orig-
inating from a perturbation, and cannot be used to model any subsequent feedback or time-
dependent reconfiguration of functional interactions. In this sense, the current model may be
thought of as a single, transient episode of synchrony following a perturbation. A simple yet
significant addition to the model would be to include a refractory state, mimicking the refrac-
tory period of single neurons. In that case, the model becomes the well-studied Susceptible-
Infected-Recovered-Susceptible (SIRS) model, a family of epidemiological models that have
also been successfully applied in the study of brain activity (Gollo, Copelli, & Roberts, 2016;
Haimovici, Tagliazucchi, Balenzuela, & Chialvo, 2013). While the addition of refractory pe-
riods introduces rich time-dependent dynamics and broadly conforms to single neuron bio-
physics, it remains to be determined whether such models and the refractory periods they
capture are applicable to populations of neurons and neuronal ensembles.
Neurosciences en réseau
423
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
un
_
0
0
0
2
2
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sensory-motor integration in the Drosophila connectome
Plus généralement, it is worth noting that the LTM belongs to a broader class of contagion mod-
le, whereby the state of a node depends on the state of its neighbors. These models range from
binary decisions in networked systems, such as the diffusion of influence or technological inno-
vations (Valente, 1995), to models of epidemic spreading (Anderson, May, & Anderson, 1992),
bootstrap percolation (Adler, 1991), and self-organized criticality (Bak, Tang, & Wiesenfeld,
1987). Unlike bootstrap percolation and self-organized criticality, where activation depends
on the absolute number of activated neighbors, in the LTM activation depends on the frac-
tion of activated neighbors. In the most general case, the LTM can be conceptualized from
the perspective of standard percolation (Watts, 2002). Percolation is a convenient model of
interactions on complex topologies and refers to the probability of the existence of a path be-
tween all nodes in a graph (Saberi, 2015). The relationship between the LTM and percolation
is therefore straightforward: The susceptibility of the network to global cascades following a
focal perturbation simply depends on the existence of a percolating vulnerable cluster, c'est,
a subgraph of nodes with degrees less than or equal to the inverse of the threshold parameter
(Watts, 2002).
En résumé, the present report offers a framework for studying communication processes
in neural circuits. As advances in imaging and tract tracing techniques propel connectomics
towards comprehensive maps of neuronal connectivity across multiple scales and for multi-
ple organisms, there is a need for general theoretical models that describe the evolution of
communication processes on the anatomical substrate. Our results add to a growing litera-
ture that the organization of neural circuits may be optimized for specific functions, y compris
sensory-motor integration.
MÉTHODES
Drosophila Connectome
The Drosophila connectome was reconstructed from the FlyCircuit 1.1 database (Chiang et al.,
2011; Shih et al., 2015), utilizing images of 12,995 projection neurons in the female Drosophila
brain.
Single neurons were labeled with green fluorescent protein (GFP) using genetic
mosaic analysis with a repressible cell marker. GFP-labeled neurons were then delineated
from whole brain three-dimensional images. Individual GFP-labeled neurons from each im-
age were coregistered to a female template brain using a rigid linear transform.
Individual
neurons were stratified into 49 local populations with distinct morphological and functional
characteristics, termed local processing units (LPUs), which constituted the nodes of the net-
travail. Specifically, LPUs were delineated as neuronal populations with their own population
of local interneurons, whose fibers are limited to that LPU (Shih et al., 2015). The resulting
connectome is represented as a weighted, directed adjacency matrix.
Multiscale Community Detection
The modular structure of
the network was estimated using the Louvain algorithm
(Blondel, Guillaume, Lambiotte, & Lefebvre, 2008), as implemented in the Brain Connec-
tivity Toolbox (Rubinov & Sporns, 2010). Briefly, the goal of the analysis was to identify
communities of LPUs that are more densely interconnected with each other than expected.
This constraint was operationalized in terms of the modularity Q (Leicht & Newman, 2008;
Newman & Girvan, 2004):
Neurosciences en réseau
Q(c) = ∑
ij
[wij − γ · ρij]d(σi, σj),
(1)
424
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
un
_
0
0
0
2
2
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sensory-motor integration in the Drosophila connectome
where wij is observed connection weight between nodes i and j, while ρij is the expected
connection weight between those nodes.
In the present study, the expected connection
weight between pairs of nodes was defined according to a configuration model, dans lequel
node strengths are preserved exactly but where connections are otherwise formed at random,
giving
ρ±
ij =
i sout
sin
j
2m .
(2)
j
i and sout
Ici, sin
are the in- and out-strengths of nodes i and j, and 2m represents the total
density of the network. Variables ci and cj are the community assignments of nodes i and j.
The Kronecker delta function, (ci, cj), is equal to 1 when the arguments ci and cj are equal,
et 0 otherwise, ensuring that modularity is only computed for pairs of nodes belonging to the
same community. The resolution parameter γ scales the relative importance of the null model
ρij, potentiating the discovery of larger (c < 1) or smaller communities (γ > 1).
We scanned the resolution parameters γ = 0.5 to γ = 2, in increments of 0.05. A chaque
scale, the Louvain algorithm was run 250 times to find a partition that maximized the modu-
larity function (Blondel et al., 2008). To select an appropriate scale, we compared the mean
modularity of partitions derived for the empirical network with the mean modularity of parti-
tions derived for a population of 1,000 randomized networks, with the tacit assumption that the
optimal scale is one where the average Q of the empirical network deviates from the average
Q of randomized networks to the greatest extent (Bassett et al., 2013). The randomized net-
works were created using a link-swapping algorithm that preserved the in-degree, out-degree,
and out-strength sequences of the network. The greatest difference was observed at resolution
c = 1.05, yielding five communities or modules.
Rich Club Detection
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
un
_
0
0
0
2
2
p
d
.
t
A consistent finding in connectomics across a range of species is the tendency for high-
degree nodes to be densely interconnected with each other, beyond what would be expected
on the basis of their degrees alone (van den Heuvel et al., 2016). This tendency for nodes
“rich” in connectivity to preferentially connect with each other leads to them being referred
to as a “rich club” (Colizza, Flammini, Serrano, & Vespignani, 2006). This architectural fea-
ture has been posited as a critical component for integrating and disseminating signal traffic
(Miši´c, Sporns, et coll., 2014; van den Heuvel et al., 2012) and stabilizing interareal functional
interactions (Gollo et al., 2015; Miši´c et al., 2016).
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
In the present study we use the rich club stratification of Shih et al. (2015), ce qui était
derived from the same network. Nodes that were classified as being part of the putative rich
club were bilateral DMP, VMP, VLP-D, and SDFP, as well as FB in the central brain. Briefly, rich
club detection was performed over a range of degrees k. Nodes with degree > k are selected
and the rich club coefficient, φ(k), is calculated as the density of the resulting subgraph. Ce
procedure is then repeated for a population of randomized networks with preserved density
et en- and out-degree sequences (Maslov & Sneppen, 2002), generating a null distribution
of rich club coefficients φ(k)random at a particular level k. This null distribution is then used
to normalize the coefficient derived for the original network, yielding a normalized rich club
coefficient φ(k)norm = φ(k)/φ(k)random. A rich club is then defined as a set of nodes with
degree ≥ k over which φ(k)norm is consistently greater than 1.
Neurosciences en réseau
425
Sensory-motor integration in the Drosophila connectome
Communicability
Communicability (Cij) between two nodes i and j is a weighted sum of all paths and walks
between those nodes (Estrada & Hatano, 2008). For a binary adjacency matrix A, communi-
cability is defined as
Cij =
∞
∑
n=0
[Un]ij
n!
= [eA]ij,
(3)
with walks of length n normalized by n!, such that shorter, more direct walks contribute more
than longer walks. This concept can be generalized to weighted networks, but requires normal-
ization to mitigate the influence of high-strength nodes (Crofts & Higham, 2009). Following
Crofts & Higham (2009), this was accomplished by defining a “reduced” adjacency matrix
Ared = S−1/2WS−1/2,
(4)
where W is the weighted adjacency matrix and S is a diagonal matrix of node strengths.
Linear Threshold Model
The linear threshold model describes how a perturbation introduced at one or more seed
nodes develops into a cascade and spreads through a network (Granovetter, 1978; Watts,
2002). The perturbation and subsequent cascade are modeled as an active state; any given
node adopts this active state only if a certain threshold proportion of its neighbors have also
adopted the active state. A family of simple models of collective behavior, LTMs have been ex-
tensively studied over a wide range of networks, including spatially embdedded brain networks
(kaiser, Goerner, & Hilgetag, 2007; kaiser & Hilgetag, 2010; Miši´c et al., 2015; O’Dea et al.,
2013). The models capture how generic focal perturbations, such as the transduction of a sen-
sory stimulus, spread through connected neuronal populations (see the Discussion section for
a discussion of the neurobiological interpretation and limitations).
Officiellement, the state of a node i at time t is denoted as a binary variable ri(t) = {0, 1}, avec
only two possible states: active (1) or inactive (0). At initialization (t = 0), the entire network is
inactive, except for a subset of activated seed nodes. The model is then updated synchronously
at each time step according to the following rule:
(cid:2)
ri(t + 1) =
1
if θsi < ∑j∈Ni
rj(t)
0 otherwise.
(5)
Thus, at each time step the state of node i depends on its neighborhood, Ni, and specifically
on the number of incident connections (in-degree or in-strength, si). The node adopts the active
state only if the proportion of inputs from active nodes exceeds the threshold θ. In the case
of binary networks, the threshold represents the proportion of a node’s neighbors that must be
active to propagate the cascade. The model can be naturally extended to weighted networks,
whereby the threshold represents the proportion of a node’s total weighted inputs (in-strength)
In all scenarios, the fundamental performance
that must be connected to active neighbors.
measure is the adoption or spread time Ai→k, from seed node i to target node k.
The threshold parameter was chosen to satisfy two criteria. At lower thresholds, nodes re-
quire fewer neighbors to be active at time t in order to become active themselves at time t + 1.
Network Neuroscience
426
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
a
_
0
0
0
2
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sensory-motor integration in the Drosophila connectome
Thus, nodes will be activated at the earliest possible time step, and the cascade will effectively
propagate along the shortest path. As the threshold is increased beyond the inverse of the
highest degree/strength in the network, cascades can no longer influence the most highly con-
nected nodes and do not spread through the whole network. Because we sought to compare
spreading times for all possible seed-target combinations, we set the threshold to the highest
value at which all perturbations will cause a complete cascade (θ = 0.01). As we discuss in
more detail in the Results section, at this threshold cascades will spread to all target nodes, but
their trajectory is only partially predicted by shortest path length (r = 0.34, p ≈ 0), with much
of the spreading process occurring via alternative paths as well.
Note that the activation of a target node depends on three factors: target node in-strength,
source node out-strength, and topology. The relative importance of these factors depends
on the threshold. Specifically, at higher thresholds it is more difficult to activate nodes, as
more of their neighbors need to be active, so the dynamics are more dependent on local
connectivity. At lower thresholds, the dynamics are less constrained by local connectivity and
more influenced by global topology. Thus, by limiting the threshold to allow spreading to all
target nodes, the dynamics are also more likely to be shaped by global topology.
The order in which individual projections contribute to the spreading of a cascade can be
inferred using asynchronous updating. In this case, the propagation of influence is not instan-
taneous, but subject to a finite transit time. In the present study, transit times were assumed
to be proportional to the ratio of projection length and projection weight. This operational-
izes the idea that transmission along short, strong projections should be faster compared with
long, weak projections. As a result, activations and signal spreading take place at nonuniform
time intervals, and the model is updated asynchronously. Differences in transit times can then
be used to infer, for any given node, exactly which of its incoming projections were used to
propagate the cascade.
Two Seeds, Same Signal
We next investigate scenarios where identical perturbations are initiated in two seed nodes
simultaneously. If the resultant cascade spread is accelerated relative to the single-seed cases,
this would indicate a synergistic relationship between the two seed nodes, that is, that those
two nodes would potentially benefit from simultaneous stimulation due to the topology of
the network. Specifically, we assess the spread time speedup (Sij→k) of a particular two-seed
combination (Aij→k) relative to the faster of the individual single-seed scenarios (Ai→k, Aj→k):
Sij→k = min(Ai→k, Aj→k) − Aij→k
min(Ai→k, Aj→k)
.
(6)
Two Seeds, Different Signals
To investigate the evolution of multiple cascades, we extend the model to include two active
states, for example, ri(t) = {0, 1, 2}. Once a node adopts a particular state, it remains in that
state indefinitely. For a node to adopt a particular state, its weighted inputs for that specific state
must be greater than the threshold. Thus, inputs from competing states cannot be combined to
exceed the threshold. If multiple competing states exceed the threshold for a particular node,
the node adopts the state associated with the greatest total weight of its inputs.
Importantly, as the cascades develop, they eventually meet and form one or more fronts. In
this scenario, we focus on the propensity of a node to mediate the integration of two cascades.
Network Neuroscience
427
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
a
_
0
0
0
2
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sensory-motor integration in the Drosophila connectome
To do so, we estimate the diversity of a node’s neighborhood as the entropy of its neighborhood
vector. Specifically, for a set of c possible active states, the probability that the neighbors of
node i will adopt state xc is given by the entropy of its neighborhood:
hi = − ∑
c
P {xc} logP {xc}.
(7)
Multiple Seeds, Multiple Signals
To investigate the propensity of nodes to coactivate, we extended the competitive spreading
scenario described above to include more than two seeds. Specifically, we initiated two to
p perturbations, each carrying a different signal. For any two nodes i and j, coactivation is
defined as the propensity of that node pair to adopt the same signal. More formally, coactiva-
tion is defined as the number of times that nodes i and j adopted the same signal across all
possible seeding scenarios. We performed this procedure for a range of scenarios, from p = 2
to p = 10 seeds. Since the number of possible seed combinations increases exponentially
with the number of seeds, we sampled, without replacement, the space of all possible seed
combinations by randomly choosing m = 10, 000 pairs for each p-seed scenario.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
a
_
0
0
0
2
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
AUTHOR CONTRIBUTIONS
Jacob C. Worrell: Formal analysis; Visualization; Writing – original draft. Jeffrey Rumschlag:
Formal analysis. Richard F. Betzel: Methodology; Writing – review & editing. Olaf Sporns:
Conceptualization; Writing – original draft; Writing – review & editing. Bratislav Miši´c: Con-
ceptualization; Formal analysis; Methodology; Supervision; Visualization; Writing – original
draft; Writing – review & editing.
FUNDING INFORMATION
BM acknowledges support from the Natural Sciences and Engineering Research Council of
Canada (NSERC Discovery Grant RGPIN #017-04265) and from the Fonds de recherche du
Québec - Santé (Chercheur Boursier). OS acknowledges support from the J.S. McDonnell
Foundation (#220020387), the National Science Foundation (#1212778), and the National
Institutes of Health (NIH R01 AT009036-01).
REFERENCES
Abdelnour, F., Voss, H., & Raj, A.
(2014). Network diffu-
sion accurately models the relationship between structural
and functional brain connectivity networks. NeuroImage, 90,
335–347.
Adler, J. (1991). Bootstrap percolation. Physica A, 171(3), 453–470.
Infectious
Anderson, R. M., May, R. M., & Anderson, B.
diseases of humans: dynamics and control (Vol. 28). Wiley
Online Library.
(1992).
Atasoy, S., Donnelly, I., & Pearson, J.
(2016). Human brain net-
works function in connectome-specific harmonic waves. Nature
Communications, 7.
Avena-Koenigsberger, A., Miši´c, B., Hawkins, R. X., Griffa, A.,
Hagmann, P., Goñi, J., & Sporns, O.
(2017). Path ensembles
and a tradeoff between communication efficiency and resilience
in the human connectome. Brain Structure Function, 222(1),
603–618.
Bacik, K. A., Schaub, M. T., Beguerisse-Díaz, M., Billeh, Y. N.,
& Barahona, M.
(2016). Flow-based network analysis of the
caenorhabditis elegans connectome. PLoS Computational Biol-
ogy, 12(8), e1005055.
Bak, P., Tang, C., & Wiesenfeld, K.
(1987). Self-organized criti-
cality: An explanation of the 1/f noise. Physical Review Letters,
59(4), 381.
Bassett, D., Porter, M., Wymbs, N., Grafton, S., Carlson, J., &
(2013). Robust detection of dynamic community
Mucha, P.
structure in networks. Chaos, 23(1), 013142.
Beggs, J., & Plenz, D. (2003). Neuronal avalanches in neocortical
circuits. Journal of Neuroscience, 23(35), 11167–11177.
Network Neuroscience
428
Sensory-motor integration in the Drosophila connectome
Bertolero, M. A., Yeo, B. T., & D’Esposito, M.
(2015). The mod-
ular and integrative functional architecture of the human brain.
Proceedings of the National Academy of Sciences, 112(49),
E6798–E6807.
Betzel, R., Griffa, A., Avena-Koenigsberger, A., Goñi, J., Thiran,
J.-P., Hagmann, P., et al.
(2013). Multi-scale community orga-
nization of the human structural connectome and its relation-
ship with resting-state functional connectivity. Network Science,
1(03), 353–373.
Betzel, R. F., & Bassett, D. S.
(2016). Multi-scale brain networks.
NeuroImage, 160, 73–83. https://doi.org/10.1016/j.neuroimage.
2016.11.006
Blondel, V., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E. (2008).
Fast unfolding of communities in large networks. Journal of Sta-
tistical Mechanics: Theory and Experiment, 2008(10), P10008.
Bota, M., Sporns, O., & Swanson, L. W.
(2015). Architecture of
the cerebral cortical association connectome underlying cogni-
tion. Proceedings of the National Academy of Sciences, 112(16),
E2093–E2101.
Chiang, A.-S., Lin, C.-Y., Chuang, C.-C., Chang, H.-M., Hsieh,
C.-H., Yeh, C.-W., . . . Hwang, J.-K. (2011). Three-dimensional
reconstruction of brain-wide wiring networks in Drosophila at
single-cell resolution. Current Biology, 21(1), 1–11.
Colizza, V., Flammini, A., Serrano, M., & Vespignani, A.
(2006).
Detecting rich-club ordering in complex networks. Nature
Physics, 2(2), 110–115.
Couzin, I., Krause, J., Franks, N., & Levin, S.
(2005). Effective
leadership and decision-making in animal groups on the move.
Nature, 433(7025), 513–516.
Crofts, J. J., & Higham, D. J. (2009). A weighted communicability
measure applied to complex brain networks. Journal of the Royal
Society Interface, 6(33), 411–414.
Crossley, N., Mechelli, A., Vértes, P., Winton-Brown, T., Patel, A.,
Ginestet, C., . . . Bullmore, E.
(2013). Cognitive relevance of
the community structure of the human brain functional coactiva-
tion network. Proceedings of the National Academy of Sciences,
110(28), 11583–11588.
Deco, G., Jirsa, V., McIntosh, A. R., Sporns, O., & Kötter, R. (2009).
Key role of coupling, delay, and noise in resting brain fluctua-
tions. Proceedings of the National Academy of Sciences, 106(25),
10302–10307.
Deco, G., Jirsa, V., Robinson, P., Breakspear, M., & Friston, K.
(2008). The dynamic brain: From spiking neurons to neural
masses and cortical fields. PLoS Computational Biology, 4(8),
e1000092.
Deco, G., Senden, M., & Jirsa, V.
(2012). How anatomy shapes
dynamics: A semi-analytical study of the brain at rest by a simple
spin model. Frontiers in Computational Neuroscience, 6, 68.
Estrada, E., & Hatano, N.
(2008). Communicability in complex
networks. Physical Review E, 77(3), 036111.
Fraiman, D., Balenzuela, P., Foss, J., & Chialvo, D. R. (2009). Ising-
like dynamics in large-scale functional brain networks. Physical
Review E, 79(6), 061922.
Fries, P., Reynolds, J., Rorie, A., & Desimone, R.
(2001). Modu-
lation of oscillatory neuronal synchronization by selective visual
attention. Science, 291(5508), 1560–1563.
Gollo, L. L., Copelli, M., & Roberts, J. A. (2016). Diversity improves
performance in excitable networks. PeerJ, 4, e1912.
Gollo, L. L., Zalesky, A., Hutchison, R. M., van den Heuvel, M., &
Breakspear, M. (2015). Dwelling quietly in the rich club: Brain
network determinants of slow cortical fluctuations. Philosophical
Transactions of the Royal Society B, 370(1668), 20140165.
Goñi,
J., van den Heuvel, M., Avena-Koenigsberger, A., de
Mendizabal, N., Betzel, R., Griffa, A., . . . Sporns, O.
(2013).
Resting-brain functional connectivity predicted by analytic mea-
sures of network communication. Proceedings of the National
Academy of Sciences, 111(2), 833–838.
Granovetter, M.
(1978). Threshold models of collective behavior.
American Journal of Sociology, 83(6), 1420–1443.
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C.,
(2008). Mapping the structural core
Wedeen, V., & Sporns, O.
of human cerebral cortex. PLoS Biology, 6(7), e159.
Haimovici, A., Tagliazucchi, E., Balenzuela, P., & Chialvo, D. R.
(2013). Brain organization into resting state networks emerges at
criticality on a model of the human connectome. Physical Review
Letters, 110(17), 178101.
Harriger, L., van den Heuvel, M. P., & Sporns, O. (2012). Rich club
organization of macaque cerebral cortex and its role in network
communication. PLoS ONE, 7(9), e46497.
Helbing, D., Farkas, I., & Vicsek, T. (2000). Simulating dynamical
features of escape panic. Nature, 407(6803), 487–490.
Honey, C., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J.-P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Proceedings
of the National Academy of Sciences, 106(6), 2035–2040.
Kaiser, M., Goerner, M., & Hilgetag, C. C.
(2007). Criticality of
spreading dynamics in hierarchical cluster networks without
inhibition. New Journal of Physics, 9(5), 110.
Kaiser, M., & Hilgetag, C. C. (2010). Optimal hierarchical modular
topologies for producing limited sustained activation of neural
networks. Frontiers in Neuroinformatics, 4(8).
Leicht, E. A., & Newman, M. E.
(2008). Community structure in
directed networks. Physical Review Letters, 100(11), 118703.
Lichtman, J. W., & Denk, W.
(2011). The big and the small:
Challenges of imaging the brain’s circuits. Science, 334(6056),
618–623.
Maslov, S., & Sneppen, K. (2002). Specificity and stability in topol-
ogy of protein networks. Science, 296(5569), 910–913.
Miši´c, B., Betzel, R. F., De Reus, M. A., van den Heuvel, M. P.,
Berman, M. G., McIntosh, A. R., & Sporns, O. (2016). Network-
level
structure-function relationships in human neocortex.
Cerebral Cortex, 26(7), 3285–3296.
Miši´c, B., Betzel, R. F., Nematzadeh, A., Goñi,
J., Griffa, A.,
Hagmann, P., . . . Sporns, O. (2015). Cooperative and compet-
itive spreading dynamics on the human connectome. Neuron,
86(6), 1518–1529.
Miši´c, B., Goñi, J., Betzel, R. F., Sporns, O., & McIntosh, A. R.
(2014). A network convergence zone in the hippocampus. PLoS
Computational Biology, 10(12), e1003982.
Miši´c, B., & Sporns, O.
(2016). From regions to connections and
networks: New bridges between brain and behavior. Current
Opinion in Neurobiology, 40, 1–7.
Network Neuroscience
429
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
a
_
0
0
0
2
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sensory-motor integration in the Drosophila connectome
Miši´c, B., Sporns O., & McIntosh, A. R.
(2014). Communication
efficiency and congestion of signal traffic in large-scale brain
networks. PLoS Computational Biology, 10(1), e1003427.
Nematzadeh, A., Ferrara, E., Flammini, A., & Ahn, Y.-Y.
(2014).
Optimal network modularity for information diffusion. Physical
Review Letters, 113(8), 088701.
Newman, M., & Girvan, M.
Finding and evaluating
community structure in networks. Physical Review E, 69(2),
026113.
(2004).
O’Dea, R., Crofts, J., & Kaiser, M.
(2013). Spreading dynamics
on spatially constrained complex brain networks. Journal of the
Royal Society Interface, 10(81), 20130016.
Pastor-Satorras, R., & Vespignani, A. (2001). Epidemic spreading in
scale-free networks. Physical Review Letters, 86(14), 3200.
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069.
Rubinov, M., Ypma, R. J., Watson, C., & Bullmore, E. T.
(2015).
Wiring cost and topological participation of the mouse brain
connectome. Proceedings of the National Academy of Sciences,
112(32), 10032–10037.
Saberi, A. A. (2015). Recent advances in percolation theory and its
applications. Physics Reports, 578, 1–32.
Schelling, T.
(1971). Dynamic models of segregation.
Journal of
Mathematical Sociology, 1(2), 143–186.
Shen, K., Miši´c, B., Cipollini, B. N., Bezgin, G., Buschkuehl, M.,
Hutchison, R. M., . . . Berman, M. G. (2015). Stable long-range
interhemispheric coordination is supported by direct anatomical
projections. Proceedings of the National Academy of Sciences,
112(20), 6473–6478.
Shih, C.-T., Sporns, O., Yuan, S.-L., Su, T.-S., Lin, Y.-J., Chuang,
C.-C., . . . Chiang, A.-S.
(2015). Connectomics-based analy-
sis of information flow in the drosophila brain. Current Biology,
25(10), 1249–1258.
Sporns, O.
(2014). Contributions and challenges for network
models in cognitive neuroscience. Nature Neuroscience, 17(5),
652–660.
Stramaglia, S., Pellicoro, M., Angelini, L., Amico, E., Aerts, H.,
Cortes, J., . . . Marinazzo, D.
Ising model with con-
served magnetization on the human connectome: Implications
on the relation structure-function in wakefulness and anesthesia.
Chaos, 27, 047407.
(2017).
Towlson, E. K., Vértes, P. E., Ahnert, S. E., Schafer, W. R., &
Bullmore, E. T. (2013). The rich club of the C. elegans neuronal
connectome. Journal of Neuroscience, 33(15), 6380–6387.
Valente, T. W. (1995). Network models of the diffusion of innova-
tions. Cresskill, NJ: Hampton, Press.
van den Heuvel, M., Kahn, R., Goñi, J., & Sporns, O.
(2012).
High-cost, high-capacity backbone for global brain communica-
tion. Proceedings of the National Academy of Sciences, 109(28),
11372–11377.
van den Heuvel, M., & Sporns, O.
(2013). Network hubs in the
human brain. Trends in Cognitive Sciences, 17(12), 683–696.
van den Heuvel, M. P., Bullmore, E. T., & Sporns, O.
(2016).
Comparative connectomics. Trends in Cognitive Sciences, 20(5),
345–361.
Varshney, L. R., Chen, B. L., Paniagua, E., Hall, D. H., & Chklovskii,
Structural properties of the Caenorhabditis
D. B.
elegans neuronal network. PLoS Computational Biology, 7(2),
e1001066.
(2010).
Váša, F., Shanahan, M., Hellyer, P. J., Scott, G., Cabral, J., & Leech,
(2015). Effects of lesions on synchrony and metastability in
R.
cortical networks. NeuroImage, 118, 456–467.
Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I., & Shochet, O.
(1995). Novel type of phase transition in a system of self-driven
particles. Physical Review Letters, 75(6), 1226.
Vogelstein, J. T., Park, Y., Ohyama, T., Kerr, R. A., Truman, J. W.,
Priebe, C. E., & Zlatic, M. (2014). Discovery of brainwide neural-
behavioral maps via multiscale unsupervised structure learning.
Science, 344(6182), 386–392.
Watts, D.
(2002). A simple model of global cascades on random
networks. Proceedings of the National Academy of Sciences,
99(9), 5766–5771.
Womelsdorf, T., Schoffelen,
J.-M., Oostenveld, R., Singer, W.,
Desimone, R., Engel, A., & Fries, P. (2007). Modulation of neu-
ronal interactions through neuronal synchronization. Science,
316(5831), 1609–1612.
Zamora-López, G., Zhou, C., & Kurths, J. (2010). Cortical hubs form
a module for multisensory integration on top of the hierarchy of
cortical networks. Frontiers in Neuroinformatics, 4(1).
Zhou, C., Zemanová, L., Zamora, G., Hilgetag, C., & Kurths, J.
(2006). Hierarchical organization unveiled by functional con-
nectivity in complex brain networks. Physical Review Letters,
97(23), 238103.
Network Neuroscience
430
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
4
1
5
1
0
9
1
8
6
5
n
e
n
_
a
_
0
0
0
2
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3