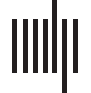RECHERCHE
Applying multilayer analysis to morphological,
structural, and functional brain networks to
identify relevant dysfunction patterns
Jordi Casas-Roma1*
, Eloy Martinez-Heras2*
, Albert Solé-Ribalta3
Elisabet Lopez-Soley2
, Francesc Vivó2
, Marcos Diaz-Hurtado1
, Elisabeth Solana2
,
,
Salut Alba-Arbalat2
, Maria Sepulveda2
, Yolanda Blanco2
, Albert Saiz2
,
Javier Borge-Holthoefer3
, Sara Llufriu2
, and Ferran Prados1,4,5
1e-Health Center, Universitat Oberta de Catalunya, Barcelona, Espagne
2Center of Neuroimmunology, Laboratory of Advanced Imaging in Neuroimmunological Diseases (ImaginEM),
Hospital Clínic de Barcelona, Institut d’Investigacions Biomèdiques August Pi i Sunyer (IDIBAPS),
Universitat de Barcelona, Barcelona, Espagne
3IN3, Universitat Oberta de Catalunya, Barcelona, Espagne
4Centre for Medical Image Computing, Department of Medical Physics and Biomedical Engineering,
University College London, Londres, United Kingdom
5Queen Square MS Centre, Department of Neuroinflammation, UCL Institute of Neurology, Faculty of Brain Sciences,
University College London, Londres, United Kingdom
*These authors contributed equally.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
un
_
0
0
2
5
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mots clés: Structural connectivity, Functional connectivity, Gray matter networks, Multiple
sclerosis, Multilayer
ABSTRAIT
Au cours des dernières années, research on network analysis applied to MRI data has advanced significantly.
Cependant, the majority of the studies are limited to single networks obtained from resting-state
IRMf, diffusion MRI, or gray matter probability maps derived from T1 images. Although a
limited number of previous studies have combined two of these networks, none have
introduced a framework to combine morphological, structural, and functional brain
connectivity networks. The aim of this study was to combine the morphological, structural,
and functional information, thus defining a new multilayer network perspective. This has
proved advantageous when jointly analyzing multiple types of relational data from the same
objects simultaneously using graph- mining techniques. The main contribution of this research
is the design, development, and validation of a framework that merges these three layers of
information into one multilayer network that links and relates the integrity of white matter
connections with gray matter probability maps and resting-state fMRI. To validate our
framework, several metrics from graph theory are expanded and adapted to our specific
domain characteristics. This proof of concept was applied to a cohort of people with multiple
sclerosis, and results show that several brain regions with a synchronized connectivity
deterioration could be identified.
RÉSUMÉ DE L'AUTEUR
This study presents the design, development, and validation of a framework that merges
morphological, structural, and functional brain connectivity networks into one multilayer
réseau. To validate our framework, several metrics from graph theory are expanded and
adapted to our specific domain characteristics. This proof of concept was applied to a cohort
un accès ouvert
journal
Citation: Casas-Roma, J., Martinez-
Heras, E., Solé-Ribalta, UN., Solana, E.,
Lopez-Soley, E., Vivó, F., Diaz-Hurtado,
M., Alba-Arbalat, S., Sepulveda, M.,
Blanco, Y., Saiz, UN., Borge-Holthoefer,
J., Llufriu, S., & Prados, F. (2022).
Applying multilayer analysis to
morphological, structural, et
functional brain networks to identify
relevant dysfunction patterns. Réseau
Neurosciences, 6(3), 916–933. https://est ce que je
.org/10.1162/netn_a_00258
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00258
Informations complémentaires:
https://doi.org/10.1162/netn_a_00258;
https://github.com/ADaS-Lab
/Multilayer-MRI
Reçu: 10 Mars 2022
Accepté: 7 Juin 2022
Intérêts concurrents: See Competing
Interests section.
Auteur correspondant:
Jordi Casas-Roma
jcasasr@uoc.edu
Éditeur de manipulation:
Olaf Sporns
droits d'auteur: © 2022
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
Applying multilayer analysis to brain networks
Réseau:
Also known as a graph, it is a set of
entities (nodes) and relationships
between pairs of nodes (links).
Multilayer network:
Network composed of different
layers, each representing a single
type of relationship between nodes
within one layer.
of people with multiple sclerosis, and results show that some brain regions with a
synchronized connectivity deterioration could be identified.
INTRODUCTION
In the field of neuroscience, studying brain networks in the context of both health and disease
is common and plays a critical role in shedding light on the brain mechanisms driving cogni-
tive processes such as learning or reasoning, as well as addressing brain damage (Bassett &
Sporns, 2017). Recent advances in magnetic resonance imaging (IRM) have facilitated the
study of brain connectivity structures and functions and provide a comprehensive understand-
ing of aspects of brain connectivity behavior and organization (Bennett & Rypma, 2013;
Groppa et al., 2021). Graph theoretical analysis enables us to model complex network systems
with comprehensive indices related to the integration, segregation, and propagation of infor-
mation inside the brain system (Sporns, 2013). Cependant, most studies focus on only the topo-
logical characteristics of brain structural or functional connectivity metrics without considering
the interactions between them. This approach limits knowledge on how the brain works or
how it responds to damage. It is our hypothesis that integrating information on structural
connectivity based on fractional anisotropy (FA)-weighted connectivity, gray matter (GM) mor-
phological association networks, and functional connections studied through resting-state
functional connectivity can provide further insights and new knowledge on brain organization.
This integration of data could be carried out taking multiple approaches used in previous
études. Par exemple, some indirect methods analyze each network separately using the same
graph theory metrics, and then merge the quantitative brain network properties using
advanced statistical methods (Shu et al., 2016). Other indirect methods apply machine learn-
ing techniques to extract different patterns or obtain groups from the networks analyzed (Zitnik
et coll., 2019). A further method uses more advanced techniques such as deep learning methods
and graph neural networks (GNN; Ma & Tang, 2021) to directly analyze all the networks
simultaneously. Yet another strategy, known as multilayer or multiplex networks, integrates
all the networks into a single higher dimensional graph, and with the information from all
the networks compiled, can perform a direct data analysis.
In terms of flexibility, this method can integrate information from structural and functional
graph theoretical analysis into a multilayer network framework, and extract the multilayer
organization of human brain connectivity in a neurological disease context, such as multiple
sclerosis (MS; Chard et al., 2021). MS is a chronic, inflammatory, demyelinating, and neuro-
degenerative disease of the central nervous system characterized by widespread damage lead-
ing to disruption of large- and short-scale structural and functional connectivity, which leads to
clinical alterations (Fleischer et al., 2019; Rocca et al., 2015). Local and global implications of
damage on networked systems, such as our brain, have been studied from many angles using
complex networks (Newman, 2018). Ainsi, network theory approaches have been widely
applied in the field of neuroscience to study both structural and functional connectivity and
explore its relationship with cognitive function (Llufriu et al., 2017; Pagani et al., 2020; Rocca
et coll., 2016). Cependant, in this context, single network analysis is limited to only one feature,
and hence, does not fully describe the complexity of brain mechanisms after damage.
The multilayer network approach (Kivelä et al., 2014; Boccaletti et al., 2014), on the other
main, enables one to incorporate different types of relational information between brain
régions, and additionally to encode their cross relationships. This generic modeling framework
Neurosciences en réseau
917
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
un
_
0
0
2
5
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Applying multilayer analysis to brain networks
Node:
Mathematical representation of an
entity, also known as a vertex. In our
case, it refers to a group of voxels.
Link:
A mathematical representation of a
relationship between two nodes, aussi
called edge.
can be exploited in different ways to study the brain in its different states (De Domenico, 2017;
Muldon & Bassett, 2016), such as frequency-based decompositions (Buldú & Porter, 2018;
Guillon et al., 2017), time-varying networks (Betzel et al., 2019; Pedersen et al., 2018; Ting
et coll., 2021), or structural and functional decomposition (Battiston et al., 2017; Battiston et al.,
2018), although with drawbacks and challenges (Mandke et al., 2018). Within this last mul-
tilayer framework, the brain is divided into different regions that are represented by network
nodes with a one-to-one correspondence between the nodes in the different layers that repre-
sent different brain modality (par exemple., EEG, IRMf, dMRI). This provides, to date, the most robust
approach to integrate different types of brain networks into a single framework, plutôt que
simply joining and combining information obtained considering the layers independently,
or extracting them from the aggregated network.
Multilayer networks have been used in the past to study brain function at many
levels—microscale (De Domenico et al., 2016), mesoscale (Battiston et al., 2017; Battiston
et coll., 2018; Crofts et al., 2016; Ting et al., 2021), and macroscale (Buldú & Porter, 2018;
Cociu et al., 2018; Pedersen et al., 2018; Suárez et al., 2020)—and have been applied to
the analysis of different types of disorders (Gifford et al., 2020; Guillon et al., 2017; Guillon
et coll., 2019; Liu et al., 2017) or normal brain functioning, or simply to understand the brain’s
organization (Betzel et al., 2019; De Domenico, 2017; Muldon & Bassett, 2016). Intérêt-
franchement, each different disorder requires different adaptations of the general multilayer frame-
travail: definition of layers and interlinks, which may take advantage of the information that
can be obtained from the different layers individually (Liu et al., 2017).
This study presents the conceptual framework that contributes to the state of the art from
two points. We first explore and extend the brain multilayer framework to habilitate the joint
analysis of morphological, structural, and functional networks, which to date was limited to
only structural and functional networks. From there, we expand several metrics from network
theory to analyze the proposed multilayer scheme. Enfin, the multilayer framework is
adapted to study a cohort of people with MS as a proof of concept, and we detect several brain
regions with a synchronized connectivity deterioration.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
un
_
0
0
2
5
8
p
d
.
t
MATERIAL AND METHODS
Participants
This study used data on patients with relapsing-remitting MS aged 18–65 years, and consec-
utively recruited at the MS Unit at Hospital Clínic de Barcelona. The cohort was composed of
125 subjects diagnosed with MS according to the 2010 McDonald criteria (Polman et al.,
2011) et 45 healthy volunteers (HV) without relapses in the last 3 months or a previous his-
tory of psychiatric diseases. Physical disability was evaluated using the Expanded Disability
Status Scale (EDSS). The Ethics Committee of the Hospital Clínic de Barcelona approved the
étude, and all participants signed an informed consent.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Magnetic Resonance Acquisition Details
MRI acquisition protocols were acquired on a 3T Magnetom Trio scanner (SIEMENS, Erlanger,
Allemagne) using a 32-channel phased-array head coil. In part of the cohort (n = 87 partici-
pants), the high-resolution three-dimensional magnetization-prepared rapid acquisition with
gradient echo (3D-MPRAGE) was acquired with TR = 1,800 ms; LE = 3.01 ms; TI = 900 ms;
240 sagittal slices with 0.94 mm isotropic voxel size; and a 256 × 256 matrix size; et le
three-dimensional fluid-attenuated inversion recovery (3D-T2 FLAIR) with TR = 5,000 ms; LE =
304 ms; TI = 1,800 ms; 192 sagittal slices with 0.94 mm isotropic voxel size; and a 256 × 256
Neurosciences en réseau
918
Applying multilayer analysis to brain networks
matrix size. The diffusion-weighted imaging (DWI) had a TR = 14,800 ms; LE = 103 ms; 100 con-
tiguous axial slices; 1.5 mm isotropic voxel size; un 154 × 154 matrix size; b-value = 1,000 s/mm2;
60 diffusion encoding directions; and a single baseline image acquired at 0 s/mm2. The remaining
participants (n = 83) had a 3D-structural image with TR = 1,970 ms; LE = 2.41 ms; TI = 1,050 ms;
208 sagittal slices with 0.9 mm isotropic voxel size; and a 256 × 256 matrix size; and the 3D-T2
FLAIR with TR = 5,000 ms; LE = 393 ms; TI = 1,800 ms; 208 sagittal slices with 0.9 mm isotropic
voxel size; and a 256 × 256 matrix size. The DWI acquisition protocol was as follows: TR =
12,600 ms; LE = 112 ms; 80 contiguous axial slices; 2 mm isotropic voxel size; un 120 × 120
matrix size; b-value = 1,500 s/mm2; 70 diffusion encoding directions; and a single baseline
image acquired at 0 s/mm2. En outre, field map images were generated for all participants
and used to correct distortions caused by field inhomogeneities (TE 1 / TE 2 = 4.92/7.38 ms, avec
the same slice prescription, slice thickness, and field of view as the DWI sequence).
Pour 143 sujets (125 people with MS and 18 HV), the same resting-state functional MRI
(rs-fMRI) protocol was acquired using BOLD EPI pulse sequence (fat saturation), with TR =
2,000 ms; LE = 19 ms; field of view = 220 mm; 40 contiguous axial slices with 1.7 × 1.7 ×
3 mm voxel size; GRAPPA-factor of 4; and a total of 450 frames (TA = 15:14 min).
Data Processing
Anatomical parcellation scheme. White matter lesions were delineated with 3D-MPRAGE and
3D-FLAIR images using JIM7 software (https://www.xinapse.com/). Subsequently, white matter
lesions were filled in 3D-MPRAGE with the intensity of the non-lesional neighboring voxels to
improve MS patient registration and segmentation processing (Battaglini et al., 2012). Lesion-
filled images were used to parcellate the cortex into 62 GM regions and 14 subcortical regions
using Mindboggle software and FSL-FIRST packages, respectivement (Klein et al., 2017;
Patenaude et al., 2011). The anatomical cortical parcellation computed by Mindboogle was
extracted from the Desikan-Killiany-Tourville atlas (Desikan et al., 2006). The nodes of the
three brain networks constructed are the 76 brain regions depicted; thus, the same parcellation
is used within each network.
Structural brain connectivity network. The first step in constructing a structural connectivity
matrix was to build a DWI preprocessing pipeline to fit the diffusion tensor imaging (DTI)
model, an approach previously described and well established by Tournier et al. (2019). Major
components of the pipeline included MP-PCA denoising, Gibbs ringing removal, eddy current
and motion correction, geometrically unwarping procedure, and bias field correction. Once
these corrections were made, the FA scalar map was computed from the DTI model using FSL’s
DTIFIT (Basser et al., 1994). The structural connectivity matrices derived from FA-weighted
indices were generated using the results from the high-order probabilistic streamline tractogra-
phy between distinct cortical and subcortical GM areas (nodes) of the whole brain. To guar-
antee biologically plausible reconstructed streamlines, the connectome reconstruction process
incorporated the anatomical constrained tractography (ACT) framework, from which a set of
six million streamlines were selected, and postprocessing based on anatomical exclusion cri-
teria (Llufriu et al., 2017; Martínez-Heras et al., 2015). The parcellation scheme (76 nodes)
from the anatomical image was aligned to the FA map to determine which streamline connec-
tions needed to be selected between pairs of nodes to create the structural connectome. Nous
defined the mean value of the FA metric along each connection to generate the FA-weighted
adjacency matrix of the network, denoted by A(DTI ). The mean FA computed along the fiber
pathway that connects each pair of brain regions enables the inclusion of the severity of the
white matter damage at the macro- and microstructural levels (Llufriu et al., 2017). In order to
FA-weighted adjacency matrix:
Square matrix where each cell
(je, j ) indicates the mean fractional
anisotropy between node i and node j.
Neurosciences en réseau
919
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
un
_
0
0
2
5
8
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Applying multilayer analysis to brain networks
Adjacency matrix:
Square matrix where each cell (je, j )
indicates the link’s weight between
node i and node j.
Gray matter morphological
adjacency matrix:
Square matrix where each cell (je, j )
indicates the correlation of the GM
patterns between node i and node j.
Gray matter functional adjacency
matrice:
Square matrix where each cell (je, j )
indicates the signal synchronization
between node i and node j.
minimize the presence of false connections in the networks, the analysis included only net-
work links that were present in more than 60% of the 45 HV subjects. Enfin, the FA measures
for the structural network were corrected for age and gender effect using a regression model
(Solana et al., 2019). The values of DTI connectivity matrices are in the range [0, 1].
Morphological gray matter brain network. The GM morphological network is based on the sim-
ilarity of GM morphological patterns according to the defined anatomical parcellation scheme
(Tijms et al., 2012). To estimate this GM connectivity network, we used an automated pipeline,
which involved four main steps: (un) re-slicing each individual’s native space GM segmentation
à 2 mm isotropic voxel in MNI space to later define small regions of interest corresponding to
3 × 3 × 3 voxel cubes (6 × 6 × 6 mm3); (b) performing statistical similarity (Pearson’s correla-
tion coefficient) between each pair of cubes of the GM mask; (c) applying an individualized
threshold to ensure a similar percentage of spurious connections (5%) across all GM networks;
et (d) averaging the remaining correlation values within each anatomical node in order to
construct the final GM morphological network, its adjacency matrix being denoted by A(GM ),
considering the defined parcellation scheme (76 × 76). The morphological networks obtained
were corrected for the effects of age and gender using a regression model. The values of GM
morphological matrices are in the range [0, 1].
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
un
_
0
0
2
5
8
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Functional brain network. Brain signal correlation/synchronization through resting-state func-
tional connectivity (rs-fMRI) matrix was obtained following Chou et al. (2012). This includes
several preprocessing steps including slice timing and motion correction, spatial normalization
to a standard space, and band-pass filtering to retain frequencies between 0.001 et 0.08 Hz
using FSL tools (Jenkinson et al., 2012). Enfin, the defined parcellation was used to extract the
average time series for each of the 76 brain regions, resulting in a functional connectivity net-
work with adjacency matrix A(rsfMRI ). Note that the values of rs-fMRI matrices are in the range
[−1, 1], indicating negative or positive correlation between nodes. Cependant, we apply the
absolute value in order to preserve only the strength of the relationship, to simplify and avoid
relevant drawbacks when computing network descriptors related to distance or shortest paths.
As with the other networks, age and gender effects were also corrected for functional connec-
tivity networks using a regression model. The final values of rs-fMRI matrices are in the range
[0, 1].
Multilayer Brain Network Definition
A multilayer network is composed of different layers, each representing a single type of rela-
tionship between nodes within one layer. Nodes represent the same exact object in each of the
different layers, and encode different types of relationships throughout their edges. In this type
of network, we differentiate between intralayer links, which encode the single type of relation-
ship the layer represents, and interlayer links, which encode how the different node perspec-
tives (types of relationships) are related within the system.
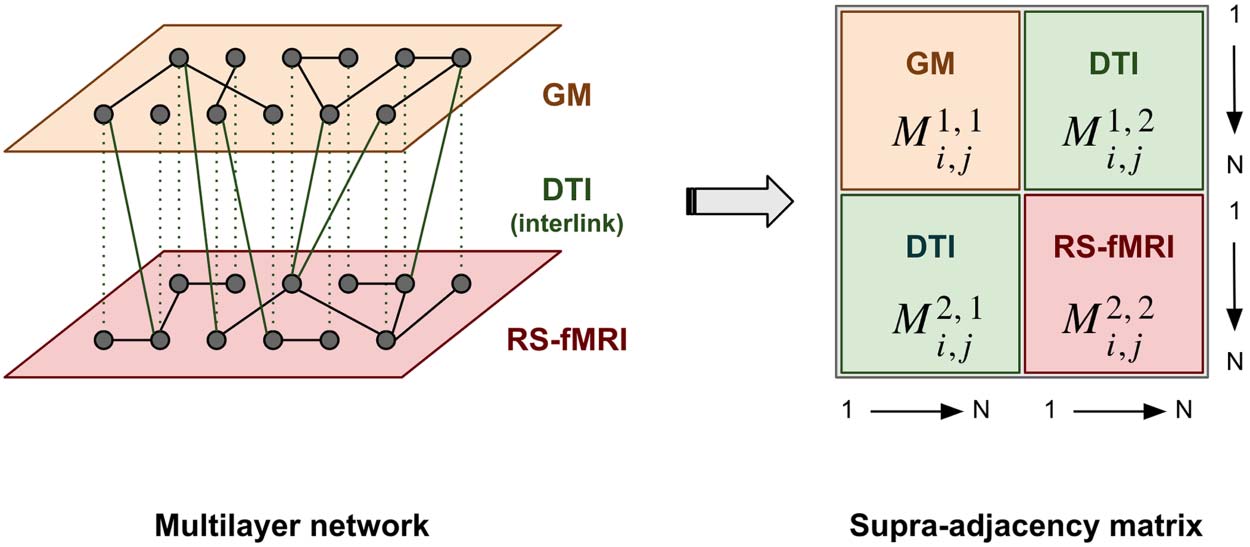
In our particular case, each subject has three single-layer networks representing GM mor-
phology, DTI structural connectivity, and rs-fMRI functional activity, which we combine to
create a multilayer network composed of two layers (Chiffre 1). We propose encoding rela-
tional data on GM tissue (GM, covariance in cortical thickness, and rs-fMRI, correlation of
functional time series) within the layers of the multilayer object, and encoding white matter
structural information (DTI) with interlayer links. This option was decided upon as DTI struc-
tural connectivity matrices represent white matter fiber pathway integrity between GM brain
regions through a range of values between 0 (isotropic diffusivity) et 1 (anisotropic diffusivity;
Llufriu et al., 2017).
Neurosciences en réseau
920
Applying multilayer analysis to brain networks
Chiffre 1. Multilayer network definition scheme using morphological, structural, and functional brain networks with the same underlying
anatomical parcellation.
Chiffre 1 shows the procedure used to assemble the multilayer object. Since the morpho-
logical GM, structural DTI, and rs-fMRI functional brain networks are already built on a com-
mon parcellation atlas, and a statistical correction for age and gender applied, the construction
of the multilayer object is not problematic. The multilayer information is represented by a
un;β
multilayer adjacency matrix, M.
je;j , composed of four indices. Two indices are the layers,
denoted by the Greek letters α and β, and two are the nodes in the layers, denoted by the Latin
letters i and j. Following on from the single-layer networks defined in the previous sections, le
multilayer adjacency matrix is defined as follows:
M.
1;1
je;j ¼ A GMð
je;j
Þ
∀i; j 2 1; …; N
F
g;
M.
rsfMRI
2;2
ð
je;j ¼ A
je;j
Þ
∀i; j 2 1; …; N
F
g;
M.
1;2
je;j ¼ M
2;1
je;j ¼ A DTI
ð
je;j
Þ
∀i; j 2 1; …; N
F
g;
un;β
je;je
where M
≈ 0, since we assume maximum connectivity between the same brain parcels cor-
responding to different layers. The morphological GM network is encoded in the first layer of
the multilayer object, and the rs-fMRI functional network in the second layer; donc, comme
stated previously, interlayer links (c'est à dire., indices α ≠ β) are defined as the DTI integrity between
the different brain areas (GM anatomical regions) represented by the structural network.
Chiffre 2 shows how this multilayer network unfolds into a supra-adjacency matrix (Kivelä
et coll., 2014). Throughout the paper, the multilayer adjacency matrix is used directly, M.
un;β
je;j .
Chiffre 2. Multilayer adjacency matrix unfolded to a supra-adjacency matrix, interlinked by struc-
tural DTI connectivity.
Neurosciences en réseau
921
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
un
_
0
0
2
5
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Applying multilayer analysis to brain networks
Path:
A path between two nodes is a list of
links that connect the source and the
target node.
un;β
defined to show minimum distances in M
In relation to the multilayer adjacency matrix, an additional object of lower dimension is
je;j . The matrix of the minimum distances (D 2 RN×N)
encodes the minimum distance between each pair of nodes in the multilayer network, inde-
pendent of the path or layer used to connect the two nodes. Despite this being an approxima-
tion, this safely simplifies the multilayer object, as connectivity between replicas of the same
node in the different layers is assumed to be maximum. Ce, donc, minimizes the cost in
≈ 0. Note that the information contained in this matrix is
partial and derived from the multilayer network and, in general, it is not possible to reconstruct
the original multilayer network from the minimum distance matrix. Officiellement, we obtain the
minimum distance matrix:
the multilayer adjacency matrix, M.
un;β
je;je
Di;j ¼ min M
un;β
je;j
: un; β 2 1; 2F
g; je; j 2 1; …; N
F
g:
As we have stated previously, all values of intra- and interlinks are encoded in the range [0, 1]
because of the preprocessing steps that we have applied to obtain the single-layer adjacency
matrice. Cependant, we underline that different or alternative preprocessing steps could be imple-
mented and integrated in the multilayer framework defined here, such as the mean or any other
relationship between values (Dimitriadis et al., 2017; Yu et al., 2017).
Graph Theoretical Analysis
Although several metrics for multilayer networks have been defined previously (De Domenico
et coll., 2013; Solé -Ribalta et al., 2014), some metrics may need to be adjusted when the par-
ticular domain characteristics are taken into account. Particularly, the complex network
descriptors related to the information flow between nodes (c'est à dire., regions of the brain) may be
within the same layers and/or different layers. Donc, we propose using well-known global
and local measures to describe the multilayer brain network properties at both local and global
levels. We formulate the following.
Strength. Node strength is one of the most basic and widely used metrics to calculate the
importance of any given node in a network, and is defined as the sum of weights of all edges
connected to the node. According to this definition, high strength indicates a highly important
node in the network. We define the strength of node i, denoted by si, as the following:
X
si ¼
αsα
je
with sα
i ¼
X
M.
un;β
je;j
:
β;j
In a multilayer network we can define node strength at two levels: a local level, sα
je , lequel
notes the importance of node i in layer α, without reducing it to the sum of the degrees of the
individual layers (De Domenico et al., 2015); and a more general level that aggregates the
overall structural importance of node i considering all layers, si. Although sα
i may be useful
to quantify the local importance of node i, this research only focuses on the aggregated
node strength si.
Degree. Node degree is one of the simplest centrality measures (often used in social network
literature) to quantify the importance of a node in a network. It is defined as the number of
edges connected to a specific node, and can be considered a binarization of strength. In a
similar way, high degree values indicate higher importance of the multilayer node. We define
the degree of node i as follows:
X
di ¼
un;β;j
(cid:2)
Θ M
(cid:3)
;
un;β
je;j
Neurosciences en réseau
922
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
un
_
0
0
2
5
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Applying multilayer analysis to brain networks
where θ is a function that returns 0 if the argument is equal to 0, et 1 otherwise. In other
words, it returns 1 if an edge exists between node i in layer α and node j in layer β, et 0
otherwise. Note that, if required, one could also define the degree per node and layer, d α
je ,
as described above for strength.
Betweenness centrality. A different concept of node importance is captured by betweenness
centrality, which measures the extent to which a node lies within paths between node pairs
(Freeman, 1977). In contrast to degree and strength, this node metric is obtained by consider-
ing the full network topology, and is related to the information flow between nodes (within the
same layer or across different layers). The betweenness centrality of node i is set out in the
following equation:
bi ¼
1
n n − 1
ð
Þ
X
o;d
σo;d ið Þ
σo;d
;
Shortest path:
Minimal path between two nodes,
where the cost is defined as the sum
of the links’ weight.
where σo,d is the number of the shortest paths from o to d, and σo,d (je) is the number of the
shortest paths from o to d that crosses node i. The betweenness centrality is a value in the
range [0, 1], où 1 indicates the highest centrality (c'est à dire., the node lies in all the shortest paths
from all pairs of nodes) et 0 denotes a node that is not in any of the network’s shortest paths.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
un
_
0
0
2
5
8
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
In our particular setup, we can efficiently compute the betweenness centrality using the
matrix of minimum distances, D, which is directly derived from the multilayer network. Par
using D, the standard betweenness centrality algorithm (Brandes, 2001) can be applied. C'est
worth noting that our definition and computation of betweenness centrality is slightly different
from the original one proposed for multilayer schemes (Solé-Ribalta et al., 2014).
Closeness centrality. Closeness centrality evaluates the average distance from one node to all
other accessible nodes in the network. Similar to the previous metric, this is a global network
descriptor, and is related to the topological location of nodes within the network. The close-
ness centrality of node i is computed as the average distance between i and all other nodes in
the network:
(cid:2)
X
ci ¼
Di;j
j≠i
(cid:3)−1
;
where values close to 1 denote very high centrality and values close to 0 indicate very low
centrality. It should be highlighted that under this metric definition, the more central a node is,
the closer it is to all other nodes.
Local efficiency. A network’s efficiency is a measure of its capacity to exchange information
between nodes (Latora & Marchiori, 2001; Stanley et al., 2015). At a global level, efficiency is
defined as the sum of the inverse of all pairwise distances between nodes and measures how
well information is exchanged within the network. At the local level, it measures how well a
node’s neighbors can exchange information between them, and it can be used to measure a
network’s resistance to failure at a local level (Latora & Marchiori, 2001). In the context of
brain networks, local and global efficiency have been linked to working memory (Stanley
et coll., 2015) and functional integration (Rubinov & Sporns, 2010). Officiellement, the local effi-
ciency of node i is computed by the following equation:
LEi ¼
1
di di − 1
Þ
ð
X
1
j;k2Gi
Dj;k
;
where Gi is the set containing the immediate neighborhood of node i (also called the ego net-
travail), but excluding the node itself, and di is the degree of node i as defined above. Analogous
923
Ego network:
Subgraph composed of a node and
the set of nodes that are directly
linked to it.
Neurosciences en réseau
Applying multilayer analysis to brain networks
to the other measures, the local efficiency of node i is in the range [0, 1], where values close to
1 indicate maximum local efficiency in the network.
Statistics
Clinical and demographic data were described through the mean and standard deviation for
quantitative variables. Comparisons of global and local network descriptors between people
with MS and HVs were performed with Student’s t tests, and the statistical significance was set
at p < 0.05. Since the FA-weighted adjacency matrices could suffer from intersite variability
because of the heterogeneity of both acquisition protocols, we harmonized the data using the
ComBat model (Fortin et al., 2017; De Stefano et al., 2022). All analyses were performed using
Python software (version 3.8.8) and the SciPy package (version 1.8.0).
Data and Code Availability
The proposed method to create a multilayer network derived from FA-weighted adjacency
matrix, GM morphological and functional brain networks, and the subsequently graph theo-
retical analysis were made publicly available by the authors in the following link:
https://github.com/ADaS-Lab/Multilayer-MRI/ (Casas-Roma, 2022).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
a
_
0
0
2
5
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
RESULTS
We analyzed a cohort of n = 125 people with relapsing-remitting MS (90 women), mean age of
45.66 ± 9.44 years, mean disease duration of 14.88 ± 8.07 years, and median EDSS of 2.0
(range 0–6.5), and a group of n = 18 HVs. The clinical and demographic from the final cohort
are summarized in Table 1. Table 2 shows the number of regions identified with significant
group differences ( p < 0.05) in the network descriptors obtained from the multilayer network
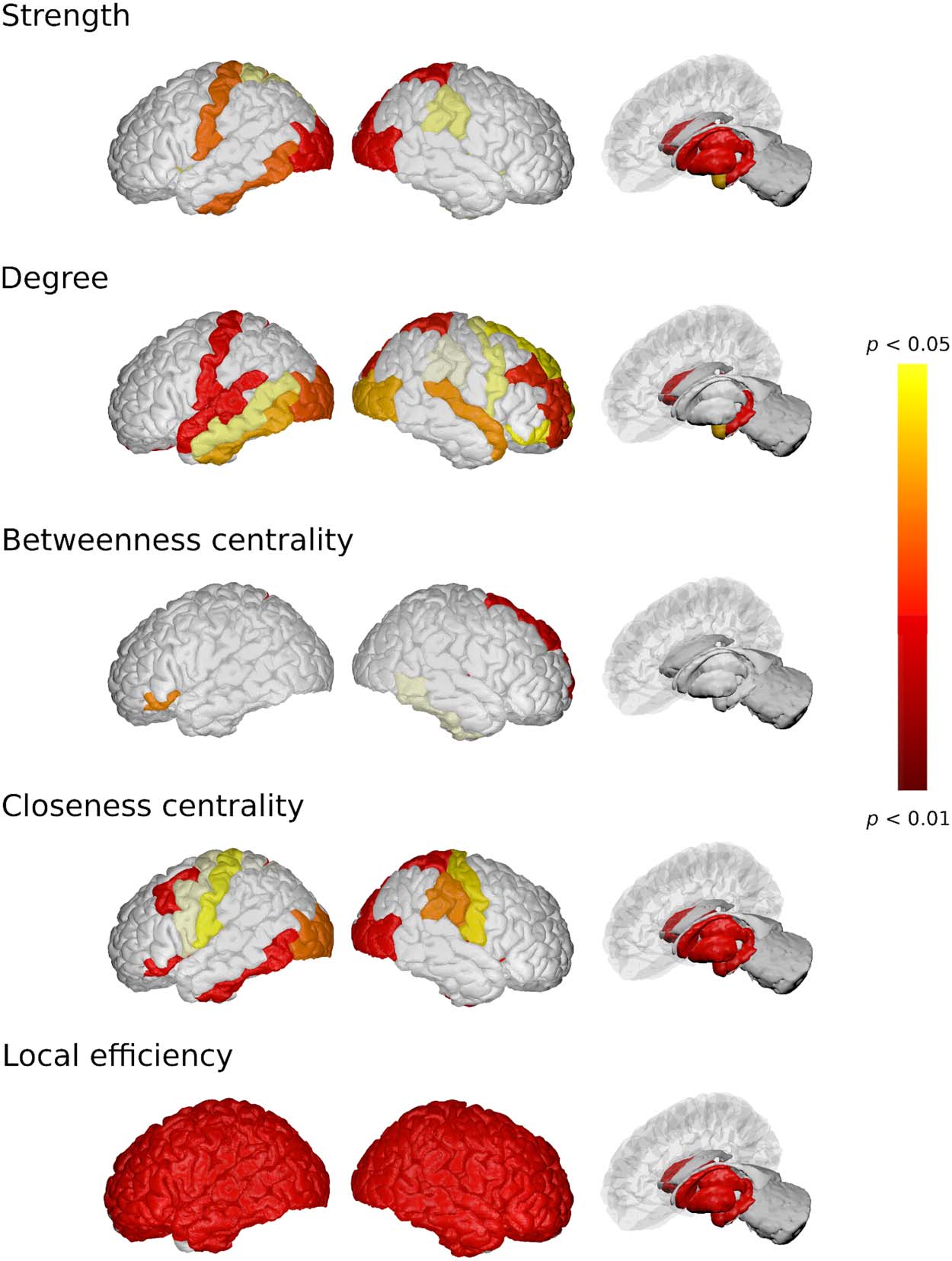
analysis. Details of these regions are depicted in Figure 3.
Upon this setup, we validate our multilayer framework proposal by comparing the number
of identified statistically different brain regions with respect to a randomized version of the
multilayer structure, in which structural DTI links are shuffled. Results show that structural
DTI data arranged as interlayer links is fundamental to identify more significant different
regions between people with MS and HV (see Appendix 1 in the Supporting Information).
Most differences among the groups were observed in local efficiency measures, closeness
centrality, node degree, and node strength (corrected p < 0.05). In all the nodes analyzed,
local efficiency was lower in people with MS compared with the HVs (corrected p < 0.05),
while closeness centrality and node degree were lower (corrected p < 0.05) in almost all deep
GM regions. Table 3 shows the p values obtained from comparing HVs with people with MS in
all deep GM regions. Regions involving left thalamus, left hippocampus, right thalamus, right
Table 1. Clinical and demographic data. Continuous variables are given as the mean ± standard deviation. EDSS = Expanded Disability
Status Scale; MS = multiple sclerosis. P values obtained from comparing the groups.
Age, years
Female, n (%)
Disease duration, years
Median EDSS score (range)
Network Neuroscience
Healthy volunteers (n = 18)
36.62 ± 9.33
People with MS (n = 125)
45.66 ± 9.44
15 (83%)
–
–
90 (66%)
14.88 ± 8.07
2.0 (0–6.5)
p value
0.001
<0.001
–
–
924
Applying multilayer analysis to brain networks
Table 2. Number of identified regions with significant differences ( p < 0.05) in network descriptors
obtained from the multilayer network analysis.
Metric
Strength
Degree
Betweenness centrality
Closeness centrality
Local efficiency
No. of regions
31 / 76
No. of deep GM
12 / 14
No. of cortical GM
19 / 62
31 / 76
6 / 76
40 / 76
76 / 76
7 / 14
0 / 14
12 / 14
14 / 14
24 / 62
6 / 62
28 / 62
62 / 62
caudate, and right accumbens were the regions with the largest differences between people
with MS and HVs (corrected p < 0.05).
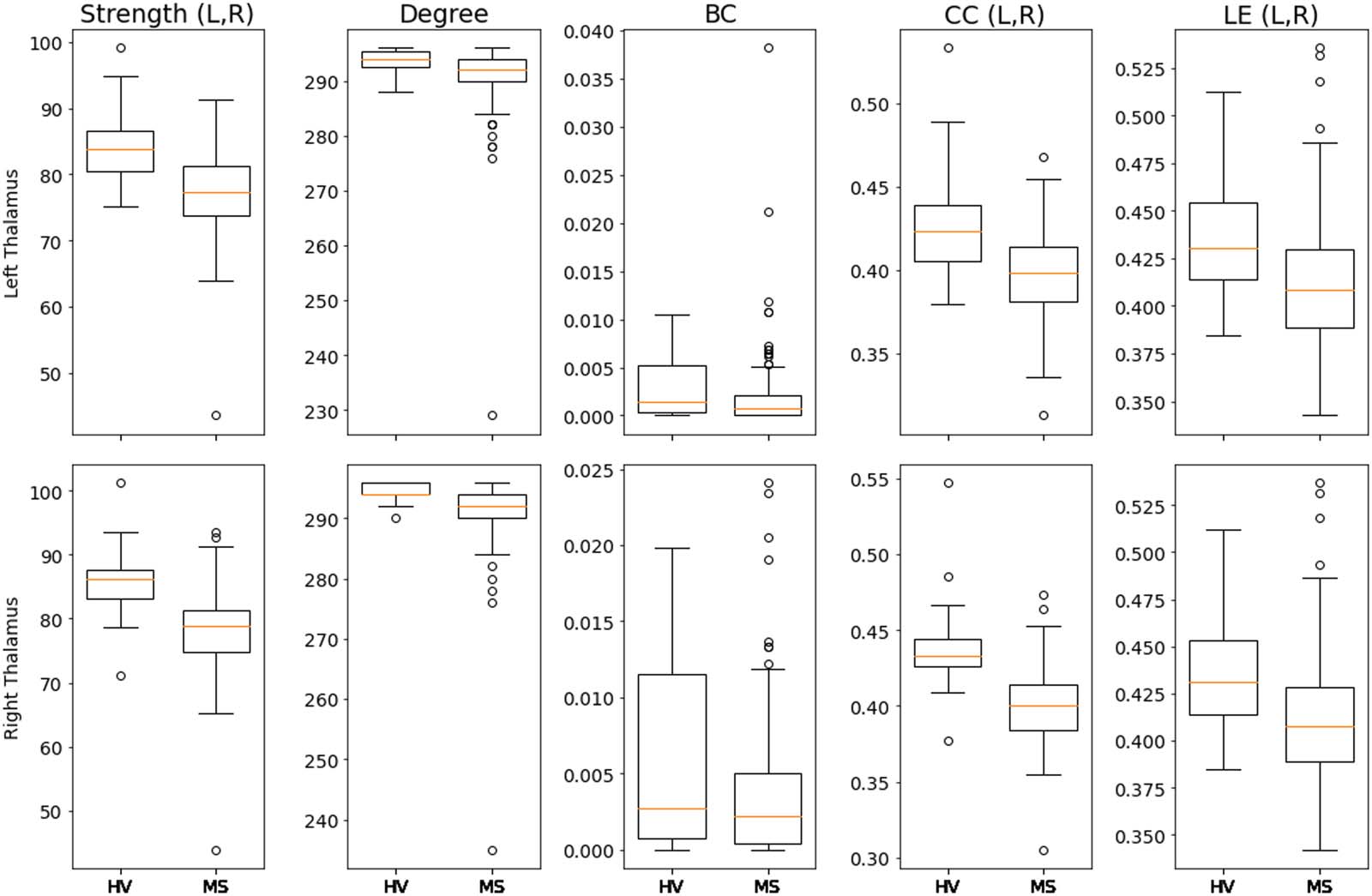
Additionally, Figure 4 shows the boxplots comparing left and right thalamus for each mul-
tilayer descriptor for HVs and people with MS. According to the data presented in Table 3, we
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
a
_
0
0
2
5
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Depiction of statistically significant anatomical regions between people with MS and
HVs using the graph theoretical descriptors obtained from the multilayer network analysis.
Network Neuroscience
925
Applying multilayer analysis to brain networks
Table 3. Detail of p values obtained from comparing healthy volunteers (HVs) with people with
MS in all deep gray matter regions for each of the multilayer metrics: strength, degree, betweenness
centrality (BC), closeness centrality (CC), and local efficiency (LE).
Nodes
Name
Left thalamus
Left caudate
Left putamen
Left pallidum
Left hippocampus
Left amygdala
Left accumbens
Right thalamus
Right caudate
Right putamen
Right pallidum
Right hippocampus
Right amygdala
Right accumbens
Strength
0.000
Degree
0.095
p values
BC
0.400
0.004
0.006
0.020
0.000
0.033
0.003
0.000
0.000
0.020
0.082
0.003
0.072
0.000
0.068
0.493
0.521
0.000
0.033
0.005
0.057
0.000
0.186
0.332
0.001
0.041
0.000
0.491
0.566
0.224
0.852
0.087
0.285
0.091
0.306
0.901
0.959
0.243
0.691
0.708
CC
0.000
0.006
0.001
0.000
0.000
0.018
0.005
0.000
0.000
0.002
0.014
0.051
0.056
0.002
LE
0.009
0.008
0.008
0.008
0.009
0.008
0.008
0.010
0.008
0.008
0.007
0.007
0.007
0.008
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
a
_
0
0
2
5
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Boxplots comparing left and right thalamus of healthy volunteers (HV) and people with MS for each of the multilayer metrics:
strength, degree, betweenness centrality (BC), closeness centrality (CC), and local efficiency (LE). For each metric, L and R stand for the sta-
tistical significance of the left and right thalamus, respectively.
Network Neuroscience
926
Applying multilayer analysis to brain networks
observe that the metrics local efficiency, closeness centrality, and degree best capture the dif-
ferences between each group (see the Supporting Information for details and boxplots of all
other regions).
We further demonstrate that the multilayer approach integrating morphological GM, struc-
tural DTI, and rs-fMRI functional networks may help to better understand the complex mech-
anisms underlying MS disease in comparison with other architectures (see Appendix 2 in the
Supporting Information).
DISCUSSION
This paper provides a multilayer approach by combining the information from different brain
networks simultaneously. We computed the graph theoretical descriptors extracted by the
combination of structural, functional, and morphological brain networks using well-
established methodological approaches. To be able to merge the information between these
three networks, we applied a common anatomical cortical atlas parcellation, and each indi-
vidual region is represented by a node in our network (31 cortical labels and 7 subcortical
regions per each brain hemisphere; Klein et al., 2017; Patenaude et al., 2011). This brain
region distribution could be substituted by other atlas templates depicted by cytoarchitectonic
or functional maps (Glasser et al., 2016). However, using this new multilayer approach, the
same graph descriptors can still be computed through other atlases to explore other outcomes
and interpretations.
The key to good multilayer architecture is combining each network efficiently. Multilayer
architecture has two main features: the set of edges within a graph (between nodes of the same
graph), and the set across graphs (between the same node in different graphs). Several
approaches have been proposed to connect nodes between layers in a multilayer network:
implicit (Battiston et al., 2017; Battiston et al., 2018) or explicit (Betzel et al., 2019; Guillon
et al., 2017; Lim et al., 2019) connections between node replicas in the different layers, iden-
tity connections with varying weights (Betzel et al., 2019; Pedersen et al., 2018), or fully con-
nected layer (Buldú & Porter, 2018; Ting et al., 2021) threshold restrictions. However, the
definition is especially difficult when layers do not represent totally equivalent information
(Damoiseaux & Greicius, 2009). Identity connections may restrict connectivity between
layers, thus reducing the impact of large-range pathological changes of WM onto GM network
properties or producing discordance (Lim et al., 2019). To overcome this challenging situation,
our multilayer approach incorporates cross interaction between functional and morphological
layers by using a structural connectivity factor that tries to mimic the WM topological organi-
zation and microstructural tissue properties within the multilayer architecture.
Another important step in our multilayer approach was to normalize the various networks,
thus merging this information within a single multilayer architecture. As such, we normalized
all values between 0 and 1 across different connectivity matrices to avoid one specific network
or negative values being more influential than the others, which could lead to significant bias
in network connectivity properties (Pedersen et al., 2018). Furthermore, statistical correction
for common confounding variables at connectivity matrix level, such as age or gender, was
applied in all the connectivity matrices to avoid bias (Solana et al., 2018).
GM morphological pipeline design produces matrices with very similar covariance patterns
between different defined regions. Thus, it is difficult to merge the GM morphological similar-
ity network with other networks, as GM network disruptions/morphological changes using
graph theory metrics are less prominent than underlying pathological MS changes derived
Network Neuroscience
927
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
a
_
0
0
2
5
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Applying multilayer analysis to brain networks
from diffusion and functional properties in mild disability patients (Zurita et al., 2018) with a
median EDSS score of 2.0 (see Table 1). Overall, this study proves that using this multilayer
approach to analyze the complex organization of the brain network could help identify abnor-
mal patterns related to structural, morphological, and functional properties.
There is a loss of significance in different areas in HV and MS patients when comparing
original and reshuffled data; this means that the nodes that remain significant after the reshuf-
fling can rely also on functional and GM network contributions (see Appendix 1 in the
Supporting Information) for their identification. Moreover, our findings show that a set of nodes
are only significant under our proposed multilayer architecture, emphasizing the key role of
DWI as interlink. Another key aspect of the proposed multilayer architecture is to analyze
whether it provides better outcomes than other architectural combinations. Extra analysis
has shown that the jointly morphological, structural, and functional brain networks provide
better results than any other data combination in a classification task (see Appendix 2 in
the Supporting Information).
As proof of concept, and to demonstrate its potential, our multilayer network approach was
used to explore the hierarchical organization of brain loss in the context of neurological
diseases such as MS. Findings point to deterioration of synchronized connectivity, which is
particularly relevant for local efficiency and shows widespread loss across the brain. More-
over, most GM regions showed connectivity changes, particularly in strength and closeness
centrality. The atrophy of deep GM areas occurs in early stages of MS, and extends to multi-
modal cortical regions over time (Eshaghi et al., 2018; Solana et al., 2021). In this context, we
demonstrated that the network metrics applied to the new multilayer framework can pick up
relevant network alterations in MS in most deep GM and in some cortical regions involved in
visual areas (bilateral occipital and lingual areas) and cognition (Gabilondo et al., 2014;
Riccitelli et al., 2020; Zhang et al., 2021). The frontal, temporal, and parietal lobes of MS
patients are closely associated with new lesions in the first 10 years (Wybrecht et al., 2017).
Furthermore, graph theory measures point out that the most atypical patterns in interconnected
multilayer networks in MS stem from a weaker topological centrality (measure of degree and
strength) and integrity (closeness centrality) measures, and increasing segregation (local effi-
ciency) of node neighbors (Riccitelli et al., 2020; Zhang et al., 2021). However, the overall
connectivity of the brain network in MS (betweenness centrality) patients is unchanged com-
pared with HV, as reported previously (Llufriu et al., 2017).
We provide a scalable multilayer network architecture that merges more than two brain
connectivity matrices in a single graph. This method enables researchers to examine multi-
modal MRI data in order to gain a better understanding of brain interactions in MS and other
brain disorders, as well as a healthy brain. We expect that the set of graph metrics obtained
from integrating connectivity matrices in a multilayer network will help detect subtle changes
in brain organization as biomarkers of neurological and neuropsychiatric diseases, thus, open-
ing the method to translation to the clinic or to clinical trials.
LIMITATIONS
Our study undertakes several processing steps to obtain the final connectivity matrices and the
multilayer network. Corrections for age and gender were applied, and the value scales and
ranges changed. Although these steps were specifically chosen following the literature, others
that would improve the sensitivity or specificity of the derived graph-mining metrics could be
added. For example, the analysis performed in the morphological GM connectivity matrix to
Network Neuroscience
928
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
a
_
0
0
2
5
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Applying multilayer analysis to brain networks
summarize the relationship between conjunctions of correlations of the cube in each brain
region could be performed through other approaches (e.g., sum or mean).
Image processing in the DWI, fMRI, and T1 data could create controversy, as a large num-
ber of similar pipelines could be applied. Thus, we designed pipelines fully aligned to current
state-of-the-art methods, without specifically tuning or optimizing any parameters for our data-
set. Cerebellum has been excluded from the analysis because of the severe distortions at the
level of brain stem region in DW images. Further research could focus on proper adjustment of
the value range for each connectivity matrix, as this may impact graph connectivity metrics,
such as considering the sign of the rs-fMRI instead of using the absolute values.
Another limitation of the study is the size of the MRI data used in the study. The single-
center MS group was small, and the number of HVs was limited, with only 18 subjects with
the three image modalities; therefore, further studies should be carried out on larger multicen-
ter datasets to confirm our findings and expound their clinical effects. Despite data size, the
findings are interesting and in line with other recently published MRI studies.
We selected the Desikan-Killiany-Tourville atlas based on an anatomical distribution. Other
atlases are available, each with underlying meanings that will affect findings (Eickhoff et al.,
2018). However, as discussed earlier, the multilayer architecture and the derived graph metrics
can be computed using the approach presented, independent of the atlas chosen.
CONCLUSIONS
This research presents a multilayer approach with corresponding graph metrics. This is the first
time a multilayer approach merges morphological, structural, and functional connectivity
information from the brain into an efficiently combined single network. Our multilayer
approach was successfully applied to a cohort of people with MS, and interestingly, the pro-
posed framework identified several brain regions showing synchronized connectivity deterio-
ration. These encouraging results indicate that larger multicentric studies are warranted. Future
work will incorporate more networks to the multilayer architecture and explore the potential of
analyzing several networks simultaneously using graph neural networks.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00258 and
https://github.com/ADaS-Lab/Multilayer-MRI/.
AUTHOR CONTRIBUTIONS
Jordi Casas-Roma: Conceptualization; Data curation; Formal analysis; Methodology; Validation;
Writing – original draft; Writing – review & editing. Eloy Martinez-Heras: Conceptualization;
Data curation; Formal analysis; Methodology; Validation; Writing – original draft; Writing –
review & editing. Albert Solé-Ribalta: Conceptualization; Data curation; Formal analysis;
Methodology; Validation; Writing – original draft; Writing – review & editing. Elisabeth Solana:
Conceptualization; Data curation; Formal analysis; Investigation; Validation; Writing – review
& editing. Elisabet Lopez-Soley: Conceptualization; Data curation; Writing – review & editing.
Francesc Vivó: Conceptualization; Data curation; Writing – review & editing. Marcos Diaz-
Hurtado: Conceptualization; Writing – review & editing. Salut Alba-Arbalat: Conceptualiza-
tion; Data curation; Writing – review & editing. Maria Sepulveda: Conceptualization; Data
curation; Writing – review & editing. Yolanda Blanco: Conceptualization; Data curation;
Network Neuroscience
929
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
a
_
0
0
2
5
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Applying multilayer analysis to brain networks
Writing – review & editing. Albert Saiz: Conceptualization; Data curation; Writing – review &
editing. Javier Borge-Holthoefer: Conceptualization; Formal analysis; Writing – review & edit-
ing. Sara Llufriu: Conceptualization; Data curation; Formal analysis; Methodology; Validation;
Writing – review & editing. Ferran Prados: Conceptualization; Data curation; Formal analysis;
Methodology; Validation; Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
Sara Llufriu, Instituto de Salud Carlos III (https://dx.doi.org/10.13039/501100004587), Award
ID: PI15/00587. Albert Saiz, Instituto de Salud Carlos III (https://dx.doi.org/10.13039
/501100004587), Award ID: PI18/01030. Albert Saiz, Red Española de Esclerosis Múltiple
(https://dx.doi.org/10.13039/501100007747), Award ID: RD16/0015/0002. Sara Llufriu, Red
Española de Esclerosis Múltiple (https://dx.doi.org/10.13039/501100007747), Award ID:
RD16/0015/0003. Albert Saiz, Red Española de Esclerosis Múltiple (https://dx.doi.org/10
.13039/501100007747), Award ID: RD12/0032/0002. Francesc Graus, Red Española de
Esclerosis Múltiple (https://dx.doi.org/10.13039/501100007747), Award ID: RD12/0060/01-02.
COMPETING INTERESTS
E. S. received travel reimbursement from Sanofi. E. L.-S. received travel reimbursement from
Sanofi and ECTRIMS. M. S. received honoraria for speaking from Roche and Biogen, and travel
reimbursement from Biogen, Sanofi, and Roche for national and international meetings. A. S.
received consulting fees for serving on a scientific advisory board, speaking, and partaking in
other activities for Merck-Serono, Sanofi, Biogen, Roche, TEVA, Novartis, Alexion, and Janssen.
S. L. received consulting fees and honoraria for speaking from Biogen Idec, Novartis, TEVA,
Genzyme, Sanofi, and Merck.
The author(s) disclose receipt of the following financial support for the research, authorship,
and/or publication of this article. This work was funded by e-Health Center at Universitat
Oberta de Catalunya, NIHR Biomedical Research Centre at University College London
Hospitals NHS Foundation Trust and University College London, a Proyecto de Investigación
en Salud (PI15/00587 to S. L. and A. S., and PI18/01030 to S. L. and A. S.), integrated into the
Plan Estatal de Investigación Científica y Técnica de Innovación I+D+I, and cofunded by the
Instituto de Salud Carlos III-Subdirección General de Evaluación and the Fondo Europeo de
Desarrollo Regional (FEDER, “Otra manera de hacer Europa”); by the Red Española de
Esclerosis Múltiple (REEM: RD16/0015/0002, RD16/0015/0003, RD12/0032/0002,
RD12/0060/01-02); and by TEVA Spain, the Ayudas Merck de Investigación 2017 from the
Fundación Merck Salud and the Proyecto Societat Catalana Neurologia 2017.
REFERENCES
Basser, P. J., Mattiello, J., & LeBihan, D. (1994). MR diffusion tensor
spectroscopy and imaging. Biophysical Journal, 66(1), 259–267.
https://doi.org/10.1016/S0006-3495(94)80775-1, PubMed:
8130344
Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353–364. https://doi.org/10.1038/nn.4502,
PubMed: 28230844
Battaglini, M., Jenkinson, M., & De Stefano, N. (2012). Evaluating
and reducing the impact of white matter lesions on brain volume
measurements. Human Brain Mapping, 33(9), 2062–2071.
https://doi.org/10.1002/hbm.21344, PubMed: 21882300
Battiston, F., Guillon, J., Chavez, M., Latora, V., & De Vico Fallani,
F. (2018). Multiplex core–periphery organization of the human
connectome. Journal of the Royal Society Interface, 15(146),
20180514. https://doi.org/10.1098/rsif.2018.0514, PubMed:
30209045
Battiston, F., Nicosia, V., Chavez, M., & Latora, V. (2017). Multi-
layer motif analysis of brain networks. Chaos, 27(4), 047404.
https://doi.org/10.1063/1.4979282, PubMed: 28456158
Bennett, I. J., & Rypma, B. (2013). Advances in functional neuro-
anatomy: A review of combined DTI and fMRI studies in healthy
younger and older adults. Neuroscience and Biobehavioral
Network Neuroscience
930
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
a
_
0
0
2
5
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Applying multilayer analysis to brain networks
Reviews, 37(7), 1201–1210. https://doi.org/10.1016/j.neubiorev
.2013.04.008, PubMed: 23628742
Betzel, R. F., Bertolero, M. A., Gordon, E. M., Gratton, C., Dosenbach,
N. U. F., & Bassett, D. S. (2019). The community structure of
functional brain networks exhibits scale-specific patterns of
inter- and intra-subject variability. NeuroImage, 202, 115990.
https://doi.org/10.1016/j.neuroimage.2019.07.003, PubMed:
31291606
Boccaletti, S., Bianconi, G., Criado, R., del Genio, C. I., Gómez-
Gardeñes, J., Romance, M., Sendiña-Nadal, I., Wang, Z., &
Zanin, M. (2014). The structure and dynamics of multilayer net-
works. Physics Reports, 544(1), 1–122. https://doi.org/10.1016/j
.physrep.2014.07.001, PubMed: 32834429
Brandes, U. (2001). A faster algorithm for betweenness centrality.
Journal of Mathematical Sociology, 25(2), 163–177. https://doi
.org/10.1080/0022250X.2001.9990249
Buldú, J. M., & Porter, M. A. (2018). Frequency-based brain net-
works: From a multiplex framework to a full multilayer descrip-
tion. Network Neuroscience, 2(4), 418–441. https://doi.org/10
.1162/netn_a_00033, PubMed: 30294706
Casas-Roma, J. (2022). Multilayer-MRI, GitHub, https://github.com
/ADaS-Lab/Multilayer-MRI/.
Chard, D. T., Alahmadi, A. A. S., Audoin, B., Charalambous, T.,
Enzinger, C., Hulst, H. E., Rocca, M. A., Rovira, À., Sastre-
Garriga, J., Schoonheim, M. M., Tijms, B., Tur, C., Gandini
Wheeler-Kingshott, C. A. M., Wink, A. M., Ciccarelli, O.,
Barkhof, F., & MAGNIMS Study Group. (2021). Mind the gap:
From neurons to networks to outcomes in multiple sclerosis.
Nature Reviews Neurology, 17(3), 173–184. https://doi.org/10
.1038/s41582-020-00439-8, PubMed: 33437067
Chou, Y.-H., Panych, L. P., Dickey, C. C., Petrella, J. R., & Chen,
N.-K. (2012). Investigation of long-term reproducibility of intrin-
sic connectivity network mapping: A resting-state fMRI study.
American Journal of Neuroradiology, 33(5), 833–838. https://
doi.org/10.3174/ajnr.A2894, PubMed: 22268094
Cociu, B. A., Das, S., Billeci, L., Jamal, W., Maharatna, K., Calderoni,
S., Narzisi, A., & Muratori, F. (2018). Multimodal functional and
structural brain connectivity analysis in autism: A preliminary inte-
grated approach with EEG, fMRI, and DTI. IEEE Transactions on
Cognitive and Developmental Systems, 10(2), 213–226. https://
doi.org/10.1109/TCDS.2017.2680408
Crofts, J. J., Forrester, M., & O’Dea, R. D. (2016). Structure-function
clustering in multiplex brain networks. EPL (Europhysics Letters),
116(1), 18003. https://doi.org/10.1209/0295-5075/116/18003
Damoiseaux, J. S., & Greicius, M. D. (2009). Greater than the sum
of its parts: A review of studies combining structural connectivity
and resting-state functional connectivity. Brain Structure and
Function, 213(6), 525–533. https://doi.org/10.1007/s00429-009
-0208-6, PubMed: 19565262
De Domenico, M. (2017). Multilayer modeling and analysis of
human brain networks. GigaScience, 6(5), gix004. https://doi
.org/10.1093/gigascience/gix004, PubMed: 28327916
De Domenico, M., Sasai, S., & Arenas, A. (2016). Mapping multi-
plex hubs in human functional brain networks. Frontiers in Neu-
roscience, 10, 326. https://doi.org/10.3389/fnins.2016.00326,
PubMed: 27471443
De Domenico, M., Solé-Ribalta, A., Cozzo, E., Kivelä, M., Moreno,
Y., Porter, M. A., Gómez, S., & Arenas, A. (2013). Mathematical
formulation of multilayer networks. Physical Review X, 3(4),
041022. https://doi.org/10.1103/PhysRevX.3.041022
De Domenico, M., Solé-Ribalta, A., Omodei, E., Gómez, S., &
Arenas, A. (2015). Ranking in interconnected multilayer net-
works reveals versatile nodes. Nature Communications, 6, 6868.
https://doi.org/10.1038/ncomms7868, PubMed: 25904405
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson,
B. C., Blacker, D., Buckner, R. L., Dale, A. M., Maguire, R. P.,
Hyman, B. T., Albert, M. S., & Killiany, R. J. (2006). An automated
labeling system for subdividing the human cerebral cortex on MRI
scans into gyral based regions of interest. NeuroImage, 31(3),
968–980. https://doi.org/10.1016/j.neuroimage.2006.01.021,
PubMed: 16530430
De Stefano, N., Battaglini, M., Pareto, D., Cortese, R., Zhang, J.,
Oesingmann, N., Prados, F., Rocca, M. A., Valsasina, P.,
Vrenken, H., Gandini Wheeler-Kingshott, C. A. M., Filippi, M.,
Barkhof, F., Rovira, À., & MAGNIMS Study Group. (2022).
MAGNIMS recommendations for harmonization of MRI data in
MS multicenter studies. NeuroImage: Clinical, 34, 102972.
https://doi.org/10.1016/j.nicl.2022.102972, PubMed: 35245791
Dimitriadis, S. I., Drakesmith, M., Bells, S., Parker, G. D., Linden,
D. E., & Jones, D. K. (2017). Improving the reliability of network
metrics in structural brain networks by integrating different net-
work weighting strategies into a single graph. Frontiers in Neuro-
science, 11, 694. https://doi.org/10.3389/fnins.2017.00694,
PubMed: 29311775
Eickhoff, S. B., Yeo, B. T. T., & Genon, S. (2018). Imaging-based
parcellations of the human brain. Nature Reviews Neuroscience,
19(11), 672–686. https://doi.org/10.1038/s41583-018-0071-7,
PubMed: 30305712
Eshaghi, A., Marinescu, R. V., Young, A. L., Firth, N. C., Prados, F.,
Jorge Cardoso, M., Tur, C., De Angelis, F., Cawley, N., Brownlee,
W. J., De Stefano, N., Laura Stromillo, M., Battaglini, M.,
Ruggieri, S., Gasperini, C., Filippi, M., Rocca, M. A., Rovira, A.,
Sastre-Garriga, J., … Ciccarelli, O. (2018). Progression of
regional grey matter atrophy in multiple sclerosis. Brain, 141(6),
1665–1677. https://doi.org/10.1093/ brain/awy088, PubMed:
29741648
Fleischer, V., Radetz, A., Ciolac, D., Muthuraman, M., Gonzalez-
Escamilla, G., Zipp, F., & Groppa, S. (2019). Graph theoretical
framework of brain networks in multiple sclerosis: A review of
concepts. Neuroscience, 403, 35–53. https://doi.org/10.1016/j
.neuroscience.2017.10.033, PubMed: 29101079
Fortin, J.-P., Parker, D., Tunç, B., Watanabe, T., Elliott, M. A.,
Ruparel, K., Roalf, D. R., Satterthwaite, T. D., Gur, R. C., Gur,
R. E., Schultz, R. T., Verma, R., & Shinohara, R. T. (2017).
Harmonization of multi-site diffusion tensor imaging data. Neu-
roImage, 161, 149–170. https://doi.org/10.1016/j.neuroimage
.2017.08.047, PubMed: 28826946
Freeman, L. C. (1977). A set of measures of centrality based on
betweenness. Sociometry, 40(1), 35–41. https://doi.org/10.2307
/3033543
Gabilondo, I., Martínez-Lapiscina, E. H., Martínez-Heras, E., Fraga-
Pumar, E., Llufriu, S., Ortiz, S., Bullich, S., Sepulveda, M., Falcon,
C., Berenguer, J., Saiz, A., Sanchez-Dalmau, B., & Villoslada, P.
(2014). Trans-synaptic axonal degeneration in the visual pathway
in multiple sclerosis. Annals of Neurology, 75(1), 98–107. https://
doi.org/10.1002/ana.24030, PubMed: 24114885
Network Neuroscience
931
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
a
_
0
0
2
5
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Applying multilayer analysis to brain networks
Gifford, G., Crossley, N., Kempton, M. J., Morgan, S., Dazzan, P.,
Young, J., & McGuire, P. (2020). Resting state fMRI based multi-
layer network configuration in patients with schizophrenia. Neu-
roImage: Clinical, 25, 102169. https://doi.org/10.1016/j.nicl
.2020.102169, PubMed: 32032819
Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D.,
Harwell, J., Yacoub, E., Ugurbil, K., Andersson, J., Beckmann,
C. F., Jenkinson, M., Smith, S. M., & Van Essen, D. C. (2016).
A multi-modal parcellation of human cerebral cortex. Nature,
536(7615), 171–178. https://doi.org/10.1038/nature18933,
PubMed: 27437579
Groppa, S., Gonzalez-Escamilla, G., Eshaghi, A., Meuth, S. G., &
Ciccarelli, O. (2021). Linking immune-mediated damage to neu-
rodegeneration in multiple sclerosis: Could network-based MRI
help? Brain Communications, 3(4), fcab237. https://doi.org/10
.1093/braincomms/fcab237, PubMed: 34729480
Guillon, J., Attal, Y., Colliot, O., La Corte, V., Dubois, B., Schwartz,
D., Chavez, M., & De Vico Fallani, F. (2017). Loss of brain
inter-frequency hubs in Alzheimer’s disease. Scientific Reports,
7(1), 10879. https://doi.org/10.1038/s41598-017-07846-w,
PubMed: 28883408
Guillon, J., Chavez, M., Battiston, F., Attal, Y., La Corte, V., de
Schotten, M. T., Dubois, B., Schwartz, D., Colliot, O., & De Vico
Fallani, F. (2019). Disrupted core-periphery structure of multi-
modal brain networks in Alzheimer’s disease. Network Neurosci-
ence, 3(2), 635–652. https://doi.org/10.1162/netn_a_00087,
PubMed: 31157313
Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W.,
& Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790. https://
doi.org/10.1016/j.neuroimage.2011.09.015, PubMed: 21979382
Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., &
Porter, M. A. (2014). Multilayer networks. Journal of Complex
Networks, 2(3), 203–271. https://doi.org/10.1093/comnet/cnu016
Klein, A., Ghosh, S. S., Bao, F. S., Giard, J., Häme, Y., Stavsky, E.,
Lee, N., Rossa, B., Reuter, M., Chaibub Neto, E., & Keshavan, A.
(2017). Mindboggling morphometry of human brains. PLoS Com-
putational Biology, 13(2), e1005350. https://doi.org/10.1371
/journal.pcbi.1005350, PubMed: 28231282
Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world
networks. Physical Review Letters, 87(19), 198701. https://doi
.org/10.1103/PhysRevLett.87.198701, PubMed: 11690461
Lim, S., Radicchi, F., van den Heuvel, M. P., & Sporns, O. (2019).
Discordant attributes of structural and functional brain connec-
tivity in a two-layer multiplex network. Scientific Reports, 9(1),
2885. https://doi.org/10.1038/s41598-019-39243-w, PubMed:
30814615
Liu, J., Li, M., Pan, Y., Lan, W., Zheng, R., Wu, F.-X., & Wang, J.
(2017). Complex brain network analysis and its applications to
brain disorders: A survey. Complexity, 2017, 8362741. https://
doi.org/10.1155/2017/8362741
Llufriu, S., Martinez-Heras, E., Solana, E., Sola-Valls, N., Sepulveda,
M., Blanco, Y., Martinez-Lapiscina, E. H., Andorra, M., Villoslada,
P., Prats-Galino, A., & Saiz, A. (2017). Structural networks
involved in attention and executive functions in multiple sclerosis.
NeuroImage: Clinical, 13, 288–296. https://doi.org/10.1016/j.nicl
.2016.11.026, PubMed: 28050344
Ma, Y., & Tang, J. (2021). Deep learning on graphs. Cambridge Uni-
versity Press. https://doi.org/10.1017/9781108924184
Mandke, K., Meier, J., Brookes, M. J., O’Dea, R. D., Van Mieghem,
P., Stam, C. J., Hillebrand, A., & Tewarie, P. (2018). Comparing
multilayer brain networks between groups: Introducing graph
metrics and recommendations. NeuroImage, 166, 371–384.
https://doi.org/10.1016/j.neuroimage.2017.11.016, PubMed:
29138088
Martínez-Heras, E., Varriano, F., Prčkovska, V., Laredo, C., Andorrà,
M., Martínez-Lapiscina, E. H., Calvo, A., Lampert, E., Villoslada,
P., Saiz, A., Prats-Galino, A., & Llufriu, S. (2015). Improved
framework for tractography reconstruction of the optic radiation.
PLoS One, 10(9), e0137064. https://doi.org/10.1371/journal
.pone.0137064, PubMed: 26376179
Muldoon, S. F., & Bassett, D. S. (2016). Network and multilayer
network approaches to understanding human brain dynamics.
Philosophy of Science, 83(5), 710–720. https://doi.org/10.1086
/687857
Newman, M. (2018). Networks. Oxford University Press. https://doi
.org/10.1093/oso/9780198805090.001.0001
Pagani, E., Rocca, M. A., De Meo, E., Horsfield, M. A., Colombo,
B., Rodegher, M., Comi, G., & Filippi, M. (2020). Structural con-
nectivity in multiple sclerosis and modeling of disconnection.
Multiple Sclerosis, 26(2), 220–232. https://doi.org/10.1177
/1352458518820759, PubMed: 30625050
Patenaude, B., Smith, S. M., Kennedy, D. N., & Jenkinson, M.
(2011). A Bayesian model of shape and appearance for subcor-
tical brain segmentation. NeuroImage, 56(3), 907–922. https://
doi.org/10.1016/j.neuroimage.2011.02.046, PubMed: 21352927
Pedersen, M., Zalesky, A., Omidvarnia, A., & Jackson, G. D. (2018).
Multilayer network switching rate predicts brain performance.
Proceedings of the National Academy of Sciences, 115(52),
13376–13381. https://doi.org/10.1073/pnas.1814785115,
PubMed: 30545918
Polman, C. H., Reingold, S. C., Banwell, B., Clanet, M., Cohen,
J. A., Filippi, M., Fujihara, K., Havrdova, E., Hutchinson, M.,
Kappos, L., Lublin, F. D., Montalban, X., O’Connor, P., Sandberg-
Wollheim, M., Thompson, A. J., Waubant, E., Weinshenker, B., &
Wolinsky, J. S. (2011). Diagnostic criteria for multiple sclerosis:
2010 revisions to the McDonald criteria. Annals of Neurology,
69(2), 292–302. https://doi.org/10.1002/ana.22366, PubMed:
21387374
Riccitelli, G. C., Pagani, E., Meani, A., Valsasina, P., Preziosa, P.,
Filippi, M., & Rocca, M. A. (2020). Cognitive impairment in benign
multiple sclerosis: A multiparametric structural and functional MRI
study. Journal of Neurology, 267(12), 3508–3517. https://doi.org
/10.1007/s00415-020-10025-z, PubMed: 32617658
Rocca, M. A., Amato, M. P., De Stefano, N., Enzinger, C., Geurts,
J. J., Penner, I.-K., Rovira, A., Sumowski, J. F., Valsasina, P.,
Filippi, M., & MAGNIMS Study Group. (2015). Clinical and
imaging assessment of cognitive dysfunction in multiple sclero-
sis. Lancet Neurology, 14(3), 302–317. https://doi.org/10.1016
/S1474-4422(14)70250-9, PubMed: 25662900
Rocca, M. A., Valsasina, P., Meani, A., Falini, A., Comi, G., &
Filippi, M. (2016). Impaired functional integration in multiple
sclerosis: A graph theory study. Brain Structure and Function,
221(1), 115–131. https://doi.org/10.1007/s00429-014-0896-4,
PubMed: 25257603
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
Network Neuroscience
932
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
a
_
0
0
2
5
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Applying multilayer analysis to brain networks
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Shu, N., Duan, Y., Xia, M., Schoonheim, M. M., Huang, J., Ren, Z.,
Sun, Z., Ye, J., Dong, H., Shi, F.-D., Barkhof, F., Li, K., & Liu, Y.
(2016). Disrupted topological organization of structural and
functional brain connectomes in clinically isolated syndrome
and multiple sclerosis. Scientific Reports, 6, 29383. https://doi
.org/10.1038/srep29383, PubMed: 27403924
Solana, E., Martinez-Heras, E., Casas-Roma, J., Calvet, L., Lopez-
Soley, E., Sepulveda, M., Sola-Valls, N., Montejo, C., Blanco,
Y., Pulido-Valdeolivas, I., Andorra, M., Saiz, A., Prados, F., &
Llufriu, S. (2019). Modified connectivity of vulnerable brain
nodes in multiple sclerosis, their impact on cognition and their
discriminative value. Scientific Reports, 9(1), 20172. https://doi
.org/10.1038/s41598-019-56806-z, PubMed: 31882922
Solana, E., Martinez-Heras, E., Martinez-Lapiscina, E. H., Sepulveda,
M., Sola-Valls, N., Bargalló, N., Berenguer, J., Blanco, Y., Andorra,
M., Pulido-Valdeolivas, I., Zubizarreta, I., Saiz, A., & Llufriu, S.
(2018). Magnetic resonance markers of tissue damage related
to connectivity disruption in multiple sclerosis. NeuroImage:
Clinical, 20, 161–168. https://doi.org/10.1016/j.nicl.2018.07
.012, PubMed: 30094165
Solana, E., Martinez-Heras, E., Montal, V., Vilaplana, E., Lopez-
Soley, E., Radua, J., Sola-Valls, N., Montejo, C., Blanco, Y.,
Pulido-Valdeolivas, I., Sepúlveda, M., Andorra, M., Berenguer,
J., Villoslada, P., Martinez-Lapiscina, E. H., Prados, F., Saiz, A.,
Fortea, J., & Llufriu, S. (2021). Regional grey matter microstructural
changes and volume loss according to disease duration in multiple
sclerosis patients. Scientific Reports, 11(1), 16805. https://doi.org
/10.1038/s41598-021-96132-x, PubMed: 34413373
Solé-Ribalta, A., De Domenico, M., Gómez, S., & Arenas, A.
(2014). Centrality rankings in multiplex networks. In Proceedings
’14
of
the 2014 ACM conference on web science: WebSci
(pp. 149–155). Association for Computing Machinery. https://doi
.org/10.1145/2615569.2615687
Sporns, O. (2013). Network attributes for segregation and integra-
tion in the human brain. Current Opinion in Neurobiology, 23(2),
162–171. https://doi.org/10.1016/j.conb.2012.11.015, PubMed:
23294553
Stanley, M. L., Simpson, S. L., Dagenbach, D., Lyday, R. G.,
Burdette, J. H., & Laurienti, P. J. (2015). Changes in brain network
efficiency and working memory performance in aging. PLoS
One, 10(4), e0123950. https://doi.org/10.1371/journal.pone
.0123950, PubMed: 25875001
Suárez, L. E., Markello, R. D., Betzel, R. F., & Misic, B. (2020). Link-
ing structure and function in macroscale brain networks. Trends
in Cognitive Sciences, 24(4), 302–315. https://doi.org/10.1016/j
.tics.2020.01.008, PubMed: 32160567
Tijms, B. M., Seriès, P., Willshaw, D. J., & Lawrie, S. M. (2012).
Similarity-based extraction of individual networks from gray
matter MRI scans. Cerebral Cortex, 22(7), 1530–1541. https://
doi.org/10.1093/cercor/bhr221, PubMed: 21878484
Ting, C.-M., Samdin, S. B., Tang, M., & Ombao, H. (2021). Detect-
ing dynamic community structure in functional brain networks
across individuals: A multilayer approach. IEEE Transactions on
Medical Imaging, 40(2), 468–480. https://doi.org/10.1109/TMI
.2020.3030047, PubMed: 33044929
Tournier, J.-D., Smith, R., Raffelt, D., Tabbara, R., Dhollander, T.,
Pietsch, M., Christiaens, D., Jeurissen, B., Yeh, C.-H., & Connelly,
A. (2019). MRtrix3: A fast, flexible and open software framework
for medical image processing and visualisation. NeuroImage,
202, 116137. https://doi.org/10.1016/j.neuroimage.2019
.116137, PubMed: 31473352
Wybrecht, D., Reuter, F., Pariollaud, F., Zaaraoui, W., Le Troter, A.,
Rico, A., Confort-Gouny, S., Soulier, E., Guye, M., Maarouf, A.,
Ranjeva, J.-P., Pelletier, J., & Audoin, B. (2017). New brain
lesions with no impact on physical disability can impact cogni-
tion in early multiple sclerosis: A ten-year longitudinal study.
PLoS One, 12(11), e0184650. https://doi.org/10.1371/journal
.pone.0184650, PubMed: 29149177
Yu, R., Zhang, H., An, L., Chen, X., Wei, Z., & Shen, D. (2017).
Connectivity strength-weighted sparse group representation-
based brain network construction for MCI classification. Human
Brain Mapping, 38(5), 2370–2383. https://doi.org/10.1002/hbm
.23524, PubMed: 28150897
Zhang, J., Cortese, R., De Stefano, N., & Giorgio, A. (2021).
Structural and functional connectivity substrates of cognitive
impairment in multiple sclerosis. Frontiers in Neurology, 12,
671894. https://doi.org/10.3389/fneur.2021.671894, PubMed:
34305785
Zitnik, M., Nguyen, F., Wang, B., Leskovec, J., Goldenberg, A., &
Hoffman, M. M. (2019). Machine learning for integrating data in
biology and medicine: Principles, practice, and opportunities.
Information Fusion, 50, 71–91. https://doi.org/10.1016/j.inffus
.2018.09.012, PubMed: 30467459
Zurita, M., Montalba, C., Labbé, T., Cruz, J. P., Dalboni da Rocha,
J., Tejos, C., Ciampi, E., Cárcamo, C., Sitaram, R., & Uribe, S.
(2018). Characterization of relapsing-remitting multiple sclerosis
patients using support vector machine classifications of
functional and diffusion MRI data. NeuroImage: Clinical, 20,
724–730. https://doi.org/10.1016/j.nicl.2018.09.002, PubMed:
30238916
Network Neuroscience
933
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
9
1
6
2
0
4
6
4
4
6
n
e
n
_
a
_
0
0
2
5
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3