RECHERCHE
Latent functional connectivity underlying
multiple brain states
Ethan M. McCormick1,2,3 †
, Katelyn L. Arnemann1 †
, Takuya Ito1,4
,
Stephen José Hanson5
, and Michael W. Cole1
1Center for Molecular and Behavioral Neuroscience, Rutgers University, Newark, New Jersey, Etats-Unis
2Department of Psychology and Neuroscience, University of North Carolina at Chapel Hill, Chapel Hill, Caroline du Nord, Etats-Unis
3Cognitive Neuroscience Department, Donders Institute for Brain, Cognition and Behavior,
Radboud University Medical Center, Nijmegen, Netherlands
4Yale University School of Medicine, Yale University, New Haven, CT, Etats-Unis
5Rutgers University Brain Imaging Center, Newark, New Jersey, Etats-Unis
†Denotes equal authorship.
un accès ouvert
journal
Mots clés: Intrinsic connectivity, Factor analysis, Resting state, Task connectivity, ActFlow
ABSTRAIT
Functional connectivity (FC) studies have predominantly focused on resting state, où
ongoing dynamics are thought to reflect the brain’s intrinsic network architecture, which is
thought to be broadly relevant because it persists across brain states (c'est à dire., is state-general).
Cependant, it is unknown whether resting state is the optimal state for measuring intrinsic FC.
We propose that latent FC, reflecting shared connectivity patterns across many brain states,
better captures state-general intrinsic FC relative to measures derived from resting state alone.
We estimated latent FC independently for each connection using leave-one-task-out factor
analysis in seven highly distinct task states (24 conditions) and resting state using fMRI data
from the Human Connectome Project. Compared with resting-state connectivity, latent FC
improves generalization to held-out brain states, better explaining patterns of connectivity
and task-evoked activation. We also found that latent connectivity improved prediction of
behavior outside the scanner, indexed by the general intelligence factor ( g). Our results
suggest that FC patterns shared across many brain states, rather than just resting state, better
reflect state-general connectivity. This affirms the notion of “intrinsic” brain network
architecture as a set of connectivity properties persistent across brain states, providing an
updated conceptual and mathematical framework of intrinsic connectivity as a latent factor.
RÉSUMÉ DE L'AUTEUR
The initial promise of resting-state fMRI was that it would reflect “intrinsic” functional
relationships in the brain free from any specific task context, yet this assumption has remained
untested until recently. Here we propose a latent variable method for estimating intrinsic
functional connectivity (FC) as an alternative to rest FC. We show that latent FC outperforms
rest FC in predicting held-out FC and regional activation states in the brain. En plus, latent
FC better predicts a marker of general intelligence measured outside of the scanner. Nous
demonstrate that the latent variable approach subsumes other approaches to combining
data from multiple states (par exemple., averaging) and that it outperforms rest FC alone in terms of
generalizability and predictive validity.
Citation: McCormick, E. M., Arnemann,
K. L., Ito, T., Hanson, S. J., & Cole, M.. W.
(2022). Latent functional connectivity
underlying multiple brain states.
Neurosciences en réseau, 6(2), 570–590.
https://doi.org/10.1162/netn_a_00234
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00234
Informations complémentaires:
https://doi.org/10.1162/netn_a_00234
Reçu: 22 Septembre 2021
Accepté: 19 Janvier 2022
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Ethan M. McCormick
ethan.mccormick@radboudumc.nl
Éditeur de manipulation:
Shella Keilholz
droits d'auteur: © 2022
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
Intrinsic connectivity:
The part of FC between a given set of
brain regions that exists
independently of current task
demands.
Functional connectivity (FC):
A measure of the degree of
relationship between the function
time course of two regions. Ici
measured with functional MRI.
Factor analysis:
A statistical framework for estimating
the properties of latent variables from
a set of correlated observed
variables.
Latent variable:
A variable (often denoted η) c'est
not directly observed but inferred by
patterns of covariation in the data.
Factor loading:
A regression-based estimate of the
relationship between latent and
observed variables (often denoted λ).
INTRODUCTION
A major goal in cognitive neuroscience in recent years has been to move away from charac-
terizing brain activation and connectivity in specific task states towards understanding
“intrinsic” or context-free brain activity. Such activity reflects the more than 95% of metabolic
brain activity that remains unchanged across cognitive demands (Raichle, 2006). This ongoing
brain activity persists across states and is not attributable to external stimuli or task demands.
Efforts to understand intrinsic function have focused primarily on statistical associations
between brain activity time series (functional connectivity; FC) during the resting state (Fox
& Raichle, 2007; but see Finn et al., 2015, and Greene, Gao, Scheinost, & Constable,
2018, for task-based investigations), which has revealed an intrinsic brain functional network
architecture that recapitulates patterns of task-evoked brain activity (Cole, Ito, Bassett, &
Schultz, 2016; Smith et al., 2009) and structural connectivity (Honey et al., 2009). As the name
implique, cependant, resting state is just one state that the brain can occupy, and a truly “intrinsic”
connectivity network should persist across the many different states a brain might assume. Dans
autres mots, a “state-general” intrinsic network. Despite its importance for understanding
brain function, many uncertainties remain on how to best estimate intrinsic FC. While some
efforts have focused on the need to obtain longer resting-state scans (Anderson, Ferguson,
Lopez-Larson, & Yurgelun-Todd, 2011; Elliott et al., 2019; Hacker et al., 2013; Laumann
et coll., 2015), more recent approaches have highlighted advantages of combining resting-state
and task data to analyze intrinsic activity.
This second set of approaches leverages functional data across different task (and rest) scans
in order to improve the reliability of FC estimates and their predictive utility (Elliott et al.,
2019). Because of the relatively high stability of FC networks across task states (Cole, Bassett,
Power, Plus courageux, & Petersen, 2014; Gratton et al., 2018; Krienen, Yeo, & Buckner, 2014), com-
bining data across task runs aims to distinguish what is common across a larger set of brain
states. What is common therefore reflects the intrinsic patterns of covariance in the brain,
while variation between different brain states is treated as noise in the combined data. Comment-
jamais, this work largely relies on averaging data from multiple scans together (Elliott et al.,
2019). While this approach has been shown to be useful, and has the advantage of simplicity,
there are potential theoretical limitations to such an approach that may limit its generaliz-
ability. Given its ubiquity and close-formed, arithmetic solution, the average is rarely thought
of as a formal statistical model. Cependant, recent work (McNeish & Loup, 2020) has shown
that the average can be thought of as a restricted case of the more general factor analytic
model. Embedding the average in a theoretically rich statistical framework is likely to offer
advantages for interpretation of results using this measure as well as insights into the mea-
sure itself.
Factor analysis has a long tradition in the behavioral sciences (Spearman, 1904; Thurstone,
1935) and is an invaluable tool in psychometrics and psychological measurement. Its key
insight is that observed measures (par exemple., behavioral responses or fMRI scans) are imperfect man-
ifestations of an unobserved (c'est à dire., latent) variable (Bollen, 2002). In the factor model, observed
indicators (yi,t; i = individual, t = task state) are modeled as dependent on the underlying latent
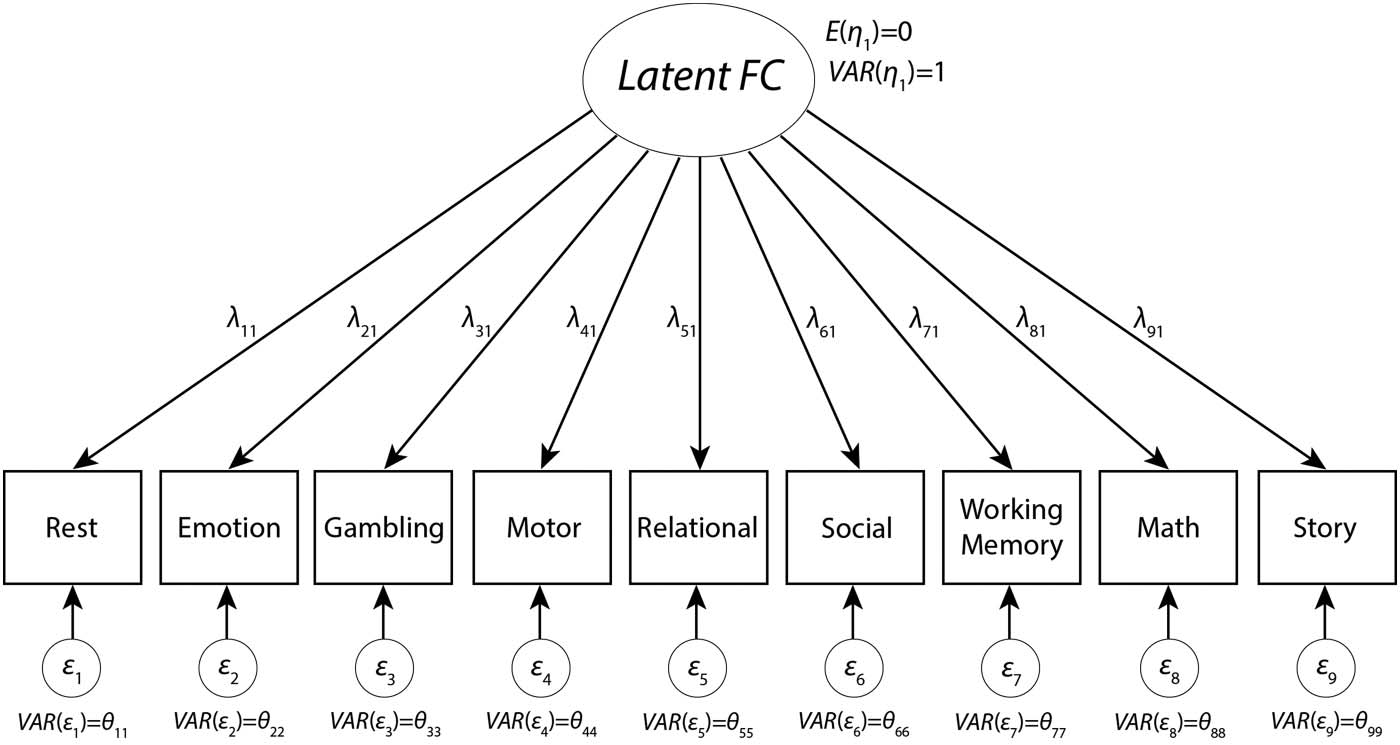
factor (η; Chiffre 1). Variability in the indicators is partitioned into common variance (transmit-
ted through the factor loading matrix, Λ) and unique variance (ɛt). In this model, latent FC
represents an unmeasured, underlying brain state that is common to all observed brain states
(c'est à dire., the indicators: resting state, motor task, etc.), but we also explicitly model additional var-
iance that is only found in each individual task state through the error terms. Factor loadings
for the individual task states (par exemple., λ11 for Rest) in this single-factor model can be interpreted as
the proportion of variance explained in each task state by latent FC (similar to R2 in regression).
Neurosciences en réseau
571
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
Factor model. A set of indicators (repos, motor task, etc.) are modeled, composed of shared
Chiffre 1.
underlying variance, as represented by the latent factor (c'est à dire., latent FC), and unique task-state var-
iance (in the errors). Factor loadings (λ) represent the percentage variance in each task state that is
explained by the underlying latent FC.
As can be seen in Figure 1, the factor analysis model of latent FC is a parameter-rich model
that allows for differentially weighted relationships between the underlying latent connectivity
and measured connectivity in each specific state. What McNeish and Wolf (2020) showed,
cependant, is that the average can be recovered using this model by setting all factor loadings
(λ) equal to 1 and the unique variances to 0. This recast of the average as a special case of the
factor model not only has the advantage of making the assumptions of the average clearer, mais
it enables a formal test of those assumptions. Par exemple, by setting all factor loadings equal,
the average assumes that each observed FC state is equally (and positively) related to the
underlying latent FC. If we want to relax that assumption, the factor analytic model can be
used to compute unique optimally weighted values for each factor loading, which suggests
that some observed states may be better (ou pire) reflections of underlying latent FC. En effet,
factor loadings may take on negative values, which implies that an observed indicator is anti-
correlated with the underlying latent FC. Cependant, if the assumption of equal, positive weight-
ing is indeed an appropriate assumption, freely estimated factor loadings will converge
towards equal values and approximate the average. Autrement dit, the flexibility of the full
factor loading does not preclude the average, but instead offers a broader range of possibility
for deriving a measure of latent FC in heterogeneous data and can be used to test the validity of
the average FC assumption of equal positive factor loadings across brain states.
Ici, we test the reliability of a factor analytic framework for modeling state-general brain
connectivity—“intrinsic” FC that generalizes across a variety of brain states. D'abord, we hypoth-
esized that latent FC reflects a positive manifold (analogous to the positive correlations across
intelligence tests in general intelligence research; Kovacs & Conway, 2016), where all state-
specific connectivity values are positively correlated with each other and so load positively
onto the underlying latent variable. This would confirm that a single common intrinsic func-
tional network architecture exists across conscious brain states. Surtout, this differs from
the idea that states are correlated (Finn et al., 2015; Gratton et al., 2018), as between-subject
variance is decomposed at each individual connection rather than correlating across connec-
tion. We further hypothesized that by combining information across task states, such as in the
factor model, a more reliable measure of “intrinsic” connectivity can be estimated than when
using resting-state data alone (the current field standard). This would suggest that resting-state
Positive manifold:
A positive manifold implies that all
variables positively correlate with
one another.
Neurosciences en réseau
572
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
Psychometric g:
A measure of generalized
intelligence underlying performance
on a set of diverse cognitive tasks.
FC is not necessarily the best state for estimating intrinsic FC, especially if resting state does not
load higher on the latent variable than other states. In testing these hypotheses, we developed
an analytic framework for estimating state-general, latent FC in whole-brain functional data.
Using multitask fMRI data from the Human Connectome Project (HCP), we compare the abil-
ity of latent and resting-state FC to predict task-evoked activation and task-state FC for held-out
brain states, as well as to explain individual differences in psychometric “g” (a measure of
human intelligence derived with a similar factor analytic model). Results demonstrate the
promise of the latent variable approach in functional neuroimaging, particularly for the esti-
mation of intrinsic FC that generalizes beyond specific brain states (par exemple., repos). Enfin, we dem-
onstrate the relationship between freely estimated latent FC and the simpler average FC
approach and discuss the theoretical advantages of casting both methods in the latent variable
framework for future work.
RÉSULTATS
Factor Analysis Model of Latent Connectivity
We ran independent factor analysis models for each connection, estimating the factor loadings
of the latent variable (c'est à dire., latent FC) onto each state. Latent FC captures the shared variance in
FC across all states (voir la figure 2). Factor analyses were run using all available data (c'est à dire., the full
time series and all states). All analyses were performed in the exploratory sample indepen-
dently and then replicated in the validation sample (both N = 176; see the Participants section
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
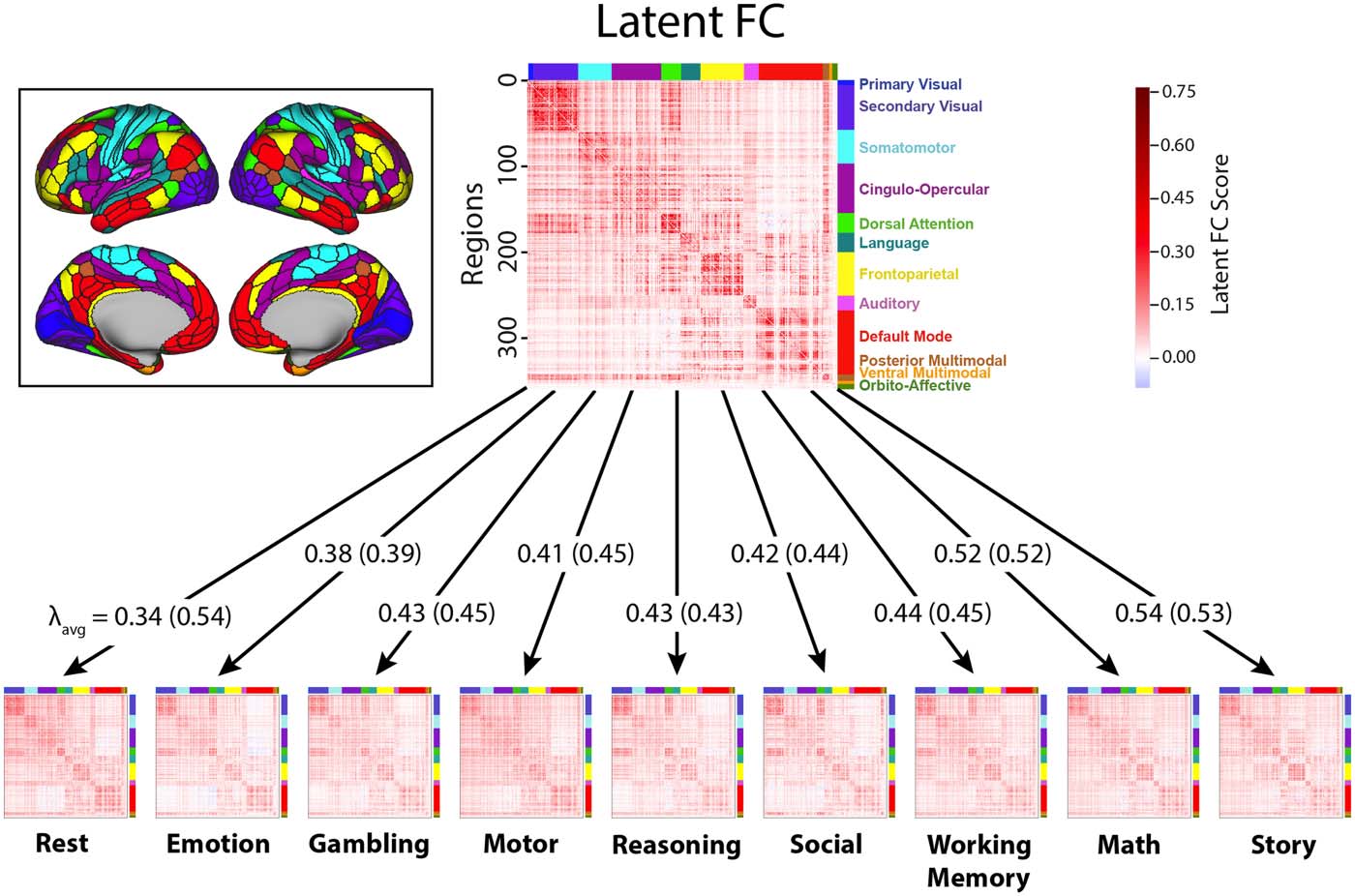
Chiffre 2. Factor analysis model of latent FC. Visualization of the latent connectivity matrix and
state-specific functional connectivity matrices (group average across subjects). Color along the axes
of each matrix corresponds to the network membership of each ROI. For each arrow, the average
loadings (λavg) for each state are shown for analyses controlling for number of TRs (d'abord) and when
not controlling for TRs (in parentheses). The average loadings for the task states were largely stable
across analyses, but the average loading for resting state increased substantially (depuis 0.34 à 0.54)
when not controlling for the number of TRs. The amount of resting-state data per participant went
depuis 4,800 TRs (58 min) à 2,112 TRs (25 min) when matching the total amount of “on-task” time.
The network mapping is shown in the cutout (gauche). Elements in the state-specific matrices represent
correlations (r) between regional time series, and elements in the latent FC matrix represent factor
scores computed from the model for each connection.
Neurosciences en réseau
573
Latent functional connectivity
for additional information). Surtout, all factor analytic models were fit for each sample
separately to avoid issues of circularity when comparing results across samples.
Consistent with our hypothesis that there is a “positive manifold” demonstrating a common
latent FC architecture across states, almost all factor loadings were positive (greater than 99%)
across all connections and all states (see Table 1). En outre, 70.7% of all factor loadings were
reasonably large in magnitude (factor loading ≥ 0.4), et 97.4% of connections had two or more
states with factor loadings ≥ 0.4 in the full latent FC model. The emotion task had the fewest large
factor loadings (47.3%), and the resting state had the most (92.6%; see Table 1 for full details).
To control for differences between states in the amount of data used to obtain state-specific
FC estimates, factor analyses were rerun while matching the number of time points from rest
and task data (2,112 TRs from rest and 264 TRs for each of the eight tasks). With this approach,
resting state had the fewest number of relatively high-magnitude factor loadings of all
states—only 31.6% of resting-state connections had factor loadings ≥ 0.4. Ainsi, resting state
had the highest factor loadings onto latent FC when a large amount of data were used to esti-
mate resting-state FC, but the lowest factor loadings when less data were used. Controlling for
the number of time points between task and rest led to less pronounced changes in the factor
loadings of the other states (voir la figure 2), likely because there was no relationship between the
number of TRs for a given task state and its average factor loading in the full TR analysis (voir
Figure S1 in the Supporting Information). Note that this drop occurs even though rest continues
to have substantially more TRs (8×) than any given task state in these analyses.
Latent FC Improves Generalization to Connectivity of Held-Out States
We next sought to test our second hypothesis: A more reliable and generalizable measure of
“intrinsic” connectivity can be estimated by combining information across task states, tel que
in the factor model, than by using resting-state data alone (the current field standard). To test
whether the measures of intrinsic FC persist across brain states, we quantified the generaliz-
ability of rest FC and latent FC to held-out brain states. To calculate the similarity of FC patterns
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
t
.
Factor loadings. Almost all factor loadings were positive regardless of whether all resting-state data were used (gauche) or we controlled
Tableau 1.
for the number of time points between task and rest (droite). Only resting state showed a substantial shift in the percentage of factor loadings
≥ 0.4 when controlling for the number of time points. The amount of resting-state data per participant went from 4,800 TRs (58 min) à 2,112 TRs
(25 min) when matching the total amount of “on-task” time.
State
Rest
Emotion
Gambling
Motor
Reasoning
Social
Working memory
Math
Language
All data
% Loadings ≥ 0
99.9
% Loadings ≥ 0.4
92.6
Controlling for no. of time points
% Loadings ≥ 0
99.0
% Loadings ≥ 0.4
31.6
99.3
99.6
99.8
99.5
99.8
99.7
99.9
99.9
47.3
65.0
68.0
62.1
66.2
67.0
82.4
86.0
98.7
99.1
99.4
99.1
99.3
99.2
99.6
99.7
46.3
62.2
54.8
62.3
58.4
64.9
82.4
86.3
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Neurosciences en réseau
574
Latent functional connectivity
Bonferroni correction:
Correction for multiple comparison
where the corrected p value
threshold is the original threshold
divided by the number of tests
performed.
Activity flow mapping:
Computational model where activity
in a target region reflects activity in
other regions weighted by their FC
with the target.
(c'est à dire., across 64,620 network connections), we computed the Pearson’s correlation of rest FC or
latent FC with state FC for each individual subject, applying Bonferroni correction to correct
for multiple comparisons. For latent FC, similarity was always computed for the state that was
held-out while running the factor analysis model. Compared with rest FC, we found that latent
FC exhibited significantly greater similarity with a variety of independent brain states (voir
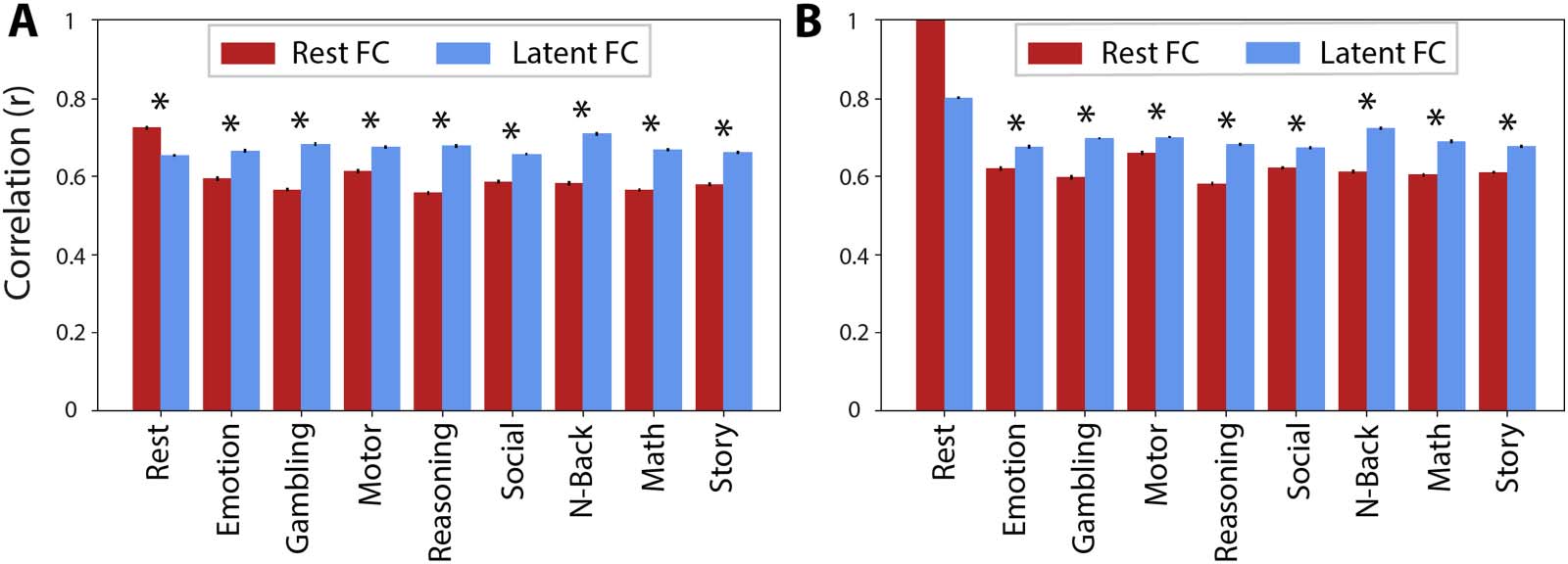
Figure 3A). Similarity of each state with latent FC was comparable across states, exhibiting
the greatest similarity to the WM task (r = 0.71) and the least similarity to the social task
(r = 0.66) and resting state (r = 0.65). Rest FC exhibited the greatest similarity to the full
resting-state data (r = 0.73), providing a measure of test-retest similarity of rest FC (c'est à dire.,
how well the restricted TR data represent the correlation matrix computed on the complete
resting-state data). For the task states, rest FC had the greatest similarity to the motor task (r =
0.61) and the least similarity to the relational task (r = 0.56).
When using the full time series (c'est à dire., not controlling for the amount of data used to obtain the
FC estimates across states), we still found greater similarity of latent FC relative to rest FC with
the task states. Cependant, latent FC exhibited the greatest similarity to the resting state (r = 0.80)
and the least similarity to the social task (r = 0.67; see Figure 3B). Alongside greater similarity
estimates with all states, this suggests that states may converge towards latent FC as we sample
substantially more data for any given state (par exemple., for resting-state FC, 26 min of data per partic-
ipant were included in the data-restricted analysis vs. 58 min of data in the unrestricted analysis).
All findings were replicated in the validation dataset (Informations complémentaires, Figure S2).
Latent FC Improves Prediction of Task Activation Patterns
We next sought to further test our hypothesis that latent FC is highly generalizable (relative to
resting-state FC), this time by testing for generalization beyond FC to patterns of task-evoked
activation. We began by using general linear models (GLMs) to estimate the pattern of
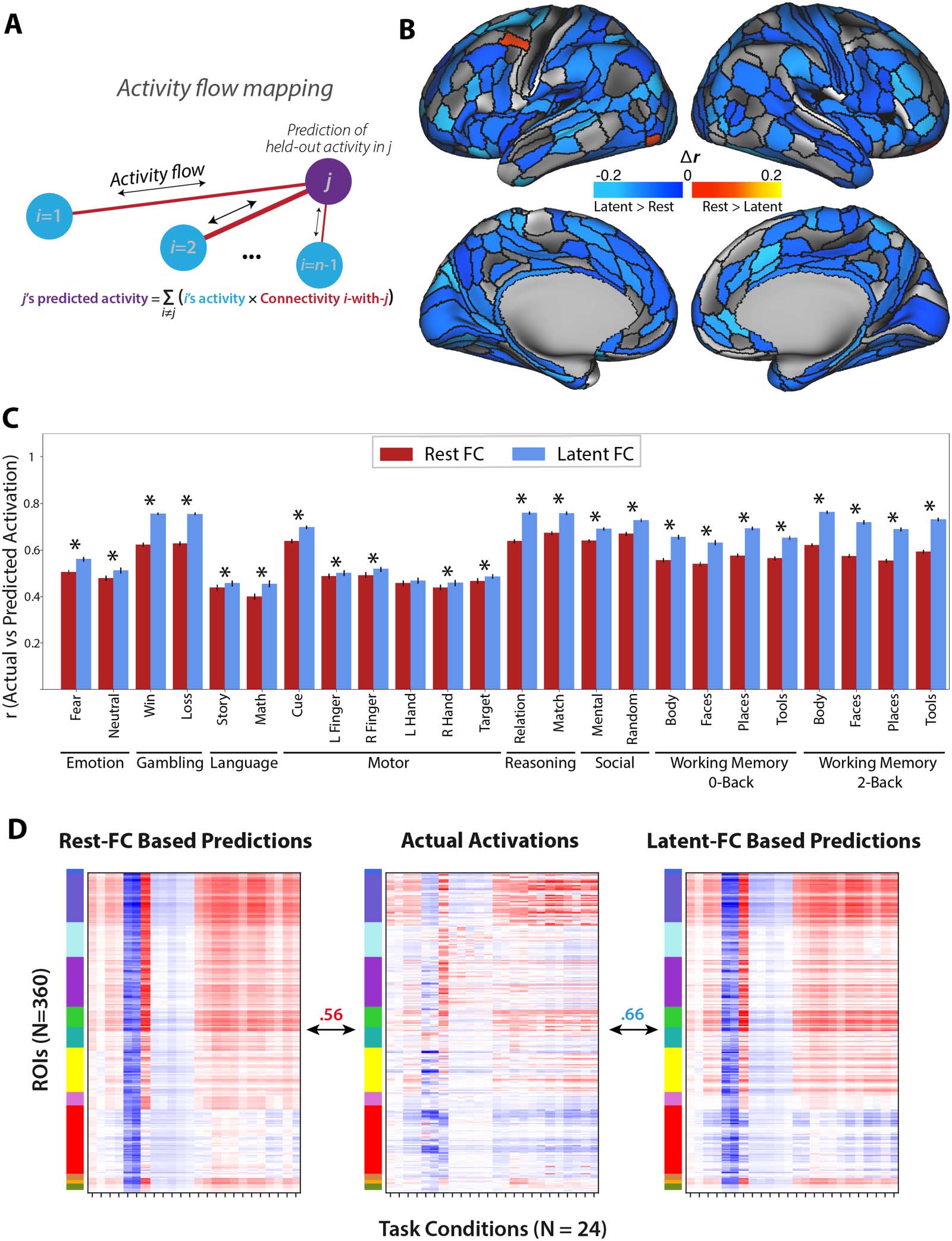
task-evoked activation for each of 24 task conditions. We then used activity flow mapping
(Figure 4A) to predict the pattern of task-evoked activation based on a simple neural network
model parameterized using either resting-state FC or latent FC. We used Pearson’s correlation
to compute the similarity of predicted-to-actual task activations of two activity flow models
with different connectivity estimates based on either latent FC or rest FC. As a global measure
Chiffre 3. Generalizability of FC patterns. Pearson’s correlation was used to quantify the similarity of latent FC (blue) and rest FC (red) to held-
out state FC. Error bars show the standard error of the mean. Asterisks indicate significant differences in similarity of latent FC and rest FC to
held-out state FC. (UN) Results when controlling for the number of time points in the resting-state data. This included 25 min of resting-state fMRI
data, matching the total amount of “on-task” time across all tasks. (B) Results when not controlling for the number of time points (y compris
58 min of resting-state data); the resting-state prediction is therefore a perfect reproduction (no error bars or comparison). These results are
consistent with resting-state FC overfitting to resting state, reducing its generalizability relative to latent FC.
Neurosciences en réseau
575
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4. Comparison of activity flow models based on latent FC versus rest FC. (UN) Conceptual model of the activity flow mapping algorithm
(Cole et al., 2016), which models the activity of a held-out region ( j) as the sum of activity in other brain regions (je) weighted by their shared
functional connectivity (ij). (B) Task activation prediction accuracies by region. Regions with prediction accuracies that were significantly
greater using the activity flow model based on latent FC are shown in cool colors. Regions with prediction accuracies that were significantly
greater using the activity flow model based on rest FC are shown in warm colors. The vast majority of regions showing a significant difference
showed prediction advantages for latent FC. (C) Task activation prediction accuracies by condition. Pearson’s correlation was used to quantify
the similarity of predicted-to-actual task activations using activity flow models with connectivity based on either rest FC (red) or latent FC
(blue). Error bars show the standard error of the mean correlation. Asterisks indicate significant differences in similarity of beta activations
from models based on latent FC versus rest FC. (D) Predicted activation patterns from activity flow models with connectivity based on latent
FC (droite; r = 0.66) outperformed predictions based on resting-state FC (gauche; r = 0.56) in reproducing the observed beta activation patterns
(center). Beta activations were averaged across individuals in the sample.
Neurosciences en réseau
576
Latent functional connectivity
Ridge regularization:
A penalized method for estimating a
linear regression model when the
number of predictors outnumbers the
number of subjects.
of performance, we first correlated the predicted activation patterns from the activity flow
model using rest and latent FC with the observed activations. Predicted activation patterns
from activity flow models with connectivity based on latent FC (r = 0.66) outperformed predic-
tions based on resting-state FC (r = 0.56) in reproducing the observed beta activation patterns
(Figure 4D). We then compared the results of the two models at the region (c'est à dire., prediction for a
given region across conditions) and condition (c'est à dire., prediction for a given condition across
régions) level.
We first estimated predicted beta activations for each region (across conditions) using the
activity flow models. This reflects the changes in activation within each region that are depen-
dent on the task condition. For each region, we compared the beta activation predictions of
the two activity flow models. For each network, we computed the percentage of regions with
significantly improved predictions for one of the two models. When using the activity flow
model based on latent FC, the predictions were significantly improved (based on a corrected
t test of z-transformed correlation coefficients) pour 68% of brain regions (246 out of 360 total),
accounting for 33% of VIS1, 69% of VIS2, 64% of SMN, 73% of CON, 70% of DAN, 62% de
LAN, 62% of FPN, 100% of AUD, 78% of DMN, 14% of PMM, 0% of VMM, et 33% de
ORA. Activity flow based on rest FC significantly improved predictions in 1% of brain regions
(4 out of 360 total), accounting for 7% of VIS2 and no other networks (Figure 4B).
When considering prediction accuracy for each task condition, we found that latent FC
significantly improved the across-region predicted activations for all task conditions—except
the left-hand condition of the motor task—when comparing the relative activations across the
topology of the brain within a condition (Figure 4C). Overlap of predicted-to-actual task acti-
vations for the activity flow models were variable by task condition. The activity flow model
based on latent FC exhibited the greatest similarity to the two-back body condition of the WM
task (r = 0.76) and the least similarity to the math condition of the language task (r = 0.45). Le
activity flow model based on rest FC exhibited the greatest similarity to the matching condition
of the relational task (r = 0.67) and the least similarity to the math condition of the language
task (r = 0.4). All findings were replicated in the validation dataset (Informations complémentaires,
Figure S3).
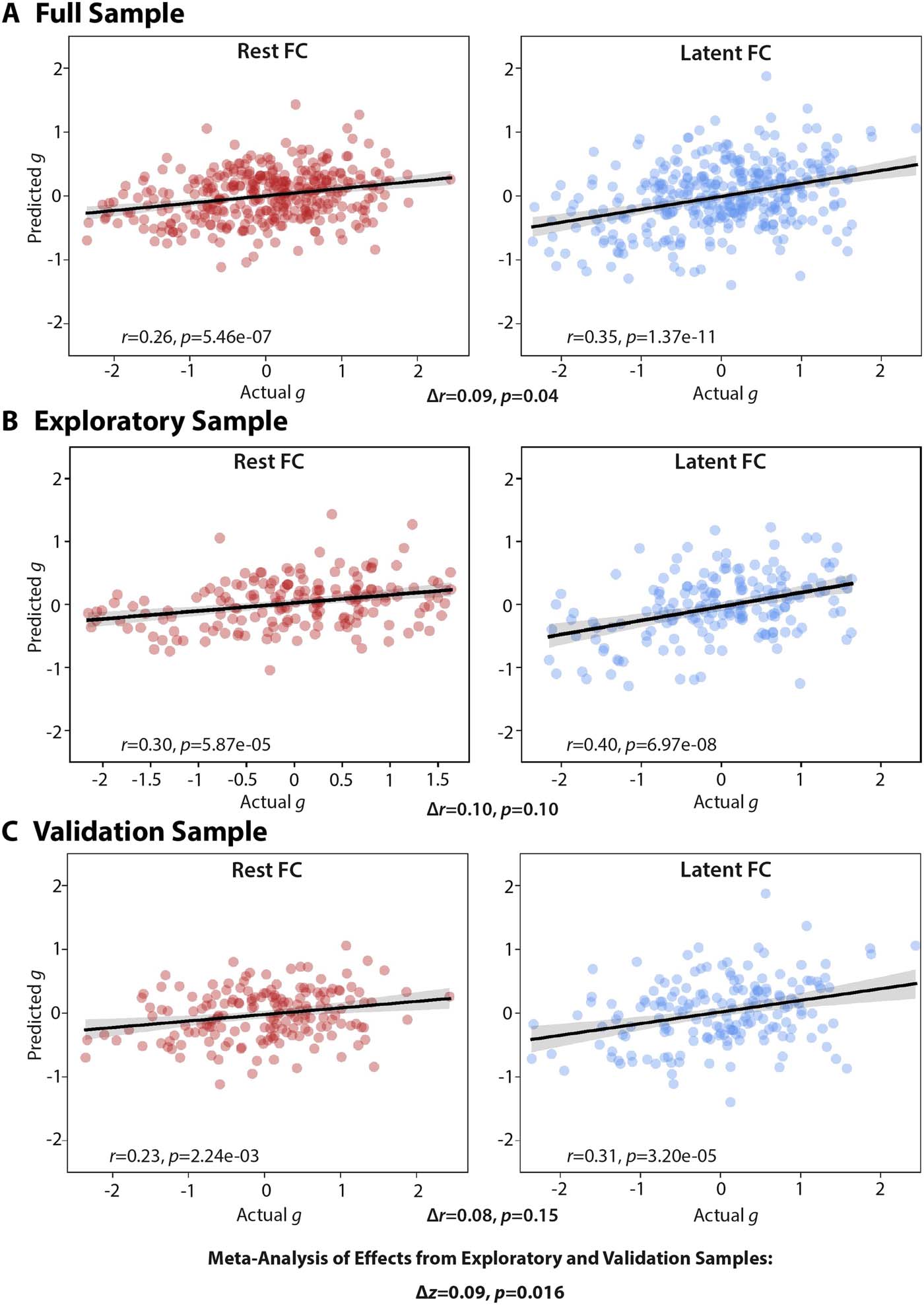
Latent FC Improves Prediction of General Intelligence
Our hypothesis that latent FC generalizes better than resting-state FC also predicts that latent
FC should be more related to general cognition and behavior, even behavior independent of
the particular tasks used for estimating the task-state FC going into the latent FC estimates. Nous
tested whether latent FC improves prediction of general intelligence using psychometric g to
capture many different behavioral and cognitive measures (Dubois, Galdi, Paul, & Adolphs,
2018; Gottfredson, 1997). We estimated general intelligence (psychometric g) using a factor
analysis model on behavioral data from a range of cognitive tasks, then tested whether latent
FC and/or rest FC measures could predict general intelligence. We combined the exploration
and validation samples to increase the number of participants to 352 for this analysis, given the
need for additional participants (relative to the other analyses in this study) to achieve reason-
able statistical power for individual difference correlations (Yarkoni, 2009). We then employed
a multiple linear regression with ridge regularization approach to predict general intelligence
from FC. Cependant, one potential confounding issue with simply pooling the full sample data is
that the estimated factor scores for latent FC and psychometric g would be influenced by the
data of to-be-predicted individuals, introducing circularity into these analyses. To avoid this,
we implemented a between-sample cross-validation approach. Ici, we estimated factor
Neurosciences en réseau
577
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
models for latent FC and psychometric g scores in each subsample separately (c'est à dire., exploratory
and validation), and predictions for the exploratory subjects were generated from the valida-
tion sample regression model and vice versa.
We found that predicted general intelligence was significantly correlated with actual gen-
eral intelligence for models using both rest FC (r = 0.26, p = 5.46e–07) and latent FC (r = 0.35,
p = 1.37e–11) (Figure 5A). Consistent with our hypothesis, the model using latent FC
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5. Relationship between actual and predicted general intelligence. Results of ridge regres-
sion models from rest FC and latent FC in the (UN) overall, (B) exploratory, et (C) validation sample.
The significance of the difference in correlation (Δr) is indicated below each plot. A meta-analysis of
the exploratory and validation samples showed a significant difference in the correlations between
actual and predicted g scores when comparing rest with latent FC (Δz = 0.09, p = 0.016).
Neurosciences en réseau
578
Latent functional connectivity
Meta-analysis:
A statistical analysis used to pool
results across multiple samples.
significantly improved prediction of general intelligence compared with the model using rest
FC (Δr = 0.09, t = 1.77, p = 0.04; see Eid, Gollwitzer, & Schmitt, 2011, for the correlation
comparison method). The magnitude of this effect was large, as the percentage linear variance
explained by latent FC (R2 = 0.123) was approximately two times the percentage linear
variance explained by rest FC (R2 = 0.067). In comparison with the overall sample results,
the correlation and difference in R2 was larger for the exploratory sample (Figure 5B), alors que
the validation set showed a more similar difference in R2 despite lower correlations between
predicted and actual psychometric g scores for both latent and rest FC data (Figure 5C). UN
meta-analysis (Field, 2001) of the exploratory and validation samples suggested that the
pooled correlation difference effect was significant (Δzpooled = 0.09, p = 0.016).
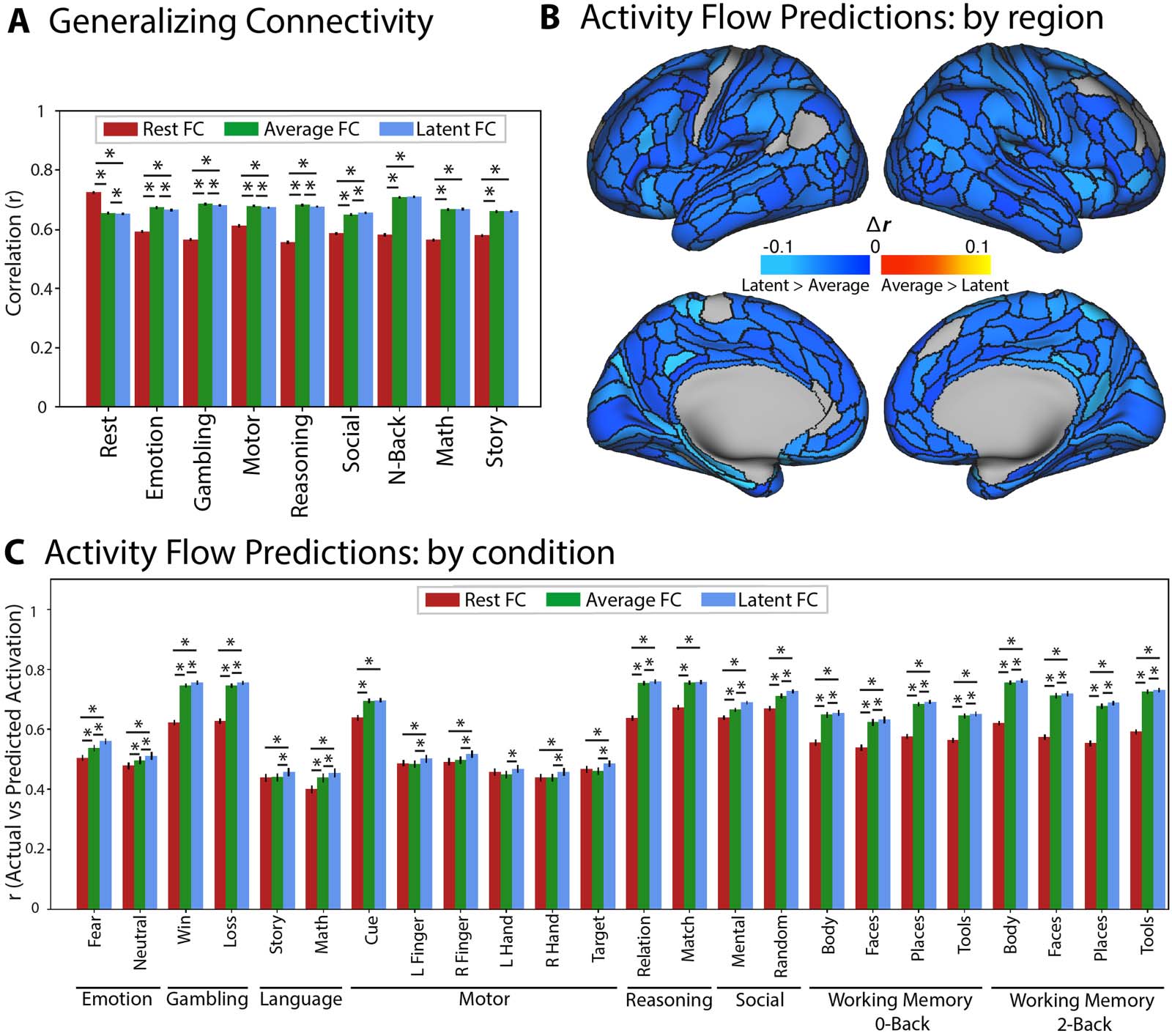
Comparing Latent and Average FC
While the factor model uses the covariance among the different states to compute optimal
weights, a simpler approach to finding consensus among states involves taking a simple
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 6. Comparison of (UN) generalizing connectivity and (B) activity flow models by region and (C) condition, based on latent FC and
average FC versus rest. (UN) Both average (vert) and latent (blue) FC outperformed rest FC on generalizing to all task states except resting
state. Average FC performed similarly or slightly better than latent FC on all held-out states (asterisks denote significant differences; the higher
position represents the test of rest versus latent FC). (B) In contrast, latent FC outperformed average FC in predicting task activation in 97% de
régions, whereas average FC outperformed in 0% of regions. (C) Across all conditions, latent FC was a better predictor than average FC of held-
out activations (lower asterisks indicate significant difference between adjacent bars; higher asterisks indicate significant difference between
latent and rest FC). All results control for the number of time points in the resting-state data. For the validation sample results, see Figure S4 in
the Supporting Information.
Neurosciences en réseau
579
Latent functional connectivity
average across states. This approach assumes the weights/loadings between measured states
are equal. Given that the computed weights in our results with latent FC were relatively uni-
form across states, we determined that this assumption was reasonable in this case. This sup-
ports the use of average FC; cependant, we directly compared latent FC with average FC to
assess whether there were any advantages to either method. To compare the factor model with
a simple average, we computed the mean value of each edge across states to construct an
average connectivity matrix. For all analyses, we controlled for the amount of data between
rest and task. Results indicated that combining across states, regardless of the approach, shows
substantial improvements over using even the full resting-state data. En effet, the average FC
approach appears to outperform the latent FC approach (albeit only slightly) in generalizing to
held-out connectivity states (Figure 6A). In the activity flow mapping results, cependant, latent
FC consistently outperforms average FC in predicting regional activity patterns, showing better
predictions in 348 out of 360 régions (97%), whereas average FC showed no improved pre-
dictions (Figure 6B). De la même manière, latent FC outperformed average FC in condition-wise activity
flow predictions in 22 out of 24 conditions (Figure 6C). Together these results suggest that the
average FC approach (sometimes termed “general functional connectivity”) is a reasonable
alternative to the more complex latent FC approach, so long as the optimal weights across
states are close to equal (an assumption not made by latent FC). This difference between
the methods would likely become more meaningful in cases wherein a particular brain state
is highly distinct from all others (par exemple., deep sleep vs. conscious states) or when one or more
states is much noisier than the others (which would be weighted lower by latent FC but not by
average FC).
DISCUSSION
Defining a map of task-independent, intrinsic functional connections in the brain is a major
aim of basic research in cognitive neuroscience. Intrinsic FC persists across task states, making
it a more reliable and generalizable measure of the underlying functional dynamics that shape
cognition and behavior. En tant que tel, measures of intrinsic FC are better candidates to serve as
stable biomarkers of important individual differences in behavioral outcomes (Elliott et al.,
2019). We utilized a factor analytic approach, a well-developed technique from measurement
psychometrics (Bollen, 2002), to define intrinsic FC as a latent variable derived from the com-
mon variances in FC across task states. We compared the factor model against the standard
approach applied in the field, FC derived from resting state. The factor model not only shows
enhanced measurement and predictive properties beyond measures of intrinsic FC derived
from resting state, it also offers a unique theoretical perspective on the relationship between
intrinsic and task-specific brain states. In a latent variable model, individual task states are
viewed as observable sample realizations of the underlying intrinsic connectivity, and task-
specific deviations from this baseline are modeled as unique errors arising from a combination
of noise and state-specific properties. The factor modeling approach allows researchers not
only to gain traction in defining intrinsic FC common among brain states, but also to separate
and explore properties that are specific to individuals and states.
Factor Analytic Model of Functional Connectivity
We began by building factor analysis models of latent FC using two approaches. Dans le premier, nous
modeled latent FC using all available data. In this model, resting-state functional connections
had the highest number of significant loadings of any condition. Cependant, when controlling
for the number of time points (by reducing the number of resting-state time points to match the
tasks with shorter durations), resting-state connections had the lowest percentage of significant
Neurosciences en réseau
580
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
factor loadings. This property of the factor model highlights one of its strengths; higher preci-
sion measurements show higher fidelity to the underlying common latent factor than do lower
precision measures. Ici, the precision appears to be driven primarily by the amount of data.
Cependant, in the absence of stringent data quality control, the factor model can also down-
weight poor-quality data (par exemple., high motion, artifacts) relative to higher quality data when var-
iability associated with noise does not replicate across task states.
Inversement, tasks that more closely represent underlying intrinsic FC will show stronger fac-
tor loadings, similar to how the Raven’s Progressive Matrices task loads highly onto the gen-
eralized intelligence factor (Dubois et al., 2018). Given its widespread use as a marker of
intrinsic FC, we might have expected that resting state would load highly onto the latent FC
factor regardless of how much data went into its estimation. Cependant, when controlling for the
amount of data used to estimate FC, the resting-state loadings were lower than all other exam-
ined states, even though there were still many more TRs of resting state than any one task state.
En plus, when using the full amount of data to estimate rest FC, the factor loadings for
resting state was similar to the story and math tasks, each of which were estimated with much
less data (Chiffre 2; values in parentheses). These results suggest that resting state is not an
especially good proxy for intrinsic FC, which aligns with its relatively poor performance com-
pared with latent FC in predicting the patterns of connectivity and evoked brain activity
observed for other states.
Latent FC as a Reliable Measure of Intrinsic Connectivity
As mentioned previously, a marker of intrinsic connectivity is its persistence across task states
(c'est à dire., generalizability), as well as its ability to accurately recapitulate observed realizations of
evoked brain activity and connectivity (Elliott et al., 2019; Elliott et al., 2020; Kragel, Han,
Kraynak, Gianaros, & Wager, 2020; Parkes, Satterthwaite, & Bassett, 2020). Our results high-
light the advantages of latent versus rest FC to reliably predict independent connectivity and
regional activations. When comparing patterns of connectivity, we showed that latent FC
showed higher correlation with held-out, task-specific connectivity states compared with rest
FC, with the sole exception of resting-state connectivity where rest FC outperformed. This pat-
tern of results suggests that resting-state FC is less generalizable as a measure of intrinsic con-
nectivity and instead there are resting-state-specific factors that shape the dynamics of rest FC
that are not present in other states.
One potential explanation for this might be that tasks as a group reliably differ from rest FC’s
more intrinsic profile, and the reduction in generalizability reflects deviations from a default
state. Under this explanation, the latent FC advantage could simply reflect that there are more
task indicators in the measurement model than rest (although note that even when controlling
for number of time points, the amount of rest data is equal to all the tasks combined) and we
would predict that latent FC would be a poorer representation of rest FC patterns of connec-
tivité. Cependant, results did not show a substantial drop in the correlation of latent and rest FC
compared with the correlations of latent FC with the various task FC patterns (blue bars,
Chiffre 3). En effet, it is when we used rest FC as the predictor that we observed reductions
in its correlation with task connectivity, compared with resting state (red bars, Chiffre 3). Ce
suggests that latent FC does a better job of representing common, stable variability in FC pro-
files across both resting and task states. Surtout, latent FC does so even though the task or
rest condition being correlated is left out of the factor model for that specific comparison to
avoid circularity. En tant que tel, the factor score analytically has different indicators across all com-
parisons, and nevertheless still outperforms rest FC. De plus, obtaining a better sample of the
Neurosciences en réseau
581
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
resting state by using the full time series resulted in the resting state having the highest factor
loadings and the strongest correlation with latent FC, which suggests that over time the resting
state converges to latent FC.
The advantages of latent FC are not, cependant, restricted to the connectivity space; the latent
measure of intrinsic FC also outperforms rest FC in predicting state-specific activation patterns.
Not only did latent FC support higher prediction accuracy by the activity flow model of task
activation globally (rlatent = 0.66 vs. rrest = 0.56), it showed condition-specific advantages in 23
out of 24 specific task conditions (Figure 4B). Rest FC, in comparison, displayed higher pre-
diction accuracy in none of the task conditions (in the left-hand motor condition, latent and
rest FC performed comparably; Figure 4C). When we examined predictions of region-specific
patterns of activation, results showed that latent FC had improved prediction over rest FC for
68% of all brain regions across a variety of distributed networks. In contrast, rest FC showed
improved prediction for only 1.1% of regions, all of which were restricted to the VIS2 network
(and constituted only 7% of that network). These improvements, as before, were not due to
circularity in the analyses, as task predictions using latent FC were done using the leave-one-
task-out approach in the factor model.
Improving External Validity with Latent FC
While latent FC has demonstrable advantages for prediction within the brain, its utility as a
method of estimating brain-based biomarkers relies on its predictive validity for outcomes
of interest. Ici, we showed that connectivity values from latent FC showed superior predic-
tion of a metric of generalized intelligence (psychometric g) than did rest FC connections.
Although both rest FC and latent FC values significantly predicted individual differences in
generalized intelligence, latent FC nearly doubled the percentage of explained variance in
the outcome over rest FC (∼12% versus ∼7%). In measurement science, this is a hallmark
advantage of the latent variable approach used in factor analysis. Methods that fail to account
for measurement error tend to show reduced relationships between variables, whereas model-
ing state-specific error terms dis-attenuates those relationships (Schmidt & Hunter, 1996).
En effet, generalized intelligence is generally modeled with a factor analytic approach for pre-
cisely this reason. We demonstrate that the framework for improving measurement properties
in behavioral measures applies equally to measures derived from functional neuroimaging
data. En tant que tel, factor analytic models are ideal for aiding the search for biomarkers across a
wide domain of individual difference outcomes. En outre, more reliable estimates of FC
may aid modeling efforts that use intermediate network metrics (par exemple., modularity, hub diversity)
to predict participant behavior (par exemple., Bertolero, Yeo, Bassett, & D'Esposito, 2018), and offer an
exciting range of possible uses for latent FC in future work.
State Aggregation Improves Predictive Performance
The performance of average FC suggests that aggregating information across states has advan-
tages over longer scan sessions of resting state, regardless of the approach used. Fait intéressant,
average FC performance is not uniform in relation to the latent FC, performing as good or
slightly better than latent FC in correlating with state-specific connectivity, but underperform-
ing latent FC in predicting held-out activity in almost all regions. A few circumstances may
predict when we would expect to see more or less pronounced differences between average
and latent FC. D'abord, data quality: We expect more pronounced differences for lower quality
data and less pronounced differences for higher quality data. The HCP data used here is of
extremely high quality, which reduces variability in noise between scans. This is reflected
in the average factor loadings, which are relatively close in value across states (Chiffre 2).
Neurosciences en réseau
582
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
Bien sûr, as the loadings converge in value, the more similar average and latent FC will
become (here the connectivity values are correlated; r = 0.98). Deuxième, the method of factor
analysis used: Ici, we opted to fit a single-factor model for each connection independently
because of the large number of operations (par exemple., separate models for each connection).
Cependant, a single factor in isolation may not be the best fit for brain data (van Kesteren &
Kievit, 2020), and the method here might represent a sort of floor performance for latent FC
relative to approaches that adopt a dependent model that tries to optimize the fit for each
factor model.
Enfin, there appear to be differences depending on the type of dependent variable in ques-
tion. Par exemple, while the factor and average models converge in their correlation with con-
nectivity for held-out states, we found that activity flow models that incorporated latent FC
performed better. Average and factor models produced similar patterns of relative connectivity
(c'est à dire., highly correlated patterns of FC); cependant, the distribution of connectivity values differ.
Latent FC estimates exhibited a sparser distribution of connectivity by zeroing out low and/or
unstable connections, which may have improved the activity flow models by reducing the
contributions of disconnected brain regions (see Figure S5 in the Supporting Information).
Despite the relatively small differences in performance between average and latent FC,
there are theoretical reasons to prefer a latent variable perspective for FC estimation. The first,
as mentioned before, is that while the average FC must assume equal loadings, latent FC
makes this a testable hypothesis. If loadings converge towards equal values, then average
and latent FC will converge (as they nearly did here). This suggests that averaging will likely
perform well under conditions similar to the HCP data (high-quality, young adult data). Comment-
jamais, as the data diverge from this baseline, latent FC should have advantages by weighting
data according to how closely they reflect intrinsic functional states and contribute to the com-
mon variance across measures. If differences among measures increase (c'est à dire., measures reflect
intrinsic FC better or worse), we would hypothesize that average and latent FC would diverge
in their performance. We can see this in a small reproducible example (see supplemental code
demonstrations in the Supporting Information), where more variable loadings impact the abil-
ity of sums scores, but not factor scores, to predict a hypothetical outcome variable. Cependant,
apart from these practical considerations, a latent variable model of FC is a good theoretical
model for how state-specific functional connections emerge from underlying, intrinsic neural
connectivité. Intrinsic connectivity is an unobserved state (Bollen, 2002) that gives rise to state-
specific phenotypes based on combinations of common (c'est à dire., the latent factor) and state-
specific (c'est à dire., the error) variance.
Conclusions
En résumé, we utilized a factor analytic approach to derive intrinsic FC from multiple task
and resting-state data. Our derived measure, termed latent FC, showed improved generaliz-
ability and reliability compared with a standard measure of resting-state FC. Not only did latent
FC do a better job of reflecting state-specific FC patterns across tasks, it also overwhelmingly
improved predictions of regional activations when utilized in activity flow models. Enfin,
connectivity derived from latent FC doubled the predictive utility of an external measure of
generalized intelligence ( g) compared with connectivity from rest FC, highlighting its suitabil-
ity for use in clinical and other individual difference research, where reliable biomarkers are
needed. These results present compelling support for the use of factor analytic models in cog-
nitive neuroscience, demonstrating the value of established tools from psychometrics for
enhancing measurement quality in neuroscience.
Neurosciences en réseau
583
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
MATERIALS AND METHODS
For clarity, portions of the text in this section are from our prior publication using the same
dataset and some identical analysis procedures: Ito et al. (2020).
Participants
Data in the present study were collected as part of the Washington University–Minnesota Con-
sortium of the Human Connectome Project (HCP; Van Essen et al., 2013). A subset of data (n =
352) from the HCP 1200 release was used for empirical analyses. Specific details and proce-
dures of subject recruitment can be found in Van Essen et al. (2013). The subset of 352 partic-
ipants was selected based on the following: quality control assessments; c'est, any participants
with any quality control flags were excluded, y compris (un) focal anatomical anomaly found in
T1w and/or T2w scans, (b) focal segmentation or surface errors, as output from the HCP struc-
tural pipeline, (c) data collected during periods of known problems with the head coil, et (d)
data in which some of the FIX-ICA components were manually reclassified; exclusion of high-
motion participants (participants that had any fMRI run in which more than 50% of TRs had
greater than 0.25-mm framewise displacement); and removal according to family relations
(unrelated participants were selected only, and those with no genotype testing were
excluded). A full list of the 352 participants used in this study will be included as part of
the code release.
All participants were recruited from Washington University in St. Louis and the surrounding
area. We split the 352 subjects into two cohorts of 176 sujets: an exploratory cohort (99
femmes) and a validation cohort (84 femmes). The exploratory cohort had a mean age of 29
years of age (range = 22–36 years of age), and the validation cohort had a mean age of 28
years of age (range = 22–36 years of age). All subjects gave signed, informed consent in accor-
dance with the protocol approved by the Washington University Institutional Review Board.
Scan Acquisition
Whole-brain multiband echo-planar imaging acquisitions were collected on a 32-channel
head coil on a modified 3T Siemens Skyra with TR = 720 ms, LE = 33.1 ms, flip angle =
52°, bandwidth = 2,290 Hz/Px, in-plane FOV = 208 × 180 mm, 72 slices, 2.0-mm isotropic
voxels, with a multiband acceleration factor of 8. Data for each subject were collected over
the span of two days. On the first day, anatomical scans were collected (including T1-weighted
and T2-weighted images acquired at 0.7-mm isotropic voxels) followed by two resting-state
fMRI scans (each lasting 14.4 min) and ending with a task fMRI component. The second
day consisted of first collecting a diffusion imaging scan, followed by a second set of two
resting-state fMRI scans (each lasting 14.4 min), and again ending with a task fMRI session.
Each of the seven tasks was collected over two consecutive fMRI runs. The seven tasks
consisted of an emotion cognition task, a gambling reward task, a language task, a motor task,
a relational reasoning task, a social cognition task, and a working memory task. Briefly, le
emotion cognition task required making valence judgments on negative (fearful and angry)
and neutral faces. The gambling reward task consisted of a card guessing game, where sub-
jects were asked to guess the number on the card to win or lose money. The language pro-
cessing task consisted of interleaving two language conditions, which involved answering
questions related to a story presented aurally, and a math condition, which involved basic
arithmetic questions presented aurally. Note that we treated the two language task conditions
as separate tasks, given the highly distinct nature of the conditions (other than that they were
presented aurally). The motor task involved asking subjects to either tap their left/right fingers,
Neurosciences en réseau
584
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
squeeze their left/right toes, or move their tongue. The reasoning task involved asking subjects
to determine whether two sets of objects differed from each other in the same dimension (par exemple.,
shape or texture). The social cognition task was a theory of mind task, where objects (squares,
circles, triangles) interacted with each other in a video clip, and subjects were subsequently
asked whether the objects interacted in a social manner. Dernièrement, the working memory task was
a variant of the N-back task. Further details on the resting-state fMRI portion can be found in
Smith et al. (2013), and additional details on the task fMRI components can be found in Barch
et autres. (2013).
Behavior: Données
To assess generalized intelligence ( g), we drew 11 measures of cognitive ability from the HCP
dataset, which are derived from the NIH Toolbox for Assessment of Neurological and Behav-
ioral Function (https://www.nihtoolbox.org; Gershon et al., 2013) and the Penn Computerized
Neurocognitive Battery (Gur et al., 2010). Tasks included picture sequence memory; dimen-
sional card sort; flanker attention and inhibitory control; the Penn Progressive Matrices; oral
reading recognition; picture vocabulary; pattern completion processing speed; variable short
Penn line orientation test; Penn word memory test (number correct and median reaction time
as separate variables); and list sorting. For all measures, the age-unadjusted score was used
where applicable. For complete information regarding all measures, see the descriptions in
the Cognition Category of the HCP Data Dictionary (https://wiki.humanconnectome.org
/display/ PublicData/ HCP+Data+Dictionary+Public-+Updated+for+the+1200+Subject
+Release).
Behavior: Factor Analysis Model of Psychometric g
We then derived a general factor of intelligence using a multiple-indicator latent factor model.
We approach the factor model using a confirmatory factor analysis (CFA) approach with a uni-
tary factor underlying all individual cognitive tasks. Factor loadings were estimated using the
psych R package (Revelle, 2017). Factor scores were computed using the regression method
(Thurstone, 1935) to obtain manifest variables for prediction.
IRMf: Preprocessing
Minimally preprocessed data for both resting-state and task fMRI were obtained from the pub-
licly available HCP data. Minimally preprocessed surface data were then parcellated into 360
brain regions using the Glasser atlas (Glasser et al., 2016). We performed additional prepro-
cessing steps on the parcellated data for resting-state fMRI and task state fMRI to conduct
neural variability and FC analyses. This included removing the first five frames of each run,
de-meaning and de-trending the time series, and performing nuisance regression on the min-
imally preprocessed data (Ciric et al., 2017). Nuisance regression removed motion parame-
ters and physiological noise. Spécifiquement, six primary motion parameters were removed,
along with their derivatives, and the quadratics of all regressors (24 motion regressors in total).
Physiological noise was modeled using aCompCor on time series extracted from the white
matter and ventricles (Behzadi, Restom, Liau, & Liu, 2007). For aCompCor, the first five prin-
cipal components from the white matter and ventricles were extracted separately and
included in the nuisance regression. En outre, we included the derivatives of each of those
components, and the quadratics of all physiological noise regressors (40 physiological noise
regressors in total). The nuisance regression model contained a total of 64 nuisance param-
eters. This was a variant of previously benchmarked nuisance regression models reported in
Ciric et al. (2017).
Neurosciences en réseau
585
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
We excluded global signal regression (GSR), given that GSR can artificially induce negative
correlations (Murphy, Birn, Handwerker, Jones, & Bandettini, 2009; Power et al., 2014), lequel
could bias analyses of whether global correlations decrease during task performance. Nous
included aCompCor as a preprocessing step here given that aCompCor does not include
the circularity of GSR (regressing out some global gray matter signal of interest) while including
some of the benefits of GSR (some extracted components are highly similar to the global sig-
nal; Power et al., 2018). This logic is similar to a recently developed temporal-ICA-based arti-
fact removal procedure that seeks to remove global artifacts without removing global neural
signals, which contains behaviorally relevant information such as vigilance (Glasser et al.,
2018; Wong, Olafsson, Tal, & Liu, 2013). We extended aCompCor to include the derivatives
and quadratics of each of the component time series to further reduce artifacts. Code to per-
form this regression is publicly available online using Python code (version 2.7.15) (https://
github.com/ito-takuya/fmriNuisanceRegression). Following nuisance regression, le temps
series for each run (task-state and rest-state) were z-normalized such that variances across runs
would be on the same scale (c'est à dire., unit variance).
Task data for task FC analyses were additionally preprocessed using a standard general lin-
ear model (GLM) for fMRI analysis. For each task paradigm, we removed the mean evoked
task-related activity for each task condition by fitting the task timing (block design) for each
condition using a finite impulse response (FIR) model (Cole et al., 2019). (Il y avait 24 task
conditions across seven cognitive tasks.) We used an FIR model instead of a canonical hemo-
dynamic response function given recent evidence suggesting that the FIR model reduces both
false positives and false negatives in the identification of FC estimates (Cole et al., 2019). Ce
is because of the FIR model’s ability to flexibly fit the mean evoked response across all blocks.
FIR-modeled task blocks were modeled separately for task conditions within each of the
seven tasks. En particulier, two conditions were fit for the emotion cognition task, where coef-
ficients were fit to either the face condition or the shape condition. For the gambling reward
task, one condition was fit to trials with the punishment condition, and the other condition
was fit to trials with the reward condition. For the language task, one condition was fit for the
story condition, and the other condition was fit to the math condition. For the motor task, six
conditions were fit: (un) cue; (b) right-hand trials; (c) left-hand trials; (d) right-foot trials; (e) gauche-
foot trials; et (F ) tongue trials. For the relational reasoning task, one condition was fit to
trials when the sets of objects were matched, and the other condition was fit to trials when
the objects were not matched. For the social cognition task, one condition was fit if the
objects were interacting socially (theory of mind), and the other condition was fit to trials
where objects were moving randomly. Dernièrement, for the working memory task, eight conditions
were fit: (un) 2-back body trials; (b) 2-back face trials; (c) 2-back tool trials; (d) 2-back place
trials; (e) 0-back body trials; (F ) 0-back face trials; (g) 0-back tool trials; et (h) 0-back place
trials. Since all tasks were block designs, each time point for each block was modeled sep-
arately for each task condition (c'est à dire., FIR model), with a lag extending up to 25 TRs after task
block offset.
IRMf: Task Activation
We performed a standard task GLM analysis on fMRI task data to estimate evoked brain activ-
ity during task states. The task timing for each of the 24 task conditions was convolved with the
SPM canonical hemodynamic response function to obtain task-evoked activity estimates
(Friston et al., 1994). Coefficients were obtained for each parcel in the Glasser et al. (2016)
cortical atlas for each of the 24 task conditions.
Neurosciences en réseau
586
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
IRMf: Functional Connectivity Estimation
Residual time series from the rest and task nuisance regressions were used to estimate func-
tional connectivity for each task. Connectivity values were estimated using zero-lag Pearson
product-moment correlations. Time series were concatenated across separate runs of the same
task to yield a single connectivity value per edge for a given task or resting-state condition. Pour
each task scan, we utilized TRs that corresponded to “on-task” time points. Par exemple, nous
extracted TRs from the working memory scan during N-back task blocks, excluding TRs from
the interblock fixation periods. For the number of TRs included in the connectivity estimates
for each condition and scan state, see Table S1 in the Supporting Information.
IRMf: Factor Analysis Model of Latent FC
Factor analysis for obtaining latent FC was conducted with the same approach used to obtain
factor scores for generalized intelligence. FC estimates from each separate fMRI task were used
as indicators on a unitary factor model, and factor scores were obtained using the regression
method in the psych R package. A separate model was computed for each edge in the con-
nectivity adjacency matrix. We took several approaches to test the predictive utility of latent
FC for activation and behavior (detailed below).
The first set of analyses tested two alternative measurement approaches for latent FC. The first
was to utilize all available data from each functional scan to estimate factor scores for each edge.
Cependant, because of the differential amount of scan time for different functional runs (par exemple., ∼58 min
of resting-state vs. ∼10 min of working memory scans), we might expect that indicators (c'est à dire., scan
les types) with more data would dominate the measurement model in the factor analysis. To control
for this potential confound, we ran additional analyses in which indicators were constrained to
have equivalent numbers of TRs used to estimate individual scan functional edges between task
and rest, and between different task states. The reasoning task had the fewest “on-task” TRs (264)
and therefore served as the limiting factor for task scan data. En tant que tel, 264 TRs of each task
(pour 2,112 TRs of task) and a corresponding 2,112 TRs of rest were used in these analyses. All
of these analyses were performed modeling all available scan types in the same factor model.
For activity flow mapping (ActFlow) analyses (Cole et al., 2016; Ito et al., 2020), where activa-
tions in held-out regions were predicted using estimated activity flowing over estimated connec-
tion, latent FC was estimated independently for each connection by applying leave-one-state-out
factor analysis (LOSO-FA) on the state FC estimates to prevent circularity in the predictive model.
Par exemple, when predicting activation in the emotion task, FC estimates were obtained without
including the emotion task as an indicator in the factor model. In all ActFlow analyses, we esti-
mated predictions per subject and then pooled results (c'est à dire., an estimate-then-average approach).
Meta-Analysis Across Samples
To appropriately combine effects of the g-prediction analysis across the validation and explor-
atory sample, we computed r-to-z-score transformations of the individual coefficients and then
combined them into a weighted z-score using the standard formula (Field, 2001) where z is the
z-score and the weight (w) corresponds to the sample size.
(cid:1)zr ¼
k
P.
i wizriP
k
i wi
:
The significance of this meta-analytic parameter was determined using a chi-square test
(Field, 2001).
Neurosciences en réseau
587
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
REMERCIEMENTS
Data were provided by the Human Connectome Project, WU-Minn Consortium (principal
investigators: D. Van Essen and K. Voiture d'Ugur; 1U54MH091657), funded by the 16 NIH Insti-
tutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the
McDonnell Center for Systems Neuroscience at Washington University. The authors acknowl-
edge the Office of Advanced Research Computing (OARC) at Rutgers, the State University of
New Jersey, for providing access to the Amarel cluster and associated research computing
resources that have contributed to the results reported here. The content is solely the respon-
sibility of the authors and does not necessarily represent the official views of any of the
funding agencies.
INFORMATIONS À L'APPUI
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00234.
CONTRIBUTIONS DES AUTEURS
Ethan M. McCormick: Analyse formelle; Méthodologie; Visualisation; Rédaction – ébauche originale;
Rédaction – révision & édition. Katelyn L. Arnemann: Conceptualisation; Analyse formelle;
Méthodologie; Logiciel; Visualisation; Rédaction – ébauche originale; Rédaction – révision & édition.
Takuya Ito: Conceptualisation; Méthodologie; Ressources; Rédaction – révision & édition. Stephen
José Hanson: Conceptualisation; Méthodologie; Rédaction – révision & édition. Michael W. Cole:
Conceptualisation; Acquisition de financement; Surveillance; Rédaction – révision & édition.
INFORMATIONS SUR LE FINANCEMENT
Michael W. Cole, National Institute on Aging (https://dx.doi.org/10.13039/100000049), Award
ID: R01 AG055556. Michael W. Cole, National Institute of Mental Health (https://dx.doi.org
/10.13039/100000025), Award ID: R01 MH109520. David C. Van Essen and Kamil Ugurbil,
National Institute of Mental Health (https://dx.doi.org/10.13039/100000025), Award ID:
1U54MH091657.
RÉFÉRENCES
Anderson, J.. S., Ferguson, M.. UN., Lopez-Larson, M., & Yurgelun-
Todd, D. (2011). Reproducibility of single-subject functional con-
nectivity measurements. American Journal of Neuroradiology,
32(3), 548–555. https://doi.org/10.3174/ajnr.A2330, PubMed:
21273356
Barch, D. M., Bourgeois, G. C., Harms, M.. P., Petersen, S. E., Schlaggar,
B. L., Corbetta, M., … WU-Minn HCP Consortium. (2013).
Function in the human connectome: Task-fMRI and individual
differences in behavior. NeuroImage, 80, 169–189. https://est ce que je
.org/10.1016/j.neuroimage.2013.05.033, PubMed: 23684877
Behzadi, Y., Restom, K., Liau, J., & Liu, T. T. (2007). A component
based noise correction method (CompCor) for BOLD and perfu-
sion based fMRI. NeuroImage, 37(1), 90–101. https://est ce que je.org/10
.1016/j.neuroimage.2007.04.042, PubMed: 17560126
Bertolero, M.. UN., Yeo, B. T. T., Bassett, D. S., & D'Esposito, M..
(2018). A mechanistic model of connector hubs, modularity and
cognition. Nature Human Behaviour, 2(10), 765–777. https://est ce que je
.org/10.1038/s41562-018-0420-6, PubMed: 30631825
Bollen, K. UN. (2002). Latent variables in psychology and the social
sciences. Revue annuelle de psychologie, 53, 605–634. https://est ce que je
.org/10.1146/annurev.psych.53.100901.135239, PubMed:
11752498
Ciric, R., Loup, D. H., Power, J.. D., Roalf, D. R., Baum, G. L.,
Ruparel, K., … Satterthwaite, T. D. (2017). Benchmarking of
participant-level confound regression strategies for the control of
motion artifact in studies of functional connectivity. NeuroImage,
154, 174–187. https://doi.org/10.1016/j.neuroimage.2017.03
.020, PubMed: 28302591
Cole, M.. W., Bassett, D. S., Power, J.. D., Plus courageux, T. S., & Petersen,
S. E. (2014). Intrinsic and task-evoked network architectures of
the human brain. Neurone, 83(1), 238–251. https://est ce que je.org/10
.1016/j.neuron.2014.05.014, PubMed: 24991964
Neurosciences en réseau
588
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
Cole, M.. W., Ito, T., Bassett, D. S., & Schultz, D. H. (2016). Activity
flow over resting-state networks shapes cognitive task activa-
tion. Neurosciences naturelles, 19(12), 1718–1726. https://doi.org
/10.1038/nn.4406, PubMed: 27723746
Cole, M.. W., Ito, T., Schultz, D., Mill, R., Chen, R., & Cocuzza, C.
(2019). Task activations produce spurious but systematic inflation
of task functional connectivity estimates. NeuroImage, 189, 1–18.
https://doi.org/10.1016/j.neuroimage.2018.12.054, PubMed:
30597260
Dubois, J., Galdi, P., Paul, L. K., & Adolphs, R.. (2018). A distributed
brain network predicts general intelligence from resting-state
human neuroimaging data. Philosophical Transactions of the
Royal Society of London. Série B, Sciences biologiques, 373(1756).
https://doi.org/10.1098/rstb.2017.0284, PubMed: 30104429
Eid, M., Gollwitzer, M., & Schmitt, M.. (2011). Statistik und
forschungsmethoden lehrbuch. Weinheim: Beltz. Retrieved from
https://www.psychometrica.de/correlation.html
Elliott, M.. L., Knodt, UN. R., Cooke, M., Kim, M.. J., Melzer, T. R.,
Keenan, R., … Hariri, UN. R.. (2019). General functional connectiv-
ville: Shared features of resting-state and task fMRI drive reliable
and heritable individual differences in functional brain networks.
NeuroImage, 189, 516–532. https://est ce que je.org/10.1016/j
.neuroimage.2019.01.068, PubMed: 30708106
Elliott, M.. L., Knodt, UN. R., Ireland, D., Morris, M.. L., Poulton, R.,
Ramrakha, S., … Hariri, UN. R.. (2020). What is the test-retest reli-
ability of common task-functional MRI measures? New empirical
evidence and a meta-analysis. Sciences psychologiques, 31(7),
792–806. https://doi.org/10.1177/0956797620916786,
PubMed: 32489141
Field, UN. P.. (2001). Meta-analysis of correlation coefficients: UN
Monte Carlo comparison of fixed- and random-effects methods.
Psychological Methods, 6(2), 161–180. https://doi.org/10.1037
/1082-989X.6.2.161, PubMed: 11411440
Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M.. D., Huang, J.,
Chun, M.. M., … Constable, R.. T. (2015). Functional connectome
fingerprinting: Identifying individuals using patterns of brain
connectivité. Neurosciences naturelles, 18(11), 1664–1671. https://
doi.org/10.1038/nn.4135, PubMed: 26457551
Fox, M.. D., & Raichle, M.. E. (2007). Spontaneous fluctuations in
brain activity observed with functional magnetic resonance
imaging. Nature Revues Neurosciences, 8(9), 700–711. https://
doi.org/10.1038/nrn2201, PubMed: 17704812
Friston, K. J., Holmes, UN. P., Worsley, K. J., Poline, J.-P., Frith, C. D., &
Frackowiak, R.. S. J.. (1994). Statistical parametric maps in func-
tional imaging: A general linear approach. Human Brain Mapping,
2(4), 189–210. https://doi.org/10.1002/hbm.460020402
Gershon, R.. C., Wagster, M.. V., Hendrie, H. C., Fox, N. UN., Cook,
K. F., & Nowinski, C. J.. (2013). NIH Toolbox for Assessment of
Neurological and Behavioral Function. Neurologie, 80(11 Supplément. 3),
S2–S6. https://doi.org/10.1212/ WNL.0b013e3182872e5f,
PubMed: 23479538
Glasser, M.. F., Coalson, T. S., Bijsterbosch, J.. D., Harrison, S. J.,
Harms, M.. P., Anticevic, UN., … Smith, S. M.. (2018). Using temporal
ICA to selectively remove global noise while preserving global
signal in functional MRI data. NeuroImage, 181, 692–717.
https://doi.org/10.1016/j.neuroimage.2018.04.076, PubMed:
29753843
Glasser, M.. F., Coalson, T. S., Robinson, E. C., Hacker, C. D.,
Harwell, J., Yacoub, E., … Van Essen, D. C. (2016). A multi-
modal parcellation of human cerebral cortex. Nature, 536(7615),
171–178. https://doi.org/10.1038/nature18933, PubMed:
27437579
Gottfredson, L. S. (1997). Mainstream science on intelligence: Un
editorial with 52 signatories, histoire, and bibliography. Intelli-
gence, 24(1), 13–23. https://doi.org/10.1016/S0160-2896(97)
90011-8
Gratton, C., Laumann, T. O., Nielsen, UN. N., Vert, D. J., Gordon,
E. M., Gilmore, UN. W., … Petersen, S. E. (2018). Functional brain
networks are dominated by stable group and individual factors,
not cognitive or daily variation. Neurone, 98(2), 439–452. https://
doi.org/10.1016/j.neuron.2018.03.035, PubMed: 29673485
Vert, UN. S., Gao, S., Scheinost, D., & Constable, R.. T. (2018).
Task-induced brain state manipulation improves prediction of
individual traits. Communications naturelles, 9(1), 2807. https://
doi.org/10.1038/s41467-018-04920-3, PubMed: 30022026
Gur, R.. C., Richard, J., Hughett, P., Calkins, M.. E., Macy, L., Bilker,
W. B., … Gur, R.. E. (2010). A cognitive neuroscience-based com-
puterized battery for efficient measurement of individual differ-
ences: Standardization and initial construct validation. Journal
of Neuroscience Methods, 187(2), 254–262. https://est ce que je.org/10
.1016/j.jneumeth.2009.11.017, PubMed: 19945485
Hacker, C. D., Laumann, T. O., Szrama, N. P., Baldassarre, UN., Snyder,
UN. Z., Leuthardt, E. C., & Corbetta, M.. (2013). Resting state network
estimation in individual subjects. NeuroImage, 82, 616–633.
https://doi.org/10.1016/j.neuroimage.2013.05.108, PubMed:
23735260
Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J.. P.,
Meuli, R., & Hagmann, P.. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Procédure
of the National Academy of Sciences, 106(6), 2035–2040. https://
doi.org/10.1073/pnas.0811168106, PubMed: 19188601
Ito, T., Brincat, S. L., Siegel, M., Mill, R.. D., Il, B. J., Miller, E. K., …
Cole, M.. W. (2020). Task-evoked activity quenches neural corre-
lations and variability across cortical areas. PLoS Computational
Biology, 16(8), e1007983. https://doi.org/10.1371/journal.pcbi
.1007983, PubMed: 32745096
Kovacs, K., & Conway, UN. R.. UN. (2016). Process overlap theory: UN
unified account of the general factor of intelligence. Psycholog-
ical Inquiry, 27(3), 151–177. https://doi.org/10.1080/1047840X
.2016.1153946
Kragel, P.. UN., Han, X., Kraynak, T. E., Gianaros, P.. J., & Wager, T. D.
(2020). fMRI can be highly reliable, but it depends on what you
measure. https://doi.org/10.31234/osf.io/9eaxk
Krienen, F. M., Yeo, B. T. T., & Buckner, R.. L. (2014). Reconfigur-
able task-dependent functional coupling modes cluster around a
core functional architecture. Philosophical Transactions of the
Royal Society of London. Série B, Sciences biologiques, 369(1653),
20130526. https://doi.org/10.1098/rstb.2013.0526, PubMed:
25180304
Laumann, T. O., Gordon, E. M., Adeyemo, B., Snyder, UN. Z., Joo,
S. J., Chen, M.-Y., … Petersen, S. E. (2015). Functional system and
areal organization of a highly sampled individual human brain.
Neurone, 87(3), 657–670. https://doi.org/10.1016/j.neuron.2015
.06.037, PubMed: 26212711
Neurosciences en réseau
589
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Latent functional connectivity
McNeish, D., & Loup, M.. G. (2020). Thinking twice about sum
scores. Behavior Research Methods, 52(6), 2674. https://doi.org
/10.3758/s13428-020-01468-3, PubMed: 32869138
Murphy, K., Birn, R.. M., Handwerker, D. UN., Jones, T. B., & Bandettini,
P.. UN. (2009). The impact of global signal regression on resting
state correlations: Are anti-correlated networks introduced? Neu-
roImage, 44(3), 893–905. https://doi.org/10.1016/j.neuroimage
.2008.09.036, PubMed: 18976716
Parkes, L., Satterthwaite, T. D., & Bassett, D. S. (2020). Towards pre-
cise resting-state fMRI biomarkers in psychiatry: Synthesizing
developments in transdiagnostic research, dimensional models
of psychopathology, and normative neurodevelopment. Actuel
Opinion in Neurobiology, 65, 120–128. https://est ce que je.org/10.1016
/j.conb.2020.10.016, PubMed: 33242721
Power, J.. D., Mitra, UN., Laumann, T. O., Snyder, UN. Z., Schlaggar,
B. L., & Petersen, S. E. (2014). Methods to detect, characterize,
and remove motion artifact in resting state fMRI. NeuroImage,
84, 320–341. https://doi.org/10.1016/j.neuroimage.2013.08
.048, PubMed: 23994314
Power, J.. D., Plitt, M., Gotts, S. J., Kundu, P., Voon, V., Bandettini,
P.. UN., & Martine, UN. (2018). Ridding fMRI data of motion-related
influence: Removal of signals with distinct spatial and physical
bases in multiecho data. Proceedings of the National Academy of
les sciences, 115(9), E2105–E2114. https://doi.org/10.1073/pnas
.1720985115, PubMed: 29440410
Raichle, M.. E. (2006). Neurosciences: The brain’s dark energy.
Science, 314(5803), 1249–1250. https://doi.org/10.1126
/science.1134405, PubMed: 17124311
Revelle, W. R.. (2017). Psych: Procedures for Personality and Psy-
chological Research. Retrieved from https://www.scholars
.northwestern.edu/en/publications/psych-procedures-for
-personality-and-psychological-research
Schmidt, F. L., & Hunter, J.. E. (1996). Measurement error in psycholog-
ical research: Lessons from 26 research scenarios. Psychological
Methods, 1(2), 199–223. https://doi.org/10.1037/1082-989X.1.2.199
Forgeron, S. M., Beckmann, C. F., Andersson, J., Auerbach, E. J.,
Bijsterbosch, J., Douaud, G., … WU-Minn HCP Consortium.
(2013). Resting-state fMRI in the Human Connectome Project.
N e u ro I m a g e , 8 0 , 1 4 4 – 1 6 8 . h t t p s : / / d o i . o rg / 1 0 . 1 0 1 6 / j
.neuroimage.2013.05.039, PubMed: 23702415
Forgeron, S. M., Fox, P.. T., Miller, K. L., Glahn, D. C., Fox, P.. M.,
Mackay, C. E., … Beckmann, C. F. (2009). Correspondence of
the brain’s functional architecture during activation and rest.
Actes de l'Académie nationale des sciences, 106(31),
13040–13045. https://doi.org/10.1073/pnas.0905267106,
PubMed: 19620724
Spearman, C. (1904). “General intelligence” objectively deter-
mined and measured. American Journal of Psychology, 15(2),
201–293. https://doi.org/10.2307/1412107
Thurstone, L. L. (1935). The vectors of mind: Multiple-factor analy-
sis for the isolation of primary traits. Retrieved from https://
psycnet.apa.org/psycinfo/2004-16228-000/. https://est ce que je.org/10
.1037/10018-000
Van Essen, D. C., Forgeron, S. M., Barch, D. M., Behrens, T. E. J.,
Yacoub, E., Voiture d'Ugur, K., & WU-Minn HCP Consortium. (2013).
The WU-Minn Human Connectome Project: An overview.
NeuroImage, 80, 62–79. https://doi.org/10.1016/j.neuroimage
.2013.05.041, PubMed: 23684880
van Kesteren, E.-J., & Kievit, R.. UN. (2020). Exploratory factor analy-
sis with structured residuals for brain imaging data. https://doi.org
/10.1101/2020.02.06.933689
Wong, C. W., Olafsson, V., Tal, O., & Liu, T. T. (2013). The ampli-
tude of the resting-state fMRI global signal is related to EEG vig-
ilance measures. NeuroImage, 83, 983–990. https://est ce que je.org/10
.1016/j.neuroimage.2013.07.057, PubMed: 23899724
Yarkoni, T. (2009). Big correlations in little studies: Inflated fMRI
correlations reflect low statistical power—Commentary on Vul
et autres. (2009). Perspectives on Psychological Science, 4(3),
294–298. https://doi.org/10.1111/j.1745-6924.2009.01127.x,
PubMed: 26158966
Neurosciences en réseau
590
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
2
5
7
0
2
0
2
8
0
7
6
n
e
n
_
un
_
0
0
2
3
4
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3