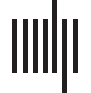RECHERCHE
Test-retest reliability of regression
dynamic causal modeling
Stefan Frässle1 and Klaas E. Stephan1,2
1Translational Neuromodeling Unit (TNU), Institute for Biomedical Engineering,
University of Zurich and ETH Zurich, Zurich, Suisse
2Max Planck Institute for Metabolism Research, Cologne, Allemagne
Mots clés: Regression dynamic causal modeling, rDCM, Generative model, Effective connectivity,
Connectomics, Test-retest reliability
un accès ouvert
journal
ABSTRAIT
Regression dynamic causal modeling (rDCM) is a novel and computationally highly efficient
method for inferring effective connectivity at the whole-brain level. While face and construct
validity of rDCM have already been demonstrated, here we assessed its test-retest reliability—
a test-theoretical property of particular importance for clinical applications—together with
group-level consistency of connection-specific estimates and consistency of whole-brain
connectivity patterns over sessions. Using the Human Connectome Project dataset for eight
different paradigms (tasks and rest) and two different parcellation schemes, we found that
rDCM provided highly consistent connectivity estimates at the group level across sessions.
Deuxième, while test-retest reliability was limited when averaging over all connections (range
of mean intraclass correlation coefficient 0.24–0.42 over tasks), reliability increased with
connection strength, with stronger connections showing good to excellent test-retest reliability.
Troisième, whole-brain connectivity patterns by rDCM allowed for identifying individual
participants with high (and in some cases perfect) accuracy. Comparing the test-retest
reliability of rDCM connectivity estimates with measures of functional connectivity,
rDCM performed favorably—particularly when focusing on strong connections. Generally, pour
all methods and metrics, task-based connectivity estimates showed greater reliability than
those from the resting state. Our results underscore the potential of rDCM for human
connectomics and clinical applications.
RÉSUMÉ DE L'AUTEUR
Test-retest reliability is an important prerequisite for the validity of connectivity estimates in
many situations, particularly in clinical applications. Ici, using different datasets from the
Human Connectome Project, we demonstrate that regression dynamic causal modeling
(rDCM) yields good to excellent test-retest reliability when focusing on strong connections.
Comparing this with the test-retest reliability of functional connectivity measures,
rDCM performed favorably in most cases. En outre, we show that reliability is not
homogeneously distributed: We identified several regions (primarily in frontal and temporal
lobe) that were linked via highly reliable connections, regardless of the paradigm. Enfin, nous
demonstrate that individual connectivity profiles are sufficiently unique that participants can
be identified with high accuracy. Our findings emphasize the potential of rDCM for robust
inference on directed “connectivity fingerprints” from fMRI data.
Citation: Frässle, S., & Stephan, K. E.
(2022). Test-retest reliability of
regression dynamic causal modeling.
Neurosciences en réseau, 6(1), 135–160.
https://doi.org/10.1162/netn_a_00215
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00215
Informations complémentaires:
https://doi.org/10.1162/netn_a_00215
https://gitlab.ethz.ch/tnu/code
/fraessleetal_rdcm_test_retest
https://gitlab.ethz.ch/tnu/analysis-plans
/fraessle_hcp_test_retest
Reçu: 1 Juin 2021
Accepté: 8 Novembre 2021
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Stefan Frässle
stefanf@biomed.ee.ethz.ch
Éditeur de manipulation:
Olaf Sporns
droits d'auteur: © 2021
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
un
_
0
0
2
1
5
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
INTRODUCTION
Computational methods for assessing whole-brain effective (directed) connectivity from nonin-
vasive neuroimaging data, such as functional magnetic resonance imaging (IRMf) or magneto-/
electroencephalography (M/EEG) data, have great potential to further our understanding of
brain function. This is because most, if not all, cognitive processes rest on widely distributed
networks of neuronal populations (Bressler & Menon, 2010; McIntosh, 1999; Mesulam, 1990;
Sporns, 2014). De la même manière, directed connectivity measures at the whole-brain level are of major
relevance for the young fields of computational psychiatry and computational neurology (Frässle,
Yao, et coll., 2018; Friston et al., 2014; Huys et al., 2016; Maia & Frank, 2011; Montague et al.,
2012; Stephan & Mathys, 2014; Stephan et al., 2015). This is because dysconnectivity in large-
scale networks has been postulated as a pathophysiological mechanism in various psychiatric and
neurological disorders, such as schizophrenia (Anticevic et al., 2015; Bullmore et al., 1997;
Friston, Brun, et coll., 2016; Friston & Frith, 1995; Stephan et al., 2006), autism (Grèzes et al.,
2009; Radulescu et al., 2013), major depression (Almeida et al., 2009; Schlösser et al., 2008;
Vai et al., 2016), Parkinson’s disease (Dirkx et al., 2016; Marreiros et al., 2013), or epilepsy
(Jirsa et al., 2016; Papadopoulou et al., 2017).
For clinical applications, computational methods for assessing functional integration in
large-scale (whole-brain) networks of individual patients have great potential (Stephan et al.,
2015). In order to leverage this potential, candidate methods need to fulfill several criteria,
y compris (un) computational efficiency (allowing assessment of large-scale networks with hun-
dreds of nodes, within clinically acceptable time frames), (b) reliability (construct and test-
retest), et (c) predictive validity (with regard to specific clinical questions).
Regression dynamic causal modeling (rDCM) is a generative model of fMRI data that was
developed with these objectives in mind (Frässle, Lomakina, Kasper, et coll., 2018; Frässle,
Lomakina, Razi, et coll., 2017). It represents a novel variant of DCM for fMRI (Friston et al.,
2003) that scales gracefully to very large networks including hundreds of nodes, enabling
whole-brain effective connectivity analyses within time frames of minutes to hours. Plus loin-
plus, the model can utilize structural connectivity information to constrain inference on
directed functional interactions or, where no such information is available, infer optimally
sparse representations of whole-brain connectivity patterns. For rDCM, we have recently dem-
onstrated the face validity of the approach in comprehensive simulation studies for both task-
based (Frässle, Lomakina, Kasper, et coll., 2018; Frässle, Lomakina, Razi, et coll., 2017) et
resting-state fMRI data (Frässle, Harrison, et coll., 2021). En outre, we have demonstrated
its construct validity in application to fMRI data from a simple hand movement paradigm
(Frässle, Manjaly, et coll., 2021), as well as to resting-state fMRI data (Frässle, Harrison,
et coll., 2021). These studies have provided promising results and suggest that rDCM might
enable the construction of clinically useful “computational assay” in psychiatry and/or neurol-
ogy (Stephan et al., 2015). Cependant, test-retest reliability of rDCM has not been assessed so far.
Test-retest reliability represents an important test-theoretical property that quantifies the sta-
bility of estimates over time at the individual-subject level. It thus has particular relevance for
clinical tests that require repeated assessments, such as monitoring treatment response over
temps. Test-retest reliability has already been assessed for classical variants of DCM for fMRI
(Almgren et al., 2018; Frässle, Paulus, et coll., 2016; Frässle, Stephan, et coll., 2015; Rowe
et coll., 2010; Schuyler et al., 2010). Dans l'ensemble, these studies have reported good reproducibility
of DCM for fMRI across sessions, although detailed work has stressed avoidance of local
extrema during optimization and the choice of the prior distributions as important factors
for achieving good test-retest reliability (Frässle, Stephan, et coll., 2015).
136
Dynamic causal modeling:
A generative model of effective
(directed) connectivity based on
neuroimaging data.
Generative model:
Describes the putative processes by
which data were generated.
Specified by the joint probability
density over model parameters and
data.
Effective connectivity:
Effective connectivity refers to the
directed influences that one neuronal
population exerts on another
neuronal population.
Test-retest reliability:
Test-theoretical property that refers to
the consistency of a test over time,
performed under identical conditions
in the same subject.
Distribution:
Refers to the probability density
function of a continuous random
variable.
Neurosciences en réseau
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
un
_
0
0
2
1
5
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
While test-retest reliability has been investigated for classical DCM for fMRI, it has not been
tested for rDCM so far. Ici, we assess the (group-level) consistency as well as the test-retest
reliability of rDCM for inferring effective connectivity from task-based as well as resting-state
fMRI data, applying the model to multiple datasets over time, acquired under the same con-
ditions in the same participants. En outre, using the same data, we examined the consis-
tency of group-level estimates of connectivity (referred to as “consistency” below). This metric
is complementary to test-retest reliability that focuses on the stability of individual estimates
au fil du temps. To this end, we made use of the comprehensive test-retest dataset from the Human
Connectome Project (HCP; Van Essen et al., 2013).
METHODS AND MATERIALS
Analysis Plan
All analyses reported in this paper have been prespecified in an analysis plan that was time-
stamped prior to the analyses (https://gitlab.ethz.ch/tnu/analysis-plans/fraessle_hcp_test_retest;
Frässle & Stephan, 2020).
Regression Dynamic Causal Modeling
General overview. Regression DCM (rDCM) is a novel variant of DCM for fMRI that enables
effective connectivity analyses in whole-brain networks (Frässle, Lomakina, Kasper, et coll.,
2018; Frässle, Lomakina, Razi, et coll., 2017). This computational efficiency is achieved by sev-
eral modifications and simplifications of the original DCM framework. These include (un) trans-
lating state and observation equations of a linear DCM from time to frequency domain, (b)
replacing the nonlinear hemodynamic model with a linear hemodynamic response function
(FRH), (c) applying a mean field approximation across regions (c'est à dire., parameters targeting dif-
ferent regions are assumed to be independent), et (d) specifying conjugate priors on neuronal
(c'est à dire., connectivity and driving input) parameters and noise precision. These modifications
reformulate a linear DCM in the time domain as a Bayesian linear regression in the frequency
domain, resulting in the following likelihood function:
ð
p Y jθ; τ; X
YR
(cid:2)
(cid:3)
;
2πi m
Þ ¼
N − 1
IN(cid:2)N
r¼1
(cid:4)
Yr ¼ e
h
N Yr ; Xθr ; τ −1
r
(cid:5) ^y r
T
h^u1; ^
; ^
X ¼ ^y 1; ^y 2; …; ^y R
θr ¼ ar;1; ar;2; …; ar;R.; cr;1; cr;2; …; cr;K
h^u2; …; ^
h^uK
(cid:6)
;
je
;
(cid:7)
(1)
:
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
un
_
0
0
2
1
5
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bayesian statistics:
Theory based on Bayes theorem,
which provides a recipe for optimally
combining prior and new
information in a probabilistic way.
Linear regression:
Statistical approach that attempts to
model the linear relationship
between a scalar response and one
or more explanatory variables.
Ici, Yr is the dependent variable in region r that is explained as a linear mixture of afferent
connections from other regions and direct (driving) inputs. Spécifiquement, Yr is the Fourier trans-
formation of the temporal derivative of the measured signal in region r. En outre, yr repre-
sents the measured BOLD signal in region r, X is the design matrix (comprising a set of regressors
and explanatory variables), uk is the kth experimental input, and the hat symbol denotes the dis-
crete Fourier transform (DFT). En plus, θr represents the parameter vector comprising all
afferent connections ar,1, …, ar,R and all driving input parameters cr,1, …, cr,K targeting region r.
Enfin, τr denotes the noise precision parameter for region r and IN×N is the identity matrix
(where N denotes the number of data points). Choosing appropriate priors on the parameters
and hyperparameters in Equation 1 (see Frässle, Lomakina, Razi, et coll., 2017) results in a gen-
erative model that can be used for inference on the directed connection strengths and inputs.
Neurosciences en réseau
137
Test-retest reliability of regression DCM
Under this formulation, inference can be done very efficiently by (iteratively) executing a
set of analytical variational Bayes ( VB) update equations of the sufficient statistics of the pos-
terior density. En outre, one can derive an expression for the negative (variational) free
energy (Friston et al., 2007). The negative free energy represents a lower bound approximation
to the log model evidence that accounts for both model accuracy and complexity. Ainsi, le
negative free energy offers a sensible metric for scoring model goodness and is frequently used
for comparing competing hypotheses (Bishop, 2006). We have recently further augmented
rDCM by introducing sparsity constraints as feature selectors into the likelihood of the model
in order to automatically prune fully connected network structures (Frässle, Lomakina, Kasper,
et coll., 2018). A comprehensive description of the generative model of rDCM, including the
mathematical details of the neuronal state equation, can be found elsewhere (Frässle,
Lomakina, Kasper, et coll., 2018; Frässle, Lomakina, Razi, et coll., 2017).
Dataset
Participants. We used the publicly available fMRI data provided by the Human Connectome
Project (HCP; Van Essen et al., 2013), specifically, all fMRI datasets from the HCP S1200 data
release for which test and retest sessions are available. In total, this included 45 participants
(31 females, 14 males). Cependant, not all participants performed all paradigms twice. Ainsi,
we excluded participants, for each paradigm individually, if not all their data from the test and
retest session of the particular paradigm were available. The experimental protocol of the HCP
was in compliance with the Declaration of Helsinki and was approved by the Institutional
Review Board at Washington University in St. Louis (CISR #20120436). Informed consent
was obtained from all participants prior to the experiment and all open-access data were de-
identified. Permission to use the open-access data for the present study was obtained from the
HCP, abiding the Data Use Terms (https://www.humanconnectome.org/data/data-use-terms).
Data acquisition. The HCP dataset comprises fMRI data acquired during the “resting state”
(c'est à dire., unconstrained cognition in the absence of experimental manipulations). During the
resting-state measurement, participants were asked to keep their eyes open and to fixate on
a crosshair projected on a screen. En outre, the HCP dataset comprises fMRI data acquired
during several cognitive tasks, y compris (un) working memory, (b) gambling, (c) moteur, (d) lan-
guage, (e) social cognition, (F ) relational processing, et (g) emotional processing. For the rest-
ing state, a total of four measurements are available per session (c'est à dire., test or retest) that differ in
the phase encoding direction during oblique axial acquisitions. Spécifiquement, two resting-state
measurements are available with phase encoding in right-to-left (RL) and two in left-to-right
(LR) direction. De la même manière, for each task, two measurements are available (c'est à dire., one per phase
encoding direction) per session.
Functional images were acquired on the HCP’s custom 3T Siemens Skyra equipped with
a 32-channel head coil. All fMRI data were acquired using a multiband accelerated 2D
echo-planar imaging sequence (72 sagittal slices, TR = 720 ms, LE = 33 ms, voxel size 2 ×
2 × 2 mm3, matrix = 104 × 90, flip angle = 52°, multiband factor = 8) sensitive to the
blood oxygen level dependent (AUDACIEUX) signal. Images covered the entire brain. The number
of volumes acquired per measurement differed between paradigms: (un) resting state =
1,200 volumes/measurement (approx. scan duration: 15 min); (b) working memory =
405 volumes/measurement (5 min); (c) gambling = 253 volumes/measurement (3 min);
(d) motor = 284 volumes/measurement (3 min); (e) language = 316 volumes/measurement
(4 min); (F ) social cognition = 274 volumes/measurement (3 min); (g) relational processing =
Neurosciences en réseau
138
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
un
_
0
0
2
1
5
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
232 volumes/measurement (3 min); et (h) emotional processing = 176 volumes/measurement
(2 min).
For detailed information on the HCP dataset, please refer to the HCP S1200 manual (https://
www.humanconnectome.org/storage/app/media/documentation/s1200/HCP_S1200_Release
_Reference_Manual.pdf) or the relevant literature (Glasser, Forgeron, et coll., 2016; Van Essen et al.,
2013).
Preprocessing. Preprocessing of the data was already performed by the HCP consortium, et
preprocessed files are released alongside the raw data. Ici, we made use of the minimally
preprocessed fMRI data (Glasser et al., 2013). The minimal preprocessing pipeline uses
different tools from various freely available software packages like FSL (Jenkinson et al.,
2012), FreeSurfer (Dale et al., 1999), and the HCP Workbench (Marcus et al., 2013) in order
to accomplish several tasks, including spatial artifact/distortion removal, realignment, surface
generation, cross-modal registration, and alignment to standard space (MNI). For the resting-
state fMRI (rs-fMRI) data, additional preprocessing steps were performed to remove noise from
the data. Spécifiquement, the preprocessing of the rs-fMRI data made use of MELODIC as part of a
single-subject spatial ICA decomposition. The resulting components were classified as signal
or noise by FIX (Griffanti et al., 2014; Salimi-Khorshidi et al., 2014) and a cleaned version of
the data is provided. The final preprocessed versions of both rs-fMRI and task data were then
stored using the HCP-internal CIFTI file format and the associated grayordinates spatial coor-
dinate system (Glasser et al., 2013). For comprehensive information on the individual prepro-
cessing steps that were performed on both the HCP resting-state and task-based fMRI data,
please refer to the manual (see above) or Glasser et al. (2013).
Time series extraction. To extract BOLD signal time series for the subsequent rDCM analyses,
we made use of two different whole-brain parcellation schemes. This allowed us to assess the
robustness of our estimates of test-retest reliability and group-level consistency to the choice of
parcellation scheme. D'abord, we made use of the Human Connectome Project parcellation (HCP
MMP 1.0; Glasser, Coalson, et coll., 2016), also known as the Glasser parcellation. HCP MMP
1.0 represents a very detailed cortical in vivo parcellation, consisting of 360 regions that were
defined based on combined information on cortical architecture (par exemple., relative cortical myelin
content, cortical thickness), connectivité, and topography within some areas (par exemple., the map of
visual space in visual cortex). Deuxième, we made use of the Schaefer 400-node parcellation
(Schaefer et al., 2018), which rests on a gradient-weighted Markov random field model that
integrates local gradient approaches (c'est à dire., transient changes in functional connectivity patterns)
and global similarity approaches (clustering of homogenous/similar functional connectivity
motifs, regardless of spatial proximity). Using task-based and resting-state fMRI, the authors
derive parcellations of the human brain at various degrees of granularity and demonstrate that
these parcels represent subcomponents of global brain networks identified by Yeo et al. (2011).
The Schaefer parcellation is optimized to align with both task-based and resting-state fMRI,
and has been found to demonstrate improved homogeneity within parcels relative to alterna-
tive parcellations (Schaefer et al., 2018).
For each of the considered whole-brain parcellation schemes, we extracted the BOLD sig-
nal time series of all regions using dedicated HCP tools for CIFTI files. Spécifiquement, we used the
command -cifti-parcellate from the HCP Workbench tool wb_command (for further informa-
tion, see https://www.humanconnectome.org/software/workbench-command/-cifti-parcellate).
The script takes the dense time series data (which is the CIFTI format in which the HCP fMRI
data are stored) and a *.dlabel file (which contains the parcellation) and extracts average
Neurosciences en réseau
139
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
un
_
0
0
2
1
5
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
BOLD signal time series from each region. The extracted time series then entered whole-brain
effective connectivity analyses using rDCM.
rDCM analysis. The extracted BOLD signal time series were then utilized for whole-brain
effective connectivity analyses using rDCM. Since neither the Glasser atlas nor the Schaefer
atlas are accompanied by an anatomical connectome that could inform the network architec-
ture of the whole-brain models (c'est à dire., the presence or absence of endogenous connections in
rDCM; the A-matrix), we assumed a fully (all-to-all) connected network. En outre, the input
(C) matrix was defined according to data type: (un) for the resting-state fMRI datasets, no driving
inputs are available and the C-matrix was set to all-zeros (as described in Frässle, Harrison,
et coll., 2021), et (b) for the task-based fMRI datasets, a full C-matrix was assumed.
For this setting, two different variants of rDCM were employed. D'abord, using the fully con-
nected network architecture, the strength of each connection and driving input was inferred
using the classical implementation of rDCM (Frässle, Lomakina, Razi, et coll., 2017). Ce
yielded a total of at least (un) 129,600 free parameters for the models based on the Glasser
atlas (y compris 129,240 connectivity parameters, 360 inhibitory self-connections, and—for
the task-based fMRI datasets—a task-dependent number of driving input parameters), et
(b) 160,000 free parameters for the models based on the Schaefer atlas (y compris 159,600
connectivity parameters, 400 inhibitory self-connections, and—for the task-based fMRI
datasets—a task-dependent number of driving input parameters).
The number of driving input parameters varied for the different tasks because a different
number of driving input regressors was available for each task. Spécifiquement, the following
regressors were included: (un) working memory = “0bk_body,” “0bk_faces,” “0bk_places,»
“0bk_tools,” “2bk_body,” “2bk_faces,” “2bk_places,” and “2bk_tools” (number of regressors =
8); (b) gambling = “win,” “loss,” and “neutral” (3); (c) motor = “cue,” “left foot,” “right foot,” “left
main,” “right hand,” and “tongue” (6); (d) language = “story” and “math” (2); (e) social cognition =
“mental” and “other” (2); (F ) relational processing = “relation” and “match” (2); et (g) emotional
processing = “fear” and “neutral” (2).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
un
_
0
0
2
1
5
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
In a second step, we utilized the sparsity constraints embedded in rDCM to automatically
prune both connections and, for the task-based fMRI data, driving inputs (Frässle, Lomakina,
Kasper, et coll., 2018). In brief, this is achieved by introducing binary indicator variables as fea-
ture selectors into the likelihood function where each indicator variable determines whether a
specific connectivity parameter is present. This resulted in the same number of neuronal
parameters (c'est à dire., connectivité, inhibitory self-connection, and driving input parameters) comme
mentioned above, plus the same number of binary indicator parameters. Notably, a Bernoulli
prior is specified on the binary indicator variables, where the Bernoulli distribution is param-
eterized by a single parameter pi
0 represents a hyperparameter of the model and
encodes the a priori belief about the network’s degree of sparseness. Since exact a priori
knowledge about the degree of sparseness of the networks is not available here, we followed
the procedure described in Frässle, Lomakina, Kasper, et autres. (2018), using a line-search proce-
dure to determine the value of pi
0 that resulted in the highest negative free energy. More spe-
cifically, pour chaque participant, we systematically varied pi
0 within a range of 0.3 à 0.9 in steps
de 0.1 and performed model inversion for each pi
0 value was then deter-
mined for each participant by selecting the one that yielded the highest negative free energy.
This yielded individual sparse effective connectivity patterns where some connections are
absent (pruned away) and thus take a value of 0, whereas other connections remain present
and thus take a nonzero connection strength.
0 valeur. The optimal pi
0. Ainsi, pi
Model inversion:
Refers to the process by which the
posterior distribution over the model
parameters of a generative model is
computed.
Neurosciences en réseau
140
Test-retest reliability of regression DCM
For either of the two rDCM variants, the whole-brain models were fitted to the extracted
BOLD signal time series by making use of the standard routines and prior settings implemented
in the rDCM toolbox. Spécifiquement, whole-brain models were inverted by utilizing the main
routine tapas_rdcm_estimate.m from the rDCM toolbox as implemented in TAPAS (Frässle,
Aponte, et coll., 2021), which is freely available as open-source software (https://www
.translationalneuromodeling.org/tapas).
Group-level consistency and test-retest reliability of individual connection strengths. D'abord, we inves-
tigated the across-session consistency of whole-brain effective connectivity patterns at the
group level. To this end, for each endogenous connection and driving input, we computed
the mean (across all participants) and then assessed the Pearson correlation between group-
level parameter estimates from Session 1 (“test”) and Session 2 (“retest”). Significance was
determined at an alpha level of 0.05, corrected for multiple comparisons (c'est à dire., number of par-
adigms) using Bonferroni correction. Ainsi, correlations with a p value smaller than 0.00625
(c'est à dire., 0.05/8) were deemed significant. These analysis steps were performed for both (un) rDCM
with fixed network architecture, ainsi que (b) rDCM with sparsity constraints. Note that we
computed the group-level effective connectivity patterns as the simple arithmetic mean across
participants; cependant, other approaches are possible as well, such as computing group-level
parameters using a parametric empirical Bayesian (PEB) approche (Friston, Litvak, et coll., 2016).
Deuxième, we assessed the test-retest reliability of the whole-brain effective connectivity pat-
terns, c'est, the stability of rDCM parameter estimates at the individual-subject level. To this
end, an intraclass correlation coefficient (ICC) was computed for each connection. Specifi-
cally, we utilized the ICC(3, 1) type (Shrout & Fleiss, 1979), quantifying the ICC as a ratio
between within-subject variability across the two sessions (σ2
w ) and between-subject
variability (σ2
b):
ICC ¼
σ2
b
σ2
b
− σ2
w
þ σ2
w
:
(2)
ICC(3, 1) values range from −1 to 1. According to conventional interpretations of ICC
valeurs, test-retest reliability is classified as “poor” for ICC < 0.4, as “fair” for 0.4 ≤ ICC <
0.6, as “good” for 0.6 ≤ ICC < 0.75, and as “excellent” for ICC ≥ 0.75 (Cicchetti, 2001).
Based on the parameter-wise ICC values, different analyses were performed. First, the dis-
tribution of ICC values across all connections was inspected and the mean of the distribution
was used to quantify the average test-retest reliability of rDCM when considering all connec-
tions. Second, reliability was tested as a function of connection strength. This was motivated
by the hypothesis that reliability should be lower for connections that are weak (close to 0) and
are thus unlikely to represent a meaningful effect that would be consistently present across
sessions. Conversely, strong connections (both inhibitory and excitatory) should be more likely
to represent meaningful effects and should thus have a greater probability to be conserved
across sessions. This hypothesis was tested using two different analyses: (a) We computed
the correlation between absolute parameter strengths and ICC values. (b) We restricted the
test-retest reliability analyses only to parameters that were significantly different from 0 (as
assessed using one-sample t tests and Bonferroni correction for the multiple comparisons).
Furthermore, for the connectivity parameters, we also further restricted the analysis to the
top 1,000 connections (i.e., the connections with the largest absolute weights).
In a final analysis, we
Inter-session consistency of whole-brain effective connectivity patterns.
tested how consistent the entire effective connectivity profiles were across the two sessions.
Network Neuroscience
141
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
This analysis follows previous work demonstrating that individual subjects can be identified by
their unique functional connectivity profiles derived from fMRI data (Finn et al., 2015). Here,
we asked whether the whole-brain connectivity profile of individual participants during the
first session (“test”) could be used to identify them from the set of all effective connectivity
profiles obtained from the second session (“retest”). To this end, we computed for each par-
ticipant in Session 1 the similarity between his/her connectivity matrix and the connectivity
matrices of all participants in Session 2. The predicted identity was that with the highest sim-
ilarity score. Following Finn et al. (2015), similarity was defined as the Pearson correlation
between two vectors of connectivity estimates taken from the participant’s adjacency matrix
from Session 1 and all adjacency matrices from Session 2. Repeating this procedure for each
participant in Session 1 allows us to construct a confusion matrix from which the identification
accuracy can be computed. To account for order effects, we performed the same analysis in
the opposite direction, testing whether a connectivity profile from the second session could be
used to identify a given individual from the set of all effective connectivity profiles obtained
from the first session.
To assess statistical significance of the identification accuracy, we performed permutation
testing. Here, an empirical null distribution of the identification accuracy was computed by
randomly permuting the participant labels of the session to be predicted and repeating the
entire prediction procedure described above. Here, we used 1,000 permutations. The p value
was then computed as the rank of the original identification accuracy in the distribution of
permutation-based identification accuracies, divided by the total number of permutations.
RESULTS
In the following, we first present our findings on group-level consistency and test-retest reli-
ability of individual connection strength estimates. Subsequently, we report the inter-session
consistency of whole-brain effective connectivity patterns. In either case, we present results
obtained using both “classical” rDCM (with a fixed network architecture) and “sparse” rDCM
(with sparsity constraints and thus variable network architecture). All results are compared
with functional connectivity estimates (Pearson correlation coefficients and L1-regularized
partial correlations).
Group-Level Consistency of Connection Strengths Across Sessions
Regression DCM with fixed (fully connected) network architecture. Group-level estimates of indi-
vidual connections were highly consistent across the two sessions, independently of the par-
adigm (i.e., task-fMRI, rs-fMRI) and whole-brain parcellation scheme. More specifically, for the
Glasser atlas, Pearson correlations (r) for the connectivity parameter estimates ranged from
0.92 for the emotional processing task to 0.97 for the language task. For the driving input
parameter estimates, Pearson correlations varied more strongly across the different paradigms
and ranged from 0.37 for the emotional processing task to 0.98 for the social cognition task.
For the Schaefer atlas, we found virtually identical results. A comprehensive list of all results
from the group-level consistency analysis is provided in Table 1.
In a second step, we assessed the across-session con-
Regression DCM with sparsity constraints.
sistency of estimated connection strengths using rDCM with embedded sparsity constraints.
Overall, we found group-level consistency of sparse rDCM to be comparable to rDCM with
fixed network architecture for all paradigms except for the resting state. More specifically, for
resting-state fMRI data, rDCM with sparsity constraints performed considerably worse (r =
0.62) than classical rDCM (r = 0.96); see Table 1. For all task-based datasets, consistency only
Network Neuroscience
142
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
Across-session consistency of group-level model parameter estimates for rDCM and
Table 1.
functional connectivity. Consistency of parameter estimates in terms of the Pearson correlation
coefficient between group-level (i.e., averaged across participants) estimates of Session 1 (“test”)
and Session 2 (“retest”). Group-level consistencies are reported for the connectivity and driving
input parameters of rDCM (middle) as well as for the functional connectivity estimates (right).
For both methods, results are shown for all HCP paradigms as well as for the two whole-brain
parcellation schemes (i.e., Glasser, Schaefer). Furthermore, results are reported for two different
“modes” of estimation (see main text for details): (a) fixed network architecture (i.e., classical
rDCM and Pearson correlation coefficient), and (b) sparsity constraints (i.e., sparse rDCM and
L1-regularized partial correlations). All correlations were significant at a significance threshold of
p < 0.05 (Bonferroni-corrected for multiple comparisons).
rDCM
Connectivity
Inputs
FC
Fixed network
REST
EMOTION
GAMBLING
LANGUAGE
MOTOR
RELATIONAL
SOCIAL
WORKING MEMORY
Sparsity constraints
REST
EMOTION
GAMBLING
LANGUAGE
MOTOR
RELATIONAL
SOCIAL
WORKING MEMORY
Glasser
Schaefer Glasser
Schaefer Glasser
Schaefer
0.96
0.92
0.97
0.97
0.96
0.97
0.97
0.95
0.61
0.90
0.95
0.94
0.94
0.95
0.95
0.90
0.96
0.91
0.96
0.96
0.95
0.96
0.97
0.95
0.62
0.89
0.94
0.94
0.93
0.94
0.95
0.90
–
0.37
0.96
0.79
0.91
0.96
0.98
0.89
–
0.66
0.93
0.86
0.83
0.97
0.97
0.92
–
0.38
0.95
0.85
0.93
0.95
0.97
0.90
–
0.61
0.94
0.88
0.84
0.97
0.97
0.92
0.95
0.89
0.91
0.92
0.90
0.92
0.92
0.90
0.98
0.91
0.93
0.94
0.94
0.94
0.95
0.95
0.94
0.87
0.89
0.90
0.88
0.90
0.90
0.88
0.98
0.91
0.93
0.94
0.95
0.93
0.95
0.95
slightly decreased for rDCM with sparsity constraints. Interestingly, for the driving input param-
eter estimates, rDCM with sparsity constraints performed comparably to rDCM with fixed net-
work architecture and, in fact, in half of the cases outperformed the latter. For the Schaefer
atlas, we again found results to be virtually identical.
In a next step, we compared the group-level consistency
Comparison to functional connectivity.
of rDCM (both with fixed [fully connected] network architecture and sparsity constraints) with
the group-level consistency of functional connectivity estimates that are frequently used for
Network Neuroscience
143
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
Connectomics:
Refers to the study of connectomes,
which represent comprehensive
maps of (anatomical or functional)
connections within the nervous
system.
human connectomics and network neuroscience. Specifically, we assessed group-level con-
sistency for functional connectivity estimates based on Pearson’s correlation coefficients (for a
full connectivity matrix) and L1-regularized partial correlations (for sparsity constraints),
respectively.
In brief, group-level Pearson correlations were highly consistent across the two sessions,
regardless of the paradigm (i.e., task-fMRI, rs-fMRI) and whole-brain parcellation scheme.
More specifically, for the Glasser atlas, group-level consistency for Pearson correlation coef-
ficients ranged from 0.89 for the emotional processing task to 0.95 for the resting state (see
Table 1). Hence, we found the group-level consistency for Pearson correlations to be some-
what lower than for rDCM. More specifically, we found differences to range between 0.01 and
0.06 (all in favor of rDCM), which was highly significant ( p < 0.001) given the high degrees of
freedom (i.e., number of connectivity parameters). For L1-regularized partial correlations,
group-level consistency ranged from 0.91 for the emotional processing task to 0.98 for the
resting state. Here, the values were generally very similar to sparse rDCM, except for the
resting-state dataset where L1-regularized partial correlations showed greater consistency.
Except for the resting state, we found differences between sparse rDCM and L1-regularized
partial correlations to range between 0.01 and 0.05 (in favor of one or the other), which
was again highly significant ( p < 0.001) given the high degrees of freedom. As for the rDCM
analysis, we found functional connectivity results for the Schaefer atlas to be virtually identical
to the ones for the Glasser atlas.
Test-Retest Reliability
In a second analysis, we
Regression DCM with fixed (fully connected) network architecture.
assessed the test-retest reliability of estimates of individual connection strengths by rDCM,
computing the ICC (Shrout & Fleiss, 1979) for each connection. Here, we report the results
for the Glasser atlas; again, the results for the Schaefer atlas are virtually identical and are
reported in the Supporting Information.
Overall, when considering all model parameters, test-retest reliability of model parameter
estimates from rDCM was relatively low (Figure 1B, left). More specifically, for the connectivity
parameters, on average test-retest reliability ranged from poor for the resting state (mean ICC =
0.24, 95% confidence interval (CI) = [−0.18, 0.59]) to fair for the social cognition task (mean
ICC = 0.42 [−0.07, 0.75]) when considering all connections. Similarly, for the intrinsic self-
connections (i.e., the diagonal of the A-matrix), on average test-retest reliability ranged from
poor for the resting state (mean ICC = 0.33 [−0.05, 0.63]) to fair for the social cognition task
(mean ICC = 0.41 [−0.15, 0.77]); hence, no systematic differences were observed for the two
types of connectivity parameters. Finally, for the driving input parameters, test-retest reliability
ranged from poor for the emotional processing task (mean ICC = 0.08 [−0.43, 0.54]) to fair for the
social cognition task (mean ICC = 0.42 [−0.03, 0.73]). Importantly, this includes weak connec-
tions and driving inputs that may not represent meaningful effects, but may be driven by noise.
In a next step, we therefore tested whether stronger parameters tended to be more reliable.
Focusing only on connections that deviated significantly from zero ( p < 0.05, Bonferroni-
corrected for multiple comparisons), we observed a clear increase in reliability (Figure 1B,
middle). While reliability of the significant connections inferred from resting-state fMRI
data was still poor on average (mean ICC = 0.32 [−0.10, 0.64]), reliability was considerably
higher for task-based fMRI data (e.g., mean ICC = 0.62 [0.10, 0.88] for the emotional pro-
cessing task). The same pattern could be observed for the significant driving inputs (although
somewhat less strongly). Finally, when restricting our reliability analysis even further to the
top 1,000 connections (i.e., the connections with the highest absolute connection strengths),
Network Neuroscience
144
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Test-retest reliability of regression DCM for a fixed network architecture. (A) Methodological overview. Resting-state and task-based
fMRI data from the Human Connectome Project (HCP) are used for the analysis. Region-wise BOLD signal time series were extracted from a
whole-brain parcellation scheme (e.g., the Glasser atlas) and whole-brain effective connectivity was inferred using rDCM. The rDCM param-
eter estimates were then analyzed with regard to group-level consistency and test-retest reliability. (B) Estimates of the probability density
functions (using the nonparametric kernel smoothing of fitdist.m implemented in MATLAB) of the connection-wise intraclass correlation coef-
ficient (ICC) for the resting state and all 7 tasks (i.e., emotional processing, gambling, language, motor, relational processing, social cognition,
and working memory) for the Glasser atlas (see Supporting Information Figure S1 for the respective results of the Schaefer atlas). Results are
shown when considering all connections (left), significant connections (middle), and the top 1,000 connections (right). (C) Mean (averaged
across all paradigms) test-retest reliability for all connections (top, left) as well as how often (i.e., in how many paradigms) a connection showed
excellent reliability (bottom, left). Mean test-retest reliability projected onto the cortical surface (top, middle) and the cortical location of all
regions that are linked via connections that show excellent reliability in all 8 paradigms (bottom, middle). Connectogram showing the con-
nections with excellent reliability in all 8 paradigms (right). The connectogram was produced using Circos (publicly available at https://circos
.ca/software/).
Network Neuroscience
145
Test-retest reliability of regression DCM
Test-retest reliability of model parameter estimates for regression DCM and functional connectivity. Test-retest reliability of parameter
Table 2.
estimates was assessed in terms of the intraclass correlation coefficient (ICC) between estimates of Session 1 (“test”) and Session 2 (“retest”)
for a fixed (full) network architecture (i.e., classical rDCM and Pearson correlation coefficient). Here, we report the mean (averaged across
parameters) ICC value and 95% confidence interval (CI). Averaging of the connection-wise ICC values as well as computing the 95% CI
was achieved by (a) transforming connection-wise ICC values to z-space using Fisher z-transformation, (b) computing mean as well as lower
and upper bound of the 95% CI in z-space, and finally (c) back-transforming estimates to r-space. Test-retest reliability is reported for the
connectivity and driving input parameter estimates of rDCM (middle) as well as for the functional connectivity estimates (right). For both
methods, results are shown for all HCP paradigms for the Glasser atlas (see Supporting Information Table S1 for the respective results of the
Schaefer atlas). Furthermore, results are shown for a all parameters (top row), b significant parameters (middle row), and c top 1,000 parameters
(bottom row).
Fixed network
REST
EMOTION
GAMBLING
LANGUAGE
MOTOR
RELATIONAL
SOCIAL
WORKING MEMORY
Connectivity
rDCM
0.24 [−0.18, 0.59]a
0.32 [−0.10, 0.64]b
0.45 [−0.02, 0.76]c
0.34 [−0.21, 0.72]
Inputs
–
0.08 [−0.43, 0.54]
0.62 [0.10, 0.88]
0.25 [0.07, 0.41]
0.74 [0.45, 0.89]
0.39 [−0.10, 0.73]
–
0.31 [−0.15, 0.65]
0.55 [0.15, 0.80]
0.41 [0.03, 0.68]
0.65 [0.35, 0.83]
0.42 [−0.09, 0.76]
0.45 [−0.08, 0.78]
0.70 [0.35, 0.83]
0.31 [−0.21, 0.70]
–
0.38 [−0.12, 0.72]
0.37 [0.08, 0.60]
–
0.25 [−0.12, 0.56]
0.53 [0.15, 0.77]
0.38 [0.04, 0.64]
0.62 [0.32, 0.81]
0.40 [−0.10, 0.73]
0.45 [−0.05, 0.77]
0.67 [0.38, 0.84]
0.42 [−0.07, 0.75]
0.46 [−0.07, 0.78]
0.69 [0.40, 0.85]
0.32 [−0.19, 0.70]
0.52 [0.13, 0.77]
0.62 [0.29, 0.82]
–
0.40 [−0.17, 0.77]
0.56 [0.12, 0.82]
–
0.42 [−0.03, 0.73]
0.51 [0.21, 0.72]
–
0.16 [−0.18, 0.46]
0.28 [−0.05, 0.55]
–
FC
0.16 [−0.25, 0.53]a
0.14 [−0.31, 0.54]b
0.22 [−0.36, 0.68]c
0.33 [−0.10, 0.66]
0.38 [−0.29, 0.80]
0.44 [−0.52, 0.91]
0.36 [−0.02, 0.65]
0.36 [−0.22, 0.75]
0.34 [−0.46, 0.83]
0.38 [−0.06, 0.69]
0.42 [−0.15, 0.78]
0.41 [−0.43, 0.87]
0.35 [−0.03, 0.64]
0.38 [−0.17, 0.75]
0.43 [−0.39, 0.87]
0.35 [−0.08, 0.67]
0.35 [−0.24, 0.76]
0.43 [−0.48, 0.89]
0.36 [−0.06, 0.67]
0.37 [−0.21, 0.76]
0.44 [−0.53, 0.91]
0.32 [−0.05, 0.65]
0.40 [−0.18, 0.77]
0.45 [−0.38, 0.88]
Network Neuroscience
146
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
we found the shift towards higher reliability to be even more pronounced (Figure 1B, right).
Specifically, we found reliability to range on average from fair for the resting state (mean ICC =
0.45 [−0.02, 0.76]) to near excellent for the emotional processing task (mean ICC = 0.74 [0.45,
0.89]). A comprehensive list of all results from the test-retest reliability analysis is provided in
Table 2.
In a post hoc analysis, we inspected which connections were most reliable across the dif-
ferent HCP paradigms. The mean ICC values (averaged across all eight paradigms) revealed a
notable pattern of connections that were consistently reliable across paradigms (Figure 1C,
left). In particular, when inspecting connections that showed excellent reliability (i.e., ICC >
0.75) in all eight paradigms, we found these connections to primarily link regions such as areas
a9-46v, a47r, p47r, and p10p near the frontal pole, AVI and FOP5 in the anterior insula and the
frontal operculum, respectivement, as well as TE1m and TE2a on the lateral surface of the tem-
poral lobe (Figure 1C, bottom left). These regions map well onto components of the multiple-
demands network, which is characterized by showing consistent activation for a number of
different cognitive tasks (Assem et al., 2020; Fedorenko et al., 2013).
These results illustrate that stronger connections (both inhibitory and excitatory) inferred by
rDCM are more reliable across sessions and, in fact, often achieve good to excellent test-retest
reliability (c'est à dire., ICC > 0.6). This is confirmed when directly testing the correlation between the
absolute mean (c'est à dire., averaged across all participants) parameter strength and the ICC value of
the parameter estimate, both for connectivity parameters (for all paradigms: r ≥ 0.26, all p <
0.001) and driving input parameters—although this was more variable for the latter (range: r =
−0.04, p = 0.29 to r = 0.40, p < 0.001).
As suggested by one of our reviewers, we repeated the above correlation analysis, but now
testing for an association between the ICC value of the parameter estimate and the mean (i.e.,
averaged across all participants) posterior precision of the parameter. In brief, we found the
correlation between ICC value and average posterior precision to be significant (for all para-
digms: r ≥ 0.17, all p < 0.001). However, this correlation was consistently (across all para-
digms) lower than the correlation between ICC value and absolute mean connection strength.
For the driving input parameters, this was more variable, showing higher correlation between
ICC value and average posterior precision for some paradigms but weaker correlation for other
paradigms (range: r = −0.08, p < 0.001 to r = 0.59, p < 0.001).
In a second step, we assessed the test-retest reliability
Regression DCM with sparsity constraints.
of connectivity estimates obtained using rDCM with embedded sparsity constraints. Overall,
the test-retest reliability of parameter estimates from sparse rDCM was lower than for rDCM
with fixed network architecture.
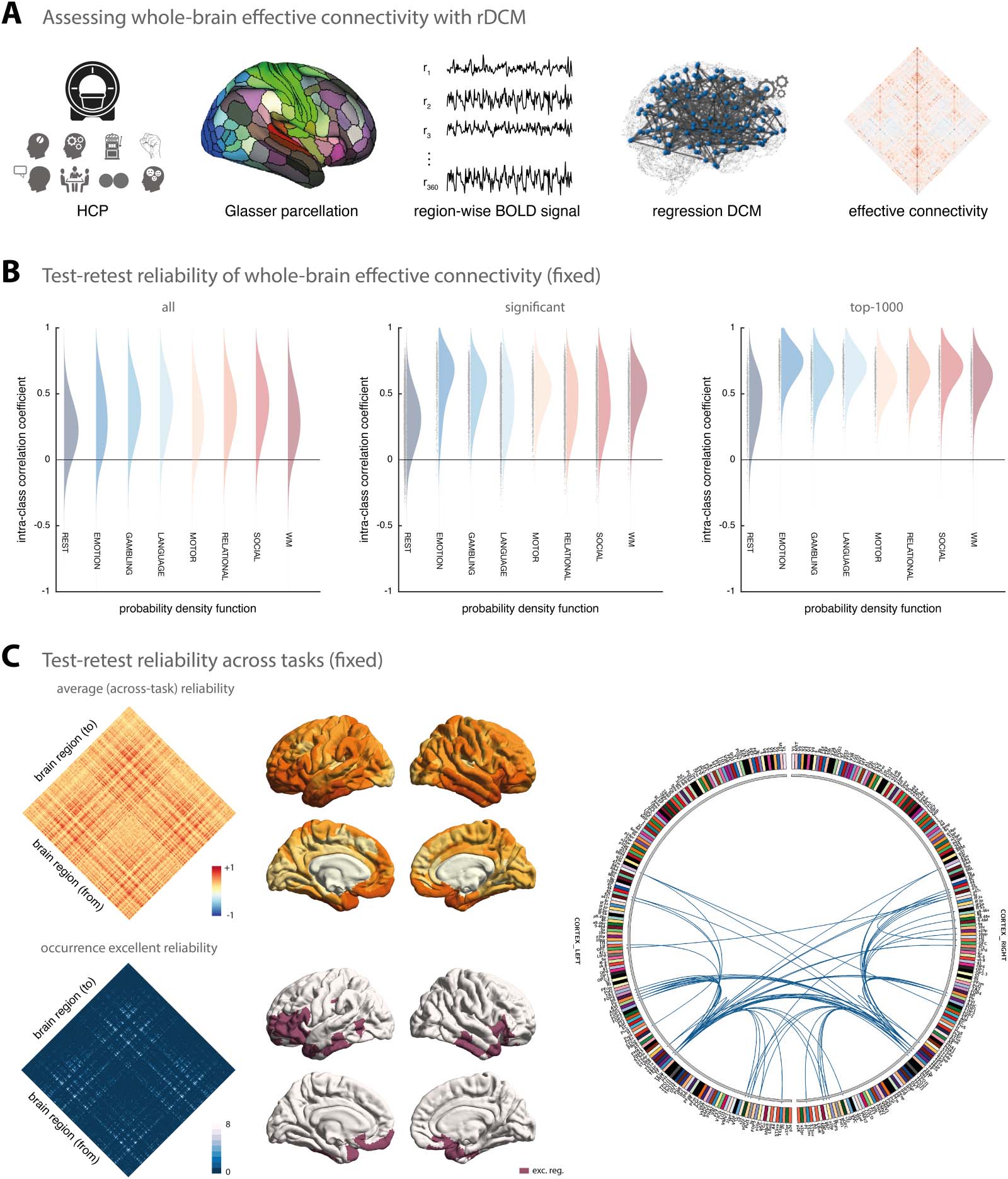
When considering all connections, test-retest reliability was on average poor for all para-
digms (Figure 2A, left). More specifically, for the connectivity parameters, test-retest reliability
ranged from mean ICC = 0.02 [−0.28, 0.33] for the resting state to mean ICC = 0.34 [−0.09,
0.66] for the motor task when considering all connections. Again, we found the test-retest reli-
ability of the intrinsic self-connections to be comparable to the (between-region) connections,
ranging from mean ICC = 0.06 [−0.28, 0.39] for the resting state to mean ICC = 0.39 [−0.31,
0.82] for the emotional processing task. Similarly, for the driving input parameters, test-retest
reliability ranged from poor for the motor task (mean ICC = 0.11 [−0.24, 0.44]) to fair for the
relational processing task (mean ICC = 0.40 [−0.16, 0.76]).
In a next step, we again tested whether stronger connections were more reliable. Focusing
only on connections that deviated significantly from zero ( p < 0.05, Bonferroni-corrected), we
Network Neuroscience
147
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Test-retest reliability of regression DCM with sparsity constraints. (A) Estimates of the probability density functions (using the non-
parametric kernel smoothing of fitdist.m implemented in MATLAB) of the connection-wise intraclass correlation coefficient (ICC) for the
resting-state and all 7 tasks (i.e., emotional processing, gambling, language, motor, relational processing, social cognition, and working mem-
ory) for the Glasser atlas (see Supporting Information Figure S2 for the respective results of the Schaefer atlas). Results are shown when con-
sidering all connections (left), significant connections (middle), and the top 1,000 connections (right). (B) Mean (averaged across all paradigms)
test-retest reliability for all connections (top, left) as well as how often (i.e., in how many paradigms) a connection showed excellent reliability
(bottom, left). Mean test-retest reliability projected onto the cortical surface (top, middle) and the cortical location of all regions that are linked
via connections that show excellent reliability in at least 6 paradigms (bottom, middle). Connectogram showing the connections with excellent
reliability in at least 6 paradigms (right). The connectogram was produced using Circos (publicly available at https://circos.ca/software/).
again observed a shift towards higher reliability (Figure 2A, middle), although less pronounced
as for rDCM with fixed network architecture. For sparse rDCM, reliability of the significant
connectivity parameters ranged on average from poor for the resting state (mean ICC = 0.16
[−0.32, 0.57]) to fair for the emotional processing task (mean ICC = 0.44 [−0.18, 0.81]). The
same pattern could be observed for the significant driving input estimates. Finally, when
restricting our reliability analysis even further to the top 1,000 connections, we found the shift
towards higher reliability to be even more pronounced, with one exception: the resting state
(Figure 2A, right). Specifically, even for the top 1,000 connections, we found poor reliability for
the resting state (mean ICC = 0.05 [−0.29, 0.38]), whereas for all task-based fMRI datasets, test-
retest reliability was considerably increased when considering only the top 1,000 connections
(e.g., mean ICC = 0.66 [0.25, 0.86] for the emotional processing task). A comprehensive list of
all results from the test-retest reliability analysis for sparse rDCM is provided in Table 3.
Network Neuroscience
148
Test-retest reliability of regression DCM
Test-retest reliability of model parameter estimates for regression DCM and functional connectivity (sparsity constraints). Test-retest
Table 3.
reliability of parameter estimates was assessed in terms of the intraclass correlation coefficient (ICC) between estimates of Session 1 (“test”) and
Session 2 (“retest”) for sparsity constraints (i.e., rDCM with sparsity constraints and L1-regularized partial correlations). Here, we report the
mean (averaged across parameters) ICC value and 95% confidence interval (CI). Averaging of the connection-wise ICC values as well as
computing the 95% CI was done in z-space (see caption of Table 2 for details). Test-retest reliability is reported for the connectivity and driving
input estimates of rDCM (middle) as well as for the functional connectivity estimates (right). For both methods, results are shown for all HCP
paradigms for the Glasser atlas (see Supporting Information Table S2 for the respective results of the Schaefer atlas). Furthermore, results are
shown for a all parameters (top row), b significant parameters (middle row), and c top 1,000 parameters (bottom row).
Sparsity constraints
REST
EMOTION
GAMBLING
LANGUAGE
MOTOR
RELATIONAL
SOCIAL
WORKING MEMORY
Connectivity
rDCM
0.02 [−0.28, 0.33]a
0.16 [−0.32, 0.57]b
0.05 [−0.29, 0.38]c
0.25 [−0.24, 0.64]
0.44 [−0.18, 0.81]
0.66 [0.25, 0.86]
0.29 [−0.15, 0.63]
0.31 [−0.12, 0.65]
0.56 [0.20, 0.79]
0.27 [−0.14, 0.61]
0.29 [−0.10, 0.61]
0.51 [0.14, 0.76]
0.34 [−0.09, 0.66]
0.38 [0.02, 0.65]
0.43 [0.06, 0.69]
0.30 [−0.13, 0.64]
0.33 [−0.07, 0.64]
0.55 [0.21, 0.78]
0.31 [−0.11, 0.64]
0.33 [−0.07, 0.63]
0.56 [0.19, 0.79]
0.24 [−0.15, 0.57]
0.26 [−0.09, 0.56]
0.32 [−0.06, 0.62]
Inputs
–
0.20 [−0.26, 0.54]
0.73 [0.73, 0.73]
–
0.26 [−0.20, 0.63]
0.42 [0.01, 0.70]
–
0.38 [−0.12, 0.73]
0.33 [−0.02, 0.61]
–
0.11 [−0.24, 0.44]
–
–
0.40 [−0.16, 0.76]
0.54 [0.08, 0.81]
–
0.36 [−0.09, 0.69]
FC
0.14 [−0.38, 0.60]a
0.50 [0.02, 0.79]b
0.55 [0.11, 0.81]c
0.08 [−0.44, 0.55]
0.30 [−0.07, 0.59]
0.31 [−0.10, 0.63]
0.08 [−0.42, 0.54]
0.32 [−0.06, 0.61]
0.32 [−0.04, 0.61]
0.08 [−0.43, 0.56]
0.36 [−0.06, 0.66]
0.37 [−0.05, 0.68]
0.07 [−0.43, 0.54]
0.33 [−0.03, 0.62]
0.35 [−0.06, 0.66]
0.07 [−0.41, 0.52]
0.34 [−0.02, 0.62]
0.33 [−0.07, 0.64]
0.09 [−0.46, 0.59]
0.46 [0.13, 0.70]
0.40 [0.03, 0.67]
–
0.16 [−0.20, 0.48]
0.27 [0.14, 0.39]
–
0.40 [0.00, 0.69]
0.08 [−0.38, 0.51]
0.35 [0.00, 0.63]
0.37 [0.00, 0.64]
Network Neuroscience
149
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
In a post hoc analysis, we again inspected which connections were most reliable across the
different HCP paradigms. Inspecting the mean (averaged across all paradigms) ICC values
revealed a similar pattern for sparse rDCM as observed above for classical rDCM—although
with somewhat lower mean ICC values (Figure 2B, left). For example, no connections were
found that showed excellent reliability in all eight paradigms. However, when inspecting those
connections that showed excellent reliability in at least six of the eight paradigms, we observed
a pattern that was highly consistent with the one obtained using rDCM with fixed network
architecture (see above). Specifically, these connections again primarily linked regions that
had previously been identified with the multiple-demands network, such as areas p10p near
the frontal pole, AVI and FOP5 in the anterior insula and the frontal operculum, respectively,
as well as TE1m and TE2a on the lateral surface of the temporal lobe (Figure 2B, bottom left).
Again, these results illustrate that stronger parameters (both inhibitory and excitatory) are more
reliable than weaker parameters. This observation was confirmed when explicitly testing the
correlation between the mean (i.e., averaged across all participants) absolute parameter strength
and the ICC values of the parameter estimate, both for connectivity strengths (resting state: r =
0.01, p < 0.001; for all task paradigms: r ≥ 0.18, p < 0.001) and for driving inputs, although
this was again more variable for the latter (range: r = 0.09; p = 0.01 to r = 0.39, p < 0.001).
Furthermore, following the suggestion by one of our reviewers, we also tested for an associ-
ation between the ICC value and the mean (i.e., averaged across all participants) posterior pre-
cision of the parameter. These results were highly consistent with the results obtained for rDCM
with fixed network architecture. More precisely, for the connectivity parameters, we found the
correlation between ICC value and average posterior precision to be significant for all task par-
adigms (r ≥ 0.06, all p < 0.001). However, the correlation became marginally negative for the
resting state (r = −0.01, p = 0.001). Furthermore, this correlation was consistently (across all par-
adigms) lower than the correlation between ICC value and absolute mean connection strength.
For the driving input parameters, the constellation was more variable, showing higher correla-
tion between ICC value and average posterior precision for some paradigms but weaker corre-
lation for other paradigms (range: r = 0.03, p = 0.113 to r = 0.50, p < 0.001).
In summary, our results indicate that, for the present datasets, connectivity estimates
obtained using sparse rDCM were less reliable than those obtained using rDCM with fixed
network architecture (see the Discussion section for potential explanations). For resting-state
data, test-retest reliability of sparse rDCM was poor—even when focusing on strong connec-
tions. Conversely, for the driving input estimates, test-retest reliability was comparable across
the two rDCM variants.
Comparison to functional connectivity. For comparison with rDCM, we investigated the test-
retest reliability of functional connectivity estimates obtained using Pearson correlations and
L1-regularized partial correlations.
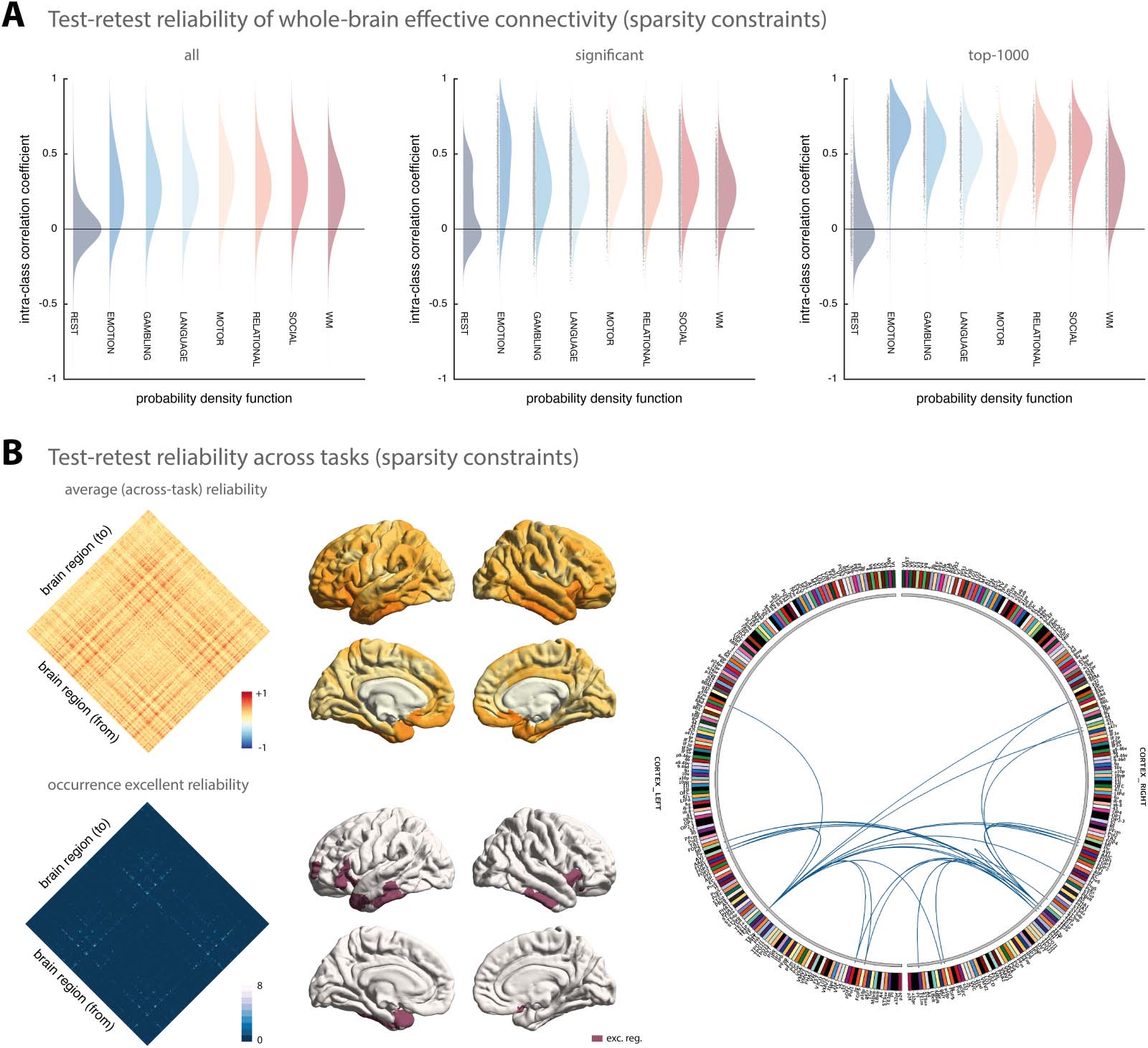
First, we compared results from rDCM with fixed network architecture to Pearson correla-
tions (Figure 3A). We found that the two methods showed similar test-retest reliability when
considering all model parameters (Figure 3A, left). Specifically, test-retest reliability of Pearson
correlations ranged from mean ICC = 0.16 [−0.25, 0.53] for the resting state to mean ICC =
0.38 [−0.06, 0.69] for the language task. Interestingly, when focusing on stronger connections,
Pearson correlations did not show the same improvement previously observed for rDCM;
instead, test-retest reliability remained mostly poor (or fair at best). More specifically, when
focusing only on significant parameter estimates, reliability ranged from mean ICC = 0.14
[−0.31, 0.54] for the resting state to mean ICC = 0.42 [−0.15, 0.78] for the language task
Network Neuroscience
150
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Comparison of test-retest reliability between regression DCM and functional connectivity. (A) Estimates of the probability density
functions (using the nonparametric kernel smoothing of fitdist.m implemented in MATLAB) of the connection-wise intraclass correlation coef-
ficient (ICC) for the resting-state and all 7 tasks (i.e., emotional processing, gambling, language, motor, relational processing, social cognition,
and working memory) for the Glasser atlas (see Supporting Information Figure S3 for the respective results of the Schaefer atlas) for fixed (full)
connectivity methods (i.e., classical rDCM and Pearson correlation coefficient), and (B) sparse connectivity methods (i.e., rDCM with sparsity
constraints and L1-regularized partial correlations). Probability density functions representing rDCM results are shown with dot-dashed lines
and lighter colors, whereas probability density functions representing functional connectivity results are shown with dashed lines and darker
colors. For each connectivity variant, results are shown when considering all connections (left), significant connections (middle), and the top
1,000 connections (right).
(Figure 3A, middle). Similarly, when restricting the analysis to the top 1,000 connections,
reliability ranged from mean ICC = 0.22 [−0.36, 0.68] for the resting state to mean ICC =
0.45 [−0.38, 0.88] for the working-memory task (Figure 3A, right). A comprehensive list of all
results from the test-retest reliability analysis is provided in Table 2 (right column).
Second, we compared sparse rDCM to L1-regularized partial correlations (Figure 3B). Inter-
estingly, we found test-retest reliability of L1-regularized partial correlations to be on average
close to zero for all paradigms when considering all connectivity parameters (Figure 3B, left).
Specifically, test-retest reliability ranged from mean ICC = 0.07 [−0.41, 0.52] for the relational
processing task to mean ICC = 0.14 [−0.38, 0.60] for the resting state. While this improved
when focusing on stronger connections, test-retest reliability remained relatively low for L1-
regularized partial correlations and, in most cases, worse than for sparse rDCM. More specif-
ically, when focusing only on significant parameters, reliability ranged from mean ICC = 0.30
[−0.07, 0.59] for the emotional processing task to mean ICC = 0.50 [0.02, 0.79] for the resting
state (Figure 3B, middle). Similarly, when restricting the analysis to the top 1,000 connections,
reliability ranged from mean ICC = 0.31 [−0.10, 0.63] for the emotional processing task to
mean ICC = 0.55 [0.11, 0.81] for the resting state (Figure 3B, right). A comprehensive list of
all results from the test-retest reliability analysis is provided in Table 3 (right column).
Network Neuroscience
151
Test-retest reliability of regression DCM
Table 4. Across-session consistency of connectivity profiles for regression DCM and functional connectivity. Consistency of the entire
connectivity profile across the two sessions. Identification accuracies are reported for predicting identity in Session 2 from Session 1 (top) and
vice versa (bottom). Results are reported for rDCM (middle) and for functional connectivity estimates (right). For both methods, results are
shown for all HCP paradigms as well as for the two whole-brain parcellation schemes (i.e., Glasser, Schaefer). Furthermore, results are reported
for two different “modes” of estimation (see main text for details): (a) fixed network architecture (i.e., classical rDCM and Pearson correlation
coefficient), and (b) sparsity constraints (i.e., rDCM with sparsity constraints and L1-regularized partial correlations).
rDCM
FC
Fixed network
Glasser
Schaefer
Glasser
Schaefer
REST
85.7% (36/42)
92.9% (39/42)
31.0% (13/42)
28.6% (12/42)
95.2% (40/42)
97.6% (41/42)
21.4% (9/42)
23.8% (10/42)
EMOTION
80.5% (33/41)
73.2% (30/41)
95.1% (39/41)
95.1% (39/41)
GAMBLING
97.7% (43/44)
97.8% (44/45)
93.3% (42/45)
93.3% (42/45)
78.0% (32/41)
75.6% (31/41)
92.7% (38/41)
90.2% (37/41)
95.5% (42/44)
95.6% (43/45)
95.6% (43/45)
93.3% (42/45)
LANGUAGE
100.0% (43/43)
100.0% (43/43)
100.0% (43/43)
95.3% (41/43)
97.7% (42/43)
97.7% (42/43)
95.3% (41/43)
95.3% (41/43)
MOTOR
93.3% (42/45)
93.3% (42/45)
93.3% (42/45)
95.6% (43/45)
95.6% (43/45)
91.1% (41/45)
95.6% (43/45)
91.1% (41/45)
RELATIONAL
97.7% (42/43)
97.7% (42/43)
95.3% (41/43)
100.0% (43/43)
97.7% (42/43)
95.3% (41/43)
97.7% (42/43)
93.0% (40/43)
SOCIAL
100.0% (44/44)
100.0% (44/44)
95.5% (42/44)
97.7% (43/44)
100.0% (44/44)
100.0% (44/44)
95.5% (42/44)
93.2% (41/44)
WORKING MEMORY
95.6% (43/45)
97.8% (44/45)
97.8% (44/45)
97.8% (44/45)
97.8% (44/45)
97.8% (44/45)
97.8% (44/45)
97.8% (44/45)
Sparsity constraints
REST
47.6% (20/42)
59.5% (25/42)
97.6% (41/42)
95.2% (40/42)
54.8% (23/42)
52.4% (22/42)
100.0% (42/42)
100.0% (42/42)
EMOTION
78.0% (32/41)
80.5% (33/41)
92.7% (38/41)
95.1% (39/41)
80.5% (33/41)
78.0% (32/41)
97.6% (40/41)
92.7% (38/41)
GAMBLING
95.6% (43/45)
97.8% (44/45)
84.4% (38/45)
97.8% (44/45)
93.3% (42/45)
93.3% (42/45)
97.8% (44/45)
100.0% (45/45)
LANGUAGE
100.0% (43/43)
100.0% (43/43)
95.3% (41/43)
95.3% (41/43)
97.7% (42/43)
100.0% (43/43)
100.0% (43/43)
100.0% (43/43)
Network Neuroscience
152
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
Table 4.
(continued )
rDCM
FC
MOTOR
95.6% (43/45)
95.6% (43/45)
93.3% (42/45)
93.3% (42/45)
97.8% (44/45)
93.3% (42/45)
100.0% (45/45)
95.6% (43/45)
RELATIONAL
97.7% (42/43)
97.7% (42/43)
95.3% (41/43)
100.0% (43/43)
97.7% (42/43)
95.3% (41/43)
97.7% (42/43)
100.0% (43/43)
SOCIAL
100.0% (44/44)
100.0% (44/44)
100.0% (44/44)
100.0% (44/44)
100.0% (44/44)
100.0% (44/44)
100.0% (44/44)
100.0% (44/44)
WORKING MEMORY
97.8% (44/45)
97.8% (44/45)
95.6% (43/45)
97.8% (44/45)
95.6% (43/45)
97.8% (44/45)
95.6% (43/45)
100.0% (45/45)
Similarity Analysis: Inter-session Consistency of Whole-Brain Effective Connectivity Patterns
In a final analysis, we shifted
Regression DCM with fixed (fully connected) network architecture.
the focus from reliability of separate connections to the consistency of the whole-brain effec-
tive connectivity profile across time. To this end, we asked whether the effective connectivity
profile of an individual person obtained in one session could be used to identify this individual
from the set of all effective connectivity profiles obtained in another session. This analysis fol-
lows previous work demonstrating that functional connectivity profiles derived from fMRI data
enable the identification of individual subjects (Finn et al., 2015).
First, we assessed identification accuracies for the whole-brain effective connectivity pat-
terns inferred using rDCM with fixed network architecture (chance level: 1/Nsub × 100%, rang-
ing from 2.4% to 2.3%, depending on the number of subjects available in each task). Overall,
entire effective connectivity profiles were highly consistent across the two sessions and
enabled identification of individual participants with high accuracies. More specifically, when
predicting identity in Session 2 from Session 1 (S1 ➔ S2), identification accuracies ranged from
80.5% (33/41) for the emotional processing task to 100% (44/44) for the social cognition task.
Similarly, when predicting identity in Session 1 from Session 2 (S2 ➔ S1), identification accu-
racies ranged from 78.0% (32/41) for the emotional processing task to 100% (44/44) for the
social cognition task. Results were almost identical for the Schaefer parcellation. All of the
identification accuracies were statistically significant at p < 0.05 (Bonferroni-corrected for
multiple comparisons), as assessed using permutation testing (see the Methods section). A
comprehensive list of all identification accuracies is provided in Table 4 (middle column, top).
Regression DCM with sparsity constraints. Second, identification accuracies were assessed for
sparse rDCM. Again, the sparse whole-brain effective connectivity profiles were highly con-
sistent across the two sessions and allowed identification of individual participants with high
accuracies, with the notable exception of the resting state. More specifically, for the resting
state, identification accuracies were around 50% (i.e., 47.6% when predicting S1 ➔ S2, and
54.8% when predicting S2 ➔ S1); please see Table 4 for details. For task-based data, identifi-
cation accuracies were considerably higher. Specifically, when predicting S1 ➔ S2, identifica-
tion accuracies ranged from 78.0% (32/41) for the emotional processing task to 100% (44/44)
for the social cognition task. Similarly, when predicting S2 ➔ S1, identification accuracies
ranged from 80.5% (33/41) for the emotional processing task to 100% (44/44) for the social
Network Neuroscience
153
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
cognition task. Again, all identification accuracies—even for the resting state—were statisti-
cally significant at p < 0.05 (Bonferroni-corrected), as assessed using permutation testing.
Comparison to functional connectivity. Finally, we compared identification accuracies between
rDCM and functional connectivity estimates obtained using Pearson correlation and L1-
regularized partial correlations. Overall, we found that functional connectivity profiles also
enabled identification of individual participants with high accuracies (Table 4). There was
one notable exception: connectivity during the resting state, as characterized by Pearson cor-
relation coefficients. More specifically, for this setting, identification accuracies were 31.0%
(13/42) when predicting S1 ➔ S2, and 21.4% (9/42) when predicting S2 ➔ S1. This is in contrast
to previous reports by Finn et al. (2015); for potential explanations of these inconsistencies,
please see the Discussion section. For all other settings, identification accuracies of functional
connectivity profiles were high and even surpassed those reported for rDCM in some cases,
particularly when using sparsity constraints. Again, all identification accuracies—even for the
resting state in combination with Pearson’s correlations—were statistically significant at p <
0.05 (Bonferroni-corrected), as assessed using permutation testing.
DISCUSSION
In this paper, we assessed the test-retest reliability and group-level consistency of connec-
tion strengths inferred from fMRI data using rDCM (Frässle, Harrison, et al., 2021; Frässle,
Lomakina, Kasper, et al., 2018; Frässle, Lomakina, Razi, et al., 2017). First, using two differ-
ent whole-brain parcellations, we demonstrated that rDCM provides highly consistent
parameter estimates at the group level across two sessions of the HCP dataset (Van Essen
et al., 2013), regardless of the exact paradigm. Second, we found, on average, relatively low
test-retest reliability when considering all connections. However, stronger connections
were more reliable, with many strong connections displaying good to excellent test-retest
reliability (ICC ≥ 0.6); see Table 2. When comparing this to the test-retest reliability of mea-
sures of functional connectivity, rDCM performed favorably—in particular, when focusing
on strong connections (see Figure 3). While these observations hold for both variants of
rDCM, we found test-retest reliability to be considerably higher for rDCM with fixed net-
work architecture as compared with rDCM with sparsity constraints.
The increase in reliability with higher connection strengths is worth emphasizing. For
example, when restricting the analysis to the top 1,000 connections, we found for all task-
based datasets on average good test-retest reliability (see Table 2). This suggests that those
connections representing meaningful effects can be reliably inferred using rDCM. These
observations are consistent with previous analyses of test-retest reliability in the context of
classical DCM for fMRI. For instance, Frässle, Paulus, et al. (2016) assessed test-retest reliabil-
ity of effective connectivity in small (six-region) networks of the core face perception system.
While finding fair to good reliability of parameter estimates on average, they observed a sim-
ilar trend of increased reliability for larger parameter estimates. Our results are also in line with
other reports on the test-retest reliability of classical DCM (Frässle, Stephan, et al., 2015; Rowe
et al., 2010; Schuyler et al., 2010) and spectral DCM (Almgren et al., 2018)—all conducted in
the context of much smaller networks than the ones considered here. Furthermore, the
observed increase in test-retest reliability with connection strength is not exclusive to DCMs.
For instance, a similar increase of test-retest reliability with effect size has also been observed
in conventional fMRI analyses (Caceres et al., 2009).
Interestingly, this pattern of increased test-retest reliability for stronger connections was less
pronounced for functional connectivity estimates (Figure 3). Test-retest reliability estimates
Network Neuroscience
154
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
based on Pearson correlations and L1-regularized partial correlations also showed an increase
of ICC values for greater connection strength, in line with previous studies of functional con-
nectivity (for a review, see Noble et al., 2019). However, this increase was only moderate and
the average test-retest reliability remained poor to fair, even for the strong connections.
With regard to the test-retest reliability of rDCM, two further observations are worth high-
lighting. First, we found connectivity estimates from task-based fMRI data to be consistently
more reliable than those from resting-state fMRI data. This is remarkable given that resting-
state measurements were considerably longer than task measurements, with longer scanning
sessions typically being associated with increased reliability (Birn et al., 2013; Noble et al.,
2017). More specifically, while (per session) approximately 1 hr of resting-state fMRI data
were collected (combined across the phase-encoding directions), task-based fMRI data
comprised just a couple of minutes. Despite these very short scanning sessions, task-based
fMRI exhibited superior reliability compared with resting-state data. These observations are
in line with previous reports demonstrating higher test-retest reliability for functional connec-
tivity patterns derived from task-based as compared with resting-state fMRI data (Noble
et al., 2019; Wang et al., 2017). Furthermore, our results are also consistent with findings
suggesting that connectivity patterns derived from task-based fMRI are more predictive of
individual traits (Greene et al., 2020; Greene et al., 2018). This indicates that—despite
its patient-friendly nature—the resting state may not be ideally suited for clinical settings since
test-retest reliability is considerably lower than for task-based fMRI—even at much longer
scanning times.
Second, we found connectivity estimates by rDCM to be more reliable when assuming a
fixed (fully connected) network architecture as compared with relying on embedded sparsity
constraints. This was surprising given that sparsity constraints prevent overfitting and should
thus increase generalizability of parameter estimates. Having said this, previous simulations
have shown that rDCM with sparsity constraints is even more demanding in terms of data
quality than rDCM with fixed network architecture (Frässle, Lomakina, Kasper, et al.,
2018). More specifically, we have demonstrated that for low signal-to-noise ratio (SNR) or
long repetition time (TR) settings, rDCM with sparsity constraints tends to yield overly sparse
connectivity matrices that result from a propensity to pruning existing connections (Frässle,
Lomakina, Kasper, et al., 2018). This may be an explanation for the diminished test-retest
reliability observed in the current study in the sense that weak connections may sometimes
be pruned and sometimes not.
Finally, moving from assessments of individual connections to whole-brain patterns, we
demonstrate that the entire connectivity profile (i.e., the whole-brain “connectivity finger-
print”) of individuals is highly consistent across the two sessions—for both effective (rDCM)
and functional connectivity measures. We show that, in many cases, it is possible to identify an
individual among all participants with close to perfect accuracy based on the inferred connec-
tivity pattern. This is consistent with a previous study demonstrating the identifiability of single
subjects from functional connectivity measures (Finn et al., 2015), as well as similar reports
(Cole et al., 2014; Horien et al., 2019; Noble et al., 2017; Pannunzi et al., 2017; Smith et al.,
2009). Interestingly, we found that one particular combination (i.e., resting state and Pearson
correlations) yielded relatively low (yet still significant) identification accuracies. This is in con-
trast to the previous report by Finn et al. (2015). These differences may be due to a number of
reasons, including differences in (a) the exact dataset, (b) preprocessing strategy, or (c) whole-
brain parcellation scheme. Despite this discrepancy, our results support the idea that individ-
ual participants may possess a unique whole-brain connectivity profile for a given cognitive
context. This underscores the exciting opportunities of whole-brain connectivity assessments
Network Neuroscience
155
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
for studying individual variability of brain networks and how this relates to cognitive pheno-
types in health and disease.
Importantly, we show that all three metrics considered—group-level consistency and test-
retest reliability of individual connections as well as whole-brain connectivity profiles—are
almost identical for two state-of-the-art parcellation schemes, that is, the Glasser parcellation
(HCP MMP 1.0; Glasser, Coalson, et al., 2016) and the Schaefer 400-node parcellation (Schaefer
et al., 2018). This is important because inference on the organizational principles of the brain has
been shown to depend on the exact parcellation scheme utilized for defining the nodes of the
network (Fornito et al., 2010; Fornito et al., 2016). Consequently, it is critical to verify that any
conclusions drawn from connectivity estimates are not dependent on this particular choice.
Here, we demonstrate that the reliability and consistency of whole-brain effective connectivity
estimates obtained using rDCM (as well as those for functional connectivity measures) general-
ize across the two parcellation schemes. Notably, these two parcellation schemes focus on the
cortex and do not cover the cerebellum and subcortical regions. The latter structures, in partic-
ular subcortical regions, are usually characterized by diminished signal-to-noise ratio of the
fMRI signal. Hence, it remains to be tested whether the reliability results reported here generalize
to parcellation schemes that include subcortical structures, like the Automated Anatomical
Labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002).
Our findings have important implications for the fields of human connectomics and network
neuroscience in general, as well as for the clinically oriented disciplines of computational
psychiatry and computational neurology in particular. Especially for the latter two, test-retest
reliability of a computational model is important for its clinical utility, particularly when longi-
tudinal measurements are required (e.g., monitoring of treatment response). Here, we showed
that rDCM provides good test-retest reliability when focusing on strong connections and enables
identification of individual participants with high accuracy based on the entire connectivity pro-
file. Importantly, rDCM shows high reliability even for very short scanning sessions of 3–4 min
when working with task-based fMRI data. This is important for potential clinical applications.
In summary, our systematic analyses indicate that, in many constellations, rDCM exhibits
good properties with regard to group-level consistency and test-retest reliability of connec-
tions, as well as the inter-session consistency of whole-brain connectivity patterns. This com-
plements previous methodological assessments of face and construct validity of rDCM (Frässle,
Harrison, et al., 2021; Frässle, Lomakina, Kasper, et al., 2018; Frässle, Lomakina, Razi, et al.,
2017; Frässle, Manjaly, et al., 2021) and underscores its potential for clinical applications. Its
ability to obtain reliable estimates of directed whole-brain connectivity may enable the
construction of computational assays for identifying pathophysiological mechanisms and for
predictions about individual treatment responses or clinical trajectories (Frässle, Marquand,
et al., 2020)—a possibility that we will examine in future studies.
CODE AND DATA AVAILABILITY
A MATLAB implementation of the regression dynamic causal modeling (rDCM) approach is
available as open-source code in the Translational Algorithms for Psychiatry-Advancing
Science (TAPAS) software package (https://www.translationalneuromodeling.org/tapas). Fur-
thermore, we will publish the code for the analysis as well as the source data files for figures
and tables online as part of an online repository that conforms to the FAIR (Findable, Acces-
sible, Interoperable, and Reusable) data principles (https://gitlab.ethz.ch/tnu/code/fraessleetal
_rdcm_test_retest; Frässle & Stephan, 2021). Additionally, the raw data are openly available
from the HCP website, which also conforms to the FAIR principles.
Network Neuroscience
156
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00215.
AUTHOR CONTRITUBUTIONS
Stefan Frässle: Conceptualization; Formal analysis; Investigation; Methodology; Software;
Validation; Visualization; Writing – original draft; Writing – review & editing. Klaas Enno Stephan:
Conceptualization; Funding acquisition; Resources; Supervision; Writing – review & editing.
FUNDING INFORMATION
Klaas Enno Stephan, René and Susanne Braginsky Foundation. Klaas Enno Stephan,
Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen Forschung (https://dx
.doi.org/10.13039/501100001711), Award ID: 320030_179377. Klaas Enno Stephan,
University of Zurich.
REFERENCES
Almeida, J. R., Versace, A., Mechelli, A., Hassel, S., Quevedo, K.,
Kupfer, D. J., & Phillips, M. L. (2009). Abnormal amygdala-
prefrontal effective connectivity to happy faces differentiates
bipolar from major depression. Biological Psychiatry, 66,
451–459. https://doi.org/10.1016/j.biopsych.2009.03.024,
PubMed: 19450794
Almgren, H., Van de Steen, F., Kuhn, S., Razi, A., Friston, K., &
Marinazzo, D. (2018). Variability and reliability of effective
connectivity within the core default mode network: A multi-site
longitudinal spectral DCM study. NeuroImage, 183, 757–768.
https://doi.org/10.1016/j.neuroimage.2018.08.053, PubMed:
30165254
Anticevic, A., Hu, X., Xiao, Y., Hu, J., Li, F., Bi, F., Cole, M. W.,
Savic, A., Yang, G. J., Repovs, G., Murray, J. D., Wang, X. J.,
Huang, X., Lui, S., Krystal, J. H., & Gong, Q. (2015). Early-course
unmedicated schizophrenia patients exhibit elevated prefrontal
connectivity associated with longitudinal change. Journal of
N e u ro s c i e n c e , 3 5 , 2 6 7 – 2 8 6 . h t t p s : / / d o i . o rg / 1 0 . 1 5 2 3
/JNEUROSCI.2310-14.2015, PubMed: 25568120
Assem, M., Glasser, M. F., Van Essen, D. C., & Duncan, J. (2020). A
domain-general cognitive core defined in multimodally Parcel-
lated human cortex. Cerebral Cortex, 30, 4361–4380. https://
doi.org/10.1093/cercor/bhaa023, PubMed: 32244253
Birn, R. M., Molloy, E. K., Patriat, R., Parker, T., Meier, T. B., Kirk,
G. R., Nair, V. A., Meyerand, M. E., & Prabhakaran, V. (2013).
The effect of scan length on the reliability of resting-state fMRI
connectivity estimates. NeuroImage, 83, 550–558. https://doi
.org/10.1016/j.neuroimage.2013.05.099, PubMed: 23747458
Bishop, C. M. (2006). Pattern recognition and machine learning.
Springer.
Bressler, S. L., & Menon, V. (2010). Large-scale brain networks in
cognition: Emerging methods and principles. Trends in Cognitive
Sciences, 14, 277–290. https://doi.org/10.1016/j.tics.2010.04
.004, PubMed: 20493761
Bullmore, E. T., Frangou, S., & Murray, R. M. (1997). The dysplastic net
hypothesis: An integration of developmental and dysconnectivity
theories of schizophrenia. Schizophrenia Research, 28, 143–156.
https://doi.org/10.1016/S0920-9964(97 )00114-X, PubMed:
9468349
Caceres, A., Hall, D., Zelaya, F., Williams, S., & Mehta, M. (2009).
Measuring fMRI reliability with the intra-class correlation coeffi-
cient. NeuroImage, 45, 758–768. https://doi.org/10.1016/j
.neuroimage.2008.12.035, PubMed: 19166942
Cicchetti, D. (2001). The precision of reliability and validity esti-
mates re-visited: Distinguishing between clinical and statistical
significance of sample size requirements. Journal of Clinical
and Experimental Neuropsychology, 23, 695–700. https://doi
.org/10.1076/jcen.23.5.695.1249, PubMed: 11778646
Cole, M. W., Bassett, D. S., Power, J. D., Braver, T. S., & Petersen,
S. E. (2014). Intrinsic and task-evoked network architectures of
the human brain. Neuron, 83, 238–251. https://doi.org/10.1016
/j.neuron.2014.05.014, PubMed: 24991964
Dale, A. M., Fischl, B., & Sereno, M. I. (1999). Cortical
surface-based analysis. I. Segmentation and surface reconstruc-
tion. NeuroImage, 9, 179–194. https://doi.org/10.1006/nimg
.1998.0395, PubMed: 9931268
Dirkx, M. F., den Ouden, H., Aarts, E., Timmer, M., Bloem, B. R.,
Toni, I., Helmich, R. C. (2016). The cerebral network of Parkin-
son’s tremor: An effective connectivity fMRI study. Journal of
Neuroscience, 36, 5362–5372. https://doi.org/10.1523
/JNEUROSCI.3634-15.2016, PubMed: 27170132
Fedorenko, E., Duncan, J., & Kanwisher, N. (2013). Broad domain
generality in focal regions of frontal and parietal cortex. Proceed-
ings of the National Academy of Sciences, 110, 16616–16621.
https://doi.org/10.1073/pnas.1315235110, PubMed: 24062451
Finn, E. S., Shen, X. L., Scheinost, D., Rosenberg, M. D., Huang, J.,
Chun, M. M., Papademetris, X., & Constable, R. T. (2015).
Functional connectome fingerprinting: Identifying individuals
using patterns of brain connectivity. Nature Neuroscience, 18,
1664–1671. https://doi.org/10.1038/nn.4135, PubMed: 26457551
Fornito, A., Zalesky, A., & Bullmore, E. T. (2010). Network scaling
effects in graph analytic studies of human resting-state FMRI data.
Network Neuroscience
157
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
Frontiers in Systems Neuroscience, 4, 22. https://doi.org/10.3389
/fnsys.2010.00022, PubMed: 20592949
Fornito, A., Zalesky, A., & Bullmore, E. (2016). Fundamentals of
brain network analysis. Elsevier.
Frässle, S., Aponte, E. A., Bollmann, S., Brodersen, K. H., Do, C. T.,
Harrison, O. K., Harrison, S. J., Heinzle, J., Iglesias, S., Kasper, L.,
Lomakina, E. I., Mathys, C., Müller-Schrader, M., Pereira, I.,
Petzschner, F. H., Raman, S., Schöbi, D., Toussaint, B., Weber,
L. A., Yao, Y., & Stephan, K. E. (2021). TAPAS: An open-source
software package for translational neuromodeling and computa-
tional psychiatry. https://doi.org/10.1101/2021.03.12.435091
Frässle, S., Harrison, S. J., Heinzle, J., Clementz, B. A., Tamminga,
C. A., Sweeney, J. A., Gershon, E. S., Keshavan, M. S., Pearlson,
G. D., Powers, A., & Stephan, K. E. (2021). Regression dynamic
causal modeling for resting-state fMRI. Human Brain Mapping,
42(7), 2159–2180. https://doi.org/10.1002/ hbm.25357,
PubMed: 33539625
Frässle, S., Lomakina, E. I., Kasper, L., Manjaly, Z. M., Leff, A.,
Pruessmann, K. P., Buhmann, J. M., & Stephan, K. E. (2018). A
generative model of whole-brain effective connectivity. Neuro-
Image, 179, 505–529. https://doi.org/10.1016/j.neuroimage
.2018.05.058, PubMed: 29807151
Frässle, S., Lomakina, E. I., Razi, A., Friston, K. J., Buhmann, J. M., &
Stephan, K. E. (2017). Regression DCM for fMRI. NeuroImage,
155, 406–421. https://doi.org/10.1016/j.neuroimage.2017.02
.090, PubMed: 28259780
Frässle, S., Manjaly, Z. M., Do, C. T., Kasper, L., Pruessmann, K. P.,
& Stephan, K. E. (2021). Whole-brain estimates of directed con-
nectivity for human connectomics. NeuroImage, 225, 117491.
https://doi.org/10.1016/j.neuroimage.2020.117491, PubMed:
33115664
Frässle, S., Marquand, A. F., Schmaal, L., Dinga, R., Veltman, D. J.,
van der Wee, N. J. A., van Tol, M. J., Schöbi, D., Penninx, B., &
Stephan, K. E. (2020). Predicting individual clinical trajectories of
depression with generative embedding. NeuroImage: Clinical,
26, 102213. https://doi.org/10.1016/j.nicl.2020.102213,
PubMed: 32197140
Frässle, S., Paulus, F. M., Krach, S., & Jansen, A. (2016). Test-retest
reliability of effective connectivity in the face perception net-
work. Human Brain Mapping, 37, 730–744. https://doi.org/10
.1002/hbm.23061, PubMed: 26611397
Frässle, S., & Stephan K. E. (2020). Robustness and reliability of
whole-brain effective connectivity, GitLab, https://gitlab.ethz.ch
/tnu/analysis-plans/fraessle_hcp_test_retest
Frässle, S., & Stephan K. E. (2021). Code for test-retest reliability
analyses, GitLab, https://gitlab.ethz.ch/tnu/code/fraessleetal
_rdcm_test_retest
Frässle, S., Stephan, K. E., Friston, K. J., Steup, M., Krach, S., Paulus,
F. M., & Jansen, A. (2015). Test-retest reliability of dynamic
causal modeling for fMRI. NeuroImage, 117, 56–66. https://doi
.org/10.1016/j.neuroimage.2015.05.040, PubMed: 26004501
Frässle, S., Yao, Y., Schöbi, D., Aponte, E. A., Heinzle, J., & Stephan,
K. E. (2018). Generative models for clinical applications in com-
putational psychiatry. Wiley Interdisciplinary Reviews: Cognitive
Science, 9, e1460. https://doi.org/10.1002/wcs.1460, PubMed:
29369526
Friston, K., Brown, H. R., Siemerkus, J., & Stephan, K. E. (2016). The
dysconnection hypothesis. Schizophrenia Research, 176, 83–94.
https://doi.org/10.1016/j.schres.2016.07.014, PubMed:
27450778
Friston, K., & Frith, C. D. (1995). Schizophrenia: A disconnection
syndrome? Clinical Neuroscience, 3, 89–97. PubMed: 7583624
Friston, K., Harrison, L., & Penny, W. (2003). Dynamic causal
modelling. NeuroImage, 19, 1273–1302. https://doi.org/10
.1016/S1053-8119(03)00202-7, PubMed: 12948688
Friston, K., Litvak, V., Oswal, A., Razi, A., Stephan, K. E., van Wijk,
B. C., Ziegler, G., & Zeidman, P. (2016). Bayesian model reduc-
tion and empirical Bayes for group (DCM) studies. NeuroImage,
128, 413–431. https://doi.org/10.1016/j.neuroimage.2015.11
.015, PubMed: 26569570
Friston, K., Mattout, J., Trujillo-Barreto, N., Ashburner, J., & Penny,
W. (2007). Variational free energy and the Laplace approxima-
tion. NeuroImage, 34, 220–234. https://doi.org/10.1016/j
.neuroimage.2006.08.035, PubMed: 17055746
Friston, K., Stephan, K. E., Montague, R., & Dolan, R. J. (2014).
Computational psychiatry: The brain as a phantastic organ. Lancet
Psychiatry, 1, 148–158. https://doi.org/10.1016/S2215-0366(14)
70275-5, PubMed: 26360579
Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D.,
Harwell, J., Yacoub, E., Ugurbil, K., Andersson, J., Beckmann,
C. F., Jenkinson, M., Smith, S. M., & Van Essen, D. C. (2016).
A multi-modal parcellation of human cerebral cortex. Nature,
536, 171–178. https://doi.org/10.1038/nature18933, PubMed:
27437579
Glasser, M. F., Smith, S. M., Marcus, D. S., Andersson, J. L.,
Auerbach, E. J., Behrens, T. E., Coalson, T. S., Harms, M. P.,
Jenkinson, M., Moeller, S., Robinson, E. C., Sotiropoulos, S. N.,
Xu, J., Yacoub, E., Ugurbil, K., & Van Essen, D. C. (2016). The
Human Connectome Project’s neuroimaging approach. Nature
Neuroscience, 19, 1175–1187. https://doi.org/10.1038/nn.4361,
PubMed: 27571196
Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,
Fischl, B., Andersson, J. L., Xu, J., Jbabdi, S., Webster, M.,
Polimeni, J. R., Van Essen, D. C., Jenkinson, M., & WU-Minn
HCP Consortium. (2013). The minimal preprocessing pipe-
lines for the Human Connectome Project. NeuroImage, 80,
105–124. https://doi.org/10.1016/j.neuroimage.2013.04.127,
PubMed: 23668970
Greene, A. S., Gao, S. Y., Noble, S., Scheinost, D., & Constable,
R. T. (2020). How tasks change whole-brain functional organiza-
tion to reveal brain-phenotype relationships. Cell Reports, 32(8),
108066. https://doi.org/10.1016/j.celrep.2020.108066, PubMed:
32846124
Greene, A. S., Gao, S., Scheinost, D., & Constable, R. T. (2018).
Task-induced brain state manipulation improves prediction of
individual traits. Nature Communications, 9, 2807. https://doi
.org/10.1038/s41467-018-04920-3, PubMed: 30022026
Grèzes, J., Wicker, B., Berthoz, S., & de Gelder, B. (2009). A failure
to grasp the affective meaning of actions in autism spectrum dis-
order subjects. Neuropsychologia, 47, 1816–1825. https://doi
.org/10.1016/j.neuropsychologia.2009.02.021, PubMed:
19428413
Griffanti, L., Salimi-Khorshidi, G., Beckmann, C. F., Auerbach, E. J.,
Douaud, G., Sexton, C. E., Zsoldos, E., Ebmeier, K. P., Filippini,
N., Mackay, C. E., Moeller, S., Xu, J., Yacoub, E., Baselli, G.,
Ugurbil, K., Miller, K. L., & Smith, S. M. (2014). ICA-based
Network Neuroscience
158
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
artefact removal and accelerated fMRI acquisition for improved
resting state network imaging. NeuroImage, 95, 232–247. https://
doi.org/10.1016/j.neuroimage.2014.03.034, PubMed: 24657355
Horien, C., Shen, X., Scheinost, D., & Constable, R. T. (2019). The
individual functional connectome is unique and stable over
months to years. NeuroImage, 189, 676–687. https://doi.org/10
.1016/j.neuroimage.2019.02.002, PubMed: 30721751
Huys, Q. J., Maia, T. V., & Frank, M. J. (2016). Computational psy-
chiatry as a bridge from neuroscience to clinical applications.
Nature Neuroscience, 19, 404–413. https://doi.org/10.1038/nn
.4238, PubMed: 26906507
Jenkinson, M., Beckmann, C. F., Behrens, T. E., Woolrich, M. W., &
Smith, S. M. (2012). FSL. NeuroImage, 62, 782–790. https://doi
.org/10.1016/j.neuroimage.2011.09.015, PubMed: 21979382
Jirsa, V. K., Proix, T., Perdikis, D., Woodman, M. M., Wang, H.,
Gonzalez-Martinez, J., Bernard, C., Bénar, C., Guye, M., Chauvel,
P., & Bartolomei, F. (2016). The Virtual Epileptic Patient: Individ-
ualized whole-brain models of epilepsy spread. NeuroImage,
145(Pt. B). https://doi.org/10.1016/j.neuroimage.2016.04.049,
PubMed: 27477535
Maia, T., & Frank, M. (2011). From reinforcement learning models
to psychiatric and neurological disorders. Nature Neuroscience,
14, 154–162. https://doi.org/10.1038/nn.2723, PubMed:
21270784
Marcus, D. S., Harms, M. P., Snyder, A. Z., Jenkinson, M., Wilson,
J. A., Glasser, M. F., Barch, D. M., Archie, K. A., Burgess, G. C.,
Ramaratnam, M., Hodge, M., Horton, W., Herrick, R., Olsen, T.,
McKay, M., House, M., Hileman, M., Reid, E., Harwell, J.,
Coalson, T., Schindler, J., Elam, J. S., Curtiss, S. W., Van Essen,
D. C., & WU-Minn HCP Consortium. (2013). Human Connec-
tome Project informatics: Quality control, database services,
and data visualization. NeuroImage, 80, 202–219. https://doi
.org/10.1016/j.neuroimage.2013.05.077, PubMed: 23707591
Marreiros, A. C., Cagnan, H., Moran, R. J., Friston, K. J., & Brown, P.
(2013). Basal ganglia-cortical interactions in Parkinsonian
patients. NeuroImage, 66, 301–310. https://doi.org/10.1016/j
.neuroimage.2012.10.088, PubMed: 23153964
McIntosh, A. R. (1999). Mapping cognition to the brain through
neural interactions. Memory, 7, 523–548. https://doi.org/10
.1080/096582199387733, PubMed: 10659085
Mesulam, M. M. (1990). Large-scale neurocognitive networks and
distributed processing for attention, language, and memory.
Annals of Neurology, 28, 597–613. https://doi.org/10.1002/ana
.410280502, PubMed: 2260847
Montague, P., Dolan, R., Friston, K., & Dayan, P. (2012). Computa-
tional psychiatry. Trends in Cognitive Sciences, 16, 72–80.
https://doi.org/10.1016/j.tics.2011.11.018, PubMed: 22177032
Noble, S., Scheinost, D., & Constable, R. T. (2019). A decade of
test-retest reliability of functional connectivity: A systematic
review and meta-analysis. NeuroImage, 203, 116157. https://doi
.org/10.1016/j.neuroimage.2019.116157, PubMed: 31494250
Noble, S., Spann, M. N., Tokoglu, F., Shen, X., Constable, R. T., &
Scheinost, D. (2017). Influences on the test-retest reliability of
functional connectivity MRI and its relationship with behavioral
utility. Cerebral Cortex, 27, 5415–5429. https://doi.org/10.1093
/cercor/bhx230, PubMed: 28968754
Pannunzi, M., Hindriks, R., Bettinardi, R. G., Wenger, E., Lisofsky,
N., Martensson, J., Butler, O., Filevich, E., Becker, M., Lochstet,
M., Kuhn, S., & Deco, G. (2017). Resting-state fMRI correlations:
From link-wise unreliability to whole brain stability. NeuroImage,
157, 250–262. https://doi.org/10.1016/j.neuroimage.2017.06
.006, PubMed: 28599964
Papadopoulou, M., Cooray, G., Rosch, R., Moran, R., Marinazzo,
D., & Friston, K. (2017). Dynamic causal modelling of seizure
activity in a rat model. NeuroImage, 146, 518–532. https://doi
.org/10.1016/j.neuroimage.2016.08.062, PubMed: 27639356
Radulescu, E., Minati, L., Ganeshan, B., Harrison, N. A., Gray,
M. A., Beacher, F. D., Chatwin, C., Young, R. C., & Critchley,
H. D. (2013). Abnormalities in fronto-striatal connectivity
within language networks relate to differences in grey-matter
heterogeneity in Asperger syndrome. NeuroImage: Clinical, 2,
716–726. https://doi.org/10.1016/j.nicl.2013.05.010, PubMed:
24179823
Rowe, J., Hughes, L., Barker, R., & Owen, A. (2010). Dynamic
causal modelling of effective connectivity from fMRI: Are results
reproducible and sensitive to Parkinson’s disease and its treat-
ment? NeuroImage, 52, 1015–1026. https://doi.org/10.1016/j
.neuroimage.2009.12.080, PubMed: 20056151
Salimi-Khorshidi, G., Douaud, G., Beckmann, C. F., Glasser, M. F.,
Griffanti, L., & Smith, S. M. (2014). Automatic denoising of func-
tional MRI data: Combining independent component analysis and
hierarchical fusion of classifiers. NeuroImage, 90, 449–468.
https://doi.org/10.1016/j.neuroimage.2013.11.046, PubMed:
24389422
Schaefer, A., Kong, R., Gordon, E. M., Laumann, T. O., Zuo, X. N.,
Holmes, A. J., Eickhoff, S. B., & Yeo, B. T. T. (2018). Local-global
parcellation of the human cerebral cortex from intrinsic func-
tional connectivity MRI. Cerebral Cortex, 28, 3095–3114.
https://doi.org/10.1093/cercor/bhx179, PubMed: 28981612
Schlösser, R. G., Wagner, G., Koch, K., Dahnke, R., Reichenbach,
J. R., & Sauer, H. (2008). Fronto-cingulate effective connectivity
in major depression: A study with fMRI and dynamic causal
modeling. NeuroImage, 43, 645–655. https://doi.org/10.1016/j
.neuroimage.2008.08.002, PubMed: 18761094
Schuyler, B., Ollinger, J., Oakes, T., Johnstone, T., & Davidson, R.
(2010). Dynamic causal modeling applied to fMRI data shows
high reliability. NeuroImage, 49, 603–611. https://doi.org/10
.1016/j.neuroimage.2009.07.015, PubMed: 19619665
Shrout, P., & Fleiss, J. (1979). Intraclass correlations: Uses in asses-
sing rater reliability. Psychological Bulletin, 86, 420–428. https://
doi.org/10.1037/0033-2909.86.2.420, PubMed: 18839484
Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M.,
Mackay, C. E., Filippini, N., Watkins, K. E., Toro, R., Laird,
A. R., & Beckmann, C. F. (2009). Correspondence of the brain’s
functional architecture during activation and rest. Proceedings of
the National Academy of Sciences, 106, 13040–13045. https://
doi.org/10.1073/pnas.0905267106, PubMed: 19620724
Sporns, O. (2014). Contributions and challenges for network
models in cognitive neuroscience. Nature Neuroscience, 17,
652–660. https://doi.org/10.1038/nn.3690, PubMed: 24686784
Stephan, K. E., Baldeweg, T., & Friston, K. (2006). Synaptic plasticity
and dysconnection in schizophrenia. Biological Psychiatry, 59,
929–939. https://doi.org/10.1016/j.biopsych.2005.10.005,
PubMed: 16427028
Stephan, K. E., Iglesias, S., Heinzle, J., & Diaconescu, A. O. (2015).
Translational perspectives for computational neuroimaging.
Network Neuroscience
159
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Test-retest reliability of regression DCM
Neuron, 87, 716–732. https://doi.org/10.1016/j.neuron.2015.07
.008, PubMed: 26291157
Stephan, K. E., & Mathys, C. (2014). Computational approaches to
psychiatry. Current Opinion in Neurobiology, 25, 85–92. https://
doi.org/10.1016/j.conb.2013.12.007, PubMed: 24709605
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F.,
Etard, O., Delcroix, N., Mazoyer, B., & Joliot, M. (2002). Auto-
mated anatomical labeling of activations in SPM using a macro-
scopic anatomical parcellation of the MNI MRI single-subject
brain. NeuroImage, 15, 273–289. https://doi.org/10.1006/nimg
.2001.0978, PubMed: 11771995
Vai, B., Bulgarelli, C., Godlewska, B. R., Cowen, P. J., Benedetti, F.,
& Harmer, C. J. (2016). Fronto-limbic effective connectivity as
possible predictor of antidepressant response to SSRI administra-
tion. European Neuropsychopharmacology, 26, 2000–2010.
https://doi.org/10.1016/j.euroneuro.2016.09.640, PubMed:
27756525
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E. J.,
Yacoub, E., Ugurbil, K., & WU-Minn HCP Consortium. (2013).
The WU-Minn Human Connectome Project: An overview.
NeuroImage, 80, 62–79. https://doi.org/10.1016/j.neuroimage
.2013.05.041, PubMed: 23684880
Wang, J., Ren, Y., Hu, X., Nguyen, V. T., Guo, L., Han, J., & Guo,
C. C. (2017). Test-retest reliability of functional connectivity
networks during naturalistic fMRI paradigms. Human Brain
Mapping, 38, 2226–2241. https://doi.org/10.1002/hbm.23517,
PubMed: 28094464
Yeo, B. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D.,
Hollinshead, M., Roffman, J. L., Smoller, J. W., Zollei, L.,
Polimeni, J. R., Fischl, B., Liu, H., & Buckner, R. L. (2011). The
organization of the human cerebral cortex estimated by intrinsic
functional connectivity. Journal of Neurophysiology, 106,
1125–1165. https://doi.org/10.1152/jn.00338.2011, PubMed:
21653723
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
1
3
5
1
9
8
4
2
3
5
n
e
n
_
a
_
0
0
2
1
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
160