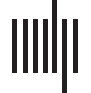RECHERCHE
Adaptive rewiring in nonuniform
coupled oscillators
MohamamdHossein Manuel Haqiqatkhah1,2
and Cees van Leeuwen1,3
1Brain and Cognition Research Unit, KU Leuven, Leuven, Belgium
2Department of Methodology and Statistics, Utrecht University, Utrecht, The Netherlands
3Center for Cognitive Science, TU Kaiserslautern, Kaiserslautern, Allemagne
Mots clés: Evolving neural networks, Neural oscillators, Dynamical systems, Complexity
un accès ouvert
journal
ABSTRAIT
Structural plasticity of the brain can be represented in a highly simplified form as adaptive
rewiring, the relay of connections according to the spontaneous dynamic synchronization in
network activity. Adaptive rewiring, au fil du temps, leads from initial random networks to brain-like
complex networks, c'est, networks with modular small-world structures and a rich-club
effect. Adaptive rewiring has only been studied, cependant, in networks of identical oscillators
with uniform or random coupling strengths. To implement information-processing functions
(par exemple., stimulus selection or memory storage), it is necessary to consider symmetry-breaking
perturbations of oscillator amplitudes and coupling strengths. We studied whether
nonuniformities in amplitude or connection strength could operate in tandem with adaptive
rewiring. Throughout network evolution, either amplitude or connection strength of a subset of
oscillators was kept different from the rest. In these extreme conditions, subsets might become
isolated from the rest of the network or otherwise interfere with the development of network
complexity. Cependant, whereas these subsets form distinctive structural and functional
communautés, they generally maintain connectivity with the rest of the network and allow the
development of network complexity. Pathological development was observed only in a small
proportion of the models. These results suggest that adaptive rewiring can robustly operate
alongside information processing in biological and artificial neural networks.
RÉSUMÉ DE L'AUTEUR
Dynamic synchronization in coupled oscillators has been studied extensively. Previously, it
has been shown how these dynamics can adaptively rewire a random network structure into a
complexe, brain-like one. For biological and artificial networks to benefit from this dynamic
self-organization, these networks must have input and memory facilities. Both functions
involve breaking the symmetry of uniform network oscillators and network connectivity
strength. We show that adaptive rewiring is generally robust against such perturbations.
Notably, we show—via novel methods of comparing network structures—that local symmetry-
breaking perturbations can develop discernible anatomical and functional connectivity
structures at the global level. Our research qualifies adaptive rewiring as a potential tool for
optimizing connectivity in biological and artificial neural networks.
Citation: Haqiqatkhah, M.. M., & van
Leeuwen, C. (2022). Adaptive rewiring
in nonuniform coupled oscillators.
Neurosciences en réseau, 6(1), 90–117.
https://doi.org/10.1162/netn_a_00211
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00211
Informations complémentaires:
https://doi.org/10.1162/netn_a_00211
https://doi.org/osf.io/625d8
Reçu: 20 Avril 2021
Accepté: 2 Octobre 2021
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
MohamamdHossein Manuel
Haqiqatkhah
mh.haqiqatkhah@gmail.com
Éditeur de manipulation:
Gustavo Deco
droits d'auteur: © 2021
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
Structural plasticity:
The brain’s ability to modify its
structure by means of forming and
pruning neuron-to-neuron
connections or changes in synaptic
strength based on neural activities.
Neural mass oscillators:
Simplified models of coarse-grained
mesoscopic or macroscopic
oscillatory activities of often large
coupled populations of excitatory
and inhibitory neurons and their
synapses.
Chaotic attractor:
An attractor (a set of values or states
that a dynamic system tends to
evolve toward) that is highly sensitive
to the initial conditions of the system.
Poincaré section:
A lower dimension in a continuous
dynamic system’s state space with
which the periodic orbit of the
system’s flow intersects.
Limit-cycle attractors:
An isolated periodic orbit or closed
trajectory of a continuous dynamical
system that has a two-dimensional
state space.
Neurosciences en réseau
INTRODUCTION
The anatomical connectivity of the brain network is shaped dynamically through structural
plasticity (Butz, Wörgötter, & van Ooyen, 2009). A variety of structural plasticity mechanisms
serve the adaptive role of accommodating the functional connectivity, the mutual statistical
dependencies between the network components (Avena-Koenigsberger, Misic, & Sporns,
2018; Rubinov, Sporns, van Leeuwen, & Breakspear, 2009). A common principle underlying
these mechanisms has become known as adaptive rewiring (Gong & van Leeuwen, 2003,
2004; Papadopoulos, Kim, Kurths, & Bassett, 2017). Adaptive rewiring implements the
Hebbian principle of “what fires together, wires together” at the level of network dynamics
(Bi & Poo, 2001; Hebb, 1949).
In networks of which the units may represent spiking model neurons (Kwok, Jurica, Raffone,
& van Leeuwen, 2007) or neural mass oscillators (Rubinov et al., 2009), adaptive rewiring
involves establishing connections between dynamically synchronized units at the expense of
currently non-synchronized ones. Over time, adaptively rewiring networks dynamically evolve
into complex architectures, showing the characteristics of small-worldness, modularity, et le
rich-club effect (Gong & van Leeuwen, 2003, 2004; Hellrigel, Jarman, & van Leeuwen, 2019;
Rubinov et al., 2009). Since small-worldness (Sporns & Zwi, 2004), modularity (Meunier,
Lambiotte, & Bullmore, 2010), and the rich-club effect (van den Heuvel & Sporns, 2011) sont
characteristics of large-scale brain connectivity, adaptive rewiring could represent a driving
force for the dynamic evolution of brain connectivity structure.
Adaptive rewiring models typically are highly simplified models, of which the units are
identical nonlinear oscillators with uniform connection weights and coupling strengths
(Rubinov et al., 2009). These simplifications severely reduce the functionality of such models.
To implement information processes in these networks, it is vital to enable nonidentical oscil-
lators and nonuniform connection strength. Cependant, the question should be asked whether
the properties of adaptive rewiring are robust to such nonuniformities. We therefore aimed to
explore adaptive rewiring of coupled oscillators with nonuniform amplitude and coupling
strengths and compare their evolution with that of uniform networks. The results will be crucial
for the utility of adaptive rewiring in biological and artificial neural networks with information-
processing functions such as pattern recognition and learning.
Adaptive Rewiring in Coupled Logistic Maps
Most adaptive rewiring studies have represented network activity by a model known as
coupled logistic maps (Kaneko, 1992). This choice was reached based on a succession of
abstractions. Mass activity was described by chaotic attractor dynamics, shown in Figure
S1A of the Supporting Information (Breakspear, Terry, & Friston, 2003). Further simplification
was obtained via the Poincaré section, yielding the mapping in Figure S1B. This mapping,
à son tour, can approximately be described, minus the noise, by a logistic map (Figure S1C).
Ainsi, the logistic map is the most straightforward possible abstract representation of neural
mass activity (Rubinov et al., 2009). Note that in coupled map networks, the couplings
provide noise perturbations to the oscillators, yielding mappings again more similar to
Figure S1B.
The version of the logistic map used in our study is shown in Equation 1, in which x is a
continuous variable in the range [−1, 1] that is updated in discrete time t, and α is the ampli-
tude. Logistic maps are known to exhibit universal dynamical properties (Feigenbaum, 1978).
For certain regimes of α, the behavior of the logistic map converges to one or more limit-cycle
attractors, but otherwise, it exhibits chaotic behavior. In these regimes, logistic maps produce
91
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
deterministic bounded time series that, en effet, qualitatively resemble the oscillations of neural
mass activity (see Figure S1).
xtþ1 ¼ 1 − αx2
t
:
(1)
Because of the universal dynamics of logistic maps, networks of such simple maps may
capture generic properties of interacting nonlinear systems (Kaneko, 1992). The logistic maps
are coupled according to Equation 2, which describes the activity of map i at time t + 1 as a
function of its activity at the previous time step and the activity of maps coupled with it. Dans ce
equation, Bi denotes the set of units connected to unit i (its neighbors in the network), et le
coupling strength ε
i sets the proportion to which the average activities of coupled units influ-
ence the activity of unit i (Hellrigel et al., 2019).
(cid:3)
(cid:3)
ð
xi;tþ1 ¼ 1 − εi
(cid:1)
Þ 1 − αix2
je;t
þ
j
εi
Bi
X
j
j2Bi
(cid:1)
1 − αix2
j;t
:
(2)
Through the effect of the neighbors, the map activity of Figure S1C regains a noisy appearance
more in line with Figure S1B. For efficiency of computation, we rewrite rewrite Equation 2 dans
matrix notation. For a network with N nodes, the activity of nodes at time t + 1 is calculated via
Équation 3 (cf. the Supporting Information for its derivation).
Xtþ1 ¼ 1N − α (cid:2) Xt (cid:2) Xt
½
(cid:3) (cid:2) 1N − ε þ Atε
ð
½
ð
Þ (cid:4)= At1N
(cid:3):
Þ
(3)
In this equation, symbols (cid:2) et (cid:4)= denote Hadamard (c'est à dire., element-wise) multiplication and
division, respectivement. The right-hand side of Equation 3 constitutes the vector form of the
logistic map, in which α is the vector of amplitudes and Xt is the vector of node’s activities at
time t. The map is Hadamard-multiplied by a coupling term. In the coupling term, ε is the vector
of coupling strengths, At is the connectivity matrix at time t, and 1N denotes a vertical unit vector
ε is Hadamard-divided by At1N, normalizing the former by the
of size N. In the coupling term, À
sum of the weights of the edges connected to each node. For binary networks, the term in the
denominator counts the number of connections for each node. We consider only binary graphs
for convenience. For adaptive rewiring in weighted networks, see Hellrigel et al. (2019).
Based on the network activity defined by Equation 3, adaptive rewiring takes the following
formulaire. After several updates to the network activity, a rewiring step is made. At each rewiring
step, the connections of a random node are updated as follows: The node is disconnected from
the neighbor most dissimilar in activity and is connected to the one most similar in activity
among those it is presently unconnected to. Dissimilarity of two nodes at a given time is de-
fined as the absolute value of the difference of their activity values. Note that although rewiring
steps are local, the most dissimilar unconnected node is obtained through a global search. Pour
algorithms using local or, instead, regional information for this purpose, see Jarman, Steur,
Trengove, Tyukin, and van Leeuwen (2017); Jarman, Trengove, Steur, Tyukin, and van
Leeuwen (2014).
All adaptive rewiring studies using coupled logistic maps have used fixed, uniform values
for the amplitude parameters α and the coupling strengths ε. In logistic map networks with
fixed architectures, these parameters have previously been allowed to vary in order to imple-
ment information-processing functions. In a perceptual organization model (van Leeuwen,
Steyvers, & Nooter, 1997), sensory input function was realized by local modulation of oscil-
lator amplitudes. The presence of sensory input to certain units brought their amplitude param-
eter values down to impose a more stable regime on the oscillators. Par conséquent, ces
oscillators showed a bias to become mutually synchronized. The synchronization was
92
Perceptual organization:
A process that, by grouping visual
elements (such as corners and
edges), facilitates determining the
meaning of the visual input as a
whole.
Neurosciences en réseau
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
understood as representing perceptual grouping. Grouping preferences followed the Gestalt
proximity principle and showed spontaneous switching in case of stimulation with bistable
motifs.
In a memory model (van Leeuwen & Raffone, 2001), connectivity parameter values were
locally incremented to represent the presence of a memory trace. This led to synchronization
biases along the incremented connections, resulting in spontaneous rehearsal and relearning
of stored pattern information. These examples demonstrate that coupled maps are capable of
performing cognitive functions based on ongoing dynamics.
The question is whether the nonidentical parameter settings involved in these functions
would dovetail with adaptive rewiring. To answer this question, we partitioned networks into
two subsets of units, a majority and a minority, each receiving a different parameter value for
the amplitude α or the coupling strength ε. Fixing these parameters at different values involves
a hardship test for adaptive rewiring. Par exemple, with one partition having increased cou-
pling strength (or decreased amplitude), we might expect connections to be established pref-
erentially within this partition and less within the other one. We may expect the opposite when
coupling strength within the partition is decreased (or amplitude increased). En outre, nous
may expect fewer connections to be established between the partitions. This might induce
network disintegration or otherwise interfere with the evolution of the network structure. Sur
the other hand, if these perturbations fail to interfere with the emergence of complexity (c'est à dire.,
small-wordness, modularity, and rich-club effect), adaptive rewiring could be used alongside
pattern detection and learning in sparse neural networks. This has implications for the func-
tioning of biological networks, as well as for the sparsification of artificial (c'est à dire., deep) neural
réseaux.
In what follows, the Method section describes details of the composition and initialization
of the models, the rewiring algorithm, and the qualitative and quantitative measures of net-
work structures used to describe, characterize, and compare models. In the Results section,
we describe our findings, mainly that nonuniformity of parameters is shown not to interfere
with the evolution of brain-like structure while giving rise to distinguishable network structures
suitable for cognitive functions. A discussion and several concluding remarks end the paper.
METHOD
Description of Networks
An unlabeled binary graph (or network) G = (V, E ) with n vertices (or nodes) and m edges
(or couplings) is defined mathematically by a set of nodes V = {1, 2, …, n} and a set of edges
E = {(je, j ) 2 V2 : i is coupled with j}. E is also known as the adjacency list of the network. We use
undirected graphs, c'est, (je, j ) 2 E () ( j, je) 2 E, and self couplings are not allowed, c'est, (je, je) =2
E. The size of the set V (c'est à dire., the number of its members) is denoted by |V|. From E, nous
may construct the adjacency matrix A of G as a square matrix of the size |V|, the elements of
which can take values of 0 ou 1. The element on its ith row and jth column (c'est à dire., aij) is equal to 1
si (je, j ) 2 E and is 0 otherwise. Since G is undirected, A is symmetrical around the main diagonal,
and since there are no self connections, its diagonal elements are zeros.
We may partition V into two nonoverlapping subsets, minority and majority, such that
|Vminority| = |V| − |Vmajority| et |Vminority| (cid:5) |Vmajority|. The edges among members of these
subsets form subgraphs within G and are henceforth called minority and majority partitions. UN
third subgraph comprises all of V but only edges between minority and majority nodes. Un tel
subgraph is called interpartition.
Neurosciences en réseau
93
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
Dynamics on the Graph
2 V, an activation value is assigned according to Equation 3. The corresponding
To each vi
parameter values, c'est, coupling strength ε and amplitude α, remain fixed in our model sim-
ulations. Models with identical parameter sets are called families. Five families of models are
simulated, each with 10 model instantiations, comprising a total of 50 model instantiations.
Each network is run for 20 million iterations. All the simulations and analyses are conducted in
R programming language version 3.6.0 (R Core Team, 2019) using computational resources
provided by VSC (Flemish Supercomputer Center).
Parameter Setting and Initialization
In our models, all Gs have |V| = 300 nodes and 5,200 edges, a connectivity density providing
robust evolution of small-world structure with uniform parameter setting (van den Berg, Gong,
Breakspear, & van Leeuwen, 2012). The model structure is initialized by randomly assigning
5,200 × 2 = 10,400 values “1” symmetrically to nondiagonal entries of A, and zeros to the
remaining entries. Each node in the network is randomly and independently assigned an initial
valeur, uniformly distributed between 0 et 1, c'est, xi1 ~ Unif (0, 1).
Previous adaptive rewiring studies have been using values of α and ε in the ranges of [1.7–1.9]
et [0.3–0.5], respectivement (Gong & van Leeuwen, 2003; Hellrigel et al., 2019; van den Berg &
van Leeuwen, 2004). Here the midpoints of these ranges, c'est, α = 1.8 and ε = 0.4, are used for
the parameters in the baseline (BL) condition. In the BL condition, all nodes have identical
parameter values.
The same applies to the majority (250 nodes) of the other conditions. Cependant, depending
on the condition, the minority subset (c'est à dire., the first 50) of nodes could have either lowered or
increased values of either the α or ε parameters. As shown in Figure S2, higher values of the
amplitude α tend to yield greater divergence in activity values; reducing the coupling parameter
ε has a similar effect (Hellrigel et al., 2019). Conditions with lowered values of α are called less
chaotic (LC), and those with increased values more chaotic (MC); conditions with lowered ε
values are called sub-coupled (SC) and those with increased values hyper-coupled (HC).
While keeping the parameters of the majority at the baseline level (un
i251:300 =
0.4), five different combinations of parameters were assigned to the minorities, each combina-
tion called a “family”: The baseline family (BL; un
i21:50 = 0.4), and the families with
less chaotic minority (LC; un
i21:50 = 1.9,
ε
i21:50 = 0.4), sub-coupled minorities (SC; un
i21:50 = 0.3), and hyper-coupled
minority (HC; un
i21:50 = 0.5). In the Results section, we identify model instantiations
by the two capitals indicating their family, together with a serial number [1-dix], Par exemple,
BL7, MC10. Le 10 model instantiations within each condition are run with different initiali-
zations, which are identical across conditions to allow matched comparison between families.
i21:50 = 0.4), more chaotic family (MC; un
i251:300 = 1.8, ε
i21:50 = 1.8, ε
i21:50 = 1.7, ε
i21:50 = 1.8, ε
i21:50 = 1.8, ε
The Adaptive Rewiring Algorithm
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A rewiring takes place after every 20 updates of the logistic maps, meaning that 1 million
rewiring attempts are performed over the 20 million updates of the model. At each rewiring
attempt, at time t, a node i is selected randomly from V, a vector of its distance from other
− xi,t1|V||, and another vector of similarities is defined as si,t =
nodes is calculated as di,t = |Xt
1|V|
− di,t.
Using these vectors, we compute two vectors: δ = [d
1, …, d
j, …, d
|V|]T = ( J.|V|
|V|]T = Adi,t for the dis-
− A)si,t for the
− I|V|
tances of node i from its neighbors; and σ = [p
1, …, p
j, …, p
Neurosciences en réseau
94
Adaptive rewiring in nonuniform coupled oscillators
similarities of node i to its non-neighbors, where J|V| is a |V| × |V| unit matrix (with all elements
equal to 1) et moi|V| is the identity matrix of size |V| (with diagonal and off-diagonal elements
− A ensures the search for the most
equal to 1 et 0, respectivement). The subtraction J|V|
similar node takes place among non-neighbors. The most dissimilar neighbor and the most
similar non-neighbor of node i, respectively denoted as ξ and ζ, are marked by finding the
index of the maxima of δ and σ:
− I|V|
ξ ¼ argmax
j
δj
ζ ¼ argmax
σj:
j
The rewiring is then changing the corresponding elements of the adjacency matrix A:
aiξ ¼ aξi ¼ 0
aiζ ¼ aζi ¼ 1:
(4)
(5)
Characterizing and Comparing Models
The state of each model at any given time t is described by adjacency matrix At (henceforth,
“anatomical connectivity”), which is subject to adaptive rewiring, and the vector of activation
valeurs, Xt. A model’s “functional connectivity” at t (represented by the |V| × |V| matrix Ft) est
defined by the momentary pairwise absolute differences of its node activation values.
Qualitative description of network structures. Network structure can be qualitatively assessed by
means of visual inspection of the wiring diagram or the adjacency matrix. Using the package
seriation (Hahsler, Hornik, & Buchta, 2008), the adjacency matrix is serialized by ordering
rows and columns according to the projection of the matrix on its first principal component.
Seriation maximizes the visual identifiability of modules within the network.
Quantitative measures of the structure. After each rewiring attempt, we calculate six network
connectivity measures (Costa, Rodrigues, Travieso, & Villas Boas, 2007): edge density, clus-
tering coefficient, average path length, small-world index, modularity, and assortativity.
En outre, we calculate an additional measure, namely, the rich-club coefficient, after
the final rewiring. All measures are calculated separately for the entire graph and the three
subgraphs (viz., the minority, majority, and interpartition subgraphs).
Edge Density. For a subset of nodes, this coefficient is the proportion of edges existing in a
subgraph to the theoretical maximum number of edges possible in the same subgraph. Pour
a subgraph with a subset of nodes |Vs| and adjacency matrix As, this value is calculated as
P.
ED ¼
ijAs
j : Vs
ð
j
Þ
j − 1
:
j
Vs
(6)
Since the total number of edges remains the same during the adaptive rewiring, this coef-
ficient gives an indication of how strongly each partition has attracted new nodes at every
rewiring step.
Clustering Coefficient. This measure can be defined either locally or globally and gives an in-
dication for the tendency of nodes to form clusters. We use the global clustering coefficient,
which is defined as the number of closed triplets of nodes (the triplets of nodes that are all
connected) divided by the number of connected triplets, either open (c'est à dire., paths of length
deux) or closed (c'est à dire., triangles). The numerator is equal to 3 times the number of triangles in
Neurosciences en réseau
95
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
the graph. Using linear algebra, the global clustering coefficient can be calculated formally
from the adjacency matrix A via
C ¼
3 (cid:6) #triangles
#triplets of connected nodes
¼ Tr A3ð
P.
Þ
(cid:4)
A2 − Tr A2
(cid:5)
:
ij
(7)
In this equation, Tr(UN) is the trace of matrix A and is defined as the sum of its diagonal ele-
ments, c'est, Tr(UN) = (cid:1)
i Aii.
Average Path Length. The average path length is the mean value of lengths of shortest paths
between all pairs of nodes, as defined in Equation 4 for a network of size N, where dij is the
length of the shortest distance between nodes i and j, and dij = 0 if there is no path between i
and j. This measure, which we calculated using the igraph package (Csardi & Nepusz, 2006),
gives an indication of how closely the nodes of a network are located from each other.
PL ¼
1
N N − 1
ð
Þ
X
i≠j2V
dij:
(8)
Small-world Index. This measure quantifies the degree to which a graph shows the optimal
combination of local and global connectedness, known as small-worldness (Watts &
Strogatz, 1998). It is defined as the proportion of clustering coefficient to average path length
for a network,
SW ¼ C
PL
:
(9)
The small-world index is often normalized by SW0 = C0
PL0
random network of the same size and density as the network in question. C0 and PL0 are,
respectivement, the expected clustering coefficient and expected average path length in such a
random network. Ainsi, the normalized small-world index is given by
, the expected small-world index of a
SWnorm ¼ SW
SW0
¼
:
C
PL
C0
PL0
(10)
The normalized index makes the comparison of networks with different sizes and densities
possible. Since all networks modeled in this study start off with random networks of equal size
and density, for computational reasons, the non-normalized small-world index (Équation 9) est
calculated and reported.
Modularity. Modularity of a network, as proposed by Newman (2006) and denoted by Q,
is a measure of to what extent the nodes tend to form interconnected communities isolated
from the other nodes of the graph. More precisely, for a network of size N (avec le
theoretical maximum number of edges m = N N−1
ð
defined as
) and adjacency matrix A, modularity is
2
Þ
Q ¼ 1
2m
(cid:6)
X
je;j
Mij − kikj
2m
(cid:7)
(cid:4)
δ ci; cj
(cid:5)
:
(11)
In this equation, ki and kj are, respectivement, degrees of nodes i and j. d(ci, cj) is the Kronecker
delta function, which is equal to 1 if nodes i and j have the same label and 0 otherwise. Le
term in square brackets is the difference between the actual number of edges between nodes
i and j and the expected number of edges between them. Ainsi, according to Equation 11,
Neurosciences en réseau
96
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
modularity equals the sum of these differences for the nodes within communities,
normalized by the theoretical maximum number of edges in the network.
This measure requires an a priori labeling of nodes that defines the communities to which
the nodes belong. A variety of algorithms have been suggested to discover module, or com-
munities, within a network so that the value of Q is maximized (for a review, cf. Zhang, Ma,
Zhang, Sun, & Yan, 2018). The communities discovered by these algorithms can thus be used
as labels for calculating modularity of the network. In line with Clauset, Newman, and Moore
(2004), we use the fast greedy algorithm to optimally detect communities and thus calculate
the modularity based on community membership of the nodes. The igraph package was used
to automatically detect communities and calculate modularity.
Assortativity. The assortativity coefficient is a measure of homophily in networks that indicates
the preferences of nodes to connect to alike nodes. The likeness can be imposed externally, pour
example, by assigning categories to the nodes using labels (known as nominal assortativity), ou
by internal criteria such as node degrees (degree assortativity). Degree assortativity is defined
as the Pearson correlation coefficient of degrees of connected nodes, thus taking values in the
range [−1, 1].
To give a formal definition, let pk be the probability that a randomly chosen node has degree
k. It can be shown that the degree distribution for a node connected to a randomly selected edge l
Þpkþ1
is thus proportional to kpk. Alors, a quantity for “remaining degree” is defined as qk = kþ1
jTjpj
which is the normalized distribution of remaining degree for the nodes connected to l. Enfin,
the joint probability of remaining degrees of the nodes at both ends of l is denoted by ejk. For an
undirected network ejk = ekj and its marginal distribution is (cid:1)
j ejk = qk. Having the variance of
− [(cid:1)
remaining degree as σ2
k kqk]2, the degree assortativity can be calculated as
k k2qk
shown in Equation 12 (Newman, 2003).
q = (cid:1)
P.
,
ð
r ¼ 1
σ2
q
X
ij
(cid:4)
jk ejk
(cid:5)
:
− qjqk
(12)
Rich-club Coefficient. This coefficient quantifies the tendency of nodes with higher than a cer-
tain degree to connect to each other. More formally, as Equation 13 shows, the coefficient is
equivalent to the edge density of the subgraph of the network where the nodes with lower
degrees than the cutoff value k are removed,
RC kð Þ ¼ ED≥k
¼
P.
ijA≥k
ð
N≥k N≥k
Þ
− 1
:
(13)
Since this coefficient is a function of club size k, it is hard to visualize its evolution over time
for all possible values of k. Ainsi, the values of this coefficient were only plotted for the final
state of the networks.
The absolute value of the rich-club coefficient is hard to interpret and is not comparable
among networks of different sizes, densities, and degree distributions. Ainsi, this coefficient is
often normalized by the average rich-club coefficient of random networks of the same size
with similar degree sequence. For each model (and its minority and majority partitions), nous
simulated 200 such networks, for each club size k, and normalized the values of the rich-club
coefficients of the network by the average rich-club coefficient among the random networks.
97
Degree sequence:
A sorted list of the degrees of nodes
(c'est à dire., the number of connections each
node has to others) in a network.
Neurosciences en réseau
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
De plus, for each k, we statistically tested whether the non-normalized RC is significantly
larger than the rich-club coefficients of randomly generated networks. Since the distribution
of RCs of random networks were non-Gaussian, the conventional one-sample t test was not
applicable. Plutôt, we performed one-sample Wilcoxon signed rank test and set α = 0.01 comme
the significance level for the p values.
For a certain k, a normalized rich-club coefficient larger than 1 indicates that nodes with
degree k tend to connect to the “rich” nodes (c'est à dire., those with degrees equal to or greater
than k), thus forming “rich clubs.” Conversely, RCnorm(k) < 1 implies that the nodes with
degree k show a tendency to connect to nodes with lower degrees. Finally, RCnorm(k) = 1 sug-
gests that nodes with degree k show no preference to connect to nodes with lower or higher
degrees.
Investigating the resemblance between models. To compare network families with each other,
we assume, in line with Berlingerio, Koutra, Eliassi-Rad, and Faloutsos (2012), that the struc-
tural information embedded in networks can be summarized by the distributions of local
network measures. Comparison of networks is thus reduced to comparing these distributions.
To obtain measures of distributional distances, we use the NetSimile method (Berlingerio
et al., 2012) and the Heller–Heller–Gorfine (HHG) algorithm (Heller, Heller, & Gorfine,
2013), both of which are discussed in the Supporting Information. In short, NetSimile indi-
cates the degree of dissimilarity between the distributions attributed to the networks being
compared via comparing signature vectors that encapsulate the distributions by their sum-
mary statistics.
HHG, on the other hand, provides p values for a test of independence among the distribu-
tions; a small p value derived from HHG (e.g., below the threshold of α = 0.05) provides ev-
idence to reject the null hypothesis of distributional independence. Thus, loosely speaking,
HHG p value can be regarded as an indicator for dissimilarity; a higher value of this measure
entails a smaller “resemblance” (or dependence) between the networks. Nevertheless, inter-
preting HHG p values as such a measure is somewhat unorthodox and is hardly meaningful
unless used along with another dissimilarity measure such as NetSimile.
We first make pairwise comparisons among the 1,225 unique pairs of model instantiations
at their final state after 1 million rewiring attempts. Having quantitative measures for dissim-
ilarities among the networks, we quantify the within-family resemblances and between-family
contrasts among the models. Finally, we define a score for family distinction in order to com-
pare how families vary with respect to this measure.
Family Resemblances and Differentiations. The outcomes of pairwise comparison of the net-
works using NetSimile and HHG were stored in four 50 × 50 matrices of form
DissimilarityG
M for networks G (either A or F, respectively for anatomical and functional con-
nectivities) based on method M (either NetSimile or HHG). To ease the visual comparison of
these measures, the matrices of NetSimile distances, that is, DissimilarityA
DissimilarityF
NetSimile, were normalized by the highest value in each matrix so their values
range from 0 to 1. Then, within- and between-family contrast aggregate scores were calculated
by averaging the elements of dissimilarity matrices that belong to the families being compared as
shown in Equation 14:
NetSimile and
Network Neuroscience
ContrastG
(cid:4)
M fi; fj
(cid:5)
¼
1
10 (cid:6) 10
X
X
(cid:4)
i2fi
j2fj
DissimilarityG
M
(cid:5)
:
ij
(14)
98
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
Finally, a differentiation score was calculated for each family to quantify the degree to
which models belonging to family fi resemble each other and, at the same time, diverge from
the members of other families, via
DifferentiationG fið Þ ¼
1
4
P
(cid:8)
1 − ContrastG
i≠j 1 − ContrastG
NetSimile fi; fi
(cid:4)
ð
NetSimile fi; fj
Þ
(cid:5)
(cid:9) :
(15)
In this equation, the numerator is the within-family resemblance of networks belonging to
family fi. The denominator is the mean of the between-family resemblance of fi to other
families. This score will be larger than 1 if family fi differentiates from other families. For
the lack of straightforward interpretation, this score was not calculated for HHG outcomes.
RESULTS
Network Structures
Using the seriation and igraph packages, we plot the raw (unserialized) and ordered (serial-
ized) adjacency matrices and the wiring diagrams of the networks in their final state. In the
plots, the minority and majority nodes are colored sky blue and pink, respectively. In both
matrix visualizations and wiring diagrams, the within-minority and within-majority edges are
colored blue and red, respectively. The interpartition edges, connecting nodes of minority
subset to nodes of majority, are colored green. Although there are variations among models,
either within- or between-families, in all models (except for the MC2, MC3, SC1, and SC3;
see below), several densely coupled sets of nodes, that is, modules, emerged. These modules
can be identified as squares in the serialized adjacency matrices. Figure 1 shows two rep-
resentative networks per family. As evident in the plots, the networks manifest a range of
different structures. Yet, similarities can be observed among models belonging to the same
families.
The baseline models (BL2 and BL8 in Figure 1) typically include three densely coupled
modules and a few larger, sparser sets of nodes. The modules are not isolated from the rest
of the network, as intermodular edges keep them connected to other nodes. The unserialized
adjacency matrices show that the density of edges is relatively uniform over subsets of nodes.
In the HC family, wherein the minority nodes have relatively higher coupling strengths, the
edge density is higher in the minority subgraph. Moreover, the HC family networks have more
distinct modules than other families. HC2 (Figure 1), for instance, has only two modules, both
of which are highly connected. Higher edge density in the minority subset and highly distinct
modules are also observed for the LC family, which has lower amplitude in the minority nodes
(LC5 and LC8, Figure 1). The similarity between the HC and LC models was expected, as the
nodes with lower amplitudes and higher coupling strengths can synchronize more easily.
However, it is worth noting that the effect is not limited to the minority nodes; highly con-
nected modules also emerge among the majority nodes.
In the MC family, the edge density in the minority partition is reduced. Moreover, the
higher level of amplitude for minority nodes resulted in highly connected modules among
the majority nodes (see MC4 in Figure 1). In the SC family, the edge density of the minority
(which had lower coupling strengths) is lower than that of the majority. Additionally, the
lower coupling strength of the minority prevented minority nodes from forming modules, and
they were absorbed into modules formed mainly by the majority nodes. See SC5 and SC7 in
Figure 1.
Network Neuroscience
99
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Network structures of representative models. Each panel shows the unserialized (top left) and serialized (top right) adjacency
matrices, and the graph representation (bottom) of the structural connectivity at the last rewiring step. The within-minority, within-majority,
and interpartition edges are colored blue, red, and green, respectively. In the graph representation, the minority and majority nodes are colored
sky blue and pink, respectively.
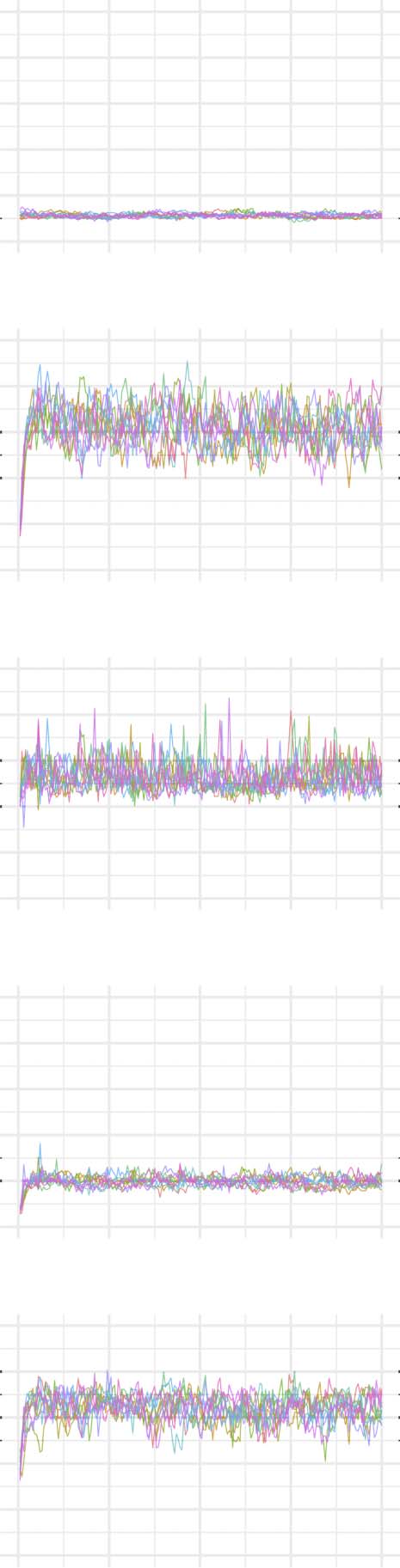
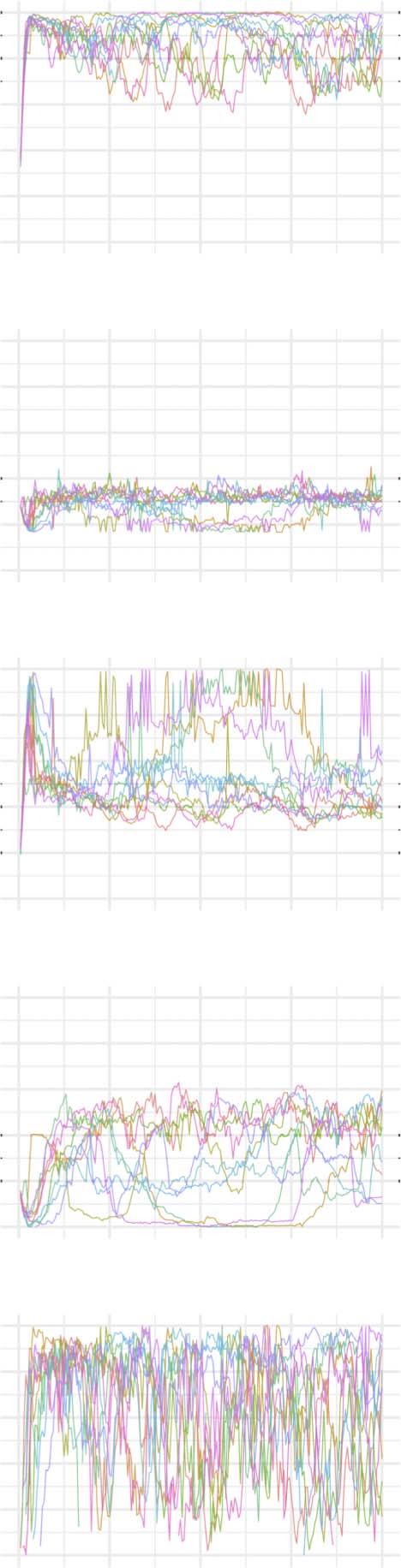
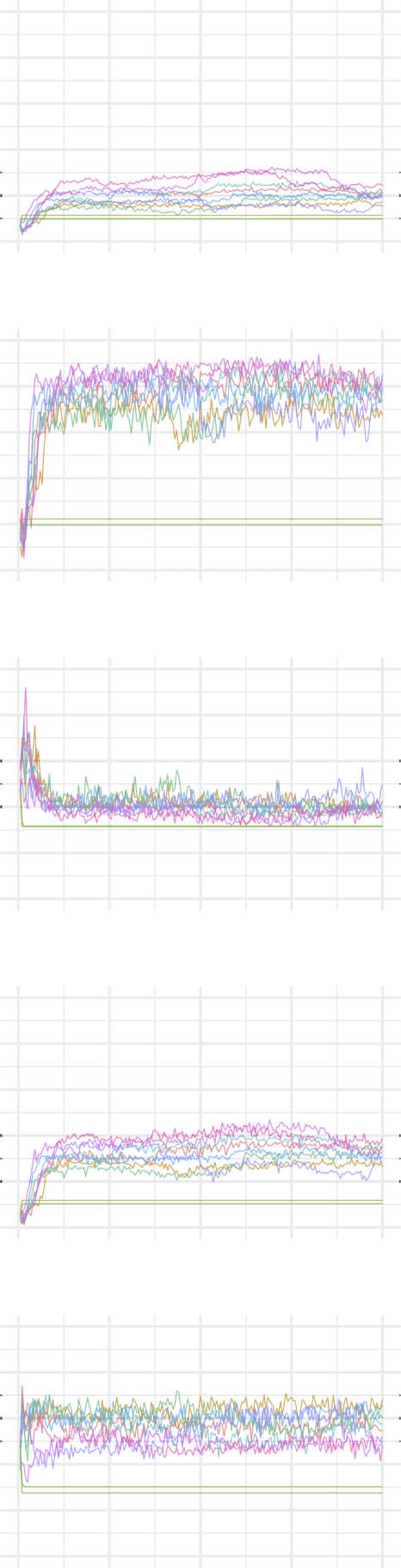
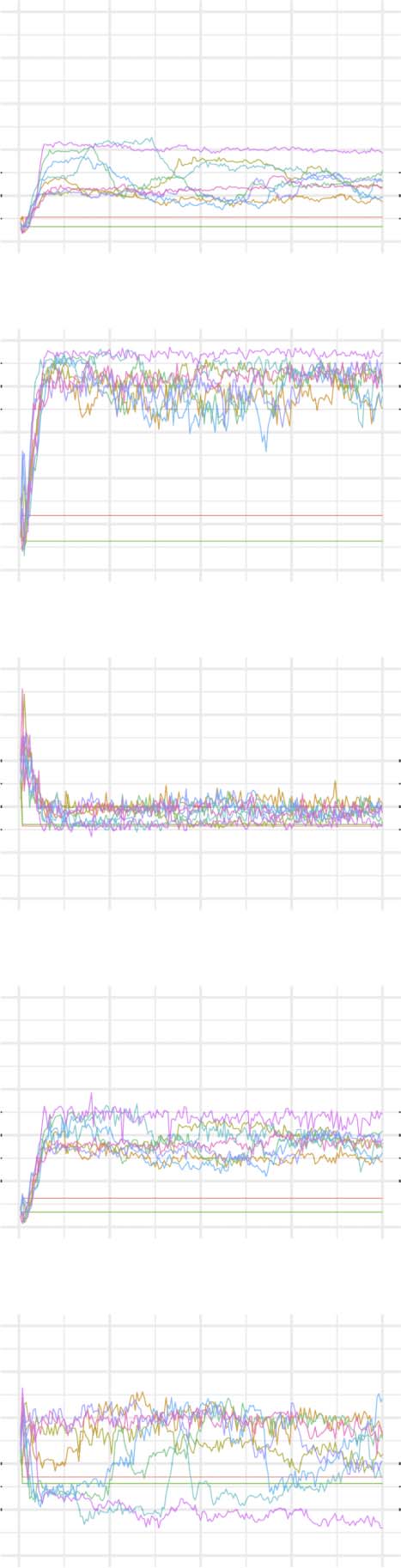
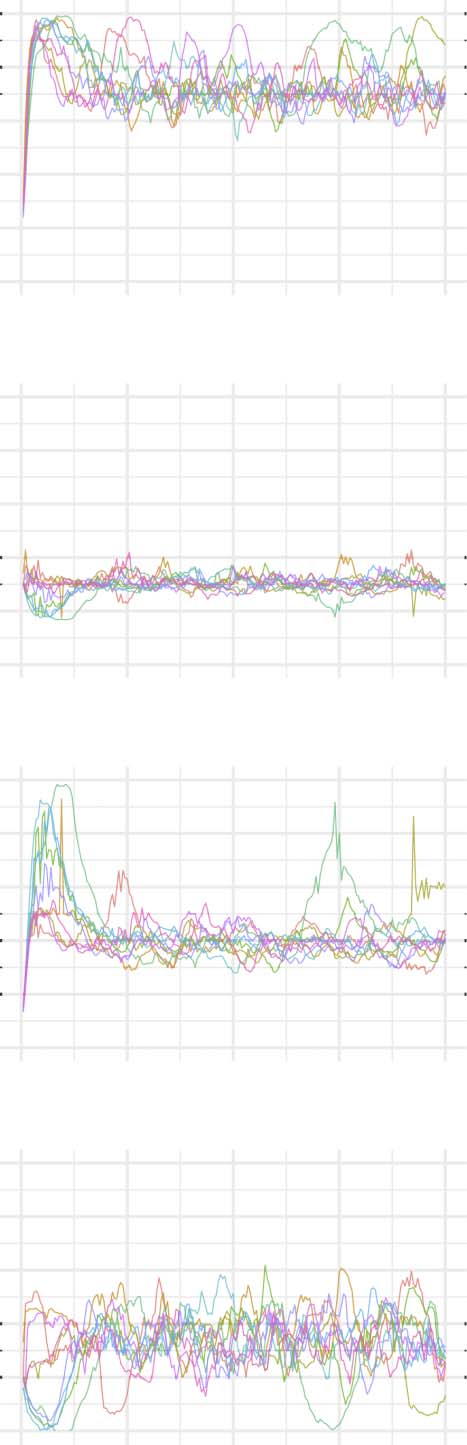
Network Statistics
The evolution of clustering coefficient, modularity, edge density, small-world index, degree
assortativity, and average path length were plotted for the structural network connectivity of
all models and their subnetworks (viz., within-minority, within-majority, and interpartition).
Figures 2–6 show these plots for the minority, majority, and whole networks, grouped per
family. Furthermore, the normalized rich-club coefficient of the final states of the minority,
majority, and whole networks are plotted in Figure 7.
Network Neuroscience
100
Adaptive rewiring in nonuniform coupled oscillators
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2.
Evolution of network statistics in the baseline (BL) condition for the whole network and majority and minority subgraphs.
Network Neuroscience
101
Adaptive rewiring in nonuniform coupled oscillators
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3.
Evolution of network statistics in the less chaotic (LC) condition for the whole network and majority and minority subgraphs.
Network Neuroscience
102
Adaptive rewiring in nonuniform coupled oscillators
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4.
Evolution of network statistics in the more chaotic (MC) condition for the whole network and majority and minority subgraphs.
Network Neuroscience
103
Adaptive rewiring in nonuniform coupled oscillators
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5.
Evolution of network statistics in the sub-coupled (SC) condition for the whole network and majority and minority subgraphs.
Network Neuroscience
104
Adaptive rewiring in nonuniform coupled oscillators
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6.
Evolution of network statistics in the hyper-coupled (HC) condition for the whole network and majority and minority subgraphs.
Network Neuroscience
105
Adaptive rewiring in nonuniform coupled oscillators
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Normalized rich-club coefficients of the whole network after the last rewiring step, grouped by condition. Solid circles mark sig-
nificant values.
Network Neuroscience
106
Adaptive rewiring in nonuniform coupled oscillators
Let us first consider the evolution of network statistics for the whole network. As evident in
the plots, modularity, clustering coefficients, and small-world index of all models increase no-
ticeably after 60,000 rewiring attempts (roughly by a factor of 4.7, 5.3, and 4.6, respectively)
and degree assortativity approaches 0.53. Meanwhile, the average path length increases no
more than 15%. The network statistics fluctuate afterward, and the fluctuation is more pro-
nounced for degree assortativity. The majority subnetworks show similar trends. In the minor-
ity subnetworks—although with higher fluctuations and instability in HC, LC, and SC—we
observe an increase in these statistics after 60,000 rewiring attempts. The network statistics
of minority subnetworks of MC and BL families resemble those of the whole networks in
the same families. Yet, clustering coefficient and small-world index show higher growth in
the minority subnetworks (more than six- and sevenfold, respectively). The exception to these
improvements is the modularity, which increases only moderately (roughly 35%) in this sub-
network. Given the finite number of nodes in this partition, this was not unexpected; a larger
subnetwork would likely have shown more improvement in modularity as well. The edge den-
sities in the minority subnetworks, although unstable, are often large, roughly 2.4 times that of
the whole network. In line with elevated edge density, average path length within the minority
subgraph drops by almost 7%. This means that the minority nodes tend to connect more
strongly to each other than to other nodes. Tables 1–3 summarize the mean and standard de-
viation of changes in network statistics after 60,000 rewiring attempts for the whole network
and the majority and minority subnetworks.
Figure 7 shows the normalized rich-club coefficient RCnorm(k) of the minority, majority, and
whole networks, grouped by families, as a function of club size k. RCnorm(k) above 1 (dashed
line) indicates rich clubs. Values significantly larger than 1 ( p < 0.01, based on one-sample
Wilcoxon signed rank test) are marked by solid circles. Despite differences among families,
they all show significant rich-club structures for larger club sizes, both in the whole network
and in the majority partition. Let us first consider the plots for the whole networks, depicted in
the left column of this figure. The HC family has clubs of sizes 30 < k < 70 (involving 10–23%
of the nodes), most of them significant, with consistent RCnorm values among members. In the
LC family, all models form rich clubs with 25 < k < 55 (roughly 8–18% of the nodes), and
some models form larger rich clubs up to the sizes of 65–85 (roughly 22–28% of the nodes).
Other families, that is, MC, BL, and SC, form clubs with sizes ranging from 30 to roughly 65
(10–22% of the nodes), with relatively higher (but less consistent) RCnorm values compared
with HC.
Table 1. Means and standard deviations (between parentheses) of network statistics of the whole graph for different conditions. Means are
from 60,000 to 1 million rewiring steps, normalized by those of 100 random networks, except degree assortativity. BL: baseline; LC: less
chaotic; MC: more chaotic; SC: sub-coupled; HC: hyper-coupled.
Condition
HC
Clustering
coefficient
5.33 (1.05)
Average
path length
1.15 (0.05)
Small-world
index
4.62 (0.80)
Modularity
4.69 (0.85)
Assortativity
0.52 (0.22)
MC
BL
LC
SC
5.34 (1.02)
1.15 (0.05)
4.63 (0.78)
4.7 (0.81)
0.53 (0.22)
5.32 (1.05)
1.14 (0.05)
4.62 (0.80)
4.68 (0.84)
0.53 (0.22)
5.35 (1.03)
1.15 (0.05)
4.63 (0.79)
4.7 (0.82)
0.53 (0.22)
5.35 (1.01)
1.15 (0.05)
4.64 (0.78)
4.69 (0.82)
0.53 (0.22)
Network Neuroscience
Edge
density
1 (0.02)
1 (0.01)
1 (0.02)
1 (0.02)
1 (0.01)
107
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
Table 2. Means and standard deviations (between parentheses) of network statistics of the majority subgraph for different conditions. Means
are from 60,000 to 1 million rewiring steps, normalized by those of 100 random networks, except degree assortativity. BL: baseline; LC: less
chaotic; MC: more chaotic; SC: sub-coupled; HC: hyper-coupled.
Condition
HC
Clustering
coefficient
5.49 (1.13)
Average
path length
1.17 (0.06)
Small-world
index
4.64 (0.85)
Modularity
4.45 (0.84)
Assortativity
0.52 (0.18)
Edge
density
1.01 (0.12)
MC
BL
LC
SC
5.51 (1.08)
1.17 (0.06)
4.66 (0.82)
4.47 (0.8)
0.52 (0.18)
1 (0.11)
5.49 (1.12)
1.17 (0.06)
4.64 (0.85)
4.44 (0.83)
0.52 (0.18)
1.01 (0.12)
5.52 (1.11)
1.18 (0.06)
4.66 (0.84)
4.47 (0.81)
0.53 (0.18)
5.53 (1.08)
1.18 (0.06)
4.67 (0.83)
4.46 (0.8)
0.54 (0.18)
1 (0.12)
1 (0.12)
In the majority partition (middle column of Figure 7), we consistently observe rich clubs
larger than 25, involving 10% of the nodes within that partition. The HC family has rich clubs
as large as 40 (16% of nodes), and other families form even larger rich clubs, with sizes span-
ning 45 to 60 (making up 18–24% of the nodes). In general, we observe more diverse values
among models for the rich-club coefficients in the majority partition. Finally, in the minority
partition (the right column of the same figure), we observe a relatively remarkable—and
consistent—rich-club effect in the HC family (12 < k < 30; 24–60% of nodes), while other
families have relatively larger rich-club coefficients for smaller club sizes (5 < k < 20; 10–
40% of nodes). Some models of the LC family form much larger rich clubs with sizes up to
40 (i.e., 80% of the nodes).
Incidental Losses
As can be observed in the evolution plots, four models (viz., MC2, MC3, SC1, and SC3) stop
evolving before 10,000 rewiring attempts. Visual inspection reveals that, at some point in their
evolution, one node reaches maximum degree and is connected to all other nodes (cf.
Figure 8). This indicates that these models reached the end point of a pathological develop-
ment, something we chose not to prevent in our algorithm. Consequently, the rewiring
Table 3. Means and standard deviations (between parentheses) of network statistics of the minority subgraph for different conditions. Means
are from 60,000 to 1 million rewiring steps, normalized by those of 100 random networks, except degree assortativity. BL: baseline; LC: less
chaotic; MC: more chaotic; SC: sub-coupled; HC: hyper-coupled.
Condition
HC
Clustering
coefficient
6.24 (1.71)
Average
path length
0.94 (0.24)
Small-world
index
7.16 (3.19)
Modularity
1.35 (0.56)
Assortativity
0.53 (0.32)
Edge
density
2.36 (1.44)
MC
BL
LC
SC
6.26 (1.69)
0.93 (0.24)
7.27 (3.24)
1.35 (0.57)
0.53 (0.31)
2.42 (1.49)
6.18 (1.72)
0.94 (0.24)
7.07 (3.03)
1.38 (0.54)
0.52 (0.32)
2.35 (1.39)
6.19 (1.70)
0.93 (0.23)
7.11 (3.11)
1.39 (0.52)
0.52 (0.32)
2.34 (1.38)
6.2 (1.67)
0.93 (0.24)
7.17 (3.25)
1.37 (0.55)
0.51 (0.31)
2.36 (1.47)
Network Neuroscience
108
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
algorithm naturally terminates, as division by 0 looms in Equation 3. Terminated models failed
to form any modules and were omitted from family-wise comparisons. We consider these
incidental losses as a sign that robustness against perturbation is not always guaranteed for
our models.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. Network structures of terminated models. Panels and color coding are similar to those of Figure 1.
Network Neuroscience
109
Adaptive rewiring in nonuniform coupled oscillators
Family-Wise Comparisons
NetSimile and HHG similarity measures were composed in new matrices wherein the lower tri-
angle belongs to DissimilarityN
HHG and the upper triangle belongs to DissimilarityN
NetSimile, that is,
DissimilaritiesN ¼ lower:tri DissimilarityN
þ upper:tri DissimilarityN
NetSimile
(cid:4)
(cid:5)
HHG
(cid:4)
(cid:5)
:
(16)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. Heat maps of pairwise dissimilarities of anatomical (top) and functional (bottom) networks.
The upper diagonal elements show normalized dissimilarity measures derived from NetSirnile algo-
rithm, and the lower diagonal elements show HHG p values. Model names and family assignments
are indicated. Lower dissimilarity (hence higher similarity) measures are coded by brighter colors.
Network Neuroscience
110
Adaptive rewiring in nonuniform coupled oscillators
The matrices of DissimilaritiesN are plotted in Figure 9 as heat maps using the ComplexHeatmap
R package (Gu, Eils, & Schlesner, 2016).
The matrices of ContrastN are plotted as upper triangular matrices in Figure 10 using the
corrplot R package (Wei & Simko, 2021). The cell colors, coded similarly to the heat maps,
denote average contrast measures derived from the NetSimile algorithm while average HHG
p values (i.e., ContrastN
HHG) are indicated in each cell. The HC family manifests the least
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
a
_
0
0
2
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 10. Heat maps of within- and between-family contrasts for anatomical (top) and functional
(bottom) connectivities. The values within cells show the average HHG p values of corresponding
family-wise comparisons. Lower contrast measures are coded by brighter colors.
Network Neuroscience
111
Adaptive rewiring in nonuniform coupled oscillators
within-family contrast. Based on the HHG test of multivariate independence, except for HC-
HC and HC-LC family pairs, no conclusive evidence exists for distributional dependence
among families. Finally, as can be seen in this figure, the within- and between-family
NetSimile contrasts of both structural and functional connectivity networks show similar pat-
terns. More specifically, both the structural and the functional connectivity of HC-BL, HC-LC,
BL-BL, BL-LC, and LC-LC all share close contrast values compared with other family pairs. This
is also the case for the BL-SC and LC-SC pairs.
The differentiation scores for structural and functional connectivity between families are
plotted in Figure 11. Differentiation values above 1 (dashed line) imply that the within-family
resemblance of network structures of family fi is higher than the average resemblance of its
members to the members of other families. We observe elevated differentiation in both struc-
tural and functional networks of HC, BL, and LC. This measure is remarkably higher for the
structural networks of the HC family while barely exceeding the threshold for the functional
network of the same family.
Finally, in order to have both family resemblance and family differentiation in a single
frame, we summarized their values in the graphs shown in Figure 12. In these graphs, individ-
ual nodes represent families of models. Edge color and size code between-family contrast and
node color captures within-family contrast. The size of each node is proportional to the value
of the differentiation score of its corresponding family. The families with DifferentiationN( fi) >
1 are marked with asterisks. It can be noticed that in both structural and functional networks,
the families with differentiation scores larger than 1 (c'est à dire., HC, BL, and LC) have lower within-
family contrast values. De plus, the pairwise contrasts among these families (c'est à dire., HC-BL,
HC-LC, and BL-LC) are lower than any other family pair. This suggests that models with in-
creased amplitude and decreased coupling strengths lead to structures less resembling the
baseline family.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 11. Between-family differentiation scores of the anatomical and functional networks.
Values above 1 (dashed line) imply above-average within-family resemblance compared with other
families.
Neurosciences en réseau
112
Adaptive rewiring in nonuniform coupled oscillators
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 12. Graph representation of family resemblance and differentiation in anatomical (top) et
functional (bottom) connectivities of the fully evolved models. Edge color and size code
between-family contrast and node color captures within-family contrast. Node size is proportional
to the differentiation score of the corresponding family. The families with ditferentiation scores
au-dessus de 1 are marked with asterisks.
DISCUSSION
We investigated the effect of nonuniformity of oscillator amplitude and connection strength on
the evolution of network structure under adaptive rewiring. The adaptive rewiring was driven
by synchronization in coupled logistic maps. The amplitude and coupling parameters of the
oscillators govern their synchronization behavior. It has amply been shown that networks
evolve to complex, brain-like structures when these parameters were fixed to uniform values.
We replicated this behavior for our baseline parameter setting. En plus, we studied how
nonuniform parametrization gets reflected in the evolving network structure and whether
adaptive rewiring is robust to these perturbations.
To this aim, a minority subset of network units had either the amplitude reduced (LC) ou
increased (MC), or the connectivity reduced (SC) or increased (HC). These perturbations may
be compared with perceptual input (modeled by increased or decreased divergence in node
activités) or memory processes (modeled by varying degrees of coupling). In all these condi-
tion, adaptive rewiring establishes the evolution of random networks into complex structures.
These structures are modular and small-world networks and show a fivefold increase in the
Neurosciences en réseau
113
Adaptive rewiring in nonuniform coupled oscillators
clustering coefficient, at the cost of an increase of less than 15% in average path length com-
pared with the original random networks. De plus, the models form rich clubs as large as 8–
28% of network size. This evolution is in accord with previous adaptive rewiring studies.
Adaptive rewiring, donc, is generally robust against the symmetry-breaking perturbations
of system parameters and thus can accommodate—and integrate—function-specific modules.
Note, cependant, that robustness is not always guaranteed. In a small proportion of our models
(four cases in total), we observed pathological development in the perturbed models, resulting
in network evolution breakdown.
On top of these findings about the whole network, the subsets of our models also developed
brain-like structures. More specifically, across families, the majority subnetwork shows improved
properties akin to the whole network. The minority subnetwork of perturbed models—with
an exception for modularity—manifests these properties to a much greater degree, especially
in the relative sizes of its rich clubs. The latter observation is indicative of more specialized
structures in the minority subnetwork as a direct result of heterogeneity in model parameters.
Despite the overall consistency in structural improvements of networks, we observed con-
siderable variability among models, both in their evolution and in the final states of structural
and functional connectivity. These variations are partly due to the family-specific parameter-
ization of models and partly due to the random initialization of the models. We quantified the
within- and between-family contrasts and defined a measure of family differentiation to score,
on average, how well models belonging to one family distinguish from others.
We found that the baseline network family and families with increased coupling strengths or
decreased amplitude (respectivement, BL, HC, and LC) differentiate themselves most from other
families, in both structural and functional connectivity. The differentiation score is the highest
for the structural connectivity of the HC family. De plus, we observe a relatively high resem-
blance between HC and LC for both structural and functional connectivity. Based on the HHG
test, there is relatively strong evidence ( p = 0.02) for distributional dependence between
structural networks of HC and LC. This means that elevated coupling strength and reduced
amplitude have similar effects on both the structural and the functional connectivity of adap-
tively rewiring oscillator models.
Altogether, perturbation to the parameters of coupled oscillators yields structural and func-
tional differences that are fundamental for implementing cognitive functions in evolving net-
travaux. De plus, for both the structural and the functional connectivity, perturbation leads to
differentiation from the baseline. Different perturbations show specific differentiations. From a
cognitive neuroscience perspective, this implies that functional and structural differentiation
can be used to identify functional components in a network, in accord with the use of struc-
tural and functional connectivity measures in neuroimaging.
CONCLUDING REMARKS
Further research may extend our findings in several ways. D'abord, the incidental occurrence of
network evolution breakdown was unexpected. Technically speaking, the matrix algebraic im-
plementation of coupled logistic maps is sensitive to minor computational errors such as un-
defined division for one node (which may stem from pathological development of models), comme
was the case for MC2, MC3, SC1, and SC3. A different implementation could have prevented
breakdown by isolating the problematic node and proceeding with the adaptive rewiring al-
gorithm for the remaining network. Cependant, rather than searching for an even more robust
version of our algorithm, we choose to keep the current implementation for the sake of
Neurosciences en réseau
114
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
Traveling waves:
Spatially coherent neural activities
that propagate across brain regions at
different scales and that are
hypothesized to coordinate brain
circuits at longer ranges.
consistency with previous work, and as a warning signal that pathologies may arise as a by-
product of neural network evolution. Future work may focus more specifically on such path-
ological development, in relation to developmental disorders in the human brain. This may
require a systematic study of the probability distribution of network breakdown under a range
of parametrization conditions, network sizes, and connectivity densities to find factors contrib-
uting to the pathological development of adaptively rewiring networks.
Deuxième, a broader range of parameter variation conditions than currently imposed should
be attempted. Par exemple, amplitude and coupling strength parameters could both deviate
from baseline values simultaneously, either for the same subset of nodes or for two (overlap-
ping or nonoverlapping) subsets. Random and patterned deviations of parameters can be stud-
ied in large-scale systems to implement perceptual and memory functions. Finalement, the aim
is to have these functions implemented in a network that simultaneously maintains its optimal
structure.
This study was limited to binary, unweighted, and undirected networks. The effect of non-
uniform parameters of logistic maps can be studied, via systematic search, on weighted net-
works with various edge weight distributions, akin to Hellrigel et al. (2019). For directed
réseaux, see Rentzeperis, Laquitaine, and van Leeuwen (2021).
We followed the strategy to provide the simplest possible model of brain structure and func-
tion in order to avoid stacking arbitrary assumptions. Simplification is inevitable in modeling;
“all models are wrong—but some are useful.” (Attributed to George Box.) For those who
consider the model to pose severe limitations on the generalization of our findings to neuro-
biological systems, more realistic neural mass models instead of coupled maps could be a
viable solution, in particular, ones that have facilities for studying the effects of traveling waves
and spatial embedding of the network topology (Calvo Tapia, Makarov, & van Leeuwen, 2020)
on network evolution, or apply phase–amplitude–frequency coupling (Chehelcheraghi,
Nakatani, Steur, & van Leeuwen, 2016; Chehelcheraghi, van Leeuwen, Steur, & Nakatani,
2017) to networks of neural mass activity (Deschle, Ignacio Gossn, Tewarie, Schelter, &
Daffertshofer, 2021).
Enfin, despite the current limitations, our study has set an essential first step in the devel-
opment of adaptively rewiring networks capable of pattern recognition and learning. Showing
the principled possibility of such networks offers scope for the study of the developing, func-
tional brain as well as for applying adaptive rewiring to sparsify artificial neural networks
(Coup de vent, Elsen, & Hooker, 2019).
REMERCIEMENTS
Part of the research leading to this review was supported by an Odysseus grant (G.0003.12)
from the Flemish Organization for Science (FWO) to Cees van Leeuwen. The computational
resources and services used in this work were provided by the VSC (Flemish Supercomputer
Centre), funded by FWO and the Flemish Government. The authors would like to thank Ilias
Rentzeperis for his feedback and comments on parts of the results.
DATA AND CODE AVAILABILITY
The reproducible scripts used in this study are available online on the study’s repository on the
Open Science Framework (https://osf.io/625d8; Haqiqatkhah & van Leeuwen, 2021). This re-
pository also includes all model files of this study (500 files amounting to 101 GB of data,
Neurosciences en réseau
115
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Adaptive rewiring in nonuniform coupled oscillators
generated using VSC computational resources) and additional plots of various qualitative and
quantitative network measures.
INFORMATIONS À L'APPUI
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00211.
CONTRIBUTIONS DES AUTEURS
MohammadHossein Manuel Haqiqatkhah: Conceptualisation; Conservation des données; Analyse formelle;
Enquête; Méthodologie; Logiciel; Visualisation; Rédaction – ébauche originale. Cees van Leeuwen:
Conceptualisation; Acquisition de financement; Enquête; Gestion de projet; Ressources;
Surveillance; Rédaction – révision & édition.
INFORMATIONS SUR LE FINANCEMENT
Cees van Leeuwen, Fonds Wetenschappelijk Onderzoek (https://dx.doi.org/10.13039
/501100003130), Award ID: G.0003.12.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
RÉFÉRENCES
Avena-Koenigsberger, UN., Misic, B., & Sporns, Ô. (2018).
Communication dynamics in complex brain networks. Nature
Reviews Neuroscience, 19(1), 17–33. https://doi.org/10.1038/nrn
.2017.149, PubMed: 29238085
Berlingerio, M., Koutra, D., Eliassi-Rad, T., & Faloutsos, C. (2012).
NetSimile: A scalable approach to size-independent network
similarité. arXiv:1209.2684.
Bi, G.-Q., & Poo, M.-M. (2001). Synaptic modification by correlated
activité: Hebb’s postulate revisited. Revue annuelle des neurosciences,
24(1), 139–166. https://doi.org/10.1146/annurev.neuro.24.1.139,
PubMed: 11283308
Breakspear, M., Terry, J.. R., & Friston, K. J.. (2003). Modulation of
excitatory synaptic coupling facilitates synchronization and com-
plex dynamics in a biophysical model of neuronal dynamics.
Réseau: Calcul dans les systèmes neuronaux, 14(4), 703–732.
https://doi.org/10.1088/0954-898X_14_4_305
Butz, M., Wörgötter, F., & van Ooyen, UN. (2009). Activity-dependent
structural plasticity. Brain Research Reviews, 60(2), 287–305.
https://doi.org/10.1016/j.brainresrev.2008.12.023, PubMed:
19162072
Calvo Tapia, C., Makarov, V. UN., & van Leeuwen, C. (2020). Basic
principles drive self-organization of brain-like connectivity
structure. Communications in Nonlinear Science and Numerical
Simulation, 82, 105065. https://doi.org/10.1016/j.cnsns.2019
.105065
Chehelcheraghi, M., Nakatani, C., Steur, E., & van Leeuwen, C.
(2016). A neural mass model of phase–amplitude coupling.
Biological Cybernetics, 110(2), 171–192. https://est ce que je.org/10
.1007/s00422-016-0687-5, PubMed: 27241189
Chehelcheraghi, M., van Leeuwen, C., Steur, E., & Nakatani, C.
(2017). A neural mass model of cross frequency coupling. PLoS
ONE, 12(4), e0173776. https://doi.org/10.1371/journal.pone
.0173776, PubMed: 28380064
Clauset, UN., Newman, M.. E. J., & Moore, C. (2004). Finding
community structure in very large networks. Physical Review E,
70(6), 066111. https://doi.org/10.1103/ PhysRevE.70.066111,
PubMed: 15697438
Costa, L. d. F., Rodrigues, F. UN., Travieso, G., & Villas Boas, P.. R..
(2007). Characterization of complex networks: A survey of mea-
surements. Advances in Physics, 56(1), 167–242. https://doi.org
/10.1080/00018730601170527
Csardi, G., & Nepusz, T. (2006). The igraph software package for
complex network research. InterJournal, Complex Systems, 1695.
Deschle, N., Ignacio Gossn, J., Tewarie, P., Schelter, B., &
Daffertshofer, UN. (2021). On the validity of neural mass models.
Frontiers in Computational Neuroscience, 14, 581040. https://est ce que je
.org/10.3389/fncom.2020.581040, PubMed: 33469424
Feigenbaum, M.. J.. (1978). Quantitative universality for a class of
nonlinear transformations. Journal of Statistical Physics, 19(1),
25–52. https://doi.org/10.1007/BF01020332
Coup de vent, T., Elsen, E., & Hooker, S. (2019). The state of sparsity in deep
neural networks. arXiv:1902.09574.
Gong, P., & van Leeuwen, C. (2003). Emergence of scale-free net-
work with chaotic units. Physica A: Statistical Mechanics and Its
Applications, 321(3), 679–688. https://doi.org/10.1016/S0378
-4371(02)01735-1
Gong, P., & van Leeuwen, C. (2004). Evolution to a small-world
network with chaotic units. EPL (Europhysics Letters), 67(2), 328.
https://doi.org/10.1209/epl/i2003-10287-7
Gu, Z., Eils, R., & Schlesner, M.. (2016). Complex heatmaps reveal
patterns and correlations in multidimensional genomic data.
Bioinformatics, 32(18), 2847–2849. https://est ce que je.org/10.1093
/bioinformatics/btw313, PubMed: 27207943
Hahsler, M., Hornik, K., & Buchta, C. (2008). Getting things in
order: An introduction to the R package seriation. Journal de
Statistical Software, 25(3). https://doi.org/10.18637/jss.v025.i03
Neurosciences en réseau
116
Adaptive rewiring in nonuniform coupled oscillators
Haqiqatkhah, M.. H. M., & van Leeuwen, C. (2021). Adaptive rewiring
on coupled logistic maps with heterogenous parameters, Open
Science Framework, https://osf.io/625d8/
073115. https://doi.org/10.1063/1.4994819, PubMed:
28764402
R Core Team. (2019). R.: A language and environment for statistical
Hebb, D. Ô.
(1949). The organization of behavior (Vol. 65).
computing. Vienna, Austria.
New York, New York: Wiley.
Heller, R., Heller, Y., & Gorfine, M.. (2013). A consistent multivar-
iate test of association based on ranks of distances. Biometrika,
100(2), 503–510. https://doi.org/10.1093/biomet/ass070
Hellrigel, S., Jarman, N., & van Leeuwen, C. (2019). Adaptive
rewiring in weighted networks. Cognitive Systems Research,
55, 205–218. https://doi.org/10.1016/j.cogsys.2019.02.004
Jarman, N., Steur, E., Trengove, C., Tyukin, je. Y., & van Leeuwen, C.
(2017). Self-organisation of small-world networks by adaptive
rewiring in response to graph diffusion. Rapports scientifiques, 7(1),
13158. https://doi.org/10.1038/s41598-017-12589-9, PubMed:
29030608
Jarman, N., Trengove, C., Steur, E., Tyukin, JE., & van Leeuwen, C.
(2014). Spatially constrained adaptive rewiring in cortical net-
works creates spatially modular small world architectures.
Cognitive Neurodynamics, 8(6), 479–497. https://est ce que je.org/10
.1007/s11571-014-9288-y, PubMed: 26396647
Kaneko, K. (1992). Overview of coupled map lattices. Chaos: Un
Interdisciplinary Journal of Nonlinear Science, 2(3), 279–282.
https://doi.org/10.1063/1.165869, PubMed: 12779975
Kwok, H. F., Jurica, P., Raffone, UN., & van Leeuwen, C. (2007).
Robust emergence of small-world structure in networks of
spiking neurons. Cognitive Neurodynamics, 1(1), 39–51. https://
doi.org/10.1007/s11571-006-9006-5, PubMed: 19003495
Meunier, D., Lambiotte, R., & Bullmore, E. T. (2010). Modular and
hierarchically modular organization of brain networks. Frontiers
in Neuroscience, 4. https://doi.org/10.3389/fnins.2010.00200,
PubMed: 21151783
Newman, M.. E. J.. (2003). Mixing patterns in networks. Physical
Review E, 67(2), 026126. https://doi.org/10.1103/PhysRevE.67
.026126, PubMed: 12636767
Newman, M.. E. J.. (2006). Modularity and community structure in
réseaux. Actes de l'Académie nationale des sciences,
103(23), 8577–8582. https://doi.org/10.1073/pnas.0601602103,
PubMed: 16723398
Papadopoulos, L., Kim, J.. Z., Kurths, J., & Bassett, D. S. (2017).
Development of structural correlations and synchronization
from adaptive rewiring in networks of Kuramoto oscillators.
Chaos: An Interdisciplinary Journal of Nonlinear Science, 27(7),
Rentzeperis, JE., Laquitaine, S., & van Leeuwen, C. (2021). Adaptive
rewiring of random neural networks generates convergent-
divergent units. arXiv:2104.01418.
Rubinov, M., Sporns, O., van Leeuwen, C., & Breakspear, M.. (2009).
Symbiotic relationship between brain structure and dynamics.
BMC Neuroscience, 10(1), 55. https://doi.org/10.1186/1471
-2202-10-55, PubMed: 19486538
Sporns, O., & Zwi, J.. D. (2004). The small world of the cerebral
cortex. Neuroinformatics, 2(2), 145–162. https://est ce que je.org/10
.1385/NI:2:2:145, PubMed: 15319512
van den Berg, D., Gong, P., Breakspear, M., & van Leeuwen, C.
(2012). Fragmentation: Loss of global coherence or breakdown
of modularity in functional brain architecture? Frontiers in
Systems Neuroscience, 6. https://doi.org/10.3389/fnsys.2012
.00020, PubMed: 22479239
van den Berg, D., & van Leeuwen, C. (2004). Adaptive rewiring in
chaotic networks renders small-world connectivity with consis-
tent clusters. EPL (Europhysics Letters), 65(4), 459. https://est ce que je
.org/10.1209/epl/i2003-10116-1
van den Heuvel, M.. P., & Sporns, Ô. (2011). Rich-club organiza-
tion of the human connectome. Journal des neurosciences, 31(44),
15775–15786. https://doi.org/10.1523/ JNEUROSCI.3539-11
.2011, PubMed: 22049421
van Leeuwen, C., & Raffone, UN. (2001). Coupled nonlinear maps as
models of perceptual pattern and memory trace dynamics.
Cognitive Processing, 2, 67–116.
van Leeuwen, C., Steyvers, M., & Nooter, M.. (1997). Stability and in-
termittency in large-scale coupled oscillator models for perceptual
segmentation. Journal of Mathematical Psychology, 41(4), 319–344.
https://doi.org/10.1006/jmps.1997.1177, PubMed: 9473396
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of
“small-world” networks. Nature, 393(6684), 440–442. https://
doi.org/10.1038/30918, PubMed: 9623998
Wei, T., & Simko, V. (2021). R package ‘corrplot’: Visualization of a
correlation matrix [Manual].
Zhang, X., Ma, Z., Zhang, Z., Sun, Q., & Yan, J.. (2018). A review of
community detection algorithms based on modularity optimiza-
tion. Journal of Physics: Conference Series, 1069, 012123.
https://doi.org/10.1088/1742-6596/1069/1/012123
Neurosciences en réseau
117
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
6
1
9
0
1
9
8
4
2
5
9
n
e
n
_
un
_
0
0
2
1
1
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3